中考数学几何选择填空压轴题配答案

合集下载

2020年中考数学选择填空压轴题汇编几何综合结论含解析

几何综合结论1. （2020深圳）如图，矩形纸片個8中,AB=6. 5（7=12.将纸片折叠，使点3落在边"的延长线上的点 G 处，折痕为肪点E 、尸分别在边血和边證上.连接％,交CD 于点、K, FG 交CD 于点、H.给出以下结论： ① EF1BG ；② GE=GF ：③ 冰和2X00的而积相等；④ 当点尸与点Q 重合时，Z/?£F=75° ,其中正确的结论共有（）【解答】解：如图，连接宓设EFG BG 交于点0,•••将纸片折叠，使点〃落在边〃的延长线上的点G 处,B. 2个 C. 3个D. 4个:.EFIBG, BO=GO. BE=EG, BF= FG,故①正确,AD//BC.:・ZEGO= ZFBO、又T ZEOG= ZBOF,:.、BOZ'GOE (ASA\:・BF=EG,:・BF=EG=GF、故②正确，•: BE=EG=BF=FG、・••四边形购沪是菱形，:•乙BEF= ZGEF,当点尸与点Q重介时，则BF=BC=BE=\2,TsinZ 遊「，•••ZM5=30° ,:・ZDEF=W,故④正确，由题意无法证明△宓和△GAZf的而积相等，故③错误：故选：C.2.（2020贵州铜仁）如图，正方形個力的边长为4,点厅在边曲上，BE=\,ZQLW=45°，点尸在射线刖上，且过点尸作“的平行线交BA的延长线于点H, 67■与初相交于点G,连接EC、EG、EF.下列结论：①尸的而积为S②△庇G的周长为&③必=亦+血：其中正确的是（）A.①(D ③B. @@C.①②【解答】解：如图，在正方形個8中，AD//BC. AB=BC=AD=49AZZ£W=90° ,HF//AD.AZ J ^=90° ,VZ2£4F=90° - ZMQ45° >AAFH=AHAF.:.AH=HF=\=BE.:.EH=AE^AH=AB- BE ・AH=4 = BC 、:AEHFg'CBE (SAS'、:・EF=EC, ZHEF= ZBCE,•:乙BCE+乙BEC=9$ ,:・HEHZBEC=9y »:.ZFEC=9Q° ,:■ \ CEF 是等腰直角三角形, 在 R 仏CBE 中，BE=1. BC=A. H 刀D.②③ ZB=ZBAD=9Q Q ,:.EC=BE+BC = 17.=i=g =兰：£g云EF・EC 2EC 2\故①正确；过点尸作FQLBC于0,交.AD于P,•••Z 时=90° = ZH= ZHAD.・••四边形北明是矩形，•: AH=HF,.•・矩形册叨是正方形，:.AP=PH=AH=\,同理：四边形测是矩形，:.PQ=AB=\y BQ=AP1、FQ=FP-PQ=z. CQ=BO BQ=3、•: AD〃BC,•••△/TVs △磁，FP _况. 五一&在RtAEAG 中，根据勾股宦理得，EG°V/i^=4,=空 Is t 2旳工空 Is 产云 :・E C 羊D C+B E,故③错误，・•・正确的有①故选：C.:.AG=AP^PG'AEG 的周长为 AG-E&rAEI r 3=8,敬②正确; 25:.DG^BE 1£7•: EC= ( 3:.DG=AD- AG3. （2020黑龙江鹤岗）如图，正方形馭7?的边长为⑦ 点&在边月万上运动（不与点川3重合），ADAM= 45°，点尸在射线凡『上，且AF ^^BE,仔■与血相交于点G,连接应'、EF 、EG.则下列结论： ① ZECF= 45° :② △近的周长为（1 <3：③ B »D C=E C ；④△轩的而积的最大值是肚其中正确的结论是（）•:BE=BH, Z 翊=90° ,:・AF=EH,⑤当BE 二;a 时，G 是线段初的中点.A.①②③B.②④⑤C.①®®D.①④⑤ 【解答】解：如图1中, 任BC 上截取BH=庞,连接筋•: ZDAM=ZEHB=45° , Z馳?=90° ,:・ZFAE=ZEHC=\35° ,•: BA=BC, BE= BH,:.AE=HC.:仏FAE^HEHC (SAS)、:・EF=EC, ZAEF= ZECH,•:乙EC出乙CEB=90° ,:.AAEF^ACEB=W y•••Z亦*90° ,:•乙ECF= ZEFC='M ,故①正确，如图2中.延长初到/ 使得BE,则厶CBMHCDH ISAS). :・ZECB= ZDCH、：.2LECH= ABCD=W ,:.ZECG=ZGCH=45° ,•: CG=CG、CE=CH.:.HGCE^HGCH (SAS),:・EG=GH,V GH=D&rDH. DH=BE、:・EG=BE+DG.故③错误，'AEG的周长=AE^EG-AG= AE-AH= AD-DH^AE= AE^E&vAD= A&rAD= 2a.故②错误,二屈设殆F 贝^AE=a-x. AF 阳=—- 十一■ ■£> 2 W.Y ax解得-Y •:.AG=GD.故⑤正确,故选:D.4. （2020黑龙江绥化）如图，在Rt △磁中，G9为斜边初的中线，过点。

填空压轴题(几何篇)-2023年中考数学压轴题专项训练(学生版)

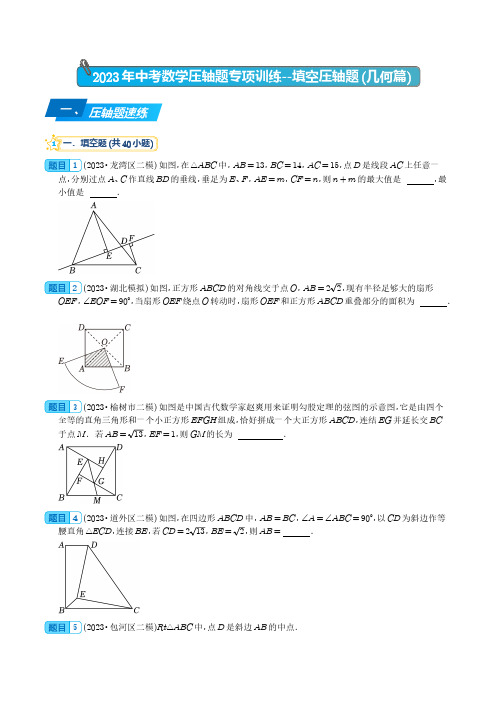
2023年中考数学压轴题专项训练--填空压轴题(几何篇)一、压轴题速练1一．填空题(共40小题)1(2023•龙湾区二模)如图，在△ABC中，AB=13，BC=14，AC=15，点D是线段AC上任意一点，分别过点A、C作直线BD的垂线，垂足为E、F，AE=m，CF=n，则n+m的最大值是，最小值是．2(2023•湖北模拟)如图，正方形ABCD的对角线交于点O，AB=22，现有半径足够大的扇形OEF，∠EOF=90°，当扇形OEF绕点O转动时，扇形OEF和正方形ABCD重叠部分的面积为．3(2023•榆树市二模)如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图，它是由四个全等的直角三角形和一个小正方形EFGH组成，恰好拼成一个大正方形ABCD，连结EG并延长交BC于点M．若AB=13，EF=1，则GM的长为．4(2023•道外区二模)如图，在四边形ABCD中，AB=BC，∠A=∠ABC=90°，以CD为斜边作等腰直角△ECD，连接BE，若CD=213，BE=2，则AB=．5(2023•包河区二模)Rt△ABC中，点D是斜边AB的中点．(1)如图1，若DE ⊥BC 与E ，DF ⊥AC 于F ，DE =3，DF =4，则AB =；(2)如图2，若点P 是CD 的中点，且CP =52，则PA 2+PB 2=．6(2023•庐江县三模)如图，四边形ABCD 中，AB =AC =AD ，点M 、N 分别是BC 、CD 的中点，连接MN ，若∠DAM =105°，∠BAN =75°，若AM AN=3+12，则∠ANM =°．7(2023•中山市二模)如图，△ABC 与△BDE 均为等腰直角三角形，点A ，B ，E 在同一直线上，BD ⊥AE ，垂足为点B ，点C 在BD 上，AB =4，BE =10．将△ABC 沿BE 方向平移，当这两个三角形重叠部分的面积等于△ABC 面积的一半时，△ABC 平移的距离为．8(2023•新都区模拟)青朱出入图，是魏晋时期数学家刘徽根据“割补术”运用数形关系证明勾股定理的几何证明法，即“勾自乘为朱方，股自乘为青方，令出入相补，各从其类，因就其余不动也，合成弦方之幂．开方除之，即弦也．”，若图中DF =1，CF =2，则AE 的长为．9(2023•黄埔区一模)△ABC为等腰直角三角形，AB=AC=6，∠BAC=90°，动点D在边BC上运动．以A为直角顶点，在AD右侧作等腰直角三角形△ADE(如图)．M为DE中点，N为BC三等分点，CN=13BC，连接MN，则线段MN的最小值为．10(2023•雁塔区校级模拟)如图，菱形ABCD的边长为5，将一个直角的顶点放置在菱形的中心O 处，此时直角的两边分别交边AD，CD于点E，F，当OE⊥AD时，OE的长为2，则EF的长是．11(2023•奉贤区二模)如果四边形有一组邻边相等，且一条对角线平分这组邻边的夹角，我们把这样的四边形称为“准菱形”．有一个四边形是“准菱形”，它相等的邻边长为2，这两条边的夹角是90°，那么这个“准菱形”的另外一组邻边的中点间的距离是　2　．12(2023•吕梁一模)如图，在正方形ABCD中，点P在对角线BD上，点E，F分别在边AB和BC 上，且∠EPF=45°，若CF=2DP=4，AE=12，则AB的长度为．13(2023•蚌埠二模)如图，点E为正方形ABCD的边CD上一点，以点A为圆心，AE长为半径画弧EF，交边BC于点F，已知正方形边长为1．(1)若∠DAE=15°，则DE的长为；(2)△AEF的面积为S的最大值是．14(2023•兰考县一模)如图，方形ABCD中，AB=8，点P为射线BC上任意一点(与点B、C不重合)，连接AP，在AP的右侧作正方形APGH，连接AG，交射线CD于E，当ED长为2时，点BP的长为．15(2023•本溪一模)由4个形状相同，大小相等的菱形组成如图所示的网格，菱形的顶点称为格点，点A，B，C，D都在格点上，∠A=60°，则cos∠CDB的值为．16(2023•沂南县校级一模)如图，矩形ABCD中，AC、BD相交于点O，过点B作BF⊥AC交CD 于点F，交AC与点M，过点D作DE∥BF交AB于点E，交AC于点N，连接FN、EM，则下列结论：①DN=BM；②EM∥FN；③AE=FC；④当AO=AD时，四边形DEBF是菱形．其中，正确结论的个数是．17(2023•琼海一模)如图，菱形ABCD，AE⊥BC，点E为垂足，点F为AE的中点，连接BF并延长交AD于点G，连接CG，CE=2，CG=211，则DG=，AG=，AF=．18(2023•镇江一模)如图，在矩形ABCD中，AB=6，BC=8，△BEF的顶点E在对角线AC上运动，且∠BFE=90°，∠EBF=∠BAC，连接AF，则AF的最小值为．19(2023•泉州模拟)如图，在菱形ABCD 中，∠A =60°，点E 在边AD 上，以BE 为边在菱形ABCD 的内部作等边三角形BEF ，若∠DEF =α，∠EBD =β，则α与β之间的数量关系可用等式表示为．20(2023•市南区一模)如图，正方形ABCD 中，E 、F 分别为BC 、CD 边上的点，∠EAF =45°，则下列结论中正确的有．(填序号)①BE +DF =EF ；②tan ∠AMD =CD DF； ③BM 2+DN 2=MN 2；④若EF =1.5，S △AEF =3，则．S 正方形ABCD =4．21(2023•大连一模)学习菱形时，我们从它的边、角和对角线等方面进行研究，可以发现并证明：菱形的每一条对角线平分一组对角．小明参考平行四边形、矩形判定方法的研究过程，得出下面的猜想：①一条对角线平分一组对角的四边形是菱形；②每一条对角线平分一组对角的四边形是菱形；③一条对角线平分一组对角的平行四边形是菱形．其中正确的是(填序号，填写一个即可)．22(2023•石景山区一模)如图，在菱形ABCD 中，点E ，F 分别在BC ，AD 上，BE =DF ．只需添加一个条件即可证明四边形AECF 是矩形，这个条件可以是(写出一个即可)．23(2023•河东区一模)已知，如图，已知菱形ABCD 的边长为6，∠ABC =60°，点E ，F 分别在AB ，CB 的延长线上，且BE =BF =13AB ，G 是DF 的中点，连接GE ，则GE 的长是．24(2023•合肥模拟)如图，点P在正方形ABCD内，∠BPC=135°，连接PA、PB、PC、PD．(1)若PA=AB，则∠CPD=；(2)若PB=2，PC=3，则PD的长为．25(2023•鄞州区一模)如图，Rt△ABC中，∠C=90°，AC=BC=8，作正方形CDEF，其中顶点E 在边AB上．(1)若正方形CDEF的边长为26，则线段AE的长是；(2)若点D到AB的距离是2，则正方形CDEF的边长是．26(2023•郓城县校级模拟)如图，在平行四边形ABCD中，对角线AC、BD交于点O．点M是BC 边的中点，连接AM、OM，作CF∥AM．已知OC平分∠BCF，OB平分∠AOM，若BD=32，则sin∠BAM的值为．27(2023•三原县二模)如图，点M是▱ABCD内一点，连接MA，MB，MC，MD，过点A作AP∥BM，过点D作DP∥CM，AP与DP交于点P，若四边形AMDP的面积为6，则▱ABCD的面积为．28(2023•和平区二模)如图，已知正方形ABCD的边长为4，点E为边BC上一点，BE=3，在AE的右侧，以AE为边作正方形AEFG，H为BG的中点，则AH的长等于．29(2023•鼓楼区校级模拟)如图，在矩形ABCD中，AD=3，AB=4，B是边AB上一点，△BCE与△FCE关于直线CE对称，连接BF并延长交AD于点G，过点F作FH⊥AD，垂足为点H，设BE=a，若点H为AG的中点，则BE的长为．30(2023•呼和浩特一模)如图在菱形ABCD中，O为对角线AC与BD的交点，点P为边AB上的任一点(不与A、B重合)，过点P分别作PM⊥AC，PN⊥BD，M、N为垂足，则可以判断四边形MPNO 的形状为．若菱形的边长为a，∠ADC=120°，则MN的最小值为．(用含a的式子表示)31(2023•洛阳一模)在扇形OAB中，∠AOB=60°，点C是半径OA上一点，且OC=6，将线段OC 沿OB方向平移，当平移距离是6时，点C的对应点C'恰好落在弧AB上，则图中阴影部分的面积为．32(2023•临渭区二模)如图，正六边形纸片ABCDEF的边长为6cm，从这个正六边形纸片上剪出一个扇形(图中阴影部分)，则这个扇形的面积为cm2．(结果保留π)33(2023•桂林二模)如图，在Rt△ABC中，∠C=90°，AB=10，BC=6，半径为1的⊙O在Rt△ABC内移动，当⊙O与∠A的两边都相切时，圆心O到点B的距离为2　．34(2023•万州区模拟)如图，在Rt△ABC中，∠ACB=90°，BC=1，AB=2，以点B为圆心，AB为半径作圆弧交CB的延长线于点D，以点A为圆心，AC为半径作圆弧交AD于点E．则图中阴影部分的面积为．35(2023•九龙坡区校级模拟)如图，AC、AD是⊙O中关于直径AB对称的两条弦，以弦AC、AD 为折线将弧AC、弧AD折叠后过圆心O，若⊙O的半径r=4，则圆中阴影部分的面积为．36(2023•烟台一模)如图，GC，GB是⊙O的切线，AB是⊙O的直径，延长GC，与BA的延长线交于点E，过点C作弦CD∥AB，连接DO并延长与圆交于点F，连接CF，若AE=2，CE=4，则CD的长度为．37(2023•历下区二模)如图，已知扇形AOB的半径OA=2，∠AOB=120°将扇形AOB绕点A顺时针旋转30°得到扇形AO′B′，则图中阴影部分的面积是．38(2023•邓州市一模)如图，在扇形AOB中，∠AOB=60°，OA=3，半径OC平分AB，点D为半径OA中点，点E为半径OC上一动点，当AE+DE取得最小值时，由AC，AE，CE围成的阴影部分的面积为．39(2023•龙口市二模)如图，由边长为1的小正方形构成的网格中，点A，B，C都在格点上，以AB 为直径的圆经过点C，D，则cos∠ADC的值为．40(2023•渝中区校级二模)如图，扇形纸片AOB的半径为2，沿AB折叠扇形纸片，点O恰好落在AB上的点C处，图中阴影部分的面积为．。

中考数学---几何选择填空压轴题精选1

中考数学---几何选择填空压轴题精选1一．选择题：1．如下图1，点O为正方形ABCD的中心，BE平分∠DBC交DC于点E，延长BC到点F，使FC=EC，连接DF交BE的延长线于点H，连接OH交DC于点G，连接HC．则以下四个结论中正确结论的个数为（）①OH=BF；②∠CHF=45°；③GH=BC；④DH2=HE•HB．A. 1个B. 2个C. 3个D. 4个2、如上图2，梯形ABCD中，AD∥BC，，∠ABC=45°，AE⊥BC于点E，BF⊥AC于点F，交AE于点G，AD=BE，连接DG、CG．以下结论：①△BEG≌△AEC；②∠GAC=∠GCA；③DG=DC；④G为AE中点时，△AGC的面积有最大值．其中正确的结论有（）A. 1个B. 2个C. 3个D. 4个3．如上图3，正方形ABCD中，在AD的延长线上取点E，F，使DE=AD，DF=BD，连接BF分别交CD，CE于H，G下列结论：①EC=2DG；②∠GDH=∠GHD；③S△CDG=S▭DHGE；④图中有8个等腰三角形．其中正确的是（）A.①③ B.②④ C.①④ D.②③4．如下图1，矩形ABCD的面积为5，它的两条对角线交于点O1，以AB，AO1为两邻边作平行四边形ABC1O1，平行四边形ABC1O1的对角线交BD于点02，同样以AB，AO2为两邻边作平行四边形ABC2O2．…，依此类推，则平行四边形ABC2009O2009的面积为（）A.B. C. D.5、如上图2，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，则下列结论：①PM=PN；②；③△PMN为等边三角形；④当∠ABC=45°时，BN=PC．其中正确的个数是（）A.1个 B.2个 C.3个 D.4个6．Rt△ABC中，AB=AC，点D为BC中点．∠MDN=90°，∠MDN绕点D旋转，DM、DN分别与边AB、AC交于E、F两点．下图1，下列结论：①（BE+CF）=BC；②S△AEF ≤S△ABC；③S四边形AEDF=AD•EF；④AD≥EF；⑤AD与EF可能互相平分，其中正确结论的个数是（）A.1个B.2个C.3个D.4个7．如上图2，在正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后折痕DE分别交AB、AC于点E、G，连接GF．下列结论①∠ADG=22.5°；②tan∠AED=2；③S△AGD =S△OGD；④四边形AEFG是菱形；⑤BE=2OG．其中正确的结论有（）A.①④⑤B.①②④C.③④⑤D.②③④8．如上图3，正方形ABCD中，O为BD中点，以BC为边向正方形内作等边△BCE，连接并延长AE 交CD于F，连接BD分别交CE、AF于G、H，下列结论：①∠CEH=45°；②GF∥DE；③2OH+DH=BD；④BG=DG；⑤．其中正确的结论是（）A.①②③B.①②④C.①②⑤D.②④⑤9．如下图1，在正方形ABCD中，AB=4，E为CD上一动点，AE交BD于F，过F作FH⊥AE于H，过H作GH⊥BD于G，下列有四个结论：①AF=FH，②∠HAE=45°，③BD=2FG，④△CEH的周长为定值，其中正确的结论有（）A.①②③B.①②④C.①③④D.①②③④10．正方形ABCD、正方形BEFG和正方形RKPF的位置如上图2所示，点G在线段DK上，正方形BEFG 的边长为4，则△DEK的面积为（）A. 10B. 12C. 14D. 16二．填空题1．如下图1，观察图中菱形的个数：图1中有1个菱形，图2中有5个菱形，图3中有14个菱形，图4中有30个菱形…，则第6个图中菱形的个数是个．2.如下图2，在△ABC 中，∠A=α．∠ABC 与∠ACD 的平分线交于点A 1，得∠A 1； ∠A 1BC 与∠A 1CD 的平分线相交于点A 2，得∠A 2； …；∠A 2011BC 与∠A 2011CD 的平分线相交于点A 2012，得∠A 2012，则∠A 2012= ．3．如下图1，已知Rt △ABC 中，AC=3，BC=4，过直角顶点C 作CA 1⊥AB ，垂足为A 1，再过A 1作A 1C 1⊥BC ，垂足为C 1，过C 1作C 1A 2⊥AB ，垂足为A 2，再过A 2作A 2C 2⊥BC ，垂足为C 2，…，这样一直做下去，得到了一组线段CA 1，A 1C 1，C 1A 2，…，则CA 1= ，= ．4、如上图2，点A 1，A 2，A 3，A 4，…，A n 在射线OA 上，点B 1，B 2，B 3，…，B n ﹣1在射线OB 上，且A 1B 1∥A 2B 2∥A 3B 3∥…∥A n ﹣1B n ﹣1，A 2B 1∥A 3B 2∥A 4B 3∥…∥A n B n ﹣1，△A 1A 2B 1，△A 2A 3B 2，…，△A n ﹣1A n B n ﹣1为阴影三角形，若△A 2B 1B 2，△A 3B 2B 3的面积分别为1、4，则△A 1A 2B 1的面为；面积小于2011的阴影三角形共有个． 5、如下图1，已知点A 1（a ，1）在直线l ：上，以点A 1为圆心，以为半径画弧，交x 轴于点B 1、B 2，过点B 2作A 1B 1的平行线交直线l 于点A 2，在x 轴上取一点B 3，使得A 2B 3=A 2B 2，再过点B 3作A 2B 2的平行线交直线l 于点A 3，在x 轴上取一点B 4，使得A 3B 4=A 3B 3，按此规律继续作下去，则①a= ；②△A 4B 4B 5的面积是．6、如下图，在梯形ABCD中，AD∥BC，EA⊥AD，M是AE上一点，F、G分别是AB、CM的中点，且∠BAE=∠MCE，∠MBE=45°，则给出以下五个结论：①AB=CM；②A E⊥BC；③∠BMC=90°；④EF=EG；⑤△BMC是等腰直角三角形．上述结论中始终正确的序号有．7、如图，边长为1的菱形ABCD中，∠DAB=60度．连接对角线AC，以AC为边作第二个菱形ACC1D1，使∠D1AC=60°；连接AC1，再以AC1为边作第三个菱形AC1C2D2，使∠D2AC1=60°；…，按此规律所作的第n个菱形的边长为．8、如图，将矩形ABCD的四个角向内折起，恰好拼成一个既无缝隙又无重叠的四边形EFGH，若EH=3，EF=4，那么线段AD与AB的比等于．9．如图，E、F分别是平行四边形ABCD的边AB、CD上的点，AF与DE相交于点P，BF与CE相交于点Q，若S△APD =15cm2，S△BQC=25cm2，则阴影部分的面积为cm2．中考数学---几何选择填空压轴题精选1答案一．选择题：1、解：作EJ⊥BD于J，连接EF①∵BE平分∠DBC ∴EC=EJ，∴△DJE≌△ECF ∴DE=FE∴∠HEF=45°+22.5°=67.5°∴∠HFE==22.5°∴∠EHF=180°﹣67.5°﹣22.5°=90°∵DH=HF，OH是△DBF的中位线∴OH∥BF ∴OH=BF②∵四边形ABCD是正方形，BE是∠DBC的平分线，∴BC=CD，∠BCD=∠DCF，∠EBC=22.5°，∵CE=CF，∴Rt△BCE≌Rt△DCF，∴∠EBC=∠CDF=22.5°，∴∠BFH=90°﹣∠CDF=90°﹣22.5°=67.5°，∵OH是△DBF的中位线，CD⊥AF，∴OH是CD的垂直平分线，∴DH=CH，∴∠CDF=∠DCH=22.5°，∴∠HCF=90°﹣∠DCH=90°﹣22.5°=67.5°，∴∠CHF=180°﹣∠HCF﹣∠BFH=180°﹣67.5°﹣67.5°=45°，故②正确；③∵OH是△BFD的中位线，∴DG=CG=BC，GH=CF，∵CE=CF，∴GH=CF=CE∵CE＜CG=BC，∴GH＜BC，故此结论不成立；④∵∠DBE=45°，BE是∠DBF的平分线，∴∠DBH=22.5°，由②知∠HBC=∠CDF=22.5°，∴∠DBH=∠CDF，∵∠BHD=∠BHD，∴△DHE∽△BHD，∴=∴DH=HE•HB，故④成立；所以①②④正确．故选C．（第5题图）2、解：根据BE=AE，∠GBE=∠CAE，∠BEG=∠CEA可判定①△BEG≌△AEC；用反证法证明②∠GAC≠∠GCA，假设∠GAC=∠GCA，则有△AGC为等腰三角形，F为AC的中点，又BF⊥AC，可证得AB=BC，与题设不符；由①知△BEG≌△AEC 所以GE=CE 连接ED、四边形ABED为平行四边形，∵∠ABC=45°，AE⊥BC于点E，∴∠GED=∠CED=45°，∴△GED≌△CED，∴DG=DC；④设AG为X，则易求出GE=EC=2﹣X 因此，S△AGC =SAEC﹣SGEC=﹣+x=﹣（x2﹣2x）=﹣（x2﹣2x+1﹣1）=﹣（x﹣1）2+，当X取1时，面积最大，所以AG等于1，所以G是AE中点，故G为AE中点时，GF最长，故此时△AGC的面积有最大值．故正确的个数有3个．故选C．3、解：∵DF=BD，∴∠DFB=∠DBF，∵AD∥BC，DE=BC，∴∠DEC=∠DBC=45°，∴∠DEC=2∠EFB，∴∠EFB=22.5°，∠CGB=∠CBG=22.5°，∴CG=BC=DE，∵DE=DC，∴∠DEG=∠DCE，∵∠GHC=∠CDF+∠DFB=90°+22.5°=112.5°，∠DGE=180°﹣（∠BGD+∠EGF）=180°﹣（∠BGD+∠BGC），=180°﹣（180°﹣∠DCG）÷2=180°﹣（180°﹣45°）÷2=112.5°，∴∠GHC=∠DGE，∴△CHG≌△EGD，∴∠EDG=∠CGB=∠CBF，∴∠GDH=∠GHD，∴S△CDG =S▭DHGE．故选D．4、解：∵矩形ABCD的对角线互相平分，面积为5，∴平行四边形ABC1O1的面积为，∵平行四边形ABC1O1的对角线互相平分，∴平行四边形ABC2O2的面积为×=，…，依此类推，平行四边形ABC2009O2009的面积为．故选B．5、解：①∵BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，∴PM=BC，PN=BC，∴PM=PN，正确；②在△ABM与△ACN中，∵∠A=∠A，∠AMB=∠ANC=90°，∴△ABM∽△ACN，∴，正确；③∵∠A=60°，BM⊥AC于点M，CN⊥AB于点N，∴∠ABM=∠ACN=30°，在△ABC中，∠BCN+∠CBM═180°﹣60°﹣30°×2=60°，∵点P是BC的中点，BM⊥AC，CN⊥AB，∴PM=PN=PB=PC，∴∠BPN=2∠BCN，∠CPM=2∠CBM，∴∠BPN+∠CPM=2（∠BCN+∠CBM）=2×60°=120°，∴∠MPN=60°，∴△PMN是等边三角形，正确；（见上图）④当∠ABC=45°时，∵CN⊥AB于点N，∴∠BNC=90°，∠BCN=45°，∴BN=CN，∵P为BC边的中点，∴PN⊥BC，△BPN为等腰直角三角形；∴BN=PB=PC，正确．故选D．6、解：∵Rt△ABC中，AB=AC，点D为BC中点，∴∠C=∠BAD=45°，AD=BD=CD，∵∠MDN=90°，∴∠ADE+∠ADF=∠ADF+∠CDF=90°，∴∠ADE=∠CDF．在△AED与△CFD中，∵，∴△AED≌△CFD（ASA），∴AE=CF，在Rt△ABD中，BE+CF=BE+AE=AB==BD=BC．故①正确；设AB=AC=a，AE=CF=x，则AF=a﹣x．∵S△AEF =AE•AF=x（a﹣x）=﹣（x﹣a）2+a2，∴当x=a时，S△AEF有最大值a2，又∵S△ABC =×a2=a2，∴S△AEF≤S△ABC．故②正确；EF2=AE2+AF2=x2+（a﹣x）2=2（x﹣a）2+a2，∴当x=a时，EF2取得最小值a2，∴EF≥a（等号当且仅当x=a时成立），而AD=a，∴EF≥AD．故④错误；由①的证明知△AED≌△CFD，∴S四边形AEDF =S△AED+S△ADF=S△CFD+S△ADF=S△ADC=AD2，∵EF≥AD，∴AD•EF≥AD2，∴AD•EF＞S四边形AEDF故③错误；当E、F分别为AB、AC的中点时，四边形AEDF为正方形，此时AD与EF互相平分．故⑤正确．综上所述，正确的有：①②⑤，共3个．故选C．7、解：∵四边形ABCD是正方形，∴∠GAD=∠ADO=45°，由折叠的性质可得：∠ADG=∠ADO=22.5°，故①正确．∵tan∠AED=，由折叠的性质可得：AE=EF，∠EFD=∠EAD=90°，∴AE=EF＜BE，∴AE＜AB，∴tan∠AED=＞2，故②错误．∵∠AOB=90°，∴AG=FG＞OG，△AGD与△OGD同高，∴S△AGD ＞S△OGD，故③错误．∵∠EFD=∠AOF=90°，∴EF∥AC，∴∠FEG=∠AGE，∵∠AGE=∠FGE，∴∠FEG=∠FGE，∴EF=GF，∵AE=EF，∴AE=GF，故④正确．∵AE=EF=GF，AG=GF，∴AE=EF=GF=AG，∴四边形AEFG是菱形，∴∠OGF=∠OAB=45°，∴EF=GF=OG，∴BE=EF=×OG=2OG．故⑤正确．∴其中正确结论的序号是：①④⑤．故选：A．8、解：①由∠ABC=90°，△BEC为等边三角形，△ABE为等腰三角形，∠AEB+∠BEC+∠CEH=180°，可求得∠CEH=45°，此结论正确；②由△EGD≌△DFE，EF=GD，再由△HDE为等腰三角形，∠DEH=30°，得出△HGF为等腰三角形，∠HFG=30°，可求得GF∥DE，此结论正确；③由图可知2（OH+HD）=2OD=BD，所以2OH+DH=BD此结论不正确；④如图，过点G作GM⊥CD垂足为M，GN⊥BC垂足为N，设GM=x，则GN=x，进一步利用勾股定理求得GD=x，BG=x，得出BG=GD，此结论不正确；⑤由图可知△BCE和△BCG同底不等高，它们的面积比即是两个三角形的高之比，由④可知△BCE的高为（x+x）和△BCG的高为x，因此S△BCE ：S△BCG=（x+x）：x=，此结论正确；故正确的结论有①②⑤．故选C．9、解：（1）连接FC，延长HF交AD于点L，∵BD为正方形ABCD的对角线，∴∠ADB=∠CDF=45°．∵AD=CD，DF=DF，∴△ADF≌△CDF．∴FC=AF，∠ECF=∠DAF．∵∠ALH+∠LAF=90°，∴∠LHC+∠DAF=90°．∵∠ECF=∠DAF，∴∠FHC=∠FCH，∴FH=FC．∴FH=AF．（上图2）（2）∵FH⊥AE，FH=AF，∴∠HAE=45°．（3）连接AC交BD于点O，可知：BD=2OA，（上图3）∵∠AFO+∠GFH=∠GHF+∠GFH，∴∠AFO=∠GHF．∵AF=HF，∠AOF=∠FGH=90°，∴△AOF≌△FGH．∴OA=GF．∵BD=2OA，∴BD=2FG．（4）延长AD至点M，使AD=DM，过点C作CI∥HL，则：LI=HC，根据△MEC≌△CIM，（见下图2）可得：CE=IM，同理，可得：AL=HE，∴HE+HC+EC=AL+LI+IM=AM=8．∴△CEH的周长为8，为定值．故（1）（2）（3）（4）结论都正确．故选D．10、解：如下图1，连DB，GE，FK，则DB∥GE∥FK，在梯形GDBE中，S△DGE =S△GEB（同底等高的两三角形面积相等），同理S△GKE=S△GFE．∴S阴影=S△DGE+S△GKE=S△GEB+S△GEF=S正方形GBEF=4×4=16 故选D．二．填空题：1、解：观察图形，发现规律：图1中有1个菱形，图2中有1+22=5个菱形，图3中有5+32=14个菱形，图4中有14+42=30个菱形，则第5个图中菱形的个数是30+52=55，第6个图中菱形的个数是55+62=91个．故答案为91．2、解：∵∠ABC与∠ACD的平分线交于点A1，∴∠A1BC=∠ABC，∠A1CD=∠ACD，根据三角形的外角性质，∠A+∠ABC=∠ACD，∠A1+∠A1BC=∠A1CD，∴∠A1+∠A1BC=∠A1+∠ABC=（∠A+∠ABC），整理得，∠A1=∠A=，同理可得，∠A2=∠A1=×=，…，∠A2012=．故答案为：．3、解：在Rt△ABC中，AC=3，BC=4，∴AB=，又因为CA1⊥AB，∴AB•CA1=AC•BC，即CA1===．∵C4A5⊥AB，∴△BA5C4∽△BCA，∴，∴==．所以应填和．4、解：由题意得，△A2B1B2∽△A3B2B3，∴==，==，又∵A1B1∥A2B2∥A3B3，∴===，==，∴OA1=A1A2，B1B2=B2B3继而可得出规律：A1A2=A2A3=A3A4…；B1B2=B2B3=B3B4…又△A2B1B2，△A3B2B3的面积分别为1、4，∴S△A1B1A2=，S△A2B2A3=2，继而可推出S△A3B3A4=8，S△A4B4A5=32，S△A5B5A6=128，S△A6B6A7=512，S△A7B7A8=2048，故可得小于2011的阴影三角形的有：△A1B1A2，△A2B2A3，△A3B3A4，△A4B4A5，△A5B5A6，△A6B6A7，共6个．故答案是：；6．5、解：如图所示：①将点A1（a，1）代入直线1中，可得，所以a=．②△A1B1B2的面积为：S==；因为△OA1B1∽△OA2B2，所以2A1B1=A2B2，又因为两线段平行，可知△A1B1B2∽△A2B2B3，所以△A2B2B3的面积为S1=4S；以此类推，△A4B4B5的面积等于64S=．6、解：∵梯形ABCD中，AD∥BC，EA⊥AD，∴AE⊥BC，即②正确．∵∠MBE=45°，∴BE=ME．在△ABE与△CME中，∵∠BAE=∠MCE，∠AEB=∠CEM=90°，BE=ME，∴△ABE≌△CME，∴AB=CM，即①正确．∵∠MCE=∠BAE=90°﹣∠ABE＜90°﹣∠MBE=45°，∴∠MCE+∠MBC＜90°，∴∠BMC＞90°，即③⑤错误．∵∠AEB=∠CEM=90°，F、G分别是AB、CM的中点，∴EF=AB，EG=CM．又∵AB=CM，∴EF=EG，即④正确．故正确的是①②④．7、解：连接DB，∵四边形ABCD是菱形，∴AD=AB．AC⊥DB，∵∠DAB=60°，∴△ADB是等边三角形，∴DB=AD=1，∴BM=，∴AM==，∴AC=，同理可得AC1=AC=（）2，AC2=AC1=3=（）3，按此规律所作的第n个菱形的边长为（）n﹣1故答案为（）n﹣1．8、解：∵∠1=∠2，∠3=∠4，∴∠2+∠3=90°，∴∠HEF=90°，（见上图3）同理四边形EFGH的其它内角都是90°，∴四边形EFGH是矩形．∴EH=FG（矩形的对边相等）；又∵∠1+∠4=90°，∠4+∠5=90°，∴∠1=∠5（等量代换），同理∠5=∠7=∠8，∴∠1=∠8，∴Rt△AHE≌Rt△CFG，∴AH=CF=FN，又∵HD=HN，∴AD=HF，在Rt△HEF中，EH=3，EF=4，根据勾股定理得HF=，∴HF=5，又∵HE•EF=HF•EM，∴EM=，又∵AE=EM=EB（折叠后A、B都落在M点上），∴AB=2EM=，∴AD：AB=5：=．故答案为：．9、解：如图，连接EF；∵△ADF与△DEF同底等高，∴S△ADF =S△DEF即S△ADF﹣S△DPF=S△DEF﹣S△DPF，即S△APD =S△EPF=15cm2，同理可得S△BQC=S△EFQ=25cm2，∴阴影部分的面积为S△EPF+S△EFQ=15+25=40cm2．故答案为40．。

2020年中考数学5.几何综合选择填空压轴题(含解析)

几何综合-填空选择压轴题51、以正方形ABCD勺边AD作等边△ ADE则/ BEC勺度数是 __________2、如图.在厶ABC中, / ACB=60 , AC=1, D是边AB的中点，E是边BC上一点.若DE平分△ ABC的周长，则DE的长是 ____ .3、已知CD是△ ABC的边AB上的高，若CD・3,AD=1AB=2AC则BC的长为__4、如图，将面积为32V2的矩形ABCC沿对角线BD折叠，点A的对应点为点P,连接AP交BC于点E.若BE=J，贝U AP的长为____ .p5、如图，△ ABC是等边三角形，△ ABD是等腰直角三角形，/ BAD=90 , AE L BD 于点E,连CD分别交AE AB于点F, G过点A作AH L CD交BD于点H.则下列结论：①/ ADC=15 :② AF=AG ③ AH=DF ④厶AF3A CBQ ⑤AF= (V3 - 1)EF.其中正确结论的个数为（）A. 5 B . 4 C . 3 D . 26 已知O 0的半径为10cm AB CD是O O的两条弦，AB// CD AB=16cm CD=12cm则弦AB和CD之间的距离是cm513 13 13 7 77、如图，将矩形ABCD 沿 EF 折叠，使点B 落在AD 边上的点G 处，点C 落在点H 处，已知/ DGH=30，连接BG 则/ AGB ________ .8、如图，？ABCD 勺对角线相交于点 0,且A 》CD 过点0作OM L AC,交AD 于点 M.如果△ CDM 勺周长为8,那么？ABCD 勺周长是 _____ .9、如图，由四个全等的直角三角形围成的大正方形的面积是169，小正方形的面积为 49，则 sin a - COS a =( ) A 13 B10、如图，P是厶ABC的内心，连接PA PB PC, △ PAB △ PBG △ PAC的面积分别为S、S、S.则Si ____ S2+S3.（填“v” 或“二”或“〉”）11、如图，△ ABC中, AB=AC AD L BC 于D点，DEL AB 于点E, BF 丄AC 于点F,DE=3cryi 则BF= ______ cm12、如图，已知半圆O与四边形ABCD勺边AD AB BC都相切，切点分别为DE、C,半径OC=1 则AE?BE=_.13、《九章算术》是我国古代数学名著，书中有下列问题：“今有勾五步，股十二步，问勾中容方几何？”其意思为：“今有直角三角形，勾（短直角边）长为5步，股（长直角边）长为12步，冋该直角二角形能容纳的正方形边长最大是多少步？”该问题的答案是____________ 步.14、如图，以AB为直径的。

2020江苏省中考数学选择填空压轴题专题：《函数的几何综合问题》(含答案)

专题: 函数的几何综合问题例1．如图，在平面直角坐标系中，直线l：y＝33x－33与x轴交于点B1，以OB1为边长作等边三角形A1OB1，过点A1作A1B2平行于x轴，交直线l于点B2，以A1B2为边长作等边三角形A2A1B2，过点A2作A2B3平行于x轴，交直线l于点B3，以A2B3为边长作等边三角形A3A2B3，…，则点A2017的横坐标是____________．同类题型1.1 如图，直线l：y＝x＋1交y轴于点A1，在x轴正方向上取点B1，使OB1＝OA1；过点B1作A2B1⊥x轴，交l于点A2，在x轴正方向上取点B2，使B1B2＝B1A2；过点B2作A3B2⊥x轴，交l 于点A3，在x轴正方向上取点B3，使B2B3＝B2A3；…记△OA1B1面积为S1，△B1A2B2面积为S2，△B2A3B3面积为S3，…则S2017等于（）A．24030B．24031C．24032D．24033同类题型1.2 如图，已知直线l：y＝33x，过点A（0，1）作y轴的垂线交直线l于点B，过点B作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线l的垂线交y轴于点A2；…；按此作法继续下去，则点A4的坐标为（）A．（0，128）B．（0，256）C．（0，512）D．（0，1024）同类题型1.3 如图，在平面直角坐标系中，直线l ：y ＝33x ＋1交x 轴于点B ，交y 轴于点A ，过点A 作AB 1 ⊥AB 交x 轴于点B 1 ，过点B 1 作B 1A 1 ⊥x 轴交直线l 于点A 2 …依次作下去，则点B n 的横坐标为____________．例2．高速公路上依次有3个标志点A 、B 、C ，甲、乙两车分别从A 、C 两点同时出发，匀速行驶，甲车从A →B →C ，乙车从C →B →A ，甲、乙两车离B 的距离y 1 、y 2 （千米）与行驶时间x （小时）之间的函数关系图象如图所示．观察图象，给出下列结论：①A 、C 之间的路程为690千米；②乙车比甲车每小时快30千米；③4.5小时两车相遇；④点E 的坐标为（7，180），其中正确的有_________（把所有正确结论的序号都填在横线上）．同类题型2.1 甲、乙两辆汽车沿同一路线从A 地前往B 地，甲车以a 千米/时的速度匀速行驶，途中出现故障后停车维修，修好后以2a 千米/时的速度继续行驶；乙车在甲车出发2小时后匀速前往B 地，比甲车早30分钟到达．到达B 地后，乙车按原速度返回A 地，甲车以2a 千米/时的速度返回A 地．设甲、乙两车与A 地相距s （千米），甲车离开A 地的时间为t （小时），s 与t 之间的函数图象如图所示．下列说法：①a ＝40；②甲车维修所用时间为1小时；③两车在途中第二次相遇时t 的值为5.25；④当t ＝3时，两车相距40千米，其中不正确的个数为（）A ．0个B ．1个C ．2个D ．3个同类题型2.2 甲、乙两车从A 地驶向B 地，并以各自的速度匀速行驶，甲车比乙车早行驶2h ，并且甲车途中休息了0.5h ，如图是甲乙两车行驶的距离y （km ）与时间x （h ）的函数图象．则下列结论：（1）a ＝40，m ＝1；（2）乙的速度是80km/h ；（3）甲比乙迟74h 到达B 地；（4）乙车行驶94 小时或194小时，两车恰好相距50km ．正确的个数是（）A ．1B ．2C ．3D ．4同类题型2.3 甲、乙两人从科技馆出发，沿相同的路线分别以不同的速度匀速跑向极地馆，甲先跑一段路程后，乙开始出发，当乙超出甲150米时，乙停在此地等候甲，两人相遇后乙又继续以原来的速度跑向极地馆．如图是甲、乙两人在跑步的全过程中经过的路程y （米）与甲出发的时间x （秒）的函数图象．则下列四种说法：①甲的速度为1.5米/秒；②a ＝750；③乙在途中等候甲100秒；④乙出发后第一次与甲相遇时乙跑了375米．其中正确的个数是（）A ．1个B ．2个C ．3个D ．4个例3．如图，已知动点P 在函数y ＝ 12x（x ＞0）的图象上运动，PM ⊥x 轴于点M ，PN ⊥y 轴于点N ，线段PM 、PN 分别与直线AB ：y ＝－x ＋1交于点E ，F ，则AF ﹒BE 的值为（）A ．4B ．2C ．1D ．12同类题型3.1 如图，在反比例函数y ＝ 32x 的图象上有一动点A ，连接AO 并延长交图象的另一支于点B ，在第二象限内有一点C ，满足AC ＝BC ，当点A 运动时，点C 始终在函数y ＝ k x的图象上运动，若tan ∠CAB ＝2，则k 的值为（）A ．－3B ．－6C ．－9D ．－12同类题型3.2 如图，在平面直角坐标系中，点A 在x 轴的正半轴上，点B 在第一象限，点C 在线段AB 上，点D 在AB 的右侧，△OAB 和△BCD 都是等腰直角三角形，∠OAB ＝∠BCD ＝90°，若函数y ＝ 6x（x ＞0）的图象经过点D ，则△OAB 与△BCD 的面积之差为（） A ．12 B ．6 C ．3 D ．2同类题型3.3 如图，在平面直角坐标系xOy 中，已知直线y ＝kx （k ＞0）分别交反比例函数y ＝ 1x 和y ＝ 9x在第一象限的图象于点A ，B ，过点B 作 BD ⊥x 轴于点D ，交y ＝ 1x的图象于点C ，连结A C ．若△ABC 是等腰三角形，则k 的值是___________．例4．如图，一次函数y ＝x ＋b 的图象与反比例函数y ＝ k x的图象交于点A （3，6）与点B ，且与y 轴交于点C ，若点P 是反比例函数y ＝ k x图象上的一个动点，作直线AP 与x 轴、y 轴分别交于点M 、N ，连结BN 、CM ．若S △ACM ＝S △ABN ，则APAN的值为__________．同类题型4.1 当12 ≤x ≤2时，函数y ＝－2x ＋b 的图象上至少有一点在函数y ＝ 1x的图象下方，则b 的取值范围为（）A ．b ＞2 2B ．b ＜ 92C ．b ＜3D ．2 2＜b ＜ 92同类题型4.2 方程x 2＋3x －1＝0的根可视为函数y ＝x ＋3的图象与函数y ＝ 1x的图象交点的横坐标，那么用此方法可推断出方程x 2＋2x －1＝0的实数根x 0 所在的范围是（）A ．－1＜x 0 ＜0B ．0＜x 0 ＜1C ．1＜x 0 ＜2D ．2＜x 0 ＜3例5．在平面直角坐标系xOy 中，抛物线y ＝－x 2＋2mx －m 2－m ＋1交y 轴于点为A ，顶点为D ，对称轴与x 轴交于点H ．当抛物线顶点D 在第二象限时，如果∠ADH ＝∠AHO ，则m ＝__________．同类题型5.1 已知抛物线y ＝ 14x 2＋1具有如下性质：该抛物线上任意一点到定点F （0，2）的距离与到x 轴的距离始终相等，如图，点M 的坐标为（ 3 ，3），P 是抛物线y ＝ 14x 2＋1上一个动点，则△PMF周长的最小值是（）A ．3B ．4C ．5D ．6同类题型5.2 抛物线y ＝ax 2＋bx ＋3（a ≠0）经过点A （－1，0），B （ 32，0），且与y 轴相交于点C ．设点D 是所求抛物线第一象限上一点，且在对称轴的右侧，点E 在线段AC 上，且DE ⊥AC ，当△DCE 与△AOC 相似时，求点D 的坐标．同类题型5.3小明家的洗手盆上装有一种抬启式水龙头（如图1），完全开启后，水流路线呈抛物线，把手端点A ，出水口B 和落水点C 恰好在同一直线上，点A 至出水管BD 的距离为12cm ，洗手盆及水龙头的相关数据如图2所示，现用高10.2cm 的圆柱型水杯去接水，若水流所在抛物线经过点D 和杯子上底面中心E ，则点E 到洗手盆内侧的距离EH 为__________cm ．参考答案例1．如图，在平面直角坐标系中，直线l ：y ＝ 33x － 33与x 轴交于点B 1 ，以OB 1 为边长作等边三角形A 1OB 1 ，过点A 1 作A 1B 2 平行于x 轴，交直线l 于点B 2 ，以A 1B 2 为边长作等边三角形A 2A 1B 2 ，过点A 2 作A 2B 3 平行于x 轴，交直线l 于点B 3 ，以A 2B 3 为边长作等边三角形A 3A 2B 3 ，…，则点A 2017 的横坐标是____________．解：由直线l ：y ＝33x －33 与x 轴交于点B 1 ，可得B 1 （1，0），D （0，－33），∴OB 1 ＝1，∠OB 1 D ＝30°，如图所示，过A 1 作A 1A ⊥OB 1 于A ，则OA ＝12OB 1＝12，即A 1 的横坐标为12＝21－12，由题可得∠A 1B 2B 1＝∠OB 1 D ＝30°，∠B 2A 1B 1＝∠A 1B 1 O ＝60°，∴∠A 1B 1B 2 ＝90°， ∴A 1B 2＝2A 1B 1 ＝2，过A 2 作A 2B ⊥A 1B 2 于B ，则A 1B ＝12A 1B 2 ＝1，即A 2 的横坐标为12＋1＝32＝22－12 ，过A 3 作A 3C ⊥A 2B 3 于C ，同理可得，A 2B 3＝2A 2B 2 ＝4，A 2C ＝12A 2B 3 ＝2，即A 3 的横坐标为12＋1＋2＝72＝23－12，同理可得，A 4 的横坐标为12＋1＋2＋4＝152＝24－12 ，由此可得，A n 的横坐标为2n－12 ，∴点A 2017 的横坐标是22017－12．同类题型1.1 如图，直线l ：y ＝x ＋1交y 轴于点A 1 ，在x 轴正方向上取点B 1 ，使OB 1＝OA 1 ；过点B 1 作A 2B 1 ⊥x 轴，交l 于点A 2 ，在x 轴正方向上取点B 2 ，使B 1B 2＝B 1A 2 ；过点B 2 作A 3B 2 ⊥x 轴，交l 于点A 3 ，在x 轴正方向上取点B 3 ，使B 2B 3＝B 2A 3 ；…记△OA 1B 1 面积为S 1 ，△B 1A 2B 2 面积为S 2 ，△B 2A 3B 3 面积为S 3 ，…则S 2017 等于（）A ．24030B ．24031C ．24032D ．24033解：∵OB 1＝OA 1 ；过点B 1 作A 2B 1 ⊥x 轴，B 1B 2＝B 1A 2；A 3B 2 ⊥x 轴，B 2B 3＝B 2A 3 ；… ∴△△OA 1B 1 ，△B 1A 2B 2 ，△B 2A 3B 3 是等腰直角三角形， ∵y ＝x ＋1交y 轴于点A 1 ， ∴A 1 （0，1）， ∴B 1 （1，0）， ∴OB 1＝OA 1 ＝1，∴S 1＝12×1×1＝12×12 ，同理S 2＝12×2×2＝12×22 ，S 3＝12×4×4＝12×42；…∴S n ＝12×22n －2＝22n －3 ，∴S 2017＝22×2017－3＝24031，选B ．同类题型1.2 如图，已知直线l ：y ＝ 33x ，过点A （0，1）作y 轴的垂线交直线l 于点B ，过点B 作直线l 的垂线交y 轴于点A 1 ；过点A 1 作y 轴的垂线交直线l 于点B 1 ，过点B 1 作直线l 的垂线交y 轴于点A2；…；按此作法继续下去，则点A4的坐标为（）A．（0，128） B．（0，256） C．（0，512） D．（0，1024）解：∵直线l的解析式为；y＝33x，∴l与x轴的夹角为30°，∵AB∥x轴，∴∠ABO＝30°，∵OA＝1，∴OB＝2，∴AB＝ 3 ，∵A1B⊥l，∴∠ABA1＝60°，∴A1O＝4，∴A1（0，4），同理可得A2（0，16），…∴A4纵坐标为44＝256，∴A4（0，256）．选B．同类题型1.3 如图，在平面直角坐标系中，直线l：y＝33x＋1交x轴于点B，交y轴于点A，过点A作AB1⊥AB交x轴于点B1，过点B1作B1A1⊥x轴交直线l于点A2…依次作下去，则点B n的横坐标为____________．解：由直线l ：y ＝33x ＋1交x 轴于点B ，交y 轴于点A ，可得A （0，1），B （－ 3 ，0），∴tan ∠ABO ＝33，即∠ABO ＝30°， ∴BA ＝2AO ＝2，又∵AB 1 ⊥AB 交x 轴于点B 1 ，AO ＝1，∴AB 1＝233 ，∴Rt △BAB 1 中，BB 1＝433 ；由题可得BA 1＝83 ，∴A 1B 2＝893 ，∴Rt △BA 1B 2 中，BB 2＝1693 ；由题可得BA 2＝329 ，∴A 2B 3＝32273 ，∴Rt △BA 2B 3 中，BB 3＝64273 ，…以此类推，BB n ＝(43)n3 ，又∵BO ＝ 3 ，∴OB n ＝(43)n3－ 3 ，∴点B n 的横坐标为(43)n3－ 3 ．例2．高速公路上依次有3个标志点A 、B 、C ，甲、乙两车分别从A 、C 两点同时出发，匀速行驶，甲车从A →B →C ，乙车从C →B →A ，甲、乙两车离B 的距离y 1 、y 2 （千米）与行驶时间x （小时）之间的函数关系图象如图所示．观察图象，给出下列结论：①A 、C 之间的路程为690千米；②乙车比甲车每小时快30千米；③4.5小时两车相遇；④点E 的坐标为（7，180），其中正确的有_________（把所有正确结论的序号都填在横线上）．解：①450＋240＝690（千米）．故A、C之间的路程为690千米是正确的；②450÷5－240÷4＝90－60＝30（千米/小时）．故乙车比甲车每小时快30千米是正确的；③690÷（450÷5＋240÷4）＝690÷（90＋60）＝690÷150＝4.6（小时）．故4.6小时两车相遇，原来的说法是错误的；④（450－240）÷（450÷5－240÷4）＝210÷（90－60）＝210÷30＝7（小时），450÷5×7－450＝630－450＝180（千米）．故点E的坐标为（7，180）是正确的，故其中正确的有①②④．同类题型2.1 甲、乙两辆汽车沿同一路线从A地前往B地，甲车以a千米/时的速度匀速行驶，途中出现故障后停车维修，修好后以2a千米/时的速度继续行驶；乙车在甲车出发2小时后匀速前往B地，比甲车早30分钟到达．到达B地后，乙车按原速度返回A地，甲车以2a千米/时的速度返回A地．设甲、乙两车与A地相距s（千米），甲车离开A地的时间为t（小时），s与t之间的函数图象如图所示．下列说法：①a＝40；②甲车维修所用时间为1小时；③两车在途中第二次相遇时t的值为5.25；④当t＝3时，两车相距40千米，其中不正确的个数为（）A．0个 B．1个 C．2个 D．3个解：①由函数图象，得a＝120÷3＝40故①正确，②由题意，得5.5－3－120÷（40×2），＝2.5－1.5，＝1．∴甲车维修的时间为1小时；故②正确， ③如图：∵甲车维修的时间是1小时， ∴B （4，120）．∵乙在甲出发2小时后匀速前往B 地，比甲早30分钟到达． ∴E （5，240）．∴乙行驶的速度为：240÷3＝80， ∴乙返回的时间为：240÷80＝3， ∴F （8，0）．设BC 的解析式为y 1＝k 1t ＋b 1 ，EF 的解析式为y 2＝k 2t ＋b 2 ，由图象，得 ⎩⎪⎨⎪⎧120＝4k 1＋b 1240＝5.5k 1＋b ，，⎩⎪⎨⎪⎧240＝5k 2＋b 20＝8k 2＋b 2 解得⎩⎪⎨⎪⎧k 1＝80b 1＝－200 ，⎩⎪⎨⎪⎧k 2＝－80b 2＝640 ，∴y 1 ＝80t －200，y 2 ＝－80t ＋640，当y 1＝y 2 时，80t －200＝－80t ＋640， t ＝5.25．∴两车在途中第二次相遇时t 的值为5.25小时，故弄③正确，④当t ＝3时，甲车行的路程为：120km ，乙车行的路程为：80×（3－2）＝80km ， ∴两车相距的路程为：120－80＝40千米，故④正确，选A ．同类题型2.2 甲、乙两车从A 地驶向B 地，并以各自的速度匀速行驶，甲车比乙车早行驶2h ，并且甲车途中休息了0.5h ，如图是甲乙两车行驶的距离y （km ）与时间x （h ）的函数图象．则下列结论：（1）a ＝40，m ＝1；（2）乙的速度是80km/h ；（3）甲比乙迟74 h 到达B 地；（4）乙车行驶94 小时或194小时，两车恰好相距50km ．正确的个数是（） A ．1 B ．2 C ．3 D ．4解：（1）由题意，得m ＝1.5－0.5＝1． 120÷（3.5－0.5）＝40（km/h ），则a ＝40，故（1）正确；（2）120÷（3.5－2）＝80km/h （千米/小时），故（2）正确；（3）设甲车休息之后行驶路程y （km ）与时间x （h ）的函数关系式为y ＝kx ＋b ，由题意，得 ⎩⎨⎧40＝1.5k+b 120＝3.5k+b解得：⎩⎨⎧k ＝40b ＝-20∴y ＝40x －20，根据图形得知：甲、乙两车中先到达B 地的是乙车，把y ＝260代入y ＝40x －20得，x ＝7， ∵乙车的行驶速度：80km/h ，∴乙车的行驶260km 需要260÷80＝3.25h ，∴7-（2+3.25）=74 h ，∴甲比乙迟74h 到达B 地，故（3）正确；（4）当1.5＜x ≤7时，y ＝40x －20．设乙车行驶的路程y 与时间x 之间的解析式为y ＝k 'x ＋b '，由题意得 ⎩⎨⎧0＝2k ′+b ′120＝3.5k ′+b ′解得：⎩⎨⎧k ′＝80b ′＝-160∴y ＝80x －160．当40x －20－50＝80x －160时，解得：x=94．当40x －20＋50＝80x －160时，解得：x=194．∴94－2＝14 ，194－2＝114．所以乙车行驶小时14 或114小时，两车恰好相距50km ，故（4）错误．选C ．同类题型2.3 甲、乙两人从科技馆出发，沿相同的路线分别以不同的速度匀速跑向极地馆，甲先跑一段路程后，乙开始出发，当乙超出甲150米时，乙停在此地等候甲，两人相遇后乙又继续以原来的速度跑向极地馆．如图是甲、乙两人在跑步的全过程中经过的路程y （米）与甲出发的时间x （秒）的函数图象．则下列四种说法：①甲的速度为1.5米/秒；②a ＝750；③乙在途中等候甲100秒；④乙出发后第一次与甲相遇时乙跑了375米．其中正确的个数是（） A ．1个 B ．2个 C ．3个D ．4个解：①根据图象可以得到：甲共跑了900米，用了600秒，则甲的速度是：900÷600＝1.5米/秒，故①正确；②甲跑500秒时的路程是：500×1.5＝750米，故②正确；③CD 段的长是900－750＝150米，时间是：560－500＝60秒，则乙速度是：150÷60＝2.5米/秒；甲跑150米用的时间是：150÷1.5＝100秒，则甲比乙早出发100秒．乙跑750米用的时间是：750÷2.5＝300秒，则乙在途中等候甲用的时间是：500－300－100＝100秒，故③正确； ④甲每秒跑1.5米，则甲的路程与时间的函数关系式是：y ＝1.5x ，乙晚跑100秒，且每秒跑2.5米，则 AB 段的函数解析式是：y ＝2.5（x －100），根据题意得：1.5x ＝2.5（x －100），解得：x ＝250秒．∴乙的路程是：2.5×（250－100）＝375（米）．∴甲出发250秒和乙第一次相遇，此时乙跑了375米，故④正确．选D ．例3．如图，已知动点P 在函数y ＝ 12x（x ＞0）的图象上运动，PM ⊥x 轴于点M ，PN ⊥y 轴于点N ，线段PM 、PN 分别与直线AB ：y ＝－x ＋1交于点E ，F ，则AF ﹒BE 的值为（）A ．4B ．2C ．1D ．12解：作FG ⊥x 轴，∵P的坐标为（a，12a），且PN⊥OB，PM⊥OA，∴N的坐标为（0，12a），M点的坐标为（a，0），∴BN＝1－12a，在直角三角形BNF中，∠NBF＝45°（OB＝OA＝1，三角形OAB是等腰直角三角形），∴NF＝BN＝1－12a，∴F点的坐标为（1－12a ，12a），同理可得出E点的坐标为（a，1－a），∴AF 2＝（1－1＋12a）2＋（12a）2＝12a2，BE2＝（a）2＋（－a）2＝2a2，∴AF 2﹒BE2＝12a2﹒2a2＝1，即AF﹒BE＝1．选C．同类题型3.1 如图，在反比例函数y＝32x的图象上有一动点A，连接AO并延长交图象的另一支于点B，在第二象限内有一点C，满足AC＝BC，当点A运动时，点C始终在函数y＝kx的图象上运动，若tan∠CAB＝2，则k的值为（）A．－3 B．－6 C．－9 D．－12解：如图，连接OC，过点A作AE⊥y轴于点E，过点C作CF⊥y轴于点F，∵由直线AB与反比例函数y＝32x的对称性可知A、B点关于O点对称，∴AO ＝BO ．又∵AC ＝BC ， ∴CO ⊥A B ．∵∠AOE ＋∠AOF ＝90°，∠AOF ＋∠COF ＝90°， ∴∠AOE ＝∠COF ，又∵∠AEO ＝90°，∠CFO ＝90°， ∴△AOE ∽△COF ，∴AE CF ＝OE OF ＝AO CO， ∵tan ∠CAB ＝OCOA＝2，∴CF ＝2AE ，OF ＝2OE ．又∵AE ﹒OE ＝32，CF ﹒OF ＝|k |，∴k ＝±6．∵点C 在第二象限， ∴k ＝－6，选B ．同类题型3.2 如图，在平面直角坐标系中，点A 在x 轴的正半轴上，点B 在第一象限，点C 在线段AB 上，点D 在AB 的右侧，△OAB 和△BCD 都是等腰直角三角形，∠OAB ＝∠BCD ＝90°，若函数y= 6x（x ＞0）的图象经过点D ，则△OAB 与△BCD 的面积之差为（） A ．12 B ．6 C ．3 D ．2解：∵△OAB 和△BCD 都是等腰直角三角形，∴OA ＝AB ，CD ＝B C ．设OA ＝a ，CD ＝b ，则点D 的坐标为（a ＋b ，a －b ），∵反比例函数y ＝6x在第一象限的图象经过点D ，∴（a ＋b ）（a －b ）＝a 2－b 2＝6，∴△OAB 与△BCD 的面积之差＝12a 2－12b 2＝12×6＝3．选C ．同类题型3.3 如图，在平面直角坐标系xOy 中，已知直线y ＝kx （k ＞0）分别交反比例函数y ＝ 1x 和y ＝ 9x在第一象限的图象于点A ，B ，过点B 作 BD ⊥x 轴于点D ，交y ＝ 1x的图象于点C ，连结A C ．若△ABC 是等腰三角形，则k 的值是___________．解：∵点B 是y ＝kx 和y ＝9x 的交点，y ＝kx ＝9x，解得：x ＝3k，y ＝3k ，∴点B 坐标为（3k，3k ），点A 是y ＝kx 和y ＝1x 的交点，y ＝kx ＝1x，解得：x ＝1k，y ＝k ，∴点A 坐标为（1k，k ），∵BD ⊥x 轴， ∴点C 横坐标为3k，纵坐标为13k＝k3， ∴点C 坐标为（3k，k3），∴BA ≠AC ，若△ABC 是等腰三角形，①AB ＝BC ，则(3k －1k )2＋(3k －k )2＝3k －k 3 ，解得：k ＝377 ；②AC ＝BC ，则(3k－1k)2＋(k －k 3)2＝3k －k 3 ，解得：k ＝155；故答案为k ＝377 或155．例4．如图，一次函数y ＝x ＋b 的图象与反比例函数y ＝ k x的图象交于点A （3，6）与点B ，且与y 轴交于点C ，若点P 是反比例函数y ＝ k x图象上的一个动点，作直线AP 与x 轴、y 轴分别交于点M 、N ，连结BN 、CM ．若S △ACM ＝S △ABN ，则APAN的值为__________．解：把A （3，6）代入到一次函数y ＝x ＋b 与反比例函数y ＝k x中，得：b ＝3，k ＝18，∴y ＝18x，y ＝x ＋3，∴C （0，3），则⎩⎪⎨⎪⎧y ＝18x y ＝x ＋3，解得：⎩⎪⎨⎪⎧x 1＝3y 1＝6 ，⎩⎪⎨⎪⎧x 2＝－6y 2＝－3 ，∴B （－6，－3），分两种情况：①点P 在第一象限时，如图1，∵S △ACM ＝S △ABN ，S △MNC －S △ACN ＝S △ACN ＋S △BCN ， S △MNC ＝2S △ACN ＋S △BCN ， 12NC ﹒OM ＝2×12NC ×3＋12 NC ×6， OM ＝6＋6＝12， ∴M （12，0），直线AM 的解析式为：y ＝－23x ＋8，∴N （0，8），则⎩⎨⎧y ＝18xy ＝－23x ＋8，18x ＝－23x ＋8，解得：x ＝3或9， ∴P （9，2），∴AN ＝32＋22＝13 ，AP ＝62＋42＝213 ， ∴AP AN ＝21313＝2；②当点P 在第三象限上时，如图2，∵S △ACM ＝S △ABN ，∴S △ACN ＋S △MNC ＝S △ACN ＋S △BCN ， S △MNC ＝S △BCN ， 12NC ﹒OM ＝12 NC ×6， ∴OM ＝6， ∴M （－6，0），直线AM 的解析式为：y ＝23x ＋4，∴N （0，4），则⎩⎨⎧y ＝18xy ＝23x ＋4 ，18x ＝23x ＋4，解得：x ＝3或－9， ∴P （－9，－2），∴AN ＝13 ，AP ＝122＋82＝413 ， ∴AP AN ＝41313＝4，综上所述，则AP AN的值为2或4．同类题型4.1 当12 ≤x ≤2时，函数y ＝－2x ＋b 的图象上至少有一点在函数y ＝ 1x的图象下方，则b 的取值范围为（）A ．b ＞2 2B ．b ＜ 92C ．b ＜3D ．2 2＜b ＜ 92解：在函数y ＝1x 中，令x ＝2，则y ＝12 ；令x ＝12，则y ＝2；若直线y ＝－2x ＋b 经过（2，12），则12 ＝－4＋b ，即b ＝92；若直线y ＝－2x ＋b 经过（12，2），则2＝－1＋b ，即b ＝3，∵直线y ＝－2x ＋92在直线y ＝－2x ＋3的上方，∴当函数y ＝－2x ＋b 的图象上至少有一点在函数y ＝1x的图象下方时，直线y ＝－2x ＋b 在直线y ＝－2x ＋92的下方，∴b 的取值范围为b ＜92．选B ．同类题型4.2 方程x 2＋3x －1＝0的根可视为函数y ＝x ＋3的图象与函数y ＝ 1x的图象交点的横坐标，那么用此方法可推断出方程x 2＋2x －1＝0的实数根x 0 所在的范围是（） A ．－1＜x 0 ＜0 B ．0＜x 0 ＜1 C ．1＜x 0 ＜2 D ．2＜x 0 ＜3解：方程x 2＋2x －1＝0的实数根可以看作函数y ＝x ＋2和y ＝1x的交点．函数大体图象如图所示：A ．由图可得，第三象限内图象交点的横坐标小于－2，故－1＜x 0 ＜0错误；B ．当x ＝1时，y 1 ＝1＋2＝3，y 2＝11＝1，而3＞1，根据函数的增减性可知，第一象限内的交点的横坐标小于1，故0＜x 0 ＜1正确；C ．当x ＝1时，y 1 ＝1＋2＝3，y 2＝11＝1，而3＞1，根据函数的增减性可知，第一象限内的交点的横坐标小于1，故1＜x 0 ＜2错误；D ．当x ＝2时，y 1 ＝2＋2＝4，y 2＝12 ，而4＞12，根据函数的增减性可知，第一象限内的交点的横坐标小于2，故2＜x 0 ＜3错误．选B ．例5．在平面直角坐标系xOy 中，抛物线y ＝－x 2＋2mx －m 2－m ＋1交y 轴于点为A ，顶点为D ，对称轴与x 轴交于点H ．当抛物线顶点D 在第二象限时，如果∠ADH ＝∠AHO ，则m ＝__________．解：（1）∵y ＝－x 2＋2mx －m 2－m ＋1＝－（x －m ）2－m ＋1， ∴顶点D （m ，1－m ）． ∵顶点D 在第二象限， ∴m ＜0．当点A 在y 轴的正半轴上，如图（1）作AG ⊥DH 于点G ，∵A （0，－m 2－m ＋1），D （m ，－m ＋1），∴H （m ，0），G （m ，－m 2－m ＋1） ∵∠ADH ＝∠AHO ，∴tan ∠ADH ＝tan ∠AHO ， ∴AG DG ＝AO HO． ∴－m 1－m －(－m 2－m ＋1)＝－m 2－m ＋1－m．整理得：m 2＋m ＝0． ∴m ＝－1或m ＝0（舍）．当点A 在y 轴的负半轴上，如图（2）．作AG ⊥DH 于点G ，∵A （0，－m 2－m ＋1），D （m ，－m ＋1），∴H （m ，0），G （m ，－m 2－m ＋1） ∵∠ADH ＝∠AHO ，∴tan ∠ADH ＝tan ∠AHO ， ∴AG DG ＝AO HO． ∴－m 1－m －(－m 2－m ＋1)＝m 2＋m －1－m．整理得：m 2＋m －2＝0． ∴m ＝－2或m ＝1（舍）．综上所述，m 的值为－1或－2．同类题型5.1 已知抛物线y ＝ 14x 2＋1具有如下性质：该抛物线上任意一点到定点F （0，2）的距离与到x 轴的距离始终相等，如图，点M 的坐标为（ 3 ，3），P 是抛物线y ＝ 14x 2＋1上一个动点，则△PMF周长的最小值是（）A ．3B ．4C ．5D ．6解：过点M 作ME ⊥x 轴于点E ，交抛物线y ＝14x 2 ＋1于点P ，此时△PMF 周长最小值，∵F （0，2）、M （ 3 ，3），∴ME ＝3，FM ＝(3－0)2＋(3－2)2 ＝2，∴△PMF 周长的最小值＝ME ＋FM ＝3＋2＝5．选C ．同类题型5.2 抛物线y ＝ax 2 ＋bx ＋3（a ≠0）经过点A （－1，0），B （ 32，0），且与y 轴相交于点C ．设点D 是所求抛物线第一象限上一点，且在对称轴的右侧，点E 在线段AC 上，且DE ⊥AC ，当△DCE 与△AOC 相似时，求点D 的坐标．解：如图2所示：延长CD ，交x 轴与点F ．∵∠ACB ＝45°，点D 是第一象限抛物线上一点，∴∠ECD ＞45°．又∵△DCE 与△AOC 相似，∠AOC ＝∠DEC ＝90°，∴∠CAO ＝∠EC D ．∴CF ＝AF ．设点F 的坐标为（a ，0），则（a ＋1）2＝32＋a 2 ，解得a ＝4．∴F （4，0）．设CF 的解析式为y ＝kx ＋3，将F （4，0）代入得：4k ＋3＝0，解得：k ＝－34 ． ∴CF 的解析式为y ＝－34x ＋3．将y ＝－34 x ＋3与y ＝－2x 2 ＋x ＋3联立：解得：x ＝0（舍去）或x ＝78．将x ＝78 代入y ＝－34 x ＋3得：y ＝7532． ∴D （78 ，7532 ）．同类题型5.3小明家的洗手盆上装有一种抬启式水龙头（如图1），完全开启后，水流路线呈抛物线，把手端点A ，出水口B 和落水点C 恰好在同一直线上，点A 至出水管BD 的距离为12cm ，洗手盆及水龙头的相关数据如图2所示，现用高10.2cm 的圆柱型水杯去接水，若水流所在抛物线经过点D 和杯子上底面中心E ，则点E 到洗手盆内侧的距离EH 为__________cm ．解：如图所示，建立直角坐标系，过A 作AG ⊥OC 于G ，交BD 于Q ，过M 作MP ⊥AG 于P ，由题可得，AQ ＝12，PQ ＝MD ＝6，故AP ＝6，AG ＝36，∴Rt △APM 中，MP ＝8，故DQ ＝8＝OG ，∴BQ ＝12－8＝4，由BQ ∥CG 可得，△ABQ ∽△ACG ，∴BQ CG ＝AQ AG ，即4CG ＝1236， ∴CG ＝12，OC ＝12＋8＝20，∴C （20，0），又∵水流所在抛物线经过点D （0，24）和B （12，24），∴可设抛物线为y ＝ax 2 ＋bx ＋24，把C （20，0），B （12，24）代入抛物线，可得⎩⎨⎧24＝144a ＋12b ＋240＝400a ＋20b ＋24 ，解得⎩⎨⎧a ＝－320b ＝95， ∴抛物线为y ＝－320x 2＋95x ＋24，又∵点E 的纵坐标为10.2，∴令y ＝10.2，则10.2＝－320x 2＋95x ＋24，解得x 1＝6＋8 2 ，x 2＝6－8 2 （舍去）， ∴点E 的横坐标为6＋8 2 ，又∵ON ＝30，∴EH ＝30－（6＋82）＝24－8 2 ．。

选择压轴题(几何篇1)-2023年中考数学压轴题专项训练(全国通用)(解析版)

2023年中考数学压轴题专项训练选择压轴题(几何篇1)一、压轴题速练1一．选择题(共40小题)1(2023•朝阳区校级三模)如图，AB是⊙O的直径，将OB绕着点O逆时针旋转40°得到OC，P是⊙O上一点，且与点C在AB的异侧，连结PA、PC、AC，若PA=PC，则∠PAB的大小是()A.20°B.35°C.40°D.70°【答案】B【分析】由圆周角定理求出∠P=70°，由等腰三角形的性质求出∴∠PAC=55°，由三角形外角的性质求出∠CAO=20°，即可得到∠PAB=∠PAC-∠CAO=35°．【详解】解：∵∠AOC+∠BOC=180°，∠BOC=40°，∴∠AOC=140°，∴∠P=12∠AOC=70°，∵PA=PC，∴∠PAC=∠PCA=12×(180°-∠P)=55°，∵OA=OC，∴∠OAO=∠ACO，∵∠BOC=∠OAO+∠ACO=2∠CAO，∴∠CAO=12∠BOC=20°，∴∠PAB=∠PAC-∠CAO=35°．故选：B．【点睛】本题考查圆周角定理，等腰三角形的性质，旋转的性质，关键是由圆周角定理，求出∠P的度数．2(2023•河北区二模)如图，在平面直角坐标系中，菱形OABC的顶点A在x轴上，且∠COA=45°，OA=4，则点B的坐标为()A.(4+22，22)B.(22，22)C.(2+22，2)D.(2，2)【答案】A【分析】作BD⊥x轴于点D，由菱形的性质得AB∥OC，AB=OA=4，则∠BAD=∠COA=45°，可求得AD=BD=AB•sin45°=22，所以OD=4+22，则B(4+22，22)，于是得到问题的答案．【详解】解：作BD⊥x轴于点D，则∠ADB=90°，∵四边形OABC是菱形，∠COA=45°，OA=4，∴AB∥OC，AB=OA=4，∴∠BAD=∠COA=45°，∴∠ABD=∠BAD=45°，∴AD=BD=AB•sin45°=4×22=22，∴OD=4+22，∴点B的坐标为(4+22，22)，故选：A．【点睛】此题重点考查图形与坐标、菱形的性质、等腰直角三角形的判定与性质、锐角三角函数与解直角三角形等知识，正确地作出所需要的辅助线是解题的关键．3(2023•奉贤区二模)如图，矩形ABCD中，AB=1，∠ABD=60°，点O在对角线BD上，圆O经过点C．如果矩形ABCD有2个顶点在圆O内，那么圆O的半径长r的取值范围是()A.0<r≤1B.1<r≤3C.1<r≤2D.3<r≤2【答案】B【分析】解直角三角形得到BD=2AB=2，AD=3，如图，当圆O的半径长r=1时，A、B、C、D四个点都在圆O上，当圆O的半径长r=3时，A、B在圆内，C在圆上，D点在圆外，观察图形即可得到结论．【详解】解：矩形ABCD中，AB=1，∠ABD=60°，∴BD=2AB=2，AD=3，∵矩形的对角线相等且平分，∴当圆O的半径长r=1时，A、B、C、D四个点都在圆O上，当圆O的半径长r=3时，A、B在圆内，C在圆上，D点在圆外，∴如果矩形ABCD有2个顶点在圆O内，那么圆O的半径长r的取值范围是1<r≤3，故选：B ．【点睛】本题考查了点与圆的位置关系，矩形的性质，解直角三角形，正确的作出图形是解题的关键．4(2023•广灵县模拟)如图，在Rt △ABC 中，∠C =90°，BC =3，AC =6，点O ，D ，E 是AB 边上的点，以点O 为圆心，DE 长为直径的半圆O 与AC 相切于点M ，与BC 相切于点N ，则图中阴影部分的面积为()A.5B.9-2πC.9-πD.5-π【答案】D【分析】连接ON ，OM ，根据切线的性质得到∠ONC =∠OMC =90°，根据正方形的性质得到ON =OM =CN =CM ，∠NOM =90°，根据相似三角形的性质得到OM =2，根据三角形和正方形以及扇形的面积公式即可得到结论．【详解】解：连接ON ，OM ，∵半圆O 与AC 相切于点M ，与BC 相切于点N ，∴∠ONC =∠OMC =90°，∵∠C =90°，ON =OM ，∴四边形CMON 是正方形，∴ON =OM =CN =CM ，∠NOM =90°，∴∠BON +∠AOM =90°，∵∠AMO =∠C =90°，∴OM ∥BC ，∴△AOM ∽△ABC ，∴OM BC =AM AC ，∴OM 3=6-OM 6，∴OM =2，∴图中阴影部分的面积=12×3×6-90⋅π×22360-2×2=5-π，故选：D ．【点睛】本题考查了切线的性质，扇形面积的计算，相似三角形的判定和性质，熟练掌握切线的性质是解题的关键．5(2023•普陀区二模)如图，△ABC 中，∠BAC =60°，BO 、CO 分别平分∠ABC 、∠ACB ，AO =2，下面结论中不一定正确的是()A.∠BOC =120°B.∠BAO =30°C.OB =3D.点O 到直线BC 的距离是1【答案】C【分析】由角平分线的定义求出∠OBC +∠OCB =12(∠ABC +∠ACB )=60°，由三角形内角和定理求出∠BOC 的度数，由三角形内心的性质求出∠BAO 的度数是30°，OB 的长在变化不一定等于3，由直角三角形的性质得到ON =1，由角平分线的性质得到OM =ON =1，得到O 到BC 的距离是1．【详解】解：作OM ⊥BC 于M ，ON ⊥AB 于N ，∵BO 、CO 分别平分∠ABC 、∠ACB ，∴∠OBC =12∠ABC ，∠OCB =12∠ACB ，∴∠OBC +∠OCB =12(∠ABC +∠ACB )=12×(180°-∠BAC )=60°，∴∠BOC =180°-(∠OBC +∠OCB )=120°，故A 正确；∵BO 、CO 分别平分∠ABC ，∴O 是△ABC 的内心，∴AO 平分∠BAC ，∵∠BAC =60°，∴∠BAO =12∠BAC =30°，故B 正确；OB 的长在变化不一定等于3，故C 不一定正确；∵∠ANO =90°，∠NAO =30°，∴ON =12AO =12×2=1，∴OM =ON =1，∴O 到BC 的距离是1，故D 正确．故选：C ．【点睛】本题考查角平分线的性质，关键是掌握角平分线的性质．6(2023•瓯海区模拟)如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD 与正方形EFGH ，连结DH 并延长交AB 于点K ，若DF 平分∠CDK ，则DH HK=()A.233B.65C.5-1D.457【答案】C【分析】过点K 作KM ⊥AH ，设DE =a ，AE =b ，先证得∠KHA =∠KAH ，可得KH =KA ，再证△EHD ∽△EDA ，可得HE DE =DE AE，即b -a a =a b ，解出b =5+12a ，再证△HED ∽△HMK ，列比例式求解即可．【详解】解：过点K 作KM ⊥AH ，设DE =a ，AE =b ，∵DF 平分∠CDK ，∴∠CDF =∠EDH ，∵四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD 与正方形EFGH ，∴∠CDF =∠ABH ，DE =AH ，∠DEA =∠EHB ，∴DF ∥HB ，∴∠EDH =∠BHK ，∴∠KBH =∠KHB ，∴KH =KB ，∵∠AHB =90°，∴∠KBH +∠KAH =90°，∠KHB +∠KHA =90°，∴∠KHA =∠KAH ，∴KH =KA ，∴HM =12AH =12a ，∵∠HED =∠DEA ，∠HDE =∠EAD ，∴△EHD ∽△EDA ，∴HE DE =DE AE ，即b -a a =a b，解得：b =5+12a ，∵DE ∥KM ，∴△HED ∽△HMK ，∴DH HK =EH HM =b -a 12a =5+12a -a 12a =5-1，故选：C ．【点睛】本题是四边形综合题，考查了正方形的性质，相似三角形的判定和性质，解题的关键是学会添加常用辅助线，构造相似三角形解决问题，属于中考压轴题．7(2023•花溪区模拟)勾股定理是人类数学文化的一颗璀璨明珠，是用代数思想解决几何问题的最重要工具也是数形结合的组带之一，如图，秋千静止时，踏板离地的垂直高度BE=1m，将它往前推6m至C处时(即水平距离CD=6m)，踏板离地的垂直高度CF=4m，它的绳索始终拉直，则绳索AC的长是()A.152mB.92mC.6mD.212m【答案】A【分析】设绳索AC的长是xm，则AB=xm，求出AD=AB+BE-DE=(x-3)m，然后在Rt△ACD中，由勾股定理得出方程，解方程即可．【详解】解：设绳索AC的长是xm，则AB=xm，∵DE=FC=4m，BE=1m，∴AD=AB+BE-DE=x+1-4=(x-3)m，在Rt△ACD中，由勾股定理得：AC2=AD2+CD2，即x2=(x-3)2+62，解得：x=15 2，即绳索AC的长是152m，故选：A．【点睛】本题考查了勾股定理的应用，由勾股定理得出方程是解题的关键．8(2023•承德一模)如图，在菱形ABCD中，AC、BD(AC>BD)相交于点O，E、F分别为OA和OC上的点(不与点A、O、C重合)．其中AE=OF．过点E作GH⊥AC，分别交AD、AB于点G、H；过点F作IJ⊥AC分别交CD、CB于点J、I；连接GJ、HI，甲、乙、丙三个同学给出了三个结论：甲：随着AE长度的变化，GH+IJ=BD始终成立．乙：随着AE长度的变化，四边形GHIJ可能为正方形．丙：随着AE长度的变化，四边形GHIJ的面积始终不变，都是菱形ABCD面积的一半．下列选项正确的是()A.甲、乙、丙都对B.甲、乙对，丙不对C.甲、丙对，乙不对D.甲不对，乙、丙对【答案】C【分析】连接HJ，GI，交于点M，根据轴对称的性质得出GE=EH，JF=FI，MG=MH，MJ=MI，GJ=HI，EO=FC，过点G作GK⊥BD于点K，过点J作JT⊥BD于点T，证明△DTJ≌△GEA，△DKG≌△JFC得出GH+IJ=BD，即可判断甲，进而得出四边形AHJD是平行四边形，四边形HJBC是平行四边形，即可判断丙，反证法证明四边形GHIJ不可能是正方形，即可求解．【详解】解：如图所示，连接HJ，GI，交于点M，∵四边形ABCD是菱形，GH⊥AC，IJ⊥AC，∴GH∥JI，根据菱形是轴对称图形，AC是GH，IJ，BD的垂直平分线，∴GE=EH，JF=FI，MG=MH，MJ=MI，GJ=HI，∵AE=OF，OA=OC，∴EO=FC，如图所示，过点G作GK⊥BD于点K，过点J作JT⊥BD于点T，则四边形GEOK，TJFO是矩形，∴GK=EO=FC，KO=GE=12GH，TJ=OF=AE，TO=JF=12JI，∵四边形ABCD是菱形，∴∠DAO=∠DCO，∵GK∥AO，TJ∥OC，∴∠DJT=∠DCA=∠GAE，∠DGK=∠DAC=∠JCF，∴△DTJ≌△GEA(ASA)，△DKG≌△JFC(ASA)，∴DJ=AG，JC=GD，GE=DT，JF=DK，∴12DB=DO=DT+TO=GE+JF=12(GH+JI)，即GH+IJ=BD，故甲正确，∵DJ=AG，又AG=AH，∴JD=AH，∴四边形AHJD是平行四边形，∴S△HCJ=12S四边形AHJD，HJ∥AD，HJ=AD，∴四边形HJBC是平行四边形，∴S△HIJ=12S四边形BHJC，∴S四边形GHIJ =S△HCJ+S△HIJ=12S四边形BHJC+12S四边形AHJD=12S菱形ABCD，即四边形GHIJ的面积始终不变，都是菱形ABCD面积的一半，故丙正确；同理可得四边形AGBI，CDGI是平行四边形，∴GI∥CD，HJ∥AD，∵当四边形GHIJ是正方形时，则GI⊥HJ，∴AD⊥DC，则四边形ABCD是正方形，∵AC>BD，∴四边形ABCD不是正方形，即四边形GHIJ不可能是正方形，故乙错误，故选：C．【点睛】本题考查了平行四边形的性质与判定，菱形的性质，正方形的性质，熟练掌握以上知识是解题的关键．9(2023•石家庄二模)如图，在平行四边形ABCD中，对角线AC，BD交于点O，E，F分别是OB与OD的中点，依连接点A，E，C，F，A，当四边形AECF是矩形时，与线段BE相等的线段有()A.4条B.5条C.6条D.7条【答案】B【分析】由平行四边形的性质得OB=OD，由E，F分别是OB与OD的中点，得OE=BE=12OB，OF=DF=12OD，则OE=OF=DF=BE，由矩形的性质得，OA=OC=12AC，OE=OF= 12EF且AC=EF，OA=OC=OE=OF=DF=BE，可知与线段BE相等的线段有5条，于是得到问题的答案．【详解】解：∵四边形ABCD是平行四边形，对角线AC，BD交于点O，∴OB=OD，∵E，F分别是OB与OD的中点，∴OE=BE=12OB，OF=DF=12OD，∴OE=OF=DF=BE，∵四边形AECF是矩形，∴OA=OC=12AC，OE=OF=12EF，AC=EF，∴OA=OC=OE=OF=DF=BE，∴与线段BE相等的线段有5条，故选：B．【点睛】此题重点考查平行四边形的性质、矩形的性质、线段中点的定义等知识，证明OB=OD、OA =OC且AC=EF是解题的关键．10(2023•青山区二模)如图，边长为2的正方形ABCD的对角线AC与BD相交于点O，E是BC边上一点，F是BD上一点，连接DE，EF．若△DEF与△DEC关于直线DE对称，则OF的长为()A.22B.22-2C.2-2D.2-1【答案】C【分析】根据正方形的性质和轴对称的性质得出DF=DC和DB=2DC，进而解答即可．【详解】解：∵四边形ABCD是正方形，DC=2，∴DB=2DC=22，OD=OB，∴OD=2∵△DEF与△DEC关于直线DE对称，∴DF=DC=2，∴OF=DF-OD=2-2，故选：C．【点睛】此题考查正方形的性质，关键是根据正方形的性质得出DB和OD解答．11(2023•柳城县一模)七巧板是我国古代劳动人民的发明之一，被誉为“东方魔板”，它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的．(清)陆以活《冷庐杂识》卷中写道：近又有七巧图，其式五，其数七，其变化之式多至千余，体物肖形，随手变幻，盖游戏之具，足以排闷破寂，故世俗皆喜为之．如图，是一个用七巧板拼成的装饰图，放入长方形ABCD内，装饰图中的三角形顶点E，F分别在边AB，BC上，三角形①的边GD在边AD上，则BFBE的值为()A.1+22B.22C.2+24D.2+22【答案】D【分析】设七巧板正方形的边长为x ，根据正方形的性质、矩形的性质分别表示出BF ，BE 的长，即可求解．【详解】解：设七巧板正方形的边长为x ，∴2BE 2=x 2，∴BE 2=x 22，∴BE =22c ，∴BF =12x +22x ，∴BF BE =1+22x 22x =1+22=2+22，故选：D ．【点睛】本题考查了矩形的性质，七巧板，勾股定理，正方形的性质，表示出BF ，BE 的长是解题的关键．12(2023•泉州模拟)如图，在矩形ABCD 中，AB =2，BC =4，将△ABC 沿BC 的方向平移至△A 'B 'C '，使得A ′E =A ′F ，其中E 是A ′B ′与AC 的交点，F 是A ′C ′与CD 的交点，则CC ′的长为()A.52-52B.112-5C.5-5D.92-5【答案】C【分析】由矩形的性质得AB ∥CD ，由平移得AB ∥A ′B ′，AC ∥A ′C ′，所以A ′B ′∥CD ，而A ′E =A ′F ，即可证明四边形A ′ECF 是菱形，因为∠EB ′C =∠ABC =90°，AB =2，BC =4，EB 'B 'C =AB BC =tan ∠ACB =12，则B ′C =2EB ′，由勾股定理得A ′E =CE =EB '2+B 'C 2=5EB ′，则EB ′+5EB ′=2，得EB ′=5-12，所以B ′C =5-1，即可求得CC ′=BB ′=5-5，于是得到问题的答案．【详解】解：∵四边形ABCD 是矩形，∴AB ∥CD ，由平移得AB ∥A ′B ′，AC ∥A ′C ′，∴A ′B ′∥CD ，A ′F ∥CE ，∴A ′E ∥CF ，∴四边形A ′ECF 是平行四边形，∵A ′E =A ′F ，∴四边形A ′ECF 是菱形，∵∠EB ′C =∠ABC =90°，AB =2，BC =4，∴EB 'B 'C =AB BC=tan ∠ACB =24=12，∴B ′C =2EB ′，∴A ′E =CE =EB '2+B 'C 2=EB '2+(2EB ')2=5EB ′，∴EB ′+5EB ′=A ′B ′=AB =2，∴EB ′=5-12，∴B ′C =2×5-12=5-1，∴CC ′=BB ′=BC -B ′C =4-(5-1)=5-5，故选：C ．【点睛】此题重点考查矩形的性质、平移的性质、平行四边形的判定、菱形的判定与性质、勾股定理、锐角三角函数与解直角三角形等知识，证明四边形A ′ECF 是菱形是解题的关键．13(2023•定远县二模)如图，在Rt △ABC 中，∠BAC =90°，AB =3，BC =5，点P 为BC 边上任意一点，连接PA ，以PA ，PC 为邻边作平行四边形PAQC ，连接PQ ，则PQ 长度的最小值为()A.3B.2.5C.2.4D.2【答案】C【分析】以PA ，PC 为邻边作平行四边形PAQC ，由平行四边形的性质可知O 是AC 中点，PQ 最短也就是PO 最短，所以应该过O 作BC 的垂线P ′O ，然后根据△P ′OC 和△ABC 相似，利用相似三角形的性质即可求出PQ 的最小值．【详解】解：∵∠BAC =90°，AB =3，BC =5，∴AC =BC 2-AB 2=52-32=4，∵四边形APCQ 是平行四边形，∴PO =QO ，CO =AO ，∵PQ 最短也就是PO 最短，∴过O 作BC 的垂线OP ′，∵∠ACB =∠P ′CO ，∠CP ′O =∠CAB =90°，∴△CAB ∽△CP ′O ，∴CO BC =OP 'AB ，∴25=OP '3，∴OP ′=65，∴则PQ 的最小值为2OP ′=2.4，【点睛】本题考查了勾股定理的运用、平行四边形的性质、相似三角形的判定和性质以及垂线段最短的性质，解题的关键是作出高线构造出相似三角形．14(2023•烟台一模)如图，在矩形ABCD中，AB=12，AD=10，点E在AD上，点F在BC上，且AE=CF，连结CE，DF，则CE+DF的最小值为()A.26B.25C.24D.22【答案】A【分析】先连接BE，将CE+DF转化为CE+BE，再利用将军饮马解决问题即可．【详解】解：如图，连接BE，∵四边形ABCD是矩形，∴AB=CD，∠BAE=∠DCF=90°，∵AE=CF，∴△ABE≌△CDF，∴BE=DF，∴CE+DF=CE+BE，如图，作点B关于A点的对称点B'，连接CB'，CB'即为CE+BE的最小值，∵AB=12，AD=10，∴BB'=24，BC=10，∴CB'=BB'2+BC2=26，∴CE+DF的最小值为26，故A正确．故选：A．【点睛】本题考查矩形的性质、勾股定理、将军饮马问题、全等三角形的判定与性质等内容，综合性较强，将CE+DF转化为CE+BE是解题的关键．15(2023•郯城县一模)如图，在Rt△ABC中，∠BAC=90°，AB=6，BC=10，点P为BC边上任意一点，连接PA，以PA，PC为邻边作平行四边形PAQC，连接PQ，则PQ长度的最小值为()A.4.8B.5C.2.4D.4【分析】利用勾股定理得到BC 边的长度，根据平行四边形的性质，得知OP 最短即为PQ 最短，利用垂线段最短得到点P 的位置，再证明△CAB ∽△CP 'O 利用对应线段的比得到OP '的长度，继而得到PQ 的长度．【详解】解：∵∠BAC =90°，AB =6，BC =10，∴AC =BC 2-AB 2=8，∵四边形APCQ 是平行四边形，∴PO =QO ，CO =AO ，∵PQ 最短也就是PO 最短，∴过O 作BC 的垂线OP '，∵∠ACB =∠P 'CO ，∠CP 'O =∠CAB =90°，∴△CAB ∽△CP 'O ，∴CO BC =OP 'AB ，∴410=OP '6，∴OP '=125，∴则PQ 的最小值为2OP '=245=4.8．故选：A ．【点睛】本题考查了平行四边形性质和相似三角形的判定与性质，垂线段最短的知识，解答此题的关键是利用垂线段最短求解．16(2023•白云区一模)如图，正方形ABCD 的面积为3，点E 在边CD 上，且CE =1，∠ABE 的平分线交AD 于点F ，点M ，N 分别是BE ，BF 的中点，则下列结论错误的是()A.FD =2MNB.△DEF 是等腰直角三角形C.BN =1D.tan ∠FBE =3【答案】D【分析】根据正方形ABCD 的面积为3，可得正方形的边长为3，根据正方形的性质可得∠A =∠ABC =∠C =∠D =90°，BC =AB =CD =AD =3，根据tan ∠CBE =CE CB=33，可知∠CBE =30°，根据tan ∠ABF =AF AB=33，可得AF =CE =1，可得DF =DE ，即可判断B 选项；根据勾股定理和三角形中位线定理可判断A 选项；求出BF 的长，进一步可得BN 的长，即可判断C 选项；根据∠FBE =30°，tan ∠FBE =33，即可判断D 选项．【详解】解：∵正方形ABCD的面积为3，∴正方形的边长为3，在正方形ABCD中，∠A=∠ABC=∠C=∠D=90°，BC=AB=CD=AD=3，∴tan∠CBE=CECB=3 3，∴∠CBE=30°，∴∠ABE=60°，∵BF平分∠ABE，∴∠ABF=∠FBE=30°，∵tan∠ABF=AFAB=33，AB=3，∴AF=1，∴AF=CE，∴DF=DE，∵∠D=90°，∴△DEF是等腰直角三角形，故B不符合题意；根据勾股定理，得EF=DE2+DF2=2DF，∵M，N分别是BE，BF的中点，∴MN是△BEF的中位线，∴MN=12EF，∴MN=22DF，即DF=2MN，故A不符合题意；在△ABF中，根据勾股定理，得BF=(3)2+12=2，∴BN=1，故C不符合题意；∵∠FBE=30°，∴tan∠FBE=33，故D符合题意，故选：D．【点睛】本题考查了正方形的性质，三角形中位线定理，等腰直角三角形的判定，角平分线，勾股定理，解直角三角形等，本题综合性较强，熟练掌握这些知识是解题的关键．17(2023•九龙坡区校级模拟)如图，在正方形ABCD中，O为AC、BD的交点，△DCE为直角三角形，∠CED=90°，OE=32，若CE•DE=6，则正方形的面积为()A.20B.22C.24D.26【答案】C【分析】过点O 作OM ⊥CE 交EC 延长线于M ，作ON ⊥DE 于N ，判断出四边形OMEN 是矩形，根据矩形的性质可得∠MON =90°，再求出∠COM =∠DON ，根据正方形的性质可得OC =OD ，然后利用“角角边”证明△COM 和△DON 全等，根据全等三角形对应边相等可得OM =ON ，CM =DN ，然后判断出四边形OMEN 是正方形，根据CE •DE =6即可解决问题．【详解】解：如图，过点O 作OM ⊥CE 交EC 延长线于M ，作ON ⊥DE 于N ，∵∠CED =90°，∴四边形OMEN 是矩形，∴∠MON =90°，∵∠COM +∠DOM =∠DON +∠DOM ，∴∠COM =∠DON ，∵四边形ABCD 是正方形，∴OC =OD ，在△COM 和△DON 中，∠COM =∠DON ∠N =∠CMO =90°OC =OD，∴△COM ≌△DON (AAS )，∴OM =ON ，CM =DN ，∴四边形OMEN 是正方形，∵OE =32，∴2NE 2=OE 2=(32)2=18，∴NE =ON =3，∵DE +CE =DE +EM +MC =DE +EM +DN =EN +EM =2EN =6，设DE =a ，CE =b ，∴a +b =6，∵CE •DE =6，CD 2=a 2+b 2=(a +b )2-2ab =62-2×6=24，∴S 正方形ABCD =24．故选：C ．【点睛】本题考查了正方形的性质，全等三角形的判定与性质，勾股定理，作辅助线构造出全等三角形是解题的关键，也是本题的难点．18(2023•杭州一模)如图，有两张矩形纸片ABCD 和EFGH ，AB =EF =2cm ，BC =FG =8cm ．把纸片ABCD 交叉叠放在纸片EFGH 上，使重叠部分为平行四边形，且B 点D与点G 重合，当两张纸片交叉所成的角α最小时，tan α等于()A.14B.815C.12D.817【答案】B【分析】由“ASA ”可证△CDM ≌△HDN ，可证MD =DN ，即可证四边形DNKM 是菱形，当点B 与点E 重合时，两张纸片交叉所成的角a 最小，由勾股定理求出MD 的长，即可得出答案．【详解】解：如图，∵四边形ABCD 和四边形EFGH 是矩形，∴∠ADC =∠HDF =90°，CD =AB =2cm ，∴∠CDM =∠NDH ，且CD =DH ，∠H =∠C =90°，∴△CDM ≌△HDN (ASA )，∴MD =ND ，且四边形DNKM 是平行四边形，∴四边形DNKM 是菱形，∴KM =MD ，∵sin α=sin ∠DMC =CD MD，∴当点B 与点E 重合时，两张纸片交叉所成的角a 最小，设MD =KM =acm ，则CM =8-a (cm )，∵MD 2=CD 2+MC 2，∴a 2=4+(8-a )2，∴a =174(cm )，∴tan α=tan ∠DMC =CD CM =28-174=815，故选：B ．【点睛】本题考查了矩形的性质，菱形的判定，勾股定理，全等三角形的判定和性质以及三角函数定义等知识；求MD 的长是本题的关键．19(2023•高明区二模)矩形ABCD 和直角三角形EFG 的位置如图所示，点A 在EG 上，点D 在EF 上，若∠2=55°，则∠1等于()A.155°B.135°C.125°D.105°【答案】C【分析】由图形可知∠ADC=90°=∠GEF，即可得出∠EAD+∠ADE=90°，∠2+∠ADE=90°，从而求得∠DAE=∠2=55°，根据平角的定义即可求得∠1=180°-∠DAE=125°．【详解】解：∵∠ADC=90°=∠GEF，∴∠EAD+∠ADE=90°，∠2+∠ADE=90°，∴∠DAE=∠2=55°，∴∠1=180°-∠DAE=125°，故选：C．【点睛】本题考查了矩形的性质，直角三角形两锐角互余，平角的定义，证得∠DAE=∠2=55°是解题的关键．20(2023•余姚市一模)如图，由两个正三角形组成的菱形内放入标记为①，②，③，④的四种不同大小的小正三角形5个，其中编号①的有2个．设未被覆盖的浅色阴影部分的周长为C1，深色阴影部分的周长为C2，若要求出C1-C2的值，只需知道其中两个小正三角形的边长，则这两个小三角形的编号为()A.①②B.②③C.①③D.②④【答案】C【分析】设标记为①，②，③，④的小正方形的边长分别是m、n、x、y，表示出C1和C2，即可解决问题．【详解】解：设标记为①，②，③，④的小正方形的边长分别是m、n、x、y，由题意得：C1=4x+m+2n=2(x+n)+2x+m，C2=2y+4m=2(y+m)+2m，∵x+n=y+m，∴C1-C2=2x-m，∴只需知道编号是①③的两个小正三角形的边长，即可求出C1-C2的值．故选：C．【点睛】本题考查菱形的性质，等边三角形的性质，关键是由菱形、等边三角形的性质，用m、n、x、y 表示出C1和C2．21(2023•衡水二模)如图，点P是正方形ABCD的边BC上一点，点M是对角线BD上一点，连接PM并延长交BA的延长线于点Q，交AD于点G，取PQ的中点N．连接AN．若AQ=PC，有下面两个结论：①DM=DG，②AN⊥BD，则这两个结论中，正确的是()A.①对B.②对C.①②都对D.①②都不对【答案】B【分析】延长AN交BD于H，在AB上取点K，使AK=AQ，由正方形ABCD，可得AB=BC，∠CBA=90°，∠DBA=45°，根据AQ=PC，AK=AQ，有BK=PB，∠BKP=45°，而AN是△QPK的中位线，知AN∥PK，故∠NAK=∠PKB=45°，即得∠AHB=180°-∠NAK-∠DBA= 90°，AN⊥BD，②正确；因∠DGM=∠AGQ=90°-∠Q，∠DMG=90°-∠HNM=90°-∠ANQ，∠Q与∠ANQ不一定相等，可得∠DGM与∠DMG不一定相等，从而DM与DG不一定相等，①错误．【详解】解：延长AN交BD于H，在AB上取点K，使AK=AQ，如图：∵正方形ABCD，∴AB=BC，∠CBA=90°，∠DBA=45°，∵AQ=PC，AK=AQ，∴PC=AK，∴AB-AK=BC-PC，即BK=PB，∴△BPK是等腰直角三角形，∴∠BKP=45°，∵N是PQ中点，AQ=AK，∴AN是△QPK的中位线，∴AN∥PK，∴∠NAK=∠PKB=45°，∴∠AHB=180°-∠NAK-∠DBA=180°-45°-45°=90°，∴AN⊥BD，故②正确；∵∠DGM=∠AGQ=90°-∠Q，∠DMG=90°-∠HNM=90°-∠ANQ，而∠Q与∠ANQ不一定相等，∴∠DGM与∠DMG不一定相等，∴DM与DG不一定相等，故①错误；故选：B．【点睛】本题考查正方形性质及应用，涉及等腰直角三角形判定与性质，三角形中位线定理等知识，解题的关键是作辅助线，构造等腰直角三角形解决问题．22(2023•新乡二模)如图，在矩形ABCD中，点B(0，4)，点C(2，0)，BC=2CD，先将矩形ABCD沿y轴向下平移至点B与点O重合，再将平移后的矩形ABCD绕点O逆时针旋转90°得到矩形EOMN，则点D的对应点N的坐标为()A.(3，3)B.(4，4)C.(3，4)D.(4，3)【答案】C【分析】过点D 作DF ⊥x 轴于点F ，如图所示，先证明△BOC ∽△CFD ，得到OB FC =OC FD =BC CD =2，进而求出FC =2，FD =1，则点D (4，1)．由题意知矩形ABCD 向下平移了4个单位长度，将点D 向下平移4个单位长度到点D '(4，-3)，连接OD '，DD '，则点F 在线段DD '上，过点N 作NP ⊥x 轴于点P ，连接ON ，如图所示证明△OD 'F ≌△NOP ．得到OP =D 'F =3，NP =OF =4，则点N 的坐标为(3，4)．【详解】解：过点D 作DF ⊥x 轴于点F ，如图所示，由题意得，∠BOC =∠BCD =∠CFD =90°，∴∠OCB +∠OBC =90°=∠FCD +∠OBC ，∴∠OBC =∠FCD ，∴△BOC ∽△CFD ，∵BC =2CD ，∴OB FC =OC FD =BC CD=2．∵B (0，4)，C (2，0)，∴OB =4，OC =2，∴FC =2，FD =1．∴点D (4，1)．由题意知矩形ABCD 向下平移了4个单位长度，将点D 向下平移4个单位长度到点D '(4，-3)，连接OD '，DD '，则点F 在线段DD '上，过点N 作NP ⊥x 轴于点P ，连接ON ，如图所示．由旋转的性质可得∠D 'ON =90°，OD ′=ON ．又∵∠D 'FO =∠OPN =90°，∴∠D 'OF +∠NOP =90°=∠D ′OF +∠OD 'F ．∴∠OD 'F =∠NOP ．∴△OD 'F ≌△NOP (AAS )．∴OP =D 'F =3，NP =OF =4．∴点N 的坐标为(3，4)，故选C ．【点睛】本题主要考查了矩形的性质，平移的性质，旋转的性质，相似三角形的判定与性质，全等三角形的判定与性质，坐标与图形，等等，正确作出辅助线构造相似三角形和全等三角形是解题的关键．23(2023•荆门一模)如图，菱形ABCD 各边的中点分别是E 、F 、G 、H ，若EH =2EF ，则下列结论错误的是()A.EH ⊥EFB.EH =ACC.∠B =60°D.AB =5EF【答案】C【分析】由中位线的性质可知AC =2EF ，结合EH =2EF 可得EH =AC ，可判断B 选项；由菱形的性质可知AC ⊥BD ，用勾股定理解Rt △AOB 可验证选项D ；先证四边形AHFB 是平行四边形，再用勾股定理的逆定理证明△FEH 是直角三角形，可判断选项A ；假设∠B =60°成立，则△FEB 是等边三角形，EF =BE =12AB ，与AB =5EF 矛盾，可判断选项C ．【详解】解：如图，连接AC ，BD 交于点O ，连接FH ，∵菱形ABCD 各边的中点分别是E 、F 、G 、H ，∴EF =HG =12AC ，EH =FG =12BD ，∴AC =2EF ，BD =2EH ，∵EH =2EF ，∴EH =AC ，故B 选项结论正确，不合题意；由菱形的性质可知AC ⊥BD ，∴OA 2+OB 2=AB 2，∵EF =12AC =OA ，EH =12BD =OB ，∴AB 2=EF 2+EH 2=EF 2+4EF 2=5EF 2，∴AB =5EF ，故D 选项结论正确，不合题意；∵AH =12AD ，BF =12BC ，AD =BC ，∴AH =BF ，又AH ∥BF ，∴四边形AHFB 是平行四边形，∴AB =HF ，∴EF 2+EH 2=AB 2=HF 2，∴△FEH 是直角三角形，∴EH ⊥EF ，故A 选项结论正确，不合题意；由已知条件可知BE =BF ，若∠B =60°，则△FEB 是等边三角形，则EF =BE =12AB ，与AB =5EF 矛盾，因此∠B =60°不成立，故C选项结论错误，符合题意．故选：C．【点睛】本题考查菱形的性质，勾股定理及其逆定理，三角形中位线的性质，平行四边形的判定与性质等，解题的关键是综合运用上述知识点，逐步进行推导论证．24(2023•中原区校级二模)如图，在Rt△ABO中，AB=OB，顶点A的坐标为(2，0)，以AB为边向△ABO的外侧作正方形ABCD，将组成的图形绕点O逆时针旋转，每次旋转45°，则第98次旋转结束时，点D的坐标为()A.(1，-3)B.(-1，3)C.(-1，2+2)D.(1，3)【答案】B【分析】过D作DH⊥x轴于H，由在Rt△ABO中，AB=OB，OA=2，得AB=OA2=2，∠BAO=45°，根据四边形ABCD是正方形，可得D(3，1)，又将组成的图形绕点O逆时针旋转，每次旋转45°，知每旋转8次回到初始位置，第98次旋转结束，相当于将D(3，1)旋转90°，即可得到答案．【详解】解：过D作DH⊥x轴于H，如图：∵在Rt△ABO中，AB=OB，OA=2，∴AB=OA2=2，∠BAO=45°，∵四边形ABCD是正方形，∴AD=AB=2，∠BAD=90°，∴∠DAH=45°，∴△ADH是等腰直角三角形，∴AH=DH=AD2=1，∴OH=OA+AH=3，∴D(3，1)，∵将组成的图形绕点O逆时针旋转，每次旋转45°，∴每旋转8次回到初始位置，∵98÷8=12......2，∴第98次旋转结束，相当于将D(3，1)旋转90°，∴第98次旋转结束时，点D的坐标为(-1，3)，故选：B．【点睛】本题考查正方形的性质及应用，涉及旋转变换，解题的关键是掌握正方形的性质，找到旋转的规律．25(2023•中原区模拟)如图，▱ABCD 的边BC 在x 轴的负半轴上，点B 与原点O 重合，DE ⊥AB ，交BA 的延长线于点E ，已知∠ABC =60°，AB =4，BC =6，则点E 的坐标为()A.(-2，-，23)B.(-3，33)C.-72，723D.-523，52【答案】C【分析】过点E 作EF ⊥y 轴于点F ，由平行四边形的性质得AD =BC =6，AD ∥BC ，再由含30°角的直角三角形的性质得AE =3，EF =72，然后由勾股定理得OF =723，即可得出结论．【详解】解：如图，过点E 作EF ⊥y 轴于点F ，则∠EFO =90°，∵四边形ABCD 是平行四边形，∴AD =BC =6，AD ∥BC ，∴∠EAD =∠ABC =60°，∵DE ⊥AB ，∴∠AED =90°，∴∠ADE =90°-∠EAD =30°，∴AE =12AD =3，∴BE =AB +AE =4+3=7，∵∠EOF =90°-∠ABC =30°，∴EF =12OE =72，∴OF =OE 2-EF 2=72-72 2=723，∴点E 的坐标为-72，723 ，故选：C ．【点睛】本题考查了平行四边形的性质、坐标与推出性质、含30°角的直角三角形的性质以及勾股定理等知识，熟练掌握平行四边形的性质和含30°角的直角三角形的性质是解题的关键．26(2023•武邑县二模)如图，N 是正六边形ABCDEF 对角线CF 上一点，延长FE ，CD 相交于点M ，若S △ABN =2，则S 五边形ABCMF =()A.10B.12C.14D.16【答案】C【分析】根据正六边形的性质得出S △ABN =S △AOB =16S 正六边形ABCDEF=S △DEM 即可．【详解】解：如图，正六边形的中心为O ，则点O 在CF 上，由正六边形的性质可知，AB ∥CF ，∴S △ABN =S △AOB =16S 正六边形ABCDEF =2=S △DEM ，∴S 五边形ABCMF =7S △AOB=14，故选：C ．【点睛】本题考查正六边形和圆，三角形面积的计算，掌握正六边形的性质以及三角形、正六边形面积的计算方法是正确解答的前提．27(2023•承德一模)如图，正六边形的两条对角线AE 、BE 把它分成Ⅰ、Ⅱ、Ⅲ三部分，则该三部分的面积比为()A.1：2：3B.2：2：4C.1：2：4D.2：3：5【答案】A【分析】根据正多边形的性质，三角形中线的性质即可求解．【详解】解：如图，连接AD ，CF 交BE 于点O ，CF ，AE 交于点P ，∵正六边形，∴△AOF ≌△EOF ≌△DOE ≌△DOC ≌BOC ≌AOB (SSS )，∵△AEF 和△AEO 是等腰三角形，FO 分别是∠AFE 和∠AOE 的角分线，∴FO ⊥AE ，AP =EP (三线合一)，∴Rt △APF ≌Rt △EPF ≌Rt △EPO ≌Rt △APO (HL )，∴S △AEF =S △AOE =12S 四边形AOEF =S △AOF ，∴S △AFE =S △AOE =S △AOB =S △COB =S △COD =S △DOE ，∴Ⅰ、Ⅱ、Ⅲ三部分的面积比为1：2：3，故选：A ．【点睛】本题考查了正多边形，三角形中线的性质，熟记图形的性质并准确识图是解题的关键．28(2023•罗湖区二模)如图，AB 为圆O 的直径，C 为圆O 上一点，过点C 作圆O 的切线交AB 的延长线于点D ，DB =13AD ，连接AC ，若AB =8，则AC 的长度为()A.23B.25C.43D.45【答案】C【分析】根据DB =13AD ，AB 为圆O 的直径可得OA =OB =DB ，结合DC 是圆O 的切线即可得到∠OCD =90°，即可得到CB =OB ，根据勾股定理即可得到答案．【详解】解：连接OC ，BC ，∵DB =13AD ，AB 为圆O 的直径，∴OA =OB =DB ，∠ACB =90°，∵DC 是圆O 的切线，∴∠OCD =90°，∵OB =DB ，∴CB =OB ，∵AB =8，∴BC =4，在Rt △ABC 中，AC =82-42=43，故选：C ．【点睛】本题考查圆周角定理，勾股定理，直角三角形斜边上的中线等于斜边一半，解题的关键是求出BC ．29(2023•杭州一模)如图，过⊙O 外一点A 作⊙O 的切线AD ，点D 是切点，连结OA 交⊙O 于点B ，点C 是⊙O 上不与点B ，D 重合的点．若∠A =α°，则∠C 的度数为()A.45-12α °B.12α°C.2α°D.45+12α°【答案】A【分析】由切线的性质定理，得到∠ADO =90°，由直角三角形的性质得到，∠AOD =90°-α°，由圆周角定理得到∠C =12∠AOD =45-12α °．【详解】解：∵AD 切圆于D ，∴半径OD ⊥AD ，∴∠ADO =90°，∵∠A =α°，∴∠AOD =90°-α°，∴∠C =12∠AOD =45-12α °．故选：A ．【点睛】本题考查切线的性质，圆周角定理，关键是掌握切线的性质定理，圆周角定理．30(2023•西宁一模)如图，扇形纸片AOB 的半径为3，沿AB 所在直线折叠扇形纸片，圆心D 恰好落在AB 上的点C 处，则阴影部分的面积是()A.3π-932B.3π-332C.2π-332D.2π-932【答案】A【分析】根据折叠变换的性质得到AC =AO ，BC =BO ，推出四边形AOBC 是菱形，连接OC 交AB 于D ，根据等边三角形的性质得到∠CAO =∠AOC =60°，求得∠AOB =120°，根据菱形和扇形的面积公式即可得到结论．【详解】解：沿AB 折叠扇形纸片，点O 恰好落在AB 上的点C 处，∴AC =AO ，BC =BO ，∵AO =BO ，∴四边形AOBC 是菱形，连接OC 交AB 于D ，∵OC =OA ，∴△AOC 是等边三角形，∴∠CAO =∠AOC =60°，∴∠AOB =120°，∵AC =3，∴OC =3，AD =32AC =332，∴AB =2AD =33，∴图中阴影部分的面积=S 扇形AOB -S 菱形AOBC =120π×32360-12×3×33=3π-932，故选：A ．【点睛】本题考查了扇形面积的计算，菱形的判定和性质，等边三角形的判定和性质，正确地作出辅助线是解题的关键．31(2023•太原一模)如图，在扇形纸片OAB 中，∠AOB =105°，OA =6、点C 是半径OA 上的点、沿直线BC 折叠△OBC 得到△DBC ，点O 的对应点D 落在AB 上，图中阴影部分的面积为()。

几何最值问题-2023年中考数学压轴题专项训练(全国通用)(解析版)

12023年中考数学压轴题专项训练1.几何最值问题一、压轴题速练1一、单选题1(2023·山东烟台·模拟预测)如图，在矩形ABCD 中，AB =8，AD =4，点E 是矩形ABCD 内部一动点，且∠BEC =90°，点P 是AB 边上一动点，连接PD 、PE ，则PD +PE 的最小值为()A.8 B.45 C.10 D.45-2【答案】A【分析】根据∠BEC =90°得到点的运动轨迹，利用“将军饮马”模型将PE 进行转化即可求解．【详解】解：如图，设点O 为BC 的中点，由题意可知，点E 在以BC 为直径的半圆O 上运动，作半圆O 关于AB 的对称图形(半圆O ')，点E 的对称点为E 1，连接O 'E 1,则PE =PE 1，∴当点D 、P 、E 1、O '共线时，PD +PE 的值最小，最小值为DE 1的长，如图所示，在Rt △DCO '中，CD =8，CO '=6，∴DO '=82+62=10，又∵O 'E 1=2，∴DE 1=DO '-O 'E 1=8，即PD +PE 的最小值为8，故选：A ．【点睛】本题考查线段和最短问题、轴对称的性质、勾股定理及圆周角定理，利用“将军饮马”模型将PE 进行转化时解题的关键．2(2023·安徽黄山·校考模拟预测)如图，在平面直角坐标系中，二次函数y =32x 2-32x -3的图象与x 轴交于点A ，C 两点，与y 轴交于点B ，对称轴与x 轴交于点D ，若P 为y 轴上的一个动点，连接PD ，则12PB +PD 的最小值为()2A.334B.32C.3D.543【答案】A【分析】作射线BA ，作PE ⊥BA 于E ，作DF ⊥BA 于F ，交y 轴于P ，可求得∠ABO =30°，从而得出PE =12PB ，进而得出PD +12PB =PD +EP ，进一步得出结果．【详解】解：如图，作射线BA ，作PE ⊥BA 于E ，作DF ⊥BA 于F ，交y 轴于P ，抛物线的对称轴为直线x =--322×32=12，∴OD =12，当x =0时，y =-3，∴OB =3，当y =0时，32x 2-32x -3=0，∴x 1=-1，x 2=2，∴A (-1,0)，∴OA =1，∵tan ∠ABO =OA OB =13=33，∴∠ABO =30°，∴PE =12PB ，∴12PB +PD =PD +PE ≥DF ，当点P 在P 时，PD +PE 最小，最大值等于DF ，在Rt △ADF 中，∠DAF =90°-∠ABO =60°，AD =OD +PA =12+1=32，∴DF =AD ⋅sin ∠DAE =32×32-334，∴12PB +PD 最小=DF =334，故选：A ．【点睛】本题以二次函数为背景，考查了二次函数与一元二次方程之间的关系，解直角三角形等知识，解决问题的关键是用三角函数构造12PB ．3(2023秋·浙江金华·九年级统考期末)如图，正方形ABCD 的边长为4，点E 是正方形ABCD 内的动点，点P 是BC 边上的动点，且∠EAB =∠EBC ．连结AE ，BE ，PD ，PE ，则PD +PE 的最小值为()3A.213-2B.45-2C.43-2D.215-2【答案】A【分析】先证明∠AEB =90°，即可得点E 在以AB 为直径的半圆上移动，设AB 的中点为O ，作正方形ABCD 关于直线BC 对称的正方形CFGB ，则点D 的对应点是F ，连接FO 交BC 于P ，交半圆O 于E ，根据对称性有：PD =PF ，则有：PE +PD =PE +PF ，则线段EF 的长即为PE +PD 的长度最小值，问题随之得解．【详解】解：∵四边形ABCD 是正方形，∴∠ABC =90°，∴∠ABE +∠EBC =90°，∵∠EAB =∠EBC ，∴∠EAB +∠EBA =90°，∴∠AEB =90°，∴点E 在以AB 为直径的半圆上移动，如图，设AB 的中点为O ，作正方形ABCD 关于直线BC 对称的正方形CFGB ，则点D 的对应点是F ，连接FO 交BC 于P ，交半圆O 于E ，根据对称性有：PD =PF ，则有：PE +PD =PE +PF ，则线段EF 的长即为PE +PD 的长度最小值，E∵∠G =90°，FG =BG =AB =4，∴OG =6，OA =OB =OE =2，∴OF =FG 2+OG 2=213，∴EF =OF -OE =213-2，故PE +PD 的长度最小值为213-2，故选：A ．【点睛】本题考查了轴对称-最短路线问题，正方形的性质，勾股定理，正确的作出辅助线，得出点E 的运动路线是解题的关键．4(2022秋·安徽池州·九年级统考期末)如图，Rt △ABC 中，∠C =90°，AC =4，BC =3，点P 为AC 边上的动点，过点P 作PD ⊥AB 于点D ，则PB +PD 的最小值为()4 A.154 B.245 C.5 D.203【答案】B【分析】作点B 关于AC 的对称点B ，过点B 作B D ⊥AB 于点D ，交AC 于点P ，点P 即为所求作的点，此时PB +PD 有最小值，连接AB ，根据对称性的性质，可知：BP =B P ，△ABC ≅△AB C ，根据S △ABB =S △ABC +S △AB C =2S △ABC ，即可求出PB +PD 的最小值．【详解】解：如下图，作点B 关于AC 的对称点B ，过点B 作B D ⊥AB 于点D ，交AC 于点P ，连接AB ，点P 即为所求作的点，此时PB +PD 有最小值，根据对称性的性质，可知：BP =B P ，在Rt △ABC 中，∠ACB =90°,AC =4,BC =3，∴AB =AC 2+BC 2=5，根据对称性的性质，可知：△ABC ≅△AB C ，∴S △ABB =S △ABC +S △ABC =2S △ABC ，即12×AB ⋅B D =2×12BC ⋅AC ，∴5B D =24，∴B D =245，故选：B ．【点睛】本题考查了轴对称一最短路线问题，解题的关键是掌握轴对称的性质．5(2023秋·甘肃定西·八年级校考期末)如图所示，在△ABC 中，∠ABC =68°，BD 平分∠ABC ，P 为线段BD 上一动点，Q 为边AB 上一动点，当AP +PQ 的值最小时，∠APB 的度数是()A.118°B.125°C.136°D.124°【答案】D【分析】先在BC 上截取BE =BQ ，连接PE ，证明△PBQ ≌△PBE SAS ，得出PE =PQ ，说明AP +PQ =AP +PE ，找出当A 、P 、E 在同一直线上，且AE ⊥BC 时，AP +PE 最小，即AP +PQ 最小，过点A 作AE ⊥BC 于点E ，交BD 于点P ，根据三角形外角的性质可得答案．【详解】解：在BC 上截取BE =BQ ，连接PE ，如图：∵BD 平分∠ABC ，∠ABC =68°，∴∠ABD =∠CBD =12∠ABC =34°，∵BP =BP ，∴△PBQ ≌△PBE SAS ，∴PE =PQ ，∴AP +PQ =AP +PE ，∴当A 、P 、E 在同一直线上，且AE ⊥BC 时，AP +PE 最小，即AP +PQ最小，过点A作AE ⊥BC 于点E ，交BD 于点P ，如图：∵∠AEB =90°，∠CBD =34°，∴∠APB =∠AEB +∠CBD =124°．故选：D ．5【点睛】本题主要考查了角平分线的定义，三角形全等的判定和性质，垂线段最短，三角形内角和定理与三角形的外角的性质，解题的关键是找出使AP +PQ 最小时点P 的位置．6(2022秋·重庆沙坪坝·八年级重庆市凤鸣山中学校联考期末)如图，E 为正方形ABCD 边AD 上一点，AE =1，DE =3，P 为对角线BD 上一个动点，则PA +PE 的最小值为()A.5B.42C.210D.10【答案】A【分析】连接EC 交BD 于P 点，根据“两点之间线段最短”，可知PA +PE 的最小值即为线段EC 的长，求出EC 的长即可.【详解】连接EC ，交BD 于P 点∵四边形ABCD 为正方形∴A 点和C 点关于BD 对称∴PA =PC∴PA +PE =PC +PE =EC根据“两点之间线段最短”，可知PA +PE 的最小值即为线段EC 的长.∵AE =1，DE =3∴AD =4∴DC =4∴CE =DE 2+CD 2=32+42=5∴PA +PE 的最小值为5故选：A【点睛】本题主要考查了正方形的性质和两点之间线段最短，这是一个将军饮马模型.熟练掌握正方形的性质并且能够识别出将军饮马模型是解题的关键.7(2023春·湖南张家界·八年级统考期中)如图，正方形ABCD 的边长为4，点M 在DC 上，且DM =1，N 是AC 上一动点，则DN +MN 的最小值为()A.4B.42C.25D.5【答案】D【分析】由正方形的对称性可知点B 与D 关于直线AC 对称，连接BM 交AC 于N ′，N ′即为所求在Rt △BCM 中利用勾股定理即可求出BM 的长即可．【详解】∵四边形ABCD 是正方形，∴点B 与D 关于直线AC 对称，6连接BD ，BM 交AC 于N ′，连接DN ′，∴当B 、N 、M 共线时，DN +MN 有最小值，则BM 的长即为DN +MN 的最小值，∴AC 是线段BD 的垂直平分线，又∵CD =4，DM =1∴CM =CD -DM =4-1=3，在Rt △BCM 中，BM =CM 2+BC 2=32+42=5故DN +MN 的最小值是5．故选：D ．【点睛】本题考查的是轴对称-最短路线问题及正方形的性质，先作出D 关于直线AC 的对称点，由轴对称及正方形的性质判断出D 的对称点是点B 是解答此题的关键．8(2022秋·浙江杭州·九年级杭州外国语学校校考开学考试)如图，在平面直角坐标系中，二次函数y =-x 2+bx +3的图像与x 轴交于A 、C 两点，与x 轴交于点C (3,0)，若P 是x 轴上一动点，点D 的坐标为(0,-1)，连接PD ，则2PD +PC 的最小值是()A.4B.2+22C.22D.32+232【答案】A【分析】过点P 作PJ ⊥BC 于J ，过点D 作DH ⊥BC 于H ，根据2PD +PC =2PD +22PC =2PD +PJ ，求出DP +PJ 的最小值即可解决问题．【详解】解：连接BC ，过点P 作PJ ⊥BC 于J ，过点D 作DH ⊥BC 于H ．∵二次函数y =-x 2+bx +3的图像与x 轴交于点C (3,0)，∴b =2，∴二次函数的解析式为y =-x 2+2x +3，令y =0，-x 2+2x +3=0，解得x =-1或3，∴A (-1，0)，令x =0，y =3，∴B (0，3)，∴OB =OC =3，∵∠BOC =90°，∴∠OBC =∠OCB =45°，∵D(0，-1)，∴OD =1，BD =4，∵DH ⊥BC ，∴∠DHB =90°，设DH =x ，则BH =x ,∵DH 2+BH 2=BD 2，7∴x =22，∴DH =22，∵PJ ⊥CB ，∴∠PJC =90°，∴PJ =22PC ，∴2PD +PC =2PD +22PC =2PD +PJ ，∵DP +PJ ≥DH ，∴DP +PJ ≥22，∴DP +PJ 的最小值为22，∴2PD +PC 的最小值为4．故选：A ．【点睛】本题考查了二次函数的相关性质，以及等腰直角三角形的判定和性质，垂线段最短等知识，得到∠OBC =∠OCB =45°，PJ =22PC 是解题的关键．9(2022·山东泰安·统考中考真题)如图，四边形ABCD 为矩形，AB =3，BC =4．点P 是线段BC 上一动点，点M 为线段AP 上一点．∠ADM =∠BAP ，则BM 的最小值为()A.52 B.125 C.13-32 D.13-2【答案】D【分析】证明∠AMD =90°，得出点M 在O 点为圆心，以AO 为半径的圆上，从而计算出答案．【详解】设AD 的中点为O ，以O 点为圆心，AO 为半径画圆∵四边形ABCD 为矩形∴∠BAP +∠MAD =90°∵∠ADM =∠BAP∴∠MAD +∠ADM =90°∴∠AMD =90°∴点M 在O 点为圆心，以AO 为半径的圆上连接OB 交圆O 与点N∵点B 为圆O 外一点∴当直线BM 过圆心O 时，BM 最短∵BO 2=AB 2+AO 2，AO =12AD =2∴BO 2=9+4=13∴BO =13∵BN =BO -AO =13-2故选：D ．【点睛】本题考查直角三角形、圆的性质，解题的关键是熟练掌握直角三角形和圆的相关知识．810(2022·河南·校联考三模)如图1，正方形ABCD 中，点E 是BC 的中点，点P 是对角线AC 上的一个动点，设AP =x ，PB +PE =y ，当点P 从A 向点C 运动时，y 与x 的函数关系如图2所示，其中点M 是函数图象的最低点，则点M 的坐标是()A.42，35B.22,35C.35,22D.35,42【答案】A【分析】根据图像，当P 与C 重合时，PB +PE =9即CB +CE =9，从而确定正方形的边长为6，根据将军饮马河原理，连接DE 交AC 于点G ，当点P 与点G 重合时，PE +PB 最小，且为DE 的长即点M 的纵坐标，利用相似三角形，计算AG 的长即为横坐标．【详解】如图，根据图像，当P 与C 重合时，PB +PE =9即CB +CE =9，∵点E 是BC 的中点，∴BC =6，连接DE 交AC 于点G ，当点P 与点G 重合时，PE +PB 最小，且为DE 的长即点M 的纵坐标，∵四边形ABCD 是正方形，AB =6，∴CE ∥AD ，AC =62+62=62，DE =62+32=35，∴△CGE ∽△AGD ，∴CG AG =CE AD =12，∴AC AG=32，∴AG =42，故点M 的坐标为(42，35)，故A 正确．故选：A ．【点睛】本题考查了正方形的性质，三角形相似的判定和性质，函数图像信息的获取，将军饮马河原理，熟练掌握正方形的性质，灵活运用三角形相似，构造将军饮马河模型求解是解题的关键．2二、填空题11(2023春·江苏宿迁·九年级校联考阶段练习)如图，矩形ABCD ，AB =4，BC =8，E 为AB 中点，F 为直线BC 上动点，B 、G 关于EF 对称，连接AG ，点P 为平面上的动点，满足∠APB =12∠AGB ，则DP 的最小值．【答案】210-22【分析】由题意可知，∠AGB =90°，可得∠APB =12∠AGB =45°，可知点P 在以AB 为弦，圆周角∠APB =45°的9圆上，(要使DP 最小，则点P 要靠近蒂点D ，即点P 在AB 的右侧)，设圆心为O ，连接OA ，OB ，OE ，OP ，OD ，过点O 作OQ ⊥AD ，可知△AOB 为等腰直角三角形，求得OA =22AB =22=OP ，AQ =OQ =22OA =2，QD =AD -AQ =6，OD =OQ 2+QD 2=210，再由三角形三边关系可得：DP ≥OD -OP =210-22，当点P 在线段OD 上时去等号，即可求得DP 的最小值．【详解】解：∵B 、G 关于EF 对称，∴BH =GH ，且EF ⊥BG∵E 为AB 中点，则EH 为△ABG 的中位线，∴EH ∥AG ，∴∠AGB =90°，∵∠APB =12∠AGB ，即∠APB =12∠AGB =45°，∴点P 在以AB 为弦，圆周角∠APB =45°的圆上，(要使DP 最小，则点P 要靠近蒂点D ，即点P 在AB 的右侧)设圆心为O ，连接OA ，OB ，OE ，OP ，OD ，过点O 作OQ ⊥AD ，则OA =OB =OP ，∵∠APB =45°，∴∠AOB =90°，则△AOB 为等腰直角三角形，∴OA =22AB =22=OP ，又∵E 为AB 中点，∴OE ⊥AB ，OE =12AB =AE =BE ，又∵四边形ABCD 是矩形，∴∠BAD =90°，AD =BC =8，∴四边形AEOQ 是正方形，∴AQ =OQ =22OA =2，QD =AD -AQ =6，∴OD =OQ 2+QD 2=210，由三角形三边关系可得：DP ≥OD-OP =210-22，当点P 在线段OD 上时去等号，∴DP 的最小值为210-22，故答案为：210-22．【点睛】本题考查轴对称的性质，矩形的性质，隐形圆，三角形三边关系，正方形的判定及性质，等腰直角三角形的判定及性质，根据∠APB =12∠AGB =45°得知点P 在以AB 为弦，圆周角∠APB =45°的圆上是解决问题的关键．12(2023春·江苏连云港·八年级期中)如图，在边长为8的正方形ABCD 中，点G 是BC 边的中点，E 、F 分别是AD 和CD 边上的点，则四边形BEFG 周长的最小值为．【答案】2410【分析】作点G 关于CD 的对称点G ，作点B 关于AD 的对称点B ，连接B G ，根据两点之间线段最短即可解决问题．【详解】作点G 关于CD 的对称点G ，作点B 关于AD 的对称点B ，连接B G∵EB =EB ,FG =FG ，∴BE +EF +FG +BG =B E +EF +FG +BG ，∵EB +EF +FG ≥B G ，∴四边形BEFG 的周长的最小值=BG +B G ，∵正方形ABCD 的边长为8∴BG =4，BB =16，BG =12，∴B G =162+122=20，∴四边形BEFG 的周长的最小值为=4+20=24．故答案为：24．【点睛】本题考查轴对称求线段和的最短问题，正方形的性质，勾股定理，解题的关键是学会利用轴对称解决最短问题．13(2022·湖南湘潭·校考模拟预测)如图，菱形草地ABCD 中，沿对角线修建60米和80米两条道路AC <BD ，M 、N 分别是草地边BC 、CD 的中点，在线段BD 上有一个流动饮水点P ，若要使PM +PN 的距离最短，则最短距离是米．【答案】50【分析】作M 关于BD 的对称点Q ，连接NQ ，交BD 于P ，连接MP ，当P 点与P 重合时，MP +NP =MP +NP =NQ 的值最小，根据菱形的性质和勾股定理求出BC 长，即可得出答案．【详解】解：作M 关于BD 的对称点Q ，连接NQ ，交BD 于P ，连接MP ，当P 点与P 重合时，MP +NP =MP +NP =NQ 的值最小，∵四边形ABCD 是菱形，∴AC ⊥BD ，∠QBP =∠MBP ，即Q 在AB 上，∵MQ ⊥BD ，∴AC ∥MQ ，∴M 为BC 中点，∴Q 为AB 中点，∵N 为CD 中点，四边形ABCD 是菱形，∴BQ ∥CD ，BQ =CN ，∴四边形BQNC 是平行四边形，∴NQ =BC ，设AC 与BD 的交点为点O ，∵四边形ABCD 是菱形，∴AC ⊥BD，OC =12AC =30米，OB =12BD =40米，∴BC =OB 2+OC 2=50米，∴PM +PN 的最小值是50米．故答案为：50．11【点睛】本题考查了轴对称-最短路线问题，平行四边形的性质和判定，菱形的性质，勾股定理的应用，解此题的关键是能根据轴对称找出P 的位置．14(2023春·江苏·九年级校考阶段练习)如图，正方形ABCD 的边长为4，⊙B 的半径为2，P 为⊙B 上的动点，则2PC -PD 的最大值是．【答案】2【分析】解法1，如图：以PD 为斜边构造等腰直角三角形△PDM ，连接MC ，BD ，连接PM 、DM ，推得2PC -PD=2PC -22PD =2PC -PM ，因为PC -PM ≤MC ，求出MC 即可求出答案．解法2：如图：连接BD 、BP 、PC ，在BD 上做点M ，使BM BP =24，连接MP ，证明△BMP ∼△BPD ，在BC 上做点N ，使BN BP=12，连接NP ，证明△BNP ∼△BPC ，接着推导出2PC -PD =22MN ，最后证明△BMN ∼△BCD ，即可求解．【详解】解法1如图：以PD 为斜边构造等腰直角三角形△PDM ，连接MC ，BD ，∴∠PDM =45，DM =PM =22PD ，∵四边形ABCD 正方形∴∠BDC =45°，DB DC=2又∵∠PDM =∠PDB +MDB ，∠BDC =∠MDB +MDC∴∠PDB =∠MDC在△BPD 与△MPC 中∠PDB =∠MDC ，DB DC=DP DM =2∴△BPD ∼△MPC∴PB MC=2∵BP =2∴MC =2∵2PC -PD =2PC-22PD =2PC -PM ∵PC -PM ≤MC ∴2PC -PD =2PC -PM ≤2MC =2故答案为：2．解法2如图：连接BD 、BP 、PC根据题意正方形ABCD 的边长为4，⊙B 的半径为2∴BP =2，BD =BC 2+CD 2=42+42=42∵BP BD =242=2412在BD 上做点M ，使BM BP=24，则BM =22，连接MP 在△BMP 与△BPD 中∠MBP =∠PBD ，BP BD =BM BP∴△BMP ∼△BPD∴PM PD =24，则PD =22PM ∵BP BC =24=12在BC 上做点N ，使BN BP=12，则BN =1，连接NP 在△BNP 与△BPC 中∠NBP =∠PBC ，BN BP =BP PC∴△BNP ∼△BPC∴PN PC=12，则PC =2PN ∴如图所示连接NM ∴2PC -PD =2×2PN -22PM =22PN -PM ∵PN -PM ≤NM ∴2PC -PD =22PN -PM ≤22NM在△BMN 与△BCD 中∠NBM=∠DBC ，BM BC =224=28，BN BD =142=28∴BM BC=BN BD ∴△BMN ∼△BCD∴MN CD=28∵CD =4∴MN =22∴22MN =22×22=2∴2PC -PD ≤22NM =2故答案为：2．【点睛】本题考查正方形的性质，相似三角形，勾股定理等知识，难度较大，熟悉以上知识点运用是解题关键．15(2023秋·广东广州·九年级统考期末)如图，四边形ABCD 中，AB ∥CD ，AC ⊥BC ，∠DAB =60°，AD =CD =4，点M 是四边形ABCD 内的一个动点，满足∠AMD =90°，则△MBC 面积的最小值为．【答案】63-4【分析】取AD 的中点O ，连接OM ，过点M 作ME ⊥BC 交BC 的延长线于点E ，过点O 作OF ⊥BC 于F ，交CD 于G ，则OM +ME ≥OF ，通过计算得出当O ,M ,E 三点共线时，ME 有最小值，求出最小值即可．【详解】解：如图，取AD 的中点O ，连接OM ，过点M 作ME ⊥BC 交BC 的延长线于点E ，过点O 作OF ⊥BC 于F ，交CD 于G ，则13OM +ME ≥OF ，∵AB ∥CD ，∠DAB =60°，AD =CD =4，∴∠ADC =120°，∵AD =CD ，∴∠DAC =30°，∴∠CAB =30°，∵AC ⊥BC ，∴∠ACB =90°∴∠B =90°-30°=60°，∴∠B =∠DAB ，∴四边形ABCD 为等腰梯形，∴BC =AD =4，∵∠AMD =90°，AD =4，OA =OD ，∴OM =12AD =2，∴点M 在以点O 为圆心，2为半径的圆上，∵AB ∥CD ，∴∠GCF =∠B =60°，∴∠DGO =∠CGF =30°，∵OF ⊥BC ，AC ⊥BC ，∴∠DOG =∠DAC =30°=∠DGO ，∴DG =DO =2，∴OG =2OD ⋅cos30°=23，GF =3，OF =33，∴ME ≥OF -OM =33-2，∴当O ,M ,E 三点共线时，ME 有最小值33-2，∴△MBC 面积的最小值为=12×4×33-2 =63-4．【点睛】本题考查了解直角三角形、隐圆、直角三角形的性质等知识点，点M 位置的确定是解题关键．16(2023春·全国·八年级专题练习)如图，在等边△ABC 中，BD ⊥AC 于D ，AD =3cm ．点P ,Q 分别为AB,AD 上的两个定点且BP =AQ =1cm ，点M 为线段BD 上一动点，连接PM ,QM ，则PM +QM 的最小值为cm ．【答案】5【分析】如图所示，作点P 关于BD 的对称点P ，且点P 在BC 上，则PM +QM =P M+QM ，当P ,M ,Q 在同一条直线上时，有最小值，证明四边形PP QA 是平行四边形，P Q =AP =AB -BP ，由此即可求解．【详解】解：如图所示，作点P 关于BD 的对称点P ，∵△ABC 是等边三角形，BD ⊥AC ，∴∠ABD =∠DBC =12∠ABC =12×60°=30°，14∴点P 在BC 上，∴P M =PM ，则PM +QM =P M +QM ，当P ,M ,Q 在同一条直线上时，有最小值，∵点P 关于BD 的对称点P ，∠ABD =∠DBC =30°，∴PP ⊥BM ，BP =BP =1cm ，∴∠BP P =60°，∴△BPP 是等边三角形，即∠BP P =∠C =60°，∴PP ∥AC ，且PP =AQ =1cm ，∴四边形PP QA 是平行四边形，∴P Q =AP =AB -BP ，在Rt △ABD 中，∠ABD =30°，AD =3，∴AB =2AD =2×3=6，∴AP =P Q =P M +QM =PM +QM =AB -BP =6-1=5，故答案为：5．【点睛】本题主要考查动点与等边三角形，对称-最短路径，平行四边形的判定和性质的综合，理解并掌握等边三角形得性质，对称-最短路径的计算方法，平行四边形的判定和性质是解题的关键．17(2022秋·山东菏泽·九年级校考阶段练习)如图，在周长为12的菱形ABCD 中，DE =1，DF =2，若P 为对角线AC 上一动点，则EP +FP 的最小值为．【答案】3【分析】作F 点关于BD 的对称点F ，连接EF 交BD 于点P ，则PF =PF ，由两点之间线段最短可知当E 、P 、F 在一条直线上时，EP +FP 有最小值，然后求得EF 的长度即可．【详解】解：作F 点关于BD 的对称点F ，则PF =PF ，连接EF '交BD 于点P ．∴EP +FP =EP +F P ．由两点之间线段最短可知：当E 、P 、F '在一条直线上时，EP +FP 的值最小，此时EP +FP =EP +F P =EF ．∵四边形ABCD 为菱形，周长为12，∴AB =BC =CD =DA =3，AB ∥CD ，∵AF =2，AE =1，∴DF =AE =1，∴四边形AEF D 是平行四边形，∴EF =AD =3．∴EP +FP 的最小值为3．故答案为：3．【点睛】本题主要考查的是菱形的性质、轴对称--路径最短问题，明确当E 、P 、F 在一条直线上时EP +FP 有最小值是解题的关键．18(2023春·上海·八年级专题练习)如图，直线y =x +4与x 轴，y 轴分别交于A和B ，点C 、D 分别为线段AB 、OB 的中点，P 为OA 上一动点，当PC +PD 的值最小时，点P 的坐标为．15【答案】(-1,0)【分析】直线y =x +4与x 轴，y 轴分别交于A 和B ，可求出点A ，B 的坐标，点C 、D 分别为线段AB 、OB 的中点，可求出点C 、D 的坐标，作点C 关于x 轴的对称点C ，连接C D 与x 轴的交点就是所求点P 的坐标．【详解】解：直线y =x +4与x 轴，y 轴分别交于A 和B ，∴当y =0，x =-4，即A (-4,0)；当x =0，y =4，即B (0,4)，∵点C 、D 分别为线段AB 、OB 的中点，∴C (-2,2)，D (0,2)，如图所示，过点C 关于x 轴的对称点C，∴C (-2,-2)，∴直线C D 的解析式为：y =2x +2，当y =0，x =-1，即P (-1,0)，故答案为：(-1,0)．【点睛】本题主要考查一次函数与最短线段的综合，掌握对称中最短线段的解题方法是解题的关键．19(2023秋·黑龙江鸡西·九年级统考期末)如图，抛物线y =x 2-4x +3与x 轴分别交于A ,B两点(点A 在点B 的左侧)，与y 轴交于点C ，在其对称轴上有一动点M ，连接MA ,MC ,AC ，则△MAC 周长的最小值是．【答案】32+10【分析】根据“将军饮马”模型，先求出A 1,0 ,B 3,0 ,C 0,3 ，由二次函数对称性，A ,B 关于对称轴对称，从而C △MAC =CA +CM +MA =CA +CM +MB ，AC =OA 2+OC 2=10，则△MAC 周长的最小值就是CM +MB 的最小值，根据两点之间线段最短即可得到CM +MB 的最小值为C ,M ,B 三点共线时线段CB 长，从而得到CB =OC 2+OB 2=32，即可得到答案．【详解】解：∵抛物线y =x 2-4x +3与x 轴分别交于A ,B 两点(点A 在点B 的左侧)，与y 轴交于点C ，16∴当y =0时，0=x 2-4x +3解得x =1或x =3，即A 1,0 ,B 3,0 ；当x =0时，y =3，即C 0,3 ，由二次函数对称性，A ,B 关于对称轴对称，即MA =MB ，∴C △MAC =CA +CM +MA =CA +CM +MB ，∵AC =OA 2+OC 2=10，∴△MAC 周长的最小值就是CM +MB 的最小值，根据两点之间线段最短即可得到CM +MB 的最小值为C ,M ,B 三点共线时线段CB 长，∵CB =OC 2+OB 2=32，∴△MAC 周长的最小值为CA +CB =32+10，故答案为：32+10．【点睛】本题考查动点最值问题与二次函数综合，涉及“将军饮马”模型求最值、二次函数图像与性质、解一元二次方程、勾股定理求线段长等知识，熟练掌握动点最值的常见模型是解决问题的关键．20(2023秋·浙江温州·九年级校考期末)如图所示，∠ACB =60°，半径为2的圆O 内切于∠ACB．P 为圆O 上一动点，过点P 作PM 、PN 分别垂直于∠ACB 的两边，垂足为M 、N ，则PM +2PN 的取值范围为．【答案】6-23≤PM +2PN ≤6+23【分析】根据题意，本题属于动点最值问题-“阿氏圆”模型，首先作MH ⊥NP 于H ，作MF ⊥BC 于F ，如图所示，通过代换，将PM +2PN 转化为PN +12PM =PN +HP =NH ，得到当MP 与⊙O 相切时，MF 取得最大值和最小值，分两种情况，作出图形，数形结合解直角三角形即可得到相应最值，进而得到取值范围．【详解】解：作MH ⊥NP 于H ，作MF ⊥BC 于F ，如图所示：∵PM ⊥AC ，PN ⊥CB ，∴∠PMC =∠PNC =90°，∴∠MPN =360°-∠PMC -∠PNC -∠C =120°，∴∠MPH =180°-∠MPN =60°，∴HP =PM ⋅cos ∠MPH =PM ⋅cos60°=12PM ，∴PN +12PM =PN +HP =NH ，∵MF =NH ，∴当MP 与⊙O 相切时，MF 取得最大和最小，①连接OP ，OG ，OC ，如图1所示：可得：四边形OPMG 是正方形，∴MG =OP =2，在Rt △COG 中，CG =OG ⋅tan60°=23，∴CM =CG +GM =2+23，在Rt △CMF 中，MF =CM ⋅sin60°=3+3，∴HN =MF =3+3，即PM +2PN =212PM +PN =2HN =6+23；②连接OP ，OG ，OC ，如图2所示：可得：四边形OPMG 是正方形，17∴MG =OP =2，由上同理可知：在Rt △COG 中，CG =OG ⋅tan60°=23，∴CM =CG -GM =23-2，在Rt △CMF 中，MF =CM ⋅sin60°=3-3，∴HN =MF =3-3，即PM +2PN =212PM +PN =2HN =6-23，∴6-23≤PM +2PN ≤6+23．故答案为：6-23≤PM +2PN ≤6+23．【点睛】本题考查动点最值模型-“阿氏圆”，难度较大，掌握解决动点最值问题的方法，熟记相关几何知识，尤其是圆的相关知识是解决问题的关键．3三、解答题21(2022春·江苏·九年级专题练习)综合与探究如图，已知抛物线y =ax 2+bx +4经过A -1,0 ，B 4,0 两点，交y 轴于点C ．(1)求抛物线的解析式，连接BC ，并求出直线BC 的解析式；(2)请在抛物线的对称轴上找一点P ，使AP +PC 的值最小，此时点P 的坐标是；(3)点Q 在第一象限的抛物线上，连接CQ ，BQ ，求出△BCQ 面积的最大值．【答案】(1)y =-x 2+3x +4；y =-x +4(2)32,52(3)8【分析】(1)将A -1,0 ，B 4,0 两点，代入抛物线解析式，可得到抛物线解析式，从而得到C 0,4 ，再设直线BC 的解析式为y =kx +b k ≠0 ，把点B 、C 的坐标代入，即可求解；(2)连接BC ，PB ，根据题意可得A 、B 关于抛物线的对称轴直线x =32对称，从而得到当P 在直线AB 上三点共线时，AP +CP 的值最小，把x =32代入直线BC 的解析式，即可求解；(3)过Q 作QD ⊥x 轴，交BC 于D ，设Q d ,-d 2+3d +4 ，其中0≤d ≤4，则D d ,-d +4 ，可得QD =-d 2+4d ，从而得到S ΔBCQ =12OB ×QD =-2d -2 2+8，即可求解；【详解】(1)解：(1)∵抛物线y =ax 2+bx +4经过A -1,0 ，B 4,0 两点，∴a -b +4=016a +4b +4=0，解得：a =-1b =3 ，18∴抛物线的解析式为y =-x 2+3x +4；∵抛物线与y 轴的交点为C ，∴C 0,4 ，设直线BC 的解析式为y =kx +b k ≠0 ，把点B 、C 的坐标代入得：4k +b =0b =4 ，解得：k =-1b =4 ，∴直线BC 的解析式为y =-x +4；(2)如图，连接BC ，PB ，∵y =-x 2+3x +4=-x -32 2+74，∴抛物线的对称轴为直线x =32，根据题意得：A 、B 关于抛物线的对称轴直线x =32对称，∴AP =BP ，∴AP +CP =BP +CP ≥BC ，即当P 在直线AB 上时，AP +CP 的值最小，∴当x =32时，y =-32+4=52，∴P 32,52 ，故答案是：32,52 ；(3)过Q 作QD ⊥x 轴，交BC 于D ，设Q d ,-d 2+3d +4 ，其中0≤d ≤4，则D d ,-d +4 ，∴QD =-d 2+3d +4 --d +4 =-d 2+4d ，∵B 4,0 ，∴OB =4，∴S ΔBCQ =12OB ×QD =-2d 2+8d =-2d -2 2+8，当d =2时，S ΔBCQ 取最大值，最大值为8，∴△BCQ 的最大面积为8；【点睛】本题主要考查了二次函数的图像和性质，利用数形结合思想和分类讨论思想是解题的关键．22(2023秋·江苏淮安·八年级统考期末)如图1，直线AB :y =-x +6分别与x ,y 轴交于A ,B 两点，过点B 的直线交x 轴负半轴于点C -3,0 ．(1)请直接写出直线BC 的关系式：(2)在直线BC 上是否存在点D，使得S △ABD =S △AOD 若存在，求出点D 坐标：若不存请说明理由；(3)如图2，D 11,0 ，P 为x 轴正半轴上的一动点，以P 为直角顶点、BP 为腰在第一象限内作等腰直角三角形△BPQ ，连接QA ,QD ．请直接写出QB -QD 的最大值：．19【答案】(1)y =2x +6(2)当D 185,665 或D -185,-65时，S △ABD =S △AOD (3)37【分析】(1)根据直线AB 与y 轴的交点，可求出点B 的坐标，再用待定系数法即可求解；(2)设D (a ,2a +6)，分别用含a 的式子表示出出S △AOD ,S △ABD ，由此即可求解；(3)△BPQ 是等腰直角三角形，设P (m ,0)(m >0)，可表示出QB ，再证Rt △BOP ≌Rt △PTQ (AAS )，如图所示，当点B ,R ,Q 在一条直线上时，QB -QD 的值最大，最大值为BR 的值，可求得点R 的坐标，根据勾股定理即可求解．【详解】(1)解：∵直线AB :y =-x +6分别与x ,y 轴交于A ,B 两点，令x =0，则y =6，∴B (0,6)，且C -3,0 ，设直线BC 的解析式为y =kx +b ，∴b =6-3k +b =0，解得，k =2b =6 ，∴直线BC 的解析式为y =2x +6，故答案为：y =2x +6．(2)解：由(1)可知直线BC 的解析式为y =2x +6，直线AB 的解析式为y =-x +6，∴A (6,0),B (0,6),C (-3,0)，∴OA =6,BO =6,OC =3，如图所示，点D 在直线BC 上，过点D 作DE ⊥x 轴于E ，∴设D (a ,2a +6)，E (a ,0)，∴S △ABC =12AC ·OB =12×(6+3)×6=27，S △ADC =12AC ·DE =12×(6+3)×a =92a ，S △AOD =12OA ·DE =12×6×a =3a ，∴S △ABD =S △ABC -S △ADC =27-92a ，若S △ABD =S △AOD ，则27-92a =3a ，当a >0时，27-92a =3a ，解得，a =185，即D 185,665 ；当a <0时，27+92a =-3a ，解得，a =-185，即D -185,-65 ；综上所述，当D 185,665 或D -185,-65时，S △ABD =S △AOD ．(3)解：已知A (6,0),B (0,6),D (11,0)，设P (m ,0)(m >0)，∴在Rt △BOP 中，OB =6,OP =m ，∵△BPQ 是等腰直角三角形，∠BPQ =90°，∴BP =QP ；如图所示，过点Q 作QT ⊥x 轴于T ，20在Rt △BOP ,Rt △PTQ 中，∠BOP =∠PTQ =90°，∠BPO +∠QPA =∠QPA +∠PQT =90°，∴∠BPO =∠PQT ，∴∠BPO =∠PQT∠BOP =∠PTQ BP =QP，∴Rt △BOP ≌Rt △PTQ (AAS )，∴OP =TQ =m ，OB =PT =6，∴AT =OP +PT -OA =m +6-6=m ，∴AT =QT ，且QT ⊥x 轴，∴△ATQ 是等腰直角三角形，∠QAT =45°，则点Q 的轨迹在射线AQ 上，如图所示，作点D 关于直线AQ 的对称点R，连接QR ,BR ,AR ，A (6,0)，B (0,6)，D (11,0)，∵△ATQ 是等腰直角三角形，即∠QAT =45°，根据对称性质，∴∠QAR =45°，∴RA ⊥x 轴，且△DQA ≌△RQA ，∴AR =AD =11-6=5，则R (6,5)，如图所示，当点B ,R ,Q 在一条直线上时，QB -QD 的值最大，最大值为BR 的值；∴由勾股定理得：BR =62+(6-5)2=37，故答案为：37．【点睛】本题主要考查一次函数，几何的综合，掌握待定系数法求解析式，将军饮马问题，等腰直角三角形的性质，勾股定理是解题的关键．23(2023春·重庆沙坪坝·九年级重庆八中校考阶段练习)△ABC 中，∠B =60°．(1)如图1，若AC >BC ，CD 平分∠ACB 交AB 于点D ，且AD =3BD ．证明：∠A =30°；(2)如图2，若AC <BC ，取AC 中点E ，将CE 绕点C 逆时针旋转60°至CF ，连接BF 并延长至G ，使BF =FG ，猜想线段AB 、BC 、CG 之间存在的数量关系，并证明你的猜想；(3)如图3，若AC =BC ，P 为平面内一点，将△ABP 沿直线AB 翻折至△ABQ ，当3AQ +2BQ +13CQ 取得最小值时，直接写出BPCQ的值．【答案】(1)见解析(2)BC =AB +CG ，理由见解析(3)213+33913【分析】(1)过点D 分别作BC ，AC 的垂线，垂足为E ，F ，易得DE =DF ，由∠B =60°，可得DE =DF =32BD ，由AD =3BD ，求得sin A =DE AD=12，可证得∠A =30°；(2)延长BA ，使得BH =BC ，连接EH ，CH ，易证△BCH 为等边三角形，进而可证△BCF ≌△HCE SAS ，可得BF =HE ，∠BFC =∠HEC ，可知∠AEH =∠CFG ，易证得△AEH ≌△CFG SAS ，可得AH =CG ，由BC =BH =AB +AH =AB +CG 可得结论；(3)由题意可知△ABC 是等边三角形，如图，作CM ⊥CA ，且CM =32CA ，作CN ⊥CQ ，且CN =32CQ ，可得CM CA=CN CQ =32，QN =CQ 2+CN 2=132CQ ，可知△ACQ ∽△MCN ，可得MN =32AQ ，由3AQ +2BQ +13CQ =232AQ +BQ +132CQ =2MN +BQ +QN ≥2BM 可知点Q ，N 都在线段BM 上时，3AQ +2BQ+13CQ 有最小值，过点C 作CR ⊥BM ，过点M 作MT ⊥BC 交BC 延长线于T ，可得CR =CQ ⋅sin ∠CQN =313CQ ，QR =CQ ⋅cos ∠CQN =213CQ ，可证△CBR ∽△MBT ，得BR CR =BT MT ，设BC =a 由等边三角形的性质，可得CM =32a ，进而可得CT =CM ⋅cos30°=334a ，MT =CM ⋅sin30°=34a ，结合BR CR=BTMT 可得：BQ +213CQ 313CQ =a +334a 34a ，可得BQ CQ =213+33913，由翻折可知，BP =BQ ，可求得BP CQ的值．【详解】(1)证明：过点D 分别作BC ，AC 的垂线，垂足为E ，F ，∵CD 平分∠ACB ，DE ⊥BC ，DF ⊥AC ，∴DE =DF ，又∵∠B =60°，∴DE =BD ⋅sin60°=32BD ，则DE =DF =32BD ，又∵AD =3BD ，∴sin A =DE AD =32BD3BD=12，∴∠A =30°；(2)BC =AB +CG ，理由如下：延长BA ，使得BH =BC ，连接EH ，CH ，∵∠ABC =60°，BH =BC ，∴△BCH 为等边三角形，∴CB =CH ，∠BCH =60°，∵CE 绕点C 逆时针旋转60°至CF ，∴CE =CF ，∠ECF =60°，则∠BCH -∠ACB =∠ECF -∠ACB ，∴∠ECH =∠FCB ，∴△BCF ≌△HCE SAS ，∴BF =HE ，∠BFC =∠HEC ，则∠AEH =∠CFG ，∵BF =FG ，∴BF =HE =FG ，又∵E 为AC 中点，∴AE =CE =CF ，∴△AEH ≌△CFG SAS ，∴AH =CG ，∴BC =BH =AB +AH =AB +CG ；(3)∵∠ABC =60°，AC =BC ，∴△ABC 是等边三角形，如图，作CM ⊥CA ，且CM =32CA ，作CN ⊥CQ ，且CN =32CQ ，则CM CA=CN CQ =32，QN =CQ 2+CN 2=132CQ ，∴sin ∠CQN =CN QN =313，cos ∠CQN =CQ QN =213，则∠ACM =∠QCN =90°，∴∠ACM -∠ACN =∠QCN -∠ACN ，则∠ACQ =∠MCN∴△ACQ ∽△MCN ，∴MN AQ =CM CA=32，即：MN =32AQ ，∴3AQ +2BQ +13CQ =232AQ +BQ +132CQ =2MN +BQ +QN ≥2BM即：点Q ，N 都在线段BM 上时，3AQ +2BQ +13CQ 有最小值，如下图，过点C 作CR ⊥BM ，过点M 作MT ⊥BC 交BC 延长线于T ，则∠BRC =∠BTM =90°，CR =CQ ⋅sin ∠CQN =313CQ ，QR =CQ ⋅cos ∠CQN =213CQ ，又∵∠CBR =∠MBT ，∴△CBR ∽△MBT ，∴BR CR=BT MT ，∵△ABC 是等边三角形，设BC =a ∴∠ACB =60°，AC =BC =a ，则CM =32a ，∵∠ACM =90°，∴∠MCT =30°，则CT =CM ⋅cos30°=334a ，MT =CM ⋅sin30°=34a ，则由BR CR=BT MT 可得：BQ +213CQ 313CQ =a +334a34a ，整理得：133BQ CQ +23=4+333，得BQ CQ=213+33913，由翻折可知，BP =BQ ，∴BP CQ =BQ CQ=213+33913．【点睛】本题属于几何综合，考查了解直角三角形，等边三角形的判定及性质，全等三角形的判定及性质，相似三角形的判定及性质，旋转的性质以及费马点问题，掌握费马点问题的解决方法，添加辅助线构造全等三角形和相似三角形是解决问题的关键．24(2023春·江苏·八年级专题练习)定义：既相等又垂直的两条线段称为“等垂线段”，如图1，在Rt △ABC 中，∠A =90°，AB =AC ，点D 、E 分别在边AB 、AC 上，AD =AE ，连接DE 、DC ，点M 、P 、N 分别为DE 、DC 、BC 的中点，且连接PM 、PN ．(1)观察猜想线段PM 与PN 填(“是”或“不是”)“等垂线段”．(2)△ADE 绕点A 按逆时针方向旋转到图2所示的位置，连接BD ，CE ，试判断PM 与PN 是否为“等垂线段”，并说明理由．(3)拓展延伸把△ADE 绕点A 在平面内自由旋转，若DE =2，BC =4，请直接写出PM 与PN 的积的最大值．。

2020年中考数学1.几何综合选择填空压轴题(含解析)

几何综合-填空选择压轴题11、如图，正方形ABCD中，E，F分别在边AD，CD上，AF，BE相交于点G，若AE=3ED，DF=CF，则AGGF的值是（）A．43B．54C．65D．762、在平面直角坐标系内，以原点O为圆心，1为半径作圆，点P在直线y=√3x+2√3上运动，过点P作该圆的一条切线，切点为A，则PA的最小值为（）A．3 B．2 C．√3D．√23、如图，等腰△ABC的底边BC=20，面积为120，点F在边BC上，且BF=3FC，EG是腰AC的垂直平分线，若点D在EG上运动，则△CDF周长的最小值为．4、如图，在▱ABCD中，CD=2AD，BE⊥AD于点E，F为DC的中点，连结EF、BF，下列结论：①∠ABC=2∠ABF；②EF=BF；③S四边形DEBC =2S△EFB；④∠CFE=3∠DEF，其中正确结论的个数共有（）A．1个B．2个C．3个D．4个5、如图，在边长为1的小正方形网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD相交于点O，则tan∠AOD= ．6、如图，△ACB和△ECD都是等腰直角三角形，CA=CB，CE=CD，△ACB的顶点A 在△ECD的斜边DE上，若AE=√2，AD=√6，则两个三角形重叠部分的面积为（）A．√2 B．3−√2 C．√3−1 D．3−√37、如图，在△ABC中，AC=3，BC=4，若AC，BC边上的中线BE，AD垂直相交于O 点，则AB= ．8、如图，正方形ABCD的边长为2，P为CD的中点，连结AP，过点B作BE⊥AP 于点E，延长CE交AD于点F，过点C作CH⊥BE于点G，交AB于点H，连接HF．下列结论正确的是（）A．CE=√5 B．EF=√22 C．cos∠CEP=√55D．HF2=EF•CF9、如图，在△ABC中，DE∥BC，BF平分∠ABC，交DE的延长线于点F．若AD=1，BD=2，BC=4，则EF= ．10、已知△ABC的三边a，b，c，满足a+b2+|c﹣6|+28=4√a−1+10b，则△ABC 的外接圆半径= ．11、如图，直线y=﹣x+1与两坐标轴分别交于A，B两点，将线段OA分成n等份，分点分别为P1，P2，P3，…，Pn﹣1，过每个分点作x轴的垂线分别交直线AB于点T 1，T 2，T 3，…，T n ﹣1，用S 1，S 2，S 3，…，S n ﹣1分别表示Rt △T 1OP 1，Rt △T 2P 1P 2，…，Rt △T n ﹣1P n ﹣2P n ﹣1的面积，则S 1+S 2+S 3+…+S n ﹣1= ．12、已知如图，在正方形ABCD 中，AD=4，E ，F 分别是CD ，BC 上的一点，且∠EAF=45°，EC=1，将△ADE 绕点A 沿顺时针方向旋转90°后与△ABG 重合，连接EF ，过点B 作BM ∥AG ，交AF 于点M ，则以下结论：①DE+BF=EF ，②BF=47，③AF=307，④S △MBF =32175中正确的是（）A ．①②③B ．②③④C ．①③④D ．①②④13、在△ABC 中，若O 为BC 边的中点，则必有：AB 2+AC 2=2AO 2+2BO 2成立．依据以上结论，解决如下问题：如图，在矩形DEFG 中，已知DE=4，EF=3，点P 在以DE 为直径的半圆上运动，则PF 2+PG 2的最小值为（）A．√10 B．192C．34 D．1014、如图，AB是半圆的直径，AC是一条弦，D是AC的中点，DE⊥AB于点E且DE交AC于点F，DB交AC于点G，若EFAE =34，则CGGB= ．15、如图，在矩形ABCD中，AB=3，CB=2，点E为线段AB上的动点，将△CBE沿CE折叠，使点B落在矩形内点F处，下列结论正确的是（写出所有正确结论的序号）①当E为线段AB中点时，AF∥CE；②当E为线段AB中点时，AF=95；③当A、F、C三点共线时，AE=13−2√133；④当A、F、C三点共线时，△CEF≌△AEF．16、如图，在边长为a正方形ABCD中，把边BC绕点B逆时针旋转60°，得到线段BM，连接AM并延长交CD于N，连接MC，则△MNC的面积为（）A．√3−12a2 B．√2−12a2 C．√3−14a2 D．√2−14a217、如图，在△ABC中，AC=BC=2，AB=1，将它沿AB翻折得到△ABD，则四边形ADBC的形状是形，点P、E、F分别为线段AB、AD、DB的任意点，则PE+PF 的最小值是．18、如图，在正方形ABCD中，E，F分别为AD，BC的中点，P为对角线BD上的一个动点，则下列线段的长等于AP+EP最小值的是（）A．AB B．DE C．BD D．AF19、如图，在边长为4的等边△ABC中，D，E分别为AB，BC的中点，EF⊥AC于点F，G为EF的中点，连接DG，则DG的长为．20、如图，在每个小正方形的边长为1的网格中，△ABC的顶点A，B，C均在格点上，（I）∠ACB的大小为（度）；（Ⅱ）在如图所示的网格中，P是BC边上任意一点，以A为中心，取旋转角等于∠BAC，把点P逆时针旋转，点P的对应点为P′，当CP′最短时，请用无刻度的直尺，画出点P′，并简要说明点P′的位置是如何找到的（不要求证明）．21、如图，点P是边长为1的菱形ABCD对角线AC上的一个动点，点M，N分别是AB，BC边上的中点，则MP+PN的最小值是（）B．1 C．√2 D．2A．1222、在△ABC中，AB=√34，AC=5，若BC边上的高等于3，则BC边的长为．23、如图直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，BC=3，将腰CD以D为中心逆时针旋转90°至ED，连AE、CE，则△ADE的面积是（）A．1 B．2 C．3 D．不能确定24、如图，已知点P是矩形ABCD内一点（不含边界），设∠PAD=θ1，∠PBA=θ2，∠PCB=θ3，∠PDC=θ4，若∠APB=80°，∠CPD=50°，则（）A．（θ1+θ4）﹣（θ2+θ3）=30°B．（θ2+θ4）﹣（θ1+θ3）=40°C．（θ1+θ2）﹣（θ3+θ4）=70°D．（θ1+θ2）+（θ3+θ4）=180°25、如图，在△ABC中，点D在AB边上，DE∥BC，与边AC交于点E，连结BE．记△ADE，△BCE的面积分别为S1，S2（）A．若2AD＞AB，则3S1＞2S2B．若2AD＞AB，则3S1＜2S2C．若2AD＜AB，则3S1＞2S2D．若2AD＜AB，则3S1＜2S226、折叠矩形纸片ABCD时，发现可以进行如下操作：①把△ADE翻折，点A落在DC边上的点F处，折痕为DE，点E在AB边上；②把纸片展开并铺平；③把△CDG翻折，点C落在线段AE上的点H处，折痕为DG，点G在BC边上，若AB=AD+2，EH=1，则AD= ．27、如图，已知在△ABC中，∠BAC＞90°，点D为BC的中点，点E在AC上，将△CDE沿DE折叠，使得点C恰好落在BA的延长线上的点F处，连结AD，则下列结论不一定正确的是（）。

2020年中考数学4.几何综合选择填空压轴题(含解析)

几何综合-填空选择压轴题41、如图，在菱形ABCD中，AB=2，∠B是锐角，AE⊥BC于点E，M是AB的中点，连结MD，ME．若∠EMD=90°，则cosB的值为．2、如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC于F，若BD=8cm，AE=2cm，则OF的长度是（）A．3cm B．√6cm C．2.5cm D．√5cm3、定义：在平面直角坐标系中，一个图形先向右平移a个单位，再绕原点按顺时针方向旋转θ角度，这样的图形运动叫作图形的γ（a，θ）变换．如图，等边△ABC的边长为1，点A在第一象限，点B与原点O重合，点C在x轴的正半轴上．△A1B1C1就是△ABC经γ（1，180°）变换后所得的图形．若△ABC经γ（1，180°）变换后得△A1B1C1，△A1B1C1经γ（2，180°）变换后得△A2B2C2，△A2B2C2经γ（3，180°）变换后得△A3B3C3，依此类推……△An﹣1Bn﹣1Cn﹣1经γ（n，180°）变换后得△AnBnCn，则点A1的坐标是，点A2018的坐标是．4、我国古代伟大的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形，得到一个恒等式．后人借助这种分割方法所得的图形证明了勾股定理，如图所示的矩形由两个这样的图形拼成，若a=3，b=4，则该矩形的面积为（）A．20 B．24 C．994D．5325、如图，直线y=﹣√33x+4与x轴、y轴分别交于A，B两点，C是OB的中点，D 是AB上一点，四边形OEDC是菱形，则△OAE的面积为．6、小明发现相机快门打开过程中，光圈大小变化如图1所示，于是他绘制了如图2所示的图形．图2中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形，若PQ所在的直线经过点M，PB=5cm，小正六边形的面积为49√3cm2，则该圆的半径为cm．27、如图，在矩形ABCD中，AB=4，AD=2，点E在CD上，DE=1，点F是边AB上一动点，以EF为斜边作Rt△EFP．若点P在矩形ABCD的边上，且这样的直角三角形恰好有两个，则AF的值是．8、如图，AB是⊙O的直径，弦CD交AB于点P，AP=2，BP=6，∠APC=30°，则CD的长为（）A．√15 B．2√5 C．2√15 D．89、如图，在矩形ABCD中，点E是边BC的中点，AE⊥BD，垂足为F，则tan∠BDE 的值是（）A．√24 B．14C．13D．√2310、如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，AF平分∠CAB，交CD于点E，交CB于点F．若AC=3，AB=5，则CE的长为（）A．32B．43C．53D．8511、如图，在正方形ABCD中，AD=2√3，把边BC绕点B逆时针旋转30°得到线段BP，连接AP并延长交CD于点E，连接PC，则三角形PCE的面积为．12、如图，P为等边三角形ABC内的一点，且P到三个顶点A，B，C的距离分别为3，4，5，则△ABC的面积为（）A．9+25√34 B．9+25√32C．18+25√3 D．18+25√3213、如图，点O 是▱ABCD 的对称中心，AD ＞AB ，E 、F 是AB 边上的点，且EF=12AB ；G 、H 是BC 边上的点，且GH=13BC ，若S 1，S 2分别表示△EOF 和△GOH 的面积，则S 1与S 2之间的等量关系是．14、如图，已知∠POQ=30°，点A 、B 在射线OQ 上（点A 在点O 、B 之间），半径长为2的⊙A 与直线OP 相切，半径长为3的⊙B 与⊙A 相交，那么OB 的取值范围是（）A ．5＜OB ＜9 B ．4＜OB ＜9C ．3＜OB ＜7D ．2＜OB ＜715、如图，在矩形ABCD 中，按以下步骤作图：①分别以点A 和C 为圆心，以大于12AC 的长为半径作弧，两弧相交于点M 和N ；②作直线MN 交CD 于点E ．若DE=2，CE=3，则矩形的对角线AC 的长为．16、如图，在菱形ABCD中，tanA=43，M，N分别在边AD，BC上，将四边形AMNB沿MN翻折，使AB的对应线段EF经过顶点D，当EF⊥AD时，BNCN的值为．17、如图，△ABC的周长为19，点D，E在边BC上，∠ABC的平分线垂直于AE，垂足为N，∠ACB的平分线垂直于AD，垂足为M，若BC=7，则MN的长度为（）A．32B．2 C．52D．318、如图，E，F是平行四边形ABCD对角线AC上两点，AE=CF=14AC．连接DE，DF并延长，分别交AB，BC于点G，H，连接GH，则S△ADGS△BGH的值为（）A．12B．23C．34D．119、如图，平面直角坐标系中，矩形OABC的顶点A（﹣6，0），C（0，2√3）．将矩形OABC绕点O顺时针方向旋转，使点A恰好落在OB上的点A1处，则点B的对应点B1的坐标为．20、如图，Rt△ABC中，∠C=90°，AC=2，BC=5，点D是BC边上一点且CD=1，点P是线段DB上一动点，连接AP，以AP为斜边在AP的下方作等腰Rt△AOP．当P从点D出发运动至点B停止时，点O的运动路径长为．21、如图，点O为正六边形ABCDEF的中心，点M为AF中点，以点O为圆心，以OM的长为半径画弧得到扇形MON，点N在BC上；以点E为圆心，以DE的长为半径画弧得到扇形DEF，把扇形MON的两条半径OM，ON重合，围成圆锥，将此圆锥的底面半径记为r1；将扇形DEF以同样方法围成的圆锥的底面半径记为r2，则r 1：r2= ．22、对角线长分别为6和8的菱形ABCD如图所示，点O为对角线的交点，过点O 折叠菱形，使B，B′两点重合，MN是折痕．若B'M=1，则CN的长为（）A．7 B．6 C．5 D．423、如图，一艘渔船正以60海里/小时的速度向正东方向航行，在A处测得岛礁P在东北方向上，继续航行1.5小时后到达B处，此时测得岛礁P在北偏东30°方向，同时测得岛礁P正东方向上的避风港M在北偏东60°方向．为了在台风到来之前用最短时间到达M处，渔船立刻加速以75海里/小时的速度继续航行小时即可到达．（结果保留根号）24、如图，点A1的坐标为（2，0），过点A1作x轴的垂线交直线l：y=√3x于点B 1，以原点O为圆心，OB1的长为半径画弧交x轴正半轴于点A2；再过点A2作x轴的垂线交直线l于点B2，以原点O为圆心，以OB2的长为半径画弧交x轴正半轴于点A3；…．按此作法进行下去，则A2019B2018̂的长是．25、如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连结PM，以点P为圆心，PM长为半径作⊙P．当⊙P与正方形ABCD的边相切时，BP 的长为．26、如图，正方形ABCD的边长为1，点A与原点重合，点B在y轴的正半轴上，点D在x轴的负半轴上，将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置，B'C′与CD相交于点M，则点M的坐标为．27、如图，在△ABC中，已知AC＝3，BC＝4，点D为边AB的中点，连结CD，过点A作AE⊥CD于点E，将△ACE沿直线AC翻折到△ACE′的位置．若CE′∥AB，则CE′＝．。

中考数学几何选择填空压轴题四边形难题(含答案))

1、《求长度》（答案）1、（容易）如图1的矩形ABCD 中，有一点E 在AD 上，今以BE 为折线将A 点往右折，如图2所示，再作过A 点且与CD 垂直的直线，交CD 于F 点，如图3所示，若AB= 36，BC=13，∠BEA=60°，则图3中AF 的长度为 4【解】作AH ⊥BC 于H2、（难）如图，矩形ABCD 与菱形EFGH 的对角线均交于点O ，且EG ∥BC ，将矩形折叠，使点C 与点O 重合，折痕MN 恰好过点G 若AB=6，EF=2，∠H=120°，则DN 的长为36-【解】长EG 交DC 于P 点，连接GC 、FH ；如图所示：则CP=DP=21CD=26，△GCP 为直角三角形，∵四边形EFGH 是菱形，∠EHG=120°，∴GH=EF=2，∠OHG=60°，EG ⊥FH ，∴OG=GH•sin60°=2×23=3，由折叠的性质得：CG=OG=3，OM=CM ，∠MOG=∠MCG ，∴PG==26，∵OG ∥CM ，∴∠MOG+∠OMC=180°，∴∠MCG+∠OMC=180°，∴OM ∥CG ，∴四边形OGCM 为平行四边形，∵OM=CM ，∴四边形OGCM 为菱形，∴CM=OG=3，根据题意得：PG 是梯形MCDN 的中位线，∴DN+CM=2PG=6，∴DN=36-3、（中等）如图，△ABC 的周长为19，点D ，E 在边BC 上，∠ABC 的平分线垂直于AE ，垂足为N ，∠ACB 的平分线垂直于AD ，垂足为M ，若BC=7，则MN 的长度为25【解】△BNA ≅△BNE∴BA=BE ，∴△BAE 是等腰三角形，同理△CAD 是等腰三角形，∴点N 是AE 中点，点M 是AD 中点（三线合一），∴MN 是△ADE 的中位线， ∵BE+CD=AB+AC=19-BC=19-7=12，∴DE=BE+CD-BC=5，∴MN=21DE=25．4、（难度）如图，在菱形ABCD 中，∠ABC=120°，将菱形折叠，使点A 恰好落在对角线BD 上的点G 处（不与B 、D 重合），折痕为EF ，若DG=2，BG=6，则BE 的长为______2.8【解】作EH ⊥BD ，设BE=x在Rt △EHG 中，EG 2=EH 2+GH 2，即(8－x )2=(23x )2+(6－21x )2，解得，x =2.8，即BE=2.8，故答案为：2.85、如图，▱ABCD 中，AB=7，BC=3，连接AC ，分别以点A 和点C 为圆心，大于21AC 的长为半径作弧，两弧相交于点M ，N ，作直线MN ，交CD 于点E ，连接AE ，则△AED 的周长是_____ 10．6、（容易）如图，ABCD 的对角线相交于点O ，且AD CD ，过点O 作OM AC ，交AD 于点M ．如果CDM 的周长为8，那么ABCD 的周长是_ 16【解】∵四边形ABCD 是平行四边形，∴OA=OC ，∵OM ⊥AC ，∴AM=CM ，∵△CDM 的周长为8， ∴CM+DM+CD=AM+DM+CD=AD+CD=8，∴平行四边形ABCD 的周长是：2×8=16.7、（中等）如图，正方形ABCD 的边长为12，点E 在边AB 上，BE=8，过点E 作EF ∥BC ，分别交BD 、CD 于G 、F 两点．若点P 、Q 分别为DG 、CE 的中点，则PQ 的长为_____ 1328、（难度）如图，在平行四边形ABCD 中，对角线AC 、BD 相交于点O ，AB=OB ，点E 、点F 分别是OA 、OD 的中点，连接EF ，∠CEF=45°，EM ⊥BC 于点M ，EM 交BD 于点N ，FN=，则线段BC 的长为_____249、（难度）如图，平行四边形ABCD 中，AM ⊥BC 于M ，AN ⊥CD 于N ，已知AB ＝10，BM ＝6，MC ＝3，则MN 的长为___________5734【方法】将目标量置入直角三角形中10、（容易）如上图，在矩形ABCD 中，AB =6，BC =8，点E 是BC 中点，点F 是边CD 上的任意一点，当△AEF 的周长最小时，则DF 的长为 4【解】以CD 为对称轴作对称变换11、如图，在矩形ABCD 中，E 是BC 边上的点，连接AE 、DE ，将△DEC 沿线段DE 翻折，点C 恰好落在线段AE 上的点F 处．若AB ＝6，BE : EC ＝4 : 1，则线段DE 的长为 ____102_______．【方法】AD = AE=10；勾股定理12、如图，矩形ABCD 中，AB ＝8，BC ＝4．点E 在边AB 上，点F 在边CD 上，点G 、H 在对角线AC 上．若四边形EGFH 是菱形，则AE 的长是 [5【解】连接EF 交AC 于O ，∵四边形EGFH 是菱形，∴EF ⊥AC ，OE =OF ， ∵四边形ABCD 是矩形，∴∠B =∠D =90°，AB ∥CD ，∴∠ACD =∠CAB ，在△CFO 与△AOE 中，，∴△CFO ≌△AOE ，∴AO =CO ，A BDCM NAE BDC F∵AC ==4，∴AO =21AC =2，∵∠CAB =∠CAB ，∠AOE =∠B =90°，∴△AOE ∽△ABC ，∴，∴，∴AE =5．13、（难度）如图，矩形ABCD 中，AB ＝2，AD ＝2．点E 是BC 边上的一个动点，连接AE ，过点D 作DF ⊥AE 于点F ．当△CDF 是等腰三角形时，BE 的长为 1、2、22-【解】①CF ＝CD 时，过点C 作CM ⊥DF ，垂足为点M ，则CM ∥AE ，DM ＝MF ，延长CM 交AD 于点G ，∴AG ＝GD ＝1，∴CE ＝1， ∵CG ∥AE ，AD ∥BC ，∴四边形AGCE 是平行四边形，∴CE ＝AG ＝1，∴BE ＝1 ∴当BE ＝1时，△CDF 是等腰三角形；②DF ＝DC 时，则DC ＝DF ＝2，∵DF ⊥AE ，AD ＝2，∴∠DAE ＝45°，则BE ＝2， ∴当BE ＝2时，△CDF 是等腰三角形；③FD ＝FC 时，则点F 在CD 的垂直平分线上，故F 为AE 中点． ∵AB ＝2，BE ＝x ，∴AE ＝，AF ＝，∵△ADF ∽△EAB ，∴＝，，x 2﹣4x +2＝0，解得：x ＝2±2，∴当BE ＝22-时，△CDF 是等腰三角形．综上，当BE ＝1、2、22-时，△CDF 是等腰三角形．14、如图，边长为1的菱形ABCD 中，∠DAB=60度．连接对角线AC ，以AC 为边作第二个菱形ACC 1D 1，使∠D 1AC=60°；连接AC 1，再以AC 1为边作第三个菱形AC 1C 2D 2，使∠D 2AC 1=60°；…，按此规律所作的第n 个菱形的边长为 1)3(-n ．解：连接DB ，∵四边形ABCD 是菱形，∴AD=AB ．AC ⊥DB ， ∵∠DAB=60°，∴△ADB 是等边三角形，∴DB=AD=1，∴BM=21， ∴AM==23，∴AC=3，同理AC 1=3AC=（3）2，AC 2=3AC 1=33=（3）3，按此规律所作的第n 个菱形的边长为1)3(-n15、如图，以Rt △ABC 的斜边BC 为一边在△ABC 的同侧作正方形BCEF ，设正方形的中心为O ，连接AO ，如果AB=4，AO=26，那么AC 的长等于 16 ．【解】如图，过O 点作OG 垂直AC ，G 点是垂足．∵∠BAC=∠BOC=90°，∴ABCO 四点共圆，∴∠OAG=∠OBC=45° ∴△AGO 是等腰直角三角形，∴2AG 2=2GO 2=AO 2=2)26(=72， ∴OG=AG=6，∵∠BAH=∠OGH=90°，∠AHB=∠OHG ，∴△ABH ∽△GOH ，∴AB/OG=AH/（AG ﹣AH ），∵AB=4，OG=AG=6，∴AH=2.4 在直角△OHC 中，∵HG=AG ﹣AH=6﹣2.4=3.6，OG 又是斜边HC 上的高， ∴OG 2=HG×GC ，而OG=6，GH=3.6，∴GC=10．∴AC=AG+GC=6+10=16．故AC 边的长是16．16、如图，在梯形ABCD 中，AD ∥BC ，∠B=90°，AD=2，BC=5，E 为DC 中点，tanC=34．则AE 的长度为265【解】过点E 作BC 的垂线交BC 于点F ，交AD 的延长线于点M ，在梯形ABCD 中，AD ∥BC ，E 是DC 的中点，∴∠M=∠MFC ，DE=CE ；在△MDE 和△FCE 中，∠M=∠MFC ，∠DEM=∠CEF ，DE=CE ；∴△MDE ≌△FCE ，∴EF=ME ，DM=CF ． ∵AD=2，BC=5，∴DM=CF=23，在Rt △FCE 中，tanC=CFEF =34，∴EF=ME=2，在Rt △AME 中，AE=265)232(222=++ 17、如图，平行四边形ABCD 中，AE 平分∠BAD 交BC 边于E ，EF ⊥AE 交CD 边于F ，延长BA 到点G ，使AG = CF ，连接GF ．若BC = 7，DF = 3，tan ∠AEB =3 ，则GF 的长为 23【解】连接AC ，羊场AE 与DC 延长线交于一点H18、（容易）如图，梯形ABCD 中，AD ∥BC ，AB = 3，BC=4，连结BD ，∠BAD 的平分线交BD 于点E ，且AE ∥CD ，则AD 的长为1DG ABCDEMABC DEF【解】构造平行四边形。

2020年中考数学2几何综合选择填空压轴题（含解析）

几何综合-填空选择压轴题21、矩形ABCD中，AB=6,BC=8.点P在矩形ABCD的内部，点E在边BC±,满足△PBE s^DBC,若AAPD是等腰三角形，则PE的长为.2、如图，CE是q ABCD的边AB的垂直平分线，垂足为点0,CE与DA的延长线交于点E.连接AC,BE,DO,DO与AC交于点F,则下列结论:四边形ACBE是菱形;①②ZACD=ZBAE；③AF：BE=2：3；④S四边形AFOE：S a C0D=2： 3.其中正确的结论有..（填写所有正确结论的序号）3、如图，点P是菱形ABCD边上的一动点，它从点A出发沿在A-B-C—D路径匀速运动到点D,设APAD的面积为y,P点的运动时间为x,则y关于x的函数)图象大致为（4、如图，在菱形ABCD中，AC=6很，BD=6,E是BC边的中点，P,M分别是AC, AB上的动点，连接PE,PM,则PE+PM的最小值是（）A.6B.3V3C.2V6D. 4.55、如图，在RtAABC中，ZACB=90°,AB=4,BC=2,将AABC绕点B顺时针方向旋转到AA，BJ的位置，此时点A，恰好在CB的延长线上，则图中阴影部分的面积为.（结果保留丸）.6、如图，ZA0B=60°,OA=OB,动点C从点0出发，沿射线OB方向移动，以AC 为边在右侧作等边AACD,连接BD,则BD所在直线与0A所在直线的位置关系是()A.平行B,相交C,垂直 D.平行、相交或垂直7、如图，正六边形ABCDEF的边长是6+4扼，点0”0?分别是^ABF,ACDE的内心，贝I0i02=.8、已知。

0的直径CD=10cm,AB是。

0的弦，AB±CD,垂足为M,且AB=8cm,则AC的长为()A.2V5cmB.4V5cmC.2-\/5cm或4扼cmD.2-\/3cm或4V3cm9、正方形AiBCO,A2B2C2G,A3B3C3C2,…按如图的方式放置,点A”A2,A3…和点G，C2,C3…分别在直线y=x+l和x轴上，则点辟的坐标为10、如图,C为半圆内一点,0为圆心,直径AB长为2cm,ZB0C=60°,NBC0=90°,将△BOC绕圆心0逆时针旋转至AB，0C'，点C'在0A上，则边BC扫过区域（图中阴影部分）的面积为cm2.A C O B11、如图，已知在AABC中，BC边上的高AD与AC边上的高BE交于点F,且/ BAC=45°,BD=6,CD=4,则AABC的面积为.12、如图，四边形ABCD中,AD〃BC,ZABC=90°,AB=5,BC=10,连接AC、BD,以BD为直径的圆交AC于点E.若DE=3,则AD的长为（）C.3V5A.5B.4 D.2V513、如图，在菱形ABCD中，ZABC=120°,将菱形折叠，使点A恰好落在对角线BD上的点G处（不与B、D重合），折痕为EF,若DG=2,BG=6,则BE的长为.14、如图，已知口AOBC的顶点0(0,0), A (-1,2),点B在x轴正半轴上按以下步骤作图：①以点0为圆心，适当长度为半径作孤，分别交边0A,0B于点D, E；②分别以点D,E为圆心，大于fDE的长为半径作弧，两孤在ZA0B内交于点F；③作射线0F,交边AC于点G,则点G的坐标为()A.(V5-1,2)B.(V5,2)C.(3-扃2)D,(扼-2,2)15、如图，ZMAN=90°,点C在边AM上，AC=4,点B为边AN上一动点，连接BC,AA Z BC与AABC关于BC所在直线对称，点D,E分别为AC,BC的中点，连接DE并延长交A'B所在直线于点F,连接A' E.当△▲'EF为直角三角形时, AB的长为.16、如图，在AABC中，ZACB=90°,AC=BC=2,将AABC绕AC的中点D逆时针旋转90。

中考数学压轴题含答案

中考数学压轴题含答案一、选择题1、下列图形中，既是轴对称图形，又是中心对称图形的是（）A.菱形B.平行四边形C.矩形（答案：C）2、如果一个三角形的三条边的平方相等，那么这个三角形一定是（）A.等边三角形B.直角三角形C.等腰三角形D.等腰直角三角形（答案：A）3、下列说法正确的是（）A.所有的质数都是奇数B.所有的偶数都是合数C.一个数的因数一定比它的倍数小D.自然数一定是正数（答案：A）二、填空题1、若a-b=2，a+b=7，则a²-b²=（答案：14）2、我们学过的数有整数和分数，整数的运算律在分数运算中（答案：同样适用）。

3、一个长方形的周长是20cm，长和宽的比是3:2，则长方形的面积是（答案：60平方厘米）。

三、解答题1、一个圆柱体底面半径为r，高为h，它的体积是多少？（答案：πr²h）2、有一块三角形的土地，底边长为120米，高为90米，这块土地的面积是多少？（答案：5400平方米）3、对于一个给定的整数n，如果它是3的倍数，那么我们就称它为“三的倍数”，否则我们就称它为“非三的倍数”。

现在有一个整数n，它是“三的倍数”，我们可以得出哪些结论？（答案：n+1、n+2、n+3、...、2n都是“三的倍数”，因为它们都可以被3整除。

）中考数学压轴题100题及答案在中考数学考试中，压轴题往往是最具挑战性和最能检验考生数学能力的题目。

为了帮助同学们更好地理解和掌握中考数学的压轴题，本文将分享100道经典的中考数学压轴题及其答案。

一、选择题1、在一个等边三角形中，边长为6，下列哪个选项的面积最接近这个等边三角形的面积？A. 20B. 25C. 30D. 35答案：B解析：等边三角形的面积可以通过计算得出，边长为6的等边三角形的面积为：436293约为28.2，因此选项B最接近。

2、如果一个多边形的内角和是外角和的2倍，那么这个多边形的边数是多少？A. 4B. 6C. 8D. 10答案：C解析：根据多边形的内角和公式和外角和为360度，可列出方程求解。

初中中考数学几何选择填空压轴题精选配包括答案.doc

2 0 1 6中考数学几何选择填空压轴题精选(配答案)一．（共13 小）1．（ 2013?春模）如，点O正方形 ABCD的中心， BE 平分∠ DBC 交 DC于点 E，延 BC到点F，使 FC=EC，接 DF交 BE的延于点 H，接 OH交 DC于点 G，接 HC．以下四个中正确的个数（）①OH= BF；②∠ CHF=45°；③ GH= BC；④ DH2=HE?HB．A． 1 个B． 2 个C． 3 个D． 4 个2．（2013?云港模）如， Rt△ABC 中， BC= ，∠ ACB=90°，∠ A=30°， D1是斜 AB的中点，D1作 D1E1⊥AC 于 E1， BE1交 CD1于 D2；D2作 D2 E2⊥AC 于 E2， BE2交 CD1于 D3； D3作D3E3⊥AC 于 E3，⋯，如此，可以依次得到点E4、 E5、⋯、 E2013，分△ BCE1、△ BCE2、△BCE3、⋯、△ BCE2013的面 S1、 S2、 S3、⋯、 S2013． S2013的大小（）A．B．C．D．3．如，梯形 ABCD中， AD∥BC，，∠ ABC=45°， AE⊥BC 于点 E，BF⊥AC 于点 F，交AE于点 G， AD=BE，接 DG、 CG．以下：①△ BEG≌△ AEC；②∠ GAC=∠GCA；③ DG=DC；④G AE 中点，△ AGC 的面有最大．其中正确的有（）A． 1 个B． 2 个C． 3 个D． 4 个4．如，正方形ABCD中，在 AD的延上取点E， F，使 DE=AD， DF=BD，接 BF 分交 CD， CE于H， G下列：①EC=2DG；②∠ GDH=∠GHD；③S△CDG=S?DHGE；④ 中有 8 个等腰三角形．其中正确的是（）A．①③B．②④C．①④D．②③5．（ 2008? 州）如，直角梯形ABCD中，∠ BCD=90°， AD∥BC， BC=CD， E 梯形内一点，且∠BEC=90°，将△ BECC点旋90°使 BC 与 DC重合，得到△ DCF，EF 交 CD于 M．已知 BC=5，CF=3， DM： MC的（）A． 5： 3 B． 3： 5 C． 4： 3 D． 3： 4 6．如，矩形ABCD的面5，它的两条角交于点O1，以 AB， AO1两作平行四形ABCO11，平行四形 ABCO11的角交 BD于点 02，同以 AB， AO2两作平行四形 ABCO22．⋯，依此推，平行四形ABC2009O2009的面（）A．B．C．D．7．如，在角△ ABC 中， AB=6，∠ BAC=45°，∠ BAC 的平分交 BC 于点 D， M， N 分是 AD和 AB上的点， BM+MN的最小是（）A．B． 6 C．D． 3 8．（ 2013? 牡丹江）如，在△ ABC 中∠ A=60°， BM⊥AC 于点 M，CN⊥AB 于点 N， P BC的中点，接 PM， PN，下列：① PM=PN；②；③△ PMN等三角形；④当∠ ABC=45° ，BN= PC．其中正确的个数是（）A． 1 个B． 2 个C． 3 个D． 4 个9．（ 2012? 黑河） Rt△ABC 中， AB=AC，点 D BC中点．∠ MDN=90°，∠ MDN 点 D 旋， DM、 DN分与 AB、AC 交于 E、 F 两点．下列：①（ BE+CF） =BC；②S△AEF≤S△ABC；③S四边形=AD?EF；AEDF④A D≥EF；⑤A D 与 EF 可能互相平分，其中正确的个数是（）A． 1 个B． 2 个C． 3 个D． 4 个10．（2012? 无一模）如，在正方形片ABCD中，角AC、 BD交于点 O，折叠正方形片ABCD，使 AD落在 BD上，点 A 恰好与 BD上的点 F 重合，展开后折痕DE分交 AB、 AC于点 E、 G，接 GF．下列①∠ ADG=°；② tan ∠AED=2；③S△AGD=S△OGD；④四形 AEFG是菱形；⑤ BE=2OG．其中正确的有（）A．①④⑤B．①②④C．③④⑤D．②③④11．如，正方形ABCD中， O BD中点，以 BC 向正方形内作等△ BCE，接并延AE 交 CD 于 F，接 BD分交 CE、AF 于 G、 H，下列：①∠ CEH=45°；② GF∥DE；③2OH+DH=BD；④ BG= DG；⑤．其中正确的是（）A．①②③B．①②④C．①②⑤D．②④⑤12．如，在正方形ABCD中， AB=4， E CD上一点， AE交 BD 于 F， F 作 FH⊥AE 于 H， H 作GH⊥BD 于 G，下列有四个：① AF=FH，②∠ HAE=45°，③ BD=2FG，④△ CEH 的周定，其中正确的有（）A．①②③B．①②④C．①③④D．①②③④13．（2013? 州模）正方形 ABCD、正方形 BEFG和正方形 RKPF的位置如所示，点G在段 DK上，正方形 BEFG的4，△ DEK 的面（）A． 10 B． 12 C． 14 D． 16 二．填空（共 16 小）14．如，在梯形ABCD中， AD∥BC，EA⊥AD， M是 AE上一点， F、 G分是 AB、 CM的中点，且∠B AE=∠MCE，∠ MBE=45°，出以下五个：① AB=CM；② A E⊥BC；③∠ BMC=90°；④ EF=EG；⑤△ BMC是等腰直角三角形．上述中始正确的序号有_________ ．15．（2012? 沟区一模）如，面 1 的△ ABC逐次行以下操作：第一次操作，分延AB、BC、 CA至 A1、 B1、 C1，使得 A1B=2AB， B1C=2BC， C1A=2CA，次接 A1、 B1、 C1，得到△A1B1C1，其面 S1；第二次操作，分延 A1B1， B1C1， C1 A1至 A2， B2， C2，使得 A2B1=2A1B1， B2C1=2B1C1，C2A1=2C1A1，次接 A2，B2， C2，得到△A2B2 C2，其面 S2⋯，按此律下去，可得到△A5B5C5，其面S5= _________ ．第 n 次操作得到△A n B n C n，△A n B n C n的面 S n =_________ ．16．（ 2009? 黑河）如， 1 的菱形 ABCD中，∠ DAB=60 度．接角 AC，以 AC作第二个菱形 ACCD11，使∠D1AC=60°；接AC1，再以 AC1作第三个菱形 AC1C2D2，使∠D2AC1 =60°；⋯，按此律所作的第n 个菱形的_________ ．17．（ 2012? 通州区二模）如，在△ ABC 中，∠ A=α．∠ ABC 与∠ ACD的平分交于点 A1，得∠A1；∠A1BC与∠A1CD的平分相交于点A2，得∠A2；⋯；∠A2011BC与∠A2011CD的平分相交于点 A2012，得∠A2012，∠A2012= _________ ．18．（ 2009?湖州）如，已知 Rt△ABC， D1是斜 AB的中点， D1作 D1E1⊥AC 于 E1，接 BE1交 CD1于 D ； D 作D E ⊥AC 于 E ，接 BE 交 CD 于 D ； D 作 D E ⊥AC 于 E ，⋯，如此，可以依次22 2 222133 3 3 3得到点 D4， D5，⋯， D n，分△ BD 1E1，△ BD2E2，△ BD3E3，⋯，△ BD n E n的面 S1， S2，S3，⋯S n． S n= _________ S△ABC（用含 n 的代数式表示）．19．（ 2011? 丰台区二模）已知：如，在Rt△ABC 中，点 D1是斜 AB 的中点，点 D1作 D1 E1⊥AC 于点 E1，接 BE1交 CD1于点 D2；点 D2作 D2E2⊥AC于点 E2，接 BE2交 CD1于点 D3；点 D3作 D3E3⊥AC于点 E3，如此，可以依次得到点D4、 D5、⋯、 D n，分△ BD 1E1、△ BD2E2、△ BD3E3、⋯、△ BD n E n的面 S1、 S2、 S3、⋯S n．△ ABC 的面是1， S1= _________ ， S n= _________ （用含 n 的代数式表示）．20．（ 2013?路北区三模）在△ ABC中， AB=6， AC=8， BC=10， PBC上一点， PE⊥AB 于 E，PF⊥AC于 F， M EF 中点， AM的最小_________ ．21．如，已知 Rt△ABC中， AC=3， BC=4，直角点 C作 CA1⊥AB，垂足 A1，再 A1作 A1C1⊥BC，垂足 C1， C1作 C1 A2⊥AB，垂足A2，再 A2作 A2 C2⊥BC，垂足 C2，⋯，一直做下去，得到了一段 CA1， A1C1， C1A2，⋯，CA1= _________ ，= _________ ．22．（ 2013? 沐川二模）如，点A1， A2， A3， A4，⋯， A n在射 OA上，点 B1， B2， B3，⋯， B n﹣1在射 OB上，且 A1B1∥A2B2∥A3B3∥⋯∥A n﹣1B n﹣1， A2B1∥A3B2∥A4B3∥⋯∥A n B n﹣1，△A1A2 B1，△A2A3B2，⋯，△A n﹣ 1A n B n﹣ 1 阴影三角形，若△A 2B1B2，△A3B2B3 的面分1、 4，△A1A2B1的面_________ ；面小于2011 的阴影三角形共有_________ 个．23．（ 2010?城区）如，已知点A1（ a， 1）在直 l ：上，以点 A1心，以半径画弧，交 x 于点 B1、 B2，点 B2作 A1B1的平行交直 l 于点 A2，在 x 上取一点 B3，使得A2B3=A2 B2，再点 B3作 A2B2的平行交直 l 于点 A3，在 x 上取一点B4，使得 A3B4 =A3B3，按此律作下去，① a= _________ ；②△A4 B4B5 的面是_________ ．24．（ 2013? 松北区二模）如，以Rt△ABC 的斜 BC 一在△ ABC 的同作正方形 BCEF，正方形的中心 O，接 AO，如果 AB=4， AO=6 ，那么 AC的等于_________ ．25．（ 2007? 淄川区二模）如，将矩形ABCD的四个角向内折起，恰好拼成一个既无隙又无重叠的四形 EFGH，若 EH=3， EF=4，那么段AD与 AB的比等于_________ ．26．（ 2009? 泰市模）梯形ABCD中 AB∥CD，∠ ADC+∠BCD=90°，以AD、 AB、 BC 斜向形外作等腰直角三角形，其面分是S1、 S2、 S3且 S1+S3 =4S2， CD= _________ AB．27．如，察中菱形的个数： 1 中有 1 个菱形， 2 中有 5 个菱形， 3 中有 14 个菱形， 4 中有 30 个菱形⋯，第 6 个中菱形的个数是_________ 个．28．（2012? 港一模）如， E、 F 分是平行四形 ABCD的 AB、 CD上的点， AF 与 DE相交于点 P，BF 与 CE 相交于点 Q，若 S△APD=15cm2，S△BQC=25cm2，阴影部分的面_________ cm2．29．（ 2012? 天津）如，已知正方形ABCD的 1，以点 A、 B 心， 1 半径的两弧交于点E，以点 C、 D 心， 1 半径的两弧交于点F， EF 的_________ ．30．如， ABCD是凸四形， AB=2， BC=4， CD=7，求段 AD 的取范（）．参考答案与试题解析一．（共 13 小）1．（ 2013?春模）如，点O正方形 ABCD的中心， BE 平分∠ DBC 交 DC于点 E，延 BC到点F，使 FC=EC，接 DF交 BE的延于点H，接 OH交 DC于点 G，接 HC．以下四个中正确的个数（）①OH= BF；②∠ CHF=45°；③ GH= BC；④ DH2=HE?HB．A． 1 个B． 2 个C． 3 个D． 4 个解答：解：作 EJ⊥BD 于 J，接 EF①∵ BE 平分∠ DBC∴E C=EJ，∴△ DJE≌△ ECF∴D E=FE∴∠ HEF=45°+°=°∴∠ HFE==°∴∠ EHF=180°﹣°﹣° =90°∵D H=HF， OH是△ DBF 的中位线∴OH∥BF∴O H= BF②∵四边形ABCD是正方形， BE 是∠ DBC的平分线，∴B C=CD，∠ BCD=∠DCF，∠ EBC=°，∵C E=CF，∴Rt△BCE≌Rt△DCF，∴∠ EBC=∠CDF=°，∴∠ BFH=90°﹣∠ CDF=90°﹣° =°，∵OH是△ DBF 的中位线， CD⊥AF，∴O H是 CD的垂直平分线，∴D H=CH，∴∠ CDF=∠DCH=°，∴∠ HCF=90°﹣∠ DCH=90°﹣° =°，∴∠ CHF=180°﹣∠ HCF﹣∠ BFH=180°﹣°﹣° =45°，故②正确；③∵ OH是△ BFD 的中位线，∴D G=CG= BC， GH= CF，∵C E=CF，∴G H= CF= CE∵C E＜ CG= BC，∴GH＜BC，故此结论不成立；④∵∠ DBE=45°， BE 是∠ DBF 的平分线，∴∠ DBH=°，由②知∠ HBC=∠CDF=°，∴∠ DBH=∠CDF，∵∠ BHD=∠BHD，∴△ DHE∽△ BHD，∴=∴D H=HE?HB，故④成立；所以①②④正确．故选 C．2．（2013?云港模）如， Rt△ABC 中， BC=，∠ ACB=90°，∠A=30°，D1是斜AB的中点，D1作 D1E1⊥AC 于 E1， BE1交 CD1于 D2； D2作 D2 E2⊥AC 于 E2， BE2交 CD1于 D3； D3作D3E3⊥AC 于E3，⋯，如此，可以依次得到点E4、 E5、⋯、E2013，分△ BCE1、△ BCE2、△BCE3、⋯、△ BCE2013的面S1、 S2、 S3、⋯、 S2013．S2013的大小（）A．B．C．D．解答：解：∵ Rt△ABC 中， BC=∴AC==BC=6，，∠ ACB=90°，∠ A=30°，∴S△ABC=AC?BC=6，∵D1 E1⊥AC，∴D1 E1∥BC，∴△ BD1E1与△ CD1E1同底同高，面相等，∵D1 是斜AB的中点，∴D1 E1=BC， CE1= AC，∴S1 =BC?CE1= BC×AC= ×AC?BC= S△ABC；∴在△ ACB 中， D2其重心，∴D2 E1=BE1，∴D E =2 2 BC， CE = AC， S =×22×AC?BC= S△，ABC∴D E =3 3BC， CE = AC， S = S△⋯；23ABC ∴S n = S△ABC；∴S2013= ×6= ．故C．3．如，梯形ABCD中， AD∥BC，AE于点 G， AD=BE，接 DG、 CG．以下：①△，∠ ABC=45°， AE⊥BC 于点 E，BF⊥AC 于点BEG≌△ AEC；②∠ GAC=∠GCA；③ DG=DC；④GF，交AE中点，△ AGC 的面有最大．其中正确的有（）A． 1 个B． 2 个C． 3 个D． 4 个解答：解：根据BE=AE，∠ GBE=∠CAE，∠ BEG=∠CEA可判定①△ BEG≌△AEC；用反法明②∠ GAC≠∠ GCA，假∠ GAC=∠GCA，有△ AGC等腰三角形，F AC 的中点，又BF⊥AC，可AB=BC，与不符；由①知△ BEG≌△ AEC 所以GE=CE 接 ED、四形ABED平行四形，∵∠ ABC=45°， AE⊥BC 于点 E，∴∠ GED=∠CED=45°，∴△ GED≌△ CED，∴D G=DC；④ AG X，易求出GE=EC=2 X 因此， S△=S S =+x=（x22x）AGC AEC GEC=﹣（x2﹣2x+1﹣1）=﹣（x﹣1）2+，当X取1时，面积最大，所以AG等于 1，所以 G是 AE 中点，故 G 为 AE 中点时， GF最长，故此时△ AGC 的面积有最大值．故正确的个数有 3 个．故选 C．4．如图，正方形ABCD中，在AD的延长线上取点E， F，使DE=AD， DF=BD，连接BF 分别交CD， CE于H， G下列结论：①EC=2DG；②∠ GDH=∠GHD；③S△CDG=S?DHGE；④图中有A．①③B．②④解答：解：∵ DF=BD，∴∠ DFB=∠DBF，8 个等腰三角形．其中正确的是（C．①④）D．②③∵AD∥BC， DE=BC，∴∠ DEC=∠DBC=45°，∴∠ DEC=2∠EFB，∴∠ EFB=°，∠ CGB=∠CBG=°，∴CG=BC=DE，∵DE=DC，∴∠ DEG=∠DCE，∵∠ GHC=∠CDF+∠DFB=90°+°=°，∠DGE=180°﹣（∠ BGD+∠EGF），=180°﹣（∠ BGD+∠BGC），=180°﹣（ 180°﹣∠ DCG）÷ 2，=180°﹣（ 180°﹣ 45°）÷ 2，=°，∴∠ GHC=∠DGE，∴△ CHG≌△ EGD，∴∠ EDG=∠CGB=∠CBF，∴∠ GDH=∠GHD，∴S△CDG=S?DHGE．故选D．5．（ 2008? 荆州）如图，直角梯形ABCD中，∠ BCD=90°， AD∥BC，BC=CD， E 为梯形内一点，且∠BEC=90°，将△ BEC 绕 C点旋转90°使BC 与 DC重合，得到△DCF，连EF 交CD于M．已知BC=5，CF=3，则 DM： MC的值为（）A．5： 3B．3： 5解答：解：由题意知△ BCE 绕点 C 顺时转动了∴△ BCE≌△ DCF，∠ ECF=∠DFC=90°，90 度，C．4： 3 D．3： 4∴CD=BC=5，DF∥CE，∴∠ ECD=∠CDF，∵∠EMC=∠DMF，∴△ECM∽△ FDM，∴D M： MC=DF： CE，∵DF==4，∴DM： MC=DF： CE=4： 3．故选 C．6．如，矩形ABCD的面5，它的两条角交于点O1，以AB， AO1两作平行四形ABC1O1，平行四形ABC1O1的角交BD于点02，同以AB， AO2两作平行四形ABC2O2．⋯，依此推，平行四形ABC O的面（20092009）A．B．C．D．解答：解：∵矩形ABCD的角互相平分，面5，∴平行四形ABC1O1的面，∵平行四形ABC1O1的角互相平分，∴平行四形ABC2O2的面×=，⋯，依此推，平行四形ABC2009O2009的面．故 B．7．如，在角△ABC 中， AB=6，∠ BAC=45°，∠ BAC 的平分交BC 于点D， M， N 分是AD和AB 上的点，BM+MN的最小是（）A．解答：B． 6解：如，作BH⊥AC，垂足H，交 AD 于 M′点，最小．C．M′点作M′N′⊥ AB，垂足D． 3N′，BM′+M′N′ 所求∵A D是∠ BAC 的平分，∴M′H=M′N′，∴BH是点 B 到直 AC的最短距离（垂段最短），∵A B=4，∠ BAC=45°，∴BH=AB?sin45°=6×=3．∵BM+MN的最小是BM′+M′N′=BM′+M′H=BH=3．故 C．8．（ 2013? 牡丹江）如，在△ ABC 中∠ A=60°， BM⊥AC 于点 M，CN⊥AB 于点 N， P BC的中点，接PM， PN，下列：①PM=PN；②；③△ PMN等三角形；④当∠ABC=45° ，BN= PC．其中正确的个数是（）A． 1 个B． 2 个C． 3 个D． 4 个解答：解：①∵ BM⊥AC 于点 M，CN⊥AB 于点 N， P BC 的中点，∴P M= BC， PN= BC，∴P M=PN，正确；②在△ABM与△ ACN中，∵∠ A=∠A，∠ AMB=∠ANC=90°，∴△ ABM∽△ ACN，∴，正确；③∵∠ A=60°， BM⊥AC 于点 M，CN⊥AB 于点 N，∴∠ ABM=∠ACN=30°，在△ ABC中，∠ BCN+∠CBM═180° 60° 30°× 2=60°，∵点 P 是 BC 的中点， BM⊥AC，CN⊥AB，∴P M=PN=PB=PC，∴∠ BPN=2∠BCN，∠ CPM=2∠CBM，∴∠ BPN+∠CPM=2（∠ BCN+∠CBM）=2×60°=120°，∴∠ MPN=60°，∴△ PMN是等边三角形，正确；④当∠ ABC=45°时，∵ CN⊥AB于点N，∴∠ BNC=90°，∠ BCN=45°，∴B N=CN，∵P为 BC边的中点，∴P N⊥BC，△ BPN 为等腰直角三角形∴B N= PB= PC，正确．故选 D．9．（ 2012? 黑河） Rt△ABC 中， AB=AC，点 D 为 BC中点．∠ MDN=90°，∠ MDN 绕点 D 旋转， DM、DN分别与边 AB、 AC 交于 E、 F 两点．下列结论：①（ BE+CF） =BC；②S△AEF≤S△ABC；③S四边形 AEDF=AD?EF；④A D≥EF；⑤A D 与 EF 可能互相平分，其中正确结论的个数是（）A． 1 解答：个B． 2 个解：∵ Rt△ABC 中， AB=AC，点 D 为∴∠ C=∠BAD=45°，AD=BD=CD，∵∠ MDN=90°，BC中点，C． 3 个D． 4 个∴∠ ADE+∠ADF=∠ADF+∠CDF=90°，∴∠ ADE=∠CDF．在△ AED与△ CFD中，∵，∴△ AED≌△ CFD（ ASA），∴A E=CF，在 Rt△ABD 中， BE+CF=BE+AE=AB==BD=BC．故①正确；设AB=AC=a， AE=CF=x，则 AF=a﹣ x ．∵S= AE?AF= x（ a﹣ x） =﹣（x﹣a）2+a2，△AEF∴当 x= a 时， S△AEF有最大值a2，又∵ S△ABC= × a2= a2，∴S△AEF≤S△ABC．故②正确；EF2=AE2+AF2=x2+（ a﹣ x）2 =2（ x﹣a）2+a2，∴当 x= a 时， EF2取得最小值a2，∴EF≥a（等号当且仅当x= a 时成立），而AD= a，∴ EF≥AD．故④错误；由①的证明知△ AED≌△ CFD，∴S四边形=S△+S△=S△+S△=S△=AD2，AEDF AED ADF CFD ADF ADC∵E F≥AD，∴A D?EF≥AD 2，∴A D?EF＞ S 四边形AEDF故③错误；当E、 F 分别为 AB、 AC 的中点时，四边形 AEDF为正方形，此时 AD与 EF 互相平分．故⑤正确．综上所述，正确的有：①②⑤，共 3 个．故选 C．10．（2012? 无锡一模）如图，在正方形纸片ABCD中，对角线AC、 BD交于点 O，折叠正方形纸片ABCD，使 AD落在 BD上，点 A 恰好与 BD上的点 F 重合，展开后折痕DE分别交 AB、 AC于点 E、 G，连接 GF．下列结论①∠ ADG=°；② tan∠AED=2；③S△AGD=S△OGD；④四边形AEFG是菱形；⑤BE=2OG．其中正确的结论有（）A．①④⑤B．①②④C．③④⑤D．②③④解答：解：∵四边形ABCD是正方形，∴∠ GAD=∠ADO=45°，由折叠的性质可得：∠ADG= ∠ADO=°，故①正确．∵tan ∠AED= ，由折叠的性质可得：AE=EF，∠ EFD=∠EAD=90°，∴A E=EF＜ BE，∴A E＜ AB，∴tan ∠AED=＞2，故②错误．∵∠ AOB=90°，∴A G=FG＞ OG，△ AGD与△ OGD同高，∴S△AGD＞S△OGD，故③错误．∵∠ EFD=∠AOF=90°，∴E F∥AC，∴∠ FEG=∠AGE，∵∠ AGE=∠FGE，∴∠ FEG=∠FGE，∴EF=GF，∵AE=EF，∴A E=GF，故④正确．∵AE=EF=GF， AG=GF，∴A E=EF=GF=AG，∴四边形 AEFG是菱形，∴∠ OGF=∠OAB=45°，∴E F=GF= OG，∴BE=EF=×OG=2OG．故⑤正确．∴其中正确结论的序号是：①④⑤．故选： A．11．如图，正方形ABCD中， O 为 BD中点，以 BC 为边向正方形内作等边△BCE，连接并延长于 F，连接BD分别交 CE、AF 于 G、 H，下列结论：①∠ CEH=45°；② GF∥DE；AE 交CD③2OH+DH=BD；④ BG= DG；⑤．其中正确的结论是（）A．①②③B．①②④C．①②⑤D．②④⑤解答：解：①由∠ ABC=90°，△ BEC为等边三角形，△ ABE为等腰三角形，∠ AEB+∠BEC+∠CEH=180°，可求得∠CEH=45°，此结论正确；②由△ EGD≌△ DFE，EF=GD，再由△ HDE 为等腰三角形，∠ DEH=30°，得出△ HGF为等腰三角形，∠ HFG=30°，可得 GF∥DE，此结论正确；③由图可知2（ OH+HD） =2OD=BD，所以 2OH+DH=BD此结论不正确；④如图，过点G作 GM⊥CD 垂足为 M，GN⊥BC 垂足为 N，设 GM=x，则 GN= x ，进一步利用勾股定理求得GD=BG= x，得出BG=GD，此结论不正确；⑤由图可知△BCE 和△ BCG同底不等高，它们的面积比即是两个三角形的高之比，由④可知△BCE 的高为（x+x ）和△ BCG的高为x ，因此S△BCE：S△BCG= （x+x ）：x= ，此结论正确；故正确的结论有①②⑤．故选 C．12．如图，在正方形ABCD中， AB=4， E 为 CD上一动点， AE交 BD 于 F，过GH⊥BD 于 G，下列有四个结论：① AF=FH，②∠ HAE=45°，③ BD=2FG，④△ CEH F 作 FH⊥AE 于 H，过 H 作的周长为定值，其中正确的结论有（）A．①②③解答：解：（ 1）连接B．①②④FC，延长 HF交 AD 于点L，C．①③④D．①②③④∵B D为正方形 ABCD的对角线，∴∠ ADB=∠CDF=45°．∵AD=CD， DF=DF，∴△ ADF≌△ CDF．∴FC=AF，∠ ECF=∠DAF．∵∠ ALH+∠LAF=90°，∴∠ LHC+∠DAF=90°．∵∠ ECF=∠DAF，∴∠ FHC=∠FCH，∴F H=FC．∴F H=AF．（2）∵ FH⊥AE，FH=AF，∴∠ HAE=45°．（3）连接 AC交 BD于点 O，可知： BD=2OA，∵∠ AFO+∠GFH=∠GHF+∠GFH，∴∠ AFO=∠GHF．∵AF=HF，∠ AOF=∠FGH=90°，∴△ AOF≌△ FGH．∴OA=GF．∵B D=2OA，∴B D=2FG．（4）延长 AD至点 M，使 AD=DM，过点 C 作 CI∥HL，则： LI=HC，根据△ MEC≌△ CIM，可得：CE=IM，同理，可得：AL=HE，∴HE+HC+EC=AL+LI+IM=AM=8．∴△ CEH的周长为8，为定值．故（ 1）（ 2）（ 3）（ 4）结论都正确．故选 D．13．（2013? 钦州模拟）正方形 ABCD、正方形BEFG和正方形RKPF的位置如图所示，点正方形 BEFG的边长为4，则△ DEK 的面积为（）G在线段DK上，A．10 B．12 C．14 D．16解答：解：如图，连DB， GE， FK，则 DB∥GE∥FK，在梯形 GDBE中， S△DGE=S△GEB（同底等高的两三角形面积相等），同理 S△GKE=S△GFE．∴S阴影 =S△+S△，DGE GKE=S△GEB+S△GEF，=S 正方形GBEF，=4×4=16故选 D．二．填空题（共16 小题）14．如图，在梯形ABCD中， AD∥BC，EA⊥AD，M是 AE上一点， F、 G分别是AB、 CM的中点，且∠BAE=∠MCE，∠ MBE=45°，则给出以下五个结论：① AB=CM；② A E⊥BC；③∠ BMC=90°；④ EF=EG；⑤△ BMC是等腰直角三角形．上述结论中始终正确的序号有①②④．解答：解：∵梯形ABCD中， AD∥BC，EA⊥AD，∴A E⊥BC，即②正确．∵∠MBE=45°，∴B E=ME．在△ ABE 与△ CME中，∵∠ BAE=∠MCE，∠ AEB=∠CEM=90°，BE=ME，∴△ ABE≌△ CME，∴AB=CM，即①正确．∵∠ MCE=∠BAE=90° ∠ ABE＜90° ∠ MBE=45°，∴∠ MCE+∠MBC＜90°，∴∠ BMC＞90°，即③⑤ ．∵∠ AEB=∠CEM=90°，F、 G分是AB、 CM的中点，∴E F= AB， EG= CM．又∵ AB=CM，∴EF=EG，即④正确．故正确的是①②④．15．（2012? 沟区一模）如，面 1 的△ ABC逐次行以下操作：第一次操作，分延 AB、BC、 CA至 A1、 B1、 C1，使得 A1B=2AB， B1C=2BC， C1A=2CA，次接 A1、 B1、 C1，得到△A1B1C1，其面 S1；第二次操作，分延 A1B1，B1C1， C1 A1至 A2， B2， C2，使得 A2B1=2A1B1， B2C1=2B1C1，C2A1=2C1A1，次接A2， B2， C2，得到△A2B2 C2，其面S2⋯，按此律下去，可得到△A5B5C5，其面S5= 2476099．第n次操作得到△A n B n C n，△A n B n C n的面S n= 19 n．解答：解：接A1C；S△AA1C=3S△ABC=3，S△AA1C1=2S△AA1C=6，所以 S△=6×3+1=19；A1B1C1同理得 S△A2B2C2=19×19=361；S△A3B3C3=361×19=6859，S△A4B4C4=6859×19=130321，S△A5B5C5=130321×19=2476099，从中可以得出一个律，延各后得到的三角形是原三角形的19 倍，所以延第 n 次后，得到△A n B n C n，其面 S n=19n?S1 =19n故答案是： 2476099 ； 19n．16．（ 2009? 黑河）如， 1 的菱形 ABCD中，∠ DAB=60 度．接角 AC，以 AC作第二个菱形 ACC1D1，使∠D1AC=60°；接AC1，再以 AC1作第三个菱形AC1C2D2，使∠D2AC1 =60°；⋯，按此律所作的第n 个菱形的（） n﹣ 1 ．解答：解：接 DB，∵四形 ABCD是菱形，∴AD=AB．AC⊥DB，∵∠ DAB=60°，∴△ ADB 是等三角形，∴D B=AD=1，∴B M= ，∴AM= = ，∴AC= ，同理可得 AC1 = AC=（）2， AC2= AC1=3=（）3，按此律所作的第n 个菱形的（n﹣ 1 ）n﹣ 1 故答案（）．∠A BC与∠A CD的平分相交于点1 1ABC 中，∠ A=α．∠ ABC 与∠ ACD的平分交于点A1，得∠A1；A2，得∠A2；⋯；∠A2011BC与∠A2011CD的平分相交于点A2012，得∠A2012，∠A2012= ．解答：解：∵∠ ABC 与∠ ACD的平分交于点A1，∴∠A1BC= ∠ABC，∠A1CD= ∠ACD，根据三角形的外角性，∠A+∠ABC=∠ACD，∠A1+∠A1BC=∠A1CD，∴∠A1+∠A1BC=∠A1 +∠ABC=（∠A+∠ABC），整理得，∠A1=∠A=，同理可得，∠A2=∠A1=×=，⋯，∠A2012=．故答案：．18．（ 2009?湖州）如，已知Rt△ABC， D1是斜 AB的中点，D1作 D1E1⊥AC 于 E1，接 BE1交 CD1 于D2； D2作 D2E2⊥AC 于 E2，接 BE2交 CD1于 D3； D3作 D3E3⊥AC 于 E3，⋯，如此，可以依次得到点 D4，D5，⋯， D n，分△ BD 1E1，△ BD2E2，△ BD3E3，⋯，△ BD n E n的面 S1， S2，S3，⋯S n． S n =S△ABC（用含n 的代数式表示）．解答：解：易知D1E1∥BC，∴△ BD 1E1与△ CD1 E1同底同高，面相等，以此推；根据直角三角形的性以及相似三角形的性可知：D1E1= BC， CE1= AC， S1=S△ABC；∴在△ ACB 中， D2其重心，∴D E = BE ，2 1 1∴D2E2=BC， CE2= AC， S2=S△ABC，∵D2E2：D1E1=2：3，D1E1：BC=1：2，∴B C： D2E2 =2D1 E1： D1E1=3，∴CD3： CD2 =D3E3： D2E2=CE3： CE2=3： 4，∴D3E3=D2E2=×BC= BC， CE3= CE2=×AC= AC， S3=S△ABC⋯；∴S n=S△ABC．19．（ 2011? 丰台区二模）已知：如，在Rt△ABC 中，点 D1是斜 AB 的中点，点D1作 D1 E1⊥AC 于点 E1，接 BE1交 CD1于点 D2；点 D2作 D2E2⊥AC于点 E2，接 BE2交 CD1于点 D3；点 D3作 D3E3⊥AC于点 E3，如此，可以依次得到点D4、 D5、⋯、 D n，分△ BD 1E1、△ BD2E2、△ BD3E3、⋯、△ BD n E n的面S1、 S2、 S3、⋯S n．△ ABC 的面是1， S1=，S n=（用含n 的代数式表示）．解答：解：易知 D1E1∥BC，∴△ BD 1E1与△ CD1 E1同底同高，面相等，以此推；∴S1=S△D1E1A= S△ABC，根据直角三角形的性以及相似三角形的性可知：D1E1= BC， CE1= AC， S1= S△ABC；∴在△ ACB 中， D2其重心，又D1E1三角形的中位，∴D1E1∥BC，∴△D2D1E1∽△ CD2B，且相似比 1： 2，即= ，∴D2E1=BE1，∴D2E2=BC， CE2= AC， S2=S△ABC，∴D E = BC， CE = AC， S =S△⋯；3 333ABC∴S=S△．n ABC故答案：，．20．（ 2013?路北区三模）在△ ABC中， AB=6， AC=8， BC=10， P BC上一点， PE⊥AB 于 E，PF⊥AC 于 F， M EF 中点，AM的最小．解答：解：∵四形AFPE是矩形∴A M= AP，AP⊥BC ， AP最短，同 AM也最短∴当 AP⊥BC ，△ ABP∽△ CAB∴A P： AC=AB： BC∴A P： 8=6： 10∴A P 最短， AP=∴当 AM最短， AM=AP÷2=．点：解决本的关是理解直外一点到直上任一点的距离，垂段最短，利用相似求解．21．如，已知 Rt△ABC中， AC=3， BC=4，直角点 C作 CA1⊥AB，垂足 A1，再 A1作 A1C1⊥BC，垂足 C1， C1作 C1 A2⊥AB，垂足 A2，再 A2作 A2 C2⊥BC，垂足 C2，⋯，一直做下去，得到了一段CA1， A1C1， C1A2，⋯，CA1=，=．解答：解：在 Rt△ABC 中， AC=3，BC=4，∴AB=，又因 CA1⊥AB，∴AB?CA=AC?BC，1即 CA1===．∵C4A5⊥AB，∴△ BA5C4∽△ BCA，∴，∴==．所以填和．22．（ 2013? 沐川二模）如，点A1， A2， A3， A4，⋯， A n在射 OA上，点 B1， B2， B3，⋯， B n﹣1在射 OB上，且 A1B1∥A2B2∥A3B3∥⋯∥A n﹣1B n﹣1， A2B1∥A3B2∥A4B3∥⋯∥A n B n﹣1，△A1A2 B1，△A A B ，⋯，△A﹣ A B ﹣阴影三角形，若△A B B ，△A B B 的面分1、 4，△A A B 的面2 3 2n 1 n n 1 2 1 2 3 2 3 1 2 1；面小于2011 的阴影三角形共有6个．解答：解：由意得，△A2B1B2∽△A3B2B3，∴==，==，又∵A1B1∥A2B2∥A3B3，∴===，==，∴OA1=A1 A2， B1B2=B2B3而可得出律：A1A2= A2A3= A3A4⋯； B1B2= B2B3= B3 B4⋯又△A2B1B2，△A3B2B3 的面分1、 4，∴S△A1B1A2=，S△A2B2A3=2，而可推出S△A3B3A4=8， S△A，4B4A5=32， S△A5B5A6=128 ，S△A6B6A7=512， S△A7B7A8=2048 ，故可得小于2011 的阴影三角形的有：△A 1 B1A2，△A2B2A3，△A3B3A4，△A4B4A5，△A5 B5 A6，△A6 B6A7，共 6 个．故答案是：； 6．23．（ 2010?城区）如，已知点A1（ a， 1）在直l ：上，以点A1心，以半径画弧，交x 于点B1、 B2，点 B2作 A1B1的平行交直l 于点 A2，在 x 上取一点B3，使得A2B3=A2 B2，再过点B3作A2B2的平行线交直线l 于点A3，在x 轴上取一点B4，使得A3B4 =A3B3，按此规律继续作下去，则①a= ；②△A4B4B5 的面积是．解答：解：如图所示：①将点A1（ a，1）代入直线 1 中，可得，所以a= ．②△A1B1B2 的面积为：S= =；因为△ OA1B1∽△ OA2B2，所以2A1 B1 =A2B2，又因为两线段平行，可知△A 1 B1B2∽△A2B2B3，所以△A 2B2B3 的面积为S1=4S；以此类推，△A4B4B5 的面积等于64S= ．BCEF，设正方24．（ 2013? 松北区二模）如图，以Rt△ABC 的斜边 BC 为一边在△ ABC 的同侧作正方形形的中心为O，连接 AO，如果AB=4， AO=6，那么AC的长等于16．解答：解：如图，过O点作 OG垂直 AC， G点是垂足．∵∠ BAC=∠BOC=90°，∴ABCO四点共圆，∴∠ OAG=∠OBC=45°∴△ AGO是等腰直角三角形，2 2 2∴2AG =2GO=AO==72，∴O G=AG=6，∵∠ BAH=∠0GH=90°，∠ AHB=∠OHG，∴△ ABH∽△ GOH，∴A B/OG=AH/（ AG﹣AH），∵AB=4，OG=AG=6，∴A H=在直角△ OHC 中，∵ HG=AG﹣ AH=6﹣ =， OG又是斜边HC上的高，2∴OG=HG×GC，而OG=6，GH=，∴GC=10．∴AC=AG+GC=6+10=16．故 AC边的长是 16．25．（ 2007? 淄川区二模）如图，将矩形ABCD的四个角向内折起，恰好拼成一个既无缝隙又无重叠的四边形 EFGH，若 EH=3， EF=4，那么线段 AD与 AB的比等于．解答：解：∵∠ 1=∠2，∠ 3=∠4，∴∠ 2+∠3=90°，∴∠ HEF=90°，同理四边形EFGH的其它内角都是90°，∴四边形EFGH是矩形．∴E H=FG（矩形的对边相等）；又∵∠ 1+∠4=90°，∠ 4+∠5=90°，∴∠ 1=∠5（等量代换），同理∠ 5=∠7=∠8，∴∠ 1=∠8，∴R t△AHE≌Rt△CFG，∴A H=CF=FN，又∵ HD=HN，∴A D=HF，在 Rt△HEF 中， EH=3， EF=4，根据勾股定理得HF=，∴H F=5，又∵ HE?EF=HF?EM，∴E M= ，又∵ AE=EM=EB（折叠后A、 B 都落在M点上），∴A B=2EM= ，∴AD： AB=5：=．故答案：．26．（ 2009? 泰市模）梯形ABCD中 AB∥CD，∠ ADC+∠BCD=90°，以等腰直角三角形，其面分是S1、 S2、 S3且 S1+S3 =4S2， CD= 3 解答：解：∵以AD、 AB、 BC斜向外作等腰直角三角形，其面分是S1、 S2、 S3，AD、 AB、 BC 斜向形外作AB．∴S1=，S2=，S3=∵S1+S3=4S2，∴A D2+BC2=4AB2点 B 作 BK∥AD 交 CD于点 K，∵A B∥CD∴AB=DK， AD=BK，∠ BKC=∠ADC∵∠ ADC+∠BCD=90°∴∠ BKC+∠BCD=90°∴B K2+BC2=CK2∴A D2+BC2=CK22 2∴C K =4AB∴C K=2AB∴C D=3AB．27．如，察中菱形的个数： 1 中有 1 个菱形， 2 中有 5 个菱形， 3 中有 14 个菱形， 4中有 30 个菱形⋯，第 6 个中菱形的个数是91个．2 222 214+4 =30 个菱形，第 5 个中菱形的个数是30+5 =55，第 6 个中菱形的个数是55+6 =91 个．4 中有故答案91．28．（2012? 港一模）如， E、 F 分是平行四形ABCD的 AB、 CD上的点， AF 与 DE相交于点22 2解答：解：如，接EFP，∵△ ADF 与△ DEF 同底等高，∴S△ADF=S△DEF即 S△﹣S△=S△﹣S△，ADF DPF DEF DPF即S△APD=S△EPF=15cm2，同理可得S△=S△=25cm2，BQC EFQ∴阴影部分的面积为S△EPF+S△EFQ=15+25=40cm2．故答案为40．29．（ 2012? 天津）如图，已知正方形ABCD的边长为1，以顶点A、 B 为圆心， 1 为半径的两弧交于点E，以顶点C、 D 为圆心， 1 为半径的两弧交于点F，则解答：解：连接AE， BE， DF， CF．∵以顶点A、 B 为圆心， 1 为半径的两弧交于点∴AB=AE=BE，∴△ AEB 是等边三角形，EF 的长为E， AB=1，．∴边 AB上的高线为EN=，延长 EF 交 AB于 N，并反向延长EF 交 DC于 M，则 E、 F、 M， N 共线，则EM=1﹣ EN=1﹣，∴NF=EM=1﹣，∴EF=1﹣ EM﹣ NF=﹣1．故答案为﹣ 1．30．如图， ABCD是凸四边形，AB=2， BC=4， CD=7，求线段AD 的取值范围．解答：解：连接AC．∵AB=2， BC=4，在△ ABC 中，根据三角形的三边关系，4﹣ 2＜ AC＜ 2+4，即 2＜ AC＜ 6．∴﹣ 6＜﹣ AC＜﹣ 2， 1＜ CD﹣ AC＜ 5， 9＜ CD+AC＜ 13 ，在△ ACD 中，根据三角形的三边关系，得CD﹣ AC＜ AD＜CD+AC，∴1＜ AD＜ 13．故 AD的取值范围是1＜ AD＜ 13．。

2024北京中考数学二轮复习专题一选择、填空压轴题 (含答案)

2024北京中考数学二轮复习专题一选择、填空压轴题类型一分析统计图(表)1.根据国家统计局2019—2023年中国普通本专科、中等职业教育及普通高中招生人数的相关数据，绘制统计图如下：2019—2023年普遍本专科、中等职业教育及普遍高中招生人数第1题图下面有四个推断：①2019—2023年，普通本专科招生人数逐年增多；②2023年普通高中招生人数比2019年增加约4%；③2019—2023年，中等职业教育招生人数逐年减少；④2019年普通高中招生人数约是中等职业教育招生人数的1.4倍．所有合理推断的序号是()A.①④ B.②③ C.①②④D.①②③④2.为了解某校学生每周课外阅读时间的情况，随机抽取该校a 名学生进行调查，获得的数据整理后绘制成统计表如下：每周课外阅读时间x (小时)0≤x <22≤x <44≤x <66≤x <8x ≥8合计频数817b 15a 频率0.080.17c 0.151表中4≤x <6组的频数b 满足25≤b ≤35.下面有四个推断：①表中a的值为100；②表中c的值可以为0.31；③这a名学生每周课外阅读时间的中位数一定不在6～8之间；④这a名学生每周课外阅读时间的平均数不会超过6.所有合理推断的序号是()A.①②B.③④C.①②③D.②③④3.密云水库是首都北京重要水源地，水源地生态保护对保障首都水源安全及北京市生态和城市可持续发展具有不可替代的作用．以下是1986—2023年密云水库水体面积和年降水量变化图．1986—2023年密云水库水体面积和年降水量变化图第3题图(以上数据来源于《全国生态气象公报(2023年)》，部分年份缺数据)对于现有数据有以下结论：①2004年的密云水库水体面积最小，仅约为20km2；②2015—2023年，密云水库的水体面积呈持续增加趋势．表明水资源储备增多；③在1986—2023年中，2023年的密云水库水体面积最大，约为170km2；④在1986—2023年中，密云水库年降水量最大的年份，水体面积也最大．其中结论正确的是()A.②③B.②④C.①②③D.③④4.某公司计划招募一批技术人员，他们对25名面试合格人员又进行了理论知识和实践操作测试，其中25名入围者的面试成绩排名，理论知识成绩排名与实践操作成绩的排名情况如图所示第4题图下面有3个推断：①甲的理论知识成绩排名比面试成绩排名靠前；②甲的实践操作成绩排名与理论知识成绩排名相同；③乙的理论知识成绩排名比甲的理论知识成绩排名靠前．其中合理的是()A.①B.①②C.①③D.①②③5.多年来，北京市以强有力的措施和力度治理大气污染，空气质量持续改善，主要污染物的年平均浓度值全面下降．下图是1998年至2019年二氧化硫(SO2)和二氧化氮(NO2)的年平均浓度值变化趋势图．第5题图下列说法错误的是()A.1998年至2019年，SO2的年平均浓度值的平均数小于NO2的年平均浓度值的平均数B.1998年至2019年，SO2的年平均浓度值的中位数小于NO2的年平均浓度值的中位数C.1998年至2019年，SO2的年平均浓度值的方差小于NO2的年平均浓度值的方差D.1998年至2019年，SO2的年平均浓度值比NO2的年平均浓度值下降得更快6.“实际平均续航里程”是指电动汽车的行驶总里程与充电次数的比值，是反映电动汽车性能的重要指标．某汽车生产厂家为了解某型号电动汽车的“实际平均续航里程”，收集了使用该型号电动汽车1年以上的部分客户的相关数据，按年龄不超过40岁和年龄在40岁以上将客户分为A，B两组，从A，B组各抽取10位客户的电动汽车的实际平均续航里程数据整理成图．其中“⊙”表示A组的客户，“*”表示B组的客户.第6题图下列推断不正确的是()A.A组客户的电动汽车的“实际平均续航里程”的最大值低于B组B.A组客户的电动汽车的“实际平均续航里程”的方差低于B组C.A组客户的电动汽车的“实际平均续航里程”的平均值低于B组D.这20位客户的电动汽车的“实际平均续航里程”的中位数落在B组7.某种预防病虫害的农药即将于三月15日之前喷洒，需要连续三天完成，又知当最低温度不低于0摄氏度，且昼夜温差不大于10摄氏度时药物效果最佳，为此农广站工作人员查看了三月1—15日的天气预报，请你结合气温图给出一条合理建议，药剂喷洒可以安排在________日开始进行．1—15日天气情况第7题图类型二分析与判断函数图象1.如图，一个小球由静止开始沿一个斜坡滚下，其速度每秒增加的值相同．用t 表示小球滚动的时间，v 表示小球的速度．下列图象中，能表示小球在斜坡上时v 与t 的函数关系的图象大致是()第1题图2.某农科所响应“乡村振兴”号召，为某村免费提供一种优质瓜苗及大棚栽培技术．这种瓜苗先在农科所的温室中生长，平均高度长到大约20cm 时，移至该村的大棚内继续生长．研究表明，60天内，这种瓜苗的平均高度y (cm)与生长时间x (天)的函数关系的图象如图所示．当这种瓜苗长到大约80cm 时，开始开花结果，此时瓜苗在该村大棚内生长的天数是()第2题图A.10天B.18天C.33天D.48天3.有一圆形苗圃如图①所示，中间有两条交叉过道AB ，CD ，它们为苗圃⊙O 的直径，且AB ⊥C D.入口K位于AD ︵中点，园丁在苗圃圆周或两条交叉过道上匀速行进．设该园丁行进的时间为t ，与入口K 的距离为S ，表示S 与t 的函数关系的图象大致如图②所示，则该园丁行进的路线可能是()第3题图A.A →O →DB.C →A →O →BC.D →O →CD.O →D →B →C4.(2023通州区一模)为满足人民对美好生活的向往，造福子孙后代，环保部门要求相关企业加强污水治理能力，污水排放未达标的企业要限期整改．甲、乙两个企业的污水排放量W 与时间t 的关系如图所示，我们用W t表示t时刻某企业的污水排放量，用－Wt1－Wt2t1－t2的大小评价在t1至t2这段时间内某企业污水治理能力的强弱．已知甲、乙两企业在整改期间排放的污水排放量与时间的关系如下图所示．第4题图给出下列四个结论：①在t1≤t≤t2这段时间内，甲企业的污水治理能力比乙企业强；②在t1时刻，乙企业的污水排放量高；③在t3时刻，甲、乙两企业的污水排放量都已达标；④在0≤t≤t1，t1≤t≤t2，t2≤t≤t3这三段时间中，甲企业在t2≤t≤t3的污水治理能力最强．其中所有正确结论的序号是()A.①②③B.①③④C.②④D.①③5.(2023房山区一模)在平面直角坐标系xOy中，若函数图象上任意两点P(x1，y1)，Q(x2，y2)均满足(x1－x2)(y1－y2)>0.下列四个函数图象中，所有正确的函数图象的序号是()第5题图A.①②B.③④C.①③D.②④类型三代数类问题1.(2023西城区期末)现有函数y ＋4（x <a ），2－2x （x ≥a ），如果对于任意的实数n ，都存在实数m ，使得当x ＝m 时，y ＝n ，那么实数a 的取值范围是()A.－5≤a ≤4 B.－1≤a ≤4 C.－4≤a ≤1D.－4≤a ≤52.在平面直角坐标系xOy 中，对于自变量为x 的函数y 1和y 2，若当－1≤x ≤1时，都满足|y 1－y 2|≤1成立，则称函数y 1和y 2互为“关联的”．下列函数中，不与y ＝x 2互为“关联的”函数是()A.y ＝x 2－1B.y ＝2x 2C.y ＝(x －1)2D.y ＝－x 2＋13.(2023人大附中模拟)在数轴上有三个互不重合的点A ，B ，C ，它们代表的实数分别为a ，b ，c ，下列结论中：①若abc >0，则A ，B ，C 三点中，至少有一个点在原点右侧；②若a ＋b ＋c ＝0，则A ，B ，C 三点中，至少有一个点在原点右侧；③若a ＋c ＝2b ，则点B 为线段AC 的中点；④O 为坐标原点且A ，B ，C 均不与O 重合，若OB －OC ＝AB －AC ，则bc >0.所有正确结论的序号是()A.①② B.③④ C.①②③D.①②③④4.(2023西城区二模)从1，2，3，4，5中选择四个数字组成四位数abcd ，其中a ，b ，c ，d 分别代表千位、百位、十位、个位数字.若要求这个四位数同时满足以下条件：①abcd 是偶数；②a >b >c ；③a ＋c ＝b ＋d ，请写出一个符合要求的数________．5.(2023燕山区期末)在实数范围内定义一种运算“*”，其运算法则为a *b ＝a 2－a b.根据这个法则，下列结论中错误的是________．(把所有错误结论的序号都填在横线上)①2*3＝2－6；②若a ＋b ＝0，则a *b ＝b *a ；③(x ＋2)*(x ＋1)＝0是一元二次方程；④方程(x ＋2)*1＝3的根是x 1＝－3－52，x 2＝－3＋52.6.(2023丰台区一模)京剧作为一门中国文化的传承艺术，常常受到外国友人的青睐．如图，在平面直角坐标系xOy 中，某脸谱轮廓可以近似地看成是一个半圆与抛物线的一部分组合成的封闭图形，记作图形G .点A ，B ，C ，D 分别是图形G 与坐标轴的交点，已知点D 的坐标为(0，－3)，AB 为半圆的直径，且AB ＝4，半圆圆心M 的坐标为(1，0)．关于图形G 给出下列四个结论，其中正确的是________(填序号)．①图形G 关于直线x ＝1对称；②线段CD 的长为3＋3；③图形G 围成区域内(不含边界)恰有12个整点(即横、纵坐标均为整数的点)；④当－4≤a ≤2时，直线y ＝a 与图形G 有两个公共点．第6题图7.(2023石景山区二模)在平面直角坐标系xOy 中，A (0，1)，B (1，1)，有以下4种说法：①一次函数y ＝x 的图象与线段AB 无公共点；②当b <0时，一次函数y ＝x ＋b 的图象与线段AB 无公共点；③当k >1时，反比例函数y ＝k x的图象与线段AB 无公共点；④当b >1时，二次函数y ＝x 2－bx ＋1的图象与线段AB 无公共点．上述说法中正确的是________．8.(2023一七一中学模拟)小聪用描点法画出了函数y ＝x (x ≥0)的图象F ，如图所示．结合旋转的知识，他尝试着将图象F 绕原点逆时针旋转90°得到图象F 1，再将图象F 1绕原点逆时针旋转90°得到图象F 2，如此继续下去，得到图象F n .在尝试的过程中，他发现点P (4，2)在图象________上(写出一个正确的即可)；若点P (a ，b )在图象F 2021上，则a ＝________(用含b 的代数式表示)．第8题图9.如图，A (0，1)，B (1，5)，曲线BC 是双曲线y ＝k x(k ≠0)的一部分，曲线AB 与BC 组成图形G ，由点C 开始不断重复图形G 形成一线“波浪线”，若点P (2023，m )，Q (x ，n )在该“波浪线”上，则m 的值为________．n 的最大值为________．第9题图类型四几何类问题1.(2023海淀区一模)如图，在平面直角坐标系xOy中，AB，CD，EF，GH是正方形OPQR 边上的线段，点M在其中某条线段上，若射线OM与x轴正半轴的夹角为α，且sinα＞cosα，则点M所在的线段可以是()第1题图A.AB和CDB.AB和EFC.CD和GHD.EF和GH2.程老师制作了如图①所示的学具，用来探究“边边角条件是否可确定三角形的形状”问题．操作学具时，点Q在轨道槽AM上运动，点P既能在以A为圆心、以8为半径的半圆轨道槽上运动，也能在轨道槽QN上运动．图②是操作学具时，所对应某个位置的图形的示意图．第2题图有以下结论：①当∠PAQ＝30°，PQ＝6时，可得到形状唯一确定的△PAQ；②当∠PAQ＝30°，PQ＝9时，可得到形状唯一确定的△PAQ；③当∠PAQ＝90°，PQ＝10时，可得到形状唯一确定的△PAQ；④当∠PAQ＝150°，PQ＝12时，可得到形状唯一确定的△PAQ.其中所有正确结论的序号是()A.②③B.③④C.②③④D.①②③④3.(2021东城区二模)数学课上，李老师提出如下问题：已知：如图，AB是⊙O的直径，射线AC交⊙O于C.求作：弧BC的中点D.同学们分享了如下四种方案：第3题图①如图①，连接BC，作BC的垂直平分线，交⊙O于点D；②如图②，过点O作AC的平行线，交⊙O于点D；③如图③，作∠BAC的平分线，交⊙O于点D；④如图④，在射线AC上截取AE，使AE＝AB，连接BE，交⊙O于点D.上述四种方案中，正确的方案的序号是________．4.(20231大兴区一模)如图，在▱ABCD中，AD>AB，E，F分别为边AD，BC上的点(E，F 不与端点重合)．对于任意▱ABCD，下面四个结论中：①存在无数个四边形ABFE，使得四边形ABFE是平行四边形；②至少存在一个四边形ABFE，使得四边形ABFE是菱形；③至少存在一个四边形ABFE，使得四边形ABFE是矩形；④存在无数个四边形ABFE，使得四边形ABFE的面积是▱ABCD面积的一半．所有正确结论的序号是________．第4题图5.(2021西城区期末)如图，在平面直角坐标系xOy中，P(4，3)，⊙O经过点P.点A，点B 在y轴上，PA＝PB，延长PA，PB分别交⊙O于点C，点D，设直线CD与x轴正方向所夹的锐角为α.(1)⊙O的半径为________；(2)tanα＝________第5题图参考答案类型一分析统计图(表)1.C【解析】由题图知2019—2023年，普通本专科招生人数逐年增多，故①正确；2023年普通高中招生人数比2019年增加约876－839×100%≈4%，故②正确；从2019—2018839年，中等职业教育招生人数逐年减少，从2019—2023年，中等职业教育招生人数在增加，故③错误；2019年普通高中招生人数约是中等职业教育招生人数的839÷600≈1.4倍，故④正确．2.A【解析】①8÷0.08＝100，故表中a的值为100，是合理推断；②25÷100＝0.25，35÷100＝0.35，1－0.08－0.17－0.35－0.15＝0.25，1－0.08－0.17－0.25－0.15＝0.35，故表中c的值为0.25≤c≤0.35，表中c的值可以为0.31，是合理推断；③∵表中4≤x<6组的频数b满足25≤b≤35，∴8＋17＋25＝50，8＋17＋35＝60，∴这100名学生每周课外阅读时间的中位数可能在4～6之间，也可能在6～8之间，故此推断不是合理推断；④这a名学生每周课外阅读时间的平均数可以超过6，故此推断不是合理推断．3.A【解析】由题图知①2004年的水体面积超过60km2，不符合题意；②2015—2023年，密云水库的水体面积呈持续增加趋势，表明水资源储备增多，符合题意；③在1986—2023年中，2023年的密云水库水体面积最大，约为170km2，符合题意；④水体面积最大的年份是2023年，但年降水量不是最大，不符合题意．4.D【解析】由题图知，甲的面试成绩排名为11，理论知识成绩排名为8，实践操作成绩排名为8；乙的面试成绩排名为7，实践操作成绩排名为15，理论知识成绩排名为5，故①②③都合理，故选D.5.C【解析】由题图可得，A.2000年至2019年，SO2的年平均浓度值都在NO2的年平均浓度值以下，由此可得SO2的年平均浓度值的平均数小于NO2的年平均浓度值的平均数，此选项正确，不合题意；B.2000年至2019年，SO2的年平均浓度值都在NO2的年平均浓度值以下，由此可得SO2的年平均浓度值的中位数小于NO2的年平均浓度值的中位数，此选项正确，不合题意；C.根据图中两折线中点的离散程度可得SO2的年平均浓度值的方差大于NO2的年平均浓度值的方差，此选项错误，符合题意；D.1998年至2019年，根据图中两折线的起止点可得SO2的年平均浓度值比NO2的年平均浓度值下降得更快，此选项正确，不合题意．6.C 【解析】由图象可得，A 组客户的电动汽车的“实际平均续航里程”的最大值在350左右，B 组客户的电动汽车的“实际平均续航里程”的最大值在450左右，故A 选项不符合题意；A 组客户的电动汽车的“实际平均续航里程”的数据波动比B 组客户的电动汽车的“实际平均续航里程”的数据波动小，即A 组客户的电动汽车的“实际平均续航里程”的方差比B 组客户的电动汽车的“实际平均续航里程”的方差小，故B 选项不符合题意；A 组客户的电动汽车的“实际平均续航里程”的平均值不一定低于B 组，故C 选项符合题意；这20位客户的电动汽车的“实际平均续航里程”按从大到小排序，第10位，第11位均在B 组，故D 选项不符合题意．7.3或12(任写一个即可)【解析】由题图可知，3日、4日、5日最低温度分别是1摄氏度、2摄氏度、0摄氏度，且昼夜温差分别是8－1＝7摄氏度，4－2＝2摄氏度，9－0＝9摄氏度，最低温度不低于0摄氏度，且昼夜温差不大于10摄氏度，可以药剂喷洒，12日、13日、14日最低温度分别是6摄氏度、7摄氏度、8摄氏度，且昼夜温差分别是12－6＝6摄氏度，16－7＝9摄氏度，14－8＝6摄氏度，最低温度不低于0摄氏度，且昼夜温差不大于10摄氏度，可以药剂喷洒．类型二分析与判断函数图象1.D 【解析】∵一个小球由静止开始沿一个斜坡滚下，其速度每秒增加的值相同，∴v t为定值，∴v 与t 是正比例函数的关系．∴选项D 符合题意．2.B 【解析】当15<x ≤60时，设y ＝kx ＋b (k ≠0)，k ＋b ＝20，k ＋b ＝170，＝103，＝－30，∴y ＝103x －30.当y ＝80时，103x －30＝80，解得x ＝33，33－15＝18(天)，∴开始开花结果，此时瓜苗在该村大棚内生长的天数是18天．3.B 【解析】若按A →O →D 路线，图象应呈现对称性，故A 错误；若按C →A →O →B ，则从C →A 距离逐渐减少，A →O →B 距离先减少，再增大，符合题图中函数图象的大致走势，故B 正确；C 、D 中，起始点处S 值小于终点处S 值，由题图可知在起点和终点时，S 值最大且相等，故C 、D 错误．4.D 【解析】①在t 1≤t ≤t 2这段时间内，甲企业的图象比乙企业的图象倾斜角度大，故①正确；②在t 1时刻，甲企业的污水排放量高，故②错误；③在t 3时刻，甲、乙两企业的污水排放量在达标量以下，故③正确；④在0≤t ≤t 1，t 1≤t ≤t 2，t 2≤t ≤t 3这三段时间中，甲企业在t 1≤t ≤t 2的图象倾斜角度最大，即治理污水能力最强，故④错误．5.D 【解析】由题意中(x 1－x 2)(y 1－y 2)>0可知，x 1－x 2>0，y 1－y 2>0或x 1－x 2<0，y 1－y 2<0，即当x 1>x 2时，y 1>y 2或当x 1<x 2时，y 1<y 2.故函数中y 随着x 的增大而增大，故②④正确．类型三代数类问题1.A 【解析】如解图，由图象可知，当－5≤a ≤4时，对于任意的实数n ，都存在实数m ，使得当x ＝m 时，函数y ＝n .第1题解图2.C 【解析】A .∵|y 1－y 2|＝|x 2－(x 2－1)|＝1≤1，故A 选项与y ＝x 2互为“关联的”函数；B .∵|y 1－y 2|＝|x 2－2x 2|＝x 2，又∵－1≤x ≤1，∴x 2≤1，故B 选项与y ＝x 2互为“关联的”函数；C .∵|y 1－y 2|＝|x 2－(x －1)2|＝|2x －1|，又∵－1≤x ≤1，∴|2x －1|≤3，故C 选项不与y ＝x 2互为“关联的”函数；D .∵|y 1－y 2|＝|x 2－(－x 2＋1)|＝|2x 2－1|，又∵－1≤x ≤1，∴|2x 2－1|≤1，故D 选项与y ＝x 2互为“关联的”函数．3.D 【解析】若全在原点的左侧，则a <0，b <0,c <0，与abc >0矛盾，∴三点中至少有一个在原点的右侧，故①正确；若全在原点的左侧，则a <0,b <0,c <0，∴a ＋b ＋c <0.又∵a ，b ，c 不全为0，与a ＋b ＋c ＝0矛盾，∴至少有一个点在原点右侧，故②正确；∵a ＋c ＝2b ，∴b ＝a ＋c 2，∴B 为AC 的中点，故③正确；由绝对值的意义：OB ＝|b |,OC ＝|c |,AB ＝|b －a |,AC ＝|c －a |，|b |－|c |＝|b －a |－|c －a |，∴A 在最左或最右时，上面等式的右边＝b －c 或c －b ，∴|b |－|c |＝b －c ，∴b >0，c >0，∴bc >0，|b |－|c |＝c －b ，∴b <0，c <0，∴bc >0，故④正确．4.4312(答案不唯一)【解析】∵abcd 是偶数，∴d ＝2或4.∵a >b >c ，a ＋c ＝b ＋d ，∴a ＝4，b ＝3，c ＝1，d ＝2，或a ＝5，b ＝4，c ＝1，d ＝2，或a ＝5，b ＝3，c ＝2，d ＝4，或a ＝5，b ＝2，c ＝1，d ＝4，∴abcd ＝4312或5412或5324或5214.5.③④【解析】根据题中的定义得：2*3＝(2)2－2×3＝2－6，①正确，不符合题意；若a ＋b ＝0，则有a ＝－b ,a *b ＝a 2－ab ＝b 2＋b 2＝2b 2,b *a ＝b 2－ab ＝b 2＋b 2＝2b 2，即a *b ＝b *a ,②正确，不符合题意；已知等式变形得：(x ＋2)2－(x ＋2)(x ＋1)＝0，即x 2＋4x ＋4－x 2－3x －2＝0，合并得：x ＋2＝0，是一元一次方程，③错误，符合题意；④方程变形得：(x ＋2)2－(x ＋2)＝3，整理得：x 2＋4x ＋4－x －2－3＝0，即x 2＋3x －1＝0，∵a ＝1,b ＝3,c ＝－1，∴x ＝－b ±b 2－4ac 2a ＝－3±132，解得x 1＝－3＋132，x 2＝－3－132，④错误，符合题意．6.①②【解析】由半圆M 可知A (－1，0)，B (3，0)，M (1，0)，且点A ，B 在抛物线上，∴图形G 关于直线x ＝1对称，故①正确；如解图，连接CM ，第6题解图在Rt △MOC 中，∵OM ＝1,CM ＝2，∴OC ＝22－12＝ 3.又∵D (0，－3)，∴OD ＝3，∴CD ＝OC ＋OD ＝3＋3，故②正确；根据题图得，图形G 围成区域内(不含边界)恰有13个整点(即横、纵坐标均为整数的点)，故③错误；由题意得A (－1，0)，B (3，0)，当a ＝－4时，直线y ＝－4与图形G 有一个公共点，当a ＝2时，直线y ＝2与图形G 有一个公共点，故④错误．综上所述，正确的有①②.7.②③【解析】一次函数y ＝x 图象经过点B (1，1)，即一次函数y ＝x 的图象与线段AB 有公共点，故①错误；一次函数y ＝x 图象刚好经过点B (1，1)，向下平移直线y ＝x ，此时b <0，直线y ＝x ＋b 与线段AB 无公共点，故②正确；反比例函数y ＝1x的图象刚好经过点B (1，1)，当k >1时，反比例函数y ＝k x的图象沿着y ＝x 向远离原点的方向平移，与线段AB 无公共点，故③正确；二次函数y ＝x 2－bx ＋1的图象一定经过A (0，1)，即二次函数的图象与线段AB 有公共点，故④错误．8.F 4，－b 【解析】根据旋转的规律得，F 1的解析式为y ＝x 2，其图象位于第二象限；F 2的解析式为y ＝－－x ，其图象位于第三象限；F 3的解析式为y ＝－x 2，其图象位于第四象限；F 4的解析式为y ＝x ，其图象位于第一象限；…则2021÷4＝505……1，即F 2021的图象位于第二象限，该图象的函数解析式是y ＝x 2.∵P (4，2)位于第一象限，∴点P 所在的图象是F 4.∵点P (a ，b )在图象F 2021上，∴b ＝a 2，∴a ＝－b .9.1，5【解析】∵B (1，5)在y ＝k x 的图象上，∴k ＝1×5＝5.当x ＝5时，y ＝55＝1.∴C (5，1)．又∵2023÷5＝404，∴m ＝1.∵Q (x ，n )在该“波浪线”上，∴n 的最大值是5.类型四几何类问题1.D 【解析】如解图，连接OQ ，则∠POQ ＝45°，sin 45°＝cos 45°＝22，当点M 在AB 和CD 上时，α＜45°，则sin α＜cos α，当点M 在EF 和GH 上时，α＞45°，sin α＞cos α.第1题解图2.C 【解析】①当∠PAQ ＝30°，PQ ＝6时，以P 为圆心，6为半径画弧，与射线AM 有两个交点，则△PAQ 的形状不能唯一确定，故①错误；②当∠PAQ ＝30°，PQ ＝9时，以P 为圆心，9为半径画弧，与射线AM 有两个交点，但左边位置的Q 不符合题意，∴Q 点位置唯一确定，则可得到形状唯一确定的△PAQ ，故②正确；③当∠PAQ ＝90°，PQ ＝10时，以P 为圆心，10为半径画弧，与射线AM 有两个交点，但此时两个三角形全等，Q 点位置唯一确定，则可得到形状唯一确定的△PAQ ，故③正确；④当∠PAQ ＝150°，PQ ＝12时，以P 为圆心，12为半径画弧，与射线AM 有两个交点，左边的Q 不符合题意，∴Q 点位置唯一确定，则可得到形状唯一确定的△PAQ ，故④正确，故选C .3.①②③④【解析】①如题图①，由作图可知，BC 的垂直平分线经过圆心O ，∵OD⊥BC ，∴点D 是BC ︵的中点；②如解图①，连接BC ，∵AB 是⊙O 的直径，∴∠ACB ＝90°.∵OD ∥AC ，∴OD ⊥BC ，∴点D 是BC ︵的中点；③如题图③，∵∠BAD ＝∠CAD ，∴点D 是BC ︵的中点；④如解图②，连接AD ，∵AB 是⊙O 的直径，∴∠ADB ＝90°.∵AE ＝AB ，∴∠BAD ＝∠CAD ，∴点D 是BC ︵的中点．图①图②第3题解图4.①②④【解析】只要满足AB ∥EF ，则四边形ABFE 是平行四边形，这样的EF 有无数条，故①正确；∵AD >AB ，∴在AD 上截取AE ＝AB ，再满足AB ∥EF ，就能使得四边形ABFE 是菱形，故②正确；∵∠B 不是直角，∴矩形ABFE 不存在，故③错误；只要当EF 经过▱ABCD 对角线交点时，四边形ABFE 的面积是▱ABCD 面积的一半，这样的EF 有无数条，故④正确．5.(1)5；(2)43【解析】(1)如解图，连接OP ，∵P (4，3)，∴OP ＝32＋42＝5；(2)如解图，设CD 交x 轴于点J ，过点P 作PT ⊥AB 交⊙O 于点T ，交AB 于点E ，连接CT ，DT ，OT ，∵P (4，3)，∴PE ＝4，OE ＝3.在Rt △OPE 中，tan ∠POE ＝PE OE ＝43，∵OE ⊥PT ，OP ＝OT ，∴∠POE ＝∠TOE ，∴∠PDT ＝12∠POT ＝∠POE ，∵PA ＝PB ，PE ⊥AB ，∴∠APT ＝∠DPT ，∴TC ︵＝DT ︵，∴∠TDC ＝∠TCD ，∵PT ∥x 轴，∴∠CJO ＝∠CKP ，∵∠CKP ＝∠TCK＋∠CTK ，∠CTP ＝∠CDP ，∠PDT ＝∠TDC ＋∠CDP ，∴∠TDP ＝∠CJO ，∴∠CJO ＝∠POE ，∴tan α＝tan ∠CJO ＝tan ∠POE ＝43.第5题解图。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2016中考数学几何选择填空压轴题精选(配答案)一．选择题（共13小题）1．（2013?蕲春县模拟）如图，点O 为正方形ABCD 的中心，BE 平分∠DBC 交DC 于点E ，延长BC 到点F ，使FC=EC ，连接DF 交BE 的延长线于点H ，连接OH 交DC 于点G ，连接HC ．则以下四个结论中正确结论的个数为（） ①OH=BF ；②∠CHF=45°；③GH=BC ；④DH 2=HE?HB ．A ． 1个B ． 2个C ． 3个D ． 4个2．（2013?连云港模拟）如图，Rt△ABC 中，BC=，∠ACB=90°，∠A=30°，D 1是斜边AB 的中点，过D 1作D 1E 1⊥AC 于E 1，连结BE 1交CD 1于D 2；过D 2作D 2E 2⊥AC 于E 2，连结BE 2交CD 1于D 3；过D 3作D 3E 3⊥AC 于E 3，…，如此继续，可以依次得到点E 4、E 5、…、E 2013，分别记△BCE 1、△BCE 2、△BCE 3、…、△BCE 2013的面积为S 1、S 2、S 3、…、S 2013．则S 2013的大小为（）A ．B ．C ．D ．3．如图，梯形ABCD 中，AD∥BC，，∠ABC=45°，AE⊥BC 于点E ，BF⊥AC于点F ，交AE 于点G ，AD=BE ，连接DG 、CG ．以下结论：①△BEG≌△AEC；②∠GAC=∠GCA；③DG=DC；④G 为AE 中点时，△AGC 的面积有最大值．其中正确的结论有（）A．1个B．2个C．3个D．4个4．如图，正方形ABCD中，在AD的延长线上取点E，F，使DE=AD，DF=BD，连接BF分别交CD，CE于H，G下列结论：①EC=2DG；②∠GDH=∠GHD；③S△CDG =S?DHGE；④图中有8个等腰三角形．其中正确的是（）A．①③B．②④C．①④D．②③5．（2008?荆州）如图，直角梯形ABCD中，∠BCD=90°，AD∥BC，BC=CD，E为梯形内一点，且∠BEC=90°，将△BEC绕C点旋转90°使BC与DC重合，得到△DCF，连EF交CD于M．已知BC=5，CF=3，则DM：MC的值为（）A．5：3B．3：5C．4：3D．3：46．如图，矩形ABCD的面积为5，它的两条对角线交于点O1，以AB，AO1为两邻边作平行四边形ABC1O1，平行四边形ABC1O1的对角线交BD于点02，同样以AB，AO2为两邻边作平行四边形ABC2O2．…，依此类推，则平行四边形ABC2009O2009的面积为（）A．B．C．D．7．如图，在锐角△ABC中，AB=6，∠BAC=45°，∠BAC的平分线交BC于点D，M，N分别是AD和AB上的动点，则BM+MN的最小值是（）A．B．6C．D．38．（2013?牡丹江）如图，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P 为BC边的中点，连接PM，PN ，则下列结论：①PM=PN；②；③△PMN为等边三角形；④当∠ABC=45°时，BN=PC．其中正确的个数是（）A．1个B．2个C．3个D．4个9．（2012?黑河）Rt△ABC中，AB=AC，点D为BC中点．∠MDN=90°，∠MDN绕点D 旋转，DM、DN分别与边AB、AC交于E、F两点．下列结论：①（BE+CF）=BC；②S△AEF ≤S△ABC；③S四边形AEDF=AD?EF；④AD≥EF；⑤AD与EF可能互相平分，其中正确结论的个数是（）A．1个B．2个C．3个D．4个10．（2012?无锡一模）如图，在正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后折痕DE分别交AB、AC于点E、G，连接GF．下列结论①∠ADG=°；②tan∠AED=2；③S△AGD =S△OGD；④四边形AEFG是菱形；⑤BE=2OG．其中正确的结论有（）A．①④⑤B．①②④C．③④⑤D．②③④11．如图，正方形ABCD中，O为BD中点，以BC为边向正方形内作等边△BCE，连接并延长AE交CD于F，连接BD分别交CE、AF于G、H，下列结论：①∠CEH=45°；②GF∥DE；③2OH+DH=BD；④BG=DG；⑤．其中正确的结论是（）A．①②③B．①②④C．①②⑤D．②④⑤12．如图，在正方形ABCD中，AB=4，E为CD上一动点，AE交BD于F，过F作FH⊥AE 于H，过H作GH⊥BD于G，下列有四个结论：①AF=FH，②∠HAE=45°，③BD=2FG，④△CEH的周长为定值，其中正确的结论有（）A ． ①②③B ． ①②④C ． ①③④D ． ①②③④13．（2013?钦州模拟）正方形ABCD 、正方形BEFG 和正方形RKPF 的位置如图所示，点G 在线段DK 上，正方形BEFG 的边长为4，则△DEK 的面积为（）A ． 10B ． 12C ． 14D ． 16二．填空题（共16小题）14．如图，在梯形ABCD 中，AD∥BC，EA⊥AD，M 是AE 上一点，F 、G 分别是AB 、CM 的中点，且∠BAE=∠MCE，∠MBE=45°，则给出以下五个结论：①AB=CM；②A E⊥BC；③∠BMC=90°；④EF=EG；⑤△BMC 是等腰直角三角形．上述结论中始终正确的序号有 _________ ．15．（2012?门头沟区一模）如图，对面积为1的△ABC 逐次进行以下操作：第一次操作，分别延长AB 、BC 、CA 至A 1、B 1、C 1，使得A 1B=2AB ，B 1C=2BC ，C 1A=2CA ，顺次连接A 1、B 1、C 1，得到△A 1B 1C 1，记其面积为S 1；第二次操作，分别延长A 1B 1，B 1C 1，C 1A 1至A 2，B 2，C 2，使得A 2B 1=2A 1B 1，B 2C 1=2B 1C 1，C 2A 1=2C 1A 1，顺次连接A 2，B 2，C 2，得到△A 2B 2C 2，记其面积为S 2…，按此规律继续下去，可得到△A 5B 5C 5，则其面积为S 5= _________ ．第n 次操作得到△A n B n C n ，则△A n B n C n 的面积S n = _________ ． 16．（2009?黑河）如图，边长为1的菱形ABCD 中，∠DAB=60度．连接对角线AC ，以AC 为边作第二个菱形ACC 1D 1，使∠D 1AC=60°；连接AC 1，再以AC 1为边作第三个菱形AC 1C 2D 2，使∠D 2AC 1=60°；…，按此规律所作的第n 个菱形的边长为 _________ ．17．（2012?通州区二模）如图，在△ABC 中，∠A=α．∠ABC 与∠ACD 的平分线交于点A 1，得∠A 1；∠A 1BC 与∠A 1CD 的平分线相交于点A 2，得∠A 2； …；∠A 2011BC 与∠A 2011CD 的平分线相交于点A 2012，得∠A 2012，则∠A 2012= _________ ．18．（2009?湖州）如图，已知Rt△ABC，D 1是斜边AB 的中点，过D 1作D 1E 1⊥AC 于E 1，连接BE 1交CD 1于D 2；过D 2作D 2E 2⊥AC 于E 2，连接BE 2交CD 1于D 3；过D 3作D 3E 3⊥AC 于E 3，…，如此继续，可以依次得到点D 4，D 5，…，D n ，分别记△BD 1E 1，△BD 2E 2，△BD 3E 3，…，△BD n E n 的面积为S 1，S 2，S 3，…S n ．则S n = _________ S △ABC （用含n 的代数式表示）．19．（2011?丰台区二模）已知：如图，在Rt△ABC 中，点D 1是斜边AB 的中点，过点D 1作D 1E 1⊥AC 于点E 1，连接BE 1交CD 1于点D 2；过点D 2作D 2E 2⊥AC 于点E 2，连接BE 2交CD 1于点D 3；过点D 3作D 3E 3⊥AC 于点E 3，如此继续，可以依次得到点D 4、D 5、…、D n ，分别记△BD 1E 1、△BD 2E 2、△BD 3E 3、…、△BD n E n 的面积为S 1、S 2、S 3、…S n ．设△ABC 的面积是1，则S 1= _________ ，S n = _________ （用含n 的代数式表示）．20．（2013?路北区三模）在△ABC 中，AB=6，AC=8，BC=10，P 为边BC 上一动点，PE⊥AB 于E ，PF⊥AC 于F ，M 为EF 中点，则AM 的最小值为 _________ ． 21．如图，已知Rt△ABC 中，AC=3，BC=4，过直角顶点C 作CA 1⊥AB，垂足为A 1，再过A 1作A 1C 1⊥BC，垂足为C 1，过C 1作C 1A 2⊥AB，垂足为A 2，再过A 2作A 2C 2⊥BC，垂足为C 2，…，这样一直做下去，得到了一组线段CA 1，A 1C 1，C 1A 2，…，则CA 1= _________ ，= _________ ．22．（2013?沐川县二模）如图，点A 1，A 2，A 3，A 4，…，A n 在射线OA 上，点B 1，B 2，B 3，…，B n ﹣1在射线OB 上，且A 1B 1∥A 2B 2∥A 3B 3∥…∥A n ﹣1B n ﹣1，A 2B 1∥A 3B 2∥A 4B 3∥…∥A n B n﹣1，△A 1A 2B 1，△A 2A 3B 2，…，△A n ﹣1A n B n ﹣1为阴影三角形，若△A 2B 1B 2，△A 3B 2B 3的面积分别为1、4，则△A 1A 2B 1的面积为 _________ ；面积小于2011的阴影三角形共有 _________ 个．23．（2010?鲤城区质检）如图，已知点A 1（a ，1）在直线l ：上，以点A 1为圆心，以为半径画弧，交x 轴于点B 1、B 2，过点B 2作A 1B 1的平行线交直线l 于点A 2，在x 轴上取一点B 3，使得A 2B 3=A 2B 2，再过点B 3作A 2B 2的平行线交直线l 于点A 3，在x 轴上取一点B 4，使得A 3B 4=A 3B 3，按此规律继续作下去，则①a= _________ ；②△A 4B 4B 5的面积是 _________ ．24．（2013?松北区二模）如图，以Rt△ABC 的斜边BC 为一边在△ABC 的同侧作正方形BCEF ，设正方形的中心为O ，连接AO ，如果AB=4，AO=6，那么AC 的长等于 _________ ．25．（2007?淄川区二模）如图，将矩形ABCD 的四个角向内折起，恰好拼成一个既无缝隙又无重叠的四边形EFGH ，若EH=3，EF=4，那么线段AD 与AB 的比等于 _________ ．26．（2009?泰兴市模拟）梯形ABCD中AB∥CD，∠ADC+∠BCD=90°，以AD、AB、BC为斜边向形外作等腰直角三角形，其面积分别是S1、S2、S3且S1+S3=4S2，则CD=_________ AB．27．如图，观察图中菱形的个数：图1中有1个菱形，图2中有5个菱形，图3中有14个菱形，图4中有30个菱形…，则第6个图中菱形的个数是_________ 个．28．（2012?贵港一模）如图，E、F分别是平行四边形ABCD的边AB、CD上的点，AF与DE相交于点P，BF与CE相交于点Q，若S△APD =15cm2，S△BQC=25cm2，则阴影部分的面积为_________ cm2．29．（2012?天津）如图，已知正方形ABCD的边长为1，以顶点A、B为圆心，1为半径的两弧交于点E，以顶点C、D为圆心，1为半径的两弧交于点F，则EF的长为_________ ．30．如图，ABCD是凸四边形，AB=2，BC=4，CD=7，求线段AD的取值范围（）．。