高考小题狂练一(附详细答案)
2021届高三数学新高考小题狂练(1)(答案解析)

2021届新高考小题狂练(1)-答案解析一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 【答案】B 【解析】{}2,3,5A =,{}2,5U B =,则{}2,5U A B ⋂=(),故选B.考点:本题主要考查集合的交集与补集运算. 2. 【答案】C 【解析】试题分析:特称命题的否定是全称命题,并将结论加以否定,所以命题的否定为:(0,)x ∀∈+∞,ln 1x x ≠- 考点:全称命题与特称命题 3. 【答案】C 【解析】分析:利用复数的除法运算法则:分子、分母同乘以分母的共轭复数,化简复数z ,然后求解复数的模.详解:()()()()1i 1i 1i2i 2i 1i 1i 1i z ---=+=++-+ i 2i i =-+=:则1z =:故选c.点睛:复数是高考中的必考知识,主要考查复数的概念及复数的运算.要注意对实部、虚部的理解,掌握纯虚数、共轭复数这些重要概念,复数的运算主要考查除法运算,通过分母实数化转化为复数的乘法,运算时特别要注意多项式相乘后的化简,防止简单问题出错,造成不必要的失分. 4. 【答案】C 【解析】二项式()1nx +的展开式的通项是1C r rr n x +T =,令2r得2x 的系数是2C n ,因为2x 的系数为15,所以2C 15n =,即,解得:6n =或5n =-,因为n +∈N ,所以6n =,故选C .【考点定位】二项式定理.5. 【答案】B 【解析】试题分析:设BA a =,BC b =,∴11()22DE AC b a ==-,33()24DF DE b a ==-, 1353()2444AF AD DF a b a a b =+=-+-=-+,∴25353144848AF BC a b b ⋅=-⋅+=-+=.【考点】向量数量积【名师点睛】研究向量的数量积问题,一般有两个思路,一是建立直角坐标系,利用坐标研究向量数量积;二是利用一组基底表示所有向量,两种实质相同,坐标法更易理解和化简. 平面向量的坐标运算的引入为向量提供了新的语言——“坐标语言”,实质是将“形”化为“数”.向量的坐标运算,使得向量的线性运算都可用坐标来进行,实现了向量运算完全代数化,将数与形紧密结合起来. 6. 【答案】A 【解析】分析:先求出A:B 两点坐标得到AB ,再计算圆心到直线距离,得到点P 到直线距离范围,由面积公式计算即可详解: 直线x y 20++=分别与x 轴:y 轴交于A :B 两点()()A 2,0,B 0,2∴--,则AB =点P圆22x 22y -+=()上∴圆心为(2:0),则圆心到直线距离1d ==故点P 到直线x y 20++=的距离2d 的范围为则[]2212,62ABPSAB d ==∈ 故答案选A.点睛:本题主要考查直线与圆,考查了点到直线的距离公式,三角形的面积公式,属于中档题. 7.【答案】C 【解析】分析:首先根据g :x )存在2个零点,得到方程()0f x x a ++=有两个解:将其转化为()f x x a =--有两个解,即直线y x a =--与曲线()y f x =有两个交点,根据题中所给函数解析式,画出函数()f x 的图像(将(0)x e x >去掉),再画出直线y x =-:并将其上下移动,从图中可以发现,当1a -≤时:满足y x a=--与曲线()y f x =有两个交点,从而求得结果.详解:画出函数()f x 的图像,xy e =在y 轴右侧的去掉,再画出直线y x =-:之后上下移动,可以发现当直线过点A 时,直线与函数图像有两个交点,并且向下可以无限移动,都可以保证直线与函数的图像有两个交点, 即方程()f x x a =--有两个解, 也就是函数()g x 有两个零点, 此时满足1a -≤:即1a ≥-:故选C.点睛:该题考查的是有关已知函数零点个数求有关参数的取值范围问题,在求解的过程中,解题的思路是将函数零点个数问题转化为方程解的个数问题,将式子移项变形,转化为两条曲线交点的问题,画出函数的图像以及相应的直线,在直线移动的过程中,利用数形结合思想,求得相应的结果. 8. 【答案】D 【解析】 【分析】先证得PB ⊥平面PAC ,再求得PA PB PC ===P ABC -为正方体一部分,进而知正方体的体对角线即为球直径,从而得解. 【详解】解法一:,PA PB PC ABC ==∆为边长为2的等边三角形,P ABC ∴-为正三棱锥,PB AC ∴⊥,又E ,F 分别为PA 、AB 中点, //EF PB ∴,EF AC ∴⊥,又EF CE ⊥,,CEAC C EF =∴⊥平面PAC ,PB ⊥平面PAC ,APB PA PB PC ∴∠=90︒,∴===,P ABC ∴-为正方体一部分,2R ==3442338R V R =∴=π=⨯=π,故选D .解法二:设2PA PB PC x ===,,E F 分别为,PA AB 中点,//EF PB ∴,且12EF PB x ==,ABC ∆为边长为2的等边三角形,CF ∴=又90CEF ∠=︒1,2CE AE PA x ∴===AEC ∆中余弦定理()2243cos 22x x EAC x+--∠=⨯⨯,作PD AC ⊥于D ,PA PC =,D 为AC 中点,1cos 2AD EAC PA x ∠==,2243142x x x x +-+∴=,22121222x x x ∴+=∴==,PA PB PC ∴===,又===2AB BC AC ,,,PA PB PC ∴两两垂直,2R ∴==2R ∴=,344338V R ∴=π=π⨯=,故选D . 【点睛】本题考查学生空间想象能力,补体法解决外接球问题.可通过线面垂直定理,得到三棱两两互相垂直关系,快速得到侧棱长,进而补体成正方体解决.二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.9. 【答案】ABD 【分析】观察折线图,掌握折线图所表达的正确信息,逐一判断各选项.【详解】由2017年1月至2019年12月期间月接待游客量的折线图得: 在A 中,年接待游客量虽然逐月波动,但总体上逐年增加,故A 正确; 在B 中,各年的月接待游客量高峰期都在8月,故B 正确;在C 中,2017年1月至12月月接待游客量的中位数小于30,故C 错误;在D 中,各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳,故D 正确. 故选:ABD【点睛】本题主要考查学生对于折线图的理解能力,考查图表的识图能力,属于基础题. 10. 【答案】ABD 【解析】 【分析】对各选项逐一作出正确的判断即可.【详解】可证AC ⊥平面11D DBB ,从而AC BE ⊥,故A 正确;由11//B D 平面ABCD ,可知//EF 平面ABCD ,B 也正确;连结BD 交AC 于O ,则AO 为三棱锥A BEF -的高,1111224BEF S =⨯⨯=△,三棱锥A BEF -的体积为1134224⨯⨯=D 正确;很显然,点A 和点B 到的EF 距离是不相等的,C 错误. 故选:ABD【点睛】本题主要考查空间线、面的位置关系及空间几何体的体积与面积,属于中档题. 11. 【答案】AC【解析】 【分析】对各选项逐一作出正确的判断即可. 【详解】如图:对于A 选项,经计算显然正确;对于B 选项,0m =时,可以得出3AFE π∠=,当1m =时,4AFE π∠<,根据对称性,存在m 使FAB 为直角三角形,故B 错误;对于C 选项,根据椭圆对称性可知,当0m =时,四边形FBEA 面积最大,故C 正确; 对于D 选项, 由椭圆的定义得:FAB 的周长(2)(2)4AB AF BF AB a AE a BE a AB AE BE =++=+-+-=+--;∵AE BE AB +≥;∴0AB AE BE --≤,当AB 过点E 时取等号; ∴44AB AF BF a AB AE BE a ++=+--≤; 即直线x m =过椭圆的右焦点E 时,FAB 的周长最大;此时直线1x m c ===;但11m -<<,所以不存在m ,使FAB 的周长最大.故D 错误.故选:AC【点睛】本题主要考查了椭圆的定义及几何性质,考查学生识图能力,属于中档题. 12. 【答案】AB 【解析】 【分析】根据题意,对各选项逐一作出正确的判断即可.【详解】对于A 选项,反例2,13()10,3x x f x x ⎧≤<=⎨=⎩,此函数满足性质P 但不连续,故A 错误;对于B 选项,()f x x =-具有该性质,但是22()f x x =-不具有该性质,故B 错误;对于C 选项,由性质P 得,()(4)2(2)2f x f x f +-≥=,且()1f x ≤,(4)1f x -≤, 故()1f x =,故C 正确;对于D 选项,121234342314++221()=()()()42222x x x x x x x x x x x x f f f f ++++++⎡⎤≤+⎢⎥⎣⎦[]12341()()()()4f x f x f x f x ≤+++,故D 正确. 故选:AB【点睛】本题主要考查函数的概念,函数的性质,考查学生分析能力,推理判断能力,属于中档题.三、填空题:本题共4小题,每小题5分,共20分.13. 【答案】16 【解析】 分析】首先想到所选的人中没有女生,有多少种选法,再者需要确定从6人中任选3人的选法种数,之后应用减法运算,求得结果.【详解】根据题意:没有女生入选有344C =种选法,从6名学生中任意选3人有3620C =种选法,故至少有1位女生入选,则不同的选法共有20416-=种,故答案是16.【点睛】该题是一道关于组合计数的题目,并且在涉及到“至多、至少”问题时多采用间接法,一般方法是得出选3人的选法种数,间接法就是利用总的减去没有女生的选法种数,该题还可以用直接法,分别求出有1名女生和有两名女生分别有多少种选法,之后用加法运算求解.14. 【答案】14【解析】 【分析】由题意首先求得3a b -的值,然后结合均值不等式的结论整理计算即可求得最终结果,注意等号成立的条件.详解】由360a b -+=可知36a b -=-:且:312228aa b b -+=+,因为对于任意x :20x >恒成立,结合均值不等式的结论可得:3122224ab-+≥==.当且仅当32236a b a b -⎧=⎨-=-⎩,即31a b =-⎧⎨=⎩时等号成立.【综上可得128ab +的最小值为14. 【点睛】在应用基本不等式求最值时,要把握不等式成立的三个条件,就是“一正——各项均为正;二定——积或和为定值;三相等——等号能否取得”,若忽略了某个条件,就会出现错误.15.【答案】 (1). 1- (2). 2【解析】分析:由正六边形性质得渐近线的倾斜角,解得双曲线中22,m n 关系,即得双曲线N 的离心率:由正六边形性质得椭圆上一点到两焦点距离之和为c +,再根据椭圆定义得2c a +=:解得椭圆M 的离心率.详解:由正六边形性质得椭圆上一点到两焦点距离之和为c +,再根据椭圆定义得2c a +=,所以椭圆M 的离心率为1.c a == 双曲线N 的渐近线方程为n y x m =±:由题意得双曲线N 的一条渐近线的倾斜角为222ππtan 333n m ∴==,:222222234 2.m n m m e e m m ++∴===∴=,点睛:解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于,,a b c 的方程或不等式,再根据,,a b c 的关系消掉b 得到,a c 的关系式,而建立关于,,a b c 的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.16.【答案】 【解析】分析:首先对函数进行求导,化简求得()()1'4cos 1cos 2f x x x ⎛⎫=+-⎪⎝⎭,从而确定出函数的单调区间,减区间为()52,233k k k Z ππππ⎡⎤--∈⎢⎥⎣⎦,增区间为()2,233k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦,确定出函数的最小值点,从而求得sin 22x x =-=-代入求得函数的最小值. 详解:()()21'2cos 2cos24cos 2cos 24cos 1cos 2f x x x x x x x ⎛⎫=+=+-=+- ⎪⎝⎭,所以当1cos 2x <时函数单调减,当1cos 2x >时函数单调增,从而得到函数的减区间为()52,233k k k Z ππππ⎡⎤--∈⎢⎥⎣⎦,函数的增区间为()2,233k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦,所以当2,3x k k Z ππ=-∈时,函数()f x 取得最小值,此时sin x x ==,所以()min 2f x ⎛=⨯= ⎝⎭,故答案是. 点睛:该题考查的是有关应用导数研究函数的最小值问题,在求解的过程中,需要明确相关的函数的求导公式,需要明白导数的符号与函数的单调性的关系,确定出函数的单调增区间和单调减区间,进而求得函数的最小值点,从而求得相应的三角函数值,代入求得函数的最小值.。
高考生物小题狂练一刻钟1 新冠病毒

高考生物小题狂练一刻钟1 新冠病毒(时间:15分钟)1.(2021·河北石家庄市质检)新型冠状病毒引发的新冠肺炎,严重危害人类健康。
在党中央领导下,我国迅速控制住了疫情。
目前,我国科学家已成功研制出多种疫苗。
下列相关叙述错误的是()A.从生命系统视角来看,病毒不属于任何结构层次B.新型冠状病毒仅含有核糖体这一种细胞器C.阻断病毒的传播可降低该病的发病率D.用咽拭子检测新型冠状病毒利用了核酸分子具有特异性的原理答案B解析细胞是生命系统最基本的结构层次,病毒无细胞结构,不属于任何结构层次,A正确;新型冠状病毒无细胞结构,不含核糖体,B错误;由新型冠状病毒引起的肺炎属于传染病,该病主要通过飞沫、接触等进行传播,阻断病毒的传播可以降低该病的发病率,C正确;用咽拭子检测新型冠状病毒利用了核酸分子具有特异性的原理,D正确。
2.(2021·河南名校联盟)针对新冠病毒的检测方式,除了核酸检测外,还有间接检测。
目前间接检测最常见的就是对IgG和IgM抗体的检测。
IgM抗体是人体感染病毒后最早出现的抗体,疾病康复后很快消失。
IgG抗体是具有保护性的抗体,感染病毒后2周开始产生,持续时间较长,有可能终生携带,表示已经感染过病毒。
下列有关叙述错误的是()A.组成新冠病毒的核酸彻底水解的产物有6种B.浆细胞产生抗体消灭新冠病毒属于免疫系统的防御功能C.若待测者IgM和IgG抗体检测均为阳性,表示新近感染过病毒,体内还有病毒D.若待测者IgG检测为阳性,表示体内含有新冠病毒,IgG抗体越多体内新冠病毒也越多答案D解析新冠病毒为RNA病毒,RNA彻底水解后产物有6种,A正确;免疫系统消灭新冠病毒属于人体的防御功能,B正确;IgM抗体是人体感染病毒后最早出现的抗体,疾病康复后很快消失,IgG抗体是具有保护性的抗体,感染病毒后2周开始产生,持续时间较长,有可能终生携带,若待测者IgM和IgG抗体检测均为阳性,表示新近感染过,体内还有病毒,C正确,D错误。
高考语文一轮总复习 小题狂练 第一周 小题天天练1(含解析)

小题天天练1一、语言文字运用(20分)阅读下面的文字,完成1~3题。
红红绿绿的“舞台”上正演着《霸王别姬》,那条紫色灯芯绒做的条幅上有几个黄色大字“横山县艺术剧团”。
寒酸的横标________地耷拉着,天太热了。
那个舞台还叫舞台吗?薄薄的一层土上铺着一些高粱秆,演员在台上深一脚浅一脚,上来下去,可真难为他们了。
我看到三伏天里,“霸王”“虞姬”穿的都是露胳肢窝的戏装,可这并没有影响他们________的演出。
我看了兵败如山倒的霸王退到乌江边,以及虞姬自刎的那一场戏。
本来秦腔的做派、唱腔就有一股豪中有悲、________之势。
霸王一上场,“哇呀呀”一声吼,见到虞姬,三步并作两步弯腰将她托起,仰天长啸,( )。
他抓住虞姬的乌丝往嘴里一叼,左腿一抬;金鸡独立……我顿时感到一股英雄气概,没想到“力拔山兮气盖世”的楚霸王也有这样落魄的一天。
但见他把头一扭,大吼一声向前冲去,自刎于滚滚乌江边,千古英雄就这么与美人同归于尽……我见到过各个剧种对霸王与虞姬永诀的艺术处理,都没有他们处理得那么悲怆。
我在这小小的山洼里竟找到创作的源泉,是现今艺术家还未开垦的处女地,即便我有八张嘴也讲不完对这几千年丰富文化积淀的感受。
演出结束后,我们赶紧去了“后台”。
我看到化着简单妆容的“演员”,千金不卖的破烂戏服和没了盖的道具箱。
我拉着“霸王”,对他说:“我们是来学习的,您一定要________……”1.文中画横线的句子有语病,下列修改最恰当的一项是(3分)( )A.我在这小小的山洼里竟找到创作的源泉,这里是现今艺术家还未开垦的处女地,即便我有八张嘴也讲不完对这几千年丰富文化积淀的感受。
B.我在这小小的山洼里竟找到创作的源泉,是现今艺术家的处女地,即便我有八张嘴也讲不完对这几千年丰富文化积淀的感受。
C.在这小小的山洼里,我竟找到创作的源泉,是现今艺术家的处女地,即便我有八张嘴也讲不完对这几千年丰富文化积淀的感受。
D.我在这小小的山洼里竟找到创作的源泉,这里是现今艺术家的处女地,即便我有八张嘴也讲不完对这几千年丰富文化积淀的感受。
高中小题狂练试题及答案

高中小题狂练试题及答案一、选择题1. 根据题目分析,下列哪个选项是正确的?A. 地球是平的B. 光速是可变的C. 氧气是可燃的D. 水在标准大气压下沸点是100℃答案:D2. 以下哪个历史事件标志着中国近代史的开端?A. 鸦片战争B. 甲午战争C. 辛亥革命D. 五四运动答案:A3. 在数学中,下列哪个表达式表示的是二次方程?A. \( x + 2 = 0 \)B. \( x^2 + 3x + 2 = 0 \)C. \( x^3 - 5x^2 + 6x = 0 \)D. \( 2x - 1 \)答案:B二、填空题4. 根据题目所给信息,中国最大的淡水湖是________。
答案:鄱阳湖5. 在化学中,元素周期表的第1族元素被称为________。
答案:碱金属6. 根据题目所给信息,下列哪个方程式表示的是光合作用?\( 6CO_2 + 6H_2O + \text{光能} \rightarrow \text{有机物} + 6O_2 \)答案:正确三、简答题7. 请简述牛顿第三定律的内容。
答案:牛顿第三定律,也称为作用与反作用定律,指出:对于任何两个相互作用的物体,它们之间的作用力和反作用力总是大小相等、方向相反。
8. 请解释什么是温室效应,并简述其对环境可能造成的影响。
答案:温室效应是指地球大气层中的某些气体(如二氧化碳、甲烷等)能够吸收和重新辐射地表反射的太阳辐射,导致地球表面温度升高的现象。
温室效应可能导致全球气候变暖,极端天气事件增多,海平面上升,生态系统受到影响等。
四、计算题9. 已知一个物体的质量为5千克,受到的重力加速度为9.8米/秒²,求该物体受到的重力大小。
答案:物体受到的重力大小可以通过公式 \( F = m \times g \) 计算,其中 \( m \) 是质量,\( g \) 是重力加速度。
所以,\( F = 5 \times 9.8 = 49 \) 牛顿。
结束语:本试题及答案涵盖了高中阶段的多个学科,旨在帮助学生巩固基础知识,提高解题能力。
2025年高考生物复习之小题狂练300题(解答题):植物生命活动的调节(10题)

2025年高考生物复习之小题狂练300题(解答题):植物生命活动的调节(10题)一.解答题(共10小题)1.水杨酸是一种小分子酚类化合物,为探究水杨酸对植物根生长的影响,科研人员取适量品质均一的油菜种子,播到含不同浓度的水杨酸的培养基上培养,种子发芽13d后对油菜幼根的侧根数目和主根长度分别进行计数,结果如下表。
测定项目水杨酸浓度/(μmol•L﹣1)00.080.40 2.0010.00侧根数目(条)15.7016.7021.3016.6210.33主根长度13.6512.6911.719.017.48(cm)回答下列问题:(1)植物激素作为参与调节植物的生命活动。
基于以上信息,还需确认,可初步判断水杨酸也属于植物激素。
(2)据表分析可得:①水杨酸对油菜侧根发生的影响为;②主根处理组中出现,表明一定浓度范围内,水杨酸对主根伸长的抑制作用随浓度增加而增强。
(3)有研究发现,水杨酸对主根伸长的抑制作用会随着主根生长时间的延长而减弱。
在上述实验基础上设计实验进行验证,实验思路是,预期实验结果是。
(4)植物根的生长还受等环境因素的调节(至少答出2点)。
2.光敏色素是一类能接受光信号的分子,主要吸收红光和远红光,具有非活化态(Pr)和活化态(Pfr)两种类型。
农田中玉米—大豆间作时,高位作物(玉米)对低位作物(大豆)具有遮阴作用,严重时引发“荫蔽胁迫”,此时,低位植物体内的光敏色素及多种激素共同响应荫蔽胁迫。
请回答下列问题。
(1)光敏色素是一类(化学本质)。
在不同的光照条件下,光敏色素接受光信号后,会经过信息传递系统传导至细胞核内,影响,从而表现出生物学效应。
(2)自然光被植物滤过后,其中红光(R)/远红光(FR)的值会下降,原因是。
发生荫蔽胁迫时,低位植物体内的光敏色素主要以形式存在。
此形式的光敏色素可(选填“减弱”或“增强”)对光敏色素互作因子(PIFs)的抑制作用,有利于多种激素共同响应荫蔽胁迫。
2020届高考英语小题狂练1:时态、语态及主谓一致单句填空+语法填空

2020届高考英语小题狂练1:时态、语态及主谓一致单句填空+语法填空技巧点拨当句子缺少谓语动词时,括号中的动词就是谓语动词。
此时,要根据语境确定用哪种时态,根据主语与该动词的主动或被动关系确定用主动语态还是用被动语态。
具体解题技巧如下:第一步:确定句中是否缺谓语或并列谓语,如缺谓语动词,则填谓语动词。
第二步:根据语境确定时态。
第三步:观察主语与谓语之间是主动关系还是被动关系,以确定用主动语态还是被动语态,同时还要根据语境考虑用哪种时态。
第四步:要注意主谓一致。
常考考点小题狂练1.【2019·全国I卷】Of the nineteen recognized polar bear subpopulations, three are declining, six ______ (be) stable, one is increasing, and nine lack enough data.2.【2019·全国I卷】In recent years some Inuit people in Nunayut ______ (report) increases in bear sightings around human settlements3.【2019·全国 II卷】I love coming here and seeing my family and all the friends I ______(make) over the years.4.【2019·浙江卷】When every pupil in the school wears the uniform, nobody_____ (have) to worry about fashion(时尚).5.【2019·浙江卷】 One study in America found that students' grades ______ (improve) a little after the school introduced uniforms.6. 【2018·全国卷I I】Diets have changed in China — and so too has its top crop. Since 2011,the country _____(grow)more corn than rice.7. In US high school, everything (record) and graded, including your grades on quizzes, tests and final examinations.8. As you go through this book, you ________ (find) that each of the millions of people who lived through World War II had a different experience.9. Just as I got to the school gate, I realized I ________ (leave) my book in the cafe.10. Shirley ________ (write) a book about China last year but I don’t know whether she has finished it.11. It was the second time that we _____ (see) her.12. Either the beautiful sights of this modern city or its local custom____ (attract) thousands of visitors during the past years.13. At this time tomorrow we_________ _ (fly) over the Atlantic Ocean.14. The father as well as his three children ____________ (go) skating on the frozen river every Sunday afternoon in winter.15. Engineers (set) up over 15,000 sensors (传感器) nationwide and wiring them into a web.16. The treatment continued and finally the deep, bloody pain ______ (be) 100% healed.直击考题passage1“extreme sports”, which we might have seen on a magazine or a website, 1 (be) becoming more and more common as the concept of extreme sports gains 2 (popular). But what are extreme sports on earth?During the 1970s and 1980s, the term was used for sports with high risks 3 (involve). Today, however, the sports also include activities that give a feeling of adventure without 4 (necessary) putting a participant’s life in danger. For every extreme sport, there is professional equipment that has been developed 5 (protect) your body, improve your performance and give you 6 advantage in the competition.Extreme sports cover a wide range. Some 7 (develop) from familiar activities so far, like mountain biking, climbing and drag race. Some may not be well known. For instance, bouldering is a kind of rock climbing 8 no rope is used. 9 usually takes place in an area with large rocks or in climbing center.Nowadays, such sports have become more popular 10 young people all over the world than ever before.passage2medieval cathedral of Notre-Dame in Paris, one of France's 1 (famous) landmarks. Thousands of people gathered in the streets around the cathedral, watching the flames in silence, some of 2 could be seen crying. Watching such a symbol of French culture burnt and its spire destroyed is extremely 3 (shock) to any French person.No other site represents France like Notre-Dame, which 4 (receive) almost 13 million visitors each year, more than the Eiffel Tower. The Eiffel Tower, is a little more than a century old 5 Notre-Dame has stood tall above Paris 6 1200s. It has given its name to one of the country’s literal 7 (masterpiece). Victor Hugo's The Hunchback of Notre-Dame is known 8 me French simply as Notre-Dame de Paris.The three large rose windows 9 (destroy) by the fire. 10 (fortunate), the main structure, including the two bell towers, has been saved. Also, the most valuable cultural relics have survived the fire. The last time the cathedral suffered major damage was during the French Revolution. It survived two world wars largely in good condition.passage3【2019-2020年吉林省长春市普通高中高三上学期质量监测(一)】Since July 2019, China’s online food-delivery platform Eleme___1___ (carry) out a new service of picking up garbage from its users in Shanghai.The service comes after___2___recently-released regulation on waste management in Shanghai. Individuals ___3___throw away their garbage without being sorted out can be fined up to 200 yuan, while companies and ___4___ (organize) can face fines up to 50,000 yuan.The trash takeaway service requires residents to sort ___5___ (they) own garbage before it ___6___ (pick) up by workers from Eleme, who will ensure the waste is disposed of in the correct garbage bins.It’s obvious that this service is ___7___ (convenience) to the old, especiallyto the disabled customers. ___8___, many netizens on Sina Weibo don’t think Eleme is providing a wonderful service, saying it just wants ___9___ (make) money. They think 12 yuan for an order is too much. Besides, many more people doubt if these collectors will wash their hands after dealing ___10___the trash.1.【答案】are【解析】考查主谓一致。
近年高考化学一轮优题小狂练(1)(含解析)新人教版(2021年整理)

2019高考化学一轮优题小狂练(1)(含解析)新人教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2019高考化学一轮优题小狂练(1)(含解析)新人教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2019高考化学一轮优题小狂练(1)(含解析)新人教版的全部内容。
人教化学2019高考一轮优题小狂练(1)李仕才一、选择题1、反应Fe(s)+CO2(g)FeO(s)+CO(g),700 ℃时平衡常数为1.47,900 ℃时平衡常数为2。
15。
下列说法正确的是( )A.升高温度该反应的正反应速率增大,逆反应速率减小B.该反应的化学平衡常数表达式为K=错误!C.该反应的正反应是吸热反应D.增大CO2浓度,平衡常数增大解析:A项,升温,正、逆反应速率均增大,不正确;B项,该化学平衡常数表达式为c COc CO2,故不正确;C项,升温,平衡常数增大,表明平衡向正反应方向移动,即正反应为吸热反应, 故正确;D项,增大反应物浓度,平衡常数不变,故不正确.答案:C2、一定温度下,在一个容积为1 L的密闭容器中,充入1 mol H2(g)和1 mol I2(g),发生反应H2(g)+I2(g)2HI(g),经充分反应达到平衡后,生成的HI(g)占气体体积的50%,该温度下,在另一个容积为2 L的密闭容器中充入1 mol HI(g)发生反应HI(g)错误!H2(g)+错误!I2(g),则下列判断正确的是( ) A.后一反应的平衡常数为1B.后一反应的平衡常数为0。
5C.后一反应达到平衡时,H2的平衡浓度为0.25 mol·L-1D.后一反应达到平衡时,HI(g)的平衡浓度为0.5 mol·L-1解析:前一反应达到平衡时c(H2)=c(I2)=0。
2025年高考地理复习之小题狂练300题(解答题):农业(10题)

2025年高考地理复习之小题狂练300题(解答题):农业(10题)一.解答题(共10小题)1.(2024•安徽)阅读图文材料,完成下列要求。
佛手为热带、亚热带植物,具有药用、食用和观赏价值。
喜暖湿,适合在土层深厚、疏松肥沃、排水良好的土壤中生长。
绿化村位于四川省乐山市沙湾区,喀斯特地貌广布。
近年来,绿化村采取了“土地流转+优先雇用+分红”的模式进行佛手种植,石缝里长出了“金果果”,“石缝经济”得到大力发展(如图),昔日“石山”变“青山”进而变“金山”,走出了一条山区发展富民产业的乡村振兴之路。
(1)分析该地佛手种植的限制性自然条件,并提出相应的治理工程措施。
(2)分析“土地流转+优先雇用+分红”模式对该地佛手种植业发展的重要作用。
(3)为进一步促进“石山”变“青山”进而变“金山”,从产业关联的视角为该地佛手产业发展提出建议。
2.(2024•选择性)阅读文字材料,完成下列要求。
山西省偏关县地处黄土高原沟壑丘陵区,沟壑占全县总面积的47.8%。
经近50年综合治理,全县绿化率由4%增加到40%。
2019年,国家实施黄河流域生态保护和高质量发展战略,偏关县坚持生态优先、绿色发展,推广优质杂粮种植,建设“非笼养”蛋鸡养殖基地,不断扩大养殖规模,并积极开拓国际市场。
“非笼养”蛋鸡养殖采用清洁化生产方式和国际先进的健康养殖技术,创造优良的养殖环境,满足消费者对产品质量和安全的需求。
产品健康、安全、可追溯,主要供给知名餐饮企业,现已获得“非笼养”国际标识许可和出口备案审核。
(1)简述偏关县发展“非笼养”蛋鸡养殖的优势条件。
(2)分析市场因素对偏关县“非笼养”蛋鸡养殖发展的影响。
(3)说明“非笼养”蛋鸡养殖对偏关县绿色发展的积极作用。
3.(2024•贵港二模)阅读图文材料,完成下列要求。
张掖位于甘肃省河西走廊中段,南靠青藏高原,北依巴丹吉林沙漠,黑河贯穿全境。
黑河从祁连山北麓奔腾而下形成了冲积扇,当地聚落多分布在祁连山山前冲积扇上。
2025年高考物理复习之小题狂练600题(解答题):机械波(10题)
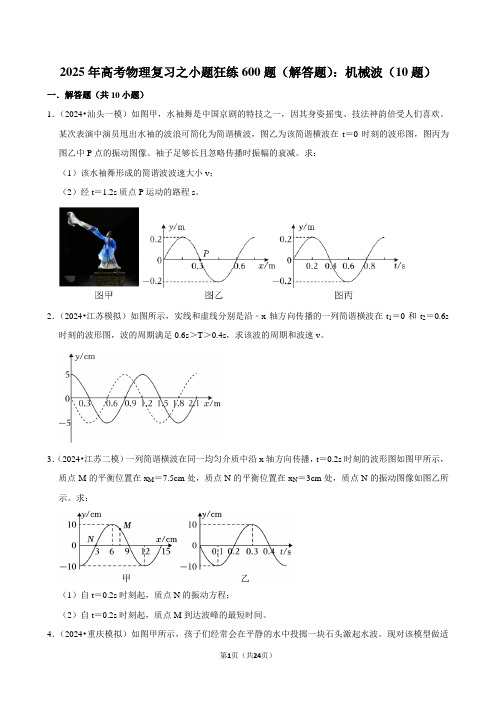
2025年高考物理复习之小题狂练600题(解答题):机械波(10题)一.解答题(共10小题)1.(2024•汕头一模)如图甲,水袖舞是中国京剧的特技之一,因其身姿摇曳、技法神韵倍受人们喜欢。
某次表演中演员甩出水袖的波浪可简化为简谐横波,图乙为该简谐横波在t=0时刻的波形图,图丙为图乙中P点的振动图像。
袖子足够长且忽略传播时振幅的衰减。
求:(1)该水袖舞形成的简谐波波速大小v;(2)经t=1.2s质点P运动的路程s。
2.(2024•江苏模拟)如图所示,实线和虚线分别是沿﹣x轴方向传播的一列简谐横波在t1=0和t2=0.6s 时刻的波形图,波的周期满足0.6s>T>0.4s,求该波的周期和波速v。
3.(2024•江苏二模)一列简谐横波在同一均匀介质中沿x轴方向传播,t=0.2s时刻的波形图如图甲所示,质点M的平衡位置在x M=7.5cm处,质点N的平衡位置在x N=3cm处,质点N的振动图像如图乙所示。
求:(1)自t=0.2s时刻起,质点N的振动方程;(2)自t=0.2s时刻起,质点M到达波峰的最短时间。
4.(2024•重庆模拟)如图甲所示,孩子们经常会在平静的水中投掷一块石头激起水波。
现对该模型做适当简化,若小孩将小石头垂直于水面投入水中,以小石头入水点为坐标原点O,以此为计时起点,沿波传播的某个方向建立O﹣x坐标轴,在x轴上离O点不远处有一片小树叶,若水波为简谐横波,如图乙所示t=0.6s时的波动图像,图丙为小树叶的部分振动图像。
(1)请判断小树叶位于P、Q两点中的哪一点?并写出合理的解释;(2)波源的振动形式第一次传到P点需要的时间;(3)求质点P在小石头入水后0.6s内运动的总路程。
5.(2024•盐城模拟)如图甲所示,两振动情况相同的波源M、N相距0.5m,波源激起的横波波长为0.4m,其振动图像如图乙所示,求:(1)波的传播速度大小v;(2)M、N连线间振动加强点的位置。
6.(2024•黑龙江三模)一列简谐横波沿x轴正方向传播,波源位于坐标原点处,t=0时波源沿y轴负方向起振,t1=2.5s时的波形如图所示。
2020届高三高考化学一轮复习小题狂练《物质及其变化》含答案及详细解析

绝密★启用前2020届高三高考化学一轮复习小题狂练《物质及其变化》1.在含有I-且能使甲基橙试液变红的溶液中能大量共存的离子组为()A. Fe3+、Na+、Br-B. NH、Na+、AlOC. Ba2+、Al3+、Cl-D. K+、MnO、NO2.下列反应的离子方程式书写正确的是()A.将Al条投入NaOH溶液中:Al+OH-+H2O===AlO+H2↑B.铜溶于稀硝酸中:Cu+4H++2NO===Cu2++2NO2↑+2H2OC.碳酸氢钙溶液中加入过量的氢氧化钠溶液:HCO+OH-===CO+H2OD.向碳酸钠溶液中逐滴加入与之等体积等物质的量浓度的稀醋酸:CO+CH3COOH===CH3COO-+HCO3.下列有关化学用语使用正确的是()A. Ca2+的电子式:B.12C的原子结构示意图:C. NH的结构式:D.甲烷分子的球棍模型:4.下列各项表述正确的是()A.羟基的电子式B.醛基官能团符号-COHC.乙醇的分子式:CH3CH2OHD.异丁烷的结构简式:CH3CH(CH3)CH35.SO2气体与足量Fe2(SO4)3溶液完全反应后,再加入K2Cr2O7溶液,发生如下两个化学反应:①SO2+2Fe3++2H2O===SO+2Fe2++4H+;②Cr2O+6Fe2++14H+===2Cr3++6Fe3++7H2O。
下列有关说法不正确的是()A. SO2发生氧化反应B.氧化性:Cr2O>Fe3+> SOC.每1 mol K2Cr2O7参加反应,转移电子的数目为6N AD.若有6.72 L SO2(标准状况)参加反应,则最终消耗0.2 mol K2Cr2O76.下列关于胶体的说法不正确的是()A.可用渗析法提纯胶体B.胶体、溶液和浊液这三种分散系的根本区别是分散质粒子直径的大小C.胶体微粒不能透过滤纸D.往25 mL沸水中逐滴加入1~2 mL FeCl3饱和溶液,继续煮沸可制得Fe(OH)3胶体7.在酸性高锰酸钾溶液中加入过氧化钠粉末,溶液褪色,其中发生反应的离子方程式为:2MnO +16H++5Na2O2===2Mn2++5O2↑+8H2O+10Na+。
2025年高考生物复习之小题狂练300题(解答题):遗传的基本规律(10题)

2025年高考生物复习之小题狂练300题(解答题):遗传的基本规律(10题)一.解答题(共10小题)1.家兔的毛色有野鼠色、黑色和褐色之分,受常染色体上两对等位基因共同控制。
D、d为控制颜色的基因,D基因控制黑色,d基因控制褐色;E、e为控制颜色分布的基因,E基因控制颜色分布不均匀,体色均为野鼠色,e基因控制颜色分布均匀,体色表现为相应颜色。
研究人员利用不同毛色的纯种家兔进行了杂交实验,结果如图。
回答下列问题:(1)基因D、d和E、e的遗传遵循定律,野鼠色兔的基因型有种。
(2)实验一中,F1野鼠色兔的基因型为,F2野鼠色兔与褐色兔杂交,其后代表型及比例为。
(3)实验二中,F2野鼠色兔中性状能稳定遗传的个体占。
若实验一F2中一只野鼠色雄兔和实验二F2中一只野鼠色雌兔杂交,后代中为野鼠色兔的概率为。
(4)研究发现,在实验二F2黑色兔群体中偶然出现一只灰色可育突变雄兔,经检测,其基因型为DdeeGg,G基因会影响D和d的表达,导致家兔黑色或褐色淡化为灰色或黄色。
为探究D、d和G、g 在染色体上的位置关系,科研人员让该雄兔与多只褐色雌兔杂交,观察并统计后代的表型及比例。
①若后代出现:,则两对基因位于两对同源染色体上。
②若后代出现:黑色兔与黄色兔数量比接近1:1,则该突变雄兔细胞中D、d和G、g在染色体上的位置关系(不考虑互换)。
2.某昆虫的体色由位于3号染色体(常染色体)上的一组复等位基因B+(黑色)、B(红色)、b(棕色)控制(复等位基因的显隐性关系是B+>B>b),只有常染色体另一基因E存在时,上述体色才能表现,否则表现为灰色。
含有B+的雌配子致死。
不考虑基因突变和其他变异。
请回答下列问题:(1)复等位基因B+、B、b的出现是的结果,若控制体色的基因符合自由组合定律,从基因的位置分析,需满足的条件是。
(2)该昆虫种群中,体色为黑色个体的基因型有种。
现有一只雄性黑色昆虫与一只雌性灰色昆虫杂交,F1中只有黑色、红色、棕色三种体色的个体,则亲本的基因型为。
2025年高考地理复习之小题狂练300题(选择题):自然灾害(10题)

2025年高考地理复习之小题狂练300题(选择题):自然灾害(10题)一.选择题(共10小题)2023年9月,第9号台风苏拉和第11号台风海葵同时登陆,极大地影响了我国南部沿海地区(如图)。
两个台风靠近时,大气旋转会受到彼此影响,呈现彼此接近甚至合并的趋势,称为“双台风效应”。
据此完成1﹣3题。
1.下列不能代表西北太平洋双台风活动形式的是()A.B.C.D.2.“双台风效应”加剧了台风的防御难度,主要原因是()A.台风影响范围变大B.台风风力变大C.台风预报难度增大D.台风降水增多3.动态监测台风“苏拉”移动路径采用的地理信息技术是()①遥感技术②地理信息系统③5G通信技术④全球卫星导航系统A.①②B.③④C.①④D.②③高架雷暴是一种强对流天气,发生时,近地面多为稳定的冷空气层,暖湿气流沿冷空气层上界急剧上升,从而触发雷暴。
美国中南部地区春季高架雷暴频发。
完成4﹣5题。
4.高架雷暴发生时近地面常出现()A.短时强降水B.气温剧烈上升C.气压骤降D.风力减小5.导致美国中南部地区春季高架雷暴频发的因素有()A.地质构造和洋流B.海陆分布和地形C.大气环流和水文D.人类活动和植被“雷打雪”是指因冷暖气团交汇产生强对流天气,并在降雪过程中伴有雷电的天气现象。
2023年12月济南市出现了“雷打雪”现象。
如图示意为济南市12月份气温变化曲线。
据此完成下面小题。
6.依据材料推测济南市出现“雷打雪”现象的时间可能是()A.12月8日B.12月14日C.12月16日D.12月25日澳大利亚是森林火灾多发的国家,近年来频繁的森林火灾不仅烧毁了大片森林、建筑等,而且造成大量动物死亡。
专业机构研究发现:较长时期内,在没有人类活动的干扰下,森林中动物数量和种类保持稳定。
现在澳大利亚政府与民间普遍开始反思林火的消防理念,将重点从灭火转向防控,学习“适应火灾”。
图示意近些年澳大利亚火灾起火点的分布。
据此完成下面小题。
7.受气候影响,8~10月森林火灾发生概率最大的林区是()A.①B.②C.③D.④8.森林中动物数量和种类保持稳定,反映了森林自然环境的()A.生产功能B.适应功能C.保护功能D.稳定功能9.下列措施属于“适应火灾”的是()A.增加专业消防队B.建立视频监控系统C.学习灭火的技术D.购买先进灭火装备环北极地区地跨亚洲、欧洲和北美洲。
2020届高三数学小题狂练试题含答案(共40份)

2020届高三数学小题狂练一姓名 得分1.已知2{230}A x x x =--≤,{}B x x a =<,若A ⊆B ,则实数a 的取值范围是 .2.已知2()|log |f x x =,则=+)23()43(f f .3.若平面向量b 与向量a =(1,2)-的夹角是180o,且|b |=b = .4.已知α,β,γ是三个互不重合的平面,l 是一条直线,给出下列四个命题: ①若αβ⊥,l β⊥,则l ∥α; ②若l α⊥,l ∥β,则βα⊥; ③若l 上有两个点到α的距离相等,则α//l ; ④若αβ⊥,α∥γ,则βγ⊥. 其中正确命题的序号是 .5.设函数()24xf x x =--,0x 是()f x 的一个正数零点,且0(,1)x a a ∈+,其中a ∈N ,则a = .6.已知α为第二象限的角,且53sin =α,则=+)4cos(πα . 7.在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,已知3A π=,3=a ,1=b ,则=c .8.已知函数()cos f x x x =,则'()3f π=_________.9.已知等差数列{n a }中,0n a ≠,若m ∈N ,1m >,2110m m m a a a -+-+=,2138m S -=,则m = .10.若关于x 的方程10kx +=有两个不相等的实数解,则实数k 的取值范围是 .11.设周期函数)(x f 是定义在R 上的奇函数,若)(x f 的最小正周期为3,且2)1(->f ,mm f 3)2(-=,则m 的取值范围是 . 12.分别在区间[1,6]和[2,4]内任取一实数,依次记为m 和n ,则m n >的概率为 .答案 1.(3,)+∞ 2.1 3.(3,6)- 4.②④ 5.26. 7.28.12 9.10 10.1[,0)2-11.)3,0()1,(⋃--∞ 12.352020届高三数学小题狂练二姓名 得分1.已知复数z 满足(2-i)z =5,则z = .2.已知向量24(),a =,11(),b =.若向量()λ⊥b a +b ,则实数λ的值是 . 3.若连续投掷两枚骰子分别得到的点数m ,n 作为点P 的坐标(,)m n ,则点P 落在圆1622=+y x 内的概率为_________.4.已知()f x 是定义在R 上的奇函数,且当0x >时,2()log f x x =,则方程()1f x =的解集是 .5.已知函数3()128f x x x =-+在区间[3,3]-上的最大值与最小值分别为M ,m ,则M m -= .6.若三条直线320x y -+=,230x y ++=,0mx y +=不能构成三角形,则m 的值构成的集合是 .7.由直线1y x =+上的一点向圆22(3)1x y -+=引切线,则切线长的最小值为 . 8.某人5次上班途中所花的时间(单位:分钟)分别为x ,y ,10,11,9,已知这组数据的平均数为10,方差为2,则||x y -的值为 .9.已知(1)(1)()sin 33x x f x ππ++=,则(1)(2)(2015)f f f +++=L .10.数列{}n a 中,11a =,1411++=+n n n a a a = .11.已知点G 是ABC ∆的重心,若120A ∠=︒,2AB AC =-u u u r u u u rg ,则||AG u u u r 的最小值是 .12.双曲线221x y n-=(1n >)的两焦点为1F ,2F ,点P 在双曲线上,且满足12PF PF +=,则12PF F ∆的面积为 .答案1.2+i 2.3- 3.294.{2,-12}5.326.{3-,1-,2} 7.7 8.4 9.010.1276411.23:1()3AG AB AC =+u u ur u u u r u u u r12.1:12PF PF +=1212S PF PF =g ,平方减2020届高三数学小题狂练三姓名 得分1.若12z a i =+,234z i =-,且12z z 为纯虚数,则实数a 的值是 . 2.抛物线2y ax =(a 为非零常数)的准线方程为 .3.设函数()log a f x x =(0a >,1a ≠)满足(9)2f =,则(9)af 的值是 . 4.曲线C :()sin xf x x e =+在0x =处的切线方程为 .5.设n S 是等比数列{}n a 的前n 项和,若3S ,9S ,6S 成等差数列,则数列{}n a 的公比q 为 .6.若a ,b≤m 的最小值是 .7.椭圆22143x y +=的右焦点为F ,点(1,1)A ,点M 是椭圆上的任意一点,则2MA MF +的最小值为 . 8.设x ,y 均为正实数,且312121=+++y x ,则xy 的最小值为 . 9.若直线l 与圆224x y +=相交于11(,)A x y ,22(,)B x y 两点,且12122x x y y +=,则AB = .10.小张、小李、小王三位同学在足球场上做传球训练,规定:持球的任何一人必须将球传给另两位同学中的一人.开始时球在小王脚下,传球4次后,则球仍然回到小王脚下的概率为 .11.已知()f x =||2x x a x -+,若()f x 在R 上恒为增函数,则a 的取值范围是 .12.已知双曲线22221x y a b-=(0a >,0b >)的左、右焦点分别为1F ,2F ,点P 在准线上,且12PF PF ⊥,124PF PF ab =g ,则该双曲线的离心率等于 .答案 1.38 2.14y a=- 3.64.210x y -+=5.2-67.38. 16(去分母)9.2(2OA OB ⋅=u u u r u u u r ,3AOB π∠=)10.38(树状图,616)11.[2,2]-(x a ≥:0x a ≤;x a <:0x a ≥)12(由射影公式得222()a m c c c =+2222c a =+,222()a n c c c=-22b =,代入222216m n a b =)或(2ab h c=,中线PO c =,2222()a h c c =-)2020届高三数学小题狂练四姓名 得分1.若集合2{5,log (3)}A a =+,集合{,}B a b =,{2}A B =I ,则A B U = . 2.若复数2(56)(3)i z m m m =-++-是纯虚数,则实数m = . 3.若10≤≤x ,且21y x -≥,则2z x y =+的最小值为 .4.若函数32()f x ax x x =-+在R 上单调递增,则a 的取值范围是 . 5.在等差数列{}n a 中,638a a a =+,则前9项之和9S = . 6.已知ABC ∆中,2a =,b =45A =︒,则B 等于 .7.曲线sin cos y t x x =+在0=x 处的切线方程为1+=x y ,则=t . 8.曲线C1+=上的点到原点的距离的最小值为_________.9.已知直线l 的倾斜角为︒120,与圆M :0222=-+y y x 交于P ,Q 两点,若0OP OQ ⋅=u u u r u u u r(O 为原点),则l 在x 轴上的截距为 .10.如图,在ABC ∆中,1tan 22C =,0AH BC ⋅=u u u r u u ur ,0)(=+⋅CB CA AB ,则过点C 以A ,H 为两焦点的双曲线的离心率为 .11.在由正整数构成的无穷数列{}n a 中,对任意的正整数n ,都有1n n a a +≤,且对任意的正整数k ,该数列中恰有21k -个k ,则2015a 的值等于 .12.已知函数()f x 满足(2016)1f =,)1(-x f 为奇函数,)1(+x f 为偶函数,则(4)f 的值等于 .BACH答案1.{1,2,5} 2.2 3.1 4.1[,)3+∞ 5.0 6.60°或120° 7.1 8.429y b =+ 10.2 11.4512.1-:(1)(1)f x f x -=---,(1)(1)f x f x -=+,于是()(2)f x f x =---,(2)()f x f x -=,所以(2)(2)f x f x -=---,进而得周期为82020届高三数学小题狂练五姓名 得分1.已知向量(1,3)m →=,(2,1)n a a →=-,若→→⊥n m ,则a = .2.已知7-,1a ,2a ,1-四个实数成等差数列,4-,1b ,2b ,3b ,1-五个实数成等比数列,则212b a a -= . 3.正方体的内切球与其外接球的体积之比为 .4.若以连续掷两次骰子分别得到的点数m ,n 作为点P 的横、纵坐标,则点P 在直线5x y +=下方的概率是 .5.若直线10x my ++=与线段AB 有公共点,其中(2,3)A -,(3,2)B ,则实数m 的取值范围是 .6.若椭圆22221(0)x y a b a b +=>>的离心率为,则双曲线22221y x a b-=的离心率为 .7.设x ,y 为实数,且511213x y i i i+=---,则x y += .8.已知向量a r 与b r 的夹角为120o,||3a =r ,||a b +=r r ||b r = .9.在ABC ∆中,3sin 4cos 6A B +=,3cos 4sin 1A B +=,则C ∠等于 . 10.与直线20x y +-=和曲线221212540x y x y +--+=都相切的半径最小的圆的标准方程是 .11.函数()f x 对于任意x 满足()(2)1f x f x +=,且(1)5f =-,则((5))f f = . 12.已知()f x 是定义在R 上的偶函数,定义在R 上的奇函数()g x 的图象过点(1,1)-且()(1)g x f x =-,则(2015)(2016)f f +=__________.答案 1.3 2.1-3.1∶ 4.165.1[2,]3-6 7.4 8.4 9.6π(若6A B π+=,1sin 2A <,4cos 4B ≤)10.22(2)(2)2x y -+-= 11.15-:1(1)5f -=-12.1-(由()(1)g x f x -=--得()(1)g x f x -=+,故(1)(1)f x f x --=+,于是(4)()f x f x +=,所以(1)(0)(0)(1)f f g g -+=+)2020届高三数学小题狂练六姓名 得分1.设集合{0,1,2}M =,{2,}N x x a a M ==∈,则集合=N M I . 2.已知∈x R ,[]x 表示不大于x 的最大整数,如[]π=3,[]-=-121,[]120=,则使[]x -=13成立的x 的取值范围是 .3.定义在R 上的奇函数)(x f 满足1)2(=f ,且)2()()2(f x f x f +=+,则(1)f = .4.已知ααcos sin 2=,则ααα2cos 12sin 2cos ++的值等于 . 5.若关于x 的不等式2260ax x a -+<的解集为(1,)m ,则实数m = .6.若向量a v ,b v满足||a =v ||1b =v ,()1a a b +=v v vg ,则向量a v ,b v 夹角大小为 .7.若cos 2sin()4απα=-,则cos sin αα+的值为 . 8.化简tan 70cos10tan 702cos 40-oo o o o= . 9.已知0a >且1a ≠,2()xf x x a =-,若当x ∈[1,1]-时均有1()2f x <,则实数a 的范围是 .10.已知正项数列{}n a 的首项11a =,前n 和为n S ,若以(,)n n a S 为坐标的点在曲线1(1)2y x x =+上,则数列{}n a 的通项公式为 . 11.已知02x π<<,且t 是大于0的常数,1()sin 1sin tf x x x=+-的最小值为9,则t = . 12.设()f x 是定义在R 上的函数,且满足(2)(1)()f x f x f x +=+-,如果3(1)lg2f =,(2)lg15f =,则(15)f = .答案 1.}2,0{ 2.[4,5) 3.21 4.3 5.2 6.135︒ 7.128.29.1(,1)(1,2)2U 讨论最大值 10.n a n = 11.412.1((3)()f x f x +=-)2020届高三数学小题狂练七姓名 得分1.若集合{1,1}M =-,11{|242x N x x +=<<∈Z},,则M N =I . 2.已知cos ,0,()(1)1,0,x x f x f x x π≤⎧=⎨-+>⎩则41()()33f f +-的值为 .3.已知()(1)(21)(31)(1)f x x x x x nx =+++⋅⋅⋅+,求=')0(f .4.设O 是ABC ∆内部一点,且2OA OC OB +=-u u u r u u u r u u u r,则AOB ∆与AOC ∆的面积之比为 .5.已知函数2()log 3f x x x =⋅+,直线l 与函数()f x 图象相切于点(1,)A m ,则直线l 的方程的一般式为 .6.扇形OAB 半径为2,圆心角60AOB ∠=︒,点D 是弧AB 的中点,点C 在线段OA 上,且3=OC .则OB CD ⋅的值为 .7.已知0x >,0y >,且211x y+=,若222x y m m +>+恒成立,则实数m 的取值范围是 .8.已知ABC ∆的面积等于3,1BC =,3π=∠B ,则tan C 的值为 .9.如果圆2244100x y x y +---=上至少有三个点到直线l :0ax by +=的距离为l 的倾斜角的取值范围是 .10.若函数)(x f 是定义在(0,+∞)上的增函数,且对一切0x >,0y >满足)()()(y f x f xy f +=,则不等式)4(2)()6(f x f x f <++的解集为 .11.若直线6x π=是函数sin cos y a x b x =+图像的一条对称轴,则直线0ax by c ++=的倾斜角为 . 12.已知正实数x ,y 满足111x y +=,则9411y xx y +--的最小值为 .答案 1.{1}- 2.2 3.1 4.1∶25.(ln 2)3ln 210x y -+-=6.3(CD CO OD =+u u u r u u u r u u u r)7.(4,2)-8.- 9.5[,]1212ππ10.(0,2)11.150°((0)()3f f π=)12.25:令10m x=>,10n y =>,则1m n +=,于是9411y x x y +--49449911m n m nm n n m++=+=+--25≥2020届高三数学小题狂练八姓名 得分1.复数z 满足方程(2)z z i =+,则z = .2.设集合{|}M x x m =≤,{|2}xN y y -==,若M N ⋂≠∅,则实数m 的取值范围是 .3.若函数2()2x x af x a+=-是奇函数,则a = .4.抛物线24x y =上一点A 的横坐标为2,则点A 与抛物线焦点的距离为 . 5.掷一个骰子的试验,事件A 表示“大于2的点数出现”,事件B 表示“大于2的奇数点出现”,则一次试验中,事件A B +发生概率为 .6.过点(1,4)A -作圆22(2)(3)1x y -+-=的切线l ,则l 的方程为 . 7.若ABC ∆的三条边长2a =,3b =,4c =,则C ab B ca A bc cos 2cos 2cos 2++的值为 .8.已知函数)(x f 的导数()(1)()f x a x x a '=+-,若()f x 在x a =处取到极大值,则常数a 的取值范围是 .9.已知二次函数2()f x ax bx c =++,且不等式()0f x <的解集为(,1)(3,)-∞+∞U ,若)(x f 的最大值小于2,则a 的取值范围是 .10.在OAB ∆中,M 为OB 的中点,N 为AB 的中点,ON ,AM 交于点P ,若AP mOA nOB =+u u u v u u u v u u u v(m ,n ∈R ),则n m -= .11.已知n S 为等差数列{}n a 的前n 项的和,n T 为等差数列{}n b 的前n 项的和,若n m S T =2(1)n m m +,则510a b =_________.12.已知()f x 是定义在R 上的偶函数,它的图象关于直线2x =对称,当[02]x ∈,时,tan [01),()(1)[12],x x f x f x x ∈⎧=⎨-∈⎩,,,,则(5)6f π--=__________.答案 1.1i -+ 2.(0,)+∞ 3.1± 4.2 5.326.4y =或34130x y +-= 7.29 8.(1,0)- 9.(2,0)-10.1:连MN ,相似 11.920(59101921929a Sb T =) 12.3(()()f x f x -=,(2)(2)f x f x +=-+,∴()(4)f x f x =-+((4))f x =--+,周期为4,(5)(1)(1)()tan 66666f f f f πππππ--=--=+===)2020届高三数学小题狂练九姓名 得分1.函数()sin(2)f x x π=+的最小正周期是 .2.若直线210x ay +-=与01)1(=+--ay x a 平行,则a 的值为 . 3.抛物线22y x =-的焦点坐标是 .4.函数20.5()log (65)f x x x =-+的单调减区间是 .5.已知3sin 5α=,(,)2παπ∈,则tan()4πα+值为 . 6.某人有甲、乙两只电子密码箱,欲存放三份不同的重要文件,则此人使用同一密码箱存放这三份重要文件的概率是 . 7.函数sin()cos()66y x x ππ=++的图象离原点最近的对称轴方程为 .8.在等比数列{}n a 中,0n a >,且211a a =-,439a a =-,则45a a += .9.若3213()32f x x x ax =-+在[1,4]-上是减函数,则实数a 的取值范围是 .10.已知向量a r ,b r 满足||1a =r ,||b =r a b +=r r,则||a b -=r r .11.已知三棱锥S ABC -的所有顶点都在球O 的球面上.若平面SCA ⊥平面SCB ,SA AC =,SB BC =,三棱锥S ABC -的体积为9,则球O 的表面积为 .12.对于任意两个实数a ,b ,定义运算“⊗”如下:,,,.a a b a b b a b ≤⎧⊗=⎨>⎩则函数2()[(6)(215)]f x x x x =⊗-⊗+的最大值为_________.答案 1.22.123.1(0,)8-4.),5(+∞5.17 6.147.12x π=8.27 9.(,4]-∞- 10.2 11.36π 12.92020届高三数学小题狂练十姓名 得分1.方程2lg(1)1lg(1)x x ++=-的解是 . 2.已知复数i z24-=(i 为虚数单位),且复数2()z ai +在复平面上对应的点在第一象限,则实数a 的取值范围为 .3.曲线x x f ln )(=在e x =处的切线方程为 .4.随机向一个正三角形内丢一粒豆子,则豆子落在此三角形内切圆内的概率为 . 5.若双曲线122=-y x 右支上一点(,)A m n 到直线x y =的距离为2,则m n += .6.函数5x y x a+=-在(1,)-+∞上单调递减,则实数a 的取值范围是 . 7.ABC ∆中,AP 为BC 边上的中线,||3AB =u u u r ,2-=⋅,则||AC =u u u r.8.直线AB 过抛物线2y x =的焦点F ,与抛物线相交于A ,B 两点,且|AB |=3,则线段AB 的中点到y 轴的距离为 .9.设数列{}n a 的通项为210n a n =-(n ∈N *),则=+++||...||||1521a a a . 10.已知函数()cos f x x =((,3)2x ππ∈),若方程a x f =)(有三个不同的实根,且三根从小到大依次构成等比数列,则a 的值为 .11.若函数()f x 满足(2)()1f x f x +=-+,且(1)2007f =-,则(2015)f = . 12.对于任意实数x ,符号[]x 表示x 的整数部分,即[]x 是不超过x 的最大整数.那么]1024[log ]4[log ]3[log ]2[log ]1[log 22222+++++Λ= .答案1.11x = 2.(2,6) 3.0x ey -=4 5.126.(5,1]--7 8.549.130 10.21-(三根:α,2πα-,2πα+) 11.2008:(2)()1f x f x +=-+,(4)(2)1f x f x +=-++,4T =,(3)(1)1f f =-+ 12.8204:1+1+2(23-22)+3(24-23)+…+9(210-29)+10=1*21+2*22+3*23+…+9*29+102020届高三数学小题狂练十一姓名 得分1.设集合1{|0}2M x x =-<,{}210N x x =+>,则M N =I . 2.幂函数()y f x =的图象经过点1(2,)8--,则满足()27f x =的x 的值是 .3.过点(1,0)且倾斜角是直线210x y --=的倾斜角的两倍的直线方程是 . 4.若椭圆221x my +=(01m <<,则它的长轴长为 . 5.从分别写有1,2,3,4,5的五张卡片中任取两张,则这两张卡片上的数字和为偶数的概率为 .6.已知复数11z i =-,2||3z =,那么||21z z -的最大值是 . 7.若函数213ln1xy x x+=+-的最大值与最小值分别为M ,m ,则M m += . 8.设1232,2,()log (1),3,x e x f x x x -⎧<⎪=⎨-≥⎪⎩则不等式()2f x >的解集为 . 9.若()sin()1f x A x ωϕ=++(0ω>,||<πϕ)对任意实数t ,都有ππ()()33f t f t +=-+.记()cos()1g x A x ωϕ=+-,则π()3g = .10.已知在同一平面上的三个单位向量a r ,b r ,c r,它们两两之间的夹角均为120o ,且 |1ka b c ++>r r r|,则实数k 的取值范围是 .11.过抛物线22(0)y px p =>的焦点F 的直线l 交抛物线于A 、B 两点,交准线于点C .若2CB BF =uu r uu u r,则直线AB 的斜率为 .12.已知ABC ∆三边a ,b ,c 的长都是整数,且a b c ≤≤,如果b m =(m ∈N *),则这样的三角形共有 个(用m 表示).答案1.11{|}22x x -<<2.133.4340x y --= 4.4 5.526.3+ 7.68.),10()2,1(+∞Y 9.1-10.{|0k k <或2}k >11.BH l ⊥,抛物线定义得sin 0.5BCH =,故倾斜角为60︒或120︒) 12.(1)2m m +(a m c ≤≤,则m c a m ≤<+,1a =时1个,…,a m =时m 个)2020届高三数学小题狂练十二姓名 得分1.若复数z 满足方程1-=⋅i i z ,则z = .2.A ,B ,C 三种不同型号的产品的数量之比依次为2:3:5,现用分层抽样的方法抽出样本容量为n 的样本,样本中A 型产品有16件,那么样本容量n 为 .3.底面边长为2的正四棱锥的体积为 .4.若点P 是曲线x x y ln 2-=上任意一点,则点P 到直线2-=x y 的最小距离为 .5.袋中有红、黄、绿色球各一个,每次任取一个有放回地抽取三次,球的颜色全相同的概率是 .6.数列{}n a 中,12a =,21a =,11112-++=n n n a a a (2n ≥,n ∈N ),则其通项公式为n a = .7.已知双曲线C 与椭圆221925y x +=有相同的焦点,它们离心率之和为145,则C 的标准方程是 .8.已知二次函数f x ()满足f x f x ()()11+=-,且f f ()()0011==,,若f x ()在区间[,]m n 上的值域是[,]m n ,则m n +的值等于 .9.已知函数()cos f x x ω=(0ω>)在区间π[0]4, 上是单调函数,且3π()08f =,则ω= . 10.已知PA ,PB ,PC 两两互相垂直,且△PAB ,△PAC ,△PBC 的面积分别为1.5cm 2,2cm 2,6cm 2,则过P ,A ,B ,C 四点的外接球的表面积为 cm2.11.设椭圆22221y x a b+=(0a b >>)的两个焦点分别为1F ,2F ,点P 在椭圆上,且120PF PF ⋅=u u u r u u u u r,12tan 2PF F ∠=,则该椭圆的离心率等于 .12.在ABC ∆中,已知4AB =,3AC =,P 是边BC 的垂直平分线上的一点,则BC AP ⋅u u u r u u u r= .答案1.1i-2.803.4 345.1 96.2 n7.221 412y x-=8.1(1n≤)9.43或410.26π(补形)1112.7 2 -2020届高三数学小题狂练十三姓名 得分1.函数2()12sin f x x =-的最小正周期为 .2.若函数()log (01)a f x x a =<<在闭区间[,2]a a 上的最大值是最小值的3倍,则a = .3.函数x y sin =的定义域为],[b a ,值域为21,1[-],则a b -的最大值和最小值之和为 .4.函数32()267f x x x =-+的单调减区间是 . 5.若2(3),6,()log ,6,f x x f x x x +<⎧=⎨≥⎩则(1)f -的值为 .6.设等差数列{}n a 的公差0d ≠,19a d =.若k a 是1a 与2k a 的等比中项,则k = .7.在直角坐标系xOy 中,i r ,j r分别是与x 轴,y 轴平行的单位向量,若直角ABC ∆中,AB i j =+u u u r r r ,2AC i m j =+u u u r r r,则实数m = .8.若函数2()x f x x a=+(0a >)在[1,)+∞上的最大值为3,则a 的值为 . 9.若不等式1,0ax x a >-⎧⎨+>⎩的解集是空集,则实数a 的取值范围是 .10.已知两圆1C :22210240x y x y +-+-=,2C :222280x y x y +++-=,则以两圆公共弦为直径的圆的方程是 .11.过抛物线22(0)y px p =>的焦点F 的直线交抛物线于A ,B 两点,交其准线于点C ,且2BC FB =u u u r u u u r,12AF =,则p 的值为 .12.从椭圆上一点A 看椭圆的两焦点1F ,2F 的视角为直角,1AF 的延长线交椭圆于B ,且2AF AB =,则椭圆的离心率为__________.答案 1.π2.43.2π 4.[0,2]5.3 6.4 7.0或2-81-讨论a 9.(,1]-∞-10.5)1()2(22=-++y x (圆心在公共弦上,3λ=-)11.6:作AH Ox ⊥,30AFH ∠=︒,12sin 30622A p px =+︒=+,12cos 30A y =︒=12269-不扣分):2AF m =,2BF =,24m a +=,故(4m a =-,12AF a m =-,22212(2)AF AF c +=2020届高三数学小题狂练十四姓名 得分1.设集合{0,}P m =,2{|250,}Q x x x x Z =-<∈,若P Q ≠∅I ,则m 的值等于 .2.若函数sin3xy π=(0x t ≤≤)的值域为[1,1]-,则正整数t 的最小值是 .3.若函数23xy t =⨯+的图象不经过第二象限,则t 的取值范围是 .4.已知()y f x =是奇函数,当0x <时,2()f x x ax =+,且(2)6f =,则a = . 5.A 是圆O 上一定点,在圆O 上其它位置任取一点B ,连接AB ,则AB 的长度不小于圆O 半径长度的概率为 .6.若数列}{n a 满足12,01,1,1,n n n n n a a a a a +≤≤⎧=⎨->⎩且167a =,则2015a = .7.已知两点(2,0)A -,(0,2)B ,点C 是圆0222=-+x y x 上任意一点,则ABC ∆面积的最小值是 .8.已知1F ,2F 分别是双曲线22221x y a b-=(0a >,0b >)的左、右焦点,P 为双曲线上的一点,若︒=∠9021PF F ,且21PF F ∆的三边长成等差数列,则双曲线的离心率是 .9.已知函数()f x ,()g x 满足(5)5f =,3)5('=f ,(5)4g =,1)5('=g ,则函数()2()f x yg x +=的图象在5x =处的切线方程为 .10.若存在[1,3]a ∈,使得不等式2(2)20ax a x +-->成立,则实数x 的取值范围是 .11.若实数a ,b 满足410ab a b --+=(1a >),则(1)(2)a b ++的最小值为 . 12.已知a ,b 是两个互相垂直的单位向量,且1⋅=c a ,1⋅=c b,||=c 正实数t ,1||t t++c a b 的最小值为 .答案1.1或2 2.53.(,2]-∞- 4.55.23 6.377.3-8.59.51630x y -+= 10.{|x 1x <-或23x >}补 11.27(消a )12.2020届高三数学小题狂练十五姓名 得分1.复数13i z =+,21i z =+,则复数12z z 在复平面内对应的点位于第___ ___象限. 2.函数224x x y -=的值域是 .3.等差数列{}n a 中,若18153120a a a ++=,则9102a a -= . 4.若不等式1420xx a +-->在[2,)+∞上恒成立,则实数a 的取值范围为 .5.函数3sin(2)([0,])6y x x ππ=+∈的单调减区间是 .6.若经过点(1,0)P -的直线与圆224230x y x y ++-+=相切,则这条直线在y 轴上的截距是 .7.若3()2f x x ax =--在区间(1,)+∞上是增函数,则实数a 的取值范围是 . 8.在ABC ∆中,角A ,B ,C 所对边的长分别为a ,b ,c ,且sin cos cos A B Ca b c==,则A ∠= .9.实数x ,y 满足350x y --=,[1,3]x ∈,则2yx -的取值范围是 . 10.若33,0,()0,xx a x f x x a -+-<⎧=⎨≥⎩(0a >且1a ≠)是),(+∞-∞上的减函数,则a 的取值范围是 . 11.已知函数||sin 1()||1x x f x x -+=+的最大值为M ,最小值为m ,则M m += .12.已知点O 在ABC ∆内部,且有24OA OB OC ++=0u u u r u u u r u u u r,则OAB ∆与OBC ∆的面积之比为 .答案1.四 2.(0,4] 3.24 4.(,8)-∞ 5.2[,]63ππ6.1 7.(,3]-∞ 8.90o9.(,2][4,)-∞+∞U 10.2(0,]311.212.4∶1(OA OB BA =+u u u r u u u r u u u r ,1477OC OB BC BO BA BC =+⇒=+u u u r u u u r u u u r u u u r u u u r u u u r,平行四边形,相似三角形)2020届高三数学小题狂练十六姓名 得分1.设复数112z i =-,2x x i =+(x ∈R ),若12z z 为实数,则x = . 2.双曲线过点P,且渐近线方程为y x =,则此双曲线的方程为 . 3.已知212cos2sin=+θθ,则cos 2θ= . 4.若关于x 的方程3sin 4cos 21x x m +=-有解,则实数m 的取值范围是 . 5.与圆22(3)(1)2x y -++=相切,且在两坐标轴上有相等截距的切线共有________条.6.已知向量a r ,b r ,c r 满足0a b c ++=r r r r,||1a =r ,||2b =r ,且a r ⊥c r ,则a r 与b r 的夹角大小是 .7.在数列}{n a 中,21=a ,其前n 项和为n S ,若数列{}nS n是公差为2的等差数列,则}{n a 的通项公式为 .8.若函数2()lg 22f x x a x =⋅-+在区间(1,2)内有且只有一个零点,那么实数a 的取值范围是 .9.已知()f x 是以2为周期的偶函数,且当[0,1]x ∈时,()f x x =.若在区间[1,3]-内,方程()1f x kx k =++有4个实数解,则实数k 的取值范围是 .10.已知(,)P x y 满足约束条件30,10,10,x y x y x +-≤⎧⎪--≤⎨⎪-≥⎩O 为坐标原点,(3,4)A ,则||cos OP AOP ⋅∠u u u r的最大值是 .11.抛物线C :2y x =上两点M ,N 满足12MN MP =u u u u r u u u r,若(0,2)OP =-u u u r ,则||MN u u u u r = . 12.若0x y >>323xy y +-的最小值为 .答案 1.12-2.2212x y -=3.81-4.[2,3]- 5.3 6.120o7.42n a n =-8. 9.1(,0)3- 10.115:1(34)5x y +11(,)N m n ,(2,22)M m n +)12.10(4)(22x y x y y xy ≤-=-,3212()f x x≥+,再求导)2020届高三数学小题狂练十七姓名 得分1.集合{3,2}aA =,{,}B a b =,若{2}A B =I ,则A B =U .2.已知函数)1(log )(+=x x f a 的定义域和值域都是[0,1],则实数a 的值是 . 3.若(1,1)a ∈-,则方程20x x a -+=有实根的概率等于 . 4.若函数m y x +=-|1|)21(的图象与x 轴有公共点,则m 的取值范围是 .5.若方程02)1(22=-+++a x a x 有一根比1大,另一根比1-小,则a 的取值范围是 .6.若函数()sin()f x x ωφ=+对任意的实数x 都有)3()3(x f x f -=+ππ,则)3(πf 的值等于 .7.若锐角α,β满足4)tan 31)(tan 31(=++βα,则βα+= . 8.设曲线3233+-=x x y 上任一点处的切线的倾斜角为α,则α的取值范围是 .9.已知1F ,2F 为椭圆2212x y +=的两个焦点,过1F 作倾斜角为4π的弦AB ,则2F AB ∆的面积为 .10.已知()f x 为奇函数,且(31)f x +是周期为3的周期函数,(3)2f =,则(60)f 的值等于 .11.已知双曲线22221x y a b-=(0a >,0b >)的左、右焦点分别为1F ,2F ,点P 在双曲线的右支上,若此双曲线的离心率为e ,且12||||PF e PF =,则e 的最大值为 . 12.已知数列{}n a 满足1111n n n n a a n a a +++-=-+(n 为正整数),且26a =,则数列{}n a 的通项公式为n a =__________.答案1.{1,2,3} 2.2 3.584.)0,1[- 5.)0,1(- 6.1±7.3π 8.),32[)2,0[πππY9.4310.()f x 周期为9,(60)(3)f f =- 11.21+(2em m a -=,2em m c +≥,相除得11e e e +≥-) 12.22n n -(由1111n n n n a a n a a +++-=-+得)2(11111≥---=++n n n a n a n n ,令na b n n =,则)2(1111≥---=+n n b n n b n n ,故)1(111---=+n n n b n b n n ,…,1211223⨯-=b b ,累加得)1)(12(1++=+n n a n ,)3(22≥-=n n n a n .又11a =,26a =也满足n n a n -=22,故对n ∈N *都有n n a n -=22)2020届高三数学小题狂练十八姓名 得分1.已知全集2{2,4,1}U a a =-+,集合{1,2}A a =+,若}7{=A C U ,则实数a 的值等于 .2.已知双曲线2221x y a-=(0a >)的一条渐近线与直线032=+-y x 垂直,则该双曲线的准线方程是 .3.在数列{}n a 中,已知17a =-,25a =,且满足22n n a a +=+(n ∈N *),则12318a a a a ++++L = .4.已知θ是第三象限角,且95cos sin 44=+θθ,那么θ2sin = . 5.将3OM OA OB OC =--u u u u r u u u r u u u r u u u r写成AM xAB y AC =+u u u u r u u u r u u u r 时,x y += .6.当228x x -<时,函数252x x y x --=+的最小值是 .7.若直角三角形的三边成等比数列,则较小内角的正弦值是 .8.已知函数()y f x =满足(3)(3)f x f x -=+,且有n 个零点1x ,2x ,…,n x (n ∈N *),则12n x x x +++L = .9.过抛物线24y x =的焦点F 作斜率为1的直线交抛物线于A ,B 两点(点A 在x 轴上方),若AF FB λ=u u u r u u u r (1)λ>,则λ= .10.若{|2}xx kx >=R ,则实数k 的取值范围是 .11.已知函数2()1f x x =-,()g x x =-,令{}()max (),()F x f x g x =(max 表示最大值),则()F x 的最小值是 .12.已知00(,)x y 是直线2x y a +=-与圆2222x y a a +=++的公共点,则00x y 的取值范围是 .答案 1.32.x = 3.1264 5.2- 6.3-7.12- 8.3n9.3+21y y -) 10.[0,ln 2)e (21log ln 2e =)1112.(,1][16,)-∞+∞U (自编:由d r ≤得a 的取值范围是6a ≤-或0a ≥,再用222000000()2x y x y x y +=++得00252ax y -=)2020届高三数学小题狂练十九姓名 得分1.设a 是实数,且211ii a +++是纯虚数,则=a . 2.已知0a >,0b <,),(a b m ∈且0≠m ,则m1的取值范围是 .3.直线2(1)(3)750m x m y m ++-+-=与直线(3)250m x y -+-=垂直的充要条件是 .4.有一棱长为a 的正方体框架,其内放置一气球,使其充气且尽可能地膨胀(气球保持为球的形状),则气球表面积的最大值为 . 5.若函数1)(2++=mx mx x f 的定义域是R ,则m 的取值范围是 .6.已知α,β均为锐角,且cos()sin()αβαβ+=-,则tan α的值等于 . 7.设数列{}n a 的前n 项和为n S ,若11a =,13n n a S +=(n =1,2,3,…),则410log S = .8.已知定义在R 上的奇函数)(x f 满足)()2(x f x f -=+,则)6(f 的值为 .9.设双曲线C :22221x y a b-=(0a >,0b >)的右顶点为E ,左准线与两渐近线的交点分别为A ,B 两点,若60AEB ∠=︒,则双曲线C 的离心率e 等于 . 10.函数)sin()(θ+=x x f (||2πθ<)满足对任意x ∈R 都有)6()6(x f x f --=+ππ,则θ= .11.在△ABC 中,AB =2BC =,CA =BC a =u u u r r ,CA b =u u u r r ,AB c =u u u r r,则a b b c c a ⋅+⋅+⋅=r r r r r r .12.过抛物线214y x =准线上任一点作该抛物线的两条切线,切点分别为M ,N ,则直线MN 过定点__________.答案 1.1-2.),1()1,(+∞⋃-∞ab 3.3m =或2m =-4.22a π 5.[0,4] 6.1 7.9 8.0 9.210.6π-11.6-12.(0,1)(解法1:(,1)a -,2240i i x ax --=,122x x a +=,2222121212()248x x x x x x a +=+-=+,于是MN中点为22(,)2a a +,21122122MN y y x x a k x x -+===-,直线MN :12ay x =+,过定点(0,1).解法2:(,1)a -,1111()2y y x x x -=-,1111122y x a y --=-,11220ax y -+=.同理可得22220ax y -+=.故直线MN 方程为220ax y -+=,过(0,1))2020届高三数学小题狂练二十姓名 得分1.已知集合2{|log 1}M x x =<,{|1}N x x =<,则M N I = .2.双曲线2213x y -=的两条渐近线的夹角大小为 .3.设a 为常数,若函数1()2ax f x x +=+在(2,2)-上为增函数,则a 的取值范围是 . 4.函数)2(log log 2x x y x +=的值域是 .5.若函数()23f x ax a =++在区间)1,1(-上有零点,则a 的取值范围是 .6.若1(1)(1)2n na n+--<+对于任意正整数n 恒成立,则实数a 的取值范围是 .7.已知函数12||4)(-+=x x f 的定义域是[,]a b (a ,b 为整数),值域是[0,1],则满足条件的整数数对),(b a 共有 个.8.设P ,Q 为ABC ∆内的两点,且2155AP AB AC =+u u u r u u u r u u u r ,AQ uuu r 23AB =u u u r 14+AC u u ur ,则ABP ∆的面积与ABQ ∆的面积之比为 . 9.在等差数列{}n a 中,59750a a +=,且95a a >,则使数列前n 项和n S 取得最小值的n 等于 . 10.设x ,y ∈R +,312121=+++y x ,则xy 11.在正三棱锥A BCD -中,E ,F 分别是AB ,BC EF DE ⊥,1BC =,则正三棱锥A BCD -的体积是 .12.设()f x 是定义在R 上的偶函数,满足(1)()1f x f x ++=,且当[1,2]x ∈时,()2f x x =-,则(2016.5)f -=_________.DCQ BAP答案1.(0,1) 2.60︒ 3.),21(+∞4.),3[]1,(+∞--∞Y 5.(3,1)-- 6.)23,2[- 7.5(||[0,2]x ∈) 8.459.610.16(8xy x y =++,8xy ≥+16xy ≥)11.242(EF DE ⊥,EF ∥AC ,∴AC DE ⊥.又AC BD ⊥,∴AC ⊥平面ABD .∵1BC =,∴2AB AC AD ===,3162V =24=)12.0.5(2T =,(0.5)(0.5)(1.5)0.5f f f =-==)2020届高三数学小题狂练二十一姓名 得分1.已知等比数列{}n a 的前三项依次为1a -,1a +,4a +,则n a = . 2.抛物线24y x =上一点M 到其焦点的距离为3,则点M 的横坐标x = . 3.已知函数)(x f y =(x ∈R )满足)()2(x f x f =+,且]1,1[-∈x 时,2)(x x f =,则5()()log F x f x x =-的零点的个数为 .4.若(2,1)a =-v与(,2)b t =-v 的夹角为钝角,则实数t 的取值范围为 .5.函数2()lg(21)f x x ax a =-++在区间(1)-∞,上单调递减,则实数a 的取值范围是 . 6.设α为锐角,54)6sin(=+πα,则)32sin(πα+的值等于 . 7.已知0a >,且1a ≠,函数,0,()(14)2,0x a x f x a x a x ⎧<=⎨-+≥⎩满足对任意12x x ≠,都有1212()[()()]0x x f x f x --<成立,则a 的取值范围是 .8.已知a b >,1a b ⋅=,则22a b a b+-的最小值是 .9.已知数列{}n a ,{}n b 都是公差为1的等差数列,其首项分别为1a ,1b ,且115a b +=,1a ,1b ∈N *,则数列{}nb a (n ∈N *)前10项的和等于 .10.设椭圆1C 和双曲线2C 具有公共焦点1F ,2F ,其离心率分别为1e ,2e ,P 为1C 和2C 的一个公共点,且满足021=⋅PF PF ,则2212221)(e e e e +的值为 . 11.设22log 1()log 1x f x x -=+,12()(2)1f x f x +=(12x >),则12()f x x 的最小值为_______.12.对于一切实数x ,令[]x 为不大于x 的最大整数,则函数()[]f x x =称为高斯函数或取整函数.若()3n na f =(n ∈N *),n S 为数列{}n a 的前n 项和,则3n S =________.答案 1.134()2n -⋅2.2 3.44.(1,4)(4,)-+∞U 5.[1,2]6.2524(若3cos()65πα+=-,cos [cos()]066ππαα=+-<;或45<3πα<)7.11(,]428.222()2a b a b +=-+)9.85(11n a a n =+-,11n b b n =+-,113n b n a a b n =+-=+)10.2(2224m n c +=,12m n a +=,2||2m n a -=,后二式平方相加得22122e e --+=)11.23(21222122log 1log (2)11log 1log (2)1x x x x --+=++,化简得22214log log 1x x =-.于是212212221214log ()log log log 5log 1x x x x x x =+=+≥-,所以21212212212log ()122()1log ()1log ()13x x f x x x x x x -==-≥++(12x >))12.232n n -(33(1)(1)(1)n n S S n n n --=-+-+,311S ⨯=,3n S =232n n-)2020届高三数学小题狂练二十二姓名 得分1.函数20.5log (2)y x x =-的单调减区间是 .2.已知函数()sin cos f x a x x =+,且()4f x π-()4f x π=+,则a 的值为 .3.设O 为坐标原点,F 为抛物线x y 42=的焦点,A 为抛物线上的一点,若4-=⋅,则点A 的坐标为 .4.从原点向圆0271222=+-+y y x 作两条切线,则该圆夹在两条切线间的劣弧长为 .5.若函数32()26f x x x m =-+(m 为常数)在[2,2]-上有最大值3,则()f x 在[2,2]-上的最小值为 .6.设等比数列{}n a 的公比为q ,其前n 项的和为n S ,若1n S +,n S ,2n S +成等差数列,则公比q 等于 . 7.规定一种运算:,,,,a a b a b b a b ≤⎧⊗=⎨>⎩则函数x x x f cos sin )(⊗=的值域为 .8.已知当x ∈R 时,函数)(x f y =满足1(2.1)(1.1)3f x f x +=++,且1)1(=f ,则)100(f 的值为 .9.设函数)(x f 是定义在R 上的奇函数,1(1)2f =,)2()()2(f x f x f +=+,则=)5(f .10.双曲线222015x y -=的左、右顶点分别为1A ,2A ,P 为其右支上一点,且12124A PA PA A ∠=∠,则12PA A ∠的大小为 .11.已知3450a b c ++=r r r r ,且||||||1a b c ===r r r,则()a b c ⋅+=r r r .12.已知α,β均为锐角,且sin cos()sin ααββ+=,则tan α的最大值是 .答案1.(2,)+∞ 2.1(取4x π=)3.(1,2)± 4.2π 5.37- 6.2- 7.]22,1[- 8.349.2.5((12)(1)(2)f f f -+=-+,故(2)1f =,(3) 1.5f =,(5)(3)1f f =+)10.12π(tan y x a α=+,tan 5y x a α=-,由222015x y -=得tan tan51αα=,于是得cos60α=)11.35-(534c a b -=+r r r ,435b a c -=+r r r ,两式分别平方得0a b =r r g,35a c =-r r g )12αβ+也为锐角,tan()αβ+存在.由cos()sin sin[()]αββαββ+=+-展开得tan()2tan αββ+=.从而有tan tan[()]ααββ=+-2tan 41tan ββ=≤+)2020届高三数学小题狂练二十三姓名 得分1.若直线30x ay ++=的倾斜角为120︒,则a 的值是 .2.已知定义在R 上的函数()f x 的图象关于点3(,0)4-对称,且(1)1f -=,则1()2f -的值等于 .3.不等式02||2<--x x 的解集是 .4.在一个水平放置的底面半径为3的圆柱形量杯中装有适量的水,现放入一个半径为R 的实心铁球,球完全浸没于水中且无水溢出,若水面高度恰好上升R ,则R = . 5.函数xx y tan 31tan 3+-=的单调减区间是 .6.在坐标平面内,已知由不等式组|2|,||y x y x a≥-⎧⎨≤-+⎩所确定的区域的面积为52,则a 的值等于 .7.若函数3()log ()(0a f x x ax a =->且1)a ≠在区间1(,0)3-内单调递增,则实数a 的取值范围是 .8.已知数列{}n a 中,12a =,前n 项和n S ,若n n a n S 2=,则n a = .9.已知函数1,1,|1|()11,x x f x x ⎧≠⎪-=⎨⎪=⎩, 若关于x 的方程2()()0f x bf x c ++=有3个不同的实数解1x ,2x ,3x ,则222123x x x ++的值等于 .10.已知函数()f x 在[2,)+∞单调递增,且对任意实数x 恒有(2)(2)f x f x +=-,若22(12)(12)f x f x x -<+-,则x 的取值范围是 .11.设非零向量a r ,b r 满足||1b =r ,a r 与b a -r r 的夹角为120︒,则||a r的最大值为 .12.已知)(x f y =是定义在R 上的函数,且对任意x ∈R ,都有1()(2)1()f x f x f x -+=+,又1(1)2f =,1(2)4f =,则(2015)(2016)f f += .答案1.32.1-3.(2,2)- 4.325.5(,)66k k ππππ-+(k ∈R ) 6.37.1[,1)38.)1(4+n n9.510.(2,0)-(12|2||2|X X -<-)11ABC ∆中,CA b =u u u r r ,CB a =u u u r r ,BA b a =-u u u r r r ,60ABC ∠=︒,||sin 601a ︒≤r ,||a ≤r )12.1415(令1=x ,则1(1)1(3)1(1)3f f f -==+,令2=x ,则1(2)3(4)1(2)5f f f -==+,)(n f 以4为周期,所以1314(3)(4)3515f f +=+=)2020届高三数学小题狂练二十四姓名 得分1.设230.0310x y -==,则11xy ---的值为 .2.已知函数()f x 对任意的x ∈R 都有11()()222f x f x ++-=成立,则127()()()888f f f +++L 的值为 . 3.设直线0=++C By Ax 与圆422=+y x 相交于M ,N 两点,若222A B C +=,0C ≠,则OM ·ON (O 为坐标原点)的值等于 . 4.若222xy ax y ≤+对任意[1,2]x ∈及[2,3]y ∈恒成立,则实数a 的范围是 .5.设数列{}n a 的通项公式为3n a n n λ=+(n ∈N *),若123n a a a a <<<<<L L ,则实数λ的取值范围是 . 6.若()2sin()f x ax =在区间[,]34ππ-上的最小值为2-,则实数a 的范围是 .7.若等比数列{}n a 满足354321=++++a a a a a ,且122524232221=++++a a a a a ,则54321a a a a a +-+-的值等于 .8.在ABC ∆中,a ,b ,c 分别为角A ,B ,C 所对边的长,若a ,b ,c 成等差数列,4sin 5B =,且ABC ∆的面积为32,则b = . 9.已知函数21,0,()(1),0,x x f x f x x -⎧-≤=⎨->⎩若方程()f x x a =+有且只有两个不相等的实数根,则实数a 的取值范围是 .10.已知1F ,2F 分别为双曲线C :12222=-by a x 的左、右焦点,P 是C 左支上的一点,若2218||PF a PF =,则C 的离心率的取值范围是 .11.已知1()41()xf x f x +=-,正实数1x ,2x 满足12()()1f x f x +=,则12()f x x +的最小值为 .12.已知实数x ,y 满足x y ,则x y +的最大值为 .。
每日一练高考语文小题狂做(一)

每日一练高考语文小题狂做(一)每日一练(一)时间:50分钟分值:50分一、语言文字运用阅读下面的文字,完成1~3题。
( ),那么故宫博物院推出的“古画会唱歌”则更进一步,古典雅致的歌词、的曲调将千年古画青山绿水的场景烘托、渲染得。
这种新形式让现代人不仅用眼睛来欣赏古画的“静美”,也用耳朵来聆听古画的旋律,更用心体会诗情画意的韵味,通过创新的艺术通感形式,传承并弘扬中华传统文化之精髓。
《千里江山图》可谓,这幅千古名画就像“最熟悉的陌生人”一样让不少人。
从中我们也深切地感受到人们对文化的渴望、对精神生活的追求。
正因如此,古画要变得更有吸引力、拉近人们的距离,就必须不断拓展人们欣赏的渠道和深度,以更好地发挥其教育、文化传播的作用。
从《国家宝藏》《如果国宝会说话》到如今的“古画会唱歌”,我们看到有越来越多的文物,借助高大上的科技手段,尊重年轻人的审美习惯,与生动有趣的故事相结合,变得更“接地气”,真正飞入寻常百姓家。
1.下列在文中括号内补写的语句,最恰当的一项是( )A.如果说此前能够让国宝开口说话使得《国家宝藏》热播B.与其说此前能够让国宝开口说话使得《国家宝藏》热播C.如果说此前大热的《国家宝藏》让国宝能够开口说话D.与其说此前大热的《国家宝藏》让国宝能够开口说话2.依次填入文中横线上的成语,全都恰当的一项是( )A.行云流水栩栩如生尽人皆知魂牵梦萦B.珠圆玉润栩栩如生妇孺皆知魂牵梦萦C.行云流水惟妙惟肖妇孺皆知朝思暮想D.珠圆玉润惟妙惟肖尽人皆知朝思暮想3.文中画横线的句子有语病,下列修改最恰当的一项是( )A.古画要变得更有吸引力、拉近人们的距离,就必须不断拓展和开掘人们欣赏的渠道和深度,以更好地发挥其教育、文化传播的作用。
B.古画要变得更有吸引力、拉近与人们的距离,就必须不断拓展和开掘人们欣赏的渠道和深度,以更好地发挥其教育、文化传播的作用。
C.古画要变得拉近人们的距离、更有吸引力,就必须不断拓展人们欣赏的渠道和深度,以更好地发挥其教育作用和文化传播的作用。
2025年高考地理复习之小题狂练300题(解答题):资源、环境与区域发展(10题)

2025年高考地理复习之小题狂练300题(解答题):资源、环境与区域发展(10题)一.解答题(共10小题)1.(2023•昌乐县校级模拟)阅读图文材料,完成下列问题。
位于新疆天山以南的沙雅县(如图)由渭干河冲积扇平原、塔里木河谷平原和80%的沙丘、沙漠三部分组成。
塔里木河自西向东流经该县,河床宽广低浅,主要有松散的粉砂组成;由于河床的冲淤变化,造成塔里木河干流在南北方向频繁改道,历史上干流河床南北移动达近百公里:沿岸地区湖泊星罗棋布,有保存世界最大、最完好的胡杨林群落。
形成由乔﹣灌﹣草组成的胡杨林群落系统。
(1)从冲淤变化角度,分析造成沙雅县塔里木河干流河床南北方向移动的原因。
(2)分析塔里木河沙雅县河段两侧沿岸地区形成众多湖泊的条件。
(3)从防风固沙角度,分析集中连片胡杨林群落系统对当地生态环境的作用。
2.(2023•东莞市校级模拟)阅读图文材料,完成下列要求。
喀斯特地区以化学风化作用为主,成土基岩主要为碳酸盐岩,其成土物质(酸性不溶物)少于碳酸盐岩总物质量10%,远低于可溶性矿物占比。
平均需8000年才能形成一厘米厚的土层,土壤石砾含量高、土质疏松。
喀斯特地区生态系统脆弱,易形成石漠化。
贵州省安顺市普定县石漠化较为严重,坡耕地于2002年前完成全部退耕工作,并开展坡面治理工程,在部分坡面修建了鱼鳞坑、梯田等。
梯田水平田面宽4~6m,田坎高70~110cm。
鱼鳞坑直径约280~340cm,高约30~50cm。
图示意为在不同石漠化治理措施下土壤有机碳含量,图中的自然坡地为无任何水土保持措施的退耕还林地。
(1)从土壤的角度,说明喀斯特地区生态脆弱的自然原因。
(2)分析该地梯田土壤有机碳含量最低的原因。
(3)请从当地坡面发展农业产业的角度,提出合理化建议。
3.(2023•雨花区校级二模)阅读图文材料,回答下列问题。
金沙江下游从上游至下游依次建设有乌东德、白鹤滩、溪洛渡、向家坝4个梯级水电站(图1)。
2022届新高考版数学小题狂练01(含解析)

小题专练01函数、导数与不等式(A)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(考点:函数的定义域,★)函数f (x )=√3-x+lg (2x +3)的定义域是( ).A .(-32,3)B .(-∞,3)C .(-32,+∞)D .(-3,-32)2.(考点:导数的几何意义,★)若曲线y=f (x )=12x 2+ax+b 在点(4,f (4))处的切线方程是2x-y+1=0,则( ). A . a=10,b=1B . a=-2,b=-9C . a=-2,b=9D . a=2,b=-93.(考点:函数单调性与奇偶性的综合应用,★★)已知定义在R 上的偶函数f (x )在区间[0,+∞)上单调递减,则满足f (3x-1)<f (8)的x 的取值范围是( ). A .(-3,73)B .(-∞,-73)∪(3,+∞)C .(-73,3)D .(-∞,-3)∪(73,+∞)4.(考点:函数的图象,★★)函数f (x )=x 32x -4的图象大致为( ).5.(考点:函数的零点,★★)已知函数f (x )={2x +6,x ≤0,x 2-2x +4,x >0.若函数g (x )=f (x )-m 有三个不同的零点,则实数m 的取值范围为( ). A .(3,4)B .(-4,-3)C .[3,4]D .(3,6)6.(考点:均值不等式,★★)设a>0,b>0,若9是3a 与3b 的等比中项,则4a +1b的最小值为( ). A .4B .2C .34D .947.(考点:利用导数研究函数的单调性,★★★)若函数f (x )=kx-sin x 在区间(-π6,π3)上单调递增,则实数k 的取值范围是( ). A .[1,+∞)B .[-12,+∞)C .(1,+∞)D .(12,+∞)8.(考点:导数的综合应用,★★★)已知奇函数f (x )的导函数为f'(x ),当x>0时,f'(x )+2f (x )x>0.若a=1e2f(-1e),b=14f(-12),c=f(-1),则a,b,c的大小关系为().A. a<b<cB. c<b<aC. c<a<bD. a<c<b二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.9.(考点:不等式的综合应用,★)已知p:1x-1>1,则p成立的一个必要不充分条件可以是().A.1<x<2B.-2<x<3C.-2<x<4D.-3<x<210.(考点:函数的基本性质,★★)下列函数中,既是偶函数,又在(0,+∞)上单调递增的是().A.f(x)=ln(√1+4x2-2x)B.f(x)=e x+e-xC.f(x)=x2+5D.f(x)=cos x11.(考点:均值不等式,★★)已知正实数x,y满足x+2y=1,则1x +1y可能的值为().A.3B.6C.7D.912.(考点:导数的应用,★★★)设f(x),g(x)分别是定义在R上的奇函数和偶函数,f'(x),g'(x)分别为其导函数,当x<0时,f'(x)·g(x)+f(x)·g'(x)<0且g(-5)=0,则使得不等式f(x)·g(x)<0成立的x的值可以是().A.-6B.-4C.4D.6三、填空题:本题共4小题,每小题5分,共20分.13.(考点:函数的基本性质,★★)函数f(x)=lo g12(-x2-2x+3)的单调递增区间是,值域是. 14.(考点:函数单调性的应用,★★)若函数f(x)=x2+4(a+2)x+3在(-∞,4]上不是单调函数,则实数a的取值范围是.15.(考点:均值不等式,★★)函数y=log a(x-3)+2(a>0且a≠1)的图象恒过定点A,若点A在直线mx+ny-2=0上,其中m, n均大于0,则1m +1n的最小值为.16.(考点:利用导数研究函数的极值,★★★)已知函数f(x)=13x3+2x2-5x+2的极大值为a,极小值为b,则a+b= .答案解析:函数、导数与不等式(A)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(考点:函数的定义域,★)函数f (x )=√3-x+lg (2x +3)的定义域是( ).A .(-32,3)B .(-∞,3)C .(-32,+∞)D .(-3,-32)【解析】要使函数有意义,则{3-x >0,2x +3>0,即{x <3,x >-32,即-32<x<3, 所以函数的定义域为(-32,3).故选A . 【答案】A2.(考点:导数的几何意义,★)若曲线y=f (x )=12x 2+ax+b 在点(4,f (4))处的切线方程是2x-y+1=0,则( ). A . a=10,b=1B . a=-2,b=-9C . a=-2,b=9D . a=2,b=-9【解析】因为f (x )=12x 2+ax+b ,所以f'(x )=x+a ,由题可知f'(4)=2,所以a=-2. 又切点坐标(4,f (4))满足切线方程2x-y+1=0,f (4)=b ,所以8-b+1=0,解得b=9. 故选C . 【答案】C3.(考点:函数单调性与奇偶性的综合应用,★★)已知定义在R 上的偶函数f (x )在区间[0,+∞)上单调递减,则满足f (3x-1)<f (8)的x 的取值范围是( ). A .(-3,73)B .(-∞,-73)∪(3,+∞)C .(-73,3)D .(-∞,-3)∪(73,+∞)【解析】因为f (x )是定义在R 上的偶函数, 所以f (3x-1)<f (8)等价于f (|3x-1|)<f (8). 又因为f (x )在[0,+∞)上单调递减, 所以|3x-1|>8, 所以3x-1<-8或3x-1>8, 解得x<-73或x>3,故x 的取值范围为(-∞,-73)∪(3,+∞).故选B . 【答案】B4.(考点:函数的图象,★★)函数f (x )=x 32x -4的图象大致为( ).【解析】由题意,函数f (x )=x 32x -4的定义域为{x|x ∈R,x ≠2},排除A;又f (1)<0,排除C;f (-1)>0,排除D.故选B .【答案】B5.(考点:函数的零点,★★)已知函数f (x )={2x +6,x ≤0,x 2-2x +4,x >0.若函数g (x )=f (x )-m 有三个不同的零点,则实数m 的取值范围为( ). A .(3,4)B .(-4,-3)C .[3,4]D .(3,6)【解析】函数g (x )=f (x )-m 有三个不同的零点等价于函数y=f (x )与y=m 的图象有三个不同的交点,作出函数f (x )的图象如图所示.函数y=m 的图象为水平的直线,由图象可知,当m ∈(3,4)时,两函数的图象有三个不同的交点,即函数g (x )有三个不同的零点.故选A . 【答案】A6.(考点:均值不等式,★★)设a>0,b>0,若9是3a 与3b 的等比中项,则4a +1b 的最小值为( ). A .4B .2C .34D .94【解析】因为9是3a 与3b 的等比中项, 所以3a ·3b =3a+b =92,即a+b=4, 所以4a +1b =14(a+b )(4a +1b )=54+144b a +ab≥54+14×4=94, 当且仅当4b a =ab ,即a=83,b=43时,等号成立,所以4a +1b的最小值为94.故选D . 【答案】D7.(考点:利用导数研究函数的单调性,★★★)若函数f (x )=kx-sin x 在区间(-π6,π3)上单调递增,则实数k 的取值范围是( ). A .[1,+∞)B .[-12,+∞)C .(1,+∞)D .(12,+∞)【解析】由题意可得f'(x )=k-cos x ,因为f (x )在(-π6,π3)上单调递增,所以f'(x )≥0在(-π6,π3)上恒成立,即f'(x )min =k-1≥0,所以k ≥1.故选A . 【答案】A8.(考点:导数的综合应用,★★★)已知奇函数f (x )的导函数为f'(x ),当x>0时,f'(x )+2f (x )x>0.若a=1e 2f (-1e ),b=14f (-12),c=f (-1),则a ,b ,c 的大小关系为( ). A . a<b<cB . c<b<aC . c<a<bD . a<c<b【解析】令g (x )=x 2f (x ),则g'(x )=2xf (x )+x 2f'(x ).由题意可知当x>0时,2xf (x )+x 2f'(x )>0,即当x>0时,g'(x )>0,所以函数g (x )在(0,+∞)上单调递增.又函数f (x )为奇函数,所以g (-x )=(-x )2·f (-x )=-x 2·f (x )=-g (x ),所以函数g (x )为奇函数,所以当x<0时,函数g (x )单调递增.因为-1e >-12>-1,所以g (-1e )>g -12>g (-1),所以a>b>c. 【答案】B二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分. 9.(考点:不等式的综合应用,★)已知p :1x -1>1,则p 成立的一个必要不充分条件可以是( ). A .1<x<2 B .-2<x<3 C .-2<x<4D .-3<x<2【解析】由1x -1>1⇔x -2x -1<0⇔(x-1)(x-2)<0⇔1<x<2,所以选项A 为p 成立的充要条件,选项B 、C 、D 为p 成立的必要不充分条件. 【答案】BCD10.(考点:函数的基本性质,★★)下列函数中,既是偶函数,又在(0,+∞)上单调递增的是( ). A .f (x )=ln(√1+4x 2-2x )B .f (x )=e x +e -xC .f (x )=x 2+5D .f (x )=cos x【解析】由题意,易知A,B,C,D 四个选项中的函数的定义域均为R,对于选项A,f(-x)+f(x)=ln(√1+4x2+2x)+ln(√1+4x2-2x)=0,则f(x)=ln(√1+4x2-2x)为奇函数,故选项A不符合题意;对于选项B,f(-x)=e-x+e x=f(x),即f(x)=e x+e-x为偶函数,当x∈(0,+∞)时,设t=e x(t>1),则y=t+1t,由对勾函数的性质可得,y=t+1t在t∈(1,+∞)时是增函数,又t=e x单调递增,所以f(x)=e x+e-x在(0,+∞)上单调递增,故选项B符合题意;对于选项C,f(-x)=(-x)2+5=x2+5=f(x),即f(x)=x2+5为偶函数,由二次函数的性质可知f(x)=x2+5在(0,+∞)上单调递增,故选项C符合题意;对于选项D,由余弦函数的性质可知y=cos x是偶函数,但不在(0,+∞)上单调递增,故选项D不符合题意.综上,BC正确.【答案】BC11.(考点:均值不等式,★★)已知正实数x,y满足x+2y=1,则1x +1y可能的值为().A.3B.6C.7D.9【解析】因为x,y都为正实数,所以1x +1y=x+2yx+x+2yy=3+2yx+xy≥3+2√2yx·xy=3+2√2(当且仅当2yx=xy,即x=√2y时取等号),显然6>3+2√2,7>3+2√2,9>3+2√2,故选项B,C,D符合题意.【答案】BCD12.(考点:导数的应用,★★★)设f(x),g(x)分别是定义在R上的奇函数和偶函数,f'(x),g'(x)分别为其导函数,当x<0时,f'(x)·g(x)+f(x)·g'(x)<0且g(-5)=0,则使得不等式f(x)·g(x)<0成立的x的值可以是().A.-6B.-4C.4D.6【解析】∵f(x),g(x)分别是定义在R上的奇函数和偶函数,∴f(-x)=-f(x),g(-x)=g(x),令h(x)=f(x)·g(x),则h(-x)=-h(x),故h(x)=f(x)·g(x)为定义在R上的奇函数.∵当x<0时,f'(x)·g(x)+f(x)·g'(x)<0,即当x<0时,h'(x)=f'(x)·g(x)+f(x)·g'(x)<0,∴h(x)=f(x)·g(x)在区间(-∞,0)上单调递减,∴奇函数h(x)在区间(0,+∞)上也单调递减,如图,∵g(-5)=0,∴g(5)=0,∴h(-5)=h(5)=0,∴当x∈(-5,0)∪(5,+∞)时,h(x)=f(x)·g(x)<0.故选BD.【答案】BD三、填空题:本题共4小题,每小题5分,共20分.13.(考点:函数的基本性质,★★)函数f(x)=lo g12(-x2-2x+3)的单调递增区间是,值域是. 【解析】令t=-x2-2x+3,则由-x2-2x+3>0,可得-3<x<1.又因为y=lo g12t为减函数,而函数t=-x2-2x+3在区间(-3,-1)上单调递增,在(-1,1)上单调递减.故f(x)=lo g12(-x2-2x+3)在区间(-3,-1)上单调递减,在(-1,1)上单调递增.易知t=-x2-2x+3在区间(-3,1)上的值域为(0,4],故f(x)=lo g12t的值域为[-2,+∞).【答案】(-1,1)[-2,+∞)14.(考点:函数单调性的应用,★★)若函数f(x)=x2+4(a+2)x+3在(-∞,4]上不是单调函数,则实数a的取值范围是.【解析】由题意可得,f(x)图象的对称轴为直线x=-2(a+2),且满足-2(a+2)<4,解得a>-4.故实数a的取值范围为(-4,+∞).【答案】(-4,+∞)15.(考点:均值不等式,★★)函数y=log a(x-3)+2(a>0且a≠1)的图象恒过定点A,若点A在直线mx+ny-2=0上,其中m, n均大于0,则1m +1n的最小值为.【解析】由题意可得点A(4,2),代入mx+ny-2=0得4m+2n-2=0,即2m+n=1.所以1m +1n=(1m+1n)(2m+n)=3+nm+2mn≥3+2√nm·2mn=3+2√2,当且仅当nm=2mn,即m=1-√22,n=√2-1时等号成立.【答案】3+2√216.(考点:利用导数研究函数的极值,★★★)已知函数f(x)=13x3+2x2-5x+2的极大值为a,极小值为b,则a+b= .【解析】∵f(x)=13x3+2x2-5x+2,∴f'(x)=x2+4x-5.令f'(x)=0,解得x=-5或x=1.列表如下:∴a=f (-5)=1063,b=f (1)=-23,∴a+b=1063-23=1043.【答案】1043。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小题狂练(一)
1.下列句子中加点成语的使用,不正确的一项是()
A.上清寺是最具传奇色彩的地方,周公馆、桂园、人民大礼堂、三峡博物馆……举手投足
....间都可以窥见历史的遗踪和时代的发展。
B.大米市场失衡,某种程度上世界贸易组织(WTO)是始作俑者
....。
世贸有一项为人诟病的规定,要求日本不论是否需要,都必须年年进口大米。
而日本为了保护国内的农业,就将进口米存仓,待变坏时再当做喂鸡的饲料出售,十分浪费。
C.“科技点燃圣火创新园梦中国”——全国科技活动周暨北京科技周大型主题展览展示活动在中国科技馆举行。
在开幕式开始前,全体与会者首先向四川地震灾区遇难者默哀一分钟,全场
鸦雀无声
....,所有人都为四川灾区默默祈祷。
D.在这次研讨会了,代表们纷纷表示,一定要牢记胡锦涛总书
记倡导的“八荣八耻”,激浊扬清
....,在全社会树立起道德新标杆。
2.下列各句中,没有语病的一句是()
A.分析当前的经济形势,就是善于发现和总结工农业经济效益有所回升的经验和第三产业发展滞后等问题。
B.各企事业单位特别是窗口服务行业,都要制定各自的职业道德和行为规范,促进从业人员养成良好的职业习惯和敬业精神。
C.中国强烈要求所有核武器国家同时谈判并缔结一项无条件不首先使用核武器及不对无核国家和无核地区使用和威胁使用核武器的条约。
D.这套网上航班查询系统和民航总局计算机订座系统相连,具有及时、准确、信息全面等特点。
3.阅读下面这首宋诗,完成问题。
春寒
陈与义
二月巴陵日日风,春寒未了怯园公。
海棠不惜胭脂色,独立蒙蒙细雨中。
[注]本诗作于宋高宗建炎三年,当时南宋朝廷正处于风雨飘摇之际。
作者几经逃难,避乱岳州,借居于郡守后园的君子亭,自
称“园公”。
(1).本诗第二句中的“怯”字用得好,请简要赏析。
(2).三、四句写出了海棠的什么特点?表达了诗人怎样的性格特征?
4.祖国的名山胜水,一直是哲人、诗人歌咏的对象。
阅读例句,根据情境,仿写两个含有描写名山胜水的诗句的句子。
面对泰山,杜甫写下“会当凌绝顶,一览众山小”,抒发了不怕困难,敢于攀登绝顶,俯视一切的雄心和气概。
漫步西湖,
搏击长空,
小题狂练(一)答案
1.正确答案为A。
(举手投足:一抬手,一动脚,形容轻而易举,毫不费力,多指人,在句中不合语境,使用对像错误。
B始作俑者:恶劣风气的创始者,贬义。
C;鸦雀无声:连乌鸦麻雀的声音都没有,形容非常静。
D.激浊扬清:冲去污水,让清水上来,比喻清除坏的,发扬好的。
)
2.正确答案为D。
(A.“发现和总结”与“经验”“问题”动宾搭配不当;B.“养成”与“敬业精神”动宾搭配不当;C.“使用”“威胁使用”语序不当之不合逻辑。
)
3.(1)“怯”字既描绘出漂泊异乡的诗人在春寒未尽时节,对料峭春寒难以忍受的畏惧,也写出了对处于风雨飘摇之际的南宋朝廷的担忧之情。
炼字题型之一;分析字的含义,表面及内里
(2)写出了海棠“不惜”损毁胭脂容颜,不畏春寒独立于细雨之中的孤高绝俗的特点,表达了诗人在朝廷处于风雨飘摇之际,勇于在这样艰难的世事中傲然挺立的性格特征。
赏析:这是一首描写风雨中海棠的咏物诗。
表面上是写风雨之中的海棠实际上是写动乱中的自己。
早春二月,大地上已经是新花嫩叶装点着春光了,这时候,人们所希望的是风和日丽,蜂蝶纷纷,把春光点缀得更加浓郁,可是事情常常不如人意,如果寒朝夹着风雨侵袭来了,就会发生“倒春寒”,这些花儿叶儿就要遭受摧残。
“二月巴陵日日风”
说的正是这“倒春寒”,“怯园公”是倒装句,说是“使园公害怕”的意思,园公害怕什么呢,结合诗文我们料想,他是担心春寒会使百花凋零,为花儿担忧,结合注释内容我们也会想到这风雨中的花朵不也暗合国情人事吗,流亡中的诗人,动乱中的国家,不都像是那风雨中的花朵。
下面,笔锋一转,写出了一个振奋人心的情景:庭院中,短篱旁,一枝铁梗海棠毫不吝惜娇艳的花朵,在寒风冷雨中傲然挺立,笑靥绽放。
诗人用“不惜”“独立”展示了雨中海棠风姿卓然,品格孤傲的神韵,同时也是诗人情怀的写照。
咏物诗鉴赏:咏物诗往往托物言志,借所咏之物表达自己的志向或品质或对生活的思考、对人事的评价。
常用比喻、拟人、象征、对比等表现手法。
要从人与物的相似点,物所具有的特点入手分析。
4.(示例)白居易喜呤“最爱湖东行不足,绿扬阴里白沙堤”,留下了对西湖美景的留恋之情。
毛泽东笔下“不管风吹浪打,胜似闲庭信步”,展示了无产阶级革命家搏击风浪的伟大气魄和襟怀。
答题思路:所写诗句要与前文规定的对像吻合,语句中先写诗人和诗句,然后写这句诗表达了怎样的情感。
