毕萨定律及其应用

合集下载

毕萨奥伐尔定律

毕萨奥伐尔定律
摘要：
1.毕萨奥伐尔定律的简介
2.毕萨奥伐尔定律的公式及含义
3.毕萨奥伐尔定律在现实生活中的应用
4.毕萨奥伐尔定律的局限性及改进方法
5.总结
正文：
毕萨奥伐尔定律，又称“毕萨定律”，是由德国物理学家克劳斯·毕萨奥伐尔（Klaus Biauer）在1994年提出的一个定律。

该定律主要用于描述在固定压力下，流体通过管道时的流量与管道长度、管道直径之间的关系。

毕萨奥伐尔定律的公式为：Q = π/8 * d * √(2gh) ，其中Q表示流量，d 表示管道直径，g表示重力加速度，h表示管道长度。

在现实生活中，毕萨奥伐尔定律广泛应用于液体和气体的输送系统设计、优化及运行管理。

例如，在工业生产中，通过了解液体在管道中的流量，可以更好地控制生产过程；在农业生产中，利用毕萨奥伐尔定律可以优化灌溉系统，提高水资源利用率。

然而，毕萨奥伐尔定律也有其局限性。

首先，该定律适用于稳态流动，而在非稳态流动中，液体的流速与管道长度、直径的关系可能会发生改变。

其次，毕萨奥伐尔定律未考虑流体的黏性对流动的影响，因此在处理粘性流体时，需要对其进行修正。

为了解决这些问题，研究人员对毕萨奥伐尔定律进行了改进。

例如，引入了考虑流体黏性的修正系数，使得该定律在处理粘性流体时具有更好的准确性。

此外，还有一些研究者提出了基于毕萨奥伐尔定律的改进公式，以适应非稳态流动的计算需求。

总之，毕萨奥伐尔定律是一个具有广泛应用价值的定律，但在实际应用中也需要注意其局限性。

11.2 毕萨定理

B= 2R
0I
2R
I I
0 (NI )
(3) 一段圆弧在圆心处产生的磁场
B=
0I φ
2R 2π
=
0Iφ
4πR
φ
如图，点的磁感应强度。例如图，求O 点的磁感应强度。解
dB =
2
O R
B =0 1
30I B2 = = 4πR 2 8R B3 = =
4π r3
I
0 Idl × r
1 3
0I 3π
dq
1
ω
b a
3
dq = λdl = λbdθ
dB = 1
v
=
dθ
4
r
O
0 dqv ×r
4π r
3
0 dqv
4π r
2
=
0 dq ωb
4π
π
0
b2
=
0λω
4π
dθ
2
B1 = ∫
0λω
1 dθ = 0λω 4π 4 1 B2 = 0λω 4
线段2：线段：同理
线段3 线段
dq = λdr
4π r 4πr
讨论
B=
0I
4πa
θ2
(cosθ1 cosθ2 )
I
(1) 无限长直导线
θ1 →0
θ2 →π
B
θ1
B=
0I
2πa
方向：方向：右螺旋法则
(2) 任意形状直导线
B = B + B2 = 0 + 1
0I
4πa
2
P
I a
B
r
1
(3) 无限长载流平板

毕奥-萨伐尔定律及毕奥-萨伐尔定律应用举例

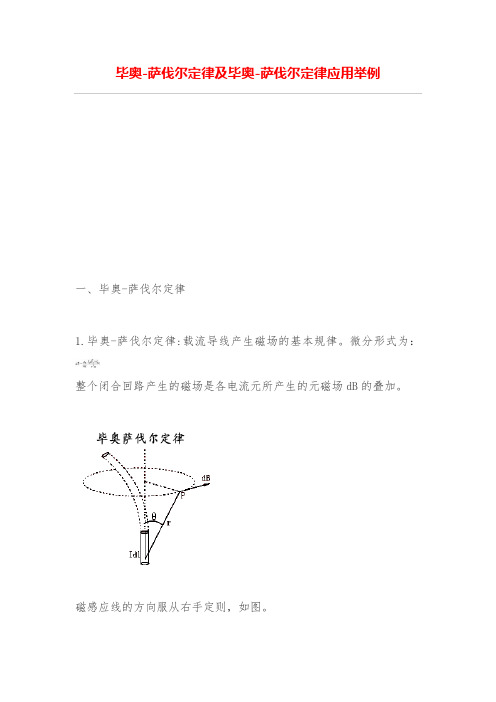
毕奥-萨伐尔定律及毕奥-萨伐尔定律应用举例一、毕奥-萨伐尔定律1.毕奥-萨伐尔定律:载流导线产生磁场的基本规律。

微分形式为：整个闭合回路产生的磁场是各电流元所产生的元磁场dB的叠加。

磁感应线的方向服从右手定则，如图。

二、毕奥-萨伐尔定律应用举例两种基本电流周围的磁感应强度的分布：载流直导线；圆电流。

例1.载流长直导线的磁场解：建立如图坐标系，在载流直导线上，任取一电流元Idz，由毕-萨定律得元电流在P点产生的磁感应强度大小为：方向为垂直进入纸面。

所有电流元在P点产生的磁场方向相同，所以求总磁感强度的积分为标量积分，即：（1）由图得：,即：此外：，代入（1）可得：讨论：（1）无限长直通电导线的磁场：（2）半无限长直通电导线的磁场：（3）其他例子例2:圆形载流导线轴线上的磁场：设在真空中，有一半径为 R ，通电流为 I 的细导线圆环，求其轴线上距圆心 O 为 x 处的P点的磁感应强度。

解：建立坐标系如图，任取电流元，由毕-萨定律得：，方向如图：，所有dB形成锥面。

将dB进行正交分解：，则由由对称性分析得：，所以有:，因为： ,r=常量，所以：，又因为：所以：，方向：沿x轴正方向，与电流成右螺旋关系。

讨论：（1）圆心处的磁场：x=0 ，。

（2）当即P点远离圆环电流时，P点的磁感应强度为：。

例3：设有一密绕直螺线管。

半径为 R ，通电流 I。

总长度L，总匝数N（单位长度绕有n 匝线圈），试求管内部轴线上一点 P 处的磁感应强度。

解：建立坐标系，在距P 点 x 处任意截取一小段 dx ，其线圈匝数为: 电流为：。

其相当于一个圆电流，它在P点的磁感应强度为：。

因为螺线管各小段在P点的磁感应强度的方向均沿轴线向右，所以整个螺线管在P点的磁感应强度的大小为：因为：代入上式得：所以：讨论：（1）管内轴线上中点的磁场:（2）当 L>>R时，为无限长螺线管。

此时,，管内磁场。

即无限长螺线管轴线上及内部为均匀磁场，方向与轴线平行满足右手定则。

11-3毕奥-萨伐尔定律及应用

真空的磁导率: π×10 真空的磁导率:o=4π× -7 π× 点的距离. (2) r是电流元到P点的距离. ) 是电流元Idl 点的距离 r是从电流元指向点的单位矢量. 是从电流元Idl 指向P点的单位矢量点的单位矢量. 是从电流元
上页下页
(3)磁场的大小: )磁场的大小:
o Idl sin θ dB = 2 θ是Idl与r 之间的夹角与之间的夹角. 4π r
在薄片中取弧长为dl的窄条, 在薄片中取弧长为的窄条, 的窄条其中通过的微元电流为: 其中通过的微元电流为:
I
I I dI = dl = dθ πR π
上页下页
y
在俯视图上建立如图坐标, 在俯视图上建立如图坐标, 电流元在O点激发的磁感应电流元在点激发的磁感应强度为: 强度为:
o
dB
θ
毕奥-萨伐尔定律及应用 §11-3 毕奥萨伐尔定律及应用
毕奥-萨伐尔定律一, 毕奥萨伐尔定律
d 真空中,电流元真空中,电流元Idl 在P点产 B 点产生的磁场为
o Idl ×r dB = 2 4π r
说明
P
r
θ
I
Idl
上式称为毕奥萨伐尔定律上式称为毕奥-萨伐尔定律毕奥
(1)公式中的系数是制要求的. 制要求的. )公式中的系数是SI制要求的
x R
0 0 I dB = dI = 2 dθ 2πR 2π R
所以: 所以:
π
dθ
方向如图所示. 方向如图所示.
0 I Bx = dBx = 2 ∫0 π R
即:
0 I dBx = dBsinθ = 2 sinθdθ 2π R
By = ∫ dB = 0

大学物理第三册第八章

7
真空中的磁导率矢量形式
0 Idl r ˆ dB 2 4 r
B dB
I
Idl r P
dB
例1 直线电流的磁场。
Idl
2
L l o
r
r
o Idl sin dB 2 4 r
方向
1
P
o Idl sin B dB 2 4r
dq dS 2rdr
dt T 2 /

dI rdr

R
r dr

o
o
x P x
0 r dI dB 3 2 2 2 r x 2
2

0
B dB R 3 s 0 r
2 r 2 x2
2 r 2 x2

r
3

3
dr
2
I内流向与L绕向成左手关系时为负； 3） B d l 中的 B 是全空间电流的贡献；
4） B d l 0 说明磁场为非保守场（涡旋场）。
L
L
例如：
I1 I2 l1

l1
B dl 0 I1 I 2
I
l2
B dl 0
电流密度 (体)电流的(面)密度
I
S
如图电流强度为I的电流通过截面S
若均匀通过电流密度为
(面)电流的(线)密度若均匀通过则
I J S
I
如图电流强度为I的电流通过截线 l
l
I J l
例2 如图所示，在无限大薄平板导体上，沿某一方向通有电流密度为J 的电流。求平板导体周围的磁场.

11.2_毕奥-萨伐尔定律及应用

第十一章稳恒磁场
B=
µ0 nI
2
(cos β 2 − cos β1 )
β1 = π − β 2
l/2
点位于管内轴线中点（1）P点位于管内轴线中点）点位于管内
cos β1 = − cos β 2
B = µ0 nI cos β 2 =
若
cos β2 =
(l / 2)
l
2
+ R2
µ0 nI
2
(l
2
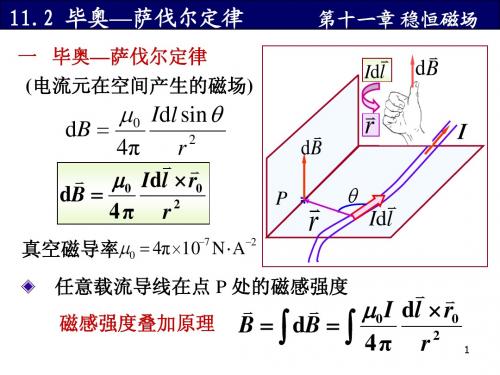
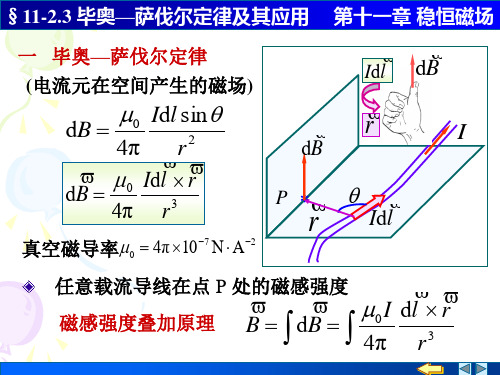
毕奥—萨伐尔定律 11.2 毕奥萨伐尔定律
毕奥—萨伐尔定律一毕奥萨伐尔定律 (电流元在空间产生的磁场电流元在空间产生的磁场) 电流元在空间产生的磁场
第十一章稳恒磁场
Idl
dB
4π r µ0 Idl × r0 dB = 4π r2
−7 −2 真空磁导率µ0 = 4π ×10 N ⋅ A
dB =
µ0 Idl sin θ
2
r
dB
P *
I
r
θ
Idl
任意载流导线在点 P 处的磁感强度磁感强度叠加原理
B = ∫ dB = ∫
µ0 I dl × r0
4π r
2
1
毕奥—萨伐尔定律 11.2 毕奥萨伐尔定律
第十一章稳恒磁场毕奥—萨伐尔定律毕奥萨伐尔定律
dB =
µ0 Idl × r0
4π
1
r
1 B = µ 0 nI 2
B=
µ0nI
2
(cos β2 − cos β1 )
B
1 µ 0 nI 2
µ0nI
x
24
O
毕奥—萨伐尔定律 11.2 毕奥萨伐尔定律

毕奥-萨伐尔定律及应用

B x = ∫ dB x B y = ∫ dB y Bz = ∫ dBz
}Байду номын сангаас
⇒
v v v v B = Bx i + B y j + Bz k
设有长为L的载流直导例1 载流长直导线的磁场设有长为的载流直导线，其中电流为I。计算距离直导线为a处的点的磁其中电流为。计算距离直导线为处的P点的磁处的感应强度。感应强度。 I 解：任取电流元 Idl 据毕奥-萨伐尔定律萨伐尔定律， r 据毕奥萨伐尔定律，此电 α Idl 流元在P 流元在P点磁感应强度dB为 r r L r
I dl
R
r
x
d B⊥
θ
θ
r dB
I
O
P
r d B//
µ0 I d l B = ∫ dB// = ∫ dB sin θ = ∫L r 2 sin θ L L 4π µ 0 I sin θ 2πR µ 0 I sin θ = 2 ∫0 d l = 4πr 2 2πR 4πr
µ0 I sin θ B= 2πR 2 4πr
单位矢量
真空中的磁导率
大小：大小： dB =
4π
µ0 Idl sin θ
r2
Idl vθ
P
v B
方向：方向：右螺旋法则
v r
r dB
r dB
r Id l
P
r r
α
r dl
I
电流元在给定点所产生的磁感应强度的大小与 I d l 成正比，与到电流元的距离平方成反比，与电 r 成正比，与到电流元的距离平方成反比， r 流元 r 矢径夹角的正弦成正比。 dB 方向垂直于 r 和 r r 组成的平面，与 Idl 组成的平面，指向为由 Idl 经 α 角转向 r 时右螺旋前进方向。右螺旋前进方向。 r

10-2毕萨定律

4）磁场应强度-----载流导体激发
二、毕奥-萨伐尔定律应用
根据毕奥-萨伐尔定律
积分得到两个基本公式：
1、直线载流导线
2、圆形载流环线
1、载流直线的磁感
一段直导线L载流I向上，求与导线垂直距离为r的任意点的磁感强度。
解：
1）建坐标系 2）电流元B大小
0 Idy r sin dB 3 4 r
BO μ0 I 角度 4π r
磁感方向（右手螺旋关系）
练习：
（1）求无限长直导线磁感
（2）求完整载流圆环在O点的磁感
计算题
电流为I的无限长载流导线弯成如图形状，求圆心O处的磁感。
解：
1）过圆心的直线 I ，在O点产生的磁感
B1 0
2）圆环在O点产生的磁感
μ0 I 3 π 4πR 2
0 Idl r B dB 3 4 L r L
B大小: B dB
0 Idl sin 2 4 r
定律说明：
0 Idl r B dB 3 4 L r L
1）磁感应强度---对载流导线的积分 2）磁感应强度取决于导线形状、电流大小. 和方向 3）磁感应强度还取决于场点的距离和方位
10-2 毕奥-萨伐尔定律
一、毕奥-萨伐尔定律二、应用举例
一、毕奥-萨伐尔定律
• 问题：研究任意形状的载流导线在任意场点P激发的磁感强度
•想法：导线分段，
强度叠加
具体过程
1）电流元
在载流导线上任取无限小长度dl .
电流元： Idl
方向—电流流向
电流元形成的磁感dB
起因： Idl
场点：位矢 r

毕奥——萨伐尔定律在极坐标系中的表达式及其应用

毕奥——萨伐尔定律在极坐标系中的表达式及其应用
毕奥萨伐尔定律是世界上最经典的物理定律之一，它可以描述磁场在极坐标系中的表达式及其应用，是物理学中不可缺少的重要组成部分。

本文主要介绍毕奥萨伐尔定律在极坐标系中的表达式及其应用。

首先，我们来介绍毕奥萨伐尔定律在极坐标系中的表达式。

首先，毕奥萨伐尔定律定义了磁场从磁极出发的表达式，它表示磁场受到磁极强度的影响而产生，而且它的值取决于磁极的强度与磁极之间的距离，而这个距离关系可以用一个抛物线表达：即磁场强度随着距离的减小而增大，而随着距离的增加而减小，用公式表示为：B=B0*(1/r^2)，其中B0为磁极强度，r为两磁极之间的距离。

此外，毕奥萨伐尔定律还可以描述磁场的产生方向，即它的向量表达式，它表明磁场是从磁极出发的，具体来说，磁场的方向是从磁极的正极指向负极的方向。

用公式表示为：B=B0*(1/r)*对应的单位
向量，其中B0为磁极强度，r为两磁极之间的距离，对应的单位向
量表示磁场方向。

接着，我们来讨论毕奥萨伐尔定律在极坐标系中的应用，首先，它可以用于研究磁性材料，因为磁性材料向外施加磁极的时候，磁场的变化遵循毕奥萨伐尔定律。

其次，毕奥萨伐尔定律可以用于研究空间磁场的变化，这对于放射性核物质的研究有着重要意义，因为空间磁场变化可以影响核子间的相互作用，从而影响放射性核物质的结构和品质，从而不同的空间磁场可以调节放射性核物质表现出不同的性质。

总而言之，毕奥萨伐尔定律可以描述磁场在极坐标系中的表达式及其应用，是物理学中不可缺少的重要组成部分。

它的表达式可以用简单的数学公式来描述，而它的应用范围也包括磁性材料和放射性核物质的研究。

毕奥—萨伐尔定律及其应用

0 I
4a
sin d
0 I
4a
(cos1
cos2 )
上式中，1 和2 分别是直导线两端的电流元与它们到 P 点的矢径之间的夹角。
毕奥—萨伐尔定律及其应用
，，
，
，
例题讲解 1
设长为 L 的直导线通有电流 I，求距离导线为 a 处一点 P 的磁感应强度。
若导线长度远大于点 P 到直导线的垂直距离（ L a ），则导线可视为无限长。
dB，Idl，r 这 3 个矢量的方向符合右手螺旋法则。
因此，矢量形式
dB
0 4
Idl r2
er
er ——由电流元指向点 P 的单位矢量。
整个载流导线在空间某点 P 的磁感应强度 B，等于导线上所有电流元在该点所产生的磁感应强度
dB
的矢量和，即
B
L
dB
L
0 4
Idl r2
er
积分是对整个载流导线进行矢量积分。
r2
式中，0 称为真空磁导率，其值为 0 4π 10–7 N A2 。磁感应强度 dB 的方向垂直于 Idl 和 r 所组
成的平面，并沿 Idl r 的方向，即当右手弯曲，四指从 Idl 方向沿小于 π 的角转向 r 时，伸直的大拇指所
指的方向为 dB 的方向。
毕奥—萨伐尔定律及其应用
1.1 毕奥—萨伐尔定律
大学物理
毕奥—萨伐尔定律及其应用
1.1 毕奥—萨伐尔定律
毕奥—萨伐尔定律指出：电流元 Idl 在真空中某点 P 所产生的磁感应强度 dB 的大小，与电流元的
大小 Idl 成正比，与电流元和从电流元到 P 点的矢径 r 之间夹角的正弦成正比，与电流元到点 P 的距离 r

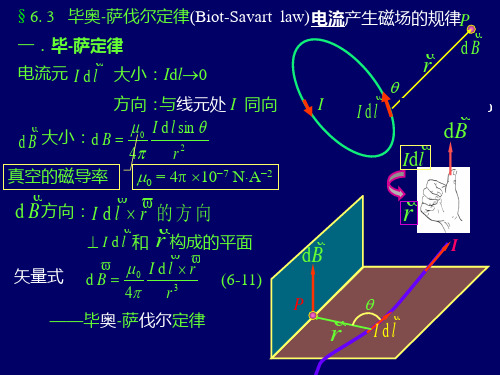
6. 3 毕奥——萨伐尔定律及其应用

L L
或：大小 B
B B B
2 x 2 y
2 z
标明方向！
关键是求出 d B
0 I d l r dB 4 r 3
(6-11)
——毕奥-萨伐尔定律
例：判断下列各点磁感应强度的方向和大小. 1 方向如图示： 8

2
大小
7 R 6 5
Id l

3
4
0 I d l sin dB 4 r2 1、5 点： dB 0
真空的磁导率
I dl
r
Байду номын сангаасdB
d B 方向：I d l r 的方向 I d l 和 r 构成的平面
0 I d l r dB 4 r 3
4 r 0 = 4 107 NA2
I※ dl d B =?
Bd dB LB
0 Ia d x 0I l arctan— l 4l ( x 2 a 2 ) = —— 2l a
4l x a
2
0 Ia d x 2 2 4l ( x 2 a 2 ) x a
a

B= — j (匀强场) 2
0
本题下去重做一下
四、运动电荷的磁场
+ + + + + + + + + + + +++ + + + + + + ++ ++++ + + + + + + + + + + + + + + + + + + + + ++ +++ + ++++ +++ + ++ + + + + + + + + + + + + ++ + + +++ ＋＋＋ +++ + ++++ + + + +++ + + + + + + + + + + + + + + ++ ++ + + + + + ++ ++ + + + + + ++ + + + + ++ v ＋＋＋设：导体单位体积内电荷数 n 0 I d l r dl 内电荷数 dN= n (Sdl) (6-11) dB 3 0 I d l 4 r sin 它们的合磁场 d B 每个电荷产生的磁场？ 4 r 2 q 的平均速度 v I = n(vS)q 矢量式运动电荷 q 产生的磁场 0 qv r (6-13) B 0 3 d B 4 r B = —— dN 4 r 2 vq sin 和 1. 说明：的方向垂直于 v B 方向与 d B 同向，仍为 I d l r 。 r 所确定的平面。

复习毕奥萨伐尔定律的应用

（4）按 Bx dBx
L
L 各坐标的分量，最后得到 B Bx i By j Bz k
L
By dBy Bz dBz ，求出 B 的
毕奥—萨伐尔定律的应用
一毕奥---萨伐尔定律应用举例
例1 载流长直导线的磁场.
dB 方向均沿
第八章
z
D
2
dz
1 B 0 nI 2
0 nI cos 2 cos 1 B 2
思考：
螺线管内部的
B 0nI
为什么？
边缘部分轴线上的 B 1 nI 0
2
毕奥—萨伐尔定律的应用
第八章
例如图载流长直导线的电流为 I , 试求通过矩形面积的磁通量. 解先求，对变磁场
B
4π
毕奥—萨伐尔定律的应用
第八章
0 I B sin d 4π r0（cos1 cos 2） 4π r0 z B 的方向沿 x 轴的负方向. D 2
0 I
2
1
无限长载流长直导线的磁场.
B
（cos1 cos 2） 4π r0
B
0 I
I
o
x
C
B
1 0 2 π
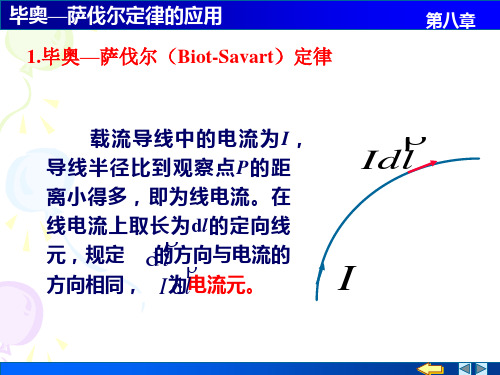
毕奥—萨伐尔定律的应用 1.毕奥—萨伐尔（Biot-Savart）定律
第八章
载流导线中的电流为 I，导线半径比到观察点P的距离小得多，即为线电流。在线电流上取长为dl的定向线
Idl
元，规定 d l 的方向与电流的
方向相同，
I 为电流元。 dl
I
毕奥—萨伐尔定律的应用
dB
I dl
r

11-2.3 毕奥-萨伐尔定律及其应用

毕奥—萨伐尔定律及其应用 §11-2.3 毕奥萨伐尔定律及其应用例3 载流直螺线管的磁场
第十一章稳恒磁场
如图所示，有一长为半径为R的载流密绕直螺如图所示，有一长为l , 半径为的载流密绕直螺线管，螺线管的总匝数为N，通有电流I. 线管，螺线管的总匝数为，通有电流设把螺线管放在真空中，求管内轴线上一点处的磁感强度. 放在真空中，求管内轴线上一点处的磁感强度
判断下列各点磁感强度的方向和大小. 例判断下列各点磁感强度的方向和大小
8 2
d 1、5 点： B = 0 、
3、7点：dB 、点 +3
+
=
µ 0 Id l
4π R
2
7
Idl
R
6 5
2、4、6、8 点：、、、
+4
dB =
µ 0 Idl
4π R
sin 450 2
毕奥—萨伐尔定律及其应用 §11-2.3 毕奥萨伐尔定律及其应用毕奥---萨伐尔定律萨伐尔定律应用举例二毕奥萨伐尔定律应用举例载流长直导线的磁场. 例1 载流长直导线的磁场
dB =
µ0
2
B = ∫ dB =
µ 0 nI
2
(R
R In d x
2
2
+x
x2 x1
2 3/2
)
B=−
µ 0 nI
2
∫ (R
2
R 2 dx
2
x = R ctg β 2 dx = − R csc βdβ
+x
2 3/ 2
∫β
β
1
R 3 csc 2 β d β R 3 csc 3 β

.毕奥-萨伐尔定律

.毕奥-萨伐尔定律
摘要：
1.毕奥- 萨伐尔定律的定义
2.毕奥- 萨伐尔定律的发现历程
3.毕奥- 萨伐尔定律的数学表达式
4.毕奥- 萨伐尔定律的应用领域
5.毕奥- 萨伐尔定律在我国的研究现状与前景
正文：
毕奥- 萨伐尔定律，又称毕萨定律，是电磁学中的一个基本定律，描述了电流在磁场中受力的规律。

该定律由法国物理学家让- 巴蒂斯特·毕奥（Jean-Baptiste Biot）和法国数学家费尔南德·萨伐尔（Ferdinand de Saussure）在1820 年同时独立发现，故以两位科学家的名字命名。

毕奥- 萨伐尔定律的数学表达式为：F = I * d * B，其中F 表示电流在磁场中受到的安培力，I 表示电流强度，d 表示电流元的长度，B 表示磁感应强度。

根据这个公式，可以计算出电流在磁场中所受的力。

毕奥- 萨伐尔定律在许多领域都有广泛的应用，如电磁制动、电磁起重机、电磁继电器等。

此外，在现代科技领域，如磁悬浮列车、电动汽车、风力发电等方面，毕奥- 萨伐尔定律的应用也越来越重要。

在我国，对毕奥- 萨伐尔定律的研究始于上世纪50 年代。

经过几十年的发展，我国在电磁学领域的研究已经取得了世界领先的成果。

目前，我国正加大对电磁学领域的研究力度，致力于推动电动汽车、磁悬浮列车等新型产业发
展，为我国经济建设和科技进步做出贡献。

总之，毕奥- 萨伐尔定律作为电磁学的基本定律之一，对我国科技发展具有重要意义。

毕奥—萨法尔定律及应用

第 8 章
8.1
磁
场
毕奥—萨法尔定律
课时：15 分钟
人类离不开磁
地磁场是地球生物的保护伞
磁技术的开发利用推动人类社会不断发展
知识回顾
磁感应强度的叠加原理
回忆：电场的叠加原理磁感应强度的叠加原理
如果有几个点电荷同时存在,它们产生的电场就相互叠加,形成合电场,这时某点的场强等于各个电荷单独存在时在该点产生的场强的矢量和.
稳恒电流产生的磁场，可把稳恒电流分割成无限多个电流元（载流导线上某一线元矢量 dl 与流经它的电流的乘积称为电流元。规定，电流元的方向为线元中电流的流向，先求出每个电流元在所求点产生的磁感应强度，再应用叠加原理计算电巴蒂斯特· 毕奥，法国物理学家。曾恪守电与磁无关系的看法，后支持他奥斯特，与萨伐尔共同提出毕奥——萨伐尔定律。是第一个发现云母独特的光学性质，因此以云母为基础的矿物黑云母就是以他命名的。 1804年，他和约瑟夫· 路易· 盖-吕萨克制造了一个热气球，上升到了五千米的高度，目的是为了研究地球的大气层。
在真空中，载流导线上任一电流元，在空间某点P处的磁感应强度的大小，与电流元的大小 Idl 成正比，与电流元和自电流元到 P点的矢量r 间的夹角的正弦成正比，而与电流元到 P点的距离 r的平方成反比。
数学表达式:
Idl sin dB k r2
0 如式中各量均用国际单位制，则 k ，其 4 7 1 中 0 4 10 N A ，为真空中磁导率。
菲利克斯· 萨伐尔（ Félix Savart ，1791年6月30日－ 1841年3月16日），法国物理学家和医生。他与让-巴蒂斯特· 毕奥共同创建了毕奥-萨伐尔定律。这是静磁学的一个基本定律，精确地描述载流导线的电流所产生的磁场。萨伐尔对于声学也很有研究。他发展出一种声学仪器，沙伐音轮 (Savart wheel) ，可以用来研究听觉的最低频率限度。现在不再常用的音程度量单位，沙伐 (savart) ，也是因他而命名。

毕奥萨伐尔定律的应用

毕奥萨伐尔定律的应用
毕奥萨伐尔定律是一个广泛应用于物理学和工程学的原理，以下是一些其应用的例子：
1. 电动机理论：毕奥萨伐尔定律可以用来确定电动机所产生的力矩和电流之间的关系。

这可以用于电动机的设计和性能优化。

2. 磁共振成像（MRI）：MRI利用了毕奥萨伐尔定律，通过物体中的原子核自旋与外加磁场之间的相互作用来产生图像。

由此可以用于医学成像、生命科学、材料科学等方面。

3. 电力工程：毕奥萨伐尔定律可以用于变压器和发电机的设计。

通过探索磁场的作用，我们可以优化电力系统的性能和效率。

4. 磁选分离技术：通过应用毕奥萨伐尔定律来制造强磁场，在该磁场中将由特定元素组成的粒子分离出来，以帮助提取或清洁物质。

这种技术可以应用于生产、环保和化学制药等领域。

5. 磁浮列车：使用毕奥萨伐尔定律可以制造出磁浮飞行的草图。

由于磁场中的气垫，磁浮列车可以悬浮在轨道上，并以高速运行，相比于传统的火车安全和效率相对提高。

6. 鸽派派论争：在哲学中，毕奥萨伐尔定律常用于指导对归因于自然色素或者文化习俗的某些现象占主导地位的讨论。

总而言之，毕奥萨伐尔定律不仅是一个理论上有趣的原则，而且在科学，工程和医学方面具有非常广泛的应用。

毕萨定律及其应用

Idl
p1
2） dB与 r 和 Idl 的夹角的有关：在与电流元垂直的方向上，磁场最强；在与电流元重合的方向上，磁场为零； 2. 关于dB 的方向：垂直于电流元和矢径构成的平面。
（下一页）
二、毕奥---萨伐尔定律的应用计算各种电流分布产生的磁场的磁感强度基本步骤： p 1）任取电流元Idl, 求出其在 ==场点 P 产生的磁感dB的 dB p r ==大小与方向； α 2 ）分析 dB方向是否变化 : ==若不变,直接积分; Idl ===若变化, 则要将dB适当= 的分解, 对各分量分别积分, 然后再合成起来.
B
dB
L

L
0 Idl r 4 r 3
（下一页）
例1. 直电流的磁场已知：真空中, I、1、 2、a 求 p点的磁感强度. 建立坐标系OXY
Y
I
2
dl l
O

1
r
dB
任取电流元 Idl
0 Idl sin 大小: dB 2 4 r
m Pm NISn
S
n
大小： B
0 IR 2
2( R 2 x 2 )3 2
则 B 0m 3 2x
方向：右手螺旋法则
（下一页）
2.）圆心处： x
0 IR B 2( R 2 x 2 )3 2 0 I B 2R
2
0
0 Idl sin =900 Bx dBx I 2 = R2 4 r 0 I 0 IR 0 IR d dl Rd 3 3 4R 2 4R 2R 4R 2
I
0 I 0 I Bo 2R 4 R

h2-1毕-萨定律的应用

12
手螺旋定则
en
en
en
说明：只有当载流线圈的面积S很小，或场点距圆电流很远时，才能把圆电流叫做磁偶极子。对比：习题10-4：电偶极子在其轴线上产生的电场
E
1 p 3 2 π 0 r
, r l
13
例3 ：真空中，载流密绕直螺线管轴上的磁场。如图所示，有一长为l , 半径为R的载流密绕直螺线管，螺线管的总匝数为N，通有电流I. 设把螺线管放在真

I
0 I B 2 R 2 4 R
0 I
10
(4) d *A
BA
0 I
4π d
(5)
I
R1
R2
* o
0 I 0 I I BO 4 R2 4 R1 4 R1
0
注：垂直纸面向里为正方向
11
闭合通电线圈的磁偶极矩:
定义：
m ISen
R
r
x
所以有
B B// d B// d B sin
O

dB dB dB
P
dB
x
R 0 IR 因为 sin ,场点一定，x一定 B r 3 4 r r 常量，所以有

2R
0
dl
0 IR2
2r 3
又，r 2 x 2 R2 , 所以有
2
0 nI
0 nI
2
B
A1
O
A2
x
直螺线管轴线上的磁场的分布
参阅课本，图13.20 在螺线管中心附近轴线上各点磁场基本是均匀的，管口附近磁场逐渐减小，出口以后磁场很快地减弱。

毕萨定律及其应用

毕萨奥伐尔定律

11.2 毕萨定理

毕奥-萨伐尔定律及毕奥-萨伐尔定律应用举例

11-3毕奥-萨伐尔定律及应用

大学物理第三册第八章

11.2_毕奥-萨伐尔定律及应用

毕奥-萨伐尔定律及应用

10-2毕萨定律

毕奥——萨伐尔定律在极坐标系中的表达式及其应用

毕奥—萨伐尔定律及其应用

6. 3 毕奥——萨伐尔定律及其应用

复习 毕奥萨伐尔定律的应用

11-2.3 毕奥-萨伐尔定律及其应用

.毕奥-萨伐尔定律

毕奥—萨法尔定律及应用

毕奥萨伐尔定律的应用

毕萨定律及其应用

h2-1毕-萨定律的应用

复习毕奥萨伐尔定律的应用