浙教版八年级下册数学第四章平行四边形测试题(附答案)
浙教版八年级下学期数学(下册)第四章平行四边形测试题(附答案)

浙教版数学八年级下册第四章平行四边形测试题(时间:100分钟满分:120分)题号 1 2 3 4 5 6 7 8 9 10 答案一、选择题(共10小题每3分共30分)1.在四边形的四个内角中,钝角个数最多为()A.4B.3C.2D.12.一个多边形的内角和是外角和的4倍,则这个多边形对角线的条数是()A.35条B.40条C.70条D.80条3.如图,已知AB∥CD,∠1=21∠CAB,∠2=21∠ACD,PE⊥AC于点E,若PE=3,则AB 与CD的距离为( )A.3 B.6 C.12 D.无法确定4.如图,□ABCD中,对角线AC和BD交于点O,若AB=5,AO=6,则边AD长的取值范围是( )A.1<AD<11 B.7<AD<17 C.6<AD<17 D.5<AD<115.张扑克牌如图1所示放在桌子上,有人将其中一张旋转180°后得到如图2所示,那么他所旋转的牌从左起是()A.第一张B.第二张C.第三张D.第四张6.在四边形ABCD中,对角线AC,BD相交于点O,若OA=OC,再添加一个条件使其成为平行四边形,则添加的条件是( )A.AB=DC B.AD=BC C.∠ADC=∠ABC D.OB=OD7.用反证法证明命题“若a+b+c≥0,abc≤0,则a、b、c三个实数中最多有一个小于零”的反设内容为()A.a、b、c三个实数中最多有一个不大于零B.a、b、c三个实数中最多有两个小于零第10题图第4题图第5题图1 第5题图2C . a 、b 、c 三个实数中至少有两个小于零D . a 、b 、c 三个实数中至少有一个不大于零8.如图,在□ABCD 中,对角线AC ,BD 交于点O ,将△AOB 平移至△CDP 的位置,连结OP , 则图中平行四边形的个数为( )A .1B .2C .3D .49.如图,O 为在□ABCD 对角线的交点, E 为AB 的中点,连接DE 交AC 于点F ,有下面的结 论:①OE =21AD ;②S △AEF =DOF S ∆;③FD =2EF ;④S △AFD =4EOF S ∆;⑤AF :FO :OC =2:1:3. 其中正确的个数为( )A .5B .4C .3D .210.如图,△ABC 中,点D ,E ,F 分别为BC ,AB ,AC 的中点,将△AEF 沿EF 折叠,使得A落在边BC 上的点A '处,连接EF ,ED ,DF ,E A '与FD 相交于点P ,有下面的结论: ①△EDF ≌△E A F ';②E A F S '∆=41ABC S ∆;③PE =PF ;④E A '⊥FD ;⑤△E A F '的周长等于 △ABC 周长的一半.其中正确的个数为 ( )A .2个B .3个C .4个D .5个二、填空题(共10小题 每题3分 共30分)11.在ABC ∆中,∠A =30°,∠C =90°,以边BC 的中点P 为中心,作出与ABC ∆成中心对称的CB A '∆,则A A '的长为 .12.如图,一块试验田的形状是五边形,管理员从CD 边上的一点P 出发,沿PD →DE →EA →AB→BC →CP 的方向走了一圈回到D 处,则管理员从出发到回到原处在途中身体转过 度. 13.已知在平面直角坐标系中,点A ,B ,C 的坐标分别是A (-3,4),B (-5,6),C (1,2),若点D 与A 、B 、C 三点构成平行四边形,则点D 的坐标是 .14.如图,在四边形ABCD 中,∠A +∠D =240°,∠B =3α,∠C =α2-5α,则α的度数为 .15.如图,点P 是□ABCD 内任意一点,若S □ABCD =16,则阴影部分的面积为 .第14题图第12题第15题图第8题图第9题图第10题图16.如图,四边形ABCD的平行四边形,直线AD的解析式为y=3,直线DC的解析式为y=-3x -3,BC=2DC,则点A的坐标为.17.如图,在□ABCD中,E在CD上,以BE为折痕把△BCE向上翻折,使点C落在AD上的点F处. 若△DEF的周长为5,△ABF的周长为13,则AF= .18.一个四边形的边长分别为a、b、c、d,其中a,c为对边,且满足a+b+c+d=2ac+2bd,则这个四边形的对角线.19.如图,□ABCD的对角线AC,BD交于点O,EF过点O且与AB,CD分别交于点E,F.已知DE=m,则BF的长为________.20.如图,△ABC中,点D,E,F分别为BC,AB,AC的中点,将△AEF沿EF折叠,使得A 落在边BC上的点A'处,连接EF,ED,DF,E A'与FD相交于点P,有下面的结论:①△EDF≌△EAF';②S△EDF =EAFS'∆;③PE=PF;④E A'⊥FD;⑤△EAF'的周长等于△ABC周长的一半.其中正确的是(填序号)三、解答题(共6题共60分)21.(满分9分) 甲、乙分别利用图①、②的不同方法求出了七边形的内角和都是900°.请你考虑在图③中再用另外一种方法求七边形的内角和.并写出求解过程.22.(满分9分)如图,一个六边形的6个内角都是120°,其相邻四边的长依次是AF=2,AB=3,BC=CD=4,求第15题图①第15题图②第15题图③第16题图第17题图第13题图第20题(1)DE和EF的长;(2)六边形ABCDEF 的面积.23.(满分10分) 18、如图,在□ABCD中,AE⊥BC于E,AF⊥CD于F.(1)若∠EAF=50°,求∠F AD的度数;(2)BP是∠ABC的平分线,分别交AE、AF、AD于点M、N、P,求证:AM=AN;(3)若□ABCD的周长为48,AE=6,AF=10,求BC的长.第23题图24.(满分10分) 如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形,即△ABD、△BCE、△ACF,连接DE,EF,求证:四边形ADEF是平行四边形.例题24图25.(满分10分) 已知△ABC与△A′BC有公共边BC,且A′B+A′C>AB+AC.用反证法证明:点A′在△ABC的外部.第25题图26.(满分12分)如图,在△ABC中,点E是BC上任意一点,连接AE,点D是BC的中点,点F是BE的中点,点P为AE的中点,点G为AC的中点. 求证:(1)PD与FG互相平分;(2)EC=2FD.第26题图参考答案一、选择题(共10小题每3分共30分)题号 1 2 3 4 5 6 7 8 9 10答案 B A B B D D C D A C二、填空题(共10小题每题3分共30分)11、13212、360 13、(-9,8)或(-3,0)或(-1,4)14、12°15、8 16、(-6,3)17、4 18、互相平行19、m 20、①、②、③、⑤.三、解答题(共6题共60分)21.(满分9分) 甲、乙分别利用图①、②的不同方法求出了七边形的内角和都是900°.请你考虑在图③中再用另外一种方法求七边形的内角和.并写出求解过程.21.解:连接GC、FD将七边形分成两个四边形和一个三角形,因为四边形的内角和是360度,三角形的内角和是180度,所以七边形ABCDEFG的内角和为360°+360°+180°=900°(方法不唯一).22.(满分9分)如图,一个六边形的6个内角都是120°,其相邻四边的长依次是AF=2,AB=3,BC=CD=4,求(1)DE和EF的长;(2)六边形ABCDEF的面积.22.解:(1)如图,延长并反向延长AB,CD,EF,分别交于M,N,∵六边形ABCDEF的每个内角都是120°,∴其每个外角均为60°,∴△AGF,△BMC,△DNE都是等边三角形,∴∠G=∠M=∠N=60°,∴△GMN是等边三角形,∴MG=MN=NG.GA+AB+BM=MC+CD+DN=NE+EF+FG=2+3+4=9DE=DN=1,EF=9-2-1=6.S六边形ABCDEF= S△GMN-S△GAF-S△BMC-S△DNE=2943⨯-2243⨯-2443⨯-2143⨯=153.23.(满分10分) 18、如图,在□ABCD中,AE⊥BC于E,AF⊥CD于F.(1)若∠EAF=50°,求∠F AD的度数;(2)BP是∠ABC的平分线,分别交AE、AF、AD于点M、N、P,求证:AM=AN;第21题图①第21题图②第21题图③第21题图④第22题图(3)若□ABCD 的周长为48,AE =6,AF =10,求BC 的长.(1)解:∵AE ⊥BC ,AF ⊥CD ,∠EAF =50° , ∴∠AEC +∠AFC =180°, ∴∠DAF +∠C =180°. ∴∠C =130°.∵四边形ACED 是平行四边形, ∴AD ∥BC , ∴∠C +∠D =180°,∴∠D =50° ∴∠F AD =40°;(2)证明:∵四边形ACED 是平行四边形, ∴AD ∥BC ,∠ABC =∠D , ∴∠3=∠1, ∴∠BAE =∠F AD .∵BP 是∠ABC 的平分线, ∴∠1=∠2,∵∠AMN =∠2+∠BAE ,∠ANM =∠3+∠F AE , ∴∠AMN =∠ANM , ∴AM =AN ;(3) ∵□ABCD 的周长为48,AE =6,AF =10, ∴BC +CD =24,设BC =x ,则CD =24-x ,由平行四边形的面积得BC ·AE =CD ·AF , ∴6x =10(24-x ),解得x =15,∴BC =15.24.(满分10分) 如图,以△ABC 的三边为边在BC 的同侧分别作三个等边三角形,即△ABD 、△BCE 、△ACF ,连接DE ,EF ,求证:四边形ADEF 是平行四边形. 证明∵△ABD ,△EBC 都是等边三角形. ∴AD =BD =AB ,BC =BE =EC , ∠DBA =∠EBC =60°.∴∠DBE +∠EBA =∠ABC +∠EBA =60°. ∴∠DBE =∠ABC . 在△DBE 和△ABC 中,∵⎪⎩⎪⎨⎧=∠=∠=BC BE ABC DBE AB DB , 例题24图∴△DBE ≌△ABC . ∴DE =AC .又∵△ACF 是等边三角形, ∴AC =AF . ∴DE =AF .同理可证:△FEC ≌△ABC . ∴EF = AD ,∴四边形ADEF 平行四边形(两组对边分别相等的四边形是平行四边形).25.(满分10分) 已知△ABC 与△A ′BC 有公共边BC ,且A ′B +A ′C >AB +AC .用反证法证明:点A ′在△ABC 的外部.25、 解答:证明:如图1,设点A ′在△ABC 的边上时, ∵AA ′+AC >A ′C , ∴A ′B +A ′C <AB +AC ,与已知矛盾,故假设不成立,原命题正确; 如图2,若点A ′在△ABC 内部时: 延长BA ′交AC 于点E在△ABE 中,AB +AE >BE =BA ′+A ′E , 在△CA ′E 中,A ′E +CE >A ′C ∴AB +AE +A ′E +CE >A ′B +A ′E +A ′C 即有:AB +AC >A ′B +A ′C ,与已知矛盾,故假设不成立,原命题正确;由此可见,与△ABC 共一条边BC 的三角形中,另一顶点A '在AB 、AC 或△ABC 内时都有A 'B +A 'C <AB +AC因此满足条件的点A '必在△ABC 外部.26.(满分12分)如图,在△ABC 中,点E 是BC 上任意一点,连接AE ,点D 是BC 的中点,点F 是BE 的中点,点P 为AE 的中点,点G 为AC 的中点. 求证: (1)PD 与FG 互相平分; (2)EC =2FD .证明(1)连接PG 、GD 、FP ,∵D 、G 、P 、F 分别是BC 、AC 、AE 、BE 的中点, ∴PG 为△AEC 的中位线, ∴PG ∥EC ,即PG ∥FD ,∴DG 与PF 分别为△ABC 与△ABE 的中位线, ∴DG ∥AB ,PF ∥AB , ∴DG ∥PF .∴四边形DGPF 为平行四边形,第25题图第26题图∴PD 与FG 互相平分. (2)由(1)得, PG =FD . ∵PG 为△AEC 的中位线, ∴PG =21EC , ∴FD =21EC .。
(汇总)浙教版八年级下册数学第四章 平行四边形含答案
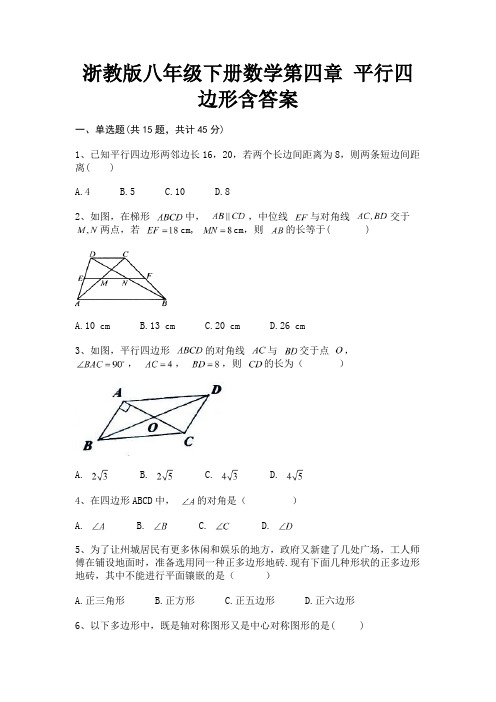
浙教版八年级下册数学第四章平行四边形含答案一、单选题(共15题,共计45分)1、已知平行四边形两邻边长16,20,若两个长边间距离为8,则两条短边间距离( )A.4B.5C.10D.82、如图,在梯形中,,中位线与对角线交于两点,若cm, cm,则的长等于( )A.10 cmB.13 cmC.20 cmD.26 cm3、如图,平行四边形的对角线与交于点,,,,则的长为()A. B. C. D.4、在四边形ABCD中,的对角是()A. B. C. D.5、为了让州城居民有更多休闲和娱乐的地方,政府又新建了几处广场,工人师傅在铺设地面时,准备选用同一种正多边形地砖.现有下面几种形状的正多边形地砖,其中不能进行平面镶嵌的是()A.正三角形B.正方形C.正五边形D.正六边形6、以下多边形中,既是轴对称图形又是中心对称图形的是( )A.正五边形B.矩形C.等边三角形D.平行四边形7、下列图案中,不是中心对称图形的是()A. B. C. D.8、一个多边形的内角和比它的外角的和的2倍还大180°,这个多边形的边数是()A.5B.6C.7D.89、如图,在平行四边形ABCD中,对角线AC,BD相交于点O,下列结论中一定正确的是()A.AB=BCB.OB=ODC.AC=BDD.AB⊥AC10、下列由一个正方形和两个相同的等腰直角三角形组成的图形中,是中心对称图形的是()A. B. C. D.11、下列图形中,是中心对称图形的是()A. B. C. D.12、若一个多边形的每个内角都为135°,则它的边数为()A.6B.8C.5D.1013、下面图形中,既是中心对称图形又是轴对称图形的是()A. B. C. D.14、将图1中五边形纸片ABCDE的A点以BE为折线往下折,A点恰好落在CD 上,如图2所示,再分别以图2的AB,AE为折线,将C,D两点往上折,使得A,B,C,D,E五点均在同一平面上,如图3所示,若图1中∠A=124°,则图3中∠CAD的度数为何()A.56B.60C.62D.6815、用反证法证明命题“三角形中最多有一个角是直角”时,下列假设正确的是()A.三角形中最少有一个角是直角B.三角形中没有一个角是直角C.三角形中三个角全是直角D.三角形中有两个或三个角是直角二、填空题(共10题,共计30分)16、若一个多边形内角和等于1260°,则该多边形边数是________ .17、已知直线a∥b∥c,a与b的距离是5cm,b与c的距离是3cm,则a与c 的距离是________18、一个三角形的三边长分别为4,5,6,则连结各边中点所得三角形的周长为________19、如图,是4×4正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是________.20、已知点P(﹣2,3)关于原点的对称点为M(a,b),则a+b=________ .21、顺次连接对角线互相垂直的四边形各边中点,得到的四边形是________.22、如图所示,线段EF过平行四边形ABCD的对角线的交点O,交AD于点E,交BC于点F。
浙教版八年级下册数学第四章平行四边形测试卷(附答案)

浙教版八年级下册数学第四章平行四边形测试卷(附答案)一、单选题(共12题;共24分)1.下列图形中,既是轴对称图形又是中心对称图形的是A. B. C. D.2.若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是( )A. 十三边形B. 十二边形C. 十一边形D. 十边形3.下列图形中,不是中心对称图形的是()A. B. C. D.4.如果一个角的两边分别垂直于另一个角的两边,那么这两个角的数量关系为()A. 相等B. 互补C. 相等或互补D. 无法确定5.如图,在平行四边形ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE 于G,BG=4 ,则四边形AECD的周长为()A. 20B. 21C. 22D. 236.已知一个正多边形的每个外角等于60°,则这个正多边形是()A. 正五边形B. 正六边形C. 正七边形D. 正八边形7.能判定四边形ABCD为平行四边形的是().A. AB∥CD,AD=BCB. ∠A=∠B,∠C=∠DC. AB=CD,AD=BCD. AB=AD,CB=CD8.n边形的每个内角都为120°,则内角和为()A. 360°B. 540°C. 720°D. 1080°9.如图,在△ABC中,∠BAC=60°,BC=18,D是AB上一点,AC=BD,E是CD的中点.则AE的长是( ).A. 12B. 9C. 9D. 以上都不对10.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于()A. 60°B. 72°C. 90°D. 108°11.如果一个多边形的内角和是外角和的3倍,那么这个多边形是()A. 五边形B. 六边形C. 七边形D. 八边形12.把边长相等的正五边形ABGHI和正六边形ABCDEF的AB边重合,按照如图的方式叠合在一起,连接EB,交HI于点K,则∠BKI的大小为()A. 90°B. 84°C. 72°D. 88°二、填空题(共8题;共18分)13.已知平行四边形ABCD中,∠C=2∠B,则∠A=________度.14.一个n边形的内角和是720°,则n=________.15.若一个多边形的内角和为360°,则这个多边形的边数为________.16.如图,在正六边形ABCDEF中,连接AD,AE,则∠DAE=________.17.六边形有m条对角线,五边形有n条对角线,则m﹣n=________ .18.如图1所示,圆上均匀分布着11个点A1,A2,A3,…,A11.从A1起每隔k个点顺次连接,当再次与点A1连接时,我们把所形成的图形称为“k+1阶正十一角星”,其中1≤k≤8(k为正整数).例如,图2是“2阶正十一角星”,那么∠A1+∠A2+…+∠A11=________;当∠A1+∠A2+…+∠A11=900°时,k=________.19.如图,已知△ABC中,BC=2,AB=AC=4,点D是BC的中点,E为AC的中点,点P为AB上的动点,则点D到AC的距离为________,DP+EP的最小值等于________.20.如图,小亮从A点出发前10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了________.三、解答题(共3题;共25分)21.如图,在平行四边形ABCD中,连接对角线BD,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足,求证:四边形AECF是平行四边形.22.在直角坐标平面内,已知点A(3,0)、B(2,3),点B关于原点对称点为C.(1)写出C点的坐标;(2)求△ABC的面积.23.已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,.E是边AB的中点,联结DE、CE,且DE⊥CE.设AD=x,BC=y.(1)如果∠BCD=60°,求CD的长;(2)求y关于x的函数解析式,并写出自变量x的取值范围;(3)联结BD.如果△BCD是以边CD为腰的等腰三角形,求x的值.四、综合题(共3题;共33分)24.如图,在平面直角坐标系中,一次函数的图象经过点,与反比例函数的图象交于.(1)求一次函数和反比例函数的表达式;(2)设是直线上一点,过作轴,交反比例函数的图象于点,若为顶点的四边形为平行四边形,求点的坐标.25.如图,E、F是四边形ABCD的对角线BD上的两点,BF=DE,AE=CF,∠1=∠2.(1)求证:△ABE≌△CDF;(2)四边形ABCD是平行四边形吗?请说明理由.26.如图,在□ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连结BE、BF。
浙教版八年级下册第4章《平行四边形》单元检测卷 附答案解析

浙教版八年级下册第4章《平行四边形》单元检测卷(满分:120分)姓名:___________班级:___________学号:___________题号一二三总分得分一.选择题(共10小题,满分30分)1.下列图形中具有稳定性的是()A.正方形B.长方形C.等腰三角形D.平行四边形2.下列图形中,是中心对称图形的是()A.B.C.D.3.如图,在▱ABCD中,若∠A+∠C=130°,则∠D的大小为()A.100°B.105°C.110°D.115°4.能判定一个四边形是平行四边形的条件是()A.一组对边相等,另一组对边平行B.一组对边平行,一组对角相等C.一组对边相等,一条对角线平分另一条对角线D.一组对角相等,一条对角线平分另一条对角线5.对于命题“已知a∥b,b∥c,求证:a∥c”,如果用反证法,应先假设()A.a不平行于b B.b不平行于c C.a不平行于c D.a⊥c6.如图,A、B两点被池塘隔开,在外选一点C,连接AC和BC,并分别找出它们的中点M、N.若测得MN=20米,则A、B两点间的距离为()A.40米B.30米C.20米D.10米7.如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是()A.点A与点A′是对称点B.BO=B′OC.AB∥A′B′D.∠ACB=∠C′A′B′8.若经过n边形的一个顶点的所有对角线可以将该n边形分成7个三角形,则n的值是()A.7B.8C.9D.109.如图,在四边形ABCD中,∠α、∠β分别是与∠BAD、∠BCD相邻的补角,且∠B+∠CDA=140°,则∠α+∠β=()A.260°B.150°C.135°D.140°10.如图,在平行四边形ABCD中,延长CD到E,使DE=CD,连接BE交AD于点F,交AC于点G.下列结论,其中正确的有()个①DE=DF;②AG=GF:③AF=DF:④BG=GC;⑤BF=EF,A.1B.2C.3D.4二.填空题(共8小题,满分24分)11.一个多边形的内角和等于1800°,则该多边形的边数n等于.12.如图,△ABC与△DEC关于点C成中心对称,若AB=2,则DE=.13.已知四边形ABCD,从下列条件中:(1)AB∥CD;(2)BC∥AD;(3)AB=CD;(4)BC=AD;(5)∠A=∠C;(6)∠B =∠D任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况有.14.如图,▱ABCD的周长是22,△ABC的周长是17,则AC的长为.15.在平面直角坐标系中,若▱ABCD的三个顶点坐标分别是A(m,﹣n)、B(2,3)、C(﹣m,n),则点D的坐标是16.△ABC中,三条中位线围成的三角形周长是15cm,则△ABC的周长是cm.17.如图所示是三个边长相等的正多边形拼成的无缝隙、不重叠的图形的一部分,正多边形①和②的内角都是108°,则正多边形③的边数是.18.如图,在▱ABCD中,AE⊥BC于E,AF⊥CD于F.若AE=3,AF=4,▱ABCD的周长为28,则▱ABCD的面积为.三.解答题(共7小题,满分66分)19.如图,在▱ABCD中,点E、F在BD上,且BE=AB,DF=CD.求证:四边形AECF是平行四边形.20.如图,在四边形ABCD中,已知BE平分∠ABC,∠AEB=∠ABE,∠D=70°.(1)试说明:AD∥BC;(2)求∠C的度数.21.用反证法求证:三角形的一个外角等于与它不相邻的两个内角的和.22.如图,在△ABC中,AB=AC,D、E分别是AB、BC的中点,EF⊥AC,垂足F;(1)求证:AD=DE;(2)求证:DE⊥EF.23.(1)从多边形的一个顶点出发,分别连接这个多边形的其余各顶点,则可以把这个多边形分成若干个三角形.若多边形是一个五边形,则可以分成个三角形;若多边形是一个六边形,则可以分割成个三角形,……;则n边形可以分割成个三角形.(2)如果从一个多边形的一个顶点出发,分别连接其余各顶点,将这个多边形分割成了2016个三角形,那么此多边形的边数为.(3)若在n边形的一条边上取一点P(不是顶点),再将点P与n边形的各顶点连接起来,则可将n边形分割成个三角形.24.如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,F A.(1)求证:四边形AECF是平行四边形.(2)若AF=EF,∠BAF=108°,∠CDF=36°,直接写出图中所有与AE相等的线段(除AE外).25.如图,在▱ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为lcm/s,连接PO并延长交BC于点Q.设运动时间为t(s)(0<t<5)(1)当t为何值时,四边形ABQP是平行四边形?(2)设四边形OQCD的面积为y(cm2),当t=4时,求y的值.参考答案一.选择题(共10小题)1.【解答】解:正方形,长方形,等腰三角形,平行四边形中只有等腰三角形具有稳定性.故选:C.2.【解答】解:A、不是中心对称图形,故此选项不合题意;B、不是中心对称图形,故此选项不合题意;C、是中心对称图形,故此选项符合题意;D、不是中心对称图形,故此选项不合题意;故选:C.3.【解答】解:∵四边形ABCD是平行四边形,∴∠A=∠C,∵∠A+∠C=130°,∴∠A=65°,∴∠D=180°﹣∠A=115°.故选:D.4.【解答】解:A、∵一组对边平行,另一组对边相等的四边形是等腰梯形,不一定是平行四边形,∴A不能判定;B、∵一组对边平行,另一组对角相等的四边形是平行四边形,∴B能判定;C、∵一组对边相等,一条对角线平分另一条对角线可能是梯形,不一定是平行四边形,∴C不能判定;D、∵一组对角相等,一条对角线平分另一条对角可能是筝形,不一定是平行四边形,∴D不能判定;故选:B.5.【解答】解:由于命题:“已知:a∥b,b∥c,求证:a∥c”的反面是:“a不平行c”,故用反证法证明:“已知:a∥b,b∥c,求证:a∥c”,应假设“a不平行c”,故选:C.6.【解答】解:∵M、N分别是AC和BC的中点,∴AB=2MN=40(米),7.【解答】解:观察图形可知,A、点A与点A′是对称点,故本选项正确;B、BO=B′O,故本选项正确;C、AB∥A′B′,故本选项正确;D、∠ACB=∠A′C′B′,故本选项错误.故选:D.8.【解答】解:依题意有n﹣2=7,解得:n=9.故选:C.9.【解答】解:∵∠B+∠D+∠DAB+∠BCD=360°,∠B+∠CDA=140°,∴∠DAB+∠BCD=360°﹣140°=220°,∵∠α+∠β+∠DAB+∠BCD=360°,∴∠α+∠β=360°﹣220°=140°.故选:D.10.【解答】解:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,即AB∥CE,∴∠ABF=∠E,∵DE=CD,∴AB=DE,在△ABF和△DEF中,∵,∴△ABF≌△DEF(AAS),∴AF=DF,BF=EF;可得③⑤正确,故选:B.二.填空题(共8小题)11.【解答】解:因为多边形的内角和公式为(n﹣2)•180°,所以(n﹣2)×180°=1800°,则该多边形的边数n等于12.故答案为:12.12.【解答】解:∵△ABC与△DEC关于点C成中心对称,∴CA=CD,CB=CE,∵∠ACB=∠DCE∴△ABC≌△DEC(SAS),∴AB=DE,∵AB=2,∴DE=2,故答案为2.13.【解答】解:根据平行四边形的判定,符合四边形ABCD是平行四边形条件的有九种:(1)(2);(3)(4);(5)(6);(1)(3);(2)(4);(1)(5);(1)(6);(2)(5);(2)(6)共9种.故答案为:9种.14.【解答】解:∵,▱ABCD的周长是22,∴AD+DC=11,∵△ABC的周长是17,∴AC=17﹣11=6,故答案为:615.【解答】解:∵A(m,﹣n),C(﹣m,n),∴点A和点C关于原点对称,∵四边形ABCD是平行四边形,∴D和B关于原点对称,∵B(2,3),∴点D的坐标是(﹣2,﹣3).故答案为(﹣2,﹣3)16.【解答】解:设△ABC三边的中点分别为E、F、G,如图,∵D、E、F分别为AB、BC、AC的中点,∴AB=2EF,BC=2DF,AC=2DE,∴AB+BC+AC=2(EF+DF+DE),∵△DEF的周长为15cm,∴EF+DF+DE=15cm,∴AB+BC+AC=2×15cm=30cm,即△ABC的周长为30cm,故答案为:30.17.【解答】解:360°﹣108°﹣108°=144°,180°﹣144°=36°,360°÷36°=10.故答案为:10.18.【解答】解:∵▱ABCD的周长=2(BC+CD)=28,∴BC+CD=14①,∵AE⊥BC于E,AF⊥CD于F,AE=3,AF=4,∴S▱ABCD=AE•BC=AF•CD,即3BC=4CD,整理得,BC=CD②,联立①②解得,CD=6,∴▱ABCD的面积=AF•CD=4×6=24.故答案为:24三.解答题(共7小题)19.【解答】证明:连接AC交BD于O,∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,AB=CD,∵BE=AB,DF=CD,∴BE=DF,∴BO﹣BE=OD﹣DF,即OE=OF,∴四边形AECF是平行四边形.20.【解答】解:(1)∵BE平分∠ABC,∴∠ABE=∠CBE,∵∠AEB=∠ABE,∴∠AEB=∠CBE,∴AD∥BC;(2)∵AD∥BC,∴∠C+∠D=180°,∵∠D=70°,∴∠C=110°.21.【解答】已知:如图,∠1是△ABC的一个外角,求证:∠1=∠A+∠B,证明:假设∠1≠∠A+∠B,在△ABC中,∠A+∠B+∠2=180°,∴∠A+∠B=180°﹣∠2,∵∠1+∠2=180°,∴∠1=180°﹣∠2,∴∠1=∠A+∠B,与假设相矛盾,∴假设不成立,∴原命题成立即:∠1=∠A+∠B.22.【解答】解:(1)∵AB=AC,∴∠B=∠C,∵D、E分别是AB、BC的中点,∴AD=AB,DE=AC,∴AD=DE;(2)∵D、E分别是AB、BC的中点,∴DE∥AC,∵EF⊥AC,∴DE⊥EF.23.【解答】解:(1)从一个五边形的同一顶点出发,分别连接这个顶点与其余各顶点,可以把这个五边形分成5﹣2=3个三角形.若是一个六边形,可以分割成6﹣2=4个三角形,n边形可以分割成(n﹣2)个三角形.故答案为:3,4,(n﹣2);(2)如果从一个多边形的一个顶点出发,分别连接其余各顶点,将这个多边形分割成了2016个三角形,那么此多边形的边数为:2016+2=2018;故答案为:2018;(3)若点P取在多边形的一条边上(不是顶点),在将P与n边形各顶点连接起来,则可将多边形分割成(n﹣1)个三角形.故答案为:(n﹣1).24.【解答】(1)证明:如图,连接AC交BD于点O,在▱ABCD中,OA=OC,OB=OD,∵BE=DF,∴OB﹣BE=OD﹣DF,即OE=OF,∴四边形AECF是平行四边形(对角线互相平分的四边形是平行四边形);(2)解:∵AB∥CD,∴∠ABF=∠CDF=36°,∵AF=EF,∴∠F AE=∠FEA=72°,∵∠AEF=∠EBA+∠EAB,∴∠EBA=∠EAB=36°,∴EA=EB,同理可证CF=DF,∵AE=CF,∴与AE相等的线段有BE、CF、DF.25.【解答】解:(1)当t=2.5s时,四边形ABQP是平行四边形,理由是:∵四边形ABCD是平行四边形,∴AD∥BC,AB=CD=3cm,AD=BC=5cm,AO=CO,BO=OD,∴∠P AO=∠QCO,在△APO和△CQO中∴△APO≌△CQO(ASA),∴AP=CQ=2.5cm,∵BC=5cm,∴BQ=5cm﹣2.5cm=2.5cm=AP,即AP=BQ,AP∥BQ,∴四边形ABQP是平行四边形,即当t=2.5s时,四边形ABQP是平行四边形;(2)过A作AM⊥BC于M,过O作ON⊥BC于N,∵AB⊥AC,AB=3cm,BC=5cm,∴在Rt△ABC中,由勾股定理得:AC=4cm,∵由三角形的面积公式得:S△BAC==,∴3×4=5×AM,∴AM=2.4(cm),∵ON⊥BC,AM⊥BC,∴AM∥ON,∵AO=OC,∴MN=CN,∴ON=AM=1.2cm,∵在△BAC和△DCA中∴△BAC≌△DCA(SSS),∴S△DCA=S△BAC==6cm2,∵AO=OC,∴△DOC的面积=S△DCA=3cm2,当t=4s时,AP=CQ=4cm,∴△OQC的面积为 1.2cm×4cm=2.4cm2,∴y=3cm2+2.4cm2=5.4cm2.。
浙教版八年级下册数学第四章 平行四边形含答案(有解析)

浙教版八年级下册数学第四章平行四边形含答案一、单选题(共15题,共计45分)1、下列图形中,不是中心对称图形的是( )A. B. C. D.2、如图所示的几何图形中,既是轴对称图形又是中心对称图形的个数是()A.4B.3C.2D.13、为了加强生活垃圾管理,改善城乡环境,保障人体健康,5月1日起,北京市实施《北京市生活垃圾管理条例》.下图分别是厨余垃圾,可回收物,有害垃圾,和其他垃圾的标识,其中是中心对称图形的是()A. B. C. D.4、已知一个正多边形一个外角是72°,则这个正多边形是()A.四边形B.五边形C.六边形D.七边形5、菱形具有而一般平行四边形不具有的性质是()A.对边相等B.对角相等C.对角线互相平分D.对角线互相垂直6、七边形的内角和是()A.360°B.540°C.720°D.900°7、如图,在▱ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于()A.1.5cmB.2cmC.2.5cmD.3cm8、下列哪一个角度可以作为一个多边形的内角和( )A.2080ºB.1240ºC.1980ºD.1600º9、下列图形中,既是中心对称图形又是轴对称图形的是()A. B. C. D.10、多边形的外角和等于()A.180°B.360°C.720°D.(n﹣2)•180°11、下列四个图形中,既是轴对称图形又是中心对称图形的是()A. B. C. D.12、如图,平行四边形四个内角平分线相交,如能构成四边形EFGH,则四边形EFGH的形状是()A.平行四边形B.矩形C.正方形D.菱形13、如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数(x>0)的图象经过点=2,则k的值是()D.已知S△BCEA.2B.﹣2C.3D.414、十二边形的内角和为()A.180°B.360°C.1800°D.无法计算15、在中,E,F是对角线AC上不同的两点,下列条件中,不能得出四边形BEDF一定为平行四边形的是()A. B. C. D.二、填空题(共10题,共计30分)16、如图,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F.且AD交EF于O,则∠AOF=________度.17、如图,▱ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=3,则AB的长是________.18、一个多边形的内角和是外角和的2倍,则这个多边形的边数为________.19、若一个多边形的内角和为900º,则这个多边形的边数是________20、如图,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D,则下列结论:①若BD=4,则AC=8;②AB=CD;③∠DBA=∠ABC;④S△ABE =S△ACE;⑤∠D=∠AEC;⑥连接AD,则AD=CD.其中正确的是________.(填写序号)21、从正三角形、正方形、正五边形、圆这四个图形中随机选出一个图形,结果是中心对称图形的概率为________.22、如图,某学校一块草坪的形状是三角形(设其为△ABC).李俊同学从BC边上的一点D出发,沿DC→CA→AB→BD的方向走了一圈回到点D处.问:李俊从出发到回到原处在途中身体转过的角度是________23、如图,在中,,,,点D是边上的动点,过点D作于E点.请探究下列问题:(1)若,则________;(2)若,设点F是边上的动点,连接、,以、为邻边作平行四边形,且使得顶点G恰好落在边上,则________.24、正五边形的一个内角是________度。
浙教版八年级下册数学第四章 平行四边形含答案

浙教版八年级下册数学第四章平行四边形含答案一、单选题(共15题,共计45分)1、在下列性质中,平行四边形不一定具有的是()A.对边相等B.对边平行C.对角互补D.内角和为360°2、下列四个命题中,正确命题的个数是①若ac>bc,则a>b;②一组对角相等一组对边平行的四边形是平行四边形;③平分弦的直径垂直于弦;④反比例函数y= ,当k<0 时,y 随x的增大而增大.A.4B.3C.2D.13、下图是天气预报中的图标,其中既是轴对称图形又是中心对称图形的是()A. B. C. D.4、下列所给图形既是中心对称图形,又是轴对称图形的是()A.正三角形B.角C.正方形D.正五边形5、已知△ABC的周长为1,连接其三边中点构成第二个三角形,再连接第二个三角形的中点构成第三个三角形,以此类推,则第2012个三角形的周长为()A. B. C. D.6、如果,E、F、G、H分别是四边形ABCD四条边的中点,要使EFGH为菱形,四边形应该具备的条件是()A.一组对边平行而另一组对边不平行B.对角线相等C.对角线互相垂直D.对角线互相平分7、下列命题中假命题是()A.对顶角相等B.直线y=x﹣5不经过第二象限C.五边形的内角和为540°D.因式分解x 3+x 2+x=x(x 2+x)8、如下图,平行四边形ABCD的周长为40,△BOC的周长比△AOB的周长多10,则AB长为()A.20B.15C.10D.59、在▱ABCD中,对角线AC,BD相交于点O,以点O为坐标原点建立平面直角坐标系,其中A(a,b),B(a﹣1,b+2),C(3,1),则点D的坐标是()A.(4,﹣1)B.(﹣3,﹣1)C.(2,3)D.(﹣4,1)10、下列说法中:①一组对边平行,另一组对边相等的四边形是平行四边形;②一组对边平行,一组对角相等的四边形是平行四边形;③对角线相等的四边形一定是平行四边形。
浙教版八年级下册数学第四章 平行四边形含答案
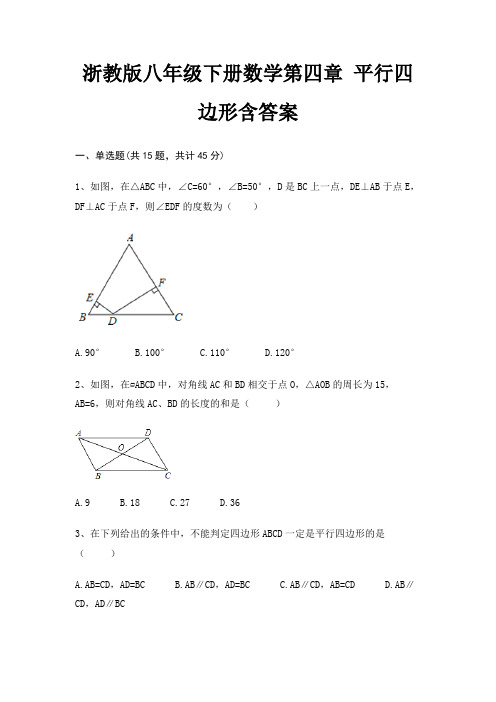
浙教版八年级下册数学第四章平行四边形含答案一、单选题(共15题,共计45分)1、如图,在△ABC中,∠C=60°,∠B=50°,D是BC上一点,DE⊥AB于点E,DF⊥AC于点F,则∠EDF的度数为()A.90°B.100°C.110°D.120°2、如图,在▱ABCD中,对角线AC和BD相交于点O,△AOB的周长为15,AB=6,则对角线AC、BD的长度的和是()A.9B.18C.27D.363、在下列给出的条件中,不能判定四边形ABCD一定是平行四边形的是()A.AB=CD,AD=BCB.AB∥CD,AD=BCC.AB∥CD,AB=CDD.AB∥CD,AD∥BC4、在平行四边形ABCD中,对角线AC,BD的长度分别为10和6,则AB长度的最大整数值是()A.8B.5C.6D.75、下列图形中是中心对称图形但不是轴对称图形的是()A. B. C. D.6、如图,点D,E,F分别为△ABC三边的中点,若△DEF的周长为15,则△ABC的周长为()A.30B.15C.7.5D.457、如图,在平行四边形ABCD中,对角线AC与BD相交于点O,则图中相等的线段共有()A.2对B.3对C.4对D.5对8、如图,▱ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①∠ACD=30°;②S▱ABCD=AC·BC;③OE∶AC=∶6;④S△OCF=2S△OEF.成立的个数有()A.1个B.2个C.3个D.4个9、在下列正方体的表面展开图中,剪掉1个正方形(阴影部分),剩余5个正方形组成中心对称图形的是()A. B. C. D..10、下列说法中,正确的有()个①两点之间直线最短;②若,则a=b;③任何一个有理数都可以用数轴上的一个点来表示;④过n边形的每一个项点有(n﹣2)条对角线.A.1B.2C.3D.411、下列图形是某设计大师的精美服装饰品,仅仅从外形上看,不属于中心对称图形的是( ).A. B. C. D.12、怀化是一个多民族聚居的地区,民俗文化丰富多彩.下面是几幅具有浓厚民族特色的图案,其中既是轴对称图形又是中心对称图形的是()A. B. C. D.13、正多边形的每个内角都等于135°,则该多边形是正()边形A.8B.9C.10D.1114、如图,在梯形ABCD中,AD∥BC,对角线BD与中位线EF交于点O,若FO-EO=3,则BC-AD等于 ( )A.4;B.6;C.8;D.10.15、下列图形中是轴对称图形但不是中心对称图形的是().A. B. C. D.二、填空题(共10题,共计30分)16、已知一个多边形的内角和是外角和的,则这个多边形的边数是________.17、若多边形的内角和为1800°,那么从这个多边形的一个顶点能引出________条对角线.18、如图,在中,,若剪去得到四边形,则________.19、如图,在平行四边形ABCD中,M、N分别是BC、DC的中点,AM=4,AN=3,且∠MAN=60°,则AB的长是________.20、如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0),点M是⊙P上的动点,点C是MB的中点,则AC的最小值是________.21、□ABCD中,∠B=45°,AB= ,E为直线BC上一点,且∠CDE=15°,则DE 的长为________.22、已知一个多边形的内角和等于1260°,则这个多边形是________边形.23、如图1六边形的内角和为度,如图2六边形的内角和为度,则m-n=________.24、如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件________(只添一个即可),使四边形ABCD是平行四边形.25、过8边形的一个顶点可作________ 条对角线,可将8边形分成________ 个三角形.三、解答题(共5题,共计25分)26、如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.若⊙O的半径为1,求图中阴影部分的面积(结果保留π).27、求证:任意三角形的三个外角中至多有一个直角.28、在▱ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H,求证:CH=EH.29、如图,平行四边形ABCD中,过点C作CE交BD于点M,交AD于点F,交BA的延长线于点E,若FM =2,EF =6,求CM的长.30、如图,∠MON=∠PMO,OP=x-3,OM=4,ON=3,MN=5,MP=11-x.求证:四边形OPMN是平行四边形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙教版八年级下册数学第四章平行四边形测试题(附答案)
一、单选题(共12题;共24分)
1.下列汽车标志中既是轴对称又是中心对称图形的是()
A. B. C. D.
2.若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是( )
A. 十三边形
B. 十二边形
C. 十一边形
D. 十边形
3.下列图形中,一定是轴对称图形,又是中心对称图形的是()
A. 等边三角形
B. 平行四边形
C. 六边形
D. 圆
4.如图是一个五边形木架,它的内角和是()
A. 180°
B. 360°
C. 540°
D. 720°
5.已知平行四边形ABCD中,∠A=4∠B,那么∠C等于()
A. 36°
B. 45°
C. 135°
D. 144°
6.每个内角都相等的多边形,它的一个外角等于一个内角的,则这个多边形是()
A. 三角形
B. 四边形
C. 五边形
D. 六边形
7.已知四边形ABCD中,AC与BD交于点O,如果只给出条件“AB∥CD”,那么可以判定四边形ABCD是平行四边形的是()
①再加上条件“BC=AD”,则四边形ABCD一定是平行四边形.
②再加上条件“∠BAD=∠BCD”,则四边形ABCD一定是平行四边形.
③再加上条件“AO=CO”,则四边形ABCD一定是平行四边形.
④再加上条件“∠DBA=∠CAB”,则四边形ABCD一定是平行四边形.
A. ①和②
B. ①③和④
C. ②和③
D. ②③和④
8.一个多边形的内角和是外角和的2倍,那么这个多边形的边数为()
A. 4
B. 5
C. 6
D. 7
9.如图,在▱ABCD中,EF∥AD,HN∥AB,则图中的平行四边形共有( )
A. 8个
B. 9个
C. 7个
D. 5个
10.四边形ABCD中,若∠A+∠C=180°且∠B:∠C:∠D=3:5:6,则∠A为().
A. 80°
B. 70°
C. 60°
D. 50°
11.一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是()
A. 27
B. 35
C. 44
D. 54
12.下图是由10把相同的折扇组成的“蝶恋花”(图1)和梅花图案(图2)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为()
A. 36°
B. 42°
C. 45°
D. 48°
二、填空题(共8题;共18分)
13.如图,▱ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是________.
14.如图,该硬币边缘镌刻的正九边形每个内角的度数是________.
15.一个正八边形每个内角的度数为________度
16.一个正多边形,它的一个外角等于与它相邻内角的,则这个多边形是________ .
17.已知一个多边形的边数恰好是从一个顶点出发的对角线条数的2倍,则这个多边形的边数是________ ,内角和是________ .
18.小燕偶然发现爸爸手机有软件可用来测量方位,于是她来到小区一处广场上.如图,小燕从P点向西直走12米后,向左转,转动的角度为α=40度,再走12米,再左转40度,如此重复,最终小燕又回到点P,则小燕一共走了________米.
19.如图,在△ABC中,AB=AC=6,中线CE=5.延长AB到点D,使BD=AB,则CD的长________.
20.一个多边形截去一个角后,所形成的一个新多边形的内角和为2520°,则原多边形有________条边。
三、解答题(共3题;共25分)
21.如图,在▱ABCD中,点O是对角线AC,BD的交点,点E是边CD的中点,点F在BC的延长线上,且CF=BC,求证:四边形OCFE是平行四边形.
22.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)图中哪两个图形成中心对称?
(2)若△ADC的面积为4,求△ABE的面积.
23.已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断
①OA=OC ②AB=CD ③∠BAD=∠DCB ④AD∥BC
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
(1)构造一个真命题,画图并给出证明;
(2)构造一个假命题,举反例加以说明.
四、综合题(共3题;共33分)
24.在□ABCD中,点E在CD上,点F在AB上,连接AE、CF、DF、BE,∠DAE=∠BCF.
(1)如图1,求证:四边形DFBE是平行四边形;
(2)如图2,若E是CD的中点,连接GH,在不添加任何辅助线的情况下,请直接写出图2中以GH为边或以GH为对角线的所有平行四边形.
25.如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°.
(1)求证:AC∥DE;
(2)过点B作BF⊥AC于点F,连结EF,试判断四边形BCEF的形状,并说明理由.
26.综合题:探索与发现
(1)如图1,以□BMDC的两相邻边CB、CD为腰,在□BMDC的外侧,作两个等腰Rt△CBF和Rt△CDH,则□ BMDC中与C相对的顶点M与这两等腰直角三角形的两顶点F、H形成一个新的等腰直角三角形FMH. 请证明△FMH为等腰直角三角形。
(2)如图2,以□BMDC的两相邻边CB、CD为腰,在□BMDC的外侧,作两个等腰△CBF和△CDH,使其顶角∠CBF=∠CDH=α,则□BMDC中与C相对的顶点M与两等腰三角形的两顶点F、H形成一个新的等腰三角形,写出顶角∠FMH的度数。
试说明理由。
答案
一、单选题
1.D
2. A
3.D
4. C
5. D
6. C
7. C
8.C
9. B 10. A 11. C 12. D
二、填空题
13. 14 14. 140°15.135 16.正十边形17.6;720 18.108 19.10 20.15或16或17
三、解答题
21.证明:∴OE∥BC,且OE=BC. 又∵CF=BC,∴OE=CF. 又∵点F在BC的延长线上,∴OE∥CF,∴四边形OCFE是平行四边形
22.(1)解:图中△ADC和三角形EDB成中心对称。
(2)解:∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8。
23.(1)解:①④作为条件时,如图,∵AD∥BC,
∴∠ADB=∠DBC,在△AOD和△COB
中,∵
, ∴△AOD≌△COB
(AAS),
∴AD=CB,
∴四边形ABCD是平行四边形.
(2)解:②④作为条件时,此时一组对边相等,一组对边平行,是等腰梯形.
四、综合题
24.(1)解:证明:∵四边形ABCD为平行四边形
∴
∴△ADE≌△CBF(ASA),
∴DE=BF,
又∵DE BF,
∴四边形DFBE是平行四边形;
(2)解:∵E是CD的中点,
∴DE=CE,
∴以GH为边的平行四边形有平行四边形GHFA、平行四边形GHBF、平行四边形GHED、平行四边形GHCE;以GH为对角线的平行四边形有GFHE.
25.(1)证明:在矩形ABCD中,AC∥DE,∴∠DCA=∠CAB.∵∠EDC=∠CAB,∴∠DCA=∠EDC,
∴AC∥DE
(2)解:四边形BCEF是平行四边形.
理由:由∠DEC=90°,BF⊥AC,可得∠AFB=∠DEC=90°,
又∠EDC=∠CAB,AB=CD,
∴△DEC≌△AFB,∴DE=AF,由(1)得AC∥DE,
∴四边形AFED是平行四边形,∴AD∥EF且AD=EF,
∵在矩形ABCD中,AD∥BC且AD=BC,
∴EF∥BC且EF=BC,∴四边形BCEF是平行四边形:
26.(1)解:由BC∥MD可得∠DMH+∠FMH+∠BMF+∠CBM=180°,由三角形内角和可得
∠CBM+∠CBF+∠BFM=180°,将两个式子整理可得∠FMH=90°.
(2)解:由BC∥MD可得∠DMH+∠FMH+∠BMF+∠CBM=180°,由三角形内角和可得
∠CBM+∠CBF+∠BFM=180°,将两个式子整理可得∠FMH=α.。
