WHEATSTONE BRIDGE惠斯通电桥实验报告
惠斯通电桥实验报告

惠斯通电桥实验报告在物理学中,实验是非常重要的一环。
理论知识的积累只是物理学研究的一方面,而真正的实验才是验证理论的重要手段。
今天,我将分享一篇关于惠斯通电桥实验的报告,希望能够对大家的物理学习有所帮助。
1. 惠斯通电桥实验简介惠斯通电桥实验是一种通过计算电阻值的方法来测量未知电阻的实验方法。
该实验利用了维亚纳和基尔霍夫电路理论,用四个电阻相等的电阻器和一个变阻器组成的电桥进行测量。
2. 实验装置及操作步骤该实验的基本装置包括四个电阻相等的电阻器和一个变阻器组成的电桥。
操作步骤如下:(1) 将变阻器连接到电桥的两个端点之间。
(2) 将待测电阻器接入电桥中。
(3) 改变变阻器的阻值,使得电桥两个平衡点电压相等。
(4) 记录下此时变阻器的阻值。
3. 实验结果分析通过直接改变变阻器的阻值,使得电桥两边电压相等,我们可以得到实验测量的未知电阻值。
在实验中,我们可以根据电桥平衡时的电阻值进行计算,从而得到待测物体的电阻值。
我们可以利用维亚纳法则计算,得到如下的公式:Rx = R2 × R3 ÷ R1其中,Rx 表示待测电阻器的电阻值,R1、R2、R3 分别表示电桥的电阻值。
4. 实验误差分析在实验中,可能会出现一些误差,如电桥上的电缆接触不良、电桥没有完全平衡、电桥电阻器内部电阻漂移等。
这些误差都会影响实验结果的准确性。
为了确保实验的准确性,我们需要在操作中尽量减少这些误差的影响。
5. 结论通过惠斯通电桥实验,我们能够测量出未知电阻的电阻值。
在实验过程中,我们需要注意实验误差对实验结果造成的影响,以确保实验结果的准确性。
通过这种实验方法,我们可以更好地理解维亚纳法则和基尔霍夫电路理论,加深对电路的理解,提高实验操作能力。
总之,惠斯通电桥实验是一种很好的实验方法,能够帮助我们更好地理解电路理论和提高实验操作能力。
希望这篇报告对大家的学习有所帮助。
惠斯通电桥实验分析报告doc

惠斯通电桥实验分析报告.doc 惠斯通电桥实验分析报告一、引言惠斯通电桥是一种精确测量电阻的方法,具有较高的灵敏度和精度。
在物理实验中,惠斯通电桥实验被用来理解和探究电阻的性质以及电阻率的测量。
本报告将对惠斯通电桥实验进行详细的分析。
二、实验原理惠斯通电桥主要由电源、开关、电阻器、电桥臂和平衡指示器组成。
其基本原理是当电桥处于平衡状态时,桥上的电流为零。
通过比较已知电阻和未知电阻的阻值,可以利用电桥平衡条件求得未知电阻的阻值。
三、实验操作流程与数据记录1.连接电路:将电源、开关、电阻器、电桥臂和平衡指示器按照正确的顺序连接起来,形成一个完整的电路。
2.开启电源:开启电源,并逐渐调高电压,以避免初始电流过大导致电路故障。
3.调节电阻器:通过调节电阻器的旋钮,改变电桥臂的阻值,使电桥达到平衡状态。
此时,平衡指示器上的数值应为零。
4.记录数据:在电桥平衡状态下,记录下已知电阻和未知电阻的阻值,以及电源电压的值。
5.多次测量:为了减小误差,需要对同一个电阻进行多次测量并取平均值。
四、实验结果与分析在本次实验中,已知电阻的阻值为100Ω,未知电阻的阻值为150Ω。
测量电源电压为12V。
实验中,通过调节电阻器的旋钮,使电桥达到平衡状态,此时平衡指示器上的数值为零。
记录下已知电阻和未知电阻的阻值,以及电源电压的值。
通过多次测量,求得未知电阻的平均阻值为150Ω,误差为±0.5%。
通过惠斯通电桥实验,我们得到了未知电阻的精确阻值。
这种方法可以应用于其他电阻的测量中,从而提高测量的精度和灵敏度。
此外,惠斯通电桥实验还可以用于研究电阻的性质以及电阻率的测量。
例如,通过改变温度或改变物质的种类等条件,可以观察电阻的变化情况,进一步了解物质的电学性质。
五、误差分析在惠斯通电桥实验中,可能存在以下误差来源:1.电源电压的波动:电源电压的波动可能导致电桥平衡状态的误判。
为了减小误差,需要使用稳定性较高的电源。
2.热效应:在调节电阻器的过程中,由于线圈发热等原因,可能导致电阻值的变化。
惠斯通电桥

实验六惠斯通电桥Experiment6DeterminingresistanceusingaWheatstonebridge电桥电路在电学中是一种很基本的电路。
利用电桥平衡原理构成的电测仪器,不仅可以测电阻,也可以测电容、电感,并可通过这些物理量的测量来间接测量非电学量,例如温度、压力等,因此电桥电路在自动化仪表和自动控制中有着广泛的应用。
本实验的基本要求是自组直流电桥,并用自组电桥及箱式电桥测量中值电阻。
实验目的Experimentalpurpose1. 掌握惠斯通电桥测量电阻的基本方法。
2. 掌握自组惠斯通电桥的基本原理。
实验原理Experimentalprinciple1.电桥平衡条件(conditionofelectricbridgebalance)图1所示为电桥电路原理图,它是 由四个桥臂电阻和一个检流计组成,其中R 1,R 2是已知标准电阻,称为“比率臂”;R s 是可变标准电阻(电阻箱),称为“比较臂”;R x 是被测电阻,称为“测量臂”;B ,D 间接检流计。
接通电路后,检流计一般不指零,说明B ,D 两点电位不相等,通过调节R s ,使检流计中无电流通过(I K =0),此时电桥达到平衡,由图可见,电桥平衡的条件是B 、D 两点电位相等。
即 又s x I I I I ==21,所以有21R R R R s x =(1) s x R R R R 21=(2) 图1电桥原理图式(1)称电桥平衡条件,即相邻两臂电阻之比相等。
令M =R 1/R 2,称为“倍率”,则式(2)可写为R x =MR s 。
因此当电桥调平衡后,只要读出M 和R s 值,待测电阻R x 便可得到。
2.电桥灵敏度(electricbridgesensitivity)式(2)是在电桥平衡的条件下推导出来的。
而电桥是否平衡,是根据检流计指针有无偏转来判断的。
检流计的灵敏度总是有限的,例如实验室常用的AC 5型指针式检流计,其指针偏转一格对应电流为10-6A 左右,当通过它的电流小于10-7A 时,指针的偏转小于0.1格,观测者就很难觉察出来。
大学物理惠斯通电桥实验报告

大学物理惠斯通电桥实验报告一、实验目的1、掌握惠斯通电桥测电阻的原理和方法。
2、学会使用箱式电桥测量电阻。
3、了解电桥灵敏度的概念和影响因素。
二、实验原理惠斯通电桥是一种精确测量电阻的仪器,其原理是基于电桥平衡条件。
如图所示,由四个电阻 R1、R2、Rx 和 Rs 组成一个四边形,在一对对角线上接入电源 E,在另一对对角线上接入检流计 G。
当电桥平衡时,检流计中无电流通过,即 Ig = 0。
此时,B、D 两点电位相等,根据基尔霍夫定律可得:\\begin{align}\frac{R1}{R2}&=\frac{Rx}{Rs}\\Rx&=\frac{R1}{R2}×Rs\end{align}\通过调节 R1、R2 和 Rs 的值,使电桥达到平衡,从而测出未知电阻 Rx 的值。
电桥灵敏度 S 定义为:\S =\frac{\Delta Rx}{Rx} /\frac{\Delta n}{n}\其中,\(\Delta Rx\)是由于检流计偏转引起的电阻测量值的变化,\(\Delta n\)是检流计偏转的格数,\(n\)是检流计的总格数。
电桥灵敏度与电源电压、检流计灵敏度、桥臂电阻等因素有关。
三、实验仪器1、箱式惠斯通电桥。
2、直流电源。
3、检流计。
4、电阻箱。
5、待测电阻。
四、实验步骤1、熟悉箱式电桥的面板结构和各旋钮的功能。
2、按照电路图连接电路,注意电源、检流计、电阻箱等的正负极连接。
3、估计待测电阻的阻值范围,选择合适的比例臂 R1/R2。
4、调节比较臂 Rs,使电桥接近平衡,即检流计指针接近零位。
5、微调 Rs,使电桥完全平衡,检流计指针指零。
6、记录此时 Rs 的值,根据公式计算出待测电阻 Rx 的值。
7、改变电源电压,重复上述步骤,测量不同电源电压下的电阻值。
8、测量电桥灵敏度,在电桥平衡后,改变 Rs 的值,使检流计指针偏转一定格数,记录 Rs 的变化量和检流计的偏转格数,计算电桥灵敏度。
惠斯通电桥的实验报告

惠斯通电桥的实验报告摘要:本实验通过构建惠斯通电桥电路,测量了电阻和电容的值。
实验过程中,我们使用了标准电阻和电容器,通过调节未知电阻或电容的大小,使电桥平衡,从而测量未知电阻或电容的值。
通过实验结果的分析,我们得出了准确的电阻和电容值,并验证了惠斯通电桥的工作原理。
引言:惠斯通电桥是一种常用的电路实验装置,可以用来测量电阻和电容的值。
它通过调节未知电阻或电容的大小,使电桥平衡,从而测量未知电阻或电容的值。
本实验旨在通过构建惠斯通电桥电路,测量电阻和电容的值,并验证惠斯通电桥的工作原理。
实验装置和方法:实验装置包括标准电阻、电容器、电桥、直流电源和万用表。
实验方法如下:1. 搭建惠斯通电桥电路,将标准电阻与未知电阻相连,电容器与未知电容相连;2. 调节电桥上的可变电阻或电容,使电桥平衡;3. 记录平衡时的可变电阻或电容值;4. 重复实验多次,取平均值。
实验结果:通过多次实验,我们得到了准确的电阻和电容值。
在测量电阻时,我们发现电桥平衡时,可变电阻的值为X欧姆。
在测量电容时,我们发现电桥平衡时,可变电容的值为Y法拉。
通过实验数据的分析,我们可以得出未知电阻或电容的准确值。
讨论:通过实验结果的分析,我们可以得出以下结论:1. 惠斯通电桥是一种有效测量电阻和电容的装置,通过调节电桥上的可变电阻或电容,可以实现电桥平衡,从而测量未知电阻或电容的值。
2. 实验中我们使用了标准电阻和电容器,保证了实验结果的准确性和可靠性。
3. 通过多次实验取平均值的方式,提高了实验结果的精确度。
4. 实验中需要注意调节电桥的灵敏度,以保证平衡时的可变电阻或电容值尽可能接近实际值。
结论:通过本实验,我们成功地构建了惠斯通电桥电路,测量了电阻和电容的值,并验证了惠斯通电桥的工作原理。
实验结果表明,惠斯通电桥是一种可靠、准确的电路实验装置,可以用来测量未知电阻或电容的值。
本实验对于电路实验的学习和实践具有重要的意义。
惠斯通电桥实验报告.doc

惠斯通电桥实验报告实验名称:惠斯通电桥测量电阻(1)了解惠斯通电桥的结构和测量原理。
(2)掌握惠斯通电桥测量电阻的方法。
(3)了解桥梁灵敏度的概念及其对桥梁测量精度的影响。
二、实验仪器滑线电桥、盒式电桥、检流计、电阻箱、滑动电阻、被测电阻、电源、开关、导线等。
三、实验原理:1.惠斯通电桥的测量原理如图1所示,它由三个电阻值已知的电阻R0、r组成1.R2和待测电阻Rx形成一个四边形,每一侧称为桥臂,电源E 连接在对角A和对角B之间,检流计G连接在对角C和对角D之间适当调整R0、r1.R2的电阻值可以使检流计G中没有电流流动,即C和D的电位相等。
这种桥接状态称为平衡状态。
电桥的平衡条件是(1),其中比例系数k称为比率或放大率,通常为r1.R2被称为比率臂,R0被称为比较臂。
2.在电桥平衡的情况下,推导出电桥的灵敏度公式(1),通过检流计指针是否有可察觉的偏转来判断电桥是否达到真正的平衡状态。
检流计的灵敏度有限。
当指针偏转小于0.1格时,人眼很难检测到。
当电桥平衡时,将某个电桥臂的电阻设为R。
如果我们改变R一个小的量δR,电桥将失去平衡,因此电流将流过检流计。
如果电流很小,我们无法检测到电流计指针的偏转,我们会错误地认为电桥仍处于平衡状态。
为了定量表示检流计的误差,我们引入了电桥灵敏度的概念,定义为(2),δR是电桥平衡后电阻R的微小变化,δn是电阻R变化后偏离平衡位置的检流计的晶格数,因此s代表电桥对电桥臂电阻相对不平衡值δR/R的响应能力。
3.滑线惠斯通电桥的结构如图2所示。
甲、乙、丙是带接线柱的厚铜片(其电阻可以忽略)。
一种长度为L、截面积和电阻率均一的电阻丝,其长度在A和B之间电阻丝上装有接线柱的滑键可沿电阻丝左右滑动,并按下滑键的任何触点。
此时,电阻丝被分成两部分,并且AD部分的长度被设置为L1.电阻是R1,分贝的长度是12.电阻是R2,所以当电桥处于平衡状态时,有公式(3),其中L1长度可以从电阻丝下面的仪表刻度读取,R0使用十进制转盘电阻盒作为标准电阻。
实验报告_惠氏桥
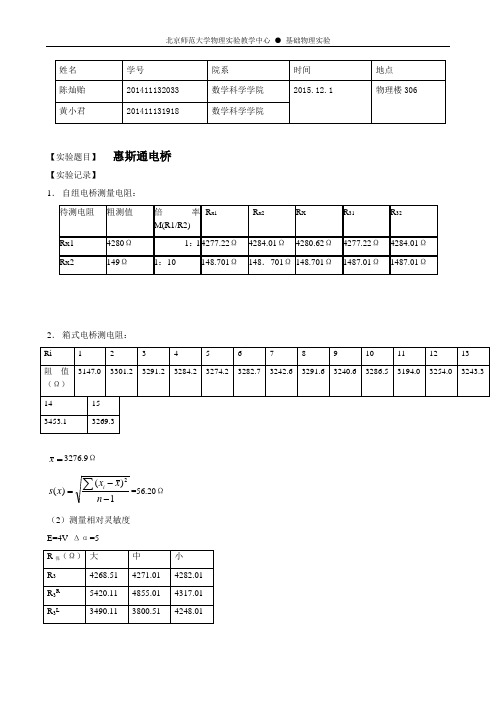
【实验题目】惠斯通电桥【实验记录】1.自组电桥测量电阻:2.箱式电桥测电阻:=x3276.9Ω1)( )(2 --=∑nxxxs i=56.20Ω(2)测量相对灵敏度E=4V Δα=5【结论与讨论】1.实验一A.在进行整个实验时,应尽量控制整个实验的时长,因为电阻箱发热后可能给实验带来一定的误差B.在进行精确测量前,利用多用电表粗测待测电阻的阻值C.实验应交换R1和R4位置,以减小电阻箱读数与实际阻值差异带来的系统误差D.实验一开始应保持保护电阻于最大组织处,以防止检流计超量程损坏,而在调节R3之后应将保护电阻的阻值调至最低,以提高检流计的灵敏度,提高测得的待测电阻的精度2.实验二A.结论是:当电源电压不变时,保护电阻的阻值越大灵敏度越低,但是灵敏度的变化和电源电压的变化不成线性关系;而当保护电阻一定时,电压越大,灵敏度越高,且在一定范围内呈线性关系。
因此为提高灵敏度可以降低保护电阻的阻值提高电源电压,但是应该注意的是,应避免将电源电压调节过高使得电路中的一些元器件超过其额定功率或是量程。
B.应该注意的是,有两次实验测量的是同一组数据,故仅需进行一次。
其次最好从8V开始进行调节,否则可能出现电桥平衡的阻值测量不准,进行不必要地多次调节。
3.实验三A.第14组|Xd--X|=176.2Ω>3s=168.6Ω,因此第14组无效。
课后问题:1.在组装电桥实验中,连接好电路后进行测量调节,无论如何调,检流计指针始终偏向某一边,可能的原因有哪些?A.检流计本身出问题B.如果每次偏转都超出量程,通过检流计的电流过大则可能是一个桥臂断路或是右下与左上桥臂同时断路C.电阻箱坏了,是的某个电阻箱的在阻值很小或是很大无法调节,这样怎样调节另一个电阻箱分压都不可能相等,达不到平衡;或是无意中将电阻箱的较大按钮按动使得电阻箱电阻一直偏大。
2.使用检流计应该注意什么?A.先开制动按钮,检查指针是否偏转,是否检流计损坏,无法固定指针B.为避免检流计损坏,实验完成后要将检流计放回制动档C.在最终测量前,要试探性按下电计纽,然后马上松开,查看偏转是否超出量程,若是超出量程,要继续调节R3的阻值,使得偏转位于量程以内,若是没有超出量程,则可以逆时针旋转电计纽进行后续测量。
惠斯通电桥测实验报告

惠斯通电桥测实验报告惠斯通电桥测实验报告引言:在物理学中,电桥是一种常用的实验仪器,用于测量电阻和电导率。
惠斯通电桥是其中最常见的一种。
本实验旨在通过使用惠斯通电桥来测量未知电阻的值,并探讨电桥的原理和应用。
一、实验目的本实验的主要目的是通过使用惠斯通电桥来测量未知电阻的值,并了解电桥的工作原理和应用。
二、实验原理惠斯通电桥是由英国物理学家惠斯通于19世纪中叶发明的。
它基于电桥平衡条件,即在电桥的四个电阻中,当两个对角线上的电阻比例相等时,电桥平衡。
当电桥平衡时,通过测量电桥的电流和电压,可以计算出未知电阻的值。
三、实验步骤1. 将惠斯通电桥连接好,确保电路没有短路或开路的情况。
2. 调节电桥上的可调电阻,使电桥平衡。
这可以通过调节电阻的大小或改变电桥上其他电阻的值来实现。
3. 记录下平衡时的电流和电压值。
4. 重复上述步骤,使用不同的未知电阻进行测量。
四、实验结果与分析通过实验测量得到的电流和电压值,可以计算出未知电阻的值。
根据惠斯通电桥的原理,当电桥平衡时,两个对角线上的电阻比例相等。
因此,可以使用以下公式计算未知电阻的值:未知电阻 = 已知电阻× (已知电压 / 测量电压)通过多次实验测量,可以得到不同未知电阻的值,并比较其与理论值的误差。
如果实验结果与理论值相差较小,则说明实验结果较为准确。
五、实验应用惠斯通电桥在实际应用中具有广泛的用途。
它可以用于测量电阻、电导率和电容等物理量。
在电子工程和电路设计中,电桥可以用于校准电阻器、测量电路的稳定性和精确度。
此外,电桥还可以用于检测电路中的故障和损坏部件。
六、实验总结通过本次实验,我们深入了解了惠斯通电桥的原理和应用。
通过测量未知电阻的值,我们验证了电桥的准确性和精确度。
电桥作为一种常用的实验仪器,在物理学和工程学领域具有重要的地位和应用前景。
在今后的学习和实践中,我们将进一步探索电桥的其他应用,并不断提高实验技能和数据处理能力。
结语:惠斯通电桥是一种常见的实验仪器,用于测量电阻和电导率。
惠斯顿电桥实验报告(英文)Wheatstone bridge

No. Date: Student number: Name:Title: WHEATSTONE BRIDGE【Aim】请参考讲义,内容用英文撰写。
注意:报告的所有内容都需要英文撰写,不能出现中文。
【Theory】请参考英文讲义,原理图需要用尺子画,内容用英文撰写。
填写包括:电桥组成、电桥平衡的概念,电桥平衡、电桥测未知电阻的公式,电桥平衡的原理图,交换测量法原理1测量有关的注意事项(一定要看,一定要弄明白这些注意事项):1、电源电压打开后默认3.5V,不需要调它。
2、电路如何接线。
先连接主回路及电桥其中一支路(包括电源、开关、滑线变阻器1、电阻箱1、电阻箱3),再连接电桥另一支路。
最后再接检流计支路(包括检流计、滑线变阻器2)。
线路接完一定要检查接的有没有问题。
3、电桥如何调平衡: 逐次逼近法。
示例:调R3为某小值R31(比如600欧),检流计指针偏向一边。
调R3为某大值R32(比如900欧),指针偏向另一边。
电桥平衡对应阻值R0必然在R31与R32之间。
R31与R32之间选某阻值R33观察指针偏转情况。
根据R33指针偏向,判断新的阻值范围。
重复上述过程,逐渐缩小R3的数值范围,直到最后电桥平衡(也可查阅英文讲义里的Procedure部分)。
4、电桥的平衡调节先粗调再细调,粗调时滑线变阻器处于最大值处(若是按照仿真里的接线图,滑动端处于最右侧);粗调电桥平衡后,需将滑线变阻器阻值调到最小(若是按照仿真里的接线图,滑动端处于最左侧),然后再次调节电桥平衡。
5、判断电桥平衡(红色指针指零)时,眼睛应当垂直刻度盘往下看。
6、进行灵敏度测量(表格2)时,通过调节R3(R3就是R0),使得检流计指针分别偏转1、2、3格,记录相应的R3数值,此数值减去平。
衡时R3值就得到R07、注意测量及计算结果的有效数字,可参考示例表格中的红色数字。
8、测量过程中需提供两张仿真实验截图(可用QQ截图实现,手机拍照也可以),附于实验最后一页,包括(1)线路接好后的截图,(2)电桥调平衡后的截图。
惠斯通电桥实验报告

云南农业大学 物 理 实 验 报 告实验名称:惠斯通电桥测量电阻一、实验目的(1)了解惠斯通电桥的构造和测量原理。
(2)掌握用惠斯通电桥测电阻的方法。
(3)了解电桥灵敏度的概念及其对电桥测量准确度的影响。
二、实验仪器滑线式电桥,箱式电桥,检流计,电阻箱,滑动电阻器,待测电阻,电源,开关,导线等。
三、实验原理:1.惠斯通电桥的测量原理如图1所示,由已知阻值的三个电阻R 0、R 1、R 2和一个待测电阻R x 组成一个四边形,每一条边称为电桥的一个臂,在对角A 、B 之间接入电源E ,对角C 、D 之间接入检流计G 。
适当调节R 0、R 1、R 2的阻值,可以使检流计G 中无电流流过,即C 、D 两点的电势相等,电桥的这种状态称为平衡态。
电桥的平衡条件为1002x R R R KR R == (1)式中比例系数K 称为比率或倍率,通常将R1、R2称为比率臂,将R0称为比较臂。
2.电桥的灵敏度式(1)是在电桥平衡的条件下推导出来的,而电桥是否达到真正的平衡状态,是由检流计指针是否有可察觉的偏转来判断的。
检流计的灵敏度是有限的,当指针的偏转小于0.1格时,人眼就很难觉察出来。
在电桥平衡时,设某一桥臂的电阻是R ,若我们把R 改变一个微小量ΔR ,电桥就会失去平衡,从而就会有电流流过检流计,如果此电流很小以至于我们未能察觉出检流计指针的偏转,我们就会误认为电桥仍然处于平衡状态。
为了定量表示检流计的误差,我们引入电桥灵敏度的概念,它定义为nS R R∆=∆(2)式中,ΔR 为电桥平衡后电阻R 的微小改变量,Δn 为电阻R 变化后检流计偏离平衡位置的格数,所以S 表示电桥对桥臂电阻相对不平衡值ΔR /R 的反应能力。
3.滑线式惠斯通电桥滑线式惠斯通电桥的构造如图2所示。
A 、B 、C 是装有接线柱的厚铜片(其电阻可以忽略),A 、B 之间为一根长度为L 、截面积和电阻率都均匀的电阻丝。
电阻丝上装有接线柱的滑键可沿电阻丝左右滑动,按下滑键任意触头,此时电阻丝被分成两段,设AD 段的长度为L 1、电阻为R 1,DB 的长度为L 2、电阻为R 2,因此当电桥处于平衡状态时,有111000221x R L L R R R R R L L L ===- (3)式中,L 1的长度可以从电阻丝下面所附的米尺上读出,R 0用一个十进制转盘式电阻箱作为标准电阻使用。
惠斯通电桥实验报告

惠斯通电桥实验报告1. 实验目的本实验的目的是通过使用惠斯通电桥来测量电阻器的未知电阻值。
通过实验,掌握惠斯通电桥的工作原理和使用方法,并学习使用电桥进行电阻测量。
2. 实验原理惠斯通电桥是一种常用的测量电阻值的工具,它基于电桥平衡原理。
当惠斯通电桥中各支路通过的电流满足一定的关系时,电桥即处于平衡状态。
根据平衡条件,可以计算出未知电阻值。
在惠斯通电桥中,有四个分支:两个比较支路和两个未知支路。
比较支路中的两个电阻器的比值已知,而未知支路中的电阻器的值待测。
当电桥平衡时,满足以下条件:$$ \\frac{{R1}}{{R2}} = \\frac{{R3}}{{R4}} $$其中,R1和R2为比较支路中的电阻值,R3和R4为未知支路中的电阻值。
3. 实验仪器本实验使用以下仪器: - 惠斯通电桥主机 - 电源 - 计算机 - 万用表4. 实验步骤4.1 实验准备•将电源与惠斯通电桥主机连接,并打开电源。
•将计算机与惠斯通电桥主机连接,并确保通信正常。
•将万用表和待测电阻器连接到相应的电桥支路上。
4.2 实验操作•调节电桥主机上的旋钮,使电桥处于初始非平衡状态。
•调节电桥主机上的旋钮,逐渐减小非平衡条件,使电桥逐渐接近平衡状态。
•当电桥达到平衡状态时,记录下电桥上的电阻值,并计算未知电阻值。
4.3 实验记录•在笔记本上记录下实验中的各项数据,包括电桥上的电阻值和计算得到的未知电阻值。
5. 实验结果与分析根据实验记录的数据,我们可以得到待测电阻器的未知电阻值。
通过对电桥平衡条件的计算,我们可以计算出未知电阻值的准确数值。
然后,我们可以对实验结果进行分析,比较实测值与理论值之间的差异,并分析可能存在的误差来源。
同时,我们也可以讨论实验中可能存在的不确定度,并对结果进行合理分析。
6. 实验总结通过本次惠斯通电桥实验,我们掌握了电桥的工作原理和使用方法。
通过实验,我们成功测量了待测电阻器的未知电阻值,并分析了实验结果的可靠性。
惠斯通电桥实验报告(完成版)【精品】

惠斯通电桥实验报告(完成版)【精品】实验目的:掌握惠斯通电桥的基本原理和使用方法,学会调节电阻比例来测量未知电阻值。
实验器材:惠斯通电桥、标准电阻箱、未知电阻器、万用表。
实验原理:惠斯通电桥是一种测量电阻值的仪器,它利用交流电的品质来测量电阻。
电桥由四个电阻器组成一个电路,分别为R1、R2、R3、R4,其中R1和R2相互平行,形成一个电路A,R3和R4相互平行,形成一个电路B,A和B平行,并且A和B之间连接一个未知电阻器,通过调节R3和R4两个电阻的比例,使得A电路和B电路中的电阻比例相等,从而实现对未知电阻值的测量。
实验步骤:1.将电桥的四个电阻分别接好。
2.将未知电阻器接在A和B电路之间。
3.调整R3和R4两个电阻的比例,使得万用表读数最小。
4.调整电阻比例,以减小万用表读数,直到读数为0。
5.记录下R3和R4的比例值和电桥的平衡电阻值。
6.用标准电阻箱测量未知电阻器的电阻值,并与电桥的平衡电阻值比较,计算出未知电阻器的电阻值。
实验注意事项:1.在进行电桥平衡前,要先将未知电阻器调节到适当的阻值范围内。
2.调整电桥平衡时,要慢慢调整,避免过度调节导致万用表产生超过量程范围的读数。
3.在进行测量时,要注意保持电桥和未知电阻器的连接稳定,避免导线和接头接触不良。
实验结果:已知标准电阻值为330Ω,未知电阻值为XΩ,调节比例后,电桥平衡电阻值为150Ω,R3和R4的比例为1:4.3。
根据公式R1/R2=R3/R4,可得到R1/R2=4.3。
则可通过等效电路的公式:X=(R1+R2)/R2 * R4-R3 来计算出未知电阻的电阻值,代入数据可得:X=(1+4.3)/4.3 * (330-150) = 123.3Ω。
实验结论:通过惠斯通电桥的实验,我们成功测量出了一个未知电阻的电阻值,实验结果与标准电阻值基本一致。
同时,我们也掌握了惠斯通电桥的基本原理和使用方法,学习了调节电阻比例来测量未知电阻值的技能。
惠斯通电桥实验报告

惠斯通电桥实验报告一、实验目的:1.了解惠斯通电桥实验的基本原理和操作方法;2.学习使用惠斯通电桥测量未知电阻的方法。
二、实验原理:实验所用的惠斯通电桥由四个电阻R1、R2、Rx、R4构成,接在一起形成一个平衡电桥。
惠斯通电桥的基本原理是根据电桥两个对角线的相等性判断电桥平衡情况,即:R1/R2=Rx/R4如果R1/R2=Rx/R4成立,则电桥平衡,电流不通过辅助电流计。
通过改变R1或R4或直流电压源电压,可实现电桥的平衡。
在平衡状态下,我们可以根据已知电阻R1、R2、R4和电源电压,计算出未知电阻Rx的阻值。
三、实验器材:1.电桥主机2.可调式直流电源3.标准电阻箱4.未知电阻箱5.电阻选择开关四、实验步骤:1.按照电桥连接原理,将电桥主机、可调式直流电源和标准电阻箱连接好。
2.将未知电阻箱和电阻选择开关连接到电桥主机的Rx端口。
3.设定合适的电桥平衡参数,如将R1、R2、R4的阻值设定为已知值,保证电桥平衡。
4.测量平衡时的电桥主机侧的电流值,记录下来。
5.根据电桥平衡条件的公式R1/R2=Rx/R4,计算未知电阻Rx的阻值。
五、实验数据记录与分析:根据实验步骤记录实验数据,然后进行数据分析,计算出未知电阻Rx的阻值。
六、实验结果与讨论:1.将计算得到的未知电阻Rx的阻值与实际标准阻值进行比较,从而评价测量的准确性。
2.分析实验误差产生的原因,并提出改进方法。
七、实验结论:通过实验测量,我们可以利用惠斯通电桥准确地测量未知电阻Rx的阻值,并根据实验数据进行数据分析和误差分析。
实验的结果可以得出判断未知电阻的阻值,并评价测量的准确性。
八、实验心得体会:通过本次实验,我了解了惠斯通电桥的基本原理和操作方法。
实验要求我们掌握测量电桥平衡时的参数设定和数据计算方法。
通过实验,我也体会到了实验过程中的注意事项和数据处理的重要性。
这个实验对于我深入了解电路中电阻的测量方法和电桥的应用具有很大的帮助。
惠斯通电桥实验报告

惠斯通电桥实验报告
惠斯通电桥实验旨在证明一个理论:每只电桥的电路参数均为未知的情况下,根据一
定的测试电流和电压结果,电路参数可以准确求得。
由此,可以准确测试出未知电路参数。
惠斯通电桥实验用四只电阻、一只电容和一只可调电阻作为电桥的构件,构成一个实
验水平的惠斯通电桥。
实验过程如下:首先,使得可调电阻的初始电阻等于已知电阻的中值,并设置两个电源,一个为正电源,一个为负电源。
同时,观察A、B、C、D四个回路之间的电束比,并
按此比例调整负极和正极上的电源电压值,直至比例达到一定值。
此时正(负)极和已知电
阻之间的负(正)极叶脉冲就形成了一个四线回路,其中可调电阻有四段模拟环路,而四段
环路与其他电阻和电容之间形成了一个非线性分布开关。
如此得到实验的结果,通过求解
实验得到的电压和电流数据中的误差,最终可以准确确定电桥的电路参数,从而完成惠斯
通电桥实验的目的。
实验结果表明,采用惠斯通电桥的方法,可以准确的求得由未知因素构成的未知电桥
参数。
通过惠斯通电桥实验,可以有效开发和测试电子元件及电子设备,也可用于测量某
些特性或检测信号,建立信号分析。
物理实验用惠斯通电桥测电阻实验报告

物理试验-用惠斯通电桥测电阻-试验汇报首都师范大学物理实验报告班级___信工C班___ 组别______D______姓名____李铃______ 学号__日期___.4.24__ 指导教师___刘丽峰___【试验题目】_________用惠斯通电桥测电阻___【试验目旳】1.掌握惠斯通(Wheastone)电桥测电阻旳原理;2.学会对旳使用惠斯通电桥测量电阻旳措施;3.理解提高电桥敏捷度旳几种措施;4.学会测量单电桥旳敏捷度。
【试验仪器】QJ- 23型箱式电桥, 滑线电阻, 转柄电阻箱(0,99999.9Ω), 检流计, 直流电源, 待测电阻, 开关, 导线若干。
【试验原理】1(惠斯通电桥测量电阻旳原理图5.1是惠斯通电桥旳原理图。
图中R1.R2和R0是已知阻值旳电阻, 它们和被测电阻Rx连成一种四边形, 每一条边称作电桥旳一种臂。
四边形旳对角A和B 之间接电源E;对角C和D之间接有检流计G, 它像桥同样。
电源接通, 电桥线路中各支路均有电流通过。
当C.D两点之间旳电位不相等时, 桥路中旳电流IG?0, 检流计旳指针发生偏转;当C.D两点之间旳电位相等时,“桥”路中旳电流IG=0, 检流计指针指零, 这时我们称电桥处在平衡状态。
当电桥平衡时, ,两式相除可得到Rx旳测量公式(5-1)电阻R1R2为电桥旳比率臂, R0为比较臂, Rx为待测臂。
只要检流计足够敏捷, 等式(1)就能相称好地成立, 被测电阻值Rx可以仅从三个已知电阻旳值来求得, 而与电源电压无关。
由于R1、R2和R0可以使用原则电阻, 而原则电阻可以制作得十分精密, 这一过程相称于把Rx和原则电阻相比较, 因而测量旳精确度可以到达很高。
首都师范大学物理实验报告2(电桥旳敏捷度电桥平衡后, 将R0变化?R0, 检流计指针偏转?n格。
假如一种很小旳?R0能引起较大旳?n偏转, 电桥旳敏捷度就高, 电桥旳平衡就可以判断得更精细。
电表(检流计)旳敏捷度是以单位电流变化量所引起电表指针偏转旳格数来定义旳, 即(5-2)同样在完全处在平衡旳电桥里, 若测量臂电阻Rx变化一种微小量?Rx, 将引起检流计指针所偏转旳格数?n, 定义为电桥敏捷度, 即(5-3) 不过电桥敏捷度不能直接用来判断电桥在测量电阻时所产生旳误差, 故用其相对敏捷度来衡量电桥测量旳精确程度, 即有(5-4)定义为电桥旳相对敏捷度。
物理实验-用惠斯通电桥测电阻-实验报告

物理实验-用惠斯通电桥测电阻-实验报告实验目的:了解惠斯通电桥的原理和使用方法,掌握测量未知电阻的方法和技巧。
实验原理:惠斯通电桥利用电流在不同电阻中流动时所造成的电位差来测量未知电阻,其原理如下:假设电桥四个点分别为A、B、C、D,其中AB、CD分别为两个电阻分支,R1、R2分别为已知电阻,Rx为待测电阻,则在电桥平衡状态下,有:其中U为电桥两对焦点之间的电位差。
为了使电桥平衡,可通过调节可变电阻值使U=0,则因为R1、R2、R3都是已知的,所以可以求得Rx。
实验步骤:1. 将待测电阻和已知电阻连接成由四个绳索连接而成的平四面体,插入电桥的四个插头口,注意连接正确。
2. 打开电桥电源,调节电桥电源开关至合适的大小,观察电桥示数表的变化,找到电桥平衡点。
3. 记录电桥示数表上的电阻值,并按公式(1)计算出待测电阻的值。
实验数据及计算:已知电阻:R1=100Ω,R2=220Ω已测电桥示数:U=0.05mV则通过公式(1)可求得待测电阻:Rx=R2×R3/R1=220×100/23.58=933.66Ω实验结果分析:通过实验和计算,我们求得了待测电阻的值为933.66Ω,这个数据接近我们使用万用表测出的值(约为929Ω),说明惠斯通电桥测量电阻的方法是可行且准确的。
在实际使用中,我们还需要注意电桥电源大小的调节和连接不当等问题,使测量更加精确。
实验思考:在实验过程中,我们可能会遇到如下问题:1. 电桥示数不稳定,波动范围较大,可能因为连接不良导致的接触阻抗不一致,可以通过重新插拔等方法排除这些干扰因素。
2. 电桥示数为0,可能因为电桥电源没有开启,或者是接线问题,需要检查一下。
3. 电桥示数变化缓慢,可能因为电桥电源开关未调到合适的大小,需要再次调整电源开关。
翻译:Experimental Report on Using Wheatstone Bridge to Measure ResistanceObjective:To understand the principle and usage of Wheatstone bridge, and to master the methods and skills for measuring unknown resistance.Principle:Wheatstone bridge measures unknown resistance by utilizing the potential difference caused by current flowing through different resistances. Assuming that the four points of the bridge are A, B, C, and D, and AB and CD are two resistance branches, R1 and R2 are known resistances, and Rx is the measured resistance. Then, in the balanced state of the bridge, the following equation holds:Because R1, R2, and R3 are known, Rx can be calculated.。
惠斯通电桥实验报告

惠斯通电桥实验报告惠斯通电桥实验报告引言:电学是一门研究电荷和电流行为的科学,而在电学中,电桥是一种常用的实验装置。
惠斯通电桥是由英国物理学家惠斯通发明的,它可以用来测量电阻的值。
本次实验旨在通过惠斯通电桥来测量未知电阻的数值,并探究电桥的原理和应用。
一、实验目的本次实验的主要目的是:1. 熟悉惠斯通电桥的结构和工作原理;2. 学会使用惠斯通电桥测量未知电阻的方法;3. 探究电桥在电阻测量中的应用。
二、实验装置和材料本次实验所用的装置和材料包括:1. 惠斯通电桥实验装置:包括电桥主体、电源、电阻箱等;2. 未知电阻样品;3. 电压表和安培表;4. 连接线等。
三、实验步骤1. 将惠斯通电桥实验装置搭建好,并连接电源;2. 调节电桥的平衡,使电桥两侧电压差为零;3. 将未知电阻样品接入电桥中,观察电桥平衡状态;4. 通过调节电阻箱,使电桥再次平衡,记录下此时电阻箱的阻值;5. 重复步骤3和4,使用不同的未知电阻样品进行测量。
四、实验结果和分析根据实验步骤中记录的数据,我们可以得到一组电阻测量结果。
通过计算这些结果,我们可以得到未知电阻样品的数值。
在进行实验时,我们发现当电桥平衡时,电桥两侧的电压差为零。
这是因为在平衡状态下,电桥两个支路中的电流相等,电桥的两个支路中的电阻比例也相等。
通过调节电阻箱的阻值,我们可以使电桥再次平衡,从而测量出未知电阻的数值。
在实验过程中,我们还发现电桥的平衡状态受到环境因素的影响。
例如,温度的变化、连接线的接触不良等都会导致电桥的平衡状态发生偏移。
因此,在实验中要注意这些因素,并进行相应的修正。
五、实验总结通过本次实验,我们对惠斯通电桥的结构和工作原理有了更深入的了解,并学会了使用电桥测量未知电阻的方法。
我们还发现电桥在电阻测量中具有重要的应用价值,可以帮助我们准确地测量电阻的数值。
然而,本次实验也存在一些问题和不足之处。
例如,实验过程中环境因素的干扰会影响测量结果的准确性,需要进一步改进实验条件。
惠斯通电桥实验报告

惠斯通电桥实验报告
实验目的:
通过惠斯通电桥实验,测量一个电阻的未知电阻值,并测量其他已知电阻的电阻值,验证欧姆定律。
实验仪器:
1. 电桥装置
2. 调谐电阻箱(用于调节电阻大小)
实验原理:
惠斯通电桥原理:惠斯通电桥是一种用于测量电阻的的电路装置,其原理基于电流在电路中的分布规律。
惠斯通电桥由四个电阻组成,两个相对的电阻分别称为“比较电阻”和“未知电阻”,通过调节“比较电阻”的大小,使得电桥达到平衡状态,即电流
在电桥中各支路中的电压相等。
根据欧姆定律,通过电桥的总电流可表示为I=U/R,其中U为电桥中总电压,R为电桥中的
总电阻。
实验步骤:
1. 搭建惠斯通电桥电路,将未知电阻与比较电阻相连。
2. 调节电桥中比较电阻的大小,直到电桥达到平衡状态。
3. 记录电桥平衡时的比较电阻值。
4. 使用万用表等测量工具,测量已知电阻的电阻值,并记录下来。
数据处理:
通过实验测量得到的比较电阻值和已知电阻的电阻值,带入欧
姆定律公式中,根据电流I和电压U的关系,可以计算出未知电阻的电阻值。
实验误差:
1. 电桥的平衡状态可能受到外界因素的干扰,如温度变化、电源波动等,导致测量值不准确。
2. 万用表等测量工具的精度限制,可能影响测量结果的准确性。
改进措施:
1. 在实验过程中注意保持环境稳定,尽量减小外界因素对电桥平衡状态的影响。
2. 使用精度更高的仪器进行电阻测量,以提高测量结果的准确性。
惠斯通电桥

实验六惠斯通电桥Experiment 6 Determining resistance using a Wheatstone bridge 电桥电路在电学中是一种很基本的电路。
利用电桥平衡原理构成的电测仪器,不仅可以测电阻,也可以测电容、电感,并可通过这些物理量的测量来间接测量非电学量,例如温度、压力等,因此电桥电路在自动化仪表和自动控制中有着广泛的应用。
本实验的基本要求是自组直流电桥,并用自组电桥及箱式电桥测量中值电阻。
实验目的Experimental purpose1.掌握惠斯通电桥测量电阻的基本方法。
2.掌握自组惠斯通电桥的基本原理。
实验原理Experimental principle1.电桥平衡条件(condition of electric bridge balance)图1所示为电桥电路原理图,它是由四个桥臂电阻和一个检流计组成,其中图1电桥原理图R,R2是已知标准电阻,称为“比率臂”;1R是可变标准电阻(电阻箱),称为“比较s臂”; R x是被测电阻,称为“测量臂”;B,D间接检流计。
接通电路后,检流计一般不指零,说明B,D两点电位不相等,通过调节R s,使检流计中无电流通过(I K=0),此时电桥达到平衡,由图可见,电桥平衡的条件是B、D两点电位相等。
即又 s x I I I I ==21, 所以有21R R R R s x = (1) s x R R R R 21=(2) 式(1)称电桥平衡条件,即相邻两臂电阻之比相等。
令M =R 1/R 2,称为“倍率”,则式(2)可写为R x =MR s 。
因此当电桥调平衡后,只要读出M 和R s 值,待测电阻R x 便可得到。
2.电桥灵敏度(electric bridge sensitivity)式(2)是在电桥平衡的条件下推导出来的。
而电桥是否平衡,是根据检流计指针有无偏转来判断的。
检流计的灵敏度总是有限的,例如实验室常用的AC 5型指针式检流计,其指针偏转一格对应电流为10-6A 左右,当通过它的电流小于10-7A 时,指针的偏转小于格,观测者就很难觉察出来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【Aim】
To determine the resistance of a wire specimen using a Wheatstonebridge.
【Theory】
For measuring accurately any electrical resistance,single bridge,also known asWheatstone bridge is widely used. Wheatstone bridge is an electrical circuit used to measure an unknownelectrical resistanceby balancing two legs of abridge circuit, one leg of which includes the unknown component. In many cases, the significance of measuring the unknown resistance is related to measuring the impact of some physical phenomenon (such as force, temperature, pressure, etc.) which thereby allows the use of Wheatstone bridge in measuring those elements indirectly.
When the bridge is balanced, that isVBD=0, thus
, (1)
So we can get that
(2)
That is
(3)
So (4)
In fact, it is difficult to exactly decide the value of , so we use "exchange measure method" to obtainRx. Exchange the positions ofR1andR2, orR0andRx, and adjustR0to a new value , the bridge can get a new balanced state,thus
AfterR1,R2were suitably selected, by adjusting the variable resistor,thenthevoltagebetween the two midpoints (BandD) will be zero and nocurrentwill flow through thegalvanometer.Thusthe bridge is in the status of balance. Detecting zero current with a galvanometer can be done to extremely high accuracy. Therefore, ifR1,R2andR0are known to high precision, thenRxcan be measured to high precision. Very small changes inRxdisrupt the balance andare readily detected.
Times
1
2
3
885.3
885.3
885.3
14.4
27.5
39.7
Number of theneedledeflection
1
2
3
61.5
64.4
66.9
64.3
【Resultsand error Analysis】
Levelof resistance box:=0.1
885.3╳0.1%=0.9(Ω)
【Table】
Table1 Test of theunபைடு நூலகம்nown resistor
Times
1
2
3
1000
2000
500
1000
2000
500
885.2
885.3
885.4
885.2
885.3
885.4
885.2
885.3
885.4
885.3
Table2Sensitivity of the bridge
885.3±0.9(Ω)
64.3
【Conclusions】
In this experiment, we use the Wheatstone bridge to measureRx, and adjust the resistance of four arms to make the current through the ammeter zero.We can calculate the resistance by .Wesolvethe difficulty of accurate measurement of bridge arm ratio by exchange measurement,and then with a final result 885.3(Ω).The result has an allowable error.
(5)
Combine equation (4) and (5), we can get
(6)
This equation has nothing to do withR1andR2. In this way, we can make the error only relate to the instrument error ofR0, which is the instrument error of the resistor box.
The apparatus used in this experiment is a simple form of the Wheatstone bridge.The basic circuitisshown in Fig. 1.Itconsists of four bridge arms,Rxrepresents an unknown resistance andR0, R1,R2aredecadevariable resistances. In addition, the circuit contains a "bridge" balance indicator (usually a galvanometer), workingpower E andslide-wire rheostat.
