上海师范大学综合实验复习

合集下载

上海上海师范大学第三附属实验学校初二生物实验探究综合题测试卷附答案

上海上海师范大学第三附属实验学校初二生物实验探究综合题测试卷附答案一、实验探究综合题1．下面是与生殖有关的结构示意图，请分析回答：（7分）（1）在甲的结构中将来发育成新植物体的是[ ]_____________，该结构是由_____________发育而来。

（2）在乙图中，[ ]_____________落在温暖、湿润的地方会发育成一个新个体。

（3）在丙图中，将来发育成新个体的结构是[ ]_____________，其发育成新个体的内在条件是_____________，在其发育过程中，所需要的营养物质来自_____________（填序号）。

（4）以上图示反映的生殖方式中，属于有性生殖的是_____________（填序号）。

2．下面是家鸽的呼吸系统示意图，请据图回答下列问题：（1）写出图中各部分名称：①_____________；②_____________；③_____________。

（2）家鸽在飞行时，空气进入肺→气囊→肺，这样的呼吸方式叫_____________。

（3）鸟类的体形呈型，可减少飞行时空气对它的阻力；体表覆盖着_________，用于飞行的羽毛主要是__________；前肢变成________。

（4）飞行时，当家鸽两翼举起时，（）________扩张，外界的空气就进入（）_______里，大量空气在其中进行气体交换。

3．如图所示A、B、C、D、E、F、G是常见的几种动物，据图回答。

（1）如将图中动物分为甲、乙两类，甲类群为：B、E、H，乙类群为：A、C、D、F、G，上述分类的依据是动物体内是否有____________；将A、C、D、F、G图中的生物按照从低等到高等的顺序排列________________________（用字母表示）。

（2）B为蚯蚓，它用_______________呼吸。

（3）C在繁殖和哺育后代的过程中具有__________、__________的特征，所以属于哺动物。

上海上海师范大学康城实验学校初二生物实验探究综合题专题

上海上海师范大学康城实验学校初二生物实验探究综合题专题一、实验探究综合题1．生物学兴趣小组的同学进行野外考察时，拍摄了如下一些动物的照片，请你利用本学期所学的动物学知识，协助兴趣小组的同学进行科学分析和研究：（1）若将图中蝗虫和河蚌归为一类，其余为另一类，则分类依据是_______。

（2）一生中用过三种器官呼吸的动物是______（用字母表示）（3）真正的陆生生活的脊椎动物的是_____（用字母表示），原因是它们的______和_____完全摆脱了水的限制。

（4）A和C虽然都可以在空中飞行，但它们在呼吸和生殖发育过程存在较大区别：例如，两者都用____进行气体交换，但C还用_____辅助呼吸：生殖发育过程中，A区别于鸟类的主要特征是_____。

（5）河蚌利用______与水流进行气体交换；蝗虫的呼吸器官是______。

（6）青蛙幼体生活在水中，用______呼吸；成体生活在潮湿陆地上，也可生活在水中，主要用______呼吸，兼用______辅助呼吸。

这种发育方式叫______。

（7）请把上述六种动物按由低等到高等的顺序排列______（用字母表示）。

2．如图A、B、C、D、E是常见的几种动物，据图回答下列问题：（1）D生活在水中，用______呼吸，用______游泳，靠______感知水流和测定方向。

（2）B的身体体表有______，具有保护和支持内部柔软器官、防止水分蒸发等作用。

（3）A的幼体生活在水中用______呼吸；成体水陆两栖生活，用______呼吸。

（4）E的身体呈______型，前肢变成______；它的身体内有发达的______与肺相通，有贮存空气，辅助呼吸的作用。

（5）C是哺动物，特有的生殖发育特点是______。

（6）F类动物的主要特征：体表覆盖角质的鳞片或甲：______；在陆地上产卵，卵表面具有______。

（7）上述动物中，体温能保持恒定的是______（填字母）。

3．如图是鲫鱼的外形图，请据图填空：（1）俗话说：“鱼儿离不开水。

上海上海师范大学第三附属实验学校初二生物期末实验探究综合题汇编

上海上海师范大学第三附属实验学校初二生物期末实验探究综合题汇编一、实验探究综合题1．下图是我们生活中常见的几种动物，请分析回答。

（1）图示动物中，不能较好地在陆地干燥环境中生活的有___________、___________（用图中字母表示），原因是___________。

（2）B、C俩类动物在发育方面的共同特征为___________。

（3）B、E两种动物都善于在空中飞行，原因是它们具有相似的运动器官。

试请简单介绍一下它们的运动器官适于飞行的共同特点：___________、___________、___________。

（4）如果以“体温是否恒定”为依据对图中的动物进行分类，则与动物A可同分一组的为___________（用图中字母表示）。

答案：（1） A C 它们都必须依靠体表黏液溶解空气中的氧气来完成呼吸（2）变态发育（3）轻薄大（4）BCD【分析】图中A蚯蚓，属于解析：（1） A C 它们都必须依靠体表黏液溶解空气中的氧气来完成呼吸（2）变态发育（3）轻薄大（4）BCD【分析】图中A蚯蚓，属于环节动物；B蝴蝶，属于昆虫类；C青蛙，属于两栖类动物；D蜥蜴属于爬行类；E鸟类；F家兔，属于哺乳动物。

（1）陆地生活的动物与陆地气候相对干燥的环境相适应一般都有防止水分散失的结构如昆虫的外骨骼、爬行动物的鳞片或甲，而A蚯蚓属于环节动物，靠湿润的体壁呼吸，在干燥的环境中蚯蚓无法进行呼吸，C青蛙的幼体蝌蚪只可以在水中生活，用鳃呼吸；成体既可以在水中生活，也可以在陆地上生活，用肺呼吸，皮肤辅助呼吸功，所以其皮肤必须保持湿润，生活在潮湿的环境中。

（2）B蝴蝶的发育历程：受精卵、幼虫、蛹、成虫，发育特点为完全变态发育；C青蛙的发育历程：受精卵、蝌蚪、幼蛙、成蛙，发育特点为变态发育，因此B\C两类动物在发育方面的共同特征为变态发育。

（3）B蝴蝶属于昆虫，胸部有发达的肌肉，附着在外骨骼上，牵引运动器官完成跳跃、飞行等多种运动，有利于觅食和避敌，蝴蝶的翅是适于飞行的扇面形结构，这种结构的运动是由肌肉的收缩和舒张引起的，在空气中都可以产生向上的升力和前进的动力，相对于自身身体的大小来说，具有轻、薄、表面积大的特点，有利于通过扇动空气产生飞行的动力，使蝴蝶能自由飞行；E鸟类有发达的胸肌，利于牵动两翼完成飞行动作，所以此两种动物翅膀的特点大、薄、轻。

上海上海师范大学第三附属实验学校初二生物实验探究综合题专题

上海上海师范大学第三附属实验学校初二生物实验探究综合题专题一、实验探究综合题1．由于家鸽飞行速度快、耐力强，并且具有良好的导航能力，自古以来常被用于通信传书。

已有研究表明家鸽的导航包括定向与定位。

家鸽主要利用太阳和地磁定向，视觉与定位有关。

（1）家鸽具有许多与飞行相适应的特点，如身体呈流线型，有利于_____；骨骼轻薄，有些骨内部_____，可减轻体重。

家鸽用肺进行气体交换，并有_____辅助呼吸，呼吸作用旺盛。

（2）科研人员研究了嗅觉与定位的关系。

他们进行多次实验：将多只家鸽分为两组，A组用含木犀草素的溶液麻醉家鸽嗅觉，B组用_____处理作为对照。

在良好天气下，选择不同距离放飞后记录归巢时间，求平均值后计算_____，结果如图1所示。

图1实验结果表明放飞距离较近时，A、B组差异不太显著，放飞距离较远时，两组差异显著，说明嗅觉与家鸽导航定位有关，而且_____。

（3）近年来，亚洲多地出现雾霾。

科研人员研究了雾霾对家鸽归巢的影响。

由于雾霾会影响家鸽的视线，因此科研人员假设随着雾霾严重程度增加，家鸽归巢速度减慢。

他们在不同雾霾程度下，从距离鸽巢200公里处，放飞大约1500只家鸽，多次实验得到如图2所示结果。

①实验中放飞多只家鸽并进行多次实验，目的都是为了_____。

②图2所示实验结果是否支持研究人员的假设，请你判断并说明理由。

_____③雾霾对家鸽产生上述影响，推测可能的原因是_____A．雾霾干扰家鸽通过太阳和地磁的定向B．雾霾的化学成分增强家鸽嗅觉定位C．家鸽主要依靠视觉进行定位2．如图是几种动物的形态结构示意图，请据图回答下列问题：（1）该类动物的共同特征是______。

（2）蚯蚓的呼吸器官是______。

（3）不是鱼，原因是其具有软体动物的______特征。

（4）下列是对图中所示的一部分动物的分类概念图，请完成概念图中A～E的相关内容，使其符合概念图的划分意图。

A～E依次为：A______、B______、C______、D______、E______。

上海上海师范大学第三附属实验学校中考二轮复习化学推断题80题专题训练(含答案)

上海上海师范大学第三附属实验学校中考二轮复习化学推断题80题专题训练(含答案)一、中考化学推断题1．已知A、B、C、D、甲为初中化学常见的物质，甲为参与大气循环的物质，它们之间的转化关系如图所示（反应条件省略）：（1）若A、B的组成元素相同，则甲为_____（填化学式）。

（2）若反应②为复分解反应，则反应②的化学方程式为____________________________。

【答案】O2Ca（OH）2+Na2CO3=CaCO3↓+2NaOH【解析】【详解】（1）A、B、C、D、甲为初中化学常见的物质，甲为参与大气循环的物质，所以甲是氧气或二氧化碳，若A、B的组成元素相同，A和甲反应生成B，一氧化碳在氧气中燃烧生成一氧化碳，所以A是一氧化碳，B是二氧化碳，甲是氧气，C可以是氧化铜，氧化铜和一氧化碳加热生成铜和二氧化碳，所以D是铜，铜和氧气加热生成氧化铜，经过验证，推导正确，所以甲是O2；（2）A、B、C、D、X是初中化学研究中常见的五种物质，X为参与大气循环的气体，X 可能是氧气或二氧化碳，反应②为复分解反应，X可能是二氧化碳，A、B是氢氧化钙或碳酸钠，氢氧化钙和碳酸钠反应生成碳酸钙沉淀和氢氧化钠，A和二氧化碳反应会生成C，所以A是氢氧化钙，B是碳酸钠，C是碳酸钙，D是氢氧化钠，经过验证，推导正确，所以反应②是氢氧化钙和碳酸钠反应生成碳酸钙沉淀和氢氧化钠，化学方程式为：Ca （OH）2+Na2CO3=CaCO3↓+2NaOH。

2．A、B、C、D是初中化学常见的物质，它们的关系如图：“﹣”表示相互之间可以反应，“→”表示可以转化生成，其中A是年产量最多的金属，C是一种常见的碱，B和C反应生成的一种物质是我们日常生活的调味品，D是一种气体，D在大气中含量的增加会导致温室效应．（1）写出D的化学式_____，C必须密封保存的原因是____________________________．（2）A放入B的溶液中，可以观察到现象是____________________________________，反应的化学方程式___________________________________．（3）写出B和C反应的化学方程式____________________________________，该反应属于___________类型（填基本反应类型）．（4）D导致温室效应，从而威胁人类生存，我们应该倡导“低碳生活”，下列做法哪些符合“低碳生活”的理念___________（填序号）．A 尽量少用一次性杯筷B 提倡步行上下学，乘坐公交车上下班C 植树造林，爱护花草树木 D大力开发太阳能、风能等新能源．【答案】CO2氢氧化钠容易吸收空气中的水分及二氧化碳有气泡产生，溶液逐渐变成浅绿色 Fe+2HCl═FeCl2+H2↑ NaOH+HCl=NaCl+H2O 复分解反应 ABCD【解析】【分析】A是年产量最多的金属，则A是铁，B和C反应生成的一种物质是我们日常生活的调味品，C是一种常见的碱，则C是氢氧化钠，B是盐酸，D是一种气体，D在大气中含量的增加会导致温室效应，则D是二氧化碳。

上海上海师范大学康城实验学校功和机械能中考综合专项复习训练

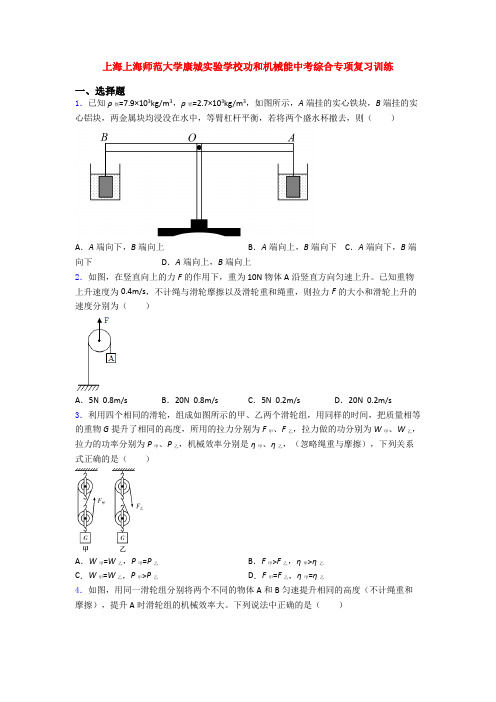
上海上海师范大学康城实验学校功和机械能中考综合专项复习训练一、选择题1．已知ρ铁=7.9×103kg/m3，ρ铝=2.7×103kg/m3，如图所示，A端挂的实心铁块，B端挂的实心铝块，两金属块均浸没在水中，等臂杠杆平衡，若将两个盛水杯撤去，则（）A．A端向下，B端向上B．A端向上，B端向下C．A端向下，B端向下D．A端向上，B端向上2．如图，在竖直向上的力F的作用下，重为10N物体A沿竖直方向匀速上升。

已知重物上升速度为0.4m/s，不计绳与滑轮摩擦以及滑轮重和绳重，则拉力F的大小和滑轮上升的速度分别为（）A．5N 0.8m/s B．20N 0.8m/s C．5N 0.2m/s D．20N 0.2m/s3．利用四个相同的滑轮，组成如图所示的甲、乙两个滑轮组，用同样的时间，把质量相等的重物G提升了相同的高度，所用的拉力分别为F甲、F乙，拉力做的功分别为W甲、W乙，拉力的功率分别为P甲、P乙，机械效率分别是η甲、η乙，（忽略绳重与摩擦），下列关系式正确的是（）A．W甲=W乙，P甲=P乙B．F甲>F乙，η甲>η乙C．W甲=W乙，P甲>P乙D．F甲=F乙，η甲=η乙4．如图，用同一滑轮组分别将两个不同的物体A和B匀速提升相同的高度（不计绳重和摩擦），提升A时滑轮组的机械效率大。

下列说法中正确的是（）①A物体比B物体轻；②提升A的拉力大；③提升A做的额外功多；④提升A做的有用功多A．只有②④B．只有①③C．只有②③D．只有①④5．如图所示，一块厚度很薄、质量分布均匀的长方体水泥板放在水平地面上，若分别用一竖直向上的动力F1、F2作用在水泥板一端的中间，欲使其一端抬离地面，则（）A．F1>F2，因为甲中的动力臂长B．F1<F2，因为乙中的阻力臂长C．F1>F2，因为乙中的阻力臂短D．F1=F2，因为动力臂都是阻力臂的2倍6．关于定滑轮、动滑轮，以下说法不正确的是A．使用定滑轮虽然不省力，但可以改变力的方向B．定滑轮实质是等臂杠杆，而动滑轮实质是不等臂杠杆C．又省力又少移动距离的动滑轮是无法实现的D．使用一个定滑轮和一个动滑轮组成的滑轮组，只能省一半力7．关于功、功率、机械效率的说法中，正确的是A．功率大的机械，机械效率一定高B．机械做功时，做的有用功越多，机械效率越大C．机械做功时，工作时间越短，功率一定越大D．利用机械做功时可以省力或省距离，但不能省功8．如图所示是某建筑工地用升降机提升大理石的滑轮组示意图。

上海上海师范大学康城实验学校初二生物实验探究综合题测试卷附答案

上海上海师范大学康城实验学校初二生物实验探究综合题测试卷附答案一、实验探究综合题1．图为蝗虫的外部形态示意图。

（1）根据动物体内有无脊柱分类，蝗虫属于_______________动物。

（2）蝗虫身体的三个部分中，[_____] (填序号)是蝗虫的运动中心；（3）蝗虫适应陆地生活的特点是身体表面有一层坚韧的___________，虽然会限制身体的发育和长大，但能保护体内柔软器官并防止体内____________蒸发（或散失）的作用；（4）蝗虫的体表有与呼吸有关的结构是____________。

2．下图是鸟的形态结构示意图。

据图回答下列问题：（1）从图A中看出鸟的身体呈流线型，这样就能减少运动时的阻力。

请再举出一类动物，通常也具有这样的形态和作用，如________类动物。

（2）图B中的①所示，鸟的前肢变成________，适于空中飞行；②所示为附着在胸骨上全身最发达的_________，它能拉动两翼产生飞行的动力。

（3）图C中所示鸟的骨骼轻、薄、坚固，有些骨______；③为胸骨上高耸的突起叫做_______。

（4）图D中表示气囊结构的序号是________，这样的结构使得鸟类能够进行________呼吸。

3．呼吸是生物的重要特征。

不同动物呼吸的结构和器官差异很大，但其功能都是最大限度地吸收氧气排出二氧化碳。

据图回答下列问题。

（1）原始的单细胞动物A用表膜呼吸，制作临时装片观察时，要用吸管从培养液的表层吸取A，原因是_____。

（2）观察B时，要经常往其体表滴水以保持湿润，原因是蚯蚓靠_____进行呼吸。

观察C 时，发现它已具有了呼吸器官____ ；观察D时，发现其体表具有与体内气管相连的_____ ，它是气体出入的门户。

（3）BTB是一种蓝色指示剂，遇二氧化碳由蓝变黄。

短时间使用对鱼无毒害。

在图E鱼口的前方滴一滴BTB溶液，根据鱼在水中的呼吸特点，预测从鱼的鰓盖后缘流出的溶液呈_______色。

上海上海师范大学第三附属实验学校初二生物期末复习综合题汇编

上海上海师范大学第三附属实验学校初二生物期末复习综合题汇编一、实验探究综合题1．我省黔东南等地的劳动人民积极探索和实践“稻田养鱼”种养模式。

该模式中稻田能为鱼提供栖息环境，鱼以水中浮游植物、杂草和浮游动物等为食；鱼的排泄物能为水稻提供有机肥，可获得水稻和鱼的双丰收，使农民在脱贫攻坚和乡村振兴的道路上迈出了坚实的步伐。

下图是某同学绘制的与鱼有关的部分生物之间关系示意图，请回答下列问题。

（1）“稻田养鱼”能减少在稻田中施用农药和化肥，请在题干中寻找证据：_____（答出一项即可）。

（2）从生态系统的成分看，A是___，B（含B1、B2）是______，C是__________。

（3）A、B遗体中含有的有机物都能被细菌和真菌分解，分解后的产物主要有_______（列出两种即可），这些产物能够被水稻等绿色植物吸收利用。

（4）通过分析，可以说明动物在生物圈中具有___________（填“促进”或“抑制"）生态系统物质循环的作用。

答案：（1）鱼以水中浮游植物、杂草等为食或：鱼的排泄物能为水稻提供有机肥（合理叙述给分）（2）生产者消费者分解者（3）水、二氧化碳、无机盐等（4）促进【分析】解析：（1）鱼以水中浮游植物、杂草等为食或：鱼的排泄物能为水稻提供有机肥（合理叙述给分）（2）生产者消费者分解者（3）水、二氧化碳、无机盐等（4）促进【分析】生态系统包括非生物成分和生物成分，生物成分包括生产者、消费者、分解者。

生产者主要指绿色植物，能够通过光合作用制造有机物，为自身和生物圈中的其他生物提供物质和能量；消费者主要指各种动物，在促进生物圈中的物质循环起重要作用；分解者是指细菌和真菌等营腐生生活的微生物，它们能将动植物残体中的有机物分解成无机物归还无机环境，促进了物质的循环。

（1）使用农药主要是消灭或控制农田里的害虫或杂草；施用化肥主要给农作物提供无机盐。

根据资料信息可知，在“稻田养鱼”种养模式中稻田能为鱼提供栖息环境，鱼以水中浮游植物、杂草和浮游动物等为食；鱼的排泄物能为水稻提供有机肥，可获得水稻和鱼的双丰收。

上海上海师范大学康城实验学校浮力中考综合专项复习训练

上海上海师范大学康城实验学校浮力中考综合专项复习训练一、选择题1．如图所示，两个底面积相同的薄壁容器甲乙分别装有密度为ρa，ρb的液体，放置在水平桌面上，现将同一物块（密度为ρ）分别放入两容器中，物块静止时两容器中液面等高。

下列说法正确的是（）A．液体密度与物体密度的关系为ρa<ρb<ρB．放入物块前，甲容器底受到液体的压强较大C．放入物块后，甲容器对桌面的压强增加量较大D．放入物块后与放入前相比，甲容器底受到液体的压力增加量较大2．如图所示是甲、乙两种物质的m﹣V图象，用这两种物质按一定比例混合制成实心小球，并将其放入水中。

下列分析正确的是（）A．若甲、乙物质质量相等，则实心小球将沉入水底B．若甲、乙物质体积相等，则实心小球静止时漂浮于水面C．若实心小球悬浮在水中，则甲、乙物质体积比为5∶3D．若实心小球悬浮在水中，则甲、乙物质质量比为3∶23．在三个完全相同的杯子中均盛满某种液体后，将一木块放在乙杯中后，木块漂浮在液体中，将另一个完全相同的木块浸没在丙杯中，并用细线将其系在丙杯的杯底，如图所示，此时三个杯子对桌面的压力分别为F甲、F乙、F丙，液体对杯子底部的压强分别为p甲、p、p丙，则( )乙A ．F F F ==甲乙丙B ．p p p >=乙甲丙C ．F F F <=甲乙丙D ．p p p =>乙甲丙4．把一个物体挂在弹簧秤下，弹簧秤示数为3N ，把它浸没在水（密度为1.0g ／cm 3）中时,弹簧秤示数变为2N 。

假设物体的质量为m ，物体的密度为ρ，浸没在水中时物体的上下表面所受的压力差和压强差分别为△F 和△P ，则无法求得的是（）A ．mB ．ρC ．△FD ．△P5．如图所示，在水平桌面上放置一个平底轻质薄塑料杯，杯子底面积为-32210m ⨯，高为0.1m ，杯中装满水，水的质量为300g ，将体积为3100cm 、重为1.8N 的小球缓慢的放入水中，当小球静止时，下列判断中正确的是（g=10N/kg ）（）A ．溢出水的体积为310cmB ．水对杯底的压力为3NC ．水对杯底的压强为1500PaD ．小球受到的浮力为1N6．如图，将装有适量水的小玻璃瓶瓶口向下，使其漂浮在大塑料瓶内的水面上，拧紧大瓶瓶盖，通过改变作用在大瓶侧面的压力大小，实现小瓶的浮与沉。

上海上海师范大学康城实验学校运动和力中考综合专项复习训练

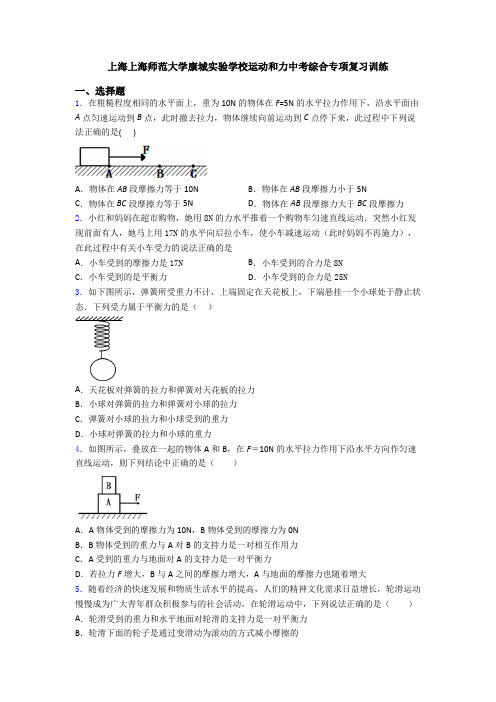
上海上海师范大学康城实验学校运动和力中考综合专项复习训练一、选择题1．在粗糙程度相同的水平面上，重为10N的物体在F=5N的水平拉力作用下，沿水平面由A点匀速运动到B点，此时撤去拉力，物体继续向前运动到C点停下来，此过程中下列说法正确的是( )A．物体在AB段摩擦力等于10N B．物体在AB段摩擦力小于5NC．物体在BC段摩擦力等于5N D．物体在AB段摩擦力大于BC段摩擦力2．小红和妈妈在超市购物，她用8N的力水平推着一个购物车匀速直线运动．突然小红发现前面有人，她马上用17N的水平向后拉小车，使小车减速运动（此时妈妈不再施力），在此过程中有关小车受力的说法正确的是A．小车受到的摩擦力是17N B．小车受到的合力是8NC．小车受到的是平衡力D．小车受到的合力是25N3．如下图所示，弹簧所受重力不计，上端固定在天花板上，下端悬挂一个小球处于静止状态．下列受力属于平衡力的是（）A．天花板对弹簧的拉力和弹簧对天花板的拉力B．小球对弹簧的拉力和弹簧对小球的拉力C．弹簧对小球的拉力和小球受到的重力D．小球对弹簧的拉力和小球的重力4．如图所示，叠放在一起的物体A和B，在F＝10N的水平拉力作用下沿水平方向作匀速直线运动，则下列结论中正确的是（）A．A物体受到的摩擦力为10N，B物体受到的摩擦力为0NB．B物体受到的重力与A对B的支持力是一对相互作用力C．A受到的重力与地面对A的支持力是一对平衡力D．若拉力F增大，B与A之间的摩擦力增大，A与地面的摩擦力也随着增大5．随着经济的快速发展和物质生活水平的提高，人们的精神文化需求日益增长，轮滑运动慢慢成为广大青年群众积极参与的社会活动，在轮滑运动中，下列说法正确的是（）A．轮滑受到的重力和水平地面对轮滑的支持力是一对平衡力B．轮滑下面的轮子是通过变滑动为滚动的方式减小摩擦的C．轮滑匀速转弯时，受到平衡力的作用D．轮滑运动时不用力仍能保持向前滑行是由于受到惯性的作用6．体检时，小宏静立在体重秤上，下列几对力中属于彼此平衡的是A．小宏对秤的压力与秤受到的支持力B．小宏对秤的压力与秤对他的支持力C．秤受到的重力与秤对小宏的支持力D．小宏受到的重力与秤对他的支持力7．汽车在平直公路上匀速行驶时，下列属于平衡力的是（）A．汽车受到的牵引力和阻力B．汽车受到的支持力和地面受到的压力C．汽车受到的牵引力和重力D．汽车受到的牵引力和地面受到的压力8．梅西在发任意球时，能使足球由静止绕过人墙钻入球门，该现象说明（）A．力的作用是相互的B．力可以改变物体的形状C．力可以改变物体的运动状态D．梅西充分发挥了惯性力的作用9．电动平衡车是一种时尚代步工具，如图所示，当人驾驶平衡车在水平路面上匀速前行时，下列说法中正确的是（）A．平衡车受到的重力与地面对它的支持力是一对平衡力B．平衡车前行时，轮子受到路面的摩擦力方向是向前的。

上海上海师范大学康城实验学校初二生物实验探究综合题专题

第1篇一、引言纲要实践教学是一种以项目为导向的教学模式，旨在培养学生的实际操作能力和团队协作精神。

在过去的一段时间里，我参与了学校组织的纲要实践教学活动，通过实践锻炼，我对自己的专业知识和技能有了更深的理解，以下是我对这次实践教学活动的个人总结。

二、实践内容与过程1. 实践项目概述本次纲要实践教学项目以“智慧校园”为主题，旨在通过实际操作，让学生了解和掌握智慧校园的建设流程、关键技术以及应用场景。

2. 实践过程（1）前期准备：在项目开始前，我们小组进行了充分的讨论和调研，明确了项目目标、任务分工以及时间节点。

（2）项目实施：在项目实施过程中，我们按照以下步骤进行：a. 确定智慧校园建设需求，包括硬件设备、软件系统、网络环境等；b. 设计智慧校园解决方案，包括系统架构、功能模块、技术选型等；c. 实施项目，包括设备采购、系统搭建、网络部署等；d. 项目验收，对智慧校园系统进行测试、调试和优化。

（3）项目总结：在项目结束后，我们对项目进行了总结和反思，分享了项目实施过程中的经验教训。

三、实践成果与收获1. 实践成果（1）完成了智慧校园系统的设计与实施，实现了校园管理、教学、科研、生活等方面的智能化；（2）掌握了智慧校园建设的关键技术，如云计算、大数据、物联网等；（3）提升了团队协作能力和沟通能力。

2. 实践收获（1）专业知识：通过实践，我对智慧校园建设的相关知识有了更深入的了解，提高了自己的专业素养；（2）实践能力：在项目实施过程中，我学会了如何将理论知识应用于实际操作，提高了自己的实践能力；（3）团队协作：在团队中，我学会了如何与他人沟通、协作，共同完成任务；（4）创新思维：在项目实施过程中，我尝试了多种解决方案，锻炼了自己的创新思维能力。

四、实践反思与改进1. 反思（1）在项目实施过程中，我们发现了一些问题，如项目进度控制、团队协作、技术难题等；（2）在项目总结阶段，我们认识到自己在某些方面的不足，如时间管理、沟通技巧等。

上海上海师范大学康城实验学校中考数学期末几何综合压轴题模拟汇编

上海上海师范大学康城实验学校中考数学期末几何综合压轴题模拟汇编一、中考几何压轴题1．综合与实践：利用矩形的折叠开展数学活动，探究体会图形在轴对称，旋转等变换过程中的变化，及其蕴含的数学思想和方法．动手操作：如图①，矩形纸片ABCD 的边AB ＝23，将矩形纸片ABCD 对折，使点A 与点D 重合，点B 与点C 重合，折痕为EF ，然后展开，EF 与AC 交于点H ；如图②，将矩形ABCD 沿过点A 的直线折叠，使点B 落在对角线AC 上，且点B 与点H 重合，展开图形，折痕为AG ，连接GH ；若在图①中连接BH ，得到如图③，点M 是线段BH 上的动点，点N 是线段AH 上的动点，连接AM ，MN ，且∠AMN ＝∠ABH ；若在图②中连接BH ，交折痕AG 于点Q ，隐去其它线段，得到如图④．解决问题：（1）在图②中，∠ACB ＝，BC ＝，AGGF＝，与△ABG 相似的三角形有个；（2）在图②中，AH 2＝AE ·（从图②中选择一条线段填在空白处），并证明你的结论；（3）在图③中，△ABH 为三角形，设BM 为x ，则NH ＝（用含x 的式子表示）；拓展延伸：（4）在图④中，将△ABQ 绕点B 按顺时针方向旋转α（0°≤α≤180°），得到△A ′BQ ′，连接DQ ′，则DQ ′的最小值为，当tan ∠CBQ ′＝时，△DBQ ′的面积最大值为． 2．类比、转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整．原题：如图1，在平行四边形ABCD 中，点E 是BC 的中点，点F 是线段AE 上一点，BF 的延长线交射线CD 于点G ．若3AFEF ，求CD CG的值．（1）尝试探究在图1中，过点E 作//EH AB 交BG 于点H ，则AB 和EH 的数量关系是_________，CG 和EH 的数量关系是_________，CDCG的值是_________．（2）类比延伸如图2，在原题的条件下，若()0AF m m EF =>，则CDCG的值是_________（用含有m 的代数式表示），试写出解答过程．（3）拓展迁移如图3，梯形ABCD 中，//DC AB ，点E 是BC 的延长线上的一点，AE 和BD 相交于点F ．若ABa CD =，BCb BE=，()0,0a b >>，则AF EF 的值是________（用含a 、b 的代数式表示）．3．综合与实践动手操作利用正方形纸片的折叠开展数学活动．探究体会在正方形折叠过程中，图形与线段的变化及其蕴含的数学思想方法．如图1，点E 为正方形ABCD 的AB 边上的一个动点，3AB =，将正方形ABCD 对折，使点A 与点B 重合，点C 与点D 重合，折痕为MN ．思考探索（1）将正方形ABCD 展平后沿过点C 的直线CE 折叠，使点B 的对应点B '落在MN 上，折痕为EC ，连接DB '，如图2．①点B '在以点E 为圆心，_________的长为半径的圆上； ②B M '=_________；③DB C '为_______三角形，请证明你的结论．拓展延伸（2）当3AB AE =时，正方形ABCD 沿过点E 的直线l （不过点B ）折叠后，点B 的对应点B '落在正方形ABCD 内部或边上．①ABB '面积的最大值为____________；②连接AB '，点P 为AE 的中点，点Q 在AB '上，连接,PQ AQP AB E '∠=∠，则2B C PQ '+的最小值为____________．4．如图，已知ABC 和ADE 均为等腰三角形，AC ＝BC ，DE ＝AE ，将这两个三角形放置在一起．（1）问题发现：如图①，当60ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，则CEB∠＝ °，线段BD 、CE 之间的数量关系是；（2）拓展探究：如图②，当90ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，请判断CEB ∠的度数及线段BD 、CE 之间的数量关系，并说明理由；（3）解决问题：如图③，90ACB AED ∠∠︒＝＝，25AC ＝，AE ＝2，连接CE 、BD ，在AED 绕点A 旋转的过程中，当DE BD ⊥时，请直接写出EC 的长．5．点E 是矩形ABCD 边AB 延长线上的一动点，在矩形ABCD 外作Rt △ECF ，其中∠ECF ＝90°，过点F 作FG ⊥BC ，交BC 的延长线于点G ，连接DF ，交CG 于点H ．（1）发现：如图1，若AB ＝AD ，CE ＝CF ，猜想线段DH 与HF 的数量关系是；（2）探究：如图2，若AB ＝nAD ，CF ＝nCE ，则（1）中的猜想是否仍然成立？若成立，请给予证明；若不成立，请说明理由．（3）拓展：在（2）的基础上，若射线FC 过AD 的三等分点，AD ＝3，AB ＝4，则直接写出线段EF 的长． 6．综合与实践动手操作利用旋转开展教学活动，探究图形变换中蕴含的数学思想方法．如图1，将等腰直角三角形ABC 的AB 边绕点B 顺时针旋转90°得到线段A B '，90ACB ∠=︒，1AC =，连接A C '，过点A '作A H CB '⊥交CB 延长线于点H ．思考探索（1）在图1中：①求证：ABC A BH '≌△△； ②A BC '的面积为______； ③tan A CB '∠=______．拓展延伸（2）如图2，若ABC 为任意直角三角形，90ACB ∠=︒．BC 、AC 、AB 分别用a 、b 、c 表示．请用a 、b 、c 表示：①A BC '的面积：______； ②A C '的长：______；（3）如图3，在ABC 中，AB AC =，AB A B '⊥，10AB =，12BC =，5A B '=，连接A C '．①A BC '的面积为______；②点D 是BC 边的高上的一点，当AD =______时，A D DB '+有最小值______． 7．如图：两个菱形ABCD 与菱形BEFG 的边AB BE ，在同一条直线上，边长分别为a 和b ，点C 在BG 上，点M 为CG 的中点．（1）观察猜想：如图①，线段BM 与线段AE 的数量关系是______________．（2）拓展探究：如图②，120ABC ∠=︒，将图①中的菱形BEFG 绕点B 顺时针旋转至图②位置，其他条件不变，连接BM ，①猜想线段BM 与线段AE 的数量关系，并说明理由． ②求出线段BM 与AE 所成的最小夹角．（3）解决问题：如图③，若将题目中的菱形改为矩形，且3BC EFAB BE=段BM 与线段AE 的数量关系．8．将抛物线y ＝ax 2的图像（如图1）绕原点顺时针旋转90度后可得新的抛物线图像（如图2），记为C ：y 2＝1ax ．（概念与理解）将抛物线y 1=4x 2和y 2=x 2按上述方法操作后可得新的抛物线图像，记为：C 1：_____________；C 2：____________．（猜想与证明）在平面直角坐标系中，点M （x ，0）在x 轴正半轴上，过点M 作平行于y 轴的直线，分别交抛物线C 1于点A 、B ，交抛物线C 2于点C 、D ，如图3所示．（1）填空：当x =1时，AB CD =______；当x =2时，ABCD=_______；（2）猜想：对任意x （x ＞0）上述结论是否仍然成立？若成立，请证明你的猜想；若不成立，请说明理由．（探究与应用）①利用上面的结论，可得△AOB 与△COD 面积比为；②若△AOB 和△COD 中有一个是直角三角形时，求△COD 与△AOB 面积之差；（联想与拓展）若抛物线C 3：y 2＝mx 、C 4：y 2＝nx （0<m<n ），M （k ，0）在x 轴正半轴上，如图所示，过点M 作平行于y 轴的直线，分别交抛物线C 3于点A 、B ，交抛物线C 4于点C 、D ．过点A 作x 轴的平行线交抛物线C 4于点E ，过点D 作x 轴的平行线交抛物线C 3于点F ．对于x 轴上任取一点P ，均有△PAE 与△PDF 面积的比值1:3，请直接写出m 和n 之间满足的等量关系是______． 9．（1）（问题发现）如图①，正方形AEFG 的两边分别在正方形ABCD 的边AB 和AD 上，连接CF ．填空：①线段CF 与DG 的数量关系为______； ②直线CF 与DG 所夹锐角的度数为_______．（2）（拓展探究）如图②，将正方形AEFG 绕点A 逆时针旋转，在旋转的过程中，（1）中的结论是否仍然成立，请利用图②进行说明．（3）（解决问题）如图③，在正方形ADBC 中，AD AC =，点M 为直线BC 上异于B ，C 的一点，以AM 为边作正方形AMEF ，点N 为正方形AMEF 的中心，连接CN ，若4,2AC CM ==，直接写出CN 的长．10．综合与实践动手实践：一次数学兴趣活动，张老师将等腰Rt AEF 的直角顶点A 与正方形ABCD 的顶点A 重合（AE AD >），按如图（1）所示重叠在一起，使点E 在CD 边上，连接BF ．则可证：ADE ≌△△______，______三点共线；发现问题：（1）如图（2），已知正方形ABCD ，E 为DC 边上一动点，DC nDE =，AF AE ⊥交CB 的延长线于F ，连结EF 交AB 于点G ．若2n =，则AG BG =______，AGE BGFS S =△△______；尝试探究：（2）如图（3），在（1）的条件下若3n =，求证：5AG GB =；拓展延伸：（3）如图（4），在（1）的条件下，当n =______时，AG 为GB 的6倍（直接写结果，不要求证明）．11．（1）尝试探究：如图①，在ABC ∆中，90ACB ∠=︒，30A ∠=︒，点E 、F 分别是边BC 、AC 上的点，且EF ∥AB ．①AF BE的值为_________；②直线AF 与直线BE 的位置关系为__________；（2）类比延伸：如图②，若将图①中的CEF ∆绕点C 顺时针旋转，连接AF ，BE ，则在旋转的过程中，请判断AF BE的值及直线AF 与直线BE 的位置关系，并说明理由；（3）拓展运用：若3BC =，2CE =，在旋转过程中，当,,B E F 三点在同一直线上时，请直接写出此时线段AF 的长．12．综合与实践操作探究（1）如图1，将矩形ABCD 折叠，使点A 与点C 重合，折痕为EF ，AC 与EF 交于点G ．请回答下列问题：①与AEG △全等的三角形为______，与AEG △相似的三角形为______．并证明你的结论：（相似比不为1，只填一个即可）：②若连接AF 、CE ，请判断四边形AFCE 的形状：______．并证明你的结论；拓展延伸（2）如图2，矩形ABCD 中，2AB =，4BC =，点M 、N 分別在AB 、DC 边上，且AM NC =，将矩形折叠，使点M 与点N 重合，折痕为EF ，MN 与EF 交于点G ，连接ME ．①设22m AM AE =+，22n ED DN =+，则m 与n 的数量关系为______； ②设AE a =，AM b =，请用含a 的式子表示b ：______； ③ME 的最小值为______．13．（问题情境）（1）如图1，四边形ABCD 是正方形，点E 是AD 边上的一个动点，以CE 为边在CE 的右侧作正方形CEFG ，连接DG 、BE ，则DG 与BE 的数量关系是；（类比探究）（2）如图2，四边形ABCD 是矩形，AB=2，BC=4，点E 是AD 边上的一个动点，以CE 为边在CE 的右侧作矩形CEFG ，且CG ：CE=1：2，连接DG 、BE ．判断线段DG 与BE 有怎样的数量关系和位置关系，并说明理由；（拓展提升）（3）如图3，在（2）的条件下，连接BG ，则2BG+BE 的最小值为．14．问题发现：（1）如图1，在Rt △ABC 中，∠BAC=30°，∠ABC ＝90°，将线段AC 绕点A 逆时针旋转，旋转角α=2∠BAC ， ∠BCD 的度数是；线段BD ，AC 之间的数量关系是．类比探究：（2）在Rt △ABC 中，∠BAC=45°，∠ABC ＝90°，将线段AC 绕点A 逆时针旋转，旋转角α=2∠BAC ，请问（1）中的结论还成立吗？；拓展延伸：（3）如图3，在Rt △ABC 中，AB ＝2，AC ＝4，∠BDC ＝90°，若点P 满足PB ＝PC ，∠BPC ＝90°，请直接写出线段AP 的长度．15．某数学学习小组在复习线段垂直平分线性质时，提出了以下几个问题，请你帮他们解决： [数学理解](1)点P 是线段AB 垂直平分线上的一点，则:PA PB 的值为； [拓展延伸](2)在平面直角坐标系xOy 中，点()6,0C ，点Q 在x 轴上，且:O 1:2QO C =，则点Q 的坐标为．(3)经小组探究发现，如图，延长线段DE 到点F ，使13EF DE =，以点F 为因心，2EF 长为半径作园，则对于OF 上任一点T ，都有2TD TE =，请你证明这个结论：[问题解决](4)如图，某人乘船以25千米/时的速度沿一笔直的河l 从码头G 到码头M ，再立即坐车沿一笔直公路以75千米/时的速度回到住处H ，已知乘船和坐车所用的时间相等请在河l 边上确定码头M 的位置．(请画出示意图并简要说明理由)16．（性质探究）如图，在矩形ABCD中，对角线AC，BD相交于点O，AE平分∠BAC，交BC于点E．作DF⊥AE于点H，分别交AB，AC于点F，G．（1）判断△AFG的形状并说明理由．（2）求证：BF=2OG．（迁移应用）（3）记△DGO的面积为S1，△DBF的面积为S2，当121 3S S 时，求ADAB的值．（拓展延伸）（4）若DF交射线AB于点F，（性质探究）中的其余条件不变，连结EF，当△BEF的面积为矩形ABCD面积的110时，请直接写出tan∠BAE的值．17．综合与实践问题情境：△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D，点E是射线AD上的一个动点(不与点A重合)将线段AE绕点A顺时针旋转90°得到线段AF，连接CF交线段AB于点G，交AD于点H、连接EG．特例分析:(1)如图1，当点E 与点D 重合时，“智敏”小组提出如下问题，请你解答： ①求证：AF=CD ；②用等式表示线段CG 与EG 之间的数量关系为：_______；拓展探究:(2)如图2，当点E 在线段AD 的延长线上，且DE=AD 时，“博睿”小组发现CF=2EG ．请你证明；(3)如图3，当点E 在线段AD 的延长线上，且AE=AB 时，EGCF的值为_______；推广应用:(4)当点E 在射线AD 上运动时，AE m AD n =，则EGCF的值为______用含m.n 的式子表示)． 18．如图1所示，边长为4的正方形ABCD 与边长为()14a a <<的正方形CFEG 的顶点C 重合，点E 在对角线AC 上．（问题发现）如图1所示，AE 与BF 的数量关系为________；（类比探究）如图2所示，将正方形CFEG 绕点C 旋转，旋转角为()030αα<<︒，请问此时上述结论是否还成立？如成立写出推理过程，如不成立，说明理由；（拓展延伸）若点F 为BC 的中点，且在正方形CFEG 的旋转过程中，有点A 、F 、G 在一条直线上，直接写出此时线段AG 的长度为________19．（教材呈现）下图是华师版八年级下册教材第89页的部分内容．例6：如图18.2.12，G 、H 是平行四边形ABCD 对角线AC 上的两点，且AG ＝CH ，E 、 F 分别是边AB 和CD 的中点．图18.2.12求证：四边形EHFG 是平行四边形．证明：连结EF 交AC 于点O ．∵四边形ABCD 是平行四边形，∴AB ＝CD ，AB ∥CD ．又∵E 、F 分别是AB 、CD 的中点，∴AE ＝CF ．又∵AB ∥CD ，∴∠EAO ＝∠FCO ．又∵∠AOE ＝∠COF ,∴AOE COF ≅．请补全上述问题的证明过程．．．．．．．．．．．．．（探究）如图①，在ABC 中，E ，O 分别是边AB 、AC 的中点，D 、F 分别是线段AO 、CO 的中点，连结DE 、EF ，将DEF 绕点O 旋转180°得到DGF △，若四边形DEFG 的面积为8，则ABC 的面积为．（拓展）如图②，GH 是正方形ABCD 对角线AC 上的两点，且AG ＝CH ，GH ＝AB ，E 、F 分别是AB 和CD 的中点．若正方形ABCD 的面积为16，则四边形EHFG 的面积为．20．在ABC 与CDE △中，90ACB DCE ∠=∠=︒且CAB CDE θ∠=∠=︒，点D 始终在线段AB 上（不与A 、B 重合）．（1）问题发现：如图1，若45θ=度，DBE ∠的度数______，BE AD =______；（2）类比探究：如图2，若30θ=度，试求DBE ∠的度数和BE AD的值；（3）拓展应用：在（2）的条件下，M 为DE 的中点，当3AC =BM 的最小值为多少？直接写出答案．【参考答案】***试卷处理标记，请不要删除一、中考几何压轴题1．（1）30°，6，4，7；（2）AG ；（3）等边，；（4）3，，6【分析】（1）由点H 为AC 中点，可得AC=2AH ，由折叠，点B 与点H 重合，与四边形ABCD 为矩形，可证GH 为AC 的垂直平分线，可解析：（1）30°，6，4，7；（2）AG ；（3）等边，2+x x ；（4）6 【分析】（1）由点H 为AC 中点，可得AC =2AH ，由折叠，点B 与点H 重合，与四边形ABCD 为矩形，可证GH 为AC 的垂直平分线，可得AG =CG ，∠GCH =∠GAH ，可求∠ACB =30°，利用三角函数可求BC =6，AG =4，BF =FC =3，可求4==41AG GF ，与△ABG 相似的三角形由7个；（2）由EF 为折痕，可证△AEH ∽△AHG ，可得2=AH AE AG ⋅即可；（3）由四边形ABCD 为矩形，点H 为对角线AC 中点，可证△ABH 为等边三角形，再证△ABM ∽△MHN ，可得x HN =即可；（4）连结BD ，当点Q′在BD 上时，Q′D 最小，先求BC =Q′D 最小=BD BQ '-BQ′⊥BD 时，△BDQ′面积最大∠CBQ′=60°，S △BDQ′最大=162BD Q B '⋅=．【详解】解（1）∵点H 为AC 中点，∴AC =2AH ，∵折叠，点B 与点H 重合，∴AB =AH BG =HG ，∠BAG =∠HAG =12BAC ∠，∠B =∠AHG ， ∵四边形ABCD 为矩形，∴∠B =90°，∴∠AHG =∠B =90°，∴GH 为AC 的垂直平分线，∴AG =CG ，∠GCH =∠GAH ，∴∠BAG =∠HAG =∠GCH ，∵∠BAH +∠BCH =180°-∠B =90°，∴3∠ACB =90°∴∠ACB =30°，∴∠BAG =∠HAG =∠GCH =30°，∴tan30°=AB BC =AB∴BC =3=6AB ， ∵tan ∠BAG =tan30°=33BG AB =， ∴BG =33=23=233AB ⨯， ∴AG =2BG =4，BF =FC =116322BC =⨯=， ∴GF =BF -BG =3-2=1，∴4==41AG GF ， ∵AD ∥BC ，∴∠DAC =∠ACB =30°，∴∠BAG =∠HAG =∠GHF =∠HCF =∠GCH =∠EAH =∠DAC =∠BCA =30°，∵∠B =∠AHG =∠HFG =∠HFC =∠AEH =∠D =∠GHC =∠CBA =90°，∴△ABG ∽△AHG ∽△HFG ∽△CFH ∽△CHG ∽△AEH ∽△ADC ∽△CBA ，∴与△ABG 相似的三角形由7个，故答案为：30°；6；4；7；（2）∵EF 为折痕，∴EH ⊥AD ，∵∠EAH =∠HAG =30°∠AHG =∠AEH =90°∴△AEH ∽△AHG ，∴AE AH AH AG=， ∴2=AH AE AG ⋅故答案为AG ；（3）∵四边形ABCD 为矩形，点H 为对角线AC 中点，∴AH =CH =BH ，由图2知AB =AH ，∴AH =BH =AB ，∴△ABH 为等边三角形，∴∠ABH =∠AHB =60°，∵∠AMN ＝∠ABH ；∴∠AMN ＝∠ABH =∠AHB =60°，∴∠BAM +∠AMB =180°-∠ABH =120°，∠AMB +∠NMH =180°-∠AMN =120°，即∠BAM +∠AMB =∠AMB +∠NMH ，∴∠BAM =∠NMH ，∴△ABM ∽△MHN ， ∴AB BM MH HN =， ∵AB =23，MH =23x -， ∴2323x HN x=-， ∴()2233==623x xHN x x --，故答案为：等边；236x x -，（4）连结BD ，当点Q′在BD 上时，Q′D 最小∵AB =23，AD =BC =6，∴BC =()2222+=23+6=43AD AB ∵AQ′=Q′H=132AB =∴Q′D 最小=43333BD BQ '-=-=当BQ′⊥BD 时，△BDQ′面积最大∵tan ∠DAC =23363CD BC ==， ∴∠DAC =30°，∴∠CBQ′=90°-∠DBC =90°-30°=60°∴tan ∠CBQ'=3S △BDQ′最大=11433622BD Q B '⋅=⨯=；故答案为3336．【点睛】本题考查折叠性质，矩形性质，线段垂直平分线，锐角三角函数，三角形相似判定与性质，等边三角形判定与性质，两图形的最小距离，最大面积，掌握查折叠性质，矩形性质，线段垂直平分线，锐角三角函数，三角形相似判定与性质，等边三角形判定与性质，两图形的最小距离，最大面积求法是解题关键．2．（1）；；；（2）；（3）．【分析】（1）本问体现“特殊”的情形，是一个确定的数值．如答图1，过E 点作平行线，构造相似三角形，利用相似三角形和中位线的性质，分别将各相关线段均统一用EH 来表示，最解析：（1）3AB EH =；2CG EH =；32；（2）2m ；（3）ab ．【分析】（1）本问体现“特殊”的情形，3AF EF =是一个确定的数值．如答图1，过E 点作平行线，构造相似三角形，利用相似三角形和中位线的性质，分别将各相关线段均统一用EH 来表示，最后求得比值；（2）本问体现“一般”的情形，AF m EF =不再是一个确定的数值，但（1）问中的解题方法依然适用，如答图2所示．（3）本问体现“类比”与“转化”的情形，将（1）（2）问中的解题方法推广转化到梯形中，如答图3所示．【详解】解：（1）依题意，过点E 作//EH AB 交BG 于点H ，如图1所示．则有ABF EHF ， ∴3AB AF EH EF==， ∴3AB EH =． ∵ABCD ，//EH AB ， ∴//EH CD ，又∵E 为BC 中点，∴EH 为BCG 的中位线，∴2CG EH =．3322CD AB EH CG CG EH ===．故答案为：3AB EH =；2CG EH =；32．（2）如图2所示，作//EH AB 交BG 于点H ，则EFH AFB △△． ∴AB AF m EH EF==， ∴AB mEH =．∵AB CD =，∴CD mEH =．∵////EH AB CD ，∴BEH BCG △△． ∴2CG BC EH BE ==， ∴2CG EH =． ∴22CD mEH m CG EH ==．故答案为：2m ．（3）如图3所示，过点E 作//EH AB 交BD 的延长线于点H ，则有////EH AB CD ． ∵//EH CD ，∴BCD BEH △△，∴=CD BC b EH BE=， ∴CD bEH =．又AB a CD =， ∴AB aCD abEH ==．∵//EH AB ，∴ABF EHF ， ∴==AF AB abEH ab EF EH EH=．故答案为：ab ．【点睛】本题的设计独特：由平行四边形中的一个特殊的例子出发（第1问），推广到平行四边形中的一般情形（第2问），最后再通过类比、转化到梯形中去（第3问）．各种图形虽然形式不一，但运用的解题思想与解题方法却是一以贯之：即通过构造相似三角形，得到线段之间的比例关系，这个比例关系均统一用同一条线段来表达，这样就可以方便地求出线段的比值．本题体现了初中数学的类比、转化、从特殊到一般等思想方法，有利于学生触类旁通、举一反三．3．（1）①；②；③等边，证明见解析；（2）①3；②．【分析】（1）①利用圆的基本性质，即可求解；②根据折叠的性质，利用勾股定理，即可求解；③利用勾股定理，求得B′D=，即可求解；（2）①由题解析：（1）①BE；②333；③等边，证明见解析；（2）①3；13【分析】（1）①利用圆的基本性质，即可求解；②根据折叠的性质，利用勾股定理，即可求解；③利用勾股定理，求得B′D=BC CD=，即可求解；（2）①由题意知点B'在以点E为圆心，半径长为2的圆上，△ABB'的面积要最大，只要以AB为底的高最长即可，此时当B'E⊥AB时，△ABB'的面积最大；②当E、B′、C三点共线时，B'C+ EB'取得最小值，即B'C+2PQ取得最小值，且最小值为EC 的长，利用勾股定理即可求解．【详解】解：（1）根据折叠的性质知：BE=B′E，BC=B′C=3，MA=MB=NC=ND=32，∠B=∠EB′C=90︒，①点B′在以点E为圆心，BE的长为半径的圆上；②B′M=MN- B′N=22MN B C NC'-=223332⎛⎫-- ⎪⎝⎭ =3332-； ③B′D=222222B N ND B C NC ND BC BC CD +=-+===''，∴△DB'C 为等边三角形；故答案为：①BE ，②3332-，③等边；（2）①∵AB=3=3AE ，∴AE=1，BE=2，故点B'在以点E 为圆心，半径长为2的圆上，∴△ABB'的面积要最大，只要以AB 为底的高最长即可，∴当B'E ⊥AB 时，△ABB'的面积最大，如图：△ABB'的面积最大值1132322AB E B =⨯=⨯⨯='； ②∵∠AQP=∠AB'E ，∴PQ ∥B'E ，∵P 为AE 的中点，∴Q 为AB'的中点， ∴PQ 为△AEB'的中位线，∴PQ=12EB'，即12EB'=2PQ ， ∴B'C+2PQ= B'C+ EB'，当E 、B′、C 三点共线时，B'C+ EB'取得最小值，即B'C+2PQ 取得最小值，且最小值为EC 的长，∴=∴B'C+2PQ故答案为：①3；【点睛】本题考查了圆的性质，矩形的性质、图形的折叠、等腰三角形的性质等，有一定的综合性，难度适中，其中（2）①当B'E ⊥AB 时，△ABB'的面积最大；②当E 、B′、C 三点共线时，B'C+2PQ 取得最小值，是解本题的关键．4．（1）；（2），理由见解析；（3）CE 的长为2或4，理由见解析．【分析】（1）证明，得出CE ＝BD ，，即可得出结论；（2）证明，得出，，即可得出结论；（3）先判断出，再求出：①当点E 在点D解析：（1）60BD CE ，＝；（2）45CEB BD ∠︒＝，，理由见解析；（3）CE 的长为【分析】（1）证明ACE ABD ≌，得出CE ＝BD ，AEC ADB ∠=∠，即可得出结论；（2）证明ACE ABD ∽，得出AEC ADB ∠=∠，BD =，即可得出结论；（3）先判断出BD =，再求出AB =：①当点E 在点D 上方时，先判断出四边形APDE 是矩形，求出AP ＝DP ＝AE ＝2，再根据勾股定理求出，BP ＝6，得出BD ＝4；②当点E 在点D 下方时，同①的方法得，AP ＝DP ＝AE ＝1，BP ＝6，进而得出BD ＝BP +DP ＝8，即可得出结论．【详解】解：（1）ABC 为等腰三角形，60AC BC ACB ∠︒＝，＝，∴ABC 是等边三角形，同理可得ADE 是等边三角形6018012060BAD DAC DAC CAE BAD CAEAD AE AB ACEAC DAB ACE ABD SAS BD CEAEC ADB ADE AEC AED CEBCEB ∠+∠=∠+∠=︒∴∠=∠=⎧⎪=⎨⎪∠∠⎩∴∴=∠=∠=︒-∠=︒∠=∠+∠∴∠=︒＝≌（）故答案为：60CEB BD CE ∠=︒=；．（2）45CEB BD ∠︒＝，，理由如下：在等腰三角形ABC 中，AC ＝BC ，90ACB ∠︒＝，45AB CAB ∴∠︒，＝，同理，45AD ADE DAE ∠∠︒，＝＝， ∴AE AC AD AB =，DAE CAB ∠∠＝，EAC DAB ∴∠∠＝，ACE ABD ∴∽ ，∴BD AD CE AE = ∴AEC ADB BD ∠∠＝，，点B 、D 、E 在同一条直线上:180135ADB ADE ∴∠︒-∠︒＝＝135AEC ∴∠︒＝45CEB AEC AED ∴∠∠-∠︒＝＝；（3）由（2）知，ACE ABD ∽，BD ∴，在Rt ABC 中，AC ＝AB ∴＝，①当点E 在点D 上方时，如图③，过点A 作AP BD ⊥交BD 的延长线于P ， DE BD ⊥，PDE AED APD ∴∠∠∠＝＝，∴四边形APDE 是矩形，AE DE ＝，∴矩形APDE 是正方形，2AP DP AE ∴＝＝＝，在Rt APB △中，根据勾股定理得，6BP ， 4BD BP AP ∴-＝＝，CE BD ∴＝ ②当点E 在点D 下方时，如图④同①的方法得，AP ＝DP ＝AE ＝2，BP ＝6， ∴BD ＝BP +DP ＝8，CE ∴＝综上CE 的长为．【点睛】本题是几何变换的综合题，主要考查了旋转的性质，全等三角形的判定和定理，相似三角形的判定和性质，勾股定理，等边三角形的性质，判断出三角形ACE 和三角形ABD 相似是关键．5．(1)DH=HF ；(2)DH=HF 仍然成立，理由见解析；(3)或．【分析】(1)证明，得，则，则证，得出即可；(2)证，则，由矩形的性质得出，证，即可得出；(3)根据矩形的性质和已知得，则解析：(1)DH =HF ；(2)DH =HF 仍然成立，理由见解析；55517．【分析】(1)证明()GCF BEC AAS ∆∆≌，得BC GF =，则CD GF =，则证()HCD HGF ASA ∆∆≌，得出DH HF =即可；(2)证FCG CEB ∆∆∽，则GF FC n BC CE ==，由矩形的性质得出CD n BC=，证()HCD HGF ASA ∆∆≌，即可得出DH HF =； (3)根据矩形的性质和已知得43AB n AD ==，则43CE CF =，分两种情况，根据勾股定理和平行线的性质进行解答即可．【详解】解：(1)DH HF =，理由如下：∵四边形ABCD 是矩形，AB AD =，∴四边形ABCD 是正方形，∴BC CD =，90ABC EBC BCD ∠=∠=∠=︒，∵FG BC ⊥，90ECF ∠=︒，∴//CD GF ，90CGF ECF EBC ∠=∠=∠=︒，∴+90GCF BCE ∠∠=︒，∵+90BCE BEC ∠∠=︒，∴=GCF BEC ∠∠，在GCF ∆和BEC ∆中，==GCF BEC CGF EBC CF CE ∠∠⎧⎪∠∠⎨⎪=⎩， ∴()GCF BEC AAS ∆∆≌，∴BC GF =，∴CD GF =，//CD GF∴=HDC HFG ∠∠，=HCD HGF ∠∠，在HCD ∆和HGF ∆中，==HDC HFG CD GFHCD HGF ∠∠⎧⎪=⎨⎪∠∠⎩， ∴()HCD HGF ASA ∆∆≌，∴DH HF =，故答案为DH HF =，(2) DH HF =仍然成立，理由如下：∵四边形ABCD 是矩形，FG BC ⊥，90ECF ∠=︒，∴90CGF ECF EBC ∠=∠=∠=︒∴+90FCG BCE ∠∠=︒，∵+90BCE CEB ∠∠=︒，∴=FCG CEB ∠∠，∴FCG CEB ∆∆， ∴GF FC n BC CE==， ∴四边形ABCD 是矩形，AB nAD =， ∴CD n BC=， ∴GF CD BC BC =， ∴GF CD =，∵四边形ABCD 是矩形，∴CD BC ⊥，∵FG BC ⊥，∴//CD FG ，∴HDC HFG ∠=∠，HCD HGF ∠=∠，在HCD ∆和HGF ∆中，==HDC HFG CD GFHCD HGF ∠∠⎧⎪=⎨⎪∠∠⎩， ∴()HCD HGF ASA ∆∆≌，∴DH HF =，(3)如图所示，延长FC 交AD 于R ，∵四边形ABCD 是矩形，∴4AB CD ==，3AD BC ==，90RDC ∠=︒，//RD CH ，∵AB nAD =，CF nCE =， ∴43AB n AD ==， ∴43CF CE =，分两种情况：①当13AR AD =时， ∵3AD =，∴1AR =，2DR =，在Rt CDR ∆中，由勾股定理得：22222425CR DR CD ++=∵//RD CH ，DH HF =， ∴25RC CF == ∴3325542CE =⨯ 由勾股定理得：EF ()222235255522CF CE ⎛⎫+=+ ⎪⎝⎭ ②当13DR AD =时，同理可得：1DR =， 4DC =，17CF RC ==∴ 317CE = 由勾股定理得：∴ 2222317517(17)()44EF CF CE =+=+=，综上所说，若射线FC 过AD 的三等分点，3AD =，4AB =，则线段EF 的长为552或5174．【点睛】本题主要考查了正方形的判定与性质、矩形的性质、平行线的性质、全等三角形的判定与性质、勾股定理、相似三角形的判定与性质等知识，熟练掌握平行线的性质和相似三角形的判定与性质是解题的关键． 6．（1）①见解析；②；③；（2）①；②；（3）①24；②，【分析】（1）①由旋转的性质，，然后利用AAS ，即可得到结论成立；②求出，即可求出面积；③求出，即可求出答案；（2）①过点作交延长线解析：（1）①见解析；②12；③12；（2）①22a ；②2222a ab b ++；（3）①24；②558，265 【分析】（1）①由旋转的性质，AB A B '=，然后利用AAS ，即可得到结论成立；②求出1AC A H '==，即可求出面积；③求出2CH =，即可求出答案；（2）①过点A '作A H CB '⊥交CB 延长线于点H ，由（1）可知ABC A BH '≌△△，求出A H '的长度，即可求出答案；②求出CH 的长度，利用勾股定理，即可求出答案；（3）①过点A 作AE ⊥BC ，过点A '作A H CB '⊥交CB 延长线于点H ，然后证明ABE BA H '△△，求出A H '，CH 的长度，即可求出面积；②点C 是点B 关于AE 的对称点，则BD =CD ，设A C '与AE 的交点为点D ，使得A D DB '+有最小值为，为线段A C '的长度，然后利用勾股定理求出A C '，再利用平行线分线段成比例求出DE 的长度即可．【详解】解：（1）如图：①由旋转的性质，则AB A B '=，90ABA '∠=︒，∵90ACB A HB '∠=∠=︒，∴90ABC A ABC A BH '∠+∠=∠+∠=︒，∴A A BH '∠=∠，∴ABC A BH '≌△△（AAS ）；②∵1AC BC ==，∴1A H BH '==，∴A BC '的面积为111122⨯⨯=；故答案为：12．③在直角三角形A CH '中，∵112CH =+=，1A H '=， ∴1tan 2A H A CB CH ''∠==；故答案为：12．（2）①过点A '作A H CB '⊥交CB 延长线于点H ，由（1）可知，ABC BA H '≌△△， ∴A H BC a '==，BH AC b ==，∴A BC '的面积为：211222a BC A H a a '•=••= 故答案为：22a ； ②∵CH BC BH ab =+=+，由勾股定理，则222222()22A C CH A H a b a a ab b ''+++=++2222a ab b ++（3）①过点A 作AE ⊥BC ，过点A '作A H CB '⊥交CB 延长线于点H ，如图与（1）同理，可证BAE A BH '∠=∠，∵90AEB A HB '∠=∠=︒，∴ABE BA H '△△， ∴AB BE AE BA A H BH ==''， ∵AB AC =，10AB =，12BC =，5A B '=， ∴1112622BE BC ==⨯=； ∴221068AE =-=， ∴10685A H BH=='， ∴3A H '=，4BH =，∴12416CH BC BH =+=+=，∴A BC '的面积为：11•1231822CB A H =⨯⨯'=；故答案为：18．②由题意，点C 是点B 关于AE 的对称点，则BD =CD ，设A C '与AE 的交点为点D ，则此时A D DB '+有最小值，如图：此时A D DB '+的最小值为线段A C '的长度，∵22316265A C '+∵AE ∥A H '，∴CE DE CH A H ='，即6163DE =， ∴98DE =， ∴955888AD =-=，∴当558AD =时，A D DB '+．故答案为：558 【点睛】本题考查了相似三角形的判定和性质，全等三角形的判定和性质，旋转的性质，勾股定理，最短路径问题等知识，解题的关键是熟练掌握所学的知识，正确的作出辅助线，从而进行解题．7．（1）；（2）①，理由见解析；②线段与所成的最小夹角为60；（3）．【分析】（1）根据已知求得AE =a+b ，CG =b-a ，根据线段中点的定义求得CM =，通过计算即可求解；（2）①延长BM解析：（1）12BM AE =；（2）①12BM AE =，理由见解析；②线段BM 与AE 所成的最小夹角为60︒；（3）BM AE =．【分析】（1）根据已知求得AE =a +b ，CG =b -a ，根据线段中点的定义求得CM =1122b a -，通过计算即可求解；（2）①延长BM 到H ，使MH =BM ，连接GH ，利用SAS 证明△CMB ≅△GMH 和△ABE ≅△HGB ，即可得到结论；②延长MB 交AE 于N ，证明∠GBE =∠BNE =60︒，即可求解；（3）延长BM 到H ，使MH =BM ，连接GH ，同理证明△CMB ≅△GMH ，再证明△ABE ~△HGB ，即可求解．【详解】（1）12BM AE =，理由如下： ∵菱形ABCD 与菱形 BEFG 的边长分别为a 和b ，∴AE =AB +BE =a +b ，CG =BG -BC =b -a ，∵点M 为CG 的中点，∴CM =12CG =1122b a -， ∴()1111122222BM BC CM a b a a b a b =+=+-=+=+， ∴12BM AE =；（2）①12BM AE =，理由如下：延长BM 到H ，使MH =BM ，连接GH ，如图：∵点M为CG的中点，∴CM=MG，∵∠CMB=∠GMH，∴△CMB≅△GMH (SAS)，∴∠BCM=∠HGM，BC=HG，∴BC∥GH，∴∠BGH+∠CBG=180︒，∵菱形ABCD与菱形BEFG中，∠ABC=120°，∠GBE=60°，∴∠ABE+∠CBG=180︒，∴∠ABE=∠BGH，∵AB=BC=HG，BE=BG，∴△ABE≅△HGB (SAS)，∴AE= HB12AE=；②线段BM与AE所成的最小夹角为60︒，理由如下：∵△ABE≅△HGB，∴∠AEB=∠BHG，延长MB交AE于N，则∠MBE=∠BNE+∠AEB，即∠HBG+∠GBE=∠BNE+∠AEB，∴∠GBE=∠BNE=60︒，∴线段BM与AE所成的最小夹角为60︒；（3）3BM AE，理由如下：延长BM到H，使MH=BM，连接GH，如图：同理可得：△CMB ≅△GMH (SAS )，∴∠BCM =∠HGM ，BC =HG ，∴BC ∥GH ，∴∠BGH +∠CBG =180︒，∵矩形ABCD 与矩形 BEFG 中，∠ABC =∠GBE =90°，∴∠ABE +∠CBG =180︒，∴∠ABE =∠BGH ， ∵3BC EF AB BE == ∴3HG B AB G BE== ∴△ABE ~△HGB ， ∴3BH BG AE BE== ∵12BM BH =， ∴3BM AE =．【点睛】本题考查四边形综合题、全等三角形的判定和性质、相似三角形的判定和性质、菱形的性质、矩形的性质等知识，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．8．【概念与理解】，；【猜想与证明】（1），；（2）成立，证明见解析；【探究与应用】①；②△COD 与△AOB 面积之差为或；【联想与拓展】n3=9m3．【分析】【概念与理解】：根据题意信息即可得出答案解析：【概念与理解】214y x =，2y x =；【猜想与证明】（1）12，12；（2）成立，证明见解析；【探究与应用】①12；②△COD 与△AOB 面积之差为116或12；【联想与拓展】n 3=9m 3．【分析】【概念与理解】：根据题意信息即可得出答案；【猜想与证明】：（1）当x =1时，求出A ，B ，C ，D 的坐标进而得出AB ,CD 即可得出答案；当x =2时，求出A ，B ，C ，D 的坐标进而得出AB ,CD 即可得出答案；（2）任意x （x ＞0），求出A ，B ，C ，D 的坐标进而得出AB ,CD 即可得出答案；【探究与应用】：①根据已知条件表示出△AOB 与△COD 面积即可得出答案；②设M （x ，0）（x ＞0），根据已知条件可得出2COD AOB x S S -=△AOB 是直角三角形时解得14x =，当△COD 是直角三角形时，解得1x =，把x 代入即可；【联想与拓展】：根据题意求出AEDF 的坐标然后表示出面积再利用△PAE 与△PDF 面积的比值1:3，即可得出关系式；【详解】【概念与理解】∵y 1=4x 2∴由题意可得C 1：214y x = ∵y 2=x 2∴由题意可得C 2：2y x =故答案为：C 1：214y x =，C 2：2y x =；【猜想与证明】（1）当x =1时，∵点A 、B 在抛物线C 1上∴令x =1，则112y =± ∴A 1(1,)2，B 1(1,)2- ∴AB =1∵点C 、D 在抛物线C 2上∴令x =1，则21y ==±∴C (1,1)，D (1,1)- ∴CD =2∴AB CD =12当x =2时，∵点A、B在抛物线C1上∴令x=2，则1y==∴A，B(2,∴AB∵点C、D在抛物线C2上∴令x=2，则2y=∴C，D(2,∴CD=∴ABCD1 2 =（2）对任意x（x＞0）上述结论仍然成立理由如下：对任意x（x＞0），1y=∴A(x，B(,x∴AB对任意x（x＞0），2y=∴C(x，D(,x∴CD=∴ABCD1 2 =【探究与应用】①连接OA，OB，OC，OD12AOB S AB OM =12COD S CD OM = ∴12AOB COD S ABS CD ==故答案为：12②设M （x ，0）（x ＞0），∵M （x ，0） ∴114xy x =∴AB x∵M （x ，0），∴2y x =±∴CD =x∵122AOB xxS AB OM ==。

上海上海师范大学第三附属实验学校九年级化学下册第十二单元《化学与生活》复习题

一、选择题1．下列说法合理的有①人体中钠元素是一种常量元素② pH＜7的降雨称为酸雨③面粉厂、纺织厂都要粘贴标有“严禁烟火”的字样或图标④向一定量的Fe(NO3)2和AgNO3的混合溶液中加入一定量的Mg和Zn，充分反应后过滤，得到滤渣和滤液，向滤液中加入铁粉，溶液颜色无变化，向滤渣中加入稀盐酸有气泡产生，则滤渣的成分组成可能有3种情况⑤某碳酸钠溶液中可能含有另一种溶质，取一定量该溶液逐滴滴加稀盐酸，观察到一段时间后产生气泡，则该碳酸钠溶液中一定含有氢氧化钠A．2个B．3个C．4个D．5个B解析：B① 常量元素包括：C H O N P K S K Ca Na Cl Mg，故人体中钠元素是一种常量元素，正确；② pH＜5.6的降雨称为酸雨，错误；③ 面粉厂、纺织厂的空气中含有大量的可燃性颗粒，混有一定量的空气，遇到明火，容易发生爆炸，故都要粘贴标有“严禁烟火”的字样或图标，正确；④ 由于金属活动性：Mg＞Zn＞Fe＞Ag，故向一定量的Fe（NO3）2和AgNO3的混合溶液中加入一定量的Mg和Zn，镁先与硝酸银反应生成硝酸镁和银，待硝酸银完全反应后，镁再与硝酸亚铁反应生成硝酸镁和铁，如果镁含量不足，待镁完全反应后，锌先与硝酸银反应生成硝酸锌和银，待硝酸银完全反应后，锌再与硝酸亚铁反应生成硝酸锌和铁，充分反应后过滤，得到滤渣和滤液，向滤液中加入铁粉，溶液颜色无变化，说明硝酸银已经完全反应，向滤渣中加入稀盐酸有气泡产生，则滤渣中一定含铁，银，可能含镁、锌，滤渣的成分组成可能有铁、银、锌；铁、银；铁、银、锌、镁共3种情况，正确；⑤某碳酸钠溶液中可能含有另一种溶质，取一定量该溶液逐滴滴加稀盐酸，观察到一段时间后产生气泡，一段时间后，才产生气体，说明该物质能与稀盐酸反应，且不产生气泡，但是不一定是氢氧化钠，可能是氢氧化钾等，错误。

故合理的有3个。

故选B。

2．元素符号和化学式是国际通用的化学符号,下列叙述正确的是（）A．一氧化碳中含有C元素B．双氧水（H2O2）、水中都含有1个氢分子C．人体中含量最高的元素是CaD．铁丝在氧气中燃烧产物的化学式是O4Fe3A解析：AA、一氧化碳的化学式为CO，从化学式中可知一氧化碳中含有C元素，选项A正确；B、化学式中元素符号右下角的数字表示该物质的一个分子中含有的该元素的原子个数，根据双氧水的化学式：H2O2，水的化学式：H2O，这两种物质的一个分子中都含有两个氢原子，不含氢分子，选项B错误；C、人体中含量最多的元素是氧元素而不是Ca，选项C错误；D、书写氧化物的化学式时，一般氧的元素符号写在右边，另一种元素的符号写在左边，因此铁丝在氧气中燃烧产物的化学式是Fe3O4而不是O4Fe3，选项D错误。

上海上海师范大学康城实验学校中考二轮复习化学推断题专题训练

上海上海师范大学康城实验学校中考二轮复习化学推断题专题训练一、中考化学推断题1．A、B、C、D是初中化学中常见的物质。

A是一种常见的盐,其水溶液显碱性,A和B反应生成的一种物质C在大气中含量的增加会导致温室效应。

D是一种常见的碱,B和D反应生成的一种物质是我们厨房常用的调味品。

(1)写出B的化学式_________；(2)A和B的反应属于________反应(填基本反应类型)；(3)B和D反应的实质是_________。

【答案】 HCl 复分解 H+和OH-结合生成水【解析】本题是推断题，解题时往往需要从题目中挖出一些明显或隐含的条件，抓住突破口（突破口往往是现象特征、反应特征等），获得结论，最后把结论代入原题中验证。

A 是一种常见的盐，其水溶液显碱性，A可能是碳酸钠，A 和B反应生成的一种物质C在大气中含量的增加会导致温室效应，B是酸，生成的C是二氧化碳，D是一种常见的碱，B和D反应生成的一种物质是我们厨房常用的调味品，厨房常用的调味品是氯化钠，B是盐酸，D是氢氧化钠，代入题文，推断合理；（1）B是盐酸，化学式是：HCl；（2）A和B的反应是碳酸钠与盐酸反应生成氯化钠、水、二氧化碳，该反应是由两种化合物互相交换成分，生成另外两种化合物的反应，属于复分解反应；（3）B是盐酸，D是氢氧化钠，氢氧化钠与盐酸反应生成水和氯化钠，反应的实质是H+和OH-结合生成水。

2．A～G是初中化学常见的物质，A和C在常温下均为无色液体，且组成元素相同；D是天然气的主要成分；E与F含有相同的两种元素，且F是有毒气体。

它们的转化关系如图，根据图示回答下列问题。

（1）A的化学式为_____；（2）反应②的化学方程式为_____；（3）反应③属于基本反应类型中的_____反应；（4）列举一项固态E在实际生活中的用途_____。

H O CH4+2O2 CO2+2H2O 化合人工降雨【答案】22【解析】【分析】A G～是初中化学常见的物质，A和C在常温下均为无色液体，且组成元素相同，由A与C的关系可知，A是过氧化氢，C是水，B是氧气；D是天然气的主要成分，D是甲烷；E 与F含有相同的两种元素，且F是有毒气体，F是一氧化碳，E是二氧化碳，G是碳酸。

上海上海师范大学第三附属实验学校九年级化学上册第三单元《物质构成的奥秘》复习题

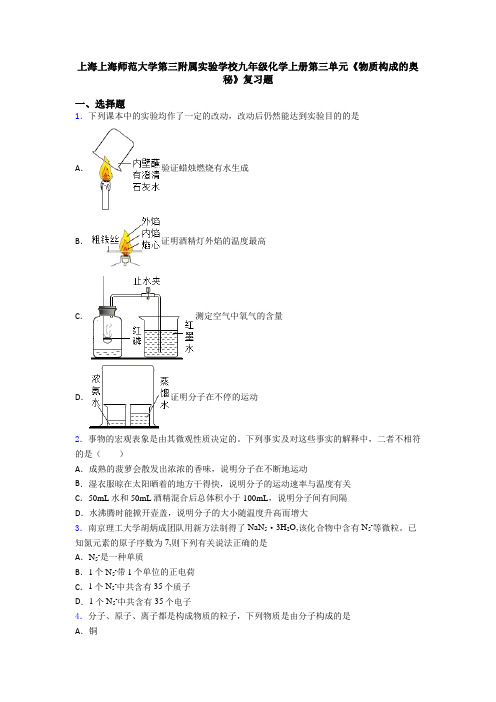
上海上海师范大学第三附属实验学校九年级化学上册第三单元《物质构成的奥秘》复习题一、选择题1．下列课本中的实验均作了一定的改动，改动后仍然能达到实验目的的是A．验证蜡烛燃烧有水生成B．证明酒精灯外焰的温度最高C．测定空气中氧气的含量D．证明分子在不停的运动2．事物的宏观表象是由其微观性质决定的。

下列事实及对这些事实的解释中，二者不相符的是（）A．成熟的菠萝会散发出浓浓的香味，说明分子在不断地运动B．湿衣服晾在太阳晒着的地方干得快，说明分子的运动速率与温度有关C．50mL水和50mL酒精混合后总体积小于100mL，说明分子间有间隔D．水沸腾时能掀开壶盖，说明分子的大小随温度升高而增大3．南京理工大学胡炳成团队用新方法制得了NaN5·3H2O,该化合物中含有N5-等微粒。

已知氮元素的原子序数为7,则下列有关说法正确的是A．N5-是一种单质B．1个N5-带1个单位的正电荷C．1个N5-中共含有35个质子D．1个N5-中共含有35个电子4．分子、原子、离子都是构成物质的粒子，下列物质是由分子构成的是A．铜B．金刚石C．氨D．硫酸铜5．分别分解高锰酸钾、氯酸钾、过氧化氢三种物质,都可以制得氧气。

这说明三种物质的组成中都含有A．氧气B．氧分子C．氧化物D．氧元素6．分子与原子的本质区别是（）A．分子比原子大B．化学变化中分子可分而原子不可分C．分子能构成物质而原子不能D．化学变化中原子可分而分子不可分7．下列叙述正确的是A．氯化氢是由一个氢原子和一个氯原子构成的B．酒精 + 氧气−−→水+ 二氧化碳，属于分解反应C．与元素的化学性质关系最密切的是原子的核外电子数D．催化剂在反应前后质量和化学性质都不发生变化8．如图为某粒子的结构示意图，下列说法正确的是（）A．一个该粒子有12个质子B．该粒子第一层的2个电子能量最高C．该粒子已达到相对稳定结构D．该元素的化学性质和氦元素相似9．下列对宏观事实的微观解释错误的是A．夏天钢轨之间的缝隙变小——原子受热时体积变大B．闻到远处饭菜的香味——分子在不断地运动C．氢气和液氢都可做燃料——相同物质的分子，其化学性质相同D．水的三态变化一一分子的间隔发生了改变10．下列图示能达到实验目的的是A．检查装置气密性B．测定空气中氧气的含量C．氧气的验满D．探究分子在不断运动二、填空题11．空气质量意味着生活质量。

上海上海师范大学第三附属实验学校九年级化学上册第七单元《燃料及其利用》复习题

上海上海师范大学第三附属实验学校九年级化学上册第七单元《燃料及其利用》复习题一、选择题1．下列说法中，合理的个数是（）①西藏是旅游胜地，平原地区的旅客到达西藏时，常出现“高原反应”，是因为空气中氧气的体积分数小于 21%②电解水时向水中加入少量氢氧化钠，反应速率加快，说明氢氧化钠作为该反应的催化剂③同种元素的原子，质子数一定相同，质子数相同的粒子一定属于同种元素④分子可分为原子，原子不可分⑤可燃性气体与空气混合点燃可能发生爆炸，所以点燃氢气前要检验其纯度⑥在化合物中，金属元素通常显正价，非金属元素通常显负价；同种元素在同种化合物中只能显一种化合价⑦金属元素的原子最外层电子数一般少于 4 个，最外层电子数少于 4 个的原子一定是金属元素的原子A．1 个B．2 个C．3 个D．4 个2．推理是学习化学的一种重要方法.以下推理正确的是（）A．单质都是由一种元素组成的，所以由一种元素组成的物质一定是单质B．点燃氢气前需要验纯，所以点燃可燃性气体前都需要验纯C．分子和原子都是不带电的微粒，所以不带电的微粒都是分子和原子D．稀有气体元素原子的最外层电子数一般为8，所以最外层电子数为8的粒子一定是稀有气体元素的原子3．据报道，天津8.12 爆炸事故现场有剧毒物氰化钠库存，则氰化钠的外包装应有下列哪种标志A．B．C．D．4．下列过程是通过物理变化获得能量的是（）A．鞭炮爆炸发声B．电水壶通电发热C．煤燃烧火力发电D．汽油燃烧驱动汽车5．鉴别一氧化碳、氧气、二氧化碳、甲烷四种气体，现有一盒火柴，还必须用到的是A．装有蒸馏水的烧杯B．装有紫色石蕊的水C．冷而干燥的烧杯D．内壁有石灰水的烧杯6．下列措施——理由之间，其因果关系不正确的是（）A．白磷要保存在水中——防止自燃B．加油站严禁烟火——防止爆炸C．真空包装食品——防止缓慢氧化D．用扇子扇煤炉火——降低可燃物的着火点7．目前，科学家提出了一种最经济最理想的获得氢能源的循环体系（如图）。

上海师范大学综合实验复习

最新上师大有机化学实验考试答案汇总

上海上海师范大学第三附属实验学校初二生物实验探究综合题测试卷附答案

上海上海师范大学康城实验学校初二生物实验探究综合题专题

上海上海师范大学第三附属实验学校初二生物期末实验探究综合题汇编

上海上海师范大学第三附属实验学校初二生物实验探究综合题专题

上海上海师范大学第三附属实验学校中考二轮复习化学推断题80题专题训练(含答案)

上海上海师范大学康城实验学校功和机械能中考综合专项复习训练

上海上海师范大学康城实验学校初二生物实验探究综合题测试卷附答案

上海上海师范大学第三附属实验学校初二生物期末复习综合题汇编

上海上海师范大学康城实验学校浮力中考综合专项复习训练

上海上海师范大学康城实验学校运动和力中考综合专项复习训练

上海上海师范大学康城实验学校初二生物实验探究综合题专题

上海上海师范大学康城实验学校中考数学期末几何综合压轴题模拟汇编

上海上海师范大学第三附属实验学校九年级化学下册第十二单元《化学与生活》复习题

上海上海师范大学康城实验学校中考二轮复习化学推断题专题训练

上海上海师范大学第三附属实验学校九年级化学上册第三单元《物质构成的奥秘》复习题

上海上海师范大学第三附属实验学校九年级化学上册第七单元《燃料及其利用》复习题