偏最小二乘法代码
偏最小二乘方法

偏最小二乘方法(PLS-Partial Least Squares))是近年来发展 起来的一种新的多元统计分析法, 现已成功地应用于分析化学, 如紫外光谱、气相色谱和电分析化学等等。该种方法,在化合 物结构-活性/性质相关性研究中是一种非常有用的手段。如美国 Tripos公司用于化合物三维构效关系研究的CoMFA (Comparative Molecular Field Analysis)方法, 其中,数据统计处 理部分主要是PLS。在PLS方法中用的是替潜变量,其数学基础 是主成分分析。替潜变量的个数一般少于原自变量的个数,所 以PLS特别适用于自变量的个数多于试样个数的情况。在此种 情况下,亦可运用主成分回归方法,但不能够运用一般的多元 回归分析,因为一般多元回归分析要求试样的个数必须多于自 变量的个数。
设矩阵X的阶为I*J,若T的阶与J相等,则主成分回归与 多元线性回归所得结果相同,并不能显示出主成分回归的优 越之处。选取的主成分数一般应该比J 小,而删去那些不重 要的主成分,因为这些主成分所包含的信息主要是噪声,由 此所得的回归方程稳定性较好。 另外,由X所定义的空间可以进一步来说明主成分回归 与多元线性回归的区别。多元线性回归应用了由X的列所定 义的全部空间,而主成分回归所占用的是一子空间。当X的J 列中,有一列可为其它J —1列的线性组合时,则X可用J -1列 的矩阵T来描述,而并不丢失信息。新的矩阵T定义了X的一 个子空间。
2 7 5 4 3 3 Y 9 12 3 6 8 2
运用式(6.3)则可得B矩阵:
0.48 0.71 0.55 B 0.42 0.41 0.24 0.08 0.28 0.05
所用数学模型有效性的量度可用Err:
分块核偏最小二乘法

文章编 号 :2 82 2 ( 0 7 0 -660 0 5 -74 2 0 ) 50 2 .5
分 块 核 偏 最 小 二 乘 法
自裔 峰 , 肖 建 , 于
摘
龙
( 西南交通大 学电气工程学 院 ,四川 成都 6 0 3 ) 1 1 要: 针对核偏 最A -  ̄- -乘法 ( P S 随核 函数矩 阵维 数膨 胀 L) 提 J 乘  ̄
中图分类号 : 2 03 文 献标识码 : A
Bl c W ie Ke ne r i lLe s- ua e e ho o k- s r lPa ta a tSq r sM t d
B Ir  ̄ , X A i , Ⅲ l g A in fg IO Ja n o n
( c ol f l tcl n . otw s J oogU iesy hnd 10 1 hn ) Sho e r a E g ,Suh et i tn nvrt,C e gu6 0 3 ,C ia oE ci a i
在使用普通 的统计 回归方法建模过程 中, 模型变量多重相关性严重 , 或者系统 中样本容量少于变量数 量, 都会给建模过程带来 困难. 偏最小二乘法 (a i atqae, L ) pra l s s r P S 是源于化工领域过程控制 的建模 t le - u s
( oen ) 回归(erso ) 判别 (i r i tn 和分类(l si tn 技术 , m dl g 、 i r ei 、 g sn d cm n i ) s i ao c sfa o ) ai i c 借助提取 主元 的思路 , 有效 地提取对系统解释性最强 的综合信息 , 从而实现对高维数据空 间的降维处理 , 较好地克服 变量 多重相关 性 , 到广 泛 的研究 J为 了提 高线 性 P S在 非线 性 的情 况下 提取 主元 的能 力 , 线 性 化 的 P S及核 偏 最 得 . L 非 L 小二乘 法 ( e e pra l s su e, P S 成 为 目前研 究 的热 点 -]K L kr l a i at qa s K L ) n t le - r 5. P S将论 域 内的输 入 数 据通 过 非 线性函数映射到特征空间 , 然后在特征空间中建立线性或者非线性的 P S回归模型 , 以更加有效地在 L 可 非线性情况下抽取主元. P S K L 算法一般 由普通 P S算法通过核方法改进而成 7 文献 [ ] 出的 K L L .. J 2提 PS 算法 由文献 [ ] 1 中的简化 P S L 算法变化而来. 与之前的方法 比较 , 该方法不需要通过迭代计算而是直接抽 取主元 , 并且根据统计学 习理论提出了实际风险的性能指标 , 不但有助于核 函数 的参数选 择 , 而且还实现 了结 构 风险最 小 化原 则 .
正交偏最小二乘法

正交偏最小二乘法正交偏最小二乘法(Orthogonal Partial Least Squares, OPLS)是一种常用的多元统计分析方法,广泛应用于数据建模、特征选择、变量筛选等领域。
本文将介绍正交偏最小二乘法的原理、应用和优势,以及其在实际问题中的应用案例。
正交偏最小二乘法是基于偏最小二乘法(Partial Least Squares, PLS)的改进方法。
偏最小二乘法是一种回归分析的方法,通过将自变量和因变量进行线性组合,建立回归模型。
但是在应用过程中,偏最小二乘法可能存在多个潜在的自变量对应一个因变量的情况,这就导致了模型的不稳定性和可解释性差。
正交偏最小二乘法通过引入正交化的步骤,解决了偏最小二乘法的不足。
其基本思想是,在建立回归模型的过程中,除了考虑与因变量相关的部分(预测分量),还引入与因变量不相关的部分(正交分量),从而提高模型的解释能力和稳定性。
通过正交化的操作,正交偏最小二乘法能够将数据进行更好的降维,去除噪声和冗余信息,提取出对预测结果有用的信息。
正交偏最小二乘法在实际问题中具有广泛的应用。
例如,在药物研发领域,研究人员可以利用正交偏最小二乘法对大量的分子结构和活性数据进行建模和预测,快速筛选出具有潜在药效的化合物。
在工业过程控制中,正交偏最小二乘法可以用于建立传感器数据与产品质量之间的关系,实现对产品质量的在线监测和控制。
此外,正交偏最小二乘法还可以应用于生物信息学、化学分析、图像处理等领域。
与其他方法相比,正交偏最小二乘法具有以下优势。
首先,正交偏最小二乘法能够解决多重共线性问题,降低模型的复杂度,提高模型的解释能力。
其次,正交偏最小二乘法能够处理高维数据,提取出对预测结果有用的特征,减少冗余信息的干扰。
此外,正交偏最小二乘法还可以进行特征选择,帮助研究人员挖掘出对预测结果具有重要影响的变量。
下面以一个实际应用案例来说明正交偏最小二乘法的应用。
假设我们需要建立一个模型来预测商品的销售量。
偏最小二乘法(PLS)简介

偏最小二乘法(PLS)简介偏最小二乘法(PLS )简介偏最小二乘法(PLS )简介简介偏最小二乘法是一种新型的多元统计数据分析方法,它于1983年由伍德(S.Wold)和阿巴诺(C.Albano)等人首次提出。
近几十年来,它在理论、方法和应用方面都得到了迅速的发展。
偏最小二乘法长期以来,模型式的方法和认识性的方法之间的界限分得十分清楚。
而偏最小二乘法则把它们有机的结合起来了,在一个算法下,可以同时实现回归建模(多元线性回归)、数据结构简化(主成分分析)以及两组变量之间的相关性分析(典型相关分析)。
这是多元统计数据分析中的一个飞跃。
偏最小二乘法在统计应用中的重要性体现在以下几个方面:偏最小二乘法是一种多因变量对多自变量的回归建模方法。
偏最小二乘法可以较好的解决许多以往用普通多元回归无法解决的问题。
偏最小二乘法之所以被称为第二代回归方法,还由于它可以实现多种数据分析方法的综合应用。
主成分回归的主要目的是要提取隐藏在矩阵X 中的相关信息,然后用于预测变量Y 的值。
这种做法可以保证让我们只使用那些独立变量,噪音将被消除,从而达到改善预测模型质量的目的。
但是,主成分回归仍然有一定的缺陷,当一些有用变量的相关性很小时,我们在选取主成分时就很容易把它们漏掉,使得最终的预测模型可靠性下降,如果我们对每一个成分进行挑选,那样又太困难了。
偏最小二乘回归可以解决这个问题。
它采用对变量X 和Y 都进行分解的方法,从变量X 和Y 中同时提取成分(通常称为因子),再将因子按照它们之间的相关性从大到小排列。
现在,我们要建立一个模型,我们只要决定选择几个因子参与建模就可以了基本概念偏最小二乘回归是对多元线性回归模型的一种扩展,在其最简单的形式中,只用一个线性模型来描述独立变量Y 与预测变量组X 之间的关系:偏最小二乘法(PLS) 简介Y = b0 + b1X1 + b2X2 + ... + bpXp在方程中,b0是截距,bi的值是数据点1到p的回归系数。
偏最小二乘回归方法(PLS)

偏最小二乘回归方法1 偏最小二乘回归方法(PLS)背景介绍在经济管理、教育学、农业、社会科学、工程技术、医学和生物学中,多元线性回归分析是一种普遍应用的统计分析与预测技术。
多元线性回归中,一般采用最小二乘方法(Ordinary Least Squares :OLS)估计回归系数,以使残差平方和达到最小,但当自变量之间存在多重相关性时,最小二乘估计方法往往失效。
而这种变量之间多重相关性问题在多元线性回归分析中危害非常严重,但又普遍存在。
为消除这种影响,常采用主成分分析(principal Components Analysis :PCA)的方法,但采用主成分分析提取的主成分,虽然能较好地概括自变量系统中的信息,却带进了许多无用的噪声,从而对因变量缺乏解释能力。
最小偏二乘回归方法(Partial Least Squares Regression:PLS)就是应这种实际需要而产生和发展的一种有广泛适用性的多元统计分析方法。
它于1983年由S.Wold和C.Albano等人首次提出并成功地应用在化学领域。
近十年来,偏最小二乘回归方法在理论、方法和应用方面都得到了迅速的发展,己经广泛地应用在许多领域,如生物信息学、机器学习和文本分类等领域。
偏最小二乘回归方法主要的研究焦点是多因变量对多自变量的回归建模,它与普通多元回归方法在思路上的主要区别是它在回归建模过程中采用了信息综合与筛选技术。
它不再是直接考虑因变量集合与自变量集合的回归建模,而是在变量系统中提取若干对系统具有最佳解释能力的新综合变量(又称成分),然后对它们进行回归建模。
偏最小二乘回归可以将建模类型的预测分析方法与非模型式的数据内涵分析方法有机地结合起来,可以同时实现回归建模、数据结构简化(主成分分析)以及两组变量间的相关性分析(典型性关分析),即集多元线性回归分析、典型相关分析和主成分分析的基本功能为一体。
下面将简单地叙述偏最小二乘回归的基本原理。
最小二乘法 c语言

最小二乘法 c语言最小二乘法是一种常用的数学方法,用于通过已知数据点拟合出一条最佳拟合曲线。
在本文中,我们将讨论如何使用C语言实现最小二乘法。
我们需要明确最小二乘法的基本原理。
最小二乘法的目标是找到一条曲线,使得该曲线上的点到已知数据点的距离之和最小。
具体地,我们假设已知数据点的集合为{(x1, y1), (x2, y2), ..., (xn, yn)},我们需要找到一条曲线y = f(x),使得f(xi)与yi的差的平方和最小。
那么,如何在C语言中实现最小二乘法呢?首先,我们需要定义一个函数来计算拟合曲线上的点f(xi)。
在这个函数中,我们可以使用多项式的形式来表示拟合曲线。
例如,我们可以选择使用一次多项式y = ax + b来拟合数据。
然后,我们可以使用最小二乘法的公式来计算出最优的a和b的值。
接下来,我们需要编写一个函数来计算拟合曲线上每个点f(xi)与已知数据点yi的差的平方和。
通过遍历已知数据点的集合,并计算每个点的差的平方,最后将所有差的平方求和,即可得到拟合曲线的误差。
然后,我们可以使用梯度下降法来最小化误差函数。
梯度下降法是一种优化算法,通过不断迭代来找到误差函数的最小值。
在每次迭代中,我们通过计算误差函数对参数a和b的偏导数,来更新a和b的值。
通过多次迭代,最终可以找到最优的a和b的值,从而得到最佳拟合曲线。
我们可以编写一个主函数来调用以上的函数,并将最终的拟合曲线绘制出来。
在这个主函数中,我们可以读取已知数据点的集合,并调用最小二乘法函数来计算拟合曲线的参数。
然后,我们可以使用绘图库来绘制已知数据点和拟合曲线,并将结果输出到屏幕上。
通过以上的步骤,我们就可以使用C语言实现最小二乘法了。
当然,在实际应用中,我们可能会遇到更复杂的数据和更高阶的多项式拟合。
但是基本的原理和方法是相同的,只是需要做一些适当的调整。
总结一下,最小二乘法是一种常用的数学方法,用于通过已知数据点拟合出一条最佳拟合曲线。
最小二乘法C语言编程

#include <hidef.h> /* common defines and macros */
#include "derivative.h" /* derivative-specific definitions */
x2=x*x*x*x;
x3+=x2;
}
*(pp++)=x3;
}
}
pp=*(b+1);
p=a9;
ppp=a8;
x3=0;
for(i=0;i<10;i++) {
x=*(p++);
x2=*(ppp++);
x3+=x*x2;
}
*pp=x3;
pp=*(b+2);
p=a9;
ppp=a8;
x3=0;
for(i=0;i<10;i++) {
*(p++)=(x1*x5-x2*x4);
p=*(b1+0);
pp=*(b4+0);
for (i=0;i<3;i++) {
for(j=0;j<3;j++){
x1=*(p++);
x=x1*c;
*(pp++)=x;
}
}
//////////////////////////求两矩阵的商//////////////////////////////////////
matlab 最小二乘法

在Matlab中,可以使用“\”或者pinv函数进行最小二乘法的求解。
下面给出一个使用“\”运算符进行最小二乘法的例子:
假设有一个线性方程组Ax = b,其中$A$ 是m×n的矩阵,x是n×1的未知向量,b 是m×1的已知向量,且m>n。
最小二乘法的目标是找到一个x,使得Ax≈b,即∥Ax−b∥最小。
使用Matlab中的“\”运算符求解最小二乘法的代码如下:
% 生成数据
x = [0:0.1:1]';
y = 2*x + randn(size(x))*0.1;
% 构造矩阵A和向量b
A = [x, ones(size(x))];
b = y;
% 求解最小二乘问题
x_ls = A \ b;
% 输出结果
fprintf('斜率:%f,截距:%f\n', x_ls(1), x_ls(2));
在这个例子中,我们生成了一个带噪声的数据集,然后构造了矩阵A 和向量b,其中A的第一列为x,第二列为常数项1。
最后,使用“\”运算符求解最小二乘问题,并输出斜率和截距的值。
需要注意的是,在实际应用中,最小二乘法的精度和稳定性可能会受到多种因素的影响,如数据噪声、矩阵奇异性等等。
因此,在使用最小二乘法时需要对数据和算法进行充分的分析和优化,以保证结果的准确性和可靠性。
各种最小二乘法汇总(算例及MATLAB程序)

图 1 一般最小二乘参数过渡过程 .....................................................4 图 2 一般最小二乘方差变化过程 ....................................................5 图 3 遗忘因子法参数过渡过程 ........................................................7 图 4 遗忘因子法方差变化过程 ........................................................8 图 5 限定记忆法参数过渡过程 ......................................................10 图 6 限定记忆法方差变化过程 ......................................................10 图 7 偏差补偿最小二乘参数过渡过程 ..........................................12 图 8 偏差补偿最小二乘方差变化过程 ..........................................12 图 9 增广最小二乘辨识模型 ..........................................................13 图 10 增广最小二乘参数过渡过程 ................................................14 图 11 广义最小二乘参数过渡过程 ................................................16 图 12 广义最小二乘方差变化过程 ................................................16 图 13 辅助变量法参数过渡过程 ....................................................18 图 14 辅助变量法方差变化过程 ....................................................18 图 15 二步法参数过渡过程 ............................................................20 图 16 二步法方差变化过程 ............................................................20
偏最小二乘算法

偏最小二乘算法偏最小二乘算法(Partial Least Squares Regression,简称PLS 回归)是一种常用的统计分析方法,用于处理多变量数据集中的回归问题。
它是在被解释变量与解释变量之间存在复杂关系的情况下,通过降维和建立线性模型来解决回归问题的一种有效手段。
下面将详细介绍偏最小二乘算法的原理和应用。
一、原理介绍偏最小二乘算法的核心思想是通过寻找解释变量与被解释变量之间最大的协方差方向,将原始变量空间转换为新的综合变量空间,从而实现降维的目的。
具体步骤如下:1. 数据预处理:对原始数据进行中心化和标准化处理,以消除量纲和变量之间的差异。
2. 求解权重矩阵:根据解释变量和被解释变量的协方差矩阵,通过迭代的方式求解权重矩阵,使得新的综合变量能够最大程度地反映原始变量之间的关系。
3. 计算综合变量:将原始变量与权重矩阵相乘,得到新的综合变量。
4. 建立回归模型:将新的综合变量作为自变量,被解释变量作为因变量,通过最小二乘法建立回归模型。
5. 预测与评估:利用建立的回归模型对新的解释变量进行预测,并通过评估指标(如均方根误差、决定系数等)评估模型的拟合效果。
二、应用案例偏最小二乘算法在多个领域都有广泛的应用,下面以药物研究为例,介绍其应用案例。
假设我们需要研究一个药物的活性与其分子结构之间的关系。
我们可以收集一系列药物分子的结构信息作为解释变量,收集相应的生物活性数据作为被解释变量。
然后利用偏最小二乘算法,建立药物活性与分子结构之间的回归模型。
通过偏最小二乘算法,我们可以找到最相关的分子结构特征,并将其转化为新的综合变量。
然后,利用建立的模型,我们可以预测新的药物的活性,从而指导药物设计和优化。
三、优缺点分析偏最小二乘算法具有以下优点:1. 能够处理多变量之间的高度相关性,避免了多重共线性问题。
2. 通过降维,提高了模型的解释能力和预测精度。
3. 对于样本量较小的情况,仍能有效建立回归模型。
机器学习:最小二乘法实际应用的一个完整例子
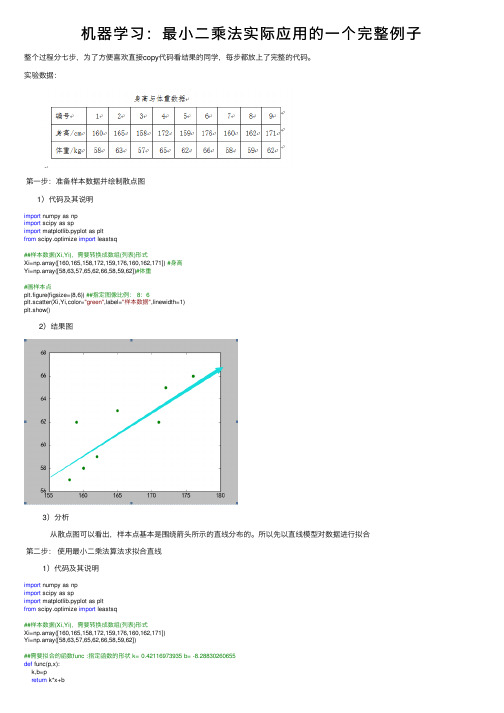
机器学习:最⼩⼆乘法实际应⽤的⼀个完整例⼦整个过程分七步,为了⽅便喜欢直接copy代码看结果的同学,每步都放上了完整的代码。
实验数据:第⼀步:准备样本数据并绘制散点图1)代码及其说明import numpy as npimport scipy as spimport matplotlib.pyplot as pltfrom scipy.optimize import leastsq##样本数据(Xi,Yi),需要转换成数组(列表)形式Xi=np.array([160,165,158,172,159,176,160,162,171]) #⾝⾼Yi=np.array([58,63,57,65,62,66,58,59,62])#体重#画样本点plt.figure(figsize=(8,6)) ##指定图像⽐例: 8:6plt.scatter(Xi,Yi,color="green",label="样本数据",linewidth=1)plt.show()2)结果图3)分析从散点图可以看出,样本点基本是围绕箭头所⽰的直线分布的。
所以先以直线模型对数据进⾏拟合第⼆步:使⽤最⼩⼆乘法算法求拟合直线1)代码及其说明import numpy as npimport scipy as spimport matplotlib.pyplot as pltfrom scipy.optimize import leastsq##样本数据(Xi,Yi),需要转换成数组(列表)形式Xi=np.array([160,165,158,172,159,176,160,162,171])Yi=np.array([58,63,57,65,62,66,58,59,62])##需要拟合的函数func :指定函数的形状 k= 0.42116973935 b= -8.28830260655def func(p,x):k,b=preturn k*x+b##偏差函数:x,y都是列表:这⾥的x,y更上⾯的Xi,Yi中是⼀⼀对应的def error(p,x,y):return func(p,x)-y#k,b的初始值,可以任意设定,经过⼏次试验,发现p0的值会影响cost的值:Para[1]p0=[1,20]#把error函数中除了p0以外的参数打包到args中(使⽤要求)Para=leastsq(error,p0,args=(Xi,Yi))#读取结果k,b=Para[0]print("k=",k,"b=",b)#画样本点plt.figure(figsize=(8,6)) ##指定图像⽐例: 8:6plt.scatter(Xi,Yi,color="green",label="样本数据",linewidth=2)#画拟合直线x=np.linspace(150,190,100) ##在150-190直接画100个连续点y=k*x+b ##函数式plt.plot(x,y,color="red",label="拟合直线",linewidth=2)plt.legend() #绘制图例plt.show()2)结果图3)分析从图上看,拟合效果还是不错的。
偏最小二乘法 python

偏最小二乘法 python偏最小二乘法(Partial Least Squares,PLS)是一种常用的多元线性回归分析方法,主要用于解决自变量之间存在多重共线性的问题。
在 Python 中,可以使用第三方库`scikit-learn`和`numpy`搭配来实现偏最小二乘法。
首先请确保你已经安装了`scikit-learn`库与`numpy`库,如果还没有安装,可以使用以下命令来进行安装:```pip install scikit-learn numpy```以下是一个使用 Python 实现偏最小二乘法的示例代码:```pythonimport numpy as npfrom sklearn.cross_decomposition import PLSRegressiondef pls_example():# 准备示例数据X = np.array([[2], [3], [4], [5], [6]])y = np.array([1, 2, 3, 4, 5])# 创建偏最小二乘回归模型pls = PLSRegression(n_components=1)# 在训练数据上拟合模型pls.fit(X, y)# 新的自变量new_X = np.array([[7]])# 使用模型进行预测predicted_y = pls.predict(new_X)return predicted_yprint(pls_example())```在这个示例中,我们首先导入所需的库。
然后,我们准备了一个示例数据集,其中`X`是自变量矩阵,`y`是因变量向量。
接下来,我们创建了一个`PLSRegression`对象,通过设置`n_components`参数来指定保留的主成分数量。
然后,我们使用`fit`方法拟合模型到训练数据上。
最后,我们可以使用`predict`方法对新的自变量`new_X`进行预测,并输出预测结果。
请注意,这只是一个简单的示例,实际应用中可能需要更复杂的数据预处理、调参和评估步骤。
两阶段最小二乘法python

两阶段最小二乘法python
两阶段最小二乘法(Two-Stage Least Squares,2SLS)是一种用于处理内生性问题的工具变量方法。
在Python中,可以使用`statsmodels`库中的`OLS`类和`IV2SLS`类来实现两阶段最小二乘法。
下面是一个使用两阶段最小二乘法的示例代码:
```python
import numpy as np
import as sm
生成样本数据
(0)
n_samples = 100
X = (n_samples)
Z = (n_samples)
Y = X + (X) + (n_samples)
第一阶段回归
X = _constant(X) 添加常数项
Z = _constant(Z) 添加常数项
XZ = _constant(_stack((X, Z))) 添加常数项和交互项
model1 = (Y, XZ)
results1 = ()
X_hat = (XZ) 预测内生解释变量的值
第二阶段回归
endog = Y - (X) + (Z) 计算外生解释变量的值
exog = X_hat 使用预测值作为工具变量
model2 = (endog, exog)
results2 = ()
print(())
```
在上面的代码中,我们首先生成了样本数据,其中`X`是内生解释变量,`Z`是工具变量,`Y`是因变量。
然后,我们使用第一阶段回归来预测内生解释变量的值,并将预测值作为工具变量。
在第二阶段回归中,我们使用外生解释变量的值作为因变量,并将工具变量的预测值作为解释变量。
最后,我们打印出第二阶段回归的结果。
偏最小二乘路径模型 python

偏最小二乘路径模型python偏最小二乘路径模型(Partial Least Squares Path Model,PLS Path Model)是一种用于研究变量间因果关系的统计模型。
在Python中,可以使用plspm库来实现偏最小二乘路径模型。
首先,需要安装plspm库。
可以使用pip命令进行安装:shell复制代码pip install plspm接下来,导入所需的库和数据集:python复制代码import pandas as pdimport numpy as npfrom plspm import PLS假设我们有一个名为data的数据集,其中包含多个变量。
首先,我们需要对数据进行标准化处理:python复制代码data = pd.DataFrame(data)data = (data - data.mean()) / data.std()接下来,使用PLS方法对数据进行拟合:python复制代码pls = PLS(data, n_comp=3) # n_comp表示主成分的数量pls.fit()在拟合完成后,我们可以使用pls.path()方法绘制路径图:python复制代码pls.path()这将绘制出变量之间的因果关系路径图。
如果需要更详细的解释和可视化,可以使用pls.explanation()方法:python复制代码pls.explanation(kind='path') # 绘制路径解释图pls.explanation(kind='corr') # 绘制相关系数解释图pls.explanation(kind='causal') # 绘制因果关系解释图此外,还可以使用pls.predict()方法对新的数据进行预测:python复制代码new_data = pd.DataFrame(np.random.rand(100, len(data.columns))) # 生成新的数据集predictions = pls.predict(new_data) # 对新数据进行预测这就是使用Python中的plspm库实现偏最小二乘路径模型的基本步骤。
偏最小二乘回归方法(PLS)

偏最小二乘回归方法1 偏最小二乘回归方法(PLS)背景介绍在经济管理、教育学、农业、社会科学、工程技术、医学和生物学中,多元线性回归分析是一种普遍应用的统计分析与预测技术。
多元线性回归中,一般采用最小二乘方法(Ordinary Least Squares :OLS)估计回归系数,以使残差平方和达到最小,但当自变量之间存在多重相关性时,最小二乘估计方法往往失效。
而这种变量之间多重相关性问题在多元线性回归分析中危害非常严重,但又普遍存在。
为消除这种影响,常采用主成分分析(principal Components Analysis :PCA)的方法,但采用主成分分析提取的主成分,虽然能较好地概括自变量系统中的信息,却带进了许多无用的噪声,从而对因变量缺乏解释能力。
最小偏二乘回归方法(Partial Least Squares Regression :PLS)就是应这种实际需要而产生和发展的一种有广泛适用性的多元统计分析方法。
它于1983年由S.Wold 和 C.Albano 等人首次提出并成功地应用在化学领域。
近十年来,偏最小二乘回归方法在理论、方法和应用方面都得到了迅速的发展,己经广泛地应用在许多领域,如生物信息学、机器学习和文本分类等领域。
偏最小二乘回归方法主要的研究焦点是多因变量对多自变量的回归建模,它与普通多元回归方法在思路上的主要区别是它在回归建模过程中采用了信息综合与筛选技术。
它不再是直接考虑因变量集合与自变量集合的回归建模,而是在变量系统中提取若干对系统具有最佳解释能力的新综合变量(又称成分),然后对它们进行回归建模。
偏最小二乘回归可以将建模类型的预测分析方法与非模型式的数据内涵分析方法有机地结合起来,可以同时实现回归建模、数据结构简化(主成分分析)以及两组变量间的相关性分析(典型性关分析),即集多元线性回归分析、典型相关分析和主成分分析的基本功能为一体。
下面将简单地叙述偏最小二乘回归的基本原理。
最小二乘法LSQ(least square)_计算公式

( 3)
∑ τ = 108, ∑ τ ∑ lg y = 10.3, ∑ τ
i 1 8= i i =1 8 i =1 i i =1
8
8
2
i
= 1836, lg yi = 122.
i
将他们代入方程组( ) 将他们代入方程组(3)得
1836a + 108b = 122, 108a + 8b = 10.3. a = 0.4343m = −0.045, 解这方程组, 解这方程组,得 b = lg k = 1.8964.
71728140273036由2式算出的函数值与实测270268265263261257253243算得2712526821265182621425911256072530325000偏差01250021001800860189009300030200偏差的平方和我们把称为均方误差它的大小在一定程度上反映了用经验公式来近似表达原来函数关系的近似程度的好坏
达到最小. 求 f ( t ),使 M = ∑ [ yi − (at i + b )] 达到最小.
2 i =1
n
注意:计算机与数据拟合. 注意:计算机与数据拟合.
(参看高等数学实验课讲义 郭锡伯 徐安农编) 徐安农编)
最小二乘法
一、经验公式
在工程问题中,常常需要根据两个变量的 在工程问题中, 几组实验数值——实验数据,来找出这两个变 实验数据, 几组实验数值 实验数据 量的函数关系的近似表达式. 量的函数关系的近似表达式.通常把这样得到 的函数的近似表达式叫做经验公式 经验公式. 的函数的近似表达式叫做经验公式. 问题:如何得到经验公式,常用的方法是什么? 问题:如何得到经验公式,常用的方法是什么?
最小二乘法曲线拟合_原理及matlab实现

曲线拟合(curve-fitting ):工程实践中,用测量到的一些离散的数据},...2,1,0),,{(m i y x i i =求一个近似的函数)(x ϕ来拟合这组数据,要求所得的拟合曲线能最好的反映数据的基本趋势(即使)(x ϕ最好地逼近()x f ,而不必满足插值原则。
因此没必要取)(i x ϕ=i y ,只要使i i i y x -=)(ϕδ尽可能地小)。
原理:给定数据点},...2,1,0),,{(m i y x i i =。
求近似曲线)(x ϕ。
并且使得近似曲线与()x f 的偏差最小。
近似曲线在该点处的偏差i i i y x -=)(ϕδ,i=1,2,...,m 。
常见的曲线拟合方法:1.使偏差绝对值之和最小2.使偏差绝对值最大的最小3.使偏差平方和最小最小二乘法:按偏差平方和最小的原则选取拟合曲线,并且采取二项式方程为拟合曲线的方法,称为最小二乘法。
推导过程:1. 设拟合多项式为:2. 各点到这条曲线的距离之和,即偏差平方和如下:3. 问题转化为求待定系数0a ...k a 对等式右边求i a 偏导数,因而我们得到了: .......4、 把这些等式化简并表示成矩阵的形式,就可以得到下面的矩阵:5. 将这个范德蒙得矩阵化简后可得到:6. 也就是说X*A=Y ,那么A = (X'*X)-1*X'*Y ,便得到了系数矩阵A ,同时,我们也就得到了拟合曲线。
MATLAB 实现:MATLAB 提供了polyfit ()函数命令进行最小二乘曲线拟合。
调用格式:p=polyfit(x,y,n)[p,s]= polyfit(x,y,n)[p,s,mu]=polyfit(x,y,n)x,y 为数据点,n 为多项式阶数,返回p 为幂次从高到低的多项式系数向量p 。
x 必须是单调的。
矩阵s 包括R (对x 进行QR 分解的三角元素)、df(自由度)、normr(残差)用于生成预测值的误差估计。
偏最小二乘法算法

偏最小二乘法 1.1 基本原理偏最小二乘法(PLS )是基于因子分析的多变量校正方法,其数学基础为主成分分析。
但它相对于主成分回归(PCR )更进了一步,两者的区别在于PLS 法将浓度矩阵Y 和相应的量测响应矩阵X 同时进行主成分分解:X=TP+E Y=UQ+F式中T 和U 分别为X 和Y 的得分矩阵,而P 和Q 分别为X 和Y 的载荷矩阵,E 和F 分别为运用偏最小二乘法去拟合矩阵X 和Y 时所引进的误差。
偏最小二乘法和主成分回归很相似,其差别在于用于描述变量Y 中因子的同时也用于描述变量X 。
为了实现这一点,数学中是以矩阵Y 的列去计算矩阵X 的因子。
同时,矩阵Y 的因子则由矩阵X 的列去预测。
分解得到的T 和U 矩阵分别是除去了大部分测量误差的响应和浓度的信息。
偏最小二乘法就是利用各列向量相互正交的特征响应矩阵T 和特征浓度矩阵U 进行回归:U=TB得到回归系数矩阵,又称关联矩阵B :B=(T T T -1)T TU因此,偏最小二乘法的校正步骤包括对矩阵Y 和矩阵X 的主成分分解以及对关联矩阵B 的计算。
1.2主成分分析主成分分析的中心目的是将数据降维,以排除众多化学信息共存中相互重叠的信息。
他是将原变量进行转换,即把原变量的线性组合成几个新变量。
同时这些新变量要尽可能多的表征原变量的数据结构特征而不丢失信息。
新变量是一组正交的,即互不相关的变量。
这种新变量又称为主成分。
如何寻找主成分,在数学上讲,求数据矩阵的主成分就是求解该矩阵的特征值和特征矢量问题。
下面以多组分混合物的量测光谱来加以说明。
假设有n 个样本包含p 个组分,在m 个波长下测定其光谱数据,根据比尔定律和加和定理有:A n×m =C n×pB p×m如果混合物只有一种组分,则该光谱矢量与纯光谱矢量应该是方向一致,而大小不同。
换句话说,光谱A 表示在由p 个波长构成的p 维变量空间的一组点(n 个),而这一组点一定在一条通过坐标原点的直线上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
sol=[ch0;xish] %显示回归方程的系数,每一列是一个方程,每一列的第一个数是常数项
disp('显示回归方程的系数,每一列是一个方程,每一列的第一个数是常数项');
save mydata x0 y0 num xishu ch0 xish
load mydata
beta_z(end,:)=[]; %删除常数项
disp('求Y关于X的回归系数,且是针对标准数据的回归系数')
xishu=w_star(:,1:r)*beta_z %求Y关于X的回归系数,且是针对标准数据的回归系数,
%每一列是一个回归方程
mu_x=mu(1:n);mu_y=mu(n+1:end);
plot(0:ymax(1),0:ymax(1),yhat(:,1),y0(:,1),'*')
subplot(2,2,2)
plot(0:ymax(2),0:ymax(2),yhat(:,2
),y0(:,2),'O')
val=diag(val); %提出对角线元素
[val,ind]=sort(val,'descend');
w(:,i)=vec(:,ind(1)) %提出最大特征值对应的特征向量
w_star(:,i)=chg*w(:,i); %计算w*的取值
t(:,i)=e0*w(:,i); %计算成分ti 的得分
beta=[t(:,1:i),ones(num,1)]\f0; %求回归方程的系数
beta(end,:)=[]; %删除回归分析的常数项
cancha=f0-t(:,1:i)*beta; %求残差矩阵
ss(i)=sum(sum(cancha.^2)); %求误差平方和
%以下计算press(i)
sig_x=sig(1:n);sig_y=sig(n+1:end);
for i=1:m
ch0(i)=mu_y(i)-mu_x./sig_x*sig_y(i)*xishu(:,i); %计算原始数据的回归方程的常数项
end
for i=1:m
xish(:,i)=xishu(:,i)./sig_x'*sig_y(i); %计算原始数据的回归方程的系数,每一列是一个回归方程
else
Q_h2(1)=1;
end
if Q_h2(i)<0.0975
fprintf('提出的成分个数r=%d',i);
r=i;
break
end
end
disp('Y 关于t 的回归系数')
beta_z=[t(:,1:r),ones(num,1)]\f0 %求Y 关于t 的回归系数
alpha=e0'*t(:,i)/(t(:,i)'*t(:,i)); %计算alpha_i
chg=chg*(eye(n)-w(:,i)*alpha'); %计算w 到w*的变换矩阵
e=e0-t(:,i)*alpha'; %计算残差矩阵
e0=e;
%以下计算ss(i)的值
num
ch0=repmat(ch0,num,1);
yhat=ch0+x0*xish; % 计算y 的预测值
y1max=max(yhat);
y2max=max(y0);
ymax=max([y1max;y2max])
cancha=yhat-y0; % 计算残差
subplot(2,2,1)
subplot(2,2,3)
plot(0:ymax(3),0:ymax(3),yhat(:,3),y0(:,3),'H')
clc
clear
load aa.txt ;%原始数据存放在纯文本文件aa.txt 中
disp('期望')
mu=mean(aa)
disp('和标准差')
sig=std(aa) %求均值和标准差
for j=1:num
t1=t(:,1(j,:);she_f=f1(j,:); %把舍去的第j 个样本点保存起来
t1(j,:)=[];f1(j,:)=[]; %删除第j 个观测值
beta1=[t1,ones(num-1,1)]\f1; %求回归分析的系数
beta1(end,:)=[]; %删除回归分析的常数项
cancha=she_f-she_t*beta1; %求残差向量
press_i(j)=sum(cancha.^2);
end
press(i)=sum(press_i);
if i>1
Q_h2(i)=1-press(i)/ss(i-1);
disp('相关系数矩阵')
rr=corrcoef(aa) %求相关系数矩阵
disp('数据标准化')
data=zscore(aa) %数据标准化
n=3;m=3; %n 是自变量的个数,m 是因变量的个数
x0=aa(:,1:n);
y0=aa(:,n+1:end);
e0=data(:,1:n);
f0=data(:,n+1:end);
num=size(e0,1);%求样本点的个数
chg=eye(n); %w 到w*变换矩阵的初始化
for i=1:n
%以下计算w,w*和t 的得分向量,
matrix=e0'*f0*f0'*e0;
[vec,val]=eig(matrix);%求特征值和特征向量
