2020届 百校联盟TOP20 高三四月联考(全国Ⅰ卷) 数学(理)试题(解析版)
【附加15套高考模拟试卷】安徽省2020届百校联盟TOP20四月联考(全国I卷)数学(理)试卷含答案

出现奇数或者同时出现偶数}.给出下列说法:
① P(A) P(B) P(C) ;
② P(AB) P(AC) P(BC) ;
③ P( ABC) 1 ; 8
④ P(A)P(B)P(C) 1 , 8
其中正确的有()
A.0 个 B.1 个 C.2 个 D.3 个
10.已知双曲线 C
:
x2 a2
y2 b2
点 P 0,t ,使得 PEF 的内心在 y 轴上,则实数 t ______.
14.若曲线 C1 : y ax3 x2 2x 与曲线 C2 : y ex 在 x 1 处的两条切线互相垂直,则实数 a 的值为
______.
15.等比数列 an 中各项均为正数,Sn 是其前 n 项和,且满足 2S3 8a1 3a2 , a4 16 ,则 S4 ______.
则 p 是 q 的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
2. “ a,b,c,d 成等差数列”是“ a d b c ”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.已知 2sin2α=1+cos2α,则 tan2α=( )
A.函数 g(x) 的最大值为 3 1
B.函数 g(x) 的最小正周期为
C.函数
g(x)
的图象关于直线
x
3
对称
D.函数
g(x)
在区间
6
,
2 3
上单调递增
9.设同时抛掷两个质地均匀的四面分别标有 1,2,3,4 的正四面体一次.记事件 A {第一个四面体向下
的一面出现偶数};事件 B {第二个四面体向下的一面出现奇数}; C {两个四面体向下的一面或者同时
百校联盟2020届高三4月教育教学质量监测考试(全国Ⅰ卷)+数学(理)+Word版含答案

百校联盟2020届普通高中教育教学质量监测考试 全国I 卷 理科数学注意事项:1.本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
2.答题前,考生务必将自己的姓名、准考证号填写在本试卷相应的位置。
3.全部答案写在答题卡上,写在本试卷上无效。
4.本试卷满分150分,测试时间120分钟。
5.考试范围:高考全部内容。
第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若复数z 满足z -1+i =2i +1,则|z|=A.5B.2C.3D.32.已知集合A ={2a -1,a 2,0},B ={1-a ,a -5,9},且A ∩B ={9},则A.A ={9,25,0}B.A ={5,9,0}C.A ={-7,9,0}D.A ∪B ={-7,9,0,25,-4}3.已知向量a =(x 2-2x ,1),b =(1,-3),则“-1<x<3”是“a ,b 的夹角为钝角”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件4.将函数y =2sin(2x +4π)的图象向右平移4π个单位长度,所得函数 A.在区间(-38π,8π)上单调递增 B.在区间(-58π,-8π)上单调递减 C.以x =8π为一条对称轴 D.以(38π,0)为一个对称中心 5.已知一个几何体的三视图如图所示,则此几何体的体积为A.83πB.8πC.163πD.12π 6.改编自中国神话故事的动画电影《哪吒之魔童降世》自7月26日首映,在不到一个月的时间,票房收入就超过了38亿元,创造了中国动画电影的神话。
小明和同学相约去电影院观看《哪吒之魔童降世》,影院的三个放映厅分别在7:30,8:00,8:30开始放映,小明和同学大约在7:40至8:30之间到达影院,且他们到达影院的时间是随机的,那么他们到达后等待的时间不超过10分钟的概率是A.13B.12C.25D.347.已知函数()()122log f x x ax a =-+在(12,+∞)上为减函数,则实数a 的取值范围是 A.(-∞,1] B.[-12,1] C.(-12,1] D.(-12,+∞) 8.在平面直角坐标系xOy 中,A 、B 为函数y =33|x|图象上的两点,若线段AB 的中点M 恰好落在曲线x 2-3y 2+3=0上,则△OAB 的面积为A.2B.3C.32D.339.一只蚂蚁从正四面体A -BCD 的顶点A 点出发,沿着正四面体A -BCD 的棱爬行,每秒爬一条棱,每次爬行的方向是随机的,则第4秒时蚂蚁在A 点的概率为A.2027B.79C.727D.2910.在梯形ABCD 中,AB//CD ,AB =2CD ,BC 3,则∠ADB 的最大值为A.4πB.3πC.2π D.23π 11.我国古代的数学著作《九章算术·商功》中,将底面是直角三角形的直三棱柱称为“堑堵”。
2020届百校联盟高三4月教育教学质量监测考试(全国Ⅰ卷) 数学(理)试题(解析版)

2020届百校联盟高三4月教育教学质量监测考试(全国Ⅰ卷)数学(理)试题一、单选题1.若复数z 满足121z i i -+=+,则||z =( )A .B .2C D .3【答案】A【解析】由条件121z i i -+=+,则211z i i =++-,求出z ,在求||z . 【详解】∵121z i i -+=+,∴2z i =+,∴z ==故选:A 【点睛】本题考查复数的加法运算和模长,属于基础题.2.已知集合{}221,,0A a a =-,{1,5,9}B a a =--,且{9}A B =I ,则( ) A .{9,25,0}A = B .{5,9,0}A =C .{7,9,0}A =-D .{7,9,0,25,4}A B ⋃=--【答案】C【解析】由{9}A B =I 可得29a =,或219a -=,则3a =±,或5a =,再检验得出结论. 【详解】由已知可得29a =,或219a -=,∴3a =±,或5a =. 当3a =时,{5,9,0}A =,{2,2,9}B =--(舍), 当5a =时,{9,25,0}A =,{4,0,9}B =-(舍), 当3a =-时,{7,9,0}A =-,{4,8,9}B =-. 故选:C 【点睛】本题考查利用集合的交集求参数,注意检验集合的元素的唯一性,属于基础题. 3.已知向量()22,1a x x →=-,(1,3)b →=-,则“13x -<<”是“a →,b →的夹角为钝角”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分又不必要条件【答案】B【解析】根据若0a b ⋅<r r,则a →,b →的夹角为钝角或平角,再求出a →,b →反向时x 的取值,从而可得到答案. 【详解】∵223x x a b →→=--⋅,∴130a b x →→⋅-<<⇔<,当//a b →→时,()2321x x -⨯-=,解得:13x =±当1x =时,1,13a →⎛⎫=- ⎪⎝⎭,此时a →,b →反向.所以a →,b →的夹角为钝角则13x -<<且1x ≠所以“13x -<<”不能得到“a →,b →的夹角为钝角. 当“a →,b →的夹角为钝角”则能得到“13x -<<”.∴“13x -<<”是“a →,b →的夹角为钝角”的必要不充分条件. 故选:B 【点睛】本题考查必要不充分条件的判断和向量的夹角与数量积的关系,属于中档题. 4.将函数2sin 24y x π⎛⎫=+⎪⎝⎭的图象向右平移4π个单位长度,所得函数( ) A .在区间3,88ππ⎛⎫-⎪⎝⎭上单调递增 B .在区间5,88ππ⎛⎫-- ⎪⎝⎭上单调递减 C .以8x π=为一条对称轴D .以3,08π⎛⎫⎪⎝⎭为一个对称中心 【答案】B【解析】由三角函数的图像平移得出解析式2sin 24y x π⎛⎫=- ⎪⎝⎭,然后再根据函数()sin y A ωx φ=+的图像性质对选项进行逐一判断,即可得出答案.【详解】将函数2sin 24y x π⎛⎫=+ ⎪⎝⎭的图象向右平移4π个单位长度,可得2sin 22sin 2444y x x πππ⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,由222()242k x k k πππππ--+∈Z 剟,得3()88k x k k ππππ-+∈Z 剟, ∴单调递增区间为3,()88k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z ,故A 错误; 由32+22()242k x k k πππππ-+∈Z 剟,得37+()88k x k k ππππ+∈Z 剟 当1k =-时,函数在5,88ππ⎛⎫-- ⎪⎝⎭上单调递减. 故B 正确 由242x k πππ-=+,得对称轴为3()28k x k ππ=+∈Z ,故C 错误; 由24x k ππ-=,得()28k x k ππ=+∈Z ,对称中心为,028k ππ⎛⎫+⎪⎝⎭,故D 错误. 故选:B 【点睛】本题考查根据三角函数的图像平移得出解析式,进一步研究函数的单调性和对称性,属于中档题.5.已知一个几何体的三视图如图所示,则此几何体的体积为( )A .83πB .8πC .163πD .12π【答案】B【解析】由三视图知,该几何体为一个圆柱挖去半个球和一个圆锥,然后求体积.【详解】由三视图知,该几何体为一个圆柱挖去半个球和一个圆锥, ∴3114164228323V ππππ=-⨯⨯-⨯⨯=. 故选:B 【点睛】本题考查根据三视图求体积,属于中档题.6.改编自中国神话故事的动画电影《哪吒之魔童降世》自7月26日首映,在不到一个月的时间,票房收入就超过了38亿元,创造了中国动画电影的神话.小明和同学相约去电影院观看《哪吒之魔童降世》,影院的三个放映厅分别在7:30,8:00,8:30开始放映,小明和同学大约在7:40至8:30之间到达影院,且他们到达影院的时间是随机的,那么他们到达后等待的时间不超过10分钟的概率是( ) A .13B .12C .25D .34【答案】C【解析】根据题意,等待时间不超过10分钟的时间段分别为7:50~8:00,8:20~8:30,共20分钟,7:40至8:30之间共50分钟,由几何概型即可求出概率. 【详解】由题意可知,满足条件的时间段为7:50~8:00,8:20~8:30,共20分钟, 7:40至8:30之间共计50分钟, 由几何概型知所求概率为202505=. 故选:C . 【点睛】本题考查几何概型求概率问题,属于基础题.7.已知函数()212()log f x x ax a =-+在1,2⎛⎫+∞ ⎪⎝⎭上为减函数,则实数a 的取值范围是( ) A .(,1]-∞ B .1,12⎡⎤-⎢⎥⎣⎦C .1,12⎛⎤-⎥⎝⎦D .1,2⎛⎫-+∞ ⎪⎝⎭【答案】B【解析】可看出该函数是由对数函数和二次函数复合而成的复合函数,这样根据二次函数、对数函数和复合函数的单调性及对数函数的定义域便可建立关于a 的不等式组,解出a 的取值范围即可. 【详解】12log y x =Q 在(0,)+∞上为减函数,2y x ax a ∴=-+在1,2⎛⎫+∞ ⎪⎝⎭上为增函数,且0y >,122a -∴-≤,且211022a a ⎛⎫-+≥ ⎪⎝⎭, 1a ∴≤,且12a ≥-,1,12a ⎡⎤∴∈-⎢⎥⎣⎦.故选:B . 【点睛】本题考查复合函数单调性的应用,涉及复合函数单调性的判断,解题关键是对数函数的定义域、二次函数的性质的运用,属于中等题.8.在平面直角坐标系xOy 中,A 、B 为函数||y x =图象上的两点,若线段AB 的中点M 恰好落在曲线22330x y -+=上,则OAB V 的面积为( )A .2BCD 【答案】B【解析】设()11,A x y ,()22,B x y ,不妨设10x <,20x >,由线段AB 的中点M ,则122122x x x x M ⎛⎫+-⎫ ⎪⎪ ⎪⎝⎭⎝⎭,将M 的坐标代入曲线22330x y -+=可得123x x =-,然后求出1OA x =,2OB x =,利用三角形的面积公式可求得答案. 【详解】设()11,A x y ,()22,B x y ,线段AB 的中点(,)M x y . 由题意,不妨设10x <,20x >.∵12121221233333222x x xx x y y x x y +⎧=⎪⎪⎨-+⎪+-⎛⎫===⎪ ⎪⎝⎭⎩, 点(,)M x y 在22330x y -+=上,则22221221123333223330x x x x x y x x ⎡⎤+-⎛⎫⎛⎫-=-+=⎢⎥ ⎪ ⎪⎝⎭⎭⎣⎦++=⎝∴123x x =-,又∵2211123OA x y x =+=-, 22222233OB x y x =+=,23AOB π∠=,∴1213sin 323OAB S OA OB AOB x x =⋅⋅∠=-=△. 故选:B 【点睛】本题考查中点坐标公式的应用和求三角形的面积,属于中档题.9.一只蚂蚁从正四面体A BCD -的顶点A 点出发,沿着正四面体A BCD -的棱爬行,每秒爬一条棱,每次爬行的方向是随机的,则第4秒时蚂蚁在A 点的概率为( )A .2027B .79C .727D .29【答案】C【解析】设第n 秒时蚂蚁不在顶点A 的概率为n P ,易知11P =.则1121(13)n n n P P P --=+⨯-,先求出n P 的通项公式,然后可得4P ,从而可得答案. 【详解】由题意知,蚂蚁每次爬行到下一个顶点的概率均为13, 设第n 秒时蚂蚁不在顶点A 的概率为n P ,易知11P =.则1121(13)n n n P P P --=+⨯-,∴1313434n n P P -⎛⎫⎛⎫-=-- ⎪ ⎪⎝⎭⎝⎭, ∴数列34n P ⎧⎫-⎨⎬⎩⎭是以为14为首项,以13-为公比的等比数列. ∴()*331443nn P n ⎛⎫=-⋅-∈ ⎪⎝⎭N ,∴第4秒时蚂蚁在A 点的概率为4207112727P -=-=. 故选:C 【点睛】本题考查概率的计算和利用数列的递推关系求通项公式,属于中档题.10.在梯形ABCD 中,//AB CD ,2AB CD =,BC =,则ADB ∠的最大值为( ) A .4π B .3π C .2π D .23π 【答案】B【解析】设CD a =,则2AB a =,BC =.取AB 的中点M ,延长AB 到N 点,使BN a =,连接CM ,CN .在MBC △,NBC V 中分别用余弦定理可得2228m n a +=,然后在ABD △中用余弦定理结合均值不等式可求解出答案. 【详解】设CD a =,则2AB a =,BC =.取AB 的中点M ,延长AB 到N 点,使BN a =,连接CM ,CN . 由平面几何知识,易知AD MC =,BD NC =. 设AD MC m ==,BD NC n ==.在MBC △中,222)2cos m a a MBC =+-⨯⋅∠,在NBC V 中,222)2cos()n a a MBC π=+-⨯⋅-∠,∴2228m n a +=,在ABD △中,222244cos 22m n a a ADB mn mn+-∠==, 又∵22228mn m n a +=„,∴222441cos 282a a ADB mn a ∠==…,∴ADB ∠的最大值为3π. 故选:B【点睛】本题考查利用余弦定理解三角形结合均值不等式求最值,属于中档题.11.我国古代的数学著作《九章算术·商功》中,将底面是直角三角形的直三棱柱称为“堑堵”.在如图所示的“堑堵”111ABC A B C -中,12AB AC AA ===,M 、N 分别是1BB 和11A C 的中点,则平面AMN 截“堑堵”111ABC A B C -所得截面图形的面积为( )A 221B .213C .273D .473【答案】A【解析】延长AN ,与1CC 的延长线交于点P ,则P ∈平面11BB C C .连接PM ,与11B C 交于点E ,连接NE ,可得截面图形,然后计算其面积. 【详解】延长AN ,与1CC 的延长线交于点P ,则P ∈平面11BB C C .连接PM ,与11B C 交于点E ,连接NE ,得到的四边形AMEN 就是平面AMN 截“堑堵”111ABC A B C -所得截面图形.由已知可求得:2215AM AN ==+=, 由1△PC E ∽1△EB M ,可得1111223B E B E ==142C E = 2221713ME ⎛⎫=+= ⎪ ⎪⎝⎭,2424217121cos 4533NE ⎛⎫=+-⨯⨯⨯︒= ⎪ ⎪⎝⎭()222115+16MN A N A M =+==.()2222161176221656222323S ⎛⎫⎛⎫⎛⎫=⨯⨯-+⨯⨯-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∴截面面积2213S =. 故选:A【点睛】本题考查作出平面截空间立体几何图形的截面并计算其面积,属于中档题.12.已知函数()ln 2f x a x x =-,若存在*x ∈N ,使()0f x >成立,则实数a 的取值范围是( ) A .(2,)e +∞ B .4,ln 2⎛⎫+∞⎪⎝⎭C .6,ln 3⎛⎫+∞⎪⎝⎭D .(2,)+∞【答案】C【解析】显然当1x =时,不成立,则当1x >时,即2ln x a x >,设2()ln xg x x=,分析出函数()g x 的单调区间,然后可得出答案. 【详解】由题意,得ln 20a x x ->,当1x =时,20->不成立; 当1x >时,2ln x a x >,设2()ln xg x x=,则22(ln 1)()(ln )x g x x -'=,当(1,)x e ∈时,()0g x '<,()g x 为减函数, 当(,)x e ∈+∞时,()0g x '>,()g x 为增函数.当2x =时,4(2)ln 2g =,当3x =时,6(3)ln 3g =,又∵4ln3ln81ln646ln2=>=,∴46ln 2ln 3>,∴6ln 3a >. 故选:C. 【点睛】本题考查利用导数分析函数的单调区间进一步解决存在性问题,属于中档题.二、填空题13.若x ,y 满足约束条件43602210210x y x y x y --≤⎧⎪-+≥⎨⎪+-≥⎩,则|1|z x y =-+的最大值为__________.【答案】2811【解析】根据条件,作出可行域,分析出可行域在直线10x y -+=的同侧,然后利用目标函数的几何意义可求解. 【详解】由线性约束条件,得到图中ABC V 所在的区域,在图中做出直线10x y -+=,可以看出三角形区域ABC 的所有点都在直线10x y -+=的同一侧,所以当直线10x y -+=平移经过点B 时,z 取得最大值.由4360210x y x y --=⎧⎨+-=⎩,解得152,1111B ⎛⎫- ⎪⎝⎭,代入1z x y =-+,得2811z =. 故答案为:2811【点睛】本题考查简单线性规划问题,属于中档题.14.在()251()x x x a +--的展开式中,含5x 项的系数为14,则实数a 的值为___________.【答案】1-或32【解析】由()2525551()()()()+x x x a x x a x x a x a =-+-----,又5()x a -的展开式的通项公式为()515rr rr T C x a -+=-,可得含5x 项,从而可得其系数,从而可得答案.【详解】()2525551()()()()+xx x a x x a x x a x a =-+-----又5()x a -的展开式的通项公式为()515rr r r T C x a -+=-由已知,含5x 的项为22324050555C ()C ()(1)C ()x x a x x a x a -+⋅-+-⋅-⋅()251051a a x =--,∴2105114a a --=,即2230a a --=,解得1a =-或32. 故答案为:1a =-或32. 【点睛】本题考查二项式展开式中指定项的系数,求参数的值,属于基础题. 15.已知实数,x y 满足20y x ≥>,则92y x x x y++的最小值为_____. 【答案】174【解析】采用换元法设yt x=,由已知可得2t ≥,可得9922y x t x x y t +=+++,令9()(2)2f t t t t =+≥+,利用导数求最值即可. 【详解】 设yt x=,由已知可得2t ≥, 9922y x t x x y t ∴+=+++,令9()(2)2f t t t t =+≥+, 29()10(2)f t t '=->+Q , 9()2f t t t ∴=++在[2,)+∞上为增函数, 917()24f t t t ∴=+≥+,即91724y x x x y +≥+.故答案为:174. 【点睛】本题考查函数的最值问题,题目含有双变量,此类问题可用换元法将其转化为函数,再利用导数求解最值,属于中等题.16.已知1F 、2F 为双曲线2214x y -=的左、右焦点,P 为双曲线右支上异于顶点的任意一点,若12PF F △内切圆的圆心为I ,则圆心I 到圆22(1)1y x +-=上任意一点的距离的最小值为____________. 【答案】1【解析】设12PF F △内切圆与12PF F △的三边1PF 、2PF 、12F F 的切点分别为D 、N 、M ,根据圆的切线性质,可得2OM =,即可得答案.【详解】由双曲线2214x y -=,则 2,1,a b c ===设12PF F △内切圆与12PF F △的三边1PF 、2PF 、12F F 的切点分别为D 、N 、M , 根据圆的切线性质,可得1224F M F M a -==,又因为1212F M F M F F +==,∴12F M =,即2OM =, ∴内切圆圆心I 在直线2x =上.又因为圆22(1)1y x +-=的圆心为(0,1),半径1r =, ∴圆心I 到圆22(1)1y x +-=上任意一点的距离的最小值为211-=. 故答案为:1 【点睛】本题考查双曲线的定义和性质,属于中档题.三、解答题17.已知n S 为数列{}n a 的前n 项和,210S =,()*1121n n n S a n N n +-=+∈+. (1)求数列{}n a 的通项公式; (2)设()*2(1)!n n n a b n N n =∈+,数列{}nb 的前n 项和为n T ,求证:112n T ≤<.【答案】(1)()*2nn a n n =⋅∈N .(2)证明见解析【解析】(1)由1121n n n S a n +-=++有()*1222,n n n S a n n n--=+∈N …两式相减可得()*122,1n n a an n n n+=⋅∈+N …,从而可求出答案. (2)由112(1)!(1)!!(1)!n n n a n b n n n n ===-+++用裂项相消可求和.【详解】(1)当1n =时,112S a ==, ∵210S =,∴28a =, 又∵()*1121n n n S a n n +-=+∈+N , ∴()*1222,n n n S a n n n--=+∈N …, ∴()*1122,1n n n n n a a a n n n n +--=-∈+N …, 整理得:()*122,1n n a an n n n+=⋅∈+N …, ∴数列n a n ⎧⎫⎨⎬⎩⎭从第二项242a =开始是公比为2的等比数列. ∴2422n n na n-=⨯= ∴()*22,nn a n n n =⋅∈N …又∵当1n =时,12a =满足2nn a n =⋅.∴()*2nn a n n =⋅∈N .(2)由(1)得()*112(1)!(1)!!(1)!n n na nb n n n n n ===-∈+++N , ∴111111112!2!3!!(1)!(1)!n T n n n =-+-+⋯+-=-++,显然当*n ∈N 时,n T 为单调递增函数,且10(1)!n >+,∴1112n T T =<…成立. 【点睛】本题考查利用n a 和n S 的递推关系求通项公式和利用裂项相消可求和,属于中档题. 18.某市为了了解该市教师年龄分布情况,对年龄在[20,60]内的5000名教师进行了抽样统计,根据分层抽样的结果,统计员制作了如下的统计表格: 年龄区间 [20,30) [30,40) [40,50) [50,60] 教师人数 2000 1300 样本人数130由于不小心,表格中部分数据被污染,看不清了,统计员只记得年龄在[20,30)的样本人数比年龄在[50,60]的样本人数多10,根据以上信息回答下列问题:(1)求该市年龄在[50,60]的教师人数;(2)试根据上表做出该市教师按照年龄的人数频率分布直方图,并求该市教师年龄的平均数x 及方差2s (同一组的数据用该组区间的中点值作代表). 【答案】(1)800.(2)频率分布直方图见解析,39x =,292s = 【解析】(1)设样本容量为x ,由130********x⨯=解得x 的值,进一步求得年龄在[30,40)的教师在样本中的人数,可得年龄在[20,30)和[50,60]的教师在样本中的人数,在列式计算.(2)分布求出各区间段的频率,即可画出频率分布直方图,再由期望与方差公式求解即可. 【详解】(1)设样本容量为x ,则130********x⨯=,解得500x =, ∴年龄在[30,40)的教师在样本中共有50020002005000⨯=(人), ∴年龄在[20,30)和[50,60]的教师在样本中共有500200130170--=(人), 设年龄在[50,60]的教师在样本中的人数为y , 由题意可知:(10)170y y ++=,∴80y =,∴该市年龄在[50,60]的教师人数为500080800500⨯=. (2)由(1)可知,年龄在[20,30)的教师人数为500020001300800900---=(人),频率为9000.185000=, 年龄在[30,40)的教师人数为2000(人),频率为20000.45000=, 年龄在[40,50)的教师人数为1300(人),频率为13000.265000=, 年龄在[50,60]的教师人数为800(人),频率为8000.165000=. 由此做出频率分布直方图.250.18350.4450.26550.1639x =⨯+⨯+⨯+⨯=;22222(2539)0.18(3539)0.4(4539)0.26(5539)0.1692s =-⨯+-⨯+-⨯+-⨯=.【点睛】本题考查频率分布直方图,利用频率分布直方图求期望与方程的估计值,属于中档题. 19.如图,将斜边长为42的等腰直角ABC V 沿斜边BC 上的高AD 折成直二面角B ADC --,E 为AD 中点.(1)求二面角A BC E --的余弦值;(2)M 为线段BC 上一动点,当直线DM 与平面BCE 所成的角最大时,求三棱锥M CDE -外接球的体积.【答案】(1)223.(2510 【解析】(1)设F 为BC 中点,连接EF 、AF 得出BD ⊥平面ADC ,由平面几何可知EF BC ⊥,AF BC ⊥,则EFA Ð就是二面角A BC E --的平面角,在EFA △中求解.(2) 设直线DM 与平面BCE 所成的角为α,点D 到平面BCE 的距离为d ,则sin d DM α=,由等体积法可得求得233d =,当DM 最小时,直线DM 与平面BCE 所成的角的正弦值最大,此时所成角也最大,从而当M 为BC 中点时,直线DM 与平面BCE 所成的角最大,此时2DM =,可求出三棱锥M CDE -外接球的体积. 【详解】 【详解】解法一:(1)设F 为BC 中点,连接EF 、AF . ∵ABC V 为等腰直角三角形, 且二面角B AD C --为直二面角, ∴BD ⊥平面ADC∴22AD BD CD ===,4AB BC CA ===, 由平面几何可知,10BE CE ==, ∴EF BC ⊥,AF BC ⊥,∴EFA Ð就是二面角A BC E --的平面角, 在EFA △中,2AE =,224223AF =-=,1046EF =-=,∴2221622cos 23122EF AF AE EFA EF AF +-∠===⨯⨯, ∴二面角A BC E --的余弦值为223.(2)设直线DM 与平面BCE 所成的角为α,点D 到平面BCE 的距离为d , 则sin d DMα=, 在三棱锥B CDE -中,1262BCE S BC EF =⨯⨯=△, 由B CDE D BCE V V --=三棱锥三棱锥,求得23d =,∴当DM 最小时,直线DM 与平面BCE 所成的角的正弦值最大,此时所成角也最大, ∴当M 为BC 中点时,直线DM 与平面BCE 所成的角最大,此时2DM =. 由平面几何知识可知,CDE △和CME △都是直角三角形,设N 为CE 的中点, 则11022ND NE NC NM CE =====, ∴三棱锥M CDE -外接球的半径为102, ∴外接球的体积3410510323V ππ⎛⎫==⎪⎝⎭.解法二:(1)∵ABC V 为等腰直角三角形,且二面角B AD C --为直二面角,∴BD ⊥平面ADC , ∴BD CD ⊥,∴以D 为坐标原点,以DA 、DC 、DB 所在直线为x 轴、y 轴、z 轴建立如图所示的空间直角坐标系.∵在平面图形中,ABC V 是斜边为42的等腰直角三角形,且E 为高AD 的中点, ∴(0,0,0)D ,(22,0,0)A,(0,0,22)B ,(0,22,0)C ,(2,0,0)E ,∴(22,22,0)AC =-,(0,22,22)BC =-u u u r,(2,22,0)EC =-,设平面ABC 的一个法向量为()111,,m x y z =u r,平面BCE 的一个法向量为()222,,n x y z =r,由00m BC m AC ⎧⋅=⎨⋅=⎩u u u v v v ,得11112222022220y z x y ⎧-=⎪⎨-+=⎪⎩,令11x =,则111y z ==∴(1,1,1)m =u r,同理可求得(2,1,1)n =r,∴22cos ,336m n m n m n ⋅〈〉===⨯⨯u r ru r r u r r , ∴二面角A BC E --的余弦值为22.(2)如图,设(01)BM BC λλ=剟, 可得(0,22,2222)M λλ-, ∴(0,22,2222)DM λλ=-,又由(1)可知平面BCE 的法向量为(2,1,1)n =r,∴2222cos ,244263(21)1DM n λλλ〈〉==-+⨯⨯-+u u r r即直线DM 与平面BCE,∵01λ剟,3,当且仅当12λ=时,等号成立. ∴当M 为BC 中点时,直线DM 与平面BCE 所成的角最大,此时2DM =. 由平面几何知识可知,CDE △和CME △都是直角三角形,设N 为CE 的中点,则122ND NE NC NM CE =====, ∴三棱锥M CDE -外接球的半径为2, ∴外接球的体积34323V π⎛==⎝⎭. 【点睛】本题考查求二面角的余弦值和三棱锥外接球的体积的求法,考查空间线线、线面、面面的位置关系,属于中档题.20.动圆P 过定点(2,0)A ,且在y 轴上截得的弦GH 的长为4. (1)若动圆圆心P 的轨迹为曲线C ,求曲线C 的方程;(2)在曲线C 的对称轴上是否存在点Q ,使过点Q 的直线l '与曲线C 的交点S T 、满足2211||||QS QT +为定值?若存在,求出点Q 的坐标及定值;若不存在,请说明理由. 【答案】(1)24y x =.(2)存在点(2,0)Q ,定值为14. 【解析】(1)设(,)P x y ,由题意知:PA PG =,利用距离公式及弦长公式可得方程,化简可得P 的轨迹方程;(2)假设存在(,0)Q a ,设()11,S x y 、()22,T x y ,由题意知直线l '的斜率必不为0,设直线l '的方程,与抛物线联立,利用根与系数关系可求得()212222121121t a QS QT a t ++=+,当2a =时,上式221114QS QT +=,与1t 无关,为定值. 【详解】(1)设(,)P x y ,由题意知:PA PG =.当P 点不在y 轴上时,过P 做PB GH ⊥,交GH 于点B ,则B 为GH 的中点,122GB GH ∴==,PG ∴=又PA =Q ,=24(0)y x x =≠;当P 点在y 轴上时,易知P 点与O 点重合.(0,0)P 也满足24y x =,∴曲线C 的方程为24y x =.(2)假设存在(,0)Q a ,满足题意.设()11,S x y 、()22,T x y .由题意知直线l '的斜率必不为0, 设直线l '的方程为()110x t y a t =+≠.由124x t y a y x=+⎧⎨=⎩得21440y t y a --=.1214y y t ∴+=,124y y a ⋅=-. ()2121121242x x t y y a t a ∴+=++=+,2221212116x x y y a ⋅=⋅=. ()()2222221111114(42)QS x a y x a x x a x a =-+=-+=+-+Q ,()()2222222222224(42)QT x a y x a x x a x a =-+=-+=+-+,()222221212(42)2QS QT x x a x x a ∴+=++-++()()22121212(42)22x x a x x x x a =++-+-+()()21212124222x x x x a x x a =+++--+ ()()22114244t a t =++, ()222221161QS QT a t ⋅=+.()()()()2222211122222222211424411221161t a t QS QT t a QS QT QS QT a t a t ++++∴+===⋅++, 当2a =时,上式221114QS QT +=,与1t 无关,为定值. ∴存在点(2,0)Q ,使过点Q 的直线l '与曲线C 的交点S T 、满足2211QS QT +为定值14. 【点睛】本题考查轨迹方程、定值问题的求解,求轨迹方程,一般是求谁设谁的坐标然后根据题目等式直接求解即可,存在性与定值问题一般设存在,代入,结合韦达定理等知识消去参数求解,属于较难题型.21.已知函数1()f x ax x =+,()1xe g x x=-. (1)讨论函数()f x 在(0,)+∞上的单调性;(2)当12a =时,设(,)P x y 为函数()1ln ((0,))()1x g x y x x f x ⋅-=∈+∞⋅-图象上任意一点.直线OP 的斜率为k ,求证:01k <<.【答案】(1)答案见解析.(2)证明见解析【解析】(1)由22211()ax f x a x x-'=-=,分0a ≤与0a >两类讨论,可求得函数()f x 在(0,)+∞上的单调区间.(2)由已知,即证0y x <<,由于2()11ln ln 1()12x x g x e x y x f x x ⋅---==⋅-,即证210ln 12x e x x x --<<,①设21()12x h x e x x =---,②构造函数21()12x x s x e x x e =---,利用导数研究这两个函数的单调性及函数取值情况,可证结论.【详解】(1)∵1()f x ax x=+, ∴22211()ax f x a x x-'=-=, 当0a ≤时,()0f x '<,函数()f x 在(0,)+∞上单调递减;当0a >时,由()0f x '=,得x a=±(舍负)当x ⎛∈ ⎝⎭时,()0f x '<,函数()f x 单调递减,当x ⎫∈+∞⎪⎪⎝⎭时,()0f x '>,函数()f x 单调递增. (2)证明:由已知,即证0y x <<. ∵2()11ln ln 1()12x x g x e x y x f x x ⋅---==⋅-, ∴即证210ln 12x e x x x --<<, ①设21()12x h x e x x =---, ∴()1x h x e x '=--, ∴()1x h x e ''=-,∵(0,)x ∈+∞,∴()10x h x e ''=->,∴()h x '为增函数∴()1(0)0x h x e x h ''=-->=, ∴()h x 为增函数 ∴21()1(0)02x h x e x x h =--->=, ∴21102x e x x --->, 即2112x e x x -->,即21112x e x x -->, ∴21ln 012x e x x -->,即0y >, ②构造函数21()12x x s x e x x e =---,∵21()12x x x s x e xe x e '=---, 21()22x x s x xe x e ''=--, ∴21()202x x s x xe x e ''=--<, ∴()s x '在(0,)+∞上为减函数,∴()(0)0s x s ''<=,∴()s x 在(0,)+∞上为减函数,∴()(0)0s x s <=, ∴2112x x e x x e --<, ∴2112x x e x e x --<,即21ln 12x e x y x x --=<成立. 由①②可知0y x <<, ∴01k <<成立.【点睛】本题考查利用导数判断函数的单调性,考查证明不等式的有关问题,考查分离讨论和构造函数,属于难题.22.在平面直角坐标系xOy 中,曲线C 的参数方程为1cos 1sin x y θθ=+⎧⎨=+⎩(θ为参数),在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,直线l的极坐标方程为sin 04πρϕ⎛⎫++= ⎪⎝⎭,P 为直线l 上的任意一点. (1)Q 为曲线C 上任意一点,求P Q 、两点间的最小距离;(2)过点P 作曲线C 的两条切线,切点为A B 、,曲线C 的对称中心为点C ,求四边形PACB 面积的最小值.【答案】(1)1.(2【解析】(1)将曲线C 的参数方程化为普通方程可得圆,直线l 的极坐标方程化为直角坐标方程,由直线与圆的位置关系可得P Q 、两点间的最小距离;(2)△P AC 与△PBC 为直角三角形,AC =BC =1,根据图形的对称性及勾股定理可知,四边形PACB的面积2PAC S S PA AC PA ==⨯==△PC 最小时面积最小,由此能求出面积的最小值.【详解】(1)由曲线C 的参数方程为1cos 1sin x y θθ=+⎧⎨=+⎩(θ为参数),得22(1)(1)1x y -+-=, ∴曲线C 是以(1,1)为圆心,以1为半径的圆.由sin 04πρϕ⎛⎫++= ⎪⎝⎭,化简得cos sin 20ρϕρϕ++=, cos sin x y ρϕρϕ=⎧⎨=⎩Q ,:20l x y ∴++=, P Q 为直线l 上的任意一点,Q 为圆C 上任意一点,min min 1PQ PC ∴=-(其中C 为圆心),又min PC ==Qmin 1PQ ∴=-.(2)由题意,△P AC 与△PBC 为直角三角形,AC =BC =1,根据图形的对称性及勾股定理可知,四边形PACB 的面积2PAC S S PA AC PA ==⨯==△由(1)知,min PC =∴四边形PACB 面积的最小值min S =.【点睛】本题考查简单曲线的极坐标方程,参数方程化成普通方程,解题关键是利用极坐标与直角坐标的关系将极坐标方程与参数方程转化为直角坐标方程,利用直线与圆位置关系求解即可,属于中等题.23.若0a >,0b >,且223a b ab ++=.(1)求2a b +的最小值;(2)是否存在a 、b ,使得33a b +=?并说明理由.【答案】(1)4.(2)不存在a ,b ,理由见解析【解析】(1) 利用均值不等式有3222ab a b =++…,从而可求解出答案.(2)由均值不等式有33a b +厖1)2ab …可得出答案. 【详解】(1)由3222ab a b =+++…,得2ab …,当且仅当22a b ==时等号成立. 故2324a b ab +=-…,当且仅当22a b ==时等号成立. 所以2a b +的最小值为4.(2)由(1)知,33a b +厖当且仅当22a b a b =⎧⎨==⎩时等号成立).因此,33a b +>.从而不存在a ,b ,使33a b +=.【点睛】本题考查利用均值不等式求最值和考查等号成立的条件,属于中档题.。
全国卷2020届高考数学4月联考试题理20200420031

PF
MN
1
的标准方程为____
三、解答题:共 70 分.解答应写出文字说明、证明过程或演算步骤.第 17~21 题为必考题,每个试题考生
都必须作答.第 22,23 题为选考题,考生根据要求作答.
(一)必考题:共 60 分.
17.(12 分)
已知正项数列{ }的前 n 项和为 满足 S a
a .等比数列{b }满足 1 1, 2 2.
C.[ , 26
] [,] 62
D.[ ,0] [0, ]
6
6
9.北宋徽宗在崇宁年间(1102 年一 1106 年)铸造崇宁通宝钱,因为崇宁通宝版别多样、铜质细腻、铸工
精良,钱文为宋徽宗亲笔书写的“瘦金体”,所以后人写诗赞美日:“风流天子书崇观,铁线银钩字字端”.
崇宁通宝被称为我国钱币铸造史上的一个巅峰铜钱直径 3.5 厘米,中间穿口为边长为 0.9 厘米的正方形.用
且 A=
, 2
60°,则△ABC 的周长为____
xy
2
2
16.已知双曲线
C:
ab
2
2
的左、右焦点分别为
1(a 0,b 0)
F F FF
P 为双曲线右支上
1, 2,| 1 2 | 10.
的一点,直线 交 y 轴于点 M,交双曲线 C 的一条渐近线于点 N,且 M 是 的中点
PF
则双曲线 C
2 N P ,1
a
S, 4
22
a ba b
n
n
n
n
n
n
( I )求数列{a }与数列{b }的通项公式;
n
n
(II )若 c a b , ,求数列{c }的前 n 项和 T .
2020届百校高考考前冲刺(四)全国i卷数学(理)试题(解析版)

第 3 页 共 21 页
5.若集合
A x | sin 2x
1
Байду номын сангаас
,
B
y
y
k
,k
Z
,则(
)
42
A. A B A
B. CRB CR A
C. A B
D. CR A CRB
【答案】B 【解析】根据正弦函数的性质可得集合 A,由集合性质表示形式即可求得 A B ,进而
可知满足 CRB CR A .
A.
17 2
,
9
B.
,
17 2
9,
C.
17 4
,
9 2
D.
,
17 4
9 2
,
【答案】C
【解析】将函数 f x 解析式化简,并求得 f x ,根据当 x1 1,3 时 f ′ x 0 可得 f x1 的值域;由函数 g x x m 2 在 x2 1,3 上单调递减可得 g x2 的值域,
是奇函数;都有 f (x)=f (- x) ,则函数 f (x) 是偶函数
(2)图象法:函数是奇(偶)函数 函数图象关于原点( y 轴)对称.
3.函数 f x 2x 3x 1 在2,1 上的最大值和最小值分别为( )
2
A. ,-2
3
【答案】B
B. 2 ,-9 3
C.-2,-9
D.2,-2
【解析】由函数解析式中含绝对值,所以去绝对值并画出函数图象,结合图象即可求得
2020 届百校高考考前冲刺全国 i 卷数学(理)试题
一、单选题
1.设集合 A {x N | (x 3)(x 2) 0}, B y | y 2 ,则 A I ðRB ( )
2020高考全国卷 4月联考数学(理科)试题(word版,含解析)

2020高考全国卷4月联考数学(理科)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数z满足1(ii i z-=-为虚数单位),则2z=()A.1+ iB.1-iC.2iD. -2i2.已知集合A=2{|13},{|2940},x x B y y y-≤<=-+≤则A∩B=()A.{x|-1≤x≤4}1.{|3}2B x x≤< C.{x|-1≤x<3} D.∅3.实数x,y满足不等式组1,22,22,x yx yx y+≤⎧⎪-≥-⎨⎪+≥-⎩则目标函数z=2x+ y的最大值为()A.3B.4C.5D.64.三只小松鼠小芳、小松和点点住在同一-棵大松树上,一天它们在一起玩智力游戏.小芳说:今天我们三个有的吃了松子;小松说:今天我们三个有的没吃松子;点点说:今天我没吃松子.已知它们三个中只有一个说的是真的,则以下判断正确的是()A.全吃了B.全没吃C.有的吃了D.有的没吃5.已知3sin(15),5α︒+=则cos(30)α︒-=()72.A2.B-72.C272.D2-6.已知函数||sin()xxf xe=,则函数y= f(x)的大致图象是7.志愿者团队安排去甲、乙、丙、丁四个精准扶贫点慰问的先后顺序,一位志愿者说:不能先去甲,甲的困难户最多;另一位志愿者说:不能最后去丁,丁离得最远.他们总共有多少种不同的安排方法( )A.14B.12C.24D.288.已知函数()sin()f x A x ωϕ=+(其中A 0,0,||)2πωϕ>>≤离原点最近的对称轴为0,x x =若满足0||,6x π≤,则称f(x)为“近轴函数”.若函数y = 2sin(2x -φ )是"近轴函数" ,则φ的取值范围是( )[,]62A ππ⋅ .[,]26B ππ-- .[,][,]2662C ππππ--⋃ .[,0][0,]66D ππ-⋃ 9.北宋徽宗在崇宁年间(1102年一1106 年)铸造崇宁通宝钱,因为崇宁通宝版别多样、铜质细腻、铸工精良,钱文为宋徽宗亲笔书写的“瘦金体”,所以后人写诗赞美日:“风流天子书崇观,铁线银钩字字端”.崇宁通宝被称为我国钱币铸造史上的一个巅峰铜钱直径3.5厘米,中间穿口为边长为0.9厘米的正方形.用一根细线把铜钱悬挂在树枝上,假定某位射手可以射中铜钱,但是射在什么位置是随机的(箭头的大小不计).这位射手射中穿口的概率最接近()1.6A 1.8B 1.10C 1.12D第9题图 第10题图 10.已知四棱锥S- ABCD 的底面是等腰梯形,AB// CD,AD= DC= BC= 1,AB =SA=2,且SA ⊥平面ABCD ,则四棱锥S - ABCD 的外接球的体积为( )A.8π 82.3B π .82C π 2.3D π 11.已知椭圆2222:1(0)x y E a b a b+=>>,直线20x -=与椭圆E 交于点P,与直线2(a x c c ==22a b -)交于点Q,O 为坐标原点,且2,OQ OP =u u u r u u r 则椭圆E 的离心率为() 1.2A 1.4B 3C 3D12.已知函数32()3f x x ax ax b =+++的图象在点(1,f(1))处的切线方程为y= -12x+ m,若函数f(x)至少有两个不同的零点,则实数b 的取值范围是()A.( -5,27)B.[-5,27]C.(-1,3]D.[-1,3] 二、填空题:本题共4小题,每小题5分,共20分.13.已知函数2,0,()(2),0,x e x f x f x x ⎧+≤=⎨->⎩则f(2020)=____14.已知点O 为坐标原点,向量(1,2),(,),OA OB x y ==u u u r u u u r 且10,OA OB ⋅=u u u r u u u r ||OB uuu r 的最小值____15.已知△ABC 中,角A,B,C 所对的边分别为a,b,c.满足2230,a c b ABC -+=V 的面积S =且A= 60°,则△ABC 的周长为____ 16.已知双曲线2222:1(0,0)x y C a b a b -=>>的左、右焦点分别为1212,,||10.F F F F =P 为双曲线右支上的一点,直线1PF 交y 轴于点M,交双曲线C 的一条渐近线于点N,且M 是1PF 的中点MN =u u u u r 2,NP uuu r 则双曲线C 的标准方程为____三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(12分)已知正项数列{}n a 的前n 项和为,n S 满足242n n n S a a =+.等比数列{}n b 满足1122,.a b a b ==( I )求数列{}n a 与数列{n b }的通项公式;(II )若,n n n c a b =⋅,求数列{}n c 的前n 项和.n T18.(12分)如图,已知四棱锥S- ABCD 的底面ABCD 为直角梯形,AB// CD,AD ⊥CD,且AB= AD= 1, SC=2,SD CD SA ===E 为SC 的中点.( I )求证: BE//平面SAD;(II)求平面SAD 与平面SBC 所成的锐二面角的正弦值.19.(12分)已知抛物线2:2(0)C x py p =>与直线l:y= kx+2交于A,B 两点,O 为坐标原点.当k= 1时,OA ⊥OB. ( I )求抛物线C 的标准方程;(II)点F 为抛物线C 的焦点,求△FAB 面积的最小值.20.(12分) 已知函数2()2(1)1x e x e f x x e x e--=+-++ (I)求函数f(x)的单调区间; (II)设函数2ln(1)()()2(1)1x F x f x x e x m x -=-++++-,若F(x)≤0对任意x> 1恒成立,求实数m 的取值范围.21.(12分)2019年6月6日,中国商务部正式下发5G 商用牌照,中国正式进入5G 商用元年.在5G 基站的建设中对零部件的要求非常严格,一次质检人员发现有1个次品部件混入了5个正品部件中.从外观看这6个部件是完全一-样的,5 个正品部件一样重,1 个次品部件略轻一些现有两个方案通过用电子秤称重的办法把次品部件挑出来.A 方案:逐一称重,称重一次不能确定是否是次品部件,称重两次,若重量相同则都是正品部件如果有1个较轻,则是次品部件,结束称重.依次进行,直到挑出次品部件. B 方案:把6个部件任意分成3组,每组2个,然后称重.(I)分析A,B两个方案,分别求出恰好称重3次挑出次品部件的概率;(II)如果称重一次需要2分钟,试比较A, B两个方案哪一个用时更少,并说明原因.(二)选考题:共10分.请考生在第22,23题中任选一题作答,如果多做,则按所做的第一题记分,作答时,请用2B铅笔在答题卡上将所选题号后的方框涂黑.22.[选修4-4:坐标系与参数方程](10分)在平面直角坐标系x0y中,已知直线l的参数方程为1cos1sinx ty tαα=+⎧⎨=+⎩(α∈R,t为参数).以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ+2cosθ=0.( I )求曲线C的直角坐标方程;(II)若曲线C上的点到直线l1,求tanα的值.23.[选修4-5:不等式选讲](10分)已知函数f(x)= |x+a| +|x-1|.( I )当a=2时,解关于x的不等式f(x)- x≥8;(II )若关于x的不等式f(x)≤|x-5|在[0,2]上恒成立,求实数a的取值范围.。
2020年百校联盟高考数学模拟试卷(理科)(4月份)(全国Ⅰ卷)(含答案解析)

2020年百校联盟高考数学模拟试卷(理科)(4月份)(全国Ⅰ卷)一、选择题(本大题共12小题,共60.0分)1.若复数z满足z−1+i=2i+1,则|z|=()A. √5B. 2C. √3D. 32.已知集合A={2a−1,a2,0},B={1−a,a−5,9},且A∩B={9},则()A. A={9,25,0}B. A={5,9,0}C. A={−7,9,0}D. A∪B={−7,9,0,25,−4}3.已知向量a⃗=(x2−2x,1),b⃗ =(1,−3),则“−1<x<3”是“a⃗,b⃗ 的夹角为钝角”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件4.将函数y=2sin(2x+π4)的图象向右平移π4个单位长度,所得函数()A. 在区间(−3π8,π8)上单调递增 B. 在区间(−5π8,−π8)上单调递减C. 以x=π8为一条对称轴 D. 以(3π8,0)为一个对称中心5.已知一个几何体的三视图如图所示,则此几何体的体积为()A. 8π3B. 8πC. 16π3D. 12π6.改编自中国神话故事的动画电影《哪吒之魔童降世》自7月26日首映,在不到一个月的时间,票房收入就超过了38亿元,创造了中国动画电影的神话.小明和同学相约去电影院观看《哪吒之魔童降世》,影院的三个放映厅分别在7:30,8:00,8:30开始放映,小明和同学大约在7:40至8:30之间到达影院,且他们到达影院的时间是随机的,那么他们到达后等待的时间不超过10分钟的概率是()A. 13B. 12C. 25D. 347.已知函数f(x)=log12(x2−ax+a)在(12,+∞)上为减函数,则实数a的取值范围是()A. (−∞,1]B. [−12,1] C. (−12,1] D. (−12,+∞)8.在平面直角坐标系xOy中,A、B为函数y=√33|x|图象上的两点,若线段AB的中点M恰好落在曲线x2−3y2+3=0上,则△OAB的面积为()A. 2B. √3C. √32D. √339.一只蚂蚁从正四面体A−BCD的顶点A点出发,沿着正四面体A−BCD的棱爬行,每秒爬一条棱,每次爬行的方向是随机的,则第4秒时蚂蚁在A点的概率为()A. 2027B. 79C. 727D. 2910.在梯形ABCD中,AB//CD,AB=2CD,BC=√3CD,则∠ADB的最大值为()A. π4B. π3C. π2D. 2π311.我国古代的数学著作《九章算术⋅商功》中,将底面是直角三角形的直三棱柱称为“堑堵”.在如图所示的“堑堵”ABC−A1B1C1中,AB=AC=AA1=2,M、N分别是BB1和A1C1的中点,则平面AMN截“堑堵”ABC−A1B1C1所得截面图形的面积为()A. 2√213B. 4√213C. 2√73D. 4√7312.已知函数f(x)=alnx−2x,若存在x∈N∗,使f(x)>0成立,则实数a的取值范围是()A. (2e,+∞)B. (4ln2,+∞) C. (6ln3,+∞) D. (2,+∞)二、填空题(本大题共4小题,共20.0分)13.若x,y满足约束条件{4x−3y−6≤02x−2y+1≥0x+2y−1≥0,则z=|x−y+1|的最大值为______.14.在(x2+x−1)(x−a)5的展开式中,含x5项的系数为14,则实数a的值为______.15.已知实数x,y满足y≥2x>0,则yx +9x2x+y的最小值为______.16.巳知F1、F2为双曲线x24−y2=1的左、右焦点,P为双曲线右支上异于顶点的任意一点,若△PF1F2内切圆的圆心为I,则圆心1到圆x2+(y−1)2=1上任意一点的距离的最小值为______.三、解答题(本大题共7小题,共82.0分)17.已知S n为数列{a n}的前n项和,S2=10,S n=n−1n+1a n+1+2(n∈N∗).(1)求数列{a n}的通项公式;(2)设b n=a n2n(n+1)!(n∈N∗),数列{bn}的前n项和为T n,求证:12≤T n<1.18.某市为了了解该市教师年龄分布情况,对年齡在[20,60]内的5000名教师进行了抽样统计,根据分层抽样的结果,统计员制作了如表的统计表格:年龄区间[20,30)[30,40)[40,50)[50,60]教师人数20001300样本人数130由于不小心,表格中部分数据被污染,看不清了,统计员只记得年龄在[20,30)的样本人数比年龄在[50,60]的样本人数多10,根据以上信息回答下列问题:(1)求该市年龄在[50,60]的教师人数;(2)试根据上表做出该市教师按照年龄的人数频率分布直方图,并求该市教师年龄的平均数x−及方差s2(同一组的数据用该组区间的中点值作代表).19.如图,将斜边长为4√2的等腰直角△ABC沿斜边BC上的高AD折成直二面角B−AD−C,E为AD中点.(1)求二面角A−BC−E的余弦值;(2)M为线段BC上一动点,当直线DM与平面BCE所成的角最大时,求三棱锥M−CDE外接球的体积.20.动圆P过定点A(2,0),且在y轴上截得的弦GH的长为4.(1)若动圆圆心P的轨迹为曲线C,求曲线C的方程;(2)在曲线C的对称轴上是否存在点Q,使过点Q的直线l′与曲线C的交点S、T满足1|QS|2+1|QT|2为定值?若存在,求出点Q的坐标及定值;若不存在,请说明理由.21.已知函数f(x)=ax+1x ,g(x)=exx−1.(1)讨论函数f(x)在(0,+∞)上的单调性;(2)当a=12时,设P(x,y)为函数y=ln x⋅g(x)−1x⋅f(x)−1(x∈(0,+∞))图象上任意一点.直线OP的斜率为k,求证:0<k<1.22.在平面直角坐标系xOy中,曲线C的参数方程为{x=1+cosθy=1+sinθ(θ为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为ρsin(φ+π4)+√2=0,P为直线l 上的任意一点(1)Q为曲线C上任意一点,求P、Q两点间的最小距离;.(2)过点P作曲线C的两条切线,切点为A、B,曲线C的对称中心为点C,求四边形PACB面积的最小值.23.若a>0,b>0,且2a+b+2=3ab.(1)求2a+b的最小值;(2)是否存在a、b,使得a3+b3=4√2?并说明理由.-------- 答案与解析 --------1.答案:A解析:解:∵z−1+i=2i+1,∴z=2+i,∴|z|=√22+12=√5,故选:A.先根据复数的基本运算求出复数z,再利用复数的模长公式即可算出结果.本题主要考查复数模长的计算,比较基础.2.答案:C解析:解:∵A∩B={9},∴9∈A,∴2a−1=9或a2=9,∴a=5或a=±3,①a=3时,A={5,9,0},B={−2,−2,9},集合B错误,不满足集合元素的互异性,∴a≠3;②a=−3时,A={−7,9,0},B={4,−8,9},满足A∩B={9},即a=−3成立;③a=5时,A={9,25,0},B={−4,0,9},A∩B={0,9},∴a=5不成立,综上得,A={−7,9,0},A∪B={−8,−7,0,4,9}.故选:C.根据条件可得出2a−1=9或a2=9,从而得出a=±3或a=5,然后对于每个a的值,求出A,B,看是否满足题意即可.本题考查了列举法的定义,交集、并集的定义及运算,元素与集合的关系,集合元素的互异性,考查看计算能力,属于基础题.3.答案:B解析:解:a⃗⋅b⃗ =x2−2x−3=(x−3)(x+1),当−1<x<3时,a⃗⋅b⃗ <0,此时a⃗,b⃗ 的夹角为钝角或平角,即充分性不成立,若a⃗,b⃗ 的夹角为钝角,则a⃗⋅b⃗ <0,得−1<x<3,即必要性成立,则“−1<x<3”是“a⃗,b⃗ 的夹角为钝角”的必要不充分条件,故选:B.根据向量数量积与夹角的关系,结合充分条件和必要条件的定义进行判断即可.本题主要考查充分条件和必要条件的判断,结合向量数量积与夹角的关系是解决本题的关键.比较基础.4.答案:B解析:解:函数y=2sin(2x+π4)的图象向右平移π4个单位长度,得到y=2sin(2x−π4),对于选项A:令−π2+2kπ≤2x−π4≤2kπ+π2(k∈Z),整理得:−π8+kπ≤x≤kπ+3π8(k∈Z),故单调增区间为:[−π8+kπ,kπ+3π8](k∈Z).故选项A错误.对于选项B:由于函数的最小正周期为π,所以单调递减区间为[−5π8+kπ,kπ−π8](k∈Z).当k=0时,在区间(−5π8,−π8)上单调递减,故正确.对于选项C:当x=π8时.2x−π4=0,所以函数没有取得最大或最小值,故错误.对于选项D:当x=3π8时,2x−π4=π2,所以f(3π8)=2≠0,故选项D错误.故选:B.首先利用三角函数关系式的恒等变换和平移变换的应用求出函数的关系式,进一步利用正弦型函数的性质的应用求出结果.本题考查的知识要点:三角函数关系式的变换,正弦型函数的性质的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.5.答案:B解析:解:根据三视图知,该几何体是一个圆柱,挖去一个半球和一个圆锥,结合三视图中的数据,计算该几何体的体积为V=V圆柱−V圆锥−V半球=π⋅22⋅4−13⋅π⋅22⋅2−12⋅4π3⋅23=8π.故选:B.根据三视图知该几何体是一个圆柱,挖去一个半球和一个圆锥,结合三视图中的数据计算该几何体的体积.本题考查了利用几何体的三视图求体积的问题,也考查了运算求解能力,是基础题.6.答案:C解析:解:由题意可知,满足条件的时间段为7:50~8:00,8:20~8:30共20分钟,由几何概型知所求的概率P=2050=25.故选:C.由满足条件的时间段为7:50~8:00,8:20~8:30共20分钟,结合与长度有关的几何概率公式可求.本题主要考查了与长度有关的几何概率公式的应用,属于基础试题.7.答案:B解析:解:∵y=log12x在(0,+∞)上为减函数,∴y=x2−ax+a在(12,+∞)上为增函数,且y>0恒成立,∴{−−a2≤12(12)2−12a+a≥0,解得−12≤a≤1.故选:B.由复合函数的单调性法则可知y =x 2−ax +a 在(12,+∞)上为增函数,由对数函数的真数大于0可知,y >0恒成立,则实数a 应满足{−−a2≤12(12)2−12a +a ≥0,解不等式组即可得到答案.本题主要考查复合函数的单调性法则以及对数函数的图象及性质,考查计算能力,属于基础题. 8.答案:B解析:解:设A(x 1,y 1),B(x 2,y 2),线段AB 的中点M(x,y), 由题意不妨设:x 1<0,x 2>0, ∵{x =x 1+x 22y =y 1+y 22,y═y 1+y 22=√33⋅x 2−x 12, 所以x 2−3y 2=x 1x 2,∴x 1x 2=−3,∵OA =√x 12+y 12=−2√33x 1,OB =2√33x 2,∠AOB =2π3,∴S △AOB =12OA ⋅OBsin∠AOB =−√33x 1x 2=√3.故选:B .设出AB 坐标,求出中点坐标,代入双曲线方程,利用已知条件,转化求解三角形的面积,推出结果即可.本题考查直线与双曲线的位置关系的应用,考查转化思想以及计算能力,是中档题. 9.答案:C解析:解:由题意可得,蚂蚁每次爬到下一个顶点的概率为13,设第n 秒时蚂蚁不在顶点A 的概率为P n ,易知P 1=1,则P n =23P n−1+1×(1−P n−1), ∴(P n −34)=−13(P n−1−34),∴数列{P n −34}是以14为首项,以−13为公比的等比数列, ∴P n −34=14×(−13)n−1, ∴P n =34−34×(−13)n ,n ∈N ∗,∴第4秒时蚂蚁在A 点的概率为1−P 4=1−2027=727, 故选:C .设第n 秒时蚂蚁不在顶点A 的概率为P n ,易知P 1=1,利用古典概型的的概率公式可得P n =23P n−1+1×(1−P n−1),即(P n −34)=−13(P n−1−34),再利用等比数列的通项公式求出P n 即可. 本题主要考查了古典概型的概率公式,是中档题.解析:解:设CD=a,则AB=2a,BC=√3a.取AB的中点M,延长AB到N点,使BN=a,连接CM,CN,由平面几何知识,易知AD=MC,BD=NC.设AD=MC=m,BD=NC=n.在△MBC中,m2=a2+(√3a)2−2×a×√3a⋅cos∠MBC,在△NBC中,n2=a2+(√3a)2−2×a×√3a⋅cos(π−∠MBC),∴m2+n2=8a2,在△ABD中,cos∠ADB=m2+n2−4a22mn =4a22mn,又2mn≤m2+n2=8a2,∴cos∠ADB=4a22mn ≥4a28a2=12,∴∠ADB的最大值为π3.故选:B.取AB的中点M,延长AB到N点,使BN=a,连接CM,CN,设CD=a,AD=m,BD=n,则AB=2a,BC=√3a,MC=m,NC=n,然后依次在△MBC和△NBC中利用余弦定理,借助∠MBC和∠NBC互补,可以得出m2+n2=8a2,再在△ABD中,利用余弦定理,表示出cos∠ADB,并结合基本不等式的性质即可求得其最大值.本题主要考查解三角形中的余弦定理,还涉及利用基本不等式求最值的问题,作出辅助线并利用互补的两个角的余弦值之和为0属于本题的难点,考查学生的分析能力和逻辑推理能力,属于中档题.11.答案:A解析:解:延长AN,与CC1的延长线交于点P,则P∈平面BB1C1C,连结PM,与B1C1交于点E,连结NE,得到的四边形AMEN是平面AMN截“堑堵”ABC−A1B1C1所得截面图形,由题意得NE=ME=√173,AM=AN=√5,MN=√6,∴AMN截“堑堵”ABC−A1B1C1所得截面图形面积为:S=12×√6×√(√5)2−(√62)2+12×√6×(√173)(√62)=2√213.故选:A.延长AN,与CC1的延长线交于点P,则P∈平面BB1C1C,连结PM,与B1C1交于点E,连结NE,得到的四边形AMEN是平面AMN截“堑堵”ABC−A1B1C1所得截面图形,由此能求出结果.本题考查平面截“堑堵”所得截面图形的面积的求法,考查“堑堵”性质、三角形面积公式等基础知识,考查运算求解能力,是中档题.解析:解:由题意可得alnx −2x >0, 当x =1时,−2>0不成立, 当x >1时,a >2xlnx , 设g(x)=2xlnx , 则g′(x)=2(lnx−1)ln 2x ,当x ∈(1,e)时,g′(x)<0,函数g(x)单调递减, 当x ∈(e,+∞)时,g′(x)>0,函数g(x)单调递增, ∵g(2)=4ln2,g(3)=6ln3, 又4ln3=ln81>ln64=6ln2, ∴4ln2>6ln3, ∴a >6ln3, 故选:C .由题意可得a >2xlnx ,设g(x)=2xlnx ,利用导数求出a 的范围即可.本题考查了函数的单调性,最值问题,考查导数的应用以及转化思想,是一道常规题.13.答案:2811解析:解:作出不等式组对应的平面区域如图: 令t =x −y +1,得y =x +1−t 表示,斜率为1纵截距为1−t 的一组平行直线,{4x −3y +6=0x +2y −1=0⇒C(1511,−211); 平移直线y =x +1−t ,当直线y =x +1−t 经过点C(1511,−211)时,直线y =x +1−t 的截距最小, 此时t max =1511−(−211)+1=2811,当直线y =x +1−t 与AB 重合时,直线y =x +1−t 的截距最大,A(0,12)此时t min =0−12+1=12,∴z =|x −y +1|的取值范围是:[12,2811]. 故z =|x −y +1|的最大值为2811.故答案为:2811.作出不等式组对应的平面区域,令t=x−y+1,利用目标函数t的几何意义,结合图象得到结论.本题主要考查线性规划的基本应用,利用数形结合,结合目标函数的几何意义是解决此类问题的基本方法.14.答案:−1或32解析:解:设(x−a)5的展开式中的通项T r+1=∁5r⋅x5−r⋅(−a)r,则当r=2时,T3=∁52⋅x3⋅(−a)2=10a2⋅x3;则当r=1时,T2=∁51⋅x4⋅(−a)1=−5ax4;则当r=0时,T1=∁50⋅x5⋅(−a)0=x5;∴(x2+x−1)(x−a)5的展开式中,含x5项的系数是:10a2−5a−1=14⇒a=−1或32;故答案为:−1或32.根据题意,利用(x−a)5的展开式中的通项T r+1=∁5r⋅x5−r⋅(−a)r,通过对r取值即可求得(x2+x−1)(x−a)5的展开式中,含x5项的系数进而求得结论.本题考查二项式定理,着重考查二项展开式中的通项公式的应用,考查分析与转化运算的能力,属于中档题.15.答案:174解析:解:设t=yx,由题意知t≥2,则yx+9x2x+y=t+9t+2,令f(t)=t+9t+2,t≥2,∵f′(x)=1−9(t+2)2>0,∴f(t)在t≥2上单调递增,∴f(t)≥f(2)=174,故答案为:174.先令t=yx ,可转化成f(t)=t+9t+2,t≥2,因为不满足不等式取等号时的条件,使用单调性求最值.本题考查导数求最值,使用不等式求最值时,注意取等号时的条件,属于中档题.16.答案:1解析:解:设△PF1F2的内切圆分别与PF1、PF2切于点A、B,与F1F2切于点M,则|PA|=|PB|,|F1A|=|F1M|,|F2B|=|F2M|.又点P在双曲线右支上,∴|PF1|−|PF2|=2a,即(|PA|+|F1A|)−(|PB|+|F2B|)=2a,∴|F1M|−|F2M|=2a,而|F1M|+|F2M|=2c,设M点坐标为(x,0),∵|F1M|−|F2M|=2a,∴(x+c)−(c−x)=2a,解得x=a,故内切圆的圆心I与在直线x=2上,故圆x2+(y−1)2=1上任意一点的距离的最小值为2−1=1故答案为:1.设△PF1F2的内切圆分别与PF1、PF2切于点A、B,与F1F2切于点M,则可知|PA|=|PB|,|F1A|=|F1M|,|F2B|=|F2M|,点P在双曲线右支上,根据双曲线的定义可得|PF1|−|PF2|=2a,因此|F1M|−|F2M|=2a,设M点坐标为(x,0),代入即可求得x,可得内切圆的圆心I与在直线x=2上,即可求解.本题考查圆与圆锥曲线的综合与双曲线的简单性质,难点在于“|PF1|−|PF2|=2a⇒|F1M|−|F2M|=2a”的分析与应用,着重考查双曲线的定义与性质的灵活运用,属于难题.17.答案:(1)解:由题意,当n=1时,a1=S1=2,∵S2=a1+a2=2+a2=10,∴a2=8,当n≥2时,由S n=n−1n+1a n+1+2,可得:S n−1=n−2na n+2,两式相减,可得:a n=S n−S n−1=n−1n+1a n+1+2−n−2na n−2,整理,得:a n+1 n+1=2⋅a nn(n≥2,n∈N∗),∴数列{a nn }从第二项a22=4开始是以2为公比的等比数列,∴a nn=4⋅2n−2=2n∴a n=n⋅2n(n≥2,n∈N∗),∵当n=1时,a1=2也满足上式,∴a n=n⋅2n,n∈N∗.(2)证明:由(1)知,b n=a n2n(n+1)!=n⋅2n2n⋅(n+1)!=n(n+1)!=1n!−1(n+1)!,则T n=b1+b2+⋯+b n=1−12!+12!−13!+⋯+1n!−1(n+1)!=1−1(n+1)!<1,∵b n=n(n+1)!>0,n∈N∗,∴由T n构造成的数列{T n}为单调递增数列,∴T n≥T1=12,∴12≤T n<1.解析:本题第(1)题先计算出a1,a2的值,再根据公式a n=S n−S n−1(n≥2),代入进行推导可得数列{a nn }从第二项a22=4开始是以2为公比的等比数列,通过计算出数列{a nn}的通项公式可得到数列{a n}的通项公式,最后将n=1代入验证最终可得数列{a n}的通项公式;第(2)题先根据第(1)题的结果计算出数列{b n}的通项公式,然后运用裂项相消法计算出前n项和T n,再根据放缩法和数列的单调性的应用即可证明结论.本题主要考查数列求通项公式,以及数列与不等式的综合问题.考查了转化与化归思想,构造法,裂项相消法求数列前n项和,放缩法,不等式的计算能力,逻辑推理能力和数学运算能力.本题属中档题.18.答案:解:(1)设样本容量为x,则x5000×1300=130,解得x=500.∴年龄在[30,40)的教师在样本中共有5005000×2000=200(人).∴年龄在[20,30)和[50,60)的教师在样本中共有500−200−130=170(人).设年龄在[50,60)的教师在样本中的人数为y,由题意知,y+(y+10)=170,则y=80.即该市年龄在[50,60]的教师人数为5000500×80=800;(2)由(1)可知,年龄在[20,30]的教师人数为5000−2000−1300−800=900(人),频率为9005000=0.18;年龄在[30,40]的教师人数为2000(人),频率为20005000=0.4;年龄在[40,50]的教师人数为1300(人),频率为13005000=0.26;年龄在[50,60]的教师人数为800(人),频率为9005000=0.18.由此作出频率分布直方图:x−=25×0.18+35×0.4+45×0.26+55×0.16=39;s2=(25−39)2×0.18+(35−39)2×0.4+(45−39)2×0.26+(55−39)2×0.16=92.解析:(1)设样本容量为x,由x5000×1300=130解得x,进一步求得年龄在[30,40)的教师在样本中的人数,可得年龄在[20,30)和[50,60)的教师在样本中的人数,再由题意列式求解;(2)分别求出各区间段的频率,即可画出频率分布直方图,再由期望与方差公式求该市教师年龄的平均数x−及方差s2.本题考查频率分布直方图,训练了利用频率分布直方图求期望与方程的估计值,考查计算能力,是中档题.19.答案:解:(1)设F为BC中点,连结EF,AF,∵△ABC为等腰直角三角形,且二面角B−AD−C为直二面角,∴BD⊥平面ADC,∴AD=BD=CD=2√2,AB=BC=CA=4,由平面几何可知,BE=CE=√10,∴EF⊥BC,AF⊥BC,∴∠EFA是二面角A−BC−E的平面角,在△EFA中,AE=√2,AF=√42−22=2√3,EF=√10−4=√6,∴cos∠EFA=EF2+AF2−AE22×EF×AF =1612√2=2√23,∴二面角A−BC−E的余弦值为2√23.(2)设直线DM与平面BCE所成角为α,点D到平面BCE的距离为d,则sinα=dDM,在三棱锥B−CDE中,S△BCE=12×BC×EF=2√6,由V B−CDE=V D−BCE,解得d=2√33当DM最小时,直线DM与平面BCE所成角的正弦值最大,此时所成角也最大,∴当M为BC中点时,直线DM与平面BCE所成角最大,此时DM=2,由平面几何知识可知,△CDE和△CME都是直角三角形,设N为CE的中点,则ND=NE=NC=NM=12CE=√102,∴三棱锥M−CDE的外接球的半径为R=√102,∴三棱锥M−CDE外接球的体积为:V=43π×(√102)3=5√103π.解析:(1)设F为BC中点,连结EF,AF,推导出BD⊥平面ADC,AD=BD=CD=2√2,AB=BC= CA=4,由平面几何可知,BE=CE=√10,从而EF⊥BC,AF⊥BC,进而∠EFA是二面角A−BC−E 的平面角,由此能求出二面角A−BC−E的余弦值.(2)设直线DM与平面BCE所成角为α,点D到平面BCE的距离为d,则sinα=dDM,由V B−CDE=V D−BCE,解得d=2√33当DM最小时,直线DM与平面BCE所成角的正弦值最大,此时所成角也最大,从而当M 为BC 中点时,直线DM 与平面BCE 所成角最大,此时DM =2,同此能求出三棱锥M −CDE 外接球的体积.本题考查二面角的余弦值、三棱锥外接球的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题. 20.答案:解:(1)设P(x,y),由题意知:PA =PG ,当P 点不在y 轴上时,过P 作PB ⊥GH ,交GH 于点B ,则B 为GH 的中点, ∴GB =12GH =2,∴PG =√x 2+4,又∵PA =√(x −2)2+y 2=√x 2+4,整理可得y 2=4x(x ≠0); 当点P 在y 轴上时,易知P 点与O 点重合,P(0,0)也满足y 2=4x , ∴曲线C 的方程为y 2=4x ,(2)假设存在Q(a,0)满足题意,设S(x 1,y 1),T(x 2,y 2),根据题意可知直线l′的斜率必不为0,设其方程为x =t 1y +a(t 1≠0),联立{x =t 1y +a y 2=4x ,整理可得y 2−4t 1y −4a =0,∴y 1+y 2=−4t 1,y 1y 2=−4a ,∴x 1+x 2=t 1(y 1+y 2)+2a =4t 12+2ax 1x 2=116y 12y 22=a 2,∵QS 2=(x 1−a)2+y 12=(x 1−a)2+4x 1=x 12+(4−2a)x 1+a 2,QT 2=(x 2−a)2+y 22=(x 2−a)2+4x 2=x 22+(4−2a)x 2+a 2,∴QS 2+QT 2=x 12+(4−2a)x 1+a 2+x 22+(4−2a)x 2+a 2=(x 1+x 2)2+(4−2a)(x 1+x 2)−2x 1x 2+2a 2=(x 1+x 2)(x 1+x 2+4−2a)−2x 1x 2+2a 2=(4t 12+2a)(4t 12++4),QS 2⋅QT 2=16a 2(t 12+1)2,则1|QS|+1|QT|=QS 2+QT 2QS ⋅QT =2t 12+a 2a (t 12+1),当a =2时,上式=14与t 1无关为定值,所以存在Q(2,0)使过点Q 的直线与曲线交于点S 、T 满足1|QS|2+1|QT|2为定值14.解析:(1)设P(x,y),过P 作PB ⊥GH ,交GH 于点B ,则B 为GH 的中点,GB =12GH =2,PG =√x 2+4,PA =√(x −2)2+y 2=√x 2+4,整理可得y 2=4x(x ≠0);(2)假设存在Q(a,0)满足题意,设S(x 1,y 1),T(x 2,y 2),设其方程为x =t 1y +a(t 1≠0),联立{x =t 1y +a y 2=4x,利用根与系数关系表示出QS 2,QT 2, 进而表示出1|QS|2+1|QT|2即可.本题考查动点轨迹方程的求法,考查韦达定理,考查换元法的应用,考查计算能力,属于中档题.21.答案:解:(1)∵f(x)=ax +1x ,∴f′(x)=a −1x 2=ax 2−1x 2,…1分;当a ≤0时,f′(x)<0,函数f(x)在(0,+∞)上的单调递减…2分; 当a >0时,由f′(x)=0,得x =±√1a =±√aa(舍负),…3分;当x ∈(0,√a a )时,f′(x)<0,函数f(x)单调递减;当x ∈(√aa ,+∞)时,f′(x)>0,函数f(x)单调递增;…5分(2)证明:由已知,即证0<y <x . ∵y =ln x⋅g(x)−1x⋅f(x)−1=lnx(e x x −1)−1x(12x+1x)−1=lne x −x−112x 2,∴即证0<lne x −x−112x 2<x …6分①设ℎ(x)=e x −x −1−12x 2,∴ℎ′(x)=e x −1−x ,ℎ″(x)=e x −1, ∵x ∈(0,+∞),∴ℎ″(x)=e x −1>0,∴ℎ′(x)=e x −1−x 为增函数. ∴ℎ′(x)=e x −1−x >ℎ′(0)=e 0−1=0, ∴ℎ(x)为增函数,∴ℎ(x)=e x−x −1−12x 2>ℎ(0)=0,即e x−x −1>12x 2,即x(e xx −1)−1x(12x+1x)−1>1,∴lnx(e x x −1)−1x(12x+1x)−1>0,即y >0,…9分②构造函数s(x)=e x −x −1−12x 2e x ,∵s′(x)=e x −1−xe x −12x 2e x ,∴s″(x)=−2xe x −12x 2e x<0,∴s′(x)在(0,+∞)上为减函数, ∴s′(x)<s′(0)=0,∴s(x)在(0,+∞)上为减函数,∴s(x)<s(0)=0, ∴e x−x −1<12x 2e x,即e x −x−112x 2<e x,即y =lne x −x−112x 2<x 成立.由①②可知,0<y <x ,∴0<k <1成立,…12分.解析:(1)由f′(x)=a −1x 2=ax 2−1x 2,分a ≤0与a >0两类讨论,即可求得函数f(x)在(0,+∞)上的单调区间;(2)由已知,即证0<y <x.由于y =lnx⋅g(x)−1x⋅f(x)−1=lnx(e xx −1)−1x(12x+1x)−1=lne x −x−112x 2,即证0<lne x −x−112x 2<x ,①设ℎ(x)=e x −x −1−12x 2;②构造函数s(x)=e x −x −1−12x 2e x ,利用导数研究由这两个函数的单调性及函数取值情况,即可证得0<k <1成立.本题考查导数的综合应用,涉及利用导数判断函数的单调性,考查分类讨论、构造函数、多次求导等方法,有一定综合性,考查学生的分析能力和逻辑推理能力,属于难题.22.答案:解:(1)曲线C 的参数方程为{x =1+cosθy =1+sinθ(θ为参数),转换为直角坐标方程为(x −1)2+(y −1)2=1.直线l 的极坐标方程为ρsin(φ+π4)+√2=0,转换为直角坐标方程为x +y +2=0. 所以圆心(1,1)到直线x +y +2=0的距离d =√2=2√2,所以最小距离d min =2√2−1.(2)由于圆心到直线的最小距离d =2√2, 所以构成的切线长为√(2√2)2−1=√7,×1×√7=√7.所以四边形PACB面积的最小值为S=2×12解析:(1)直接利用转换关系的应用,把参数方程极坐标方程和直角坐标方程之间的进行转换.(2)利用点到直线的距离公式的应用和三角形的面积公式的应用求出结果.本题考查的知识要点:参数方程极坐标方程和直角坐标方程之间的转换,点到直线的距离公式的应用,三角形面积公式的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.23.答案:解:(1)由3ab=2a+b+2≥2√2ab+2,得ab≥2,当且仅当2a=b=2时成立,所以2a+b=3ab−2≥6−2=4,当且仅当2a=b=2时成立,所以2a+b的最小值为4.(2)由(1)知a3+b3≥2√a3b3≥4√2,当且仅当2a=b=2,a=b时成立,因为2a=b=2,a=b不同时成立,所以a3+b3>4√2,不存在a,b使a3+b3=4√2成立.解析:根据基本不等式求解ab的值域,然后求解(1)(2).本题考查基本不等式,属于中等题.。
【2020年数学高考】安徽省2020届百校联盟TOP20四月联考(全国I卷)数学理.doc
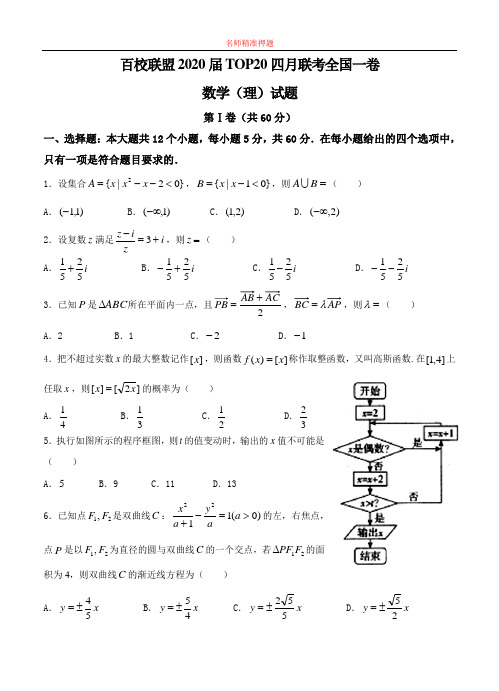
百校联盟2020届TOP20四月联考全国一卷数学(理)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合}02|{2<--=x x x A ,}01|{<-=x x B ,则=B A ( ) A .)1,1(- B .)1,(-∞ C .)2,1( D .)2,(-∞2.设复数z 满足i ziz +=-3,则=z ( ) A .i 5251+ B .i 5251+- C .i 5251- D .i 5251--3.已知P 是ABC ∆所在平面内一点,且2ACAB PB +=,AP BC λ=,则=λ( ) A .2 B .1 C .2- D .1-4.把不超过实数x 的最大整数记作][x ,则函数][)(x x f =称作取整函数,又叫高斯函数.在]4,1[上任取x ,则]2[][x x =的概率为( ) A .41 B .31 C .21 D .32 5.执行如图所示的程序框图,则t 的值变动时,输出的x 值不可能是( )A .5B .9C .11D .136.已知点21,F F 是双曲线C :)0(1122>=-+a ay a x 的左,右焦点,点P 是以21,F F 为直径的圆与双曲线C 的一个交点,若21F PF ∆的面积为4,则双曲线C 的渐近线方程为( ) A .x y 54±= B .x y 45±= C .x y 552±= D .x y 25±=7.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为( )A .58248++B .2424+C .2208+D .28 8.已知定义域为R 的函数)(x f 满足)()2(x f x f =-,且1≥x 时,22)(2+-+=x x x f x ,若0(6)2(log ><a a f a 且)1≠a ,则实数a 的取值范围是( )A.)2,1()1,21(B.),2()21,0(+∞C.)2,1()21,0( D.),2()1,21(+∞ 9.已知实数y x ,满足约束条件⎪⎩⎪⎨⎧≤--≥+-≥-+0220101y x y x y x ,若y mx z +=,z 的取值范围为集合A ,且]6,31[⊆A ,则实数m 的取值范围是( )A .]32,31[B .]32,911[-C .]31,911[-D .]6,32[10.已知数列}{n a 满足048,102141=+-<<a a a n ,且数列}4{22nn a a +是以8为公差的等差数列,设}{n a 的前n 项和为n S ,则满足10>n S 的n 的最小值为( )A .60B .61C .121D .12211.已知x A x f cos )(=,若直线π-=x y 2与)(x f 的图象有3个交点,且交点横坐标的最大值为t ,则( )A .1tan )(),,2(=-∈t t A ππB .1tan )2(),,2(=-+∞∈t t A ππC .1tan )(),,2(=-∈t t A ππD .1tan )2(),,2(=-+∞∈t t A ππ12.在三棱锥BCD A -中,BD AB DB AB DC DB AC AB ⊥=+==,4,,,则三棱锥BCD A -外接球的体积的最小值为( ) A .3264π B .332π C .328π D .34π二、填空题(每题4分,满分20分,将答案填在答题纸上)13.已知⎪⎩⎪⎨⎧≤+>-=1,11,11)(x x x x x f ,若)0)(1()1(>+=-a a f a f ,则实数a 的值为 .14.已知nx )3(+的展开式中所有偶数项系数之和为496,则展开式中第3项的系数为 . 15.已知B A ,是椭圆C 上关于原点对称的两点,若椭圆C 上存在点P ,使得直线PB PA ,斜率的绝对值之和为1,则椭圆C 的离心率的取值范围是 .16.已知四边形ABCD 中,133====DA CD BC AB ,设ABD ∆与BCD ∆面积分别为21,S S ,则2221S S +的最大值为 .三、解答题 (本大题共6题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知数列}{n a 满足31a a =,11232++=-n n n a a ,设n n n a b 2=. (1)求数列}{n b 的通项公式; (2)求数列}{n a 的前n 项和n S .18.每年的寒冷天气都会带热“御寒经济”,以餐饮业为例,当外面太冷时,不少人都会选择叫外卖上门,外卖商家的订单就会增加,下表是某餐饮店从外卖数据中抽取的5天的日平均气温与外卖订单数.(1)经过数据分析,一天内平均气温)(0C x 与该店外卖订单数y (份)成线性相关关系,试建立y关于x 的回归方程,并预测气温为C 012-时该店的外卖订单数(结果四舍五入保留整数); (2)天气预报预测未来一周内(七天),有3天日平均气温不高于C 010-,若把这7天的预测数据当成真实数据,则从这7天任意选取3天,预测外卖订单数不低于160份的天数为X ,求X 的分布列与期望.附注:回归方程a x b yˆˆˆ+=中斜率和截距的最小二乘估计公式分别为:x b y ax xy y x xbni ini i iˆˆ,)())((ˆ121-=---=∑∑==. 19.如图,在几何体ABCDEF 中,底面CDEF 是平行四边形,CD AB //,4,52,2,1====DF DE CD AB ,⊥DB 平面CDEF ,CE 与DF 交于点O .(1)求证://OB 平面ACF ;(2)若平面CAF 与平面DAF 所成的锐二面角余弦值为1030,求线段DB 的长度. 20.已知动圆M 与直线03=+x 相切,且与圆015822=+-+x y x 外切. (1)求动圆M 圆心轨迹C 的方程;(2)若直线l :m x y +=与曲线C 交于B A ,两点,且曲线C 上存在两点E D ,关于直线l 对称,求实数m 的取值范围及||||DE AB -的取值范围. 21.已知e ax x g ax e x f x -=-=2)(,)(.(1)若)(x f 的图象在1=x 处的切线与)(x g 的图象也相切,求实数a 的值;(2)若)()()(x g x f x F -=有两个不同的极值点)(,2121x x x x <,求证:2421a e e x x <.请考生在22、23二题中任选一题作答,如果都做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,直线l 的参数方程为⎩⎨⎧+=+=ααsin 1cos 1t y t x (t 为参数,πα<≤0),以原点O为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为θθρsin 2cos 2+=. (1)若直线l 过点)0,2(,求直线l 的极坐标方程;(2)若直线l 与曲线C 交于B A ,两点,求||||OB OA +的最大值. 23.选修4-5:不等式选讲 已知函数|2|)(2-+=x x x f . (1)解不等式||2)(x x f >;(2)若22232)(c b a x f ++≥(0,0,0>>>c b a )对任意R x ∈恒成立,求证:3227<⋅c ab .数 学(理科)参考答案一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.二、填空题:本大题共4小题,每小题5分,共20分. 把答案填在答题卡中对应题号后的横线上. 13.1 14.270 15.)1,23[16.87 三、解答题:本大题共70分,解答应写出文字说明、证明过程或演算步骤.17.解:(Ⅰ)由n nn a b 2=,得n n n b a 2=,代入11232++=-n n n a a 得 1112322+++=-n n n n a b ,即31=-+n n b b , 所以数列}{n b 是公差为3的等差数列, 又31a a =,所以8231b b =,即86211+=b b ,所以21=b , 所以13)1(31-=-+=n n b b n . (Ⅱ) 由13-=n b n 得nnn n n b a 2132-==, 所以n n n S 21328252232-++++=, 143221328252221+-++++=n n n S , 两式相减得113225325213)212121(3121+++-=--++++=n n n n n n S 所以nn n S 2535+-=. 18.(Ⅰ) 由题意可知65108642-=-----=x ,11051601401158550=++++=y ,40)4()2(024)(22222512=-+-+++=-∑=i ix x,55050)4(30)2(50)25(2)60(4))((1-=⨯-+⨯-+⨯+-⨯+-⨯=--∑=ni i iy y x x,所以75.1340550)())((ˆ12401-=-=---=∑∑==ni ini iix xy y x x b, 5.27)6(75.13110ˆˆ=-⨯+=-=x b y a, 所以y 关于x 的回归方程为5.2775.13ˆ+-=x y当12-=x 时,1935.1925.27)12(75.135.2775.13ˆ≈=+-⨯-=+-=x y. 所以可预测当平均气温为C 012-时,该店的外卖订单数为193份. (Ⅱ)由题意知,X 的取值可能为0,1,2,3.354)0(3734===C C X P ,3518)1(372413===C C C X P ,3512)2(371423===C C C X P ,351)3(3733===C C X P 所以X 的分布列为79351335122351813540)(=⨯+⨯+⨯+⨯=X E . 19.解:(Ⅰ)取CF 中点G ,连接OG AG ,, 在CDF ∆中,O 是DF 的中点,G 是CF 的中点, 所以CD OG CD OG 21,//=, 又2,1,===CD AB CD AB , 所以AB OG AB OG =,//所以四边形ABOG 为平行四边形, 所以AG OB //,又因为⊂AG 平面ACF ,⊄OB 平面ACF , 故//OB 平面ACF .(Ⅱ)由2=CD ,52==DE CF ,4=DF 可得222CF DF CD =+,所以DF CD ⊥,又⊥DB 平面CDEF ,故以D 为坐标原点,直线DB DC DF ,,分别为z y x ,,轴建立如图所示的空间直角坐标系xyz D -,则)0,0,0(D ,)0,0,4(F ,)0,2,0(C ,设a DB =,则),0,0(a B ,),1,0(a A , 所以)0,2,4(-=CF ,),1,4(a AF --=,)0,0,4(=DF . 设平面CAF 的一个法向量),,(111z y x m =,则⎪⎩⎪⎨⎧=⋅=⋅00AF m CF m 即⎩⎨⎧=--=-0402411111az y x y x ,取21=z 得)2,2,(a a m =,设平面DAF 的一个法向量),,(222z y x n =,则⎪⎩⎪⎨⎧=⋅=⋅00AF n DF n 即⎩⎨⎧=--=04042222az y x x ,取12=z 得)1,,0(a n -=,设平面CAF 与平面DAF 所成的锐二面角为θ, 则1030145|22|||||cos 222=++-==a a a n m n m θ, 整理得0281072524=+-a a , 解得42=a 或2572=a ,所以2=DB 或57.20.解:(Ⅰ)圆015822=+-+x y x 化为标准方程为1)4(22=+-y x ,设动圆M 圆心坐标为),(y x P ,由动圆M 与直线03=+x 相切,且与圆015822=+-+x y x 外切, 得41|3|)4(22+=++=+-x x y x , 两边平方整理得x y 162=.所以动圆M 圆心轨迹C 的方程为x y 162=. (Ⅱ)m x y +=与x y 162=联立得,0)162(22=+-+m x m x ,因为直线l 与曲线C 交于B A ,两点, 所以04)162(22>--m m ,解得4<m ,① 设),(),,(2211y x B y x A ,则16221+-=+m x x ,221m x x =, 所以m x x x x x x AB -=-+=-=4284)(2||2||2122121,因为点E D ,关于直线l 对称, 设直线DE 方程为n x y +-=,与x y 162=联立得,0)162(22=++-n x n x ,由04)162(22>-+n n ,得4->n , 设),(),,(4433y x E y x D ,DE 中点),(00y x G 则8,8200430-=+-=+=+=n x y n x x x , 因为点G 也在直线m x y +=上,所以m n ++=-88, 所以m n --=16,代入4->n 得12-<m ,②由①②得,实数m 的取值范围为)12,(--∞. 又12284284)(2||2||4324343--=+=-+=-=m n x x x x x x DE ,所以mm m m DE AB --+-=----=-1242128)124(28||||,因为12-<m ,所以4124>--+-m m , 所以23212421280<--+-<mm ,所以||||DE AB -的取值范围是)232,0(. 21.解:(Ⅰ) 因为ax e x f x -=)(,所以a e x f x-=)('所以a e f -=)1(,a e f -=)1(',所以)(x f 的图象在1=x 处的切线方程为)1)(()(--=--x a e a e y ,即x a e y )(-=,与e ax x g -=2)(联立得,0)(2=---e x a e ax ,因为直线x a e y )(-=与)(x g 的图象相切, 所以04)(2=+-ea a e ,解得e a -=.(Ⅱ) e ax ax e x g x f x F x +--=-=2)()()(,a ax e x F x --=2)(',若0≤a ,)('x F 是增函数,0)('=x F 最多有一个实根,)(x F 最多有一个极值点,不满足题意,所以0>a ,由题意知02,022121=--=--a ax ea ax e x x,两式相减得21212x x e e a x x --=,由21221222124212121212121x x e e x x e e ea ea ee x x x x x x x x x x x x --<⇔--<⇔<⇔<--++,设t x x =-221,则0<t , 要证2421a e e x x <,即证0<t 时,t e e t t212-<恒成立, 即te e tt 21--<恒成立,即02<---t e e t t 恒成立, 设t e e t h t t 2)(--=-,则02)('>-+=-t t e e t h ,所以)(t h 在)0,(-∞上是增函数,所以0)0()(=<h t h ,所以0<t 时,02<---t e e t t 恒成立,即2421a ee x x <.22.解:(Ⅰ)由直线l 过点)0,2(,得所以1tan -=α,结合πα<≤0, 得43πα=,所以直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧+=-=t y t x 221221(t 为参数),消去t ,得2=+y x , 把θρθρsin ,cos ==y x ,代入2=+y x 得直线l 的极坐标方程为2)sin (cos =+θθρ.(Ⅱ)曲线C 的普通方程为2)1()1(22=-+-y x ,所以曲线C 是以)1,1(为圆心且经过原点的圆, 因为直线l 过圆心)1,1(,所以OB OA ⊥,所以8||||22=+OB OA ,16|)||(|2||||2|||||)||(|2222=+≤⋅++=+OB OA OB OA OB OA OB OA所以4||||≤+OB OA (当且仅当2||||==OB OA 时取等号),故||||OB OA +的最大值为4.23.解:(Ⅰ) ||2|2|||2)(2x x x x x f >-+⇔> ⎩⎨⎧>-+≥⇔x x x x 2222或⎩⎨⎧>-+<<x x x x 22202或⎩⎨⎧->-+≤xx x x 22022>⇔x 或10<<x 或20>⇔≤x x 或1<x所以不等式||2)(x x f >的解集为),2()1,(+∞-∞ .(Ⅱ)当2≥x 时,42222)(22=-+≥-+=x x x f ,当2<x 时,4747)21(2)(22≥+-=+-=x x x x f ,所以)(x f 的最小值为47,因为22232)(c b a x f ++≥对任意R x ∈恒成立, 所以4732222≤++c b a , 又222222222442)(232abc bc ac c b c a c b a ≥+≥+++=++,且等号不能同时成立, 所以47242<abc ,即3227<⋅c ab .“”——。
河南省百校联盟2020届高三4月教学质量监测(理数)

河南省百校联盟2020届高三4月教学质量监测数 学(理科)注意事项:1.本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
2.答题前,考生务必将自己的姓名、准考证号填写在本试卷相应的位置。
3.全部答案写在答题卡上,写在本试卷上无效。
4.本试卷满分150分,测试时间120分钟。
5.考试范围:高考全部内容。
第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若复数z 满足z -1+i =2i +1,则|z|= 5 B.2 3 D.32.已知集合A ={2a -1,a 2,0},B ={1-a ,a -5,9},且A∩B ={9},则A.A ={9,25,0}B.A ={5,9,0}C.A ={-7,9,0}D.A ∪B ={-7,9,0,25,-4}3.已知向量a =(x 2-2x ,1),b =(1,-3),则“-1<x<3”是“a ,b 的夹角为钝角”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件4.将函数y =2sin(2x +4π)的图象向右平移4π个单位长度,所得函数 A.在区间(-38π,8π)上单调递增 B.在区间(-58π,-8π)上单调递减 C.以x =8π为一条对称轴 D.以(38π,0)为一个对称中心 5.已知一个几何体的三视图如图所示,则此几何体的体积为 A.83π B.8π C.163π D.12π6.改编自中国神话故事的动画电影《哪吒之魔童降世》自7月26日首映,在不到一个月的时间,票房收入就超过了38亿元,创造了中国动画电影的神话。
小明和同学相约去电影院观看《哪吒之魔童降世》,影院的三个放映厅分别在7:30,8:00,8:30开始放映,小明和同学大约在7:40至8:30之间到达影院,且他们到达影院的时间是随机的,那么他们到达后等待的时间不超过10分钟的概率是 A.13 B.12 C.25 D.347.已知函数()()122log f x x ax a =-+在(12,+∞)上为减函数,则实数a 的取值范围是 A.(-∞,1] B.[-12,1] C.(-12,1] D.(-12,+∞) 8.在平面直角坐标系xOy 中,A 、B 为函数y =3|x|图象上的两点,若线段AB 的中点M 恰好落在曲线x 2-3y 2+3=0上,则△OAB 的面积为A.2B.3C.32D.339.一只蚂蚁从正四面体A -BCD 的顶点A 点出发,沿着正四面体A -BCD 的棱爬行,每秒爬一条棱,每次爬行的方向是随机的,则第4秒时蚂蚁在A 点的概率为A.2027B.79C.727D.2910.在梯形ABCD 中,AB//CD ,AB =2CD ,BC =3CD ,则∠ADB 的最大值为A.4πB.3πC.2π D.23π 11.我国古代的数学著作《九章算术·商功》中,将底面是直角三角形的直三棱柱称为“堑堵”。
2020届全国大联考高三4月联考理科数学试题

2020届全国大联考高三4月联考理科数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题 1.不等式110x->成立的充分不必要条件是( ) A .1x >B .1x >-C .1x <-或01x <<D .10x -≤≤或1x >2.复数 12z i =+的共轭复数是z ,则z z ⋅=( )A B .3C .5D 3.已知随机变量()22,X N σ,若()130.36P X <<=,则()3P X ≥=( )A .0.64B .0.32C .0.36D .0.724.设,m n 是两条不同的直线,,αβ是两个不同的平面,由下列四个命题,其中正确的是( )A .若,m m n α⊥⊥,则//n αB .若//,//m n αα,则//m nC .若//,m αβα⊂,则//m β.D .若//m β,m α⊂,则//αβ.5.已知sin 32πα⎛⎫-=⎪⎝⎭cos 3πα⎛⎫+= ⎪⎝⎭( )A .2B .C .12D .-126.右图是计算某年级500名学生期末考试(满分为100分)及格率q 的程序框图,则图中空白框内应填入( )A .N q M=B .M q N=C .Nq M N=+D .Mq M N=+7.下图是某几何体的三视图,该几何体的体积为( )A .112B .16C .13D .128.设不等式组02201x y x y x -≤⎧⎪-+≥⎨⎪≥⎩表示的平面区域为w ,则( )A .w 的面积是92B .w 内的点到x 轴的距离有最大值C .点(,)A x y 在w 内时,22yx <+ D .若点00(,)p x y w ∈,则002x y +≠9.已知2313a ⎛⎫= ⎪⎝⎭,1314b ⎛⎫= ⎪⎝⎭,3log c π=,则a ,b ,c 的大小关系为( )A .a b c >>B .a c b >>C .c a b >>D .c b a >>10.函数()y f x =的定义域为R ,且()()()x f x f x a ϕ=-+,对任意0a <,()x ϕ在R 上是增函数,则函数()y f x =的图象可以是( )A .B .C .D .11.双曲线E :22221(0,0)x y a b a b-=>>的左、右焦点分别为12,F F ,过1F 作一条直线与两条渐近线分别相交于,A B 两点,若112F B F A =,122F F OB =,则双曲线的离心率为( )AB C .2 D .312.已知函数()()()2ln 110f x a x a x a =+-+<,在函数()f x 图象上任取两点,A B ,若直线AB 的斜率的绝对值都不小于5,则实数a 的取值范围是( )A .,0B .⎛-∞ ⎝⎦C .2,4⎛--∞- ⎝⎦D .2,04⎛⎫- ⎪ ⎪⎝⎭二、填空题13.已知()525012531x a a x a x a x -=+++⋅⋅⋅+,则135a a a ++=__________14.已知P 是抛物线24y x =上的动点,(A ,若点P 到y 轴的距离为1d ,点P 到点A 的距离为2d ,则12d d +的最小值是__________.15.已知定义在实数集R 上的函数()f x 满足(1)0f =,且()f x 的导函数()f x '满足()10f x '+<,则不等式(ln )ln 1f x x +>的解集为____________.(结果用区间..表示) 16.如图点P 是正方体1111ABCD A B C D -外的一点,过点P 作直线l ,记直线l 与直线1,AC BC 的夹角分别为12,θθ,若()()121sin 50cos 1402θθ︒︒-=-=,则满足条件的直线l 有________条.三、解答题17.在ABC ∆中,角,,A B C ,的对边分别为,,a b c ,且sin cos c A C =(1)求角C 的值(2)若6ABC S a b ∆=+=,求c 的值18.现有甲、乙两种不同规格的产品,其质量按测试指标分数进行划分,其中分数不小于82分的为合格品,否则为次品.现随机抽取两种产品各100件进行检测,其结果如下:(1)根据以上数据,完成下边的22⨯列联表,并判断是否有95%的有把握认为两种产品的质量有明显差异?(2)已知生产1件甲产品,若为合格品,则可盈利40元,若为次品,则亏损5元;生产1件乙产品,若为合格品,则可盈利50元,若为次品,则亏损10元.记X 为生产1件甲产品和1件乙产品所得的总利润,求随机变量X 的分布列和数学期望(将产品的合格率作为抽检一件这种产品为合格品的概率)参考公式:()()()()()()22n ad bc K n a b c d a b c d a c b d -===+++++++19.如图所示的多面体中,底面ABCD 为正方形,GAD ∆为等边三角形,BF ⊥平面ABCD ,90GDC ︒∠=,点E 是线段GC 上除两端点外的一点.(1)若点P 为线段GD 的中点,证明:AP ⊥平面GCD ; (2)若二面角B DE C --,试通过计算说明点E 的位置. 20.设1F 、2F 分别是椭圆222:14x y E b+=的左、右焦点.若P 是该椭圆上的一个动点,12PF PF 的最大值为1.(1)求椭圆E 的方程;(2)设直线:1l x ky =-与椭圆交于不同的两点A 、B ,且AOB ∠为锐角(其中O 为坐标原点),求直线l 的斜率k 的取值范围. 21.已知函数2()8ln ().f x x x a x a R =-+∈(1)当1x =时,()f x 取得极值,求a 的值并判断1x =是极大值点还是极小值点; (2)当函数()f x 有两个极值点1212,(),x x x x <且11x ≠时,总有21111ln (43)1a x t x x x >+--成立,求t 的取值范围.22.在平面直角坐标系xOy 中,直线l的参数方程为121x t y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数).以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,圆C 的极坐标方程为2sin ρθ=.()1判断直线l 与圆C 的交点个数;()2若圆C 与直线l 交于A ,B 两点,求线段AB 的长度.23.已知函数()53f x x x =--+. (1)解关于x 的不等式()1f x x +≥;(2)记函数()f x 的最大值为m ,若440,0,a b ab ma b e e e ->>⋅=,求ab 的最小值.参考答案1.A 【分析】 求解不等式110x->的解集,其充分不必要条件即该解集的真子集即可. 【详解】 解110x->,()10,10x x x x ->->, 得()(),01,x ∈-∞+∞,其充分不必要条件即该解集的真子集,结合四个选项A 符合题意. 故选:A 【点睛】此题考查充分不必要条件的辨析,关键在于准确求解分式不等式,根据充分条件和必要条件的集合关系判定. 2.C 【分析】根据 12z i =+,写出其共轭复数 12z i =-,即可求解. 【详解】由题 12z i =+,其共轭复数 12z i =-,()()21212145z z i i i ⋅=+-=-=.故选:C 【点睛】此题考查共轭复数的概念和复数的基本运算,关键在于熟练掌握复数的乘法运算. 3.B 【分析】根据正态分布密度曲线性质()3P X ≥=()()11130.322P X -<<=. 【详解】 由题:随机变量()22,X N σ,若()130.36P X <<=,则()3P X ≥=()()11130.322P X -<<=.故选:B 【点睛】此题考查根据正态分布密度曲线性质求解概率,关键在于熟练掌握正态分布密度曲线的相关性质,结合对称性求解. 4.C 【分析】A 选项可能n ⊂α,B 选项两条直线位置关系不能确定,C 选项正确,D 选项两个平面相交也能满足//m β,m α⊂. 【详解】A 选项,当,m m n α⊥⊥可能n ⊂α,所以该选项不正确;B 选项,平行于同一平面的两条直线可能平行,可能相交,可能异面,所以该选项不正确;C 选项,根据面面平行的性质,说法正确;D 选项,当两个平面相交,m α⊂且平行于交线,也满足//m β,m α⊂,所以不能推出面面平行. 故选:C 【点睛】此题考查空间点线面位置关系的辨析,根据已知条件判断线面平行,线线平行和面面平行,关键在于熟练掌握相关定理公理. 5.C 【解析】 因为=2[]3232πππαα⎛⎫+-- ⎪⎝⎭, 所以221cos 2cos []12sin 13232322πππαπαα⎛⎫⎛⎫⎛⎫+=---=--= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,故选C. 6.D 【解析】试题分析:程序执行的过程是如果 输入的成绩不小于60分即及格,就把变量M 的值增加1,即变量M 为成绩及格的人数,否则,由变量N 统计不及格的人数,但总人数由变量i 进行统计,不超过500就继续输入成绩,直到输入完500个成绩停止循环,输出变量q ,变量q 代表的含义为及格详细地址,也就是MM N=+及格人数总人数考点:程序框图. 7.B 【分析】借助正方体,根据三视图还原几何体,根据体积公式求解体积. 【详解】根据三视图,借助棱长为1的正方体,还原其几何体为图中11D A BB -, 其中平面11A BB 即为观察正面:所以该几何体的体积11111111326D A BB V -=⨯⨯⨯⨯= 故选:B 【点睛】此题考查三视图,根据三视图求几何体的体积,关键在于准确还原几何体,常借助正方体还原几何体. 8.C 【解析】 【分析】画出可行域,通过求出可行域的面积、可行域内点到x 轴的距离、可行域内点和()2,0-连线的斜率的范围、通过特殊点判断00x y +的值是否为2,根据四个结果判断四个选项的正误. 【详解】画出可行域如下图所示:有图可知,可行域面积是无限大的,可行域内的点到x 轴的距离也是没有最大值的,故,A B 两个选项错误.注意到()1,1在可行域内,而112+=,故D 选项错误.有图可知,可行域内的点和()2,0-连线的斜率比22y x =+的斜率要小,故C 选项正确.所以选C.【点睛】本小题主要考查线性规划的问题,考查方向有可行域的面积,点到直线的距离,两点连线的斜率还有特殊点等几个方向.属于基础题. 9.D 【分析】利用指数函数、对数函数的单调性直接求解. 【详解】解:因为22103331111013244a b ⎛⎫⎛⎫⎛⎫⎛⎫<=<==<= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,33log log 31c π=>=,所以a ,b ,c 的大小关系为c b a >>.故选:D. 【点睛】本题考查三个数的大小比较,考查指数函数、对数函数的单调性等基础知识,属于基础题. 10.A 【解析】 【分析】对于四个选项,举出对应的具体函数()f x ,然后利用函数的单调性验证()x ϕ是否在R 上递增,由此得出正确选项. 【详解】对于A 选项,取()2xf x =,则()()22222122xx ax a x a x x ϕ+=-=-⋅=-⋅,由于0a <,故120a ->,故()()122axx ϕ=-⋅为增函数,符合题意.对于B 选项,取()122xf x ⎛⎫=-+ ⎪⎝⎭,则()11111122222x a x a x x ϕ⎛⎫=-+⋅=-⋅ ⎪⎝⎭,由于10,102a a -,故()11122a x x ϕ⎛⎫=-⋅ ⎪⎝⎭为减函数,不符合题意.对于C 选项,取()3f x x =,则()()332233x x x a ax a x a ϕ=-+=---,这是一个开口向上的二次函数,在对称轴两侧单调性相反,不符合题意.对于D 选项,取()f x x =,则()x a ϕ=-,是常数函数,不符合题意.综上所述,选A.【点睛】本小题考查函数的图像与性质,考查利用特殊值法解选择题,考查了函数单调性.属于中档题. 11.C 【详解】如图所示,连接2F B ,又由122F F OB =,且O 为12F F 的中点,所以01290F BF ∆=,因为112F B F A =,即112F B F A =,所以A 为线段1F B 的中点, 又由于O 为12F F 的中点,所以2//OA F B ,所以1OA F B ⊥,所以1AOF AOB ∠=∠, 又由直线OA 与OB 是双曲线的两条渐近线,则12AOF BOF ∠=∠,所以0260BOF ∠=,则2tan bBOF a=∠=,所以双曲线的离心率为2c e a ===,故选C.【点睛】本题主要考查了双曲线的标准方程及其简单的几何性质的应用,其中解答本题的关键在于将问题的几何要素进行合理转化,得到,a b 的关系式,着重考查了推理与计算能力,属于中档试题. 12.B 【分析】求出导函数得该函数在定义域内单调递减,将问题转化为()()5g x f x x =+在()0,∞+上单调递减求参数的取值范围. 【详解】()()221'0a x af x x-+=<,在()0,∞+单调递减()()()()12112212,,,,5f x f x A x y B x y x x -≥-设120x x >>,则()()112255f x x f x x +≤+ 设()()5g x f x x =+,则()g x 在()0,∞+上单调递减则()()2215'0a x x ag x x-++=≤对()0,x ∈+∞恒成立则()22150a x x a -++≤对()0,x ∈+∞恒成立,因为0a <,()5041a ->-则0∆≤,即288250a a --≥解得a ≤24a +≥,又0a <,所以a ≤. 故选:B 【点睛】此题考查根据不等式恒成立求参数的取值范围,关键在于熟练掌握利用导函数讨论函数单调性解决恒成立问题,涉及转化与化归思想. 13.528 【分析】设()()525012531f x x a a x a x a x =-=+++⋅⋅⋅+,()()()135112a a f a f -+=+-,即可得解. 【详解】由题:设()()525012531f x x a a x a x a x =-=+++⋅⋅⋅+()()5012513132f a a a a =-=+++⋅⋅⋅+=, ()()550123451314f a a a a a a -=--=-+-+-=-()()()15351123241056a a a f f ++--==+=所以135a a a ++=528 故答案为:528 【点睛】此题考查求二项式展开式的系数关系,关键在于整体考虑,利用特殊值处理求解系数之和. 14.3 【分析】根据抛物线的几何性质P 到1x =-的距离为11d d PF =+=,121d d PA PF +=+-,即可求得最小值的情况. 【详解】抛物线24y x =的准线方程为1x =-,焦点坐标()1,0FP 到1x =-的距离为11d d PF =+=,所以121d d PA PF +=+-,其最小值为113AF -=, 当P 为AF 与抛物线交点时取得最小值. 故答案为:3 【点睛】此题考查抛物线的几何性质,根据几何性质关系求解抛物线相关的距离之和的最值问题,关键在于熟练掌握抛物线的几何性质,等价转化求解. 15.()0,e 【解析】 【分析】构造函数()()h x f x x =+,求导后利用已知条件得到函数()h x 的单调性,由此求得不等式()ln ln 1f x x +>的解集. 【详解】构造函数()()h x f x x =+,依题意可知()()10h x f x '+'=<,故函数()h x 在R 上单调递减,且()()1111h f =+=,故不等式()ln ln 1f x x +>可变为()()ln 1h x h >,即ln 1x <,解得()0,x e ∈. 【点睛】本小题主要考查利用函数导数求解不等式,考查构造函数法,属于中档题.在阅读题目过程中,()1f 提供一个函数值,()10f x '+<给的是函数导数小于零,这个可以说明一个函数是递减函数,由此可以考虑构造函数()()h x f x x =+,因为()()10h x f x '+'=<,就可以把已知和求串联起来了. 16.4 【分析】求出1280θθ==︒,将问题转化为求过某点作直线与已知两直线夹角相等的直线条数. 【详解】由题直线l 与直线1,AC BC 的夹角分别为12,0,2πθθ⎡⎤∈⎢⎥⎣⎦,()()121sin 50cos 1402θθ︒︒-=-=,所以1280θθ==︒直线1,AC BC 的夹角等于11AC B ∠记为θ,11tan tan 60AC B θθ=∠︒<<︒, 将直线1,AC BC 平移至过P ,如图所示,4560,22.530,609067.522θθθ︒<<︒︒<<︒︒<︒-<︒则过点P 作两条角平分线与两条直线的夹角均小于80°,所以满足题意的直线共四条,在经过角平分线且垂直于该平面内的两个平面内各两条. 故答案为:4 【点睛】此题考查异面直线夹角问题,关键在于根据题意求出1280θθ==︒,通过平移直线求满足夹角关系的直线数.17.(1)3C π=(2)c =【分析】(1)利用正弦定理原式化为sin sin cos C A A C =,即可得解;(2)根据面积公式得8ab =,结合余弦定理变形()2222cos c a b ab ab C =+--即可求解. 【详解】(1)在ABC ∆中,sin cos c A C =∴结合正弦定理得sin sin cos C A A C =0A π<< sin 0A ∴>又cos 0C ≠,tan 3C C π∴=∴=()23ABC S C π∆==1sin 2ab C ∴=8ab ∴=又6a b +=2222cos c a b ab C ∴=+-()222cos a b ab ab C =+--3616812.=--=c ∴=【点睛】此题考查利用正余弦定理解三角形,涉及三角形面积公式的应用,关键在于熟练掌握定理公式及其变形的应用.18.(1)填表见解析;没有95%的有把握认为两种产品的质量有明显差异(2)详见解析 【分析】(1)根据已知数据得出加甲乙产品数和合格品与次品数,根据公式计算2K 并下结论; (2)随机变量X 可能取值90,45,30,15-,分别计算概率并写出分布列,计算相关期望. 【详解】(1)列联表如下:()22200802575200.717 3.84110010015545K ⨯⨯-⨯=≈<⨯⨯⨯∴没有95%的有把握认为两种产品的质量有明显差异()2依题意,生产一件甲,乙产品为合格品的概率分别为43,54随机变量X 可能取值90,45,30,15-()43390545P X ==⨯=()133455420P X ==⨯=()41130545P X ==⨯=()111155420P X =-=⨯=X 的分布列为:()33119045301566520520E X ∴=⨯+⨯+⨯-⨯=【点睛】此题考查独立性检验和随机变量及其分布,根据已知数据完善列联表,计算2K ,离散型随机变量及其分布列的问题关键在于准确找出随机变量可能的取值,并准确求出其概率,根据公式计算期望.19.(1)证明见解析(2)E 为线段GC 的中点,详见解析 【分析】(1)通过证明AP GD ⊥,,CD AP ⊥即可得证;(2)建立空间直角坐标系,利用法向量解决二面角相关探索问题. 【详解】(1)因为GAD ∆是等边三角形,点P 为线段CD 的中点, 故,AP GD ⊥因为,AD CD GD CD ⊥⊥,且AD GD D ⋂=,故CD ⊥平面GAD 又AP ⊂平面GAD , 故,CD AP ⊥ 又CD GD D ⋂=, 故AP ⊥平面GCD .()2取AD 的中点O ,以OA 所在直线为x 轴,过O 点作平行于AB 的直线为y 轴,OG 所在直线为z 轴,建立如图所示的空间直角坐标系,设2AD =,则((),1,2,0G C -故(1,2,GC =-设()(),2,01GE GC λλλλ==-<<故(),2E λλ=-又()()()1,2,0,1,0,0,1,2,0B D C --故()1,2DE λλ=-,()2,2,0BD =--设(,,)m x y z =为平面BDE 的法向量,则·0·0m DE m BD ⎧=⎨=⎩故())120x y z x y λλ⎧-++=⎪⎨+=⎪⎩令1x =,故1,y z =-=故1,m ⎛=- ⎝为平面BDE 的一个法向量.由()1可知,3,0,22AP ⎛⎫=- ⎪ ⎪⎝⎭为平面DEC 的一个法向量,故7cos ,7m AP =,((33231λ=-+-311t λλ-=- 2322323tt -+=+214130,113t t t -+==或,解得1728λ=或,经检验知12λ=,此时点E 为线段GC 的中点 【点睛】此题考查证明线面垂直,根据二面角的大小求点的位置,关键在于熟练掌握判定定理,合理使用向量法求解二面角相关问题.20.(1)2214x y +=;(2)11(,)22-.【分析】(1)由标准方程可得()1F,)2F ,设(),P x y ,则可得222121244b PF PF x b ⎛⎫⋅=-+- ⎪⎝⎭,结合12PF PF ⋅有最大值1,得22114244b b ⎛⎫=-⨯+- ⎪⎝⎭,解得21b =,从而可得结果;(2)设()11,A x y ,()22,B x y ,由22114x ky x y =-⎧⎪⎨+=⎪⎩得()224230ky ky +--=,根据平面向量数量积公式结合AOB ∠为锐角,利用韦达定理可得221404k OA OB k-⋅=>+,从而可得结果. 【详解】(1)易知2a =,c ,24b <所以()1F,)2F ,设(),P x y ,则()12,PF PF x y ⋅=--,)22222222222,4412444b x b x y x y b x b b x b ⎛⎫-=+-+=+--+=-+- ⎪⎝⎭因为[]2,2x ∈-,故当2x =±,即点P 为椭圆长轴端点时,12PF PF ⋅有最大值1,即 22114244b b ⎛⎫=-⨯+- ⎪⎝⎭,解得21b =故所求的椭圆方程为2214x y +=.(2)设()11,A x y ,()22,B x y ,由22114x ky x y =-⎧⎪⎨+=⎪⎩得 ()224230ky ky +--=,故12224k y y k +=+,12234y y k -⋅=+. ()()222212416480k k k ∆=++=+>又AOB ∠为锐角cos 00AOB OA OB ⇔∠>⇔⋅>,∴12120OA OB x x y y ⋅=+>又()()()212121212111x x ky ky k y y k y y =--=-++ ∴()()()222121212122232111144k x x y y k y y k y y k k k-+=+-++=+⋅-+++ 222222332414044k k k k k k ---++-==>++, ∴214k <,解得1122k -<<∴k 的取值范围是11,22⎛⎫- ⎪⎝⎭. 【点睛】点睛:求参数取值范围常用的方法和思路:①直接法:直接根据题设条件构建关于参数的不等式,可列出相应的不等式组,再通过解不等式确定参数范围;②分离参数法:先将参数分离,转化成求函数值域问题加以解决.21.(Ⅰ)6a =,1x =为极大值点(Ⅱ)1t ≤-.【分析】(Ⅰ)求出函数的导数,求出a 的值,得到函数的单调区间,求出函数的极值点即可; (Ⅱ)求出函数极值点,问题转化为111x x -[2lnx 1211(1)t x x -+]>0,根据0<x 1<1时,111x x ->0.1<x 1<2时,111x x -<0.即h (x )=2lnx 2(1)t x x-+(0<x <2),通过讨论t 的范围求出函数的单调性,从而确定t 的范围即可.【详解】(Ⅰ)()228(0)x x a f x x x-+=>',()10f '=,则6a = 从而()()()213(0)x x f x x x --=>',所以()0,1x ∈时,()0f x '>,()f x 为增函数;()1,3x ∈时,()0f x '<,()f x 为减函数,所以1x =为极大值点.(Ⅱ)函数()f x 的定义域为()0,+∞,有两个极值点1x ,212()x x x <,则()2280t x x x a =-+=在()0,+∞上有两个不等的正实根,所以08a <<, 由12121242x x a x x x x +=⎧⎪⎪=⎨⎪<⎪⎩可得()1110224x a x x <<⎧⎨=-⎩ 从而问题转化为在102x <<,且11x ≠时()21111ln 431a x t x x x >+--成立. 即证()()111211124ln 431x x x t x x x ->+--成立. 即证()11112ln 11x x t x x >+- 即证()11112ln 101x x t x x -+>- 亦即证 ()21111112ln 01t x x x x x ⎡⎤-⎢⎥+>-⎢⎥⎣⎦. ① 令()()212ln (02)t x h x x x x -=+<<则()222(02)tx x t h x x x++<<'= 1)当0t ≥时,()0h x '>,则()h x 在()0,2上为增函数且()10h =,①式在()1,2上不成立.2)当0t <时,244t ∆=-若0∆≤,即1t ≤-时,()0h x '≤,所以()h x 在()0,2上为减函数且()10h =, 111x x -、()211112ln t x x x -+在区间()0,1及()1,2上同号,故①式成立. 若0∆>,即10t -<<时,22y tx x t =++的对称轴11x t=->, 令1min ,2a t ⎧⎫=-⎨⎬⎩⎭,则1x a <<时,()0h x >,不合题意.综上可知:1t ≤-满足题意.【点睛】本题考查了利用导数研究函数的单调性极值与最值、方程与不等式的解法、等价转化方法、分类讨论方法,考查了推理能力与计算能力,属于难题.22.()()1?22?2 【分析】(1)先求出直线的普通方程,再求出圆的直角坐标方程,由于圆心()0,1在直线l 上, 所以直线l 与圆C 的交点个数为2.(2)直接求圆的半径和直径得解.【详解】()1∵直线l的参数方程为1212x t y t ⎧=⎪⎪⎨⎪=-⎪⎩(t 为参数). ∴消去参数t 得直线l10y +-=,∵圆C 的极坐标方程为2sin ρθ=,即22sin ρρθ=,∴由222x y ρ=+,sin y ρθ=,得圆C 的直角坐标方程为2220x y y +-=.∵圆心()0,1在直线l 上,∴直线l 与圆C 的交点个数为2.()2由()1知圆心()0,1在直线l 上,∴AB 为圆C 的直径,∵圆C 的直角坐标方程为2220x y y +-=.∴圆C的半径1r ==,∴圆C 的直径为2,∴2AB =. 【点睛】(1)本题主要考查直线和圆的位置关系和弦长的计算,意在考查学生对这些知识的掌握水平和基本计算能力.(2)求直线和圆相交的弦长,一般解直角三角形,利用公式||AB =求解.但是本题由于圆心在直线上,所以弦长就是直径.23.(1)1,3⎛⎤-∞ ⎥⎝⎦(2)4 【解析】分析:(1)通过讨论x 的范围,解不等式,求出不等式的解集即可;(2)根据a >0,b >0,得到a 2)≥0.解出即可.详解:解:(1)当3x ≤-时,由531x x x -++≥+,得7x ≤,所以3x ≤-;当35x -<<时,由531x x x ---≥+ ,得13x ≤, 所以133x -<≤; 当5x ≥时,由531x x x ---≥+ ,得9x ≤-,无解. 综上可知,13x ≤,即不等式()1f x x ≥+的解集为1,3⎛⎤-∞ ⎥⎝⎦. (2)因为53538x x x x --+≤---=,所以函数()f x 的最大值8m =.因为448·a b ab e e e -=,所以448a b ab +=-.又0,0a b >>,所以4a b +≥=所以480ab --≥,即20ab ≥.所以有)120≥.0>2,4ab ≥≥,即ab 的最小值为4.点睛:|x -a |+|x -b |≥c (或≤c )(c >0),|x -a |-|x -b |≤c (或≤c )(c >0)型不等式的解法, 零点分区间法的一般步骤①令每个绝对值符号的代数式为零,并求出相应的根;②将这些根按从小到大排列,把实数集分为若干个区间;③由所分区间去掉绝对值符号得若干个不等式,解这些不等式,求出解集;④取各个不等式解集的并集就是原不等式的解集.。
百校联盟2020届高三4月教育教学质量监测考试(全国Ⅰ卷)数学(理)试卷(有答案)

百校联盟2020届高三4月教育教学质量监测考试(全国Ⅰ卷)数学(理)试卷注意事项:1.本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
2.答题前,考生务必将自己的姓名、准考证号填写在本试卷相应的位置。
3.全部答案写在答题卡上,写在本试卷上无效。
4.本试卷满分150分,测试时间120分钟。
5.考试范围:高考全部内容。
第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若复数z 满足z -1+i =2i +1,则|z|=B.2 D.32.已知集合A ={2a -1,a 2,0},B ={1-a ,a -5,9},且A ∩B ={9},则A.A ={9,25,0}B.A ={5,9,0}C.A ={-7,9,0}D.A ∪B ={-7,9,0,25,-4}3.已知向量a =(x 2-2x ,1),b =(1,-3),则“-1<x<3”是“a ,b 的夹角为钝角”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件4.将函数y =2sin(2x +)的图象向右平移个单位长度,所得函数 A.在区间(-,)上单调递增 B.在区间(-,-)上单调递减 C.以x =为一条对称轴 D.以(,0)为一个对称中心5.已知一个几何体的三视图如图所示,则此几何体的体积为4π4π38π8π58π8π8π38πA. B.8π C. D.12π 6.改编自中国神话故事的动画电影《哪吒之魔童降世》自7月26日首映,在不到一个月的时间,票房收入就超过了38亿元,创造了中国动画电影的神话。
小明和同学相约去电影院观看《哪吒之魔童降世》,影院的三个放映厅分别在7:30,8:00,8:30开始放映,小明和同学大约在7:40至8:30之间到达影院,且他们到达影院的时间是随机的,那么他们到达后等待的时间不超过10分钟的概率是A. B. C. D. 7.已知函数在(,+∞)上为减函数,则实数a 的取值范围是 A.(-∞,1] B.[-,1] C.(-,1] D.(-,+∞) 8.在平面直角坐标系xOy 中,A 、B 为函数y|x|图象上的两点,若线段AB 的中点M 恰好落在曲线x 2-3y 2+3=0上,则△OAB 的面积为A.29.一只蚂蚁从正四面体A-BCD 的顶点A 点出发,沿着正四面体A -BCD 的棱爬行,每秒爬一条棱,每次爬行的方向是随机的,则第4秒时蚂蚁在A 点的概率为A. B. C. D. 10.在梯形ABCD 中,AB//CD ,AB =2CD ,BC CD ,则∠ADB 的最大值为A. B. C. D. 11.我国古代的数学著作《九章算术·商功》中,将底面是直角三角形的直三棱柱称为“堑堵”。
百师联盟2020届高三理数模拟试卷四(全国卷Ⅰ)附答案
第 1 页 共 4 页百师联盟2020届高三理数模拟试卷四(全国卷Ⅰ)一、选择题:本题共12小题,每小题5分,共60分。
(共12题;共60分)1.若用列举法表示集合 A ={(x,y)|{2x +y =6x −y =3} ,则下列表示正确的是( )A. {x=3,y=0}B. {(3,0)}C. {3,0}D. {0,3} 2.已知复数z=5i 3+i,则 z̅ =( )A. −12+32iB. −12−32i C. 12+32i D. 12−32i3.新高考改革后,某校2000名学生参加物理学考,该校学生物理成绩的频率分布直方图如图所示,若规定分数达到90分以上为A 级,则该校学生物理成绩达到A 级的人数是( )A. 600B. 300C. 60D. 304.掷硬币实验是很常见却又非常有名的一个概率实验,许多著名的科学家都做过这个实验,比如蒲丰、德摩根等.通过掷硬币的实验,可以让人们感受到随机事件的发生,形成可能性的概率观念.若抛掷一枚硬币出现正面向上记为1,反面向上记为0.现抛掷一枚硬币6次,出现两个0和四个1的概率为( ) A. 1564B. 516C. 916 D. 585.已知凸四边形ABCD 的面积为S ,点P 是四边形内部任意一点,若点P 到四条边AB ,BC ,CD ,DA 的距离分别为d 1 , d 2 , d 3 , d 4 , 且满足 AB 1=BC 2=CD 3=DA 4=k ,利用分割法可得d 1+2d 2+3d 3+4d 4=2S k;类比以上性质,体积为V 的三棱锥P-ABC ,点Q 是三棱锥内部任意一点,Q 到平面PAB ,PBC ,PAC ,ABC 的距离分别为D 1 , D 2 , D 3 , D 4 , 若S ΔPAB 1=S ΔPBC 2=S ΔPAC 3=S ΔABC 4=K ,则D 1+2D 2+3D 3+4D 4=( )A. VK B. 2V K C. 3VK D. 4VK 6.已知F 1 , F 2是椭圆C :x 2a 2+y 2b 2=1 (a>b>0)的两个焦点,C 的上顶点A 在圆(x-2)2+(y-1)2=4上,若∠F 1AF 2= 2π3,则椭圆C 的标准方程为( )A. x 22+y 2=1 B.x 24+y 23=1 C.x 24+y 2=1 D.x 23+y 2=17.如图是某几何体的三视图,其中正视图和侧视图均为矩形,俯视图由半圆和直角三角形组成,则该几何体的表面积为( )A. 6π+12B. 10π+36C. 5π+36D. 6π+18 8.执行如图所示的程序框图,则输出的a=( )A. - 32B. - 13C. 2D. -29.已知函数f (x )=sinπx6cos πx6- √3 sin 2 πx6+ √32,x ∈[-1,a],a ∈N*,若函数f (x )图象与直线y=1至少有2个交点,则a 的最小值为( )A. 7B. 9C. 11D. 1210.在如图所示的圆锥中,平面ABC 是轴截面,底面圆O'的面积为4π,∠ABC= π3 ,则该圆锥的外接球的表面积为( )A.64π3B.16π3C.128π3D. 32π11.已知点P是双曲线C:x2a2−y2=1(a>1)上的动点,点M为圆O:x2+y2=1上的动点,且OM⃗⃗⃗⃗⃗⃗ ⋅PM⃗⃗⃗⃗⃗⃗ =0,若|PM|的最小值为√3,则双曲线C的离心率为()A.5√33B. √3C. √52D. √512.已知f(x)是定义在R上的偶函数,且满足f(x)=f(2-x),当x∈[0,1]时,f(x)=x·2x.则方程f(x)-|lgx|=0的根的个数为()A. 99B. 100C. 198D. 200二、填空题:本题共4小题,每小题5分,共20分。
百校联盟2020届高考复习全程精练模拟卷理科数全国卷1模拟答案解析(5页)

a !M
]
N
O
*%#'
# #
c
d
e
f
g
&&#%&!'%
&#%!'%+NO)&#'c d e f g&"%#'%&!%('%+ N O)&#'%#!#'&##&#:KLhi$ 2 j!
0!2
!!
" "k
j
l &# !
&
) #
'1
mnl:oj$
+,'#
%,,1&#!
'1&,&&
) #
', %,,1
&# !
'1&,
&&)',#1&!,%p
1
& !, %
& #%[
, % *%+
# #
j
:
q
O
$
,*1&#!'1&*&&)'*%!44)(!
1!5 !!""#$Qr s Q r %&*%0'S t%& ' u, % &!-%)-'!M +%#*%[ &!-%)-'+
&&(%#'%#*%[ &1-%#*%! [ -% &!!+ %
) *
%""2"$2""%
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020届百校联盟 top20高三四月联考(全国i 卷) 数学(理)试题一、单选题1.已知集合{}29A x x =∈≤Z ,{}ln 1B x x =<,则A B =I ( ) A .{}0e x x << B .{}1,2C .{}0,1,2,3D .{}3,2,1,0,1,2---【答案】B【解析】解一元二次不等式、对数不等式化简集合,A B 的表示,结合集合交集的定义进行求解即可. 【详解】集合{}3,2,1,0,1,2,3A =---,集合{}0B x x e =<<,故{}1,2A B =I . 故选:B 【点睛】本题考查了集合交集的定义,考查了一元二次不等式、对数不等式的解法,考查了数学运算能力. 2.已知复数i1im z =-(m ∈R ),若满足1z ≤,则复数z 的虚部取值范围为( )A .[]1,1-B .11,22⎡⎤-⎢⎥⎣⎦C .22⎡-⎢⎣⎦D .⎡⎣【答案】C【解析】运用复数的除法的运算法则化简复数z 的表示,根据复数模的定义,结合已知条件进行求解即可. 【详解】由题意知i i 1i 22m m m z ==-+-,1z ==≤即m ≤≤z 的虚部,222m ⎡∈-⎢⎣⎦.故选:C本题考查了复数的除法运算法则、复数模的计算公式,考查了数学运算能力.3.支付宝和微信支付已经成为现如今最流行的电子支付方式,某市通过随机询问100名居民(男女居民各50名)喜欢支付宝支付还是微信支付,得到如下的22⨯列联表:附表及公式:()()()()()22n ad bc K a b c d a c b d -=++++,n a b c d =+++.则下面结论正确的是( )A .有99.9%以上的把握认为“支付方式与性别有关”B .在犯错误的概率超过1%的前提下,认为“支付方式与性别有关”C .在犯错误的概率不超过1%的前提下,认为“支付方式与性别有关”D .有99%以上的把握认为“支付方式与性别无关” 【答案】C【解析】根据题中所给的公式和列联表计算出2K 的值,然后根据观测值的比较进行求解即可. 【详解】由22⨯列联表得到40a =,10b =,25c =,25d =,则代入()()()()()22n ad bc K a b c d a c b d -=++++,解得2K 的观测值()210010002509.8950506535k ⨯-=≈⨯⨯⨯.因为6.6359.8910.828<<,所以有99%以上的把握认为“支付方式与性别有关”. 故选:C本题考查了2K 的计算,属于基础题.4.已知曲线C :221x y m n+=表示焦点在y 轴上且离心率大于2的双曲线,则下列不等关系正确的是( ) A .0m n +> B .0m n +< C .0m n -> D .20m n ->【答案】B【解析】根据曲线方程表示焦点在y 轴的双曲线,得到,m n 的正负性,再根据双曲线的离心率,结合不等式的性质进行求解即可. 【详解】由题意知0m <,0n >,又因为212m e n =->,故1mn->,即0m n +<. 故选:B 【点睛】本题考查了已知曲线表示双曲线求参数取值范围,考查了双曲线离心率公式,考查了不等式的性质,考查了数学运算能力.5.执行如图所示的程序框图,则输出结果为( )A .32B .64C .128D .256【答案】C【解析】先判断后执行循环体,可以判断出程序的功能,最后求值即可. 【详解】阅读程序框图知,因为234560222222100S =++++++≥,故最后输出128.【点睛】本题考查了循环结构的输出问题,考查了数学运算能力.6.已知两个锐角α,β(αβ<),且tan α,tan β为方程2401310x x -+=的两根,如果钝角γ的始边与x 轴正半轴重合,终边经过点()2,1-,则αβγ+-=( ) A .4π- B .23π-C .34π-D .4π 【答案】C【解析】根据一元二次方程根与系数关系,结合两角和与差的正切公式、正切的定义,特殊角的三角函数值进行求解即可. 【详解】由tan α,tan β为方程2401310x x -+=的两根,解得1tan 8α=,1tan 5β=,则()11185tan 13140αβ++==-,又1tan 2γ=-,则()1132tan 1116αβγ++-==-.因为 06παβ<+<,56πγπ<<,则23ππαβγ-<+-<-,故34παβγ+-=-. 故选:C 【点睛】本题考查了两角和与差的正切公式,考查了正切函数的定义,考查了数学运算能力. 7.设等差数列{}n a 的前n 项和为n S ,且满足20180S >,20190S <,记n n b a =,则n b 最小时,n 的值为( ) A .1009 B .1010C .1011D .2019【答案】B【解析】根据等差数列的前n 项和公式,结合等差数列的下标性质、绝对值的性质进行求解即可. 【详解】由2019101020190S a =<,10100a <;由()120182018201802a a S +=>,即101010090a a +>,10101009a a >-,故10091010a a >.故选:B 【点睛】本题考查了等差数列的前n 项和公式,考查了等差数列的下标性质,考查了绝对值的性质,考查了数列最小项问题,考查了数学运算能力.8.某几何体的三视图如图所示,则该几何体的体积为( )A .83B .3C .103D .113【答案】C【解析】由三视图可知; 该几何体为一个直三棱柱削去一个三棱锥,运用棱柱和棱锥的体积公式进行求解即可. 【详解】如图,该几何体为一个直三棱柱削去一个三棱锥,故体积为11111022222223223⨯⨯⨯-⨯⨯⨯⨯⨯=. 故选:C【点睛】本题考查了由三视图还原空间几何体求体积问题,考查了棱柱和棱锥的体积公式,考查了空间想象能力和数学运算能力.9.已知()()()()1521501215111x a a a x a x a x +=+-+-+⋅⋅⋅+-中0a >,若13945a =-,则a 的值为()A .2B .3C .4D .5【答案】A【解析】根据()1515[(1)(1)]x a a x +=--++-利用二项展开式的通项公式、二项式系数的性质、以及13945a =-,即可求得a 的值,得到答案. 【详解】由题意,二项式()()()()1521501215111x a a a x a x a x +=+-+-+⋅⋅⋅+-,又由()1515[(1)(1)]x a a x +=--++-,所以()()()2151501215[(1)(1)]111a x a a x a x a x --++-=+-+-+⋅⋅⋅+-,其中0a >,由13945a =-,可得:1321315[(1)]945a C a =-⋅-+=-,即2105(1)945a -+=-,即2(1)9a +=,解得2a =, 故选A . 【点睛】本题主要考查了二项式定理的应用,二项展开式的通项公式,二项式系数的性质,其中解答中熟记二项展开式的通项及性质是解答的关键,着重考查了推理与运算能力,属于中档试题.10.设抛物线C :22y px =(0p >)的焦点为F ,已知P ,Q ,T 为抛物线C 上三个动点,且满足F 为PQT ∆的重心,PQT ∆三边PQ ,PT ,TQ 的中点分别为1M ,2M ,3M ,分别过1M ,2M ,3M 作抛物线C 准线的垂线,垂足分别为1N ,2N ,3N ,若11223312M N M N M N ++=,则p =( ) A .2 B .3 C .4 D .6【答案】C【解析】设P ,Q ,T 的横坐标分别为1x ,1x ,1x ,过点P ,Q 作抛物线C 准线的垂线,垂足分别为1P ,1Q ,运用梯形中位线定理,结合抛物线的定义求出11M N 的表达式,同理求出2233,M N M N 的表达式,最后利用已知进行求解即可.【详解】设P ,Q ,T 的横坐标分别为1x ,1x ,1x ,过点P ,Q 作抛物线C 准线的垂线,垂足分别为1P ,1Q ,在梯形11PPQ Q 中,11112PP QQ M N +=,由抛物线定义知1PP PF =,1QQ QF =,故112PF TFM N +=. 同理可知222PF TF M N +=,332TF QFM N +=, 故11223312M N M N M N PF QF TF ++=++=.再由焦半径公式可得1233122x x x p +++=,又123132x x x p ++=,故312p =,解得4p =. 故选:C【点睛】本题考查了抛物线的定义的应用,考查了梯形中位线定理,考查了数学运算能力. 11.函数()f x 在定义域R 内的导函数为()f x ',若4()(),(2),(1)f x f x a e f b ef '>=-=,(2)c f =,A .a c b >>B .b a c >>C .a b c >>D .c b a >>【答案】D 【解析】由题得()[]0x f x e '>,设()()xf xg x e=,得函数g(x)在R 上是增函数,再利用函数的单调性分析得解. 【详解】由题得()()0,f x f x '-> 所以()e ()e 0,x x f x f x '-> 所以()[]0x f x e '>,设()()xf xg x e =,所以函数g(x)在R 上是增函数, 所以(2)(1)(2)g g g >>-, 所以212(2)(1)(2)f f f e e e-->>, 所以c b a >>. 故选:D 【点睛】本题主要考查导数的运算和性质,考查函数的单调性,意在考查学生对这些知识的理解掌握水平和分析推理能力.12.如图,在三棱锥A BCD -中,AB ⊥平面BCD ,BC CD ⊥,2AB BD ==,M 为AD 中点,H 为线段AC 上一点(除AC 的中点外),且MH HB ⊥.当三棱锥M HAB -的体积最大时,则三棱锥M ABC -的外接球表面积为( )A .4πB .6πC .8πD .12π【答案】B【解析】利用线面垂直的判定定理和性质,可以证明AM ⊥平面BHM ,利用三棱锥的等积性,结合基本不等式,这样可以求出1BH HM ==,过点C 作CK BD ⊥,取AB ,AC 的中点T ,N ,连接MN ,MT ,过点T 作CK 的平行线交MN 于点O .利用线面垂直的性质和判定定理可以证明出O 为三棱锥M ABC -的外接球的球心,运用正切函数的定义,球的表面积公式进行求解即可. 【详解】在Rt ABD ∆中,因为M 为AD 中点,故BM AD ⊥,且2BM =CD BC ⊥,CD AB ⊥,所以CD ⊥平面ABC ,故CD BH ⊥,又因为MH BH ⊥,所以BH ⊥平面ACD ,因此BH AD ⊥,故AM ⊥平面BHM ,三棱锥M HAB -的体积等于三棱锥A BHM -的体积,即只需底面BHM ∆面积最大即可.因为2222BH HM BM +==,则22BH HM ≥⋅,故1122BHM S BH HM ∆=⋅≤,当且仅当1BH HM ==时取等号.在Rt ABC ∆中,30CAB ∠=︒,故3BC =,过点C 作CK BD ⊥,取AB ,AC 的中点T ,N ,连接MN ,MT ,过点T 作CK 的平行线交MN 于点O .由CK ⊥平面ABD 知OT ⊥平面ABD .又DC ⊥平面ABC ,故MN ⊥平面ABC .因此O 为三棱锥M ABC -的外接球的球心,由tan tan tan 2CDTOM KCD CBK BC∠=∠=∠==,因为1TM =,所以2tan 2TM OT TOM ==∠,故2232R OA ==,即三棱锥M ABC -的外接球表面积为6π.故选:B【点睛】本题考查三棱锥外接球的表面积问题,考查了基本不等式的应用,考查了线面垂直的判定定理和性质,考查了数学运算能力.二、填空题13.已知向量()1,a t =-r ,()1,2b =r,且()2a b b +⊥r r r ,则实数t 的值为______.【答案】92-【解析】根据平面向量加法、数乘、数量积的坐标表示公式,结合两个平面向量垂直的性质进行求解即可. 【详解】由题意知()21,4a b t +=+r r ,再由()2a b b +⊥r r r 得290t +=,解得92t =-.故答案为:92-【点睛】本题考查了平面向量加法、数乘、数量积的坐标表示公式,考查了两个平面向量垂直的性质,考查了数学运算能力.14.设数列{}n a 的前n 项和为n S ,若21n n S a +=,则使不等式427m a ≥(m *∈N )成立的m 最大值为______. 【答案】3【解析】对递推关系21n n S a +=再递推一步,得到新的等式,两个等式相减,结合等比数列的定义进行求解即可. 【详解】当1n =时,111231S a a +==,故113a =;当2n ≥时,1121,21,n n n n S a S a --+=⎧⎨+=⎩两式相减得123n n a a -=.故数列{}n a 为首项为13,公比为23的等比数列,故11233n n a -⎛⎫=⋅ ⎪⎝⎭,故12341237m -⎛⎫⋅ ⎪⎝⎭≥,即12439m -⎛⎫ ⎪≥⎝⎭,则3m ≤,故m 的最大值为3. 故答案为:3 【点睛】本题考查了由数列递推公式求数列通项公式,考查了等比数列的定义,考查了数学运算能力.15.设函数()22sin sin 3f x x x πωω⎛⎫=+⎪⎝⎭(0>ω),若()f x 在区间0,24π⎛⎫⎪⎝⎭上单调递增,则下列说法中正确的是______(填所有正确选项的序号). ①存在ω使得函数()f x 为奇函数;②函数()f x 的最大值为12;③ω的取值范围为(]0,4;④存在4个不同的ω使得函数()f x 的图象关于2x π=对称. 【答案】②③④【解析】根据正弦型函数的单调性、奇偶性、对称性进行逐一判断即可. 【详解】由题意()212sin sin sin 2362f x x x x ππωωω⎛⎫⎛⎫=+=+- ⎪ ⎪⎝⎭⎝⎭,显然不存在ω使得函数()f x 为奇函数,故①错误;()12f x ≤,故②正确;由于()f x 在区间0,24π⎛⎫⎪⎝⎭上单调递增,故26221262k k ππππππωπ⎧≥-+⎪⎪⎨⎪+≤+⎪⎩(k ∈Z ),解得04ω<≤,故③正确:;令62m πππωπ+=+,m ∈Z ,解得13m ω=+,由04ω<≤知ω的取值为13,43,73,103,故④正确. 故答案为:②③④ 【点睛】本题考查了正弦型函数的单调性、奇偶性、最值、对称性,考查了数学运算能力. 16.已知函数()ln xf x x=,函数()y g x =与()y f x =的图象关于原点对称,若函数()222log e G x g x m e x ⎛⎫=+++ ⎪⎝⎭(e 为自然对数的底数)有4个不同的零点,则实数m 的取值范围为______.【答案】()(),4222,e e -∞---+∞U【解析】根据对称性可以求出()y g x =的解析式,对该函数进行求导,判断单调性,利用换元法,结合基本不等式、双勾函数的单调性,最后求出实数m 的取值范围. 【详解】由题意知()()()ln xg x f x x =--=-,()()()2ln 1ln x g x x --'=-⎡⎤⎣⎦,当()1,0x ∈-时,()0g x '<,()g x 单调递减且()0g x >;当(),1x e ∈--时,()0g x '<,()g x 单调递减;当(),e -∞-时,()0g x '>,()g x 单调递增.令(][)2,,22,e t x m t m e m e x=++∈-∞-++∞U ,由()()()224ln 2g t g g =-=-=-,故2t =-或4t =-.由2e t x m x =++图象知22m e ->-或24m e +<-,解得22m e >-或42m e <--.故答案为:22m e >-或42m e <-- 【点睛】本题考查了利用对称性求函数的解析式,考查了已知函数零点的个数求参数取值范围问题,考查了数学运算能力.三、解答题17.在ABC ∆中,三个内角A ,B ,C 的对边分别为a ,b ,c ,若22tan tan b A a B =,22sin 1cos 22A BC +=+. (1)求角A 的大小;(2)若点D 为AB 边上一点,满足45BCD ∠=︒且CD =ABC ∆的面积.【答案】(1)30A =︒;(2)【解析】(1)根据降幂公式,结合三角形内角和定理,通过解一元二次方程,结合特殊角的余弦值、正弦定理、同角三角函数关系式中商关系进行求解即可;(2)由(1),可以得知ABC ∆为等腰三角形,顶角120C =︒,由ABC ∆的面积建立等式关系,结合三角形面积公式进行求解即可. 【详解】 (1)由22sin1cos 22A BC +=+得()21cos 2cos A B C -+=, 即22cos cos 10C C --=,解得1cos 2C =-, 故120C =︒. 根据正弦定理知sin sin a b A B=,代入22tan tan b A a B =得22sin sin sin sin cos cos A BB A A B⋅=⋅, 即sin cos sin cos A A B B =,故sin 2sin 2A B =, 因此A B =或90A B +=︒(舍去),故30A =︒. (2)由(1)知ABC ∆为等腰三角形,顶角120C =︒. 设BC AC m ==,由ABC BCD ACD S S S ∆∆∆=+, 即2111sin120sin 45sin 75222m m CD m CD ⋅︒=⋅⋅︒+⋅⋅︒,(32CD ⎛=⋅+== ⎝⎭,解得m =故21sin120332ABC S m ∆=⋅︒=. 【点睛】本题考查了降幂公式,考查了三角形面积公式,考查了正弦定理,考查了同角三角函数关系式中的商关系,考查了数学运算能力.18.如图,在平行六面体1111ABCD A B C D -中,1B A ⊥底面ABCD ,12BB BC AB ==,60ABC ∠=︒.(1)求证:1AB A D ⊥;(2)求二面角1A A D C --的余弦值.【答案】(1)见解析;(210【解析】(1)连接11A C ,1C D ,AC ,通过勾股定理得到AB AC ⊥,再由条件推得1AB C D ⊥进而得到线面垂直,线线垂直;(2)建立坐标系,分别求得两个面的法向量,进而求得夹角的余弦值. 【详解】(1)连接11A C ,1C D ,AC ,以为原几何体是平行六面体,故得到1111AA CC AC CA=∴P 是平行四边形,进而得到11AC AC ∥,因为2BC AB =且60ABC ∠=︒, 在三角形ABC 中由余弦定理得到边22222122AC AB BC AB BC BC AB =+-⨯⨯=-,222AB AC BC AB AC ∴+=∴⊥,进而得到11AB A C ⊥,又因为1B A ⊥底面ABCD ,1111,B A AB B A C D AB C D ∴⊥∴⊥Q P1111AC C D C AB ⋂=∴⊥面11AC D .1AB A D ∴⊥.(2)根据题干,以及第一问可建立如图坐标系:设122BB BC AB ===,13AB =,()()1,0,0,0,0,0B A,()()10,0,3,0,3,0B C 根据()1111,0,3A B AB A =⇒-,设面1AA D 的法向量为(),,n x y z =r()()11,0,3,1,3,0AA AD BC =-==-u u u r u u u r u u u r()303,1,130x z n x y ⎧-+=⎪⇒=⎨-+=⎪⎩v设面1A CD 的法向量为(),,m x y z =u r()1,0,0AB DC ==u u u r u u u r ,()11,3,3CA =--u u u r ,()00,1,1330x m x y z =⎧⎪⇒=⎨--+=⎪⎩v则两个半平面的夹角余弦值为:10cos .5||||n m n m θ⋅==⋅r u r r u u r【点睛】这个题目考查了空间中直线和面的位置关系的应用,涉及线面垂直的性质的应用,以及线线垂直的证明,和二面角的求法,一般求二面角,可以利用几何方法,做出二面角,或者建立空间坐标系得到法向量进而求得二面角的大小.19.已知椭圆C :22221x y a b+=(0a b >>)的左,右焦点为1F ,2F ,且焦距为3点2B ,1B 分别为椭圆C 的上、下顶点,满足111212111212B F B F B B B F B F B B +=u u u u r u u u u r u u u u r u u u u r u u u u r u u u u r . (1)求椭圆C 的方程;(2)已知点()2,0E -,椭圆C 上的两个动点M ,N 满足EM EN ⊥,求证:直线MN 过定点.【答案】(1)2214x y +=;(2)见解析【解析】(1)设111111B F B FB F =u u u u ru u u u r u u u u r ,121212B F B F B F =u u u u r u u u u r u u u u r ,121212B B B B B B =u u u u ru u u ur u u u u r ,结合已知的向量表达式,根据平面向量加法的几何意义可知四边形1122B F B F '''为菱形,结合已知条件进行求解即可;(2)根据直线MN 是否存在斜率进行分类讨论.设直线MN 的方程,与椭圆方程联立,结合一元二次方程根与系数的关系,结合两平面向量垂直的性质进行求解即可. 【详解】(1)设111111B F B F B F =u u u u ru u u u r u u u u r ,121212B F B F B F =u u u u r u u u u r u u u u r ,121212B B B B B B =u u u u ru u u ur u u u u r , 由1112121112121B F B F B B B F B F B B ===u u u u r u u u u r u u u u r u u u u r u u u u ru u u u r 可知四边形1122B F B F '''为菱形且11260F B B ''∠=︒, 故33=,解得1b =,故2a =, 椭圆C 的方程为2214x y +=.(2)当直线MN 斜率存在时,设MN :y kx m =+,()11,M x y ,()22,N x y .联立2244y kx m x y =+⎧⎨+=⎩消去y 得 ()222148440k xkmx m +++-=,()()()222222641611416140k m m k k m ∆=--+=+->,122814km x x k +=-+,21224414m x x k -=+, 由EM EN ⊥,则0EM EN ⋅=u u u u r u u u r, 即()()1212220x x y y +++=, 整理得()()()2212121240kx x km x x m++++++=,将122814km x x k +=-+,21224414m x x k-=+代入整理得22121650k km m -+=, 即()()2650k m k m --=, 解得2m k =或65m k =. 当2m k =时,直线MN :2y kx k =+过点E ,舍去; 当65m k =时,直线MN :65y kx k =+过定点6,05⎛⎫- ⎪⎝⎭. 当直线MN 斜率不存在时,不妨设()11,M x y ,()11,N x y -, 则由EM EN ⊥,则0EM EN ⋅=u u u u r u u u r,即()221120x y +-=,即()22112104x x ⎛⎫+--= ⎪⎝⎭,即211516120x x ++=,解得12x =-(舍去)或165x =-,也过定点6,05⎛⎫- ⎪⎝⎭. 综上,直线MN 过定点6,05⎛⎫- ⎪⎝⎭. 【点睛】本题考查了平面向量加法的几何意义,考查求椭圆的标准方程,考查了直线与椭圆的位置关系,考查了椭圆中直线过定点问题,考查了数学运算能力,考查了分类讨论思想. 20.新疆小南瓜以沙甜闻名全国,小田计划从新疆运输小南瓜去上海,随机从某瓜农的瓜地里挑选了100个,其质量分别在[)100,200,[)200,300,[)300,400,[)400,500,[)500,600,[]600,700(单位:克)中,经统计得频率分布直方图如图所示,将频率视为概率.(1)请根据频率分布直方图估计该瓜农的小南瓜的平均质量;(2)已知瓜地里还有2万个小南瓜已经成熟,可以采摘,小田想全部购买,可是瓜农要求超过400克的小南瓜以5元一个的价格出售,其他的以3元一个的价格出售.将频率视为概率,若新疆到上海往返的运费约2000元,请问这2万个小南瓜在上海以每斤(500克)多少元定价才能保证小田的利润不少于5000元?(结果保留一位小数) (3)某天王阿姨在上海某超市的蔬菜柜台上看到小田从新疆采摘的新疆小南瓜,已知柜台上有若干个,若质量超过500克的小南瓜为“优质品”,王阿姨随机购买了20个小南瓜,求王阿姨购买的小南瓜中“优质品”个数的期望. 【答案】(1)415克;(2)至少定价每斤5.6元;(3)5【解析】(1)根据每组取中点为代表,根据平均数的定义进行求解即可;(2)求出每个小南瓜质量超过400克的概率,再求出2万个小南瓜中质量超过400克的个数,最后结合已知条件进行求解即可;(3)由频率分布直方图可求出小南瓜质量超过500克的概率,结合二项分布的性质进行求解即可. 【详解】(1)小南瓜的平均质量为1500.12500.13500.154500.45500.26500.05415⨯+⨯+⨯+⨯+⨯+⨯=(克)(2)每个小南瓜质量超过400克的概率为0.65, 故2万个小南瓜中质量超过400克的个数为13000个,价值为130********⨯=(元),质量低于400克的价值为7000321000⨯=(元), 则小田运到上海总的费用为6500021000200088000++=(元). 由(1)知,2万个小南瓜的总质量为2000041550016600⨯÷=(斤), 因为8800050005.616600+≈,所以小田至少定价每斤5.6元才能保证利润不少于5000元.(3)由频率分布直方图知,小南瓜质量超过500克的概率0.25P =,由题意知,王阿姨购买的小南瓜中“优质品”个数X 服从二项分布()20,0.25B , 则()200.255E X =⨯=,故王阿姨购买的小南瓜中“优质品”个数的期望为5. 【点睛】本题考查了二项分布的性质,考查了利用频率直方图求平均数,考查了数学运算能力.21.已知函数()2e ,02,0x m x f x x x x ⎧+≤=⎨-+>⎩(e 为自然对数的底数).(1)当1m =-时,设()()g x xf x =,求()g x 的单调区间;(2)若()f x 的图象在两点()()11,P x f x ,()()22,Q x f x (120x x ≤<)处的切线重合,求证:314m -≤<. 【答案】(1)增区间40,3⎛⎫ ⎪⎝⎭,减区间(),0-∞,4,3⎛⎫+∞⎪⎝⎭;(2)见解析 【解析】(1)求出函数()g x 的解析式,然后分类讨论,结合导数进行求解即可; (2)根据题意,利用导数求出两点处切线的斜率,再求出Q 点处的切线方程,这样可以得到()()2222222ln 2222m x x x x =-+-++-+,通过换元法,构造函数,再求导,求出新函数的单调性,利用单调性进行求解即可. 【详解】(1)由题意知()32e ,0,2,0,x x x x g x x x x ⎧-≤=⎨-+>⎩ 当0x ≤时,()()1e 10xg x x '=+-≤,故()g x 在(),0-∞上单调递减;当0x >时,()234g x x x '=-+,故()g x 在40,3⎛⎫ ⎪⎝⎭上单调递增,在4,3⎛⎫+∞ ⎪⎝⎭上单调递减.(2)由题意知()11e xf x '=,()2222f x x '=-+,则(]12e 220,1xx =-+∈,Q 点处的切线方程为()()22222222y x x x x x =-+--+,则有()()1221222e 222xm x x x x x +=-++-+,将12e 22xx =-+代入整理得()()2222222ln 2222m x x x x =-+-++-+,令(]2220,1t x =-+∈,则2ln 214t m t t t =-++,令()2ln 214t G t t t t =-++((]0,1t ∈),则()ln 102tG t t '=-+<, 故()G t 在(]0,1上单调递减, 故()()314G t G ≥=-, 又因为()1ln 204t G t t t ⎛⎫-=-+< ⎪⎝⎭, 所以()1G t <,即3,14m ⎡⎫∈-⎪⎢⎣⎭. 【点睛】本题考查了利用导数求函数的单调性,考查了曲线的切线求法,考查了数学运算能力.22.在平面直角坐标系xOy 中,直线l的参数方程是1212x t y ⎧=-⎪⎪⎨⎪=+⎪⎩(t 为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程是4πρθ⎛⎫=+⎪⎝⎭. (1)证明:直线l 与曲线C 相切;(2)设直线l 与x 轴、y 轴分别交于点A ,B ,点P 是曲线C 上任意一点,求22PA PB +的取值范围.【答案】(1)见解析;(2)[]4,8【解析】(1)利用加减消元法把直线l 化成普通方程,再根据极坐标与直角坐标互化公式把曲线C 化成直角坐标方程形式,最后通过圆心到直线的距离进行证明即可;(2)由(Ⅰ)知()2,0A ,()0,2B ,设点P坐标为11cos ,sin 2222θθ⎛⎫++ ⎪ ⎪⎝⎭,根据两点间距离公式,结合辅助角公式进行求解即可. 【详解】(1)直线l 的普通方程为20x y +-=, 根据cos x ρθ=,sin y ρθ=,222x y ρ+=,代入得曲线C 的直角坐标方程为220x y x y +--=, 即22111222x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭,圆心为11,22C ⎛⎫ ⎪⎝⎭,半径为2,圆心C 到直线l 的距离d ==, 故直线l 与曲线C 相切.(2)由(Ⅰ)知()2,0A ,()0,2B ,设点P 坐标为11cos ,sin 2222θθ⎛⎫++ ⎪ ⎪⎝⎭, 22231cos 2222PA θθ⎛⎫⎛⎫=-++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭32θθ-=+2221322PB θθ⎛⎫⎫=+- ⎪⎪ ⎪⎪⎝⎭⎝⎭32θθ-=+,则)226sin cos PA PB θθ+=+[]62sin 4,84πθ⎛⎫=-+∈ ⎪⎝⎭,故22PA PB +的取值范围为[]4,8.【点睛】本题考查了参数方程、极坐标方程化成普通直角坐标方程,考查了辅助角公式的应用,考查了数学运算能力. 23.已知函数()4f x x x a a=+--(0a >) (1)求证:()4f x ≥;(2)当4a =时,解不等式()9f x ≥. 【答案】(1)见解析;(2)(][),27,-∞-+∞U第 21 页 共 21 页 【解析】(1)利用绝对值的性质进行求解即可;(2)利用绝对值的性质把函数()f x 的解析式化简为分段函数的形式,最后分类讨论求解即可.【详解】(1)()4f x x x a a=+-- 444x x a a a a≥-++=+≥(当且仅当2a =且()40x x -≤时“=”成立), 故()4f x ≥成立.(2)当4a =时,()5f x x x =+-52,0,5,05,25,5,x x x x x -≤⎧⎪=<<⎨⎪-≥⎩则0529x x ≤⎧⎨-≥⎩或5,259,x x ≥⎧⎨-≥⎩ 解得2x -≤或7x ≥,故()9f x ≥的解集为(][),27,-∞-+∞U .【点睛】本题考查了绝对值的性质,考查了解绝对值不等式,考查了数学运算能力.。
