江南十校2019届高三第一次联考
精品解析:【校级联考】安徽省江南十校2019届高三3月综合素质检测理科综合物理试题(解析版)

安徽省“江南十校”2019年综合素质检测理科综合能力测试物理试卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、考号、考试科目涂写在答题卡上。
2.第Ⅰ卷每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试卷上。
3.考试结束,监考人只将答题卡收回。
一、选择题1.下列说法中正确的是A. 光电效应揭示了光的粒子性B. 用光子能量为11.0eV的光照射时,可使处于基态的氢原子跃迁到激发态C. 氡原子核的半衰期为3.8天,4个氡原子核经过7.6天一定只剩下1个未发生衰变D. 研究原子的结构是从发现放射性现象开始的【答案】A【解析】【详解】A:光电效应揭示了光的粒子性,故A项正确。
B:在基态时氢原子能量,在n=2激发态时氢原子能量,在n=3激发态时氢原子能量;n=2激发态氢原子与基态氢原子间的能量差,n=3激发态氢原子与基态氢原子间的能量差;氢原子跃迁时吸收(或放出)光子能量需等于两个能级的能量差,,用光子能量为11.0eV的光照射时,处于基态的氢原子不会跃迁。
故B项错误。
C:半衰期描述的是统计规律,少量原子核发生衰变时不一定遵守。
故C项错误。
D:研究原子核的结构是从发现放射性现象开始的,故D项错误。
2.将固定在水平地面上的斜面分为四等份,如图所示,AB=BC=CD=DE,在斜面的底端A点有一个小滑块以初速度v0沿斜面向上运动,刚好能到达斜面顶端E点。
则小滑块向上运动经过D点时速度大小是A. B. C. D.【答案】D【解析】【分析】根据题中“在斜面的底端A点有一个小滑块以初速度v0沿斜面向上运动,刚好能到达斜面顶端E点”可知,本题考察匀减速直线运动。
根据匀减速直线运动的规律,应用逆向思维法、速度位移公式等知识分析求解。
【详解】将末速度为零的匀减速直线运动看作初速度为零的匀加速直线运动,则、,又,解得:。
故D项正确,ABC三项错误。
3.如图所示,游乐场中有一半球形的碗状装置固定在水平地面上,装置的内半径为R,在其内表面有一个小孩(可视为质点)从底部向上爬行,小孩与内表面之间的动摩擦因数为0.75,设小孩所受的最大静摩擦力等于滑动摩擦力,则小孩沿该装置缓慢向上爬行的最大高度是A. 0.2RB. 0.25RC. 0.75RD. 0.8R【答案】A【解析】【分析】根据题中“沿该装置缓慢向上爬行”可知,本题考察平衡问题。
江南十校2019届高三第一次联考(理科)

2019年安徽省“江南十校”综合素质检测数学(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、设集合}{2,1,0,1,2--=U ,{}U x x x A ∈>=,12,则=A C U{}2,2.-A {}1,1.-B {}2,0,2.-C {}1,0,1.-D2、复数iiz -=1(i 为虚数单位),则=-z22.A 2.B 21.C 2.D 3、抛物线22x y =的焦点坐标是⎪⎭⎫ ⎝⎛21,0.A ⎪⎭⎫ ⎝⎛0,21.B ⎪⎭⎫ ⎝⎛81,0.C ⎪⎭⎫ ⎝⎛0,81.D 4、在ABC ∆中,角C B A ,,的对边分别为c b a ,,,若C B c b 2,3,72===,则C 2cos 的值为37.A 95.B 94.C 47.D 5、已知边长为1的菱形ABCD 中,︒=∠60BAD ,点E 满足→→=EC BE 2,则→→•BD AE 的值是31.-A 21.-B 41.-C 61.-D5、我国南北朝时期的科学家祖暅,提出了计算体积的祖暅原理:“幂势既同,则积不容异.” 意思是:如果两个等高的几何体,在等高处的截面积恒等,则这两个几何体的体积相等.利用此原理求以下几何体的体积:曲线)0(2L y x y ≤≤=绕y 轴旋转一周得几何体Z ,将Z 放在与y 轴垂直的水平面α上,用平行于平面α,且与Z 的顶点O 距离为l 的平面截几何体Z ,的截面圆的面积为l l ππ=2)(.由此构造右边的几何体1Z :其中⊥AC 平面α,πα=⊂=11,,AA AA L AC ,它与Z 在等高处的截面面积都相等,图中EFPQ 为矩形,且l FP PQ ==,π,则几何体Z 的体积为2.L A π3.L B π 221.L C π 321.L D π7、已知函数)0)(32cos()(>+=ωπωx x f 的最小正周期为π4,则下面结论正确的是.A 函数)(x f 在区间()π,0上单调递增 .B 函数)(x f 在区间()π,0上单调递减 .C 函数)(x f 的图像关于直线32π=x 对称 .D 函数)(x f 的图像关于点⎪⎭⎫⎝⎛032,π对称 8、设函数1313)(2+-•=x x x x f ,则不等式0)log 1()log 3(22<-+x f x f 的解集是⎪⎪⎭⎫⎝⎛22,0.A ⎪⎪⎭⎫ ⎝⎛+∞,22.B ()2,0.C ()+∞,2.D9、已知双曲线14222=-by x 的左、右焦点分别为21,F F ,P 为右支上一点且直线2PF 与x 轴垂直,若21PF F ∠的角平分线恰好过点()0,1,则21F PF ∆的面积为12.A 24.B 36.C 48.D10. 已知函数()()xeInx x x g x k x x f -=+-=4,11(e 是自然对数的底数),若对()[]3,1,1,021∈∃∈∀x x ,使得)()(21x g x f ≥成立,则正数k 的最小值为21.A 1.B 324.-C 324.+D11. 如图,网格线上的小正方形的边长为1,粗线(实线、虚线)画出的某几何体的三视图, 其中的曲线都是半径为1的圆周的四分之一,则该几何体的表面积为20.A 420.π+B 4320.π+C 4520.π+D12. 计算机内部运算通常使用的是二进制,用1和0两个数字与电脑的通和断两种状态相对应。
最新-22019019江南十校联考 精品

2104江南十校联考篇一:2019年安徽省“江南十校”高三联考2019年安徽省“江南十校”高三联考理科综合能力测试第卷(选择题共126分)一、选择题:本题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列有关实验和研究方法,叙述正确的是.绿叶中色素提取的原理是色素在层析液中溶解度越大,在滤纸上扩散越快.盐酸在“观察根尖分生组织细胞的有丝分裂”和“低温诱导植物染色体数目的变化”中的作用原理相同.萨顿用假说演绎法证实了基因在染色体上.探究酵母菌的呼吸方式可以用是否产生二氧化碳予以确定2.已知与人体血红蛋白合成有关的一对等位基因是和。
只有纯合子()患镰刀型细胞贫血症,患者大多于幼年期死亡。
只含一个致病基因的个体不表现镰刀型细胞贫血症,并对疟疾具有较强的抵抗力。
以下说法不正确的是.该致病基因的出现是基因突变的结果,可以用显微镜检测镰刀型细胞贫血症.杂合子不易感染疟疾,显性纯合子易感染疟疾.基因和不可能存在于一个染色体组中.非洲某流行疟疾的地区消灭疟疾后,基因频率会上升3.小肠上皮细胞跨膜运输葡萄糖的过程如图所示,判断下列说法正确的是.由图可知,葡萄糖进出小肠上皮细胞的方式是主动运输.图中同向转运蛋白可同时转运+和葡萄糖,所以该载体蛋白不具有特异性.人体温发生变化时,不会影响+进出小肠上皮细胞.小肠上皮细胞+排出的方式和神经细胞+外流的方式不同4.科学家在癌细胞培养液中加入维生素(实验组)以研究其对癌细胞生长的影响。
培养过程中定时检测处于分裂期细胞的百分比,得到如图曲线。
据此分析,下列有关说法正确的是实验组细胞培养液中的尿嘧啶在0-消耗速率比其他时间段快在0-时,实验组细胞正在进行复制,而对照组细胞复制已完成.在0时,对照组细胞中染色体上的等位基因随着同源染色体的分开而分离由图可推测,维生素可在一定程度上抑制癌细胞增殖5.红圆蚧是美国加州南部的一种柑桔害虫,蔷薇轮蚧小蜂能寄生红圆蚧而抑制其爆发。
安徽省江南十校2019届高三3月联考理科数学试题

2019安徽省“江南十校”综合素质测试数学(理科)解析及评分标准一、选择题1. 答案 D 【解析】{2,2}A =−,故选D.2. 答案A 【解析】|i ||||||1i |2z z ====−,故选A.3. 答案C 【解析】标准方程为212x y =,故选C. 4. 答案B 【解析】由正弦定理知,sin sin 22cos sin sin 3B C C C C ===,cos 3C ∴= 25cos 22cos 1,9C C ∴=−=故选B. 5. 答案D 【解析】12AB AD ⋅=,2+3AE AB AD =,BD AB AD =−+ 212211(+)()1323326AE BD AB AD AB AD ⋅=⋅−+=−+−⨯=−,故选D. 6. 答案C 【解析】11121=2ABC A B C V L π−⋅三棱柱,故选C 7 .答案C 【解析】由已知得,24ππω=,112,()cos().223f x x πω∴==+故选C. 8 .答案A 【解析】由已知得()(),()f x f x y f x R −=−=且在上单调递增,22(3log )(log 1)f x f x ∴<−由可得223log log 1x x <−21log 2x ∴<−,解得:0x <<故选A. 9 .答案B 【解析】记(1,0)A ,则2224||2b c PF a −==,2214||22b c PF a a +=+=,1||1F A c =+, 2||1F A c =−,由角平分线性质得21122||||404||||PF F A c c c PF F A =⇒−=⇒=, 或作1AD PF ⊥于D ,由角平分线的对称性质知1112||||||||||24DF PF PD PF PF a =−=−==,2||||1AD AF c ==−,在1Rt ADF ∆中,222112||1,||||||AF c AF AF AD =+=+,解得4c =故12212214||||24.22PF F c S F F PF c ∆−=⨯=⋅=故选B. 10 .答案C 【解析】由已知,min min ()()f x g x ≥,由已知可得2min ()1),f x =+min ()3g x =,21)3,4k ∴+≥∴≥−故选C.11 .答案B 【解析】由已知得原几何体是由一个棱长为2的正方体挖去一个四分之一圆柱及一个八分之一球体得到的组合体,216245420,484S ππππ∴=⨯−−⨯+⨯+=+表故选B. 12 .答案C 【解析】前44组共含有数字:44(441)1980⨯+=个,198044(20191980)2019441975,S ∴=−+−=−=故选C.二、填空题13. 答案2 【解析】0,2x y ==时,min 3022z =⨯+=14. 答案1− 【解析】22sin cos 1sin 4cos 4αααα⋅=+,2tan 14tan 4αα=+,tan 2α=, []123tan =tan ()11123βαβα−+−==−+⨯. 15. 答案240 【解析】[]66()=()x y z x y z ++++,含2z 的项为24226T C()x y z =+⋅,所以形如2a b x y z 的项的系数之和为246C 2=240⋅.16.【解析】由已知动点P 落在以AB 为轴、该侧面与三棱锥侧面ACD 的交线为椭圆的一部分,设其与AC 的交点为P ,此时PB 最大,由P 到AB P 为AC 的中点,且2cos ,5BAC ∠=在BAP ∆中,由余弦定理可得 PB ==. 三、解答题17【解析】(1)由1232n n a a a a b ++++=①2n ≥时,123112n n a a a a b −−++++=②①−②可得:12()n n n a b b −=−(2)n ≥,∴3322()8a b b =−=∵12,0n a a =>,设{}n a 公比为q ,∴218a q =,∴2q =…………………………3分 ∴1222n n n a −=⨯=∴12312(12)222222212n nn n b +−=++++==−−,∴21n n b =−.…………6分 (2)证明:由已知:111211(21)(21)2121n n n n n n n n n a c b b +++===−⋅−−−−. ………………9分 ∴12312231111111212121212121n n n c c c c +++++=−+−++−−−−−−− 111121n +=−<−………………………………………………………………………………12分18 【解析】(1)∵2AB =,1A B ,160A AB ∠=,由余弦定理:22211112cos A B AA AB AA AB A AB =+−⋅∠,即21112303AA AA AA −−=⇒=或1−,故13AA =.………2分取BC 中点O ,连接1,OA OA ,∵ABC ∆是边长为2的正三角形, ∴AO BC ⊥,且AO =1BO =,由11A AB A AC ∆≅∆得到11A B AC ==1A O BC ⊥, 且1AO =, ∵22211AO A O AA +=,∴1AO A O ⊥,…………………4分又BC AO O =,故1A O ⊥平面ABC ,∵1A O ⊂平面1A BC , ∴平面1A BC ⊥平面ABC . ………………………………………6分(2)解法一:以O 为原点,OB 所在的直线为x 轴,取11B C 中点K ,以OK 所在的直线为y 轴,过O 作1OG AA ⊥,以OG所在的直线为z 轴建立空间直角坐标系.则111(1,0,0),(1,3,0),(1,3,0),B B C A −111(2,3,0),(0,3,0),(BC BB BA ∴=−==−……………………………………………8分设平面11ABB A 的一个法向量为(,,1)m x y =,则1130(2,0,1)020m BB y x m y m BA x y ⎧⋅==⎧=⎪⎪⇒⇒=⎨⎨=⎪⋅=−+=⎪⎩⎩设所求角为θ,则11||2sin39||||13BC m BC m θ⋅===…………………………………………………12分1解法二:以O 为原点,OB 所在的直线为x 轴,以1OA 所在的直线为y 轴,以OA 所在的直线为z 轴建立空间直角坐标系.则1(1,0,0),(1,0,0)B A A C ,设1(,,)C x y z ,由11=C A CA可得1(C −,11(2,6,3),(1,0,3),(1,BC AB BA ∴=−−=−=−……………………8分设平面11ABB A 的一个法向量为(,,)m x yz =,则110,(6,1,0y m AB x x m z m BA x ⎧=⎧⋅=−=⎪⎪==⎨⎨=⎪⋅=−=⎪⎩⎩取 设所求角为θ,则11||2sin 39||||13BC m BC m θ⋅===…………………………………………………12分 解法三:由(1)111111332C ABA AOA V BCS BC AO A O −==⨯⨯⨯⨯=设C 到平面11ABB A 的距离为h ,则由111//CC ABB A 面知1C 到平面11ABB A 的距离也为h ,则 111111sin 60332CABA ABA V hS h AB A A h −===⨯⨯⨯⨯︒==………………………………9分 设所求角为θ,则1sin h BC θ===………………………………………………………12分 19【解析】(1)由数据可知,2012,2013,2016,2017,2018五个年份考核优秀,故ξ的所有可能取值为0123,,,. 0353381(0)56C C P C ξ===,12533815(1),56C C P C ξ=== 2130535333883010(2),(3)5656C C C C P P C C ξξ======………………………………………………………………4分 故ξ的分布列为:所求0123.565628288E ξ=⨯+⨯+⨯+⨯=………………………………………………………………6分(2)解法一:8882222111()72()8360i ii i i i x x x x x x ===−=⇒=−+⨯=∑∑∑ 888111()()34.5()()8226.5i i i i i i i i i xx y y x y x x y y x y ===−−=⇒=−−+⨯⨯=∑∑∑ 故去掉2015年的数据之后686483296,777x y ⨯−⨯−==== 2222255()736067672i i i i x x x x ≠≠−=−=−−⨯=∑∑ 5529()()7226.5637634.57i i i i i i x x y y x y x y ≠≠−−=−=−⨯−⨯⨯=∑∑…………………………9分 所以^34.50.4872b =≈,^^2934.56 1.27772a y b x =−⋅=−⨯≈ 从而回归方程为:^0.48+1.27.y x =…………………………………………………………………………12分 解法二: 因为66x x ==,所以去掉2015年的数据后不影响^b 的值, 所以^34.50.4872b =≈, …………………………………………………………………………9分 而去掉2015年的数据之后686483296,777x y ⨯−⨯−====, ^^2934.56 1.27772a yb x =−⋅=−⨯≈ 从而回归方程为:^0.48+1.27.y x =…………………………………………………………………………12分注: 若有学生在计算^a 时用^0.48b ≈计算得^^290.486 1.267a yb x =−⋅=−⨯≈也算对。
安徽省江南十校2019届高三第一次模拟考试文科综合地理
安徽省江南十校2019届高三第一次模拟考试文科综合地理本试题卷共24页,47题(含选考题)。
全卷满分300分。
考试用时150分钟。
★祝考试顺利★注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B铅笔将答题卡上试卷类型A后的方框涂黑。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑.答案写在答题纸上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本大题共35 个小题,每小题4 分,共140 分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
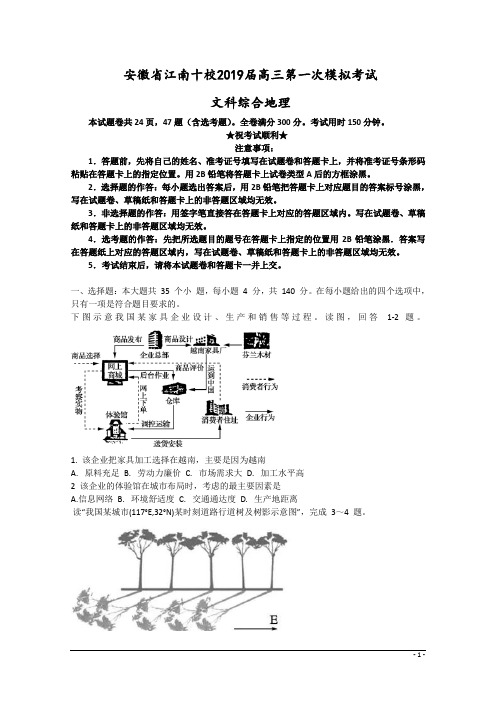
下图示意我国某家具企业设计、生产和销售等过程。
读图,回答1-2 题。
1. 该企业把家具加工选择在越南,主要是因为越南A. 原料充足B. 劳动力廉价C. 市场需求大D. 加工水平高2 该企业的体验馆在城市布局时,考虑的最主要因素是A.信息网络B. 环境舒适度C. 交通通达度D. 生产地距离读“我国某城市(117°E,32°N)某时刻道路行道树及树影示意图”,完成3~4 题。
3.根据行道树及树影推断该城市此时的北京时间可能是A.1 月1 日16:00 B.3 月1 日6:00C.7 月1 日6:00 D. 8 月1 日16:004.此时A.非洲热带草原动物正在向南迁徙B.澳大利亚北部天气高温多雨C.从澳大利亚西岸向中国航行的轮船顺风顺水D.南极中山站正值科考繁忙季节肯尼亚山位于东非高原,是距离赤道最近的雪山。
图2 为非洲肯尼亚山植被的垂直分布示意图。
【校级联考】安徽省江南十校2019届高三3月综合素质检测数学(理)试题-490329328b3745d3b943781280a7a6b7

绝密★启用前【校级联考】安徽省江南十校2019届高三3月综合素质检测数学(理)试题试卷副标题注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 一、单选题1.设集合 , ,则 ( ) A . B . C . D . 2.复数( 为虚数单位),则 ( )A .B .C .D .2 3.抛物线 的焦点坐标是( ) A .B .C .D .4.在 中,角 、 、 的对边分别为 、 、 ,若 , , ,则 的值为( )A .B .C .D .5.已知边长为1的菱形 中, ,点 满足 ,则 的值是( ) A .B .C .D .6.我国南北朝时期的科学家祖暅,提出了计算体积的祖暅原理:“幂势既同,则积不容异.”意思是:如果两个等高的几何体,在等高处的截面积恒等,则这两个几何体的体积相等.利用此原理求以下几何体的体积:曲线 绕 轴旋转一周得几何体 ,将 放在与 轴垂直的水平面 上,用平行于平面 ,且与 的顶点 距离为 的平面截几何体 ,得截面圆的面积为 .由此构造右边的几何体 :其中 平面 ,…………外…………线……………………内…………线………… , , ,它与 在等高处的截面面积都相等,图中 为矩形,且 , ,则几何体 的体积为( )A .B .C .D .7.已知函数的最小正周期为 ,则下面结论正确的是( )A .函数 在区间 上单调递增B .函数 在区间 上单调递减C .函数 的图象关于直线对称 D .函数 的图象关于点对称 8.设函数,则不等式 的解集是( )A .B .C .D .9.已知双曲线的左、右焦点分别为 , , 为右支上一点且直线 与 轴垂直,若 的角平分线恰好过点 ,则 的面积为( ) A .12 B .24 C .36 D .48 10.已知函数,( 是自然对数的底数),若对 ,,使得 成立,则正数 的最小值为( ) A .B .1C .D .11.如图,网格纸上的小正方形的边长为1,粗线(实线、虚线)画出的是某几何体的三视图,其中的曲线都是半径为1的圆周的四分之一,则该几何体的表面积为( )A .20B .C .D .12.计算机内部运算通常使用的是二进制,用1和0两个数字与电路的通和断两种状态相对应.现有一个2019位的二进制数,其第一个数字为1,第二个数字为0,且在第个0和第个0之间有个1(),即个,则该数的所有数字之...和.为()A.1973B.1974C.1975D.1976………外………○…………订…※※订※※线※※内※※答………内………○…………订…第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题13.设 , 满足约束条件,则 的最小值为_______.14.已知,且,则 的值为______.15.在 的展开式中,所有形如 的项的系数之和是_____(用数字作答).16.如图,三棱锥 中, , , ,点 在侧面 上,且到直线 的距离为 ,则 的最大值是_______.三、解答题17.已知数列 与 满足: ,且 为正项等比数列, , .(Ⅰ)求数列 与 的通项公式; (Ⅱ)若数列 满足, 为数列 的前 项和,证明: .18.斜三棱柱 中,底面是边长为2的正三角形, , .(Ⅰ)证明:平面 平面 ;(Ⅱ)求直线 与平面 所成角的正弦值.秀,现获得该公司2011-2018年的相关数据如下表所示:Array注:年返修率年返修台数年生产台数(Ⅰ)从该公司2011-2018年的相关数据中任意选取3年的数据,以表示3年中生产部门获得考核优秀的次数,求的分布列和数学期望;(Ⅱ)根据散点图发现2015年数据偏差较大,如果去掉该年的数据,试用剩下的数据求出年利润(百万元)关于年生产台数(万台)的线性回归方程(精确到0.01).附:线性回归方程中,,. 20.设是坐标原点,圆:,椭圆的焦点在轴上,左、右顶点分别为,,离心率为,短轴长为4.平行轴的直线与椭圆和圆在轴右侧的交点分别为,,直线与轴交于点,直线与轴交于点.(Ⅰ)求椭圆的标准方程;(Ⅱ)当时,求的取值范围.21.已知定义在区间上的函数,.(Ⅰ)证明:当时,;(Ⅱ)若曲线过点的切线有两条,求实数的取值范围.22.[选修4-4:坐标系与参数方程]在直角坐标系中,曲线的参数方程为(为参数),以坐标原点极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.(Ⅱ)点为曲线上一点,若曲线上存在两点,,使得,求的取值范围.23.[选修4-5:不等式选讲]设函数.(Ⅰ)当时,求函数的定义域;(Ⅱ)若函数的定义域为,求的取值范围.参考答案1.D【解析】【分析】求解出集合的范围,根据补集定义求解.【详解】或又,则本题正确选项:【点睛】本题考查集合基本运算中的补集,属于基础题. 2.A【解析】【分析】将整理成的形式,与模长相同,求即可.【详解】本题正确选项:【点睛】本题考查复数的基本运算,属于基础题.3.C【解析】【分析】将方程化为标准形式,然后可得焦点坐标.【详解】抛物线标准方程为,焦点在轴上焦点坐标为本题正确选项:【点睛】本题考查利用抛物线方程求焦点,易错点是忽略了原方程是否为标准方程,而直接去求解. 4.B【解析】【分析】由正弦定理可推导出的取值,再利用二倍角公式求得结果.【详解】由正弦定理可得:即本题正确选项:【点睛】本题考查正弦定理和二倍角公式的应用,属于基础题.5.D【解析】【分析】将通过线性运算进行拆解,转变成与向量和相关的数量积和模长求解即可.【详解】由题意可得大致图像如下:;又,本题正确选项:【点睛】本题考查向量的数量积的求解,处理此类问题的关键是将所求向量进行线性拆解,拆解为已知模长和夹角的两个向量的问题.6.C【解析】【分析】通过截面面积相等可求得的长度,再利用三棱柱体积公式即可求解.【详解】由题意可知:在高为处,截面面积为,且截面面积相等本题正确选项:【点睛】本题考查空间几何体中柱体体积的求解,属于基础题.7.C【解析】【分析】最小正周期为,可求得函数解析式;再依次将四个选项代入,与进行对比,得到正确结果.【详解】由题意知:选项和选项:当时,,当时,单调递减;时,单调递增.因此,和都错误;选项:时,;是的对称轴,则是的对称轴.因此,正确;选项:由可知,是对称轴的位置,则必不是对称中心.错误.本题正确选项:【点睛】本题考查的图像与性质,处理此类问题的关键是采用整体代入的方式,将范围代入函数,得到整体所处的范围,进而与图像相对应,确定最终结果.8.A【解析】【分析】判断出的奇偶性与单调性,然后将不等式转化为,通过单调性变成自变量的比较,从而得到关于的不等式,求得最终结果.【详解】为上的奇函数又可知与在上都单调递增,即与在上都单调递增当时,,;假设则即:在上单调递增又为奇函数,则在上单调递增,即在上单调递增由可得:即本题正确选项:【点睛】本题考查利用函数单调性与奇偶性求解函数不等式的问题,解题关键在于将不等式转化为符合单调性定义的形式,利用单调性转变为自变量的比较.9.B【解析】【分析】根据双曲线几何性质及定义,可用表示出与,再利用角平分线定理,求得,即可用表示出所求面积.【详解】记,则,由题意可知,为双曲线通径长的一半,即由双曲线定义可知:由角平分线性质定理可得:本题正确选项:【点睛】本题主要考查双曲线的几何性质,关键在于能够熟练应用双曲线的定义表示长度,同时涉及角平分线问题时,角平分线定理是常用的比例关系.10.C【解析】【分析】,,使得成立,说明,分别求出与的最小值,建立不等关系求解.【详解】“,,使得成立”等价于当时,令,解得:,在上单调递减,上单调递增当时,令,解得:在上单调递减,上单调递增当时,此时在上单调递增,上单调递增减,,无最小值,不合题意综上所述:,令,解得:在上单调递减,在上单调递增本题正确选项:【点睛】本题考查导数中的恒成立和能成立的综合问题,关键在于通过成立条件,将问题转化为最值之间的比较;难点在于求解时,需要对的范围进行讨论,才能最终确定取值. 11.B【解析】【分析】通过三视图还原几何体后,用正方体表面积减掉去除的面积,再加上因割正方体而增加的面的面积即可得到结果.【详解】由三视图可得几何体如图所示:由已知得原几何体是由一个棱长为2的正方体挖去一个四分之一圆柱及一个八分之一球体得到的组合体本题正确选项:【点睛】本题考查组合体的表面积问题,关键在于能够通过三视图准确还原组合体.12.C【解析】【分析】通过分组将问题变为等差数列求和的问题,先利用数位求解出分组的组数,再根据每组数字之和为首项为,公差为的等差数列,求解出最终结果.【详解】将数字从左只有以为分界进行分组第一组为,数字和为;第二组为,数字之和为;第三组为,数字之和为;以此类推数字共位,则,前组共有位则前位数字之和为:剩余数位为:则所有数字之和为:本题正确选项:【点睛】本题考查数列求和的问题,关键在于能够将数据进行合理分组,构建出等差数列的模型,从而解决问题.13.2【解析】【分析】通过约束条件,画出可行域,将问题转化为直线在轴截距最小的问题,通过图像解决.由题意可得可行域如下图所示:令,则即为在轴截距的最小值由图可知:当过时,在轴截距最小本题正确结果:【点睛】本题考查线性规划中的型最值的求解问题,关键在于将所求最值转化为在轴截距的问题.14.-1【解析】【分析】通过,的齐次式,求得的值;再利用两角和差的正切公式求解.【详解】又解得:本题正确结果:本题考查同角三角函数关系以及两角和差公式的应用,属于基础题.15.240【解析】【分析】将变为,将所求问题转变为的所有系数之和,通过赋值法可求得结果.【详解】则展开式通项为:含的项的为:则形如项的系数之和即为展开式的系数之和令,,则:本题正确结果:【点睛】本题考查二项式定理的相关知识,求解系数之和问题的关键方法是赋值法,通过赋值,消除变量的影响,得到系数之和.16.【解析】【分析】通过点到直线距离为定值,确定点在圆柱侧面上,同时确定点轨迹;根据椭圆性质可知,当落在上时,最大;根据距离可确定为中点,然后利用余弦定理解出结果.【详解】动点到直线的距离为定值动点落在以为轴、底面半径为的圆柱的侧面上可知侧面与三棱锥侧面的交线为椭圆的一部分设其与的交点为,此时最大由题意可得,点到的距离为:则到的距离为可知:为的中点又在中,由余弦定理可得本题正确结果:【点睛】本题考查立体几何中的直线与平面的位置关系,难点在于确定点在侧面上的轨迹类型,锁定最值取得的点,对学生的空间想象能力要求较高.17.(1);(2)见证明【解析】【分析】(1)通过作差的方式得到,从而求解出公比,进而得到;可利用等比数列求和推导得到;(2)通过裂项相消的方式,得到,通过放缩得到所证结果.【详解】(1)由……①时,……②①-②可得:,,设公比为(2)证明:由已知:当时,即:【点睛】本题考查等比数列以及裂项相消法求和,解题关键在于能够通过通项公式的形式确定可以进行裂项,从而可以前后相消,得到最终关系式.18.(1)见证明;(2)【解析】【分析】(1)利用等腰三角形三线合一和勾股定理分别证明和,得到平面,进而得到面面垂直;(2)利用空间向量法,得到所求正弦值等于的值;也可以利用体积桥的方式,求出到平面的距离,从而求得正弦值.【详解】(1),,由余弦定理:即或故取中点,连接,,如图所示:是边长为的正三角形,可得:,由得到又为中点,且又,平面平面平面平面(2)解法一:以为原点,所在的直线为轴,取中点,以所在的直线为轴,过作,以所在的直线为轴建立空间直角坐标系则,,,,,设平面的一个法向量为则设所求角为,则解法二:以为原点,所在的直线为轴,以所在的直线为轴,以所在的直线为轴建立空间直角坐标系则,,,设,由可得,,设平面的一个法向量为则,取,则设所求角为,则解法三:由(1)设到平面的距离为,则由面知到平面的距离也为,则设所求角为,则【点睛】本题考查立体几何中面面垂直的证明和直线与平面所成角问题.立体几何求解角度问题常常采用空间向量法来求解,线面角的正弦值即为直线与平面法向量所成角的余弦值;也可以求解出直线上的点到平面的距离,再利用直角三角形求解.19.(1)见解析;(2)【解析】【分析】(1)根据数据,确定考核优秀的年份数量,利用超几何分布来求解分布列和数学期望;(2)确定去掉年数据后,公式各个构成部分的数值,代入公式求解回归直线.【详解】(1)由数据可知,,,,,五个年份考核优秀的所有可能取值为,,,,,,故的分布列为:则数学期望(2)解法一:故去掉年的数据之后:,所以,从而回归方程为:解法二:因为,所以去掉年的数据后不影响的值所以而去掉年的数据之后,从而回归方程为:【点睛】本题考查概率统计部分的超几何分布和线性回归问题,关键在于根据题意确定好概率模型,选择合适的模型来进行计算.20.(1)(2)【解析】【分析】(1)根据椭圆的几何性质,得到关于的方程,求得结果;(2)解法一:假设方程和坐标,利用得到和的坐标,从而将转化为关于的式子,求得范围;解法二:假设方程和坐标,与椭圆方程联立解出点坐标,进一步推导出坐标,将转化为关于的式子,求得范围.【详解】(1)设椭圆的标准方程为由题意得,解得椭圆的标准方程为(2)解法一:设且,,,,设,共线,得,同理得解法二:设,,联立得:,,令得又由,令得又轴【点睛】本题考查直线与椭圆中的求解参数范围类问题,求解范围类问题的关键是能够根据已知关系,构造出关于参数的不等式;常见的已知关系有向量关系、位置关系、长度关系等. 21.(1)见证明;(2)【解析】【分析】(1)利用导数求得函数单调性,可证得;(2)利用假设切点的方式写出切线方程,原问题转化为方程在上有两个解;此时可采用零点存在定理依次判断零点个数,得到范围,也可以先利用分离变量的方式,构造新的函数,然后讨论函数图像,得到范围.【详解】(1)证明:时,在上递减,在上递增(2)当时,,,明显不满足要求;当时,设切点为(显然),则有,整理得由题意,要求方程在区间上有两个不同的实数解令①当即时,在上单调递增,在上单调递减或先单调递减再递增而,,,在区间上有唯一零点,在区间上无零点,所以此时不满足题要求.②当即时,在上单调递增,在上单调递减,在上单调递增.,在区间上有唯一零点,所以此时不满足题要求.③当时,在上单调递减,在上单调递增,,,当即时,在区间上有唯一零点,此时不满足题要求.当即时,在区间和上各有一个零点设零点为,又这时显然在区间上单调递减,此时满足题目要求.综上所述,的取值范围是(2)解法二:设切点为由解法一的关于的方程在区间内有两解显然不是方程的解故原问题等价于在区间内有两解设,且则,且令,,则又,;,,故,;,从而,递增,,递减令,由于时,时故,;,,而时,,时,故在区间内有两解解得:【点睛】本题主要考查导数的几何意义、导数在研究函数中的应用.难点在于将原问题转化为方程根的个数的问题,此时根无法确切的得到求解,解决此类问题的方式是灵活利用零点存在定理,在区间内逐步确定根的个数.22.(1) :,:.(2)【解析】【分析】(1)根据和直接化简求得结果;(2)过作圆切线,此时两切线夹角为临界状态,需大于等于才能出现的情况,利用角的正弦的范围求出的范围.【详解】(1)由题意得:(2)由(1),过作曲线的两条切线,切点分别记为曲线上存在两点,使得即,即【点睛】本题考查极坐标与参数方程部分的知识,关键在于通过临界值将问题转移到直角三角形内的角的范围问题,构造不等式求解出最终结果.23.(1) (2)【解析】【分析】(1)利用零点分段法讨论各个区间的解析式,得到取值范围;(2)利用恒成立思想,根据绝对值不等式的性质求得最值,得到的范围.【详解】(1)当时,定义域基本要求为:当时,当时,,无解当时,综上:的定义域为(2)由题意得:恒成立【点睛】本题考查含绝对值不等式的解法和绝对值不等式的性质,关键在于本题定义域为等价于恒成立,利用恒成立中的分离变量法求解.。
2019年安徽省“江南十校”高三联考语文试题

2019年安徽省“江南十校”高三联考语文试题第I卷(阅读题共66分)一、(9分)阅读下面的文字,完成l一3题。
徽派建筑的宗法意识韩文杰在封建宗法制度阴影的笼罩下,徽派建筑的最大特点是规范化、系统化,具体表现为:一、聚族而居,杂姓不得混居。
即使同一村落,各族宗祠、民居亦界域分明。
二、无论宗族人丁多寡,象征宗法势力的祠堂,展现宗族荣耀的水口等“基础设施”一应俱全。
三、讲究群体布局,即以封建“风水”术为理论依据,在封建族权的制约下强调宗族建筑整体轮廓必须像模像样。
如不符合要求,则需设法修改或弥补。
站远了看,徽派建筑总体布局与封建城池模式如出一辙:以祠堂为中心放射状散开的民居群类似于拱卫内城的外廓;地势险要,易守难攻的水口类似于护城河,具有抵御外族入侵的防卫功能;被民居众星拱月般团团簇拥着的祠堂则以其优越的地理位置,表明了宗法势力的至高无上,不容侵犯,也便于在此召集宗族成员议事、祠祭,公布村规民约,行使族权。
祠堂在徽派建筑中的地位'也体现在其建筑规模上。
词堂的外观形象、内部设施直接反映了一个宗族的社会地位、文化素质、经济实力,是宗族间相互攀比争雄的首要内容。
各族各姓对祠堂建设毫不含糊,尽力而为,从族产收入,挨家摊派到主动捐赠,族人有钱出钱,没钱交粮卖力,修得高大雄伟,壮观亮堂。
囿于族权的约束,徽派民居的地势、规模均不得超过祠堂,且不能遮挡与其遥相辉映的山峰河流,影响风水,妨碍宗族的繁荣昌盛。
民居外廓大,住房多,却井然有序,有回廊彼此连通,按男女长幼,房系嫡庶有序排列,主人住正(厢)房,佃仆散居四周,缜密繁杂,等级森严,堪称封建王室寝宫位序结构的翻版。
水口是走官道进村的必经之地。
学子赶考,高官归省,巨贾还乡,族人在此迎来送往,举行欢庆仪式。
显示族威荣耀,宗族凝聚力的同时,觋身说法,教育族中晚辈笃学敬业,勤勉执著,将来光宗耀祖。
宗族的荣誉和荫护使族人沾沾自喜,忘乎所以,对水口建设热情洋溢,不遗余力;功成名就的高官巨贾更是慷慨解囊,._掷千金,支持家乡的水口建设:育林、砌桥、修亭、刻碑、撰联……大力弘扬水口文化,以协调宗族内部关系,淡化阶级矛盾。
安徽江南十校2019高三第一次联考试题-政治(文综)

安徽江南十校2019高三第一次联考试题-政治(文综)本卷共32小题,每题4分,共128分。
在每题给出的四个选项中,只有一项为哪一项最符合题目要求的。
1.假定其他条件不变,在一般情况下,以下选项中与图1曲线反映的变动关系相一致的是①P甲为人民币汇率Q乙为商品进口量②P甲为个别劳动时间Q乙为商品价值总量③P甲为某种商品价格Q乙为替代品需求量④P甲为恩格尔系数Q乙为居民生活水平A.①②B.①③C.②④D.③④2.2017年9月1日起我国实行修改后的个人所得税法,将起征点由2000元调整为3500元,部分税率的变动情况见表1。
假定甲2017年每月工资为5500元,个税调整前后,其每月应缴纳的个税数额变化为,这个变化凸显个税的作用是()A.少缴305元调节个人收入分配的有效手段B.多缴305元国家财政收入的重要来源C.少缴325元调节个人收入分配的有效手段D.多缴325元国家财政收入的重要来源2017年是中国加入世界贸易组织(WTO)10周年,也是中国加入亚太经合组织(APEC)20周年。
回答3—4题。
3.从1991年至2017年,中国进出口总额从1357亿美元增长至29740亿美元,年均增长L7.6%;吸收外商直接投资从43.7亿美元增长到1057.4亿美元,年均增长18.3%:中国关税总水平从42.5%降至9.8%。
这说明()A.世界经济组织在国际经贸领域发挥了重要作用B.降低关税就能促进世界自由贸易C.我国积极参与国际经济竞争与合作的成效显著D.经济全球化实质已发生根本改变4.近年来,中国国家领导人每年都要出席APEC会议、G20峰会、中国一东盟(L0+1)领导人会议、上海合作组织会议等,在世界经济政治舞台上对国际事务发挥着重要的建设性作用。
这是因为()①国家利益是对外活动的出发点和落脚点②国际政治经济新秩序已经建立③和平与发展是我国外交政策的首要目标④世界格局多极化趋势不可逆转A.①②B.②③C.③④D.①④5.2017年9月至2018年2月,安徽省委部署开展“五级书记带头大走访”活动,做到“访民情、汇民智、释民惑、解民忧、惠民生”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年安徽省“江南十校”综合素质检测
数学(理科)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、设集合}{2
,1,0,1,2--=U ,{}U x x x A ∈>=,12,则=A C U
{}2,2.-A {}1,1.-B {}2,0,2.-C {}1,0,1.-D
2、复数i
i
z -=1(i 为虚数单位),则=-z
22.
A 2.
B 2
1
.C 2.D 3、抛物线2
2x y =的焦点坐标是
⎪⎭⎫ ⎝⎛21,0.A ⎪⎭⎫ ⎝⎛0,21.B ⎪⎭⎫ ⎝⎛81,0.C ⎪⎭
⎫ ⎝⎛0,81.D 4、在ABC ∆中,角C B A ,,的对边分别为c b a ,,,若C B c b 2,3,72===,则C 2cos 的值为
37.
A 95.
B 9
4
.C 47.D 5、已知边长为1的菱形ABCD 中,︒
=∠60BAD ,点E 满足→→=EC BE 2,则→
→•BD AE 的值是
31.-A 21.-B 41.-C 6
1.-D
5、我国南北朝时期的科学家祖暅,提出了计算体积的祖暅原理:“幂势既同,则积不容异.” 意思是:如果两个等高的几何体,在等高处的截面积恒等,则这两个几何体的体积相等.利用此原理求以下几何体的体积:曲线)0(2
L y x y ≤≤=绕y 轴旋转一周得几何体Z ,将Z 放在与y 轴垂直的水平面α上,用平行于平面α,且与Z 的顶点O 距离为l 的平面截几何
体Z ,的截面圆的面积为l l ππ=2
)(.由此构造右边的几何体1Z :其中⊥AC 平面
α,πα=⊂=11,,AA AA L AC ,它与Z 在等高处的截面面积都相等,图中EFPQ 为矩形,
且l FP PQ ==,π,则几何体Z 的体积为
2.L A π
3.L B π 221.L C π 32
1
.L D π
7、已知函数)0)(3
2cos()(>+
=ωπ
ωx x f 的最小正周期为π4,则下面结论正确的是 .A 函数)(x f 在区间()π,0上单调递增
.B 函数)(x f 在区间()π,0上单调递减 .C 函数)(x f 的图像关于直线3
2π
=
x 对称 .D 函数)(x f 的图像关于点⎪⎭
⎫
⎝⎛032,π对称 8、设函数1
31
3)(2
+-•=x x x x f ,则不等式0)log 1()log 3(22<-+x f x f 的解集是
⎪⎪⎭⎫
⎝⎛22,0.A ⎪⎪⎭
⎫ ⎝⎛+∞,22.B ()2,0.C ()
+∞,2.D
9、已知双曲线142
2
2=-b y x 的左、右焦点分别为21,F F ,P 为右支上一点且直线2PF 与x 轴垂直,若21PF F ∠的角平分线恰好过点()0,1,则21F PF ∆的面积为
12.A 24.B 36.C 48.D
10. 已知函数()()x
eInx
x x g x k x x f -=
+-=
4,11(e 是自然对数的底数),若对()[]3,1,1,021∈∃∈∀x x ,使得)()(21x g x f ≥成立,则正数k 的最小值为
2
1
.A 1.B 324.-C 324.+D 11. 如图,网格线上的小正方形的边长为1,粗线(实线、虚线)画出的某几何体的三视图, 其中的曲线都是半径为1的圆周的四分之一,则该几何体的表面积为
20.A 4
20.π
+
B 4320.π+
C 4
520.π
+D
12. 计算机内部运算通常使用的是二进制,用1和0两个数字与电脑的通和断两种状态相对应。
现有一个2019位的二进制,其第一个数字位1,第二个数字为0,且在第k 个0和第k+1个0之间有2k+1个1)(*
∈N k ,即4
434421Λ个
2019101011101111,则该数的所有数字之和为 1973.A 1974.B 1975.C 1976.D
二.填空题(本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应
位置)
13. 设x ,y 满足约束条件⎪⎩
⎪
⎨⎧≥+-≤+-≥-+02201202y x y x y x ,则y x z +=3的最小值为
14. 已知
41cos 31cos sin 2=+⋅ααα,且3
1
)tan(=
+βα,则βtan 的值为 15. 在()6
z y x ++的展示式中,所有形如2z y x b a ),(*
∈N b a 的项的系数之和是 (用
数字作答)
16. 如图,三棱锥BCD A -中,,12,8,10======CD AB BD BC AD AB 点P 在侧面ACD 上,且到直线AB 的距离是21,则PB 的最大值是
17、已知数列{}n a 与{}n b 满足)(2.......*
321N n b a a a a n n ∈=++++,且{}n a 为正项等
比数列,21=a ,423+=b b . (1)求数列{}n a 与{}n b 的通项公式;
(2)若数列{}n c 满足)(*1
N n b b a c n n n
n ∈=
+,n T 为数列{}n c 的前n 项和,证明:1<n T .
二、简答题:共70分.解答应写出必要的文字说明、证明过程或演算步骤.第17-21题为必做题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
18、斜三棱柱111C B A ABC -中,底面是边长为2的正三角形,71=
B A ,
ο6011=∠=∠AC A AB A .
(1)证明:平面⊥BC A 1平面ABC ;
(2)求直线1BC 与平面11A ABB 所成角的正弦值.
19、某公司生产的某种产品,如果年返修率不超过千分之一,则其生产部门当年考核优秀,现获得该公司2011-2018年的相关数据如下表所示:
注:年返修率=
年生产台数
年返修台数
(1)从该公司2011-2018年的相关数据中任意选取3年的数据,以ξ表示3年中生产部门获得考核优秀的次数,求ξ的分布列和数学期望;
(2)根据散点图发现2015年数据偏差较大,如果去掉该年的数据,试用剩下的数据求出年利润y (百万元)关于年生产台数x (万台)的线性回归方程(精确到).
附:线性回归方程∧∧+=a x b y 中,∑∑∑∑====∧
⋅-⋅⋅-=
---=
n
i i
n
i i
i n
i i
n
i i i
x
n x
y x n y
x x x
y y x x
b 1
2
_2
1
_
_2
1
_
_
1
_)()
)((,
._
_x b y a ⋅-=∧∧
20、设O 是坐标原点,圆O :)3(2
2
2
≥=+r r y x ,椭圆C 的焦点在x 轴上,左、右顶点分
别为A ,B ,离心率为
3
5
,短轴长为4.平行x 轴的直线l 与椭圆C 和圆O 在y 轴右侧的交点分别为E ,F ,直线AE 与y 轴交于点M ,直线BE 与y 轴交于点N . (1)求椭圆C 的标准方程;
(2)当1612≤•≤→
→
FN FM 时,求r 的取值范围.
21、已知定义在区间)2,0(上的函数R m x x
m
x f ∈+=
,ln )(. (1)证明:当1=m 时,1)(≥x f ;
(2)若曲线)(x f y 过点)0,1(A 的切线有两条,求实数m 的取值范围.
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所作的第一题计分.
22、(选修4-4:坐标系与参数方程)在直角坐标系xoy 中,曲线1C 的参数方程为⎪⎩⎪⎨⎧+=+=α
αsin 104y cos 101x (α为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标为5cos =θρ.
(1)求曲线1C 的普通方程和曲线2C 的直角坐标方程;
(2)点()n m P ,为曲线2C 上一点,若曲线1C 上存在两点B A ,,使得︒=∠90APB ,求n 的取值范围.
23、(选修4-5:不等式选讲)设函数)1212lg()(a x x x f -++-=.
(1)当4=a 时,求函数()x f 的定义域;
(2)若函数()x f 的定义域R 为,求a 的取值范围.。
