模型预测控制快速求解算法
预测控制之模型算法控制

• 1982年,Meral等在MPHC基础上进一步提出模型算法控制 (MAC,Model Algorithm Control)
• 1987年,Clarke等提出广义预测控制(GPC,Generalized Predictive Control)
模型描述
• 对于一个线性定常系统,其所有动静态特性可以完全由其单位脉冲响应函数表达。若该系 统还是稳定的(此处指系统的极点具有负实部的情形,不包括临界稳定), 其单位脉冲响应函 数满足:
• 若对于离散时间控制系统,则相应的脉冲响应序列趋于零。根据控制原理,基于单位脉冲 响应函数的系统输出响应等于单位脉冲响应函数与系统输入的卷积,即有
• 内模控制是直接针对控制系统存在建模误差和外部干扰的情况下研究系 统的闭环稳定、提高相应性能指标的控制方法,可显著提高控制系统对 建模误差和外部干扰的鲁棒性。
• 传统控制系统
• 内模控制系统结构框图
非参数模型之单位脉冲响应函数
• 在MAC中对被控对象可采用单位脉冲响应函数(在离散情形也称为单位脉冲 响应序列)作为其数学模型描述。
模型算法控制(MAC)
• MAC系统(预测控制)的主要四个部分:内部模型、模型校正 与输出预测、参考轨迹\轨迹优化、控制优化目标\滚动优化
一、内模原理
• 所谓内模原理,是针对传统控制理论对被控对象模型及建模误差处理的 不足而提出的一种新的处理方法。
• 当建模所存在的误差控制在较小范围时,传统的控制系统设计方法具有 较好的克服建模误差和抗干扰的能力。建模误差超过一定程度时,所设 计的控制系统的反馈本身的抗干扰能力及系统的稳定性裕量则不能很好 地将系统稳定,并保持所期望的系统性能指标。
8讲 预测控制主要算法

令此误差最小,即令 e(P)=0,得最优控制律:
u(k ) a P [ y s (k ) y (k ) ( g P i g i )u(k i )]
1 i 1 N
(2-12)
g i 为系统第 P 步的阶跃响应值。这就是单值预测控 其中 a P i 1
P
制算法,对 SISO 系统, a P 为标量;对 MIMO 系统,在输入输出 维数均为 m 时, a P 为 m×m 阵,这时计算可得到一定的简化。
1. 模型预测 DMC 中的预测模型是用被控对象的单位阶跃响应来描述的。 当在系统的输入端加上一控制增量后,在各采样时刻 t T 、 2T 、…、 NT 分别可在系统的输出端测得一系列采样值,它们可 用动态系数 a1、a2、…、aN 来表示,这种用动态系数和输入量来 描述各个采样时刻的系统输出和输入关系的过程特性,就是被控 对象的非参数数学模型。
(2-7)
3. 最优控制 通常采用下述二次型指标函数:
J k E T QE U (k )T RU(k )
J k 为得到最优解,令 U 0 ,得:
U (k ) (G1 QG1 R) 1 G1 Q[Ys (k 1) G2U (k 1) He(k )]
T T
(2-8)
U (k ) [u(k ) u(k M 1)
U (k 1) [u(k 1) u(k 1 N )]T
g1 g g1 2 G1 g g M M 1 g P g P 1
0 g2 g g 1 G2 3 P M 1 g P 1 g i i 1 PM
6. 闭环系统特性 对式(2-11)作 Z 变换:
mpc控制算法

mpc控制算法模型预测控制(MPC)是一种可以用来控制复杂过程的算法。
它可以根据设定的控制参数来实时地调整过程参数,从而最大限度地达到控制系统预期的输出目标。
MPC算法是一种智能控制系统,它综合考虑影响现实系统的动态变化参数,而不仅仅是考虑其瞬时量。
MPC控制算法是一种能够预测未来状态的控制方法,它可以根据不同的模型参数和控制策略,模拟出影响系统性能的多种变量,并可以在这些变量的影响下实时调整系统状态,从而达到系统性能最优化的目的。
MPC控制算法是一种智能控制,其中包括优化技术(像线性规划)、数学建模、系统参数调节等多种技术。
MPC控制算法既可以应用于离散系统,也可以应用于持续系统。
它以模型预测为基础,通过计算来预测和控制系统的输出,从而达到最佳控制系统性能的目的。
MPC控制算法的主要步骤包括:建立模型、分析调节器的特性,定义控制变量;其次,根据前面步骤构建模型,并通过数值求解来测试模型准确性;最后,根据求解结果,调整调节器参数,实现系统的控制目标。
MPC控制算法的应用领域很广,主要包括机械系统控制、电力系统控制、运距控制、航迹跟踪控制、位置跟踪控制、多机协调控制、空间结构控制等。
例如,MPC控制算法可以用于电力系统的有功功率调节;也可以用于航迹跟踪控制,实现无人机根据预设路径自动跟踪;还可以应用于多机协调、空间结构控制等领域,从而达到最大效果。
由于MPC控制算法可以模拟不同的过程参数,实时调整系统状态,因此具有杰出的优势。
首先,MPC控制算法有效的降低了模型的不确定性,使得模型的性能更稳定;其次,MPC控制算法可以有效地处理参数模糊性和运算误差;第三,MPC控制算法具有良好的自动调节能力,可以有效地抵抗环境和过程中的变化;最后,MPC控制算法可以控制复杂并发过程,有效地实现最优化控制。
可以看出,MPC控制算法在智能控制领域具有重要的作用。
它无需过多的参数设置,能够根据不断变化的状态实现自动调节,而且可以有效地降低参数不确定性,有效地抵抗外部和过程变化,实现性能最优化。
汽车轨迹跟踪模型预测控制的加速求解方法
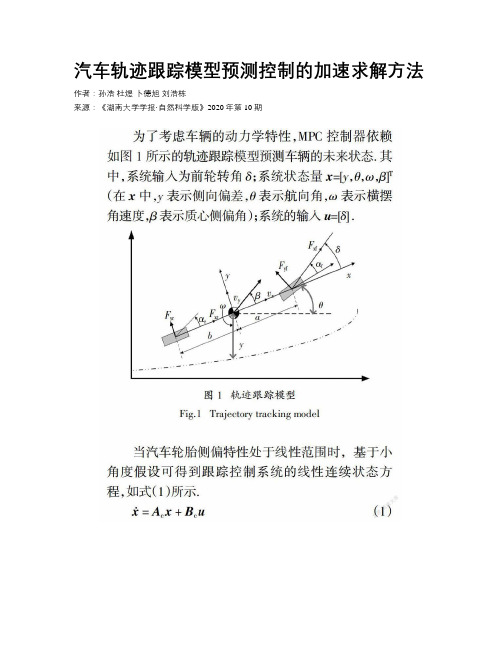
汽车轨迹跟踪模型预测控制的加速求解方法作者:孙浩杜煜卜德旭刘浩栋来源:《湖南大学学报·自然科学版》2020年第10期摘要:针对汽车轨迹跟踪模型预测控制求解中存在的规模较大、求解效率较低的问题,提出一种基于时域分解的加速计算方法提高求解效率. 首先引入全局一致性变量,将模型预测控制中邻接控制周期的时域耦合约束转化为全局一致性约束,实现时域解耦;随后在交叉方向乘子法框架下推导了时域分解后优化问题的分块更新方法,并设计了分块更新数值求解问题的停止准则,从而将大规模优化问题转化为小规模子问题;最后搭建了Simulink-CarSim平台进行了算法的仿真验证. 仿真结果表明,在求解精度不变的情况下,求解耗时下降24.21%,从而实现模型预测控制问题的加速求解.关键词:模型预测控制;自动驾驶汽车;轨迹跟踪;交叉方向乘子法;时域分解中图分类号:U461.99 文献标志码:AAccelerated Solution Method for Vehicle TrajectoryTracking Based on Model Predictive ControlSUN Hao1,2,DU Yu1,2†,BU Dexu3,LIU Haodong1,2(1. Beijing Key Laboratory of Information Service Engineering,Beijing Union University,Beijing 100101,China;2. College of Robotics,Beijing Union University,Beijing 100027,China;3. College of Traffic and Transportation Engineering,Central South University,Changsha 410076,China)Abstract:To solve the problems of large scale and low efficiency in the solution of intelligent vehicle trajectory tracking algorithm based on model predictive control,this paper proposes a time-domain splitting method to accelerate the calculation. First,global consistency variables are introduced to transform the time-domain coupling constraints of the adjacent control cycles into global consistency constraints,thus to achieve time-domain decoupling. Then,under the framework of Alternating Direction Method of Multipliers,the block updating method of optimization problem after time domain splitting is derived,and the stop criterion of block updating numerical solution is designed. Therefore,the large-scale optimization problem is converted into several small-scale sub-problems. Finally,the Simulink-CarSim platform is set up and the algorithm is verified by simulation. The simulation results show that,under the same accuracy of the solution,the efficiency of solution is improved by 24.21% on average with the proposed method,achieving accelerated solution for vehicle trajectory tracking based on model predictive control.Key words:model predictive control; autonomous vehicles; path tracking; alternating direction method of multipliers; time splitting自動驾驶汽车是提高交通系统安全、效率、经济等性能的有效途径,而轨迹跟踪是实现智能驾驶的核心技术之一[1],其目标是在满足汽车复杂动力学约束、行驶安全性约束前提下,以较小的偏差、较高的舒适性跟踪所规划的轨迹[2]. 模型预测控制(ModelPredictive Control,MPC)最早被应用在成本不敏感的大型工程中(如化工产业),并被认为是当年最具影响力的现代控制算法之一[3]. MPC通过引入参考模型,对约束的处理直接简单,不仅能够有效处理被控模型特性、约束带来影响,还能够通过滚动求解优化问题找到当前的最优控制量[4].基于上述优点,MPC在汽车轨迹跟踪问题的研究中得到国内外研究者的广泛关注.求解MPC问题的主流思路是将其转化为二次规划(Quadratic Programming,QP)问题. 其中,无约束MPC求解相对简单. Xu等以跟踪误差为性能指标实现AGV的轨迹跟踪控制[5],Shen等则建立了综合考虑跟踪精度和舒适性的目标函数[6],也有研究将输入量的边界建模为目标函数中代价值,构成“软约束”,但其数学原问题仍是无约束二次规划. 无约束二次规划问题可通过梯度下降等方法直接求解,但其局限在于仅考虑车辆的运动及动力学约束,没有考虑运动过程中所受到的其它约束,局限性较强. 因此,约束MPC更具备实际意义. 如Bo等建立了基于动力学的增量模型,考虑了执行机构的动力学特性约束[7]; Cai等则通过4自由度车辆模型加入车辆运动的侧翻约束,提高车辆跟踪控制的安全性[8]. 约束MPC的数学原问题是约束QP问题(MPC-QP问题),需要通过数值优化方法计算求解. 求解约束二次规划问题主要采用主动集法、内点法等方法,迭代次数较多. Wang和Boyd的研究表明,对于状态维数为m、控制输入维数为n、求解时域为T的MPC问题,状态转移形式及控制输入形式的MPC-QP问题求解的时间复杂度分别为O([T(n+m)]3)和O([Tn]3)[9]. 综上,虽然MPC在轨迹跟踪问题研究中得到广泛关注,但MPC-QP问题存在规模大、求解所需的浮点运算多、求解效率低的缺点,制约了MPC的性能. 因此,提高轨迹跟踪MPC问题的求解效率具有重要的意义.针对上述问题,本文提出一种加速求解方法以提高求解效率. 该方法通过交叉方向乘子法(Alternating Direction Method of Multipliers,ADMM)实现汽车轨迹跟踪问题的时域分解,将集中大规模的优化问题转为分块小规模优化问题,从而降低汽车轨迹跟踪MPC问题的时间复杂度,实现求解加速.1 模型预测控制问题的时域分解1.1 问题建模为了考虑车辆的动力学特性,MPC控制器依赖如图1所示的轨迹跟踪模型预测车辆的未来状态. 其中,系统输入为前轮转角δ;系统状态量x=[y,θ,ω,β]T(在x中,y表示侧向偏差,θ表示航向角,ω表示横摆角速度,β表示质心侧偏角);系统的输入u=[δ] .当汽车轮胎侧偏特性处于线性范围时,基于小角度假设可得到跟踪控制系统的线性连续状态方程,如式(1)所示.式(1)中各矩阵如式(2)所示. 其中,k1、k2分别为二自由度模型中车辆前、后轮等效侧偏刚度;a、b分别为二自由度模型中车辆直线到前、后轴的距离.那么,可得线性离散时间系统的狀态空间模型,如式(3)所示.x(k+1) = Ad x(k) + Bd u(k)(3)且连续与离散系统矩阵转换关系如式(4)所示,其中Ts为离散系统的采样时间.不失一般性,假设当前时刻系统状态为x0,根据离散系统的状态方程(3),在预测时域N内系统的输入与系统状态之间的转移关系如图 2所示,其中x∈Rm,u∈Rn.设离散时刻t下系统的参考状态为rt,那么综合考虑跟踪精度、舒适性的优化目标函数J 可用式(5)表示. 式中Q∈Rm × m、R∈Rn × n分别为状态变量、输入变量的权重对角矩阵.在轨迹跟踪问题中,代价函数越小越好. 对式(5)进行展开,轨迹跟踪的MPC问题可转化为如式(6)所示的约束二次规划问题. 在目标函数中,省略了不影响极值求解的常数项. 在约束条件中,(6a)表示汽车的动力学约束,(6b)表示不同时刻下状态变量及控制变量的可行域约束. 可以看出,虽然目标函数J在时域上解耦,但由于约束条件(6a)的存在(即t周期的终止状态为t+1周期的初始状态),并不能在求解过程中实现问题的分块解耦计算.1.2 时域分解为了实现问题的时域解耦,本文引入全局一致性变量,将汽车动力学带来的时域耦合约束转为全局一致性约束,从而实现问题的分块求解. 图 3为ADMM时域分解示意图.首先,以控制周期为单位对状态变量、控制变量进行分块表达. 对于所关注预测时域内的N个控制周期,按照次序给予编号1到N. 对于每个控制周期,该周期初始状态量、输入状态量和输出状态量可分别用x(t)t表达,其中上角标(t)表示为变量所属的分块编号,且块内变量之间的关系由汽车动力学特性决定,如式(7)所示:而块间关系由时域耦合约束决定,满足式(8):为解耦式(8)所示的时域耦合约束,引入全局一致性变量[z][~] = (z0,z1,…,zN)T ,并使x与z之间满足如式(9)所示的关系,其中:(9a)表示分块(t)的输入变量与zt-1的一致性约束;(9b)表示分块(t)的输出变量与zt的一致性约束.因此,联合式(7)~式(9),问题(6)可重写为如式(10)所示形式. 此时,邻接块之间不存在直接关系,其耦合约束通过一致性变量间接表达,从而实现控制周期之间时域解耦.2 分块求解方法2.1 问题求解综上所述,本文已经构建了MPC问题的时域分解范式,本节的工作则是基于ADMM求解时域分解后的问题. ADMM的标准构型如式(11)所示.为了方便地将式(10)转换为ADMM标准构型,引入块变量:[x][~]t = (x(t)求解MPC问题的主流思路是将其转化为二次规划(Quadratic Programming,QP)问题.其中,无约束MPC求解相对简单. Xu等以跟踪误差为性能指标实现AGV的轨迹跟踪控制[5],Shen等则建立了综合考虑跟踪精度和舒适性的目标函数[6],也有研究将输入量的边界建模为目标函数中代价值,构成“软约束”,但其数学原问题仍是无约束二次规划. 无约束二次规划问题可通过梯度下降等方法直接求解,但其局限在于仅考虑车辆的运动及动力学约束,没有考虑运动过程中所受到的其它约束,局限性较强. 因此,约束MPC更具备实际意义. 如Bo等建立了基于动力学的增量模型,考虑了执行机构的动力学特性约束[7]; Cai等则通过4自由度车辆模型加入车辆运动的侧翻约束,提高车辆跟踪控制的安全性[8]. 约束MPC的数学原问题是约束QP问题(MPC-QP问题),需要通过数值优化方法计算求解. 求解约束二次规划问题主要采用主动集法、内点法等方法,迭代次数较多. Wang和Boyd的研究表明,对于状态维数为m、控制输入维数为n、求解时域为T的MPC问题,状态转移形式及控制输入形式的MPC-QP问题求解的时间复杂度分别为O([T(n+m)]3)和O([Tn]3)[9]. 综上,虽然MPC在轨迹跟踪问题研究中得到广泛关注,但MPC-QP问题存在规模大、求解所需的浮点运算多、求解效率低的缺点,制约了MPC的性能. 因此,提高轨迹跟踪MPC问题的求解效率具有重要的意义.针对上述问题,本文提出一种加速求解方法以提高求解效率. 该方法通过交叉方向乘子法(Alternating Direction Method of Multipliers,ADMM)实现汽车轨迹跟踪问题的时域分解,将集中大规模的优化问题转为分块小规模优化问题,从而降低汽车轨迹跟踪MPC问题的时间复杂度,实现求解加速.1 模型预测控制问题的时域分解1.1 问题建模为了考虑车辆的动力学特性,MPC控制器依赖如图1所示的轨迹跟踪模型预测车辆的未来状态. 其中,系统输入为前轮转角δ;系统状态量x=[y,θ,ω,β]T(在x中,y表示侧向偏差,θ表示航向角,ω表示横摆角速度,β表示质心侧偏角);系统的输入u=[δ] .当汽车轮胎侧偏特性处于线性范围时,基于小角度假设可得到跟踪控制系统的线性连续状态方程,如式(1)所示.式(1)中各矩阵如式(2)所示. 其中,k1、k2分别为二自由度模型中车辆前、后轮等效侧偏刚度;a、b分别为二自由度模型中车辆直线到前、后轴的距离.那么,可得线性离散时间系统的状态空间模型,如式(3)所示.x(k+1) = Ad x(k) + Bd u(k)(3)且连续与离散系统矩阵转换关系如式(4)所示,其中Ts为离散系统的采样时间.不失一般性,假设当前时刻系统状态为x0,根据离散系统的状态方程(3),在预测时域N内系统的输入与系统状态之间的转移关系如图 2所示,其中x∈Rm,u∈Rn.設离散时刻t下系统的参考状态为rt,那么综合考虑跟踪精度、舒适性的优化目标函数J 可用式(5)表示. 式中Q∈Rm × m、R∈Rn × n分别为状态变量、输入变量的权重对角矩阵.在轨迹跟踪问题中,代价函数越小越好. 对式(5)进行展开,轨迹跟踪的MPC问题可转化为如式(6)所示的约束二次规划问题. 在目标函数中,省略了不影响极值求解的常数项. 在约束条件中,(6a)表示汽车的动力学约束,(6b)表示不同时刻下状态变量及控制变量的可行域约束. 可以看出,虽然目标函数J在时域上解耦,但由于约束条件(6a)的存在(即t周期的终止状态为t+1周期的初始状态),并不能在求解过程中实现问题的分块解耦计算.1.2 时域分解为了实现问题的时域解耦,本文引入全局一致性变量,将汽车动力学带来的时域耦合约束转为全局一致性约束,从而实现问题的分块求解. 图 3为ADMM时域分解示意图.首先,以控制周期为单位对状态变量、控制变量进行分块表达. 对于所关注预测时域内的N个控制周期,按照次序给予编号1到N. 对于每个控制周期,该周期初始状态量、输入状态量和输出状态量可分别用x(t)t表达,其中上角标(t)表示为变量所属的分块编号,且块内变量之间的关系由汽车动力学特性决定,如式(7)所示:而块间关系由时域耦合约束决定,满足式(8):为解耦式(8)所示的时域耦合约束,引入全局一致性变量[z][~] = (z0,z1,…,zN)T ,并使x与z之间满足如式(9)所示的关系,其中:(9a)表示分块(t)的输入变量与zt-1的一致性约束;(9b)表示分块(t)的输出变量与zt的一致性约束.因此,联合式(7)~式(9),问题(6)可重写为如式(10)所示形式. 此时,邻接块之间不存在直接关系,其耦合约束通过一致性变量间接表达,从而实现控制周期之间时域解耦.2 分块求解方法2.1 问题求解综上所述,本文已经构建了MPC问题的时域分解范式,本节的工作则是基于ADMM求解时域分解后的问题. ADMM的标准构型如式(11)所示.为了方便地将式(10)转换为ADMM标准构型,引入块变量:[x][~]t = (x(t)求解MPC问题的主流思路是将其转化为二次规划(Quadratic Programming,QP)问题.其中,无约束MPC求解相对简单. Xu等以跟踪误差为性能指标实现AGV的轨迹跟踪控制[5],Shen等则建立了综合考虑跟踪精度和舒适性的目标函数[6],也有研究将输入量的边界建模为目标函数中代价值,构成“软约束”,但其数学原问题仍是无约束二次规划. 无约束二次规划问题可通过梯度下降等方法直接求解,但其局限在于仅考虑车辆的运动及动力学约束,没有考虑运动过程中所受到的其它约束,局限性较强. 因此,约束MPC更具备实际意义. 如Bo等建立了基于动力学的增量模型,考虑了执行机构的动力学特性约束[7]; Cai等则通过4自由度车辆模型加入车辆运动的侧翻约束,提高车辆跟踪控制的安全性[8]. 约束MPC的数学原问题是约束QP问题(MPC-QP问题),需要通过数值优化方法计算求解. 求解约束二次规划问题主要采用主动集法、内点法等方法,迭代次數较多. Wang和Boyd的研究表明,对于状态维数为m、控制输入维数为n、求解时域为T的MPC问题,状态转移形式及控制输入形式的MPC-QP问题求解的时间复杂度分别为O([T(n+m)]3)和O([Tn]3)[9]. 综上,虽然MPC在轨迹跟踪问题研究中得到广泛关注,但MPC-QP问题存在规模大、求解所需的浮点运算多、求解效率低的缺点,制约了MPC的性能. 因此,提高轨迹跟踪MPC问题的求解效率具有重要的意义.针对上述问题,本文提出一种加速求解方法以提高求解效率. 该方法通过交叉方向乘子法(Alternating Direction Method of Multipliers,ADMM)实现汽车轨迹跟踪问题的时域分解,将集中大规模的优化问题转为分块小规模优化问题,从而降低汽车轨迹跟踪MPC问题的时间复杂度,实现求解加速.1 模型预测控制问题的时域分解1.1 问题建模为了考虑车辆的动力学特性,MPC控制器依赖如图1所示的轨迹跟踪模型预测车辆的未来状态. 其中,系统输入为前轮转角δ;系统状态量x=[y,θ,ω,β]T(在x中,y表示侧向偏差,θ表示航向角,ω表示横摆角速度,β表示质心侧偏角);系统的输入u=[δ] .当汽车轮胎侧偏特性处于线性范围时,基于小角度假设可得到跟踪控制系统的线性连续状态方程,如式(1)所示.式(1)中各矩阵如式(2)所示. 其中,k1、k2分别为二自由度模型中车辆前、后轮等效侧偏刚度;a、b分别为二自由度模型中车辆直线到前、后轴的距离.那么,可得线性离散时间系统的状态空间模型,如式(3)所示.x(k+1) = Ad x(k) + Bd u(k)(3)且连续与离散系统矩阵转换关系如式(4)所示,其中Ts为离散系统的采样时间.不失一般性,假设当前时刻系统状态为x0,根据离散系统的状态方程(3),在预测时域N内系统的输入与系统状态之间的转移关系如图 2所示,其中x∈Rm,u∈Rn.设离散时刻t下系统的参考状态为rt,那么综合考虑跟踪精度、舒适性的优化目标函数J 可用式(5)表示. 式中Q∈Rm × m、R∈Rn × n分别为状态变量、输入变量的权重对角矩阵.在轨迹跟踪问题中,代价函数越小越好. 对式(5)进行展开,轨迹跟踪的MPC问题可转化为如式(6)所示的约束二次规划问题. 在目标函数中,省略了不影响极值求解的常数项. 在约束条件中,(6a)表示汽车的动力学约束,(6b)表示不同时刻下状态变量及控制变量的可行域约束. 可以看出,虽然目标函数J在时域上解耦,但由于约束条件(6a)的存在(即t周期的终止状态为t+1周期的初始状态),并不能在求解过程中实现问题的分块解耦计算.1.2 时域分解为了实现问题的时域解耦,本文引入全局一致性变量,将汽车动力学带来的时域耦合约束转为全局一致性约束,从而实现问题的分块求解. 图 3为ADMM时域分解示意图.首先,以控制周期为单位对状态变量、控制变量进行分块表达. 对于所关注预测时域内的N个控制周期,按照次序给予编号1到N. 对于每个控制周期,该周期初始状态量、输入状态量和输出状态量可分别用x(t)t表达,其中上角标(t)表示为变量所属的分块编号,且块内变量之间的关系由汽车动力学特性决定,如式(7)所示:而块间关系由时域耦合约束决定,满足式(8):为解耦式(8)所示的时域耦合约束,引入全局一致性变量[z][~] = (z0,z1,…,zN)T ,并使x与z之间满足如式(9)所示的关系,其中:(9a)表示分块(t)的输入变量与zt-1的一致性约束;(9b)表示分块(t)的输出变量与zt的一致性约束.因此,联合式(7)~式(9),问题(6)可重写为如式(10)所示形式. 此时,邻接块之间不存在直接关系,其耦合约束通过一致性变量间接表达,从而实现控制周期之间时域解耦.2 分块求解方法2.1 问题求解综上所述,本文已经构建了MPC问题的时域分解范式,本节的工作则是基于ADMM求解时域分解后的问题. ADMM的标准构型如式(11)所示.为了方便地将式(10)转换为ADMM标准构型,引入块变量:[x][~]t = (x(t)。
模型预测控制算法

模型预测控制算法
模型预测控制(Model Predictive Control, MPC)是一种先进的控制算法,它可以在复杂的系统中实现有效的运动控制。
MPC是一种运动控制算法,它可以根据预设的目标参数和实时的反馈信息,在实时的情况下预测未来的状态,并根据这些预测结果调整控制参数,以实现最佳的控制效果。
MPC是一种基于模型的控制算法,它通过建立一个模型来模拟系统的行为,并基于这个模型来预测未来的情况。
这个模型可以是确定性模型,也可以是不确定性模型,不管哪种模型都可以帮助MPC 更好地预测未来的情况。
MPC可以在系统处于不同状态时,根据预设的目标参数,自动选择最佳的控制策略。
MPC算法的优点在于可以实现更快的反应,更高的精度,更少的误差,更稳定的控制效果,可以更好地满足复杂系统的需求。
MPC 算法还可以实现自适应控制,即根据实时反馈信息自动调整控制参数,以达到最优的控制效果。
模型预测控制算法的应用非常广泛,可以用于汽车、机器人、飞机等运动控制,也可以用于温度、压力等过程控制等不同领域。
总之,MPC算法是一种非常有效的控制算法,可以有效地解决复杂系统的控制问题,为系统提供更好的性能。
mpc快速求解方法

mpc快速求解方法
MPC(Model Predictive Control)是一种基于预测的控制算法,用于优化具有约束条件的非线性系统。
由于其计算复杂度较高,因此需要采用快速求解方法来提高计算效率。
以下是几种常用的MPC快速求解方法:
1. 块坐标下降法(Block Coordinate Descent):将多维的MPC问题分解为多个一维子问题,逐个求解每个子问题,从而降低计算复杂度。
2. 内点法(Interior Point Method):将MPC问题转化为一个二次规划问题,并使用内点法进行求解。
相比于传统的线性规划方法,内点法可以更好地处理约束条件,并且具有更快的收敛速度。
3. 序列二次规划(Sequential Quadratic Programming,SQP):将MPC问题转化为一个二次规划问题,并使用SQP方法进行求解。
SQP方法通过迭代优化当前时刻的二次规划子问题来逐步推进整个问题的求解过程,具有较高的计算效率和精度。
4. 蒙特卡洛模拟(Monte Carlo Simulation):对于一些复杂的MPC问题,可以通过蒙特卡洛模拟来进行快速求解。
该方法利用随机采样的思想,通过多次模拟来逼近真实的最优解,具有较好的鲁棒性和适应性。
以上是常用的MPC快速求解方法,不同的方法适用于不同类型的MPC问题,选择合适的方法可以提高计算效率和精度。
控制工程中的模型预测控制算法

控制工程中的模型预测控制算法随着工业化和数字化的高速发展,涉及自动化控制的应用越来越广泛,越来越深入。
不论是在实践中还是理论研究中,控制工程一直是一个备受关注的领域。
控制工程是研究如何在自动化装置中运用控制理论和技术对生产和生活中的控制问题进行分析、设计和实现的学科。
而控制算法作为控制工程的核心,尤其是模型预测控制算法,已经成为现代自动化控制中的重要技术手段之一。
模型预测控制算法(MPC)是一种基于模型的控制策略,通过将过程变量的状态预测与控制相结合,并对未来一段时间内的控制变量作出预测,最后对预测与实际变量进行比对,调整控制变量以达到最优控制目标。
MPC拥有突出的优点,如对控制变量作出预测、处理非线性、处理多变量等,使其在化工、石油、电子、材料、制造等领域具有广泛的应用。
MPC的实现MPC的实现同样是一个需要重视的问题。
对于MPC,其优化算法决定了控制系统的性能。
因此,MPC的实现过程中一个重要的考虑因素就是如何求解优化问题。
求解MPC中的优化问题可以采用数学优化算法,如线性规划、二次规划或非线性规划等。
而MPC的关键问题就是如何带约束的最优控制问题与上述数学方法相结合。
针对这个问题,MPC前瞻控制算法提供了一种有效的解决方案。
MPC前瞻控制算法MPC前瞻控制算法(MPC-PR)将数学优化算法与基于约束的控制(MPC)相结合,可轻松地解决MPC的实现问题。
对于复杂的物理系统,MPC-PR综合了高级预测模型、状态估计技术、多模型预测和优化控制算法,实现了一系列复杂动态约束的精确解决。
通过MPC-PR算法(如下图)的分层分解、扩展线性化和非线性规划,可以得到合适的状态估计和最优控制输入。
在任何时间点,该控制策略都能够考虑各种限制条件,并且考虑外部干扰、控制过程和多求解器并行处理等传统算法无法处理的约束条件。
MPC在工业领域的应用MPC在化工、石油、电子、材料、制造等领域的广泛应用,使它已成为工业制造领域中的重要技术手段之一。
工业控制中的模型预测控制算法研究

工业控制中的模型预测控制算法研究随着信息技术和智能化技术的迅速发展,工业控制在现代工业中起到了越来越重要的作用,其中模型预测控制算法(Model Predictive Control, MPC)被广泛应用于各种工业控制领域。
本文将探讨MPC算法的原理、优点和应用以及现有的研究成果。
一、MPC算法原理MPC算法是一种基于预测模型的控制方法,其核心思想是在考虑预测模型的同时将未来一段时间(通常为1秒至数十秒)的最优控制输入计算出来,并将其实施到被控制对象上。
简单来说,就是通过对系统的动态方程进行建模和优化,来实现对被控制对象的最优控制。
和传统的PID控制相比,MPC算法的主要优点在于它能够处理更为复杂的控制系统,因为它可以利用模型来预测未来的系统状态,并在这个基础上计算出最优控制输入。
此外,MPC算法还能够以动态的方式处理多个约束条件,并根据不同的权重进行优化,从而实现对系统的更加精细的控制。
二、MPC算法优点与应用由于MPC算法具有灵活性、准确性和多变量控制的能力,所以被广泛应用于各种工业控制领域,如化工、能源、制造等。
下面来看一些实际应用。
1、化工厂提高产能以苯乙烯生产为例,苯乙烯生产过程中,温度、压力、流量等因素都对产品质量和产量产生影响。
传统的PID控制无法解决多变量控制和约束条件的问题,MPC算法就可以完美解决这个问题。
通过合理预测未来的系统状态并计算出最优控制输入,可以让化工厂在不违反约束条件的情况下提高产能。
2、电网频率稳定控制电网频率是电网稳定运行的重要指标。
磁悬浮风机作为具有较大惯性和容量的电压变频器负载,其电压、电流信号具有一定的不确定性和时变性,对于电力系统的动态响应和频率控制影响是非常显著的。
而MPC算法可以更好地对电压、电流等变量进行优化控制,从而实现电网频率稳定控制。
三、MPC算法研究进展MPC算法自问世以来,在理论和应用方面都有着广泛的研究。
下面将列举一些近年来的研究成果。
模型预测控制算法

模型预测控制算法
模型预测控制算法
模型预测控制(Model Predictive Control,MPC)是一种基于模型的面向未来的控制策略,它通过对未来的预测和规划来调节系统性能。
它是目前运用较为广泛的一种控制算法,以它的实时性,自适应性和可扩展性而备受关注。
MPC算法主要由两部分组成:模型预测和控制算法。
在模型预测部分,MPC算法会根据当前状态来建立系统的模型,在控制算法部分,MPC算法会根据建立的模型去规划最优的控制策略。
MPC的优势在于能够根据系统的模型来预测未来的趋势,从而调整控制参数,并且它可以根据系统的变化来实时优化控制策略,从而提高系统的性能。
MPC算法可以用于多种不同的应用场景,例如,它可以用于自动驾驶,电力系统,石油和天然气系统,工业控制等。
在自动驾驶技术中,MPC可以用来预测车辆的未来行驶路线,从而更好地控制车辆的行驶方向和速度。
在电力系统中,MPC可以帮助优化电力系统的运行,使得能源的利用更加合理和高效。
总之,MPC算法是一种非常有效的控制算法,它可以在不同领域中得到广泛应用,并能够帮助优化系统的性能。
模型预测控制公式

模型预测控制公式模型预测控制(Model Predictive Control,简称 MPC)公式,听起来是不是有点高大上?但其实它在很多领域都有着重要的应用。
咱们先来说说模型预测控制到底是个啥。
简单来讲,它就像是一个聪明的“指挥官”,能够根据系统当前的状态和未来的目标,提前规划出一系列的控制动作。
MPC 的核心公式可以表示为:\[\begin{align*}\min_{u(k),\cdots,u(k+N_c-1)} & \sum_{i=1}^{N_p} \left( y(k+i|k) - r(k+i) \right)^2 + \sum_{i=0}^{N_c-1} \lambda_i u^2(k+i) \\\text{s.t.} & x(k+1|k) = Ax(k) + Bu(k) \\& y(k) = Cx(k) \\& u_{\min} \leq u(k+i) \leq u_{\max} \\& x_{\min} \leq x(k+i) \leq x_{\max} \\\end{align*}\]哎呀,别被这一堆公式给吓住啦!我来给您慢慢解释解释。
这里面的 \(y(k+i|k)\) 表示在 \(k\) 时刻对未来 \(i\) 时刻的输出预测,\(r(k+i)\) 则是未来 \(i\) 时刻的期望输出。
我们的目标就是让预测输出和期望输出的差距尽可能小,同时还要考虑控制动作 \(u(k)\) 的大小,不能太大也不能太小,得在允许的范围内。
我给您讲个我自己的经历吧。
有一次,我参加了一个智能机器人的研发项目。
这个机器人要在一个复杂的环境中自主移动,避开各种障碍物,到达指定的目标点。
这时候,模型预测控制就派上用场了。
我们通过各种传感器获取机器人当前的位置、速度、姿态等信息,然后把这些数据输入到模型预测控制的公式中。
就像是给这个“聪明的大脑”提供了思考的素材。
然后,公式开始运算,计算出接下来一段时间内机器人应该怎么移动,转向多少角度,速度是多少等等。
模型预测控制算法

模型预测控制算法
模型预测控制算法是一种基于模型的计算方法,主要用于控制系统建模和控制。
它提供了一种更加精确和高效的方法,可以有效地预测和控制系统的行为,从而提高系统的性能和可靠性。
模型预测控制算法的核心思想是根据输入信息来预测系统的行为,以此来调整系统的状态,从而实现目标控制。
它可以帮助控制工程师更加准确地估计系统输出值,从而更有效地控制系统。
模型预测控制算法的核心部分是建立一个预测模型,用于预测系统的行为。
这种模型可以是从实验数据中获得的,也可以是基于一些数学方程的模型。
在预测模型建立完成后,控制工程师需要根据系统的实际行为来调整模型的参数,以便使其输出更加准确。
模型预测控制算法也可以用来处理复杂的系统,比如生产流水线,机器人和自动驾驶汽车等。
在这些系统中,控制工程师可以利用预测模型来预测系统的行为,并调整系统的参数,以获得更加精确的控制。
总之,模型预测控制算法是一种强大的工具,可以帮助控制工程师更加有效地控制系统,从而提高系统的性能和可靠性。
它的应用范围非常广泛,可以应用于各种各样的控制系统,从而实现更加高效的控制。
mpc算法原理公式解析

mpc算法原理公式解析
MPC(模型预测控制)算法是一种先进的控制策略,其原理和公式解析如下:
一、原理:
MPC算法基于模型预测和控制重构的思想,通过在线求解有限时间开环优化问题来实现对系统的控制。
在每个采样时刻,MPC算法会根据当前时刻的测量信息,预测系统未来的动态行为,然后求解一个优化问题,得到控制序列,并将控制序列的第一个元素作用于被控对象。
在下一个采样时刻,算法会用新的测量值更新预测模型并重新求解优化问题。
MPC算法的三个主要步骤是预测系统未来动态、求解开环优化问题和将优化解的第一个元素作用于系统。
二、公式解析:
1. 预测系统未来动态:基于系统的动态模型,预测系统在未来一段时间内的状态变化。
常用的预测模型有线性回归模型、神经网络模型等。
2. 求解开环优化问题:根据预测模型和设定的优化目标,求解一个开环优化问题,以得到控制序列。
开环优化问题的求解可以使用各种优化算法,如梯度下降法、牛顿法等。
3. 将优化解的第一个元素作用于系统:将得到的控制序列的第一个元素作用于被控对象,以实现对系统的控制。
在数学公式方面,MPC算法通常涉及到状态方程、预测模型和控制目标函数的建立和优化。
状态方程描述了系统动态行为的数学模型,预测模型用于预测未来一段时间内的系统状态,而控制目标函数则是优化问题的核心,旨在最大化某些性能指标或满足某些约束条件。
模型预测控制快速求解算法

模型预测控制快速求解算法模型预测控制(Model Predictive Control,MPC)是一种基于在线计算的控制优化算法,能够统一处理带约束的多参数优化控制问题。
当被控对象结构和环境相对复杂时,模型预测控制需选择较大的预测时域和控制时域,因此大大增加了在线求解的计算时间,同时降低了控制效果。
从现有的算法来看,模型预测控制通常只适用于采样时间较大、动态过程变化较慢的系统中。
因此,研究快速模型预测控制算法具有一定的理论意义和应用价值。
虽然MPC方法为适应当今复杂的工业环境已经发展出各种智能预测控制方法,在工业领域中也得到了一定应用,但是算法的理论分析和实际应用之间仍然存在着一定差距,尤其在多输入多输出系统、非线性特性及参数时变的系统和结果不确定的系统中。
预测控制方法发展至今,仍然存在一些问题,具体如下:①模型难以建立。
模型是预测控制方法的基础,因此建立的模型越精确,预测控制效果越好。
尽管模型辨识技术已经在预测控制方法的建模过程中得以应用,但是仍无法建立非常精确的系统模型。
②在线计算过程不够优化。
预测控制方法的一大特征是在线优化,即根据系统当前状态、性能指标和约束条件进行在线计算得到当前状态的控制律。
在在线优化过程中,当前的优化算法主要有线性规划、二次规划和非线性规划等。
在线性系统中,预测控制的在线计算过程大多数采用二次规划方法进行求解,但若被控对象的输入输出个数较多或预测时域较大时,该优化方法的在线计算效率也会无法满足系统快速性需求。
而在非线性系统中,在线优化过程通常采用序列二次优化算法,但该方法的在线计算成本相对较高且不能完全保证系统稳定,因此也需要不断改进。
③误差问题。
由于系统建模往往不够精确,且被控系统中往往存在各种干扰,预测控制方法的预测值和实际值之间一定会产生误差。
虽然建模误差可以通过补偿进行校正,干扰误差可以通过反馈进行校正,但是当系统更复杂时,上述两种校正结合起来也无法将误差控制在一定范围内。
自动化控制系统的模型预测控制算法研究

自动化控制系统的模型预测控制算法研究摘要:自动化控制系统在工业生产和日常生活中扮演着至关重要的角色。
模型预测控制算法是一种有效的控制算法,广泛应用于工业过程控制和实时系统控制中。
本文将对模型预测控制算法的原理、应用以及研究进展进行详细介绍,并重点讨论几种常见的模型预测控制算法。
1. 引言自动化控制系统的发展已经极大地提高了工业生产的效率和质量。
模型预测控制算法是一种基于系统模型的优化方法,通过预测模型对未来的系统行为进行预测,并根据优化准则进行控制输入的优化。
这种控制算法在工业过程控制、流程控制以及实时系统控制中被广泛应用。
2. 模型预测控制算法原理模型预测控制算法的基本原理是利用数学模型对系统进行建模,并根据模型对未来的行为进行预测,然后依据预测结果进行控制输入的优化。
模型预测控制算法的核心是优化问题的求解,通常使用数学规划方法进行求解。
3. 模型预测控制算法应用场景模型预测控制算法广泛应用于各个领域的控制系统中。
在工业过程控制中,模型预测控制算法可以实现对复杂工艺过程的高效控制;在电力系统控制中,模型预测控制算法可以实现对电网负载和频率的优化调节;在智能交通系统中,模型预测控制算法可以实现对交通流的优化调度。
4. 常见的模型预测控制算法4.1 微分动态规划微分动态规划是模型预测控制算法中的常用方法之一,其核心思想是通过离散化状态空间和控制空间,并利用动态规划方法求解最优控制输入。
微分动态规划算法对于非线性系统的控制有很好的效果,但由于其计算复杂度较高,在实时控制系统中的应用相对有限。
4.2 无约束优化无约束优化是模型预测控制算法的常用技术之一,其基本思想是将控制系统建模为一个无约束优化问题,并通过数学规划方法求解最优控制输入。
无约束优化算法对于线性系统和凸优化问题的求解效果较好,在实时控制系统中应用广泛。
4.3 基于模型的预测控制基于模型的预测控制是一种常用的模型预测控制算法,其核心思想是建立系统的数学模型,并根据模型进行预测和优化控制。
mpc计算例题

以下是一个简单的MPC(模型预测控制)计算例题:
假设我们有两个机器人A和B,它们都装备了激光雷达传感器。
机器人A的坐标为(0,0),而机器人B的坐标为(10,0)。
机器人A和B都以恒定速度向对方移动,并且它们都希望避免碰撞。
现在,我们要使用MPC来计算机器人A和B的轨迹,以确保它们不会碰撞。
建立模型:
机器人的运动模型可以表示为:x(t+1) = x(t) + v * dt
其中,x(t)表示机器人t时刻的位置,v表示机器人的速度,dt表示时间步长。
预测未来轨迹:
对于每个机器人,我们可以使用上述模型来预测其在未来一段时间内的轨迹。
优化问题:
我们需要解决一个优化问题,以确定每个机器人在每个时间步长上的最佳速度v。
优化目标可以是使机器人之间的距离最大化,或者使机器人的轨迹与参考轨迹之间的误差最小化。
更新控制:
根据优化结果,我们可以更新每个机器人的速度,并观察其轨迹是否发生变化。
如果轨迹发生变化,我们可以再次解决优化问题,并更新控制。
重复步骤4,直到达到收敛条件或达到预定的迭代次数。
以上是一个简单的MPC计算例题。
在实际应用中,MPC通常用于更复杂的系统,例如无人机、车辆、机器人等。
模型预测控制

z 1 g ( z 1 )u (k ) (k )
输出预测
预测模型:
ˆ ( z 1 )u (k ) (k ) y (k ) G ˆ ( z 1 )u (k ) (k ) z g
1
第1步输出预测:
ˆ ˆ m ( k 1) G ( z 1 )u ( k 1) (k 1) y ˆ g ( z 1 )u ( k ) (k 1)
受控过程越来越复杂,难以建模 不确定因素多 能源危机 经济效益
• 70年代
开始关注工业过程复杂性控制问题 串级控制、前馈控制等在过程控制中得到应用 现代控制理论仍很少在过程控制领域应用
• 80年代
Richalet和Cutler两人几乎同时报道研究成果
MPHC(模型预测启发式控制)
DMC(动态矩阵控制)
MAC主要包括内部预测模型、反馈校正、滚动优 化和参考轨迹等几个部分。 MAC采用系统脉冲响应作为内部预测模型,是一 种非参数模型。 用过去和当前的输入输出状态,根据内部模型, 预测系统未来的输出状态。 经过用模型输出误差进行反馈校正以后,再与 参考轨迹进行比较,应用二次型性能指标进行 滚动优化,然后再计算当前时刻加于系统的控 制,完成整个动作循环。
反馈校正
2
3
y u k k+1
4 1
ˆ y(k 1) ym (k 1) e(k 1) ˆ e(k 1) y(k 1) ym (k 1)
t/T
1─k时刻的预测输出 2─k+1时刻实际输出 3─预测误差 4─k+1时刻校正后的预测输出
反馈校正
y(k) y(k-j) ym(k ) u (k+j ) u(k-j) e(k)
模型预测控制快速求解算法

模型预测控制快速求解算法模型预测控制(Model Predictive Control,MPC)是一种基于在线计算的控制优化算法,能够统一处理带约束的多参数优化控制问题。
当被控对象结构和环境相对复杂时,模型预测控制需选择较大的预测时域和控制时域,因此大大增加了在线求解的计算时间,同时降低了控制效果。
从现有的算法来看,模型预测控制通常只适用于采样时间较大、动态过程变化较慢的系统中。
因此,研究快速模型预测控制算法具有一定的理论意义和应用价值。
虽然MPC方法为适应当今复杂的工业环境已经发展出各种智能预测控制方法,在工业领域中也得到了一定应用,但是算法的理论分析和实际应用之间仍然存在着一定差距,尤其在多输入多输出系统、非线性特性及参数时变的系统和结果不确定的系统中。
预测控制方法发展至今,仍然存在一些问题,具体如下:①模型难以建立。
模型是预测控制方法的基础,因此建立的模型越精确,预测控制效果越好。
尽管模型辨识技术已经在预测控制方法的建模过程中得以应用,但是仍无法建立非常精确的系统模型。
②在线计算过程不够优化。
预测控制方法的一大特征是在线优化,即根据系统当前状态、性能指标和约束条件进行在线计算得到当前状态的控制律。
在在线优化过程中,当前的优化算法主要有线性规划、二次规划和非线性规划等。
在线性系统中,预测控制的在线计算过程大多数采用二次规划方法进行求解,但若被控对象的输入输出个数较多或预测时域较大时,该优化方法的在线计算效率也会无法满足系统快速性需求。
而在非线性系统中,在线优化过程通常采用序列二次优化算法,但该方法的在线计算成本相对较高且不能完全保证系统稳定,因此也需要不断改进。
③误差问题。
由于系统建模往往不够精确,且被控系统中往往存在各种干扰,预测控制方法的预测值和实际值之间一定会产生误差。
虽然建模误差可以通过补偿进行校正,干扰误差可以通过反馈进行校正,但是当系统更复杂时,上述两种校正结合起来也无法将误差控制在一定范围内。
强化学习算法中的模型预测控制方法详解(五)

强化学习算法中的模型预测控制方法详解强化学习是一种通过与环境交互学习最优决策策略的机器学习方法。
在强化学习中,模型预测控制方法是一种重要的技术手段,用于通过预测环境的变化来指导智能体的决策,从而实现最优的控制效果。
本文将详细探讨强化学习算法中的模型预测控制方法,包括其基本原理、算法框架和应用场景。
模型预测控制的基本原理模型预测控制是一种基于模型的控制方法,其基本原理是通过建立环境的动态模型,对未来的状态进行预测,并基于这些预测结果来制定最优的控制策略。
在强化学习中,模型预测控制方法通常用于解决连续状态和动作空间的问题,例如机器人路径规划、交通信号控制等。
模型预测控制的算法框架模型预测控制方法的算法框架通常包括以下几个步骤:首先,建立环境的动态模型,通常采用基于神经网络的函数逼近方法来近似环境的动态特性;其次,利用建立的动态模型对未来的状态进行预测,得到状态-动作序列的预测结果;最后,基于预测结果通过优化方法(如强化学习算法)来制定最优的控制策略。
这一框架能够有效地处理连续状态和动作空间的问题,并且能够在具有不确定性的环境中取得良好的控制效果。
模型预测控制方法的应用场景模型预测控制方法在强化学习中有着广泛的应用场景。
例如,智能体在复杂环境中的路径规划问题中,可以利用模型预测控制方法来预测未来的状态,从而制定最优的移动策略;在交通信号控制中,可以利用模型预测控制方法来预测车辆的行驶轨迹,从而优化交通信号的控制策略;在机器人控制中,可以利用模型预测控制方法来预测机器人的运动轨迹,从而实现精准的操作控制。
这些应用场景都需要智能体能够对环境的动态特性进行准确的预测,并能够在不确定性环境中做出最优的决策,模型预测控制方法能够很好地满足这些需求。
模型预测控制方法的发展趋势随着人工智能技术的不断发展,模型预测控制方法在强化学习中的应用也在不断深化和拓展。
未来,随着深度学习和强化学习算法的不断完善,模型预测控制方法将更加准确和高效,能够处理更加复杂和多样化的环境;同时,模型预测控制方法还将更加注重与实际应用场景的结合,能够为实际问题提供更加有效的解决方案。
列出模型预测控制计算的概述步骤

列出模型预测控制计算的概述步骤
ModelPredictiveControl(MPC)引入以解决控制问题。
MPC一种
基于模型预测的控制计算方法,它基于连续变化的模型,通过对未来发展状况的预测来计算当前的控制指令。
本文将讨论MPC的概述步骤以及它的优点。
MPC的步骤概述包括:
1)建立模型:建立MPC模型之前,需要建立系统的数学模型,并使用数学模型来描述系统运行的特征。
2)定义目标函数、约束条件和变量:一步将定义最大化或最小化目标函数、约束条件以及变量,以满足所需的控制要求。
3)求解模型:此步骤中,将使用线性规划算法或非线性规划算法来求解MPC模型,以计算最佳控制指令。
4)实施控制指令:一步将检查预测的控制指令,以确保它工作的效果。
5)根据新的输入重复以上步骤: 一旦控制指令实施,MPC将继
续根据新的输入数据来重复以上步骤,以持续提供最新的控制指令。
MPC有许多优点,其中包括:
1)准确性:于MPC可以基于模型预测来计算当前的控制指令,因此它可以更准确地预测实际情况,从而提高控制精度。
2)实时性: MPC可以根据新的输入数据来重复以上步骤,以确
保控制的实时性。
3)反应性:于MPC可以根据输入数据的变化来实时调整控制指令,
因此它可以较快地响应环境的变化,从而有效控制系统的运行状况。
4)防止过度控制: MPC可以有效地防止过度控制,从而避免额外的控制成本。
总之,MPC有准确性、实时性、反应性和防止过度控制的优点,是一种非常有用的控制计算方法。
本文概述了MPC的步骤,并简要介绍了它的优点,以帮助读者了解和使用MPC的方法以解决控制问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模型预测控制快速求解算法模型预测控制(Model Predictive Control,MPC)是一种基于在线计算的控制优化算法,能够统一处理带约束的多参数优化控制问题。
当被控对象结构和环境相对复杂时,模型预测控制需选择较大的预测时域和控制时域,因此大大增加了在线求解的计算时间,同时降低了控制效果。
从现有的算法来看,模型预测控制通常只适用于采样时间较大、动态过程变化较慢的系统中。
因此,研究快速模型预测控制算法具有一定的理论意义和应用价值。
虽然MPC方法为适应当今复杂的工业环境已经发展出各种智能预测控制方法,在工业领域中也得到了一定应用,但是算法的理论分析和实际应用之间仍然存在着一定差距,尤其在多输入多输出系统、非线性特性及参数时变的系统和结果不确定的系统中。
预测控制方法发展至今,仍然存在一些问题,具体如下:①模型难以建立。
模型是预测控制方法的基础,因此建立的模型越精确,预测控制效果越好。
尽管模型辨识技术已经在预测控制方法的建模过程中得以应用,但是仍无法建立非常精确的系统模型。
②在线计算过程不够优化。
预测控制方法的一大特征是在线优化,即根据系统当前状态、性能指标和约束条件进行在线计算得到当前状态的控制律。
在在线优化过程中,当前的优化算法主要有线性规划、二次规划和非线性规划等。
在线性系统中,预测控制的在线计算过程大多数采用二次规划方法进行求解,但若被控对象的输入输出个数较多或预测时域较大时,该优化方法的在线计算效率也会无法满足系统快速性需求。
而在非线性系统中,在线优化过程通常采用序列二次优化算法,但该方法的在线计算成本相对较高且不能完全保证系统稳定,因此也需要不断改进。
③误差问题。
由于系统建模往往不够精确,且被控系统中往往存在各种干扰,预测控制方法的预测值和实际值之间一定会产生误差。
虽然建模误差可以通过补偿进行校正,干扰误差可以通过反馈进行校正,但是当系统更复杂时,上述两种校正结合起来也无法将误差控制在一定范围内。
模型预测控制区别于其它算法的最大特征是处理多变量多约束线性系统的能力,但随着被控对象的输入输出个数的增多,预测控制方法为保证控制输出的精确性,往往会选取较大的预测步长和控制步长,但这样会大大增加在线优化过程的计算量,从而需要更多的计算时间。
因此,预测控制方法只能适用于采样周期较大且动态变化过程较慢的系统中。
为使预测控制方法能在更多场合中应用,快速模型预测控制算法成为了一个新的研究方向。
国内外研究现状近年来人们对预测控制算法的不足有了越来越清晰的认识,为了将该算法应用到更多领域,越来越多的学者对其进行不断研究和改进。
阅读近些年国内外核心期刊的文献可知,人们对预测控制方法能够在更大更复杂的系统中应用寄予了很高期望,同时也在其不足方面做了很多探究和尝试,发展出了多种智能预测控制方法。
快速模型预测控制算法作为目前智能预测控制方法之一,其研究方向主要有以下几个方面:(1)显式模型预测控制(Explicit Model Predictive Control,EMPC)2002年Alberto Bemporad等学者[1]提出了显式模型预测控制,该方法在预测控制基础之上,在线性时不变系统优化求解过程中引入多参数二次规划理论,对系统的状态区域进行凸划分,根据最优控制问题计算得到状态分区上相应的控制律。
EMPC将模型预测控制的在线计算过程转化为离线和在线计算相结合的过程,大大减少了算法的在线计算时间,弥补了MPC方法反复在线计算的不足,EMPC 也在电力电子[2]、电机控制[3]等领域得到了很好应用。
但随着被控对象问题规模(如输入、状态维数、约束等)的增大,EMPC算法在离线计算过程中所求的状态分区数会呈指数倍增加,而状态分区数的增加不仅会导致存储状态分区所需的存储空间增加,还会导致EMPC算法在线查找最优解所需的计算时间增加,因此该算法很难适用于状态约束较多(状态变量往往不超过5)、预测步长较大的复杂系统。
基于以上原因,许多学者提出用近似的显式模型预测控制方法[4,5]来代替精确的EMPC算法,即通过牺牲一定的控制精度来降低计算过程中的复杂度,从而简化整个求解过程。
如文献[6]提出了显式模型预测控制的多尺度近似方法,通过引入分段线性插入法和自适应分层函数近似法,运用重心插值理论对EMPC离线计算出的状态空间进行网格划分,得到近似的状态分区和近似控制律。
基于同样的思想,文献[7]提出了显式模型预测控制多胞体近似方法,主要利用双描述法对最优控制问题进行近似处理,再通过重心插值得到近似控制律。
文献[8]基于小波的多分辨率分析提出了近似EMPC,通过二次插值和网格划分得到低复杂度且可保证系统稳定的近似控制律。
上述文献提出的方法均能在误差允许的范围内保证系统的控制性能,在一定程度上解决了EMPC随着问题规模增大而带来的复杂度和存储空间增大的问题。
(2)模型预测控制的简化算法MPC算法采用的是在线滚动优化的控制策略,但随着工业模型和环境越来越复杂,其在线计算量越来越大,所以限制了MPC算法在动态变化较快系统中的应用。
为减少MPC在线优化求解的计算量,有学者考虑对参数进行优化,提出了预测控制的简化算法,如将参数分块化的blocking技术[9],其思想是将越远离当前时刻的控制输入越粗略计算,从而减少在线计算量。
在此基础上,又有学者提出了移动blocking方法,其核心是限制系统优化变量个数同时增大系统的有效输入步长[10]。
相较于blocking技术,文献[11]提出的简化方法主要把约束分为起作用约束集、不起作用约束集和不确定约束集,对不起作用的约束集进行忽略操作,对起作用约束集和不确定约束集进行优化计算,从而降低在线计算量,加快控制进程。
(3)改进的在线优化算法模型预测控制的核心是采用反复的迭代优化进行在线求解,选取适当的在线优化方法可以提高在线计算速度。
近年来,有学者试图对模型预测控制的标准形式做适当变形或者近似处理,继而降低预测控制方法的在线计算量。
如文献[12]提出了一种用扩展的牛顿拉夫逊(Newton-Raphson)方法来代替传统的二次规划方法,当问题规模增大时,不仅能够保证优化问题总是收敛,还可以有效解决MPC在线计算量过大的问题。
文献[13]提出了将表存储和在线优化相结合的部分枚举法(Partial Enumeration,PE),对于规模较大的线性模型不仅有很好的控制效果,而且求解速度是传统MPC算法的5倍以上。
文献[14]提出了基于降精度求解准则的序列二次规划法,主要通过牺牲一定的精确度来降低在线优化所需的迭代次数,从而提高在线求解速度。
文献[15]提出了可用于预测控制在线优化过程的有效内点法,该内点法不仅可以减少代码量,而且可以使在线计算时间提高2-5倍。
理论基础凸集与凸函数首先给出凸优化理论中凸集、凸函数和仿射的定义。
凸集:假设C 为n 维实数空间n R 中的集合,若C 中任意两点之间的线段仍然在集合C 中,即对于任意12,x x C ∈且对任意实数[]0,1λ∈,都满足:12(1)x x C λλ+-∈ (3-1)则称集合C 为凸集,反之则为非凸集。
满足凸集的集合具有以下性质:(1)若集合1C 、2C 都是凸集则集合{}12121122|,,C C x x y y y C y C +==+∈∈也是凸集。
(2)两个或多个凸集的交集仍为凸集。
(3)空集也是凸集。
凸函数:设()f x 是定义在非空凸集n C R ∈上的函数,对于凸集C 中任意的1x 和2x 以及任意实数[]0,1λ∈均满足1212((1))()(1)()f x x f x f x λλλλ+-≤+-(3-2)则称()f x 为凸函数,反之则为非凸函数(或称凹函数)。
若对12x x ≠和任意实数[]0,1λ∈均满足1212((1))()(1)()f x x f x f x λλλλ+-<+-(3-3)则称()f x 为严格凸函数。
同样,根据凸函数的定义可以推导出凸函数的几个性质,具体如下:(1)若1(),,()m f x f x 是定义在凸集C 上的凸函数,则11()()m m f x f x αα++也是凸集C 上的凸函数,其中α为任意实数。
(2)若函数()f x 是定义在凸集C 上的凸函数,则对于任意实数α,函数()f x α也是凸集C 上的凸函数。
(3)若()g x 是单调递增的凸函数,()f x 也是凸函数,则复合函数[]()g f x 也是凸函数。
(4)若()f x 和()g x 都是定义在凸集C 中非单调递增的凸函数,则()()f x g x 也是定义在凸集C 中的凸函数。
仿射:对于集合C 中任意两点1x 和2x 且任意实数R λ∈,若满足12(1)x x C λλ+-∈ (3-4)则称集合C 是仿射的。
也就是说,通过集合n C R ⊆中任意两点的直线仍在集合C 中。
凸优化问题凸优化问题是指性能指标函数和不等式约束函数均为凸函数且由约束条件所得到的集合是凸集的最优化问题。
由于凸优化问题的局部最优解就是全局最优解,因此对于一个实际问题,如果能表示成凸优化问题,则意味着该问题可以得到彻底解决,对实际应用有着十分重要的意义。
凸优化问题有多种形式,其基本形式可表示为:min ().. ()0 1,, ()0 1,,i i f x s t g x i m h x i p≤===(3-5)其中()f x 为性能指标函数,()0i g x ≤为不等式约束条件,()0i h x =为等式约束条件,()0 1,,()0 1,,ii g x i m C x h x i p ≤=⎧⎫=⎨⎬≤=⎩⎭为可行域(也称可行集或约束集)。
如果上述问题中性能指标函数()f x 和不等式约束()i g x 都是仿射函数,则该问题又称线性规划问题(Linear Programming ,LP ),其形式可表示为:min .. T c x ds t Gx h Ax b+≤=(3-6)其中,m n p n G R A R ⨯⨯∈∈,对于线性规划问题而言,通常将性能指标函数中常数项d 忽略,因为其不影响最优解的集合。
该问题的几何解释可由图表示,图中阴影多面体为可行域P ,若性能指标函数中T c x 为线性的,则其等位曲线是和c正交的超平面(图中的虚线),点*x对即为最优点。
图线性规划的几何解释如果性能指标函数()f x是凸二次型且约束条件是仿射函数,则该问题又称二次规划问题(Quadratic Programming,QP)。
对于二次规划问题,其标准形式可表示为:1min2..T Tx Qx q x rs t Ax bGx h++=≤(3-7)其中,,,,,n n m n m p n pQ S q R A R b R G R h R⨯⨯+∈∈∈∈∈∈。
