高数微积分基本公式大全

合集下载

高等数学常用微积分公式

高等数学常用微积分公式一、极限1.无穷大与无穷小：当x→∞时，若极限值L=0，则称函数f(x)是无穷小。

常见无穷小有：x→0时的无穷小o(x)、无穷次可导的无穷小O(x^n)；当x→∞时，若极限值L≠0或不存在，则称函数f(x)是无穷大；2.函数极限：若函数f(x)当x→a时的极限存在稳定的常数L，则称L为f(x)当x→a时的极限，记作：lim(x→a) f(x) = L；3.等价无穷小：若 f(x) 和 g(x) 都是x→a 时的无穷小，并且lim(x→a)(f(x)/g(x))=1，则称 f(x) 和 g(x) 是x→a 时的等价无穷小。

二、导数1.导数的定义：若函数f(x)在点x处的函数值可近似表示为f(x+Δx)≈f(x)+f'(x)Δx，其中f'(x)为f(x)在点x处的导数，则称f'(x)是函数f(x)在点x处的导数。

2.常见函数的导数：(1)和差法则：(u±v)'=u'±v'；(2)乘法法则：(u*v)'=u'*v+u*v'；(3)除法法则：(u/v)'=(u'*v-u*v')/v^2，其中v≠0；(4) 链式法则：若 y=f(u)，u=g(x) ，则 y=f(g(x)) 的导数为dy/dx = f'(u)*g'(x)。

3.高阶导数：函数f(x)的导数f'(x)的导数称为f(x)的二阶导数，记为f''(x)。

可以依此类推，得到函数f(x)的n阶导数f^(n)(x)。

三、微分1.微分的定义：函数 f(x) 在点 x 处的微分记为 dx，根据导数的定义，有 df(x) = f'(x)dx。

2.微分的性质：(1)常数微分：d(c)=0，其中c为常数；(2) 取单项微分：d(x^n) = nx^(n-1)dx，其中 n 为实数，x 为变量；(3) 和差微分：d(u ± v) = du ± dv；(4) 乘法微分：d(uv) = u*dv + v*du；(5) 除法微分：d(u/v) = (v*du - u*dv)/v^2，其中v ≠ 0；(6) 复合函数微分：若 y=f(u)，u=g(x)，则 dy = f'(u)du =f'(g(x))g'(x)dx。

高等数学微积分公式

高等数学微积分公式高等数学微积分公式微积分是数学中的一个重要分支，它研究的是函数的变化规律。

在微积分的学习中，我们需要掌握许多公式，在处理函数的变化过程中起到了非常重要的作用。

下面是高等数学中常见的微积分公式。

一、导数公式1.常数函数的导数公式：\[\frac{d}{dx} C=0\]其中C为常数。

2.幂函数的导数公式：\[\frac{d}{dx} x^{n}=nx^{n-1}\]其中n为常数。

3.自然指数函数的导数公式：\[\frac{d}{dx} e^{x}=e^{x}\]4.对数函数的导数公式：\[\frac{d}{dx} ln(x)=\frac{1}{x}\]5.三角函数的导数公式：\[\frac{d}{dx} sin(x)=cos(x)\]\[\frac{d}{dx} cos(x)=-sin(x)\]6.反三角函数的导数公式：\[\frac{d}{dx} sin^{-1}(x)=\frac{1}{\sqrt{1-x^{2}}}\] \[\frac{d}{dx} cos^{-1}(x)=-\frac{1}{\sqrt{1-x^{2}}}\]7.复合函数的导数公式（链式法则）：设y=f(u)和u=g(x)，则有\[\frac{dy}{dx}=\frac{dy}{du}\times \frac{du}{dx}\]二、微分公式1.常数函数的微分公式：\[d(C)=0\]其中C为常数。

2.幂函数的微分公式：\[d(x^{n})=nx^{n-1}dx\]其中n为常数。

3.指数函数的微分公式：\[d(e^{x})=e^{x}dx\]4.三角函数的微分公式：\[d(sin(x))=cos(x)dx\]\[d(cos(x))=-sin(x)dx\]5.反三角函数的微分公式：\[d(sin^{-1}(x))=\frac{dx}{\sqrt{1-x^{2}}}\]\[d(cos^{-1}(x))=-\frac{dx}{\sqrt{1-x^{2}}}\]6.复合函数的微分公式（链式法则）：设y=f(u)和u=g(x)，则有\[dy=\frac{dy}{du}\times du\]三、泰勒公式泰勒公式是微积分中的一个重要定理，它可以将一个函数在某点的值表示为一系列关于该点的导数的和。

高数微积分公式大全

高等数学微积分公式大全一、基本导数公式⑴ c0 ⑵ x x 1⑶sin x cos x⑷ cos x sin x ⑸ tan x sec2x ⑹ cot x csc2 x⑺ secx sec x tan x ⑻ csc x csc x cot x⑼ e x e x⑽ a x a x ln a ⑾ ln x1x⑿ log a x1⒀ arcsin x1⒁ arccos x1x ln a1x2 1 x2⒂ arctanx12⒃ arccot x12⒄ x1⒅x11x 1 x2x二、导数的四则运算法例三、高阶导数的运算法例（1）u x v x nn v xn（2）cu x n cu n x u x（3）u ax b n ax b （4） u x v x n nc n k u n k x v(k ) xa n u nk 0四、基本初等函数的n 阶导数公式（1）x nnn! （） e ax b n(3)a x nax n n a2(4) (6)sin n a n sin ax b n(5)cos ax b nax b a n cos ax b n221n n a n n!n n 1 a n n 1 !1(7)ln ax bax axn 11axnb b b五、微分公式与微分运算法例⑴ d c 0 ⑵ d x x1 dx ⑶ d sin x cos xdx⑷ d cosx sin xdx ⑸ d tan x sec2 xdx ⑹ d cot x csc2 xdx ⑺ d secx secx tan xdx ⑻ d cscx cscx cot xdx⑼ d e x e x dx ⑽ d a x a x ln adx ⑾d ln x 1 dxx⑿⒂d log a x1dx⒀ d arcsin x11dx ⒁ d arccos x1dx x ln a x21x2d arctan x1dx ⒃ d arccot x1dx1x212x六、微分运算法例⑴ d u v du dv⑵ d cu cdu⑶ d uv vdu udv u vdu udv⑷ dv2v七、基本积分公式⑴kdx kx c ⑵x dx x 1 c ⑶dxln x c1x⑷a x dx a x c ⑸e x dx e x c ⑹ cosxdx sin x cln a⑺⑼sin xdx cosx c ⑻1dx sec2xdx tan x ccos2x1csc2 xdx cot x c ⑽1dx arctan x c sin 2 x1x2⑾1dx arcsin x c1x2八、增补积分公式九、以下常用凑微分公式积分型换元公式十、分部积分法公式⑴形如x n e ax dx ，令u x n， dv e ax dx 形如x n sin xdx 令u x n，dv sin xdx 形如x n cosxdx 令u x n，dv cosxdx⑵形如x narctan，令 u arctanx ，dvndx xdx x形如 x n ln xdx，令u ln x ，dv x n dx⑶形如 e ax sin xdx ，e ax cosxdx 令u e ax ,sin x,cos x 均可。

高数微积分基本公式大全

∫
⑻
1 ⑼∫ = csc2 xdx = − cot x + c sin 2 x ∫
⑾
x 1 ⑽∫ dx = arctan x + c 1 + x2
∫ cos
1
2
dx = ∫ sec 2 xdx = tan x + c
∫
1 1 − x2
dx = arcsin x + c
六、补充积分公式
∫ tan xdx = − ln cos x + c ∫ sec xdx = ln sec x + tan x + c
2.二倍角公式
cos( A − B ) = cos A cos B + sin A sin B
tan( A − B ) = tan A − tan B 1 + tan A tan B cot A ⋅ cot B + 1 cot( A − B ) = cot B − cot A
sin 2 A = 2sin A cos A tan 2 A = 2 tan A 1 − tan 2 A
2
u = cos x
xdx = ∫ f ( tan x )d ( tan x ) xdx = ∫ f ( cot x )d ( cot x )
1
2
u = tan x u = cot x
2
∫ f ( arctan x ) ⋅ 1 + x
dx = ∫ f ( arc ta n x )d ( arc ta n x )
tan
cot
4.和差化积公式
sin a + sin b = 2sin
a+b a−b ⋅ cos 2 2 a+b a −b cos a + cos b = 2 cos ⋅ cos 2 2

高数微积分公式大全

∫ duv = uv = ∫ udv + ∫ vdu →∫ udv = uv - ∫ vdu cos2θ-sin2θ=cos2θ cos2θ+ sin2θ=1 cosh2θ-sinh2θ=1 cosh2θ+sinh2θ=cosh2θ
sin 3θ=3sinθ-4sin3θ cos3θ=4cos3θ-3cosθ
x
sin α + sin β = 2 sin ½(α+β) cos ½(α-β) sin α - sin β = 2 cos ½(α+β) sin ½(α-β) cos α + cos β = 2 cos ½(α+β) cos ½(α-β) cos α - cos β = -2 sin ½(α+β) sin ½(α-β) tan (α±β)= tan α ± tan β ∓ cot α cot β , cot (α±β)= ∓ tan α tan β cot α ± cot β
2
∞
0
∫
∞
0
1 (ln ) x-1 dt t
(1+x)r =1+rx+
π 1 r ( r − 1) 2 r ( r − 1)( r − 2) 3 x+ x +… -1<x<1 β(m, n) = ∫ x m-1(1-x)n-1 dx=2 ∫ 2 sin 2m-1x cos2n-1x dx 0 0 2! 3!
1 + x2 x 1 )=ln( + ) |x| >0 x2 a x duv = udv + vdu csch-1 (
∫ tanh x dx = ln | cosh x |+ C coth x = -csch x ∫ coth x dx = ln | sinh x | + C sech x = -sech x tanh x ∫ sech x dx = -2tan-1 (e-x) + C csch x = -csch x coth x 1 + e− x ∫ csch x dx = 2 ln | |+C 1 − e −2 x x 1 Dx sinh-1( )= ∫ sinh-1 x dx = x sinh-1 x- 1 + x 2 + C 2 2 a a +x x 1 cosh-1( )= ∫ cosh-1 x dx = x cosh-1 x- x 2 − 1 + C 2 2 a x −a x ±a tanh-1( )= 2 a a − x2

高等数学中所涉及到的微积分公式汇总

高等数学中所涉及到的微积分公式汇总微积分是高等数学中的一门重要学科，涉及到很多重要的公式和定理。

下面是一些微积分中常用的公式的汇总：1.导数公式：- 函数f(x)在点x处的导数：f'(x) = lim (f(x+h)-f(x))/h,其中h -> 0- 常见函数的导数公式：常数函数导数为0，幂函数导数为nx^(n-1)，三角函数的导数等-乘法法则：(f*g)'(x)=f'(x)*g(x)+f(x)*g'(x)-商法则：(f/g)'(x)=(f'(x)g(x)-f(x)g'(x))/(g(x))^22.积分公式：- 不定积分和定积分的基本定理：若F'(x) = f(x)，则∫f(x) dx = F(x) + C- 基本不定积分：∫x^n dx = (1/n+1)*x^(n+1) + C （其中n不等于-1）- 定积分的性质：∫(a to b) f(x) dx = -∫(b to a) f(x) dx，∫(a to b) [f(x) ± g(x)] dx = ∫(a to b) f(x) dx ± ∫(a to b)g(x) dx3.微分学的基本定理：- 导数的基本定理：如果F(x)是f(x)的一个原函数，那么∫(a to b) f(x) dx = F(b) - F(a)- 牛顿-莱布尼茨公式：若F(x)是f(x)的一个原函数，那么∫(a tob) f(x) dx = F(x)，_(a to b) = F(b) - F(a)4.极限定理：- 极限的四则运算定理：设lim (x -> a) f(x) = L，lim (x -> a) g(x) = M，则lim (x -> a) [f(x)±g(x)] = L±M，lim (x -> a)[f(x)*g(x)] = L*M，lim (x -> a) [f(x)/g(x)] = L/M （其中M不等于0）- L'Hospital法则：设lim (x -> a) f(x) = 0，lim (x -> a) g(x) = 0，并且lim (x -> a) f'(x)/g'(x) 存在，则lim (x -> a) f(x)/g(x) = lim (x -> a) f'(x)/g'(x)- 夹逼定理：如果数列{a_n}、{b_n}、{c_n}满足a_n <= b_n <=c_n，并且lim (n -> ∞) a_n = lim (n -> ∞) c_n = L，则lim (n -> ∞) b_n = L5.泰勒级数：-函数f(x)的泰勒级数展开：f(x)=f(a)+f'(a)(x-a)+f''(a)*(x-a)^2/2!+...+f^n(a)*(x-a)^n/n!+...，其中f^n(a)表示函数f(x)在点a处的n阶导数以上仅是微积分中涉及到的一些公式，实际上微积分的公式和定理非常丰富，还有更多的公式可以在相关的教材和文献中找到。

高数微积分公式大全dy

高等数学微积分公式大全一、基本导数公式⑴()0c '= ⑵1x x μμμ-= ⑶()sin cos x x '= ⑷()cos sin x x '=- ⑸()2tan sec x x '= ⑹()2cot csc x x '=-⑺()sec sec tan x x x '=⋅ ⑻()csc csc cot x x x '=-⋅ ⑼()xxe e '= ⑽()ln xxa aa '= ⑾()1ln x x'=⑿()1log ln xax a'= ⒀()arcsin x '= ⒁()arccos x '=⒂()21arctan 1x x '=+ ⒃()21arc cot 1x x '=-+⒄()1x '=⒅'=二、导数的四则运算法则()u v u v '''±=± ()uv u v uv '''=+ 2u u v uv v v '''-⎛⎫= ⎪⎝⎭三、高阶导数的运算法则（1）()()()()()()()n n n u x v x u x v x ±=±⎡⎤⎣⎦ （2）()()()()n n cu x cu x =⎡⎤⎣⎦（3）()()()()n n nu ax b a uax b +=+⎡⎤⎣⎦（4）()()()()()()()0nn n k k k n k u x v x c u x v x -=⋅=⎡⎤⎣⎦∑四、基本初等函数的n 阶导数公式（1）()()!n nxn = （2）()()n ax b n ax b e a e ++=⋅ (3)()()ln n x x n a a a =(4)()()sin sin 2n n ax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (5) ()()cos cos 2n nax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (6)()()()11!1n n nn a n ax b ax b +⋅⎛⎫=- ⎪+⎝⎭+ (7) ()()()()()11!ln 1n n n na n axb ax b -⋅-+=-⎡⎤⎣⎦+五、微分公式与微分运算法则⑴()0d c = ⑵()1d x x dx μμμ-= ⑶()sin cos d x xdx =⑷()cos sin d x xdx =- ⑸()2tan sec d x xdx = ⑹()2cot csc d x xdx =-⑺()sec sec tan d x x xdx =⋅ ⑻()csc csc cot d x x xdx =-⋅⑼()x x d e e dx = ⑽()ln x xd a a adx = ⑾()1ln d x dx x=⑿()1logln xad dx x a =⒀()arcsin d x = ⒁()arccos d x =⒂()21arctan 1d x dx x =+ ⒃()21arc cot 1d x dx x=-+ 六、微分运算法则⑴()d u v du dv ±=± ⑵()d cu cdu = ⑶()d uv vdu udv =+ ⑷2u vdu udvd v v -⎛⎫= ⎪⎝⎭七、基本积分公式⑴kdx kx c =+⎰ ⑵11x x dx c μμμ+=++⎰ ⑶ln dx x c x =+⎰⑷ln xxa a dx c a=+⎰ ⑸x x e dx e c =+⎰ ⑹cos sin xdx x c =+⎰ ⑺sin cos xdx x c =-+⎰ ⑻221sec tan cos dx xdx x c x ==+⎰⎰⑼221csc cot sin xdx x c x ==-+⎰⎰⑽21arctan 1dx x c x =++⎰ ⑾arcsin x c =+八、补充积分公式tan ln cos xdx x c =-+⎰ cot ln sin xdx x c =+⎰ sec ln sec tan xdx x x c =++⎰ csc ln csc cot xdx x x c =-+⎰2211arctan x dx c a x a a=++⎰ 2211ln 2x adx c x a a x a-=+-+⎰arcsin xc a =+ln x c =+十、分部积分法公式⑴形如n ax x e dx ⎰，令nu x =，ax dv e dx =形如sin n x xdx ⎰令nu x =，sin dv xdx =形如cos n x xdx ⎰令nu x =，cos dv xdx =⑵形如arctan n x xdx ⎰，令arctan u x =，ndv x dx =形如ln n x xdx ⎰，令ln u x =，ndv x dx =⑶形如sin ax e xdx ⎰，cos ax e xdx ⎰令,sin ,cos axu e x x =均可。

高数微积分公式大全

高等数学微积分公式大全一、基本导数公式⑴()0c '= ⑵1x x μμμ-= ⑶()sin cos x x '= ⑷()cos sin x x '=- ⑸()2tan sec x x '= ⑹()2cot csc x x '=- ⑺()sec sec tan x x x '=⋅ ⑻()csc csc cot x x x '=-⋅⑼()x x e e '= ⑽()ln x x a a a '= ⑾()1ln x x'=⑿()1log ln xa x a'= ⒀()arcsin x '= ⒁()arccos x '=⒂()21arctan 1x x '=+ ⒃()21arccot 1x x '=-+⒄()1x '=⒅1'= 二、导数的四则运算法则()u v u v '''±=± ()u v u v u v '''=+ 2u u v u v v v '''-⎛⎫= ⎪⎝⎭三、高阶导数的运算法则（1）()()()()()()()nn n u x v x u x v x ±=±⎡⎤⎣⎦ （2）()()()()nn cu x cu x =⎡⎤⎣⎦（3）()()()()n n nu ax b a uax b +=+⎡⎤⎣⎦（4）()()()()()()()0nn n k k k n k u x v x c u x v x -=⋅=⎡⎤⎣⎦∑四、基本初等函数的n 阶导数公式（1）()()!n nx n = （2）()()n ax b n ax b e a e ++=⋅ (3)()()ln n x x n a a a =(4)()()sin sin 2n n ax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (5) ()()cos cos 2n nax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (6)()()()11!1n n nn a n ax b ax b +⋅⎛⎫=- ⎪+⎝⎭+ (7) ()()()()()11!ln 1n n n na n axb ax b -⋅-+=-⎡⎤⎣⎦+五、微分公式与微分运算法则⑴()0d c = ⑵()1d x x dx μμμ-= ⑶()sin cos d x xdx =⑷()cos sin d x xdx =- ⑸()2tan sec d x xdx = ⑹()2cot csc d x xdx =-⑺()sec sec tan d x x xdx =⋅ ⑻()csc csc cot d x x xdx =-⋅⑼()x x d e e dx = ⑽()ln x xd a a adx = ⑾()1ln d x dx x=⑿()1logln x a d dx x a =⒀()arcsin d x =⒁()arccos d x = ⒂()21arctan 1d x dx x =+ ⒃()21arccot 1d x dx x=-+ 六、微分运算法则⑴()d u v du dv ±=± ⑵()d cu cdu = ⑶()d uv vdu udv =+ ⑷2u vdu udvd v v -⎛⎫= ⎪⎝⎭七、基本积分公式⑴kdx kx c =+⎰ ⑵11x x dx c μμμ+=++⎰ ⑶ln dxx c x=+⎰⑷ln xxa a dx c a=+⎰ ⑸x x e dx e c =+⎰ ⑹cos sin xdx x c =+⎰⑺sin cos xdx x c =-+⎰ ⑻221sec tan cos dx xdx x c x ==+⎰⎰⑼221csc cot sin xdx x c x ==-+⎰⎰ ⑽21arctan 1dx x c x=++⎰ ⑾arcsin x c =+八、补充积分公式tan ln cos xdx x c =-+⎰ c o t l n s i n x d x x c =+⎰ sec ln sec tan xdx x x c =++⎰ c s c l n c s cc o t xd x x x c=-+⎰ 2211arctan xdx c a x a a=++⎰ 2211ln 2x adx c x a a x a-=+-+⎰arcsinxc a=+ ln x c =++九、下列常用凑微分公式十、分部积分法公式⑴形如n ax x e dx ⎰，令n u x =，ax dv e dx =形如sin n x xdx ⎰令n u x =，sin dv xdx =形如cos n x xdx ⎰令n u x =，cos dv xdx =⑵形如arctan n x xdx ⎰，令arctan u x =，ndv x dx =形如ln n x xdx ⎰，令ln u x =，ndv x dx =⑶形如sin ax e xdx ⎰，cos ax e xdx ⎰令,sin ,cos axu e x x =均可。

高数微积分公式

高数微积分公式以下是一些高数微积分中常用的公式：1. 极限求导公式：- $\\displaystyle \\frac{d}{dx}(x^{n})=nx^{n-1}$- $\\displaystyle \\frac{d}{dx}(\\sin x)=\\cos x$- $\\displaystyle \\frac{d}{dx}(\\cos x)=-\\sin x$- $\\displaystyle \\frac{d}{dx}(\\ln x)=\\frac{1}{x}$ - $\\displaystyle \\frac{d}{dx}(e^{x})=e^{x}$2. 基本导数法则：- $\\displaystyle \\frac{d}{dx}(cf(x))=cf'(x)$ （常数的导数）- $\\displaystyle \\frac{d}{dx}(f(x)\\pmg(x))=f'(x)\\pm g'(x)$ （和差法则）- $\\displaystyle\\frac{d}{dx}(f(x)g(x))=f'(x)g(x)+f(x)g'(x)$ （乘积法则）- $\\displaystyle\\frac{d}{dx}\\left(\\frac{f(x)}{g(x)}\\right)=\\frac{f'(x)g( x)-f(x)g'(x)}{g^{2}(x)}$ （商法则）- $\\displaystyle \\frac{d}{dx}(f(g(x)))=f'(g(x))\\cdot g'(x)$ （链式法则）3. 积分公式：- $\\displaystyle \\intx^{n}dx=\\frac{1}{n+1}x^{n+1}+C$- $\\displaystyle \\int \\sin xdx=-\\cos x+C$- $\\displaystyle \\int \\cos xdx=\\sin x+C$- $\\displaystyle \\int \\frac{1}{x}dx=\\ln |x|+C$- $\\displaystyle \\int e^{x}dx=e^{x}+C$这些只是一些常用的公式，高数微积分中还有更多的公式和定理。

高数微积分基本公式大全

高数微积分基本公式大全1.导数的基本公式：-基本导数：(常数)' = 0, (x^n)' = nx^(n-1), (e^x)' = e^x, (a^x)' = a^xln(a), (ln(x))' = 1/x, (sin(x))' = cos(x),(cos(x))' = -sin(x), (tan(x))' = sec^2(x), (cot(x))' = -csc^2(x), (sec(x))' = sec(x)tan(x), (csc(x))' = -csc(x)cot(x).-乘法法则：(uv)' = u'v + uv'.-除法法则：(u/v)' = (u'v - uv') / v^2.-链式法则：(f(g(x)))' = f'(g(x)) * g'(x).2.不定积分的基本公式：-基本积分：∫(k) dx = kx + C, ∫(x^n) dx =(1/(n+1))x^(n+1) + C, ∫(e^x) dx = e^x + C, ∫(1/x) dx =ln(|x|) + C, ∫(sin(x)) dx = -cos(x) + C, ∫(cos(x)) dx =sin(x) + C.-分部积分：∫(uv') dx = uv - ∫(u'v) dx.-特殊积分：∫(1/(1+x^2)) dx = arctan(x) + C,∫(1/(sqrt(1-x^2))) dx = arcsin(x) + C.3.微分方程的基本公式：-一阶线性微分方程：dy/dx + P(x)y = Q(x),解为y = e^(-∫P(x)dx) * (∫Q(x)e^(∫P(x)dx)dx + C).-齐次方程：dy/dx = f(y/x),令v = y/x，化为可分离变量的形式求解.-常系数线性齐次微分方程：ay'' + by' + cy = 0，其特征方程为ar^2 + br + c = 0，解为y = C1e^(r1x) + C2e^(r2x)。

高数微积分公式大全

微積分公式希腊字母 (Greek Alphabets)倒数关系: sin θcsc θ=1; tan θcot θ=1; cos θsec θ=1 商数关系: tan θ=θθcos sin ; cot θ= θθsin cos 平方关系: cos 2θ+ sin 2θ=1; tan 2θ+ 1= sec 2θ; 1+ cot 2θ= csc 2θ順位低順位高; ⎰ 顺位高d 顺位低 ;1 000 000 000 000 000 000 000 000 10 yotta Y1 000 000 000 000 000 000 000 1021 zetta Z1 000 000 000 000 000 000 1018 exa E1 000 000 000 000 000 1015 peta P1 000 000 000 000 1012 tera T 兆1 000 000 000 109 giga G 十亿1 000 000 106 mega M 百万1 000 103 kilo K 千100 102 hecto H 百10 101 deca D 十0.1 10-1 deci d 分，十分之一0.01 10-2 centi c 厘（或写作「厘」），百分之一0.001 10-3 milli m 毫，千分之一0.000 001 10-6 micro ? 微，百万分之一0.000 000 001 10-9 nano n 奈，十亿分之一0.000 000 000 001 10-12 pico p 皮，兆分之一0.000 000 000 000 001 10-15 femto f 飞（或作「费」），千兆分之一0.000 000 000 000 000 001 10-18 atto a 阿0.000 000 000 000 000 000 001 10-21 zepto z0.000 000 000 000 000 000 000 001 10-24 yocto y重点在三方面：一、函数与反函数的关系：(Function and Inverse Function)以前我们学过的相反运算有：加<------->减；乘<------->除；平方<----->开方；指数<----->对数；三角<----->反三角。

【精品】高数微积分公式大全96065

高等数学微积分公式大全一、基本导数公式⑴()0c '=⑵1x x μμμ-=⑶()sin cos x x '=⑷()cos sin x x '=-⑸()2tan sec x x '=⑹()2cot csc x x '=-⑺()sec sec tan x x x '=⋅⑻()csc csc cot x x x '=-⋅⑼()x x e e '=⑽()ln x x a a a '=⑾()1ln x x'=⑿()1log ln x a x a '=⒀()arcsin x '=⒁()arccos x '=⒂()21arctan 1x x '=+⒃()21arccot 1x x'=-+⒄()1x '=⒅'=二、导数的四则运算法则()u v u v '''±=±()uv u v uv '''=+2u u v uv v v '''-⎛⎫= ⎪⎝⎭三、高阶导数的运算法则（1）()()()()()()()n n n u x v x u x v x ±=±⎡⎤⎣⎦（2）()()()()n n cu x cu x =⎡⎤⎣⎦（3）()()()()n n nu ax b a uax b +=+⎡⎤⎣⎦（4）()()()()()()()0nn n k k k n k u x v x c u x v x -=⋅=⎡⎤⎣⎦∑ 四、基本初等函数的n 阶导数公式（1）()()!n n x n =（2）()()n ax b n ax b e a e ++=⋅(3)()()ln n x x n a a a =(4)()()sin sin 2n n ax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭(5)()()cos cos 2n nax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (6)()()()11!1n n nn a n ax b ax b +⋅⎛⎫=- ⎪+⎝⎭+(7)()()()()()11!ln 1n n n na n axb ax b -⋅-+=-⎡⎤⎣⎦+五、微分公式与微分运算法则⑴()0d c =⑵()1d x x dx μμμ-=⑶()sin cos d x xdx =⑷()cos sin d x xdx =-⑸()2tan sec d x xdx =⑹()2cot csc d x xdx =-⑺()sec sec tan d x x xdx =⋅⑻()csc csc cot d x x xdx =-⋅ ⑼()xxd ee dx =⑽()ln xxd a aadx =⑾()1ln d x dx x=⑿()1logln x a d dx x a =⒀()arcsin d x =⒁()arccos d x dx = ⒂()21arctan 1d x dx x =+⒃()21arccot 1d x dx x =-+ 六、微分运算法则⑴()d u v du dv ±=± ⑵()d cu cdu = ⑶()d uv vdu udv =+ ⑷2u vdu udvd v v -⎛⎫= ⎪⎝⎭七、基本积分公式⑴kdx kx c =+⎰⑵11x x dx c μμμ+=++⎰⑶ln dxx c x=+⎰ ⑷ln xxa a dx c a=+⎰⑸x x e dx e c =+⎰⑹cos sin xdx x c =+⎰ ⑺sin cos xdx x c =-+⎰⑻221sec tan cos dx xdx x c x ==+⎰⎰ ⑼221csc cot sin xdx x c x ==-+⎰⎰⑽21arctan 1dx x c x=++⎰ ⑾arcsin x c =+八、补充积分公式tan ln cos xdx x c =-+⎰cot ln sin xdx x c =+⎰sec ln sec tan xdx x x c =++⎰csc ln csc cot xdx x x c =-+⎰2211arctan xdx c a x a a=++⎰2211ln 2x a dx c x a a x a -=+-+⎰arcsinxc a=+ln x c =++⎰十、分部积分法公式⑴形如n ax x e dx ⎰，令nu x =，axdv e dx =形如sin n x xdx ⎰令nu x =，sin dv xdx =形如cos n x xdx ⎰令nu x =，cos dv xdx = ⑵形如arctan n x xdx ⎰，令arctan u x =，ndv x dx =形如ln n x xdx ⎰，令ln u x =，ndv x dx =⑶形如sin ax e xdx ⎰，cos ax e xdx ⎰令,sin ,cos axu e x x =均可。

高数微积分公式大全

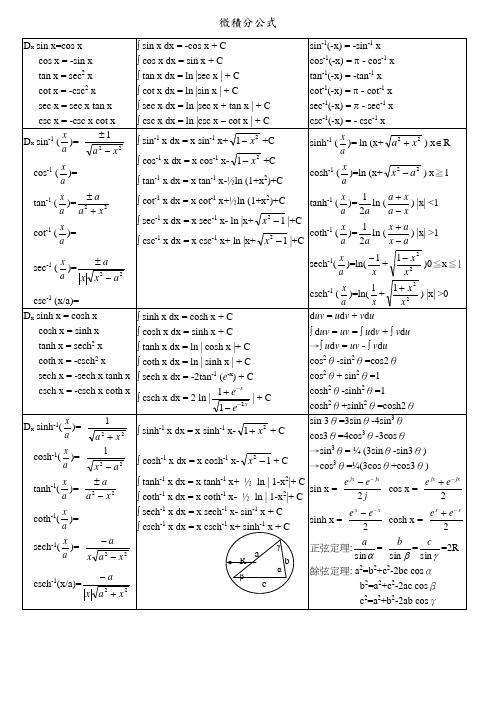
微积分公式D x sin x=cos x cos x = -sin x tan x = sec 2 x cot x = -csc 2 x sec x = sec x tan x csc x = -csc x cot x⎰ sin x dx = -cos x + C ⎰ cos x dx = sin x + C ⎰ tan x dx = ln |sec x | + C ⎰ cot x dx = ln |sin x | + C⎰ sec x dx = ln |sec x + tan x | + C ⎰ csc x dx = ln |csc x – cot x | + C sin -1(-x) = -sin -1 x cos -1(-x) = π - cos -1 x tan -1(-x) = -tan -1 x cot -1(-x) = π - cot -1 x sec -1(-x) = π - sec -1 x csc -1(-x) = - csc -1 xD x sin -1 (a x )= 221xa -±cos -1 (a x)=tan -1 (a x )=22x a a +±cot -1 (ax )=sec -1 (a x )=22a x x a-±csc -1 (x/a)= ⎰ sin -1 x dx = x sin -1 x+21x -+C ⎰ cos -1 x dx = x cos -1 x-21x -+C ⎰ tan -1 x dx = x tan -1 x-½ln (1+x 2)+C ⎰ cot -1 x dx = x cot -1 x+½ln (1+x 2)+C ⎰ sec -1 x dx = x sec -1 x- ln |x+12-x |+C⎰ csc -1 x dx = x csc -1 x+ ln |x+12-x |+Csinh -1 (a x)= ln (x+22x a +) x ∈Rcosh -1 (a x)=ln (x+22a x -) x ≧1tanh -1 (a x )=a 21ln (xa xa -+) |x| <1coth -1 (a x )=a 21ln (a x a x -+) |x| >1 sech -1(a x )=ln(x 1-+221xx -)0≦x ≦1 csch -1(a x )=ln(x 1+221xx +) |x| >0 D x sinh x = cosh xcosh x = sinh xtanh x = sech 2 x coth x = -csch 2 x sech x = -sech x tanh x csch x = -csch x coth x ⎰ sinh x dx = cosh x + C ⎰ cosh x dx = sinh x + C⎰ tanh x dx = ln | cosh x |+ C ⎰ coth x dx = ln | sinh x | + C ⎰ sech x dx = -2tan -1 (e -x ) + C ⎰ csch x dx = 2 ln |xxee 211---+| + Cd uv = u d v + v d u⎰ d uv = uv = ⎰ u d v + ⎰ v d u →⎰ u d v = uv - ⎰ v d u cos 2θ-sin 2θ=cos2θ cos 2θ+ sin 2θ=1 cosh 2θ-sinh 2θ=1cosh 2θ+sinh 2θ=cosh2θD x sinh -1(a x )= 221xa + cosh -1(ax)=221ax - tanh -1(a x )= 22x a a -±coth -1(ax )=sech -1(a x )= 22x a x a --csch -1(x/a)=22xa x a +-⎰ sinh -1 x dx = x sinh -1 x-21x ++ C⎰ cosh -1 x dx = x cosh -1 x-12-x + C ⎰ tanh -1 x dx = x tanh -1 x+ ½ ln | 1-x 2|+ C⎰ coth -1 x dx = x coth -1 x- ½ ln | 1-x 2|+ C⎰ sech -1 x dx = x sech -1 x- sin -1 x + C⎰ csch -1 x dx = x csch -1 x+ sinh -1 x + Csin 3θ=3sin θ-4sin 3θ cos3θ=4cos 3θ-3cos θ →sin 3θ= ¼ (3sin θ-sin3θ) →cos 3θ=¼(3cos θ+cos3θ)sin x = j e e jxjx 2-- cos x = 2jx jx e e -+sinh x = 2x x e e -- cosh x = 2xx e e -+正弦定理:αsin a = βsin b =γsin c=2R余弦定理: a 2=b 2+c 2-2bc cos α b 2=a 2+c 2-2ac cos β c 2=a 2+b 2-2ab cos γa b cαβγ Rsin (α±β)=sin α cos β ± cos α sin β cos (α±β)=cos α cos β sin α sin β 2 sin α cos β = sin (α+β) + sin (α-β) 2 cos α sin β = sin (α+β) - sin (α-β) 2 cos α cos β = cos (α-β) + cos (α+β) 2 sin α sin β = cos (α-β) - cos (α+β)sin α + sin β = 2 sin ½(α+β) cos ½(α-β)sin α - sin β = 2 cos ½(α+β) sin ½(α-β)cos α + cos β = 2 cos ½(α+β) cos ½(α-β) cos α - cos β = -2 sin ½(α+β) sin ½(α-β)tan (α±β)=βαβαtan tan tan tan ±, cot (α±β)=βαβαcot cot cot cot ±e x=1+x+!22x +!33x +…+!n x n+ …sin x = x-!33x +!55x -!77x +…+)!12()1(12+-+n x n n + …cos x = 1-!22x +!44x -!66x +…+)!2()1(2n x nn -+ …ln (1+x) = x-22x +33x -44x +…+)!1()1(1+-+n x n n + …tan -1x = x-33x +55x -77x +…+)12()1(12+-+n x n n + …(1+x)r=1+r x+!2)1(-r r x 2+!3)2)(1(--r r r x 3+… -1<x<1 ∑=ni 11= n∑=ni i 1= ½n (n +1)∑=ni i 12=61n (n +1)(2n +1) ∑=ni i13= [½n (n +1)]2Γ(x) = ⎰∞t x-1e -t d t = 2⎰∞t 2x-12t e -d t =⎰∞)1(ln tx-1 d t β(m , n ) =⎰10x m -1(1-x)n -1 d x =2⎰20sin π2m -1x cos 2n -1x d x =⎰∞+-+01)1(nm m x x d x 希腊字母 (Greek Alphabets)大写小写读音大写小写读音大写小写读音 Α α alpha Ι ι iota Ρ ρrhoΒ β beta Κ κ kappa Σ σ, ς sigmaΓ γ gamma Λ λ lambda Τ τtau Δ δ delta Μ μ mu Υ υ upsilonΕ ε epsilon Ν ν nu Φ φphi Ζ ζ zeta Ξ ξ xi Χ χkhi Η η eta Ο ο omicron Ψ ψpsi ΘθthetaΠπpiΩω omega倒数关系: sin θcsc θ=1; tan θcot θ=1; cos θsec θ=1 商数关系: tan θ=θθcos sin ; cot θ= θθsin cos 平方关系: cos 2θ+ sin 2θ=1; tan 2θ+ 1= sec 2θ; 1+ cot 2θ= csc 2θ順位低順位高; ⎰ 顺位高d 顺位低 ;0*∞ =∞1 *∞ = ∞∞ = 0*01 = 0000 = )(0-∞e ; 0∞ = ∞⋅0e ; ∞1 = ∞⋅0e顺位一: 对数; 反三角(反双曲) 顺位二: 多项函数; 幂函数顺位三: 指数; 三角(双曲)算术平均数(Arithmetic mean) nX X X X n+++= (21)中位数(Median) 取排序后中间的那位数字众数(Mode)次数出现最多的数值几何平均数(Geometric mean) n n X X X G ⋅⋅⋅= (21)调和平均数(Harmonic mean))1...11(1121nx x x n H +++=平均差(Average Deviatoin)nX Xni||1-∑变异数(Variance)nX Xni21)(-∑ or1)(21--∑n X Xni标准差(Standard Deviation)nX Xni21)(-∑ or1)(21--∑n X Xni分配机率函数f (x )期望值E(x )变异数V(x )动差母函数m (t )Discrete Uniform n1 21(n +1) 121(n 2+1) tnt t e e e n --1)1(1Continuous Uniform a b -1 21(a +b ) 121(b -a )2 ta b e e atbt )(--Bernoulli p x q 1-x (x =0, 1)p pq q +pe t Binomial ⎪⎪⎭⎫ ⎝⎛x n p x q n -x npnpq(q+ pe t )nNegative Binomial ⎪⎪⎭⎫ ⎝⎛-+x x k 1p k q x pkq 2p kq k t kqe p )1(-Multinomialf (x 1, x 2, …, x m -1)= m xm x x m p p p x x x n ...!!...!!212121np inp i (1-p i )三项 (p 1e t 1+ p 2e t 2+ p 3)nGeometric pq x-1p1 2p q ttqe pe -1 Hypergeometric⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛n N x n k N x k n ⎪⎭⎫ ⎝⎛N k ⎪⎭⎫ ⎝⎛--1N n N n ⎪⎭⎫ ⎝⎛N kPoissone xλλ- λ λ)1(--t e eλNormal 2)(21 21σμπσ--x eμ σ222 21 t t eσμ+Beta 11)1(),(1---βαβαx x Bβαα+2))(1(βαβααβ+++Gammax e x λαλαλ--Γ1)()( λα 2λα αλλ-⎪⎭⎫ ⎝⎛-t Exponentxeλλ-λ121λ t-λλ Chi-Squared χ2 =f (χ2)=212222)(221χχ--⎪⎭⎫⎝⎛Γen n nE(χ2)=nV(χ2)=2n2)21(n t --Weibullαβα--x e1⎪⎭⎫⎝⎛+Γ+111λαβλ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+Γ-⎪⎭⎫ ⎝⎛+Γ111222λλαλ1 000 000 000 000 000 000 000 000 1024 yotta Y1 000 000 000 000 000 000 000 1021 zetta Z 1 000 000 000 000 000 000 1018 exa E 1 000 000 000 000 000 1015 peta P 1 000 000 000 000 1012 tera T 兆 1 000 000 000 109 giga G 十亿 1 000 000 106 mega M 百万 1 000 103 kilo K 千 100 102 hecto H 百 10 101 deca D 十0.1 10-1 deci d 分，十分之一 0.01 10-2 centi c 厘（或写作「厘」），百分之一 0.001 10-3 milli m 毫，千分之一0.000 001 10-6 micro ? 微，百万分之一 0.000 000 001 10-9 nano n 奈，十亿分之一 0.000 000 000 001 10-12 pico p 皮，兆分之一0.000 000 000 000 001 10-15 femto f 飞（或作「费」），千兆分之一 0.000 000 000 000 000 001 10-18 atto a 阿 0.000 000 000 000 000 000 001 10-21 zepto z 0.000 000 000 000 000 000 000 001 10-24 yocto y。

微积分公式大全(高数)

公式，所有一、基本导数公式⑴()0c '= ⑵1x x μμμ-= ⑶()sin cos x x '= ⑷()cos sin x x '=- ⑸()2tan sec x x '= ⑹()2cot csc x x '=-⑺()sec sec tan x x x '=⋅ ⑻()csc csc cot x x x '=-⋅ ⑼()xxe e '= ⑽()ln xxa aa '= ⑾()1ln x x'=⑿()1log ln xax a'= ⒀()arcsin x '= ⒁()arccos x '=⒂()21arctan 1x x '=+ ⒃()21arc cot 1x x '=-+⒄()1x '=⒅'=二、四则运算法则()u v u v '''±=± ()uv u v uv '''=+ 2u u v uv v v '''-⎛⎫= ⎪⎝⎭三、运算法则（1）()()()()()()()n n n u x v x u x v x ±=±⎡⎤⎣⎦ （2）()()()()n n cu x cu x =⎡⎤⎣⎦（3）()()()()n n nu ax b a uax b +=+⎡⎤⎣⎦（4）()()()()()()()0nn n k k k n k u x v x c u x v x -=⋅=⎡⎤⎣⎦∑四、n 阶导数公式（1）()()!n nxn = （2）()()n ax b n ax b e a e ++=⋅ (3)()()ln n x x n a a a =(4)()()sin sin 2n n ax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (5) ()()cos cos 2n nax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (6)()()()11!1n n nn a n ax b ax b +⋅⎛⎫=- ⎪+⎝⎭+ (7) ()()()()()11!ln 1n n n na n axb ax b -⋅-+=-⎡⎤⎣⎦+五、微分公式与微分运算法则⑴()0d c = ⑵()1d x x dx μμμ-= ⑶()sin cos d x xdx =⑷()cos sin d x xdx =- ⑸()2tan sec d x xdx = ⑹()2cot csc d x xdx =-⑺()sec sec tan d x x xdx =⋅ ⑻()csc csc cot d x x xdx =-⋅⑼()x x d e e dx = ⑽()ln x xd a a adx = ⑾()1ln d x dx x=⑿()1logln xad dx x a =⒀()arcsin d x = ⒁()arccos d x =⒂()21arctan 1d x dx x =+ ⒃()21arc cot 1d x dx x=-+ 六、微分运算法⑴()d u v du dv ±=± ⑵()d cu cdu = ⑶()d uv vdu udv =+ ⑷2u vdu udvd v v -⎛⎫= ⎪⎝⎭七、基本公式⑴kdx kx c =+⎰ ⑵11x x dx c μμμ+=++⎰ ⑶ln dx x c x =+⎰⑷ln xxa a dx c a=+⎰ ⑸x x e dx e c =+⎰ ⑹cos sin xdx x c =+⎰ ⑺sin cos xdx x c =-+⎰ ⑻221sec tan cos dx xdx x c x ==+⎰⎰⑼221csc cot sin xdx x c x ==-+⎰⎰⑽21arctan 1dx x c x =++⎰ ⑾arcsin x c =+八、补充公式tan ln cos xdx x c =-+⎰ cot ln sin xdx x c =+⎰ sec ln sec tan xdx x x c =++⎰ csc ln csc cot xdx x x c =-+⎰2211arctan x dx c a x a a=++⎰ 2211ln 2x adx c x a a x a-=+-+⎰arcsin xc a =+ln x c =+十、分部积分法公式⑴形如n ax x e dx ⎰，令nu x =，ax dv e dx =形如sin n x xdx ⎰令nu x =，sin dv xdx =形如cos n x xdx ⎰令nu x =，cos dv xdx =⑵形如arctan n x xdx ⎰，令arctan u x =，ndv x dx =形如ln n x xdx ⎰，令ln u x =，ndv x dx =⑶形如sin ax e xdx ⎰，cos ax e xdx ⎰令,sin ,cos axu e x x =均可。

高数微积分公式大全

高数微积分公式大全1.极限和连续：- 函数f(x)在x=a处连续的充分必要条件是：$\lim_{x\toa}f(x)=f(a)$- 若$\lim_{x\to a}f(x)=A$，$\lim_{x\to a}g(x)=B$，则$\lim_{x\to a}[f(x)\pm g(x)]=A\pm B$- $\lim_{x\to a}[f(x)g(x)]=\lim_{x\to a}f(x)\cdot\lim_{x\to a}g(x)$- 若$\lim_{x\to a}f(x)=A$，$\lim_{x\to a}g(x)=B\neq0$，则$\lim_{x\to a}\frac{f(x)}{g(x)}=\frac{A}{B}$- $f(x)$在$a$点附近可导的充分必要条件是：存在常数$A$和$B$，使得$x\to a$时，$f(x)-f(a)=A(x-a)+o(x-a)$，且$A=B$-若$f(x)$在$a$点可导，则$f(x)$在$a$点连续2.微分中值定理：- 若$f(x)$在闭区间$[a,b]$上连续，在开区间$(a,b)$上可微，则在$(a,b)$内存在一点$c$，使得$f'(c)=\frac{f(b)-f(a)}{b-a}$ - 若$f(x)$在闭区间$[a,b]$上连续，且在开区间$(a,b)$上可导，且存在常数$M$，使得$，f'(x)，\leq M$，则$f(x)$在闭区间$[a,b]$上有界3.微分法：-$(C)'=0$，其中$C$为常数- $(x^n)'=nx^{n-1}$，其中$n$为实数- $(\sin x)'=\cos x$，$(\cos x)'=-\sin x$，$(\tan x)'=\sec^2 x$- $(e^x)'=e^x$，$(a^x)'=a^x\ln a$- $(\ln x)'=\frac{1}{x}$，$(\log_a x)'=\frac{1}{x\ln a}$4.积分法：- $\int k\,dx=kx+C$，其中$k$为常数，$C$为常数- $\int x^n\,dx=\frac{1}{n+1}x^{n+1}+C$，其中$n$为实数，$C$为常数- $\int \frac{1}{x}\,dx=\ln ，x，+C$，其中$C$为常数- $\int e^x\,dx=e^x+C$- $\int \sin x\,dx=-\cos x+C$，$\int \cos x\,dx=\sin x+C$，$\int \sec^2 x\,dx=\tan x+C$- $\int \frac{1}{\sqrt{1-x^2}}\,dx=\arcsin x+C$5.微分方程：- $y'+P(x)y=Q(x)$的通解为$y=e^{-\int P(x)\,dx}\left(\intQ(x)e^{\int P(x)\,dx}\,dx+C\right)$，其中$P(x)$和$Q(x)$是已知函数- $y''+P(x)y'+Q(x)y=R(x)$的通解是$y=e^{-\intP(x)\,dx}\left[A\int e^{\intP(x)\,dx}R(x)\,dx+B\right]+C_1e^{kx}+C_2e^{kx}$，其中$k$为$P(x)$的重根，$A$和$B$为任意常数，$C_1$和$C_2$为任意常数这只是微积分中的一些重要公式，还有许多其他的公式和定理可以用于不同的问题和应用中。

微积分公式大全(高数)

公式,所有一、基本导数公式⑴()0c '= ⑵1x x μμμ-= ⑶()sin cos x x '= ⑷()cos sin x x '=- ⑸()2tan sec x x '= ⑹()2cot csc x x '=-⑺()sec sec tan x x x '=⋅ ⑻()csc csc cot x x x '=-⋅ ⑼()xxe e '= ⑽()ln xxa aa '= ⑾()1ln x x'=⑿()1log ln xax a'= ⒀()arcsin x '= ⒁()arccos x '=⒂()21arctan 1x x '=+ ⒃()21arc cot 1x x '=-+⒄()1x '=⒅'=二、四则运算法则()u v u v '''±=± ()uv u v uv '''=+ 2u u v uv v v '''-⎛⎫= ⎪⎝⎭三、运算法则 (1）()()()()()()()n n n u x v x u x v x ±=±⎡⎤⎣⎦ (2)()()()()n n cu x cu x =⎡⎤⎣⎦（3)()()()()n n nu ax b a uax b +=+⎡⎤⎣⎦（4）()()()()()()()0nn n k k k n k u x v x c u x v x -=⋅=⎡⎤⎣⎦∑四、n 阶导数公式（1）()()!n nxn = （2)()()n ax b n ax b e a e ++=⋅ （3)()()ln n x x n a a a =（4）()()sin sin 2n n ax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (5） ()()cos cos 2n nax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (6)()()()11!1n n nn a n ax b ax b +⋅⎛⎫=- ⎪+⎝⎭+ （7） ()()()()()11!ln 1n n n na n axb ax b -⋅-+=-⎡⎤⎣⎦+五、微分公式与微分运算法则⑴()0d c = ⑵()1d x x dx μμμ-= ⑶()sin cos d x xdx =⑷()cos sin d x xdx =- ⑸()2tan sec d x xdx = ⑹()2cot csc d x xdx =-⑺()sec sec tan d x x xdx =⋅ ⑻()csc csc cot d x x xdx =-⋅⑼()x x d e e dx = ⑽()ln x xd a a adx = ⑾()1ln d x dx x=⑿()1logln xad dx x a =⒀()arcsin d x = ⒁()arccos d x =⒂()21arctan 1d x dx x =+ ⒃()21arc cot 1d x dx x=-+ 六、微分运算法⑴()d u v du dv ±=± ⑵()d cu cdu = ⑶()d uv vdu udv =+ ⑷2u vdu udvd v v -⎛⎫= ⎪⎝⎭七、基本公式⑴kdx kx c =+⎰ ⑵11x x dx c μμμ+=++⎰ ⑶ln dx x c x =+⎰⑷ln xxa a dx c a=+⎰ ⑸x x e dx e c =+⎰ ⑹cos sin xdx x c =+⎰ ⑺sin cos xdx x c =-+⎰ ⑻221sec tan cos dx xdx x c x ==+⎰⎰⑼221csc cot sin xdx x c x ==-+⎰⎰⑽21arctan 1dx x c x =++⎰ ⑾arcsin x c =+八、补充公式tan ln cos xdx x c =-+⎰ cot ln sin xdx x c =+⎰ sec ln sec tan xdx x x c =++⎰ csc ln csc cot xdx x x c =-+⎰2211arctan x dx c a x a a=++⎰ 2211ln 2x adx c x a a x a-=+-+⎰arcsin xc a =+ln x c =+十、分部积分法公式⑴形如n ax x e dx ⎰，令n u x =，axdv e dx =形如sin n x xdx ⎰令nu x =，sin dv xdx =形如cos n x xdx ⎰令nu x =,cos dv xdx =⑵形如arctan n x xdx ⎰，令arctan u x =，ndv x dx =形如ln n x xdx ⎰，令ln u x =，ndv x dx =⑶形如sin ax e xdx ⎰，cos axe xdx ⎰令,sin ,cos ax u e x x =均可。

高等数学微积分公式大全

高等数学微积分公式大全微积分是高等数学中的重要分支，是研究函数变化规律以及求解各种问题的一种数学工具。

微积分公式是微积分学习中最为基础和重要的内容之一，掌握这些公式可以帮助我们更好地理解和应用微积分知识。

本文将为大家逐一介绍高等数学微积分公式大全。

1. 导数公式导数是函数在某一点上的变化速率，反映了函数的局部特征。

以下是常见的导数公式：- 常数函数导数公式：若y = C，C为常数，则导数dy/dx = 0。

- 幂函数导数公式：若y = x^n，n为实数，则导数dy/dx = nx^(n-1)。

- 指数函数导数公式：若y = a^x，a>0且a≠1，则导数dy/dx = a^x * ln(a)。

- 对数函数导数公式：若y = loga(x)，a>0且a≠1，则导数dy/dx = 1 / (x * ln(a))。

- 三角函数导数公式：若y = sin(x)，则导数dy/dx = cos(x)。

若y = cos(x)，则导数dy/dx = -sin(x)。

若y = tan(x)，则导数dy/dx = sec^2(x)。

2. 积分公式积分是反导数的计算过程，可以计算函数的面积、曲线长度、体积等。

以下是常见的积分公式：- 幂函数积分公式：∫x^n dx = (1/(n+1))x^(n+1) + C，其中C为常数。

- 指数函数积分公式：∫a^x dx = (1/ln(a))a^x + C，其中C为常数。

- 对数函数积分公式：∫(1/x) dx = ln|x| + C，其中C为常数。

- 三角函数积分公式：∫sin(x) dx = -cos(x) + C，其中C为常数。

∫cos(x) dx = sin(x) + C，其中C为常数。

∫tan(x) dx = -ln|cos(x)| + C，其中C为常数。

3. 极限公式极限是函数在某一点附近的近似取值，是微积分理论的基础。

以下是常见的极限公式：- 基本极限公式：lim(x→0) (sin(x)/x) = 1。

高等数学微积分公式大全

高等数学微积分公式大全高等数学微积分公式是高等数学中重要的一部分，也是我们在研究数学问题和应用数学技术时必须掌握的基础。

下面就让我们来看看高等数学微积分中常用的公式吧。

第一部分：导数公式1. 导数的定义公式$$f'(x)=\lim_{\Delta x\rightarrow0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$$2. 导数的四则运算公式$$\left(f(x)\pm g(x)\right)'=f'(x)\pm g'(x)$$$$\left(f(x)g(x)\right)'=f'(x)g(x)+f(x)g'(x)$$$$\left(\frac{f(x)}{g(x)}\right)'=\frac{f'(x)g(x) -f(x)g'(x)}{g^2(x)}(g(x)\neq 0)$$$$\left(g(f(x))\right)'=g'(f(x))f'(x)$$3. 高阶导数公式$$f''(x)=(f'(x))'$$$$f'''(x)=(f''(x))'$$$$f^{(n)}(x)=\left(f^{(n-1)}(x)\right)'$$4. 链式法则$$\frac{d}{dx}f(g(x))=f'(g(x))g'(x)$$5. 反函数求导若$f(x)$的反函数为$y=g(x)$，则有$$\frac{d}{dx}g(x)=\frac{1}{f'(g(x))}$$6. 隐函数求导设有方程$F(x,y)=0$，其中$y$是$x$的隐函数，则有$$\frac{dy}{dx}=-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}}$$第二部分：微分公式7. 微分的定义公式$$df(x)=f'(x)dx$$8. 微分的四则运算公式$$(u\pm v)'=u'dx\pm v'dx$$$$(uv)'=(u'v+uv')dx$$$$\left(\frac{u}{v}\right)'=\frac{u'v-uv'}{v^2}dx(v\neq 0)$$$$(g\circ f)'=(g'\circ f)f'dx$$9. 高阶微分公式$$d^2y=d(dy)=d\left(\frac{dy}{dx}\right)=\frac{d^ 2y}{dx^2}dx$$$$d^3y=d(d^2y)=d\left(\frac{d^2y}{dx^2}\right)=\f rac{d^3y}{dx^3}dx$$$$d^ny=d(d^{n-1}y)=d\left(\frac{d^{n-1}y}{dx^{n-1}}\right)=\frac{d^ny}{dx^n}dx$$10. 多元函数微分公式设$z=f(x,y)$，则有$$dz=\frac{\partial z}{\partialx}dx+\frac{\partial z}{\partial y}dy$$其中，$\frac{\partial z}{\partial x}$表示$f(x,y)$对$x$的偏导数，$\frac{\partial z}{\partialy}$表示$f(x,y)$对$y$的偏导数。

高数微积分公式大全

微積分公式希腊字母 (Greek Alphabets)倒数关系: sin θcsc θ=1; tan θcot θ=1; cos θsec θ=1 商数关系: tan θ=θθcos sin ; cot θ= θθsin cos平方关系: cos 2θ+ sin 2θ=1; tan 2θ+ 1= sec 2θ; 1+ cot 2θ= csc 2θ順位低順位高; ⎰ 顺位高d 顺位低 ;1 000 000 000 000 000 000 000 000 10 yotta Y1 000 000 000 000 000 000 000 1021 zetta Z1 000 000 000 000 000 000 1018 exa E1 000 000 000 000 000 1015 peta P1 000 000 000 000 1012 tera T 兆1 000 000 000 109 giga G 十亿1 000 000 106 mega M 百万1 000 103 kilo K 千100 102 hecto H 百10 101 deca D 十0.1 10-1 deci d 分，十分之一0.01 10-2 centi c 厘（或写作「厘」），百分之一0.001 10-3 milli m 毫，千分之一0.000 001 10-6 micro ? 微，百万分之一0.000 000 001 10-9 nano n 奈，十亿分之一0.000 000 000 001 10-12 pico p 皮，兆分之一0.000 000 000 000 001 10-15 femto f 飞（或作「费」），千兆分之一0.000 000 000 000 000 001 10-18 atto a 阿0.000 000 000 000 000 000 001 10-21 zepto z0.000 000 000 000 000 000 000 001 10-24 yocto y重点在三方面：一、函数与反函数的关系：(Function and Inverse Function)以前我们学过的相反运算有：加<------->减；乘<------->除；平方<----->开方；指数<----->对数；三角<----->反三角。