matlab课后习题答案(1-9章)

合集下载

matlab课后习题标准答案(1-9章)

1 数字1.5e ２，１.５e3 中的哪个与1500相同吗?1.５e32 请指出如下５个变量名中，哪些是合法的?ａbcd-2ﻩ ｘyz ＿3ﻩ ３chan ﻩａ变量ﻩ A ＢC Ｄe ｆｇh ﻩ2、5是合法的。

3 在MATL ＡB 环境中,比１大的最小数是多少？ 1＋ep ｓ4 设ａ = -8 , 运行以下三条指令，问运行结果相同吗？为什么？w １=a^(2/３）ﻩ w2=(ａ＾２)^(1/３)ﻩ w ３＝(ａ^(１/3)）^2w1 = -2.0000 ＋ 3.464１i ;ｗ2 = 4.0000 ;ｗ3 =－２.0000 ＋ 3．4641i 5 指令clea ｒ，ｃｌf ， clc 各有什么用处?cle ａr 清除工作空间中所有的变量。

clf 清除当前图形。

ｃｌc ﻩ 清除命令窗口中所有显示。

第二章1 说出以下四条指令产生的结果各属于哪种数据类型，是“双精度”对象,还是“符号”符号对象？3/７+0.1双; s ｙm(3/7+0.1）符; sym('3/7+0.１') 符;; ｖpa(s ｙｍ(3/７+0.１)）符;2 在不加专门指定的情况下，以下符号表达式中的哪一个变量被认为是自由符号变量.ｓｙｍ('sin(w ＊t)＇),sym(＇a ＊exp(－X ）＇）,ｓym('z*exp （j*th)'）s ｙm ｖａr(sym('sin(ｗ*t)'）,１) w a z3 (1）试写出求三阶方程05.443=-x 正实根的程序。

注意：只要正实根,不要出现其他根。

（２)试求二阶方程022=+-a ax x 在0>a 时的根。

(1)reset(symengine) ﻩﻩ sy ｍｓ x ｐosi ｔiveﻩs ｏlve （x ＾3-４4.5)ﻩﻩans =ﻩ (２^（２／3）*8９^（１/3）)/2（2）求五阶方程022=+-a ax x 的实根syms a p ｏsi ｔiv ｅﻩ %注意：关于x 的假设没有去除solve(ｘ^2-a*x ＋a^2）Wa ｒning ： E ｘｐl ｉci ｔ solu ｔｉon co ｕｌd not be found.> Ｉｎ so ｌv ｅ at 83ans =［ em ｐty ｓym ]ｓｙm ｓ x ｃl ｅa ｒｓym ｓ a positiv ｅso ｌve （x^２-ａ*x+a^2）a ｎs =a/2 ＋ (3^(1/2)*a ＊ｉ）/２a/2 - (3＾(1/2)*ａ*i)/24 观察一个数（在此用＠记述）在以下四条不同指令作用下的异同。

matlab课后习题及答案

第一章 5题已知a=4.96，b=8.11，计算)ln(b a eba +-的值。

解：clear clc a=4.96; b=8.11;exp(a-b)/log(a+b) ans =0.0167 6题已知三角形的三边a=9.6,b=13.7, c=19.4,求三角形的面积。

提示：利用海伦公式area =))()((c s b s a s s ---计算，其中S=(A+B+C)/2. 解：clear clc a=9.6; b=13.7; c=19.4; s=(a+b+c)/2area=sqrt(s*(s-a)*(s-b)*(s-c)) s =21.3500 第二章 8题已知S=1+2+2^2+2^3+……+2^63,求S 的值解：clear clc S=0;for i=0:1:63 S=S+2^i; end S S =1.8447e+019 9题分别用for 和while 循环结构编写程序，计算∑=-1001n 1n 2）（的值。

解：clear clc s=0;for n=1:100 s=s+(2*n-1); end s s =10000 clear clc n=1; s=0;while n<=100 s=s+(2*n-1); n=n+1; end s s =10000 第三章 2题在同一坐标下绘制函数x ,,2x-,2x xsin(x)在()∏∈,0x 的曲线。

解：clear clcx=0:0.2:pi; y1=x; y2=x.^2; y3=-(x.^2); y4=x.*sin(x);plot(x,y1,'-' ,x,y2,'-' ,x,y3,'-' ,x,y4,'-')0.511.522.53-10-8-6-4-202468109题用不同的线型和颜色在同一坐标内绘制曲线y1=2ex5.0 、y2=sin(2∏x )的图形。

(完整版)汽车理论课后作业答案MATLAB

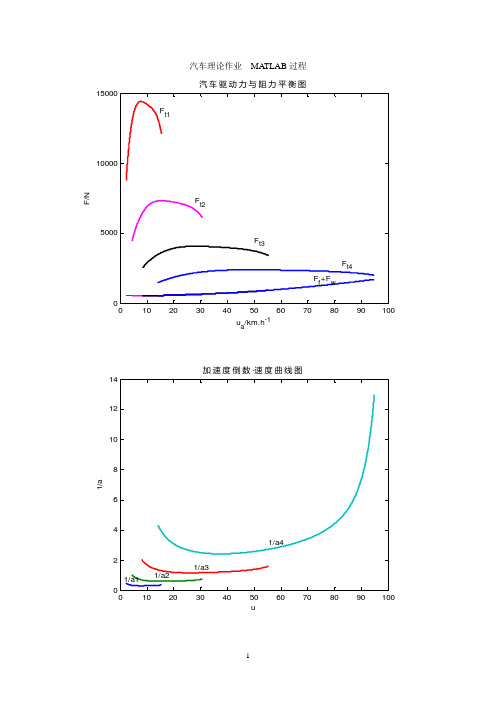
汽车理论作业 MA TLAB 过程010203040506070809010050001000015000汽车驱动力与阻力平衡图u a /km.h -1F /N10203040506070809010002468101214加速度倒数-速度曲线图u1/a0102030405060708090100102030405060u/(km/h)P /k W汽车功率平衡图10203040506070809010012141618202224最高档等速百公里油耗曲线Ua/(km/h)Q s /L2324252627282912131415161718燃油积极性-加速时间曲线燃油经济性(qs/L)动力性--原地起步加速时间 (s t /s )源程序：《第一章》m=3880; g=9.8; r=0.367; x=0.85; f=0.013; io=5.83; CdA=2.77; If=0.218; Iw1=1.798; Iw2=3.598; Iw=Iw1+Iw2;ig=[6.09 3.09 1.71 1.00]; %变速器传动比 L=3.2; a=1.947; hg=0.9; n=600:1:4000;T=-19.313+295.27*n/1000-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000).^4; Ft1=T*ig(1)*io*x/r;%计算各档对应转速下的驱动力Ft2=T*ig(2)*io*x/r;Ft3=T*ig(3)*io*x/r;Ft4=T*ig(4)*io*x/r;u1=0.377*r*n/(io*ig(1));u2=0.377*r*n/(io*ig(2));u3=0.377*r*n/(io*ig(3));u4=0.377*r*n/(io*ig(4));u=0:130/3400:130;F1=m*g*f+CdA*u1.^2/21.15;%计算各档对应转速下的驱动阻力F2=m*g*f+CdA*u2.^2/21.15;F3=m*g*f+CdA*u3.^2/21.15;F4=m*g*f+CdA*u4.^2/21.15;figure(1);plot(u1,Ft1,'-r',u2,Ft2,'-m',u3,Ft3,'-k',u4,Ft4,'-b',u1,F1,'-r',u2,F2,'-m',u3,F3,'-k',u4,F4,'-b','LineWidth',2)title('汽车驱动力与阻力平衡图');xlabel('u_{a}/km.h^{-1}')ylabel('F/N')gtext('F_{t1}')gtext('F_{t2}')gtext('F_{t3}')gtext('F_{t4}')gtext('F_{f}+F_{w}')%由汽车驱动力与阻力平衡图知，他们无交点，u4在最大转速时达到最大umax=u4(3401)Ft1max=max(Ft1);imax=(Ft1max-m*g*f)/(m*g)disp('假设是后轮驱动');C=imax/(a/L+hg*imax/L) % 附着率delta1=1+(Iw1+Iw2)/(m*r^2)+If*ig(1)*r^2*io^2*x/(m*r^2);delta2=1+(Iw1+Iw2)/(m*r^2)+If*ig(2)*r^2*io^2*x/(m*r^2);delta3=1+(Iw1+Iw2)/(m*r^2)+If*ig(3)*r^2*io^2*x/(m*r^2);delta4=1+(Iw1+Iw2)/(m*r^2)+If*ig(4)*r^2*io^2*x/(m*r^2);a1=(Ft1-F1)/(delta1*m); %加速度a2=(Ft2-F2)/(delta2*m);a3=(Ft3-F3)/(delta3*m);a4=(Ft4-F4)/(delta4*m);h1=1./a1; %加速度倒数h2=1./a2;h3=1./a3;h4=1./a4;figure(2);plot(u1,h1,u2,h2,u3,h3,u4,h4,'LineWidth',2); title('加速度倒数-速度曲线图');xlabel('u')ylabel('1/a')gtext('1/a1')gtext('1/a2')gtext('1/a3')gtext('1/a4')%由加速度倒数-速度曲线图可知u1min=min(u1);u1max=max(u1);u2min=u1max;u2min=min(u2);u2max=max(u2);u3min=u2max;u3max=max(u3);u4min=u3max;u4max=70;x1=[];x2=[];x3=[];x4=[];y=3401;for i=1:3401;if u3(i)<=u3min;x1=[i];endendq1=max(x1);ua3=u3(q1:y);a3=h3(q1:y);for i=1:3401;if u4(i)<=u4min;x2=[i];elseif u4(i)<=u4max;x3=[i];endendq2=max(x2);q3=max(x3);ua4=u4(q2:q3);a4=h4(q2:q3);s1=trapz(h2,u2 ); %二挡运行时间s2=trapz(ua3,a3);s3=trapz(ua4,a4);s=[s1 s2 s3];disp('积分得')t=sum(s)*1000/3600 %总时间《第二章》Pe1=Ft1.*u1./3600;%计算各档对应转速下的功率Pe2=Ft2.*u2./3600;Pe3=Ft3.*u3./3600;Pe4=Ft4.*u4./3600;P1=F1.*u1./(3600*x);%计算各档对应的各个车速下的行驶功率P2=F2.*u2./ (3600*x);P3=F3.*u3./ (3600*x);P4=F4.*u4./ (3600*x);figure(3);plot(u1,Pe1,'-r',u2,Pe2,'-m',u3,Pe3,'-k',u4,Pe4,'-b',u1,P1,'k',u2,P2,'k',u3,P3,'k', u4,P4,'k','linewidth',2);gtext('Pe1')gtext('Pe2')gtext('Pe3')gtext('Pe4')xlabel('u/(km/h)');ylabel('P/kW');title('汽车功率平衡图');n=[815 1207 1614 2012 2603 3006 3403 3804];Ua=[];Ua=0.377*r*n./(io*ig(4))ft=[];ft=m*g*f+(2.77/21.15)*Ua.^2;%计算各转速对应的各个车速下的行驶阻力Pe(1)=ft(1).*Ua(1)./(3600*x);%计算各转速对应的各个车速下的行驶阻力功率Pe(2)=ft(2).*Ua(2)./(3600*x);Pe(3)=ft(3).*Ua(3)./(3600*x);Pe(4)=ft(4).*Ua(4)./(3600*x);Pe(5)=ft(5).*Ua(5)./(3600*x);Pe(6)=ft(6).*Ua(6)./(3600*x);Pe(7)=ft(7).*Ua(7)./(3600*x);Pe(8)=ft(8).*Ua(8)./(3600*x)B0=[1326.8 1354.7 1284.4 1122.9 1141.0 1051.2 1233.9 1129.7];B1=[-416.46 -303.98 -189.75 -121.59 -98.893 -73.714 -84.478 -45.291];B2=[72.739 36.657 14.525 7.0035 4.4763 2.8593 2.9788 0.7113];B3=[-5.8629 -2.0533 -0.51184 -0.18517 -0.091077 -0.05138 -0.047449 -0.00075215];B4=[0.17768 0.043072 0.0068164 0.0018555 0.00068906 0.00035032 0.00028230-0.000038568];b1=(B0(1))+(B1(1)*Pe(1))+(B2(1)*Pe(1)^2)+(B3(1)*Pe(1)^3)+(B4(1)*Pe(1)^4);b2=(B0(2))+(B1(2)*Pe(2))+(B2(2)*Pe(2)^2)+(B3(2)*Pe(2)^3)+(B4(2)*Pe(2)^4);b3=(B0(3))+(B1(3)*Pe(3))+(B2(3)*Pe(3)^2)+(B3(3)*Pe(3)^3)+(B4(3)*Pe(3)^4);b4=(B0(4))+(B1(4)*Pe(4))+(B2(4)*Pe(4)^2)+(B3(4)*Pe(4)^3)+(B4(4)*Pe(4)^4);b5=(B0(5))+(B1(5)*Pe(5))+(B2(5)*Pe(5)^2)+(B3(5)*Pe(5)^3)+(B4(5)*Pe(5)^4);b6=(B0(6))+(B1(6)*Pe(6))+(B2(6)*Pe(6)^2)+(B3(6)*Pe(6)^3)+(B4(6)*Pe(6)^4);b7=(B0(7))+(B1(7)*Pe(7))+(B2(7)*Pe(7)^2)+(B3(7)*Pe(7)^3)+(B4(7)*Pe(7)^4);b8=(B0(8))+(B1(8)*Pe(8))+(B2(8)*Pe(8)^2)+(B3(8)*Pe(8)^3)+(B4(8)*Pe(8)^4);p=0.7;Qs=[];Qs(1)=(Pe(1)*b1)/(1.02*Ua(1).*p*g);Qs(2)=(Pe(2)*b2)/(1.02*Ua(2).*p*g);Qs(3)=(Pe(3)*b3)/(1.02*Ua(3).*p*g);Qs(4)=(Pe(4)*b4)/(1.02*Ua(4).*p*g);Qs(5)=(Pe(5)*b5)/(1.02*Ua(5).*p*g);Qs(6)=(Pe(6)*b6)/(1.02*Ua(6).*p*g);Qs(7)=(Pe(7)*b7)/(1.02*Ua(7).*p*g);Qs(8)=(Pe(8)*b8)/(1.02*Ua(8).*p*g);M=polyfit(Ua,Qs,2);UA=0.377*r*600/(ig(4)*io):1:0.377*r*4000/(ig(4)*io);%UA表示车速QS=polyval(M,UA);%QS表示油耗figure(4);plot(UA,QS,'linewidth',2);title('最高档等速百公里油耗曲线');xlabel('Ua/(km/h)');ylabel('Qs/L');《第三章》io=[5.17 5.43 5.83 6.17 6.33];Va=0.377*r*n(7)./(io.*ig(4));Ps=46.9366;disp('假设以最高档，较高转速（n取3401 ），最经济负荷（即90%负荷大约 46.9366Kw）行驶时油耗')qs=[];qs(1)=(Ps*b7)/(1.02*Va(1).*p*g);qs(2)=(Ps*b7)/(1.02*Va(2).*p*g);qs(3)=(Ps*b7)/(1.02*Va(3).*p*g);qs(4)=(Ps*b7)/(1.02*Va(4).*p*g);qs(5)=(Ps*b7)/(1.02*Va(5).*p*g);st=[ 17.5813 16.2121 14.5126 13.3775 12.9185];%加速时间：（这里以最高档〈四档〉、速度由0加速到94.93Km/h 的时间）因与题1.3第三问求法相同，这里不在累述，可直接有计算机求得：figure(5);plot(qs,st,'+','linewidth',2)hold on plot(qs,st,); gtext('5.17') gtext('5.43') gtext('5.83') gtext('6.17') gtext('6.33')title('燃油积极性-加速时间曲线'); xlabel('燃油经济性(qs/L)');ylabel('动力性--原地起步加速时间 (st/s)');《第四章》 4-31）前轴利用附着系数为：gf zh b zL +=βϕ后轴利用附着系数为： ()gr zh a zL --=βϕ1空载时：g h b L -=βϕ0=413.0845.085.138.095.3-=-⨯所以0ϕϕ>空载时后轮总是先抱死。

matlab第二版习题答案

matlab第二版习题答案Matlab是一种强大的数学软件工具，被广泛应用于科学计算、数据分析和工程设计等领域。

对于学习和掌握Matlab的人来说，习题是不可或缺的一部分。

本文将为大家提供Matlab第二版习题的答案，帮助读者更好地理解和应用Matlab。

第一章：基本操作1.1 Matlab的启动和退出启动Matlab的方法有多种，可以通过桌面图标、命令行或者启动器来打开Matlab。

退出Matlab可以直接关闭窗口或者使用命令"exit"。

1.2 Matlab的基本语法Matlab的基本语法与其他编程语言相似，包括变量的定义、运算符的使用、条件语句和循环语句等。

例如，定义一个变量x并赋值为5可以使用语句"x = 5;"。

1.3 Matlab的数据类型Matlab支持多种数据类型，包括数值型、字符型和逻辑型等。

数值型可以是整数或者浮点数，字符型用单引号或双引号表示，逻辑型只有两个值true和false。

第二章：向量和矩阵操作2.1 向量的定义和运算向量是一维数组，可以通过一对方括号来定义。

Matlab提供了丰富的向量运算函数，如加法、减法、乘法和除法等。

2.2 矩阵的定义和运算矩阵是二维数组，可以通过方括号和分号来定义。

Matlab提供了矩阵的加法、减法、乘法、转置和求逆等运算。

2.3 矩阵的索引和切片可以使用索引和切片来访问矩阵中的元素。

索引从1开始，可以使用冒号表示全部元素。

切片可以用来选择矩阵的一部分。

第三章：函数和脚本文件3.1 函数的定义和调用函数是一段独立的代码块，可以接受输入参数并返回输出结果。

在Matlab中，函数的定义以关键字"function"开头，调用函数使用函数名和参数。

3.2 脚本文件的编写和运行脚本文件是一系列Matlab语句的集合，可以保存为.m文件。

通过运行脚本文件，可以一次性执行多个语句，提高效率。

第四章：图形绘制和数据可视化4.1 图形绘制函数Matlab提供了丰富的图形绘制函数，可以绘制线图、散点图、柱状图等。

matlab课后习题及答案详解

matlab课后习题及答案详解第1章练习题1.安装matlab时，在选择组件窗口中哪些部分必须勾选，没有勾选的部分以后如何补安装？在安装matlab时，安装内容由选择组件窗口中个复选框是否被勾选来决定，可以根据自己的需要选择安装内容，但基本平台（即matlab选项）必须安装。

第一次安装没有选择的内容在补安装时只需按照安装的过程进行，只是在选择组件时只勾选要补装的组件或工具箱即可。

2.matlab操作方式桌面存有几个窗口？如何并使某个窗口瓦解桌面沦为单一制窗口？又如何将瓦解过来的窗口再次置放至桌面上？与其他计算机语言相比较，matlab语言注重的特点就是什么？matlab系统由那些部分共同组成？在matlab操作桌面上有五个窗口，在每个窗口的右上角有两个小按钮，一个是关闭窗口的close按钮，一个是可以使窗口成为独立窗口的undock按钮，点击undock按钮就可以使该窗口脱离桌面成为独立窗口，在独立窗口的view菜单中选择dock……菜单项就可以将独立的窗口重新防止的桌面上。

matlab具备功能强大、使用方便、输出简便、库函数多样、开放性弱等特点。

matlab系统主要由开发环境、matlab数学函数库、matlab语言、图形功能和应用程序接口五个部分组成。

3.如何设置当前目录和搜寻路径，在当前目录上的文件和在搜寻路径上的文件存有什么区别？命令历史窗口除了可以观测前面键入的命令外，除了什么用途？当前目录可以在当前目录浏览器窗口左上方的输入栏中设置，搜索路径可以通过选择操作桌面的file菜单中的setpath菜单项来完成。

在没有特别说明的情况下，只有当前目录和搜索路径上的函数和文件能够被matlab运行和调用，如果在当前目录上有与搜索路径上相同文件名的文件时则优先执行当前目录上的文件，如果没有特别说明，数据文件将存储在当前目录上。

命令历史窗口除了用作查阅以前键入的命令外，还可以轻易执行命令历史窗口中选取的内容、将选取的内容拷贝到剪贴板中、将选取内容轻易拷贝到m文件中。

Matlab习题答案

(1) (3− 5i)(4 + 2i) (2) sin (2 − 8i)
参考答案：（1） >> (3-5*i)*(4+2*i) ans =
22.0000 -14.0000i
（2） >> sin(2-8*i) ans =
1.3553e+003 +6.2026e+002i
5．判断下面语句的运算结果。 (1) 4 < 20 (2) 4 <= 20 (3) 4 == 20 (4) 4 ~= 20 (5) 'b'<'B' 参考答案：（1） >> 4<20 ans =
y_nearest(i)=interp1(x,y,scalar_x(i),'nearest'); y_linear(i) =interp1(x,y,scalar_x(i),'linear'); y_spline(i) =interp1(x,y,scalar_x(i),'spline'); y_cubic(i) =interp1(x,y,scalar_x(i),'cubic'); end subplot(2,2,1),plot(x,y,'*'),hold on,plot(scalar_x,y_nearest),title('method=nearest'); subplot(2,2,2),plot(x,y,'*'),hold on,plot(scalar_x,y_linear),title('method=linear'); subplot(2,2,3),plot(x,y,'*'),hold on,plot(scalar_x,y_spline),title('method=spline'); subplot(2,2,4),plot(x,y,'*'),hold on,plot(scalar_x,y_cubic),title('method=cubic'); 得到结果为：

matlab第二版课后习题答案

matlab第二版课后习题答案
《MATLAB第二版课后习题答案》
MATLAB是一种强大的数学软件，被广泛应用于工程、科学和金融等领域。

《MATLAB第二版》是一本经典的教材，为了帮助学生更好地掌握MATLAB的使用，书中提供了大量的课后习题。

下面我们将为大家总结一些MATLAB第二版课后习题的答案，希望能对大家的学习有所帮助。

1. 第一章课后习题答案
第一章主要介绍了MATLAB的基本操作，包括变量的定义、矩阵的运算、函数的使用等。

在课后习题中，有一道题目是要求计算一个矩阵的逆矩阵。

答案是使用MATLAB中的inv函数，将原矩阵作为参数传入即可得到逆矩阵。

2. 第二章课后习题答案
第二章介绍了MATLAB中的绘图功能，包括二维和三维图形的绘制。

有一道课后习题是要求绘制一个正弦曲线和余弦曲线，并在同一张图上显示。

答案是使用MATLAB中的plot函数，分别绘制正弦曲线和余弦曲线，并使用legend函数添加图例。

3. 第三章课后习题答案
第三章介绍了MATLAB中的控制流程，包括if语句、for循环和while循环等。

有一道课后习题是要求编写一个程序，计算1到100之间所有偶数的和。

答案是使用for循环遍历1到100之间的所有数，判断是否为偶数并累加。

通过以上几个例子，我们可以看到MATLAB第二版课后习题的答案涵盖了各种基本和高级的操作，对于学习MATLAB是非常有帮助的。

希望大家在学习MATLAB的过程中能够多加练习，掌握更多的技巧和方法。

MATLAB第1-8章答案

第1章一、思考题4. （1） B=A(2:5,1:2:5)（2）A(7)=[]（3） A=A+30（4）size(A)（5） t(find(t==0))=eps（6）t=reshape(x,3,4)（7）abs('matlab')（8）char(93)5. A=[97,67,34,10;-78,75,65,5;32,5,-23,-59;0,-12,54,7](1) B=A(1:3,:)C=A(:,1:2)D=A(2:4,3:4)E=B*C(2)A(find(A>=50 & A<=100))二、实验题1.x=-74/180*pi;y=-27/180*pi;sin(x*x+y*y)/sqrt(tan(abs(x+y)))+pi2.a=-3.0:0.1:3.0;exp(-0.3*a).*sin(a+0.3)3.x=[2,4;-0.45,5];log(x+sqrt(1+x.*x))/24. A=[3,54,2;34,-45,7;87,90,15];B=[1,-2,67;2,8,74;9,3,0]; （1）A*Bans =129 432 41977 -407 -1052402 591 12489A.*Bans =3 -108 13468 -360 518783 270 0（2） A^3ans =-28917 240246 -4368137883 -259101 27669171333 252504 38673A.^3ans =27 157464 839304 -91125 343658503 729000 3375（3）A/Bans =-5.8845 5.3549 -0.20286.3554 -5.6596 4.3293-6.6325 6.2078 9.0241B/Aans =30.2855 19.2643 -8.561433.4394 21.1547 -9.3974-0.7443 -0.3938 0.2830（4）[A,B]ans =3 54 2 1 -2 6734 -45 7 2 8 7487 90 15 9 3 0[A([1,3],:);B^2]ans =3 54 287 90 15600 183 -81684 282 72615 6 8255.a=1+2i;b=3+4i;c=exp(pi*i/6)c =0.8660 + 0.5000ic+a*b/(a+b)ans =1.6353 + 1.8462i第2章一、思考题3.s=0;for n=0:63s=s+2^n;enddisp(s)n=0:63;s=sum(2.^n)二、实验题1.x=input('输入一个四位整数：');y=[fix(x/1000),mod(fix(x/100),10),mod(fix(x/10),10),mod(x,10)] z=mod((y+7),10)x=z(3)*1000+z(4)*100+z(1)*10+z(2)2.gh=input('输入工号');h=input('输入工时');dj=84;if h>120gz=dj*120+1.15*dj*(h-120);elseif h<60gz=dj*h-700;elsegz=dj*h;endformat bank;display([gh,gz])3.循环结构n=input('input n:');s=0;for k=1:ns=s+1/k^2;enddisplay(sqrt(s*6))向量运算n=input('input n:');k=1:n;display(sqrt(sum(1./k.^2)*6))4.y=0;k=0;while y<3k=k+1;y=y+1/(2*k-1);enddisplay([k-1,y-1/(2*k-1)])5.x0=0;x=1;k=0;a=input('a=');b=input('b=');while abs(x-x0)>=1e-5 && k<500x0=x;x=a/(b+x0);k=k+1;enddisplay([k,x]);display([(-b+sqrt(b^2+4*a))/2,(-b-sqrt(b^2+4*a))/2]);6.y=fun(40)/(fun(30)+fun(20))（1）函数文件fun.mfunction f=fun(n)f=n+log(n^2+5);（2）函数文件fun.mfunction f=fun(n)a=1:n;f=sum(a.*(a+1));第3章一、思考题4.t=0:0.01:1.5;y=sqrt(3)/2*exp(-4*t).*sin(4*sqrt(3)*t+pi/3);5.x=-10:0.01:10;y=linspace(-6,6,size(x,2))z=x.^3+3*x.*y.^2;plot3(x,y,z)6.x=100:100:400;y=100:100:400;z=[636,697,624,478;698,712,630,478;680,674,598,412;662,626,552,334]; [X,Y]=meshgrid(x,y);mesh(X,Y,z)二、实验题1.（1）x=-10:0.01:10;plot(x,x-x.^3/3/2)（2）plot(x,exp(-x.*x/2)/2/pi)（3）x=-8:0.01:8;plot(x,sqrt((64-x.*x)/2))（4）t=0:pi/100:6*pi;plot(t.*sin(t),t.*cos(t))2. （1）x1=linspace(0,1,100);y1=2*x1-0.5;t=linspace(0,pi,100);x=sin(3*t).*cos(t);y=sin(3*t).*sin(t);plot(x1,y1,'r-',x,y,'b:');text(0.4,1,'y=2x-0.5');text(-0.4,0.5,'x=sin(3t)cos(t)');text(-0.4,0.3,'y=sin(3t)sin(t)');（2）subplot(1,2,1);scatter(x1,y1,10)title('y=2x-0.5');subplot(1,2,2);scatter(x,y,10)3.subplot(1,21);x=1:1:100; y=sin(1./x);plot(x,y)subplot(1,2,2);fplot('sin(1/x)',[1,100])4.subplot(2,2,1);bar(t,y);subplot(2,2,2);stairs(t,y);subplot(2,2,3);stem(t,y)subplot(2,2,4);semilogy(t,y);5.theta=linspace(-pi,pi,100);ro=5.*cos(theta)+4;polar(theta,ro);fi=linspace(0,2*pi,100);a=1r=a.*(1+cos(fi));polar(fi,r);6.t=0:pi/20:2*pi;x=exp(-t./20).*cos(t);y=exp(-t./20).*sin(t);z=t; plot3(x,y,z);t=0:0.01:1;x=t;y=t.^2;z=t.^3;plot3(x,y,z);7.x=-30:0.1:0;y=0:0.1:30;[x,y]=meshgrid(x,y);z=10.*sin(sqrt(x.^2+y.^2))./sqrt(1+x.^2+y.^2); meshc(x,y,z);8.x=linspace(-3,3,100);y=linspace(-3,3,100);[x y]=meshgrid(x,y);fxy=-5./(1+x.^2+y.^2);i=find(abs(x)<=0.8 & abs(y)<=0.5);fxy(i)=NaN;surf(x,y,fxy)9.u=linspace(1,10,100);v=linspace(-pi,pi,100);[u,v]=meshgrid(u,v);x=3.*u.*sin(v);y=2.*u.*cos(v);z=4*u.^2;x=3*u.*sin(v);y=2*u.*cos(v);z=4*u.^2;surf(x,y,z);shading interp;light('position',[1,0,1]);10.t=0:pi/100:2*pi;y=sin(t);comet(t,y)第4章一、思考题5.（1）A=eye(3);（2）C=100+(200-100)*rand(5,6);（3）D=1+sqrt(0.2)*randn(1,500);（4）E=ones(size(A));（5）A=A+30*eye(size(A));（6）B=diag(diag(A))二、实验题1.P=pascal(5);H=hilb(5);Dp=det(P);Dh=det(H);Kp=cond(P);Kh=cond(H);P矩阵的性能更好，因为Kp较小2.A=[1,-1,2,3;0,9,3,3;7,-5,0,2;23,6,8,3]B=[3,pi/2,45;32,-76,sqrt(37);5,72,4.5e-4;exp(2),0,97]A1=diag(A);B1=diag(B);A2=triu(A);B2=triu(B);A3=tril(A);B3=tril(B);rA=rank(A);rB=rank(B);nA=norm(A);nb=norm(B);cA=cond(A);cB=cond(B);3.A=[31,1,0;-4,-1,0;4,-8,-2]；[V,D]=eig(A);4.A=diag([-1,-1,-1,-1],-1)+diag([-1,-1,-1,-1],1)+diag([2,2,2,2,2]) b=[1,0,0,0,0]';x1=inv(A)*b;x2=A\b;[L,U]=lu(A);x3=U\(L\b);[Q,R]=qr(a);[Q,R]=qr(A);x4=R\(Q\b)R=chol(A);x5=R\(R'\b)5.B=sparse(A);x1=inv(B)*b;x2=B\b;[L,U]=lu(B);x3=U\(L\b);第5章一、思考题3.A=randn(10,5);mean(A)std(A)max(max(A))min(min(A))sum(A,2)sum(sum(A))sort(A,1)sort(A,2,'descend')二、实验题1.A=rand(1,30000);mean(A)std(A)max(A)min(A)size(find(A>0.5))/size(A)2.h=[466,715,950,1422,1635];w=[7.04,4.28,3.40,2.52,2.13];hh=[500,900,1500];ww=interp1(h,w,hh,'spline')3.x=linspace(1,10,50);y=log(x);f=polyfit(x,y,5);yy=polyval(f,x);plot(x,y,'r-',x,yy,'g.')4.N=64; % 采样点数T=5; % 采样时间终点t=linspace(0,T,N); % 给出N个采样时间ti(I=1:N) x=3*exp(-t); % 求各采样点样本值xdt=t(2)-t(1); % 采样周期f=1/dt; % 采样频率(Hz)X=fft(x); % 计算x的快速傅立叶变换XF=X(1:N/2+1); % F(k)=X(k)(k=1:N/2+1) f=f*(0:N/2)/N; % 使频率轴f从零开始plot(f,abs(F),'-*') % 绘制振幅-频率图xlabel('Frequency');ylabel('|F(k)|')5.（1）p1=[1 2 0 0 7];p2=[1 -2];p3=[1 0 0 5 1];p12=conv(p1,p2);p=p12+[zeros(1,size(p12,2)-size(p3,2)),p3];roots(p)（2）A=[-1,4,3;2,1,5;0,5,6];Px=polyval(p,A)Pxm=polyvalm(p,A)6.（1）z=fzero('3*x-sin(x)+1',0)（2）建立函数文件myfun.mfunction F=myfun(X)x=X(1);y=X(2);F(1)=x*x+y*y-9;F(2)=x+y-1;在命令窗口中输入以下命令：x=fsolve(@myfun,[3,0]',optimset('Display','off')) 第6章一、思考题2.fx=inline('1./(1+x.^2)');[I,n]=quad(fx,-100000,100000,1e-3);[I,n]=quadl(fx,-100000,100000,1e-3);x=-100000:0.01:100000;y=1./(1+x.*x);trapz(x,y);3.(1)fx=inline('-2*y+2*x*x+2*x');[t,y]=ode23(fx,[0,0.5],1)(2)fx=inline('y-exp(x)*cos(x)');[t,y]=ode23(fx,[0,3],1)二、实验题1.for x=1:3fx=[x,x^2,x^3;1,2*x,3*x;0,2,6*x];diff(fx)end2.（1）x=0:0.01:1;y=x.^10+10.^x+1./log10(x);dy=diff(y)/0.01;（2）x=0:0.01:1;y=log(1+x);dy=diff(y,2)/0.01;plot(x(1:99),dy)3.（1）fx=inline('x.^2.*sqrt(2*x.*x+3)');quad(fx,1,5)（2）fx=inline('x./sin(x).^2');quad(fx,pi/4,pi/3)（3）fx=inline('abs(cos(x+y))');dblquad(fx,0,pi,0,pi)（4）syms x y ;fx=x*y;int(int(fx,y^2,y+2),-1,2)x 的积分区间为【0，2】时fx=inline('x.*y');dblquad(fx,0,2,-1,2)4.x=0.3:0.2:1.5;y=[0.3895,0.6598,0.9147,1.1611,1.3971,1.6212,1.8325]; trapz(x,y)5.（1）yp=inline('-(1.2+sin(10*x))*y');[t,y]=ode23(yp,[0,5],1);（2）令''3,,21y x y x y x ='==，则可写出原方程的状态方程形式：123233221sin 31)1(2cos 5cos x tx x t t t x x x x x +--++='='='⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+-+-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡'''t x x x t t t x x x cos 00)1(2cos 51sin 311000103212321 建立函数文件ztfun.mfunction y=ztfun(t,x)b=[0;0;cos(t)];y=[0,1,0;0,0,1;-1/(3+sin(t)),-1,5*cos(2*t)/(t+1)^2]*x+b; 解微分方程组[t,y]=ode23(@ztfun,[0,5],[1;0;2]);6.建立函数文件ztfun.mfunction yy=ztfun(t,y)yy=[y(2)*y(3);-y(1)*y(3);-0.51*y(1)*y(2)];解微分方程组[t,y]=ode23(@ztfun,[0,5],[0;1;1])第7章一、思考题3.（1）数值积分fx=inline('exp(x).*(1+exp(x)).^2');quad(fx,0,log(2))符号积分f=sym('exp(x)*(1+exp(x))^2');v=int(f,0,log(2));eval(v)（2）略二、实验题1.A=sym('[1,2,3;x,y,z;3,2,1]')rank(A)inv(A)det(A)2.(1) y=sym('sqrt(x+sqrt(x+sqrt(x)))');y1=diff(y)y2=diff(y,'x',2)(2) syms x y;fxy=sin(x^2*y)*exp(-x^2-y);diff(diff(fxy,x),y)3.(1) syms xint(1/(1+x^4))(2) syms x tint((-2*x*x+1)/(2*x*x-3*x+1)^2,x,cos(t),exp(2*t)) 4.syms n xsymsum(1/(2*n+1)/(2*x+1)^(2*n+1),n,0,inf)symsum(1/(2*n+1)/(2*x+1)^(2*n+1),n,0,5)5.(1) syms xtaylor((exp(x)+exp(-x))/2,5,0)(2) syms a xtaylor(exp(-5*x)*sin(3*x+pi/3),5,a)6.(1)x=solve(sym('x^3+a*x+1=0'))(2) [x y]=solve(sym('sqrt(x^2+y^2)-100=0,3*x+5*y-8=0'))7. 方程转化为： π21'11't y y y y -=+=⎩⎨⎧符号解[y1,y11]=dsolve('Dy=y1,Dy1+y=1-t^2/pi','y(-2)=5,y1(-2)=5','t') 数值解编写函数文件ztfun.mfunction yy=ztfun(t,y)yy=[y(2);1-t^2/pi-y(1)];在命令窗口输入以下命令[t,y]=ode45(@ztfun,[-2,7],[-5;5]);t=linspace(-2,7,49)y2=y8.[x,y]=dsolve('Dx=3*x+4*y,Dy=-4*x+3*y','x(0)=0,y(0)=1')。

matlab课后答案完整版

matlab课后答案完整版ones表⽰1矩阵zeros表⽰0矩阵ones(4)表⽰4x4的1矩阵zeros(4)表⽰4x4的0矩阵zeros(4,5)表⽰4x5的矩阵eye(10,10)表⽰10x10的单位矩阵rand(4,5)表⽰4x5的伴随矩阵det(a)表⽰计算a的⾏列式inv(a)表⽰计算a的逆矩阵Jordan(a)表⽰求a矩阵的约当标准块rank(a)表⽰求矩阵a的秩[v,d]=eig(a)对⾓矩阵b=a’表⽰求a矩阵的转置矩阵sqrt表⽰求平⽅根exp表⽰⾃然指数函数log⾃然对数函数abs绝对值第⼀章⼀、5（1）b=[97 67 34 10;-78 75 65 5;32 5 -23 -59]; >> c=[97 67;-78 75;32 5;0 -12]; >> d=[65 5;-23 -59;54 7];>> e=b*ce =5271 11574-11336 6641978 3112（2）a=50:1:100⼆、1 、x=-74;y=-27;z=(sin(x.^2+y.^2))/(sqrt(tan(abs(x+y)))+pi) z =-0.09012、a=-3.0:0.1:3.0;>> b=exp(-0.3*a).*sin(a+0.3)y =0.7218 1.0474-0.2180 1.15624、a*b表⽰a矩阵和b矩阵相乘a.*b表⽰a矩阵和b矩阵单个元素相乘A(m,n)表⽰取a矩阵第m⾏，第n列A(m,:)表⽰取a矩阵第m⾏的全部元素A(:,n)表⽰取a矩阵的第n列全部元素A./B表⽰a矩阵除以b矩阵的对应元素，B.\A等价于A./BA.^B表⽰两个矩阵对应元素进⾏乘⽅运算A.^2表⽰a中的每个元素的平⽅A^2表⽰A*A例：x=[1,2,3];y=[4,5,6];z=x.^yz=1 32 729指数可以是标量（如y=2）.底数也可以是标量（如x=2）5、a=1+2i;>> b=3+4i;>> c=exp((pi*i)/6)c =0.8660 + 0.5000id=c+a*b/(a+b)d =1.6353 + 1.8462i第⼆章⼆、4、（1）y=0;k=0;>> while y<3k=k+1;>> display([k-1,y-1/(2*k-1)])ans =56.0000 2.9944第三章⼆1（1） x=0:pi/10:2*pi; >> y=x-x.^3/6; >> plot(x,y)1234567-40-35-30-25-20-15-10-505（2）x=0:pi/10:2*pi; y=(exp(-x.^2/2))/2*pi;plot(x,y)012345670.20.40.60.811.21.41.6（3）x=-8:0.01:8; y=sqrt((64-x.^2)/2);plot(x,y)-8-6-4-2024680123456（4）t=0:0.1:8*pi; >> x=t.*sin(t); >> y=t.*cos(t);-25-20-15-10-50510152025-30-20-10102030例3.4x=0:pi/100:2*pi; y1=exp(-0.5*x);y2=exp(-0.5*x).*sin(2*x); plot(x,y1,x,y2)>> title('x from 0 to 2{\pi} '); >> xlabel('variable x'); >> ylabel('variable y'); >> text(1.5,0.5,'曲线y1=e^(-0.5x)'); >> text(3,0.1,'曲线y2=cos(4{\pi}x)e^{-0.5x}'); >> legend('y1','y2')1234567-0.4-0.20.20.40.60.81x from 0 to 2πvariable xv a r i a b l e y曲线y1=e (-0.5x)曲线y2=cos(4πx)e -0.5xy1y22、(1)y1=2*x-0.5;t=linspace(0,pi,100); x=sin(3*t).*cos(t); y=sin(3*t).*sin(t);>> k=find(abs(y-x)<1e-2); >> t1=t(k) t1 =0 0.7933 1.04722.0944>> z=sin(3.*(t1)).*cos(t1) z =0 0.4841 0.0000 0.0000 -0.0000>> plot(t,x,t,y,'k:',t1,z,'bp');0.511.522.533.5-1-0.8-0.6-0.4-0.200.20.40.60.81（2）subplot(1,2,1); >> scatter(x1,y1,10)； >> title('y=2x-0.5')； >> subplot(1,2,2); >> scatter(x,y,10)-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.63、subplot(1,2,1); x=0:0.01:pi; y=sin(1./x); plot(x,y)subplot(1,2,2);fplot('sin(1./x)',[1,100])1234-1-0.8-0.6-0.4-0.200.20.40.60.81204060801000.10.20.30.44、t=0:pi:2*pi; y=1./(1+exp(-t));subplot(2,2,1);%图形窗⼝的分割bar(t,'group'); %绘制柱形图（分组） subplot(2,2,2);barh(t,'stack');%绘制柱形图（堆积） subplot(2,2,3);loglog(t,y); %函数使⽤全对数坐标，x,y 均采⽤常⽤对数刻度 subplot(2,2,4); semilogy(t,y); %函数使⽤半对数坐标，y 轴为常⽤对数刻度，x 轴仍为线性刻度1230246802468123100.5100.710-0.01810-0.0010246810-0.310-0.210-0.15、（1）theta=linspace(-pi,pi,100); ro=5.*cos(theta)+4; polar(theta,ro); （2）x=linspace(0,2*pi,100);a=1>> r=a.*(1+cos(x)); polar(x,r);3021060240902701203001503301806、（1）t=0:pi/10:2*pi;>> x=exp((-t)/20).*cos(t); >> y=exp((-t)/20).*sin(t); >> z=t; >> plot3(x,y,z);-1-0.50.51-1-0.50.5102468（2）t=0:0.01:1; x=t;>> y=t.^2; >> z=t.^3;>> plot3(x,y,z);0.20.40.60.800.20.40.60.817、x=-30:0.1:0; >> y=0:0.1:30;>> [x,y]=meshgrid(x,y); >>z=10.*sin(sqrt(x.^2+y.^2))./sqrt(1+x.^2+y.^2);>> meshc(x,y,z);绘制曲⾯图和等⾼线-30-20-10102030-4-202468、x=linspace(-3,3,100); >> y=linspace(-3,3,100); >> [x y]=meshgrid(x,y); %可以将向量转化为矩阵 >> fxy=-5./(1+x.^2+y.^2); >> i=find(abs(x)<=0.8 & abs(y)<=0.5); >> fxy(i)=NaN; >>surf(x,y,fxy) %绘制三维曲⾯图-4-224-4-224-4-3-2-19、u=linspace(1,10,100); v=linspace(-pi,pi,100);[u v]=meshgrid(u,v); x=3.*u.*sin(v); y=2.*u.*cos(v); z=4*u.^2; surf(x,y,z); shading interp;-40-20-1010200100200300400第五章⼆1、a=rand(1,30000);mean(a) %求平均数 ans =0.5010 >>b=std(a) %求标准差 b =0.2882 >> c=max(a) c =0.9999 >> d=min(a) d =3.5706e-005size(find(a>0.5))/size(a) %求⼤于0.5的随机数个数占总数的百分⽐ans =0.50322、h=[466,715,950,1422,1635]; >> w=[7.04,4.28,3.40,2.52,2.13]; >> hh=[500,900,1500]; >> ww=interp1(h,w,hh,'spline')ww =6.4903 3.5226 2.3845 3、x=linspace(1,10,50); y=log(x);f=polyfit(x,y,5); %求曲线的拟合 >> yy=polyval(f,x); >> plot(x,y,'r-',x,yy,'g.') 123456789100.511.522.55、（1）、（2） p1=[1,2,0,7]; p2=[1,-2]; p3=[1,0,5,1]; p12=conv(p1,p2); >>p=p12+[zeros(1,size(p12,2)-size(p3,2)),p3]; >> roots(p) ans =-3.4656 0.6128 + 1.6278i 0.6128 - 1.6278i 1.2400-29 291 95 19 -3 697 -13 697 1427 >>y2=polyvalm(p,a)%以矩阵a 为⾃变量 y2 =391 2084 3273 502 2693 4207 720 3775 5892 6、（1）z=fzero('3*x-sin(x)+1',0) %求x=0时附近的根 z =-0.4903 第⼋章⼆、2t=0:pi/20:2*pi; x=sin(t); y=cos(t); x1=sin(7*t); y1=cos(7*t);h=plot(x,y,x1,y1);set(h,'marker','x','linewidth',2); set(gca,'xtick',-1:0.1:1); title('篮筐')-1-0.9-0.8-0.7-0.6-0.5-0.4-0.3-0.2-0.100.10.20.30.40.50.60.70.80.91 -1-0.8-0.6-0.4-0.200.20.40.60.81篮筐3、x=0:pi/10:5*pi;y=exp(-0.2*x).*cos(x)+2; h=plot(x,y);set(gca,'color','red','linestyle','-','linewidth',3);text(5,2.4,'y=exp(-0.2*x).*cos(x)+2');02468101214161.41.61.822.22.42.62.83y=exp(-0.2*x).*cos(x)+24、t=-pi:pi/100:pi; x=cos(t); y=sin(t); z=t;h=plot(t,x,t,y,t,z);set(h,'linestyle','-','linewidth',3);-4-3-2-101234-4-3-2-101234字符串例ch='Welcome to Beijing';subch=ch(12:18) 选12~18个字符串（空格也算）ans =WELCOME TO BEIJING >> length(k)统计⼩写字母的个数ans = 14 例：已知y=1-1/2+1/3-1/4.........-1/100求y 的值y=0; >> n=100; >> for i=1:100; y=y+(-1)^(i-1)/i; end>> disp(y)0.6882绘制⼆维曲线图x=0:pi/100:2*pi; >> y1=0.2*exp(-0.5*x).*cos(4*pi*x); >> y2=1.5*exp(-0.5*x).*cos(pi*x); >> plotyy(x,y1,x,y2); 7-0.20.20123456-202绘制三维图像例：x=sint+tcost y=cost-tsint z=tt=0:pi/10:10*pi; x=sin(t)+t.*cos(t); y=cos(t)-t.*sin(t); z=t; plot3(x,y,z); axis([-30 30 -30 30 0 35]); 坐标轴的最⼤值与最⼩值title('line in 3-D space'); 图形的题⽬ >> xlabel('x');ylabel('y');zlabel('z'); 标注坐标>> grid on; 加⽹格线 -30-20-10102030-20205101520253035xline in 3-D spaceyz三维例]2/,0[],,0[,cos sin 22ππ∈∈+=y x y x z [x,y]=meshgrid(0:pi/100:pi,0:pi/100:pi/2);>> z=sin(x.^2)+cos(y.^2);>> mesh(x,y,z);>> axis([0 4 0 1.8 -1.5 1.5]); 012340.511.5-1.5-1-0.500.511.5例3.16t=0:pi/20:2*pi; subplot(1,2,1);[x,y,z]=cylinder(sin(t),30);surf(x,y,z); 绘制三维曲⾯图subplot(1,2,2);>> [x,y,z]=peaks(100);>> mesh(x,y,z); 绘制三维⽹格图-11-10100.20.40.60.81-55-505-10-5510多项式求导例：f(x)=1/x^2+5 p=[1];>> q=[1,0,5];>> [p,q]=polyder(p,q)注：c=conv(a,b) 表⽰a 多项式与b 多项式乘积[p,r]=deconv(a,b) 表⽰a 多项式与b 多项式相除其中p 为商向量 r 为余数向量p=polyder(p) 表⽰求p 的导数 p=poleder(p,q) 表⽰求p 乘以q 的导数[p,q]=poleder(p,q) 表⽰p 除以q 的导数多项式求根例：f(x)=2x^4-12x^3+3x^2+5 p=[2,-12,3,0,5]; >> x=roots(p); >> p=[2,-12,3,0,5]; x=roots(p) 求⽅程f(x)=0的根 x =5.7246 0.8997 -0.3122 + 0.6229i -0.3122 - 0.6229i>> g=poly(x) 已知多项式的根求多项式 g =1.0000 -6.0000 1.5000 -0.00002.5000符号求导例7.3x=a(t-tsint)y=b(1-cost) 求y 对x 的⼀阶导数 syms x y a b t;>> f21=a*(t-sin(t)); >> f22=b*(1-cos(t));>> diff(f22)/diff(f21) 求y 对x 的⼀阶导数ans =b*sin(t)/a/(1-cos(t))注：diff(f1,x,2) 表⽰f1对x 的⼆阶导数diff （f3,x ）表⽰z 对x 的偏导 diff （f3,y ）表⽰z 对y 的偏导求不定积分int(f) 求f 的不定积分 f1=int(f,a,b) 求f 在a ，b 之间的定积分eval （f1）计算积分值符号求极限例7.2 syms x h>> f=(sin(x+h)-sin(x))/h;>> limit(f,h,0) h 趋向于0ans =cos(x)例2f=sym('(1+t/x)^x');limit(f,inf) f趋向于⽆穷ans =exp(t)例3f=sym('x*(sqrt(x^2+1)-x)');limit(f,sym('x'),inf,'left') x 趋向于正⽆穷ans =1/2⼤⼩写ch='Welcome to Beijing';subch=ch(12:18)subch =Beijing>> k=find(ch>='A'&ch<='Z'); ch(k)=ch(k)-('A'-'a');>> char(ch)ans =welcome to beijing>> length(k)ans =2。

MATLAB课后题答案整理

第一章1.利用MATLAB 的帮助功能分别查询inv 、plot 、max 、round 等函数的功能及用法。

Help+函数2.简述MATLAB 的主要功能。

①数值计算和符号计算功能。

②绘图功能。

③编程语言功能。

④扩展功能。

3.help 命令和lookfor 命令有何区别？Help 命令只搜索出那些与关键字完全匹配的结果，lookfor 命令对搜索范围内的M 文件进行关键字搜索，条件比较宽松。

Lookfor 命令只对M 文件的第一行进行关键字搜索。

若在lookfor 命令后加上-all 选项，则可对M 文件进行全文搜索。

第二章1（1）)1034245.01(26-⨯+⨯=ww=sqrt(2)*(1+0.34245*10^(-6)) w = 1.4142（2）ac b e abc c b a x ++-+++=)tan(22ππ，其中a=3.5，b=5，c=-9.8。

a=3.5;b=5;c=-9.8;x=(2*pi*a+(b+c)/(pi+a*b*c)-exp(2))/(tan(b+c)+a) x =0.9829（3）])48333.0()41[(22απβππα---=y ，其中α=3.32，β=-7.9。

a=3.32;b=-7.9;y=2*pi*a^2*((1-pi/4)*b-(0.8333-pi/4)*a) y = -128.4271（4）)1ln(2122t t e z t ++=，其中t=]65.05312[--i 。

t=[2,1-3i;5,-0.65];z=0.5*exp(2*t)*log(t+sqrt(1+t.*t)) z = 1.0e+004 * 0.0048 + 0.0002i 0.0048 - 0.0034i1.58992.0090 - 1.3580i2.已知]023352138[],7613870451[--=--=B A 求下列表达式的值。

（1）B A 6+和I B A +-2。

MATLAB第一章作业答案

第一章M A T L A B概况与基本操作1.选择题：(1)最初的MATLAB核心程序是采用A语言编写的。

(2)即将于2011年9月发布的MATLAB新版本的编号为D。

2011Ra 2011Rb R2011a R2011b(3)在默认设置中，MATLAB中的注释语句显示的颜色是D。

A.黑色B.蓝色C.红色D.绿色(4)如果要以科学计数法显示15位有效数字，使用的命令是B。

long long e long g long d(5)在命令窗口新建变量a、b，如果只查看变量a的详细信息，使用的命令为B。

a a(6)如果要清除工作空间的所有变量，使用的命令为 C 。

all C.两者都可 D.两者都不可(7)在创建变量时，如果不想立即在命令窗口中输出结果，可以在命令后加上D。

A.冒号B.逗号C.空格D.分号(8)如果要重新执行以前输入的命令，可以使用B键。

A.下箭头↓B.上箭头↑C.左箭头←D.右箭头→(9)如果要查询函数inv的相关信息，并显示在命令窗口，应使用命令A。

D.三者均可(10)如果要启动Notebook文档，下列D操作是可行的。

A.在命令窗口输入notebook命令B.在命令窗口输入notebook filename命令C.在Word中启动M-book文档D.三者均可2.填空题：(1)MATLAB是MATrix和LABoratory两个单词前三个字母的组合，意为“矩阵实验室”，它的创始人是Cleve Moler和Jack Little。

(2)在MATLAB的默认设置中，关键字显示的字体为蓝色，命令、表达式、计算结果显示的字体为黑色，字符串显示的字体为紫色，注释显示的字体为绿色，错误信息显示的字体为红色。

(3)在命令窗口中，输出结果显示为各行之间添加空行的命令为format compact，各行之间不添加空行的命令为format compact。

备注：本题布置给大家时有一点小错误，现在予以更正。

MATLAB 课后部分答案

P77 第2章1、>> x=2;>> y=power(x,3)+(x-0.98).^2./(x+1.35).^3-5*(x+1./x)>> x=4;>> y=power(x,3)+(x-0.98).^2./(x+1.35).^3-5*(x+1./x)7、>> mat=rand(4,5);>> m=1;>> for i=1:2for j=1:5if mat(i,j)>0.3b(m)=mat(i,j);m=m+1;endendend>> b8、>> V=inv(A)>> A=rand(5,5);10、>> A=[1 4 8 13;-3 6 -5 -9;2 -7 -12 -8];B=[5 4 3 -2;6 -2 3 -8;-1 3 -9 7]; >> C=A*B??? Error using ==> mtimesInner matrix dimensions must agree.>> C=A.*BC =5 16 24 -26-18 -12 -15 72-2 -21 108 -5611、>> x=linspace(0,2*pi,125);>> y=cos((x).*(0.5+3*sin(x)./(1+x.^2)));>> plot(x,y)13、>> x=-2:0.1:2;y=-2:0.1:2;>> [X,Y]=meshgrid(x,y);>> Z=X.^2.*exp(-X.^2-Y.^2);>> mesh(Z)建立一个M函数文件mycos.m，程序如下：function y=mycos(x)clear allx=input('请输入x的值')y=1./((x-2).^2+0.1)+1./((x-3).^3+0.01)在命令窗口输入：mycosP123 第3章1、>> x=[446 714 950 1422 1634];y=[7.04 4.28 3.40 2.54 2.13];>> xi=500:500:1500;>> yi=interp1(x,y,xi,'linear')4、>> p=[3 4 7 2 9 12];>> roots(p)8、>> a=[2 4 9;4 2 4;9 4 18];>> [V,D]=eig(a) %V的列向量是相应的特征向量,对角阵D的对角元素为a的特征值10、>> p1=[-1 4 0];p2=[-1 -4 0];>> A=polyder(p1);B=polyder(p2);>> A1=roots(A);B1=roots(B);>> y=4*A1-4*B1-A1.^2-B1.^213、>> syms x y>> Ex=int(int(x.*12.*y.^2,y,0,x),x,0,1)>> Ey=int(int(y.*12.*y.^2,x,y,1),y,0,1)>> Exy=Ex.*Ey14、>> A=rand(4,4);>> [L,U]=lu(A)>> [Q,R]=qr(A)P183 第4章1、>> n=-2*pi:0.01:2*pi;>> N=12;x=cos(n*pi./6);>> X=fft(x,N)>> nx=((n>=0)&(n<=11)); hx=((n>=0)&(n<=5)); >> xn=0.8*nx;hn=hx;>> y=conv(xn,hn)4、>> n=0:11;h=0:5;>> nx=((n>=0)&(n<=11)); hx=((n>=0)&(n<=5)); >> xn=0.8*nx;hn=hx;>> M=length(xn);N=length(hn);>> L=pow2(nextpow2(M+N-1));>> Xk=fft(xn,L);Hk=fft(hn,L);>> Yk=Xk.*Hk;>> yn=ifft(Yk,L)5、>> num=[2 3 0];den=[1 0.4 1];>> [z,p,k]=tf2zp(num,den)6、>> num=[4 15.6 6 2.4 -6.4];den=[3 2.4 6.3 -11.4 6]; >> [z,p,k]=tf2zp(num,den)>> zplane(z,p)7、>> num=[18 0 0 0];den=[18 3 -4 -1];>> [r,p,k]=residuez(num,den)9、建立一个M函数文件，程序如下：clear allN=10;[z,p,k]=buttap(N);[A,B,C,D]=zp2ss(z,p,k);wc1=100;wc2=200;[At,Bt,Ct,Dt]=lp2bp(A,B,C,D,wc1,wc2);[num1,den1]=ss2tf(At,Bt,Ct,Dt);[num2,den2]=impinvar(num1,den1);dimpulse(num2,den2)10、建立一个M函数文件，程序如下：clear allwp=100*2*pi;ws=200*2*pi;Rp=2;Rs=15;Fs=500;[N,Wc]=buttord(wp,ws,Rp,Rs,'s'); %选择滤波器的最小阶数[z,p,k]=buttap(N);[B,A]=zp2tf(z,p,k);[num,den]=bilinear(B,A,Fs); %模拟滤波器的传递函数转换为数字滤波器的传递函数freqz(num,den)11、建立一个M函数文件，程序如下：clear allN=48;w=[0.35,0.65];B=fir1(N,w,'bandpass'); %返回一个N阶的带通滤波器freqz(B) %绘制滤波器的频率响应曲线12、建立一个M函数文件，程序如下：clear allN=37;wc=0.3*pi;B=fir1(N,wc);freqz(B) %绘制滤波器的频率响应曲线13、建立一个M函数文件，程序如下：clear allN=55;F=[0:1/55:1];A=[ones(1,28),zeros(1,N-27)];B=fir2(N,F,A);freqz(B) %绘制滤波器的频率响应曲线15、建立一个M函数文件，程序如下：clear allwc=0.4*pi/(2*pi);N=12;[B,A]=butter(N,wc);%设计N阶截止频率为wc的Butterworth低通数字滤波器的传递函数模型m=dimpulse(B,A,101);stem(m,'.')P277 第6章2、建立一个M函数文件，程序如下：function [h,l]=huffmancode(P)if length(find(P<0))~=0,error('Not a prod.vector')endif abs(sum(P)-1)>10e-10error('Not a prod.vector')endn=length(P);for i=1:n-1for j=i:nif P(i)<=P(j)p=P(i);P(i)=P(j);P(j)=p;endendenddisp('概率分布'),PQ=P;m=zeros(n-1,n);for i=1:n-1[Q,l]=sort(Q);m(i,:)=[l(1:n-i+1),zeros(1,i-1)];Q=[Q(1)+Q(2),Q(3:n),1];endfor i=1:nc(i,:)=blanks(n*n);endc(n-1,n)='0';c(n-1,2*n)='1';for i=2:n-1c(n-i,1:n-1)=c(n-i+1,n*(find(m(n-i+1,:)==1))-(n-2):n*(find(m(n-i+1,:)==1)));c(n-1,n)='0';c(n-i,n+1:2*n-1)=c(n-i,1:n-1);c(n-i,2*n)='1';for j=1:i-1c(n-i,(j+1)*n+1:(j+2)*n)=c(n-i+1,n*(find(m(n-i+1,:)==j+1)-1)+1:n*find(m(n-i+1,:)==j+1));endendfor i=1:nh(i,1:n)=c(1,n*(find(m(1,:)==i)-1)+1:find(m(1,:)==i)*n);ll(i)=length(find(abs(h(i,:))~=32));endl=sum(P.*ll); %计算平均码长在命令窗口中输入：>> P=[0.20 0.15 0.13 0.12 0.1 0.09 0.08 0.07 0.06];>> [h,l]=huffmancode(P)3、建立一个M函数文件，程序如下：function[sqnr,a_quan,code]=u_pcm(a,n)% U_PCM 一个序列均匀的PCM编码.% n=量化级数的数目（偶数）.% sqnr=输入信号量化噪声比（偶数）。

matlab课后习题答案到章

m a t l a b课后习题答案到章Last updated on the afternoon of January 3, 2021习题二1.如何理解“矩阵是MATLAB最基本的数据对象”2.答：因为向量可以看成是仅有一行或一列的矩阵，单个数据（标量）可以看成是仅含一个元素的矩阵，故向量和单个数据都可以作为矩阵的特例来处理。

因此，矩阵是MATLAB最基本、最重要的数据对象。

3.设A和B是两个同维同大小的矩阵，问：(1)A*B和A.*B的值是否相等(2)答：不相等。

(3) A./B和B.\A的值是否相等？答：相等。

(4)A/B和B\A的值是否相等(5)答：不相等。

(6)A/B和B\A所代表的数学含义是什么？答：A/B等效于B的逆右乘A矩阵，即A*inv(B)，而B\A等效于B矩阵的逆左乘A矩阵，即inv(B)*A。

4.写出完成下列操作的命令。

(1)将矩阵A第2~5行中第1,3,5列元素赋给矩阵B。

答：B=A(2:5,1:2:5);或B=A(2:5,[135])(2)删除矩阵A的第7号元素。

答：A(7)=[](3)将矩阵A的每个元素值加30。

答：A=A+30;(4)求矩阵A的大小和维数。

答：size(A);ndims(A);(5)将向量t的0元素用机器零来代替。

答：t(find(t==0))=eps;(6)将含有12个元素的向量x转换成34⨯矩阵。

答：reshape(x,3,4);(7)求一个字符串的ASCII码。

答：abs(‘123’);或double(‘123’);(8)求一个ASCII码所对应的字符。

答：char(49);5.下列命令执行后，L1、L2、L3、L4的值分别是多少？A=1:9;B=10-A;...L1=A==B;L2=A<=5;L3=A>3&A<7;L4=find(A>3&A<7);答：L1的值为[0,0,0,0,1,0,0,0,0]L2的值为[1,1,1,1,1,0,0,0,0]L3的值为[0,0,0,1,1,1,0,0,0]L4的值为[4,5,6]6.已知完成下列操作：(1)取出A的前3行构成矩阵B，前两列构成矩阵C，右下角32⨯子矩阵构成矩阵D，B与C的乘积构成矩阵E。

MATLAB语言基础与应用(第二版)第1章习题答案

第1章习题与答案1.1 MA TLAB桌面主要有哪些窗口构成？这些窗口主要功能是什么？请参考1.3节1.2计算下列表达式(1) 3+6 (2) sin(1+i)(3) (1+2i)×(2-i) (4) 2×4+3解答：(1) >> 3+6ans = 9(2) >> sin(1+i)ans = 1.2985 + 0.6350i(3) >> (1+2*i)*(2-i)ans = 4.0000 + 3.0000i(4) >> 2*4+3ans = 111.3借助“help”函数了解“meshgrid”函数的意义。

解答：>> help meshgridmeshgrid Cartesian grid in 2-D/3-D space[X,Y] = meshgrid(xgv,ygv) replicates the grid vectors xgv and ygv toproduce the coordinates of a rectangular grid (X, Y). The grid vectorxgv is replicated numel(ygv) times to form the columns of X. The gridvector ygv is replicated numel(xgv) times to form the rows of Y.[X,Y,Z] = meshgrid(xgv,ygv,zgv) replicates the grid vectors xgv, ygv, zgvto produce the coordinates of a 3D rectangular grid (X, Y, Z). The gridvectors xgv,ygv,zgv form the columns of X, rows of Y, and pages of Zrespectively. (X,Y,Z) are of size numel(ygv)-by-numel(xgv)-by(numel(zgv).[X,Y] = meshgrid(gv) is equivalent to [X,Y] = meshgrid(gv,gv).[X,Y,Z] = meshgrid(gv) is equivalent to [X,Y,Z] = meshgrid(gv,gv,gv).The coordinate arrays are typically used for the evaluation of functionsof two or three variables and for surface and volumetric plots.meshgrid and NDGRID are similar, though meshgrid is restricted to 2-Dand 3-D while NDGRID supports 1-D to N-D. In 2-D and 3-D the coordinates output by each function are the same, the difference is the shape of theoutput arrays. For grid vectors xgv, ygv and zgv of length M, N and Prespectively, NDGRID(xgv, ygv) will output arrays of size M-by-N whilemeshgrid(xgv, ygv) outputs arrays of size N-by-M. Similarly,NDGRID(xgv, ygv, zgv) will output arrays of size M-by-N-by-P whilemeshgrid(xgv, ygv, zgv) outputs arrays of size N-by-M-by-P.Example: Evaluate the function x*exp(-x^2-y^2)over the range -2 < x < 2, -4 < y < 4,[X,Y] = meshgrid(-2:.2:2, -4:.4:4);Z = X .* exp(-X.^2 - Y.^2);surf(X,Y,Z)Class support for inputs xgv,ygv,zgv:float: double, singleinteger: uint8, int8, uint16, int16, uint32, int32, uint64, int64 See also surf, slice, ndgrid.Overloaded methods:codistributed/meshgridgpuArray/meshgridReference page in Help browserdoc meshgrid1.4通过帮助浏览器窗口了解函数sin和cos。

matlab课后习题参考答案

Matlab课后习题部分参考答案习题二2．student=struct('name',{'zhang','wang','li'},'age',{18,21,[] },'email',{['zh ang@','zhang@'],'',''})5、a=[1 0 0;1 1 0;0 0 1];b=[2 3 4;5 6 7;8 9 10];c=[a b]d=[a;b]c =1 0 023 41 1 0 5 6 70 0 1 8 9 10d =1 0 01 1 00 0 12 3 45 6 78 9 1010、reshape(c,2,9)1 0 1 0 1 5 3 9 71 0 0 02 8 6 4 10 reshape(d,2,9)ans =1 0 5 0 0 6 0 1 71 2 8 1 3 9 0 4 10 (注意：重新排列矩阵，是将原来的矩阵按列排序)11、a.’12、a+b a.*ba\b (即inv(a)*b，考试时，要求能自己手算出a的逆)ans =2 3 43 3 38 9 1013、c=4*ones(3);a>=cb>=c14．strcat('The picture is ','very good')a=['The picture is ','very good']18．double('very good')1．norm（A），det（A），rank（A）2．b=[1 1 1 1 1];c=b';a=[17,24,1,8,50;23,5,7,14,49;4,6,13,20,43;10,12,19,21,62;11,18,25,2,56]; x=a\c习题四1、a=14*rand(1,10)-5;for i=1:9max=i;for j=i+1:10if a(j)>a(max)max=j;endendtemp=a(i);a(i)=a(max);a(max)=temp;enda将上述脚本保存为script41.m2、function y=function42(n)3*randn(1,n)+3;for i=1:n-1max=i;for j=i+1:nif a(j)>a(max)max=j;endendtemp=a(i);a(i)=a(max);a(max)=temp;endy=a;将上述函数保存为function42.m 3、r=input(‘please input 1/2: ’);if r= =1script41;elsen=input(‘please input the length: ’);y=funtion42(n);end4．function f=function1(x,y)if y==1f=sin(x);elseif y==2f=cos(x);elsef=sin(x).*cos(x);end在命令窗口调用函数f=function1(1,3) 5．function result=function3(x,n)result=0;for i=1:nresult=result+sin(x.*i)+(-1).^i.*cos(i.*x); endfunction result=function4(n,t)result=0;A=[1 2 3;0 1 2;0 0 1];for i=1:nresult=result+A*i.*exp(A*i.*t);end习题五3．x1=-2:0.01:2;x2=-2:0.01:2;y1=x1.*sin(x2);y2=x2.*cos(x1);plot3(x1,x2,y 1,'-d',x1,x2,y2,'-d')14、x=8*rand(1,100)-2;y=reshape(x,10,10);save mydata.mat yclearclcload mydatak=y>ones(10);totel=0;for i=1:100if k(i)==1totel=totel+1;endend15、x=rand(5); %生成5*5均匀分布的随机矩阵（该处只作举例，未按题目要求）fid=fopen(‘text.txt’,’w’);count=fwrite(fid,x,’int32’); closestatus=fclose(fid);清除内存，关闭所有窗口fid=fopen(‘text.txt’,’r’);x=fread(fid,[5,5],’int32’); closestatus=fclose(fid); inv(x)16．随便生成一个矩阵，x1=-1:0.2:0.8;x2=-1:0.2:0.8;y1=x1.*sin(x2)；y2=x2.*cos(x1)；a=reshape([y1;y2],10,10)；fid=fopen('table.txt','w'); fprintf (fid,‘%f’，a); fclose(fid) ;清除内存，关闭所有窗口a=fscanf('table.txt','%f') ; exp(a) ;fclose(fid) ;习题六1.c=ploy2str(A)；B=[2,0,0,1,3,5]；2.x=1:10;B=ployval(A，x)；。

matlab课后练习习题及答案详解

matlab课后习题及答案详解第1章MATLAB概论与其余计算机语言对比较，MATLAB语言突出的特色是什么？MATLAB拥有功能强盛、使用方便、输入简捷、库函数丰富、开放性强等特色。

MATLAB系统由那些部分构成？MATLAB系统主要由开发环境、MATLAB数学函数库、MATLAB语言、图形功能和应用程序接口五个部分组成。

安装MATLAB时，在选择组件窗口中哪些部分一定勾选，没有勾选的部分此后怎样补安装？在安装MATLAB时，安装内容由选择组件窗口中个复选框能否被勾选来决定，能够依据自己的需要选择安装内容，但基本平台（即MATLAB选项）一定安装。

第一次安装没有选择的内容在补安装时只要依据安装的过程进行，不过在选择组件时只勾选要补装的组件或工具箱即可。

MATLAB操作桌面有几个窗口？怎样使某个窗口离开桌面成为独立窗口？又怎样将离开出去的窗口从头搁置到桌面上？在MATLAB操作桌面上有五个窗口，在每个窗口的右上角有两个小按钮，一个是封闭窗口的Close按钮，一个是能够使窗口成为独立窗口的Undock 按钮，点击Undock按钮就能够使该窗口离开桌面成为独立窗口，在独立窗口的view菜单中选择Dock,,菜单项就能够将独立的窗口从头防备的桌面上。

怎样启动M文件编写/调试器？在操作桌面上选择“成立新文件”或“翻开文件”操作时，M文件编写/调试器将被启动。

在命令窗口中键入edit命令时也能够启动M文件编写/调试器。

储存在工作空间中的数组能编写吗？怎样操作？储存在工作空间的数组能够经过数组编写器进行编写：在工作空间阅读器中双击要编写的数组名翻开数组编写器，再选中要改正的数据单元，输入改正内容即可。

命令历史窗口除了能够察看前方键入的命令外，还有什么用途？命令历史窗口除了用于查问从前键入的命令外，还能够直接履行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中。

怎样设置目前目录和搜寻路径，在目前目录上的文件和在搜寻路径上的文件有什么差别？目前目录能够在目前目录阅读器窗口左上方的输入栏中设置，搜寻路径能够经过选择操作桌面的file菜单中的SetPath菜单项来达成。

MATLAB习题答案(清华大学)

高等应用数学问题MATLAB 求解习题参考解答（薛定宇著）目录第1 章计算机数学语言概述2第2 章MATLAB 语言程序设计基础5第3 章微积分问题的计算机求解17第4 章线性代数问题的计算机求解29第5 章积分变换与复变函数问题的计算机求解43第6 章代数方程与最优化问题的计算机求解53第7 章微分方程问题的计算机求解71第8 章数据插值、函数逼近问题的计算机求解93第9 章概率论与数理统计问题的计算机求解114第10 章数学问题的非传统解法127第A章自由数学语言Scilab 简介136第1 章计算机数学语言概述1 在你的机器上安装MATLAB 语言环境，并键入demo 命令，由给出的菜单系统和对话框原型演示程序，领略MATLAB 语言在求解数学问题方面的能力与方法。

【求解】在MATLAB 提示符>> 下键入demo 命令，则将打开如图1-1 所示的窗口，窗口左侧的列表框可以选择各种不同组合的演示内容。

图1-1 MATLAB 演示程序界面例如，用户选择MATLAB ! Graphics ! Volume Vlsulization 演示，则将得出如图1-2 所示的演示说明，单击其中的Run this demo 栏目，则将得出如图1-3 所示的演示界面。

用户可以在该界面下按按钮，逐步演示相关内容，而实现这样演示的语句将在该程序界面的下部窗口中给出。

2 作者用MATLAB 语言编写了给出例子的源程序，读者可以自己用type 语句阅读一下源程序，对照数学问题初步理解语句的含义，编写的源程序说明由下表列出。

第1 章计算机数学语言概述3图1-2 MATLAB 演示程序界面举例序号文件名程序说明例1.1 c1ex1.m 利用MATLAB 的符号运算工具箱求解微分问题例1.2 c1ex2.m 分别利用MATLAB 的符号运算工具箱和数值运算功能求解多项式方程，其中用数值方法得出的结果有误差例1.3 c1ex3.m 分别利用MATLAB 的符号运算工具箱和数值运算功能计算Hilbert 矩阵的行列式，其中用数值方法得出的结果有很大误差例1.4 c1ex4.m 令x1 = y; x2 = y_，则可以将原来的二阶微分方程转换成一阶微分方程组，然后就可以求解微分方程的数值解了，原方程是非线性微分方程，故不存在解析解。

MATLAB课后习题集附标准答案

第2章MATLAB概论1、与其他计算机语言相比较，MA TLAB 语言突出的特点是什么？答：起点高、人机界面适合科技人员、强大而简易的作图功能、智能化程度高、功能丰富，可扩展性强.2、MA TLAB 系统由那些部分组成？答：开发环境、MATLAB数学函数库、MATLAB语言、图形功能、应用程序接口3、安装MATLAB 时，在选择组件窗口中哪些部分必须勾选，没有勾选的部分以后如何补安装？答：在安装MATLAB时，安装内容由选择组件窗口中各复选框是否被勾选来决定，可以根据自己的需要选择安装内容，但基本平台（即MATLAB选项）必须安装. 第一次安装没有选择的内容在补安装时只需按照安装的过程进行，只是在选择组件时只勾选要补装的组件或工具箱即可. 矚慫润厲钐瘗睞枥庑赖。

4、MATLAB 操作桌面有几个窗口？如何使某个窗口脱离桌面成为独立窗口？又如何将脱离出去的窗口重新放置到桌面上？聞創沟燴鐺險爱氇谴净。

答：在MATLAB 操作桌面上有五个窗口，在每个窗口的右下角有两个小按钮，一个是关闭窗口的Close 按钮，一个是可以使窗口称为独立的Undock 按钮，点击Undock 按钮就可以使该窗口脱离桌面称为独立窗口，在独立窗口的view 菜单中选择Dock，菜单项就可以将独立的窗口重新防止的桌面上.残骛楼諍锩瀨濟溆塹籟。

5、如何启动M 文件编辑/调试器？答：在操作桌面上选择“建立新文件”或“打开文件”操作时，M 文件编辑/调试器将被启动.在命令窗口中键入edit 命令时也可以启动M 文件编辑/调试器.酽锕极額閉镇桧猪訣锥。

6、存储在工作空间中的数组能编辑吗？如何操作？答：存储在工作空间的数组可以通过数组编辑器进行编辑：在工作空间浏览器中双击要编辑的数组名打开数组编辑器，再选中要修改的数据单元，输入修改内容即可.彈贸摄尔霁毙攬砖卤庑。

7、命令历史窗口除了可以观察前面键入的命令外，还有什么用途？答：命令历史窗口除了用于查询以前键入的命令外，还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中. 謀荞抟箧飆鐸怼类蒋薔。

matlab课后答案

matlab课后答案第二章习题1．观察一个数（在此用@记述）在以下四条不同指令作用下的异同：a=@b=sym(@)c=sym(@,’d’)d=sym(‘@’)在此，@分别代表具体数值7/3，pi/3，pi*3^(1/3)；而异同通过vpa(abs(a-d)),vpa(abs(b-d)),vpa(abs(c-d))等来观察。

a=7/3b=sym(7/3)c=sym(7/3,'d')d=sym('7/3')vpa(abs(a-d))vpa(abs(a-b))vpa(abs(c-d))a =2.3333b =7/3c =2.3333333333333334813630699500209d =7/3ans =0.0ans =0.00.00000000000000014802973661668756666666667788716a=pi/3b=sym(pi/3)c=sym(pi/3,'d')d=sym('pi/3')vpa(abs(a-d))vpa(abs(a-b))vpa(abs(c-d))a =1.0472b =pi/3c =1.047197551196597631317786181171d =pi/3ans =0.0ans =0.0ans =0.000000000000000114836428279922167628066158185542．说出以下三条指令产生的结果各属于那种数据类型，是“双精度”对象，还是“符号”对象？3/7+0.1，sym(3/7+0.1),vpa(sym(3/7+0.1))a=3/7+0.1b=sym(3/7+0.1)c=vpa(sym(3/7+0.1))class(a)class(c)a =0.5286b =37/70c =0.52857142857142857142857142857143ans =doubleans =symans =sym3．在不加专门指定的情况下，以下符号表达中的那一个变量是独立自由变量。

MATLAB习题参考答案（胡良剑

第一章 MATLAB 入门4、求近似解解：>> x=-2:0.05:2;y=x.^4-2.^x两个近似解：y1=f(-0.85)= -0.0328; y2=f(1.250)= 0.0630第二章 MATLAB 编程与作图1、设x 是数组，求均值和方差解：函数文件如下：function [xx,s]=func1(x)n=length(x);xx=sum(x)/n;s=sqrt((sum(x.^2)-n*xx^2)/(n-1));命令窗口：>> x=[1 2 3 4 5];[xx,s]=func1(x)2、求满足的最小m 值 100)1ln(0>+∑=m n n s=0;n=0;while(s<=100)s=s+log(1+n);n=n+1;endn,s3、用循环语句形成Fibonacci 数列,....4,3,,12121=+===−−k F F F F F k k k 。

并验证极限2511+→−k k F F （提示：计算至两边误差小于精度1e-8为止）解：求Fibonacci 数列的函数文件：function f=fun(n)if n<=2f=1;elsef=fun(n-1)+fun(n-2);end验证极限的函数文件：function [k,a]=funTest(e)a=abs(1-(1+sqrt(5))/2);k=2;while(a>e)k=k+1;a=abs(fun(k)/fun(k-1)-(1+sqrt(5))/2);end命令行：>> [k,a]=funTest(10^-8)k =21a =9.7719e-009或者M 文件如下：clear; F(1)=1;F(2)=1;k=2;x=0;e=1e-8; a=(1+sqrt(5))/2;while abs(x-a)>ek=k+1; F(k)=F(k-1)+F(k-2); x=F(k)/F(k-1);enda,x,k4、分别用for 和while 循环结构编写程序，求出∑==610123i i K ，并考虑一种避免循环语句的程序设计，比较各种算法的运行时间。