【精品管理学】spss因子分析案例 共(13页)
spss因子分析案例

spss因子分析案例在进行SPSS因子分析时,我们通常遵循以下步骤:数据准备、因子提取、因子旋转、因子得分和结果解释。
下面是一个因子分析的案例,展示了如何使用SPSS软件进行这一统计分析。
首先,我们需要准备数据。
这通常涉及收集问卷调查数据,其中包含多个项目或变量,这些变量被认为是潜在因子的指标。
在SPSS中,数据应该以数据集的形式输入,每个变量代表一个问卷项目,每个案例代表一个受访者的回答。
接下来,我们进行因子提取。
在SPSS中,我们可以通过“分析”菜单选择“降维”然后选择“因子”来开始因子分析。
在因子分析对话框中,我们需要指定分析的变量,并决定提取因子的方法。
常见的提取方法包括主成分分析和最大似然法。
此外,我们还需要决定因子提取的标准,如特征值大于1的规则或基于特定比例的方差提取。
因子提取后,我们通常需要进行因子旋转。
旋转的目的是使因子结构更加清晰,便于解释。
SPSS提供了多种旋转方法,如正交旋转(如Varimax)和斜交旋转(如Promax)。
旋转后,每个变量的因子载荷(即变量与因子的相关系数)将被重新估计。
然后,我们可以计算因子得分。
因子得分是每个受访者在每个因子上的估计得分,它可以帮助我们了解每个受访者在潜在因子上的位置。
在SPSS中,可以通过“保存”选项来保存因子得分,以便进一步分析。
最后,我们需要解释因子分析的结果。
这包括解释每个因子的含义,以及哪些变量与每个因子最相关。
我们可以通过查看因子载荷矩阵来完成这一步骤。
通常,载荷值较高的变量被认为是该因子的良好指标。
在实际应用中,因子分析可以帮助我们识别数据中的潜在结构,简化数据集,并为进一步的分析提供基础。
例如,在市场研究中,因子分析可以用来识别消费者行为的潜在维度,从而帮助企业更好地理解其客户群体。
通过上述步骤,我们可以使用SPSS软件有效地进行因子分析,从而揭示数据背后的潜在结构,并为决策提供支持。
【管理学】spss因子分析案例共
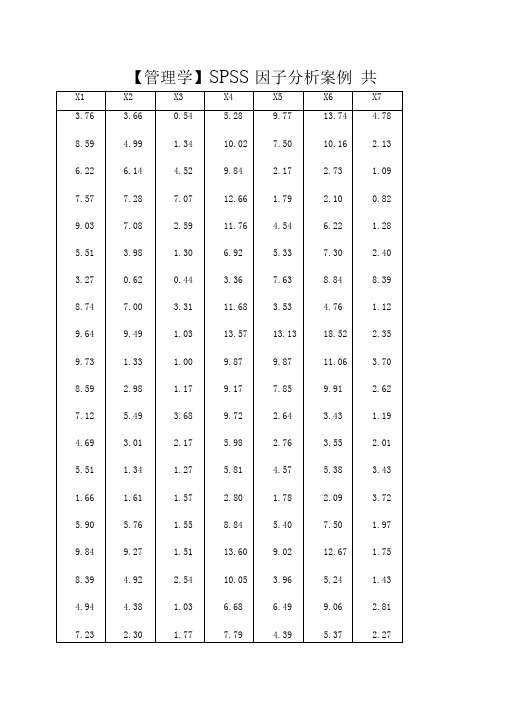
【管理学】SPSS因子分析案例共11.2.1 数据预备激活数据治理窗口,定义变量名:分不为 XI 、X2、X3、X4、X5、X6、X7,按顺序输入相应数值,建立数据库,结果见图11.1。
图11.1 原始数据的输入激活Statistics 菜单选 Data Reduction 的 Factor..命令项,弹出 Factor An alysis 对话框(图 11.2) X7,点击?钮使之进入 Variabl图11.3 描述性指标选择对话框点击 Extraction …钮,弹出 Factor Analysis:Extraction 对话框(图11.4),系统提供如下因子提取方法:图 11.4 因子提取方法选择对话框在对话框左侧的变量列表中选变量 X1至 es 框。
图11.2 因子分析对话框出 Factor Analysis:Descriptives 对话框(图 11. tedescriptives 项要求输出各变量的均数与标 内选Coefficients 项要求运算有关系数矩阵, 在Statistics 中选 UI口I 耐||的財血准差;在 Correlation"CnrtEititlv ii Mtfhrix ( 并选KMO E“「and Bartlett ' s test of sphericity 项,要求对有关系数矩阵进行 3), 统计Matrix 栏pCnr-rcl-fl liciin MirfirixPrincipal components 主成分分析法;Un weighted least squares未加权最小平方法;Generalized least squares 综合最小平方法;Maximumlikelihood :极大似然估量法;Principal axis factoring: 主轴因子法;Alpha factoring : a 因子法;Image fa cto ri n g :多元回来法。
spss因子分析案例

spss因子分析案例SPSS因子分析是一种用于探索或验证潜在结构的数据分析方法。
它将一组观测变量分解为几个潜在变量(或因子),以便更好地理解这些变量之间的关系。
假设我们有一个数据集,其中包含了一些心理测量量表的数据。
我们对这些测量量表进行因子分析,以了解是否可以将它们归类为几个互相关联的潜在因子。
我们将使用SPSS进行因子分析。
首先,我们打开SPSS,并加载数据集。
然后,我们选择'Analyze'菜单下的'Dimension Reduction',再选择'Factor'。
在'Factor'对话框中,我们将选择要进行因子分析的测量量表变量,并将它们添加到'Variables'框中。
然后,我们单击'Extraction'选项卡。
在'Extraction'选项卡中,我们需要选择一个因子抽取方法。
常用的方法包括主成分分析和最大似然估计。
在本例中,我们选择最大似然估计。
然后,我们单击'Rotation'选项卡。
因子旋转是为了使因子之间更易解释。
我们可以选择'Varimax'或'Promax'旋转方法。
在本例中,我们选择'Varimax'。
接下来,我们单击'Summary'选项卡,然后单击'Continue'。
最后,我们单击'OK'按钮开始进行因子分析。
SPSS将计算因子分析,并提供一个结果表。
在结果表中,我们可以看到每个测量量表变量在每个因子上的载荷值。
载荷值表示变量与因子之间的关联强度。
我们还可以看到每个因子的解释方差比例。
这个比例表示每个因子解释了多大比例的变量的方差。
我们希望尽可能多的方差被解释,以便更好地理解数据。
此外,结果表还提供了每个因子的特征值。
特征值表示因子的重要性,越大的特征值表示该因子在解释数据中起到更重要的作用。
心理统计SPSS-第九章 因子分析PPT课件

第六步:点击“Options”设置因子载荷系数的显示格式:
(1) 选中“Sorted by size”,则因子载荷系数按照大小顺序排 列,并构成矩阵,使得在同一因子上具有较高载荷的变量排在一 起,便于得到结论;
(2) 选中“Suppress absolute values less than:”并在其后的方 格中输入一个0~1间的一个数,则因子载荷矩阵中就不再显示那 些小于这个数值的载荷系数了,而只显示那些比此数值大的载荷 值,从而使因子所解释的主要变量一目了然。
出发点
13 15 17 17 16 16 16 18 15 20 14 18 15 12 14 13 15 15 18 13
工作投入
18 16 14 16 16 17 20 17 19 14 14 16 17 14 15 18 16 17 15 18
发展机会
16 18 17 19 18 18 15 18 19 18 16 18 15 14 16 17 14 16 17 16
在相关基础上可计算三个用于判断因子分析适合度的指标: 巴特利特球形检验(Bartlett Test of Sphericity); KMO(Kaiser-Meyer-Olkin)检验。
巴特利特球形检验(Bartlett Test of Sphericity)
该检验首先假设变量相关矩阵为单位阵(对角线为1、非对 角线为0),然后检验实际相关矩阵与此差异性。如果差异性显 著,则拒绝单位阵假设 ,即认为原变量间的相关性显著 ,适合 于作因子分析,否则不能作因子分析。
四、因子分析的实例分析
对20名大学生进行的有关价值观的测验,包括9个项目,测试 结果如下页所示。要求根据这9项内容进行因子分析,得到维度较 少的几个因子。
统计学-用SPSS进行因子分析

对SPSS因素分析结果的解释
1. 2. 3. 4. 5. 6. 适当性(KMO)检验 共同性(公共度)检查 因子陡坡(碎石图)检查 方差贡献率检验 显示未转轴的因素矩阵 分析转轴后的因素矩阵
“因子分析:抽取”( Factor Analyze: Extraction )对话框的有关选 项: ① “Method”(方法)选项框:下拉式选项内有其中抽取因子的方法: A “Principal components”法:主成分法,此为SPSS默认方法。 B “Unweighted least squares”法:未加权最小二乘法。 C “Generalized least square”法:广义最小二乘法。 D “Maximum likelihood”法:极大似然法。 E “Principal-axis factoring”法:主轴因子法。 F “Alpha factoring”法:α因子抽取法。 G “Image factoring”法:映像因子抽取法。 ② “Analyze”(分析)选项框 A “Correlation matrix”(相关矩阵):以相关矩阵来抽取因子 B “Covariance matrix”(协方差矩阵):以协方差矩阵来抽取因子。 ③ “Display”(显示)选项框 A “Unrotated factor solution”(未旋转因子解):显示未旋转时因子载荷、 特征值及共同性。 B “Scree plot”(碎石图):显示碎石图。 ④ “Extract”(抽取)选项框 A “Eigenvalues over”(特征值):后面的空格默认为1,表示因子抽取时, 只抽取特征值大于1者,使用者可随意输入0至1之间的值。 B “Number of factors”(因子个数):选取此项时,后面的空格内输入限 定的因子个数。
统计学案例——SPSS因子分析

《统计学》案例——SPSS因子分析基于因子分析的宜昌与中西部城市竞争力比较研究1引言随着武汉城市圈被国家批准为“全国资源节约型和环境友好型”社会建设综合配套改革实验区后,湖北省11个地级城市有5个进入“8+1”城市圈,享受着“两型社会”实验区和中部崛起双重政策扶持,今后一段时期会得到很好的发展。
作为发展基础比较好的宜昌市,在目前的大环境下,要争当省内同类城市第一,走在中西部城市的前列,迫切需要客观、准确地评价宜昌市社会经济发展现状,探寻中西部城市间社会经济发展的差异以及形成差异的内在原因,拟定适合城市可持续发展的各项对策。
本文在对比样本城市选择的基础上,利用反映城市经济、社会、环境等方面指标体系,借助SPSS软件因子分析法进行定量分析,探讨宜昌城市如何建设成为省域副中心城市。
2样本城市和评价指标的选择2.1样本城市的选择中部地区包括湖北、湖南、江西、安徽、河南、山西六省,西部地区包括内蒙古、广西、四川、贵州、云南、西藏、陕西、甘肃、宁夏、新疆、青海、重庆市十二个省市自治区。
中西部共有地级以上城市166个,其中有17个省会城市和1个直辖市,148个地级市。
为了增加城市之间的可比性,以对比城市宜昌市作参照系,地级市中2007年地区生产总值在700万元以上作为样本城市(宜昌市2007年地区生产总值为820万元),共有20个城市分布于6个省市自治区,具体见表1:表1 2008年地区生产总值700万元以上的中西部地区地级城市资料来源:《中国城市统计年鉴2008》,中国统计出版社,20092.2评价指标的选择城市竞争力评价指标不同的学者观点不一,朱红根等(2005)用国内生产总值、海关进出口总额等14个指标对江西省各城市综合竞争力进行比较研究,陈晓林(2007)提出地区生产总值、全社会固定资产投资总额等14个指标构成城市评价指标体系,颜丙胜等(2007)认为城市经济实力评价指标应包括城乡居民储蓄余额等在内的13项统计指标,张旭亮(2009)认为城市群城市综合竞争力评价应涵盖经济、社会、文化、环境等方面,由人均图书、城市化水平等20项指标组成。
SPSS课件因子分析
此时,12287213df n n =+−=+−=2222(1)(1)7 3.9076 5.559221211//22.482()87S n S n ωω+×+0025216=4315(13)。
,0.025(13) 2.16t 0.0254.315t t =>n0.250.20.150.10.050.0250.010.0050.00250.0010.00051 1.000 1.376 1.963 3.078 6.31412.7131.8263.66127.3318.3636.620.816 1.061 1.386 1.886 2.920 4.303 6.9659.92514.0922.3331.6030.7650.978 1.250 1.638 2.353 3.182 4.541 5.8417.45310.2112.9240.7410.941 1.190 1.533 2.132 2.776 3.747 4.604 5.5987.1738.61050.7270.920 1.156 1.476 2.015 2.571 3.365 4.032 4.773 5.893 6.86960.7180.906 1.134 1.440 1.943 2.447 3.143 3.707 4.317 5.208 5.95970.7110.896 1.119 1.415 1.895 2.365 2.998 3.499 4.029 4.785 5.40880.7060.889 1.108 1.397 1.860 2.306 2.896 3.355 3.833 4.501 5.04190.7030.883 1.100 1.383 1.833 2.262 2.821 3.250 3.690 4.297 4.781100.7000.879 1.093 1.372 1.812 2.228 2.764 3.169 3.581 4.144 4.587110.6970.876 1.088 1.363 1.796 2.201 2.718 3.106 3.497 4.025 4.437120.6950.873 1.083 1.356 1.782 2.179 2.681 3.055 3.428 3.930 4.31830.690.870.079.350.77.60.650 3.0 3.37 3.85. 130.694 1.079 1.350 1.771 2.160 2.650 3.012 3.372 3.852 4.221140.6920.868 1.076 1.345 1.761 2.145 2.624 2.977 3.326 3.787 4.140150.6910.866 1.074 1.341 1.753 2.131 2.602 2.947 3.286 3.733 4.073160.6900.865 1.071 1.337 1.746 2.120 2.583 2.921 3.252 3.686 4.015170.6890.863 1.069 1.333 1.740 2.110 2.567 2.898 3.222 3.646 3.965180.6880.862 1.067 1.330 1.734 2.101 2.552 2.878 3.197 3.610 3.922190.6880.861 1.066 1.328 1.729 2.093 2.539 2.861 3.174 3.579 3.883200.6870.860 1.064 1.325 1.725 2.086 2.528 2.845 3.153 3.552 3.850衣长臂长身高胸围体重颈围臀围筛选裤长颈围衣(裤)长变量例如,在企业形象或品牌形象的研究中,消费者可以通过一个例如在形象或牌形象的研究中消费者可个有24个指标构成的评价体系,评价百货商场的24个方面的优劣。
SPSS因子分析法-内容及案例

实验课:因子分析实验目的理解主成分〔因子〕分析的根本原理,熟悉并掌握SPSS中的主成分〔因子〕分析方法及其主要应用。
因子分析一、根底理论知识1 概念因子分析〔Factor analysis〕:就是用少数几个因子来描述许多指标或因素之间的联系,以较少几个因子来反映原资料的大局部信息的统计学分析方法。
从数学角度来看,主成分分析是一种化繁为简的降维处理技术。
主成分分析〔Principal ponent analysis〕:是因子分析的一个特例,是使用最多的因子提取方法。
它通过坐标变换手段,将原有的多个相关变量,做线性变化,转换为另外一组不相关的变量。
选取前面几个方差最大的主成分,这样到达了因子分析较少变量个数的目的,同时又能与较少的变量反映原有变量的绝大局部的信息。
两者关系:主成分分析〔PCA〕和因子分析〔FA〕是两种把变量维数降低以便于描述、理解和分析的方法,而实际上主成分分析可以说是因子分析的一个特例。
2 特点〔1〕因子变量的数量远少于原有的指标变量的数量,因而对因子变量的分析能够减少分析中的工作量。
〔2〕因子变量不是对原始变量的取舍,而是根据原始变量的信息进展重新组构,它能够反映原有变量大局部的信息。
〔3〕因子变量之间不存在显著的线性相关关系,对变量的分析比拟方便,但原始局部变量之间多存在较显著的相关关系。
〔4〕因子变量具有命名解释性,即该变量是对某些原始变量信息的综合和反映。
在保证数据信息丧失最少的原那么下,对高维变量空间进展降维处理〔即通过因子分析或主成分分析〕。
显然,在一个低维空间解释系统要比在高维系统容易的多。
3 类型根据研究对象的不同,把因子分析分为R 型和Q 型两种。
当研究对象是变量时,属于R 型因子分析;当研究对象是样品时,属于Q 型因子分析。
但有的因子分析方法兼有R 型和Q 型因子分析的一些特点,如因子分析中的对应分析方法,有的学者称之为双重型因子分析,以示与其他两类的区别。
4分析原理假定:有n 个地理样本,每个样本共有p 个变量,构成一个n ×p 阶的地理数据矩阵 :当p 较大时,在p 维空间中考察问题比拟麻烦。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[例11-1]下表资料为25名健康人的7项生化检验结果,7项生化检验指标依次命名为X1至X7,请对该资料进行因子分析。
图
???对话框(图框。
图
钮返回
图11.3?描述性指标选择对话框
???点击Extraction...钮,弹出FactorAnalysis:Extraction对话框(图11.4),系统提供如下因子提取方法:
图11.4?因子提取方法选择对话框
???Principalcomponents:主成分分析法;
???Unweightedleastsquares:未加权最小平方法;
???Generalizedleastsquares:综合最小平方法;
???Maximumlikelihood:极大似然估计法;
???Principalaxisfactoring:主轴因子法;
???Alphafactoring:α因子法;
???对话框。
???5种因图
???旋转的目的是为了获得简单结构,以帮助我们解释因子。
本例选正交旋转法,之后点击Continue钮返回FactorAnalysis对话框。
???点击Scores...钮,弹出弹出FactorAnalysis:Scores对话框(图11.6),系统提供3种估计因子得分系数的方法,本例选Regression(回归因子得分),之后点击Continue钮返回FactorAnalysis对话框,再点击OK钮即完成分析。
图11.6?估计因子分方法对话框?
?11.2.3?结果解释
??在输出结果窗口中将看到如下统计数据:
??系统首先输出各变量的均数(Mean)与标准差(StdDev),并显示共有25例观察单位进入分析;接着输出相关系数矩阵(CorrelationMatrix),经Bartlett检验表明:Bartlett值=326.28484,P<0.0001,即相关矩阵不是一个单位矩阵,故考虑进行因子分析。
好。
今KMO值
NumberofCases?=?????25
CorrelationMatrix:
X1???????X2???????X3???????X4???????X5???????X6???????X7
X1????????1.00000
X2?????????.58026??1.00000
X3?????????.20113???.36379??1.00000
X4?????????.90900???.83725???.43611??1.00000
X5?????????.28347???.16590??-.70423???.16328??1.00000
X6?????????.28656???.26119??-.68058???.20309???.99020??1.00000
X7????????-.53321??-.60846??-.64918??-.67758???.42733???.35732??1.00000
-0.88644
???在
X1?????????????.74646???????.48929
X2?????????????.79644???????.37219
X3?????????????.70890??????-.59727
X4?????????????.91054???????.38865
X5????????????-.23424???????.96350
X6????????????-.17715???????.97172
X7????????????-.88644???????.21921
FinalStatistics:
Variable????Communality?* Factor Eigenvalue PctofVar CumPct
*
替代了X1、X2
VARIMAX rotation 1forextraction 1 inanalysis 1-KaiserNormalization.
VARIMAXconvergedin3iterations.
RotatedFactorMatrix:
Factor 1 Factor 2
X1 .87795 .16064
X2 .87848 .03332 X3 .42098 -.82586 X4 .99001 .00414 X5 .15872 .97878 X6 .21452 .96415
[3]吴士元.我国省级服务业竞争力的综合评价[J].统计与决策,2003(10):57-58.
[4]中国统计年鉴编辑部.中国统计年鉴[J].北京:中国统计出版社,2006.
[5]朱建平,殷瑞飞.SPSS在统计分析中的应用[M].北京:清华大学出版社,2007:155-170.
EvaluationonServiceIndustryCompetitivenessintheWest
RegionsBasedonFactorAnalysis
管理学是系统研究管理活动的基本规律和一般方法的科学。
管理学是适应现代
科。
尔)
地》)
管理是指根据一个系统所固有的客观规律,施加影响于这个系统,从而使这个系统呈现一种新状态的过程。
(系统论学者)
管理是社会组织中,为了实现既定目标,以人为中心进行的协调活动。
(周三多)
管理职能
职能是指“活动”、“行为”,也就是各种基本活动及其功能。
最早是法国的亨利·法约尔提出的“五职能”说,后有“三功能派”、“四功能派”、“七功能派”等。
总的来看,关于管理职能划分有:计划、组织、指挥、协调、控制、激励、人事、调集资源、沟通、决策、创新。
我国从宏观上分为计划、组织、领导、控制四个方面。
对所必
(
的冲突。
(四)控制职能就是按既定的目标和标准,对组织的各种活动进行监督、检查,及时纠正执行偏差,使工作能按照计划进行,或适当调整计划以确保计划目标的实现。
控制是重要的,因为它是管理职能环节中最后的一环。
管理对象
人力:育人、选人、用人。
财力:生财、聚财、用财。
物力:采购、保管、供应、分配。
时间:合理分配。
空间:学科领域、技术服务项目。
信息:搜集、分析、利用和反馈。
健康),运用专家们的知识、智力、经验、阅历,为决策部门提供有科学根据的计划、方案、意见的一种管理方法。
特点:针对性、综合性、时效性。
(五)思想工作方法
思想工作的主要方法:(1)思想教育、启发自觉。
(2)树立榜样、典型示范。
(3)运用社会舆论,形成健康的社会风气。
(4)研究合理需要,把工作做在前头。
思想工作的主要方式:(1)演讲报告。
(2)座谈讨论。
(3)个别谈心。
(4)各种文化活动。
(5)参观访问。
(6)评比竞赛。
1
2
概念技能(ConceptualSkills):分析和诊断复杂情况的心智能力。
管理者的角色
(一)人际的角色:(1)头面人物角色。
(2)领导角色;(3)联络人角色。
(二)信息角色:(1)监听者(2)传播者(3)发言人
(三)决策者角色:(1)企业家(2)纠纷调解人(3)资源分配者(4)谈判者。
