2018年春人教版九年级数学下《第27章相似》专训3相似三角形与函数的综合应用含答案
九年级人教版数学第二学期第27章相似三角形整章知识详解

=A′C′:AC=B′C′:BC.求证:△ABC∽△A′B′C′.
A′
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
过点D作DE∥BC交AC于点E.
B′
C′
∴AD:AB=AE:AC=DE:BC,△ADE∽△ABC
A
∵AD=A′B′∴AD:AB=A′B′:AB
又A′B′:AB=B′C′:BC=C′A′:CA
A
D
E
∵ DE∥BC,
A
D
E ∴ △ADE∽△ABC.
B
C
B
C
思考:有没有其他简单的办法判断两个三角形相似?
九年级数学第27章相似三角形
A
三边对应成
A′
比例
B
C
B′
C′
A' B' B'C' A'C' AB BC AC
是否有△ABC∽△A′B′C′?
九年级数学第27章相似三角形
已知:如图△ABC和△A′B′C′中A′B′:AB
成的三角形与原三角形相似.
九年级数学第27章相似三角形
平行于三角形一边的直线与其他两边(或延长线)相交,所得 的三角形与原三角形___相__似___.
“A”型 A
D
E
“X”型
D
E
O
B
C
(图1)
B
(图2)
C
九年级数学第27章相似三角形
已知:如图,AB∥EF ∥CD,
图中共有__3__对相似三角形.
AB∥EF
△AOB∽△FOE
AB∥CD
△AOB∽△DOC
EF∥CD
△EOF∽△COD
A E C
(完整版)人教版九年级数学下《第27章相似》专项训练含答案,推荐文档

(第 3 题) 相似三角形与反比例函数 4.如图,矩形 OABC 的顶点 A,C 分别在 x 轴和 y 轴上,点 B 的坐标为
1 DE=2BC.
建议收藏下载本文,以便随时学习!
(第 3 题)
4.如图,AM 为△ABC 的角平分线,D 为 AB 的中点,CE∥AB,CE 交 DM 的延 长线于 E.
求证:AC=2CE.
(第 4 题)
证明两线段的位置关系 类型1:证明两线段平行 5.如图,已知点 D 为等腰直角三角形 ABC 的斜边 AB 上一点,连接 CD,DE⊥CD,DE=CD,连接 CE,AE.求证:AE∥BC.
k (2,3),双曲线 y=x(x>0)经过 BC 的中点 D,且与 AB 交于点 E,连接 DE.
(1)求 k 的值及点 E 的坐标; (2)若点 F 是 OC 边上一点,且△FBC∽△DEB,求直线 FB 对应的函数解析 式.
(第 4 题)
我去人也就有人!为UR扼腕入站内信不存在向你偶同意调剖沙
(第 1 题) 2.如图,一直线和△ABC 的边 AB,AC 分别交于点 D,E,和 BC 的延长线交 于点 F,且 AECE=BFCF. 求证:AD=DB.
(第 2 题) 类型2:证明两线段的倍分关系
我去人3也.如就图,有在人△AB!C 中为,BUD⊥R扼AC 于腕点入D,站CE⊥内AB 信于点不E,存∠A在=6向0°,你求偶证:同意调剖沙
建议收藏下载本文,以便随时学习! (第 11 题)
人教版数学九年级下册数学:第27章 相似 专题练习(附答案)

专题1 相似三角形的基本模型模型1 A 字型及其变形(1)如图1,公共角所对的边平行(DE ∥BC),则△ADE ∽△ABC ;(2)如图2,公共角的对边不平行,且有另一组角相等(∠AED =∠ABC 或∠ADE =∠ACB),则△AED ∽△ABC.【例1】 如图,在△ABC 中,AB =5,D ,E 分别是边AC 和AB 上的点,且∠ADE =∠B ,DE =2,求AD ·BC 的值.解:∵∠ADE =∠B ,∠EAD =∠CAB , ∴△ADE ∽△ABC. ∴DE BC =AD AB. ∴AD ·BC =DE ·AB. 又∵DE =2,AB =5, ∴AD ·BC =2×5=10.1.如图,在△ABC 中,DE ∥BC ,DF ∥AC ,AE =3,AC =5,BC =10,则BF 的长为 .2.如图,在锐角△ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.求证:△ADE∽△ABC.模型2 X字型及其变形(1)如图1,对顶角的对边平行(AB∥CD),则△ABO∽△DCO;(2)如图2,对顶角的对边不平行,且有另一对角相等(∠B=∠D或∠A=∠C),则△ABO∽△CDO.【例2】如图,在四边形ABCD中,AB∥CD,对角线AC与BD相交于点O.求证:△ABO∽△CDO.证明:∵AB∥CD,∴∠OAB=∠OCD,∠OBA=∠ODC.∴△ABO∽△CDO.【补充设问】△AOD与△BOC相似吗?试说明理由.解:△AOD 与△BOC 不相似. 理由如下:∵∠AOD =∠COB , 要使△AOD 与△BOC 相似, ∴当满足DO CO =AO BO 或DO BO =AOCO时,即DO ·BO =AO ·CO 或DO ·CO =AO ·BO 时,△AOD 与△BOC 相似.由已证可知△ABO ∽△CDO ,∴AO CO =BO DO, 即AO ·DO =BO ·CO ,不满足证明△AOD 与△BOC 相似的条件. ∴△AOD 与△BOC 不相似.【变式】 如图,在四边形ABDC 中,若AB 不平行于CD ,∠ABC =∠ADC ,则图中的相似三角形有△COD ∽△AOB ,△AOC ∽△BOD .3.如图,在正方形ABCD 中,G 为CD 边中点,连接AG 并延长交BC 边的延长线于点E ,对角线BD 交AG 于点F ,已知FG =2,则线段AE 的长度为( )A .6B .8C .10D .124.将一副三角尺如图所示叠放在一起,则BEEC的值是 .5.如图,已知∠ADE =∠ACB ,BD =8,CE =4,CF =2,求DF 的长.模型3 子母型若两个三角形有一个公共角和一条公共边,且有另一对角相等,则这两个三角形相似.如图,若∠ACD =∠B ,则△ACD ∽△ABC ,从而可得结论:AC 2=AD ·AB.【例3】 如图,P 是△ABC 的边AB 上的一点.(1)如果∠ACP =∠B ,△ACP 与△ABC 是否相似?为什么?(2)如果AP AC =AC AB ,△ACP 与△ABC 是否相似?为什么?如果AC CP =BCAC呢?解:(1)△ACP ∽△ABC.理由如下: ∵∠ACP =∠ABC , ∠PAC =∠CAB , ∴△ACP ∽△ABC.(2)AP AC =ACAB 时,△ACP ∽△ABC.理由如下:∵∠PAC =∠CAB ,且AP AC =ACAB ,∴△ACP ∽△ABC.由AC CP =BCAC不能得到△ACP 与△ABC 相似. ∵AC 与CP 的夹角为∠ACP ,BC 与AC 的夹角为∠ACB , 而∠ACP 与∠ACB 不相等,∴由AC CP =BCAC不能得到△ACP 与△ABC 相似.6.如图,在△ABC 中,AD 是中线,BC =8,∠B =∠DAC ,则线段AC 的长为( )A .4B .4 2C .6D .4 37.如图,在△ABC 中,D 为AB 边上一点,且∠BCD =∠A ,若BC =22,AB =3,则BD 的长为 .模型4 双垂直型直角三角形被斜边上的高分成的两个直角三角形与原三角形相似.如图,Rt △ABC 中,CD 为斜边AB 上的高,则有△ACD ∽△ABC ∽△CBD ,从而可得结论:CD 2=BD ·AD ,BC 2=BD ·AB ,AC 2=AD ·AB.【例4】 如图,在△ABC 中,∠BAC =90°,AD ⊥BC ,垂足为D. (1)请指出图中所有的相似三角形;(2)你能得出AD2=BD·DC吗?解:(1)△BAD∽△BCA∽△ACD.(2)能得出AD2=BD·DC.理由如下:∵∠BAC=90°,∴∠BAD+∠DAC=90°.∵AD⊥BC,∴∠DAC+∠ACD=90°,∠BDA=∠ADC=90°.∴∠BAD=∠ACD.又∵∠BDA=∠ADC,∴△BAD∽△ACD.∴ADCD=BDAD,即AD2=BD·DC.8.如图,在Rt△ABC中,CD⊥AB,D为垂足,且AD=3,AC=35,则斜边AB的长为() A.3 6B.15C.9 5D.3+3 59.如图,在△ABC中,∠ACB=90°,CD是斜边AB上的高,AD=9,BD=4,那么CD=,AC=.模型5 一线三等角型(1)如图1,AB⊥BC,CD⊥BC,AP⊥PD,垂足分别为B,C,P,且三个垂足在同一直线上,则有△ABP∽△PCD(此图又叫作“三垂图”).(2)如图2,∠B=∠APD=∠C,且B,P,C在同一直线上,则①△ABP∽△PCD;②连接AD,当点P为BC的中点时,△ABP∽△PCD∽△APD.【例5】如图,在正方形ABCD中,E为边AD上的点,点F在边CD上,且CF=3FD,∠BEF =90°.(1)求证:△ABE∽△DEF;(2)若AB=4,延长EF交BC的延长线于点G,求BG的长.解:(1)证明:∵四边形ABCD为正方形,∴∠A=∠D=90°.∴∠ABE+∠AEB=90°.又∵∠BEF=90°,∴∠AEB+∠DEF=90°.∴∠ABE=∠DEF.∴△ABE∽△DEF.(2)∵AB=BC=CD=AD=4,CF=3FD,∴DF =1,CF =3. ∵△ABE ∽△DEF , ∴AE DF =AB DE ,即4-DE 1=4DE . ∴DE =2.又∵ED ∥CG ,∴△EDF ∽△GCF. ∴ED GC =DFCF.∴GC =6. ∴BG =BC +CG =10.10.如图,在等腰△ABC 中,点E ,F ,O 分别是腰AB ,AC 及底BC 边上任意一点,且∠EOF =∠B =∠C.求证:OE ·FC =FO ·OB.1.如图,在矩形ABCD 中,作DF ⊥AC ,垂足为F ,延长DF 交AB 于点E ,在图中一定和△DFC 相似的三角形有 个.2.如图,已知△ABC,△DCE,△FEG,△HGI是4个全等的等腰三角形,底边BC,CE,EG,GI在同一条直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI=.3.【分类讨论思想】如图,在△ABC中,AC=6,AB=4,点D,A在直线BC同侧,且∠ACD =∠ABC,CD=2,点E是线段BC延长线上的动点.若△DCE和△ABC相似,则线段CE的长为.4.如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D,F分别在边AB,AC上.(1)求证:△BDE∽△CEF;(2)当点E移动到BC的中点时,求证:FE平分∠DFC.专题2 相似三角形的性质与判定类型1 利用相似三角形求线段长1.如图,在△ABC 中,AB =6,点D 是AB 的中点,过点D 作DE ∥BC ,交AC 于点E ,点M 在DE 上,且ME =13DM.当AM ⊥BM 时,则BC 的长为 .2.如图,已知菱形BEDF 内接于△ABC ,点E ,D ,F 分别在AB ,AC 和BC 上.若AB =15 cm ,BC =12 cm ,则菱形的边长为 cm.3.如图,在△ABC 中,AB =AC ,点D ,E 分别在边BC ,AB 上,且∠ADE =∠B.如果DE ∶AD =2∶5,BD =3,那么AC = .4.如图,在Rt △ABC 中,∠ABC =90°,AB =3,BC =4,在Rt △MPN 中,∠MPN =90°,点P 在AC 上,PM 交AB 于点E ,PN 交BC 于点F ,当PE =2PF 时,AP = .5.如图,在△ABC 中,点D 是BA 边延长线上一点,过点D 作DE ∥BC ,交CA 的延长线于点E ,点F 是DE 延长线上一点,连接AF. (1)如果AD AB =23,DE =6,求边BC 的长;(2)如果∠FAE =∠B ,FA =6,FE =4,求DF 的长.类型2 利用相似三角形求角度6.如图,A ,B ,C ,P 四点均在边长为1的小正方形网格格点上,则∠BAC 的度数是 .7.如图,在等腰△ABC 中,AB =AC ,D 为CB 延长线上一点,E 为BC 延长线上一点,且AB 2=BD ·CE.若∠BAC =40°,则∠DAE = . 类型3 利用相似三角形求比值8.如图,AB ∥DC ,AC 与BD 交于点E ,EF ∥DC 交BC 于点F ,CE =5,CF =4,AE =BC ,则DCAB 等于( )A.23B.14C.13D.359.如图,D ,E 分别是△ABC 的边AB ,BC 上的点,且DE ∥AC ,AE ,CD 相交于点O.若S △DOE ∶S △COA =1∶25,则S △BDE 与S △CDE 的比是( )A .1∶3B .1∶4C .1∶5D .1∶2510.如图,在矩形ABCD 中,对角线AC ,BD 交于点O ,过点A 作EA ⊥CA 交DB 的延长线于点E.若AB =3,BC =4,则AOAE的值为 .类型4 利用相似三角形证明等积式与比例式11.如图,在△ABC 中,D ,E 分别是AB ,AC 上的点,且BD =2AD ,CE =2AE.求证: (1)△ADE ∽△ABC ; (2)DF ·BF =EF ·CF.12.如图,在△ABC 中,∠ACB =90°,CD ⊥AB 于点D ,E 为AC 的中点,ED ,CB 的延长线交于点F.求证:DF CF =BCAC.类型5 利用相似求点的坐标13.如图,在平面直角坐标系xOy 中,A(-4,0),B(0,2),连接AB 并延长到点C ,连接CO.若△COB ∽△CAO ,则点C 的坐标为( )A .(1,52)B .(43,83)C .(5,25)D .(3,23)14.如图,已知直线y =-12x +2与x 轴交于点A ,与y 轴交于点B ,在x 轴上有一点C ,使B ,O ,C 三点构成的三角形与△AOB 相似,则点C 的坐标为专题3 圆与相似1.如图,⊙O 是△ABC 的外接圆,已知AD 平分∠BAC 交⊙O 于点D ,交BC 边于点E ,AD =5,BD =2,则DE 的长为( )A.35B.425 C.225 D.452.如图,已知⊙O 是等腰Rt △ABC 的外接圆,D 是AC ︵上一点,BD 交AC 于点E.若BC =4,AD =45,则AE 的长是( ) A .3 B .2 C .1 D .1.23.如图,⊙O 的两弦AB ,CD 交于点P ,连接AC ,BD ,得S △ACP ∶S △DBP =16∶9,则AC ∶BD = .4.如图,已知AB 是⊙O 的直径,C 是⊙O 上一点,∠ACB 的平分线交⊙O 于点D ,作PD ∥AB ,交CA 的延长线于点P ,连接AD ,BD.求证: (1)PD 是⊙O 的切线; (2)△PAD ∽△DBC.5.如图,以△ABC的边AC为直径的⊙O交AB边于点M,交BC边于点N,连接AN,过点C 的切线交AB的延长线于点P,∠BCP=∠BAN.求证:(1)△ABC为等腰三角形;(2)AM·CP=AN·CB.6.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.(1)求证:AC是⊙O的切线;(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.参考答案:专题1 相似三角形的基本模型1. 4.2.证明:∵AF ⊥DE ,AG ⊥BC ,∴∠AFE =∠AGC =90°. ∵∠EAF =∠GAC , ∴∠AEF =∠ACG. 又∵∠DAE =∠BAC , ∴△ADE ∽△ABC.3.D4.35.解:∵∠ADE =∠ACB ,∴180°-∠ADE =180°-∠ACB , 即∠BDF =∠ECF. 又∵∠BFD =∠EFC , ∴△BDF ∽△ECF. ∴BD EC =DF CF ,即84=DF 2. ∴DF =4. 6.B7.83. 8.B910.证明:∵∠EOC =∠EOF +∠FOC ,∠EOC =∠B +∠BEO ,∠EOF =∠B , ∴∠FOC =∠OEB. 又∵∠B =∠C , ∴△BOE ∽△CFO. ∴OE OF =OB FC, 即OE ·FC =FO ·OB.1. 5 . 2.43. 3.43或3. 4.解:(1)证明:∵AB =AC , ∴∠B =∠C.∵∠BDE =180°-∠B -∠DEB ,∠CEF =180°-∠DEF -∠DEB ,且∠DEF =∠B , ∴∠BDE =∠CEF. ∴△BDE ∽△CEF.(2)∵△BDE ∽△CEF ,∴BE CF =DEEF .∵点E 是BC 的中点,∴BE =CE.∴CE CF =DE EF .∴CE DE =CF EF. ∵∠DEF =∠B =∠C ,∴△DEF ∽△ECF. ∴∠DFE =∠CFE ,即FE 平分∠DFC.专题2 相似三角形的性质与判定1.8. 2.203.3.152.4.3.5.解:(1)∵DE ∥BC , ∴△ADE ∽△ABC. ∴AD AB =DE BC .∴23=6BC . ∴BC =9.(2)∵∠FAE =∠B ,∠B =∠D , ∴∠FAE =∠D. 又∵∠F =∠F , ∴△FAE ∽△FDA. ∴FE FA =FA DF . ∴DF =FA2FE=9.6.135°. 7.110°. 8.B 9.B 10.724.11.证明:(1)∵BD =2AD ,CE =2AE ,∴AB =3AD ,AC =3AE. ∴AD AB =AE AC =13. ∵∠A =∠A , ∴△ADE ∽△ABC. (2)∵AD AB =AE AC =13,∴DE ∥BC. ∴△DEF ∽△CBF. ∴DF CF =EF BF. ∴DF ·BF =EF ·CF.12.证明:∵∠ACB =90°,CD ⊥AB ,∴∠A +∠ACD =∠ACD +∠BCD ,∠ACB =∠BDC =90°. ∴∠A =∠BCD. ∴△ABC ∽△CBD. ∴BC BD =AC CD ,即BC AC =BD CD . 又∵E 为AC 的中点,∴AE =CE =ED.∴∠A =∠EDA.∵∠EDA =∠BDF ,∴∠FCD =∠BDF.又∵∠F 为公共角,∴△FDB ∽△FCD.∴DF CF =BD CD. ∴DF CF =BC AC. 13.B14. (-4,0)或(4,0)或(-1,0)或(1,0).专题3 圆与相似1.D2.C3.4∶3.4.证明:(1)连接OD.∵∠DCA =∠DCB ,∴AD ︵=BD ︵.∴OD ⊥AB.∵AB∥PD,∴OD⊥PD.∵点D在⊙O上,OD为⊙O的半径,∴PD是⊙O的切线.(2)∵∠PAD+∠CAD=180°,∠DBC+∠CAD=180°,∴∠PAD=∠DBC.由(1)可得:∠PDA=∠BCD=45°,∴△PAD∽△DBC.5.证明:(1)∵AC为⊙O的直径,∴∠ANC=90°.∵PC是⊙O的切线,∴∠BCP=∠CAN.∵∠BCP=∠BAN,∴∠BAN=∠CAN.又∵AN⊥BC,∴AB=AC.∴△ABC为等腰三角形.(2)连接MN∵△ABC为等腰三角形,AB=AC,∴∠ABC=∠ACB.∵∠PBC+∠ABC=∠AMN+∠ACN=180°,∴∠PBC=∠AMN.由(1)知∠BCP=∠BAN,∴△BPC∽△MNA.∴CBAM =CPAN,即AM·CP=AN·CB.6.解:(1)证明:连接OE ,∵OB =OE ,∴∠OBE =∠OEB.∵BE 平分∠ABC ,∠OBE =∠EBC.∴∠OEB =∠EBC.∴OE ∥BC. 又∵∠C =90°,∴∠OEA =90°,即AC ⊥OE.又∵OE 是⊙O 的半径,∴AC 是⊙O 的切线.(2)在△BCE 与△BED 中,∵∠C =∠BED =90°,∠EBC =∠DBE ,∴△BCE ∽△BED.∴BE BD =BC BE ,即BC =BE 2BD. ∵BE =4,BD 是⊙O 的直径,即BD =5,∴BC =165. 又∵OE ∥BC ,∴AO AB =OE BC .∵AO =AD +2.5,AB =AD +5,∴AD +2.5AD +5=2.5165. 解得AD =457.。
九年级数学下册第二十七章相似27.2相似三角形27.2.1相似三角形的判定第3课时相似三角形判定定

2018-2019学年九年级数学下册第二十七章相似27.2 相似三角形27.2.1 相似三角形的判定第3课时相似三角形判定定理3同步练习(新版)新人教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018-2019学年九年级数学下册第二十七章相似27.2 相似三角形27.2.1 相似三角形的判定第3课时相似三角形判定定理3同步练习(新版)新人教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018-2019学年九年级数学下册第二十七章相似27.2 相似三角形27.2.1 相似三角形的判定第3课时相似三角形判定定理3同步练习(新版)新人教版的全部内容。
课时作业(十)[27。
2.1 第3课时相似三角形判定定理3]一、选择题1.已知一个三角形的两个内角分别是40°,60°,另一个三角形的两个内角分别是60°,80°,则这两个三角形()A.一定不相似 B.不一定相似C.一定相似 D.全等2.下列各组图形可能不相似的是()A.两个等边三角形B.各有一个角是45°的两个等腰三角形C.各有一个角是105°的两个等腰三角形D.两个等腰直角三角形3.在△ABC和△A1B1C1中,∠A=∠A1=90°,添加下列条件不能判定两个三角形相似的是()A.∠B=∠B1 B.错误!=错误!C。
错误!=错误! D.错误!=错误!4.如图K-10-1,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有()图K-10-1A.1对 B.2对 C.3对 D.4对5.如图K-10-2,在△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为()错误!图K-10-2A.4 B.4 错误! C.6 D.4 错误!6.如图K-10-3,在△ABC中,∠A=78°,AB=4,AC=6。
2017-2018学年新人教版九年级下册第二十七章相似27.2《相似三角形的性质》名师课件_(新人教版九年级下册数

MF DC
,∴
EM MF
BD DC
又∵DF∥AB,∴
BD DC
EN NC
,
∴ EM EN
MF NC
,∴ EM EN
EF EC
.
点拨又:∵∠要M证E两N=直∠线F平EC行,,∴可△证ME其N同∽位△F角E或C. 内错角相等,而相似 三角∴形∠E可M得N=角∠相E等FC,.∴因M此N可∥A设C法. 证三角形相似.
已知:△ABC∽ ABC,相似比为k. AD⊥BC于D,AD BC
于 D .
求:(1)AABBCC的的周周长长;(2)
SABC的周长 SABC的周长
解: (1)由△ABC∽△A′B′C ′,
得
AB AB
BC BC
AC AC
k,
∴
ABC的周长 ABC的周长
k
;
∴
AB BC AC AB BC AC
知识回顾 问题探究 课
重点、难点知识★▲
活动1 合作探究 利用相似三角形证线段的数量关系和位置关系
4.证明两线垂直
例4.如图,在△ABC中,D是AB上一点,且AC2=AB•AD,BC2=
BA•BD,求证:CD⊥AB.
证明:∵AC2=AB•AD,∴
AC AD
点拨∴:S△A此BC题= 是841 由×2平0=行40得5(三cm角2)形.相似,再由“线段比等于面积比 的算故数答案平为方:根4”05求cm得2.线段比,最后由相似三角形性质“面积比 等于相似比的平方”,求得所求三角形面积.
知识回顾 问题探究 课堂小结 随堂检测
探究三:如何应用三角形相似证题?
重点、难点知识★▲
探究三:如何应用三角形相似证题?
重点、难点知识★▲
人教九下数学 第27章 相似三角形的判定及有关性质综合测试(含答案)

人教九下数学 第27章 相似三角形的判定及有关性质综合测试(含答案)一、选择题(每小题6分,共48分)1.在△ABC 中,D 、F 是AB 上的点,E 、H 是AC 上的点,直线DE//FH//BC ,且DE 、FH 将△ABC 分成面积相等的三部分,若线段FH=65,则BC 的长为( ) A .15 B .10 C.6215 D .15322.在△ABC 中,DE//BC ,DE 交AB 于D ,交AC 于E ,且S △ADE :S 四边形DBCE=1:2,则梯形的高与三角形的边BC 上的高的比为( )A .1:2B .1:)12(-C .1:)13(-D .)13(-:33.在Rt △ABC 中,∠C=90°,CD 是斜边AB 上的高,AC=5,BC=8,则S △ACD :S △CBD 为( ) A .85B .6425 C .3925 D .8925 4.如图1—5—1,D 、E 、F 是△ABC 的三边中点,设△DEF 的面积为4,△ABC 的周长为9,则△DEF 的周长与△ABC 的面积分别是( )A.29,16 B. 9,4 C. 29,8 D. 49,165.如图1—5—2,在△ABC 中,AD ⊥BC 于D ,下列条件:(1)∠B+∠DAC=90°;(2)∠B=∠DAC ; (3)ABAC AD CD =;(4)AB 2=BD ·BC 。
其中一定能够判定△ABC 是直角三角形的共有( ) A .3个B .2个C .1个D .0个6.如图1—5—3,在正三角形ABC 中,D ,E 分别在AC ,AB 上,且31AC AD =,AE=BE ,则有( )A. △AED ∽△BED B .△AED ∽△CBD C. △AED ∽△ABD D .△BAD ∽△BCD7.如图1—5—4,PQ//RS//AC ,RS=6,PQ=9,SC 31QC =,则AB 等于( ) A. 415B. 436C. 217D. 58.如图1—5—5,平行四边形ABCD 中,O 1、O 2、O 3是BD 的四等分点,连接AO 1,并延长交BC 于E ,连接EO 2,并延长交AD 于F ,则FDAD等于( )A .3:1B .3:1C .3:2 D. 7:39.如果一个三角形的一条高分这个三角形为两个相似三角形,那么这个三角形必是( ) A .等腰三角形 B. 任意三角形C .直角三角形D .直角三角形或等腰三角形10.在△ABC 和△A'B'C'中,AB : AC=A'B':A'C',∠B=∠B',则这两个三角形( ) A .相似,但不全等 B .全等C .一定相似D .无法判断是否相似11.如图1—6—1,正方形ABCD 中,E 是AB 上的任一点,作EF ⊥BD 于F ,则BEEF为( )A .22B .21C .36D .2图1—6—112.如图1—6—2,把△ABC 沿边AB 平移到△A'B'C'的位置,它们的重叠部分(图中阴影部分)的面积是△ABC 的面积的一半,若2AB =,则此三角形移动的距离AA'是( )A .12-B .22C .1D .21 图1—6—213.如图1—6—3,在四边形ABCD 中,∠A=135°,∠B=∠D=90°,BC=32,AD=2,则四边形ABCD 的面积是( )A .24B .34C .4D .6 图1—6—314.如图1—6—4,平行四边形ABCD 中,G 是BC 延长线上一点,AG 与BD 交于点E ,与DC 交于点F ,则图中相似三角形共有( )A .3对B .4对C .5对D .6对15.在直角三角形中,斜边上的高为6cm ,且把斜边分成3:2两段,则斜边上的中线的长为( )A.265cm B .64cm C .65cmD .325cm16.AD 为Rt △ABC 斜边BC 上的高,作DE ⊥AC 于E ,45AC AB =,则EACE=( ) A .2516 B .54C .45D .162517.如图1—6—5,△ABC 中,AB=AC ,∠A=36°,BD 平分∠ABC ,已知AB=m ,BC=n ,求CD 的长。
人教版九年级数学下册 第27章 相 似 相似三角形 相似三角形的判定 第3课时 由两角判定三角形相似

第二十七章 相 似
27.2 相似三角形
27.2.1 相似三角形的判定
第3课时 由两角判定三角形相似
知识点❶:两角对应相等的两个三角形相似
1.在△ABC和△A′B′C′中,∠A=68°,∠B=40°,∠A′=68°,∠C′=72°,
则这两个三角形( )
B
A.全等 B.相似
C.不相似 D.无法确定
14.如图,等边三角形 ABC 的边长为 6,在 AC,BC 边上各取一点 E,F, 使 AE=CF,连接 AF,BE 相交于点 P.
(1)求证:AF=BE,并求∠APB 的度数; (2)若 AE=2,试求 AP·AF 的值.
解:(1)∵△ABC 为等边三角形,∴AB=AC,∠C=∠CAB=60°,在△ABE 和
4.(南京中考)如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分 ∠ACB.若AD=2,BD=3,则AC的长为__1_0_.
5.(通辽中考)如图,⊙O的直径AB交弦(不是直径)CD于点P,且PC2=PB·PA, 求证:AB⊥CD.
证 明 : 连 接 AC , BD , ∵ ∠ A = ∠ D , ∠ C = ∠ B , ∴ △ APC∽△DPB , ∴ PC∶PB = PA∶PD , ∴ PC·PD = PA·PB , ∵ PC2 = PB·PA , ∴ PC = PD , ∵ AB 为 直 径 , ∴AB⊥CD
解:(1)在△AOF 和△EOF 中,
பைடு நூலகம்
OA=OE, ∠AOD=∠EOD, ∴△AOF≌△EOF(SAS),∴∠OAF=∠OEF,∵BC 与⊙O 相 OF=OF,
切,∴OE⊥FC,即∠OEF=90°,∴∠OAF=90°,即 OA⊥AF,又∵OA 是⊙O 的半径,
2017-2018学年新人教版九年级下册第二十七章相似2.72《相似三角形的应用》名师课件(共39张PPT)

知识回顾 问题探究 课堂小结 随堂检测
探究三:什么是视点、视角、盲区?它们是如何应用的?
活动2 例题讲解
重点、难点知识★▲
解:如图,假设观察者从左向右走到点E时,她的眼睛的位置点F与
两棵树的顶端A,C恰在一条直线上.
∵AB⊥l,CD ⊥l,∴AB∥CD. ∴△AFH ∽△CFK. ∴ FH AH .
分析:(1)设直线AD的解析式为y=kx+b, 用待定系数法将A( 4,5),D(0,1)的
33
坐标代入即可;
知识回顾 问题探究 课堂小结 随堂检测 探究四:如何解相似三角形与函数的综合应用? 重点、难点知识★▲
活动1 合作探究,相似三角形与函数的综合应用
例1.如图,在平面直角坐标系xOy中,直线y=﹣x+3与x轴交于点C,与直
问题:1、本题中是利用什么构造相似三角形的? 2、本题的突破点在哪里? 3、如何测量旗杆的高度?(设计出你的测量方案,画出图形 与同伴交流) 4、你发现了什么规律?
知识回顾 问题探究 课堂小结 随堂检测 探究一:如何测量不能到达顶部的物体的高度? 重点、难点知识★▲
活动1 探究利用三角形相似测量物高
——利用三角形相似测宽
测距的方法:测量不能到达两点间的距离,常构造相似三角形求解.
解相似三角形实际问题的一般步骤: (1)审题; (2)构建图形; (3)利用相似解决问题.
知识回顾 问题探究 课堂小结 随堂检测
探究二:如何测量不能直接到达的两点间的距离?
活动2 例题讲解
重点、难点知识★▲
例:如图,已知零件的外径为a,要求它的厚度x,需先求出内孔的直 径AB,现用一个交叉卡钳(两条尺长AC和BD相等)去量,若 OA:OC=OB:OD=n,且量得CD=b,求厚度x。
人教版 九年级数学 第27章 相似 综合训练(含答案)
如果别人思考数学的真理像我一样深入持久,他也会找到我的发现。
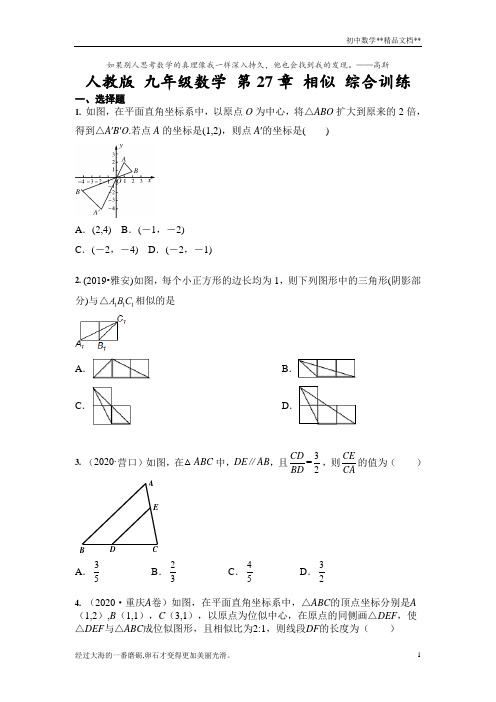
——高斯人教版九年级数学第27章相似综合训练一、选择题1. 如图,在平面直角坐标系中,以原点O为中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是()A.(2,4) B.(-1,-2)C.(-2,-4) D.(-2,-1)2. (2019•雅安)如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与相似的是A.B.C.D.3. (2020·营口)如图,在△ABC中,DE∥AB,且CDBD=32,则CECA的值为()AEA.35B.23C.45D.324. (2020·重庆A卷)如图,在平面直角坐标系中,△ABC的顶点坐标分别是A (1,2),B(1,1),C(3,1),以原点为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2:1,则线段DF的长度为()A.5B.2C.4D.255. (2019•沈阳)已知△ABC∽△A'B'C',AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的周长比是A.3∶5 B.9∶25C.5∶3 D.25∶96. (2019•巴中)如图ABCD,F为BC中点,延长AD至E,使13DE AD=∶∶,连接EF交DC于点G,则:DEG CFGS S△△=A.2∶3 B.3∶2C.9∶4 D.4∶97. (2020·铜仁)已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为()A.3 B.2 C.4 D.58. (2020•丽水)如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH.连结EG,BD相交于点O、BD与HC相交于点P.若GO=GP,则ABCDEFGHSS正方形正方形的值是()A.12+B.22+C.52-D.154二、填空题9. (2020·南通)如图,在正方形网格中,每个小正方形的边长均为1,△ABC 和△DEF的顶点都在网格线的交点上,设△ABC的周长为C1,△DEF的周长为C2,则12CC的值等于▲ .ABCD EF10. (2020·绥化)在平面直角坐标系中,△ABC和△A1B1C1的相似比等于12,并且是关于原点O的位似图形,若点A的坐标为(2,4),则其对应点A1的坐标是______.11.(2020·临沂)如图,在ABC∆中,D,E为边AB的三等分点,////EF DG AC,H为AF与DG的交点.若6AC=,则DH=_________.12. (2020·郴州)在平面直角坐标系中,将AOB∆以点O为位似中心,32为位似比作位似变换,得到11OBA∆.已知)3,2(A,则点1A的坐标是.13. (2019•台州)如图,直线123l l l∥∥,A,B,C分别为直线1l,2l,3l上的动点,连接AB,BC,AC,线段AC交直线2l于点D.设直线1l,2l之间的距离为m,直线2l,3l之间的距离为n,若90ABC∠=︒,4BD=,且32mn=,则m n+的最大值为__________.14. (2019•烟台)如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,ABO △与'A'B'O △是以点P 为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P 的坐标为__________.三、解答题 15. (2020·苏州)如图,在矩形ABCD 中,E 是BC 的中点,DF AE ⊥,垂足为F .(1)求证:ABE DFA ∆∆∽;(2)若6AB =,4BC =,求DF 的长.16.(2020·攀枝花)三角形三条边上的中线交于一点,这个点叫三角形的重心.如图G 是ABC ∆的重心.求证:3AD GD =.GDECBA17. (2020·通辽)如图,⊙O的直径AB交弦(不是直径)CD于点P,且PC2=PB•P A,求证:AB⊥CD.PDCBOA18.(2020·泰州)如图,在ABC∆中,90C∠=︒,3AC=,4BC=,P为BC边上的动点(与B、C不重合),//PD AB,交AC于点D,连接AP,设CP x=,ADP∆的面积为S.(1)用含x的代数式表示AD的长;(2)求S与x的函数表达式,并求当S随x增大而减小时x的取值范围.人教版九年级数学第27章相似综合训练-答案一、选择题1. 【答案】C 解析:根据以原点O 为位似中心,图形的坐标特点得出,对应点的坐标应乘以-2,故点A 的坐标是(1,2),则点A ′的坐标是(-2,-4).2. 【答案】B【解析】因为111A B C △中有一个角是135°,选项中,有135°角的三角形只有B ,且满足两边成比例夹角相等,故选B .3. 【答案】A【解析】利用平行截割定理求CECA的值.∵DE ∥AB ,∴CE AE =CD BD =32,∵CE+AE=AC ,∴CE CA =35.4. 【答案】D【解析】∵A (1,2),B (1,1),C (3,1),∴AB=1,BC=2,AC=5.∵△DEF 与△ABC 成位似图形,且相似比为2,∴DF=2AB=2.5. 【答案】C【解析】∵△ABC ∽△A'B'C',AD 和A'D'是它们的对应中线,AD =10,A'D'=6,∴△ABC 与△A'B'C'的周长比=AD ∶A ′D ′=10∶6=5∶3.故选C .6. 【答案】D【解析】设DE x =,∵13DE AD =∶∶,∴3AD x =, ∵四边形ABCD 是平行四边形,∴AD BC ∥,3BC AD x ==, ∵点F 是BC 的中点,∴1322CF BC x ==, ∵AD BC ∥,∴DEG CFG △∽△, ∴224()()392DEG CFG S DE x S CF x ===△△,故选D .7. 【答案】A 【解析】相似三角形的周长之比等于相似比,所以△FHB 和△EAD的相似比为30∶15=2∶1,所以FH ∶EA=2∶1,即6∶EA=2∶1,解得EA=3.因此本题选A .8. 【答案】C【解析】∵四边形EFGH 为正方形,∴∠EGH =45°,∠FGH =90°,∵OG =GP ,∴∠GOP =∠OPG =67.5°,∴∠PBG =22.5°,又∵∠DBC =45°,∴∠GBC =22.5°,∴∠PBG =∠GBC ,∵∠BGP =∠BG =90°,BG =BG ,∴△BPG ≌△BCG ,∴PG =CG .设OG =PG =CG =x ,∵O 为EG ,BD 的交点,∴EG =2x ,FG 2=x .∵四个全等的直角三角形拼成“赵爽弦图”,∴BF =CG =x ,∴BG =x 2+x ,∴BC2=BG2+CG2()2222(21)422x x x =++=+,∴()22422222ABCD EFGHx S S x +==+正方形正方形D .二、填空题9. 【答案】2 【解析】由图形易证△ABC 与△DEF 相似,且相似比为1:2,所以周长比为1:2.故答案为:2.10. 【答案】(-4,-8)或(4,8)【解析】∵△ABC 和△A1B1C1的相似比等于12,∴△A1B1C1和△ABC 的相似比等于2.因此将点A(2,4)的横、纵坐标乘以±2即得点A1的坐标,∴点A1的坐标是(-4,-8)或(4,8).11. 【答案】1【解析】 ∵D 、E 为边AB 的三等分点, ∴BE=ED=AD=13AB.∵////EF DG AC ,∴123EF AC ==∴112DH EF ==.12. 【答案】(,2) 【解析】∵将△AOB 以点O 为位似中心,为位似比作位似变换,得到△A 1OB 1,A (2,3),∴点A 1的坐标是:(×2,×3),即A 1(,2).故答案为:(,2).13. 【答案】253【解析】如图,过B 作1BE l ⊥于E ,延长EB 交3l 于F ,过A 作2AN l ⊥于N ,过C 作2CM l ⊥于M ,设AE x =,CF y =,BN x =,BM y =, ∵4BD =,∴4DM y =-,4DN x =-,∵90ABC AEB BFC CMD AND ∠=∠=∠=∠=∠=︒, ∴90EAB ABE ABE CBF ∠+∠=∠+∠=︒, ∴EAB CBF ∠=∠,∴ABE BFC △∽△, ∴AE BEBF CF=,即x m n y =,∴xy mn =,∵ADN CDM ∠=∠,∴CMD AND △△, ∴AN DNCM DM=,即4243m x n y -==-, ∴3102y x =-+,∵23m n =,∴32n m =, ∴5()2m n m +=最大, ∴当m 最大时,5()2m n m +=最大, ∵22333(10)10222mn xy x x x x m ==-+=-+=,∴当1010332()2x =-=⨯-时,250332mn m ==最大, ∴103m =最大, ∴m n +的最大值为51025233⨯=.故答案为:253.14. 【答案】(32)-,【解析】如图,连接B'B 并延长,A'A 并延长,B'B 与A'A 的交点即为位似中心P点,由图可知B'、B 、P 在一条直线上,则P 点横坐标为–3, 由图可得ABO △和'A'B'O △的位似比为3162''OB O B ==,2BB '=, 所以12PB PB PB'PB BB'==+,解得PB =2, 所以P 点纵坐标为2,即P 点坐标为(32)-,.故答案为:(32)-,.三、解答题15. 【答案】解: 证明:(1)∵四边形ABCD 是矩形,∴90B ∠=︒,AD BC .∴AEB DAF ∠=∠,∵DF AE ⊥,∴90DFA ∠=︒.∴B DFA ∠=∠,∴ABE DFA ∆∆∽.解:(2)∵ABE DFA ∆∆∽,∴AB AEDF AD =. ∵4BC =,E 是BC 的中点,∴114222BE BC ==⨯=.∴在Rt ABE ∆中,222262210AE AB BE =+=+=.又∵4AD BC ==,∴6104DF=,∴105DF =.16. 【答案】证明:连接DE ,∵点G 是△ABC 的重心,∴点E 和点D 分别是AB 和BC 的中点, ∴DE 是△ABC 的中位线,∴DE ∥AC 且DE=12AC ,∴△DEG ∽△ACG , ∴2AG AC DG ED ==, ∴2AG GD =∴AD=3DG , 即AD=3GD .17. 【答案】解:如图,连结AC ,BD .∵∠A =∠D ,∠C =∠B ,∴△ACP ∽△DBP ,∴AP DP =CPBP,∴PC •PD =PB •P A ,∵PC 2=PB •P A ,∴PC =PD ,即AB 平分CD ,∵CD 是弦(不是直径),AB 是直径,∴AB ⊥CD .BA18. 【答案】解: (1)∵DP ∥AB ∴△DCP ∽△ACB ∴CD CP AC CB =∴34CD x =∴34CD x =∴AD =3-34x(2)∵△DCP ∽△ACB,且相似比为x :4. ∴S △DCP :S △ACB =x 2:16∴S △ABC =13462⨯⨯=∴S △DCP =238x∴S △APB =13(4)22PB AC x ⨯⨯=-∴S =S △ABC -S △ABP -S △CDP22336(6)283382x x x x=---=-+当2x ≥ 时,S 随x 增大而减少.一天,毕达哥拉斯应邀到朋友家做客。
人教版数学九年级下册27.2.3相似三角形的应用举例说课稿

(三)教学重难点
根据对学生的了解和教学内容的分析,本节课的教学重点为相似三角形的应用方法和实际问题的解决。难点在于如何引导学生运用相似三角形的性质进行问题的分析和解决。
1.重点:
(1)相似三角形的应用方法,如求线段长度、角度大小等。
(三)学习动机
为了激发学生的学习兴趣和动机,我将采取以下策略或活动:
1.引入生活中的实际案例,让学生感受到相似三角形在生活中的广泛应用,提高他们的学习兴趣。
2.设计具有挑战性的问题,引导学生积极参与,培养他们的探究精神和解决问题的能力。
3.组织小组合作交流,让学生在互动中互相学习、互相启发,提高他们的合作能力和沟通能力。
3.采用几何画板软件,动态展示相似三角形的性质,帮助学生形象理解。
4.结合教材例题,引导学生独立思考、小组讨论,总结解题步骤和技巧。
(三)巩固练习
我计划设计以下巩固练习或实践活动,以帮助学生巩固所学知识并提升应用能力:
1.课堂练习:设计具有代表性的习题,让学生当堂完成,巩固相似三角形的应用方法。
2.小组竞赛:开展小组间的解题竞赛,鼓励学生积极思考、合作交流,提高解题速度和准确率。
四、教学过程设计
(一)导入新课
为快速吸引学生的注意力和兴趣,我采用以下方式导入新课:
1.生活实例引入:向学生展示一张具有相似三角形特征的建筑图片,如古希腊神庙的三角形门廊,引导学生观察并思考这些三角形之间的关系。
2.提问互动:询问学生:“你们在生活中还见到过类似的三角形吗?它们之间有什么共同特点?”通过问题引导学生回顾相似三角形的性质,为新课的学习做好铺垫。
主要知识点包括:1.相似三角形的判定方法;2.相似三角形的应用,如求线段长度、角度大小等;3.实际问题的解决,如测量高度、距离等。
人教版九年级下册数学作业课件 第27章 综合滚动练习:相似三角形的性质与判定

(2)求证:2BG2=BH·BD. 证明:∵∠BEH=∠EDB=45°,∠EBH=∠DBE, ∴△BEH∽△BDE.∴BBDE=BBHE. ∴BE2=BD·BH. ∵BE= 2BG, ∴2BG2=BH·BD.(12 分)
15.(14 分)如图,在 Rt△ABC 中,∠ACB=90°,AC= BC,P 为△ABC 内部一点,且∠APB=∠BPC=135°. (1)求证:△PAB∽△PBC; 证明:∵∠ACB=90°,AC=BC, ∴∠ABC=45°=∠PBA+∠PBC. 又∠APB=135°, ∴∠PAB+∠PBA=45°.∴∠PBC=∠PAB. 又∵∠APB=∠BPC=135°,∴△PAB∽△PBC.(4 分)
一、选择题(每小题 5 分,共 30 分) 1.已知△ABC∽△A′B′C′,AB=8,A′B′=6,则 BB′CC′=( B ) A.2 B.43 C.3 D.196
2.如图,已知∠1=∠2,欲证△ADE∽△ACB,可 补充的条件是( D ) A.∠B=∠D B.DE=AB C.AADB=DBCE D.∠D=∠C
5.如图,⊙O 是△ABC 的外接圆,已知 AD 平分
∠BAC 交⊙O 于点 D,交 BC 边于点 E,AD=5,
BD=2,则 DE 的长为( D )
A.35
B.245
C.225
D.45
6.如图,在 Rt△ABC 中,∠ACB=90°,AC=6, BC=12,点 D 在边 BC 上,点 E 在线段 AD 上, EF⊥AC 于点 F,EG⊥EF 交 AB 于点 G.若 EF=EG, 则 CD 的长为( B ) A.3.6 B.4 C.4.8 D.5 解析:如图,作 DH∥EG 交 AB 于点 H, 则△AEG∽△ADH,∴AADE=DEGH.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
OB BA
,∴
P4O=
3 2.
又易得
P4 在 P3M
上,∴ P4M =
3 4.
∴ P4
3, 4
3 4
.
(第 1 题③ )
当∠ BOP= 90°时,点 P 在 x 轴上,不符合要求.
综上得,符合条件的点有四个,分别是:
P1(3,
3), P2(1,
3) ,P3
34,
3
3 4
, P4
34,
3 4
.
2. 解: (1) 由题意得 A(3 , 0), B(0, 3),∵抛物线经过 A ,B , C 三点,∴把 A(3 , 0),
(1)求直线 BD 和抛物线对应的函数解析式;
(2)在第一象限内的抛物线上,是否存在一点
M ,作 MN 垂直于 x 轴,垂足为点 N, 使
得以 M , O, N 为顶点的三角形与△ BOC 相似?若存在,求出点 M 的坐标;若不存在,请
说明理由.
(第 3 题 )
相似三角形与反比例 函数
4.如图,矩形 OABC 的顶点 A, C 分别在 x 轴和 y 轴上,点 B 的坐标为 (2, 3),双曲
m=2,
k=- 2,
得
解得
k+m=0,
m= 2.
∴直线 BD 对应的函数解析式为 y=- 2x+ 2. ∵抛物线对应的函数解析式为 y=- x2+ bx+ c, ∴把 B(0 , 2), D(3 ,- 4)的坐标分别代入 y =- x 2+bx + c,
c=2,
b= 1,
得
解得
- 9+ 3b+ c=- 4,
线
y=
k x
(x>0)
经过
BC
的中点
D ,且与
AB 交于点
E,连接
DE.
(1)求 k 的值及点 E 的坐标;
(2)若点 F 是 OC 边上一点,且△ FBC∽△ DEB ,求直线 FB 对应的函数解析式.
(第 4 题 )
答案
1. 解: (1) 设直线 AB 对应的函数解析式为 y= kx+ b,将 A(3 , 0), B(0 , 3) 的坐标分
重合,∴ P2(1, 2),∴点 P 的坐标为 (- 1, 4)或 (1, 2).
(第 2 题) 3. 解: (1) 易得 A( - 1, 0), B(0 , 2),C(1 , 0). 设直线 BD 对应的函数解析式为 y= kx + m. 把 B(0 , 2), C(1 , 0)的坐标分别代入 y= kx + m,
别代入得
3k + b= 0, 解得
b= 3,
k=-
3, 3
b= 3.
∴直线 AB 对应的函数解析式为
y=-
3 3 x+
3.
(2)设点 C 的坐标为
3 x,- 3 x+
3
, [来源 学* 科*网 Z*X*X*K][
来源 :Z&xx&]ຫໍສະໝຸດ 那么 OD = x, CD=-
3 3 x+
3.
( OB + CD) ·OD
BP 1= OA
=
3,
∴ P1(3, 3).
Ⅱ.
若
△ BP2O∽△ OBA
,
则
BP 2
=
OB
BO OA
,
∴
BP2=
OB
2
=
OA
1,∴
P2
(1,
3).
当∠ OPB= 90°时,
Ⅲ .若△ P3BO ∽△ OBA( 如图② ),过点 P3 作 P3M ⊥ OA 于点 M.
(第 1 题② )
则
PO3BB=
专训 3 相似三角形与函数的综合应用
名师点金: 解涉及相似三角形与函数的综合题时,由于这类题的综合性强,是中考压轴题重点命 题形式之一,因此解题时常结合方程思想、分类讨论思想进行解答.
相似三角形与一次函数 1.如图,在平面直角坐标系中,直线 AB 与 x 轴, y 轴分别交于 A(3 , 0), B(0 , 3) 两点,点 C 为线段 AB 上的一动点,过点 C 作 CD⊥ x 轴于点 D. (1)求直线 AB 对应的函数解析式;
ABO
∽△
AP 1D
,则
AO AD
=
OB , DP 1
∴DP 1=AD = 4,∴ P1(-1, 4);若△ ABO ∽△ ADP 2,过点 P2 作 P2M ⊥x 轴于 M ,∵△ ABO
为等腰直角三角形,∴△ ADP 2 是等腰直角三角形,∴ DM = AM = 2= P2M ,即点 M 与点 C
43 (2)若 S 梯形 OBCD= 3 ,求点 C 的坐标; (3)在第一象限内是否存在点 P,使得以 P, O,B 为顶点的三角形与△ OBA 相似.若存 在,请求出所有符合条件的点 P 的坐标;若不存在,请说明理由.
(第 1 题)
[来源 学科网 ]
相似三角形与二次函数 2.如图,直线 y =- x +3 交 x 轴于点 A ,交 y 轴于点 B,抛物线 y= ax2+ bx+ c 经过
BO BA
=
P3O OA
又易知 AB = 2
3
,∴
P3B
=
OB AB
2
=
3 2
,
P3O=
OA·OB AB
=
3 2.
∴ P3A = 2
3-
3= 2
3
2
3 .
∵
OP3·P3A
=
P3M·OA
,∴
P3M
=
3
4
3 .
∴ OM
=
3 4.
∴
P3
34, 3 4 3
.
Ⅳ .若△ P4OB ∽△ OBA(
如图③
),则
PO4BO=
B(0 , 3) , C(1, 0) 三点的坐标分别代入
y = ax2+ bx+ c ,得方程组
9a+ 3b+ c= 0,
c=3,
解得
a+ b+c= 0,
a= 1, b=- 4,∴抛物线对应的函数解析式为 c= 3,
y= x 2- 4x+3.
(2) 如图,由题意可得△ ABO 为等腰直角三角形.若△
c= 2.
∴抛物线对应的函数解析式为 y=- x2+ x+ 2.
∴ S 梯形 OBCD =
2
=-
3x2+ 6
3x.
由题 意得-
3 6
x2+
3x= 4 3,解得 3
x1 =2, x2= 4(舍去 ).
∴C
2,
3 3
.
(3)存在.当∠ OBP= 90°时,如图① .易知 OB = 3, OA= 3.
(第 1 题① )
Ⅰ
.若△
BOP
1∽△
OBA
,则
BP 1= OA
BO ,∴ OB
A , B, C(1 ,0) 三点.
(1)求抛物线对应的函数解析式;
[来源 学科网 ZXXK]
(2)若点 D 的坐标为 (- 1, 0),在直线 y=- x+3 上有一点 P,使△ ABO 与△ ADP 相
似,求出点 P 的坐标.
(第 2 题 )[来源 学科网]
3.如图,直线 y= 2x+ 2 与 x 轴交于点 A ,与 y 轴交于点 B ,把△ AOB 沿 y 轴翻折, 点 A 落到点 C 处,过点 B 的抛物线 y=- x 2+ bx +c 与直线 BC 交于点 D(3 ,- 4).
