实验四 函数
实验四 Matlab编程

实验四Matlab编程【实验目的】1、了解Matlab运行方式2、熟悉Matlab程序流程与结构3、会编写简单的Matlab程序4、掌握M文件编辑器及程序的调试工具【实验内容】1、关系运算与逻辑运算2、m函数文件(function file)和m命令文件(script file)以及m文件的调试3、分支结构和循环结构4、相关语句或函数5、根据要求,完成实验报告中的内容【实验指导】1)关系运算与逻辑运算关系运算符>(大于) <(小于) >=(大于等于) <=(小于等于) ==(等于) ~=(不等于) 逻辑运算符& (与) |(或) ~(非) xor(异或)% 逻辑结果以“1”或者“非零数字”表示真, 以“0”表示假。
测试函数2)m函数文件(function file)基本数学函数自定义函数:以m文件形式出现✓格式:function [y1, y2, ..., yn]=fun_name(x1, x2, ..., xn)✓说明:◆函数名必须符合Matlab变量命名规则。
◆m文件名必须与函数名相同。
◆输出参数只有一个或者没有时,可以省略方括号。
◆输入参数可为0、1、2、...个,但不能省略圆括号。
◆M函数文件第一行必须以funtion开头。
◆函数有自已的工作空间,它与Matlab系统本身的工作空间是分开的。
◆当m文件到终点或者遇到return时结束调用。
◆函数可以调用其他函数,也可以调用自己。
◆一个m文件中可以定义多个函数,第一个出现的为主函数,其他的为子函数。
注意文件名与主函数名相同,子函数只能被主函数调用,而不能被该m文件外的函数或者m文件调用。
✓调用:[y1, y2, ..., yn]=fun_name(x1, x2, ..., xn)3)m命令文件(script file)该文件仅是一连串Matlab指令的集合,执行时按顺序执行。
它没有输入参数与输出参数,中间可以调用函数。
数值分析实验四(龙格函数)

实验名称:龙格反例的数值实验实验目的与要求:1、了解切比雪夫多项式零点插值;2、运用切比雪夫多项式零点插值法避免龙格现象。
3、与等距节点构造插值多项式比较。
实验内容:龙格反例的数值实验在区间[–5,5 ]上分别取11阶切比雪夫多项式的零点22)12(cos 5π+=k x k ( k = 0,1,2,……,10) 和等距节点作插值结点,计算函数211)(xx f +=在结点处的值 y k = f (x k )。
构造插值多项式L 10(x ),∑==10010)()(k k k y x l x L 其中,∏≠=--=n k j j j k j k x x x x x l 0)()()(。
取自变量点 t k = – 5 + 0.05k ( k =0,1,…,201),分别计算切比雪夫零点、等距节点插值多项式L k (x )和被插值函数f (x )在离散点t k ( k =0,1,…,201)上的值,并绘出三条曲线比较。
实验环境与器材:9#505机房、《数值分析》实验过程(步骤)或程序代码:function y=Lagrange(x,n,xx,yy)sum=0; %初始化for k=1:n+1lk=1; %初始化for i=1:n+1if k~=ilk=lk*(x-xx(i))/(xx(k)-xx(i));endendsum=lk*yy(k)+sum;endy=sum;clcclearfor i=1:11 %下标只能从1开始x1(i)=-5+10*(i-1)/10;x2(i)=5*cos((2*i-1)*pi/22);y1(i)=1/(1+x1(i)*x1(i));y2(i)=1/(1+x2(i)*x2(i)); %y1,y2分别是在两种节点处得到的函数值endh=0.05;for k=1:202x3(k)=-5+(k-1)*h;y11(k)=Lagrange(x3(k),10,x1,y1);y22(k)=Lagrange(x3(k),10,x2,y2);y(k)=1/(1+x3(k)*x3(k));%y11,y22分别为利用切比雪夫零点和等距节点构造出的插值多项式在离散点处的值endplot(x3,y11,'r');hold onplot(x3,y22,'g');hold onplot(x3,y,'b')%被插值函数在离散点处值的曲线图hold onxlabel('-5<=x<=5');ylabel('y');legend('f(x)=1/(1+x^2)','等距节点插值多项式','切比雪夫多项式零点插值多项式'); xlim([-5,5])实验结果与分析:分析:由高次插值的病态性质,我们知道次数n太高时会出现龙格现象,即L n(x)并不收敛于f(x),由上图我们也可以看到运用等距节点构造的插值多项式的确出现了龙格现象,因此并不适用。
实验四基于Simulink进行系统仿真微分方程传递函数
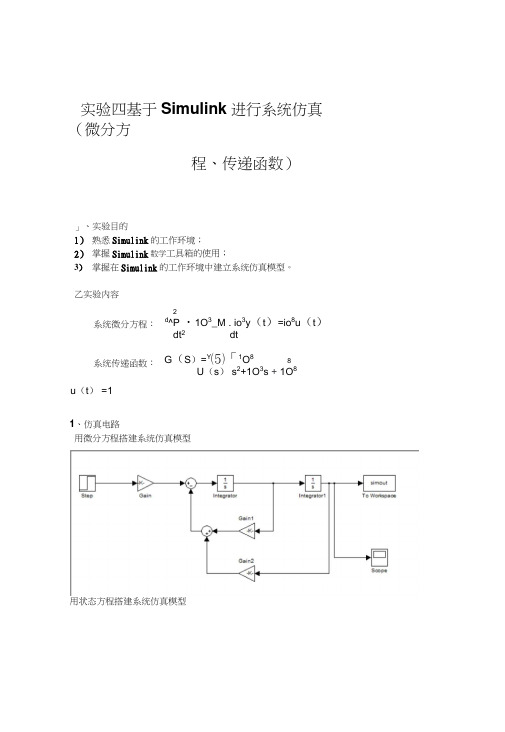
实验四基于Simulink进行系统仿真(微分方程、传递函数)」、实验目的1)熟悉Simulink的工作环境;2)掌握Simulink数学工具箱的使用;3)掌握在Simulink的工作环境中建立系统仿真模型。
乙实验内容系统微分方程:2d^P ・1O3_M . io3y(t)=io8u(t)dt2dt系统传递函数:G(S)=Y⑸「1O88U(s) s2+1O3s + 1O8 u(t) =11、仿真电路用微分方程搭建系统仿真模型用状态方程搭建系统仿真模型2、电路元件参数的设置1)设置Gain 参数■7) Function Block Parameters: Gai Gain2)设置Gainl参数X Element-wise gain (y = K* *uj or matrin gain Cy = K*u or y = 口*K)・3)设置Gain2的参数吕 Function Block Parameters: Gain2_________ __________________________________________________________________ GainElement-ifise gain Cy = K* *uj or mat r ix gain (y = K*u or y = u*K).Nlain Signal Att nbutes Paranet er kttribut BSGain: le8 Multiplication : Elejnent-wise(K, *u)Sample time 1 for inherited):-14)设置State-Space 的参数H ^unction Block Parameters: GainlApplyCancel磊=unction Block Parameters: State-Space5)设置Transfer Fcr t勺参数[Ie8]OK [1 le3 le8]3、仿真结果微分方程状态方程-unction Block Parameters: Tr^nsfer -cnTransfer FenParametersNmerator coefficients:Denominator coefficients :Absolut& tolerance ;autoHelp | ApplyCancel The numerator coefficient can be a vector or matrix expression ・ Thedenomiriator coefficient must be a vector ・ The output width equals theriumber uf rovs in the riumerator coefficient» You should specify the coefficients in descending order of powers of s.State Nane: (e. ? ' posit inn 7 )D(E传递函数4、仿真结果的分析用微分方程和状态方程搭建系统仿真模型的仿真结果一样,而用传递函数搭建系统仿真模型的仿真结果发散。
函数实验报告总结

函数实验报告总结函数实验报告总结引言:函数是计算机编程中的重要概念,它能够将一组输入映射为输出,是程序设计中模块化和可重用性的基石。
为了更好地理解函数的概念和使用方法,我们进行了一系列的函数实验。
本文将对这些实验进行总结和归纳,探讨函数在实际编程中的应用。
实验一:函数的定义和调用在这个实验中,我们学习了函数的基本概念和语法。
通过定义一个简单的函数,我们了解了如何使用关键字“def”来定义函数,并通过调用函数来执行其中的代码块。
这个实验让我们明白了函数的封装性和可复用性,可以将一段代码封装成函数,供其他地方调用。
实验二:函数的参数传递在这个实验中,我们学习了函数的参数传递方式。
通过定义带有参数的函数,我们了解了函数参数的不同类型,包括位置参数、关键字参数和默认参数。
我们还学习了如何在函数调用时传递参数,并探讨了参数传递的机制和注意事项。
这个实验让我们对函数的灵活性和可变性有了更深入的理解。
实验三:函数的返回值在这个实验中,我们学习了函数的返回值。
通过定义带有返回值的函数,我们了解了如何使用关键字“return”来返回函数执行的结果。
我们还学习了函数返回值的类型和用途,包括返回单个值、返回多个值和返回空值。
这个实验让我们明白了函数的结果可以被其他代码使用,提高了代码的灵活性和可扩展性。
实验四:递归函数在这个实验中,我们学习了递归函数的概念和用法。
通过定义递归函数来解决问题,我们了解了递归的原理和应用场景。
我们还学习了递归函数的优缺点,包括代码简洁但可能导致性能问题。
这个实验让我们对递归思想和算法有了更深入的认识,提高了问题解决的能力。
实验五:高阶函数在这个实验中,我们学习了高阶函数的概念和用法。
通过定义接受函数作为参数或返回函数的函数,我们了解了高阶函数的特点和应用场景。
我们还学习了匿名函数和函数式编程的基本概念,以及如何使用内置函数和自定义函数来实现高级功能。
这个实验让我们对函数的扩展性和灵活性有了更深入的理解。
实验四 基于感知函数准则线性分类器设计

实验四、基于感知函数准则线性分类器设计4.1 实验类型:设计型:线性分类器设计(感知函数准则)4.2 实验目的:本实验旨在让同学理解感知准则函数的原理,通过软件编程模拟线性分类器,理解感知函数准则的确定过程,掌握梯度下降算法求增广权向量,进一步深刻认识线性分类器。
4.3 实验条件:matlab 软件4.4 实验原理:感知准则函数是五十年代由Rosenblatt 提出的一种自学习判别函数生成方法,由于Rosenblatt 企图将其用于脑模型感知器,因此被称为感知准则函数。
其特点是随意确定的判别函数初始值,在对样本分类训练过程中逐步修正直至最终确定。
感知准则函数利用梯度下降算法求增广权向量的做法,可简单叙述为: 任意给定一向量初始值)1(a ,第k+1次迭代时的权向量)1(+k a 等于第k 次的权向量)(k a 加上被错分类的所有样本之和与k ρ的乘积。
可以证明,对于线性可分的样本集,经过有限次修正,一定可以找到一个解向量a ,即算法能在有限步内收敛。
其收敛速度的快慢取决于初始权向量)1(a 和系数k ρ。
4.5 实验内容已知有两个样本空间w1和w2,这些点对应的横纵坐标的分布情况是:x1=[1,2,4,1,5];y1=[2,1,-1,-3,-3];x2=[-2.5,-2.5,-1.5,-4,-5,-3];y2=[1,-1,5,1,-4,0];在二维空间样本分布图形如下所示:(plot(x1,y1,x2,y2))2 -6-4-20246-6-4-22464.6 实验任务:1、 用matlab 完成感知准则函数确定程序的设计。
2、 请确定sample=[(0,-3),(1,3),(-1,5),(-1,1),(0.5,6),(-3,-1),(2,-1),(0,1),(1,1),(-0.5,-0.5),( 0.5,-0.5)];属于哪个样本空间,根据数据画出分类的结果。
3、 请分析一下k ρ和)1(a 对于感知函数准则确定的影响,并确定当k ρ=1/2/3时,相应的k 的值,以及)1(a 不同时,k 值得变化情况。
上机实训四--printf()函数的应用

上机实训四格式化输出函数printf( )的应用一、实验概要1、掌握格式化输出函数printf( )的应用,能用printf( )函数来正确输出数据。
2、掌握printf()的使用格式以及常见的错误的解决办法。
二、实验内容1、写出下面程序的运行结果,并分析原因。
#include"stdio.h"main(){int a=12345;double b=116800000.123456789;printf("%d\n",a);printf("%4d\n",a);printf("%12d\n",a);printf("%012d\n",a);printf("%e\n",b);printf("%4f\n",b);printf("%20.7f\n",b);printf("%-20.7f\n",b);}2、格式字符%s、%d、%u等的应用。
读懂程序,写出运行结果。
#include"stdio.h"main(){int a=1508,b=-1;printf("%15s%d\n","Decimal:a=",a);printf("%15s%x\n","Hexadecimal:a=",a);printf("%15s%o\n","Octal:a=",a);printf("%15s%u\n","Unsinged:a=",a);printf("%15s%d,%x,%o,%u\n","b=",b,b,b,b);}3、读懂程序,写出结果,并上机进行实验验证。
数学实验第四章函数和方程习题MATLAB编码(胡良剑版)

%p0,p1是初始值
%delta是给定允许误差
%m是p1-p0的误差估计?
%k是所需
%要的迭代次数?%y=f(p1)
% K=0,p0,p1,feval('f',p0),feval('f',p1)
% for k=1:max1
% if(f1==0)
% root=a;
% end
% if(f2==0)
% root=b;
% end
% if(f1*f2>0)
% disp('两端点函数值乘积大于0!');
% return;
% else
% tol=1;
% fun=diff(sym(f));
% fa=subs(sym(f),findsym(sym(f)),a);
% x=fminsearch(fun,[0 0]) %求极小值
% fun2=inline('-(x(2)^3/9+3*x(1)^2*x(2)+9*x(1)^2+x(2)^2+x(1)*x(2)+9)');
% x=fminsearch(fun2,[0 -5]) %求极大值
%第10题
% t=0:24;
% c=[15 14 14 14 14 15 16 18 20 22 23 25 28 ...
% x(2)=fminsearch(fun2,-2.5);
% x(4)=3;
% feval(fun,x)
%第8题(3)
% fun=inline('abs(x^3-x^2-x-2)');
% fplot(fun,[0 3]);grid on; %作图观察
实验四 函数

}
int area(int x)
{
return PI*x*x;
}
float area(float x)
{
return PI*x*x;
}
思考:
编写重载函数实现对两个整型数、三个整型数、两个实型数、三个实型数等求最小值。
5.使用内联函数计算长方形的面积。
分析:C++编译器在调用遇到内联函数的地方,会用函数体中的代码替换函数。
5、编写一个用户自定义函数,该函数有一个整数参数,函数的功能是:判断这个整数是否素数,函数的返回值为判断结果。编写一个程序,求3到100之间的所有素数。
解:
阶乘函数定义如下:
double fact(int k)
{
int p=1;
if((k==0)||(k==1))
return p;
else
{
for(int i=1;i<=k;i++)
p=p*i;
return p;
}
}
一个完整的参考程序如下:
#include <iostream.h>
double fact(int);
return p;
}
}
思考:
分别输入n=0,1,3,m=0,1,2测试程序。
试用静态存储变量设计阶乘函数。
3.编写程序,求两个自然数m和n的最大公约数和最小公倍数。
分析:
最大公约数就是能同时整除m和n的最大正整数,可用欧几里德算法(也称辗转相除法)求解。应用欧几里德算法计算两个数的最大公约数的方法是:求两个数(m、n)相除的余数r(r=m/n m>n),当余数不为零时,m取n的值,n取r的值,再求两个数相除的余数,反复进行直到余数为零,除数n是最大公约数。
C语言_实验四、函数程序设计

实验四函数一、实验目的1.掌握函数的定义、函数的说明和调用。
2.掌握函数的参数及其传递方式,函数值的正确返回。
二、实验内容1.[目的]掌握标准库函数的说明和调用方法。
[题目内容]编写一个程序,首先显示一个菜单,然后根据用户的选择,输入数据后,执行相应的操作。
[输入]用户选择和函数自变量值[输出]如下菜单:=======MENU======1.。
sin2.。
cos3.。
pow4.。
sqrt0.。
exit==================[提示]使用标准库函数、多分支选择结构。
2.[目的]掌握用户自定义函数的定义、函数的说明和调用方法。
[题目内容]编写一个用户自定义函数,该函数有一个整型参数,函数的功能是:当这个整型数的值是偶数时,函数的返回值为0,当这个整型数的值是奇数时,返回值为1 。
编写一个程序,从键盘输入任意10个整数,分别调用用户自定义函数来判断这10个整数的奇偶性。
[输入]任意10个整数[输出]这10个整数的奇偶性[提示]在主函数中使用循环结构输入10个整数。
根据子函数的返回值输出相应的判断结果信息。
3.[目的]掌握用户自定义函数的定义、函数的说明和调用方法。
[题目内容]编写一个用户自定义函数,该函数有三个整数参数,函数的功能是:求解这三个整数的最大值,函数的返回值为三个参数的最大值。
编写一个程序,从键盘输入任意5个整数,分别两次调用用户自定义函数来求出这5个整数中的最大值。
[输入]任意5个整数[输出]这5个整数的最大值[提示]先用前三个整数调用函数,求出的最大值作为参数之一,再与另两个整数一起求出最大值即为所求。
4.[目的]掌握用户自定义函数的定义、函数的说明和调用方法。
[题目内容]nA表示从m各元素中抽出n个元素的排列的个数。
它的计算公式为:m)!(!n m m A n m -=。
编写一个用户自定义函数,该函数有一个整数参数,函数的功能是:求解这个整数的阶乘,函数的返回值为这个整数的阶乘。
实验四 函数和运算符重载

实验四函数重载和运算符重载(2学时)一、实验目的1.掌握函数的定义和调用方法。
2.练习重载函数的使用,注意与缺省参数的区别。
3.练习函数模板的使用。
4.练习运算符重载。
5.练习使用系统函数。
6.学习使用VC++的debug调试功能,使用step into追踪到函数内部。
二、实验任务1.定义一个简单的菜单类,运行时显示主菜单,可通过选择进入子菜单(可模仿ATM柜员机的模式,菜单内容可自行设定,相关功能函数可不用实现):主菜单:取现的子菜单1.转账 1.5002.余额查询 2.10003.取现 3.1500Q(退出) 4.返回主菜单请选择(A/S/F/Q)?选择相应的选项后悔执行相应模块并回到主菜单,选择Q则退出。
2.编写重载函数Maxl可分别求取两个整数,三个整数,两个双精度数,三个双精度数的最大值。
3.使用重载函数模板重新实现上小题中的函数Maxl。
4.使用系统函数pow(X,y)计算X y的值,注意包含头文件math.h。
5.用递归的方法编写函数求Fibonacci级数,观察递归调用的过程。
6.写一个点point的类,并重载+实现两个点的坐标相加,和-实现求两点间的距离, >>、<<输入输出点的信息,(1)和(2)分别取点的x和y轴坐标。
三、实验步骤1.考虑抽取菜单的数据和相关操作。
2.分别编写四个同名函数maxl,实现函数重载,在main()函数中测试函数功能。
程序名:lab3_2.cpp。
3.使用函数模板实现求任意类型数的最大值,针对不同的参数个数,编写两个同名函数模板maxl,其参数个数不同,实现函数重载,在main()函数中测试函数功能。
程序名:lab3_3.cpp。
4.在main()函数中提示输入两个整数x、y,使用cin语句得到x、y的值,调用pow(x,y)函数计算x的Y次幂的结果,再显示出来。
程序名.1ab3_4.cpp。
5.编写递归函数int fib(int n),在主程序中输入n的值,调用fib函数计算Fibonacci级数。
实验四工作表中的公式和函数解读

实验四工作表中的公式和函数一、实验要求1.掌握工作表中公式的输入方法。
2,熟悉工作表中公式的复制、移动和填充。
3.掌握常用函数的使用方法。
二、实验内容工作表中的公式输入是以“=”开始的,公式中的表达式可以包含:数字、字符、运算符、单元格地址、区域、以及各种函数。
除了直接输入公式外,还可以对公式进行复制、移动、填充等操作,达到快速输入公式的目的。
打开保存在D盘EXCEL文件夹中的ex1.xls工作簿文件,完成下列操作后存盘。
(一)公式的输入与填充。
在Sheet1工作表中完成下列操作:1.使用公式计算每个学生的总分(1)在单元格G3中输入:=C3+D3+E3+F3 ,按Enter键,在G3单元格中显示计算结果。
(2)用鼠标单击G3单元格,在编辑栏查看公式是否正确。
(3)选中G3单元格,拖拽填充柄到G10,可将填充公式到G4:G10。
2.计算各个学生的平均分(1)在H3单元格中输入:=G3/4 ,按Enter键,在H3单元格中显示计算结果。
(2)选中单元格H3,双击填充柄,可将公式自动填充到H4:H10。
3.字符连接(1)在A14单元格中输入文字:计算机,B14单元格中输入文字:专业。
(2)在单元格D14中输入公式:=A14&B14 ,按Enter键,则在D14中显示连接结果。
4.数据比较(1)在单元格F14中输入“成绩比较”(2)在F15单元格中输入公式:=C3>D3,选中F15拖拽填充柄到F22。
(3)用鼠标分别单击F15、F16、…,查看编辑栏中的公式及C列和D列的相应数据,并与计算结果进行对照,验证计算结果的正确性。
(二)复制或移动公式公式中引用了单元格或区域,则在复制或移动公式时,单元格中的相对地址、绝对地址和混合地址会根据调整规则进行调整。
在工作表Sheet2中完成下列操作:1.复制公式(1)在H2单元格中输入公式:=C2+D2,选中H2拖拽填充柄到H9,将公式复制到H3:H9。
实验四 过程、函数、触发器和程序包

实验四过程、函数、触发器和程序包实验目的:(1)了解存储过程的作用;(2)了解函数的作用;(3)掌握存储过程的创建;(4)掌握存储过程的调用;(5)掌握函数的建立;(6)掌握函数的调用。
(7) 掌握触发器的基本作用及使用方法。
(8) 掌握触发器的建立、修改、查看、删除操作。
实验内容:一、过程、歪数(1)无参数的存储过程创建一个存储过程proc_execution,要求能够将empno为‘9010’的员工姓名更改为'yourname',并调用执行这个存储过程。
(2)带输入参数的存储过程创建一个存储过程,参数为员工编号,该存储过程能够删除指定的员工信息。
请编写并调用该存储过程。
(3)带输入输出的存储过程创建一个存储过程,要求能够查询并返回EMP中给定职工号的姓名、工资和佣金。
请编写并调用该存储过程。
(4)带输入参数的函数:创建一个函数get_sal,要求能够查询并返回EMP中给定职工号的工资,请编写该函数并正确调用。
(5)用异常处理完善程序请将第任务1中的程序完善,如果输入的员工号不存在,则执行异常处理,显示“此员工不存在”。
(6)创建函数,实现功能为:在scott.emp表和scott.dept 表中查询出任意给定职工号的职工姓名及职工所在部门的名称。
(7)对存储过程、函数及触发器实现查看、修改、删除等基本操作。
二、触发器1. 以SCOTT帐号登录,完成以下操作:(1)利用以下SQL语句,创建emp_copy表和emp_bak表(2)在emp表中创建一个触发器tg_insert_emp,当向emp表中添加一条记录时,自动向emp_copy表也自动添加一条记录。
当向emp表中更新一条记录时,自动更新emp_copy表中相关记录。
(3)当删除emp表中一条记录时,自动删除emp_copy表中相关记录,并且将删除的记录自动添加到emp_bak表。
2.请编写相关触发器,完成下列操作:利用下面的命令创建一个表OP_LOGCREATE OR REPLACE TABLE op_log(ID V ARCHAR2(20) PRIMARY KEY, op_dae date,op_type varchar2(200),op_user varhcar2(50));(1)编写一个触发器,当系统关闭时,记录系统关闭的时间及操作用户。
实验四函数的迭代、混沌与分形解读
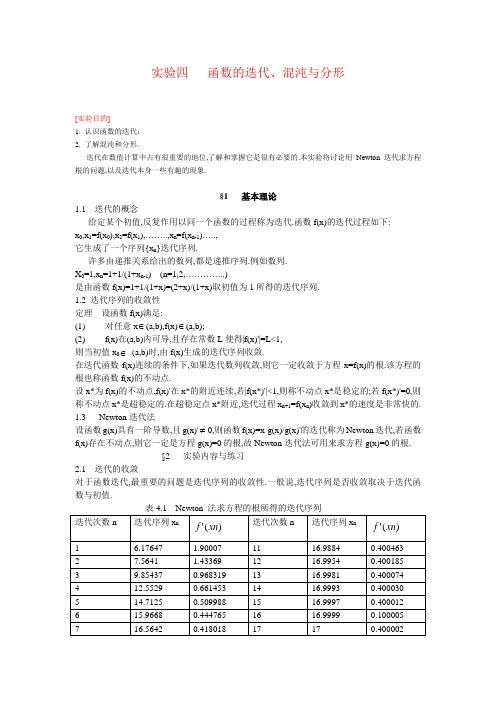
实验四函数的迭代、混沌与分形[实验目的]1. 认识函数的迭代;2. 了解混沌和分形.迭代在数值计算中占有很重要的地位,了解和掌握它是很有必要的.本实验将讨论用Newton迭代求方程根的问题,以及迭代本身一些有趣的现象.§1 基本理论1.1 迭代的概念给定某个初值,反复作用以同一个函数的过程称为迭代.函数f(x)的迭代过程如下:x0,x1=f(x0),x2=f(x1),……..,x n=f(x n-1)…..,它生成了一个序列{x n}迭代序列.许多由递推关系给出的数列,都是递推序列.例如数列.X0=1,x n=1+1/(1+x n-1) (n=1,2,…………..)是由函数f(x)=1+1/(1+x)=(2+x)/(1+x)取初值为1所得的迭代序列.1.2 迭代序列的收敛性定理设函数f(x)满足:(1)对任意x∈(a,b),f(x)∈(a,b);(2)f(x)在(a,b)内可导,且存在常数L使得|f(x)'|=L<1,则当初值x0∈(a,b)时,由f(x)生成的迭代序列收敛.在迭代函数f(x)连续的条件下,如果迭代数列收敛,则它一定收敛于方程x=f(x)的根.该方程的根也称函数f(x)的不动点.设x*为f(x)的不动点,f(x)'在x*的附近连续,若|f(x*)'|<1,则称不动点x*是稳定的;若f(x*)'=0,则称不动点x*是超稳定的.在超稳定点x*附近,迭代过程x n+1=f(x n)收敛到x*的速度是非常快的.1.3 Newton迭代法设函数g(x)具有一阶导数,且g(x)'≠0,则函数f(x)=x-g(x)/g(x)'的迭代称为Newton迭代,若函数f(x)存在不动点,则它一定是方程g(x)=0的根,故Newton迭代法可用来求方程g(x)=0的根.§2 实验内容与练习2.1 迭代的收敛对于函数迭代,最重要的问题是迭代序列的收敛性.一般说,迭代序列是否收敛取决于迭代函数与初值.作为一个例子,我们用来讨论用Newton迭代法求函数g(x)=(x-17)5/3(x-5)-2/3的根,其Mathematica程序为:Clear[g,x];g[x_]:=(x-17)^(5/3)*(x-5)^(-2/3);f[x_]=Factor[x-g(x)]/D[g[x],x]];x0=5.5;n=20;For[i=1,i<=n,i++,x0=N[f[x0]];Print[i,”“,x0,”“,D[f[x],x]/.x->x0]]执行结果见表4.1.表4.1的结果说明迭代序列收敛于g(x)的零点17.我们注意到程序中取的迭代处值为5.5,如果其它的数作为初值,所得的迭代序列是否收敛于17呢?我们可以取其它初值做实验,结果得到表4.2(表中第三列是迭代序列的前6位有效数字首次为17.0000的步数).从表4.2中可看出,只要初值不取5,迭代序列都收敛于17,且收敛速度与初值的选取关系不大.前面程序中使用的f(x)为g(x)的化简过的Newton迭代函数,用Mathematica命令可检查出它为(25x-85)/(x+3)(注意,这个式子扩充了原迭代函数在x=5,x=17处的定义),解方程f(x)=x.得到x=17,与x=5.即17和5是f(x)的两个不动点,有前面的讨论知这两个不动点是有区别的:对于17,不管初值取为多少(只要不为5),迭代序列总是收敛于它;而对于5,只要初值取为5时,迭代序列才以它为极限,这样一种现象在函数的迭代中普遍存在,为方便区分起见,我们给这样两种点各一个名称:像17这样的所有附近的点在迭代过程中都趋向于它的不动点,称为吸引点;而像5这样的所有附近的点在迭代过程中都远离它的不动点,称为排斥点.上面的f(x)=(25x-85)/(x+3)是一个分式线性函数,对于一般的分式线性函数,迭代序列是否总是收敛呢?练习1 编程判断函数f(x)=(x-1)/(x+1)的迭代序列是否收敛.在上节我们已经指出,如果迭代序列收敛,一定收敛到函数的某个不动点,这就是说,迭代函数存在不动点是迭代序列收敛的必要条件.那么如果迭代函数存在不动点,迭代序列是否一定收敛呢?练习2 先分别求出分式线性函数f1(x)=(x-1)/(x+3),f2(x)=(-x+15)/(x+1)的不动点,再编程判断它们的迭代序列是否收敛.运用上节的收敛定理可以证明:如果迭代函数在某不动点处具有连续的导数且导数值介于-1与1之间,那么取该不动点附近的点为初值所得到的迭代序列一定收敛到该不动点.练习3 你能否说明为什么17是f(x)=(25x-85)/(x+3)的吸引点,而5是f(x)的排斥点?尽量多找些理由支持这个结论.练习4 能否找到一个分式线性函数(ax+b)/(cx+d),使它产生的迭代序列收敛到给定的数?用这种办法计算2.2.2迭代的”蜘蛛图”对函数的迭代过程,我们可以用几何图象来直观地显示它.在xoy平面上,先作出函数y=f(x)与y=x的图象,对初值x0,在曲线y=f(x)上可确定一点p0,它以x0为横坐标,过p0引平行x轴的直线,设该直线与y=x交与点Q1作平行于y轴的直线它与曲线y=f(x)的交点记为p1,重复上面的过程,就在曲线y=f(x)上得到点列p1,p2,……,如图4.1,不难知道,这些点的横坐标构成的序列x0,x1,x2,……,xn……就是迭代序列.若迭代序列收敛,则点列p1,p2,……趋向于y=f(x)与y=x的交点p*,因此迭代序列是否收敛,可以在图上观查出来,这种图因其形状像蜘蛛网而被称为“蜘蛛网”图。
实验四_ 传递函数的零极点对系统过渡过程的影响
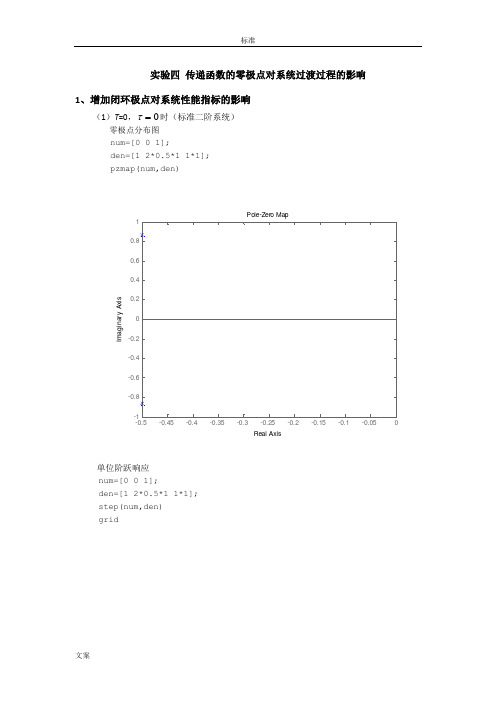
实验四 传递函数的零极点对系统过渡过程的影响1、增加闭环极点对系统性能指标的影响(1)T =0,0=τ时(标准二阶系统)零极点分布图 num=[0 0 1]; den=[1 2*0.5*1 1*1]; pzmap(num,den)单位阶跃响应num=[0 0 1]; den=[1 2*0.5*1 1*1]; step(num,den) grid-0.5-0.45-0.4-0.35-0.3-0.25-0.2-0.15-0.1-0.050Pole-Zero MapReal AxisI m a g i n a r y A x i s(2)当0=τ时,增加附加闭环极点:①n T ζω51> ②n T ζω≈1 ③n Tζω<1零极点图num2=[0 0 1];den2=conv([0 1/3 1],[1 1 1]); num3=[0 0 1];den3=conv([0 1/0.5 1],[1 1 1]); num4=[0 0 1];den4=conv([0 1/0.1 1],[1 1 1]); pzmap(num1,den1) hold onpzmap(num2,den2) hold onpzmap(num3,den3) hold onpzmap(num4,den4)0246810120.20.40.60.811.21.4Step ResponseTime (sec)A m p l i t u d e单位阶跃响应num2=[0 0 1];den2=conv([0 1/3 1],[1 1 1]); num3=[0 0 1];den3=conv([0 1/0.5 1],[1 1 1]); num4=[0 0 1];den4=conv([0 1/0.1 1],[1 1 1]); step(num2,den2) hold on step(num3,den3) hold on step(num4,den4)-3-2.5-2-1.5-1-0.50Pole-Zero MapReal AxisI m a g i n a r y A x i s(3)一阶系统)1(,11)()(n TTs s X s Y ζω<+= 闭环零极点num=[0 1]; den=[1/0.1 1]; pzmap(num,den)01020304050600.20.40.60.811.21.4Step ResponseTime (sec)A m p l i t u d e单位阶跃响应num=[0 1]; den=[1/0.1 1]; step(num,den) gridPole-Zero MapReal AxisI m a g i n a r y A x i s-0.1-0.09-0.08-0.07-0.06-0.05-0.04-0.03-0.02-0.010010********600.10.20.30.40.50.60.70.80.91Step ResponseTime (sec)A m p l i t u d e(2)与标准二阶系统进行比较,说明增加闭环极点对系统性能的影响。
05【实验四】 二元函数的图形
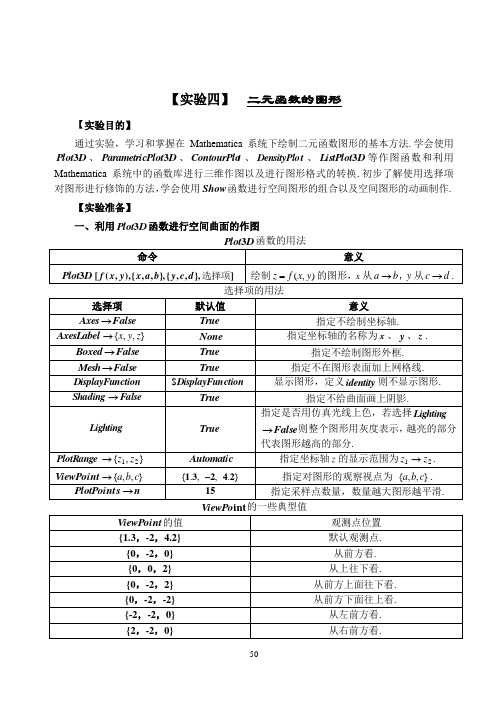
【实验四】 二元函数的图形【实验目的】通过实验,学习和掌握在Mathematica 系统下绘制二元函数图形的基本方法.学会使用D Plot 3、D Plot Parametric 3、t ContourPlo 、t DensityPlo 、D ListPlot 3等作图函数和利用Mathematica 系统中的函数库进行三维作图以及进行图形格式的转换.初步了解使用选择项对图形进行修饰的方法,学会使用Show 函数进行空间图形的组合以及空间图形的动画制作.【实验准备】一、利用D Plot 3函数进行空间曲面的作图例1 作出22),(y xe y xf --=的图形,并利用选择项对所作图形进行修饰.解 In[1]:= Plot3D Exp x ^2y^2,x,2,2,y,2,2Out[1]:= ?SurfaceGraphics ? 去掉刻度In[2]:= Plot3D Exp x ^2y^2,x,2,2,y,2,2,TicksFalseOut[2]:= ?SurfaceGraphics ?去掉图形上的网格线Plot3D Exp x^2y^2,x,2,2,y,2,2,Mesh False不画出图形上的阴影In[4]:=Plot3D Exp x^2y^2,x,2,2,y,2,2,Shading FalseOut[4]:=? SurfaceGraphics?不用仿真光线上色In[4]:=Plot3D Exp x^2y^2,x,2,2,y,2,2,Lighting FalseOut[4]:=? SurfaceGraphics?去掉外框In[5]:=Plot3D Exp x^2y^2,x,2,2,y,2,2,Boxed False分别以x、y 、z定义坐标轴的名称In[6]:=Plot3D Exp x^2y^2,x,2,2,y,2,2,Boxed False,AxesLabel x,y,zOut[6]:=? SurfaceGraphics?定义以每个方向以36个点绘图,观测点为从前方看.In[7]:=Plot3D Exp x^2y^2,x,2,2,y,2,2,PlotPoints36,ViewPoint0,2,0,Boxed FalseOut[7]:=? SurfaceGraphics?将绘图的范围限制在2≤z0≤In[8]:=Plot3D Exp x^2y^2,x,2,2,y,2,2,PlotRange0,2Out[8]:= ?SurfaceGraphics ? 二、利用D Plot Parametric 3函数进行空间曲面(曲线)的参数作图如果函数是),(y x f z =的形式,则可以利用D Plot 3命令绘制这个函数的曲面.但有些空间曲面(曲线)无法表示成),(y x f z =的形式,例如球面、螺旋线等.对于这种空间曲面(曲线),有时可以利用一组参数方程来表示.关于这类用参数方程表示的曲面(曲线),我们用D Plot Parametric 3函数进行作图,其格式如下:由上表可以看出,如果参数方程有两个变量,所作图形为空间曲面.如果参数方程只有一个变量,所作图形为空间曲线.选择项与D Plot 3作图选择项类似,只是所取样点的默认值有所不同,曲面参数作图的默认值为→s int PlotPo },{1515,而曲线参数作图的默认值为75→s int PlotPo ,必要时可加大此值以求得更平滑的曲面或曲线.例2 作出由参数方程⎪⎩⎪⎨⎧===v cos z v sin u sin y v sin u cos x ,πππ≤≤≤≤v u 5.0,20所确定的曲面图形.解 In[1]:=ParametricPlot3D @8C os @u DSin @v D ,Sin @u D Sin @v D ,Cos @v D <,8u ,0,2Pi <,8v ,0.5 Pi,Pi <D例3 作出由参数方程⎪⎩⎪⎨⎧===t .z t cos y tsin x 10,π≤≤80t 所确定的圆柱螺旋线的图形.解 In[1]:= ParametricPlot3DSin t ,Cos t ,0.1t ,t,0,8三、使用Show 函数拼合多张曲面使用函数可以将已作好的一些图形组合在一起,其格式如下:例4 作出由参数方程⎪⎪⎪⎩⎪⎪⎪⎨⎧===2cos 2sin sin 2cos sin v z u v y u v x ,π≤≤π≤≤v u 0,20所确定的曲面,并与例2中所作的曲面进行拼合.解 In[1]:= f1ParametricPlot3DSin v Cos u 2,Sin v Sin u2,Cos v 2,u,0,2,v,0,,DisplayFunctionIdentityOut[1]:= ?Graphics3D ? In[2]:= f2ParametricPlot3D Cos u Sin v ,Sin u Sin v ,Cos v ,u,0,2,v,0.5,,DisplayFunction IdentityOut[2]:= ?Graphics3D ? In[3]:= Show f1,f2,DisplayFunction$DisplayFunctionOut[3]:= ?Graphics3D ? 注:利用Show 命令可以作出两个曲面的交线以及曲面的切平面.方法是:分别作出两个空间曲面或一个曲面与其切平面,然后用Show 命令再现这组已作好的空间图形.四、绘制空间曲面的等高线图等高线图(t ContourPlo )是将三维空间中高度相等的点连接起来.等高线图在弹性力学(力的分布),热传学(温度的分布)以及空间曲面求最值问题中有着广泛的应用.下面介绍作图格式:例 5 作出函数22122)2(),(y xe y x y xf --+=在22(≤≤-x ,)22≤≤-y 范围内所表示的空间曲面及等高线图,并对等高线图进行适当的修饰.解 In[1]:= f x_,y_:x^22y^21x 2y 2; (为作图方便先定义函数)In[2]:= Plot3D f x,y ,x,2,2,y,2,2Out[2]:= ?Graphics3D ? 作出等高线图In[3]:= ContourPlot f x,y ,x,2,2,y,2,2Out[3]:=? ContourGraphics?图形中较亮的部分为空间曲面中较高的位置,较暗的部分为空间曲面中较低的位置. 加大sPlotPo的值可以使等高线图形更加平滑,如下图:intIn[4]:=ContourPlot f x,y,x,2,2,y,2,2,PlotPoints400Out[4]:=? ContourGraphics?改变Contours 的值可以指定等高线的数目,如下图:In[5]:= ContourPlot f x,y ,x,2,2,y,2,2,Contours20Out[5]:= ?ContourGraphics ?五、绘制空间曲面的密度图密度图)(t DensityPlo 和等高线图有些类似,只是密度图用了一个上了色的方格数组,配合颜色的深浅代表函数值的大小.其作图格式如下:选择项例6 作出函数22122)2(),(y x e y x y x f --+=在22(≤≤-x ,)22≤≤-y 范围内的密度图,并注意选择项的效果.解 In[1]:= f x_,y_:x^22y^21x 2y 2;In[2]:= DensityPlot f x,y ,x,2,2,y,2,2,MeshFalse,PlotPoints50Out[2]:= ?DensityGraphics ?六、图形格式的转换如果图形是以D Plot 3、t ContourPlo 和)(t DensityPlo 等命令绘制的,则可以在这三者之间做图形转换.例如可以把一个空间曲面图形转换成等高线图,或把一个密度图转换为空间曲面图形.其转换图形格式的命令如下:例7 作出由函数y x y x f cos sin ),(=确定的空间曲面,并将其转换为等高线图和密度图.解 In[1]:= Plot3D @S in @x DCos @y D ,8x ,0,2 Pi <,8y ,0,2 Pi <DOut[1]:= ?SurfaceGraphics ?In[2]:= Show @C ontourGraphics @%DOut[2]:= ?ContourGraphics ?In[3]:= Show @DensityGraphics @%DOut[3]:= ?DensityGraphics ? 七、利用函数库绘制三维图形1. 利用`D t ContourPlo `Graphics 3绘图函数库绘制空间曲面对于用方程表示的曲面,如:椭球面、椭圆抛物面和双曲抛物面等不能用D Plot 3函数进行作图,而要用Mathematica 系统函数库中提供的D t ContourPlo 3命令进行作图. 在使用D t ContourPlo 3函数之前,首先要加载`D t ContourPlo `Graphics 3绘图函数库,其格式如下:注:1.选择项与D Plot 3函数作图的选择项相同.2.s int PlotPo 的默认值为}5,3{较为粗糙,可加大s int PlotPo 的值使图形更加平滑. 例8 绘制由方程12222=+--z y x 所确定的在)22,22,33(≤≤-≤≤-≤≤-z y x 区域内的双叶双曲面,并进行适当的修饰.解 In[1]:= <<Graphics`ContourPlot3D` In[2]:= ContourPlot3Dx 22y 2z 21,x,3,3,y,2,2,z,2,2,PlotPoints6,8,Boxed FalseOut[2]:= ?Graphics3D ? 2.由曲线生成的旋转曲面首先加载`volution Re SurfaceOf `Graphics <<函数库,然后使用volution Re SurfaceOf 命令进行作图,其格式如下:例9 作出正弦曲线x sin z =,]2,0[π∈x 绕z 轴旋转一周形成的曲面解 In[1]:= <<Graphics`SurfaceOfRevolution`In[2]:= SurfaceOfRevolution@S in @x D ,8x ,0,2 Pi <,AxesLabel ?8x ,y,z <DOut[2]:= ?Graphics3D ?*例10 作出曲线2x z =绕起点在原点的向量}1,1,1{旋转的曲面 解 In[1]:=<<Graphics`SurfaceOfRevolution`In[2]:= SurfaceOfRevolution@x ^2,8x ,0,1<, RevolutionAxis ?81,1,1<,AxesLabel ?8x ,y,z<D3.空间曲面在坐标面上的投影绘制空间曲面在各个坐标面上的投影需要使用投影函数Shadow .在利用Shadow 绘制空间曲面的投影之前,需要加载Graphics`Graphics3D`函数库. 例11 按照下列要求作出椭圆抛物面12222=++z y x 在坐标面上的投影.(1)三个坐标平面上的投影;(2)一个坐标面上的投影.解 In[1]:= <<Graphics`ContourPlot3D` In[2]:= A 8<(1)In[3]:= <<Graphics`Graphics3D` In[4]:= Shadow @u D(2)In[5]:=*例12 绘制由参数方程⎪⎩⎪⎨⎧--===)sin 2(3sin cos 22t r z t r y t r x 与⎪⎩⎪⎨⎧+===)sin 1(sin cos 22t r z t r y tr x )10(≤≤r ,)20π≤≤t 所确定的两个曲面围成的立体图形,并将它投影到坐标面上.解 In[1]:= <<Graphics`Graphics3D`In[2]:= u1ParametricPlot3Dr Cos t ,r Sin t ,3r22Sin t ^2, r,0,1,t,0,2Pi ,DisplayFunction Identity Out[2]:= Graphics3DIn[3]:=u2ParametricPlot3Dr Cos t,r Sin t,r21Sin t^2,r,0,1,t,0,2Pi,DisplayFunction Identity Out[3]:=Graphics3DIn[4]:=u Show u1,u2,DisplayFunction$DisplayFunctionIn[5]:=八、空间图形的动画制作制作空间图形的动画可以用有关循环结构的命令(如:For 、Table 、Do 等),将作图函数作出的图形按照时间顺序生成动画,下面举例说明例13 制作在区域1010≤≤-x ,1010≤≤-y 内,由函数22221)sin(10),(yx y x y x f +++=所确定的曲面变化的动画过程.解 In[1]:= For i1,i30,i,Plot3D10Sinx ^2y^21x^2y ^2,x,10,10i 30,y,10,10i 30,PlotPoints50,Boxed False执行程序后得到一组图形,鼠标左键双击工作区右端包含全部图形的兰色线框,保留最上面的图形(如上图)而关闭其它图形,然后用鼠标左键双击该图即可播放动画.注:In[1]中的“30/i ”的含义是每隔单位长度的30i作出一张图形,根据i 的不同取值得到多幅图形,读者可以根据不同情况自行设置.【实验任务】一、作出下列函数所确定的空间曲面,并根据下列要求修饰图形:(1)去掉网格;(2)使图形平滑;(3)指定坐标轴的名称为“x 、y 、z ”;(4)去掉图形外框.1.228sin 41),(y x y x f +=,11≤≤-x ,11≤≤-y ; 2.y xy y x y x f +-+=6),(22,30≤≤x ,30≤≤y ;3.)sin(),(y x y x f +=,ππ≤≤-x , ππ≤≤-y ;4.22),(y x y x f +=,ππ22≤≤-x ,ππ22≤≤-y .二、作出由参数方程⎪⎪⎩⎪⎪⎨⎧===t z t y t x 51cos sin 所确定的空间曲线的图形.三、根据给出的参数方程作出下列曲面的图形.1. 椭圆抛物面⎪⎩⎪⎨⎧===24cos 2sin 3u z v u y vu x ,π≤≤≤≤-20,11v u ;2.双曲抛物面⎪⎪⎩⎪⎪⎨⎧-===322v u z v y u x ,22,11≤≤-≤≤-v u ;3.圆锥面⎪⎩⎪⎨⎧===u z v u y vu x cos sin ,π≤≤≤≤-20,11v u .四、作出由方程z y x 422=+确定的空间曲面,并去掉网格、外框,使图形更加平滑. 五、已知球面由方程14222=++z y x 确定,球面的切平面由方程01432=-++z y x 确定,在同一坐标系下作出球面及其切平面的图形.六、作出由曲线x z cos =,]2,0[π∈x 绕z 轴旋转一周形成的曲面. 七、作出由直线x z =绕x 轴旋转一周形成的一个锥面,并标注三个坐标轴.*八、作出曲面:⎪⎩⎪⎨⎧==+=u z v y v x sin 1cos )20,31(π≤≤≤≤v u ;与曲面:⎪⎩⎪⎨⎧===u z v u y vu x sin sin cos sin)20,0(ππ≤≤≤≤v u ;围成的立体图形,并将其投影到xOy 面上.九、制作由函数22sin y x y +=在)20,20(π≤≤π≤≤y x 区域内的动画.。
matlab实验四函数编写与程序设计

实验四:函数编写与程序设计一、实验目的1 . 掌握M文件的创建。
2.掌握函数的编写规则。
3.掌握函数的调用。
4 . 掌握基本的输入输出函数以及显示函数的用法。
5.会用Matlab程序设计实现一些工程算法问题。
二、实验内容1 . 设计程序,完成两位数的加、减、乘、除四则运算,即产生两个两位随机整数,再输入一个运算符号,做相应的运算,显示相应的结果,并要求结果显示类似于“a=x+y=34”。
a=input('请输入一个数:')b=input('请输入一个数:');fuhao=input('请输入一个运算符号(+-*/):','s');switch fuhaocase {'+'}he=a+b;disp(['和=',num2str(a),'+',num2str(b),'=',num2str(he)]);case {'-'}he=a-b;disp(['减=',num2str(a),'-',num2str(b),'=',num2str(he)]) case {'*'}he=a*b;disp(['乘=',num2str(a),'*',num2str(b),'=',num2str(he)]) case {'/'}he=a/b;disp(['除=',num2str(a),'/',num2str(b),'=',num2str(he)]) otherwise disp('请输入正确的符号');end2 . 求下列分段函数的值2 2 26,0 56,1,yχχχχχχχχχχχ⎧+-<≠⎪=-+≤≠≠⎨⎪--⎩且-30<10,2且3其他要求:用if语句实现,分别输出x = -5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
包头师范学院信息科学与技术学院实验报告
实验课程名称:C语言程序设计实验指导教师:于方
实验院系:信息科学与技术学院实验班级:
学号:姓名:
实验地点:博学楼西109
一、实验题目:实验四函数(4学时)
二、实验要求:①掌握函数定义、说明及调用的方法;②了解函数调用时参数传递的本质;③掌握正确使用变量存储属性的方法。
三、实验内容及实验过程
1、实验11函数及其测试
2+4+6。
要求:①编写函数f1和f2实现
(1)完善程序,实现求解222
所求功能;②给出正确的函数调用实参值(与所给a相关)。
(2)实参调用测试。
要求:分别使用f1(a+++1,a+++2,a+++3)和
f1(++a+1,++a+2,++a+3)两种实参调用函数f1,记录程序运行结果,给出相关分析。
(3)参数传递和函数返回测试。
要求:在程序中合适位置插入输出
语句,能够验证函数间参数传递和函数返回是否正确。
(4)多文件编译、链接的方法和步骤。
要求:将程序中的main函
数、f1函数和f2函数分别保存在三个文件中,给出正确的多程序文件的编译、链接方法。
(5)递归函数测试。
要求:①设计一个递归程序实现同样的功能,
2+4+6的值;②使用输出语句显示递归调用的过程。
即求解222
2、实验12变量的存储属性
(1)变量存储属性测试练习。
要求:①找出实验内容(1)所给程序中
的错误;②分析每个错误原因。
(2)分析变量的作用域和存储属性。
要求:①调试程序,给出程序
运行结果;②分析每个变量“i”的存储属性和作用域。
(3)分析变量的作用域和存储属性。
要求:①根据实验内容(3)给出
的程序框架,分别在a~f各个函数中添加printf语句,将每个函数范围内的所有有效变量值打印出来;②删除file3.c中的extern int y,给出程序运行结果和相关原因分析。
四、分析与总结:
1、总结函数调用时,参数的计算顺序。
2、总结测试函数的一般方法。
(通过函数功能、参数传递和函数
返回是否正确等几方面分析)
3、总结不同存储属性变量的使用方法。
4、自己在实验过程中出现的错误及解决方法。
