两级开环比较器的设计
运放的开环闭环

运放的开环闭环运放的开环闭环是电子电路中常见的概念。
运放(Operational Amplifier)是一种高增益、差分输入、差模输出的电子器件,广泛应用于模拟电路和信号处理领域。
它可以实现信号放大、滤波、积分、微分等功能,是许多电路设计中重要的基础元件。
一、运放的基本结构和特性运放通常由一个差分输入级和一个差模输出级组成。
差分输入级包含两个输入端和一个差分放大器,用于将输入信号转换为差分信号。
差模输出级包含一个输出端和一个输出级,用于将差分信号转换为单端输出信号。
运放具有以下特性:1. 高增益:运放的开环增益非常高,通常在几万到几百万倍之间。
2. 大输入阻抗:运放的输入端具有很高的阻抗,可以减小外部电路对输入信号的影响。
3. 小输出阻抗:运放的输出端具有很小的阻抗,可以提供较大的输出功率。
4. 宽带宽:运放具有较宽的频带宽度,能够处理高频信号。
5. 高共模抑制比:运放可以有效抑制共模信号的干扰。
二、运放的开环和闭环1. 开环运放:当运放的输出端未连接到反馈回路时,称为开环运放。
开环运放的特点是增益非常高,但稳定性较差,容易受到噪声和温度变化的影响。
在实际应用中,很少直接使用开环运放。
2. 闭环运放:当运放的输出端连接到反馈回路时,称为闭环运放。
闭环运放通过反馈回路将一部分输出信号送回输入端,使得输出信号与输入信号之间存在负反馈关系。
闭环运放的特点是增益稳定、精确可控,能够提供稳定且精确的放大功能。
三、运放的反馈类型根据反馈回路的连接方式,可以将运放的反馈分为正反馈和负反馈两种类型。
1. 正反馈:正反馈是指将一部分输出信号直接或间接地送回到输入端,使得输出信号与输入信号之间存在正相关关系。
正反馈会增强系统的不稳定性,容易产生自激振荡等问题,在实际应用中很少使用。
2. 负反馈:负反馈是指将一部分输出信号送回到输入端,并与输入信号相减,使得输出信号与输入信号之间存在负相关关系。
负反馈能够提高系统的稳定性、减小非线性失真、扩大带宽等。
比较器工作原理及应用

电压比较器以下简称比较器是一种常用的集成电路;它可用于报警器电路、自动控制电路、测量技术,也可用于V/F变换电路、A/D变换电路、高速采样电路、电源电压监测电路、振荡器及压控振荡器电路、过零检测电路等;本文主要介绍其基本概念、工作原理及典型工作电路,并介绍一些常用的电压比较器;什么是电压比较器简单地说, 电压比较器是对两个模拟电压比较其大小也有两个数字电压比较的,这里不介绍,并判断出其中哪一个电压高,如图1所示;图1a是比较器,它有两个输入端:同相输入端“+”端及反相输入端“-”端,有一个输出端Vout输出电平信号;另外有电源V+及地这是个单电源比较器,同相端输入电压VA,反相端输入VB;VA和VB的变化如图1b所示;在时间0~t1时,VA>VB;在t1~t2时,VB>VA;在t2~t3时,VA>VB;在这种情况下,Vout的输出如图1c 所示:VA>VB时,Vout输出高电平饱和输出;VB>VA时,Vout输出低电平;根据输出电平的高低便可知道哪个电压大;如果把VA输入到反相端,VB输入到同相端,VA及VB的电压变化仍然如图1b所示,则Vout输出如图1d所示;与图1c比较,其输出电平倒了一下;输出电平变化与VA、VB的输入端有关;图2a是双电源正负电源供电的比较器;如果它的VA、VB 输入电压如图1b那样,它的输出特性如图2b所示;VB>VA时,Vout 输出饱和负电压;如果输入电压VA与某一个固定不变的电压VB相比较,如图3a所示;此VB称为参考电压、基准电压或阈值电压;如果这参考电压是0V地电平,如图3b所示,它一般用作过零检测;比较器的工作原理比较器是由运算放大器发展而来的,比较器电路可以看作是运算放大器的一种应用电路;由于比较器电路应用较为广泛,所以开发出了专门的比较器集成电路;图4a由运算放大器组成的差分放大器电路,输入电压VA经分压器R2、R3分压后接在同相端,VB通过输入电阻R1接在反相端,RF 为反馈电阻,若不考虑输入失调电压,则其输出电压Vout与VA、VB 及4个电阻的关系式为:Vout=1+RF/R1·R3/R2+R3VA-RF/R1VB;若R1=R2,R3=RF,则Vout=RF/R1VA-VB,RF/R1为放大器的增益;当R1=R2=0相当于R1、R2短路,R3=RF=∞相当于R3、RF开路时,Vout=∞;增益成为无穷大,其电路图就形成图4b的样子,差分放大器处于开环状态,它就是比较器电路;实际上,运放处于开环状态时,其增益并非无穷大,而Vout输出是饱和电压,它小于正负电源电压,也不可能是无穷大;从图4中可以看出,比较器电路就是一个运算放大器电路处于开环状态的差分放大器电路;同相放大器电路如图5所示;如果图5中RF=∞,R1=0时,它就变成与图3b一样的比较器电路了;图5中的Vin相当于图3b中的VA;比较器与运放的差别运放可以做比较器电路,但性能较好的比较器比通用运放的开环增益更高,输入失调电压更小,共模输入电压范围更大,压摆率较高使比较器响应速度更快;另外,比较器的输出级常用集电极开路结构,如图6所示,它外部需要接一个上拉电阻或者直接驱动不同电源电压的负载,应用上更加灵活;但也有一些比较器为互补输出,无需上拉电阻;这里顺便要指出的是,比较器电路本身也有技术指标要求,如精度、响应速度、传播延迟时间、灵敏度等,大部分参数与运放的参数相同;在要求不高时可采用通用运放来作比较器电路;如在A/D变换器电路中要求采用精密比较器电路;由于比较器与运放的内部结构基本相同,其大部分参数电特性参数与运放的参数项基本一样如输入失调电压、输入失调电流、输入偏置电流等;比较器典型应用电路这里举两个简单的比较器电路为例来说明其应用;1.散热风扇自动控制电路一些大功率器件或模块在工作时会产生较多热量使温度升高,一般采用散热片并用风扇来冷却以保证正常工作;这里介绍一种极简单的温度控制电路,如图7所示;负温度系数NTC热敏电阻RT粘贴在散热片上检测功率器件的温度散热片上的温度要比器件的温度略低一些,当5V电压加在RT及R1电阻上时,在A点有一个电压VA;当散热片上的温度上升时,则热敏电阻RT的阻值下降,使VA上升;RT 的温度特性如图8所示;它的电阻与温度变化曲线虽然线性度并不好,但是它是单值函数即温度一定时,其阻值也是一定的单值;如果我们设定在80℃时应接通散热风扇,这80℃即设定的阈值温度TTH,在特性曲线上可找到在80℃时对应的RT的阻值;R1的阻值是不变的它安装在电路板上,在环境温度变化不大时可认为R1值不变,则可以计算出在80℃时的VA值;R2与RP组成分压器,当5V电源电压是稳定电压时电压稳定性较好,调节RP可以改变VB的电压电位器中心头的电压值;VB 值为比较器设定的阈值电压,称为VTH;设计时希望散热片上的温度一旦超过80℃时接通散热风扇实现散热,则VTH的值应等于80℃时的K值;一旦VA>VTH,则比较器输出低电平,继电器K吸合,散热风扇直流电机得电工作,使大功率器件降温;VA、VTH电压变化及比较器输出电压Vout的特性如图9所示;这里要说清楚的是在VA开始大于VTH时,风扇工作,但散热体有较大的热量,要经过一定时问才能把温度降到80℃以下;从图7可看出,要改变阈值温度TTH十分方便,只要相应地改变VTH值即可;VTH值增大,TTH增大;反之亦然,调整十分方便;只要RT确定,RT的温度特性确定,则R1、R2、RP可方便求出设流过RT、R1及R2、RP的电流各为0.1~0.5mA;2.窗口比较器窗口比较器常用两个比较器组成双比较器,它有两个阈值电压VTHH高阈值电压及VTHL低阈值电压,与VTHH及VTHL比较的电压VA输入两个比较器;若VTHL≤VA≤VTHH,Vout输出高电平;若VA<VTHL,VA>VTHH,则Vout输出低电平,如图10所示;图10是一个冰箱报警器电路;冰箱正常工作温度设为0~5℃,0℃到5℃是一个“窗口”,在此温度范围时比较器输出高电平表示温度正常;若冰箱温度低于0V或高于5℃,则比较器输出低电平,此低电平信号电压输入微控制器μC作报警信号;温度传感器采用NTC热敏电阻RT,已知RT在0℃时阻值为333.1kΩ;5℃时阻值为258.3kΩ,则按1.5V工作电压及流过R1、RT的电流约1.5 uA,可求出R1的值;R1的值确定后,可计算出0℃时的VA值为0.5V按图10中R1=665kΩ时,5℃时的VA值为0.42V,则VTHL=0.42V,VTHH=0.5V;若设R2=665kΩ,则按图11,可求出流过R2、R3、R4电阻的电流I=1.5V-0.5V/665kΩ=0.0015mA,按R4×I/=0.42V,可求出R4=280kΩ再按0.5V=R3+R40.0015mA,则可求出R3=53.3kΩ;本例中两个比较器采用低工作电压、低功耗、互补输出双比较器LT1017,无需外接上拉电阻;。
两级开环比较器的设计

两级开环比较器的设计初级比较器设计比较器的电路符号如右图所示,它的功能是比较输入端的信号差异,输出以之对应的数值上离散的两种信号之一,当Vin+>Vin-时,比较器输出为高电平(Voh);当Vin+<="">(Vol);比较器广1泛用于模拟电路和数字电路的接口部分即连续和离散的交接部分。
1.比较器静态特性(1)理想比较器模型理想比较器的电路模型如下图所示:C 理想比较器模型它的传输曲线如下图所示:A VoVo hVin+ -Vin-传输曲线可以用数学函数表示如下:本文主要包括:(1)分析说明比较器工作原理; 器的HSPICE莫拟;(4)比较器物理版图设计实现;(1)(2)比较器的设计计算方法;(5)设计文件列表说明。
(3)比较.比较器的原理简述比较器电路符号理想比较器的传输曲线Vo lB2f八,V)V oh ,when(V n V n ) 0To (V inVin ) - --- - TT ; - —: TTV ol ,when(V n V n ) 0A V oh V olV ih V il(2)有限增益比较器模型有限增益比较器的电路模型如下图所示:有限增益比较器模型它的传输曲线如下图所示:传输曲线可以用数学函数表示如下:f l (V in V in ) 1 rV oh,when(V in V in ) V ih ]A (V inV in ), whenV il M % )V,1V ol,,when(V inV in ) V^AVoh Vo1,为一个有限值V ih V il(3)包含输入失调电压的比较器包含输入失调电压比较器电路模型如下图所示:223 42包含输入失调电压比较器模型它的传输曲线如下图所示:包含输入失调电压比较器的传输曲线其中的Vos 为输入失调电压,它被定义为:实际比较器输出电压为零时,输入端所加的电压, 它是比较器的一个重要参数,跟比较器的精度有密切的关系,而且它的温漂很难补偿。
lm393的工作原理

lm393的工作原理
LM393是一种常用的比较器芯片,用于电路中的电压比较功能。
它具有两个比较输入引脚VIN+和VIN-,以及一个输出引脚OUT。
LM393工作原理如下:
1. 当VIN+的电压大于VIN-时,输出引脚OUT会产生高电平;
2. 当VIN+的电压小于VIN-时,输出引脚OUT会产生低电平。
具体而言,工作原理如下:
1. 比较器的两个输入引脚VIN+和VIN-都与一个内部的基准电压源Vref相连;
2. LM393的比较器使用开环放大器的结构,即没有反馈回路;
3. 当VIN+的电压高于VIN-时,Vref会被放大并输出到输出引脚OUT上,产生高电平信号;
4. 当VIN+的电压低于VIN-时,Vref不会被放大并输出到输出引脚OUT上,产生低电平信号。
由于LM393是一个开环比较器,所以它适用于需要简单的电
压参考和比较的应用,例如电池电量检测、温度控制、光强检测等。
它的工作原理简单而稳定,使用方便,因此在实际电子电路设计中被广泛应用。
两级放大器的设计

两级放大器的设计摘要:两级放大器在实际生活中有着非常重要的作用,它可以把我们生活中需要的信号进行放大来便利人们的生活。
在生活中有着非常广泛的应用。
该设计是两级放大器的设计,首先是对设计方案的选择和设计,详细分析了两级放大器的所需数据,然后在multisim中选择所需的元器件来进行电路的设计。
通过改变电路的电压来进行动态的分析。
仿真结果表明:在电路中输入的电压在第二级放大器的输出端可以准确的看到放大了1000倍,实现了题目的要求。
关键词:两级放大器;电路仿真;设计目录1.设计任务与要求2.方案设计与论证3.单元电路的设计与仿真3.1第一级放大器的设计3.2第二级放大器的3.3桥式整流电源的设计4.总电路设计及其仿真调试过程4.1总体电路的设计4.2仿真结果及其分析5.结论和心得6.参考文献1.设计任务与要求(1)中频带电压的放大增益1000(2)通频带30HZ—30KHZ(3)输出电阻10(4)输入电阻20K(5)负载电阻20K(6)最大不失真输出电压5V(7)用桥式整流电容滤波集成稳压块电路设计所需的正负直流电源2.方案的设计与论证两级放大器的设计具有组装简单,调试方便,工作稳定的实验电路。
设计中包括电源输入电路,一级同相放大电路,二级反相放大电路三部分。
电路原理图如下图2.1所示:图2.1 两级放大器电路原理由设计与要求可以知道,两级放大器设计的实验主要分为三部分,即对于电源输入信号和第一级放大电路,第二级放大电路的设计。
进过分析,电源输入信号电路是桥式整流滤波集成稳压块所设计出来的正负直流电源。
第一级放大电路可以是由同相放大电路的组成,第二级放大电路是由反相放大电路所组成。
由于所需要的电压放大倍数是1000,而同相放大器的电压放大倍数在1—100之间,反相放大器的电压放大倍数在0.1—100之间,因此放大1000倍的设计就可以使用这两个放大器来实现。
因为设计初稿有很多东西都是借鉴书上或者网站上的东西,Multisim 则是第一次接触的仿真软件,因此有的某些电器元件只能够使用Multisim 中所有的。
运放常用电路过零比较器

运放常用电路过零比较器运放是一种常用的电子元器件,它在电子电路中起着放大信号、滤波、比较、积分、微分等作用。
运放有很多种常用电路,其中比较器是一种重要的电路之一,它常常用于在电路中进行信号的比较和判断。
本文将重点介绍运放常用电路中的过零比较器,并对其工作原理、特点以及应用进行详细讲解。
一、过零比较器的工作原理过零比较器是一种利用运放制作的开环比较器,它的工作原理是当输入信号为零时,输出信号为零;当输入信号为正时,输出信号为正;当输入信号为负时,输出信号为负。
过零比较器通常使用在信号波形的过零检测和相位判断上,是一种非常常见的电路。
二、过零比较器的特点1.简单易制作。
过零比较器只需要一个运放和几个电阻就可以组成,成本低廉,制作简单。
2.输出准确。
过零比较器能够对信号进行准确的比较和判断,输出结果精准可靠。
3.性能稳定。
由于过零比较器采用了运放,因此其性能稳定,能够长时间稳定地工作。
4.电路灵活。
过零比较器可以根据需要进行调整和改动,具有一定的灵活性。
三、过零比较器的电路图和原理图过零比较器的电路图如下所示:其中,R1和R2为输入电阻,R3为反馈电阻,R4为固定电阻。
Vcc 为正电源,Vee为负电源。
过零比较器采用反相输入,负反馈的方式,从而可以得到稳定的输出结果。
其原理图如下:四、过零比较器的应用1.信号检测。
过零比较器可以用于检测信号波形的过零点,通常用于音频设备和测量仪器中。
2.相位判断。
过零比较器可以用于判断两路信号的相位关系,常用于相位同步电路的设计中。
3.数字电路。
过零比较器还可以用于数字电路中,如数字电子钟、数字频率计等。
五、总结通过本文的介绍,我们可以了解到过零比较器是一种常用的运放电路,在电子电路中有着重要的应用。
它具有简单易制作、输出准确、性能稳定、电路灵活等特点,在信号检测、相位判断、数字电路等领域有广泛的应用。
对于电子工程师来说,掌握过零比较器的工作原理和应用技巧是非常重要的。
高速比较器的分析与设计

本章小结 ............................................................. 29 结 致 论 .................................................................. 30 谢 .................................................................. 31
1.2
国内外发展现状分析
比较器是所有模数转换器的关键模块。其性能,尤其是速度、功耗,对整个模数转 换器的速度和功耗都有着至关重要的影响。但是传统的比较器很难同时满足模数转换器 对速度和功耗的要求,因此需要对传统的电路结构进行更新和改进,以满足应用要求。 传统的预放大锁存比较器有较小的延迟时间和低失调、低回踢噪声,但是这些高指标是 以高损耗和大的芯片面积为代价的;动态比较器虽然具有速度快、功耗低的优点,但是 失调电压和回踢噪声都很大,限制了其在高精度模数转换器中的应用;静态比较器具有 较小的回踢噪声,然而其功耗大,比较速度慢,不适于高速模数转换器。 关于比较器的研究,综合国际和国内模数转换器发展的情况来看,其趋势是高速和
关键词:高速比较器;CMOS;失调电压
I
兰omparator is one of the most important units in ADCs and widely used in electronic systems.The performances of comparators,such as speed, power consumption,noise, and offset,strongly influence the speed,precision and power consumption of ADCs. Voltage detectors,voltage level transformer,voltage-frequency transformer,sampling/track and hold circuit, zero detectors, peak and delay line detectors all utilize comparators. Based on preamplifier-latch theory,this design of the comparator useing pre-amplifier stage with the structure and dynamic latch structure,on the basis of the traditional structure of high-speed comparator circuit switch,application switching operational amplifier technology, improve the resolution and reduce the transmission delay. the comparator includes a preamplifier circuit of fully differential structure,a regenerative latch whose key components are inverters connected end to end,and a simple output stage which is made up of two cross-coupled NMOS transistor and the PMOS common source amplifier.When clock is low, the difference between input signal and reference signal amplified by preamplifier circuit,Preamplifier circuit get a big bandwidth to achieve high gain in the same time,improve the speed of the comparator effectively,Reduces the input offset voltage of the comparator,comparator output corresponding to logic level.When the clock signal is high,the comparator output is latched to high. Key words: high-speed comparator; CMOS; Offset voltag
比较器

模拟比较器:将模拟量与一标准值进行比较,当高于该值时,输出高(或低)电平.反之,则输出低(或高)电平.例如,将一温度信号接于运放的同相端,反相端接一电压基准(代表某一温度),当温度高于基准值时,运放输出高电平,控制加热器关闭,反之当温度信号低于基准值时,运放输出低电平,将加热器接通.这一运放就是一个简单的比较器,因为输入与输出同相,称为同相比较器..有的模拟比较器具有迟滞回线,称为迟滞比较器,用这种比较器,有助于消除寄生在信号上的干扰.数字比较器:用来比较二组二进制数是否相同,相同时输出(或低)高电平,反之,则输出相反的电平.最简单的数字比较器是一位二进制数比较器,是一个异或门(或同或门).电压比较器的作用:它可用作模拟电路和数字电路的接口,还可以用作波形产生和变换电路等。
利用简单电压比较器可将正弦波变为同频率的方波或矩形波电压比较器是集成运放非线性应用电路,他常用于各种电子设备中,那么什么是电压比较器呢?下面我给大家介绍一下,它将一个模拟量电压信号和一个参考固定电压相比较,在二者幅度相等的附近,输出电压将产生跃变,相应输出高电平或低电平。
常用的电压比较器有过零电压比较器、具有滞回特性的过零比较器、滞回电压比较器,窗口(双限)电压比较器.1.模拟比较器将模拟量与一标准值进行比较,当高于该值时,输出高(或低)电平.反之,则输出低(或高)电平.例如,将一温度信号接于运放的同相端,反相端接一电压基准(代表某一温度),当温度高于基准值时,运放输出高电平,控制加热器关闭,反之当温度信号低于基准值时,运放输出低电平,将加热器接通.这一运放就是一个简单的比较器,因为输入与输出同相,称为同相比较器..有的模拟比较器具有迟滞回线,称为迟滞比较器,用这种比较器,有助于消除寄生在信号上的干扰.2.数字比较器用来比较二组二进制数是否相同,相同时输出(或低)高电平,反之,则输出相反的电平.最简单的数字比较器是一位二进制数比较器,是一个异或门(或同或门).电压比较器可以看作是放大倍数接近“无穷大”的运算放大器。
比较器工作原理及应用

电压比较器(以下简称比较器)是一种常用的集成电路。
它可用于报警器电路、自动控制电路、测量技术,也可用于V/F变换电路、A/D 变换电路、高速采样电路、电源电压监测电路、振荡器及压控振荡器电路、过零检测电路等。
本文主要介绍其基本概念、工作原理及典型工作电路,并介绍一些常用的电压比较器。
什么是电压比较器简单地说,电压比较器是对两个模拟电压比较其大小(也有两个数字电压比较的,这里不介绍),并判断出其中哪一个电压高,如图1所示。
图1(a)是比较器,它有两个输入端:同相输入端(“+”端) 及反相输入端(“-”端),有一个输出端Vout(输出电平信号)。
另外有电源V+及地(这是个单电源比较器),同相端输入电压VA,反相端输入VB。
VA和VB的变化如图1(b)所示。
在时间0~t1时,VA>VB;在t1~t2时,VB>VA;在t2~t3时,VA>VB。
在这种情况下,Vout的输出如图1(c)所示:VA>VB时,Vout输出高电平(饱和输出);VB>VA时,Vout输出低电平。
根据输出电平的高低便可知道哪个电压大。
如果把VA输入到反相端,VB输入到同相端,VA及VB 的电压变化仍然如图1(b)所示,则Vout输出如图1(d)所示。
与图1(c)比较,其输出电平倒了一下。
输出电平变化与VA、VB的输入端有关。
图2(a)是双电源(正负电源)供电的比较器。
如果它的VA、VB输入电压如图1(b)那样,它的输出特性如图2(b)所示。
VB>VA 时,Vout输出饱和负电压。
如果输入电压VA与某一个固定不变的电压VB相比较,如图3(a)所示。
此VB称为参考电压、基准电压或阈值电压。
如果这参考电压是0V(地电平),如图3(b)所示,它一般用作过零检测。
比较器的工作原理比较器是由运算放大器发展而来的,比较器电路可以看作是运算放大器的一种应用电路。
由于比较器电路应用较为广泛,所以开发出了专门的比较器集成电路。
两级开环比较器地设计

初级比较器设计一.前言本文主要包括:(1)分析说明比较器工作原理;(2)比较器的设计计算方法;(3)比较器的HSPICE模拟;(4)比较器物理版图设计实现;(5)设计文件列表说明。
传输曲线可以用数学函数表示如下:1()in in f V V +--=,()oh in in ihV when V V V +-->(),()v in in il in in ih A V V whenV V V V +-+--<-< ,,()ol in in il V when V V V +--<(0)(0)()11v v v c cA A A s s s w τ==++ 那么,我们下面就可以分析比较器的时延:根据时延的定义和()v A s ,进行拉普拉斯逆变换,得到输入为阶跃信号min in V 的时域响应如三.比较器的设计比较器的传输时延始终是我们关注的一个重点指标,以下侧重分析时延的限制因素和设计时常常引用的公式。
66()[1oh DD DS DD DD G MIN TP V V V V V V V ⇒=-=---v v2根据基尔霍夫电压环路(KVL )和电流节点(KCL )定理,可以得到该小信号等效电路的方程组并解得:1624676224567624675656()(1/)()()1[(')][()]out m m ds ds c m v in ds n c ds n ds ds n n c n n V s g g r r sC g A s V s s r C M C r C s r r C C C C C -==++++++M ’为密勒因子, (3)估算时延为了计算的方便,()v A s 可以采用节点时间常数近似方法估算,它的另一种表示方式如下:12(0)()(1)(1)v v A A s s s p p =++其中:低频增益161246672467(0)(//)(//)()()m m v m ds ds m ds ds ds ds ds ds g g A g r r g r r g g g g ==++,2411ds ds g g p C +=-,6722ds ds g g p C +=-,1C 为第一级输出极点5的电容,2C 为为第二级输出节点6的电容。
过零比较器,单限比较器,滞回比较器,窗口比较器

一、过零比较器过零比较器,顾名思义,其阈值电压U T=0V。
电路如图(a)所示,集成运放工作在开环状态,其输出电压为+U OM或-U OM。
当输入电压u I<0V时,U O=+U OM;当输入电压u I>0V时,U O=-U OM。
因此,电压传输特性如图(b)所示。
为了限制集成运放的差模输入电压,保护其输入级,可加二极管限幅电路,如右图所示。
★两只稳压管稳压值不同在实用电路中为了满足负载的需要,常在集成运放的输出端加稳压管限幅电路,从而获得合适的U OH和U OL,如图(725)(a)所示。
图中R为限流电阻,两只稳压管的稳定电压均应小于集成运放的最大输出电压U OM。
设稳压管D Z1的稳定电压为U Z1,稳压管D Z2的稳定电压为U Z2,U Z1和U Z2的正向导通电压均为U D。
当u I<0时,由于集成运放的输出电压u/O=+U OM,D Z1使工作在稳压状态,D Z2工作在正向导通状态,所以输出电压u O=U OH=(U Z1+U D)当u I>0时,由于集成运放的输出电压u/O=-U OM,D Z2使工作在稳压状态,D Z1工作在正向导通状态,所以输出电压u O=U OL=-(U Z2+U D)★两只稳压管稳压值相同若要求,U Z1=U Z2则可以采用两只特性相同而又制作在一起的稳压管,其符号如图(b)所示,稳定电压标为±U Z。
当u I<0时,u O=U OH=U Z;当u I>0时,u O=U OL=-U Z。
★稳压管接在反馈通路中限幅电路的稳压管还可跨接在集成运放的输出端和反相输入端之间,如右图所示。
假设稳压管截止,则集成运放必然工作在开环状态,输出电压不是+U OM,就是-U OM。
这样,必将导致稳压管击穿而工作在稳压状态,D Z构成负反馈通路,使反相输入端为“虚地”,限流电阻上的电流i R等于稳压管的电流i Z,输出电压u O=±U Z。
CMOS比较器解读

自动调零技术
理想比较器
-
+ VOS
+ -
(a) VIN
理想比较器 -
+
CAZ -
+ VOS VOS
+ -
(c)
理想比较器
-
VOS
+ +-
VOS
(b)
失调消除方法 (a)包含失调的比较器简单模型;(b)前半个自动较 零周期内存储失调;(c)后半个自动较零周期内输入端抵消失调
迟滞比较器
非迟滞比较器对含有噪声的输入的响应
几种比较器结构的性能比较
开环比较器,特别是多级开环比较器容易做到高速高精度。然而,由于 这类比较器中运放的增益和带宽的折衷,很难做到超高速。此外,多级 开环比较器相比于其他结构的比较器功耗较大,这限制了这类比较器在 超高速高精度中的应用。
迟滞比较器在抗噪声抗干扰环境中具有广泛的应用。然而,它是放大器 在闭环情况下的应用,速度受限。
2 VO Spream p
2 2 VO Slatch V
增益越大越大越好?
预放大级减小比较器输入失调电压原理图
正反馈锁存器前边加一级预放大器,预放大器内部和输出端加载隔离电 路,使得其输出信号多次衰减后到达信号的输入端。加载的隔离电路越 多,回踢噪声衰减的就越大
预放大再生锁存比较器分类
静态预放大再生锁存比较器
VIL
t VIH
t
比较器的传输延迟
比较器的分类及结构
根据放大器的不同应用形式,可以分为开环和闭环两种 按照工作原理划分,可以分为开环比较器和可再生比较器 按照电路结构划分,可以分为单端输出结构比较器和双端输出结
构比较器两种 从功耗的角度,比较器可以分为静态比较器和动态比较器两种
开环比较器
C
20_开环与闭环的比较讲课ppt课件

练习三:台灯控制系统
(1)按钮式台灯控制系统是 __(开环/闭环)控制系统。 (2旋钮式可调光台灯控制系统是 __(开环/闭环)控制
系统。
14
• 练习四: 投篮活动
(3) 在画圆过程人对粉笔的控制可视为一个
__ 关有键检看 测1其装检置测就篮到是的闭球信环号控赛是制来系上自统于?,输入球端 员的一次投篮活动是
系统的输出量返回到系统的输入端并对控制过程产生影 响的控制。
4
定义特征化:
开环控制系统: 1、是个单程的控制流向。 2、不能对控制结果加以修正、调节。 闭环控制系统: 1、有反馈; 2、会调整; 3、被控量会被控制在一定的值——结果稳定; 4、“结果”会影响“结果”; 5、给定量与被控量是可比较的同一种性质的量。
被控量
对控制对象所产生作用
控制量
7
3.关于检测装置 【探究】
有检测装置就是闭环控制系统?
P103.案例分析• 当人走进自动门时,红外线装置检测到人体红外
线信号,然后通过处理电路,启动电机的正转和 反转,实现开门和关门。 • [思考] • 这个控制系统中也存在检测装置,案例分析为何定 其为开环控制系统?
• 练习五: 十字路口的红路灯控制系统
1 红路灯定时控制系统是 __(开环/闭环)控制系统。 2 根据车流量而改变的红路灯控制系统 __(开环/闭环)控
制系统。
16
四、拓展延伸
【 辨析】
开环控制系统都是人工控制系统, 闭环控制系统都是自动控制系统。
17
驾驶汽车
手动驾驶汽车
“斯坦利”无人自动驾驶汽车
开环与闭环的比较
1
一、导入
小游戏 ——“画圆”
要求:某同学分别在睁眼和闭眼的情况下, 在黑板上给正方形画内切圆。
两级开环比较器的设计.pptx
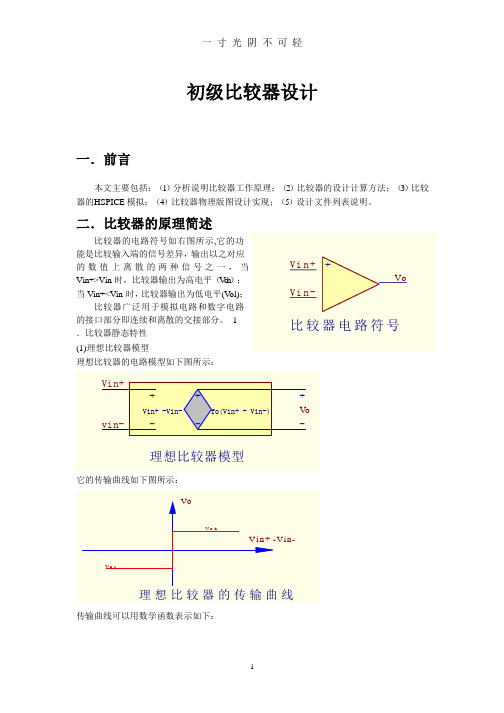
Av (Vin Vin ), whenVil (Vin Vin ) Vih
Vol, , when(Vin Vin ) Vil
Av
Voh Vol VihV il
,为一个有限值
(3)包含输入失调电压的比较器 包含输入失调电压比较器电路模型如下图所示:
2
一 寸 光 阴 不 可轻
Vin+ +
+ - V in+'
+
+
Vin+'-Vin-'
fo(Vin+' - Vin-') Vo
vin-
-v in-'
-
-
包含输入失调电压比较器模型
它的传输曲线如下图所示:
Vo
Vo s
Vo h
V il V ih
Vo l
Vin+ -Vin-
包含输入失调电压比较器的传输曲线
其中的 Vos 为输入失调电压,它被定义为:实际比较器输出电压为零时,输入端所加的电压, 它是比较器的一个重要参数,跟比较器的精度有密切的关系,而且它的温漂很难补偿。 (4)比较器其他的静态特性 差分输入电阻和电容,输出电阻,共模输入电阻,共模输入电压范围,还有和过度区特性相 关联的噪声。这些和运放很相似,可以同样建模。 2.单极点简单比较器动态特性
5
一寸光阴不可轻
Vol Vss
(2)两级比较器的特性 A 部分 .第一级简单CMOS OTA 特性 由以上的电路原理图可以得到第一级简单 COMS OTA 的小信号等效电路如下图所示:
1 + Vg s1
比较器动态特性中的重要特性之一为传输时延,定义比较器的时延为:比较器的输入激 励和输出转换之间的时延,如下图所示:
四电压比较器LM339的常用方法

四电压比较器LM339的常用方法LM339是一种四电压比较器,常用于逻辑电路、信号处理和测量等领域。
它具有低功耗、高精度、快速响应和可靠性等特点,同时支持单电源运作。
本文将介绍LM339的常用方法。
1.基本比较器电路:LM339是一种开环比较器,它有四个独立的比较器,每个比较器都有一个非反相输入端(IN-)和一个反相输入端(IN+)。
基本比较器电路由一个电阻分压电路决定,可以将输入电压映射到比较电压。
当输入电压超过比较电压时,输出电平将翻转。
2.阈值电平偏置:在一些应用中,我们希望在一个中心电压附近进行比较。
为此,可以使用阈值电平偏置电路。
通过将一个电阻分压电路连接到非反相输入端,可以设置比较电压的阈值。
3.反馈电路:反馈电路可用于增加LM339的增益和稳定性。
一个常见的反馈电路是焊接电桥,它使用负反馈来提供精确的比较功能。
焊接电桥的输入电压通过一个电阻分压电路进行比较,通过负反馈调整电阻值来匹配所需的电压比较。
4.窗口比较器:窗口比较器是一种特殊的应用,可以同时比较两个不同的电压范围。
该应用通常用于电池管理、温度控制等。
窗口比较器可以通过将两个基本比较器连接在一起实现。
每个比较器负责限制输入电压的上下限,当输入电压超出所设置的范围时,相应的比较器输出将翻转。
5.电流传感:由于LM339的高精度和可靠性,它常用于电流传感应用。
通过将电阻与电流传感器连接在一起,可以将电流转换为电压,并通过LM339比较器输出电平来表示电流大小。
6.器件保护:为了确保LM339的正常工作,需要采取一些保护措施。
例如,可以在输入端添加电流限制电阻,用于限制输入电流的大小。
此外,还可以添加电源去耦电容来消除电压噪声和功率供应波动对性能的影响。
7.应用扩展:除了上述常见的应用方法之外,LM339还可以通过级联多个比较器来实现更复杂的功能。
例如,可以使用它们来实现数字模拟转换(ADC)或脉冲宽度调制(PWM)等功能。
总结:LM339是一种高性能的四电压比较器,常用于逻辑电路、信号处理和测量等领域。
基本比较器电路

基本比较器电路基本比较器电路是一种常用的电子电路,用于比较两个输入电压的大小,并输出相应的电平信号。
它在数字电路设计、模拟电路设计以及传感器信号处理等领域中广泛应用。
本文将从基本比较器电路的工作原理、常见类型以及应用方面展开介绍。
基本比较器电路的工作原理是通过将输入电压与参考电压进行比较,然后根据比较结果输出高电平或低电平信号。
常见的基本比较器电路有几种类型,包括差动比较器、开环比较器和窗口比较器。
差动比较器是最简单的一种基本比较器电路,它由一个差动放大器和一个阈值电压组成。
当输入电压高于阈值电压时,输出为高电平;当输入电压低于阈值电压时,输出为低电平。
差动比较器常用于模拟电路中的信号处理,如滤波、增益等。
开环比较器是另一种常见的基本比较器电路,它由一个比较器和一个正反馈网络组成。
开环比较器可以提供较高的增益和灵敏度,但容易产生振荡。
在数字电路设计中,开环比较器常用于模拟信号的转换和处理。
窗口比较器是一种特殊的基本比较器电路,它可以同时比较两个阈值电压。
当输入电压在两个阈值电压之间时,输出为高电平;当输入电压在两个阈值电压之外时,输出为低电平。
窗口比较器常用于传感器信号处理中,如温度、光强等传感器。
基本比较器电路的应用非常广泛。
在模拟电路设计中,基本比较器电路常用于信号的比较和转换。
在数字电路设计中,基本比较器电路常用于逻辑门电路、计数器和时序电路等。
此外,基本比较器电路还可以应用于传感器信号的处理和控制系统中。
基本比较器电路是一种常用的电子电路,通过比较输入电压和参考电压的大小,输出相应的电平信号。
它具有简单、稳定和可靠的特点,在数字电路设计、模拟电路设计以及传感器信号处理等领域中有着广泛的应用。
希望本文可以为读者提供一些关于基本比较器电路的基础知识和应用方面的参考。
电路中的比较器设计与分析

电路中的比较器设计与分析在电子电路设计中,比较器是一种常用的电路元件,用于比较输入信号,并产生输出信号以表示两个信号的关系。
比较器广泛应用于模拟电路和数字电路中,具有很高的实用性。
本文将介绍比较器的设计原理和分析方法,为读者提供一些有关电路中比较器的设计与分析的基本知识和技巧。
一、比较器的基本原理和分类比较器是一种电子设备,它的输入有两个或多个信号,而输出则是一个用于表示输入信号关系的二进制位。
比较器的基本原理是将两个输入信号进行比较,并产生相应的输出信号。
根据输入信号的类型和输出信号的形式,比较器可以分为模拟比较器和数字比较器两种类型。
1. 模拟比较器:模拟比较器适用于将输入电压信号进行比较,并产生相应的模拟输出信号。
模拟比较器的输出信号通常是一个连续变化的模拟电压信号,可以用于模拟电路中的各种应用,如比较两个模拟信号的大小、判断输入信号的高低电平等。
2. 数字比较器:数字比较器适用于将输入信号进行数字比较,并产生相应的数字输出信号。
数字比较器的输出信号通常是一个二进制位,用于表示两个或多个输入信号的大小关系。
数字比较器主要应用于数字电路或微处理器系统中,用于实现逻辑比较、数据排序和状态判断等功能。
二、模拟比较器的设计与分析模拟比较器是电路中常见的一种元件,用于对输入电压进行比较,并产生相应的输出电压。
常见的模拟比较器电路包括基本比较器、窗限比较器和振荡比较器等。
下面分别介绍这三种常见的模拟比较器电路的设计与分析。
1. 基本比较器:基本比较器是一种最简单的比较器电路,由一个比较元件和电压供应电源组成。
比较元件通常是根据输入电压产生不同输出电压的二极管或晶体管。
基本比较器的设计原理是根据输入电压与参考电压之间的关系,产生相应的输出电压。
2. 窗限比较器:窗限比较器是一种能够对输入电压进行范围限制的比较器电路。
窗限比较器通常由两个比较元件和两个参考电压组成,用于判断输入信号是否在指定的范围内。
窗限比较器的设计原理是通过比较输入电压与两个参考电压之间的关系,判断输入信号是否在指定的范围内,并产生相应的输出信号。
运算比较器电路

运算比较器电路全文共四篇示例,供读者参考第一篇示例:运算比较器电路是一种常见的电子电路,用于比较两个输入信号的大小,并输出一个相应的电压信号。
它被广泛应用于电子设备中的各种功能模块,如自动控制系统、传感器信号处理、数字信号处理等领域。
本文将介绍运算比较器电路的工作原理、特点、应用和设计方法。
一、工作原理运算比较器电路是由运算放大器和电阻网络组成的电路。
运算放大器是一种特殊的集成电路,具有高输入阻抗、高增益、低输出阻抗等特点。
它的工作原理是将两个输入信号分别连接到运算放大器的两个输入端,通过反馈电阻网络实现信号的比较和放大,最终输出一个比较结果。
在运算比较器电路中,通常将一个输入信号作为比较器的基准信号,另一个输入信号作为被比较的信号。
当被比较的信号大于基准信号时,输出信号为高电平;当被比较的信号小于基准信号时,输出信号为低电平。
通过这种方式,可以实现对输入信号的比较和判断。
二、特点1.高精度:运算比较器电路采用运算放大器作为比较器的核心组件,具有高增益、低漂移、高稳定性等特点,可以实现高精度的比较和判断。
2.快速响应:由于运算放大器具有高速度和快速响应的特点,运算比较器电路可以实现快速的信号比较和输出,适用于对输入信号的实时判断。
3.灵活性:运算比较器电路可以根据实际需求进行灵活设计和调整,可实现不同的比较功能和输出模式,满足不同应用场景的需求。
4.低功耗:运算比较器电路采用集成电路和低功耗元件设计,具有低功耗、高效率的特点,适用于电池供电和功耗敏感的应用。
5.可靠性:运算比较器电路具有简单、稳定、可靠的特点,具有抗干扰、抗干扰能力,适用于工业控制、仪器仪表和传感器领域。
三、应用领域1.模拟比较器电路:用于模拟信号的比较和检测,常用于电压比较、电流检测、阈值控制等应用。
3.自动控制系统:用于实现对输入信号的比较和判断,常用于自动控制、过程控制、传感器信号处理等应用。
4.信号处理系统:用于对输入信号进行滤波、增益、补偿等处理,常用于仪器仪表、音频处理、图像处理等应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初级比较器设计一.前言本文主要包括:(1)分析说明比较器工作原理;(2)比较器的设计计算方法;(3)比较器的HSPICE模拟;(4)比较器物理版图设计实现;(5)设计文件列表说明。
1()in in f V V +--=,()oh in in ihV when V V V +-->(),()v in in il in in ih A V V whenV V V V +-+--<-<(0)(0)()11v v v c cA A A s s s w τ==++ 那么,我们下面就可以分析比较器的时延:根据时延的定义和()v A s ,进行拉普拉斯逆变换,得到输入为阶跃信号min in V 的时域响应如下式://min (0)[1](0)[1]2(0)tp c tp c oh ol oh ol v in v v V V V VA e V A e A ττ----=-=- ⇒max ln(2)0.693tp c c ττ==同理可以得到更为普遍的结果:当输入激励信号为阶跃信号min in kV ,相应得输出响应时延为:三.比较器的设计比较器的传输时延始终是我们关注的一个重点指标,以下侧重分析时延的限制因素和设计时常常引用的公式。
1.两级开环比较器的线性响应设计NMOS输入管两极开环比较器的电路拓扑结构如下图所示:66()[1oh DD DS DD DD G MIN TP V V V V V V V ⇒=-=--- 显然,ol ss V V =(2)两级比较器的特性 A 部分.第一级简单CMOS OTA 特性v v 效电路中的所有电容为0,于是可以得到如下的方程组:2244541141221()out m gs m gs n gs m gs n m m gs gs V g V g V r V g V r g g V V =-+=-==-114114511445()(1)out m gs m m gs n n m gs m n n V g V g g V r r g V g r r ⇒=+=+12ings V V =----------------------------------------------------------------关;M3二极管连接方式决定了节点4的时间常数很小也不可能形成主极点;最有可能形成主极点的地方为节点5和节点6,即第一级的节点电容对整体电路的特性没有决定作用,利用A部分的分析结果可以得到整体电路的小信号等效电路如下图所示:组并解得:1624676224567624675656()(1/)()()1[(')][()]out m m ds ds c m v in ds n c ds n ds ds n n c n n V s g g r r sC g A s V s s r C M C r C s r r C C C C C -==++++++ M ’为密勒因子, (3)估算时延为了计算的方便,()v A s 可以采用节点时间常数近似方法估算,它的另一种表示方式如下:12(0)()(1)(1)v v A A s s s p p =++其中:低频增益161246672467(0)(//)(//)()()m m v m ds ds m ds ds ds ds ds ds g g A g r r g r r g g g g ==++,2411ds ds g g p C +=-,6722ds ds g g p C +=-,1C 为第一级输出极点5的电容,2C 为为第二级输出节点6的电容。
假设输入激励信号为Vin,那么在S 域的电路响应为:Vo(s)= ()v A s Vin(s),对它进行拉普拉斯逆变换可以得到时域的响应为:/1/2211212()(0)[1]()t t o v in p e p e V t A V t p p p p ττ--=+---,其中2416721(//),2(//)ds ds ds ds r r C r r C ττ==,根据这个时域响应可以估算比较器的线性响应传输时延,为了计算方便,对该式进行级数展开得 :2221()(0)[1(1...)(1...)]1212n n o n v in n n t m t m V t A V t mt m m ≈--+++-++--,其中,211,1n p p tm t t p τ=== 再进一步简化得:2(0)()2n v ino n mt A V V t ≈令()()/2o n oh ol V t V V =+,解得:pn t ===1pn tp t τ⇒==,(21min,in p Vinm k p V ==),这就是估算线性线性响应传输时延的关系式。
附带说明一下如何选择摆率受限或线性响应受限来估算比较器的传输时延:为了比较线性响应受限和摆率受限,我们对/1/2211212()(0)[1]()t t o v in p e p e V t A V t p p p p ττ--=+---进行归1化处理得:()'21(0)11()1,1,111o n n n v inV t t mt o n n A V p m tV t e e m t tp m m p τ--==-+=≠==--其中:, 对上式进行两次求导并令其等于0可以得到归一化响应的最大斜率为:ln ln '11max()[]1m mm o n m m ndV t me e dt m ----=--------------()而两级开环比较器的输出摆率为:72I SR C -=-------------() 26676722()DD G MINTP V V V I I ISR C C β+----==------------ 比较()、和(),当min in in V V >且摆率比()小时,则应采用摆率来估算比较器电路的时延。
需要特别强调的是:如果是线性响应受限则极点的位置十分重要,如果是摆率受限则对电容的充放电的能力变得更为重要。
(4)设计常用公式:为设计方便,现将常用的设计公式及步骤总结如下:①276212N Pp C p p I I λλ====+ ②667722667722,'()'()P SD SAT N DS SAT W I W I L K V L K V ==,67,SD SAT dd oh DS SAT ol ss V V V V V V =-=- ③115722C C I I C =假设一个的值,计算 ④3542343'()P SG TP W I W L L K V V ==-,3SG dd icm TN V V V V +=-+⑤2467166(0)()(),v ds ds ds ds m m m A g g g g g g g ++==2112125min,(0)m oh ol v N in g V V W W A L L K I V -=== ⑥124624gd gd gs bd bd C C C C C C =++++22123221234412344123()2()()2()AD W L L L PD W L L L AD W L L L PD W L L L =++=+++=++=+++计算出C1,如果计算出的C1大于在第三步中假设的C1,则必须加大C1且重复3~6的步骤,直道计算出来的C1小于假设的C1为止。
⑦55512552,'()DS SAT icm GS ss N DS SAT W I V V V V L K V -=--=,如果5DS SATV 小于100mV 则增大11W L 2.两级开环比较器的摆率响应设计 (1)设计中用到的分析方法设计中的分析法方法法和“1”部分讲解的类同,重点要理解电路的小信号等效电路,并利用根据基尔霍夫电压环路(KVL )和电流节点(KCL )定理来求解,并进行设计计算。
(2)时延的估算在大多数的情况下,两级开环比较器会被驱动到摆率受限,此时,传输时延由下式计算:i i i ii idv vi C C dt t ∆==∆,其中:Ci 为第i 级的对地电容,由该式可以得到第i 级的传输时延为:i i i ii V t t C I ∆=∆=,总的传输时延为ii i iV tp C I ∆=∑。
(2)设计常用公式为设计方便,现将常用的设计公式及步骤总结如下: ①2762()out oh ol dv C V V I I C dt tp-=== ②667722667722,'()'()P SD SAT N DS SAT W I W I L K V L K V ==,67,SD SAT dd oh DS SAT ol ss V V V V V V =-=- ③假设一个C1值并在以后检查 ④1151()o oh ol dv C V V I C dt tp-=≈ ⑤3542343'()P SG TP W I W L L K V V ==-,3SG dd icm TN V V V V +=-+⑥2467166(0)()(),v ds ds ds ds m m m A g g g g g g g ++==2112125min,(0)m oh ol v N in g V V W W A L L K I V -===⑦124624gd gd gs bd bd C C C C C C =++++22123221234412344123()2()()2()AD W L L L PD W L L L AD W L L L PD W L L L =++=+++=++=+++计算出C1,如果计算出的C1大于在第三步中假设的C1,则必须加大C1且重复3~6的步骤,直道计算出来的C1小于假设的C1为止。
⑧55512552,'()DS SAT icm GS ss N DS SAT W I V V V V L K V -=--=,如果5DS SATV 小于100mV 则增大11W L 3.复合比较器(前置线性放大级+锁存再生级)设计M9和M10构成,而其他的M5、M6和M11是动态时钟控制开关管。
为了保证最小的传输时延,它的设计思想在于:强调前级的大带宽和后级的高摆率,前级按负指数响应把输入信17921111792111111()()()'0o m m o o o m m o o o o g g V GV sC V g g V GV sC V C V s +++-=+++-=2810122228101222222'()()()'0o m m o o o m m o o o o V g g V G V sC V g g V G V sC V C V s+++-=+++-=⇒79179111112121111()()1''111111m m m m o o o o o g g R g g R R C V V V V V sR C sR C s s τττ++=-=-++++8102810222221212222()()2''112121m m m m o o o o o g g R g g R R C V V V V V sR C sR C s s τττ++=-=-++++其中:11221,2R C R C ττ==假设MOS 管采用对称设计使他们的跨导相等,令:79810m m m m m g g g g g ====,12,R R R ==12,12C C C τττ====,2121,''o o o i o o V V V V V V ∆=-∆=-,则可以解得:12'(12)'1112iim o m m V V g R V V s s g R s g Rττττττ∆∆-∆∆===+-++-,其中:'12m g R ττ=-求上式的拉普拉斯逆变换的时域响应为:(12)/2///'()'m m L t g R g Rt t t o i i i i v t V e V e e V e V ττττ---∆=∆=∆≈∆=∆,即: /()L t o i v t e V τ∆=∆其中:0.342L m C g Rττ=== 要求锁存器级的传输时延,可以令:/()()/2Lt o i oh ol v t e V V V τ∆=∆=-,解得传输时延为:ln()2oh olL iV V tp V τ-=∆,显然要改善传输时延应该从L τ和i V ∆两方面着手解决。
