第一讲答案
高思奥数一年级下册含答案第1讲 认识奇与偶

第一讲认识奇与偶前续知识点:一年级第一讲;XX模块第X讲后续知识点:X年级第X讲;XX模块第X讲林林你看!我今天买了一个魔法棒!按一下会变成紫色,再按一下会变成黄色!我也好想玩啊!啊!你怎么在偷玩田田的魔法棒!总是按会坏的!林林怎么知道我说谎了?萱萱卡莉娅卡莉娅萱萱阿呆阿呆阿呆萱萱我只按了4下……你说谎!我要去告诉田田!萱萱小高小高把相应的人物换成红字标明的人物. 魔法棒的颜色不要改变.大家还记得我们的好朋友单数和双数吗?今天我们来学习它们的另一个名字:奇数和偶数.单数的另一个名字叫做奇数,双数的另一个名字叫做偶数.大家记住了吗?例题1下面有10个数,请你分一分,哪些是奇数,哪些是偶数?【提示】奇数就是单数,偶数就是双数.练习1下面有8个数,请你分一分,哪些是奇数,哪些是偶数?大家认识奇数与偶数了吗?关于奇数与偶数,其中有许多规律,在生活中也是经常会用到的!我们一起来探索一下它们的规律吧!1256 314 5 238 567871 49682102153 6721524 93618例题2灰灰回到家,发现灯不亮,于是他按一下开关,灯就亮了,再按一下又不亮了……淘气的灰灰一连按了6下开关,请你说说,这时灯是亮的,还是不亮的?如果连按了9下呢?【提示】按的次数和灯是否亮有什么关系?找一找规律吧!练习2圣诞节的时候,商店门口挂了一排彩灯,它们按照红黄红黄红黄……的顺序进行排列.你知道第9个是什么颜色的灯吗?第18个呢?例题3小企鹅呆呆在南极一条小河的两岸之间来回的游.若规定呆呆从一岸游到另一岸就叫渡河一次,请想一想:如果呆呆最初在左岸,那么渡河13次后,它最后游到了左岸,还是游到了右岸?【提示】小企鹅第1次渡河后游到了哪一岸呢?小河右岸左岸练习3一只小青蛙在小河的两岸之间来回的游.从一岸游到另一岸叫渡河一次,请想一想:如果小青蛙最初在右岸,那么渡河16次后,小青蛙最后游到了左岸,还是游到了右岸?前面我们研究了奇数与偶数的规律在生活中的应用,在加减法计算中,奇数与偶数也有巧妙的运用哦!例题4不用计算,你能判断下列算式的结果是奇数还是偶数吗?在对的下面画“√”.7+9 (奇数,偶数) 4+18(奇数,偶数) 4+15(奇数,偶数) 5+11(奇数,偶数) 16+26(奇数,偶数) 12+13(奇数,偶数) 15-7(奇数,偶数) 18-6 (奇数,偶数) 27-12(奇数,偶数) 29-5(奇数,偶数) 30-14(奇数,偶数) 23-8 (奇数,偶数)【提示】算式中的每个数是奇数还是偶数?练习4不用计算,你能判断下列算式的结果是奇数还是偶数吗?在对的下面画“√”.9+13(奇数,偶数) 28+12(奇数,偶数) 16+11(奇数,偶数)7+21(奇数,偶数) 26+34(奇数,偶数) 18+29(奇数,偶数) 11-3(奇数,偶数) 24-12(奇数,偶数 ) 36-11(奇数,偶数) 23-7(奇数,偶数) 38-24(奇数,偶数) 34-19(奇数,偶数)你发现上面的规律了吗?奇数+奇数=偶数,偶数+偶数=偶数,奇数+偶数=奇数.减法也是这样的规律.小 河右岸左岸在题目中,我们也会遇到多个数相加的情况,怎样才能在不算出结果的情况下,快速判断出一个算式的结果是奇数还是偶数呢?我们一起来看看下面的题目吧!例题5算式1+2+3+4+5+6+7+8+9的结果是奇数还是偶数?【提示】两两相加,试一试.例题6美美买了15瓶饮料,全部分给亮亮和欢欢,想要分给每人奇数瓶饮料,她能成功吗?为什么呢?【提示】15是奇数还是偶数?课堂内外谁说谎了?唐僧师徒四人取经路上在一个道观借宿,观中童子端出15个人参果招待他们.全部吃完后,唐僧和沙僧都说自己吃了奇数个人参果,孙悟空和猪八戒都说自己吃了偶数个人参果,童子马上对他们四个人说:“你们有人说谎!”你知道童子是怎样知道他们当中有人说谎的吗?我们都吃了奇数个人参果.我们都吃了偶数个人参果.作业1. 下面有10个数,请你分一分,哪些是奇数,哪些是偶数?2. 小熊买了一个可爱的手电筒,手电筒上有一个按钮.手电筒现在不亮,按一下按钮,就亮了,再按一下又不亮了……淘气的小熊一连按了5下按钮,这时手电筒是亮的,还是不亮的?如果连按了8下,手电筒是亮的,还是不亮的?3. 小鸭子松松在一条小河的两岸之间来回的游.若规定松松从一岸游到另一岸叫渡河一次,请想一想:如果松松最初在左岸,渡河11次后,松松最后游到了左岸,还是游到了右岸?4. 不计算,你能判断下列算式的结果是奇数还是偶数吗?在对的下面画“√”.右岸小 河左岸24 71 273 1676529530 19 56 188奇数偶数21-7(奇数,偶数)21-18(奇数,偶数)11+13(奇数,偶数)12+6(奇数,偶数)21+22(奇数,偶数)19-17(奇数,偶数)8+13(奇数,偶数)20-10(奇数,偶数)29-4 (奇数,偶数)5. 算式11+14+19+26+37的结果是奇数还是偶数?第一讲认识奇与偶1.例题1答案:奇数:9、15、21、53、67;偶数:2、10、18、24、36详解:奇数是单数的大名,偶数是双数的小名.判断一个数是奇数还是偶数,应该从这个数的个位入手.个位为1、3、5、7、9的数就是奇数,个位为0、2、4、6、8的数就是偶数.2.例题2答案:连按6下,灯是不亮的,连按9下,灯是亮的详解:记录初始状态(可记为0),如下图:观察表格规律容易发现,亮和不亮是交替出现的,结合奇数与偶数的规律,即可发现,按奇数下灯是亮的,按偶数下灯是不亮的.3.例题3答案:渡河13次后,它游到了右岸详解:记录初始状态(可记为0),如下图:本题的难点在于理解渡河几次,渡河1次的时候是从左岸到右岸的过程,最终状态是在右岸.按规律发现,渡河奇数次后在右岸,渡河偶数次后是在左岸.4.例题4答案:7+9 (偶数)4+18(偶数)4+15(奇数)5+11(偶数)16+26(偶数)12+13(奇数)15-7(偶数)18-6 (偶数)27-12(奇数)29-5(偶数)30-14(偶数)23-8 (奇数)详解:奇数+奇数=偶数,偶数+偶数=偶数,奇数+偶数=奇数奇数-奇数=偶数,偶数-偶数=偶数,奇数-偶数=奇数.5.例题5答案:结果是奇数详解:这个算式中一共有5个奇数:1、3、5、7、9.这5个奇数两两配对,那么一共可以配成2对和1个单独的奇数.奇数的个数与结果的奇偶有关系:当奇数的个数为奇数时,结果为奇数;当奇数的个数为偶数时,结果为偶数.6.例题6答案:不能详解:因为15是奇数,奇数=奇数+偶数=偶数+奇数,不可能都是奇数,所以不会成功的.7.练习1答案:奇数:5、49、567、871;偶数:238、314、682、1256简答:个位为1、3、5、7、9的数就是奇数,个位为0、2、4、6、8的数就是偶数.8.练习2答案:第9个是红色的彩灯,第18个是黄色的彩灯简答:商店彩灯是按照红黄红黄……的顺序排列的,第1个是红色的;第2个是黄色的,第3个是红色的;第4个是黄色的,第5个是红色的;第6个是黄色的,由此可以看出第奇数个灯是红色的;第偶数个灯是黄色的.第9个是红色,第18个是黄色.9.练习3答案:渡河16次后,它游到了右岸简答:小青蛙最初在右岸,渡河16次,说明小青蛙游的次数是偶数,那么小青蛙最后游到了右岸.10.练习4答案:9+13(偶数)28+12(偶数)16+11(奇数)7+21(偶数)26+34(偶数)18+29(奇数)11-3(偶数)24-12(偶数)36-11(奇数)23-7(偶数)38-24(偶数)34-19(奇数)简答:奇数+奇数=偶数,偶数+偶数=偶数,奇数+偶数=奇数奇数-奇数=偶数,偶数-偶数=偶数,奇数-偶数=奇数.11.作业1答案:奇数:19、71、95、167、273;偶数:24、30、56、188、652简答:个位为1、3、5、7、9的数就是奇数,个位为0、2、4、6、8的数就是偶数.12.作业2答案:亮;不亮简答:按1下,手电筒是亮的,按2下,手电筒是不亮的,按3下,手电筒是亮的,按4下,手电筒是不亮的……由此可推出,按奇数次,手电筒是亮的,按偶数次,手电筒是不亮的.13.作业3答案:右简答:如果松松最初在左岸,渡河1次后,松松在右岸,渡河2次后,松松在左岸,渡河3次后,松松在右岸,渡河4次后,松松在左岸……由此可推出,渡河奇数次,松松在右岸,渡河偶数次,松松在左岸.14.作业4答案:21-7(偶数)21-18(奇数)11+13(偶数)12+6(偶数)21+22(奇数)19-17(偶数)8+13(奇数)20-10(偶数)29-4 (奇数)简答:奇数+奇数=偶数,偶数+偶数=偶数,奇数+偶数=奇数奇数-奇数=偶数,偶数-偶数=偶数,奇数-偶数=奇数15.作业5答案:奇简答:这个算式中一共有3个奇数:11、19、37.这3个奇数两两配对,那么一共可以配成1对和1个单独的奇数.奇数的个数与结果的奇偶有关系:当奇数的个数为奇数时,结果为奇数;当奇数的个数为偶数时,结果为偶数.。
第一讲绪论(参考答案)

第一讲绪论(13级临床1-10班、麻醉)参考答案一单项选择题试题1 满分值:1.0分状态:已答实际得分:分试题: 遗传病最基本的特征是()先天性家族性遗传物质改变罕见性不治之症[参考答案] 遗传物质改变[我的答案] 遗传物质改变试题2 满分值:1.0分状态:已答实际得分:分试题: 遗传病特指()先天性疾病家族性疾病遗传物质改变引起的疾病不可医治的疾病既是先天的,也是家族性的疾病[参考答案] 遗传物质改变引起的疾病[我的答案] 遗传物质改变引起的疾病试题3 满分值:1.0分状态:已答实际得分:分试题: *有些遗传病家系看不到垂直遗传的现象,这是因为()该遗传病是体细胞遗传病该遗传病是线粒体病该病是性连锁遗传病该遗传病具有传染性以上都不是[参考答案] 该遗传病是体细胞遗传病[我的答案] 以上都不是试题4 满分值:1.0分状态:已答实际得分:分试题: *种类最多的遗传病是()单基因病多基因病染色体病体细胞遗传病线粒体病[参考答案] 单基因病[我的答案] 单基因病试题5 满分值:1.0分状态:已答实际得分:分试题: *下列发病率最高的遗传病是()单基因病多基因病染色体病线粒体病不能确定[参考答案] 多基因病[我的答案] 多基因病试题6 满分值:1.0分状态:已答实际得分:分试题: 关于先天性疾病、家族性疾病和遗传性疾病,下列哪种说法是正确的()先天性疾病一定是遗传性疾病家族性疾病都是遗传性疾病大多数遗传性疾病为先天性疾病,且往往表现为家族性疾病遗传性疾病一定是先天性疾病,但不一定是家族性疾病遗传性疾病一定是家族性疾病,但不一定是先天性疾病[参考答案] 大多数遗传性疾病为先天性疾病,且往往表现为家族性疾病[我的答案] 大多数遗传性疾病为先天性疾病,且往往表现为家族性疾病试题7 满分值:1.0分状态:已答实际得分:分试题: 先天性疾病是指()出生时即表现出来的疾病先天畸形遗传性疾病非遗传性疾病以上都不是[参考答案] 出生时即表现出来的疾病[我的答案] 出生时即表现出来的疾病试题8 满分值:1.0分状态:已答实际得分:分试题: 有关遗传病不正确的说法是( )遗传病是一种先天性疾病遗传病具有家族聚集的特征先天性疾病不一定都是遗传病遗传病的发生必定涉及DNA序列的改变家族性疾病不一定都是遗传病[参考答案] 遗传病是一种先天性疾病[我的答案] 遗传病的发生必定涉及DNA序列的改变试题9 满分值:1.0分状态:已答实际得分:分试题: 下列哪种病不是遗传病()白化病Down综合征精神分裂症坏血病线粒体病[参考答案] 坏血病[我的答案] 坏血病试题10 满分值:1.0分状态:已答实际得分:分试题: 下列哪类疾病可能不是遗传病()单基因病多基因病染色体病先天性疾病线粒体病[参考答案] 先天性疾病[我的答案] 先天性疾病试题11 满分值:1.0分状态:已答实际得分:分试题: 下列哪类疾病可能不是遗传病()染色体病单基因病多基因病家族性疾病线粒体病[参考答案] 家族性疾病[我的答案] 家族性疾病试题12 满分值:1.0分状态:已答实际得分:分试题: 完全由环境因素决定发病的疾病是()乙型肝炎抑郁症高血压外伤肿瘤[参考答案] 外伤[我的答案] 外伤试题13 满分值:1.0分状态:已答实际得分:分试题: *乙型肝炎发病()仅受遗传因素控制主要受遗传因素影响,但需要环境因素的调节以遗传因素影响为主和环境因素为辅以环境因素影响为主和遗传因素为辅仅受环境因素影响[参考答案] 以环境因素影响为主和遗传因素为辅[我的答案] 以遗传因素影响为主和环境因素为辅试题14 满分值:1.0分状态:已答实际得分:分试题: 环境因素诱导发病的单基因病为()Huntington舞蹈病蚕豆病白化病血友病A镰形细胞贫血[参考答案] 蚕豆病[我的答案] 蚕豆病试题15 满分值:1.0分状态:已答实际得分:分试题: 美国白种人冠心病发病率较当地华人高,由此判断其发病与遗传因素有关,得此结论是基于()医学遗传学研究方法群体普查法双生子法种族差异比较法疾病组分分析法伴随性状研究法[参考答案] 种族差异比较法[我的答案] 种族差异比较法试题16 满分值:1.0分状态:已答实际得分:分试题: O型血型者十二指肠溃疡发病率较其他血型高30%~40%,由此判断其发病与遗传因素有关,得此结论是基于()医学遗传学研究方法伴随性状研究法基因分析法疾病组分分析法系谱分析法群体筛查法[参考答案] 伴随性状研究法[我的答案] 伴随性状研究法试题17 满分值:1.0分状态:已答实际得分:分试题: 下列哪一项不是判断疾病是否具有遗传基础的研究方法()生化检查法系谱分析法双生子法疾病组分分析法群体筛查法[参考答案] 生化检查法[我的答案] 生化检查法试题18 满分值:1.0分状态:已答实际得分:分试题: 对一些发病机理不清的复杂疾病,要研究其遗传基础可采取的方法是( )群体普查法系谱分析法双生子法疾病组分分析法染色体分析法[参考答案] 疾病组分分析法[我的答案] 疾病组分分析法试题19 满分值:1.0分状态:已答实际得分:分试题: 用比较发病的一致性的差异来估计某种疾病是否有遗传基础,通常采用的方法是()群体普查法系谱分析法双生子法疾病组分分析法关联分析法[参考答案] 双生子法[我的答案] 双生子法试题20 满分值:1.0分状态:已答实际得分:分试题: 哪些人是你的二级亲属()父母子女外祖父母曾祖父母表兄弟姐妹[参考答案] 外祖父母[我的答案] 外祖父母二不定项选择题试题1 满分值:1.0分状态:已答实际得分:分试题: *关于遗传病,下列说法正确的有()由于遗传物质发生改变所引起的疾病在上下代之间垂直传递遗传病的发生与环境因素无关在世代间进行传递的不是表型,而是异常改变的遗传物质终生携带[参考答案]由于遗传物质发生改变所引起的疾病在上下代之间垂直传递在世代间进行传递的不是表型,而是异常改变的遗传物质终生携带[我的答案]终生携带在世代间进行传递的不是表型,而是异常改变的遗传物质在上下代之间垂直传递由于遗传物质发生改变所引起的疾病试题2 满分值:2.0分状态:已答实际得分:分试题: 判断是否是遗传病的指标为()患者亲属发病率随亲属级别下降而下降患者亲属发病率随亲属级别下降而升高患者亲属发病率不随亲属级别变化而变化患者家族成员发病率高于一般群体患者血缘亲属发病率高于非血缘亲属[参考答案]患者亲属发病率随亲属级别下降而下降患者家族成员发病率高于一般群体患者血缘亲属发病率高于非血缘亲属[我的答案]患者血缘亲属发病率高于非血缘亲属患者家族成员发病率高于一般群体患者亲属发病率随亲属级别下降而下降试题3 满分值:2.0分状态:已答实际得分:分试题: 遗传病的特征多表现为( )家族性先天性传染性不累及非血缘关系者同卵双生率高于异卵双生率[参考答案]家族性先天性不累及非血缘关系者同卵双生率高于异卵双生率[我的答案]同卵双生率高于异卵双生率不累及非血缘关系者先天性家族性试题4 满分值:2.0分状态:已答实际得分:分试题:下列哪些人之间是二级亲属()姨妈与侄儿之间祖孙之间同父异母兄弟之间表兄妹之间同父母的同胞之间[参考答案]姨妈与侄儿之间祖孙之间同父异母兄弟之间[我的答案]同父异母兄弟之间祖孙之间姨妈与侄儿之间试题5 满分值:2.0分状态:已答实际得分:分试题:下列哪些人之间为一级亲属()父母与子女之间同卵双生子之间同胞之间祖孙之间舅舅与侄儿之间[参考答案]父母与子女之间同胞之间[我的答案]同胞之间同卵双生子之间父母与子女之间试题6 满分值:2.0分状态:已答实际得分:分试题: 下列哪些遗传病不是先天性疾病()甲型血友病Huntington舞蹈病重症肌无力糖尿病白化病[参考答案]Huntington舞蹈病重症肌无力糖尿病[我的答案]糖尿病Huntington舞蹈病试题7 满分值:2.0分状态:已答实际得分:分试题: 由遗传和环境因素共同作用决定发病的包括()白化病冠心病艾滋病精神分裂症恶性肿瘤[参考答案]冠心病艾滋病精神分裂症恶性肿瘤[我的答案]恶性肿瘤精神分裂症艾滋病冠心病试题8 满分值:2.0分状态:已答实际得分:分试题下列哪些疾病可能不是家族性疾病():常染色体显性遗传病X-连锁隐性遗传病多基因病染色体病常染色体隐性遗传病[参考答案]染色体病常染色体隐性遗传病[我的答案]染色体病多基因病试题9 满分值:2.0分状态:已答实际得分:分试题: 识别疾病遗传基础的方法包括()双生子法种族差异比较疾病组分分析法伴随性状研究[参考答案]群体普查法双生子法种族差异比较疾病组分分析法伴随性状研究[我的答案]伴随性状研究疾病组分分析法种族差异比较双生子法群体普查法试题10 满分值:2.0分状态:已答实际得分:分试题: 下列哪些病不遵从孟德尔式遗传( )地中海贫血Leber遗传性视神经病克雅病(一种蛋白折叠病,与疯牛病类似)帕金森病Tunner综合征[参考答案]Leber遗传性视神经病帕金森病Tunner综合征[我的答案]Tunner综合征帕金森病克雅病(一种蛋白折叠病,与疯牛病类似)Leber遗传性视神经病。
中央财经大学国际金融学第一讲习题集和答案

第一讲一、单选题1.国际收支系统记录的是一定时期内一国居民与非居民之间的()。
A.贸易收支B.外汇收支C.国际交易D.经济交易答案与解析:选D。
2.一国使用国际货币基金组织的信贷和贷款记录包括在该国国际收支平衡表的()中。
A.经常账户B.资本金融账户C.储备与相关项目 D.净差错与遗漏项目答案与解析:选C。
3.国际收支平衡表中,记入贷方的项目是()。
A.对外资产的增加B.对外负债的增加C.官方储备的增加D.对外无偿转移增加答案与解析:选B。
凡是有利于国际收支顺差增加或逆差减少的资金来源增加或资金占用减少均记入贷方,凡是有利于国际收支逆差增加或顺差减少的资金占用增加或资金来源减少均记入借方。
所以ACD三项应该记入借方。
4.债务注销记录在国际收支平衡表的()。
A.资本账户B.金融账户C.错误与遗漏账户D.国际储备账户答案与解析:选A。
5.建国后我国首次公布国际收支平衡表是在()。
A.1979年B.1980年C.1983年D.1985年答案与解析:选D。
6.各国政府间的无偿经济援助包含在国际收支平衡表的()中。
A.经常转移项目B.资本转移项目C.官方储备项目D.融投资项目答案与解析:选A。
7.国际收支平衡表中一项人为设置的项目是()。
A.经常项目B.资本金融项目C.储备与相关项目D.错误与遗漏项目答案与解析:选B。
8.政府间贷款在国际收支平衡表中应列入()。
A.经常项目B.资本金融项目C.储备与相关项目D.错误与遗漏项目答案与解析:选A。
9.一国使用国际货币基金组织的信贷和贷款记录包括在该国国际收支平衡表的()中。
A.经常账户B.资本金融账户C.储备与相关项目D.净差错与遗漏项目答案与解析:选C。
10.若国际收支不平衡是由于总需求大于总供给而形成的收入性不平衡,可采取的措施是()。
A.紧缩的财政货币政策B.扩张的财政货币政策C.直接管制政策D.货币贬值的汇率政策答案与解析:选A。
二、多选题1..国际收支平衡表中的官方储备项目是()。
第一讲 数字谜答案

数字谜(一)数字谜的内容在三年级和四年级都讲过,同学们已经掌握了不少方法。
例如用猜想、拼凑、排除、枚举等方法解题。
数字谜涉及的知识多,思考性强,所以很能锻炼我们的思维。
这两讲除了复习巩固学过的知识外,还要讲述数字谜的代数解法及小数的除法竖式问题。
例1 把+,-,×,÷四个运算符号,分别填入下面等式的○内,使等式成立(每个运算符号只准使用一次):(5○13○7)○(17○9)=12。
分析与解:因为运算结果是整数,在四则运算中只有除法运算可能出现分数,所以应首先确定“÷”的位置。
当“÷”在第一个○内时,因为除数是13,要想得到整数,只有第二个括号内是13的倍数,此时只有下面一种填法,不合题意。
(5÷13-7)×(17+9)。
当“÷”在第二或第四个○内时,运算结果不可能是整数。
当“÷”在第三个○内时,可得下面的填法:(5+13×7)÷(17-9)=12。
例2 将1~9这九个数字分别填入下式中的□中,使等式成立:□□□×□□=□□×□□=5568。
解:将5568质因数分解为5568=26×3×29。
由此容易知道,将 5568分解为两个两位数的乘积有两种:58×96和64×87,分解为一个两位数与一个三位数的乘积有六种:12×464, 16×348, 24×232,29×192, 32×174, 48×116。
显然,符合题意的只有下面一种填法:174×32=58×96=5568。
例3 在443后面添上一个三位数,使得到的六位数能被573整除。
分析与解:先用443000除以573,通过所得的余数,可以求出应添的三位数。
由443000÷573=773 (71)推知, 443000+(573-71)=443502一定能被573整除,所以应添502。
第一讲习题参考答案

= E(X Y = yj ) 由 y j , zk 的任意性, 可得
E[E( X Y , Z ) Y ] = E(X Y ) = E[E( X Y ) Y , Z ]
得证.
上式中第一个等式的直观意义为: 分的较“粗”的区域上的 平均等于分的其更“细”的局部区域上的加权平均的加权平均.
更准确地说,将 ω ∈{ω : Y (ω) = y j}=Bj 按照 ω ∈{ω : Z (ω) = zk } = Ck 划分为若干个 Ck Bj , 在每个 Ck 上 X (ω ) 有均值, 则在 Bj 上对这些均值再求加权平均, 等于直接在 Bj 上求 X (ω ) 的加权 平均.
第一个等式可以看作是条件概率的全概率公式的推广.
上式中第二个等式的直观意义为: 在 ω ∈{ω : Y (ω) = y j , Z (ω) = zk } = BjCk 上, 其中{ω : Y (ω) = y j }=Bj , {ω : Z (ω) = zk }=Ck , 则 Bj 上 X (ω ) 的均值, 与 Ck 无关.
∫ µ =2,σ =1 +∞ x ⋅ e−( x−2)2 / 2dx =0 2π ⋅ Φ(2)
= 2+
e−2
= 2.0553
2π ⋅ Φ(2)
∆x → 0
∆y
→
0
,
f X (1),X (n) (x, y) = n(n −1)(F ( y) − F (x))n−2 f (x) f ( y) ⋅ I{x< y} 代入
f (x) = λe−λx ⋅ I{x≥0}
∫ F (x) = x λe−λtdt = 1− e−λx 0
得
f (x, y) = n(n −1)λ 2 (e−λx − e−λ y )n−2 e−λ x−λ y ⋅ I{0≤x< y}
第一讲 直线型面积的计算-(带完整答案)五年级奥数
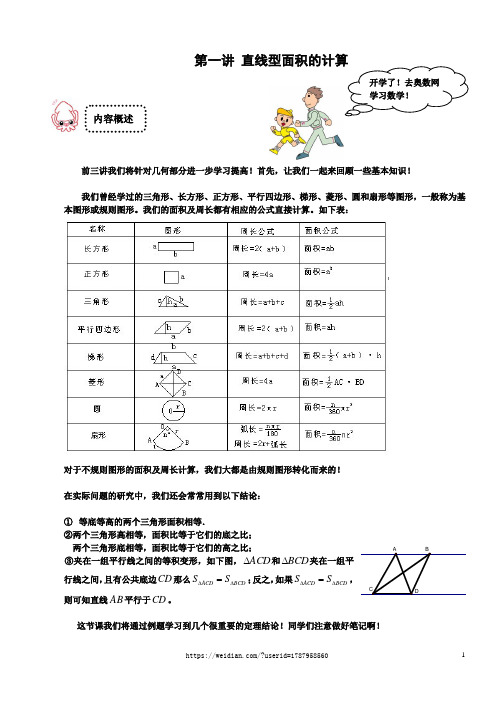
第一讲直线型面积的计算内容概述前三讲我们将针对几何部分进一步学习提高!首先,让我们一起来回顾一些基本知识!我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形。
我们的面积及周长都有相应的公式直接计算。
如下表:对于不规则图形的面积及周长计算,我们大都是由规则图形转化而来的!在实际问题的研究中,我们还会常常用到以下结论:① 等底等高的两个三角形面积相等.②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比;③夹在一组平行线之间的等积变形,如下图,ACD ∆和BCD ∆夹在一组平行线之间,且有公共底边CD 那么BCD ACD S S ∆∆=;反之,如果BCD ACD S S ∆∆=,则可知直线AB 平行于CD 。
这节课我们将通过例题学习到几个很重要的定理结论!同学们注意做好笔记啊!开学了!去奥数网学习数学!CDB例题精讲【例1】你有多少种方法将任意一个三角形分成(1)2个面积相等的三角形;(2)3个面积相等的三角形;(3)4个面积相等的三角形。
分析:(1)如右图,D、E、F分别是对应边上的中点,这样就将三角形分成了2个面积相等的三角形;(2)如右图,D、E是BC的三等分点,F、G分别是对应线段的中点;答案不唯一;(3)如下图,答案不唯一,以下仅供参考;前四种答案学生都容易得到,在这里我们需要特别说明的是第五个答案。
请看例2 。
【例2】在学习三角形时,很多同学都听说过中位线,所谓中位线就是三角形两边中点的连线。
如右图所示,D、E、F分别是AB、AC、BC边的中点,根据定义可知DE、DF、EF就是三角形ABC的中线。
那么请你说明:(1)DE与BC平行(2)DE= 1/2 BC(3)S△ADE= 1/4 S△ABC分析:(1)在解答一些几何问题时,我们常常需要添加一些辅助线帮助我们分析解决。
如右图(1),连接DC、BE。
因为D、E分别是AB、AC的中点,所以S△BDC= 1/2S△ABC= S△BEC,又因为△BDC与△BEC同用BC做底,根据“内容概述”部分常用结论③可得:DE与BC平行。
第一讲 计算综合 提高班 教师版(带完整答案)_5年级奥数讲义与课件

第一讲计算问题在历届的小升初选拔、迎春杯和希望杯中,考察学生的计算能力是必不可少的。
这部分的题目难度不大,但是方法很巧妙,目的是考察大家的基本运算和巧算的能力。
要做好这些题目,就需要同学们在掌握好最基本的计算知识和方法的基础上多做题,从而锻炼自己的运算能力。
在计算的过程中也有许多巧方法可以帮助我们加快计算速度、提高正确率。
知识说明:计算中的提取公因数法是近几年来迎春杯、希望杯和小升初中经常考的题目,但是通过分析我们发现在考试中不仅仅是只考提取公因数这样简单的题,这类题目往往是同积不变的规律、商不变的规律等结合着出的综合题。
和不变的规律:如果一个加数增加另一个加数减少同一个数,它们的和不变.积不变的规律:如果一个因数扩大几倍,另一个因数缩小相同的倍数,积不变.商不变的规律:如果除数和被除数同时扩大或缩小相同的倍数,商不变.【例1】(05 年希望杯 2 试)计算(1)2.005×390+20.05×41+200。
5×2(2)2000×1999-1999×1998 + 1998×1997-1997×1996+1996×1995-1995×1994分析: (1)根据提取公因数的方法和积不变的规律知道,原式=200.5×3.9+200.5×4.1+2=200.5×(3.9+4.1+2)=200.5×10=2005 (2)题目是六项乘积的和差运算 , 其中 , 每两项中都有公因数 , 于是 , 我们先分组简算 .原式 =1999×(2000-1998)+1997×(1998-1996)+1995×(1996-1994)=1999×2+1997×2+1995×2 =2× (1999+1997+1995) =2×(2000+2000+2000-9) =2× (6000-9) =2×6000-2×9 =12000-18 =11982【例2】计算(1)(04 年希望杯 2 试)12.5 ÷ 3.6 - 7 ÷ 9 + 8.3 ÷ 3.6(2)2003×2001÷111+2003×73÷37分析:(1)原式=125÷36-28÷36+83÷36=(125-28+83)÷36=5125 7 83 125 - 28 + 83 180 或12.5 ÷ 3.6 - 7 ÷ 9 + 8.3 ÷ 3.6 = - + = = = 536 9 36 36 36(2)原式=2003×2001÷111+2003×73×3÷(37×3)=2003×(2001+73×3)÷111=2003×2220÷111=40060知识说明提取公因数[前铺](05 年希望杯 1 试)计算 78.16×1.45+3.14×21.84+169×0.7816 分析:不难看出式子中 7816 出现过两次:78.16 和 0.7816,由此可以联想到提取公因数原式=78.16×1.45+3.14×21.84+1.69×78.16=78.16×(1.45+1.69)+3.14×21.84=78.16×3.14 +3.14×21.84=3.14×100=314[巩固](06 年希望杯 2 试)8.1×1.3-8÷1.3+1.9×1.3+11.9÷1.3 分析:原式=(8.1+1.9)×1.3+(11.9-8)÷1.3=13+3=16【例3】 计算 412×0.81+11× 9 1+53.7×1.94分析:原式=41.2×8.1+11×(9+0.25)+(41.2+12.5)×1.9=41.2×8.1+41.2×1.9+12.5×1.9+11×9+11×0.25 =41.2×(8.1+1.9)+(10+2.5)×1.9+99+11×0.25=412+10×1.9+2.5×1.9+99+11×0.25=412+19+99+(11+19)×0.25=410+2+20-1+100-1+7.5=537.5[前铺]计算 31.4×36+64×43.9 分析:观察发现题中有 36 和 64,试想如果出现 64×31.4,就太完美了,所以我们可以构造出 64×31.4这就是提取公因数的构造法。
城市化与城市现代化第一讲 城市化概论答案完整版

第一部分 ;判断题1. 工业革命的开始意味着现代城市化阶段的到来。
A. 正确 B. 错误 您的答案:A 答案分析: 无 正确答案:A正确 √2. 城市化就是大城市化、城市行政辖区的扩展。
A. 正确 B. 错误 您的答案:B 答案分析: 无 正确答案:B正确 √3. 过度城市化是指工业化和经济发展水平明显超过城市化水 平的城市化模式。
A. 正确 B. 错误 您的答案:B 答案分析: 无 正确答案:B正确 √4. “线型城市”源于有机疏散理论,是为缓解城市过度集中 而提出的。
A. 正确 B. 错误 您的答案:B 答案分析: 无 正确答案:B正确 √5. 离心型城市化一般出现在城市化的低级阶段。
A. 正确正确 √B. 错误 您的答案:B 答案分析: 无 正确答案:B6. 农村劳动力转移法是指根据农村剩余劳动力可能转移量的 计算,来预测相应的城市化水平提高数值。
A. 正确 B. 错误 您的答案:A 答案分析: 无 正确答案:A正确 √7. 城市是一个复杂的巨系统,是以非农产业和非农业人口集 聚为主要特征的居民点。
A. 正确 B. 错误 您的答案:A 答案分析: 无 正确答案:A正确 √8. 在我国计划经济体制下,工业化明显滞后于城市化。
A. 正确 B. 错误 您的答案:B 答案分析: 无 正确答案:B正确 √9. 城市化水平越高,城市的发展层次越高。
A. 正确 B. 错误 您的答案:B 答案分析: 无 正确答案:B正确 √10. 城市郊区化是指人口、就业岗位和工商业等从大城市的中 正确 心区向郊区迁移,中心区的人口增长相对低于人口迁出的一种√离心分散化的过程。
A. 正确 B. 错误 您的答案:A 答案分析: 无 正确答案:A11. 城市化的过程不都是集中过程,也包括分散,集中和分散 正确 是经济社会不同发展阶段的表现。
A. 正确 B. 错误 您的答案:A 答案分析: 无 正确答案:A√12. 总的来看,我国还处在向心型城市化的阶段,但一些较发 正确 达的大城市,也出现了一些离心型城市郊区化的现象。
小学四年级奥数举一反三第1讲至第20讲参考答案

小学四年级奥数举一反三第1讲至第20讲参考答案小学四年级奥数举一反三参考答案第1讲练习1:(1)2,6,10,14,(18 ),22,26(2)3,6,9,12,(15),18,21(3)33,28,23,(18),13,(8 ),3(4)55,49,43,(37),31,(25 ),19(5)3,6,12,(24 ),48,(96),192(6)2,6,18,(54),162,(486 )(7)128,64,32,(16 ),8,( 4 ),2(8)19,3,17,3,15,3,(13),(3),11,3..练习2:(1)10,11,13,16,20,(25 ),31(2)1,4,9,16,25,(36 ),49,64(3)3,2,5,2,7,2,(9 ),( 2 ),11,2(4)53,44,36,29,(23),18,(14),11,9,8(5)81,64,49,36,(25 ),16,(9),4,1,0(6)28,1,26,1,24,1,(22 ),( 1 ),20,1(7)30,2,26,2,22,2,(18 ),( 2 ),14,2(8)1,6,4,8,7,10,(10 ),(12),13,14练习3:(1)1,6,5,10,9,14,13,(18 ),(17)(2)13,2,15,4,17,6,(19 ),(8 )(3)3,29,4,28,6,26,9,23,(13),(20 ),18,14 (4)21,2,19,5,17,8,(15 ),(11 )(5)32,20,29,18,26,16,(23 ),(14 ),20,12(6)2,9,6,10,18,11,54,(12),(162),13,486 (7)1,5,2,8,4,11,8,14,(16 ),(17)(8)320,1,160,3,80,9,40,27,(20 ),(81)练习4:(1)2,2,4,6,10,16,(26),(42)(2)34,21,13,8,5,( 3 ),2,( 1 )前一个数减第二个数等于第三个数(3)0,1,3,8,21,(55),144.前一个数的2倍加前两个数的差。
第1讲 有理数的概念和性质和答案

第一讲有理数的概念和性质一、【概念和性质】1、正数和负数正数:比0大的数。
如+3、+1.5、+12、+584(正号可以省略)负数:比0小的数。
如-3、-1.5、-12、-584(负号不可以省略)零:既不是正数,也不是负数。
零是正数和负数的分界。
【实际意义】如“零上”和“零下”“高出”和“低于”“上升”和“下降”“超出”和“不足”“盈利”和“亏损”“收入”和“支出”▲如正数表示某种意义,那么负数表示它的相反的意义。
例:用正数表示向南,那么向北3km可以用负数表示为-3km,向南-5km表示向北5km填空(1)若汽车向东行驶2.5千米记作+2.5千米,则向西行驶1.5千米记作;汽车原地不动记作。
(2)某人转动转盘,如果+2圈表示沿顺时针转2圈,那么圈-3表示。
2、整数和分数统称为有理数。
▲有理数可以写成mn(m、n是整数,n≠0)。
▲有理数的两种分类:①按定义分:②按符号分(常用):几个重要概念(1)非负数:正数和零(2)非正数:负数和零(3)非负整数:正整数和零(4)非正整数:负整数和零3、规定了原点、正方向和单位长度的直线叫做数轴。
所有有理数都可以用数轴上的点表示,但不是数轴上所有点都是有理数。
左边的数〈右边的数整数分数正整数负整数正分数负分数有理数正有理数正整数正分数负整数负分数有理数负有理数0(零既不是正数,也不是负数)-2 -1 0 1 2大小有限小数无限小数分数(分子是1时,这个分数就是正数)无限循环小数无限不循环小数(无理数)小数自然数▲ 正数大于0,0大于负数,正数大于负数。
两个负数,绝对值大的反而小。
4、绝对值的意义与性质:① 数轴上表示a 的点与原点的距离叫做a 的绝对值,记作||a 。
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0。
②③ 非负性 2(||0,0)a a ≥≥④ 非负数的性质: i )非负数的和仍为非负数。
ii )几个非负数的和为0,则他们都为0。
第一讲 行程问题专项练习题(含答案)

第一讲:行程问题一、基本公式1.路程=速度×时间;2.速度=路程÷时间;3.时间=路程÷速度。
关键问题二、相遇问题1.基本公式:相遇总路程=甲行的路程+乙行的路程,2.相遇总路程=速度之和×相遇时间,即(甲速+乙速)×相遇时间。
3.速度之和=相遇路程÷相遇时间,4.相遇时间=相遇路程÷速度之和,即相道路程÷(甲速十乙速)5.甲速=相遇总路程÷相遇时间-乙速;乙速=相遇总路程÷相遇时间-甲速。
三、追及问题(一)基本公式1.追及时间=追及时的距离差÷速度差2.速度差=追及时的距离差÷追及时间3.追及时间×速度差=追及时的距离差四、往返的平均速度基本公式:平均速度=总路程÷总时间,即往返的平均速度=甲乙之间的路程×2÷(路程÷去时速度+路程÷回时速度)五、流水问题顺水行程=(船速+水速)×顺水时间逆水行程=(船速-水速)×逆水时间行程问题专项练习一、求时间:1.甲乙两地相距405千米,一辆汽车从甲地开往乙地,4小时行驶了180千米.照这样的速度,再行驶多少小时,这辆汽车就可以到达乙地?2.甲、乙两辆汽车从相距255千米的A、B两地同时相向开出,甲车的速度是45千米/时,乙车的速度是40千米/时,他们几小时后相遇?3.小强有一本书要给小刚,他们约好同时从家出发迎面而行.已知两家之间的路程是960米,小强的速度是80米/分,小刚的速度是70米/分,经过几分两人相遇?相遇地点距小刚家多少米?4.上海至天津铁路长1375千米.一列火车从上海开往天津,当行了总路程的时,接到通知要求火车提速到每小时行110千米,再经过多少小时到达天津?5.甲乙两人骑自行车从相距90千米的南北两地同时出发,相向而行.甲每小时行10千米乙的速度是甲的1.25倍,经过多长时间两人相遇?6.A、B二人从相距900米的两地同时相对而行,A的速度是60米/秒,B的速度是90米/秒,请问两人多长时间相遇?(请用两种方法解答)二、求距离7.一辆小汽车每小时行98千米,这辆小汽车往返A、B两地一次要6小时,A、B两地之间的距离是多少千米?8.甲、乙两车同时从A地开往B地,乙车6小时达到,甲车每小时比乙车慢8千米,因此比乙车迟到一小时达到.A、B两地间的路程是多少千米?9.甲乙两人从东西两地同时出发,相向而行,甲每分钟行75米,乙每分钟行的是甲的,经过1小时相遇,求东西两地的距离是多少?10.客车每小时行65千米,货车每小时行60千米,客车从甲站先开出2小时,货车从乙站开出后,经4小时,两车相遇,甲乙两站相距多少千米?11.客车和货车同时从甲、乙两城相向而行,货车每小时行85千米,客车每小时行90千米,两车相遇时距全程中点8千米。
高校物理强基计划讲义:第1讲运动学(带答案详解)

=
( v12
+ v22
+
) 2(v1v2 cos α l2 − l2 (v1)+ v12 + v22 + 2v1v2 cos α
v2 cos α)2
=
v12
l2v22 sin2 α + v22 + 2v1v2 cos α
故此过程中甲、乙两质点间距离的最小值为
rmin
=
√ v12
+
lv2 sin α v22 + 2v1v2 cos α
2. 如图所示,三位芭蕾演员 A、B、C 同时从边长为 l 的三角形顶点 A、B、C 出发,以相同的速 率 v 运动,运动中始终保持 A 朝着 B,B 朝着 C,C 朝着 A.试问:经多少时间三人相聚?
第3页
解: 【分析】由三位舞者运动的对称性可知,他们的会合点在三角形 ABC 的中心 O,每人的运 动均可看做绕 O 转动并且同时向 O 运动.
微元法的好处是把曲线变成直线,非线性变成线性,非理想模型变成理想模型,把线性的变量 变成常量。这个也是微积分的一个基本思想。
1. 累加求和:我们用符号 ∑ 来表示累加求和,用法如下:
∑n n (n + 1) i=
(1)
2
i=1
其中 i 可以理解成是一个变量,只能整数的从 1 变到 n.
常用的一些结论如下:
角度为
α = DD′ = vD∆t
ρ
ρ
因为 ∆t 很小,所以狐狸运动的距离为
vF ∆t
=
αL
=
vD∆t L ρ
即 所以
【解答】(1)由三位舞者运动的对称性可知,他们的会合点在三角形 ABC 的中心 O,每人
2023年新高考数学大一轮复习专题二平面向量与三角函数第1讲平面向量(含答案)

新高考数学大一轮复习专题:第1讲 平面向量[考情分析] 1.平面向量是高考的热点和重点,命题突出向量的基本运算与工具性,在解答题中常与三角函数、直线和圆锥曲线的位置关系问题相结合,主要以条件的形式出现,涉及向量共线、数量积等.2.常以选择题、填空题形式考查平面向量的基本运算,中低等难度;平面向量在解答题中一般为中等难度. 考点一 平面向量的线性运算 核心提炼1.平面向量加减法求解的关键是:对平面向量加法抓住“共起点”或“首尾相连”.对平面向量减法应抓住“共起点,连两终点,指向被减向量的终点”,再观察图形对向量进行等价转化,即可快速得到结果.2.在一般向量的线性运算中,只要把其中的向量当作一个字母看待即可,其运算方法类似于代数中合并同类项的运算,在计算时可以进行类比.例1 (1)如图所示,AD 是△ABC 的中线,O 是AD 的中点,若CO →=λAB →+μAC →,其中λ,μ∈R ,则λ+μ的值为( )A .-12B.12 C .-14D.14答案 A解析 由题意知,CO →=12(CD →+CA →)=12×⎝ ⎛⎭⎪⎫12CB →+CA →=14(AB →-AC →)+12CA →=14AB →-34AC →, 则λ=14,μ=-34,故λ+μ=-12.(2)已知e 1,e 2是不共线向量,a =m e 1+2e 2,b =n e 1-e 2,且mn ≠0.若a ∥b ,则m n=________. 答案 -2解析 ∵a ∥b ,∴m ×(-1)=2×n ,∴m n=-2.(3)A ,B ,C 是圆O 上不同的三点,线段CO 与线段AB 交于点D ,若OC →=λOA →+μOB →(λ∈R ,μ∈R ),则λ+μ的取值范围是________.答案 (1,+∞)解析 由题意可得,OD →=kOC →=kλOA →+kμOB →(0<k <1),又A ,D ,B 三点共线,所以kλ+kμ=1,则λ+μ=1k>1,即λ+μ的取值范围是(1,+∞).易错提醒 在平面向量的化简或运算中,要根据平面向量基本定理恰当地选取基底,变形要有方向,不能盲目转化.跟踪演练1 (1)如图,在平行四边形ABCD 中,E ,F 分别为边AB ,BC 的中点,连接CE ,DF ,交于点G .若CG →=λCD →+μCB →(λ,μ∈R ),则λμ=________.答案 12解析 由题意可设CG →=xCE →(0<x <1), 则CG →=x (CB →+BE →)=x ⎝ ⎛⎭⎪⎫CB →+12CD →=x 2CD →+xCB →.因为CG →=λCD →+μCB →,CD →与CB →不共线,所以λ=x 2,μ=x ,所以λμ=12.(2)如图,在扇形OAB 中,∠AOB =π3,C 为弧AB 上的一个动点,若OC →=xOA →+yOB →,则x +3y的取值范围是________.答案 [1,3]解析 设扇形的半径为1,以OB 所在直线为x 轴,O 为坐标原点建立平面直角坐标系(图略), 则B (1,0),A ⎝ ⎛⎭⎪⎫12,32,C (cos θ,sin θ)⎝ ⎛⎭⎪⎫其中∠BOC =θ,0≤θ≤π3.则OC →=(cos θ,sin θ)=x ⎝ ⎛⎭⎪⎫12,32+y (1,0),即⎩⎪⎨⎪⎧x 2+y =cos θ,32x =sin θ,解得x =23sin θ3,y =cos θ-3sin θ3,故x +3y =23sin θ3+3cos θ-3sin θ=3cos θ-33sin θ,0≤θ≤π3. 令g (θ)=3cos θ-33sin θ, 易知g (θ)=3cos θ-33sin θ在⎣⎢⎡⎦⎥⎤0,π3上单调递减,故当θ=0时,g (θ)取得最大值为3, 当θ=π3时,g (θ)取得最小值为1,故x +3y 的取值范围为[1,3].考点二 平面向量的数量积 核心提炼1.若a =(x ,y ),则|a |=a ·a =x 2+y 2. 2.若A (x 1,y 1),B (x 2,y 2),则|AB →|=x 2-x 12+y 2-y 12.3.若a =(x 1,y 1),b =(x 2,y 2),θ为a 与b 的夹角, 则cos θ=a ·b |a ||b |=x 1x 2+y 1y 2x 21+y 21x 22+y 22. 例2 (1)(2020·全国Ⅲ)已知向量a ,b 满足|a |=5,|b |=6,a ·b =-6,则cos 〈a ,a +b 〉等于( )A .-3135B .-1935C.1735D.1935答案 D解析 ∵|a +b |2=(a +b )2=a 2+2a ·b +b 2=25-12+36=49, ∴|a +b |=7,∴cos〈a ,a +b 〉=a ·a +b |a ||a +b |=a 2+a ·b|a ||a +b |=25-65×7=1935. (2)已知扇形OAB 的半径为2,圆心角为2π3,点C 是弧AB 的中点,OD →=-12OB →,则CD →·AB →的值为( )A .3B .4C .-3D .-4 答案 C解析 如图,连接CO ,∵点C 是弧AB 的中点, ∴CO ⊥AB ,又∵OA =OB =2,OD →=-12OB →,∠AOB =2π3,∴CD →·AB →=(OD →-OC →)·AB →=-12OB →·AB →=-12OB →·(OB →-OA →)=12OA →·OB →-12OB →2=12×2×2×⎝ ⎛⎭⎪⎫-12-12×4=-3. (3)已知在直角梯形ABCD 中,AB =AD =2CD =2,∠ADC =90°,若点M 在线段AC 上,则|MB →+MD →|的取值范围为________________.答案 ⎣⎢⎡⎦⎥⎤255,22 解析 以A 为坐标原点,AB ,AD 所在直线分别为x 轴,y 轴, 建立如图所示的平面直角坐标系,则A (0,0),B (2,0),C (1,2),D (0,2),设AM →=λAC →(0≤λ≤1),则M (λ,2λ), 故MD →=(-λ,2-2λ),MB →=(2-λ,-2λ), 则MB →+MD →=(2-2λ,2-4λ), ∴|MB →+MD →|=2-2λ2+2-4λ2=20⎝⎛⎭⎪⎫λ-352+45,0≤λ≤1, 当λ=0时,|MB →+MD →|取得最大值为22, 当λ=35时,|MB →+MD →|取得最小值为255,∴|MB →+MD →|∈⎣⎢⎡⎦⎥⎤255,22.易错提醒 两个向量的夹角的范围是[0,π],在使用平面向量解决问题时要特别注意两个向量的夹角可能是0或π的情况,如已知两个向量的夹角为钝角时,不仅要求其数量积小于零,还要求不能反向共线.跟踪演练2 (1)(2019·全国Ⅰ)已知非零向量a ,b 满足|a |=2|b |,且(a -b )⊥b ,则a 与b 的夹角为( )A.π6B.π3C.2π3D.5π6 答案 B解析 方法一 设a 与b 的夹角为θ,因为(a -b )⊥b ,所以(a -b )·b =a ·b -|b |2=0, 又因为|a |=2|b |,所以2|b |2cos θ-|b |2=0, 即cos θ=12,又θ∈[0,π],所以θ=π3,故选B. 方法二 如图,令OA →=a ,OB →=b ,则BA →=OA →-OB →=a -b .因为(a -b )⊥b ,所以∠OBA =π2,又|a |=2|b |,所以∠AOB =π3,即a 与b 的夹角为π3,故选B.(2)(2020·新高考全国Ⅰ)已知P 是边长为2的正六边形ABCDEF 内的一点,则AP →·AB →的取值范围是( ) A .(-2,6) B .(-6,2) C .(-2,4) D .(-4,6)答案 A解析 如图,取A 为坐标原点,AB 所在直线为x 轴建立平面直角坐标系,则A (0,0),B (2,0),C (3,3),F (-1,3). 设P (x ,y ),则AP →=(x ,y ),AB →=(2,0),且-1<x <3. 所以AP →·AB →=(x ,y )·(2,0)=2x ∈(-2,6).(3)设A ,B ,C 是半径为1的圆O 上的三点,且OA →⊥OB →,则(OC →-OA →)·(OC →-OB →)的最大值是( ) A .1+ 2 B .1- 2 C.2-1 D .1答案 A解析 如图,作出OD →,使得OA →+OB →=OD →.则(OC →-OA →)·(OC →-OB →)=OC →2-OA →·OC →-OB →·OC →+OA →·OB →=1-(OA →+OB →)·OC →=1-OD →·OC →,由图可知,当点C 在OD 的反向延长线与圆O 的交点处时,OD →·OC →取得最小值,最小值为-2,此时(OC →-OA →)·(OC →-OB →)取得最大值,最大值为1+ 2.故选A.专题强化练一、单项选择题1.已知四边形ABCD 是平行四边形,点E 为边CD 的中点,则BE →等于( )A .-12AB →+AD →B.12AB →-AD →C.AB →+12AD →D.AB →-12AD →答案 A解析 由题意可知,BE →=BC →+CE →=-12AB →+AD →.2.(2020·广州模拟)加强体育锻炼是青少年生活学习中非常重要的组成部分,某学生做引体向上运动,处于如图所示的平衡状态时,若两只胳膊的夹角为π3,每只胳膊的拉力大小均为400 N ,则该学生的体重(单位:kg)约为(参考数据:取重力加速度大小为g =10 m/s 2,3≈1.732)( )A .63B .69C .75D .81 答案 B解析 设该学生的体重为m ,重力为G ,两臂的合力为F ′,则|G |=|F ′|,由余弦定理得|F ′|2=4002+4002-2×400×400×cos 2π3=3×4002,∴|F ′|=4003,∴|G |=mg =4003,m =403≈69kg.3.已知向量a =(1,2),b =(2,-2),c =(λ,-1),若c ∥(2a +b ),则λ等于( ) A .-2B .-1C .-12D.12答案 A解析 ∵a =(1,2),b =(2,-2),∴2a +b =(4,2),又c =(λ,-1),c ∥(2a +b ),∴2λ+4=0,解得λ=-2,故选A.4.(2020·潍坊模拟)在平面直角坐标系xOy 中,点P (3,1),将向量OP →绕点O 按逆时针方向旋转π2后得到向量OQ →,则点Q 的坐标是( )A .(-2,1)B .(-1,2)C .(-3,1)D .(-1,3) 答案 D解析 由P (3,1),得P ⎝⎛⎭⎪⎫2cos π6,2sin π6,∵将向量OP →绕点O 按逆时针方向旋转π2后得到向量OQ →,∴Q ⎝ ⎛⎭⎪⎫2cos ⎝ ⎛⎭⎪⎫π6+π2,2sin ⎝ ⎛⎭⎪⎫π6+π2, 又cos ⎝⎛⎭⎪⎫π6+π2=-sin π6=-12,sin ⎝ ⎛⎭⎪⎫π6+π2=cos π6=32,∴Q (-1,3).5.(2020·泰安模拟)如图,在△ABC 中,点O 是BC 的中点,过点O 的直线分别交直线AB ,AC 于不同的两点M ,N ,若AB →=mAM →,AC →=nAN →,则m +n 等于( )A .0B .1C .2D .3 答案 C解析 如图,连接AO ,由O 为BC 的中点可得,AO →=12(AB →+AC →)=m 2AM →+n 2AN →, ∵M ,O ,N 三点共线, ∴m 2+n2=1. ∴m +n =2.6.在同一平面中,AD →=DC →,BE →=2ED →.若AE →=mAB →+nAC →(m ,n ∈R ),则m +n 等于( ) A.23B.34C.56D .1 答案 A解析 由题意得,AD →=12AC →,DE →=13DB →,故AE →=AD →+DE →=12AC →+13DB →=12AC →+13(AB →-AD →)=12AC →+13⎝ ⎛⎭⎪⎫AB →-12AC →=13AB →+13AC →,所以m =13,n =13,故m +n =23.7.若P 为△ABC 所在平面内一点,且|PA →-PB →|=|PA →+PB →-2PC →|,则△ABC 的形状为( ) A .等边三角形 B .等腰三角形 C .直角三角形 D .等腰直角三角形答案 C解析 ∵|PA →-PB →|=|PA →+PB →-2PC →|,∴|BA →|=|(PA →-PC →)+(PB →-PC →)|=|CA →+CB →|,即|CA →-CB →|=|CA →+CB →|,两边平方整理得,CA →·CB →=0,∴CA →⊥CB →,∴△ABC 为直角三角形.故选C. 8.已知P 是边长为3的等边三角形ABC 外接圆上的动点,则||PA →+PB →+2PC →的最大值为( )A .23B .33C .43D .5 3 答案 D解析 设△ABC 的外接圆的圆心为O , 则圆的半径为332×12=3,OA →+OB →+OC →=0, 故PA →+PB →+2PC →=4PO →+OC →.又||4PO →+OC→2=51+8PO →·OC →≤51+24=75, 故||PA →+PB →+2PC →≤53, 当PO →,OC →同向共线时取最大值.9.如图,圆O 是边长为23的等边三角形ABC 的内切圆,其与BC 边相切于点D ,点M 为圆上任意一点,BM →=xBA →+yBD →(x ,y ∈R ),则2x +y 的最大值为( )A.2B.3C .2D .2 2 答案 C解析 方法一 如图,连接DA ,以D 点为原点,BC 所在直线为x 轴,DA 所在直线为y 轴,建立如图所示的平面直角坐标系.设内切圆的半径为r ,则圆心为坐标(0,r ),根据三角形面积公式,得12×l △ABC ×r =12×AB ×AC ×sin60°(l △ABC 为△ABC 的周长),解得r =1.易得B (-3,0),C (3,0),A (0,3),D (0,0), 设M (cos θ,1+sin θ),θ∈[0,2π),则BM →=(cos θ+3,1+sin θ),BA →=(3,3),BD →=(3,0), 故BM →=(cos θ+3,1+sin θ)=(3x +3y ,3x ),故⎩⎨⎧cos θ=3x +3y -3,sin θ=3x -1,则⎩⎪⎨⎪⎧x =1+sin θ3,y =3cos θ3-sin θ3+23,所以2x +y =3cos θ3+sin θ3+43=23sin ⎝⎛⎭⎪⎫θ+π3+43≤2.当θ=π6时等号成立.故2x +y 的最大值为2.方法二 因为BM →=xBA →+yBD →,所以|BM →|2=3(4x 2+2xy +y 2)=3[(2x +y )2-2xy ]. 由题意知,x ≥0,y ≥0, |BM →|的最大值为232-32=3,又2x +y 24≥2xy ,即-2x +y 24≤-2xy ,所以3×34(2x +y )2≤9,得2x +y ≤2,当且仅当2x =y =1时取等号. 二、多项选择题10.(2020·长沙模拟)已知a ,b 是单位向量,且a +b =(1,-1),则( ) A .|a +b |=2 B .a 与b 垂直C .a 与a -b 的夹角为π4D .|a -b |=1 答案 BC解析 |a +b |=12+-12=2,故A 错误;因为a ,b 是单位向量,所以|a |2+|b |2+2a ·b =1+1+2a ·b =2,得a ·b =0,a 与b 垂直,故B 正确;|a -b |2=a 2+b 2-2a ·b =2,|a -b |=2,故D 错误;cos 〈a ,a -b 〉=a ·a -b |a ||a -b |=a 2-a ·b 1×2=22,所以a 与a -b 的夹角为π4,故C 正确. 11.设向量a =(k,2),b =(1,-1),则下列叙述错误的是( )A .若k <-2,则a 与b 的夹角为钝角B .|a |的最小值为2C .与b 共线的单位向量只有一个为⎝ ⎛⎭⎪⎫22,-22 D .若|a |=2|b |,则k =22或-2 2 答案 CD解析 对于A 选项,若a 与b 的夹角为钝角,则a ·b <0且a 与b 不共线,则k -2<0且k ≠-2,解得k <2且k ≠-2,A 选项正确;对于B 选项,|a |=k 2+4≥4=2,当且仅当k =0时等号成立,B 选项正确;对于C 选项,|b |=2,与b 共线的单位向量为±b |b |,即与b 共线的单位向量为⎝⎛⎭⎪⎫22,-22或⎝ ⎛⎭⎪⎫-22,22,C 选项错误;对于D 选项,∵|a |=2|b |=22,∴k 2+4=22,解得k =±2,D 选项错误.12.已知△ABC 是边长为2的等边三角形,D ,E 分别是AC ,AB 上的两点,且AE →=EB →,AD →=2DC →,BD 与CE 交于点O ,则下列说法正确的是( )A.AB →·CE →=-1B.OE →+OC →=0C .|OA →+OB →+OC →|=32D.ED →在BC →方向上的投影为76答案 BCD解析 因为AE →=EB →,△ABC 是等边三角形,所以CE ⊥AB ,所以AB →·CE →=0,选项A 错误;以E 为坐标原点,EA →,EC →的方向分别为x 轴,y 轴正方向建立平面直角坐标系,如图所示,所以E (0,0),A (1,0),B (-1,0),C (0,3),D ⎝ ⎛⎭⎪⎫13,233, 设O (0,y ),y ∈(0,3),则BO →=(1,y ),DO →=⎝ ⎛⎭⎪⎫-13,y -233, 又BO →∥DO →,所以y -233=-13y ,解得y =32, 即O 是CE 的中点,OE →+OC →=0,所以选项B 正确;|OA →+OB →+OC →|=|2OE →+OC →|=|OE →|=32, 所以选项C 正确;ED →=⎝ ⎛⎭⎪⎫13,233,BC →=(1,3),ED →在BC →方向上的投影为ED →·BC →|BC →|=13+22=76,所以选项D 正确. 三、填空题13.(2020·全国Ⅱ)已知单位向量a ,b 的夹角为45°,k a -b 与a 垂直,则k =________. 答案 22解析 由题意知(k a -b )·a =0,即k a 2-b ·a =0.因为a ,b 为单位向量,且夹角为45°,所以k ×12-1×1×22=0,解得k =22. 14.在△ABC 中,AB =1,∠ABC =60°,AC →·AB →=-1,若O 是△ABC 的重心,则BO →·AC →=________.答案 5解析 如图所示,以B 为坐标原点,BC 所在直线为x 轴,建立平面直角坐标系.∵AB =1,∠ABC =60°,∴A ⎝ ⎛⎭⎪⎫12,32.设C (a,0). ∵AC →·AB →=-1,∴⎝ ⎛⎭⎪⎫a -12,-32·⎝ ⎛⎭⎪⎫-12,-32 =-12⎝ ⎛⎭⎪⎫a -12+34=-1,解得a =4. ∵O 是△ABC 的重心,延长BO 交AC 于点D ,∴BO →=23BD →=23×12()BA →+BC → =13⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫12,32+4,0=⎝ ⎛⎭⎪⎫32,36. ∴BO →·AC →=⎝ ⎛⎭⎪⎫32,36·⎝ ⎛⎭⎪⎫72,-32=5. 15.(2020·石家庄模拟)在锐角三角形ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,点O为△ABC 的外接圆的圆心,A =π3,且AO →=λAB →+μAC →,则λμ的最大值为________. 答案 19解析 ∵△ABC 是锐角三角形,∴O 在△ABC 的内部,∴0<λ<1,0<μ<1.由AO →=λ(OB →-OA →)+μ(OC →-OA →), 得(1-λ-μ)AO →=λOB →+μOC →,两边平方后得,(1-λ-μ)2AO →2=(λOB →+μOC →)2=λ2OB →2+μ2OC →2+2λμOB →·OC →,∵A =π3,∴∠BOC =2π3,又|AO →|=|BO →|=|CO →|. ∴(1-λ-μ)2=λ2+μ2-λμ,∴1+3λμ=2(λ+μ),∵0<λ<1,0<μ<1,∴1+3λμ≥4λμ,设λμ=t ,∴3t 2-4t +1≥0,解得t ≥1(舍)或t ≤13, 即λμ≤13⇒λμ≤19,∴λμ的最大值是19.16.(2020·浙江)已知平面单位向量e 1,e 2满足|2e 1-e 2|≤2,设a =e 1+e 2,b =3e 1+e 2,向量a ,b 的夹角为θ,则cos 2θ的最小值是________. 答案 2829解析 设e 1=(1,0),e 2=(x ,y ),则a =(x +1,y ),b =(x +3,y ).由2e 1-e 2=(2-x ,-y ),故|2e 1-e 2|=2-x 2+y 2≤2,得(x -2)2+y 2≤2.又有x 2+y 2=1,得(x -2)2+1-x 2≤2,化简,得4x ≥3,即x ≥34,因此34≤x ≤1.cos 2θ=⎝ ⎛⎭⎪⎫a ·b|a |·|b |2=⎣⎢⎡⎦⎥⎤x +1x +3+y 2x +12+y 2x +32+y 22=⎝ ⎛⎭⎪⎫4x +42x +26x +102=4x +12x +13x +5=4x +13x +5=433x +5-833x +5=43-833x +5,。
四年级奥数第一讲_速算与巧算含答案解析

第一讲 速算与巧算一、 知识点:1. 要认真观察算式中数的特点,算式中运算符号的特点。
2. 掌握基本的运算定律:乘法交换律、乘法结合律、乘法分配律。
3. 掌握速算与巧算的方法:如等差数列求知、凑整、拆数等等。
二、典例剖析:例(1) 19199199919999199999++++分析:运用凑整法来解十分方便,也不容易出错误。
解:原式()()()() =(201)+2001+20001+200001+2000001 -----=20+200+2000+20000+2000005 =2222205 =222215--练一练:898998999899998999998+++++=答案:1111098例(2)10099989796321+-+-++-+分析:暂不看头尾两个数,就会发现中间都是先加后减,并且加数与减数相差1,所以就算这题可以先把中间部分分组凑成若干个1,再与其余部分进行计算。
解:原式100(9998)(9796)(32)1=+-+-++-+100491=++150=练一练:989796959493929190894321+--++--++---++答案:99例(3) 1111111111⨯分析:111,1111121,11111112321⨯=⨯=⨯= 解:1111111111123454321⨯=练一练:2222222222⨯答案:493817284例(4) 1234314243212413+++分析:数字1、2、3、4,在个位、十位、百位、千位上均各出现一次。
解:原式1111222233334444=+++ 1111(1234)=⨯+++ 111110=⨯ 11110=练一练:5678967895789568956795678++++答案:388885例(5) 339340341342343344345++++++分析:这七个数均差1,且个数为7个,所以中间数就是七个数的中位数。
解:原式3427=⨯ 2394=练一练:(445443440439433434)6+++++÷答案:439例(6) 482594115932359⨯+⨯-⨯分析:先改变运算顺序,把4159⨯与32359⨯交换位置,48259⨯与32359⨯都有公共因素59,将48259⨯与32359⨯的差算出再与41159⨯求和。
2019年中考数学专题复习第1讲《实数及有关概念》(含详细参考答案)

2019年中考数学精品专题复习第一章 数与式第一讲 实数及有关概念★★★核心知识回顾★★★知识点一、实数的分类 1.按实数的定义分类:⎧⎧⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪⎨⎬⎪⎨⎪⎪⎨⎪⎪⎪⎩⎭⎪⎪⎪⎩⎪⎩整数有限小数或无限循环小数有理数实数:无限不循环小数 2.按实数的正负分类:⎧⎧⎪⎪⎨⎪⎪⎩⎪⎨⎪⎧⎪⎪⎨⎪⎪⎩⎩正实数正无理数实数零负有理数负实数知识点二、实数的基本概念和性质1.数轴:规定了 、 、 的直线叫做数轴,实数和数轴上的点是一一对应的。
2.相反数:(1)只有 不同的两个数叫做互为相反数,a 的相反数是 ,0的相反数是 ; (2)a+b=0⇔a 、b 互为 ;(3)在数轴上,表示相反数的两个点位于原点两侧,且到原点的距离 。
3.倒数:(1)乘积为 的两个数互为倒数,用数学语言表述为:1ab =,则a ,b 互为 ; (2)1和 的倒数还是它本身, 没有倒数。
4.绝对值:(1)一般地,数轴上表示数a 的点与原点的 叫做数a 的绝对值。
(2)(0)||0(0)(0)a a a a >⎧⎪==⎨⎪<⎩(3)因为绝对值表示的是距离,所以一个数的绝对值是 数,我们学过的非负数有三个: 、 和 。
知识点三、平方根、算术平方根、立方根 1.平方根: (1)一般地,如果一个数的 等于a ,那么这个数就叫做a 的平方根或二次方根,记作 ; (2)正数的平方根有两个,它们互为 ,0的平方根为 , 没有平方根。
2.算术平方根:(1)一般地,如果一个正数x 的平方等于a ,即2x a =,那么这个正数x 叫做a 的算术平方根,记作 ;(2)正数的算术平方根为 ,0的算术平方根为 。
3.立方根: (1)一般地,如果一个数的立方等于a ,那么这个数就叫做a 的立方根或三次方根,记作 ; (2)正数的立方根为 , 0的立方根为 ,负数立方根为 ;每个实数有且只有一个立方根。
知识点四、科学记数法科学记数法:把一个较大或较小的数写成写成10na ⨯的形式(其中a 大于或等于1且小于10,n 是正整数),使用的是科学记数法。
数学五年级下册 第一讲 观察物体 基础版(含答案、学生版+教师版)人教版

第1讲观察物体1.根据从一个方向(正面、左面或上面)看到的图形摆几何体根据从一个方向看到的图形摆几何体,使小正方体的行数、列数、层数符合要求,所摆的几何体通常不止一种。
2.根据从不同方向看到的图形摆几何体先根据从上面看到的图形确定小正方体的列数和行数,再根据从正面和左面看到的图形确定各列和各行小正方的层数,所摆的几何体通常只有一种。
3.做简单图形的三视图三视图怎么看: 1.从正面看,为主视图2.从侧面看,为左视图3.从上面看,为俯视图展开图为空间形体的表面在平面上摊平后得到的图形.考点1:画几何体的三视图【典例1】把如图的的立体图形在方格纸上画出从正面、上面、左面看到的图形.【分析】这个立体图形由5个相同的小正方体组成。
从正面能看到4个相同的小正方形,分两层,上层1个,下层3个,右齐;从上面能看到4个相同的小正方形,分两层,上层3个,下层1个,左齐;从左面能看到3个相同的小正方形,分两层,上层1个,下层2个,左齐。
【解答】解:【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形。
【典例2】分别画出从上面和右面看到的立体图形的形状.【分析】这个立体图形由4个相同的小正方体组成。
从上面能看到3个相同的小正方形,分两层,上层2个,下层1个,右齐;从右面能看到3个相同的小正方形,分两层,上层1个,下层2个,右齐。
【解答】解:【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形。
【典例3】分别从前面、右面、上面观察如图,再在方格纸中画出看到的图形。
【分析】这个立体图形由5个相同的小正方体构成。
从前面能看到4个正方形,分两层,上层1个,下层3个,左齐;从右面能看到3个正方形,分两层,上层1个,下层2个,左齐;从上面能看到4个正方形,分两层,上层3个,下层1个,左齐。
【解答】解:【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形。
第一讲游戏(商店打烊时)答案

附件二 (答案)1. 店主将店堂内的灯关掉后,一男子到达。
不确定. 商人可能是店主, 可能不是.2. 抢劫者是一男子。
不确定. ‘一男子’ 不一定是抢劫者, 可能是乞丐.3. 来的那个男子没有索要钱款。
错. ‘到店堂并索要钱款’.4. 打开收银机的那个男子是店主。
不确定. 店主的性别不确定.5. 店主倒出收银机中的东西后逃离。
不确定. 不知是谁倒出来.6. 故事中提到了收银机,但没有说里面具体有多少钱。
对.7. 抢劫者向店主索要钱款。
不确定. 可能是’乞丐’索要钱款.8. 索要钱款的男子倒出收银机中的东西后,急忙离开。
不确定. 东西被倒了出来, 但不知是谁倒的.9. 抢劫者打开了收银机。
错. 是店主打开收银机.10. 店堂灯关掉后,一个男子来了。
对.11. 抢劫者没有把钱随身带走。
不确定. 不一定是抢劫.12. 故事涉及三个人物:店主、一个索要钱款的男子、以及一个警察。
不确定. 也可能是四个人: 一个商人, 一个索要钱款的男子, 店主, 警察.是下巴还是面颊1、讲师一边示范,一遍请学员站起来,伸出双臂,与地面保持水平。
讲师说:“现在,请用你们的大拇指和食指围成一个圈。
”(在你说的时候,示范该动作)然后继续说:“请将上臂举起,完成直角。
”(继续示范该动作)2、看看学员是否都做正确,然后继续说:“好,请用掌心托住你的下巴》”注意,当你说“托住下巴”时,你自己用掌心托住面颊。
3、你四处看看,但什么也不要说。
5——10秒后,学员中有些人会意识到错误并转而用掌心托住下巴。
再过几秒。
学员会大笑起来。
这时,你可以强调指出:“一位讲师的行为往往比他的言语更为有效。
”相关讨论:1、你们刚才有没有听到我说“请不要跟着我做,请根据我说的做”之类的话?为什么会跟着我做呢?2、我们都知道行动胜于雄辩,我们在工作中如何应用这一原则,来取得更好的相互理解?3、很多时候,行为上发生的问题会导致沟通的失误。
通过这个游戏,启发了我们认识到阻碍有效沟通的困难有哪些?4、我们应当如何克服这些困难?。
2019届高考一轮讲义:第1讲-中国早期政治制度的特点(含答案)
第1讲中国早期政治制度的特点一、早期国家形态(夏商周的国家制度)夏:公元前2070年,禹建立夏朝,都阳城(今河南登封),这是中国历史上第一个国家,政治制度的形成时期。
禹死后,其子启强行夺取了王位,父传子的“王位世袭制”取代“禅让制”,“家天下”取代“公天下”。
(二里头考古遗址被史学界普遍认为是夏王朝遗迹。
)夏朝最后一个国王是桀,昏庸无道,于公元前1600年被商灭朝。
商:公元前1600年,商汤建立,首都为亳,后商王盘庚迁都于殷(今河南安阳)。
商代是当时世界上的大国,可惜纣王无道(助纣为虐),建鹿台、造酒池肉林、创炮烙之刑压制百姓,最终“武王伐纣”,纣王自焚于鹿台,商朝灭亡。
西周:“凤鸣岐山,天命所归”,公元前1046年,武王姬发在姜尚等人辅佐下推翻商朝,建立周朝,史称西周,都城镐(今陕西西安)。
并在后世君主努力下建立起一套完整的国家体制,主要包含:分封制、宗法制、井田制、礼乐制。
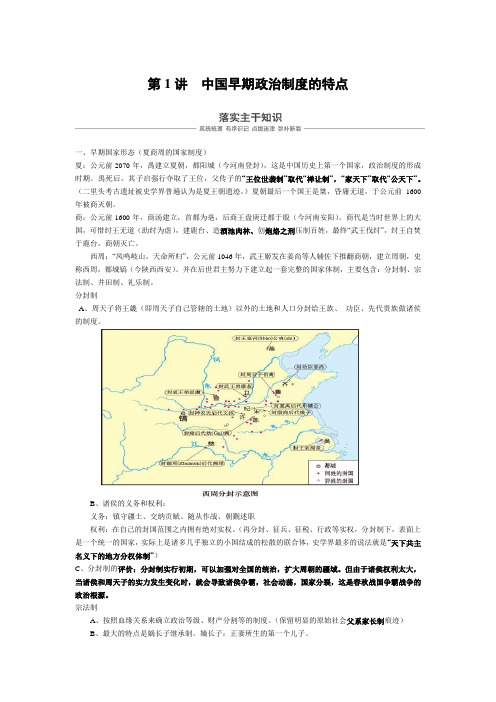
分封制A、周天子将王畿(即周天子自己管辖的土地)以外的土地和人口分封给王族、功臣、先代贵族做诸侯的制度。
B、诸侯的义务和权利:义务:镇守疆土、交纳贡赋、随从作战、朝觐述职权利:在自己的封国范围之内拥有绝对实权。
(再分封、征兵、征税、行政等实权,分封制下,表面上是一个统一的国家,实际上是诸多几乎独立的小国结成的松散的联合体,史学界最多的说法就是“天下共主名义下的地方分权体制”)C、分封制的评价:分封制实行初期,可以加强对全国的统治,扩大周朝的疆域。
但由于诸侯权利太大,当诸侯和周天子的实力发生变化时,就会导致诸侯争霸,社会动荡,国家分裂,这是春秋战国争霸战争的政治根源。
宗法制A、按照血缘关系来确立政治等级、财产分割等的制度。
(保留明显的原始社会父系家长制痕迹)B、最大的特点是嫡长子继承制。
嫡长子:正妻所生的第一个儿子。
周天子→嫡长子庶子诸侯→嫡长子庶子卿大夫→嫡长子庶子士→嫡长子庶子平民C、作用:利于凝聚宗族,防止内部纷争,强化王权D、宗法观念影响国人甚深。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ex. 1C
1. Walden Pond, once praised by Thoreau for its natural beauty, is now the site of many tourist stands.
2. Almost every summer night the cooling northeast wind swept through our bedroom windows , marking air conditioning unnecessary and a light blanket welcome. / Swepping through our bedr oom windows almost every summer night, the cooling northeast wind made…
3. The steep surrounding slopes were capped with snow, which fed two streams plunging down to join in the valley below.
4. With the river on one side and a large tree providing shade, this is a good spot for a picnic, a nd we can spread our blanket on the grassy knoll.
5. Panting for breath after running up the stairs, Mr wood stood at his neighbour’s door and knocked again and again till someone opened it.
6. The town folk envied horace, who had come into a small fortune with which he bought a big house and obtained a partnership in the biggest grocery in town.
7. Standing in front of the mirror, Jim looked at his image, wondering at the big change that ha
d com
e over him in recent years.
8. The idea that his only daughter whom he had greatly wronged might never forgive him almo st drove hime mad.
9. The story, written in plain language, consists of three parts with an interesting plot centering。
