语音信号处理实验三
语音信号处理实验报告.docx
在实验中,当P值增加到一定程度,预测平方误差的改善就不很明显了,而且会增加计算量,一般取为8~14,这里P取为10。
5.基音周期估计
①自互相关函数法
②短时平均幅度差法
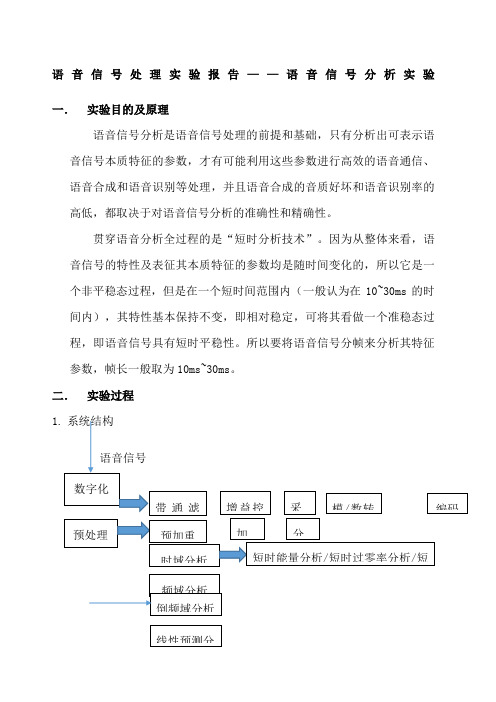
二.实验过程
1. 系统结构
2.仿真结果
(1)时域分析
男声及女声(蓝色为时域信号,红色为每一帧的能量,绿色为每一帧的过零率)
某一帧的自相关函数
3.频域分析
①一帧信号的倒谱分析和FFT及LPC分析
②男声和女声的倒谱分析
③浊音和清音的倒谱分析
④浊音和清音的FFT分析和LPC分析(红色为FFT图像,绿色为LPC图像)
从男声女声的时域信号对比图中可以看出,女音信号在高频率分布得更多,女声信号在高频段的能量分布更多,并且女声有较高的过零率,这是因为语音信号中的高频段有较高的过零率。
2.频域分析
这里对信号进行快速傅里叶变换(FFT),可以发现,当窗口函数不同,傅里叶变换的结果也不相同。根据信号的时宽带宽之积为一常数这一性质,可以知道窗口宽度与主瓣宽度成反比,N越大,主瓣越窄。汉明窗在频谱范围中的分辨率较高,而且旁瓣的衰减大,具有频谱泄露少的有点,所以在实验中采用的是具有较小上下冲的汉明窗。
三.实验结果分析
1.时域分析
实验中采用的是汉明窗,窗的长度对能否由短时能量反应语音信号的变化起着决定性影响。这里窗长合适,En能够反应语音信号幅度变化。同时,从图像可以看出,En可以作为区分浊音和清音的特征参数。
短时过零率表示一帧语音中语音信号波形穿过横轴(零电平)的次数。从图中可以看出,短时能量和过零率可以近似为互补的情况,短时能量大的地方过零率小,短时能量小的地方过零率较大。从浊音和清音的时域分析可以看出,清音过零率高,浊音过零率低。
语音信号处理实验报告
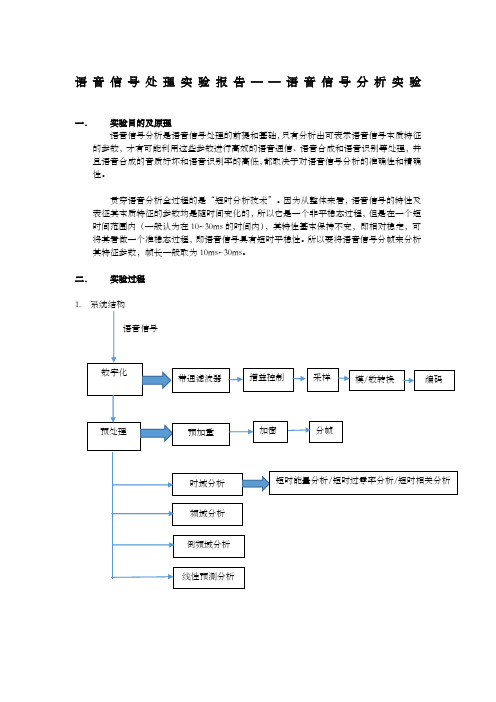
语音信号处理实验报告——语音信号分析实验一.实验目的及原理语音信号分析是语音信号处理的前提和基础,只有分析出可表示语音信号本质特征的参数,才有可能利用这些参数进行高效的语音通信、语音合成和语音识别等处理,并且语音合成的音质好坏和语音识别率的高低,都取决于对语音信号分析的准确性和精确性。
贯穿语音分析全过程的是“短时分析技术”。
因为从整体来看,语音信号的特性及表征其本质特征的参数均是随时间变化的,所以它是一个非平稳态过程,但是在一个短时间范围内(一般认为在10~30ms的时间内),其特性基本保持不变,即相对稳定,可将其看做一个准稳态过程,即语音信号具有短时平稳性。
所以要将语音信号分帧来分析其特征参数,帧长一般取为10ms~30ms。
二.实验过程1.2. 仿真结果(1) 时域分析男声及女声(蓝色为时域信号,红色为每一帧的能量,绿色为每一帧的过零率)x 104-0.6-0.4-0.200.20.40.60.81x 105-0.4-0.200.20.40.60.811.2某一帧的自相关函数-1-0.8-0.6-0.4-0.200.20.40.60.813. 频域分析①一帧信号的倒谱分析和FFT 及LPC 分析对应的倒谱系数:119.2,-7.6895,……对应的LPC 预测系数:1,-0.1,-0.02,-0.4,-0.27,……②男声和女声的倒谱分析③浊音和清音的倒谱分析原语音波形一帧语音波形一帧语音的倒谱④浊音和清音的FFT分析和LPC分析(红色为FFT图像,绿色为LPC图像)三.实验结果分析1.时域分析实验中采用的是汉明窗,窗的长度对能否由短时能量反应语音信号的变化起着决定性影响。
这里窗长合适,En能够反应语音信号幅度变化。
同时,从图像可以看出,En可以作为区分浊音和清音的特征参数。
短时过零率表示一帧语音中语音信号波形穿过横轴(零电平)的次数。
从图中可以看出,短时能量和过零率可以近似为互补的情况,短时能量大的地方过零率小,短时能量小的地方过零率较大。
语音信号处理实验讲义

for m=1:N
sum=sum+b1(m)*b1(m+k-1);
end
A(k)=sum;
end
for k=1:320
A1(k)=A(k)/A(1);
end
%画图
figure(1)
subplot(3,1,1)
plot(A1);
xlabel('延时k')
ylabel('R(k)')
legend('N=320')
e=fra(256,128,x);
ee=e(20,:);
subplot(2,2,1)
ee1=ee/max(ee);
plot(ee1)
xlabel('样点数')
ylabel('幅度')
title('原始语音')
axis([0,256,-1.5,1.5])
%矩形窗傅立叶变换
r=fft(ee,1024);
axis([0,320,-0.5,1])
图2-2 修正的自相关函数(参加自相关运算的点数N取不同值)
四、思考题
1、自相关函数的作用是什么?互相关函数的作用是什么?
2、浊音信号分别加矩形窗和汉明窗时自相关函数有什么不同?
3、清音信号的自相关函数和浊音信号的有什么区别?
实验三语音信号频域特征分析
一、实验目的
plot(s2)
title('一帧语音信号');
xlabel('样点数');
ylabel('幅度');
axis([0,320,-1,1]);
subplot(3,1,2)
语音信号处理实验报告

实验一 显示语音信号的语谱图一、实验目的综合信号频谱分析和滤波器功能,对语音信号的频谱进行 分析,并对信号含进行高通、低通滤波,实现信号特定处理 功能。
加深信号处理理论在语音信号中的应用;理解语谱图 与时频分辨率的关系。
二、实验原理语谱图分析语音又称语谱分析,语谱图中显示了大量的与语音的语句特性有关的信息,它总额了频谱图和时域波形的优点,明显地显示出语音频谱随时间的变化情况。
语谱图实际上是一种三维频谱,即同时在时间和频率上显示出语音的特性,或者说是一种动态的频谱。
窄带语谱图可以得到较好的频域分辨率,窗长通常为至少两个基音周期的“长窗”;而宽带语谱图可以给出较好的时域分辨率,窗长为小于一个基音周期的“短窗”。
三、实验内容实验数据为工作空间 ex3M2.mat 中数组 we_be10k 是单词“we ”和“be ”的语音波形(采样率为10000 点/秒) 。
1、 听一下 we_be10k (可用 sound )2、使用函数 specgram_ex3p19.显示语谱图和语音波形,如图一。
图一、参数窗长 20ms (200 点) 、帧间隔 1ms (10 点)0.511.5-2-1012Time (s)SPEECHTime (ms)F r e q u e n c y (H z )SPECTROGRAM00.51 1.5200040002、 对比调用参数窗长 20ms (200 点) 、帧间隔 1ms (10 点),(如图一)和参数窗长5ms (50点) 、帧间隔 1ms (10点)(如图二) ;图二、参数窗长5ms (50点) 、帧间隔 1ms (10点)图三、参数窗长30ms (300点) 、帧间隔 1ms (10点)0.511.5-2-1012Time (s)SPEECHTime (ms)F r e q u e n c y (H z )SPECTROGRAM00.51 1.5200040000.511.5-2-1012Time (s)SPEECHTime (ms)F r e q u e n c y (H z )SPECTROGRAM00.51 1.520004000图四、参数窗长20ms (200点) 、帧间隔 5ms (50点)3、 再对比窗长>20ms 或小于5ms ,以及帧间隔>1ms 时的语谱图说明宽带语谱图、窄带语谱图与时频分辨率的关系及如何得到时频折中。
语音信号处理综合实验

语音信号处理综合实验电子信息科学与技术09380049 陈俊浩一:实验目的通过利用matlab设计仿真实验,理解如下知识点:1.信号的采样及混迭2.信号的频谱分析3.信号的幅度调制解调的方法4.理想滤波器的时频域特性5.数字滤波器的设计二:实验要求1.录制一段个人自己的语音信号2.采用合适的频率,对录制的信号进行采样,画出采样后语音信号的时域波形和频谱图3.给原始语音信号加噪声,画出加噪声后的语音信号和频谱图4.设计一个频域的理想带通信道5.对这语音信号进行幅度调制,画出调制后的语音信号和频谱图6.利用理想带通信道对信号进行传输7.对接受到的信号进行解调,画出解调后的语音信号和频谱图8.设计性能良好的滤波器对信号进行滤波9.对语音进行回放,并与滤波后的语音信号进行对比三:实验过程1.首先利用windows操作系统自带的录音机录取一段声音,保存为‘cjh.wav’;再利用wavread函数将这个语音文件读进matlab中,然后对这段语音进行采样,采样频率为fs=22050Hz,语音持续时间为2.5s,用sound函数听这段语音信号;2.用plot函数画出这段语音信号的时域波形,用fftshift函数对信号进行快速傅里叶变换,并调整y轴的幅度,画出原始信号的频谱图;3.为了给原始信号加噪声,用randn函数产生一段随机噪声,然后加到原始信号中,然后用sound函数听加了噪音以后的信号,和原始信号相对比,可听到有一些“沙沙”的噪声;用plot函数画出加了噪音以后的时域波形,然后再将其进行快速傅里叶变换,然后画出其频域波形4.直接用matlab的逻辑语句,设计一个理想的带通信号,其截至频率为fl=4000Hz,fh=8000Hz;5.设定载波频率,用matlab的modulate函数对其进行幅度调制,画出调制以后的信号的时域波形,然后再将其通过傅里叶变换,然后画出其频谱图;6.用matlab中的demod函数将已经调制以后的信号进行解调,在用和上述一致的方法画出解调以后的时域和频域波形;7.由于人的声音频率一般比较低,而且由画出来的原始信号的频域波形可知,信号的能量都集中在低频的范围,我们可以考虑设计一个低通滤波器对其进行滤波,然后将滤波以后的信号就行回放,与原始信号进行对比。
哈尔滨工程大学语音信号处理实验报告讲述

实验报告实验课程名称:语音信号处理实验姓名:班级: 20120811 学号:Array指导教师张磊实验教室 21B#293实验时间 2015年4月12日实验成绩实验一 语音信号的端点检测一、实验目的1、掌握短时能量的求解方法2、掌握短时平均过零率的求解方法3、掌握利用短时平均过零率和短时能量等特征,对输入的语音信号进行端点检测。
二、实验设备 HP 计算机、Matlab 软件 三、实验原理 1、短时能量语音信号的短时能量分析给出了反应这些幅度变化的一个合适的描述方法。
对于信号)}({n x ,短时能量的定义如下:∑∑∞-∞=∞-∞=*=-=-=m m n n h n x m n h m xm n w m x E )()()()()]()([2222、短时平均过零率短时平均过零率是指每帧内信号通过零值的次数。
对于连续语音信号,可以考察其时域波形通过时间轴的情况。
对于离散信号,实质上就是信号采样点符号变化的次数。
过零率在一定程度上可以反映出频率的信息。
短时平均过零率的公式为:∑∑-+=∞-∞=--=---=1)]1(sgn[)](sgn[21 )()]1(sgn[)](sgn[21N n nm w w m n m x m x m n w m x m x Z其中,sgn[.]是符号函数,即⎩⎨⎧<-≥=0)(10)(1)](sgn[n x n x n x3、端点检测原理能够实现这些判决的依据在于,不同性质语音的各种短时参数具有不同的概率密度函数,以及相邻的若干帧语音应具有一致的语音特性,它们不会在S 、U 、V 之间随机地跳来跳去。
要正确判断每个输入语音的起点和终点,利用短时平均幅度参数E 和短时平均过零率Z 可以做到这一点。
首先,根据浊音情况下的短时能量参数的概率密度函数)|(V E P 确定一个阈值参数H E ,H E 值一般定的较高。
当一帧输入信号的短时平均幅度参数超过H E 时,就可以判定该帧语音信号不是无声,而有相当大的可能是浊音。
语音信号处理实验报告集锦

语音信号处理实验报告集锦【实验一】一、实验题目Short time analysis(短时间分析)二、实验要求Write a MA TLAB program to analyze a speech and simultaneously, on a single page, plot the following measurements:1. the entire speech waveform2. the short-time energy, En3. the short-time magnitude, Mn4. the short-time zero-crossing, Zn5. the narrowband spectrogram6. the wideband spectrogramUse both the speech waveforms in the wznjdx_normal.wav. Choose appropriate window sizes, window shifts, and window for the analysis. Explain your choice of these parameters.写一个程序来分析语音的同时,在一个单页,情节如下措施:1。
整个语音波形2。
短时间能量3。
短时幅度,锰4。
短时过零,锌5。
窄带语谱图6。
宽带语谱图在wznjdx_normal.wav使用语音波形。
选择合适的窗口大小,窗口移动和窗口进行分析。
解释你对这些参数的选择。
三、实验程序clear[x,fs]=wavread('wznjdx_normal.wav');n=length(x);N=320;subplot(4,1,1);plot(x);h=linspace(1,1,N);En=conv(h,x.*x);subplot(4,1,2);plot(En);Mn=conv(h,abs(x));subplot(4,1,3);plot(Mn);for i=1:n-1if x(i)>=0 y(i)=1;else y(i)=-1;endif x(i+1)>=0 y(i+1)=1;else y(i+1)=-1;endw(i)=abs(y(i+1)-y(i));endk=1;j=0;while (k+N-1)<nZm(k)=0;for i=0:N-1Zm(k)=Zm(k)+w(k+i);endj=j+1;k=k+N/2;endfor w=1:jQ(w)=Zm(160*(w-1)+1)/(2*N);endsubplot(4,1,4);plot(Q);grid;figure(2);subplot(2,1,1);spectrogram(x,h,256,200,0.0424*fs); subplot(2,1,2);spectrogram(x,h,256,200,0.0064*fs);四、实验结果语谱图:(Matlab 7.0 用不了spectrogram)【实验二】一、实验题目Homomorphic analysis同态分析二、实验要求Write a MATLAB program to compute the real cepstrums of a section of voiced speech and unvoiced speech.Plot the signal, the log magnitude spectrum, the real cepstrum, and the lowpass liftered log magnitude spectrum.写一个程序来计算实际倒谱一段浊音和清音。
lpc

语音信号处理实验报告实验二:语音信号的LPC分析学院:电子与信息学院专业:信息工程提交日期:2014./实验三:语音信号的LPC 分析1、 实验内容线性预测分析是最有效的语音分析技术之一,在语音编码、语音合成、语音识别和说话人识别等语音处理领域中得到了广泛的应用。
语音线性预测的基本思想是:一个语音信号的抽样值可以用过去若干个取样值的线性组合来逼近。
通过使实际语音抽样值与线性预测抽样值的均方误差达到最小,可以确定唯一的一组线性预测系数。
采用线性预测分析不仅能够得到语音信号的预测波形,而且能够提供一个非常好的声道模型。
如果将语音模型看作激励源通过一个线性时不变系统产生的输出,那么可以利用LP 分析对声道参数进行估值,以少量低信息率的时变参数精确地描述语音波形及其频谱的性质。
此外,LP 分析还能够对共振峰、功率谱等语音参数进行精确估计,LP 分析得到的参数可以作为语音识别的重要参数之一。
2、 实验方法2.1线性预测分析的基本原理线性预测分析为线性时不变因果稳定系统V (z )建立一个全极点模型,并利用均方误差准则,对已知的语音信号s(n)进行模型参数估计。
如果利用P 个取样值来进行预测,则称为P 阶线性预测。
假设用过去P 个取样值()()(){}1,2,S n S n S n p ---的加权之和来预测信号当前取样值()S n,则预测信号()S n∧为:()()1pk k S n a n k ∧==-∑ (1)其中加权系数用k a 表示,称为预测系数,则预测误差为:()()()()()1pk k e n s n S n s n a n k ∧==-=--∑ (2)要使预测最佳,则要使短时平均预测误差最小有:()2min E e n ε⎡⎤==⎣⎦ (3)()20,(1)ke n k p a ⎡⎤∂⎣⎦=≤≤∂ (4)令()()(),,i k E s n i S n k φ=--⎡⎤⎣⎦(5)最小的ε可表示成:()()min 10,00,pk k a k εφφ==-∑ (6)显然,误差越接近于零,线性预测的准确度在均方误差最小的意义上为最佳,由此可以计算出预测系数。
(完整版)语音信号进行倒谱分析

实验三 语音信号进行倒谱分析一、 实验目的、要求1.理解倒谱分析的作用 2. 掌握倒谱分析求基音周期的方法3. 了解LPC 倒谱分析方法二、实验原理1.倒谱分析原理同态信号处理也称为同态滤波,实现将卷积关系变换为求和关系的分离处理,即解卷。
如 进行如下3步处理)(ˆ)(ˆ)(ˆ)](ˆ)(ˆ[)](ˆ[)3()(ˆ)(ˆ)(ˆ)(ln )(ln )(ln )2()()()()]([)1(212111212121n x n x n x z X z X Z z X Z z X z X z Xz X z X z X z X z X z X n x Z =+=+==+=+=⋅==--对于语音信号进行解卷,可将语音信号的声门激励信息及声道响应信息分离开来,从而求得声道共振特征和基音周期,用于语音编码、合成和识别.同态信号处理的基本原理(1)第一个子系统D *[](特征系统)完成将卷积信号转化为加性信号的运算。
)(ˆ1n x 和 )(ˆ2n x信号也均是时域序列,但它们所处的离散时域显然不同于x(n )所处的离散时域,故把它称之为复倒频谱域。
)(ˆn x是x(n)的复倒频谱,简称为复倒谱,有时也称为对数复倒谱.复倒谱具体计算公式其中倒谱计算公式为:2 线性预测原理12()()()x n x n x n 1ˆ()[ln (())]x n Z Z x n [()]()ˆ()ln ()ˆˆ()[()]jw jw jw jw DFT x n X e X e X e x n IDFT X e线性预测分析的基本思想由于语音样点之间存在相关性,所以可以用过去的样点值来预测现在或未来的样点值。
通过使实际语音抽样和线性预测抽样之间的误差在某个准则下达到最小值来决定唯一的一组预测系数,而这组系数就能反映语音信号的特性,可以作为语音信号特征参数来用于语音编码、语音合成和语音识别等应用中去。
线性预测分析的基本原理每个采样值由前面的p 个采样值线性组合所构成。
语音信号处理实验报告

语⾳信号处理实验报告语⾳信号处理实验报告【实验⼀】⼀、实验题⽬Short time analysis⼆、实验要求Write a MA TLAB program to analyze a speech and simultaneously, on a single page, plot the following measurements:1. the entire speech waveform2. the short-time energy, En3. the short-time magnitude, Mn4. the short-time zero-crossing, Zn5. the narrowband spectrogram6. the wideband spectrogramUse both the speech waveforms in the wznjdx_normal.wav. Choose appropriate window sizes, window shifts, and window for the analysis. Explain your choice of these parameters.三、实验程序clear[x,fs]=wavread('wznjdx_normal.wav');n=length(x);N=320;subplot(4,1,1);plot(x);h=linspace(1,1,N);En=conv(h,x.*x);subplot(4,1,2);plot(En);Mn=conv(h,abs(x));subplot(4,1,3);plot(Mn);for i=1:n-1if x(i)>=0 y(i)=1;else y(i)=-1;endif x(i+1)>=0 y(i+1)=1;else y(i+1)=-1;endw(i)=abs(y(i+1)-y(i));endk=1;j=0;while (k+N-1)Zm(k)=0;for i=0:N-1Zm(k)=Zm(k)+w(k+i);endj=j+1;k=k+N/2;endfor w=1:jQ(w)=Zm(160*(w-1)+1)/(2*N);endsubplot(4,1,4);plot(Q);grid;figure(2);subplot(2,1,1);spectrogram(x,h,256,200,0.0424*fs); subplot(2,1,2);spectrogram(x,h,256,200,0.0064*fs);四、实验结果语谱图:(Matlab 7.0 ⽤不了spectrogram)【实验⼆】⼀、实验题⽬Homomorphic analysis⼆、实验要求Write a MATLAB program to compute the real cepstrums of a section of voiced speech and unvoiced speech. Plot the signal, the log magnitude spectrum, the real cepstrum, and the lowpass liftered log magnitude spectrum.三、实验程序nfft=256;[x,fs] = wavread('wznjdx_normal.wav');fx=x;Xvm=log(abs(fft(fx,nfft)));xhv=real(ifft(Xvm,nfft));lifter=zeros(1,nfft);lifter(1:30)=1;lifter(nfft-28:nfft)=1;fnlen=0.02*fs; % 20mswin=hamming(fnlen);%加窗n=fnlen;%窗宽度赋给循环⾃变量nnoverlap=0.5*fnlen;while(n<=length(x)-1)fx=x(n-fnlen+1:n).*win;n=n+noverlap;endxhvp=xhv.*lifter';figure;subplot(4,1,1)plot(lifter);title('倒谱滤波器');subplot(4,1,2)plot(x);title('语⾳信号波形');subplot(4,1,3)plot(Xvm);title('Xvm');subplot(4,1,4)plot(xhv);title('xhv');四、实验结果【实验三】⼀、实验题⽬LP analysis⼆、实验要求Write a MATLAB program to convert from a frame of speech to a set of linear prediction coefficients. Plot the LPC spectrum superimposed on the corresponding STFT.三、实验程序clear;[x,fs]=wavread('wznjdx_normal.wav');fx=x(4000:4160-1);p=10;[a,e,k]=aryule(fx,p);G=sqrt(e*length(fx));f=log(abs(fft(fx)));h0=zeros(1,160);h=log(G)-log(abs(fft(a,160)));figure(1);subplot(211);plot(fx);subplot(212);plot(f);hold on;plot((0:160-1),h,'r');四、实验结果【实验四】⼀、实验题⽬Pitch estimation⼆、实验内容Write a program to implement the pitch estimation and the voiced/unvoiced decision using the LPC-based method.三、实验程序clear[x,fs]=wavread('wznjdx_normal.wav');n=length(x);Q = x';NFFT=512;N = 256;Hamm = hamming(N);frame = 30;M = Q(((frame -1) * (N / 2) + 1):((frame - 1) * (N / 2) + N)); Frame = M .* Hamm';% lowpass filter[b2,a2]=butter(2,900/4000);speech2=filter(b2,a2,Frame); % filter% residual[a,e] = lpc(speech2,20);errorlp=filter(a,1,speech2); % residual% Short-term autocorrelation.re = xcorr(errorlp);% Find max autocorrelation for lags in the interval minlag to maxlag. minlag = 17; % F0: 450Hzmaxlag =160; % F0: 50Hz[remax,idx] = max(re(fnlen+minlag:fnlen+maxlag));figuresubplot(3,1,1);plot(Frame);subplot(3,1,2);plot(speech2);subplot(3,1,3);plot(re);text(500,0,'idx');idx=idx-1+minlagremax四、实验结果【实验五】⼀、实验题⽬Speech synthesis⼆、实验内容Write a program to analyze a speech and synthesize it using the LPC-based method.三、实验程序主程序clear;[x,sr] = wavread('wznjdx_normal.wav');p=[1 -0.9];x=filter(p,1,x);N=256;inc=128;y=lpcsyn(x,N,inc);wavplay(y,sr);⼦程序lpcsynfunction y=lpcsyn(x,N,inc)%[x,sr] = wavread('wznjdx_normal.wav');%pre = [1 -0.97];%x = filter(pre,1,x);%N=256;%inc=128;fn=floor(length(x)/inc);y=zeros(1,50000);for (i=1:fn)x(1:N,i)=x((i-1)*inc+1:(i+1)*inc);[A(i,:),G(i),P(i),fnlen,fnshift] = lpcana(x(1:N,i),order); if (P(i)) % V oiced frame.e = zeros(N,1);e(1:P(i):N) = 1; % Impulse-train excitation.else % Unvoiced frame.e = randn(N,1); % White noise excitation.endyt=filter(G(i),A(i,:),e);j=(i-1)*inc+[1:N];y(j) = y(j)+yt';end;end⼦程序lpcanafunction [A,G,P,fnlen,fnshift] = lpcana(x,order) fnlen=256;fnshift=fnlen/2;n=length(x);[b2,a2]=butter(2,900/4000);speech2=filter(b2,a2,x);[A,e]=lpc(speech2,order);errorlp=filter(A,1,speech2);re=xcorr(errorlp);G=sqrt(e*length(speech2));minlag=17;maxlag=160;[remax,idx]=max(re(n+minlag:n+maxlag));P=idx-1+minlag;end四、实验结果【实验六】⼀、实验题⽬Speech enhancement⼆、实验内容Write a program to implement the basic spectral magnitude subtraction.三、实验程序clear[speech,fs,nbits]=wavread('wznjdx_normal.wav');%读⼊数据alpha=0.04;%噪声⽔平winsize=256;%窗长size=length(speech);%语⾳长度numofwin=floor(size/winsize);%帧数hamwin=zeros(1,size);%定义汉明窗长度enhanced=zeros(1,size);%定义增强语⾳的长度ham=hamming(winsize)';%%产⽣汉明窗x=speech'+alpha*randn(1,size);%信号加噪声noisy=alpha*randn(1,winsize);%噪声估计N=fft(noisy);nmag=abs(N);%噪声功率谱%分帧for q=1:2*numofwin-1frame=x(1+(q-1)*winsize/2:winsize+(q-1)*winsize/2);%对带噪语⾳帧间重叠⼀半取值hamwin(1+(q-1)*winsize/2:winsize+(q-1)*winsize/2)=...hamwin(1+(q-1)*winsize/2:winsize+(q-1)*winsize/2)+ham;%加窗y=fft(frame.*ham);mag=abs(y);%带噪语⾳功率谱phase=angle(y);%带噪语⾳相位%幅度谱减for i=1:winsizeif mag(i)-nmag(i)>0clean(i)=mag(i)-nmag(i);else clean(i)=0;endend%频域中重新合成语⾳spectral=clean.*exp(j*phase);%反傅⾥叶变换并重叠相加enhanced(1+(q-1)*winsize/2:winsize+(q-1)*winsize/2)=...enhanced(1+(q-1)*winsize/2:winsize+(q-1)*winsize/2)+real(ifft(spectral));endfigure(1);subplot(3,1,1);plot(speech);xlabel('样点数');ylabel('幅度');title('原始语⾳波形'); subplot(3,1,2);plot(x);xlabel('样点数');ylabel('幅度');title('语⾳加噪波形'); subplot(3,1,3);plot(enhanced);xlabel('样点数');ylabel('幅度');title('增强语⾳波形');四、实验结果。
语音信号处理 实验报告

实验一、语音信号采集与分析一、实验目的:1)了解语音信号处理基本知识:语音信号的生成的数学模型。
2)在理论学习的基础上,进一步地理解和掌握语音信号的读入、回放、波形显示。
语音信号时域和频域分析方法。
二、实验原理一定时宽的语音信号,其能量的大小随时间有明显的变化。
其中清音段(以清音为主要成份的语音段),其能量比浊音段小得多。
短时过零数也可用于语音信号分析中,发浊音时,其语音能量约集中于3kHz以下,而发清音时,多数能量出现在较高频率上,可认为浊音时具有较低的平均过零数,而清音时具有较高的平均过零数,因而,对一短时语音段计算其短时平均能量及短时平均过零数,就可以较好地区分其中的清音段和浊音段,从而可判别句中清、浊音转变时刻,声母韵母的分界以及无声与有声的分界。
这在语音识别中有重要意义。
FFT在数字通信、语音信号处理、图像处理、匹配滤波以及功率谱估计、仿真、系统分析等各个领域都得到了广泛的应用。
本实验通过分析加噪的语音信号频谱,可以作为分离信号和噪声的理论基础。
三、实验内容:Matlab编程实验步骤:1.新建M文件,扩展名为“.m”,编写程序;2.选择File/Save命令,将文件保存在F盘中;3.在Command Window窗中输入文件名,运行程序;程序一、用MATLAB对原始语音信号进行时域分析,分析短时平均能量及短时平均过零数。
程序二、用MATLAB对原始语音信号进行频域分析,画出它的时域波形和频谱给原始的语音信号加上一个高频余弦噪声,频率为5kHz。
画出加噪后的语音信号时域和频谱图。
程序1.a=wavread(' D:\II.wav'); %读取语音信号的数据,赋给变量x1,这里的文件的全路径和文件名由个人设计n=length(a);N=320;subplot(3,1,1),plot(a);h=linspace(1,1,N);%形成一个矩形窗,长度为NEn=conv(h,a.*a);%求卷积得其短时能量函数Ensubplot(3,1,2),plot(En);for i=1:n-1if a(i)>=0b(i)= 1;elseb(i) = -1;endif a(i+1)>=0b(i+1)=1;elseb(i+1)=-1;endw(i)=abs(b(i+1)-b(i));end%求出每相邻两点符号的差值的绝对值k=1;j=0;while (k+N-1)<nZm(k)=0;for i=0:N-1;Zm(k)=Zm(k)+w(k+i);endj=j+1;k=k+160; %每次移动半个窗endfor w=1:jQ(w)=Zm(160*(w-1)+1)/640;%短时平均过零率endsubplot(3,1,3),plot(Q);实验结果打印粘贴到右侧:程序2:fs=22050; %语音信号采样频率为22050x1=wavread('D:\II.wav'); %读取语音信号的数据,赋给变量x1sound(x1,22050); %播放语音信号f=fs*(0:511)/1024;t=0:1/22050:(size(x1)-1)/22050; %将所加噪声信号的点数调整到与原始信号相同Au=0.03;d=[Au*cos(2*pi*5000*t)]'; %噪声为5kHz的余弦信号x2=x1+d;sound(x2,22050); %播放加噪声后的语音信号y2=fft(x2,1024); %对信号做1024点FFT变换figure(1)subplot(2,1,1);plot(x1) %做原始语音信号的时域图形title('原始语音信号');xlabel('time n');ylabel('幅值 n');subplot(2,1,2);plot(t,x2)title('加噪后的信号');xlabel('time n');ylabel('幅值 n');figure(2)subplot(2,1,1);plot(f,abs(x1(1:512)));title('原始语音信号频谱');xlabel('Hz');ylabel('幅值');subplot(2,1,2);plot(f,abs(y2(1:512)));title('加噪后的信号频谱');xlabel('Hz'); ylabel('幅值');实验结果打印粘贴到右侧:050010001500200025003000350040004500原始语音信号time n幅值 n加噪后的信号time n幅值 n020004000600080001000012000原始语音信号频谱Hz幅值加噪后的信号频谱Hz幅值四、实验分析加入噪声后音频文件可辨性下降,波形的平缓,频谱图上看,能量大部分集中在2000HZz到4000Hz之间。
语音信号信号处理实验报告

实验一 语音信号的端点检测一、实验目的1、掌握短时能量的求解方法2、掌握短时平均过零率的求解方法3、掌握利用短时平均过零率和短时能量等特征,对输入的语音信号进行端点检测。
二、仪器设备HP 计算机、Matlab 软件三、实验原理3.1、短时能量3.1.1、原理:语音信号能量随时间有相当大的变化,特别是清音段的能量一般比浊音段的小得多。
语音信号的短时能量定义:3.1.2、短时能量序列反映了语音振幅或能量随着时间缓慢变化的规律。
从原始语音信号图中可以看到语音信号幅度随时间有相当大的变化,特别是清音段的幅度一般比浊音段的幅度小很多,语音信号的短时能量给出了反映这些幅度变化的一个合适的描述方法。
3.1.3、短时平均幅度函数和能量函数的作用(1)区分清/浊音。
En 、Mn 大,对应浊音; En 、Mn 小,对应清音。
其中Mn 是短时幅度差。
(2)在信噪比高的情况下,能进行有声/无声判决。
无声时,背景噪声的En 、Mn 小;有声时,En 、Mn 显著增大。
判决时可设置一个门限。
(3)大致能定出浊音变为清音的时刻,或反之。
3.2、短时过零率:3.2.1、定义:过零就是信号通过零值。
连续语音信号,考察其时域波形通过时间轴的情况;离散时间信号,相邻的 值改变符号则称为过零。
12()n N n w m nE x m +-==∑()()()01w x n w n x n m N =⋅≤≤-101() 0n N w n ≤≤-⎧=⎨⎩其它窄带信号,平均过零数作为信号频率的一种简单度量是很精确的,语音信号序列是宽带信号, 则不能简单用上面的公式,但是可以用短时平均过零数来得到频谱的粗略估计。
3.2.2、短时过零分析的意义:(1)、可以区分清音与浊音:浊音时具有较低的平均过零数,而清音时具有较高的平均过零数。
(2)、利用它可以从背景噪声中找出语音信号,可用于判断寂静无语音和有语音的起点和终点位置。
(3)、在背景噪声较小时用平均能量识别较为有效,而在背景噪声较大时用平均过零数识别较为有效。
语音信号处理实验报告

一、实验目的1. 理解语音信号处理的基本原理和流程。
2. 掌握语音信号的采集、预处理、特征提取和识别等关键技术。
3. 提高实际操作能力,运用所学知识解决实际问题。
二、实验原理语音信号处理是指对语音信号进行采集、预处理、特征提取、识别和合成等操作,使其能够应用于语音识别、语音合成、语音增强、语音编码等领域。
实验主要包括以下步骤:1. 语音信号的采集:使用麦克风等设备采集语音信号,并将其转换为数字信号。
2. 语音信号的预处理:对采集到的语音信号进行降噪、去噪、归一化等操作,提高信号质量。
3. 语音信号的特征提取:提取语音信号中的关键特征,如频率、幅度、倒谱等,为后续处理提供依据。
4. 语音信号的识别:根据提取的特征,使用语音识别算法对语音信号进行识别。
5. 语音信号的合成:根据识别结果,合成相应的语音信号。
三、实验步骤1. 语音信号的采集使用麦克风采集一段语音信号,并将其保存为.wav文件。
2. 语音信号的预处理使用MATLAB软件对采集到的语音信号进行预处理,包括:(1)降噪:使用谱减法、噪声抑制等算法对语音信号进行降噪。
(2)去噪:去除语音信号中的杂音、干扰等。
(3)归一化:将语音信号的幅度归一化到相同的水平。
3. 语音信号的特征提取使用MATLAB软件对预处理后的语音信号进行特征提取,包括:(1)频率分析:计算语音信号的频谱,提取频率特征。
(2)幅度分析:计算语音信号的幅度,提取幅度特征。
(3)倒谱分析:计算语音信号的倒谱,提取倒谱特征。
4. 语音信号的识别使用MATLAB软件中的语音识别工具箱,对提取的特征进行识别,识别结果如下:(1)将语音信号分为浊音和清音。
(2)识别语音信号的音素和音节。
5. 语音信号的合成根据识别结果,使用MATLAB软件中的语音合成工具箱,合成相应的语音信号。
四、实验结果与分析1. 语音信号的采集采集到的语音信号如图1所示。
图1 语音信号的波形图2. 语音信号的预处理预处理后的语音信号如图2所示。
语音信号处理实验指导书

语音信号处理实验指导书实验一:语音信号的采集与播放实验目的:了解语音信号的采集与播放过程,掌握采集设备的使用方法。
实验器材:1. 电脑2. 麦克风3. 扬声器或者耳机实验步骤:1. 将麦克风插入电脑的麦克风插孔。
2. 打开电脑的录音软件(如Windows自带的录音机)。
3. 在录音软件中选择麦克风作为录音设备。
4. 点击录音按钮开始录音,讲话或者唱歌几秒钟。
5. 点击住手按钮住手录音。
6. 播放刚刚录制的语音,检查录音效果。
7. 将扬声器或者耳机插入电脑的音频输出插孔。
8. 打开电脑的音频播放软件(如Windows自带的媒体播放器)。
9. 选择要播放的语音文件,点击播放按钮。
10. 检查语音播放效果。
实验二:语音信号的分帧与加窗实验目的:了解语音信号的分帧和加窗过程,掌握分帧和加窗算法的实现方法。
实验器材:1. 电脑2. 麦克风3. 扬声器或者耳机实验步骤:1. 使用实验一中的步骤1-5录制一段语音。
2. 将录制的语音信号进行分帧处理。
选择合适的帧长和帧移参数。
3. 对每一帧的语音信号应用汉明窗。
4. 将处理后的语音帧进行播放,检查分帧和加窗效果。
实验三:语音信号的频谱分析实验目的:了解语音信号的频谱分析过程,掌握频谱分析算法的实现方法。
实验器材:1. 电脑2. 麦克风3. 扬声器或者耳机实验步骤:1. 使用实验一中的步骤1-5录制一段语音。
2. 将录制的语音信号进行分帧处理。
选择合适的帧长和帧移参数。
3. 对每一帧的语音信号应用汉明窗。
4. 对每一帧的语音信号进行快速傅里叶变换(FFT)得到频谱。
5. 将频谱绘制成图象,观察频谱的特征。
6. 对频谱进行谱减法处理,去除噪声。
7. 将处理后的语音帧进行播放,检查频谱分析效果。
实验四:语音信号的降噪处理实验目的:了解语音信号的降噪处理过程,掌握降噪算法的实现方法。
实验器材:1. 电脑2. 麦克风3. 扬声器或者耳机实验步骤:1. 使用实验一中的步骤1-5录制一段带噪声的语音。
语音信号处理实验报告

实验报告一、 实验目的、要求(1)掌握语音信号采集的方法(2)掌握一种语音信号基音周期提取方法(3)掌握短时过零率计算方法(4)了解Matlab 的编程方法二、 实验原理基本概念:(a )短时过零率:短时内, 信号跨越横轴的情况, 对于连续信号, 观察语音时域波形通过横轴的情况;对于离散信号, 相邻的采样值具有不同的代数符号, 也就是样点改变符号的次数。
对于语音信号, 是宽带非平稳信号, 应考察其短时平均过零率。
其中sgn[.]为符号函数⎪⎩⎪⎨⎧<=>=0 x(n)-1sgn(x(n))0 x(n)1sgn(x(n))短时平均过零的作用1.区分清/浊音:浊音平均过零率低, 集中在低频端;清音平均过零率高, 集中在高频端。
2.从背景噪声中找出是否有语音, 以及语音的起点。
(b )基音周期基音是发浊音时声带震动所引起的周期性, 而基音周期是指声带震动频率的倒数。
基音周期是语音信号的重要的参数之一, 它描述语音激励源的一个重要特征, 基音周期信息在多个领域有着广泛的应用, 如语音识别、说话人识别、语音分析与综合以及低码率语音编码, 发音系统疾病诊断、听觉残障者的语音指导等。
因为汉语是一种有调语言, 基音的变化模式称为声调, 它携带着非常重要的具有辨意作用的信息, 有区别意义的功能, 所以, 基音的提取和估计对汉语更是一个十分重要的问题。
由于人的声道的易变性及其声道持征的因人而异, 而基音周期的范围又很宽, 而同—个人在不同情态下发音的基音周期也不同, 加之基音周期还受到单词∑--=-=10)]1(sgn[)](sgn[21N m n n n m x m x Z发音音调的影响, 因而基音周期的精确检测实际上是一件比较困难的事情。
基音提取的主要困难反映在: ①声门激励信号并不是一个完全周期的序列, 在语音的头、尾部并不具有声带振动那样的周期性, 有些清音和浊音的过渡帧是很难准确地判断是周期性还是非周期性的。
语音信号处理实验三

一.实验目的1.熟悉前一个实验程序以及中心削波的意义。
.2.用Matlab实现用修正的短时自相关检测语音的基音周期。
3.分析修正的短时自相关在基音周期检测中的应用。
4.能够对程序进行重新编制。
二.实验原理如果x(n) 是一个周期为P 的信号,则其自相关函数也是周期为P的信号,且在信号周期的整数倍处,自相关函数取最大值。
语音的浊音信号具有准周期性,其自相关函数在基音周期的整数倍处取最大值。
计算两相邻最大峰值间的距离,就可以估计出基音周期。
观察浊音信号的自相关函数图,其中真正反映基音周期的只有少数几个峰,而其余大多数峰都是由于声道的共振特性引起的。
因此为了突出反映基音周期的信息,同时压缩其他无关信息,减小运算量,有必要对语音信号进行适当预处理后再进行自相关计算以获得基音周期。
第一种方法是先对语音信号进行低通滤波,再进行自相关计算,因为语音信号包括十分丰富的谐波分量,基音频率的范围分布宰0~500Hz左右,即使女高音升c调最高也不会超过1Kz,所以采用1Kz 的低通滤波器先对语音信号进行滤波,保留基音频率,再用2Kz采样频率进行采样;最后用2~20ms的滞后时间计算短时自相关,帧长取10~20ms,即可估计出基音周期。
且中心削波函数如式(3-1)一般削波电平 X L取本帧语音幅度的60%~70%。
将削波后的序列f(x) 用短时自相关函数估计基音周期,在基音周期位置的峰值更加尖锐,可以有效减少倍频或半频错误。
三.实验要求1.实验前自己用Cool Edit 音频编辑软件录制浊音部分,并把它保存为.txt文件。
2.分别取长度N=160和N’=N+K的矩形窗函数作用于语音信号上,首先对其进行中心削波,比较削波前和削波后语音信号波形,并使得削波后的信号进行乘积并求和,计算延迟为0<K<160时的相关值,并且用得到的相关值来检测语音信号的基音周期,用MATLAB画出图形。
3.写出实验报告,分析实验结果。
语音信号处理实验报告

语音信号处理实验报告 The Standardization Office was revised on the afternoon of December 13, 2020语音信号处理实验报告——语音信号分析实验一.实验目的及原理语音信号分析是语音信号处理的前提和基础,只有分析出可表示语音信号本质特征的参数,才有可能利用这些参数进行高效的语音通信、语音合成和语音识别等处理,并且语音合成的音质好坏和语音识别率的高低,都取决于对语音信号分析的准确性和精确性。
贯穿语音分析全过程的是“短时分析技术”。
因为从整体来看,语音信号的特性及表征其本质特征的参数均是随时间变化的,所以它是一个非平稳态过程,但是在一个短时间范围内(一般认为在10~30ms的时间内),其特性基本保持不变,即相对稳定,可将其看做一个准稳态过程,即语音信号具有短时平稳性。
所以要将语音信号分帧来分析其特征参数,帧长一般取为10ms~30ms。
二.实验过程男声及女声(蓝色为时域信号,红色为每一帧的能量,绿色为每一帧的过零率)某一帧的自相关函数3.频域分析①一帧信号的倒谱分析和FFT及LPC分析②男声和女声的倒谱分析对应的倒谱系数:,,……对应的LPC预测系数:1,,,,,……原语音波形一帧语音波形一帧语音的倒谱③浊音和清音的倒谱分析④浊音和清音的FFT分析和LPC分析(红色为FFT图像,绿色为LPC图像)三.实验结果分析1.时域分析实验中采用的是汉明窗,窗的长度对能否由短时能量反应语音信号的变化起着决定性影响。
这里窗长合适,En能够反应语音信号幅度变化。
同时,从图像可以看出,En可以作为区分浊音和清音的特征参数。
短时过零率表示一帧语音中语音信号波形穿过横轴(零电平)的次数。
从图中可以看出,短时能量和过零率可以近似为互补的情况,短时能量大的地方过零率小,短时能量小的地方过零率较大。
从浊音和清音的时域分析可以看出,清音过零率高,浊音过零率低。
从男声女声的时域信号对比图中可以看出,女音信号在高频率分布得更多,女声信号在高频段的能量分布更多,并且女声有较高的过零率,这是因为语音信号中的高频段有较高的过零率。
语音信号实验报告

一、实验目的1. 理解语音信号的基本特性和处理方法。
2. 掌握语音信号的采样、量化、编码等基本过程。
3. 学习使用相关软件对语音信号进行时域和频域分析。
4. 了解语音信号的降噪、增强和合成技术。
二、实验原理语音信号是一种非平稳的、时变的信号,其频谱特性随时间变化。
语音信号处理的基本过程包括:信号采集、信号处理、信号分析和信号输出。
三、实验仪器与软件1. 仪器:计算机、麦克风、耳机。
2. 软件:Matlab、Audacity、Python。
四、实验步骤1. 信号采集使用麦克风采集一段语音信号,并将其存储为.wav格式。
2. 信号处理(1)使用Matlab读取.wav文件,提取语音信号的采样频率、采样长度和采样数据。
(2)将语音信号进行时域分析,包括绘制时域波形图、计算信号的能量和过零率等。
(3)将语音信号进行频域分析,包括绘制频谱图、计算信号的功率谱密度等。
3. 信号分析(1)观察时域波形图,分析语音信号的幅度、频率和相位特性。
(2)观察频谱图,分析语音信号的频谱分布和能量分布。
(3)计算语音信号的能量和过零率,分析语音信号的语音强度和语音质量。
4. 信号输出(1)使用Audacity软件对语音信号进行降噪处理,比较降噪前后的效果。
(2)使用Python软件对语音信号进行增强处理,比较增强前后的效果。
(3)使用Matlab软件对语音信号进行合成处理,比较合成前后的效果。
五、实验结果与分析1. 时域分析从时域波形图可以看出,语音信号的幅度、频率和相位特性随时间变化。
语音信号的幅度较大,频率范围一般在300Hz~3400Hz之间,相位变化较为复杂。
2. 频域分析从频谱图可以看出,语音信号的能量主要集中在300Hz~3400Hz范围内,频率成分较为丰富。
3. 信号处理(1)降噪处理:通过对比降噪前后的时域波形图和频谱图,可以看出降噪处理可以显著降低语音信号的噪声,提高语音质量。
(2)增强处理:通过对比增强前后的时域波形图和频谱图,可以看出增强处理可以显著提高语音信号的幅度和频率,改善语音清晰度。
语音信号处理实验报告

语音信号处理实验报告语音信号处理实验报告一、引言语音信号处理是一门研究如何对语音信号进行分析、合成和改善的学科。
在现代通信领域中,语音信号处理起着重要的作用。
本实验旨在探究语音信号处理的基本原理和方法,并通过实验验证其有效性。
二、实验目的1. 了解语音信号处理的基本概念和原理。
2. 学习使用MATLAB软件进行语音信号处理实验。
3. 掌握语音信号的分析、合成和改善方法。
三、实验设备和方法1. 设备:计算机、MATLAB软件。
2. 方法:通过MATLAB软件进行语音信号处理实验。
四、实验过程1. 语音信号的采集在实验开始前,我们首先需要采集一段语音信号作为实验的输入。
通过麦克风将语音信号输入计算机,并保存为.wav格式的文件。
2. 语音信号的预处理在进行语音信号处理之前,我们需要对采集到的语音信号进行预处理。
预处理包括去除噪声、归一化、去除静音等步骤,以提高后续处理的效果。
3. 语音信号的分析语音信号的分析是指对语音信号进行频谱分析、共振峰提取等操作。
通过分析语音信号的频谱特征,可以了解语音信号的频率分布情况,进而对语音信号进行进一步处理。
4. 语音信号的合成语音信号的合成是指根据分析得到的语音信号特征,通过合成算法生成新的语音信号。
合成算法可以基于传统的线性预测编码算法,也可以采用更先进的基于深度学习的合成方法。
5. 语音信号的改善语音信号的改善是指对语音信号进行降噪、增强等处理,以提高语音信号的质量和清晰度。
常用的语音信号改善方法包括时域滤波、频域滤波等。
六、实验结果与分析通过实验,我们得到了经过语音信号处理后的结果。
对于语音信号的分析,我们可以通过频谱图观察到不同频率成分的分布情况,从而了解语音信号的特点。
对于语音信号的合成,我们可以听到合成后的语音信号,并与原始语音信号进行对比。
对于语音信号的改善,我们可以通过降噪效果的评估来判断处理的效果。
七、实验总结通过本次实验,我们深入了解了语音信号处理的基本原理和方法,并通过实验验证了其有效性。
语音信号处理实验

3 实验过程
1)读语音数 wavread 2)听语音 sound 3)写语音 wavwrite 4)对语音信号进行分帧处理 5)对语音信号进行预加重
分帧处理流程
1 读语音数据。 2 求语音长度。 3 确定帧长和帧移。 4 确定可以分多少帧 5 for 循环实现各帧信号的取出。先确定各帧信号的起点和终点坐标,然后利 用矩阵操作函数将各帧信号取出。
[x,fs,bits]=wavread(' c:\windows\media\dig.wav '); x=x(:,1); x=x'; len=length(x); N=256; M=128; Fn=fix((len-N)/M+1); y=[]; for i=1:Fn
实验一 语音信号的预处理
1 实验目的
通过 Matlab 编程掌握语音信号的预处理方法,包括对信号进行分帧、预加 重,加窗处理。
2 实验原理
由于语音信号从整体上来看是一个非平稳过程,但是在一个短的时间内,其 特性保持相对不变,所以语音信号具有短时平稳性,对语音信号的分析和处理必 须建立在“短时”的基础上,将信号分为一段一段来分析其特征参数。
down=1+(i-1)*M; up=down+N-1; temp=x(down:up); y=[y;temp]; end % K=100; M=[]; for i=1:Fn temp=sum(abs(y(i,:)),2)
1
M=[M,temp]; end plot(M)
%短时过零率 [x,fs,bits]=wavread('c:\WINDOWS\Media\chimes.wav'); x=x(:,1); x=x'; len=length(x); N=256; M=128; Fn=fix((len-N)/M+1); y=[]; for i=1:Fn
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三语音信号的同态处理
一、实验目的
1.熟悉语音信号求其倒谱与复倒谱的方法;
2.计算一段语音信号的频谱与倒谱;
3.比较由加窗语音信号求得的对数幅度谱与倒谱域滤波后得到的对数幅度谱的各自特点。
二、实验原理及内容
本实验同学们可以自己设计怎么去求语音信号的频谱与倒谱,实验方案与步骤自己发挥确定。
没有思路的同学可以按一下步骤完成:
1.读入语音,选取一段浊音:读入一段语音(例如6.wav,其它也可以),选取其中一段浊
音,例如可以选取256点。
2.给这段浊音信号加汉明窗,求对数幅度谱:利用fft求对数幅度谱。
3.求倒谱:根据求倒谱的原理,即通过fft、取模、取log、ifft得到倒谱。
改变帧长、帧移
重复上述步骤。
4.由倒谱滤波得到声道对数幅度谱的估值,与由fft得到的对数幅度谱比较。
利用subplot
画出窗选时域波形图、对数幅度谱、倒谱及由倒谱滤波得到的声道对数幅度谱的估值。
5. 由倒谱分别得到声道冲激响应的估值与声门激励脉冲的估值,利用subplot画出原始信号波形、窗选时域波形、对数幅度谱、倒谱、声道冲激响应的估值与声门激励脉冲的估值。
6. 取一段清音重复上述步骤,分析清音与浊音的对数幅度谱、倒谱有什么不同。
7. (选做)学习matlab自带的复倒谱与倒谱分析函数cceps与rceps。
三、实验报告要求
报告中要有实验目的、实验原理及步骤、实验程序、实验中得出的图形结果及结论等。
另外,总结本次上机实验的收获。
1。
