小学奥数第18周 面积计算
小学奥数举一反三B版5年级数学

目录第1周平均数 (1)第2周等差数列 (3)第3周长方形、正方形的周长 (5)第4周长方形、正方形的面积 (8)第5周分类数图形 (11)第6周尾数和余数 (14)第7周一般应用题(一) (16)第8周一般应用题(二) (18)第9周一般应用题(三) (20)第10周数阵 (22)期中测试(一) (25)第11周周期问题 (27)第12周盈亏问题 (30)第13周长方体和正方体(一) (32)第14周长方体和正方体(二) (34)第15周长方体和正方体(三) (36)第16周倍数问题(一) (38)第17周倍数问题(二) (40)第18周组合图形的面积(一) (42)第19周组合图形的面积(二) (45)第20周数字趣味题 (48)期末测试(一) (50)第21周假设法解题 (52)第22周作图法解题 (54)第23周分解质因数(一) (56)第24周分解质因数(二) (58)第25周最大公约数 (60)第26周最小公倍数(一) (62)第27周最小公倍数(二) (64)第28周行程问题 (66)第29周行程问题(二) (68)期中测试(二) (72)第31周行程问题(四) (74)第32周算式谜 (76)第33周包含与排除 (78)第34周转换问题 (80)第35周估值问题 (82)第36周火车行程问题 (84)第37周简单列举 (86)第38周最大最小问题 (88)第39周推理问题 (90)期末测试(二) (92)第1周平均数基础卷1.期中考试过后,李玲同学语文、数学的平均成绩为91分,语文、英语的平均成绩为88分,数学、英语的成绩为93分,李玲三门功课各得多少分?2.奶糖和水果糖混合起来,成为什锦糖,平均每千克售价9.13元,已知奶糖有35千克,每千克10.3元,水果糖每千克8.5元,那么有多少千克水果糖?3.7位同学进行跳绳比赛,平均每人跳148下。
由于记录失误,李强的成绩被错记成121下,因此他们的平均成绩变成145下,问:李强实际上跳了多少下?4.几位裁判员为一位体操运动员评分,去掉一个最高分后,平均成绩为8.82分。
小学六年级奥数练习-举一反三A版练习题

达标测试卷(一)第1周~第5周(定义新运算、简便运算)(本卷满分100分,建议测试时间80分钟)1.(10分)规定②=1*2*3,③=2*3*4,④=3*4*5……如果⑦-⑥=6A,那么A等于多少?2.(10分)规定a*b=(a+b)(a-b),求49*9等于多少?3.(10分)设A,B是两个数,规定A*B= ,求5*10等于多少?4.(10分)规定a b=3a-4b,求(157)10等于多少?5.(10分)设a b=2ab,已知(3x)2=96,求x的值?6.(10分)对两个整数a和b定义新运算“#”;a#b=,求2#6+3#9.7.(40分)下列各题怎样算简便就怎样算。
(1)8.75-8.57+(11.25-1.43)(2)0.999*0.7+0.111*3.7(3)875*0.25+8.75*76-8.75(4)72*1.09+2.4*67.3 (5)4123+3412+2341+1234(6)999*375+6375(7)*2000(8)1/2+1/4+1/8+…+1/128(9)(10)1/99+2/99+3/99+…+98/99是达标测试卷(二)第6周~第8周(转化单位“1”)(本卷满分100分,建议测试时间80分钟)1.(8分)一本书第一次看了全书的0.6,第二次看了第一次的0.6,两次一共看了多少?2.(8分)已知a=3/4b,c=2/3a,b-c=16,求a=()。
3.(8分)甲、乙、丙三位同学手机画片,甲的张数占三人总数的1/6,丙的张数是甲的3/2,乙比丙多30多张,三人一共有多少张画片?4.(8分)水果店有275千克苹果,梨的质量是苹果和橘子的8/21,橘子的质量是梨和苹果总质量的10/19,梨和橘子的质量分别是多少?5.(8分)六年级学生分成甲、乙两组,如果从甲组调14人到乙组,则甲组的人数是乙组的3/5,如果从乙组调12人到甲组,则乙组人数是甲组的3/5,甲、乙两组原来分别有多少人?6.(8分)弟弟有51快糖,哥哥有21块糖,两人每天分别吃一块糖,多少天以后哥哥的块数是弟弟糖的块数的1/3?7.(8分)百货商场进了一批童装,按进价的50%作为利润来定价,当售出这批童装的80%以后,决定降价出售,按照定价的60%出售,这批服装全部售完后实际获利百分之几?8.(8分)阅览室里看书的同学中,男生人数占女生人数的1/2,若走出16位女生,走进16位男生,女生人数是男生的1/2,现在男、女生各有几人?9.(8分)王明参加班干部竞选,需要超过3/4的选票才能当选,在计算了总选票的1/3后,他得到的选票已达到当选票数的3/5,他还要得到剩下选票的几分之几才能当选?10.(8分)某公司女职员比总人数的3/5少18人,男职员人数是女职员的5/3,这个公司一共有职员多少人?11.(10分)有两筐苹果,一筐苹果的个数是甲筐的2/5,从甲筐取出10个苹果放入乙筐后,乙筐苹果的个数是甲筐的3/4,甲、乙两筐一共有多少苹果?12.(10分)有两根彩带,一根长8米,另一根长4米,从两根彩带上剪去同样长的一段后,短彩带剩下的长度是长彩带剩下长度的1/3,两根彩带各剪去多少米?达标测试卷(三)第9周~第11周(设数法解题、假设法解题)(本卷满分100分,建议测试时间80分钟)1.(8分)一次数学竞赛,某班全班平均分为80分,其中4/5的人及格,及格的同学平均分为88分,那么不及格的同学平均分是多少分?2.(8分)王叔叔翻越一座山,他上山的速度是每分钟100米,下山的速度是每分钟150米。
四年级奥数专题--图形周长与面积

第一讲图形周长和面积知识导航亲爱的同学们,我们已经学会长方形、正方形的周长与面积的计算,利用公式很容易算出它们的面积与周长。
但在遇到一些较复杂的有关长方形和正方形的周长和面积计算时,一些同学就会感到棘手。
这一讲我们将学习用平移、转化、分解、合并等技巧解决难题,使大家在解题中能顺利地找到突破口,化难为易,化繁为简。
精典例题例1:下图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是多少厘米?思路点拨每个正方形的面积为:400÷16=25(平方厘米),所以每个正方形的边长是5厘米。
从上下方向来看有14条边是周长的一部分,从左右方向来看有20条边是周长的一部分,所以……模仿练习计算右面图形的周长(单位:厘米)。
例2:有9个小长方形,它们的长和宽分别相等,用这9个小长方形拼成的大长方形(如图)的面积是45平方厘米,求这个大长方形的周长。
思路点拨从图上可以知道,小长方形的长的4倍等于宽的5倍,所以长是宽的5÷4=1.25倍。
每个小长方形的面积为45÷9=5平方厘米,所以1.25×宽×宽=5,所以宽为2厘米,长为2.5厘米。
模仿练习下图的长方形被分割成5个正方形,已知原长方形的面积为120平方厘米,求原长方形的长与宽。
例3:一块正方形的苗圃(如右图实线所示),若将它的边长各增加30米,则面积增加9900平方米,问原来这块正方形苗圃的面积是多少平方米?思路点拨通过画图可以算出:小正方形的面积为:30×30=900平方米。
用增加的面积减去小正方形的面积就得到增加的两个长方形的面积之和,9900-900=9000平方米。
而增加的两个长方形的面积相等,于是其中一个长方形的面积为9000÷2=4500平方米。
模仿练习喜阳阳小学的操场长90米,宽45米。
改造后,长增加10米,宽增加5米。
现在操场面积比原来增加了多少平方分米?例4:如下图,用标号为1,2,3,4,5的五种大小不同的正方形拼成一个大长方形,大长方形的长和宽分别是18,14,则标号为5的正方形的面积是多少?(2006年“希望杯”第二试)思路点拨如果标号为5的正方形的边长是a ,那么1号比2号大a ,2号比3号大a ,所以1号比3号大2a ,又因为2号和3号的边长之和是14,1号和2号的边长之和是18,所以1号比3号大18-14=4。
小学六年级奥数 第十八章 圆的周长和面积

第十八章 圆的周长和面积知识要点如右图所示,当一条线段OA 绕着固定端点O 在平面内旋转一周,它的另一端点A 在平面内画出了一条封闭的曲线,这条封闭的曲线叫做圆。
围成圆的曲线叫做圆周,线段OA 叫做圆的半径,通常用r 或R 表示。
O 点是这个圆的圆心。
在同一个圆中,所有的半径都相等。
通过圆心,并且两端都在圆上的线段叫做直径。
在同一个圆内,所有直径都相等,且等于半径的2倍。
圆心决定圆的位置,半径决定圆的大小。
无论什么圆,它的周长除以直径的商是一个固定的数,这个数叫圆周率,用π表示。
如果用C 表示圆周的长度,d 表示这个圆的直径,那么,π=C d 。
π是一个无限不循环小数:π=3.14159265358979323846…圆的周长:C =2πr 或C =πd 圆的面积:S =πr 2=π(2d )2=π(2C π)2=24C π 扇形是由圆心角的两条半径和圆心角所对的弧围成的图形。
如果扇形的圆心角是n ,那么当圆周长C =2πr 时,扇形的弧长计算方法:L =360n ×2πr =180n ×πr 例1 (第五届“希望杯”邀请赛试题)如图,ABCD 是边长为10厘米的正方形,且AB 是半圆的直径,则阴影部分的面积是 平方厘米。
(π取3.14)点拨 过E 点作AB 的垂线,垂足为O ,因为∠CAB=45°,所以点O 是半圆的圆心,则阴影部分的面积等于梯形OECB 的面积,减去圆O 面积的14。
解 过E 点作AB 的垂线,垂足为0。
∵∠CAB =45°,∴点0是半圆的圆心。
则S 阴影=S 梯形OECB -14S ⊙O=(5+10)×5÷2- ×52=17.875(平方厘米)例2 将半径分别是4厘米和3厘米的两个半圆,如图放置。
求阴影部分的周长。
点拨阴影部分的周长为小半圆的弧长加上大半圆的弧长,再加两条线段的长。
两个半圆的半径分别为4厘米和3厘米;两条线段分别是4厘米和3×2-4=2(厘米)。
小学数学举一反三第18周 组合图形面积一

P107举一反三2
• 1.如下图所示,已知大正方形的边长是 12厘米,求中间最小正方形的面积。
P108举一反三2
• 2. 下图正方形ABCD的面积是16平方厘米,E、 F都是所在边的中点。求三角形AEF的面积。
P108 举一反三2
• 3.求下图长方形ABCD的面积。(单位:厘米)
A
D
68
B
C
• 例3 图中的甲和乙都是正方形,求阴影部 分的面积。(单位:厘米)
B 6厘米 C
P111举一反三5
• 1. 如图所示,平行四边形BCEF中,BC=8厘 米,直角三角形中,AC=10厘米,阴影部分 面积比三角形ADH的面积大8平方厘米。求 AH长多少厘米?
P112举一反三5
• 2. 下图中三个正方形的边长分别是1厘米、 2厘米、和3厘米。求图中阴影部分的面积。
P112举一反三5
C D
10
A
40
B
P111举一反三4
• 3. 如图所示,BC=10厘米,EC=8厘米,且阴 影部分面积比三角形EFG的面积大10平方厘 米。求平行四边形ABCD的面积。
E
A
G
F
D
B
• 例5 • 图中ABCD是长方形,三角形EFD的面积比
三角形ABF的面积大6平方厘米,求ED的长。
E
AF D 4厘米
第18周 组合图形一
• 例1
• 一个等腰直角三角形,最长的边是12 厘米,这个三角形的面积是多少平方 厘米?
P106 举一反三1
• 1.求四边形ABCD的面积。(单位:厘米)
3D A
B
450 7
C
P106举一反三1
• 2.已知正方形ABCD的边长是7厘米,求 正方形EFGH的面积。
三年级奥数第18讲简单列举(教师版)

三年级奥数第18讲简单(jiǎndān)列举(教师版)教学目标用列举解决简单(jiǎndān)实际问题,能不重复(chóngfù)、不遗漏的找到符合要求的答案。
发展学生(xué sheng)思维的条理性和严密性。
知识梳理养鸡场的工人(gōng rén),小心翼翼地把鸡蛋从筐里一个一个往外拿,边拿边数筐里的鸡蛋拿光了,有多少个鸡蛋也就数清了,这种计数的方法就是枚举法。
一般地,根据问题要求,一一列举问题,并加以解决,最终达到解决整个问题的目的。
这种分析问题、解决问题的方法,称之为枚举法。
运用枚举法解决应用题时,必须注意无重复、无遗漏。
为此必须力求有次序、有规律地进行枚举。
典例分析例1、从小华家到学校有3条路可走,从学校到文峰公园有4条路可走。
从小华家到文峰公园,有几种不同的走法?【解析】为了帮助理解题意,我们可以画出如上示意图。
我们把小华的不同走法一一列举如下:根据列举(lièjǔ)可知,从小(cóngxiǎo)明家经学校到文峰公园,走①路有4种不同(bù tónɡ)走法,走②路有4种不同(bù tónɡ)走法,走③路也有4种不同(bù tónɡ)走法,共有4×3=12种不同走法。
例2、用红、绿、黄三种信号灯组成一种信号,可以组成多少种不同的信号? 【解析】要使信号不同,要求每一种信号颜色的顺序不同,我们可以把这些信号进行列举。
可以看出,红色信号灯排在第一个位置时,有两种不同的信号;绿色信号灯排在第一个位置时,也有两种不同的信号;黄色信号灯排在第一个位置时,也有两种不同的信号,因而共有3个2种不同排列方法,即2×3=6种。
例3、一个长方形的周长是22米,如果它的长和宽都是整米数,那么这个长方形的面积有多少种可能?【解析】由于长方形的周长是22米,可知它的长与宽之和为11米。
小学数学竞赛:基本图形的面积计算.教师版解题技巧 培优 易错 难

模块二、简单的割补
【例 12】图中“风车”(阴影部分)的面积等于 。
【考点】基本图形的面积计算【难度】2星【题型】填空
【关键词】希望杯,4年级,初赛,18题
【解析】由割补法知:这个风车可以拼成一个长为2厘米的正方形,所以它的面积是4平方厘米。
【答案】 平方厘米
【例 13】如图,正方形硬纸片ABCD的每边长20厘米,点E、F分别是AB、BC的中点,现沿图a中的虚线剪开,拼成图b所示的一座“小别墅”,则图b中阴影部分的面积是平方厘米。
【答案】 厘米
【例 10】如图3,边长为4的正方形 和边长为6的正方形 并排放在一起, 和 分别是两个正方形的中心(正方形对角线的交点),则阴影部分的面积是______.
【考点】基本图形的面积计算【难度】4星【题型】填空
【关键词】希望杯,六年级,初赛,第10题,6分
【解析】等于一个直角梯形减去两个直角梯形的面积,(2+3)×5÷2-2×2÷2-3×3÷2=6.
【考点】基本图形的面积计算【难度】3星【题型】填空
【关键词】希望杯,五年级,复赛,第17题,10分
【解析】方法一、先计算四个长条形面积之和,再减去重叠部分.
=3×25+1×25+2×15+3×15-2×l-2×3-3×1-3×3=155.
方法二、可将四组平行线分别移至端线处,如图所示,移动后阴影部分面积不变。
【考点】基本图形的4年级,初赛,19题
【解析】四个边角的面积和为2×2×4=16,则水池的边长为:104÷2÷4=13,所以水池的面积是:13×13=169平方米。
【答案】 平方米
【例 3】每边长是10厘米的正方形纸片,正中间挖了一个正方形的洞,成为一个宽1厘米的方框。把五个这样的方框放在桌面上,成为一个这样的图案(如图所示)。问桌面上被这些方框盖住的部分面积是多少平方厘米?
六年级奥数举一反三第18周面积计算

六年级奥数举一反三第18周面积计算专题简析;计算平面图形的面积时,有些问题乍一看,在已知条件与所求问题之间找不到任何联系,会使你感到无从下手。
这时,如果我们能认真观察图形,分析·研究已知条件,并加以深化,再运用我们已有的基本几何知识,适当添加辅助线,搭一座连通已知条件与所求问题的小“桥”,就会使你顺利达到目的。
有些平面图形的面积计算必须借助于图形本身的特征,添加一些辅助线,运用平移旋转·剪拼组合等方法,对图形进行恰当合理的变形,再经过分析推导,方能寻求出解题的途径。
例题1。
已知图18-1中,三角形ABC 的面积为8平方厘米,AE =ED ,BD=23BC ,求阴影部分的面积。
【思路导航】阴影部分为两个三角形,但三角形AEF 的面积无法直接计算。
由于AE=ED,连接DF ,可知S △AEF =S △EDF 【等底等高】,采用移补的方法,将所求阴影部分转化为求三角形BDF 的面积。
因为BD=23BC ,所以S △BDF =2S △DCF 。
又因为AE =ED ,所以S △ABF =S △BDF =2S △DCF 。
因此,S △ABC =5 S △DCF 。
由于S △ABC =8平方厘米,所以S △DCF =8÷5=1,6【平方厘米】,则阴影部分的面积为1,6×2=3,2【平方厘米】。
练习11·如图18-2所示,AE =ED ,BC=3BD ,S △ABC =30平方厘米。
求阴影部分的面积。
2·如图18-3所示,AE=ED ,DC =13BD ,S △ABC =21平方厘米。
求阴影部分的面积。
3·如图18-4所示,DE =12AE ,BD =2DC ,S △EBD =5平方厘米。
求三角形ABC 的面积。
C D18-1例题2。
两条对角线把梯形ABCD 分割成四个三角形,如图18-5所示,已知两个三角形的面积,求另两个三角形的面积各是多少?【思路导航】已知S △BOC 是S △DOC 的2倍,且高相等,可知;BO =2DO ;从S △ABD 与S △ACD相等【等底等高】可知;S △ABO 等于6,而△ABO 与△AOD 的高相等,底是△AOD的2倍。
四年级奥数举一反三第1718周之数数图形(可编辑修改word版)

四年级奥数举一反三第1718 周之数数图形第 17 讲数数图形(一)一、知识要点我们已经认识了线段、角、三角形、长方形等基本图形,当这些图形重重叠叠地交错在一起时就构成了复杂的几何图形。
要想准确地计数这类图形中所包含的某一种基本图形的个数,就需要仔细地观察,灵活地运用有关的知识和思考方法,掌握数图形的规律,才能获得正确的结果。
要准确、迅速地计数图形必须注意以下几点:1.弄清被数图形的特征和变化规律。
2.要按一定的顺序数,做到不重复,不遗漏。
二、精讲精练【例题 1】数出下面图中有多少条线段。
【思路导航】要正确解答这类问题,需要我们按照一定的顺序来数,做到不重复,不遗漏。
从图中可以看出,从 A 点出发的不同线段有 3 条:AB、AC、AD;从 B 点出发的不同线段有 2 条:BC、BD;从 C 点出发的不同线段有 1 条:CD。
因此,图中共有3+2+1=6 条线段。
练习 1::数出下列图中有多少条线段。
(2)(3)【例题 2】数一数下图中有多少个锐角。
【思路导航】数角的方法和数线段的方法类似,图中的五条射线相当于线段上的五个点,因此,要求图中有多少个锐角,可根据公式1+2+3……(总射线数- 1)求得:1+2+3+4=10(个).练习 2::下列各图中各有多少个锐角?【例题 3】数一数下图中共有多少个三角形。
【思路导航】图中AD 边上的每一条线段与顶点O 构成一个三角形,也就是说,AD 边上有几条线段,就构成了几个三角形,因为 AD 上有4 个点,共有 1+2+3=6条线段,所以图中有 6 个三角形。
练习 3::数一数下面图中各有多少个三角形。
【例题 4】数一数下图中共有多少个三角形。
【思路导航】与前一个例子相比,图中多了一条线段 EF,因此三角形的个数应是 AD 和 EF 上面的线段与点 O 所围成的三角形个数的和。
显然,以 AD 上的线段为底边的三角形也是 1+2+3=6 个,所以图中共有6×2=12个三角形。
五年级奥数举一反三专题 第18周 组合图形面积(一)

第18周组合图形面积(一)专题简析:组合图形是由两个或两个以上的简单的几何图形组合而成的。
组合的形式分为两种:一是拼合组合,二是重叠组合。
由于组合图形具有条件相等的特点,往往使得问题的解决无从下手。
要正确解答组合图形的面积,应该注意以下几点:1,切实掌握有关简单图形的概念、公式,牢固建立空间观念;2,仔细观察,认真思考,看清所求图形是由哪几个基本图形组合而成的;3,适当采用增加辅助线等方法帮助解题;4,采用割、补、分解、代换等方法,可将复杂问题变得简单。
例1 一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?分析与解答由于此三角形中只知道最长的边是12厘米,所以,不能用三角形的面积公式来计算它的面积。
我们可以假设有4个这样的三角形,且拼成了下图正方形。
显然,这个正方形的面积是12×12,那么,一个三角形的面积就是12×12÷4=36平方厘米。
练习一1,求四边形ABCD的面积。
(单位:厘米)2,已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
3,有一个梯形,它的上底是5厘米,下底7厘米。
如果只把上底增加3厘米,那么面积就增加4.5平方厘米。
求原来梯形的面积。
例2 正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
分析与解答图中的两个小三角形平移后可拼得一个小正方形,两个大三角形平移后可拼得一个大正方形。
这两个正方形的边长分别是12÷(1+2)=4(厘米)和4×2=8(厘米)。
中间长方形的面积只要用总面积减去这两个拼起来的正方形的面积就可以得到。
即:12×12-(4×4+8×8)=64(平方厘米)练习二1,(如下图)已知大正方形的边长是12厘米,求中间最小正方形的面积。
2,正图长方形ABCD的面积是16平方厘米,E、F都是所在边的中点,求三角形AEF的面积。
小学奥数三年级 01 数数图形

第39周 抽屉原理 第40周 一题多解
第一讲 数数图形
精讲精练
【例题1】 数出下图中有多少条线段?
【练习1】 (1)数出下图中有多少条线段?
【练习1】 (2)数出下图中有几个长方形?
【例题2】 数出图中有几个角?
【练习2】 (1)数出图中有几个角?
【练习2】 (2)数出图中有几个角?
小学奥数举一反三 (三年级)
目录
第1周 数数图形 第2周 寻找规律 第3周 加减巧算
第4周 巧添符号 第5周 算式之谜 第6周 文字之谜 第7周 填数游戏 第8周 有余除法 第9周 周期问题 第10周 数学趣题
第11周 火柴游戏
第12周 乘法速算
第13周 乘除巧算
第14周 解决问题(一) 第15周 解决问题(二) 第16周 植树问题 第I7周 数字趣谈 第18周 重叠问题 第19周 简单枚举 第20周 等量代换
目录
第21周 错中求解 第22周 “对应”解题 第23周 盈亏问题 第24周 简单推理(一) 第25周 和倍问题 第26周 差倍问题(一) 第27周 差倍问题(二) 第28周 和差问题 第29周 年龄问题 第30周 “还原”解题
第31周 “假设”解题 第32周 平均数问题(一) 第33周 平均数问题(二) 第34周 简单推理(二) 第35周 巧求周长(一) 第36周 巧求周长(二) 第37周 面积计算
【练习5】
(1)银海学校三年级有9个班,每两个班要比赛拔河一次, 这样一共要拔河几次?
(2)有1,2,3,4,5,6,7,8等8个数字,能组成多少个 不同的两位数?
【例题3】 数出下图中有几个三角形?
【练习3】 数出图中共有多少个三角形?
【练习3】 数出图中共有多少个三角形?
小学奥数举一反三五年级 完整版

第一周平均数(一)第2周平均数(二)第3周长方形、正方形的周长第4周长方形、正方形的面积第5周分类数图形第6周尾数和余数第7周一般应用题(一)第8周一般应用题(二)第9周一般应用题(三)第10周数阵第11周周期问题第12周盈亏问题第13周长方体和正方体(一)第十四周长方体和正方体(二)第十五周长方体和正方体(三)第16周倍数问题(一)第17周倍数问题(二)第18周组合图形面积(一)第十九周组合图形的面积第二十周数字趣题第二十一讲假设法解题第二十二周作图法解题第二十三周分解质因数第二十四周分解质因数(二)第25周最大公约数第二十六周最小公倍数(一)第二十七周最小公倍数(二)第28周行程问题(一)第二十九周行程问题(二)第三十周行程问题(三)第三十一周行程问题(四)第三十二周算式谜第33周包含与排除(容斥原理)第34周置换问题第35周估值问题第36周火车行程问题第37周简单列举第三十八周最大最小问题第三十九周推理问题第40周杂题第一周平均数(一)专题简析:把几个不相等的数,在总数不变的条件下,通过移多补少,使它们完全相等,求得的相等的数就是平均数。
如何灵活运用平均数的数量关系解答一些稍复杂的问题呢?下面的数量关系必须牢记:平均数=总数量÷总份数总数量=平均数×总份数总份数=总数量×平均数例1有4箱水果,已知苹果、梨、橘子平均每箱42个,梨、橘子、桃平均每箱36个,苹果和桃平均每箱37个。
一箱苹果多少个?练习一1,一次考试,甲、乙、丙三人平均分91分,乙、丙、丁三人平均分89分,甲、丁二人平均分95分。
问:甲、丁各得多少分?2,甲、乙、丙、丁四人称体重,乙、丙、丁三人共重120千克,甲、丙、丁三人共重126千克,丙、丁二人的平均体重是40千克。
求四人的平均体重是多少千克?3,甲、乙、丙三个小组的同学去植树,甲、乙两组平均每组植树18棵,甲、丙两组平均每组植树17棵,乙、丙两组平均每组植树19棵。
小学圆的面积奥数题100道及答案(完整版)

小学圆的面积奥数题100道及答案(完整版)题目1一个圆的半径是3 厘米,它的面积是多少平方厘米?答案:圆的面积= π×半径×半径,即3.14×3×3 = 28.26(平方厘米)题目2圆的直径是8 分米,求面积。
答案:半径= 8÷2 = 4 分米,面积= 3.14×4×4 = 50.24(平方分米)题目3一个圆的周长是18.84 米,求其面积。
答案:周长= 2×π×半径,所以半径= 18.84÷(2×3.14)= 3 米,面积= 3.14×3×3 = 28.26(平方米)题目4圆的面积是12.56 平方厘米,求半径。
答案:3.14×半径×半径= 12.56,半径×半径= 4,半径= 2 厘米题目5直径为10 厘米的圆,面积比半径为6 厘米的圆的面积小多少?答案:直径10 厘米的圆半径为5 厘米,面积为 3.14×5×5 = 78.5 平方厘米;半径6 厘米的圆面积为3.14×6×6 = 113.04 平方厘米,小113.04 - 78.5 = 34.54 平方厘米题目6一个圆的半径扩大3 倍,面积扩大多少倍?答案:原来面积= π×半径×半径,半径扩大3 倍后,面积= π×(3×半径)×(3×半径)= 9×π×半径×半径,面积扩大9 倍题目7两个圆的半径分别是2 厘米和3 厘米,它们面积的和是多少?答案:面积分别为3.14×2×2 = 12.56 平方厘米,3.14×3×3 = 28.26 平方厘米,和为12.56 + 28.26 = 40.82 平方厘米题目8一个圆的面积是50.24 平方分米,在里面画一个最大的正方形,正方形的面积是多少?答案:圆的半径= √(50.24÷3.14)= 4 分米,正方形的对角线是圆的直径为8 分米,正方形面积= 对角线×对角线÷2 = 8×8÷2 = 32 平方分米题目9圆的半径由4 厘米增加到6 厘米,面积增加了多少平方厘米?答案:原来面积= 3.14×4×4 = 50.24 平方厘米,新面积= 3.14×6×6 = 113.04 平方厘米,增加了113.04 - 50.24 = 62.8 平方厘米题目10在一个边长为8 厘米的正方形中画一个最大的圆,圆的面积是多少?答案:圆的直径= 8 厘米,半径= 4 厘米,面积= 3.14×4×4 = 50.24 平方厘米题目11已知圆的面积是28.26 平方米,求周长。
《数学小学三年级奥数专题》第37讲面积计算(附答案)

《数学小学三年级奥数专题》第37讲面积计算一、知识要点:我们已经学会了计算长方形、正方形的面积,知道长方形的面积=长乂宽,正方形的面积=边长x边长。
利用这些知识我们能解决许多有关面积的问题。
在解答比较复杂的关于长方形、正方形的面积计算的问题时,生搬硬套公式往往不能奏效,可以添加辅助线或运用割补、转化等解题技巧。
因此,敏锐的观察力和灵活的思维在解题中十分重要。
二、精讲精练例1把一张长为4米,宽为3米的长方形木板,剪成一个面积最大的正方形。
这个正方形木板的面积是多少平方米?练习一1、把一张长6厘米,宽4厘米的长方形纸剪成一个面积最大的正方形,这张正方形纸的面积是多少平方厘米?2、把一块长2米、宽6分米的长方形铁板切割成一个面积最大的正方形,这个正方形铁板的面积是多少?例2学校里有一个正方形花坛,四周种了一圈绿篱,绿篱总长20米。
花坛的面积是多少平方米?练习二1、一个正方形的周长为36厘米,那么这个正方形的面积是多少平方厘米?2、运动场有一个正方形的游泳池,在游泳池四周粘上瓷砖,瓷砖总长400米,求游泳池的面积是多少平方米。
例3求下面图形的面积。
(单位:厘米)14321、计算下面图形的面积。
(单位:厘米)(2)⑴例4有两个相同的长方形,长是8厘米,宽是3厘米。
如果把它们按下图叠放,这个图形的面积是多少?1、两张边长8厘米的正方形纸,一部分叠在一起放在桌上(如下图),桌面被盖住的面积是多少?2、求下图中阴影部分的面积。
(单位:分米)例5一个长方形若长增加2厘米,面积就增加10平方厘米,若宽减少3厘米,面积就减少18平方厘米。
求原来长方形的面积。
3厘米18平方厘米10平方厘米2厘米1、一个长方形,若长减少5厘米,面积就减少50平方厘米,若宽增加7厘米,面积就增加28平方厘米。
原来长方形的面积是多少平方厘米?2、一个正方形若边长都增加4厘米,面积就增加56平方厘米。
原来正方形的面积是多少平方厘米?三、课后作业1、将一张长10厘米、宽8厘米的长方形纸片剪成一个面积最大的正方形,那么剪下的另一个小长方形的面积是多少?2、在公园里有两个花圃,它们的周长相等。
小学奥数:不规则图形的面积

4-2-6.不规则图形的面积例题精讲本讲主要通过求一些不规则图形的面积,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求面积的技巧,提高学生的观察能力、动手操作能力、综合运用能力.【例 1】你有什么好的方法计算所给图形的面积呢?(单位:厘米)4993499349934993图1图2图3【巩固】如图是学校操场一角,请计算它的面积(单位:米)40303020【巩固】如右图所示,图中的ABEFGD是由一个长方形ABCD及一个正方形CEFG拼成的,线段的长度如图所示(单位:厘米),求ABEFGD的周长和面积.A D4A D4HFE10GCFE10GCB10B10【巩固】求图中五边形的面积.3645【例 2】这是一个楼梯的截面图,高280厘米,每级台阶的宽和高都是20厘米.问,此楼梯截面的面积是多少?【巩固】如图是一个楼梯的截面图,每级台阶的宽和高都是20厘米.这楼梯的截面积是多少平方厘米?【例 3】有一块菜地长16米,宽8米,菜地中间留了宽2米的路,把菜地平均分成四块,每一块地的面积是多少?2米2米8米2米2米8米16米16米【例 4】有10张长3厘米,宽2厘米的纸片,将它们按照下图的样子摆放在桌面上,那么这10张纸片所盖住的桌面的面积是多少平方厘米?【例 5】下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.20-55820820【巩固】两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积.ADBO32ECF【例 6】如图,李大伯给一块长方形田地喷药,喷药器所能喷洒的范围是以李大伯的落脚点为中心,边长2米的正方形区域,他从图中的A点出发,沿最短路线(图中虚线)走,走过88米到达B点,恰好把这块田地全部喷完,这块田地的面积是多少平方米?A1米1米B【例 7】右图中甲的面积比乙的面积大__________平方厘米.4厘米乙8厘米甲6厘米【例 8】右图中,矩形ABCD的边AB为4厘米,BC为6厘米,三角形ABF比三角形EDF 的面积大9平方厘米,求ED的长.A FEDB C【巩固】如图所示,CA=AB=4厘米,△ABE比△CDE的面积小2平方厘米,求CD的长为多少厘米?D CEA B【巩固】如图,平行四边形ABCD种,BC=10cm,直角三角形ECB的边EC=8cm,已知阴影部分的总面积比三角形EFG的面积大10cm2,求平行四边形ABCD的面积.EA F G DB C【例 9】如图,ABCD是7⨯4的长方形,DEFG是10⨯2的长方形,求VBCO与VEFO的面积差.A B A BD G C O EFD C O EFG【例 10】有一个长方形菜园,如果把宽改成50米,长不变,那么它的面积减少680平方米,如果使宽为60米,长不变,那么它的面积比原来增加2720平方米,原来的长和宽各是多少米?5060680平方米2720平方米【巩固】有一个长方形,如果宽减少2米,或长减少3米,则面积均减少24平方米,求这个长方形的面积?3【例 11】一块长方形铁板,长15分米,宽12分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?12215【例 12】一个长方形,如果长减少5厘米,宽减少2厘米,那么面积就减少66平方厘米,这时剩下的部分恰好成为一个正方形,求原来长方形的面积?522×5【巩固】一块长方形纸片,在长边剪去5cm,宽边剪去2cm后(如图),得到的正方形面积比原长方形面积少31cm2.求原长方形纸片的面积.552 A22BC【巩固】一个正方形,如果把它的相邻两边都增加6厘米,就可以得到一个新正方形,新正方形的面积比原正方形大120平方厘米.求原正方形的面积?6厘米6厘米6厘米6厘米【例 13】一块正方形的钢板,先截去一个宽5分米的长方形,又截去一个宽8分米的长方形(如图),面积就比原来正方形减少181平方分米.原正方形的边长是多少分米?58【巩固】一张长方形纸片,先把长剪去8厘米,这时面积减少了72平方厘米,又把宽剪去5厘米,这时面积又减少了60平方厘米,原来这张长方形纸片的面积是多少平方厘米?长5宽8【巩固】如右图所示,在一个正方形上先截去宽11分米的长方形,再截去宽7分米的长方形,所得图形的面积比原正方形减少301平方分米.原正方形的边长是______分米.711【例 14】如图长方形被分成两部分,已知阴影面积比空白部分面积大34平方厘米,求阴影部分的面积.10cm18cm【例 15】一张长方形纸片,把它的右上角往下折叠(如图甲),阴影部分面积占原纸片面积2的;再把左下角往上折叠(如图乙),乙图中阴影部分面积占原纸片面积的7________(答案用分数表示).甲乙【巩固】折叠后,原平行四边形面积是折叠后图形面积的1.5倍.已知阴影部分面积之和为1,则重叠部分(即空白部分)的面积是多少?【巩固】如图,一张长方形纸片,长7厘米,宽5厘米.把它的右上角往下折叠,再把左下角往上折叠,未盖住的阴影部分的面积是多少平方厘米?75【例 16】如图,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?【例 17】如图所示,直角三角形中有一个长方形,求长方形的面积?464BAD6F C 64【例 18】一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个、第四个、第五个正方形.求第五个正方形的面积??【巩固】如图是由5个大小不同的正方形叠放而成的,如果最小的正方形(阴影部分)的周长是8,那么最大的正方形的边长是.第6题【巩固】图中有6个正方形,较小的正方形都由较大的正方形的4边中点连接而成.已知最大的正方形的边长为16厘米,那么最小的正方形的面积等于多少平方厘米?【例 19】已知图中大正方形的面积是22平方厘米,小正方形面积是多少平方厘米?【巩固】如图所示,外侧大正方形的边长是10cm ,在里面画两条对角线、一个圆、两个正方形,阴影的总面积为26cm 2,最小的正方形的边长为多少厘米?A BCZ Y X D【例 20】有一个边长为16厘米的正方形,连接每边的中点构成第二个正方形,再连接每边的中点构成第三个正方形,第四个正方形.求图中阴影部分的面积?【例 21】如图,边长为10的正方形中有一等宽的十字,其面积(阴影部分)为36,则十字中央的小正方形面积为.第2题【例 22】下图大小两个正方形有一部分重合,两块没有重合的阴影部分面积相差是多少?(单位:厘米)663【巩固】如图所示,四个相叠的正方形,边长分别是5、7、9、11.问灰色区与黑色区的面积的差是多少?11975【例 23】甲、乙、丙三个正方形,它们的边长分别是6、8、10厘米,乙的一个顶点在甲的中心上,丙的一个顶点在乙的中心上.这三个正方形的覆盖面积是多少平方厘米?甲6甲6乙8丙10乙8丙10【巩固】将20张边长为10厘米的正方形纸片,按顺序一张一张地摆放在地板上,摆的时候,要求后摆的纸片必须有一个顶点与前一张的中心重合,且每一张只与其前一张和后一张有重合部分(右图表示已经摆好的5张).地板被这20张纸片所覆盖部分的面积是多少?【例 24】有2个大小不同的正方形A 和B .如下左图所示的那样,在将B 正方形的对角线的交点与A 正方形的一个顶点相重叠时,相重叠部分的面积为A 正方形面积的1.求A 与B 的边长之比.如果当按下右图那样,将A 和B 反向重叠的话,所重9叠部分的面积是B 的几分之几?BAABAB左图右图【例 25】有一个正方形水池(图中阴影部分),在它的周围修一个宽是8米的草地,草地的面积为480平方米,求水池的边长?8888【巩固】一块长方形草坪(图中阴影部分)长是宽的2倍,它的四周围的总面积是34平方米的1米宽的小路.求草坪的面积是多少平方米?A C BA CB AA【例 26】如图所示,一个长方形广场的正中央有一个长方形的水池.水池长8米、宽3米.水池周围用边长为1米的方砖一圈一圈地向外铺.恰好铺了若干圈,共用了152块方砖,那么共铺了圈.水池【例 27】用四个相同的长方形拼成一个面积为100cm 2的大正方形,每个长方形的周长是多少平方厘米?【巩固】如图所示,4个相同的长方形和一个小正方形拼成一个大的正方形,大正方形的面积是100平方分米,小正方形的面积是36平方分米,求一个小长方形的面积及周长.【例 28】四个完全相同的长方形拼成右图,大正方形的面积是l00平方分米,小正方形的面积是l6平方分米,求每个长方形的面积是多少?长方形的短边是多少分米?16【巩固】如图,4个相同的长方形和1个小正方形拼成一个大正方形,已知其中小正方形的面积为4平方厘米,大正方形的面积为400平方厘米,则其中长方形的长为厘米,宽厘米.【例 29】街心花园里有一个正方形花坛,四周有一条宽1米的甬道(如图),如果甬道的面积是12平方米,那么中间花坛的面积是多少平方米?第19题1米【巩固】在一个正方形的小花园周围,环绕着宽5米的水池,水池面积为300平方米,那么正方形花园的面积是多少平方米?5【巩固】有大、小两个长方形(如图),对应边的距离均为1cm ,已知两个长方形之间部分的面积是16cm 2,且小长方形的长是宽的2倍,求大长方形的面积.AB【例 30】已知大正方形比小正方形边长多4厘米,大正方形面积比小正方形面积大96平方厘米.问大、小正方形面积各是多少?44ABC4D 4【巩固】两个正方形的面积相差9cm 2,边长相差1cm .求两个正方形的面积和.C AB【巩固】有一大一小两个正方形,它们的周长相差20厘米,面积相差55平方厘米.小正方形的面积是多少平方厘米?【例 31】在一个正方形中放入一个四个顶点与大正方形相接的一个小正方形(如图),如果两个正方形的周长相差16厘米,面积相差96平方厘米,求小正方形的面积是多少平方厘米?(1)(2)cabc【例 32】用两块长方形纸片和一块正方形纸片拼成一个大正方形,长方形纸片面积分别为44平方厘米与28平方厘米,原正方形纸片面积是多少平方厘米?【例 33】计划修建一个正方形的花坛,并在花坛周围种上3米宽的草坪,草坪的面积为300平方米,那么修建这个花坛需要占地多少平方米?(1)(2)【巩固】有大、小两个长方形(右图),对应边的距离均为1厘米,已知两个长方形之间部分的面积是16平方厘米,且小长方形的长是宽的2倍,求大长方形的面积.【巩固】一块长方形的草坪(见图中阴影部分),长是宽的2倍,它的四周围的总面积是34平方米的1米宽的小路,求草坪的总面积是多少平方米?A C AB BA C A【例 34】一块正方形的苗圃(如右图实线所示),若将它的边长各增加30米(如图虚线所示),则面积增加9900平方米,问原来这块正方形苗圃的面积是多少平方米?3030【例 35】从一块正方形的玻璃板上锯下宽为0.5米的一个长方形玻璃条后,剩下的长方形的面积为5平方米,请问锯下的长方形玻璃条的面积等于多少?0.55【巩固】从一个正方形的木板上锯下宽1m 的一个长方形木条后,剩下的长方形面积为6m 2,问锯下的长方形木条面积是多少?【巩固】从一块正方形木板锯下宽为165米的一个木条以后,剩下的面积是平方米.问锯218下的木条面积是多少平方米?【例 36】图中,甲、乙两个正方形的边长的和是20厘米,甲正方形比乙正方形的面积大40平方厘米.求乙正方形的面积.【例 37】有一大一小两块正方形试验田,他们的周长相差40米,面积相差220平方米,那么小正方形试验田的面积是多少平方米?图a图b【例 38】如图,边长是整数的四边形AFED的面积是48平方厘米,FB为8厘米.那么,正方形ABCD的面积是平方厘米.F8AB48C【例 39】如图,一个正方形被分成4个小长方形,它们的面积分别是ED11平方米、平方米、10532平方米和平方米.已知图中的阴影部分是正方形,那么它的面积是多少平105方米?【例 40】长方形ABCD 的周长是30厘米,以这个长方形的每一条边为边长向外画正方形.已知这四个正方形的面积之和为290平方厘米,那么长方形ABCD 的面积是多少平方厘米?E 1D 1EDC 1C BA 1A【巩固】如图,长方形ABCD 的周长是16厘米,在它的每一条边上各画一个以该边为边长的正方形,已知这四个正方形的面积和是68平方厘米,求长方形ABCD 的面积?IH DG FADAB C B C E【例 41】一条白色的正方形手帕,它的边长是18厘米,手帕上横竖各有二道黑条,黑条宽都是2厘米,这条手帕白色部分的面积是多少?【例 42】用同样大小的瓷砖铺一个正方形地面,两条对角线上铺黑色的,其它地方铺白色的,如图所示.如果铺满这块地面共用101块黑色瓷砖,那么白色瓷砖用了多少块?图1图2【例 43】7个完全相同的长方形拼成了图中阴影部分,图中空白部分的面积是多少平方厘米?24【巩固】如图所示,7个完全相同的长方形拼成了图中的阴影部分,图中空白部分的面积是多少平方厘米?【例 44】如右图所示,在长方形ABCD中,放入六个形状大小相同的长方形(尺寸如图),图中阴影部分的面积是__________.D C6A14B【例 45】若干同样大小的长方形小纸片摆成了如图所示的图形.已知小纸片的宽是12厘米,问阴影部分的总面积是多少平方厘米?【例 46】一个大长方形若能分割成若干个大小不同的小正方形,则称为完美长方形.下面一个长方形是由9个小正方形组成的完美长方形.图中正方形A 和B 的边长分别是7厘米和4厘米,那么这个完美长方形的面积分别是多少平方厘米?DABE A HBFCG【巩固】如图:有一个矩形可以被分割为11个正方形,其中最小的正方形(阴影部分)面积为81cm 2,请问这个矩形之面积为多少平方厘米?jg ehca bif d教师寄语:拼一个春夏秋冬,换一生无怨无悔。
小学奥数教材三年级全册

数学思维训练(三年级全册)前言成为数学优等生的正确方法一. 学会主动预习。
在老师讲新知识之前,学生要认真阅读要学的内容,课前自学例题,在看书时,要动脑思考,步步深入。
学会运用自己有的知识去独立探究新的知识。
二. 注意听讲,在老师的引导下掌握思考问题的方法。
一些学生对公式.性质.法则等背的很熟,但遇到实际问题时又无从下手,不知如何应用所学知识去解题,因此要注意上课听讲时在老师的指导下掌握思考问题的方法。
一些学生之所以那么优秀,就是因为他们把老师讲的知识都应用到了自己解题的过程中了。
课堂上的40分钟就决定了你的成败,所以必须消化和理解老师在课堂上讲的内容。
&三.及时总结解题规律在解题时,要注意总结解题规律,在解决每一道练习题后,要回顾以下问题:(1).本题最重要的特点时什么(2).解本题用了哪些基本知识(3).解本题最关键的一步在哪里(4).以前有没有做过跟本题类似的题目异同点在哪里(5).本题除了这种方法之外,还有没有其他解法把这一连串的问题贯穿于解题。
四.善于质疑问难学启于思,思源于疑。
也就是说学生的积极思维往往思由疑问开始的,学生的发现和提出问题思学会创新的关键。
着名教育家顾明远说:“不会提问的学生,不是一个好学生。
”因此,学生从小开始,就要学会质疑。
比如学习“角的度量”,认识学习量角器时,认真观察它,问:“我发现了什么刻度有什么用”在学习时,经常这样提出问题,就可以开拓自己的思维空间,进而提高分析问题解决问题的能力。
此外还要养成良好的学习习惯:1.良好的学习习惯是很关键的,它对于孩子学习数学起到很关键的作用。
2.自觉学习的习惯是一种良好的学习习惯。
从小学开始养成这种习惯,对以后的学习甚至是以后工作都有很好的帮助。
3.良好的解题习惯对于学习也是很有帮助的。
比如,在书写解题步骤时,要正确.规范。
>兴趣是最好的老师,是学好数学的前提。
正确的学习方法,良好的学习习惯是学好的关键。
目录第1周平均数(一)第2周平均数(二)第3周长方形、正方形的周长第4周长方形、正方形的面积第5周分类数图形第6周尾数和余数>第7周生活中的数学(一)第8周生活中的数学(二)第9周生活中的数学(三)第10周数阵第11周周期问题第12周盈亏问题第13周长方体和正方体(一)第14周长方体和正方体(二)¥第15周长方体和正方体(三)第16周倍数问题(一)第17周倍数问题(二)第18周组合图形面积(一)第19周组合图形面积(二)第20周数字趣味题第21周假设法解题第22周作图法解题@第23周分解质因数(一)第24周分解质因数(二)第25周最大公约数第26周最小公倍数(一)第27周最小公倍数(二)第28周行程问题(一)第29周行程问题(二)第30周行程问题(三)?第31周行程问题(四)第32周算式谜题第33周包含与排除第34周置换问题第35周估值问题第36周火车行程问题第37周简单列举第38周最大最小问题'第39周推理问题第40周数学杂题第1讲找规律一、知识要点按照一定次序排列起来的一列数,叫做数列。
小学奥数:第18讲四年级数学图形的周长和面积教案 ;;
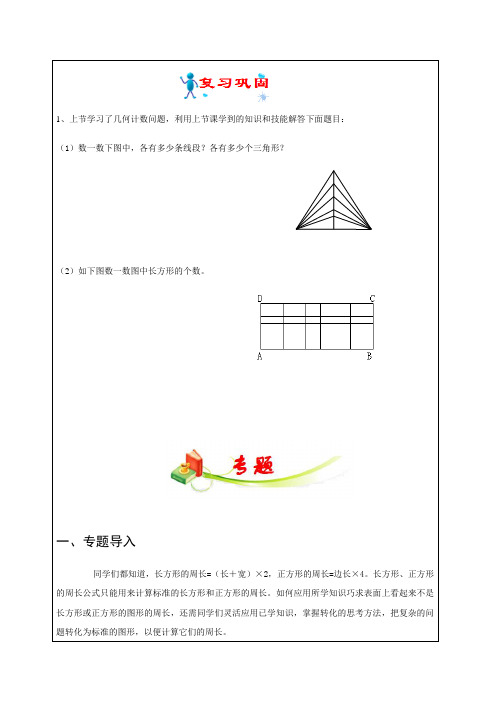
1、上节学习了几何计数问题,利用上节课学到的知识和技能解答下面题目:(1)数一数下图中,各有多少条线段?各有多少个三角形?(2)如下图数一数图中长方形的个数。
一、专题导入同学们都知道,长方形的周长=(长+宽)×2,正方形的周长=边长×4。
长方形、正方形的周长公式只能用来计算标准的长方形和正方形的周长。
如何应用所学知识巧求表面上看起来不是长方形或正方形的图形的周长,还需同学们灵活应用已学知识,掌握转化的思考方法,把复杂的问题转化为标准的图形,以便计算它们的周长。
二、专题精讲【例1】有5张同样大小的纸如下图(a)重叠着,每张纸都是边长6厘米的正方形,重叠的部分为边长的一半,求重叠后图形的周长。
分析解答:根据题意,我们可以把每个正方形的边长的一半同时向左、右、上、下平移(如图b),转化成一个大正方形,这个大正方形的周长和原来5个小正方形重叠后的图形的周长相等。
因此,所求周长是18×4=72厘米。
【例2 】一块长方形木板,沿着它的长度不同的两条边各截去4厘米,截掉的面积为192平方厘米。
现在这块木板的周长是多少厘米?分析解答:思路导航把截掉的192平方厘米分成A、B、C三块(如图),其中AB的面积是192-4×4=176(平方厘米)。
把A和B移到一起拼成一个宽4厘米的长方形,而此长方形的长就是这块木板剩下部分的周长的一半。
176÷4=44(厘米),现在这块木板的周长是44×2=88(厘米)。
【例3 】已知下图中,甲是正方形,乙是长方形,整个图形的周长是多少?分析解答:从图中可以看出,整个图形的周长由六条线段围成,其中三条横着,三条竖着。
三条横着的线段和是(a+b)×2,三条竖着的线段和是b×2。
所以,整个图形的周长是(a+b)×2+b×2,即2a+4b。
【例4 】下图是边长为4厘米的正方形,求正方形中阴影部分的周长。
小学四年级奥数第18讲 方阵问题(含答案分析)

第18讲方阵问题一、知识概要1、方阵可以分为实心方阵和空心方阵。
2、方阵的基本特点是:方阵中,里一层总比外一层的一边少2个物体,里一层物体的个数一定比上一层物体总个数少8个。
3、实心方阵中,物体个数=最外层的一边个数×最外层一边的个数;(每边数—1)×4=每层数;每层数÷4+1=每边数4、空心方阵中物体的个数=(最外层一边个数—层数)×层数×45、去掉一行、一列的总人数=去掉的每边人数×2-1二、典型例题1、有一个正方形的稻田,四个角上都放1个稻草人,如果每边放5个,四边共放多少个稻草人?2、有一个正方形池塘,四个角上都栽1棵树,一共栽了28棵树,那么每边栽多少棵?3、同学们排成一个两层空心方阵,外层每边8人,这个方阵一共有多少人?4、把若干个棋子摆成一个三层的空心方阵,最外层每边12个棋子,求这个方阵共有多少个棋子?5、同学们在军训时排成了一个由204人组成的三层空心方阵,求最外面一层每边有多少人?6、某小学举行运动会,同学们排成正方形队列参加团体操表演。
如果在这个正方形队列中减少一行一列,则要减少15人,问参加团体操表演的有多少同学?7、在儿童公园的一次菊花展上,用120盆菊花摆成一个三层空心方阵,这个方阵最外层每边有多少盆花?8、一个中空方阵的队列,最外层每边18人,最内层每边10人。
这个队列共有多少人?9、用64枚棋子摆成一个两层中空方阵,如果想在外面再增加一层,问需要增加多少枚棋子?10、学校组织一次团体操表演,把男生排列成一个实心方阵,又在这个实心方阵四周站一排女生。
女生有72人参加表演,男生有多少人?三、针对练习1、在正方形的广场四周装彩灯,四个角上都装一盏,每边装25盏,问这个广场一共需装彩灯多少盏?2、小强用棋子排成了一个每边11枚的中空方阵,共2层,求这个方阵共用多少枚棋子?3、小刚在用棋子摆好的实心阵上又填了17枚棋子,使它的横竖各增加一排,成了大一点的实心方阵,求原来实心方阵有多少枚棋子?4、解放军进行排队表演,组成一个外层有48人,内层有16人的多层中空方阵,这个方阵有几层?一共有多少人?5、有一个用圆片摆成的两层中空方阵,外层每边有16个圆片,如果把内层的圆片取出来,在外层再摆一层,变成一个新的中空方阵,应再增加多少圆片?6、用棋子摆成方阵,恰好每边24粒的实心方阵,若改为3层的空心方阵,它的最外层每边应改放多少粒?7、有学生若干名,排成中实的方阵则多2人,若在这正方阵纵横两个方向个增加一行还缺五人,问有学生多少人?8、仪仗队员组成两个实心方阵,甲方阵每边12人,后来两队合在一起排成一个中空方阵的丙方阵,丙方阵最外层一边人数比乙方阵最外层一边人数多4人,又原来甲方阵的人正好填满丙方阵空心。
小学四年级奥数竞赛班作业第18讲:巧求面积(一)

巧求面积练习题一.夯实基础:1. 如图是学校操场一角,请计算它的面积(单位:米)2. 一块长方形铁板,长15分米,宽12分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?3. 一块长方形纸片,在长边剪去5cm ,宽边剪去2cm 后(如图),得到的正方形面积比原长方形面积少231cm .求原长方形纸片的面积.4. 一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个、第四个、第五个正方形.求第五个正方形的面积?30203040525. 如图所示,把一个正方形各边中点顺次相连,可得一个新的较小的正方形;把这个小正方形的各边中点顺次相连,又可以得到一个新的更小一些的正方形……如此依次连下去,一直连到第三个新正方形为止。
如果图中阴影的面积等于1,那么图中最大的正方形面积等于多少?二. 拓展提高:6. 甲、乙、丙三个正方形,它们的边长分别是6、8、10厘米,乙的一个顶点在甲的中心上,丙的一个顶点在乙的中心上.这三个正方形的覆盖面积是多少平方厘米?7. 如图,四边形ABCD 的周长是60厘米,点M 到各边的距离都是4.5厘米,这个四边形的面积是 平方厘米.8. 有一个长方形,如果宽减少2米,或长减少3米,则面积均减少24平方米,求这个长方形的面积?1086丙乙甲9. 有大、小两个长方形(如图),对应边的距离均为1cm ,已知两个长方形之间部分的面积是216cm ,且小长方形的长是宽的2倍,求大长方形的面积.10. 空白处每个方格都是边长为4厘米的正方形,黑条的宽度为2厘米,求阴影部分的面积和周长。
11. 如图,一块正方形地砖,上面印有四周对称的花纹,正中心红色小正方形面积是8,四块绿色等腰直角三角形均相同,面积总和是36,那么图中阴影部分的面积是多少?三.超常挑战:12. 下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.13. 两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积.四.杯赛演练:14. (2008年第七届”小机灵杯”数学竞赛决赛)如图是由5个大小不同的正方形叠放而成的,如果最小的正方形(阴影部分)的周长是8,那么最大的正方形的边长是 .15. (2008年全国小学生”我爱数学夏令营”数学竞赛)如图,边长为 10的正方形中有一等宽的十字,其面积(阴影部分)为36,则十字中央的小正方形面积为 .16. (武汉明心奥数挑战赛)如图所示,四个相叠的正方形,边长分别是5、7、9、11.问灰色区与黑色区的面积的差是多少?FBA第6题第2题1017.(第四届《小数报》数学竞赛决赛试题)有一大一小两个正方形,它们的周长相差20厘米,面积相差55平方厘米.小正方形的面积是多少平方厘米?18.(第五届”祖冲之杯”数学邀请赛)如右图所示,在长方形ABCD中,放入六个形状大小相同的长方形(尺寸如图),图中阴影部分的面积是__________.B答案:1. 这是一个不规则图形,怎样使它能转化为我们熟悉的基本图形呢?可以在图中添上一条辅助线,把多边形切割成上下两个长方形或左右两个长方形;也可以把多边形补充完整,成为一个长方形;图一 图二 图三方法一:如图一,3040203040120014002600⨯+⨯+=+=()(平方米) 方法二:如图二,203040203060020002600⨯+⨯+=+=()(平方米) 方法三:如图三,40302030303035009002600+⨯+-⨯=-=()()(平方米)2. (方法一)如图,铁板面积比原来减少的面积就是阴影部分的面积,阴影部分的面积是用原长方形 的面积减去空白部分的面积.即: 1512(152)(122)⨯--⨯-180130=-=50(平方分米).(方法二)也可把阴影部分分割成两个长方形,求两个长方形的面积.3. 通过对图形进行分割,可以发现C 的长与宽分别是5cm 和2cm ,则它的面积是5210⨯=(2cm ),那么A B +的面积是311021-=(2cm ),如给B 移到A 的旁边,则知正方形的边长:(cm ),正方形的面积是339⨯=(2cm ),原长方形的面积是31940+=(2cm ).4. 第一个正方形的面积是2020400⨯=(平方厘米),第二个正方形的面积如图,实际上是第一个正方形面积的一半.依次类推,第五个正方形的面积为:400222225÷÷÷÷=(平方厘米).5. 最小的正方形面积等于2,每往外扩一层,面积就会增加一倍。
小学四年级奥数

例1、人民路小学操场长90米,宽45米,改造后,长增加10米,宽增加5米,现在操场的面积比原来操场的面积增加了多少平方米?例2、一个长方形,如果宽不变,长增加6米,那么它的面积增加54平方米,如果长不变,宽减少3米,那么它的面积减少36平方米,这个长方形原来的面积是多少平方米?例3、右图是一个养殖专业户用一段长16米的篱笆围成的一个长方形养鸡场,宽为4米,求占地面积有多大?例4、街心花园中一个正方形的花坛周围有1米宽的水泥路,如果水泥路的总面积是12平方米,中间花坛的面积是多少平方米?例5、一块长方形的钢板,先截去宽5分米的长方形,又截去宽8分米的长方形(如图),面积比原来的正方形减少181平方分米,原来正方形的边长是多少?课后练习:1、一块长方形铁板,长18分米,宽13分米,如果长和宽各减少2分米,面积比原来减少多少分米?2、一个长方形,如果宽不变,长增加5米,那么它的面积增加30平方米,如果长不变,宽增加3米,那么它的面积增加48平方米,这个长方形原来的面积是多少平方米?3、用56米长额木兰围成长或宽是20米的长方形,其中一边利用围墙,怎样才能使围成的面积最大?4、四个完全相同的长方形和一个小正方形拼成了一个大正方形,(如图)大正方形的面积是64平方米,小正方形的面积是2平方米,长方形的短边是多少米?5、一个长方形木板,如果长减少5分米,宽减少2分米,那么它的面积就减少66平方分米,这时剩下的部分恰好是一个正方形,求原来长方形的面积?例1、数出右图中有多少条线段?例2、数一数右图中有多少个锐角?例3、数一数右图中共有多少个三角形?例4、数一数右图中共有多少个三角形?例5、数一数右图中有多少个长方形?例6、数一数右图中有多少个长方形?注:公式一:长方形的个数=长边上的线段数*短边上的线段数例7、一数下图中有多少个正方形(每个小方格为边长是1的正方形)?注:由相同的n行n列个小方格组成的n行n列的正方形其中所含有的正方形总数为:公式二:正方形个数=1*1+2*2+3*3+…+n*n例8、数一数下图中有多少个正方形(每个小方格都是边长为1的小正方形)?注:如果一个长方形的长边分成m份,短边分成n份,(长和宽的每一份都是相等的),那么正方形的总数为(n<m)公式三:正方形的个数=mn+(m-1)(n-1)+(m-2)(n-2)+…+(m-n+1)n例9、从广州到北京的某次快车中途要停靠8个站,铁路局要为这次快车准备多少中不同的车票?这些车票中有多少种不同的票价?课后习题:1、数出右图中有多少条线段。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
因此,S△ABC=5 S△DCF。由于 S△ABC=8 平方厘米,所以 S△DCF=8÷5=1.6(平方厘 米),则阴影部分的面积为 1.6×2=3.2(平方厘米)。 练习 1 1、 如图 18-2 所示,AE=ED,BC=3BD,S△ABC=30 平方厘米。求阴影部分的面积。
A
DA
DA
D
F
F
F
B
E
C
B
E
C
B
E
C
18-18
18-19
18-20
答案:
练1
1、 30÷5×2=12 平方厘米
2、 21÷7×3=9 平方厘米
21
3、
5×3÷3=22
平方厘米 2
练2
1、 4÷2=2 8÷2=4
2、 8×2=16 16+8×2+4=36
3、 15×3=45 15+5+15+45=80
1 2、 如图 18-3 所示,AE=ED,DC=3BD,S△ABC=21 平方厘米。求阴影部分的面积。
1 3、 如图 18-4 所示,DE=2AE,BD=2DC,S△EBD=5 平方厘米。求三角形 ABC 的面积。
A F
E
A F
E
A
E
F
B D 18-2
C B
18D-3
B C
C D 18-4
例题 2。 两条对角线把梯形 ABCD 分割成四个三角形,如图 18-5 所示,已知两个三角形的面
的面积是 4,求三角形 ABC 的面积。
A
F
A
F
C
C
DB
E
D
E
18-17
【思路导航】连接 AE。仔细观察添加辅助线 AE 后,使问题可有如下解法。 由图上看出:三角形 ADE 的面积等于长方形面积的一半(16÷2)=8。用 8 减去 3 得到
三角形 ABE 的面积为 5。同理,用 8 减去 4 得到三角形 AEC 的面积也为 4。 因此可知三角形 AEC 与三角形 ACF 等底等高,C 为 EF 的中点,而三角形 ABE 与三角形 BEC 等底,高是三角形 BEC 的 2 倍,三角形 BEC 的面积为 5÷ 2=2.5,所以,三角形 ABC 的面积为 16-3-4-2.5=6.5。 练习 5 1、 如图 18-18 所示,长方形 ABCD 的面积是 20 平方厘米,三角形 ADF 的面积为 5 平 方厘米,三角形 ABE 的面积为 7 平方厘米,求三角形 AEF 的面积。 2、 如图 18-19 所示,长方形 ABCD 的面积为 20 平方厘米,S△ABE=4 平方厘米,S△AFD= 6 平方厘米,求三角形 AEF 的面积。 3、 如图 18-20 所示,长方形 ABCD 的面积为 24 平方厘米,三角形 ABE、AFD 的面积 均为 4 平方厘米,求三角形 AEF 的面积。
第十八周 面积计算(一)
专题简析: 计算平面图形的面积时,有些问题乍一看,在已知条件与所求问题之间找不到任何联
系,会使你感到无从下手。这时,如果我们能认真观察图形,分析、研究已知条件,并加以 深化,再运用我们已有的基本几何知识,适当添加辅助线,搭一座连通已知条件与所求问题 的小“桥”,就会使你顺利达到目的。有些平面图形的面积计算必须借助于图形本身的特征, 添加一些辅助线,运用平移旋转、剪拼组合等方法,对图形进行恰当合理的变形,再经过分 析推导,方能寻求出解题的途径。
练习 3 1、 四边形 ABCD 的对角线 BD 被 E、F、G 三点四等分,且四边形 AECG 的面积为 15 平
方厘米。求四边形 ABCD 的面积(如图 18-10)。 2、 已知四边形 ABCD 的对角线被 E、F、G 三点四等分,且阴影部分面积为 15 平方厘米。
求四边形 ABCD 的面积(如图 18-11 所示)。 3、 如图 18-12 所示,求阴影部分的面积(ABCD 为正方形)。
米。求四边形 ABCD 的面积(如图 18-9 所示)。 D
A F
E
B
C
18-9
【思路导航】由于 E、F 三等分 BD,所以三角形 ABE、AEF、AFD 是等底等高的三角形, 它们的面积相等。同理,三角形 BEC、CEF、CFD 的面积也相等。由此可知, 三角形 ABD 的面积是三角形 AEF 面积的 3 倍,三角形 BCD 的面积是三角形 CEF 面积的 3 倍,从而得出四边形 ABCD 的面积是四边形 AECF 面积的 3 倍。 15×3=45(平方厘米) 答:四边形 ABCD 的面积为 45 平方厘米。
因为 S△ABD 与 S△ACD 等底等高
所以 S△ABO=6
因为 S△BOC 是 S△DOC 的 2 倍
所以△ABO 是△AOD 的 2 倍
所以△AOD=6÷2=3。
答:△AOD 的面积是 3。
练习 2
1、 两条对角线把梯形 ABCD 分割成四个三角形,(如图 18-6 所示),已知两个三角形的
面积,求另两个三角形的面积是多少?
例题 1。 2
已知图 18-1 中,三角形 ABC 的面积为 8 平方厘米,AE=ED,BD=3BC,求阴影部分 的面积。
A
F E
B C
D 18-1
【思路导航】阴影部分为两个三角形,但三角形 AEF 的面积无法直接计算。由于 AE=ED, 连接 DF,可知 S△AEF=S△EDF(等底等高),采用移补的方法,将所求阴影部分 转化为求三角形 BDF 的面积。 2
质,可知 S△DBC=S△CDA;S△COB=S△DOA=4,类推可得每个三角形的面积。 所以,
S△CDO=4÷2=2(平方厘米)
S△DAB=4×3=12 平方厘米
S 梯形 ABCD=12+4+2=18(平方厘米)
答:梯形 ABCD 的面积是 18 平方厘米。
练习 4
1、 如图 18-14 所示,阴影部分面积是 4 平方厘米,OC=2AO。求梯形面积。
2、 已知 OC=2AO,S△BOC=14 平方厘米。求梯形的面积(如图 18-15 所示)。
3、 已知 S△AOB=6 平方厘米。OC=3AO,求梯形的面积(如图 18-16 所示)。
A
D
A
D
O
A
D
O
O
B 18-14
CB 18-15
CB
18-16
C
例题 5。 如图 18-17 所示,长方形 ADEF 的面积是 16,三角形 ADB 的面积是 3,三角形 ACF
14+7+7+3.5=31.5 平方厘米
3、 6×(3+1)=24 6÷3=2 24+6+2=32
练5
1 1、 20÷2-7=3 3× =1.5 20-7-5-1.5=6.5
2
10-6 2
23
2、 20÷2=10 (10-4)× 10 =25 20-6-4-25=75
3、 24÷2=12 平方厘米
4
练3
1、 15×2=30 平方厘米
2、 15×4=60 平方厘米
3、 6×6÷2-6×4÷2=6 平方厘米 6×2÷4=3 平方厘米
(6+3)×6÷2=27 平方厘米
练4
1、 4×2=8 平方厘米 8×2=16 平方厘米
16+8+8+4=36 平方厘米
2、 14÷2=7 平方厘米 7÷2=3.5 平方厘米
积,求另两个三角形的面积各是多少?
A
D
O 6
12
B
C
18-5
【思路导航】已知 S△BOC 是 S△DOC 的 2 倍,且高相等,可知:BO=2DO;从 S△ABD 与 S△ACD
相等(等底等高)可知:S△ABO 等于 6,而△ABO 与△AOD 的高相等,底是△AOD
的 2 倍。所以△AOD 的面积为 6÷2=3。
1
(12-4)×(1- )=5 平方厘米
12
3
12 24-4-4-5 =10 平方厘米
33
D
A
G
F
E
B 18-10
A
D
E
A6
D
E
CB
F
4
G·
18-11
C
B
C
18-12
例题 4。
如图 18-13 所示,BO=2DO,阴影部分的面积是 4 平方厘米。那么,梯形 ABCD 的
面积是多少平方厘米?
A
D
O
E
B
C
18-13
【思路导航】因为 BO=2DO,取 BO 中点 E,连接 AE。根据三角形等底等高面积相等的性
1 2、 已知 AO= OC,求梯形 ABCD 的面积(如图 18-7 所示)。
3
3、 已知三角形 AOB 的面积为 15 平方厘米,线段 OB 的长度为 OD 的 3 倍。求梯形 ABCD
的面积。(如图 18-8 所示)。
A
D
A
D
A
D
O
O 4
4O 8
8
B 18-6
CB
18-7
CB
18-8
C
例题 3。 四边形 ABCD 的对角线 BD 被 E、F 两点三等分,且四边形 AECF 的面积为 15 平方厘
