圆曲线测设
圆曲线

第十章 曲线测设曲线测设是施工测量中的常用方法,是测量工作的一项重要技术。
它是几何大地测量学中建立国家大地控制网的主要方法之一,也是为地形测图、测量和各种工程测量建立控制点的常用方法第一节 线路平面组成和平面位置的标志铁路与公路线路的平面通常由直线和曲线构成,这是因为在线路的定线中,由于受地形、地物或其他因素限制,需要改变方向。
在改变方向处,相邻两直线间要求用曲线连结起来,以保证行车顺畅安全。
这种曲线称平面曲线。
铁路与公路中线上采用的平面曲线主要有圆曲线和缓和曲线。
如图10-1所示,圆曲线是具有一定曲率半径的圆弧;缓和曲线是连接直线与圆曲线的过渡曲线,其曲率半径由无穷大(直线的半径)逐渐变化为圆曲线半径。
根据铁道部公布的《铁路工程技术规范》规定,在铁路干线线路中都要加设缓和曲线;但在地方专用线、厂内线路及站场内线路中,由于列车速度不高,有时可不设缓和曲线,只设圆曲线。
在地面上标定线路的平面位置时,常用方木桩打入地下,并在桩面上钉一小钉,以表示线路中心的位置,在线路前进方向左侧约0.3 m 处打一标志桩,写明主桩的名称及里程。
所谓里程是指该点离线路起点的距离,通常以线路起点为K 0+000.0。
图10-2中的主桩为直线上的一个转点(ZD ),它的编号为31;里程为K 3+402.31,K 3表示3 km ;402.31 表示公里以下的米数,即注明此桩离开线路起点的距离为3 402.31 m 。
第二节 圆曲线及其测设一、圆曲线概述 (一)圆曲线半径我国《新建铁路测量工程规范》和《铁路技术管理规程》中规定,在正线上采用的圆曲线半径为4000、3000、2500、2000、1800、1500、1200、1000、800、700、600、550、500、450、400和350米。
各级铁路曲线的最大半径为4000米。
Ⅰ、Ⅱ级铁路的最小半径在一般地区分别为1000米和800米,在特殊地段为400米;Ⅲ级铁路的最小半径在一般地区为600米,在特殊困难地区为350米。
圆曲线及其主点的测设

第二节圆曲线及其主点的测设§11—2 圆曲线及其主点的测设一、圆曲线概述1.圆曲线半径铁路:我国《新建铁路测量工程规范》和《铁路技术管理规程》中规定:采用的圆曲线半径为:4000、3000、2500、2000、1800、1500、1200、1000、800、700、600、550、500、450、400和350米。
各级铁路曲线的最大半径为4000米。
Ⅰ、Ⅱ级铁路的最小半径:在一般地区分别为1000米和800米,在特殊地段为400米;Ⅲ级铁路的最小半径:在一般地区为600米,在特殊困难地区为350米。
公路:我国《公路工程技术标准》中规定:高速公路的最小半径:在平原微丘区为650米,在山岭重丘区为250米;一级公路在上述两种地区分别为400米和125米;二级公路分别为250米和60米;三级公路分别为125米和30米;四级公路分别为60米和15米。
2.圆曲线主点圆曲线的主点:ZY——直圆点, 即直线与圆曲线的分界点;QZ——曲中点,即圆曲线的中点;YZ——圆直点,即圆曲线与直线的分界点。
圆曲线的控制点:ZY、QZ、YZ、JD。
JD——两直线方向的交点,也是一个重要的点,但不在线路上。
图11-3圆曲线及其主点和要素3.圆曲线要素T——切线长,即交点至直圆点或圆直点的直线长度(JD--ZY,JD—YZ之距离);见图11-3L——曲线长,即圆曲线的长度(ZY—QZ—YZ圆弧的长度);E0——外矢距,即交点至曲中点的距离(JD至QZ之距离);α——转向角,即直线方向转变的水平角;R——圆曲线半径。
T、L、E0总称为圆曲线要素.4、圆曲线要素的计算:α和R分别根据实际测定和线路设计时选定,可按公式法或查表法确定圆曲线的要素T、L、E o1)公式法:切线长曲线长外矢距2)查表法:在《铁路曲线测设用表》(以下简称曲线表)中以α、R为引数,查得相应的圆曲线要素。
[例11-1]:已知α=55o43'24",R=500 m,求圆曲线各要素T,L,E o。
三、圆曲线测设

曲线长L
圆直点 YZ
量取外矢距E,得QZ点。
α/2 半径R α R
圆心O
p
四、圆曲线的详细测设
x
T
切线支距法
一种直角坐标法 N
T
JD
x E
α
原点:ZY或YZ
yi
QZ
X轴:过原点切线
Y轴:过原点半径
桩点坐标计算
v
p
YZ
பைடு நூலகம்
li
ZY
xi
M
li 180 i R
i
α/2 R α R
xi R sin i
一、圆曲线元素的计算
圆曲线主点: 直圆点ZY、 曲中点QZ、 圆直点YZ 圆曲线元素: 切线长T、 曲线长L、 外矢距E、 切曲差D 已 知元素: 圆曲线半径R和偏角α
交点JD
α
切线长T 外矢距E 曲中点QZ 曲线长L 圆直点YZ 切线长T
切线长度: T R tan 曲线长度:L=R
外矢距:E= R cos
直圆点ZY
180
R R (sec
1)
R
a 2
切曲差: 2T-L D=
α O
二、圆曲线主点里程的计算
已知:交点JD里程、圆曲线半径R、偏角α
交点JD
ZY点里程=JD点里程-T
切线长T
α
L 2
YZ点里程=ZY点里程+L
直圆点ZY
曲中点QZ
曲线长L
QZ点里程=YZ点里程-
yi R(1 cos i )
y O
四、圆曲线的详细测设
x
T
圆曲线的主点测设

圆曲线的主点测设摘要:一、圆曲线测设的意义与要求1.圆曲线测设的重要性2.圆曲线测设的主要要求二、圆曲线的主点测设方法1.主点的概念与作用2.测设主点的步骤与工具3.主点测设的注意事项三、圆曲线主点测设的实践应用1.道路工程中的圆曲线测设2.桥梁工程中的圆曲线测设3.其他工程中的圆曲线测设四、圆曲线主点测设的案例分析1.案例一:某道路工程圆曲线主点测设2.案例二:某桥梁工程圆曲线主点测设正文:圆曲线的主点测设是测量工作中一个重要的环节,涉及到道路、桥梁等各类工程的建设。
本文首先介绍了圆曲线测设的意义与要求,然后详细阐述了圆曲线的主点测设方法,并给出了实践应用与案例分析。
一、圆曲线测设的意义与要求圆曲线测设对于道路、桥梁等工程的建设具有重要意义。
准确地测设圆曲线,可以为工程设计提供可靠的数据支持,保证工程的质量和安全。
在进行圆曲线测设时,需要遵循一定的测量规范和要求,确保测设结果的准确性。
二、圆曲线的主点测设方法1.主点的概念与作用主点是指圆曲线上起决定作用的点,用于确定曲线的形状和位置。
主点在圆曲线测设中具有重要作用,它是测设其他点位的依据。
2.测设主点的步骤与工具圆曲线主点的测设步骤主要包括:选择测设方法、设置测量仪器、进行测量观测、计算主点坐标等。
测设主点所需的工具主要包括:经纬仪、全站仪、测距仪等。
3.主点测设的注意事项在进行圆曲线主点测设时,需要注意以下几点:确保测量仪器的精度和稳定性;根据实际情况选择合适的测设方法;注意测量数据的记录和整理。
三、圆曲线主点测设的实践应用圆曲线主点测设广泛应用于道路、桥梁、隧道等各类工程中。
例如,在道路工程中,测设圆曲线主点可以为道路的设计和施工提供重要依据;在桥梁工程中,测设圆曲线主点可以确保桥梁的线形和位置满足设计要求。
四、圆曲线主点测设的案例分析1.案例一:某道路工程圆曲线主点测设在某道路工程中,圆曲线主点测设的步骤如下:首先,采用全站仪进行测量;然后,根据测量数据计算主点坐标;最后,对测设结果进行检验。
圆曲线主点的测设

1、偏角法
(A)短弦偏角法 无全站仪时,用经 纬仪配合钢尺测设, 适合于测设场地起 伏不大。
特点: 测点误差积 累。
偏角法测设圆 曲线是以曲线 起点ZY或终点 YZ作为测站, 计δ算出测站至 曲线上任一细 部点i的弦线与 切线的夹角
(弦切角,也 称偏角)和弦 线Ci。据此确定 点的位置。
O
R
QZ
例题:已知交点的桩号为K3+182.76,测得转折角α =25°48′10″ 设计圆曲线半径R=300m。JD,ZD1和ZD2坐标如图。
求:曲线主点和细部点的坐标。
解:由图中数据计算出两条切线及点至点的方位角分别为 计算出主点、圆曲线细部点的坐标列于下表
测设曲线上整桩和加桩称为圆曲线详细最常用的方法有偏角法偏角法又有短弦偏角法和长弦偏角法切线支最常用的方法有偏角法偏角法又有短弦偏角法和长弦偏角法切线支直角坐标法直角坐标法和极坐标法等
平面圆曲线的测设
任务一:偏角法测设平面单圆曲线 任务二:极坐标法测设平面单圆曲线 任务三:切线支距法测设平面单圆曲线
2R sin i或展开为 ci
li
li3 24 R2
宜以QZ 为界,将曲线分两部分进行测设。
平面圆曲线的测设
任务一:偏角法测设平面单圆曲线 任务二:极坐标法测设平面单圆曲线 任务三:切线支距法测设平面单圆曲线
任务二:切线支距法测设平面单圆曲线
切线支距法(也称直角坐标法) 以曲线起点ZY(或终点YZ)为 独立坐标系的原点,切线指向JD 方向为X轴,通过原点的方向为Y 轴,建立局部直角坐标系,计算 出曲线细部点Pi在该独立坐标系 中的坐标(Xi,Yi)进行测设。 一、计算测设数据
后进行详细测设,即再依据 主点测设曲线上每隔一定距 离的里程桩,详细标定曲线 位置。
圆曲线详细测设的基本要求

3
道路桥梁工程技术专业教学资源库
工程测量
整桩距法
整桩距法
➢ 整桩距法:
➢ 从圆曲线起点ZY和终点YZ 开始,分别以桩距 l0 连续 向圆曲线中点QZ设桩。
道路桥梁工程技术专业教学资源库
工程测量
整桩距法
工程测量
例: 已知某JD的里程为K2+968.43,测得转角������ =34°1 2‘,圆曲线半径R=200m,若按整桩距法加桩,试确定加 桩桩号。
间按规定桩距加密设桩,
并进行测设。
➢ 加密设桩的桩距 l0 ,应符 合下述规定。
直线(m)
曲线(m)
平原、微丘 重丘、山岭 不设超高的曲线
R>60
30<R<60
R<30
50
25
25
20
10
5
道路桥梁工程技术专业教学资源库 Nhomakorabea工程测量
2
道路桥梁工程技术专业教学资源库
工程测量
整桩号法
整桩号法
➢ 整桩号法:
道路桥梁工程技术专业教学资源库
工程测量
谢谢观看
道路桥梁工程技术专业教学资源库
➢ 将靠近圆曲线起点(ZY) 的第一个桩的桩号凑整成 为 l0 倍数的整桩号
➢ 且与ZY点的桩距小于l0 , 然后按桩距 l0 连续向圆 曲线终点YZ设桩。
道路桥梁工程技术专业教学资源库
工程测量
整桩号法
工程测量
例: 已知某JD的里程为K2+968.43,测得转角������=34°1 2‘, 圆曲线半径R=200m,若按整桩号法加桩,试确定加桩桩号。
工程测量
道路桥梁工程技术专业教学资源库
圆曲线测设

圆曲线测设1. 引言圆曲线是道路、铁路和运动赛道等曲线的基本类型之一。
在工程测量中,圆曲线的测设是非常重要的一项任务。
圆曲线测设的目的是确定曲线的半径、切线长以及缓和曲线的相对位置,以确保道路设计的安全性和顺畅性。
本文将介绍圆曲线测设的基本原理、测量方法以及注意事项。
2. 圆曲线测设的基本原理圆曲线测设是基于圆曲线的几何性质进行的。
根据圆曲线的定义,任意一点到圆心的距离都相等,这个距离就是圆曲线的半径。
圆曲线还具有切线的概念,即曲线上每一点的切线方向都与该点的切线相切。
在圆曲线测设中,测量人员通过测量切线长、切线与缓和曲线的交点等信息来确定圆曲线的位置和参数。
3. 圆曲线测设的测量方法圆曲线测设通常使用电子测量设备进行。
下面介绍主要的测量步骤:3.1 设置测量起点测量起点是圆曲线的起始位置,通常选择在道路或铁路的直线段上。
测量人员使用测量杆、经纬仪或全站仪等设备准确记录起点位置的坐标。
3.2 测量切线长测量人员沿着直线段逐步前进,使用测量杆或激光测距仪测量每一段切线的长度。
切线长是圆曲线测设的重要参数之一。
3.3 确定切线与缓和曲线的交点切线与缓和曲线的交点确定了曲线的位置。
测量人员继续测量切线的长度,直到切线与缓和曲线相交。
使用全站仪或经纬仪测量交点的坐标,以确定圆曲线的位置。
3.4 计算圆曲线参数根据测得的切线长和切线与缓和曲线的交点,可以计算出圆曲线的半径、切线坡度等参数。
常用的计算方法有各种数学公式和计算软件,如CAD软件、测绘软件等。
4. 圆曲线测设的注意事项在进行圆曲线测设时,需要注意以下几点:4.1 测量精度圆曲线测设需要高精度的测量数据,因此必须使用精密的测量设备,并进行合理的校准和误差补偿。
4.2 安全措施在进行圆曲线测设时,要注意交通安全和工作人员的安全。
必要时应设置警示标志,避免发生交通事故。
4.3 数据处理测量得到的数据需要经过严格的处理和分析。
对于测量误差进行合理的处理,避免对工程设计和施工产生不良影响。
单圆曲线详细测设

单圆曲线详细测设曲线详细测设是指为满足施工要求,利用主点桩放样曲线上中线桩的工作。
中桩间距的要求:平曲线上中桩间距宜为20 m;当地势平坦且曲线半径大于800 m时,其中桩间距可为40 m;一般公路的曲线半径较小,应按测规要求钉设,中桩间距一般为5 m或10 m。
圆曲线要求设桩位置为从曲线起点(终点)算起,第一点的里程应凑成整数桩号,并为中桩间距的整倍数,然后按整桩号设桩。
例如:ZY里程为K18+197.36,中桩间距为20 m,第1点里程为K18+200,第2点为K18+220,…以此类推。
(里程符号铁路为定线里程冠以DK、公路冠以K。
)一、切线支距法切线支距法(直角坐标法)是以ZY或YZ为坐标原点,以切线为x轴,且指向交点为x轴正向,过原点的半径方向为y轴,建立切线坐标系。
利用在这一坐标系内曲线上各点的直角坐标值测设点的平面位置的方法称切线支距法。
1.坐标计算公式如图4.4.1所示,各点的坐标(xi ,yi)按下式计算:式中 li——待测点里程桩号;φi ——li所对圆心角;lA——ZY或YZ里程桩号。
【例4.4.1】按例4.3.1计算成果,圆曲线要求每20 m测设1点,且桩号为整桩号,现以DK18+200、DK18+220为例说明计算方法。
【解】(1)根据式(4.4.2)计算各弧长il所对圆心角:(2)根据式(4.4.1)计算各点的直角坐标:2.测设方法(1)置镜于ZY或YZ照准切线,沿切线方向测设横坐标xi,得待测点垂足。
(2)在各垂足点上用量角器,分别定出垂足方向,量取纵坐标yi即可定出各待测点的位置。
(3)测量相邻各桩之间的距离,并与相应桩号间的距离进行比较,其精度应满足规范要求。
这种方法适用于平坦地区,优点是积累误差小。
二、偏角法1.偏角法测设圆曲线的基本原理偏角法是传统曲线详细测设的方法之一。
偏角是指过置镜点的切线与置镜点到测设点的弦长之间的夹角,几何学中称为弦切角。
如图4.4.2所示,偏角法测设曲线的基本原理是根据偏角δ和弦长C交会出曲线点。
第四讲2、圆曲线

24 图12-
Байду номын сангаас
• 1、要增加曲线测设例题 • 2、极坐标法用例题介绍 • 3、曲线测设技巧和方法
2 1
δ 3 = 3 ⋅ δ1
L
δ n = n ⋅ δ1
•
由于《测规》规定,圆曲线的中桩里程宜为20 m的整倍数,而通常在ZY、QZ、YZ附近的曲 线点与主点间的曲线长不足20 m,则称其所对应的弦为分弦。分弦所对应的偏角可按式(11 -8)来计算。
(二)圆曲线详细测设举例
• • • • •
圆曲线详细测设前,曲线主点ZY、QZ、YZ己测设好,因此通常以ZY为测站,分别测设ZY~ QZ和YZ~QZ曲线段,并闭合于QZ作检核。 以上例资料为依据,举例说明测设的步骤与方法。 1.以ZY为测站 (1)偏角计算 已知ZY里程为DK53+621.56,QZ为DK 53+864.70,R = 500 m,曲线ZY QZ为顺时针转 (图12-20)。偏角资料计算见表12-12。由于偏角值与度盘读数增加方向一致,故称“正 拨”。
左 右
• •
•
R——圆曲线的半径。 α 、R为计算曲线要素的必要资料,是已 知值。α 可由外业直接测出,亦可由纸上 定线求得;R为设计时采用的数据。 圆曲线要素的计算公式,由图12-18得: • α
切线长 曲线长 外矢距 T=R ⋅ tan π L = R ⋅α ⋅ • o 180 α E0 = R ⋅ sec − R 2 2
(12-7) 图12-18
•
α 式中计算L时, 以度为单位。
(三)圆曲线主点里程计算
• •
•
主点里程计算是根据计算出的曲线要素,由一已知点里程来推算,一般沿里程增加的方向由 ZY QZ Y2进行推算。 如上例己知ZY点的里程为DK53+621.56,则各主点里程计算如下: • ZY DK53+621.56 • +L/2 243.14 • QZ DK53+864.70 • +L/2 243.14 • YZ DK 54+107.84 若已知交点JD的里程,则需计算出ZY或YZ的里程,由此推算其它主点的里程。
圆曲线测设

偏 角(°′″)
正拨
反拨
0 00 00
360 00 00
0 23 25
359 36 35
0 57 48
359 02 12
1 32 10
358 27 50
2 06 33
357 53 27
2 40 56
357 19 04
3 15 18
356 44 32
3 49 41
356 10 19
4 24 04
355 35 56
(2)偏角法
偏角法测设圆曲线是以
曲线起点ZY或曲线终点
YZ为测站,计算出测站
至曲线上任一点弦线与
切线的夹角(弦切角,
也称偏角)和弦长C,据
此确定点位。 1)计算公式:
偏角:
l 180
2 2R π
弦长:
C 2R sin 2
2R sin
弧弦差:
l
C
l3 24R 2
4、主点放样
(1)用盘左位后视直线上的转点(ZD), 固定水平制动螺旋,沿视线方向定线,并 用钢尺量出切线长初步定出曲线起点 (ZY),钉下木桩,用铅笔标记点位,并 返测该段距离,当相对误差小于1/2000时, 取两次丈量结果的平均值准确定出ZY点。
(2)用望远镜瞄准另一切线的转点,固定水 平制动螺旋,按上法定出曲线终点(YZ) (打ZY或YZ点桩,用盘左、盘右其中一个盘 位即可)。
(3)把望远镜从切线方向转(180-α )/2 的角值,定出方向线(分角线),从交点沿 分角线方向量出外矢距E0,初步得曲中点 (QZ),(定下木桩,用铅笔定出点位)再 用另一盘位瞄准切线方向,转(180-α )/ 2角再定出分角线又得一曲中点位置,取正、 倒镜分中位置钉下小钉作为曲中点QZ。
道路中线测量—圆曲线测设(工程测量课件)

01
交点和转点的测设
02
03
道路中
线测量
04
05
06
08
09
路线转角的测定和里程桩设置
圆曲线测设
圆曲线详细测设的基本要求
虚交点的测设
带有缓和曲线的平曲线测设
回头曲线的测设
道路中线逐桩坐标计算
C
目
录 ONTENTS
1
圆曲线详细测设
2
整桩号法
3
整桩距法
4
特点及适用性
1
圆曲线详细测设
➢ 圆曲线详细测设:
3
整桩距法
➢ 整桩距法:
➢ 从圆曲线起点ZY和终点YZ
开始,分别以桩距 l 0 连续
向圆曲线中点QZ设桩。
例: 已知某JD的里程为K2+968.43,测得转角 =34°1
2‘,圆曲线半径R=200m,若按整桩距法加桩,试确定加
桩桩号。
解:
由前例已知ZY里程=K2+906.9,QZ里程=K2+966.59,
2
圆曲线主点测设
➢ ZY点的测设:
➢ 将仪器置于JD上,望远镜照准
后视JD或此方向上的转点,沿
望远镜视线方向量取切线长T,
得ZY,先插一测钎标志。
➢ 用钢尺丈量ZY至最近一个直线
桩的距离,如两桩号之差等于
所丈量的距离或相差在容许范
围内,即可在测钎处打下ZY桩。
➢ YZ点的测设:
➢ 在ZY点测设完后,转动望远镜
C
目
录 ONTENTS
1
直角坐标系的建立
2
加密桩点坐标的计算
3
测设方法
4
优缺点及适用性
圆曲线测设
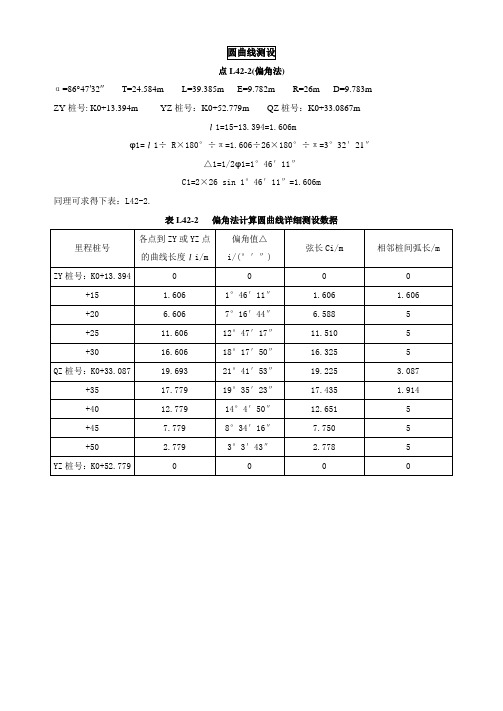
点L42-2(偏角法)α=86°47′32″T=24.584m L=39.385m E=9.782m R=26m D=9.783m ZY桩号: K0+13.394m YZ桩号:K0+52.779m QZ桩号:K0+33.0867mι1=15-13.394=1.606mφ1=ι1÷ R×180°÷π=1.606÷26×180°÷π=3°32′21″△1=1/2φ1=1°46′11″C1=2×26 sin 1°46′11″=1.606m同理可求得下表:L42-2.表L42-2 偏角法计算圆曲线详细测设数据点L42-3A和点L42-3B(虚交测设/偏角法)α=95°11′22″T=32.848m L=49.841m R=30mZY桩号:K0+66.616m QZ桩号:K0+91.537m YZ桩号:K0+116.457mι1=70-66.616=3.384mφ1=ι1÷ R×180°÷π=3.384÷30×180°÷π=6°27′47″△1=1/2φ1=3°13′53″C1=2×30 sin 3°13′53″=3.382m同理可求得下表:L42-3A/L42-3B.表L42-3A/L42-3B 法计算圆曲线详细测设数据点L42-4(偏角法)α= 82°32′14″T=15.796m L=25.930m E=5.948m R=18m D=5.662m ZY桩号:K0+136.585m QZ桩号:K0+149.550m YZ桩号:K0+162.515mι1=140-136.585=3.4156mφ1=ι1÷ R×180°÷π=3.415÷18×180°÷π=10°42′14″△1=1/2φ1=5°26′7″C1=2×18 sin 5°26′7″=3.410m同理可求得下表:L42-4.表L42-4 偏角法计算圆曲线详细测设数据α= 144°25′15″T=28.049m L=22.686m E=20.458m R=9m D=33.412mZY桩号:K0+180.030m QZ桩号:K0+191.373m YZ桩号:K0+202.716mι1=183-180.030=2.97 mφ1=ι1÷ R×180°÷π=2.97÷9×180°÷π=18°54′27″χ1=Rsinφ1=2.916m, y1=R(1-cosφ1)= 0.586m同理可求得下表:L42-5.表L42-5 切线支距法计算圆曲线详细测设数据ZY桩号:K0+220.106m QZ桩号:K0+232.629m YZ桩号:K0+245.151mι1=224-220.106=3.894mφ1=ι1÷ R×180°÷π=3.894÷41×180°÷π=5°26′30″χ1=Rsinφ1=3.888m, y1=R(1-cosφ1)= 0.185m同理可求得下表:L42-5.表L42-6 切线支距法计算圆曲线详细测设数据ZY桩号:K0+295.572m QZ桩号:K0+319.63m YZ桩号:K0+343.688mι1=300-295.572=4.428mφ1=ι1÷ R×180°÷π=4.428÷32×180°÷π=7°55′42″χ1=Rsinφ1=4.414m, y1=R(1-cosφ1)= 0.306m同理可求得下表:L42-7.表L42-7 切线支距法计算圆曲线详细测设数据。
圆曲线测设

JD
P2
α
P3 P4
P1 P2
41624 1 20812 2 2
1
ZY
1
YZ
41624 C1 2 R sin 2 120 sin 8.95( m) 2 2
2 1
2 41624 9 32 57 65441 2
(m) xi 0 5.95 45.77 48.92 29.09 9.14 0
y(m) i
0 0.06 1.12 3.51 4.02 1.41 0.14 0
§2-4 圆曲线测设
• 三、圆曲线的详细测设
2.圆曲线详细测设的方法 (2)切线支距法 测设步骤 ①从ZY(或YZ)点开始用钢尺或皮尺沿切线方向量 取 Pi的 横坐标xi ,得垂足Ni 。 ②在各垂足Ni上用方向架定出垂直方向,量取纵坐 标yi,即 可定出Pi点。
※分弦的偏角:
图2-5
K4=039.52-020.00=19.52m,相应的偏角值
K 4 180 4 = · 2 2R
(2)弦长计算 (如图2-4)
严密计算公式: C 2R sin 近似计算: Ck
c sin 2 , 2 R
c 2 R sin
(2-3)
图2-8 切线支距原理
图2-9 切线支距法测设圆曲线
2.测设方法:
以图2-9为例,设在圆曲线上每10m测设一点。
(1)先沿切线上每1Om量一点,将半个曲线长度测 设完毕; (2)于每10m处回量Li-xi,可得各曲线点在X轴上 的投影,即各曲线点的X值;
(3)过各曲线点在X轴上的投影点做切线的垂直方 向,并在垂直方向上量取yi ,即测设出圆曲线的各点。
圆曲线测设实验报告

实验一圆曲线测设一、目的和要求(1)掌握圆曲线主点元素的计算和主点的测设方法。
(2)掌握用偏角法进行圆曲线的详细测设二、计划和设备(1)试验时数安排为4学时,实验小组由5人组成(2)实验设备为DJ6经纬仪1台,钢尺1把,标杆2支,测钎10支,木桩3支,榔头1把,记录板1块,计算器1支。
三、方法和步骤1.圆曲线主点测设道路圆曲线主点测设之前,需要有标定路线方向的交点(JD)和转点(ZD)。
在空旷地面打一木桩作为路线交点JD1,然后向两个方向(路线的转折角约等于)延伸30 m以上,定出两个转点ZD1和ZD2,插上测钎。
如图1-1所示。
图1-1 圆曲线的主点测设元素在JD1点安置经纬仪,以一个测回测定转折角,计算路线偏角。
设计圆曲线的半径,按下列公式计算圆曲线元素(切线长T、曲线长L、外距E、切曲差q,记录于附录表2中。
用安置于JD1点的经纬仪先后瞄准ZD1,ZD2定出方向,用钢尺在该方向上测设且切线长T,定出圆曲线的起点(直圆点)ZY和圆曲线的终点(圆直点)YZ,打下木桩,重新测设一次,在木桩顶上标出ZY 和YZ的精确位置。
用经纬仪瞄准YZ,水平读盘读数置于,照准部旋转,定出转折角的分角线方向,用钢尺测设外距E,定出圆曲线中点QZ 。
1.主点桩号计算位于道路中线上的曲线主点桩号由交点的桩号推算而得。
设交点JD1的桩号为,根据圆曲线元素,计算曲线主点的桩号:(检核)1.用偏角法详细测设圆曲线设圆曲线上里程每整需要测设里程桩,则,为曲线上第一个整桩与圆曲线起点ZY间的弧长,如图1-2所示。
图1-2 用偏角法详细测设圆曲线用偏角法详细测设圆曲线,按下式计算测设点的偏角和以后每增加弧长的各点的偏角增量:等细部点的偏角按下式计算:……曲线起点至曲线上任一细部点的弦长按下式计算:曲线上相邻整桩间的弦长按下式计算:曲线上任两点间的弧长与弦长之差(弦弧差)按下式计算:根据以上这些公式和算得的曲线主点桩号,计算圆曲线偏角法测设数据,记录于附录表2中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆曲线测设
摘要:在公路、铁路的路线圆曲线测设中,一般是在测设出曲线各主点后,随之在直圆点或圆直点进行圆曲线详细测设。
本文通过仪器安置不同地方进行多种圆曲线测设,提出了交点偏角法详细测设圆曲线的方法,其中主要运用了偏角法测设法。
关键词:安置交点偏角法圆曲线测设
前言
《礼记》有云:大学之道,在明德,在亲民。
在提笔撰写我的毕业设计论文的时候,我也在向我的大学生活做最后的告别仪式。
我不清楚过去的一切留给现在的我一些什么,也无从知晓未来将赋予我什么,但只要流泪流汗,拼过闯过,人生才会少些遗憾!
非常幸运能够加入水利工程这个古老
而又新兴的行业,即将走向工作岗位的时刻,我仿佛感受到水利行业对我赋予新的历史
使命,水利是一项以除害兴利、趋利避害,协调人与水、人与大自然关系的高尚事业。
水利工作,既要防止水对人的侵害,更要防止人对水的侵害;既要化解自然灾害对人类生命财产的威胁,又要善待自然、善待江河、善待水,促进人水和谐,实现人与自然和谐相处。
这种使命,更让我用课堂中的知识用于实际生产中来。
特别是这两个月来的毕业设计,我越发感觉到学会学精测量基础知识对于我贡献水利是多么的重要。
所以,我越发不愿放弃不多的大学时光,努力提高自己的实践动手能力,而本学期的毕业设计,为我提供了绝好的机会,我又怎能放弃?
刚刚从老师那里得到毕业设计的题目
和任务时,我的心里真的没底。
作为毕业设计的主体工作,我们主要运用电子水准仪对某幢建筑物进行变形观测与计算,布设控制点进行平面控制测量和高程控制测量;用全站仪进行了中心多边行角度和距离的测量,并用条件平差原理进行平差,通过控制点的放样来计算土的挖方量,还有圆曲线的计算与测设。
而我研究的毕业课题是圆曲线测设。
大学的最后一个学期过得特别快,几乎每天扛着仪器,奔走在校园的每个角落,生
活亦很有节奏。
今天我提笔写毕业论文,我的毕业设计也接近尾声。
不管成果如何,毕竟心里不再是没底了,挑着两个多月的辛苦换来的数据和成果,并不断的完善他们,心里感觉踏实多了。
在本次毕业设计论文的设计中要感谢
水利系为我们的工作提供了测量仪器,还有各指导老师的教导和同学的帮助。
开题报告
一、研究课题:《微分曲线的应用》
二、学科地位和研究应用领域
1.学科定义
工程测量学是研究地球空间中具体几
何实体的测量描绘和抽象几何实体的测设
实现的理论方法和技术的一门应用性学科。
它主要以建筑工程、机器和设备为研究服务对象。
2.学科地位
测绘科学和技术是一门具有悠久历史
和现代发展的一级学科。
该学科无论怎样发展,服务领域无论怎样拓宽,与其他学科的
交叉无论怎样增多或加强,学科无论出现怎
样的综合和细分,学科名称无论怎样改变,
学科的本质和特点都不会改变。
3.研究应用领域
目前国内把工程建设有关的工程测量
按勘测设计、施工建设和运行管理三个阶段划分;也有按行业划分成:线路工程测量、水利工程测量、桥隧工程测量、建筑工程测量、矿山测量、海洋工程测量、军事工程测量、三维工业测量等,几乎每一行业和工程测量都有相应的著书或教材。
国际测量师联合会的第六委员会称作
工程测量委员会,过去它下设4个工作组:测量方法和限差;土石方计算;变形测量;地下工程测量。
此外还设了一个特别组:变形分析与解释。
现在,下设了6个工作组和2个专题组。
6个工作组是:大型科学设备的高精度测量技术与方法;线路工程测量与优化;
变形测量;工程测量信息系统;激光技术在
工程测量中的应用;电子科技文献和网络。
2个专题组是:工程和工业中的特殊测量仪器;工程测量标准。
工程测量学主要包括以工程建筑为对。
