第五章多原子分子结构
第五章多原子分子的结构和性质

甲烷分子中四个成键轨道定域在C-H之间,每个 定域轨道中有两个成键电子,电子分布分别对C-H键 轴对称,为四个等性单键。几何构型为正四面体。 四个H的1s轨道分别对键轴对称。
C的2s,2px,2py和2pz除2s轨道外,与键轴是不
平面型有机共轭分子中,σ 键定域,构成分子骨架,每个 C 余下的 一个垂直于平面的 p 轨道往往以肩并肩的型式形成多原子离域π 键。 用 HMO法处理共轭分子结构时,假定: (1) 假定π电子是在核和σ 键所形成的整个骨架中运动,可将σ 键和π 键 分开处理; (2) 假定共轭分子的σ 键骨架不变,分子的性质由π电子状态决定; (3) 假定每个π 电子k 的运动状态用k 描述,其Schrö dinger方程为: ˆ H k Ek k HMO法还假定: •各C原子的α积分相同,各相邻C原子的β积分也相同; •不相邻C原子的β 积分和重叠积分S均为0。
A
四个杂化轨道分别与四个氢原子1s 轨道组合成四个分子轨道
A C1 A C21SA B C1B C21SB C C1C C21SC D C1D C21SD
1sA——氢原子A的1S轨道,以此类推。 A——由两个原子轨道线性组合而成的分子轨道,称为定域分子轨道
a1 C1S C2 1SA 1SB 1SC 1SD t2 x C3Px C4 1SA 1SB 1SC 1SD t2 z C3Pz C4 1SA 1SB 1SC 1SD t2 y C3Py C4 1SA 1SB 1SC 1SD
成键能力: F 3 ; 键角: cos
结构化学第五章 多原子分子中的化学键3

此刻再对它施加反映操作
可知它对于镜面反映已变为非对称
点击动画按钮,用播放键分步观察
(2)在相关图上,按轨道对称性守恒要求, 将反应物 和产物的MO由低到高关联,即S与S连线、A与A连线. 相
关轨道的能量应相近;
(3)各连线遵守不相交规则.
例1. 丁二烯-环丁烯顺旋电环化的轨道相关图:对称性允许
例2. 丁二烯-环丁烯对旋电环化的轨道相关图:对称性禁阻
4m+2
C2
C2
S A A S
A S S A
加热 光照 加热 光照
顺旋 对旋 对旋 顺旋
在加热条件下,丁二烯衍生物处于基态,HOMO是 ψ2 。闭环要求轨道同位相重叠,只能以顺旋方式进行:
丁二烯基态的HOMO ψ2
请单击按钮观看动画
若在光照下进行反应,分子被激发,ψ3 成为HOMO. 闭环要求轨道同位相重叠,以对旋方式进行:
丁二烯激发态的HOMO ψ3
请单击按钮观看动画
己 三 烯 衍 生 物 的 电 环 化 反 应
C2H4 HOMO π
例4.丁二烯与乙烯环加成生成环己烯
乙烯 LUMO π* 丁二烯 LUMO ψ3
丁二烯 HOMO ψ2
乙烯 HOMO π
轨道对称性允许,加热即能进行.
例5.呋喃的生成反应
+ H2 O O
+ H2 O O
通过热消去H2生成呋喃的下列两个反应, 第一个容易而 第二个困难. 根据微观可逆性原理,从逆反应来考虑. 在加 氢反应中, 呋喃起变化的部分只是Π 44共轭体系而与O无关:
5.5 离域 p 键和共轭效应
5.5.1 离域p键的形成和表示法
• 当形成化学键的p 电子不局限于两个原子的区域,而 是在参加成键的多个原子的分子骨架中运动,从而形 成p型化学键,称为离域p键。 • 离域p键的表示:
结构化学习题解答5(北大)

NH3 N(CH3)3 C6H5NH2 CH3CONH2
[解]: 碱性的强弱和提供电子对能力大小有关,当N原子提供孤
对电子的能力大,碱性强。分子的几何够习惯内和有关性质主 要决定于分子中骨干原子的成键情况。下面将分析4个分子中的 骨干原子特别是N原子的成键轨道以及所形成的化学键的类型, 并结合有关原子或基团的电学性质,比较N原子上电荷密度的大 小,从而推断出4个分子碱性强弱的次序。
=-152.2 KJ•mol-1 [5.20] 试分析下列分子中的成键情况,指出C—Cl键键长大小
次序,并说明理由。
(a)H3CCl (b)H2C=CHCl (c)HC≡CCl [解]: (a)H3CCl:该分子为CH4分子的衍生物。同时CH4分子一样, C原子也采用sp3杂化轨道成键。4个sp3杂化轨道分别与3个H原 子的1s轨道及Cl原子的3p轨道重叠共形成4个σ键。分子呈四面 体构型,属C3v点群。 (b) H2C=CHCl:该分子为H2C=C H2分子的衍生物,其成键情况 与C2H4分子的成键情况即有相同之处又有差别。在C2H3Cl分子 中,C原子(1)的3个sp2杂化轨道分别与两个H原子的1s轨道
H
H
βc1+(α-E) c2+βc3=0
βc1+βc2+(α-E)c3=0 用β除各式并令x = (α-E)/β,则得:
xc1+c2+c3=0 c1+xc2+c3=0
c1+c2+xc3=0
欲使ci为非0解,则必须师其系数行列式为零,即:x 1 1
解此行列式,得:
1 x 10
x1=-2,x2=1,x3=1 将x值代入x=(α-E)/β,得: E1=α+2β,E2=α-β,E3=α-β 能级及电子分布简图如下:
第五章 多原子分子结构与性质习题解答

第五章 多原子分子结构与性质习题解答070601306 何梅华 070601307游梅芳 070601308 陈风芳 070601309黄丽娜 070601310 郑海霞 070601311 黄秀娟 070601312 尤丽君1.以CH 4为例,讨论定域分子轨道和离域分子轨道间的区别和联系。
答:杂化轨道理论将CH 4分子中的C 原子进行了sp 杂化,每个杂化轨道和1个H 原子的1s 杂化形成一个定域分子轨道,在此成键轨道中的一对电子形成定域键C-H ,四个C-H 键轨道能量等同。
离域分子轨道处理CH 4分子所得的能级图说明4个轨道能量高低不同。
定域分子和离域分子两种模型是等价的,只是反应的物理图像有所区别。
2.试讨论杂化轨道构成三原则。
解:若以{i φ}表示某原子参加杂化的原子轨道集合,k Φ为杂化轨道,则:∑=Φni i k cki φ i =1,2,3,…,n (1)(1) 杂化轨道要满足归一化条件 杂化轨道是一种原子轨道,它描述了处于价态原子中单电子的可能状态。
归一化的数学表达式为:1)(222===Φ∑⎰∑⎰ki c d cki d ninii kτφτ (2) 上面的计算用到了同一原子中原子轨道间满足正交、归一的条件。
ki c 为i φ在第k个杂化轨道中的组合系数,而2ki c 表示i φ在k Φ中的成分。
当把k Φ轨道中s 轨道的成分记为k α、p 轨道的成分记为k β时,就有2ks k c =α (3)222kzky kx k c c c ++=β (4) (2)参加杂化的轨道贡献之和为1参加杂化的i φ轨道是归一化的,杂化后的在新形成的所有杂化轨道里的成分之和——即i φ电子“分散”到各杂化轨道中的概率之和应为1。
故有12=∑kkic(5)由(2)式和(5)式可知,有n 个i φ轨道参与杂化应得n 个杂化轨道。
(2) 同一原子中杂化轨道间正交正交的杂化轨道间排斥作用能最小,使原子体系稳定。
多原子分子的结构与性质

多原子分子的结构与性质一、分子结构:1.长链结构:一些多原子分子如碳酸盐(CO3^2-)、多聚芳醚等,它们的分子结构呈线性长链状。
这种结构使得分子具有较高的分子量和高度的拉伸强度,使得这些物质适用于制备高强度的材料、纤维和聚合物。
2.环状结构:多原子分子还可以形成环状结构,如环氧烷、苯等。
这种结构使得分子呈现闭合环状,具有较高的稳定性和刚性。
环状结构还可以影响分子的化学性质,如苯环结构使得苯具有共轭平面结构,从而赋予苯具有稳定的芳香性和较高的反应活性。
3.分支结构:一些多原子分子如维生素C等呈现分支结构。
分支结构可以增加分子的立体构型和表面积,增强物质的活性和溶解性。
这使得分支结构的多原子分子在生物体内能够更好地发挥作用,如维生素C具有较高的抗氧化性和溶解性。
二、分子性质:1.分子极性:多原子分子中,如果原子之间存在较大的电负性差异,化学键就会呈极性,导致分子整体带有一个正负极。
这种极性会使分子在外电场的作用下发生取向和形状改变,具有静电相互作用和氢键相互作用等,从而影响分子的化学和物理性质,如溶解度、沸点、熔点等。
2.分子对称性:分子内部原子的排列方式对分子的性质具有重要影响。
分子对称性常常决定着分子的振动、旋转和反应方式等。
对称性分子具有如以下特性:属于同一个对称元素的原子之间的键长和键角相等;对称元素平分分子;中心对称元素过属于同一个原子的键。
对称性分子具有较低的能量和较高的稳定性。
3.分子的化学反应活性:多原子分子在化学反应中通常会通过化学键的形成和断裂来改变分子的结构和性质。
多原子分子通过与其他分子的化学反应,可以进一步转化为其他更复杂的化合物。
例如,脂肪酸分子中含有多个碳碳双键,通过加氢反应可以将双键还原为饱和脂肪酸。
4.分子的热学性质:多原子分子具有比较复杂的热学性质。
其热容常常取决于分子内部的振动、旋转等模式的能级。
例如,多原子分子的热容常常会出现阶梯状的变化,且热容的变化幅度较大。
多原子分子的结构和性质

5.1 价电子对互斥理论
价电子对包括成键电子对(bp)和孤电子对(lp)。 原子周围各个价电子对之间由于互相排斥,在键长一 定的条件下,互相间距越远越稳定。
价电子对之间斥力的来源:静电排斥;Pauli斥力。
为使价电子对间互相远离,可将价电子对看作等距排 布在一个球面上,形成多面体。
于sp1,sp2,sp3杂化来说,上式等价于:
cosij pip jd (i j ) / (i j )
其中pi是杂化轨道i中的归一化的p轨道组合。
等性杂化轨道:以sp3杂化为例
每个杂化轨道中,有1/4是s轨道,3/4是p轨道
i
1s 2
3 2 pi;
i 1, 2, 3, 4
pi aipx px aipy p y aipz pz
由于是不等性杂化,杂化轨道的成分与等性杂化不 同,轨道间的夹角也不同,一般情况下,要么已知 轨道间夹角,求出轨道成分,要么已知轨道成分, 求出轨道夹角。以前一种情况为例。
水分子中,两根H-O键间的夹角为104.5°
首先建立坐标系,将其中一根H-O键的杂化轨道放 在x轴上,另一个在x-y平面,则
1 1s 1p1
1 1
cos104.5
0
11
0.2002 0.7998
不妨取 1 2 0.4474; 1 2 0.8943
夹角公式 cos104.5 p1p2d a2 px 0.2504
a2 py 1 a22px 0.9681(任意取其中一个)
结果: 每个H-O键中s轨道成分占20.02%,p轨道占79.98% 每对孤对电子中s轨道占(1-2×20.02%)/2=29.98%, p轨道占(3-2×79.98%)/2=70.02%
多原子分子的结构和性质习题解答
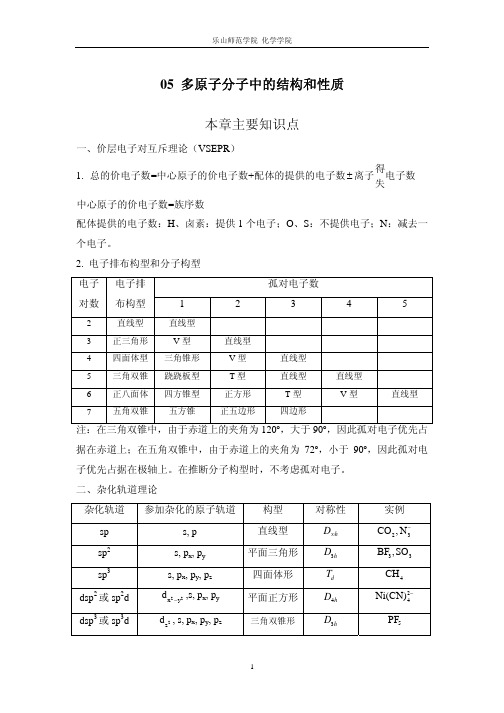
五、离域 π
键的表示:
π
n m
,其中
m
表示形成离域 π
键的
p
轨道数,n
表示填充
在离域π 键的电子数(要求会写)。
2
乐山师范学院 化学学院
六、前线轨道理论: 分子的最高占据轨道(HOMO)和最低空轨道(LUMO)统称为前线轨道。 两个分子要发生化学反应,首先要相互接近,在两个分子相互接近时,一个
四方锥
C4v
IF5
d2sp3 或 sp3d2 dz2 , dx2 −y2 , s, px, py, pz 正八面体
Oh
SF6
三、离域分子轨道理论:
用分子轨道理论处理多原子分子时,最一般的方法是用非杂化的原子轨道进
行线性组合,构成分子轨道,它们是离域化的,即这些分子轨道的电子并不定域
于多原子分子的两个原子之间,而是在几个原子间离域运动。
7+3=10 5
三角双锥
3
2
O H
H H 三角锥型
F
Br F
F T型
NF3
5+3=8
4
四面体
3
1
N F
F F 三角锥型
ICl4− 7+4+1=12 6
八面体
4
2
IF4+
7+4-1=10 5
三角双锥
4
1
SbF4− 5+4+1=10 5
三角双锥
4
1
Cl
Cl
I Cl
Cl
正方形
F F
I F
F
跷跷板型
F F
周公度第四版结构化学第五章_多原子分子的结构和性质总结

·价电子对互斥理论不能应用的化合物
·过渡金属化合物(具有全充满、半充满或全空的 d轨道除外)。
§5.2 杂化轨道理论
一、杂化概念的提出 1931年和Slater提出杂化概念,为了解
释键角的变化。
为了解释甲烷的正四面体结构,说明碳原子四个 键的等价性,鲍林在1928一1931年,提出了杂化轨道 的理论。
例:如右图:
A(1,2,3) 124.1 A(1,2,4) 124.1 A(3,2,4) 111.9
3. 成键电子对和孤对电子对的分布情况不同,前者受 到2个成键原子核的吸引,比较集中在键轴的位置, 而孤对电子对没有这种限制,显得比较肥大(空间 分布范围广),所以孤对电子对对相邻电子对的排 斥较大。
目录
1 价电子对互斥理论(VSEPR) 2 杂化轨道理论 3 离域分子轨道理论 4 休克尔分子轨道法(HMO法) 5 离域π键和共轭效应 6 分子轨道对称性和反应机理
5.1 价层电子对互斥理论(VSEPR)
VSEPR: (Valence Shell Electron Pair Repulsion) 判断多原子分子几何构型的近代学说。
三、判断分子几何构型的原则:
ALmEn
当中心原子A周围存在m个配位体L及n个孤 对电子对E(ALmEn)时,提出判断分子几何构型 的原则如下:
1.为使价电子对间斥力最小,可将价电子对看作等距 离地排布在同一个球面上,形成规则的多面体形式。
★ 当m+n=2 时,直线形; ★ 当m+n=3 时,三角形; ★ 当m+n=4 时,四面体形;★ 当m+n=5 时,三方双锥形; ★ 当m+n=6 时,八面体形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 多原子分子结构5001NF 3和NH 3分子中, 键角∠FNF 比∠HNH 要 (a ) , 这是因为(b )。
5002写出下列分子的结构式(标明单键和多重键等键型)和立体构型:(1) Al 2Cl 6 ,(2) HN 3 ,(3) Fe(CO)3(η4- C 4H 4) ,(4) XeOF 4 ,(5) XeF 4 5003NH 3和PH 3分子键角值大者为___________________分子。
5004用价电子对互斥理论推断: PF 4+的构型为_________________, 中心原子采用的杂化轨道为_____________________: XeF 4的构型为___________________,中心原子采用的杂化轨道为________________________。
5005写出下述分子中中心原子的杂化方式及分子的几何构型:HgCl 2_________________: Co(CO)4-__________________:BF 3___________________: Ni(CN)42-__________________。
5006sp 2(s ,p x ,p y )等性杂化轨道中,若1ψ和x 轴平行,2ψ和y 轴成30°,1ψ,2ψ,3ψ互成120°。
请写出满足正交归一化条件的三个杂化轨道表达式:1ψ______________________________:2ψ______________________________:3ψ______________________________。
5007O 3的键角为116.8°,若用杂化轨道ψ=c 1s 2ψ+c 2p 2ψ描述中心O 原子的成键轨道,试按键角与轨道成分关系式cos θ=-c 12/c 22,计算:(1) 成键杂化轨道中c 1和c 2值;(2) ψ2s 和ψ2p 轨道在杂化轨道ψ中所占的比重。
5008已知 H 2O 的键角为104.5°,O 原子进行了不等性sp 3杂化,其中两个与氢原子成键的杂化轨道中,O 原子的p 成分的贡献为:------------------------------ ( )(A) 0.21 (B) 0.80 (C) 0.5 (D) 0.75( 已知键角和轨道成分的关系式为 cos θ= -c 12/c 22 )5009实验测得乙烯(C 2H 4)分子∠CCH=121.7°,∠HCH=116.6°,分子处在xy 平面,C ═C轴和x 轴平行。
试计算C 原子 sp 2杂化轨道的系数。
( 已知键角和轨道成分的关系式为 cos θ=-c 12/c 22 )5011判断:在形成CH 4分子的过程中, C 原子的2p 轨道和H 原子的1s 轨道组合成sp 3杂化轨道。
------------------------------ ( )5012sp 2等性杂化是指同一杂化轨道中s 成分和p 成分相等。
这一说法是否正确? 5013等性的d 2sp 3杂化的杂化轨道波函数的一般形式为:-------------( )(A)ψ=6/1s ψ +2/1p ψ+3/1d ψ (B)ψ=1/2s ψ+1/4p ψ+1/3d ψ (C)ψ=1/6s ψ+1/2p ψ+1/3d ψ (D) ψ=2/1s ψ+6/1p ψ+3/1d ψ5015杂化轨道是:------------------------------------------------- ( )(A) 两个原子的原子轨道线性组合形成一组新的原子轨道(B) 两个分子的分子轨道线性组合形成一组新的分子轨道(C) 两个原子的原子轨道线性组合形成一组新的分子轨道(D) 一个原子的不同类型的原子轨道线性组合形成的一组新的原子轨道5016定域分子轨道模型和价键理论对于成键区电子运动的描述是完全相同的。
这一说法是否正确?5018写出下列分子休克尔行列式。
(用x 表示,x =(α-E )/β,自己给原子编号)(1) CH 3—CH ═CH —CH 3(2) CH 2═CH —CH ═CH 2(3)5019已知烯丙基阳离子的三个π分子轨道为: (A =1/2, B =1/2)3211φφφψA B A ++=312φφψB B -= 3211φφφψA B A +-=问亲电反应发生在哪个原子上:------------------------------------ ( )(A) 1 (B) 2 (C) 3 (D) 1,3 (E) 1,2,35020Huckel 行列式有以下几个特点:(A) 行列式的阶由参加离域大π键的原子数决定(B) 行列式的主对角元为α-E(C) 行列式的非对角元为β和0,且β的分布总是紧挨着主对角元α-E(D) 如有杂原子参加, 诸α,β须分别标记清楚上述说法有错误的是:------------------------------------ ( )5021试用HMO 法求丙二烯双自由基 H C═C ═C H 的 (1) 电子分子轨道能级能量;(2) 离域能;(3) 分子轨道波函数;(4) 键键级。
5022在三次甲基甲烷分子中, 中心C 原子与邻近三个次甲基组成大π键。
试证明中心C 原子的键级为4.732。
5024环丙烯基的三个C 原子各位于等边三角形的顶点上,π分子轨道可用C 原子的2p z 轨道的线性组合, 用Huckel MO 法确定该π键的波函数和能级。
5025用HMO 法计算H C═C ═C H 双自由基的π电子的分子轨道和能量,并作出分子图。
5026若环丁二烯是平面正方形构型, 用HMO 求其π电子能级及其最低能级的分子轨道。
5027试用HMO 法求环丁二烯C 4H 4的π分子轨道和能级, 再求其共轭能, 由此预测:(1) 该分子的稳定性如何(需要简单说明);(2) 该分子的基态是三重态还是单态?5028画出下列久期行列式对应的共轭分子碳原子骨架:0011001100110=x x x x [ x =(α-E ) / β ]5029利用分子的对称性, 求环丁二烯分子的大π键分子轨道和能量。
5030求烯丙基阳离子(CH 2CHCH 2)+的电荷密度、键级、自由价和分子图。
已知:321331232112122212222212221φφφψφφψφφφψ+-=-=++=5031乙烯的吸收光谱λ极大约为193?nm , 而丁二烯的λ极大约为217?nm 。
(1) 用HMO 法计算出乙烯和丁二烯能级;(2) 根据以上结果,定性说明为什么λ极大(丁二烯)> λ极大(乙烯)(设丁二烯、乙烯中的β相等)(3) 用前线轨道理论讨论,在加热条件下,顺-丁二烯和乙烯二分子进行环加成的可能性如何?5032用HMO 求烯丙基分子( ) π电子能级和分子轨道。
5033用 Huckel MO 法, 求烯丙基的(1) π电子能级;(2) π分子轨道;(3) 电荷密度;(4) 键级。
5035已知丁二烯的四个π分子轨道为:43211φφφφψA B B A +++=43212φφφφψB A A B --+=43213φφφφψB A A B +--= 43214φφφφψA B B A -+-=则其第一激发态的键级P 12,P 23为何者?(π键级) ---------------------------------- ( ) P 12 P 23(A) 2AB 2B 2(B) 4AB 2(A 2+B 2)(C) 4AB 2(B 2-A 2)(D) 0 2(B 2+A 2)(E) 2AB B 2+A 25036基态丁二烯有一电子从最高成键轨道激发到最低反键轨道, 求此激发态丁二烯的电荷密度、键级、自由价和分子图。
已知:432113717.06515.06515.03717.0φφφφψ+++=432126015.03717.03717.06015.0φφφφψ--+=432136015.03717.03717.06015.0φφφφψ+--= 432143717.06515.06515.03717.0φφφφψ-+-=5037在HMO 法中⎩⎨⎧≠===⎰s r s r 01d s r rs τS φφ 是因为r φ与s φ正交归一。
这种说法是否正确?5038(1) 写出N 3-的几何构型、成键情况;(2) 用HMO 法计算出N 3-中离域π键的离域能(不用公式直接代);(3) 写出N 3-中离域键的波函数形式。
5039试用HMO 法计算基态戊二烯基负离子的总能量和离域能。
5040用HMO 法处理环戊二烯基负离子,其久期方程的解 x =-2,-0.618,-0.618,1.618,1.618。
求:(1) ∏65键能,(2) 离域能。
5041用HMO 法对丁二烯进行分析,计算用α和β表示的轨道能级,已知丁二烯最前二个光电子谱带是 9.03?eV 和 11.46?eV ,计算β值。
5042在用HMO 法计算共轭分子各碳原子的自由价时,都以三次甲基甲烷自由基中心碳原子的总键级 4.732 为最大成键度。
现发现双自由基H C=C=C H 中心碳原子的成键度更大, 请用HMO 法计算之。
5048已知富烯的三个能量最低的π轨道为:ψ1=0.245φ1+0.523φ2+0.429(φ3+φ6)+0.385(φ4+φ5)ψ2=0.5(φ1+φ2)-0.5(φ4+φ5) ψ3=0.602(φ3-φ6)+0.372(φ4-φ5)若用亲核试剂与其反应, 则反应位在:------------------------------------ ( )(A) 1 (B) 2 (C) 3,6 (D) 4,5 (E) 都可能5049用HMO法计算分子的π轨道能级以及基态时的离域能。
5050已解得苯分子的三个已占π分子轨道如下,试求苯的分子图。
ψ1=1/6(φ1+φ2+φ3+φ4+φ5+φ6)ψ2=1/12(2φ1+φ2-φ3-2φ4-φ5+φ6)ψ3=1/4(φ2+φ3-φ5-φ6)5051试用HMO法确定基态戊二烯基负离子的HOMO 和LUMO 波函数,并标出这两个轨道的节面位置。
5052由HMO法计算可得环戊二烯基的五个π轨道的能量分别为:E1=α+2β,E2=E3=α+0.618β,E4=E5=α-1.618β,试求基组态时的最高占有轨道波函数,并标出节面位置。
5053在用HMO法处理某共轭分子时,它的久期行列式为:101110 1111 01111=xxxxxx试给出该共轭分子的结构式(只画出σ骨架) 。
5054试用HMO法计算环丁二烯基组态时的离域能。
