蒋中一《数理经济学的基本方法》(第4版)课后习题详细分析和解答(第1章 数理经济学的实质)【圣才出品
概率论与数理统计(第四版)习题答案全

概率论与数理统计(第四版)习题答案全概率论与数理统计习(第四版)题解答第一章 随机事件及其概率·样本空间·事件的关系及运算一、任意抛掷一颗骰子,观察出现的点数。
设事件A 表示“出现偶数点”,事件B 表示“出现的点数能被3整除”.(1)写出试验的样本点及样本空间;(2)把事件A 及B 分别表示为样本点的集合;(3)事件B A AB B A B A ,,,,分别表示什么事件?并把它们表示为样本点的集合.解:设i ω表示“出现i 点”)6,,2,1( =i ,则(1)样本点为654321,,,,,ωωωωωω;样本空间为}.,,,,,{654321ωωωωωω=Ω (2)},,{642ωωωA =; }.,{63ωωB =(3)},,{531ωωωA =,表示“出现奇数点”;},,,{5421ωωωωB =,表示“出现的点数不能被3整除”;},,,{6432ωωωωB A =⋃,表示“出现的点数能被2或3整除”;}{6ωAB =,表示“出现的点数能被2整除且能被3整除”;},{B A 51ωω= ,表示“出现的点数既不能被2整除也不能被3整除”二、写出下列随机试验的样本空间及各个事件中的样本点:(1)同时掷三枚骰子,记录三枚骰子的点数之和.A —“点数之和大于10”,B —“点数之和小于15”.(2)一盒中有5只外形相同的电子元件,分别标有号码1,2,3,4,5.从中任取3只,A —“最小号码为1”.解:(1) 设i ω表示“点数之和等于i ”)18,,4,3( =i ,则},,,{1843ωωω =Ω;},,,{181211ωωωA =;}.,,,{1443ωωωB =(2) 设ijk ω表示“出现号码为k j i ,,”);5,,2,1,,(k j i k j i ≠≠= ,则},,,,,,,,,{345245235234145135134125124123ωωωωωωωωωω=Ω }.,,,,,{145135134125124123ωωωωωωA =三、设C B A ,,为三个事件,用事件之间的运算表示下列事件: (1) A 发生, B 与C 都不发生; (2) C B A ,,都发生;(3) C B A ,,中至少有两个发生; (4) C B A ,,中至多有两个发生. 解:(1) C B A ;(2) ABC ;(3) ABC C AB C B A BC A ⋃⋃⋃或CA BC AB ⋃⋃(4) BC A C B A C AB C B A C B A C B A C B A ⋃⋃⋃⋃⋃⋃或C B A ⋃⋃或.ABC四、一个工人生产了n 个零件,以i A 表示他生产的第 i 个零件是合格品(n i ≤≤1).用i A 表示下列事件:(1)没有一个零件是不合格品; (2)至少有一个零件是不合格品; (3)仅有一个零件是不合格品;(4)至少有一个零件不是不合格品. 解:(1) n A A A 21;(2) n A A A 21或n A A A ⋃⋃⋃ 21; (3) n n n A A A A A A A A A 212121⋃⋃⋃ (4) n A A A ⋃⋃⋃ 21或.21n A A A第二章 概率的古典定义·概率加法定理一、电话号码由七个数字组成,每个数字可以是0,1,2,…,9中的任一个数(但第一个数字不能为0),求电话号码是由完全不同的数字组成的概率.解:基本事件总数为611011011011011011019109⨯=C C C C C C C 有利事件总数为456789214151617181919⨯⨯⨯⨯⨯=C C C C C C C 设A 表示“电话号码是由完全不同的数字组成”,则0605.0109456789)(62≈⨯⨯⨯⨯⨯⨯=A P 二、把十本书任意地放在书架上,求其中指定的三本书放在一起的概率.解:基本事件总数为!101010=A 指定的三本书按某确定顺序排在书架上的所有可能为!777=A 种;这三本书按确定的顺序放在书架上的所以可能的位置共818=C 种;这三本书的排列顺序数为!333=A ;故有利事件总数为!3!8!38!7⨯=⨯⨯(亦可理解为)3388P P设A 表示“指定的三本书放在一起”,则067.0151!10!3!8)(≈=⨯=A P三、为了减少比赛场次,把二十个队任意分成两组(每组十队)进行比赛,求最强的两个队被分在不同组内的概率.解:20个队任意分成两组(每组10队)的所以排法,构成基本事件总数1020C ;两个最强的队不被分在一组的所有排法,构成有利事件总数91812C C 设A 表示“最强的两队被分在不同组”,则526.01910)(102091812≈==C C C A P四、某工厂生产的产品共有100个,其中有5个次品.从这批产品中任取一半来检查,求发现次品不多于1个的概率.解:设i A 表示“出现的次品为i 件”)5,4,3,2,1,0(=i ,A 表示“取出的产品中次品不多于 1个”,则 .10A A A ⋃=因为V A A =10,所以).()()(10A P A P A P +=而0281.0979942347)(5010050950≈⨯⨯⨯==C C A P 1529.09799447255)(501004995151≈⨯⨯⨯⨯==C C C A P故 181.01529.00281.0)(=+≈A P五、一批产品共有200件, 其中有6件废品.求 (1) 任取3件产品恰有1件是废品的概率; (2) 任取3件产品没有废品的概率; (3) 任取3件产品中废品不少于2件的概率. 解:设A 表示“取出的3件产品中恰有1件废品”;B 表示“取出的3件产品中没有废品”;C 表示“取出的3件产品中废品不少于2件”,则 (1) 0855.019819920019319418)(3200219416≈⨯⨯⨯⨯==C C C A P (2) 912.0198199200192193194)(32003194≈⨯⨯⨯⨯==C C B P(3) 00223.019819920012019490)(3200019436119426≈⨯⨯⨯⨯=+=C C C C C C P六、设41)( ,0 ,31)()()(======BC P P(AC)P(AB)C P B P A P .求A , B , C 至少有一事件发生的 概率.解:因为0==P(AC)P(AB),所以V AC V AB ==,,从而V C AB =)(可推出0)(=ABC P设D 表示“A , B , C 至少有一事件发生”,则C B A D ⋃⋃=,于是有)()()()()()()()()(ABC P CA P BC P AB P C P B P A P C B A P D P +---++=⋃⋃=75.04341313131==-++=第三章 条件概率与概率乘法定理·全概率公式与贝叶斯公式一、设,6.0)|(,4.0)(,5.0)(===B A P B P A P 求)|(,)(B A A P AB P . 解:因为B A AB B B A A +=+=)(,所以)()()(B A P AB P A P +=,即14.06.0)4.01(5.0)()()()()()(=⨯--=-=-=B A P B P A P B A P A P AB P68.074.05.036.0)4.01(5.05.0)()()()()()]([)|(≈=--+=-+==B A P B P A P A P B A P B A A P B A A P二、某人忘记了电话号码的最后一个数字,因而他随意地拨号,求他拨号不超过两次而接通所需电话的概率.若已知最后一个数字是奇数,那么此概率是多少? 解:设A 表示“第一次拨通”,B 表示“第二次拨通”,C 表示“拨号不超过两次而拨通”(1)2.0101101)()()(19111101911011=+=⋅+=+=C C C C C C A B P A P C P(2)4.05151)()()(2511141511=+=+=+=A A A A A A B P A P C P三、两台车床加工同样的零件,第一台出现废品的概率是0.03,第二台出现废品的概率是0.02.加工出来的零件放在一起,并且已知第一台加工的零件比第二台加工的零件多一倍.(1)求任意取出的零件是合格品的概率;(2)如果任意取出的零件是废品,求它是第二台车床加工的概率. 解:设i A 表示“第i 台机床加工的零件”)2,1(=i ;B 表示“出现废品”;C 表示“出现合格品”(1))()()()()()()()(22112121A C P A P A C P A P C A P C A P C A C A P C P +=+=+= 973.0)02.01(31)03.01(32≈-⨯+-⨯=(2)25.002.03103.03202.031)()()()()()()()()(22112222=⨯+⨯⨯=+==A B P A P A B P A P A B P A P B P B A P B A P四、猎人在距离100米处射击一动物,击中的概率为0.6;如果第一次未击中,则进行第二次射击,但由于动物逃跑而使距离变为150米;如果第二次又未击中,则进行第三次射击,这时距离变为200米.假定击中的概率与距离成反比,求猎人三次之内击中动物的概率.解:设i A 表示“第i 次击中”)3,2,1(=i ,则由题设,有1006.0)(1kA P ==,得60=k ,从而有4.015060150)(2===k A P ,.3.020060200)(3===k A P设A 表示“三次之内击中”,则321211A A A A A A A ++=,故有)()()()()()()(321211A P A P A P A P A P A P A P ++=832.03.0)4.01()6.01(4.0)6.01(6.0=⨯-⨯-+⨯-+= (另解)设B 表示“猎人三次均未击中”,则168.0)3.01)(4.01)(6.01()(=---=B P故所求为 832.0)(1)(=-=B P B P五、盒中放有12个乒乓球,其中有9个是新的.第一次比赛时从其中任取3个来用,比赛后仍放回盒中.第二次比赛时再从盒中任取3个,求第二次取出的都是新球的概率. 解:设i A 表示“第一次取得i 个新球”)3,2,1,0(=i ,则2201)(312330==C C A P 22027)(31219231==C C C A P 220108)(31229132==C C C A P 22084)(31239033==C C C A P 设B 表示“第二次取出的都是新球”,则312363123731238312393022084220108220272201)()()(C C C C C C C C A B P A P B P i i i ⋅+⋅+⋅+⋅==∑=146.0532400776161112208444722010855142202755212201≈=⋅+⋅+⋅+⋅=第四章 随机事件的独立性·独立试验序列一、一个工人看管三台车床,在一小时内车床不需要工人照管的概率:第一台等于0.9,第二台等于0.8,第三台等于0.7.求在一小时内三台车床中最多有一台需要工人照管的概率. 解:设i A 表示“第i 台机床不需要照管”)3,2,1(=i ,则9.0)(1=A P 8.0)(2=A P 7.0)(3=A P再设B 表示“在一小时内三台车床中最多有一台需要工人照管”,则321321321321A A A A A A A A A A A A B +++= 于是有)()()()()()()()()()()()()(321321321321A P A P A P A P A P A P A P A P A P A P A P A P B P +++= )7.01(8.09.07.0)8.01(9.07.08.0)9.01(7.08.09.0-⨯⨯+⨯-⨯+⨯⨯-+⨯⨯=902.0=.(另解)设i B 表示“有i 台机床需要照管”)1,0(=i ,B 表示“在一小时内三台车床中最多有一台需要工人照管”,则10B B B +=且0B 、1B 互斥,另外有 504.07.08.09.0)(0=⨯⨯=B P398.0)7.01(8.09.07.0)8.01(9.07.08.0)9.01()(1=-⨯⨯+⨯-⨯+⨯⨯-=B P 故902.0398.0504.0)()()()(1010=+=+=+=B P B P B B P B P .二、电路由电池a 与两个并联的电池b 及c 串联而成.设电池c b a ,,损坏的概率分别是0.3、0.2、0.2,求电路发生间断的概率. 解:设1A 表示“a 损坏”;2A 表示“b 损坏”;3A 表示“c 损坏”;则3.0)(1=A P 2.0)()(32==A P A P 又设B 表示“电路发生间断”,则321A A A B += 于是有)()()()()(321321321A A A P A A P A P A A A P B P -+=+=)()()()()()(321321A P A P A P A P A P A P -+=328.02.02.03.02.02.03.0=⨯⨯-⨯+=.三、三个人独立地去破译一个密码,他们能译出的概率分别为51、31、41,求能将此密码译出的概率.解:设A 表示“甲能译出”;B 表示“乙能译出”;C 表示“丙能译出”,则51)(=A P 31)(=B P 41)(=C P设D 表示“此密码能被译出”,则C B A D ⋃⋃=,从而有)()()()()()()()()(ABC P CA P BC P AB P C P B P A P C B A P D P +---++=⋃⋃=)()()()()()()()()()()()(C P B P A P A P C P C P B P B P A P C P B P A P +---++= 6.0413151415141513151413151=⨯⨯+⨯-⨯-⨯-++=. (另解)52)411)(311)(511()()()()()(=---===C P B P A P C B A P D P ,从而有6.053521)(1)(==-=-=D P D P四、甲、乙、丙三人同时对飞机进行射击,三人的命中概率分别为7.0,5.0,4.0.飞机被一人击中而被击落的概率为2.0,被两人击中而被击落的概率为6.0,若三人都击中,则 飞机必被击落.求飞机被击落的概率. 解:设1A 表示“甲命中”;2A 表示“乙命中”;3A 表示“丙命中”;则4.0)(1=A P5.0)(2=A P 7.0)(3=A P 设i B 表示“i 人击中飞机” )3,2,1,0(=i ,则09.0)7.01)(5.01)(4.01()())(()()(3213210=---===A P A P A P A A A P B P)()(3213213211A A A A A A A A A P B P ++=)()()(321321321A A A P A A A P A A A P ++=)()()()()()()()()(321321321A P A P A P A P A P A P A P A P A P ++=36.07.0)5.01)(4.01()7.01(5.0)4.01()7.01)(5.01(4.0=⨯--+-⨯⨯-+--⨯=)()(3213213212A A A A A A A A A P B P ++= )()()(321321321A A A P A A A P A A A P ++=)()()()()()()()()(321321321A P A P A P A P A P A P A P A P A P ++=41.07.0)5.01)(4.01()7.01(5.0)4.01()7.01)(5.01(4.0=⨯--+-⨯⨯-+--⨯=14.07.05.04.0)()()()()(3213213=⨯⨯===A P A P A P A A A P B P 设A 表示“飞机被击落”,则由题设有0)(0=B A P 2.0)(1=B A P 6.0)(2=B A P 1)(3=B A P故有458.0114.06.041.02.036.0009.0)()()(30=⨯+⨯+⨯+⨯==∑=i i i B A P B P A P .五、某机构有一个9人组成的顾问小组,若每个顾问贡献正确意见的概率都是0.7,现在该机构内就某事可行与否个别征求每个顾问的意见,并按多数人意见作出决策,求作 出正确决策的概率.解:设i A 表示“第i 人贡献正确意见”,则7.0)(=i A P )9,,2,1( =i .又设m 为作出正确意见的人数,A 表示“作出正确决策”,则)9()8()7()6()5()5()(99999P P P P P m P A P ++++=≥=+⋅⋅+⋅⋅+⋅⋅=277936694559)3.0()7.0()3.0()7.0()3.0()7.0(C C C 9991889)7.0()3.0()7.0(⋅+⋅⋅+C C+⋅⋅+⋅⋅+⋅⋅=273645)3.0()7.0(36)3.0()7.0(84)3.0()7.0(126918)7.0()3.0()7.0(9+⋅⋅+0403.01556.02668.02668.01715.0++++= 901.0=.六、每次试验中事件A 发生的概率为p ,为了使事件A 在独立试验序列中至少发生一次的概率不小于p ,问至少需要进行多少次试验? 解:设做n 次试验,则n p A P A P )1(1}{1}{--=-=一次都不发生至少发生一次要p p n ≥--)1(1,即要p p n -≤-1)1(,从而有.1)1(log )1(=-≥-p n p 答:至少需要进行一次试验.第五章离散随机变量的概率分布·超几何分布·二项分布·泊松分布一、一批零件中有9个合格品与3个废品.安装机器时从这批零件中任取1个.如果每次取出的废品不再放回去,求在取得合格品以前已取出的废品数的概率分布.解:设X表示“在取得合格品以前已取出的废品数”,则X的概率分布为即亦即二、自动生产线在调整以后出现废品的概率为p.生产过程中出现废品时立即进行调整.求在两次调整之间生产的合格品数的概率分布.解:设X表示“在两次调整之间生产的合格品数”,且设=1,则ξ的概率分布为q-p三、 已知一批产品共20个,其中有4个次品.(1)不放回抽样.抽取6个产品,求样品中次品数的概率分布;(2)放回抽样.抽取6个产品,求样品中次品数的概率分布. 解:(1)设X 表示“取出的样本中的次品数”,则X 服从超几何分布,即X 的概率函数为)4,3,2,0()(6206164===-x CCC x X P x x从而X 的概率分布为即(2)设X 表示“取出的样本中的次品数”,则X 服从超几何分布,即X 的概率函数为)6,5,4,3,2,0()2.01()2.0()(66=-==-x C x X P xxx从而X 的概率分布为即四、 电话总机为300个电话用户服务.在一小时内每一电话用户使用电话的概率等于0.01,求在一小时内有4个用户使用电话的概率(先用二项分布计算,再用泊松分布近似计算,并求相对误差). 解:(1)用二项分布计算)01.0(=p168877.0)01.01()01.0()1()4(2964430029644300≈-=-==C p p C ξP(2)用泊松分布计算)301.0300(=⨯==np λ168031355.0!43)4(34≈==-e ξP 相对误差为.5168877.0168031355.0168877.000≈-=δ五、 设事件A 在每一次试验中发生的概率为0.3,当A 发生次数不少于3次时,指示灯发出信号.现进行了5次独立试验,求指示灯发出信号的概率. 解:设X 表示“事件A 发生的次数”,则3.0)(==p A P ,5=n ,).3.0,5(~B X 于是有)5()4()3()3(=+=+==≥X P X P X P X P5554452335)1()1(p C p p C p p C +-+-=16308.000243.002835.01323.0≈++≈(另解) )2()1()0(1)3(1)3(=-=-=-=<-=≥X P X P X P X P X P 32254115505)1()1()1(11p p C p p C p p C ------=16308.0≈六、 设随机变量X 的概率分布为2, 1, ,0 , !)(===k k ak X P kλ;其中λ>0为常数,试确定常数a .解:因为∑∞===01)(k k X P ,即∑∞==01!k kk λa ,亦即1=λae ,所以.λe a -=第六章 随机变量的分布函数·连续随机变量的概率密度一、 函数211x +可否是连续随机变量X 的分布函数?为什么?如果X 的可能值充满区间: (1)(∞+∞- ,);(2)(0,∞-). 解:(1)设211)(x x F +=,则1)(0<<x F因为0)(lim =-∞→x F x ,0)(lim =+∞→x F x ,所以)(x F 不能是X 的分布函数.(2)设211)(x x F +=,则1)(0<<x F 且0)(lim =-∞→x F x ,1)(lim 0=-→x F x因为)0( 0)1(2)('22<>+-=x x x x F ,所以)(x F 在(0,∞-)上单增.综上述,故)(x F 可作为X 的分布函数.二、函数x x f sin )(=可否是连续随机变量X 的概率密度?为什么?如果X 的可能值充满区间:(1)⎥⎦⎤⎢⎣⎡2,0π; (2)[]π,0; (3)⎥⎦⎤⎢⎣⎡23,0π. 解:(1)因为⎥⎦⎤⎢⎣⎡∈2,0πx ,所以sin )(≥=x x f ;又因为1cos )(2020=-=⎰ππx dx x f ,所以当⎥⎦⎤⎢⎣⎡∈2,0πx时,函数x x f sin )(=可作为某随机变量X 的概率密度.(2)因为[]πx ,0∈,所以0sin )(≥=x x f ;但12cos )(00≠=-=⎰ππx dx x f ,所以当[]πx ,0∈时,函数x x f sin )(=不可能是某随机变量X 的概率密度.(3)因为⎥⎦⎤⎢⎣⎡∈23,0πx ,所以x x f sin )(=不是非负函数,从而它不可能是随机变量X 的概率密度.二、 一批零件中有9个合格品与3个废品.安装机器时从这批零件中任取1个.如果每次取出的废品不再放回去,求在取得合格品以前已取出的废品数的分布函数,并作出分布函数的图形. 解:设X 表示“取出的废品数”,则X 的分布律为⎪⎪⎪⎩⎪⎪⎪⎨⎧>≤<≤<≤<≤=3,132,22021921,222110,430,0)(x x x x x x F四、(柯西分布)设连续随机变量X 的分布函数为+∞<<∞-+=x x B A x F ,arctan )(.求:(1)系数A 及B ;(2)随机变量X 落在区间)1 ,1(-内的概率;(3) X 的概率密度.解:(1) 由0)2()(lim =-⋅+=-∞→πB A x F x ,12)(lim =⋅+=-∞→πB A x F x ,解得.1,21πB A == 即)( ,arctan 121)(+∞<<-∞+=x x πx F . (2).21)]1arctan(121[]1arctan 121[)1()1()11(=-+-+=--=<<-ππF F X P(3) X 的概率密度为)1(1)()(2x x F x f +='=π.五、(拉普拉斯分布)设随机变量X 的概率密度为+∞<<∞-=-x Ae x f x,)(.求:(1)系数A ;(2)随机变量X 落在区间)1,0(内的概率;(3)随机变量X 的分布函数.解:(1) 由1)(⎰+∞∞-=dx x f ,得1220⎰⎰+∞∞-+∞--===A dx e A dx Ae xx,解得21=A ,即有).( ,21)(+∞<<-∞=-x e x f x(2)).11(21)(2121)()10(101010ee dx e dx xf X P x x -=-===<<--⎰⎰(3) 随机变量X 的分布函数为⎪⎩⎪⎨⎧>-≤===-∞--∞-⎰⎰21102121)()(x e x e dx e dx x f x F x xx xx .第七章 均匀分布·指数分布·随机变量函数的概率分布一、公共汽车站每隔5分钟有一辆汽车通过.乘客到达汽车站的任一时刻是等可能的.求乘客候车时间 不超过3分钟的概率.解:设随机变量X 表示“乘客的候车时间”,则X 服从]5,0[上的均匀分布,其密度函数为⎩⎨⎧∉∈=]5,0[,0]5,0[,51)(x x x f 于是有.6.053)()30(3===≤≤⎰dx x f X P二、已知某种电子元件的使用寿命X (单位:h)服从指数分布,概率密度为⎪⎩⎪⎨⎧≤>=-.0,0;0,8001)(800x x e x f x任取3个这种电子元件,求至少有1个能使用1000h 以上的概率. 解:设A 表示“至少有1个电子元件能使用1000h 以上”;321A 、A 、A 分别表示“元件甲、乙、丙能使用1000h 以上”.则287.08001)1000()()()(4510008001000800321≈=-==>===-∞+-∞+-⎰e e dx e X P A P A P A P xx)()()()()()()()()(321313221321321A A A P A A P A A P A A P A P A P A P A A A P A P +---++=⋃⋃=638.0287.0287.03287.0332≈+⨯-⨯=(另解)设A 表示“至少有1个电子元件能使用1000h 以上”.则287.08001)1000(4510008001000800≈=-==>-∞+-∞+-⎰e e dx e X P xx从而有713.01)1000(1)1000(45≈-=>-=≤-eX P X P ,进一步有 638.0713.01)]1000([1)(33≈-≈≤-=X P A P三、(1) 设随机变量X 服从指数分布)(λe .证明:对于任意非负实数s 及t ,有).()(t X P s X t s X P ≥=≥+≥这个性质叫做指数分布的无记忆性.(2) 设电视机的使用年数X 服从指数分布)10(.e .某人买了一台旧电视机,求还能使用5年以上的概率.解:(1)因为)(~λe X ,所以R x ∈∀,有xe x F λ--=1)(,其中)(x F 为X 的分布函数.设t s X A +≥=,t X B ≥=.因为s 及t 都是非负实数,所以B A ⊂,从而A AB =.根据条件概率公式,我们有)(1)(1)()()()()()()()(s X P t s X P s X P t s X P B P A P B P AB P B A P s X t s X P <-+<-=≥+≥====≥+≥tst s e e e λλλ--+-=----=]1[1]1[1)(. 另一方面,我们有tt e e t F t X P t X P t X P λλ--=--=-=≤-=<-=≥)1(1)(1)(1)(1)(.综上所述,故有)()(t X P s X t s X P ≥=≥+≥. (2)由题设,知X 的概率密度为⎩⎨⎧≤>=-.,;,0001.0)(1.0x x e x f x设某人购买的这台旧电视机已经使用了s 年,则根据上述证明的(1)的结论,该电视机还能使用5年以上的概率为6065.01.0)()5()5(5.051.051.05≈=-===≥=≥+≥-∞+-∞+-∞+⎰⎰e e dx e dx x f X P s X s X P x x.答:该电视机还能使用5年以上的概率约为6065.0. 四、 设随机变量X 服从二项分布)4.0 ,3(B ,求下列随机变量函数的概率分布: (1)X Y 211-=;(2)2)3(2X X Y -=.解:X 的分布律为(1)X Y 211-=的分布律为(2)2)3(2X X Y -=的分布律为即五、设随机变量X 的概率密度为⎪⎩⎪⎨⎧≤>+=.0,0;0,)1(2)(2x x x x f π求随机变量函数X Y ln =的概率密度.解:因为)()()(ln )()(yXyYe F e X P y X P y Y P y F =<=<=<= 所以随机变量函数X Y ln =的概率密度为)( )1(2)()()()(2''+∞<<-∞+====y e e e e f e e F y F y f yyyyyyXYY π,即)( )1(2)(2+∞<<-∞+=y e e y f y yY π.第八章 二维随机变量的联合分布与边缘分布一、把一颗均匀的骰子随机地掷两次.设随机变量X 表示第一次出现的点数,随机变量Y 表示两次出现点数的最大值,求二维随机变量),(Y X 的联合概率分布及Y 的边缘概率分布.解:二维随机变量),(Y X 的联合概率分布为Y的边缘概率分布为二、设二维随机变量(X ,Y )的联合分布函数)3arctan )(2arctan (),(yC x B A y x F ++=. 求:(1)系数A 、B 及C ;(2)(X ,Y )的联合概率密度:(3)边缘分布函数及边缘概率密度. 解:(1)由0)0,(,0),0(,1),(=-∞=∞-=∞+-∞F F F ,得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=--=++0)2(0)2)(0(1)2)(2(πB AC πC B A πC πB A 解得2πC B ==,.12πA =(2)因为)3arctan 2)(2arctan 2(1),(2yx y x F ++=πππ,所以(X ,Y )的联合概率密度为.)9)(4(6),(),(222"y x y x F y x f xy ++==π(3)X 及Y 的边缘分布函数分别为xxxXx dx x dy y x f dx x F ∞-∞-∞-+∞∞-=+==⎰⎰⎰2arctan 1)4(2),()(2ππ2arctan 121x π+=yxy Y ydy y dx y x f dy x F ∞-∞-∞-+∞∞-=+==⎰⎰⎰3arctan1)9(3),()(2ππ3arctan 121y π+=X 及Y 的边缘概率密度分别为⎰⎰⎰+∞+∞∞-+∞∞-++⋅=++==0222222)9(1)4(112)9)(4(6),()(dy y x dy y x dy y x f x f X ππ)4(2)3arctan 31()4(1122022x y x +=+⋅=∞+ππ⎰⎰⎰+∞+∞∞-+∞∞-++=++==022222241)9(12)9)(4(6),()(dxx y dx y x dx y x f y f Y ππ)9(3)2arctan 21()9(122022y x y +=+=∞+ππ三、设),(Y X 的联合概率密度为⎩⎨⎧>>=+-.,00;0,,Ae ),(3y)(2x 其它y x y x f求:(1)系数A ;(2)),(Y X 的联合分布函数;(3)X及Y 的边缘概率密度;(4)),(Y X落在区域R :632 ,0 ,0<+>>y x y x 内的概率. 解:(1)由1),(=⎰⎰+∞∞-+∞∞-dy dx y x f ,有1610032==⎰⎰∞+∞+--A dy e dx e A yx,解得.6=A (2)),(Y X 的联合分布函数为⎪⎩⎪⎨⎧>>==⎰⎰⎰⎰--∞-∞-其它0,06),(),(0032y x dy e dx e dy y x f dx y x F x yy x xy⎩⎨⎧>>--=--其它00,0)1)(1(32y x e e y x(3)X 及Y 的边缘概率密度分别为⎩⎨⎧≤>=⎪⎩⎪⎨⎧≤>==-+∞--∞+∞-⎰⎰020006),()(2032x x ex x dye e dy y xf x f xy x X⎩⎨⎧≤>=⎪⎩⎪⎨⎧≤>==-+∞--∞+∞-⎰⎰030006),()(3032y y ex x dxe e dx y xf y f yy x Y(4)⎰⎰⎰⎰---==∈x y xRdye dx edxdy y x f R Y X P 322033026),(}),{( 6306271)(2---⎰-=-=e dx e e x四、设二维随机变量),(Y X 在抛物线2x y =与直线2+=x y 所围成的区域R 上服从均匀分布.求:(1) ),(Y X 的联合概率密度;(2) 概率)2(≥+Y X P . 解:(1) 设),(Y X 的联合概率密度为⎩⎨⎧∉∈=.),(, 0;),(,),(R y x R y x C y x f 则由129)322()2(21322122212==-+=-+==--+-⎰⎰⎰⎰⎰Cx x x C dx x x C dy dx C Cdxdy x x R解得92=C .故有⎪⎩⎪⎨⎧∉∈=.),(, 0;),(,92),(R y x R y x y x f(2) ⎰⎰⎰⎰⎰⎰++-≥++==≥+x x x x y x dydx dy dx dxdy y x f Y X P 2212210229292),()2(⎰⎰-++=21210)2(92292dx x x xdx481.02713)322(92922132102≈=-++=x x x x .第九章 随机变量的独立性·二维随机变量函数的分布一、 设X 与Y 是两个相互独立的随机变量,X 在]1,0[上服从均匀分布,Y 的概率密度为⎪⎩⎪⎨⎧≤>=-.0,0;0,21)(2y y e y f yY求 (1) ),(Y X 的联合概率密度; (2) 概率)(X Y P ≥. 解: (1)X 的概率密度为⎩⎨⎧∉∈=)1,0(,0)1,0(,1)(x x x f X,),(Y X 的联合概率密度为(注意Y X ,相互独立)⎪⎩⎪⎨⎧><<==-其它,00,10,21)()(),(2y x e y f x f y x f yY X(2)dxedx edy e dx dxdy y x f X Y P x xyxyxy ⎰⎰⎰⎰⎰⎰-∞+-∞+-≥=-===≥102102212)(21),()(7869.0)1(2221122≈-=-=--e ex二、 设随机变量X 与Y 独立,并且都服从二项分布:.,,2 ,1 ,0 ,)(;,,2 ,1 ,0 ,)(212211n j q p C j p n i q p C i p j n j j n Y in i i n X====--证明它们的和Y X Z +=也服从二项分布. 证明: 设j i k +=, 则ik n i k i k n ki i n i i n ki Y X Z q p C q p C i k P i P k Z P k P +---=-=∑∑=-===22110)()()()(∑=-+=ki kn n k in i n q p C C 02121)(由k nm ki ik nk m C C C +=-=∑0, 有 kn nki in i n C C C21210+==∑. 于是有),,2,1,0( )(212121n n k q p C k P k n n k in n Z +==-++由此知Y X Z +=也服从二项分布.三、设随机变量X 与Y 独立,并且X 在区间[0,1]内服从均匀分布,Y 在区间[0,2]内服从辛普森分布:⎪⎩⎪⎨⎧><≤<-≤≤=.20 0,;2 1 ,2;10 ,)(y y y y y y y f Y 或求随机变量Y X Z +=的概率密度.解: X 的概率密度为 ⎩⎨⎧∉∈=]1,0[,0]1,0[,1)(x x y f ξ. 于是),(Y X 的联合概率密度为⎪⎩⎪⎨⎧≤<≤≤-≤≤≤≤=. 0,2 1,10 ,210,10,),(其它当当y x y y x y y x fYX Z +=的联合分布函数为}),{(}{}{)(D y x P z Y X P z Z P z F Z∈=≤+=≤=,其中D 是z y x ≤+与),(y x f 的定义域的公共部分.故有⎪⎪⎪⎩⎪⎪⎪⎨⎧≤<+-≤<-+-≤≤><=3229321212331023,00)(222z z z z z z z zz z z F Z从而随机变量Y X Z +=的概率密度为⎪⎪⎩⎪⎪⎨⎧≤<-≤<+-≤≤><=3232132103,00)(z z z z z z z z z f Z三、 电子仪器由六个相互独立的部件ijL (3,2,1;2,1==j i )组成,联接方式如右图所示.设各个部件的使用寿命ijX 服从相同的指数分布)(λe ,求仪器使用寿命的概率密度.解: 由题设,知ij X 的分布函数为⎩⎨⎧≤>-=-0,00,1x x e F x X ij λ 先求各个并联组的使用寿命)3,2,1( =i Y i 的分布函数.因为当并联的两个部件都损坏时,第i 个并联组才停止工作,所以有)3,2,1(),m ax (21==i Y i i i ξξ从而有)3,2,1( =i Y i 的分布函数为⎩⎨⎧≤>-==-0,00,)1()(221y y e F F y F y X X Y i i i λ设Z "仪器使用寿命".因为当三个并联组中任一个损坏时,仪器停止工作.所以有),,min(321Y Y Y Z =.从而有Z 的分布函数为⎩⎨⎧≤>---=⎩⎨⎧≤>----=-0,00,])1(1[10,00)],(1)][(1)][(1[1)(32321z z e z z z F z F z F z F z Y Y Y Z λ故Z 的概率密度为⎩⎨⎧≤>--=---0,00,)2)(1(6)(23z z e e e z f z z z Z λλλλ第十章 随机变量的数学期望与方差一、 一批零件中有9个合格品与3个废品.安装机器时从这批零件中任取一个.如果取出的废品不再放回去,求在取得合格品以前已取出的废品数的数学期望、方差与标准差.解:设X 表示“在取得合格品以前已取出的废品数”,则X 的概率分布为即于是有1103322013220924491430=⨯+⨯+⨯+⨯=EX 即3.0004.03041.02205.0175.00≈⨯+⨯+⨯+⨯=EX 2X 的分布为即于是有229220192209444914302=⨯+⨯+⨯+⨯=EX 即4091.0004.09041.04205.0175.002≈⨯+⨯+⨯+⨯=EX从而有3191.013310042471)11033(229)(222≈=-=-=EX EX DX 565.03191.0≈==DX Xσ二、 对某一目标进行射击,直至击中为止.如果每次射击命中率为p ,求射击次数的数学期望及方差. 解:设X 表示“第i 次击中”),2,1( =i ,则X 的分布为于是有p q p q q p q p iq p ipq EX i ii i i i 1)1()1()(211111=-='-='===∑∑∑∞=∞=-∞=- 2X于是有pp p p q q p q p q q p pqi EX i i i ii i 122)1()1()(])([223111122-=-=-+='=''==∑∑∑∞=∞=∞=-进一步有pp p p p EX EX DX 11)1(12)(22222-=--=-=三、设离散型随机变量X 的概率函数为,,2,1,21]2)1([ ==-=k k X P kk k问X 的数学期望是否存在?若存在,请计算)(X E ;若不存在,请解释为什么.解:因为∑∑∑∑∞=∞=∞=∞=-=⋅-=-=-==1111)1(212)1(]2)1([2)1()(k kkk k kkkk kki iik k k X P k x X P x 不绝对收敛,所以ξ没有数学期望. 四、设随机变量X 的概率密度为⎪⎩⎪⎨⎧≥<-=.1, 0;1,11)(2x x x x f π 求数学期望)(X E 及方差)(X D . 解:011)()(112=-⋅==⎰⎰-+∞∞-dx xx dx x xf X E πdxx x dx xx dx x f x X D ⎰⎰⎰-=-⋅==-∞+∞-1022112221211)()(πππ21]arcsin 2112[2102=+--=x x x π五、(拉普拉斯分布)设随机变量X 的概率密度为)( ,21)(+∞<<-∞=-x e x f x.求数学期望)(X E 及方差)(X D . 解:021)(===⎰⎰+∞∞--+∞∞-dx xe dx x xf EX x2!2)3(21)(0222==Γ====⎰⎰⎰+∞-+∞∞--+∞∞-dx e x dx e x dx x f x DX x x(分部积分亦可)第十一章 随机变量函数的数学期望·关于数学期望与方差的定理一、设随机变量X 服从二项分布)4.0,3(B ,求2)3(X X Y -=的数学期望及方差. 解:X 的概率分布为Y 的概率分布为2Y 的分布为于是有72.072.0128.00=⨯+⨯=EY72.072.0128.002=⨯+⨯=EY2016.0)72.0(72.0)(222=-=-=EY EY DY二、过半径为R 的圆周上一点任意作这圆的弦,求所有这些弦的平均长度.解:在圆周上任取一点O ,并通过该点作圆得直径OA .建立平面直角坐标系,以O 为原点,且让OA 在x 轴的正半轴上.通过O 任作圆的一条弦OB ,使OB 与x 轴的夹角为θ,则θ服从]2,2[ππ-上的均匀分布,其概率密度为 ⎪⎩⎪⎨⎧-∉-∈=]2,2[,0]2,2[,1)(ππθππθπθf .弦OB 的长为]2,2[cos 2)(ππθθθ-∈=R L ,故所有弦的平均长度为⎰⎰-∞+∞-⋅==22cos 21)()()]([ππθθπθθθθd R d L f L EπθπθθπππRR d R4sin 4cos 42020===⎰.三、一工厂生产的某种设备的寿命X (以年计)服从指数分布,概率密度为⎪⎩⎪⎨⎧≤>=-. 0,0 ; 0 ,41)(4x x e x f x工厂规定,出售的设备若在售出一年之内损坏可予以调换.若工厂售出一台设备赢利100元,调换一台设备厂方需花费300元.试求厂方出售一台设备的平均净赢利. 解:由题设,有⎰⎰---∞--=-===<14110441141)()1(e e dx e dx x f X P x x进而有 41)1(1)1(-=<-=≥e X P X P 设Y 表示“厂方出售一台设备获得的净赢利”,则Y 的概率分布为从而有64.33200300100)1(200414141≈-⨯=⨯+-⨯-=---e e e EY答:厂方出售一台设备获得的平均净赢利约为64.33元.四、设随机变量nX X X ,,21相互独立,并且服从同一分布,数学期望为μ,方差为2σ.求这些随机变量的算术平均值∑==ni iX nX 11的数学期望与方差. 解:因为μ=)(i X E ,2)(σ=i X D ,且随机变量nX X X,,21相互独立.所以有μμ=====∑∑∑∑====ni n i i ni i n i i n X E n X E n X n E X E 11111)(1)(1)1()(,nn X D n X D n X n D X D ni ni in i i n i i 2122121211)(1)(1)1()(σσ=====∑∑∑∑====.五、一民航送客车载有20位旅客自机场开出,沿途有10个车站可以下车,到达一个车站时如没有旅客下车就不停车.假设每位旅客在各车站下车是等可能的,且各旅客是否下车相互独立.求该车停车次数的数学期望.解: 设iX 表示"第i 站的停车次数" (10,,2,1 =i ). 则iX 服从"10-"分布. 其中⎩⎨⎧=站有人下车若在第站无人下车若在第i i X i,1,0 于是iX 的概率分布为设∑==ni iX X 1, 则X 表示沿途停车次数, 故有]})10110(1[1)10110(0{10)(2020101101--⨯+-⨯===∑∑==i i i i EX X E EX748.8)9.01(1020≈-=即停车次数的数学期望为748.8.第十二章 二维随机变量的数字特征·切比雪夫不等式与大数定律一、 设二维随机变量),(Y X 的联合概率密度为()(). 1,222++=y x Ay x f求:(1)系数A ;(2)数学期望)(X E 及)(Y E ,方差)(X D 及)(Y D ,协方差),cov(Y X . 解: (1) 由⎰⎰+∞∞-+∞∞-=1),(dxdy y x f . 有()()⎰⎰⎰⎰∞+∞-∞+∞-∞+==+=++11120022222A dr r rd A dxdy y x A πθπ解得, π1=A .(2)()11),()(222⎰⎰⎰⎰∞+∞-∞+∞-∞+∞-∞+∞-=++==dx y xxdy dxdy y x xf X E π.由对称性, 知)(=Y E .⎰⎰+∞∞-+∞∞-==-=dxdy y x f x EX EX X E X D ),(])[()(222()⎰⎰∞+∞-∞+∞-++=dxy xx dy 222211π()()+∞=+++=+-+=+=∞+∞+∞+⎰⎰⎰022022220223]11)1ln([1)1(211r r dr r r r r dr r r d πθπ同理, 有 +∞=)(Y D .)()])([(),cov(XY E EY Y Ex X E Y X =--=⎰⎰+∞∞-+∞∞-=dxdy y x xyf ),(()011),(222⎰⎰⎰⎰∞+∞-∞+∞-∞+∞-∞+∞-=++==dx y x xydy dxdy y x xyf π.二、 设二维随机变量),(Y X 的联合概率密度为⎩⎨⎧<<<=其它.,0;10,,1),(x x y y x f求(1) ),cov(Y X ;(2) X 与Y 是否独立,是否相关,为什么?解: (1) 因为 ⎰⎰⎰⎰⎰====-∞+∞-∞+∞-121322),(dx x dy xdx dxdy y x xf EX xx0),(1===⎰⎰⎰⎰-+∞∞-+∞∞-xx ydy dx dxdy y x yf EY 0),()(1===⎰⎰⎰⎰-+∞∞-+∞∞-xxydy xdx dxdy y x xyf XY E所以有])32[()])([(),cov(Y X E EY Y EX X E Y X -=--=⎰⎰+∞∞-+∞∞-=dxdyy x xyf ),(10==⎰⎰-xxydy xdx .(2) 当)1,0(∈x 时,有⎰⎰+∞∞--===xdy dy y x f x f x xX 2),()(; 当)1,0(∉x 时,有0)(=x f X.即⎩⎨⎧∉∈=)1,0(0)1,0(2)(X x x x x f同理有 ⎩⎨⎧∉+∈-=⎪⎩⎪⎨⎧∉∈=⎰⎰-)1,0(1)1,0(1)1,0()1,0()(11Y x y x y x dx x dx y f y y 因为),()()(y x f y f x f Y X ≠, 所以X 与Y 不是独立的.又因为0),cov(=Y X , 所以X 与Y 是不相关的.三、 利用切比雪夫不等式估计随机变量X 与其数学期望)(X E 的差的绝对值大于三倍标准差 )(X σ的概率.解:91)3()3(2=≤>-ξξξξξD DD E P .四、为了确定事件A 的概率,进行10000次重复独立试验.利用切比雪夫不等式估计:用事件A在10000次试验中发生的频率作为事件A 的概率的近似值时,误差小于0.01的概率.解:设ξ表示“在10000次试验中事件A 的次数”,则)5.0,10000(~B ξ且有50005.010000=⨯==np E ξ 2500)5.01(5.010000=-⨯⨯==npq D ξ 于是有npq p npq p np m P p n m P 22)01.0(1)01.0(1)01.0()01.0(-=-≥<-=<- 75.025.011=-=-=pq五、 样检查产品质量时,如果发现次品多于10个,则认为这批产品不能接受.应该检查多少 个产品,可使次品率为10%的一批产品不被接受的概率达到0.9?解:设ξ表示“发现的次品件数”,则)1.0,(~n B ξ,现要求.nn ξE 1.0= n ξD 09.0=要使得9.0)10(=>ξP ,即9.0)10(=≤<n ξP ,因为9.0)10(=≤<n ξP ,所以)3.01.03.01.03.01.010()10(nn n n n ξn n P ξD ξE n ξD ξE ξξD ξE P -≤-<-=-≤-<-)3.01.010()3()33.01.03.01.010(1,01,0nn n n n n ξn n P --≈≤-<-=ΦΦ 1)3.0101.0()3(1,01,0--+nn n ΦΦ (德莫威尔—Laplace 定理) 因为10>n ,所以53>n ,从而有1)3(1,0≈n Φ,故9.0)3.0101.0(1,0≈-nn Φ.查表有8997.0)28.1(1,0=Φ,故有28.13.0101.0≈-nn ,解得.146≈n答:应该检查约146个产品,方可使次品率为10%的一批产品不被接受的概率达到0.9.第十三章 正态分布的概率密度、分布函数、数学期望与方差一、 设随机变量X 服从正态分布)2,1(2N ,求(1))8.56.1(<≤-X P ;(2))56.4(≥X P .解:(1) )4.2213.1()8.416.2()8.56.1(<-≤-=<-≤-=<≤-X P X P X P8950.09032.019918.0)]3.1(1[)4.2()3.1()4.2(1,01,01,01,0=+-=--=--=ΦΦΦΦ(2) )78.12178.2(1)56.4(1)56.4(<-<--=<-=≥X P X P X P)]78.2(1)78.1(1)]78.2()78.1([11,01,01,01,0ΦΦΦΦ-+-=---=.0402.09973.09625.02=--二、 已知某种机械零件的直径X (mm )服从正态分布)6.0,100(2N .规定直径在2.1100±(mm )之间为合格品,求这种机械零件的不合格品率.解:设p 表示这种机械零件的不合格品率,则)2.1100(1)2.1100(≤--=>-=X P X P p .而)26.01002()6.02.16.01006.02.1()2.1100(≤-≤-=≤-≤-=≤-X P X P X P 1)2(2)]2(1[)2()2()2(-Φ=Φ--Φ=-Φ-Φ= 9544.019772.02=-⨯= 故0456.09544.01=-=p .三、测量到某一目标的距离时发生的误差X (m)具有概率密度3200)20(22401)(--=x ex f π求在三次测量中至少有一次误差的绝对值不超过30m 的概率.解:三次测量中每次误差绝对值都超过30米可表为}30{}30{}30{>⋃>⋃>=ξξξD 第三次第二次第一次因为)40,20(~2N ξ,所以由事件的相互独立性,有31,01,033)]25.0(1)25.1([})3030{(})30{()(ΦΦ-+-=>+-<=>=ξξP ξP D P 13025.05069.0)8944.05987.02(33≈=--= 于是有86975.013025.01)(1}30{=-=-=<D P P 米至少有一次绝对值三次测量中ξ.四、设随机变量),(~2σμN X ,求随机变量函数Xe Y =的概率密度(所得的概率分布称为对数正态分布). 解:由题设,知X 的概率密度为)(21)(222)(+∞<<-∞=--x ex f x X σμσπ从而可得随机变量Y 的分布函数为)()()(y e P y Y P y F XY≤=≤=.当0≤y 时,有0)(=y F Y ;此时亦有0)(='y F Y. 当0>y 时,有dx ey X P y F yx Y⎰∞---=≤=ln 2)(2221)ln ()(σμσπ. 此时亦有222)(ln 21)(σμσπ--='y Yeyy F .从而可得随机变量Y 的概率密度为⎪⎩⎪⎨⎧>≤=--.0,21;0,0)(222)(ln y e yy y f y Y σμσπ五、设随机变量X 与Y 独立,),(~211σμN X ,),(~222σμN Y ,求: (1) 随机变量函数bY aX Z +=1的数学期望与方差,其中a 及b 为常数;(2) 随机变量函数XY Z =2的数学期望与方差.解:由题设,有211)(,)(σμ==X D X E ;222)(,)(σμ==Y D Y E .从而有 (1)211)()()()()()(μμb a Y bE X aE bY E aX E bY aX E Z E +=+=+=+=; 222212221)()()()()()(σσb a Y D b X D a bY D aX D bY aX D Z D +=+=+=+=. (2)212)()()()(μμ===Y E X E XY E Z E ;)()()()()()()()(22222222Y E X E Y E X E XY E Y X E XY D Z D -=-== )()()]()()][()([2222Y E X E Y E Y D X E X D -++= )()()()()()(22X E Y D Y E X D Y D X D ++= 212222212221μσμσσσ++=.第十四章二维正态分布·正态随机变量线性函数的分布中心极限定理一、设二维随机变量),(Y X 服从二维正态分布,已知0)()(==Y E X E ,16)(=X D ,25)(=Y D ,并且12),cov(=Y X ,求),(Y X 的联合概率密度.。
概率与数理统计第四版(简明版)课后习题答案

随机变量的函数及其分布
总结词
描述通过函数变换得到的随机变量的概率分 布情况。
详细描述
对于一个或多个随机变量,通过函数变换可 以得到新的随机变量。这些新随机变量的概 率分布可以通过对原随机变量的概率分布进 行函数变换得到。例如,如果X是一个随机 变量,f(X)是关于X的函数,那么f(X)的概率 分布可以通过对X的概率分布进行函数变换 得到。常见的函数变换包括线性变换、幂函 数变换等。在得到新随机变量的概率分布后, 可以进一步分析其性质和特征。
多元线性回归分析的假设包括线性关系、误差项独立同分 布以及误差项的无偏性。
详细描述
在进行多元线性回归分析之前,需要检验各因变量与自变 量之间的线性关系,并确保误差项独立且服从相同的分布 ,同时误差项的均值为零,以保证估计的回归系数是无偏 和有效的。
总结词
多元线性回归分析的应用范围广泛,包括经济、金融、生 物、医学和社会科学等领域。
随机变量的定义与性质
随机变量是定义在样本 空间上的一个实值函数 ,其取值随试验结果的 变化而变化。
随机变量具有可加性、 独立性、有限可加性等 性质,这些性质在随机 变量的计算和推导中有 着重要的应用。
离散型随机变量是取有 限个或可数个值的随机 变量,其分布律是一个 离散的概率分布。常见 的离散型随机变量包括 二项分布、泊松分布等 。
边缘概率分布与条件概率分布
总结词
描述随机变量的边缘概率分布和条件概 率分布,即考虑某些变量的取值对其他 变量的概率分布的影响。
VS
详细描述
边缘概率分布是指考虑某些随机变量的取 值后,其他随机变量的概率分布情况。对 于两个随机变量X和Y,X的边缘概率分布 表示为P(X),表示在给定Y取某个值的条件 下,X的概率分布。条件概率分布则表示在 给定某个事件发生的条件下,其他随机变 量的概率分布情况。条件概率分布表示为 P(X|Y),表示在Y取某个值的条件下,X的 概率分布。
蒋中一《数理经济学的基本方法》(第4版)课后习题详细分析和解答(第10章 指数函数与对数函数)【圣才
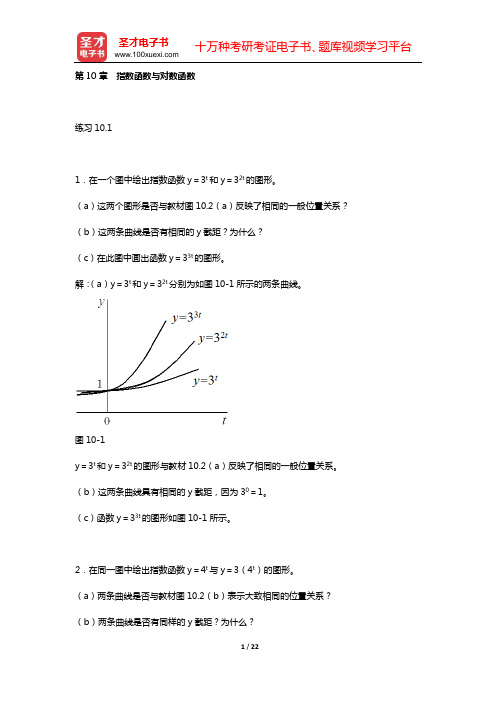
第10章指数函数与对数函数练习10.11.在一个图中绘出指数函数y=3t和y=32t的图形。
(a)这两个图形是否与教材图10.2(a)反映了相同的一般位置关系?(b)这两条曲线是否有相同的y截距?为什么?(c)在此图中画出函数y=33t的图形。
解:(a)y=3t和y=32t分别为如图10-1所示的两条曲线。
图10-1y=3t和y=32t的图形与教材10.2(a)反映了相同的一般位置关系。
(b)这两条曲线具有相同的y截距,因为30=1。
(c)函数y=33t的图形如图10-1所示。
2.在同一图中绘出指数函数y=4t与y=3(4t)的图形。
(a)两条曲线是否与教材图10.2(b)表示大致相同的位置关系?(b)两条曲线是否有同样的y截距?为什么?(c)在同一图中绘出函数y=3(4t)/2的图形。
解:(a)y=4t和y=3(4t)曲线为如图10-2所示的两条曲线。
y=4t和y=3(4t)的曲线与教材10.2(b)中的曲线有大致相同的位置关系。
图10-2(b)两条曲线不具有同样的y截距,因为40=1,3×40=3。
(c)函数y=3(4t)/2的图形如图10-2所示。
3.认可e t的导数为其自身,运用链式法则求下列函数的dy/dt:(a)y=e5t;(b)y=4e3t;(c)y=6e-2t。
解:(a)dy/dt=[dy/d(5t)][d(5t)/dt]=5e5t。
(b)dy/dt=[dy/d(3t)][d(3t)/dt]=12e3t。
(c)dy/dt=[dy/d(-2t)][d(-2t)/dt]=-12e-2t。
4.根据我们对(10.1)的讨论,你能预期函数y=e t是以递增速率单调地递增吗?通过确定此函数的一阶和二阶导数的符号验证你的答案。
在验证答案时,记住此函数的定义域为全体实数的集合,即区间(-∞,+∞)。
解:y′=e t>0,y″=e t>0。
所以,函数是以递增速率单调地递增。
5.在(10.2)中,若a与c被赋予负值,则教材图10.2中的曲线图形便不再适用。
数理经济学的基本方法蒋中一

数理经济学的基本方法蒋中一1.引言1.1 概述数理经济学作为一门交叉学科,涵盖了经济学、数学和统计学等多个领域的知识与方法。
它通过运用数理工具和模型,对经济现象进行深入分析和解释,为经济决策提供科学依据。
数理经济学的发展使得经济学研究更加系统化、定量化,能够更准确地理解和解释经济现象,进而制定更科学的经济政策。
数理经济学的基本方法主要包括数理建模、假设检验和经济模拟等。
数理建模是数理经济学中最关键的方法之一,通过建立数学模型来描述经济行为和市场机制,进而进行定量分析和预测。
假设检验则是用来验证数理模型的适用性和有效性,通过对经济数据进行统计分析,从而得出对经济理论的验证或修正。
另外,经济模拟是一种应用数理方法来模拟经济系统的行为和演化过程,通过构建合理的数学模型,进行计算和仿真,以便更好地理解和预测经济发展的趋势。
数理经济学的应用领域广泛,涵盖了市场结构、价格理论、产业组织、经济增长等方面。
它在经济学理论的发展、政策制定和企业决策等方面都发挥了重要的作用。
但需要注意的是,数理经济学并不是解决所有经济问题的万能工具,它只是经济学领域中的一个工具和方法,需要与其他经济学理论和经验相结合,共同分析和解决实际问题。
本文旨在介绍数理经济学的基本方法,通过对其定义和背景的探讨,进一步了解其在经济学研究中的地位和作用。
接下来的章节将重点介绍数理经济学的基本方法,并总结其应用和展望未来的发展方向。
通过对数理经济学的深入研究,我们可以更好地理解和应用数理工具,以推动经济学的进一步发展和实践应用。
1.2 文章结构:本文主要分为引言、正文和结论三个部分。
在引言部分,首先会对数理经济学的概念进行概述,介绍数理经济学的背景及其在经济学研究中的重要性。
接着,对本文的结构进行说明,简要介绍各个部分的内容安排。
最后,明确本文的目的,即介绍数理经济学的基本方法,为读者提供一个全面了解数理经济学的基础。
在正文部分,首先会详细阐述数理经济学的定义和背景,介绍数理经济学作为一门交叉学科的特点和重要性。
经济学基础第四版习题答案

第一章1,一般的,相对于人类社会的无限欲望而言,生产人类所需物品的资源总是不足的。
这就是资源的稀缺性。
资源的稀缺性不是指资源绝对数量的多少,而是指相对于无限的欲望而言,再多的资源也是不足的。
即稀缺性是就相对意义而言的。
欲望的基本特点在于无限性,即人们得欲望永远没有完全得到满足的时候,人的欲望要用各种物品或劳务来满足,而物品要用各种资源来生产,这些资源包括人力资源和自然资源。
然而,人类赖以生存的地球的资源是有限的,这样无限的欲望与有限的资源的矛盾就形成了经济学所说的稀缺性。
2,人类社会作面临的基本问题。
面对资源稀缺性的事实,人类社会都必须面对和解决三个基本的经济问题。
他们是:生产什么,如何生产和为谁生产。
(1)生产什么商品和生产多少。
一个社会必须决定,在诸多可能的物品和劳务中,每一种应该生产多少以及何时生产,生产多少消费品和投资品。
(2)如何生产物品。
一个社会必须决定谁来生产,使用何种资源,以及采用何种生产技术。
(3)为谁生产。
谁来享用经济活动的成果?收入和财富的分配是公平合理的吗?社会产品如何在不同的居民之间进行分配?是否会出现贫富差距?3,微观经济学以单个经济单位为研究对象,通过研究单个经济单位的经济行为和相应的经济变量数值的决定来说明价格机制如何解决社会的资源配置问题。
可见,微观经济学研究的对象是单个经济单位的经济行为,即家庭和企业的经济行为。
微观经济学解决的问题是资源配置。
微观经济学的中心理论是价格理论。
微观经济学的研究方法是个量分析。
相对而言,宏观经济学以整个国民经济为研究对象,通过研究经济中各有关总量的决定及其变化,来说明资源如何才能得到充分利用。
可见,与微观经济学的几个方面相对应的,宏观经济学研究的对象是整个经济。
而不是经济中的各个单位。
宏观经济学解决的问题是资源利用。
它把资源配置最为既定的前提,研究现有资源未能得到充分利用的原因,大到充分利用的途径,以及如何增长等问题。
宏观经济学的中心理论是国民收入决定理论。
蒋中一《数理经济学的基本方法》(第4版)课后习题详细分析和解答(第20章 最优控制理论)【圣才出品】

第20章 最优控制理论练习20.2找出下面问题的控制变量、状态变量和协状态变量的最优路径:1.,且y (0)=2,y (1)自由。
解:这个问题的哈密尔顿函数为H =y -u 2+λu,对于u 是凹的,并且u 没有任何限制,所以应用一阶条件使H 最大化:∂H/∂u =-2u +λ=0,从而u (t )=λ/2或y ′=λ/2①λ的运动方程是λ′=-∂H/∂y =-1,对其积分可解出λ=c 1-t 。
又横截性条件为λ(1)=0,从而c 1=0,最优协状态变量的路径是λ*(t )=1-t 。
由①式,得到y′=(1/2)(1-t ),通过积分得到y (t )=(1/2)t -(1/4)t 2+c 2,通过初始条件y (0)=2可确定c 2=2。
这样状态变量的最优路径为y *(t )=(1/2)t -(1/4)t 2+2。
对应的最优控制路径是u *(t )=(1/2)(1-t )。
2.,且y (0)=10,y (8)自由,u (t )∈[0,2]。
解:哈密尔顿函数为H =6y +λ(y +u )=(6+λ)y +λu ,是关于u 的线性函数,斜率为λ。
为使H 最大化,当λ>0时,取u =2;当λ<0时,取u =0。
λ的运动方程是λ′=-∂H/∂y =-6-λ,该方程的通解是λ(t )=Ae -t -6。
通过横截性条()120Max d ..y u t s t y u -' =⎰80Max 6d ..y t s t y y u ' =+⎰件λ(T )=λ(8)=0可以确定A =6e 8,从而协状态变量的最优路径是λ*(t )=6e 8-t -6。
这是一个关于t 的单减函数,且λ*(8)=0,从而对于t ∈[0,8],λ*(t )≥0。
所以取控制变量u 的最优路径为u *=2。
由运动方程有y ′=y +u =y +2,该方程的通解为y (t )=ce t -2。
由初始条件y (0)=10可确定出c =12,从而状态变量的最优路径为y *(t )=12e t -2。
概率论与数理统计第四版第一章答案

习题解答1. 将一枚均匀的硬币抛两次,事件C,分别表示“第一次A,B出现正面”,“两次出现同一面”,“至少有一次出现正面”。
试写出样本空间及事件CA,,中的样本点。
B解:{=Ω(正,正),(正,反),(反,正),(反,反)}{=A(正,正),(正,反)};{=B(正,正),(反,反)}{=C(正,正),(正,反),(反,正)}2. 在掷两颗骰子的试验中,事件D,,分别表示“点数之BCA,和为偶数”,“点数之和小于5”,“点数相等”,“至少有一颗骰子的点数为3”。
试写出样本空间及事件-AB-A,,中的样本点。
,+,-BCBADACBC解:{})6,6(,2,1(),1,1(Ω;),=2,6(),1,6(,6,1(,),),6,2(,2,2(),1,2(),),{})1,3(),2,2(),3,1(),1,1(AB;={})1,2(),2,1(),6,6(),4,6(),2,6(,+B=A;),3,1(),1,1(5,1(),CA;{})2,2(),1,1(=ΦBC;={})4,6(),2,6(),1,5(),6,4(),2,4(),6,2(),4,2(),5,1(=---D C B A3. 以C B A ,,分别表示某城市居民订阅日报、晚报和体育报。
试用C B A ,,表示以下事件:(1)只订阅日报; (2)只订日报和晚报; (3)只订一种报; (4)正好订两种报; (5)至少订阅一种报; (6)不订阅任何报; (7)至多订阅一种报; (8)三种报纸都订阅; (9)三种报纸不全订阅。
解:(1)C B A ;(2)C AB ; (3)C B A C B A C B A ++;(4)BC A C B A C AB ++; (5)C B A ++;(6)C B A ; (7)C B A C B A C B A C B A +++或C B C A B A ++(8)ABC ; (9)C B A ++4. 甲、乙、丙三人各射击一次,事件321,,A A A 分别表示甲、乙、丙射中。
蒋中一《数理经济学的基本方法》(第4版)课后习题详细分析和解答(第6~9章)【圣才出品】

v7 v 7
v7
v7
v7
因为左极限与右极限相等,所以 v→7 时 q 十万种考研考证电子书、题库视频学习平台
2.已知 q=[(v+2)3-8]/v,(v≠0),求:
(a)
lim
v0
q
;
(b)
lim
v2
q
;
(c)
lim
va
q
。
解
:
(
a
(c)求 f′(3)和 f′(4)。
解:(a)Δy=4(x+Δx)2+9-(4x2+9)=8xΔx+4Δx2,差商为:Δy/Δx=(8xΔ
x+4Δx2)/Δx=8x+4Δx。
(b) dy f x lim y lim 8x 4x 8x
dx
x x0
x 0
(c)f′(3)=3×8=24,f′(4)=4×8=32。
2.已知函数 y=5x2-4x: (a)求作为 x 和Δx 的函数的差商; (b)求导数 dy/dx; (c)求 f′(2)和 f′(3)。 解:(a)Δy=5(x+Δx)2-4(x+Δx)-(5x2-4x)=10xΔx+5Δx2-4Δx。 差商为:Δy/Δx=(10xΔx+5Δx2-4Δx)/Δx=10x+5Δx-4。
(a)
lim
v
q
;
(b)
lim q
v
。
解:(a) lim q lim 5 1 5
v
v
v
(b) lim q lim 5 1 5
v
v
v
4.运用教材图 6.3 证明:我们不能将(L+a2)看做当 v 趋近于 N 时 q 的极限。 证:教材中图 6.3 如下所示:
3 / 66
蒋中一《数理经济学的基本方法》(第4版)课后习题详细分析和解答(第17~20章)【圣才出品】

蒋中一《数理经济学的基本方法》(第4版)课后习题详细分析和解答第17章离散时间:一阶差分方程练习17.21.将下列差分方程变换为(17.2″)的形式。
(a)Δy t=7(b)Δy t=0.3y t(c)Δy t=2y t-9解:(a)y t+1=y t+7。
(b)y t+1=1.3y t。
(c)y t+1=3y t-9。
2.用迭代法解下列差分方程:(a)y t+1=y t+1(y0=10);(b)y t+1=αy t(y0=β);(c)y t+1=αy t-β(当t=0时,y t=y0)。
解:(a)y1=y0+1,y2=y1+1=y0+2,y3=y2+1=y0+3。
不难看出,一般而言,对任意时期t,y t=y0+t=10+t。
(b)y1=αy0,y2=αy1=α2y0,y3=αy2=α3y0。
不难看出,一般而言,对任意时期t,y t=αt y0=βαt。
(c)y 1=αy 0-β,y 2=αy 1-β=α2y 0-αβ-β,y 3=αy 2-β=α3y 0-α2β-αβ-β。
不难看出,一般而言,对任意时期t,()120=1t t t t y y αβααα---++++ 3.按(17.6)式改写上题中的差分方程,并用公式(17.8′)或(17.9′)解之(哪个方便用哪个)。
答案与用迭代法求得的答案一致吗?解:(a)改写:y t+1-y t =1(y 0=10)。
a=-1,c=1,由(17.9′),定解为y t =y 0+ct=10+t。
答案与用迭代法求得的答案一致。
(b)改写:y t+1-αy t =0(y 0=β)。
a=-α,c=0。
若α≠1,由(17.8′),定解为y t =y 0αt =βαt 。
若α=1,则a=-1,由(17.9′),定解为y t =y 0+ct=β。
不难发现,定解的形式可以统一为y t =βαt 。
答案与用迭代法求得的答案一致。
(c)改写:y t+1-αy t =-β(当t=0时,y t =y 0)。
蒋中一《数理经济学的基本方法》(第4版)课后习题详细分析和解答(第9章 最优化:一类特殊的均衡分析)

第9章最优化:一类特殊的均衡分析练习9.21.假设定义域为全部实数的集合,求下列函数的稳定值,并检验其为相对极大值、极小值还是拐点:(a)y=-2x2+8x+7;(b)y=5x2+x;(c)y=3x2+3;(d)y=3x2-6x+2。
解:(a)令y′=-4x+8=0,解得x=2。
当x<2时,y′>0;当x>2时,y′<0。
所以,稳定值y=-2×22+8×2+7=15是函数的极大值。
(b)令y′=10x+1=0,解得x=-1/10。
当x<-1/10时,y′<0;当x>-1/10时,y′>0。
所以,稳定值y=5×(-1/10)2-1/10=-1/20是函数的极小值。
(c)令y′=6x=0,解得x=0。
当x<0时,y′<0;当x>0时,y′>0。
所以,稳定值y =3是函数的极小值。
(d)令y′=6x-6=0,解得x=1。
当x<1时,y′<0;当x>1时,y′>0。
所以,稳定值y=3×1-6×1+2=-1是函数的极小值。
2.假设定义域为区间[0,∞),求下列函数的稳定值,并检验其为相对极小值、极大值,还是拐点:(a)y=x3-3x+5;(b)y=x3/3-x2+x+10;(c)y=-x3+4.5x2-6x+6。
解:(a)令y′=3x2-3=0,解得x=1。
当0≤x<1时,y′<0;当x>1时,y′>0。
所以,稳定值y=1-3+5=3是函数的极小值。
(b)令y′=x2-2x+1=0,解得x=1。
当0≤x<1时,y′>0;当x>1时,y′>0。
所以,稳定值y=1/3-1+1+10=31/3是函数的拐点。
(c)令y′=-3x2+9x-6=0,解得x1=1,x2=2。
当0≤x<1时,y′<0;当1<x<2时,y′>0;当x>2时,y′<0。
所以,稳定值y=-1+4.5-6+6=3.5是函数的极小值,稳定值y=-23+4.5×22-6×2+6=4是函数的极大值。
数理经济学习题参考答案

1
2
则有
6
x >0 ⇒ u =1 2
⇒ 2−x −x = 0
⇒
(2x
) 1
2
−1 x
=0
1
1
⇒ x = 0 or x = 1
1
12
⇒ x = 2 or x = 3
2
1
2
其中所用到的条件依次为第二互补条件, 第三互补条件, 第一互补条件. 由于 x = (0,2)T
不满足梯度差非负的第一个条件, 删去. 同理
kλ
l =1 1l
= 1,
kλ
l =1 2l
= 1,
且使得
∑k
y1 = λ xl 1l l =1 ∑k
y2 = λ xl 2l l =1
对于任意 λ ∈ (0,1), 由于 λλ + (1 − λ)λ ≥ 0, l = 1, 2, ", k , 且
1l
2l
因此
( ) ( ) ( ) ∑k λλ + (1−λ)λ = ∑k λλ + ∑k (1− λ)λ
11. 证明: 显然所有包含 S 的半空间的交集仍然包含 S . 现证该交集也包含于 S , 否则必存 在 x 属于半空间的交集但不属于 S , 则根据凸集分离定理, 存在实数 α 与不为 0 的向量 u 使得对于任意 z ∈ S 都有
uT z > α > uT x
{ } { } 这表明 S ⊂ y : uTy ≥ α , x ∉ y : uTy ≥ α , 或者说我们找到了一个新的包含了 S 的半
x1 x1
⎞⎠⎟⎟⎟⎟⎟⎟ + (1 − λ)⎛⎝⎜⎜⎜⎜⎜f
x2 x2
⎞⎠⎟⎟⎟⎟⎟⎟ = ⎛⎜⎜⎜⎜⎜⎝λf
蒋中一《数理经济学的基本方法》(第4版)课后习题详细分析和解答(第12章 具有约束方程的最优化)【圣

第12章具有约束方程的最优化练习12.21.运用拉格朗日乘数法求z的稳定值:(a)z=xy,满足约束x+2y=2;(b)z=x(y+4),满足约束x+y=8;(c)z=x-3y-xy,满足约束x+y=6;(d)z=7-y+x2,满足约束x+y=0。
解:(a)拉格朗日函数为:Z=xy+λ(2-x-2y),稳定值的必要条件为:Zλ=2-x-2y=0Z x=y-λ=0Z y=x-2λ=0解得:λ*=1/2,x*=1,y*=1/2,故z的稳定值为z*=1/2。
(b)拉格朗日函数为:Z=xy+4x+λ(8-x-y),稳定值的必要条件为:Zλ=8-x-y=0Z x=y+4-λ=0Z y=x-λ=0解得:λ*=6,x*=6,y*=2,故z的稳定值为z*=36。
(c)拉格朗日函数为:Z=x-3y-xy+λ(6-x-y),稳定值的必要条件为:Zλ=6-x-y=0Z x=1-y-λ=0y解得λ*=-4,x*=1,y*=5,故z的稳定值为z*=-19。
(d)拉格朗日函数为:Z=7-y+x2+λ(-x-y),稳定值的必要条件为:Zλ=-x-y=0Z x=2x-λ=0Z y=-1-λ=0解得λ*=-1,x*=-1/2,y*=1/2,故z的稳定值为z*=27/4。
2.在上题中,约束条件略微放松是增加还是降低了z的最优值,增加或降低的速率是多少?解:(a)增加,增加的速率为:dz*/dc=λ*=1/2。
(b)增加,增加的速率为:dz*/dc=λ*=6。
(c)降低,降低的速率为:dz*/dc=λ*=-4。
(d)降低,降低的速率为:dz*/dc=λ*=-1。
3.写出下列函数的拉格朗日函数和稳定值的一阶条件(不必解方程):(a)z=x+2y+3w+xy-yw,满足约束x+y+2w=10;(b)z=x2+2xy+yw2,满足约束2x+y+w2=24和x+w=8。
解:(a)拉格朗日函数为:Z=x+2y+3w+xy-yw+λ(10-x-y-2w)稳定值的一阶条件为:Zλ=10-x-y-2w=0Z x=1+y-λ=0y Z w =3-y -2λ=0 (b )拉格朗日函数为:Z =x 2+2xy +yw 2+λ(24-2x -y -w 2)+v (8-x -w ) 稳定值的一阶条件为: Z λ=24-2x -y -w 2=0 Z v =8-x -w =0 Z x =2x +2y -2λ-v =0 Z y =2x +w 2-λ=0 Z w =2yw -2λw -v =04.若将约束条件写成G (x ,y )=0,而不是写成g (x ,y )=c 的形式,那么,拉格朗日函数和一阶条件应如何修正? 解:拉格朗日函数应修正为:一阶条件应修正为: Z λ=-G (x ,y )=0 Z x =f x -λG x =0 Z y =f y -λG y =05.在讨论全微分法时,我们曾指出已知约束条件g (x ,y )=c ,可以推导出dg =0。
蒋中一《数理经济学的基本方法》(第4版)课后习题详细分析和解答(第8章 一般函数模型的比较静态分析)

5.上题中两个偏弹性如何随 P 和 R 的变化而变化?若 P 和 R 为正,变化是严格单调的吗? 解:∂εQP/∂P=4bP(a+R1/2)/(a+bP2+R1/2)2,∂εQP/∂R=-bP2R-1/2/(a+bP2+R1/2) 2<0。 所以,供给的价格弹性随 R 增大而减小;如果 a+R1/2>0,则随 P 的增大而增大,如果 a +R1/2<0,则随 P 的增大而减小,如果 a+R1/2=0,则不随 P 变化。但是供给的价格弹性 关于 R 和 P 的变化都是单调的。
4.某商品的供给函数为: Q=a+bP2+R1/2(a<0,b>0)[R:降雨量] 求供给的价格弹性 εQP,供给的降雨量弹性 εQR。 解:供给的价格弹性为:εQP=(∂Q/∂P)/(Q/P)=2bP/[(a+bP2+R1/2)/P]=2bP2/ (a+bP2+R1/2)。 供给的降雨量弹性为:εQR=(∂Q/∂R)/(Q/R)=(R-1/2/2)/[(a+bP2+R1/2)/R]= R1/2/8.2
1.以梯度向量▽U 表示全微分 dU。
dx1
dx2
解:▽U 为行向量(U1,U2,…,Un),而 dx 为列向量 dxn
那么全微分
dU U1,U2 ,
dx1
,U
数理经济学_茹少峰_第1章课后题及答案

第1章习题答案1.什么是数理经济学?解:什么是数理经济学尚无统一的定义,以下是几种代表性的定义。
美国经济学家Kenneth J. Arrow(阿罗)等人在《数理经济学手册》一书中指出:数理经济学是包括数学概念和方法在经济学,特别是在经济理论中的各种应用。
Alpha C. Chiang(蒋中一)、Kevin Wainwright(凯尔文·温赖特)在《数理经济学的基本方法》一书中指出:数理经济学是一种经济分析方法,是经济学家利用数学符号描述经济问题,运用已知的数学定理进行推理的一种方法。
就分析的具体对象而言,它可以是微观或宏观经济理论,也可以是公共财政、城市经济学或其他学科方面的理论。
路甬祥、杜瑞芝分别在《现代科学技术大众百科—科技与社会卷》和《数学史辞典》指出:数理经济学是运用数学符号、数学方法和数学图形表述和论证经济现象及其相互依存关系的一门综合性边缘学科,研究经济活动中的数量关系并从中寻找规律。
杨小凯在《数理经济学基础》中指出:数理经济学主要是进行定性分析的理论经济学,它研究最优经济效果、利益协调和最优价格的确定这些经济学基本理论问题,为经济计量学、管理科学、经济控制论提供模型框架、结构和基础理论,它实在是经济学的基础之基础。
由以上定义可以看出:数理经济学主要是介绍数学方法如何应用到经济分析中,如经济问题如何用数学模型表示,一个变量的变化如何影响另一变量的变化等问题。
因此,数理经济学与其说是一门经济学分支学科,不如说它是一种经济学分析方法。
2.数理经济学是如何诞生的?简述其发展过程。
解:数理经济学的诞生和发展是数学在经济学中应用的过程,也是经济学发展的必然结果。
因为经济学家不仅仅要关心现实生活中的许多经济现象,更要对经济现象的数量,如价格、产量、收入、就业、失业、CPI、GDP等进行度量,要和数量打交道,便要研究数量之间的变化与关系,以此来把握经济运行规律,故数学就必然进入经济学的领域。
蒋中一《数理经济学的基本方法》(第4版)课后习题详细分析和解答(第4章 线性模型与矩阵代数)【圣才出

4 30
CB 也有定义:
CB
7 6
2 2
2 3
3 3
7 6
0 0
2 8 3 8
20
21
16 24
BC=CB 不成立。
3.在例 9 给出的矩阵的基础上,判断 BA 是否有定义?若有,计算其积。在此例中,我们 是否有 AB=BA?
4 / 27
圣才电子书
1 4
1 2
5.在例 7 中,如果我们将数量和价格写成列向量而非行向量,Q·P 有定义吗?我们能否将 总采购成本表示为 Q·P?或 Q′·P?或 Q·P′? 答:Q·P 有定义。两个元素个数相同的向量的内积是对应元素的积的和,两个行向量、两个 列向量、一个行向量和一个列向量、一个列向量和一个行向量的内积均有定义。所以能将采 购成本表示为 Q·P 或 Q′·P 或 Q·P′。
1 / 27
圣才电子书 十万种考研考证电子书、题库视频学习平台
Qd1 Qs1 Qd1
Qs1
0
a1P1 a2 P2 a0
b1P1 b2 P2 b0
Qd 2 Qs2
0
Qd 2
1P1 2 P2 0
Qs2 1P1 2 P2 0
则系数矩阵为
1 1 0 0 0 0
Qd-Qs=0
Qd+bP=a
Qs-dP=-c
1 1 0
0
1 0
b
a
如果系数矩阵为 0 1 d ,则常数向量为 c 。
2.变量按下列顺序排列:Qd1,Qs1,Qd2,Qs2,P1,P2。按(4.1)方式改写方程组(3.12)。 写出系数矩阵、变量向量和常数向量。 解:将方程组(3.12)改写为:
,常数向量为
《数理经济学的基本方法》作业题答案

凸函数,或者都不是。
(������)������ = ������������
解:此题可采用海塞行列式或一阶导数判断。
方法 1:由题目可知������������ = −������,������������ = −������,������������������ = 0,������������������ = 0,������������������ = ������������������ = −1。
������′(3) = ������"(3) = ������(3)(3) = ������(4)(3) = ������(5)(3) = 0, ������(6)(3) = 720 > 0
故������(3) = 7为函数的相对极小值点。
(������)������ = (������ − ������������)������ + ������
������(������)
=
−3
+
(−2)
∙
(������
+
2)
+
(−4) 2!
∙
(������
+
2)2
+
(−12) 3!
∙
(������
+
2)3
+
(−48) 4!
∙
(������
+
2)4
+
⋯
= −3 − 2(������ + 2) − 2(������ + 2)2 − 2(������ + 2)3 − 2(������ + 2)4 − ⋯
4
������"(������) =
数理经济学参考答案

(x y) (x (1)y ) = x (1)y = x y
(6) 证明
0 (x (x)) = x ( x ) = x x
=0
2.2 证明下列集合是线性空间:(Expl.1.67~1.69) (1)
n 维实向量空间 n ;
xy yz x (x y ) x (x z ) ( x x) y ( x x) z 0y 0z yz
(2)证明
1
x = y
( x) 1
( y )
1 1 ( )x ( )y
(2) 所有实数序列的集合 x1 , x2 ,... ,对任意 i , xi ; (3) 所有多项式 x a0 a1t a2t 2 an t n 的集合。
2.3 设 X 1 和 X 2 是线性空间,它们的乘积 X X 1 X 2 的加法和乘法定义如下:
( x1 , x2 ) ( y1 , y2 ) ( x1 y1 , x2 y2 )
N / RN 5. 不是。因为 x ∈ RN ++ 故 R+ 在标量乘法的意义上不是闭的。 ++ , α < 0 ⇒ αx ∈
6. 证明:∀x, y ∈ S1 ∩ S2 ,S1 是 X 的子空间 ⇒ αx + β y ∈ S1 , 同理, αx + β y ∈ S2 7. 证明: (a) ∀x ∈ intS ⇒ ∃Br (x) ⊆ intS ; S ⊆ T ⇒ Br (x) ∈ T ⇒ intS ⊆ intT ¯ ⇒ x ∈ intS ∪ ∂ (S ), 若 x ∈ intS , S ⊆ T ⇒ x ∈ T ⊆ T ¯; 若 x ∈ ∂ (S ) ⇒ ∀Br (x) 包 (b) ∀x ∈ S ¯⊆T ¯ 含 S 中的某些点,由于 S ⊆ T, 因此或者 x ∈ intT, 或者 x ∈ ∂ (T )。综上,S 8. ∂ (S ) = S ∪ {0} 9. 若 ∂ (S ) ̸= ∅ ⇒ ∃x ∈ ∂ (S ), 由于 S = intS ∪∂ (S ), 因此 x ∈ S , 这与 S 是开集矛盾,故 ∂ (S ) = ∅ 10. 证明: (a) 令 G = ∪α Gα , ∀Gα 为开集。∀x ∈ G ⇒ ∃α, x ∈ Gα ; Gα 开 ⇒ ∃Br (x) ∈ Gα ⊆ G ⇒ G 为开集 (b) 令 H = ∩N i=1 Hi , Hi 为开集。∀x ∈ H ⇒ x ∈ Hi , i = 1, . . . , N ; Hi 开 ⇒ ∃Br (x) ∈ Hi ⇒ Br (x) ∈ H ⇒ x 为内点 ⇒ H 为开集 ( )C C C (c) (2) 利用 ∩N = ∪N i=1 Gi i=1 Gi ,(∪α Hα ) = ∩α Hα 2
