PCB数控钻孔最佳走刀路线的建模与求解
走刀路线的选择方法

走刀路线的选择方法在数控加工中,刀具(严格说是刀位点)相对于工件的运动轨迹和方向称为加工路线,即刀具从对刀点开始运动起,直至结束加工程序所经过的路径,包括切削加工的路径及刀具引入、返回等非切削空行程。
走刀路线是刀具在整个加工工序中相对于工件的运动轨迹,不但包括了工序的内容,而且也反映出工序的顺序。
走刀路线是编写程序的依据之一。
确定加工路线时首先必须保证被加工零件的尺寸精度和表面质量,其次应考虑数值计算简单、走刀路线尽量短、效率较高等。
工序顺序是指同一道工序中各个表面加工的先后次序。
工序顺序对零件的加工质量、加工效率和数控加工中的走刀路线有直接影响,应根据零件的结构特点和工序的加工要求等合理安排。
工序的划分与安排一般可随走刀路线来进行,在确定走刀路线时,主要考虑以下几点:1、对点位加工的数控机床,如钻床、镗床,要考虑尽可能使走刀路线最短,减少刀具空行程时间,提高加工效率如图1-a所示,按照一般习惯,总是先加工均布于外圆周上的8个孔,再加工内圆周上的4个孔。
但是对点位控制的数控机床而言,要求定位精度高,定位过程应该尽可能快,因此这类机床应按空程最短来安排走刀路线,以节省时间,如图1-b所示。
图1.走刀路线示意图2、应能保证零件的加工精度和表面粗糙度要求当铣削零件外轮廓时,一般采用立铣刀侧刃切削。
刀具切入工件时,应沿外廓曲线延长线的切向切入,避免沿零件外廓的法向切入,以免在切入处产生刀具的刻痕而影响表面质量,保证零件外廓曲线平滑过渡。
同理,在切离工件时,应该沿零件轮廓延长线的切向逐渐切离工件,避免在工件的轮廓处直接退刀影响表面质量,如图2所示。
图2.外轮廓铣削走刀路线铣削封闭的内轮廓表面时,如果内轮廓曲线允许外延,则应沿切线方向切入或切出。
若内轮廓曲线不允许外延,则刀具只能沿内轮廓曲线的法向切入或切出,此时刀具的切入切出点应尽量选在内轮廓曲线两几何元素的交点处。
若内部几何元素相切无交点时,刀具切入切出点应远离拐角,以防止刀补取消时在轮廓拐角处留下凹口,如图3所示。
数控铣削加工的走刀路线

数控铣削加工的刀路线反映了工序的加工过程,走刀路线合理与否,关系到工件的加工质量与生产效率。
尤其在数控铣削曲面零件过程中,应认真分析零件的加工要求及其结构特点,找出走刀路线中影响加工效率的因素,在保证零件加工精度和表面粗糙度要求的前提下,应尽量缩短加工路线,从而提高数控机床的加工效率,降低加工成本。
数控加工过程中刀具相对于工件的运动轨迹称为走刀路线。
走刀路线反映了工序的加工过程,确定合理的走刀路线是保证铣削加工精度和表面质量的重要工艺措施之一,也是确定数控编程的前提。
数控铣削加工中走刀路线对工件的加工精度和表面质量有直接的影响,走刀路线合理与否,还关系到加工的生产效率,因此每道工序走刀路线的确定都是非常重要的。
一、走刀路线的确定原则影响走刀路线的因素很多,有工艺方法、工件材料及状态、加工精度及表面粗糙度要求、工件刚度、加工余量、刀具的刚度及耐用度、机床类型和工件的轮廓形状等。
在确定走刀路线时,主要应遵循以下原则:(1)保证产品质量,应将保证工件的加工精度和表面粗糙度要求放在首位。
(2)在保证工件加工质量的前提下,应力求走刀路线最短,并尽量减少空行程时间,提高加工效率。
(3)在满足工件加工质量、生产效率等条件下,尽量简化数学处理的数值计算工作量,以简化编程工作。
此外,在确定走刀路线时,还要综合考虑工件、机床与刀具等多方面因素,确定一次走刀还是多次走刀,以及设计刀具的切入点与切出点,切入方向与切出方向。
在铣削加工中,还要确定是采用顺铣还是逆铣等。
二、铣削方式的选择铣削有顺铣和逆铣两种方式。
铣削加工中是采用顺铣还是逆铣,对工件表面粗糙度有较大的影响。
确定铣削方式应根据工件的加工要求,材料的性质、状态、使用机床及刀具等条件综合考虑。
由于采用顺铣方式,工件加工表面质量较好,刀齿磨损小,因此,一般情况下,尽可能采用顺铣,尤其是精铣内外轮廓、精铣铝镁合金、钛合金或耐热合金时,应尽量按顺铣方式安排走刀路线。
三、铣削曲面类零件走刀路线的确定铣削曲面类零件的走刀路线加工面为空间曲面的零件称为曲面类零件。
数控加工技术基础:第三章4:走刀路线和加工参数1

毛坯与加工余量 切削用量 走刀路线 切人与切出 非切运动
一、加工余量
加工余 量
加工过程中,所切 去的金属层厚度
工序余量
相邻两工序的工序尺寸之差
加工总余量
毛坯尺寸与零件图样 的设计尺寸之差
◆前工序的尺寸公差Ta(Ta越大, 就越大); ◆前工序的位置误差; ◆前工序的表面质量(Ra+Ha); ◆本工序的安装误差; ◆其它:如热处理引起的工件变形(若变形过大而余量 不足而报废)
◆Vc的选择 主要根据工件材料、刀具材料和机床功率来选
●刀具材料好,可选得高些; ● Ra值要求小的,要避开积屑瘤、鳞刺产生的Vc ,高速钢刀取小Vc<5 m/min ,硬质合金取较高的Vc=130~160 m/min; ●表面有硬皮或断续切削时,应适当降低; ●工艺系统刚性差的,应减小Vc
平面铣削加工的计算式
(一)确定走刀路线的一般原则
1)保证零件的加工精度和表面粗糙度要求; 2) 方便数值计算,减少编程工作量。 3) 寻求最短加工路线,减少空刀时间以提高加工效率。 4) 尽量减少程序段数。 5) 保证工件轮廓表面加工后的粗糙度的要求,最终轮廓 应安排最后一走刀连续加工出来。 6 ) 注意拐角的变化 7) 刀具的进退刀(切入与切出)路线也要认真考虑,以 尽量减少在轮廓处停刀(切削力突然变化造成弹性变形) 而留下刀痕,也要避免在轮廓面上垂直下刀而划伤工件。
切削速度(vc)
D1(mm);铣刀直径 π(3.14):圆周率 n(min-1):主轴转速 vc(m/min):切削速度
(例题) 主轴转速350min-1、铣刀直径Ø125,求此时的切 削速度。
(答) π=3.14、D1=125、n=350代入公式 vc=(π×D1×n)÷1000=(3.14×125×350)÷100 0 =137.4(m/min) 切削速度为137.4m/min
PCB数控钻孔最佳走刀路线的建模与求解

第13卷第7期2001年7月计算机辅助设计与图形学学报JO U RN A L OF CO M P U T ER -A IDED D ESI GN &CO M PU T ER G RA PHICSV o l.13,N o.7July ,2001PCB 数控钻孔最佳走刀路线的建模与求解王 霄 刘会霞(江苏理工大学机械工程学院 镇江 212013)摘要 目前,采用PCB 数控钻自动编程系统生成的钻孔路线并非最佳走刀路线.通过分析,将P CB 数控钻孔最佳走刀路线问题归结为大型T SP 问题,其目标函数定为钻头的总走刀时间最短.由于T SP 问题在理论上属于N P 完备问题,因此很难用一般的算法求解.文中详细介绍了用模拟退火方法求解该问题的具体算法,并以此为基础开发了P CB 最优化的自动编程系统.关键词 PCB,最佳走刀路线,T SP 问题,模拟退火方法中图法分类号 T P 391.73Modeling and Solving Optimal Moving Path for NC Drilling of PCBWANG Xiao LIU H ui-Xia(S chool of M ec hanical E ngineering ,Jiang su Univ er sity of S cience and T echnology ,Zh enj iang 212013)Abstract U p to now ,the gener ation of drilling path by automatic prog ramm ing system for pr inted circuit bo ards (PCB)did not give optim al solutio n.T he problem of optimizing the m oving path of NC drilling fo r PCB can be formulated as a larg e scale trav elling salesm an problem (T SP),and the g oal function is defined as the shortest total tim e o f mo ving drill.Because T SP is know n to be a NP-co mplete pro blem ,it w ould be too difficult to tackle it w ith traditional opti-mization metho ds.In this paper,an algo rithm of solving TSP for PCB by sim ulated annealing is pr esented in detail.Based on the research,an optim al autom atic pr ogram ming system for PCB is developed.Key words PCB ,optimal m oving path ,T SP ,Sim ulated Annealing (SA ) 原稿收到日期:2000-03-25;修改稿收到日期:2001-03-05.王 霄,男,1964年生,讲师,主要研究方向为CAD/CAM 、虚拟制造.刘会霞,女,1964年生,副教授,主要研究方向为网络辅助设计与制造、多媒体CAI .1 引 言目前,国内外广泛采用PROT EL ,T ANGO ,ORCAD,P-CADEE 等印刷电路板CAD 软件设计PCB .将PCB -CAD 生成的PCB 图形文件输入光绘仪可获得光绘正片;生成的钻孔数控文件经自动编程处理生成NC 指令,以供PCB 专用数控钻床进行敷铜版焊盘孔的加工.然而在生成NC 指令方面,现有的PCB 自动编程软件采用按孔位的X Y 坐标以某种约定逐次编排的方法确定钻孔的走刀顺序.显然,这样生成的钻孔走刀路线并非最佳路线,影响生产效率.这对于那些年产几千块到几十万块PCB 的中、大批量生产规模的专用生产厂家来说,其影响相当可观.关于这一问题,国外学者进行了不少研究与探讨,足见其整体工艺过程优化的强烈意识.2 最佳走刀路线模型的建立PCB 上通常有多种不同直径的孔,对某一种孔径所构成的孔系,PCB 数控钻问题可描述为:从换刀点出发,不重复又不遗漏地加工完所有孔,再回到换刀点,进行下一种孔径换刀和加工.这对数控编程而言,就存在如何安排孔的加工顺序(路线),使空程移动时间最短,即所谓最佳走刀路线问题.显然,这一问题可归结为著名的旅行售货员问题,其中钻头扮演了售货员的角色,而最佳走刀路线的目标函数可选为刀具的空行程最短或空行程花费的时间最短.现讨论分析:PCB 数控钻都是具有点位控制的数控机床,这种机床的刀具由一点(孔)运动到另一点(孔)时,通常是沿X Y 轴方向同时快速移动.当沿X Y 轴各自距离不同时,坐标值小者先完成运动,到达某一中间点(如图1中由0点到A 点).另一坐标将沿坐标轴方向从中间点继续向终点(如图1中1点)运动,由换刀点0经过1→2→3→4→5返回换刀点0的运动轨迹如图1所示.从图1可知,刀具从一孔到另一孔,其快速移动的走刀路线一般不是直线,而是折线.以0到1为例,其两点间的空行程S (0,1)=S 0a +S a 1=(X 1-X 0)/co s45°+[(Y 1-Y 0)-(X 1-X 0)×tan45°],而两点间的空行程时间t (I ,J )=m ax{ûX J -X I û/V X ,ûY J -Y I û/V Y }.其中,V 为工作台相对刀具的X 或Y 方向的快移速度,一般V X =V Y =V .由于求最短路线的目的是为了减少空程时间,因此,采用计算比较简单的最短空程时间作为衡量最佳走刀路线的目标函数能提高计算效率.显然,最小化t (I ,J )相对于最小化DT (I ,J )=max {ûX J -X I û,ûY J -Y I û}作为衡量最佳走刀路线的目标函数更简化.3 最佳走刀路线的求解方法TSP 问题是实际应用中出现的复杂问题的集中概括和简化形式,是一个容易定义但难于处理的问题,属于NP 完备问题.在迄今所提出的TSP 的各种解法中基本可分为3类:精确求解法、启发式求解法以及神经网络算法.精确求解法仅能解较小规模的T SP 问题,显然对PCB 问题不适合.PCB 的最佳走刀路线问题属于大规模T SP 问题.国外学者对这一问题作了不少研究[2—5],基本上都是采用启发式求解法,并且其算法都建立在两点间欧几里德距离的基础上,即d I J =SQRT [(X J -X I )2+(Y J -Y I )2].从前面分析可知,这与数控钻所走的路径不符.这样,利用其位置信息或利用三角不等式的几何特征提出的算法就很难有效地解决这一问题.本系统以空行程时间为目标函数,采用模拟退火方法[1,6]有效地解决了这一问题.3.1 模拟退火算法SA (Simulated Annealing )SA 算法将组合优化问题与统计力学中的热平衡问题相类比,开辟了一条求解组合优化问题的新途径.它通过模拟退火过程,可以找到全局(或近似)最优解.SA 算法是基于M ontecar lo 迭代求解法的一种启发式随机搜索算法.设S ={s 1,…,s k }为所有可能的组合状态集合,C :S →R 为非负目标函数,即C (s i )≥0反映取状态s i 为解的代价,则组合优化问题可形式地表述为寻找s *∈S ,使得C (s *)=m in C (s i ),P s i ∈S .SA 算法的基本思想是:将每种组合状态s i 看成某一物体体系的微观状态,C (s i )看成该物质体系在状态s i 下的能量,并用控制参数T 表示伪温度.让T 从一个足够高的值慢慢下降,对每个T ,用M etropolis 抽样法模拟该体系在此T 下的热平衡状态,即对当前状态s 做随机扰动,生成一个新状态s ′,计算增量$C ′=C (s ′)-C (s ),并以概率ex p(-$C /bT )接受s ′作为新的当前状态.当这样的随机扰动重复足够多的次数后,系统将达到该温度下的热平衡状态,并且系统的状态将导致Bo ltzmann 分布,b 是Boltzm ann 常数.SA 算法的主要步骤描述如下.算法1.SA-Algo rithmpr ocedur e SA _A lgor ithm (i 0,T 0);/*s i 0为任一初态,T 0为初始控制参数*/beg in(1)s ←s i 0;C *←C i ;k ←0/*简记C i =C (s i ),C *为当前代价值.*/(2)repeat (2.1)repeat5917期王 霄等:P CB 数控钻孔最佳走刀路线的建模与求解 (2.1.1)s j←Gener ate(s);(2.1.2)if C j≤C*then s←s j else if A ccep t(j,s)t hen s←s j endifendif(2.1.3)until 内循环结束条件;(2.2)T K+1←Up date(T k);k←k+1(3)until T k≤Eend其中,(1)为初始化;(2.1.1)的Gener ate(s)表示从s的邻域中随机产生下一个状态s j.若C j≤C*,则接受j为新的当前状态;否则仅以一定的概率接受j为新的当前状态,这也就是Accep t(j,s)函数的功能;(2.1.3)中的内循环结束条件是指在每一度T k下迭代多少次以达到平衡态;(2.2)中的Up date(T k)函数则表示温度每次下降的速率.由此可知,SA算法有3个重要函数:产生函数Gen-erate,接受函数A ccep t和温度更新函数Up d ate.在实际应用中,初始温度T0、内循环次数和终止条件也是影响SA算法性能的重要参数.3.2 用SA算法求解TSP问题传统的启发式算法主要有两种:一种是先自顶向下的分而治之,再自底向上的组合求解的分治法;第二种是步步贪心,以达到全局最优的迭代法.SA 算法可看成是上述两种方法的综合.在高温下,它是大粒度的分治法;而在低温下,是细粒度的贪心法.由于SA算法中能做概率性的扰动以跳出局部极小,因而可获得全局最优解.用SA求解T SP问题的关键是如何确定函数形式与各参数.(1)目标函数.设R=(i0,i1,…,i N)为顶点的一个排列,则优化目标函数就可取为路径长度,即c(s i)=∑j ‖A j A Ri(j)‖,j∈[1,N].(2)产生函数Gener ate.function T SP-Gener ate(s i);/*令s i=(i1,…,i N)*/begini←Rando m(1,N-1);j←R andom(i+1,N);ret ur n(S wap(i,j,s i,s j))end它表示交换顶点A i和A j,看能否产生较短的周游路径,即可用弧(X i-1,X j),(X j,X i+1),(X j-1,X i), (X i,X j+1)去替代弧(X i-1,X i),(X i,X i+1),(X j-1,X j),(X j,X j+1).(3)接受函数A ccep t.A ccep t函数通常取如下形式functio n A ccep t(j,s);begin$C′←C j-C*;if ex p(-$C′/bT K)>Ra ndom(0,1)/*b为Boltzmann常数*/then A ccep t←tr ueelse A ccep t←falseendifend(4)温度更新函数Up date.Up date实质就是退火策略,这种策略的选择是最关键的,因为算法中影响解收敛质量的温度由退火策略控制.常见的退火策略有:a.T k+1=AõT K (0<A<1),b.T k+1=T k/(H BõT k) (B<<T0),c.T k+1=T kõex p(0.7T k/R) (R为目标函数值的标准偏差[6]).其中c是一种自适应的退火策略,本文即选用这种退火策略.SA算法是一个通用的、与领域无关的具有概率爬山的、能逃离局部最优的强有力的组合优化算法,对T SP而言,它是较好的模型之一,目前能处理的城市数目已达6000个之多.3.3 运行实例算法1用Visual C++ 5.0编写,在奔腾III处理器650M Hz计算机上调试并运行通过.图2是某一PCB(N o.Citys=64)按一般PCB-CAD软件所生成的钻孔走刀路线图.图3是利用本文算法生成的钻孔走刀路线图.比较图2,3可以看出,其走刀空行程缩短了36.5%.通过大量实例比较,发现用该算法所得的优化走刀路线比用一般PCB-CAD软件按孔位的X Y坐标,以某种约定逐次编排的方法确592计算机辅助设计与图形学学报2001年定的走刀路线节省的行程显著,一般在25%以上,该方法实用、可靠并能获得较好的解.4 PCB 最优数控编程系统PCB 数控钻孔最佳走刀路线的确定,有效地解决了PCB 加工工艺过程的优化数控编程问题.在此基础上开发了PCB 自动编程系统,其工作流程如图4所示.图4的工作原理是将不同类型的PCB-CAD 系统中生成的不同格式的PCB 钻孔数据文件交给前置处理器.前置处理器的作用是分析识别不同CAD 系统产生的钻孔数据文件内容,并按不同孔径族提取位置信息,将其转化为统一的数据文件形式,作为确定某一钻头最佳走刀路线模型的数据源;再经最佳走刀路线模块确定钻孔的最佳走刀路线,然后交给后置处理器处理.后置处理器的任务是由扫描器读入不同的钻头直径、最佳走刀路线模型位置信息及具体数控机床的数控特性文件,由语义分析器进行分析并产生对应数控机床的数控指令,最后由DNC 通讯程序将数控指令传输给对应的数控机床.5 结束语本文将PCB 数控钻孔最佳路线归结为TSP 问题,给出了利用SA 算法求解最佳走刀路线的目标函数及3个重要函数:产生函数Gener ate 、接受函数A ccep t 及温度更新函数Up date .其中,退火策略在模拟退火中起重要作用,直接影响TSP 解的质量.该算法已成功应用于激光数控打孔中,并在PCB 数控钻孔CAM 系统中试用.该算法有效地解决了多孔加工中刀具路径冗长、空行程导致加工效率低的问题,使数控钻孔加工工艺得以优化.参考文献1S Kirk patrick,et al .Optimiz ation by simu lated an nealing.S ci-ence,1983,220(4598):671-6802Conley W C.Programming an au tomated pun ch or drill.In ter-national J ou rnal of Systems Science,1991,22(11):2039-20563J D litke.An improved solution to the traveling salesman prob-lem w ith thous ands of n munications of the ACM ,1984,2(12):1227-12364Vangelis F M agirou.T he efficient dr illing of printed cir cuit boards .Inter faces ,1988,16(4):13-235S urya Danusaputro,et al .An efficient algorithm for drilling printed circu it boards .Computer s and Indus trial Engin eering ,1990,18(2):145-1516S zykman S ,Cagan J .A s imulated annealing -based approach to three-d imens ional componentpacking.T ransaction of theAS M E ,1995,117(3):308-3145937期王 霄等:P CB 数控钻孔最佳走刀路线的建模与求解。
零件数控加工的走刀路线设计

零件数控加工的走刀路线设计摘要:走刀路线是指切削加工过程中刀具相对于被加工零件的运动轨迹和运动方向,即指刀具从对刀点开始运动起,直至返回该点并结束加工程序所经过的路径,包括切削加工的路径及刀具引入、返回等非切削空行程。
走刀路线是编制程序的依据之一。
关键词:数控加工;走刀路线1.确定走刀路线设计原则(1)走刀路线应保证被加工工件的精度和表面粗糙度。
(2)应尽量使加工路线最短,减少空行程时间,以提高加工效率;(3)合理选用铣削加工中的顺铣或逆铣方式。
(4)选择工件加工变形小的加工路线。
(5)使数值计算最简单和减少程序段,以减少编程工作量。
(6)根据工件情况,确定循环加工次数。
(7)合理设计刀具的切入与切出的方向。
2铣削加工中加工路线的选择要点2.1在数控铣床上铣削外轮廓零件时,为了保证轮廓表面质量的要求,应设计合理的刀具切入和切出时的进、退刀位置。
2.2铣削封闭内轮廓表面零件时也要注意刀具切入和切出时的运动轨迹。
为了提高加工精度和减少表面粗糙度,在铣削封闭的内轮廓时,因刀具切入、切出不允许外延,此时刀具的切入和切出点尽量选在内轮廓曲线两几何元素的交点处或者以圆弧切向进刀。
用行切法加工凹槽,其加工路线最短,但表面租糙度差,适用于对表面粗糙度要求不太高的粗加工或半精加工。
用环切法加工凹槽,其表面粗糙度最好,但加工路线最长。
用综合法加工凹槽,即先采用行切法粗加工,最终轮廓用环切法再沿轮廓切削一周进行精加工,使凹槽轮廓表面光整,易保证凹槽侧面达到所要求的表面质量。
见图2.1。
图2.1综合法2.3用圆弧插补铣削整圆时,当整圆加工完毕后,要让刀具最好沿切线方向多运动一段距离,以免取消刀具补偿时,刀具与工件表面发生碰撞,造成工件报废。
2.4在铣削零件时,要根据工件的材料等因素考虑铣削方式,顺铣效率高节能性好,但当工件表面有硬皮时,应采用逆铣的加工路线进行加工。
2.5在铣削圆弧与直线的连接处,应选用直径较小的刀具,采用补加工的方式消除欠切现象。
20.走刀路线的选择
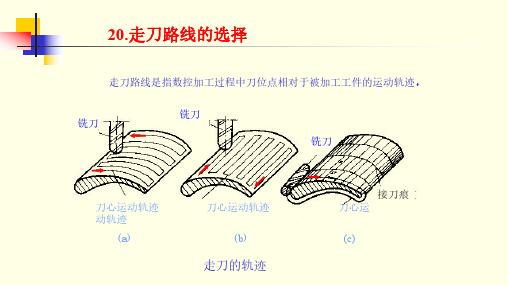
接刀痕
铣刀铣刀铣刀
走刀的轨迹 刀心运动轨迹 刀心运动轨迹 刀心运动轨迹
(a) (b) (c)
20.走刀路线的选择
走刀路线是指数控加工过程中刀位点相对于被加工工件的运动轨迹。
行距是铣刀走完一切削行后转向加工下一切削行,所跨越的间距。
决定行距大小的主要因素是事先给定的加工结束后零件表面上相邻切削行之间的最大刀痕残留高度h。
L =2(h(2r 刀-h ))1/2 l ≈ L*ρ /(r 刀
±ρ)
走刀路线的选择原则:
① 保证零件的加工精度和表面租糙度;
②方便数值计算,减少编程工作量;
③缩短走刀路线,减少空行程。
有缘学习更多+谓ygd3076或关注桃报:奉献教育(店铺)。
数控加工刀具路径拟定

2. 3数控加工刀具路径拟定CNC加工的刀具路径指,加工过程中,刀具刀位点相对于工件进给运动的轨迹和方向。
刀具路径一般包括:从起始点快速接近工件加工部位,然后以工进速度加工工件结构,完成加工任务后,快速离开工件,回到某一设定的终点。
可归纳为两种典型的运动:点到点的快速定位运动一一空行程;工作进给速度的切削加工运动一一切削行程。
确定刀具走刀路线的原则主要有以下几点:⑴规划安全的刀具路径,保证刀具切削加工的正常进行。
⑵规划适当的刀具路径,保证加工零件满足加工质量要求。
⑶规划最短的刀具路径,减少走刀的时间,提高加工效益。
2. 3. 1规划安全的刀具路径在数控加工拟定刀具路径时,把安全考虑放在首要地位更切BI荷坏叨刨电域实际。
规划刀具路时,最值得注意的安全问题就是刀具在快速的点定位过程中与障碍物的碰撞。
为了节省时间,刀具加工前接近工件加工部位,完成加工任务后,快速离开工件,常用快速—' ----- ----------- ~点定位路线。
快速点定位时,刀具以最快的设定速图2-3-1车削加工X、Z向安全间隙设计度移动,一旦发生碰撞后果不堪设想。
1 .快速的点定位路线起点、终点的安全设定工艺编程时,对刀具快速接近工件加工部位路线的终点和刀具快速离开工件路线的起点的位置应精心设计,应保证刀具在该点与工件的轮廓应有足够的安全间隙,避免刀具与工件的碰撞。
在拟定刀具快速趋近工件的定位路径时,趋向点与工件实体表面的安全间隙大小应有谨慎的考虑。
如图2-3-1,刀具相对工件在Z向或X向的趋近点的安全间隙设置多少为宜呢?间隙量小可缩短加工时间,但间隙量太小对操作工来说却是不太安全和方便,容易带来潜在的撞刀危险。
对间隙量大小设定时,应考虑到Z0的加工面是否已经加工到位,若没有加工,还应考虑可能的最大的毛坯余量。
若程序控制是批量生产,还应考虑更换新工件后Z向尺寸带来的新变化,以及操作员是否有足够的经验。
在铳削工艺编程,刀具从 X 、Y 向快速趋于工件轮廓时的情况,与Z 向趋近相比较,同 样应精心设计安全间隙,但情况又有所不同,因为刀具X 、Y 向刀位点在圆心,始终与刀具 切削工件的点相差一个半径, 刀具快速趋近的同时, 又需建立半径补偿, 因此设计刀具趋近工件点与工件的安全间隙时,除了要考虑毛坯余量的大小,又应考虑刀具半径值的大小。
数控加工走刀路线图介绍

14.4 数控加工走刀路线图
数控加工走刀路线图零件图号工序号 2 工步号 2 程序号O0002 机床型号KV650 程序段号加工内容铣心型轮廓共 6 页第 2 页
编程
校对
审批
符号
含义抬刀下刀编程原点起刀点
走刀
方向
走刀线
相交
爬斜坡铰孔行切数控加工走刀路线图零件图号工序号 3 工步号 3 程序号O0003 机床型号KV650 程序段号加工内容挖槽共 6 页第 3 页
编程
校对
审批符号
含义抬刀下刀编程原点起刀点走刀
方向
走刀线
相交
爬斜坡铰孔行切
数控加工走刀路线图零件图号工序号 5 工步号5-8 程序号O0005
钻孔
编程
校对
审批符号
含义抬刀下刀编程原点起刀点走刀
方向
走刀线
相交
爬斜坡铰孔行切
数控加工走刀路线图零件图号工序号 6 工步号13 程序号O0006 机床型号KV650 程序段号加工内容加工内球面共 6 页第 6 页
编程
校对
审批。
数控木工钻孔机床的刀具路径规划与优化

数控木工钻孔机床的刀具路径规划与优化随着科技的不断进步和发展,数控木工钻孔机床逐渐取代了传统的手工操作方式。
它的出现不仅简化了工作流程,提高了工作效率,而且保证了产品的精度和质量。
在数控木工钻孔机床的运行中,刀具路径的规划和优化对于完美的加工结果至关重要。
刀具路径规划是数控木工钻孔机床加工过程中的重要环节。
当我们输入设计好的CAD图纸数据后,程序会自动生成刀具路径。
刀具路径规划需要考虑钻孔的位置、顺序、深度等因素,确保钻孔的精度和效率。
同时,刀具路径规划也应该根据不同的木材材质、孔径等因素进行调整,以达到最佳的加工效果。
首先,在刀具路径规划中,确定钻孔位置是必不可少的。
通过CAD图纸数据,我们可以确定木材的几何结构和孔洞要求。
根据这些信息,钻孔位置可以精确计算,避免出现误差。
同时,考虑到木材的密度和强度等因素,我们可以在刀具路径规划中调整孔洞的间距和深度,以确保加工出的孔洞均匀、牢固。
其次,在确定钻孔位置后,刀具路径的顺序也需要进行规划。
通常情况下,我们会根据钻孔的位置和孔洞要求,对刀具路径做一个合理的排序。
这样做可以减少刀具在加工过程中的移动距离,提高加工效率,并减少加工误差的发生。
同时,我们还可以根据木材的特性,在刀具路径规划过程中进行合理的削减方式选择,以确保木材的表面光滑和精细度。
此外,刀具路径规划还应考虑刀具的选择和刀具路径的优化。
在数控木工钻孔机床中,刀具的选择对于加工效果和速度有着重要的影响。
我们需要根据木材的硬度和孔洞要求,选择合适的刀具。
同时,在刀具路径规划中,我们也应考虑如何优化刀具路径,以减少加工时间和提高加工效率。
例如,利用曲线轨迹和有效的曲线连接方式,可以减少刀具在加工过程中的停顿时间,并降低刀具磨损和损坏的风险。
最后,对于数控木工钻孔机床的刀具路径规划与优化,我们也应关注人性化设计和操作的实现。
保证操作人员能够轻松理解和操作机床系统,提高其工作效率和工作质量。
还要注重系统的稳定性和安全性,确保操作过程中不会发生任何意外事故。
PCB线路板雕刻钻孔教程

雕刻机使用电路设计网整理:淘宝店的配套雕刻机产品:(1)掌握雕刻机的软件使用,生成加工文件;(2)掌握雕刻机的前期准备工作,固定空白电路板、选择安装钻头;(3)掌握雕刻机的冲定位孔、试雕、过孔、隔离、镂空、割边等技能;重点(1)钻头的选择与安装;(2)对刀、设定原点;(3)试雕、过孔、割边;14.3.1 雕刻机的简单工作原理PCB线路板雕刻机可根据PCB线路设计软件(如PROTEL)设计生成的线路文件,自动、精确地制作单、双面印制电路板。
用户只需在计算机上完成PCB文件设计并据其生成加工文件后,通过LPT通讯接口传送给雕刻机的控制系统,雕刻机就能快速的自动完成雕刻、钻孔、隔边的全部功能,制作出一块精美的线路板来,真正实现了低成本、高效率的自动化制板。
该设备操作简单,可靠性高,是高校电子、机电、计算机、控制、仪器仪表等相关专业实验室、电子产品研发企业及科研院所、军工单位等的理想工具。
线路板雕刻机是一种机电、软硬件互相结合的高新科技产品,它利用PCB线路设计软件(如PROTEL)生成的PCB文件信息,转换为国际通用的G代码加工文件,直接输出给雕刻机,来控制雕刻机自动完成雕刻、钻孔、切边等工作。
它利用物理雕刻方法,通过计算机控制,在空白的敷铜板上把不必要的铜箔铣去,形成用户设计的线路板。
使用简单、精度高、省时、省料。
14.3.2.1 关于空白线路板空白线路板是在绝缘基体上粘贴覆盖一层导电的铜。
从原理上看,制作一张线路板的过程,就是利用铣刻的原理,把线路板上多余的不必要覆铜部分铣去。
这一过程跟传统的雕刻过程相似,区别在于传统雕刻利用手工,本机则利用数控原理让机器自动完成。
14.3.2.2 计算机雕刻路径要完成一张线路板的制作,第一步首先是要知道哪些部分是要保留的,哪些部分是要铣去的,让刀具沿什么路线运动才能达到我们的目的。
在本系统中,我们利用个人计算机的高速运算性能,从保存的PCB文件中获取相关信息,经过算法的转换,获得主轴刀头运动的路线,这一过程称计算机雕刻路径。
数控加工刀具路径拟定

图2-3-1车削加工X 、Z 向安全间隙设计 2.3 数控加工刀具路径拟定CNC 加工的刀具路径指,加工过程中,刀具刀位点相对于工件进给运动的轨迹和方向。
刀具路径一般包括:从起始点快速接近工件加工部位,然后以工进速度加工工件结构,完成加工任务后,快速离开工件,回到某一设定的终点。
可归纳为两种典型的运动:点到点的快速定位运动——空行程;工作进给速度的切削加工运动——切削行程。
确定刀具走刀路线的原则主要有以下几点:⑴规划安全的刀具路径,保证刀具切削加工的正常进行。
⑵规划适当的刀具路径,保证加工零件满足加工质量要求。
⑶规划最短的刀具路径,减少走刀的时间,提高加工效益。
2.3.1规划安全的刀具路径在数控加工拟定刀具路径时,把安全考虑放在首要地位更切实际。
规划刀具路时,最值得注意的安全问题就是刀具在快速的点定位过程中与障碍物的碰撞。
为了节省时间,刀具加工前接近工件加工部位,完成加工任务后,快速离开工件,常用快速点定位路线。
快速点定位时,刀具以最快的设定速度移动,一旦发生碰撞后果不堪设想。
1.快速的点定位路线起点、终点的安全设定工艺编程时,对刀具快速接近工件加工部位路线的终点和刀具快速离开工件路线的起点的位置应精心设计,应保证刀具在该点与工件的轮廓应有足够的安全间隙,避免刀具与工件的碰撞。
在拟定刀具快速趋近工件的定位路径时,趋向点与工件实体表面的安全间隙大小应有谨慎的考虑。
如图2-3-1,刀具相对工件在Z 向或X 向的趋近点的安全间隙设置多少为宜呢?间隙量小可缩短加工时间,但间隙量太小对操作工来说却是不太安全和方便,容易带来潜在的撞刀危险。
对间隙量大小设定时,应考虑到Z0的加工面是否已经加工到位,若没有加工,还应考虑可能的最大的毛坯余量。
若程序控制是批量生产,还应考虑更换新工件后Z 向尺寸带来的新变化,以及操作员是否有足够的经验。
在铣削工艺编程,刀具从X 、Y 向快速趋于工件轮廓时的情况,与Z 向趋近相比较,同样应精心设计安全间隙,但情况又有所不同,因为刀具X 、Y 向刀位点在圆心,始终与刀具切削工件的点相差一个半径,刀具快速趋近的同时,又需建立半径补偿,因此设计刀具趋近工件点与工件的安全间隙时,除了要考虑毛坯余量的大小,又应考虑刀具半径值的大小。
基于模拟退火算法的 PCB 钻孔机空行路径优化

基于模拟退火算法的 PCB 钻孔机空行路径优化杨婷;贾朝川【摘要】为提高其工作效率,提出了基于模拟退火算法对 PCB 钻孔机钻头的空行路径进行优化,首先,结合 PCB 钻孔机的机械结构原理图,描述了其运动过程;其次,根据 PCB 板上焊孔的位置坐标信息,设计出模拟退火算法实现对钻孔机钻头空行路径进行优化;最后,结合具体的实例验证仿真优化过程,实验结果显示该算法收敛速度较快,能够在很大程度上提高 PCB 钻孔机的工作效率。
PCB 钻孔机是在 PCB 板加工过程中必不可少的加工机器之一,其工作效率直接影响整体效率。
%The path optimization algorithm was designed based on the simulated annealing algorithm in or-der to improve the work efficiency.Firstly,the movement process was described according to the mechani-cal structure principle diagram of PCB drillingmachine.Secondly,the path optimization algorithm was de-signed based on the simulated annealing algorithm with using the hole position coordinates information on the printed circuit board.Finally,the path optimization algorithm was validated with simulation results on a printed circuit board.The working efficiency of the PCB drilling machine was improved.The PCB drill-ing machine is a indispensable machine in the process of PCB processing,the overall efficiency of process-ing will affect its work efficiency.【期刊名称】《蚌埠学院学报》【年(卷),期】2016(005)005【总页数】4页(P6-9)【关键词】钻孔机;模拟退火算法;路径优化【作者】杨婷;贾朝川【作者单位】皖西学院机械与电子工程学院,安徽六安 237012;皖西学院机械与电子工程学院,安徽六安 237012; 山东科技大学机械电子工程学院,山东青岛266590【正文语种】中文【中图分类】TG527PCB钻孔机是在PCB板加工过程中必不可少的机器之一,主要负责制作PCB板上的焊孔或者不同层面的线路导通(VIA)孔。
数控走刀路线图

数控走刀路线图
数控走刀路线图 零件 图号
工序号
工步号
程序号 机床 型号
CK6150
程序 段号
加工 内容
共 页
第页
编 程
校 对
审 核
符号
含义 循环点
编程 原点
换刀点
快速走刀方向 进给走 刀方向
数控走刀路线图 零件 图号
工序号
工步号
程序号 机床 型号
CK6150
程序 段号
加工 内容
共 页
第页
编 程
校 对
审 核
符号
含义 循环点
编程 原点
换刀点
快速走刀方向 进给走 刀方向
数控走刀路线图 零件 图号
工序号
工步号
程序号 机床 型号
CK6150
程序 段号
加工 内容
共 页
第页
编 程
校 对
审 核
符号
含义 循环点
编程 原点
换刀点
快速走刀方向 进给走 刀方向
数控走刀路线图 零件 图号
工序号
工步号
程序号 机床 型号
CK6150
程序 段号
加工 内容
共 页
第页
编 程 校 对
审 核
符号
含义 循环点
编程 原点
换刀点
快速走刀方向 进给走 刀方向。
数控加工走刀路线图说明
数控加工走刀路线图
零件图号
工序号
2
工步号
2
程序号
O0002
机床型号
KV650
程序段号
加工内容
铣心型轮廓
共6页
第2页
编程
校对
审批
符号
含义
抬刀
下刀
编程原点
起刀点
走刀
方向
走刀线
相交
爬斜坡
铰孔
行切
数控加工走刀路线图
零件图号
工序号
3工Biblioteka 号3程序号O0003
机床型号
KV650
程序段号
加工内容
下刀
编程原点
起刀点
走刀
方向
走刀线
相交
爬斜坡
铰孔
行切
工序号
5
工步号
5-8
程序号
O0005
机床型号
KV650
程序段号
加工内容
钻孔
共6页
第5页
编程
校对
审批
符号
含义
抬刀
下刀
编程原点
起刀点
走刀
方向
走刀线
相交
爬斜坡
铰孔
行切
数控加工走刀路线图
零件图号
工序号
6
工步号
13
程序号
O0006
机床型号
KV650
程序段号
加工内容
加工内球面
共6页
第6页
编程
校对
审批
符号
含义
抬刀
挖槽
共6页
第3页
编程
校对
审批
符号
含义
走刀路线的确定(精)

Produced by Miss Xie
刀路线的确定
二 、数控车削加工走刀路线
(三)车削圆锥的加工路线
图1-2 粗车正锥进给路线示意图
图1-3 粗车倒锥进给路线示意图
在数控车床上车削外圆锥可以分为车削正圆锥和车削倒圆锥两种情况 ,而每一种情况又有两种加工路线。图1-2所示为车削正圆锥的两种 加工路线。按图1-2a车削正圆锥时,需要计算终刀距 。设圆锥大径为 ,小径为 ,锥长为 ,背吃刀量为 ,则由相似三角形可知: 根据上述公式,便可计算出终刀距S的大小。
Produc控车削加工走刀路线
(四)车削圆弧的加工路线
1、车锥法粗车圆弧 2.矩形法粗车圆弧 3.圆法粗车圆弧
Produced by Miss Xie
刀路线的确定
二 、数控车削加工走刀路线
(五)车螺纹时的加工路线
在数控车床上车螺纹时,沿螺距方向的Z向进给应和车床主轴的转速 保持严格的速比例关系,因此应避免在进给机构加速或减速的过程中 切削。为此要有升速进刀段和降速进刀段,如图示1-7所示, 一般为2 ~5㎜, 一般为1~2㎜。这样在切削螺纹时,能保证在升速后使刀肯 接触工件,刀具离开工件后再降速。
Produced by Miss Xie
刀路线的确定
二 、数控车削加工走刀路线
(一)轮廓粗车进给路线 (二)轮廓精车进给路线
(三)车削圆锥的加工路线
(四)车削圆弧的加工路线 (五)车螺纹时的加工路线 (六)车槽加工路线
Produced by Miss Xie
刀路线的确定
二 、数控车削加工走刀路线
Produced by Miss Xie
刀路线的确定
二 、数控车削加工走刀路线
(二)轮廓精车进给路线
浅述数控车床加工中走刀路线的合理确定

浅述数控车床加工中走刀路线的合理确定作者:杨艳华来源:《中国新技术新产品》2011年第15期摘要:在数控加工中,刀具刀位点相对于工件运动的轨迹称为进给路线,也称走刀路线。
它不但包括了工步的内容,而且也反映出工步的顺序。
在数控加工中,进给路线是由数控系统控制的。
它对零件的加工质量、加工效率有直接影响,因此,工序设计时必须拟定好刀具合理的进给路线。
关键词:数控车床;走刀路线;原则;确定方法中图分类号:TG659 文献标识码:A1确定走刀路线的原则工步的划分与安排一般可随走刀路线来进行,在确定走刀路线时,主要遵循以下几点原则:1.1加工路线应保证被加工工件的精度和表面粗糙度;1.2应使加工路线最短,以减少空行程时间,提高加工效率;1.3尽量简化数学处理时的数值计算工作量,以简化编程工作;1.4当进给路线重复时,为了简化编程,缩短程序长度,应使用子程序。
此外,确定加工路线时,还要考虑工件的形状与刚度、加工余量的大小,机床与刀具的刚度,合理的切入与切出方向等。
2走刀路线的确定方法走刀路线的确定原则是在保证加工质量的前提下,使加工程序具有最短的走刀路线,这样不仅可以节省整个加工过程的执行时间,还能减少一些不必要的刀具消耗及机床进给滑动部件的磨损等。
2.1粗车走刀路线2.1.1外圆粗车G71适于切削区轴向余量较大的细长轴套类零件的粗车,使用该方式加工可减少径向分层次数,使走刀路线变短2.1.2端面粗车G72用于切削区径向余量较大的轮盘类零件的粗车加工,并使得轴向分层次数少。
2.1.3环状粗车G73适合周边余量较均匀的铸锻坯料的粗车加工,对从棒料开始粗车加工,则会有很多空行程的切削进给路线。
如图1所示。
图1粗车走刀路线若按图2(a)所示,从右往左由小到大逐次车削,由于受背吃刀量不能过大的限制,所剩的余量就必然过多;按图2(b)所示,从大到小依次车削,则在保证同样背吃刀量的条件下,每次切削所留余量就比较均匀,是正确的阶梯切削路线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第13卷第7期2001年7月计算机辅助设计与图形学学报JO U RN A L OF CO M P U T ER -A IDED D ESI GN &CO M PU T ER G RA PHICSV o l.13,N o.7July ,2001PCB 数控钻孔最佳走刀路线的建模与求解王 霄 刘会霞(江苏理工大学机械工程学院 镇江 212013)摘要 目前,采用PCB 数控钻自动编程系统生成的钻孔路线并非最佳走刀路线.通过分析,将P CB 数控钻孔最佳走刀路线问题归结为大型T SP 问题,其目标函数定为钻头的总走刀时间最短.由于T SP 问题在理论上属于N P 完备问题,因此很难用一般的算法求解.文中详细介绍了用模拟退火方法求解该问题的具体算法,并以此为基础开发了P CB 最优化的自动编程系统.关键词 PCB,最佳走刀路线,T SP 问题,模拟退火方法中图法分类号 T P 391.73Modeling and Solving Optimal Moving Path for NC Drilling of PCBWANG Xiao LIU H ui-Xia(S chool of M ec hanical E ngineering ,Jiang su Univ er sity of S cience and T echnology ,Zh enj iang 212013)Abstract U p to now ,the gener ation of drilling path by automatic prog ramm ing system for pr inted circuit bo ards (PCB)did not give optim al solutio n.T he problem of optimizing the m oving path of NC drilling fo r PCB can be formulated as a larg e scale trav elling salesm an problem (T SP),and the g oal function is defined as the shortest total tim e o f mo ving drill.Because T SP is know n to be a NP-co mplete pro blem ,it w ould be too difficult to tackle it w ith traditional opti-mization metho ds.In this paper,an algo rithm of solving TSP for PCB by sim ulated annealing is pr esented in detail.Based on the research,an optim al autom atic pr ogram ming system for PCB is developed.Key words PCB ,optimal m oving path ,T SP ,Sim ulated Annealing (SA ) 原稿收到日期:2000-03-25;修改稿收到日期:2001-03-05.王 霄,男,1964年生,讲师,主要研究方向为CAD/CAM 、虚拟制造.刘会霞,女,1964年生,副教授,主要研究方向为网络辅助设计与制造、多媒体CAI .1 引 言目前,国内外广泛采用PROT EL ,T ANGO ,ORCAD,P-CADEE 等印刷电路板CAD 软件设计PCB .将PCB -CAD 生成的PCB 图形文件输入光绘仪可获得光绘正片;生成的钻孔数控文件经自动编程处理生成NC 指令,以供PCB 专用数控钻床进行敷铜版焊盘孔的加工.然而在生成NC 指令方面,现有的PCB 自动编程软件采用按孔位的X Y 坐标以某种约定逐次编排的方法确定钻孔的走刀顺序.显然,这样生成的钻孔走刀路线并非最佳路线,影响生产效率.这对于那些年产几千块到几十万块PCB 的中、大批量生产规模的专用生产厂家来说,其影响相当可观.关于这一问题,国外学者进行了不少研究与探讨,足见其整体工艺过程优化的强烈意识.2 最佳走刀路线模型的建立PCB 上通常有多种不同直径的孔,对某一种孔径所构成的孔系,PCB 数控钻问题可描述为:从换刀点出发,不重复又不遗漏地加工完所有孔,再回到换刀点,进行下一种孔径换刀和加工.这对数控编程而言,就存在如何安排孔的加工顺序(路线),使空程移动时间最短,即所谓最佳走刀路线问题.显然,这一问题可归结为著名的旅行售货员问题,其中钻头扮演了售货员的角色,而最佳走刀路线的目标函数可选为刀具的空行程最短或空行程花费的时间最短.现讨论分析:PCB 数控钻都是具有点位控制的数控机床,这种机床的刀具由一点(孔)运动到另一点(孔)时,通常是沿X Y 轴方向同时快速移动.当沿X Y 轴各自距离不同时,坐标值小者先完成运动,到达某一中间点(如图1中由0点到A 点).另一坐标将沿坐标轴方向从中间点继续向终点(如图1中1点)运动,由换刀点0经过1→2→3→4→5返回换刀点0的运动轨迹如图1所示.从图1可知,刀具从一孔到另一孔,其快速移动的走刀路线一般不是直线,而是折线.以0到1为例,其两点间的空行程S (0,1)=S 0a +S a 1=(X 1-X 0)/co s45°+[(Y 1-Y 0)-(X 1-X 0)×tan45°],而两点间的空行程时间t (I ,J )=m ax{ûX J -X I û/V X ,ûY J -Y I û/V Y }.其中,V 为工作台相对刀具的X 或Y 方向的快移速度,一般V X =V Y =V .由于求最短路线的目的是为了减少空程时间,因此,采用计算比较简单的最短空程时间作为衡量最佳走刀路线的目标函数能提高计算效率.显然,最小化t (I ,J )相对于最小化DT (I ,J )=max {ûX J -X I û,ûY J -Y I û}作为衡量最佳走刀路线的目标函数更简化.3 最佳走刀路线的求解方法TSP 问题是实际应用中出现的复杂问题的集中概括和简化形式,是一个容易定义但难于处理的问题,属于NP 完备问题.在迄今所提出的TSP 的各种解法中基本可分为3类:精确求解法、启发式求解法以及神经网络算法.精确求解法仅能解较小规模的T SP 问题,显然对PCB 问题不适合.PCB 的最佳走刀路线问题属于大规模T SP 问题.国外学者对这一问题作了不少研究[2—5],基本上都是采用启发式求解法,并且其算法都建立在两点间欧几里德距离的基础上,即d I J =SQRT [(X J -X I )2+(Y J -Y I )2].从前面分析可知,这与数控钻所走的路径不符.这样,利用其位置信息或利用三角不等式的几何特征提出的算法就很难有效地解决这一问题.本系统以空行程时间为目标函数,采用模拟退火方法[1,6]有效地解决了这一问题.3.1 模拟退火算法SA (Simulated Annealing )SA 算法将组合优化问题与统计力学中的热平衡问题相类比,开辟了一条求解组合优化问题的新途径.它通过模拟退火过程,可以找到全局(或近似)最优解.SA 算法是基于M ontecar lo 迭代求解法的一种启发式随机搜索算法.设S ={s 1,…,s k }为所有可能的组合状态集合,C :S →R 为非负目标函数,即C (s i )≥0反映取状态s i 为解的代价,则组合优化问题可形式地表述为寻找s *∈S ,使得C (s *)=m in C (s i ),P s i ∈S .SA 算法的基本思想是:将每种组合状态s i 看成某一物体体系的微观状态,C (s i )看成该物质体系在状态s i 下的能量,并用控制参数T 表示伪温度.让T 从一个足够高的值慢慢下降,对每个T ,用M etropolis 抽样法模拟该体系在此T 下的热平衡状态,即对当前状态s 做随机扰动,生成一个新状态s ′,计算增量$C ′=C (s ′)-C (s ),并以概率ex p(-$C /bT )接受s ′作为新的当前状态.当这样的随机扰动重复足够多的次数后,系统将达到该温度下的热平衡状态,并且系统的状态将导致Bo ltzmann 分布,b 是Boltzm ann 常数.SA 算法的主要步骤描述如下.算法1.SA-Algo rithmpr ocedur e SA _A lgor ithm (i 0,T 0);/*s i 0为任一初态,T 0为初始控制参数*/beg in(1)s ←s i 0;C *←C i ;k ←0/*简记C i =C (s i ),C *为当前代价值.*/(2)repeat (2.1)repeat5917期王 霄等:P CB 数控钻孔最佳走刀路线的建模与求解 (2.1.1)s j←Gener ate(s);(2.1.2)if C j≤C*then s←s j else if A ccep t(j,s)t hen s←s j endifendif(2.1.3)until 内循环结束条件;(2.2)T K+1←Up date(T k);k←k+1(3)until T k≤Eend其中,(1)为初始化;(2.1.1)的Gener ate(s)表示从s的邻域中随机产生下一个状态s j.若C j≤C*,则接受j为新的当前状态;否则仅以一定的概率接受j为新的当前状态,这也就是Accep t(j,s)函数的功能;(2.1.3)中的内循环结束条件是指在每一度T k下迭代多少次以达到平衡态;(2.2)中的Up date(T k)函数则表示温度每次下降的速率.由此可知,SA算法有3个重要函数:产生函数Gen-erate,接受函数A ccep t和温度更新函数Up d ate.在实际应用中,初始温度T0、内循环次数和终止条件也是影响SA算法性能的重要参数.3.2 用SA算法求解TSP问题传统的启发式算法主要有两种:一种是先自顶向下的分而治之,再自底向上的组合求解的分治法;第二种是步步贪心,以达到全局最优的迭代法.SA 算法可看成是上述两种方法的综合.在高温下,它是大粒度的分治法;而在低温下,是细粒度的贪心法.由于SA算法中能做概率性的扰动以跳出局部极小,因而可获得全局最优解.用SA求解T SP问题的关键是如何确定函数形式与各参数.(1)目标函数.设R=(i0,i1,…,i N)为顶点的一个排列,则优化目标函数就可取为路径长度,即c(s i)=∑j ‖A j A Ri(j)‖,j∈[1,N].(2)产生函数Gener ate.function T SP-Gener ate(s i);/*令s i=(i1,…,i N)*/begini←Rando m(1,N-1);j←R andom(i+1,N);ret ur n(S wap(i,j,s i,s j))end它表示交换顶点A i和A j,看能否产生较短的周游路径,即可用弧(X i-1,X j),(X j,X i+1),(X j-1,X i), (X i,X j+1)去替代弧(X i-1,X i),(X i,X i+1),(X j-1,X j),(X j,X j+1).(3)接受函数A ccep t.A ccep t函数通常取如下形式functio n A ccep t(j,s);begin$C′←C j-C*;if ex p(-$C′/bT K)>Ra ndom(0,1)/*b为Boltzmann常数*/then A ccep t←tr ueelse A ccep t←falseendifend(4)温度更新函数Up date.Up date实质就是退火策略,这种策略的选择是最关键的,因为算法中影响解收敛质量的温度由退火策略控制.常见的退火策略有:a.T k+1=AõT K (0<A<1),b.T k+1=T k/(H BõT k) (B<<T0),c.T k+1=T kõex p(0.7T k/R) (R为目标函数值的标准偏差[6]).其中c是一种自适应的退火策略,本文即选用这种退火策略.SA算法是一个通用的、与领域无关的具有概率爬山的、能逃离局部最优的强有力的组合优化算法,对T SP而言,它是较好的模型之一,目前能处理的城市数目已达6000个之多.3.3 运行实例算法1用Visual C++ 5.0编写,在奔腾III处理器650M Hz计算机上调试并运行通过.图2是某一PCB(N o.Citys=64)按一般PCB-CAD软件所生成的钻孔走刀路线图.图3是利用本文算法生成的钻孔走刀路线图.比较图2,3可以看出,其走刀空行程缩短了36.5%.通过大量实例比较,发现用该算法所得的优化走刀路线比用一般PCB-CAD软件按孔位的X Y坐标,以某种约定逐次编排的方法确592计算机辅助设计与图形学学报2001年定的走刀路线节省的行程显著,一般在25%以上,该方法实用、可靠并能获得较好的解.4 PCB 最优数控编程系统PCB 数控钻孔最佳走刀路线的确定,有效地解决了PCB 加工工艺过程的优化数控编程问题.在此基础上开发了PCB 自动编程系统,其工作流程如图4所示.图4的工作原理是将不同类型的PCB-CAD 系统中生成的不同格式的PCB 钻孔数据文件交给前置处理器.前置处理器的作用是分析识别不同CAD 系统产生的钻孔数据文件内容,并按不同孔径族提取位置信息,将其转化为统一的数据文件形式,作为确定某一钻头最佳走刀路线模型的数据源;再经最佳走刀路线模块确定钻孔的最佳走刀路线,然后交给后置处理器处理.后置处理器的任务是由扫描器读入不同的钻头直径、最佳走刀路线模型位置信息及具体数控机床的数控特性文件,由语义分析器进行分析并产生对应数控机床的数控指令,最后由DNC 通讯程序将数控指令传输给对应的数控机床.5 结束语本文将PCB 数控钻孔最佳路线归结为TSP 问题,给出了利用SA 算法求解最佳走刀路线的目标函数及3个重要函数:产生函数Gener ate 、接受函数A ccep t 及温度更新函数Up date .其中,退火策略在模拟退火中起重要作用,直接影响TSP 解的质量.该算法已成功应用于激光数控打孔中,并在PCB 数控钻孔CAM 系统中试用.该算法有效地解决了多孔加工中刀具路径冗长、空行程导致加工效率低的问题,使数控钻孔加工工艺得以优化.参考文献1S Kirk patrick,et al .Optimiz ation by simu lated an nealing.S ci-ence,1983,220(4598):671-6802Conley W C.Programming an au tomated pun ch or drill.In ter-national J ou rnal of Systems Science,1991,22(11):2039-20563J D litke.An improved solution to the traveling salesman prob-lem w ith thous ands of n munications of the ACM ,1984,2(12):1227-12364Vangelis F M agirou.T he efficient dr illing of printed cir cuit boards .Inter faces ,1988,16(4):13-235S urya Danusaputro,et al .An efficient algorithm for drilling printed circu it boards .Computer s and Indus trial Engin eering ,1990,18(2):145-1516S zykman S ,Cagan J .A s imulated annealing -based approach to three-d imens ional componentpacking.T ransaction of theAS M E ,1995,117(3):308-3145937期王 霄等:P CB 数控钻孔最佳走刀路线的建模与求解。
