2017-2018学年福建省春季高考高职单招数学模拟试题 (14) Word版含答案
高职单招数学模拟试题

2018年高职单招《数学》试题一、单项选择题(本大题共10小题,每小题5分,共50分。
) 姓名:姓名:1.函数y=x 的定义域是(的定义域是() A.{0}x x £ B. {0}x x < C.{0}x x ³ D. {0}x x > 2. 已知平面向量a(1,3),(1,1)b -,则a b ·=( ) A. (0,4) B.(-1,3) C.0 D.2 3. 3log 9=( ) A.1 B.2 C.3D.4 4.下列函数在其定义域内是增函数的是(下列函数在其定义域内是增函数的是( ) A. y=x B. y=sinx C.2y x = D. 1y x = 5.不等式(x-1)(x-2)<0的解集为( ) A. (1,2) B.[1,2] C.(-¥,1)(2,)È+¥D. (-¥,1]∪(2,]+¥ 6.直线31y x =+的倾斜角为(的倾斜角为( ) A. 6p B. 4p C. 3p D. 34p 7.已知某高职院校共有10个高职单招文化考试考场,每名考试每名考试被安排到每个考场的可能性相同,两名考生一同前往该校参加单招文化考试,则他们在同一个考场考试的概率为(同前往该校参加单招文化考试,则他们在同一个考场考试的概率为() A.19 B. 110 C. 190 D. 11008.过点A (-1,1)和点B (1,3),且圆心在x 轴上的圆的方程为(轴上的圆的方程为() A.22x (2)2y +-= B. 22x (2)10y +-= C. 22(x-2x-2))2y += D. 22(x-2x-2))10y += 9.某报告统计的2009年至2017年我国高速铁路运营里程如下图所示:年我国高速铁路运营里程如下图所示:根据上图,以下关于2010年至2017年我国高速铁路运营里程的说法错误的是(年我国高速铁路运营里程的说法错误的是() A.高速铁路运营里程逐年增加高速铁路运营里程逐年增加B.高速铁路运营里程奶奶增长量最大的年份是2014年C.与2014年相比,2017年高速铁路运营的里程增加了1倍以上倍以上D. .与2012年相比,2017年高速铁路运营的里程增加了1倍以上倍以上10.已知函数-ì£=<-=í>î2,0f ()若,为实数,且为实数,且a a 0,0,则则f (a b)()2,0x x x x a b b x A .f ()()a f b - B. f ()()a f b C. f ()()a f b D. f (b)()f a二、填空题(本大题共12小题,每小题2分,共24分。
福建省春季高考高职单招数学模拟试题(十二)及答案.pdf

20.(本小题满分 8 分) 已知函数 f (x) = sin( − x) − cos x,(x R) .
(1) 求函数 f (x) 的最小正周期; (2) 求函数 f (x) 的最大值和最小值;
(3) 若 f ( ) = 1 , (0, ) ,求 sin + cos 的值.
学海无涯
福建省春季高考高职单招数学模拟试题(十二)
班级:
姓名:
座号:
一.选择题:本大题共14小题,每小题5分,满分70分.
成绩:
1.已知集合 A ={−1,0,1},则( )
A.1+ i A
B.1+ i2 A
C.1+ i3 A D.1+ i4 A
2.已知命题 P:“ x R, x2 + 2x + 3 0 ”,则命题 P 的否定为( )
0 0.065 0.070 0.075 0.0800.0850.0900.0950.1000.105
于等于 2.5 微米的颗粒物).右图是某市某月(按 30 天计)根据对“pm2.5” 24 小时平均浓度值测试
的结果画成的频率分布直方图,若规定空气中“pm2.5”24 小时平均浓度值不超过 0.075 毫克/立方米
学海无涯
22. (本小题满分 10 分) 如图①边长为 1 的正方形 ABCD 中,点 E、F 分别为 AB、BC 的中点,将△BEF 剪去,将△AED、△DCF
分别沿 DE、DF 折起,使 A、C 两点重合于点 P 得一三棱锥如图②示.
A. 3
B. 4
C. 6
D. 10
9.已知向量 a = (x − z,1),b = (2, y + z) ,且 a ⊥ b ,若变量 x,y
福建省春季高考数学高职单招模拟试题14

福建省高考高职单招数学模拟试题准考证号 姓名(在此卷上答题无效)2015年福建省高等职业教育入学考试数学适应性试卷 (面向普通高中考生)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至3页,第Ⅱ卷4至5页.考试时间120分钟,满分150分.注意事项:1.答题前,考生务必在试卷、答题卡规定的地方填写自己准考证号、姓名.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.非选择题用0.5毫米的黑色签字笔在答题卡上书写作答.在试卷上作答,答案无效.3.保持答题卡卡面清洁,不折叠、不破损.考试结束,考生必须将试卷和答题卡一并交回.参考公式:样本数据12,,...,n x x x 的标准差 锥体体积公式s =13V Sh = 其中x 为样本平均数 其中S 为底面面积,h 为高 柱体体积公式球的表面积、体积公式 V Sh =24S R =π,343V R =π其中S 为底面面积,h 为高其中R 为球的半径第Ⅰ卷(选择题 共70分)一.单项选择题(本大题共14小题,每小题5分,共70分.在每小题给出的四个备选答案中,选出一个正确答案,并将答题卡上对应题目的答案标号涂黑) 1.复数2i i +等于A .1i +B .1i -C .1i -+D .1i --2.已知函数()22xf x =+,则(1)f 的值为A .2B .3C .4D .63. 函数y =的定义域为 A .[)1,0- B .()0,+∞ C .[)()1,00,-+∞ D .()(),00,-∞+∞4.执行如图所示的程序框图,若输入的x 的值为3,则输出的y 的值为A .4B .5C .8D .10 5.若x ∈R ,则“x =1”是“x =1”的A .充分而不必要条件B .必要而不充分条件C .充要条件D . 既不充分又不必要条件6.下列函数中,在其定义域内既是奇函数,又是减函数的是A .3y x =- B .sin y x = C .tan y x = D .1()2xy =7. 函数y =⎝ ⎛⎭⎪⎫12x+1的图象关于直线y =x 对称的图象大致是8. 已知cos α=45,(,0)2απ∈-,则sin α+cos α等于A .-15B . 15C .-75D .759. 函数()23-+=x x f x的零点所在的一个区间是A .(-2,-1)B .(-1,0)C .(0,1)D .(1,2)10.若变量,x y 满足约束条件2,2,2,x y x y ≤⎧⎪≤⎨⎪+≥⎩则y x z +=2的最大值是A .2B .4C .5D .611.若双曲线方程为221916x y -=,则其离心率等于 A .53 B .54 C .45 D . 35 12.如右图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度h 随时间t变化的可能图象是13.过原点的直线与圆03422=+++x y x 相切,若切点在第三象限,则该直线的方程是A .x y 3=B .x y 3-=C .y =D . y x = 14. 已知()f x 是奇函数,且当0x ≥时,2()f x x x =-+,则不等式()0xf x <的解集为A .(,1)(0,1)-∞-B .(1,0)(1,)-+∞C .(1,0)(0,1)-D .(,1)(1,)-∞-+∞2015年福建省高等职业教育入学考试数学适应性试卷 (面向普通高中考生)第Ⅱ卷(非选择题 共80分)注意事项:请用0.5毫米黑色签字笔在答题卡上书写作答.在试卷上作答,答案无效.二、填空题(本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置上) 15.若集合},0{m A =,}2,0{=B ,}2,1,0{=B A ,则实数=m .16.已知已知向量(3,1)=a ,(,3)x =-b ,若⊥a b ,则x =_________.17.如图,在边长为5的正方形中随机撒1000粒黄豆,有200粒落到阴影部分,据此估计阴影部分的面积为 .18.若lg lg 2,x y +=则x y +的最小值为 .三、解答题(本大题共6小题,共60分.解答应写出文字说明,证明过程或演算步骤) 19.(本小题满分8分)已知△ABC 的内角,,A B C 的对边分别为,,a b c ,且2,4,60a b C ===. (Ⅰ)求△ABC 的面积; (Ⅱ)求c 的值.20.(本小题满分8分)在等比数列{}n a 中,公比2q =,且2312a a +=. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)求数列{}n a 的前2015项和2015S .21.(本小题满分10分)某机器零件是如图所示的几何体(实心),零件下面是边长为10cm 的正方体,上面是底面直径为4cm ,高为10cm 的圆柱. (Ⅰ)求该零件的表面积;(Ⅱ)若电镀这种零件需要用锌,已知每平方米用锌0.11kg ,问制造1000个这样 的零件,需要锌多少千克?(注:π取3.14)22.(本小题满分10分)题21图甲乙两台机床同时生产一种零件,5天中,两台机床每天的次品数分别是:甲 1 0 2 0 2 乙 1 0 1 0 3(Ⅰ)从甲机床这5天中随机抽取2天,求抽到的2天生产的零件次品数均不超过1个的概率;(Ⅱ)哪台机床的性能较好?23.(本小题满分12分)已知函数()ln af x x x=-,a ∈R . (Ⅰ)当0a >时,判断()f x 在定义域上的单调性; (Ⅱ)若()f x 在[1,e]上的最小值为2,求a 的值. (Ⅰ)证明OA OB ⋅的值与(Ⅱ)记直线MN 的斜率为福建省高考高职单招数学模拟试题1.C 2.C 3.C 4.C 5.A 6.A 7.A 8.B 9.C 10.D 11.D 12.B 13.D 14.D 15.1 16.1 17.5 18.20 19.解:(Ⅰ)因为2,4,60a b C ===,所以1sin 2ABCSab C =……………………………………………2分124sin 602︒=⨯⨯⨯=. ……………………………………4分(Ⅱ)因为2222cos c a b ab C =+- ……………………………………………6分 2224224cos60︒=+-⨯⨯⨯ 12=,所以c =. ……………………………………………8分201622=-. …………………………………8分21.解:(Ⅰ)零件的表面积610104 3.1410S =⨯⨯+⨯⨯ ……………………4分 725.6=(2cm ) ………………………………6分 0.07256=2m . 该零件的表面积0.072562m .(Ⅱ)电镀1000个这种零件需要用的锌为0.072560.111000⨯⨯ ………………………………8分 7.9816=(kg ). ………………………………10分所以制造1000个这样的零件,需要锌7.9816千克. 22.解:(Ⅰ)从甲机床这5天中随机抽取2天,共有(1,0),(1,2),(1,0),(1,2) ,(0,2),(0,0),(0,2),(2,0),(2,2), (0,2) 等10个基本事件, …………………………………..2分其中所取的两个零件均为合格品的事件有(1,0),(1,0),(0,0)等3个. …………..4分记“从甲机床这5天中随机抽取2天,抽到2天生产的零件次品数均不超过1个”为事件A ,则3()10P A =. …………………………5分(Ⅱ)因为=1x x =乙甲,2222221[(11)(01)(21)(01)(21)]0.45s =-+-+-+-+-=甲, ………7分2222221[(11)(01)(11)(01)(31)]0.85s =-+-+-+-+-=乙, ………9分所以22s s <乙甲,即甲台机床的性能较好. ………10分23.解:(Ⅰ)由题意:()f x 的定义域为(0,)+∞,且221()a x af x x x x+'=+=.………………2分0,()0a f x '>∴>,故()f x 在(0,)+∞上是单调递增函数.…………………5分(Ⅱ)因为2()x af x x+'=① 若1a ≥-,则0x a +≥,即()0f x '≥在[1,e]上恒成立,此时()f x 在[1,e]上为增函数,()min ()12f x f a ==-= , 2-=∴a (舍去). ……………7分 题21图② 若e a ≤-,则0x a +≤,即()0f x '≤在[1,e]上恒成立,此时()f x 在[1,e]上为减函数,()min ()e 12eaf x f ∴==-= 所以,e a =- ……………………9分 ③ 若e 1a -<<-,令()0f x '=得x a =-,当1x a <<-时,()0,()f x f x '<∴在(1,)a -上为减函数,当e a x -<<时,()0,()f x f x '>∴在(,e)a -上为增函数,()min ()ln()12f x f a a =-=-+=,e a =-(舍去), …………………11分 综上可知: e a =- . ……………………12分24.解:证明:(Ⅰ)依题意,设直线AB 的方程为2(0)x my m =+≠. ……………1分将其代入24y x =,消去x ,整理得 2480y my --=.…………2分从而128y y =-,于是2212126444416y y x x =⋅==, ………………3分 ∴1212484OA OB x x y y ⋅=+=-=-与1k 无关. ………………5分(Ⅱ)证明:设33( )M x y ,,44( )N x y ,. 则223434341121222212341234124444y y x x y y k y y y yk x x y y y yy y y y --+--=⨯=⨯=---+-.…………8分 设直线AM 的方程为1(0)x ny n =+≠,将其代入24y x =,消去x , 整理得 2440y ny --=∴134y y =-. 同理可得 244y y =-. ………………10分故341122121212444y y k y y k y y y y y y --++-===++, ………………11分 由(Ⅰ)知,128y y =-,∴1212k k =为定值. ………………12分第24题图。
(完整版)春季高考数学模拟试卷(综合训练含答案),推荐文档

f(x)=f (2-x) ,f(-1)=2f(1), 求 (1)f(x)的解析式,(2)当 f (x) 12 时,求 x 的取值范围
26.(7 分)已知 y= a · b ,其中 a =(cosx, 3 (sinx+cosx)), b =(2sinx,sinx-cosx),xR (1)把 y= a · b 化成 y=Asin(wx+ ),其中(A,w, )都是常数的形式
春季高考数学模拟试卷(综合训练 3)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷 1 至 4 页,第Ⅱ 卷 5 至 8 页。满分 100 分,考试时间 90 分钟。考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题,共 60 分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名.准考证号.考试科目用铅笔涂写在答题卡
22
5
83
46
28、(1)
(2)
5
5
)
(A) (-2,-1) (3,4)
(B)(-2,3) (-1,4)
(C) R 2.a>b 是 ac2>bc2 的(
)条件
(D) (- ,1) (3,)
(A)充分条件
(B) 必要条件
(C) 充要条件
(D)非充分非必要条件
3.方程 ax2+bx+c=0 ,(a<0)有两个实根-2,4,则不等式 ax2+bx+c<0 的解集为(
的中点,点 A 的坐标为( z
DD
28.(7 分)已知斜率为 1 的直线过椭圆
x2 3
y2 2
1 的右焦点 F2,交椭圆于 A 和 B 两点,
福建省春季高考高职单招数学模拟试题(十四)及答案
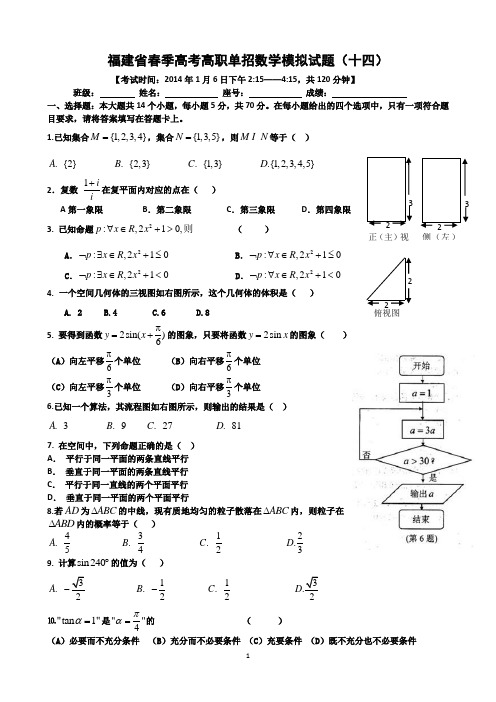
福建省春季高考高职单招数学模拟试题(十四)【考试时间:2014年1月6日下午2:15——4:15,共120分钟】班级: 姓名: 座号: 成绩:一、选择题:本大题共14个小题,每小题5分,共70分。
在每小题给出的四个选项中,只有一项符合题目要求,请将答案填写在答题卡上。
1.已知集合{1,2,3,4}M =,集合{1,3,5}N =,则M N 等于( ) .{2}A .{2,3}B .{1,3}C .{1,2,3,4,5}D 2.复数1ii+在复平面内对应的点在( ) A 第一象限 B .第二象限 C .第三象限 D .第四象限 3. 已知命题2:,210,p x R x ∀∈+>则 ( ) A .2:,210p x R x ⌝∃∈+≤ B .2:,210p x R x ⌝∀∈+≤C .2:,210p x R x ⌝∃∈+<D .2:,210p x R x ⌝∀∈+<4. 一个空间几何体的三视图如右图所示,这个几何体的体积是( )A. 2B.4C.6D.85. 要得到函数2sin()6y x π=+的图象,只要将函数2sin y x =的图象( ) (A )向左平移6π个单位 (B )向右平移6π个单位(C )向左平移3π个单位 (D )向右平移3π个单位6.已知一个算法,其流程图如右图所示,则输出的结果是( ).3A .9B .27C .81D7. 在空间中,下列命题正确的是( )A . 平行于同一平面的两条直线平行B . 垂直于同一平面的两条直线平行C . 平行于同一直线的两个平面平行D . 垂直于同一平面的两个平面平行8.若AD 为ABC ∆的中线,现有质地均匀的粒子散落在ABC ∆内,则粒子在ABD ∆内的概率等于( )4.5A 3.4B 1.2C 2.3D 9. 计算sin 240︒的值为( ).A 1.2B - 1.2CD ⒑"tan 1"α=是""4πα=的 ( )正(主)视侧(左)俯视图11. 下列函数中,在),0(+∞上是减函数的是( ).A xy 1=.B 12+=x y .C xy 2= .D x y 3l o g =⒓已知直线的点斜式方程是21)y x -=-,那么此直线的倾斜角为( ).6A π.3B π2.3C π 5.6D π 13.已知实数x 、y 满足04x y x y ⎧⎪⎨⎪+⎩≥≥0≥4,则z x y =+的最小值等于( ).0A .1B .4C .5D14、设椭圆的两焦点为F 1、F 2,过F 2作椭圆长轴的垂线交椭圆于点P ,若△F 1PF 2为等腰直角三角形,则椭圆的离心率为( )A 、22 B 、212-C 、22-D 、12-厦门市海沧中学高职高考 数学模拟试卷答题卡一、 请将选择题答案填入:二、 填空题:本大题共4个小题,每小题5分,共20分。
福建省春季高考高职单招数学模拟试题(六)及答案
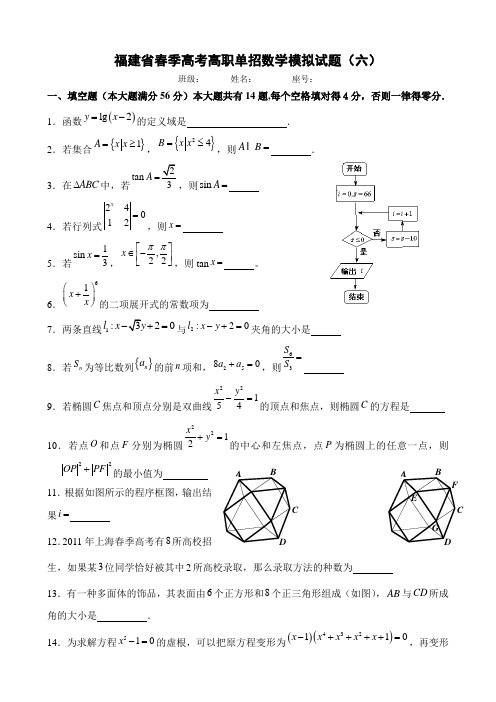
福建省春季高考高职单招数学模拟试题(六)班级: 姓名: 座号:一、填空题(本大题满分56分)本大题共有14题,每个空格填对得4分,否则一律得零分. 1.函数()lg 2y x =-的定义域是 . 2.若集合{}1A x x =≥,{}24B x x =≤,则A B = .3.在ABC ∆中,若tan A =,则sin A =4.若行列式24012x=,则x =5.若1sin 3x =,,22x ππ⎡⎤∈-⎢⎥⎣⎦,则tan x = 。
6.61x x ⎛⎫+ ⎪⎝⎭的二项展开式的常数项为 7.两条直线1:20l x +=与2:20l x y -+=夹角的大小是8.若n S 为等比数列{}n a 的前n 项和,2580a a +=,则63S S =9.若椭圆C 焦点和顶点分别是双曲线22154x y -=的顶点和焦点,则椭圆C 的方程是 10.若点O 和点F 分别为椭圆2212x y +=的中心和左焦点,点P 为椭圆上的任意一点,则22OP PF +的最小值为11.根据如图所示的程序框图,输出结果i =12.2011年上海春季高考有8所高校招生,如果某3位同学恰好被其中2所高校录取,那么录取方法的种数为13.有一种多面体的饰品,其表面由6个正方形和8个正三角形组成(如图),AB 与CD 所成角的大小是 . 14.为求解方程510x-=的虚根,可以把原方程变形为()()432110x x x x x -++++=,再变形DCBAG F EDC BA为()()()221110x x ax x bx -++++=,由此可得原方程的一个虚根为二、选择题(本大题满分20分)本大题共有4题,每题只有一个正确答案,考生应在答题纸相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.15.若向量()2,0a =,()1,1b = ,则下列结论正确的是 ( )A.1a b ⋅= B.a b = C.()a b b -⊥D.//a b16.函数()412x xf x -=的图象关于 ( ) A.原点对称 B.直线y x =对称 C.直线y x =-对称 D.y 轴对称17.直线1:2l y k x ⎛⎫=+ ⎪⎝⎭与圆22:1C x y +=的位置关系为 ( ) A.相交或相切 B.相交或相离 C.相切 D.相交18.若123,,a a a 均为单位向量,则1a =⎝⎭ 是123a a a ++= 的 ( )A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分又不必要条件 三、解答题(本大题74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.19.(本题满分12分)向量()sin 21,cos a x x =- ,()1,2cos b x = .设函数()f x a b =⋅.求函数()f x 的最小正周期及0,2x π⎡⎤∈⎢⎥⎣⎦时的最大值.20.(14分)某甜品店制作一种蛋筒冰激凌,其上部分是半球形,下半部分呈圆锥形(如图),现把半径为10cm 的圆形蛋皮等分成5个扇形,用一个蛋皮围成圆锥的侧面(蛋皮的厚度忽略不计),求该蛋筒冰激凌的表面积和体积(精确到0.01)21.(本题满分14分)本题共有2个小题,第1小题满分4分,第2小题满分10分.已知抛物线2:4F x y =.(1) ABC ∆的三个顶点在抛物线F 上,记ABC ∆的三边,,AB BC CA 所在直线的斜率分别为,,AB BC CA k k k ,若点A 在坐标原点,求AB BC CA k k k -+的值;(2) 请你给出一个以()2,1P 为顶点,且其余各顶点均为抛物线F 上的动点的多边形,写出多边形各边所在直线的斜率之间的关系式,并说明理由.说明:第(2)题将根据结论的一般性程度给与不同的评分.22.(本题满分16分)定义域为R ,且对任意实数12,x x 都满足不等式()()121222f x f x x x f ++⎛⎫≤⎪⎝⎭的所有函数()f x 组成的集合记为M .例如()f x kx b M =+∈.(1) 已知函数(),0,1,02x x f x x x ≥⎧⎪=⎨<⎪⎩证明:()f x M ∈;(2) 写出一个函数()f x ,使得()f x M ∉,并说明理由;23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8分, 第3小题满分6分.对于给定首项)00x a >>,由递推式112n n x x +⎛=+⎝()n +∈N 得到数列{}n x ,且对于任意的n +∈N ,都有n x >{}n x(1) 取05x =,100a =,计算123,,x x x 的值(精确到0.01),归纳出n x ,1n x +的大小关系;(2) 当1n ≥时,证明()1112n n n n x x x x +--<-;(3) 当[]05,10x ∈时,用数列{}n x4110n n x x -+-<,请你估计n ,并说明理由.福建省春季高考高职单招数学模拟试题(六)参考答案1、【解】()2,+∞.函数()lg 2y x =-的定义域满足20x ->,即2x >,所以函数()lg 2y x =-的定义域为()2,+∞.2、【解】{}12x x ≤≤.{}{}2422B x x x =≤=-≤≤,所以A B = {}12x x ≤≤.3、【解】11.因为tan 03A =>,则A ∠是锐角,于是2221111tan 199cos A A+=+==, 则29cos 11A =,cos A =,sin tan cos A A A =⋅==. (或由29cos 11A =得22sin 11A =,因为sin 0A >,则sin 11A =.)4、【解】1.242214012x x =⨯-⨯=,则22x =,1x =.5、【解】1arcsin3.因为1sin 3x =,,22x ππ⎡⎤∈-⎢⎥⎣⎦,则1arcsin 3x =. 6、【解】20.61x x ⎛⎫+ ⎪⎝⎭的二项展开式的通项为662166C C r r r r rr T x x x---+==. 令620r -=得3r =.所以61x x ⎛⎫+ ⎪⎝⎭的二项展开式的常数项为36C 20=.7、【解】12π.直线1l 的倾斜角为6π,直线2l 的倾斜角为4π,夹角为4612πππ-=. 8、【解】7-.设公比为q ,则4118a q a q =-,所以38q =-.63633118171S q q S q -==+=-+=--. 9、【解】22194x y +=.双曲线22154x y -=的顶点和焦点坐标分别是()和()3,0±.设椭圆C 的方程为22221x y a b +=,则由题设,3a ==2b =,所以椭圆C 的方程为22194x y +=.10、【解】2设(),P x y ,由()1,0F -得()2222221OP PF x y x y +=++++①因为点P 为椭圆上的任意一点,则2212x y =-,于是①式化为2222221212x OP PF x x ⎛⎫+=+++- ⎪⎝⎭223x x =++()212x =++.因为x ≤≤,而()212x ++图象的对称轴1x ⎡=-∈⎣,所以当1x =-时,22OP PF +有最小值为2.11、【解】7.根据如图所示的程序框图,所得的数据如下表所以输出的7i =.12、【解】168.第一步:从8所高校取2所高校的方法有28C 28=种,第二步:3位同学分配到2所高校的方法有2位同学被分配到同一所高校,所以有2132C C 6=种,所以录取方法的种数为286168⨯=种.13、【解】3π.AB 与CD 是正方形的边,则//AB EF ,//CD FG , 因为EF 和FG 是正三角形EFG 的两边,则AB 与CD 所成的角为3π. 14、【解中的一个.由题设,有()()43222111x x x x x ax x bx ++++=++++,即()()()432432121x x x x x a b x ab x a b x ++++=+++++++,对应相应项的系数得1,21a b ab +=⎧⎨+=⎩解得1,2a b ⎧=⎪⎪⎨⎪=⎪⎩或12a b ⎧=⎪⎪⎨⎪=⎪⎩解210x x +=,因为1004--∆=<,所以5i x =,同理,解21102x x ++=得中的一个.15、【解】2a b ⋅= ,A不正确;2a =,b = ,则a b ≠ ,B不正确;()1,1a b -=-,()()()1,11,10a b b -⋅=-⋅= ,所以()a b b -⊥,C正确;不存在实数λ,使a b λ= ,D不正确.故选C.16、【解】()41222x x x xf x --==-,则()()f x f x -=-,其图象关于原点对称.故选A. 17、【解】解法1.因为直线l 过点1,02⎛⎫-⎪⎝⎭,而点1,02⎛⎫- ⎪⎝⎭在圆22:1C x y +=的内部,所以直线与圆相交.故选D.解法2.圆心为()0,0,半径为1,圆心到直线的距离为11212kd k =≤=<,所以直线与圆相交.故选D.18、【解】若123a a a ++=,当123a a a ==时,得1a =⎝⎭,若133a ⎛⎫= ⎪⎪⎝⎭,当()231,0a a ==,则123a a a ++≠,所以133a ⎛= ⎝⎭是123a a a ++=的必要不充分条件.故选B.19、【解】()2sin 212cos f x a b x x =⋅=-+ sin 2cos2x x =+24x π⎛⎫=+ ⎪⎝⎭.所以,函数()f x 的最小正周期22T ππ==.因为0,2x π⎡⎤∈⎢⎥⎣⎦,所以52,444x πππ⎡⎤+∈⎢⎥⎣⎦,当242x ππ+=,即8x π=时,函数有最大值max y =.20、【解】设圆锥的底面半径为r ,高为h .由题意,圆锥的侧面扇形的周长为121045ππ⋅⋅=()cm ,圆锥底面周长为2r π()cm ,则24r ππ=,2r =()cm .圆锥的=()cm ,圆锥的侧面扇形的面积为11410202S ππ=⨯⨯=()2cm ,半球的面积为 2214282S ππ=⨯⨯=.该蛋筒冰激凌的表面积122887.96S S S π=+=≈()2cm ;圆锥的体积为21123V π=⨯⨯=()3cm ,半球的体积为3214162233V ππ=⨯⨯=()3cm ,所以该蛋筒冰激凌的体积为)1216157.803V V V π=+=≈()3cm .因此该蛋筒冰激凌的表面积约为287.96cm , 体积约为357.80cm . 21、【解】(1) 设(),B B B x y ,(),C C C x y .则B C CB AB BC CA B B C Cy y y y k k k x x x x --+=-+- ()2222444B C C B B B C C x x x x x x x x -=-+-()104B B C C x x x x =-++=⎡⎤⎣⎦.(2) ① 研究PBC ∆.B C C PB P PB BC CP B P B C C Py y y y y y k k k x x x x x x ----+=-+--- ()()()222222444B C C P B PB P BC C P x x x x x x x x x x x x ---=-+---()()()14B P BC C P x x x x x x =+-+++⎡⎤⎣⎦12P x ==. ② 研究四边形PBCD .4444B C C D B P D PPB BC CD DP x x x x x x x x k k k k ++++-+-=-+-0= ③ 研究五边形PBCDE .PB BC CD DE EP k k k k k -+-+ 44444B C C D B P D E E P x x x x x x x x x x +++++=-+-+12Px ==. ④ 研究2n k =边形122k PP P (),2k k +∈≥N ,其中1P P =.()12233421211k k P P P P P P P P k k k k --+-+- ()233421122114444k k P P P P P P P P x x x x x x x x -++++=-+-+- ()1211104k P x -⎡⎤=+-=⎣⎦.⑤研究21n k =-边形1221k PP P - (),2k k +∈≥N ,其1P P =.()1223342112111k k P P P P P P P P k k k k ----+-+- ()23342111221114444k k P P P P P P P P x x x x x x x x ---++++=-+-+- ()12111114k P x --⎡⎤=+-=⎣⎦.⑥研究n 边形12n PP P (),3k n +∈≥N ,其中1P P =.()122334111n n P P P P P P P P k k k k --+-+-()2334121114444n P P P P P P Pn P x x x x x x x x -++++=-+-+- ()()111111142n n P x --+-⎡⎤=+-=⎣⎦.22、【解】(1) 当120x x ≤≤时,()()1212121202244f x f x x x x x x x f ++++⎛⎫-=-=⎪⎝⎭,则不等式()()121222f x f x x x f ++⎛⎫≤⎪⎝⎭成立;当120x x ≤≤时,()()1212121202222f x f x x x x x x x f ++++⎛⎫-=-= ⎪⎝⎭,则不等式()()121222f x f x x x f ++⎛⎫≤ ⎪⎝⎭成立; 当120x x ≤≤,且1202x x +<时,()()1212121221120222224x xf x f x x x x x x f ++++⎛⎫-=-⋅=≥ ⎪⎝⎭,则 不等式()()121222f x f x x x f ++⎛⎫≤⎪⎝⎭成立; 当120x x ≤≤,且1202x x +≥时,()()12121212112022224x x f x f x x x x x x f ++++⎛⎫-=-=-≥ ⎪⎝⎭,则 不等式()()121222f x f x x x f ++⎛⎫≤⎪⎝⎭成立. 综合以上,不等式()()121222f x f x x x f ++⎛⎫≤ ⎪⎝⎭成立.所以()f x M ∈ (2) 例如函数()2f x x =-,取11x =-,21x =,则()()121222f x f x x x f ++⎛⎫- ⎪⎝⎭()()()110102f f f -+=-=-<. 所以()fx M ∉.也可以从()2f x x =-的图象看出,()()121222f x f x x x f ++⎛⎫> ⎪⎝⎭,不满足()()121222f x f x x x f ++⎛⎫≤ ⎪⎝⎭.所以()2f x x M =-∉.(3) 例如函数()2,1,, 1.x x f x x x ⎧≥⎪=⎨<⎪⎩满足()f x M ∈,()222limlim 1n n f n n n n →∞→∞==,()lim lim 1n n f nn nn →∞→∞--==--. 23、【解】(1) 1234.74, 4.67, 4.65x x x ===,猜想1n n x x +<; (2) ()1112n n n n x x x x +----1111222n n n n x x x x -⎛=--+ ⎝112n n x x -=-111122n n x x --⎛=+- ⎝==①因为n x >11110222n n n n n x x x x x +⎛⎛-=-== ⎝⎝,所以1n n x x +>. 由①式,()11102n n n n x x x x +----=<,所以()1112n n n n x x x x +--<-.(3) 由(2)()()()()1121120121111102222n n n n n n n n x x x x x x x x x x +----<-<-<-<<-<- , 所以只要()4011102nx x --<即可,于是()401210n x x >-,因为01012x x x ⎛⎫-= ⎝,所以42log 1015.1n ⎛>≈ ⎝⎭.所以16n =.。
福建省2018年高职单招数学试题 推荐

福建省2018年高职单招数学试题一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干后的括号内,本大题12小题,每小题4分,共48分)1、设全集},5,4,2{},5,2,1{},5,4,3,2,1{===B A I 则)()(B C A C I I =( )A 、}5,4,2,1{B 、}3{C 、}4,3{D 、}3,1{2、若a>b>0,则( ) A、ba 11> B、b a < C、33b a < D、b a 33> 3、已知,54)sin(-=+απ则( ) A、54)sin(=-απ B、53cos =α C、34tan =α D、35sec -=α 4、椭圆364922=+y x 的离心率是( ) A、25 B、313 C、553 D、35 5、函数x x f cos 21)(+=的值域是( )A、[0,2] B、[-1,2] C、[-1,3] D、[-1,1]6、平面内到两定点)0,5(),0,5(21F F -的距离之差的绝对值等于6的点的轨迹方程是( ) A、116922=-y x B、191622=-y x C、116922=+y x D、192522=+y x 7、把一枚均匀的硬币连掷3次,恰有两次正面向上的概率是( ) A、41 B、83 C、43 D、32 8、若二次函数22++-=mx x y 是偶函数,则此函数的单调递增区间是( )A、),0[+∞ B、]0,(-∞ C、),1[+∞ D、]1,(-∞9、已知点A(1,-1),B(-1,-7),C(0,x),D(2,3),且向量CD 与AB 平行,则x=( ).A、-4 B、4 C、-3 D、310、在等差数列}{n a 中,若10121=+a a ,则=+++111032a a a a ( )A、10 B、20 C、30 D、4011、下列命题中正确的是( )A、过平面外一点有且仅有一个平面与这个平面平行B、若三条直线两两相交,则这三条直线共面C、若直线L 与平面α平行,则直线L 与平面α上任何直线都平行D、已知三个平面γβα,,,若,,γβγα⊥⊥则βα//12、如果函数x y a log =在区间[1,9]上的最大值与最小值之和为2,那么a 的值是( )A、9 B、91 C、3 D、31 二、填空题(把答案写在横线上,本大题8小题,每小题5分,共40分) 1、函数)23lg(2x x y --=的定义域是____________________. 2、15tan 115tan 1+-的值等于_______________。
2017年高职高考数学模拟试[卷]和参考答案解析三
![2017年高职高考数学模拟试[卷]和参考答案解析三](https://img.taocdn.com/s3/m/e7baaf224a7302768e993979.png)
2017年高职高考数学模拟试题三数 学本试卷共4页,24小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(A)填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、选择题(本大题共15小题,每题只有一个正确答案,请将其序号填在答题卡上,每小题5分,满分75分)1、已知全集U =R ,M={x|x 21+≤,x ∈R},N ={1,2,3,4},则C U M ∩N= ( ) A. {4} B. {3,4} C. {2,3,4} D. {1,2,3,4}2、“G =ab ±”是“a,G,b 成等比数列”的 ( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件3、函数y=)32(log 3-x 的定义域为区间 ( )A. ),23(+∞B. ),23[+∞ C. ),2(+∞ D. ),2[+∞4、函数y=sin3xcos3x 是 ( ) A. 周期为3π的奇函数 B. 周期为3π的偶函数 C. 周期为32π的奇函数 D. 周期为32π的偶函数 5、已知平面向量与的夹角为90°,且=(k,1),=(2,6),则k 的值为 ( )A. -31B. 31C. -3D. 36、在等差数列{a n }中,若S 9=45,则a 5= ( ) A. 4 B. 5 C. 8 D. 107、已知抛物线y=mx 2的准线方程为y=-1,则m = ( ) A. -4 B. 4 C.41 D. -418、在△ABC 中,内角A 、B 所对的边分别是a 、b ,且bcosA=acosB ,则△ABC 是( ) A. 等腰三角形 B. 直角三角形 C. 等边三角形 D. 等腰直角三角形9、函数y=sin3x 的图像平移向量后,新位置图像的解析式为y=sin(3x-4π)-2,则平移向量= ( )A. (6π,-2) B. (12π,2) C. (12π,-2) D. (6π,2)10、设项数为8的等比数列的中间两项与2x 2+7x+4=0的两根相等,则该数列的各项的积为 ( )A. 8B. 16C. 32D. 64 11、过原点的直线与圆x 2+y 2+4x+3=0相切,若切点在第二象限,则该直线的方程是( )A. y=x 3B. y=-x 3C. y=x 33D. y=-x 3312、函数y=3sinx+cosx ,x ∈[-6π,6π]的值域是 ( ) A. [-3,3] B. [-2,2] C. [0,3] D. [0,2] 13、已知tan α=5,则sin α·cos α= ( ) A. -526 B. 526 C. -265 D. 265 14、椭圆4x 2+y 2=k 上任意两点间的最大距离为8,则k 的值为 ( ) A. 4 B. 8 C. 16 D. 32 15、若α、β都是锐角,且sin α=734,cos(α+β)=1411-,则β= ( ) A.3π B. 8πC. 4πD. 6π第二部分(非选择题,共75分)二、填空题(本大题共5小题,每小题5分,满分25分)16、第四象限点A(2,y)到直线3x+4y-5=0的距离为3,则y 的值为 . 17、顶点在圆x 2+y 2=16上,焦点为F(±5,0)的双曲线方程为 . 18、向量与的夹角为60°,||=2,||=3,则|+|= . 19、经过点M(1,0),且与直线x-2y+3=0垂直的直线方程为y= . 20、若log 3x+log 3y=4,则x+y 的最小值为 .三、解答题(21、22小题各10分,23、24小题各15分,满分50分) 21、解不等式 8x 2+2ax-3a 2≤0 (a ≠0)22、求以椭圆114416922=+y x 的右焦点为圆心,且与双曲线116922=-y x 的渐近线相切的圆的方程.23、如图,甲船以每小时230海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A 1处时,乙船位于甲船的北偏西105°方向的B 1处,此时两船相距20海里.当甲船航行20分钟到达A 2处时,乙船航行到甲船的北偏西120°方向的B 2处,此时两船相距210海里,问乙船每小时航行多少海里?沿什么方向航行?24、设数列{a n }是等差数列,)(21N k ka a ab kk ∈+++=(1)求证:数列{b n }也是等差数列. (2)若23132113211=++++++=b b b a a a a ,求数列{a n },{b n }的通项公式.高三高职类高考班第二次模拟考试数学 参考答案一、选择题BBDAC BCACB DCDCA 二、选择题(5×5´=25´)16、 -4 17、 191622=-y x 18、 19 19、 -2x+2 20、 18三、解答题(21、22小题各10分,23、24小题各15分,共50分) 21、解:原不等式可化为 (4x+3a)(2x-a)≤0∴x 1=a 43-,x 2=a 21(1)当a>0时,则a 21>a 43-故原不等式的解集为[a 43-,a 21](2)当a<0时,则a 21<a 43-故原不等式的解集为[a 21,a 43-]22、解:椭圆114416922=+y x 的右焦点为(5,0) 令016922=-y x ,则双曲线的渐近线方程为:x y 34±= 即4x+3y=0及4x-3y=0由题意知,所求圆的圆心坐标为(5,0) 半径为 r=2234|0354|+⨯+⨯=4故所求圆的方程为(x-5)2+y 2=1623、解:如图,在△A 2B 2A 1中,已知∠B 2A 2A 1=60°,A 1A 2=302×31=102,B 2A 2=102,则△A 2B 2A 1是等边三角形,故A 1B 2=102,∠B 2A 1A 2=60°∴在△B 2A 1B 1中,∠B 2A 1B 1=45°,A 1B 1=20 设B 1B 2=x 由余弦定理知,x 2=202+(102)2-2×20×102×cos45°=200 ∴ x=102易知△B 1A 1B 2为等腰直角三角形,即∠A 1B 1B 2=45° 故乙船每小时行驶31210=302海里,沿“北偏东30°”的方向航行.24、设数列{a n }的首项为a 1,公差为d ,则(1)a 1+a 2+…+a k =ka 1+d k k 2)1(-∴b k =kdk k ka 2)1(1-+= a 1+2)1(d k - 即b n =a 1+2)1(dn -当n =1时,b 1=a 1;当n>1时,b n -b n-1= [a 1+2)1(d n -]-[a 1+2)2(d n -]=2d∴数列{b n }是首项为a 1,公差为2d的等差数列.(2)由题意知:2322)113(13132)113(131311132113211=⨯-+-+=++++++=d a da b b b a a a a ,易得:d=21故a n =1+n 21,b n =n 4145+。
高考高职单招数学模拟试题及答案word版,〔4〕

〔1〕
上存在点, 使得平面, 点是线段的中点. …1 分 下面证明平面: 取
由题设知:,又,将代入, 得到:,即,所以,, 故椭圆方程
线段的中点, 连接, ………2 分
为,。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
∵点是线段的中点,
3 分 焦点 F1、F2 的坐标分别为〔-1,0〕和〔1,0〕,。。。。。。。。。。。。。。。。。。。。。。。 ∴是△的中位线. ………3 分
从得分在区间内的运动员中随机抽取人 , 求这人得分之和大于的概率. 大题共14 个小题,每题 5 分,共 70 分。〕
21.如下图,F1、F2 分别为椭圆 C:的左、右两个焦点,、B 为两个顶点,
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 答案 D A C
该椭圆的离心率为,的面积为. 〔Ⅰ〕求椭圆 C 的方程和焦点坐标; D C D C B B B B 二,填空题〔本大题共5个小题,每题4分,共2
〔C〕
共 4 个小题,每题 5 分,共 20 分〕
〔D〕
15. 函数的定义域是 . 16. 把函数的图象向左平移个单位,得到
y x O 1 12.已知,那么以下各式中,对任意不为零的实数都成立 的函数解析式为________________. 17. 某公司生产、、三种不同型号的
的是 〔 〕
轿车,产量之比依次为,为了检验该公司的产品质量,用分层抽样的方法
〔Ⅱ〕作与 B 平行的直线交椭圆于 P、Q 两点,,求直线的方程. 22. 〔10 0分。〕
分〕已知函数 〔1〕
15. 16. 17. 18. 三,解答题〔共五个大题,共 40 分〕
求其最小正周期;
19.〔10 分〕本小题主要考查等差数列、数列求和、不等式等基础
2018高职高考数学模拟考试题和参考答案解析一

2017年高职高考数学模拟试题数 学本试卷共4页,24小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(A)填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、选择题:本大题共15小题,每小题5分,满分75分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1、已知集合{1,1},{0,1,2},M N =-=则MN =( )A .{0 } B.{1 } C.{0,1,2 } D.{-1,0,1,2 } 2、函数y=的定义域为( ).(2,2).[2,2].(,2).(2,)A B C D ---∞-+∞3、设a ,b ,是任意实数,且a<b,则下列式子正确的是( )22..1.lg()0.22a b b A a b B C a b D a><-><4、()sin30︒-=( )11...22A B C D -5、=(2,4),=(4,3),+=a b a b 若向量则( ).(6,7).(2,1).(2,1).(7,6)A B C D --6、下列函数为奇函数的是( ) ..lg .sin .cos xA y eB y xC y xD y x ====7、设函数21,1()2,1x x f x x x⎧+≤⎪=⎨>⎪⎩,则f(f(—1))=( )A .-1B .-2C .1 D. 2 8、 “3x>”是“5x >”的( )A.充分非必要条件B.必要非充分条件C.充分必要条件D.非充分非必要条件 9、若向量a ,b 满足|a+b|=|a-b|,则必有( ).0.0.||||.0A a B b C a b D a b ====10、若直线l 过点(1, 4),且斜率k=3,则直线l 的方程为( ).310.310.10.10A x yB x yC x yD x y --=-+=--=-+=11、对任意x R ∈,下列式子恒成立的是( )22121.210.|1|0.10.log (1)02xA x xB xCD x ⎛⎫ ⎪⎝⎭⎛⎫-+>->+>+> ⎪⎝⎭12a +a =( ).2.4.24.24A B C D ---或或13、抛物线28yx =-的准线方程是( ).2.2.2.2A x B x C y D y ==-==-14、已知x 是1210,,,x x x 的平均值,1a 为123456,,,,,x x x x x x 的平均值,2a 为78910,,,x x x x 的平均值,则x =( )121212122332....552a a a a a a A B C a a D ++++15)( ).0.45.0.55.0.65.0.75A B C D二、填空题:本大题共5小题,每小题5分,满分25分.16、函数()3sin 4f x x =的最小正周期为__________17、不等式2280x x -->的解集为________18、若sin θ=35,tan θ< 0,则cos θ=_________ 19、已知等差数列{}n a 满足3285,30,a a a =+=则n a =_______20、设袋子内装有大小相同,颜色分别为红,白,黑的球共100个,其中红球35个,从袋子内任取1个球,若取出白球的概率为0.25,择取黑球的概率为____________三、解答题:本大题共4小题,第21~23题各12分,第24题14分,满分50分.解答须写出文字说明、证明过程和演算步骤. 21.(本小题满分12分),,,3(1)(2)cos B ABC a b c ABC C a π∆∆∠∠∠=∠=已知是中,A 、B 、C 的对边,b=1,c 求的值;求的值.22.(本小题满分12分){}{}(){}(){}21-12n n n =132n 6n+3(n=2,3,)b 1b 2b n S n n n n n n a a a a a =+-⋅⋅⋅已知数列的首项,数列的通项公式b =+n :证明数列是等比数列.求数列的前项和.23.(本小题满分12分)2212x=19A B AB C F (3,0)F (3,0)4D C D C D C xoy y +=-在平面直角坐标系中,直线与圆x 交于两点,,记以为直径的圆为,以点和为焦点,短半轴为的椭圆为。
2018年福建省高等职业教育入学考试数学卷

机密★本科目考试启用前2018年福建省高等职业教育入学考试数学试卷(面向普通高中考生)注意事项:请用0.5毫米黑色签字笔在答题卡上书写作答、在试上作答、答案走效一、单项选择题(本大题共14小题,每小题5分,共70分,在每小题列出的四个备选项中只有一个是符合题目要求的,请选出并将答题卡上对应的答案代码涂黑,错涂、多涂或未涂的均不得分)1、已知集合A={1,2,3},B={2,3,4},则AB()A、{2,3}B、{1,2,3}C、{2,3,4}D、{1,2,3,4}2、在区间[0,4]上随机抽取一个数x,则事件“x<1”发生的概率是()A、B、C、D、3、若向量a=(1,-1),b=(2,1),则a.b=()A、-3B、-1C、1D、34、不等式(x-1)(x+1)<0的解集是()A、(-1,1)B、[-1,1]C、D、5、函数的图像大致为()6、某单位有三个部门,其中甲部门有30人,乙部门有50人,丙部门有20人,现按部门用分层抽样的方法,从中抽取10人进行健康检查,则甲部门应抽取的人数为()A、2B、3C、4D、57、等比数列{}中,,则( )A、3 B、6 C、9 D、128一个几何体的三视图如右图所示,则该几何体可以是()A、棱柱B、棱锥C、圆柱D、圆锥9、A、B、C、D、110、双曲线的渐近线方程为()A、B、C、D、11、已知函数f(x)是偶函数,且当x>0时,,则f(-2)=( )A、-5 B、-3 C、3 D、512、函数f(x)=2sinxcosx的最小正周期是()A、B、C、D、13、若变量x,y满足约束条件则z=x-y的最小值为()A、-3B、-1C、0D、114、设m ,n表示两条不同的直线,表示平面,则下列命题中的真命题是()A、若α,则B、若α,则αC、若α,则D、若α,则α二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卡的相应位置上)15、复数:,则∣z∣=__________.16、函数,,则f(1)=______________.17、若抛物线的焦点为圆(-)的圆心,则a=______________.18、观察下列等式:…………据此规律,第n个等式可为____________.三、解答题(本大題共6小题,共60分,解答应写出文字说明、证明过程或演算步骤)19、(本小题满分8分)已知数列{}是等差数列、其前n项和为、且=1,=9(1)求数列{}的通项公式(Ⅱ)求的值20、(本小题满分8分)△ABC的内角A,B,C的对边分别为a,b,C,且a=4,b=,C=(1)求△ABC的面积(2)求c的值21、(本小题满分10分)甲、乙两人同时生产内径为10.10mm的一种零件、为了对两人生产的质量进行评比,从他们生产的零件中各抽取5件,量得其内径尺寸如下:分别计算这两组数据的平均数与方差.从计算结果看,谁生产的质量较高?22.(本小题满分10分)如图是某实心零件的直观图(单位:厘米),它的上部是正四棱锥(底面是正方形,侧面是全等的等腰三角形)形,下部是长方体形(I)求此零件的表面积;(Ⅱ)电镀这种零件需要用锌,已知每平方厘米用锌.千克,问电镀10000个这种零件需锌多少千克?23、(本小题满分12分)已知椭圆F经过点(,0),离心率为是(1)求F的方程;(I)过F右焦点的直线l交F于P,Q两点、若线段PQ的中点的積坐标为,求直线l 的方程24、(本小分12分)知函数在x=1处取得极值,a,b R(1)求a的值,并求f(x)的单调区()讨论f(x)的零点个数,并说明理由。
福建省春季高考高职单招数学模拟试题及答案

过椭圆的焦点作直线交椭圆于、两点,是椭圆另一焦x y F A B F 221236251+=福建省春季高考高职单招数学模拟试题班级: 姓名: 座号:一、选择题(本大题共14个小题。
每小题5分,共70分) 1, 下列各函数中,与x y =表示同一函数的是( )(A)xx y 2= (B)2x y = (C)2)(x y = (D)33x y =2,抛物线241x y -=的焦点坐标是( )(A) ()1,0- (B)()1,0 (C)()0,1 ( D)()0,1-3,设函数216x y -=的定义域为A,关于X的不等式a x <+12log 2的解集为B,且A B A = ,则a 的取值范围是( )(A)()3,∞- (B)(]3,0 (C)()+∞,5 (D)[)+∞,54,已知x x ,1312sin =是第二象限角,则=x tan ( ) (A)125 (B) 125- (C) 512 (D)512-5,等比数列{}n a 中,30321=++a a a ,120654=++a a a ,则=++987a a a ( ) (A)240 (B)240± (C) 480 (D)480± 6, tan330︒= ( )(A(B(C) (D)7,设b >a >0,且a +b =1,则此四个数21,2ab ,a 2+b 2,b 中最大的是( ) (A )b (B )a 2+b 2 (C)2ab (D )218,数列1,n +++++++ 3211,,3211,211的前100项和是:( ) (A)201200 (B)201100 (C)101200 (D1011009, 点,则△ABF 2的周长是 ( )(A ).12 (B ).24 (C ).22 (D ).1010, 函数sin 26y x π⎛⎫=+ ⎪⎝⎭图像的一个对称中心是( )(A )(,0)12π-(B )(,0)6π- (C )(,0)6π(D )(,0)3π11.已知0a >且1a ≠,且23a a >,那么函数()x f x a =的图像可能是 ( )12.已知()1f x x x=+,那么下列各式中,对任意不为零的实数x 都成立的是 ( )(A )()()f x f x =- (B )()1f x f x ⎛⎫=⎪⎝⎭(C )()f x x > (D )()2f x >13.如图,D 是△ABC 的边AB 的三等分点,则向量CD 等于 ( )(A )23CA AB + (B )13CA AB +(C )23CB AB +(D )13CB AB +14.如果执行右面的程序框图,那么输出的S 等于( )(A )45 (B )55 (C )90 (D )110 二,填空题(本大题共4个小题,每小题5分,共20分) 15. 函数()ln 21y x =-的定义域是 . 16. 把函数s i n 2y x =的图象向左平移6π个单位,得到的函数解析式为________________.17. 某公司生产A 、B 、C 三种不同型号的轿车,产量之比依次为2:3:4,为了检验该公司的产品质量,用分层抽样的方法抽取一个容量为n 的样本,样本中A 种型号的轿车比B 种型号的轿车少8辆,那么n = .18. 已知函数1(0x y a a -=>且1)a ≠的图象恒过点A . 若点A 在直线 上, 则12m n+的最小值为 .三,解答题(共六个大题,共60分)(A ) (B ) (C ) (D )ADB ()100mx ny mn +-=>19.(10分)已知等差数列{}n a 的前n 项和为n S ,且1310a a +=, 424S =. (1)求数列{}n a 的通项公式;(2)令12111n n T S S S =+++,求证:34n T <.20. (本小题满分10分)编号分别为12312,,,,A A A A 的12名篮球运动员在某次篮球比赛中的得分记录如下:(1) 完成如下的频率分布表:(2)从得分在区间[)10,20内的运动员中随机抽取2人 , 求这2人得分之和大于25的概率.21.如图所示,F 1、F 2分别为椭圆C :)0(12222>>=+b a by a x 的左、右两个焦点,A 、BABO ∆(Ⅰ)求椭圆C 的方程和焦点坐标;(Ⅱ)作与AB 平行的直线l 交椭圆于P 、Q两点,PQ =,求直线l 的方程.22.(10分)已知函数.cos sin sin )(2x x x x f += (1) 求其最小正周期; (2) 当20π≤≤x 时,求其最值及相应的x 值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
福建省高考高职2017-2018学年单招数学模拟试题准考证号 姓名(在此卷上答题无效)2017-2018学年福建省高等职业教育入学考试数学适应性试卷 (面向普通高中考生)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至3页,第Ⅱ卷4至5页.考试时间120分钟,满分150分.注意事项:1.答题前,考生务必在试卷、答题卡规定的地方填写自己准考证号、姓名.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.非选择题用0.5毫米的黑色签字笔在答题卡上书写作答.在试卷上作答,答案无效.3.保持答题卡卡面清洁,不折叠、不破损.考试结束,考生必须将试卷和答题卡一并交回.参考公式:样本数据12,,...,n x x x 的标准差 锥体体积公式s =222121()()()n x x x x x x n ⎡⎤-+-++-⎣⎦ (13)V Sh = 其中x 为样本平均数 其中S 为底面面积,h 为高 柱体体积公式球的表面积、体积公式 V Sh =24S R =π,343V R =π其中S 为底面面积,h 为高其中R 为球的半径第Ⅰ卷(选择题 共70分)一.单项选择题(本大题共14小题,每小题5分,共70分.在每小题给出的四个备选答案中,选出一个正确答案,并将答题卡上对应题目的答案标号涂黑)1.复数2i i +等于A .1i +B .1i -C .1i -+D .1i --2.已知函数()22xf x =+,则(1)f 的值为A .2B .3C .4D .6 3. 函数1x y x+=的定义域为 A .[)1,0- B .()0,+∞ C .[)()1,00,-+∞ D .()(),00,-∞+∞4.执行如图所示的程序框图,若输入的x 的值为3,则输出的y 的值为A .4B .5C .8D .10 5.若x ∈R ,则“x =1”是“x =1”的A .充分而不必要条件B .必要而不充分条件C .充要条件D . 既不充分又不必要条件6.下列函数中,在其定义域内既是奇函数,又是减函数的是A .3y x =- B .sin y x = C .tan y x = D .1()2xy =7. 函数y =⎝ ⎛⎭⎪⎫12x+1的图象关于直线y =x 对称的图象大致是8. 已知cos α=45,(,0)2απ∈-,则sin α+cos α等于A .-15B . 15C .-75D .759. 函数()23-+=x x f x的零点所在的一个区间是A .(-2,-1)B .(-1,0)C .(0,1)D .(1,2)10.若变量,x y 满足约束条件2,2,2,x y x y ≤⎧⎪≤⎨⎪+≥⎩则y x z +=2的最大值是A .2B .4C .5D .611.若双曲线方程为221916x y -=,则其离心率等于 A .53 B .54 C .45 D . 35 12.如右图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度h 随时间t变化的可能图象是13.过原点的直线与圆03422=+++x y x 相切,若切点在第三象限,则该直线的方程是A .x y 3=B .x y 3-=C .3y x =-D . 3y x = 14. 已知()f x 是奇函数,且当0x ≥时,2()f x x x =-+,则不等式()0xf x <的解集为A .(,1)(0,1)-∞-B .(1,0)(1,)-+∞C .(1,0)(0,1)-D .(,1)(1,)-∞-+∞2015年福建省高等职业教育入学考试数学适应性试卷 (面向普通高中考生)第Ⅱ卷(非选择题 共80分)注意事项:请用0.5毫米黑色签字笔在答题卡上书写作答.在试卷上作答,答案无效.二、填空题(本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置上) 15.若集合},0{m A =,}2,0{=B ,}2,1,0{=B A ,则实数=m .16.已知已知向量(3,1)=a ,(,3)x =-b ,若⊥a b ,则x =_________. 17.如图,在边长为5的正方形中随机撒1000粒黄豆,有200粒落到阴影部分,据此估计阴影部分的面积为 .18.若lg lg 2,x y +=则x y +的最小值为 .三、解答题(本大题共6小题,共60分.解答应写出文字说明,证明过程或演算步骤) 19.(本小题满分8分)已知△ABC 的内角,,A B C 的对边分别为,,a b c ,且2,4,60a b C ===. (Ⅰ)求△ABC 的面积; (Ⅱ)求c 的值.20.(本小题满分8分)在等比数列{}n a 中,公比2q =,且2312a a +=. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)求数列{}n a 的前2015项和2015S .21.(本小题满分10分)某机器零件是如图所示的几何体(实心),零件下面是边长为10cm 的正方体,上面是底面直径为4cm ,高为10cm 的圆柱. (Ⅰ)求该零件的表面积;(Ⅱ)若电镀这种零件需要用锌,已知每平方米用锌0.11kg ,问制造1000个这样 的零件,需要锌多少千克?(注:π取3.14)22.(本小题满分10分)题21图甲乙两台机床同时生产一种零件,5天中,两台机床每天的次品数分别是:甲 1 0 2 0 2 乙 1 0 1 0 3(Ⅰ)从甲机床这5天中随机抽取2天,求抽到的2天生产的零件次品数均不超过1个的概率;(Ⅱ)哪台机床的性能较好?23.(本小题满分12分)已知函数()ln af x x x=-,a ∈R . (Ⅰ)当0a >时,判断()f x 在定义域上的单调性; (Ⅱ)若()f x 在[1,e]上的最小值为2,求a 的值.24.(本小题满分12分)如图,已知抛物线24y x =的焦点为F ,过点(2 0)P ,且斜率为1k 的直线交抛物线于22(Ⅰ)证明OA OB ⋅的值与(Ⅱ)记直线MN 的斜率为题24福建省高考高职单招数学模拟试题2015年福建省高等职业教育入学考试 数学适应性试卷答案及评分参考(面向普通高中考生)说明:一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则.二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分. 三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数.选择题和填空题不给中间分. 一、单项选择题(本大题共14小题,每小题5分,共70分)1.C 2.C 3.C 4.C 5.A 6.A 7.A 8.B 9.C 10.D 11.D 12.B 13.D 14.D 二、填空题(本大题共4小题,每小题5分,共20分)15.1 16.1 17.5 18.20三、解答题(本大题共6小题,共60分.解答应写出文字说明,证明过程或演算步骤) 19.解:(Ⅰ)因为2,4,60a b C ===,所以1sin 2ABCSab C = ……………………………………………2分124sin 602︒=⨯⨯⨯=. ……………………………………4分(Ⅱ)因为2222cos c a b ab C =+- ……………………………………………6分 2224224cos60︒=+-⨯⨯⨯ 12=,所以23c =. ……………………………………………8分 20.解:(Ⅰ)因为公比2q =,且2312a a +=, 所以112412a a +=,解得12a =, ……………………………………………2分所以2nn a =. ……………………………………………4分(Ⅱ)由(Ⅰ)知12a =,2q =, 2015201512015(1)2(12)112a q S q --==-- …………………………………6分201622=-. …………………………………8分21.解:(Ⅰ)零件的表面积610104 3.1410S =⨯⨯+⨯⨯ ……………………4分 725.6=(2cm ) ………………………………6分 0.07256=2m . 该零件的表面积0.072562m . (Ⅱ)电镀1000个这种零件需要用的锌为0.072560.111000⨯⨯ ………………………………8分 7.9816=(kg ). ………………………………10分所以制造1000个这样的零件,需要锌7.9816千克.22.解:(Ⅰ)从甲机床这5天中随机抽取2天,共有(1,0),(1,2),(1,0),(1,2) ,(0,2),(0,0),(0,2),(2,0),(2,2), (0,2) 等10个基本事件, …………………………………..2分其中所取的两个零件均为合格品的事件有(1,0),(1,0),(0,0)等3个. …………..4分记“从甲机床这5天中随机抽取2天,抽到2天生产的零件次品数均不超过1个”为事件A ,则3()10P A =. (21)……5分(Ⅱ)因为=1x x =乙甲,2222221[(11)(01)(21)(01)(21)]0.45s =-+-+-+-+-=甲, ………7分2222221[(11)(01)(11)(01)(31)]0.85s =-+-+-+-+-=乙, ………9分所以22s s <乙甲,即甲台机床的性能较好. ………10分23.解:(Ⅰ)由题意:()f x 的定义域为(0,)+∞,且221()a x af x x x x+'=+=.………………2分0,()0a f x '>∴>,故()f x 在(0,)+∞上是单调递增函数.…………………5分(Ⅱ)因为2()x af x x+'=① 若1a ≥-,则0x a +≥,即()0f x '≥在[1,e]上恒成立,此时()f x 在[1,e]上为增函数,()min ()12f x f a ==-= , 2-=∴a (舍去). ……………7分 ② 若e a ≤-,则0x a +≤,即()0f x '≤在[1,e]上恒成立,此时()f x 在[1,e]上为减函数,()min ()e 12eaf x f ∴==-= 所以,e a =- ……………………9分 ③ 若e 1a -<<-,令()0f x '=得x a =-,当1x a <<-时,()0,()f x f x '<∴在(1,)a -上为减函数,当e a x -<<时,()0,()f x f x '>∴在(,e)a -上为增函数,()min ()ln()12f x f a a =-=-+=,e a =-(舍去), …………………11分 综上可知: e a =- . ……………………12分24.解:证明:(Ⅰ)依题意,设直线AB 的方程为2(0)x my m =+≠. ……………1分将其代入24y x =,消去x ,整理得 2480y my --=.…………2分从而128y y =-,于是2212126444416y y x x =⋅==, ………………3分第24题图∴1212484OA OB x x y y ⋅=+=-=-与1k 无关. ………………5分(Ⅱ)证明:设33( )M x y ,,44( )N x y ,. 则223434341121222212341234124444y y x x y y k y y y yk x x y y y yy y y y --+--=⨯=⨯=---+-.…………8分 设直线AM 的方程为1(0)x ny n =+≠,将其代入24y x =,消去x , 整理得 2440y ny --=∴134y y =-. 同理可得 244y y =-. ………………10分故341122121212444y y k y y k y y y y y y --++-===++, ………………11分 由(Ⅰ)知,128y y =-,∴1212k k =为定值. ………………12分。
