(完整版)分数乘法讲义
人教版六年级数学讲义-6分数乘法计算

分数乘法计算学生姓名年级学科授课教师日期时段教学核心分数乘法计算课型培训辅导/课堂讲解教学目标1、理解分数的乘法意义和性质;2、掌握分数乘法的运算方法.重点难点教学重点:分数与带分数或小数的乘法计算及分数简便运算;教学难点:带分数与小数的乘法计算法则及分数的基本性质.课前引导同学们.暑假玩得开心吗?马上进入新学期.是不是很期待啊?对于分数乘法计算法则.了解多少呢?我们今天就来探究学习一下分数乘法.比异分母分数加减法计算其实还更简单哦!知识导图课前检测1.把5米长的绳子平均分成6份.每份占全长的.每份长米.2.一块木头锯成两段需小时.如果同样的速度把木头锯成10段需要()小时.3.“小羊只数是大羊只数的”.()是单位“1”.A、小羊只数B、大羊只数C、无法确定4.把一根绳子剪成两段.第一段长米.第二段占全长的.那么()长.A.第一段B.第二段C.两段一样D.无法确定导学一:分数乘法的意义重点讲解 1:分数乘法意义(2) ) 1、分数乘整数与整数乘法的意义相同;2、一个数乘分数.就是求这个数的几分之几是多少.例 1. + + + =()×()=()例 2. 把3米长的木头平均锯成5份.每份占全长的.每份长 米.例 3. 有两根6米长的绳子.第一根剪去米.第二根剪去全长的 .那么剩下的第( )根长.课堂练习1. 有两根同样长的绳子.第一根剪去米.第二根剪去全长的 .那么剩下的( ) . A .第一根长B .第二根长C .两根一样长D .无法确定2. (1)12个是()(2)24的 是()(3) 的3倍是()重点讲解 2:分数乘法计算法则1、两个分数相乘.将分子相乘的积作分子.分母相乘的积作分母.能约分的要先约分再乘;2、整数与分数相乘.整数与分数的分子的积作分子.分母不变.能约分的要先约分再乘;3、带分数与分数(或带分数)相乘.先把带分数化成假分数.再利用分数乘以分数的运算法则进行计算.例 1.例 2. =例 3. (1)= (2)例 4. × ×课堂练习1. (1)(4) (5 (62.(1) × × (2) ×22×(3))导学二:分数乘法简便计算和混合运算重点讲解 1:分数乘法简算1、简算法:能约分的要先约分.再计算.计算结果一定是最简分数.2、乘法结合律、分配律的运用;3、乘法分配律和积不变规律的拓展运用.例 1. (1)(2)例 2. (1)(2)课堂练习1. (1)(2)2. (1)(2)重点讲解 2:稍复杂分数乘法简便计算1、运用乘法交换律、结合律和分配律进行计算;2、积不变规律和乘法分配律的综合拓展运用.例 1. (1)(2)课堂练习1. (1)(2)2. (1)(2)(3)重点讲解 3:分数乘法与加减混合运算1、分数乘法与加减混合运算跟整数乘法和加减混合运算法则一样;2、没有括号的混合运算.先算乘法.再算加减法.有括号的就先算括号里面的.再算括号外面的.例 1. +×例 2. 与的和乘36.积是多少?课堂练习1. 44-72×2. 与的积的21倍再减去2.差是多少?限时考场模拟: 10分钟完成1.一根1米的绳子.先剪去.又接上米后.还是1米.()2.3千克铁块的和1千克棉花的是一样重的.()3.运走一堆货物的与运走吨货物.运走的重量一定相等.()4.一个数乘一个真分数.所得的积一定小于这个数.()5. = = ()6.的分子加上21.要使分数的大小不变.分母应加上().A.27 B.21 C.36 D.307.一根绳子连续对折三次后.每段占全长的().A.B.C.D.8. 与比较. () .A.< B.> C.= D.无法确定9. 把5米长的钢筋.锯成每段一样长.锯了7次.每段是这根钢筋的().每段长()米.如果锯成2段需要3 分钟.那么锯成6段.需要()分钟.10. 小时=()分公顷=()平方米11. (1)(2)课后作业1.把3米长的铁丝平均分成8份.每份是这根铁丝的().每份长()米.2.一个正方形的边长是dm.它的周长是()dm.面积是()dm2.3. (1)小时=()分(2)千米=()米(3)公顷=()平方米(4)千米=()米(5)分钟=()秒(6)升=()毫升4. 六(1)班的男生人数是全班人数的.那么女生人数占全班人数的().5.把5米长的钢筋锯成每段一样长的小段.共锯6次.每段占全长的().每段长()米.6.与的计算结果相等的式子是().A.B.C.D.7. (1)○ (2)○ (3)○8.一根绳子被剪成两段.其中第一段长米.第二段占.比较两段绳子.(). A.第一段长B.第二段长C.一样长D.无法判断9. ()÷8=0.75===.10. 12×(+)=3+4=7.这是根据()计算的.A、乘法交换律B、乘法分配律C、乘法结合律11. 一块长方形菜地.长20米.宽是长的.求面积的算式是().A、20×B、20×+20C、20×(20×)12. (1)(2)(3)(4)1、了解学生课后掌握情况;2、课后是否按时完成作业;3、完成作业方面是否遇到什么困难.课前检测1. ;2.3解析:把木头锯成10段.即锯了9次.段数比次数多1.算出一次需要多少时间.再乘以9即可.3.B4.A解析:一根绳子剪成两段.主要看哪一段占的分率大.不要受具体量的干扰.所以选A导学一重点讲解 1:分数乘法意义例题1. ;4;解析:4个相加的简便运算2. ;3.一解析:两根6米长的绳子.有具体长度.可以算出来.再比较是第一根剩下的长.课堂练习1.D解析:两根同样长的绳子.没有具体长度.要分三种情况讨论.所以无法比较.2.(1)10;(2)16;(3)重点讲解 2:分数乘法计算法则例题1.2.3.(1)4;(2)0.6解析:分数乘带分数或小数.先把带分数或小数化成假分数或分数.再按照分数乘以分数的计算法则进行计算.4. 解析:三个分数连乘.可以交叉约分.使计算简便.课堂练习1.(1)26;(2);(3);(4)6;(5)1.4;(6)2.(1);(2)导学二重点讲解 1:分数乘法简算例题1.(1);(2)10解析:第(1)题中含有带分数.先化成假分数.再用乘法分配律的逆运算进行计算;第(2)题直接运用乘法分配律展开计算.2.(1);(2)17解析:第(1)题中把2016裂项成(2015+1).再用乘法分配律计算.第(2)题是易错题.可以用捆绑法.免得出错.把5×6看成一个整体.都跟括号里的两个分数相乘.课堂练习1.(1);(2)442.(1);(2)4解析:第(1)题可以把小数化成分数后.再运用乘法分配律计算.第(2)题是分数连乘.可以交叉约分.从而实现化简.使计算简便.重点讲解 2:稍复杂分数乘法简便计算例题1.(1)6300 ;(2)解析:第(1)题可以先运用积不变的性质.再运用分配律逆运算;第(2)题中后面两个分数相乘.可以交换分子的位置.使题中出现两个.再运用乘法分配律计算.课堂练习1.(1)10 ;(2)2.(1);(2)26;(3)20解析:第(1)题第一步没有简便运算.先算乘法.第二步再运用减法性质计算.第(2)和第(3)题都可以直接运用乘法分配律.重点讲解 3:分数乘法与加减混合运算例题1.解析:混合运算中.先算乘法.再算加法2.59解析:由题意得.列式为(+ )×36.计算可以用乘法分配律进行简算.课堂练习1.142.4解析:由题意得.列式为××21-2.计算即可.限时考场模拟1.对2.对解析:3千克铁块的和1千克棉花的都是千克3.错解析:这堆货物具体是多少吨不知道.所以无法比较.判断是错的.4.错5.错解析:运算顺序搞错.6.A解析:由分数的基本性质计算可得.答案选A.7.C8.D解析:这是个陷阱题.稍不小心就会出错.没有说明具体是多少.所以无法确定.9. ;;1510.36; 1250解析:单位换算中.由高级单位到低级单位转化.要乘这两个单位间的进率.11.(1);(2)课后作业1. ;2. ;3.(1)25;(2)375;(3)2500;(4)625;(5)40;(6)350解析:单位换算中.由高级单位到低级单位转化.要乘这两个单位间的进率.4.解析:把全班看作整体”1”.男生占全班人数的.则女生占全班人数的5. ;6.C解析:这是一道简便运算.可以把99裂项成(100-1).再用乘法分配律展开后.选C.7.(1)<;(2)>;(3)>8.B解析:一根绳子剪成两段.主要看哪一段占的分率大.不要受具体量米的干扰.所以选B.9.6;4; 12; 1510.B解析:一目了然.选B11.C解析:由长方形的面积公式可得.选C 12.(1);(2)70;(3);(4)。
人教版六年级数学讲义-5分数乘法

分数乘法解决问题学生姓名年级学科授课教师日期时段教学核心分数乘法解决问题课型培训辅导/课堂讲解教学目标(1)、理解分数乘法的意义.使学生掌握分数乘法的计算方法.并能运用这个方法能熟练、灵活地进行相关计算.和计算法则.倒数的认识.(2)、使学生能分辨清楚先乘后加减的运算顺序.并能熟练地应用乘法运算定律进行简便计算.(3)、引导学生准确地找到单位“1”.并能熟练地解答一步和二步的乘法应用题.重点难点重点:回顾和整理本单元的知识.牢记知识点.熟练计算和应用.难点:找准单位“1”.正确分析应用题的数量关系.课前引导1.上次学习的分数乘法的应用题都掌握了吗?2.今天我们将复习一下分数乘法的有关内容.你准备好了吗?知识导图课前检测1. ×5表示:(). ×表示:().2. kg的是()kg. m的是()m.3.计算.×100=()×=()×=()4. (判断)1吨的和3吨的一样重.()5. (判断)×=×=()6. 一种正方形方砖的边长是米.它的周长是多少?面积是多少?导学一:分数乘法重点讲解 1:分数乘整数1.分数乘整数的意义与整数乘法的意义().都是求().2.分数乘整数.用分数的()乘整数的积作分子.()不变.例 1. 小新、爸爸和妈妈一起吃一个蛋糕.每人吃个.3人一共吃多少个?列式:列式:课堂练习1. 看图写算式.).4. 一根包装带长米.6根这样的包装带长多少米?5. 小时=( )分. 千米=( )米6. 口算下面各题. ×2=2==重点讲解 2:一个数乘分数一个数乘几分之几.表示求这个数的几分之几是多少.例 1. 1桶水有12升.算式:12×3想:求3个12L.就是求12L 的( )倍是多少.桶是多少升?求: ( )+( )+( )=( )( 2.)×( )=( ×4表示( )3.算式:12×想:求12L的一半.就是求12L的是多少.桶是多少升?算式:想:求12L 的是多少.课堂练习米.2根长多少? 根长多少? 根长多少? 算式:()算式:()算式:()2. 列出乘法算式.(只列式.不计算) ①80厘米的 是多少? ② 的 是多少? 算式:()算式:()重点讲解 3:分数乘分数分数乘分数.用分子相乘的积作分子.分母相乘的积作分母.能约分的先约分.例 1.李伯伯家有一块 公顷的地.(1) 种土豆的面积是多少公顷?求: 1. 一根木棍长×× = × =× =×× =公顷的 是多少公顷?(2) 种玉米的面积是多少公顷?课堂练习1.×3表示:()× 表 示:().2. 先涂色表示计算结果.再填空.3. 口算 = =4. 一辆汽车每小时行90千米.从甲地到乙地行了 小时.甲乙两地相距多少千米?从乙地到丙地行了40分钟.乙、丙两地相距多少千米?重点讲解 4:一个数(0除外)乘大于1或小于的数一个数(0除外)乘大于1的数.积比原来的数().一个数(0除外)乘小于1的数(0除外).积比原来的数( ).例1.课堂练习1. 在○里填上“>”“<”或“=”.导学二:分数乘法应用题重点讲解 1:确定单位“1”(1)“的”字前面是单位“1”.(2)“是”、“占”、“相当于”、“比”的后面是单位“1”.例 1. 女生人数是男生的.把()看作单位“1”.例 2. 一袋大米.吃了.把()看作单位“1”. 例 3. 甲比乙多.把()看作单位“1”.课堂练习1.男生人数是女生的.把()看作单位“1”.2.一条路.修完了.是把()看作单位“1”.3.铅笔数量比圆珠笔多.把()看作单位“1”.重点讲解 2:求一个数的的几分之几是多少的应用题1.找分率句.写数量关系式.2.根据题目中的数量关系.按照:单位“1”×分率=分率对应量.列出算式求出所要求的对应量.例 1. 两班各收集多少个?例 2. 某班有男生20人.女生人数是男生的.求女生有多少人?列式:课堂练习1.甲乙两地相距420千米.一辆汽车行驶了全程的.行驶了多少千米?2.一个果园占地20公顷.其中的种苹果树. 种梨树.苹果树和梨树各种了多少公顷?重点讲解 3:比单位“1”多(或少)几分之几的应用题例 1. 学校春季给学生做体检.量得小东的体重是36千克.小远的体重比小东轻.小远的体重是多少千克?小东的体重比小远多多少千克?课堂练习1.一件西服原价180元.现在的价格比原来降低了 .现在的价格是多少元?2.希望小学三年级有学生216人.四年级的人数比三年级多 .四年级有学生多少人?重点讲解 4:连续求一个数的的几分之几是多少的应用题例 1.3个同学跳绳.小明跳了120下.小红跳了多少下?课堂练习1.小军的爷爷今年65岁.爸爸的年龄是爷爷的.小军的年龄是爸爸的.小军今年多少岁?2.公牛有30头.母牛的头数相当于公牛的.小牛的头数相当于母牛的.小牛有多少头?重点讲解 5:分数应用题综合运用例 1. 小明看一本书.共240页.第一天看了这本书的.第二天看了这本书的.小明这两天共看了多少页?还剩几页未看?第三天.他从第几页开始看起?例 2. 一袋大米20千克.第一次吃去它的.第二次吃去它的千克.还剩多少千克?课堂练习1.一堆煤重40吨.第一天运走这堆煤的.第二天运走吨.两天一共运了多少吨煤?2.果园里有梨树40棵.(1)如果桃树的棵数是梨树的.那么桃树有多少棵?(2)如果桃树的棵数比梨树多.那么桃树有多少棵?(3)如果桃树的棵数比梨树少 .那么桃树有多少棵?(4)如果桃树的棵数比梨树少.那么桃树比梨树少多少棵?限时考场模拟1.2. 两根都是2米长的绳子.第一根截去它的.第二根截去米.比较两根绳子余下的部分.则()A. 一样长B. 第一根长C. 第二根长D. 不能确定3. 一根绳子截成两根.一段占全长的.一段长米.比较这两根绳子.则()A. 一样长B. 第一根长C. 第二根长D. 不能确定4. 把5米长的绳子平均分成6段.每段长()米.每段占全长的.5.一根铁丝长米.截去 .还剩下.截去米.还剩下()米.6.修一条路.原计划投资56万元.实际比原计划节约投资 .修这条路实际比原计划节约投资多少万元?7.一块平行四边形的木板.高是米.底比高长 .这块木板的面积是多少平方米?8.修一条长400米的环形跑道.已经铺好了150米.再铺多少米就正好铺完了全长的?课后作业1. +++ =()×()=()2. 12个是().24的是().3. 的倒数是().()和互为倒数.4. ×()= ×()=0.5×()5.在○里填上>、<或=6.边长分米的正方形的周长是()分米.7.六(1)班有50人.女生占全班人数的.女生有()人.男生有().8.(判断)60的相当于80的 .()9.(判断)冰箱的数量相当于电视机的,冰箱的数量比电视机少.()10.看图列式计算.11.某鞋店进来皮鞋600双.第一周卖出总数的.第二周卖出总数的.⑴两周一共卖出总数的几分之几?⑵两周一共卖出多少双?⑶还剩多少双?12.六年级同学给灾区的小朋友捐款.六一班捐了500元.六二班捐的是六一班的.六三班捐的是六二班的 .六三班捐款多少元?13.甲乙两个仓库.甲仓存粮30吨.如果从甲仓中取出放入乙仓.则两仓存粮数相等.两仓一共存粮多少千克?1.上次的课后作业完成了吗?还有什么不懂得吗?2.今天学习的内容是复习分数的乘法.你掌握了吗?3.回去记得完成课后练习.做到温故而知新.课前检测1.5个的和是多少.的是多少.2. .3.40. .4.对5.错6. (米). (平方米)导学一重点讲解 1:分数乘整数例题1.解析:.课堂练习1. . .. .2.4个的和是多少3.1. ..3. .4. 米解析:求6根同样长的包装就是求6个是多少.用乘法计算. (米)5.24.700解析: 把小时转换分钟.用乘法.×60=24(分)把千米转换米.用乘法. ×1000=700(米) 6. ,, ,重点讲解 2:一个数乘分数1.. 2. .. 例题1.3. . 12×.课堂练习重点讲解 3:分数乘分数例题1. 公顷. 公顷解析: (1)求 公顷的 .就是把 公顷平均分成5份.取其中的1份.也就是把1公顷平均分成(2×5)份.取其中的1 份.即. (2)(公顷)课堂练习1.3个 的和是多少.的 是多少.2. .解析: = . × =3. .. . . .4.75千米.60千米解析: (千米). . (千米) 重点讲解 4:一个数(0除外)乘大于1或小于的数例题1. . . . .解析:在分数乘法的时候需要把结果约成最简分数.课堂练习1.<.>.=.<.>.<导学二重点讲解 1:确定单位“1”例题1.男生的人数解析: “是”、“占”、“相当于”、“比”的后面是单位“1”.所以单位“1”是男生的人数.需要具体.2.一袋大米3.乙课堂练习1.女生的人数2.一条路3.圆珠笔数量重点讲解 2:求一个数的的几分之几是多少的应用题例题1.一班:60个.二班:72个解析:一班:180×=60(个).二班:180×=72(个) 2.课堂练习1.420×=300(千米)2.8公顷. 5公顷解析:苹果树:20×=8(公顷).梨树:20×=5(公顷)重点讲解 3:比单位“1”多(或少)几分之几的应用题例题1.小远体重: 30(千克).相差重量: 6(千克)解析:小远体重:36×=30(千克).相差重量:36-30=6(千克)或36×=6(千克)课堂练习1.144元解析:比单位“1”少.用1- 表示.180×(1- )=144(元)2.264(人)解析:比单位“1”多.用1+ 表示.216×(1+ )=264(人)重点讲解 4:连续求一个数的的几分之几是多少的应用题例题1.50(下)解析:先求120的是多少.再求“120的”的是多少.最后用连乘的方法.120××=50(下)课堂练习1.12岁解析:先求65的是多少.再求“65的”的是多少.最后用连乘的方法.65××=12(岁)2.16(头)解析:先求30的是多少.再求“30的”的是多少.最后用连乘的方法.30××=16(头)重点讲解 5:分数应用题综合运用例题1.140(页).100(页).141(页)解析:两天共看页数240×=140(页).还剩页数240-140=100(页). 第3天.从第141页开始看起140+1=141(页)2.(千克)解析:20×-= (千克)课堂练习1. (吨)解析:40×+= (吨)2.(1)40×=24(棵). (2)40×=64(棵).(3)40×=16(棵). (4)40×=24(棵)限时考场模拟.2.29.571.2.C解析: 第一根剩下的:2×(1-)= 米.第二根剩下的:2- = 米3.C解析: 因为第一段占全长的.所以第二段段占全长的.4. .5. .解析: 1- = . - =6.49(万元)解析:56×(1- )=49(万元)7. (平方米)解析:底:×(1+ )= 米.面积:×= (平方米) 8.90(米)解析:400×-150=90(米)课后作业1. .3.2.10.163. .44. ..0.65.>.=.<6.2解析: ×4=2(分米) 7.女生20人.男生: 30人解析: 女生:50×=20(人).男生:50-20=30(人)8.对解析: 60×=24. 80×=249.对10.160(米).306(吨)解析:400×(1- )=160(米).168×(1+ )=306(吨)11.(1).(2)345双.(3)255双解析:(1)+= .(2)600×(+ )=345(双).(3)600-345=255(双)12.450元解析:500×× =450(元)13.一共有54000千克.解析:甲仓库现在的存粮=乙仓库现在的存粮:30×(1- )=27(吨).两个仓库的总数没变.所以一共有27×2=54(吨).54吨=54000千克.。
分数乘法讲义

教学内容
教学内容
教学内容
教学内容
第一课时分数乘整数
一、旧知铺垫
1、计算下列各题
+++++
过程要求:
(1)写出计算过程。
(2)说一说分数加法的计算方法。
2、想一想,能不能把++改写成乘法算式呢?
二、探索新知
1、例1
(1)根据题意列出解答算式:
++==
×3=
(2)探索分数乘整数的计算方法。
×=
1发现分数乘分数的计算方法。
2引导学生观察算式和结果,看一看其中的联系。
×==
想一想:虚线框中,应该是怎样的一个计算过程呢?
×==
然后,联系以上的算式,让学生说一说计算方法。
分数乘分数,用分子相乘的积作分子,分母相乘的积作分母。
问题二:小时粉刷多少呢?(引导学生列出算式)
×==
总结分数乘分数的计算方法
(3)一辆汽车,每小时行驶全程的,4小时行驶全程的几分之几?
二、探索新知
1、教学例3。
问题一:小时粉刷这面墙的几分之几?怎样列式?
×
分数乘分数怎样计算?
×表示什么?使学生理解×,就是求的是多少,也就是说把平均分成4份,取其中一份是多少?
画示意图分析。
每小时粉刷这面墙的
这面墙的的
从图上可以看出,这面墙的的,是占整面墙的
1
×10×7==60(kg)
1
2、课本练习二第1、2题
四、课堂练习设计
1、填空:看图写算式
++=
++=
×( ) =
2、计算
六年级数学上册精品讲义(完整版)

第1讲分数乘法一,整数、小数乘分数【知识梳理】1.分数乘分数的计算方法:用分子相乘的积作分子,用分母相乘的积作分母。
用字母表示为:b d b da c a c⨯⨯=⨯()0,0a c≠≠【注意】计算分数乘分数时,为了简便,可以先约分,再计算。
2.分数乘整数:求几个相同加数和的运算;分数乘分数的计算方法同样适用于分数乘整数,即先把整数化为分母是1的分数,再计算。
3.小数乘分数的计算方法:(1)把小数化成分数计算;(2)如果所乘分数能化成有限小数,也可以把分数化成小数计算;(3)小数和分母能约分的,先约分再计算比较简便。
例1.计算:(1)7384⨯;(2)7489⨯;(3)3475⨯;(4)314×718;例2.计算:(1)126×213;(2)292314⨯;(3)211135⨯;(4)533174⨯.例3.计算:(1)71339⨯;(2)51012⨯. (3)133×9;(4)2897⨯.例4.计算:422417⨯ 321615⨯ 659⨯ 1430⨯例5:某食堂原有煤212吨,烧去了85,还剩几分之几?剩下多少吨?例6.一块冰,每小时失去其质量的一半,8小时后的质量为kg 165,一开始这块冰的质量是多少千克? 例7. 1. 判断题.(1)小数乘分数,可以把小数化成分数计算,但不可以把分数化成小数计算 ( ) (2)小数乘分数的意义就是求这个小数的几分之几是多少 ( )2.用三种方法计算2.4×433.计算下面各题:__________ ____________________ ____________________ __________试一试: 1、分数乘以整数112×11= 92×27= 6017×8= 509×8= 187×3= 9825×7=52×2500= 3×97= 127×6= 174×5= 545×6= 5027×2=2、分数乘以分数85×154= 209×215= 56×35= 257×1415= 113×21=2811×338= 3920×1513= 187×143= 165×158= 3925×3013=3. 分数乘以小数 (1)把小数画成分数0.6 1.8 0.45 0.125 2.5(2)把分数化成小数43 57 83 21 41 87 52(3)计算0.8×43 57×1.5 83×2.4 2.6×21 3.5×75 0.45×530.625×154 8.8×225 0.56×7552×0.15 87×0.24 2.6×1310达标检测一、计算(直接写出得数)73× 65 = 95 × 43 = 258 × 245 = 107 × 143=87 × 73= 2120 × 83 = 209 × 154 = 145 × 2521=二、填空1、看图列式计算( )×( )=( )( )×( )=()2、先涂色表示计算结果,再填空。
人教版六年级上册数学第一单元 分数乘法 课件(共30张PPT)

练习3:计算下列各题
2
5
3
6
5 14 1 2 2 7 15 1 3 3
11 2 5 2 51 5 43 43 23 6 3 6 25 1 2 5 10 57 9 171 7
10 7
分数乘分数三部曲: 1、将带分数化成假分数 2、看分子和分母能否约分 3、分子乘分子,分母乘分母
答:长方形桌布比正方形桌布的面积多 5 m2
18
练习8:折一只千纸鹤要用 3 张纸。他们一共用了多少张
8
纸?
葫芦娃:15 3 = 45(张) 88
蜡笔小新:23 3 = 69(张) 88
一共:45 + 69 = 57(张) 884
答:他们一共用了
57 4
张纸
我折了15只
我折了23只
能力提升
一块冰,每小时融化掉其质量的一半,4小时后其质量为 5 千克,那
7
13
分数乘整数三部曲:1、先把分数化为最简分数 2、再看整数能否和分母约分 3、用约分后的整数乘分数的分子做分子,分母不变
例题2:瓶子中装有一种孢子,每小时分裂一次,体积增大 一倍。如果最初孢子的体积占瓶子的 ,3小时后孢子的体 积占瓶子的几分之几?
乘2
乘2
乘2 ?
三小时
例题2:瓶子中装有一种孢子,每小时分裂一次,体积增大 一倍。如果最初孢子的体积占瓶子的 ,3小时后孢子的体 积占瓶子的几分之几?
例题7:计划修一条2.7千米的路,已经修了这条路的 2 ,
已经修了多少千米?
3
2.7 2 =1.8(千米) 3
答:已经修了1.8千米
求一个数的几分之几用乘法 小数能和分母约分的先约分再相乘
练习7:王老师家八月份用水4.5吨,九月份的用水量是八 月份的 8 。九月份用水多少吨?
《分数乘法》课件

计算$frac{2}{3} times frac{3}{4}$,分子为 $2 times 3 = 6$,分母为$3 times 4 = 12$,约分为$frac{6}{12} = frac{1}{2}$。
分数乘法的简便算法
整数与分数相乘
将整数与分数的分子相乘,分母 保持不变。
举例
计算$2 times frac{3}{4}$,分子
(2/5) × (3/4) = 3/10
两个分数相乘,分子乘分子,分母乘分母, 结果是最简分数。
5/6 × 3/5 = 1/2
两个分数相乘,分子乘分子,分母乘分母, 结果是最简分数。
(5/8) × (4/7) = 20/56
两个分数相乘,分子乘分子,分母乘分母, 结果是最简分数。
THANK YOU
此外,分数乘法还可以用于计算化学键的强度和稳定性。 例如,在分子力学中,分数乘法可以用于计算分子结构和 分子间相互作用力。在材料科学中,分数乘法可以用于计 算材料的物理性质和化学性质。
04
分数乘法的扩展知识
分数乘法的推广
分数乘法的定义
分数乘法是指将一个分数的分子与另一个分数的分子相乘,分母 与分母相乘。
为$2 times 3 = 6$,分母仍为
$4$,结果为$frac{6}{4}
=
frac{3}{2}$。
分数乘法的注意事项
注意运算符号
分数乘法中,正正得正,负负得正, 正负得负。
注意运算顺序
先乘除后加减,有括号先算括号内的 。
03
分数乘法在生活中的应用
分数乘法在数学中的应用
分数乘法在数学中有着广泛的应用,它涉及到许多数学概念 和问题。例如,在几何学中,分数乘法可以用于计算面积和 体积。在统计学中,分数乘法可以用于计算概率和频率。
分数乘法(讲义)

分数乘法(讲义)小学数学教案主题:分数乘法适用年级:四年级教学目标:1. 理解分数乘法的概念;2. 掌握分数乘法的运算方法;3. 能够运用分数乘法解决实际问题。
教学内容:1. 什么是分数乘法?分数乘法是指将两个或多个分数相乘的运算。
例如:⅔ × ½ = 1/32. 如何计算分数乘法?方法一:直接将分子相乘,分母相乘得到分数积即可。
例如:2/3 × 1/2 = (2 × 1) / (3 × 2) = 1/3方法二:将分数化为带分数,再进行乘法运算。
例如:2/3 × 1/2 = 2 ÷ 3 × 1 ÷ 2 = 4 ÷ 6 = 2/3方法三:将分数化为小数,再进行乘法运算。
例如:2/3 × 1/2 = 0.666… × 0.5 = 0.333…3. 几个实际的分数乘法例子①. 小明有5/6个苹果,小红有2/3个苹果,两人共有多少苹果?解:小明和小红共有的苹果数为:5/6 × 2/3 = (5 × 2) / (6 × 3) = 10/18 = 5/9答:两人共有5/9个苹果。
②. 三个人所分得的一块披萨面积分别为2/5、3/5和1/5,共分到多少面积?解:三个人分得的披萨面积之和为:2/5 + 3/5 + 1/5 = (2 + 3 + 1) / 5 = 6/5答:三个人共分到6/5面积的披萨。
③. 一种糖果每盒有3/4磅,共有10盒,求这种糖果的总重量。
解:一盒这种糖果的重量为:3/4磅十盒这种糖果的总重量为:3/4 × 10 = 30/4 = 7.5磅答:这种糖果的总重量为7.5磅。
教学步骤:1. 引入:玩海盗游戏,分数相乘。
2. 提出问题:如果有⅔的小朋友去绿地玩,而⅕的小朋友去了华山游玩,(⅔ × ⅕ = ?)会有几个小朋友既去了绿地,又去了华山?3. 让学生依次进行计算。
第一讲分数乘法讲义(完整资料).doc

4、一个平行四边形的高是 分米,它的底是高的 ,这个平行四边形的面积是多少?
【家庭作业】
1、在○里填上“>”、“<”或“=”。
×10○ ×1○ ×0○
2、 + + + =( )×( )=( )
3、 + + +……+ =( )×( )=( )
100个
3、实验小学有一长方形花坛,花坛的宽是 米,长是宽的20倍,花坛的面积是多少平方米?
(5)一个长方形正好可以平均分割成六个边长是 米的正方形,求这个长方形的面积和周长。
【最新整理,下载后即可编辑】
个性化教学辅导教案
学科 数学 任课教师: 授课时间:2014 年 月 日( ) 部长审核签字:
姓名
年级
课题
分数乘整数及一个数乘分数
第_ _课
教学
目标
1、结合具体情境,借助示意图理解分数乘整数的意义,渗透数形结合思想,并借助转化的方法理解分数乘整数的算理,并能正确地进行计算,提高计算能力。
【例1】小明、小红和小芳是三个好朋友,一天小明过生日买了一个蛋糕,他们三人一起吃蛋糕,每人吃 个,3人一共吃多少个?
【小结】1、分数乘整数的意义与整数乘法的意义相同,都是求几个相同加数和的简便运算。
2、分数乘整数的计算方法:用分子乘整数的积作为分子,分母不变。能约分的,可以先约分,再计算。
【例2】计算
第二部分
【课堂练习】
练一、
1、 ×7表示;
2、 + + =( )×( )=( ) + + =( )×( )=( )
3、计算。
×6 ×8 12×
4、解答下列应用题。
分数乘法讲义

课前检测:回顾整数乘法和小数乘法运算知识梳理:1、什么叫乘法多个相同加数求和的简便运算例:7+7+7+7+7=7×56+6+6+6+6=6×52、小数乘法和分数加法推导分数乘法一个物体每分钟移动0.6千米,5分钟移动多少千米?0.6×5=3(千米)分析:0.6千米=610千米=600米 600×5=3000米即:610×5=3(千米)另:610×5=610+610+610+610+610=6+6+6+6+610=5×610=3010=3(千米)总结:分数乘以整数,分母不变,分子和整数相乘。
3 8×6=3×63=94能约分的时候,要先约分,使计算简便3、分数乘以分数课本第10页,例3我每小时刷这面墙的15,14小时刷这面墙的几分之几?拿出一张纸,用它表示这面墙,涂出它的15涂出1的1是多少想:14小时刷这面墙的几分之几,就是求15的14是多少 列式:15×14=1×15×4=120 总结:分数乘以分数,应该分子和分子相乘,分母和分母相乘。
例4:蜂鸟是目前所发现的世界上最小的鸟,也是唯一能倒飞的鸟,蜂鸟每分钟可飞行310千米,23分钟能飞行多少千米? 310×23=3×2510×3=15(千米) 注:分数和分数相乘,能约分的要先约分,使计算简便课外拓展:1、单位换算45千米=( )米 45×1000=800米 56小时=( )分 56×60=50分2、一个不为0的数乘以大于1的数,积比原数大乘以小于1的数,积比原数小。
在分数乘法中同样适用,即一个数乘以真分数,积小于这个数,一个数乘以大于1的假分数,积大于这个数。
3、分数乘整数的意义和整数(或分数)乘分数的意义比较:分数乘整数的意义表示几个相同的分数相加的和整数(或分数)乘分数的意义表示一个数的几分之几是多少4、分数后带单位和没带单位的问题34吨和34是不能进行比较的 一段绳子,用了34,还剩34米,问用去的和剩下的谁更长?(无法比较)分数乘法的简便运算乘法交换律:a ×b =b ×a乘法结合律:a ×(b ×c)=(a ×b)×c乘法交换律:a ×(b +c )=a ×b +a ×c。
第一单元:分数乘法(讲义)-2024-2025学年人教版六年级数学上册

分数乘法(思维导图+知识梳理+典例分析+高频真题+答案解析)【分数乘法-知识点归纳】1、分数乘法的意义:分数乘法的意义与整数乘法的意义相同,就是求几个相同加数和的简便运算.2、乘积是1的两个数叫做互为倒数.3、分数乘法法则:(1)带分数乘法:先把带分数化成假分数,然后再乘.结果是假分数时,要把假分数化成带分数或整数.(2)(2)分数乘以分数:用分子相乘的积作为分子,用分母相乘的积作为分母.为了使计算简便,在计算的过程中,能够约分的,要约分.(3)分数乘以整数或整数乘以分数:由于任何整数(0除外)都可以化成分母是1的假分数,分数乘以整数或整数乘以分数,都可以转化成分数乘以分数的形式.因此,在计算中,是用分数的分子和整数相乘的积作为分子,分母不变.在乘的过程中,如果有可以约分的数,可以先约分,这样,可以使计算的数字缩小,从而使计算变得简便.【分数乘整数-知识点归纳】1、分子乘整数,可以求出一共有多少个这样的分数单位,而分数单位的个数其实就是分子乘整数的积,因此整数乘分子作分子。
求几个分数单位的和,分数单位不变,也就是分母不变。
2、分数乘整数的意义:分数乘整数,也是表示几个相同加数相加,与整数乘法的意义相同。
3、分数乘整数的计算方法:分数乘整数,用分子乘整数的积作分子,分母不变。
其实就是计算分数单位的个数。
【整数乘分数-知识点归纳】1、一个数乘分数的意义就是求一个数的几分之几是多少。
2、“一个数乘分数”指的是第二个因数必须是分数,不能是整数。
(第一个因数是什么都可以)3、方法总结;(1)、整数与分数相乘,用分数的分子与整数相乘,分母不变;(2)、计算时能约分的可以先约分再计算出结果。
【分数乘分数-知识点归纳】分数乘法的计算法则1、整数和分数相乘:整数和分子相乘的积作分子,分母不变。
2、分数和分数相乘:分子相乘的积作分子,分母相乘的积作分母。
【典例1】在“世界无烟日”健康知识竞赛中,小星答对了50道题,小铭答对的题数比小星少15。
第1讲 分数乘法-六年级上册数学讲义(含答案)
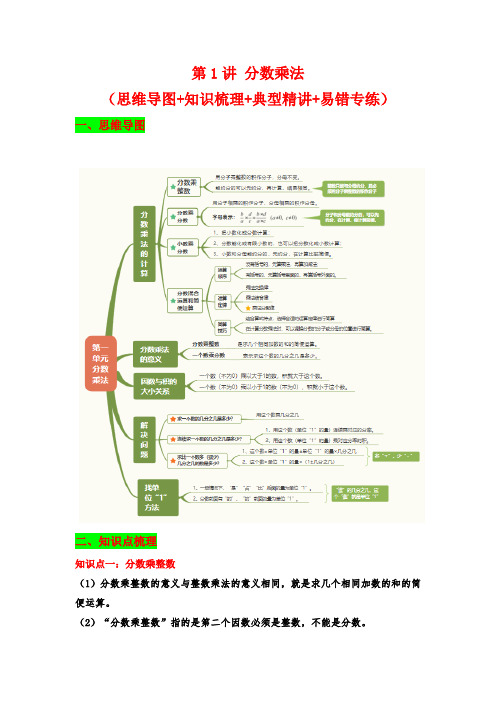
第1讲分数乘法(思维导图+知识梳理+典型精讲+易错专练)一、思维导图二、知识点梳理知识点一:分数乘整数(1)分数乘整数的意义与整数乘法的意义相同,就是求几个相同加数的和的简便运算。
(2)“分数乘整数”指的是第二个因数必须是整数,不能是分数。
分数乘整数,就是用分子乘整数作分子,分母不变。
(3)能约分的可以先约分,再计算,这样可以简便些。
(4)一个数乘分数的意义:就是求一个数的几分之几是多少。
“一个数乘分数”指的是第二个因数必须是分数,不能是整数。
知识点二:分数与分数1、分数乘分数用分子相乘的积做分子,分母相乘的积做分母。
(分子乘分子,分母乘分母)(1)如果分数乘法算式中含有带分数,要先把带分数化成假分数再计算。
(2)分数化简的方法是:分子、分母同时除以它们的最大公因数。
(3)在乘的过程中约分,是把分子、分母中,两个可以约分的数先划去,再分别在它们的上、下方写出约分后的数。
(约分后分子和分母必须不再含有公因数,这样计算后的结果才是最简单分数)。
(4)分数的基本性质:分子、分母同时乘或者除以一个相同的数(0除外),分数的大小不变。
知识点三:积与因数的关系1、一个数(0除外)乘大于1的数,积大于这个数。
a×b=c,当b >1时,c>a。
2、一个数(0除外)乘小于1的数,积小于这个数。
a×b=c,当b <1时,c<a(b ≠0)。
3、一个数(0除外)乘等于1的数,积等于这个数。
a×b=c,当b =1时,c=a 。
在进行因数与积的大小比较时,要注意因数为0时的特殊情况。
知识点四:分数乘法混合运算1、分数合运算顺序:(与整数相同),先乘、除后加、减,有括号的先算括号里面的。
2、整数乘法运算定律对分数乘法同样适用;运算定律可以使一些计算简便。
乘法交换律:a×b=b×a乘法结合律:(a×b)×c=a×(b×c)乘法分配律:a×(b±c)=a×b±a×c知识点五:用分数乘法解决问题1、求一个数的几分之几是多少?用单位“1”的量与分数相乘。
人教6上分数乘法讲义

《分数乘法》知识点一:分数乘整数1. 分数乘整数的意义分数乘整数的意义与整数乘法的意义相同,都是求几个相同加数的和的简便运算。
2. 分数乘整数的计算方法分数乘整数,用分数的分子和整数相乘的积作分子,分母不变。
3. 分数乘整数的简便算法能约分的可以先约分,再计算,这样可以简便些。
知识点二:分数乘分数1. 分数乘分数的意义分数乘分数,表示求这个数的几分之几是多少。
2. 分数乘分数的计算方法用分子相乘的积作分子,用分母相乘的积作分母。
3. 分数乘法的简便运算能约分的要先约分,后计算,计算结果必须是最简分数或整数。
知识点三:小数乘分数1. 能约分的先约分再计算比较简便。
2. 可以把小数转化成分数来计算;如果分数能化成有限小数,也可以把分数化成小数来计算。
知识点四:分数乘法运算定律1. 应用乘法的运算定律时要做到:一看符号:看运算符号是不是符合运算定律的要求;二看数:看参与计算的数是否符合简便计算;三选定律:根据参与运算的数和符号,选择合适的运算定律;四计算:运用运算定律进行计算。
2. 连续求一个数的几分之几是多少的实际问题有两种解法:(1)用已知量(原始单位“1”的量)依次乘已知分率。
(2)先把各分率按顺序相乘,求出所求问题占原始单位“1”的量的分率,再用原始单位“1”的量乘这个分率。
(2.1)解题关键是明确每一步中谁是单位“1”。
(2.2)每一步中的数量关系是:单位“1”的量×比较量占单位“1”的几分之几=比较量。
3. 求比一个数多(或少)几分之几的数是多少的问题;已知一个部分量是总量的几分之几,求另一个部分量的问题。
两类问题都可以用以下两种解法:(1)单位“1”的量+单位“1”的量×这个数量比单位“1”的量多(或少)几分之几=这个数量(2)单位“1”的量× (1+这个数量比单位“1”的量多(或少)几分之几)=这个数量考点01:分数乘法及运算律1.52×54×2×4=(52×2)×(54×4)=5×5=25,在计算过程中应用了()进行简便计算。
2024版分数乘法ppt课件小学数学PPT课件

在数学中的应用
分数乘法在数学中有着广 泛的应用,如在几何、代 数、概率等领域中都有着
重要的作用。
05
常见问题解答与误区纠正
学生常见错误类型
直接相乘
学生可能直接将两个分数的分子和分母分 别相乘,忽略了分数乘法的规则。
忽略约分
在得出结果后,学生可能会忘记将结果进 行约分至最简分数。
混淆运算顺序
示例:$frac{a}{b} times frac{c}{d} = frac{a times c}{b times d}$
注意点
约分后相乘法
示例:$frac{6}{8} times frac{10}{12} = frac{3}{4} times frac{5}{6} = frac{3 times 5}{4 times 6}$
配料比例调整
根据不同口味或需求调整配料比例,例如原食谱中糖和盐的比例为2:1,若需要减少糖分增加盐分,修或农业种植等场景中,需要计算面积时可以用到分数乘法,例如一个房间的长和 宽分别为3米和4米,则房间面积计算为3 × 4 = 12平方米。若另一个房间面积是第一
示例
$frac{11}{4} = 2frac{3}{4}$,$frac{15}{3} = 5$
特殊情况处理
注意点
在处理特殊情况时,要保持清晰的思路和 步骤。
确保每一步的计算都是正确的,避免因为 粗心而导致的错误。
03
分数乘法在生活中的应用
购物折扣计算
商品打折
一件原价为100元的商品,打9折后的价格计算为100 × (9/10) = 90元。
06
课堂互动环节
小组讨论:分享学习心得
小组讨论的目的
鼓励学生互相交流学 习分数乘法的心得和 体会,共同提高学习 效果。
人教版六年级上数学分数与乘法讲义(完整版)

人教版六年级上数学分数与乘法讲义专题一 知识体系一、分数乘法(一)分数乘法的意义:1、分数乘整数与整数乘法的意义相同。
都是求几个相同加数的和的简便运算。
例如: 98×5表示求5个98的和是多少? 2、分数乘分数是求一个数的几分之几是多少。
例如: 98×43表示求98的43是多少? (二)分数乘法的计算法则:1、分数与整数相乘:分子与整数相乘的积做分子,分母不变。
(整数和分母约分)2、分数与分数相乘:用分子相乘的积做分子,分母相乘的积做分母。
3、为了计算简便,能约分的要先约分,再计算。
注意:当带分数进行乘法计算时,要先把带分数化成假分数再进行计算。
(三)规律:(乘法中比较大小时) 一个数(0除外)乘大于1的数,积大于这个数。
一个数(0除外)乘小于1的数(0除外),积小于这个数。
一个数(0除外)乘1,积等于这个数。
(四)分数混合运算的运算顺序和整数的运算顺序相同。
(五)整数乘法的交换律、结合律和分配律,对于分数乘法也同样适用。
乘法交换律: a × b = b × a乘法结合律:( a × b )×c = a × ( b × c )乘法分配律:( a + b )×c = a c + b c二、分数乘法的解决问题(已知单位“1”的量(用乘法),求单位“1”的几分之几是多少)1、画线段图:(1)两个量的关系:画两条线段图;(2)部分和整体的关系:画一条线段图。
2、找单位“1”:在句中几分之几的前面;或“占”、“是”、“比”的后面3、求一个数的几倍:一个数×几倍;求一个数的几分之几是多少:一个数×几几。
4、已知一个数比另一个数多(或少)几分之几,求这个数是多少?(1)单位“1”的量±单位“1”的量×另一个数比单位“1”的量多(或少)的几分之几=另一个数(2)单位“1”的量×(1±另一个数比单位“1”的量多(或少)的几分之几)=另一个数5、写数量关系式技巧:(1)“的”相当于“×”“占”、“是”、“比”相当于“÷”(2)几分之几前是“的”:单位“1”的量×几分之几=几分之几对应量(3)几分之几前是“多或少”的意思:单位“1”的量×(1±几分之几)=几分之几对应量练一、看图列式计算。
2024版课件分数乘法

课件分数乘法contents •分数乘法基本概念•分数乘法计算方法•分数乘法在生活中的应用•分数乘法与其他运算关系•常见问题及解决方法•总结回顾与拓展延伸目录01分数乘法基本概念分数定义及性质分数定义分数性质分数乘法意义分数乘法的意义分数乘法的应用场景运算规则与性质运算规则分数乘法运算时,分子乘分子作为积的分子,分母乘分母作为积的分母。
运算性质分数乘法满足交换律、结合律和分配律。
即两个分数相乘,交换因数的位置,积不变;三个分数相乘,先乘前两个数,再乘第三个数,或者先乘后两个数,再乘第一个数,积不变;一个数与两个分数的和相乘,等于把这个数分别与两个分数相乘再相加。
02分数乘法计算方法定义示例注意事项030201定义交叉相乘法是指将第一个分数的分子与第二个分数的分母相乘,再将第二个分数的分子与第一个分数的分母相乘,最后将两个乘积相加。
示例对于分数a/b 和c/d,它们的乘积可以表示为(a*d + b*c)/(b*d)。
注意事项交叉相乘法通常用于解决一些特殊的数学问题,如求解方程组等。
在实际应用中,需要根据具体情况选择合适的计算方法。
简化计算过程提取公因数约分在计算过程中,可以提取分子或分母中的公因数以简化计算。
例如,对于分数(a*c)/(b*c)因数c,得到利用分配律03分数乘法在生活中的应用日常生活中的例子烹饪01时间管理02分配物品03商业和金融领域应用折扣计算投资回报商业计划其他领域应用科学实验工程设计艺术创作04分数乘法与其他运算关系分数与小数相乘,可以将小数转换为分数形式进行运算。
小数转换为分数时,根据小数的位数确定分母,分子则为小数去掉小数点后的数值。
运算结果可以化为小数或分数形式,根据需要选择。
在数学中的应用分数乘法是解决数学问题中涉及比例、百分数、折扣等问题的基本运算之一。
在几何中,分数乘法可用于计算图形的面积、体积等。
在代数中,分数乘法可用于解方程、不等式等问题。
05常见问题及解决方法寻找共同分母当两个分数的分母不同时,可以寻找它们的共同分母,以便进行相加或相减。
五年级数学分数乘法讲义

第十讲 预习篇2 分数乘法学习要求1. 掌握分数乘整数,用分数的分子和整数相乘的积做分子,分母不变。
分母与整数能约分时,可以先约分,再计算。
2. 掌握分数乘分数的计算,用分子相乘的积作分子,分母相乘的积做分母。
计算时,能约分的可以先约分再乘。
3. 知道分数的运算方法:分数混合运算的顺序和整数混合运算顺序相同,整数乘法的交换律、结合律和分配律,对于分数乘法也适用。
讲练互动例1 计算。
(1)41×28 65×15×2 (2)53×43 98×87×21 分析:分数乘整数,先将分数的分母与整数进行约分,再计算;分数乘分数,用分子相乘的积作分子,分母相乘的积做分母,能约分的先约分再乘,计算更简便。
解:(1)41×28=41×28 =7 65×15×2=65×15×2=25×5×2=25 1 7 2 5 1 11(2) 53×43=4533X X =209 98×87×21=98×87×21=219171X X X X =187 1即时练习1 计算。
76×28 367×3×6 32×23×43例2 (1)43×(94+54+154) (2)2517×3729+2517×378 (3)100×9998 分析:可以运用乘法的分配律计算。
解:(1)43×(94+54+154) (2)2517×3729+2517×378 (3)100×9998 = 43×94+43×54+43×154 =2517×(3729+378) =(99+1)×9998 = 31+53+51 =2517×1 =99×9998+1×9998=155+159+153 =2517 =98+9998 =1152 基础过关训练1. 画图并填数。
六年级分数乘法讲义

课本【2 】学科:数学任课教师:讲课时光:教学过程一、常识回想盘算107×2=1615×0=43+74=34×43= 9×65=187×149=31-51=145×57=75×2×57= 24×83=二、新课讲授分数乘整数分数乘整数,用分子乘整数的积作分子,分母不变.能约分的可以先约分,再盘算,成果雷同.如:103+103+103=103×3=1033⨯分数乘分数一个数乘几分之几表示的是求这个数的几分之几是若干.分数乘分数,用分子相乘的积作分子,用分母相乘的积作分母.如:每小时粉刷这面墙的51,43小时粉刷这面墙的几分之几?依据公式“工作效力×工作时光=工作总量”,列式:51×43=4531⨯⨯=203分数乘法混杂运算应遵守整数混杂运算定律:1、先算乘后算加减2、乘法交流律3、乘法联合律4、乘法分派律5、能约分的先约分6、含有带分数的要先把带分数化为假分数◆【典范例题】例1:例2: 例3:例4:◆【巩固演习】一.填空1.38 +38 +38 +38 =( )×( )=( )2.12个 56 是( );24的 23 是( ). 3.1013 的倒数是( );( )和 14 互为倒数. 4.12 ×( )= 35 ×( )=0.5×( ) 5.在○里填上>.<或=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
个性化教学辅导教案
初夏早上六点,清亮透明的月儿还躲藏在云朵里,不忍离去,校园内行人稀少,我骑着单车,晃晃悠悠的耷拉着星松的睡眼。
校园内景色如常,照样是绿意盈盈,枝繁叶茂,鸟儿歌唱。
经过西区公园,看那碧绿的草地,飞翔中的亭子,便想起十七那年,在这里寻找春天的日子。
本想就此停车再感受一遍,可惜心中记挂北区的荷塘。
回想起冬日清理完荷塘的枯枝败叶,一片萧条的景色:湖水变成墨绿色,没有鱼儿游动,四处不见了鸟儿的踪影,只有莲藕躺在湖底沉沉睡去。
清洁大叔撑着竹竿,乘一叶扁舟,把一片片黑色腐烂的枯叶残枝挑上船。
几个小孩用长长的铁钩把莲蓬勾上岸,取下里头成熟的莲子。
