理论力学动力学复习题.doc
理论力学复习题(含答案)
《理论力学》复习题A一、填空题1、二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是 二力平衡是作用在一个物体上,作用效果能抵消、作用力与反作用力是作用在两个物体上,作用效果不能抵消。
2、平面汇交力系平衡的几何条件是顺次将表示各个力Fi 的有向线段首尾相接,可以构成闭合n 边形;平衡的解析条件是 ∑Fxi=0;且∑Fyi=o 。
3、静滑动摩擦系数与摩擦角之间的关系为 tanφ=fs 。
4、点的切向加速度与其速度的 方向 变化率无关,而点的法向加速度与其速度 大小 的变化率无关。
5、点在运动过程中,满足0,0=≠n a a 的条件,则点作 牵连 运动。
6、动点相对于的 定系 运动称为动点的绝对运动;动点相对于 动系 的运动称为动点的相对运动;而 动系 相对于 定系 的运动称为牵连运动。
7、图示机构中,轮A (只滚不滑)作 平面 运动;杆DE 作 定轴转动 运动。
题7图 题8图8、图示均质圆盘,质量为m ,半径为R ,则其对O 轴的动量矩为 。
9、在惯性参考系中,不论初始条件如何变化,只要质点不受力的作用,则该质点应保持 静止或等速直线 运动状态。
10. 任意质点系(包括刚体)的动量可以用 其质心 的动量来表示。
二、选择题1. 在下述公理、规则、原理和定律中,对所有物体都完全适用的有( D )。
A.二力平衡公理B.力的平行四边形规则C.加减平衡力系原理D.力的可传性2. 分析图中画出的5个共面力偶,与图(a )所示的力偶等效的力偶是(B )。
A. 图(b ) B. 图(c ) C.图(d ) D. 图(e )题2图3. 平面力系向点1简化时,主矢0='RF ,主矩01≠M ,如将该力系向另一点2简化,则( D )。
A. 12,0M M F R≠≠' B. 12,0M M F R ≠='C. 12,0M M F R=≠' D. 12,0M M F R ==' 4. 将大小为100N 的力F 沿x 、y 方向分解,若F 在x 轴上的投影为86.6 N ,而沿x 方向的分力的大小为115.47 N ,则F 在y 轴上的投影为( B )。
《理论力学》期末复习资料

a
L
T k(2b cos b a)
L
L F k(2b x b a)
b
2L L
x
a
FL2 k b2
例16、试用牛顿方法和拉氏方法证明单摆的运动微分方程 g sin 0
l
其中为摆线与铅直线之间的夹角,l为摆线长度。
解: (1)用牛顿法:
l
ml mg sin
T
g sin 0
l
mg
3
3
33
v2 x2 y 2 an
v2
2 2m
9
11
例4、一质点受有心力 轨道的微分方程。
F
km r2
作用,列出求解其
解:
h2u
2
(
d 2u
d 2
u)
F (r) m
F km kmu2 r2
d 2u u k
d 2
h2
例5、如下图所示,船长为L=2a,质量为M的小船,在船头上站一质量为m的人,
cos3 d
L
o
x
mg
y
18
例12、如下图所示的机构,已知各杆长为L,弹簧的原长L,弹性系数 k,若忽略各处摩擦不计,各杆的重量忽略不计。试用虚功原理求平衡
时p的大小与角度之间的关系。
y
TT
解: 2TxD pyA 0
xD L cos xD L sin yA 2L sin yA 2L cos
x
(2TLsin 2 pLcos ) 0
o
2TLsin 2 pLcos 0
p T tan k(2L cos L) tan kL(2sin tan )
19
例13、如下图所示的机构,已知各杆长为L,弹簧的原长也L,弹性系数为 k,若忽略各处摩擦不计,各杆的重量也忽略不计。试用虚功原理求平衡时
理论力学题库(完整资料).doc
【最新整理,下载后即可编辑】
【最新整理,下载后即可编辑】
【最新整理,下载后即可编辑】
【最新整理,下载后即可编辑】
【最新整理,下载后即可编辑】
【最新整理,下载后即可编辑】
【最新整理,下载后即可编辑】
【最新整理,下载后即可编辑】
【最新整理,下载后即可编辑】
【最新整理,下载后即可编辑】
【最新整理,下载后即可编辑】
【最新整理,下载后即可编辑】
【最新整理,下载后即可编辑】
【最新整理,下载后即可编辑】
【最新整理,下载后即可编辑】
【最新整理,下载后即可编辑】
【最新整理,下载后即可编辑】
13-1 圆盘的半径r=0.5m,可绕水平轴O 转动。
在绕过圆盘的绳上吊有两物块A,B,质量分别为m A=3 kg ,m B=2 kg。
绳与盘之间无相对滑动。
在圆盘上作用一力偶,力偶矩按的规律变化(M以N·m计,以rad计)。
求到时,力偶M与物块A,B的重力所做的功之总和。
13-2 图示坦克的履带质量为m,两个车轮的质量均为,车轮视为均质盘,半径为R,两车轮轴间距离为.设坦克前进速度为,计算此质点系的动能。
【最新整理,下载后即可编辑】
解:
1.先研究车轮,车轮作平面运动,角速度
;两车轮的动能为
2.再研究坦克履带,AB部分动能为零,CD部分为平动,其速度为2v ;圆弧AD与BC
部分和起来可视为一平面运动圆环,环心速度为v ,角速度为,则履带的动能为
3.此质点系的动能为
【最新整理,下载后即可编辑】
【最新整理,下载后即可编辑】。
理论力学动力学部分试题及答案

1物体自地球表面以速度眄铅直上抛.试求该物体返回地面时的速度巧・假定空气阻力R=mkv2,其中k是比例常量,搜数值它等于单位质量在单位速度时所受的阻力。
m是物体质V 是物体速度,重力加速度认为不变.答:叮解:阻力方向在上升与下降阶段不同(其方向与速度y相反),故分段考虑(1)上升阶段:tn— - -tng一dt通过坐标变换有加V字二-刃护-加£ ,积分得axvdv(2)下落阶段:(1)g2.静止中心0以引力F=k2mr吸弓I质量是m的质点M,其中k是比例常量,r=OM是点M的矢径.运动开始时OMo=b,初速度时呵并与阪成夹角求质点M的运动方程。
x = b cos 处 + —cosasin ktky = —sinasin^k解:取坐标如图,质点M在任意位貳将fna = F 沿x、y轴投彫,得mx = 一F cos<p= -k2fnrcos (p= -Qmxfny = 一Fsin cp= -k2fnr sin (p= -k^my艮卩x+k2x = 0 , y+^2y = 0徽分方程得通解为:x = s coskt+c2 sin kt求导得x = -kc x sin kt + kc2 coskt , y = -kc3 sin kt + kc^ cos kt (2)已知初始条件f=0 z 妒b z /o=0,x0 = v0 sin a ,代入方程(1),(2)得点M的运动方程为v =—cosax = 2?cos Ar/ +—kcos ar sin kt -I sin asin kt y =c3 cos kt + c^ sin kt (1)九=v0 sin a3单摆M 的悬线长/,摆重G 支点B 具有水平向左的均加速度a.如将摆在&=0处静止 释啟,试确定悬线的张力T (表示成&的函数).解:质点的相对徴分方程为 ma r = mg+f +©投影到法线方向由式(2)得T = Gsin3 + —acos0 + — v 2g 0T = G 3 sin + 3 — cos — 2 —\ g S )答・ T - G(3sin3-cos^- 2-) g g投影到切线方向= T-Gsin^-0e cosB g !(2)由式(1)得 妙=gcos^-usin 0分离变量并积分|*V Xiv = \ f geos^10- [ asm Odd v 2 = 2"gsin &+ocos&-a 1(3)将式(3)代入上式代入式(2)得dt dt积分得4.水平面内弯成任意形状的细管以匀角速度G 绕点0转动.光滑小球M 在管內可自由 运动.设初瞬时小球在吆处,OMo=©相对初速^v o =0,求小球相对速度大小冬与极径r的关系。
动力学试题参考

10质点动力学10-1【是非题】不受力作用的质点将静止不动。
()10-2【是非题】质量是质点惯性的气宇。
质点的质量越大,惯性就越大。
()10-3【是非题】质点的连累惯性力和科氏惯性力与作用在质点上的主动力和约束力一样,都与参考系的选择无关。
()10-4【是非题】由于地球自转的阻碍,自由落体的着地址在北半球偏南,在南半球偏西。
()10-5【填空题】质量为m的质点沿直线运动,其运动规律为x= b ln(l +tbv)其中0v为初速度,b为常数。
那么作用于质点上的力F = 。
10-6【填空题】飞机以匀速v在铅垂平面内沿半径为r的大圆弧飞行。
驾驶员的体重为F P。
那么驾驶员对座椅的最大压力为。
10-7 重物M重力为10 N,系于30 cm长的细线上,线的另一端系于固定点O。
重物在水平面内作圆周运动,且细线与铅垂线成30º角。
求重物的速度与线的张力。
10-8 如下图,在三棱柱ABC的粗糙斜面上放一质量为m的物块M,三棱柱以匀加速度a沿水平方向运动。
设摩擦系数为f s,且f s<tanθ。
为使物块M在三棱柱上处于相对静止,试求a的最大值,和这时物块M对三棱柱的压力。
10-9 图示水平圆盘绕O轴转动,转动角速度ω为常量。
在圆盘上沿某直径有一滑槽,一质量为m的质点M在光滑槽内运动。
如质点在开始时离轴心O的距离为a,且无初速度。
求质点的相对运动方程和槽的水平反力。
′11 动量定理11-1【是非题】质点系内各质点动量的矢量和,即质点系的动量系的主矢,称为质点系的动量。
()11-2【是非题】质点系的质量与其质心速度的乘积等于质点系的动量。
()11-3【选择题】设有质量相等的两物体AB,在同一段时刻内,A物体发生水平移动,而B物体发生铅直移动,那么此两物体的重力在这段时刻内的冲量。
A.不同 B.相同C.A物体重力的冲量大D.B物体重力的冲量大11-4【选择题】系统在某一运动进程中,作用于系统的所有外力的冲量和方向与系统在此运动进程中的方向相同。
理论力学复习题(答案)

理论力学复习题一、填空题1、力对物体的作用效果一般分为力的外效应和力的内效应。
2、作用在刚体上的力可沿其作用线任意移动,而不改变该力对刚体的作用效果。
3、质点动力学的三个基本定律:惯性定律、力与加速度之间的关系定律、作用力与反作用力定律4、质点系动能定理建立了质点系动能的改变量和作用力的功之间的关系。
5、一对等值、反向、不共线的平行力组成的特殊力系,称为力偶6、两个或两个以上力偶的组合称为力偶系。
7、力矩与矩心的位置有关,力偶矩与矩心的位置无关。
8、物体质量的改变与发生这种改变所用合外力的比值叫做加速度。
9、力的三要素为大小、方向和作用点。
10、物体相对于地球静止或作匀速直线运动称为平衡状态。
11、作用在一个物体上的两个力使物体平衡,这两个力一定是大小相等、方向相反、作用在同一条直线上。
12、平面运动的速度分析法有三种方法基点法、速度瞬心法和速度投影法。
13、在刚体的平面运动中,刚体的平移和转动是两种最基本运动。
14、动力学的三个基本定律:动量定理、动量矩定理、动能定理。
15、空间力系分为空间汇交力系和空间力偶。
16、带传动中,带所产生的约束力属于柔性约束,带只能承受拉约束。
17、质点动力学的三个基本定律:惯性定律、力与加速度之间的关系定律、作用力与反作用力定律18、质点系动能定理建立了质点系动能的改变量和作用力的功之间的关系。
19、当力为零或力的作用线过矩心时,力矩为零,物体不产生效果。
二、判断题1实际位移和虚位移是位移的两种叫法(×)2.作用力和反作用力等值、反向、共线、异体、且同时存在。
(√)3.力偶无合力。
(×)4.运动物体的加速度大,它的速度也一定大。
(×)5.平面任意力系的合力对作用面内任一点之矩等于力系中各分力对于同一点之矩的代数和。
(√)6.若力偶有使物体顺时针旋转的趋势,力偶矩取正号;反之,取负号。
(×)7.既不完全平行,也不完全相交的力系称为平面一般力系(√)8.二力构件是指两端用铰链连接并且只受两个力作用的构件。
理论力学复习题

理论力学复习题1(总13页) -本页仅作为预览文档封面,使用时请删除本页-《理论力学复习参考题》(10土本)一、填空题(每题5分,共计20分)1、如图所示,已知力F及其作用点A的坐标为(1、1、0),求力F在三个坐标轴上的投影和对三个轴之矩。
=Fz=)F(mxF(my)==)F(mz2、如图所示各杆,其长度为,LDOCDABAO31====2L,CO2=AO1杆的转动角速度为ω,试确定其余杆作什么运动它们的角速度为多少(填入下表)=yF=xF23二、判断题1.当某平面一般力系的主矢量0F F /R ==∑i时,则该力系一定有合力偶。
( ) 2.力偶只能使刚体转动,而不能使刚体移动.( )3. 当一物体上有几处与周围物体接触时,这几个接触面的摩擦力同时达到临界平衡状态。
( )4.只要点作匀速运动,其加速度总为零。
( )5、在点的合成运动问题中,某瞬时动坐标上一点的速度称为动点的牵连速度。
( )6、摩擦力作为未知的约束反力,其大小和方向完全可以由平衡方程确定。
( )7、运动学只研究物体运动的几何性质,而不涉及引起运动的物理原因。
( )8.牵连运动是指动系上在该瞬时与动点重合的点对于静系的运动。
( )9.动系相对于静系的运动称为牵连运动。
( )10.平面图形的角速度与图形绕基点的角速度始终相等。
( )11.不管质点系作什么样的运动,也不管质点系内各质点的速度如何,只要知道质点系的总质量和质心速度,即可得知质点系的动量。
( )12.内力不改变质点系的动量,却能改变质点系内各部分的动量。
( )13.变力的冲量为零时则变力F 必为零。
( )14.质点系的动量等于外力的矢量和。
( )15.质点系的质心位置保持不变的条件是作用于质点系的外力主矢恒为零及质心的初速度为零。
16. 质点系的内力不能改变质点系的动量与动量矩17.若系统的动量守恒,则其对任意点的动量矩一定守恒;若系统对某点的动量矩守恒;则其动量一定守恒。
《理论力学》动力学典型习题+答案
学习 资料 整理 分享《动力学I 》第一章 运动学部分习题参考解答1-3 解:运动方程:θtan l y =,其中kt =θ。
将运动方程对时间求导并将030=θ代入得34cos cos 22lklk l y v ====θθθ 938cos sin 2232lk lk y a =-==θθ1-6证明:质点做曲线运动,所以n t a a a +=, 设质点的速度为v ,由图可知:a a v v yn cos ==θ,所以: yv va a n =将c v y =,ρ2n v a =代入上式可得 ρc v a 3=证毕 1-7证明:因为n2a v =ρ,v a a v a ⨯==θsin n所以:va ⨯=3v ρ证毕1-10解:设初始时,绳索AB 的长度为L ,时刻t 时的长度 为s ,则有关系式:t v L s 0-=,并且 222x l s +=将上面两式对时间求导得: 0v s-= ,x x s s 22= 由此解得:xsv x-= (a ) (a)式可写成:s v x x 0-= ,将该式对时间求导得: 2002v v s x x x =-=+ (b)将(a)式代入(b)式可得:3220220xlv x x v x a x -=-==(负号说明滑块A 的加速度向上)1-11解:设B 点是绳子AB 与圆盘的切点,由于绳子相对圆盘无滑动,所以R v B ω=,由于绳子始终处于拉直状态,因此绳子上A 、B 两点的速度在 A 、B 两点连线上的投影相等,即: θcos A B v v = (a ) 因为xR x 22cos -=θ (b ) 将上式代入(a )式得到A 点速度的大小为: 22Rx x Rv A -=ω (c )由于x v A -=,(c )式可写成:Rx R x xω=--22 ,将该式两边平方可得: 222222)(x R R x xω=- 将上式两边对时间求导可得:x x R x x R x xx 2232222)(2ω=-- 将上式消去x2后,可求得:22242)(R x xR x --=ω由上式可知滑块A 的加速度方向向左,其大小为 22242)(R xxR a A -=ω1-13解:动点:套筒A ;动系:OA 杆; 定系:机座; 运动分析:绝对运动:直线运动;o vo va ve vr vxovxot学习 资料 整理 分享 相对运动:直线运动; 牵连运动:定轴转动。
理论力学--动力学习题+答案

A
B
2g 5r
aC
4 5
g
(2)选圆柱A为研究对象
1 2
P g
r 2 A
M
Tr
(1)
选圆柱B为研究对象
1 2
P g
r
2
B
T
'r
(2)
P g
aC
T 'P
(3)
运动学关系:
aC ae ar r A r B (4)
由(1)~(4)式得:
B
4gM 2g 5 Pr2
mv1x
py 0
mv2x mv3x
5 2
ml1()
所以
p
px
5 2
ml1
A
方向水平向左
B
O
例9-5在静止的小船中间站着两个人,其中甲m1=50kg,面向船首方向走动1.5m。 乙m2=60kg,面向船尾方向走动0.5m。若船重M=150kg,求船的位移。水的阻力不计。
【解受】力有三个重力和一个水的浮力,因无水平力,水平方向质心运动守恒,
0 3.67rad/s
如图所示,均质杆AB质量为m,长为l,由图示位置( )无初速度地倒下4,5求0 该瞬
时A端所受到地面的约束反力。
B
C C
A
例10-13 如图所示均质细长杆,质量为M,长为l,放置在光滑水平面上。若在A 端 作用一垂直于杆的水平力F,系统初始静止,试求B端的加速度。
Pr
A
6gM 5
2g Pr2
Pr
aC
理论力学总复习(3).

R ,质量为
m的匀质圆盘在其自身平面内作平面运动。
点速度大小为 B
在图示位置时,若已知图形上 A、B 二点的速度方向如图所示。
45 ,且知
v B ,则圆轮的动能为
②
2、已知匀质杆长L,质量为m,端点B的速度为v,则杆的动能为 ②
3、图示三棱柱重P,放在光滑的水平面上,重Q的匀质圆柱体静止释放后
(a 0 g ) sin / L 0
1、倾角为 的楔形块A质量为 m1 ,置于光滑水平面上,物块B的 质量为 m2 ,放置在楔块斜面上。系统由静止开始运动。求A、 B的相互作用力。(不计两物块之间的摩擦)
第九章 质点系动力学基础
一、是非题
1、任意质点系(包括刚体)的动量可以用其质心(具有系统的质量)的动量来 表示。 (√ ) 2、质点系中各质点都处于静止时,质点系的动量为零。于是可知如果质点系的 动量为零,则质点系中各质点必须静止。 ( ×) 3、不管质点系作什么样的运动,也不管质点系内各质点的速度如何,只要知道 质点系的总质量和质点系质心的速度,即可求得质点系的动量。 (√ ) √ 4、冲量的量纲与动量的量纲相同。 ( ) 5、质点系对某轴的动量矩等于质点系中各质点的动量对同一轴之矩的代数和。 (√ ) 6、刚体的质量是刚体平动时惯性大小的度量,刚体对某轴的转动惯量则是刚体 绕该轴转动时惯性大小的度量。 ( ) √
1、半径为r,质量为M的光滑圆柱放在光滑水平面上,如图所示。一质 量为m的小球从圆柱顶点无初速下滑,试求小球离开圆柱前的轨迹。
2、重为 W1 的物体A,沿三棱体D的光滑斜面下降,同时借一绕过滑轮 C的绳子使重为 W2 的物块B运动。三棱体D重为 W 0 ,斜面与水平 面成 角,如略去绳子和滑轮的重量,求三棱体D给凸出部分E
理论力学10动力学
N F
F = 0.14 kN
N1
W1
N2
26
例题4.均质杆AD 和 BD长为l 质量分别为6m和4m ,
铰接如图.开始时维持在铅垂面内静止.设地面光滑, 两杆被释放后将分开倒向地面.求D点落地时偏移 多少.
D
(系统的质心的 x坐标守衡.沿y 方向运动)
60 B
T1 m1
O
T2 m2
C T3 m3
m1g
m2 g
x
m3 g
4
2 x1 2 m / s
解上述方程组得:
2 6 m / s 2 x 3 2 m / s 2 x
Fo o ' T1 ' Tc T2' Tc
c
T3'
5
例题3:细绳长为l,上端固定在O点,下端系一质量为m的小 球,在铅垂面内作微幅摆动。初时,绳的偏角为o,小球无初 速释放。求:绳微小摆动时的运动规律。 解:取小球为研究对象,进行运动 受力分析,如图。
P POC PAB PA PB
POC
A
I
vC
vD
O
D t
C
B
1 m1l 2
PAB PA PB (2m1 m2 m2 )l = 2(m1+m2)l
P = (2.5m1 + 2m2)l
23
例题3. 小车重W1= 2kN, 车上有一装沙的箱重 W2=1kN,以3.5km/h的速度在光滑直线轨道上匀速 行驶.今有一重W3= 0.5kN的物体铅垂落入沙箱中, 如图.求此后小车的速度. 又设重物落人沙箱后,沙 箱在小车上滑动 0.2 s 后,始与车面相对静止, 求车 面与箱底间相互作用的摩擦力.
理论力学 动力学复习

3.质点系动能定理
1 或 T J P 2 2 2 J P J C md )
T2 T1 W i
四、达朗贝尔原理
Fi FIi 0
(e )
MO (Fi )MO (FIi )0
(e )
刚体惯性力系的简化 1、刚体作平动 2、刚体绕定轴转动
FIR maC
构件的自重与各处摩擦,试应用虚位移原理,求当机构 在图示位置平衡时,力F1与F2的关系。
F1 B
,
解:虚功方程(几何法)
δrB
C
F2
F1δrBcos45 F2δrC 0
45° 45° A
δrC
δrB δrC cos45
F1 F2 2
[例] 质量为m的均质球半径为R,放在墙与AB杆之间,B端用 水平绳索BD拉住,杆长为l ,杆重不计,各处摩擦不计。 试用虚位移原理求绳子的拉力。 解:虚功方程(解析法)
解:研究对象:整体
受力分析: Fx
(e )
P
0 , 运动分析:
vC
mg FN mg FN
初始静止,所以水平方向质心位置守恒。
1 2 2 vA 1 2 T1 0 ,T2 ( J B ) 2 ml 2 3 1 2 vC l T2 mvC 3 h mg W12 mg 2 mgh 2
4
2h ( ) R1
R2
C
11 2 2 Mh mvC 3mgh 4 R1
11 mvC aC ( 2 M 3mg ) dh 2 R1 dt
2( M 3mgR 2 ) aC 11mR 2
(2)O轮子,动量矩定理(定轴转动微分方程)
J O O M O
理论力学复习题目动力学判断选择填空

适用标准文案一、是非题1.只需知道作用在质点上的力,那么质点在任一刹时的运动状态就完整确立了。
(错)2.在惯性参照系中,无论初始条件怎样变化,只需质点不受力的作用,则该质点应保持静止或等速直线运动状态。
(对)3.作用于质点上的力越大,质点运动的速度越高。
(错)4.牛顿定律合用于随意参照系。
(错)5.一个质点只需运动,就必定受有力的作用,并且运动的方向就是它受力的方向。
(错)6.圆盘在圆滑的水平面上平动,其质心作等速直线运动。
若在此圆盘平面上作用一力偶,则今后圆盘质心的运动状态是变速直线运动。
(错)7.若系统的总动量为零,则系统中每个质点的动量必为零。
(错)8.质系动量关于时间的变化率,只与作用于系统的外力相关,而与内力没关。
(对)9.刚体在一组力作用下运动,只需各个力的大小和方向不变,无论各力的作用点如何变化,刚体质心的加快度的大小和方向不变。
(对)10.冲量的量纲与动量的量纲同样。
(对)11.平动刚体各点的动量对一轴的动量矩之和能够用质心对该轴的动量矩表示。
(对)12.质点系关于随意动点的动量矩对时间的导数,等于作用于质点系的全部外力关于同一点的矩的矢量和。
(错)13.因为质点系的动量为p m v C,所以质点系对O 点的动量矩为L O M O m v C。
(错)14.质点系的内力不可以改变质点系的动量与动量矩。
(对)15.刚体的质量是刚体平动时惯性大小的胸怀,刚体对某轴的转动惯量则是刚体绕该轴转动时惯性大小的胸怀。
(对)16.机械能守恒定理是,当质点系不受外力作用时,则动能与势能之和等于零。
(错)17.系统内力所做功之代数和总为零。
(错)18.假如某质点系的动能很大,则该质点系的动量也很大。
(错)19.在使用动静法时,凡是运动着的质点都应加上惯性力。
(错)20.平移刚体惯性力系可简化为一个协力,该协力必定作用在刚体的质心上。
(对)21.拥有垂直于转轴的质量对称面的转动刚体,其惯性力系可简化为一个经过转轴的力和一个力偶,此中力偶的矩等于对转轴的转动惯量与刚体角加快度的乘积,转向与角加快度相反。
最新理论力学动力学复习题

1.在图示平面机构中,菱形板分别与杆AA1和BB 1铰接,两杆可分别绕轴A 1 和轴B 1作定轴转动。
AB =BD =20cm ,AA 1=25cm 。
当ϕ=30°,AA 1⊥BB 1时,设平板的角速度ω=2rad/s 。
试求此瞬时点D 的速度和杆AA 1的角速度。
解:菱形板的速度瞬心在P 点,故s cm /2030sin =⋅︒⋅=⋅=ωωAB AP v A杆AA 1的角速度 s rad/8.0AA 11==Av ω(顺钟向)D 点的速度 s cm/720=⋅=ωDP v D(斜向左下方)2.等腰三角形平板ABC 的腰长AB =BC =5 cm ,AC =6 cm ,端点A 和端点B 分别在水平面上和斜面上运动。
斜面与铅垂线之间的夹角ϕ=⎪⎭⎫ ⎝⎛43arctan 。
在图示位置时,AC 边铅垂,平板的角速度ω=4 rad/s ,角加速度α=5 rad/s 2。
试求该瞬时A ,B 和C 三点的加速度的大小。
解:平板取A 为基点 t n BA BA A B a a a a +==式中2n ωAB a BA =,αAB a BA =tBC : ()()ϕθϕθϕ---+=cos sin cos 0t n BA BA A a a a故 2cm /s 1.2=A ay : ϕϕϕcos sin cos t n BA BA B a a a --=-故 2cm/s 85=B a取A 为基点 t n CA CA A C a a a a ++=式中 2n ωAC a CA =,αAC a CA =tx :2t cm/s 9.27=+-=CA A C a a a xy : 2n cm/s 96-=-=CA C a a y 2cm/s 100=C a3.在图示平面机构中,已知:杆OA 以匀角速度0ω绕定轴O 转动,OA =AC =r ,O 1B =2r , β=30°。
在图示位置时,OA ,CB 水平,O 1B ,AC 铅垂。
《理论力学》动力学典型习题 答案_图文.

《动力学 I 》第一章运动学部分习题参考解答1-3 解:运动方程:θtan l y =,其中kt =θ。
将运动方程对时间求导并将 030=θ代入得34cos cos 22lk lk l y v ====θθθ98cos sin 2232lk lk y a =-==θθ1-6证明:质点做曲线运动 , 所以 n t a a a +=, 设质点的速度为 v , 由图可知 : a a vv y n cos ==θ,所以 : yv va a n = 将c v y =, ρ2n va =代入上式可得ρc v a 3=证毕 1-7证明:因为 n2a v=ρ, va a v a ⨯==θsin n所以:va ⨯=3v ρ证毕1-10解:设初始时 , 绳索 AB 的长度为 L , 时刻 t 时的长度为 s , 则有关系式: t v L s 0-=,并且 222x l s +=将上面两式对时间求导得:0v s-= , x x s s 22= 由此解得:xsv x-= (a (a式可写成:s v x x 0-= ,将该式对时间求导得: 2002v v s x x x=-=+ (b 将 (a式代入 (b式可得:3220220xlv x x v x a x -=-==(负号说明滑块 A 的加速度向上1-11解:设 B 点是绳子 AB 与圆盘的切点,由于绳子相对圆盘无滑动,所以R v B ω=,由于绳子始终处于拉直状态,因此绳子上 A 、 B 两点的速度在 A、 B 两点连线上的投影相等,即: θcos A B v v = (a 因为xR x 22cos -=θ (b 将上式代入(a 式得到 A 点速度的大小为: 22Rx x Rv A -=ω (c由于 x v A -=, (c 式可写成:Rx R x xω=--22 ,将该式两边平方可得: 222222 (x R R x x ω=- 将上式两边对时间求导可得:x x R x x R x xx 2232222 (2ω=-- 将上式消去 x 2后,可求得:22242(R x xR x--=ω由上式可知滑块 A 的加速度方向向左,其大小为 2 2242(R x xR a A -=ω1-13解:动点:套筒 A ;动系:OA 杆; 定系:机座; 运动分析:绝对运动:直线运动; 相对运动:直线运动; 牵连运动:定轴转动。
理论力学复习.doc

《理论力学》复习题一、是非题1.合力不一定比分力大。
-------------------------------------------------- ()2.平动刚体上的点的运动轨迹也可能是空间曲线。
----------------------------- ()3.某平面力系向一点简化的结果与简化中心无关,则该力系一定平衡。
----------- ()4.约束反力的方向一定与被约束体所限制的运动方向相反。
---------------------- ()5.如果作用在刚体上的三个力共面且汇交于一点,则刚体一定平衡。
-------------- ()6.力偶可以用一个合力来平衡。
---------------------------------------------- ()7.若点的法向加速度为零,则该点轨迹的曲率必为零。
-------------------------- ()8.经过的时间越长,变力的冲量也一定越大。
---------------------------------- ()9. 在点的合成运动中,动点的绝对加速度总是等于牵连加速度与相对加速度的矢量和。
()10.牛顿第一定律适用于任何参照系。
------------------------------------------ ()二、选择题1.已知F1、F2、F3、F4为作用于刚体上的平面汇交力系,其力多边形如图所示,由此可知()A:力系的合力为零,力系平衡;B:力系可合成为一个力;C:力系可简化为一个力和一个力偶;D:力系可合成一个力偶。
2.如图所示,物块 A 重P=200N,放在与水平面成30 的粗糙斜面上,物块 A 与斜面间的静摩擦系数为f=1,则摩擦力的大小为()A:0 B:86.6N C:150N D:100N3.平面一般力系的二力矩式平衡方程的附加使用条件是( )。
A:二个矩心的连线和投影轴不能垂直B:二个矩心的连线和投影轴可以垂直C:没有什么条件限制4.既限制物体任何方向移动,但不限制物体转动的支座称()支座。
理论力学动力学测试

第三篇动力学一、选择题(每题2分,共20分)1。
在铅直面内得一块圆板上刻有三道直槽AO,BO,CO,三个质量相等得小球M1,M2,M3在重力作用下自静止开始同时从A,B,C三点分别沿各槽运动,不计摩擦,则________到达O 点、(A)M1小球先; (B)M2小球先; (C)M3小球先; (D)三球同时。
题1 题2 题32、质量分别为m1=m,m2=2m得两个小球M1,M2用长为L而重量不计得刚杆相连。
现将M1置于光滑水平面上,且M1M2与水平面成角。
则当无初速释放,M2球落地时,M1球移动得水平距离为____________。
(A);ﻩﻩ(B);ﻩﻩ(C);ﻩﻩ(D)0。
3、质量为m,长为b得匀质杆OA,以匀角速度ω绕O轴转动。
图示位置时,杆得动量及对O 轴得动量矩得大小为________。
(A),; (B),;(C),;ﻩ(D),。
4.在_____情况下,跨过滑轮得绳子两边张力相等,即F1=F2(不计轴承处摩擦)。
(A)滑轮保持静止或以匀速转动或滑轮质量不计;(B)滑轮保持静止或滑轮质量沿轮缘均匀分布;(C)滑轮保持静止或滑轮质量均匀分布;(D)滑轮质量均匀分布。
题4 题55.均质杆长L,重P,均质圆盘直径D=L,亦重P,均放置在铅垂平面内,并可绕O轴转动。
初始时杆轴线与圆盘直径均处于水平位置,而后无初速释放,则在达到图示位置瞬时,杆得角速度ω1________圆盘得角速度ω2。
(A)大于;ﻩ(B)小于; (C)等于;ﻩ(D)小于或等于。
6.均质杆AB,长L,质量m,沿墙面下滑,已知A端速度,B端高度h,AB对过杆端A,质心C,瞬心I得水平轴得转动惯量分别为JA,J C,J I,则图示瞬时杆得动能为__________、(A); (B); (C);(D)题6题7 题87.已知均质杆长L,质量为m,端点B得速度为,则AB杆得动能为___________。
(A);ﻩﻩ(B);ﻩ(C); (D)8、质量为m1得均质杆OA,一端铰接在质量为m2得均质圆盘中心,另一端放在水平面上,圆盘在地面上作纯滚动。
922144-理论力学之动力学-第二章d大纲习题

1.质点系的动量
n
p mivi
i 1
2.微分形式
dp
dt
n
Fi (e)
i 1
FR(e)
3.积分形式
pt2
pt1
n
I
(e) i
i 1
t2 t1
FR(e)dt
动量守恒
当:FRe 0
n
当: Fxei 0
i 1
则: p p0
则: px p0x
9
小结
一、动量定理
质点系相对定点与相对运动点动量矩的关系
Lo rA mvC rAC mvA LrA
Lo rC mvC LrC
质点系相对于动点的动量矩定理
dLrA
dt
n i1
M A(Fi(e) ) rAC
(maA)
质点系相对于质心的动量矩定理
dLrC
dt
n i1
MC (Fi(e) )
12
小结
三、动能定理
绳索AM的拉力与未剪断绳索 BM时相比,是增大了还是减
小了? =?绳索AM的拉力
不变。
剪断前: F mg
2 cos 剪断后: F mg cos
2
物块A、B放在半径为R处于静
止的水平圆盘的边缘,两者间的静
滑动摩擦因数为f,物块的质量分别
为mA > mB,将物块视为质点。圆盘
以角速度ω=αt 绕铅垂轴转动。
i1
Lo rC mv
Lz J z
2.相对于惯性参考系中定点的动量矩定理
dLo
dt
n
Mo (Fi(e))
i1 n
守恒情况: Mo (Fi(e)) 0 则:Lo (t) Lo (t0 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
OC
r
cos
因
vC
vCe
vCr
得
vCr
vCe
r
cos
cos2
vD C
vC
vCrsin
2r
3
又有aeC
0 , aeC
OC2
r
2
cos2
C
r
2r
2
aC
2 vC
cos2
a
ae
ae
C
ar
ac
C
C
C
C
x:aCcos
ae
Ccos
aCc
故
aDC
aC
a
e
aCc
10 3 r2
C
cos
9
6.在图示平面机构中,半径为R的半圆环OC
-------------精选文档-----------------
1.在图示平面机构中, 菱形板分别与杆
AA1和BB1铰接,
两杆可分别绕轴A1和轴B1
作定轴转动。
AB=BD =20cm,AA =25cm。当=30°,AA
BB
时,
1
1
1
设平板的角速度=2rad/s。试求此瞬时点D
的速度和
杆AA1的角速度。
0
vB3
1
O1B6
1(顺钟向)
可编辑
-------------精选文档-----------------
ABCvA30(顺钟向)
PA3
选点A为基点,则
aBaBnaBtaAaBAnaBAt
将上式向BA方向投影,得
aBnsin
aBt
cos
aAcosaBAn
aBt
1
7
3r
02
18
1
aBt
0.837
02(顺钟向)
中央。试求该瞬时:
(1)轮中心的加速度;
(2)接触处A的摩擦力。
.解:由动能定理:dT=ΣδWi
d [m( 2v)2+m v2+JA(v)2] =
r
2m g? 2 ds? sin
+ 2m gds? sin
对上式两边同除dt得:a=dv=3g
d t
11
可编辑
-------------精选文档-----------------
绕O轴转动,并带动套在其上的小圈M沿固
可编辑
-------------精选文档-----------------
定的竖直杆AB滑动。若角速度为已知常量,试求图示位置(OC
⊥AB)时,小圈M的绝对速度和绝对加速度。
பைடு நூலகம்解:
取M为动点,半圆环OC为动系。
ve
2 R
M
由
得
又有
vMvMevMr
vMvMrR
r2
e2r(vM)2
解:对系统按动能定理:d
T
=Σ δi
W
d (1m vA2+1m vo2+1Joω2) =
2
2
2
m g
d
l
sin
+
m g
d
l
sin
-
cos·d
l
β
βf m g
β
对上式两边同除dt得:
aO=
dvA
=
2(2 sinβf cosβ) g
dt
5
可编辑
-------------精选文档-----------------
O1B
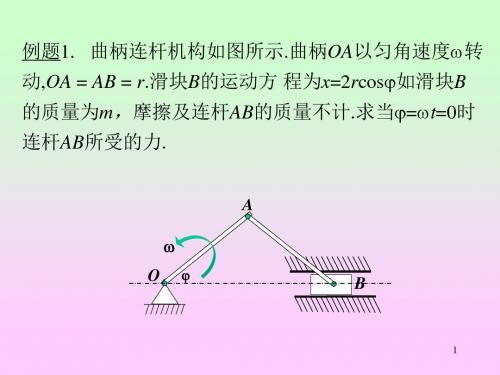
4.曲柄滑块机构如图,已知:OA=r,AB=L,OA以匀角速度转动。试求=90°
时杆AB的角加速度。
解:
因杆AB作瞬时平动,故
AB0
取点A为基点aBaAaBAt
由加速度矢量合成关系,得
aBAt
aA
r
2L
cos
L2
r2
可编辑
-------------精选文档-----------------
角加速度
3.在图示平面机构中,已知:杆OA以匀角速度0绕定轴O转动,OA=AC=r,O1B=2r,
=30°。在图示位置时,OA,CB水平,O1B,AC铅垂。试求此瞬时:
⑴板上点C的速度;
⑵杆O1B的角速度;
⑶杆O1B的角加速度。
解:
板ABC的速度瞬心在P点
vC
vA
PC
2
3r
3
PA
vB
vA
PB
3r
3
PA
1(方向如图示)
故
aA
2.1cm/s2
y:
aBcos
aBAnsin
aBAtcos
故
aB
85cm/s2
取A为基点
aC
aA
aCAn
aCAt
式中
aCAn
AC
2,aCAt
AC
x:aCxaAaCAt27.9 cm/s2
可编辑
-------------精选文档-----------------
y:aCyaCAn96cm/s2
aC100 cm/s2
12
(1)平板的角加速度;
(2)支座A的约束力。2012运动学与动力学
解:由
MA(F)=0
MgA-mgl
= 0
JC+m(l
2
式中:MgA=JA
)2
)
6gl
2
得:
=
4l2
b2
由
Fx= 0
得:
FAx= 0
由Fy= 0
FAy+FgA-mg= 0
可编辑
AB
aBAt
r
2
AB
L2
r2
(逆钟向)
5.在图示平面机构中,直角杆OAB绕轴O转动,套筒C可在AB段滑动,O、C、D位于同一铅垂线上。已知OA=r,当= 30°时,直角杆OAB的角速度为,角加速度为零。试求该瞬
时杆CD的速度和加速度。
解:
以铰链C为动点,杆OAB为动系。
可编辑
-------------精选文档-----------------
对滑块A按质心运动定理:
F-FSA+m g? sinβ=m aA其中:aA=aOFNA-m g? cosβ= 0
由上可得:F=(3 fcosβsinβ)mg
5
9.图示匀质平板位于铅直面内的水平位置。已知:平板长为l,宽为b,质量为m,
对质心C的转动惯量为JC=1m(l2+b2)。试用达朗贝尔原理求在撤去B支座销钉瞬时:
解:
菱形板的速度瞬心在P点,故
vAAPAB sin 3020 cm/ s
杆AA1的角速度
1
vA
0.8rad/ s
AA1
(顺钟向)
D点的速度
vDDP207 cm/ s
(斜向左下方)
可编辑
-------------精选文档-----------------
2.等腰三角形平板ABC的腰长AB=BC=5 cm,AC=6 cm,端点A和端点B分别在水平面
分别由板、轮平面运动微分方程:
2m g? sin
-2F
s 1
= 2
m? 2a
1
○
(
F
1
+F
A
)
mr2a
2
r =
○
2r
得:
FA=
2mg
11
8.在图示机构中, 已知:纯滚动的匀质轮与物A的质量均为m,轮半径为r,斜面倾角为β,物A与斜面间的动摩擦因数为f,不
计杆OA的质量。试求:
(1)O点的加速度;
(2)杆OA的内力。
aM2R, aMR
aMc
2 vMr
2R
2
由
aM
aeM
arM
arM
aMc
aM方向投影得:aM
aeMcos45 arMaMc
得
aM
0
可编辑
-------------精选文档-----------------
7\在图示机构中,已知:两纯滚动匀质轮的质量各为m,板
的质量为2m,倾角β=30 ?,初瞬时板的质心C1位于图示CD的
上和斜面上运动。斜面与铅垂线之间的夹角=arctan3。在图示位置时,AC边铅垂,
4
平板的角速度=4 rad/s,角加速度=5 rad/s2。试求该瞬时A,B和C三点的加速度
的大小。
解:
平板取A为基点
aBaAaBAnaBAt
式中
aBAnAB2,aBAtAB
BC:
0
aAcos
aBAnsin
aBAtcos
