算法复习题
复习题2(算法部份)

D.一个算法不能有多个开始处,也不能有多个结束处
答案:B
14.算法中通常需要三种不同的执行流程,即:_____。
A.连续模式、分支模式和循环模式
B.顺序模式、结构模式和循环模式
C.结构模式、分支模式和循环模式
D.顺序模式、分支模式和循环模式
答案:D
15.算法中通常需要三种不同的执行流程,下面说法正确的是:_____。
答案:B
2.计算机是一种按照设计好的程序,快速、自动地进行计算的电子设备,计算机开始计算之前,必须把解决某个问题的程序存贮在计算机的_____中。
A.硬盘B.软盘C.内存D.CPU
答案:C
3.计算机程序由以下两部分即:_____组成。
A.执行部分和数据部分
B.数据部分和程序部分
C.指令部分和数据部分
第1章计算机和算法
1.使用计算机解题的步骤,以下描述正确的是:_____。
A.正确理解题意→设计正确算法→寻找解题方法→编写程序→调试运行
B.正确理解题意→寻找解题方法→设计正确算法→编写程序→调试运行
C.正确理解题意→寻找解题方法→设计正确算法→调试运行→编写程序
D.正确理解题意→寻找解题方法→设计正确算法→编写程序→调试运行
答案:B
10.关于算法的确定性特征,以下不符合算法确定性的是:_____。
A.D←(B * B–4 * A * C)
B.S←(L * H) / 10
C.输入:X
D.输出:L /正整数
答案:D
11.可以用多种不同的方法来描述一个算法,算法的描述可以用:_____。
A.流程图、分支和循环
B.顺序、流程图和自然语言
算法(复习题)1

平均情况:设待查找的元素在数组中的概率为P,不在数组中的概率为1-P,若出现在数组中每个位置的概率是均等的为p/nT(n)=P1D1+P2D2+...+PiDi+(1-P)Dn+1=p/2+n(1-p/2)1.叙述分治算法和动态规划算法的基本思想,并比较两种算法的异同。
答:分治法将待求解的问题划分成K个较小规模的子问题,对这K个子问题分别求解,再将子问题的解合并为一个更大规模的问题的解,自底向上逐步求出原问题的解. 动态规划将待求解的问题分解成若干的子问题,自底向上地通过求解子问题的解得到原问题的解。
动态规划将每个子问题只求解一次并将其解保存在一个表格中,当需要再次求解此子问题时,只是简单的通过查表过的该子问题的解,避免了大量的重复计算.异同:分治法求解的问题分解后的子问题都是独立的,而使用动态规划求解的问题分解后得到的子问题往往不是相互独立的。
分治法是自顶向下用递归的方法解决问题,而动态规划则是自底向上非递归解决问题。
1.简述分治算法求解过程的三个阶段。
答:(1)划分:既然是分治,当然需要把规模为n的原问题划分为k个规模较小的子问题,并尽量使这k个子问题的规模大致相同。
(2)求解子问题:各子问题的解法与原问题的解法通常是相同的,可以用递归的方法求解各个子问题,有时递归处理也可以用循环来实现。
(3)合并:把各个子问题的解合并起来,合并的代价因情况不同有很大差异,分治算法的有效性很大程度上依赖于合并的实现。
2.叙述分治法的基本思想,并分析分治法与减治法二者的区别。
答:分治法将待求解的问题划分成K个较小规模的子问题,对这K个子问题分别求解,再将子问题的解合并为一个更大规模的问题的解,自底向上逐步求出原问题的解.区别:分治法是把一个大问题划分成若干个子问题,分别求解各个子问题,然后把子问题的解进行合并并得到原问题的解。
减治法同样是把一个大问题划分成若干个子问题,但是这些子问题不需要分别求解,只需求解其中的一个子问题,因而也无需对子问题的解进行合并。
算法复习题

算法复习试题一、名词解释:1、算法:就是一组有穷的规则,它规定了解决某一特定类型问题的一系列运算。
2、贪心算法:能够得到某种量度意义下的最优解的分级处理方法称为贪心算法。
3、分治法:分治法的求解思想就是把整个问题分成若干个小问题后分的治之4、递归过程:一个递归过程的执行类似于多个子程序的嵌套调用,递归过程是自己调用自己本身代码。
递归算法的特点:思路清晰,算法的描述简洁且易理解。
5、集合:在研究某一类对象时,可把这类对象的整体称为集合。
6、生成树:设G=(V,E)是一个无向连通图。
如果G的生成子图T=(V,E')是一棵树,则称T是G的一棵生成树。
7、算法具有以下5个属性:有穷性:一个算法必须总是在执行有穷步之后结束,且每一步都在有穷时间内完成。
确定性:算法中每一条指令必须有确切的含义。
不存在二义性。
只有一个入口和一个出口可行性:就是算法描述的操作是可以通过已经实现的基本运算执行有限次来实现的。
输入:一个算法有零个或多个输入,这些输入取自于某个特定对象的集合。
输出:一个算法有一个或多个输出,这些输出同输入有着某些特定关系的量。
8、迭代法:称辗转法,是一种不断用变量的旧值递推出新值的解决问题的方法。
9、贪婪法: 是一种不追求最优解,只希望得到较为满意解的方法。
贪婪法不要回溯10、动态规划:是一种将问题实例分解为更小的、相似的子问题,并存储子问题的解而避免计算重复的子问题,以解决最优化问题的算法策略。
11、分支限界法:是一种用于求解组合优化问题的排除非解的搜索算法。
12、树:树是一个或多个结点的有限集合。
12、二元树:它是结点的有限集合,它或者为空,或者由一个根和两棵树(左子树和右子树)的不相交的二元树所组成。
13、二分检索树:T是一棵二元树,它或者为空,或者其每个结点含有一个可比较大小的数据元素。
14、图:图是数据结构,一个图G是由称之为结点V和边E的两个集合组成的15、最优解:使目标函数取极值(极大值或极小值)的可行解。
算法期末复习题2

填空题:1.一个算法就是一个有穷规则的集合,其中之规则规定了解决某一特殊类型问题的一系列运算,此外,算法还应具有以下五个重要特性:确定性有穷性可行性 0个或多个输入一个或多个输出2.算法的复杂性有时间复杂性和空间复杂性之分,衡量一个算法好坏的标准是时间复杂度高低。
3.某一问题可用动态规划算法求解的显著特征是该问题具有最优子结构性质。
5.用回溯法解问题时,应明确定义问题的解空间,问题的解空间至少应包含一个(最优)解6.动态规划算法的基本思想是将待求解问题分解成若干子问题_,先求解子问题,然后从这些子问题的解得到原问题的解。
7.以深度优先方式系统搜索问题解的算法称为回溯法。
8.0-1背包问题的回溯算法所需的计算时间为o(n*2n),用动态规划算法所需的计算时间为o(min{nc,2n})。
9.动态规划算法的两个基本要素是最优子结构和重叠子问题。
10.二分搜索算法是利用动态规划法实现的算法。
11.一个算法复杂性的高低体现在计算机运行该算法所需的时间和存储器资源上,因此算法的复杂性有时间复杂性和空间复杂性之分。
12.出自于“平衡子问题”的思想,通常分治法在分割原问题,形成若干子问题时,这些子问题的规模都大致相同。
13.动态规划算法有一个变形方法备忘录方法。
这种方法不同于动态规划算法“自底向上”的填充方向,而是“自顶向下”的递归方向,为每个解过的子问题建立了备忘录以备需要时查看,同样也可避免相同子问题的重复求解。
14、这种不断回头寻找目标的方法称为回溯法。
15、直接或间接地调用自身的算法称为递归算法。
16、 记号在算法复杂性的表示法中表示渐进确界或紧致界。
17、由分治法产生的子问题往往是原问题的较小模式,这就为使用递归技术提供了方便。
18、建立计算模型的目的是为了使问题的计算复杂性分析有一个共同的客观尺度。
19、下列各步骤的先后顺序是②③④①。
①调试程序②分析问题③设计算法④编写程序。
20、最优子结构性质的含义是问题的最优解包含其子问题的最优解。
算法设计与分析期末复习题

算法设计与分析期末考试复习题1.算法有哪些特点?为什么说一个具备了所有特征的算法,不一定就是使用的算法?2.证明下面的关系成立:(参考例题1.5--1.6)(1)logn!=Θ(nlogn) (2)2n=Θ(2n+1)(3)n!=Θ(n n) (4)5n2-6n=Θ(n2)3.考虑下面的算法:输入:n个元素的数组A输出:按递增顺序排序的数组A1. void sort(int A[],int n)2. {3. int i,j,temp;4. for(i=0;i<n-1;i++)5. for(j=i+1;j<n;j++)6. if(A[j]<A[i]) {7. temp=A[i];8. A[i]=A[j];9. A[j]=temp;10. }11. }(1)什么时候算法所执行的元素赋值的次数最少?最少多少次?(2)什么时候算法所执行的元素赋值的次数最多?最多多少次?4.考虑下面的算法:输入:n个元素的数组A输出:按递增顺序排序的数组A1. void bubblesort(int A[],int n)2. {3. int j,i,sorted;4. i=sorted=0;5. while(i<n-1 && !sorted) {6. sorted=1;7. for(j=n-1;j>i;j--) {8. if(A[j]<A[j-1]) {9. temp=A[j];10. A[j]=A[j-1];11. A[j-1]=temp;12. sorted=0;13. }14. }15. i=i+1;16. }17. }(1)算法所执行的元素比较次数最少是多少次?什么时候达到最少?(2)算法所执行的元素比较次数最多是多少次?什么时候达到最多?(3)算法所执行的元素赋值次数最少是多少次?什么时候达到最少?(4)算法所执行的元素赋值次数最多是多少次?什么时候达到最多?(5)用О、和Ω记号表示算法的运行时间。
算法设计与分析复习题目及答案

分治法1、二分搜索算法是利用(分治策略)实现的算法。
9. 实现循环赛日程表利用的算法是(分治策略)27、Strassen矩阵乘法是利用(分治策略)实现的算法。
34.实现合并排序利用的算法是(分治策略)。
实现大整数的乘法是利用的算法(分治策略)。
17.实现棋盘覆盖算法利用的算法是(分治法)。
29、使用分治法求解不需要满足的条件是(子问题必须是一样的)。
不可以使用分治法求解的是(0/1背包问题)。
动态规划下列不是动态规划算法基本步骤的是(构造最优解)下列是动态规划算法基本要素的是(子问题重叠性质)。
下列算法中通常以自底向上的方式求解最优解的是(动态规划法)备忘录方法是那种算法的变形。
(动态规划法)最长公共子序列算法利用的算法是(动态规划法)。
矩阵连乘问题的算法可由(动态规划算法B)设计实现。
实现最大子段和利用的算法是(动态规划法)。
贪心算法能解决的问题:单源最短路径问题,最小花费生成树问题,背包问题,活动安排问题,不能解决的问题:N皇后问题,0/1背包问题是贪心算法的基本要素的是(贪心选择性质和最优子结构性质)。
回溯法回溯法解旅行售货员问题时的解空间树是(排列树)。
剪枝函数是回溯法中为避免无效搜索采取的策略回溯法的效率不依赖于下列哪些因素(确定解空间的时间)分支限界法最大效益优先是(分支界限法)的一搜索方式。
分支限界法解最大团问题时,活结点表的组织形式是(最大堆)。
分支限界法解旅行售货员问题时,活结点表的组织形式是(最小堆)优先队列式分支限界法选取扩展结点的原则是(结点的优先级)在对问题的解空间树进行搜索的方法中,一个活结点最多有一次机会成为活结点的是( 分支限界法).从活结点表中选择下一个扩展结点的不同方式将导致不同的分支限界法,以下除( 栈式分支限界法)之外都是最常见的方式.(1)队列式(FIFO)分支限界法:按照队列先进先出(FIFO)原则选取下一个节点为扩展节点。
(2)优先队列式分支限界法:按照优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点。
算法分析与设计复习题及参考答案

《算法分析与设计》课程复习资料一、名词解释:1.算法2.程序3.递归函数4.子问题的重叠性质5.队列式分支限界法6.多机调度问题7.最小生成树 二、简答题:1.备忘录方法和动态规划算法相比有何异同?简述之。
2.简述回溯法解题的主要步骤。
3.简述动态规划算法求解的基本要素。
4.简述回溯法的基本思想。
5.简要分析在递归算法中消除递归调用,将递归算法转化为非递归算法的方法。
6.简要分析分支限界法与回溯法的异同。
7.简述算法复杂性的概念,算法复杂性度量主要指哪两个方面? 8.贪心算法求解的问题主要具有哪些性质?简述之。
9.分治法的基本思想是什么?合并排序的基本思想是什么?请分别简述之。
10.简述分析贪心算法与动态规划算法的异同。
三、算法编写及算法应用分析题:1.已知有3个物品:(w1,w2,w3)=(12,10,6),(p1,p2,p3)=(15,13,10),背包的容积M=20,根据0-1背包动态规划的递推式求出最优解。
2.按要求完成以下关于排序和查找的问题。
①对数组A={15,29,135,18,32,1,27,25,5},用快速排序方法将其排成递减序。
②请描述递减数组进行二分搜索的基本思想,并给出非递归算法。
③给出上述算法的递归算法。
④使用上述算法对①所得到的结果搜索如下元素,并给出搜索过程:18,31,135。
3.已知1()*()i i k k ij r r A a +=,k =1,2,3,4,5,6,r 1=5,r 2=10,r 3=3,r 4=12,r 5=5,r 6=50,r 7=6,求矩阵链积A 1×A 2×A 3×A 4×A 5×A 6的最佳求积顺序(要求给出计算步骤)。
4.根据分枝限界算法基本过程,求解0-1背包问题。
已知n=3,M=20,(w1,w2,w3)=(12,10,6),(p1,p2,p3)=(15,13,10)。
算法分析复习题

算法分析复习题⼀、单项选择题:1、算法的五⼤特征是确定性、有穷性、输⼊、输出和可⾏性。
其输⼊⾄少是( A )个。
A、0B、1C、n D、-12、⼤整数的乘法是利⽤的算法( C )。
A、贪⼼法B、动态规划法C、分治策略D、回溯法3、采⽤贪⼼算法的最优装载问题的主要计算量在于将集装箱依其重量从⼩到⼤排序,故算法的时间复杂度为( B )。
A、O(n2n)B、O(nlogn)C、O(2n)D、O(n)4、⼀个问题可⽤动态规划算法或贪⼼算法求解的关键特征是问题的( B )。
A、重叠⼦问题B、最优⼦结构性质C、贪⼼选择性质D、定义最优解5、设⼀个算法的输⼊规模为n,Dn是所有输⼊的集合,任⼀输⼊I∈Dn,P(I)是I出现的概率,有=1,T(I)是算法在输⼊I下所执⾏的基本语句次数,则该算法的平均执⾏时间为(D)。
A、B、C、D、6、把递归算法转化为⾮递归算法有如下两种基本⽅法:(1)直接⽤循环结构的算法替代递归算法。
(2)⽤( A )模拟系统的运⾏过程,通过分析只保存必须保存的信息,从⽽⽤⾮递归算法替代递归算法。
A、栈B、队列C、顺序表D、链表7、算法分析中,记号表⽰(A)。
A、渐进下界B、渐进上界C、⾮紧上界D、紧渐进界9、贪⼼算法与动态规划算法的主要区别是(B )。
A、最优⼦结构B、贪⼼选择性质C、构造最优解D、定义最优解10、回溯法在问题的解空间树中,按(D)策略,从根结点出发搜索解空间树。
A、⼴度优先B、活结点优先C、扩展结点优先D、深度优先11. 回溯法的问题的解空间树是(B),并不需要在算法运⾏时构造⼀棵真正的树结构,然后再在该解空间树中搜索问题的解,⽽是只存储从根结点到当前结点的路径。
A、顺序⽅式的⼆叉树B、虚拟的树C、满⼆叉树D、完全⼆叉树12. 应⽤回溯法求解问题时,⾸先应该明确问题的解空间。
解空间中满⾜约束条件的决策序列称为(C)。
A、最优解B、局部最优解C、可⾏解D、最优⼦序列解13. ⼀个问题的最优解包含其⼦问题的最优解,则称此问题具有(D)性质。
算法复习题(精炼版)

填空题动态规划算法的基本要素为:最优子结构性质与重叠子问题性质1)算法分析中,记号O表示渐进上界,记号Ω表示渐进下界,记号Θ表示紧渐进界。
2)回溯法在问题的解空间树中,按深度优先策略,从根结点出发搜索解空间树。
3)分支限界法在问题的解空间树中,按广度优先策略,从根结点出发搜索解空间树。
所谓贪心选择性质是指(所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到)。
所谓最优子结构性质是指(问题的最优解包含了其子问题的最优解)。
回溯法是指(具有限界函数的深度优先生成法)。
回溯法的算法框架按照问题的解空间一般分为(子集树)算法框架与(排列树)算法框架。
4)二分搜索算法是利用分治策略实现的算法。
5)衡量一个算法好坏的标准是时间复杂度低6)最长公共子序列算法利用的算法是动态规划法7)Strassen矩阵乘法是利用分治策略实现的算法8)回溯法搜索状态空间树是按照深度优先遍历的顺序。
9)算法中通常以自底向下的方式求解最优解的是动态规划法10)背包问题的贪心算法所需的计算时间为O(nlogn)11)0-1背包问题的回溯算法所需的计算时间为O(n2n)12)用动态规划算法解决最大字段和问题,其时间复杂性为n13)一个算法就是一个有穷规则的集合,其中之规则规定了解决某一特殊类型问题的一系列运算,此外,算法还应具有以下五个重要特性:_有穷性,确定性,可行性,输入,输出。
1.算法的复杂性有时间复杂性和空间复杂性之分。
2、程序是算法用某种程序设计语言的具体实现。
3、算法的“确定性”指的是组成算法的每条指令是清晰的,无歧义的。
4.矩阵连乘问题的算法可由动态规划设计实现。
6、算法是指解决问题的一种方法或一个过程。
7、从分治法的一般设计模式可以看出,用它设计出的程序一般是递归算法。
8、问题的最优子结构性质是该问题可用动态规划算法或贪心算法求解的关键特征。
9、以深度优先方式系统搜索问题解的算法称为回溯法。
10、数值概率算法常用于数值问题的求解。
算法分析复习题目及答案16-12-10

一。
选择题1、二分搜索算法是利用( A )实现的算法。
A、分治策略B、动态规划法C、贪心法D、回溯法2、下列不是动态规划算法基本步骤的是( D )。
A、找出最优解的性质B、构造最优解C、算出最优解D、定义最优解3、最大效益优先是( A )的一搜索方式。
A、分支界限法B、动态规划法C、贪心法D、回溯法5. 回溯法解旅行售货员问题时的解空间树是()。
A、子集树B、排列树C、深度优先生成树D、广度优先生成树6.下列算法中通常以自底向上的方式求解最优解的是( B )。
A、备忘录法B、动态规划法C、贪心法D、回溯法注意:动态规划采用的是自底向上的方式求解,而贪心算法采用的是自顶向下的方式来求解问题。
7、衡量一个算法好坏的标准是(C )。
A 运行速度快B 占用空间少C 时间复杂度低D 代码短8、以下不可以使用分治法求解的是(D )。
A 棋盘覆盖问题B 选择问题C 归并排序D 0/1背包问题9. 实现循环赛日程表利用的算法是( A )。
A、分治策略B、动态规划法C、贪心法D、回溯法11.下面不是分支界限法搜索方式的是( D )。
A、广度优先B、最小耗费优先C、最大效益优先D、深度优先12.下列算法中通常以深度优先方式系统搜索问题解的是( D )。
A、备忘录法B、动态规划法C、贪心法D、回溯法13.备忘录方法是那种算法的变形。
( B )A、分治法B、动态规划法C、贪心法D、回溯法注意:备忘录是动态规划方法的一个步骤。
14.哈弗曼编码的贪心算法所需的计算时间为( B )。
A、O(n2n)B、O(nlogn)C、O(2n)D、O(n)15.分支限界法解最大团问题时,活结点表的组织形式是( B )。
A、最小堆B、最大堆C、栈D、数组16.最长公共子序列算法利用的算法是( B )。
A、分支界限法B、动态规划法C、贪心法D、回溯法17.实现棋盘覆盖算法利用的算法是( A )。
A、分治法B、动态规划法C、贪心法D、回溯法18.下面是贪心算法的基本要素的是( C )。
算法复习题

一、选择题1、衡量一个算法好坏的标准是( )。
(A )运行速度快 (B )占用空间少 (C )时间复杂度低 (D )代码短2、函数n n 1032 的渐进表达式是( )。
(A )O(23n ) (B )O(3) (C )O(n 10) (D )O(2n )3、以下不可以使用分治法求解的是( )。
(A )棋盘覆盖问题 (B )选择问题 (C )归并排序 (D ) 0/1背包问题4、二分搜索算法是利用( )实现的算法。
(A )分治策略 (B )动态规划法 (C )贪心法 (D )回溯法5、二分搜索算法的时间复杂性为( )。
(A )O(2n ) (B )O(n ) (C )O(n log ) (D )O(n n log )6、快速排序算法的时间复杂性为( )。
(A )O(2n ) (B )O(n ) (C )O(n log ) (D )O(n n log )7、实现大整数的乘法是利用( )的算法。
(A )分治策略 (B )动态规划法 (C )贪心法 (D )回溯法8、矩阵连乘问题的算法可由( )设计实现。
(A )分支界限算法 (B )动态规划算法 (C )贪心算法 (D )回溯算法9、实现循环赛日程表利用的算法是( )。
(A )分治策略 (B )动态规划法 (C )贪心法(D )回溯法10、下列是动态规划算法基本要素的是( )。
(A )定义最优解 (B )构造最优解 (C )算出最优解 (D )子问题重叠性质11、最长公共子序列算法利用的算法是( )。
(A )分治法 (B )动态规划法 (C )贪心法 (D )回溯法12、下列算法中通常以自底向上的方式求解最优解的是( )。
(A )备忘录法 (B )动态规划法 (C )贪心法 (D )回溯法13、以下不可以使用分治法求解的是( )。
(A )棋盘覆盖问题 (B )选择问题 (C )归并排序 (D )0/1背包问题14、下列算法中不能解决0/1背包问题的是( )(A )贪心法 (B )动态规划 (C )回溯法 (D )分支限界法15、算法是由若干条指令组成的有穷序列,而且满足以下性质( )(A )输入:有0个或多个输入 (B )输出:至少有一个输出(C )确定性:指令清晰,无歧义 (D )有限性:指令执行次数有限,而且执行时间有限A (1)(2)(3) B(1)(2)(4) C(1)(3)(4) D (1) (2)(3)(4)16、函数32n +10nlog n 的渐进表达式是( ).A. 2nB. 32nC. nlog nD. 10nlog n17、能采用贪心算法求最优解的问题,一般具有的重要性质为:( )(A )最优子结构性质与贪心选择性质 (B )重叠子问题性质与贪心选择性质(C )最优子结构性质与重叠子问题性质 (D )预排序与递归调用18、回溯法在问题的解空间树中,按()策略,从根结点出发搜索解空间树。
算法设计与分析考试题目及答案

算法设计与分析考试题目及答案Revised at 16:25 am on June 10, 2021I hope tomorrow will definitely be better算法分析与设计期末复习题一、 选择题1.应用Johnson 法则的流水作业调度采用的算法是DA. 贪心算法B. 分支限界法C.分治法D. 动态规划算法塔问题如下图所示;现要求将塔座A 上的的所有圆盘移到塔座B 上,并仍按同样顺序叠置;移动圆盘时遵守Hanoi 塔问题的移动规则;由此设计出解Hanoi 塔问题的递归算法正确的为:B3. 动态规划算法的基本要素为C A. 最优子结构性质与贪心选择性质 B .重叠子问题性质与贪心选择性质 C .最优子结构性质与重叠子问题性质 D. 预排序与递归调用4. 算法分析中,记号O 表示B , 记号Ω表示A , 记号Θ表示D ; A.渐进下界 B.渐进上界 C.非紧上界 D.紧渐进界 E.非紧下界5. 以下关于渐进记号的性质是正确的有:A A.f (n)(g(n)),g(n)(h(n))f (n)(h(n))=Θ=Θ⇒=Θ B. f (n)O(g(n)),g(n)O(h(n))h(n)O(f (n))==⇒= C. Ofn+Ogn = Omin{fn,gn} D. f (n)O(g(n))g(n)O(f (n))=⇔=Hanoi 塔A. void hanoiint n, int A, int C, int B { if n > 0 {hanoin-1,A,C, B; moven,a,b;hanoin-1, C, B, A; } B. void hanoiint n, int A, int B, int C { if n > 0 {hanoin-1, A, C, B; moven,a,b; hanoin-1, C, B, A; }C. void hanoiint n, int C, int B, int A { if n > 0 { hanoin-1, A, C, B; moven,a,b; hanoin-1, C, B, A; }D. void hanoiint n, int C, int A, int B { if n > 0 {hanoin-1, A, C, B; moven,a,b;hanoin-1, C, B, A; }6.能采用贪心算法求最优解的问题,一般具有的重要性质为:AA. 最优子结构性质与贪心选择性质B.重叠子问题性质与贪心选择性质C.最优子结构性质与重叠子问题性质D. 预排序与递归调用7. 回溯法在问题的解空间树中,按D策略,从根结点出发搜索解空间树;广度优先 B. 活结点优先 C.扩展结点优先 D. 深度优先8. 分支限界法在问题的解空间树中,按A策略,从根结点出发搜索解空间树;A.广度优先 B. 活结点优先 C.扩展结点优先 D. 深度优先9. 程序块A是回溯法中遍历排列树的算法框架程序;A.B.C.D.10.xk的个数;11. 常见的两种分支限界法为DA. 广度优先分支限界法与深度优先分支限界法;B. 队列式FIFO分支限界法与堆栈式分支限界法;C. 排列树法与子集树法;D. 队列式FIFO分支限界法与优先队列式分支限界法;12. k带图灵机的空间复杂性Sn是指BA.k带图灵机处理所有长度为n的输入时,在某条带上所使用过的最大方格数;B.k带图灵机处理所有长度为n的输入时,在k条带上所使用过的方格数的总和;C.k带图灵机处理所有长度为n的输入时,在k条带上所使用过的平均方格数;D.k带图灵机处理所有长度为n的输入时,在某条带上所使用过的最小方格数;13. N P类语言在图灵机下的定义为DA.NP={L|L是一个能在非多项式时间内被一台NDTM所接受的语言};B.NP={L|L是一个能在多项式时间内被一台NDTM所接受的语言};C.NP={L|L是一个能在多项式时间内被一台DTM所接受的语言};D.NP={L|L是一个能在多项式时间内被一台NDTM所接受的语言};14. 记号O的定义正确的是A;A.Ogn = { fn | 存在正常数c和n0使得对所有n≥n0有:0≤ fn ≤cgn };B.Ogn = { fn | 存在正常数c和n0使得对所有n≥n0有:0≤ cgn ≤fn };>0使得对所有n≥n0C.Ogn = { fn | 对于任何正常数c>0,存在正数和n有:0 ≤fn<cgn };>0使得对所有n≥n0D.Ogn = { fn | 对于任何正常数c>0,存在正数和n有:0 ≤cgn < fn };15. 记号Ω的定义正确的是B;A.Ogn = { fn | 存在正常数c和n0使得对所有n≥n0有:0≤ fn ≤cgn };B.Ogn = { fn | 存在正常数c和n0使得对所有n≥n0有:0≤ cgn ≤fn };>0使得对所有n≥n0有:C.gn = { fn | 对于任何正常数c>0,存在正数和n0 ≤fn<cgn };D.gn = { fn | 对于任何正常数c>0,存在正数和n0 >0使得对所有n≥n0有:0 ≤cgn < fn };二、 填空题1. 下面程序段的所需要的计算时间为 2O(n ) ;2.3.4. 5.6. 用回溯法解题的一个显着特征是在搜索过程中动态产生问题的解空间;在任何时刻,算法只保存从根结点到当前扩展结点的路径;如果解空间树 中从根结点到叶结点的最长路径的长度为hn,则回溯法所需的计算空间通常为Ohn ;7. 回溯法的算法框架按照问题的解空间一般分为子集树算法框架与排列树算法框架;8. 用回溯法解0/1背包问题时,该问题的解空间结构为子集树结构; 9.用回溯法解批处理作业调度问题时,该问题的解空间结构为排列树结构; 10.用回溯法解0/1背包问题时,计算结点的上界的函数如下所示,请在空格中填入合适的内容:11. n m12. 用回溯法解图的m着色问题时,使用下面的函数OK检查当前扩展结点的每一个儿子所相应的颜色的可用性,则需耗时渐进时间上限Omn;13.;设分分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用fn个单位时间;用Tn表示该分治法解规模为|P|=n的问题所需的计算时间,则有:(1)1 ()(/)()1O nT nkT n m f n n=⎧=⎨+>⎩通过迭代法求得Tn的显式表达式为:log1log()(/)nmk j jmjT n n k f n m-==+∑试证明Tn的显式表达式的正确性;2. 举反例证明0/1背包问题若使用的算法是按照p i/w i的非递减次序考虑选择的物品,即只要正在被考虑的物品装得进就装入背包,则此方法不一定能得到最优解此题说明0/1背包问题与背包问题的不同;证明:举例如:p={7,4,4},w={3,2,2},c=4时,由于7/3最大,若按题目要求的方法,只能取第一个,收益是7;而此实例的最大的收益应该是8,取第2,3 个;3. 求证:Ofn+Ogn = Omax{fn,gn} ;证明:对于任意f1n∈ Ofn ,存在正常数c1和自然数n1,使得对所有n≥n1,有f1n≤ c1fn ;类似地,对于任意g1n ∈ Ogn ,存在正常数c2和自然数n2,使得对所有n≥n2,有g1n ≤c2gn ;令c3=max{c1, c2}, n3 =max{n1, n2},hn= max{fn,gn} ;则对所有的 n ≥ n3,有f1n +g1n ≤ c1fn + c2gn≤c3fn + c3gn= c3fn + gn≤ c32 max{fn,gn} = 2c3hn = Omax{fn,gn} .4. 求证最优装载问题具有贪心选择性质;最优装载问题:有一批集装箱要装上一艘载重量为c 的轮船;其中集装箱i 的重量为Wi;最优装载问题要求确定在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船; 设集装箱已依其重量从小到大排序,x 1,x 2,…,x n 是最优装载问题的一个最优解;又设1min{|1}i i nk i x ≤≤== ;如果给定的最优装载问题有解,则有1k n ≤≤;证明: 四、 解答题1. 机器调度问题;问题描述:现在有n 件任务和无限多台的机器,任务可以在机器上得到处理;每件任务的开始时间为s i ,完成时间为f i ,s i <f i ;s i ,f i 为处理任务i 的时间范围;两个任务i,j 重叠指两个任务的时间范围区间有重叠,而并非指i,j 的起点或终点重合;例如:区间1,4与区间2,4重叠,而与4,7不重叠;一个可行的任务分配是指在分配中没有两件重叠的任务分配给同一台机器;因此,在可行的分配中每台机器在任何时刻最多只处理一个任务;最优分配是指使用的机器最少的可行分配方案;问题实例:若任务占用的时间范围是{1,4,2,5,4,5,2,6,4,7},则按时完成所有任务最少需要几台机器提示:使用贪心算法画出工作在对应的机器上的分配情况;2. 已知非齐次递归方程:f (n)bf (n 1)g(n)f (0)c =-+⎧⎨=⎩ ,其中,b 、c 是常数,gn 是n 的某一个函数;则fn 的非递归表达式为:nnn i i 1f (n)cb b g(i)-==+∑;现有Hanoi 塔问题的递归方程为:h(n)2h(n 1)1h(1)1=-+⎧⎨=⎩ ,求hn 的非递归表达式;解:利用给出的关系式,此时有:b=2, c=1, gn=1, 从n 递推到1,有: 3. 单源最短路径的求解;问题的描述:给定带权有向图如下图所示G =V,E,其中每条边的权是非负实数;另外,还给定V 中的一个顶点,称为源;现在要计算从源到所有其它各顶点的最短路长度;这里路的长度是指路上各边权之和;这个问题通常称为单源最短路径问题;解法:现采用Dijkstra 算法计算从源顶点1到其它顶点间最短路径;请将此过程填入下表中;4. 请写出用回溯法解装载问题的函数; 装载问题:有一批共n 个集装箱要装上2艘载重量分别为c1和c2的轮船,其中集装箱i 的重量为wi,且121ni i w c c =≤+∑;装载问题要求确定是否有一个合理的装载方案可将这n 个集装箱装上这2艘轮船;如果有,找出一种装载方案;解:void backtrack int i{用分支限界法解装载问题时,对算法进行了一些改进,下面的程序段给出了改进部分;试说明斜线部分完成什么功能,以及这样做的原因,即采用这样的方式,算法在执行上有什么不同;初始时将;也就是说,重量仅在搜索进入左子树是增加,因此,可以在算法每一次进入左子树时更新bestw 的值;43 2 110030maxint10 - {1} 初始 dist5 dist4 dist3 dist2 u S 迭代7. 最长公共子序列问题:给定2个序列X={x 1,x2,…,xm }和Y={y 1,y2,…,yn },找出X 和Y 的最长公共子序列;由最长公共子序列问题的最优子结构性质建立子问题最优值的递归关系;用cij 记录序列Xi 和Yj 的最长公共子序列的长度;其中, Xi={x1,x2,…,xi};Y j={y1,y2,…,yj};当i=0或j=0时,空序列是Xi 和Yj 的最长公共子序列;故此时Cij=0;其它情况下,由最优子结构性质可建立递归关系如下:00,0[][][1][1]1,0;max{[][1],[1][]},0;i j i ji j c i j c i j i j x y c i j c i j i j x y ⎧==⎪=--+>=⎨⎪-->≠⎩在程序中,bij 记录Cij 的值是由哪一个子问题的解得到的;8.1.2.3.4.5.用回溯法解问题时,应明确定义问题的解空间,问题的解空间至少应包含___________;6.动态规划算法的基本思想是将待求解问题分解成若干____________,先求解___________,然后从这些____________的解得到原问题的解;7.以深度优先方式系统搜索问题解的算法称为_____________;背包问题的回溯算法所需的计算时间为_____________,用动态规划算法所需的计算时间为____________;9.动态规划算法的两个基本要素是___________和___________;10.二分搜索算法是利用_______________实现的算法;二、综合题50分1.写出设计动态规划算法的主要步骤;2.流水作业调度问题的johnson算法的思想;3.若n=4,在机器M1和M2上加工作业i所需的时间分别为ai 和bi,且a 1,a2,a3,a4=4,5,12,10,b1,b2,b3,b4=8,2,15,9求4个作业的最优调度方案,并计算最优值;4.使用回溯法解0/1背包问题:n=3,C=9,V={6,10,3},W={3,4,4},其解空间有长度为3的0-1向量组成,要求用一棵完全二叉树表示其解空间从根出发,左1右0,并画出其解空间树,计算其最优值及最优解;5.设S={X1,X2,···,Xn}是严格递增的有序集,利用二叉树的结点来存储S中的元素,在表示S的二叉搜索树中搜索一个元素X,返回的结果有两种情形,1在二叉搜索树的内结点中找到X=Xi ,其概率为bi;2在二叉搜索树的叶结点中确定X∈Xi ,Xi+1,其概率为ai;在表示S的二叉搜索树T中,设存储元素Xi的结点深度为C i ;叶结点Xi,Xi+1的结点深度为di,则二叉搜索树T的平均路长p为多少假设二叉搜索树Tij={Xi ,Xi+1,···,Xj}最优值为mij,Wij= ai-1+bi+···+bj+aj,则mij1<=i<=j<=n递归关系表达式为什么6.描述0-1背包问题;三、简答题30分1.流水作业调度中,已知有n个作业,机器M1和M2上加工作业i所需的时间分别为ai 和bi,请写出流水作业调度问题的johnson法则中对ai和bi的排序算法;函数名可写为sorts,n2.最优二叉搜索树问题的动态规划算法设函数名binarysearchtree答案:一、填空1.确定性有穷性可行性 0个或多个输入一个或多个输出2.时间复杂性空间复杂性时间复杂度高低3. 该问题具有最优子结构性质4.{BABCD}或{CABCD}或{CADCD}5.一个最优解6.子问题子问题子问题7.回溯法8. on2n omin{nc,2n}9.最优子结构重叠子问题10.动态规划法二、综合题1.①问题具有最优子结构性质;②构造最优值的递归关系表达式;③最优值的算法描述;④构造最优解;2. ①令N1={i|ai<bi},N2={i|ai>=bi};②将N1中作业按ai的非减序排序得到N1’,将N2中作业按bi的非增序排序得到N2’;③N1’中作业接N2’中作业就构成了满足Johnson法则的最优调度;3.步骤为:N1={1,3},N2={2,4};N 1’={1,3}, N2’={4,2};最优值为:384.解空间为{0,0,0,0,1,0,0,0,1,1,0,0,0,1,1,1,0,1, 1,1,0,1,1,1}; 解空间树为:该问题的最优值为:16 最优解为:1,1,0 5.二叉树T 的平均路长P=∑=+ni 1Ci)(1*bi +∑=nj 0dj *aj{mij=0 i>j6.已知一个背包的容量为C,有n 件物品,物品i 的重量为W i ,价值为V i ,求应如何选择装入背包中的物品,使得装入背包中物品的总价值最大; 三、简答题 1.void sortflowjope s,int n {int i,k,j,l;fori=1;i<=n-1;i++ag=0 k++; ifk>n break;ag==0ifsk.a>sj.a k=j; swapsi.index,sk.index; swapsi.tag,sk.tag;} }l=i;<sj.b k=j;swapsi.index,sk.index; ag,sk.tag; }mij=Wij+min{mik+mk+1j} 1<=i<=j<=n,mii-1=0}2.void binarysearchtreeint a,int b,int n,int m,int s,int w{int i,j,k,t,l;fori=1;i<=n+1;i++{wii-1=ai-1;mii-1=0;}forl=0;l<=n-1;l++Init-single-sourceG,s2. S=Φ3. Q=VGQ<> Φdo u=minQS=S∪{u}for each vertex 3do 4四、算法理解题本题10分根据优先队列式分支限界法,求下图中从v1点到v9点的单源最短路径,请画出求得最优解的解空间树;要求中间被舍弃的结点用×标记,获得中间解的结点用单圆圈○框起,最优解用双圆圈◎框起;五、算法理解题本题5分设有n=2k个运动员要进行循环赛,现设计一个满足以下要求的比赛日程表:①每个选手必须与其他n-1名选手比赛各一次;②每个选手一天至多只能赛一次;③循环赛要在最短时间内完成;1如果n=2k,循环赛最少需要进行几天;2当n=23=8时,请画出循环赛日程表;六、算法设计题本题15分分别用贪心算法、动态规划法、回溯法设计0-1背包问题;要求:说明所使用的算法策略;写出算法实现的主要步骤;分析算法的时间;七、算法设计题本题10分通过键盘输入一个高精度的正整数nn的有效位数≤240,去掉其中任意s个数字后,剩下的数字按原左右次序将组成一个新的正整数;编程对给定的n 和s,寻找一种方案,使得剩下的数字组成的新数最小;样例输入178543S=4样例输出13一、填空题本题15分,每小题1分1.规则一系列运算2. 随机存取机RAMRandom Access Machine;随机存取存储程序机RASPRandom Access Stored Program Machine;图灵机Turing Machine3. 算法效率4. 时间、空间、时间复杂度、空间复杂度5.2n6.最好局部最优选择7. 贪心选择最优子结构二、简答题本题25分,每小题5分1、分治法的基本思想是将一个规模为n的问题分解为k个规模较小的子问题,这些子问题互相独立且与原问题相同;对这k个子问题分别求解;如果子问题的规模仍然不够小,则再划分为k个子问题,如此递归的进行下去,直到问题规模足够小,很容易求出其解为止;将求出的小规模的问题的解合并为一个更大规模的问题的解,自底向上逐步求出原来问题的解;2、“最优化原理”用数学化的语言来描述:假设为了解决某一优化问题,需要依次作出n个决策D1,D2,…,Dn,如若这个决策序列是最优的,对于任何一个整数k,1 < k < n,不论前面k个决策是怎样的,以后的最优决策只取决于由前面决策所确定的当前状态,即以后的决策Dk+1,Dk+2,…,Dn也是最优的;3、某个问题的最优解包含着其子问题的最优解;这种性质称为最优子结构性质;4、回溯法的基本思想是在一棵含有问题全部可能解的状态空间树上进行深度优先搜索,解为叶子结点;搜索过程中,每到达一个结点时,则判断该结点为根的子树是否含有问题的解,如果可以确定该子树中不含有问题的解,则放弃对该子树的搜索,退回到上层父结点,继续下一步深度优先搜索过程;在回溯法中,并不是先构造出整棵状态空间树,再进行搜索,而是在搜索过程,逐步构造出状态空间树,即边搜索,边构造;5、PPolynomial问题:也即是多项式复杂程度的问题;NP就是Non-deterministicPolynomial的问题,也即是多项式复杂程度的非确定性问题;NPCNP Complete问题,这种问题只有把解域里面的所有可能都穷举了之后才能得出答案,这样的问题是NP里面最难的问题,这种问题就是NPC问题;三、算法填空本题20分,每小题5分1、n后问题回溯算法1 Mj&&Li+j&&Ri-j+N2 Mj=Li+j=Ri-j+N=1;3 tryi+1,M,L,R,A4 Aij=05 Mj=Li+j=Ri-j+N=0 2、数塔问题; 1c<=r2trc+=tr+1c 3trc+=tr+1c+1 3、Hanoi 算法 1movea,c2Hanoin-1, a, c , b 3Movea,c 4、1pv=NIL 2pv=u3 v ∈adju 4Relaxu,v,w四、算法理解题本题10分五、18天2分;2当n=23=8时,循环赛日程表3分;六、算法设计题本题15分 1贪心算法 Onlogn ➢ 首先计算每种物品单位重量的价值Vi/Wi,然后,依贪心选择策略,将尽可能多的单位重量价值最高的物品装入背包;若将这种物品全部装入背包后,背包内的物品总重量未超过C,则选择单位重量价值次高的物品并尽可能多地装入背包;依此策略一直地进行下去,直到背包装满为止; ➢ 具体算法可描述如下:void Knapsackint n,float M,float v,float w,float x {Sortn,v,w; int i;for i=1;i<=n;i++ xi=0; float c=M;for i=1;i<=n;i++ {if wi>c break; xi=1; c-=wi; }if i<=n xi=c/wi; }2动态规划法 Oncmi,j 是背包容量为j,可选择物品为i,i+1,…,n 时0-1背包问题的最优值;由0-1背包问题的最优子结构性质,可以建立计算mi,j 的递归式如下;void KnapSackint v,int w,int c,int n,int m11 {int jMax=minwn-1,c;for j=0;j<=jMax;j++ /mn,j=0 0=<j<wn/ mnj=0;1 2 3 4 5 6 7 82 1 43 6 5 8 73 4 1 2 7 8 5 64 3 2 1 8 7 6 55 6 7 8 1 2 3 4 6 5 8 7 2 1 4 37 8 5 6 3 4 1 28 7 6 5 4 3 2 1for j=wn;j<=c;j++ /mn,j=vn j>=wn/mnj=vn;for i=n-1;i>1;i--{ int jMax=minwi-1,c;for j=0;j<=jMax;j++ /mi,j=mi+1,j 0=<j<wi/mij=mi+1j;for j=wi;j<=c;j++/mn,j=vn j>=wn/mij=maxmi+1j,mi+1j-wi+vi;}m1c=m2c;ifc>=w1m1c=maxm1c,m2c-w1+v1;}3回溯法 O2ncw:当前重量 cp:当前价值 bestp:当前最优值voidbacktrack int i//回溯法 i初值1{ifi>n //到达叶结点{ bestp=cp; return; }ifcw+wi<=c //搜索左子树{cw+=wi;cp+=pi;backtracki+1;cw-=wi;cp-=pi;}ifBoundi+1>bestp//搜索右子树backtracki+1;}七、算法设计题本题10分为了尽可能地逼近目标,我们选取的贪心策略为:每一步总是选择一个使剩下的数最小的数字删去,即按高位到低位的顺序搜索,若各位数字递增,则删除最后一个数字,否则删除第一个递减区间的首字符;然后回到串首,按上述规则再删除下一个数字;重复以上过程s次,剩下的数字串便是问题的解了;具体算法如下:输入s, n;while s > 0{ i=1; //从串首开始找while i < lengthn && ni<ni+1{i++;}deleten,i,1; //删除字符串n的第i个字符s--;}while lengthn>1&& n1=‘0’deleten,1,1; //删去串首可能产生的无用零输出n;。
人工智能核心算法复习题含答案

人工智能核心算法复习题含答案一、单选题(共40题,每题1分,共40分)1、假设我们有一个使用ReLU激活函数(ReLU activation function)的神经网络,假如我们把ReLU激活替换为线性激活,那么这个神经网络能够模拟出同或函数(XNOR function)吗A、可以B、不能C、不好说D、不一定正确答案:B2、EM算法是()A、半监督B、都不是C、有监督D、无监督正确答案:D3、让学习器不依赖外界交互、自动地利用未标记样本来提升学习性能,就是(___)?A、监督学习B、倍监督学习C、无监督学习D、半监督学习正确答案:D4、YOLOv3在coco数据集上聚类了()个矛框?A、9B、nanC、80D、3正确答案:A5、在一个神经网络中,知道每一个神经元的权重和偏差是最重要的一步。
如果知道了神经元准确的权重和偏差,便可以近似任何函数,但怎么获知每个神经的权重和偏移呢?A、以上都不正确的B、搜索每个可能的权重和偏差组合,直到得到最佳值C、随机赋值,听天由命D、赋予一个初始值,然后检查跟最佳值的差值,不断迭代调整权重正确答案:D6、执行完语句X_train, X_test, y_train, y_test = train_test_split( ... iris.data, iris.target, test_size=0.4, random_state=0),训练集占比多少?A、50%B、70%C、60%D、40%正确答案:C7、如果一个模型在测试集上偏差很大,方差很小,则说明该模型?A、过拟合B、刚好拟合C、可能过拟合可能欠拟合D、欠拟合正确答案:C8、下列哪个神经网络结构会发生权重共享A、卷积神经网络B、循环神经网络C、全连接神经网络D、卷积和循环神经网络正确答案:D9、混沌度(Perplexity)是一种常见的应用在使用深度学习处理NLP问题过程中的评估技术,关于混沌度,哪种说法是正确的?A、混沌度越高越好B、混沌度对于结果的影响不一定C、混沌度没什么影响D、混沌度越低越好正确答案:D10、关于递归函数基例的说明,以下选项中错误的是A、递归函数的基例不再进行递归B、每个递归函数都只能有一个基例C、递归函数的基例决定递归的深度D、递归函数必须有基例正确答案:B11、通过以下哪些指标我们可以在层次聚类中寻找两个集群之间的差异?()A、以上都行B、均链接C、单链接D、全链接正确答案:A12、考虑以下问题:假设我们有一个5层的神经网络,这个神经网络在使用一个4GB显存显卡时需要花费3个小时来完成训练。
计算机算法复习题

计算机算法复习题## 计算机算法复习题### 一、选择题1. 在排序算法中,时间复杂度为O(nlogn)的算法是:A. 冒泡排序B. 快速排序C. 选择排序D. 插入排序2. 以下哪个算法是用于解决最近邻问题的?A. Dijkstra算法B. A*算法C. 动态规划D. 贪心算法### 二、填空题1. 在图的遍历中,深度优先搜索(DFS)使用的栈是_________。
2. 快速排序算法的核心思想是_________。
3. 在动态规划中,解决背包问题通常使用_________方法。
### 三、简答题1. 描述二分查找算法的基本步骤,并说明其时间复杂度。
二分查找算法的基本步骤如下:- 首先,设定查找区间的左右端点。
- 在查找区间的中间位置取一个值,与目标值进行比较。
- 如果中间值等于目标值,则查找成功。
- 如果中间值小于目标值,则在右半区间继续查找。
- 如果中间值大于目标值,则在左半区间继续查找。
- 重复以上步骤,直到找到目标值或查找区间为空。
二分查找算法的时间复杂度为O(logn)。
2. 什么是动态规划?请举例说明其应用场景。
动态规划是一种通过将复杂问题分解为更简单的子问题来求解的方法。
它适用于具有重叠子问题和最优子结构特性的问题。
在动态规划中,我们首先解决子问题,并将结果存储在一个表格中,以避免重复计算。
这样,当需要解决更大的子问题时,可以直接使用表格中的结果。
一个典型的动态规划应用场景是斐波那契数列的计算。
传统的递归方法会重复计算很多子问题,而使用动态规划,我们可以存储已计算的斐波那契数,从而大大提高计算效率。
### 四、编程题给定一个未排序的整数数组,请使用快速排序算法对其进行排序,并输出排序后的结果。
```pythondef quick_sort(arr):if len(arr) <= 1:return arrpivot = arr[len(arr) // 2]left = [x for x in arr if x < pivot]middle = [x for x in arr if x == pivot]right = [x for x in arr if x > pivot]return quick_sort(left) + middle + quick_sort(right)# 示例arr = [3, 6, 8, 10, 1, 2, 1]sorted_arr = quick_sort(arr)print(sorted_arr)```通过以上复习题,可以对计算机算法的基本概念、原理和应用有一个全面的回顾和理解。
算法分析与设计考试复习题及参考答案jing

一、填空题1、算法的复杂性是算法效率2、的度量,是评价算法优劣的重要依据。
1、设n为正整数,利用大“O(·)”记号,将下列程序段的执行时间表示为n的函数,则下面程序段的时间复杂度为O(n)2、。
i=1; k=0;while(i<n) { k=k+10*i;i++; }3、计算机的资源最重要的是时间和空间资源。
因而,算法的复杂性有时间复杂度和空间复杂度之分。
3、f(n)= 6×2n+n2,f(n)的渐进性态f(n)= O( 2n4、 )5、递归是指函数直接或者间接通过一些语句调用自身。
4、分治法的基本思想是将一个规模为n的问题分解为k个规模较小的子问题,这些子问题互相独立6、且与原问题相同。
二、选择题(本题20分,每小题2分)1、分支限界法与回溯法都是在问题的解空间树T上搜索问题的解,二者( B )。
A.求解目标不同,搜索方式相同B.求解目标不同,搜索方式也不同C.求解目标相同,搜索方式不同D.求解目标相同,搜索方式也相同2、回溯法在解空间树T上的搜索方式是( A)。
A.深度优先B.广度优先C.最小耗费优先D.活结点优先3、在对问题的解空间树进行搜索的方法中,一个活结点最多有一次机会成为活结点的是( B )。
A.回溯法B.分支限界法C.回溯法和分支限界法D.回溯法求解子集树问题4、以下关于判定问题难易处理的叙述中正确的是( C )。
A.可以由多项式时间算法求解的问题是难处理的B.需要超过多项式时间算法求解的问题是易处理的C.可以由多项式时间算法求解的问题是易处理的D.需要超过多项式时间算法求解的问题是不能处理的5、设f(N),g(N)是定义在正数集上的正函数,如果存在正的常数C和自然数N0,使得当N≥N0时有f(N)≤Cg(N),则称函数f(N)当N充分大时有上界g(N),记作f(N)=O(g(N)),即f(N)的阶( A )g(N)的阶。
A.不高于B.不低于C.等价于D.逼近6、对于含有n个元素的子集树问题,最坏情况下其解空间的叶结点数目为( B )。
算法设计复习题

一、单选题1、下面关于算法的描述,正确的是(d )A、一个算法只能有一个输入B、算法只能用框图来表示C、一个算法的执行步骤可以是无限的D、一个完整的算法,不管用什么方法来表示,都至少有一个输出结果2、一位爱好程序设计的同学,想通过程序设计解决“韩信点兵”的问题,他制定的如下工作过程中,更恰当的是(c )A、设计算法,编写程序,提出问题,运行程序,得到答案B、分析问题,编写程序,设计算法,运行程序,得到答案C、分析问题,设计算法,编写程序,运行程序,得到答案D、设计算法,提出问题,编写程序,运行程序,得到答案3、有5位运动员100米成绩依次为13.8,12.5,13.0,13.2,13.4,(c)若采用选择排序算法对其进行从小到大排序,则第二趟的排序结果是(A) 12.5 13.8 13.2 13.4 13.0 (B) 12.5 13.4 13.2 13.8 13.0(C) 12.5 13.0 13.8 13.2 13.4 (D) 12.5 13.2 13.8 13.4 13.04、下面说法正确的是(a )A、算法+数据结构=程序B、算法就是程序C、数据结构就是程序D、算法包括数据结构5、数列1,4,7,10,13,……的递推公式为( d )。
(A) f(1)=1;f(n)=n+3 (B) f(1)=1;f(n)=n*2-1(C) f(1)=1;f(n)=n*2+1 (D) f(1)=1;f(n)=f(n-1)+36、用选择排序法对数据7,6,3,9,2从大到小排序,共需经过多少次数据对调。
a(A) 3 (B) 4 (C) 5 (D) 107、动态规划算法的基本要素为(c )。
A、最优子结构性质与贪心选择性质B、重叠子问题性质与贪心选择性质C、最优子结构性质与重叠子问题性质D.、预排序与递归调用8、算法分析中,记号O表示( b ),记号Ω表示(a),记号Θ表示(d )。
A、渐进下界B、渐进上界C、非紧上界D、紧渐进界E、非紧下界9、以下关于渐进记号的性质是正确的有:(a)A、f(n)(g(n)),g(n)(h(n))f(n)(h(n))=Θ=Θ⇒=ΘB、f(n)O(g(n)),g(n)O(h(n))h(n)O(f(n))==⇒=C、O(f(n))+O(g(n)) = O(min{f(n),g(n)})D、f(n)O(g(n))g(n)O(f(n))=⇔=10、下列算法中通常以自底向上的方式求解最优解的是( b )。
算法复习题选择题

算法复习题选择题一、选择题1. 下列哪种排序算法具有最差时间复杂度为O(n^2)?A. 快速排序B. 归并排序C. 堆排序D. 冒泡排序答案:D. 冒泡排序解析:冒泡排序是一种简单直观的排序算法,它的基本思想是通过不断比较相邻的两个元素,将较大的元素向右移动,较小的元素向左移动,直到整个序列按照从小到大的顺序排列。
冒泡排序的最差时间复杂度为O(n^2),当待排序序列已经有序时,冒泡排序的最坏情况就会出现,需要进行n-1趟排序,每趟比较n-1次。
2. 下列哪种排序算法不属于比较排序?A. 计数排序B. 插入排序C. 选择排序D. 希尔排序答案:A. 计数排序解析:计数排序是一种非比较排序算法,它通过确定每个元素之前有多少个元素小于它来确定元素的位置。
计数排序的时间复杂度为O(n+k),其中n为待排序序列的长度,k为待排序序列中的最大值大小。
3. 下列哪个算法通常用来解决最短路径问题?A. Dijkstra算法B. Kruskal算法C. Prim算法D. Floyd-Warshall算法答案:A. Dijkstra算法解析:Dijkstra算法是一种用于求解单源最短路径问题的算法。
它基于贪心策略,通过选择当前最短路径上的顶点来逐步扩展最短路径树。
Dijkstra算法的时间复杂度为O(V^2),其中V为图的顶点数。
4. 下列哪种数据结构通常用于实现图的遍历?A. 队列B. 栈C. 链表D. 数组答案:B. 栈解析:图的遍历包括深度优先遍历和广度优先遍历两种方式。
其中,深度优先遍历(DFS)通常使用栈来实现,广度优先遍历(BFS)通常使用队列来实现。
栈是一种后进先出(LIFO)的数据结构,适合将深度优先遍历的节点存储起来。
5. 下列哪种查找算法具有最坏时间复杂度为O(log n)?A. 二分查找B. 线性查找C. 哈希查找D. 顺序查找答案:A. 二分查找解析:二分查找是一种基于分治思想的查找算法,它通过将查找区间逐步缩小为左右两个子区间,并与目标元素进行比较,从而确定目标元素的位置。
算法复习题
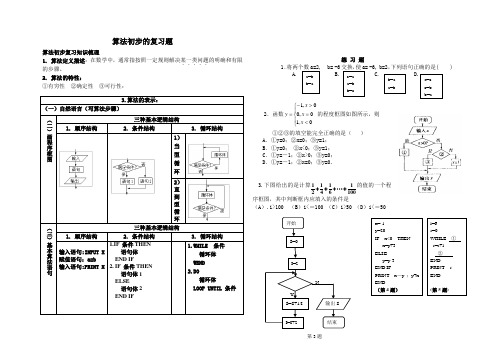
算法初步的复习题算法初步复习知识梳理1. 算法定义描述:在数学中,通常指按照一定规则解决某一类问题.....的明确和有限的步骤。
2. 算法的特性:①有穷性 ②确定性 ③可行性:练 习 题1.-6-6, b=2,下列语句正确的是( )2.函数⎪⎩⎪⎨⎧<=>-=0,10,00,1x x x y 的程度框图如图所示,则①②③的填空能完全正确的是( )A .①y=0;②x=0;③y=1;B .①y=0; ②x<0;③y=1;C .①y=-1;②x>0;③y=0;D .①y=-1;②x=0;③y=0.3.下图给出的是计算0101614121+⋅⋅⋅+++的值的一个程 序框图,其中判断框内应填入的条件是(A ).i>100 (B )i<=100 (C )i>50 (D )i<=50第3题4.图中程序运行后输出的结果为( )(A)3 43 (B)43 3(C)-18 16 (D)16 -185.图中程序是计算2+3+4+5+6的值的程序。
在WHILE后的①处和在s=s+i之后的②处所就填写的语句可以是( )A.①i>1 ②i=i-1 B.①i>1 ②i=i+1C.①i>=1 ②i=i+1 D.①i>=1 ②i=i-16、按如下图所示的程序框图,在运行后输出的结果为()A.36 B.45 C.55 D.56第7题7.上面的程序框图,如果输入三个实数a、b、c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的()A. c > xB. x > cC. c > bD. b > c8.如果下边程序执行后输出的结果是990,那么在程序中UNTIL后面的“条件”应为( )A. i>10B. i<8C. i<=9D. i<99.右边程序运行后输出的的结果是( ) A.17B.19C.21D.2310.如右图所示的程序是用来( )A.计算3×10的值B.计算93的值C.计算103的值D.计算1×2×3×…×10的值11.为了在运行程序之后得到输出16,键盘输入x应该是( ) INPUT xIF x<0 THENy=(x+1)*(x+1)ELSEy=(x-1)*(x-1)END IFPRINT yENDA.3或-3 B.-5 C.5或-3 D.5或-5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.什么是算法?算法必须满足的五个特性是什么?算法:一组有穷的规则,规定了解决某一特定类型问题的一系列运算。
(有限指令的集合,遵循它可以完成一个特定的任务).必须满足的五个特性是(遵循以下五条准则):1.有穷(限)性2.确定性3.可(能)行性4.输入(n≥0)5.输出(n≥1)2.对算法进行分析分哪两个阶段?各自完成什么任务(分别得到什么结果)?对一个算法要作出全面的分析可分成两个阶段进行,即:事前分析和事后测试。
事前分析求出该算法的一个时间界限函数;事后测试搜集此算法的执行时间和实际占用空间的统计资料。
3.证明:若f1(n)=O(g1(n))并且f2(n)= O(g2(n)),那么f1(n) +f2(n)=O(max{g1(n), g2(n)}证明:根据f1(n)=O(g1(n))可知,存在正常数C1,当n≥n0时,使得|f1(n)|≤C1|g1(n)|;同理,根据f2(n)= O(g2(n))可知,存在正常数C2,当n≥n0时,使得|f2(n)|≤C2|g2(n)|当n≥n0时,|f1(n)+f2(n)|≤|f1(n)|+|f2(n)|≤C1|g1(n)|+C2|g2(n)|≤C1|g k(n)|+C2|g k(n)|≤(C1+C2)|g k(n)|,其中g k(n)=max{g1(n),g2(n)},k={1,2}当n≥n0时,取C=(C1+C2),据定义命题得证。
4.如果f1(n)= Θ(g1(n))并且f2(n)= Θ(g2(n)),下列说法是否正确?试说明之。
(a) f1(n) +f2(n)= Θ(g1(n)+ g2(n))(b) f1(n) +f2(n)= Θ(min{g1(n), g2(n)})(c) f1(n) +f2(n)= Θ(max{g1(n), g2(n)})答:(a)和(c)均正确,(b)错误。
(a)正确可以根据定义直接证得。
(b)错误可举反例。
例:f1(n)= 2n,f2(n)=2 n2下面证明(c)正确性.根据上题已经证明f1(n)+f2(n)= O(max{g1(n),g2(n)}),下面只需证明f 1(n)+f2(n)= Ω(max{g1(n), g2(n)}),即存在正常数C,使得|f1(n)+f2(n)|≥C(max{g1(n), g2(n)})根据f1(n)= Θ(g1(n))并且f2(n)= Θ(g2(n)) 得到,当n≥n0时,存在正常数C1、C2、C3、C4C 1|g1(n)|≤|f1(n)|≤C3|g1(n)|C2|g2(n)|≤|f2(n)|≤C4|g2(n)|不妨设max{g1(n), g2(n)}= g1(n)由于|f1(n)+f2(n)|≥||f1(n)|-|f2(n)||≥|C1|g1(n)|-C3|g2(n)||=C|max{g1(n), g2(n)}|取C≥|C1-C3|的正常数,由定义得f 1(n)+f2(n) = Ω(max{g1(n), g2(n)})命题得证。
5.证明 |「log2n」|= O(n) 证明:对于任意的正整数n,|「log2n」|≤|log2(n+1)|≤|n+1|≤2|n|取n0=1,C=2,根据定义知命题成立。
6.证明 3n「log2n」= O(n2)证明:对于任意的正整数n,|3n「log2n」|≤|3n「log2n」|≤3|n2| 取n0=1,C=3,根据定义知命题成立。
7.用数学归纳法证明:当n≥1时,∑=+ =ninni12/)1(.证明:当n=1时,∑==nii11,n(n+1)/2=1,命题成立;假设n=k-1时,∑=+ =ninni12/)1(成立;(k≥2)当n=k时,∑=+ =ninni12/)1(=kkkini+-=∑=12/)1(=k(k+1)/2综上可知,命题成立。
8.在下列情况下求解递归关系式T(n)=()2(/2)()g nT n f n⎧⎨+⎩否则足够小n当①n=2k g(n)= O(1)和f(n)= O(n);②n=2k g(n)= O(1)和f(n)= O(1)。
解: T(n)=T(2k)=2 T(2k-1)+f(2k)=2(2 T(2k-2)+f(2k-1)) +f(2k)=22T(2k-2)+21 f(2k-1)+ f(2k)=……=2k T(1)+2k-1f(2)+2k-2f(22)+…+20f(2k ) =2k g(n)+ 2k-1f(2)+2k-2f(22)+…+20f(2k ) ①当g(n)= O (1)和f(n)= O (n)时,不妨设g(n)=a ,f(n)=bn ,a ,b 为正常数。
则T(n)=T(2k )= 2k a+ 2k-1*2b+2k-2*22b+…+20*2k b =2k a+kb2k=an+bnlog 2n= O (nlog 2n) ②当g(n)= O (1)和f(n)= O (1)时,不妨设g(n)=c ,f(n)=d ,c ,d 为正常数。
则 T(n)=T(2k )=c2k + 2k-1d+2k-2d+…+20d=c2k +d(2k -1)=(c+d)n-d= O (n)9.求解递推关系式:解:构造生成函数∑∞==++=12)()2()1()(k k x k h x h x h x H求解)(x H+--=-++=322)2(2)1(2)(2)2()1()(x h x h x xH x h x h x Hxxx x x x H x -=+++=-1)()21(32 )1(<x )1)(21()(x x xx H --=分解)(x H 成幂级数 令xBx A x H 211)(-+-=则A=-1 B=1))2()2(21()1(21111)(322 ++++++++-=-+--=∴x x x x x xx x H1)1(2)(1)1(+-==n h n h h∑∞=-=+-++-+-=122)12()12()12()12(k kk n n x x x x所以12)(-=∴n n h10.求解递推关系式:⎩⎨⎧+==-22111n nT T T解:22*3)22(22222)2(222111122221-=+++=++=++=+=------n n n n n n n T T T T T11.求解递推关系式:⎪⎩⎪⎨⎧>+===--)2(112121n F F F F F n n n解:以n F 为系数,构成生成函数)(x F++=-++=++=423123221221)()()(x F x F x F x x F x F x xF x F x F x F251251)251)(251(1)()()()(1(231232121)2+++-+=++-+-=--==+--+-+=--x Bx A x x x xx xx F x x F F F x F F x F x F x x )511(21+-=A )511(21--=B +-+-=222)()((51)(x x x F βαβα 其中251+=α 251-=βnn n n n n F F )251(51)(51+≈-=∞→βα12.分治法的三个步骤是什么?给出使用SPARKS 语言描述的分治策略抽象化控制。
答:分治法的三个步骤是: ① 分解 ②解决 ③合并 用SPARKS 语言描述的分治策略抽象化控制为:Procedure DANDC(p,q)Global n,A(1:n);integer m,p,q; If SMALL(p,q)Then return(G(p,q)) Else m ←DIVIDE(p,q)Return(COMBINE(DANDC(p,m), DANDC(m+1,q)))Endif End DANDC13.根据教材中所给出的二分检索策略,写一个二分检索的递归过程。
Procedure BINSRCH(A, low, high, x, j) integer mid if low ≤high then mid ←⎣⎦2/)(high low +if x=A(mid) then j ←mid; endifif x>A(mid) then BINSRCH(A, mid+1, high, x, j); endif if x<A(mid) then BINSRCH(A, low, mid-1, x, j); endifelse j ←0; endif end BINSRCH14.作一个“三分”检索算法。
它首先检查n/3处的元素是否等于某个x 的值,然后检查2n/3处的元素;这样,或者找到x ,或者把集合缩小到原来的1/3。
分析此算法在各种情况下的计算复杂度。
Procedure ThriSearch(A, x, n, j) integer low, high, p1, p2 low ←1; high ←n while low ≤high dop1←⎣⎦3/)2(high low + ; p2←⎣⎦3/)2(high low + case:x=A(p1): j ←p1; return :x=A(p2): j ←p2; return :x<A(p1): high ←p1-1 :x>A(p2): low ←p2+1:else: low ←p1+1; high ←p2-1end caserepeat j ←0 end ThriSearchT(n)= ⎩⎨⎧+)()3/()(n f n T n g 否则足够小ng(n)= O (1) f(n)= O (1)成功:O(1), O(log3(n)), O(log3(n))最好,平均,最坏失败:O(log3(n)), O(log3(n)), O(log3(n))最好,平均,最坏15.对于含有n个内部结点的二元树,证明E=I+2n,其中,E,I分别为外部和内部路径长度。
证明:数学归纳法①当n=1时,易知E=2,I=0,所以E=I+2n成立;②假设n≤k(k>0)时,E=I+2n成立;③则当n=k+1时,不妨假定找到某个内结点x为叶结点(根据二元扩展树的定义,一定存在这样的结点x,且设该结点的层数为h),将结点x及其左右子结点(外结点)从原树中摘除,生成新二元扩展树。
此时新二元扩展树内部结点为k个,则满足E k=I k+2k,考察原树的外部路径长度为E k+1= E k-(h-1)+2h,内部路径长度为Ik+1=Ik+(h-1),所以Ek+1= Ik+2k+h+1= Ik+1+2k+2=Ik+1+2(k+1),综合①②③知命题成立。
16.以比较为基础(基本操作)的分类算法最坏情况的时间下界是什么?答:)(nn logθ17对线性存储的有序表中元素的以比较为基础的检索算法最坏时间的下界是什么?简要说明理由。
