大学电路与电子学第二章课件
合集下载
【精品课件】电子线路第二章

ICn2 ICp
ICBO
C
R1 VBE IB
VCB R2
B
总结两个PN结,共同形成流入基区的载流子电流为
IEp +( IEn – ICn1) – ( ICp + ICn2 ) 为满足电中性条件,必须通过外电路向基区补充空穴,因 此,外电路的电流为:
IB = IEp +( IEn – ICn1) – ( ICp + ICn2 ) = IEp +( IEn – ICn1) –ICBO IB 的方向为基极流入。
§2.1 放大模式晶体管的工作原理
JE
JC
IE
N
P
E
IEn IEp
IC
ICBNO
C
电子流
空穴流 复合
B IB
漂移
VBE
VCB
(3)集电结收集电子的过程:
集电结加较大的反偏,结电场很强,由基区扩散到集电结
边缘的电子,迅速漂移越过集电结进入集电区。形成从外电路
流进集电区的集电极电流IC;另一方面,集电结两边的少数载 流子也要经集电结漂移,构成反向饱和电流ICBO。
= IEn + IEp = IE 即 IE = IC + IB
§2.1 放大模式晶体管的工作原理
分析讨论:
(1)只有发射区中的多子自由电子通过发射结 基区
集电结
集电区。即:将IEn 转化为ICn1,
第二章 晶体三极管
2.0 引言 2.1 放大模式下晶体三极管工作原理 2.2 晶体三极管的其它工作模式 2.3 埃伯尔斯—莫尔模型 2.4 晶体三极管的伏安特性曲线 2.5 晶体三极管的小信号电路模型 2.6 晶体三极管电路分析方法 2.7 晶体三极管应用原理
南通大学模电第二章PPT课件
12.02当 R4 R3 , R1 R2
则
vo
R4 R1
(vi2
vi1)
若继续有 R4 R1, 则 vovi2vi1
12.02.2021
.
14
R 4 R 3 时, 从R放1 大vo器R2角RR度14 (看vi2vi1)
增益为
Avd
vo vi2vi1
R4 R1
(该电路也称为差分电路或减法电路)
第二章 运算放大电路
2. 运放的开环电压增益很高
若(vP-vN)>0 则 vO= +Vom=V+ 若(vP-vN)<0 则 vO= –Vom=V-
3. 若V-< vO <V+ 则 (vP-vN)0
4. 输入电阻ri的阻值很高 使 iP≈ 0、iN≈ 0
5. 输12出.02.电2021阻很小, ro ≈ 0
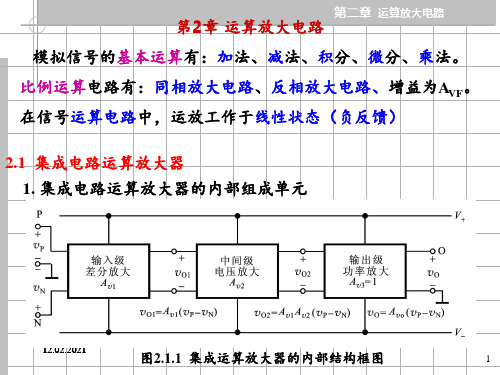
图2.2.1 运放的简化电路模型
第二章 运算放大电路
根据虚短和虚断的概念有
所v以i vvpp≈vvn,nipR =1-R in1=R20 vo
Avv voi
R1R2 1R2
R1
R1
(2)输入电阻Ri
(可作为公式直接使用)
输入电阻定义
Ri
vi ii
根据虚短和虚断有
所以
Ri
vi ii
(3)输出电阻Ro
12v.02i=.202v1 p,ii = ip≈0
.
Ro→0
8
3. 电压跟随器 根据虚短和虚断有
vo=vn≈ vp= vi
Av
vo vi
1
(可作为公式直接使用)
第二章 运算放大电路
12.02.2021
.
9
电压跟随器的作用
电工学ppt(第七版)第二章:电路的分析方法

1 A 3
返回
(b)
2.2电阻星形连结与三角形连结的等效变换
1
Y-变换
1
2
3
A
2
3
A
C
D B
Rd
C D
Rd
B
I
r2
+
1 r1 r3 3
Y- 等效变换
I
R12
+
1 R31
-
2
-
2
R23
3
r1 r2 R12 // R31 R23
原
则
r2 r3 R23 // R12 R31
1 1 1 1 E5 VB VA R R R R R5 4 5 3 3
其中未知数仅有:VA、VB 两个。
结点电位法列方程的规律
以A结点为例:
方程左边:未知节点的电
位乘上聚集在该节点上所 有支路电导的总和(称自 电导)减去相邻节点的电 E1 位乘以与未知节点共有支 路上的电导(称互电导)。
U Is I R0
我们可以用下面的图来表示这一伏安 关系 等效电流源
a I U R0
R0
E Is R0
+
a
负载两端的电压
和电流没有发生
RL
U
改变。
b
当R0 》 L 或R0=∞,这样的电源被称为理想电 R 流源,也称恒流源。理想电流源的特点是无论负载 或外电路如何变化,电流源输出的电流不变。
1 R7 3
R 3456 2
(d)
(c)
U 由(d)图可知 R 15 , I 2A R
由(b) 图可知
I
3V
返回
(b)
2.2电阻星形连结与三角形连结的等效变换
1
Y-变换
1
2
3
A
2
3
A
C
D B
Rd
C D
Rd
B
I
r2
+
1 r1 r3 3
Y- 等效变换
I
R12
+
1 R31
-
2
-
2
R23
3
r1 r2 R12 // R31 R23
原
则
r2 r3 R23 // R12 R31
1 1 1 1 E5 VB VA R R R R R5 4 5 3 3
其中未知数仅有:VA、VB 两个。
结点电位法列方程的规律
以A结点为例:
方程左边:未知节点的电
位乘上聚集在该节点上所 有支路电导的总和(称自 电导)减去相邻节点的电 E1 位乘以与未知节点共有支 路上的电导(称互电导)。
U Is I R0
我们可以用下面的图来表示这一伏安 关系 等效电流源
a I U R0
R0
E Is R0
+
a
负载两端的电压
和电流没有发生
RL
U
改变。
b
当R0 》 L 或R0=∞,这样的电源被称为理想电 R 流源,也称恒流源。理想电流源的特点是无论负载 或外电路如何变化,电流源输出的电流不变。
1 R7 3
R 3456 2
(d)
(c)
U 由(d)图可知 R 15 , I 2A R
由(b) 图可知
I
3V
电路分析大学教材第二章

感谢您的观看
THANKS
电路元件及其特性
总结词
电路元件包括电阻Biblioteka 电容、电感等,它们具有不同的特性, 如电阻限制电流、电容存储电荷、电感阻碍电流的变化。
详细描述
电阻是表示导体对电流阻碍作用的元件,其特性是电压与电 流成正比;电容是表示电场储能能力的元件,其特性是电流 与电压的变化率成正比;电感是表示磁场储能能力的元件, 其特性是电压与电流的变化率成正比。
04
一阶动态电路分析
一阶电路的微分方程
要点一
总结词
描述一阶电路中电压或电流随时间变化的数学模型。
要点二
详细描述
一阶电路的微分方程是描述电路中电压或电流随时间变化 的数学模型,通常表示为 dy/dt = f(y,t) 的形式,其中 y 代表电压或电流,t 代表时间,f(y,t) 是与 y 和 t 相关的函 数。
线性电阻电路的分析方法
基尔霍夫定律
基尔霍夫电流定律和基尔霍夫电 压定律是线性电阻电路的基本定 律,用于描述电路中电流和电压 的关系。
节点分析法
节点分析法是一种求解线性电阻 电路中电压和电流的方法,通过 列写节点电压方程来求解。
网孔分析法
网孔分析法是一种求解线性电阻 电路中电压和电流的方法,通过 列写网孔电流方程来求解。
电路分析大学教材第二章
目录
• 电路分析的基本概念 • 电路的等效变换 • 电路定理 • 一阶动态电路分析 • 二阶动态电路分析
01
电路分析的基本概念
电路的定义与组成
总结词
电路是由若干个元件按照一定的方式 连接而成的闭合回路,用于传输和转 换电能。
详细描述
电路由电源、负载、开关、导线等组 成,其中电源提供电能,负载消耗电 能,开关控制电路的通断,导线则用 于连接各元件。
电工与电子技术基础第二章课件

第二章
1.了解磁场的基本概念,理解磁感应强度、磁通、磁导率的概念。 2.掌握磁场的产生及磁场(或磁力线)方向的判断。 3.掌握磁场对通电直导体的作用及方向的判断。 4.了解铁磁材料的性质。 5.理解电磁感应定律,掌握感应电动势的计算公式。 6.了解自感现象和互感现象及其在实际中的应用。 7.理解互感线圈的同名端概念。 1.能用右手螺旋定则(安培定则)判断磁场方向。 2.能用左手定则判断电磁力方向。 3.能正确判断导体中感应电动势的方向。 4.会正确判断绕组的同名端。 一、磁的基本知识 二、电流的磁场
五、互感
8)楞次定律的基本内容是:感应磁通总是企图阻止原磁通的变化。 9)直导体产生的感应电动势的方向用右手定则来判断,其大小为e= BLvsinα,当直导体垂直于磁场方向切割磁力线时,产生的感应电动 势最大。 10)自感是由于流过线圈本身的电流变化而引起的电磁感应,对于线 性电感来说,自感电动势的大小与电流的变化率成正比。 11)互感是由于一个线圈中的电流变化在另一个线圈中引起的电磁感 应,互感电动势的方向可用楞次定律来判别,但比较复杂,通常用 同名端判别法来判断互感电动势的方向。 12)同名端就是绕在同一铁心上的线圈其绕向一致而产生感应电动势 极性相同的接线端。
一、磁的基本知识
1)磁铁的两端磁性最强,叫做磁极。 2)同性磁极互相排斥,异性磁极互相吸引。 3)任何磁铁都具有两个磁极,而且无论把磁铁怎样分割总保持有两 个异性磁极,也就是说N极和S极总是成对出现的。 2.磁场与磁力线 1)磁力线是无头无尾互不交叉,假想闭合的曲线,在磁铁外部由N 极指向S极,在磁铁内部由S极转向N极。 2)磁力线上任意一点的切线方向,就是该点的磁场方向,即小磁针 N极的指向。 3)磁力线越密,磁场越强;磁力线越疏,磁场越弱。
1.了解磁场的基本概念,理解磁感应强度、磁通、磁导率的概念。 2.掌握磁场的产生及磁场(或磁力线)方向的判断。 3.掌握磁场对通电直导体的作用及方向的判断。 4.了解铁磁材料的性质。 5.理解电磁感应定律,掌握感应电动势的计算公式。 6.了解自感现象和互感现象及其在实际中的应用。 7.理解互感线圈的同名端概念。 1.能用右手螺旋定则(安培定则)判断磁场方向。 2.能用左手定则判断电磁力方向。 3.能正确判断导体中感应电动势的方向。 4.会正确判断绕组的同名端。 一、磁的基本知识 二、电流的磁场
五、互感
8)楞次定律的基本内容是:感应磁通总是企图阻止原磁通的变化。 9)直导体产生的感应电动势的方向用右手定则来判断,其大小为e= BLvsinα,当直导体垂直于磁场方向切割磁力线时,产生的感应电动 势最大。 10)自感是由于流过线圈本身的电流变化而引起的电磁感应,对于线 性电感来说,自感电动势的大小与电流的变化率成正比。 11)互感是由于一个线圈中的电流变化在另一个线圈中引起的电磁感 应,互感电动势的方向可用楞次定律来判别,但比较复杂,通常用 同名端判别法来判断互感电动势的方向。 12)同名端就是绕在同一铁心上的线圈其绕向一致而产生感应电动势 极性相同的接线端。
一、磁的基本知识
1)磁铁的两端磁性最强,叫做磁极。 2)同性磁极互相排斥,异性磁极互相吸引。 3)任何磁铁都具有两个磁极,而且无论把磁铁怎样分割总保持有两 个异性磁极,也就是说N极和S极总是成对出现的。 2.磁场与磁力线 1)磁力线是无头无尾互不交叉,假想闭合的曲线,在磁铁外部由N 极指向S极,在磁铁内部由S极转向N极。 2)磁力线上任意一点的切线方向,就是该点的磁场方向,即小磁针 N极的指向。 3)磁力线越密,磁场越强;磁力线越疏,磁场越弱。
电路课件 第二章(第四版 邱关源 高等教育出版社)

B
i
+ u -
等效 C
i
+ u -
对A电路中的电流、电压和功率而言,满足
B
A (1)电路等效变换的条件
C
A
两电路具有相同的VCR 未变化的外电路A中 的电压、电流和功率 化简电路,方便计算
明 确
(2)电路等效变换的对象 (3)电路等效变换的目的
2.3 电阻的串联、并联和串并联
1. 电阻串联( Series Connection of Resistors )
(4) 功率
p1=G1u2, p2=G2u2,, pn=Gnu2 p1: p2 : : pn= G1 : G2 : :Gn
总功率
p=Gequ2 = (G1+ G2+ …+Gn ) u2
=G1u2+G2u2+ +Gnu2
=p1+ p2++ pn 表明
(1) 电阻并连时,各电阻消耗的功率与电阻大小成反比 (2) 等效电阻消耗的功率等于各串连电阻消耗功率的总和
第2章 电阻电路的等效变换
重点: 1. 电路等效的概念; 2. 电阻的串、并联; 3. Y— 变换; 4. 电压源和电流源的等效变换;
2.1 引言
电阻电路 分析方法 (1)欧姆定律和基尔霍夫定律是分 析电阻电路的依据; (2)等效变换的方法,也称化简的方法 仅由电源和线性电阻构成的电路
2. 电阻并联 (Parallel Connection)
(1) 电路特点
i + u _
R1
i1 R2
i2 Rk
ik Rn
in
(a) 各电阻两端分别接在一起,两端为同一电压 (KVL); (b) 总电流等于流过各并联电阻的电流之和 (KCL)。
大学电路课件第2章-1

叠加定理
1. 叠加定理
在线性电路中, 在线性电路中 , 任一支路的 电流或电压(响应) 电流或电压(响应)可以看成是电路中每一个独立 电源单独作用于电路时,在该支路产生的电流( 电源单独作用于电路时,在该支路产生的电流(或 电压)的代数和。 电压)的代数和。 1 i G i3 G G
.定理的证明 2 .定理的证明
+21V– + + us R2 – – u '=34V s 解
采用倒推法: 采用倒推法: i'=1A
i us 则 = ' i ' us
us 51 即 i = ' i ' = × 1 = 1 .5 A us 34
返 回 上 页 下 页
替代定理
1.替代定理 1.替代定理
对于给定的任意一个电路, 对于给定的任意一个电路 , 若某一支路电 压为u 电流为i 压为 k、电流为 k, 那么这条支路就可以用一个 电压等于u 的独立电压源, 电压等于 k的独立电压源,或者用一个电流等于 ik的独立电流源,或用 的独立电流源,或用R=uk/ik的电阻来替代,替 的电阻来替代, 代后电路中全部电压和电流均保持原有值( 代后电路中全部电压和电流均保持原有值(解答 唯一) 唯一)。
a R1 R2 R4 IS b 无源二端网络 有源二端网络 + E – R3 a + E – R1 R2 IS R3 b
1、戴维宁定理
任何一个线性含源一端口网络(二端网络) 任何一个线性含源一端口网络(二端网络), 对外电路来说, 对外电路来说 , 总可以用一个电压源和电阻的串 联组合来等效置换; 此电压源的电压等于外电路 联组合来等效置换 ; 断开时端口处的开路电压u 断开时端口处的开路电压 uoc, 而电阻等于端口的 输入电阻(或等效电阻R 输入电阻(或等效电阻 eq)。 i a i + Req a + + u A u Uoc b b
电工电子学第二章 41页PPT文档

23
4、理想电流源与任何一条支路串联后,其等效电源仍
为电流源;
R
a
E a
a
a
IS
IS
IS
IS
b
b
b
b
2019/9/5
电工电子学C
24
例1:将电源模型等效转换为另一形式。
a
5
10 V
b
a
5 2A
b
c
10
3A
d
c
10
30 V
d
2019/9/5
电工电子学C
25
例2:求电流I。
应用:分流
2019/9/5
电工电子学C
21
二、电压源和电流源的等效变换:
Ia
Ia
R0 U
E
b
电压源模型
IS
R0 U
b
电流源模型
I Is UR0'
UUsR0I (1)
UIsR'0IR'0 (2)
比较两式,可知,满足:
R0 R0'
(3)
EIsR0'或Is
E R0
电压源和电流源对外电路就等效
任何一个线性有源二端口网络,对外电路来说,可
以用一个电动势为E、内阻为R0的等效电压源来代替;其
中电压源的电动势等于端口开路电压Uoc,内阻等于端口
中所有独立电源置零后两端之间的等效电阻。
aI
aI
N
R0
U RL + E-
U RL
I E R0 RL
b
b
2019/9/5
不作用的电压源要视为短路,不作用的电流源要视
(2) 4A电流源单独作用, 10V电压源短路; 6
武汉理工大学电子电工课件第2章

据此可推出两者的关系
总目录 章目录 返回 上一页 下一页
2.2 电阻星形联结与三角形联结的等效变换
Ia
a
Ra Rc
Ia
a
Rab RbcRca b
等效变换
c
Ib Ic
Ib
Ic
Rab Rbc Rca
b
Rb
c
Y
Y
Rab Rca Ra Rab Rbc Rca Rbc Rab Rb Rab Rbc Rca Rca Rbc Rc Rab Rbc Rca
Rc c
等效变换
Ib Ic
Rb
c
将Y形联接等效变换为形联结时 若 Ra=Rb=Rc=RY 时,有Rab=Rbc=Rca= R = 3RY; 将形联接等效变换为Y形联结时 若 Rab=Rbc=Rca=R 时,有Ra=Rb=Rc=RY =R/3
总目录 章目录 返回 上一页 下一页
例 1: 对图示电路求总电阻R12
1
2 R12 1 2 D 0.8
C
2
1
R12
1
0.4 2 2
0.4
2 1
1 0.8 1
1
1
R12
2.4
1.4
2.684 2
由图: R12=2.68
总目录 章目录 返回 上一页 下一页
1
2
例2:计算下图电路中的电流 I1 。 a a I1 I1
4 8 4
Ra Rb
RL
电流源模型 由上图电路可得: I
U O I IS IS R0 若 R0 = 电流源的外特性 理想电流源 : I IS 若 R0 >>RL ,I IS ,可近似认为是理想电流源。
总目录 章目录 返回 上一页 下一页
2.2 电阻星形联结与三角形联结的等效变换
Ia
a
Ra Rc
Ia
a
Rab RbcRca b
等效变换
c
Ib Ic
Ib
Ic
Rab Rbc Rca
b
Rb
c
Y
Y
Rab Rca Ra Rab Rbc Rca Rbc Rab Rb Rab Rbc Rca Rca Rbc Rc Rab Rbc Rca
Rc c
等效变换
Ib Ic
Rb
c
将Y形联接等效变换为形联结时 若 Ra=Rb=Rc=RY 时,有Rab=Rbc=Rca= R = 3RY; 将形联接等效变换为Y形联结时 若 Rab=Rbc=Rca=R 时,有Ra=Rb=Rc=RY =R/3
总目录 章目录 返回 上一页 下一页
例 1: 对图示电路求总电阻R12
1
2 R12 1 2 D 0.8
C
2
1
R12
1
0.4 2 2
0.4
2 1
1 0.8 1
1
1
R12
2.4
1.4
2.684 2
由图: R12=2.68
总目录 章目录 返回 上一页 下一页
1
2
例2:计算下图电路中的电流 I1 。 a a I1 I1
4 8 4
Ra Rb
RL
电流源模型 由上图电路可得: I
U O I IS IS R0 若 R0 = 电流源的外特性 理想电流源 : I IS 若 R0 >>RL ,I IS ,可近似认为是理想电流源。
电路与电子技术课件-第二章电路的分析方法

12
当一个电源单独作用时,其余电源不作用,就意味着取零
值。即对电压源看作短路,而对电流源看作开路。
BUCT
例如下图:
R1 +
us1 –
i1
i3
i2 R2
+ us2
–
R3
+ us3
–
三个电源共同作用
i1 = i1' + i1" + i1"' i2 = i2' + i2" + i2"' i3 = i3' + i3" + i3"'
5 15
5 15
+U –
10A
+ U
'–
2
4
2
4
+–
20V
+–
20V
解: 20V电压源单独作用时,U '
U '= 20×
5 5+15
=5V
电流源不作用 应相当于开路
18
例2. 求图示电路中5电阻的电压U及功率P。
BUCT
5 15
5 15
+U –
10A
+U ''–
10A
电压源不 作用应相
2
4
当于短路
该一端口的全部独立电源置零后的输入电导(电阻)。
a 外
NS
电 路
a Isc Gi(Ri)
a
NS b Isc
a
b 开路、短路法计算
b
NO
Ri
输入电阻
b
诺顿等效电路可由戴维宁等效电路经电源等效变换得
电路与电子学基础第二章

【例2-2】已知某交流电路两端的电压u和通入的电流i分别为
u(ut)(t)UmUsimn(sint (1t35)1,3i(5t) ), iI(mt)cos(Imt co3s0() t 30 )
画出该电路电流和电压的相量图。
u(t) U m sin(t 135 ) U m cos(t 135 90 ) U m cos(t 45 )
式中的Em,Um和Im称为正弦交流电量的最大值或振幅; ω称为角频率,角频率ω和频率f的关系是ω=2πf; φe、φu和φi称为初相位。
最大值、角频率和初相位正弦交流电量的三要素
1.最大值(幅值)
最大值是描述正弦交流电量变化的范围和幅度的物理量。用大写的字母并加下标m 来表示 。
2.周期、频率和角频率
与x轴正方向的夹角为Φ0,对应于正弦交流电量的初相位等于Φ0,当有向线段 以正弦交流电量的角频率ω在平面内作逆时针方向旋转时,有向线段 I m
在y轴上的投影对应于
i(t) Im sin(t 0 )
注意:表示交流电的旋转向量与表示力, 电场强度等物理量的矢量有着不同的概念。 矢量在空间上的指向是固定的,而旋转向 量在空间上的指向是不固定的,是按ω的 角频率沿逆时针方向旋转的。
上式表明:同频正弦交流电量的相位差等于它们的初相差,是一个与时间t无关 的常数。电路课程中常采用“超前”和“滞后”的概念,来说明两个同频率正 弦交流电量相位比较的结果。
当▽φ21>0时,说明φ2>φ1,称i2超前u1;当▽φ21<0时,说明φ2<φ1,称i2滞 后u1;当▽φ21=0时,说明φ2=φ1,称i2和u1同相;当|▽φ21|=π/2时,说明i2 和u1的夹角为π/2,称i2和u1正交;当|▽φ21|=π时,说明i2和u1的夹角为π,称 i2和u1反相。
电路与电工技术全书课件完整版ppt全套教学教程最全电子教案电子讲义最新

当电压的参 考方向与电动势
电压正方向表示电位降
的参考方向相反
A
时 A
UE
当电压的参
E
U
E
U
考方向与电动 势的参考方向
B
相同时 B
E 5V
E 5V
U E
U VA VB 5V U VB VA 5V
UE
U E
电路与电工技术
注意:
1. i、u、e 的参考方向可任意假定。但一经选定,分析过程
线性电阻(过原点的直线) 分类: 非线性电阻
电路与电工技术
2)电阻的电压电流关系 (1)伏安特性曲线
i
i
f (u, i) 0
电阻的伏安 特性曲线
0
u
0
u
非线性电阻
线性电阻
电阻元件的 u、i 关系可由 u – i 平面的一条曲线确定。
电路与电工技术
3)欧姆定律(线性电阻)
u
R tg u
i
G 1 R
36
电路Байду номын сангаас电工技术
第2章 直流电路的基本分析和计算
学习目的: 1. 掌握基尔霍夫定律,它是分析电路最基本的定律;能运用支路 电流法分析电路。 2. 能正确应用叠加定理和戴维南定理分析和计算两个网孔以上的 电路。 3. 建立电压源和电流源的概念,了解它们的特性及等效变换。 学习重点:基尔霍夫的两大定律,支路电流法、叠加定理和戴维 南定理;电压源和电流源的等效变换。 学习难点:基尔霍夫电压定律,支路电流法和戴维南定理;电压 源和电流源的等效变换。
电感
i
亨利(H)
(安)A
+
u
L
–
电路与电工技术
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电路中按开路处理,电感在电路中按短路处理, 计算出uC(0−)和iL(0−),图中uC(0+)=0V
大学电路与电子学第二章
10
2.非独立初始值(非状态变量)
(1)定义:非独立初始条件是指一阶电路
中除uC(0+)和iL(0+)以外,电路中其它响应在
t
=
0+时刻的值都称为非独立初始值。
电路中uC(0+)为独立初
一定的时间来完成。
状态
大学电路与电子学第二章
8
2.1.2 动态电路的初始条件
换路一瞬间记为:t = 0
换路前的一瞬间记为: t = 0−
初换始路条后件的是一指瞬在间换记路为后:一t =瞬0+间一阶电路中响应
值y(0+)——即t = 0+时刻的uC(0+) 、 i(0+)、 uR(0+)
初始条件由初始值确定
常用动态元件:电容元件、电感元件
电阻电路——由电阻元件和电源构
集中电路
成的电路
动态电路——电路中包含有动态元
件,至少一个动态元
件
大学电路与电子学第二章
2
电阻电路用代数方程描述其性能,并计算电
路变量 UR=IR 动态电路用微分方程描述其性能,并计算电
路变量
R1
R2
iC
C
duC dt
R1
R2
+ uS
K
14
2.2 一阶电路的时域分析 主要内容:研究一节电路换路后,电路中电 流、电压随时间而变化的情况,即一节电路的 响应。
电路的激励不同,其响应也不同,一节电路 有零状态响应、零输入响应和全响应三种。
大学电路与电子学第二章
15
2.2 一阶电路的时域分析
2.2.1 零输入响应
1.零输入响应:一阶电路在没有外加激励情况
i(t) C duC dt
i(t)与uC非关联
R0 +
RC
duC dt
uC
0
t 0
U0
K
i u+c C
R
duC dt
1 RC
uC
0
通解为:uC(tt)KeAt
为一阶线性齐次微分方程
其中A 1 RC
uC Ke RC
解得:K=U0
即t =: 0u时C ,Uu0Ce(0R)t=CU0
U0为电容 的初始值
下,仅由电路中动态元件初始储能所引起的响应
K (t 0)
2.RC电路的零输入响应
t 0 电路稳态uC U0
uC(0−)=U0 ——电容储能
R0 ①
i
②
U0 C
uC
R
t 0时发生换路,
即开关K由1倒向2
uC 0 uC 0 uC 0 U0
大学电路与电子学第二章
16
KVL方程: Ri(t) uC 0
第一章 直流电路
§1.1 电路与电路模型 §1.2 电路变量 §1.3 电路元件 §1.4 基尔霍夫定律 §1.6 叠加定理 §1.7 等效电源定理
大学电路与电子学第二章
1
第二章 一阶电路的过渡过程 动态元件:元件的电流、电压之间的关系涉 及到对电流、电压的微分或者积分。
uRiiCCd dC u t uLLd dLit
+
uS
C
K
一阶电路:当动态电路只含有一个动态元件 时,描述其性能的为一节微分方程,所以称为 一节电路;RC电路与RL电路。
大学电路与电子学第二章
3
大学电路与电子学第二章
4
大学电路与电子学第二章
5
大学电路与电子学第二章
6
②动态电路的换路 t =0 R i K未动作前,电路处于稳定状态
+K US
t =0
R
i
始条件;i(0+)与uR(0+)为 非独立初始条件。
+ US
K
u+C C
非独立初始值是由电路的独立初始值与电路 在t = 0+时刻的状态决定
如:i(0)USu RC(0)U RS
大学电路与电子学第二章
11
3.非独立初始值确定的基本步骤
(1)确定独立初始值
通过t=0−时刻的电路,计算出uC(0−)或iL(0−), 则uC(0+)= uC(0−), iL(0+)= iL(0−)
t =0 R i
独立初始条件(值)+ K
初始条件
US
u+C C
非独立初始条件(值)
大学电路与电子学第二章
9
1.独立初始条件(状态变量)
独立初始条件是指电容电 压和电感电流在t = 0+时刻的 响应值uC(0+)和iL(0+)
电容电压不能突变,所以 uC (0 ) uC (0 )
电感电流电能突变,所以 iL (0 ) iL (0 ) 独立初始条件是由其t=0−时刻的值确定的 独立初始值的求解方法:在t=0−时,将电容在
12
例2-1-1:图示电路原处于稳定状态。t=0时
开关闭合,求 uC(0+)和电流i(0+)。 解:(1)计算独立初
始值:uc (0 ) 将电容开路处理
2Ω i(t)
uC(0) uC(0)
2A
248V
4Ω
+
+ 10V
uC(0-) 4Ω
(2)用8V电压源替代
电容,画出t=0+的等 2A 效电路
4Ω
+ 8V
(2)画出t=0+的等效电路
电容用电压源代替,电压源电压US= uC(0+)
电感用电流源代替,电流源电流 IS= iL(0+)
(3)求解t=0+的等i 效电路
t=0 R +
++
uS2
uS1
uC
++
uS2
uS1
i R+
uS1
uC (0)uC (0)u 大学S1 电路与电子学第二章 t=i0(0+时)的uS等2R效uS电1 路
大学电路与电子学第二章
17
解得:
t
uC(t) U0e RC
当t=0时:e
流激励的作用下,响应是同频率的正弦交流
过度状态(暂态):一阶电路由一个稳定状
态转换为另一个稳定状态所经历的中间状态
3.过渡t过=0程产R 生i的原因:
uc
US
? U③能②①S+电发电电路生路路K在突发中换 变生含路 ,了有后 要换动u+C一 增路态瞬 大;C元稳间 或第件定电 减一L状、个小容态C到电;新压0过的、渡稳电t1 态感稳第定值电二状需流个态要不 t
2Ω i(0+)
+ 10V 4Ω
大学电路与电子学第二章
13
(3)计算i(0+)
i(0
)
10 2
8
1A
2A
4Ω
+ 8V
用KVL计算:
A
2Ω i(0+)
+ 10V 4Ω
小结:熟悉换路、过渡过程、初始条件的 概念,掌握独立初始值和非独立初始值的确 定计算方法
大学电路与电子学第二章
u+C
i=0 ,
C
US
uC = 0
uc
形成一 U过S 渡期
R?
i
K接通电源后一定 第一个 0 时间,电容充电完 稳定状态
t1 第二个 t 稳定状态
毕,电路达到新的
过渡
稳定状态
状态
t=t1: i = 0 , uC= Us
大学电路与电子学第二章
7
稳定状态(稳态):是指一阶电路在直流激
励作用下,电路中的响应也为直流;在正弦交
大学电路与电子学第二章
10
2.非独立初始值(非状态变量)
(1)定义:非独立初始条件是指一阶电路
中除uC(0+)和iL(0+)以外,电路中其它响应在
t
=
0+时刻的值都称为非独立初始值。
电路中uC(0+)为独立初
一定的时间来完成。
状态
大学电路与电子学第二章
8
2.1.2 动态电路的初始条件
换路一瞬间记为:t = 0
换路前的一瞬间记为: t = 0−
初换始路条后件的是一指瞬在间换记路为后:一t =瞬0+间一阶电路中响应
值y(0+)——即t = 0+时刻的uC(0+) 、 i(0+)、 uR(0+)
初始条件由初始值确定
常用动态元件:电容元件、电感元件
电阻电路——由电阻元件和电源构
集中电路
成的电路
动态电路——电路中包含有动态元
件,至少一个动态元
件
大学电路与电子学第二章
2
电阻电路用代数方程描述其性能,并计算电
路变量 UR=IR 动态电路用微分方程描述其性能,并计算电
路变量
R1
R2
iC
C
duC dt
R1
R2
+ uS
K
14
2.2 一阶电路的时域分析 主要内容:研究一节电路换路后,电路中电 流、电压随时间而变化的情况,即一节电路的 响应。
电路的激励不同,其响应也不同,一节电路 有零状态响应、零输入响应和全响应三种。
大学电路与电子学第二章
15
2.2 一阶电路的时域分析
2.2.1 零输入响应
1.零输入响应:一阶电路在没有外加激励情况
i(t) C duC dt
i(t)与uC非关联
R0 +
RC
duC dt
uC
0
t 0
U0
K
i u+c C
R
duC dt
1 RC
uC
0
通解为:uC(tt)KeAt
为一阶线性齐次微分方程
其中A 1 RC
uC Ke RC
解得:K=U0
即t =: 0u时C ,Uu0Ce(0R)t=CU0
U0为电容 的初始值
下,仅由电路中动态元件初始储能所引起的响应
K (t 0)
2.RC电路的零输入响应
t 0 电路稳态uC U0
uC(0−)=U0 ——电容储能
R0 ①
i
②
U0 C
uC
R
t 0时发生换路,
即开关K由1倒向2
uC 0 uC 0 uC 0 U0
大学电路与电子学第二章
16
KVL方程: Ri(t) uC 0
第一章 直流电路
§1.1 电路与电路模型 §1.2 电路变量 §1.3 电路元件 §1.4 基尔霍夫定律 §1.6 叠加定理 §1.7 等效电源定理
大学电路与电子学第二章
1
第二章 一阶电路的过渡过程 动态元件:元件的电流、电压之间的关系涉 及到对电流、电压的微分或者积分。
uRiiCCd dC u t uLLd dLit
+
uS
C
K
一阶电路:当动态电路只含有一个动态元件 时,描述其性能的为一节微分方程,所以称为 一节电路;RC电路与RL电路。
大学电路与电子学第二章
3
大学电路与电子学第二章
4
大学电路与电子学第二章
5
大学电路与电子学第二章
6
②动态电路的换路 t =0 R i K未动作前,电路处于稳定状态
+K US
t =0
R
i
始条件;i(0+)与uR(0+)为 非独立初始条件。
+ US
K
u+C C
非独立初始值是由电路的独立初始值与电路 在t = 0+时刻的状态决定
如:i(0)USu RC(0)U RS
大学电路与电子学第二章
11
3.非独立初始值确定的基本步骤
(1)确定独立初始值
通过t=0−时刻的电路,计算出uC(0−)或iL(0−), 则uC(0+)= uC(0−), iL(0+)= iL(0−)
t =0 R i
独立初始条件(值)+ K
初始条件
US
u+C C
非独立初始条件(值)
大学电路与电子学第二章
9
1.独立初始条件(状态变量)
独立初始条件是指电容电 压和电感电流在t = 0+时刻的 响应值uC(0+)和iL(0+)
电容电压不能突变,所以 uC (0 ) uC (0 )
电感电流电能突变,所以 iL (0 ) iL (0 ) 独立初始条件是由其t=0−时刻的值确定的 独立初始值的求解方法:在t=0−时,将电容在
12
例2-1-1:图示电路原处于稳定状态。t=0时
开关闭合,求 uC(0+)和电流i(0+)。 解:(1)计算独立初
始值:uc (0 ) 将电容开路处理
2Ω i(t)
uC(0) uC(0)
2A
248V
4Ω
+
+ 10V
uC(0-) 4Ω
(2)用8V电压源替代
电容,画出t=0+的等 2A 效电路
4Ω
+ 8V
(2)画出t=0+的等效电路
电容用电压源代替,电压源电压US= uC(0+)
电感用电流源代替,电流源电流 IS= iL(0+)
(3)求解t=0+的等i 效电路
t=0 R +
++
uS2
uS1
uC
++
uS2
uS1
i R+
uS1
uC (0)uC (0)u 大学S1 电路与电子学第二章 t=i0(0+时)的uS等2R效uS电1 路
大学电路与电子学第二章
17
解得:
t
uC(t) U0e RC
当t=0时:e
流激励的作用下,响应是同频率的正弦交流
过度状态(暂态):一阶电路由一个稳定状
态转换为另一个稳定状态所经历的中间状态
3.过渡t过=0程产R 生i的原因:
uc
US
? U③能②①S+电发电电路生路路K在突发中换 变生含路 ,了有后 要换动u+C一 增路态瞬 大;C元稳间 或第件定电 减一L状、个小容态C到电;新压0过的、渡稳电t1 态感稳第定值电二状需流个态要不 t
2Ω i(0+)
+ 10V 4Ω
大学电路与电子学第二章
13
(3)计算i(0+)
i(0
)
10 2
8
1A
2A
4Ω
+ 8V
用KVL计算:
A
2Ω i(0+)
+ 10V 4Ω
小结:熟悉换路、过渡过程、初始条件的 概念,掌握独立初始值和非独立初始值的确 定计算方法
大学电路与电子学第二章
u+C
i=0 ,
C
US
uC = 0
uc
形成一 U过S 渡期
R?
i
K接通电源后一定 第一个 0 时间,电容充电完 稳定状态
t1 第二个 t 稳定状态
毕,电路达到新的
过渡
稳定状态
状态
t=t1: i = 0 , uC= Us
大学电路与电子学第二章
7
稳定状态(稳态):是指一阶电路在直流激
励作用下,电路中的响应也为直流;在正弦交
