简单图的判定
图论重要结论

定理1: 图G= (V, E)中所有顶点的度的和等于边数m 的2倍,即:推论1 在任何图中,奇点个数为偶数。
推论2 正则图的阶数和度数不同时为奇数 。
定理2 若n 阶简单图G 不包含Kl+1,则G 度弱于某个完全 l 部图 H ,且若G 具有与 H 相同的度序列,则: 定理3设T 是(n, m)树,则:偶图判定定理: 定理4图G 是偶图当且仅当G 中没有奇回路。
敏格尔定理: 定理5 (1) 设x 与y 是图G 中的两个不相邻点,则G 中分离点x 与y 的最小点数等于独立的(x, y)路的最大数目; (2)设x 与y 是图G 中的两个不相邻点,则G 中分离点x 与y 的最小边数等于G 中边不重的(x, y)路的最大数目。
欧拉图、欧拉迹的判定: 定理6 下列陈述对于非平凡连通图G 是等价的:(1) G 是欧拉图;(2) G 的顶点度数为偶数; (3) G 的边集合能划分为圈。
推论: 连通非欧拉图G 存在欧拉迹当且仅当G 中只有两个顶点度数为奇数。
H 图的判定: 定理H 图,则对V(G)的任一非空顶点子集S定理8 (充分条件) 对于n ≧3的单图G ,如果G 定理9 (充分条件) 对于n ≧3的单图G ,如果G 中的任意两个不相邻顶点u 与v ,有:定理10 (帮迪——闭包定理) 图G 是H 图当且仅当它的闭包是H 图。
定理11(Chv átal ——度序列判定法) 设简单图G 的度序列是(d1,d2,…,dn), 这里,d1≦d2≦…≦m<n/2,或者 dm>m,或者dn-m ≧ n-m,则定理12 设G 是n 阶单图。
若n ≧3且则G 是H 图;并且,具有n 个顶点 条边的非H 图只有C1,n 以及C2,5.定理13 (Hall G 存在饱和X 每个顶推论:若G 是k (k>0)正则偶图,则G 存在完美匹配。
定理14 (哥尼,1931) 在偶图中,最大匹配的边数等于最小覆盖的顶点数。
(完整版)图论复习提纲

复习课件 数学科学学院
1
本次课主要内容 期末复习
(一)、重点概念 (二)、重要结论 (三)、应用
2
(一)、重点概念
1、图、简单图、图的同构与自同构、度序列与图序列、 补图与自补图、两个图的联图、两个图的积图、偶图;
(1) 图:一个图是一个序偶<V,E>,记为G=(V,E),其中: 1) V是一个有限的非空集合,称为顶点集合,其元素称为顶点或点。
G1 G2
例1 指出4个顶点的非同构的所有简单图。 分析:四个顶点的简单图最少边数为0,最多边数为6,所以 可按边数进行枚举。
5
(6) 补图与自补图
1) 对于一个简单图G =(V, E),令集合 E1 uv u v,u,vV
则图H =(V,E1\E)称为G的补图,记为 H G
2) 对于一个简单图G =(V, E),若 G G ,称G为自补图。
(5) 根树
一棵非平凡的有向树T,如果恰有一个顶点的入度为0,而其余所有顶 点的入度为1,这样的的有向树称为根树。其中入度为0的点称为树根, 出度为0的点称为树叶,入度为1,出度大于1的点称为内点。又将内点 和树根统称为分支点。
9
(6) 完全m元树
对于根树T,若每个分支点至多m个儿子,称该根树为m元根树; 若每个分支点恰有m个儿子,称它为完全m元树。
(2) 森林
称无圈图G为森林。
8
(3) 生成树
图G的一个生成子图T如果是树,称它为G的一棵生成树;若T 为森林,称它为G的一个生成森林。
生成树的边称为树枝,G中非生成树的边称为弦。
(4) 最小生成树
在连通边赋权图G中求一棵总权值最小的生成树。该生成树称 为最小生成树或最小代价树。
离散数学——图论

提示:反证法。
设有两个连通分支,这两个分支至多是完 全图。由此得到图中点与边之间的数量关系。
§8.3欧拉图
欧拉图产生的背景就是前面的七桥问题。
定义:图G的回路,若它通过G中的每条边一 次,这样的回路称为欧拉回路。具有欧拉回 路的图称为欧拉图。
定义欧拉通路:通过图G中每条边一次的通 路(非回路)称为欧拉通路。
基本通路:通路中没有重复的点。
简单回路和基本回路。
基本通路一定是简单通路,但反之简单通路 不一定是基本通路。基本回路必是简单回路。
定理:一个有向(n,m)图中任何基本通路长 度≤n-1。任何基本回路的长度≤n。 任一通路中如果删去所有回路,必得基本通 路。 任一回路中如删去其中间的所有回路,必得 基本回路。
例1:教材121页。
结点次数
引出次数:有向图中以结点v为起点的边的条数称为 v的引出次数,记 deg(v) 引入次数:有向图中以结点v为终点的边的条数称为 v的引出次数,记 deg(v)
结点次数:有向图中引出次数和引入次数之和称为 结点次数;无向图中与结点v相关联的边的条数称为 V的次数。统一为记deg(v)。
图论的发展
图论的产生和发展经历了二百多年的历史, 从1736年到19世纪中叶是图论发展的第一阶 段。 第二阶段大体是从19世纪中叶到1936年,主 要研究一些游戏问题:迷宫问题、博弈问题、 棋盘上马的行走线路问题。
一些图论中的著名问题如四色问题(1852年)和哈密 尔顿环游世界问题(1856年)也大量出现。同时出现 了以图为工具去解决其它领域中一些问题的成果。
有向连通图
图论期末考试整理复习资料

目录第一章图的基本概念 (1)二路和连通性 (3)第二章树 (3)第三章图的连通度 (4)第四章欧拉图与哈密尔顿图 (5)一,欧拉图 (5)二.哈密尔顿图 (6)第五章匹配与因子分解 (9)一.匹配 (9)二.偶图的覆盖于匹配 (10)三.因子分解 (11)第六章平面图 (14)二.对偶图 (16)三.平面图的判定 (17)四.平面性算法 (20)第七章图的着色 (24)一.边着色 (24)二.顶点着色 (25)第九章有向图 (30)二有向树 (30)第一章图的基本概念1.点集与边集均为有限集合的图称为有限图。
2.只有一个顶点而无边的图称为平凡图。
3.边集为空的图称为空图。
4.既没有环也没有重边的图称为简单图。
5.其他所有的图都称为复合图。
6.具有二分类(X, Y)的偶图(或二部图):是指该图的点集可以分解为两个(非空)子集X 和Y ,使得每条边的一个端点在X 中,另一个端点在Y 中。
7.完全偶图:是指具有二分类(X, Y)的简单偶图,其中X的每个顶点与Y 的每个顶点相连,若|X|=m,|Y|=n,则这样的偶图记为Km,n8. 定理1 若n 阶图G 是自补的(即),则n = 0, 1(mod 4)9. 图G 的顶点的最小度。
10. 图G 的顶点的最大度。
11. k-正则图: 每个点的度均为 k 的简单图。
例如,完全图和完全偶图Kn,n 均是正则图。
12. 推论1 任意图中,奇点的个数为偶数。
13.14. 频序列:定理4 一个简单图G 的n 个点的度数不能互不相同。
15. 定理5 一个n 阶图G 相和它的补图有相同的频序列。
16.17.18. 对称差:G1△G2 = (G1∪G2) - (G1∩G2) = (G1-G2)∪(G2-G1)19. 定义: 联图 在不相交的G1和G2的并图G1+G2中,把G1的每个顶点和G2的每个顶点连接起来所得到的图称为G1和G2的联图,记为G1∨G220. 积图:积图 设G1= (V1, E1),G2 = (V2, E2),对点集V = V1×V2中的任意两个点u =(u1,u2)和v = (v1,v2),当(u1 = v1和 u2 adj v2) 或 (u2 = v2 和 u1 adj v1) 时就把 u 和 v 连接起来所得到的图G 称为G1和G2积图。
图论及其应用
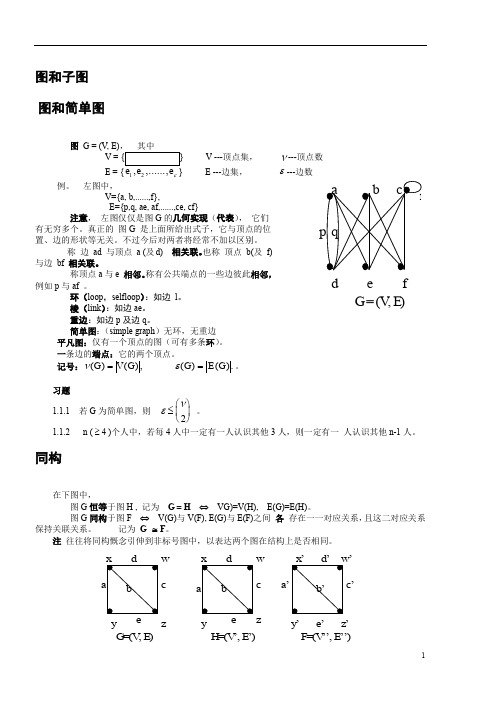
图和子图 图和简单图图 G = (V, E)V ---顶点集,ν---顶点数12ε E ---边集, ε---边数例。
左图中, V={a, b,......,f}, E={p,q, ae, af,......,ce, cf} 注意, 左图仅仅是图G 的几何实现(代表), 它们有无穷多个。
真正的 图G 是上面所给出式子,它与顶点的位置、边的形状等无关。
不过今后对两者将经常不加以区别。
称 边 ad 与顶点 a (及d) 相关联。
也称 顶点 b(及 f) 与边 bf 相关联。
称顶点a 与e 相邻。
称有公共端点的一些边彼此相邻,例如p 与af 。
环(loop ,selfloop ):如边 l 。
棱(link ):如边ae 。
重边:如边p 及边q 。
简单图:(simple graph )无环,无重边 平凡图:仅有一个顶点的图(可有多条环)。
一条边的端点:它的两个顶点。
记号:νε()(),()().G V G G E G ==。
习题1.1.1 若G 为简单图,则εν≤⎛⎝ ⎫⎭⎪2 。
1.1.2 n ( ≥ 4 )个人中,若每4人中一定有一人认识其他3人,则一定有一 人认识其他n-1人。
同构在下图中, 图G 恒等于图H , 记为 G = H ⇔ VG)=V(H), E(G)=E(H)。
图G 同构于图F ⇔ V(G)与V(F), E(G)与E(F)之间 各 存在一一对应关系,且这二对应关系保持关联关系。
记为 G ≅F。
注 往往将同构慨念引伸到非标号图中,以表达两个图在结构上是否相同。
de f G = (V , E )yz w cG =(V , E )w cyz H =(V ’, E ’)’a ’c ’y ’e ’z ’F =(V ’’, E ’’)注 判定两个图是否同构是NP-hard 问题。
完全图(complete graph) Kn空图(empty g.) ⇔ E = ∅ 。
V’ ( ⊆ V) 为独立集 ⇔ V’中任二顶点都互不相邻。
简单连通平面图

v3 u3 u4 v4 (b)是(c) (a)
v1
的细分图
v3 u3 u4 v4
(b)
v1
v4
v3
v6
v2
v5 同构
v3
v4
(c)
2019/11/30
计算机学院
v2
v5 K3,3
(d)
v6
14
对偶图
定义12.3 若图G=<V,E>是一个平面图,构造
图 G*=<V*,E*>如下:
①
G的面F1,F2,‥‥,Ff与V*中的结点v1*
推论12.5.1 任何简单连通平面图中,至少存在 一个其度不超过5的结点
2019/11/30
计算机学院
9
围长:一个图的围长为它包含的最短圈的长度。 一个图若不含圈,则规定其围长为无穷大。
定理12.6 设G是一个(n,m)简单连通平面 图,其围长k>2,则有
m k (n - 2) k-2
2019/11/30
2019/11/30
计算机学院
8
定理12.5
设G是一个(n,m)简单连通平面图,若m>1,则有
m≤3n-6 证明 设G有k个面,因为G是平面图,所以G的每
个面至少由3条边围成,而G中各面度之和是边
数的二倍,所以
2m≥3k,即k≤2m/3,代入欧拉公式有
整理得
2nmk nm 2m 3
m≤3n-6
2019/11/30
计算机学院
23
1890年,Heawood 建立了“五色定理” ( Heawood定理)。 定理12.15
任何连通平面图都是可以五着色的。
2019/11/30
计算机学院
几何——第一讲 几何基本概念与简单图形
(2)点 A、B 在直线 m 同侧:
第 4 页 共 29 页
(3)两个点都在内侧:
形式二:已知点 A 位于直线 m、n 的内侧, 在直线 m、n 上分别求点 P、Q,使得三角形 APQ 的周长最短。
3. 台球两次碰壁模型 形式一:已知点 A、B 位于直线 m、n 的内侧,在
直线 n、m 上分别求点 D、E 点,使得围成的四边形 ADEB 的周长最短。
果它们有一个公共点,我们就说他们相交,它们是相交 直线,这个公共点叫做它们的交点。
相交关系中最重要的是垂直相交,与垂直有关的知 识,有以下两个重要的结论: ⑴过一点有且仅有一条直线与已知直线垂直; ⑵直线外一点与直线上各点连结的所有线段中,垂线段 最短。
两条直线相交,可形成两组对顶角,它们分别相等, 也可以形成邻补角,即一条直线与端点在这条直线上的 一条射线组成的两个角。也就是说,邻补角是具有特殊 位置关系的两个互补角,一个角的邻补角有且只有两个。
如果两个角的和是一个平角,这两个角叫做互为补角; 如图(b): BDC ABD A ACD
如果两个角的和是一个直角,这两个角叫做互为余角。
第 8 页 共 29 页
⑶“8 字形”模型 如图(c): A B C D
⑷“内角平分线”模型 点 P 是 ABC 和 ACB 的角平分线的交点。 如图(d): BPC 90 1 A
第 20 页 共 29 页
四、面积初步
由于多边形可以分割成若干个三角形,所以多边形
在中学数学里,面积是非常重要的内容,除简单的 的面积可转化为三角形面积来研究。
面积计算外,还要学会使用“等积变换”的思想方法来处
关于三角形的面积,有以下几个重要性质:
理几何问题。
⑴等底等高的两个三角形面积相等;
小学一年级简单的图形推理

小学一年级简单的图(Tu)形推理一、每种水果都(Du)表示一个数,你能知道这个数是几吗?— 6 = 15 =12 — = 8 =+ 12 = 35 =25 — = 11 =二、每个图形代表一个数,你能算出这个数是多少(Shao)吗??( 1 ) △一(Yi)7=5 o+△=17 ( 2 )☆+☆=12 ☆一(Yi)△=6 △=( ) o=( ) ☆=( ) △=( )( 3 )△一(Yi)4=11 o+△=16 ( 4 )☆+☆=24 ☆一(Yi)△=6 △=( ) o=( ) ☆=( ) △=( )(5)5+o=12 △+o=10 ( 6 ) o 一(Yi)☆=5 12一☆=8o=( ) △=( ) o =( ) ☆=( )( 7 )5+o=12 △+o=10 ( 8 ) o 一☆=5 12一☆=8o=( ) △=( ) o =( ) ☆=( )( 9 )△+△=18 △=( ) (10)口+口+△+△=14☆+ o =13 o =( ) △+△+口=10△+ o =15 ☆=( ) △=( ) 口(Kou)=( )三、每个图形代表一(Yi)个数,你能算出这个数是多少吗?( 1 )△+□=9 ○-△=1 △+△+△=9△=()□=()○=()( 2 )△ + ○ = 12 ○ + ☆ = 8 △ + ○ + ☆ = 21△ =( ) ○= ( ) ☆=( )( 3 )你 + 我(Wo) = 7 你 + 他 = 18 你 + 我 + 他 = 24 你(Ni) = ()我 = ()他 = ()( 4 )○+□=10,□+△=12,○+□+△=15。
○=(),□=(),△=()。
( 5 )△+○=9 △+△+○+○+○=25△=()○=()四(Si)、每个图(Tu)形代表一个数,你能算出这个数是多少吗?(1)△+△+△+△=28 △=()△+△+□=20 □=()(2)○+○+○=6 ○=()△+△+△=12 △=()(3)△-○=1 △=()△+△-○=9 ○=()△+○-□=10 □=()二(Er)、下图中每种水果各代表一个(Ge)数,算一算,它们各代表几?+ = 7+= 10+= 9=()=()=()已(Yi)知:☆+☆+☆=6,△+△+△+△=20,则(Ze)△-☆=( )已(Yi)知:△+○=14 △-○=2 则(Ze)△=( ) ○=( )已(Yi)知:▲=●+●+●,▲+●=12,则(Ze)●=(),▲=()已(Yi)知:△ + ○ = 5 ○ + ☆ = 9 △ + ○ + ☆ = 13△ =( ) ○= ( ) ☆=( )七、张老师把红、白、蓝各一个气球分别送给三位小朋友(You)。
图论期末复习题

17.任何简单平面图,均有. G 3
二、解答题
1.同构的判定及理由
3.左图称作什么图?两图是否同 构?为什么?
x
y
z
x
c
a
a
b
c
z
y b
2、给定图 :
(1)给出图 的一个生成树 。 (2)给出图 的顶点的最大度数 。
(3)给出图 的最长链。 (4)给出图 的一个边数最多的割集。
d
f
a
e1 b
在或不存在〕完美匹配.
35.在计算平面图面的次数之和时,每条边边计算了______ 次.
36.一个图是平面图当且仅当它既没有收缩到K5的子图, 也没有收缩到 的子图.
37.如果一个平面图有一个面的次数为4,那么该图______ 〔填是或不是〕极大平面图.
三、判断题
1.假设途径中的所有点互不相同,那么称此途径为一 条链.
31.设M1和M2是图G的两个不同匹配, 由M1 M2导出的G的边导出子图记作H, 那么H的任意连通分支是以下情况之一: (1)边在M1和M2中交错出现的偶圈;(2)边 在M1和M2中交错出现的 .
32.二部图G中假设满足V1= V2,那么G必有完美匹配. 33. (G)=2 G是 . 34.假设最大匹配的边数为p(G)/2,那么说明该图___〔填存
点连通度、边连通度与最小顶点的度数。
四、应用题
1. (蚂蚁比赛问题)甲、乙两只蚂蚁分别位于如以下图 中的顶点A,B处,并设图中的边长度是相等的。甲、 乙进行比赛:从它们所在的顶点出发,走过图中的所 有边最后到达顶点C处。如果它们的速度相同,问谁 先到达目的地?
甲A
乙
C
B
2.某地要兴建5个工厂,拟修筑道路连接这5 处。经勘测其道路可依如以下图无向边铺设。 为使这5处都有道路相通,问至少要铺几条路?
简单无向图的同构判定方法

简单无向图的同构判定方法王 卓 1王成红2摘 要 给出了矩阵同构变换、简单无向图距离矩阵、距离矩阵列和向量以及图的距离谱的定义, 将基于邻接矩阵的同构判定条件推广到简单无向图距离矩阵. 针对简单无向连通图的同构判定问题: 给出了基于距离矩阵特征多项式的同构判定条件; 进一步, 为避免计算误差对判定结果的影响, 给出了基于距离矩阵的秩与列和向量的同构判定条件. 上述两个判定条件均是充要条件且均具有多项式时间复杂度.关键词 简单无向图, 同构判定条件, 距离矩阵列和向量, 图的距离谱, 特征多项式引用格式 王卓, 王成红. 简单无向图的同构判定方法. 自动化学报, 2023, 49(9): 1878−1888DOI 10.16383/j.aas.c230025Isomorphism Determination Methods for Simple Undirected GraphsWANG Zhuo 1 WANG Cheng-Hong 2Abstract This work gives the definitions of matrix isomorphic transformation, distance matrix of the simple undir-ected graph, column sum vector of the distance matrix, and distance spectrum of the graph, which extend the adja-cency matrix-based isomorphism determination conditions to the distance matrix-based ones for simple undirected graphs. For the isomorphism determination problem of simple undirected connected graphs: One determination con-dition based on the characteristic polynomial of distance matrix is proposed; Further, another determination condi-tion based on the rank and the column sum vector of distance matrix is proposed to avoid the influence of calcula-tion error on the determination result. These two determination conditions are both necessary and sufficient condi-tions and both have polynomial time complexity.Key words Simple undirected graphs, isomorphism determination conditions, column sum vector of distance mat-rix, distance spectrum of graph, characteristic polynomialCitation Wang Zhuo, Wang Cheng-Hong. Isomorphism determination methods for simple undirected graphs. Acta Automatica Sinica , 2023, 49(9): 1878−1888图的同构判定在化学分析、计算机科学、人工智能以及智能决策与控制等领域有着广泛的应用[1−3].上世纪前半叶, 与图同构相关的问题主要围绕图的邻接矩阵及其性质、邻接矩阵(拉普拉斯矩阵)特征值及其应用展开[4], 取得了若干重要的理论成果和一大批应用成果.P NP 上世纪70年代, Karp 、Garey 和Johnson 等认为图的同构判定问题是少数几个既不能归类为 ,也不能归类为 的问题[1, 3]. 自此之后, 该问题成为理论计算机领域的公开问题并受到广泛重视.exp (O (√n log n ))n exp ((log n )O (1))1982年, Luks 使用有限群等数学工具给出了一个当时最好的两图同构判定算法, 该算法的时间复杂度是 ( 为图的顶点数)[5−6].此后40年来, 图的同构判定问题引起了众多学者的关注, 几百篇这方面的文章得以在不同的学术期刊上发表[1]. 2015年, Babai 在Luks 算法的基础上,利用群作用下轨道间的局部关系和群的正则分解技术, 给出了两图同构判定问题的拟多项式算法, 该算法的时间复杂度是 [5]. 上述算法的目的在于给出同构判定问题的复杂度上界, 并不能直接用于具体图的同构判定[5]. Babai 的工作虽然是一个重要进展, 但图的同构判定问题是否在多项式时间内可解仍然悬而未决[1].图的同构判定问题的另一研究路径是设计可执行的具体判定算法, 大致可以分为传统判定算法和非传统判定算法两种情况. 传统判定算法有两类:1) 针对一些特殊图(如树和极大外平面图等)[7−8]的同构判定算法(如Ullman 算法、Schmidt 算法、收稿日期 2023-01-18 录用日期 2023-07-22Manuscript received January 18, 2023; accepted July 22, 2023广东省重点领域研发计划(2021B010*******), 国家自然科学基金(61673041)资助Supported by Key Area Research and Development Program of Guangdong Province (2021B010*******) and National Natur-al Science Foundation of China (61673041)本文责任编委 孙健Recommended by Associate Editor SUN Jian1. 北京航空航天大学仪器科学与光电工程学院 北京 1001912. 国家自然科学基金委员会 北京 1000831. School of Instrumentation and Optoelectronic Engineering,Beihang University, Beijing 1001912. National Natural Sci-ence Foundation of China, Beijing 100083第 49 卷 第 9 期自 动 化 学 报Vol. 49, No. 92023 年 9 月ACTA AUTOMATICA SINICASeptember, 2023Falkenhainer 算法和Messmer 算法等)[9]. 这些算法主要使用“搜索、标号和回溯”技术且被证明具有多项式时间复杂度; 2) 针对一般简单图的判定算法,如一些放在因特网上用于测试两图是否同构的程序(如Nauty 、Saucy 、Bliss 、Conauto 和Traces 等)[3, 5]. 这些程序运行速度很快, 但算法的时间复杂度分析和正确性证明却没有公开报道. 非传统判定算法也有两类: 1) 基于遗传算法、神经网络和粒子群算法等的智能同构判定算法. 这些算法将图的同构判定问题转化为一类优化求解问题, 但其判定结果并不完全可靠. 2) 基于生物(DNA)计算[9]和量子计算的判定算法. 这类算法虽然高效, 但实现比较困难而且也不能回答图的同构判定是P 还是NP 问题.本文的主要思路和贡献是: 1) 给出了矩阵同构变换和简单无向图距离矩阵的定义, 将基于邻接矩阵的同构判定条件推广到简单无向图距离矩阵. 2) 针对简单无向连通图的同构判定问题, 给出了基于距离矩阵特征多项式的同构判定条件. 因用数值方法求解特征多项式会产生计算误差, 故该判定条件仅适合中小规模简单无向连通图的同构判定[10−11]. 3) 为避免计算误差对判定结果的影响, 给出了简单无向连通图距离矩阵列和向量与图的距离谱的定义, 并进而给出了基于距离矩阵的秩与列和向量的同构判定条件. 该判定条件不产生计算误差, 因而适合大规模简单无向连通图的同构判定. 上述两个判定条件均是充要条件且均具有多项式时间复杂度, 将这些条件用于简单无向不连通图的各个连通子图, 就可解决简单无向不连通图的同构判定问题.1 相关概念和预备知识1.1 相关概念若仅考虑顶点间的邻接关系和拓扑结构, 则图可视为由若干个顶点和若干条边连接成的网络.G G =⟨V,E ⟩定义 1[4, 12−13]. 图 是一个二元组, 记作 , 其中:V ={v 1,v 2,···,v n ||V |=n,n ≥1}v i ∈V G V G 1) , 称为 的顶点, 称为 的顶点集;E ={e 1,e 2,···,e m ||E |=m,m ≥0}e j ∈E G E G 2) , 称为 的边, 称为 的边集;∀e j ∈E e j G e jG 3) : 为无向边时, 称 为无向图, 为有向边时, 称 为有向图;4) 连接同一个顶点的边称为自环, 两个顶点间的多条无向边或多条方向相同的有向边称为重边.无自环和重边的图称为简单图, 否则称为复杂图.本文分析和讨论的图均是顶点和边为有限数的无向图.G =⟨V,E ⟩V ={v 1,v 2,···,v n }v i v j (1≤i,j ≤n )k k ≥0a ij =k a ij A (a ij )∈R n ×n G 定义 2[12−14]. 设 为无向图, . 若顶点 和 之间有 ( 为非负整数)条边, 令 ; 称由元素 构成的矩阵 为无向图 的邻接矩阵.k =0a ii =k v i k 在定义2中, 表示无边, 表示顶点 有 个自环. 如此, 定义2既适合简单无向图也适合复杂无向图.G =⟨V,E ⟩V ={v 1,v 2,···,v n }(n ≥2)E ={e 1,e 2,···,e m }(m ≥1)G W =v 1e 1v 2e 2···v k e k v k +1(k ≤n −1)G W W k W k =|W |v i v j V v i v j s W p (1≤p ≤s )d (v i ,v j )=min {k p =|W p ||1≤p ≤s }v i v j v i v j G d (v i ,v j )=∞d (G )=max {d (u,v )|u v ∈V }G 定义 3[4, 12−14]. 设 为无向图, , .1) 中顶点与边的交替序列 称为 的链, 各边互异的链称为迹, 各顶点互异的链称为路; 当 是路时, 中的边数 称为 的长度, 记作 . 2) 设 和 是 中的任意两个顶点, 当 和 之间有 条路 时, 称 为 和 之间的距离; 若 和 之间无路( 不连通), 约定 . 3) 称 , 为 的直径.图的同构问题可以这样表述: 给定两个图, 当忽略图中顶点的标号、顶点间的相对位置、边的长短和曲直信息时, 问这两个图是否具有相同的结构? 现有文献中关于简单图的同构定义已有多个[4, 13−14],这些定义虽然表述略有不同但彼此等价. 下面, 我们给出一个既适合简单图又适合复杂图的同构定义.G 1=⟨V 1,E 1⟩G 2=⟨V 2,E 2⟩V 1V 2g ∀v i ,v j ∈V 1v i v j k g (v i )g (v j )∈V 2g (v i )g (v j )k G 1G 2G 1∼=G 2定义 4[4]. 设 和 是两个无向(有向)图. 若存在一个从 到 的一一映射 : , 至 有 条无向(有向)边, 当且仅当 , , 且 至 也有 条无向(有向)边, 则称 和 同构, 记作 .1.2 预备知识I n ∈R n ×n I n i j i j P (i,j )定义 5[15]. 设 为单位矩阵, 交换 的第 行与第 行(或第 列与第 列)所得的矩阵 称为对换矩阵, 对换矩阵的乘积称为置换矩阵.引理 1[15]. 对换矩阵和置换矩阵具有如下性质:det (P (i,j ))=−1P −1(i,j )=P (i,j )1) , ;2) 置换矩阵的乘积仍是置换矩阵;Q det (Q )=±13) 设 是置换矩阵, 则 ;Q Q T Q −1Q T =Q −14) 设 是置换矩阵, 则 和 也是置换矩阵, 且 ;5) 置换矩阵是正交矩阵;Q Q m =I n m 6) 置换矩阵是幂幺矩阵, 即若 是置换矩阵,则 , 是自然数.9 期王卓等: 简单无向图的同构判定方法1879I n 由引理1中的性质2)和性质6)可知, 对换矩阵和 也是置换矩阵.A,B ∈R n ×n Ω⊂R n ×n n Q ∈ΩA =Q T BQ A B A ∼=B Q T BQ B 定义 6. 设 , 为全体 阶置换矩阵的集合. 若存在置换矩阵 , 使得, 则称 与 同构, 记作 ; 此外,称 是对 的同构变换.G =⟨V,E ⟩|V |=n ≥2V n πTi =[σi 1σi 2···σin ]∈R 1×n {σi 1,···,σin }{1,2,···,n }A ∈R n ×n π1π2V A B G π1π2π1=π2A =B π1=π2A =B A =B 任给一个无向(有向)图 , . 对 中每个顶点指定一个1 ~ 的标号, 可以得到一个标号向量 ( 是 的一个置换)和一个邻接矩阵 . 设 和 是 的任意两个标号向量, 与 分别是图 相应于 和 的邻接矩阵. 当 时, ; 当 时, (或 ).π1=π2π1π1π2A B v i v j π1P (i,j )π1P (i,j )A P (i,j )AP T (i,j )P (i,j )AP T (i,j )A i j i j m (m ≥1)π1π2s (1≤s ≤m )P s π2=P m P m −1···P 1π1=Qπ1(Q =P m P m −1···P 1)B =P m P m −1···P 1AP T 1···P Tm −1×P T m =QAQ T Q ∈Ωπ1=Q T π2A =Q T BQ 设 . 逐次不重复地对调 中两个分量的位置(对换两个顶点的标号), 经有限次对调就可将 变成 , 同时将 变成 . 对调顶点 与 的标号, 将变为 ( 为对换矩阵), 将变为 . 其中, 是对调 的第 行和第 行之后, 再对调第 列和第 列所得的矩阵. 设顶点标号经 次对调之后 变成 , 并且第 次对调所对应的对换矩阵为 , 则 , . 由引理1可知, 为置换矩阵. 如此, , .G A B G Q ∈ΩA =Q T BQ 由上述分析和定义6可知: 任给无向图 , 若 和 是 的两个邻接矩阵, 则存在置换矩阵 , 使得 , 即同一图的任意两个邻接矩阵彼此同构; 邻接矩阵的行列同时互换是同构变换,邻接矩阵的同构变换还是邻接矩阵.G 1=⟨V 1,E 1⟩G 2=⟨V 2,E 2⟩|V 1|=|V 2|=n A B G 1G 2G 1∼=G 2n Q ∈ΩA =Q T BQ A =Q −1BQ 引理 2[12]. 设 和 是两个图, , 与 分别是 和 的邻接矩阵. 则 的充要条件是存在 阶置换矩阵 , 使得 , 或 .n Q ∈ΩA =Q T BQ Q T BQ B A =Q T BQ G 2G 1G 2A G 1G 2G 1∼=G 2证明. 设存在 阶置换矩阵 , 使得 . 由定义6可知, 是对 的同构变换.因邻接矩阵的同构变换还是同一图的邻接矩阵, 故 是 的邻接矩阵. 如此, 和 有相同的邻接矩阵 , 即 和 是同一个图; 换言之,.G 1∼=G 2G 1G 2B A n Q ∈ΩA =Q T BQ 设 . 当 和 同构时, 可经有限次行列同时互换转化为 , 即存在 阶置换矩阵, 使得 .□引理2表明, 两个图同构当且仅当该两图的邻接矩阵同构; 若两个图有相同的邻接矩阵, 则这两Q 个图同构. 容易证明, 引理2中的 是唯一的.2 简单无向图的同构判定方法由定义3可知, 复杂无向图中的自环和多重边中的重边对顶点间的距离没有影响. 为区分起见,本节仅讨论简单无向图.G =⟨V,E ⟩V ={v 1,v 2,···,v n }d ij =d (v i ,v j )v i v j (1≤i,j ≤n )i =j d ii =0i =j d (v i ,v j )=k (d (v i ,v j )=∞)d ij =k (d ij =∞)k ≥1d ij D (d ij )∈R n ×n G G 定义 7. 设 是简单无向图, , 表示顶点 和 之间的距离: 当 时, 令 ; 当 且 时, 令 , 其中 为正整数; 称由元素 构成的矩阵 为简单无向图 的顶点距离矩阵, 简称 的距离矩阵.i =j d (v i ,v j )=d (v j ,v i )d ij =d ji G D G 因 时, , 所以 ,简单无向图 的距离矩阵 是对称矩阵. 与邻接矩阵一样, 顶点标号不同时, 的距离矩阵通常也互不相同.G 1=⟨V 1,E 1⟩G 2=⟨V 2,E 2⟩|V 1|=|V 2|=n ≥2D 1D 2G 1G 2G 1∼=G 2n Q ∈ΩD 1=Q T D 2Q D 1=Q −1D 2Q 定理 1. 设 和 是两个简单无向图, , 与 分别是 和 的距离矩阵; 则 的充要条件是存在 阶置换矩阵 , 使得 , 或.n Q ∈ΩD 1=Q T D 2Q Q ∈ΩQ T D 2Q D 2Q T D 2Q D 2D 2Q T D 2Q =D 1G 2D 2=QD 1Q T G 1D 1D 2G 1G 2G 1π1D 1A 1G 2π2D 2A 2D 1D 2G 1D 1=Q T D 2Q π1=Q T π2A 1=Q T A 2Q.Q ∈Ω,D 1=Q T D 2Q,A 1=Q T A 2Q.G 1∼=G 2.证明. 设存在 阶置换矩阵 , 使得 . 因 , 由定义6可知, 是对 的同构变换. 因 只改变 行与列的排列而不改变 的元素, 故 也是 的距离矩阵. 同理, 也是 的距离矩阵. 如此, 和 既是 的距离矩阵也是 的距离矩阵. 设 的顶点标号向量为 , 相应的距离矩阵和邻接矩阵分别是 和 ; 的顶点标号向量为 ,相应的距离矩阵和邻接矩阵分别是 和 . 因 和 均是 的距离矩阵, 类似第1.2节的分析可得,当 时, , 如此,若存在 使得 则 由引理2可知, G 1∼=G 2Q ∈ΩA 1=Q T A 2Q A 1=Q T A 2Q π1=Q T π2D 1=Q T D 2Q G 1∼=G 2Q ∈ΩD 1=Q T D 2Q D 1=Q −1D 2Q 设 . 由引理2可知, 存在 , 使得. 同上分析可得, 当 时,, . 这表明, 若 , 则存在 , 使得 , 或 .□定理1表明, 两个简单无向图同构当且仅当这两个图的距离矩阵同构; 距离矩阵的同构变换还是距离矩阵; 距离矩阵的同构性与邻接矩阵的同构性保持一致.不难理解, 定理1即是引理2在简单无向图距1880自 动 化 学 报49 卷离矩阵上的推广.G =⟨V,E ⟩|V |=n ≥2D (d ij )∈R n ×n G D G D d (G )=max {d ij |1≤i,j ≤n }D G G 设 是简单无向连通图, , 是 的距离矩阵. 由定义7可知, 是对角线元素均为零而其他元素全为正整数的对称矩阵. 由定义3和定义7可知, 的直径可由 的元素求取, 即 . 此外,由 的元素还可求出 中各顶点的离心率和 的半径[4, 13].G =⟨V,E ⟩D (d ij )∈R n ×n G d j =∑ni =1d ij (1≤j ≤n )d j d o (D )=[¯d1¯d 2···¯dn ](¯d 1≤¯d 2≤···≤¯d n )d o (D )D d o (D )D 定义 8. 设 是简单无向连通图,是 的距离矩阵, ; 对 进行升序排列, 可得 , 则 是 的列元素之和按升序排列所得的向量, 简称 是 的列和向量.G 1=⟨V 1,E 1⟩G 2=⟨V 2,E 2⟩|V 1|=|V 2|=n ≥2D 1D 2G 1G 2d o (D 1)=d o (D 2)G 1G 2推论 1. 设 和 是两个简单无向连通图, , 与 分别是 和 的距离矩阵; 若 ,则 和 不同构.d o (D 1)=d o (D 2)G 1∼=G 2G 1∼=G 2n Q ∈ΩD 1=Q T D 2Q E 1={d (1)1,d (1)2,···,d (1)n }E 2={d (2)1,d (2)2,···,d (2)n }D 1D 2E 2Q T D 2Q E 2G 1∼=G 2D 1=Q T D 2Q E 1=E 2E 1E 2d o (D 1)=d o (D 2)G 1∼=G 2d o (D 1)=d o (D 2)G 1G 2证明. 设 时, . 由定理1可知, 当 时, 存在 阶置换矩阵 ,使得 . 设 与分别是 和 列元素之和构成的集合. 因同构变换只改变矩阵列的排序而不改变列元素之和, 故在不考虑 元素的排序时, 列元素之和构成的集合仍是 . 如此, 当 时, , (两集合相等当且仅当它们的元素一一对应相等), 和 元素的升序排列相等, 即 , 与推论1条件矛盾, 则 的假设不成立. 综上可知, 当 时, 和 不同构. □T ⊂R n ×n (n ≥2)n Ω−={−S |S ∈Ω}n Φ=Ω∪Ω−n n Θ=T −ΦT Φn 定义 9. 设 表示全体 阶正交矩阵的集合; 表示全体 阶负置换矩阵的集合; 表示全体 阶置换矩阵和全体 阶负置换矩阵的并集; 表示 中除 之外全体 阶正交矩阵的集合.Θ∩Φ=∅∅Θ∪Φ=T ∀Q 1,Q 2∈ΦQ 1Q 2∈Φ∀Q ∈Φ∀P ∈ΘQP,P Q ∈Θ∀P ∈Θ∀E ∈Φ∀Q ∈T Q =EP T QP,P Q ∈Θ由定义9和正交矩阵的性质可知: ( 为空集), ; , ;, , ; , , 且 , .A ∈R n ×n A P ∈T 引理 3[15]. 设 , 则 为正交矩阵的充要条件是存在正交矩阵 , 使得I s I t s t 其中, 与 分别是 阶和 阶单位矩阵,[]s +t +2k=n θj ∈R (1≤j ≤k ) , 为实数.P θH θ由正交矩阵的定义可知, 和 均是正交矩阵.A (a ij )∈R n ×n (n ≥2)∀P ∈ΘP T AP P T AP 定理 2. 设 是对角线元素均为1而其他元素均为正整数的对称矩阵, 则, 不是正整数矩阵( 的元素不全是正整数).n =2证明. 当 时, 设a θ∈R 其中, 为正整数, . 如此,θ=±lπ(l =0,1,2,···)P ∈ΘP T AP P ∈ΘE ∈ΦC ∈T C =EP −1Q 1=CP ∈ΘQ 2=P C ∈ΘQ 3=C T P C ∈ΘQ T 1AQ 1Q T 2AQ 2Q T3AQ 3Q ∈ΘQ T AQ 当 时, , 不是正整数矩阵. 当 时, 由定义9和引理3可知,对一切2阶正交矩阵 、 且 ,则: 1) , , ; 2) 、 和 均不是正整数矩阵. 故对一切2阶正交矩阵 , 不是正整数矩阵.n =3当 时, 设a 1a 2a 3δ=±1θ∈R 其中, , , 为正整数, , . 如此,α1(θ)=a 1cos θ−a 2sin θα2(θ)=a 1sin θ+a 2cos θα3(θ)=a 3sin 2θδ=1θ=±2lπ(l =0,1,2,···)δ=−1θ=±hπh P ∈ΘP T AP n =2Q ∈ΘQ T AQ 其中, , , . 当 且 , 或 且 ( 为奇数)时,, 不是正整数矩阵. 类似 时的分析可得, 对一切3阶正交矩阵 , 不是正整数矩阵.n ≥4当 时, 设A 11∈R s ×s A 22∈R t ×t A 33∈R 2k ×2k 其中, , , 均是9 期王卓等: 简单无向图的同构判定方法1881A 12A 13A 23P θH θs+t +2k =n θj ∈R (1≤j ≤k )对角线元素为1而其他元素为正整数的分块对称矩阵, , , 均是分块正整数矩阵; 和为形如引理3中的矩阵, , 为实数. 如此,s =n 1≤s <n t =0θj =±2lπ(1≤j ≤k,l =0,1,2,···)s =t =0θj =±2lπ(1≤j ≤k,l =0,1,2,···)P θ=I n ∈Ωt =n 1≤t <n s =0θj =±hπ1≤j ≤k h t =s =0θj =±hπ1≤j ≤k h P θ=−I n ∈Φs t k θj (1≤j ≤k )P θ∈ΘP TθAP θP ∈Θn ≥4E ∈ΦZ ∈T Z =EP −1Q 1=ZP ∈ΘQ 2=P Z ∈ΘQ 3=Z T P Z ∈ΘQ T 1AQ 1Q T 2AQ 2Q T 3AQ 3n ≥4Q ∈ΘQ T AQ 当 或 、 且所有的 , 或 且所有的 时, ;当 , 或 , 且所有的 ( , 为奇数), 或 且所有的 ( , 为奇数)时, . 当 ,, 和 的取值不是前两种情况时,, 不是正整数矩阵. 当 时, 由定义9和引理3可知, 对一切 阶正交矩阵 , 且 , 则: 1) , , ; 2) , , 均不是正整数矩阵. 如此, 对一切 阶正交矩阵 , 不是正整数矩阵.n ≥2∀P ∈ΘP T AP 综合上述各种情况可得, 当 时, ,不是正整数矩阵.□n ≥2∀Q ∈ΦQ T AQ 此外, 不难证明, 当 时, , 是正整数矩阵.A,B ∈R n ×n det (λI n −A )=det (λI n −B )P ∈T A =P T BP =P −1BP 引理 4[15]. 设 为对称矩阵, 则 的充要条件是存在正交矩阵 , 使得 .基于定理1、定理2和引理4, 下面给出两个简单无向连通图是否同构的判定条件.G 1=⟨V 1,E 1⟩G 2=⟨V 2,E 2⟩|V 1|=|V 2|=n ≥2D 1D 2G 1G 2G 1∼=G 2det (λI n −D 1)=det (λI n −D 2)定理 3. 设 和 是两个简单无向连通图, , 与 分别是 和 的距离矩阵, 则 的充要条件是 .det (λI n −D 1)=det (λI n −D 2)D 1D 2det (λI n −D 1)=det (λI n −D 2)n P ∈T D 1=P T D 2P ∀n ≥2P ∈ΩP =−S S ∈ΩP ∈ΘD 1=P T D 2P I n +D 1=P T P +P T D 2P =P T (I n +D 2)P I n +D 1In +D 2P T (I n +D 2)P P /∈ΘΘ∩Φ=∅Θ∪Φ=T P ∈T P /∈ΘP ∈Φ∀n ≥2D 1D 2det (λI n −D 1)=det (λI n −D 2)P ∈ΩP =−S S ∈Ω证明. 设 . 因 和 均是实对称矩阵, 由引理4可知, 当 时, 存在 阶正交矩阵 ,使得 . 下面证明, , (或, ). 假设存在一个 , 使得 , 则 . 因 和 均是正整数矩阵, 故 也是正整数矩阵, 这与定理2的结论矛盾. 如此, . 因 , , 故当 且 时, 必有 . 换言之, , 当 和 均是距离矩阵且 时, 一定存在 (或 , ), 使得D 1=P T D 2P G 1∼=G 2. 由定理1可知, .G 1∼=G 2n P ∈ΩD 1=P T D 2P det (λI n −D 1)=det (λI n −D 2)设 . 由定理1可知, 存在 阶置换矩阵, 使得 . 如此, .□B ∈R n ×n I n +B 需要强调的是, 距离矩阵特征多项式和邻接矩阵特征多项式是两种完全不同的多项式; 邻接矩阵特征多项式相等并不总能确定两个简单无向连通图(特别是无向树)同构[4, 16]. 设 是简单无向连通图的邻接矩阵, 因 一般不是正整数矩阵(完全图除外, 完全图的邻接矩阵等于其距离矩阵), 故定理3的充分性证明方法不能用于邻接矩阵.D det (λI n −D )因求解距离矩阵 [13−14]和特征多项式 [10−11]均有多项式时间算法, 故定理3的判定条件具有多项式时间复杂度.因用数值方法求解特征多项式会产生计算误差[10−11], 故当图的规模很大时, 这种计算误差可能会对定理3的判定结果产生影响. 因此, 寻找一种无误差判定条件无疑具有重要的应用价值.G 1=⟨V 1,E 1⟩G 2=⟨V 2,E 2⟩|V 1|=|V 2|=n ≥2D 1D 2G 1G 2r (D 1)=r (D 2)r (D )D G 1G 2推论 2. 设 和 是两个简单无向连通图, , 与 分别是 和 的距离矩阵; 若 ( 表示 的秩), 则 和 不同构.D 1D 2D 1D 2D 1D 2r 1r 2λi (1≤i ≤r 1)µj (1≤j ≤r 2)D 1D 2n P 1,P 2∈T 证明. 因 和 均是实对称矩阵, 故 和 的特征值均是实数[15, 17]. 设 和 的非零特征值个数分别是 和 , 和分别是 和 的非零特征值, 则存在 阶正交矩阵 , 使得r (D 1)=r (P −11D 1P 1)=r 1r (D 2)=r (P −12D 2P 2)=r 2r (D 1)=r (D 2)D 1D 2det (λI n −D 1)=det (λI n −D 2)G 1G 2如此可得, , . 当 时, 和 的非零特征值个数不相等, . 由定理3可知, 和 不同构.□G =⟨V,E ⟩|V |=n ≥2D (d ij )∈R n ×n G d (G )=max {d ij }G m s d ij =s (1≤s ≤d (G ),1≤i,j ≤n )d s (D )=[m 1m 2···m d (G )]G G 定义 10. 设 是简单无向连通图, , 是 的距离矩阵, 是 的直径, 是 的元素总数; 称 是 的距离谱向量, 简称 的距离谱.m s ∑n i,j d ij =∑d (G )s =1m s s ∑n i,j d 2ij =∑d (G )s =1m s s 2由定义7和定义10可知: 均是正整数,, .G 1=⟨V 1,E 1⟩G 2=⟨V 2,E 2⟩|V 1|=|V 2|=n ≥2D 1D 2G 1G 2d s (D 1)=d s (D 2)G 1G 2推论 3. 设 和 是两个简单无向连通图, , 与 分别是 和 的距离矩阵; 若 ,则 和 不同构.d s (D 1)=d s (D 2)G 1∼=G 2.证明. 设 时, 由定理1882自 动 化 学 报49 卷G 1∼=G 2Q ∈ΩD 1=Q T ×D 2Q d s (D 1)=d s (Q T D 2Q )=d s (D 2)d s (D 1)=d s (D 2)G 1∼=G 2d s (D 1)=d s (D 2)G 1G 21可知, 当 时, 存在 , 使得 . 因同构变换不改变图的距离谱, 故 , 即 , 与推论3的条件矛盾, 的假设不成立. 换言之, 当时, 和 不同构.□d o (D 1)=d o (D 2)r (D 1)=r (D 2)d s (D 1)=d s (D 2)由推论1 ~ 3可知, , , 均是两个简单无向连通图同构的必要条件.A ∈R n ×n (n ≥2)n P ∈Ω定义 11[17]. 设 , 若存在 阶置换矩阵 , 使得A 11k ×k (1≤k ≤n −1)A 22(n −k )×(n −k )A A 其中, 是 阶子矩阵, 是 阶子矩阵, 则称 是可约矩阵;否则, 称 是不可约矩阵.D 由定义7和定义11可知, 简单无向连通图的距离矩阵 是非负不可约矩阵.A ∈R n ×n k ρ(A )k =1A k >1A k 定义 12[17]. 设 是非负不可约矩阵且有 个模等于 的特征值: 若 , 则称 是素矩阵; 若 , 则称 是指数为 的循环矩阵.A ∈R n ×n A m A m >0A m 引理 5[17]. 设 是非负不可约矩阵, 则 为素矩阵的充要条件是存在某正整数 , 使得 ( 的所有元素大于零).n ≥3D D 2>0容易证明, 当 时, 一切距离矩阵 均是素矩阵( ).A ∈R n ×n λ1,λ2,···,λn A ρ(A )>0A |λi |=ρ(A )|λi |<ρ(A ).引理 6[17]. 设 是素矩阵, 是 的特征值, 则谱半径 是 的单特征值, 且对一切 , 均有 A (a ij )∈R n ×n (A T A =AA T )λ1,λ2,···,λn A ∑ni,j a 2ij =∑ni =1λ2i 引理 7[17]. 设 为正规矩阵 , 是 的特征值, 则 .r (D )=k ∆k =∆r (D )D k ∆k 设 , 表示 的所有 阶主子式的和. 使用符号 并依据引理5 ~ 7, 可以得到简单无向连通图的另一个同构判定条件.G 1=⟨V 1,E 1⟩G 2=⟨V 2,E 2⟩|V 1|=|V 2|=n ≥2D 1D 2G 1G 2G 1∼=G 2d s (D 1)=d s (D 2)r (D 1)=r (D 2)∆r (D 1)=∆r (D 2)定理 4. 设 和 是两个简单无向连通图, , 与 分别是 和 的距离矩阵, 则 的充要条件是 , 且 .n =2D 1=D (a ij )D 2=D (b ij )n ≥3证明. 当 时, 定理4的结论显然成立. 设, , 下面证明 时, 定理4的结论也成立.d s (D 1)=d s (D 2)r (D 1)=r (D 2)∆r (D 1)=∆r (D 2).d s (D 1)=d s (D 2)d (G 1)=d (G 2)∑d (G 1)s =1m s s 2=∑ni,j a 2ij∑d (G 2)s =1m s s 2=∑n i,j b 2ij ∑n i,j a 2ij =∑n i,j b 2ij .D 1D 2设 , 且 当 时, 由定义10可得, , , , 因 和 均是对称r (D 1)=r (D 2)=m ∆r (D 1)=∆r (D 2)=∆D 1矩阵和素矩阵, 故当 且 时, 可设 的非零特征值和特征多项式分别为D 2的非零特征值和特征多项式分别为n i,ja 2ij =n i,j b 2ij m i =1λ2i =∑m i =1µ2i D 1D 2∑m i =1λi =∑mµi =0∏m λi =∏mµi =∆由 和引理7可得, . 因 和的对角线元素全为零, 故由特征值和特征多项式系数之间的关系可得, , . 如此,λi =µi (1≤i ≤m )不难发现, 是上述3个方程的一组公共解. 下面分4步证明该组解是唯一解.∀n ≥31≤i ≤m ¯λi =−µi .µ1≤···≤µm −1<µm (µ1<0)∀i =m |µi |<µm =ρ(D 2)>0¯λ1≥···≥¯λm −1>¯λm ¯λ1>0¯λm <0¯λ1=|µ1|<µm =|¯λm |¯λ1<|¯λm |¯λi (1≤i ≤m )D 1¯λi =−µi (1≤i ≤m )(1)(2)(3)1) 和 , 设 因已假设, 且 , ; 故 , 且 . 因 , 即 , 由引理6可知, 不是或不全是对称素矩阵 的特征值. 如此, 不可能是式, , 的公共解.∀n ≥3∀l ∈{1,···,m −1}¯λi =−µi (1≤i ≤l )¯λj =µj (l +1≤j ≤m ),¯λi µi ∑m i =1¯λi =∑m i =1µi −2∑l i =1µi .∑m i =1µi =0l <m ∑l i =1µi =∑m i =1µi ,∑m i =1¯λi =−2∑li =1µi =0¯λi (1≤i ≤m )D 1(2)(3)2) 和 , 若设 , 则 和 是式(1)的解, 因 且 , 故 . 如此, 不是或不全是 的特征值, 式 和式 均不成立.∀ε∈R ε=0∀i =j t =i t =j ¯λt =λt ¯λi =λi −ε¯λj =λj +ε¯µt =µt ¯µi =µi −ε¯µj =µj +ε¯λt ¯µt (1≤t ≤m )(2)(1)(3)3) 且 ; , 且 ; 设 , , , , ,, 则 和 满足式 , 但不能同时满足式 和式 .|λi |=|µi |(1≤i ≤m )|λi |=|µi |λi =αµi λj =α−1µj α=1(3)(1)(2)4) 若有奇数个 , 则式(1) ~(3)均不成立; 若有偶数个 (如 ,, )使得式 成立, 则式 和式 均不成立.λi =µi (1≤i ≤m )综合上述4种情况可知, 9 期王卓等: 简单无向图的同构判定方法1883∀n ≥3det (λI n −D 1)=det (λI n −D 2)是同时满足式(1) ~ (3)的一组唯一解. 如此, , .∀n ≥2d s (D 1)=d s (D 2)r (D 1)=r (D 2)∆r (D 1)=∆r (D 2)det (λI n −D 1)=det (λI n −D 2)G 1∼=G 2.总之, , 当 , 并且 时, . 由定理3可知, G 1∼=G 2.G 1∼=G 2n P ∈ΩD 1=P T D 2P d s (D )r (D )∆r (D )D 1=P T D 2P ds (D 1)=d s (D 2)r (D 1)=r (D 2)∆r (D 1)=∆r (D 2)设 由定理1可知, 当 时, 存在 阶置换矩阵 , 使得 . 因 , 和 均在矩阵同构变换下保持不变, 故当时, , 且 . □n r (D )0.5n ∆r (D )当图的顶点数 很大且 接近 时, 求解 的计算量将异常大. 因此, 还需寻找更易计算的同构判定条件.G 1=⟨V 1,E 1⟩G 2=⟨V 2,E 2⟩|V 1|=|V 2|=n ≥2D 1D 2G 1G 2G 1∼=G 2r (D 1)=r (D 2)d o (D 1)=d o (D 2)定理 5. 设 和 是两个简单无向连通图, , 与 分别是 和 的距离矩阵, 则 的充要条件是 且 .n =2n ≥3证明. 当 时, 定理5的结论显然成立. 下面证明 时, 定理5的结论也成立. 为方便起见, 下面仍使用证明定理4时所用的符号和术语.r (D 1)=r (D 2)d o (D 1)=d o (D 2)G 1G 2r (D 1)=r (D 2)=m d o (D 1)=d o (D 2)G 1G 2D 1D 2|λi ||µi |(1≤i ≤m )∑m i =1λ2i =∑m i =1µ2i∑m i =1λ2i =∑m i =1µ2i ∑n i,j a 2ij =∑n i,j b 2ij ∑n i,j a 2ij =∑n i,j b 2ij ∑d (G 1)s =1m s s 2=∑d (G 2)t =1m t t 2d s (D 1)=d s (D 2)∑n i,j a ij =∑ni,j b ij d o (D 1)=d o (D 2)G 1G 2r (D 1)=r (D 2)d o (D 1)=d o (D 2)G 1∼=G 2设 且 , 但 和 不同构. 由定理4的证明可知, 若 且 时, 和 不同构, 则对称素矩阵 与 的非零特征值的绝对值 和不全部相等, .由引理7可知, 当 时, . 由定义7和定义10可知, 当 时, , , . 如此, ,与假设矛盾, 和 不同构的假设不成立. 换言之,若 且 , 则 .G 1∼=G 2.G 1∼=G 2n P ∈ΩD 1=P T D 2P r (D )d o (D )D 1=P T D 2P r (D 1)=r (D 2)d o (D 1)=d o (D 2).设 由定理1可知, 当 时, 存在 阶置换矩阵 , 使得 . 因 和 均是矩阵同构变换下的不变量, 故当 时, 且 □D r (D )d o (D )det (λI n −D )r (D )d o (D )因距离矩阵 是非负整数矩阵, 故求解 和 均不会产生计算误差. 如此, 定理5为无误差判定条件. 此外, 因求解 比求解 和 困难得多, 故定理5比定理3在计算便利性方面更具优势. 上述两个优点表明, 定理5更适合大规模简单无向连通图的同构判定.D ∈R n ×n r (D )d o (D ).D O (n 4)D O (n 3)r (D )定理5主要涉及3种运算, 求解距离矩阵, 以及 现对定理5的算法复杂度做一些简要说明: 1) 用Floyd 算法[14]求解 的算法复杂度是 , 用Warshall 算法[14]求解 的算法复杂度是 ; 2) 求解 的算法复杂度O (n 3)d o (D )O (1.5n 2)d o (D 1)d o (D 2)O (n )O (2n 4)是 [11]; 3) 由定义8和排序算法可知, 求解 的算法复杂度是 ; 4) 比较 和 是否相等的算法复杂度是 . 总之, 使用定理5判定两个简单无向连通图是否同构的算法复杂度不会超过 .A ∈R n ×n (n ≥2)引理 8[18]. 设 具有如下分块形式:A 11k ×k (1≤k ≤n −1)A 22(n −k )×(n −k )A 11det (A )=det (A 11)det (A 22−A 21A −111A 12).其中, 是 阶子矩阵, 是 阶子矩阵. 若 可逆, 则G =⟨V,E ⟩|V |=n ≥2,D G det (D )=(−1)n −1(n −1)2n −2定理 6. 设 是无向树, 是 的距离矩阵, 则 .D k ∈R k ×k (k ≥2)n =2r (D 2)=2det (D 2)=−1n =3r (D 3)=3det (D 3)=4n =4r (D 4)=4det (D 4)=−122≤n ≤4det (D )=(−1)n −1(n −1)2n −2r (D )=n 证明. 1) 设 为无向树的距离矩阵. 经直接验证可得[16]: 时, ,; 时, , (2顶点和3顶点无向树只有1个自同构类); 时, , (4顶点无向树有2个自同构类). 上述结果表明, 时, , 且与树的拓扑结构无关.n =k (k ≥5)r (D k )=k det (D k )=(−1)k −1(k −1)2k −2n =k +1r (D k +1)=k +1det (D k +1)=(−1)kk ×2k −1n =k +1G 2) 设 时, , 且与树的拓扑结构无关; 下面证明, 时, , 且与树的拓扑结构无关. 设 时, 的距离矩阵为ςT =[ς1ς2···ςk ]ςi (1≤i ≤k )r (D k )=k det (D k )=0D k det (D k +1)=−det (D k )det (ςT D −1k ς)ςD −1k =0det (ςT D −1k ς)=0det (D k +1)=(−1)kk ×2k −1r (D k +1)=k +1其中, , 为正整数.因已假设 , 故 , 可逆. 由引理8可得, .因 为正整数向量并且 , 故 , , ,且与树的拓扑结构无关.D ∈R n ×n (n ≥2)det (D )=(−1)n −1(n −1)2n −2由归纳步骤1)和步骤2)可得, 对一切无向树的距离矩阵 , .□G 1=⟨V 1,E 1⟩G 2=⟨V 2,E 2⟩|V 1|=|V 2|=n ≥2D 1D 2G 1G 2G 1∼=G 2d s (D 1)=d s (D 2)推论 4. 设 和 是两个无向树, , 与 分别是 和 的距离矩阵, 则 的充要条件是 .G 1G 2|V 1|=|V 2|=n ≥2r (D 1)=r (D 2)=n 证明. 因 和 均是无向树且 , 故由定理6可知, , 且r (D 1)=r (D 2)∆r (D 1)=∆r (D 2)恒成立, 即 且 恒成立.1884自 动 化 学 报49 卷d s (D 1)=d s (D 2)r (D 1)=r (D 2)∆r (D 1)=∆r (D 2)d s (D 1)=d s (D 2)G 1∼=G 2d s (D 1)=d s (D 2)如此, “ 、 且 ”与“ ”等价. 因无向树是简单无向连通图, 由定理4立即可得, 无向树 的充要条件是 . □有了推论4, 两个无向树的同构判定问题就变为一个简单的算术问题.不难理解, 将定理3特别是定理5用于简单无向不连通图的各个连通子图或将推论4用于无向森林的各个无向树, 就可解决任意简单无向不连通图的同构判定问题.例 1. 试判定下列各对应图(如图1所示)是否同构.G 1G 2G 1G 2解. 1) 和 均是无向树(毛虫形[4, 16, 19]), 按图中顶点标号, 经计算可得 和 的距离矩阵分别为D 1D 2由 和 可得,d s (D 1)=d s (D 2)G 1G 2因 , 由推论3或推论4均可判定 和 不同构.G 1G 2ϕ(G 1,λ)=ϕ(G 2,λ)=λ10−9λ8+26λ6−27λ4+8λ2G 1G 2此外, 和 的邻接矩阵同谱, 即 . 若将邻接矩阵特征多项式相等作为判据来判定 和 是否同构[16, 19], 就会得出错误的结果.G 3G 4G 3G 42) 和 均是3正则无向图(Wagner 图[1, 20]).按图中顶点标号, 经计算可得 和 的距离矩阵分别为det (λI 8−D 3)=det (λI 8−D 4)=(λ−11)(λ+1)(λ+3)2(λ2+2λ−1)2G 3∼=G 4因为 , 故由定理3可以判定 .r (D 3)=r (D 4)=8d o (D 3)=[1111111111111111]d o (D 4)=[1111111111111111]d o (D 3)=d o (D 4)G 3∼=G 4另一方面, 因 ; , , ; 由定理5可轻松判定.G 5G 6G 5G 63) 和 均是3正则简单无向连通图[3]. 按图中顶点标号, 经计算可得 和 的距离矩阵分别为det (D 5)=0det (D 6)=−4352det (D 5)=det (D 6)G 5G 6经计算可得, , .因 , 由定理3可以判定 和 不同构.d s (D 5)=d s (D 6)=[304020]r (D 5)=因 , 但 9 期王卓等: 简单无向图的同构判定方法1885r (D 6)G 5G 6, 故由推论2或定理5亦可判定 和 不同构.G 7G 8G 7G 84) 和 均是3正则简单无向连通图(Pe-tersen 图[4, 13]). 按图中顶点标号, 经计算可得 和 的距离矩阵为D 7=D 8G 7∼=G 8因 , 由定理1、定理3或定理5均可判定 .G 7G 8G 5G6此外, 因图的距离谱不同, 故由定理5可轻松判定 和 与 或 不同构.G 9G 10G 9G 105) 和 均是简单无向连通图, 按图中标号可得 和 的距离矩阵分别为G 1G 2G 3G 4G 5G 6G 7G 8G 9G10822478963124810742135910图 1 例1各对应图Fig. 1 Corresponding figures of Example 11886自 动 化 学 报49 卷det (D 9)=37det (D 10)=−7det (D 9)=det (D 10)det (λI 8−D 9)=det (λI 8−D 10).G 9G 10经计算可得, , . 因, 故 由定理3可以判定 和 不同构.d o (D 9)=[1010101011111111],d o (D 10)=[711111*********],d o (D 9)=d o (D 10)G 9G 10此外, 经计算还可得, . 由推论1或定理5亦可判定 和 不同构.3 结束语图的同构关系是一种等价关系. 图论在自然科学和社会科学的诸多领域中有着广泛的应用, 凡与图的结构相关的分类、聚类、识别与学习等问题均与图的同构判定问题有关. 时至今日, 图的同构判定问题仍然具有重要的理论和应用价值.本文给出了简单无向图距离矩阵的定义, 将基于邻接矩阵的同构判定条件推广到简单无向图距离矩阵. 由简单无向连通图的距离矩阵很容易求得该图的直径(求图的直径是图论中的难题[13])、半径和离心率等[4], 而这些整体性结构参数不可能由邻接矩阵得到. 此外, 距离矩阵是素矩阵而邻接矩阵一般不是素矩阵. 正是利用了这些邻接矩阵所没有的整体结构性质, 本文给出了基于距离矩阵特征多项式的同构判定条件(定理3). 距离矩阵特征多项式不同于邻接矩阵特征多项式, 邻接矩阵特征多项式相等仅是两个简单无向连通图同构的必要条件. 就无向树而言, 随着顶点数趋于无穷大, 几乎没有树可被它的邻接矩阵特征值唯一确定[4]. 为避免特征多项式计算误差对判定结果的影响, 本文率先给出了简单无向连通图距离矩阵列和向量与图的距离谱的定义, 并进一步给出了基于距离矩阵的秩与列和向量的同构判定条件(定理5). 该条件易于验证且不产生计算误差, 故更适合大规模简单无向连通图的同构判定. 定理3和定理5均是充要条件且均具有多项式时间复杂度. 针对无向树的同构判定问题,本文还给出了基于距离谱的判定条件(推论4). 容易理解, 将定理3特别是定理5用于简单无向不连通图的各个连通子图或将推论4用于无向森林的各个无向树, 就可解决任意简单无向不连通图的同构判定问题. 最后, 本文用一些典型例图说明了定理3、定理5、推论4及其他相关结论的使用方法, 其中部分例图(如Wagner 图和Petersen 图)曾被多位学者深入研究或引用过.P P NP 本文的主要创新点和贡献可概括为: 1)给出了简单无向图的同构判定条件, 这些条件均具有多项式时间复杂度, 间接地证明了简单无向图的同构判定问题是 问题; 2) 不同于现有的图上操作算法(搜索−标号−回溯算法), 本文所给的同构判定条件均是数学方程式, 不仅便于分析和应用而且便于计算机编程; 3) 因简单无向图是一大类常见的图且无向树和极大无向外平面图均是简单无向图的真子集,故本文的主要结果是现有工作的一个重要进展. 需要说明的是, 虽然本文在简单无向图的同构判定问题上有较大进展, 但一般(任意)无向或有向图的同构判定是 还是 问题仍然没有得到解决.今后, 我们将针对简单有向强连通图的同构判定问题开展研究, 期望得到一些有理论和实用价值的新结果.ReferencesGrohe M, Schweitzer P. The graph isomorphism problem. Com-munications of the ACM , 2020, 63(11): 128−1341McKay B D, Piperno A. Practical graph isomorphism, Ⅱ. Jour -nal of Symbolic Computation , 2014, 60: 94−1122Rosen K H [Author], Xu Liu-Tong, Yang Juan, Wu Bin [Trans-lator]. Discrete Mathematics and Its Applications . Beijing:China Machine Press, 2016.(Rosen K H [著], 徐六通, 杨娟, 吴斌 [译]. 离散数学及其应用.北京: 机械工业出版社, 2016.)3West D B. Introduction to Graph Theory , 2nd Edition . Pearson Education, Inc., 2018.4Babai L. Graph isomorphism in quasipolynomial time. arXiv preprint arXiv: 1512.03547v2 [cs. Ds], 2016.5Luks E M. Isomorphism of graphs of bounded valance can be tested in polynomial time. Journal of Computer and System Sci-ences , 1982, 25(1): 42−656Beyer T, Jones W, Mitchell S. Linear algorithms for isomorph-ism of maximal outerplanar graphs. Journal of the ACM , 1979,26(4): 603−6107Buss S R. Alogtime algorithms for tree isomorphism, comparis-on, and canonization. In: Proceedings of the 5th Kurt Cödel Col-loquium on Computational Logic and Proof Theory. Berlin, Ger-many: Springer-Verlag, 1997. 18−338Liu G W, Yin Z X, Xu J, Dong Y F. Algorithm of graph iso-morphism with three dimensional DNA graph structures. Pro-gress in Natural Science , 2005, 15(2): 181−1849Liu Chun-Feng, Chang Jin-Cai, Yang Ai-Min, Gong Dian-Xuan,Yan Shao-Hong. Numerical Methods . Beijing: Higher Education Press, 2016.(刘春凤, 常锦才, 杨爱民, 龚佃选, 阎少宏. 数值计算方法. 北京:高等教育出版社, 2016.)10Wang Ming-Hui, Wang Guang-Bin, Zhang Wen. Applied Nu-merical Analysis . Beijing: Chemical Industry Press, 2015.(王明辉, 王广彬, 张闻. 应用数值分析. 北京: 化学工业出版社,2015.)11Wang Chao-Rui. Graph Theory, 2nd Edition . Beijing: Beijing129 期王卓等: 简单无向图的同构判定方法1887。
【图论】度序列可简单图化判断

【图论】度序列可简单图化判断Havel−Hakimi定理学习资料:判断给定度序列是否可简单图化可简单图化:⼀个由⾮负整数组成的有限序列如果是某个⽆向图的序列,则称该序列是可简单图化的。
定理描述:由⾮负整数组成的有限⾮递增序列, S={d1,d2,...,d n} , 当且仅当S1={d2−1,d3−1,...,d d+1−1,d d1+2,...,d n} 也是可图的, 也就是说, 序1列S1也是由⾮负整数组成的有限⾮递增序列。
判定过程:对当前序列S排序, 使其呈递减,若⾸元素为0, 则判断该序列可简单图化, 否则继续下⼀步。
删除序列⾸元素d1 ,并使序列之后的d1个数的值均减 1, 若出现了负数, 则该可判断该序列是不可简单图化, 否则,继续上⼀步。
例题:⼀句话题意: 给n+1 个数,问哪些数满⾜删除它之后所剩下的长度为n的序列可简单图化, 输出这些数的下标。
其中 1≤n≤500 .code://#pragma GCC optimize("-O2")#include<bits/stdc++.h>#define reg registerusing namespace std;typedef long long ll;const int inf=0x3f3f3f3f;const int mod=1e9+7;const int maxn=2e5+5;struct A{int v,id;}a[maxn];int p[maxn],t[maxn],n;bool check(){int x,st=1,l1,l2,r1,r2,cnt;while(p[st]>0){x=p[st];for(int i=st+1;i<=st+x;i++)p[i]--;if(p[st+x]<0)return 0;//归并排序O(n)替换快排O(nlogn)l1=st+1;l2=st+x+1;cnt=0;while(l1<=st+x||l2<=n){if(l1<=st+x&&p[l1]>=p[l2]||l2>n)t[++cnt]=p[l1++];else t[++cnt]=p[l2++];}for(int i=1;i<=cnt;i++)p[st+i]=t[i];st++;// sort(p+st,p+1+n,greater<int>());}return 1;}vector<int>ans;int main(){scanf("%d",&n);for(int i=1,v;i<=n+1;i++){scanf("%d",&a[i].v);a[i].id=i;}sort(a+1,a+1+n+1,[](A a1,A a2)->bool{return a1.v>a2.v;});for(int i=1;i<=n+1;i++){for(int j=1,cnt=0;j<=n+1;j++){if(i==j)continue;p[++cnt]=a[j].v;}if(check())ans.push_back(a[i].id);}sort(ans.begin(),ans.end()); printf("%d\n",ans.size());for(int u:ans)printf("%d\n",u); }Processing math: 100%。
图论基础知识点

基本知识点:一、图的基本定义:平凡图:只有一个顶点无边的图。
非平凡图:其他所有图。
空图:边集合为空的图。
简单图:既没有环也没有重边的图。
复合图:其他所有的图。
同构图:顶点集合之间存在双射(一一对应关系),对应边重数和端点对应相等。
标定图:给图的点和边标上符号。
非标定图:不标号。
非标定图代表一类相互同构的图。
完全图:每两个不同顶点之间都有一条边相连的简单图。
N 个顶点的完全图只有一个,记为n K 。
偶图(二部图):具有二分类(,)X Y 的图,他的点集可以分解为两个(非空)子集X 和Y ,使得每条边的一个端点在X 中,另一个端点在Y 中。
完全偶图 :指具有二分类(,)X Y 的简单偶图,其中X 的每个顶点与Y 的每个顶点相连。
若,X m Y n ==,则这样额完全偶图记为:,m n K 。
k —正则图:设(,)G V E =为简单图,如果对所有的结点v V ∈,有()d v k =,称G 为k —正则图。
完全图和完全偶图,n n K 均是正则图。
图划分:若一个n 阶简单图G 各点的度为i d ,则分正整数k 为n 个部分的划分i d ∑称为是图划分。
子图:边集合和点集合均是原图的子集,且待判定图中的边的重数不超过原图中对应的边的重数。
生成子图:点集合相等,边集合为原图子集的图。
导出子图:由顶点集为原图G 真子集的所有点,及两端点均在该集合中的边的全体组成的子图V ‘。
'[]G V 和G v -。
边导出子图:由原图G 边的真子集,该图中边的断点全体为顶点组成的子图E ‘。
'[]G E 和{}G e -。
图的运算:并,交,差,对称差,联图,积图,合成图,极图路与图的联通性:途径:迹:边互不相同的途径。
路:边和点都互不相同的途径。
连通的:两个顶点之间存在路。
连通图:每一对顶点之间都有一条路。
连通分支:将V 划分为一些等价类12,,...k V V V 。
两个顶点u 和v 是连通的当且仅当他们属于同一个子集i V ,称子图()i G V 为连通分支。
电子科技大学图论及其应用 第1章

例 判断下面两图是否同构。
u1
v1
解 两图不同构。 若两图同构,则两图中唯一的与环关联的两个点u1与v1一定 相对应,而u1的两个邻接点与v1的两个邻接点状况不同,u1 邻接有4度点,而v1没有。 所以,两图不同构。
例 指出4个顶点的非同构的所有简单图。
分析:四个顶点的简单图最少边数为0,最多边数为6,所以 可按边数进行枚举。 解 (a) (b) (c)
四、顶点的度、度序列
设v为G 的顶点,G 中以v为端点的边的条数(环计算两次)称 为点v的度数,简称为点v的度,记为dG (v),简记为d(v)。 相关术语和记号
G : 图G 的顶点的最小度
G :图G 的顶点的最大度
奇点:度数为奇数的顶点 偶点:度数为偶数的顶点 k-正则图: 每个点的度均为k 的简单图 例如,完全图和完全偶图Kn, n 均是正则图。
完全偶图是指具有二分类(X, Y )的简单偶图,其中X的 每个顶点与Y 的每个顶点相连,若 |X|=m,|Y|=n,则这 样的偶图记为Km,n。
例
偶图
不是偶图
例
G1
G2
K1, 3
K3, 3
四个图均为偶图
K1, 3, K3, 3为完全偶图
偶图是一种常见数学模型。
例 学校有6位教师将开设6门课程。六位教师的代号分别是 xi (i=1,2,3,4,5,6 ),六门课程代号是yi (i=1,2,3,4,5,6 )。已知教 师x1能够胜任课程y2和y3;教师x2能够胜任课程y4和y5;教师 x3能够胜任课程y2;教师x4能够胜任课程y6和y3;教师x5能够 胜任课程y1和y6;教师x6能够胜任课程y5和y6。请画出老师和 课程之间的状态图。 解
dG (v) dG (v) n 1 。
图论基础知识汇总(适合建模)

图与网络模型及方法§1 概论图论起源于18世纪。
第一篇图论论文是瑞士数学家欧拉于1736 年发表的“哥尼斯堡的七座桥”。
1847年,克希霍夫为了给出电网络方程而引进了“树”的概念。
1857年,凯莱在计数烷22 n n H C 的同分异构物时,也发现了“树”。
哈密尔顿于1859年提出“周游世界”游戏,用图论的术语,就是如何找出一个连通图中的生成圈,近几十年来,由于计算机技术和科学的飞速发展,大大地促进了图论研究和应用,图论的理论和方法已经渗透到物理、化学、通讯科学、建筑学、生物遗传学、心理学、经济学、社会学等学科中。
图论中所谓的“图”是指某类具体事物和这些事物之间的联系。
如果我们用点表示这些具体事物,用连接两点的线段(直的或曲的)表示两个事物的特定的联系,就得到了描述这个“图”的几何形象。
图论为任何一个包含了一种二元关系的离散系统提供了一个数学模型,借助于图论的概念、理论和方法,可以对该模型求解。
哥尼斯堡七桥问题就是一个典型的例子。
在哥尼斯堡有七座桥将普莱格尔河中的两个岛及岛与河岸联结起来问题是要从这四块陆地中的任何一块开始通过每一座桥正好一次,再回到起点。
当然可以通过试验去尝试解决这个问题,但该城居民的任何尝试均未成功。
欧拉为了解决这个问题,采用了建立数学模型的方法。
他将每一块陆地用一个点来代替,将每一座桥用连接相应两点的一条线来代替,从而得到一个有四个“点”,七条“线”的“图”。
问题成为从任一点出发一笔画出七条线再回到起点。
欧拉考察了一般一笔画的结构特点,给出了一笔画的一个判定法则:这个图是连通的,且每个点都与偶数线相关联,将这个判定法则应用于七桥问题,得到了“不可能走通”的结果,不但彻底解决了这个问题,而且开创了图论研究的先河。
图与网络是运筹学(Operations Research )中的一个经典和重要的分支,所研究的问题涉及经济管理、工业工程、交通运输、计算机科学与信息技术、通讯与网络技术等诸多领域。
图论第一章 图的基本概念

0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
图论及其应用
1
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
第一章 图的基本概念
本次课主要内容
图的概念与图论模型
(一)、图论课程简介
(二)、图的定义与图论模型 (三)、图的同构 (四)、完全图、偶图与补图 (五)、顶点的度与图的度序列
0.5
00
1 0.8
0.6 0.4 x 0.2
(四)、完全图、偶图与补图
1、每两个不同的顶点之间都有一条边相连的简单图称为 完全图 .
在同构意义下,n个顶点的完全图只有一个,记为 Kn
K2
K3
K5
容易求出: m(Kn )
1 2
n(n
1)
20
1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
定理:若n阶图G是自补图( G G ),则有:
n 0,1(mod 4)
证明:n阶图G是自补图,则有:
22
H G 1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
m(G)
m(G)
m(Kn )
1 2
n(n
1)
所以:
m(G) 1 n(n 1) 4
由于n是正整数,所以:n 0,1(mod 4)
推论2 正则图的阶数和度数不同时为奇数 。
电子科技大学《图论及其应用》复习总结--第一章图的基本概念

电⼦科技⼤学《图论及其应⽤》复习总结--第⼀章图的基本概念⼀、重要概念图、简单图、图的同构、度序列与图序列、偶图、补图与⾃补图、两个图的联图、两个图的积图1.1 图⼀个图G定义为⼀个有序对(V, E),记为G = (V, E),其中(1)V是⼀个有限⾮空集合,称为顶点集或边集,其元素称为顶点或点;(2)E是由V中的点组成的⽆序点对构成的集合,称为边集,其元素称为边,且同⼀点对在E中可出现多次。
注:图G的顶点数(或阶数)和边数可分别⽤符号n(G) 和m(G)表⽰。
连接两个相同顶点的边的条数,叫做边的重数。
重数⼤于1的边称为重边。
端点重合为⼀点的边称为环。
1.2 简单图⽆环⽆重边的图称为简单图。
(除此之外全部都是复合图)注: 1.顶点集和边集都有限的图称为有限图。
只有⼀个顶点⽽⽆边的图称为平凡图。
其他所有的图都称为⾮平凡图。
边集为空的图称为空图。
2.n阶图:顶点数为n的图,称为n阶图。
3.(n, m) 图:顶点数为n的图,边数为m的图称为(n, m) 图1.3 邻接与关联:顶点u与v相邻接:顶点u与v间有边相连接(u adj v);其中u与v称为该边的两个端点。
注:1.规定⼀个顶点与⾃⾝是邻接的。
2.顶点u与边e相关联:顶点u是边e的端点。
3.边e1与边e2相邻接:边e1与边e2有公共端点。
1.4 图的同构设有两个图G1=(V1,E1)和G2=(V2,E2),若在其顶点集合间存在双射,使得边之间存在如下关系:u1,v1∈V1,u2,v2∈ V2 ,设u1↔u2,v1↔v2,; u1v1∈E1 当且仅当u2v2∈E2,且u1v1与u2v2的重数相同。
称G1与G2同构,记为:G1≌G2注:1、图同构的两个必要条件: (1) 顶点数相同;(2) 边数相同。
2、⾃⼰空间的理解:通过空间的旋转折叠可以进⾏形态转换1.5 完全图、偶图1、在图论中,完全图是⼀个简单图,且任意⼀个顶点都与其它每个顶点有且只有⼀条边相连接。
总结-图论

生成树
设 T 为无向连通图 G 中一棵生成树,e 为 T 的任意一条弦,则 T ∪e 中含 G 中只含一条弦其余边均为树枝的圈,而且不同的弦对应的圈 也不同。
设 T 是连通图 G 的一棵生成树,e 为 T 的树枝,则G 中存在只含树 枝 e,其余边都是弦的割集,且不同的树枝对应的割集也不同。
r 叉完全正则树——树叶的层数均为树高的 r 叉正则树
r 叉完全正则有序树——r 叉完全正则树是有序的的
平面图
G 是可平面图或平面图——如果能将无向图 G 画在平面 上,使得除顶 点处外无边相交。
G 的平面嵌入——画出的无边相交的平面图。 非平面图——无平面嵌入的图。
K5 和 K3,3 都不是平面图。
平面图
(1)设 T 为根树,若将 T 中层数相同的顶点都标定次序,
则称 T 为有序树。 (2)分类:根据根树 T 中每个分支点儿子数以及是否有序 r 叉树——每个分支点至多有 r 个儿子
r 叉有序树——r 叉树是有序的
r 叉正则树——每个分支点恰有 r 个儿子 r 叉正则有序树——r 叉正则树是有序的
T 是 n (n≥2) 阶有向树, (1) T 为根树— T 中有一个顶点入度为 0, 其余顶点的入度均为 1
(2) 树根——入度为 0 的顶点
(3) 树叶——入度为 1,出度为 0 的顶点 (4) 内点——入度为 1,出度不为 0 的顶点 (5) 分支点——树根与内点的总称 (6) 顶点v的层数——从树根到v的通路长度 (7) 树高——T 中层数最大顶点的层数 (8) 根树——平凡树(规定)
d
i 1
n
i
0( mod 2)
图的基本概念
图同构、子图、生成子图、导出子图等。
简单流程图的七个基本符号

简单流程图的基本符号
开始/结束使用此形状表示流程中的第一步和最后一步。
流程此形状表示流程中的一个步骤。
子流程此形状用于表示一组步骤,这些步骤组合起来创建一个在其他位置(通常在同一绘图的另一页上)定义的子流程。
文档此形状表示一个生成文档的步骤。
数据此形状指示信息从外部进入流程或者指示信息离开流程。
此形状还可用来表示材料,有时候称之为“输入/输出”形状。
判定此形状制信息进入流程判定状态,yes流程自动向下个动作继续执行,no流程返回上一步骤重新判定,达到yes后继续执行。
连接线是带有箭头表示的流程走向以及顺序表示。
图论第2章 基本概念

2.2 点和边的关联关系
[定义] 对无向图 G=(V, E) ,若其任一顶点的度都为 r, 则称 G 为一个 r度正则图。
[例] n 阶完全图是 n1 度正则图。 [推论2] 3度正则图中有偶数个顶点。
11
2.3 同构
➢ 图解法具有不唯一性。例:
➢ 一一对应的两个关系,具有相同的代数性质,在 一定意义上可视为同一。
= v0 a1 v1 a2 v2 …… ak vk (k1)
其中 viV ( i = 0.. k ), ajA ( j = 1..k ) 且 aj= <vj1, vj> ( j=0.. k )
v0 和 vk分别称为 的起点和终点(或端点), vj ( j = 1.. k-1 ) 称为 的内顶点。k 称为 的长度。 在简单图中,也可记作 = ( v0 v1 v2 …… vp ) 或
Deg(vi) =|Inc(vi)|
➢ 对有向图 G=(V, A),有
deg(vi) deg(vi)vivFra bibliotekviv
9
2.2 点和边的关联关系
[定理2-1] 对 G=(V, E) ,有:
deg(vi ) 2| E|
viv
➢ 对 G=(V, A) 有同样的结论; [推论1] 图中度为奇数的顶点必为偶数个。
[证明](构造法)
25
2.5 Euler 回路
[有向图的 Euler 回路] 若有向连通图 G=(V, A) 中存在 一条有向闭迹经过 G 的所有弧,则称该闭迹为 G 中的一条 Euler 回路,称该图为 Euler 有向图。
[定理2-6-2] 设连通有向图 G=(V, A), 则下述命题等价: (1) G 是一个 Euler 有向图; (2) G 的每一个顶点的入度等于出度; (3) G 的弧集能被划分成若干有向回路。
小学数学图形的简单描绘

小学数学图形的简单描绘一、基本概念与术语1.平面图形:在平面内,由直线和曲线围成的图形。
2.立体图形:在空间内,由平面图形围成的图形。
3.点:没有长度、宽度和高度的简单几何形态。
4.线段:有两个端点的直线部分,具有长度。
5.射线:有一个端点,无限延伸的直线。
6.直线:无限延伸的线,无端点。
7.角:由两条具有公共端点的射线组成的图形。
8.边:图形的最外部分,由线段或射线组成。
9.顶点:多边形的角上的一点。
10.面:图形所覆盖的平面区域。
二、基本图形的性质与特征1.矩形:四个角都是直角,对边平行且相等。
2.正方形:四条边相等,四个角都是直角。
3.三角形:由三条边和三个角组成。
4.等边三角形:三条边相等,三个角都相等。
5.等腰三角形:两条边相等,两个角都相等。
6.圆形:所有点到圆心的距离都相等。
7.椭圆形:两个焦点到椭圆上任意一点的距离之和相等。
8.线段的长度:用尺子或直尺测量。
9.角度的度量:用量角器度量。
三、图形的画法与表示1.画线段:用尺子和铅笔,两点确定一条线段。
2.画射线:以一个点为端点,向一个方向无限延伸。
3.画直线:无端点,向两个方向无限延伸。
4.画角:以一点为顶点,两条射线为边。
5.画多边形:按照一定的顺序连接多个点。
6.画圆:以一个点为圆心,一个距离为半径,旋转一周。
7.画椭圆:以两个焦点为中心,连接两点成椭圆。
8.图形的大小和形状:用字母和数字表示。
9.图形的位置:用坐标系表示。
四、图形的变换1.平移:将图形沿着某一方向移动一定的距离。
2.旋转:将图形绕着某一点旋转一定的角度。
3.翻转:将图形沿着某一条线翻转。
4.缩放:将图形的尺寸按照一定的比例放大或缩小。
五、图形的对称性1.轴对称:图形关于某条直线对称。
2.中心对称:图形关于某个点对称。
六、图形的组合与分解1.组合:将多个简单的图形组合成一个复杂的图形。
2.分解:将一个复杂的图形分解成多个简单的图形。
七、图形的实际应用1.计算图形的面积和周长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图序列判定的三个简单方法综合理科062班 张芳芳摘要:图的度序列是图论研究中的一个重要课题,至今有很多学者对其性质及应用进行了一系列的研究和探索,而简单图的度序列是图论研究中的一个难点,本文具体介绍了两个图序列的判定和例题应用,并给出了图序列的另外6个判定。
关键词:图;度序列;图序列1.引言图论是一门应用十分广泛,内容非常丰富的数学分支,这里所讨论的图并不是几何学中的图形,而是客观世界中某些具体事物间联系的一个数学抽象。
下面给出图的定义:定义1 用顶点(小圆点)代表事物,用边表示各事物间的二元关系,若所讨论的事物之间有某种二元关系,我们就把相应的顶点连成一条边,这种由顶点及连接这些顶点的边所组成的图就是图论中所研究的图。
定义2 度序列:设图G,其顶点的集合为123(){,,,,}n V G v v v v =⋅⋅⋅,iv 的度为(),1,2,G i d v i n =⋅⋅⋅,则称非负整数序列n ϕ12((),(),,())G G G n d v d v d v =⋅⋅⋅为图G 的度序列;若图G 是简单图,则称之为图序列或可图序列。
2. 图序列问题及判定首先不妨设,i j ∀,若i j <,则()()G i G j d v d v ≤记为条件(1),而一个边数为q 的图G ,其各点的度数的和12nii dq ==∑,显然是偶数。
所以对给定的一个非负整数序列n ϕ12(,,,)n d d d =⋅⋅⋅,若12,n i i d k k =≠∑为自然数,则n ϕ一定不是度序列,从而不是图序列,记为条件(2),且对于一个简单图而言,必有1}1:)(max{-≤≤≤n n i v d i G 记为条件(3),将1()2,nGi i dv k k N ==∈∑记为条件(4)。
本文在以上条件成立的基础上进行讨论,将其称为前提条件。
对于这些条件成立的图的度序列对应的图的一个实现有很多,例如,图1所示的12G ,G 的度序列均是(7,3,1,4,6,5)。
图1 简单图的度序列称为图序列,已知一个序列nϕ12(,,,)n d d d =⋅⋅⋅,若存在简单图G ,使得n ϕ是图G 的度序列,则称n ϕ是可图的,而图G 就是度序列nϕ12(,,,)n d d d =⋅⋅⋅的一个实现。
图序列的讨论或判断要比度序列的讨论困难得多。
下面定理1是Erdos 和Callai 在1960年给出的图序列的一个判别方法: 定理1[1]设12()()()G G G n d v d v d v ≥≥⋅⋅⋅≥,非负整数序列12((),(),,())G G G n d v d v d v ⋅⋅⋅是图序列当且仅当1()nG i i d v =∑是偶数,且对一切整数k ,11k n ≤≤-,有11()(1)min{,()}knG i Gi i i k d v k k k dv ==+≤-+∑∑。
例题应用:例1 证明非负整数序列(7,6,5,4,3,3,2)和(6,6,5,4,3,3,1)不是图序列。
证:1对序列(7,6,5,4,3,3,2),1()30nGi i dv ==∑,为偶数,当1k =时,1()7kG i i d v ==∑,1(1)min(,())6nG i i k k k d v =-+=∑,不满足11()(1)min{,()}knGi Gi i i k dv k k k d v ==+≤-+∑∑,所以序列(7,6,5,4,3,3,2)不是图序列。
2序列(6,6,5,4,3,3,1),1()28nGi i dv ==∑为偶数,当2k =时,1()12kG i i d v ==∑,1(1)min(,())11nG i i k k k d v =-+=∑,不满足11()(1)min{,()}knGi Gi i i k dv k k k dv ==+≤-+∑∑,所以序列(6,6,5,4,3,3,1)不是图序列。
定理2 利用分配——减点法得出的判定条件简单叙述。
以下给出利用分配——减点法得出的判定条件的过程:定义3 对n ϕ进行变换,令:1111''''''12211110,,1,1,,1,1n d n d n d n d n n n n d d d d d d d d d d d ---+-+--==⋅⋅⋅=-=-⋅⋅⋅=-=-记'''''121{,,,,}nn n d d d d ϕ-=⋅⋅⋅,因为'10d =,不妨记为''''121{,,,}n n n d d d ϕ--=⋅⋅⋅,不妨将'''21,,,n n d d d -⋅⋅⋅重新自小到大排列,并记为:1111121{,,,}n n n d d d ϕ--=⋅⋅⋅。
这样由n ϕ变换为11n ϕ-的方法即为分配——减点法;并且我们称11n ϕ-为n ϕ的一个分配——减点子列。
更一般的1i j ϕ+为1ij ϕ+的分配——减点子列。
定义4 准简单图序列正整数序列*n ϕ满足简单图序列的前提条件,对其进行2n -次的分配——减点操作,得到*n ϕ的1次,2次,……3n -次,2n -次分配——减点子列,分别为*11n ϕ-,*22n ϕ-,……*(3)(3)n n n ϕ---,*(2)(2)n n n ϕ---,若,12i i n ∀≤≤-,in i ϕ-满足条件(1),(2),则称这样的正整数序列*n ϕ为准简单图序列。
引理1121{(),(),,(),()}i G G G i G i d v d v d v d v ϕ-∀=⋅⋅⋅,若,1,()G j j j i d v i ∃≤≤≥,则i ϕ一定不是图序列。
引理2 任意正整数序列n ϕ与其分配——减点子列11n ϕ-有相同的简单图化性质,即:n ϕ是图序列的充要条件为11n ϕ-是图序列。
由引理1与引理2易知一个推论:设1in ϕ-是n ϕ的i 次分配——减点子列,则n ϕ是图序列的充要条件为1in ϕ-是图序列。
证明:分别对n ϕ进行1次,2次……1i -次,i 次分配——减点操作,则分别得其1次,2次……1i -次,i 次分配——减点子列11n ϕ-,22n ϕ-,……,11i n i ϕ--+,in i ϕ-。
由引理2知:11n ϕ-是图序列⇔22n ϕ-是图序列⇔33n ϕ-是图序列,……,⇔11i n i ϕ--+是图序列⇔i n iϕ-是图序列,根据等价的传递性知:n ϕ是图序列⇔1in ϕ-是图序列。
设nϕ12(,,,)n d d d =⋅⋅⋅是一正整数序列,且满足条件(3),(4),n ϕ是图序列的充要条件是n ϕ是准简单图序列,且其2n -次的分配——减点子列222212{,}n n n d d ϕ---= 满足:22121n n d d --=≤。
证明:1需证准简单图正整数序列*n ϕ是图序列的充要条件为*n ϕ的其2n -次的分配——减点子列*(2)*(2)22(2)212{,}n n n n n n d d ϕϕ------==满足22121n n d d --=≤。
由引理的推论知:*n ϕ是图序列的充要条件为*n ϕ的分配——减点子列*(2)2n ϕ-是图序列。
而*(2)22212{,}n n n d d ϕ---=满足:22121n n d d --=≤。
若22121n n d d --==,则*(2)2n ϕ-对应着2阶完全图;若22120n n d d --==,则*(2)2n ϕ-对应着2阶空图,显然*(2)2n ϕ-均是图序列。
因此,*n ϕ是图序列。
2 进行定理证明。
n ϕ是准简单图序列,且2n -次的分配——减点子列222212{,}n n n d d ϕ---=满足:22121n n d d --=≤,则由上面的证明可知n ϕ是图序列。
例题应用:任意一正整数序列10{1,2,3,4,5,6,6,7,8,8}ϕ=,判断其是否为图序列。
解:110ϕ满足图序列的前提条件,2 对其进行8次分配——减点操作,其各次分配——减点子列如下:19{2,3,4,5,6,6,7,7,8}ϕ= 28{3,4,5,6,6,6,7,7}ϕ= 37{4,5,5,6,6,6,6}ϕ= 46{5,5,5,5,5,5}ϕ=55{4,4,4,4,4}ϕ=64{3,3,3,3}ϕ=73{2,2,2}ϕ=82{1,1}ϕ=3 由以上操作可知:10ϕ是准简单图序列且82{1,1}ϕ=满足判定的条件,所以10ϕ是图序列。
如下图为10ϕ对应的一个简单图图2对定理2有一个更简单直接的判定方法即: 定理3 非负整数序列12((),(),,())G G G n d v d v d v ⋅⋅⋅,且1()nGi i dv =∑是偶数,121()()()G G G n n d v d v d v -≥≥≥⋅⋅⋅≥,它是图序列的充要条件为231(()1,()1,()1,())G G G n G n d v d v d v d v ---⋅⋅⋅-是图序列。
例题应用:任然用方法一中的例题的第二个序列,对序列(6,6,5,4,3,3,1),231(()1,()1,()1,())(5,4,3,2,2,1)G G G n G n d v d v d v d v ---⋅⋅⋅-=,对原序列有1()28nGi i dv ==∑,为偶数,且121()()()G G G n n d v d v d v -≥≥≥⋅⋅⋅≥,新产生的序列(5,4,3,2,2,1),对其求和为17,是奇数,不是图序列,所以序列(6,6,5,4,3,3,1)不是图序列。
下面给出图序列的另外几个判定: 1) 基本定义:(1) 设12(,,,)n x x x x =⋅⋅⋅,12(,,,)n y y y y =⋅⋅⋅是两个非负整数序列,若x 与y经重排为12n x x x ≥≥⋅⋅⋅≥与12n y y y ≥≥⋅⋅⋅≥,有11,1,2,3,,k ki i i i x y k n ==≤=⋅⋅⋅∑∑,其中当k n=时取等号,则称x优超y,记作x y。
同理,x y表示11,1,2,3,,kki ii i x y k n ==≥=⋅⋅⋅∑∑,当k n =时等号成立。
(2) 对非负整数序列12(,,,)n x x x x =⋅⋅⋅,记*{:1}j i x i i n x j =≤≤≥且,{:111}{:1}j i i x i i j x j i j i n x j -=≤≤-≥-++≤≤≥且且,1j j x x -=+当1j m ≤≤时,且j j x x -=当1m j n +≤≤,其中max{:1}i m i i n x i =≤≤≥且,则****12(,,,)nx x x x =⋅⋅⋅与12(,,,)n x x x x ----=⋅⋅⋅分别是x 的共轭序列与约束共轭序列。
