大学物理学第版修订版北京邮电大学出版社 下册 第十章 习题答案
大学物理学下册答案(北邮大赵近芳)

v E0′
=
ρ 3ε 0
OO '
题 8-13 图(a)
题 8-13 图(b)
(3)设空腔任一点 P 相对 O′ 的位矢为 rv′ ,相对 O 点位矢为 rv (如题 8-13(b)
图)
则
v E PO
=
ρrv 3ε 0
,
v E PO′
=
− ρrv′ 3ε 0
,
∴
v EP
=
v E PO
+
v E PO′
=
通过圆平面的电通量.(α = arctan R ) x
∫ 解: (1)由高斯定理
Ev
⋅
v dS
=
q
s
ε0
立方体六个面,当 q 在立方体中心时,每个面上电通量相等
∴
各面电通量 Φ e
=
q 6ε 0
.
(2)电荷在顶点时,将立方体延伸为边长 2a 的立方体,使 q 处于边长 2a 的立
方体中心,则边长 2a 的正方形上电通量 Φ e
0
∑ r = 8 cm 时,
q = p 4π (r3 3
− r内3 )
∴
( ) E
=
ρ
4π 3
r 3 − r内2
≈ 3.48 ×10 4 N ⋅ C −1 , 方向沿半径向外.
4πε 0r 2
∑ r = 12 cm 时,
q
=
ρ
4π 3
(r外3
−
r内3)
( ) ∴
E
=
ρ
4π 3
r外 3
− r内3
≈ 4.10 ×104
+
4d
2 2
以 λ = 5.0 ×10−9 C ⋅ cm −1 , l = 15 cm , d2 = 5 cm 代入得
大学物理课后习题答案北京邮电大学出版社

习题十三13-1 衍射的本质是什么?衍射和干涉有什么联系和区别?答:波的衍射现象是波在传播过程中经过障碍物边缘或孔隙时所发生的展衍现象.其实质是由被障碍物或孔隙的边缘限制的波阵面上各点发出的无数子波相互叠加而产生.而干涉则是由同频率、同方向及位相差恒定的两列波的叠加形成.13-2 在夫琅禾费单缝衍射实验中,如果把单缝沿透镜光轴方向平移时,衍射图样是否会 跟着移动?若把单缝沿垂直于光轴方向平移时,衍射图样是否会跟着移动?答:把单缝沿透镜光轴方向平移时,衍射图样不会跟着移动.单缝沿垂直于光轴方向平移时,衍射图样不会跟着移动.13-3 什么叫半波带?单缝衍射中怎样划分半波带?对应于单缝衍射第3级明条纹和第4级暗 条纹,单缝处波面各可分成几个半波带?答:半波带由单缝A 、B 首尾两点向ϕ方向发出的衍射线的光程差用2λ来划分.对应于第3级明纹和第4级暗纹,单缝处波面可分成7个和8个半波带. ∵由272)132(2)12(sin λλλϕ⨯=+⨯=+=k a13-4 在单缝衍射中,为什么衍射角ϕ愈大(级数愈大)的那些明条纹的亮度愈小?答:因为衍射角ϕ愈大则ϕsin a 值愈大,分成的半波带数愈多,每个半波带透过的光通量就愈小,而明条纹的亮度是由一个半波带的光能量决定的,所以亮度减小.13-5 若把单缝衍射实验装置全部浸入水中时,衍射图样将发生怎样的变化?如果此时用公式),2,1(2)12(sin Λ=+±=k k a λϕ来测定光的波长,问测出的波长是光在空气中的还是在水中的波长?解:当全部装置浸入水中时,由于水中波长变短,对应='='λϕk a sin n k λ,而空气中为λϕk a =sin ,∴ϕϕ'=sin sin n ,即ϕϕ'=n ,水中同级衍射角变小,条纹变密.如用)12(sin +±=k a ϕ2λ),2,1(⋅⋅⋅=k 来测光的波长,则应是光在水中的波长.(因ϕsin a 只代表光在水中的波程差).13-6 在单缝夫琅禾费衍射中,改变下列条件,衍射条纹有何变化?(1)缝宽变窄;(2)入 射光波长变长;(3)入射平行光由正入射变为斜入射.解:(1)缝宽变窄,由λϕk a =sin 知,衍射角ϕ变大,条纹变稀;(2)λ变大,保持a ,k 不变,则衍射角ϕ亦变大,条纹变稀;(3)由正入射变为斜入射时,因正入射时λϕk a =sin ;斜入射时,λθϕk a '=-)sin (sin ,保持a ,λ不变,则应有k k >'或k k <'.即原来的k 级条纹现为k '级.13-7 单缝衍射暗条纹条件与双缝干涉明条纹的条件在形式上类似,两者是否矛盾?怎样说明?答:不矛盾.单缝衍射暗纹条件为k k a 2sin ==λϕ2λ,是用半波带法分析(子波叠加问题).相邻两半波带上对应点向ϕ方向发出的光波在屏上会聚点一一相消,而半波带为偶数,故形成暗纹;而双缝干涉明纹条件为λθk d =sin ,描述的是两路相干波叠加问题,其波程差为波长的整数倍,相干加强为明纹.13-8 光栅衍射与单缝衍射有何区别?为何光栅衍射的明条纹特别明亮而暗区很宽?答:光栅衍射是多光束干涉和单缝衍射的总效果.其明条纹主要取决于多光束干涉.光强与缝数2N 成正比,所以明纹很亮;又因为在相邻明纹间有)1(-N 个暗纹,而一般很大,故实际上在两相邻明纹间形成一片黑暗背景.13-9 试指出当衍射光栅的光栅常数为下述三种情况时,哪些级次的衍射明条纹缺级?(1) a+b=2a;(2)a+b=3a;(3)a+b=4a.解:由光栅明纹条件和单缝衍射暗纹条件同时满足时,出现缺级.即 可知,当k a b a k '+=时明纹缺级.(1)a b a 2=+时,⋅⋅⋅=,6,4,2k 偶数级缺级;(2)a b a 3=+时,⋅⋅⋅=,9,6,3k 级次缺级;(3)a b a 4=+,⋅⋅⋅=,12,8,4k 级次缺级.13-10 若以白光垂直入射光栅,不同波长的光将会有不同的衍射角.问(1)零级明条纹能 否分开不同波长的光?(2)在可见光中哪种颜色的光衍射角最大?不同波长的光分开程度与什 么因素有关?解:(1)零级明纹不会分开不同波长的光.因为各种波长的光在零级明纹处均各自相干加强.(2)可见光中红光的衍射角最大,因为由λϕk b a =+sin )(,对同一k 值,衍射角λϕ∞. 13-11 一单色平行光垂直照射一单缝,若其第三级明条纹位置正好与6000οA 的单色平行光的第二级明条纹位置重合,求前一种单色光的波长. 解:单缝衍射的明纹公式为当6000=λoA 时,2=k x λλ=时,3=k重合时ϕ角相同,所以有得 4286600075=⨯=x λoA 13-12 单缝宽0.10mm ,透镜焦距为50cm ,用5000=λoA 的绿光垂直照射单缝.求:(1)位于透镜焦平面处的屏幕上中央明条纹的宽度和半角宽度各为多少?(2)若把此装置浸入水中(n=1.33),中央明条纹的半角宽度又为多少?解:中央明纹的宽度为f na x λ2=∆ 半角宽度为na λθ1sin -=(1)空气中,1=n ,所以(2)浸入水中,33.1=n ,所以有13-13 用橙黄色的平行光垂直照射一宽为a=0.60mm 的单缝,缝后凸透镜的焦距f=40.0cm ,观察屏幕上形成的衍射条纹.若屏上离中央明条纹中心1.40mm 处的P 点为一明条纹;求:(1)入射光的波长;(2)P 点处条纹的级数;(3)从P 点看,对该光波而言,狭缝处的波面可分成几个半波带?解:(1)由于P 点是明纹,故有2)12(sin λϕ+=k a ,⋅⋅⋅=3,2,1k 由ϕϕsin tan 105.34004.13≈=⨯==-f x 故3105.3126.0212sin 2-⨯⨯+⨯=+=k k a ϕλ 当 3=k ,得60003=λoA 4=k ,得47004=λoA (2)若60003=λoA ,则P 点是第3级明纹;若47004=λoA ,则P 点是第4级明纹. (3)由2)12(sin λϕ+=k a 可知,当3=k 时,单缝处的波面可分成712=+k 个半波带;当4=k 时,单缝处的波面可分成912=+k 个半波带.13-14 用5900=λoA 的钠黄光垂直入射到每毫米有500条刻痕的光栅上,问最多能看到第几级明条纹? 解:5001=+b a mm 3100.2-⨯=mm 4100.2-⨯=o A由λϕk b a =+sin )(知,最多见到的条纹级数m ax k 对应的2πϕ=, 所以有39.35900100.24max ≈⨯=+=λba k ,即实际见到的最高级次为3max =k .13-15 波长为5000oA 的平行单色光垂直照射到每毫米有200条刻痕的光栅上,光栅后的透镜焦距为60cm . 求:(1)屏幕上中央明条纹与第一级明条纹的间距;(2)当光线与光栅法线成 30°斜入射时,中央明条纹的位移为多少? 解:3100.52001-⨯==+b a mm 6100.5-⨯m(1)由光栅衍射明纹公式λϕk b a =+sin )(,因1=k ,又f x ==ϕϕtan sin所以有λ=+f x b a 1)(即 62101100.51060105000---⨯⨯⨯⨯=+=b a fx λ (2)对应中央明纹,有0=k正入射时,0sin )(=+ϕb a ,所以0sin =≈ϕϕ斜入射时,0)sin )(sin (=±+θϕb a ,即0sin sin =±θϕ因︒=30θ,∴21tan sin ±==≈f x ϕϕ故22103010602121--⨯=⨯⨯==f x m 30=cm这就是中央明条纹的位移值.13-16 波长6000=λo A 的单色光垂直入射到一光栅上,第二、第三级明条纹分别出现在20.0sin =ϕ与30.0sin =ϕ处,第四级缺级.求:(1)光栅常数;(2)光栅上狭缝的宽度;(3)在90°>ϕ>-90°范围内,实际呈现的全部级数.解:(1)由λϕk b a =+sin )(式对应于20.0sin 1=ϕ与30.0sin 2=ϕ处满足:得 6100.6-⨯=+b a m(2)因第四级缺级,故此须同时满足解得 k k b a a '⨯='+=-6105.14取1='k ,得光栅狭缝的最小宽度为6105.1-⨯m (3)由λϕk b a =+sin )( 当2πϕ=,对应max k k =∴ 10106000100.6106max =⨯⨯=+=--λba k因4±,8±缺级,所以在︒︒<<-9090ϕ范围内实际呈现的全部级数为9,7,6,5,3,2,1,0±±±±±±±=k 共15条明条纹(10±=k 在︒±=90k 处看不到).13-17 一双缝,两缝间距为0.1mm ,每缝宽为0.02mm ,用波长为4800oA 的平行单色光垂直入射双缝,双缝后放一焦距为50cm 的透镜.试求:(1)透镜焦平面上单缝衍射中央明条纹的宽度;(2)单缝衍射的中央明条纹包迹内有多少条双缝衍射明条纹?解:(1)中央明纹宽度为(2)由缺级条件知即⋅⋅⋅=,15,10,5k 缺级.中央明纹的边缘对应1='k ,所以单缝衍射的中央明纹包迹内有4,3,2,1,0±±±±=k 共9条双缝衍射明条纹.13-18 在夫琅禾费圆孔衍射中,设圆孔半径为0.10mm ,透镜焦距为50cm ,所用单色光波长为5000oA ,求在透镜焦平面处屏幕上呈现的爱里斑半径. 解:由爱里斑的半角宽度∴ 爱里斑半径5.1105.30500tan 24=⨯⨯=≈=-θθf f d mm 13-19 已知天空中两颗星相对于一望远镜的角距离为4.84×10-6rad ,它们都发出波长为5500oA 的光,试问望远镜的口径至少要多大,才能分辨出这两颗星? 解:由最小分辨角公式∴86.131084.4105.522.122.165=⨯⨯⨯==--θλD cm 13-20 已知入射的X 射线束含有从0.95~1.30oA 范围内的各种波长,晶体的晶格常数为2.75oA ,当X 射线以45°角入射到晶体时,问对哪些波长的X 射线能产生强反射? 解:由布喇格公式 λϕk d =sin 2 得k d ϕλsin 2=时满足干涉相长当1=k 时, 89.345sin 75.22=⨯⨯=︒λoA 2=k 时,91.1245sin 75.22=⨯⨯=︒λo A3=k 时,30.1389.3==λo A4=k 时, 97.0489.3==λo A故只有30.13=λo A 和97.04=λo A 的X 射线能产生强反射.。
大学物理课后习题答案(北邮第三版)下

大学物理习题及解答习题八8-1 电量都是q 的三个点电荷,分别放在正三角形的三个顶点.试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系? 解: 如题8-1图示(1) 以A 处点电荷为研究对象,由力平衡知:q '为负电荷20220)33(π4130cos π412a q q a q '=︒εε解得q q 33-='(2)与三角形边长无关.题8-1图 题8-2图8-2 两小球的质量都是m ,都用长为l 的细绳挂在同一点,它们带有相同电量,静止时两线夹角为2θ,如题8-2图所示.设小球的半径和线的质量都可以忽略不计,求每个小球所带的电量.解: 如题8-2图示⎪⎩⎪⎨⎧===220)sin 2(π41sin cos θεθθl q F T mg T e解得θπεθtan 4sin 20mg l q =8-3 根据点电荷场强公式204r qE πε=,当被考察的场点距源点电荷很近(r →0)时,则场强→∞,这是没有物理意义的,对此应如何理解?解:20π4r r q E ϖϖε=仅对点电荷成立,当0→r 时,带电体不能再视为点电荷,再用上式求场强是错误的,实际带电体有一定形状大小,考虑电荷在带电体上的分布求出的场强不会是无限大.8-4 在真空中有A ,B 两平行板,相对距离为d ,板面积为S ,其带电量分别为+q 和-q .则这两板之间有相互作用力f ,有人说f =2024d q πε,又有人说,因为f =qE ,S qE 0ε=,所以f=Sq2ε.试问这两种说法对吗?为什么?f到底应等于多少?解: 题中的两种说法均不对.第一种说法中把两带电板视为点电荷是不对的,第二种说法把合场强SqEε=看成是一个带电板在另一带电板处的场强也是不对的.正确解答应为一个板的电场为SqE2ε=,另一板受它的作用力SqSqqf222εε==,这是两板间相互作用的电场力.8-5 一电偶极子的电矩为l qpϖϖ=,场点到偶极子中心O点的距离为r,矢量rϖ与lϖ的夹角为θ,(见题8-5图),且lr>>.试证P点的场强E在r方向上的分量r E和垂直于r的分量θE 分别为rE=32cosrpπεθ, θE=34sinrpπεθ证: 如题8-5所示,将pϖ分解为与rϖ平行的分量θsinp和垂直于rϖ的分量θsinp.∵lr>>∴场点P在r方向场强分量3π2cosrpErεθ=垂直于r方向,即θ方向场强分量30π4sinrpEεθ=题8-5图题8-6图8-6 长l=15.0cm的直导线AB上均匀地分布着线密度λ=5.0x10-9C·m-1的正电荷.试求:(1)在导线的延长线上与导线B端相距1a=5.0cm处P点的场强;(2)在导线的垂直平分线上与导线中点相距2d=5.0cm 处Q点的场强.解:如题8-6图所示(1)在带电直线上取线元x d,其上电量q d在P点产生场强为2)(dπ41dxaxEP-=λε222)(dπ4dxaxEEllPP-==⎰⎰-ελ]2121[π4lala+--=ελ)4(π220l a l-=ελ用15=l cm ,9100.5-⨯=λ1m C -⋅, 5.12=a cm 代入得21074.6⨯=P E 1C N -⋅ 方向水平向右(2)同理2220d d π41d +=x xE Q λε 方向如题8-6图所示 由于对称性⎰=lQx E 0d ,即QE ϖ只有y 分量,∵22222220d d d d π41d ++=x x x E Qyλε22π4d d ελ⎰==lQyQy E E ⎰-+2223222)d (d ll x x2220d 4π2+=l lελ以9100.5-⨯=λ1cm C -⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Qy Q E E 1C N -⋅,方向沿y 轴正向8-7 一个半径为R 的均匀带电半圆环,电荷线密度为λ,求环心处O 点的场强.解: 如8-7图在圆上取ϕRd dl =题8-7图ϕλλd d d R l q ==,它在O 点产生场强大小为20π4d d R R E εϕλ=方向沿半径向外则 ϕϕελϕd sin π4sin d d 0R E E x ==ϕϕελϕπd cos π4)cos(d d 0R E E y -=-=积分R R E x 000π2d sin π4ελϕϕελπ==⎰0d cos π400=-=⎰ϕϕελπR E y∴REExπ2ελ==,方向沿x轴正向.8-8 均匀带电的细线弯成正方形,边长为l,总电量为q.(1)求这正方形轴线上离中心为r 处的场强E;(2)证明:在lr>>处,它相当于点电荷q产生的场强E.解: 如8-8图示,正方形一条边上电荷4q在P点产生物强P Eϖd方向如图,大小为()4π4coscosd2221lrEP+-=εθθλ∵22cos221lrl+=θ12coscosθθ-=∴24π4d2222lrllrEP++=ελPEϖd在垂直于平面上的分量βcosddPEE=⊥∴424π4d222222lrrlrlrlE+++=⊥ελ题8-8图由于对称性,P点场强沿OP方向,大小为2)4(π44d42222lrlrlrEEP++=⨯=⊥ελ∵lq4=λ∴2)4(π42222lrlrqrEP++=ε方向沿OP8-9 (1)点电荷q位于一边长为a的立方体中心,试求在该点电荷电场中穿过立方体的一个面的电通量;(2)如果该场源点电荷移动到该立方体的一个顶点上,这时穿过立方体各面的电通量是多少?*(3)如题8-9(3)图所示,在点电荷q的电场中取半径为R的圆平面.q在该平面轴线上的A 点处,求:通过圆平面的电通量.(x Rarctan=α)解: (1)由高斯定理0d εq S E s⎰=⋅ϖϖ 立方体六个面,当q 在立方体中心时,每个面上电通量相等∴ 各面电通量06εqe =Φ.(2)电荷在顶点时,将立方体延伸为边长a 2的立方体,使q 处于边长a 2的立方体中心,则边长a 2的正方形上电通量06εq e =Φ对于边长a 的正方形,如果它不包含q 所在的顶点,则024εqe =Φ,如果它包含q 所在顶点则0=Φe .如题8-9(a)图所示.题8-9(3)图题8-9(a)图 题8-9(b)图 题8-9(c)图(3)∵通过半径为R 的圆平面的电通量等于通过半径为22x R +的球冠面的电通量,球冠面积*]1)[(π22222xR x x R S +-+=∴)(π42200x R Sq +=Φε02εq=[221x R x +-]*关于球冠面积的计算:见题8-9(c)图ααα⎰⋅=0d sin π2r r S ααα⎰⋅=02d sin π2r)cos 1(π22α-=r8-10 均匀带电球壳内半径6cm ,外半径10cm ,电荷体密度为2×510-C ·m -3求距球心5cm ,8cm ,12cm 各点的场强.解: 高斯定理0d ε∑⎰=⋅q S E sϖϖ,02π4ε∑=qr E当5=r cm 时,0=∑q ,=E ϖ8=r cm 时,∑q 3π4p=3(r )3内r -∴()2023π43π4r r r E ερ内-=41048.3⨯≈1C N -⋅, 方向沿半径向外. 12=r cm 时,3π4∑=ρq -3(外r )内3r∴ ()420331010.4π43π4⨯≈-=r r r E ερ内外 1C N -⋅ 沿半径向外.8-11 半径为1R 和2R (2R >1R )的两无限长同轴圆柱面,单位长度上分别带有电量λ和-λ,试求:(1)r <1R ;(2) 1R <r <2R ;(3) r >2R 处各点的场强.解: 高斯定理0d ε∑⎰=⋅q S E sϖϖ取同轴圆柱形高斯面,侧面积rl S π2=则rlE S E Sπ2d =⋅⎰ϖϖ对(1) 1R r < 0,0==∑E q(2) 21R r R <<λl q =∑∴r E 0π2ελ=沿径向向外(3) 2R r > 0=∑q ∴ 0=E题8-12图8-12 两个无限大的平行平面都均匀带电,电荷的面密度分别为1σ和2σ,试求空间各处场强.解: 如题8-12图示,两带电平面均匀带电,电荷面密度分别为1σ与2σ,两面间, nE ϖϖ)(21210σσε-= 1σ面外, nE ϖϖ)(21210σσε+-=2σ面外, nE ϖϖ)(21210σσε+=n ϖ:垂直于两平面由1σ面指为2σ面.8-13 半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为r <R 的小球体,如题8-13图所示.试求:两球心O 与O '点的场强,并证明小球空腔内的电场是均匀的.解: 将此带电体看作带正电ρ的均匀球与带电ρ-的均匀小球的组合,见题8-13图(a).(1) ρ+球在O 点产生电场010=E ϖ,ρ- 球在O 点产生电场'd π4π3430320OO r E ερ=ϖ∴ O 点电场'd 33030OO r E ερ=ϖ;(2) ρ+在O '产生电场'd π4d 3430301OO E ερπ='ϖρ-球在O '产生电场002='E ϖ∴ O ' 点电场003ερ='E ϖ'OO题8-13图(a) 题8-13图(b)(3)设空腔任一点P 相对O '的位矢为r ϖ',相对O 点位矢为r ϖ(如题8-13(b)图)则03ερrE PO ϖϖ=,03ερr E O P '-='ϖϖ,∴0003'3)(3ερερερd OO r r E E E O P PO P ϖϖϖϖϖϖ=='-=+=' ∴腔内场强是均匀的.8-14 一电偶极子由q =1.0×10-6C 的两个异号点电荷组成,两电荷距离d=0.2cm ,把这电偶极子放在1.0×105N ·C -1的外电场中,求外电场作用于电偶极子上的最大力矩.解: ∵ 电偶极子p ϖ在外场E ϖ中受力矩E p M ϖϖϖ⨯= ∴ qlE pE M ==max代入数字 4536max 100.2100.1102100.1---⨯=⨯⨯⨯⨯⨯=M m N ⋅8-15 两点电荷1q =1.5×10-8C ,2q =3.0×10-8C ,相距1r =42cm ,要把它们之间的距离变为2r =25cm ,需作多少功?解:⎰⎰==⋅=2221212021π4π4d d r r r r q q r r q q r F A εεϖϖ)11(21r r - 61055.6-⨯-=J外力需作的功 61055.6-⨯-=-='A A J题8-16图8-16 如题8-16图所示,在A ,B 两点处放有电量分别为+q ,-q 的点电荷,AB 间距离为2R ,现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点,求移动过程中电场力作的功.解: 如题8-16图示0π41ε=O U 0)(=-R qR q 0π41ε=O U )3(R q R q -R q 0π6ε-=∴R qq U U q A o C O 00π6)(ε=-=8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中心O 点处的场强和电势.解: (1)由于电荷均匀分布与对称性,AB 和CD 段电荷在O 点产生的场强互相抵消,取θd d R l =则θλd d R q =产生O 点E ϖd 如图,由于对称性,O 点场强沿y 轴负方向题8-17图θεθλππcos π4d d 2220⎰⎰-==R R E E y R 0π4ελ=[)2sin(π-2sinπ-] R 0π2ελ-=(2) AB 电荷在O 点产生电势,以0=∞U⎰⎰===AB 200012ln π4π4d π4d R R x x x x U ελελελ同理CD 产生 2ln π402ελ=U半圆环产生0034π4πελελ==R R U∴0032142ln π2ελελ+=++=U U U U O8-18 一电子绕一带均匀电荷的长直导线以2×104m ·s -1的匀速率作圆周运动.求带电直线上的线电荷密度.(电子质量0m =9.1×10-31kg ,电子电量e =1.60×10-19C)解: 设均匀带电直线电荷密度为λ,在电子轨道处场强r E 0π2ελ=电子受力大小r e eE F e 0π2ελ==∴ r v mre 20π2=ελ 得1320105.12π2-⨯==e mv ελ1m C -⋅ 8-19 空气可以承受的场强的最大值为E =30kV ·cm -1,超过这个数值时空气要发生火花放电.今有一高压平行板电容器,极板间距离为d =0.5cm ,求此电容器可承受的最高电压.解: 平行板电容器内部近似为均匀电场∴ 4105.1d ⨯==E U V8-20 根据场强E ϖ与电势U 的关系U E -∇=ϖ,求下列电场的场强:(1)点电荷q 的电场;(2)总电量为q ,半径为R 的均匀带电圆环轴上一点;*(3)偶极子ql p =的l r >>处(见题8-20图).解: (1)点电荷r qU 0π4ε=题 8-20 图∴ 0200π4r r q r r U E ϖϖϖε=∂∂-= 0r ϖ为r 方向单位矢量.(2)总电量q ,半径为R 的均匀带电圆环轴上一点电势220π4x R qU +=ε∴ ()ix R qx i x U E ϖϖϖ2/3220π4+=∂∂-=ε(3)偶极子l q p ϖϖ=在l r >>处的一点电势200π4cos ])cos 21(1)cos 2(1[π4r ql l l r q U εθθθε=+--=∴ 30π2cos r p r U E r εθ=∂∂-=30π4sin 1r p U r E εθθθ=∂∂-=8-21 证明:对于两个无限大的平行平面带电导体板(题8-21图)来说,(1)相向的两面上,电荷的面密度总是大小相等而符号相反;(2)相背的两面上,电荷的面密度总是大小相等而符号相同.证: 如题8-21图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ,2σ,3σ,4σ题8-21图(1)则取与平面垂直且底面分别在A 、B 内部的闭合柱面为高斯面时,有)(d 32=∆+=⋅⎰S S E sσσϖϖ∴ +2σ03=σ 说明相向两面上电荷面密度大小相等、符号相反;(2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即0222204030201=---εσεσεσεσ又∵ +2σ03=σ∴ 1σ4σ=说明相背两面上电荷面密度总是大小相等,符号相同.8-22 三个平行金属板A ,B 和C 的面积都是200cm 2,A 和B 相距4.0mm ,A 与C 相距2.0mm .B ,C 都接地,如题8-22图所示.如果使A 板带正电3.0×10-7C ,略去边缘效应,问B 板和C 板上的感应电荷各是多少?以地的电势为零,则A 板的电势是多少?解: 如题8-22图示,令A 板左侧面电荷面密度为1σ,右侧面电荷面密度为2σ题8-22图(1)∵ AB AC U U =,即∴AB AB AC AC E E d d =∴ 2d d 21===AC ABAB AC E E σσ且 1σ+2σS q A=得,32S q A=σ S q A 321=σ 而7110232-⨯-=-=-=A C q S q σC C10172-⨯-=-=S q B σ(2)301103.2d d ⨯===AC AC AC A E U εσV 8-23 两个半径分别为1R 和2R (1R <2R )的同心薄金属球壳,现给内球壳带电+q ,试计算:(1)外球壳上的电荷分布及电势大小;(2)先把外球壳接地,然后断开接地线重新绝缘,此时外球壳的电荷分布及电势; *(3)再使内球壳接地,此时内球壳上的电荷以及外球壳上的电势的改变量.解: (1)内球带电q +;球壳内表面带电则为q -,外表面带电为q +,且均匀分布,其电势题8-23图⎰⎰∞∞==⋅=22020π4π4d d R R R qr r q r E U εεϖϖ(2)外壳接地时,外表面电荷q +入地,外表面不带电,内表面电荷仍为q -.所以球壳电势由内球q +与内表面q -产生:π4π42020=-=R qR qU εε(3)设此时内球壳带电量为q ';则外壳内表面带电量为q '-,外壳外表面带电量为+-q q '(电荷守恒),此时内球壳电势为零,且π4'π4'π4'202010=+-+-=R q q R q R q U A εεε得 q R R q 21='外球壳上电势()22021202020π4π4'π4'π4'R qR R R q q R q R q U B εεεε-=+-+-=8-24 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量.解: 如题8-24图所示,设金属球感应电荷为q ',则球接地时电势0=O U8-24图由电势叠加原理有:=O U 03π4π4'00=+R qR q εε得 -='q 3q8-25 有三个大小相同的金属小球,小球1,2带有等量同号电荷,相距甚远,其间的库仑力为0F.试求:(1)用带绝缘柄的不带电小球3先后分别接触1,2后移去,小球1,2之间的库仑力; (2)小球3依次交替接触小球1,2很多次后移去,小球1,2之间的库仑力.解: 由题意知2020π4r q F ε=(1)小球3接触小球1后,小球3和小球1均带电2q q =',小球3再与小球2接触后,小球2与小球3均带电qq 43=''∴ 此时小球1与小球2间相互作用力0220183π483π4"'2F rqr q q F =-=εε (2)小球3依次交替接触小球1、2很多次后,每个小球带电量均为32q.∴ 小球1、2间的作用力0294π432322F r qq F ==ε *8-26 如题8-26图所示,一平行板电容器两极板面积都是S ,相距为d ,分别维持电势A U =U ,B U =0不变.现把一块带有电量q 的导体薄片平行地放在两极板正中间,片的面积也是S ,片的厚度略去不计.求导体薄片的电势.解: 依次设A ,C ,B 从上到下的6个表面的面电荷密度分别为1σ,2σ,3σ,4σ,5σ,6σ如图所示.由静电平衡条件,电荷守恒定律及维持U U AB =可得以下6个方程题8-26图⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++++==+=+-==+=+===+6543215432065430021001σσσσσσσσσσεσσσσεσσd US q S qdU U C S S q B A解得S q261==σσ S qd U 2032-=-=εσσ S qd U 2054+=-=εσσ所以CB 间电场S q d U E 00422εεσ+== )2d (212d 02S q U E U U CB C ε+===注意:因为C 片带电,所以2U U C ≠,若C 片不带电,显然2UU C =8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳,介质相对介电常数为r ε,金属球带电Q .试求: (1)电介质内、外的场强; (2)电介质层内、外的电势; (3)金属球的电势. 解: 利用有介质时的高斯定理∑⎰=⋅qS D Sϖϖd(1)介质内)(21R r R <<场强303π4,π4r rQ E r r Q D r εεϖϖϖϖ==内;介质外)(2R r <场强303π4,π4r r Q E r Qr D εϖϖϖ==外 (2)介质外)(2R r >电势r Q E U 0rπ4r d ε=⋅=⎰∞ϖϖ外介质内)(21R r R <<电势rd r d ϖϖϖϖ⋅+⋅=⎰⎰∞∞rrE E U 外内2020π4)11(π4R Q R rqr εεε+-=)11(π420R r Q r r -+=εεε(3)金属球的电势rd r d 221ϖϖϖϖ⋅+⋅=⎰⎰∞R R R E E U 外内⎰⎰∞+=222020π44πdrR R R r r Qdrr Q εεε )11(π4210R R Q r r -+=εεε8-28 如题8-28图所示,在平行板电容器的一半容积内充入相对介电常数为r ε的电介质.试求:在有电介质部分和无电介质部分极板上自由电荷面密度的比值.解: 如题8-28图所示,充满电介质部分场强为2E ϖ,真空部分场强为1E ϖ,自由电荷面密度分别为2σ与1σ 由∑⎰=⋅0d q S D ϖϖ得11σ=D ,22σ=D而101E D ε=,202E D r εε=d 21UE E ==∴ r D D εσσ==1212题8-28图 题8-29图8-29 两个同轴的圆柱面,长度均为l ,半径分别为1R 和2R (2R >1R ),且l >>2R -1R ,两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时,求: (1)在半径r 处(1R <r <2R =,厚度为dr ,长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量; (2)电介质中的总电场能量; (3)圆柱形电容器的电容. 解: 取半径为r 的同轴圆柱面)(S 则 rlDS D S π2d )(=⋅⎰ϖϖ当)(21R r R <<时,Q q =∑∴rl Q D π2=(1)电场能量密度22222π82l r Q D w εε== 薄壳中rl rQ rl r l r Q w W εευπ4d d π2π8d d 22222=== (2)电介质中总电场能量⎰⎰===211222ln π4π4d d R R V R R l Q rl r Q W W εε(3)电容:∵C Q W 22=∴)/ln(π22122R R lW Q C ε== *8-30 金属球壳A 和B 的中心相距为r ,A 和B 原来都不带电.现在A 的中心放一点电荷1q ,在B 的中心放一点电荷2q ,如题8-30图所示.试求:(1) 1q 对2q 作用的库仑力,2q 有无加速度;(2)去掉金属壳B ,求1q 作用在2q 上的库仑力,此时2q 有无加速度. 解: (1)1q 作用在2q 的库仑力仍满足库仑定律,即2210π41r q q F ε=但2q 处于金属球壳中心,它受合力为零,没有加速度.(2)去掉金属壳B ,1q 作用在2q 上的库仑力仍是2210π41r q q F ε=,但此时2q 受合力不为零,有加速度.题8-30图 题8-31图8-31 如题8-31图所示,1C =0.25μF ,2C =0.15μF ,3C =0.20μF .1C 上电压为50V .求:AB U .解: 电容1C 上电量111U C Q =电容2C 与3C 并联3223C C C +=其上电荷123Q Q =∴355025231123232⨯===C U C C Q U86)35251(5021=+=+=U U U AB V8-32 1C 和2C 两电容器分别标明“200 pF 、500 V ”和“300 pF 、900 V ”,把它们串联起来后等值电容是多少?如果两端加上1000 V 的电压,是否会击穿? 解: (1) 1C 与2C 串联后电容1203002003002002121=+⨯=+='C C C C C pF(2)串联后电压比231221==C C U U ,而100021=+U U∴ 6001=U V ,4002=U V即电容1C 电压超过耐压值会击穿,然后2C 也击穿.8-33 将两个电容器1C 和2C 充电到相等的电压U 以后切断电源,再将每一电容器的正极板与另一电容器的负极板相联.试求: (1)每个电容器的最终电荷; (2)电场能量的损失.解: 如题8-33图所示,设联接后两电容器带电分别为1q ,2q题8-33图则⎪⎪⎩⎪⎪⎨⎧==-=-=+2122112121201021U U U C U C q q U C U C q q q q解得 (1) =1q UC C C C C q U C C C C C 21212221211)(,)(+-=+-(2)电场能量损失W W W -=∆0)22()2121(2221212221C q C q U C U C +-+= 221212U C C C C +=8-34 半径为1R =2.0cm 的导体球,外套有一同心的导体球壳,壳的内、外半径分别为2R =4.0cm 和3R =5.0cm ,当内球带电荷Q =3.0×10-8C时,求:(1)整个电场储存的能量;(2)如果将导体壳接地,计算储存的能量; (3)此电容器的电容值.解: 如图,内球带电Q ,外球壳内表面带电Q -,外表面带电Q题8-34图(1)在1R r <和32R r R <<区域0=E ϖ在21R r R <<时 301π4r rQ E εϖϖ=3R r >时 302π4r rQ E εϖϖ=∴在21R r R <<区域⎰=21d π4)π4(21222001R R r r r Q W εε⎰-==21)11(π8π8d 2102202R R R R Q rr Q εε 在3R r >区域⎰∞==32302220021π8d π4)π4(21R R Q r r rQ W εεε ∴ 总能量)111(π83210221R R R Q W W W +-=+=ε 41082.1-⨯=J(2)导体壳接地时,只有21R r R <<时30π4r rQ E εϖϖ=,02=W∴ 4210211001.1)11(π8-⨯=-==R R Q W W ε J(3)电容器电容)11/(π422102R R Q W C -==ε 121049.4-⨯=F习题九9-1 在同一磁感应线上,各点B ϖ的数值是否都相等?为何不把作用于运动电荷的磁力方向定义为磁感应强度B ϖ的方向?解: 在同一磁感应线上,各点B ϖ的数值一般不相等.因为磁场作用于运动电荷的磁力方向不仅与磁感应强度B ϖ的方向有关,而且与电荷速度方向有关,即磁力方向并不是唯一由磁场决定的,所以不把磁力方向定义为B ϖ的方向.题9-2图9-2 (1)在没有电流的空间区域里,如果磁感应线是平行直线,磁感应强度B ϖ的大小在沿磁感应线和垂直它的方向上是否可能变化(即磁场是否一定是均匀的)? (2)若存在电流,上述结论是否还对?解: (1)不可能变化,即磁场一定是均匀的.如图作闭合回路abcd 可证明21B B ρϖ=∑⎰==-=⋅0d 021I bc B da B l B abcd μϖϖ ∴ 21B B ρϖ= (2)若存在电流,上述结论不对.如无限大均匀带电平面两侧之磁力线是平行直线,但B ϖ方向相反,即21B B ρϖ≠.9-3 用安培环路定理能否求有限长一段载流直导线周围的磁场?答: 不能,因为有限长载流直导线周围磁场虽然有轴对称性,但不是稳恒电流,安培环路定理并不适用.9-4 在载流长螺线管的情况下,我们导出其内部nI B 0μ=,外面B =0,所以在载流螺线管 外面环绕一周(见题9-4图)的环路积分⎰外B L ϖ·d l ϖ=0但从安培环路定理来看,环路L 中有电流I 穿过,环路积分应为⎰外B L ϖ·d l ϖ=I 0μ这是为什么?解: 我们导出nl B 0μ=内,0=外B 有一个假设的前提,即每匝电流均垂直于螺线管轴线.这时图中环路L 上就一定没有电流通过,即也是⎰∑==⋅LI l B 0d 0μϖϖ外,与⎰⎰=⋅=⋅Ll l B 0d 0d ϖϖϖ外是不矛盾的.但这是导线横截面积为零,螺距为零的理想模型.实际上以上假设并不真实存在,所以使得穿过L 的电流为I ,因此实际螺线管若是无限长时,只是外B ϖ的轴向分量为零,而垂直于轴的圆周方向分量rIB πμ20=⊥,r 为管外一点到螺线管轴的距离.题 9 - 4 图9-5 如果一个电子在通过空间某一区域时不偏转,能否肯定这个区域中没有磁场?如果它发 生偏转能否肯定那个区域中存在着磁场?解:如果一个电子在通过空间某一区域时不偏转,不能肯定这个区域中没有磁场,也可能存在互相垂直的电场和磁场,电子受的电场力与磁场力抵消所致.如果它发生偏转也不能肯定那个区域存在着磁场,因为仅有电场也可以使电子偏转.9-6 已知磁感应强度0.2=B Wb ·m -2的均匀磁场,方向沿x 轴正方向,如题9-6图所示.试求:(1)通过图中abcd 面的磁通量;(2)通过图中befc 面的磁通量;(3)通过图中aefd 面的磁通量.解: 如题9-6图所示题9-6图(1)通过abcd 面积1S 的磁通是 24.04.03.00.211=⨯⨯=⋅=S B ϖϖΦWb(2)通过befc 面积2S 的磁通量 022=⋅=S B ϖϖΦ(3)通过aefd 面积3S 的磁通量24.0545.03.02cos 5.03.0233=⨯⨯⨯=θ⨯⨯⨯=⋅=S B ϖϖΦWb (或曰24.0-Wb )题9-7图9-7 如题9-7图所示,AB 、CD 为长直导线,C B )为圆心在O 点的一段圆弧形导线,其半径为R .若通以电流I ,求O 点的磁感应强度.解:如题9-7图所示,O 点磁场由AB 、C B )、CD 三部分电流产生.其中AB 产生 01=B ϖCD 产生RIB 1202μ=,方向垂直向里CD 段产生 )231(2)60sin 90(sin 24003-πμ=-πμ=︒︒R I R I B ,方向⊥向里∴)6231(203210ππμ+-=++=R I B B B B ,方向⊥向里. 9-8 在真空中,有两根互相平行的无限长直导线1L 和2L ,相距0.1m ,通有方向相反的电流,1I =20A,2I =10A ,如题9-8图所示.A ,B 两点与导线在同一平面内.这两点与导线2L 的距离均为5.0cm .试求A ,B 两点处的磁感应强度,以及磁感应强度为零的点的位置.题9-8图解:如题9-8图所示,A B ϖ方向垂直纸面向里42010102.105.02)05.01.0(2-⨯=⨯+-=πμπμI I B A T(2)设0=B ϖ在2L 外侧距离2L 为r 处则02)1.0(220=-+rIr I πμπμ解得 1.0=r m题9-9图9-9 如题9-9图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连.已知圆环的粗细均匀,求环中心O 的磁感应强度. 解: 如题9-9图所示,圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生,但∞A 和∞B 在O 点产生的磁场为零。
大学物理学答案(北京邮电大学第3版)赵近芳等编著#(精选.)

大学物理学(北邮第三版) 习题及解答(全)习题一1-1 |r ∆|与r ∆有无不同?t d d r 和t d d r 有无不同? t d d v 和t d d v有无不同?其不同在哪里?试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r -=∆; (2)t d d r 是速度的模,即t d d r ==v tsd d . t rd d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则t ˆrˆt r t d d d d d d r r r += 式中t rd d 就是速度径向上的分量,∴t r td d d d 与r 不同如题1-1图所示.题1-1图(3)t d d v 表示加速度的模,即t v a d d =,t v d d 是加速度a 在切向上的分量. ∵有ττ (v =v 表轨道节线方向单位矢),所以t v t v t v d d d d d d ττ +=式中dt dv就是加速度的切向分量.(t tr d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论) 1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =t rd d ,及a =22d d t r 而求得结果;又有人先计算速度和加速度的分量,再合成求得结果,即v =22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x 你认为两种方法哪一种正确?为什么?两者差别何在?解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r+=,jt y i t x t r a jt y i t x t r v222222d d d d d d d d d d d d +==+==∴故它们的模即为222222222222d d d d d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=t y t x a a a t y t x v v v y x y x而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作22d d d d t r a trv ==其二,可能是将22d d d d t r tr 与误作速度与加速度的模。
最新大学物理(北邮大)答案习题9

大学物理(北邮大)答案习题9习题九9-1 在同一磁感应线上,各点B的数值是否都相等?为何不把作用于运动电荷的磁力方向定义为磁感应强度B的方向?解: 在同一磁感应线上,各点B的数值一般不相等.因为磁场作用于运动电荷的磁力方向不仅与磁感应强度B的方向有关,而且与电荷速度方向有关,即磁力方向并不是唯一由磁场决定的,所以不把磁力方向定义为B的方向.题9-2图9-2 (1)在没有电流的空间区域里,如果磁感应线是平行直线,磁感应强度B的大小在沿磁感应线和垂直它的方向上是否可能变化(即磁场是否一定是均匀的)? (2)若存在电流,上述结论是否还对?解: (1)不可能变化,即磁场一定是均匀的.如图作闭合回路abcd 可证明21B B=∑⎰==-=⋅0d 021I bc B da B l B abcdμ∴ 21B B=(2)若存在电流,上述结论不对.如无限大均匀带电平面两侧之磁力线是平行直线,但B方向相反,即21B B≠.9-3 用安培环路定理能否求有限长一段载流直导线周围的磁场?答: 不能,因为有限长载流直导线周围磁场虽然有轴对称性,但不是稳恒电流,安培环路定理并不适用.9-4 在载流长螺线管的情况下,我们导出其内部nI B 0μ=,外面B =0,所以在载流螺线管 外面环绕一周(见题9-4图)的环路积分⎰外B L·d l =0但从安培环路定理来看,环路L 中有电流I 穿过,环路积分应为⎰外B L·d l =I 0μ这是为什么?解: 我们导出nl B 0μ=内,0=外B 有一个假设的前提,即每匝电流均垂直于螺线管轴线.这时图中环路L 上就一定没有电流通过,即也是⎰∑==⋅LI l B 0d 0μ 外,与⎰⎰=⋅=⋅Ll l B 0d 0d外是不矛盾的.但这是导线横截面积为零,螺距为零的理想模型.实际上以上假设并不真实存在,所以使得穿过L 的电流为I ,因此实际螺线管若是无限长时,只是外B的轴向分量为零,而垂直于轴的圆周方向分量rIB πμ20=⊥,r 为管外一点到螺线管轴的距离.题 9 - 4 图9-5 如果一个电子在通过空间某一区域时不偏转,能否肯定这个区域中没有磁场?如果它发 生偏转能否肯定那个区域中存在着磁场?解:如果一个电子在通过空间某一区域时不偏转,不能肯定这个区域中没有磁场,也可能存在互相垂直的电场和磁场,电子受的电场力与磁场力抵消所致.如果它发生偏转也不能肯定那个区域存在着磁场,因为仅有电场也可以使电子偏转.9-6 已知磁感应强度0.2=B Wb ·m -2的均匀磁场,方向沿x 轴正方向,如题9-6图所示.试求:(1)通过图中abcd 面的磁通量;(2)通过图中befc 面的磁通量;(3)通过图中aefd 面的磁通量. 解: 如题9-6图所示题9-6图(1)通过abcd 面积1S 的磁通是24.04.03.00.211=⨯⨯=⋅=S BΦWb(2)通过befc 面积2S 的磁通量022=⋅=S BΦ(3)通过aefd 面积3S 的磁通量24.0545.03.02cos 5.03.0233=⨯⨯⨯=θ⨯⨯⨯=⋅=S B ΦWb (或曰24.0-Wb )题9-7图9-7 如题9-7图所示,AB 、CD 为长直导线,C B为圆心在O 点的一段圆弧形导线,其半径为R .若通以电流I ,求O 点的磁感应强度.解:如题9-7图所示,O 点磁场由AB 、C B、CD 三部分电流产生.其中AB产生 01=BBC 产生RIB 1202μ=,方向垂直向里CD段产生 )231(2)60sin 90(sin 24003-πμ=-πμ=︒︒R I R I B ,方向⊥向里 ∴)6231(203210ππμ+-=++=R I B B B B ,方向⊥向里. 9-8 在真空中,有两根互相平行的无限长直导线1L 和2L ,相距0.1m ,通有方向相反的电流,1I =20A,2I =10A ,如题9-8图所示.A ,B 两点与导线在同一平面内.这两点与导线2L 的距离均为5.0cm .试求A ,B 两点处的磁感应强度,以及磁感应强度为零的点的位置.题9-8图解:如题9-8图所示,A B方向垂直纸面向里42010102.105.02)05.01.0(2-⨯=⨯+-=πμπμI I B A T(2)设0=B在2L 外侧距离2L 为r 处则02)1.0(220=-+rI r Iπμπμ 解得 1.0=r m题9-9图9-9 如题9-9图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连.已知圆环的粗细均匀,求环中心O 的磁感应强度.解: 如题9-9图所示,圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生,但∞A 和∞B 在O 点产生的磁场为零。
大学物理学[第3版.修订版]北京邮电大学出版社(下册)第十章习题10答案解析..
![大学物理学[第3版.修订版]北京邮电大学出版社(下册)第十章习题10答案解析..](https://img.taocdn.com/s3/m/23e3d607a4e9856a561252d380eb6294dd8822ad.png)
大学物理学[第3版.修订版]北京邮电大学出版社(下册)第十章习题10答案解析..习题1010.1选择题(1) 对于安培环路定理的理解,正确的是:(A )若环流等于零,则在回路L 上必定是H 处处为零;(B )若环流等于零,则在回路L 上必定不包围电流;(C )若环流等于零,则在回路L 所包围传导电流的代数和为零;(D )回路L 上各点的H 仅与回路L 包围的电流有关。
[答案:C](2) 对半径为R 载流为I 的无限长直圆柱体,距轴线r 处的磁感应强度B ()(A )内外部磁感应强度B 都与r 成正比;(B )内部磁感应强度B 与r 成正比,外部磁感应强度B 与r 成反比;(C )内外部磁感应强度B 都与r 成反比;(D )内部磁感应强度B 与r 成反比,外部磁感应强度B 与r 成正比。
[答案:B](3)质量为m 电量为q 的粒子,以速率v 与均匀磁场B 成θ角射入磁场,轨迹为一螺旋线,若要增大螺距则要()(A )增加磁场B ;(B )减少磁场B ;(C )增加θ角;(D )减少速率v 。
[答案:B](4)一个100匝的圆形线圈,半径为5厘米,通过电流为0.1安,当线圈在1.5T 的磁场中从θ=0的位置转到180度(θ为磁场方向和线圈磁矩方向的夹角)时磁场力做功为()(A )0.24J ;(B )2.4J ;(C )0.14J ;(D )14J 。
[答案:A]10.2 填空题(1)边长为a 的正方形导线回路载有电流为I ,则其中心处的磁感应强度。
[答案:aIπμ220,方向垂直正方形平面](2)计算有限长的直线电流产生的磁场用毕奥——萨伐尔定律,而用安培环路定理求得(填能或不能)。
[答案:能, 不能](3)电荷在静电场中沿任一闭合曲线移动一周,电场力做功为。
电荷在磁场中沿任一闭合曲线移动一周,磁场力做功为。
[答案:零,正或负或零](4)两个大小相同的螺线管一个有铁心一个没有铁心,当给两个螺线管通以电流时,管内的磁力线H 分布相同,当把两螺线管放在同一介质中,管内的磁力线H 分布将。
大学物理学 北京邮电大学出版社(赵近芳主编)课后习题答案(1-5章)

习题解答 习题一1-1 |r ∆|与r ∆ 有无不同?t d d r 和t d d r 有无不同? t d d v 和td d v 有无不同?其不同在哪里?试举例说明.解:(1)r ∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r-=∆;(2)t d d r 是速度的模,即t d d r ==v ts d d . trd d 只是速度在径向上的分量. ∵有r r ˆr =(式中r ˆ叫做单位矢),则tˆr ˆt r t d d d d d d rrr += 式中trd d 就是速度径向上的分量, ∴tr t d d d d 与r 不同如题1-1图所示.题1-1图(3)t d d v 表示加速度的模,即t v a d d=,tv d d 是加速度a 在切向上的分量.∵有ττ(v =v 表轨道节线方向单位矢),所以tvt v t v d d d d d d ττ += 式中dt dv就是加速度的切向分量. (tt r d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论) 1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =tr d d ,及a =22d d t r 而求得结果;又有人先计算速度和加速度的分v =22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x 你认为两种方法哪一种正确?为什么?两者差别何在?解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r +=,jty i t xt r a jty i t x t r v222222d d d d d d d d d d d d +==+==∴ 故它们的模即为222222222222d d d d d d d d ⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=+=t y t x a a a t y t x v v v yxyx而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作22d d d d tr a trv ==其二,可能是将22d d d d t r t r 与误作速度与加速度的模。
大学物理学-(第3版.修订版)-北京邮电大学出版社-下册--第十章-习题10标准答案..

习题1010.1选择题(1) 对于安培环路定理的理解,正确的是:(A )若环流等于零,则在回路L 上必定是H 处处为零; (B )若环流等于零,则在回路L 上必定不包围电流;(C )若环流等于零,则在回路L 所包围传导电流的代数和为零; (D )回路L 上各点的H 仅与回路L 包围的电流有关。
[答案:C](2) 对半径为R 载流为I 的无限长直圆柱体,距轴线r 处的磁感应强度B () (A )内外部磁感应强度B 都与r 成正比;(B )内部磁感应强度B 与r 成正比,外部磁感应强度B 与r 成反比; (C )内外部磁感应强度B 都与r 成反比;(D )内部磁感应强度B 与r 成反比,外部磁感应强度B 与r 成正比。
[答案:B](3)质量为m 电量为q 的粒子,以速率v 与均匀磁场B 成θ角射入磁场,轨迹为一螺旋线,若要增大螺距则要() (A ) 增加磁场B ;(B )减少磁场B ;(C )增加θ角;(D )减少速率v 。
[答案:B](4)一个100匝的圆形线圈,半径为5厘M ,通过电流为0.1安,当线圈在1.5T 的磁场中从θ=0的位置转到180度(θ为磁场方向和线圈磁矩方向的夹角)时磁场力做功为() (A )0.24J ;(B )2.4J ;(C )0.14J ;(D )14J 。
[答案:A]10.2 填空题(1)边长为a 的正方形导线回路载有电流为I ,则其中心处的磁感应强度。
[答案:aIπμ220,方向垂直正方形平面] (2)计算有限长的直线电流产生的磁场用毕奥——萨伐尔定律,而用安培环路定理求得(填能或不能)。
[答案:能, 不能](3)电荷在静电场中沿任一闭合曲线移动一周,电场力做功为。
电荷在磁场中沿任一闭合曲线移动一周,磁场力做功为。
[答案:零,正或负或零](4)两个大小相同的螺线管一个有铁心一个没有铁心,当给两个螺线管通以电流时,管内的磁力线H 分布相同,当把两螺线管放在同一介质中,管内的磁力线H 分布将。
大学物理下册第10章课后题答案

习题10-3图第10章 静电场中的导体和电介质习 题一 选择题10-1当一个带电导体达到静电平衡时,[ ] (A) 表面上电荷密度较大处电势较高 (B) 表面曲率较大处电势较高(C) 导体内部的电势比导体表面的电势高(D) 导体内任一点与其表面上任一点的电势差等于零 答案:D解析:处于静电平衡的导体是一个等势体,表面是一个等势面,并且导体内部与表面的电势相等。
10-2将一个带正电的带电体A 从远处移到一个不带电的导体B 附近,导体B 的电势将[ ](A) 升高 (B)降低 (C)不会发生变化 (D)无法确定 答案:A解析:不带电的导体B 相对无穷远处为零电势。
由于带正电的带电体A 移到不带电的导体B 附近的近端感应负电荷;在远端感应正电荷,不带电导体的电势将高于无穷远处,因而正确答案为(A )。
10-3将一带负电的物体M 靠近一不带电的导体N ,在N 的左端感应出正电荷,右端感应出负电荷。
若将导体N 的左端接地(如图10-3所示),则[ ](A) N 上的负电荷入地 (B) N 上的正电荷入地 (C) N 上的所有电荷入地 (D) N 上所有的感应电荷入地 答案:A解析:带负电的带电体M 移到不带电的导体N 附近的近端感应正电荷;在远端感应负电荷,不带电导体的电势将低于无穷远处,因此导体N 的电势小于0,即小于大地的电势,因而大地的正电荷将流入导体N ,或导体N 的负电荷入地。
故正确答案为(A )。
10-4 如图10-4所示,将一个电荷量为q电的导体球附近,点电荷距导体球球心为d 。
设无穷远 处为零电势,则在导体球球心O 点有[ ] (A) 0E =,04πε=q V d(B) 204πε=qE d ,04πε=qV d(C) 0E =,0V = (D) 204πε=q E d , 04πε=qV R答案:A解析:导体球处于静电平衡状态,导体球内部电场强度为零,因此0E =。
导体球球心O 点的电势为点电荷q 及感应电荷所产生的电势叠加。
大学物理答案第10章北京邮电大学出版社主编:罗益民余燕

⼤学物理答案第10章北京邮电⼤学出版社主编:罗益民余燕第10章波动光学10-1 (1)由λdDkx =得 A kD xd 6000m 1060.12102.0106733=?===---λ(2) m m )(3103102.0106337=?=??==?---λd D x 10-2 若在下缝处置⼀折射率为n 厚度为t 的透明薄膜,则光从下缝到屏上的光程将增加(n -1)t ,屏上的条纹均要向下移动。
依题意中央明条纹多到屏中⼼下⽅原来第3级明条纹位置,则从双缝到该位置的光程差[]t n r r r t n r )1()()1(1212-+-=--+=δ0)1(3=-+-=t n λ故 m 3.2m 1016.316.110328.631367µλ≈?=-??=-=-n t 10-3 屏上1λ的经三级明绿纹中⼼的位置m 103.310550106.02.133933---?===λd D kx 依题意屏上1λ的第六级明条纹和波长为λ的第五级明条纹重合于x 处则有λλdDk d D k x 516== 即λλ516k k = m 106.6105505679156--?=??==λλk k 10-4 由λdDk10)0.46.7(1025.010501)(---?-=-=-紫红紫红λλd D k x x m 102.74-?=10-5 光源S 0和其在镜中的虚光源等价⼀对相⼲光源,它们在屏上的⼲涉条纹的计算与杨⽒双缝条纹基本相同,只是明暗条纹分布完全相反,故屏上第⼀条明纹位置就是双缝⼲涉的零级暗条纹位置. 即2102.7104)3.02.0(22)12(73--+==+=λλd D d D k x(m)105.45-?=上⾯表达式也可直接由光程差推导⽽得.10-6 (1)由题10-6图可以看出αβθ22221-====r C S C S SC∴αθβ+=⼜εαβ+=∴εθ=等效双缝间距εsin 2r d =(2)λεελsin 2cos r r L d D x +==(3)λεεελεεε)cos (sin 22sin 2cos 22r L r Ltg r r L Ltg x x +?=+=? 3105)15.05.1(105.02105.12733=+??=--- 屏上共可看到3条明条纹,除中央明条纹外,在其上、下侧还可看到⼀级明条纹. 10-7 ∵ 321n n n <<,故有,3,2,1,02)12(21112=+==k k e n λδ① 3,2,12222222===k k e n λδ②由上两式21312k k =+?但由于λ是连续可调的,在1λ和2λ间⽆其他波长消失与增强,所以取,1,121==k k 把11=k 或12=k 代⼊①式或②式)m (10333.121079027922--?≈??==n e λ10-8 在反射光中产⽣⼲涉加强的波长应满⾜习题10-6图习题10-7图λλk e n =+222 故 122021612380033.141242-=-??=-=k k k e n λ当k =2时,A 67392=λ(红光);k =3时,A 40433=λ(紫光)故肥皂膜正⾯呈紫红⾊在透射光中产⽣⼲涉加强的波长应满⾜λk e n =22kk k e n 10108380033.1222=??==λ当k =2时,A 50542=λ(绿光),故肥皂膜背⾯呈绿⾊. 10-9 ∵ 321n n n <<透射光中产⽣⼲涉加强的条件应满⾜λλk e n =+222故冰层厚度 A k k n k e 2053)2/1(33.125460)2/1(2)2/1(2?-=??-=-=令k =1,可得冰层的最⼩厚度为A e 1027min =10-10 根据题中折射间的关系,对A 5500=λ黄绿光的增透膜应满⾜关系λλk e n =+2/22)2/1(2)2/1(2?-=??-=-=λ令A e k 996,1==即为增透膜的最薄厚度.另解:要使透射光增强,必须的射光⼲涉减弱. ∵321n n n << ∴2 )12(22λδ+==k e n996)12(4122+=+=k n k e λA k )9961992(+=, k =0,1,2, …A e 996min =10-11 由22sin n l λθ=得8rad 1088.31088.310552.1210893.52sin 55372''=?=?===----θλθl n 10-12 ∵212n e e k k λ=-=+,∴ 20条明条纹对应平晶厚度差为5.1210328.619219)(19721==-=?-+n e e d k k λ (m)100.46-?=10-13 (1)12.010048.013-?==≈L d tg θθ21068027921--+?=??==-n e e k k λ(3)0.85(mm)m 105.8104121068024492=?===---θλn l (4)141105.812.04=?=-N10-14 (1)∵ 321n n n <<∴反射光中明条纹的条件为:λk e n =22 油膜边缘 e =0 ∴ k =0 油膜中⼼ m 102.16-?==h e∴ 8.4106102.12.122762===--λen k 故共可看到五条明条纹(k =0,1,2,3,4) (2)对应各明条纹中⼼油膜的厚度22n k e λ=当k =0,1,2,3,4时,对应油膜的厚度分别为:0,2500A ,5000A ,7500A ,10000A .(3)油膜逐渐展开时,圆条纹向外扩展,条纹间间距增⼤,条纹级数减⼩,油膜中⼼由半明半暗向暗、明、暗、明……依次变化,直⾄整个油膜呈现⼀⽚明亮区域. 10-15 依题意 1144d R R r r =-= -λλ2144d R R r r ='-'='-'λλ由上两式可解得未知单⾊光波长A d d 545958931041085.333212==???='--λλ 10-16 依题意有/)2/110(210110D n R r D R r =-='=-=λλ由上两式可解得液体折射率22.11027.1104.1222221==? ??=--D D n 10-17 由2λN d =得A N d 6290m 1029.6102410322.02273=?=??==--λ10-18 设放⼊厚度为d 玻璃⽚后,则来⾃⼲涉仪两臂相应的光程差变化为λN d n =-)1(2m 1093.5)1632.1(2105150)1(257--?=-=-=n N d λ10-19 ∵衍射⾓0?很⼩,∴中央明条纹的半⾓宽度rad 105101.01053370---?=??==a λ中央明条纹的宽度afftg x λ220≈=?mm 5m 1053=?=- 若单缝装置浸⼊⽔中,中央明条纹的半⾓宽度rad 1076.3101.033.11053370---?===na λ10-20 (1)设⼊射光波长为λ,离屏中⼼x =1.4mm 处为明条纹,则由单缝衍射明条纹条件,x 应满⾜12(sin λ+=k atg f x = ∵sin ?很⼩∴λ??ak ff ftg x 2)12(sin +=≈= )12(4.0104.1106.02)12(233+=+=--k k f ax λ m 12102.46+?=-k 当m 106,373-?==λk 恰在橙黄⾊波长范围内,所以⼊射光波长为A 6000. (2)p 点的条纹级数为3(3)从p 点看,对该光波⽽⾔,狭缝处波阵⾯可分成(2k +1)=7个半波带. 10-21 由单缝衍射明条纹条件,2 )12(sin λ+=k a ,可分别求得21λλ、两单⾊光第⼀级明条纹离屏中⼼的距离分别为4711110210435.02)12(--=+==a k f ftg x λ?mm)(3m 1033=?=-47222102106.735.02)12(--=+==a k f ftg x λ? mm)(7.5m 107.53=?=-这两条明条纹之间的距离mm)(7.2m 107.210)37.5(3312=?=?-=-=?--x x x若⽤光栅代替单缝,光栅常数(m)10cm 1000+b a 则由光栅⽅程λ?k b a =+sin )(,可分别求得21,λλ两单⾊光的第⼀级明条纹离屏中⼼的距离分别为cm)(2m 102101045.0257111=?=??+==---b a k f ftg x λ? m 108.310106.75.0257222---?=??+==b a k f ftg x λ?cm)(8.3=cm)(8.128.312=-=-=?x x x 10-22 光栅常数m 102mm 50016-?==+b a ,由光栅⽅程λ?k b a =+sin )( 4.3109.51102sin )(76==+=--λb a k 即最多可看到第3级明条纹. 10-23 光栅常数m 105mm 20016-?==+b a (1)由光栅⽅程λ?k b a =+sin )(可得第⼀级明条纹与中央明条纹的距离,即第⼀级明条纹离屏中⼼的距离cm)(6m 10610510516.0267=?==+==---b a k f ftg x λ? (2)当光线与光栅法线成30°斜⼊射时,光栅⽅程为λθ?k b a =±+)sin )(sin (0上式取负号,且当k =0,可得中央明条纹的衍射⽅向;即0θ?=,所以中央明条纹离屏中⼼距离为m 35.0306.0=?==tg ftg x ?10-24 (1)由光栅⽅程λ?k b a =+sin )(,对应于20.0sin 1=?与30.0sin 2=?处满⾜771063)(30.01062)(20.0--??=+??=+b a b a∴ m 1066-?=+b a (2)因为明条纹第四级缺级,应满⾜缺级条件= 因第⼆级明条纹不缺级,取1='k ,可得光栅上狭缝的宽度为m 105.1410666--?=?=+'=k b a k aor m 105.436-?=?='a k(3)由λ?k b a =+sin )(,且当2π=,则10106106sin )(76=??=+=--λb a k ∴在?<±6, ±7, ±9级明条纹(k =±10的明条纹在?=90?处)10-25 光栅常数m 105.2cm 400016-?==+b a 设A A 7600,40001='=λλ,由光栅⽅程可得λ?λ?''='+=+k b a k b a k k s i n )(s i n)(2.3106.7105.2sin )(2.6104105.2sin )(7676=??=''+='=??='+=----λ?λ?k k b a k b a k亦即λ的(k +1)级条纹要在λ'的k 级条纹之后∴λλλλ)1()1(+<'++<+'k k ba kb a k)1(40007600+只有k =1才满⾜上式,所以屏上只可能出现⼀个完整⽽不重迭的第⼀级光谱,第⼆级和第三级光谱均有重迭现象.10-26 (1)由单缝衍射可确定中央明条纹的宽度为371002.0108.45.0222--===?a f ftg x λcm 4.2m 104.22=?=- (2)由缺级条件,且取1='k502.01.0==+'=a b a k k 可见第5级缺级;∴在单缝衍射的中央明条纹包迹内共有9条双缝衍射明条纹(4,3,2,1,0±±±±=k )10-27 设A A 7600,400021==λλ,由光栅⽅程可求得21,λλ第⼀级谱线的位置分别为:ba fftg x +==111λ? )sin (11tg ,≈很⼩ba fftg x +==222λ?依题意 m 100.6212-?=-=?x x x∴ m 10610771212----?=??-??=--=+x x f b a λλ 10-28 爱⾥班半径m 1053.1101.021055.022.122.13371---?==?=D f r λ若mm 0.122?=D ,则m 1053.11021055.022.122.14372---?===D f r λ10-29 ⼈眼最⼩分辨⾓为rad 1022.110510522.122.14370---?===D λθ⽽x l ?=?0θ,所以眼睛恰可分辨两灯的距离为km 84.91084.91022.12.134=?=?==-θxl 10-30 由最⼩分辨⾓公式Dλθ22.10=可得m 139.01084.4105.522.122.1670===--θλD10-31 由布拉格公式λ?k d =sin 2得kAk k d89.32/275.22sin 2=??==λ当A k A k 94.1,2;89.3,12====λλ; 当;97.0,4;3.1,343A k A k ====λλ所以只有λ为1.30A 和0.97A 的谱线在x 射线波长范围内,能产⽣强反射.10-32 设⾃然光强度为0I ,通过第⼀偏振⽚后光强度为2/0I ,依题意,由马吕斯公式可得透过第⼆偏振⽚后的光强为=60cos 2201I I ∴ 108I I =今在两偏振⽚之间再插⼊另⼀偏振⽚,则通过该偏振⽚后的光强为102038330cos 2I I I I ==?=' 再通过第三偏振⽚后的光强1214930cos 3I I I == ∴25.21=I I10-33 (1)强度为0I 的⾃然光通过两重迭偏振⽚后,透射光的最⼤光强为2I ,按题意当两偏振⽚的偏振化⽅向夹⾓为α时,透过检偏器的光强231cos 2020I I I ?==α∴ 4454'?=α(2)按题意,由马吕斯公式 3cos 2020II I ==α∴ 6135'?=α 10-34 设⾃然光强度为0I ,线偏振光强度为1I ,该混合光通过偏振⽚时,若其偏振化⽅向与线偏振光的振动⽅向⼀致,则透射光强度102I I +,若其偏振化⽅向与线偏振光的振动⽅向垂直,则透射光强度为2I ,依题意 252010I I I ?=+ ∴ 012I I =故⾃然光和线偏振光的光强各占总光强的31和32. 10-35 当光由⽔射向玻璃时,按布儒斯特定律可求得起偏振⾓724833.15.111'?===--tg n n tgb ⽔玻璃θ当光由玻璃射向⽔时43415.133.111'?===--tg n n tg b 玻璃⽔θ 10-36 (1)这时反射线与折射线相互垂直∴ ?=?-?=-?=58329090r b θθ(2)由布儒斯特公式60.158=?==tg tg n b θ10-37 设⼊射线偏振光的振幅为E ,则射⼊晶⽚后e 光和o 光的振幅分别为 ?=?=30sin 30cos 0E E E E e ∴ 73.1300=?=ctg E E e。
北京邮电大学大学物理学习题答案10
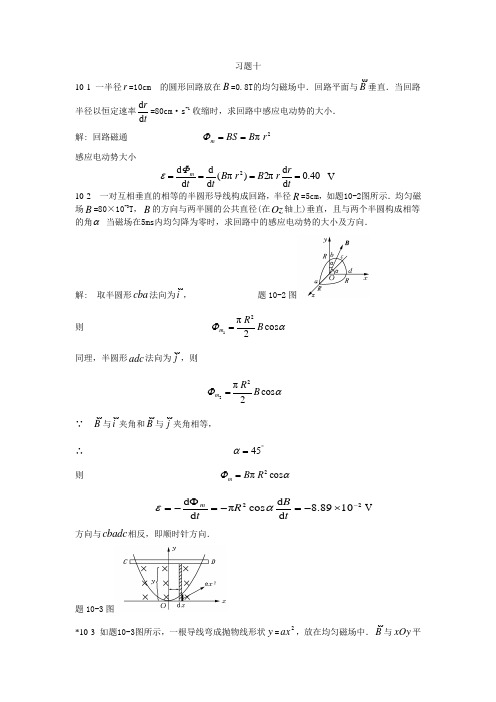
习题十10-1 一半径r =10cm 的圆形回路放在B =0.8T 的均匀磁场中.回路平面与B垂直.当回路半径以恒定速率tr d d =80cm ·s -1 收缩时,求回路中感应电动势的大小.解: 回路磁通 2πr B BS m ==Φ 感应电动势大小40.0d d π2)π(d d d d 2====tr rB r B ttm Φε V10-2 一对互相垂直的相等的半圆形导线构成回路,半径R =5cm ,如题10-2图所示.均匀磁场B =80×10-3T ,B 的方向与两半圆的公共直径(在Oz 轴上)垂直,且与两个半圆构成相等的角α 当磁场在5ms 内均匀降为零时,求回路中的感应电动势的大小及方向.解: 取半圆形cba 法向为i, 题10-2图则 αΦcos 2π21B R m =同理,半圆形adc 法向为j,则αΦcos 2π22B R m =∵ B 与i夹角和B 与j 夹角相等,∴ ︒=45α则 αΦcos π2R B m =221089.8d d cos πd d -⨯-=-=Φ-=tB RtmαεV方向与cbadc 相反,即顺时针方向.题10-3图*10-3 如题10-3图所示,一根导线弯成抛物线形状y =2ax ,放在均匀磁场中.B与xOy 平面垂直,细杆CD 平行于x 轴并以加速度a 从抛物线的底部向开口处作平动.求CD 距O 点为y 处时回路中产生的感应电动势.解: 计算抛物线与CD 组成的面积内的磁通量⎰⎰=-==aym y B x x y B S B 0232322d )(2d 2ααΦ∴ v y Bty y Btm 21212d d d d ααε-=-=Φ-=∵ ay v 22=∴ 212y a v =则 ααεaByy a yBi 8222121-=-= i ε实际方向沿ODC .题10-4图10-4 如题10-4图所示,载有电流I 的长直导线附近,放一导体半圆环MeN 与长直导线共面,且端点MN 的连线与长直导线垂直.半圆环的半径为b ,环心O 与导线相距a .设半圆环以速度v 平行导线平移.求半圆环内感应电动势的大小和方向及MN 两端的电压NM UU -.解: 作辅助线MN ,则在MeNM 回路中,沿v方向运动时0d =m Φ ∴ 0=MeNM ε 即 MN MeN εε=又∵ ⎰+-<+-==ba ba MN ba b a Ivl vB 0ln2d cos 0πμπε所以MeN ε沿NeM 方向,大小为ba b a Iv-+ln20πμM 点电势高于N 点电势,即ba b a IvU U N M -+=-ln20πμ题10-5图10-5如题10-5所示,在两平行载流的无限长直导线的平面内有一矩形线圈.两导线中的电流方向相反、大小相等,且电流以tI d d 的变化率增大,求:(1)任一时刻线圈内所通过的磁通量; (2)线圈中的感应电动势. 解: 以向外磁通为正则 (1) ]ln[lnπ2d π2d π2000da db ab Ilr l r Ir l r Iab b ad d m +-+=-=⎰⎰++μμμΦ(2) tIb a b d a d l t d d ]ln [ln π2d d 0+-+=-=μΦε 10-6 如题10-6图所示,用一根硬导线弯成半径为r 的一个半圆.令这半圆形导线在磁场中以频率f 绕图中半圆的直径旋转.整个电路的电阻为R .求:感应电流的最大值.题10-6图解: )cos(2π02ϕωΦ+=⋅=t r B S B m∴Bfr f r B r B t r B tm m i 222202ππ22π2π)sin(2πd d ===+=-=ωεϕωωΦε∴ RBf r RI m 22π==ε10-7 如题10-7图所示,长直导线通以电流I =5A ,在其右方放一长方形线圈,两者共面.线圈长b =0.06m ,宽a =0.04m ,线圈以速度v =0.03m ·s -1垂直于直线平移远离.求:d =0.05m 时线圈中感应电动势的大小和方向.题10-7图解: AB 、CD 运动速度v方向与磁力线平行,不产生感应电动势. DA 产生电动势⎰==⋅⨯=A D Ivb vBb l B v d2d )(01πμεBC 产生电动势)(π2d )(02d a I vbl B v CB+-=⋅⨯=⎰με∴回路中总感应电动势8021106.1)11(π2-⨯=+-=+=ad dIbvμεεεV方向沿顺时针.10-8 长度为l 的金属杆ab 以速率v 在导电轨道abcd 上平行移动.已知导轨处于均匀磁场B中,B 的方向与回路的法线成60°角(如题10-8图所示),B的大小为B =kt (k 为正常).设t =0时杆位于cd 处,求:任一时刻t 导线回路中感应电动势的大小和方向.解: ⎰==︒=⋅=22212160cos d klvt lv kt Blvt S B m Φ∴ klvt tm -=-=d d Φε即沿abcd 方向顺时针方向.题10-8图10-9 一矩形导线框以恒定的加速度向右穿过一均匀磁场区,B的方向如题10-9图所示.取逆时针方向为电流正方向,画出线框中电流与时间的关系(设导线框刚进入磁场区时t =0). 解: 如图逆时针为矩形导线框正向,则进入时0d d <Φt,0>ε;题10-9图(a)题10-9图(b)在磁场中时0d d =tΦ,0=ε;出场时0d d >tΦ,0<ε,故t I -曲线如题10-9图(b)所示.题10-10图10-10 导线ab 长为l ,绕过O 点的垂直轴以匀角速ω转动,aO =3l 磁感应强度B 平行于转轴,如图10-10所示.试求: (1)ab 两端的电势差; (2)b a ,两端哪一点电势高? 解: (1)在Ob 上取dr r r +→一小段则 ⎰==320292d lOb l B r rB ωωε同理 ⎰==32181d lOa l B r rB ωωε∴ 2261)92181(l B l B Ob aO ab ωωεεε=+-=+=(2)∵ 0>ab ε 即0<-b a U U ∴b 点电势高.题10-11图10-11 如题10-11图所示,长度为b 2的金属杆位于两无限长直导线所在平面的正中间,并以速度v平行于两直导线运动.两直导线通以大小相等、方向相反的电流I ,两导线相距2a .试求:金属杆两端的电势差及其方向. 解:在金属杆上取r d 距左边直导线为r ,则 ba b a Ivr ra rIv l B v ba ba BAAB -+-=-+-=⋅⨯=⎰⎰+-lnd )211(2d )(00πμπμε∵ 0<AB ε ∴实际上感应电动势方向从A B →,即从图中从右向左,∴ ba ba Iv U AB -+=ln 0πμ题10-12图10-12 磁感应强度为B的均匀磁场充满一半径为R 的圆柱形空间,一金属杆放在题10-12图中位置,杆长为2R ,其中一半位于磁场内、另一半在磁场外.当tB d d >0时,求:杆两端的感应电动势的大小和方向.解: ∵ bc ab ac εεε+=tB R B R ttab d d 43]43[d d d d 21=--=-=Φε=-=tab d d 2ΦεtB R B R td d 12π]12π[d d 22=--∴ tB R R ac d d ]12π43[22+=ε∵0d d >tB∴ 0>ac ε即ε从c a → 10-13 半径为R 的直螺线管中,有dtdB >0的磁场,一任意闭合导线abca ,一部分在螺线管内绷直成ab 弦,a ,b 两点与螺线管绝缘,如题10-13图所示.设ab =R ,试求:闭合导线中的感应电动势.解:如图,闭合导线abca 内磁通量)436π(22R R B S B m-=⋅= Φ∴ tB R R i d d )436π(22--=ε∵ 0d d >tB∴0<i ε,即感应电动势沿acba ,逆时针方向.题10-13图题10-14图10-14 如题10-14图所示,在垂直于直螺线管管轴的平面上放置导体ab 于直径位置,另一导体cd 在一弦上,导体均与螺线管绝缘.当螺线管接通电源的一瞬间管内磁场如题10-14图示方向.试求:(1)ab 两端的电势差;(2)cd 两点电势高低的情况.解: 由⎰⎰⋅-=⋅l S t Bl Ed d d d 旋知,此时旋E 以O 为中心沿逆时针方向.(1)∵ab 是直径,在ab 上处处旋E与ab 垂直 ∴ ⎰=⋅ll 0d旋∴0=ab ε,有b a U U =(2)同理, 0d >⋅=⎰l Ecddc旋ε∴ 0<-c d U U 即d c U U >题10-15图10-15 一无限长的直导线和一正方形的线圈如题10-15图所示放置(导线与线圈接触处绝缘).求:线圈与导线间的互感系数.解: 设长直电流为I ,其磁场通过正方形线圈的互感磁通为⎰==32300122ln π2d π2aa Ia r rIa μμΦ∴ 2ln π2012aIM μΦ==10-16 一矩形线圈长为a =20cm ,宽为b =10cm ,由100匝表面绝缘的导线绕成,放在一无限长导线的旁边且与线圈共面.求:题10-16图中(a)和(b)两种情况下,线圈与长直导线间的互感.解:(a)见题10-16图(a),设长直电流为I ,它产生的磁场通过矩形线圈的磁通为2ln π2d 2πd 020)(12Iarr Ia S B bbS μμΦ⎰⎰==⋅=∴ 6012108.22ln π2-⨯===aNIN M μΦ H(b)∵长直电流磁场通过矩形线圈的磁通012=Φ,见题10-16图(b) ∴ 0=M题10-16图题10-17图10-17 两根平行长直导线,横截面的半径都是a ,中心相距为d ,两导线属于同一回路.设两导线内部的磁通可忽略不计,证明:这样一对导线长度为l 的一段自感为πμl L 0=Inaa d -.解: 如图10-17图所示,取r l S d d = 则 ⎰⎰-----=--=-+=ad aad aad d aa d Il r r rIl r l r I r πI )ln(ln2πd )d11(π2d ))d (π22(0000μμμμΦaa d Il-=lnπ0μ∴ aa d lI L -==lnπ0μΦ10-18 两线圈顺串联后总自感为1.0H ,在它们的形状和位置都不变的情况下,反串联后总自感为0.4H .试求:它们之间的互感. 解: ∵顺串时 M L L L 221++= 反串联时M L L L 221-+='∴ M L L 4='-15.04='-=L L M H10-19图10-19 一矩形截面的螺绕环如题10-19图所示,共有N 匝.试求: (1)此螺线环的自感系数;(2)若导线内通有电流I ,环内磁能为多少? 解:如题10-19图示 (1)通过横截面的磁通为 ⎰==baab NIhr h r NIlnπ2d π200μμΦ磁链 ab Ih N N ln π220μΦψ==∴ ab h N IL lnπ220μψ==(2)∵ 221LIW m =∴ ab hI N W m ln π4220μ=10-20 一无限长圆柱形直导线,其截面各处的电流密度相等,总电流为I .求:导线内部单位长度上所储存的磁能. 解:在R r <时 20π2RI B rμ=∴ 4222002π82RrI Bw m μμ==取 r r V d π2d =(∵导线长1=l ) 则 ⎰⎰===RRm I Rr r I r r w W 0204320π16π4d d 2μμπ。
大学物理课后习题10第十章答案

习题1010.1选择题(1)在双缝干涉实验中,为使屏上的干涉条纹间距变大,可以采取的办法是[](A)使屏靠近双缝.(B)使两缝的间距变小.(C)把两个缝的宽度稍微调窄.(D)改用波长较小的单色光源.[答案:C](2)两块平玻璃构成空气劈形膜,左边为棱边,用单色平行光垂直入射.若上面的平玻璃以棱边为轴,沿逆时针方向作微小转动,则干涉条纹的[](A)间隔变小,并向棱边方向平移.(B)间隔变大,并向远离棱边方向平移.(C)间隔不变,向棱边方向平移.(D)间隔变小,并向远离棱边方向平移.[答案:A](3)一束波长为的单色光由空气垂直入射到折射率为n的透明薄膜上,透明薄膜放在空气中,要使反射光得到干涉加强,则薄膜最小的厚度为[](A).(B)/(4n).(C).(D)/(2n).[答案:B](4)在迈克耳孙干涉仪的一条光路中,放入一折射率为n,厚度为d 的透明薄片,放入后,这条光路的光程改变了[](A)2(n-1)d.(B)2nd.(C)2(n-1)d+/2.(D)nd.(E)(n-1)d.[答案:A](5)在迈克耳孙干涉仪的一条光路中,放入一折射率为n的透明介质薄膜后,测出两束光的光程差的改变量为一个波长,则薄膜的厚度是[](A).(B)/(2n).(C)n.(D)/[2(n-1)].[答案:D](6)在夫琅禾费单缝衍射实验中,对于给定的入射单色光,当缝宽度变小时,除中央亮纹的中心位置不变外,各级衍射条纹[](A)对应的衍射角变小.(B)对应的衍射角变大.(C)对应的衍射角也不变.(D)光强也不变.[答案:B](7)波长nm(1nm=10-9m)的单色光垂直照射到宽度a=0.25mm的单缝上,单缝后面放一凸透镜,在凸透镜的焦平面上放置一屏幕,用以观测衍射条纹。
今测得屏幕上中央明条纹一侧第三个暗条纹和另一侧第三个暗条纹之间的距离为d=12mm,则凸透镜的焦距是[](B)平行于入射面的振动占优势的部分偏振光.(C)垂直于入射面振动的完全线偏振光.(D)垂直于入射面的振动占优势的部分偏振光.[答案:C](12)一束自然光自空气射向一块平板玻璃(如图),设入射角等于布儒斯特角i0,则在界面2的反射光是[](A)自然光。
大学物理(赵近芳北京邮电大学出版社)下册课后习题答案

- 1 -习题八8-1 电量都是q 的三个点电荷,分别放在正三角形的三个顶点.试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系? 解: 如题8-1图示(1) 以A 处点电荷为研究对象,由力平衡知:q '为负电荷20220)33(π4130cos π412a q q a q '=︒εε解得q q 33-='(2)与三角形边长无关.题8-1图 题8-2图8-2 两小球的质量都是m ,都用长为l 的细绳挂在同一点,它们带有相同电量,静止时两线夹角为2θ,如题8-2图所示.设小球的半径和线的质量都可以忽略不计,求每个小球所带的电量.解: 如题8-2图示⎪⎩⎪⎨⎧===220)sin 2(π41sin cos θεθθl q F T mg T e解得θπεθtan 4sin 20mg l q =8-3 根据点电荷场强公式204r qE πε=,当被考察的场点距源点电荷很近(r →0)时,则场强→∞,这是没有物理意义的,对此应如何理解?解:20π4r r q E ε=仅对点电荷成立,当0→r 时,带电体不能再视为点电荷,再用上式求场强是错误的,实际带电体有一定形状大小,考虑电荷在带电体上的分布求出的场强不会是无限大.8-4 在真空中有A ,B 两平行板,相对距离为d ,板面积为S ,其带电量分别为+q 和-q .则这两板之间有相互作用力f ,有人说f =2024d q πε,又有人说,因为f =qE ,S qE 0ε=,所以f =S q 02ε.试问这两种说法对吗?为什么? f 到底应等于多少?解: 题中的两种说法均不对.第一种说法中把两带电板视为点电荷是不对的,第二种说法把合场强S qE 0ε=看成是一个带电板在另一带电板处的场强也是不对的.正确解答应为一个板的电场为S qE 02ε=,另一板受它的作用力S q S q q f 02022εε==,这是两板间相互作用的电场力.8-5 一电偶极子的电矩为l q p =,场点到偶极子中心O 点的距离为r ,矢量r 与l 的夹角为θ,(见题8-5图),且l r >>.试证P 点的场强E 在r 方向上的分量r E 和垂直于r 的分量θE 分别为r E =302cos r p πεθ, θE =304sin r p πεθ证: 如题8-5所示,将p 分解为与r 平行的分量θsin p 和垂直于r 的分量θsin p .∵ l r >> ∴ 场点P 在r 方向场强分量30π2cos r p E r εθ=垂直于r 方向,即θ方向场强分量300π4sin r p E εθ=题8-5图 题8-6图8-6 长l =15.0cm 的直导线AB 上均匀地分布着线密度λ=5.0x10-9C ·m -1的正电荷.试求:(1)在导线的延长线上与导线B 端相距1a =5.0cm 处P 点的场强;(2)在导线的垂直平分线上与导线中点相距2d =5.0cm 处Q 点的场强. 解: 如题8-6图所示(1)在带电直线上取线元x d ,其上电量q d 在P 点产生场强为20)(d π41d x a x E P -=λε2220)(d π4d x a xE E llP P -==⎰⎰-ελ ]2121[π40l a l a +--=ελ)4(π220l a l-=ελ 用15=l cm ,9100.5-⨯=λ1m C -⋅, 5.12=a cm 代入得21074.6⨯=P E 1C N -⋅ 方向水平向右(2)同理2220d d π41d +=x xE Q λε 方向如题8-6图所示 由于对称性⎰=l QxE 0d ,即Q E只有y 分量,∵22222220d d d d π41d ++=x x xE Qyλε22π4d d ελ⎰==lQy Qy E E ⎰-+2223222)d (d ll x x2220d 4π2+=l lελ以9100.5-⨯=λ1cm C -⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Q y Q E E 1C N -⋅,方向沿y 轴正向8-7 一个半径为R 的均匀带电半圆环,电荷线密度为λ,求环心处O 点的场强.解: 如8-7图在圆上取ϕRd dl =题8-7图ϕλλd d d R l q ==,它在O 点产生场强大小为20π4d d R R E εϕλ=方向沿半径向外则 ϕϕελϕd sin π4sin d d 0R E E x ==ϕϕελϕπd cos π4)cos(d d 0R E E y -=-=积分R R E x 000π2d sin π4ελϕϕελπ==⎰0d cos π400=-=⎰ϕϕελπR E y∴R E E x 0π2ελ==,方向沿x 轴正向.8-8 均匀带电的细线弯成正方形,边长为l ,总电量为q .(1)求这正方形轴线上离中心为r处的场强E ;(2)证明:在l r >>处,它相当于点电荷q 产生的场强E .解: 如8-8图示,正方形一条边上电荷4q 在P 点产生物强P Ed 方向如图,大小为()4π4cos cos d 22021l r E P +-=εθθλ∵22cos 221l r l +=θ 12cos cos θθ-= ∴24π4d 22220l r ll r E P ++=ελ P Ed 在垂直于平面上的分量βcos d d P E E =⊥∴424π4d 222222l r rl r l r lE +++=⊥ελ题8-8图由于对称性,P 点场强沿OP 方向,大小为2)4(π44d 422220l r l r lrE E P ++=⨯=⊥ελ ∵l q 4=λ ∴2)4(π422220l r l r qrE P ++=ε 方向沿 8-9 (1)点电荷q 位于一边长为a 的立方体中心,试求在该点电荷电场中穿过立方体的一个面的电通量;(2)如果该场源点电荷移动到该立方体的一个顶点上,这时穿过立方体各面的电通量是多少?*(3)如题8-9(3)图所示,在点电荷q 的电场中取半径为R 的圆平面.q 在该平面轴线上的A 点处,求:通过圆平面的电通量.(x Rarctan=α)解: (1)由高斯定理0d εq S E s⎰=⋅立方体六个面,当q 在立方体中心时,每个面上电通量相等∴ 各面电通量06εqe =Φ.(2)电荷在顶点时,将立方体延伸为边长a 2的立方体,使q 处于边长a 2的立方体中心,则边长a 2的正方形上电通量06εq e =Φ对于边长a 的正方形,如果它不包含q 所在的顶点,则024εqe =Φ,如果它包含q 所在顶点则0=Φe .如题8-9(a)图所示.题8-9(3)图题8-9(a)图 题8-9(b)图 题8-9(c)图(3)∵通过半径为R 的圆平面的电通量等于通过半径为22x R +的球冠面的电通量,球冠面积*]1)[(π22222xR x x R S +-+=∴)(π42200x R Sq +=Φε02εq=[221x R x +-]*关于球冠面积的计算:见题8-9(c)图ααα⎰⋅=0d sin π2r r S ααα⎰⋅=02d sin π2r)cos 1(π22α-=r8-10 均匀带电球壳内半径6cm ,外半径10cm ,电荷体密度为2×510-C ·m -3求距球心5cm ,8cm ,12cm 各点的场强.解: 高斯定理0d ε∑⎰=⋅qS E s,02π4ε∑=qr E当5=r cm 时,0=∑q ,0=E8=r cm 时,∑q 3π4p=3(r )3内r -∴()2023π43π4r r r E ερ内-=41048.3⨯≈1C N -⋅, 方向沿半径向外.12=r cm 时,3π4∑=ρq -3(外r )内3r∴()420331010.4π43π4⨯≈-=r r r E ερ内外 1C N -⋅ 沿半径向外.8-11 半径为1R 和2R (2R >1R )的两无限长同轴圆柱面,单位长度上分别带有电量λ和-λ,试求:(1)r <1R ;(2) 1R <r <2R ;(3) r >2R 处各点的场强.解: 高斯定理0d ε∑⎰=⋅qS E s取同轴圆柱形高斯面,侧面积rl S π2= 则rlE S E Sπ2d =⋅⎰对(1) 1R r < 0,0==∑E q(2) 21R r R <<λl q =∑∴r E 0π2ελ=沿径向向外 (3) 2R r > 0=∑q∴ 0=E题8-12图8-12 两个无限大的平行平面都均匀带电,电荷的面密度分别为1σ和2σ,试求空间各处场强.解: 如题8-12图示,两带电平面均匀带电,电荷面密度分别为1σ与2σ,两面间, nE )(21210σσε-=1σ面外, nE )(21210σσε+-= 2σ面外, nE )(21210σσε+=n:垂直于两平面由1σ面指为2σ面.8-13 半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为r <R 的小球体,如题8-13图所示.试求:两球心O 与O '点的场强,并证明小球空腔内的电场是均匀的.解: 将此带电体看作带正电ρ的均匀球与带电ρ-的均匀小球的组合,见题8-13图(a).(1) ρ+球在O 点产生电场010=E ,ρ- 球在O 点产生电场'd π4π3430320OO r E ερ=∴ O 点电场d 33030r E ερ= ;(2) ρ+在O '产生电场d π4d 3430301E ερπ=' ρ-球在O '产生电场002='E∴ O ' 点电场003ερ='E 'OO题8-13图(a) 题8-13图(b)(3)设空腔任一点P 相对O '的位矢为r ',相对O 点位矢为r(如题8-13(b)图)则03ερrE PO =, 03ερr E O P '-=' ,∴00033)(3ερερερd r r E E E O P PO P=='-=+=' ∴腔内场强是均匀的.8-14 一电偶极子由q =1.0×10-6C 的两个异号点电荷组成,两电荷距离d=0.2cm ,把这电偶极子放在1.0×105N ·C -1的外电场中,求外电场作用于电偶极子上的最大力矩.解: ∵ 电偶极子p 在外场E 中受力矩E p M⨯=∴ qlE pE M ==max代入数字 4536max 100.2100.1102100.1---⨯=⨯⨯⨯⨯⨯=M m N ⋅8-15 两点电荷1q =1.5×10-8C ,2q =3.0×10-8C ,相距1r =42cm ,要把它们之间的距离变为2r =25cm ,需作多少功?解:⎰⎰==⋅=22210212021π4π4d d r r r r q q r r q q r F A εε)11(21r r - 61055.6-⨯-=J外力需作的功 61055.6-⨯-=-='A A J题8-16图8-16 如题8-16图所示,在A ,B 两点处放有电量分别为+q ,-q 的点电荷,AB 间距离为2R ,现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点,求移动过程中电场力作的功.解: 如题8-16图示0π41ε=O U 0)(=-R qR q 0π41ε=O U )3(R q R q -R q 0π6ε-=∴R qq U U q A oC O 00π6)(ε=-= 8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中心O 点处的场强和电势.解: (1)由于电荷均匀分布与对称性,AB 和CD 段电荷在O 点产生的场强互相抵消,取θd d R l =则θλd d R q =产生O 点Ed 如图,由于对称性,O 点场强沿y 轴负方向题8-17图θεθλππcos π4d d 2220⎰⎰-==R R E E y R 0π4ελ=[)2sin(π-2sinπ-] R 0π2ελ-=(2) AB 电荷在O 点产生电势,以0=∞U⎰⎰===AB 200012ln π4π4d π4d R R x x x x U ελελελ同理CD 产生 2ln π402ελ=U半圆环产生 0034π4πελελ==R R U∴0032142ln π2ελελ+=++=U U U U O8-18 一电子绕一带均匀电荷的长直导线以2×104m ·s -1的匀速率作圆周运动.求带电直线上的线电荷密度.(电子质量0m =9.1×10-31kg ,电子电量e =1.60×10-19C)解: 设均匀带电直线电荷密度为λ,在电子轨道处场强r E 0π2ελ=电子受力大小r e eE F e 0π2ελ== ∴r v m r e 20π2=ελ 得1320105.12π2-⨯==e mv ελ1m C -⋅ 8-19 空气可以承受的场强的最大值为E =30kV ·cm -1,超过这个数值时空气要发生火花放电.今有一高压平行板电容器,极板间距离为d =0.5cm ,求此电容器可承受的最高电压.解: 平行板电容器内部近似为均匀电场∴ 4105.1d ⨯==E U V8-20 根据场强E与电势U 的关系U E -∇= ,求下列电场的场强:(1)点电荷q 的电场;(2)总电量为q ,半径为R 的均匀带电圆环轴上一点;*(3)偶极子ql p =的l r >>处(见题8-20图).解: (1)点电荷r qU 0π4ε=题 8-20 图∴ 0200π4r r q r r U E ε=∂∂-= 0r 为r 方向单位矢量.(2)总电量q ,半径为R 的均匀带电圆环轴上一点电势220π4x R qU +=ε∴ ()ix R qx i x U E 2/3220π4+=∂∂-=ε(3)偶极子l q p=在l r >>处的一点电势200π4cos ])cos 21(1)cos 2(1[π4r ql l l r q U εθθθε=+--=∴ 30π2cos r p r U E r εθ=∂∂-=30π4sin 1r p U r E εθθθ=∂∂-=8-21 证明:对于两个无限大的平行平面带电导体板(题8-21图)来说,(1)相向的两面上,电荷的面密度总是大小相等而符号相反;(2)相背的两面上,电荷的面密度总是大小相等而符号相同.证: 如题8-21图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ,2σ,3σ,4σ题8-21图(1)则取与平面垂直且底面分别在A 、B 内部的闭合柱面为高斯面时,有)(d 32=∆+=⋅⎰S S E sσσ∴ +2σ03=σ 说明相向两面上电荷面密度大小相等、符号相反;(2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即0222204030201=---εσεσεσεσ又∵ +2σ03=σ∴ 1σ4σ=说明相背两面上电荷面密度总是大小相等,符号相同.8-22 三个平行金属板A ,B 和C 的面积都是200cm 2,A 和B 相距4.0mm ,A 与C 相距2.0mm .B ,C 都接地,如题8-22图所示.如果使A 板带正电3.0×10-7C ,略去边缘效应,问B 板和C 板上的感应电荷各是多少?以地的电势为零,则A 板的电势是多少?解: 如题8-22图示,令A 板左侧面电荷面密度为1σ,右侧面电荷面密度为2σ题8-22图(1)∵ AB AC U U =,即∴AB AB AC AC E E d d =∴ 2d d 21===AC ABAB AC E E σσ且 1σ+2σS q A=得,32S q A =σ S q A321=σ 而7110232-⨯-=-=-=A C q S q σC C10172-⨯-=-=S q B σ(2)301103.2d d ⨯===AC AC AC A E U εσV8-23 两个半径分别为1R 和2R (1R <2R )的同心薄金属球壳,现给内球壳带电+q ,试计算:(1)外球壳上的电荷分布及电势大小;(2)先把外球壳接地,然后断开接地线重新绝缘,此时外球壳的电荷分布及电势; *(3)再使内球壳接地,此时内球壳上的电荷以及外球壳上的电势的改变量.解: (1)内球带电q +;球壳内表面带电则为q -,外表面带电为q +,且均匀分布,其电势题8-23图⎰⎰∞∞==⋅=22020π4π4d d R R R qr r q r E U εε(2)外壳接地时,外表面电荷q +入地,外表面不带电,内表面电荷仍为q -.所以球壳电势由内球q +与内表面q -产生:0π4π42020=-=R qR qU εε(3)设此时内球壳带电量为q ';则外壳内表面带电量为q '-,外壳外表面带电量为+-q q '(电荷守恒),此时内球壳电势为零,且π4'π4'π4'202010=+-+-=R q q R q R q U A εεε得 q R R q 21='外球壳上电势()22021202020π4π4'π4'π4'R qR R R q q R q R q U B εεεε-=+-+-=8-24 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量.解: 如题8-24图所示,设金属球感应电荷为q ',则球接地时电势0=O U8-24图由电势叠加原理有:=O U 03π4π4'00=+R qR q εε得 -='q 3q8-25 有三个大小相同的金属小球,小球1,2带有等量同号电荷,相距甚远,其间的库仑力为0F.试求:(1)用带绝缘柄的不带电小球3先后分别接触1,2后移去,小球1,2之间的库仑力; (2)小球3依次交替接触小球1,2很多次后移去,小球1,2之间的库仑力.解: 由题意知 2020π4r q F ε=(1)小球3接触小球1后,小球3和小球1均带电2q q =',小球3再与小球2接触后,小球2与小球3均带电qq 43=''∴ 此时小球1与小球2间相互作用力00220183π483π4"'2F r qr q q F =-=εε(2)小球3依次交替接触小球1、2很多次后,每个小球带电量均为32q.∴ 小球1、2间的作用力0294π432322F r qq F ==ε *8-26 如题8-26图所示,一平行板电容器两极板面积都是S ,相距为d ,分别维持电势A U =U ,B U =0不变.现把一块带有电量q 的导体薄片平行地放在两极板正中间,片的面积也是S ,片的厚度略去不计.求导体薄片的电势.解: 依次设A ,C ,B 从上到下的6个表面的面电荷密度分别为1σ,2σ,3σ,4σ,5σ,6σ如图所示.由静电平衡条件,电荷守恒定律及维持U U AB =可得以下6个方程题8-26图⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++++==+=+-==+=+===+6543215432065430021001σσσσσσσσσσεσσσσεσσd US q S qdU U C S S q B A解得S q261==σσ S qd U 2032-=-=εσσ S qd U 2054+=-=εσσ所以CB 间电场S q d U E 00422εεσ+== )2d(212d 02S q U E U U CB C ε+===注意:因为C 片带电,所以2U U C ≠,若C 片不带电,显然2UU C =8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳,介质相对介电常数为r ε,金属球带电Q .试求: (1)电介质内、外的场强; (2)电介质层内、外的电势; (3)金属球的电势. 解: 利用有介质时的高斯定理∑⎰=⋅qS D Sd(1)介质内)(21R r R <<场强303π4,π4r rQ E r r Q D r εε ==内;介质外)(2R r <场强303π4,π4r r Q E r Qr D ε ==外 (2)介质外)(2R r >电势r Q E U 0rπ4r d ε=⋅=⎰∞外介质内)(21R r R <<电势rd r d ⋅+⋅=⎰⎰∞∞rrE E U 外内2020π4)11(π4R Q R r qr εεε+-=)11(π420R r Q r r -+=εεε(3)金属球的电势rd r d 221 ⋅+⋅=⎰⎰∞R R R E E U 外内⎰⎰∞+=222020π44πdrR R R r r Qdrr Q εεε )11(π4210R R Q r r -+=εεε8-28 如题8-28图所示,在平行板电容器的一半容积内充入相对介电常数为r ε的电介质.试求:在有电介质部分和无电介质部分极板上自由电荷面密度的比值. 解: 如题8-28图所示,充满电介质部分场强为2E ,真空部分场强为1E,自由电荷面密度分别为2σ与1σ由∑⎰=⋅0d q S D 得11σ=D ,22σ=D而101E D ε=,202E D r εε=d 21U E E ==∴ r D D εσσ==1212题8-28图 题8-29图8-29 两个同轴的圆柱面,长度均为l ,半径分别为1R 和2R (2R >1R ),且l >>2R -1R ,两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时,求: (1)在半径r 处(1R <r <2R =,厚度为dr ,长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量; (2)电介质中的总电场能量; (3)圆柱形电容器的电容. 解: 取半径为r 的同轴圆柱面)(S 则 rlDS D S π2d )(=⋅⎰当)(21R r R <<时,Q q =∑∴rl Q D π2=(1)电场能量密度22222π82l r Q D w εε== 薄壳中rl rQ rl r l r Q w W εευπ4d d π2π8d d 22222=== (2)电介质中总电场能量⎰⎰===211222ln π4π4d d R R V R R l Q rl r Q W W εε(3)电容:∵C Q W 22=∴)/ln(π22122R R lW Q C ε== *8-30 金属球壳A 和B 的中心相距为r ,A 和B 原来都不带电.现在A 的中心放一点电荷1q ,在B 的中心放一点电荷2q ,如题8-30图所示.试求:(1) 1q 对2q 作用的库仑力,2q 有无加速度;(2)去掉金属壳B ,求1q 作用在2q 上的库仑力,此时2q 有无加速度. 解: (1)1q 作用在2q 的库仑力仍满足库仑定律,即2210π41r q q F ε=但2q 处于金属球壳中心,它受合力为零,没有加速度.(2)去掉金属壳B ,1q 作用在2q 上的库仑力仍是2210π41r q q F ε=,但此时2q 受合力不为零,有加速度.题8-30图 题8-31图8-31 如题8-31图所示,1C =0.25μF ,2C =0.15μF ,3C =0.20μF .1C 上电压为50V .求:AB U .解: 电容1C 上电量111U C Q =电容2C 与3C 并联3223C C C +=其上电荷123Q Q =∴355025231123232⨯===C U C C Q U86)35251(5021=+=+=U U U AB V8-32 1C 和2C 两电容器分别标明“200 pF 、500 V ”和“300 pF 、900 V ”,把它们串联起来后等值电容是多少?如果两端加上1000 V 的电压,是否会击穿? 解: (1) 1C 与2C 串联后电容1203002003002002121=+⨯=+='C C C C C pF(2)串联后电压比231221==C C U U ,而100021=+U U∴ 6001=U V ,4002=U V即电容1C 电压超过耐压值会击穿,然后2C 也击穿.8-33 将两个电容器1C 和2C 充电到相等的电压U 以后切断电源,再将每一电容器的正极板与另一电容器的负极板相联.试求: (1)每个电容器的最终电荷; (2)电场能量的损失.解: 如题8-33图所示,设联接后两电容器带电分别为1q ,2q题8-33图则⎪⎪⎩⎪⎪⎨⎧==-=-=+2122112121201021U U U C U C q q U C U C q q q q解得 (1) =1q UC C C C C q U C C C C C 21212221211)(,)(+-=+-(2)电场能量损失W W W -=∆0)22()2121(2221212221C q C q U C U C +-+= 221212U C C C C +=8-34 半径为1R =2.0cm 的导体球,外套有一同心的导体球壳,壳的内、外半径分别为2R =4.0cm 和3R =5.0cm ,当内球带电荷Q =3.0×10-8C 时,求:(1)整个电场储存的能量;(2)如果将导体壳接地,计算储存的能量; (3)此电容器的电容值.解: 如图,内球带电Q ,外球壳内表面带电Q -,外表面带电Q题8-34图(1)在1R r <和32R r R <<区域0=E在21R r R <<时 301π4r rQ E ε =3R r >时 302π4r rQ E ε =∴在21R r R <<区域⎰=21d π4)π4(21222001R R r r r QW εε⎰-==21)11(π8π8d 2102202R R R R Q rr Q εε 在3R r >区域⎰∞==32302220021π8d π4)π4(21R R Q r r rQ W εεε ∴ 总能量)111(π83210221R R R Q W W W +-=+=ε 41082.1-⨯=J(2)导体壳接地时,只有21R r R <<时30π4r rQ E ε=,02=W∴ 4210211001.1)11(π8-⨯=-==R R Q W W ε J(3)电容器电容)11/(π422102R R Q W C -==ε 121049.4-⨯=F习题九9-1 在同一磁感应线上,各点B的数值是否都相等?为何不把作用于运动电荷的磁力方向定义为磁感应强度B的方向?解: 在同一磁感应线上,各点B的数值一般不相等.因为磁场作用于运动电荷的磁力方向不仅与磁感应强度B的方向有关,而且与电荷速度方向有关,即磁力方向并不是唯一由磁场决定的,所以不把磁力方向定义为B的方向.题9-2图9-2 (1)在没有电流的空间区域里,如果磁感应线是平行直线,磁感应强度B的大小在沿磁感应线和垂直它的方向上是否可能变化(即磁场是否一定是均匀的)? (2)若存在电流,上述结论是否还对?解: (1)不可能变化,即磁场一定是均匀的.如图作闭合回路abcd 可证明21B B=∑⎰==-=⋅0d 021I bc B da B l B abcd μ∴ 21B B= (2)若存在电流,上述结论不对.如无限大均匀带电平面两侧之磁力线是平行直线,但B方向相反,即21B B≠.9-3 用安培环路定理能否求有限长一段载流直导线周围的磁场?答: 不能,因为有限长载流直导线周围磁场虽然有轴对称性,但不是稳恒电流,安培环路定理并不适用.9-4 在载流长螺线管的情况下,我们导出其内部nI B 0μ=,外面B =0,所以在载流螺线管 外面环绕一周(见题9-4图)的环路积分⎰外B L·d l =0但从安培环路定理来看,环路L 中有电流I 穿过,环路积分应为⎰外B L·d l =I 0μ这是为什么?解: 我们导出nl B 0μ=内,0=外B 有一个假设的前提,即每匝电流均垂直于螺线管轴线.这时图中环路L 上就一定没有电流通过,即也是⎰∑==⋅LI l B 0d 0μ外,与⎰⎰=⋅=⋅Ll l B 0d 0d外是不矛盾的.但这是导线横截面积为零,螺距为零的理想模型.实际上以上假设并不真实存在,所以使得穿过L 的电流为I ,因此实际螺线管若是无限长时,只是外B 的轴向分量为零,而垂直于轴的圆周方向分量rIB πμ20=⊥,r 为管外一点到螺线管轴的距离.题 9 - 4 图9-5 如果一个电子在通过空间某一区域时不偏转,能否肯定这个区域中没有磁场?如果它发 生偏转能否肯定那个区域中存在着磁场?解:如果一个电子在通过空间某一区域时不偏转,不能肯定这个区域中没有磁场,也可能存在互相垂直的电场和磁场,电子受的电场力与磁场力抵消所致.如果它发生偏转也不能肯定那个区域存在着磁场,因为仅有电场也可以使电子偏转.9-6 已知磁感应强度0.2=B Wb ·m -2的均匀磁场,方向沿x 轴正方向,如题9-6图所示.试求:(1)通过图中abcd 面的磁通量;(2)通过图中befc 面的磁通量;(3)通过图中aefd 面的磁通量.解: 如题9-6图所示题9-6图(1)通过abcd 面积1S 的磁通是 24.04.03.00.211=⨯⨯=⋅=S BΦWb(2)通过befc 面积2S 的磁通量 022=⋅=S BΦ(3)通过aefd 面积3S 的磁通量24.0545.03.02cos 5.03.0233=⨯⨯⨯=θ⨯⨯⨯=⋅=S B ΦWb (或曰24.0-Wb )题9-7图9-7 如题9-7图所示,AB 、CD 为长直导线,C B为圆心在O 点的一段圆弧形导线,其半径为R .若通以电流I ,求O 点的磁感应强度.解:如题9-7图所示,O 点磁场由AB 、C B、CD 三部分电流产生.其中AB 产生 01=BCD 产生RIB 1202μ=,方向垂直向里CD 段产生 )231(2)60sin 90(sin 24003-πμ=-πμ=︒︒R I I B ,方向⊥向里∴)6231(203210ππμ+-=++=R I B B B B ,方向⊥向里.9-8 在真空中,有两根互相平行的无限长直导线1L 和2L ,相距0.1m ,通有方向相反的电流,1I =20A,2I =10A ,如题9-8图所示.A ,B 两点与导线在同一平面内.这两点与导线2L 的距离均为5.0cm .试求A ,B 两点处的磁感应强度,以及磁感应强度为零的点的位置.题9-8图解:如题9-8图所示,A B方向垂直纸面向里42010102.105.02)05.01.0(2-⨯=⨯+-=πμπμI I B A T(2)设0=B在2L 外侧距离2L 为r 处则 02)1.0(220=-+rIr I πμπμ解得 1.0=r m题9-9图9-9 如题9-9图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连.已知圆环的粗细均匀,求环中心O 的磁感应强度. 解: 如题9-9图所示,圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生,但∞A 和∞B 在O 点产生的磁场为零。
大学物理学第版修订版北京邮电大学出版社下册习题答案.docx

习题9 9.1 选择题(1)正方形的两对角线处各放置电荷 Q,另两对角线各放置电荷 q,若 Q 所受到合力为零,则 Q与 q 的关系为:()( A) Q=-23/2 q (B) Q=23/2 q(C) Q=-2q(D) Q=2q[ 答案: A](2)下面说法正确的是:()(A)若高斯面上的电场强度处处为零,则该面内必定没有电荷;(B)若高斯面内没有电荷,则该面上的电场强度必定处处为零;(C)若高斯面上的电场强度处处不为零,则该面内必定有电荷;(D)若高斯面内有电荷,则该面上的电场强度必定处处不为零。
[ 答案: D](3)一半径为 R 的导体球表面的面点荷密度为σ,则在距球面 R处的电场强度()(A)σ / ε0(B)σ /2ε 0(C)σ /4ε 0(D)σ /8ε0 [ 答案: C](4)在电场中的导体内部的()(A)电场和电势均为零;(B)电场不为零,电势均为零;(C)电势和表面电势相等;(D)电势低于表面电势。
[ 答案: C]9.2 填空题(1) 在静电场中,电势不变的区域,场强必定为。
[ 答案:相同 ](2) 一个点电荷 q 放在立方体中心,则穿过某一表面的电通量为,若将点电荷由中心向外移动至无限远,则总通量将。
[ 答案: q/6 ε0 ,将为零](3) 电介质在电容器中作用(a)——( b)——。
[ 答案: (a) 提高电容器的容量;(b)延长电容器的使用寿命](4) 电量 Q均匀分布在半径为R 的球体内,则球内球外的静电能之比。
[ 答案: 5: 6]9.3电量都是q的三个点电荷,分别放在正三角形的三个顶点.试问:(1) 在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡( 即每个电荷受其他三个电荷的库仑力之和都为零)?(2) 这种平衡与三角形的边长有无关系?解 :如题9.3图示(1)以A处点电荷为研究对象,由力平衡知:q 为负电荷解得q 3 q3(2)与三角形边长无关.题 9.3 图题9.4图9.4两小球的质量都是m ,都用长为l的细绳挂在同一点,它们带有相同电量,静止时两线夹角为 2, 如题 9.4 图所示.设小球的半径和线的质量都可以忽略不计,求每个小球所带的电量.解: 如题 9.4 图示解得q 2 sin 40mgtan l9.5 根据点电荷场强公式E q,当被考察的场点距源点电荷很近(r →0) 时,则0r 24场强→∞,这是没有物理意义的,对此应如何理解?解 :qr0仅对点电荷成立,当r0 时,带电体不能再视为点电荷,再用上Er24π式求场强是错误的,实际带电体有一定形状大小,考虑电荷在带电体上的分布求出的场强不会是无限大.9.6在真空中有 A , B 两平行板,相对距离为 d ,板面积为 S ,其带电量分别为+ q 和q 2- q.则这两板之间有相互作用力 f ,有人说 f =40d 2,又有人说,因为f = qE , E q,所以 f =q2.试问这两种说法对吗 ?为什么 ? f 到底应等于多少?0 SS解 :题中的两种说法均不对.第一种说法中把两带电板视为点电荷是不对的,第二种说法把合场强E q看成是一个带电板在另一带电板处的场强也是不对的.正确0S解答应为一个板的电场为 Eq,另一板受它的作用力 f qq q22 0 S 2 0 S,这是两2 0 S板间相互作用的电场力.9.7 长l =15.0cm的直导线 AB上均匀地分布着线密度=5.0x10-9-1的正电C·m荷.试求: (1) 在导线的延长线上与导线 B端相距a1=5.0cm处P点的场强;(2)在导线的垂直平分线上与导线中点相距 d 2=5.0cm 处Q点的场强.解:如题 9.7 图所示(1) 在带电直线上取线元dx ,其上电量dq在 P 点产生场强为dE P1dx4π0(a x) 2l dxE P dE P2题 9.7图l(a x)24π02用 l 15 cm, 5.0 10 9 C m 1,a12.5 cm代入得E P 6.74102N C1方向水平向右(2) 同理dE Q1dx方向如题 9.7图所示4π0x 2 d 22由于对称性dE Qx 0 ,即 E Q只有 y 分量,l2∵dE Qy1dx dπ 0x2 d 22x 2d224以 5.0 10 9 C cm 1,l 15 cm,d2 5 cm 代入得E Q E Qy14.96 102N C1,方向沿 y 轴正向9.8一个半径为R的均匀带电半圆环,电荷线密度为, 求环心处O点的场强.解: 如 9.8 图在圆上取dl Rd题9.8 图dq dl R d,它在O点产生场强大小为RddE方向沿半径向外24π0 R则dE x dE sinsin d4π0 R积分E x sin d04π0 R2π0 R∴ E E x,方向沿 x 轴正向.2π0 R9.9均匀带电的细线弯成正方形,边长为l ,总电量为q .(1)求这正方形轴线上离中心为r 处的场强 E ;(2)证明:在r l 处,它相当于点电荷q 产生的场强 E .解 :如9.9图示,正方形一条边上电荷q在P点产生物强dE P方向如图,大小为4l∵cos212r 2l2∴dE Pl2 l 22 l 24π0r r42 dE P在垂直于平面上的分量dE dE P cos∴l rdE4π0r 2l 2r 2l 2r 2l 2424题9.9 图由于对称性,P 点场强沿 OP 方向,大小为q∵4l∴E P qr方向沿 OP4π0 ( r 2l 2) r2 l 2429.10 (1)点电荷q位于一边长为a的立方体中心,试求在该点电荷电场中穿过立方体的一个面的电通量;(2) 如果该场源点电荷移动到该立方体的一个顶点上,这时穿过立方体各面的电通量是多少?解: (1)由高斯定理qE dSs立方体六个面,当q 在立方体中心时,每个面上电通量相等∴ 各面电通量e q.60(2) 电荷在顶点时,将立方体延伸为边长2a 的立方体,使 q 处于边长 2a 的立方体中心,则边长 2a 的正方形上电通量qe60q对于边长 a 的正方形,如果它不包含q 所在的顶点,则e,24 0如果它包含 q 所在顶点则e0 .如题 9.10 图所示.题9.10图9.11 均匀带电球壳内半径6cm,外半径 10cm,电荷体密度为 2×105-3求距球心C· m5cm,8cm ,12cm 各点的场强.解 :高斯定理 E dS q, E4πr2qs00当 r 5 cm时,q 0 ,E0r 8 cm时, q p 4π(r3r内3 ) 34πr3r内2∴E323.48 104N C1,方向沿半径向外.4π0 rr 12cm时 ,4π33q( r外内3r )4πr外3r内3∴E324.10 104N C1沿半径向外 .4π0 r9.12半径为R1和R2(R2>R1)的两无限长同轴圆柱面,单位长度上分别带有电量和- , 试求 :(1)r < R1;(2)R1< r < R2;(3)r > R2处各点的场强.解 :高斯定理q E dSs取同轴圆柱形高斯面,侧面积S2πrl则 E dSSE2πrl对 (1)r R1q 0, E0(2)R1r R2q l∴E沿径向向外2π0 r(3)r R2q0∴ E 0题9.13 图9.13两个无限大的平行平面都均匀带电,电荷的面密度分别为 1 和 2 ,试求空间各处场强.解 :如题9.13图示,两带电平面均匀带电,电荷面密度分别为 1 与 2 ,两面间, E1( 12 ) n201面外, E1( 12 )n202面外, E1( 12 ) n20n :垂直于两平面由 1 面指为 2 面.9.14半径为R 的均匀带电球体内的电荷体密度为, 若在球内挖去一块半径为r <R 的小球体,如题9.14 图所示.试求:两球心O 与 O点的场强,并证明小球空腔内的电场是均匀的.解 :将此带电体看作带正电的均匀球与带电的均匀小球的组合,见题9.14图(a).(1)球在O点产生电场E100 ,4 π3球在 O 点产生电场E2033OO'4π0dr 3∴O点电场EOO';030d34d3(2)在O产生电场E1033 OO '4π0d球在 O 产生电场E200∴O点电场E03OO '题 9.14 图(a)题9.14图(b)(3)设空腔任一点 P 相对 O 的位矢为 r ,相对 O 点位矢为 r (如题8-13(b)图)则E PO r ,30EPO r,30∴EPEPOEPO( r r )dOO'3 0 3 0 3 0∴腔内场强是均匀的.9.15一电偶极子由 q =1.0×10-6C的两个异号点电荷组成,两电荷距离d=0.2cm,把这电偶极子放在 1.0 × 105N·C-1的外电场中,求外电场作用于电偶极子上的最大力矩.解 :∵电偶极子p在外场E中受力矩∴M max pE qlE 代入数字9.16两点电荷q1=1.5× 10-8C,q2=3.0× 10-8C,相距r1=42cm,要把它们之间的距离变为 r2=25cm,需作多少功?解 : Ar2F dr r2 q1q2drq1q2 (11 )r1r2 4π0r24π0 r1r2外力需作的功A A 6.55 10 6J题9.17 图9.17如题9.17图所示,在A,B两点处放有电量分别为+q ,- q的点电荷,AB间距离为 2 R,现将另一正试验点电荷q0从O点经过半圆弧移到 C 点,求移动过程中电场力作的功.解: 如题 9.17 图示∴ A q0 (U Oq o q U C )6π0 R9.18如题9.18图所示的绝缘细线上均匀分布着线密度为的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中心 O 点处的场强和电势.解 : (1)由于电荷均匀分布与对称性,AB 和 CD 段电荷在 O 点产生的场强互相抵消,取dl Rd则 dq Rd产生O点dE如图,由于对称性,O点场强沿 y 轴负方向题9.18 图[sin() sin ]4π0 R22(2)AB 电荷在 O 点产生电势,以U0同理 CD 产生U 2ln 24π 0πR 半圆环产生U 34π 0 R4 0∴U O U 1 U 2 U 3ln 22π 04 04-1的匀速率作圆周运动.求带9.19 一电子绕一带均匀电荷的长直导线以 2× 10 m ·s电直线上的线电荷密度.-31-19( 电子质量 m 0 =9.1 × 10 kg ,电子电量 e =1.60 × 10 C)解 :设均匀带电直线电荷密度为,在电子轨道处场强电子受力大小F ee eE2π 0 r∴e v 2 2π 0 rmr得2π 0 mv 212.5 10 13 C m 1e-19.20 空气可以承受的场强的最大值为E =30kV · cm ,超过这个数值时空气要发生火花放电.今有一高压平行板电容器,极板间距离为 d =0.5cm ,求此电容器可承受的最高电压.解 :平行板电容器内部近似为均匀电场9.21 证明:对于两个无限大的平行平面带电导体板 ( 题9.21 图 ) 来说, (1) 相向的两面上,电荷的面密度总是大小相等而符号相反;(2) 相背的两面上,电荷的面密度总是大小相等而符号相同.证 :如题 9.21 图所示,设两导体A 、 的四个平面均匀带电的电荷面密度依次为1,B2,3,4题 9.21 图(1) 则取与平面垂直且底面分别在 A 、 B 内部的闭合柱面为高斯面时,有∴230说明相向两面上电荷面密度大小相等、符号相反;(2) 在 A 内部任取一点 P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即又∵230∴14说明相背两面上电荷面密度总是大小相等,符号相同.9.22 三个平行金属板2A ,B 和C 的面积都是 200cm , A 和 B 相距 4.0mm , A 与 C 相距 2.0 mm . B , C 都接地,如题 9.22 图所示.如果使 A 板带正电 3.0 ×10-7 C ,略去边缘效应,问 B 板和 C 板上的感应电荷各是多少?以地的电势为零,则 A 板的电势是多少?解 :如题9.22图示,令A板左侧面电荷面密度为 1 ,右侧面电荷面密度为2题9.22 图(1)∵∴∴且得而(2)U AC U AB,即E AC d AC E AB d AB1 E AC d AB2EABdAC21+q A2S2qA ,12q A3S3Sq C 1 S2q A 2 10 7C3q B 2 S 1 10 7 CU A E AC d AC 1 d AC 2.3103V9.23 两个半径分别为R1和 R2( R1< R2)的同心薄金属球壳,现给内球壳带电+ q,试计算: (1) 外球壳上的电荷分布及电势大小;(2)先把外球壳接地,然后断开接地线重新绝缘,此时外球壳的电荷分布及电势;*(3) 再使内球壳接地,此时内球壳上的电荷以及外球壳上的电势的改变量.解: (1)内球带电q ;球壳内表面带电则为q ,外表面带电为q ,且均匀分布,其电势U E dr qdr qR2 4π0 r24π0RR2题9.23 图(2) 外壳接地时,外表面电荷q 入地,外表面不带电,内表面电荷仍为q .所以球壳电势由内球q 与内表面q 产生:(3) 设此时内球壳带电量为q ;则外壳内表面带电量为q ,外壳外表面带电量为q q (电荷守恒),此时内球壳电势为零,且得q R1qR2外球壳上电势9.24半径为R的金属球离地面很远,并用导线与地相联,在与球心相距为d3R处有一点电荷 + q,试求:金属球上的感应电荷的电量.解 :如题9.24图所示,设金属球感应电荷为q ,则球接地时电势U O0题9.24 图由电势叠加原理有:得q q39.25 有三个大小相同的金属小球,小球 1,2带有等量同号电荷,相距甚远,其间的库仑力为 F 0 .试求:(1) 用带绝缘柄的不带电小球 3先后分别接触 1, 2后移去,小球 1, 2之间的库仑力;(2) 小球 3依次交替接触小球 1,2很多次后移去,小球 1, 2之间的库仑力.解 : 由题意知q 2F 00 r 24π (1) 小球 3 接触小球 1后,小球 3和小球 1均带电qq,2小球 3 再与小球 2 接触后,小球 2 与小球 3 均带电∴此时小球 1与小球 2 间相互作用力(2) 小球 3 依次交替接触小球 1、 2 很多次后,每个小球带电量均为2q .32 q 2 q4 ∴ 小球 1、 2间的作用力3 3F 24π 0 r 29F9.26 在半径为 R 1 的金属球之外包有一层外半径为 R 2 的均匀电介质球壳,介质相对介电常数为r ,金属球带电 Q .试求:(1) 电介质内、外的场强;(2) 电介质层内、外的电势;(3) 金属球的电势.解 : 利用有介质时的高斯定理D dSqS(1) 介质内 ( R 1r R 2 ) 场强DQr , E 内Qrr3;4π 34π0 rr介质外 (rR 2 ) 场强(2) 介质外 (r R 2 ) 电势介质内 (R 1 r R 2 ) 电势(3) 金属球的电势9.27 如题 9.27 图所示,在平行板电容器的一半容积内充入相对介电常数为 r 的电介质.试求:在有电介质部分和无电介质部分极板上自由电荷面密度的比值.解 : 如题 9.27 图所示,充满电介质部分场强为 E 2 ,真空部分场强为 E 1 ,自由电荷面密度分别为2 与1由 D dSq 0 得D1 1,D2 2而D1 0E 1 ,D2 0 rE2∴20 r E2r10 E1题 9.27 图题9.28图9.28两个同轴的圆柱面,长度均为l,半径分别为R1和R2(R2>R1),且l>>R2-R1,两柱面之间充有介电常数的均匀电介质 . 当两圆柱面分别带等量异号电荷Q 和- Q 时,求:(1)在半径 r 处( R1< r < R2=,厚度为dr,长为l的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量;(2)电介质中的总电场能量;(3)圆柱形电容器的电容.解 :取半径为r的同轴圆柱面( S)则D S rlD( S)d2π当 (R1r R2 ) 时,q Q∴(1)电场能量密度QD2πrlD 2Q 2w22l228π r薄壳中 dW wdQ 2Q 2 dr22l22πrdrl8π r4π rl(2)电介质中总电场能量(3) 电容:∵Q 2W2CQ 2πl∴C22W ln( R2 / R1 )题9.29 图9.29如题9.29图所示,C1=0.25F,C2 =0.15 F,C3 =0.20 F .C1上电压为50V.求:U AB.解 :电容C1上电量电容 C 2与 C3并联 C 23 C 2C3其上电荷 Q 23Q1∴Q23C1U 125 50 U 2C 2335C 239.30C1和 C 2两电容器分别标明“200 pF 、 500 V ”和“ 300 pF 、 900 V ”,把它们串联起来后等值电容是多少?如果两端加上 1000 V的电压,是否会击穿?解 : (1)C1与 C 2串联后电容(2)串联后电压比U 1C23,而 U 1 U 2 1000U 2C12∴U 1600 V, U 2400V即电容 C1电压超过耐压值会击穿,然后 C 2也击穿.9.31 半径为R1 =2.0cm 的导体球,外套有一同心的导体球壳,壳的内、外半径分别为R2=4.0cm和 R3=5.0cm,当内球带电荷 Q =3.0×10-8C时,求:(1)整个电场储存的能量;(2)如果将导体壳接地,计算储存的能量;(3)此电容器的电容值.解: 如图,内球带电Q,外球壳内表面带电Q ,外表面带电 Q题9.31 图(1) 在r R1和 R2r R3区域在 R1 r R2时QrE134π0 rr R3时QrE234π0 r∴在 R1r R2区域在 r R3区域∴总能量 W W1 W2Q 2(11 1 )8π0R1R2R3(2) 导体壳接地时,只有 R 1 r R 2 时 E Qr , W 2 0 4π 0 r 3∴W W 1 Q 2 ( 1 1 ) 1.01 10 4 J 8π 0 R 1 R 2(3) 电容器电容C 2W 4π 0 /( 1 1 ) Q 2 R 1 R 2。
大学物理第十章课后习题答案

10.1 解:O O B B B B 出圆弧进++=0其中两直线电流在O 点产生的磁感应强度为0,1/4圆电流在O 点产生的磁感应强度方向垂直纸面向里,大小为R IRIB B O 841200μμ=⨯==圆弧。
10.2解:d b c a B B B B B +++=中心如图a I a I B B a πμπμ0022/22224)45cos 22===︒(中心过中心平行于ad (如图竖直向上)。
10.3 解:1PI B方向垂直纸面向里,大小为d I πμ2102PI B方向纸面向右,大小为d I πμ220 21PI PI P B B B +=T I I d d I d I B B B PI PI P 52221022021022102.72)2()2(21-⨯=+=+=+=πμπμπμ方向在过P 垂直于1I 的平面内与2PI B 夹α角︒===--7.33)32()(1121tna B B tna PI PI α10.4解:两线圈在P 点产生的磁感应强度方向都在两圆心的连线上指向小圆(向左)}])([])([{22322122223221211021x b R R I x b R R I B B B PR PR P -++++=+=μ10.5 解:a bc d2I P 2PIra Idy r dya I rdI B d πμπμπμ422200===20044cos r a Iydyr y r a Idy dB dB x πμπμα=== 20044sin r a Ixdyr x r a Idy dB dB y πμπμα===由对称性可知⎰==0x Px dB Bx a a I x a x a a I x y x a Ix y x dy a Ix y x a Ixdy r a Ixdy dB B aaa aa a aa y Py 101101022022020tan 2)tan (tan 4]tan 144)(44--------=--==+=+===⎰⎰⎰⎰πμπμπμπμπμπμ10.6解:对于无限大平面载流导体板,即上题结果中a x <<,2π=x a arctgi u a I u B 00214==∴(i 为电流密度)(1) 在两面之间1i 产生的磁感强度大小为10121i u B =,方向垂直纸面向里。
大学物理课后习题答案 北京邮电大学出版社

习题五5-1 振动和波动有什么区别和联系?平面简谐波动方程和简谐振动方程有什么不同?又有什么联系?振动曲线和波形曲线有什么不同?解: (1)振动是指一个孤立的系统(也可是介质中的一个质元)在某固定平衡位置附近所做的往复运动,系统离开平衡位置的位移是时间的周期性函数,即可表示为;波动是振动在连续介质中的传播过程,此时介质中所有质元都在各自的平衡位置附近作振动,因此介质中任一质元离开平衡位置的位移既是坐标位置,又是时间的函数,即.(2)在谐振动方程中只有一个独立的变量时间,它描述的是介质中一个质元偏离平衡位置的位移随时间变化的规律;平面谐波方程中有两个独立变量,即坐标位置和时间,它描述的是介质中所有质元偏离平衡位置的位移随坐标和时间变化的规律.当谐波方程中的坐标位置给定后,即可得到该点的振动方程,而波源持续不断地振动又是产生波动的必要条件之一.(3)振动曲线描述的是一个质点的位移随时间变化的规律,因此,其纵轴为,横轴为;波动曲线描述的是介质中所有质元的位移随位置,随时间变化的规律,其纵轴为,横轴为.每一幅图只能给出某一时刻质元的位移随坐标位置变化的规律,即只能给出某一时刻的波形图,不同时刻的波动曲线就是不同时刻的波形图.5-2 波动方程=cos[()+]中的表示什么?如果改写为=cos (),又是什么意思?如果和均增加,但相应的[()+]的值不变,由此能从波动方程说明什么?解: 波动方程中的表示了介质中坐标位置为的质元的振动落后于原点的时间;则表示处质元比原点落后的振动位相;设时刻的波动方程为则时刻的波动方程为其表示在时刻,位置处的振动状态,经过后传播到处.所以在中,当,均增加时,的值不会变化,而这正好说明了经过时间,波形即向前传播了的距离,说明描述的是一列行进中的波,故谓之行波方程.5-3 波在介质中传播时,为什么介质元的动能和势能具有相同的位相,而弹簧振子的动能和势能却没有这样的特点?解: 我们在讨论波动能量时,实际上讨论的是介质中某个小体积元内所有质元的能量.波动动能当然是指质元振动动能,其与振动速度平方成正比,波动势能则是指介质的形变势能.形变势能由介质的相对形变量(即应变量)决定.如果取波动方程为,则相对形变量(即应变量)为.波动势能则是与的平方成正比.由波动曲线图(题5-3图)可知,在波峰,波谷处,波动动能有极小(此处振动速度为零),而在该处的应变也为极小(该处),所以在波峰,波谷处波动势能也为极小;在平衡位置处波动动能为极大(该处振动速度的极大),而在该处的应变也是最大(该处是曲线的拐点),当然波动势能也为最大.这就说明了在介质中波动动能与波动势能是同步变化的,即具有相同的量值.题5-3图对于一个孤立的谐振动系统,是一个孤立的保守系统,机械能守恒,即振子的动能与势能之和保持为一个常数,而动能与势能在不断地转换,所以动能和势能不可能同步变化.5-4 波动方程中,坐标轴原点是否一定要选在波源处? =0时刻是否一定是波源开始振动的时刻? 波动方程写成=cos()时,波源一定在坐标原点处吗?在什么前提下波动方程才能写成这种形式?解: 由于坐标原点和开始计时时刻的选全完取是一种主观行为,所以在波动方程中,坐标原点不一定要选在波源处,同样,的时刻也不一定是波源开始振动的时刻;当波动方程写成时,坐标原点也不一定是选在波源所在处的.因为在此处对于波源的含义已做了拓展,即在写波动方程时,我们可以把介质中某一已知点的振动视为波源,只要把振动方程为已知的点选为坐标原点,即可得题示的波动方程.5-5 在驻波的两相邻波节间的同一半波长上,描述各质点振动的什么物理量不同,什么物理量相同?解: 取驻波方程为,则可知,在相邻两波节中的同一半波长上,描述各质点的振幅是不相同的,各质点的振幅是随位置按余弦规律变化的,即振幅变化规律可表示为.而在这同一半波长上,各质点的振动位相则是相同的,即以相邻两波节的介质为一段,同一段介质内各质点都有相同的振动位相,而相邻两段介质内的质点振动位相则相反.5-6 波源向着观察者运动和观察者向波源运动都会产生频率增高的多普勒效应,这两种情况有何区别?解: 波源向着观察者运动时,波面将被挤压,波在介质中的波长,将被压缩变短,(如题5-6图所示),因而观察者在单位时间内接收到的完整数目()会增多,所以接收频率增高;而观察者向着波源运动时,波面形状不变,但观察者测到的波速增大,即,因而单位时间内通过观察者完整波的数目也会增多,即接收频率也将增高.简单地说,前者是通过压缩波面(缩短波长)使频率增高,后者则是观察者的运动使得单位时间内通过的波面数增加而升高频率.题5-6 图多普勒效应5-7 一平面简谐波沿轴负向传播,波长= m,原点处质点的振动频率为=2. 0 Hz,振幅=,且在=0时恰好通过平衡位置向轴负向运动,求此平面波的波动方程.解: 由题知时原点处质点的振动状态为,故知原点的振动初相为,取波动方程为则有5-8 已知波源在原点的一列平面简谐波,波动方程为=cos(),其中,,为正值恒量.求:(1)波的振幅、波速、频率、周期与波长;(2)写出传播方向上距离波源为处一点的振动方程;(3)任一时刻,在波的传播方向上相距为的两点的位相差.解: (1)已知平面简谐波的波动方程()将上式与波动方程的标准形式比较,可知:波振幅为,频率,波长,波速,波动周期.(2)将代入波动方程即可得到该点的振动方程(3)因任一时刻同一波线上两点之间的位相差为将,及代入上式,即得.5-9 沿绳子传播的平面简谐波的波动方程为=(10),式中,以米计,以秒计.求:(1)波的波速、频率和波长;(2)绳子上各质点振动时的最大速度和最大加速度;(3)求=处质点在=1s时的位相,它是原点在哪一时刻的位相?这一位相所代表的运动状态在=时刻到达哪一点?解: (1)将题给方程与标准式相比,得振幅,频率,波长,波速.(2)绳上各点的最大振速,最大加速度分别为(3)m处的振动比原点落后的时间为故,时的位相就是原点(),在时的位相,即π.设这一位相所代表的运动状态在s时刻到达点,则5-10 如题5-10图是沿轴传播的平面余弦波在时刻的波形曲线.(1)若波沿轴正向传播,该时刻,,,各点的振动位相是多少?(2)若波沿轴负向传播,上述各点的振动位相又是多少?解: (1)波沿轴正向传播,则在时刻,有题5-10图对于点:∵,∴对于点:∵,∴对于点:∵,∴对于点:∵,∴(取负值:表示点位相,应落后于点的位相)(2)波沿轴负向传播,则在时刻,有对于点:∵,∴对于点:∵,∴对于点:∵,∴对于点:∵,∴(此处取正值表示点位相超前于点的位相)5-11 一列平面余弦波沿轴正向传播,波速为5m·s-1,波长为2m,原点处质点的振动曲线如题5-11图所示.(1)写出波动方程;(2)作出=0时的波形图及距离波源处质点的振动曲线.解: (1)由题5-11(a)图知,m,且时,,∴,又,则题5-11图(a)取,则波动方程为(2) 时的波形如题5-11(b)图题5-11图(b) 题5-11图(c)将m代入波动方程,得该点处的振动方程为如题5-11(c)图所示.5-12 如题5-12图所示,已知=0时和=时的波形曲线分别为图中曲线(a)和(b) ,波沿轴正向传播,试根据图中绘出的条件求:(1)波动方程;(2)点的振动方程.解: (1)由题5-12图可知,,,又,时,,∴,而,,∴故波动方程为(2)将代入上式,即得点振动方程为题5-12图5-13 一列机械波沿轴正向传播,=0时的波形如题5-13图所示,已知波速为10 m·s -1,波长为2m,求:(1)波动方程;(2) 点的振动方程及振动曲线;(3) 点的坐标;(4) 点回到平衡位置所需的最短时间.解: 由题5-13图可知,时,,∴,由题知,,则∴(1)波动方程为题5-13图(2)由图知,时,,∴(点的位相应落后于点,故取负值)∴点振动方程为(3)∵∴解得(4)根据(2)的结果可作出旋转矢量图如题5-13图(a),则由点回到平衡位置应经历的位相角题5-13图(a)∴所属最短时间为5-14 如题5-14图所示,有一平面简谐波在空间传播,已知P点的振动方程为=cos().(1)分别就图中给出的两种坐标写出其波动方程;(2)写出距点距离为的点的振动方程.解: (1)如题5-14图(a),则波动方程为如图(b),则波动方程为题5-14图(2) 如题5-14图(a),则点的振动方程为如题5-14图(b),则点的振动方程为5-15 已知平面简谐波的波动方程为(SI).(1)写出= s时各波峰位置的坐标式,并求此时离原点最近一个波峰的位置,该波峰何时通过原点?(2)画出= s时的波形曲线.解:(1)波峰位置坐标应满足解得 (…)所以离原点最近的波峰位置为.∵故知,∴,这就是说该波峰在前通过原点,那么从计时时刻算起,则应是,即该波峰是在时通过原点的.题5-15图(2)∵,∴,又处,时,又,当时,,则应有解得,故时的波形图如题5-15图所示5-16 题5-16图中(a)表示=0时刻的波形图,(b)表示原点(=0)处质元的振动曲线,试求此波的波动方程,并画出=2m处质元的振动曲线.解: 由题5-16(b)图所示振动曲线可知,,且时,,故知,再结合题5-16(a)图所示波动曲线可知,该列波沿轴负向传播,且,若取题5-16图则波动方程为5-17 一平面余弦波,沿直径为14cm的圆柱形管传播,波的强度为×10-3J·m-2·s-1,频率为300 Hz,波速为300m·s-1,求:(1)波的平均能量密度和最大能量密度?(2)两个相邻同相面之间有多少波的能量?解: (1)∵∴(2)5-18 如题5-18图所示,和为两相干波源,振幅均为,相距,较位相超前,求:(1) 外侧各点的合振幅和强度;(2) 外侧各点的合振幅和强度解:(1)在外侧,距离为的点,传到该点引起的位相差为(2)在外侧.距离为的点,传到该点引起的位相差.5-19 如题5-19图所示,设点发出的平面横波沿方向传播,它在点的振动方程为;点发出的平面横波沿方向传播,它在点的振动方程为,本题中以m计,以s计.设=,= m,波速=·s-1,求:(1)两波传到P点时的位相差;(2)当这两列波的振动方向相同时,处合振动的振幅;*(3)当这两列波的振动方向互相垂直时,处合振动的振幅.解: (1)题5-19图(2)点是相长干涉,且振动方向相同,所以(3)若两振动方向垂直,又两分振动位相差为,这时合振动轨迹是通过Ⅱ,Ⅳ象限的直线,所以合振幅为5-20 一平面简谐波沿轴正向传播,如题5-20图所示.已知振幅为,频率为波速为.(1)若=0时,原点处质元正好由平衡位置向位移正方向运动,写出此波的波动方程;(2)若从分界面反射的波的振幅与入射波振幅相等,试写出反射波的波动方程,并求轴上因入射波与反射波干涉而静止的各点的位置.解: (1)∵时,,∴故波动方程为m题5-20图(2)入射波传到反射面时的振动位相为(即将代入),再考虑到波由波疏入射而在波密界面上反射,存在半波损失,所以反射波在界面处的位相为若仍以点为原点,则反射波在点处的位相为,因只考虑以内的位相角,∴反射波在点的位相为,故反射波的波动方程为此时驻波方程为故波节位置为故 (…)根据题意,只能取,即5-20 一驻波方程为=(SI),求:(1)形成此驻波的两列行波的振幅和波速;(2)相邻两波节间距离.解: (1)取驻波方程为故知,则,∴(2)∵所以相邻两波节间距离5-22 在弦上传播的横波,它的波动方程为=(13+ (SI)试写出一个波动方程,使它表示的波能与这列已知的横波叠加形成驻波,并在=0处为波节.解: 为使合成驻波在处形成波节,则要反射波在处与入射波有的位相差,故反射波的波动方程为5-23 两列波在一根很长的细绳上传播,它们的波动方程分别为=()(SI), =()(SI).(1)试证明绳子将作驻波式振动,并求波节、波腹的位置;(2)波腹处的振幅多大?=处振幅多大?解: (1)它们的合成波为出现了变量的分离,符合驻波方程特征,故绳子在作驻波振动.令,则,k=0,±1,±2…此即波腹的位置;令,则,…,此即波节的位置.(2)波腹处振幅最大,即为m;处的振幅由下式决定,即5-24 汽车驶过车站时,车站上的观测者测得汽笛声频率由1200Hz变到了1000 Hz,设空气中声速为330m·s-1,求汽车的速率.解: 设汽车的速度为,汽车在驶近车站时,车站收到的频率为汽车驶离车站时,车站收到的频率为联立以上两式,得5-25 两列火车分别以72km·h-1和54 km·h-1的速度相向而行,第一列火车发出一个600 Hz 的汽笛声,若声速为340 m·s-1,求第二列火车上的观测者听见该声音的频率在相遇前和相遇后分别是多少?解: 设鸣笛火车的车速为,接收鸣笛的火车车速为,则两者相遇前收到的频率为两车相遇之后收到的频率为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题10选择题(1) 对于安培环路定理的理解,正确的是:(A )若环流等于零,则在回路L 上必定是H 处处为零; (B )若环流等于零,则在回路L 上必定不包围电流;(C )若环流等于零,则在回路L 所包围传导电流的代数和为零; (D )回路L 上各点的H 仅与回路L 包围的电流有关。
[答案:C](2) 对半径为R 载流为I 的无限长直圆柱体,距轴线r 处的磁感应强度B () (A )内外部磁感应强度B 都与r 成正比;(B )内部磁感应强度B 与r 成正比,外部磁感应强度B 与r 成反比; (C )内外部磁感应强度B 都与r 成反比;(D )内部磁感应强度B 与r 成反比,外部磁感应强度B 与r 成正比。
[答案:B](3)质量为m 电量为q 的粒子,以速率v 与均匀磁场B 成θ角射入磁场,轨迹为一螺旋线,若要增大螺距则要()(A ) 增加磁场B ;(B )减少磁场B ;(C )增加θ角;(D )减少速率v 。
[答案:B](4)一个100匝的圆形线圈,半径为5厘米,通过电流为安,当线圈在的磁场中从θ=0的位置转到180度(θ为磁场方向和线圈磁矩方向的夹角)时磁场力做功为() (A );(B );(C );(D )14J 。
[答案:A]填空题(1)边长为a 的正方形导线回路载有电流为I ,则其中心处的磁感应强度 。
[答案:aIπμ220,方向垂直正方形平面](2)计算有限长的直线电流产生的磁场 用毕奥——萨伐尔定律,而 用安培环路定理求得(填能或不能)。
[答案:能, 不能](3)电荷在静电场中沿任一闭合曲线移动一周,电场力做功为 。
电荷在磁场中沿任一闭合曲线移动一周,磁场力做功为 。
[答案:零,正或负或零](4)两个大小相同的螺线管一个有铁心一个没有铁心,当给两个螺线管通以 电流时,管内的磁力线H 分布相同,当把两螺线管放在同一介质中,管内的磁力线H 分布将 。
[答案:相同,不相同]在同一磁感应线上,各点B ϖ的数值是否都相等?为何不把作用于运动电荷的磁力方向定义为磁感应强度B ϖ的方向?解: 在同一磁感应线上,各点B ϖ的数值一般不相等.因为磁场作用于运动电荷的磁力方向不仅与磁感应强度B ϖ的方向有关,而且与电荷速度方向有关,即磁力方向并不是唯一由磁场决定的,所以不把磁力方向定义为B ϖ的方向.题图(1)在没有电流的空间区域里,如果磁感应线是平行直线,磁感应强度B ϖ的大小在沿磁感应线和垂直它的方向上是否可能变化(即磁场是否一定是均匀的)? (2)若存在电流,上述结论是否还对?解: (1)不可能变化,即磁场一定是均匀的.如图作闭合回路abcd 可证明21B B ρϖ=∴ 21B B ρϖ=(2)若存在电流,上述结论不对.如无限大均匀带电平面两侧之磁力线是平行直线,但B ϖ方向相反,即21B B ρϖ≠.用安培环路定理能否求有限长一段载流直导线周围的磁场?答: 不能,因为有限长载流直导线周围磁场虽然有轴对称性,但不是稳恒电流,安培环路定理并不适用.在载流长螺线管的情况下,我们导出其内部nI B 0μ=,外面B =0,所以在载流螺线管外面环绕一周(见题图)的环路积分⎰外B L ϖ·d l ϖ=0但从安培环路定理来看,环路L 中有电流I 穿过,环路积分应为 ⎰外B L ϖ·d l ϖ=I 0μ这是为什么? 解: 我们导出nl B 0μ=内,0=外B 有一个假设的前提,即每匝电流均垂直于螺线管轴线.这时图中环路L 上就一定没有电流通过,即也是⎰∑==⋅LI l B 0d 0μϖϖ外,与⎰⎰=⋅=⋅Ll l B 0d 0d ϖϖϖ外是不矛盾的.但这是导线横截面积为零,螺距为零的理想模型.实际上以上假设并不真实存在,所以使得穿过L的电流为I ,因此实际螺线管若是无限长时,只是外B ϖ的轴向分量为零,而垂直于轴的圆周方向分量rIB πμ20=⊥,r 为管外一点到螺线管轴的距离. 题 图如果一个电子在通过空间某一区域时不偏转,能否肯定这个区域中没有磁场?如果它发 生偏转能否肯定那个区域中存在着磁场?解:如果一个电子在通过空间某一区域时不偏转,不能肯定这个区域中没有磁场,也可能存在互相垂直的电场和磁场,电子受的电场力与磁场力抵消所致.如果它发生偏转也不能肯定那个区域存在着磁场,因为仅有电场也可以使电子偏转.已知磁感应强度0.2=B Wb ·m-2的均匀磁场,方向沿x 轴正方向,如题9-6图所示.试求:(1)通过图中abcd 面的磁通量;(2)通过图中befc 面的磁通量;(3)通过图中aefd 面的磁通量.解: 如题图所示题图(1)通过abcd 面积1S 的磁通是 (2)通过befc 面积2S 的磁通量 (3)通过aefd 面积3S 的磁通量24.0545.03.02cos 5.03.0233=⨯⨯⨯=θ⨯⨯⨯=⋅=S B ϖϖΦWb (或24.0-Wb )题图如题图所示,AB 、CD 为长直导线,C B )为圆心在O 点的一段圆弧形导线,其半径为R .若通以电流I ,求O 点的磁感应强度.解:如题图所示,O 点磁场由AB 、C B )、CD 三部分电流产生.其中AB产生 01=B ϖCD产生RIB 1202μ=,方向垂直向里CD段产生 )231(2)60sin 90(sin 24003-πμ=-πμ=︒︒R I R I B ,方向⊥向里 ∴)6231(203210ππμ+-=++=R I B B B B ,方向⊥向里. 在真空中,有两根互相平行的无限长直导线1L 和2L ,相距0.1m ,通有方向相反的电流,1I =20A,2I =10A ,如题图所示.A ,B 两点与导线在同一平面内.这两点与导线2L 的距离均为5.0cm .试求A ,B 两点处的磁感应强度,以及磁感应强度为零的点的位置.题图解:如题图所示,A B ϖ方向垂直纸面向里 (2)设0=B ϖ在2L 外侧距离2L 为r 处 则02)1.0(220=-+rI r Iπμπμ 解得 1.0=r m题图如题图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连.已知圆环的粗细均匀,求环中心O 的磁感应强度.解: 如题图所示,圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生,但∞A 和∞B 在O 点产生的磁场为零。
且θ-πθ==21221R R I I 电阻电阻. 1I 产生1B ϖ方向⊥纸面向外πθπμ2)2(2101-=R I B ,2I 产生2B ϖ方向⊥纸面向里∴1)2(2121=-=θθπI I B B 有 0210=+=B B B ϖϖϖ在一半径R =1.0cm的无限长半圆柱形金属薄片中,自上而下地有电流I =5.0 A 通过,电流分布均匀.如题图所示.试求圆柱轴线任一点P 处的磁感应强度.题图解:因为金属片无限长,所以圆柱轴线上任一点P 的磁感应强度方向都在圆柱截面上,取坐标如题图所示,取宽为l d 的一无限长直电流l RII d d π=,在轴上P 点产生B ϖd 与R 垂直,大小为 ∴ 520202221037.6)]2sin(2[sin 22d cos -ππ-⨯=πμ=π--ππμ=πθθμ=⎰RI RI RI B x T ∴ i B ϖϖ51037.6-⨯= T氢原子处在基态时,它的电子可看作是在半径a =×10-8cm 的轨道上作匀速圆周运动,速率v =×108cm ·s -1.求电子在轨道中心所产生的磁感应强度和电子磁矩的值.解:电子在轨道中心产生的磁感应强度 如题图,方向垂直向里,大小为电子磁矩m P ϖ在图中也是垂直向里,大小为题图 题图两平行长直导线相距d =40cm ,每根导线载有电流1I =2I =20A ,如题图所示.求: (1)两导线所在平面内与该两导线等距的一点A 处的磁感应强度;(2)通过图中斜线所示面积的磁通量.(1r =3r =10cm,l =25cm).解:(1) 5210104)2(2)2(2-⨯=+=d I d I B Aπμπμ T 方向⊥纸面向外(2)取面元r l S d d =一根很长的铜导线载有电流10A ,设电流均匀分布.在导线内部作一平面S ,如题图所示.试计算通过S 平面的磁通量(沿导线长度方向取长为1m 的一段作计算).铜的磁导率0μμ=.解:由安培环路定律求距圆导线轴为r 处的磁感应强度 ∴202R IrB πμ=题 图磁通量 60020)(1042-===⋅=Φ⎰⎰πμπμIdr R Ir S d B Rs m ϖϖ Wb设题图中两导线中的电流均为8A ,对图示的三条闭合曲线a ,b ,c ,分别写出安培环路定理等式右边电流的代数和.并讨论:(1)在各条闭合曲线上,各点的磁感应强度B ϖ的大小是否相等? (2)在闭合曲线c 上各点的B ϖ是否为零?为什么?解: ⎰μ=⋅al B 08d ϖϖ(1)在各条闭合曲线上,各点B ϖ的大小不相等.(2)在闭合曲线C 上各点B ϖ不为零.只是B ϖ的环路积分为零而非每点0=B ϖ.题图题图题图中所示是一根很长的长直圆管形导体的横截面,内、外半径分别为a ,b ,导体内载有沿轴线方向的电流I ,且I 均匀地分布在管的横截面上.设导体的磁导率0μμ≈,试证明导体内部各点)(b r a <<的磁感应强度的大小由下式给出:解:取闭合回路r l π2= )(b r a <<则 ⎰π=⋅lr B l B 2d ϖϖ∴ )(2)(22220a b r a r I B --=πμ 一根很长的同轴电缆,由一导体圆柱(半径为a )和一同轴的导体圆管(内、外半径分别为b ,c )构成,如题图所示.使用时,电流I 从一导体流去,从另一导体流回.设电流都是均匀地分布在导体的横截面上,求:(1)导体圆柱内(r <a ),(2)两导体之间(a <r <b ),(3)导体圆筒内(b <r <c )以及(4)电缆外(r >c )各点处磁感应强度的大小解: ⎰∑μ=⋅LI l B 0d ϖϖ(1)a r < 2202RIr r B μπ=(2) b r a << I r B 02μπ=(3)c r b << Ibc b r I r B 0222202μμπ+---=(4)c r > 02=r B π题图题图在半径为R 的长直圆柱形导体内部,与轴线平行地挖成一半径为r 的长直圆柱形空腔,两轴间距离为a ,且a >r ,横截面如题图所示.现在电流I 沿导体管流动,电流均匀分布在管的横截面上,而电流方向与管的轴线平行.求:(1)圆柱轴线上的磁感应强度的大小;(2)空心部分轴线上的磁感应强度的大小.解:空间各点磁场可看作半径为R ,电流1I 均匀分布在横截面上的圆柱导体和半径为r 电流2I -均匀分布在横截面上的圆柱导体磁场之和. (1)圆柱轴线上的O 点B 的大小: 电流1I 产生的01=B ,电流2I -产生的磁场 ∴ )(222200r R a Ir B -=πμ(2)空心部分轴线上O '点B 的大小:电流2I 产生的02='B ,电流1I 产生的222022r R Ia a B -πμ=')(2220r R Ia -=πμ ∴ )(22200r R IaB -='πμ题图如题图所示,长直电流1I 附近有一等腰直角三角形线框,通以电流2I ,二者 共面.求△ABC 的各边所受的磁力.解: ⎰⨯=ABAB B l I F ϖϖϖd 2daI I d I aI F AB πμπμ22210102== 方向垂直AB 向左 ⎰⨯=CAAC B l I F ϖϖϖd 2 方向垂直AC 向下,大小为同理 BC F ϖ方向垂直BC 向上,大小∵ ︒=45cos d d r l∴ ⎰++πμ=︒πμ=ad aBC d ad I I r r I I F ln 245cos 2d 210120题图在磁感应强度为B ϖ的均匀磁场中,垂直于磁场方向的平面内有一段载流弯曲导线,电流为I ,如题9-19图所示.求其所受的安培力.解:在曲线上取l ϖd则 ⎰⨯=baab B l I F ϖϖϖd∵ l ϖd 与B ϖ夹角l ϖd <,2π>=B ϖ不变,B ϖ是均匀的.∴ ⎰⎰⨯=⨯=⨯=b ab aab B ab I B l I B l I F ωϖϖϖϖ)d (d方向⊥ab 向上,大小BI F ab=ab题图如题图所示,在长直导线AB 内通以电流1I =20A ,在矩形线圈CDEF 中通有电流2I =10 A ,AB 与线圈共面,且CD ,EF 都与AB 平行.已知a =9.0cm,b =20.0cm,d =1.0 cm ,求:(1)导线AB 的磁场对矩形线圈每边所作用的力;(2)矩形线圈所受合力和合力矩.解:(1)CD F ϖ方向垂直CD 向左,大小同理FE F ϖ方向垂直FE 向右,大小 CF F ϖ方向垂直CF 向上,大小为ED F ϖ方向垂直ED 向下,大小为5102.9-⨯==CF ED F F N(2)合力ED CFFE CD F F F F F ϖϖϖϖϖ+++=方向向左,大小为合力矩B P M m ϖϖϖ⨯=∵ 线圈与导线共面∴ B P m ϖϖ//0=M ϖ.题图边长为l =0.1m的正三角形线圈放在磁感应强度B =1T 的均匀磁场中,线圈平面与磁场方向平行.如题图所示,使线圈通以电流I =10A ,求: (1) 线圈每边所受的安培力; (2) 对O O '轴的磁力矩大小;(3)从所在位置转到线圈平面与磁场垂直时磁力所作的功.解: (1) 0=⨯=B l I F bc ϖϖϖB l I F ab ϖϖϖ⨯= 方向⊥纸面向外,大小为 B l I F ca ϖϖϖ⨯=方向⊥纸面向里,大小(2)IS P m =B P M m ϖϖϖ⨯= 沿O O '方向,大小为(3)磁力功 )(12ΦΦ-=I A∵ 01=Φ B l 2243=Φ ∴ 221033.443-⨯==B l I A J一正方形线圈,由细导线做成,边长为a ,共有N 匝,可以绕通过其相对两边中点的一个竖直轴自由转动.现在线圈中通有电流I ,并把线圈放在均匀的水平外磁场B ϖ中,线圈对其转轴的转动惯量为J .求线圈磁矩与磁场B ϖ的夹角为θ时,线圈受到的转动力矩.解:由线圈所受磁力矩B P Mm ϖϖϖ⨯=得到一长直导线通有电流1I =20A ,旁边放一导线ab ,其中通有电流2I =10A ,且两者共面,如题图所示.求导线ab 所受作用力对O 点的力矩.解:在ab 上取r d ,它受力ab F ⊥ϖd 向上,大小为 F ϖd 对O 点力矩F r M ϖϖϖ⨯=d M ϖd 方向垂直纸面向外,大小为题图电子在B =70×10-4T 的匀强磁场中作圆周运动,圆周半径r =3.0cm .已知B ϖ垂直于纸面向外,某时刻电子在A 点,速度v ϖ向上,如题图.(1) 试画出这电子运动的轨道; (2) 求这电子速度v ϖ的大小; (3)求这电子的动能k E .题图解:(1)轨迹如图(2)∵ rv mevB 2=∴ 7107.3⨯==m eBrv 1s m -⋅ (3) 162K 102.621-⨯==mv E J一电子在B =20×10-4T 的磁场中沿半径为R =2.0cm 的螺旋线运动,螺距h=5.0cm ,如题图.(1)求这电子的速度;(2)磁场B ϖ的方向如何?解: (1)∵ eBmv R θcos =θπcos 2v eBmh =题 图∴ 6221057.7)2()(⨯=+=meBh m eBR v π1s m -⋅ (3)磁场B ϖ的方向沿螺旋线轴线.或向上或向下,由电子旋转方向确定.在霍耳效应实验中,一宽1.0cm ,长4.0cm ,厚×10-3cm 的导体,沿长度方向载有3.0A 的电流,当磁感应强度大小为B =的磁场垂直地通过该导体时,产生×10-5V 的横向电压.试求:(1) 载流子的漂移速度; (2) 每立方米的载流子数目.解: (1)∵ evB eE H =∴lBU B E v HH ==l 为导体宽度,0.1=l cm∴ 425107.65.110100.1---⨯=⨯⨯==lB U v H -1s m ⋅ (2)∵ nevS I = ∴ evSI n =两种不同磁性材料做成的小棒,放在磁铁的两个磁极之间,小棒被磁化后在磁极间处于不同的方位,如题图所示.试指出哪一个是由顺磁质材料做成的,哪一个是由抗磁质材料做成的?解: 见题图所示.题图题图题图中的三条线表示三种不同磁介质的H B -关系曲线,虚线是B =H 0μ关系的曲线,试指出哪一条是表示顺磁质?哪一条是表示抗磁质?哪一条是表示铁磁质?答: 曲线Ⅱ是顺磁质,曲线Ⅲ是抗磁质,曲线Ⅰ是铁磁质.螺绕环中心周长L =10cm ,环上线圈匝数N =200匝,线圈中通有电流I =100 mA .(1)当管内是真空时,求管中心的磁场强度H ϖ和磁感应强度0B ϖ;(2)若环内充满相对磁导率r μ=4200的磁性物质,则管内的B ϖ和H ϖ各是多少?*(3)磁性物质中心处由导线中传导电流产生的0B ϖ和由磁化电流产生的B ϖ′各是多少?解: (1) I l H l∑=⋅⎰ϖϖd(2)200=H 1m A -⋅05.1===H H B o r μμμ T(3)由传导电流产生的0B ϖ即(1)中的40105.2-⨯=B T∴由磁化电流产生的05.10≈-='B B B T螺绕环的导线内通有电流20A ,利用冲击电流计测得环内磁感应强度的大小是Wb ·m -2.已知环的平均周长是40cm ,绕有导线400匝.试计算:(1) 磁场强度; (2) 磁化强度; *(3)磁化率; *(4)相对磁导率.解: (1)4102⨯===I lNnI H 1m A -⋅(2)51076.7⨯≈-=H BMμ1m A -⋅(3)8.38≈=HMx m (3)相对磁导率 8.391=+=m rx μ一铁制的螺绕环,其平均圆周长L =30cm ,截面积为1.0 cm 2,在环上均匀绕以300匝导线,当绕组内的电流为安培时,环内的磁通量为×10-6Wb .试计算:(1)环内的平均磁通量密度; (2)圆环截面中心处的磁场强度;解: (1) 2102-⨯=Φ=SB T (2) 0d NI l H =⋅⎰ϖϖ。
