四年级奥数.计数综合.几何计数

合集下载

四年级奥数第二讲图形的计数问题含答案

四年级奥数第⼆讲图形的计数问题含答案第⼆讲图形的计数问题⼀、知识点：⼏何图形计数问题往往没有显⽽易见的顺序，⽽且要数的对象通常是重叠交错的，要准确计数就需要⼀些智慧了．实际上，图形计数问题，通常采⽤⼀种简单原始的计数⽅法－⼀枚举法．具体⽽⾔，它是指把所要计数的对象⼀⼀列举出来，以保证枚举时⽆⼀重复、．⽆⼀遗漏，然后计算其总和．正确地解答较复杂的图形个数问题，有助于培养同学们思维的有序性和良好的学习习惯．⼆、典例剖析：例（1）数出右图中总共有多少个⾓分析：在∠AOB内有三条⾓分线OC1、OC2、OC3，∠AOB被这三条⾓分线分成4个基本⾓，那么∠AOB内总共有多少个⾓呢？⾸先有这4个基本⾓，其次是包含有2个基本⾓组成的⾓有3个（即∠AOC2、∠C1OC3、∠C2OB），然后是包含有3个基本⾓组成的⾓有2个（即∠AOC3、∠C1OB），最后是包含有4个基本⾓组成的⾓有1个（即∠AOB），所以∠AOB内总共有⾓：4＋3＋2＋1＝10（个）解：4＋3＋2＋1＝10（个）答：图中总共有10个⾓。

练⼀练：数⼀数右图中总共有多少个⾓？答案: 总共有⾓：10+9+8+…+4+3+2+1=55（个）例（2 ）数⼀数共有多少条线段？共有多少个三⾓形？分析：①要数多少条线段：先看线段AB、AD、AE、AF、AC、上各有2个分点，各分成3条基本线段，再看BC、MN、GH这3条线段上各有3个分点，各分成4条基本线段.所以图中总共有线段是：（3+2+1）×5+（4+3+2+1）×3=30+30=60（条）.②要数有多少个三⾓形，先看在△AGH中，在GH上有3个分点，分成基本⼩三⾓形有4个.所以在△AGH中共有三⾓形4+3+2+1=10（个）.在△AMN与△ABC中，三⾓形有同样的个数，所以在△ABC中三⾓形个数总共：（4+3+2+1）×3=10×3=30（个）解：：①在△ABC中共有线段是：（3+2+1）×5+（4+3+2+1）×3=30+30=60（条）②在△ABC中共有三⾓形是：（4+3+2+1）×3=10×3=30（个）答：在△ABC中共有线段60条，共有三⾓形30个。

小学四年级奥数知识点第八讲几何中的计数问题(二)

（1+2+3+…+m）×（1+2+3+…+n）.
例2 如右图数一数图中长方形的个数.
解：AB边上分成的线段有：
5+4+3+2+1=15.
BC边上分成的线段有：
3+2+1=6.
所以共有长方形：
（5+4+3+2+1）×（3+2+1）=15×6=90（个）.
二、数正方形
例3 数一数下页各个图中所有正方形的个数.（每个小方格为边长为1的正方形）
分析图Ⅰ中，边长为1个长度单位的正方形有：
2×2=4（个），边长为2个长度单位的正方形有：
1×1=1（个）.
所以，正方形总数为1×1+2×2=1+4=5（个）.
图Ⅱ中，边长为1个长度单位的正方形有3×3=9（个）；
最后把每一步中每个图形所包含三角形个数求出相加再乘以4就是整个图形中所包含的三角形的个数.
解：Ⅰ.在小矩形AEOH中：
①由一个三角形构成的有8个.
②由两个三角形构成的三角形有5个.
③由三个或三个以上三角形构成的三角形有5个.
这样在一个小矩形内有17个三角形.
Ⅱ.在由两个小矩形组合成的图形中，如矩形AEGD，共有5个三角形.
尖朝下的三角形的个数也是从1开始的连续自然数的和，它的第一个和恰是尖朝上的第二个和，依次各个和都比上一个和少最大的两个加数，以此类推直到零为止.
例7 页图数一数图中有多少个三角形.
解：参考例6所总结的规律把图中三角形分成尖朝上和尖朝下的两类：
Ⅰ.尖朝上的三角形有五种：

小学奥数教程之-几何计数(三)教师版 (162) 全国通用(含答案)

四年级奥数—几何中的计数问题

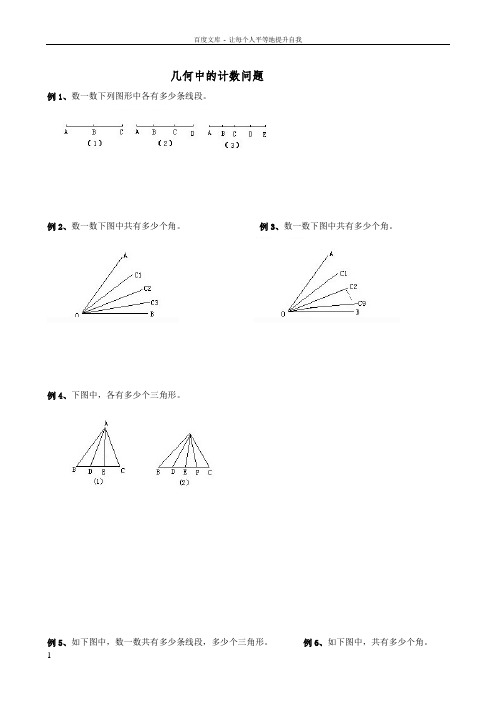
几何中的计数问题
例1、数一数下列图形中各有多少条线段。

例2、数一数下图中共有多少个角。

例3、数一数下图中共有多少个角。

例4、下图中，各有多少个三角形。

例5、如下图中，数一数共有多少条线段，多少个三角形。

例6、如下图中，共有多少个角。

例7、如下图，数一数共有多少个长方形。

例8、数一数下图中长方形的个数。

例9、数一数下面各图中所有正方形的个数。

例10、数一数下图中有多少个正方形。

例11、数一数下图三角形的个数。

例12、数一数下图中三角形的个数。

例13、数一数下图中三角形的个数。

例14、数一数下图中三角形的个数。

练：1、数一数下面各图中有多少条线段。

2、数一数下面各图中有多少个角。

3、数一数下面各图中，各有多少条线段。

4、数一数下面各图中，各有多少条线段，各有多少个三角形。

5、下面图中有多少个正方形。

6、下图中有多少个长方形。

7、下图中有多少个三角形。

8、下图中有多少个长方形。

9、下图中各有多少个三角形。

小学奥数几何计数(三) 精选练习例题含答案解析(附知识点拨及考点)

(完整word版)四年级奥数第二讲_图形的计数问题含答案,推荐文档

第二讲图形的计数问题一、知识点：几何图形计数问题常常没有不言而喻的次序，并且要数的对象往常是重叠交织的，要正确计数就需要一些智慧了．实质上，图形计数问题，往常采纳一种简单原始的计数方法－一列举法．详细而言，它是指把所要计数的对象一一列举出来，以保证列举时无一重复、．无一遗漏，而后计算其总和．正确地解答较复杂的图形个数问题，有助于培育同学们思想的有序性和优秀的学习习惯．二、典例解析：例（ 1）数出右中共有多少个角解析：在∠ AOB内有三条角分线 OC1、OC2、OC3，∠ AOB被这三条角分线分红 4 个基本角，那么∠ AOB内总合有多少个角呢？第一有这 4 个基本角，其次是包括有 2 个基本角构成的角有 3 个（即∠ AOC2、∠ C1OC3、∠ C2OB），而后是包括有 3 个基本角构成的角有 2 个（即∠ AOC3、∠C1OB），最后是包括有 4 个基本角构成的角有 1 个（即∠ AOB），所以∠ AOB内总合有角：4＋3＋2＋1＝10（个）解：4＋3＋ 2＋ 1＝10（个）答：中共有10 个角。

一：数一数右中共有多少个角？答案 :共有角：10+9+8+⋯ +4+3+2+1=55（个）例（ 2）数一数共有多少条线段？共有多少个三角形？解析：①要数多少条线段：先看线段3 条基本线段，再看 BC、 MN、GH 这AB、AD、 AE、AF、 AC、上各有3 条线段上各有 3 个分点，各分红2 个分点，各分红4 条基本线段 .所以图中总合有线段是：（3+2+1）× 5+（ 4+3+2+1）× 3=30+30=60（条） .②要数有多少个三角形，先看在△ AGH中，在 GH上有 3 个分点，分红基本小三角形有 4 个. 所以在△ AGH中共有三角形 4+3+2+1=10（个） . 在△ AMN与△ ABC中，三角形有相同的个数，所以在△ ABC中三角形个数总合：（4+3+2+1）× 3=10× 3=30（个）解：：①在△ ABC中共有线段是：（3+2+1）×5+（4+3+2+1）×3=30+30=60（条）②在△ ABC中共有三角形是：（4+3+2+1）× 3=10× 3=30（个）答：在△ ABC中共有线段60 条，共有三角形30 个。

4年级奥数几何计数问题例题

例1．用3根等长的火柴可以摆成一个等边三角形．如图19-1,用这样的等边三角形拼合成一个更大的等边三角形．如果这个大等边三角形昀每边由20根火柴组成，那么一共要用多少根火柴?[分析与解]把大的等边三角形分为20“层”分别计算火柴的根数：最上一“层”只用了3根火柴；从上向下数第二层用了3×2＝6根火柴；从上向下数第三层用了3×3＝9根火柴；……从上向下数第20层用了3×20＝60根火柴．所以，总共要用火柴3×(1+2+3+…+20)＝630根．【巩固提高】1．如下图,一个三角形分成36个小三角形.把每个小三角形涂上红色或蓝色,两个有公共边的小三角形要涂上不同的颜色,已知涂成红色的三角形比涂成蓝色的三角形多,那么多_____个.2.右图是由小立方体码放起来的,其中有一些小方体看不见.图中共有_____个小立方体.3.数一数,下图是由_____个小立方体堆成的.要注意那些看不见的.例2．如图19-2，用长短相同的火柴棍摆成3×1996的方格网，其中每个小方格的边都由一根火柴棍组成，那么一共需用多少根火柴棍?[分析与解]横放需1996×4根，竖放需1997×3根，共需1996×4+1997×3＝13975根．【巩固与提高】1．如图下图是一个4×328的长方形，每个小正方形的边长为1厘米，请你计算这个图形中所有线段的长度之和是多少？例3．图19-3是一个跳棋棋盘，请你计算出棋盘上共有多少个棋孔?[分析与解]把棋盘分割成一个平行四边形和四个小三角形，如下图．平行四边形中棋孔数为9×9＝81，每个小三角形中有10个棋孔，所以棋孔共有81+10×4＝121个．或直接数出有121个．例4．如图19-4，在桌面上，用6个边长为l的正三角形可以拼成一个边长为1的正六边形．如果在桌面上要拼出一个边长为6的正六边形，那么，需要边长为1的正三角形多少个？[分析与解]如图AB＝6，组成△AOB需要边长为1的正三角形共：1+3+5+7+9+11＝36个，而拼成边长为6的正六边形需要6个△AOB，因此总共需要边长为1的正三角形36×6＝216个．【巩固提高】如图一个正六边形，每条边上均与分布着998个点（不包括两个端点），分别连接不相邻的两条边上相互对应的两点，这样就把这个六边形分割成多个等边三角形，请问可以分割出多少个等边三角形？例5．如图19-5，其中的每条线段都是水平的或竖直的，边界上各条线段的长度依次为5厘米、7厘米、9厘米、2厘米和4厘米、6厘米、5厘米、1厘米．求图中长方形的个数，以及所有长方形面积的和．[分析与解]确定好长方形的长和宽，长方形就唯一确定，而图中只需确定好横向线段，竖向线段，即可．于是横向线段有(1+2+3+4)＝10种选法，竖向线段也有(1+2+3+4)＝10种选法，则共有10×10＝100个长方形．这些长方形的面积和为：(5+7+9+2+12+16+11+21+18+23)×(4+6+5+1+10+11+6+15+12+16)＝124×86＝10664(平方厘米)．例6．如图19-6，18个边长相等的正方形组成了一个3×6的方格表，其中包含“*”的长方形及正方形共有多少个?[分析与解]我们把所求的长、正方形按占有的行数分为三类，每类的长、正方形的个数相等．其中只占有下面一行的有如下12种情况：于是共有12×3＝36个正、长方形包含“*”．【巩固提高】1.下图中长方形（包括正方形）总个数是_____.2．如图19-10，AB，CD，EF，MN互相平行，则图中梯形个数与三角形个数的差是多少?[分析与解]图中共有三角形(1+2+3+4)×4＝40个，梯形(1+2+3+4)×(1+2+4)＝60个，梯形比三角形多60－40＝20个．例7．图19-7是由若干个相同的小正方形组成的．那么，其中共有各种大小的正方形多少个?[分析与解]每个4×4正方形中有：边长为1的正方形4×4个；边长为2的正方形3×3个；边长为3的正方形2×2个，边长为4的正方形1×1个．总共有4×4+3×3+2×2+1×1＝30个正方形．现在5个4×4的正方形，它们重叠部分是4个2×2的正方形．因此，图中正方形的个数是30×5－5×4＝130．例8．图19-8中共有多少个三角形?[分析与解]边长为1的正三角形，有16个．边长为2的正三角形，尖向上的有3个，尖向下的也有3个．因此共有16+3+3＝22个．例9．图19-9是由18个大小相同的小正三角形拼成的四边形，其中某些相邻的小正三角形可以拼成较大的正三角形．那么，图中包含“*”的各种大小的正三角形一共有多少个?[分析与解]设小正三角形的边长为1，分三类计算计数包含*的三角形中，边长为1的正三角形有1个；边长为2的正三角形有4个，边长为3的正三角形有1个；因此，图中包含“*”的所有大、小正三角形一共有1+4+1＝6个．【巩固提高】1.图形中有_____个三角形.2．下图中共有_____个正方形.例10．在图19-1l中，共有多少个不同的三角形?[分析与解]下图中共有35个三角形，两个叠加成题中图形时，又多出5+5×2＝15个三角形，共计35×2+15＝85个三角形．【巩固提高】在下图中有多少条线段，有多少个三角形？例11．如图19-12，一块木板上有13枚钉子．用橡皮筋套住其中的几枚钉子，可以构成三角形、正方形、梯形等等，如图19-13．那么，一共可以构成多少个不同的正方形?[分析与解]按正方形的面积分类，设最小的正方形面积为1，面积为1的正方形有5个，如图a所示；面积为2的正方形有4个，如图b所示；面积为4的正方形有1个，如图c所示；还有1个面积比4大的正方形，如图d所示；于是，一共可以构成5+4+1+1＝11个不同的正方形．【巩固提高】1.如下图,方格纸上放了20枚棋子,以棋子为顶点的正方形共有_____个.3．如图19-14，用9枚钉子钉成水平和竖直间隔都为1厘米的正方阵．用一根橡皮筋将3枚不共线的钉子连结起来就形成一个三角形．在这样得到的三角形中，面积等于1平方厘米的三角形共有多少个?[分析与解]我们分三种情况来找面积为1平方厘米的三角形，这些三角形的底与高分别为1厘米或2厘米，利用正方形的对称性：(1)等腰直角三角形，如下图a所示有△AOC，△COE，△EOG，△GOA，△BOH，△DFB，△FHD，△HBF，共计8个，其中以AC，CF，FG，GA为底的各一个，以BF，DH为底的各两个．(2)直角三角形，如图b所示有△ACH，△CHD，△ACD，△DHA，△BEF，△BCE，△CEF，△CFB，△DEG，△DGH，△EGH，△EHD，△GAB，△GBF，△FAB，△FGA，共计16个，其中以AD、CH、BE、CF、DG、EH、FA、GB为斜边的各两个．(3)钝角三角形，如图c所示有△ABE，△AHE，△ADE，△AFE，△CBG，△CFG，△CDG，△CHG共计8个，其中以AE、CG为边的各四个．于是，综上所述，共有面积为1平方厘米的三角形32个．例12．如图19-15，木板上钉着12枚钉子，排成三行四列的长方阵．那么用橡皮筋共可套出多少个不同的三角形?[分析与解]我们先任意选取三个点，那么第1个点有12个位置可以选择，第2个点有11个位置可以选择，第3个点有10个位置可以选择，但是每6种选法对应的都是同一个图形，如下图，ABC，ACB，BAC，BCA，CAB，CBA 均是同一个图形．所以有12×11×10÷6＝220种选法，但是如果这3点在同一条直线上就无法构成三角形，其中每行有4种情况，共3×4；每列有1种情况，共1×4；2个边长为2的正方形的4条对角线，共4种情况．所以，可以套出220－3×4－1×4－4＝200个不同的三角形．【巩固提高】1.下图中的正方形被分成9个相同的小正方形,它们一共有16个顶点(共同的顶点算一个),以其中不在一条直线上的3个点为顶点,可以构成三角形.在这些三角形中,与阴影三角形有同样大小面积的有多少个?例13．如图19-16，正方形ACEG的边界上有A，B，C，D，E，F，G这7个点，其中B，D，F分别在边AC，CE，EG上．以这7个点中的4个点为顶点组成的不同四边形的个数等于多少?[分析与解]如果暂时不考虑点之间的排列位置关系，从7个点中任取4个点，则第一个点有7个位置可选，第二个点有6个位置可选，第三个点有5个位置可选，第四个点有4个位置可选，而不考虑先后，那么有4×3×2×1＝24种选法的实质是一样的，所有可能的组合数目应该是(7×6×5×4)÷24＝35．我们只要从中减去不能构成四边形的情形．对图19-16而言，任取4个点而又不构成四边形的情形只能发生在所取的4个点中有3个来自正方形ACEG的一条边，而另一个则任意选取的时候，例如选定A、B、C3点，第4个点无论如何选取都不能构成四边形．正方形的4条边中有3条都存在这样的情况．而每次这种情况发生时，第4个顶点的选取有4种可能．所取的顶点只有4个，因此不可能出现同时选择了2条有3点共线的边的情况．那么需要排除的情况有4×3＝12种．所以，满足题意的四边形个数有35－12＝23个．【巩固提高】如下图，在三角形AFJ的边界上有A，B，C，……J，K，L共12个点，以这12个点中的3个点位顶点的三角形共有多少个？。

小学奥数全国推荐四年级奥数通用学案附带练习题解析答案33几何计数(一)

年级四年级学科奥数版本通用版课程标题几何计数（一）在几何中，有许多有趣的计数问题，如计算线段的条数，满足某种条件的三角形的个数，若干个图分平面所成的区域数等等。

这类问题看起来似乎没有什么规律可循，但是通过认真分析，还是可以找到一些处理方法的。

通常采用一种简单原始的计数方法——枚举法。

具体而言，它是指把所要计数的对象一一列举出来，以保证枚举时无一重复、无一遗漏，然后计算其总数。

我们把直线上两点间的部分称为线段，这两个点称为线段的端点。

线段是组成三角形、正方形、长方形、多边形等图形最基本的元素。

因此，观察图形中的线段，探寻线段与线段之间、线段与其他图形之间的联系，对于了解图形、分析图形是很重要的。

数线段：如果一条线段上有n＋1个点（包括两个端点）（或含有n条“基本线段”），那么这n＋1个点把这条线段一共分成的线段总数为n＋（n－1）＋…＋2＋1条。

数角：数角与数线段相似，线段图形中的点类似于角图形中的边。

数三角形：可用数线段的方法（对应法）数如图所示的三角形，因为DE上有15条线段，每条线段的两端点与点A相连，可构成一个三角形，共有15个三角形。

同样一边在BC 上构成的三角形也有15个，所以图中共有30个三角形。

例1数出下图中有多少条线段。

A B CD分析与解：方法一：我们可以采用以线段左端点分类来数的方法。

以A点为左端点的线段有：AB、AC、AD 3条；以B点为左端点的线段有：BC、BD 2条；以C点为左端点的线段有：CD 1条。

所以，图中共有线段3＋2＋1＝6（条）。

方法二：把图中线段AB、BC、CD看做基本线段来数，那么，由1条基本线段构成的线段有：AB、BC、CD 3条；由2条基本线段构成的线段有：AC、BD 2条；由3条基本线段构成的线段有：AD 1条。

所以，图中一共有3＋2＋1＝6（条）线段。

例2 数出下图中总共有多少个角。

分析与解：在∠AOB 内有三条角分线1OC 、2OC 、3OC ，∠AOB 被这三条角分线分成4个基本角，那么∠AOB 内总共有多少个角呢？首先有OB C OC C OC C AOC 332211∠∠∠∠、、、这4个基本角，其次是由2个基本角组成的角有3个（即∠2AOC 、∠31OC C 、∠OB C 2），然后是由3个基本角组成的角有2个（即∠3AOC 、∠OB C 1），最后是由4个基本角组成的角有1个（即∠AOB ），所以∠AOB 内总共有角：4＋3＋2＋1＝10（个）。

小学四年级奥数第41讲：几何计数

2
★
1
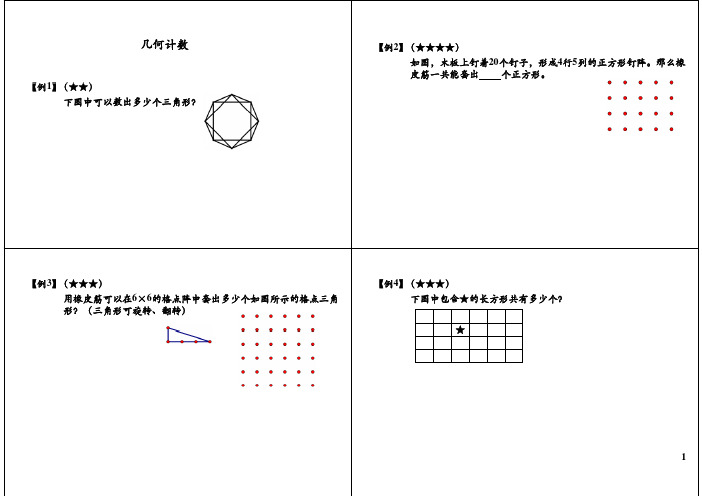
【例5】（★★★★）在下图中只包含一个★的长方形有多少个？
★ ★
【例6】（★★★★）如图，用9枚钉子钉成水平和竖直间隔都为1的正方阵。用一根橡皮筋将3枚不共线的钉子连接起来就形成一个三角形。其中面积为 1的三角形有多少个？
【例7】（★★★★★）图中一共有多少个三角形？
本讲总结枚举法——按照大小和位置对应法——找到对应关系容斥原理——不重不漏和面积相关——熟悉公式利用图形对称性重点例题：例4，例5，例6
几何计数
【例1】（★★）下图中可以数出多少个三角形？
【例2】（★★★★）如图，木板上钉着20个钉子，形成4行5列的正方形钉阵。那么橡皮筋一共能套出个正方形。
【例3】（★★★）用橡皮筋可以在6×6的格点阵中套出多少个如图所示的格点三角形？（三角形可旋转、翻转）
【例4】（★★★）下图中包含★的长方形共有多少个？

小学奥数知识体系之几何计数-四五年级组

几何计数几何计数分类数线段：如果一条线段上有n+1个点(包括两个端点)（或含有n个“基本线段”），那么这n+1个点把这条线段一共分成的线段总数为n+(n-1)+…+2+1条数角：数角与数线段相似，线段图形中的点类似于角图形中的边．数三角形：可用数线段的方法数如右图所示的三角形（对应法），因为DE上有15条线段，每条线段的两端点与点A相连，可构成一个三角形，共有15个三角形，同样一边在BC上的三角形也有15个，所以图中共有30个三角形．数长方形、平行四边形和正方形：一般的，对于任意长方形（平行四边形），若其横边上共有n条线段，纵边上共有m条线段，则图中共有长方形（平行四边形）mn个．【例1】数出右图中有多少条线段练习1：数出右图中有多少个锐角练习2：数一数下面图中各有多少个三角形。

练习3：从上海至青岛的某次直快列车，中途要停靠6个大站，这次列车有几种不同票价？【例题2】数一数，下图中有多少个正方形？（每个小方格是边长为1的正方形）练习1：下图中共有____个正方形．练习2：图中有______个正方形．【例3】下面的55⨯和64⨯图中共有____个正方形．练习1：在图中(单位：厘米)： ①一共有几个长方形?②所有这些长方形面积的和是多少?练习2：如图，其中的每条线段都是水平的或竖直的，边界上各条线段的长度依次为5厘米、7厘米、9厘米、2厘米和4 厘米、6厘米、5厘米、1厘米．求图中长方形的个数，以及所有长方形面积的和．【例4】如图，其中同时包括两个☆的长方形有个．练习1：在下图中，不包含☆的长方形有________个．（6级）练习2：图中含有“※”的长方形总共有________个．（6级）练习3：由20个边长为1的小正方形拼成一个45 长方形中有一格有“☆”图中含有“☆”的所有长方形(含正方形)共有个，它们的面积总和是． (第六届走美决赛试题)作业题：1：如图是由18个大小相同的小正三角形拼成的四边形．其中某些相邻的小正三角形可以拼成较大的正三角形若干个．那么，图中包含“*”号的大、小正三角形一共有______个．※※*2：如图AB，CD，EF，MN互相平行，则图中梯形个数与三角形个数的差是多少?3：图中共有多少个三角形？4：下图中的正方形被分成9个相同的小正方形，它们一共有16个顶点（共同的顶点算一个），以其中不在一条直线上的3个点为顶点，可以构成三角形．在这些三角形中，与阴影三角形有同样大小面积的有多少个？。

小学奥数几何计数(二) 精选练习例题含答案解析(附知识点拨及考点)

1.掌握计数常用方法；2.熟记一些计数公式及其推导方法；3.根据不同题目灵活运用计数方法进行计数．本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等，并渗透分类计数和用容斥原理的计数思想．一、几何计数在几何图形中，有许多有趣的计数问题，如计算线段的条数，满足某种条件的三角形的个数，若干个图分平面所成的区域数等等．这类问题看起来似乎没有什么规律可循，但是通过认真分析，还是可以找到一些处理方法的．常用的方法有枚举法、加法原理和乘法原理法以及递推法等．n 条直线最多将平面分成21223(2)2n n n ++++=++……个部分；n 个圆最多分平面的部分数为n (n -1)+2；n 个三角形将平面最多分成3n (n -1)+2部分；n 个四边形将平面最多分成4n (n -1)+2部分……在其它计数问题中，也经常用到枚举法、加法原理和乘法原理法以及递推法等．解题时需要仔细审题、综合所学知识点逐步求解．排列问题不仅与参加排列的事物有关，而且与各事物所在的先后顺序有关；组合问题与各事物所在的先后顺序无关，只与这两个组合中的元素有关．二、几何计数分类数线段：如果一条线段上有n +1个点(包括两个端点)（或含有n 个“基本线段”），那么这n +1个点把这条线段一共分成的线段总数为n +(n -1)+…+2+1条数角：数角与数线段相似，线段图形中的点类似于角图形中的边．数三角形：可用数线段的方法数如右图所示的三角形（对应法），因为DE 上有15条线段，每条线段的两端点与点A 相连，可构成一个三角形，共有15个三角形，同样一边在BC 上的三角形也有15个，所以图中共有30个三角形．ED CBA数长方形、平行四边形和正方形：一般的，对于任意长方形（平行四边形），若其横边上共有n 条线段，纵边上共有m 条线段，则图中共有长方形（平行四边形）mn 个．教学目标知识要点7-8-2.几何计数（二）例题精讲模块二、复杂的几何计数【例1】如下图在钉子板上有16个点，每相邻的两个点之间距离都相等，用绳子在上面围正方形，你可以得到个正方形．【考点】复杂的几何计数【难度】4星【题型】填空【关键词】学而思杯，2年级，第4题【解析】先看横着的正方形如下图⑴，可以得到94114++=个正方形，再看斜着的正方形如下图⑵可以得到4个正方形，如下图⑶可以得到2个正方形．这样一共可以得到144220++=个正方形．⑴⑵⑶<考点> 图形计数【答案】20个【巩固】如图，44⨯的方格纸上放了16枚棋子，以棋子为顶点的正方形有个．【解析】根据正方形的大小，分类数正方形．共能组成五种大小不同的正方形(如右图)．⨯的正方形：1个；⨯的正方形：4个；33⨯的正方形：9个；2211以11⨯正方形对角线为边长的正方形：4个；以12⨯长方形对角线为边长的正方形：2个．故可以组成9414220++++=(个)正方形．【巩固】下图是3×3点阵，同一行(列)相邻两个点的距离均为1。

四年级上册奥数知识点总结第7课-几何中的计数问题.doc

奥数知识点第7课・几何中的计数问题（1）笫七讲几何中的计数问题（一）几何中的计数问题包括：数线段、数角、数长方形、数正方形、数三角形、数综合图形等•通过这一讲的学习，可以帮助我们养成按照一定顺序去观察、思考问题的良好习惯，逐步学会通过观察、思考探寻事物规律的能力.一、数线段我们把直线上两点间的部分称为线段，这两个点称为线段的端点•线段是组成三角形、正方形、长方形、多边形等最基本的元素•因此，观察图形中的线段，探寻线段与线段之间、线段与其他图形之间的联系，对于了解图形、分析图形是很重要的.例1数一数下列图形中各有多少条线段.A B C A B C p A B C DE（1）（2）（3）例2数出右图中总共有多少个角•ClC2C3例3数一数右图中总共有多少个角?三、数三角形例4如右图中，各个图形内各有多少个三角形?A例5如右图中，数一数共有多少条线段？共有多少个三角形?例6如右图中，共有多少个角?习题七1 •数一数下图中，各有多少条线段?2.数一数下图中各有多少角?3•数一数下图中，各有多少条线段?4•数一数下图中，各有多少条线段，各有多少个三角形?(1) (2)课后作业:(1) (2)CB答案：第七讲几何中的计数问题（一）形、曙麟「專湃羯蟲聽辟思考问题的良好习惯, 逐歩学会通过观察、思考探寻事物规律的能力.一、数线段我们把直线上两点间的部分称为线段，这两个点称为线段的端点•线段是组成三角形、正方形、长方形、多边形等最基本的元素•因此，观察图形中的线敲犧評之间' 线段煮他图形之间的联系’对于了解图形' 分析例1数一数下列图形中各有多少条线段.B C A B C D A B C DE（1）（2）（3）分析要想使数出的每一个图形中线段的总条数，不重复、不遗漏，就需要按照一定的顺序、按照一定的规律去观察、去数•这样才不至于杂乱无章、毫无头绪•我们可以按照两种顺序或两种规律去数.第一种：按照线段的端点顺序去数，如上图（1）中，线段最左边的端点是A,即以A为左端点的线段有AB、AC两条以B为左端点的线段有BC—条，所以上图（1）中共有线段2 +1 = 3条•同样按照从左至右的顺序观察图（2）中，以A为左端点的线段有AB、AC、AD三条，以B为左端点的线段有BC、BD两条，以C为左端点曲线段有CD—条・E斤以上页图〔2）中共有殳腰为3 +2 +1 = 6条.第二种：按照基本线段多少的顺序去数•所谓基本线段是指一条大线段中若有n个分点，则这条大线段就被这n个分点分成n+1条小线段，这每条小线段称为基本线段•如上页图（2）中，线段AD上有两个分点B、C,这时分点B、C把AD 分成AB、BC^ CD三条基本线巖，那么线段AD总箕有参少条线段？首宪有三条基本线段，其次是包含有二条基本线段的是：AC、BD二条，然后是包含有三条基本线段的是AD这样一条•所以线段AD上总共有线段3+2 + 1 = 6条，又如上页图（3）中线段AE上有三个分点B、C、D,这样分点B、C、D把线段AE分为AB、BC、CD、DE四条基本线段，那么线段AE上总共有多少条线段？按照基本线段多少的顺序是：首先有4条基本线段，其次是包含有二条基本线段的有3条，然后是包含有三条基本线段的有2条，最后是包含有4条基本线段的有一条，所以线段AE 上总共有线段是4 + 3 + 2 + 1 = 10条.解：①2 + 1 = 3 （条）・②3 + 2+1 = 6 （条）・第一种：按照线段的端点顺序去数，如上图（1）中，线段最左边的端点是A,即以A 为左端点的线段有AB、AC两条以B为左端点的线段有BC—条，所以上图（1）中共有线段2 +1 = 3条•同样按照从左至右的顺序观察图（2）中，以A为左端点的线段有AB、AC、AD三条，以B为左端点的线段有BC、BD两条，以C为左端点商线段有CD—条•所以上页图⑵ 申共有妄腰为3 +2 +1 = 6条.第二种：按照基本线段多少的顺序去数•所谓基本线段是指一条大线段中若有门个分点，则这条大线段就被这n个分点分成门+1条小线段，这每条小线段称为基本线段•如上页图（2）中，线段AD上有两个分点B、C,这时分点B、C把AD 分成AB、BC、CD三条基本线農，邮么线段AD总唉有参少条线段？音晁有三条基本殘段，其次是包备有二条基本殁段的是：AC、BD二条，然后是包含有三条基未线段0勺是AD这样一秦•所以线腰AD丄总共有线段3 + 2 + 1 = 6条，又如上页图（3）中线段AE上有三个分点B、C、D,这样分点B、C、D把线段AE分为AB、BC、CD、DE四条基本线段，那么线段AE上总共有多少条线段？按照基本线段多少的顺序是：音先有4素量本线段，箕次是包•备有二累盘未殳陵馬有3氯然后是包鸟有三条基车塚凌6勺有2条，最后是窃含有4条基未线段的有一条，紡以冬段AE 上总共有线段是4丄3 + 2丄1 = 10条.解：①2 + 1 = 3 （条）・②3 + 2 + 1 = 6〔条）・③ 4+3+2+1=10（条）・小结：上述三例说明：要想不重复、不遗漏地数出所有线段，必须按照一定顺序有规律的去数，这个规律就是：线段的总条数等于从1开始的连续几个自然数的和，这个连续自然数的和的最大的加数是线段分点数加1或者是线段所有点数（包括线段的两个端点）减1 •也就是基本线段的条数•例如右图中线段AF上麻有点数（包岳两个端点A、F）共有6个，所以从1开始的连续自然数的和申最大的加数是6-1 = 5,或者线段AF上的分点有4个（B、C、D、E）•所以从1开始的连续自然数的和中最大的加数是4 + 1 = 5.也就是线段AF上基本线段（AB、BC、CD、DE、EF）的条数是5•所以线段AF上总共有线段的条数是5+4 +3 +2 + 1 =15 （条）・二数角例2数出右图中总共有多少个角.分析在ZAOB内有三条角分线OC1、OC2、OC3, ZAOB被这三条角分线分成4 个基本角，那么ZAOB内总共有多少个角呢？首先有这4个基本角，其次是包含有2个基本角组成的角有3个〔即ZAOC2. ZC1OC3、ZC2OB）,然后是包含有3 个基本角组成的角有2个（即ZAOC3、ZC1OB）,最后是包含有4个基本角组成的角有1个（即ZAOB）,所以ZAOB内总共有角：4+3+2+1=10（个）・解：4+3+2+1=10（个）・小结：数角的方法可以采用例1数线段的方法来数，就是角的总数等于从1 开始的几个连续自然数的和，这个和里面的最大的加数是角分线的条数加1,也就是基本角的个数.例3数一数右图中总共有多少个角？W：因为ZAOB内角分线0C1、OC2-OC9共有9条，即9+1二10个基本角.所以总共有角:10+9+8+…+4+3+2+1=55 （个）.三.数三角形例4如右图中，各个图形内各有多少个三角形?分析可以采用类似例1数线段的两种方法来数，如图（2）:第一种方法：先数以AB为一条边的三角形共有：△ABD、ZXABE、Z\ABF、ZXABC四个三角形.再数以AD为一条边的三角形共有：△ADE、ZXADF、ZXADC三个三角形.以AE为一条边的三角形共有：△AEF、ZXAEC二个三角形.最后以AF为一条边的三角形共有AAFC—个三角形.所以三角形的个数总共有4+3+2+1=10.第二种方法：先数图中小三角形共有：△ABD、ZXADE、Z\AEF、ZXAFC四个三角形.再数由两个小三角形组合在一起的三角形共有：△ABE、AADF. ZXAEC三个三角形，以三个小三角形组合在一起的三角形共有： △ABF 、ZXADC 二个三角形，最后数以四个小三角形组合在一起的只有AABC —个. 所以图中三角形的个数总共有：4+3+2+1=10 （个）・解：①3+2+1 二6 （个） ② 4+3+2+1=10 （个）・答：图（1）及图（2）中各有三角形分别是6个和10个.小结：计算三角形的总数也等于从1开始的几个连续自然数的和，其中最大例5如右图中，数一数共有多少条线段？共有多少个三角形?分析在数的过程中应充分利用上几例总结的规律，明确数什么？怎么数？这样两个问题•数：就是要数出图中基本线段（基本三角形）的条数，算：就是以基本线段（基本三角形）条数为最大加数的从1开始的连续几个自然数的和.①要数多少条线段：先看线段AB 、AD 、AE 、AF 、AC 、上各有2个分点，各分成3条基本线段，再看BC 、MN 、GH 这3条线段上各有3个分点，各分成4条基本线最・0T 以鹵中总共有第段是:（3+2+1） X5+（4+3+2+1） X 3二30+30=60 （条）.②要数有多少个三角形，先看在AAGH 中，在GH 上有3个分点，分成基本小三的加数就是三角形一边上的分点数加1,也就是三角形这边上分成的基本线段的条数.角形有4个•所以在ZXAGH中共有三角形4+3+2+1=10 （个）•在ZXAMN与ZXABC 中，三角形有同样的个数，所以在ZXABC中三角形个数总共：〔4+3+2+1） X 3=10X3=30 （个）・解：①在△ ABC中共有线段是：〔3+2+1） X5+（4+3+2+1） X 3二30+30二60〔条）②在△ABC中共有三角形是：（4+3+2+1） X 3=10X3=30〔个）・例6如右图中，共有多少个角？分析本题虽然与上几例有区别，但仍可以采用上几例所总结的规律去解决.Zl、Z2、Z3、Z4我们可视为4个基本角，由2个基本角组成的有：Z1与Z2、Z2与Z3、Z3与Z4、Z4与Z1,共4个角•由3个基本角组成的角有：Z 1、上2与Z3； Z2. Z3与上4； Z3、上4与Z1；上4、Z1与上2,共4个角，由4个基本角组成的角只有一个.所以图中总共有角是：4X3+1二13 （个）・解：所以图中共有角是：4X3+1二13 （个）・小结：由本题可以推出一般情况：若周角中含有n个基本角，那么它上面角的总薮是n （n-1） +1.课后作业答案：习题七解答1 •①在AB线段上有4个分点，所以它上面线段的总条数为：5+4+3+2+1二15 （条）・②在线段AB上有3个分点，所以它上面线段的总条数为：4+3+2+1=10 （条）・在线段CD上有4个分点：所以它上面线段的总条数为：5+4+3+2+1=15 （条）・・・・整个图（2）共有线段10+15二25 （条）・③在线段AB上有3个分点，它上面线段的条数为:44-34-2+1=10 （条）・在线段CD上有2个分点，它上面线段的条数为:占。

石头老师四年级奥数竞赛班图形计数专题

航创四年级竞赛班图形计数专题一、知识点：几何图形计数问题往往没有显而易见的顺序，而且要数的对象通常是重叠交错的，要准确计数就需要一些智慧了．实际上，图形计数问题，通常采用一种简单原始的计数方法－一枚举法．具体而言，它是指把所要计数的对象一一列举出来，以保证枚举时无一重复、．无一遗漏，然后计算其总和．正确地解答较复杂的图形个数问题，有助于培养同学们思维的有序性和良好的学习习惯．二、典例剖析：例（1）数出右图中总共有多少个角练一练：数一数右图中总共有多少个角？例（2 ）数一数共有多少条线段？共有多少个三角形？练一练：共有多少个三角形？例（3）数一数图中长方形的个数练一练：数一数图中长方形的个数例（4）数一数图中有多少个正方形（其中每个小方格都是边长为1个长度单位的正方形）.练一练：下图共有几个正方形?例（5）数一数图中三角形的个数练一练：数一数图中三角形的个数例（6）数一数图中一共有多少个三角形？练一练：数一数图中一共有多模拟测试（ 2 ）一、填空题（每小题5分）1、.下列图形各有几条线段( )条 ( )条 ( )条2、一条直线上共有50个点,可以数出( )条线段.3、数一数下图共有( )条线段.( )条. ( )条.4、下图中各有（）个三角形.5、数一数下图有（）个长方形.6、右图一共有( )个长方形?7、右图一共有( )个正方形？8、下图共有( )个平行四边形.9、一共有( )个梯形.10、下图共有( )个三角形.二、简答题(每小题10分)1、右图的图形中一共有多少个三角形?2、下图共有几个正方形?3、下图共有多少个长方形?4、下图中一共有多少个三角形?5、下图共有几个三角形?.6. 下图中有几个长方形？7.下图中有几个含星号的三角形或者长方形？模拟测试（ 2 ）解答一、填空题1、a有10条, b有15条, c有21条.2、50⨯49÷2=1225(条).3、36; 27.4. 33;5、30个.图中AB边上共有线段4+3+2+1=10条.BC边上共有线段: 2+1=3(条),把AB 上的每一条线段作为长, BC边上每一条线段作为宽,每一个长配一个宽,就组成一个长方形,所以图中共有长方形为:(4+3+2+1)⨯(2+1)=10⨯3=30(个).6、一共有64个.7、一共有18个.解:分三类计算,边长是1的正方形有2+4=13(个),边长为2的正方形有4(个),边长为3 的正方形有1个.因此,图中共有正方形13+4+1=18(个).8、315个=7(=÷⨯÷⨯(个)⨯⨯)215315621)26(59、45个最好的办法是先数出长方形和梯形的总数,再减去长方形的个数.长方形和梯形的总数为:(1+2+3+4+5+6)×(1+2)=63(个)长方形的个数为:(1+2+3)×(1+2)=18(个)梯形的总数为:63-18=45(个)10、 126个Ⅰ.尖朝上的三角形有五种:=8+7+6+5+4=30(1)W①上=7+6+5+4=22(2)W②上(3)W=6+5+4=15③上(4)W=5+4=9④上(5)W=4⑤上∴尖朝上的三角形共有:30+22+15+9+4=80(个)Ⅱ.尖朝下的三角形有四种:(1) W=3+4+5+6+7=25①下=2+3+4+5=14(2)W②下=1+2+3=6(3)W③下=1(4)W④下尖朝下的三角形共有25+14+6+1=46(个)∴80+46=126个.二、简答题1、解：①单个三角形有6个.②两个图形组成的有4个.③三个图形组成的有1个.④四个图形组成的有2个.⑤八个图形组成的有1个.答：一共有: 6+4+1+2+1=14个.2、解：一共有正方形52+42+32+22+12=25+16+9+4+1=55(个).答：一共有正方形55个。

小学奥数--几何计数25道

【题型】应用题【题目】用3根等长的火柴可以摆成一个等边三角形．如图19-1,用这样的等边三角形拼合成一个更大的等边三角形．如果这个大等边三角形昀每边由20根火柴组成，那么一共要用多少根火柴?【答案】630【解析】把大的等边三角形分为20“层”分别计算火柴的根数：最上一“层”只用了3根火柴；从上向下数第二层用了3×2＝6根火柴；从上向下数第三层用了3×3＝9根火柴；……从上向下数第20层用了3×20＝60根火柴．所以，总共要用火柴3×(1+2+3+…+20)＝630根．【难度】难度3【知识点】几何计数【题目】如图19-2，用长短相同的火柴棍摆成3×1996的方格网，其中每个小方格的边都由一根火柴棍组成，那么一共需用多少根火柴棍?【答案】13975【解析】横放需1996×4根，竖放需1997×3根，共需1996×4+1997×3＝13975根．【难度】难度2【知识点】几何计数【题目】图19-3是一个跳棋棋盘，请你计算出棋盘上共有多少个棋孔?【答案】【解析】把棋盘分割成一个平行四边形和四个小三角形，如下图．平行四边形中棋孔数为9×9＝81，每个小三角形中有10个棋孔，所以棋孔共有81+10×4＝121个．或直接数出有121个．【难度】难度3【知识点】几何计数【题目】如图19-4，在桌面上，用6个边长为l的正三角形可以拼成一个边长为1的正六边形．如果在桌面上要拼出一个边长为6的正六边形，那么，需要边长为1的正三角形多少个？【答案】【解析】如图AB＝6，组成△AOB需要边长为1的正三角形共：1+3+5+7+9+11＝36个，而拼成边长为6的正六边形需要6个△AOB，因此总共需要边长为1的正三角形36×6＝216个．【难度】难度4【知识点】几何计数【题目】如图19-5，其中的每条线段都是水平的或竖直的，边界上各条线段的长度依次为5厘米、7厘米、9厘米、2厘米和4厘米、6厘米、5厘米、1厘米．求图中长方形的个数，以及所有长方形面积的和．【答案】100，10664【解析】确定好长方形的长和宽，长方形就唯一确定，而图中只需确定好横向线段，竖向线段，即可．于是横向线段有(1+2+3+4)＝10种选法，竖向线段也有(1+2+3+4)＝10种选法，则共有10×10＝100个长方形．这些长方形的面积和为：(5+7+9+2+12+16+11+21+18+23)×(4+6+5+1+10+11+6+15+12+16)＝124×86＝10664(平方厘米)．【难度】难度4【知识点】几何计数【题目】如图19-6，18个边长相等的正方形组成了一个3×6的方格表，其中包含“*”的长方形及正方形共有多少个?【答案】36【解析】我们把所求的长、正方形按占有的行数分为三类，每类的长、正方形的个数相等．其中只占有下面一行的有如下12种情况：于是共有12×3＝36个正、长方形包含“*”．【难度】难度4【知识点】几何计数【题目】图19-7是由若干个相同的小正方形组成的．那么，其中共有各种大小的正方形多少个?【答案】130【解析】每个4×4正方形中有：边长为1的正方形4×4个；边长为2的正方形3×3个；边长为3的正方形2×2个，边长为4的正方形1×1个．总共有4×4+3×3+2×2+1×1＝30个正方形．现在5个4×4的正方形，它们重叠部分是4个2×2的正方形．因此，图中正方形的个数是30×5－5×4＝130．【难度】难度4【知识点】几何计数【题目】图19-8中共有多少个三角形?【答案】22【解析】边长为1的正三角形，有16个．边长为2的正三角形，尖向上的有3个，尖向下的也有3个．因此共有16+3+3＝22个．【难度】难度2【知识点】几何计数【题目】图19-9是由18个大小相同的小正三角形拼成的四边形，其中某些相邻的小正三角形可以拼成较大的正三角形．那么，图中包含“*”的各种大小的正三角形一共有多少个?【答案】6【解析】设小正三角形的边长为1，分三类计算计数包含*的三角形中，边长为1的正三角形有1个；边长为2的正三角形有4个，边长为3的正三角形有1个；因此，图中包含“*”的所有大、小正三角形一共有1+4+1＝6个．【难度】难度2【知识点】几何计数【题目】如图19-10，AB，CD，EF，MN互相平行，则图中梯形个数与三角形个数的差是多少?【答案】20【解析】图中共有三角形(1+2+3+4)×4＝40个，梯形(1+2+3+4)×(1+2+4)＝60个，梯形比三角形多60－40＝20个．【难度】难度3【知识点】几何计数【题目】在图19-1l中，共有多少个不同的三角形?【答案】85【解析】下图中共有35个三角形，两个叠加成题中图形时，又多出5+5×2＝15个三角形，共计35×2+15＝85个三角形．【难度】难度5【知识点】几何计数【题目】如图19-12，一块木板上有13枚钉子．用橡皮筋套住其中的几枚钉子，可以构成三角形、正方形、梯形等等，如图19-13．那么，一共可以构成多少个不同的正方形?【答案】11【解析】按正方形的面积分类，设最小的正方形面积为1，面积为1的正方形有5个，如图a所示；面积为2的正方形有4个，如图b所示；面积为4的正方形有1个，如图c所示；还有1个面积比4大的正方形，如图d所示；于是，一共可以构成5+4+1+1＝11个不同的正方形．【难度】难度3【知识点】几何计数【题目】如图19-14，用9枚钉子钉成水平和竖直间隔都为1厘米的正方阵．用一根橡皮筋将3枚不共线的钉子连结起来就形成一个三角形．在这样得到的三角形中，面积等于1平方厘米的三角形共有多少个?【答案】32【解析】我们分三种情况来找面积为1平方厘米的三角形，这些三角形的底与高分别为1厘米或2厘米，利用正方形的对称性：(1)等腰直角三角形，如下图a所示有△AOC，△COE，△EOG，△GOA，△BOH，△DFB，△FHD，△HBF，共计8个，其中以AC，CF，FG，GA为底的各一个，以BF，DH为底的各两个．(2)直角三角形，如图b所示有△ACH，△CHD，△ACD，△DHA，△BEF，△BCE，△CEF，△CFB，△DEG，△DGH，△EGH，△EHD，△GAB，△GBF，△FAB，△FGA，共计16个，其中以AD、CH、BE、CF、DG、EH、FA、GB为斜边的各两个．(3)钝角三角形，如图c所示有△ABE，△AHE，△ADE，△AFE，△CBG，△CFG，△CDG，△CHG共计8个，其中以AE、CG为边的各四个．于是，综上所述，共有面积为1平方厘米的三角形32个．【难度】难度4【知识点】几何计数【题目】如图19-15，木板上钉着12枚钉子，排成三行四列的长方阵．那么用橡皮筋共可套出多少个不同的三角形?【答案】200【解析】我们先任意选取三个点，那么第1个点有12个位置可以选择，第2个点有11个位置可以选择，第3个点有10个位置可以选择，但是每6种选法对应的都是同一个图形，如下图，ABC，ACB，BAC，BCA，CAB，CBA均是同一个图形．所以有12×11×10÷6＝220种选法，但是如果这3点在同一条直线上就无法构成三角形，其中每行有4种情况，共3×4；每列有1种情况，共1×4；2个边长为2的正方形的4条对角线，共4种情况．所以，可以套出220－3×4－1×4－4＝200个不同的三角形．【难度】难度2【知识点】几何计数【题目】如图19-16，正方形ACEG的边界上有A，B，C，D，E，F，G这7个点，其中B，D，F分别在边AC，CE，EG上．以这7个点中的4个点为顶点组成的不同四边形的个数等于多少?【答案】12【解析】如果暂时不考虑点之间的排列位置关系，从7个点中任取4个点，则第一个点有7个位置可选，第二个点有6个位置可选，第三个点有5个位置可选，第四个点有4个位置可选，而不考虑先后，那么有4×3×2×1＝24种选法的实质是一样的，所有可能的组合数目应该是(7×6×5×4)÷24＝35．我们只要从中减去不能构成四边形的情形．对图19-16而言，任取4个点而又不构成四边形的情形只能发生在所取的4个点中有3个来自正方形ACEG的一条边，而另一个则任意选取的时候，例如选定A、B、C3点，第4个点无论如何选取都不能构成四边形．正方形的4条边中有3条都存在这样的情况．而每次这种情况发生时，第4个顶点的选取有4种可能．所取的顶点只有4个，因此不可能出现同时选择了2条有3点共线的边的情况．那么需要排除的情况有4×3＝12种．所以，满足题意的四边形个数有35－12＝23个．【难度】难度4【知识点】几何计数【题目】数一数下列图形中各有多少条线段.【答案】15【解析】要想使数出的每一个图形中线段的总条数，不重复、不遗漏，就需要按照一定的顺序、按照一定的规律去观察、去数.这样才不至于杂乱无章、毫无头绪.我们可以按照两种顺序或两种规律去数.第一种：按照线段的端点顺序去数，如上图（1）中，线段最左边的端点是A，即以A为左端点的线段有AB、AC两条以B为左端点的线段有BC一条，所以上图（1）中共有线段2＋1＝3条.同样按照从左至右的顺序观察图（2）中，以A 为左端点的线段有AB、AC、AD三条，以B为左端点的线段有BC、BD两条，以C为左端点的线段有CD一条.所以上页图（2）中共有线段为3＋2＋1＝6条. 第二种：按照基本线段多少的顺序去数.所谓基本线段是指一条大线段中若有n 个分点，则这条大线段就被这n个分点分成n＋1条小线段，这每条小线段称为基本线段.如上页图（2）中，线段AD上有两个分点B、C，这时分点B、C把AD 分成AB、BC、CD三条基本线段，那么线段AD总共有多少条线段？首先有三条基本线段，其次是包含有二条基本线段的是：AC、BD二条，然后是包含有三条基本线段的是AD这样一条.所以线段AD上总共有线段3＋2＋1＝6条，又如上页图（3）中线段AE上有三个分点B、C、D，这样分点B、C、D把线段AE分为AB、BC、CD、DE四条基本线段，那么线段AE上总共有多少条线段？按照基本线段多少的顺序是：首先有4条基本线段，其次是包含有二条基本线段的有3条，然后是包含有三条基本线段的有2条，最后是包含有4条基本线段的有一条，所以线段AE上总共有线段是4＋3＋2＋1＝10条.解：①2＋1＝3（条）.② 3＋2＋1＝6（条）.③ 4＋3＋2＋1＝10（条）.小结：上述三例说明：要想不重复、不遗漏地数出所有线段，必须按照一定顺序有规律的去数，这个规律就是：线段的总条数等于从1开始的连续几个自然数的和，这个连续自然数的和的最大的加数是线段分点数加1或者是线段所有点数（包括线段的两个端点）减1.也就是基本线段的条数.例如右图中线段AF 上所有点数（包括两个端点A、F）共有6个，所以从1开始的连续自然数的和中最大的加数是6—1＝5，或者线段AF上的分点有4个（B、C、D、E）.所以从1开始的连续自然数的和中最大的加数是4＋1＝5.也就是线段AF上基本线段（AB、BC、CD、DE、EF）的条数是5.所以线段AF上总共有线段的条数是5＋4＋3＋2＋1＝15（条）.【难度】难度3【知识点】几何计数【题目】数出下图中总共有多少个角.【答案】10【解析】在∠AOB内有三条角分线OC1、OC2、OC3，∠AOB被这三条角分线分成4个基本角，那么∠AOB内总共有多少个角呢？首先有这4个基本角，其次是包含有2个基本角组成的角有3个（即∠AOC2、∠C1OC3、∠C2OB），然后是包含有3个基本角组成的角有2个（即∠AOC3、∠C1OB），最后是包含有4个基本角组成的角有1个（即∠AOB），所以∠AOB内总共有角：4＋3＋2＋1＝10（个）.解：4＋3＋2＋1＝10（个）.小结：数角的方法可以采用例1数线段的方法来数，就是角的总数等于从1开始的几个连续自然数的和，这个和里面的最大的加数是角分线的条数加1，也就是基本角的个数.【难度】难度3【知识点】几何计数【题目】数一数下图中总共有多少个角？【答案】55【解析】因为∠AOB内角分线OC1、OC2…OC9共有9条，即9+1=10个基本角. 所以总共有角：10+9+8+…+4+3+2+1=55（个）.【难度】难度3【知识点】几何计数【题目】如下图中，各个图形内各有多少个三角形？【答案】（1）6（2）10【解析】可以采用类似例1数线段的两种方法来数，如图（2）：第一种方法：先数以AB为一条边的三角形共有：△ABD、△ABE、△ABF、△ABC四个三角形.再数以AD为一条边的三角形共有：△ADE、△ADF、△ADC三个三角形.以AE为一条边的三角形共有：△AEF、△AEC二个三角形.最后以AF为一条边的三角形共有△AFC一个三角形.所以三角形的个数总共有4+3+2+1=10.第二种方法：先数图中小三角形共有：△ABD、△ADE、△AEF、△AFC四个三角形.再数由两个小三角形组合在一起的三角形共有：△ABE、△ADF、△AEC三个三角形，以三个小三角形组合在一起的三角形共有：△ABF、△ADC二个三角形，最后数以四个小三角形组合在一起的只有△ABC一个.所以图中三角形的个数总共有：4+3+2+1=10（个）.解：①3+2+1=6（个）② 4+3+2+1=10（个）.答：图（1）及图（2）中各有三角形分别是6个和10个.小结：计算三角形的总数也等于从1开始的几个连续自然数的和，其中最大的加数就是三角形一边上的分点数加1，也就是三角形这边上分成的基本线段的条数.【难度】难度3【知识点】几何计数【题目】如下图中，数一数共有多少条线段？共有多少个三角形？【答案】60,30【解析】分析在数的过程中应充分利用上几例总结的规律，明确数什么？怎么数？这样两个问题.数：就是要数出图中基本线段（基本三角形）的条数，算：就是以基本线段（基本三角形）条数为最大加数的从1开始的连续几个自然数的和.①要数多少条线段：先看线段AB、AD、AE、AF、AC、上各有2个分点，各分成3条基本线段，再看BC、MN、GH这3条线段上各有3个分点，各分成4条基本线段.所以图中总共有线段是：（3+2+1）×5+（4+3+2+1）×3=30+30=60（条）.②要数有多少个三角形，先看在△AGH中，在GH上有3个分点，分成基本小三角形有4个.所以在△AGH中共有三角形4+3+2+1=10（个）.在△AMN与△ABC 中，三角形有同样的个数，所以在△ABC中三角形个数总共：（4+3+2+1）×3=10×3=30（个）.解：①在△ABC中共有线段是：（3+2+1）×5+（4+3+2+1）×3=30+30=60（条）②在△ABC中共有三角形是：（4+3+2+1）×3=10×3=30（个）.【难度】难度3【知识点】几何计数【题目】如右图中，共有多少个角？【答案】13【解析】分析本题虽然与上几例有区别，但仍可以采用上几例所总结的规律去解决. ∠1、∠2、∠3、∠4我们可视为4个基本角，由2个基本角组成的有：∠1与∠2、∠2与∠3、∠3与∠4、∠4与∠1，共4个角.由3个基本角组成的角有：∠1、∠2与∠3；∠2、∠3与∠4；∠3、∠4与∠1；∠4、∠1与∠2，共4个角，由4个基本角组成的角只有一个.所以图中总共有角是：4×3+1=13（个）.解：所以图中共有角是：4×3+1=13（个）.小结：由本题可以推出一般情况：若周角中含有n 个基本角，那么它上面角的总数是 n （n-1）+1.【难度】难度4【知识点】几何计数【题目】在图中(单位：厘米)：①一共有几个长方形?②所有这些长方形面积的和是多少?374218125【答案】100,12384【解析】①一共有(4321)(4321)100+++⨯+++=(个)长方形；②所求的和是[][]51281(512)(128)(81)(5128)(1281)(51281)2473(24)(47)(73)(247)(473)(2473)+++++++++++++++++++⨯+++++++++++++++++++ 1448612384=⨯=(平方厘米)。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

几何计数
知识结构
一、公式计算法
几何计数内容很广，包括数线段的条数，角的个数，长方形、正方形、三角形、平行四边形、梯形等图形的个数，也包括数立体图形的个数。

图形的计数一般有两种思考方法：公式计算法和分类计数法。

三年级学习的线段、长方形和正方形的计数就属于公式计算法。

（1）一条线段有两个端点，若这条线段上有n个点，那么线段总数是
（n－1）＋（n＋2）＋…＋3＋2＋1
（2）如果一个长方形的长边上有n个小格，宽边上有m个小格，那么长方形的总数是
（1＋2＋3＋…＋n）×（1＋2＋…＋m）
（3）如果把正方形各边都n等分，那么正方形的总数是
n2＋（n－1）2＋（n－2）2＋…＋32＋22＋12
上面计算线数的方法也可用于计算角的个数，而且，根据这些计数方法在以后还可以类推出立体图形的计算方法。

二、对应法
将难以计数的数量与某种可计量的事物联系起来，只要能建立一一对应的关系，那么这两种事物在数量上是相同的．事实上插入法和插板法都是对应法的一种表现形式．
重难点
（1）分类数图形。

（2）对应法数图形。

例题精讲
一、分类数图形
【例 1】下图的两个图形（实线）是分别用10根和16根单位长的小棍围成的．如果按此规律（每一层比上面一层多摆出两个小正方形）围成的图形共用了60多根小棍，那么围成的图形有几层，共
用了多少根小棍？
【巩固】如图所示，用长短相同的火柴棍摆成3×1996的方格网，其中每个小方格的边都由一根火柴棍组成，那么一共需用多少根火柴棍?
【例 2】图中有______个正方形．
【巩固】数一数：图中共有________ 个正方形。

【例 3】右图中三角形共有个．
【巩固】数一数图中有_______个三角形．
【例 4】图中共有多少个三角形？
C
B A
【巩固】下图是由边长为1的小三角形拼成，其中边长为4的三角形有_____个。

【例 5】如图，每个小正方形的面积都是l 平方厘米。

则在此图中最多可以画出__________个面积是4平
方厘米的格点正方形(顶点都在图中交叉点上的正方形)。

【巩固】图中的每个小方格都是面积为1的正方形，面积为2的矩形有个。

二、对应法数图形
【例 6】在8×8的方格棋盘中，取出一个由三个小方格组成的“L”形（如图），一共有多少种不同的方法？
【例 7】在8×8的黑白相间染色的国际象棋棋盘中，以网格线为边的、恰包含两个白色小方格与一个黑色小方格的长方形共有多少个？
【巩固】用一张如图所示的纸片盖住66 方格表中的四个小方格，共有多少种不同的放置方法？
三、几何计数综合
【例 8】如图，连接一个正六边形的各顶点．问图中共有多少个等腰三角形(包括等边三角形)？
【巩固】如右图是一个跳棋棋盘，请你算算棋盘上共有多少个棋孔？
【例 9】如图所示，在直线AB上有7个点，直线CD上有9个点．以AB上的点为一个端点、CD上的点为另一个端点的所有线段中，任意3条线段都不相交于同一个点，求所有这些线段在AB与CD
之间的交点数．
A
B
C D 【巩固】图中可数出的三角形的个数为．
【例 10】用9个钉子钉成相互间隔为1厘米的正方阵(如右图)．如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形，这样得到的三角形中，面积等于1平方厘米的三角形的个数有多少？面
积等于2平方厘米的三角形有多少个？
【巩固】下图中的正方形被分成9个相同的小正方形，它们一共有16个顶点（共同的顶点算一个），以其中不在一条直线上的3个点为顶点，可以构成三角形．在这些三角形中，与阴影三角形有同样大小面积的有多少个？
【例 11】一张长方形纸片，长是宽的2倍，先对折成正方形，再对折成长方形，再对折成正方形，……，共对折7次，将纸打开展平，数一数用折痕分割成的正方形共有多少个？
【巩固】将正方形纸片由下往上对折，再由左向右对折，称为完成一次操作．按上述规则完成五次操作后，剪去所得的小正方形的左下角．问：当展开这张正方形纸后，一共有多少个小洞孔？
【例 12】一个圆上有12个点A1，A2，A3，…，A11，A12．以它们为顶点连三角形，使每个点恰好是一个三角形的顶点，且各个三角形的边都不相交．问共有多少种不同的连法?
A 12
A 11A 10A 9
A 8
A 7
A 6
A 5
A 4
A 3A 2
A 1
【随练1】数一数，图中有_________________个三角形。

【随练2】用3根等长的火柴可以摆成一个等边三角形．如图用这样的等边三角形拼合成一个更大的等边
三角形.如果这个大等边三角形的每边由20根火柴组成，那么一共要用多少根火柴?
【作业1】图中共有个三角形。

课堂检测
家庭作业
【作业2】右图是半个正方形，它被分成一个一个小的等腰直角三角形，图中，正方形有个，三角形有个。

【作业3】图中共有个正方形。

【作业4】用三根火柴可拼成一个小“△”，若用108根火柴拼成如图所示形状的大三角形，请你数一数共有多少个三角形？
【作业5】图中每个小正方形的边长都是l厘米，则在图中最多可以画出面积是3平方厘米的格点三角形(顶点在图中交叉点上的三角形)____个。

【作业6】如图所示，在边长为1的小正方形组成的4×4方格图中，共有25个格点。

在以格点为顶点的直角三角形中，两条直角边长分别是1和3的直角三角形共有个。

教学反馈
学生对本次课的评价
○特别满意○满意○一般
家长意见及建议
家长签字：。