二次函数 直角三角形
二次函数中求直角三角形的方法

求直角三角形的方法中的特定函数在二次函数中求直角三角形的方法中,可以使用特定的函数来计算直角三角形的各个属性,例如边长、角度、面积等。
这些函数可以帮助我们快速准确地解决直角三角形相关的问题。
本文将详细介绍几个常用的函数,包括函数的定义、用途和工作方式等。
1. 求斜边长的函数求斜边长的函数是用来计算直角三角形斜边的长度的。
根据勾股定理,直角三角形的斜边长度可以通过已知的两个直角边的长度来计算。
函数的定义如下:def hypotenuse(a, b):"""计算直角三角形的斜边长:param a: 直角三角形的直角边a的长度:param b: 直角三角形的直角边b的长度:return: 直角三角形的斜边长"""c = math.sqrt(a**2 + b**2)return c该函数接受两个参数a和b,分别表示直角三角形的直角边a和直角边b的长度。
函数内部使用勾股定理来计算斜边的长度,并返回结果。
2. 求角度的函数求角度的函数是用来计算直角三角形中某个角度的大小的。
根据三角函数的定义,我们可以通过已知的两个直角边的长度来计算角度的大小。
函数的定义如下:def angle(a, b):"""计算直角三角形中的角度:param a: 直角三角形的直角边a的长度:param b: 直角三角形的直角边b的长度:return: 直角三角形中的角度(弧度制)"""radians = math.atan(a / b)return radians该函数接受两个参数a和b,分别表示直角三角形的直角边a和直角边b的长度。
函数内部使用反正切函数来计算角度的大小,并返回结果(以弧度制表示)。
3. 求面积的函数求面积的函数是用来计算直角三角形的面积的。
根据直角三角形的面积公式,我们可以通过已知的两个直角边的长度来计算面积。
二次函数压轴之直角三角形的存在性问题,方法集锦

②
AF BG
BF CG
得
3 m
3
3 (m2 3m)
解得m1 2 7(舍去), m 2 7
C2 (2 7,5 7)
方法一:一线三角构相似
① ②合并
第一种情况
E
设C(m, m2 3m)如图可得AOB : BEC
C
AO BO 得
3
3
BE EC |m2 3m 3| |m|
①
解得m1 2 7, m 2 7
C=900, AC2 CB2 AB2 (m 3)2 (m2 3m)2 m2 (m2 3m 3)2 18
m1
0,
m2
3 2
17
,
m3
3 2
17
C(0, 0),C(3 17 , 2)C(3 17 , 2)
2
2
ቤተ መጻሕፍቲ ባይዱ
方法三:利用勾股定理
设C(m,m2 -3m)A(3,0)B(0,3) AB2 18, AC 2 (m 3)2 (m2 3m)2 BC 2 m2 (m2 3m 3)2
如图,抛物线y x2 3x,与x轴交于O、A,直线y=-x+3与y轴交于点B, 与抛物线交于A、D, 问:抛物线上是否存在点P使ABC为直角三角形,并求出P点的坐标
如图,抛物线y x2 3x,与x轴交于O、A,直线y=-x+3与y轴交于点B, 与抛物线交于A、D, 问:抛物线上是否存在点P使ABC为直角三角形,并求出P点的坐标
如图,抛物线y x2 3x,与x轴交于O、A,直线y=-x+3与y轴交于点B, 与抛物线交于A、D, 问:抛物线上是否存在点P使ABC为直角三角形,并求出P点的坐标
如图,抛物线y x2 3x,与x轴交于O、A,直线y=-x+3与y轴交于点B, 与抛物线交于A、D, 问:抛物线上是否存在点P使ABC为直角三角形,并求出P点的坐标
二次函数中等腰直角三角形 -回复

二次函数中等腰直角三角形 -回复
您好,关于二次函数中等腰直角三角形,我们可以通过以下步骤来解决:
1. 二次函数一般式:$y=ax^2+bx+c$。
2. 因为中位线长度为右腰,所以这个中位线对应的$x$可以用平移的方法求出:设中位线长度为$t$,则该中位线对应的$x$值为$-\frac{b}{2a}+t$。
3. 由直角三角形性质可知,斜边的平方等于直角腰的平方和,即$(\frac{t}{2})^2+(at^2+c)^2=(\frac{t}{2}+b)^2$。
4. 将第3步中的方程式化简后解出$t$,再带回第2步中的式子,求出该中位线对应的$x$值。
5. 根据对称性,可以得出第二条中位线的长度与第一条中位线相等,且对应的$x$值也相等。
6. 根据中位线长度与底边长度相等的定义,可以得出三角形的底边长度为$2\times(\frac{t}{2}+b)$。
7. 最终,我们就可以得出该等腰直角三角形的底边长、两条直角边长及其顶点的坐标。
希望以上解释能够解决您的问题,任何疑问,请随时追问。
二次函数存在性——直角三角形ppt课件
精选ppt课件
22
精选ppt课件
9
自学指导4(4分钟)
在抛物线y=x2-x-2上是否存在点P ,使△PAC是以AC为
直角边的三角形?若存在,求出所有符合条件的点P的
坐标;
情况 :当 一 PC 9A 00 时
y=x2-x-2
P1
(
3 2
,
7 2
)
情况 :当 二 PA 9 C00 时
P2
(
5 2
,
7 4
)
(-1,0)A O
④在抛物线上求点Q,使△BCQ是以BC为直角边的 直角三角形.
yx2 2xk
精选ppt课件 yx2 2xk
19
4.如图,矩形OABC的顶点A在x轴的正半轴上,点B的坐 标为(1,3),把矩形绕点B旋转一定的角度,使它的 顶点O落在x轴的点D处,已知M是第四象限内纵坐标为-1 的点,以M为顶点的抛物线正好过O、D两点. (1)求点D的坐标; (2)求抛物线的解析式; (3)在抛物线上是否存在点N,使以O、M、N为顶点的 三角形为直角三角形?若存在,求出所有满足条件的点 N的坐标;若不存在,请说明理由.
精选ppt课件
14
当堂训练(6分钟)
(2012•赤峰改编)如图,抛物线y=x2-bx-5与x轴交于A、 B两点(点A在点B的左侧),与y轴交于点C,点C与点F 关于抛物线的对称轴对称,直线AF交y轴于点E,|OC|: |OA|=5:1. (1)求抛物线的解析式; (2)求直线AF的解析式; (3)在直线AF上是否存在 点P,使△CFP是直角三角形? 若存在,求出P点坐标;若不 存在,说明理由.
(4)在抛物线上是否存在点M,
使△ACM是以AC为直角边的三
二次函数13---直角三角形问题

二次函数与直角三角形的探究问题“某函数图象(或对称轴)上是否存在一点,使之与另两个定点构成直角三角形或”的问题”(1):利用坐标系中两点距离公式,得到所求三角形三边平方的关系式(勾股定理);确定三角形中的直角顶点,若无法确定则分情况讨论;根据勾股定理得到方程,然后解方程,若方程有解,此点存在;否则不存在;(2):利用两直线垂直,k 值互为负倒数(121-=k k ),先确定点所在的直线表达式,将直线与抛物线的表达式联立方程组,若求出交点坐标,此点存在;否则不存在;注:若夹直角的两边中有一边与y 轴平行,此时不能使用斜率公式。
补救措施是:过余下的那一个点(没在平行于y 轴的那条直线上的点)直接向平行于y 的直线作垂线或过直角点作平行于y 轴的直线的垂线与另一相关图象相交,则相关点的坐标可轻松搞定。
如图,已知抛物线()02≠++=a c bx ax y 的对称轴为直线1-=x ,且经过()0,1A ,()3,0C 两点,与x 轴的另一个交点为B 。
(1)若直线n mx y +=经过C B ,两点,求抛物线和直线BC 的解析式;(2)设点P 为抛物线的对称轴1-=x 上的一个动点,求使BPC ∆为直角三角形的点P 的坐标.如图,直线3+=x y 与两坐标轴交于A ,B 两点,抛物线c bx x y ++-=2过点B A 、,且交x 轴的正半轴于点C 。
(1)直接写出B A 、两点的坐标;(2)求该抛物线的解析式和顶点D 的坐标;(3)在抛物线上是否存在动点P ,使得PAB △是以AB 为直角边的直角三角形?若存在,请求出所有符合条件的点P 的坐标;若不存在,请说明理由。
如图,直线2+=x y 与抛物线)0(62≠++=a bx ax y 相交于)25,21(A ,),4(cB 两点,点P 是线段AB 上异于B A 、的动点,过点P 作x PC ⊥轴于点D ,交抛物线于点C 。
(1)求该抛物线的解析式;(2)求PAC △为直角三角形时点P的坐标。
二次函数直角三角形问题

1、已知抛物线与x轴交于A、 B两点,与y轴交于点C.是否存在实数a,使得△ABC为直角三角形.若存在,请求出a的值;若不存在,请说明理由.由,解得,.∴点A、B的坐标分别为(-3,0),(,0).∴,,.∴,,.〈ⅰ〉当时,∠ACB=90°.由,得.解得.∴当时,点B的坐标为(,0),,,.于是.∴当时,△A BC为直角三角形.〈ⅱ〉当时,∠ABC=90°.2:如图,抛物线与x轴交与A(1,0),B(-3,0)两点,顶点为D。
交Y轴于C,在抛物线第二象限图象上是否存在一点M,使△MBC是以∠BCM为直角的直角三角形,若存在,求出点P的坐标。
若没有,请说明理由抛物线y=-x^2+bx+c与x轴交予A(1,0),B(-3,0)两点,得-1+b+c=0-9-3b+c=0得b=-2,c=3该抛物线的解析式y=-x^2-2x+3点C为(0.3)△ABC的面积为1/2AB*OC=6设在抛物线第二象限图象上存在点M(x0,y0)使△MBC是以∠BCM为直角的直角三角形则x0<0,y0>0y0=-x0^2-2x0+3(1)再由MB^2=MC^2+BC^2得(x0+3)^2+(y0-0)^2=(x0-0)^2+(y0-3)^2+(0+3)^2+(3-0)^2(2)(3)由(1)和(2)可解得y0=3,x0=0或者y0=4,x0=-1又x0<0,y0>0所以y0=4,x0=-1在抛物线第二象限图象上存在点M(-1,4)使△MBC是以∠BCM为直角的直角三角形.3:(2012云南)如图,在平面直角坐标系中,直线交x轴于点P,交y轴于点A.抛物线的图象过点E(-1,0),并与直线相交于A、B两点(1)求抛物线的解析式(关系式);(2)过点A作AC⊥AB交x轴于点C,求点C的坐标;(3)除点C外,在坐标轴上是否存在点M,使得△MAB是直角三角形?若存在,请求出点M的坐标;若不存在,请说明理由.解答:解:(1)直线解析式为y=x+2,令x=0,则y=2,∴A(0,2),∵抛物线y=x2+bx+c的图象过点A(0,2),E(﹣1,0),∴,解得.∴抛物线的解析式为:y=x2+x+2.(2)∵直线y=x+2分别交x轴、y轴于点P、点A,∴P(6,0),A(0,2),∴OP=6,OA=2.∵AC⊥AB,OA⊥OP,∴Rt△OCA∽Rt△OPA,∴,∴OC=,又C点在x轴负半轴上,∴点C的坐标为C(,0).(3)抛物线y=x2+x+2与直线y=x+2交于A、B两点,令x2+x+2=x+2,解得x1=0,x2=,∴B(,).如答图①所示,过点B作BD⊥x轴于点D,则D(,0),BD=,DP=6﹣=.点M在坐标轴上,且△MAB是直角三角形,有以下几种情况:①当点M在x轴上,且BM⊥AB,如答图①所示.设M(m,0),则MD=﹣m.∵BM⊥AB,BD⊥x轴,∴,即,解得m=,∴此时M点坐标为(,0);②当点M在x轴上,且BM⊥AM,如答图①所示.设M(m,0),则MD=﹣m.∵BM⊥AM,易知Rt△AOM∽Rt△MDB,∴,即,化简得:m2﹣m+=0,解得:x1=,x2=,∴此时M点坐标为(,0),(,0);(说明:此时的M点相当于以AB为直径的圆与x轴的两个交点)③当点M在y轴上,且BM⊥AM,如答图②所示.此时M点坐标为(0,);④当点M在y轴上,且BM′⊥AB,如答图②所示.设M′(0,m),则AM=2﹣=,BM=,MM′=﹣m.易知Rt△ABM∽Rt△MBM′,∴,即,解得m=,∴此时M点坐标为(0,).综上所述,除点C外,在坐标轴上存在点M,使得△MAB是直角三角形.符合条件的点M有5个,其坐标分别为:(,0)、(,0)、(,0)、(0,)或(0,).4:(2012?河池)如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线经过A、B两点.(1)写出点A、点B的坐标;(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;(3)在(2)的条件下,抛物线上是否存在一点P,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.解:(1)抛物线y=﹣x2+x+4中:令x=0,y=4,则 B(0,4);令y=0,0=﹣x2+x+4,解得 x1=﹣1、x2=8,则 A(8,0);∴A(8,0)、B(0,4).△ABC中,AB=AC,AO⊥BC,则OB=OC=4,∴C(0,﹣4).由A(8,0)、B(0,4),得:直线AC:y=﹣x+4;依题意,知:OE=2t,即 E(2t,0);∴P(2t,﹣2t2+7t+4)、Q(2t,﹣t+4),PQ=(﹣2t2+7t+4)﹣(﹣t+4)=﹣2t2+8t;S=S△ABC+S△PAB=×8×8+×(﹣2t2+8t)×8=﹣8t2+32t+32=﹣8(t﹣2)2+64;∴当t=2时,S有最大值,且最大值为64.(3)∵PM∥y轴,∴∠AMP=∠ACO<90°;而∠APM是锐角,所以△PAM若是直角三角形,只能是∠PAM=90°;由A(8,0)、C(0,﹣4),得:直线AC:y=x﹣4;所以,直线AP可设为:y=﹣2x+h,代入A(8,0),得:﹣16+h=0,h=16∴直线AP:y=﹣2x+16,联立抛物线的解析式,得:,解得、∴存在符合条件的点P,且坐标为(3,10).5:(2012?海南)如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON,(1)求该二次函数的关系式;(2)若点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:①证明:∠ANM=∠ONM;②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.1)∵二次函数图象的顶点为P(4,-4),∴设二次函数的关系式为。
2019数学中考复习——二次函数中直角三角形存在性问题

二次函数中直角三角形存在性问题
解题方法
一、代数法:
(1)根据条件用坐标表示三边或三边的平方
(2)以直角顶点分三种情况,根据勾股定理列方程,解方程
(3)根据题目条件及方程解确定坐标
二、几何法:
(1)先分三种情况进行构造:若已知边做直角边,过直角边的两端点作垂线,则第三个顶点在垂线上,若已知边为斜边,可取斜边为直径作圆,直角顶点在圆上
(2)计算:注意题目的几何背景,如有直接的相似则表示线段长度,进行相似求解,无直接相似则围绕顶点分别做坐标轴的平行线,构造一线三角模型进行相似求解。
专题训练
例1.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,与x轴的另一个交点为B.设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
几何法:
例2.如图,在平面直角坐标系中,已知点A 的坐标是(4,0),并且OA=OC=4OB ,动点P 在过A ,B ,C 三点的抛物线上.
(1)求抛物线的解析式;
(2)是否存在点P ,使得△ACP 是以AC 为直角边的直角三角形?若存在,求出所有符合条件的点P 的坐标;若不存在,说明理由;
例3.如图,在平面直角坐标系中,直线交轴于点,交轴于点,抛物线的图象过点,并与直线相交于、两点. 求抛物线的解析式(关系式);
过点作交轴于点,求点的坐标;
除点外,在坐标轴上是否存在点,使得是直角三角形?若存在,请求出点的坐标,若不存在,请说明理由.
123y x =-
+x P y A 212
y x bx c =-++(1,0)E -A B ⑴⑵A AC AB ⊥x C C ⑶C M MAB ∆M。
二次函数三角形面积最大值公式

二次函数三角形面积最大值公式二次函数三角形面积最大值公式是指在已知三角形两边和夹角的情况下,求出三角形面积最大值的公式。
这个公式在数学中有着广泛的应用,特别是在优化问题中经常出现。
首先,我们来看一下二次函数的基本形式:y=ax^2+bx+c。
其中,a、b、c都是常数,x是自变量,y是因变量。
二次函数的图像是一个开口向上或向下的抛物线。
接下来,我们来考虑如何利用二次函数求解三角形面积最大值。
假设已知三角形两边的长度分别为a和b,夹角为θ。
我们可以将三角形分成两个直角三角形,其中一个直角三角形的底边长度为x,高为h1;另一个直角三角形的底边长度为a-x,高为h2。
由于两个直角三角形的高相等,所以h1=h2=h。
根据正弦定理,我们可以得到:a/sinθ=b/sin(π-θ)=(a-x)/sinθ化简后得到:x=a/2(1-cosθ)将x代入三角形面积公式S=1/2ab*sinθ中,得到:S=a^2sinθ/4(1-cosθ)将二次函数的基本形式代入上式中,得到:S=a^2/4(1-cosθ)×sinθ将sinθ和cosθ表示为自变量x的函数,得到:sinθ=2t/(1+t^2),cosθ=(1-t^2)/(1+t^2)其中,t=tan(θ/2)。
将sinθ和cosθ代入S的公式中,得到:S=a^2/4(1-t^2)/(1+t^2)×2t/(1+t^2)化简后得到:S=a^2t/(2(1+t^2))由于t=tan(θ/2),所以t的取值范围是(-∞,+∞)。
因此,S的最大值可以通过求解二次函数y=ax^2+bx+c的顶点坐标来得到。
其中,a=a^2/2,b=0,c=0。
因此,顶点坐标为(x,y)=(0,a^2/4)。
将x=tan(θ/2)代入上式中,得到:S=a^2/8sin(θ/2)这就是二次函数三角形面积最大值公式。
通过这个公式,我们可以在已知三角形两边和夹角的情况下求出三角形面积的最大值。
二次函数中求直角三角形的方法

二次函数中求直角三角形的方法以二次函数中求直角三角形的方法为标题,我们将介绍如何利用二次函数来求解直角三角形的相关问题。
在二次函数中,我们常常会遇到求解直角三角形的问题。
直角三角形是指其中一个角为90度的三角形。
对于直角三角形,我们可以利用二次函数的性质来解决一些与其相关的问题。
我们来讨论直角三角形的三边关系。
根据勾股定理,直角三角形的两直角边的平方和等于斜边的平方。
假设直角三角形的两直角边分别为a和b,斜边为c,则有a^2 + b^2 = c^2。
这个关系式在解决直角三角形问题时非常重要。
在二次函数中,我们经常会遇到求解两点之间的距离的问题。
对于直角三角形,我们可以利用二次函数的距离公式来求解两点之间的距离。
假设直角三角形的两个顶点坐标分别为(x1, y1)和(x2, y2),则两点之间的距离可以通过以下公式来计算:d = sqrt((x2 - x1)^2 + (y2 - y1)^2)接下来,我们将介绍如何利用二次函数来解决直角三角形的面积问题。
直角三角形的面积可以通过以下公式来计算:S = 1/2 * a * b其中,a和b分别为直角三角形的两直角边的长度。
当我们已知直角三角形的两直角边的长度时,可以利用二次函数来求解斜边的长度。
根据勾股定理,我们可以得到以下公式:c = sqrt(a^2 + b^2)其中,c为直角三角形的斜边的长度。
当我们已知直角三角形的两个直角边的长度时,可以利用二次函数来求解直角三角形的两个锐角的正弦、余弦和正切值。
根据三角函数的定义,我们可以得到以下公式:sinA = a / ccosA = b / ctanA = a / b其中,A为直角三角形的一个锐角。
在二次函数中,我们也常常会遇到求解直角三角形的最大值或最小值的问题。
对于直角三角形,我们可以通过二次函数的顶点来求解其最大值或最小值。
在直角三角形中,顶点即为直角三角形的顶点,其x坐标为a/2,y坐标为b/2,其中a和b分别为直角三角形的两直角边的长度。
2抛物线(二次函数)中的直角三角形

抛物线中的直角三角形基本题型:已知AB ,抛物线()02≠++=a c bx ax y ,点P 在抛物线上(或坐标轴上,或抛物线的对称轴上),若ABP ∆为直角三角形,求点P 坐标。
分两大类进行讨论:(1)AB 为斜边时(即PA PB ⊥):点P 在以AB 为直径的圆周上。
(2)AB 为直角边时,分两类讨论:①以A ∠为直角时(即AP AB ⊥):②以B ∠为直角时(即BP BA ⊥):利用两点的斜率公式求出AB k ,因为两直线垂直斜率乘积为1-,进而求出PA (或PB )的斜率k ;进而求出PA (或PB )的解析式;将PA (或PB )的解析式与抛物线(或坐标轴,或抛物线的对称轴)的解析式联立即可求出点P 坐标。
典型例题:例1、在平面直角坐标系xOy 中,已知抛物线y=2(1)(0)a x c a ++>与x 轴交于A 、B 两点(点A 在点B 左侧),与y 轴交于点C ,其顶点为M,若直线MC 的函数表达式为3y kx =-,与x 轴的交点为N ,且COS∠BCO=10。
(1)求抛物线的解析式;(2)在此抛物线上是否存在异于点C 的点P ,使以N 、P 、C 为顶点的三角形是以NC 为一条直角边的直角三角形?若存在,求出点P 的坐标:若不存在,请说明理由;(3)过点A 作x 轴的垂线,交直线MC 于点Q.若将抛物线沿其对称轴上下平移,使抛物线与线段NQ ?(2009年成都)例2、如图,抛物线两点轴交于与B A x bx ax y ,32-+=,与y 轴交于点C ,且OA OC OB 3==.(I )求抛物线的解析式;(II )探究坐标轴上是否存在点P ,使得以点C A P ,,为顶点的三角形为直角三角形?若存在,求出P 点坐标,若不存在,请说明理由;(III )直线131+-=x y 交y 轴于D 点,E 为抛物线顶点.若α=∠DBC ,βαβ-=∠求,CBE 的值.例3、在平面直角坐标系中,现将一块等腰直角三角板ABC 放在第二象限,斜靠在两坐标轴上,且点A (0,2),点C (-1,0),如图所示,抛物线22y ax ax =+-经过点B 。
二次函数中直角三角形存在性问题.doc

二次函数中直角三角形存在性问题1. 找点:在己知两定点,确定第三点构成直角三角形时,要么以两定点为直角顶点,要么以动点为直角顶点•以定点为直角顶点时,构造两条直线与已知直线垂直;以动点为直角顶点时,以已知线段为直 径构造圆找点2. 方法:以两定点为直角顶点时,两直线互相垂直,则k1*k2=-1以已知线段为斜边时,利用K 型图,构造双垂直模 型,最后利用相似求解,或者三条边分别表示Z 后,利用勾股定理求解例一:如图,抛物线y =加空一2加兀+3加 与x 轴交于A 、B 两点,与y 轴交于C 点.(1) 请求出抛物线顶点M 的坐标(用含m 的代数式表示),A 、B 两点的坐标;(2) 经探究可知,A BC M 与A ABC 的而积比不变,试求出这个比值;(1) 求该抛物线的解析式; (2) M 为第一象限内抛物线上一动点,点M 在何处时,△ ACM 的面积最大;(3) 在抛物线的对称轴上是否存在这样的点P,使得△ PAC 为直角三角形?若存在,请求出所有可能点P 的坐标; 若不存在,请说明理由.(3)是否存在使A BCM 为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由0), B(4, 0),与y 轴交于点C.练习:1.如图.C知抛物线y=ar±bx+c (a«)的顶点M在第一象限,抛物线bx轴相交FA、B两点(点A 住点B的左边),f jy轴交万点C, O为唯标原点,如果ZkABM是何角二角形,AB=2, OM= J5(1)求点M的坐标;(2)求抛物线y=ax2+bx+c的解析式;(3)在抛物线的对称轴匕是否存在点P,使W APAC为直角三角形?若存在.请求出所有符合条件的点P 的坐标:若不存在•请说明理由.2.如图,抛物线y =〒一2加兀(m>0)与x轴的另一个交点为A,过P(l, -m)作PM丄x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.(1)若m二2,求点A和点C的坐标;(2)令m>l,连接CA,若AACP为直角三角形,求m的值;(3)在坐标轴上是否存在点E,使得APEC是以P为直角顶点的等腰直角三角形?若存在,求出点E的坐标;若不存在,请说明理由.3.如图,抛物线y =衣+分+2与x轴交于点A(l, 0)和B(4, 0).(1)求抛物线的解析式;(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC〃x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标;(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使AOCP是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.4、在平面直角坐标系中,抛物线y = ++仗一1)兀一比与直线y二kx+1交于A, B两点,点A在点B的左侧.(1)如图1,当k二1吋,直接写出A, B两点的坐标;(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求岀AABP面积的最大值及此时点P 的坐标;(3)如图2,抛物线y =兀2+仗_1)兀一比(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y二kx+1 使得Z0QC=90° ?若存在,请求出此吋k的值;若不存在,请说明理由.5.如图,直线y=x+2与抛物线y = ajc^-bx^6 (a#0)相交于A (2, 2)和B(4, m),点P是线段AB上异于A、B的动点,过点P作PC丄x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;(3)求厶PAC为直角三角形时点P的坐标.6、如图,抛物线y = ci^+bx+c经过A(-3, 0)、C(0, 4),点B在抛物线上,。
第2章二次函数直角三角形存在问题(教案)

此外,学生在解决实际问题时,对于二次函数性质的运用还不够熟练。这提示我在今后的教学中,需要加强对二次函数性质的讲解和练习,让学生在实际问题中更好地运用这一知识点。
第2章二次函数直角三角形存在问题(教案)
一、教学内容
第2章二次函数直角三角形存在问题
1.教材章节:本节课选自人教版八年级数学下册第2章“二次函数与直角三角形”。
2.教学内容:
(1)掌握二次函数与直角三角形的联系,理解二次函数在直角三角形中的应用。
(2)能够利用二次函数的性质解决直角三角形中存在的问题,如求斜边长、面积等。
2.教学难点
本节课的教学难点包括以下内容:
a.理解二次函数与直角三角形之间的联系,对于初学者来说,这部分内容较为抽象,难以理解。
b.建立数学模型解决实际问题时,学生可能会感到困惑,不知道如何将实际问题转化为数学表达式。
c.在解决直角三角形问题时,学生可能会忘记二次函数的相关性质,导致解题困难。
例:在直角三角形ABC中,已知斜边AB=5,∠C=30°,求该直角三角形的面积。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了二次函数与直角三角形的基本概念、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对这一知识点的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
二次函数与直角三角形有关的问题

二次函数的综合——与直角三角形有关的问题一.知识回顾(一)证明直角三角形(或直角)的定理:1.勾股定理的逆定理:如果三角形的三边长a ,b ,c 满足a 2+b 2=c 2, 那么这个三角形是直角三角形;两腰的夹角叫做顶角,腰和底边 的夹角叫做底角.2.半圆(或直径)所对的圆周角是直角. (二)与直角三角形(或直角)有关的线段关系:1. 勾股定理:如果直角三角形的两条直角边长分别为a ,b ,斜边长为c ,那么a 2+b 2=c 2 ;2. 辅助线构造“一线三垂直”相似三角形模型(如下图),对应边的比相等.二.例题解析例1.如图,在平面直角坐标系xOy 中,抛物线y =-x 2+2x +3与x 轴交于A ,B 两点,与y 轴交于点C ,抛物线的顶点为D ,连接BC 、CD 、BD .证明:△BCD 是直角三角形. 解:x =0时,y =3;y =0时,x 1=-1,x 2=3; ∴C 为(0,3),点B 为(3,0).∵y =-x 2+2x +3=-(x -1)2+4,∴抛物线的顶点D 为(1,4),方法一:∵BC 2=(3-0)2+(0-3)2=18,CD 2=(1-0)2+(4-3)2=2,BD 2=(3-1)2+(0-4)2=20, ∴BC 2+CD 2=BD 2,即∠DCB =90°,△BCD 是直角三角形.方法二:过点D 做DE ⊥y 轴于点E , 则DE =CE =1,OB =OC =3,∴∠DCE =∠BCO =45°,即∠BCD =90°,△BCD 是直角三角形.方法三:过点D 做DE ⊥y 轴于点E ,则DE =CE =1,OB =OC =3,∴CE DEBO CO =,又∵∠CED =∠BOC =90°,∴△CED ∽△BOC ,∠ECD =∠OBC , 而∠OBC+∠OCB =90°,∴∠BCD =180°-(∠ECD+∠OCB )=90°, △BCD 是直角三角形.已知三个顶点判断直角三角的方法:(1) 用勾股定理逆定理证明;(2)构造“一线三垂直”相似证明;(3)根据坐标判断某些特殊角,求出直角.交于点C ,点E 是抛物线对称轴上一点,若△ACE 是直角三角形,求出点E 的坐标. 解:x =0时,y =3,y =0时,x 1=-1,x 2=3; ∴C 为(0,3),点A 为(-1,0). ∵y =-x 2+2x +3=-(x -1)2+4, ∴抛物线的的对称轴为直线x =1. 设点E 的坐标为(1,a ), 方法一:AC 2=[0-(-1)]2+(3-0)2=10, EA 2=[1-(-1)]2+(a -0)2=a 2+4, CE 2=(1-0)2+(a -3)2=a 2-6a +10, 若∠CAE =90°,则CE 2=AC 2+EA 2, 即a 2-6a +10=10+a 2+4,解得:a =-32,点E 为(1,-32); 若∠ACE =90°,则AE 2=AC 2+CE 2,即a 2+4=10+a 2-6a +10,解得:a =38,点E 为(1,38);若∠CEA =90°,则AC 2=CE 2+EA 2,即10=a 2-6a +10+a 2+4,解得:a 1=1,a 2=2,点E 为(1,1)或(1,2);综上所述,点E 为(1,-32),(1,38),(1,1)或(1,2).方法二:若∠CAE =90°,过点A 作直线l //y 轴,分别过点C 、点E 作CM ⊥l 于点M ,EN ⊥l 于点N , 可证△AMC ∽△ENA , ∴MA NECM NA =,即3)1(11−−=−a , 解得:a =-32,∴点E 为(1,-32);若∠ACE =90°,过点C 作直线l //x 轴,分别过点A 、点E 作AM ⊥l 于点M ,EN ⊥l 于点N , 可证△AMC ∽△CNE ,∴AMCNMC NE =,即3113=−a ,解得:a =38,∴点E 为(1,38); 若∠AEC =90°,过点E 作直线l //y 轴,分别过点A 、点C 作AM ⊥l 于点M ,CN ⊥l 于点N ,可证△AME ∽△ENC ,∴EN AM NC ME =,即aa −=321, 解得:a 1=1,a 2=2,点E 为(1,1)或(1,2); 综上所述,点E 为(1,-32),(1,38),(1,1)或(1,2). 直角三角形已知两个顶点,求第三个顶点坐标的方法:(1)按直角顶点分类(“一圆两垂直”);(2)用勾股定理或构造“一线三垂直”相似列方程计算.交于点C ,连接BC ,点M ,N 分别是线段AB ,BC 上的动点,且AM =BN ,连接MN .当△BMN 是直角三角形时,求点M 的坐标. 方法一:解:x =0时,y =3;y =0时,x 1=-1,x 2=3; ∴A 为(-1,0),B 为(3,0),C 为(0,3). 设点M 坐标为(m ,0),∴BN =AM =m -(-1)=m +1,BM =3-m , ∵OB =OC =3,∠BOC =90°, ∴∠CBO =∠BCO =45°. 若∠MNB =90°, △BMN ∽△BCO ,则BN BM 2=,即()123+=−m m ,解得524−=m , ∴点M 的坐标为(524−,0); 若∠NMB =90°,△BMN ∽△BOC ,则BM BN 2=, 即()m m −=+321,解得247−=m ,∴点M 的坐标为(247−,0);综上所述,点M 坐标为(524−,0)或(247−,0).方法二:解:x =0时,y =3;y =0时,x 1=-1,x 2=3; ∴A 为(-1,0),B 为(3,0),C 为(0,3). ∴直线BC 的解析式为y =-x +3, ∵OB =OC =3,∠BOC =90°, ∴∠CBO =∠BCO =45°. 设点A M =BN=m ,过点N 作NG ⊥x 轴于点G , 在Rt △BNG 中,m BN BG NG 2222===, ∴点M 为(m -1,0),N 为(m 223−,m 22), ∴BM 2=(3-m +1)2=m 2-8m +16, BN 2=2222m =m 2, MN 2=22222231+ +−−m m m=162482222+−−+m m m m , 若∠MNB =90°,则MN 2+BN 2=MB 2,G即162482222+−−+m m m m +m 2=m 2-8m+16, 解得m 1=0(舍去),m 2=424−, ∴点M 的坐标为(524−,0); 若∠NMB =90°, 则MN 2+BM 2=NB 2,即162482222+−−+m m m m +m 2-8m+16=m 2, 解得m 1=4(舍去),m 2=248−, ∴点M 的坐标为(247−,0);综上所述,点M 坐标为(524−,0)或(247−,0).直角三角形已知一个顶点,另两个点伴随运动,求动点坐标的方法: (1)按直角顶点分类;(2)用勾股定理或相似列方程计算.三.方法总结:四.变式训练:1.如图,已知抛物线经过原点O ,顶点为A (1,1),且与直线y =x ﹣2交于B ,C 两点. (1)求抛物线的解析式及点C 的坐标; (2)求证:△ABC 是直角三角形.【分析】(1)可设顶点式,把原点坐标代入可求得抛物线解析式,联立直线与抛物线解析式,可求得C 点坐标;(2)分别过A 、C 两点作x 轴的垂线,交x 轴于点D 、E 两点,结合A 、B 、C 三点的坐标可求得∠ABO =∠CBO =45°,可证得结论;解:(1)∵顶点坐标为(1,1), ∴设抛物线解析式为y =a (x ﹣1)2+1, 又抛物线过原点,∴0=a (0﹣1)2+1,解得a =﹣1, ∴抛物线解析式为y =﹣(x ﹣1)2+1, 即y =﹣x 2+2x ,联立抛物线和直线解析式可得,解得或,∴B (2,0),C (﹣1,﹣3);(2)如图,分别过A、C两点作x轴的垂线,交x轴于点D、E两点,则AD=OD=BD=1,BE=OB+OE=2+1=3,EC=3,∴∠ABO=∠CBO=45°,即∠ABC=90°,∴△ABC是直角三角形.2.如果抛物线C1的顶点在拋物线C2上,抛物线C2的顶点也在拋物线C1上时,那么我们称抛物线C1与C2“互为关联”的抛物线.如图1,已知抛物线C1:y1=x2+x与C2:y2=ax2+x+c是“互为关联”的拋物线,点A,B分别是抛物线C1,C2的顶点,抛物线C2经过点D(6,﹣1).(1)直接写出A,B的坐标和抛物线C2的解析式;(2)抛物线C2上是否存在点E,使得△ABE是直角三角形?如果存在,请求出点E的坐标;如果不存在,请说明理由.【分析】(1)由抛物线C1:y1=x2+x可得A(﹣2,﹣1),将A(﹣2,﹣1),D(6,﹣1)代入y2=ax2+x+c,求得y2=﹣+x+2,B(2,3);(2)易得直线AB的解析式:y=x+1,①若B为直角顶点,BE⊥AB,E(6,﹣1);②若A为直角顶点,AE⊥AB,E(10,﹣13);③若E为直角顶点,设E(m,﹣m2+m+2)不符合题意;解:由抛物线C1:y1=x2+x可得A(﹣2,﹣1),将A(﹣2,﹣1),D(6,﹣1)代入y2=ax2+x+c得,解得,∴y2=﹣+x+2,B(2,3);(2)易得直线AB的解析式:y=x+1,①若B为直角顶点,BE⊥AB,k BE•k AB=﹣1,∴k BE=﹣1,直线BE解析式为y=﹣x+5联立,解得x=2,y=3或x=6,y=﹣1,∴E(6,﹣1);②若A为直角顶点,AE⊥AB,同理得AE解析式:y=﹣x﹣3,联立,解得x=﹣2,y=﹣1或x=10,y=﹣13,∴E(10,﹣13);③若E为直角顶点,设E(m,﹣m2+m+2)由AE⊥BE得k BE•k AE=﹣1,即,,,(m﹣2)2(m﹣6)(m+2)=﹣16(m+2)(m﹣2),(m+2)(m﹣2)[(m﹣2)(m﹣6)+16]=0,∴m+2=0或m﹣2=0,或(m﹣2)(m﹣6)+16=0(无解)解得m=2或﹣2(不符合题意舍去),∴点E的坐标E(6,﹣1)或E(10,﹣13).3.如图,抛物线y=ax2﹣5ax+c与坐标轴分别交于点A,C,E三点,其中A(﹣3,0),C (0,4),点B在x轴上,AC=BC,过点B作BD⊥x轴交抛物线于点D,点M,N分别是线段CO,BC上的动点,且CM=BN,连接MN.(1)求抛物线的解析式及点D的坐标;(2)当△CMN是直角三角形时,求点M的坐标.【分析】(1)利用待定系数法求抛物线解析式;利用等腰三角形的性质得B(3,0),然后计算自变量为3所对应的二次函数值可得到D点坐标;(2)利用勾股定理计算出BC=5,设M(0,m),则BN=4﹣m,CN=5﹣(4﹣m)=m+1,由于∠MCN=∠OCB,根据相似三角形的判定方法,当=时,△CMN∽△COB,于是有∠CMN=∠COB=90°,即=;当=时,△CMN∽△CBO,于是有∠CNM=∠COB=90°,即=,然后分别求出m的值即可得到M点的坐标;解:(1)把A(﹣3,0),C(0,4)代入y=ax2﹣5ax+c得,解得,∴抛物线解析式为y=﹣x2+x+4;∵AC=BC,CO⊥AB,∴OB=OA=3,∴B(3,0),∵BD⊥x轴交抛物线于点D,∴D点的横坐标为3,当x=3时,y=﹣×9+×3+4=5,∴D点坐标为(3,5);(2)在Rt△OBC中,BC===5,设M(0,m),则BN=4﹣m,CN=5﹣(4﹣m)=m+1,∵∠MCN=∠OCB,∴当=时,△CMN∽△COB,则∠CMN=∠COB=90°,即=,解得m =,此时M点坐标为(0,);当=时,△CMN∽△CBO,则∠CNM=∠COB=90°,即=,解得m=,此时M点坐标为(0,);综上所述,M点的坐标为(0,)或(0,).4.如图1,在平面直角坐标系中,直线l1:y=x+1与直线l2:x=﹣2相交于点D,点A是直线l2上的动点,过点A作AB⊥l1于点B,点C的坐标为(0,3),连接AC,BC.设点A 的纵坐标为t,△ABC的面积为s.(1)当t=2时,请直接写出点B的坐标;(2)在l2上是否存在点A,使得△ABC是直角三角形?若存在,请求出此时点A的坐标和△ABC的面积;若不存在,请说明理由.【分析】(1)先根据t=2可得点A(﹣2,2),因为B在直线l1上,所以设B(x,x+1),利用y=0代入y=x+1可得G点的坐标,在Rt△ABG中,利用勾股定理列方程可得点B 的坐标;(2)先把(7,4)代入s=中计算得b的值,计算在﹣1<t<5范围内图象上一个点的坐标值:当t=2时,根据(1)中的数据可计算此时s=,可得坐标(2,),代入s=a(t+1)(t﹣5)中可得a的值;解:(1)如图1,连接AG,当t=2时,A(﹣2,2),设B(x,x+1),在y=x+1中,当x=0时,y=1,∴G(0,1),∵AB⊥l1,∴∠ABG=90°,∴AB2+BG2=AG2,即(x+2)2+(x+1﹣2)2+x2+(x+1﹣1)2=(﹣2)2+(2﹣1)2,解得:x1=0(舍),x2=﹣,∴B(﹣,);(2)存在,设B(x,x+1),分两种情况:①当∠CAB=90°时,如图4,∵AB⊥l1,∴AC∥l1,∵l1:y=x+1,C(0,3),∴AC:y=x+3,∴A(﹣2,1),∵D(﹣2,﹣1),在Rt△ABD中,AB2+BD2=AD2,即(x+2)2+(x+1﹣1)2+(x+2)2+(x+1+1)2=22,解得:x1=﹣1,x2=﹣2(舍),∴B(﹣1,0),即B在x轴上,∴AB==,AC==2,∴S△ABC===2;②当∠ACB=90°时,如图5,∵∠ABD=90°,∠ADB=45°,∴△ABD是等腰直角三角形,∴AB=BD,∵A(﹣2,t),D(﹣2,﹣1),∴(x+2)2+(x+1﹣t)2=(x+2)2+(x+1+1)2,(x+1﹣t)2=(x+2)2,x+1﹣t=x+2或x+1﹣t=﹣x﹣2,解得:t=﹣1(舍)或t=2x+3,Rt△ACB中,AC2+BC2=AB2,即(﹣2)2+(t﹣3)2+x2+(x+1﹣3)2=(x+2)2+(x+1﹣t)2,把t=2x+3代入得:x2﹣3x=0,解得:x=0或3,当x=3时,如图5,则t=2×3+3=9,∴A(﹣2,9),B(3,4),∴AC==2,BC==,∴S△ABC===10;当x=0时,如图6,此时,A(﹣2,3),AC=2,BC=2,∴S△ABC===2.。
解直角三角形在二次函数中的应用

解直角三角形在二次函数中的应用解直角三角形在二次函数中的应用直角三角形是初中数学中比较基础的概念之一,二次函数则是高中数学中比较重要的一个概念,两者貌似毫无联系,但实际上它们之间却有着紧密的联系。
接下来,我们将通过以下几个方面来探讨解直角三角形在二次函数中的应用。
一、直角三角形的勾股定理勾股定理是解直角三角形中最重要的公式之一。
根据此定理,我们可以得到判断一个三角形是否为直角三角形的方法。
在二次函数中,我们可以通过勾股定理来求解关于二次函数的方程。
这个过程主要是利用勾股定理将三角形的边长转化为二次函数表达式中平方项的系数,从而解出方程。
二、三角函数的基本关系式三角函数是解直角三角形的重要工具,二次函数中也有许多与三角函数相关的公式。
三角函数中的正弦、余弦函数定义中包含直角三角形的边长,通过推导,我们可以得到正弦、余弦函数中另一个角度的值。
在求解包含三角函数的二次函数中,我们可以通过将其化简成标准形式后,利用三角函数的基本关系式,将方程转化为仅包含正弦或余弦函数的方程,从而解出方程。
三、二次函数的最值问题二次函数的图像是一个带有对称轴的抛物线,它的最值点为对称轴上的顶点。
在计算直角三角形的过程中,我们经常需要求解最大值或最小值,因此我们可以将这个过程与二次函数的最值问题联系起来。
通过将直角三角形中的某一个角度和对应的边长代入已知的二次函数中,我们可以得到二次函数的顶点坐标。
这个过程既可以被用来求解最大值和最小值的问题,也可以用于计算直角三角形中中位线的长度。
综上所述,在二次函数中,解直角三角形的知识和技能将起到重要的作用。
通过解三角函数和二次函数的方程来确定直角三角形中的角度和边长,通过二次函数的最值问题来计算直角三角形的某些特殊值,这些都是我们为了更好地理解和掌握二次函数而应该掌握的重要技巧。
中考二次函数与直角三角形有关的问题知识解读

二次函数与直角三角形有关的问题知识解读【专题说明】二次函数之直角三角形存在性问题,主要指的是在平面直角坐标系下,已知一条边(或两个顶点)的直角三角形存在,求第三个顶点的坐标的题型.主要考察学生对转化思想、方程思想、几何问题代数化的数形结合思想及分类讨论思想的灵活运用。
【解题思路】直角三角形的存在性问题1.找点:在已知两定点,确定第三点构成直角三角形时,要么以两定点为直角顶点,要么以动点为直角顶点.以定点为直角顶点时,构造两条直线与已知直线垂直;以动点为直角顶点时,以已知线段为直径构造圆找点2.方法:(1)以两定点为直角顶点时,两直线互相垂直,则k1*k2=-1(2)以已知线段为斜边时,利用K型图,构造双垂直模型,最后利用相似求解,或者三条边分别表示之后,利用勾股定理求解下面主要介绍2种常用方法:【方法1 几何法】“两线一圆”(1)若∠A 为直角,过点A 作AB 的垂线,与x 轴的交点即为所求点C;(2)若∠B 为直角,过点B 作AB 的垂线,与x 轴的交点即为所求点C;(3)若∠C 为直角,以AB 为直径作圆,与x 轴的交点即为所求点C.(直径所对的圆周角为直角)如何求得点坐标?以C2为例:构造三垂直.),坐标为(故代入得:坐标得、由,易证0213232222C C C BN AM B A N MB BN AM BN AMB ===∆≈∆()),坐标为(,,坐标为故或故又即代入得:设,,坐标得、由求法相同,如下:易证、040231a ,4a ,3ab ,3ab 1N a,31,4333333343C C C C C C C C C C b b M BN AM B A NBM N AMNB AM ==+=======∆≈∆【方法2 代数法】点-线-方程23m 20352235110,m 135-m 1-m 35-m 11-m 22222122111=+=+=+=+==,解得:)代入得方程(,,,)表示线段:();,()、,(),又坐标为()表示点:设(:不妨来求下)()()()(BC C C C A AB B A【典例分析】【方法1 勾股定理】【典例1】(2021秋•建华区期末)抛物线y=x2+bx+c经过A、B(1,0)、C(0,﹣3)三点.点D为抛物线的顶点,连接AD、AC、BC、DC.(1)求抛物线的解析式;(2)在y轴上是否存在一点E,使△ADE为直角三角形?若存在,请你直接写出点E的坐标;若不存在,请说明理由.【解答】解(1)∵抛物线y=x2+bx+c经过B(1,0)、C(0,﹣3),∴,解得,∴抛物线的解析式为:y=x2+2x﹣3.(4)在y轴上存在点E,使△ADE为直角三角形,理由如下:∵抛物线的解析式为y=x2+2x﹣3=(x+1)2﹣4,∴D(﹣1,﹣4),设E点坐标为(0,m),∴AE2=m2+9,DE2=m2+8m+17,AD2=20,当∠EAD=90°时,有AE2+AD2=DE2,∴m2+9+20=m2+8m+17,解得m=,∴此时点E的坐标为(0,);当∠ADE=90°时,DE2+AD2=AE2,m2+8m+17+20=m2+9,解得m=﹣,∴此时点E的坐标为(0,﹣);当∠AED=90°时,AE2+DE2=AD2,m2+9+m2+8m+17=20,解得m=﹣1或m=﹣3,∴此时点E的坐标为(0,﹣1)或(0,﹣3).【变式1-1】(2022•灞桥区校级模拟)如图,抛物线与x轴交于点A(1,0),B(3,0),与y轴交于点C(0,3).(1)求二次函数的表达式及顶点坐标;(2)连接BC,在抛物线的对称轴上是否存在一点E,使△BCE是直角三角形?若存在,请直接写出点E的坐标;若不存在,请说明理由.【解答】解:(1)设抛物线的解析式为y=a(x﹣1)(x﹣3),将点C(0,3)代入y=a(x﹣1)(x﹣3),∴3a=3,∴a=1,∴y=(x﹣1)(x﹣3)=x2﹣4x+3,∵y=x2﹣4x+3=(x﹣2)2﹣1,∴顶点为(2,﹣1);(2)存在一点E,使△BCE是直角三角形,理由如下:∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的对称轴为直线x=2,设E(2,t),∵△BCE是直角三角形,∴BE⊥CE,∵B(3,0),C(0,3),∴BC=3,BE=,CE=,①当BC为斜边时,∴18=()2+()2,解得t=,∴E点坐标为(2,)或(2,);②当BE为斜边时,∴18+()2=()2,解得t=5,∴E点坐标为(2,5);③当CE为斜边时,∴18+()2=()2,解得t=﹣1,∴E点坐标为(2,﹣1);综上所述:E点坐标为(2,)或(2,)或(2,5)或(2,﹣1)【变式1-2】(2022•广安)如图,在平面直角坐标系中,抛物线y=ax2+x+m(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,﹣4),点C坐标为(2,0).(1)求此抛物线的函数解析式.(2)点P为该抛物线对称轴上的动点,使得△P AB为直角三角形,请求出点P的坐标.【解答】解:(1)∵抛物线y=ax2+x+m(a≠0)的图象经过点B(0,﹣4),点C(2,0),∴,解得,∴抛物线的解析式为y=x2+x﹣4;(2)如图2中,设抛物线的对称轴交x轴于点N,过点B作BM⊥抛物线的对称轴于点M.则N(﹣1.0).M(﹣1,﹣4);∵OA=OB=4,∠AOB=90°,∴∠OAB=∠OBA=45°,当∠P1AB=90°时,△ANP1是等腰直角三角形,∴AN=NP1=3,∴P1(﹣1,3),当∠ABP2=90°时,△BMP2是等腰直角三角形,可得P2(﹣1,﹣5),当∠APB=90°时,设P(﹣1,n),设AB的中点为J,连接PJ,则J(﹣2,﹣2),∴PJ=AB=2,∴12+(n+2)2=(2)2,解得n=﹣2或﹣﹣2,∴P3(﹣1,﹣2),P4(﹣1,﹣﹣2),综上所述,满足条件的点P的坐标为(﹣1,3)或(﹣1,﹣5)或(﹣1,﹣2)或(﹣1,﹣﹣2).【方法2 构造“K”字型利用相似作答】【典例2】(2022•碑林区校级四模)如图,在平面直角坐标系中,抛物线C1:y=ax2+bx+c 交x轴于点A(﹣5,0),B(﹣1,0),交y轴于点C(0,5).(1)求抛物线C1的表达式和顶点D的坐标.(2)将抛物线C1关于y轴对称的抛物线记作C2,点E为抛物线C2上一点若△DOE是以DO为直角边的直角三角形,求点E的坐标.【解答】解:(1)将点A(﹣5,0),B(﹣1,0),C(0,5)代入y=ax2+bx+c,∴,解得,∴y=x2+6x+5,∵y=x2+6x+5=(x+3)2﹣4,∴顶点D(﹣3,﹣4);(2)设抛物线C2上任意一点(x,y),则(x,y)关于y轴对称的点为(﹣x,y),∵点(﹣x,y)在抛物线C1上,∴抛物线记作C2的解析式为y=x2﹣6x+5,设E(t,t2﹣6t+5),过点D作DG⊥x轴交于点G,过点E作EH⊥x轴交于点H,∵∠DOE=90°,∴∠GOD+∠HOE=90°,∵∠GOD+∠GDO=90°,∴∠HOE=∠GDO,∴△GDO∽△HOE,∴=,∵DG=4,GO=3,HE=﹣t2+6t﹣5,OH=t,∴=,∴t=4或t=,∴E(4,﹣3)或E(,﹣).【变式2-1】(2022•济南)抛物线y=ax2+x﹣6与x轴交于A(t,0),B(8,0)两点,与y轴交于点C,直线y=kx﹣6经过点B.点P在抛物线上,设点P的横坐标为m.(1)求抛物线的表达式和t,k的值;(2)如图1,连接AC,AP,PC,若△APC是以CP为斜边的直角三角形,求点P的坐标;【解答】解:(1)将B(8,0)代入y=ax2+x﹣6,∴64a+22﹣6=0,∴a=﹣,∴y=﹣x2+x﹣6,当y=0时,﹣t2+t﹣6=0,解得t=3或t=8(舍),∴t=3,∵B(8,0)在直线y=kx﹣6上,∴8k﹣6=0,解得k=,∴y=x﹣6;(2)作PM⊥x轴交于M,∵P点横坐标为m,∴P(m,﹣m2+m﹣6),∴PM=m2﹣m+6,AM=m﹣3,在Rt△COA和Rt△AMP中,∵∠OAC+∠P AM=90°,∠APM+∠P AM=90°,∴∠OAC=∠APM,∴△COA∽△AMP,∴=,即OA•MA=CO•PM,3(m﹣3)=6(m2﹣m+6),解得m=3(舍)或m=10,∴P(10,﹣);【变式2-2】(2022•滨州)如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,连接AC、BC.(1)求线段AC的长;(2)若点M为该抛物线上的一个动点,当△BCM为直角三角形时,求点M的坐标.【解答】解:(1)针对于抛物线y=x2﹣2x﹣3,令x=0,则y=﹣3,∴C(0,﹣3);令y=0,则x2﹣2x﹣3=0,∴x=3或x=﹣1,∵点A在点B的左侧,∴A(﹣1,0),B(3,0),∴AC==;(2)由(1)知,B(3,0),C(0,﹣3),∴OB=OC=3,设M(m,m2﹣2m﹣3),∵△BCM为直角三角形,∴①当∠BCM=90°时,如图1,过点M作MH⊥y轴于H,则HM=m,∵OB=OC,∴∠OCB=∠OBC=45°,∴∠HCM=90°﹣∠OCB=45°,∴∠HMC=45°=∠HCM,∴CH=MH,∵CH=﹣3﹣(m2﹣2m﹣3)=﹣m2+2m,∴﹣m2+2m=m,∴m=0(不符合题意,舍去)或m=1,∴M(1,﹣4);②当∠CBM=90°时,过点M作M'H'⊥x轴,同①的方法得,M'(﹣2,5);③当∠BMC=90°时,如图2,Ⅰ、当点M在第四象限时,过点M作MD⊥y轴于D,过点B作BE⊥DM,交DM的延长线于E,∴∠CDM=∠E=90°,∴∠DCM+∠DMC=90°,∵∠DMC+∠EMB=90°,∴∠DCM=∠EMB,∴△CDM∽△MEB,∴,∵M(m,m2﹣2m﹣3),B(3,0),C(0,﹣3),∴DM=m,CD=﹣3﹣(m2﹣2m﹣3)=﹣m2+2m,ME=3﹣m,BE=﹣(m2﹣2m﹣3)=﹣m2+2m+3,∴,∴m=0(舍去)或m=3(点B的横坐标,不符合题意,舍去)或m=(不符合题意,舍去)或m=,∴M(,﹣),Ⅱ、当点M在第三象限时,M(,﹣),即满足条件的M的坐标为(1,﹣4)或(﹣2,5)或(,﹣),或(,﹣).。
二次函数中的直角三角形
二次函数中的直角三角形
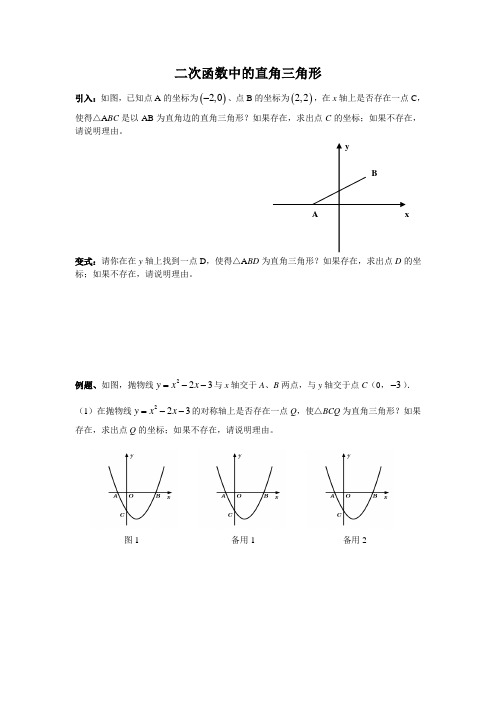
引入:如图,已知点A 的坐标为()2,0-、点B 的坐标为()2,2,在x 轴上是否存在一点C ,使得△A BC 是以AB 为直角边的直角三角形?如果存在,求出点C 的坐标;如果不存在,请说明理由。
变式:请你在在y 轴上找到一点D ,使得△A BD 为直角三角形?如果存在,求出点D 的坐标;如果不存在,请说明理由。
例题、如图,抛物线2
23y x x =--与x 轴交于A 、B 两点,与y 轴交于点C (0,3-).
(1)在抛物线223y x x =--的对称轴上是否存在一点Q ,使△BCQ 为直角三角形?如果存在,求出点Q 的坐标;如果不存在,请说明理由。
x y A x B 图1 备用1 备用2
(2)、变式:在抛物线223y x x =--上是否存在一点P ,使△BCP 是以BC 为直角边的直角三角形?如果存在,求出点P 的坐标;如果不存在,请说明理由。
练习:、
已知抛物线:122-+-=m x x y 与x 轴只有一个交点,且与y 轴交于A 点,如图,设它的顶点为B
(1)求m 的值;
(2)过A 作x 轴的平行线,交抛物线于点C ,求证是ABC ∆是等腰直角三角形;
(3)将此抛物线向下平移4个单位后,得到抛物线C',且与x 轴的左半轴交于E 点,与y 轴交于F 点,如图.请在抛物线C'上求点P ,使得EFP ∆是以EF 为直角边的直角三角形.
图1 备用1 备用 2 x C E A O B F。
二次函数中等腰直角三角形 -回复

二次函数中等腰直角三角形 -回复1.二次函数的图像可以是一个等腰直角三角形。
2.等腰直角三角形的特点是两边长度相等且夹角为90度。
3.二次函数的图像可以在坐标平面上形成等腰直角三角形的形状。
4.在二次函数的图像中,两边长度相等的线段可以表示为x轴上的两个解。
5.二次函数图像中的等腰直角三角形的斜边可以表示为顶点到x轴的最短距离。
6.二次函数图像中的等腰直角三角形的顶点处的坐标可以表示为函数的最小值或最大值。
7.二次函数图像中的等腰直角三角形的斜边长度可以通过函数的求导来计算。
8.二次函数中等腰直角三角形的形状取决于函数的系数。
9.如果二次函数的系数相等,那么等腰直角三角形的两边长度相等。
10.如果二次函数的系数为正数,那么等腰直角三角形是正放大的。
11.如果二次函数的系数为负数,那么等腰直角三角形是反转的。
12.等腰直角三角形的斜边长度与二次函数的平方项系数成正比。
13.二次函数中的等腰直角三角形在坐标平面上可以有不同的位置。
14.二次函数中的等腰直角三角形可以在x轴上有一个或两个交点。
15.等腰直角三角形的斜边长度可以通过计算顶点到两个x轴交点的距离来确定。
16.二次函数中的等腰直角三角形的斜边长度与x轴的交点位置相关。
17.二次函数的图像中等腰直角三角形的夹角为90度。
18.在二次函数中,等腰直角三角形的顶点处的横坐标可以通过求导来找到。
19.二次函数中的等腰直角三角形只有在函数是平方项系数为正数时存在。
20.等腰直角三角形的形状可以帮助我们理解二次函数的图像。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数直角三角形
二次函数是一种常见的数学模型,其图像呈现出连续的曲线,可以用于描述许多实际问题,如物体的运动轨迹、物体的抛射运动、电子电路等。
而直角三角形是一个三角形中的一种特殊情况,其中一个角为90度。
在这篇文章中,我们将讨论二次函数与直角三角形之间的关系,以及如何利用二次函数和三角函数求解直角三角形问题。
一、二次函数
二次函数是一种以自变量x的二次多项式的形式表示的函数,其一般式为:y=ax²+bx+c,其中a、b、c为常数,且a≠0。
二次函数的图像通常呈现出抛物线状,其开口向上或向下取决于系数a的正负性。
当a>0时,抛物线开口朝上;当a<0时,抛物线开口朝下。
二、二次函数与直角三角形之间的关系
二次函数可以用于描述许多物理问题,如自由落体运动、抛体运动等。
这些物理问题中通常包含有物体的高度、速度、加速度等数值。
而这些数值往往与直角三角形有直接关系。
例如,在自由落体运动中,当一个物体从高度h自由落下时,其高度与时间的关系可以表示为二次函数y=-
gt²/2 + h,其中g为重力加速度,t为时间。
同时,当物体与地面碰撞时,其速度可以表示为v=gt,即与时间t存
在线性关系。
这些物理问题中的二次函数常常与直角三角形有关,我们可以将物体高度与时间关系中的高度看作直角三角形中的斜边,将时间看作直角三角形中的一条直角边,将落地时的高度看作直角三角形中的另一条直角边。
这样,我们就可以将二次函数转化为三角函数的形式,利用三角函数求解直角三角形的问题。
三、利用三角函数求解直角三角形的问题
在直角三角形中,我们通常会用三角函数来计算三角形的各边和角度的大小。
其中最常用的三角函数包括正弦函数、余弦函数和正切函数。
通过利用三角函数可以快速地求解直角三角形的各项参数,如角度、斜边、直角边以及三角形的面积等。
下面是利用三角函数求解直角三角形的常用公式:
1.正弦定理:a/sin(A)=b/sin(B)=c/sin(C)。
2.余弦定理:a²=b²+c²-2bc·cos(A);b²=a²+c²-
2ac·cos(B);c²=a²+b²-2ab·cos(C)。
3.正切:tan(A)=a/b;tan(B)=b/a;tan(C)=c/a。
三角函数的应用十分广泛,可以用于求解数学、物理、工程等领域的诸多问题。
通过将二次函数与直角三角形相结合,我们可以更深入地理解这些问题,并找到更为精确的解决方法。
四、总结
二次函数与直角三角形之间存在着密切的联系,通过将二次函数转化为三角函数的形式,我们可以快速地求解直角三角形的多种问题。
这种联系不仅仅是数学的抽象概念,还有着重要的实际应用价值。
我们希望通过对这些知识的深入学习,掌握更多有用的工具和技能,为解决实际问题提供更为实用和可靠的方法。
