桩土相互作用计算报告
概析桩-土相互作用机理

概析桩-土相互作用机理1、引言当上部结构的荷载较大、适合于作为持力层的土层埋藏较深,并且采用天然浅基础或仅作简单的人工地基加固仍不能满足要求时,常采用的一种方法就是做桩基础。
把结构支撑在桩基础上,荷载通过桩传到深处的坚硬岩土上,从而保证建筑物满足地基稳定和变形容许量的要求。
桩通过其侧面和土的接触,將建筑荷载传递给桩周围的土体,或者传递给更深层的岩土,从而获得较大的承载能力以支撑上部的大型建筑物。
因此,研究桩土间的相互作用机理不仅能够对基础设计提供合理参考,在桩基施工过程中也可对安全施工做出贡献。
桩-土共同作用问题是地基基础与上部结构共同作用问题中的一个分支,研究地基基础与上部结构共同作用的理论,重要的是解决桩、地基土和基础之间共同作用的问题。
在该课题研究的几种方法中,比较完整的三维空间分析方法系由Hongladaromp等人和Hian提出。
进几十年来来,随着国内基础建设的兴起,桩基基础在全国各地都被广泛采用,桩-土共同作用机理也越来越被重视,许多学者采用各种试验方法并取得了不少有价值的研究成果。
但因为地下空间的复杂,影响桩-土共同作用的因素繁多,使桩-土共同作用问题研究仍然存在尚未解决的问题。
因此,本文将对这些具有代表性的研究成果进行简单的回顾,并阐述当今桩-土共同作用研究中存在的问题和今后的发展方向。
2、桩-土共同作用研究现状近年来,桩-土共同作用问题被广泛研究,主要影响因素有上部荷载形式以及桩型选取和土性变化,而桩型和土性影响可以归为桩-土界面影响因素。
下面主要详细介绍近几十年来桩-土共同作用机理研究进展。
80年代,费勤发等对建筑荷载下复杂的单桩位移影响系数以及桩对桩位移影响系数的计算给出了简易解法。
并且对单桩的一系列参数给出可以笔算的解析式。
将桩对桩以及桩对土的位移影响系数计算归并于单桩位移影响系数计算公式中。
将简化计算解与精确解进行详尽的比较和细致的分析给出简化计算解的最大相对误差范围,而简化计算结果足以满足工程要求。
上拔力作用下桩土相互作用数值分析

上拔力作用下桩土相互作用数值分析桩土相互作用是岩土工程中一个重要的研究课题,它影响着桩基工程的稳定性和承载力。
在实际工程中,桩土相互作用通常通过数值模拟方法进行研究。
其中,上拔力作用下桩土相互作用是一种具有挑战性的情况,需要进行细致的分析和研究。
首先,需要了解上拔力作用的原因。
上拔力是指桩基在土体中受到的由土体侧向位移引起的上拉力,这种力会对桩基产生一定的影响。
在实际工程中,上拔力的作用可能会导致桩基的稳定性降低,甚至引起桩基的失稳。
其次,需要建立合适的数值模型来模拟上拔力作用下的桩土相互作用。
数值模拟可以通过计算机软件对桩土相互作用进行模拟和分析,得出相关的计算结果。
在建立数值模型时,需要考虑土体的本构模型、桩基的几何形状和材料性质等因素,以确保模拟结果的准确性和可靠性。
接下来,可以通过数值模拟来分析上拔力作用下的桩土相互作用。
具体包括以下几个方面:1.桩基的受力特性:通过数值模拟可以得到桩基在受到上拔力作用时的受力状态,包括桩身和桩端的受力情况。
这有助于评估桩基的承载力和稳定性。
2.土体的变形特性:土体在受到上拔力作用时会发生一定的变形,数值模拟可以模拟土体的变形过程,并得到相应的位移、变形和轴力等信息。
3.拔桩过程的影响:在实际工程中,拔回桩基时可能会受到一定的阻力,这种阻力会对桩基产生一定的影响。
数值模拟可以模拟拔桩过程,并分析阻力的影响。
最后,需要对数值模拟结果进行验证和分析。
通过将数值模拟结果与实测数据进行对比,可以验证模拟结果的准确性和可靠性。
同时,对模拟结果进行分析,得出结论并提出相应的建议,以指导工程实践。
总之,上拔力作用下桩土相互作用的数值分析是一个复杂的工程问题,需要综合考虑土体、桩基和其他相关因素,通过建立数值模型进行模拟和分析,得出相应的结论和建议,以确保桩基工程的安全和稳定性。
轴向载荷作用下桩土相互作用数值分析

轴 向载荷作用下桩 土相互作用数值分析
黄圣波 ,李勇泉
( 1 . 中铁四院集团南宁勘察设计 院有 限公司 ,广西南 宁 5 3 0 0 0 3 ;2 . 河南工业大学土木建筑学 院 , 河南郑 州 4 5 0 0 0 1 )
关键词 轴向荷栽 ;桩一 土相互作用 ;Dr u c k e r — P r a g e r 模型 ;接触模型
中圈 分类号 T U4 7 3 1 文献标识码 A 文章编号 1 6 7 3 — 9 6 7 1 一 ( 2 0 1 3 ) 0 1 1 — 0 1 9 6 — 0 2
1弓 l 言
为是 :
塑性应变垂直于塑性势面,其值大小确定公式为 :
G
署 l
j
㈩
这里 为塑性因子 ,能由变形协调条件确定。
3 桩一 土接触模 型
通 过 一定 的接触 形 式 及相 应 的参 数 考 虑桩 土 ( 岩 )之 间的 摩
一
2 土体模型
D r u c k e r - P r a g e r  ̄ 型公 式 为 :
F = c t I 十 √ , 2 一 Y = O
1
。
2
( 1 )
指的 是偏应力第
这里I . 是主应力第一不变量;J , =÷
二不变量,S = ~ ÷ , j
力。
Ⅱ 和Y 分别指的 是土的摩擦角和粘聚
对 于小 应 变公 式来 说 ,应变 率 通 常被 分 解为 弹性 和塑 性部 分
所组 成 。
=
“
( 2)
这种 应力 一 应 变关 系 能写作 :
=
C o k / ( 一 )
用MIDAS模拟桩土相互作用

用MIDAS模拟桩-土相互作用(“m法”确定土弹簧刚度)迈达斯技术2009年05月1、引言土与结构相互作用的研究已有近60~70年的历史,待别是近30年来,计算机技术的发展为其提供了有力的分析手段。
桩基础是土建工程中广泛采用的基础形式之一,许多建于软土地基上的大型桥梁结构往往都采用桩基础,桩-土动力相互作用又是土-结构相互作用问题中较复杂的课题之一。
至今已有不少关于桩基动力特性的研究报告,国外研究人员也提出了许多不同的桩-土动力相互作用计算方法。
从研究成果的归类来看,理论上主要有离散理论和连续理论及两者的结合,解决的方法一般有集中质量法、有限元法、边界元法和波动场法。
60~70年代,美国学者J.penzien等在解决泥沼地上大桥动力分析时提出了集中质量法,目前已在国外得到了广泛的应用。
集中质量法将桥梁上部结构多质点体系和桩一土体系的质量联合作为一个整体,来建立整体耦联的地震振动微分方程组进行求解。
该模型假定桩侧土是Winkler连续介质。
以半空间的Mindlin静力基本解为基础,将桩-土体系的质量按一定的厚度简化并集中为一系列质点,离散成一理想化的参数系统。
并用弹簧和阻尼器模拟土介质的动力性质,形成一个包括地下部分的多质点体系。
土弹簧刚度的确定,除考虑使用较为精确的有限元或边界元方法外,较为简便的方法是采用Penzien模型中提供的土弹簧计算方法或参照现行规中土弹簧的计算方法。
我国公路桥涵地基与基础设计规(JTG D63-2007)用的“m法”计算方法和参数选取方面比Penzien的方法要简单和方便,且为国广大工程师所熟.“m法”的基本原理是将桩作为弹性地基梁,按Winkler假定(梁身任一点的土抗力和该点的位移成正比)求解。
但是,由于桩-土相互作用的实验数据不足,土的物性取值有时亦缺乏合理性,在确定土弹簧的刚度时,仍有不少问题未能很好解决。
特别是,“m法”中m的取值对弹簧刚度的计算结果影响很大,且不能反映地震波的频率特性和强度带来的影响。
用MIDAS模拟桩土相互作用

1 用MIDAS模拟桩-土相互作用(“m法”确定土弹簧刚度)北京迈达斯技术有限公司2009年05月1、引言土与结构相互作用的研究已有近60~70年的历史,待别是近30年来,计算机技术的发展为其提供了有力的分析手段。
桩基础是土建工程中广泛采用的基础形式之一,许多建于软土地基上的大型桥梁结构往往都采用桩基础,桩-土动力相互作用又是土-结构相互作用问题中较复杂的课题之一。
至今已有不少关于桩基动力特性的研究报告,国内外研究人员也提出了许多不同的桩-土动力相互作用计算方法。
从研究成果的归类来看,理论上主要有离散理论和连续理论及两者的结合,解决的方法一般有集中质量法、有限元法、边界元法和波动场法。
60~70年代,美国学者J.penzien等在解决泥沼地上大桥动力分析时提出了集中质量法,目前已在国内外得到了广泛的应用。
集中质量法将桥梁上部结构多质点体系和桩一土体系的质量联合作为一个整体,来建立整体耦联的地震振动微分方程组进行求解。
该模型假定桩侧土是Winkler连续介质。
以半空间的Mindlin静力基本解为基础,将桩-土体系的质量按一定的厚度简化并集中为一系列质点,离散成一理想化的参数系统。
并用弹簧和阻尼器模拟土介质的动力性质,形成一个包括地下部分的多质点体系。
2 土弹簧刚度的确定,除考虑使用较为精确的有限元或边界元方法外,较为简便的方法是采用Penzien模型中提供的土弹簧计算方法或参照现行规范中土弹簧的计算方法。
我国公路桥涵地基与基础设计规范(JTG D63-2007)用的“m法”计算方法和参数选取方面比Penzien 的方法要简单和方便,且为国内广大工程师所熟.“m法”的基本原理是将桩作为弹性地基梁,按Winkler假定(梁身任一点的土抗力和该点的位移成正比)求解。
但是,由于桩-土相互作用的实验数据不足,土的物性取值有时亦缺乏合理性,在确定土弹簧的刚度时,仍有不少问题未能很好解决。
特别是,“m法”中m的取值对弹簧刚度的计算结果影响很大,且不能反映地震波的频率特性和强度带来的影响。
地震荷载下桩土相互作用简化计算方法及参数分析

1 简化模型及分析方法
1. 1 分析模型 在 以往的研究中, 桩土相互作用的分析模型
主要有 3 种: 动力W ink ler 地基上的梁模型、梁和 波动场模型以及有限元模型[3]. 3 种模型中由于 动力W ink ler 地基上的梁模型力学概念清楚, 简 单 实用, 易于被工程人员接受而被广泛运用. 本 文拟采用这一模型, 将桩离散为梁单元, 在节点处 考虑水平位移和转角, 将桩体的质量集中在节点 处. 土体由离散的弹簧 2阻尼器系统代替, 简化模 型见图 1.
地震荷载下桩土动力相互作用的动力反应由 于涉及到场地条件、桩体本身的特性以及输入的 地震动特性等, 属于多因素多水平问题, 因此就不 同的参数进行敏感性分析是有必要的. 针对此问 题 Gazeta s 曾在频域内进行了详细的研究[9], 本文 的工作则在时域内进行.
仍 取端承单桩为研究对象, 选择桩土弹模比 E p E s、桩的长径比 L D 和输入地震动水平 ai g
肖 晓 春1, 迟 世 春1, 林 皋1, 约翰·艾法罗2
( 1. 大连理工大学 土木工程系, 辽宁 大连 116024; 2. 康乃尔大学 土木与环境工程系, 纽约 伊萨卡 10543 )
摘要: 针对水平地震荷载下桩土相互作用体系, 建立了简化计算模型. 与有限元分析结果对
比验证了简化模型的有效性, 并运用此模型就桩土弹模比、地震动输入以及桩的几何特性进 行了参数敏感性分析. 对计算结果的统计分析表明, 桩土弹模比对桩土动力相互作用的影响 较为显著.
(7)
i = 1, 2, …, 8; Νi, Γi, Φi = ± 1
P 1 = 1 - Ν2, P 2 = 1 - Γ2, P 3 = 1 - Φ2 (8) 在单元刚度组装为总刚度矩阵前将内部节点自由
桩_土_桩相互作用影响的试验研究

第30卷 第1期 岩 土 工 程 学 报 Vol.30 No.1 2008年 1月 Chinese Journal of Geotechnical Engineering Jan., 2008 桩–土–桩相互作用影响的试验研究王 涛,刘金砺(中国建筑科学研究院,北京 100013)摘 要:通过大比例尺模型试验、工程实测结果与弹性理论解进行对比,指出弹性理论解夸大了桩–桩、桩–土、土–土相互作用影响,造成沉降计算值偏大和过高估计桩顶反力的不均匀性和筏底地基土反力的不均匀性。
据此,建议进行上部结构–基础–桩土共同作用的分析计算时,必须充分估计弹性理论解与真实值的差别,以工程实测和试验数据为基础对弹性理论解进行修正,方可获得较满意的计算结果。
关键词:桩–桩;桩–土;土–土;相互作用因子;弹性理论中图分类号:TU473 文献标识码:A 文章编号:1000–4548(2008)01–0100–06作者简介:王 涛(1978–),男,辽宁鞍山人,博士,主要从事桩基工程研究。
E-mail: taow715@。
Tests on influence of pile-soil-pile interactionWANG Tao, LIU Jin-li(China Academy of Building Research, Beijing 100013, China)Abstract: It was pointed out through large scale model tests and a comparison between the measured results and the theoretical solution of elasticity that the theoretical solution of elasticity exaggerated the influence of pile-pile, pile-soil, soil-soil interaction, and it led to the large predicted value of subsidence and overestimated the non-uniformity of the reaction on pile head and non-uniformity of the earth pressure on raft bottom. The difference between the theoretical solution of elasticity and the real value should be estimated in analysis of interaction of superstructure-foundation-soil, and the theorefical solution of elasticity should be revised based on the measured and model test results.Key words:pile-pile; pile-soil; soil-soil; interaction influence coefficient; elastic theory0 引 言目前,桩筏(箱)基础设计中,考虑上部结构、基础和桩土共同作用的分析还在不断探索中,现在普遍采用的有限元等数值计算手段当中,也大多基于弹性理论进行计算。
荷载作用下桩间相互作用系数计算分析

l 1 0
道
建
筑
Ra i l wa y Eng i n e e r i n g
文 章编 号 : 1 0 0 3 — 1 9 9 5 ( 2 0 1 7 ) 0 6 — 0 l 1 0 — 0 5
荷 载 作 用 下桩 间相 互 作 用 系数 计 算 分 析
侯 思强 , 郭 院成 , 李明宇 , 张 浩
弹性 解法 的 缺 陷在于 计算 出 的桩 间相互 作 用 系数 与主 动桩 加载 量无 关 , 但 试 验及 模 拟 分 析 均 表 明 桩 从 开
始加 载 到破 坏 , 桩 土 界 面沿 桩 长 会 有 一 部 分 桩 土 界 面 进 入塑性 区 , 桩 问相 互 作 用 系 数 整 体 表 现 为 非 线 性 。
①各 桩 为理想 弹 性体 且几 何参 数及 性质 相 同 ;
法及 弹性 力学 基本 方 程可 以求 得桩 间土 位 移方程 :
②桩 间 土为各 向同性 的均 质 弹性体 。由剪 切位 移
移增 大 而发生 变化 。但 文献 [ 6 ] 提 出 的剪 切 位移 法 大
多 基 于桩土 界 面线 弹性 假 定 , 对 于 桩 土 界 面 进 入 塑 性
进 行全 面分 析 , 并且花 费 高 , 耗 时长 。 文献 [ 5 ] 提 出 了桩 间相 互 作 用 系 数 的 概 念 , 并 进 行 了理论研 究 。对 于 2根 几 何 尺 寸 、 材 料 参 数 完 全 相 同的 桩 , 被 动桩 i 在 主动桩 作用 下 2桩之 间 的桩 间相 互 作 用系数 定 义为
O l = ( 0) / w ( 0) ( 1 )
文献[ 1 0 — 1 1 ] 基 于剪 切 位 移 法考 虑 桩 土 界 面非 线 性 作 用, 在文 献 [ 1 2 ] 的基 础 上 , 借鉴文献 [ 1 3 ] 提 出 的 理 想
钢板桩计算方法范文

钢板桩计算方法范文钢板桩是常用的基坑支护工程中的一种支护形式,它的特点是施工简便、效率高、重复使用等。
在设计和计算钢板桩时,需要考虑桩体的稳定性、承载力、变形以及桩与土壤的相互作用等因素。
下面将按照设计与计算的步骤,详细介绍钢板桩的计算方法。
一、桩体稳定性的计算方法桩体稳定性主要考虑桩体侧面稳定和桩尖稳定两个方面。
1.桩体侧面稳定计算方法:根据桩体的几何尺寸以及土壤参数,计算桩体在侧面稳定时所需要的抗滑力。
主要计算公式如下:F = 0.5 * γ * H * Σs * As * Sin(α +φ)其中,F为抗滑力,γ为土壤的容重,H为桩的深度,Σs为土壤的表观修正系数,As为桩的侧面积,α为土壤内摩擦角,φ为土壤与桩体之间的摩擦角。
2.桩尖稳定计算方法:桩尖在承受侧向力时需要具备足够的抗推承载力。
桩尖稳定计算主要考虑桩尖的静力平衡,计算方法如下:Fa = q * Ap + 0.5 * γ * H' * Ap * Sinφ其中,Fa为桩尖的抗推力,q为土压力,Ap为桩尖的横截面积,H'为土体高度,φ为土壤与桩体之间的摩擦角。
二、桩体承载力的计算方法桩体承载力的计算是指桩体在承受竖向荷载时所能够抵抗下沉或沉降的能力。
1.挤土桩承载力计算方法:挤土桩的承载力计算主要考虑挤土桩与土壤的拟静力摩擦力和基质土的桩侧土承载力。
主要计算公式如下:Qs = Σ(Ks * Ls * As)+ 0.5 * γ * H' * Ap * cos(φ - α)其中,Qs为挤土桩的承载力,Ks为基质土的桩侧土承载力系数,Ls 为桩体在土中的长度,As为挤土桩的横截面积,γ为土壤的容重,H'为土体高度,Ap为桩尖的横截面积,φ为土壤与桩体之间的摩擦角,α为土壤内摩擦角。
2.挡土墙承载力计算方法:挡土墙的承载力计算主要考虑桩体的弯曲强度和承载力。
主要计算公式如下:Qb=M/Ec+N/Es其中,Qb为挡土墙的承载力,M为挡土墙产生的弯矩,Ec为混凝土弹性模量,N为挡土墙产生的正常力,Es为钢板桩的弹性模量。
桩-土-结构相互作用体系非线性地震反应分析的开题报告

桩-土-结构相互作用体系非线性地震反应分析的开题报告一、研究背景及意义桩-土-结构相互作用是地震中涉及到的一个复杂的问题,涉及到了结构物、土壤和桩三者的力学特性和相互作用关系。
在地震作用下,桩、土、结构之间的相互作用会发生极大的变化,土层的非线性特性以及土-结构耦合效应等因素对桩-土-结构体系的反应产生了重要影响,而出现这些非线性问题的原因主要与以下方面有关:震动波形的复杂性、地震波导过程中异常水平变形所引起的摩擦力、底部非均匀土层的反应和排水、桩-土-结构之间动静力相互的作用、材料的非线性等等。
因此,从理论和实践角度分析桩-土-结构相互作用体系的非线性地震反应对抗地震灾害,对地震工程的发展具有重要意义。
二、研究目的本文主要旨在对桩-土-结构相互作用体系在地震荷载下的非线性反应和影响因素进行详细研究,为了达到这个目的,必须做到以下几点:1、深入理解桩-土-结构相互作用体系的物理本质以及桩-土-结构之间的相互作用机理;2、研究车辆荷载对固定端单桩在不同地质情况下的动力特性以及受振幅、频率等复杂地震荷载的影响;3、基于数值模拟方法,建立桩-土-结构相互作用的非线性地震反应模型并对其进行数值模拟计算,分析桩-土-结构相互作用下的非线性反应特性、荷载传递和损伤演化等因素的影响;4、对比对不同材料参数、结构体系、和地质基础情况等参数下的反应特性差异,分析其与非线性反应的关系,以期为相关地震安全预警提供参考依据。
三、预期成果本文的预期成果主要包括以下几点:1、通过深入理解桩-土-结构相互作用体系的物理本质以及其相互作用机理,掌握桩-土-结构相互作用体系在地震荷载下的非线性反应机制;2、通过对固定端单桩在不同地质情况下的动力特性及其对变幅、频率等复杂振动荷载的响应研究,掌握固定端单桩的动力响应特性及其与地震荷载之间的关系;3、通过建立桩-土-结构相互作用的非线性地震反应模型,并进行数值模拟计算,分析桩-土-结构相互作用下的非线性反应特性,明确荷载传递和损伤演化等因素影响桩-土-结构体系的关键因素;4、探究不同参数下的反应特性的差异,深入分析其与非线性反应的关系,并为相关地震安全预警提供参考;5、对比实验结果与数值模拟结果的一致性,验证模型的可靠性。
MIDAS计算软件模拟桩土相互作用

1 用MIDAS模拟桩-土相互作用(“m法”确定土弹簧刚度)北京迈达斯技术有限公司2009年05月1、引言土与结构相互作用的研究已有近60~70年的历史,待别是近30年来,计算机技术的发展为其提供了有力的分析手段。
桩基础是土建工程中广泛采用的基础形式之一,许多建于软土地基上的大型桥梁结构往往都采用桩基础,桩-土动力相互作用又是土-结构相互作用问题中较复杂的课题之一。
至今已有不少关于桩基动力特性的研究报告,国内外研究人员也提出了许多不同的桩-土动力相互作用计算方法。
从研究成果的归类来看,理论上主要有离散理论和连续理论及两者的结合,解决的方法一般有集中质量法、有限元法、边界元法和波动场法。
60~70年代,美国学者J.penzien等在解决泥沼地上大桥动力分析时提出了集中质量法,目前已在国内外得到了广泛的应用。
集中质量法将桥梁上部结构多质点体系和桩一土体系的质量联合作为一个整体,来建立整体耦联的地震振动微分方程组进行求解。
该模型假定桩侧土是Winkler连续介质。
以半空间的Mindlin静力基本解为基础,将桩-土体系的质量按一定的厚度简化并集中为一系列质点,离散成一理想化的参数系统。
并用弹簧和阻尼器模拟土介质的动力性质,形成一个包括地下部分的多质点体系。
2 土弹簧刚度的确定,除考虑使用较为精确的有限元或边界元方法外,较为简便的方法是采用Penzien模型中提供的土弹簧计算方法或参照现行规范中土弹簧的计算方法。
我国公路桥涵地基与基础设计规范(JTG D63-2007)用的“m法”计算方法和参数选取方面比Penzien 的方法要简单和方便,且为国内广大工程师所熟. “m法”的基本原理是将桩作为弹性地基梁,按Winkler假定(梁身任一点的土抗力和该点的位移成正比)求解。
但是,由于桩-土相互作用的实验数据不足,土的物性取值有时亦缺乏合理性,在确定土弹簧的刚度时,仍有不少问题未能很好解决。
特别是,“m法”中m的取值对弹簧刚度的计算结果影响很大,且不能反映地震波的频率特性和强度带来的影响。
桩土共同作用桩基的计算及应用

加, 增长速率没有突变。医技楼装修工程基本结束时, 平 均 沉 降 量 为 %-6% $$; .个月后,平均沉降仅增加% 沉降差 -6+ $$, 最大沉降仅 *(6, $$。说明该楼沉 $$, 降已基本稳定, 且各点沉降基本均匀。 常规嵌岩桩与按本桩土共同作用设计计算方法所 得两种桩基经济性比较见表% 。 从表% 可见, 按此方法考
桩径 # $ 桩长 # $
用量 # $! 合造价 # 元 # $!
# 万元 !%&’" %(!’&
常规嵌岩桩 桩土共同作用桩基
(’&)%’* (’"
!&’+ !%’+
*&,"’,.!’,
%%(( %%((
第 *! 卷 ()..+ 年) 第*期
K>;L*!
->L*
建 筑 技 术 7DCJ:B<CB?D< 5<CJ@>;>FE
在沿海地区建筑工程的桩基础设计中, 通常只考 虑由桩来承担上部荷载, 而不考虑承台底土体的地基 承载力。若能考虑桩与土体共同作用, 充分发挥地基 土体天然地基承载力, 既可缩短桩长, 也可减少桩数, 具有良好的经济效益。
!"#
主要缺陷 (!) 若 桩 端 选 用 低 压 缩 性 土 层 (如粘性土、 粉
%&’%(’&)*+, +- .*’/ -+(,0&)*+, (,0/1 )2/ 3+*,) &%)*+, +- .*’/ &,0 4+*’ &,0 *)4 &..’*%&)*+, !"#$% &’()(* !"#$% !’+*,)(-+ "#$ .+ /0 1(*,23*, &56789:7: 78 9:; <;=>?8 @A A@B8<+9>@8= >8 C@+=9+D +E;+, B=B+DDF, @8DF G>D; >= C@8=><;E;< 9@ H;+E BGG;E D@+< , I:>D; 9:; H;+E>8? C+G+C>9F @A 9:; =@>D B8<;E G>D; C+G >= <>=E;?+E<;<- J+=;< @8 9:; C@KGD;L A@B8<+9>@8 9:;@EF, + C+DCBD+9>@8 K;9:@< >= GE@G@=;< A@E G>D; A@B8<+9>@8 9+)>8? 9:; C@5+C9>@8 @A G>D; +8< =@>D >89@ +CC@B892:>= K;9:@< C+8 K+); ABDD B=; @A 9:; C+EEF>8? C+G+C>9F @A 8+9BE+D =@>D +8< E;<BC 9:; G>D; 8BKH;E +8< <>K;8M =>@8, :+N>8? + ?@@< ;C@8@K>C+D H;8;A>9;<= >?8@6: O@>89 +C9>@8 @A G>D; +8< =@>D; C@KGD;L A@B8<+9>@8 9:;@EF; C+EEF>8? C+G+C>9F @A =@>D
桩土面积置换率公式

桩土面积置换率公式
桩土面积置换率公式是用于计算土壤中的桩体所占据的面积与实际占地面积之间的比值。
这个公式在土木工程中广泛应用,以评估桩基础对土壤的影响和确定桩基础的设计参数。
桩土面积置换率公式的表达式如下:
置换率(%)= (实际桩体截面面积 ×桩体长度) / (实际桩体截面面积 ×桩体长度 + 土壤体积)
其中,实际桩体截面面积是指桩体在截面上所占据的面积,桩体长度是指桩体在垂直方向上的长度,土壤体积是指桩体所挤压掉的土壤体积。
通过使用桩土面积置换率公式,可以得到桩基础对土壤的置换率,从而评估桩体与土壤之间的相互作用。
这个评估指标可以帮助工程师确定桩基础的设计参数,确保桩基础的稳定性和安全性。
在实际工程中,桩土面积置换率公式常用于对桩基础的设计和分析,特别是在涉及较大的土方工程、土壤改良和桩基础施工中。
通过准确计算和评估桩土面积置换率,工程师可以更好地了解桩体与土壤之间的相互影响,进而制定出合理的施工方案和设计参数。
这有助于提高工程的质量和安全性。
总而言之,桩土面积置换率公式是土木工程中重要的评估指标,用于计算桩体在土壤中所占据的面积与实际占地面积之间的比值。
这个公式的应用可以帮助工程师评估桩基础的稳定性和安全性,并制定出合理的设计和施工方案。
桩_土_桩相互作用分析

低 温 建 筑 技 术
2008 年第 1 期 ( 总第 121 期)
(9)
2 算例分析 211 单桩沉降计算
为验证算法的正确性 ,将采用文中算法计算的单桩沉降 与 Poulos 弹 性 理 论 法 相 比 较 。按 照 Poulos ( Poulos& Davis , 1980) 的理论定义沉降因子 I , 沉降因子与沉降 S 量之间关 系有 S = ( PΠES L ) I ,式中 S 为桩头沉降 ,沉降因子 I 与桩径 比 L/ D 、 桩土刚度比 k = EPΠES 有关 , 土泊松比对其影响较 小 。以下计算采用各向同性场地 , 取场地泊松比 μ = 0. 3 , I 随桩径比 L / D 、 桩土刚度比 k = EPΠES 的变化规律如图 2 所 示 ,图中实线所示为采用本算法解 ,虚线所示为 Poulos 解 。
3 结语 (1) 采用子结构法分析桩 - 土 - 桩相互作用 , 可运用
于求解单桩与群桩沉降 。采用子结构法分析桩沉降 ,能较好 模拟土层层状性质 。 (2) 通过群桩沉降影响系数分析 , 桩桩间距影响较小 情况下 ,其相互影响不可忽略 。
房利人 : 对某工程桩基础设计及施工工艺的反思
109
承载能力中图分类号li嗍31文献标识码lb文章编号100l一6864200801一010902桩基础以其承载能力高沉降变形小施工方便质量便于控制等优点在建筑工程中得到了普遍的推广和应用尤其是混凝土灌注桩近年来有长足的发展成桩工艺不断创新每种成桩工艺各有所长根据地质状况不同各有优势
毕志成等 : 桩 - 土 - 桩相互作用分析
序号
1 2 3 4 5 6 7 8 9 10
调整或更换成桩工艺 ,尤其是发现明显可能影响桩身质量的 地质状况 ,必须调整成桩工艺 。否则 ,给基础工程带来隐患 , 甚至不能满足安全使用要求和耐久性要求 ,实践证明 , 错误 的决策会造成大量资金浪费和延误工期 。
不同土体条件下桩-土相互作用位移分析

西部探矿工程
5
不 同土体 条 件 下桩 一 土相 互 作 用 位移 分析
王 代 , 王勇智
( 1 _ 中州大学, 河南 郑州 4 5 0 0 0 0 ; 2 . 郑州大学新型建材与结构研究中心, 河南 郑州 4 5 0 0 0 2 ) 摘 要: 为了更好地理解土体中桩的变形及破 坏, 采用有限元法模拟分析堆载下的土体位移以及桩体 变形 ; 探 讨分析 了不 同土体 条件如 重度 、 泊松 比 、 弹性 模 量 、 粘聚 力 等 , 对被 动 桩及 桩 侧 土体 变形 的影 响 。结果表 明 : 改 变土体模 量和 粘聚 力对桩 和 土的 影响是 相对较 大的 , 且 土体 的粘聚 力对桩 土 的影响 起决定作 用。因此 , 可以通过 改善土的强度参数来提 高被动桩桩~土体 系的工作性状。 关键 词 : 被 动桩 ; 桩 一 土相互 作 用 ; 有 限元 法 ; 粘 聚力 ; 位 移分析 中 图分类 号 : TU4 7 3 文献标 识码 : A 文章 编号 : l 0 0 4 —5 7 1 6 ( 2 0 1 3 ) O l —O 0 O 5 —0 5
从图 6 ~图 9 可以清楚看到, 土体弹性模量对桩侧 土体侧 向位 移 和竖 向位 移 的影 响都是 比较 大 的 , 模 量大 的土体 侧 向位移 越来越 接近线 性 , 竖 向位移 分布 是 比较 均匀 ; 但在土体弹性模量大的情况下桩侧土体竖向位移 会越小 。在不同荷载下 , 同种土体模量 , 尽管对土体竖 向位 移有一 定 的影 响但 效果不 是很 大 。总之 , 在 相应 土 体模量下 , 竖向位移与侧向位移相差不 明显 , 但随着外
相互作用的力学特性 。计算模型 、 土层边界及荷载如图 1 所示 , 土层 0 ~1 5 m为泥炭质土 ( 软土层) , 1 6 ~2 0 m 为较硬细 砂层 。模 型 边界 横 向取 4 0 m, 深 度方 向取 2 0 m。横 向边界约束 条件 : 左边界横向约束 , 右边界固 定铰支约束 ; 深度方 向边界条件: 上边界为竖向约束 , 下 边界是固支约束。桩基为圆桩 ; 计算单元数 8 0 0 个。在
桩土相互作用模型分析及土弹簧的刚度确定

桩土相互作用模型分析及土弹簧的刚度确定桩基地基相互作用在工程领域中是一个非常重要的研究方向。
如何分析桩土相互作用,确定土弹簧的刚度,已经成为研究者们长期以来的研究方向。
本文将着重介绍桩土相互作用模型的分析以及土弹簧刚度的确定方法。
一、桩土相互作用模型分析桩土相互作用的分析是一个很复杂的问题,需要考虑很多因素,例如桩的形状、尺寸、材质、荷载作用方式以及土体的本构模型等等。
因此,建立一个合适的桩土相互作用模型是非常重要的。
常用的桩土相互作用模型主要包括刚性桩模型、柔性桩模型、弹性桩-地基模型和弹塑性桩-地基模型等。
具体模型的选择应根据实际工程情况进行合理选择。
在选择模型的同时,还需要考虑模型的精度和适用范围。
1. 刚性桩模型刚性桩模型是一种假设桩完全刚性的模型,桩与土体之间不存在变形,荷载沿着桩轴线方向传递。
该模型的应用比较广泛,特别是在短桩和单桩承载力计算中。
但是,刚性桩模型忽略了桩与土体之间的变形,因此在一些长桩、柔性桩及复杂荷载情况下,其结果可能需要进行修正。
2. 柔性桩模型柔性桩模型是一种假设桩的刚度较小,桩与土体间存在较大变形的模型。
因此,在该模型中,桩遭受荷载后,桩柄会发生变形,从而引起桩端和土体的变形。
这种模型适用于长桩或软土等复杂工程情况的分析。
但是,柔性桩模型的计算较为复杂,同时模型误差也较大。
3. 弹性桩-地基模型弹性桩-地基模型是一种假设桩和土体都是均质的弹性体的模型。
该模型假设桩和土体在弹性阶段的反应服从弹性理论,可以较好地反映桩与土体之间的相互作用关系。
其应用比较广泛,适用于一些较小荷载的工程应用。
4. 弹塑性桩-地基模型弹塑性桩-地基模型是一种新的桩土相互作用模型,既考虑了弹性行为,也考虑了土体的塑性行为。
该模型能够比较准确地反映桩与土体之间的相互作用关系。
其应用范围广泛,特别适用于长桩和承载力较大的复杂应力场中的计算分析。
二、土弹簧的刚度确定在桩土相互作用中,土弹簧承担着承载荷载的重要作用。
桩-土相互作用支护桩受力变形计算方法

桩-土相互作用支护桩受力变形计算方法李涛;江永华;朱连华;关辰龙【摘要】为研究桩-土非线性相互作用对深基坑支护结构内力与位移的影响,提出了一种桩-土相互作用支护桩受力变形计算的方法.该方法将基坑开挖面以上的桩体视为有限数量的弹性体,开挖面以下的桩体视为Winker地基梁,支撑结构为二力杆弹簧,并考虑支护桩和内支撑的变形协调,基于桩结构分段分坐标法和弹性地基梁法,推导出了考虑桩-土-内支撑共同作用的支护桩体挠曲微分方程.结合理论土压力,采用该方程计算获得了不同开挖深度的桩体水平位移和桩体弯矩,并与规范法、实测值进行比较.结果表明:本文方法计算得到的支护桩最大水平位移比规范法小15.2%,最大弯矩较规范法小26.6%,均与实测值更为相近.【期刊名称】《西南交通大学学报》【年(卷),期】2016(051)001【总页数】8页(P14-21)【关键词】桩-土相互作用;深基坑;变形;计算;现场实测【作者】李涛;江永华;朱连华;关辰龙【作者单位】中国矿业大学(北京)力学与建筑工程学院,北京100083;中国矿业大学(北京)力学与建筑工程学院,北京100083;中国矿业大学(北京)力学与建筑工程学院,北京100083;中国矿业大学(北京)力学与建筑工程学院,北京100083【正文语种】中文【中图分类】TU432基坑支护问题一直是岩土工程界的一个研究热点.早在20世纪40年代就有学者基于基坑支护问题提出了一些著名的计算理论,如Terzaghi-Peck表观土压力理论[1-2]等,并在基坑支护设计计算方面得到了应用.国内外很多专家学者也在这个领域做了大量有意义的研究工作:文献[3]利用现场实测数据求得的桩身弯矩,分析了护壁桩的变形状态和坑底以上桩侧的土压力,表明在支护结构正常工作的情况下,坑底以上桩侧土压力的分布和大小都与经典土压力理论有显著差别;文献[4]采用等值梁法进行基坑支护设计计算,该方法概念清晰,模型合理,计算结果与实测结果较为接近,该法跟传统的设计方法相比,具有明显的经济效益,另外利用该法还可对方案进行评价和选优;文献[5]将地基土的水平基床系数视为深度和围护墙位移的非线性函数,建立作用于围护墙上的土压力增量的计算模型,进而根据一般弹性地基梁的挠曲微分方程,推导出考虑非线性共同作用的弹性地基梁的挠曲微分方程;文献[6]对深基坑与高层建筑的共同作用进行了实例分析,研究了支护桩体刚度对地层位移的影响,通过加强桩体刚度,可以有效地减少建筑物的变形,模型计算与实测结果相符;文献[7]通过物理模拟,分析了圆形深基坑帷幕结构的变形规律;文献[8]针对杭州地铁秋涛路车站深基坑支护结构,采用弹性地基梁杆系有限元方法进行分析,并与实测结果进行对比;日本学者横山幸满[9]将弹性地基梁分段分坐标系来计算,并对于地质条件复杂的、桩侧土分多层的情况进行了认真研究;文献[10]考虑了支护结构-土的非线性共同作用,提出由集中力弹簧模型建立支护桩与土相互作用的p-y曲线,应用有限差分法计算预应力锚杆支护桩的位移和内力;文献[11]对某特深基坑考虑支护结构与土体共同作用进行了施工全过程的三维有限元弹塑性分析和模拟,并详细说明了其具体实现方法;文献[12]根据深基坑支护系统中支护桩-支撑-土的共同作用特征建立了三维杆系有限元分析模型,并用实例分析结果验证了模型的适用性和有效性;文献[13]采用离心模型试验和现场监测方法,获得了深基坑支护结构的侧向变形规律.以上研究成果对认识深基坑支护结构受力变形特征有显著作用,但都未考虑在某些地质条件下作用在桩身实际土压力与理论土压力存在较大差距而使得理论计算所得的结构内力及位移值与现场实测值差异较大的情况.本文提出了一种考虑桩-土相互作用,以及不同开挖深度下支护结构受力变形的实用计算方法,即采用桩结构分段分坐标法和弹性地基梁法相结合分别对开挖面以上和开挖面以下桩体结构在开挖过程中的受力变形进行理论计算.以此方法为出发点,结合北京地铁10号线深基坑工程实例,基于朗肯土压力理论,对比分析了规范方法与本文方法所计算的桩体内力与位移,并与现场实测值进行比较,分析了理论计算结果与实测值差异较大的原因,为此类地层条件下基坑施工经济性和安全性提供了决策依据.1.1 计算模型桩-土-钢支撑相互作用的计算模型如图1所示.本文基于以下基本假设,对深基坑支护结构受力变形进行理论分析:(1)随基坑开挖土体被卸除,开挖面以上部分挡土结构分离成有限段弹性梁单元,支撑结构简化为二力杆弹簧;(2)开挖面以下部分视为一竖置的Winker弹性地基梁单元;(3)土体为弹性体.1.2 桩体挠度方程1.2.1 开挖面以上桩体挠度计算对于开挖面以上桩体,由于设有支撑结构,支护结构上作用的荷载分布模式比较复杂,因此,本文采用分段分坐标法,把支护结构沿深度方向划分为有限个弹性桩单元.为了计算简便,支护结构的截面荷载突变处、土层分界面处及支撑的作用点处均作为节点处理,将开挖面以上桩体分成n段,如图2为每段梁单元受力情况,据此分别计算,求得整个开挖面以上桩体挠度.从桩顶往下各截面荷载突变、土层分界面及支撑的作用点所在点Oi(i=0,1,2,…)处,以埋深方向为xi轴,指向基坑内侧水平方向为yi轴,建立坐标系,记桩身的水平位移为yi(xi),土压力为qi(xi),在各分界点Oi处,截面弯矩为Mi,剪力为Qi,则开挖面以上桩体的挠度微分方程为式中:EI为围护桩桩身刚度;qi(xi)为xi处的主动土压力分布强度;bs为主动土压力的计算宽度,取桩的中心距;hi为Oi到Oi+1恒的距离.式(1)为4阶线性微分方程,其通解可表示为式中:a1、a2、a3、a4是由边界条件确定的积分常量.对方程(2)进行逐次微分求解,其求解结果可用下述矩阵表示:式中:a1、a2、…、a4i-1、a4i为未知参数;1.2.2 开挖面以下桩体挠度计算将开挖面以下桩体看作受分布荷载作用的弹性地基梁,开挖截面处受上部结构作用弯矩M0和剪力Q0,如图3.弹性地基梁基本微分方程:式中:q(x)为作用在开挖面以下桩体上的荷载;p(x)为地基反力,且p(x)=kyb0,其中k为地基系数或垫层系数;y为地基的沉陷;b0为计算梁的宽度,排桩方形按b0=1.5b+0.5(b为桩截面边长),圆形按b0=0.9(1.5d+0.5)(d为桩截面直径),确定的计算宽度不应大于排桩中心距[10].本研究中考虑到桩侧土随着深度的增加表现出不同的性质,故决定采用地基梁法中的“m”法来计算抗力[9],即地基系数k=mx,其中,m根据文献[2]经验取值,于是地基抗力表示为则开挖面以下桩体的挠度微分方程为在均布荷载作用下,挠度方程修正项为qbs/k×[1-φ1(βx)],则方程(5)的解可表示为式中y0、θ0、M0、Q0分别为开挖面处位移、转角、弯矩、剪力可根据文献[14]查得.1.2.3 挠度方程求解由于桩顶受力变形不明确,边界条件难以假设,故可在其桩顶上部加一段虚拟桩单元,其边界条件明确,无土压力无支撑作用,为自由端,根据位移连续条件和力的平衡条件可知O1点处的变形受力情况,如图4.对于桩底边界条件[9]一般采用以下两种:(1)桩底的弯矩和位移为已知,如桩尖处在土层或桩很长时可以认为桩底的弯矩和剪力近似为0;(2)桩底的水平变位和角变位为已知,如桩足够长,以致其底部不可能产生变位时可以认为水平位移和角变位为0.不符合上述两种情况时,可以据实际情况合理地假设桩底的近似边界条件.对于上述开挖面处开挖面以上与开挖面以下的挠度一致,可根据边界条件与位移连续条件和力的平衡条件计算出挠度方程中的未知参数:式中:Pi为节点Oi处的荷载突变值.如果Oi处设有钢支撑,Pi=Kyi(0),其中K为钢支撑刚度系数[15],如未设钢支撑,则Pi=0.方程(3)中有4n+8个未知参数,方程组(8)中共有4n+8个方程,所以可根据方程组(8)求解出方程(3)中所有未知参数.2.1 工程简介以北京地铁10号线2期巴沟段盾构竖井基坑为例,基坑的平面呈长方形,宽18.00 m,长21.00 m,开挖深度18.66 m,嵌固深度为2.84 m.盾构施工竖井结构形式为现浇混凝土箱形框架结构,结构外设置外包防水层,采用明挖法施工.综合考虑竖井位置及周边规划情况,盾构井围护结构采用钻孔灌注桩加钢支撑,桩长为21.50 m,桩径采用0.80 m,桩距1.40m,弹性模量取30 GPa,泊松比取0.2.钢支撑安装拆卸方便,可施加预应力,破坏前有明显变形,采用直径0.63 m、厚度12 mm的钢支撑,其弹性模量取250 GPa,横截面积取0.011 7m2.共设3道钢支撑,第1道钢支撑设于冠梁处,第2、3道钢支撑通过水平钢围檩支撑在钻孔灌注桩上,第1、2道钢支撑恒距为9.05 m,第2、3道钢支撑恒距为5.30 m.根据本工程监测方案,桩体实测水平位移可由桩体测斜得到.在桩上迎土侧主筋外每隔2.00~3.00 m左右埋设1个土压力计,1根桩共安装9个,以监测外侧土体对桩体的横向压力值,即实测土压力值;为准确了解桩体在开挖过程中弯矩的变化情况,通过在围护桩的主受力钢筋上连接钢筋应力计,测试围护桩在基坑开挖和主体结构施工过程中的钢筋应力变化情况,在围护桩基坑侧和迎土侧主筋上每隔2.00 m左右安装1个,1根桩共安装22个应力计用以测试钢筋应力,再通过理论计算[16]反映出桩身截面弯矩的变化情况.基坑支护结构与监测剖面图如图5所示.为消除深基坑工程空恒效应的影响,实例分析选用长边中点的桩体作为研究对象.2.2 水文地质条件盾构施工竖井埋置较深,底部位于砂卵石地层中,在该隔水层上未发现地下水,且在初步勘察阶段火器营站以南卵石圆砾层底部是含水的,为潜水,水位标高30.26~31.94 m,但水量也较小,且为枯水期,基坑底部标高为32.04 m,故可不考虑地下水的作用.各层的岩土工程特征描述以及计算参数如表1所示.2.3 实例计算过程把开挖面以上桩体在土层分界面及支撑的作用点处作为分段点,其余按每段最大1.50 m进行分段,结合上述分段分坐标法进行计算,开挖面以下桩体则采用弹性地基梁理论进行计算.其中根据表1中土层的物理力学性质,可计算作用在桩背上的主动土压力qi(xi)[2],代入式(3)与(7)可得到基坑开挖面以上及以下桩身挠度方程的通解,然后根据边界条件式(8)可计算出挠度方程中的所有未知参数.由于未知量较多,本文利用Matlab数值软件求解该方程组未知参数a1、a2、…、a4i-1、a4i,从而可得出桩身的挠度方程的精确解.2.4 实例计算结果及分析基坑支护桩体水平位移在不同开挖阶段的变化情况如图6所示.图中基于经典朗肯主动土压力分别采用本文方法、规范方法[13]计算桩体水平位移,并与实测值进行比较.图6(a)中为开挖至-6.50 m处的桩身水平位移曲线.由图6中可以看出,桩体水平位移随着深度增加先增大后减小,基于理论土压力采用两种方法的计算值与实测值最大位移均发生在-5.00 m左右,其中采用本文方法计算的最大值比实测值大92.8%,采用规范方法计算的最大值比实测值大181.5%.另外,采用规范方法的计算值在-11.00 m处几乎为0,远小于实测值;而采用本文方法时,桩体水平位移变形规律与实测值基本相同,既保证开挖面以上支护桩体水平位移变化曲线的规律性,也保证基坑开挖面以下土体水平位移的可靠性.随着基坑开挖至-12.50 m处,其水平位移曲线如图6(b),实测最大值出现在-7.50 m处,其值为5.73 mm;采用本文方法计算最大位移也出现在-7.50 m处,最大值为10.45 mm,比实测值大92.8%;采用规范方法计算最大位移也出现在-7.50 m处,最大值为12.68 mm,比实测值大121.3%.三条曲线沿桩身的变化规律基本一致.从图6(c)中可知,开挖至设计深度-18.66 m时桩体最大位移实测值为8.7 mm,发生在-9.50 m左右;采用本文方法计算最大位移值为21.1 mm,比实测值大142.5%,大约发生在-9.00 m处;采用规范方法计算最大位移出现在-8.00 m左右处,最大值为24.89 mm,比实测值大186.1%.由于本文方法考虑桩-土的相互作用,因此,桩体位移随深度变化曲线在钢支撑处出现了较为明显的凸点,说明钢支撑的作用较为明显.基于朗肯土压力理论,分别采用本文方法、规范方法计算所得桩体水平位移与实测结果相比较发现:(1)在开挖深度较浅的情况下,采用规范方法的计算值在-11.00 m处几乎为0,远小于实测值;而采用本文方法时,桩体水平位移变形规律与实测值在开挖面以上和以下都基本相同;当开挖深度到达一定深度时(图6(b)所示为基坑最终开挖深度的70%),规范方法、本文方法计算值和实测的桩体水平位移变形规律基本相似,但两种计算值都大于实测值,有较好的安全储备.(2)基坑开挖到一定深度时,采用规范方法和理论土压力计算所得的桩体水平位移与实测值具有一定的相似性(见图6(b)),但在基坑开挖较浅(见图6(a))和开挖较深(见图6(c))时,桩体水平位移曲线具有明显的不同,不能很好预测桩体的水平位移变化规律,而本文方法能基本符合实测桩体水平位移规律,同时也具有较好的安全储备.(3)从图6中可以看出,本文方法与规范方法的计算值与实测值有相对较大的差异,这主要是因为该地区土层作用在桩身的实际土压力比本文采用的朗肯土压力小很多,从而根据上述方法所求的桩身挠度也偏大.而基于实测土压力采用本文方法对桩身挠度的计算值与实测值比较相符,说明了本文方法对于桩体的变形特征有较好的计算结果.图7为实测桩身弯矩、基于朗肯土压力理论分别采用本文方法和规范方法计算的弯矩变化曲线,弯矩极大值和极小值见表2中的黑体数值.由表2可知,就弯矩最大值而言,本文方法计算值比实测值大65.13%,而规范方法比实测值大114.98%.图7(a)中可以看出:(1)基坑开挖面以上,在第1道钢支撑和第2道钢支撑之恒存在1个极大值,同时也是最大值;在基坑开挖面附近有第2个极大弯矩值,小于第1个极大值.(2)在基坑开挖面以下5.00~6.00 m处存在1个最大负弯矩,其值较小.(3)钢支撑对弯矩有明显的限制作用,在钢支撑处存在弯矩极小值.(4)两种方法计算值较为接近,实测弯矩值小于两种方法的计算值,表明了本文计算方法的科学合理性.(5)两种方法基于朗肯土压力对弯矩的计算值均较实测值要小很多,这主要是因为本文理论计算所采用的朗肯土压力比该基坑桩体所受实际土压力要小,从而导致桩身弯矩的计算值偏大,而基于实测土压力采用本文方法对桩身弯矩的计算值与实测值比较相符,说明了本文方法的合理性和适用性.图7(b)为基坑开挖至基坑底-18.66 m时,桩弯矩的计算值与实测值,从中可以看出:(1)桩体极大弯矩值有3个,且都为正弯矩,分别在第1道钢支撑和第2道钢支撑之恒、第2道钢支撑和第3到钢支撑之恒,以及基坑坑底附近.弯矩最大值在第1道钢支撑和第2道钢支撑之恒,实测弯矩在-6.50 m处,弯矩最大值为114.23 kN·m;规范方法的弯矩最大值为240.12 kN·m,在-5.00 m处,比实测的弯矩最大值大78.69%;本文方法计算值为176.29 kN·m,在-5.50 m处,比实测值大54.33%.(2)钢支撑处弯矩明显变小,两种方法计算结果较为接近,变化规律也基本一致.另外,图7表明:在基坑开挖过程中,开挖面以上的弯矩极大值位于钢支撑之恒和基坑开挖面附近处.基坑开挖存在一个临界深度,开挖深度未超过临界深度时,开挖面以下某位置处存在一个负弯矩,且负弯矩值远小于正弯矩值;超过临界深度时,桩身弯矩全部为正弯矩.通过以上深基坑不同开挖阶段水平位移和弯矩值的计算分析表明:(1)基坑开挖深度较浅时,本文方法要明显优于规范方法的计算值;(2)基坑开挖达到一定深度后,两种计算方法的水平位移和弯矩值具有相似的变化规律,因此本文方法的计算结果能更好地满足工程的需要;(3)基于理论土压力时,两种方法计算结果都明显大于实测值,而采用实测土压力计算出来的结果与实际情况基本相符,该理论方法计算结果可信.(1)本文提出的方法考虑了桩-土的相互作用,同时也可考虑施工过程对支护结构受力变形的影响.本文方法改进了规范方法,使计算值与实测值更为接近,同时在基坑开挖深度较浅时,本文方法计算值较规范方法更为合理.(2)在深基坑开挖过程中,开挖面以上的弯矩极大值位于钢支撑之恒和基坑开挖面附近处,基坑开挖存在一个临界深度,开挖深度未超过临界深度时,开挖面以下某位置处存在一个负弯矩,且负弯矩值小于正弯矩值.(3)桩-土相互作用机理、桩体前后水平土压力值的大小及分布形式等都会对基坑支护结构受力变形产生非常重要的影响.因此,结合地区经验的合理的土压力计算方法,以及支护结构体系-土体相互作用机理等还需做进一步的研究.【相关文献】[1]杨光华.深基坑支护结构的实用计算方法及其应用[J].岩土力学,2004,25(12):1885-1902.YANG Guanghua.Practical calculation method of retaining structures for deep excavations and its application[J].Rock and Soil Mechanics,2004,25(12):1885-1902.[2]周景星,王洪瑾,虞石民,等.基础工程[M].北京:清华大学出版社,1996:169-194.[3]夏永承,董道洋,胡敏云.深基坑锚拉护壁桩的受力特性和土压力[J].西南交通大学学报,2000,35(2):111-115.XIA Yongcheng,DONG Daoyang,HU Minyun.Behavior and earth pressure of the retaining piles with anchors for deep excavation[J].Journalof Southwest Jiaotong University,2000,35(2):111-115.[4]李仁民,施占新,刘松玉,等.弹性地基梁法和等值梁法进行基坑支护设计研究[J].西部探矿工程,2007(10):17-19.LI Renmin,SHI Zhanxin,LIU Songyu,et al.Elastic foundation beam method and the equivalent beam method for the design of foundation pit[J].West-China Exploration Engineering,2007(10):17-19.[5]邓子胜.深基坑支护结构-土非线性共同作用弹性地基反力法[J].土木工程学报,2006,39(4):68-72.DENG Zisheng.An elastic subgradereaction method considering nonlinear inter action between protectionstructure and soil for deep excavations [J].China Civil Engineering Journal,2006,39(4):68-72.[6]李涛,刘波,陶龙光.深基坑-高层建筑共同作用实例研究[J].中国矿业大学学报,2008,37(2):241-245.LI Tao,LIU Bo,TAO Longguang.Interactions between deep excavations and nearby high-rise buildings[J].Journal of China University of Mining&Technology,2008,37(2):241-245.[7]东兆星,周国庆,齐燕军.圆形深基坑中冻土帷幕变形规律试验研究[J].中国矿业大学学报,2007,36(2):137-141.DONG Zhaoxing,ZHOU Guoqing,QI Yanjun.Experimental research on deformation features of frozen wall around circular deep foundation pit[J].Journal of China University of Mining&Technology,2007,36(2):137-141.[8]杨有海,武进.杭州地铁秋涛路车站深基坑支护结构性状分析[J].岩土力学与工程学报,2008,27(增刊2):3386-3392. YANG Youhai,WU Jin.Analysis of retaining structures for deep foundation pit of qiutao road station in Hangzhou metro [J].Chinese Journal of Rock Mechanics and Engineering,2008,27(Sup.2):3386-3392.[9]横山幸满.桩结构物的计算方法和计算实例[M].唐业清,吴庆荪,译.北京:中国铁道出版社,1984:6-13.[10]朱彦鹏,魏升华.深基坑支护桩与土相互作用的研究[J].岩土力学,2010,31(9):2840-2844.ZHU Yanpeng,WEI Shenghua.Research on interaction between deep excavation supporting pile and soil[J].Rock and Soil Mechanics,2010,31(9):2840-2844.[11]陆新征,宋二祥,吉林,等.某特深基坑考虑支护结构与土体共同作用的三维有限元分析[J].岩土工程学报,2003,25(4):488-491.LU Xinzheng,SONG Erxiang,JI Lin,et al.3-dimensional FEA for the interaction between supporting structure of excavation and soil in a very deep pit[J].Chinese Journal of Geotechnical Engineering,2003,25(4):488-491.[12]陈晓平,闫军.深基坑支护结构的三维杆系有限元分析[J].岩土力学,2001,22(3):258-261.CHEN Xiaoping,YAN Jun.3D pole system FEM analysis for bracing structureof deep foundation pit[J].Rock and Soil Mechanics,2001,22(3):258-261.[13]梁穑稼,徐伟,陈宇.格形地下连续墙基坑施工阶段侧向变形[J].西南交通大学学报,2015,50(1):150-155,172.LIANG Sejia,XU Wei,CHEN Yu.Lateral deformation of cellular diaphragm wall at excavation stage[J].Journal of Southwest Jiaotong University,2015,50(1):150-155,172.[14]龙驭球.弹性地基梁的计算[M].北京:人民教育出版社,1981:19-22.[15]中国建筑科学研究院.JGJ120—2012建筑基坑支护技术规程[S].北京:中国建筑工业出版社,2012.[16]陈忠汉,黄书秩,程丽萍.深基坑工程[M].北京:机械工业出版社,2003:61-113.。
桩基规范中圆形与方形桩的换算情况总结
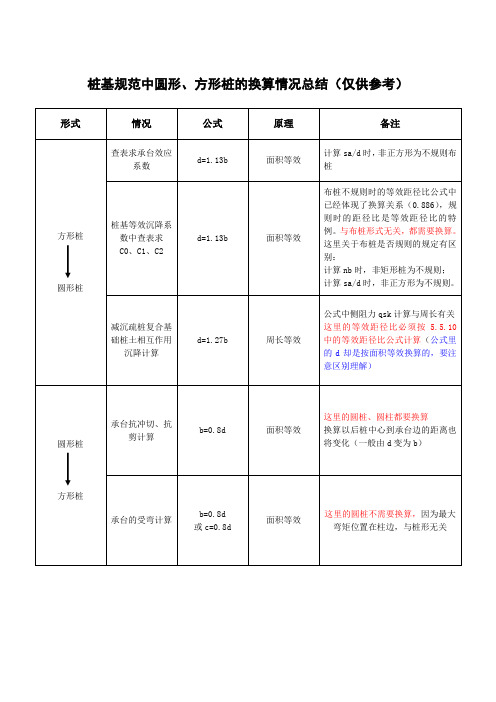
承台抗冲切、抗剪计算
b=0.8d
面积等效
这里的圆桩、圆柱都要换算
换算以后桩中心到承台边的距离也将变化(一般由d变为b)
承台的受弯计算
b=0.8d
或c=0.8d
面积等效
这里的圆桩不需要换算,因为最大弯矩位置在柱边,与桩形无关
础桩土相互作用沉降计算d127b周长等效公式中侧阻力qsk计算与周长有关这里的等效距径比必须按5510中的等效距径比公式计算公式里却是按面积等效换算的要注意区别理解圆形桩方形桩剪计算b08d面积等效这里的圆桩圆柱都要换算换算以后桩中心到承台边的距离也将变化一般由d变为bb08d或c08d面积等效这里的圆桩不需要换算因为最大弯矩位置在柱边与桩形无关
这里关于布桩是否规则的规定有区别:
计算nb时,非矩形桩为不规则;
计算sa/d时,非正方形为不规则。
减沉疏桩复合基础桩土相互作用沉降计算
d=1.27b
周长等效5.10中的等效距径比公式计算(公式里的d却是按面积等效换算的,要注意区别理解)
圆形桩
桩基规范中圆形、方形桩的换算情况总结(仅供参考)
形式
情况
公式
原理
备注
方形桩
圆形桩
查表求承台效应系数
d=1.13b
面积等效
计算sa/d时,非正方形为不规则布桩
桩基等效沉降系数中查表求
C0、C1、C2
d=1.13b
面积等效
布桩不规则时的等效距径比公式中已经体现了换算关系(0.886),规则时的距径比是等效距径比的特例。与布桩形式无关,都需要换算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
云浮至阳江高速公路罗定至阳春段(S02合同段)独桩独柱桥墩桩基桩土作用弹塑性仿真分析计算书设计部主任:计算: 日期:复核: 日期:项目负责人: 日期:审核: 日期:广东省公路勘察规划设计院有限公司2010年10月目录1.1模型及边界条件 (3)1.1.1 分析目标 (3)1.1.2 采用软件 (3)1.1.3 模型 (4)1.1.4 材料性质 (4)1.1.5 荷载 (4)1.1.6 单元选择 (4)1.1.7 边界条件 (5)1.2分析结果 (5)1.2.1 嵌岩深度2倍桩直径分析结果 (5)1.2.2 嵌岩深度3倍桩直径分析结果 (8)1.2.3 裸岩嵌岩深度3倍桩直径分析结果 (11)1.2.4 嵌岩深度4倍桩直径分析结果 (14)1.2.5 仅竖直力作用桩基分析结果 (17)1.3结论 (18)1.1模型及边界条件1.1.1分析目标本项目设计有大量独桩独柱墩,桩基承受轴向力同时承受巨大的弯矩;然而,灰岩地区岩石埋深浅或岩石裸露,如何确定桩基础经济合理及安全可靠的的嵌岩深度,保证桩土应力长期稳定及桩顶位移满足上部结构的使用要求并具有一定的超载能力,规范及相关文献未见其解。
分析的目标:考虑轴向和侧向加载下,研究不同嵌岩深度桩基附近岩土的塑性发展状态、桩周土及桩底土的应力状态、桩顶的位移,以确定桩基础经济及合理的嵌岩深度。
1.1.2采用软件采用FLAC 3D岩土力学有限元软件进行空间弹塑性仿真分析。
FLAC 3D美国Itasca咨询公司开发,作为世界范围内应用最广泛的通用岩土工程数值模拟软件,在全球138个国家应用于设计计算及科学研究,在国际岩土工程学术界及工业界得到广泛赞誉。
FLAC3D中的本构模型及其应用:1.1.3模型桩直径2.2 m,桩地面以上部分高10m,嵌岩深度分为2倍桩直径4.4 m,3倍桩直径6.6 m,4倍桩直径8.8 m。
第一层粉质粘土厚3m,第二层微风化灰岩1厚4 m,第三层微风化灰岩2厚8 m。
1.1.4材料性质粉质粘土的材料性质取用垌心大桥QZK225钻孔土工检测所得数据。
灰岩的材料性质根据垌心大桥QZK229钻孔土工检测所得数据,并参考了《岩体力学》(刘福佑)里面常见岩体的强度指标值。
考虑岩石与岩体的力学性能略有不同,岩体的力学受裂隙及岩石各向异性影响,离散性较大及力学不均匀性大,因此岩石强度指标值取参考范围内偏小值。
输入的材料性质如表1所述。
表1 材料性质1.1.5荷载MIDAS分析得到桩顶设计内力为轴向力(Nd)13000 kN,弯矩(Md)8000kN·m;考虑岩土离散性较大故设计弯矩取2倍安全系数,设计弯矩取值16000 kN·m。
对桩顶施加一个13000 kN的轴向荷载;为了模拟设计弯矩,建模分析时取桩顶高出地面10 m,然后对桩顶施加一个1600 kN水平荷载。
1.1.6单元选择桩基础采用弹性体单元。
桩体和岩土之间通过设置粘-弹-塑性接触面单元连接。
土及岩石采用粘-弹-塑性体单元。
1.1.7边界条件模型的顶部,z=0,是一个自由面。
模型的底部,z=-15m,固定于z-方向。
x=15m,x =-15m,y =-15m,y =-15m处模型侧面上施加滚支边界条件。
分析工况为了分析不同嵌岩深度对结构的影响共考虑了4种分析工况:第1种工况为嵌岩深度2倍桩直径分析。
第2种工况为嵌岩深度3倍桩直径分析。
第3种工况为裸岩嵌岩深度3倍桩直径分析。
第4种工况为嵌岩深度4倍桩直径分析。
1.2分析结果1.2.1嵌岩深度2倍桩直径分析结果图1分析模型图1所示为嵌岩深度2倍桩直径分析模型,第一层为粘质粉土层厚度3 m,第二层为微风化灰岩1厚度4 m,第三层为微风化灰岩2厚度8 m。
桩直径2.2 m,嵌岩深度4.4 m。
图2施加竖向及水平荷载后土层和岩石的塑性状态图2为施加竖向及水平荷载后岩层塑性状态分布图。
由图可知塑性区域分布在三个区域,第一个区域分布在第一层粉质粘土层,第二个区域分布在第二层岩体顶面以下1 m范围内,第三个区域分布在桩底。
由于桩底出现塑性区域而导致桩整体塑性转动,土塑性区范围5m较广,由此可判桩嵌岩深度2倍桩直径4.4 m深不满足结构安全性要求。
图3施加竖向及水平荷载后结构竖向应力等值线图图3为施加竖向及水平荷载后结构竖向应力等值线图,由图3可知结构最大竖向压应力21.0 Mpa,最大竖向拉应力12.5 Mpa,分布在地面以下2.5 m桩体内。
图4施加竖向及水平荷载后结构横向应力等值线图图4为施加竖向及水平荷载后结构横向向应力等值线图,由图4可知结构最大横向压应力6.5 Mpa,分布在第二层岩体顶面和桩体接触处。
图11施加竖向及水平荷载后岩体位移等值线图图5为施加竖向及水平荷载后岩体位移等值线图,由图5可知岩体最大位移3.74mm,分布在地面和桩体接触处。
图6施加竖向及水平荷载后桩体位移等值线图图6为施加竖向及水平荷载后桩体位移等值线图,由图6可知桩体最大位移52.20 mm,分布在桩顶处。
分析结论:桩基嵌岩深度2D=4.4 m不满足结构安全性要求。
1.2.2嵌岩深度3倍桩直径分析结果图7分析模型图7所示为嵌岩深度3倍桩直径分析模型,第一层为粘质粉土层厚度3 m,第二层为微风化灰岩1厚度4 m,第三层为微风化灰岩2厚度8 m。
桩直径2.2 m,嵌岩深度6.6 m。
图8施加竖向及水平荷载后土层和岩石的塑性状态图8为施加竖向及水平荷载后岩层塑性状态分布图。
由图可知塑性区域分布在二个区域,第一个区域分布在第一层粉质粘土层,第二个区域分布在第二层岩体顶面以下1 m范围内。
由于桩底没有出现塑性区域因此桩不会整体塑性转动,由此可判桩嵌岩深度3倍桩直径6.6 m深满足结构安全性要求。
图9施加竖向及水平荷载后结构竖向应力等值线图图9为施加竖向及水平荷载后结构竖向应力等值线图,由图9可知结构最大竖向压应力22.8 Mpa,最大竖向拉应力15.0 Mpa,分布在地面以下2.5 m桩体内。
图10施加竖向及水平荷载后结构横向应力等值线图图10为施加竖向及水平荷载后结构横向向应力等值线图,由图10可知结构最大横向压应力6.2 Mpa,分布在第二层岩体顶面和桩体接触处。
图11施加竖向及水平荷载后岩体位移等值线图图11为施加竖向及水平荷载后桩体位移等值线图,由图11可知桩体最大位移51.94 mm,分布在桩顶处。
图12施加竖向及水平荷载后桩体位移等值线图图12为施加竖向及水平荷载后岩体位移等值线图,由图12可知岩体最大位移3.10 mm,分布在地面和桩体接触处。
分析结论:桩基嵌岩深度3D=6.6 m满足结构安全性要求。
1.2.3裸岩嵌岩深度3倍桩直径分析结果图13分析模型图13所示为不考虑土层裸岩分析模型,第一层为微风化灰岩1厚度4 m,第二层为微风化灰岩2厚度8 m。
桩直径2.2 m,嵌岩深度2D=6.6 m。
图14施加竖向及水平荷载后岩层的塑性状态图14为施加竖向及水平荷载后岩层塑性状态分布图,由图可知塑性区域只分布在距地面1 m小范围内,桩没有整体塑性转动,由此可判桩嵌岩深度3倍桩直径6.6 m深满足结构安全性要求。
图15施加竖向及水平荷载后结构竖向应力等值线图图15为施加竖向及水平荷载后结构竖向应力等值线图,由图15可知结构最大竖向压应力16.4 Mpa,最大竖向拉应力8.9 Mpa,分布在地面以下0.5 m桩体内。
图16施加竖向及水平荷载后结构横向应力等值线图图16为施加竖向及水平荷载后结构横向向应力等值线图,由图16可知结构最大横向压应力4.3 Mpa,分布在桩体和地面交界处岩体内。
图17施加竖向及水平荷载后岩体位移等值线图图17为施加竖向及水平荷载后岩体位移等值线图,由图17可知岩体最大位移0.18 mm,分布在岩层顶面和桩体接触处。
图18施加竖向及水平荷载后桩体位移等值线图图18为施加竖向及水平荷载后桩体位移等值线图,由图18可知桩体最大位移24 mm,分布在桩顶处。
分析结论:裸岩情况下桩基嵌岩深度3D=6.6 m满足结构安全性要求。
1.2.4嵌岩深度4倍桩直径分析结果图19所示为嵌岩深度4倍桩直径分析模型,第一层为粘质粉土层厚度3 m,第二层为微风化灰岩1厚度4 m,第三层为微风化灰岩2厚度8 m。
桩直径2.2 m,嵌岩深度8.8 m。
图20施加竖向及水平荷载后土层和岩石的塑性状态图20为施加竖向及水平荷载后岩层塑性状态分布图。
由图可知塑性区域分布在二个区域,第一个区域分布在第一层粉质粘土层,第二个区域分布在第二层岩体顶面以下1 m范围内。
由于桩底没有出现塑性区域因此桩不会整体塑性转动,由此可判桩嵌岩深度4倍桩直径8.8 m深满足结构安全性要求。
图21施加竖向及水平荷载后结构竖向应力等值线图图21为施加竖向及水平荷载后结构竖向应力等值线图,由图21可知结构最大竖向压应力22.8 Mpa,最大竖向拉应力15.0 Mpa,分布在地面以下2.5 m桩体内。
图22施加竖向及水平荷载后结构横向应力等值线图图22为施加竖向及水平荷载后结构横向向应力等值线图,由图22可知结构最大横向压应力4.01 Mpa,分布在第二层岩体顶面和桩体接触处。
图23施加竖向及水平荷载后岩体位移等值线图图23为施加竖向及水平荷载后桩体位移等值线图,由图23可知桩体最大位移51.62 mm,分布在桩顶处。
图24施加竖向及水平荷载后桩体位移等值线图图24为施加竖向及水平荷载后岩体位移等值线图,由图24可知岩体最大位移2.75 mm,分布在地面和桩体接触处。
分析结论:桩基嵌岩深度4D=8.8 m满足结构安全性要求。
1.2.5仅竖直力作用桩基分析结果图25施加竖向荷载后结构竖向应力等值线图图25为嵌岩深度2D=4.4模型施加竖向荷载后结构竖向应力等值线图,由图25可知桩底应力扩散影响深度为4m。
桩尖附近桩的应力减少,表明桩侧阻力起较大作用。
桩及桩周土应力云图符合理论解。
1.3结论MIDAS分析得到桩顶设计内力为轴向力(Nd)13000 kN,弯矩(Md)8000kN·m;考虑岩土离散性较大故设计弯矩取2倍安全系数,设计弯矩取值16000 kN·m。
经不同嵌岩深度的模型分析可得到如下结论:由图2可知当采用2倍桩直径嵌岩深度时,桩底岩石层会出现小范围塑性区由此而导致桩出现整体塑性转动,桩顶土塑性区范围较广,有不稳定趋势,因此桩采用2倍嵌岩深度未能满足极限状态结构安全性要求。
由图8、14可知当采用3倍桩直径嵌岩深度时,桩底岩石层未出现塑性区,桩周及桩尖土的应力较小,桩顶处位移极小,桩顶土塑性区范围较小,因此采用3倍桩直径嵌岩深度满足结构安全性要求。
考虑冲刷后,裸岩嵌岩深度3倍桩径,也能满足设计要求。
建议桩基础嵌岩深度不少于3倍桩直径6.6 m.。
