人教版九年级上学期第九周周测试卷
24-25九年级数学第一次月考卷(考试版A4)【人教版九年级上册第二十一章~第二十二章】(贵州专用)

2024-2025学年九年级数学上学期第一次月考卷(贵州专用)(考试时间:120分钟试卷满分:150分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:人教版九年级上册第二十一章~第二十二章。
5.难度系数:0.8。
第一部分(选择题共36分)一、选择题:本题共12小题,每小题3分,共36分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若关于x的方程(m﹣2)x2+mx﹣1=0是一元二次方程,则m的取值范围是( )A.m≠2B.m=2C.m≥2D.m≠02.将抛物线y=x2+2x﹣1向右平移3个单位后得到新抛物线的顶点坐标为( )A.(﹣4,﹣1)B.(﹣4)C.(2,1)D.(2,﹣2)3.若一元二次方程ax2+bx+c=0(a≠0)的一个根是x=1,则a+b+c的值是( )A.0B.﹣1C.1D.不能确定4.延时课上,4个同学以接龙的方式解一元二次方程,每人负责完成一个步骤,如图所示,其中有一位同学所负责的步骤是错误的,则这位同学是( )A.小张B.小王C.小李D.小赵5.关于x的一元二次方程x2+bx﹣8=0的根的情况,下列判断正确的是( )A.只有一个实数根B.没有实数根C.有两个相等的实数根D.有两个不相等的实数根6.已知a,b,c为实数,且b+c=5﹣4a+3a2,c﹣b=1﹣2a+a2,则a,b,c之间的大小关系是( )A.a<b≤c B.b<a≤c C.b≤c<a D.c<a≤b7.新能源汽车销量的快速增长,促进了汽车企业持续的研发投入和技术创新.某上市公司今年1月份一品牌的新能源车单台的生产成本是13万元,由于技术改进和产能增长,生产成本逐月下降,3月份的生产成本为12.8万元.假设该公司今年一季度每个月生产成本的下降率都相同,设每个月生产成本的下降率为x,则根据题意所列方程正确的是( )A.13(1﹣x)2=12.8B.13(1﹣x2)=12.8C.12.8(1﹣x2)=13D.13(1+x)2=12.88.一次函数y=ax+b与二次函数y=ax2+bx在同一坐标系中的图象大致为( )A.B.C.D.9.已知抛物线y=ax2﹣2ax+b(a<0)的图象上三个点的坐标分别为A(3,y1),,C,则y1,y2,y3的大小关系为( )A.y3<y1<y2B.y2<y1<y3C.y1<y3<y2D.y1<y2<y310.点A(a,b1),B(a+2,b2)在函数y=﹣x2+2x+3的图象上,当a≤x≤a+2时,函数的最大值为4,最小值为b1,则a的取值范围是( )A.0≤a≤2B.﹣1≤a≤2C.﹣1≤a≤1D.﹣1≤a≤011.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c >0;④b2﹣4ac>0;其中正确的结论有( )A.1个B.2个C.3个D.4个12.如图所示,在菱形ABCD中,AB=6,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC.CD上滑动,且E、F不与B.C、D重合.当点E、F在BC、CD上滑动时,△CEF的面积最大值是( )A.4B.C.3D.第二部分(非选择题共114分)二、填空题:本题共4小题,每小题4分,共16分。
(全国通用)中考英语 第九周 阅读周周练(A、B卷)-人教版初中九年级全册英语试题

阅读周周练一、完形填空。
通读下面短文,从A、B、C三个选项中选出可以填入空白处的正确答案。
The picture shows eighteen-year-old Katy Ross in Nepal, a small country north of India. Katy 1 school eight months ago and soon she will go to university. She loves traveling and decides to visit Asia 2 she goes to university.Katy is living with a family in the capital of Nepal. She has 3 a lot about the country since she arrived four months ago. The family has two children but many uncles and cousins live with 4 in their big house. They have taken Katy to many parties.Katy teaches for four hours a day at a small 5 . All the classes are in English, and the pupils have spoken English since the 6 of six. The older children speak English very 7 . Katy has taught writing, grammar, and art, all in English. She enjoys art the most, and she thinks the children like these lessons best, too!Katy has not had a lot of time to 8 Nepal, but soon, she will stop teaching and travel around Nepal9 a friend. “After that,” Katy says, “we’ll visit more countries in Asia. We’re not 10 which ones yet.”( ) 1. A. left B. found C. visited( ) 2. A. before B. when C. after( ) 3. A. used B. learnt C. made( ) 4. A. us B. him C. them( ) 5. A. shop B. cinema C. school( ) 6. A. life B. age C. number( ) 7. A. bad B. good C. well( ) 8. A. see B. hear C. look( ) 9. A. of B. on C. with( ) 10. A. tired B. sure C. afraid二、阅读理解。
部编人教版2024--2025学年度第一学期九年级语文期中测试卷及答案

部编人教版2024--2025学年度第一学期期中测试卷九年级 语文(满分:100分 时间:120分钟)一、名句名篇默写(共8分)1.(本题8分)古诗文默写。
中国是诗文的国度,也是酒酿的故乡,《行路难》中,面对精心陈列的饯行酒,李白却“① ,② ”,其内心愁苦,可见一斑;《水调歌头》中,苏轼在中秋夜举杯遥祝,希望普天之下家家团圆,“③ ,④”,其乐观博爱,明月可鉴;《岳阳楼记》中,文人骚客“登斯楼也,则有⑤ ,⑥ ,把酒临风,其喜洋洋者矣”,其愉悦心境,隔空可感;《湖心亭看雪》中,张岱与亭中客人共饮三大白,难怪舟子感慨“⑦ ,⑧ ”,其故国之思,令人叹惋。
二、诗歌鉴赏(共8分)浣溪沙① 苏轼簌簌衣巾落枣花,村南村北响缫车②,牛衣③古柳卖黄瓜。
酒困路长惟欲睡,日高人渴漫思茶④,敲门试问野人家。
【注释】①公元1078年,徐州春旱,太守苏轼曾率众求雨。
得雨后,他又与百姓同赴石潭谢雨。
此为词人在赴徐门石潭谢雨路上所作。
②缫车:缫丝所用的器具。
③牛衣:蓑衣,这里泛指用粗麻织成的衣服。
④漫思茶:想随便去哪儿找点茶喝。
漫,随意。
2.(3分)下列对诗歌的理解不正确...的一项是( ) A .全词从农村习见的典型事物入手,意趣盎然地表现了淳厚的乡村风味。
B .上片写枣花、缫丝、黄瓜这些富有时令特色的事物,点染出了一幅初夏时节农村风俗画。
C .“村南村北响缫车”通过写嘈杂的“缫车”声,含蓄地表达了词人的烦躁郁闷之情。
D .这首词上片写景,重在路途之声;下片记事,重在行人之态。
3.(5分)这首词清新朴实,明白如话,“敲门试问野人家”中“试问”两字就让词人形象栩栩传神。
请结合本句内容,分析词人形象。
三、文言文阅读(共26分)(本题26分)【甲】行路难【其一】金樽清酒斗十千,玉盘珍羞直万钱。
停杯投箸不能食,拔剑四顾心茫然。
欲渡黄河冰塞川,将登太行雪满山。
闲来垂钓碧溪上,忽复乘舟梦日边。
行路难!行路难!多歧路,今安在?长风破浪会有时,直挂云帆济沧海。
2024-2025学年九年级数学上学期第三次月考卷(广东省卷专用,人教版九上第21~24章)考试版

2024-2025学年九年级数学上学期第三次月考卷(广东省卷专用)(考试时间:120分钟 试卷满分:120分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:人教版,第21~24章。
5.难度系数:0.69。
第Ⅰ卷一、选择题:本大题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.第十九届亚运会于2023年9月23日至10月8日在杭州隆重举行,下列图标是亚运会上常见的运动图标,其中是轴对称图形的是( )A .B .C .D .2.如图,在O e 中,弦AB CD ∥,若40ABC Ð=°,则BOD Ð的度数是( )A .80°B .50°C .40°D .20°3.抛物线()278y x =-+-的顶点坐标是( )A .()7,8-B .()7,8-C .()7,8D .()7,8--4.把方程2470x x --=化成2()x m n -=的形式,则点(,)P m n 关于x 轴对称的点的坐标为( )A .(2,11)B .(2,11)-C .(2,11)-D .(2,11)--5.若点()10,A y ,()21,B y ,()32,C y -是抛物线22y x x c =-+上的三点,则( )A .321y y y >>B .123y y y >>C .132y y y >>D .312y y y >>6.已知12,x x 是方程2420x x -+=的两个根,则12x x +的值是( )A .4-B .2-C .4D .27.如图,PA 、PB 切⊙O 于点A 、B ,10PA =,CD 切O e 于点E ,交PA 、PB 于C 、D 两点,则PCD △的周长是( )A .10B .18C .20D .228.如图,P ,Q 分别是O e 的内接正五边形的边AB ,BC 上的点,BP CQ =,则POQ Ð=( )A .75°B .54°C .72°D .60°9.如图,在平面直角坐标系xOy 中,直线AB 经过点()6,0A 、()0,6B ,O e 的半径为2(O 为坐标原点),点P 是直线AB 上的一动点,过点P 作O e 的一条切线PQ ,Q 为切点,则切线长PQ 的最小值为( )A .7B .3C .D 10.如图,二次函数y =﹣x 2+2x +m +1的图象交x 轴于点A (a ,0)和B (b ,0),交y 轴于点C ,图象的顶点为D .下列四个命题:①当x >0时,y >0;②若a =﹣1,则b =4;③点C 关于图象对称轴的对称点为E ,点M 为x 轴上的一个动点,当m =2时,△MCE 周长的最小值为;④图象上有两点P (x 1,y 1)和Q (x 2,y 2),若x 1<1<x 2,且x 1+x 2>2,则y 1>y 2,其中真命题的个数有( )A .1个B .2个C .3个D .4个第Ⅱ卷二、填空题:本大题共5小题,每小题3分,共15分。
九年级数学上学期周练试卷(4)(含解析) 新人教版

2015-2016学年北京市北达资源中学九年级(上)周练数学试卷(4)一、选择题(每题4分,共24分)1.已知⊙O的半径是5,OP的长为7,则点P与⊙O的位置关系是()A.点P在圆内B.点P在圆上C.点P在圆外D.不能确定2.若两圆没有公共点,则两圆的位置关系是()A.外离B.外切C.内含D.外离或内含3.如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠OCB的度数为()A.40°B.50°C.65°D.75°4.如图所示,O是线段AB上的一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于()A.50°B.40°C.60°D.70°5.如图,正三角形的内切圆半径为1,那么三角形的边长为()A.2 B.3 C.D.26.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB,CA分别相交于点E,F,则线段EF长度的最小值是()A.B.4.75 C.5 D.4.8二、填空题(每小题4分,共40分)7.如图,△ABC中,∠A=45°,I是内心,则∠BIC=°.8.如图,PA、PB分别切⊙O于点A、B,若∠P=70°,则∠C的大小为(度).9.如图所示,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的直径是cm.10.如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知PA=7cm,则△PCD的周长等于cm.11.如图,已知⊙O是△ABC的内切圆,切点为D、E、F,如果AE=2,CD=1,BF=3,则内切圆的半径r=.12.如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于.13.如图,在△ABC中,已知∠ABC=90°,在AB上取一点E,以BE为直径的☉O恰与AC相切于点D.若AE=2,AD=4.则☉O的直径BE=;△ABC的面积为.14.平面上有⊙O及一点P,P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为cm.15.直线AB与⊙O相切于B点,C是⊙O与OA的交点,点D是⊙O上的动点(D与B,C 不重合),若∠A=40°,则∠BDC的度数是.16.已知⊙O的半径OA=1,弦AB、AC的长分别是、,则∠BAC的度数是.三、解答题(第17题16分,第18、19题每题10分,共36分)17.如图,C为圆周上一点,BD是☉O的切线,B为切点.(1)在图(1)中,AB是☉O的直径,∠BAC=30°,则∠DBC的度数为.(2)在图(2)中,∠BA1C=40°,求∠DBC的度数.(3)在图(3)中,∠BA1C=α,求∠DBC的大小.(4)通过(1)、(2)、(3)的探究,你发现的结论是(5)如图(4),AC是☉O的直径,∠ACB=60°,连接AB,过A、B两点分别作☉O的切线,两切线交于点P.若已知☉O的半径为1,则△PAB的周长为.(6)如图(5),C是⊙O的直径AB延长线上的一点,CD切⊙O于D,∠ACD的平分线分别交AD、BD于E、F,试猜想∠DEF的度数并说明理由.18.如图,直线AB、BC、CD分别与⊙O相切于A、E、D,且AB∥CD,若OB=6cm,OC=8cm,求(1)∠BOC 的度数;(2)⊙O的半径;(3)AB+CD的值.19.如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上,CE=CA,AB,CE的延长线交于点F.(1)求证:CE与⊙O相切;(2)若⊙O的半径为3,EF=4,求BD的长.2015-2016学年北京市北达资源中学九年级(上)周练数学试卷(4)参考答案与试题解析一、选择题(每题4分,共24分)1.已知⊙O的半径是5,OP的长为7,则点P与⊙O的位置关系是()A.点P在圆内B.点P在圆上C.点P在圆外D.不能确定【考点】点与圆的位置关系.【分析】直接根据点与圆的位置关系即可得出结论.【解答】解:∵⊙O的半径是5,OP的长为7,5<7,∴点P在圆外.故选C.2.若两圆没有公共点,则两圆的位置关系是()A.外离B.外切C.内含D.外离或内含【考点】圆与圆的位置关系.【分析】此题要求两个圆的位置关系,可观察两个圆之间的交点个数,一个交点两圆相切(内切或外切),两个交点两圆相交,没有交点两圆相离(外离或内含).【解答】解:外离或内含时,两圆没有公共点.故选D.3.如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠OCB的度数为()A.40°B.50°C.65°D.75°【考点】切线的性质.【分析】根据切线的性质可判断∠OBA=90°,再由∠BAO=40°可得出∠O=50°,在等腰△OBC 中求出∠OCB即可.【解答】解:∵AB是⊙O的切线,B为切点,∴OB⊥AB,即∠OBA=90°,∵∠BAO=40°,∴∠O=50°,∵OB=OC(都是半径),∴∠OCB==65°.故选C.4.如图所示,O是线段AB上的一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于()A.50°B.40°C.60°D.70°【考点】切线的性质;圆周角定理.【分析】连接OC,由CE为圆O的切线,根据切线的性质得到OC垂直于CE,即三角形OCE 为直角三角形,再由同弧所对的圆心角等于所对圆周角的2倍,由圆周角∠CDB的度数,求出圆心角∠COB的度数,在直角三角形OCE中,利用直角三角形的两锐角互余,即可求出∠E的度数.【解答】解:连接OC,如图所示:∵圆心角∠BOC与圆周角∠CDB都对弧BC,∴∠BOC=2∠CDB,又∠CDB=20°,∴∠BOC=40°,又∵CE为圆O的切线,∴OC⊥CE,即∠OCE=90°,则∠E=90°﹣40°=50°.故选A.5.如图,正三角形的内切圆半径为1,那么三角形的边长为()A.2 B.3 C.D.2【考点】三角形的内切圆与内心;锐角三角函数的定义.【分析】欲求三角形的边长,已知内切圆半径,可过内心向正三角形的一边作垂线,连接顶点与内切圆心,构造直角三角形求解.【解答】解:过O点作OD⊥AB,则OD=1;∵O是△ABC的内心,∴∠OAD=30°;Rt△OAD中,∠OAD=30°,OD=1,∴AD=OD•cot30°=,∴AB=2AD=2.故选D.6.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CB,CA分别相交于点E,F,则线段EF长度的最小值是()A.B.4.75 C.5 D.4.8【考点】切线的性质;勾股定理的逆定理;圆周角定理.【分析】设EF的中点为O,圆O与AB的切点为D,连接OD,连接CO,CD,则有OD⊥AB;由勾股定理的逆定理知,△ABC是直角三角形OC+OD=EF,由三角形的三边关系知,CO+OD >CD;只有当点O在CD上时,OC+OD=EF有最小值为CD的长,即当点O在直角三角形ABC 的斜边AB的高上CD时,EF=CD有最小值,由直角三角形的面积公式知,此时CD=BC•AC÷AB=4.8.【解答】解:如图,∵∠ACB=90°,∴EF是直径,设EF的中点为O,圆O与AB的切点为D,连接OD,CO,CD,则OD⊥AB.∵AB=10,AC=8,BC=6,∴∠ACB=90°,∴EF为直径,OC+OD=EF,∴CO+OD>CD=4.8,∵当点O在直角三角形ABC的斜边AB的高上CD时,EF=CD有最小值∴由三角形面积公式得:CD=BC•AC÷AB=4.8.故选D.二、填空题(每小题4分,共40分)7.如图,△ABC中,∠A=45°,I是内心,则∠BIC=115°.【考点】三角形的内切圆与内心.【分析】由三角形内切定义可知:IB、IC是∠ABC、∠ACB的角平分线,所以可得到关系式∠IBC+∠ICB=(∠ABC+∠ACB),把对应数值代入即可解出∠BIC的值.【解答】解:∵IB、IC是∠ABC、∠ACB的角平分线,∴∠IBC+∠ICB=(∠ABC+∠ACB)==65°,∴∠BIC=180°﹣65°=115°.故答案为:115.8.如图,PA、PB分别切⊙O于点A、B,若∠P=70°,则∠C的大小为55(度).【考点】切线的性质.【分析】首先连接OA,OB,由PA、PB分别切⊙O于点A、B,根据切线的性质可得:OA⊥PA,OB⊥PB,然后由四边形的内角和等于360°,求得∠AOB的度数,又由圆周角定理,即可求得答案.【解答】解:连接OA,OB,∵PA、PB分别切⊙O于点A、B,∴OA⊥PA,OB⊥PB,即∠PAO=∠PBO=90°,∴∠AOB=360°﹣∠PAO﹣∠P﹣∠PBO=360°﹣90°﹣70°﹣90°=110°,∴∠C=∠AOB=55°.故答案为:55.9.如图所示,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的直径是10 cm.【考点】切线的性质;勾股定理;垂径定理.【分析】本题先根据垂径定理构造出直角三角形,然后在直角三角形中已知弦长和弓形高,根据勾股定理求出半径,从而得解.【解答】解:如图,设圆心为O,弦为AB,切点为C.如图所示.则AB=8cm,CD=2cm.连接OC,交AB于D点.连接OA.∵尺的对边平行,光盘与外边缘相切,∴OC⊥AB.∴AD=4cm.设半径为Rcm,则R2=42+(R﹣2)2,解得R=5,∴该光盘的直径是10cm.故答案为:1010.如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知PA=7cm,则△PCD的周长等于14cm.【考点】切线长定理.【分析】由于DA、DC、BC都是⊙O的切线,可根据切线长定理,将△PCD的周长转换为PA、PB的长,然后再进行求解.【解答】解:如图,设DC与⊙O的切点为E;∵PA、PB分别是⊙O的切线,且切点为A、B;∴PA=PB=7cm;同理,可得:DE=DA,CE=CB;则△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=14cm;故△PCD的周长是14cm.11.如图,已知⊙O是△ABC的内切圆,切点为D、E、F,如果AE=2,CD=1,BF=3,则内切圆的半径r=1.【考点】三角形的内切圆与内心;切线长定理.【分析】根据切线长定理得出AF=AE,EC=CD,DB=BF,进而得出△ABC是直角三角形,再利用直角三角形内切圆半径求法得出内切圆半径即可.【解答】解:∵⊙O是△ABC的内切圆,切点为D、E、F,∴AF=AE,EC=CD,DB=BF,∵AE=2,CD=1,BF=3,∴AF=2,EC=1,BD=3,∴AB=BF+AF=3+2=5,BC=BD+DC=4,AC=AE+EC=3,∴△ABC是直角三角形,∴内切圆的半径r==1,故答案为:1.12.如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于69°.【考点】圆内接四边形的性质.【分析】由∠BOD=138°,根据在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠A的度数,又由圆的内接四边四边形的性质,求得∠BCD的度数,继而求得∠DCE的度数【解答】解:∵∠BOD=138°,∴∠A=∠BOD=69°,∴∠BCD=180°﹣∠A=111°,∴∠DCE=180°﹣∠BCD=69°.故答案为:69°.13.如图,在△ABC中,已知∠ABC=90°,在AB上取一点E,以BE为直径的☉O恰与AC相切于点D.若AE=2,AD=4.则☉O的直径BE=6;△ABC的面积为24.【考点】切线的性质.【分析】连接OD,由切线的性质可知△OAD为直角三角形,设半径为x,在Rt△AOD中由勾股定理可列方程,可求得x的值,则可求得BE的长;再由条件可证明△AOD∽△ACB,由相似三角形的性质可求得BC的长,则容易求得△ABC的面积.【解答】解:如图,连接OD,∵AC与⊙O相切,∴OD⊥AC,设⊙O的半径为x,则OE=OB=OD=x,∴AO=AE+OE=2+x,在Rt△AOD中,由勾股定理可得AO2=OD2+AD2,即(2+x)2=x2+42,解得x=3,∴BE=2x=6,∴AB=AE+BE=2+6=8,∵∠ABC=∠ADO=90°,∠OAD=∠CAB,∴△AOD∽△ACB,∴=,即=,解得BC=6,∴S△ABC=AB•BC=×8×6=24,故答案为:6;24.14.平面上有⊙O及一点P,P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为4或2cm.【考点】点与圆的位置关系.【分析】解答此题应进行分类讨论,点P可能位于圆的内部,也可能位于圆的外部.【解答】解:当点P在圆内时,则直径=6+2=8cm,因而半径是4cm;当点P在圆外时,直径=6﹣2=4cm,因而半径是2cm.所以⊙O的半径为4或2cm.故答案为:4或2.15.直线AB与⊙O相切于B点,C是⊙O与OA的交点,点D是⊙O上的动点(D与B,C 不重合),若∠A=40°,则∠BDC的度数是25°或155°.【考点】切线的性质.【分析】连结OB,根据切线的性质得OB⊥BA,可求出∠AOB=50°,然后讨论:当点D在优弧BC上时,根据圆周角定理即可得到∠BDC=∠AOB=25°;当点D在劣弧BC上时,即在D′点处,则可根据圆内接四边形的性质求出∠BD′C=180°﹣25°=155°.【解答】解:当点D在优弧BC上时,如图,连结OB,∵直线AB与⊙O相切于B点,∴OB⊥BA,∴∠OBA=90°,∵∠A=40°,∴∠AOB=50°,∴∠BDC=∠AOB=25°;当点D在劣弧BC上时,即在D′点处,如图,∵∠BDC+∠BD′C=180°,∴∠BD′C=180°﹣25°=155°,∴∠BDC的度数为25°或155°.故答案为:25°或155°.16.已知⊙O的半径OA=1,弦AB、AC的长分别是、,则∠BAC的度数是15°或75°.【考点】垂径定理;勾股定理.【分析】根据垂径定理和勾股定理可得.【解答】解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E.∵OE⊥AC,OD⊥AB,根据垂径定理得AE=AC=,AD=AB=,∴sin∠AOE===,sin∠AOD==,根据特殊角的三角函数值可得∠AOE=60°,∠AOD=45°,∴∠BAO=45°,∠CAO=90°﹣60°=30°,∴∠BAC=45°+30°=75°,或∠BAC′=45°﹣30°=15°.故答案为:15°或75°.三、解答题(第17题16分,第18、19题每题10分,共36分)17.如图,C为圆周上一点,BD是☉O的切线,B为切点.(1)在图(1)中,AB是☉O的直径,∠BAC=30°,则∠DBC的度数为30°.(2)在图(2)中,∠BA1C=40°,求∠DBC的度数.(3)在图(3)中,∠BA1C=α,求∠DBC的大小.(4)通过(1)、(2)、(3)的探究,你发现的结论是弦切角等于它夹的弧所对的圆周角(5)如图(4),AC是☉O的直径,∠ACB=60°,连接AB,过A、B两点分别作☉O的切线,两切线交于点P.若已知☉O的半径为1,则△PAB的周长为3.(6)如图(5),C是⊙O的直径AB延长线上的一点,CD切⊙O于D,∠ACD的平分线分别交AD、BD于E、F,试猜想∠DEF的度数并说明理由.【考点】圆的综合题.【分析】(1)由切线的性质和圆周角定理以及角的互余关系得出∠DBC=∠A=30°即可;(2)连接AC,由(1)得出∠DBC=∠A,由圆周角定理得出∠A=∠A1,即可得出∠DBC=∠BA1C=40°;(3)由(2)得出∠DBC=∠BA2C=α即可;(4)∠DBC等于所对的圆周角,得出弦切角定理;(5)先在RtABC求出BC,再判断出三角形PAB是等边三角形即可求出结论;(6)先判断出∠CAD=∠COD,∠ACE=∠ACD,再利用切线得出∠COD+∠ACD=90°,最后用三角形的外角的性质即可得出结论;【解答】解:(1)∵BD是⊙0的切线,∴∠ABO=90°,即∠ABC+∠DBC=90°,∵AB是⊙O的直径,∴∠ACB=90°∴∠A+∠ABC=90°,∴∠DBC=∠A=30°;故答案为:30°,(2)连接BO交⊙O于A,连接AC,如图所示:由(1)得:∠DBC=∠A,又∵∠A=∠A1,∴∠DBC=∠BA1C=40°;(3)由(2)得:∠DBC=∠BA2C=α;(4)∠DBC等于所对的圆周角;弦切角等于它夹的弧所对的圆周角,故答案为:弦切角等于它夹的弧所对的圆周角;(5)连接如图OB,在Rt△ABC中,AC=2OA=2,∠ACB=60°,∴AB=,∠AOB=120°∵PA,PB分别与⊙O相切,∴∠PAO=∠PBO=90°,PA=PB∴∠APB=60°,∴△PAB是等边三角形,∴PA=PB=AB=,∴△PAB的周长为3,故答案为3;(6)如图5,连接OD,∴∠DAC=∠COD,∵CD是⊙O的切线,∴∠ODC=90°,∴∠ACD+∠COD=90°,∵CE是∠ACD的角平分线,∴∠ACE=∠ACD∴∠DEF=∠DAC+∠ACE=∠COD+∠ACD=(∠COD+∠ACD)=45°.18.如图,直线AB、BC、CD分别与⊙O相切于A、E、D,且AB∥CD,若OB=6cm,OC=8cm,求(1)∠BOC 的度数;(2)⊙O的半径;(3)AB+CD的值.【考点】切线的性质.【分析】(1)连接OA,OE,证明Rt△OAB≌Rt△OEB,由此可得∠ABO=∠OBE,再由平行的性质即可求解∠BOC 的度数;(2)由勾股定理求得BC,再由三角形的面积求得⊙O的半径.(3)利用(1)中所得AB=BE、CE=CD即可.【解答】解:(1)连接OA,OE.∵直线AB、BC、CD分别与⊙O相切于A、E、D,∴OA⊥AB,OE⊥BC,∴∠OAB=∠OEB=90°,OA=OE在Rt△OAB 与Rt△OEB中∴Rt△OAB≌Rt△OEB(HL)∴∠ABO=∠OBE,AB=BE同理可证:∠OCE=∠OCD,CE=CD,又∵AB∥CD,∴∠ABC+∠DCB=180°,∴∠OBC+∠OCB=90°,∴∠BOC=90°(2)在Rt△BOC中,BC==10∴OB•OC=BC•rr==4.8即:⊙O的半径为4.8(3)由(1)可知:AB=BE,CE=CD,∴AB+CD=BE+CE=BC=10即:BC的值为1019.如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上,CE=CA,AB,CE的延长线交于点F.(1)求证:CE与⊙O相切;(2)若⊙O的半径为3,EF=4,求BD的长.【考点】切线的判定;勾股定理.【分析】(1)连接OE,OC,通过三角形求得证得∠OEC=∠OAC,从而证得OE⊥CF,即可证得结论;(2)根据勾股定理求得OF,解直角三角形求得.进而求得AC=6,从而求得△ABC是等腰直角三角形,根据勾股定理求得BC,然后根据等腰三角形三线合一的性质求得DB即可.【解答】(1)证明:连接OE,OC.在△OEC与△OAC中,∴△OEC≌△OAC(SSS),∴∠OEC=∠OAC.∵∠OAC=90°,∴∠OEC=90°.∴OE⊥CF于E.∴CF与⊙O相切.(2)解:连接AD.∵∠OEC=90°,∴∠OEF=90°.∵⊙O的半径为3,∴OE=OA=3.在Rt△OEF中,∠OEF=90°,OE=3,EF=4,∴,.在Rt△FAC中,∠FAC=90°,AF=AO+OF=8,∴AC=AF•tanF=6,∵AB为直径,∴AB=6=AC,∠ADB=90°.∴BD=.在Rt△ABC中,∠BAC=90°,∴.∴BD=.文本仅供参考,感谢下载!。
人教版数学九年级上册《圆》单元综合检测(附答案)

人教版数学九年级上学期《圆》单元测试(满分120分,考试用时120分钟)一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分)1.在同圆或等圆中,如果弧AB的长度=弧CD的长度,则下列说法正确的个数是()弧AB的度数等于弧CD的度数;所对的圆心角等于弧CD所对的圆心角;弧AB和弧CD是等弧;弧AB所对的弦的弦心距等于弧CD所对的弦的弦心距.A. 1个B. 2个C. 3个D. 4个2.、是直线上的两个不同的点,且,的半径为,下列叙述正确的是()A. 点在外B. 点在外C. 直线与一定相切D. 若,则直线与相交3. 如图,已知⊙O的半径为5,点O到弦AB的距离为2,则⊙O上到弦AB所在直线的距离为3的点有()A. 1个B. 2个C. 3个D. 4个4.如图,在中,已知,是圆周上的一点,则为()A. B. C. D.5.如图,正六边形内接于圆,圆的半径为,则这个正六边形的边心距和的长分别为()A. 、B. 、C. 、D. 、6.高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,净高米,则此圆的半径A. 米B. 米C. 米D. 米7.已知和三点、、,的半径为,,,,经过这三点中的一点任意作直线总是与相交,这个点是()A. B. C. D. 或8.如图,,是的直径,的半径为,,以为圆心,以为半径作,则与围成的新月形的面积为()平方单位.A. B. C. D.9.如图,已知:是的直径,、是上的三等分点,,则是()A. B. C. D.10.如图,点,,在上,点在圆外,则下列结论正确的是()A. ∠C>∠DB. ∠C<∠DC. ∠C=∠DD. ∠C=2∠D二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分)11.在,,,,点是的外心,现在以为圆心,分别以、、为半径作,则点与的位置关系分别是________.12.如下图,在以为圆心的两个同心圆中,大圆的弦交小圆于和两点,,,则长为________.13.已知:如图,为半的直径,、、为半圆弧上的点,,,则的度数为________度.14.如图,边长为的正方形的顶点、在一个半径为的圆上,顶点、在圆内,将正方形沿圆的内壁逆时针方向作无滑动的滚动.当点第一次落在圆上时,点运动的路径长为________.15.已知中,,,,直线过点且与平行,若以为轴将旋转一周,则所得的几何体的表面积为________.(不求近似值)16.如图,已知是的直径,为弦,度.过圆心作交于点,连接,则________度.17.如图,的边位于直线上,,,,若由现在的位置向右无滑动地旋转,当第次落在直线上时,点所经过的路线的长为________(结果用含有的式子表示)18.如图,圆柱底面半径为,高为,点、分别是圆柱两底面圆周上的点,且、在同一母线上,用一棉线从顺着圆柱侧面绕圈到,求棉线最短为________.19.以矩形的顶点为圆心作,要使、、三点中至少有一点在内,且至少有一点在外,如果,,则的半径的取值范围为________.20.如图,在中,是弦,,,那么圆心到的距离是________,弦的长是________.三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分)21.一圆柱形排水管的截面如图所示,已知排水管的半径为,水面宽为.由于天气干燥,水管水面下降,此时排水管水面宽变为,求水面下降的高度.22.如图,在中,弦、于点,且.求证:.23.如图,在中,,,求分别以、、为圆心,以为半径画弧,三条弧与边所围成的阴影部分的面积.24.已知:如图,的外接圆,弦的长为,,求圆心到的距离.25.如图,已知为的直径,是弦,于,于,.求证:;求证:;若,,设,求值及阴影部分的面积.26.如图,内接于,,,.求的度数;将沿折叠为,将沿折叠为,延长和相交于点;求证:四边形是正方形;若,,求的长.参考答案一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分)1.在同圆或等圆中,如果弧AB的长度=弧CD的长度,则下列说法正确的个数是()弧AB的度数等于弧CD的度数;所对的圆心角等于弧CD所对的圆心角;弧AB和弧CD是等弧;弧AB所对的弦的弦心距等于弧CD所对的弦的弦心距.A. 1个B. 2个C. 3个D. 4个【答案】D【解析】【分析】由在同圆或等圆中,的长度=的长度,根据弧长公式得到它们所对的圆心角相等,再根据在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等,即可对选项进行判断.【详解】∵在同圆或等圆中,的长度=的长度,∴弧AB和弧CD所对的圆心角相等,∴的度数等于的度数;∴和是等弧;∴所对的弦的弦心距等于所对的弦的弦心距.故选D.【点睛】本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等.在圆中经常利用此结论把圆心角、弧、弦之间进行转化.2.、是直线上的两个不同的点,且,的半径为,下列叙述正确的是()A. 点在外B. 点在外C. 直线与一定相切D. 若,则直线与相交【答案】D【解析】【分析】由P、Q是直线l上的两个不同的点,且OP=5,⊙O的半径为5,可得点P在⊙O上,直线l与⊙O相切或相交;若OQ=5,则直线l与⊙O相交.【详解】∵OP=5,⊙O的半径为5,∴点P在⊙O上,故A错误;∵P是直线l上的点,∴直线l与⊙O相切或相交;∴若相切,则OQ>5,且点Q在⊙O外;若相交,则点Q可能在⊙O上,⊙O外,⊙O内;故B、C错误.∴若OQ=5,则直线l与⊙O相交;故D正确.故选D.【点睛】此题考查了直线与圆的位置关系,注意掌握分类讨论思想的应用是解题关键.3. 如图,已知⊙O的半径为5,点O到弦AB的距离为2,则⊙O上到弦AB所在直线的距离为3的点有()A. 1个B. 2个C. 3个D. 4个【答案】C【解析】考点:垂径定理;勾股定理.分析:根据垂径定理计算.解答:解:如图OD=OA=OB=5,OE⊥AB,OE=3,∴DE=OD-OE=5-3=2cm,∴点D是圆上到AB距离为2cm的点,∵OE=3cm>2cm,∴在OD上截取OH=1cm,过点H作GF∥AB,交圆于点G,F两点,则有HE⊥AB,HE=OE-OH=2cm,即GF到AB的距离为2cm,∴点G,F也是圆上到AB距离为2cm的点.故选C.点评:本题利用了垂径定理求解,注意圆上的点到AB距离为2cm的点不唯一,有三个.4.如图,在中,已知,是圆周上的一点,则为()A. B. C. D.【答案】B【解析】【分析】首先根据题画出图形,然后在优弧上取点D,连接AD,BD,根据圆周角的性质,即可求得∠ADB的度数,又由圆的内接四边形的性质,即可求得∠ACB的度数.【详解】如图:在优弧上取点D,连接AD,BD,∵∠AOB=100°,∴∠ADB=∠AOB=55°,∵四边形ADBC是⊙O的内接四边形,∴∠ADB+∠ACB=180°,∴∠ACB=125°.故选B.【点睛】此题考查了圆周角定理与圆的内接四边形的性质,根据题意作出图形,掌握数形结合思想的应用及圆周角定理是解题关键.5.如图,正六边形内接于圆,圆的半径为,则这个正六边形的边心距和的长分别为()A. 、B. 、C. 、D. 、【答案】D【解析】试题解析:连接OC,OD,∵正六边形ABCDEF是圆的内接多边形,∴∠COD=60°,∵OC=OD,OM⊥CD,∴∠COM=30°,∵OC=6,∴OM=6cos30°=3,∴=2π故选D.考点:1.正多边形和圆;2.弧长的计算.6.高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,净高米,则此圆的半径A. 米B. 米C. 米D. 米【答案】B【解析】【分析】根据垂径定理可知AD的长,设半径为r,利用勾股定理列方程求出r的值即可.【详解】∵CD⊥AB,∴由垂径定理得AD=6米,设圆的半径为r,则OD2+AD2=OA2,即(9-r)2+62=r2,解得r=米.故选B.【点睛】考查了垂径定理、勾股定理.根据题意构造一个由半径、半弦、弦心距组成的直角三角形进行计算是解题关键.7.已知和三点、、,的半径为,,,,经过这三点中的一点任意作直线总是与相交,这个点是()A. B. C. D. 或【答案】A【解析】【分析】根据⊙O的半径为3,OP=2,OQ=3,OR=4,可以知道点P在圆内,点Q在圆上,点R在圆外,因而这三点中P的一点任意作直线总是与⊙O相交.【详解】∵的半径为,,,,∴Q点在圆上;R点在圆外;P点在圆内,∴经过P点任意作直线总是与⊙O相交.故选A.【点睛】本题考查了对点与圆的位置关系的判断.设点到圆心的距离为d,则当d=R时,点在圆上;当d>R 时,点在圆外;当d<R时,点在圆内.准确判断P、Q、R三点与⊙O的位置关系是解决本题的关键.8.如图,,是的直径,的半径为,,以为圆心,以为半径作,则与围成的新月形的面积为()平方单位.A. B. C. D.【答案】B【解析】【分析】新月形ACED的面积是圆O半圆的面积-弓形CED的面积,弓形CED的面积又=扇形BCD面积-三角形BCD 的面积,然后依面积公式计算即可.【详解】∵OC=OB=R,,∴BC=R,)∴新月形ACED的面积=S半圆-(S扇形BCD-S△BCD=-(-)=R2.故选B.【点睛】本题的关键是看出:新月形ACED的面积是圆O半圆的面积-弓形CED的面积,然后逐一求面积即可.9.如图,已知:是的直径,、是上的三等分点,,则是()A. B. C. D.【答案】C【解析】【分析】先求出∠BOE=120°,再运用“等弧对等角”即可解.【详解】∵∠AOE=60°,∴∠BOE=180°-∠AOE=120°,∴的度数是120°,∵C、D是上的三等分点,∴弧CD与弧ED的度数都是40度,∴∠COE=80°,故选:C.【点睛】本题主要考查圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.熟练掌握圆周角定理是解题关键.10.如图,点,,在上,点在圆外,则下列结论正确的是()A. ∠C>∠DB. ∠C<∠DC. ∠C=∠DD. ∠C=2∠D【答案】A【解析】【分析】根据三角形外角的性质得到∠BEC>∠BDC,根据圆周角定理得到∠BAC=∠BEC,得到答案【详解】如图:连接AE,∵∠BEA是△ADE的外角,∴∠BEA>∠D,∵∠C=∠BEA,∴∠C>∠D,故A选项正确,则B、C、错误,∵不确定D点的位置,∴∠C不一定等于2∠D,故D选项错误,故选A.【点睛】本题考查的是圆周角定理和三角形的外角的性质的应用,掌握同弧所对的圆周角相等和三角形的一个外角大于与它不相邻的任何一个内角是解题的关键.二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分)11.在,,,,点是的外心,现在以为圆心,分别以、、为半径作,则点与的位置关系分别是________.【答案】圆外,圆上,圆内【解析】【分析】由点是的外心,可知O为△ABC的外接圆的圆心,因为∠C=90°,由圆周角定理可知AB为外接圆的直径,根据勾股定理可求出AB的长,根据直角三角形斜边中线等于斜边一半可知OC的长度,根据半径的长判断点C的位置即可.【详解】∵,点是的外心,∴AB为⊙O的直径,且O为AB中点,∵,,∴AB==5,∴OC=2.5,∵2.5>2;2.5=2.5; 2.5<3,∴以、、为半径作,则点与的位置关系分别是圆外、圆上、圆内.故答案为:圆外、圆上、圆内【点睛】本题考查了对点与圆的位置关系的判断.设点到圆心的距离为d,则当d=R时,点在圆上;当d>R 时,点在圆外;当d<R时,点在圆内.根据圆周角定理确定O点的位置是解题关键.12.如下图,在以为圆心的两个同心圆中,大圆的弦交小圆于和两点,,,则长为________.【答案】【解析】【分析】如图:作OE⊥AB于E,根据垂径定理可知CE=CD,AE=AB,根据AC=AE-CE求出AC的长即可.【详解】如图:作OE⊥AB于E,∴根据垂径定理得:CE=CD=3,AE=AB=5,∴AC=AE-CE=2.故答案为:2【点睛】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧,熟练掌握垂径定理是解题关键.13.已知:如图,为半的直径,、、为半圆弧上的点,,,则的度数为________度.【答案】【解析】【分析】根据同圆中,等弧所对的圆心角相等可知∠BOC的度数,即可求出∠AOC的度数.【详解】∵,∠BOE=55°,∴∠COD=∠DOE=∠BOE=55°,∴∠BOC=165°,∴∠AOC=180°-165°=15°,故答案为:15【点睛】本题考查圆周角定理,在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等.在圆中经常利用此结论把圆心角、弧、弦之间进行转化.14.如图,边长为的正方形的顶点、在一个半径为的圆上,顶点、在圆内,将正方形沿圆的内壁逆时针方向作无滑动的滚动.当点第一次落在圆上时,点运动的路径长为________.【答案】【解析】【分析】设圆心为O,连接AO,BO,AC,AE,易证三角形AOB是等边三角形,确定∠GFE=∠EAC=30°,再利用弧长公式计算即可.【详解】如图所示:设圆心为O,连接AO,BO,AC,AE,∵AB=,AO=BO=,∴AB=AO=BO,∴△AOB是等边三角形,∴∠AOB=∠OAB=60°同理:△FAO是等边三角形,∠FAB=2∠OAB=120°,∠DAF=120°-90°=30°,即旋转角为30°,∴∠EAC=30°,∠GFE=∠FAD=120°-90°=30°,∵AD=AB=,∴AC=2,∴当点C第一次落在圆上时,点C运动的路径长为=()π;故答案为:()π【点睛】本题考查了正方形的性质、旋转的性质、等边三角形的判定和性质、勾股定理的运用以及弧长公式的运用,题目的综合性较强,解题的关键是正确的求出旋转角的度数.15.已知中,,,,直线过点且与平行,若以为轴将旋转一周,则所得的几何体的表面积为________.(不求近似值)【答案】【解析】【分析】根据,,,可求出△ABC的其余边长,表面积为一个圆锥的侧面积+一个圆的底面积+圆柱的侧面积,按照公式计算即可.【详解】∵Rt△ABC中,∠C=90°,∠A=30°,AB=10,∴BC=5,AC=5,∴所得几何体的表面积为:π×5×10+π×52+2π×5×5=75π+50.故答案为75π+50.【点睛】考查圆锥的计算;画出相关图形,判断出表面积的组成是解决本题的关键.16.如图,已知是的直径,为弦,度.过圆心作交于点,连接,则________度.【答案】【解析】【分析】先根据直角三角形两锐角互余求出∠BOD,再根据圆周角定理∠DCB=∠BOD即可得答案.【详解】∵OD⊥BC交弧BC于点D,∠ABC=30°,∴∠BOD=90°-∠ABC=90°-30°=60°,∴∠DCB=∠BOD=30°.故答案为:30【点睛】本题主要考查圆周角定理,在同圆或等圆中同弧所对的圆周角的度数是圆心角的一半,熟练掌握圆周角定理是解题关键.17.如图,的边位于直线上,,,,若由现在的位置向右无滑动地旋转,当第次落在直线上时,点所经过的路线的长为________(结果用含有的式子表示)【答案】【解析】【分析】根据含30度的直角三角形三边的关系得到BC=1,AB=2BC=2,∠ABC=60°;点A先以B点为旋转中心,顺时针旋转120°到A1,再以点C1为旋转中心,顺时针旋转90°到A2,然后根据弧长公式计算两段弧长,从而得到点A第3次落在直线上时,点A所经过的路线的长.【详解】∵Rt△ABC中,AC=,∠ACB=90°,∠A=30°,∴BC=1,AB=2BC=2,∠ABC=60°;∵Rt△ABC由现在的位置向右无滑动的翻转,且点A第3次落在直线l上时,有3个的长,2个的长, ∴点A经过的路线长=×3+×2=(4+)π.故答案为:(4+)π.【点睛】本题考查了旋转的性质与弧长的计算,解题的关键是熟练的掌握旋转的性质与弧长的计算方法. 18.如图,圆柱底面半径为,高为,点、分别是圆柱两底面圆周上的点,且、在同一母线上,用一棉线从顺着圆柱侧面绕圈到,求棉线最短为________.【答案】【解析】【分析】将圆柱体展开,然后利用两点之间线段最短解答即可.【详解】圆柱体的展开图如图所示:用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:AC→CD→DB;即在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B的路线最短;∵圆柱底面半径为2cm,∴长方形的宽即是圆柱体的底面周长:2π×2=4πcm;又∵圆柱高为9πcm,∴小长方形的一条边长是3πcm;根据勾股定理求得AC=CD=DB=5πcm;∴AC+CD+DB=15πcm;故答案为:15π.【点睛】本题主要考查了圆柱的计算、平面展开--路径最短问题.圆柱的侧面展开图是一个长方形,此长方形的宽等于圆柱底面周长,长方形的长等于圆柱的高.本题就是把圆柱的侧面展开成长方形,“化曲面为平面”,用勾股定理解决.19.以矩形的顶点为圆心作,要使、、三点中至少有一点在内,且至少有一点在外,如果,,则的半径的取值范围为________.【答案】【解析】【分析】先求出矩形对角线的长,然后由B、C、D与⊙A的位置,确定⊙A的半径的取值范围.【详解】根据题意画出图形如下所示:∵AB=CD=5,AD=BC=12,∴AC=BD==13.∵B、C、D中至少有一个点在⊙A内,且至少有一个点在⊙A外,∴点B在⊙A内,点C在⊙A外.∴5<r<13.故答案是:5<r<13.【点睛】本题考查的是点与圆的位置关系,要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.20.如图,在中,是弦,,,那么圆心到的距离是________,弦的长是________.【答案】(1). (2).【解析】【分析】过O作OC⊥AB交AB于C点,根据垂径定理可知OC垂直平分AB,根据OA=OB,∠AOB=120°可求出∠OAB=30°,根据30°角所对直角边等于斜边一半即可求得圆心到的距离;根据勾股定理求出AC的长即可求出AB的长.【详解】过O作OC⊥AB交AB于C点,如图所示:由垂径定理可知,OC垂直平分AB,∵OA=OB,∠AOB=120°∴∠OAB=30°∴OC=OA=cm∴由勾股定理可得:AC= =cm∴AB=2AC=5cm.故答案为:;5;【点睛】本题考查垂径定理,垂直于弦的直径,平分弦且平分这条弦所对的两条弧,熟练掌握垂径定理是解题关键.三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分)21.一圆柱形排水管的截面如图所示,已知排水管的半径为,水面宽为.由于天气干燥,水管水面下降,此时排水管水面宽变为,求水面下降的高度.【答案】水面下降了米.【解析】【分析】如图:过点O作ON⊥CD于N,交AB于M,先根据垂径定理求得AM、CN,然后根据勾股定理求出OM、ON的长,即可得出结论【详解】如图,下降后的水面宽CD为6m,连接OA,OC,过点O作ON⊥CD于N,交AB于M.∴∠ONC=90°.∵AB∥CD,∴∠OMA=∠ONC=90°.∵AB=8m,CD=6m,∴AM=AB=4,CN=CD=3,在Rt△OAM中,∵OA=5,∴OM==3.同理可得ON=4,∴MN=ON-OM=1(米).答:水面下降了1米.【点睛】本题考查的是垂径定理的应用以及勾股定理的应用,熟知垂直于弦的直径平分弦,并且平分这条弦所对的两条弧是解答此题的关键.22.如图,在中,弦、于点,且.求证:.【答案】见解析【解析】【分析】根据,可证明,进而证明AC=BD,通过证明即可证明结论.【详解】∵,∴,,∴在与中,∵,∴,∴.【点睛】本题考查的是圆心角、弧、弦的关系及全等三角形的判定与性质,熟练掌握,圆心角、弧、弦的关系是解题关键.23.如图,在中,,,求分别以、、为圆心,以为半径画弧,三条弧与边所围成的阴影部分的面积.【答案】.【解析】【分析】由于三条弧所对的圆心角的和为180°,根据扇形的面积公式可计算出三个扇形的面积和,而三条弧与边AB 所围成的阴影部分的面积=S△ABC-三个扇形的面积和,再利用三角形的面积公式计算出△ABC的面积,然后代入即可得到答案.【详解】∵∠C=90°,CA=CB=2,∴AC=1,S△ABC==2,∵三条弧所对的圆心角的和为180°,三个扇形的面积和==,∴三条弧与边AB所围成的阴影部分的面积=S△ABC-三个扇形的面积和=2-,【点睛】本题考查扇形面积,熟练掌握面积公式并明确三条弧所对的圆心角的和为180°是解题关键.24.已知:如图,的外接圆,弦的长为,,求圆心到的距离.【答案】圆心到的距离为.【解析】【分析】连接,,过点作于点,根据圆周角定理可知∠BOC=60°,进而证明△OBC是等边三角形,根据垂径定理可知CD的长度,利用勾股定理求出OD的长即【详解】连接,,过点作于点,∵,∴.∵,∴是等边三角形,∴,∵OD⊥BC,∴CD=BC=2,∴=,即圆心到的距离为.【点睛】本题考查圆周角定理及垂径定理,在同圆中,同弧所对的圆周角的度数等于圆心角的一半,垂直于弦的直径,平分弦且平分这条弦所对的两条弧,熟练掌握定理是解题关键.25.如图,已知为的直径,是弦,于,于,.求证:;求证:;若,,设,求值及阴影部分的面积.【答案】(1)见解析;(2)见解析;(3)x=5,.【解析】【分析】(1)根据直径所对的圆周角是90°可知∠ACB=∠AFO=90°,由平行线判定定理即可证明OF//BC;(2)由可知∠CBE=∠FOA,利用,,即可证明;(3)在Rt△OCE中,利用勾股定理列方程即可求出x的值,根据OC=2OE可知∠OCE=30°,即可求出∠COD的度数,利用扇形面积及三角形面积公式求出阴影面积即可.【详解】证明:∵为的直径,∴又∵∴证明:∵∴∠CBE=∠FOA∵,,∴解:连接.设,∵∴.在中,,根据勾股定理可得:解得:,即,∵OC=5+5=10,∴OC=2OE,∴∠OCE=30°,∴,∴扇形的面积是:的面积是:∴阴影部分的面积是:.【点睛】本题考查圆周角定理、垂径定理及扇形面积,熟练掌握定理和公式是解题关键.26.如图,内接于,,,.求的度数;将沿折叠为,将沿折叠为,延长和相交于点;求证:四边形是正方形;若,,求的长.【答案】(1);(2)见解析;(3).【解析】【分析】(1)连接和,由OE=BC,可知OE=BE,进而可知∠OBE=45°,同理可证∠OCE=45°,即可证明∠BOC=90°,根据圆周角定理即可求得∠BAC的度数;(2)由折叠性质可知AG=AD=AF,∠AGH=∠AFH=90°,∠DAC=∠CAF,∠BAD=∠BAG,由∠BAD+∠DAC=45°,可证明∠GAF=90°,即可证明四边形AFHG 是正方形;(3)由折叠性质可知,;由(2)可知∠BHC=90°,设AD长为x,利用勾股定理列方程求出x的值即可得解.【详解】(1)连接和;∵,∴;∵,∴,∴;∵,∴;由折叠可知,,,,,∴;∴;∴四边形是正方形;解:由得,,,,;设的长为,则,.在中,,∴;解得,,(不合题意,舍去);∴.【点睛】本题主要考查圆周角定理及折叠性质,在同圆中,同弧所对的圆周角的度数等于圆心角的一半;折叠后的图形与原图形全等,熟练掌握折叠的性质是解题关键.。
九年级道法上册第一学期期中综合测试卷(人教版 2024年秋)

九年级道法上册第一学期期中综合测试卷(人教版2024年秋)一、选择题。
(下列各题的备选答案中,只有一项最符合题意。
每小题3分,共48分)1.习近平主席在向2023年中国国际服务贸易交易会全球服务贸易峰会发表的视频致辞中指出,今年(2023年)是中国改革开放45周年,中国将坚持推进高水平对外开放,以高质量发展全面推进中国式现代化,为各国开放合作提供新机遇。
习近平主席的致辞表明改革开放()①推动中国和世界共同发展②让中国人民过上幸福生活③是当代中国最鲜明的特色④改变中国并主导世界发展A.①②B.①③C.②④D.③④2.在某中央国家机关官网上,同学们查到下面新闻。
同学们对此发表了不同看法,其中你不认同的是()去年10月24日,某会议表决通过了关于批准国务院增发国债和2023年中央预算调整方案的决议。
增发国债资金精准聚焦灾后恢复重建和提升防灾减灾救灾能力。
A.小道:批准国务院增发国债的国家机关是全国人民代表大会常务委员会B.小德:此次增发国债有利于保障国家安全、促进民生改善C.小法:国务院增发国债体现了市场在资源配置中起宏观调控作用D.小治:增发国债有利于加强我国基础设施建设,助推经济高质量发展3.去年,我国中央对地方转移支付首次突破10万亿元。
每年,地方都要向中央缴纳财政,而中央会把税收等财政收入重新分配给各个省份,经济发展好、税收高的地方多交少拿,经济发展差、税收低的地方少交多拿。
我国的中央对地方转移支付政策()A.有利于促进共同富裕B.不利于社会公平正义C.在经济困难时才实施D.目的是消除绝对贫困4.漫步繁华都市,5G智慧校园初具规模,远程诊断加速落地;深入美丽山乡,高速光纤入户,直播拓展销路;走进生产一线,千兆网络直通矿井,5G赋能数字车间。
对此理解不正确的是()A.信息技术大大改变了生产生活B.数字经济越来越受人们的青睐C.生活中的各个领域都需要创新D.城乡区域的发展基本没有差距5.品质优,销路好,苹果丰产丰收离不开科技“金点子”。
人教版数学九年级上册《圆》单元测试卷带答案

A. ①B. ③C. ②D. ④
9.已知正六边形的边长为 ,则这个正六边形的边心距是( )
A. B. C. D.
10.如图,直线 , 与 和 分别相切于点 和点 .点 和点 分别是 和 上的动点, 沿 和 平移. 的半径为 , .下列结论错误的是( )
【详解】解:连结OA、OB,如图1,
∵⊙O与l1和l2分别相切于点A和点B,
∴OA⊥l1,OB⊥l2,
∵l1∥l2,
∴点A、O、B共线,
∴AB为⊙O的直径,
∴l1和l2的距离为2;故C正确,
作NH⊥AM于H,如图1,
则NH=AB=2,
∵∠AMN=60°,
∴sin60°= ,
∴MN= ;故A正确,
当MN与⊙O相切,如图2,连结OM,ON,
求证: 是 的切线;
当点 在劣弧 上运动时,其他条件不变,若 .求证:点 是 的中点;
在满足 条件下, , ,求 的长.
参考答案
一、选择题(共 16 小题,每小题 3 分,共 48 分 )
1.下列语句中,不正确的有( )
①直径 弦;
②弧是半圆;
③经过圆内一定点可以作无数条弦;
④长度相等的弧是等弧.
A.①③④B.②③C.②D.②④
∴AC= AB= ×60=30,
CO=AO-10,
在Rt△AOC中,AO2=AC2+OC2,
AO2=302+(AO-10)2,解得AO=50cm.
∴内径为2×50=100cm.
故选C.
【点睛】本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
24-25学年九年级数学上学期期中模拟卷(湖北省卷专用,人教版九上第21章~24.2)(考试版A4)

2024-2025学年九年级数学上学期期中模拟卷(湖北省卷专用)(考试时间:120分钟试卷满分:120分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:人教版第21章一元二次方程+第22章二次函数+第23章旋转+第24章24.2。
5.难度系数:0.65。
第一部分(选择题共30分)一、选择题(本大题共10小题,每小题3分,满分30分.在每个小题给出的四个选项中,只有一项符合题目要求的)1.二次函数y=2(x﹣2)2﹣1图象的顶点坐标为( )A.(﹣2,1)B.(2,1)C.(2,﹣1)D.(﹣2,﹣1)2.中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )A.B.C.D.3.如图,EF、CD是⊙O的两条直径,A是劣弧DF的中点,若∠EOD=32°,则∠CDA的度数是( )A .37°B .74°C .53°D .63°4.关于x 的一元二次方程ax 2﹣x +1=0有实数根,则a 的取值范围是( )A .a ≤14且a ≠0B .a ≤14C .a ≥14且a ≠0D .a ≥145.关于二次函数y =﹣(x +1)2+3的图象,下列说法错误的是( )A .开口向下B .对称轴为直线x =﹣1C .当x <﹣1时,y 随x 的增大而增大D .当x =﹣1时,函数有最小值,最小值为y =36.如图,将△ABC 绕点A 顺时针旋转90°得到△ADE ,若∠DAE =50°,则∠CAD =( )A .30°B .40°C .50°D .90°7.若m 是方程2x 2﹣3x ﹣1=0的一个根,则6m 2﹣9m +2024的值为( )A .2025B .2026C .2027D .20288.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点M 表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O 为圆心,5米为半径的圆,且圆心在水面上方,若圆被水面截得的弦AB 长为8米,则筒车工作时,盛水桶在水面以下的最大深度为( )A.1米B.2米C.3米D.4米9.如图,小程的爸爸用一段10m长的铁丝网围成一个一边靠墙(墙长5.5m)的矩形鸭舍,其面积为15m2,在鸭舍侧面中间位置留一个1m宽的门(由其它材料制成),则BC长为( )A.5m或6m B.2.5m或3m C.5m D.3m10.如图,已知开口向下的抛物线y=ax2+bx+c与x轴交于点(6,0),对称轴为直线x=2.则下列结论:①abc<0;②a﹣b+c>0;③4a+b=0;④抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<2<x2且x1+x2>4,则y1<y2.其中正确的有( )A.1个B.2个C.3个D.4个第二部分(非选择题共90分)二、填空题(本大题共5小题,每小题3分,满分15分)11.方程(m+2)x|m|+3mx+1=0是关于x的一元二次方程,则m的值为 .12.在平面直角坐标系中,将二次函数y=(x﹣2023)(x﹣2024)+5的图象向下平移5个单位长度,所得抛物线与x轴有两个公共点P、Q,则PQ= .13.如图,将△ABC绕点A逆时针旋转45°得到△ADE,∠BAC=45°,AB=3,AC=4.连接BE,则BE 的长为 .14.一个菱形的边长是方程x2﹣9x+18=0的一个根其中一条对角线长为6,则该菱形的面积为 .15.如图,矩形ABCD中,AD=,点E是矩形内部一动点,且∠BAE=∠CBE,已知DE的最小值等于2,则矩形ABCD的周长= .三、解答题(本大题共9小题,满分75分.解答应写出文字说明,证明过程或演算步骤)16.(每小题4分,共8分)解下列方程:(1)x2﹣4x+1=0;(2)(x+2)2=6+3x.17.(6分)已知关于x的一元二次方程mx2+2(m+1)x+m﹣1=0有两个不相等的实数根.(1)求m的取值范围;(2)若该方程的两个实数根分别为x1、x2,且x21+x22=8,求m的值.18.(7分)如图,在平面直角坐标系中,已知点A(2,0),B(1,1),C(4,2).(1)画出△ABC关于原点O成中心对称的△A1B1C1,并写出点B的对应点B1的坐标 ;(2)画出将△ABC绕点Q(0,﹣1)逆时针旋转90°后得到的△A2B2C2;(3)求△ABC的面积.19.(7分)我国快递行业迅速发展,经调查,某快递公司今年2月份投递快递总件数为20万件,4月份投递快递总件数33.8(1)求该公司投递快递总件数的月增长率;(2)若该公司每月投递快递总件数的增长率保持不变,那么5月份投递快递总件数是否达到45万件?20.(7分)已知抛物线y=ax2﹣4x与x轴交于点A(4,0),其顶点记作点P.(1)求此抛物线的顶点P的坐标.(2)将抛物线y=ax2﹣4x向左平移m(m>0)个单位,使其顶点落在直线y=x上,求平移后新抛物线的表达式.21.(8分)如图,AB为⊙O的直径,OC⊥AB交⊙O于点C,D为OB上一点,延长CD交⊙O于点E,延长OB至F,使DF=FE,连接EF.(1)求证:EF为⊙O的切线;(2)若OD=1且BD=BF,求⊙O的半径.22.(10分)某超市在“元宵节”来临前夕,购进一种品牌元宵,每盒进价是20元,超市规定每盒售价不得少于25元,根据以往销售经验发现;当售价定为每盒25元时,每天可卖出250盒,每盒售价每提高1元,每天要少卖出10盒.(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?(3)为稳定物价,有关管理部门限定:这种元宵的每盒售价不得高于38元,如果超市想要每天获得不低于2000元的利润,那么超市每天至少销售元宵多少盒?23.(10分)已知△AOB和△MON<OM<OA),∠AOB=∠MON=90°.(1)如图①,连AM,BN AOM≌△BON;(2)若将△MON绕点O顺时针旋转.①如图②,当点N恰好在AB边上时,求证:BN2+AN2=2ON2;②当点A,M,N在同一条直线上时,若OB=5,ON=4,请直接写出线段BN的长.24.(12分)平面直角坐标系中,抛物线y=a(x―1)2+92与x轴交于A,B(4,0)两点,与y轴交于点C.(1)求抛物线的解析式,并直接写出点A,C的坐标;(2)在抛物线的对称轴上是否存在点P,使△BCP是直角三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由;(3)如图,点M是直线BC上的一个动点,连接AM,OM,是否存在点M使AM+OM最小,若存在,请求出点M的坐标,若不存在,请说明理由.。
2024-2025学年人教版历史九年级上册 期中测试卷

2024-2025 学年九年级历史上学期期中模拟卷(考试时间:100 分钟试卷满分:100 分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.测试范围:九上全册。
5.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题:本题共25 小题,每小题2 分,共50 分。
在每小题给出的四个选项中,只有一项符合题目要求。
1.同苏美尔人的法律相比,古巴比伦《汉谟拉比法典》规定的契约形式很多,内容详尽,包括租佃契约、债务、抵押、损害赔偿、借贷、合伙经营、保管、继承、雇佣等等。
这()A.源于商品经济的较大发展B.体现出罗马法体系的影响C.加强古巴比伦的君主专制统治D.说明古巴比伦法律体系的成熟2.古代亚非地区的文明古国创造了辉煌灿烂的文明成果,如埃及的象形文字和金字塔,两河流域的楔形文字和《汉谟拉比法典》,中国的甲骨文和青铜器,印度的梵文和佛教等。
这表明古代文明具有()A.统一性B.稳定性C.多元性D.延续性3.“连续不断地对外征服扩张使其超出了一个城邦的概念,成为环地中海的一个多民族、多宗教、多语言、多文化的大帝国。
全盛时期控制了大约500 万平方千米的土地。
”材料中的帝国是()A.亚历ft大帝国B.古罗马帝国C.奥斯曼帝国D.拜占庭帝国4.罗马因为其历史悠久,被称为“永恒之城”。
下列文化遗产属于古代罗马的是()A.金字塔B.楔形文字C.帕特农神庙D.大竞技场5.时空观念是历史学科五大核心素养之一。
如图是某个帝国发展的时空定位。
据此判断,这个帝国是()A.罗马帝国B.亚历ft大帝国C.奥斯曼帝国D.阿拉伯帝国6.雅典对担任各种公职的人给予不同的公职津贴,还向公民发放“观剧津贴",这些措施都获得了雅典公民的广泛支持。
人教版九年级数学上册单元测试题全套及答案

九年级数学上册半月测试题姓名:分数:时间:120分钟满分:120分一、选择题(每小题3分,共30分)1.一元二次方程x2-8x-1=0配方后为( )A.(x-4)2=17 B.(x+4)2=15C.(x+4)2=17 D.(x-4)2=17或(x+4)2=172.若二次函数y=x2+bx+5配方后为y=(x-2)2+k,则b,k的值分别为( )A.0,5 B.0,1 C.-4,5 D.-4,13.已知关于x的一元二次方程x2+mx-8=0的一个实数根为2,则另一实数根及m的值分别为( ) A.4,-2 B.-4,-2 C.4,2 D.-4,24.已知x为实数,且满足(x2+3x)2+2(x2+3x)-3=0,那么x2+3x的值为( )A.1 B.-3或1 C.3 D.-1或35.抛物线y=x2+bx+c(其中b,c是常数)过点A(2,6),且抛物线的对称轴与线段y=0(1≤x≤3)有交点,则c的值不可能是( )A.4 B.6 C.8 D.106.已知关于x的一元二次方程x2+2x-(m-2)=0有实数根,则m的取值范围是( )A.m>1 B.m<1 C.m≥1 D.m≤17.如图,抛物线y=x2+bx+c与x轴交于点A,B,与y轴交于点C,∠OBC=45°,则下列各式成立的是( )A.b-c-1=0 B.b+c+1=0C.b-c+1=0 D.b+c-1=08.如图,在▱ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则▱ABCD的周长为( )A.4+2 2 B.12+6 2C.2+2 2 D.2+2或12+6 29.当x取何值时,代数式x2-6x-3的值最小?( )A.0 B.-3 C.3 D.-910.如图,将边长为12 cm的正方形ABCD沿其对角线AC剪开,再把ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为32 cm2,则它移动的距离AA′等于()A .4 cmB .8 cmC .6 cmD .4 cm 或8 cm二、填空题(每小题3分,共24分)11.把方程3x(x -1)=(x +2)(x -2)+9化成ax 2+bx +c =0的形式为__ __.12.方程2x -4=0的解也是关于x 的方程x 2+mx +2=0的一个解,则m 的值为__ __.13.若抛物线y =ax 2+bx +c 的顶点是A(2,1),且经过点B(1,0),则抛物线的函数关系式为__ __. 14.下面是某同学在一次测试中解答的填空题:①若x 2=a 2,则x =a ;②方程2x(x -2)=x -2的解为x =0;③已知x 1,x 2是方程2x 2+3x -4=0的两根,则x 1+x 2=32,x 1x 2=-2.其中错误的答案序号是____.15.已知一元二次方程x 2+3x -4=0的两根为x 1,x 2,则x 12+x 1x 2+x 22=___.16.如图,一个矩形铁皮的长是宽的2倍,四角各截去一个正方形,制成高是5 cm ,容积是500 cm 3的无盖长方体容器,那么这块铁皮的长为__ __,宽为__ __.17.三角形的每条边的长都是方程x 2-6x +8=0的根,则三角形的周长是__ _.18.若二次函数y =2x 2-4x -1的图象与x 轴交于A(x 1,0),B(x 2,0)两点,则1x 1+1x 2的值为__ __.三、解答题(共66分)19.(8分)用适当的方法解下列方程:(1)(x +1)(x -2)=x +1; (2)2x 2-4x =4 2.20.(8分) 已知:如图,二次函数y=ax2+bx+c 的图象与x 轴交于A 、B 两点,其中A 点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M 为 它的顶点.(1)求抛物线的解析式; (2)求△MCB 的面积S △MCB.21.(6分)随着国家“惠民政策”的陆续出台,为了切实让老百姓得到实惠,国家卫计委通过严打药品销售环节中的不正当行为,某种药品原价200元/瓶,经过连续两次降价后,现仅卖98元/瓶,现假定两次降价的百分率相同,求该种药品平均每次降价的百分率.22.(8分)关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2.(1)求m的取值范围;(2)若2(x1+x2)+x1x2+10=0,求m的值.23.(8分) 已知二次函数y=x2+bx-c的图象与x轴两交点的坐标分别为(m,0),(-3m,0)(m≠0).(1)求证:4c=3b2;(2)若该函数图象的对称轴为直线x=1,试求二次函数的最小值.24.(8分) 某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.(1)求y关于x的函数解析式;(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.25.(10分)端午节期间,某食品店平均每天可卖出300只粽子,卖出1只粽子的利润是1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获取的利润更多,该店决定把零售单价下降m(0<m<1)元.(1)零售单价下降m元后,该店平均每天可卖出__ __只粽子,利润为__ __元;(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元,并且卖出的粽子更多?26.(10分)要在一块长52 m,宽48 m的矩形绿地上,修建同样宽的两条互相垂直的甬路,下面分别是小亮和小颖的设计方案.(1)求小亮设计方案中甬路的宽度x;(2)求小颖设计方案中四块绿地的总面积.(友情提示:小颖设计方案中的x与小亮设计方案中的x取值相同)。
(精)新人教版九年级数学上册全单元测试卷(含答案)

新人教版九年级数学上个单元测试卷(含答案)第二十一章过关自测卷 (100分,45分钟)一、选择题(每题3分,共21分)1.下列方程是关于x 的一元二次方程的是( ) A.ax 2+bx +c =0 B.211x x=2 C.x 2+2x =y 2-1 D.3(x +1)2=2(x +1)2.若一元二次方程ax 2+bx +c =0有一根为0,则下列结论正确的是( ) A.a =0 B.b =0 C.c =0 D.c ≠03.一元二次方程x 2-2x -1=0的根的情况为( ) A.有两个相等的实数根 B.有两个不相等的实数根 C.只有一个实数根 D.没有实数根4.方程x 2+6x =5的左边配成完全平方式后所得方程为( ) A.(x +3)2=14 B.(x -3)2=14C.(x +6)2=12D.以上答案都不对 5.已知x =2是关于x 的方程32x 2-2a =0的一个根,则2a -1的值是( ) A.3 B.4 C.5 D.66.某县为发展教育事业,加强了对教育经费的投入,2012年投入3亿元,预计2014年投入5亿元.设教育经费的年平均增长率为x ,根据题意,下面所列方程正确的是( ) A .3(1+x )2=5 B .3x 2=5C. 3(1+x %)2=5D. 3(1+x ) +3(1+x )2=57.使代数式x 2-6x -3的值最小的x 的取值是( ) A.0 B.-3 C.3 D.-9 二、填空题(每题3分,共18分)8.已知x =1是一元二次方程x 2+mx +n =0的一个根,则m 2+2mn +n 2的值为________. 9.如果方程ax 2+2x +1=0有两个不等实数根,则实数a 的取值范围是____________.10.已知α、β是一元二次方程x 2-4x -3=0的两实数根,则代数式(α-3)(β-3)=________.11.在一幅长50 cm ,宽30 cm 的风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图1所示,如果要使整个挂图的面积是1 800 cm 2,设金色纸边的宽为x cm ,那么x 满足的方程为________________.112.已知x 是一元二次方程x 2+3x -1=0的实数根,那么代数式2352362x x x x x -⎛⎫÷+- ⎪--⎝⎭的值为________.13.三角形的每条边的长都是方程x 2-6x +8=0的根,则三角形的周长是_______________.三、解答题(14、19题每题12分,15题8分,16题9分,其余每题10分,共61分)14.我们已经学习了一元二次方程的四种解法:因式分解法,开平方法,配方法和公式法.请从以下一元二次方程中任选一个..,并选择你认为适当的方法解这个方程. ①x 2-3x +1=0;②(x -1)2=3;③x 2-3x =0;④x 2-2x =4.15.已知关于x 的方程x 2+kx -2=0的一个解与方程11x x +-=3的解相同. (1)求k 的值;(2)求方程x 2+kx -2=0的另一个解.16.关于x的一元二次方程x2-3x-k=0有两个不相等的实数根.(1)求k的取值范围;(2)请选择一个k的负整数值,并求出方程的根.17.〈绍兴〉某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5 000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5 000元.(1)当每间商铺的年租金定为13万元时,能租出多少间?(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)为275万元?18.中秋节前夕,旺客隆超市采购了一批土特产,根据以往销售经验,每天的售价与销售量之间有如下表的关系:(2)如果这种土特产的成本价是20元/千克,为使某一天的利润为780元,那么这一天的销售价应为多少元/千克?(利润=销售总金额-成本)19.如图2,A、B、C、D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P、Q分别从点A、C同时出发,点P以3 cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向点D移动.(1)P、Q两点从出发开始到几秒时四边形PBCQ的面积为33 cm2?图2 (2)P、Q两点从出发开始到几秒时,点P和点Q的距离是10 cm?第二十二章过关自测卷(100分,45分钟)一、选择题(每题4分,共32分)1.抛物线y=ax2+bx-3过点(2,4),则代数式8a+4b+1的值为()A.-2B.2C.15D.-152.图1是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2 m,水面宽4 m.如图2建立平面直角坐标系,则抛物线的关系式是()图1 图2A.y=-2x2B.y=2x2C.y=-12x2 D.y=12x23.〈恩施州〉把抛物线y=12x2-1先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为()A.y=12(x+1)2-3B.y=12(x-1)2-3C.y=12(x+1)2+1D.y=12(x-1)2+12a≠0)中的x与y的部分对应值如下表:给出了结论:(1)二次函数y=ax2+bx+c有最小值,最小值为-3;(2)当-12<x<2时,y<0;(3)二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴两侧.则其中正确结论的个数是()A.3 B.2C.1D.05.〈舟山〉若一次函数y=ax+b(a≠0)的图象与x轴的交点坐标为(-2,0),则抛物线y=ax2+bx的对称轴为()A.直线x=1B.直线x=-2C.直线x=-1D.直线x=-46.设一元二次方程(x-1)(x-2)=m(m>0)的两实根分别为α,β,且α<β,则α,β满足()C.α<1<β<2D.α<1且β>27.〈内江〉若抛物线y=x2-2x+c与y轴的交点为(0,-3),则下列说法不正确的是()A.抛物线开口向上B.抛物线的对称轴是直线x=1C.当x=1时,y的最大值为-4D.抛物线与x轴的交点为(-1,0),(3,0)8.〈南宁〉已知二次函数y=ax2+bx+c(a≠0)的图象如图3所示,下列说法错误的是()A.图象关于直线x=1对称B.函数y=ax2+bx+c(a≠0)的最小值是-4C.-1和3是方程ax2+bx+c=0(a≠0)的两个根D.当x<1时,y随x的增大而增大图3二、填空题(每题4分,共32分)9.已知抛物线y=-13x2+2,当1≤x≤5时,y的最大值是______.10.已知二次函数y=x2+bx-2的图象与x轴的一个交点为(1,0),则它与x轴的另一个交点坐标是__________.11.已知函数y=(k-3)x2+2x+1的图象与x轴有公共点,则k的取值范围是________.12.一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式:h=-5(t-1)2+6,则小球距离地面的最大高度是________.13.二次函数y=ax2+bx的图象如图4,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为__________.图4 图514.如图5,已知函数y=-3x与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+3x=0的解为_______.15.将一条长为20 cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是__________ cm2.16.如图6,把抛物线y=12x2平移得到抛物线m,抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=12x2交于点Q,则图中阴影部分的面积为__________.图6三、解答题(每题12分,共36分)17.〈牡丹江〉如图7,已知二次函数y=x2+bx+c的图象过点A(1,0),C(0,-3). (1)求此二次函数的解析式;(2)在抛物线上存在一点P使△ABP的面积为10,请求出点P的坐标.图718.在平面直角坐标系xOy中,O为坐标原点,已知抛物线y=x2-(k+2)x+14k2+1.(1)k取什么值时,此抛物线与x轴有两个交点?(2)若此抛物线与x轴交于A(x1,0)、B(x2,0)两点(点A在点B左侧),且x1+x2=3,求k的值.19.〈广州〉已知抛物线y 1=ax 2+bx +c 过点A (1,0),顶点为B ,且抛物线不经过第三象限. (1)使用a 、c 表示b ;(2)判断点B 所在象限,并说明理由;(3)若直线y 2=2x +m 经过点B ,且与该抛物线交于另一点C ,8c b a ⎛⎫+ ⎪⎝⎭,求当x ≥1时y 1的取值范围.第二十三章过关自测卷(100分,45分钟)一、选择题(每题3分,共24分)1.已知下列命题:①关于一点对称的两个图形一定不全等;②关于一点对称的两个图形一定是全等图形;③两个全等的图形一定关于一点对称.其中真命题的个数是()A.0 B.1 C.2 D.32.〈江苏泰州〉下列标志图(图1)中,既是轴对称图形,又是中心对称图形的是()图13.如图2,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为()图2A.10°B.15°C.20°D.25°4.如图3①,将正方形纸片两次对折,并剪出一个菱形小洞后铺平,得到的图形是图3②中的()图35.如图4所示的图案中,绕自身的某一点旋转180°后还能与自身重合的图形的个数是()图4A.1B.2C.3D.4C.第三象限D.第四象限7.将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图5①.在图5②中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换.若骰子的初始位置为图5①所示的状态,那么按上述规则连续完成10次变换后,骰子朝上一面的点数是()图5A.6 B.5 C.3 D.28.如图6,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,此时,点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为()A. 30,2B.60,2C.60D.60图6二、填空题(每题4分,共24分)9.如图7,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF.将△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α(0°<α<180°),则α=_______.图710.如图8,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△A′B′C,那么点A的对应点A′的坐标是_______.图8A′、C′仍落在格点上,则线段AB扫过的图形的面积是_______平方单位(结果保留π).图9 图1012.直线y=x+3上有一点P(3,n),则点P关于原点的对称点P′为_______.13.如图10,△ABC是直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,若AP=3,则PP′的长是_______.14.如图11①,在△AOB中,∠AOB=90°,OA=3,OB=4.将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图11②、图11③、…,则旋转得到的图11⑩的直角顶点的坐标为_______.图11三、解答题(17题10分,18题12分,19题14分,其余每题8分,共52分)15.如图12,在平面直角坐标系中,三角形②③是由三角形①依次旋转后所得的图形.图12(1)在图中标出旋转中心P的位置,并写出它的坐标;(2)在图中画出再次旋转后的三角形④.16.如图13所示,(1)观察图①~④中阴影部分构成的图案,请写出这四个图案都具有的两个共同特征:图13(2)借助图⑤的网格,请设计一个新的图案,使该图案同时具有你在解答(1)中所给出的两个共同特征.(注意:①新图案与图①~④的图案不能重合;②只答第(2)问而没有答第(1)问的解答不得分)17.如图14,矩形ABCD和矩形AEFG关于点A中心对称,(1)四边形BDEG是菱形吗?请说明理由;图14(2)若矩形ABCD面积为2,求四边形BDEG的面积.18.如图15,在平面直角坐标系中,O为坐标原点,每个小方格的边长为1个单位长度.正方形ABCD顶点都在格点上,其中,点A的坐标为(1,1).(1)若将正方形ABCD绕点A顺时针方向旋转90°,点B到达点B1,点C到达点C1,点D到达点D1,求点B1、C1、D1的坐标;图15(2)若线段AC1的长度与点D1的横坐标的差恰好是一元二次方程x2+ax+1=0的一个根,求a的值.19.〈潍坊〉如图16①所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至长方形CE′F′D′,旋转角为α.图16(1)当点D′恰好落在EF边上时,求旋转角α的值;(2)如图16②,G为BC中点,且0°<α<90°,求证:GD′= E′D;(3)小长方形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△CBD′能否全等?若能,直接写出旋转角α的值;若不能,说明理由.第二十四章过关自测卷(100分,45分钟)一、选择题(每题4分,共32分)1.〈重庆〉如图1,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠OCB的度数为()A.40°B.50°C.65°D.75°图1 图22.〈甘肃兰州〉如图2是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8 cm,水面最深地方的高度为2 cm,则该输水管的半径为()A.3 cm B.4 cm C.5 cm D.6 cm3.〈甘肃兰州〉圆锥底面圆的半径为3 cm,其侧面展开图是半圆,则圆锥母线长为()A.3 cm B.6 cm C.9 cm D.12 cm图3 图44.如图3,边长为a的六角螺帽在桌面上滚动(没有滑动)一周,则它的中心O点所经过的路径长为()A.6a B.5a C.2aπD aπEB的中点,则下列结论不成立的是()5.〈山东泰安〉如图4,已知AB是⊙O的直径,AD切⊙O于点A,点C是⌒A.OC//AE B.EC=BCC.∠DAE=∠ABE D.AC⊥OE6.〈2013,晋江市质检〉如图5,动点M,N分别在直线AB与CD上,且AB//CD,∠BMN与∠MND的平分线相交于点P,若以MN为直径作⊙O,则点P与⊙O的位置关系是()图5A.点P在⊙O外B.点P在⊙O内C.点P在⊙O上D.以上都有可能7.△ABC中,AB=AC,∠A为锐角,CD为AB边上的高,I为△ACD的内切圆圆心,则∠AIB的度数是()A.120°B.125°C.135°D.150°8.〈贵州遵义〉如图6,将边长为1 cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为()图6A.32πcm B.322⎛⎫+⎪⎝⎭πcm C.43πcm D.3 cm二、填空题(每题4分,共24分)9.〈四川巴中〉如图7,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD 等于________.图7 图810.〈重庆〉如图8,一个圆心角为90°的扇形,半径OA=2,那么图中阴影部分的面积为________(结果保留π).11.〈贵州遵义〉如图9,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为________(结果保留根号).图9 图1012.如图10,△ABC为等边三角形,AB=6,动点O在△ABC的边上从点A出发沿着A→C→B→A的路线匀速运动一周,速度为每秒1个单位长度,以O ABC的边第二次相切时是出发后第________秒.13.如图11,正六边形ABCDEF中,AB=2,P是ED的中点,连接AP,则AP的长为________.图11 图1214.如图12,AB为半圆O的直径,C为半圆的三等分点,过B,C两点的半圆O的切线交于点P,若AB的长是2a,则P A的长是________.三、解答题(15题9分,16题10分,17题11分,18题14分,共44分)15. 如图13所示,△ABC中,∠ACB=90°,AC=2 cm,BC=4 cm,CM是AB边上的中线,以C长为半径画圆,则点A,B,M与⊙C的位置关系如何?图1316. 如图14,已知CD是⊙O的直径,点A为CD延长线上一点,BC=AB,∠CAB=30°.(1)求证:AB是⊙O的切线;图14(2)若⊙O的半径为2,求⌒BD的长.17.如图15,从一个直径为4的圆形铁片中剪下一个圆心角为90°的扇形ABC.(1)求这个扇形的面积;图15(2)在剩下的材料中,能否从③中剪出一个圆作为底面,与扇形ABC围成一个圆锥?若不能,请说明理由;若能,请求出剪的圆的半径是多少.18. 如图16,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O上一动点,且P在第一象限内,过点P作⊙O的切线与x轴相交于点A,与y轴相交于点B.(1)点P在运动时,线段AB的长度也在发生变化,请写出线段AB长度的最小值,并说明理由;图16(2)在⊙O上是否存在一点Q,使得以Q,O,A,P为顶点的四边形是平行四边形?若存在,请求出Q点的坐标;若不存在,请说明理由.第二十五章过关自测卷(100分,45分钟)一、选择题(每题3分,共24分)1.〈大连〉一个不透明的袋子中有3个红球和2个黄球,这些球除颜色外完全相同.从袋子中随机摸出一个球,它是黄球的概率为()A.13B.25C.12D.352.〈牡丹江〉小明制作了十张卡片,上面分别标有1~10这十个数.从这十张卡片中随机抽取一张恰好能被4整除的概率是()A.110B.25C.15D.3103.〈贵阳〉一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是()A.6 B.10 C.18 D.204.一纸箱内有红、黄、蓝、绿四种颜色的纸牌,且图1所示为各颜色纸牌数量的统计图.若小华自箱内抽出一张牌,且每张牌被抽出的机会相等,则他抽出红色牌或黄色牌的机(概)率为()A.15B.25C.13D.12图15.小江玩投掷飞镖的游戏,他设计了一个如图2所示的靶子,点E、F分别是矩形ABCD的两边AD、BC上的点,EF∥AB,点M、N是EF上任意两点,则投掷一次,飞镖落在阴影部分的概率是()A. 13B.23C.12D.34图26.〈临沂〉如图3,在平面直角坐标系中,点A1,A2在x轴上,点B1,B2在y轴上,其坐标分别为A1(1,0),A2(2,0),B1(0,1),B2(0,2),分别以A1、A2、B1、B2其中的任意两点与点O为顶点作三角形,所作三角形是等腰三角形的概率是()A. 34B.13C.23D.12图3 图47.在学习概率时,老师说:“掷一枚质地均匀的硬币,正面朝上的概率是12”,小明做了下列三个模拟试验来验证.①取一枚新硬币,在桌面上进行抛掷,计算正面朝上的次数与总次数的比值;②把一个质地均匀的圆形转盘平均分成偶数份,并依次标上奇数和偶数,转动转盘,计算指针落在奇数区域的次数与总次数的比值;③将一个圆形纸板放在水平的桌面上,纸板正中间放一个圆锥(如图4),从圆锥的正上方往下撒米粒,计算其中一半纸板上的米粒数与纸板上总米粒数的比值.上面的试验中,不科学的有()A.0个B.1个C.2个D.3个8.小强、小亮、小文三位同学玩投硬币游戏.三人同时各投出一枚均匀硬币,若出现三个正面向上或三个反面向上,则小强赢;若出现两个正面向上一个反面向上,则小亮赢;若出现一个正面向上两个反面向上,则小文赢.下面说法正确的是()A.小强赢的概率最小B.小文赢的概率最小C.小亮赢的概率最小D.三人赢的概率相等二、填空题(每题3分,共18分)9.〈长沙〉在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复试验后发现,摸到红球的频率稳定于0.2,那么可以推算出n大约是_______.10.一只昆虫在如图5所示的树枝上爬行,假定昆虫在每个岔路口都会随机地选择一条路径,则它停留在A 叶面的概率是_______.图5 图611.如图6,电路图上有编号为①②③④⑤⑥共6个开关和一个小灯泡,闭合开关①或同时闭合开关②③或同时闭合开关④⑤⑥都可使这个小灯泡发光,问任意闭合电路上其中的两个开关,小灯泡发光的概率为_______.12.王红和刘芳两人在玩转盘游戏,如图7,把转盘甲、乙分别分成3等份,并在每一份内标上数字,游戏规则是:转动两个转盘,停止后,指针所指的两个数字之和为7时,王红胜;数字之和为8时,刘芳胜.那么这二人中获胜可能性较大的是_______.图713.〈重庆〉在平面直角坐标系xOy中,直线y=-x+3与两坐标轴围成一个△AOB.现将背面完全相同,正面分别标有数1、2、3、12、13的5张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P的横坐标,将该数的倒数作为点P的纵坐标,则点P落在△AOB内的概率为_______.14.〈济宁〉甲、乙、丙三人站成一排合影留念,则甲、乙二人相邻的概率是_______.三、解答题(18题10分,19,20题每题12分,其余每题8分,共58分)15.已知口袋内装有黑球和白球共120 个,请你设计一个方案估计一下口袋内有多少个黑球,多少个白球?16.在一个口袋中有4个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸出一个小球然后放回,再随机地摸出一个小球,求下列事件的概率:(1)两次摸出的小球的标号相同;(2)两次摸出的小球标号的和等于4.17.〈扬州〉端午节期间,扬州某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图8).规定:同一日内,顾客在本商场每消费满100元就可以转转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.(1)该顾客最少可得_______元购物券,最多可得______元购物券;(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.图818.〈包头〉甲、乙两人在玩转盘游戏时,把两个可以自由转动的转盘A、B分成4等份、3等份的扇形区域,并在每一小区域内标上数字(如图9所示),指针的位置固定.游戏规则:同时转动两个转盘,当转盘停止后,若指针所指两个区域的数字之和为3的倍数,则甲胜;若指针所指两个区域的数字之和为4的倍数,则乙胜.如果指针落在分割线上,则需要重新转动转盘.(1)试用列表或画树状图的方法,求甲获胜的概率;图9(2)请问这个游戏规则对甲、乙双方公平吗?试说明理由.19.有三张正面分别写有数-2 ,-1,1的卡片,它们的背面完全相同,将这三张卡片背面朝上洗匀后随机抽取一张,以其正面的数作为x的值,放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数作为y的值,两次结果记为(x,y).(1)用画树状图法或列表法表示(x,y)所有可能出现的结果;(2)求使代数式2223x xy yx y x y-+--有意义的(x ,y )出现的概率;(3)化简代数式2223x xy yx y x y-+--,并求使代数式的值为整数的(x ,y )出现的概率.20.〈潍坊〉 随着我国汽车产业的发展,城市道路拥堵问题日益严峻,某部门对15个城市的交通状况进行了调查,得到的数据如下表所示.(1)根据上班花费时间,将下面的频数分布直方图(如图10)补充完整;图10(2)求15个城市的平均上班堵车时间(计算结果保留一位小数);(3)规定:城市的堵车率=-上班堵车时间上班花费时间上班堵车时间×100%,比如,北京的堵车率=145214-×100%≈36.8%;沈阳的堵车率=123412-×100%≈54.5%,某人欲从北京,沈阳,上海,温州四个城市中任意选取两个作为出发目的地,求选取的两个城市的堵车率都超过30%的概率.期末选优拔尖测试(120分,90分钟)一、选择题(每题3分,共24分)1.如图1所示的图形中,既是轴对称图形又是中心对称图形的是( )图12.下列成语所描述的事件是必然事件的是()A.水中捞月B.拔苗助长C.守株待兔D.瓮中捉鳖3.如图2,AB是⊙O的直径,∠ACD=15°,则∠BAD的度数为()A.75°B.72°D.65°图2 图34.有一块长为30 m,宽为20 m的矩形菜地,准备修筑同样宽的三条直路(如图3),把菜地分成六块作为试验田,种植不同品种的蔬菜,并且种植蔬菜面积为矩形菜地面积的34,设道路的宽度为x m,下列方程:①30x+20x×2=30×20×14;②30x+20x×2-2x2=30×20×14;③(30-2x)(20-x)=30×20×34,其中正确的是()A.①②B.①③C.②③D.①②③5.已知关于x的一元二次方程x2-2x=m有两个不相等的实数根,则m的取值范围是()A.m<1 B.m<-2C.m=0 D.m>-16.半径相等的圆内接正三角形、正方形、正六边形的边长之比为()A.1B∶1C.3∶2∶1 D.1∶2∶3图47.如图4,点A、B、C、D为圆O的四等分点,动点P从圆心O出发,沿O-C-D-O的路线作匀速运动.设运动时间为t秒,∠APB的度数为y度,则如图5所示图象中表示y与t之间函数关系最恰当的是()图5 图68.二次函数y=ax2+bx+c(a≠0)的图象如图6所示,则下列5个代数式:ab,ac,a-b+c,b2-4ac,2a+b中,值大于0的个数为()A.5 B.4 C.3 D.2二、填空题(每题3分,共21分)9.(陕西)在平面直角坐标系中,将抛物线y=x2-x-6向上(下)或向左(右)平移m个单位,使平移后的抛物线恰好经过原点,则m的最小值为_______.10.已知点P(a,-3)关于原点的对称点为P1(-2,b),则a+b的值是_______.11.已知2x2-4x+c=0的一个根,则方程的另一个根是_______.12.如图7所示,某工厂的大门是抛物线形水泥建筑物,大门的地面宽度为8 m,两侧距地面3 m高处各有一壁灯,两壁灯间的水平距离为6 m,则厂门的高度约为_______.(精确到0.1 m)图713.一圆锥的侧面展开后是扇形,该扇形的圆心角为120°,半径为6 cm,则此圆锥的表面积为_______cm2.14.已知⊙O1和⊙O2的半径分别是一元二次方程x2-5x+6=0的两根,且O1O2=1,则⊙O1和⊙O2的位置关系是_______.15.如图8,Rt△ABC的边BC位于直线l上,AC∠ACB=90°,∠A= 30°;若Rt△ABC由现在的位置向右无滑动地翻转,当点A第3次落在直线l上时,点A所经过的路线的长为_______ (结果用含π的式子表示).图8三、解答题(16~18题每题6分,19~22题每题8分,23题11分,24题14分,共75分)16.已知抛物线经过两点A(1,0),B(0,-3),且对称轴是直线x=2,求此抛物线的解析式.17.解方程x2-4x+2=0.(用配方法)18.已知:△ABC的两边AB、AC的长是关于x的一元二次方程x2-(2k+1)x+k(k+1)=0的两个实数根,第三边BC的长为5.(1)k为何值时,△ABC是以BC为斜边的直角三角形?(2)k为何值时,△ABC是等腰三角形?并求△ABC的周长.19.现有形状、大小和颜色完全一样的三张卡片,上面分别标有数字“1”“2”“3”,第一次从这三张卡片中随机抽取一张,记下数字后放回;第二次再从这三张卡片中随机抽取一张并记下数字.请用列表或画树状图的方法表示出上述试验所有可能的结果,并求第二次抽取的数字大于第一次抽取的数字的概率.20.已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.(1)如图9(1),连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;图9(2)若将正方形AEFG绕点A按顺时针方向旋转,连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图9(2)为例说明理由.21.如图10,AC是⊙O的直径,P A切⊙O于点A,点B是⊙O上的一点,且∠BAC=30°,∠APB=60°.(1)求证:PB是⊙O的切线;图10(2)若⊙O的半径为2,求弦AB及P A,PB的长.22.“五一”期间,小明和同学一起到游乐场游玩.如图11为某游乐场大型摩天轮的示意图,其半径是20m,它匀速旋转一周需要24分钟,最底部点B离地面1m.小明乘坐的车厢经过点B时开始计时.(1)计时4分钟后小明离地面的高度是多少?图11 (2)在旋转一周的过程中,小明将有多长时间连续保持在离地面31m以上的空中?23.为了实现“畅通市区”的目标,市地铁一号线准备动工,市政府现对地铁一号线第15标段工程进行招标,施工距离全长为300米.经招标协定,该工程由甲、乙两公司承建,甲、乙两公司施工方案及报价分别为:(1)甲公司施工单价y1(万元/米)与施工长度x(米)之间的函数关系为y1=27.8-0.09x,(2)乙公司施工单价y2(万元/米)与施工长度x(米)之间的函数关系为y2=15.8-0.05x.(注:工程款=施工单价×施工长度)(1)如果不考虑其他因素,单独由甲公司施工,那么完成此项工程需工程款多少万元?(2)考虑到设备和技术等因素,甲公司必须邀请乙公司联合施工,共同完成该工程.因设备共享,两公司联合施工时市政府可节省工程款140万元(从工程款中扣除).①如果设甲公司施工a米(0<a<300),那么乙公司施工______米,其施工单价y2=_______万元/米,试求市政府共支付工程款P(万元)与a(米)之间的函数关系式;②如果市政府支付的工程款为2 900万元,那么应将多长的施工距离安排给乙公司施工?24.如图12,y关于x的二次函数y=-3m (x+m)(x-3m)图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于点D.以AB为直径作圆,圆心为点C,定点E的坐标为(-3,0),连接ED.(m>0)(1)写出A、B、D三点的坐标;。
九年级物理上学期第11周校本作业(含解析)-新人教版-新人教版初中九年级全册物理试题精选全文完整版

可编辑修改精选全文完整版2014-2015学年某某省某某市武平县实验中学九年级(上)第11周物理校本作业一、选择题.1.滑动变阻器实现变阻是利用了改变接入电路中电阻线的()A.电压 B.电流 C.长度 D.材料2.如图所示,当滑动变阻器的滑片P向右移动,接入电路中的电阻值变小的是()A.B.C.D.3.图所示的电路是研究导线的电阻大小是否与导线材料有关.其中除了AB、CD导线的长度相同外,还应满足的条件是()A.横截面积不同,材料不同B.横截面积相同,材料不同C.横截面积不同,材料相同D.横截面积相同,材料相同4.为维护消费者权益,某技术质量监督部门对市场上的电线产品进行抽查,发现有一个品牌电线中的铜芯直径明显比电线规格上标定的直径要小,引起电阻偏大.从影响导体电阻大小的因素来分析,引起这种电线电阻不符合规格的主要原因是()A.电线的长度B.电线的横截面积C.电线的材料D.电线的温度5.由公式I=可以推导出R=,关于其说法下列正确的是()A.导体的电阻R与导体两端的电压U成正比B.导体的电阻R与导体中的电流I成反比C.当导体两端的电压为0时,导体的电阻也为0D.导体的电阻R是导体本身的性质,与导体两端的电压U、导体中的电流I无关6.研究电流跟电压、电阻的关系,用右图电路,实验时,分保持电阻不变和保持电压不变两步进行,在保持电阻不变这一步中实验要求()A.保持电路中的电流不变B.保持电阻R两端的电压不变C.保持滑动变阻器R′的滑片位置不变D.保持电阻R的电阻值不变,调节R′的滑片到不同的适当位置7.如图实验中,在保持电压不变这一步中,实验要求()A.调节R′的滑片到适当位置,使R两端电压保持不变B.调节R′的滑片到适当位置,使R′两端的电压不变C.换用不同电压的电源,调节R′的滑片,保持R上的电压不变D.改变电阻R电阻的大小,调节R′的滑片,保持R两端的电压不变二、填空题.8.小雨同学为了探究温度对电阻的影响,他对实验做了如图所示的改进,用酒精灯给线圈加热.(1)观察到随着线圈的温度升高,灯泡渐渐变暗电流表表的示数(2)通过实验得出结论:金属导体的电阻随温度的升升高而.9.实验证明:导体的电阻是导体本身的一种性质,它的大小决定于导体的,和.导体的电阻还跟有关.10.在材料、横截面积相同的情况下,导体的电阻跟长度有关,长度越长,电阻越;在材料、长度相同的情况下,导体的电阻跟横截面积有关,横截面积越大,电阻越.11.滑动变阻器(如图)是通过改变接入电路的来改变电路中电阻的.滑动变阻器的“铭牌”上有两个重要数据,是选用滑动变阻器的依据.如“50Ω 1.5A”,表示的物理意义是“50Ω”表示该滑动变阻器的阻值变化X围是,“1.5A”表示是1.5A.12.如图的电阻箱连入电路的电阻是Ω.三、实验题.13.如图所示,是练习使用滑动变阻器改变灯泡亮度的未完成电路,请用笔画线代替导线完成电路连接.要求:灯L1和L2并联,开关同时控制两灯,滑动变阻器只控制L1的亮度,导线不能交叉.14.某同学在做研究电流跟电压、电阻关系的实验时,得到如表两组数据.表1电阻电压电流10Ω2V4V6V表2电压电阻电流6V 5Ω10Ω15Ω(1)分析表1数据可得出结论:.(2)分析表2数据可得出结论:.(3)根据表1中的数据画出电流电压关系图象:15.某导体两端的电压为4V时,通过导体的电流为0.4A,此导体的电阻为Ω,当它两端的电压变为2V时,该导体的电阻是Ω,切断电源,当导体两端的电压为0时,此导体中的电流是A,导体的电阻为Ω.16.如图为“研究电流与电阻关系”的实验电路图.(1)为了达到研究的目的,实验过程中必须保持不变;(2)当开关S闭合后,移动滑动变阻器使电压表的读数是2.5V,此时观察到电流表的读数是0.5A,现在将阻值为5Ω的电阻R换成阻值为10Ω的电阻接入电路,闭合开关发现电压表的示数(填“变大”、“不变”、“变小”)了,则下一步应进行的操作是.17.一盏电灯正常发光时的电流是0.11A,灯丝电阻为1936Ω,该电灯两端的电压是多少?18.某电加热器在220V电压下工作,其电热丝电阻是100Ω,那么通过该电热丝的电流是多大?2014-2015学年某某省某某市武平县实验中学九年级(上)第11周物理校本作业参考答案与试题解析一、选择题.1.滑动变阻器实现变阻是利用了改变接入电路中电阻线的()A.电压 B.电流 C.长度 D.材料【考点】滑动变阻器的工作原理.【专题】应用题;电压和电阻.【分析】滑动变阻器的原理:改变连入电路中的电阻线的长度来改变电阻的大小,再根据电阻是阻碍电路中电流大小的原因进行分析.【解答】解:滑动变阻器是通过改变接入电流部分电阻丝的长度来改变电阻大小,从而逐渐改变电路中的电流强度.故选C.【点评】牢记滑动变阻器的工作原理,掌握变阻器在电路中的作用.2.如图所示,当滑动变阻器的滑片P向右移动,接入电路中的电阻值变小的是()A.B.C.D.【考点】滑动变阻器的使用.【分析】滑动变阻器有四个接线柱,选择一上一下接线柱接入电路,滑动变阻器接入电路的部分取决于接入的下面接线柱.移动滑片时,改变连入电路的电阻丝的长度,改变连入电路电阻的大小.【解答】解:A、滑动变阻器被短路,滑动变阻器没有电阻接入电路.移动滑片不能改变电路的电阻.不符合题意.B、滑动变阻器为定值电阻接入了电路,滑片移动,连入电路的电阻丝不变,电阻不变.不符合题意.C、滑动变阻器接入了左半段,滑片右移,连入电路的电阻丝变长,电阻变大.不符合题意.D、滑动变阻器接入了右半段,滑片右移,连入电路的电阻丝变短,电阻变小.符合题意.故选D.【点评】滑动变阻器连入电路的电阻取决于接入电路的下面接线柱,和上面接入电路的接线柱无关.本题明确接入电路的部分,然后判断滑片移动时,连入电路的电阻丝长度的变化,来判断电阻的变化.3.图所示的电路是研究导线的电阻大小是否与导线材料有关.其中除了AB、CD导线的长度相同外,还应满足的条件是()A.横截面积不同,材料不同B.横截面积相同,材料不同C.横截面积不同,材料相同D.横截面积相同,材料相同【考点】影响电阻大小的因素.【专题】实验题;压轴题;图析法;转换法.【分析】决定导体电阻大小的因素有三个:导体的材料、长度、横截面积,并且与长度成正比,与横截面积成反比.由于导体的电阻与三个因素有关,所以探究时要用到控制变量法.探究电阻大小与哪个因素有关时,就要控制其他的因素不变,只让这一个因素变化.可以通过比较这三根导线的异同点来确定探究的目的.【解答】解:根据控制变量法的思路,要探究导体的电阻与材料的关系,就要让其它的因素即:长度和横截面积都相同,只让两根电阻丝的材料不同.因此在控制了长度相同的前提下,还要控制横截面积相同,材料不同.综上分析故选B.【点评】当探究一个物理量与多个物理量之间的关系时,要用到控制变量法,此时的电阻与三个因素有关,所以符合控制变量法使用的条件.在此实验中,电阻丝阻值的大小是通过电流表示数的大小来体现的,这里又用到了转换法.4.为维护消费者权益,某技术质量监督部门对市场上的电线产品进行抽查,发现有一个品牌电线中的铜芯直径明显比电线规格上标定的直径要小,引起电阻偏大.从影响导体电阻大小的因素来分析,引起这种电线电阻不符合规格的主要原因是()A.电线的长度B.电线的横截面积C.电线的材料D.电线的温度【考点】影响电阻大小的因素.【专题】信息给予题;控制变量法.【分析】根据影响电阻大小的因素来判断.即影响电阻大小的因素共有:材料、长度、横截面积、温度.【解答】解:当导体的长度、材料、温度不变时,横截面积越小,电阻越大.本题中的条件即为直径小,电阻大.故选 B.【点评】本题考查影响电阻大小有关因素的掌握情况,注意探究电阻大小时,用控制变量法进行分析.5.由公式I=可以推导出R=,关于其说法下列正确的是()A.导体的电阻R与导体两端的电压U成正比B.导体的电阻R与导体中的电流I成反比C.当导体两端的电压为0时,导体的电阻也为0D.导体的电阻R是导体本身的性质,与导体两端的电压U、导体中的电流I无关【考点】欧姆定律的应用.【专题】欧姆定律.【分析】电阻是导体本身的一种性质,它与两端的电压和通过电流无关,R=这个导出公式只说明导体电阻的大小是导体两端的电压与通过导体的电流大小的比值.【解答】解:AB、电阻是导体本身的一种性质,其大小只与导体的材料、长度、横截面积和温度有关,与导体两端的电压和流过的电流大小无关,因此,不能说导体的电阻与电压成正比,也不能说与电流成反比,故AB错误;C、电阻是导体本身的一种性质,当导体两端的电压为0时,导体的电阻也不为0,故C错误;D、导体的电阻R是导体本身的性质,与导体两端的电压U、导体中的电流I无关,但在数值上可以用公式R=来进行计算.故D正确.故选D.【点评】本题考查我们对欧姆定律导出公式R=的理解,要注意公式R=只是表示出了三者之间的数值关系,而并非是它们间的正、反比关系.6.研究电流跟电压、电阻的关系,用右图电路,实验时,分保持电阻不变和保持电压不变两步进行,在保持电阻不变这一步中实验要求()A.保持电路中的电流不变B.保持电阻R两端的电压不变C.保持滑动变阻器R′的滑片位置不变D.保持电阻R的电阻值不变,调节R′的滑片到不同的适当位置【考点】探究电流与电压、电阻的关系实验.【专题】探究型实验综合题.【分析】电流跟电压、电阻有关,用控制变量法研究电流跟电压和电阻的关系.(1)研究电流跟电压的关系时,保持电阻不变,改变定值电阻两端的电压,讨论电流跟电压的关系.(2)研究电流跟电阻的关系时,保持电阻两端的电压不变,改变电阻大小,讨论电流跟电阻的关系.【解答】解:研究电流跟电压的关系时,保持电阻不变,通过移动滑动变阻器的滑片,改变定值电阻的电压和电流,讨论电流跟电压的关系.所以ABC错误,D正确.故选D.【点评】(1)正确掌握欧姆定律的电流跟电压、电阻的关系.(2)导体两端的电压一定时,导体中的电流跟导体的电阻成反比,在电阻一定时,导体中的电流跟导体的电压成正比.7.如图实验中,在保持电压不变这一步中,实验要求()A.调节R′的滑片到适当位置,使R两端电压保持不变B.调节R′的滑片到适当位置,使R′两端的电压不变C.换用不同电压的电源,调节R′的滑片,保持R上的电压不变D.改变电阻R电阻的大小,调节R′的滑片,保持R两端的电压不变【考点】探究电流与电压、电阻的关系实验.【专题】欧姆定律.【分析】电流与电压和电阻有关,要探究电流与电阻的关系,需保持电阻两端的电压不变.【解答】解:导体中的电流与电压和电阻两个因素有关,由题意知,实验中保持电压不变,可知在探究电流与电阻的关系;要探究电流与电阻的关系,应改变电阻的大小,同时调节滑动变阻器保持电阻两端的电压不变.所以ABC错误,D正确.故选D.【点评】此题是探究电流与电阻关系的实验,考查了控制变量法的应用,是考试中经常出现的问题,须掌握.二、填空题.8.小雨同学为了探究温度对电阻的影响,他对实验做了如图所示的改进,用酒精灯给线圈加热.(1)观察到随着线圈的温度升高,灯泡渐渐变暗电流表表的示数变小(2)通过实验得出结论:金属导体的电阻随温度的升升高而增大.【考点】影响电阻大小的因素.【专题】电压和电阻.【分析】电阻大小与导体的长度、材料、横截面积和温度有关,在电压相同的情况下,电路中的电阻越大,其电流越小,则灯泡越暗.【解答】解:(1)用酒精灯给铁丝加热,在铁丝温度升高并发热的过程中,观察到电流表的示数变小了,灯泡变暗了;(2)通过实验得出结论:金属导体的电阻随温度的升升高而增大.故答案为:(1)变小;(2)增大.【点评】本题通过实验探究得出电阻的大小与温度有关,同时会灵活应用欧姆定律分析电学中三个基本物理量的关系.9.实验证明:导体的电阻是导体本身的一种性质,它的大小决定于导体的材料,长度和横截面积.导体的电阻还跟温度有关.【考点】影响电阻大小的因素.【分析】解答本题应掌握:导体的电阻由导体的材料、长度、横截面积及温度决定.【解答】解:导体的电阻为导体本身的一种性质,它的大小取决于导体的材料、长度及横截面积;并且电阻大小还与温度有关;故答案为:材料,长度,横截面积;温度.【点评】本题考查影响电阻大小的因素,为基础题目,要求能熟记相关内容.10.在材料、横截面积相同的情况下,导体的电阻跟长度有关,长度越长,电阻越大;在材料、长度相同的情况下,导体的电阻跟横截面积有关,横截面积越大,电阻越小.【考点】影响电阻大小的因素.【专题】电压和电阻.【分析】导体的电阻是导体本身的一种性质,电阻大小取决于内因是:导体的材料、长度、横截面积;外因是:温度.【解答】解:导体的电阻跟它的长度、材料、横截面积、温度有关系,在材料、横截面积相同的情况下,导体的电阻跟长度有关,长度越长,电阻越大;在材料、长度相同的情况下,导体的电阻跟横截面积有关,横截面积越大,电阻越小.故答案为:大;小.【点评】电阻是导体本身的属性,导体的电阻大小与导体的长度、横截面积和材料等有关,与电流以及电压的大小无关.11.滑动变阻器(如图)是通过改变接入电路的电阻丝的长度来改变电路中电阻的.滑动变阻器的“铭牌”上有两个重要数据,是选用滑动变阻器的依据.如“50Ω 1.5A”,表示的物理意义是“50Ω”表示该滑动变阻器的阻值变化X围是0~50Ω,“1.5A”表示允许通过的最大电流是1.5A.【考点】滑动变阻器的工作原理;变阻器.【专题】应用题;电压和电阻.【分析】(1)滑动变阻器在电路中的作用是通过改变电路中电阻线的长度来改变电阻的大小,从而改变电路中的电流;其在电路中的正确连接方式是连接一“上”一“下”两个接线柱;(2)滑动变阻器标有“50Ω、2A”,标明最大电阻值和允许通过的最大电流.【解答】解:(1)影响电阻大小的因素:长度、横截面积、材料.在材料和横截面积一定时,滑动变阻器依靠改变电阻线的长度来改变电阻大小,总电压不变,从而改变了电路中的电流;(2)滑动变阻器标有“50Ω、1.5A”,意思指滑动变阻器的最大电阻值是50Ω;允许通过的最大电流值是1.5A.故答案为:电阻丝的长度;0~50Ω;允许通过的最大电流.【点评】(1)掌握电阻大小的影响因素,根据影响因素能判断电阻大小变化.(2)掌握滑动变阻器的结构、接线柱的接法、连入电路的方法、原理、作用、铭牌参数的含义等等.12.如图的电阻箱连入电路的电阻是5058 Ω.【考点】变阻器.【专题】电压和电阻.【分析】解答本题应掌握电阻箱的读数方法:分别读出旋钮对应的读数,用数字乘以底下的倍数,最后将四个数据相加.【解答】解:由图可知,总电阻R=5×1000Ω+0×100Ω+5×10Ω+8×1Ω=5058Ω;故答案为:5058.【点评】本题考查了电阻箱的读数方法:把对应的数字乘以倍数,然后相加即可.三、实验题.13.如图所示,是练习使用滑动变阻器改变灯泡亮度的未完成电路,请用笔画线代替导线完成电路连接.要求:灯L1和L2并联,开关同时控制两灯,滑动变阻器只控制L1的亮度,导线不能交叉.【考点】实物的电路连接.【专题】作图题.【分析】两灯并联,要求电流有两条路径;开关同时控制两盏电灯,开关必须接在干路上;滑动变阻器只控制L1的亮度,因此滑动变阻器与灯L1串联.【解答】解:经过分析,电流路径有两条:从电源正极出发,依次连接开关、L1、滑动变阻器直到电源负极:从正极出发,依次连接开关、L2、电源负极;找出电路的分支点和汇合点,整理如下图:【点评】连接电路时,首先要通过题目中的已知条件,明确用电器是串联还是并联的,开关在支路还是干路上,电表测量谁的电压和电流,滑动变阻器控制哪个用电器.14.某同学在做研究电流跟电压、电阻关系的实验时,得到如表两组数据.表1电阻电压电流10Ω2V4V6V表2电压电阻电流6V 5Ω10Ω15Ω(1)分析表1数据可得出结论:电阻一定时,电流与导体两端电压成正比.(2)分析表2数据可得出结论:在电压一定时,电流与电阻成反比.(3)根据表1中的数据画出电流电压关系图象:【考点】探究电流与电压、电阻的关系实验.【专题】探究型实验综合题.【分析】(1)分析表1实验数据,看在电阻一定时,电流与电压的关系,然后得出结论;(2)分析表2实验数据,看在电压一定时,电流与电阻的关系,然后得出结论;(3)根据表1中数据,描点连线画出图象即可.【解答】解:(1)由表1实验数据可知,在电阻R一定时,电压与电流的比值是定值,即可出结论:电阻一定时,电流与导体两端电压成正比;(2)由表2实验数据可知,在电压一定时,电流与电阻的乘积是定值,即可出结论:在电压一定时,电流与电阻成反比;(3)根据表1中数据,描点连线画出图象,如图所示:故答案为:(1)电阻一定时,电流与导体两端电压成正比;(2)在电压一定时,电流与电阻成反比;(3)见上图.【点评】应用控制变量法,认真分析实验数据,即可得出正确结论.本题还考查了图象的绘制能力.15.某导体两端的电压为4V时,通过导体的电流为0.4A,此导体的电阻为10 Ω,当它两端的电压变为2V时,该导体的电阻是10 Ω,切断电源,当导体两端的电压为0时,此导体中的电流是0 A,导体的电阻为10 Ω.【考点】欧姆定律的应用.【专题】欧姆定律.【分析】(1)已知导体两端的电压和通过的电流,根据欧姆定律求出导体的电阻;(2)电阻是导体本身的一种性质,与两端的电压和通过的电流无关,所以当加在导体两端的电压变为2V或为0时,电阻仍不变.【解答】解:(1)根据欧姆定律I=可得,导体的电阻:R===10Ω;(2)因为电阻是导体本身的一种性质,与两端的电压和通过的电流无关,所以导体两端的电压变为2V时或切断电源时,电阻的阻值不变,仍为10Ω,但当切断电源,导体两端的电压为0时,此导体中的电流也为0.故答案为:10;10;0;10.【点评】本题考查电阻、电流的计算,关键是欧姆定律及其变形的灵活运用,要知道影响电阻大小的因素是导体的材料、长度、横截面积和温度.16.如图为“研究电流与电阻关系”的实验电路图.(1)为了达到研究的目的,实验过程中必须保持电压不变;(2)当开关S闭合后,移动滑动变阻器使电压表的读数是2.5V,此时观察到电流表的读数是0.5A,现在将阻值为5Ω的电阻R换成阻值为10Ω的电阻接入电路,闭合开关发现电压表的示数变大(填“变大”、“不变”、“变小”)了,则下一步应进行的操作是闭合开关,移动滑片P使电压表示数为2.5V .【考点】探究电流与电压、电阻的关系实验.【专题】探究型实验综合题.【分析】(1)根据控制变量法可知研究电流与电阻关系应控制什么;(2)当电阻增大时,根据串分压的知识可知其分得电压的变化情况,从而确定下一步的操作.【解答】解:(1)电流与电压和电阻有关,根据控制变量法,在研究电流与电阻关系进,应控制电压不变,改变电阻;(2)将阻值为5Ω的电阻R换成阻值为10Ω的电阻接入电路,根据分压原理可知,电压表的示数将变大,此时应该移动滑动变阻器的滑片,增大变阻器连入阻值,使电压表的示数为2.5V不变.故答案为:(1)电压;(2)变大;闭合开关,移动滑片P使电压表示数为2.5V.【点评】此题是探究电流与电阻关系的实验,考查了控制变量法的应用,同时考查了串分压的知识,特别是(2)问,在判断时,首先分析出电压表的示数变化情况,然后再判断滑动变阻器的阻值变化.17.一盏电灯正常发光时的电流是0.11A,灯丝电阻为1936Ω,该电灯两端的电压是多少?【考点】欧姆定律的应用.【专题】欧姆定律.【分析】知道电流与电阻,根据欧姆定律的变形公式U=IR可计算电压的大小.【解答】解:由欧姆定律I=得电灯两端的电压:U=IR=0.11A×1936Ω≈220V.答:该电灯两端的电压是220V.【点评】本题考查欧姆定律及其变形公式的应用,是基础知识的考查.18.某电加热器在220V电压下工作,其电热丝电阻是100Ω,那么通过该电热丝的电流是多大?【考点】欧姆定律的应用.【专题】欧姆定律.【分析】知道电热器两端的电压和电热丝电阻,根据欧姆定律求出该用电器的电流.【解答】解:根据欧姆定律可得,通过该电热丝的电流:I===2.2A.答:通过该电热丝的电流是2.2A.【点评】本题考查了欧姆定律的直接应用,是一道基础题目,熟练掌握公式,正确进行计算即可.。
人教版(2024新版)2024--2025学年度第一学期九年级化学上册期中测试卷及答案
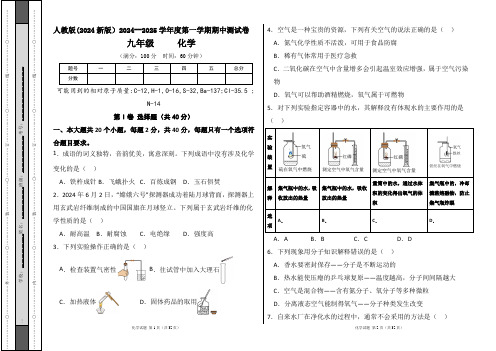
…○………………内………………○………………装………………○………………订………………○………………线………………○…………………○………………外………………○………………装………………○………………订………………○………………线………………○………………… 学校:______________姓名:_____________班级:_______________考号:______________________人教版(2024新版)2024--2025学年度第一学期期中测试卷 九年级 化学(满分:100分 时间:60分钟)题号 一 二 三 四 五 总分 分数可能用到的相对原子质量:C-12,H-1,O-16,S-32,Ba-137;Cl-35.5 ;N-14第I 卷 选择题(共40分)一、本大题共20个小题,每题2分,共40分,每题只有一个选项符合题目要求。
1.成语的词义独特,音韵优美,寓意深刻。
下列成语中没有..涉及化学变化的是( )A .铁杵成针B .飞蛾扑火C .百炼成钢D .玉石俱焚2.2024年6月2日,“嫦娥六号”探测器成功着陆月球背面,探测器上用玄武岩纤维制成的中国国旗在月球竖立。
下列属于玄武岩纤维的化学性质的是( ) A .耐高温 B .耐腐蚀C .电绝缘D .强度高3.下列实验操作正确的是( ) A .检查装置气密性B .往试管中加入大理石C .加热液体D .固体药品的取用4.空气是一种宝贵的资源,下列有关空气的说法正确的是( ) A .氮气化学性质不活泼,可用于食品防腐 B .稀有气体常用于医疗急救C .二氧化碳在空气中含量增多会引起温室效应增强,属于空气污染物D .氧气可以帮助酒精燃烧,氧气属于可燃物5.对下列实验指定容器中的水,其解释没有体现水的主要作用的是( )实验 装置解释 集气瓶中的水,吸收放出的热量集气瓶中的水,吸收放出的热量量筒中的水,通过水体积的变化得出氧气的体积集气瓶中的,冷却溅落熔融物,防止集气瓶炸裂选项A .B .C .D .A .AB .BC .CD .D6.下列现象用分子知识解释错误的是( ) A .香水要密封保存——分子是不断运动的B .热水能使压瘪的乒乓球复原——温度越高,分子间间隔越大C .空气是混合物——含有氮分子、氧分子等多种微粒D .分离液态空气能制得氧气——分子种类发生改变7.自来水厂在净化水的过程中,通常不会采用的方法是( )……○………………内………………○………………装………………○………………订………………○………………线………………○…此卷只装订不密封……○………………外………………○………………装………………○………………订………………○………………线………………○…A.吸附B.蒸馏C.消毒D.沉淀8.银针曾是中医针灸的常用器械。
九年级数学期中模拟卷02(全解全析)【测试范围:九年级上册第二十一章~第二十四章】(人教版)

2024-2025学年九年级数学上学期期中模拟卷02(人教版)(考试时间:120分钟 试卷满分:120分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:人教版九年级上册第二十一章~第二十四章。
5.难度系数:0.75。
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.下列图形中,既是轴对称又是中心对称图形的是( )A .B .C .D .【答案】B 【详解】解:A .不是中心对称图形,是轴对称图形,故此选项不合题意;B .既是中心对称图形,也是轴对称图形,故此选项符合题意;C .是中心对称图形,但不是轴对称图形,故此选项不合题意;D .不是中心对称图形,是轴对称图形,故此选项不合题意;故选:B .2.方程2430x x ++=的两个根为( )A .121,3x x ==B .121,3x x =-=C .121,3x x ==-D .121,3x x =-=-【答案】D【详解】∵243=(1)(3)x x x x ++++∴(1)(3)=0x x ++∴12=1=3x x --,故选:D .3.抛物线y=(x+2)2﹣3可以由抛物线y=x2平移得到,则下列平移过程正确的是( )A .先向左平移2个单位,再向上平移3个单位B .先向左平移2个单位,再向下平移3个单位C .先向右平移2个单位,再向下平移3个单位D .先向右平移2个单位,再向上平移3个单位【答案】B【详解】解:将2y x =的图象向左平移2个单位后得函数()22y x =+的函数图象,将()22y x =+的图象向下平移3个单位得到()223y x =+-的函数图象,∴平移过程为:先向左平移2个单位,再向下平移3个单位.故选:B .4.如图,△AOB 中,25B Ð=°,将AOB V 绕点O 顺时针旋转60°,得到A OB ¢¢△,边A B ¢¢与边OB 交于点C (A ¢不在OB 上),则A CO ¢∠的度数为( )A .105°B .95°C .85°D .75°【答案】C【详解】解:∵将AOB V 绕点O 顺时针旋转60°,得到A OB ¢¢△,∴2560B B BOB ¢¢Ð=Ð=°Ð=°,,∴85A CO B BOB ¢¢¢Ð=Ð+Ð=°,故选:C .5.若关于x 的一元二次方程2210kx x --=有两个不相等的实数根,则k 的取值范围是( )A .1k >-B .1k <C .1k >-且0k ¹D .1k <且0k ¹【答案】C 【详解】解:∵关于x 的一元二次方程 2210kx x --= 有两个不相等的实数根,2∴ 1k >- 且 0k ¹ .故答案为:C .6.如图,点A 、B 、C 、D 在⊙O 上,120AOC Ð=°,点B 是 AC 的中点,则D Ð的度数是( )A .30°B .40°C .50°D .60°【答案】A【详解】连接OB ,∵点B 是 AC 的中点,∴∠AOB =12∠AOC =60°,由圆周角定理得,∠D =12∠AOB =30°,故选:A .7.抛物线()=-+2y 2x 31过()14,y ,()23,y ,()31,y -三点,则123,,y y y 大小关系是( )A .231y y y >>B .132y y y >>C .213y y y >>D .312y y y >>【答案】D【详解】在二次函数()2231y x =-+,对称轴3x =,20a =>,开口向上,在图象上的三点()14,y ,()23,y ,()31,y -,点()31,y -离对称轴的距离最远,点()23,y 离对称轴的距离最近,312,y y y \>>故选:D .8.如图,90,25AOB B Ð=°Ð=°,A OB ¢¢△可以看做是由AOB V 绕点O 顺时针旋转α角度得到的,若点A ¢在AB 上,则旋转角α的大小是( )A .50°B .65°C .30°D .40°【答案】A【详解】解:Q A OB ¢¢△是由AOB V 绕点O 顺时针旋转α角度得到,\AO A O ¢=,A OA a =Т,Q 点A ¢在AB 上,\AOA ¢△是等腰三角形,A OA A ¢\Ð=Ð,Q 90,25AOB B Ð=°Ð=°,18065A AOB B \Ð=°-Ð-Ð=°,65A OA A ¢\Ð=Ð=°,\18050AOA A OAA ¢¢Ð=°-Ð-Ð=°,50a \=°,故选:A .9.如图,边长为1的正六边形ABCDEF 放置于平面直角坐标系中,边AB 在x 轴正半轴上,顶点F 在y 轴正半轴上,将正六边形ABCDEF 绕坐标原点O 顺时针旋转,每次旋转45°,那么经过第2026次旋转后,顶点D 的坐标为( )A .3,2æ-çèB .3,2æ-ççèC .32æöç÷èøD .32ö-÷ø【答案】D 【详解】解:连接BD ,OD ,把OD 绕点O 顺时针旋转90°至OD ¢,过点D 作DG y ^轴于点G ,过点D ¢作DH y ^轴于点H ,在正六边形ABCDEF 中,1AF AB BC CD ====,120FAB BCD Ð=Ð=°,60,30,FAO AFO \Ð=°Ð=°11,22OA AF BD BD OB \===^,33,(22OB OA AB D =+=,3,2DG OG ==将正六边形ABCDEF 绕坐标原点O 顺时针旋转,每次旋转45°,360458¸=Q ,即8次旋转一周,20268253¸=余2,45290°´=°,故经过第2026次旋转后,顶点D 在D ¢的位置,90,90,GDO DOG D OH DOG ¢Ð+Ð=°Ð+Ð=°Q ,90,,GDO D OH DGO OHD OD OD ¢¢¢Ð=ÐÐ=Ð=°=()≌A A S DGO OHD ¢V V ,3,2OH DG OG HD ¢====即3)2D ¢-,故选:D .10.如图为二次函数2y ax bx c =++的图象,在下列说法中:①0ac <;②方程20ax bx c ++=的根是11x =-,23x =;③0a b c ++<;④当1x >时,y 随x 的增大而减小;⑤20a b -=;⑥240b ac ->.下列结论一定成立的是( )A .①②④⑥B .①②③⑥C .②③④⑤⑥D .①②③④【答案】B【详解】解:①由图象可得,00a c ><,,0ac \<,故①正确,②2y ax bx c =++与x 轴的交点是()()1,03,0-,,∴方程20ax bx c ++=的根是1213x x =-=,,故②正确,③当1x =时,0y a b c =++<,故③正确,④∵该抛物线的对称轴是直线1312x -+==∴当x >1时,y 随x 的增大而增大,故④错误,⑤12b a -=则2a b =-,那么20a b +=,故⑤错误,⑥∵抛物线与x 轴两个交点,∴240b ac ->,故⑥正确,正确的为. ①②③⑥故选:B .二、填空题(本大题共5小题,每小题3分,共15分)11.若点3P m (,)与点32Q n -(,)关于原点成中心对称,则m n +的值是__________.【答案】2【详解】解:∵点3P m (,)与点32Q n -(,)关于原点成中心对称,∴323m n =--=-,,∴5n =,则352m n +=-+=.故答案为:2.12.已知m 为一元二次方程2310x x --=的一个根,则代数式2262023m m -+的值为__________.【答案】2025【详解】解:∵m 是一元二次方程2310x x --=的一个根,2310m m \--=,∴231m m -=,∴()222620232320232120232025m m m m -+=-+=´+=.故答案为:2025.13.二次函数y=ax2+bx+c 和一次函数y=mx+n 的图像如图所示,则ax2+bx+c≤mx+n 时,x 的取值范围是__________.【答案】21x ££﹣【详解】解:依题意得求关于x 的不等式2ax bx c mx n ++£+的解集,实质上就是根据图像找出函数2y ax bx c =++的值小于或等于y mx n =+的值时x 的取值范围,由两个函数图像的交点及图像的位置可以得到此时x 的取值范围是21x ££﹣.故答案为:21x ££﹣.14.如图,在菱形OABC 中,OB 是对角线,2OA OB ==,⊙O 与边AB 相切于点D ,则图中阴影部分的面积为【答案】p【详解】解:如图,连接OD ,∵AB 是切线,则OD ⊥AB ,在菱形OABC 中,∴2AB OA OB ===,∴△AOB 是等边三角形,∴∠AOB=∠A=60°,∴1AD =,OD ==,∴122AOB S D =´=,2p =,∴阴影部分的面积为:22pp ´=-;故答案为:p .15.如图,已知正方形ABCD 中,两动点M 和N 分别从顶点B 、C 同时出发,以相同的速度沿BC 、CD 向终点C 、D 运动,连接AM 、BN ,交于点P ,再连接PC ,若4AB =,则PC 长的最小值为__________.【答案】2-【详解】解:由题意得:BM CN =,∵四边形ABCD 是正方形,90,4ABM BCN AB BC \Ð=Ð=°==,在ABM V 和BCN △中,AB BC ABM BCN BH CN =ìïÐ=Ðíï=î,∴△ABM≅△BCN(SAS),BAM CBN \Ð=Ð,90ABP CBN Ð+Ð=°Q ,90ABP BAM \Ð+Ð=°,90ABP \Ð=°,∴点P 在以AB 为直径的圆上运动,设圆心为O ,运动路径一条弧 BG ,是这个圆的14,如图所示:连接OC 交圆O 于P ,此时PC 最小,4AB =Q ,2OP OB \==,由勾股定理得:OC ==2PC OC OP \=-=-;故答案为:2.三、解答题(本大题共8小题,共75分)16.(7分)解下列方程:(1)()()121x x x +-=+;2【详解】解:(1)原方程可化为:()()130x x +-=,∴x+1=0或x ﹣3=0,解得:x1=﹣1,x2=3;(3分)(2)原方程可化为:22530x x +-=,∴(x+3)(2x ﹣1)=0,∴x+3=0,2x ﹣1=0,解得:x1=﹣3,x2=12.(7分)17.(7分)如图,将ABC V 绕点A 逆时针旋转一个角度a ,得到△ADE ,点B 的对应点D 恰好落在BC 边上.且点A 、B 、E 在同一条直线上.(1)求证:AD 平分BDE Ð;(2)若AC DE ^,求旋转角a 的度数.【详解】(1)证明:∵△ADE 是由△ABC 旋转得到,1B Ð=Ð∴,AD AB =,2B \Ð=Ð,12\Ð=Ð,AD \平分BDE Ð.(3分)(2)解:如图,由旋转可知:34a Ð=Ð=,C E Ð=Ð,∵AC ⊥DE ,90C E a \Ð=Ð=-°,(4分)∵在ABD △中,AB AD =,()111809022B a a \Ð=°-=°-,(5分)Q 点,,A B E 在同一条直线上,∴4B C Ð=Ð+Ð,即190902a a a °-=°-+,(7分)解得72a =°.(8分)18.(8分)已知关于x 的一元二次方程210x ax a -+-=.(1)求证:方程总有两个实数根;(2)若该方程有一实数根大于2,求a 的取值范围.【详解】(1)解:210x ax a -+-=,根据题意得:()()()222414420a a a a a D =---=-+=-³,∴方程总有两个实数根;(4分)(2)解:210x ax a -+-=,∴()()110x x a --+=,解得:121,1x x a ==-,∵该方程有一实数根大于2,∴12a ->,3a >19.(9分)某商场销售一种商品,进价为每个20元,规定每个商品售价不低于进价,且不高于60元.经调查发 现,每天的销售量y(个)与每个商品的售价x(元)满足一次函数关系,其部分数据如下表所示:(1)求y 与x 之间的函数关系式;(2)设商场每天获得的总利润为w (元),求w 与x 之间的函数关系式;(3)不考虑其他因素,当商品的售价为多少元时,商场每天获得的总利润最大,最大利润是多少?【详解】(1)∵y 与x 满足一次函数关系.∴设y 与x 的函数表达式为y kx b =+()0k ¹.将()30,100,()40,80代入y kx b =+中,得10030.8040.k b k b =+ìí=+î 解得 2.160.k b =-ìí=î(2分)∴y 与x 之间的函数表达式为2160y x =-+.(3分)(2)由题意,得()()()22021602022003200w y x x x x x =-=-+-=-+-.∴w 与x 之间的函数表达式为222003200w x x =-+-.(5分)(3)()22220032002501800w x x x =-+-=--+.(7分)∵20-<,∴抛物线开口向下.由题可知:2060x ££,∴当x =50时,w 有最大值,=1800w 最大元. (8分)答:当售价定为50元时,商场每天获得总利润最大,最大利润是1800元. (9分)20.(10分)如图,已知△ABC 中,90BAC AB AC D E Ð=°=,,、是BC 边上的点,将ABD △绕点A 旋转,得到ACD ¢△.(1)当45DAE =°∠时,求证:DE D E ¢=;(2)在(1)的条件下,猜想:BD DE CE 、、有怎样的数量关系?请写出,并说明理由.【详解】(1)证明:由旋转性质得,△ABD≌△ACD ′,,AD AD BAD CAD ¢¢\=Ð=Ð,(2分)90,45BAC DAE Ð=°Ð=°Q ,904545BAD EAC \Ð+Ð=°-°=°,45CAD EAC DAE \Ð+Ð=°=Т,D AE DAE ¢\Ð=Ð,在EAD ¢△和EAD V 中AD =AD ′∠D ′AE =∠DAE AE =AE,()SAS EAD EAD ¢\△≌△,(3分)DE ED \=¢;(4分)(2)222DE BD CE =+,理由如下:(5分)AB AC =Q ,且90BAC Ð=°,45B ACB \Ð=Ð=°,(6分)由(1)得,45ACD B Ð=Ð=¢°,90ECD ACB ACD ¢\+ТÐ=Ð=°,ECD \¢△是直角三角形,(7分)222D E CE D C \=+¢¢,(8分)22221.(10分)如图,AC 是四边形ABCD 外接圆O 的直径,,30AB BC DAC =Ð=°,延长AC 到E 使得CE CD =,作射线ED 交BO 的延长线与,F BF 交AD 与G .(1)求证:△ADE 是等腰三角形;(2)求证:EF 与O e 相切;(3)若3AO =,求FGD V 的周长.【详解】(1)证明:∵AC 是四边形ABCD 外接圆O 的直径,30DAC Ð=°,∴90ADC Ð=°,60ACD Ð=°,(2分)∵CE CD =,∴E CDE Ð=Ð,∵E CDE ACD Ð+Ð=Ð,∴30E CDE DAC Ð=Ð=°=Ð,∴AD DE =,∴△ADE 是等腰三角形;(3分)(2)证明:如图,连接OD ,(4分)∵60OC OD OCD =Ð=°,,∴△OCD 是等边三角形,∴60DOC Ð=°,∴18090EDO E DOC Ð=°-Ð-Ð=°,(4分)又∵OD 是半径,∴EF 与⊙O 相切;(5分)(3)解:∵AC 为直径,AB BC =,∴BF AC ^,∴18060AGO DAC AOG Ð=°-Ð-Ð=°,(6分)∵3OD AO ==,∴30ODA DAC Ð=Ð=°,∴30GOD AGO ADO ADO Ð=Ð-Ð=°=Ð,∴GD OG =,(7分)∵30DOF Ð=°,90ODF Ð=°,∴12DF OF =,由勾股定理得,OD =3=,解得DF =∴OF =(8分)∴△FGD的周长为FD FG GD FD FG OG FD OF ++=++=+=∴△FGD的周长为(10分)22.(12分)已知AOB V 和MON △都是等腰直角三角形,90OM ON AOB MON ö<=Ð=Ð=÷ø°.(1)如图1:连,AM BN ,求证:AM BN =;(2)若将MON △绕点O 顺时针旋转,①如图2,当点N 恰好在AB 边上时,若1,2AN ON ==,请求出线段BN 的长;②当点,,A M N在同一条直线上时,若AB ON ==BN的长.【详解】(1)证明:Q △AOB 和MON △都是等腰直角三角形,\OA OB =,OM ON =,Q 90AOB MON Ð=Ð=°,\MON AON AOB AON Ð+Ð=Ð+Ð,\AOM BON Ð=Ð,(2分)在AMO V 和△BNO 中,OM ON AOM BONOA OB =ìïÐ=Ðíï=î,\AMO BNO ≌△△()SAS ,\AM BN =;(4分)(2)解:①如图,连接AM ,Q △AOB 和MON △都是等腰直角三角形,\OA OB =,OM ON =, 45OAB OBA Ð=Ð=°,\MN ==.(5分)Q 90AOB MON Ð=Ð=°,\MON AON AOB AON Ð-Ð=Ð-Ð,\AOM BON Ð=Ð,在AMO V 和△BNO 中,OM ON AOM BONOA OB =ìïÐ=Ðíï=î,\AMO BNO ≌△△()SAS ,(6分)\AM BN =,45OAM OBN °Ð=Ð=,\454590MAN OAM OAN °+°=°Ð=Ð+Ð=,在Rt △AMN 中,222A M A N MN +=,\AM ===,\BN AM ==(8分)②分两种情况,当点N 在线段AM 上时,连接BN ,过点O 作OH M N ^于点H ,同(1)可得AM BN =,Q △AOB 和MON △都是等腰直角三角形,AB =ON =,\4MN ==,OA =OB ==5,Q O H M N ^,\MH =NH =OH =12MN =2,\AH ===\BN =AM =AH +MH =+2;(10分)当点M 在线段AN 上时,连接BN ,过点O 作O H M N ^于点H ,同①可证AMO BNO ≌△△()SAS ,\AM BN =,Q △AOB 和MON △都是等腰直角三角形,AB =ON =,\4MN ==,5OA OB AB ===,Q O H M N ^,\122MH NH OH MN ====,\AH ==\2BN AM AH MH ==-=.(11分)综上可知,BN22.(12分)23.(12分)如图所示,抛物线2y ax bx c =++与x 轴相交于()()1,03,0A B -与y 轴相交于点C (0,―3),点M 为抛物线的顶点.(1)求抛物线的解析式及顶点M 的坐标;(2)如图2,若点N 是第四象限内抛物线上的一个动点,过点N 作x 轴的垂线,垂足为D ,并与直线BC 交于点Q ,连接BN CN 、.求BCN △面积的最大值及此时点N 的坐标;(3)若点P 在y 轴上,PBC △为等腰三角形,请直接写出P 点的坐标.【详解】(1)解:把点(1,0)A -和点(0,3)C -,点(3,0)B 代入抛物线2(0)y ax bx c a =++¹,则09303a b c a b c c -+=ìï++=íï=-î,解得123a b c =ìï=-íï=-î,∴抛物线的解析式为:2=23y x x --,故()1,4M -;(3分)(2)由(1)知抛物线的顶点为()1,4M -,设直线BC 的解析式为令y kx b ¢=+,将()(3,0),0,3B C -代入,得303k b b ¢¢+=ìí=-î,解得13k b =ìí=-¢î,设点2(,23),N m m m --,则(,3),Q m m -∴223233,NQ m m m m m =--++=-+∴CBN △面积22211393327(3)32222228QN OB m m m m m æö=××=-+×=-+=--+ç÷èø,∵302-<,∴当32m =时,CBN △面积的最大值为278.此时315,24N æöç÷èø;(6分)(3)设点P 坐标为()0,t ,∵(3,0),(0,3)B C -,∴222223318,9BC BP t =+==+,22(3)CP t =+,(7分)①当BC BP =时,即22BC BP =,∴2189t =+,解得123,3t t ==-(不合题意,舍去),∴点P 的坐标为(0,3);(8分)②当BC CP =时,即22BC CP =,∴()2183t =+,(9分)解得123,3t t ==(),∴点P的坐标为3)或3);(10分)③当CP BP =时,即22CP BP =,∴()2293t t +=+,解得0t =,∴点P 的坐标为()0,0.(11分)综上,存在,点P 的坐标为(0,3)或3)或3)+或()0,0.(12分)。
人教版九年级上册数学《圆》单元测试卷(含答案)
人教版九年级上册数学《圆》单元测试卷姓名:__________班级:__________考号:__________一 、选择题(本大题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.如图,边长为1的菱形ABCD 绕点A 旋转,当B C ,两点恰好落在扇形AEF 的弧EF 上时,弧BC 的长度等于( )A .6π B .4π C .3π D .2π2.已知和的半径分别为1和,如果两圆的位置关系为相交,那么圆心距的取值范围在数轴上表示正确的是( ) A . B . C .D .3.如图,35BAC ∠=︒,40CED ∠=︒,则BOD ∠的度数是( )A .75︒B .80︒C .150︒D .135︒4.如图,O 中,弦AB CD 、相交于点P 若3070A APD ∠=︒∠=︒,,则B ∠等于( )A.30︒B.35︒C.40︒D.50︒FDCBEA1O 2O 412O OC5.已知在直角坐标系中,以点为圆心,以为半径作,则直线()与的位置关系是( ) A .相切 B .相交 C .相离 D .与值有关6.如图,一量角器放置在AOB ∠上,角的一边OA 与量角器交于点C 、D ,且点C处的度数是20︒,点D 处的度数为110°,则AOB ∠的度数是( ) A 、20° B 、25° C 、45° D 、55°7.在数轴上,点A 所表示的实数为3,点B 所表示的实数为a ,A 的半径为2.下列说法中不正确的是( ) A .当5a <时,点B 在A 内 B .当5a 1<<点B 在A 内 C .当a <1时,点B 在A 外 D .当5a >时,点B 在A 外8.如图已知扇形的半径为6cm ,圆心角的度数为,若将此扇形围成一个圆锥,则围成的圆锥的侧面积为( )A .B .C .D .9.如图,⊙O 是△ABC 的外接圆,已知∠B=60°,则∠CAO 的度数是( )B()03A ,3A 2y kx =+0k ≠Ak D AOB 12024πcm 26πcm 29πcm 212πcm OBA6cm120°A .15︒B .30︒ C.40︒ D .60︒10.如图所示,点A 、B 、P 在O 上,且50APB ∠=︒.若点M 是O 上的动点,要使ABM ∆为等腰三角形,则所有符合条件的点M 有( ) A .1 个 B .2 个 C .2 个 D .4个二 、填空题(本大题共5小题,每小题3分,共15分)11.如图,CD 是O 的直径,弦AB CD ⊥于点H ,若30D ∠=︒,1CH cm =,则AB =12.一个已知点到圆周上的点的最大距离为5cm ,最小距离为1cm ,则此圆的半径为______.13.将ABC △绕点B 逆时针旋转到A BC ''△使A B C '、、在同一直线上,若90BCA ∠=°,4cm 30AB BAC ︒=∠=,,则图中阴影部分面积为 cm 2.14.如图,O 的两条弦AB CD 、互相垂直,垂足为E ,且AB CD =,已知PDC13CE ED ==,,则O 的半径是15.已知:如图,直角ABC ∆中,90ACB ∠=︒,1AC BC ==,DEF 的圆心为A ,如果图中两个阴影部分的面积相等,那么AD 的长是 (结果不取近似值).三 、解答题(本大题共7小题,共55分)16.如图,点A B ,在直线MN 上,11AB =厘米,A B ,的半径均为1厘米.A 以每秒2厘米的速度自左向右运动,与此同时,B 的半径也不断增大,其半径r (厘米)与时间t (秒)之间的关系式为1r t =+(0)t ≥.(1)试写出点A B ,之间的距离d (厘米)与时间t (秒)之间的函数表达式; (2)问点A 出发后多少秒两圆相切?17.已知:如图,点C 在以AB 为直径的⊙O 上,点D 在AB 的延长线上,BCD A ∠=∠.(1)求证:CD 为⊙O 的切线;(2) 过点C 作CE AB ⊥于E .若42,cos 5CE D ==,求⊙O 的半径.FC B18.从ABC △的顶点A 到BC 引垂线AD ,从D 向AB 、AC 引垂线DE DF 、,垂足为E F 、,求证:B E F C 、、、四点共圆.19.已知:如图,AB 为O 的直径,弦AC OD ∥,BD 切O 于B ,联结CD .(1)判断CD 是否为O 的切线,若是请证明;若不是请说明理由. (2)若2AC =,6OD =,求O 的半径.20.如图,在中,直径垂直于弦,垂足为,连接,将沿翻折得到,直线与直线相交于点.若,求的长.DCFEDCBAODCABO AB CD E AC ACD △ACACF △FC AB G 2OB BG ==CD21.如图,在△ABC 中,分别以AB ,AC 为直径在△ABC 外作半圆1O 和半圆2O ,其中1O 和2O 分别为两个半圆的圆心.F 是边BC 的中点,点D 和点E 分别为两个半圆圆弧的中点.过点A 作半圆2O 的切线,交CE 的延长线于点Q ,过点Q 作直线FA 的垂线,交BD 的延长线于点P ,连结PA . 求证:PA 是半圆1O 的切线.22.正方形ABCD 的四个顶点都在O 上,E 是O 上的一点.(1)如图①,若点E 在AB 上,F 是DE 上的一点,DF BE =.求证:ADF ABE ≌△△;(2)在(1)的条件下,小明还发现线段DE BE AE 、、之间满足等量关系:DE BE -.请你说明理由;(3)如图②,若点E 在AD 上.写出线段DE BE AE 、、之间的等量关系.(不必证明)Q图1 图2人教版九年级上册数学《圆》单元测试卷答案解析一 、选择题1.C;【解析】连接AC ,根据菱形的性质得知1AB BC ==,由于在扇形AEF 中,AB AC ,均为半径,故1AB AC ==,所以得知ABC ∆是等边三角形.所以弧BC的长度就可以看做是A Θ周长的16去计算了. 2.A;∵,,∴, ∴数轴上表示为.【解析】根据两圆的位置关系是相交,则这两个圆的圆心距d 大于两半径之差小于两半径之和,从而解决问题.【点评】本题考查了由两圆半径和圆心距之间数量关系判断两圆位置关系的方法.3.D;35BAC ∠=︒,40CED ∠=︒.BC ∴所对圆心角为70︒.CD 所对的圆心角为80︒.∴150BOD ∠=︒ .【解析】考查同弧所对圆周角是圆心角的一半.4.C;同弧所对的圆周角相等,30,180110,D A BPD APD ∠=∠=︒∠=︒-∠=︒ 在BPD ∆中,18040B BPD D ∠=︒-∠-∠=︒.5.B;因为直线与y 轴的交点是,所以. 则圆心到直线的距离一定小于1,所以直线和一定相交.故选. 【解析】要判断直线()与的位置关系,只需求得直线和轴的交点与圆心的距离,再根据点到直线的所有线段中,垂线段最短,进行分析.【点评】考查了直线和圆的位置关系与数量之间的联系. 6.B;【解析】连接CE 、ED∵角的一边OA 与量角器交于点C 、D ,且点C 处的度数是20°,点D 处的度数为110°,413-=415+=35P <<A 2y kx =+()02B ,1AB =A B 2y kx =+0k ≠A y即4∠=20°,OED ∠=110°,∴∠3=∠OED -∠4=110°-20°=90°. ∴∠1=∠2=45°,∠5=∠2+∠3=45°+90°=135° 故∠AOB =180°-∠5-∠4=180°-135°-20°=25° 故选B .7.A;由图可知B .当5a 1<<时点B 在A 内;当5a =或1时点B 在A 上;当a <1或5a >,点B 在A 外8.D;【解析】此题考查的是扇形的面积公式:2360n R S π=︒,把题中的已知条件带入求解即可. 9.B;【解析】此题综合考查了圆周角定理和三角形的内角和定理解:连接OC ,由圆周角定理,得2120AOC B ∠=∠=︒,OAC ∆中,OA OC =, ∴30CAO ACO ∠=∠=︒. 10.D【解析】50APB ∠=︒,∴弦AB 不是直径,APB ∆不是等边三角形.(1)当MA MB =时,MAB ∆是等腰三角形,这时M 点是弦AB 的垂直平分线与圆O 的交点,有两个;(2)当AB AM =时,这样的M 点只有一个.(3)当AB MB =时,这样的M 点只有一个.综上可得符合条件的点M 有4个.二 、填空题11.cm【解析】利用直径所对圆周角是90︒.CB连结AC ,90CAD ∠=︒,30D ∠=︒,∴60ACD ∠=︒,在Rt AHC ∆中,tan 60AH CH =︒=2AB AH ∴==12.2cm 或3cm .【关键词】分类讨论思想 【解析】(1)当点在圆外时,512cm 2r -==,(2)当点在圆内时,513cm 2r +==.13.3π;【解析】此题需要把BC 所在的圆补充完整,设它与线段AB 的交点为D ,与'A B 的交点为E .从而看出整个阴影部分可以割补成扇形'ABA 的面积-扇形BDE 的面积.即221(42)34ππ-=.14.;作OF CD ⊥于F ,OG AE ⊥于G ,由垂径定理得,11(13)222CD DF CD ===+=1.OF EF ∴==连结OD ,在ODF ∆中,由勾股定理得,OD =.【解析】利用ABC ADF S S =扇形△三 、解答题16.(1)211d t =-;(2)点A 出发后3秒、113秒、11秒、13秒两圆相切.DC【解析】(1)当0 5.5t ≤≤时,函数表达式为112d t =-; 当 5.5t >时,函数表达式为211d t =-. (2)两圆相切可分为如下四种情况:①当两圆第一次外切,由题意,可得112113t t t -=++=,; ②当两圆第一次内切,由题意,可得11112113t t t -=+-=,; ③当两圆第二次内切,由题意,可得2111111t t t -=+-=,; ④当两圆第二次外切,由题意,可得2111113t t t -=++=,. 所以,点A 出发后3秒、113秒、11秒、13秒两圆相切. 17.(1)证明:连接CO .∵AB 是⊙O 直径, ∴190OCB ∠+∠=︒. ∵AO CO =,∴1A ∠=∠.∵5A ∠=∠, ∴590OCB ∠+∠=︒. 即90OCD ∠=︒. ∴OC CD ⊥.又∵OC 是⊙O 半径, ∴CD 为⊙O 的切线. (2)∵OC CD ⊥于C , ∴390D ∠+∠=︒. ∵CE AB ⊥于E , ∴3290∠+∠=︒. ∴2D ∠=∠. ∴cos 2cos D ∠=.DC在△OCD 中,90OCD ∠=︒, ∴cos 2CECO∠=, ∵4cos 5D =,2CE =, ∴245CO =. ∴52CO =. ∴⊙O 的半径为5218.∵180AED AFD ∠+∠=︒∴A E D F 、、、四点共圆,∴AFE ADE ∠=∠,又∵AD BC DE AB ⊥⊥,∴ADE ABC ∠=∠,∴AFE ABC ∠=∠,∴B E F C 、、、四点共圆【解析】结合双垂直ABD △及四点共圆A E D F 、、、即可得出答案 19.(1)判断:CD 是O 的切线证明:联结OC ∵ AC OD ∥∴A BOD ∠=∠,ACO COD ∠=∠ ∵ OA OC = ∴A ACO ∠=∠∴BOD COD ∠=∠∵ OB OC =, OD 为公共边∴BOD COD ∆∆≌ ∴B OCD ∠=∠∵ BD 是O 的切线,AB 为直径∴ ∠90ABD =︒ ∴ ∠90OCD =︒∴ CD 是O 的切线 (2) 联结BC 交OD 于E ∵ CD 和BD 都是O 的切线 ∴CD =BD ,CDO BDO ∠=∠∴ BC ⊥OD ,BE CE =,90OBD ∠=︒∴OBE ODB ∆∆∽ ∴OB OEOD OB=由BE CE =, OA OB =得OE 为ABC ∆的中位线即112OE AC == ∴16OB OB=得OB =(舍负) ∴O .20.连接∵,∴.由翻折得,,. ∴,∴. ∴. ∴直线与相切. 在中,, ∴.在中,. ∵直径垂直于弦, ∴.【解析】连接,证即可.根据题意,证可得,从而,得证;根据垂径定理可求后求解.在中,根据三角函数可得.结合求,从而得解. 【点评】此题考查了切线的判定、垂径定理、解直角三角形等知识点,难度中等.21.设直线FA 与PQ 的垂足为M ,过C 作CS ⊥MF 于S ,过B 作BR ⊥MF 于R ,连接DR 、AD 、DMCO OA OC =12∠=∠13∠=∠90F AEC ∠=∠=︒23∠=∠OC AF ∥90OCG F ∠=∠=︒FC O Rt OCG △1cos 22OC OC COG OG OB ∠===60COG ∠=︒Rt OCE△sin 602CE OC =⋅︒==ABCD 2CD CE ==OC OC FG ⊥AF FG ⊥FAC ACO ∠=∠OC AF ∥OC FG ⊥CE Rt OCG △60COG ∠=︒2OC =CE.∵F 是BC 边的中点,∴ABF ACF S S △△.∴BR=CS , 由(2)已证∠CAQ=90°, AC=AQ, ∴∠2+∠3=90°.∵FM ⊥PQ, ∴∠2+∠1=90°, ∴∠1=∠3. 同理:∠2=∠4, ∴AMQ CSA △≌△. ∴AM=CS, ∴AM=BR.同(2)可证AD=BD ,∠ADB=∠ADP=90°, ∴∠ADB=∠ARB=90°, ∠ADP=∠AMP=90°.∴A 、D 、B 、R 四点在以AB 为直径的圆上,A 、D 、P 、M 四点在以AP 为直径的圆上,且∠DBR+∠DAR=180°, ∴∠5=∠8, ∠6=∠7, ∵∠DAM+∠DAR=180°, ∴∠DBR=∠DAM. ∴DBR DAM △≌△. ∴∠5=∠9. ∴∠RDM=90°. ∴∠5+∠7=90°.∴∠6+∠8=90°. ∴∠PAB=90°. ∴PA ⊥AB.又AB 是半圆1O 直径, ∴PA 是半圆1O 的切线.【解析】利用BRF CSF ≌△△得出BR CS =,然后利用ASC QMA ≌△△得出CS AM =,即可得BR AM =,然后证出DBR DAM ≌△△,得出59∠=∠,然后利用两次四点共圆,得出58∠=∠,9APM ∠=∠,即得到8APM ∠=∠,即PA AB ⊥ 22.(1)在正方形ABCD 中,AB AD =∵12DF BE =∠=∠,, ∴ADF ABE ≌△△.(2)由(1)有ADF ABE ≌△△,∴34AF AE =∠=∠,. 在正方形ABCD 中,90BAD ∠=︒. ∴390BAF ∠+∠=︒. ∴490BAF ∠+∠=︒. ∴90EAF ∠=︒.∴EAF △是等腰直角三角形. ∴222EF AE AF =+. ∴222EF AE =.∴EF =.即DE DF -=.∴DE BE -.(3)BE DE -.理由如下:在BE 上取点F ,使BF DE =,连接AF . 易证ADE ABF ≌△△,∴AF AE DAE BAF =∠=∠,,在正方形ABCD 中,90BAD ∠=︒. ∴90BAF DAF ∠+∠=︒. ∴∠DAE+∠DAF=90°. ∴90EAF ∠=︒.∴EAF △是等腰直角三角形. ∴222EF AE AF =+. ∴222EF AE =.∴EF =.即BE BF -=.∴BE DE -.【解析】(1)中易证AD AB =,EB DF =,所以只需证明ADF ABE ∠=∠,利用同弧所对的圆周角相等不难得出,从而证明全等;(2)中易证AEF △是等腰直角三角形,所以EF =,所以只需证明DE BE EF -=即可,由BE DF =不难证明此问题;(3)类比(2)不难得出(3)的结论.【点评】本题主要考查圆周角定理,全等三角形的判定及勾股定理,难度适中.。
部编人教版2024--2025学年度第一学期九年级语文期中测试卷及答案6

部编人教版2024--2025学年度第一学期期中测试卷九年级 语文(满分:120分 时间:120分钟)一、积累和运用(共5小题,计24分)1.阅读语段,完成小题。
(4分)大自然的四季各具风情。
惊蛰时节,河边新芽吐绿,澄清的河水荡起层层涟漪;芒种之时,湖上红莲绽放,娉.婷的乔木掩映着似锦繁花;立秋,梧桐树在风中摇曳,月朗风清的秋夜,古老的白塔讲述着岁月的故事;冬天,红装素裹的大地,润如油膏的沃土孕育着丰收的希望。
人生亦有不同的风景。
不管生活给了我们怎样的人生,只要我们能朝着目标,心无旁w ù,k è守时间,拥有一颗淡然的心,遇事不成不以客观理由宽宥.自己,我相信我们一定能更好地把握人生,把握幸福……(1)请根据语境,选出加点字正确的读音。
(只填序号)(2分) ①芒种之时,湖上红莲绽放,娉.(A.p īn B.pīng )婷的乔木掩映着似锦繁花。
( )②拥有一颗淡然的心,遇事不成不以客观理由宽宥.(A.yòu B.yǒu )自己。
( )(2)请根据语境,写出下面词语中拼音所对应的汉字。
(2分) ①心无旁w ù___ ②k è___守2.经典诗文默写。
[在(1)~(6)题中,任选四题....;在(7)~(8)题中,任选一题。
](6分)(1)欲为圣明除弊事,_____________!(韩愈《左迁至蓝关示侄孙湘》)(2)___________,边秋一雁声(杜甫《月夜忆舍弟》) (3)_____________,佳木秀而繁阴。
(欧阳修《醉翁亭记》)(4)不应有恨,_____________?[苏轼《水调歌头(明月几时有)》](5)须晴日,_____________,分外妖娆。
(毛泽东《沁园春·雪》)(6)为什么我的眼里常含泪水?__________________________……(艾青《我爱这土地》)(7)面对挫折,我们要有刘禹锡在《酬乐天扬州初逢席上见赠》“_____________,_____________”中所表现出来的不屈服于现实的豁达胸襟。
人教版数学九年级上册单元测试卷15套含答案

第21章一元二次方程测试卷(1)一、精心选一选,相信自己的判断!(每小题3分,共30分)1.(3分)方程2x2﹣3=0的一次项系数是()A.﹣3ﻩ B.2ﻩ C.0D.32.(3分)方程x2=2x的解是()A.x=0B.x=2C.x1=0,x2=2D.x1=0,x2=3.(3分)方程x2﹣4=0的根是()A.x=2B.x=﹣2 C.x1=2,x2=﹣2ﻩD.x=44.(3分)若一元二次方程2x(kx﹣4)﹣x2+6=0无实数根,则k的最小整数值是( )A.﹣1ﻩB.0ﻩC.1D.25.(3分)用配方法解一元二次方程x2﹣4x﹣5=0的过程中,配方正确的是()A.(x+2)2=1B.(x﹣2)2=1C.(x+2)2=9ﻩD.(x﹣2)2=96.(3分)在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,做成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )A.x2+130x﹣1400=0ﻩB.x2+65x﹣350=0C.x2﹣130x﹣1400=0ﻩD.x2﹣65x﹣350=07.(3分)已知直角三角形的三边长为三个连续整数,那么,这个三角形的面积是()A.6ﻩB.8ﻩC.10D.128.(3分)方程x2﹣9x+18=0的两个根是等腰三角形的底和腰,则这个三角形的周长为( )A.12ﻩB.12或15ﻩ C.15ﻩ D.不能确定9.(3分)若关于一元二次方程x2+2x+k+2=0的两个根相等,则k的取值是( )A.1B.1或﹣1C.﹣1D.210.(3分)科学兴趣小组的同学们,将自己收集的标本向本组的其他成员各赠送一件,全组共互赠了132件,那么全组共有()名学生.A.12 B.12或66C.15ﻩD.33二、耐心填一填:(把答案填放相应的空格里.每小题3分,共15分).11.(3分)写一个一元二次方程,使它的二次项系数是﹣3,一次项系数是2: .12.(3分)﹣1是方程x2+bx﹣5=0的一个根,则b=,另一个根是.13.(3分)方程(2y+1)(2y﹣3)=0的根是.14.(3分)已知一元二次方程x2﹣3x﹣1=0的两根为x1、x2,x1+x2= .15.(3分)用换元法解方程+2x=x2﹣3时,如果设y=x2﹣2x,则原方程可化为关于y的一元二次方程的一般形式是.三、按要求解一元二次方程:(20分)16.(20分)按要求解一元二次方程(1)4x2﹣8x+1=0(配方法)(2)7x(5x+2)=6(5x+2)(因式分解法)(3)3x2+5(2x+1)=0(公式法)(4)x2﹣2x﹣8=0.四、细心做一做:17.(6分)有一面积为150m2的长方形鸡场,鸡场的一边靠墙(墙长18m),另三边用竹篱笆围成,如果竹篱笆的总长为35 m,求鸡场的长与宽各为多少?18.(6分)如图所示,在一块长为32米,宽为15米的矩形草地上,在中间要设计一横二竖的等宽的、供居民散步的小路,要使小路的面积是草地总面积的八分之一,请问小路的宽应是多少米?19.(7分)某企业2006年盈利1500万元,2008年克服全球金融危机的不利影响,仍实现盈利2160万元.从2006年到2008年,如果该企业每年盈利的年增长率相同,求:(1)该企业2007年盈利多少万元?(2)若该企业盈利的年增长率继续保持不变,预计2009年盈利多少万元?20.(7分)中华商场将进价为40元的衬衫按50元售出时,每月能卖出500件,经市场调查,这种衬衫每件涨价4元,其销售量就减少40件.如果商场计划每月赚得8000元利润,那么售价应定为多少?这时每月应进多少件衬衫?21.(9分)如图1,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动.(1)经过几秒△PCQ的面积为△ACB的面积的?(2)经过几秒,△PCQ与△ACB相似?(3)如图2,设CD为△ACB的中线,那么在运动的过程中,PQ与CD有可能互相垂直吗?若有可能,求出运动的时间;若没有可能,请说明理由.参考答案与试题解析一、精心选一选,相信自己的判断!(每小题3分,共30分)1.(3分)方程2x2﹣3=0的一次项系数是( )A.﹣3B.2C.0D.3【考点】一元二次方程的一般形式.【分析】一元二次方程的一般形式是ax2+bx+c=0(a,b,c是常数且a≠0)特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.【解答】解:方程2x2﹣3=0没有一次项,所以一次项系数是0.故选C.【点评】要特别注意不含有一次项,因而一次项系数是0,注意不要说是没有.2.(3分)方程x2=2x的解是( )A.x=0B.x=2C.x1=0,x2=2D.x1=0,x2=【考点】解一元二次方程-因式分解法;因式分解-提公因式法.【专题】因式分解.【分析】把右边的项移到左边,用提公因式法因式分解,可以求出方程的两个根.【解答】解:x2﹣2x=0x(x﹣2)=0∴x1=0,x2=2.故选C.【点评】本题考查的是用因式分解法解一元二次方程,把右边的项移到左边,用提公因式法因式分解,可以求出方程的根.3.(3分)方程x2﹣4=0的根是( )A.x=2B.x=﹣2 C.x1=2,x2=﹣2D.x=4【考点】解一元二次方程-直接开平方法.【分析】先移项,然后利用数的开方解答.【解答】解:移项得x2=4,开方得x=±2,∴x1=2,x2=﹣2.故选C.【点评】(1)用直接开方法求一元二次方程的解的类型有:x2=a(a≥0),ax2=b (a,b同号且a≠0),(x+a)2=b(b≥0),a(x+b)2=c(a,c同号且a≠0).法则:要把方程化为“左平方,右常数,先把系数化为1,再开平方取正负,分开求得方程解”;(2)运用整体思想,会把被开方数看成整体;(3)用直接开方法求一元二次方程的解,要仔细观察方程的特点.4.(3分)若一元二次方程2x(kx﹣4)﹣x2+6=0无实数根,则k的最小整数值是()A.﹣1B.0C.1D.2【考点】根的判别式;一元二次方程的定义.【分析】先把方程变形为关于x的一元二次方程的一般形式:(2k﹣1)x2﹣8x+6=0,要方程无实数根,则△=82﹣4×6(2k﹣1)<0,解不等式,并求出满足条件的最小整数k.【解答】解:方程变形为:(2k﹣1)x2﹣8x+6=0,当△<0,方程没有实数根,即△=82﹣4×6(2k﹣1)<0,解得k>,则满足条件的最小整数k为2.故选D.【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.5.(3分)用配方法解一元二次方程x2﹣4x﹣5=0的过程中,配方正确的是()A.(x+2)2=1 B.(x﹣2)2=1ﻩC.(x+2)2=9D.(x﹣2)2=9【考点】解一元二次方程-配方法.【分析】先移项,再方程两边都加上一次项系数一半的平方,即可得出答案.【解答】解:移项得:x2﹣4x=5,配方得:x2﹣4x+22=5+22,(x﹣2)2=9,故选D.【点评】本题考查了解一元二次方程,关键是能正确配方.6.(3分)在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,做成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )A.x2+130x﹣1400=0B.x2+65x﹣350=0C.x2﹣130x﹣1400=0D.x2﹣65x﹣350=0【考点】由实际问题抽象出一元二次方程.【专题】几何图形问题.【分析】本题可设长为(80+2x),宽为(50+2x),再根据面积公式列出方程,化简即可.【解答】解:依题意得:(80+2x)(50+2x)=5400,即4000+260x+4x2=5400,化简为:4x2+260x﹣1400=0,即x2+65x﹣350=0.故选:B.【点评】本题考查的是一元二次方程的运用,解此类题目要注意运用面积的公式列出等式再进行化简.7.(3分)已知直角三角形的三边长为三个连续整数,那么,这个三角形的面积是()A.6B.8ﻩC.10ﻩD.12【考点】勾股定理.【分析】设三边长分别为x,x+1,x+2,根据勾股定理可得(x+2)2=(x+1)2+x2,解方程可求得三角形的三边长,利用直角三角形的性质直接求得面积即可.【解答】解:设这三边长分别为x,x+1,x+2,根据勾股定理得:(x+2)2=(x+1)2+x2解得:x=﹣1(不合题意舍去),或x=3,∴x+1=4,x+2=5,则三边长是3,4,5,∴三角形的面积=××4=6;故选:A.【点评】本题考查了勾股定理、直角三角形面积的计算方法;熟练掌握勾股定理,由勾股定理得出方程是解决问题的关键.8.(3分)方程x2﹣9x+18=0的两个根是等腰三角形的底和腰,则这个三角形的周长为()A.12ﻩB.12或15 C.15ﻩD.不能确定【考点】等腰三角形的性质;解一元二次方程-因式分解法;三角形三边关系.【专题】分类讨论.【分析】先解一元二次方程,由于未说明两根哪个是腰哪个是底,故需分情况讨论,从而得到其周长.【解答】解:解方程x2﹣9x+18=0,得x1=6,x2=3∵当底为6,腰为3时,由于3+3=6,不符合三角形三边关系∴等腰三角形的腰为6,底为3∴周长为6+6+3=15故选C.【点评】此题是一元二次方程的解结合几何图形的性质的应用,注意分类讨论.9.(3分)若关于一元二次方程x2+2x+k+2=0的两个根相等,则k的取值是()A.1ﻩB.1或﹣1 C.﹣1ﻩD.2【考点】根的判别式.【分析】根据判别式的意义得到△=22﹣4(k+2)=0,然后解一次方程即可.【解答】解:根据题意得△=22﹣4(k+2)=0,解得k=﹣1.故选C.【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2﹣4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.10.(3分)科学兴趣小组的同学们,将自己收集的标本向本组的其他成员各赠送一件,全组共互赠了132件,那么全组共有()名学生.A.12ﻩB.12或66ﻩC.15 D.33【考点】一元二次方程的应用.【分析】设全组共有x名学生,每一个人赠送x﹣1件,全组共互赠了x(x﹣1)件,共互赠了132件,可得到方程,求解即可.【解答】解:设全组共有x名学生,由题意得x(x﹣1)=132解得:x1=﹣11(不合题意舍去),x2=12,答:全组共有12名学生.故选:A.【点评】本题考查一元二次方程的实际运用,找出题目蕴含的数量关系是解决问题的关键.二、耐心填一填:(把答案填放相应的空格里.每小题3分,共15分).11.(3分)写一个一元二次方程,使它的二次项系数是﹣3,一次项系数是2:﹣3x2+2x﹣3=0.【考点】一元二次方程的一般形式.【专题】开放型.【分析】根据一元二次方程的一般形式和题意写出方程即可.【解答】解:由题意得:﹣3x2+2x﹣3=0,故答案为:﹣3x2+2x﹣3=0.【点评】本题考查了一元二次方程的一般形式,一元二次方程的一般形式是:ax2+b x+c=0(a,b,c是常数且a≠0)特别要注意a≠0的条件.在一般形式中a,b,c分别叫二次项系数,一次项系数,常数项.12.(3分)﹣1是方程x2+bx﹣5=0的一个根,则b=﹣4,另一个根是 5 .【考点】一元二次方程的解.【分析】把x=﹣1代入方程得出关于b的方程1+b﹣2=0,求出b,代入方程,求出方程的解即可.【解答】解:∵x=﹣1是方程x2+bx﹣5=0的一个实数根,∴把x=﹣1代入得:1﹣b﹣5=0,解得b=﹣4,即方程为x2﹣4x﹣5=0,(x+1)(x﹣5)=0,解得:x1=﹣1,x2=5,即b的值是﹣4,另一个实数根式5.故答案为:﹣4,5;【点评】本题考查了一元二次方程的解的概念:使方程两边成立的未知数的值叫方程的解.13.(3分)方程(2y+1)(2y﹣3)=0的根是y1=﹣,y2=.【考点】解一元二次方程-因式分解法.【专题】因式分解.【分析】解一元二次方程的关键是把二次方程化为两个一次方程,解这两个一次方程即可求得.【解答】解:∵(2y+1)(2y﹣3)=0,∴2y+1=0或2y﹣3=0,解得y1=,y2=.【点评】解此题要掌握降次的思想,把高次的降为低次的,把多元的降为低元的,这是解复杂问题的一个原则.14.(3分)已知一元二次方程x2﹣3x﹣1=0的两根为x1、x2,x1+x2=3.【考点】根与系数的关系.【分析】根据一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两,x2,则x1+x2=﹣,代入计算即可.根为x1【解答】解:∵一元二次方程x2﹣3x﹣1=0的两根是x1、x2,∴x1+x2=3,故答案为:3.【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=﹣,x1•x2=.15.(3分)用换元法解方程+2x=x2﹣3时,如果设y=x2﹣2x,则原方程可化为关于y的一元二次方程的一般形式是y2﹣3y﹣1=0.【考点】换元法解分式方程.【专题】换元法.【分析】此题考查了换元思想,解题的关键是要把x2﹣2x看作一个整体.【解答】解:原方程可化为:﹣(x2﹣2x)+3=0设y=x2﹣2x﹣y+3=0∴1﹣y2+3y=0∴y2﹣3y﹣1=0.【点评】此题考查了学生的整体思想,也就是准确使用换元法.解题的关键是找到哪个是换元的整体.三、按要求解一元二次方程:(20分)16.(20分)按要求解一元二次方程(1)4x2﹣8x+1=0(配方法)(2)7x(5x+2)=6(5x+2)(因式分解法)(3)3x2+5(2x+1)=0(公式法)(4)x2﹣2x﹣8=0.【考点】解一元二次方程-因式分解法;解一元二次方程-配方法;解一元二次方程-公式法.【分析】(1)首先将常数项移到等号的右侧,将等号左右两边同时加上一次项系数一半的平方,即可将等号左边的代数式写成完全平方形式.(2)方程移项变形后,采用提公因式法,可得方程因式分解的形式,即可求解.(3)方程化为一般形式,找出二次项系数,一次项系数及常数项,计算出根的判别式,发现其结果大于0,故利用求根公式可得出方程的两个解.(4)方程左边分解因式,即可得出两个一元一次方程,求出方程的解即可.【解答】解:(1)4x2﹣8x+1=0(配方法)移项得,x2﹣2x=﹣,配方得,x2﹣2x+1=﹣+1,(x﹣1)2=,∴x﹣1=±∴x=1+,x2=1﹣.1(2)7x(5x+2)=6(5x+2)(因式分解法)7x(5x+2)﹣6(5x+2)=0,(5x+2)(7x﹣6)=0,∴5x+2=0,7x﹣6=0,∴x=﹣,x2=;1(3)3x2+5(2x+1)=0(公式法)整理得,3x2+10x+5=0∵a=3,b=10,c=5,b2﹣4ac=100﹣60=40,∴x===,∴x1=,x2=;(4)x2﹣2x﹣8=0.(x+4)(x﹣2)=0,∴x+4=0,x﹣2=0,∴x1=﹣4,x2=2.【点评】本题考查了解一元二次方程的应用,解此题的关键是能把一元二次方程转化成一元一次方程.四、细心做一做:17.(6分)有一面积为150m2的长方形鸡场,鸡场的一边靠墙(墙长18 m),另三边用竹篱笆围成,如果竹篱笆的总长为35 m,求鸡场的长与宽各为多少?【考点】一元二次方程的应用.【专题】几何图形问题.【分析】设养鸡场的宽为xm,则长为(35﹣2x),根据矩形的面积公式即可列方程,列方程求解.【解答】解:设养鸡场的宽为xm,则长为(35﹣2x),由题意得x(35﹣2x)=150解这个方程;x2=10当养鸡场的宽为时,养鸡场的长为20m不符合题意,应舍去,当养鸡场的宽为x1=10m时,养鸡场的长为15m.答:鸡场的长与宽各为15m,10m.【点评】本题考查的是一元二次方程的应用,难度一般.18.(6分)如图所示,在一块长为32米,宽为15米的矩形草地上,在中间要设计一横二竖的等宽的、供居民散步的小路,要使小路的面积是草地总面积的八分之一,请问小路的宽应是多少米?【考点】一元二次方程的应用.【专题】几何图形问题.【分析】本题可根据关键语“小路的面积是草地总面积的八分之一”,把小路移到一起正好构成一个矩形,矩形的长和宽分别是(32﹣2x)和(15﹣x),列方程即可求解.【解答】解:设小路的宽应是x米,则剩下草总长为(32﹣2x)米,总宽为(15﹣x)米,由题意得(32﹣2x)(15﹣x)=32×15×(1﹣)即x2﹣31x+30=0解得x1=30 x2=1∵路宽不超过15米∴x=30不合题意舍去答:小路的宽应是1米.【点评】找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.19.(7分)某企业2006年盈利1500万元,2008年克服全球金融危机的不利影响,仍实现盈利2160万元.从2006年到2008年,如果该企业每年盈利的年增长率相同,求:(1)该企业2007年盈利多少万元?(2)若该企业盈利的年增长率继续保持不变,预计2009年盈利多少万元?【考点】一元二次方程的应用.【专题】增长率问题.【分析】本题为增长率问题,一般用增长后的量=增长前的量×(1+增长率).(1)可先求出增长率,然后再求2007年的盈利情况.(2)有了2008年的盈利和增长率,求出2009年的就容易了.【解答】解:(1)设每年盈利的年增长率为x,根据题意,得1500(1+x)2=2160.=0.2,x2=﹣2.2(不合题意,舍去).解得x1∴1500(1+x)=1500(1+0.2)=1800.答:2007年该企业盈利1800万元.(2)2160(1+0.2)=2592.答:预计2009年该企业盈利2592万元.【点评】本题考查的是增长率的问题.增长率问题,一般形式为a(1+x)2=b,a为起始时间的有关数量,b为终止时间的有关数量.20.(7分)中华商场将进价为40元的衬衫按50元售出时,每月能卖出500件,经市场调查,这种衬衫每件涨价4元,其销售量就减少40件.如果商场计划每月赚得8000元利润,那么售价应定为多少?这时每月应进多少件衬衫?【考点】一元二次方程的应用.【专题】销售问题.【分析】设涨价4x元,则销量为(500﹣40x),利润为(10+4x),再由每月赚8000元,可得方程,解方程即可.【解答】解:设涨价4x元,则销量为(500﹣40x),利润为(10+4x),由题意得,(500﹣40x)×(10+4x)=8000,整理得,5000+2000x﹣400x﹣160x2=8000,解得:x1=,x2=,当x1=时,则涨价10元,销量为:400件;当x2=时,则涨价30元,销量为:200件.答:当售价定为60元时,每月应进400件衬衫;售价定为80元时,每月应进200件衬衫.【点评】本题考查的是一元二次方程的应用,根据题意正确找出等量关系、列出方程是解题的关键,注意分情况讨论思想的应用.21.(9分)如图1,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C 匀速移动,当一个点到达终点时另一个点也随之停止移动.(1)经过几秒△PCQ的面积为△ACB的面积的?(2)经过几秒,△PCQ与△ACB相似?(3)如图2,设CD为△ACB的中线,那么在运动的过程中,PQ与CD有可能互相垂直吗?若有可能,求出运动的时间;若没有可能,请说明理由.【考点】一元二次方程的应用;相似三角形的判定.【专题】几何动点问题.【分析】(1)分别表示出线段PC和线段CQ的长后利用S△PCQ =S△ABC列出方程求解;(2)设运动时间为ts,△PCQ与△ACB相似,当△PCQ与△ACB相似时,可知∠CPQ=∠A或∠CPQ=∠B,则有=或=,分别代入可得到关于t的方程,可求得t的值;(3)设运动时间为ys,PQ与CD互相垂直,根据直角三角形斜边上的中线的性质以及等腰三角形的性质得出∠ACD=∠A,∠BCD=∠B,再证明△PCQ∽△BCA,那么=,依此列出比例式=,解方程即可.【解答】解:(1)设经过x秒△PCQ的面积为△ACB的面积的,由题意得:PC=2xm,CQ=(6﹣x)m,则×2x(6﹣x)=××8×6,解得:x=2或x=4.故经过2秒或4秒,△PCQ的面积为△ACB的面积的;(2)设运动时间为ts,△PCQ与△ACB相似.当△PCQ与△ACB相似时,则有=或=,所以=,或=,解得t=,或t=.因此,经过秒或秒,△OCQ与△ACB相似;( 3)有可能.由勾股定理得AB=10.∵CD为△ACB的中线,∴∠ACD=∠A,∠BCD=∠B,又PQ⊥CD,∴∠CPQ=∠B,∴△PCQ∽△BCA,∴=,=,解得y=.因此,经过秒,PQ⊥CD.【点评】本题考查了一元二次方程的应用,相似三角形的判定与性质,三角形的面积,勾股定理,直角三角形、等腰三角形的性质,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.第21章一元二次方程测试卷(2)一.选择题(本题共12小题,每小题3分,共36分.每小题给出4个选项,其中只有一个是正确的)1.(3分)把方程x(x+2)=5(x﹣2)化成一般式,则a、b、c的值分别是()A.1,﹣3,10B.1,7,﹣10C.1,﹣5,12D.1,3,22.(3分)一元二次方程x2﹣6x﹣5=0配方可变形为()A.(x﹣3)2=14ﻩB.(x﹣3)2=4C.(x+3)2=14ﻩD.(x+3)2=43.(3分)如果关于x的一元二次方程k2x2﹣(2k+1)x+1=0有两个不相等的实数根,那么k的取值范围是()A.k>B.k>且k≠0ﻩC.k<D.k≥且k≠04.(3分)用换元法解方程﹣=3时,设=y,则原方程可化为()A.y﹣﹣3=0B.y﹣﹣3=0C.y﹣+3=0ﻩD.y﹣+3=05.(3分)等腰三角形的底和腰是方程x2﹣7x+12=0的两个根,则这个三角形的周长是()A.11B.10ﻩC.11或10ﻩD.不能确定6.(3分)若分式的值为零,则x的值为()A.3ﻩB.3或﹣3ﻩC.0ﻩD.﹣37.(3分)一元二次方程x2﹣x﹣1=0的根的情况为()A.有两个不相等的实数根B.有两个相等的实数根C.只有一个实数根D.没有实数根8.(3分)在某次聚会上,每两人都握了一次手,所有人共握手10次,设有x人参加这次聚会,则列出方程正确的是()A.x(x﹣1)=10B.=10ﻩC.x(x+1)=10ﻩD.=109.(3分)某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是()A.50(1+x)2=182ﻩB.50+50(1+x)+50(1+x)2=182C.50(1+2x)=182ﻩD.50+50(1+x)+50(1+2x)2=18210.(3分)已知x1,x2是关于x的方程x2+ax﹣2b=0的两实数根,且x1+x2=﹣2,x1•x2=1,则b a的值是( )A.B.﹣ C.4D.﹣111.(3分)定义运算:aﻩb=a(1﹣b).若a,b是方程x2﹣x+m=0(m<0)的两根,则bﻩb﹣aﻩa的值为()A.0B.1 C.2ﻩD.与m有关12.(3分)使用墙的一边,再用13m的铁丝网围成三边,围成一个面积为20m2的长方形,求这个长方形的两边长.设墙的对边长为xm,可得方程()A.x(13﹣x)=20B.x•=20C.x(13﹣x)=20D.x•=20二.填空题(每小题3分,共12分)13.(3分)方程x2﹣3=0的根是.14.(3分)当k= 时,方程x2+(k+1)x+k=0有一根是0.15.(3分)设m,n分别为一元二次方程x2+2x﹣2018=0的两个实数根,则m2+3m+n=.16.(3分)写出以4,﹣5为根且二次项的系数为1的一元二次方程是.三.解答题(本题有7小题,共52分)17.(10分)解方程(1)x2﹣4x﹣5=0(2)3x(x﹣1)=2﹣2x.18.(5分)试证明关于x的方程(a2﹣8a+20)x2+2ax+1=0无论a取何值,该方程都是一元二次方程.19.(6分)某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1.在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道.当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是288m2?20.(8分)某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.(1)求该种商品每次降价的百分率;(2)若该种商品进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3210元.问第一次降价后至少要售出该种商品多少件?21.(6分)阅读下面的例题,范例:解方程x2﹣|x|﹣2=0,解:(1)当x≥0时,原方程化为x2﹣x﹣2=0,解得:x1=2,x2=﹣1(不合题意,舍去).(2)当x<0时,原方程化为x2+x﹣2=0,解得:x1=﹣2,x2=1(不合题意,舍去).∴原方程的根是x1=2,x2=﹣2请参照例题解方程x2﹣|x﹣1|﹣1=0.22.(8分)龙华天虹商场以120元/件的价格购进一批上衣,以200元/件的价格出售,每周可售出100件.为了促销,该商场决定降价销售,尽快减少库存.经调查发现,这种上衣每降价5元/件,每周可多售出20件.另外,每周的房租等固定成本共3000元.该商场要想每周盈利8000元,应将每件上衣的售价降低多少元? 23.(9分)如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿A边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从C点开始沿CB边向点B以2厘米/秒的速度移动(到达点C即停止运动).(1)如果P、Q分别从A、C两点同时出发,经过几秒钟,△PBQ的面积等于是△ABC的三分之一?(2)如果P、Q两点分别从A、C两点同时出发,而且动点P从A点出发,沿AB移动(到达点B即停止运动),动点Q从C出发,沿CB移动(到达点C即停止运动),几秒钟后,P、Q相距6厘米?(3)如果P、Q两点分别从A、C两点同时出发,而且动点P从A点出发,沿A B移动(到达点B即停止运动),动点Q从C出发,沿CB移动(到达点B即停止运动),是否存在一个时刻,PQ同时平分△ABC的周长与面积?若存在求出这个时刻的t值,若不存在说明理由.ﻩ参考答案与试题解析一.选择题(本题共12小题,每小题3分,共36分.每小题给出4个选项,其中只有一个是正确的)1.(3分)把方程x(x+2)=5(x﹣2)化成一般式,则a、b、c的值分别是() A.1,﹣3,10ﻩB.1,7,﹣10ﻩC.1,﹣5,12 D.1,3,2【考点】一元二次方程的一般形式.【专题】压轴题;推理填空题.【分析】a、b、c分别指的是一元二次方程的一般式中的二次项系数、一次项系数、常数项.【解答】解:由方程x(x+2)=5(x﹣2),得x2﹣3x+10=0,∴a、b、c的值分别是1、﹣3、10;故选A.【点评】本题考查了一元二次方程的一般形式.一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0),在一般形式中ax2叫二次项,bx叫一次项,c 是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.2.(3分)一元二次方程x2﹣6x﹣5=0配方可变形为()A.(x﹣3)2=14B.(x﹣3)2=4ﻩC.(x+3)2=14D.(x+3)2=4【考点】解一元二次方程-配方法.【分析】先把方程的常数项移到右边,然后方程两边都加上32,这样方程左边就为完全平方式.【解答】解:x2﹣6x﹣5=0,x2﹣6x=5,x2﹣6x+9=5+9,(x﹣3)2=14,故选:A.【点评】本题考查了利用配方法解一元二次方程ax2+bx+c=0(a≠0):先把二次系数变为1,即方程两边除以a,然后把常数项移到方程右边,再把方程两边加上一次项系数的一半.3.(3分)如果关于x的一元二次方程k2x2﹣(2k+1)x+1=0有两个不相等的实数根,那么k的取值范围是()A.k>ﻩB.k>且k≠0ﻩC.k<D.k≥且k≠0【考点】根的判别式.【专题】压轴题.【分析】若一元二次方程有两不等根,则根的判别式△=b2﹣4ac>0,建立关于k的不等式,求出k的取值范围.【解答】解:由题意知,k≠0,方程有两个不相等的实数根,所以△>0,△=b2﹣4ac=(2k+1)2﹣4k2=4k+1>0.又∵方程是一元二次方程,∴k≠0,∴k>且k≠0.故选B.【点评】总结:一元二次方程根的情况与判别式△的关系:(1)△>0⇔方程有两个不相等的实数根;(2)△=0⇔方程有两个相等的实数根;(3)△<0⇔方程没有实数根.注意方程若为一元二次方程,则k≠0.4.(3分)用换元法解方程﹣=3时,设=y,则原方程可化为()A.y﹣﹣3=0ﻩB.y﹣﹣3=0 C.y﹣+3=0ﻩD.y﹣+3=0【考点】换元法解分式方程.【分析】把y=代入原方程,移项即可得到答案.【解答】解:设=y,则原方程可化为:y﹣=3,即y﹣﹣3=0,故选:A.【点评】本题主要考查换元法解分式方程,用换元法解一些复杂的分式方程是比较简单的一种方法,根据方程特点设出相应未知数,解方程能够使问题简单化.5.(3分)等腰三角形的底和腰是方程x2﹣7x+12=0的两个根,则这个三角形的周长是()A.11B.10C.11或10ﻩD.不能确定【考点】解一元二次方程-因式分解法;三角形三边关系;等腰三角形的性质.【专题】计算题;一次方程(组)及应用.【分析】利用因式分解法求出方程的解得到x的值,确定出底与腰,即可求出周长.【解答】解:方程分解得:(x﹣3)(x﹣4)=0,解得:x1=3,x2=4,若3为底,4为腰,三角形三边为3,4,4,周长为3+4+4=11;若3为腰,4为底,三角形三边为3,3,4,周长为3+3+4=10.故选C.【点评】此题考查了解一元二次方程﹣因式分解法,熟练掌握因式分解法是解本题的关键.6.(3分)若分式的值为零,则x的值为()A.3 B.3或﹣3C.0ﻩD.﹣3【考点】分式的值为零的条件;解一元二次方程-直接开平方法;解一元一次不等式.【专题】计算题.【分析】分式的值为0的条件是:(1)分子为0;(2)分母不为0.两个条件需同时具备,缺一不可.据此可以解答本题.【解答】解:由题意,可得x2﹣9=0且2x﹣6≠0,解得x=﹣3.故选D.【点评】本题主要考查分式的值为0的条件.由于该类型的题易忽略分母不为0这个条件,所以常以这个知识点来命题.7.(3分)一元二次方程x2﹣x﹣1=0的根的情况为()A.有两个不相等的实数根 B.有两个相等的实数根C.只有一个实数根D.没有实数根【考点】根的判别式.【分析】先求出△的值,再判断出其符号即可.【解答】解:∵a=1,b=﹣1,c=﹣1,∴△=b2﹣4ac=(﹣1)2﹣4×1×(﹣1)=5>0,∴方程有两个不相等的实数根,故选:A.【点评】本题考查的是根的判别式,熟知一元二次方程ax2+bx+c=0(a≠0)的根与△的关系是解答此题的关键.8.(3分)在某次聚会上,每两人都握了一次手,所有人共握手10次,设有x人参加这次聚会,则列出方程正确的是()A.x(x﹣1)=10B.=10ﻩC.x(x+1)=10D.=10【考点】由实际问题抽象出一元二次方程.【专题】其他问题;压轴题.【分析】如果有x人参加了聚会,则每个人需要握手(x﹣1)次,x人共需握手x(x﹣1)次;而每两个人都握了一次手,因此要将重复计算的部分除去,即一共握手:次;已知“所有人共握手10次”,据此可列出关于x的方程.【解答】解:设x人参加这次聚会,则每个人需握手:x﹣1(次);依题意,可列方程为:=10;故选B.【点评】理清题意,找对等量关系是解答此类题目的关键;需注意的是本题中“每两人都握了一次手”的条件,类似于球类比赛的单循环赛制.9.(3分)某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是()A.50(1+x)2=182ﻩB.50+50(1+x)+50(1+x)2=182C.50(1+2x)=182D.50+50(1+x)+50(1+2x)2=182【考点】由实际问题抽象出一元二次方程.【专题】增长率问题;压轴题.【分析】主要考查增长率问题,一般增长后的量=增长前的量×(1+增长率),如果该厂五、六月份平均每月的增长率为x,那么可以用x分别表示五、六月份的产量,然后根据题意可得出方程.【解答】解:依题意得五、六月份的产量为50(1+x)、50(1+x)2,∴50+50(1+x)+50(1+x)2=182.故选B.【点评】增长率问题,一般形式为a(1+x)2=b,a为起始时间的有关数量,b为终止时间的有关数量.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020学年第一学期初三化学第9周周清试卷
一、选择题(每空2分,共60分)
1.下列图中的和O分别表示不同元素的原子,其中可能表示氧化物的是()A.B.
C.D.
2.下列有关水的说法正确的是()
A.可以用肥皂水来检验硬水和软水 B.地球淡水资源取之不尽,用之不竭C.常用过滤的方法降低水的硬度 D.自然界中的水都是纯水
3.水是最常见的物质,以下与水有关的说法正确的是()
A.地球上水资源丰富,人类不缺淡水
B.电解水是验证水的组成的方法之一
C.生活中可以用食盐水区分硬水和软水
D.自来水厂用沉淀、过滤、吸附和蒸馏等方法净化水
4.“绿水青山就是金山银山”。
下列做法符合这一理念的是()A.直接排放生活污水B.露天焚烧垃圾
C.开发利用清洁能源D.深埋处理废旧电池5.(2020•黄石)下列化学用语正确的是()
A.2个氢原子:H2 B.1个硫酸根离子:SO4﹣2
C.2个氨分子:2NH3 D.五氧化二氮的化学式:O5N2 6.(2020•盘锦)如图所示的原子,在化学反应中易得到电子的是()
A.B.C.D.
7.氮元素形成的化合物种类较多,下列化合物中氮元素化合价为+2价的是()A.NO B.N2O3C.NH3D.N2O5
8.(2020•兴安盟)如图为某粒子结构示意图,下列说法错误的是()A.该粒子属于非金属元素
B.该粒子核外电子数为17
C.该粒子具有3个电子层
D.在化学反应中,该元素原子易得电子形成Cl﹣
9.(2020•泰州)制造北斗三号卫星使用了钛合金材料,钛原子的质子数为22,相对原子质量为48,则钛原子的核外电子数为()
A.22 B.48 C.70 D.26
10.以模型代表水分子,水电解时发生改变的微粒是()
A.B.C.D.
11.(2020•宜宾)下列物质属于氧化物的是()
A.HNO3B.KMnO4C.P2O5D.Cu(OH)2
12.通过研究氢气的燃烧来认识水的组成,下列说法正确的是()
A.氢气在纯氧中安静地燃烧,产生黄色火焰
B.点燃纯净的氢气,在火焰上方罩一个干冷烧杯,可以看到白烟
C.点燃氢气,罩在火焰上的干冷烧杯只出现水珠,可见水由氢元素和氧元素组成
D.由实验可知水是由氢气和氧气组成的
13.(2020•营口)下列关于电解水实验的描述,正确的是()
A.正极产生的气体是氢气 B.该实验能证明水中含有氢、氧元素
C.生成氧气、氢气的体积比约为2:1 D.电解过程中水分子没有发生改变14.(2020•海南)海南岛存在大面积富硒土壤。
富硒土壤中的“硒”指的是()A.元素B.分子C.原子D.单质
15.极光是一种绚丽多彩的发光现象,其发生是由于太阳带电粒子流进入地球磁场。
在地球南北两极附近地区的高空,夜间出现的灿烂美丽的光辉,在南极被称为南极光,在北极被称为北极光。
下列这些微粒中,会引起极光的是()
A.水分子B.氢离子C.氢原子D.中子16.(2020•黄冈)下面是萌萌同学的一次化学用语练习的部分内容,其中正确的是()
A.氦气:He2 B.硝酸铵中﹣3价氮元素:C.N2:两个氮原子 D.2Fe2+:两个铁离子
NH4NO3 -3
17.下列说法正确的是()
A.分子是化学变化中的最小粒子 B.原子核是由质子和电子构成
C.NaCl由NaCl分子构成 D.水蒸发过程中,水分子的间隔变大18.(2020•苏州)某净水装置如图所示。
下列说法正确的是()
A.该装置能对水进行杀菌消毒 B.该装置能除去水中的颜色和异味
C.硬水经过该装置后可转化为软水D.自来水经过该装置后可得蒸馏水
19.用分子原子的观点分析下列变化,其中分子本身发生改变的是()A.水蒸发B.石蜡熔化C.水通电分解D.试管破裂20.(2020•海南)口罩能有效阻隔病毒传播,其作用原理相当于下列实验操作中的()A.溶解B.过滤C.蒸发D.结晶21.(2020•温州)中医药在治疗新冠肺炎中,为全球抗击疫情贡献了中国智慧。
下列中药煎制步骤与实验室过滤操作原理相同的是()
A.冷水浸泡B.加热煎制
C.取液弃渣D.装袋保存22.(2019•南京)过滤实验中,不需要使用的仪器是()
A.烧杯B.漏斗C.玻璃棒D.蒸发皿23.(2019•河池)净水的操作:①静置②蒸馏③过滤,相对净化程度由低到高的顺序是()A.①②③B.③②①C.③①②D.①③②24.(2018•上海)自来水生产中起杀菌消毒作用的是()
A.明矾B.氯气C.活性炭D.氯化铁
25.新冠肺炎疫情要求测量体温。
从微观角度解释温度计受热时水银柱上升的原因是()
A.汞原子体积变大B.汞原子数目增多
C.汞原子间间隔变大D.汞原子在不断运动
26.(2019•绥化)下列符号既能表示一种元素,又能表示该元素的一个原子,
还能表示一种物质的是()
A.H B.2H C.2N2D.S
27.电解水实验装置如图所示。
下列说法不正确的是()
A.水中可加入少量硫酸钠以增强导电性
B.a玻璃管中的电极与直流电源的负极相连
C.将燃着的木条放在b玻璃管尖嘴口,开启活塞,木条燃烧更旺
D.a、b两玻璃管中产生的气体质量之比是8:1
28.下列物质按照混合物、氧化物、单质顺序排列的是()
A.海水、氯酸钾、氢气 B.氧化铁、锰酸钾、水
C.硫酸铜、高锰酸钾、二氧化碳 D.空气、二氧化锰、氧气
29..理论上电解水得到氧气和氢气的体积比为1∶2。
某同学用碳棒作电极进行电解水实验,得到氧气和氢气的体积比小于1∶2,对产生此现象原因猜想不合理的是()
A. 部分氧气溶于水
B. 部分氧气与碳棒反应
C. 部分氧气被碳棒吸附
D. 部分氧气与氢气反应重新生成了水
30.下列物质中,前者属于纯净物,后者属于混合物的是()
A.液态氧,加热高锰酸钾后的固体物质 B.稀有气体,矿泉水
C.双氧水,五氧化二磷 D.汽水,四氧化三铁
二、填空题(共40分)
31.(每空1分,共5分)请用化学用语填空。
(1)2个氦原子。
(2)保持水的化学性质的最小粒子。
(3)硫酸铜中含有的阴离子。
(4)地壳中含量最多的金属元素与含量最多的非金属元素形成化合物的化学式。
(5)标出水中氢元素的化合价。
32.(每空2分,共8分)元素周期表是学习和研究化学的重要工具,根据下表回答问题:
(1)8号元素属于______(填“金属元素”或“非金属元素”)。
(2)11号元素与17号元素组成化合物的化学式为:___________。
(3)某粒子结构示童图为,该粒子所表示的符号是:__________
(4)决定元素化学性质的是_______________________________
33.(每空2分,共14分)建立宏观、微观和符号之间的相互联系是化学学科的特点。
(1)图甲为粒子之间的转化关系图,其中①表示的是。
(2)图乙中D为某粒子的结构示意图,当X=时,该粒子是原子。
符号为______ (3)图乙中B、C属于同种元素,因为相同。
B对应的微粒符号为_______ (4)由A、B形成的化合物的化学式为。
该物质是由_______(分子、原子还是离子)构成。
34.(每空1分,共13分).根据名称写化学式
(1)过氧化氢________(2)硝酸钠________(3)四氧化三铁_______ (4)氧化铁________ (5)碳酸钙_______ (6)氧化钙_____ (7)氯化铵_________ (8)硫酸钡______ (9)氢氧化钙_______ (10)氦气_________(11)高锰酸钾________ (12)锰酸钾_______(13)氯酸钾_________。
