龙贝格算法
龙贝格算法

第1章 龙贝格算法研究问题阐述计算二重积分⎰⎰=b adcdxdy y x f I ),(------------------------------------(1-1)对工科生要求计算如下3个二重积分:算例1:1110()1I x y dxdy =+=⎰⎰算例2:/2200()I x y dxdy πππ=+=⎰⎰-----------------------(1-2)算例3: 1130sin()x y I dxdy x y+=+⎰⎰通常将积分区间等分数依次取2k ,并得到相应的递推式子如(2-5)所示,相应对到过程不再累述详情可以参考教材。
1112221[()()],21[(21)]222k k k k k i b a T f a f b b a b a T T f a i --=-⎧=+⎪⎪⎨--⎪=++-⎪⎩∑----------------------------(2-5) 最终得到计算机计算步骤如下:(1)计算初值T1; (2)K 1;(3)计算新的T2,一直迭代计算2kT ;(4)精度控制:如果122||kk T T ε--<,则停止计算,并将2k T 作为积分的近似数值,否则循环将不停止。
对第四点,通常可以加入一个循环最高次数,防止程序陷入死循环。
function f=fxy(x,y,w) if w==1f=x+y; %函数1elseif w==2f=sin(abs(x-y)); %函数2elseif w==3f=sin(x+y)/(x+y); %函数3if x+y==0f=1;end;end;function gy=gy(y,a,b,w,error)k=1;lock=0;count=0;T1=(b-a)*(fxy(a,y,w)+fxy(b,y,w))/2;while lock==0&&count<100 %限定最多迭代20次T2=T2kx(y,T1,a,b,k,w);if abs(T2-T1)<errorgy=T2;lock=1;elseT1=T2;count=count+1;k=k+1;end;end% count%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%% 龙贝格算法%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%% 作者:XXXX %%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%% 时间:2012/4/16 %%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%clear all; clc;%% 详情见报告Romberg公式介绍部分clear all;clc;which=1; %表示计算的函数f1,f2,f3%积分区间a=0;if which==1||which==3b1=1;b2=1; %函数1和2的区间elseb1=pi;b2=pi/2; %函数2的区间end%% 计算主程序k=1;lock=0;count=0; %辅助量error=0.0001; %计算精度% gy=gy(y,a,b,w,error)T1=(b2-a)*(gy(a,a,b1,which,error)+gy(b2,a,b1,which,error))/2; while lock==0&&count<100 %限定最多迭代20次T2=T2ky(T1,a,b1,b2,k,which,error);if abs(T2-T1)<errorI=T2;lock=1;elseT1=T2;function T2kx=T2kx(y,T2kx_1,a,b,k,w)temp1=0;for i=1:2^(k-1)temp1=temp1+fxy(a+(2*i-1)*(b-a)/2^k,y,w);endT2kx=0.5*T2kx_1+temp1*(b-a)/2^k;function T2ky=T2ky(T2ky_1,a,b1,b2,k,w,error)temp1=0;for i=1:2^(k-1)temp1=temp1+gy(a+(2*i-1)*(b2-a)/2^k,a,b1,w,error);endT2ky=0.5*T2ky_1+temp1*(b2-a)/2^k;。
龙贝格积分算法实验[1]
![龙贝格积分算法实验[1]](https://img.taocdn.com/s3/m/1c3c3ec18bd63186bcebbcf8.png)
且 ( 为等份次数)
2.按梯形公式的递推关系,计算
3.按龙贝格公式计算加速值
4.精度控制。对给定的精度 ,若
则终止计算,并取 作为所求结果;否则 ,重复2~4步,直到满足精度为止。
问题
(1)程序运行如下:
I = Romberginterg(inline('x.^2.*exp(x)'),0,1,25,1e-6)
function I = GaussInterg(fun, type, a, b, tol)
% GaussInterg用Gauss型求积公式求积分,具体形式由使用者选取
%
% Synopsis: I = GaussInterg(fun, type, a, b)
% I = GaussInterg(fun, type, a, b, tol)
if nargin < 4
npanel = 25;
end
if nargin < 5
tol = 5e-9;
end
if nargin < 6
flag = 0;
end
T(1,1) = TrapezoidInteg(fun, a, b, npanel); %T0(h) = T(h)
err = 1; %初始化误差值
if nargin < 4
npanel = 25;
end
nnode = npanel + 1; %节点数=段数+ 1
h = (b-a)/(nnode-1); %步长
x = a:h:b; %将积分区间分段
f = feval(fun,x);%求节点处被积函数的值
I = h * ( 0.5*f(1) + sum(f(2:nnode-1)) + 0.5*f(nnode) );
龙贝格观测器离散算法

龙贝格观测器离散算法
龙贝格观测器是一种用于估计系统状态的观测器,常用于系统控制和滤波问题中。
它基于离散时间的模型,通过对系统输入输出信号进行观测和处理,得到对系统状态的估计。
龙贝格观测器的离散算法可以描述为以下步骤:
1. 定义系统模型:首先需要确定系统的离散状态空间模型,包括状态方程和输出方程。
状态方程用于描述系统状态的更新,输出方程用于描述系统输出信号和状态之间的关系。
2. 初始化观测器状态:将观测器的状态初始化为系统初值的估计值。
3. 观测器更新:根据观测器的状态和系统的输入信号,使用状态方程对观测器的状态进行更新。
观测器状态的更新可以通过状态方程的离散形式来实现。
4. 估计输出:根据观测器的状态和系统的输入信号,使用输出方程计算观测器的输出信号的估计值。
输出方程的计算可以通过观测器的状态和输入信号进行线性组合得到。
5. 更新观测器状态估计值:将观测器的状态估计值更新为观测器的状态和系统输出信号的估计值之间的误差。
6. 重复步骤3至5,直到达到预设的停止条件。
通过不断重复上述步骤,龙贝格观测器可以逐步优化状态估计值,使其接近真实的系统状态。
同时,龙贝格观测器还可以根据系统的输出进行校正,提高状态估计的准确性。
需要注意的是,龙贝格观测器的性能与状态方程和输出方程的准确性密切相关,对于有较大噪声或不确定性的系统,需要在模型中考虑噪声或不确定性,以提高观测器的鲁棒性。
同时,也需要根据具体应用场景对观测器的采样周期和参数进行选择和调整。
4.4龙贝格求积公式

4 1 T1 ( k − 1) = T0 ( k ) − T0 ( k − 1) 3 3 16 1 T2 ( k − 1) = T1 ( k ) − T1 ( k − 1) 15 15 64 1 T3 ( k − 1) = T2 ( k ) − T2 ( k − 1) 63 63
k = 1 ,2 ,L
因此有如下递推公式 b−a [ f ( a ) + f (b )] T0 (0) = 2
1 T0 (k ) = T0 (k − 1) + hk 2
2 k −1 −1 j =0
∑ f (a + (2 j + 1)h )
k
k = 1, 2 ,L
上式称为递推的梯形公式
思考
递推梯形公式加上一个控制精度,即 可成为自动选取步长的复合梯形公式
带权)正交。 不大于n 不大于 的多项式 P(x) (带权)正交。
k =0
n
x 证明: 证明: “⇒”0 … xn 为 Gauss 点, 则公式 ∫a ρ( x) f ( x)dx ≈ ∑Ak f ( xk ) k=0 次代数精度。 至少有 2n+1 次代数精度。 对任意次数不大于 的多项式 不大于n 对任意次数不大于 ⇔ 求w(x) Pm(x), Pm(x) w(x)的次数 , 的次数 求 Gauss 点 不大于2n+1,则代入公式应精确成立: 精确成立: 不大于 ,则代入公式应精确成立 n 0 b ∫ ρ ( x ) Pm ( x ) w ( x )dx = ∑ Ak Pm ( x k ) w ( x k ) = 0
外推加速公式
由复合梯形公式的余项公式
I − T2 n 1 ≈ I − Tn 4 1 I − T2 n ≈ (T2 n − Tn ) 3 4 1 I ≈ T2 n − Tn 3 3 1 f ( x 1 )) − Tn j+ 3 2
龙贝格算法

龙贝格积分1. 算法原理采用复化求积公式计算时,为使截断误差不超过ε,需要估计被积函数高阶导数的最大值,从而确定把积分区间[]b a ,分成等长子区间的个数n 。
首先在整个区间[]b a ,上应用梯形公式,算出积分近似值T1;然后将[]b a ,分半,对 应用复化梯形公式算出T2;再将每个小区间分半,一般地,每次总是在前一次的基础上再将小区间分半,然后利用递推公式进行计算,直至相邻两个值之差小于允许误差为止。
实际计算中,常用ε≤-n n T T 2作为判别计算终止的条件。
若满足,则取n T f I 2][≈;否则将区间再分半进行计算,知道满足精度要求为止。
又经过推导可知,∑=-++=ni i i n n x x f h T T 112)2(221,在实际计算中,取kn 2=,则k a b h 2-=,112)1*2(2++--+=+k i i ab i a x x 。
所以,上式可以写为∑=++--+-+=+kk i k k ab i a f a b T T 211122)2)12((2211k开始计算时,取())()(21b f a f ab T +-=龙贝格算法是由递推算法得来的。
由梯形公式得出辛普森公式得出柯特斯公式最后得到龙贝格公式。
根据梯形法的误差公式,积分值n T 的截断误差大致与2h 成正比,因此步长减半后误差将减至四分之一,即有21114n n T T -≈-将上式移项整理,知2211()3n n n T T T -≈-由此可见,只要二分前后两个积分值n T 和2n T 相当接近,就可以保证计算保证结果计算结果2n T 的误差很小,这种直接用计算结果来估计误差的方法称作误差的事后估计法。
按上式,积分值2n T 的误差大致等于21()3n n T T -,如果用这个误差值作为2n T 的一种补偿,可以期望,所得的()222141333n n n n n T T T T T T =+-=-应当是更好的结果。
龙贝格算法求数值积分程序说明及流程图
In(k,2)=4*In(k+1,1)/3-In(k,1)/3;
end
flag(2)=i+3;
for k=flag(3)+1:i+2
In(k,3)=16*In(k+1,2)/15-In(k,2)/15;
end
flag(3)=i+2;
for k=flag(4)+1:i+1
end
In(i+5,1)=In(i+5,1)/2^(i+5)+In(i+4,1)/2;
In(i+4,2)=4*In(i+5,1)/3-In(i+4,1)/3;
In(i+3,3)=16*In(i+4,2)/15-In(i+3,2)/15;
In(i+2,4)=64*In(i+3,3)/63-In(i+2,3)/63;
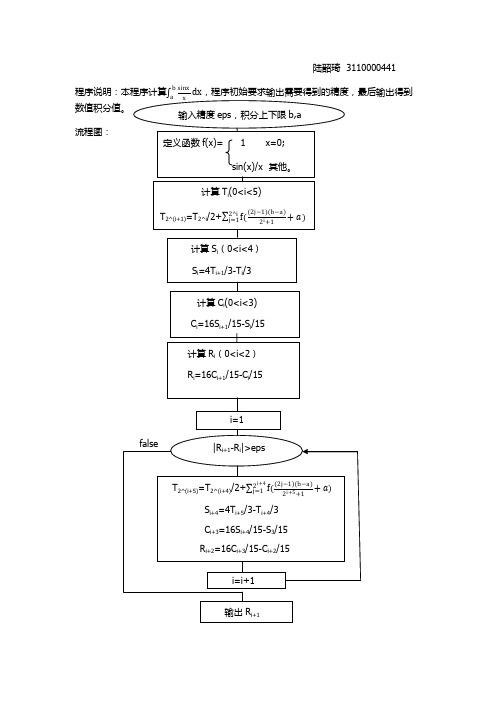
陆韶琦 3110000441
程序说明:本程序计算
数值积分值。
b sinx
a x
dx,程序初始要求输出需要得到的精度,最后输出得到
输入精度 eps,积分上下限 b,a
流程图:
定义函数 f(x)=
1
x=0;
sin(x)/x 其他。
计算 Ti(0<i<5)
T2^(i+1)=T2^i/2+
2j−1 b−a
2^i
j=1 f(
2 i +1
+ )
计算 Si(0<i<4)
Si=4Ti+1/3-Ti/3
计算 Ci(0<i<3)
龙贝格求积算法

龙贝格求积算法
龙贝格求积算法(Romberg Integration Algorithm)是用于数
值积分的一种高效的迭代方法。
它通过连续的二分、四分、八分等等
区间的方式,逐渐逼近最终的积分值,从而提高计算的精度。
该算法的基本思想是利用Richardson外推技术,结合复合梯形
法则,逐渐缩小区间并增加采样点数,以得到更精确的积分值。
下面
我们来介绍龙贝格求积算法的步骤:
1. 将积分区间[a, b]进行二分,得到初始的两个子区间;
2. 对每个子区间应用复合梯形公式进行数值积分,可以得到初始的近似积分值;
3. 利用Richardson外推技术,对不同精度的积分值进行线性组合,得到更高精度的积分值;
4. 重复步骤2和3,将积分区间不断地二分,并逐步增加采样点数,直到达到所需的精度要求。
龙贝格求积算法的主要优点是在保持高精度的能够有效减少计算量。
该算法还可以通过预先计算一些常见函数在一些固定的点上的值,以进一步提高计算速度。
总结起来,龙贝格求积算法通过利用复合梯形法则和Richardson 外推技术,逐渐逼近积分值的精确结果。
它是一种高效且精确的数值
积分方法,广泛应用于科学计算和工程领域。
龙贝格算法实验报告

实验二:龙贝格算法一、实验目的1、通过本实验理解数值积分与微分的基本原理2、掌握数值积分中常见的复合求积公式的编程实现3、掌握龙贝格算法的基本思路和迭代步骤二、实验原理三、运行结果三、代码using System;using System.Collections.Generic;using System.Linq;using System.Text;namespace ConsoleApplication4{public delegate double F(double x);class Program{const double Precision = 0.00000000001;const int MAXRepeat = 10;static double f1(double x){double s=4/(1+x*x );return s;}static double Romberg(double a,double b, F f){int m,n,k;double[] y = new double[MAXRepeat];double h,ep,p,xk,s,q=0;h=b-a;y[0]=h*(f(a)+f(b))/2.0;//计算T`1`(h)=1/2(b-a)(f(a)+f(b));m=1;n=1;ep=Precision+1;while((ep>=Precision)&&(m<MAXRepeat)){p=0.0;for(k=0;k<n;k++){xk = a + (k + 0.5) * h; // n-1p = p + f(xk); //计算∑f(xk+h/2),T} // k=0p = (y[0] + h * p) / 2.0; //T`m`(h/2),变步长梯形求积公式s = 1.0;for (k = 1; k <= m; k++){s = 4.0 * s;// pow(4,m)q = (s * p - y[k - 1]) / (s - 1.0);//[pow(4,m)T`m`(h/2)-T`m`(h)]/[pow(4,m)-1],2m阶牛顿柯斯特公式,即龙贝格公式y[k - 1] = p;p = q;}ep = Math.Abs(q - y[m - 1]);//前后两步计算结果比较求精度m = m + 1;y[m - 1] = q;n = n + n; // 2 4 8 16h = h / 2.0;//二倍分割区间}return q;}static void Main(string[] args){double a, b, result;Console.WriteLine("请输入积分下限:");a = Convert.ToDouble(Console.ReadLine());Console.WriteLine("请输入积分上限:");b = Convert.ToDouble(Console.ReadLine());result = Romberg(a, b, new F(f1));Console.Write("定积分计算结果为:{0}:", result);Console.ReadLine();}}}四、分析本次试验使我认识到了计算机计算能力的强大,通过本次实验对数值积分与微分的基本原理有了深刻理解。
龙贝格观测器离散算法

龙贝格观测器离散算法1. 介绍龙贝格观测器(Longberg observer)是一种用于状态估计的离散算法。
它通过测量系统的输出和输入,利用差分方程来估计系统的状态。
该算法广泛应用于控制系统、信号处理和机器学习领域。
龙贝格观测器离散算法的核心思想是通过对系统状态的离散估计,从而实现对系统行为的预测和控制。
该算法基于系统的动态模型和测量值,使用递推方程来更新状态估计值。
2. 算法原理2.1 系统模型龙贝格观测器离散算法的前提是系统模型已知。
系统模型可以表示为以下离散时间方程:x(k+1) = Ax(k) + Bu(k)y(k) = Cx(k) + Du(k)其中,x(k)是系统的状态向量,u(k)是输入向量,y(k)是输出向量,A、B、C和D是系统的参数矩阵。
2.2 离散观测器方程龙贝格观测器的离散方程可以表示为以下形式:x^(k+1) = (A - L*C) * x^(k) + L * y(k)其中,x^(k)是状态估计向量,L是观测器增益矩阵,通过调整观测器增益可以优化状态估计的性能。
2.3 观测器增益矩阵的计算观测器增益矩阵L的计算可以通过最小二乘法或者极小化估计误差的指标来实现。
常用的方法有最小二乘法、极小化误差平方和、极小化误差方差等。
2.4 状态估计误差状态估计误差可以通过以下公式计算:e(k) = x(k) - x^(k)其中,e(k)是状态估计误差向量。
3. 算法步骤龙贝格观测器离散算法的步骤如下:1.初始化状态估计向量x^(0)和观测器增益矩阵L。
2.根据系统模型和测量值,计算观测器增益矩阵L。
3.根据观测器方程,更新状态估计向量x^(k)。
4.根据状态估计向量x^(k)和观测器方程,计算状态估计误差e(k)。
5.重复步骤2至4,直到达到预定的收敛条件。
4. 算法优势和应用4.1 优势龙贝格观测器离散算法具有以下优势:•适用于离散时间系统:该算法适用于离散时间系统,可以对系统的状态进行准确估计。
龙贝格积分算法实验

实验题目2 Romberg 积分法摘要考虑积分()()b aI f f x dx =⎰欲求其近似值,可以采用如下公式: (复化)梯形公式 11[()()]2n ii i hT f x f x-+==+∑2()12b a E h f η-''=-[,]a b η∈ (复化)辛卜生公式 11102[()4()()]6n i i i i hS f x f x f x -++==++∑4(4)()1802b a h E f η-⎛⎫=- ⎪⎝⎭ [,]a b η∈ (复化)柯特斯公式 111042[7()32()12()90n i i i i hC f x f x f x -++==+++∑31432()7()]i i f xf x +++6(6)2()()9454b a h E f η-⎛⎫=- ⎪⎝⎭[,]a b η∈ 这里,梯形公式显得算法简单,具有如下递推关系121021()22n n n i i h T T f x -+==+∑因此,很容易实现从低阶的计算结果推算出高阶的近似值,而只需要花费较少的附加函数计算。
但是,由于梯形公式收敛阶较低,收敛速度缓慢。
所以,如何提高收敛速度,自然是人们极为关心的课题。
为此,记0,k T 为将区间[,]a b 进行2k等份的复化梯形积分结果,1,k T 为将区间[,]a b 进行2k等份的复化辛卜生积分结果,2,k T 为将区间[,]a b 进行2k等份的复化柯特斯积分结果。
根据李查逊(Richardson )外推加速方法,可得到1,11,,0,1,2,40,1,2,41m m k m km k m k T T T m -+-=-⎛⎫=⎪=-⎝⎭可以证明,如果()f x 充分光滑,则有,lim ()m k k T I f →∞= (m 固定),0lim ()m m T I f →∞=这是一个收敛速度更快的一个数值求积公式,我们称为龙贝格积分法。
5.3龙贝格(Romberg)算法

|R1-C2|<ε
否 k=4 计算 T
、S2k -1、C2k −2、R2k −3 2
k
输出积分值 I
结束
| R2k −3 − C2k −2 |< ε
否 k=k+1
是
17
龙贝格算法源程序
#include "stdio.h" #include "math.h" main() { double f(double x); double t0fun(int k,double t0[50]);
k −3
if(fabs(t3[k-3]-t2[k-2])<0.000000001) // 若 | R2 { printf("k=%3d,I=%12.9f\n",k,t3[k-3]); break; } } } double f(double x) { double y; y=sqrt(1.0+x*x); return y; }
龙贝格romberg算法等份分割为的积分区间将定积分不变等份而分割为如果将上式称为递推的梯形公式递推梯形公式加上一个控制精度即可成为自动选取步长的复合梯形公式具体的方法请同学们完成思考因此由复合simpson公式的余项可得151615161516自己证明当然同样由复合cotes公式的余项63646364636415166364加速公式以上整个过程称为龙贝格romberg算法1012龙贝格算法可用下表表示
1 b − a n −1 1 b − a n −1 1 = Tn + ∑ f ( x j + 1 ) = 2 Tn + 2 n ∑ f ( a + ( j + 2 )h) 2 2n j =0 j =0 2
龙贝格求积法

h p
)
Fk
q pk 1
(h)
,k
0,1, 2,L
定义的序列{Fk(h)}有
Fk (h) F (0) an(n)1h pn1
a h (n) pn2 n2
a h (n) pn3 n3
L
,
其中an(n)k (k 1, 2, 3,L )与h 无关,q>1.
Richardson外推法应用非常广泛且有效,下面介绍应用 于数值积分的情形。
16 15
S4
1 15
S2
3.1415946
64 1 R1 63 C2 63 C1 3.141586292
1 sin x
算例结2 果用见R表om4-b5(ekr代g算表法二计分算次I数)。0 计x算值dx.的得误到差的不梯超形过值,计
0.510-6.
表4-5
k
T2k
S k 1 2
§4.4 外推原理与Romberg求积方法
4.4.1 外推原理
在科学与工程计算中,很多算法与步长h有关,特别是数值 积分、数值微分和微分方程数值解的问题。对于这些算法,我 们可以通过外推技巧提高计算精度。
例1 计算的近似值。
龙贝格(Romberg)算法的应用实验报告

Lab4 龙贝格(Romberg)算法的应用下面图1中的塑料雨蓬材料是由图2中所示的长方形平板塑料材料压制而成。
图1 图2已知图1的横截面曲线形状满足函数,则给定了雨蓬的长度后,要求需要平板原材料的长度。
函数接口定义:double Integral(double a, double b, double (*f)(double x, double y, double z), double TOL, double l, double t)在接口定义中:a、b分别为定积分的上、下界,f是积分核函数,其中x是积分哑元,y、z是本题目定义的特殊参数,分别对应中的l和t;TOL是要求积分达到的精度;l和t传入裁判输入的参数l和t的值。
另注意:的单位是厘米,输出的长度值要求以米为单位。
裁判程序样例如下:#include<stdio.h>#include<math.h>double f0( double x, double l, double t ){ /* 弧长积分的核函数*/return sqrt(1.0+l*l*t*t*cos(t*x)*cos(t*x));}double Integral(double a, double b, double (*f)(double x, double y, double z), double TOL, double l, double t);int main(){double a=0.0, b, TOL=0.005, l, t;while (scanf("%lf %lf %lf", &l, &b, &t) != EOF)printf("%.2f\n", Integral(a, b, f0, TOL, l, t));return 0;}裁判输入样例:2 100 1标准输出样例:1.68实验报告:1.求解步骤参照书上的龙贝格求积算法2.步骤①利用k=0;h=b-a;T[0][0]=(h/2)*(f(a,l,t)+f(b,l,t));求解T0(0)3.求解T0(0)到T0(k)的值由公式h=b−an 及h=b−a2k可得n=2k其中h为步长,n为二分次数又由递推公式:T2n=12T n+ℎ2∑f(xk+12)n−1k=0得T2k+1=12T2k+b−a2k+1∑f[a+b−a2k+1(2i−1)]2k−1i=1,k=0,1,2,3~其中xk+12= a+ℎ2(2i−1)。
龙贝格算法及应用

龙贝格算法及应用龙贝格算法是一种数值计算方法,用于计算数值积分的近似解。
它的应用范围广泛,涉及到物理、工程、金融等领域。
在下面的回答中,我将详细介绍龙贝格算法的原理、步骤和一些应用实例。
原理:龙贝格算法是一种基于复化梯形公式的数值积分算法。
它通过不断提高插值点数目,逐步提高数值积分的精度。
步骤:1. 首先,我们选择一个足够小的初始步长h,然后根据复化梯形公式计算积分的近似值I(h)。
2. 接下来,我们将步长h减半,再次计算积分的近似值I(h/2)。
3. 然后,根据复化梯形公式,通过I(h/2)和I(h)计算出一个更高阶的数值积分近似值I(2h)。
4. 重复上述步骤,每次将步长减半,直到达到所需的精度。
应用:龙贝格算法广泛应用于数值积分问题,特别是对于某些复杂函数,无法通过解析方法求得精确解的情况下。
以下是一些具体的应用实例:1. 物理学中的轨道运动描述:龙贝格算法可以用来计算行星围绕太阳的轨道运动,以及其他天体运动的数值积分问题。
2. 工程学中的电路分析:通过对电路中的电流和电压的积分,可以计算电路中的功率、能量等物理量。
3. 金融学中的期权定价:龙贝格算法可以用于计算期权定价模型中的积分,以估计期权的市场价值。
4. 数理统计学中的概率密度函数估计:通过计算概率密度函数的积分,可以对数据的分布进行建模和估计。
5. 计算机图形学中的曲线绘制:龙贝格算法可以用来计算曲线的长度、面积、甚至绘制曲线的插值。
总结:龙贝格算法是一种常用的数值积分算法,通过逐步提高插值点数目,能够对于复杂函数进行积分近似。
它在物理、工程、金融等领域有广泛的应用。
通过应用龙贝格算法,我们可以获得数值计算问题的近似解,从而解决实际问题中的积分计算需求。
龙贝格求 积分

龙贝格(Romberg )求积法1.算法理论Romberg 求积方法是以复化梯形公式为基础,应用Richardson 外推法导出的数值求积方法。
由复化梯形公式 )]()(2)([2222b f h a f a f h T +++=可以化为)]()]()([2[212112h a f h b f a f hT +++==)]([21211h a f h T ++一般地,把区间[a,b]逐次分半k -1次,(k =1,2,……,n )区间长度(步长)为kk m a b h -=,其中mk =2k -1。
记k T =)1(k T 由)1(k T =]))12(([21211)1(1∑=---++km j k k k h j a f h T 从而⎰badxx f )(=)1(kT-)(''122k f h a b ξ- (1)按Richardson 外推思想,可将(1)看成关于k h ,误差为)(2k h O 的一个近似公式,因而,复化梯形公式的误差公式为⎰badxx f )(-)1(k T =......4221++k k h K h K =∑∞=12i i k i h K (2)取1+k h =k h 21有 ⎰ba dx x f )(-)1(1+k T =∑∞=+121221i ik ii hK (3)误差为)(2jh O 的误差公式 )(j kT=)1(-j kT+141)1(1)1(------j j k j k T T2.误差及收敛性分析(1)误差,对复化梯形公式误差估计时,是估计出每个子区间上的误差,然后将n 个子区间上的误差相加作为整个积分区间上的误差。
(2)收敛性,记h x i =∆,由于∑=++=ni i i n x f x f h f T 01))]()([2)(=))()((21101∑∑-==∆+∆n i ni i i i i x x f x x f上面两个累加式都是积分和,由于)(x f 在区间],[b a 上可积可知,只要],[b a 的分划的最大子区间的长度0→λ时,也即∞→n 时,它们的极限都等于积分值)(f I 。
龙贝格观测器离散算法

龙贝格观测器离散算法(最新版)目录一、龙贝格观测器概述1.龙贝格观测器的定义2.龙贝格观测器的作用二、离散化龙贝格观测器的原理1.离散化龙贝格观测器的构造方法2.离散化龙贝格观测器的输出信号三、离散化龙贝格观测器在无传感器控制中的应用1.基于 PMSM 的数学模型2.利用观测器模型进行无传感器控制四、离散化龙贝格观测器的优点1.避免系统抖振2.提高动态响应和估算精度正文一、龙贝格观测器概述龙贝格观测器(Luong-Berg 观测器)是一种用于估计线性时变系统的状态的观测器。
它可以实时观测到系统的状态,并通过反馈控制来调整系统的输出,使其达到预期的目标。
龙贝格观测器被广泛应用于控制系统中,例如,机器人控制、电力系统控制等领域。
二、离散化龙贝格观测器的原理离散化龙贝格观测器是一种基于离散时间系统的观测器。
它可以通过构造一个观测器模型,对系统的状态进行实时估计。
观测器模型的输出信号可以用来反馈调整系统的输入,从而实现对系统状态的跟踪。
离散化龙贝格观测器的构造方法主要有两种:一种是基于系统输入输出数据的观测器,另一种是基于系统数学模型的观测器。
基于输入输出数据的观测器主要通过观测系统的输入输出数据,来估计系统的状态。
而基于数学模型的观测器则是通过构造一个与系统数学模型相对应的观测器模型,来估计系统的状态。
三、离散化龙贝格观测器在无传感器控制中的应用在无传感器控制中,观测器的作用尤为重要。
由于没有传感器的反馈信息,系统的状态无法直接观测到。
因此,需要借助观测器来估计系统的状态。
离散化龙贝格观测器在无传感器控制中的应用,主要是基于 PMSM (永磁同步电机)的数学模型。
PMSM 是一种常用的电机类型,其数学模型可以用来描述电机的动态行为。
通过将 PMSM 的数学模型与离散化龙贝格观测器相结合,可以实现对电机状态的实时估计。
在无传感器控制中,观测到的电机状态可以用来调整电机的输入,从而实现对电机的精确控制。
四、离散化龙贝格观测器的优点离散化龙贝格观测器具有以下优点:1.避免系统抖振:由于离散化龙贝格观测器采用线性控制策略,因此可以避免系统抖振的现象。
龙贝格算法

龙贝格算法龙贝格算法是一种用于求解数值积分的高效算法。
它是由龙格(Richardson)和贝格(Bulirsch)两位数学家发明的,因此得名为龙贝格算法。
算法原理龙贝格算法的核心思想是通过不断迭代、细化步长来逼近积分值。
其具体步骤如下:1.设定初始步长ℎ和阶数k:选择合适的初始步长ℎ和阶数k,通常会根据被积函数的性质和精度要求来确定。
2.计算第一次迭代结果:根据初始步长ℎ和阶数k,计算第一次迭代的积分值。
3.递推计算迭代结果:利用迭代公式,不断调整步长ℎ和次数k,计算更高阶的近似积分值。
4.检查收敛性:根据一定的收敛准则,判断当前近似积分值是否满足精度要求,若满足则停止迭代,否则继续调整步长和次数。
5.输出最终结果:当迭代满足精度要求后,输出最终的数值积分结果。
算法优势龙贝格算法具有以下优势:•高效性:通过迭代细化步长和阶数,可以快速求得较为精确的数值积分结果。
•适用性:对于各种类型的函数,龙贝格算法都有较好的适用性,能够处理不同的积分情况。
•精度控制:通过调整步长和阶数,可以灵活控制算法的精度,满足不同精度要求的积分计算。
算法应用龙贝格算法在数学、物理、工程等领域有着广泛的应用。
它常用于求解复杂函数的数值积分、积分方程求解、数值微分方程的数值解等问题。
在科学计算、模拟仿真、优化等领域都有着重要的地位。
结语龙贝格算法作为一种经典的数值积分算法,凭借其高效性、适用性和精度控制等优势,为数值计算领域提供了重要的工具。
在实际问题中,合理应用龙贝格算法可以提高计算效率,得到准确的数值结果。
希望本文能够让读者更深入了解龙贝格算法的原理和应用,为相关领域的数值计算工作提供帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2)理查森外推加速 从梯形公式出发, 将区间[a,b]逐次二分可以提高求积公式精度, 当[a,b] 分为 n 等份时,若记T������ = T ℎ ,当区间[a,b]分为 2n 等份时,则有 T2������ = T
ℎ 2
。再有泰勒公式展开为: T ℎ = ������ + ������1 ℎ2 + ������2 ℎ+ ⋯ +
建立一个命名为Romberg.m的function文件:
function[T]=Romberg(f,a,b,e) T=zeros(10,10); T(1,1)=(b-a)/2*(f(a)+f(b)); for k=2:10, sum=0; for i=1:2^(k-2), x=a+(2*i-1)*(b-a)/2^(k-1); sum=sum+f(x); end T(k,1)=T(k-1,1)/2+[(b-a)/2^(k-1)]*sum; for j=2:k, end %第一列用递推梯形公式 %定义龙贝格函数 %定义10阶的零元矩阵
1 3/2 ������ 0
������������。
算,并取������ ������, ������ ≈ ������ ;否则令 k=k+1,转(3)继续计算。 6)下图为我按照自己的算法所设计的示意表: 算法设计表:
k 1 2 3 4 …
h b-a (b-a)/2 (b-a)/4 (b-a)/8 …
������ ������, 1 T(1,1) T(2,1) T(3,1) T(4,1)
������ ������, 2
������ ������, 3
������ ������, 4
������ ������, 5
T(2,2) T(3,2) T(4,2) T(3,3) T(4,3) T(4,4)
注:同一列表示求梯形值的递推过程,同一行表示外推加速的过程。
三、算法的 matlab 程序代码及实例
四、Romberg公式讨论
龙贝格公式是在梯形公式, 辛普森公式以及柯特斯公式关系的基 础上,构造出的一中加速计算积分的方法。相对于利用递推的复合梯 形公式计算积分时,需要多次二分才能达到预定的精度。龙贝格积分 利用外推加速可以极大的提高收敛的速度。 也就是说在不增加计算量 的前提下极大地提高了误差的精度。 而且龙贝格公式在计算积分时,区间不断二分,这样前一次分半 以后的函数值仍然能够保存下来,可以继续利用,这一点非常利于编 程。 当然对于f(x)不是特别光滑的函数也可以用龙贝格算法计算, 不过收敛速度相对会慢一点。 这种情况下直接使用复合辛普森公式也 可以计算。比如说上述计算的积分I =
T(k,j)=T(k,j-1)*4^(j-1)/(4^(j-1)-1)-T(k-1,j-1)/(4^(j-1)-1); %外推加速 if k>5 %从第6行开始判断下面的精度要求,如果没有这个判断,计算可能发生错误 if(abs(T(k,k)-T(k-1,k-1))<e)%判断是否达到精度要求 disp(‘当绝对误差e<10^(-5)时,龙贝格算法求得积分值为:’); fprintf('%7.6f', T(k,k)); break; end end end if(k>=11) disp('溢出'); end %超过矩阵大小则自动提示
Romberg 算法
一、 算法思路
1)梯形法的递推化 为了提高求积精度,实际计算时若精度不够可以将步长逐次分半,以 此求积分
b ������ (������)的近似值。 首先将[a,b]分为 n 等份, 共有 n+1 个分点, ������
2
注意到每个子区间 [ ������k , ������������ +1 ] 经过二分只增加了一个分点: ������������ +1 =
(������ ) (������ ) (������ )
的 m 次加速值,则依理查森外推加速公式,可以得到: ������m =
(������ ) 4 ������ 4 ������ −1
������������ −1 −
(������−1)
������ ������ ,k 4 ������ −1 ������ −1
1)计算积分I =
1 3/2 ������ 0
������������
注: 利用函数f=inline(‘’)输入函数, 再用Romberg (f,a,b,e) 实现函数调用来计算积分值。 2)计算积分I =
2������ 0
������������������������������������������
(0) (������ )
=
h 2
������ ������ + ������ (������) . 表示初始时的
梯形值,k → 10逐渐往后递推求梯形值; 3) 求梯形值������1
������−������ 2(������−1)
, 即按照递推公式 (1.1) 计算T k, 1 = ������0 ;
ℎ 2
,然后记 C ℎ =
16S
ℎ 2
−S ℎ 3
,易知 C ℎ = C������ ,即将 [a,b]
分为 n 等份得到的复合柯特斯公式……如此继续下去就可以得到龙 贝格公式。我们重新引入记号������0 ℎ = T ℎ , ������1 ℎ = S ℎ 等,从而
可以将上述公式写成统一的形式: ������������ ℎ = ������ + ������1 ℎ2(������ +1) + ������2 ℎ2(������ +2) + ⋯. 上述处理方法就称为理查森外推加速法。 3)龙贝格求积算法 设以 ������0 表示二分 k 次后求得的梯形值,且以 ������������ 表示序列 ������0
1
= 1,2 ⋯.(1.2)
这就是龙贝格求积算法。
二、 算法的程序设计(matlab 实现)
1 )我们在 matlab 中定义函数 function[T]=Romberg(f,a,b,e) 。令 T=zeros(10,10), 将其初始化为一个 10 阶的零元方阵, 以此保存������m 。 f 代表被积函数,a,b 分别是积分限,e 是我们要求的绝对误差; 2)取 k=1,h=b-a,求T 1,1 = ������0
ℎ 2
������������ ℎ2������ + ⋯ , 然 后 用 h/2 代 替 h 有 T
2������ ������������ ℎ 2
= ������ + ������1
ℎ2 4
+ ������2
ℎ4 16
+⋯+
+ ⋯。再记S ℎ =
4T
ℎ 2
−T ℎ 3
,这将复合梯形公式的的误差阶
O(ℎ2 )提高到了 O(ℎ4 ),并且易知S ℎ = S������ ,即将[a,b]分为 n 等份得到 的复合辛普森公式。 与上述做法类似,从S ℎ 出发,当 n 在增加一倍,即 h 减少一半 时得到 S
1 2
(������k , +������������ +1 )。 然后利用复合梯形求积公式可以推导出二分前后的积分
值递推关系(h 代表二分前的步长) : T2������ = T������ +
2 1 ℎ 2 ������−1 (1.1) ������ =0 ������ (������������ +1 )。
������
4)求加速值,按公式(1.2)逐个求出 T 矩阵的第 k 行其余各元素 ������ ������, ������ (j = 2,3 ⋯ k. ); < ������ (预先给定的精度),则终止计
5)若 ������ ������, ������ − ������ ������ − 1, ������ − 1
