数据结构实验(矩阵的运算)
数据结构实验五矩阵的压缩存储与运算学习资料

数据结构实验五矩阵的压缩存储与运算第五章矩阵的压缩存储与运算【实验目的】1. 熟练掌握稀疏矩阵的两种存储结构(三元组表和十字链表)的实现;2. 掌握稀疏矩阵的加法、转置、乘法等基本运算;3. 加深对线性表的顺序存储和链式结构的理解。
第一节知识准备矩阵是由两个关系(行关系和列关系)组成的二维数组,因此对每一个关系上都可以用线性表进行处理;考虑到两个关系的先后,在存储上就有按行优先和按列优先两种存储方式,所谓按行优先,是指将矩阵的每一行看成一个元素进行存储;所谓按列优先,是指将矩阵的每一列看成一个元素进行存储;这是矩阵在计算机中用一个连续存储区域存放的一般情形,对特殊矩阵还有特殊的存储方式。
一、特殊矩阵的压缩存储1. 对称矩阵和上、下三角阵若n阶矩阵A中的元素满足= (0≤i,j≤n-1 )则称为n阶对称矩阵。
对n阶对称矩阵,我们只需要存储下三角元素就可以了。
事实上对上三角矩阵(下三角部分为零)和下三角矩阵(上三角部分为零),都可以用一维数组ma[0.. ]来存储A的下三角元素(对上三角矩阵做转置存储),称ma为矩阵A的压缩存储结构,现在我们来分析以下,A和ma之间的元素对应放置关系。
问题已经转化为:已知二维矩阵A[i,j],如图5-1,我们将A用一个一维数组ma[k]来存储,它们之间存在着如图5-2所示的一一对应关系。
任意一组下标(i,j)都可在ma中的位置k中找到元素m[k]= ;这里:k=i(i+1)/2+j (i≥j)图5-1 下三角矩阵a00 a10 a11 a20 … an-1,0 … an-1,n-1k= 0 1 2 3 …n(n-1)/2 …n(n+1)/2-1图5-2下三角矩阵的压缩存储反之,对所有的k=0,1,2,…,n(n+1)/2-1,都能确定ma[k]中的元素在矩阵A中的位置(i,j)。
这里,i=d-1,(d是使sum= > k的最小整数),j= 。
2. 三对角矩阵在三对角矩阵中,所有的非零元素集中在以主对角线为中心的带内状区域中,除了主对角线上和直接在对角线上、下方对角线上的元素之外,所有其它的元素皆为零,见图5-3。
数据结构矩阵实验报告

一、实验目的和要求(1)掌握各种特殊矩阵如对称矩阵、上下三角矩阵和对角矩阵的压缩存储方法。
(2)掌握稀疏矩阵的各种存储结构以及基本运算实现算法。
(3)掌握广义表的递归特性、存储结构以及基本运算实现算法。
二、实验环境、内容和方法实验内容:①打开Visual C++6.0并输入实验指导书上的程序,并进行调试和运行。
②自行尝试编写第六个实验。
实验方法:(一)综合运用课本所学的知识,用不同的算法实现在不同的程序功能。
(二)结合指导老师的指导,解决程序中的问题,正确解决实际中存在的异常情况,逐步改善功能。
(三)根据实验内容,编译程序。
实验环境:Windows xp Visual C++6.0三、实验过程描述实验①以下是一个5*5阶的螺旋方阵。
设计一个程序输出该形式的n*n阶方阵。
1 2 3 4 516 17 18 19 615 24 25 20 714 23 22 21 813 12 11 10 9一、打开Visual C++6.0并输入如下程序#include <stdio.h>#define MaxLen 10void fun(int a[MaxLen][MaxLen],int n){int i,j,k=0,m;if (n%2==0)m=n/2;elsem=n/2+1;for (i=0;i<m;i++){for (j=i;j<n-i;j++){k++;a[i][j]=k;}for (j=i+1;j<n-i;j++){k++;a[j][n-i-1]=k;}for (j=n-i-2;j>=i;j--){k++;a[n-i-1][j]=k;}for (j=n-i-2;j>=i+1;j--){k++;a[j][i]=k;}}}void main(){int n,i,j;int a[MaxLen][MaxLen];printf("\n");printf("输入n(n<10):");scanf("%d",&n);fun(a,n);printf("%d阶数字方阵如下:\n",n);for (i=0;i<n;i++){for (j=0;j<n;j++)printf("%4d",a[i][j]);printf("\n");}printf("\n");}二、,编译并连接此程序,如图三、运行此程序,如图实验②假设n*n的稀疏矩阵A采用三元组表示,设计一个程序实现如下功能:(1)生成如下两个稀疏矩阵的三元组a和b:a:1 0 3 0 b: 3 0 0 00 1 0 0 0 4 0 00 0 1 0 0 0 1 00 0 1 1 0 0 0 2(2)输出a转置矩阵的三元组(3)输出a+b的三元组(4) 输出a*b的三元组一、输入如图所示程序#include <stdio.h>#define N 4typedef int ElemType;#define MaxSize 100typedef struct{ int r;int c;ElemType d;} TupNode;typedef struct{ int rows;int cols;int nums;TupNode data[MaxSize];} TSMatrix;void CreatMat(TSMatrix &t,ElemType A[N][N]){int i,j;t.rows=N;t.cols=N;t.nums=0;for (i=0;i<N;i++){for (j=0;j<N;j++)if (A[i][j]!=0){t.data[t.nums].r=i;t.data[t.nums].c=j;t.data[t.nums].d=A[i][j];t.nums++;}}}void DispMat(TSMatrix t){int i;if (t.nums<=0)return;printf("\t%d\t%d\t%d\n",t.rows,t.cols,t.nums);printf("\t------------------\n");for (i=0;i<t.nums;i++)printf("\t%d\t%d\t%d\n",t.data[i].r,t.data[i].c,t.data[i].d); }void TranMat(TSMatrix t,TSMatrix &tb){int p,q=0,v;tb.rows=t.cols;tb.cols=t.rows;tb.nums=t.nums;if (t.nums!=0){for (v=0;v<t.cols;v++)for (p=0;p<t.nums;p++)if (t.data[p].c==v){tb.data[q].r=t.data[p].c;tb.data[q].c=t.data[p].r;tb.data[q].d=t.data[p].d;q++;}}}int MatAdd(TSMatrix a,TSMatrix b,TSMatrix &c) {int i=0,j=0,k=0;ElemType v;if (a.rows!=b.rows || a.cols!=b.cols)return 0;c.rows=a.rows;c.cols=a.cols;while (i<a.nums && j<b.nums){if (a.data[i].r==b.data[j].r){if(a.data[i].c<b.data[j].c){c.data[k].r=a.data[i].r;c.data[k].c=a.data[i].c;c.data[k].d=a.data[i].d;k++;i++;}else if (a.data[i].c>b.data[j].c){c.data[k].r=b.data[j].r;c.data[k].c=b.data[j].c;c.data[k].d=b.data[j].d;k++;j++;}else{v=a.data[i].d+b.data[j].d;if (v!=0){c.data[k].r=a.data[i].r;c.data[k].c=a.data[i].c;c.data[k].d=v;k++;}i++;j++;}}else if (a.data[i].r<b.data[j].r){c.data[k].r=a.data[i].r;c.data[k].c=a.data[i].c;c.data[k].d=a.data[i].d;k++;i++;}else{c.data[k].r=b.data[j].r;c.data[k].c=b.data[j].c;c.data[k].d=b.data[j].d;k++;j++;}c.nums=k;}return 1;}int value(TSMatrix c,int i,int j){int k=0;while (k<c.nums && (c.data[k].r!=i || c.data[k].c!=j)) k++;if (k<c.nums)return(c.data[k].d);elsereturn(0);}int MatMul(TSMatrix a,TSMatrix b,TSMatrix &c){int i,j,k,p=0;ElemType s;if (a.cols!=b.rows)return 0;for (i=0;i<a.rows;i++)for (j=0;j<b.cols;j++){s=0;for (k=0;k<a.cols;k++)s=s+value(a,i,k)*value(b,k,j);if (s!=0){c.data[p].r=i;c.data[p].c=j;c.data[p].d=s;p++;}}c.rows=a.rows;c.cols=b.cols;c.nums=p;return 1;}void main(){ElemType a1[N][N]={{1,0,3,0},{0,1,0,0},{0,0,1,0},{0,0,1,1}};ElemType b1[N][N]={{3,0,0,0},{0,4,0,0},{0,0,1,0},{0,0,0,2}};TSMatrix a,b,c;CreatMat(a,a1);CreatMat(b,b1);printf("a的三元组:\n");DispMat(a);printf("b的三元组:\n");DispMat(b);printf("a转置为c\n");TranMat(a,c);printf("c的三元组:\n");DispMat(c);printf("c=a+b\n");MatAdd(a,b,c);printf("c的三元组:\n");DispMat(c);printf("c=a*b\n");MatMul(a,b,c);printf("c的三元组:\n");DispMat(c);}二、程序运行结果如图实验③编写一个程序实现广义表的各种运算,并在此基本上设计一个程序完成如下功能:(1)建立广义表g=“(b,(b,a,(#),d),((a,b),c,((#))))”的链式存储结构;(2)输出广义表g的长度;(3)输出广义表g的深度;(4)输出广义表g的最大原子;一、输入如图所示程序#include <stdio.h>#include <malloc.h>typedef char ElemType;typedef struct lnode{ int tag;union{ElemType data;struct lnode *sublist;}val;struct lnode *link;} GLNode;GLNode *CreatGL(char *&s){GLNode *h;char ch;ch=*s++;if (ch!='\0'){h=(GLNode *)malloc(sizeof(GLNode));if (ch=='('){h->tag=1;h->val.sublist=CreatGL(s);}else if (ch==')')h=NULL;else{h->tag=0;h->val.data=ch;}}else h=NULL;ch=*s++;if (h!=NULL)if (ch==',')h->link=CreatGL(s);elseh->link=NULL;return h;}int GLLength(GLNode *g){int n=0;g=g->val.sublist;while (g!=NULL){n++;g=g->link;}return n;}int GLDepth(GLNode *g){int max=0,dep;if (g->tag==0)return 0;g=g->val.sublist;if (g==NULL)return 1;while (g!=NULL){if (g->tag==1){dep=GLDepth(g);if (dep>max) max=dep;}g=g->link;}return(max+1);}void DispGL(GLNode *g){if (g!=NULL){if (g->tag==1){printf("(");if (g->val.sublist==NULL) printf("");else DispGL(g->val.sublist);}else printf("%c", g->val.data);if (g->tag==1) printf(")");if (g->link!=NULL){printf(",");DispGL(g->link);}}}void main(){GLNode *g;char *str="(b,(b,a,a),((a,b),c))";g=CreatGL(str);printf(" 广义表g:");DispGL(g);printf("\n");printf(" 广义表g的长度:%d\n",GLLength(g));printf(" 广义表g的深度:%d\n",GLDepth(g));printf("\n");}二、程序运行结果如图。
数据结构矩阵加法

数据结构矩阵加法
一、数据结构矩阵加法是什么呢?
嘿呀,宝子们!今天咱们来唠唠数据结构里的矩阵加法。
矩阵就像是一个方格阵,里面装着好多数字呢。
矩阵加法呢,可不是简单地把两个矩阵放在一块儿就完事儿啦。
它是要把对应的方格里面的数字相加哦。
比如说有矩阵A和矩阵B,A的第一行第一列的数字就要和B的第一行第一列的数字相加,得到新矩阵相应位置的数字。
二、怎么去做矩阵加法呢?
这就像是玩数字对对碰的游戏。
首先得保证两个矩阵的行数和列数是一样的。
要是不一样的话,就像两个人玩游戏,规则都不一样,那可没法玩加法这个游戏啦。
假设矩阵A是一个2行3列的矩阵,矩阵B也得是2行3列的。
然后就一个一个方格对着加呗。
就像给每个小方格里面的数字找个小伙伴,然后把它们凑一块儿。
三、矩阵加法在实际中有啥用呢?
这用处可大了去了。
在计算机图形学里,矩阵加法就像魔法一样。
比如说我们要把一个图形移动到另一个位置,就可以用矩阵来表示这个图形,然后通过矩阵加法来计算它移动后的新位置。
还有在物理学里,矩阵加法也能用来计算一些物理量的叠加呢。
就好比两个力作用在一个物体上,我们可以用矩阵来表示这两个力,然后用矩阵加法算出它们叠加后的效果。
概括来说呀,矩阵加法虽然看起来就是数字的相加,但是在很多领域都是超级重要的小能手呢。
它就像一把万能钥匙,能打开好
多不同领域的大门。
矩阵的乘法实验报告

一、实验目的1. 理解矩阵乘法的概念和运算规则。
2. 掌握矩阵乘法的编程实现方法。
3. 通过实验验证矩阵乘法的正确性。
二、实验环境1. 操作系统:Windows 102. 编程语言:Python3. 库:NumPy三、实验原理矩阵乘法是指两个矩阵相乘的运算。
设矩阵A为m×n的矩阵,矩阵B为n×p的矩阵,则它们的乘积C为一个m×p的矩阵。
矩阵乘法的运算规则如下:C[i][j] = Σ(A[i][k] B[k][j]),其中k为1到n的整数。
四、实验步骤1. 导入NumPy库。
```pythonimport numpy as np```2. 定义矩阵A和B。
```pythonA = np.array([[1, 2], [3, 4]])B = np.array([[5, 6], [7, 8]])```3. 计算矩阵A和B的乘积C。
```pythonC = np.dot(A, B)```4. 打印结果。
```pythonprint("矩阵A:")print(A)print("矩阵B:")print(B)print("矩阵C(A乘B):")print(C)```五、实验结果与分析1. 运行实验程序,得到以下结果:```矩阵A:[[1 2][3 4]]矩阵B:[[5 6][7 8]]矩阵C(A乘B):[[19 22][43 50]]```2. 分析结果:- 矩阵A为2×2的矩阵,矩阵B为2×2的矩阵,它们的乘积C为2×2的矩阵。
- 根据矩阵乘法的运算规则,我们可以计算出矩阵C的每个元素。
- 实验结果与理论计算相符,说明矩阵乘法的编程实现是正确的。
六、实验总结1. 本实验成功实现了矩阵乘法的编程,验证了矩阵乘法的正确性。
2. 通过实验,加深了对矩阵乘法概念和运算规则的理解。
3. NumPy库在矩阵运算方面具有强大的功能,为编程提供了便利。
数据结构课程设计报告---矩阵的运算

数据结构课程设计报告题目:专业:班级:学号:姓名:指导老师:时间:一、课程设计题目及所涉及知识点设计题目是“矩阵的运算”;所涉及的知识点主要是:1、利用数组的形式来储存数据,在main函数里面,实现对于数据的输入操作,利用switch语句进行选择来执行操作,利用for语句与do……while语句来实现功能的循环操作。
2、矩阵的加法、减法、乘法、数乘、转置的基本算法方式。
3、通过switch语句进行选择来执行操作,来实现每个算法的功能。
二、课程设计思路及算法描述设计思路:用程序实现矩阵能够完成矩阵的转置运算;矩阵的数乘运算;矩阵的加法运算;矩阵的减法运算;矩阵的乘法运算;这几种矩阵的简单的运算。
用数组把将要运算的矩阵储存起来,然后实现矩阵的这几种运算。
在main函数里面,来实现对于数据的输入操作,利用switch语句进行选择来执行操作,利用for语句来实现功能的循环操作。
算法:算法1:矩阵的转置运算;首先是把将要运算的矩阵存放在数组中,矩阵的转置运算,就是把你将要进行运算的A矩阵的行ar和列ac,把A矩阵的行ar作为B矩阵的bc,A矩阵的列ac作为B矩阵的br,这样得到的新矩阵B的行br和列bc就是矩阵A的转置。
算法如下:for(i=0;i<ar;i++)for(j=0;j<ac;j++)B[j][i]=A[i][j];算法2:矩阵的数乘运算;首先是把将要运算的矩阵存放在数组中,矩阵的数乘运算,就是实现用一个实数k 去A矩阵。
实数k去乘矩阵的每一行和每一列,得到的一个新的矩阵B,这样就解决了矩阵的数乘运算。
算法如下:for(i=0;i<ar;i++)for(j=0;j<ac;j++)B[i][j]=k*A[i][j];算法3:矩阵的加法运算;首先是把将要运算的矩阵存放在数组中,矩阵的加法运算,就是要实现A矩阵与B 矩阵进行加法运算。
事实上就是A矩阵的每一行ar与B矩阵的每一行br进行加法运算,而得到的一个新的矩阵C的每一行cr就是A矩阵的ar行与B矩阵的br行的和;A矩阵的每一列ac与B矩阵的每一列bc进行加法运算,而得到的一个新的矩阵C的每一列cc 就是A矩阵的ac列与B矩阵的bc列的和。
数据结构实验报告稀疏矩阵运算

数据结构实验报告稀疏矩阵运算实验目的:1.学习并理解稀疏矩阵的概念、特点以及存储方式。
2.掌握稀疏矩阵加法、乘法运算的基本思想和算法。
3.实现稀疏矩阵加法、乘法的算法,并进行性能测试和分析。
实验原理:稀疏矩阵是指矩阵中绝大多数元素为0的矩阵。
在实际问题中,有许多矩阵具有稀疏性,例如文本矩阵、图像矩阵等。
由于存储稀疏矩阵时,对于大量的零元素进行存储是一种浪费空间的行为,因此需要采用一种特殊的存储方式。
常见的稀疏矩阵的存储方式有三元组顺序表、十字链表、行逻辑链接表等。
其中,三元组顺序表是最简单直观的一种方式,它是将非零元素按行优先的顺序存储起来,每个元素由三个参数组成:行号、列号和元素值。
此外,还需要记录稀疏矩阵的行数、列数和非零元素个数。
稀疏矩阵加法的原理是将两个稀疏矩阵按照相同的行、列顺序进行遍历,对于相同位置的元素进行相加,得到结果矩阵。
稀疏矩阵乘法的原理是将两个稀疏矩阵按照乘法的定义进行计算,即行乘以列的和。
实验步骤:1.实现稀疏矩阵的三元组顺序表存储方式,并完成稀疏矩阵的初始化、转置、打印等基本操作。
2.实现稀疏矩阵的加法运算,并进行性能测试和分析。
3.实现稀疏矩阵的乘法运算,并进行性能测试和分析。
4.编写实验报告。
实验结果:经过实验测试,稀疏矩阵的加法和乘法算法都能正确运行,并且在处理稀疏矩阵时能够有效节省存储空间。
性能测试结果表明,稀疏矩阵加法、乘法的运行时间与非零元素个数有关,当非零元素个数较少时,运算速度较快;当非零元素个数较多时,运算速度较慢。
实验分析:稀疏矩阵的运算相对于普通矩阵的运算有明显的优势,可以节省存储空间和运算时间。
在实际应用中,稀疏矩阵的存储方式和运算算法都可以进行优化。
例如,可以采用行逻辑链接表的方式存储稀疏矩阵,进一步减少存储空间的占用;可以采用并行计算的策略加快稀疏矩阵的运算速度。
总结:通过本次实验,我深入学习了稀疏矩阵的概念、特点和存储方式,掌握了稀疏矩阵加法、乘法的基本思想和算法,并通过实验实现了稀疏矩阵的加法、乘法运算。
最新数据结构实验五矩阵的压缩存储与运算

精品资料数据结构实验五矩阵的压缩存储与运算........................................第五章矩阵的压缩存储与运算【实验目的】1. 熟练掌握稀疏矩阵的两种存储结构(三元组表和十字链表)的实现;2. 掌握稀疏矩阵的加法、转置、乘法等基本运算;3. 加深对线性表的顺序存储和链式结构的理解。
第一节知识准备矩阵是由两个关系(行关系和列关系)组成的二维数组,因此对每一个关系上都可以用线性表进行处理;考虑到两个关系的先后,在存储上就有按行优先和按列优先两种存储方式,所谓按行优先,是指将矩阵的每一行看成一个元素进行存储;所谓按列优先,是指将矩阵的每一列看成一个元素进行存储;这是矩阵在计算机中用一个连续存储区域存放的一般情形,对特殊矩阵还有特殊的存储方式。
一、特殊矩阵的压缩存储1. 对称矩阵和上、下三角阵若n阶矩阵A中的元素满足= (0≤i,j≤n-1 )则称为n阶对称矩阵。
对n阶对称矩阵,我们只需要存储下三角元素就可以了。
事实上对上三角矩阵(下三角部分为零)和下三角矩阵(上三角部分为零),都可以用一维数组ma[0.. ]来存储A的下三角元素(对上三角矩阵做转置存储),称ma为矩阵A的压缩存储结构,现在我们来分析以下,A和ma之间的元素对应放置关系。
问题已经转化为:已知二维矩阵A[i,j],如图5-1,我们将A用一个一维数组ma[k]来存储,它们之间存在着如图5-2所示的一一对应关系。
任意一组下标(i,j)都可在ma中的位置k中找到元素m[k]= ;这里:k=i(i+1)/2+j (i≥j)图5-1 下三角矩阵a00 a10 a11 a20 … an-1,0 … an-1,n-1k= 0 1 23 …n(n-1)/2 …n(n+1)/2-1图5-2下三角矩阵的压缩存储反之,对所有的k=0,1,2,…,n(n+1)/2-1,都能确定ma[k]中的元素在矩阵A中的位置(i,j)。
这里,i=d-1,(d是使sum= > k的最小整数),j= 。
数据结构实验报告-魔方阵
数据结构与程序设计实验实验报告
哈尔滨工程大学
实验报告三
c. 如果按上述方法找到的位置已填入数据,则在同一列下一行填入下一个数字。
(3). 以3×3魔方阵为例,说明其填数过程,如下图所示。
三阶魔方阵的生成过程
由三阶魔方阵的生成过程可知,某一位置(x,y)的左上角的位置是(x-1,y-1),如果x-1≥0,不用调整,否则将其调整为x-1+m;同理,如果y-1≥0,不用调整,否则将其调整为y-1+m。
所以,位置(x,y)的左上角的位置可以用求模的方法获得,即:
x=(x-1+m)%m
y=(y-1+m)%m
如果所求的位置已经有数据了,将该数据填入同一列下一行的位置。
这里需要注意的是。
此时的x和y已经变成之前的上一行上一列了,如果想变回之前位置的下一行同一列,x需要跨越两行,y需要跨越一列,即:
x=(x+2)%m
printf("%d\t",a[i][j]);
printf("\n");
}
四、界面设计
程序需要获取魔方阵的阶数(包括错误判断),输出结果,均在执行过程中给出提示。
五、运行测试与分析
1. 获取阶数并给出错误提示
2. 获取正确阶数,并输出结果
六、实验收获与思考
本次实验采用的数据结构为二维数组,在使用过程中巩固了学习的知识,在用C语言实现魔方阵算法时对C语言的使用更加熟悉。
七、附录(原程序)。
矩阵运算基础实验报告

一、实验目的1. 理解矩阵的基本概念和性质。
2. 掌握矩阵的创建、基本运算和常用函数。
3. 熟悉MATLAB软件在矩阵运算中的应用。
二、实验环境1. 操作系统:Windows 102. 软件环境:MATLAB R2020b三、实验内容1. 矩阵的创建与基本运算(1)创建矩阵在MATLAB中,可以使用多种方式创建矩阵,如:- 使用方括号[]直接输入矩阵元素。
- 使用冒号(:)生成向量。
- 使用linspace()、logspace()、zeros()、ones()等函数生成特殊矩阵。
(2)矩阵的基本运算- 矩阵加减法:两个矩阵的对应元素相加或相减。
- 矩阵乘法:包括标量乘法、矩阵乘法和转置运算。
- 矩阵除法:使用除号(/)或乘方运算符()实现。
- 矩阵求逆:使用inv()函数计算矩阵的逆。
2. 矩阵的常用函数(1)矩阵转置:使用T()或'符号实现。
(2)矩阵求行列式:使用det()函数。
(3)矩阵求特征值和特征向量:使用eig()函数。
(4)矩阵求条件数:使用cond()函数。
3. 矩阵的应用实例(1)求解线性方程组给定线性方程组:$$\begin{cases}2x + 3y = 8 \\x - y = 1\end{cases}$$在MATLAB中,可以使用以下代码求解:```A = [2, 3; 1, -1];b = [8; 1];x = A\b;disp(x);```(2)求解矩阵的逆给定矩阵A:```A = [4, 7; 2, 6];A_inv = inv(A);disp(A_inv);```四、实验结果与分析1. 创建矩阵(1)创建一个3x3矩阵:```A = [1, 2, 3; 4, 5, 6; 7, 8, 9];```(2)创建一个向量:```v = [1, 2, 3, 4, 5];```2. 矩阵的基本运算(1)矩阵加减法:```A = [1, 2; 3, 4];B = [5, 6; 7, 8];disp(A + B); % 结果为[6, 8; 10, 12] disp(A - B); % 结果为[-4, -4; -2, -4] ```(2)矩阵乘法:```A = [1, 2; 3, 4];B = [5, 6; 7, 8];disp(A B); % 结果为[19, 22; 43, 50] ```(3)矩阵求逆:```A = [4, 7; 2, 6];disp(inv(A)); % 结果为[-3, 7; 2, -1] ```3. 矩阵的常用函数(1)矩阵转置:```A = [1, 2, 3; 4, 5, 6];disp(A'); % 结果为[1, 4; 2, 5; 3, 6] ```(2)矩阵求行列式:```A = [4, 7; 2, 6];disp(det(A)); % 结果为-12```(3)矩阵求特征值和特征向量:```A = [1, 2; 3, 4];[V, D] = eig(A);disp(V); % 特征向量disp(D); % 特征值```五、实验总结通过本次实验,我们掌握了矩阵的基本概念、创建方法、基本运算和常用函数。
数据结构课程设计(矩阵的运算)

数据结构课程设计报告题目:_____________________________________专业:_____________________________________班级:_____________________________________学号:_____________________________________姓名:_____________________________________指导老师:__________________________________时间:_____________________________________、课程设计题目及所涉及知识点设计题目是“矩阵的运算” ,所涉及的知识点主要是:1、数据结构中的对于结构体的定义,用typedef struct 来实现,根据所设计的问题在结构体里面定义数据类型及其变量,用define 定义数组的大小,然后利用typedef 来实现对于变量的未知类型确定正确的类型。
2、利用数组的形式来储存数据,在实现不同操作过程中,有的用一维结构体数组(三元组顺序表)来存储,有的用二维数组来储存。
3、转置的过程中利用的是快速转置的方法,附设了num 和cpot 两个辅助变量。
4、矩阵的加法、减法、乘法、逆运算的基本算法方式。
5、通过调用每个函数,来实现每个算法的功能。
、课程设计思路及算法描述设计思路:1、首先是对于转置的考虑,要运用快速转置的方法实现,必须用三元组顺序表来储存数据,所以在第一个结构体中存在int 类型的行数(mu )列数(nu )以及非零元素的个数(tu );然后第二个结构体中分别有非零元素的行下标(i)、列下标(j)和元素数值(e),最后在第一个结构体中实现对第二个结构体成为数组结构体类型。
2、对于其余加法、减法、乘法和逆运算则是运用另一个结构体来实现,里面只有矩阵的行数、列数和一个二维数组(用float 来定义类型)。
数据结构矩阵
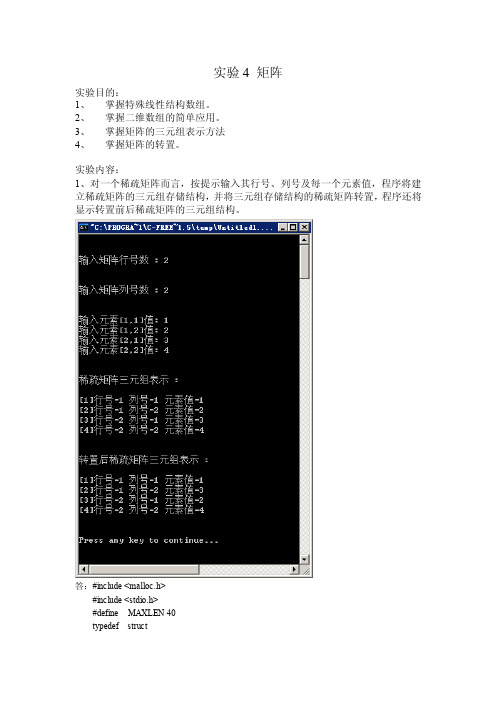
实验4 矩阵实验目的:1、掌握特殊线性结构数组。
2、掌握二维数组的简单应用。
3、掌握矩阵的三元组表示方法4、掌握矩阵的转置。
实验内容:1、对一个稀疏矩阵而言,按提示输入其行号、列号及每一个元素值,程序将建立稀疏矩阵的三元组存储结构,并将三元组存储结构的稀疏矩阵转置,程序还将显示转置前后稀疏矩阵的三元组结构。
答:#include <malloc.h>#include <stdio.h>#define MAXLEN 40typedef struct{ int i, j;int v;}NODE;typedef struct{ int m, n, t;NODE data[MAXLEN];}SPMA TRIX;SPMA TRIX transpose(SPMA TRIX a){/*稀疏矩阵(三元组存储结构)转置算法*/int p, q, col;SPMA TRIX b;b.m=a.n; b.n=a.m; b.t=a.t;if(a.t!=0){q = 1;for (col=1; col<=a.n; col++) //访问b三元组的每一行for (p=1; p<=a.t; p++) //访问a三元组的每一行if(a.data[p].j==col) //如果b三元组的行对应a数组的列,就进行转置{ b.data[q].j=a.data[p].i;b.data[q].i=a.data[p].j;b.data[q].v=a.data[p].v;q++;}}return b;}void printmatrix(SPMA TRIX c){/*稀疏矩阵(三元组存储结构)显示*/int n,i;n=c.t;for(i=1;i<=n;i++)printf("[%d]行号=%d 列号=%d 元素值=%d\n",i,c.data[i].i,c.data[i].j,c.data[i].v);}void main(){ SPMA TRIX a;SPMA TRIX b;int i,j,r,c,t,n;n=1;printf("\n\n输入矩阵行号数: ");scanf("%d",&r);printf("\n\n输入矩阵列号数: ");scanf("%d",&c);a.m=r; a.n=c;printf("\n\n");for(i=0;i<r;i++) /*输入矩阵元素值*/for(j=0;j<c;j++){printf("输入元素[%d,%d]值: ",i+1,j+1);scanf("%d",&t);if(t!=0) {a.data[n].i=i+1; /*非零元素存入稀疏矩阵三元组存储结构中*/a.data[n].j=j+1; a.data[n].v=t; n=n+1;}}n=n-1; a.t=n; /*a.t中为稀疏矩阵非零元素个数*/printf("\n\n稀疏矩阵三元组表示: \n\n");printmatrix(a); /*稀疏矩阵(三元组存储结构)转置*/b=transpose(a);printf("\n\n转置后稀疏矩阵三元组表示: \n\n");printmatrix(b);printf("\n\n");}文- 汉语汉字编辑词条文,wen,从玄从爻。
矩阵式实验报告

一、实验目的1. 理解矩阵的基本概念和性质。
2. 掌握矩阵的运算方法,包括加法、减法、乘法等。
3. 学习矩阵的应用,如线性方程组的求解。
4. 提高数学建模和解决问题的能力。
二、实验内容本次实验主要围绕矩阵的运算和应用展开,具体内容包括:1. 矩阵的加法与减法2. 矩阵的乘法3. 矩阵的逆4. 线性方程组的求解三、实验步骤1. 矩阵的加法与减法(1)选择两个矩阵A和B,确保它们具有相同的行数和列数。
(2)将矩阵A和B对应位置的元素相加或相减,得到新的矩阵C。
(3)验证矩阵C的行数和列数与矩阵A和B相同。
2. 矩阵的乘法(1)选择两个矩阵A和B,确保矩阵A的列数等于矩阵B的行数。
(2)计算矩阵A的每一行与矩阵B的每一列的点积,得到新的矩阵C。
(3)验证矩阵C的行数等于矩阵A的行数,列数等于矩阵B的列数。
3. 矩阵的逆(1)选择一个可逆矩阵A。
(2)使用高斯-约当消元法求解矩阵A的逆。
(3)验证矩阵A与其逆矩阵的乘积为单位矩阵。
4. 线性方程组的求解(1)选择一个线性方程组,例如:AX = B,其中A是系数矩阵,X是未知数矩阵,B是常数矩阵。
(2)使用高斯-约当消元法求解线性方程组。
(3)验证求解得到的X矩阵是否满足原方程组。
四、实验结果与分析1. 矩阵的加法与减法通过实验,我们发现矩阵的加法与减法运算满足交换律和结合律,且结果矩阵的行数和列数与原矩阵相同。
2. 矩阵的乘法实验结果表明,矩阵的乘法运算满足交换律和结合律,且结果矩阵的行数等于第一个矩阵的行数,列数等于第二个矩阵的列数。
3. 矩阵的逆实验发现,对于可逆矩阵,其逆矩阵存在,且满足A A^(-1) = A^(-1) A = E(单位矩阵)。
4. 线性方程组的求解通过高斯-约当消元法,我们成功求解了线性方程组,并验证了求解结果的正确性。
五、实验结论1. 理解了矩阵的基本概念和性质,掌握了矩阵的运算方法。
2. 学会了使用矩阵求解线性方程组,提高了数学建模和解决问题的能力。
数据结构稀疏矩阵基本运算实验报告

课程设计课程:数据结构题目:稀疏矩阵4 三元组单链表结构体(行数、列数、头) 矩阵运算重载运算符优班级:姓名:学号:设计时间:2010年1月17日——2010年5月XX日成绩:指导教师:楼建华一、题目二、概要设计1.存储结构typedef struct{int row,col;//行,列datatype v;//非0数值}Node;typedef struct{Node data[max];//稀疏矩阵int m,n,t;//m 行,n 列,t 非0数个数……2.基本操作⑴istream& operator >>(istream& input,Matrix *A)//输入⑵ostream& operator <<(ostream& output,Matrix *A){//输出⑶Matrix operator ~(Matrix a,Matrix b)//转置⑷Matrix operator +(Matrix a,Matrix b)//加法⑸Matrix operator -(Matrix a,Matrix b)//减法⑹Matrix operator *(Matrix a,Matrix b)//乘法⑺Matrix operator !(Matrix a,Matrix b)//求逆三、详细设计(1)存储要点position[col]=position[col-1]+num[col-1];三元组表(row ,col ,v)稀疏矩阵((行数m ,列数n ,非零元素个数t ),三元组,...,三元组)1 2 3 4 max-1(2)乘法运算要点已知稀疏矩阵A(m1× n1)和B(m2× n2),求乘积C(m1× n2)。
稀疏矩阵A、B、C及它们对应的三元组表A.data、B.data、C.data如图6所示。
由矩阵乘法规则知:C(i,j)=A(i,1)×B(1,j)+A(i,2)×B(2,j)+…+A(i,n)×B(n,j)=这就是说只有A(i,k)与B(k,p)(即A元素的列与B元素的行相等的两项)才有相乘的机会,且当两项都不为零时,乘积中的这一项才不为零。
数据结构 矩阵运算 C C++

#include<stdio.h>#include<stdlib.h>#define MAXSIZE_row 20#define MAXSIZE_col 20typedef struct //定义三元组{int i,j,e;} Triple;typedef struct //定义一个包含MAXSIZE 个三元组的距阵{Triple data[MAXSIZE_row*MAXSIZE_col+1]; //假定三元组的最大值为MAXSIZE_row*MAXSIZE_colint rops[MAXSIZE_row+1];int mu,nu,tu;}TSMatrix;void GetRops(TSMatrix &T) //获得rops{for(int n=1;n<MAXSIZE_row+1;n++)T.rops[n]=0;T.rops[T.data[1].i]=1;for(n=2;n<=T.tu;n++)if(T.data[n].i!=T.data[n-1].i){T.rops[T.data[n].i]=n;}T.rops[T.data[T.tu].i+1]=T.tu+1;}void PrintMeun(){printf("\t*****************************\n");printf("\t*** 1 矩阵的加法***\n");printf("\t*** 2 矩阵的减法***\n");printf("\t*** 3 矩阵的乘法***\n");printf("\t*** 4 矩阵的转置***\n");printf("\t*****************************\n");printf(" 请选择:");}void TripleOutput(TSMatrix T) //打印三元组{for(int n=1;n<=T.tu;n++){printf("%d,%d,%d\n",T.data[n].i,T.data[n].j,T.data[n].e);}}void TSInput(TSMatrix &T) //nrow 行ncol 列以三元组的形式输入矩阵{int nrow=0,ncol=0;printf("Input the row col:");scanf("%d %d",&nrow,&ncol);while(nrow>MAXSIZE_row || ncol>MAXSIZE_col ){printf("Erorr the row<=%d and col must <=%d\n",MAXSIZE_row,MAXSIZE_col);printf("Input agian\n");printf("Input the row col:");scanf("%d %d",&nrow,&ncol);}for(int i=1;i<=nrow*ncol+1;i++){printf("Input the %d Matrix in triple:",i);//以三元组的形式输入scanf("%d %d %d",&T.data[i].i,&T.data[i].j,&T.data[i].e);if(T.data[i].i>nrow || T.data[i].j>ncol){ printf("Erorr the row<=%d and col must <=%d\n",nrow,ncol);printf("Input agian\n");i--;}if(T.data[i].i==0 || T.data[i].j==0 || T.data[i].e==0){i--;break;}}printf("\n");T.mu=nrow;T.nu=ncol;T.tu=i;}void TSDeliver(TSMatrix S,int &n,TSMatrix &T,int k) //将M->T{T.data[k].i=S.data[n].i;T.data[k].j=S.data[n].j;T.data[k].e=S.data[n].e;n++;T.tu++;}void TSAdd(TSMatrix &M,TSMatrix &N,TSMatrix &T) //M+N->T{// TSAddif(!(M.mu==N.mu && M.nu==N.nu)) {printf("输入的两个矩阵不能做加法!");exit(1);} M.data[M.tu+1].i=21;N.data[N.tu+1].i=21;T.mu=M.mu;T.nu=M.nu;T.tu=0;printf("N.tu=%d\n",N.tu);for(int im=1,in=1,k=1;im<=M.tu || in<=N.tu;k++){ //forif(M.data[im].i<N.data[in].i)TSDeliver(M,im,T,k);else if(M.data[im].i>N.data[in].i)TSDeliver(N,in,T,k);else{//else_1if(M.data[im].j<N.data[in].j)TSDeliver(M,im,T,k);else if(M.data[im].j>N.data[in].j)TSDeliver(N,in,T,k);else{//else_2if(M.data[im].e+N.data[in].e){//ifT.data[k].i=M.data[im].i;T.data[k].j=M.data[im].j;T.data[k].e=M.data[im].e+N.data[in].e;T.tu++;im++;in++;}//end ifelse{im++;in++;k--;}}//end else_2}//end esle_1}//end for}void TSSub(TSMatrix M,TSMatrix &N,TSMatrix &T) //M-N->T{for(int i=1;i<=N.tu;i++)N.data[i].e=-N.data[i].e;TSAdd(M,N,T);}void TSMul(TSMatrix &M,TSMatrix &N,TSMatrix &T) //M*N->T{if(M.nu!=N.mu) {printf("M.nu!=N.mu");exit(1);}//尝试调用main()T.mu=M.mu;T.nu=N.nu;T.tu=0; //初始化int ctemp[MAXSIZE_col+1],p,q,brow,ccol;GetRops(M);GetRops(N);for(int arow=1;arow<=M.mu;arow++){//for_1for(int i=1;i<=MAXSIZE_col;i++) //ctemp清零ctemp[i]=0;T.rops[arow]=T.tu+1;if(p=M.rops[arow]){//if_1for(;p<M.rops[arow+1];p++){//for_2brow=M.data[p].j;if(brow<=N.mu)for(q=N.rops[brow];q<N.rops[brow+1];q++)if(q<N.rops[brow+1]){ccol=N.data[q].j;ctemp[ccol]+=M.data[p].e*N.data[q].e;} }//for_2}//if_1for(ccol=1;ccol<T.nu;ccol++)if(ctemp[ccol]){if(++T.tu>MAXSIZE_row*MAXSIZE_col){printf("The T.tu>%d",MAXSIZE_row*MAXSIZE_col);exit(1);}T.data[T.tu].i=arow;T.data[T.tu].j=ccol;T.data[T.tu].e=ctemp[ccol];}}//for_1}void TSTranspos(TSMatrix M,TSMatrix &T){int num[MAXSIZE_row+1],cpot[MAXSIZE_col+1],q;T.mu=M.nu;T.nu=M.mu;T.tu=M.tu;for(int col=1;col<=M.nu;col++) num[col]=0;for(int t=1;t<=M.tu;t++) num[M.data[t].j]++;cpot[1]=1;for(col=2;col<=M.nu;col++) cpot[col]=cpot[col-1]+num[col-1];for(int p=1;p<=M.tu;p++){col=M.data[p].j;q=cpot[col];T.data[q].i=M.data[p].j;T.data[q].j=M.data[p].i;T.data[q].e=M.data[p].e;cpot[col]++;}}void TSOutput(TSMatrix T) //输出函数{int n=1;for(int row=1;row<=T.mu;row++){for(int col=1;col<=T.nu;col++){if(T.data[n].i==row && T.data[n].j==col){printf("%3d ",T.data[n].e);n++;}else{printf("%3d ",0);}}printf("\n");}}void main(){TSMatrix M,N,T;PrintMeun();int choose;scanf("%d",&choose);if(choose==4){TSInput(M);TSTranspos(M,T);TSOutput(M);printf("转置\n");TSOutput(T);}else{TSInput(M);TSInput(N);switch(choose){case 1:{TSAdd(M,N,T);TSOutput(M);printf("+\n");TSOutput(N);printf("=\n"); TSOutput(T);break;}case 2:{TSSub(M,N,T);TSOutput(M);printf("-\n");TSOutput(N);printf("=\n");TSOutput(T);break;}case 3:{TSMul(M,N,T);TSOutput(M);printf("*\n");TSOutput(N);printf("=\n");TSOutput(T);break;}}}}。
数据结构程序设计-矩阵的运算

二.概要设计:
1、抽象数据类型定义如下: ADT SparseMatrix{ 数据对象D:D={aij|i=1,2,3…,m;j=1,2,3…,n; ai ∈ElemSet,m和n分别称为矩阵的行数和列数} 数据关系R: R={Row,Col} Row={<ai,j,ai,j+1>|1≤i≤m, 1≤j≤n-1} Col={<ai,ai+1,j>|1≤i≤m-1, 1≤j≤n} 基本操作 本程序中,用三元组顺序表作为存储结构。 (1)、CreatSMatrix (TSMatrix &M) 操作结果:创建矩阵M。 (2)、AddSMatrix(TSMatrix A,TSMatrix B,TSMatrix &C,int n) 初始条件:矩阵A和B的行数和列数对应相等。 操作结果:求矩阵A、B的和C=A+B。 (3)、SubMatrix (TSMatrix *a,TSMatrix *b) 初始条件:矩阵A和B的行数和列数对应相等。 操作结果:求矩阵A、B的和C=A+B。 (4)、MultiplicationMatrixPow (TSMatrix *a,TSMatrix *b,TSMatrix *c) 初始条件:矩阵A和B的行数和列数匹配 操作结果:求矩阵A、B的和C=A*B。 (5) OutputSMatrix(TSMatrix M) 初始条件:矩阵M已存在 操作结果:输出矩阵M 2、 本程序包含5个模块
for(i=1;i<=M->mu;i++)//输出矩阵 { for(j=1;j<=M->nu;j++) printf("%5d",a[i][j]); printf("\n"); } } //*************矩阵的求和运算*****************// int AddSMatrix(TSMatrix *M,TSMatrix *N,TSMatrix *Q)//求 采用三元组顺序表存储表示的稀疏矩阵M和N的和,结果赋给矩阵Q { int i,j,p,q,x=0,y=0; if((M->mu<=0)||(M->nu<=0)||(M->tu<=0)||(N->mu<=0)||(N>nu<=0)||(N->tu<=0))//判断行数列数非零元素个数是否符合匹配 return ERROR; if(M->mu!=N->mu||M->nu!=N->nu)//判断A与B的行列数 是否相等的 return ERROR; Q->mu=M->mu;//矩阵Q的初始化 Q->nu=M->nu; Q->tu=0; for(i=1;i<=Q->mu;i++) { for(j=1;j<=Q->nu;j++)//寻找矩阵M,N中非零元素相等 的行列 { for(p=1;p<=M->tu;p++)//求矩阵M行列中所对应的 非零元素的值 赋值给X { if((i==M->data[p].row)&&(j==M->data[p].col))// 如果i是矩阵M中非零元素行,j是其列 { x=M->data[p].e;
数据结构课程设计 特殊矩阵运算

特殊矩阵运算1.1程序功能简介对特殊矩阵能够在界面上以人们熟悉的方式显示,可以对特殊矩阵进行加法运算和减法运算,矩阵转置。
按照要求使用了多种数据结构来求解问题,具体为二维数组和类似图的数据结构。
由于题目要求使用多种数据结构,因此分开写了两段程序,均实现了上述要求的功能,以下将分开说明。
先说明的是用二维数组实现的程序,后说明的是用图结构实现的程序。
1.2关于输入、输出形式及数据范围1.2.1使用二维数组实现的程序输入、输出范围为:-73786976294838206000到73786976294838206000,足以解决绝大多数的矩阵运算问题。
1.2.2输入的格式进入程序后首先展现的是功能选择界面,如下图:此时可通过输入对应功能的数字来选择功能。
在此程序中不同功能输入格式不同:选择功能 1.矩阵转置时需要输入要进行转置操作的矩阵,首先输入矩阵的行数和列数,以逗号隔开,之后依次按矩阵形式输入矩阵即可,各数值之间以空格隔开。
选择功能2.矩阵数乘时需要输入要进行数乘操作的矩阵,此输入格式同上,之后输入一个实数,即要进行数乘的数即可。
功能3.矩阵加法与4.矩阵减法输入格式和5.矩阵乘法相同,按上述操作输入两个矩阵即可,需要注意的是矩阵减法默认顺序为先输入的矩阵减去后输入的矩阵。
当按照格式输入时可以实现以上功能,但输入错误数据时,例如进行行列数不同的矩阵相加减时则会返回无法操作,请重新输入的提示。
具体情况见下文测试部分。
1.3.1使用图结构实现的稀疏矩阵运算器程序输入、输出范围同上。
1.3.2输入的格式进入程序后首先展现的是功能选择界面,如下图:选择功能部分输入同上。
在进行矩阵输入时采取三元组的形式,这是由于稀疏矩阵的多零元性质。
首先输入矩阵的行数、列数、非零元个数,以空格隔开,输入完毕后确认,开始输入各个非零元。
输入非零元时按“所在行下标所在列下标值”的形式输入,需要注意的是输入时只能从所在行小的开始按顺序输入,不能先输入行数大的数据再输入行数小的数据。
矩阵运算实验报告

矩阵运算实验报告实验目的:通过矩阵运算实验,探究矩阵的基本运算规则、性质及应用,并加深对矩阵运算的理解。
实验原理:矩阵是一个由元素按照行和列排列成的矩形阵列,可以进行加法、减法、乘法等基本的运算。
矩阵的加法与减法满足交换律、结合律和分配律;矩阵的乘法满足结合律、分配律和左乘右乘不一定相等的性质。
实验步骤:1. 实验前的准备:准备两个矩阵A和B,并确定其维度。
2. 进行矩阵加法运算:将矩阵A与矩阵B的对应元素相加,得到新的矩阵C。
3. 进行矩阵减法运算:将矩阵A与矩阵B的对应元素相减,得到新的矩阵D。
4. 进行矩阵乘法运算:将矩阵A的行元素与矩阵B的列元素对应相乘,并将结果相加,得到新的矩阵E。
5. 对矩阵进行转置:将矩阵A的行与列互换,得到新的矩阵F。
6. 求矩阵的逆:若矩阵A可逆,则找到矩阵A的逆矩阵G。
实验结果:1. 矩阵加法运算的结果:得到新的矩阵C,其维度与矩阵A和B相同,且C(i,j) = A(i,j) + B(i,j)。
2. 矩阵减法运算的结果:得到新的矩阵D,其维度与矩阵A和B相同,且D(i,j) = A(i,j) - B(i,j)。
3. 矩阵乘法运算的结果:得到新的矩阵E,其维度为A的行数乘以B的列数,且E(i,j) = Σ(A(i,k)*B(k,j)),k的取值范围为1到B的行数(或A的列数)。
4. 矩阵转置的结果:得到新的矩阵F,其维度与矩阵A相反,即F的行数等于A的列数,F的列数等于A的行数,且F(i,j) = A(j,i)。
5. 矩阵逆矩阵的结果:得到新的矩阵G,其与矩阵A的乘积为单位矩阵,即A*G = G*A = I,其中I为单位矩阵。
实验分析:1. 从矩阵加法与减法运算的结果可以看出,矩阵的加法和减法满足交换律、结合律和分配律。
这说明矩阵加法和减法具有良好的运算性质。
2. 从矩阵乘法运算的结果可以看出,矩阵的乘法满足结合律和分配律,但左乘右乘不一定相等,即AB≠BA。
矩阵计算实验报告

一、实验目的1. 掌握矩阵的基本概念和性质。
2. 熟悉MATLAB软件在矩阵计算中的应用。
3. 熟练运用MATLAB进行矩阵的创建、运算和可视化。
二、实验内容1. 矩阵的创建与引用(1)创建矩阵在MATLAB中,可以使用多种方法创建矩阵,如直接输入矩阵元素、使用冒号操作符、使用linspace和logspace函数等。
例如,创建一个3x4的矩阵A:A = [1, 2, 3, 4; 5, 6, 7, 8; 9, 10, 11, 12];(2)引用矩阵元素可以使用行列索引来引用矩阵元素。
例如,引用矩阵A的第1行第2列元素:A(1, 2)2. 矩阵的运算(1)矩阵的加法与减法矩阵的加法与减法运算满足交换律和结合律,且只适用于相同维度的矩阵。
例如,计算矩阵A与矩阵B的和:B = [1, 2, 3; 4, 5, 6];C = A + B(2)矩阵的乘法矩阵乘法满足分配律,且左乘和右乘满足结合律。
例如,计算矩阵A与矩阵B的乘积:D = A B(3)矩阵的逆若矩阵A是可逆的,则存在矩阵A的逆,记为A^(-1)。
A^(-1)满足以下性质:A A^(-1) = A^(-1) A = I其中,I是单位矩阵。
例如,计算矩阵A的逆:E = inv(A)(4)矩阵的秩矩阵的秩是指矩阵中线性无关的行(或列)的最大数目。
例如,计算矩阵A的秩:rank(A)(5)矩阵的迹矩阵的迹是指矩阵对角线元素之和。
例如,计算矩阵A的迹:trace(A)3. 矩阵的可视化(1)绘制矩阵元素可以使用MATLAB的scatter函数绘制矩阵元素。
例如,绘制矩阵A的元素:scatter(1:size(A, 1), 1:size(A, 2), A)(2)绘制矩阵特征值可以使用MATLAB的eig函数计算矩阵的特征值,并使用plot函数绘制特征值。
例如,计算矩阵A的特征值并绘制:[V, D] = eig(A);plot(diag(D))三、实验步骤1. 打开MATLAB软件,创建一个新的M文件。
矩阵运算实验报告

实验报告--矩阵运算一.实验目的。
1.通过实践加强对程序设计语言课程知识点的理解和掌握,培养对课程知识综合运用能力、实际分析问题能力及编程能力,养成良好的编程习惯。
2.通过实践进一步领会程序设计的特点和应用,提高运用C++ 语言以及面向对象知识解决实际问题的能力。
3.通过实践掌握用C++ 语言编写面向对象的实用程序的设计方法,对面向对象方法和思想增加感性的认识;4.学会利用C++程序设计语言编写出一些短小、可靠的Windows实用程序,切实提高面向对象的程序设计能力。
为后续的相关课程的学习打下基础。
二.实验要求。
1.学会建立模板类;2.实现矩阵的“加”、“减”、“乘”、“数乘”、“转置” ;3.动态内存分配并用随机数填充;4.注意“加”、“减”、“乘” 要进行条件的判断;三.设计思路。
3.1算法基本流程1)获取用户输入的矩阵1的行数和列数,动态生成一个一维数组2)利用随机数生成数组成员,并利用两个循环输出数组,使其符合矩阵的格式3)矩阵2同矩阵1的处理方法4)通过两个矩阵的行数和列数比较来判断能否进行加减乘等运算,如不能,输出相关信息5)如能够进行计算,则利用数组进行相应运算,并按照正确格式输出6)通过改变一维数组中元素的顺序来实现转置并输出3.2算法流程图四.基本界面。
五.关键代码。
5.1关键类的声明class CMatrixclass{public:CMatrixclass(){int m_Row = 0; //行int m_Col = 0; //列m_pElements = NULL; //一维数组};virtual ~CMatrixclass(){delete [] m_pElements;}public:int m_Row;int m_Col;int * m_pElements;};5.2关键函数代码void CMyView::OnCHECKadd(){m_nums.SetCheck(0);m_combine.SetCheck(0);m_subtrict.SetCheck(0);}void CMyView::OnCHECKsubtrict(){m_add.SetCheck(0);m_combine.SetCheck(0);m_nums.SetCheck(0);}void CMyView::OnCHECKcombine(){m_add.SetCheck(0);m_nums.SetCheck(0);m_subtrict.SetCheck(0);}void CMyView::OnCHECKnums(){m_add.SetCheck(0);m_combine.SetCheck(0);m_subtrict.SetCheck(0);}void CMyView::OnBUTTONcompute(){UpdateData(TRUE);// TODO: Add your control notification handler code hereif(m_add.GetState()==1){if(op1->imax!=op2->imax||op1->jmax!=op2->jmax||op1==NULL||op2==NU LL){m_result="行数列数不等无法相加!";}else{matrix<int> c(op1->imax,op1->jmax);c=*op1+*op2;m_result="matrix1+matrix2";m_result+="\r\n";m_result+=c.my_show();}}else if(m_subtrict.GetState()==1){if(op1->imax!=op2->imax||op1->jmax!=op2->jmax||op1==NULL||op2==NU LL){m_result="行数列数不等无法相减!";}else{matrix<int> c(op1->imax,op1->jmax);c=*op1-*op2;m_result="matrix1-matrix2";m_result+="\r\n";m_result+=c.my_show();}}else if(m_combine.GetState()==1){if(op1->jmax!=op2->imax||op1==NULL||op2==NULL){m_result="以上无法相乘!";}else{matrix<int> c(op1->imax,op2->jmax);c=(*op1)*(*op2);m_result="matrix1*matrix2";m_result+="\r\n";m_result+=c.my_show();}}else if(m_nums.GetState()==1){if(op2==NULL){m_result="运算不出结果!";}else{matrix<int> c(op2->imax,op2->jmax); c=m_k*(*op2);m_result="k*matrix2";m_result+="\r\n";m_result+=c.my_show();}}else{m_result="请先选定一个算法!";}UpdateData(FALSE);}void CMyView::OnBUTTONrotate(){UpdateData(TRUE);if(m_r1.GetState()==1){if(op1==NULL){m_result="请先输入矩阵!";}else{matrix<int> c=rotate(*op1);m_result="matrix1转置";m_result+="\r\n";m_result+=c.my_show();}}else if(m_r2.GetState()==1){if(op2==NULL){m_result="请先输入矩阵!";}else{matrix<int> c=rotate(*op2);m_result="matrix2转置";m_result+="\r\n";m_result+=c.my_show();}}else{m_result="请选择一个矩阵!";}UpdateData(FALSE);}void CMyView::OnCHECKr1(){UpdateData(TRUE);m_r2.SetCheck(0);UpdateData(FALSE);}void CMyView::OnCHECKr2(){UpdateData(TRUE);m_r1.SetCheck(0);UpdateData(FALSE);}六.实验心得与编程收获。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
cout<<"相乘后:"<<endl;
//相乘运算
double **r=new double *[a1];
for(int i=0;i<a1;i++)
r[i]=new double[b2];
for(int q=0;q<a1;q++)
for(int w=0;w<b2;w++)
{
delete []x1[i];
delete []r[i];
}
for(int i=0;i<a2;i++)
delete []x2[i];
delete x1;x1=0;
delete x2;x2=0;
delete r;r=0;
}
算法的选择:switch(c)
{
case 1:Addition();break;
x2[i]=new double[b2];
cout<<"输入第二个矩阵:\n";
for(int i=0;i<a2;i++)
for(int j=0;j<b2;j++)
cin>>x2[i][j];
cout<<"相加后:"<<endl;
矩阵的加法:for(int i=0;i<a1;i++)
{
for(int j=0;j<b1;j++)
3.倘若选择加(减)法,若两个矩阵的行、列数不相等的话,软件会报错
4.注意输入矩阵的每一个成员是要以空格(space)键隔开。
5.依次输入完两个矩阵成员后,按下回车键,结果将出现显示屏。
附录:
#include <iostream.h>
//矩阵加法
void Addition()
{
int a1,b1,a2,b2;
Multiplication()实现两个任意矩阵的乘法运算
Main()主函数
主要
矩阵的构建:int a1,b1,a2,b2;
double **x1,**x2;
cout<<"输入第一个行数,列数:";
cin>>a1>>b1;
cout<<"输入第二个行数,列数:";
cin>>a2>>b2;
if(a1!=a2 ||b1 !=b2)
cout<<"\t(1)矩阵加法\n\t(2)矩阵减法\n\t(3)矩阵乘法\n\t(0)退出"<<endl;
cout<<"***************************\n";
for(int i=0;i<a1;i++)
x1[i]=new double [b1]; //为x1的每个元素动态分配数组空间
cout<<"输入第一个矩阵:\n";
forห้องสมุดไป่ตู้int i=0;i<a1;i++)
for(int j=0;j<b1;j++)
cin>>x1[i][j];
//分配地址空间
x2=new double *[a2]; //x2[][]
{
r[q][w]=0;
for(int j=0;j<b1;j++)
r[q][w]+=x1[q][j]*x2[j][w];
}
//输出相乘后结果
for(int q=0;q<a1;q++)
{
for(int w=0;w<b2;w++)
{
cout<<r[q][w]<<"\t";
}
cout<<endl;
}
for(int i=0;i<a1;i++)
for(int i=0;i<a2;i++)
x2[i]=new double[b2];
cout<<"输入第二个矩阵:\n";
for(int i=0;i<a2;i++)
for(int j=0;j<b2;j++)
cin>>x2[i][j];
cout<<"相加后:"<<endl;
//相加运算
for(int i=0;i<a1;i++)
for(int j=0;j<b1;j++)
cin>>x1[i][j];
x2=new double *[a2]; //x2[][]
for(int i=0;i<a2;i++)
x2[i]=new double[b2];
cout<<"输入第二个矩阵:\n";
for(int i=0;i<a2;i++)
for(int j=0;j<b2;j++)
{
cout<<"无法相加!"<<endl;return;
}
/**************分配地址空间********************/
x1=new double *[a1]; //x1[][],动态分配指针数组
for(int i=0;i<a1;i++)
x1[i]=new double [b1]; //为x1的每个元素动态分配数组空间
if(b1!=a2)
{
cout<<"无法相乘!"<<endl;return;
}
x1=new double *[a1]; //x1[][]
for(int i=0;i<a1;i++)
x1[i]=new double[b1];
cout<<"输入第一个矩阵:\n";
for(int i=0;i<a1;i++)
cin>>x1[i][j];
x2=new double *[a2]; //x2[][]
for(int i=0;i<a2;i++)
x2[i]=new double[b2];
cout<<"输入第二个矩阵:\n";
for(int i=0;i<a2;i++)
for(int j=0;j<b2;j++)
cin>>x2[i][j];
{
r[q][w]=0;
for(int j=0;j<b1;j++)
r[q][w]+=x1[q][j]*x2[j][w];
}
//输出相乘后结果
for(int q=0;q<a1;q++)
{
for(int w=0;w<b2;w++)
{
cout<<r[q][w]<<"\t";
}
cout<<endl;
}
for(int i=0;i<a1;i++)
{
delete []x1[i];
delete []r[i];
}
for(int i=0;i<a2;i++)
delete []x2[i];
delete x1;x1=0;
delete x2;x2=0;
delete r;r=0;
}
int main()
{
int c=1;
while(c)
{
cout<<"***************************\n";
for(int j=0;j<b1;j++)
cin>>x1[i][j];
x2=new double *[a2]; //x2[][]
for(int i=0;i<a2;i++)
x2[i]=new double[b2];
cout<<"输入第二个矩阵:\n";
for(int i=0;i<a2;i++)
for(int j=0;j<b2;j++)
cin>>a2>>b2;
if(b1!=a2)
{
cout<<"无法相乘!"<<endl;return;
}
x1=new double *[a1]; //x1[][]
for(int i=0;i<a1;i++)
x1[i]=new double[b1];
cout<<"输入第一个矩阵:\n";
for(int i=0;i<a1;i++)
delete []x2[i];
}
delete x1;x1=0;
delete x2;x2=0;
}
//矩阵乘法
void Multiplication()
{
