自动控制原理课后习题答案,第5章(西南科技大学)
自动控制原理 课后习题答案(2020年7月整理).pdf

第1章控制系统概述【课后自测】1-1 试列举几个日常生活中的开环控制和闭环控制系统,说明它们的工作原理并比较开环控制和闭环控制的优缺点。
解:开环控制——半自动、全自动洗衣机的洗衣过程。
工作原理:被控制量为衣服的干净度。
洗衣人先观察衣服的脏污程度,根据自己的经验,设定洗涤、漂洗时间,洗衣机按照设定程序完成洗涤漂洗任务。
系统输出量(即衣服的干净度)的信息没有通过任何装置反馈到输入端,对系统的控制不起作用,因此为开环控制。
闭环控制——卫生间蓄水箱的蓄水量控制系统和空调、冰箱的温度控制系统。
工作原理:以卫生间蓄水箱蓄水量控制为例,系统的被控制量(输出量)为蓄水箱水位(反应蓄水量)。
水位由浮子测量,并通过杠杆作用于供水阀门(即反馈至输入端),控制供水量,形成闭环控制。
当水位达到蓄水量上限高度时,阀门全关(按要求事先设计好杠杆比例),系统处于平衡状态。
一旦用水,水位降低,浮子随之下沉,通过杠杆打开供水阀门,下沉越深,阀门开度越大,供水量越大,直到水位升至蓄水量上限高度,阀门全关,系统再次处于平衡状态。
开环控制和闭环控制的优缺点如下表1-2 自动控制系统通常有哪些环节组成?各个环节分别的作用是什么?解:自动控制系统包括被控对象、给定元件、检测反馈元件、比较元件、放大元件和执行元件。
各个基本单元的功能如下:(1)被控对象—又称受控对象或对象,指在控制过程中受到操纵控制的机器设备或过程。
(2)给定元件—可以设置系统控制指令的装置,可用于给出与期望输出量相对应的系统输入量。
(3)检测反馈元件—测量被控量的实际值并将其转换为与输入信号同类的物理量,再反馈到系统输入端作比较,一般为各类传感器。
(4)比较元件—把测量元件检测的被控量实际值与给定元件给出的给定值进行比较,分析计算并产生反应两者差值的偏差信号。
常用的比较元件有差动放大器、机械差动装置和电桥等。
(5)放大元件—当比较元件产生的偏差信号比较微弱不足以驱动执行元件动作时,可通过放大元件将微弱信号作线性放大。
《自动控制原理》5章课后习题参考答案.

+
1(
10000(6
.311
2e +=
S S S G
1001.0(11.0(1(1.0(d +++=
S S S S S G 61
.054
.0154.0,
11(2
2
=+==+=
K K
A ω
ωω010
s
900.257.3180 2.16rad
tg ωωω----∙︒=-=,(
(
5
.1,
(5
(6 (7
5.12
K增大和T减少
((1(1(1m K
K s s Ts Ts K
s T s K
Φ=
≈
+++++
K
T m 21=
ζ ,不变(稳定裕度不变
2
22
(12(121b n ωωξξ=-+
-+
5.13
11=+=
p
ssr K e 35
.01
12
416==
=
v
ssr K e %
8.4%100%2
1=⨯=--ξ
πξ
σe 05
.006.13
==≈
ቤተ መጻሕፍቲ ባይዱεξ
ω,S t n s s
rad n n c 8.2707.0707.02=∙=ωωω=0
63
=γdB K g s rad g ∞=∞=ω0,1==r r M ωs
rad n b 4==ωω0
1
1
11006
.787.53.841001.01001.0180180=-=∙-=-+-=----tg
自动控制原理课后习题答案,第5章(西南科技大学).

(T1 T2 T3 ) T1T2T3 K (1 2T12 )(1 2T22 )
令 ()= 180
化成 G( j)
X () jY () 形式,
4.03 求出相角穿越频率 g==
将 g 代入 A( ) ,求出
令 Y ( ) 0,可获得 g 及相应h
A(g )=0.32
1 则幅值裕度 h 3.12 A(ห้องสมุดไป่ตู้ )
5-10 用奈式稳定判据判断反馈系统的稳定条件,系统的开环
1 0.4 1 L( ) 3 2 10 3 4 20 5
0.4
2 ( ) arctan 90 arctan arctan 5 10 2 将 c 代入 ( )
相角裕度:
(c )+ 180 104
5-5 已知最小相位系统的对数幅频渐近特性曲线如图所示, L() 试确定系统的开环传递函数。
解(a) :系统最左端直线的斜率为0dB/dec, 40 0 得 v=0,系统无积分环节。1、2 1 100 和3 分别是惯性、微分和惯性环节 -20 的转折频率,系统开环传递函数为:
10000 2
G( s)
其中
因 因
Ks
2 2
2 n
1 ( s 2n s )( s 1) 1 1 10n 1
2 n
得 K 10 20lg K 20
20lg M r 40 20
由M
2
r
1 2 1
2
得
0.05
K (T3s 1) 传递函数: G( s ) (T3 T1 T2 ) s(T1s 1)(T2 s 1)
自动控制原理完整版课后习题答案

1 请解释下列名字术语:自动控制系统、受控对象、扰动、给定值、参考输入、反馈。
解:自动控制系统:能够实现自动控制任务的系统,由控制装置与被控对象组成;受控对象:要求实现自动控制的机器、设备或生产过程扰动:扰动是一种对系统的输出产生不利影响的信号。
如果扰动产生在系统内部称为内扰;扰动产生在系统外部,则称为外扰。
外扰是系统的输入量。
给定值:受控对象的物理量在控制系统中应保持的期望值参考输入即为给定值。
反馈:将系统的输出量馈送到参考输入端,并与参考输入进行比较的过程。
2 请说明自动控制系统的基本组成部分。
解:作为一个完整的控制系统,应该由如下几个部分组成:①被控对象:所谓被控对象就是整个控制系统的控制对象;②执行部件:根据所接收到的相关信号,使得被控对象产生相应的动作;常用的执行元件有阀、电动机、液压马达等。
③给定元件:给定元件的职能就是给出与期望的被控量相对应的系统输入量(即参考量);④比较元件:把测量元件检测到的被控量的实际值与给定元件给出的参考值进行比较,求出它们之间的偏差。
常用的比较元件有差动放大器、机械差动装置和电桥等。
⑤测量反馈元件:该元部件的职能就是测量被控制的物理量,如果这个物理量是非电量,一般需要将其转换成为电量。
常用的测量元部件有测速发电机、热电偶、各种传感器等;⑥放大元件:将比较元件给出的偏差进行放大,用来推动执行元件去控制被控对象。
如电压偏差信号,可用电子管、晶体管、集成电路、晶闸管等组成的电压放大器和功率放大级加以放大。
⑦校正元件:亦称补偿元件,它是结构或参数便于调整的元件,用串联或反馈的方式连接在系统中,用以改善系统的性能。
常用的校正元件有电阻、电容组成的无源或有源网络,它们与原系统串联或与原系统构成一个内反馈系统。
3 请说出什么是反馈控制系统,开环控制系统和闭环控制系统各有什么优缺点?解:反馈控制系统即闭环控制系统,在一个控制系统,将系统的输出量通过某测量机构对其进行实时测量,并将该测量值与输入量进行比较,形成一个反馈通道,从而形成一个封闭的控制系统;开环系统优点:结构简单,缺点:控制的精度较差;闭环控制系统优点:控制精度高,缺点:结构复杂、设计分析麻烦,制造成本高。
自动控制原理第五章课后答案

五 频域分析法2-5-1 系统单位阶跃输入下的输出)0(8.08.11)(94≥+-=--t e e t c tt ,求系统的频率特性表达式。
【解】: 98.048.11)]([L )(1+++-==-s s s t c s C 闭环传递函数)9)(4(36198.048.11)()()(++=+++-==s s ss s s s R s C s G )9tg 4(tg 2211811636)9)(4(36)(ωωωωωωω--+-+⨯+=++=j ej j j G2-5-2系统时,系统的稳态输出(1))30sin()(0+=t t r ; (2))452cos(2)(0+=t t r ;(3))452cos(2)30sin()(00--+=t t t r 。
【解】:求系统闭环传递函数5tg 21254)5(4)(54)(1)()()()(14)(ωωωω--+=+=+=+==+=j B K K B K ej j G s s G s G s R s C s G s s G根据频率特性的定义,以及线性系统的迭加性求解如下:(1)︒===30,1,11θωr A︒--====-3.1151tg )1(178.0264)1()(1j j j B e eeA j G θωω[])7.18sin(78.0)1(sin )1()sin()(12︒+=++=+=t t A A t A t c r c s θθθ(2)︒===45,2,21θωr A︒--==+=-8.2152tg 274.02544)(1j j B e ej G ωω)2.232cos(48.1)(︒+=t t c s(3))8.662cos(48.1)7.18sin(78.0)(︒--︒+=t t t c s2-5-3 试求图2-5-3所示网络的频率特性,并绘制其幅相频率特性曲线。
【解】:(1)网络的频率特性1)(111)(212212+++=+++=ωωωωωC R R j C jR C j R R C j R j G(2)绘制频率特性曲线)tg (tg 22212121111)(1)(11)(ωωωωωωωT T j eT T jT jT j G ---++=++= 其中1221221,)(,T T C R R T C R T >+==。
自动控制原理第五版课后答案完整版

1-1 图1-2是液位自动控制系统原理示意图。在任意情况下,希望液面高度c维持不变,试说明系统工作原理并画出系统方块图。
图1-2 液位自动控制系统
解:被控对象:水箱;被控量:水箱的实际水位;给定量电位器设定水位(表征液位的希望值);比较元件:电位器;执行元件:电动机;控制任务:保持水箱液位高度不变。
(4)因为c(t)的表达式中r(t)的系数为非线性函数,所以该系统为非线性系统。
(5)因为该微分方程不含变量及其导数的高次幂或乘积项,且各项系数均为常数,所以该系统为线性定常系统。
(6)因为c(t)的表达式中包含变量的二次项,表示二次曲线关系,所以该系统为非线性系统。
(7)因为c(t)的表达式可写为,其中,所以该系统可看作是线性时变系统。
解:(1)
① n=3,根轨迹有3条分支,且均趋于无穷远处;
② 实轴上的根轨迹:[-50,0],(00];
③ 渐进线:,;
④ 分离点:
求解得:,(舍去);
作出根轨迹如图所示:
(2)临界开环增益为根轨迹与虚轴交点对应的开环增益。
令,代入,并令其实部、虚部分别为零,即
,
解得:(舍去)
当时,
当时,
当时,
3-11设随动系统的微分方程为
其中,T1、T2和K2为正常数。若要求r(t)=1+ t时,c(t)对r(t)的稳态误差不大于正常数ε0,试问K1应满足什么条件?
分析:先求出系统的误差传递函数,再利用稳态误差计算公式,根据题目要求确定参数。
解: 由题意知:
因为该系统为Ⅰ型系统,且输入为单位速度信号时,系统的稳态误差为0.1,即
所以:
自动控制原理 课后习题及答案

第一章 绪论1-1 试比较开环控制系统和闭环控制系统的优缺点.解答:1开环系统(1) 优点:结构简单,成本低,工作稳定.用于系统输入信号及扰动作用能预先知道时,可得到满意的效果。
(2) 缺点:不能自动调节被控量的偏差.因此系统元器件参数变化,外来未知扰动存在时,控制精度差.2 闭环系统⑴优点:不管由于干扰或由于系统本身结构参数变化所引起的被控量偏离给定值,都会产生控制作用去清除此偏差,所以控制精度较高。
它是一种按偏差调节的控制系统。
在实际中应用广泛。
⑵缺点:主要缺点是被控量可能出现波动,严重时系统无法工作.1—2 什么叫反馈?为什么闭环控制系统常采用负反馈?试举例说明之。
解答:将系统输出信号引回输入端并对系统产生控制作用的控制方式叫反馈。
闭环控制系统常采用负反馈。
由1-1中的描述的闭环系统的优点所证明。
例如,一个温度控制系统通过热电阻(或热电偶)检测出当前炉子的温度,再与温度值相比较,去控制加热系统,以达到设定值.1-3 试判断下列微分方程所描述的系统属于何种类型(线性,非线性,定常,时变)?(1)22()()()234()56()d y t dy t du t y t u t dt dt dt ++=+(2)()2()y t u t =+(3)()()2()4()dy t du t ty t u t dt dt +=+(4)()2()()sin dy t y t u t t dt ω+=(5)22()()()2()3()d y t dy t y t y t u t dt dt ++=(6)2()()2()dy t y t u t dt +=(7)()()2()35()du t y t u t u t dt dt =++⎰解答: (1)线性定常 (2)非线性定常 (3)线性时变 (4)线性时变 (5)非线性定常 (6)非线性定常 (7)线性定常1-4 如图1—4是水位自动控制系统的示意图,图中Q1,Q2分别为进水流量和出水流量.控制的目的是保持水位为一定的高度。
自动控制原理第五章课后习题答案(免费)[1]
![自动控制原理第五章课后习题答案(免费)[1]](https://img.taocdn.com/s3/m/11139471f46527d3250ce001.png)
自动控制原理第五章课后习题答案(免费)5-1设单位反馈系统的开环传递函数为对系统进行串联校正,满足开环增益 及 解:① 首先确定开环增益K,00()12lim v s K SG S k →===② 未校正系统开环传函为:012()(1)G s s s =+M a g n i t u d e (d B )1010101010P h a s e (d e g )Bode DiagramGm = 70.5 dB (at 200 rad/sec) , P m = 16.5 deg (at 3.39 rad/sec)Frequency (rad/sec)③ 绘制未校正系统的开环对数频率特性,得到幅穿频率 3.4c ω=,对应相位角'0()164,16c G j ωγ∠=-∴=,采用超前校正装置,最大相角 0(180())4016630m c G j ϕγωγ=-+∠+=-+=④ 11sin ,31m αϕαα--=∴=+ 0()(1)KG s s s =+40γ=︒112K s -=⑤ 在已绘图上找出10lg 10lg3 4.77α-=-=-的频率 4.4m ω=弧度/秒 令c m ωω=⑥0.128/,0.385/m T s T s ωα=⇒==∴=校正装置的传函为:110.385()110.128Ts s G s Ts s α++==++校正后的开环传函为:012(10.39)()()()(1)(10.13)c s G s G s G s s s s +==++ 校正后1801374340γ=-=>,满足指标要求.-100-50050100M a g n i t u d e (d B )101010101010P h a s e (d e g )Bode DiagramGm = 99.2 dB (at 1.82e+003 rad/sec) , P m = 42.4 deg (at 4.53 rad/sec)Frequency (rad/sec)5-2设单位反馈系统的开环传递函数为要求 设计串联迟后校正装置。
《自动控制原理》第5章习题答案

G0 ( s ) =
1 s (0.1s + 1)
特征方程为, D( s ) = 0.1s 2 + s + 1 = 0 ,即,s + 10 s + 10 = 0 ,
2
ω n = 10 = 3.162 , ζ =
10 = 1.58 ,原系统为过阻尼系统, 2ω n
2
σ % = 0 , ts >
4
ζω n
解: G ( jω ) =
ω=0 时, G (0) = 0.4 ,在低频段, L(ω ) = 20 lg 0.4 = −8dB ; ω → ∞ 时, G ( j∞) = 1 ,
在高频段, L(ω ) = 20 lg1 = 0dB 。转折频率 ω1 = 2 ,ω 2 = 5 。串联校正装置是超前校正装 置。
-j 3.46
②计算期望主导极点位置。 系统期望闭环主导极点具有阻尼系数 ζ =
2 ,自然振荡频率 ω n = 4 2 , 2
θ = arccosζ = arccos
2 = 450 , 则 一 个 具 有 期 望 极 点 的 2 阶 系 统 特 征 方 程 为 , 2
s 2 + 8s + 32 = 0
jω
期望极点
期望极点
− p3
j
600
j0.58
− p2
-1
− p1
0 -j
-3
-2
σ
-2
19.150 -1
40.880 0.33 0
119.640
校核相角条件: 根据在图中主导极点位置的近似值-0.33 ± j 0.58 和开环极点的位置, 作由各开环极点到期望主导极点的向量,
Φ = -119.640 -40.880 -19.150 = -179.670≈-1800
自动控制原理课后习题答案第五章

第 五 章5-2 若系统单位阶跃响应为49()1 1.80.8tth t ee--=-+试确定系统的频率特性。
分析 先求出系统传递函数,用j ω替换s 即可得到频率特性。
解:从()h t 中可求得:(0)0,(0)0h h '==在零初始条件下,系统输出的拉普拉斯变换()H s 与系统输出的拉普拉斯变换()R s 之间的关系为()()()H s s R s =Φ⋅即()()()H s s R s Φ=其中()s Φ为系统的传递函数,又1 1.80.836()[()]49(4)(9)H s L h t s s s s s s ==-+=++++1()[()]R s L r t s ==则()36()()(4)(9)H s s R s s s Φ==++令s j ω=,则系统的频率特性为()36()()(4)(9)H j j R j j j ωωωωωΦ==++5-7 已知系统开环传递函数为)1s T (s )1s T (K )s (G 12++-=;(K、T1、T2>0)当取ω=1时, o180)j (G -=ω∠,|G(jω)|=0.5。
当输入为单位速度信号时,系统的稳态误差为0.1,试写出系统开环频率特性表达式G(jω)。
分析:根据系统幅频和相频特性的表达式,代入已知条件,即可确定相应参数。
解: 由题意知:()G j ω=21()90arctan arctan G j T T ωωω∠=---因为该系统为Ⅰ型系统,且输入为单位速度信号时,系统的稳态误差为0.1,即1()lim ()0.1ss s e E s K→∞===所以:10K =当1ω=时,(1)0.5G j ==21(1)90arctan arctan 180G j T T ∠=---=-由上两式可求得1220,0.05T T ==,因此10(0.051)()(201)j G j j j ωωωω-+=+5-14 已知下列系统开环传递函数(参数K 、T 、T i>0,i=1,2,…,6)(1))1s T )(1s T )(1s T (K)s (G 321+++=(2))1s T )(1s T (s K)s (G 21++=(3))1Ts (s K )s (G 2+=(4))1s T (s )1s T (K )s (G 221++=(5)3s K )s (G =(6)321s)1s T )(1s T (K )s (G ++=(7))1s T )(1s T )(1s T )(1s T (s )1s T )(1s T (K )s (G 432165++++++=(8)1Ts K)s (G -=(9)1Ts K )s (G +--=(10))1Ts (s K)s (G -=其系统开环幅相曲线分别如图5-6(1)~(10)所示,试根据奈氏判据判定各系统的闭环稳定性,若系统闭环不稳定,确定其s 右半平面的闭环极点数。
自动控制原理_第5章习题解答-

第5章频率特性法教材习题同步解析一放大器的传递函数为:G (s )=1+Ts K测得其频率响应,当ω=1rad/s 时,稳态输出与输入信号的幅值比为12/2,稳态输出与输入信号的相位差为-π/4。
求放大系数K 及时间常数T 。
解:系统稳态输出与输入信号的幅值比为A ==222172K T ω=+ 稳态输出与输入信号的相位差arctan 45T ϕω=-=-︒,即1T ω=当ω=1rad/s 时,联立以上方程得T =1,K =12放大器的传递函数为:G (s )=121s +已知单位负反馈系统的开环传递函数为5()1K G s s =+ 根据频率特性的物理意义,求闭环输入信号分别为以下信号时闭环系统的稳态输出。
(1)r (t )=sin (t +30°); (2)r (t )=2cos (2t -45°);(3)r (t )= sin (t +15°)-2cos (2t -45°); 解:该系统的闭环传递函数为65)(+=Φs s 闭环系统的幅频特性为365)(2+=ωωA闭环系统的相频特性为6arctan )(ωωϕ-=(1)输入信号的频率为1ω=,因此有37375)(=ωA ,()9.46ϕω︒=- 系统的稳态输出537()sin(20.54)37ss c t t ︒=+ (2)输入信号的频率为2ω=,因此有10()A ω=,()18.43ϕω︒=- 系统的稳态输出10()cos(263.43)2ss c t t ︒=- (3)由题(1)和题(2)有对于输入分量1:sin (t +15°),系统的稳态输出如下5371()sin( 5.54)37ss c t t ︒=+ 对于输入分量2:-2cos (2t -45°),系统的稳态输出为102()cos(263.43)ss c t t ︒=-- 根据线性系统的叠加定理,系统总的稳态输出为)4363.632cos(210)537.5sin(37375)(︒︒--+=t t t c ss绘出下列各传递函数对应的幅相频率特性与对数频率特性。
自动控制原理课后参考答案

第一章1-1图1-2是液位自动控制系统原理示意图。
在任意情况下,希望液面高度c维持不变, 试说明系统工作原理并画岀系统方块图。
图1-2 液位自动控制系统解:被控对象:水箱;被控量:水箱的实际水位;给定量电位器设定水位U r(表征液位的希望值C r);比较元件:电位器;执行元件:电动机;控制任务:保持水箱液位高度不变。
工作原理:当电位电刷位于中点(对应U r)时,电动机静止不动,控制阀门有一定的开度,流入水量与流出水量相等,从而使液面保持给定高度C r,一旦流入水量或流出水量发生变化时,液面高度就会偏离给定高度C r。
当液面升高时,浮子也相应升高,通过杠杆作用,使电位器电刷由中点位置下移,从而给电动机提供一定的控制电压,驱动电动机,通过减速器带动进水阀门向减小开度的方向转动,从而减少流入的水量,使液面逐渐降低,浮子位置也相应下降,直到电位器电刷回到中点位置,电动机的控制电压为零,系统重新处于平衡状态,液面恢复给定高度r。
反之,若液面降低,则通过自动控制作用,增大进水阀门开度,加大流入水量,使液面升高到给定高度C r。
系统方块图如图所示:1-10 下列各式是描述系统的微分方程,其中c(t)为输岀量,r (t)为输入量,试判断哪些是线性定常或时变系统,哪些是非线性系统?2c(t) =5 r2(t) t d2(^(1) dt ;3 2d c(t) 3d c(t) 6dc(t) --- 3 3 ---- 2 6 — dt dt dt xdc(t) dr(t)t c(t) =r(t) 3 dt dtc(t) = r(t)cos t 5 ;dr (t) tc(t) =3r(t)6 5 r(.)d. (5) dt =;(6)c(t)訂 2 ⑴;0, t ::: 6c(t)= “r(t), t 畠 6.(7) -解:(1)因为c(t)的表达式中包含变量的二次项 『(t),所以该系统为非线性系统。
(2) 因为该微分方程不含变量及其导数的高次幕或乘积项,且各项系数均为常数,所以该 系统为线性定常系统。
《自动控制原理》第二版课后习题答案
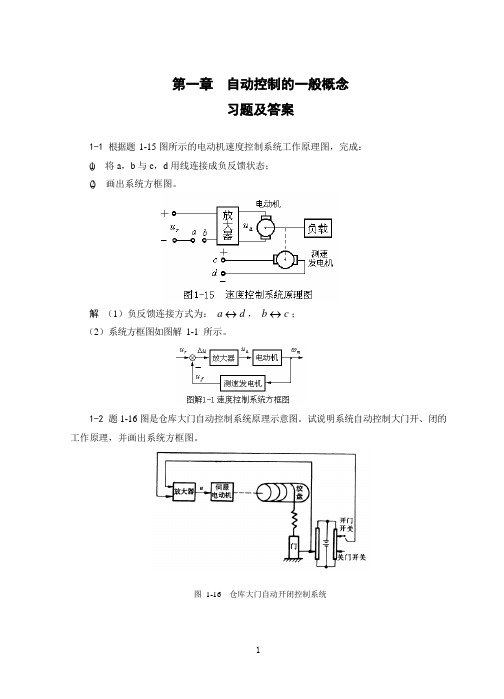
动电位器 P2 的滑臂转过一定的角度 o ,直至 o i 时, ui uo ,偏差电压ue 0 ,电动 机停止转动。这时,导弹发射架停留在相应的方位角上。只要 i o ,偏差就会产生调节作
3
用,控制的结果是消除偏差 e ,使输出量 o 严格地跟随输入量 i 的变化而变化。 系统中,导弹发射架是被控对象,发射架方位角 o 是被控量,通过手轮输入的角度 i 是
大,提高发电机的端电压,使发电机 G 的端电压回升,偏差电压减小,但不可能等于零,因
为当偏差电压为 0 时, i f =0,发电机就不能工作。即图(b)所示系统的稳态电压会低于 110
伏。 1-8 图 1-22 为水温控制系统示意图。冷水在热交换器中由通入的蒸汽加热,从而得到一
定温度的热水。冷水流量变化用流量计测量。试绘制系统方块图,并说明为了保持热水温度 为期望值,系统是如何工作的?系统的被控对象和控制装置各是什么?
图 1-16 仓库大门自动开闭控制系统
1
解 当合上开门开关时,电桥会测量出开门位置与大门实际位置间对应的偏差电压,偏 差电压经放大器放大后,驱动伺服电动机带动绞盘转动,将大门向上提起。与此同时,和大 门连在一起的电刷也向上移动,直到桥式测量电路达到平衡,电动机停止转动,大门达到开 启位置。反之,当合上关门开关时,电动机带动绞盘使大门关闭,从而可以实现大门远距离 开闭自动控制。系统方框图如图解 1-2 所示。
征炉温的希望值)。系统方框图见图解 1-3。
1-4 图 1-18 是控制导弹发射架方位的电位器式随动系统原理图。图中电位器 P1 、 P2 并 联后跨接到同一电源 E0 的两端,其滑臂分别与输入轴和输出轴相联结,组成方位角的给定元件
《自动控制原理》课后习题答案(5章)
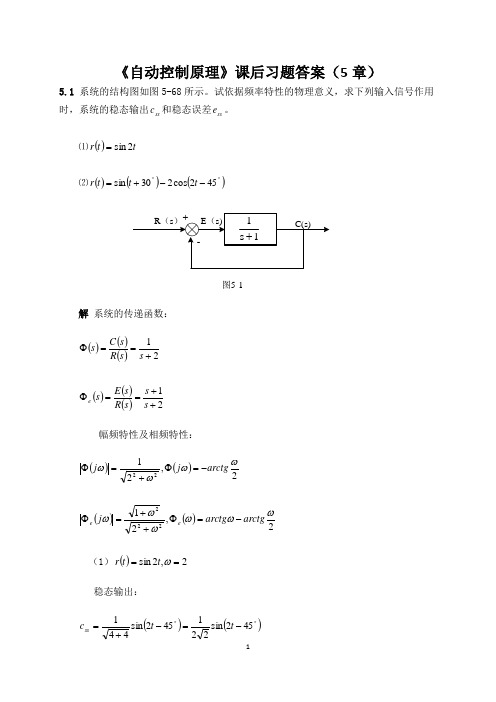
《自动控制原理》课后习题答案(5章)5.1 系统的结构图如图5-68所示。
试依据频率特性的物理意义,求下列输入信号作用时,系统的稳态输出ss c 和稳态误差ss e 。
⑴()t t r 2sin =⑵()()()︒︒--+=452cos 230sin t t t r图5-1解 系统的传递函数:()()()21+==Φs s R s C s ()()()21++==Φs s s R s E s e 幅频特性及相频特性:()()2,2122ωωωωarctgj j -=Φ+=Φ()()2,21222ωωωωωωarctgarctg j e e -=Φ++=Φ(1)()2,2sin ==ωt t r 稳态输出:()()︒︒-=-+=452sin 221452sin 441t t c ss()︒-≈452sin 354.0t稳态误差:⎪⎭⎫ ⎝⎛-+++=2222sin 2221222arctg arctg t e ss()()︒︒+≈+=43.182sin 791.043.182sin 225t t(2)()()()()()︒︒︒︒+-+=--+=452sin 230sin 452cos 230sin t t t t t r⎪⎪⎭⎫ ⎝⎛+∠+++•-⎪⎪⎭⎫ ⎝⎛+∠+++=︒︒221452sin 221212130sin 211222j t j t c ss ()t t 2sin 225.3sin 55-+=︒ ()t t 2sin 708.05.3sin 447.0-+≈︒⎪⎭⎫ ⎝⎛-++++•-⎪⎭⎫ ⎝⎛-++++=︒︒222452sin 2221221130sin 12112222222arctg arctg t arctg arctg t e ss ()()︒︒︒︒︒︒-++•--++=4543.63452sin 410257.264530sin 510t t ()()︒︒+-+≈43.632sin 582.143.48sin 632.0t t ()()︒︒--+=57.1162sin 582.143.48sin 632.0t t5.2 若系统的单位阶跃响应:()t t e e t h 948.08.11--+-=()0≥t 试求系统的频率特性。
自动控制原理第五、六章答案

第五、六章 线性系统的频域分析与校正习题与解答5-1 试求下图(a)、(b)网络的频率特性。
解 (a)依图:⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(R R C R R T C R R R R K s T s K sCR sC R R R s U s U r c ττωωτωωωωω11121212121)1()()()(jT j K C R R j R R C R R j R j U j U j G r c a ++=+++==(b)依图:⎩⎨⎧+==++=+++=C R R T CR s T s sCR R sC R s U s U r c )(1111)()(2122222212ττ ωωτωωωωω2221211)(11)()()(jT j C R R j C R j j U j U j G r c b ++=+++==5-2 某系统结构图如图所示,试根据频率特性的物理意义,求下列输入信号作用时,系统的稳态输出)(t c s 和稳态误差)(t e s(1) t t r 2s i n)(= (2) )452cos(2)30sin()(︒--︒+=t t t r解 系统闭环传递函数为:21)(+=Φs s 频率特性:2244221)(ωωωωω+-++=+=Φj j j 幅频特性:241)(ωω+=Φj相频特性:)2arctan()(ωωϕ-= 系统误差传递函数:,21)(11)(++=+=Φs s s G s e则 )2a r c t a n (a r c t a n )(,41)(22ωωωϕωωω-=++=Φj j e e(1)当t t r 2sin )(=时, 2=ω,r m =1 则 ,35.081)(2==Φ=ωωj 45)22arctan()2(-=-=j ϕ4.1862arctan )2(,79.085)(2====Φ=j j e e ϕωω )452sin(35.0)2sin()2(-=-Φ=t t j r c m ss ϕ )4.182sin(79.0)2sin()2(+=-Φ=t t j r e e e m ss ϕ (2) 当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5.26)21arctan()1(45.055)1(-=-===Φj j ϕ4.18)31arctan()1(63.0510)1(====Φj j e e ϕ)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t c m m s ϕϕ+-⋅Φ-++⋅Φ=)902cos(7.0)4.3sin(4.0 --+=t t)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t e e e m e e m s ϕϕ+-⋅Φ-++⋅Φ=)6.262cos(58.1)4.48sin(63.0 --+=t t5-3 若系统单位阶跃响应如下,试求系统频率特性。
自动控制原理 4-5章习题与解答习题课后校对稿

可知: K 增大时, % , t p 。
4
4-9 设电子心率起搏器系统如图 4-41 所示,其中模仿心脏的传递函数相当于一个纯积 分器。要求:
(1)若 0.5 对应于最佳响应情况,问该情况下起搏器的增益 K 应为多大?
(2)若期望心速为 60 次/min,并突然接通起搏器,问 1 s 后实际心速为多少?瞬时最大 心率为多大?
10(s 2) , s2 (s 20)
以及 R(s) 1 s
2 s2
则 T (s) Y (s) 10 。 R(s) s 20
4-5 某控制系统结构图如图 4-38 所示,其中 K1 5 , T1 0.5 。 (1)求系统的单位阶跃响应; (2)计算系统的性能指标 tr , t p , ts ( 5% ), % ;
T1 5T1
(1)该系统的单位阶跃响应为
y(t) 2.51
e nt 1 2
sin(d t
)
2.51
23 3
e nt
sin(
3t
)
3
2.51
1.1547e t
sin(1.7321t
3
)
(2)系统的性能指标为:
解之得: K 25 , n 25
(2)闭环传递函数写为: T (s)
s2
625 25s 625
,闭环极点 s1,2
12.5
j12.5
3。
方法一:系统的阶跃响应为
y(t) 1
1 1
2
e nt
sin( n
自动控制原理参考答案-第5章

第五章题5-1:试绘制下列开环传递函数的幅相频率特性曲线。
(1) 10G(s)H(s)(s 1)(0.2s 1)=++ (2) 25(s 1)G(s)H(s)(s 3)(s 2s 2)+=+++(3) 100G(s)H(s)(s 1)(s 3)(s 4)=+++ 题5-6:试绘制题5-1各开环传递函数的对数幅频特性渐近线和半对数相频特性曲线。
(1) 2221010122()()(1)(0.21)(1)(10.04)j G j H j j j ωωωωωωωω--==++++实频特性:)04.01)(1(210)(222ωωωω++-=P虚频特性:)04.01)(1(12)(22ωωωω++-=Q 相频特性:()arctan arctan 0.2ϕωωω=-- Nyqist 曲线:起点:0ω=(0)10P ⇒=,(0)0Q =,(0)0ϕ=终点:ω=∞()0P ⇒∞=,()0Q ∞=,()180ϕ∞=- 与虚轴交点:()0P ω= 2.236ω⇒=() 3.73Q ω⇒=- Nyqist 曲线如下:转折频率1:111T ω==;转折频率2:215T ω==对数幅频特性:()20lg ()20lg10L A ωω==-半对数相频特性:()arctan arctan 0.2ϕωωω=-- Bode 图如下:(2) 25(1)()()(3)(22)j G j H j j j ωωωωωω+=+-+ 222222225(3)(2)202(12)(9)[(2)4]j ωωωωωωωω+-+-+=+-+ 实频特性:]4)2)[(9(20)2)(3(5)(2222222ωωωωωωω+-++-+=P 虚频特性:]4)2)[(9()21(10)(22222ωωωωωω+-++-=Q相频特性:2()arctan arctan arctan 310.5ωωϕωωω=--- Nyqist 曲线:起点:0ω=5(0)6P ⇒=,(0)0Q =,(0)0ϕ=终点:ω=∞()0P ⇒∞=,()0Q ∞=,()180ϕ∞=-与虚轴交点:()0P ω= 2.09ω⇒=()0.66Q ω⇒=- Nyqist 曲线如下:225(1)0.83(1)()()(3)(22)(0.331)[(0.7)1]j j G j H j j j j j j ωωωωωωωωωω++==+-++++ 转折频率1:11 1.414T ω==;转折频率2:213T ω==对数幅频特性:5()20lg ()20lg 6L A ωω==+半对数相频特性:2()arctan arctanarctan310.5ωωϕωωω=---Bode 图如下:(3) 23222100100[128(19)]()()(1)(3)(4)(1)(3)(4)j G j H j j j j ωωωωωωωωωωω-+-==++++++实频特性:)4)(3)(1()812(100)(2222ωωωωω+++-=P虚频特性:)4)(3)(1()19(100)(2223ωωωωωω+++-=Q 相频特性:()arctan arctan 0.33arctan 0.25ϕωωωω=--- Nyqist 曲线:起点:0ω=(0)8.33P ⇒=,(0)0Q =,(0)0ϕ= 终点:ω=∞()0P ⇒∞=,()0Q ∞=,()270ϕ∞=- 与虚轴交点:()0P ω= 1.22ω⇒=() 4.77Q ω⇒=- 与实轴交点:()0Q ω= 4.36ω⇒=()0.71P ω⇒=- Nyqist 曲线如下:8.33()()(1)(0.331)(0.251)G j H j j j j ωωωωω=+++转折频率1:111T ω==;转折频率2:213T ω==;转折频率3:314T ω==对数幅频特性:()20lg ()18.4L A ωω==-半对数相频特性:()arctan arctan 0.33arctan 0.25ϕωωωω=--- Bode 图如下:题5-2:已知某一控制系统的单位阶跃响应为4t 9t c(t)1 1.8e 0.8e --=-+试求该系统的开环频率特性。
自动控制原理答案完全版_第二版
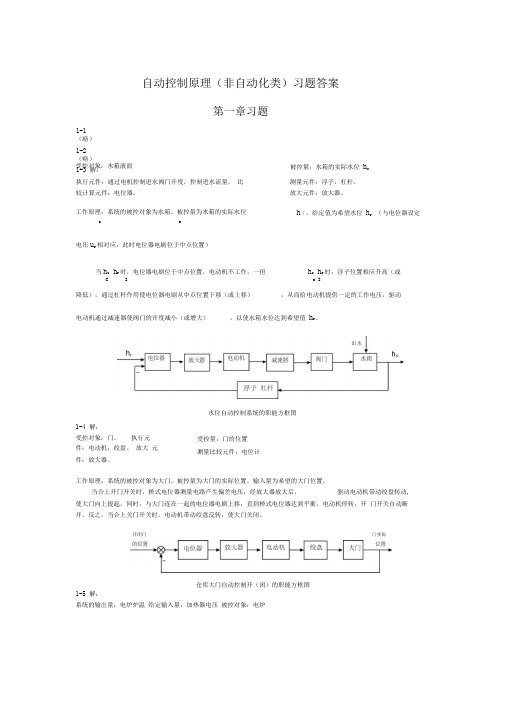
自动控制原理(非自动化类)习题答案第一章习题被控量:水箱的实际水位 h c执行元件:通过电机控制进水阀门开度,控制进水流量。
比较计算元件:电位器。
h 「。
给定值为希望水位 h r (与电位器设定cr电压u r 相对应,此时电位器电刷位于中点位置)当h c h r 时,电位器电刷位于中点位置,电动机不工作。
一但h c h r 时,浮子位置相应升高(或CIc I降低),通过杠杆作用使电位器电刷从中点位置下移(或上移) ,从而给电动机提供一定的工作电压,驱动电动机通过减速器使阀门的开度减小(或增大),以使水箱水位达到希望值 h r 。
水位自动控制系统的职能方框图受控量:门的位置 测量比较元件:电位计工作原理:系统的被控对象为大门。
被控量为大门的实际位置。
输入量为希望的大门位置。
当合上开门开关时,桥式电位器测量电路产生偏差电压,经放大器放大后,驱动电动机带动绞盘转动,使大门向上提起。
同时,与大门连在一起的电位器电刷上移,直到桥式电位器达到平衡,电动机停转,开 门开关自动断开。
反之,当合上关门开关时,电动机带动绞盘反转,使大门关闭。
1-5 解:系统的输岀量:电炉炉温 给定输入量:加热器电压 被控对象:电炉1-1 (略) 1-2(略)1-3 解: 受控对象:水箱液面 测量元件:浮子,杠杆。
放大元件:放大器。
工作原理:系统的被控对象为水箱。
被控量为水箱的实际水位1-4 解:受控对象:门。
执行元件:电动机,绞盘。
放大 元件:放大器。
开闭门门实际仓库大门自动控制开(闭)的职能方框图放大元件:电压放大器,功率放大器,减速器比较元件:电位计测量元件:热电偶职能方框图:KK3 2 Ts (T 1)s s K1K 3电位器电压放大炉温热电偶第二章习题2-1解:对微分方程做拉氏变换:X,(s) R(s) C(s) N,(s)X 2 (s) Q X/s)X 3 (s) X2 (s) X5(s TsX4 (s) X 3 (s)X5 (s) X4 (s) K2 N2(s k 3 X5 (s) s2C (s) sC(s) C(s) / R(s) 功率放大加热器'电机电炉R(s)绘制上式各子方程的方块图如下图所示:C(s) / N i (s) C(s) / R(s),K 2K 3TSTs 3~~T 1)s 2s K 1K 32-2解:对微分方程做拉氏变换X i (s) K[R(s) C (s)] X 2 (s)sR(s)(s 1) X 3(s) X i (s) X 2 (s) (Ts 1)X 4 (s)X 3 (s) X 5 (s)C(s) X 4 (s) N (s) X 5 (s) (Ts 1) N(s)(b) C (s)字红R(s) 1 G 1G 3 G G 4 G 2 G 3 G 2G 4X3(s) 绘制上式各子方程的方块如下图:将方块图连接得出系统的动态结构图:..R(s)1(s 1):Ts 1)C(s)N (s) 02-3解:(过程略)K____________C(s) (s 1)<Js 1) (s 1XTs 1) K ____________ Ts 2(T s1)s (K 1)C(s) / N 2 (s)R(s) ms fs K(c)誤 R(s) G 2 G 1G 2 1 G-i G 2G-I (d 普 R(s)G 1 G 2 1 G 2G 3(e)R^ R(s)G 1G 2G 3G 4 1 G<|G 2 G 2G 3 G 3G 4 G 1G 2G 3G 4 2-4 解:(1)求 C/R ,令 N=0 KK K 3s(Ts 1) C (s) / R(s) G(s)1 G(s) 求C/N ,令R=0,向后移动单位反馈的比较点 K C(s) / N (s) (K n G n K 1 0 ) — J s 1 亠 K 1G(s)K 1K 2 K 3 Ts 2K i K 2 K 3K n K 3s K 1K 2 K 3G K 2 n2 一Ts 2s K 1K 2 K 3 Ts 1 s (2)要消除干扰对系统的影响C(s) / N (s) K n K3s K1K2 K3GnTs 2 s K 1K 2 K 3G n (s) KnsK 1K 22-5 解:(a ) (1 )系统的反馈回路有三个,所以有3L a L 1 L 2 L 3 a 1G 1G 2G 5 G 2G 3G 4 G 4G 2G 5三个回路两两接触,可得 1 L a 1 GG 2G 5 G 2G 3G 4 G 4G 2G 5(2) 有两条前向通道,且与两条回路均有接触,所以P P 2 G 1G 2G 3,11, 2 1(3) 闭环传递函数C/R 为GGG 3 11 G 1G 2G 5 G 2G 3G 4 G 4G 2G 5(b)(1) 系统的反馈回路有三个,所以有3L aa 1L 1L 3 G 1G 2 G 1 G 1三个回路均接触,可得 1 L a 1 G-i G 2 2G-)(2 )有四条前向通道,且与三条回路均有接触,所以R G 1G 2 , 11P 2G, 21PG2,3 1P 4G 1,41(3)闭环传递函数C/R 为C G 1G 2 G 1 G 2 GG-i G 2 G 2 R 1 G 1G 22G 1 1 G-|G 2 2G.2-6解:用梅逊公式求,有两个回路,且接触,可得1L a 1 GG 2G 3 G 2,可得第三章习题采用K 0 , K H 负反馈方法的闭环传递函数为1OK o要使过渡时间减小到原来的 0.1倍,要保证总的放大系数不变,则:(原放大系数为10,时间常数为0.2)3-2解:系统为欠阻尼二阶系统(书上改为“单位负反馈……”,“已知系统开环传递函数”)% e / 1 $100%100% 1C(s) G-|G 2G 3 G 2G 3 R(s) 1 G 1G 2G 3 G 2 C (s)(1 G 2 )G 3N 2 (s) 1 GG 2G 3 G 2 E(s) 1 G 2 G 2G 3 R(s) 1 G-|G 2G :3 G 2 E(s) C(s) (1 G 2 G N 2 (s)N 2 (s)1 G 1G 2G 3 G 2C (s) NQC(s) / R(s)C(s) 1 (1 GG 2G 3 G 2 ) 1N 3 (s) 1 G 1G 2G 3 G 2 E(s) C(s) G 2G 3 G 1G 2G 3 N 1 (s) N 1(s) 1 G 1G 2G 3 G 2E(s)C(s) 1N 3 (s)N 3 (s)3-1解:(原书改为G(s) 100.2s 1)(s)C(s) K G(s) R(s) 01 G(S )K H1 10K H 0.2s1 10K10K 。
中文版教材习题五答案

z
*
30 199
30
(2)分离点为: d 0.4 ,分离角为: (2k 1)
l
2
起始角: p4 268 , p5 268
与虚轴的交点:
K1*
0 0
K2,3*
1.034 73.04
K4*,5165.553104
K(3s 1)
s(2s 1) K(3s 1)
闭环特征方程: 2s 2 (1 3K)s K 0
闭环特征根: s1,2 (1 3K)
(1 3K)2 8K (1 3K) 9K 2 2K 1
4
4
当
K=0
时,特征根
s1
0, s2
1 2
(1 3K ) (3K 1)2 8
(1)
G(s)
K s(s 1)2
(2)
G(s)
K(s s(s2 4s
4) 29)
(3) G(s)
K
s(s 2 4s 8)
试概略画出闭环系统根轨迹图。 5-4 参考答案:
(a) G(s)H (s) K s(s 1)2
(4) G(s) K (s 5)(s 4) s(s 1)(s 3)
-4 -3
Im
-1
0
Re 5
44
“自动控制原理”第五章习题参考答案
5-5
已知开环传递函数为 G(s)H (s)
K s(s 4)(s2 4s 20)
,请概略画出闭环系统根轨。
5-5 参考答案:
与虚轴交点:
K
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(T1 T2 T3 ) T1T2T3 K (1 2T12 )(1 2T22 )
3
1 T1T2 T3 (T1 T2 ) jK 2 2 2 2 (1 T1 )(1 T2 )
2 2
(3) 起点: G ( 终点: G (
j0)= 90
G( s)
其中
因 因
Ks
2 2
2 n
1 ( s 2n s )( s 1) 1 1 10n 1
2 n
得 K 10 20lg K 20
20lg M r 40 20
由M
2
r
1 2 1
2
得
0.05
得K= 100
K (1 1 s 1) G( s ) 2 s (1 2 s 1)
-40dB/dec 20 0 -20 -20dB/dec 1 10 2
s (0.00316s 1)
解(c) :系统最左端直线的斜率为40dB/dec,得 v = -2,系统有两 个纯微分环节。1 和n 分别是振荡和惯性环节的转折频 率,则系统开环传递函数为:
5-5 已知最小相位系统的对数幅频渐近特性曲线如图所示, L() 试确定系统的开环传递函数。
解(a) :系统最左端直线的斜率为0dB/dec, 40 0 得 v=0,系统无积分环节。1、2 1 100 和3 分别是惯性、微分和惯性环节 -20 的转折频率,系统开环传递函数为:
10000 2
1
10 5 40
60
5 时,直线斜率由-
40dB/dec变为-20dB/dec 。
相频特性曲线由各环节的相频特性相加获得,计算几个点 的值绘出大致曲线。
num=[20 20]; den=[1 7 20 50 0]; bode(num,den) grid
Bode Diagram 50
Magnitude (dB)
பைடு நூலகம்
j (
0.4( j 1) j 2 2 j ) j 1( 1) 10 10 5
系统由比例、微分、积分、惯性、振荡五个典型环节组成。
1,K 0.4,T1 1,T2 1 10,T3 0.2 则 1 1 1 1 1 2 10 3 5 20lg K 20lg0.4dB T1 T2 T3
j)=0 180
因此,开环频率特性的相频范围为:90
2
180
(4) 与实轴的交点,令 G(j) 的虚部为零,得
1 = 0 (T3 T1 T2 ) T1T2-T ( 3 T1+T2)
即与实轴无交点。 (5) 系统极坐标图如右图所示。 (6) 开环频率特性曲线不包围(-1, j0)点,R=0,此时 Z = P –R = 0, 故闭环系统是稳定的。
由
40 ( 20) 3 得 2 10 1 1000 20 lg 1 lg 2
( s 1)(0.0001s 1)
解(b) :系统最左端直线的斜率为- 40dB/dec,得 v = 2,系统有 两个积分环节。1 和2 分别是微分和惯性环节的转折 L() 频率,则系统开环传递函数为:
G( j)=0 180
5-13 设系统的开环幅相频率特性如图所示,判断闭环系统 是否稳定。图中,P 为开环传递函数右半 s 平面的极点数, v 为其 s=0 的极点数。
(a) P =1,v=0
(b) P =1,v=0
解:(a) P =1,Nyquist图逆时针包围(-1, j0)点半圈,Z=P-2R=1-2 *0.5=0,所以系统稳定 (b) P =1,Nyquist图顺时针包围(-1, j0)点半圈, Z=P-2R=1-2
令 ()= 180
化成 G( j)
X () jY () 形式,
4.03 求出相角穿越频率 g==
将 g 代入 A( ) ,求出
令 Y ( ) 0,可获得 g 及相应h
A(g )=0.32
1 则幅值裕度 h 3.12 A(g )
5-10 用奈式稳定判据判断反馈系统的稳定条件,系统的开环
K (T3s 1) 传递函数: G( s ) (T3 T1 T2 ) s(T1s 1)(T2 s 1)
(2) 系统开环频率特性为
解: (1) 由开环传递函数知,其在右半 s 平面的极点数 P=0。
K ( jT3 1) G ( j ) j( jT1 1)( jT2 1)
最小相位系统 Nyquist 图的结论:
(1) 开环含有v 个积分环节系统,Nyquist曲线起自幅角为-v 90° 的无穷远处。 (2) n=m 时, Nyquist 曲线起自实轴上的某一有限远点,且止于 实轴上的某一有限远点。 (3) n>m时,Nyquist曲线终点幅值为0,而相角为-(n-m)*90°。
低频渐近线:斜率为 20 20 dB ,过点 (1, 20lg0.4)。
1, 10,5 分 别 是
一阶微分环节、振荡环节、 伯德图如下图所示:
惯性环节的交接频率。当
L( )
20
1 1 时 , 直 线 斜 率 由 20dB/dec变为0dB/dec、当 20lg 0.4 2 10 时,直线斜率由 0dB/dec 变 为 -40dB/dec 、 当 3
1 0.4 1 L( ) 3 2 10 3 4 20 5
0.4
2 ( ) arctan 90 arctan arctan 5 10 2 将 c 代入 ( )
相角裕度:
(c )+ 180 104
0
c
g
h( dB )
-50
-100 -45
-90
Phase (deg)
-135
-180
-225
-270 10
-2
10
-1
10
0
10
1
10
2
Frequency (rad/sec)
计算稳定裕度:
G ( j ) H ( j )
j (
0.4( j 1) j 2 2 j ) j 1( 1) 10 10 5
K (1 2 s 1) 其中 3 10000 G( s) (1 1 s 1)(1 3 s 1) 因20lg K 40 得K 100 40 20 由 得 1 1 lg 1 lg100 100(0.001s 1)
G( s)
20 由 得 1 10 40 lg 1 lg10 20 (20) 由 20 得 2 100 10 lg 1 lg 2 20 lg K 100(0.316s 1) 40 由 G( s) 2 lg1 lg10
解:
由频率特性可得:
0. 4 1 20 lg 1 10 20 lg 0.4 L( ) 4 20 lg 2 10 5 20 lg 20 5 3
可见:c
(f) P =0,v=2
(g) P =1,v=0
(h) P =2,v=0
(f) P =0,Nyquist图顺时针包围(-1, j0)点 1圈, Z=P-2R=0-2* (-1) =2,系统不稳定 (g) P =1,Nyquist图逆时针包围(-1, j0)点半圈, Z=P-2R=1-2*0.5 =0,系统稳定 (h) P =2,Nyquist图逆时针包围(-1, j0)点 0 圈, Z=P-2R=2-2*0= 2,系统不稳定
(4) 不含一阶或二阶微分环节的系统,相角滞后量单调增加。含 有一阶或二阶微分环节的系统,由于相角非单调变化,Nyquist 曲线可能出现凹凸。
K (T3s 1) G( s ) (T3 T1 T2 ) s(T1s 1)(T2 s 1)
G( j0)= 90
10s G( s) 2 (s 0.1s 1)(0.1s 1)
5-8 已知单位反馈系统开环传递函数
20( s 1) G( s)H ( s) 2 s( s 2s 10)( s 5)
试绘制开环系统的 Bode图,并确定系统的幅值裕度和相角 裕度。
解:G (
j ) H ( j )
*(-0.5)=2,系统不稳定
(c) P =1,v=0
(d) P =0,v=2
(e) P =2,v=1
(c) P =1,Nyquist图顺时针包围(-1, j0)点半圈,Z = P-2R =1-2* (-0.5)=2,系统不稳定 (d) P =0,Nyquist图逆时针包围(-1, j0)点 0 圈, Z=P-2R=0-2*0 =0,系统稳定 (e) P =2,Nyquist图逆时针包围(-1, j0)点 1 圈, Z=P-2R=2-2*1 =0,系统稳定
