金融计量经济第五讲虚拟变量模型和Probit、Logit模型
logit 和probit模型的系数解释 -回复

logit 和probit模型的系数解释-回复Logit和Probit模型是常用的二元选择模型,用于分析二元变量的选择行为。
它们通常用于解释个体在做出选择时的决策,可以帮助我们理解各种影响因素对选择行为的影响。
在这篇文章中,我将逐步回答有关Logit和Probit模型的系数解释的问题,介绍这两个模型的基本原理、模型形式、系数解释和使用注意事项,以及如何解读模型中的系数。
首先,让我们从基本原理开始,了解Logit和Probit模型的背后逻辑。
Logit 和Probit模型都属于广义线性模型(Generalized Linear Models),它们基于一个相似的假设:选择行为是一个概率事件,可以由一组解释变量进行解释。
这些解释变量可以是个体特征(如年龄、性别、教育水平等),也可以是一些特定的因素(如收入水平、市场利率等)。
模型的目的是通过对这些解释变量的分析,预测和解释个体做出选择的概率。
接下来,让我们详细了解Logit和Probit模型的模型形式。
Logit模型使用的是逻辑函数(Logistic Function),而Probit模型使用的是标准正态分布的累积分布函数。
具体来说,Logit模型的形式为:p(y=1 x) = F(xβ) = 1 / (1 + e^(-xβ))其中,p(y=1 x)表示个体在给定解释变量x的情况下选择y=1的概率,F(x β)表示Logistic函数,x是解释变量的值,β是模型的系数。
相比之下,Probit模型的形式稍有不同:p(y=1 x) = Φ(xβ)其中,Φ(xβ)表示标准正态分布的累积分布函数,其他符号的含义与Logit 模型相同。
两个模型的模型形式不同,但它们都具有类似的特点:在x 趋近于正无穷时,概率趋近于1,而在x 趋近于负无穷时,概率趋近于0。
这种形式可以帮助我们理解个体选择行为的变化趋势。
现在让我们转向系数解释的问题。
模型的系数代表着解释变量对选择行为的影响程度。
金融计量经济第五讲虚拟变量模型和Probit、Logit模型

原始模型:
YX (5.8)
• 其中Y为观测值取1和0的虚拟被解释变量,X为 解释变量。
• 模型的样本形式: yi Xii
(5.9)
• 因为E(i)0
,E所(y以i)Xi
• 令: p i P ( y i 1 ) 1 p i P ( y i 0 )
• 于是有: E ( y i) 1 P ( y i 1 ) 0 P ( y i 0 ) p i
其它季度
1, 三季度
D3
0,
其它季度
• 小心“虚拟变量陷阱”!
精品课件
三、虚拟变量的应用
• 1、在常数项引入虚拟变量,改变截距。
y i0D 1 x 1 i kx k iu i (5.1)
• 对上式作OLS,得到参数估计值和回归模型:
y ˆiˆ0ˆD ˆ1 x 1 i ˆkx ki(5.2)
金融计量经济第五讲
虚拟变量模型和Probit、Logit模 型
精品课件
第一节 虚拟变量的一般应用
一、虚拟变量及其作用 1.定义:取值为0和1的人工变量,表示非量化
(定性)因素对模型的影响,一般用符号D表 示。例如:政策因素、地区因素、心理因素、 季节因素等。 2.作用: ⑴描述和测量定性因素的影响; ⑵正确反映经济变量之间的相互关系,提高模型 的精度; ⑶便于处理异常数据。
yˆt ˆ ˆxt yˆt ˆ ˆxt ˆ2 yˆt ˆ ˆxt ˆ3 yˆt ˆ ˆxt ˆ4
精品课件
一季度 二季度 三季度 四季度
例题:美国制造业的利润—销售额行为
• 模型:利 t 1 润 2 D 2 t 3 D 3 t 4 D 4 t ( 销 ) t u t售
0.503543 0.500354 1.13E+03 1.99E+09 -13241.74 1.648066
probit模型与logit模型

probit模型与lo git模型2013-03-30 16:10:17probit模型是一种广义的线性模型。
服从正态分布。
最简单的pr obit模型就是指被解释变量Y是一个0,1变量,事件发生地概率是依赖于解释变量,即P(Y=1)=f(X),也就是说,Y=1的概率是一个关于X的函数,其中f(.)服从标准正态分布。
若f(.)是累积分布函数,则其为Log istic模型Logit模型(Logitmodel,也译作“评定模型”,“分类评定模型”,又作Logi sticregres sion,“逻辑回归”)是离散选择法模型之一,属于多重变量分析范畴,是社会学、生物统计学、临床、数量心理学、市场营销等统计实证分析的常用方法。
逻辑分布(Logist ic distri butio n)公式P(Y=1│X=x)=exp(x’β)/1+exp(x’β)其中参数β常用极大似然估计。
Logit模型是最早的离散选择模型,也是目前应用最广的模型。
Logit模型是Luc e(1959)根据IIA特性首次导出的;Marsch ark(1960)证明了Log it模型与最大效用理论的一致性;Marley (1965)研究了模型的形式和效用非确定项的分布之间的关系,证明了极值分布可以推导出Logi t 形式的模型;McFadd en(1974)反过来证明了具有Log it形式的模型效用非确定项一定服从极值分布。
此后Logi t模型在心理学、社会学、经济学及交通领域得到了广泛的应用,并衍生发展出了其他离散选择模型,形成了完整的离散选择模型体系,如Probi t模型、NL模型(Nest Logitmodel)、MixedLogit模型等。
模型假设个人n对选择枝j的效用由效用确定项和随机项两部分构成:Logit模型的应用广泛性的原因主要是因为其概率表达式的显性特点,模型的求解速度快,应用方便。
Logit和Probit模型的比较结果
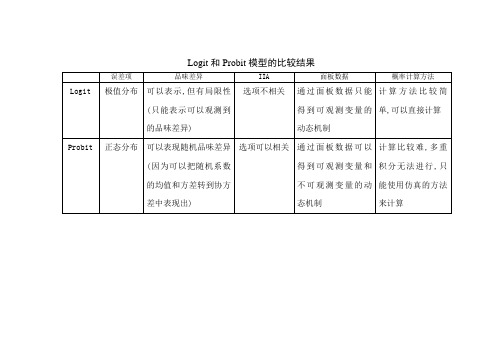
误差项
品味差异
IIA
面板数据
概率计算方法
Logit
极值分布
可以表示,但有局限性(只能表示可以观测到的品味差异)
选项不相关
通过面板数据只能得到可观测变量的动态机制
计算方法比较简单,可以直接计算
Probit
正态分布
可以表现随机品味差异(因为可以把随机系数的均值和方差转到协方差中表现出)
选项可以相关
通过面板数据可以得到可观测变量和不可观测变量的动态机制
计算比较难,多重积分无法进行,只能使用仿真的方法来计算
虚拟变量回归模型:计量经济学3

3、虚拟变量的实际应用
(1)虚拟变量可以用于研究制度变迁的影响
如:研究2001年中国加入WTO事件对中国进出 口贸易的影响,可以建立如下方程:
+d 主要贸易伙伴国 GDP+e DWTO
中国的进出口贸易总值 =a b 人民币汇率 c 中国GDP
计量经济学专题:
虚拟变量的回归与Probit模型、 Logit模型
1、虚拟变量的性质
与有明确尺度量化了的变量(GDP、产 量、价格、成本、汇率等)不同,虚拟 变量是一种定性性质的变量,如性别、 种族、国籍等只涉及“是”与“非”两 种状态的变量。 虚拟变量的取值只取0或1。1表示某种性 质出现,0表示某种性质不出现。
(3)对一个普通变量与两个两分虚拟变 量的回归
例:种族及性别差异对薪金的影响。 假定薪金除了受工作年限、性别的影响 之外,还受种族的影响。
yi 1 2 D2i 3D3i xi ui
yi 为某人的工资水平,xi 为工作年限。
yi 1 2 D2i 3D3i xi ui 虚拟变量模型:
白人女性的工资水平:
E( yi D2 0, D3 1) (1 3) xi
yi 1 2 D2i 3D3i xi ui 虚拟变量模型:
其他人种男性的平均工资:
E( yi D2 1, D3 0) (1 2) xi
其他人种女性的平均工资:
Pi P r(Y 1) P r(I i * I i ) F ( I i ) 1 2 1 2
Ii
金融计量经济第五讲虚拟变量模型和Probit、Logit模型

第二节 虚拟被解释变量模型
• 问题1:对于商业银行,企业贷款可能出现违约,也就是说一家企 业贷款后有违约和不违约两种可能,如何甄别?(李萌,2005)
• 问题2:证券投资者在特定时期内的投资选择是买或不买,如何确 定这样的选择?(王冀宁等,2003)
• 问题3:上市公司出现经营问题,可能成为ST、PT,是什么原因导 致这样的结果?
6563.76 1597.98
16.904 16.9416 157.922
0
应用例题2:股息税削减对股价的影响
• 背景资料—2005年6月14日,财政部、税务总局发文,规定对个人投资者从
上市公司取得的股息红利所得,暂减按50%计入个应纳税所得额(红利税从 20%降为10%)。
• 利用事件分析法分析该政策对股价有无显著影响,即政策出台前后股票有无 异常收益。时间窗口为发布日及前后各二天。
E( yi ) P( yi 1) X i
• 但因为
i
1 X
Xi i
当yi 1,其概率为X i 当yi 0,其概率为1 X i
• 模型具有明显的异方差性,故而用模型(5.8)直接进行参数估计 是不合适的。
• 另外,由于要求
E( yi ) P( yi 1) Xi 1
亦
难以达到。
Di 0, 其它季度的数据
, i 2,3,4
• •
原 则模 引型 入若 虚为 拟变量后的y模t 型为:
xt
ut
yt xt 2 D2t 3 D3t 4 D4t ut (5.6)
• 回归模型可视为:
yˆt ˆ ˆxt
一季度
yˆt ˆ ˆxt ˆ2 二季度
yˆt ˆ ˆxt ˆ3 三季度
二、虚拟变量的设置原则
计量经济学虚拟变量模型课件

计量经济学虚拟变量模型
21
1 正常年份 D1i 0 非正常年份
式(5.2)也可表示为
1 非正常年份 D2i 0 正常年份
Y i 0 X 1 i 1 X 2 i 2 X 3 i 3 X i u i (5.3)
其中,X 1i1 ,X 2iD 1i,X 3iD 2i,显然如下等式成立。
X1i X2i X3i
计量经济学虚拟变量模型
3
例如,性别可表现为男或女;人种可表 现为白种人和非白种人;宗教信仰可表 现为教徒和非教徒;政府的经济政策可 表现为改革开放前和改革开放后,如此 等等。
Hale Waihona Puke 计量经济学虚拟变量模型4
显然,这种不同的具体形式是无法直接引 入经济计量模型中去的。但由于这类变量 通常表现为品质、属性、种类的出现或者 未出现,所以我们可以根据质量变量的这 一特征将其数量化。
Y i1 D 1 i2 D 2 i3 X i u i (5.5)
显然模型(5.5)中,解释变量D1,D2和X之间 无完全的多重共线性。可以使用普通最小二乘 法估计式(5.5)的参数。
第五章 虚拟变量模型
在经济计量模型中除了有量的因素外 还有质的因素,质的因素包括被解释变量 为质的因素和解释变量为质的因素。如果 被解释变量为质的因素,主要是逻辑回归 要涉及的内容。
计量经济学虚拟变量模型
1
第一节 虚拟变量的概念与设定
一、虚拟变量的概念 在经济计量分析中, 经常会碰到所建模
型的被解释变量不仅受诸如收入、产量 、价格、 成本、需求、投资等数量变量
(5.4)
计量经济学虚拟变量模型
22
式(5.4)表明模型(5.3)即原模型(5.2)中有 完全的多重共线性,将导致最小二乘估计无 解。我们称该情景为掉入虚拟变量陷阱。所 以,在有截距项的情况下,如果一个质的因 素有多少个特征就引入多少个虚拟变量是行 不通的。
金融计量经济第五讲虚拟变量模型和Probit、Logit模型

• 括号内为t统计值。 • 显然,三季度和四季度与一季度差异并不明显,重 新回归,仅考虑二季度,有结果:
例子:佣金与销售额的关系:
• 模型:
Yi = α1 + β1 xi + β 2 ( xi − x* ) Di + ui 其中 : Yi是销售佣金, X i是销售额, X*是销售额基数值. 若X i > X * , 则Di = 1
• 样本回归函数: ˆ ˆ α +β x
ˆ Yi =
1
1 i
xi < x* xi ≥ x*
D1 = , 0, S < S1 , S ≥ S2 D2 = 0, S < S2
• 工资模型为: • I i = β 0 + β1[ S1 + (1 − D1i − D2i )(Si − S1 )]
+ β 2 [ D2i ( S 2 − S1 ) + D1i ( Si − S1 )] + β 3 D2i ( Si − S 2 ) + ui (5.7)
t t
一季度 ˆ β2 ˆ β3 二季度 三季度 四季度
ˆ ˆ ˆ ˆ y t = α + β xt + β 4
例题:美国制造业的利润—销售额行为 • 模型:利润t = α1 + α 2 D2t + α 3 D3t + α 4 D4t + β (销售)t + ut • 利用1965—1970年六年的季度数据,得结果:
probit 地区虚拟变量

Probit 地区虚拟变量1. 引言在统计学和经济学中,Probit模型是一种用于分析二元变量的回归模型。
它基于一个隐含的概率分布函数,通常是标准正态分布函数,来描述一个二元变量取值为1的概率。
地区虚拟变量则是指将地理区域划分为多个虚拟的分类变量,用于衡量地区对某一现象或行为的影响。
本文将介绍Probit模型中如何使用地区虚拟变量,并解释其应用和解读。
2. Probit 模型Probit模型是一种广义线性模型(Generalized Linear Model),它假设一个二元变量Y服从一个潜在的连续随机变量Z,且Z服从标准正态分布。
Probit模型可以表示为:P(Y=1|X) = Φ(βX)其中,P(Y=1|X)表示当给定自变量X时,因变量Y取值为1的概率;Φ(·)表示标准正态累积分布函数;β表示回归系数;X表示自变量。
3. 地区虚拟变量地区虚拟变量是一种将地理区域划分为多个离散分类的虚拟变量。
在Probit模型中,我们可以使用地区虚拟变量来衡量地区对某一现象或行为的影响。
例如,我们可以将一个国家划分为多个地区,并引入相应的虚拟变量来表示不同地区之间的差异。
假设我们有一个因变量Y表示某一商品是否被购买(1表示购买,0表示未购买),而自变量X包含了商品的价格、广告投入等因素。
如果我们想要探究不同地区对购买行为的影响,可以引入地区虚拟变量D1、D2、D3等,分别代表不同的地理区域。
那么Probit模型可以表示为:P(Y=1|X, D1, D2, D3) = Φ(βX + γ1D1 + γ2D2 + γ3D3)其中,γ1、γ2、γ3分别是地区虚拟变量D1、D2、D3对应的回归系数。
4. 地区虚拟变量的应用地区虚拟变量在实际应用中有着广泛的应用。
以下是几个常见领域中使用地区虚拟变量的例子:4.1 经济学在经济学中,研究人员常常使用地区虚拟变量来分析不同地区的经济发展状况。
通过引入地区虚拟变量,可以控制其他因素对经济发展的影响,从而更准确地评估不同地区之间的差异。
虚拟应变量

实际 Y、估计 Y 以及权重 wi
ob
Y
w
w
Y s
Y
w
w
0.214502 0.095809 0.146158 0.201550 0.005170 0.236080 0.069905 0.165586 0.095809
0.463143 0.309530 0.382306 0.448943 0.071906 0.485881 0.264395 0.406923 0.309530
为了消除异方差性的影响,我们可利用前面有关修正异方差的方法。这里 我们仅介绍利用加权最小二乘法(WLS)修正异方差。 根据前面的讨论,我们知道 LPM 中 u i 的方差是 Yi 条件期望的函数,故选 择权重的一种方法是:
wi E (Yi X i )[1 E (Yi X i )]
其中, wi 为权重。
21 22 23 24 25 26 27 28 29 30 31 32
1 1 0 0 1 0 1 1 0 0 1 0
1.301195 0.688410 0.279886 0.177755 0.688410 0.177755 1.096933 0.892672 0.177755 0.075624 0.790541 0.382017
0.214502 0.201550 0.146158 0.214502 0.146158 0.095809 0.146158 0.069905 0.165586 0.236080
(8.3.6)
此时,当 Yi=1 时
ui 1 1 2 X i
当 Yi=0 时
u i 1 2 X i
显然,u i 不遵从正态分布, 而是服从两点分布。 线性概率模型中的随机扰动项 u i 不遵从正态分布, 对参数估计不会产生太大的影响,此时参数的 OLS 估计量(点估计)仍是无偏估计量。并且,可以证 明,随着样本容量的无限增大,这种 OLS 点估计量 的概率分布将趋近于正态分布。
二值因变量模型_14.2Probit和Logit模型

对外经济贸易大学计量经济学I n t r o d u c t i o n t o E c o n o m e t r i c s导论二值因变量模型:Probit和Logit模型Probit和Logit回归在线性概率模型中,y=1 的概率是x 的线性函数:P (y= 1|x) = β0+ β1x在非线性概率模型中:对于β1>0,Pr(y= 1|x)是x的单增函数;010 ≤ P(y= 1|x) ≤ 1 对所有的x都成立。
02我们希望构造一个非线性函数来刻画此概率。
例如一个“S-curve”的函数。
Probit回归用标准正态分布的累积分布函数Φ(z)来建模y=1 的概率。
令z= β+ β1x,那么Probit回归模型的形式为P(y= 1|x) = Φ(β0+ β1x)其中Φ为标准正态分布的分布函数,z= β0+ β1x是probit模型的“z-value” or “z-index”.例如: 假设β= -2, β1= 3, x=0.4, 那么P(y= 1|x=0.4) = Φ(-2 + 3×0.4) = Φ(-0.8)Pr(z≤ -0.8) = 0.2119该函数的“S-shape”满足了我们的需要:对于β1>0,P(y = 1|x ) 是x 的单增函数010 ≤ P(y = 1|x ) ≤ 1 对于所有的x 都成立02为什么要使用标准正态分布的累积分布函数?便于使用–可以查正态分布表的到相关的概率值(在相关的软件中也很容易得到)相对直观的理解:β0+ β1x = z-value01β1对应于x变化一个单位时z-value 的变化02给定x,β0+β1x是预测的z-value 03. probit deny p_irat, r;Iteration 0: log likelihood = -872.0853Iteration 1: log likelihood = -835.6633Iteration 2: log likelihood = -831.80534Iteration 3: log likelihood = -831.79234Probit estimates Number of obs= 2380Wald chi2(1) = 40.68Prob> chi2 = 0.0000 Log likelihood = -831.79234 Pseudo R2 = 0.0462 ------------------------------------------------------------------------------| Robustdeny | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+----------------------------------------------------------------p_irat| 2.967908 .4653114 6.38 0.000 2.055914 3.879901 _cons | -2.194159 .1649721 -13.30 0.000 -2.517499 -1.87082 ----------------------------------------------------------------------------P(deny=1|P Iratio)= Φ(-2.19 + 2.97×P/I ratio)(0.16) (0.47)还款收入比前面的系数是正的: 是否符合实际?01标准差的理解和普通的回归一样02 P(deny=1| P Iratio)= Φ(-2.19 + 2.97×P/I ratio )(0.16) (0.47)STATA Example: HMDA data 当P/I ratio 从0.3 增加到0.4:04 P(deny=1| P Iratio =0.4)= Φ (-2.19+2.97×0.4) = Φ (-1.00) =0.159被拒概率的预测值从0.097 升至0.15905概率预测值:03 P(deny=1| P Iratio =0.3)= Φ (-2.19+2.97×0.3) = Φ (-1.30) = 0.097多个自变量的Probit回归模型Pr(Y= 1|X1, X2) = Φ (β0+ β1X1+ β2X2)Φ 是正态分布的累积分布函数.01z= β0+ β1X1+ β2X2是此probit模型的“z-value”或者“z-index”.02β1是固定X2,X1变化一个单位对z-score 的效应。
logit 和probit模型的系数解释 -回复

logit 和probit模型的系数解释-回复【logit 和probit 模型的系数解释】1. 引言在统计学和经济学中,logit模型和probit模型是两种常见的二元选择模型,它们被广泛应用于解释和预测离散选择的行为。
本文将详细介绍logit 和probit模型的系数解释步骤,并对其应用领域和优缺点进行讨论。
2. 模型背景logit模型和probit模型是建立在二元选择数据上的概率模型。
在这两种模型中,我们假设个体i选择某个选项的概率是一个关于自变量X的非线性函数F(X)的模型,其中F(X)是一个累积分布函数(CDF)。
logit模型和probit模型是两种常见的CDF函数选择,分别使用逻辑函数(logistic function)和正态分布函数(normal distribution function)进行建模。
3. logit模型的系数解释logit模型的系数解释可以通过观察变量系数的大小、正负以及显著性水平来进行。
首先,系数的大小可以表示预测变量在选择行为中的影响程度。
一个正的系数表示该变量与选择行为正相关,即该变量的增加会增加选择某个选项的概率。
一个负的系数表示该变量与选择行为负相关,即该变量的增加会降低选择某个选项的概率。
其次,系数的正负可以表明变量对选择行为的方向性影响。
最后,统计显著性测试可以帮助我们确定该系数是否显著不等于零,即该变量对选择行为的影响是否存在。
4. probit模型的系数解释probit模型的系数解释与logit模型类似。
同样,我们可以通过观察变量系数的大小、正负以及显著性水平来解释系数。
不同的是,probit模型中的系数解释基于正态分布函数的特性。
具体而言,一个正的系数表示该变量的增加会使选择某个选项的概率上升,并且该上升符合正态分布函数的曲线形状。
一个负的系数则说明选择行为概率会下降。
同样,系数的正负可以揭示变量对选择行为的方向性影响。
最后,显著性测试也可以用来确认系数的显著性。
probit logit 解析表达式

probit logit 解析表达式(最新版)目录1.介绍 Probit 和 Logit 模型2.解析 Probit 和 Logit 模型的表达式3.比较 Probit 和 Logit 模型的异同正文Probit 和 Logit 模型是两种常用的概率回归模型,常用于处理二元变量的预测问题。
在这两种模型中,我们都需要解析它们的表达式,以便更好地理解模型的预测机制。
首先,我们来看 Probit 模型。
Probit 模型是一种用于二元响应变量预测的线性模型。
它的表达式可以解析为:Probit(Y=1|X=x) = Φ(β0 + β1X1 + β2X2 +...+ βnXn)其中,Y 代表二元响应变量,X 代表自变量,β0、β1、β2 等为模型参数,Φ为标准正态分布函数的逆函数。
接着,我们看 Logit 模型。
Logit 模型也是一种用于二元响应变量预测的线性模型。
它的表达式可以解析为:Logit(Y=1|X=x) = ln(π1 / π0) = β0 + β1X1 + β2X2 +...+ βnXn其中,Y 代表二元响应变量,X 代表自变量,β0、β1、β2 等为模型参数,π0 和π1 分别为两个类别的概率。
通过比较 Probit 和 Logit 模型的表达式,我们可以发现两者的主要区别在于概率计算的方式。
Probit 模型使用的是标准正态分布函数的逆函数,而 Logit 模型则使用的是对数函数。
此外,Probit 模型的截距项为β0,而 Logit 模型的截距项为 ln(π1 / π0)。
总的来说,Probit 和 Logit 模型都是用于解决二元变量预测问题的有效工具。
离散因变量模型(Logit 模型,Probit模型)PPT课件

20
二、 二元选择模型的估计(ML)
样本 i Y
x
样本取值
形式如图: 1 2
…
n
1
x1
0
x2
……
1
xn
Yi 值
1
0
P
F(X
B)
i
1 F(XiB)
(成功)
(失败)
样本每次取值设为 贝努里分布取值。
21
P( yi 1 Xi ) F (Xi)
P( y1 , y2 , , yn ) (1 F( X i )) F( X i )
j
p x j
dp dZ
Z x j
f (Z
) j
eZ (1 eZ )2
j
(z)(1-(z)) j
2、对Logit模型系数的解释:
ln( p )
odds
L x j
1 p x j
ln(odds) x j
odds x j
j
当 xj 增加一个单位时机会比率的增长率为 j 12
例1: 南开大学国际经济研究所1999级研究生考试分 数及录取情况见数据表(N = 95)。
当=0.05时查表可得 z1 1.96 2
因为 Z=2.05>1.96,所以score 变量在0.05的显著水平下 对Y的影响是显著的。
(5) 对参数加以解释: 0.6771 2
说明当考生分数增加一分,被录取的机会比率增长率增加0.6771.
另外,是否应届生对录取与否没有显著影响。
17
3. Probit模型
0
74
0
261
1
25
0
348
1
50
0
303
计量经济学(probit,logit,异方差问题)

• 联合概率:
n
f ( yi , xi , )
i 1
• 那样的参数beta是合理的?最大化上面这个 联合概率的。
. #;
• 最大化联合概率实际上就是最大化它的对 数(增函数)
n
L [ yi log G( Xi ) (1 yi ) log(1 G( Xi ))] i 1
. #;
系数估计值的含义
• 但logit和probit不是。
• 应该这样比:
n
n
LPM [n1 glogit ( XB)] [n1 g probit ( XB)]
i 1
log it
i 1
probit
• 对probit来说,g(0)=0.4,对logit来说, g(0)=0.25。
0.4 * probit 0.25* logit
var(u | x1, x2...xk ) E(u2 ) 2
. #;
• 看下面的思路
– 估计原模型,得到残差平方和 uˆi2
– 作下面的回归:
uˆi2 0 1x1 2 x2 ...k xk vi
– 去检验这个回归的系数是不是显著?
1 0,2 0,...,k 0
– 现在再使用普通的F检验或者LM检验。
. #;
异方差问题
• (一)异方差的定义 • (二)异方差的影响 • (三)如何在异方差下求OLS估计值的方
差 • (四)如何检验异方差 • (五)如何估计系数?
– 知道h(x) – 不知道h(x)
. #r(u | x1, x2...xk ) 2
同方差假定意味着条件于解释变量,不可观测误差的方差为常数
rˆ
2 ij
uˆ
2 i
S
probit logit 解析表达式

probit logit 解析表达式摘要:1.概述Probit 和Logit 模型2.介绍Probit 和Logit 模型的解析表达式3.对比Probit 和Logit 模型的解析表达式4.总结Probit 和Logit 模型的解析表达式正文:Probit 和Logit 模型是两种广泛应用于二元选择模型的统计方法,如个体是否选择某项服务,是否购买某件商品等。
这两种模型都是基于概率理论的线性模型,其主要区别在于它们对概率的估计方式不同。
Probit 模型使用正态分布来估计概率,而Logit 模型则使用逻辑斯蒂函数来估计概率。
Probit 模型的解析表达式为:P(Y=1|X=x) = Phi(β0 + β1X1 + β2X2 +...+ βnXn)其中,Y 表示二元变量(通常为0 或1),X 表示自变量,β0、β1、...、βn 是模型参数,Φ是标准正态分布的累积分布函数。
Logit 模型的解析表达式为:Log(P(Y=1|X=x)) = β0 + β1X1 + β2X2 +...+ βnXn其中,P(Y=1|X=x) 表示给定X 的情况下Y 等于1 的概率,其他符号含义与Probit 模型相同。
对比Probit 和Logit 模型的解析表达式,我们可以发现,两者在形式上存在明显差异。
Probit 模型的解析表达式中包含了标准正态分布的累积分布函数Φ,而Logit 模型的解析表达式中则包含了对数函数。
这两种表达式在实际应用中的计算过程也有所不同。
Probit 模型需要通过查表或计算器等工具获取Φ值,而Logit 模型则可以直接进行计算。
总的来说,Probit 和Logit 模型的解析表达式是它们在二元选择问题中的核心部分。
金融计量经济第五讲虚拟变量模型和Probit,Logit模型

yˆi ˆ0 (ˆ ˆ1)x1i ˆk xki D 1
yˆi ˆ0 ˆ1x1i ˆk xki
D0
• 可考虑同时在截距和斜率引入虚拟变量:
yi 0 0Di (1Di 1)x1i k xki ui (5.5)
• 3、虚拟变量用于季节性因素分析。
0.503543 0.500354 1.13E+03 1.99E+09 -13241.74 1.648066
Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic)
• 即有: E(yi ) P(yi 1) Xi
• 但因为
i
1 X
Xi i
当yi 1,其概率为X i 当yi 0,其概率为1 X i
• 模型具有明显的异方差性,故而用模型(5.8)直 接进行参数估计是不合适的。
• 另外,由于要求 E( yi ) P( yi 1) Xi 1 亦难以 达到。
yˆi ˆ0 ˆ ˆ1x1i ˆk xki D 1 yˆi ˆ0 ˆ1x1i ˆk xki D 0
• 2、在斜率处引入虚拟变量,改变斜率。
yi 0 (D 1)x1i k xki ui (5.3)
• 作OLS后得到参数估计值,回归模型为:
yˆi ˆ0 (ˆD ˆ1)x1i ˆk xki (5.4)
• 步骤:在回归分析结果窗口,点 View\Stabiliti Test\Chow Breakpoint Test
• 注:邹氏应是邹至庄。
例1:储蓄余额与国民收入的关系
• CXYE = -1878.817965 + 5.965038605*GMSR + 812.1046287*D1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、虚拟变量的设置原则
• 引入虚拟变量一般取0和1。
• 对定性因素一般取级别数减1个虚拟变量。例 子1:性别因素,二个级别(男、女)取一个 虚拟变量,D=1表示男(女),D=0表示女 (男)。
• 例子2:季度因素,四个季度取3个变量。
1, 一季度 D1 0, 其它季度
1, 二季度
D2
0,
其它季度
.
例题:美国制造业的利润—销售额行为
• 模型:利 t 1 润 2 D 2 t 3 D 3 t 4 D 4 t ( 销 ) t u t售
• 利用1965—1970年六年的季度数据,得结果:
利 t 6 润 6 .3 8 1 88 3 .8D 2 2 9 t 2 2.8 1 D 3 t 7 1.8 8D 4 6 3 t 0 .03 (销 8 )t 3 售 (3.9 (2 ) .0(7 -0 ) .(4 04 .2 5 (8 3 )).33
.
例子:佣金与销售额的关系:
• 模型:
Yi 11xi 2(xi x*)Di ui
其中 :Yi是销售佣 ,Xi是 金销售 ,X额 *是销售额基 . 数值 若Xi X*,则Di 1
• 样本回归函数:
Yˆi
ˆ1 ˆ1xi ˆ1ˆ2x*(ˆ1ˆ2)xi
xi x* xi x*
.
附录:Chow检验(邹氏检验)
• 同样可以写成二个模型:
y ˆi ˆ0(ˆˆ1)x1iˆkxki D1
y ˆi ˆ0ˆ1x1iˆkxki
D0
• 可考虑同时在截距和斜率引入虚拟变量:
y i 0 0 D i (1 D i 1 ) x 1 i k x k iu i (5.
.
.
• 3、虚拟变量用于季节性因素分析。
•取
1, 当样本 i季为 度第 的数据 Di 0,其它季度的, i数 2,3据 ,4
金融计量经济第五讲
虚拟变量模型和Probit、Logit模型
.
第一节 虚拟变量的一般应用
一、虚拟变量及其作用 1.定义:取值为0和1的人工变量,表示非量化
(定性)因素对模型的影响,一般用符号D表 示。例如:政策因素、地区因素、心理因素、 季节因素等。 2.作用: ⑴描述和测量定性因素的影响; ⑵正确反映经济变量之间的相互关系,提高模型 的精度; ⑶便于处理异常数据。
量为: 1,
D 0,
t T0 tT 0
• b. 用虚拟变量表示某个特殊时期的影响;
1, D0,
tT1,T2 tT1,T2
• 模型中虚拟变量可放在截距项或斜率处。
.
• 5、分阶段计酬问题。
• 若工作报酬与业务量挂钩,且不同业务量提成比例 不一样(递增),设S1、S2为二个指标临界点
•
D 1 1 0 ,,S S 1 S S 1, S S 2S 2, D 2 1 0 ,, S S S S 2 2
• 工资模型为:
• Ii01 [S 1 (1 D 1 i D 2 i)S ( i S 1 )] 2 [D 2 i(S 2 S 1 ) D 1 i(S i S 1 ) ]3 D 2 i(S i S 2 ) u i (5.7
.
D2=1
S0
D1=1
S1
S2
.
• 作OLS得到参数估计值后,三个阶段的 报酬回归模型为: Iˆi ˆ0ˆ1Si, Si S1 Iˆi ˆ0ˆ1S1ˆ2(Si S1), S2Si S1 Iˆi ˆ0ˆ1S1ˆ2(S2S1)ˆ3(Si S2), Si S2
• 原模型若为 yt xt ut
• 则引入虚拟变量后的模型为:
y tx t2 D 2 t3 D 3 t4 D 4 t u t (5.6)
• 回归模型可视为: yˆt ˆ ˆxt
一季度
yˆt ˆ ˆxt ˆ2 二季度
yˆt ˆ ˆxt ˆ3 三季度
yˆt ˆ ˆxt ˆ4 四季度
1, 三季度
D3
ቤተ መጻሕፍቲ ባይዱ
0,
其它季度
• 小心“虚拟变量陷阱”!
.
三、虚拟变量的应用
• 1、在常数项引入虚拟变量,改变截距。
y i0D 1 x 1 i kx k iu i (5.1)
• 对上式作OLS,得到参数估计值和回归模型:
y ˆiˆ0ˆD ˆ1 x 1 i ˆkx ki(5.2)
• (5.2)相当于两个回归模型:
• 括号内为t统计值。 • 显然,三季度和四季度与一季度差异并不明显,重
新回归,仅考虑二季度,有结果:
利t 润 65.6 4 6 113.4 1D 21 t0.03(销 93)t售 (4.01()2.7)(3.717)
.
• 4、引用虚拟变量处理“时间拐点”问题。
• 常见的情况:
• a. 若T0为两个时间段之间的某个拐点,虚拟变
.
虚拟变量用于斜率
• CXYE = -1217.425 + 5.209*GMSR + 1.13*(D1*GMSR)
• 1952—1977: • CXYE = -1217.425 + 6.339*GMSR • 1978—1990: • CXYE = -1217.425 + 5.209*GMSR
.
CXYE
GMSR
.
应用例题1:Hedonic住宅价格模型
• 也称特征价格模型。其核心认为住宅价格由若干 hedonic(可享受的)特征构成,包括房屋建筑 特征、区位特征、社区特征等。
• Chow检验有二个内容,断点检验和预测检 验。和虚拟变量模型作用有相近之处的是 断点检验(Chow Breakpoint Test)。
• 步骤:在回归分析结果窗口,点 View\Stabiliti Test\Chow Breakpoint Test
• 注:邹氏应是邹至庄。
.
例1:储蓄余额与国民收入的关系
y ˆi ˆ0ˆˆ1x1iˆkxk i D1 y ˆi ˆ0ˆ1x1iˆkxk i D0
.
.
• 2、在斜率处引入虚拟变量,改变斜率。
y i0 (D 1 )x 1 i k x k iu i (5.3)
• 作OLS后得到参数估计值,回归模型为:
y ˆiˆ0 (ˆD ˆ1 )x 1 i ˆkx ki(5.4)
• CXYE = -1878.817965 + 5.965038605*GMSR + 812.1046287*D1
• 1952—1977: • CXYE = -1066.71 + 5.965*GMSR • 1978—1990: • CXYE = -1878.82 + 5.965*GMSR
.
GMSR
