平行四边形的性质判定知识结构图
平行四边形的判定PPT

∴ ∠OAD=∠OCB ∴AD∥ BC
∴同理可证:AB∥ CD
∴四边形ABCD是平行四边形
D O
C
由上述证明可以得到平行四边形的判定定理: 对角线互相平分的四边形是平行四边形。
几何语言描述判定:
A
D
O
B
C
AO=CO BO=DO
ABCD
学以致用 1、在下列条件中,能判定四边形ABCD为平行四 边形的是( C ) A.AB=AD,CB=CD
由上述证明可以得到平行四边形的判定定理: 一组对边平行且相等的四边形是平行四边形。
几何语言描述判定:
A
D
B
C
AD BC
ABCD
“ ”读作“平行且相等”.
探究3
A
已知:四边形ABCD中,OA=OC,OD=OB,
试问:四边 形ABCD是平行四边形吗?请说
明理由。
B
解:是平行四边形。理由如下:
在△ADO和△CBO中, AO=CO(已知) ∠AOD=∠COB (对顶角相等) DO=BO(已知)
定义:
有两组对边分别平行的四边形叫做平行四边形.
性质:
对边平行 边
对边相等 对角相等 角 邻角互补
对角线: 对角线互相平分
创设情境,引入新课
通过前面的学习,我们知道,平行 四边形对边相等、对角相等、对角线互相 平分。那么反过来,对边相等或对角相等 或对角线互相平分的四边形是不是平行四 边形呢?
探究1:
那么四边形ABCD是平行四边形。
点评:两组对边相等的四边形是平行四边形
② 若 ∠ A=1200, 则 ∠ B=__6_0_0,∠C=_1_2_0_0 , ∠ D=__6_0_0 时 , 四 边 形ABCD是平行四边形。
《平行四边形的性质》PPT课件

一位饱经苍桑的老人,经过一辈子的辛勤劳动, 到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
老大
老二
老三
老四
当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么?
叙述平行四边形的性质
性质
平行四边形的对边平行;对边相等;对角相等; 对角线互相平分
∵四边形ABCD是平行四边形∴AB∥CD,AD∥BC AB=CD,AD= BC ∠A=∠C,∠B=∠DOA=OC,OB=OD
ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F.求证:OE=OF
x
Y
C
O (0,0)
B(5,0)
D(2,3)
A. (3,7) B. (5,3)C. (7,3) D. (8,2)
C
O
D
B
A
C
如图,在 ABCD中, 对角线AC﹑BD相交于点O,且AC+BD=20, △AOB的周长等于15,则CD=______.
5
说一说
如图,在 ABCD中, BC=10cm, AC=8cm, BD=14cm, (1)△ BOC的周长是多少? 说明理由?( 2) △ ABC与△ DBC的周长哪个长, 长多少?
符号语言:
O
O
●
老大
老四
老三
老二
M
老人分地合理吗?
比一比,谁最棒?
如图,在 ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是 _________.
1<AD<9
选择:平行四边形具有而一般四边形不具有 的特征是( ) A、不稳定性 B、对角线互相平分C、内角的为360度 D、外角和为360度
平行四边形单元知识结构
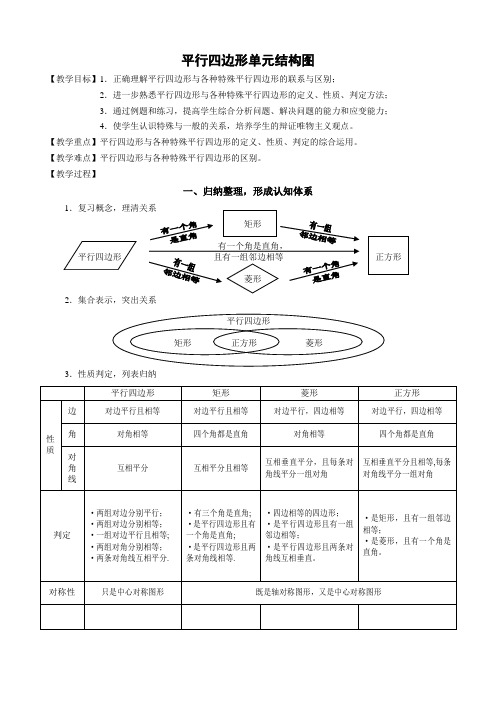
平行四边形单元结构图
【教学目标】1.正确理解平行四边形与各种特殊平行四边形的联系与区别;
2.进一步熟悉平行四边形与各种特殊平行四边形的定义、性质、判定方法; 3.通过例题和练习,提高学生综合分析问题、解决问题的能力和应变能力; 4.使学生认识特殊与一般的关系,培养学生的辩证唯物主义观点。
【教学重点】平行四边形与各种特殊平行四边形的定义、性质、判定的综合运用。
【教学难点】平行四边形与各种特殊平行四边形的区别。
【教学过程】
一、归纳整理,形成认知体系
1.复习概念,理清关系
矩形
有一个角是直角,
平行四边形 且有一组邻边相等 正方形
菱形
2.集合表示,突出关系
平行四边形
矩形 正方形 菱形
3.性质判定,列表归纳。
平行四边形的判定ppt课件

∴AE=EF.
又∵BE=CE,
∴四边形ABFC是平行四边形.
4.如图所示,四边形ABCD是平行四边形,延长AD至点E,使DE=AD,连接BD.
(1)求证:四边形BCED是平行四边形;
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵DE=AD,
∴DE=BC,DE∥BC.
∴AD=BC,AE=CF.
∵E,F分别为边AB,CD的中点,
∴AB=2AE,CD=2CF.
∴AB=CD.
∴四边形ABCD是平行四边形.
新知应用
如 图 所 示 , 已 知 E,F,G,H 分 别 是 ▱ ABCD 的 边 AB,BC,CD,DA 上 的 点 , 且
AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
别在直线AD,BC上,EH平分∠FEG,线段EH的长是否是两条平行线AD,BC之
间的距离?为什么?
解:是.理由如下:
∵AB∥EF,CD∥EG,
∴∠AEF+∠A=180°,∠DEG+∠D=180°.
∵∠A=∠D,∴∠AEF=∠DEG.
∵EH 平分∠FEG,∴∠FEH=∠GEH.
∴∠AEF+∠FEH= ×180°=90°,即∠AEH=90°.∴EH⊥AD.
O,BE⊥AC,DF⊥AC,垂足分别为E,F,且AF=CE,∠BAC=∠DCA.求证:四边形
ABCD是平行四边形.
证明:∵AF=CE,∴AF-EF=CE-EF.∴AE=CF.
∵BE⊥AC,DF⊥AC,∴∠AEB=∠CFD=90°.
∵∠BAC=∠DCA,∴AB∥CD.∴∠BAE=∠DCF.
∠ = ∠,
《 平行四边形的判定》课件(共48张PPT)

将两长两短的四根细木条用小钉绞合在一起,做成一个四边形,使等长的木条成为对边.
OA=OC,AB∥CD (2010·怀化中考)如图,平行四边形ABCD的对角线
E,F. 于点 ∴AB=B′C, AB=A′C(平行四边形的对边相等). AECF . 上两的组两 对点角,分求并别且相证等A:E的=四C四F边。形边是平形行四边形。是平行四边形
从实验结果得出什么结论? ∵ AO=OC,BO=OD 判定一个四边形是平行四边形应具备几个条件? 两组对角分别相等的四边形是平行四边形。 你认为下面四个条件中可选择的是( ) 证明:连结BD,交AC于点O ∵AB CD, ∴四边形ABCD是平行四边形 两组对边分别相等的四边形是平行四边形 求证:四边形BFDE是平行四边形 ∴四边形ABCD是平行四边形
A B
证明:∵四边形ABCD是
E
D
平行四边形
∴AD∥BC AD=BC
∵ DE=1/2AD
BF=1/2BC
∴DE∥BF DE=BF
F
C
∴四边形EBFD是平
行四边形
∴EB=DF
如图,在 ABCD中,已知AE、CF分别是
∠DAB、∠BCD的角平分线,
求证:四边形AECF是平行四边形。
A
F
D
256
1
34
8 7
∵AB ﹦∥CD, ∴四边形ABCD是平行四边形
A
通过了本节课学习,
你有哪些收获?
B
D
O
C
1、两组对边分别平行的 ∵AB∥CD,AD∥BC
平行四边形知识结构图

一、知识结构图:二、平行四边形的性质三、平行四边形的常用判定方法1.三角形的中位线平行且等于第三边的一半2.直角三角形斜边上的中线等于斜边的一半3.菱形的面积公式:对角线乘积的一半练习题:1.不能判定四边形ABCD 为平行四边形的题设是( ) (A )AB 平行且等于CD 。
(B )∠A=∠C ,∠B=∠D 。
(C )AB=AD ,BC=CD 。
(D )AB=CD ,AD=BC 。
2.下面性质中菱形有而矩形没有的是( )(A )邻角互补(B )内角和为360°(C )对角线相等 (D )对角线互相垂直 3.正方形具有而菱形不一定具有的性质是( ) (A )四条边相等 (B )对角线互相垂直平分 (C )对角线平分一组对角 (D )对角线相等4、顺次连结任意四边形四边中点所得的四边形一定是( ) A 、平行四边形 B 、矩形 C 、菱形 D 、正方形5.如图,□ABCD 中,∠C=108°,BE 平分∠ABC,则∠ABE 等于( ) A.18° B.36° C.72° D.108° 6.下列命题中,真命题是( )A 、有两边相等的平行四边形是菱形B 、对角线垂直的四边形是菱形C 、四个角相等的菱形是正方形D 、两条对角线相等的四边形是矩形 7、□ABCD 中,∠A =50°,则∠B =__________,∠C =__________。
8.已知菱形两条对角线的长分别为5cm 和8cm ,则这个菱形的面积是______cm .9、菱形ABCD 的周长为36,其相邻两内角的度数比为1:5,则 此菱形的面积为_________。
10、对角线长为22的正方形的周长为___________,面积为__________。
11.如图,过矩形ABCD 的对角线BD 上一点K 分别作矩形两边的平行线MN 与PQ ,那么图中矩形AMKP 的面积S 1与矩形QCNK 的面积S 2的关系是S 1 S 2(填“>”或“<”或“=” )B第11题图 第12题图12.如图,在矩形ABCD 中,点E 、F 分别在AB 、DC 上,BF ∥DE ,若AD=12cm ,AB=7cm ,NMQDCBEDCB A•且AE:EB=5:2,则阴影部分的面积为_______cm例1:(1)如图,已知四边形ABCD为平行四边形,∠A+∠C=80°,平行四边形ABCD的周长为46 cm,且AB-BC=3 cm,求平行四边形ABCD的各边长和各内角的度数.例2(1)如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=2∠BOC,若对角线AC=6cm,则该矩形的周长和面积各是多少?(2):如图,菱形ABCD的边长为8㎝,∠BAD=120°,则菱形ABCD的面积为例3:如图,矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且DP=OC,连结CP。
(完整版)平行四边形的性质和判定

平行四边形的性质和判定基础知识点知识点1平行四边形的定义:两组对边分别平行的四边形叫做平行四边形。
记作“口 ABCD 。
边:两组对边分别平行的四边形是平行四边形。
两组对边分别相等的四边形是平行四边形。
一组对边平行且相等的四边形是平行四边形。
角:两组对角分别相等的四边形是平行四边形。
对角线:对角线互相平分的四边形是平行四边形。
知识点4 两条平行线的距离。
知识点5 三角形的中位线定义:连接三角形两边中点的线段是三角形的中位线。
性质:三角形的中位线平行于第三边且等于第三边的一半。
典型例题例1、如图,E , F 是平行四边形 ABCD 的对角线 AC 上的点,CE AF •猜想:BE 与DF 有怎样的位置.关 系和数量 关系?并对你的猜想加以证明。
知识点2平行四边形的性质:知识点3 边:对边平行且相等。
角:对角相等,邻角互补。
对角线:对角线互相平分。
平行四边形的判定:【变式练习】已知,在口ABCD中,点E、F分别在AD、CB的延长线上,且/ 仁/2, DF交AB于G, BE交CD 于H。
求证:EH=FG。
例2、已知如图,0为平行四边形ABCD的对角线AC的中点,EF经过点0,且与AB交于E,与CD交于F。
求证: 四边形AECF是平行四边形。
例3、?ABCD中,/ BAD的平分线交直线BC于点E,线DC于点F(1) 求证:CE=CF ;(2) 若/ ABC=120 ° FG// CE, FG=CE,求/ BDG .【变式练习】1、如图,在二ABCD中,AE=CF, M、N分别ED、FB的中点.求证:四边形ENFM是平行四边形.2、在?ABCD中,/ ADC的平分线交直线BC于点E、交AB的延长线于点F,连接AC .(1)如图1,若/ ADC=90 ° G是EF的中点,连接AG、CG .①求证:BE=BF .②请判断△ AGC的形状,并说明理由;(2)如图2,若/ ADC=60 °将线段FB绕点F顺时针旋转60°至FG ,连接AG、CG .那么△ AGC又是怎样的形状.【变式练习】1.在平行四边形ABCD中, AB=3cm BC=5cm对角线AC, BD相交于点0,贝U 0A的取值范围是()A. 2cm v 0A< 5cm B . 2cm< 0A< 8cm C . 1cm v 0A< 4cm D . 3cm v 0A< 8cm例4、如图,点E、F、G H分别是四边形ABCD的四边中点,求证四边形EFGH是平行四边形。
