特殊平行四边形知识结构图
平行四边形+特殊平行四边形+梯形(更新版)

卓越个性化教案GFJW0901学生姓名年级授课时间教师姓名课时教学目标让学生进一步理解平行四边形的有关性质,掌握平行四边形、矩形、菱形、正方形、梯形的判定重点难点重点:平行四边形的性质,平行四边形的判定;矩形的性质及判定;菱形的性质及判定;正方形的性质及判定,梯形的性质及判定难点:平行四边形、矩形、菱形、正方形性质及判定的综合。
教学过程: 1、课前小测(知识点)2、例子讲解3、练习巩固(运用)知识结构:平行四边形:平行四边形特征及角和边有关计算例题1:平行四边形得周长为50cm,两邻边之差为5cm,求各边长。
作业教学效果/课后反思学生自评针对本堂收获和自我表现(对应指数上打√)①②③④⑤⑥⑦⑧⑨⑩学生/家长签名AB CD变题1:平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2:3,则AB=_______,BC=________.变题2:四边形ABCD 是平行四边形,∠BAC=90°,AB=3,AC=4,求AD 的长及∠ACD 度数。
例题2.平行四边形ABCD 中,∠A-∠B=40°,求平行四边形各内角的度数。
变题1.:平行四边形ABCD 中,BE 平分∠ABC, ∠BEA=30°,则∠C=_________,∠D_________.变题2.如图,在平行四边形ABCD 中,∠BAC=74°, ∠ACB=36°,求∠DAC 与∠D 的度数。
变题3. 如图,平行四边形ABCD 的周长为50,其中AB=15,∠ABC=60°,求平行四边形面积。
变题4、如图,在ABCD 中,已知对角线AC 和BD 相交于点O ,△BOC 的周长为24,BC=10,求对角线AC 与BD 的和是多少?ABCDEABCD ABCDAB C D ABCDABCDOA B CD课后自主练习:1、如图,ABCD的周长为60㎝,△AOB的周长比△BOC大8㎝,求AB、BC的长。
第十八章四边形章节复习辅导讲义

第十八章、四边形章节复习辅导讲义一、四边形知识框架: 1.四边形的知识结构 2.平行四边形的知识结构 二、四边形1. 定义:有不在同一直线上的四条首尾依次连接的线段构成的封闭图形。
2. 四边形的表示:四边形一般由依次的四个大写的字母表示,如四边形ABCD 等。
3. 四边形的分类:(1) 按照四边形的凹凸性将四边形分为凸四边形和凹四边形。
注意:中学阶段学习的四边形都是凸四边形。
(2) 按照四边形对边的平行性将四边形分为: ① 一般四边形:任何对边都不平行的四边形。
② 梯形:只有一组对边平行的四边形; A. 梯形分类: a .一般的梯形b .等腰梯形:一组对边平行,另一组对边相等的四边形。
c. 直角梯形:有一个内角为直角的梯形。
(3) 平行四边形:两组对边分别平行的四边形。
① 平行四边形的分类: A. 一般的平行四边形 B. 矩形(长方形):有一个较为直角的平行四边形。
C. 菱形:邻边相等的平行四边形。
D. 正方形:四条边都相等,四个内角也相等的四边形。
4. 四边形的内角和与外角和: (1) 四边形的内角和为360度 (2) 四边形的外角和为360度。
5. 四边形的性质:依次连接四边形各边中点所得的四边形称为中点四边形。
不管原四边形的形状怎样改变,中点四边形的形状始终是平行四边形【基础练习】1. 顺次连接一个任意四边形四边的中点,得到一个_______四边形. 2.顺次连接对角线相等的四边形的各边中点,所得四边形是_________.3. 如图1,已知:在ABCD 中,AB=4cm ,AD=7cm ,∠ABC 的平分线交AD•于点E ,交CD 的延长线于点F ,则DF=______cm .4. 如图,四边形ABCD 为正方形,△ADE 为等边三角形,AC 为正方形ABCD 的对角线,则∠EAC =___度.5. 四边形ABCD 的对角线AC BD ,的长分别为m n ,,可以证明当AC BD ⊥时(如图1),四边形ABCD 的面积12S mn =,那么当AC BD ,所夹的锐角为θ时(如图2),四边形ABCD 的面积S = .(用含m n θ,,的式子表示)1250°1 2A BC DB F C6.在如图所示的四边形中,若去掉一个50的角得到一个五边形,则12+=∠∠ 度.7.如图,已知AC 平分BAD ∠,12∠=∠,3AB DC ==, 则BC = . 8.已知四边形ABCD 中,90A B C ∠=∠=∠=︒,若添加一个条件即可判定该四边形是正方形,那么这个条件可以是____________.三、平行四边形(一) 平行四边形:1. 定义:两组对边分别平行的四边形。
平行四边形的应用

平行四边形的应用平行四边形是一种特殊的四边形,它具有许多实际应用。
本文将探讨平行四边形在几何学、建筑设计和工程领域中的应用,以及其在解决实际问题中的重要性。
一、几何学中的平行四边形应用在几何学中,平行四边形是研究四边形性质的重要基础。
它具有以下几个应用:1. 平行线判定:利用平行四边形的特性可以方便地判定两条直线是否平行。
当一对对边分别平行且相等时,即可确定两条直线平行。
2. 测量角度:平行四边形的对角线相交处形成的角是等于180度的。
因此,可以利用平行四边形来测量角度并进行准确的角度计算。
3. 计算面积:平行四边形的面积计算简单,可通过底边长度和高度的乘积来计算。
这在计算图形面积时非常实用。
二、建筑设计中的平行四边形应用平行四边形在建筑设计中有广泛的应用,具体包括以下几个方面:1. 地基设计:在房屋或建筑物的地基设计中,平行四边形常用来布置地基块状,以提高地基的稳定性和均匀性。
2. 墙面设计:平行四边形的特殊结构使得其在墙面设计中能够提供相对稳定的支撑,同时具有美观性,常用于建筑物外墙和内部隔墙的设计。
3. 护栏设计:平行四边形可以用于护栏的设计,一方面能够提供有效的防护功能,另一方面也能够赋予护栏更加美观的外观。
三、工程领域中的平行四边形应用平行四边形在工程领域中也具有重要的应用,主要体现在以下几个方面:1. 桥梁设计:在桥梁设计中,平行四边形可用于梁体和支撑结构的设计,能够提高桥梁的承重能力和结构稳定性。
2. 道路规划:平行四边形在道路规划中常用于设计交叉口和平行路段,能够提高交通流畅性和减少车辆拥堵。
3. 水利工程:在水利工程中,平行四边形可用于设计渠道和水坝,配合水流方向优化水流状况,提高水利设施的功能性。
总结:通过以上分析,平行四边形在几何学、建筑设计和工程领域中都有广泛的应用。
对于几何学而言,平行四边形是研究四边形性质的基础;在建筑设计中,平行四边形能够提供稳定的结构和美观的外观;而在工程领域中,平行四边形可以用于桥梁、道路和水利工程的设计,提高各类工程的效能。
图形的变化知识结构图

称轴垂直平分.
画轴对称图形:〔2〕关于x轴对称: ;
〔3〕关于y轴对ห้องสมุดไป่ตู้: .
旋转的定义:把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的旋转.
旋转的性质
图
图形的旋转定义:把一个图形绕着某一点旋转1800,如果它能够与另一个图形重合,那么就说这两个图形关于这个点
形中心对称 中心对称.
的中心对称图形:把一个图形绕着某一个点旋转1800,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心
称图形〔如线段、平行四边形〕.
变关于原点对称的点的坐标: .
相似多边形:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
化
相似三角形判定定理
图形的相似
定义:如果一个图形上的点A、B、…、P、…和另一个图形上的点 分别对应,并且它们的连线
位似 都经过同一点O, ,那么这两个图形叫做位似图形.
结论:在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k,
那么与原图形上的点〔x,y〕对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky).
图形的变化 知识结构图
平移的定义
图形的平移点的平移:
图形的平移:
定义:一个平面图形沿一条直线折叠,直线两旁的局部能够互相重合.
轴对称图形:性质:轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
两个图形成轴对称:
图形的轴对称〔1〕线段垂直平分线上的点与这条线段两个端点的距离相等;
线段垂直平分线的性质〔2〕与一条线段两个端点的距离相等的点,在这条线段的垂直平分线上.
五年级数学上册知识结构图
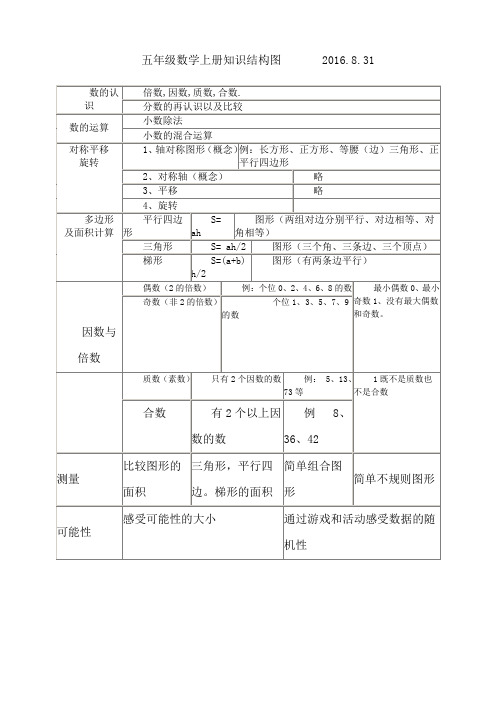
S= ah/2
图形(三个角、三条边、三个顶点)
梯形
S=(a+b)h/2
图形(有两条边平行)
因数与倍数
偶数(2的倍数)
例:个位0、2、4、6、8的数
最小偶数0、最小奇数1、没有最大偶数和奇数。
奇数(非2的倍数)
个位1、3、5、7、9的数
质数(素数)
只有2个因数的数
例:5、13、73等
1既不是质数也不是合数
合数
有2个以上因数的数
例8、36、42
测量
比较图形的面积
三角形,平行四边。梯形的面积
简单组合图形
简单不规则图形
可能性
感受可能性的大小
通过游戏和活动感受数据的随机性
五年级数学上数,因数,质数,合数.
分数的再认识以及比较
数的运算
小数除法
小数的混合运算
对称平移
旋转
1、轴对称图形(概念)
例:长方形、正方形、等腰(边)三角形、正平行四边形
2、对称轴(概念)
略
3、平移
略
4、旋转
多边形
及面积计算
平行四边形
S= ah
图形(两组对边分别平行、对边相等、对角相等)
不同版本教材知识点设置的比较研究—以初中数学平行四边形为例

摘要随着课程改革不断推进,各地出现了各有特点的数学教材,教材的编写者有不同的思路,因此教材在各个方面也会存在一定的差异,同时不同版本的教材对比也有助于教师更好地教学与进行教学研究.通过对人教版、北师大版、苏科版中的“平行四边形”部分进行比较研究,从而帮助对该部分知识点的全面把握,以便更好地把握数学教材内容,优化教学设计.通过文献分析法、对比分析法、统计法、问卷调查法对不同版本初中数学教材从结构、引入、探究及习题设置进行了比较,从而发现三个版本教材的特色以及各自的异同点.通过对此课题的研究,提供一些有益的数学教学建议.关键词平行四边形教材对比人教版北师大版苏科版A comparative study on the set of knowledge points in different editionsof textbooks—— A case study of Parallelogram in junior middle schoolAbstract With the continuous advancement of the curriculum reform, mathematics textbooks with their own characteristics have appeared in various places. The compilers of the textbooks have different ideas, so there are certain differences in various aspects of the textbooks, at the same time, the comparison of different versions of teaching materials is helpful to teachers. This paper makes a comparative study of the "Parallelogram" section in the people s education press, the Beijing Normal University press and the Soviet section press, so as to help us grasp the knowledge points of this section in anall-round way, so as to better grasp the contents of the mathematics teaching materials and optimize the teaching design. Through literature analysis, Comparative Analysis, Statistics and Questionnaire survey, this paper compares the structure, Introduction, exploration and problem setting of different editions of junior middle school mathematics textbooks, thus discovered three edition teaching material's characteristic as well as respective similarities and differences. Through the research on this subject, some useful suggestions on mathematics teaching are provided.Key words Parallelogram textbook comparison People's Education Edition Beijing Normal University Edition Suke edition目录摘要 (II)Abstract (III)引言 (1)1绪论 (1)1.1问题的提出 (1)1.2国内外研究现状 (1)1.2.1国外研究概况 (1)1.2.2国内研究概况 (2)2研究对象、研究维度、研究思路与研究方法 (2)2.1研究对象 (2)2.2研究维度 (2)2.3研究思路 (2)2.4研究方法 (3)3平行四边形内容设置的比较研究 (3)3.1教材内容结构比较 (3)3.2引入的比较 (5)3.3探究活动的比较 (12)3.4习题的比较 (14)4初中不同版本数学教材比较的实证研究 (16)4.1问卷调查对象 (16)4.2问卷调查数据整理 (16)4.3问卷调查数据分析 (17)5结论 (17)5.1三个版本教材的横向比较 (17)5.2三个版本教材的纵向比较 (18)6建议 (18)6.1内容结构方面 (18)6.2引入方式方面 (18)6.3习题设置方面 (19)6.4探究活动方面 (19)结语 (20)参考文献 (21)致谢 (22)附录 (23)引言教育改革的核心是课程改革,课程改革促进了教材的优化 [1]P10.结合不同的地域特点和教育现状,国家支持相关部门编写不同特征的教材,不同教材的编写思路决定了教材在各个方面也会存在一定差异[2]P59-66.目前有很多专家学者对不同版本的初中数学教材进行了对比研究,很多一线教师也在关注不同教材下同一知识点的异同点.目前各种教材是怎样设计的,有什么样的优缺点、异同点,编写意图是什么?这些有待作进一步研究.在实际教学过程中应如何选用和使用教材是值得每一个基础教育工作者思考的问题.作为一名未来从事教育事业的毕业生,我结合自身学习的理论经验和实习期间的实践教学经验,对人民教育出版社[3]P41-67(以下简称人教版)、北京师范大学出版社[4]P135-140(以下简称北师版)、江苏风凰科学技术出版社[5]P56-90(以下简称苏科版)三个版本教材中“平行四边形”的内容进行比较研究,在研究过程中主要运用内容分析和统计分析法,并且结合一定的实践经验,通过对不同教材进行比较,希望可以深入的理解教材,找到不同之处,取长补短,对初中数学教材进行优化与反思.1绪论1.1问题的提出教科书是教师教和学生学的主要载体[6].现如今,越来越多的人去研究教材,新版本的初中数学教材有哪些特点,现在各种教材是怎样设计的,有什么样的优缺点、异同点?这些有待作进一步研究.平行四边形是四边形内容中的重要部分.它在教材中有着呈上启下的作用.研究发现,这部分研究较缺乏,因此,本文通过对三个版本初中数学教材中“平行四边形”部分进行对比研究,分析不同版本教材的特点.1.2 国内外研究现状现在对教材的研究较多,研究的方面也很多,作者搜集了大量的资料,通过分析整理,对国内外已有的教材对比研究现状进行了分析概括.1.2.1国外研究概况近年来,我国教育事业有了很大的发展,因为我们不断与国外教材进行比较研究,比较研究大多是对某一个具体的模块进行具体的分析比较,从而找出国内外教材之间的差异.2002年, Hoyles等学者,借助TIMSS这种手段对多国教材进行有针对性的比较,分析了这些国家的数学教科书与学生的成绩测试以及评价结果,对异同点进行了详细的比较[7]P61-P65;2006年,梁贯成等学者对日本、韩国等国家的教材进行了多方面比较,同时也对比了中澳数学教材中的价值观和中新数学教材的知识架构等等[8]P32-34;2007年,范良火等学者通过对三个国家的初中数学教材内容中的“问题解决步骤的呈现方式”进行比较,发现这三个国家在这方面的异同点,同时也提供了建议[9]P61-75;2013年,曹一鸣等人对不同国家初中数学的数与代数、统计与概率和图形与几何的整体布局进行了比较[10]P29-36。
小学数学知识结构图(知识树PPT)

工程 问题
浓度 问题
溶液=溶剂+溶质
浓度=溶质÷溶液×100%
解决问题----列方程解决问题
*弄清题意,找出要求的的未知数用X表示 *找出题中数量间的等量关系,列出方程 *解方程 *检验或验算,写出答案
列 方 程 解 决 问 题
一般步骤
找等量关系 常用方法
关键语句 常见的加、减、乘、除的数量关系 常用的等量关系 利用图形周长、面积、体积公式
分数问题 类型
利息
*求a的几分之几(或百分之几)是多少 *一个数的几分之几(或百分之几)是a,求这个数 *求a是b的几分之几(或百分之几) *比a多(少)几分之几(或百分之几)的 数是多少 *a比b多(少)几分之几(或百分之几),求b *求a比b多(少)几分之几(或百分之几)。
利息=本金×利率×时间
图形的认识
测量 空间与图形 图形与位置
图形与变换
基本图形
线:直线,射线,线段,平行线, 垂线。(相交,垂直,平行) 角:角的概念,角的分类 平行四边形,长方形,正方形 三角形 梯形 圆和圆环 长方体,正方体 圆柱
图形的 认识
平面图形
立体图形
圆锥
球
基本图形
线 角 平行四边形,长方形,正方形的周长和面积 三角形的周长和面积
一般不给出具体的的工作总量用单位1表示用分数表示工效工作效率工作时间工作总量工作总量工作效率工作时间工作总量工作时间工作效率数量关系浓度问题溶液溶剂溶质浓度溶质溶液100解决问题列方程解决问题列方程解决问题题弄清题意找出要求的的未知数用x表示找出题中数量间的等量关系列出方程解方程检验或验算写出答案找等量关系常用方法关键语句常见的加减乘除的数量关系常用的等量关系利用图形周长面积体积公式一般步骤典型应用题平均数问题归一问题归总问题和差问题差倍问题和倍问题倍比问题行程问题流水问题还原问题植树问题盈亏问题年龄问题鸡兔同笼问题解决问题行程问题行程问题一般行程问题火车过桥问题相遇问题追及问题路程速度时间速度路程时间时间路程速度路程桥长车长车速桥长车长通过时间通过时间桥长车长车速桥长车速通过时间车长车长车速通过时间桥长相遇路程速度和相遇时间相遇时间相遇路程速度和速度和相遇路程相遇时间速度差追及时间追及路程追及路程速度差追及时间追及路程追及时间速度差量与计量常见的量计量进率与换算度量衡名数与名数的改写常见的量量计量单位及进率率长度
简单几何体知识结构图

简单几何体知识结构图:
柱体:
1、棱柱:有两个面相互平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,有这些面所围成的多面体叫做棱柱;
(1)直棱柱:侧棱垂直底面;
(2)正棱柱:底面是多边形的直棱柱;
(3)斜棱柱:侧棱与底面不垂直;
注意:四棱柱之间的关系
底面是平行四边形侧棱垂直底面
四棱柱平行六面体直平行六面体底面是正方形侧棱与底面边长相等
正四棱柱正方体
2、圆柱:以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱;
椎体:
1、棱锥:有一个面是多边形,其余各面都是有一个公共点的三角形,由这些面所围成的多面体叫做棱锥;
(1)正棱锥:棱锥的底面是正多边形,并且顶点在底面上的射影是底面的中心,这样的棱锥叫做正棱锥;
2、圆锥:以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥;
台体:用一个平行底面的平面去截棱锥或者圆锥,得到的几何体叫做棱台或者圆台;。
完整版初中数学知识点结构图
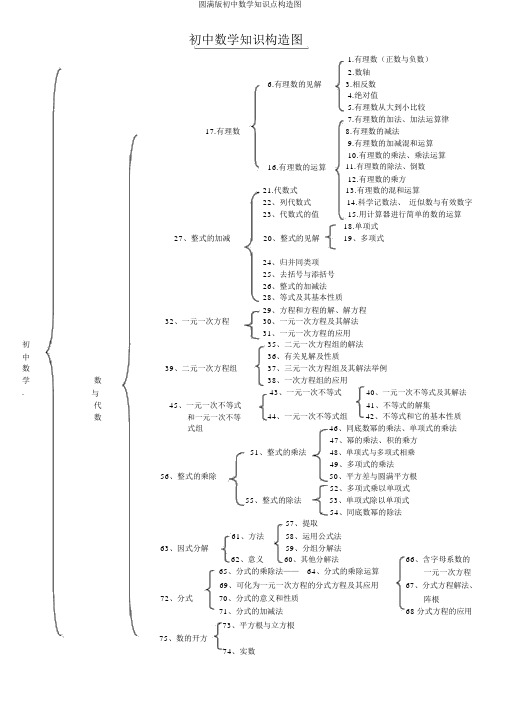
初中数学知识构造图1.有理数(正数与负数)2.数轴6.有理数的见解 3.相反数4.绝对值5.有理数从大到小比较7.有理数的加法、加法运算律17.有理数8.有理数的减法9.有理数的加减混和运算10.有理数的乘法、乘法运算16.有理数的运算11.有理数的除法、倒数12.有理数的乘方21.代数式22、列代数式23、代数式的值13.有理数的混和运算14.科学记数法、近似数与有效数字15.用计算器进行简单的数的运算18.单项式27、整式的加减20、整式的见解19、多项式初中数学.数与代数32、一元一次方程39、二元一次方程组45、一元一次不等式和一元一次不等24、归并同类项25、去括号与添括号26、整式的加减法28、等式及其基本性质29、方程和方程的解、解方程30、一元一次方程及其解法31、一元一次方程的应用35、二元一次方程组的解法36、有关见解及性质37、三元一次方程组及其解法举例38、一次方程组的应用43、一元一次不等式40、一元一次不等式及其解法41、不等式的解集44、一元一次不等式组42、不等式和它的基本性质式组46、同底数幂的乘法、单项式的乘法47、幂的乘法、积的乘方51、整式的乘法48、单项式与多项式相乘49、多项式的乘法56、整式的乘除50、平方差与圆满平方根52、多项式乘以单项式55、整式的除法53、单项式除以单项式54、同底数幂的除法63、因式分解61、方法57、提取58、运用公式法59、分组分解法72、分式62、意义60、其他分解法65、分式的乘除法——64、分式的乘除运算69、可化为一元一次方程的分式方程及其应用70、分式的意义和性质71、分式的加减法73、平方根与立方根66、含字母系数的一元一次方程67、分式方程解法、阵根68 分式方程的应用75、数的开方74、实数87、二次根式86、二次根式的意义79、二次根式的乘除法76、最简二次根式77、二次根式的除法78、二次根式的加减法82、二次根式的加减法85、二次根式的混淆运算80、二次根式的加减法81、同类二次根式83、二次根式的混淆运算84、有理化因式数与102、一元二次方程93、一元二次方程的解法98、一元二次方程的意义100、二元二次方程组99、一元二次方程组的根与系数的关系代94、分式方程的解法数97、可化为一元二次方程的分式方程式和无理方程96、分式方程、无理方程的应用101、一元二次方程的应用103、一次函数与一元一次不等式106、一次函数104、一次函数图像的图像和性质108、二次函数——105、正比率函数的图像和性质107 二次函数的有关见解113、函数及其图像109、平面直角坐标系110、函数初111、函数的图像中112、反比率函数数114、线段学116、线段、角115、角117、订交线、对顶角、邻角、补角120、订交线118、垂线、点到直线的距离126、订交、平行123、平行线119、同位角、内错角、同旁内角121、平行线见解及性质122、平行线的判断空124、空间直线、平面的地址关系125、命题、公义、定理间129、与三角形有关的边与图形138、三角形134、全等三角形135、等腰三角形133、直角三角形——132、勾股定理131、与三角形有关的角——130、三角形的内角136、轴对称151、四边形137、基本作图144、平行四边形149、多边形150、中心对称139、平行四边形的见解及其性质140、平行四边形的判断141、矩形的见解、性质和判断142、菱形的见解、性质和判断143、正方形的见解、性质和判断145、梯形的有关见解148、梯形146、等腰梯形的见解、性质和判断147、三角形、梯形的中位线156、比率线段158、相像图形157、相像多边形152、相像三角形的有关见解155、相像三角形153、三角形相像的判断163、解直角三角形154、相像三角形的性质159、解直角三角形161、解直角三角形160、解直角三角形的应162、锐角三角形164、圆的有关见解及对称性空间172、圆的有关性质165、点和圆的地址关系166、过不在同素来线上三点的圆167、三角形的外接圆168、垂径定理及其逆定理初中数与图形169、圆心角、弧、弦、弦心距170、圆周角定理171、圆内接四边形及其性质173.直线和圆的地址关系学185、圆174.切线的判断和性质177.直线和圆的地址关系175.三角形的内切圆176. * 切线长定理179.正多边形和圆——183.弧长和扇形的面积178.正多边形的有关计算180.圆周长、弧长181.圆、扇形、弓形的面积182.圆柱和圆锥的侧面张开图、侧面积184.圆和圆的地址关系186.几何体、几何图形187.平均数188.众数和中位数191.统计初步189.级差、方差、标准差195.统计与概率190.频数、频次、频次散布直方图192.概率初步——概率计算。
初中数学《平行四边形》单元教学设计以及思维导图

平行四边形主题单元设计与思维导图适用年八年级级所需时课内共用5课时间主题单元学习概述“平行四边形”主题单元结构包括“相关概念”、“探究性质”、“探究判定”三部分,这与课本的内容安排有所不同。
教材的编写顺序是“平行四边形及其性质、判定”、“矩形定义、性质、判定”、“菱形的定义、性质、判定”顺次展开,是先学特殊的四边形---平行四边形的定义、性质、判定,再学特殊的平行四边形的定义性质和判定.而新的结构是一种专题式设计,更多考虑到知识之间的关联,打破教材的原有安排,平行四边形、矩形、菱形、正方形等有关的概念放在一起作为专题一集中处理,把具有探究性的平行四边形、矩形、菱形、正方形的性质定理作为专题二集中处理,把平行四边形、矩形、菱形、正方形的判定定理作为专题三集中处理,这是考虑到平行四边形与特殊平行四边形等概念与概念之间、性质与性质之间、判定与判定之间都有紧密的联系,符合学生的“最近发展区”认识规律。
比如学完平行四边形的边、角、对角线的性质后,学生自然会想到特殊平行四边形矩形、菱形、正方形的边、角、对角线有哪些特殊的性质?因此,将这些内容紧密联系,层层递进,易于激发学生的学习兴趣也有利于帮助学生理解知识之间的联系,从而更好的展示数学知识的整体性。
主题单元规划思维导图主题单元目标知识与技能:1.理解平行四边形、矩形、菱形、正方形的概念.2.理解平行四边形与矩形、菱形、正方形之间的关系.过程与方法:1.探索并证明平行四边形的性质定理和判定定理.2.探索并证明矩形、菱形、正方形的性质定理和判定定理.3.体会并掌握转化、类比等数学思想方法.情感态度与价值观:1.通过平行四边形等概念的学习过程,体会数学知识来源于生活.2.通过平行四边形及特殊平行四边形的性质、判定的推导过程,培养学生思维的严谨性和逻辑性.3.通过研究平行四边形及特殊平行四边形的对称性,让学生体会数学和生活中的“对称美”.对应课标1.理解平行四边形、矩形、菱形、正方形的概念以及它们之间的关系2.探索并证明平行四边形的性质定理:平行四边形的对边相等、对角相等、对角线互相平分3.探索并证明矩形、菱形、正方形的性质定理:矩形的四个角都是直角、对角线相等;菱形的四条边相等、对角线互相垂直;正方形具备矩形和菱形的一切性质4.探索并证明矩形、菱形、正方形的判定定理:三个角是直角的四边形是矩形,对角线相等的平行四边形是矩形;四边相等的四边形是菱形,对角线互相垂直的平行四边形是菱形等主题单元问题设计1.理解平行四边形、矩形、菱形、正方形的概念以及它们之间的关系2.探索并证明平行四边形的性质定理:平行四边形的对边相等、对角相等、对角线互相平分3.探索并证明矩形、菱形、正方形的性质定理:矩形的四个角都是直角、对角线相等;菱形的四条边相等、对角线互相垂直;正方形具备矩形和菱形的一切性质4.探索并证明矩形、菱形、正方形的判定定理:三个角是直角的四边形是矩形,对角线相等的平行四边形是矩形;四边相等的四边形是菱形,对角线互相垂直的平行四边形是菱形等专题划分专题一:平行四边形、矩形、菱形、正方形的概念(1课时)专题二:探究平行四边形、矩形、菱形、正方形的性质(2课时)专题三:探究平行四边形、矩形、菱形、正方形的判定(2课时).......其中,专题(或专题二中的活动1 作为研究性学习)专题一平行四边形、矩形、菱形、正方形的概念所需课时课内1课时专题学习目标1.理解平行四边形、矩形、菱形、正方形的概念2.理解平行四边形与矩形、菱形、正方形之间的关系专题问题设计1.什么叫平行四边形、矩形、菱形、正方形?2.平行四边形、矩形、菱形、正方形之间的关系?所需教学环境和教学资源1.多媒体教室2.几何画板3.画图工具及一些细木条学习活动设计第一课时平行四边形、矩形、菱形、正方形的概念活动1.说说生活中的平行四边形生活中有哪些平行四边形的例子?由于学生对生活中的平行四边形的例子比较熟悉,小学里对平行四边形也有了初步的认识,本活动主要在于唤起学生的好奇心和学习的兴趣。
平行四边形制作方法

平行四边形制作方法平行四边形是一种特殊的四边形,它的对边是平行的,并且相等。
在几何学中,平行四边形是一种基本图形,也是许多其他图形的基础。
制作平行四边形的方法其实非常简单,下面我将详细介绍如何制作平行四边形。
首先,我们需要准备一张纸和绘图工具,比如铅笔和尺子。
然后,按照下面的步骤来制作平行四边形:步骤一:画出一条任意长度的线段作为平行四边形的一条边,这条线段可以是任意方向的。
步骤二:在这条线段的一端,用尺子画出一条与它平行的线段作为另一条边。
这条线段的长度可以与第一条边相等,也可以是任意长度,但要保持与第一条边平行。
步骤三:在第二条线段的一端,用尺子画出一条与它垂直的线段作为第三条边。
这条线段的长度可以与第一条边相等,也可以是任意长度。
步骤四:在第三条边的一端,用尺子画出一条与它平行的线段作为第四条边。
这条线段的长度可以与第二条边相等,也可以是任意长度,但要保持与第三条边平行。
经过以上四个步骤,我们就完成了一个平行四边形的制作过程。
这个平行四边形的对边是平行的,并且相等,符合平行四边形的定义。
除了用尺子和铅笔在纸上制作平行四边形,我们还可以用其他方法来制作平行四边形。
比如利用建筑工地上的围栏,可以在地面上画出一个平行四边形。
还可以利用角铁、木棍等材料,可以在桌面或地面上搭建出一个平行四边形的模型。
这些方法都可以帮助我们更直观地理解平行四边形的性质和特点。
在日常生活中,平行四边形的制作方法还可以通过一些实际的应用来感受。
比如在制作家具或建筑结构的过程中,设计师和工程师经常会遇到平行四边形的制作问题。
他们需要根据设计图纸,精确地绘制出各种形状的平行四边形,以确保建筑或家具的结构稳固、美观。
此外,制作平行四边形的方法也可以通过制作手工艺品或DIY项目来体验。
比如可以利用木板、剪刀、胶水等材料,制作一个简单的平行四边形模型,这不仅可以锻炼我们的动手能力,还可以加深对平行四边形的理解。
总之,平行四边形是几何学中的一种基本图形,它的制作方法非常简单。
提高对平行四边形的认识

提高对平行四边形的认识平行四边形是几何学中的一个重要概念,它有着特殊的性质和应用。
在本文中,我们将深入探讨平行四边形的定义、特征以及一些常见的应用场景。
一、平行四边形的定义平行四边形是指具有两对对边平行的四边形。
具体地说,如果一个四边形的两对对边分别平行,则该四边形就是平行四边形。
二、平行四边形的性质1. 对边平行性质:平行四边形的对边是一一对应的,即每一对对边都是平行的。
2. 对角线性质:平行四边形的对角线相交于一点,并且相交点将对角线平分。
3. 垂直性质:平行四边形的任意一条边与其对角线垂直。
4. 边长性质:平行四边形的对边长度相等。
5. 内角性质:平行四边形的内角和为360度。
三、平行四边形的分类根据边长和角度的性质,平行四边形可以分为以下几类:1. 矩形:矩形是一种特殊的平行四边形,它的四个角都是直角。
2. 正方形:正方形是一种特殊的矩形,它既是矩形又是菱形。
3. 菱形:菱形是具有对角线相等且对角线垂直的平行四边形。
4. 长方形:长方形是一种具有对边平行且相等的平行四边形。
四、平行四边形的应用平行四边形在实际生活中有广泛的应用,以下是其中一些例子:1. 建筑设计:在建筑设计中,平行四边形常被用于设计房间的地板、天花板、墙面等。
2. 制图和测量:在制图和测量领域,平行四边形可以用来绘制、测量和定位各种图形和物体。
3. 物体稳定性分析:平行四边形的稳定性使其成为分析物体平衡和支撑的工具。
4. 工程结构设计:平行四边形可以用于工程结构设计中的支撑框架和平面结构。
五、总结平行四边形是几何学中一个重要的概念,具有多种特征和应用。
通过对平行四边形的定义、性质和分类的学习,我们能够更好地理解和应用它们。
同时,了解平行四边形的应用领域,可以帮助我们将几何学知识与实际问题相结合,提高问题解决的能力。
希望通过本文的阐述,能够提高大家对平行四边形的认识,并将其应用于实际生活和学习中。
