二元关系习题课答案
数据库原理及习题答案

6.设有学生关系:S(SNO,SNAME,SSEX,SAGE,SL)。在这个关系中,SNO 表示学号, SNAME 表示姓名,SSEX 表示性别,SAGE 表示年龄,SL 表示寝室。则查询学生姓名和所 在寝室的投影操作的关系运算式是( ) 。 三、简答题 1.解释下述名词概念:关系模型、关系、属性、域、元组、候选码、码、实体完整性 规则、参照完整性规则。 2.为什么关系中的元组没有先后顺序? 3.为什么关系中不允许有重复的元组? 4.等值连接、自然连接二者之间有什么区别? 5.已知关系 R 和 S,分别计算①R∪S,② R∩S,③ R-S,④ R×S。 R A a1 a1 a2 a3 B b1 b2 b3 b3 6 8 9 6 C A a1 a2 a3 S B 1 b2 b4 C 7 8 6
A.1NF B.2NF C.3NF D.BCNF 8.下列不是 1NF 可能存在的问题 ( )。 A.更新异常 B.删除异常 C.插入异常 D.实体联系少 9.BCNF 符合 3NF,是对( )关系进行投影,将消除原关系中主属性对码的部分与传 递依赖,得到一组 BCNF 关系。 A .1NF B.2NF C.3NF D.BCNF 10.关系模式的候选码可以有 1 个或多个,而主码有( )。 A .1 个 B. 多个 C.0 个 D.1 个或多个 11.设 U 是所有属性的集合,X,Y,Z 都是 U 的子集, 若 X→→Y,则 X→→Z,其中 Z=U-X-Y,则这是多值依赖 ( ) 特性? A.对称性 B.传递性 C.特殊性 D.相反性 12.关系数据库规范化是为了解决关系数据库中的( )问题而引入的。 A.提高查询速度 B. 减少或消除插入异常、删除异常和数据冗余 C.保证数据的安全性和完整性 D.数据库管理的需要 13.关系的规范化中,各个范式之间的关系是( )。 A. 5NF 4NF BCNF 3NF 2NF 1NF B. 5NF 4NF BCNF 3NF 2NF 1NF C. 5NF 4NF BCNF 3NF 2NF 1NF D. BCNF 5 NF 4 NF 3NF 2NF 1NF 14.下列( )不属于分解规范化方法。 A.对 1NF 关系模式进行投影,消除原关系模式中的非主属性对码的部分函数依赖,将 1NF 关系模式转换成 N 个 2NF 关系模式。 B.对 2NF 关系模式进行投影,消除原关系模式中的主属性对码的传递函数依赖,将 2NF 关系模式转换成 N 个 3NF 关系模式。 C.对 3NF 关系模式进行投影,消除原关系模式中的主属性对码的部分函数依赖和传递 函数依赖,使决定因素都包含一个候选码,得到比 3NF 更高级别的 BCNF 关系模式。 D.对 BCNF 关系模式进行投影,消除关系模式中非平凡且非函数依赖的多值依赖,得 到一组 4NF。 二、填空题 1. 一个关系就是一个实体。客观事物之间彼此联系,这种联系包含两种联系:一是 ( )的联系,二是( )的联系。 2.在一个关系 R 中,若每个数据项都是不可再分割的,那么 R 一定属于( )。 3. 数据操作过程出现的操作异常是指 ( )、( )和 ( )。 4.若关系 R 为 1NF, R 中的每个非主属性都完全依赖于任意一个候选码,则称关系 R 是属于( )。 5.如果有一个关系模式属于 BCNF 范式,那么它一定属于( )范式。 6.如果 X→Y 和 X→Z 成立,那么 X→YZ 也成立,这个推理规则称为( )。 7.范式(normal form),它是英国人( )在 20 世纪 70 年代提出关系数据库模型后 总结出来的。 8. 若关系模式 R 是 2NF,R 中的每个非主属性对任何候选关键字都不存在传递依赖,
关系数据理论练习题及答案(详细完整版)

第一部分:一、求最小依赖集例:设有依赖集:F={AB→C,C→A,BC→D,ACD→B,D→EG,BE→C,CG→BD,CE→AG},计算与其等价的最小依赖集。
解:1、将依赖右边属性单一化,结果为:F1={AB→C,C→A,BC→D,ACD→B,D→E,D→G,BE→C,CG→B,CG→D,CE→A,CE→G }2、在F1中去掉依赖左部多余的属性。
对于CE→A,由于C →A成立,故E是多余的;对于ACD→B,由于(CD)+=ABCEDG,故A是多余的。
删除依赖左部多余的依赖后:F2={AB→C,C→A,BC→D,CD→B,D→E,D→G,BE→C,CG→B,CG→D,CE→G }3、在F2中去掉多余的依赖。
对于CG→B,由于(CG)+=ABCEDG,故CG→B是多余的。
删除依赖左部多余的依赖后:F3={AB→C,C→A,BC→D,CD→B,D→E,D→G,BE→C,CG→D,CE→G }CG→B与CD→B不能同时存在,但去掉任何一个都可以,说明最小依赖集不唯一。
二、求闭包例:关系模式R(U,F),其中U={A,B,C,D,E,I},F={A →D,AB→E,BI→E,CD→I,E→C},计算(AE)+。
解:令X={AE},X(0)=AE;计算X(1);逐一扫描F集合中各个函数依赖,在F中找出左边是AE子集的函数依赖,其结果是:A →D,E→C。
于是X(1)=AE∪DC=ACDE;因为X(0)≠X(1),且X(1)≠U,所以在F中找出左边是ACDE子集的函数依赖,其结果是:CD→I。
于是X(2)=ACDE∪I=ACDEI。
虽然X(2)≠X(1),但在F中未用过的函数依赖的左边属性已没有X(2)的子集,所以不必再计算下去,即(AE)+=ACDEI。
三、求候选键例1:关系模式R(U,F),其中U={A,B,C,D},F={A→B,C→D},试求此关系的候选键。
解:首先求属性的闭包:(A)+=AB,(B)+ =B,(C)+ =CD,(D)+ =D(AB)+ =AB,(AC)+=ABCD=U,(AD)+ =ABD,(BC)+ =BCD,(BD)+ =BD,(CD)+ =CD(ABD)+ =ABD,(BCD)+ =BCD,因(AC)+=ABCD=U,且(A)+=AB,(C)+ =CD,由闭包的定义,AC→A,AC→B,AC→B,AC→D,由合并规则得AC→ABCD=U;由候选码的定义可得AC 为候选码。
离散数学课后习题答案(第三章)之欧阳治创编

时间2021.03.10
创作:欧阳治
<<x,y>, <u,v>>∈R =
1对任意<x,y>∈A,因为 = ,所以
<<x,y>, <x,y>>∈R
即R是自反的。
2设<x,y>∈A,<u,v>∈A,若
<<x,y>, <u,v>>∈R = = <<u,vБайду номын сангаас,<x,y>>∈R
b)设 A={a,b,c}
R1={<a,b>,<b,a>,<b,c>,<c,b>,<a,c>,<c,a>,<a,a>,<b,b>,<c,c>}
R2={<a,a>,<b,b>,<c,c>,<b,c>,<c,b>}
R1-R2={<a,b>,<b,a>,<a,c>,<c,a>}
所以R1和R2是A上等价关系,但R1-R2不是A上等价关系。
c)若R1是A上等价关系,则
<a,a>∈R1<a,a>∈R1○R1
所以R12是A上自反的。
若<a,b>∈R12则存在c,使得<a, c>∈R1∧<c,b>∈R1。因R1对称,故有
<b, c>∈R1∧<c,a>∈R1<b, a>∈R12
即R12是对称的。
若<a,b>∈R12∧<b, c>∈R12,则有
设S=[a]R,则SS
这就证明了Π细分Π。
3-10.10 设Rj是表示I上的模j等价关系,Rk是表示I上的模k等价关系,证明I/Rk细分I/Rj当且仅当k是j的整数倍。
证明:由题设Rj={<x,y>|x≡y(modj)}
Rk={<x,y>|x≡y(modk)}
故<x,y>∈Rjx-y=cj (对某个c∈I)
证明 :对任意a∈A,必存在一个b∈A,使得<a,b>∈R.
离散数学第四版课后答案(第4章)

第4章 习题解答4.1 A :⑤; B :③; C :①; D :⑧; E :⑩4.2 A :②; B :③; C :⑤; D :⑩; E :⑦4.3 A :②; B :⑦; C :⑤; D :⑧; E :④分析 题4.1-4.3 都涉及到关系的表示。
先根据题意将关系表示成集合表达式,然后再进行相应的计算或解答,例如,题4.1中的}2,2,1,2,2,1,1,1{},2,2,1,1{><><><><=><><=s s E I};2,2,2,1,1,1{><><><=s I而题4.2中的}.1,4,4,3,1,2,4,1,1,1{><><><><><=R为得到题4.3中的R 须求解方程123=+y x ,最终得到}.1,9,2,6,3,3{><><><=R求R R 有三种方法,即集合表达式、关系矩阵和关系图的主法。
下面由题4.2的关系分别加以说明。
1°集合表达式法将ranR ran domR domR,, 的元素列出来,如图4.3所示。
然后检查R 的每个有序对,若R y x >∈<,,则从domR 中的x 到ranR 中的y 画一个箭头。
若danR 中的x 经过2步有向路径到达ranR 中的y ,则R R y x >∈<,。
由图4.3可知}.1,3,4,2,1,2,4,4,1,44,1,1,1{><><><><>><<><=R R如果求G F ,则将对应于G 中的有序对的箭头画在左边,而将对应于F 中的有序对的箭头画在右边。
对应的三个集合分别为ranF domF ran domG ,, ,然后,同样地寻找domG 到ranF 的2步长的有向路径即可。
《课程与教学论》期末考试题

《课程与教学论》期末考试题练习题(一)1.第1题“三要素说”认为,教学系统由下面三个要素构成的A.教师、学生、课程B.教师、学生、教材C.教师、教材、教学手段D.教师、学生、环境答案:A2.第2题课程与教学论的产生和发展可以分为A.萌芽期、建立期和繁荣期B.古代、近代和现代C.原始、古代和现代D.原始、封建、资本主义和社会主义答案:A3.第3题教学过程的“新三中心”是A.教师、课本、课堂B.学生、经验、活动C.教师、学生、课程D.教师、教材、教学手段答案:B4.第4题在课程研制模式中大力倡导目标模式的美国学者是A.泰勒B.司腾浩斯C.沃克D.施瓦布答案:A5.第5题学科中心说的代表人物是A.杜威B.赫尔巴特C.施瓦布D.夸美纽斯答案:C6.第6题下列课程设计模式中,属于问题中心课程设计模式的是A.学科设计B.生活领域设计C.科目设计D.学习者中心设计答案:B7.第7题在某一教学思想和原理的指导下,围绕某一主题,为实现教学目标而形成的相对稳定的规范化教学程序和操作体系就是A.教学内容B.教学模式C.教学形式D.教学方法答案:B8.第15题在学完某门课程或某个重要部分之后进行的旨在评价学生是否已经达到教学目标要求的概括水平较高的测试和成绩评定是A.终结性评价B.形成性评价C.诊断性评价D.相对性评价答案:A9.第16题现代教学的基本组织形式是A.现场教学B.个别教学C.分组教学D.班级授课答案:D10.第17题17世纪,《大教学论》,这本被认为是历史上专门而系统研究和阐述教育问题的专门著作问世,一般人将这本专著的发表看作是教学论诞生的标志。
这本著作的作者是A.昆体良B.夸美纽斯C.裴斯泰洛齐D.赫尔巴特答案:B11.第18题认为课程与教学必须重视学科结构、直觉思维和发现学习的学者是A.杜威B.赫尔巴特C.布鲁纳D.罗杰斯答案:C12.第19题在课程与教学论发展的萌芽时期,产生了一批论述课程与教学问题的专著,其中,世界上已发现的最早的课程与教学论专著是A.《理想国》B.《论语》C.《学记》D.《雄辩术原理》答案:C13.第27题在课程研制中以价值判断和选择为核心的、对理论指导、目标、内容或经验、组织与结构、活动样式或策略、评价等多种可能性和方案进行选择、确定和应用的过程被称为A.课程决策B.课程开发C.课程实施D.课程评价答案:A14.第28题在评价对象群体之外,预定一个客观的或者理想的标准,并运用这个固定的标准去评价每个评价对象的评价类型是A.绝对评价B.相对评价C.他评价D.元评价答案:A15.第29题典型的自学辅导式的教学组织形式是A.班级授课B.个别教学C.道尔顿制D.分组教学答案:C16.第30题“四要素说”认为,构成教学系统的四个要素是A.教师、学生、课程和物质条件B.教师、学生、教材和媒体C.教师、教材、教学手段和目的D.教师、学生、环境和反馈答案:A17.第8题关于课程与教学论的关系问题,西方课程与教学研究领域主要______________、______________、____________和二元循环联系模式等四种不同主张。
db第6章习题答案

第六章关系数据理论一、选择题1. 为了设计出性能较优的关系模式,必须进行规范化,规范化主要的理论依据是(A)。
A. 关系规范化理论B. 关系代数理论C.数理逻辑 D. 关系运算理论2. 规范化理论是关系数据库进行逻辑设计的理论依据,根据这个理论,关系数据库中的关系必须满足:每一个属性都是(B )。
A. 长度不变的B. 不可分解的C.互相关联的 D. 互不相关的3. 已知关系模式R(A,B,C,D,E)及其上的函数相关性集合F={A→D,B→C ,E →A },该关系模式的候选关键字是(B )。
B. BE D. DE4. 设学生关系S(SNO,SNAME,SSEX,SAGE,SDPART)的主键为SNO,学生选课关系SC(SNO,CNO,SCORE)的主键为SNO和CNO,则关系R(SNO,CNO,SSEX,SAGE,SDPART,SCORE)的主键为SNO和CNO,其满足(A )。
A. 1NFC. 3NFD. BCNF5. 设有关系模式W(C,P,S,G,T,R),其中各属性的含义是:C表示课程,P表示教师,S表示学生,G表示成绩,T表示时间,R表示教室,根据语义有如下数据依赖集:D={ C →P,(S,C)→G,(T,R)→C,(T,P)→R,(T,S)→R },关系模式W的一个关键字是( D)。
A. (S,C)B. (T,R)C. (T,P)D. (T,S)6. 关系模式中,满足2NF的模式(B )。
A. 可能是1NFB. 必定是1NFC. 必定是3NFD. 必定是BCNF7. 关系模式R中的属性全是主属性,则R的最高范式必定是(C )。
A. 1NFB. 2NFC. 3NFD. BCNF8. 消除了部分函数依赖的1NF的关系模式,必定是(B )。
A. 1NFB. 2NFC. 3NFD. BCNF9. 如果A->B ,那么属性A和属性B的联系是(B )。
A. 一对多B. 多对一C.多对多 D. 以上都不是10. 关系模式的候选关键字可以有1个或多个,而主关键字有(C )。
离散数学课后习题答案(第三章)(doc)

a) 用矩阵运算和作图方法求出 R 的自反、对称、传递闭包; b) 用 Warshall 算法,求出 R 的传递闭包。
解 a) 0 1 00
MR= 1 0 1 0 0 0 01
0 0 00
R 的关系图如图所示。
a
b
d
c
MR+MIA=
0 1 00 1 0 10
反之,若 S∩ScIX,设<x,y>∈S 且 <y,x>∈S,则 <x,y>∈S∧<x,y>∈Sc <x,y>∈S∩Sc <x,y>∈IX 故 x=y,即 S 是反对称的。
3-7.3 设 S 为 X 上的关系,证明若 S 是自反和传递的,则 S○S=S,其逆为真 吗?
证明 若 S 是 X 上传递关系,由习题 3-7.2a)可知(S○S)S, 令<x,y>∈S,根据自反性,必有< x,x> ∈S, 因此有< x,y >∈S○S, 即 SS○S。得到 S=S○S.
自反的; b)若 R1 和 R2 是反自反的,则 R1○R2 也
是反自反的; c)若 R1 和 R2 是对称的,则 R1○R2 也是
对称的; d)若 R1 和 R2 是传递的,则 R1○R2 也是
传递的。
证明 a)对任意 a∈A,设 R1 和 R2 是自 反的,则<a,a>∈R1,<a,a>∈R2 所以,<a,a>∈R1○R2,即 R1○R2 也是 自反的。
解:L= {<1,2>,<1,3>,<1,6>,<2,3>,<2,6>, <3,6>,<1,1>,<2,2>,<3,3>,<6,6>} D={<1,2>,<1,3>,<1,6>, <2,6>,<3,6>,<1, 1>,<2,2>,<3,3>,<6,6>} L∩D= {<1,2>,<1,3>,<1,6>,<2,6>,<3,6>,<1,1>, <2,2>,<3,3>,<6,6>}
哈工大集合论习题课-第三章 关系习题课(学生)

习 题 课例1设{,,}A a b c =,给出A 上的一个二元关系,使其同时不满足自反性、反自反性、对称性、反对称和传递性的二元关系,并画出R 的关系图。
解:{(,),(,),(,),(,)}R a a b c c b a c =,关系图如图所示。
例2 设X 是一个集合,X =n ,求:1.X 上的二元关系有多少?()22n 2. X 上的自反的二元关系有多少? 3. X 上的反自反的二元关系有多少?解:因为把所有的反自反的二元关系的每个都加上对角线上的序对,就变成了自反的关系,因此,自反的与反自反的个数一样多。
即22nn-4. X 上的对称的二元关系有多少?2222n n n nn -++=,故共有222n n+个对称的关系。
5. X 上的反对称的二元关系有多少?22(32)n n n -∙6. X 上既是自反的也是反自反的二元关系的个数;(0)个7.X 上既不是自反的也不是反自反的二元关系有多少?2(2(22))n nn --解:解:可用容斥原理来计算设B 表示所有自反关系构成的集合,C 表示所有反自反关系构成的集合,则22nnB C -==。
而B C φ=,故B C B C =+,从而CC B C S B C S B C =-=--2222222222222(22)n n n n n n n n n n n ----=--=-=-于是,既不是自反的,也不是反自反关系共有22(22)n nn --个。
8.自反的且对称的关系有多少?[此结果与“反自反的且对称的关系有多少?”是一样多]即有222n n -(对角线上全去掉)9.自反的或对称的关系有多少?解:设B 表示自反关系的集合,C 表示对称关系的集合,则自反或对称关系的集合为:22222222n n n n nnB C B C B C +--=+-=+-。
10.X 上既是反自反的也是反对称的二元关系的个数为:223n n -;11.X 上既是对称的也是反对称的关系个数;解:X 上既是对称的也是反对称的关系X R I ⊆,故有2n 。
二元关系习题课答案课件市公开课一等奖省赛课微课金奖PPT课件

54
90
135
6
9
15
3
{6,15,90}上确界:90
二元关系习题课答案课件
下确界:3 第6页
四、证实题
⒈ 设R是集合A上关系。证实:R是偏序关系,iff R-1∩R=IA且R=rt(R)。 ⒉ 设R是集合A上关系。证实:R是拟序关系,iff R-1∩R=Φ且R=t(R)。
二元关系习题课答案课件
① 线序 ② 等价 ③ 偏序 ④ 拟序 ⑤ 良序 ( 2,4) 8. {1,2,3,4,5}上全序关系一定是 关系。
①等价 ②偏序 ③拟序 ④良序 (1,4,5)9. {1,2,3,4,5}上良序关系一定是
① 自反 ② 反自反 ③ 对称 ④ 反对称 ⑤ 传递
(1,2,3,4)10. 设R和S都是A到B关系,以下关系式中正确有:
第7页
二元关系习题课答案课件
第3页
( 2 )⒌ 若R和S是集合A上等价关系,则以下关系中一定是等价关 系有
① R∪S ② R∩S ③ R-S ④ R⊕S (1,2,4)⒍ 若R是集合A上等价关系,则
① R2=R ② t(R)=R ③ IA R ④ R-1=R ( 1,2,3,4,5)⒎ 空集上空关系是 关系。
( 1,2,3 )⒊ 设R={<1,2>}是A={1,2,3}上关系,则
① rst(R)是等价关系 ② R10=Φ ③ r(R)是偏序 ④ tr(R)是良序
( 5 )⒋ 设R和S分别是A到B和B到C关系,且R·S=Φ,那么
① R是空关系 ② S是空关系 ③ R和S都是空关系
④ R和S中最少有一个是空关系 ⑤ 以上答案都不对
二元关系习题课答案课件
第2页
二、多项选择题
第三章书后答案详解
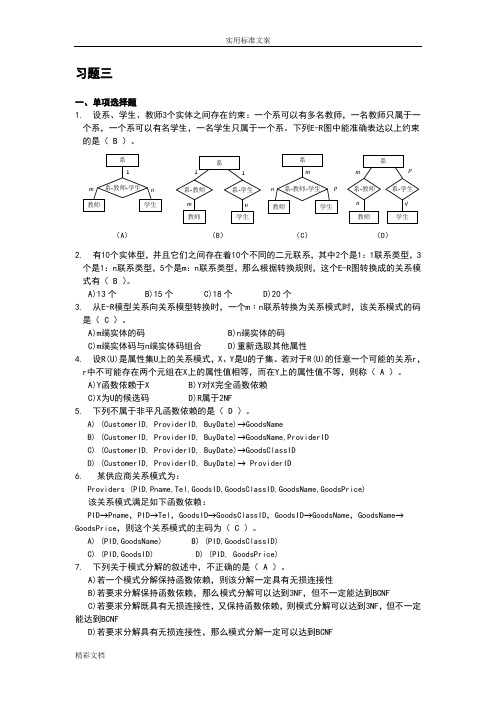
习题三一、单项选择题1.设系、学生、教师3个实体之间存在约束:一个系可以有多名教师,一名教师只属于一个系,一个系可以有名学生,一名学生只属于一个系。
下列E-R图中能准确表达以上约束的是( B )。
PID→Pname,PID→Tel,GoodsID→GoodsClassID,GoodsID→GoodsName,GoodsName→GoodsPrice,则这个关系模式的主码为( C )。
A) (PID,GoodsName) B) (PID,GoodsClassID)C) (PID,GoodsID) D) (PID, GoodsPrice)7.下列关于模式分解的叙述中,不正确的是( A )。
A)若一个模式分解保持函数依赖,则该分解一定具有无损连接性B)若要求分解保持函数依赖,那么模式分解可以达到3NF,但不一定能达到BCNFC)若要求分解既具有无损连接性,又保持函数依赖,则模式分解可以达到3NF,但不一定能达到BCNFD)若要求分解具有无损连接性,那么模式分解一定可以达到BCNF8.下列关于部分函数依赖的叙述中,正确的是( C )。
A)若 X→Y,且存在属性集 Z,Z⋂Y≠φ,X→Z,则称 Y 对 X 部分函数依赖B)若 X→Y,且存在属性集 Z,Z⋂Y=φ,X→Z,则称 Y 对 X 部分函数依赖C)若 X→Y,且存在 X 的真子集 X′,X′→Y,则称 Y 对 X 部分函数依赖D)若 X→Y,且对于 X 的任何真子集 X′,都有 X′→Y,则称 Y 对 X 部分函数依赖9.设U是所有属性的集合,X、Y、Z 都是 U 的子集,且 Z=U-X-Y,下列关于多值依赖的叙述中,正确的是( D )。
此题不用做Ⅰ. 若 X→→Y,则 X→Y Ⅱ. X→Y,则 X→→YⅢ .若 X→→Y,且 Y'→→Y,则 X→→ Y' Ⅳ .若 X→→Y,则 X→→ZA)只有Ⅱ B)只有Ⅲ C)Ⅰ和Ⅲ D)Ⅱ和Ⅳ10.设有关系模式SC(Sno, Sname, Sex, Birthday, Cno, Cname, Grade, Tno, Tname)满足函数依赖集:{Sno→Sname, Sno→Sex, Sno→Birthday, Cno→Cname, (Sno, Cno)→Grade, Tno→Tname}。
(完整版)《数据库原理及应用》课后习题参考答案解析

《数据库原理与应用》课后习题参考答案第一章作业参考答案1. 单选题 C C D B C2. 判断题对错错错对3填空题网状模型用户商业智能数据挖掘系统设计4简答题1)数据模型是指描述事物对象的数据组成、数据关系、数据约束的抽象结构及其说明。
数据模型是指描述事物对象的数据组成、数据关系、数据约束的抽象结构及其说明。
数据模型是指描述事物对象的数据组成、数据关系、数据约束的抽象结构及其说明。
3)数据约束:用于描述数据结构中数据之间的语义联系、数据之间的制约和依存关系,以及数据动态变化的规则。
主流数据库采用关系图模型。
数据库典型数据模型:层次数据模型网状数据模型关系数据模型其它数据模型(如对象数据模型、键值对数据模型、列式数据模型。
)2)数据库——是一种依照特定数据模型组织、存储和管理数据的文件,数据库文件一般存放在辅助存储器以便长久保存。
数据库具有如下特点:数据不重复存放;提供给多种应用程序访问;数据结构独立于使用它的应用程序;对数据增、删、改、检索由统一软件进行管理和控制。
3)数据库(Database)是一种依照特定模型组织、存储和管理数据的数据结构。
在数据库中,不仅存放了数据,而且还存放了数据与数据之间的关系。
数据库内部元素:用户表:用户在数据库中创建的数据库表;系统表:数据库中系统自带的数据库表;视图:数据库中用于对数据进行查询的虚拟表;索引:数据库中用于加快数据查询的索引项;约束:数据库中对数据、数据关系施加的规则;存储过程:数据库内部完成特定功能处理的程序;触发器:数据库内部因数据变化自动执行的一类存储过程等等4)数据库系统包括:用户、数据库应用程序、数据库管理系统和数据库四个组成要素。
5)数据库管理系统(Database Manage System,DBMS )——是一种专门用来创建数据库、管理数据库、维护数据库,并提供对数据库访问的系统软件。
数据库管理系统(DBMS)主要功能:创建数据库和表; 创建支持结构,如索引等; 读取数据库数据 ; 修改数据库数据; 维护数据库结构; 执行规则; 并发控制; 提供安全性;执行备份和恢复等等第二章作业参考答案1 单选题 C B D A A2. 判断题对对错对错3填空题全外连接数据约束候选键用户定义完整性4简答题外码键1)在关系模型中,使用“关系”来存储“实体”中的数据。
二元关系 (3)

150-3
电子科技大学离散数学课程组——国家精品课程
例6.4.2
设A={a,b},试计算A上所有具有自反性的关系R的 个数。 解 因为A2={<a,a>,<b,b>,<a,b>,<b,a>},所以A上 具有自反性的关系R的个数为:
C(2,0) + C(2,1) + C(2,2) = 4。
2020/1/12
2020/1/12
2020/1/12
150-5
电子科技大学离散数学课程组——国家精品课程
例6.4.2
设A={1,2,3,4}, 定义A上的关系R,S,T和V如下: (1)R={<1,1>,<1,3>,<3,1>,<4,4>}; (2)S={<1,1>,<1,3>,<1,4>,<2,4>}; (3)T={<1,1>,<1,2>,<1,3>,<3,1>,<1,4>}; (4)V={<1,1>,<2,2>,<3,3>,<4,4>}。 试判定它们是否具有对称性和反对称性
(a)
a
b
c
(b)
a
b
c
(c)
a
b
c
(d)
a
b
c
(e)
(f)
(g)
(h)
2020/1/12
150-15
电子科技大学离散数学课程组——国家精品课程
例6.4.9
设R={<1,1>,<2,2>},试判断R在集合A和B上具备的 特殊性质,其中A={1,2},B={1,2,3}。 解 当R是定义在集合A上的关系时,R是自反、对称、 反对称和传递的; 当R是定义在集合B上的关系时,R是对称、反对称 和传递的。 注意:绝对不能脱离基集(即定义关系的集合)来 谈论关系的性质。
数据库第五章习题及答案

第五章 关系数据理论一、 单项选择题1、设计性能较优的关系模式称为规范化,规范化主要的理论依据是 ( )A 、关系规范化理论B 、关系运算理论C 、关系代数理论D 、数理逻辑2、关系数据库规范化是为解决关系数据库中( )问题而引入的。
A 、插入、删除和数据冗余B 、提高查询速度C 、减少数据操作的复杂性D 、保证数据的安全性和完整性3、当关系模式R (A ,B )已属于3NF ,下列说法中( )是正确的。
A 、它一定消除了插入和删除异常B 、一定属于BCNFC 、仍存在一定的插入和删除异常D 、A 和C 都是4、在关系DB 中,任何二元关系模式的最高范式必定是( )A 、1NFB 、2NFC 、3NFD 、BCNF5、当B 属性函数依赖于A 属性时,属性A 与B 的联系是( )A 、1对多B 、多对1C 、多对多D 、以上都不是6、在关系模式中,如果属性A 和B 存在1对1的联系,则说( )A 、A B B 、B A C 、A B D 、以上都不是7、关系模式中,满足2NF 的模式,( )A 、可能是1NFB 、必定是1NFC 、必定是3NFD 、必定是BCNF8、关系模式R 中的属性全部是主属性,则R 的最高范式必定是( )A 、2NFB 、3NFC 、BCNFD 、4NF9、关系模式的候选关键字可以有( c ),主关键字有( 1个 )A 、0个B 、1个C 、1个或多个D 、多个10、如果关系模式R 是BCNF 范式,那么下列说法不正确的是( )。
A 、R 必是3NFB 、R 必是1NFC 、R 必是2NFD 、R 必是4NF11、图4.5中给定关系R ( )。
A 、不是3NFB 、是3NF 但不是2NFC 、是3NF 但不是BCNFD 、是BCNF12、设有如图4.6所示的关系R ,它是( )A 、1NFB 、2NFC 、3NFD 、4NF二、 填空题1、如果模式是BCNF ,则模式R 必定是(3NF ),反之,则( 不一定 )成立。
第5章关系数据理论习题参考答案.docx

第5章关系数据理论习题参考答案规范化定义小结:定义1:设R(U)是属性集U上的关系模式。
X, Y是属性集U的子集。
若对于R(U)的任意一个可能的关系r, r中不可能存在两个元组在X 上的属性值相等,而在Y上的属性值不等,则称X函数确定Y或Y函数依赖于X,记作XTY。
(即只要X上的属性值相等,Y上的值一定相等。
) 术语和记号:(P173页)•XTY,但Y不是X的子集,则称XTY是非平凡的函数依赖。
若不特别声明,总是讨论非平凡的函数依赖。
•XTY,但Y是X的子集,则称XTY是平凡的函数依赖。
•若XTY,则X叫做决定因素(Determinant)。
•若X-»Y, Y->X,则记作XG9Y。
•若Y不函数依赖于X,则记作2 Y。
定义2:在R(U)中,如果X^Y,并且对于X的任何一个真子集X,,都有X,p Y,则称Y对X完全函数依赖,记作:FXTY若XTY,但Y不完全函数依赖于X,则称Y对X部分函数依赖,记作:PX^Y定义3:若关系模式R的每一个分量是不可再分的数据项,则关系模式R属于第一范式(lNF)o定义4:若关系模式ReiNF,且每一个非主属性完全函数依赖于码,则关系模式RE2NF。
(即1NF消除了非主属性对码的部分函数依赖则成为2NF)o定义5:关系模式R〈U, F>中若不存在这样的码X、属性组Y及非主属性Z(Z不是Y的子集)使得XTY, Y 9 X, Yp Z成立,则称R<lbF>e3NF.定义6:关系模式R〈U, F>G1NF。
若XPY且Y不是X的子集时,X必含有码,则R<U, F>wBCNF。
定义7:关系模式伙1), F>G1NF,如果对于R的每个非平凡多值依赖XTTY(Y不是X的子集,Z=U-X-Y不为空),X都含有码,则称R〈U,F>e4NFo习题如下:2.建立一个关于系、学生.班级.学会等诸信息的关系数据库。
学生:学号.姓名、出生年月、系名、班号、宿舍区。
集合论-第三四章习题

例7 是否存在一个偏序关系≤,使得(X,≤)中有唯一 的极大元素,但没有最大元素?若有请给出一个具体 例子;若没有,请证明之。 例8 设R是X上的偏序关系,证明:
R是X上的全序关系X×X=R∪R-1。
例9设(A,≤)是偏序集,a∈A,f(a)={x|x∈A,x≤a},
证明:f:A→2A是一个单射,且当a≤b时,有
二、性质 定理1 设A,B,C是三个任意的集合,则 (1)若A⊆B,则|A|≤|B| ; (2)若|A|≤|B|,|B|≤|C|,则|A|≤|C| ; 推论:设A是无穷集合,则|N|≤|A|。 前面介绍了要证明两个集合基数相等必须在两个集 合之间建立起一个一一对应,但这往往是比较困难的。 下面介绍证明两个集合基数相等的一个比较简单的方 法,表示成下面的两个定理形式,这两个定理的证明 是冗长和复杂的,故略去。 定理2 (Zermelo)设A,B是两个任意集合,则|A|=|B|, |A|>|B|, |A|<|B|,三者中恰有一个成立。 这种性质称为三歧性,故这个定理称为三歧性定理。
习题课(2)
例1 设R是A上的二元关系,下面的结论是否正确?并 证明你的结论. (1)R是自反的,则R· R也是自反的 (2)R是对称的,则R· R也是对称的。 (3)R是反自反和传递的,则R是反对称的。 (正确\正确\正确) 例2 设R是集合A上的反对称关系,则t(R)一定是反对 称的吗? 例3 是否可以定义二元关系的反自反闭包与二元关系 的反对称闭包?为什么? 例4 是否存在X(|X|=n)上的一个二元关系R,使得 R1,R2,…,Rn两两不相等。 例5 证明:如果R是对称的,则R+也是对称的。
例3 设集合A={a,b,c,d,e}上关系R定义如下: R={(a,a),(a,b),(a,c),(a,d),(a,e),(b,b),(b,c),(b,e), (c,c),(c,e),(d,d),(d,e),(e,e)}。 1.写出R的关系矩阵; 2.验证(A,R)是偏序集; 3.画出Hasse图; 4.若A上的关系如下: R={(a,a),(a,b),(a,c),(a,d),(a,e),(b,b),(b,c),(b,e), (c,c), (c,d),(c,e),(d,d),(d,e),(e,e)},则有如何? 例4 证明:每个由n2+1个实数组成的数列中必有一个 长至少为n+1的不减子序列,或有一个长至少为n+1 的不增子序列。
离散数学课件第四章二元关系习题

闭包的定义基于关系的传递 性,即如果关系R满足传递性, 那么对于任何元素x,如果存 在元素y和z,使得xRy和yRz, 那么一定存在一个元素z',使 得xRz'。闭包就是由给定关系 和所有满足闭包定义的新元 素构成的关系集合。
闭包具有一些重要的性质, 这些性质决定了闭包在数学 和计算机科学中的广泛应用 。
同余关系的应用
应用1
在密码学中,同余关系可用于生成加 密密钥。例如,通过选择两个同余的 数作为密钥,可以确保加密和解密操 作的一致性。
应用2
在计算机科学中,同余关系可用于实 现数据校验。例如,通过将数据与一 个已知的校验值进行同余运算,可以 检测数据是否在传输过程中被篡改。
THANKS
感谢观看
反对称性
如果对于关系中的每一对 元素,如果元素x与元素y 有关系,且元素y与元素x 也有关系,但元素x与元 素y的关系不等于元素y与 元素x的关系,则称该关 系具有反对称性。
习题解析
习题1
判断给定的关系是否具有自反性、反自反性、对称性和反对称性。通过举例和推理,分析 给定的关系是否满足这些性质。
习题2
表示方法
总结词
掌握二元关系的表示方法是解题的关键。
详细描述
在数学中,我们通常使用笛卡尔积来表示二元关系。例如,如果A和B是两个集合, 那么A和B的笛卡尔积可以表示为A×B,它包含了所有形如(a, b)的元素,其中a属于 A,b属于B。
习题解析
总结词
通过解析具体习题,可以加深对二元关系定义和表示方法的理解。
有着广泛的应用。
05
习题五:关系的同余
同余关系的定义与性质
定义
反身性
对称性
传递性
如果对于任意元素$x$, 都有$f(x) = g(x)$,则 称$f$和$g$是同余的。
《数据库系统概论》第六章关系数据理论复习题及答案

《数据库系统概论》第六章关系数据理论复习题及答案一、选择题1、关系规范化中的删除操作异常是指①,插入操作异常是指②。
A.不该删除的数据被删除 B.不该插入的数据被插入 C.应该删除的数据未被删除 D.应该插入的数据未被插入答案:①A ②D2、设计性能较优的关系模式称为规范化,规范化主要的理论依据是。
A.关系规范化理论 B.关系运算理论 C.关系代数理论 D.数理逻辑答案:A3、规范化过程主要为克服数据库逻辑结构中的插入异常,删除异常以及冗余度大的缺陷。
A.数据的不一致性 B.结构不合理 C.冗余度大 D.数据丢失答案:C4、当关系模式R(A,B)已属于3NF,下列说法中是正确的。
A.它一定消除了插入和删除异常 B.仍存在一定的插入和删除异常 C.一定属于BCNF D.A 和C都是答案:B5、关系模型中的关系模式至少是。
A.1NF B.2NF C.3NF D.BCNF 答案:A 6、在关系DB中,任何二元关系模式的最高范式必定是。
A.1NF B.2NF C.3NF D.BCNF 答案:D7、在关系模式R中,若其函数依赖集中所有候选关键字都是决定因素,则R最高范式是。
A.2NF B.3NF C.4NF D.BCNF 答案:C8、候选关键字中的属性称为。
A.非主属性 B.主属性 C.复合属性 D.关键属性答案:B9、消除了部分函数依赖的1NF的关系模式,必定是。
A.1NF B.2NF C.3NF D.4NF 答案:B10、关系模式的候选关键字可以有①,主关键字有②。
A.0个B.1个 C.1个或多个 D.多个答案:①C ②B 11、关系模式的分解不惟一。
A.惟一 B.不惟一答案:B12、根据关系数据库规范化理论,关系数据库中的关系要满足第一范式。
下面“部门”关系中,因哪个属性而使它不满足第一范式? 。
部门(部门号,部门名,部门成员,部门总经理)A.部门总经理 B.部门成员 C.部门名 D.部门号答案:B二、填空题1、在关系A(S,SN,D)和B(D,CN,NM中,A的主键是S,B的主键是D,则D在S中称为。
离散数学之3—二元关系

R10={(1,1)}
既对称, 也反对称。 R9={(1,2), (2,1), (1,4)} 既不是对称, 也不是反对称。
5。如果(x, y) R (y, z) R (x, z) R, 就说 R是A上的一个传递关系。 例:设A={a, b, c}, S1 ={ (a, c), (a, b), (b, b), (c, b), (c, c) }, S2 ={ (a, a), (b, a), (b, c), (c, b), (c, c) }, S3 ={ (a, c), (a, b) }, 则 S1, S3 都是传递的, 而 S2 不是传递的。
(a, c) (R T) (S T)。
⑵ (a, c) (R S) T
( b)[ bA (a, b) R S (b, c) T ] ( b)[ bA ( (a, b) R (a, b)S ) (b, c)T ] ( b)[ bA (a, b) R ( b, c)T ) ] ( b)[ bA
R = { (a, a), (a, c), (b, a), (b, b), (c, b), (c, c) }, S = { (a, a), (a, c), (b, a), (b, c), (c, b), (c, c) }, 则 R S ={ (a, a), (a, c), (b, a), (b, c), (b, b), (c, b), (c, c) },
那么,详细写出即是 R={(2, 4), (5, 25), (2, 1), (5, 4)}。
例 2:设A={2,3,4,5,6,8},定义A到自身的一 个
二元关系为 MOD3={(a, b)a, bA (a b(mod 3))},
那么,MOD3={(2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (8, 8),
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、计算与作图
1.若集合A={1,2,3,4,5}上的等价关系R ={<1,1>,<2,2>,<3,3>,<4,4>,<5,5>,<1,2>,<2,1>,<3,4>,<4,3 >},求商集A/R 解:A/R= {{1,2},{3,4},{5}} 2.R为集合A={1,2,3,4,5}上的等价关系,已知商集A/R ={{1,2},{3},{4,5}},求R 解:R=IA ∪ {<1,2>,<2,1>,<5,4>,<4,5>}
④ R和S中至少有一个是空关系
( 2 )⒌ 若R和S是集合A上的等价关系,则下列关系中一定是等价 关系的有 ① R∪S ② R∩S ③ R-S ④ R⊕S (1,2,4)⒍ 若R是集合A上的等价关系,则 ① R2=R ② t(R)=R ③ IA ⊂ R ④ R-1=R ( 1,2,3,4,5)⒎ 空集上的空关系是 关系。 ① 线序 ② 等价 ③ 偏序 ④ 拟序 ⑤ 良序 ( 2,4) 8. {1,2,3,4,5}上的全序关系一定是 关系。 ①等价 ②偏序 ③拟序 ④良序 (1,4,5)9. {1,2,3,4,5}上的良序关系一定是 ① 自反的 ② 反自反的 ③ 对称的 ④ 反对称的 ⑤ 传递的 (1,2,3,4)10. 设R和S都是A到B的关系,下列关系式中正确的有: ① (R∪S)-1=R-1∪S-1 ③ (R-S)-1=R-1-S-1 ② (R∩S)-1=R-1∩S-1 ④ (R⊕S)-1=R-1⊕S-1
二元关系习题课
一. 判断题
( F)⒈ 设A、B、C和D是四个非空集合, 且A×C⊂B×D,则A⊂B且C⊂D。 ( F )⒉ 设A、B、C和D是四个集合,则A×C=B×D,iff A=B且C=D。 ( F ) 3. 传递关系的对称闭包仍是传递的。 ( F ) 4. 非空集合上的关系不是对称的,则必是反对称的。 ( T ) 5. 非空集合上的自反关系必不是反自反的。 ( F ) 6. 若R和S是二个有完全相同的二元组的集合,则称它们是相等的二 元关系。 ( F ) 7. 设A是一个非空集合,则A上的等价关系都不是偏序关系。 ( T ) 8. 有限集上的全序关系必是良序关系。 ( F ) 9. 有限集上的偏序关系必是全序关系。 ( F ) 10. <A;R>是偏序集,则A的任何非空子集必有极小元。 ( F ) 11. <A;R>是偏序集,则A的非空子集B的上确界必是B的最大元。 ( F ) 12. <A;R>是全序集,则A的任何非空子集必有唯一极小元。 ( F ) 13. <A;R>是全序集,则A的非空子集B的下确界必是B的最小元。
3.设A={3,6,9,15,54,90,135,180},|为自然数的整除 关系。画出<A;|>的Hasse图,并求{6,15,90}的 上、下确界。
180
54Leabharlann 901356
9
15
3
{6,15,90}的上确界:90 下确界:3
四、证明题
⒈ 设R是集合A上的关系。证明:R是偏序关系, iff R-1∩R=IA且R=rt(R)。 ⒉ 设R是集合A上的关系。证明:R是拟序关系, iff R-1∩R=Φ且R=t(R)。
二、多项选择题 (1,2 )⒈ 下列说法中正确的有: ① 任何集合都不是它自身的元素 ③ 若A×B=Φ,则A=B=Φ 是空集 ② 任何集合的幂集都不是空集 ④ 任意两集合的迪卡尔积都不
( 4,5 )⒉ {1,2,3,4,5}上的关系R={<1,1>,<1,3>,<2,3>}是 ① 自反的 ② 反自反的 ③ 对称的 ④ 反对称的 ⑤ 传递的 ( 1,2,3 )⒊ 设R={<1,2>}是A={1,2,3}上的关系,则 ① rst(R)是等价关系 ② R10=Φ (5 ① R是空关系 ② S是空关系 ③ r(R)是偏序 ④ tr(R)是良序 ③ R和S都是空关系 ⑤ 以上答案都不对 )⒋ 设R和S分别是A到B和B到C的关系,且R·S=Φ,那么
