2017-2018 第二学期 错题汇总(一)
苏教版小学数学四年级下册课本易错题(2017~2018学年度第二学期)

苏教版小学数学四年级下册课本易错题(2017~2018学年度第二学期)命题人:王秀月成绩:第一单元:平移、旋转和轴对称 一、填空: 1.钟面上的时针从6:00到9:00旋转了()。
2.正方形有( )条对称轴,长方形有( )条对称轴,圆有( )条对称轴。
二、实践与操作:1.(1)画出左边三角形绕点A 逆时针旋转90º后的图形。
(2)画出右边三角形绕点B 顺时针旋转90º后的图形。
2.画出下面每个轴对称图形的所有对称轴。
3.把下面的图形补充完整,使它成为一个轴对称图形。
A B第二单元:认识多位数一、填空:1.先读一读下面各数,再选择合适的数填在括号里。
90090000900000(1)北江市的人口总数大约是( )人。
(2)荷塘村的人口总数大约是( )人。
(3)湖滨镇的人口总数大约是( )人。
2.(1)15040800里面有()个千万、()个百万、()个万和()个百。
(2)一个数的千万位、万位位和千位上都是2,其他各位上都是0,这个数是( )(3)最大的七位数是( ),最小的八位数是( )。
3.(1)在数位顺序表上,从个位起,第五位是()位,第九位是()位。
(2)千万位位的左边一位是()位,右边一位是()位。
(3)一个十位数,它的最高位是()位。
(4)最高位是千亿位的数是()位数。
4.(1)18个亿和3个千万组成的数是()。
(2)200600000里面有()个亿和()个万。
(3)一个数的亿位和万位上都是6,其他各位上都是0,这个数是( )。
二、写出下面各数:1.目前,全世界可确认的昆虫大约九十二万种。
大约六千五百万年前,恐龙突灭绝了,原因到现在还是个谜。
2.写一写、比一比。
五十五十万五十亿四百零三四百零三万四百零三亿一千零七十九一千零七十九万一千零七十九亿3.地球绕太阳公转一周的行程大约九亿八千万千米。
4.太阳和地球之间的平均距离大约是一亿四千九百六十万千米。
三、读出下面各数:1.杭州湾跨海大桥全长36000米。
江苏省射阳县第二中学2017-2018学年高二化学学业测试错题训练1 Word版缺答案

高二化学学测错题训练(1)一、有机物的性质及方程式的正误1、下列反应的化学方程式或反应类型的叙述错误的是A .,该反应是取代反应 B .CH 2=CH 2+H 2OCH 3CH 2OH ,该反应是加成反应 C .2CH 3CH 2OH +O 22CH 3CHO +2H 2O ,该反应是氧化反应 D .,该反应是酯化反应 2、苯是重要的有机化工原料。
下列有关苯的叙述正确的是A .常温常压下,密度比水的小B .分子中含有3个碳碳双键C .不能在空气中燃烧D .能使酸性高锰酸钾溶液褪色3、甲烷、乙烯是重要的化工原料。
下列叙述正确的是A .甲烷、乙烯是同分异构体B .可用酸性高锰酸钾溶液来区别甲烷和乙烯C .甲烷与氯气在光照条件下发生置换反应D .乙烯与水在一定条件下发生取代反应生成乙醇4、下列有机化学方程式书写错误..的是 A . CH 2=CH 2 CH 3CH 2ClB .C 12H 22O 11 + H 2催化剂 C 6H 12O 6 + C 6H 12O 6C . Br 2+Br FeBr 322D . CH 3COOH +CH 3CH 23COOCH 2CH 3+H 2O5、关于乙醇的说法正确的是A. 可用来萃取碘水中的碘B. 可以发生酯化反应C. 是食醋的主要成分D. 不能发生氧化反应6、乙醇和乙酸是生活中两种常见的有机物。
下列说法正确的是A .乙醇、乙酸互为同分异构体B .乙醇、乙酸都能与钠反应C .乙醇、乙酸都能与NaOH 溶液反应D .乙醇、乙酸都能使紫色石蕊试液变红色7、下列有机反应属于加成反应的是蔗糖 葡萄糖 果糖A .Br 2+Br FeBr 3HBr +B .CH 2=CH 2催化剂3CH 2ClC .CH3COOH + CH 3CH 23COOCH 2CH 3 + H 2O D .2CH3CH 2OH + O 23CHO + 2H 2O8、下列关于乙烯的说法正确的是A .是天然气的主要成分B .能使溴的四氯化碳溶液褪色C .不能发生燃烧反应D .不能发生加聚反应9、下列有机反应属于取代反应的是A .CH ≡CH + Cl 2 → CHCl==CHClB .CH 2==CH 2+HBr →CH 3CH 2BrC .2CH 3CH 2OH +O 2――→Cu △2CH 3CHO +2H 2O D .CH 3COOH +CH 3CH 2OH 浓硫酸ΔCH 3COOCH 2CH 3+H 2O 10、下列关于乙醇的说法错误的是A. 工业酒精可作为汽车燃料B. 可以和乙酸反应制备香料C. 75%的酒精可用于医疗消毒D. 工业酒精可用于配制饮料11、下列有机反应属于加成反应的是A. CH 2===CH 2+HBr ―→CH 3CH 2BrB. CH 3CH 3+Cl 2――→光照CH 3CH 2Cl +HClC. 2CH 3CH 2OH +O 2――→Cu △2CH 3CHO +2H 20 D. CH 3COOH +CH 3CH 2OH ????浓硫酸△CH 3COOCH 2CH 3+H 2O12、下列关于苯的说法正确的是A .一定条件下能与液溴发生取代反应B .能与溴水反应而褪色C .苯存在单双建交替结构D .苯不能发生加成反应13、下列有机反应属于加成反应的是 A .CH 3CH 3 + Cl 2 CH 3CH 2Cl + HCl 光照 B .CH 2=CH 2 + HBr CH 3CH 2BrC .2CH 3CH 2OH + O 22CH 3CHO + 2H 2OD .CH 3COOH + CH 3CH 23COOCH 2CH 3 + H 2O14.下列关于乙酸与乙醇的说法正确的是A .互为同分异构体B .都能氧化为乙醛C .水溶液均显酸性D .可用石蕊溶液加入鉴别15、下列有机反应不属于...取代反应的是 A .C 2H 5OH + CH 3COOH 浓硫酸△CH 3COOC 2H 5 + H 2OB .H -C≡C-H + HCl H 2C = CHClC .+ HNO 3NO 2 + H 2OD .FeBr 3+ Br 2Br + HBr16、下列关于乙醇性质的说法正确的是A. 乙醇是无色无味的液体B. 乙醇能使紫色石蕊试液变红C. 乙醇不能与金属钠反应D. 乙醇能被酸性高锰酸钾溶液氧化17、下列有关甲烷的说法正确的是A .易溶于水B .是天然气的主要成分C .与氯气发生加成反应D .与乙烷互为同分异构体18、下列关于乙醇性质的化学方程式正确的是A .与金属钠反应: 2CH 3CH 2OH +2Na 2CH 3CH 2ONa +H 2↑B .与氧气的燃烧反应:2CH 3CH 2OH +O 2 点燃2CH 3CHO +2H 2O C .与氧气的催化氧化:CH 3CH 2OH +3O 2Cu Ag ∆−−−→或2CO 2+3H 2O D .与乙酸的酯化反应:CH 3CH 2OH +CH 3COOHCH 3CH 2OCH 2CH 3 19、下列有机化学反应属于水解反应的是A. 2CH 3CH 2OH +O 2――→催化剂△2CH 3CHO +2H 2OB.C. CH 2==CH 2+H 2O ――→催化剂CH 3—CH 2OHD. CH 3COOCH 2CH 3+NaOH ――→△CH 3COONa +CH 3CH 2OH20、下列关于乙醇和乙酸的说法中,正确的是A. 乙醇和乙酸分子中都含有CO 键B. 乙酸能溶于水,但不溶于乙醇C. 乙醇和乙酸均能使紫色石蕊试液变红D. 乙醇和乙酸在一定条件下能发生酯化反应21、下列反应中,属于加成反应的是A .CH 3Cl+Cl 光照CH 2Cl 2+HClB .CH 2=CH 2+HOCl HOCH 2—CH 2ClC.2CH3CH2OH+O22CH3CHO+2H2O D.Br+催化剂+ HBrBr222、下列事实可以说明甲烷分子具有正四面体结构的是A.CH4 没有同分异构体 B.CH3Cl没有同分异构体C.CH2Cl2没有同分异构体 D.CCl4 没有同分异构体23、下列关于苯的说法中,正确的是A. 在空气中燃烧时产生较浓的黑烟B. 分子中含有三个C—C键和三个C==C键C. 分子中C、H元素的质量比为6∶1D. 通入氢气即可发生加成反应24、下列关于乙醇和乙酸的说法中,正确的是A.乙醇和乙酸在一定条件下能发生酯化反应 B.乙酸能溶于水,但不溶于乙醇C.乙醇和乙酸均能使紫色石蕊试液变红 D.乙醇和乙酸分子中都含有碳氧双键25、下列反应的化学方程式或反应类型叙述错误的是A.取代反应B.CH2=CH2+H2O CH3CH2OH 加成反应C.2CH3CH2OH+O22CH3CHO+2H2O 氧化反应D.酯化反应(选做题)26、向500 mL稀硝酸中加入一定质量的铁粉,铁粉完全溶解后,放出NO气体5.6 L(标准状况),同时溶液质量增加9.3 g。
2017-2018学年度第二学期期末考试.doc

2017-2018学年度第二学期期末考试汽车发动机构造与维修姓名_______ 班级____________ 成绩 ___________一、填空题(每题3分,共30分)1 •根据发动机中各运动副工作条件的不同,发动机一般采用___________ 润滑和________ 润滑方式。
2润滑系统_般由_______ _________ __________ __________ __________ ________ 和_____________ 等组成。
3•汽车上的常用机油泵有______________ 和____________ ,它们都属于________ 泵,都是依靠__________ 的变化完成吸油和泵油。
4•与主油道串联的滤清器称为________________ 一般为___________ ,与主油道并联的滤清器称为_______________ _ 般为___________ .5. ______________________________________________ 曲轴箱通风装置有两种通风方式,一种是______________________________________________________ ,另一种是__________6•从曲轴箱抽出的气体直接导入大气中的通风方式称为 ____________ -7. ___________________ 柴油机多采用通风方式。
8. _____________________________________________________ 冷却系的作用是.9. 通常,冷却水在冷却系内的循环路线有两条,一条为,另一条为________ •不经过____________ 的为 __________ .经过____________ 的为____________ .10•目前,汽车发动机一般采用___________ 节温器。
贵阳学院生物工程专业2017-2018第二学期分析化学考试题

贵阳学院生物工程专业2017-2018第二学期分析化学考试题1.按照测定原理,分析化学常分为化学分析和仪器分析两大类。
[判断题] *对(正确答案)错2.分析化学的任务包括定性分析、定量分析、结构分析和形态分析。
[判断题] *对错(正确答案)3.用高锰酸钾法测定双氧水中过氧化氢的含量是属于滴定分析。
[判断题] *对(正确答案)错4.偶然误差是定量分析中误差的主要来源,它影响分析结果的精密度。
[判断题] *对(正确答案)错5.只要是可疑值(或逸出值)一定要舍去。
[判断题] *对错(正确答案)6.被分析的物质称为样品,与样品发生化学反应的物质称为试剂,以化学反应为基础的分析方法称为化学分析法。
[判断题] *对(正确答案)错7、偏差是测量值与平均值之差。
[判断题] *对错(正确答案)8、绝对误差是测量值与真实值之差。
[判断题] *对(正确答案)错9、增加平行测定次数,可以减少系统误差。
[判断题] *对错(正确答案)10、当偶然误差消除后,分析结果的精密度越高,准确度越高。
[判断题] *对错(正确答案)11、在滴定分析中,测定结果的精密度越高,其准确度也越高。
[判断题] *对错(正确答案)12、相对平均偏差、样本标准偏差、总体标准偏差都可用来表示测定值的分散程度。
[判断题] *对错(正确答案)13.增加测定次数可以提高分析结果的准确度。
[判断题] *对错(正确答案)14.用20ml移液管移取NaOH溶液,体积数记为20ml。
[判断题] *对错(正确答案)15.按照测定原理,分析化学常分为化学分析和仪器分析两大类。
[判断题] *对(正确答案)错16.用酸碱滴定法测定醋酸的含量,属于化学分析。
[判断题] *对(正确答案)错17.化学分析是分析化学的基础,仪器分析是分析化学发展的方向。
[判断题] *对(正确答案)错18.在一定称量范围内,被称样品的质量越大,称量的相对误差就越小。
2017-2018学年度第二学期期末考试初一数学试题及答案

2017—2018学年度第二学期期末考试初一数学试题一、填空题(每空1分,共22分)1、如果下降5米,记作-5米,那么上升4米记作()米;如果+2千克表示增加2千克,那么-3千克表示()。
2、从80减少到50,减少了()%;从50增加到80,增加了()%。
3、某班有60人,缺席6人,出勤率是()%。
4、如果3a=5b(a、b≠0),那么a:b=()。
5、一个圆锥的体积12dm3 ,高3dm,底面积是()。
6、甲、乙两数的比是5:8,甲数是150,乙数是()。
7、比较大小:-7○-5 1.5○5 20○-2.4 -3.1○3.18、某服装店一件休闲装现价200元,比原价降低了50元,相当于打()折。
照这样的折扣,原价800元的西装,现价()元。
9、一个圆柱和一个圆锥的体积相等,底面积也相等,圆柱的高是4米,圆锥的是高()米。
10、一桶油连桶称7.5千克,用去一半油后,连桶称还重4.5千克。
桶重()千克,油重()千克。
11、13只鸡放进4个鸡笼里,至少有()只鸡要放进同一个笼子里。
12、一个圆柱形的木料,底面半径是3厘米,高是8厘米,这个圆柱体的表面积是()平方厘米。
如果把它加工成一个最大的圆锥体,削去部分的体积是()立方厘米。
13、找出规律,填一填。
3,11,20,30,(),53,()。
二、判断题:对的在括号打√,错的打×。
(每小题1分共5分)1、0是负数。
()2、书店以50元卖出两套不同的书,一套赚10%,一套亏本10%,书店是不亏也不赚。
()3、时间一定,路程和速度成正比例。
()4、栽120棵树,都成活了,成活率是120%。
()5、圆柱的体积大于与它等底等高的圆锥的体积。
()三、选择题(每题3分,共15分)1、规定10吨记为0吨,11吨记为+1吨,则下列说法错误的是()A、9吨记为-9吨B、12吨记为+2吨C、6吨记为-4吨D、+3吨表示重量为13吨2、在a12=13中,a的值是()A、12B、4C、6D、83、把长1.2米的圆柱形钢材按2:3:7截成三段,表面积比原来增加56平方厘米,这三段圆钢中最长的一段比最短的一段体积多()A、700立方厘米B、800立方厘米C、840立方厘米D、980立方厘米4、小刚把1000元钱按年利率2.4%存入银行,存期为两年,那么计算到期时她可以从银行取回多少钱(不计利息税),列式正确的是()。
2018新人教版五年级数学下学期(100道)重点错题解析

人教版五年级数学下册因数和倍数、长方体和正方体、分数的意义和性质重点易错题解析【1】倍数一定比因数大。
(×)错题解析:倍数和因数的概念不清,倍数和因数是根据整除法a÷b=c(a、b、c≠0)来定义的,对于一个任意的非零自然数,它的最大因数和最小公倍数相等,即此时,除法的被除数和除数(或商)相等。
订正:一个数的倍数可能和它的一个因数相等。
【2】26÷8=3……2,26是8的倍数,8是26的因数。
5.7÷3=1.9的倍数。
(×)错题解析:倍数和因数的概念不清,倍数和因数是根据整数除法a÷b=c(a、b、c≠0)来定义的,即要求两个数必须是非零自然数,且其中一个数一定能整除另一个数,不能有余数,此时这个数才有相互依存的倍数和因数关系。
订正:26÷8=3……2,这里将26改成可以被3整除的数,如24,就可以说24是8的倍数,8是24的因数。
5.7÷3=1.9,将5.7改成3的倍数57,就可以说57是3的倍数,3是57的因数。
【3】3是因数,24是倍数。
(×)错题解析:倍数和因数的概念掌握得不扎实,倍数和因数代表的是两种相互依存的关系。
不能孤立地说A是因数,B是倍数,订正:3是24的因数,24是3的倍数。
【4】1是所有自然数的因数。
(×)错题解析:倍数和因数的概念不清,倍数和因数是根据整数除法a÷b=c(a、b、c≠0)来定义的,即要求两个数必须首先满足是非零自然数这个条件,且一个数整除另一个数,才能说其中一个数是另一个数的因数(或倍数)。
订正:1是所有非零自然数的因数。
【5】1既没有因数,也没有倍数。
(×)错题解析:1=1×1,所以1只有1个因数,1的倍数是所有非零自然数。
订正:1只有1个因数,1有无数个倍数。
【6】一个自然数至少有两个因数。
(×)错题解析:因数和倍数是在非零自然数整除非零自然数的范畴内定义的,所以本题要补充上零除外这个条件,并且在非零自然数中,1只有1个因数,除此以外的非零自然数中的质数只有2个因数,合数至少有3个因数,因此原题的判断是错误的。
2017-2018学年七年级历史下学期期末模拟试卷及答案(一)

2017-2018学年七年级历史下学期期末模拟试卷及答案(一)一、单项选择(每小题2分,共40分)1.结束了自东汉末年以来的长期分裂局面,使中国重新统一的朝代是()A.西汉B.东汉C.隋朝D.唐朝2.“主明臣直”,在下面的哪一组君臣身上表现的最为充分()A.唐太宗﹣魏征B.武则天﹣魏征C.唐玄宗﹣狄仁杰D.朱元璋﹣胡惟庸3.中国历史上有一位著名的皇帝,他登基前一统江山,登基后开科举、修运河,他是()A.汉武帝B.隋文帝C.隋炀帝D.唐玄宗4.孙中山说过:现在各国的考试制度,差不多都是学英国的.穷流溯源,英国的考试制度,原来是从我们中国学过去的.其历史依据是我国古代实行的()A.禅让制B.分封制C.郡县制D.科举制5.我国历史上唯一的女皇帝是()A.隋文帝B.唐太宗C.武则天D.唐玄宗6.唐玄宗前期,政局稳定,经济繁荣。
被誉为()A.文景之治B.贞观之治C.开元盛世D.康乾盛世7.火药的发明与古代的炼丹术有密切关系,唐初有个人第一次把火药的配方记录在《丹经》中,此人是()A.李春B.孙思邈C.毕昇D.关汉卿8.1951年西藏的和平解放,标志着祖国大陆获得了统一,各族人民实现了大团结。
其实西藏早在元朝时就正式纳入了中国版图,元朝还专门设置了机构加强对它的管辖,该机构是()A.驻藏大臣B.伊犁将军C.宣政院D.军机处9.郭靖和杨康是金庸先生脍炙人口的小说《射雕英雄传》中的两个重要人物。
他们名字中的“靖”、“康”与下列历史事件有直接联系的是()A.西夏的建立 B.澶渊之盟C.金灭北宋D.元朝建立10.某班举行辩论会,同学们的辩论题目中哪一个准确概括了两宋时期的特征()A.盛世危机B.短暂繁荣C.帝国中兴D.政权并立11.王安石在《元日》中写道:“爆竹声中一岁除,春风送暖入屠苏.千门万户曈曈日,总把新桃换旧符.“诗中描述的节日是我们今天的()A.元宵节B.中秋节C.春节D.冬至12.《东京梦华录》记载,东京城州桥夜市每天热闹非凡,买卖交易直到凌晨。
2017_2018学年高二数学下学期期中试题基错理

吴起高级中学2017-2018学年第二学期中期考试高二数学(理科基础卷)试题第I卷(选择题共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.函数的导函数是()A. B. C. D.2.从10名学生中挑选出3名学生参加数学竞赛,不同的选法有()A. 种B. 3!C. 种D. 以上均不对3.证明不等式“”最适合的方法是()A. 综合法B. 分析法C. 反证法D. 数学归纳法4.5名同学排成一排照相,不同的排法种数是( )A.1B.5C.60D.1205.的二项式系数之和为().A. B. C. D.6.21.如图是函数的导函数的图象,给出下列命题:①-2是函数的极值点;②1是函数的极值点;③的图象在处切线的斜率小于零;④函数在区间上单调递增.则正确命题的序号是()A. ①③B. ②④C. ②③D. ①④7.5名运动员争夺3项比赛冠军,获得冠军的可能种数为: ( )A.B.C. D.8.已知曲线上一点,则点处的切线斜率等于( )A. B. C. D. 69.由曲线y=x2与直线y=2x所围成的平面图形的面积为( )A. B. C. D.10.设函数,则()A. B. C. 1 D. ﹣111.已知函数,则它的单调递减区间是()A. B. C. D.,12.用数学归纳法证明时,由到,不等式左端应增加的式子为()A. B.C. D.第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每小题5分,共20分.)13.在的展开式中,的系数是。
14.在区间上的最大值是。
15.观察下列等式,根据上述规律,________。
16.若是函数的一个极值点,则实数_______。
三、解答题(解答应写出文字说明,证明过程或演算步骤,本大题共70分.)17.(本小题10分)已知函数,求:函数的图象在点处的切线方程。
18. (本小题12分)有10名教师,其中男教师6名,女教师4名,(1)现要从中选2人去参加会议,有多少种不同的选法?(2)现要从中选出男、女教师各两名去参加会议,有多少种不同的选法?19. (本小题12分)用数学归纳法证明:(n是正整数)。
最新浙教版七年级下册2018经典易错题汇总(Word版-无答案)
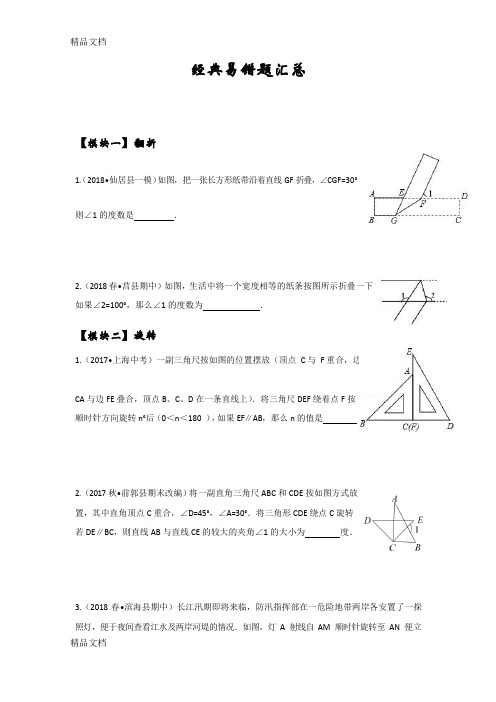
精品文档【模块一】翻折经典易错题汇总1(. 2018•仙居县一模)如图,把一张长方形纸带沿着直线 GF 折叠,∠CGF=30°则∠1 的度数是 .2.(2018 春•莒县期中)如图,生活中将一个宽度相等的纸条按图所示折叠一下如果∠2=100°,那么∠1 的度数为 .【模块二】旋转1.(2017•上海中考)一副三角尺按如图的位置摆放(顶点 C 与 F 重合,边CA 与边 FE 叠合,顶点 B 、C 、D 在一条直线上).将三角尺 DEF 绕着点 F 按顺时针方向旋转 n°后(0<n <180 ),如果 EF ∥AB ,那么 n 的值是2.(2017 秋•前郭县期末改编)将一副直角三角尺 ABC 和 CDE 按如图方式放置,其中直角顶点 C 重合,∠D=45°,∠A=30°.将三角形 CDE 绕点 C 旋转若 DE ∥BC ,则直线 AB 与直线 CE 的较大的夹角∠1 的大小为 度.3.(2018 春•滨海县期中)长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯 A 射线自 AM 顺时针旋转至 AN便立精品文档即回转,灯B 射线自BP 顺时针旋转至BQ 便立即回转,两灯不停交叉照射巡视.若灯A 转动的速度是a°/秒,灯B 转动的速度是b°/秒,且a、b 满足|a﹣3b|+(a+b﹣4)2=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°(1)求a、b 的值;(2)若灯B 射线先转动20 秒,灯A 射线才开始转动,在灯B 射线到达BQ 之前,A 灯转动几秒,两灯的光束互相平行?(3)如图,两灯同时转动,在灯A 射线到达AN 之前.若射出的光束交于点C,过C 作CD⊥AC 交PQ 于点D,则在转动过程中,∠BAC 与∠BCD 的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.【模块三】压轴题——平行线的性质1.(2017 春•南沙区期末)已知,直线AB∥DC,点P 为平面上一点,连接AP 与CP.(1)如图1,点P 在直线AB、CD 之间,当∠BAP=60°,∠DCP=20°时,求∠APC.(2)如图2,点P 在直线AB、CD 之间,∠BAP 与∠DCP 的角平分线相交于点K,写出∠AKC 与∠APC 之间的数量关系,并说明理由.(3)如图3,点P 落在CD 外,∠BAP 与∠DCP 的角平分线相交于点K,∠AKC 与∠APC 有何数量关系?并说明理由.2. (2017 春•武侯区校级期中)如图,已知AB∥CD,CE、BE 的交点为E,现作如下操作:第一次操作,分别作∠ABE 和∠DCE 的平分线,交点为E1,第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,第n次操作,分别作∠ABE n﹣1和∠DCE n﹣1的平分线,交点为E n.若∠E n=1 度,那∠BEC 等于度3.(2018 春•黄陂区期中)已知直线AB∥CD.(1)如图1,直接写出∠BME、∠E、∠END 的数量关系为;(2)如图2,∠BME 与∠CNE 的角平分线所在的直线相交于点P,试探究∠P 与∠E 之间的数量关系,并证明你的结论;(3)如图3,∠ABM=∠MBE,∠CDN= ∠NDE,直线MB、ND 交于点F,则= .4.(2017春•丰城市期末)数学思考:(1)如图1,已知AB∥CD,探究下面图形中∠APC和∠PAB、∠PCD 的关系,并证明你的结论推广延伸:(2)①如图2,已知AA1∥BA1,请你猜想∠A1,∠B1,∠B2,∠A2、∠A3的关系,并证明你的猜想;、∠A n的关系②如图3,已知AA1∥BA n,直接写出∠A1,∠B1,∠B2,∠A2、…∠B n﹣1拓展应用:(3)①如图4所示,若AB∥EF,用含α,β,γ的式子表示x,应为()A.180°+α+β﹣γB.180°﹣α﹣γ+βC.β+γ﹣αD.α+β+γ②如图5,AB∥CD,且∠AFE=40°,∠FGH=90°,∠HMN=30°,∠CNP=50°,请你根据上述结论直接写出∠GHM 的度数是.【模块四】平移1.如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP 和∠PBN,分别交射线AM 于点C,D.(1)求∠CBD 的度数;(2)当点P 运动时,∠APB 与∠ADB 之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.(3)当点P 运动到使∠ACB=∠ABD 时,∠ABC 的度数是.【模块五】作图1.(1)如图1,一个牧童从P 点出发,赶着羊群去河边喝水,则应当怎样选择饮水路线,才能使羊群走的路程最短?请在图中画出最短路线.(2)如图2,在一条河的两岸有A,B 两个村庄,现在要在河上建一座小桥,桥的方向与河岸方向垂直,桥在图中用一条线段CD 表示.试问:桥CD 建在何处,才能使A 到B 的路程最短呢?请在图中画出桥CD 的位置.【模块六】几何巩固1.(2018春•洪山区期中)如图,AB∥DE,∠ABC的角平分线BP和∠CDE的角平分线DK 的反向延长线交于点P 且∠P﹣2∠C=57°,则∠C 等于()A.24°B.34°C.26°D.22°第1 题图第2 题图2.(2018春•高新区校级期中)如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK 的角平分线CF 的反向延长线交于点H,∠K﹣∠H=27°,则∠K=()A.76°B.78°C.80°D.82°3.(2013春•汉阳区期末)如图,AB⊥BC,AE平分∠BAD交BC于点EAE⊥DE,∠1+∠2=90°,M,N 分别是BA,CD 延长线上的点,∠EAM和∠EDN 的平分线交于点F.下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE 平分∠ADC;④∠F 为定值其中结论正确的有()A.1 个B.2 个C.3 个D.4 个4.(2018 春•开福区校级期末)学习了平行线后,小敏想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的,如图所示,由操作过程可知小敏画平行线的依据可以是.(把所有正确结论的序号都填在横线上)①如果两条直线和第三条直线平行,那么这两条直线平行;②同位角相等,两直线平行;③ 内错角相等,两直线平行;④同旁内角互补,两直线平行.5.(2018春•宁波期中)如图(1)所示为长方形纸带,将纸带沿EF折叠成图(2),再沿BF 折叠成图(3),继续沿EF折叠成图(4),按此操作,最后一次折叠后恰好完全盖住∠EFG;整个过程共折叠了9 次,问图(1)中∠DEF 的度数是.6.(2017春•成都期中)已知AM∥CN,点B为平面内一点,AB⊥BC于B.(1)如图1,直接写出∠A 和∠C 之间的数量关系;(2)如图2,过点B 作BD⊥AM 于点D,求证:∠ABD=∠C;(3)如图3,在(2)问的条件下,点E、F 在DM 上,连接BE、BF、CF,BF 平分∠DBC,BE 平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC 的度数.7.(2017春•乐亭县期中)已知,∠AOB=90°,点C在射线OA上,CD∥OE.(1)如图1,若∠OCD=120°,求∠BOE 的度数;(2)把“∠AOB=90°”改为“∠AOB=120°”,射线OE 沿射线OB 平移,得O′E,其他条件不变,(如图2所示),探究∠OCD、∠BO′E的数量关系;(3)在(2)的条件下,作PO′⊥OB 垂足为O′,与∠OCD 的平分线CP 交于点P,若∠BO′E=α,请用含α的式子表示∠CPO′(请直接写出答案).8.(2017春•碑林区校级期中)探究:如图①,已知直线l1∥l2,直线l3和l1,l2分别交于点C 和D,直线l3上有一点P.(1)若点P 在C、D 之间运动时,问∠PAC,∠APB,∠PBD 之间有怎样的关系?并说明理由.(2)若点P在C、D两点的外侧运动时(点P与点C、D不重合),请尝试自己画图,写出∠PAC,∠APB,∠PBD 之间的关系,并说明理由.(3)如图②,AB∥EF,∠C=90°,我们可以用类似的方法求出∠α、∠β、∠γ之间的关系,请直接写出∠α、∠β、∠γ之间的关系.9.(2017春•锡山区校级月考)将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):(1)若∠DCE=35°,求∠ACB 的度数;(2)猜想∠ACB 与∠DCE 的数量关系,并说明理由;(3)请你动手操作,现将三角尺ACD 固定,三角尺BCE 的CE 边与CA 边重合,绕点C 顺时针方向旋转,当0°<∠ACE<180°且点E 在直线AC 的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由10.如图,把△A B C纸片沿D E折叠,当点A落在四边形B C D E的外部时,则与和之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是A.2∠A =∠1 -∠2 C.3∠A = 2∠1 -∠2 B.3∠A = 2(∠1 -∠2) D.∠A =∠1 -∠211. 小宇同学在一次手工制作活动中,先把一张矩形纸片按图 1 的方式进行折叠,使折痕的左侧部分比右侧部分短 1cm ;展开后按图 2 的方式再折叠一次,使第二次折痕的左侧部分比右 侧 部 分 长 1cm , 再 展 开 后 , 在 纸 上 形 成 的 两 条 折 痕 之 间 的 距 离 是 ( )A .0.5cmB .1cmC .1.5cmD .2cm【模块七】阅读理解1. 先阅读下列材料,然后解题:阅读材料:因为(x -2)(x +3)=x 2+x -6,所以(x 2+x -6)÷(x -2)=x +3,即 x 2+x -6 能被 x -2 整除,所以 x -2 是 x 2+x -6 的一个因式,且当 x =2 时,x 2+x -6=0.(1)类比思考:(x +2)(x +3)= x 2+5x +6 ,所以(x 2+5x +6)÷(x +2)= x +3,即 x 2+5x+6 能被 整除,所以 是 x 2+5x +6 的一个因式,且当 x = 时,x 2+5x +6=0.(2)拓展探究:根据以上材料,已知多项式 x 2+mx -14 能被 x +2 整除,试求 m 的值.2.求 1+2+22+23+…+22012 的值,可令 S =1+2+22+23+…+22012,则 2S =2+22+23+24+…+22013,因 此 2S -S =22013-1.仿照以上推理,计算出 1+5+52+53+…+52012 的值为.【模块八】求值问题1.已知 x 2-5x -1997=0,则代数式(x -2)2-(x -1)2+1的值为( ) x -2A. 1999B. 2000C. 2001D. -2 2. 若 , 则 n + m 的 值为. m n3.已知(x -1)7 = a+ a x + a x 2 + a x 3 +..... + a x 7 ,精品文档+ =3 × + =10 ×求 a + a + a + a的值。
2018新人教版五年级数学下学期(100道)重点错题解析

2018新人教版五年级数学下学期(100道)重点错题解析人教版五年级数学下册因数和倍数、长方体和正方体、分数的意义和性质重点易错题解析1.倍数和因数的概念容易混淆。
实际上,倍数是指一个数可以被另一个数整除的次数,而因数是指能够整除一个数的数。
同时,一个数的最大因数和最小公倍数相等。
2.在进行倍数和因数的计算时,需要满足整除法的定义,即两个数必须是非零自然数,且其中一个数必须能够整除另一个数,不能有余数。
例如,26÷8=3……2,24是8的倍数,8是24的因数。
3.倍数和因数代表的是两种相互依存的关系,不能孤立地说一个数是因数,另一个数是倍数。
例如,3是24的因数,24是3的倍数。
4.倍数和因数的定义要求两个数必须首先满足是非零自然数这个条件,且一个数整除另一个数,才能说其中一个数是另一个数的因数或倍数。
因此,1是所有非零自然数的因数。
5.1只有一个因数,但有无数个倍数,因为任何数的倍数都包括1.6.在非零自然数中,1只有1个因数,质数只有2个因数,合数至少有3个因数。
因此,非零自然数至少有两个因数。
7.最大因数和最小倍数的定义需要满足整除法的条件,即两个数必须是非零自然数。
因此,任何自然数的最大因数和最小倍数都是它本身。
错题解析:做长和宽都是4分米的长方体框架需要用到4根铁丝,每根铁丝长度为10分米,而不是36分米。
因此原题的列式是错误的。
订正:用4根长度为10分米的铁丝做一个长和宽都是4分米的长方体框架,它的高是4分米。
错因分析:分子相同的分数,表示的分数单位大小相同,但所含的分数单位的个数不一定相同,因为分母的大小不同。
订正:分子相同的分数,表示的分数单位大小相同,但所含的分数单位的个数不一定相同,与分母的大小有关。
的分子加上8,如果要使这个分数的大小不变,分母应加上24.12】分数加减法中,只要分母相同,就可以直接加减分子。
(√)13】分数乘法中,分子相乘,分母相乘。
(√)14】分数除法中,被除数的分子乘以除数的分母,被除数的分母乘以除数的分子。
人教版2017-2018学年六年级(下)期末数学试卷(含答案)

六年级期末数学试卷(65)一、判断.(正确的打√,错误的打×.每题1分,共10分.)1.(1分)圆、三角形和平行四边形都是轴对称图形.(判断对错)2.(1分)吨,可以写作17%吨.(判断对错)3.(1分)用110粒种子做发芽试验,结果有100粒发芽,发芽率是100%.(判断对错)4.(1分)10:的比值是50:3.(判断对错)5.(1分)=0.6,b比a多约66.7%.(判断对错)6.(1分)射线比直线短.(判断对错)7.(1分)a和b是两种相关联的量,a=5b,a和b成正比例.(判断对错)8.(1分)甲数的等于乙数的(甲、乙两数均不为0),则甲数与乙数的比是6:5.(判断对错)9.(1分))一种商品,先提价10%,再降价10%,售价与原价相等.(判断对错)10.(1分)6个同学相互之间都要握手一次,一共要握手15次.(判断对错)二、选择.(把正确答案的序号填到括号里.)(每题1分,共16分.)11.(1分)A是一个非零的自然数,下列算式中得数最大的是()A.A÷ B.A×C.A÷112.(1分)一种彩电先涨价,又降价,现价和原价相比()A.便宜了B.贵了 C.价格不变13.(1分)等底等高的圆锥和圆柱,体积相差10立方厘米,圆柱的体积是()A.30立方厘米B.5立方厘米C.15立方厘米14.(1分)把7米长的钢筋锯4次,平均分成一些小段,每小段的长度是()A.米B.米C.米15.(1分)鸡兔同笼,共有24个头,68只脚,鸡有()只.A.10B.14C.1216.(1分)从家去超市,爸爸用了0.4时,淘气用了小时,爸爸和淘气速度的比是()A.:B.8:5 C.5:817.(1分)一个圆柱和一个圆锥的底面半径之比是2:3,体积之比是3:2,它们高的比是()A.1:3 B.3:4 C.9:818.(1分)下面哪组中的三条线段不可以围成一个三角形.()A.5厘米、6厘米、7厘米B.5厘米、5厘米、10厘米C.3厘米、6厘米、4厘米19.(1分)把一根木材截成两段,第一段长米,第二段占全长的,那么两根木材相比()A.第一段长 B.第二段长 C.同样长20.(1分)从下列图形中,不是轴对称图形的是()A.平行四边形B.半圆性C.环形21.(1分)(2009邵阳)一个三角形的三个内角的度数比是1:2:1,这个三角形是()A.锐角三角形B.直角三角形C.钝角三角形22.(1分)东东和明明分别从A、B出发,沿半圆弧走到C、D,两人走过的路程相差约多少米?()A.6.28B.12.56C.150.7223.(1分)小金从家出发,骑车到达书店,选好书后发现忘记带钱,马上又骑车回家取钱,再返回书店购书,下面哪幅图表示了他的这一行为过程?()A.B.C.24.(1分)图形A怎样变换得到图形B?()A.以M点为中心,顺时针旋转90°B.以直线OM为对称轴,画图形A的轴对称图形C.向右平移3格25.(1分)图是某校学生午餐各套餐的销售情况统计图(每人限买1份),已知有80名学生选择A套餐,则选择B套餐的学生有多少名?()A.50B.70C.12026.(1分)把圆分成若干等份,剪拼成一个近似的长方形,已知长方形的宽是1分米,长是()分米.A.3.14B.6.28C.3D.4三、计算.(共36分)27.(21分)直接写出得数.3.14×8= 1.2÷4=0.1=﹣=240%+12.5%=9.42÷3=14×=72÷6=×=1﹣25%=8×12.5%=(+)×4=15﹣4=×=51÷34=1÷0.01=15×6=×40=÷=22亿+58亿=5.28×10=28.(6分)解方程.50%x ﹣25%x=102x ﹣6=20.29.(9分)用你喜欢的方法进行计算.÷[×(﹣)]907+907×936×(+﹣)四、填空.(每空1分,共10分)30.(3分)2014年天猫双十一成交总额是57112181350元,这个数读作,改写成用“亿”作单位的数是,省略“亿”后面的尾数约是.31.(2分)xy=3,则想,x 与y 成比例,时间一定,路程和速度成比例.32.(2分)8.06立方米=升,1350千克=吨.33.(2分)一个圆柱体的侧面展开图是一个正方形,这个正方形的边长是6.28cm ,那么这个圆柱体的底面半径是cm ,体积是立方厘米.34.(1分)每袋味精的标准质量是100克,记作“0”.为了检验味精重量是否合格,一个检验员抽查了5袋,记录数据如下:﹣2,+2,﹣5,+3,﹣4,这5袋味精的总重量是克.五、图与数学.(共12分)35.(3分)图形A 以为对称轴,作轴对称图形,得到图形B .图形B 绕O 点沿方向旋转度得到图形C .36.(4分)画一画.(1)画出将图形A 向右平移10格得到的图形B .(2)以直线a 为对称轴,画图形B 的轴对称图形,得到图形C .37.(3分)晚上,陈叔叔(图中用竖线表示)在路灯下散步,请分别画出他在A、B两处时的影子.当他从A处向B处走去时,他的影子逐渐.38.(2分)画出从上面和左面看到的立体图形的形状.六、解决问题.(每题4分,共16分)39.(4分)学校食堂购买一堆煤,原计划每天烧1.25吨,可以烧16天,开展节约活动后,食堂每天可节约0.25吨,照这样计算这堆煤可以烧多少天?40.(4分)张大伯家有一堆小麦,堆成圆锥形.张大伯量得麦堆的底面周长是12.56米,高2米,这堆小麦的体积是多少立方米?如果每立方米小麦的质量为700千克,这堆小麦有多少千克?41.(4分)把一块三角形的地画在比例尺是1:500的图纸上,量得图上三角形的底是12厘米,高8厘米,这块地的实际面积是多少?42.(4分)把一块底面半径和高都是2分米的圆柱形铁块铸造成一块横截面是边长为2分米的方钢,这块方钢的长是多少分米?某次数学竞赛共20道题,评分标准是:每做对一题得5分,43.(6分)每做错或不做一题扣1分。
2017-2018学年高二下学期数学复习(理)易错大题30题(江苏版)Word版含解析

2017-2018学年高二下学期数学复习(理) 易错大题30题(江苏版)Word 版含解析1.观察以下3个等式:1(1)照以上式子规律,猜想第n 个等式(n ∈N *);(2)用数学归纳法证明上述所猜想的第n 个等式成立(n ∈N *).【答案】(1)第n 2)见解析②假设当n =k (k ∈N *且k ≥1)时等式成立,即有++…+=,则当n =k +1时,++…++=+====, 所以当n =k +1时,等式也成立. 由(1)(2)可知,对一切n ∈N *等式都成立.点睛:数学归纳法被用来证明与自然数有关的命题:递推基础不可少,归纳假设要用到,结论写明莫忘掉.2.已知函数()f x 满足()()233log log .f x x x =-(1).求函数()f x 的解析式;(2).当*n N ∈时,试比较()f n 与3n 的大小,并用数学归纳法证明你的结论. 【答案】(1) ()32xf x x =-;(2)详见解析.(2)当1n =时, ()11f =, 31n =,此时 ()31f n =;当2n =时, ()25f =, 31n =,此时 ()31f n <;当3n =时, ()321f =, 327n =,此时 ()33f n <;当4n =时, ()473f =, 364n =,此时 ()34f n >;猜想:当4n ≥, *n R ∈,都有()3f n n >. 要证明:当4n ≥, *n R ∈,都有()3f n n >,即要证:当4n ≥, *n R ∈, 332n n n ->,即要证:当4n ≥, *n R ∈, 332n n n >+.证明:①当4n =时, 381n =, 3272n n +=,显然, 332n n n >+成立;②假设当n k =时, 332k k k >+成立,那么,当1n k =+时, ()1333333236k k k k k k +=⨯>⨯+=+,又当4k ≥时,()()()33322236121233233k k k k k k k k k k k ⎡⎤+-+++=-+-=⋅-+-⎣⎦2224233530k k k k k ≥⋅-+-=+->,故()()3336121k k k k +>+++,所以1n k =+时, ()()313336121k k k k k +>+>+++结论成立,由①②,根据数学归纳法可知,当4n ≥, *n R ∈,都有()3f n n >.3.在数列{a n },{b n }中,a 1=2,b 1=4,且a n ,b n ,a n +1成等差数列,b n ,a n +1,b n +1成等比数列{n ∈N +}. 求a 2,a 3,a 4及b 2,b 3,b 4,由此猜测{a n },{b n }的通项公式,并证明你的结论; 【答案】a 2=6,b 2=9,a 3=12,b 3=16,a 4=20,b 4=25.证明见解析. 猜测a n =n(n +1),b n =(n +1)2,n ∈N *.②假设当n =k(k≥2且k ∈N *)时,结论成立,即 a k =k(k +1),b k =(k +1)2, 那么当n =k +1时,a k +1=2b k -a k =2(k +1)2-k(k +1)=(k +1)(k +2), b k +1(k +2)2.解:由条件得2b n =a n +a n +1, 21n a +=b n b n +1,由此可得a 2=6,b 2=9,a 3=12,b 3=16,a 4=20,b 4=25. 猜测a n =n(n +1),b n =(n +1)2,n ∈N *. 4分 用数学归纳法证明:①当n =1时,由已知a 1=2,b 1=4可得结论成立. ②假设当n =k(k≥2且k ∈N *)时,结论成立,即 a k =k(k +1),b k =(k +1)2, 那么当n =k +1时,a k +1=2b k -a k =2(k +1)2-k(k +1)=(k +1)(k +2),b k +1(k +2)2.所以当n =k +1时,结论也成立.由①②可知,a n =n(n +1),b n =(n +1)2对一切n ∈N *都成立. 10分4.已知n S 是数列1n ⎧⎫⎨⎬⎩⎭的前n 项和,是否存在关于正整数n 的函数()f n ,使得()()1211n n S S S f n S ++++=-对于大于1的正整数n 都成立?证明你的结论.【答案】()f n n =猜测: ()f n n =,使得()()()1211,2n n S S S f n S n N n -+++=-∈≥成立.下面用数学归纳法证明:①=2,3时,上面已证,猜测正确.②假设=( 2,k k N ≥∈)时, ()f k k =,使得即()1211k k S S S k S -++⋅⋅⋅+=-成立,则 当1n k =+时, ()11f k k +=+,由()1211k k k k S S S S k S S -++⋅⋅⋅++=-+ ()1k k S k =+-()1111k k S k ⎛⎫=++- ⎪+⎝⎭ ()()()()111111k k k S f k S ++=+-=+-.即=1k +时,猜测也正确. 综上所述,存在=,使得()()1211n n S S S f n S -+++=-对于大于1的正整数都成立.5.用数学归纳法证明: ()3171nn +⋅-(*n N ∈)能被9整除. 【答案】详见解析.【解析】试题分析:利用数学归纳法的步骤首先验证n=1时成立,然后假设n k = 命题成立,验证1n k =+ 等式成立即可. 试题解析:(1)当1n =时, ()317127+⨯-=能被9整除,所以命题成立由归纳假设()3171kk +⋅-(n N +∈)能被9整除及()18277kk +⋅是9的倍数所以()()317118277k kk k ⎡⎤+⋅-++⋅⎣⎦能被9整除 即1n k =+时,命题成立由(1)(2)知命题对任意的n N +∈均成立点睛:数学归纳法是一种重要的数学思想方法,主要用于解决与正整数有关的数学问题.证明时步骤(1)和(2)缺一不可,步骤(1)是步骤(2)的基础,步骤(2)是递推的依据.在用数学归纳法证明时,第(1)步验算n =n 0的n 0不一定为1,而是根据题目要求选择合适的起始值,.第(2)步,证明n =k +1时命题也成立的过程,一定要用到归纳假设,否则就不是数学归纳法.6.甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束.除第五局甲队获胜的概率是12外,其余每局比赛甲队获胜的概率都是23.假设各局比赛结果相互独立. (1)分别求甲队以3:0,3:1,3:2获胜的概率;(2)若比赛结果为3:0或3:1,则胜利方得3分、对方得0分;若比赛结果为3:2,则胜利方得2分、对方得1分.求甲队得分X 的分布列及数学期望. 【答案】(1)827, 827, 427;(2)详见解析;【解析】试题分析:(1)甲队获胜有三种情形:3:0,3:1,3:2,其每种情形的最后一局肯定是甲队获胜,粉笔求出相应的概率,即可得到结果;(2)X的取值可能为0,1,2,3,然后利用相互独立事件的概率乘法公式求解相应的概率,列出分布列,最后根据期望的公式即可求解数学期望.试题解析:(1)记“甲队以3∶0胜利”为事件A1,“甲队以3∶1胜利”为事件A2,“甲队以3∶2胜利”为事件A3,所以甲队以3∶0胜利、以3∶1胜利的概率都为827,以3∶2胜利的概率为427.(2)设“乙队以3∶2胜利”为事件A4,由题意知,各局比赛结果相互独立,所以P(A4)=22242214 C1133227⎛⎫⎛⎫⎛⎫-⨯-=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.由题意知,随机变量X的所有可能的取值为0,1,2,3,根据事件的互斥性得P(X=0)=P(A1+A2)=P(A1)+P(A2)=16 27.又P(X=1)=P(A3)=4 27,P(X=2)=P(A4)=4 27,P(X=3)=1-P(X=0)-P(X=1)-P(X=2)=3 27,故X的分布列为所以E(X)=0×1627+1×427+2×427+3×327=79. 考点:相互独立事件的概率;离散型随机变量的分布列.【方法点晴】本题主要考查了相互独立事件的概率的乘法公式,以及离散型随机变量的分布列、数学期望的求解,其中正确理解赛制的最后一局的比赛情况是解答此类问题的关键,着重考查了分析问题和解答问题的的能力、分类讨论的思想数学思想方法的应用,应该认真试题、仔细解答,试题比较基础,属于基础题. 7.袋中有4个红球,3个黑球,从袋中随机地抽取4个球,设取到一个红球得2分,取到一个黑球得1分. (1)求得分不大于的概率; (2)求得分的数学期望.【答案】(1(2【解析】试题分析:(1)取到一个红球得(2.试题解析:(1),,(2)得分的所有可能值为:5,6,7,8,,,,得分的分布列为8.从参加数学竞赛的学生中抽出20名学生,将其成绩(均为整数)整理后画出的频率分布直方图如图所示.观察图形,回答下列问题:(1(2)估计该次数学竞赛的及格率(60分及以上为及格);(3)若从第一组和第三组的所有学生中随机抽取两人,求他们的成绩相差不超过10分的概率.【答案】(1(2(3(2(3人,第三组有学生从5人中随机抽取2人共有10种情况,记抽取的2人成绩相差不超过10分为事件A,共包含4即抽取的2人成绩相差不超过109.在某次问卷调查中,有a,b两题为选做题,规定每位被调查者必须且只需在其中选做一题,其中包括甲乙在内的4名调查者选做a b(1)求甲、乙两位被调查者选做同一道题的概率;(2)设这4名受访者中选做b.【答案】(12)见解析(20,1,2,3,4所以变量的分布表为:点睛:判断一个随机变量是否服从二项分布,要看两点:一是是否为n次独立重复试验.在每次试验中事件A发生的概率是否均为p.二是随机变量是否为在这n次独立重复试验中某事件发生的次数.且P(X=k)p k(1-p)n-k表示在独立重复试验中,事件A恰好发生k次的概率.10(1(2的二项式系数和大992,若(3【答案】(1)T4==,(2)242(3)见解析【解析】试题分析:(1)由杨辉三角的性质可得展开式中二项式系数最大的项为T4(2)有题意可得m=2;(3)利用题意结合二项式展开式的性质即可证得题中的结论.则由,又,且,所以,则;(3)(1+m)n=m n(1+)n=(m+)n,则1+m=m+,所以m=,(1+)2 017=(1+)2 0171++()2()+2+2+1=6,(1+)-2 017<1,11.为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:估计该地区老年人中,需要志愿者提供帮助的老年人的比例;请根据上面的数据分析该地区的老年人需要志愿者提供帮助与性别有关吗?0.10【答案】(12)有关【解析】试题分析:(1)(2)99%的把握认为该地区的老年人是否需要帮助与性别有关.试题解析:点睛:独立性检验得出的结论是带有概率性质的,只能说结论成立的概率有多大,而不能完全肯定一个结论,因此才出现了临界值表,在分析问题时一定要注意这点,不可对某个问题下确定性结论,否则就可能对统计计算的结果作出错误的解释.12M,二项式系数之和为N,若M-N=240.(1(2)求展开式中所有.【答案】(1)4(2【解析】试题分析:(1)利用题意得到关于实数n;(2)试题解析:解:(1)令二项系数之和为所以得(2)所以当r=0时当r=2时当r=4时所以展开式有理项为,,13.在6⎛⎝6的展开式中,求:(1)第3项的二项式系数及系数;(2)含x2的项.【答案】(1)第3项的系数为2426C=240.(2)含x2的项为第2项,且T2=-192x2.所以第3项的系数为24C=240.(2)T k+1=C(2)6-k k=(-1)k26-k C x3-k,令3-k=2,得k=1.所以含x2的项为第2项,且T2=-192x2.14.喜羊羊家族的四位成员与灰太狼、红太狼进行谈判,通过谈判他们握手言和,准备一起照合影像(排成一排). (1)要求喜羊羊家族的四位成员必须相邻,有多少种排法? (2)要求灰太狼、红太狼不相邻,有多少种排法?(3)记灰太狼和红太狼之间的喜羊羊家族的成员个数为ξ,求ξ的概率分布. 【答案】(1)144(2)见解析试题解析:(1)把喜羊羊家族的四位成员看成一个元素,排法为A .又因为四位成员交换顺序产生不同排列,所以共有A ·A =144种排法.(2)第一步,将喜羊羊家族的四位成员排好,有A 种排法;第二步,让灰太狼、红太狼插入四人形成的空(包括两端),有A 种排法,共有A ·A =480种排法.(3)ξ的概率分布表如下:15.如图,四边形ABCD 的两条对角线,AC BD 相交于O ,现用五种颜色(其中一种为红色)对图中四个三角形,,ABO BCO CDO ADO ,进行染色,且每个三角形用一种颜色图染.(1)若必须使用红色,求四个三角形,,ABO BCO CDO ADO ,中有且只有一组相邻三角形同色的染色方法的种数;(2)若不使用红色,求四个三角形,,ABO BCO CDO ADO ,中所有相邻三角形都不同色的染色方法的种数.【答案】(1)144(2)84种②若,ABO BCO ∆∆同时染的不是红色,则它们的染色有4种,另外两个三角形一个必须染红色,所以这两个三角形共有326⨯=,因此这种情况共有4624⨯=种染色方法.综上可知有且只有一组相邻三角形同色的染色方法的种数为()41224144⨯+=种; (2)因为不用红色,则只有四种颜色.若一共使用了四种颜色,则共有4424A =种染色方法;若只使用了三种颜色,则必有一种颜色使用了两次,且染在对顶的区域,所以一共有312432248C C A ⨯⨯⨯=种染色方法;若只使用了两种颜色,则两种颜色都使用了两次,且各自染在一组对顶区域,所以共有24212C ⨯=种染色方法.综上可知所有相邻三角形都不同色的染色方法的种数为84种.【方法点睛】本题主要考查分类计数原理与分步计数原理及排列组合的应用,属于难题.有关排列组合的综合问题,往往是两个原理及排列组合问题交叉应用才能解决问题,解答这类问题理解题意很关键,一定多读题才能挖掘出隐含条件.解题过程中要首先分清“是分类还是分步”、“是排列还是组合”,在应用分类计数加法原理讨论时,既不能重复交叉讨论又不能遗漏,这样才能提高准确率.16.某房屋开发公司根据市场调查,计划在2017年开发的楼盘中设计“特大套”、“大套”、“经济适用房”三类商品房,每类房型中均有舒适和标准两种型号.某年产量如下表:若按分层抽样的方法在这一年生产的套房中抽取50套进行检测,则必须抽取“特大套”套房10套, “大套”15套.(1)求,的值;(2)在年终促销活动中,奖给了某优秀销售公司2套舒适型和3套标准型“经济适用型”套房,该销售公司又从中随机抽取了2套作为奖品回馈消费者.求至少有一套是舒适型套房的概率;(3)今从“大套”类套房中抽取6套,进行各项指标综合评价,并打分如下:现从上面6个分值中随机的一个一个地不放回抽取,规定抽到数9.6或9.7,抽取工作即停止.记在抽取到数9.6或9.7所进行抽取的次数为,求的分布列及数学期望.【答案】(123【解析】【试题分析】(1)借助频率分布中数据与频率计算公式求解;(2)运用古典概型的计算公式计算;(3)先运用古典概型的计算公式求出概率,再写出随机变量的概率分布:(1)由题设有(2)1,2,3,4,5所以的分布列为:17.已知函数()()()()()21,ln xf x x e kxk R g x a x a R =--∈=∈.(1)当1a =时,求()y xg x =的单调区间;(2)若对[]1,x e ∀∈,都有()()22g x x a x≥-++成立,求a 的取值范围;(3时,求()f x 在[]0,k 上的最大值. 【答案】(12)a 1≤- (3) ()()3max 1k f x k e k ⎡⎤=--⎣⎦【解析】试题分析:(1)将a=1代入求出函数的表达式,通过求导令导函数大于0,从而求出函数的单调递增区间;(21≤x ≤e 恒成立.记h (x )h (x )的单调性,从而求出a 的范围;(3)先求出函数的导数,通过讨论当0<x <ln2k 时,当ln2k<x <k 时的情况,从而得到函数f (x )的最大值. 试题解析:⑴1a =时, ln yx x =, ln 1y x '=+,令0y '>,得ln 1x >- 所以函数ln y x x =的单调增区间为⑵由题意 ()2ln 2a x x a x ≥-++对1x e ≤≤恒成立,因为1x e ≤≤时, ln 0x x ->, 1x e ≤≤对1x e ≤≤恒成立,当且仅当1x =时()0h x '=,所以()h x 在[]1,e 上是增函数,所以()()min11h x h ⎡⎤==-⎣⎦,因此1a ≤-.所以()()(){}(){}3max max 0,max 1,1k f x f f k k e k ⎡⎤==---⎣⎦,记()()311x p x x e x =--+, 01x ≤≤,以下证明当01x ≤≤时, ()0p x ≥.()()233x x p x xe x x e x '=-=-,记()3x r x e x =-, ()30x r x e ='-<对01x <<恒成立,所以()r x 在[]0,1上单调减函数, ()010r =>, ()120r =-<,所以()00,1x ∃∈,使0030x e x -=, 当00x x <<时, ()0p x '>, ()p x 在()00,x 上是单调增函数;当01x x <<时, ()0p x '<, ()p x 在()0,1x 上是单调减函数.又()()010p p ==,所以()0p x ≥对01x <≤恒成立,即()311x x e x --≥-对01x <≤恒成立,所以()()3max1k f x k e k ⎡⎤=--⎣⎦. 点睛:导数问题经常会遇见恒成立的问题:(1)根据参变分离,转化为不含参数的函数的最值问题;(2)若()0f x >就可讨论参数不同取值下的函数的单调性和极值以及最值,最终转化为()min 0f x >,若()0f x <恒成立,转化为()max 0f x <;(3)若()()f x g x >恒成立,可转化为()()min max f x g x >.18,其中k R ∈. (1)当3k =时,求函数()f x 在[]0,5上的值域;(2)若函数()f x 在[]1,2上的最小值为3,求实数k 的取值范围. 【答案】(1) []1,21 ;(2) 2k ≥ . 【解析】试题分析:(1)由导函数讨论函数的单调性,然后可得函数的值域为[]1,21;(2)由题意得到关于实数k 的不等式组,求解不等式组可得实数k 的取值范围是2k ≥ . 试题解析:(1)3k = 时, ()32691f x x x x =-++则()()()23129313f x x x x x =-+=--'令()0f x '=得121,3x x ==列表由上表知函数()f x 的值域为[]1,21 (2)方法一: ()()()()2331331f x x k x k x x k =-++=--'①当1k ≤时, []()1,2,'0x f x ∀∈≥,函数()f x 在区间[]1,2单调递增②当2k ≥时, []()1,2,'0x f x ∀∈≤,函数()f x 在区间[]1,2单调递减 所以()()()min 28613213f x f k k ==-++⋅+= 符合题意即()()2120k k +-= 所以1k =-或2k =(舍) 注:也可令()3234g k k k =-+则()()23632g k k k k k =='--对()()1,2,0k g k ∀∈'≤()3234g k k k =-+在()1,2k ∈单调递减所以()02g k <<不符合题意综上所述:实数k 取值范围为2k ≥ 方法二: ()()()()2331331f x x k x k x x k =-++=--'①当2k ≥时, []()1,2,'0x f x ∀∈≤,函数()f x 在区间[]1,2单调递减 所以()()()min 28613213f x f k k ==-++⋅+= 符合题意②当1k ≤时, []()1,2,'0x f x ∀∈≥,函数()f x 在区间[]1,2单调递增 所以()()min 23f x f <= 不符合题意 ③当12k <<时,当[)1,x k ∈时, ()'0f x < ()f x 区间在[)1,k 单调递减 当(],2x k ∈时, ()'0f x > ()f x 区间在(],2k 单调递增所以()()()min 23f x f k f =<= 不符合题意 综上所述:实数k 取值范围为2k ≥ 19.已知函数()2ln f x x ax ax =+- ,其中a R ∈ .(1)当1a = 时,求函数()f x 在1x = 处的切线方程;(2)若函数()f x 在定义域上有且仅有一个极值点,求实数a 的取值范围. 【答案】(1) 1y x =- ;(2) 0a < .(2)()2ln f x x ax ax =+-, 0x >,则令()221t x ax ax =-+,①若0a =,则()22110t x a x a x =-+=>,故()'0f x >,函数()f x 在()0+∞,上单调递增,所以函数()f x 在()0+∞,上无极值点,故0a =不符题意,舍去;②若0a <, ,该二次函数开口向下,对称轴,所以()0t x =在()0+∞,上有且仅有一根,故()0'0f x =,且当00x x <<时, ()0t x >, ()'0f x >,函数()f x 在()00x ,上单调递增; 当0x x >时, ()0t x <, ()'0f x <,函数()f x 在()0x +∞,上单调递减; 所以0a <时,函数()f x 在定义域上有且仅有一个极值点③若0a >, ,即08a <≤,,故()'0f x ≥,函数()f x 在()0+∞,上单调递增,所以函数()f x 在()0+∞,上无极值点,故08a <≤不符题意,舍去;所以函数()f x 在()0+∞,上有两个不同的极值点,故8a >不符题意,舍去, 综上所述,实数a 的取值范围是0a <.点睛:导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,所以在历届高考中,对导数的应用的考查都非常突出 ,本专题在高考中的命题方向及命题角度 从高考来看,对导数的应用的考查主要从以下几个角度进行: (1)考查导数的几何意义,往往与解析几何、微积分相联系. (2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数. (3)利用导数求函数的最值(极值),解决生活中的优化问题. (4)考查数形结合思想的应用.20(1)求曲线()y f x =在点 (2)若函数()f x 在R 上单调递增,求实数a 的取值范围.【答案】(1)5330x y a π-+-=;(2试题解析:(1即5330x y a π-+-=;(2)因为函数()f x 在R 上单调递增,所以()0f x '≥在R 上恒成立,在R 上恒成立, 令[]cos ,1,1x t t =∈-,即24350t at --≤ 对任意的[]1,1t ∈-恒成立, 令()2435g t t at =--,则需()()1310{ 1310g a g a -=-≤=--≤,【方法点晴】本题主要考查利用导数求曲线切线以及利用导数研究函数的单调性,属于难题.求曲线切线方程的一般步骤是:(1)求出()y f x =在0x x =处的导数,即()y f x =在点P ()()00,x f x 出的切线斜率(当曲线()y f x =在P 处的切线与y 轴平行时,在 处导数不存在,切线方程为0x x =);(2)由点斜式求得切线方程()()00•y y f x x x '-=-.。
2018.07.15 2018教育综合知识经典易错题解析(7月) 谢梦 (笔记)

2018教育综合知识经典易错题解析(7月)(讲义)课前的话1.题目来源及难度问题2.NO刷屏,保证课堂的完整性3.课程2小时,每1小时休息两首歌的时间目录01 单项选择题02 多项选择题03 判断题01 单项选择题1.影响人的身心发展的因素是多种多样的,促进个体发展从潜在的可能状态转向现实状态的决定性因素是()。
A.遗传素质B.环境C.个体主观能动性D.教育2.幼儿时期孩子从学会爬到学会走,童年时期孩子从学习拼音到学会识字,少年时期孩子从直观思维转向到抽象思维,这些都体现了个体身心发展具有()。
A.不平衡性B.阶段性C.个别差异性D.顺序性顺序性VS阶段性(1)儿童心理发展先具体后抽象属于儿童身心发展的()。
B.顺序性C.不平衡性D.差异性(2)小学教学通常采用直观形象的方式,中学以后则进行抽象的讲解,这体现了儿童身心发展的( )。
A.顺序性B.阶段性C.不平衡性D.个别差异性(3)在幼儿园的门口经常会挂有“杜绝幼儿园教育小学化”的横幅,这体现了人身心发展的()。
A.顺序性B.阶段性C.互补性D.不平衡性阶段性VS不平衡性(4)儿童身心发展有两个高速发展期:新生儿与青春期,这是身心发展()规律的反映。
A.阶段性B.顺序性C.不平衡性D.差异性(5)我国历史上著名的大思想家王阳明5岁还不能开口说话,却能默背祖父的众多藏书。
这说明人的发展具有()。
B.不平衡性C.顺序性D.整体性差异性VS其他规律(6)“聪明早慧”与“大器晚成”,体现了个体身心发展的( )规律。
A.顺序性B.不平衡性C.互补性D.个别差异性(7)四年级一班的班主任张老师在班主任教育教学工作过程中,对班级的学生从不采取“一刀切”的办法,因为他深刻认识到个体的身心发展具有()。
A.阶段性B.不平衡性C.差异性D.顺序性3.对“男子私刻公章救病妻”的讨论中,栗子认为这位男子犯错就应受到法律的制裁,不然其他人也这么做社会就乱套了,这说明栗子的道德认识处于()。
2017-2018年第二学期六年级数学试卷分析

2017-2018年第二学期六年级数学试卷分析时光如白驹过隙,转瞬之间,期末考试结束了。
为更好地总结本学期工作中的成败得失,提高今后的教学质量,现对本次考试的数学试卷做如下分析:一、试题分析(一)从试卷结构看,本试卷试题总分120分,共六道大题,所占分值分别为填空题(34分)、选择题(14分)、判断题(16分)、计算题(30分)、操作题(6分)、解决问题(30分)。
试卷结构较为科学、合理。
(二)从试卷内容看,试题科学、严谨,体现了以《数学课程标准》为指导,知识与技能并重的新课程理念,较好地发挥了对教学的指导作用。
二、学生答题情况分析从总体来看,这次考试学生发挥正常,但仍存在许多不足之处。
下面就学生答卷中出现的问题逐一分析:(一)填空本题涵盖了单位换算、圆的周长和面积、圆柱(圆锥)的体积、比例尺、按比例分配、正(反)比例等多方面内容,主要考查学生对基础知识的掌握情况。
典型错题及成因分析:(16)已知a的和b的相等(a、b均不为0),那么a:b=(),a和b成()比例。
错误原因:在求a:b=()时,没有将最终结果化成最简整数比。
(17)找规律:1,3,2,6,4,(),(),12,16……错误原因:学生因没能发现其中规律而无从下笔。
其实,在平时练习中出现过类似题目,可见学生并没有真正掌握,今后教学中一定要注意加强针对性练习。
(二)选择本题共7道小题,其中1~3小题答题情况较理想。
4~7小题欠佳,得分率仅为70%。
典型错题及成因分析:(6)一个圆柱和一个圆锥体积的比是3:2,它们高的比是2:3,那么圆锥的底面积是圆柱的()。
A、3/2B、3/4C、4/3错误原因:其一,学生没有深入理解题意,综合分析、灵活运用能力较差;其二,缺乏答题技巧。
如:可采用“排除法”,先将选项A代入题目,根据“圆锥的底面积是圆柱的,圆柱和圆锥高的比是2:3”这些条件再计算,看看圆柱和圆锥的体积比是不是3:2,如果是,证明选项A是正确答案,如果不是则排除该选项。
半期考后错题整理建议

福建省厦门第一中学2017—2018学年第二学期半期考高二地理试卷湖泊与湖岸之间存在着局部环流,下图为我国某大湖(东西宽约90km)和周边湖岸某时刻实测风速(m/s)垂直剖面图,完成6-7题。
6. 影响湖泊东西岸风向差异的主要因素为A.海陆位置B.大气环流C.季风环流D.热力环流7. 在夏季,此时最可能为地方时A.0点B.5点C.15点D.20点赤道辐合带(ITCZ)是两半球信风气流形成的辐合地带的总称。
下图示意非洲某月ITCZ的分布状况,读图完成8-10题。
8. 该月为A. 1月B. 4月C. 7月D. 10月9. 该月,下列四地中月平均风速最小的是A. ①B. ②C. ③D. ④10. 该月,下列城市中月降水量最多的是A. 阿尔及尔B. 喀土穆C. 金沙萨D. 开普敦31.(14分)阅读图文材料,完成下列要求。
茉莉喜高温,抗寒性差,25℃以上才能孕育花蕾,32~37℃是花蕾成熟开放的最适温度。
喜光,根系发达。
生长旺季要求水分充足,但土壤过湿不利于其根系发育。
开花季节,于天黑之前采成熟花蕾,花蕾开放吐香时间从20时左右至次日10时左右,是将茶叶染上花香、制作茉莉花茶的最佳时间。
下图示意横县在广西的位置和范围。
(1)与江苏、浙江相比,说明横县有利于茉莉生长的气候条件。
(6分)(2)横县地形以河流冲积平原为主,茉莉主要种植在平原地势较高的旱地上。
试解释冲积平原地势较高的旱地有利于茉莉种植的原因。
(8分)31.(12分)第(1)题,农业发展的气候条件主要包括气温、热量、降水等,结合材料提示,与江苏、浙江相比,横县纬度低,气温高,热量充足,降水量大。
第(2)题,根据材料“生长旺季要求水分充足,但土壤过湿不利于其根系发育”可推断冲积平原地形平坦易于耕种,同时土壤肥沃,但地势较低处易积水,导致土壤水分过湿,故平原地势较高的旱地有利于茉莉花的生长。
第(3)题,问题①,根据材料提示,横县茉莉花茶产业的发展经验主要是突出因地制宜,发挥当地农业优势,推进农产品加工业,延长产业链,增加附加值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018 三(下)错题汇总(1)
1. 口算。
23×4= 54-9= 20×39= 20×41=
81+89+95=
2.买11个皮球一共要用多少元?买11个皮球的钱够买5个足球吗?
皮球
18元42元
够不够
3.用竖式计算。
85×79=
4.小红家养了38张蚕,每张蚕大约能产茧52千克。
小红家的蚕大约一共能产茧多少千克?
1500千克2000 千克2400千克
5.甲、乙两地之间的铁路长1600千米。
一列火车从甲地开往乙地,平均每小时行驶180千米,8小时后距离乙地还有多少千米?
6.根据所求问题选择需要的条件。
(1)小丽比小华多用了多少元?
小丽买3小华买1支钢笔和3本笔记本
营业员找给小丽14元小华买1支钢笔用去28元
(2
买1个足球和4个皮球4个皮球76元
1个足球78元一共付出200元,找回36元
7.修一条长4千米的路,已经修了8天,平均每天修300米。
是剩下的长,还是已经修好的长?长多少米?
8.看图填写数量关系。
黄花
红花
()+ ()=红花和黄花一共的朵数
红花
蓝花
()+ ()= 红花和蓝花一共的朵数
紫花
红花
()-()= 紫花比红花少的朵数
9.计算下面各题。
11×5+120 185-23×4 90×3-135 900-4×136
10.把下面的两道算式合并成综合算式。
(1)14+6=20
15×20=300
11.小丽看一本童话书,第一天看到第16页,第二天看到第54页。
小丽第二天比第一天多看了多少页?
12.为了锻炼自己的记忆力,小华打算每天记2个英语单词。
(1)今年1月小华一共能记多少个英语单词?今年2月呢?
(2)照这样坚持下去,今年上半年小华一共能记多少个英语单词?今年全年呢?
13. 想一想,填一填。
(1) 去年的上半年有( )天,下半年有( )天;去年的上半年与下半年相差 ( )天。
(2) 求15颗玻璃球的1/5是多少颗,就要把( )颗玻璃球平均分成5分,求出这样的1份。
(3) 求25颗玻璃球的1/5是多少颗,就要把( )颗玻璃球平均分成5份,求出这样的一份。
(4) 求16颗水果糖的3/4 是多少课,就要把( )颗水果糖平均分成4份,求出这样的 3份。
(5) 求24颗水果糖的3/4是多少颗,就要把( )颗水果糖平均分成4份,求出这样的3份。
(6) 把15个苹果平均分成3个小朋友,每个小朋友分得( )个,每个小朋友分得这些苹果的( )/( )。
(7) 写出三个大于0.4而小于1的小数:( )、( )、( )。
写出三个接近3的小数:( )、( )、( )。
(8)7.4+1.7的和处于整数( )与整数( )之间。
14. 选择正确答案的序号填在括号里。
(1)一个旅游团打算用1个半小时参观一个景点。
如果到达景点的时间是11;00,那么大约( )能够离开景点。
A. 1时
B. 13时
C. 11时30分
(2)下面的图形中,( )图中的涂色部分表示0.3。
A
B
C
(3)小英的身高是1.3米,小军比小英高1分米,小军的身高是(
)。
A. 1.4米
B. 2.3米
C. 2.4 米
(4)一块正方形桌布的面积是2( )。
A 平方厘米
B 平方分米
C 平方米
15. 星期天早上,小军打算做以下几件家务;用煤气灶烧开水,整理房间,擦地。
完成每件家务需要的时间如下表;
小军至少需要( )分钟才能做完这些家务。
16. 下面的说法是否正确?正确的画“√”,错误的画“×”
(1)用同样大的方砖铺地,甲房间铺了350块,乙房间铺了450块,甲房间的面积一定小于乙房间的面积。
( )
(2)把两个完全一样的正方形拼成一个长方形,长方形的面积一定是每个正方形的2倍。
( )
17. 选择合适的单位填在括号里。
(1)一支铅笔的长度大约是20 ( )。
(2)一幢楼房高9( ),长60( ),宽20( ),占地面积是1200( )。
(3)一个运动场长80( ), 宽40( ), 占地面积是3200 ( ), 绕操场跑一圈大约是240( )。
(4)北京到广州的铁路长2313( );途中有条隧道,全长1800( )。
(5)一个信封的面积大约是2( ), 一枚邮票的面积大约是6 ( )。
18. 下面每个小方格都表示1平方厘米,分别写出涂色部分与空白部分的面积。
① ②
图1 的涂色部分是( )平方厘米,空白部分是( )平方厘米。
图2的涂色部分是( )平方厘米,空白部分是( )平方厘米。
19. 如图,小宁用若干张同样大的画片铺满一块玻璃。
如果每张画片的面积是40平方厘米,那么这块玻璃的面积是多少平方厘米?
20. 小红用1平方分米的正方形纸片测量课桌面的大小,结果如下图。
估计课桌面的面积是多少平方分米?
21. 用36个边长1厘米的正方形拼成一个大正方形,大正方形的面积是多少平方厘米?
22. 一间教室的地面是长方形,长9米,宽6米。
如果用边长5分米的方砖铺地,每行需要铺多少块?要铺几行?一共要铺多少块?
23. 下图中每个小方格表示1平方厘米。
先数一数,算一算,再填表。
24. 一辆汽车从甲地开往乙地,平均每小时行驶95千米,2小时后距离乙地还有128千米。
甲、乙两地之间的公路长多少千米?
25. 看图列式计算。
(1) 苹果 (2)黄彩带
香蕉 红彩带
(2)如果用的时间不多于9.1秒算优秀,多于11.2秒算不及格,这个班男生50米跑成绩优秀的有多少人?不及格的呢?
27. 在>”,“<”或“=” 。
9平方厘米 5千米米
36××25 35+35÷÷5。
