2014北京石景山区数学二模试卷
2014石景山区中考数学二模

2014石景山区中考数学二模一、选择题(本题共32分,每小题4分)在每个小题给出的四个备选答案中,只有一个是正确的,请将所选答案前的字母填在题后括号内.1.(4分)的倒数是()A.5 B.C. D.2.(4分)某省去年底森林面积为2801700公顷,将2801700用科学记数法表示应为()A.28017×102B.2.8017×106C.28.017×105D.0.28017×1073.(4分)四张质地、大小、背面完全相同的卡片上,正面分别画有圆、矩形、等腰三角形、平行四边形四个图案.现把它们的正面向下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案是中心对称图形的概率为()A.B.C.D.14.(4分)关于x的一元二次方程x2+(m﹣2)x+m+1=0有两个相等的实数根,则m的值是()A.0 B.8 C.4±2D.0或85.(4分)如图,已知△ABC中,∠B=50°,若沿图中虚线剪去∠B,则∠1+∠2等于()A.130°B.230°C.270°D.310°6.(4分)如图是石景山当代商场地下广场到地面广场的手扶电梯示意图.其中AB、CD分别表示地下广场、地面广场电梯口处的水平线,已知∠ABC=135°,BC的长约是m,则乘电梯从点B到点C上升的高度h是()m.A.6 B. C. D.7.(4分)下面一组数据是10名学生测试跳绳项目的成绩(单位:个/分钟).176 180 184 180 170 176 172 164 186 180该组数据的众数、中位数、平均数分别为()A.180,180,178 B.180,178,178C.180,178,176.8 D.178,180,176.88.(4分)在平面直角坐标系xOy中,矩形ABCD的位置如图1所示,点A的坐标为(﹣2,0),点B的坐标为(0,2),点D的坐标为(﹣3,1).矩形ABCD以每秒1个单位长度的速度沿x轴正方向运动,设运动时间为x(0≤x≤3)秒,第一象限内的图形面积为y,则下列图象中表示y与x的函数关系的图象大致是()A.B.C. D.二、填空题(本题共16分,每小题4分)9.(4分)分解因式:ax2﹣4ay2=.10.(4分)已知二次函数y=x2+bx+8的图象的顶点在y轴右侧,则b的一个值可为(只需写出符合条件的一个b的值).11.(4分)已知A(﹣1,m)与B(2,m﹣3)是反比例函数图象上的两个点.则m的值.12.(4分)如图,已知直线l:y=x,过点A1(1,0)作x轴的垂线交直线l于点B1,以A1 B1为边作正方形A1B1C1A2,过点A2作x轴的垂线交直线l于点B2,以A2 B2为边作正方形A2B2C2A3,…;则点A5的坐标为,点C n的坐标为.三、解答题(本题共30分,每小题5分)13.(5分)计算:+2sin60°+()﹣1﹣(﹣3)0.14.(5分)解不等式组.15.(5分)已知:如图,点C是线段AB的中点,CE=CD,∠ACD=∠BCE,求证:AE=BD.16.(5分)已知当x=1时,2ax2+bx的值为﹣2,求当x=2时,ax2+bx的值.17.(5分)已知关于x的方程x2﹣(m+2)x+(2m﹣1)=0.(1)求证:方程恒有两个不相等的实数根;(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.18.(5分)北京某郊区景点门票价格:成人票每张40元,学生票每张是成人票的半价.小明和小华两家人买了12张门票共花了420元,求两家人的学生和成人各有几人?四、解答题(本题共20分,每小题5分)19.(5分)如图1,在△OAB中,∠OAB=90°,∠AOB=30°,BA=2.以OB为边,向外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.(1)求证:四边形ABCE是平行四边形;(2)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.20.(5分)以下是根据北京市国民经济和社会发展统计公报中的相关数据,绘制的北京市年生产总值统计图的一部分.请你根据以上信息解答下列问题:(1)根据北京市2009﹣﹣2013年生产总值年增长率,请计算出2011年北京市年生产总值是(结果精确到1百亿元),并补全条形统计图;(2)若从2013年以后,北京市年生产总值都按15%的年增长率增长,则请你估算,若年生产总值不低于2009年的2倍,至少要到年.(填写年份)(3)在(1)的条件下,2009﹣﹣2013这四年间,比上一年增长的生产总值的平均数为多少百亿元?若按此平均数增长,请你预测2014年北京地区的生产总值多少百亿元?21.(5分)如图,在△ABC中,∠BCA=90°,以BC为直径的⊙O交AB于点P,Q是AC的中点.(1)求证:直线PQ与⊙O相切;(2)连结PO并延长交⊙O于点E、交AC的延长线于点F,连结PC,若OC=,tan∠OPC=,求EF的长.22.(5分)阅读下列材料:小明同学遇到了这样一个问题:如图,M是边长为a的正方形ABCD内一定点,请在图中作出两条直线(要求其中一条直线必须过点M),使它们将正方形ABCD的面积分割成面积相等的四个部分.小明是这样思考的:数学课曾经做过一道类似的题目.如图2,O是边长为a的正方形ABCD的中心,将以点O为顶点的直角绕点O任意旋转,且直角两边与BA,CB相交,与正方形重叠部分(即阴影部分)的面积为一个确定的值.可以类比此问题解决.(1)请你回答图2中重叠部分(即阴影部分)的面积为;参考小明同学的想法,解答问题:(2)请你在图3中,解决原问题(3)如图4.在四边形ABCD中,AB∥CD,AB+CD=BC,点P是AD的中点,如果AB=a,CD=b,且b>a,那么在边BC上存在一点Q,使PQ所在直线将四边形ABCD的面积分成相等的两部分,请你画出该直线,保留作图痕迹.五、解答题(本题共22分,第23题7分,第24题8分,第25题7分)23.(7分)关于x的一元二次方程x2﹣3(m+1)x+3m+2=0.(1)求证:无论m为何值时,方程总有一个根大于0;(2)若函数y=x2﹣3(m+1)x+3m+2与x轴有且只有一个交点,求m的值;(3)在(2)的条件下,将函数y=x2﹣3(m+1)x+3m+2的图象沿直线x=2翻折,得到新的函数图象G.在x,y轴上分别有点P(t,0),Q(0,2t),其中t>0,当线段PQ与函数图象G只有一个公共点时,求t的值.24.(7分)将△ABC绕点A顺时针旋转α得到△ADE,DE的延长线与BC相交于点F,连接AF.(1)如图1,若∠BAC=α=60°,DF=2BF,请直接写出AF与BF的数量关系;(2)如图2,若∠BAC<α=60°,DF=3BF,猜想线段AF与BF的数量关系,并证明你的猜想;(3)如图3,若∠BAC<α,DF=mBF(m为常数),请直接写出的值(用含α、m的式子表示).25.(8分)在平面直角坐标系xOy中,射线l:.点A是第一象限内一定点,,射线OA 与射线l的夹角为30°.射线l上有一动点P从点O出发,以每秒个单位长度的速度沿射线l匀速运动,同时x 轴上有一动点Q从点O出发,以相同的速度沿x轴正方向匀速运动,设运动时间为t秒.(1)用含t的代数式表示PQ的长.(2)若当P、Q运动某一时刻时,点A恰巧在线段PQ上,求出此时的t值.(3)定义M抛物线:顶点为P,且经过Q点的抛物线叫做“M抛物线”.若当P、Q运动t秒时,将△PQA绕其某边中点旋转180°后,三个对应顶点恰好都落在“M抛物线”上,求此时t的值.参考答案与试题解析一、选择题(本题共32分,每小题4分)在每个小题给出的四个备选答案中,只有一个是正确的,请将所选答案前的字母填在题后括号内.1.【解答】的倒数是﹣,故选:D.2.【解答】将2801700用科学记数法表示为:2.8017×106.故选:B.3.【解答】∵四张质地、大小、背面完全相同的卡片上,正面分别画有圆、矩形、等腰三角形、平行四边形四个图案.中心对称图形的是圆、矩形、平行四边形,∴从中任意抽出一张,则抽出的卡片正面图案是中心对称图形的概率为:.故选C.4.【解答】∵一元二次方程x2+(m﹣2)x+m+1=0有两个相等的实数根,∴△=0,即(m﹣2)2﹣4×1×(m+1)=0,整理,得m2﹣8m=0,解得m1=0,m2=8.故选D.5.【解答】∠BDE+∠BED=180°﹣∠B,=180°﹣50°,=130°,∠1+∠2=360°﹣(∠BDE+∠BED)=360°﹣130°=230°.故选:B.6.【解答】过点C作AB的延长线的垂线CE,即乘电梯从点B到点C上升的高度h,∵∠ABC=135°,∴∠CBE=180°﹣∠ABC=45°,∴CE=BC•sin∠CBE=6•sin45°=6•=6(m).∴h=6(m).故选A.7.【解答】∵180出现了3次,出现的次数最多,∴众数是180;把这组数据从小到大排列为:164,170,172,176,176,180,180,180,184,186,最中间两个数的平均数是(176+180)÷2=178,则中位数是178;这组数据的平均数是(176+180+184+180+170+176+172+164+186+180)÷10=176.8;故选C.8.【解答】如图1,∵点A的坐标为(﹣2,0),点B的坐标为(0,2),点D的坐标为(﹣3,1),∴OA=OB=2,△AOB是等腰直角三角形,AD==,∴AB=2.∵四边形ABCD是矩形,∴AD=BC=,AB=CD=2,∠DAB=∠ABC=∠C=∠D=90°.分三种情况:①当0≤x≤1时,矩形ABCD落在第一象限内的图形是三角形PB′Q,如图2∵OA′=2﹣x,△A′OP是等腰直角三角形,∴A′P=OA′=(2﹣x),∴PB′=A′B′﹣A′P=2﹣(2﹣x)=x,∵△PB′Q是等腰直角三角形,∴y=PB′2=×(x)2=x2;②当1<x≤2时,矩形ABCD落在第一象限内的图形是梯形PB′CQ,如图3∵OA′=2﹣x,△A′OP是等腰直角三角形,∴A′P=OA′=(2﹣x),∴PB′=A′B′﹣A′P=2﹣(2﹣x)=x,D′Q=(2﹣x)+=3﹣x,∴C′Q=2﹣(3﹣x)=x﹣,∴y=(C′Q+B′P)•B′C′=(x﹣+x)×=2x﹣1;③当2<x≤3时,矩形ABCD落在第一象限内的图形是五边形PA′B′CQ,如图4.∵OA′=x﹣2,△A′OP是等腰直角三角形,∴A′P=OA′=(x﹣2),∴PD′=A′D′﹣A′P=﹣(x﹣2)=3﹣x,∴S△PD′Q=PD′2=×(3﹣x)2=x2﹣6x+9;∴y=S矩形A′B′C′D′﹣S△PD′Q=2×﹣(x2﹣6x+9)=﹣x2+6x﹣5;纵观各选项,只有D选项图形符合.故选D.二、填空题(本题共16分,每小题4分)9.【解答】ax2﹣4ay2=a(x2﹣4y2)=a(x+2y)(x﹣2y).10.【解答】二次函数y=x2+bx+8的图象的顶点在y轴右侧,∴,b<0,b=﹣1,故答案为:﹣1.11.【解答】∵A(﹣1,m)与B(2,m﹣3)是反比例函数图象上的两个点,∴(﹣1)×m=2×(m﹣3),解得m=2.故答案为:2.12.【解答】直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,可知B1点的坐标为(1,1),以A1 B1为边作正方形A1B1C1A2,A1B1=A1A2=1,OA2=1+1=2,点A2的坐标为(2,0),C1的坐标为(2,1),这种方法可求得B2的坐标为(2,2),故点A3的坐标为(4,0),C2的坐标为(4,2),此类推便可求出点点A5的坐标为(16,0),点C n的坐标为(2n,2n﹣1).故答案为(16,0),(2n,2n﹣1).三、解答题(本题共30分,每小题5分)13.【解答】原式=3+2×+6﹣1=4+5.14.【解答】∵解不等式2x﹣1≥x+1得:x≥2,解不等式x+8≤4x﹣1得:x≥3,∴不等式组的解集为x≥3.15.【解答】证明:∵点C是线段AB的中点,∴AC=BC,∵∠ACD=∠BCE,∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠BCD,在△ACE和△BCD中,∴△ACE≌△BCD(SAS),∴AE=BD.16.【解答】将x=1代入2ax2+bx=﹣2中,得2a+b=﹣2,当x=2时,ax2+bx=4a+2b,=2(2a+b),=2×(﹣2),=﹣4.17.【解答】(1)证明:∵△=(m+2)2﹣4(2m﹣1)=(m﹣2)2+4,∴在实数范围内,m无论取何值,(m﹣2)2+4>0,即△>0,∴关于x的方程x2﹣(m+2)x+(2m﹣1)=0恒有两个不相等的实数根;(2)解:根据题意,得12﹣1×(m+2)+(2m﹣1)=0,解得,m=2,则方程的另一根为:m+2﹣1=2+1=3;①当该直角三角形的两直角边是1、3时,由勾股定理得斜边的长度为:;该直角三角形的周长为1+3+=4+;②当该直角三角形的直角边和斜边分别是1、3时,由勾股定理得该直角三角形的另一直角边为2;则该直角三角形的周长为1+3+2=4+2.18.【解答】设两家人有学生x人,成人y人,据题意得:,解得:.答:两家人的学生有3人,成人有9人.四、解答题(本题共20分,每小题5分)19.【解答】(1)证明:在Rt△OAB中,D为OB的中点,∴DO=DA,∴∠DAO=∠DOA=30°,∠EOA=90°,∴∠AEO=60°又∵△OBC为等边三角形∴∠BCO=∠AEO=60°,∴BC∥AE,∵∠BAO=∠COA=90°,∴OC∥AB,∴四边形ABCE是平行四边形.(2)解:在Rt△ABO中,∵∠OAB=90°,∠AOB=30°,AB=2,∴OA=AB•tan60°=2×=.在Rt△OAG中,OA2+OG2=AG2,设OG=x,由折叠可知:AG=GC=4﹣x,可得,解得,∴OG=.20.【解答】(1)141×15.6%+141≈22+141=163(百亿元).统计图补充如图:(2)年生产总值2009年的2倍是:122×2=244(百亿元),而195(1+15%)=224.25(百亿元),195(1+15%)2=257.8875(百亿元)>244(百亿元),2013+2=2015,即若年生产总值不低于2009年的2倍,至少要到2015年;(3)增长的生产总值的平均数:(195﹣122)÷4=18.25,即2009﹣2013这四年间,比上一年增长的生产总值的平均数为18.25百亿元;195+18.25=213.25,故预测2014年北京地区的生产总值为213.25百亿元.故答案为163百亿元;2015.21.【解答】(1)证明:连结PO、PC,如图,∵BC是⊙O的直径,∴∠BPC=90°,∴∠APC=90°,又∵Q是AC的中点,∴PQ=CQ,∴∠CPQ=∠PCQ,∵OP=OC∴∠OPC=∠OCP,∴∠OPC+∠CPQ=∠OCP+∠PCQ=∠BCA=90°,∴OP⊥PQ,∴直线PQ与⊙O相切;、(2)解:连结CE,如图,∵EP是直径,∴∠ECP=90°,即∠ECO+∠OCP=90°,又∵∠ECO+∠ECF=90°,∴∠ECF=∠OCP=∠OPC,而∠F=∠F∴△FEC∽△FCP,∴==,在Rt△EPC中,tan∠OPC==,∴==,∴CF=2EF,PF=2CF,∴PF=4EF,∴PE=3EF,即3EF=2×,∴EF=.22.【解答】(1)如图2,连接BO,∵O是边长为a的正方形ABCD的中心,∴BO=CO,∠ABO=∠ACB=45°,∵∠CON+∠BON=90°,∠MOB+∠BON=90°,∴∠MOB=∠CON,在△BOM和△CON中,∴△BOM≌△CON(ASA),∴重叠部分的面积为:S△BOC=S正方形ABCD=;故答案为:;(2)如图3所示:(3)如图4所示:当BQ=CD=b时,PQ将四边形ABCD面积二等分.五、解答题(本题共22分,第23题7分,第24题8分,第25题7分)23.【解答】(1)解方程x2﹣3(m+1)x+3m+2=0,得x1=1,x2=3m+2,∵x1=1>0∴无论m为何值时,方程总有一个根大于0;(2)∵若函数y=x2﹣3(m+1)x+3m+2与x轴有且只有一个交点,∴△=9(m+1)2﹣4(3m+2)=0,∴m=﹣,(3)当时,函数y=x2﹣2x+1=(x﹣1)2,依题意,沿直线x=2翻折后的解析式为:y=(x﹣3)2=x2﹣6x+9,可得,y=(x﹣3)2=x2﹣6x+9与x,y轴的交点分别为(3,0),(0,9).设直线PQ的解析式为y=kx+b(k≠0),由P(t,0),Q(0,2t).∴直线PQ的解析式为y=﹣2x+2t,①当线段PQ与函数图象相切时,有:﹣2x+2t=x2﹣6x+9,整理得:x2﹣4x+9﹣2t,△=16﹣4(9﹣2t)=0∴②当线段PQ经过点(0,9)时,2t=9∴当t>时,P(t,0)在(3,0)的右侧,线段PQ只与图象G的右侧有交点,即当t>时,线段PQ与函数图象G只有一个公共点.综上:当或t>时,线段PQ与函数图象G只有一个公共点.24.【解答】解:(1)AF=BF.理由如下:在DF上截取DG=BF,连接AG,(如图1),由旋转得AD=AB,∠D=∠B,在△ADG和△ABF中,,∴△ADG≌△ABF(SAS),∴AG=AF,∠DAG=∠BAF,∴∠GAF=∠GAB+∠BAF=∠GAB+∠DAG=∠DAB=60°.∴△GAF是等边三角形,又∵DF=2BF,∴AF=GF=DF﹣DG=DF﹣BF=BF,即AF=BF;(2)解:猜想:AF=2BF.证明:在DF上截取DG=BF,连接AG(如图2).由旋转得AD=AB,∠D=∠B,在△ADG和△ABF中,,∴△ADG≌△ABF(SAS),∴AG=AF,∠DAG=∠BAF,∴∠GAF=∠GAB+∠BAF=∠GAB+∠DAG=∠DAB=60°,∴△GAF是等边三角形,又∵DF=3BF,∴AF=GF=DF﹣DG=DF﹣BF=2BF,即AF=2BF;(3)在DF上截取DG=BF,连接AG,(如图3),由旋转得AD=AB,∠D=∠B,在△ADG和△ABF中,,∴△ADG≌△ABF(SAS),∴AG=AF,∠DAG=∠BAF,∴∠GAF=∠GAB+∠BAF=∠GAB+∠DAG=∠DAB=α,∴△GAF是等腰三角形,∵DF=mBF,∴GF=DF﹣DG=mBF﹣BF=(m﹣1)BF,过点A作AH⊥DF于H,则FH=GF=(m﹣1)BF,∠FAH=∠GAF=α,∵sin∠FAH=,∴sin=,∴=.25.【解答】(1)∵射线l解析式为,∴∠POQ=60°.∵P,Q运动速度相同,∴OP=OQ=2t,∴△OPQ是等边三角形,∴PQ=2t;(2)由题意:A(6,2),P(,3t),Q(2t,0),过点A作AB⊥x轴于B,如图1,则AB=2,∵在Rt△ABQ中,∠ABQ=90°,∠AQB=60°,∴,∴OQ=OB+BQ=8,∴秒;(3)由抛物线的对称性知:抛物线经过P、Q、O三点P(,3t),Q(2t,0),O(0,0),如图2,不妨设:抛物线M的解析式为y=ax(x﹣2t),将P(,3t)代入可得,得到抛物线的解析式为:y=﹣x2+2x,显然:△PQA绕PQ中点旋转180°后,三个对应顶点在抛物线上,设A的对应点为A′,如图3,得到四边形PAQA′是平行四边形,∵P(,3t),Q(2t,0),A(6,2),∴A′(3t﹣6,3t﹣2),将A′(3t﹣6,3t﹣2),代入抛物线y=﹣x2+2x,解得或,∴当经过秒或秒时,△PQA绕PQ中点旋转180°后,三个对应顶点在“M抛物线”上.。
2014北京石景山中考二模数学(含解析)

点 A5 的坐标为_________,点 Cn 的坐标为_______________. 三、解答题(本题共 30 分,每小题 5 分)
1 13.计算: 27 2sin 60 ( )1 6
12 3 .
0
2 / 15
2 x 1≥x 1 14.解不等式组 . x 8≤4 x 1
1 / 15
C
y 4 3 2 B D'
y 4 C' 3 2 1 2 1 A' 3 x –3 –2 –1 O
图2
B'
D
1 A –3 –2 –1 O
图1
1
y 4
2
3 x
y 4 y 2 1 O 1 2
A.
3 2 1 3 x O 1 2
y 2 1 3 x O 1 2
3 2 1 3 x O 1
D.
2
3 x
B.
备用图
备用图 1
7 / 15
备用图 2
2014 年北京石景山区中考二模数学试卷答案
一、选择题(本题共 8 道小题,每小题 4 分,共 32 分) 题 号 答 案 1 D 2 B 3 C 4 D 5 B 6 A 7 C 8 D
二、填空题(本题共 4 道小题,每小题 4 分,共 16 分) 9. a( x 2 y)( x 2 y) ; 10. b 0 即可,答案不唯一; 11. m 2 ; 12. (16 , 0) ; (2n , 2n1 ) .
y
O
x
6 / 15
24.将 △ABC 绕点 A 顺时针旋转 得到 △ADE , DE 的延长线与 BC 相交于点 F ,连接 AF . (1)如图 1 ,若 BAC 60 , DF 2BF ,请直接写出 AF 与 BF 的数量关系; (2) 如图 2 , 若 BAC 60 ,DF 3BF , 猜想线段 AF 与 BF 的数量关系, 并证明你的猜想; (3)如图 3 ,若 BAC , DF mBF ( m 为常数) ,请直接写出 表示) .
北京市13份中考数学二模试题

适用精选文件资料分享2014 年北京市 13 份中考数学二模试题昌平区 2014 年初三年级第二次一致练习数学试卷2014.6考生须知 1 .本试卷共 6 页,共五道大题, 25 个小题,满分 120 分,考试时间 120 分钟。
2 .在答题卡上仔细填写学校名称、姓名和考试编号。
3 .试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4.在答题卡上,选择题、作图题用2B 铅笔作答,其余试题用黑色字迹署名笔作答。
5 .考试结束,请将答题卡交回。
一、选择题(共8 道小题,每题 4 分,共 32 分)以下各题均有四个选项,此中只有一个是吻合题意的. 1 .的相反数是 A . B . C. D. 2 .植树造林可以净化空气、美化环境 . 据统计一棵 50 年树龄的树,以累计计算,除去花、果实与木材价值,总计创值约196 000 美元.将 196 000 用科学记数法表示应为 A . B . C. D. 3 .若右图是某几何体的三视图,则这个几何体是 A .三菱锥 B .圆柱 C.球 D.圆锥4.六边形的内角和为 A . B . C. D.5.如图,一个可以自由转动的转盘被均分成 6 个扇形地域,并涂上了相应的颜色,转动转盘,随机转盘停止后,指针指向蓝色地域的概率是 A. B. C. D.6.如图,把一块直角三角板的直角极点放在直尺的一边上,假如∠1=35°,那么∠2的度数为 A .35° B.45° C.55° D.65° 7.10名同学分成 A、B 两队进行篮球竞赛,他们的身高(单位: cm)以下表所示:队员 1 队员 2 队员 3 队员 4 队员 5 A队 177 176 175172 175 B 队 170 175 173 174 183 设 A、B 两队队员身高的均匀数分别为,,身高的方差分别为,,则以下关系中完整正确的选项是 A .,B.,C.,D.,8.如图 1,已知点 E、F、G、H是矩形 ABCD各边的中点, AB=6,AD=8.动点 M从点 E 出发,沿 E→F→G→H→E匀速运动,设点 M运动的行程为 x, 点 M到矩形的某一个极点的距离为 y, 假如 y 关于 x 的函数图象如图 2 所示,则矩形的这个极点是图 1 图 2 A.点AB. 点BC. 点CD. 点D二、填空题(共 4 道小题,每题 4 分,共 16 分) 9 .函数 y= 中,自量 x 的取范是.10.如,⊙O的直径 CD⊥弦 AB,∠AOC=50°,∠ CDB的大小.11.如,李大要借助院成一个矩形菜园 ABCD,用笆成的别的三24m, BC的 x m,矩形的面 y m2, y与 x 之的函数表达式. 12 .如,在平面直角坐系中,已知点,△ AOB作旋化,挨次获得三角形①、②、③、④、⋯,第⑦个三角形的直角点的坐是;第个三角形的直角点的坐是.三、解答(共 6 道小,每小 5 分,共 30 分) 13. 算:.14.解不等式: 15. 如, AD⊥BC于点 D,BE⊥AC于点 E,AD与BE订交于点 F,且 BF=AC. 求:.已知,求的. 17 .已知关于的一元二次方程有两个相等的数根,求的及方程的根. 18 .如,已知□ ABCD,E,F 是角 BD上的两点,且 BE=DF.(1)求:四形 AECF是平行四形;(2)当 AE垂直均分 BC且四形AECF菱形,直接写出 AE∶AB的 .四、解答(共4道小,每小 5 分,共 20 分) 19 .如,定:若双曲与直 y=x 订交于 A、B 两点,段 AB的度双曲的径. (1) 求双曲的径; (2) 若双曲的径是,求 k 的.20.在某中学展开的“ 香伴我行” 活中,认识九年300名学生状况,随机了九年 50 名学生的册数.数据以下表所示:册数01234 人数 11316173 (1) 50个本数据的众数是,中位数是;(2)依据本数据,估校九年 300 名学生在本次活中多于 2 册的人数;(3)学校广播站的小者被的 50 名学生中册数最少和最多的人行随即采,利用状或列表,求被采的两人恰好都是册数最多的学生的概率.21.如,已知 BC⊙O的直径, EC 是⊙O的切, C是切点, EP 交⊙O于点A,D,交 CB延于点 P. 接 CD,CA,AB. (1)求:∠ECD=∠EAC;(2)若PB=OB=2,CD=3,求 PA的 .22.如右,把 a=2 的正方形剪成四个全等的直角三角形,在下边的正方形网格(每个小正方形的均 1)中画出用四个直角三角形按要求分拼成的新的多形(要求所有用上,互不重叠,互不留隙) . (1)矩形(非正方形);(2)菱形(非正方形);(3)四形(非平行四形) .五、解答(共 3 道小,第 23 7 分,第 24 7 分,第 25 8 分,共 22 分)23 .已知抛物 . (1)求:无 a 任何非零数,抛物与 x 都有交点;(2)若抛物与 x 交于 A(m,0) 、B(n,0 )两点, m、n、a 均整数,一次函数y=kx+b(k ≠0) 的象点 P(n-l ,n+l )、Q(0,a ),求一次函数的表达式 .24 .【研究】如 1,在△ ABC中, D 是 AB的中点, AE⊥BC于点 E,BF⊥AC于点 F,AE,BF订交于点 M,接 DE,DF. DE,DF的数目关系 . 【拓展】如 2,在△ ABC 中,CB=CA ,点 D是AB的中点,点 M在△ A B C 的内部,且∠MBC =∠MAC . 点 M作 ME⊥BC于点 E,MF⊥AC于点 F,接 DE,DF. 求:DE=DF;【推行】如 3,若将上边【拓展】中的条件“ CB=CA” “ CB≠CA”,其余条件不,研究 DE与 DF之的数目关系,并明你的 .25.如,已知点 A(1,0),B(0,3),C(-3 ,0),点 P(x,y)在段 AB上,CP交 y 于点 D, BD的 t. (1)求 t 关于点 P 的横坐 x 的函数表达式;(2)若 S△BCD:S△AOB=2: 1,求点 P的坐,并判断段 CD与段 AB的数目及地点关系,明原由;(3)在( 2)的条件下,若 M x 上的点,且∠BMD最大,直接写出点 M的坐 . 昌平区 2013―2014 学年初三第二次一数学卷参照答案及分准 2014 .6 一、(共 8 个小,每小4分,共 32分)号12345678答案ACDCBCBA二、填空(共 4 个小,每小 4 分,共 16 分)号9 10 11 12答案,(各2分)三、解答(共 6 道小,每小 5 分,共 30 分) 13 .解:原式= ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分=.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分 14 .解:由①得, . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分由②得, .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分∴原不等式的解集: . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分 15 .明:∵ AD⊥BC于 D,BE⊥AC于 E,∴在和中,∠ C=∠C,∴ ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分在△ 和△中,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分∴△≌△ .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分∴DF=DC. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分 16 .解:原式= ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分=. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分∵,∴ . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分∴原式= . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分 17. 解:∵关于的一元二次方程有两个相等的数根,∴ . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∴ . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分∴方程可化 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分∴ .∴ . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分注:正确求出一个根,扣 1 分. 18. (1)明:接角 AC交角 BD于点 O. ∵四形 ABCD是平行四形,∴OA=OC,OB=OD⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯.2 分∵点 E,F 是角 BD上的两点,且 BE=DF, ∴即OE=OF. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分∴四形 AECF是平行四形. ⋯⋯⋯⋯⋯⋯⋯⋯ 4 分(2)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分四、解答(共4道小,每小 5 分,共20 分) 19. 解:(1) ∵与 y=x 订交于 A、B 两点,∴A(1,1),B( -1,- 1). ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分∴A B= . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分 (2)∵双曲的径是,∴AB= .OA= . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分 , ∴m=5.∴k=25. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分 20. 解:(1)众数 3,中位数2.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分(2)在 50 名学生中,多于 2 本的学生有 20 名,因此, 300×=120. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分答:校八年 300 名学生在本次活中多于 2 册的有 120 名. (3)最少的人 A,最多的人 B1,B2,B3. A B1 B2 B3 A (A,B1)(A,B2)(A,B3) B1 (B1,A)(B1,B2)(B1,B3) B2 (B2,A)(B2,B1)( B2,B3) B3 (B3,A)(B3,B1)(B3,B2)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分被采的两人恰好都是册数最多的学生的状况以下:(B1,B2)、(B1,B3)、(B2,B1)、(B2,B3)、(B3,B1)、(B3,B2),共 6 种,因此,被采的两人恰好都是册数最多的学生的概率P= = .⋯⋯⋯⋯⋯⋯⋯5分 21. (1)明:接 BD. ∵BC⊙O的直径,∴⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∵EC与⊙O相切 , ∴ ∵ ∴ ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分∵∴∠ ECD=∠EAC. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分(2)作 DF⊥BC于点 F. 在 Rt△CDB中,在 Rt△CDF中,∴在 Rt△DFP中,∵ ∴ ∽ ∴ ∴ .∴ ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分 22 .解:如,(1)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分(2)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分(3)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分五、解答(共 3 道小,第 23 7 分,第247 分,第 258,共 22 分) 23 .解:(1)明:∵△ = ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分 = = ∴无 a 任何非零数,抛物与 x 都有交点. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分(2)解:∵抛物与 x 交于 A(m,0) 、 B (n,0 )两点,∴ . 令中 y=0, 有: . 解得:x=2, ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分∵m、 n、a 均整数,∴a=-1,m=0,n=2 或m=2,n=0. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分∵一次函数 y=kx+b(k ≠0) 的象点 P(n-l ,n+l )、Q(0,a ),∴当 a=-1,n=2 , 有 P(1,3) 、Q(0,-1 ),解得:⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分当 a=-1,n=0 , 有P(-1,1) 、Q(0,-1 ),解得:⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分24.【研究】DE=DF. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分【拓展】如 2,接 CD.∵在△ A B C中,C B = C A ,∴∠ CAB=∠CBA. ∵∠ MBC =∠MAC ,∴∠ MAB=∠MBA. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分∴AM=BM.∵点 D 是 AB 的中点,∴点 M在 CD上. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分∴CM均分∠ FCE. ∴∠FCD=∠ECD. ∵ME⊥BC于 E,MF⊥AC于 F,∴MF=ME.又∵CM=CM,∴△ CMF≌△ CME. ∴CF=CE. ∵CD=CD,∴△ CFD≌△ CED. ∴DE=DF. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分【推行】 DE=DF. 如3,作 AM的中点 G,BM的中点 H. ∵点 D 是AB的中点,∴同理可得:∵ME⊥BC于 E,H 是 BM的中点,∴在 Rt△BEM中,∴DG=HE.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分同理可得:∵DG//BM,DH//GM,∴四形DHMG是平行四形.∴∠ DGM=∠DHM. ∵∠ MGF=2∠MAC, ∠MHE=2∠MBC, 又∵∠ MBC=∠MAC ,∴∠ MGF=∠MHE. ∴∠ DGM+∠MGF =∠DHM+∠MHE.∴∠ DGF=∠DHE.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分∴△ DHE≌△ FGD.∴DE=DF.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分25 .解:(1)如,∵点(A1,0),(B0,3),∴直 AB的分析式:∵OB=3,BD=t,∴OD=3-t.P(x,-3x+3),作PE⊥AC于E,OE=x,PE=-3x+3.∵PE//y ,∴△ COD∽△ CEP. ∴ ∴∴ ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分 (2) 如, CD=AB,CD⊥AB.∵S △BCD:S△AOB=2: 1,∴ ∴BD=2. ∴解得: .∴ ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分∵OD=OA=1,OC=OB=3,∠COD=∠BOA=90°,∴△ COD≌△ BOA.∴CD=AB. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分∵△ COD≌△ BOA, ∴∠ OCD=∠ABO. 又∵∠ CDO=∠BDP,∴∠ BPD=∠COD=90°.∴CD⊥AB. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分 (3)M,M . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8 分。
石景山区14年7月初二数学期末考试试题
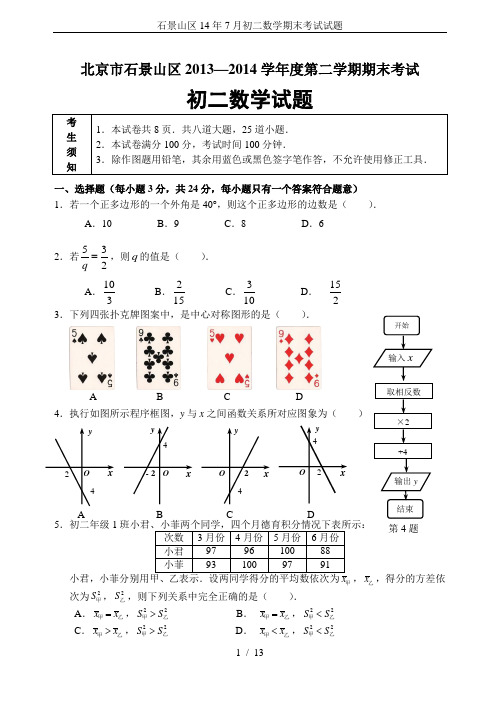
北京市石景山区2013—2014学年度第二学期期末考试初二数学试题一、选择题(每小题3分,共24分,每小题只有一个答案符合题意) 1.若一个正多边形的一个外角是40°,则这个正多边形的边数是( ).A .10B .9C .8D .6 2.若532q =,则q 的值是( ). A .103B .215 C .310D .1523.下列四张扑克牌图案中,是中心对称图形的是( ).A B C D4.执行如图所示程序框图,y 与x 之间函数关系所对应图象为( )5.初二年级1x 甲,x 乙,得分的方差依次为2S 甲,2S 乙,则下列关系中完全正确的是( ).A .x x =乙甲,22S S >乙甲B . x x =乙甲,22S S <乙甲 C .x x >乙甲,22S S >乙甲 D . x x <乙甲,22S S <乙甲A D CB 第4题6.综合实践课上,小超为了测量某棵树的高度,用长为2m 的竹竿作测量工具,移动竹竿,使竹竿顶端、树的顶端的影子恰好落在地面的同一点(如图).此时竹竿与这一点相距6m,与树相距15m ,则树的高度为 ( ) .A . 4mB . 5mC . 7mD . 9m 7.王老师组织摄影比赛,小语上交的作品如下:七寸照片(长7英寸,宽5英寸);将照片贴在一张矩形衬纸的正中央,照片四周外露衬纸的宽度相同;矩形衬纸的面积为照片面积的3倍.设照片四周外露衬纸的宽度为x 英寸(如图),下面所列方程正确是( ) .A .(7)(5)375x x ++⨯=⨯B .(72)(52)375x x ++=⨯⨯C .(72)(52)375x x ++⨯=⨯D .(7)(5)375x x ++=⨯⨯8.如图:已知P 是线段AB 上的动点(P 不与A,B 重合),4AB =,分别以AP ,PB 为边在线段AB 的同侧作等边△AEP 和等边△PFB ,连结EF ,设EF 的中点为G ;连结PG ,当动点P 从点A 运动到点B 时,设 PG=m ,则m 的取值范围是( ).A2m ≤< B .2m << C .4m ≤< D32m ≤< 二、填空题(本题共21分,每空3分) 9.方程22x x =的解为_________________.10.函数y =x 的取值范围是___________.11.在菱形ABCD 中, AC =6,BD =8,则菱形ABCD的周长为__________,面积为________.12. 如图,在△ABC 中,∠ACB=58°,D ,E 分别是AB , AC 中点.点F 在线段DE 上,且AF ⊥CF ,则∠F AE = °.13.在平面直角坐标系xOy 中,O 是坐标原点,将直线y x =绕原点O 逆时针旋转15°,再向上平移3个单位得到直线l ,则直线l 的解析式为_______________________. 14.给出定义:若直线与一个图形有且只有两个公共点,则直线与该图形位置关系是相交.坐标系xOy 中, 以()1,1A --, B (3,0), ()1,1C , D (0,3)为顶点,顺次连结AB 、BC 、CD 、DA 构成图形M .若直线y x b =-+与M 相交,则b 的取值范围是____________.第6题 第7题 第8题第12题15.用配方法...解方程:23630x x --= 解:16.已知:关于x 的一元二次方程2230x x m --+=有实数根.(1)求m 的取值范围;(2)若m 为符合条件的最小整数,求此时方程的根. 解:(1)(2)17.如图,直线x y l 2:1=与直线3:2+=kx y l 在同一平面直角坐标系内交于点P . (1)直接..写出..不等式2x > kx +3的解集 (2)设直线2l 与x 轴交于点A ,求△OAP 的面积. 解:(1)______________________ (2)18.我们把依次连接任意一个四边形各边中点得到的四边形叫做中点四边形.如图,在四边形ABCD 中,E ,F ,G ,H 分别是AB ,BC ,CD ,DA 的中点,依次连接各边中点得到中点四边形EFGH . (1)这个中点四边形EFGH 的形状是_________________(2)请证明你的结论.证明:19.如图,在矩形ABCD 中,AB =5,BC =4,将矩形ABCD 翻折,使得点B 落在CD 边上的点E 处,折痕AF 交BC 于点F ,求FC 的长.解:20.如图,在平面直角坐标系xOy 中,O 是坐标原点,一次函数y kx b =+的图象与x 轴交 于点A (3-,0),与y 轴交于点B ,且与正比例函数43y x =的图象的交点为C (m ,4) (1) 求一次函数y kx b =+的解析式;(2) D 是平面内一点,以O 、C 、D 、B 四点为顶点的四边形 是平行四边形,直接写出....点D 的坐标.(不必写出推理过程)(1)解:(2)点D 的坐标为_____________________________________________________B五、列方程解应用题(本题5分)21.小明对新发地水果批发市场某种水果销售情况调查发现:如果每千克盈利10元,每天可售出500千克.对市场进一步调查发现,在进价不变的情况下,若每千克这种水果在原售价的基础上每涨价1元,则日销售量将减少20千克.如果市场每天销售这种水果盈利了6 000元,同时顾客又得到了实.........惠.,那么每千克这种水果涨了多少元? 解:六、解答题(本题10分,每题5分)22.小辰根据北京市统计局发布的有关数据制作的统计图表的一部分,请你结合下面图表中提供的信息解答下列问题.(注:能源消费量的单位是万吨标准煤,简称标煤).(1)2010年北京市新能源和可再生能源消费量是____________万吨;并补全条形统计图并在图中标明相应数据......; (2)2010年北京市能源消费总量约是____________万吨标煤(结果精确到百位)? (3)据 “十二五”规划,到2015年,本市能源消费总量比2010年增长31%,其中新能源和可再生能源利用量占全市能源消费总量的6%.小辰调查发现使用新能源每替代一万吨标煤,可减少二氧化碳排放量约为2万吨,到2015年,由于新能源和可再生能源的开发利用,北京市可减少二氧化碳排放量约为多少万吨? 解:“十一五”期间北京市新能源和可再生能源消费量统计图2010年北京市各类能源消费量占能源消费总量的百分比统计图23.已知关于x 的方程 03)13(2=+++x m mx .(1)求证: 不论m 为任何实数, 此方程总有实数根;(2)若方程()23130mx m x +++=有两个不同的整数根,且m 为正整数,求m 的值. 解:(1)证明:(2)解:图1CFE图324. 数学课外选修课上李老师拿来一道问题让同学们思考.原问题:如图1,已知△ABC ,在直线BC 两侧..,分别画出两个..等腰三角形△DBC ,△EBC 使其面积与△ABC 面积相等;(要求:所画的两个三角形一个以BC 为底.一个以BC 为腰);小伟是这样思考的:我们学习过如何构造三角形与已知三角形面积相等.如图2,过点A 作直线l ∥BC ,点D 、E 在直线l 上时,ABC DBC EBC S S S ∆∆∆==,如图3,直线l ∥BC ,直线l 到BC 的距离等于点A 到BC 的距离,点D 、E 、F 在直线l 上,则A B C D B C E B CF BS S S S ∆∆∆∆===.利用此方法也可以计算相关三角形面积,通过做平行线,将问题转化,从而解决问题.(1)请你在下图中,解决李老师提出的原问题;参考小伟同学的想法,解答问题:(2)如图4,由7个形状,大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,若每个正六边形的边长为1, △ABC 的顶点都在格点上,则△ABC 的面积为________.(3)在平面直角坐标系xOy 中,O 是坐标原点,()()1,0,0,2,A B -D 是直线l :321+=x y 上一点,使△ABO 与△ABD 面积相等,则D 的坐标为_______________.图2B 备用图1 备用图2 B备用图325.已知:在正方形ABCD 中,E 、G 分别是射线CB 、DA 上的两个动点,点F 是CD 边上,满足EG ⊥BF , (1)如图1,当E 、G 在CB 、DA 边上运动时(不与正方形顶点重合),求证:GE =BF . (2)如图2,在(1)的情况下,连结GF,求证:FG BE +>.(3)如图3. 当E 、G 运动到BC 、AD 的反向延长线时,请你直接写出....FG 、BE 、BF 三者的数量关系(不必写出证明过程). (1)证明:(2)证明:(3)FG 、BE 、BF 三者的数量关系为______________________________________A 图1A 图2图3北京市石景山区2013—2014学年度第二学期期末考试初二数学答案及评分参考一、选择题(本题共8道小题,每小题3分,共24分)二、填空题(本题共21分,每空3分)9. 120,2x x ==(漏解扣1分,出现错解0分) 10.3x ≥; 11.20,24.12.61° 13.3y =+ 14.22b -<<或3b =(对一种得2分); 三、解答题(本题共3个小题,每小题5分,共15分)15.解:原方程化为:2210x x --= ………………………………………………1分 22111x x -+=+ ………………………………………………2分 ()212x -= ………………………………………………3分∴1211x x == ………………………………………………5分 16.解:(1)由题意:0∆≥ ………………………………………………1分 即:()4430m --≥解得 2m ≥ ………………………………………………3分 (2)当2m =时,原方程化为2210x x -+=解得121x x == ………………………………………………5分(阅卷说明:若考生答案为1x =,扣1分)17. 解:(1)x > 1;………………………………………………1分(2)把1=x 代入x y 2=,得2=y .∴点P (1,2). ……………………………………………………………2分 ∵点P 在直线3+=kx y 上, ∴32+=k . 解得 1-=k .∴3+-=x y . ………………………………………………………………3分 当0=y 时,由30+-=x 得3=x .∴点A (3,0). ……………………4分∴32321=⨯⨯=∆OAP S ………………………………………………5分 四、解答题(本题共15分,每小题5分)18. (1)平行四边形; (1)分(2)证明:连结AC ……………………………………… 2分∵E 是AB 的中点,F 是BC 中点,∴EF ∥AC ,EF =12AC .同理HG ∥AC ,HG =12AC .……… 4分∴EF ∥HG ,EF =HG ,∴四边形EFGH 是平行四边形. ……………………………………… 5分 19.解法一:由题意,△ABF ≌△AEF得AE =AB =5,AD =BC =4,EF =BF . …………………………… 1分 在Rt △ADE 中,由勾股定理,得DE =3. …………………………………… 2分 在矩形ABCD 中,DC =AB =5.∴CE =DC -DE =2. …………………………………………………………… 3分设FC =x ,则EF =4-x .在Rt △CEF 中,()22242x x -=+. .……… ……… 4分 解得23=x . ………………………………… …… 5分即FC =23.解法二:由题意,△ABF ≌△AEF得AE =AB =5,AD =BC =4,EF =BF . …………………………… 1分 在Rt △ADE 中,由勾股定理,得DE =3. …………………………………… 2分 在矩形ABCD 中,DC =AB =5.∴CE =DC -DE =2. ………………………………… 3分 由题意∠AED +∠FEC =90°在Rt △CEF 中,∠EFC +∠FEC =90° ∴∠EFC =∠AED . 又∵∠D =∠C =90°, ∴Rt △AED ∽Rt △EFC∴CF CEDE DA= .……… ………4分 ∴FC =23.………………………………… …… 5分20. 解:(1)∵点C (m ,4)在直线43y x =上,B11 / 13 ∴443m =,解得3m =. ……………………………………………… 1分 ∵点A (3-,0)与C (3,4)在直线(0)y kx b k =+≠上,∴03,43.k b k b =-+⎧⎨=+⎩ 解得2,32.k b ⎧=⎪⎨⎪=⎩ ……………………………………………… 2分 ∴一次函数的解析式为223y x =+. ………………………………………………3分 (2) 点D 的坐标为(3-,2-)或(3,6)(3,2)…………………………………………… 5分(阅卷说明:出现正确解得1分,三个点计算都正确得2分)五、列方程解应用题(本题5分)21.解:设市场某天销售这种水果盈利了6 000元,同时顾客又得到了实惠时,每千克这种水果涨了x 元 …………………………………………… 1分 由题意得 (10)(50020)6000x x +-=……………………………………………3分 整理,得 215500x x -+=.解得 15x =,210x =. ……………………………………………4分 因为顾客得到了实惠,应取 5x =答:销售这种水果盈利6 000元,同时顾客又得到了实惠时,每千克这种水果涨5元. .…………………………………………… 5分六、解答题(本题10分,每题5分)22.解:⑴ 补全统计图如右图,所补数据为98+36+78.5+8+2.8=223.3. ………2分⑵ 2010年北京市总能耗量约是223.3÷3.2%≈7000(万吨标煤).………3分⑶到2015年,由于新能源和可再生能源的开发利用北京市可减少二氧化碳排放量约为7000×(1+31%)×6%×2=1100.4(万吨).………………………5分23. 解:(1)当m =0时,原方程化为,03=+x此时方程有实数根 x =3-. ……………………………………… 1分当m ≠0时,原方程为一元二次方程.∵()()222311296131m m m m m ∆=+-=-+=-≥0.∴ 此时方程有两个实数根. …………………………………………3分综上, 不论m为任何实数时, 方程03)13(2=+++xmmx总有实数根.(2)∵mx2+(3m+1)x+3=0.解得13x=-,21xm=-………………………………………4分∵方程()23130mx m x+++=有两个不同的整数根,且m为正整数,∴1m=…………………………………5分七、解答题(本题5分)24.(1)……………………………2分(2) △ABC的面积为………………………3分(3) 则D的坐标为()2,428,33⎛⎫- ⎪⎝⎭………………………5分八、几何探究(本题5分)25.(既可以理解为平移也可以理解为旋转)(1)证明:延长DA至M,使AM=CF,连结MB∵四边形ABCD是正方形∴BA=BC,∠MAB=∠C=90°,∠ABC=90°∴△BAM≌△BCF∴BM=BF,∠MBA=∠FBC ……………1分∴∠MB F=90°,∴MB∥GE∴四边形MBEG是平行四边形∴MB=GE∴GE=BF ……………………2分(2)连结MF∵BM=BF ,且∠MBF=90°∴△MBF是等腰直角三角形∴MF=…………………3分∵四边形MBEG是平行四边形∴MG=BE在△MGF中,MG+FG>MF∴FG BE+>…………………4分13 / 13(3BE FG +> …………………5分选择第8题思路提示:8. 将AE ,BF 延长交于C ,连结GC ,△ABC 是等边三角形。
北京市石景山区2014届九年级上期末考试数学试题

石景山区2013—2014学年第一学期期末考试试卷初一数学考生 1.本试卷为闭卷考试,满分为 100分,考试时间为100分钟. 须知 2.本试卷共6页,各题答案均写在试卷相应位置上.一、选择题(本大题共 8个小题,每小题 3分,共24分•在每小题给出的四个选项中,只 有一项是符合题目要求的,把正确选项前的字母填在题后括号内) 1. -2的相反数是()11A. 2B .C .D . -22 22•当A 地高于海平面152米时,记作“海拔+152米”那么B 地低于海平面23米时,记作 ( )A .海拔23米B .海拔-23米C .海拔175米D .海拔129米 3.下列各式中,不相等的是 ( ) A . (— 3)2 和一32 B . (-3)2 和 32 C . (-2)3和一23 D .—2’和一2’4.长城总长约为6700000米,用科学计数法表示为( )567A . 6.7 10 米B . 6.7 10 米C . 6.7 10 米 5.方程2x+a-4=0的解是 x=-2,贝U a 等于( ) A . -8 B . 0C . 2D . 86.下列各组整式中不是同类项的是 ( )2.2 〔2—122. 3 .A . 3m n 与 3nmB . - xy 与—x yC . — 5ab 与—5X10 abD . 35 与—12337. 如图,点C 是线段AB 上的点,点D 是线段BC 的中点,AB=10 , AC=6,则线段CD 的 长是()D . 6.7 108 米A C D B第7题图A.4B.3C.2D.11二、填空题(本大题共 6个小题,每小题9. 如图,Z a =120o , / 3=90 o . 则/ Y 勺度数是 ______ .10. 125 十 4= ________ __________ '11•数a 、b 在数轴上的位置如图所示,化简b-a+b = _______________b O a第11题图12.如果a-b=3,ab=-1,则代数式 3ab-a+b-2的值是 _____________13.有一个正方体,A, B, C 的对面分别是X, y,z 三个字母,如图所示,将这个正方体置依此翻到第1,2,3 ,4,5,6格, ^A~当正方体翻到第3格时正方体B C向上一面的字母是/ 7^57^-671 / 4/ /第13题图14.用“•”“■”别表▲种种不同的物体,如图所示,前两架天平保持平衡,若要使第三架天平也平衡,那么? ”处应放■ ____ 个.第14题图三、探究题(本题 4分,每空1分,把答案填在题中横线上)8.下列基本几何体中,从正面、上面、左面观察都是相同图形的是( )圆柱 三棱柱 球 长方体 A B C D3分,共18分.把答案填在题中横线上)第10题图15•有若干个数,第1个数记为a1,第二个数记为a2,第三个数记为a3 ,第n个记为a n ,1若a i,从第二个数起,每个数都等于“1与它前面的那个数的差的倒数。
北京市石景山区实验中学2014—2015学年初三第一学期期末数学模拟题(二)及答案

北京市石景山区实验中学2014——2015学年初三第一学期期末模拟题(二)班级___________姓名____________学号____________成绩___________ 一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1. 以下是回收、绿色包装、节水、低碳四个标志,其中为中心对称图形的是2. 反比例函数ky x=(k ≠0)的图象过点(-1,1),则此函数的图象在直角坐标系中的 A .第二、四象限 B .第一、三象限 C .第一、二象限D .第三、四象限3. 某电视台举行歌手大奖赛,每场比赛都有编号为1~10号共10道综合素质测试题供选手随机抽取作答.在某场比赛中,前两位选手分别抽走了2号,7号题,第3位选手抽中8号题的概率是 A .17B .18C .19D .1104. 如图,在4×4的正方形网格中,△MNP 绕某点旋转90︒,得到△M 1N 1P 1 ,则其旋转中心可以是A. 点EB. 点FC. 点GD. 点H5. 如图,为估算学校的旗杆的高度,身高1.6米的小红同学沿着旗杆在地面的影子AB 由A 向B 走去,当她走到点C 处时,她的影子的顶端正好与旗杆的影子的顶端重合,此时测得AC =2m ,BC =8m ,则旗杆的高度是A .6.4mB .7mC . 8mD .9 m 6.将二次函数1822--=x x y 化成k h x a y +-=2)(的形式,结果为 A .32)4(22+-=x y B .1)2(22--=x y11C .33)4(22--=x yD . 9)2(22--=x y7. 如图,D 是△ABC 边AB 上一点,则下列四个条件不.能单独判定.....△ABC ∽△ACD 的是 A .B ACD ∠=∠ B .ADC ACB ∠=∠C .2AC AD AB =⋅ D .AC ABCD BC= 8. 在平面直角坐标系xOy 中,矩形ABCD 的位置如图1所示,点A 的坐标为)0,2(-,点B的坐标为)2,0(,点D 的坐标为(-3,1).矩形ABCD 以每秒1个单位长度的速度沿x 轴正方向运动,设运动时间为x (0≤x ≤3)秒,第一象限内的图形面积为y ,则下列图象中表示y 与x 的函数关系的图象大致是( ).二、填空题(本题共16分,每小题4分)9. 如图是某个几何体的三视图,该几何体是__________.10. 如图,P 是反比例函数图象上第二象限内的一点,且矩形PEOF 的面积为3,则反比例函数的解析式是________.A B C D俯视图左视图主视图Q PNMOCBA11. 如图,AB 为⊙O 的弦,半径OC ⊥AB 于点D ,AB =32,∠A =30°,则⊙O 的直径为 . 12.如图,在Rt △ABC 中,∠ACB =90°,∠ABC =30°,直角∠MON 的顶点O 在AB 上, OM 、ON 分别交CA 、CB 于点P 、Q ,∠MON 绕点O 任意旋转.当12OA OB =时, OP OQ的值为 ;当1OA OB n =时,OP OQ的值为 .(用含n 的式子表示)三、解答题(本题共30分,每小题5分) 13. 计算:︒-︒+︒30cos 245sin 60tan 2.14. 如图,在平面直角坐标系中,△ABC 和△'''C B A 是以坐标原点O 为位似中心的位似图形,且点B (3,1),B ′(6,2). (1)若点A (25,3),则A ′的坐标为 ; (2)若△ABC 的面积为m ,则△A ′B ′C ′的面积= .15. 已知2240x x +-=,求22(1)(6)3x x x ---+的值.16. 如图,在□ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.(1)求证:△ABE∽△ECF;(2)若AB=5,AD=8,BE=2,求FC的长.17.如图,在平面直角坐标系xOy中,一次函数y kx=-2的图象与x、y轴分别交于点A、B,与反比例函数32yx=-(x<0)的图象交于点3()2M n-,.(1)求A、B两点的坐标;(2)设点P是一次函数y kx=-2图象上的一点,且满足△APO的面积是△ABO的面积的2倍,直接写出点P的坐标.18. 列方程解应用题:学校要围一个矩形花圃,花圃的一边利用10米长的墙,另三边用总长为20米的篱笆恰好围成(如图所示).若花圃的面积为48平方米,AB边的长应为多少米?四、解答题(本题共20分,每小题5分)19. 如图,在平行四边形ABCD 中,5AB =,8BC =,AE BC ⊥于点E ,53cos =B ,求tan CDE ∠的值.20. 甲、乙两名同学玩抽纸牌比大小的游戏,规则是:“甲将同一副牌中正面分别标有数字1,3,6的三张牌洗匀后,背面朝上放置在桌面上,随机抽一次且一次只抽一张,记下数字;乙将同一副牌中正面分别标有数字2,3,4的三张牌洗匀后,背面朝上放置在桌面上,随机抽一次且一次只抽一张,记下数字;若甲同学抽得的数字比乙同学抽得的数字大,甲获胜,反之乙获胜,若数字相同,视为平局.”(1)请用画树状图或列表的方法计算出平局的概率;(2)说明这个规则对甲、乙双方是否公平.21.如图,⊙O是△ABC是的外接圆,BC为⊙O直径,作∠CAD=∠B,且点D在BC的延长线上.(1)求证:直线AD是⊙O的切线;(2)若sin∠CAD,⊙O的半径为8,求CD长.22. 阅读下面材料:问题:如图①,在△ABC中,D是BC边上的一点,若∠BAD=∠C=2∠DAC=45°,DC=2.求BD的长.小明同学的解题思路是:利用轴对称,把△ADC进行翻折,再经过推理、计算使问题得到解决.(1)请你回答:图中BD 的长为 ;(2)参考小明的思路,探究并解答问题:如图②,在△ABC 中,D 是BC 边上的一点,若∠BAD =∠C =2∠DAC =30°,DC =2,则BD=______、AB =_______.图① 图②五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23. 已知关于x 的一元二次方程22(41)30x m x m m -+++=.(1)求证:无论m 取何实数时,原方程总有两个实数根;(2)若原方程的两个实数根一个大于2,另一个小于7,求m 的取值范围;(3)抛物线22(41)3y x m x m m =-+++与x 轴交于点A 、B ,与y 轴交于点C ,当m取(2)中符合题意的最小整数时,将此抛物线向上平移n 个单位,使平移后得到的抛物线顶点落在△ABC 的内部(不包括△ABC 的边界),求n 的取值范围(直接写出答案即可).24. 已知:在△ABC 中,AB =AC ,点D 为BC 边的中点,点F 是AB 边上一点,点E 在线段DF 的延长线上,点M 在线段DF 上,且∠BAE =∠BDF ,∠ABE =∠DBM . (1) 如图1,当∠ABC =45°时,线段 DM 与AE 之间的数量关系是 ; (2) 如图2,当∠ABC =60°时,线段 DM 与AE 之间的数量关系是 ;(3)① 如图3,当ABC α∠=(0<<90α︒︒)时,线段 DM 与AE 之间的数量关系是 ;② 在(2)的条件下延长BM 到P ,使MP =BM ,连结CP ,若AB =7,AE=求sin ∠ACP 的值.25. 设a ,b 是任意两个不等实数,我们规定:满足不等式a ≤x ≤b 的实数x 的所有取值的全体叫做闭区间,表示为[]b a ,. 对于一个函数,如果它的自变量x 与函数值y 满足:当m ≤x ≤n 时,有m ≤y ≤n ,我们就称此函数是闭区间[]n m ,上的“闭函数”. (1)反比例函数xy 2014=是闭区间[]1,2014上的“闭函数”吗?请判断并说明理由; A BCDEF M MFED CBA ABCD EF M图1图2图3(2)若一次函数()0≠+=k b kx y 是闭区间[]n m ,上的“闭函数”,求此函数的表达式; (3)若二次函数5754512--=x x y 是闭区间[]b a ,上的“闭函数”,直接写出实数a ,b 的值.参考答案一、选择题(本题共32分,每小题4分)1.C2.A3. B4.C5. C6.D7. D8. D 二、填空题(本题共16分,每小题4分)9. 圆柱 10. 3y x =-11.4 12.2n; 三、解答题(本题共30分,每小题5分) 13.12. 14.(1)(5,6);(2)4m . 15.化简得225x x ++,求值为9. 16. (1)略;(2)125. 17.(1)A (-1,0)、B (0,-2);(2)(3,4)-或(1,4)- 18. 6米四、解答题(本题共20分,每小题5分)19. 解: 在△ABE 中,AE BC ⊥,5AB =,53cos =B ∴BE=3,AE=4.∴EC=BC -BE =8-3=5. ∵平行四边形ABCD, ∴CD=AB=5.∴△CED 为等腰三角形.∴∠CDE =∠CED . ∵ AD//BC, ∴∠ADE =∠CED . ∴∠CDE =∠ADE .在Rt △ADE 中,AE =4,AD=BC =8,41tan .82CDE ∴∠== 20. (1)19;(2)公平. 21. (1)证明:连接OA .∵BC 为⊙O 的直径, ∴∠BAC =90°.∴∠B +∠ACB =90°.∵OA=OC , ∴∠OAC =∠OCA . ∵∠CAD =∠B , ∴∠CAD +∠OAC =90°. 即∠OAD =90°. ∴OA ⊥AD .∴AD 是⊙O 的切线.(2) 解:过点C 作CE ⊥AD 于点E . ∵∠CAD =∠B , ∴sinB =sin ∠CAD=4. ∵⊙O 的半径为8, ∴BC=16.∴AC =sin BC B ⋅=∴在Rt △ACE 中,CE=sin AC CAD ⋅∠=2. ∵CE ⊥AD ,∴∠CED =∠OAD =90°.∴CE ∥OA . ∴△CED ∽△OAD .∴CD CEOD OA=. 设CD =x ,则OD =x +8.即288x x =+. 解得x =83.所以CD =83.22. (1)22=BD . (2)BD =2. 22=AB .23. 解:(1)证明: Δ=[]22(41)4(3)m m m -+-+=2441m m ++B=2(21)m +∵ 2(21)m +≥0,∴ 无论m 取何实数时,原方程总有两个实数根.(2) 解关于x 的一元二次方程22(41)30x m x m m -+++=,得 1231,= x m x m =+. 由题意得 312,3177. 2.m mm m +>+>⎧⎧⎨⎨<<⎩⎩或 解得173m <<. (3)符合题意的n 的取值范围是 91544n <<.24. 解:(1)DM AE =. (2)12DM AE =. (3)① cos DM AE =α.② 如图,连结AD 、EP . ∵AB =AC ,∠ABC =60°, ∴△ABC 为等边三角形.又∵D 为BC 的中点,∴AD ⊥BC ,∠DAC =30°,BD =DC =12BC =72. ∵∠BAE =∠BDM ,∠ABE =∠DBM ,∴△ABE ∽△DBM . ∴12BM DB BE AB ==.∴EB =2BM . 又∵PB =2BM ,∴EB =PB .∵60EBP ABE ABP PBC ABP ABC ∠=∠+∠=∠+∠=∠=︒, ∴△BEP 为等边三角形. ∴EM ⊥BP .∴∠BMD =90°.∵D 为BC 的中点,M 为BP 的中点,∴DM ∥PC .∴∠BPC =∠BMD = 90°. ∵AB CB =,BE BP =,∠ABE =∠DBM , ∴△ABE ≌△CBP .∴BCP BAE ∠=∠,∠BPC =∠BEA = 90°.在Rt △AEB 中,∵∠BEA =90°,AE=AB =7,∴cos EAB ∠∴cos cos PCB BAE ∠=∠ 在Rt △ABD中,sin AD AB ABD =⋅∠=在Rt △NDC中,cos DC CN NCD =∠,∴ND∴NA AD ND =-.过点N 作NH ⊥AC 于H .∴12NH AN =∴sin NH ACP CN ∠== 25. 解:(1)反比例函数x y 2014=在第一象限,y 随x 的增大而减小. ∵当1=x 时, 201412014==y当2014=x 时, 120142014==y∴当1≤x ≤2014,有1≤y ≤2014,符合闭函数的定义,xy 2014=是闭函数.(2)分两种情况讨论,k >0或者k <0.①当k >0时,此一次函数y 随x 的增大而增大,根据闭函数定义可得:⎩⎨⎧=+=+n b kn mb km ,解得k =1,b =0,所以此时一次函数表达式为x y =. ②当k <0时,此一次函数y 随x 的增大而减小,根据闭函数定义可得:⎩⎨⎧=+=+mb kn nb km ,解得k =-1,b =m +n ,所以此时一次函数表达式为n m x y ++= (3)⎩⎨⎧=-=12b a ,⎪⎪⎩⎪⎪⎨⎧+=-=21099511b aHP ACEF M N图2。
2015年石景山区初三二模数学试卷和答案

友 诚信 信 爱 国善石景山区2014-2015学年初三综合练习数学试卷学校班级姓名考生须知1.本试卷共8页,共五道大题,29道小题.满分120分,考试时间120分钟. 2.在试卷和答题卡上准确填写学校名称、姓名和准考证号. 3.试卷答案一律填涂或书写在答题卡上,在试卷上作答无效.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答.4.考试结束,将本试卷和答题卡一并交回.第Ⅰ卷(共30分)一、选择题(本题共30分,每小题3分)在每个小题给出的四个备选答案中,只有一个是正确的,请将所选答案前的字母填在题后括号内. 1.4的相反数是 A .4- B .4C .41 D .41-2.将800000用科学记数法表示为 A .70.810⨯B .5810⨯C .60.810⨯D .48010⨯3.有四张背面完全相同且不透明的卡片,每张卡片的正面分别写有数字2-,3,0,8-,将它们背面朝上,洗均匀后放置在桌面上,若随机抽取一张卡片,则抽到的数字恰好是无理数的概率是 A .41 B .21C .43D .14.如图是每个面上都有一个汉字的正方体的一种展开图, 那么在正方体的表面,与“友”相对的面上的汉字是 A .爱B .国 C .善 D .诚5.如图,CD AB //,AC 的垂直平分线交CD 于点F ,交AC 于点E ,连接AF ,若︒=∠80BAF ,则C ∠的度数为A .︒40B .︒50C .︒60D .︒806.如图,△ABC 中,∠C =90°,∠B =60°,AC =23,点D 在ACFEDC BA B上,以CD 为直径作⊙O 与BA 相切于点E ,则BE 的长为 A .2 B .3 C .2 D .37.在某校科技节“知识竞赛”中共进行四次比赛,甲、乙两个参赛同学,四次比赛成绩情况下表所示:次数 第一次 第二次 第三次 第四次 甲 9.7 10 10 8.4 乙9.2109.79.2设两同学得分的平均数依次为x 甲,x 乙,得分的方差依次为2S 甲,2S 乙,则下列关系中完全正确的是A .x x =乙甲,22S S >乙甲B .x x =乙甲,22S S <乙甲 C .x x >乙甲,22S S >乙甲D .x x <乙甲,22S S <乙甲8.等腰三角形一个角的度数为50︒,则顶角的度数为 A .50︒ B .80︒ C .65︒ D .50︒或80︒9.如图,等边△ABC 及其内切圆与外接圆构成的图形中,若外接圆的半径为3,则阴影部分的面积为 A .π2B .π3 C .π4D .π610.在平面直角坐标系中,四边形ABCD 是菱形,其中点B 的坐标是(0,2),点D 的坐标是(34,2),点M 和点N 是两个动点,其中点M 从点B出发沿BA 以每秒1个单位的速度做匀速运动,到点A 后停止,同时点N 从B 点出发沿折线BC →CD 以每秒2个单位的速度做匀速运动,如果其中一点停止运动,则另一点也停止运动,设M 、N 两点的运动时间为x ,BMN ∆的面积是y ,下列图象中能表示y 与x 的函数关系的图象大致是A B C DOCDBA xyM NCBA第Ⅱ卷(共90分)二、填空题(本题共18分,每小题3分) 11.分解因式:=+-22882y xy x .12.分式211x x --的值为零的条件是___________.13.如图,四边形ABCD 为矩形,添加一个条件:, 可使它成为正方形.14.如图所示,已知函数y x b =+和1y ax =-的图象交点为M ,则不等式1x b ax +<-的解集为___________.15.综合实践课上,小宇设计用光学原理来测量公园假山的高度,把一面镜子放在与假山AC 距离为21米的B 处,然后沿着射线CB 退后到点E ,这时恰好在镜子里看到山头A ,利用皮尺测量 2.1BE =米,若小宇的身高是1.7米,则假山AC 的高度为________________. 16.在平面直角坐标系xOy 中,我们把横,纵坐标都是整数的点叫做整点,已知在函数()50050<<+-=x x y 上有一点()n m P ,(,m n 均为整数),过点P 作x PA ⊥轴于点A ,y PB ⊥轴于点B ,当2=m 时,矩形PAOB 内部(不包括边界)有47个整点,当3=m 时,矩形PAOB 内部有92个整点,当4=m 时,矩形PAOB 内部有个整点,当=m 时,矩形PAOB 内部的整点最多. 三、解答题(本题共30分,每小题5分)17.已知:如图,OM 是AOB ∠的平分线,C 是OM 上一点,且OA CD ⊥于D ,OB CE ⊥于E ,EB AD =.求证:CB AC =.18.计算:231824cos603-⎛⎫--+-︒ ⎪⎝⎭19.用配方法解方程:0142=-+x x20.若23a b =,求代数式2221244a a a b a ab b⎛⎫-÷ ⎪+++⎝⎭的值. 21.在平面直角坐标系xOy 中,O 是坐标原点;一次函数()0y kx b k =+≠图象与反比例函数()0my m x =≠的图象交于(),21A a a -、()3,B a a . (1)求一次函数与反比例函数的表达式;(2)求ABO ∆的面积.BD CAEyDCB A AEODCBM22.列方程或方程组解应用题小明到学校的小卖部为班级运动会购买奖品,若购买4根荧光笔和8个笔记本需要100元,若购买8根荧光笔和4个笔记本需要80元,请问荧光笔和笔记本的单价各是多少元?四、解答题(本题共20分,每小题5分)23.如图,在ABC ∆中,M ,N 分别是边AB 、BC 的中点,E 、F 是边AC 上的三等分点,连接ME 、NF 且延长后交于点D ,连接BE 、BF (1)求证:四边形BFDE 是平行四边形(2)若32AB =,︒=∠45A ,︒=∠30C ,求:四边形BFDE 的面积24. 2014年,移动电商发展迅速。
2014年北京市各城区中考二模数学——填空题12题汇总

x2014年北京市各城区中考二模数学——填空题12题汇总1、(2014年门头沟二模)12. 我们知道,一元二次方程12-=x 没有实数根,即不存在一个实数的平方 等于-1,若我们规定一个新数“i ”,使其满足12-=i (即方程12-=x 有一个根为i ),并且进一步规定: 一切实数可以与新数进行四则运算,且原有的运算律和运算法则仍然成立,于是有,1i i =12-=i ,,).1(23i i i i i -=-=⋅=.1)1()(2224=-==i i 从而对任意正整数n ,则6i =______________;由于,.)(.4414i i i i i i n n n ===+同理可得,1,,143424=-=-=++n n n i i i i 那么,20132012432i i i i i i +⋅⋅⋅++++的值为________________2、(2014年丰台二模)12.如图,在数轴上,从原点A 开始,以AB=1为边长画等边三角形,记为第一个等边三角形;以BC=2为边长画等边三角形,记为第二个等边三角形;以CD=4为边长画等边三角形,记为第三个等边三角形;以DE=8为边长画等边三角形,记为第四个等边三角形;……按此规律,继续画等边三角形,那么第五个等边三角形的面积是 ,第n 个等边三角形的面积是.3、(2014年平谷二模)12.如图,□ABCD 的面积为16,对角线交于点O ;以AB 、AO 为邻边做□AOC 1B ,对角线交于点O 1;以AB 、AO 1为邻边做□AO 1C 2B ,对角线交于点O 2;…;依此类推.则□AOC 1B 的面积为_______;□AO 4C 5B 的面积为_______;□AO n C n+1B 的面积为___________.4、(2014年顺义二模) 12.如图,正方形ABCD 的边长为3,点E ,F 分别在边AB ,BC 上,AE =BF =1,小球P 从点E 出发沿直线向点F 运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P 第一次碰到BC 边时,小球P 所经过的路程为 ;当小球P 第一次碰到AD 边时,小球P 所经过的路程为 ;当小球P 第n (n为正整数)次碰到点F 时,小球P 所经过的路程为 .5、(2014年石景山二模)12.如图,已知直线l :y =x ,过点A 1(1,0)作x 轴的垂线交直线l 于点B 1,以A 1 B 1为边作正方形A 1 B 1C 1 A 2,过点A 2作x 轴的垂线交直线l 于点B 2,以A 2 B 2为边作正方形A 2 B 2 C 2 A 3,…;则点A 5的坐标为 , 点C n 的坐标为 .6、(2014年海淀二模)12.平面直角坐标系中有一点(1, 1)A ,对点A 进行如下操作:C 3C 2C 1y=xB 3B 2B 1A 4A 3A 2A 1O xy第12题图A BC D1-1E-2(2,0)xy O 第一步,作点A 关于x 轴的对称点1A , 延长线段1AA 到点2A ,使得122A A =1AA ; 第二步,作点2A 关于y 轴的对称点3A , 延长线段23A A 到点4A ,使得34232A A A A =; 第三步,作点4A 关于x 轴的对称点5A , 延长线段45A A 到点6A ,使得56452A A A A =; ·······则点2A 的坐标为________,点2014A 的坐标为________.7、(2014年西城二模)12.如图,在平面直角坐标系xOy 中,已知抛物线y =-x (x -3)(0≤x ≤3)在x 轴上方的部分,记作C 1,它与x 轴交于点O ,A 1,将C 1绕点A 1旋转180°得C 2,C 2与x 轴交于另一点A 2.请继续操作并探究:将C 2绕点A 2旋转180°得C 3,与x 轴交于另一点A 3;将C 3绕点A 2旋转180°得C 4,与x轴交于另一点A 4,这样依次得到x 轴上的点A 1,A 2,A 3,…,A n ,…,及抛物线C 1,C 2,…,C n ,….则点A 4的坐标为 ;C n 的顶点坐标为 (n 为正整数,用含n 的代数式表示) .8、(2014年通州二模)12.如图,二次函数(2)(02)y x x x =-≤≤的图象,记为C 1,它与x 轴交于点O ,A 1;将C 1绕点A 1旋转180°得C 2,交x 轴于点A 2;将C 2绕点A 2旋转180°得C 3,交x 轴于点A 3;……如此进行下去,直至得C 14. 若P (27,m )在第14段图象C 14上,则m = .9、(2014年东城二模)12.如图,矩形BCDE 的各边分别平行于x 轴或y 轴,物体甲和物体乙由点A (2,0)同时出发,沿矩形BCDE 的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2次相遇地点坐标是 ;第2014次相遇地点的坐标是 .yxO第12题图 C 1A 1C 2A 2A 3……C 310、(2014年朝阳二模)12.把长与宽之比为2的矩形纸片称为标准纸.如果将一张标准纸ABCD 进行如下操作:即将纸片对折并沿折痕剪开,则每一次所得到的两个矩形纸片都是标准纸(每一次的折痕如下图中的虚线所示).若宽AB =1,则第2次操作后所得到的其中一个矩形纸片的周长是_________;第3次操作后所得到的其中一个矩形纸片的周长是_________;第30次操作后所得到的其中一个矩形纸片的周长是_________.11、(2014年密云二模)12.如图,设四边形ABCD 是边长为1的正方形,以正方形ABCD 的对角线AC 为边作第二个正方形ACEF ,再以第二个正方形的对角线AE 为边作第三个正方形AEGH ,如此下去L L . (1)记正方形ABCD 的边长为11a =,按上述方法所作的正方形的边长依次为2a ,3a ,4a ,L ,n a ,求出4a = ;(2) 根据以上规律写出第n 个正方形的边长n a 的表达式 .(n>=1)(n 是自然数)12、(2014年延庆二模)13、(2014年房山二模) 12.矩形A 1B 1C 1O ,A 2B 2C 2C 1,A 3B 3C 3C 2,…按如图所示放置.点A 1,A 2,A 3,A 4…和点C 1,C 2,C 3,C 4…,分别在直线y kx b =+ (k >0)和x 轴上,若点B 1(1,2),B 2(3,4),且满足2334n 1122334451n n n A A A A A A A A A A A A A A A A -+====L ,则直线y kx b =+的解析式为 ,点3B 的坐标为 ,点n B 的坐标为_ .C 4B4y=kx+bC 3C 2B 3B 2C 1A 4B 1A 3A 2A 1yxO第一次第二次 第三次…JIEAH GF D14、(2014年昌平二模)12.如图,在平面直角坐标系中,已知点()()3,00,4A B -,,对△AOB 连续作旋转变化,依次得到三角形①、②、③、④、…,则第⑦个三角形的直角顶点的坐标是 ;第 个三角形的直角顶点的坐标是 .xy ②④③①-19121614O BA15、(2014年怀柔二模)12.如图(a ),有一张矩形纸片ABCD ,其中AD=6cm ,以AD 为直径的半圆,正好与对边BC 相切,将矩形纸片ABCD 沿DE 折叠,使点A 落在BC 上,如图(b ).则半圆被覆盖部分(阴影部分)的面积为_____________.错误!未找到引用源。
北京市各区县2014年中考数学二模试题分类汇编 简单计算

简单计算整理一、计算:13、212cos602-︒⎛⎫+- ⎪⎝⎭.13(顺义)计算:)1cos 60211π--++-°.13.(东城)计算:1012014tan 602-︒⎛⎫-+-- ⎪⎝⎭.13.(通州)计算:()022sin 45π+︒14.(平谷)计算:1012014tan 603-⎛⎫-+︒ ⎪⎝⎭.13.(昌平)计算:013sin60(-1)2π-︒+-.13(海淀).计算:011|π12cos302--+--()()13.(西城)计算:101()(3)3tan304-+-π-+︒13. (门头沟)计算:()011()33-2cos 454π-----+︒.13.)0112sin 60()36-︒+-14.(丰台)计算: 112sin 60(2014)3-⎛⎫+-- ⎪⎝⎭ 13(大兴).计算:10)41()25(45cos 28---+︒-π.13.(怀柔)+︒30tan 32-+212--()14.(某某)计算:︒+-+--30tan 220145310.13(密云). 计算:-1001-4+-2())二、解不等式或不等式组14(顺义).解不等式34(23)x --≥3(32)x -,并把它的解集在数轴上表示出来.-3-2-132115(平谷).求不等式组2(2)43251x x x x -≤-⎧⎨--⎩<的整数解.14. (昌平) 解不等式组:34,554 2.x x x x +>⎧⎨-<-⎩14.(石景山)解不等式组211841x x x x -≥+⎧⎨+≤-⎩.15.(密云)解不等式:5(x ﹣2)+8<6(x ﹣1)+7;三、化简求值:16.(顺义)已知2(20a b +-=,求2(2)(3)(3)a a b a b a b +-+-的值. 16(房山)已知:12=m ,求代数式)3)(2()1(2+--+m m m 的值.16.(东城)22[()()(2)](2)x y x y x y y x y y +--++-÷-已知2=4,求的值. 15(通州).已知32=-a a ,求)3()1)(1(---+a a a 的值. 16.(平谷)已知a 2+2a =3,求代数式22(1)(2)a a a ---的值.16(昌平).已知3=y x ,求22222()x y x y xy xy y --÷-的值.16.(海淀)已知22440a ab b -+=,0ab ≠,求222()a ba b a b+⋅--的值. 15. (门头沟)已知13x y =,求y x y y x y x y xy x x-++-⋅+-2222222的值. 16.(石景山)已知当1=x 时,22ax bx +的值为2-,求当2x =时,2ax bx + 的值.16(丰台).已知2220a a --=,求代数式321a (1)121a a a -÷+++的值. 16.(大兴)已知01722=-+x x ,求代数式1)3()23)(1(2+---+x x x 的值.16(怀柔).已知20+5+4=x x ,求代数式2(21)(1)(-2)2x x x -+--的值.16.(某某)已知50x y -=,求222232x y x yx xy y x y-+⋅-++的值.16.(密云)先化简,再计算:已知:210x x --=求代数式2(2)(2)(1)x x x +-+-的值.四、解分式方程 14(房山) 解方程:12242=---x xx x .14.(通州)解方程:5113--=-x xx15(西城).解分式方程:22142xx x +=-- 14.(门头沟)解分式方程26111x x x -=+- 15(怀柔).解方程:11312=-+-xxx .15.(某某)解分式方程:xx x -=+--23123. 解方程14.(东城)解方程:21080x x -+=.14.(海淀)解方程组:3,23 1.x y x y +=⎧⎨-=⎩15.(丰台)解方程:2420x x -+=.14. (大兴)解方程组212x y x y +=⎧⎨-=⎩,.一、计算答案: 13.(房山)1+42⨯解:原式 ......................................4分.....................................5分13.(顺义)解:)1cos 60211π--++-°111122π=-++-……………………………………………………… 4分 π=…………………………………………………………………………5分13(东城)..解:原式=21-+ ……………………………………4分=1分13(通州).解:()︒--+-+45sin 22820π= 1+2222-+………………………………..(3分) = 221+………………………………..(4分) 14.(平谷) (本小题满分5分)解:1012014tan 603-⎛⎫-︒ ⎪⎝⎭=31-+-------------------------4分=2+-----------------------------5分 13(昌)解:原式=1312+-…………………………………………………4分12+. ……………………………………………………………5分13(海淀). 解:011|π12cos302--++-()()122=+-4分 =1.…………………………………………………………………………………5分13.(西城)解:101()(3)3tan304-+-π-+︒=4133++⨯······················ 4分=3+······················· 5分13. (门头沟)解= 431---4分=8-……………………………………………………5分13.(石景山)解: 原式1623233-+⨯+= …………………………………4分 534+= ………………………………………………………5分14(丰台).解:原式213=+-…………………4分2=………………………………………5分13. 解: 1)41()25(45cos 28---+︒-π=41222-+-………………………………………………… 4分 =32- .……………………………………………………………5分13.(怀柔) 3tan30︒+2-+212--()=3+333⨯2++4………………………………4分9…………………………………………5分 14.(某某) 解:原式13531323………………………………………… 4分=112. …………………………………………………………………… 5分 13.(密云)二、解不等式或不等式组答案:14.(顺义)解:去括号,得 3812x -+≥96x -. ………………………………… 1分移项,得 86x x -+≥9312--. ………………………………………2分 合并同类项,得 2x -≥6-. ……………………………………………… 3分 系数化1,得 x ≤3. ………………………………………………………… 4分 把它的解集在数轴上表示为…………………………………………… 5分15(平谷).(本小题满分5分)解:2(2)43251x x x x -≤-⎧⎨--⎩<由①得 21-≥x ; ----------------------------------------------------------------------------2分由②得 x<2.-----------------------------------------------------------------------------------3分∴ 此不等式组的解集为221<≤-x -------------------------------------------------------4分 ∴此不等式组的整数解为0,1. ----------------------------------------------------5分14.(昌平)解:34,554 2.x x x x +>⎧⎨-<-⎩①②①=3.............................5原式分分由①得,2x >-. ………………………………………………………………… 2分 由②得,3x <. …………………………………………………………………… 4分 ∴原不等式组的解集为:23x -<<. ……………………………………………… 5分 14(石景山).解:21 1 84 1 x x x x -≥+⎧⎨+≤-⎩①②,解①得:2x ≥, ………………………………………2分 解②得:3x ≥. …………………………………………4分 则不等式组的解集是:3x ≥. …………………………………5分 15(密云).10x-10+8<6x-6+7…………………1分 10x-6x<10-8-6+7………………2分 4x<3………………4分34x <………………5分 三、化简求值答案:16(顺义)解:2(2)(3)(3)a a b a b a b +-+-222249a ab a b =+-+………………………………………………………… 2分 2249a ab b =++……………………………………………………………… 3分∵2(20a b +-=,∴,2a b ==.……………………………………………………………… 4分∴原式22429233639=++⨯=+=+ 5分16. (房山)解:原式=m ²+2m +1-m ²-m +6=m +7 ...............................................................2分 ∵12=m ,∴m =±1 .................................................................3分当m =1时,原式=8; ..............................................................4分 当m =-1时,原式=6; 原式的值为8或6 ...............................................................5分16.(东城)22216.[()()(2)](2)(2)(2)1.3224,12.52x y x y y x y y xy y y x y x y x y --++-÷-=--÷-=++=∴+=解:分分15. (通州)解:)3()1)(1(---+a a a312+--=a a ………………………………..(2分)= 22+-a a ……………………………..(3分)32=-a a∴原式=22+-a a ………………………………..(4分)= 5 ………………………..(5分) 16.(平谷) (本小题满分5分) 解:22(1)(2)a a a ---=2222(44)a a a a ---+--------------------------------------------------------------------2分=222244a a a a --+---------------------------------------------------------------------------3分=224a a +-------------------------------------------------------------------------------------4分 ∵223a a += ∴原式=341-=-------------------------------------------------------------------------------5分16.(昌)解:原式=()()2()()2y x y x y x y xy x y -+-⋅-…………………………………………………………2分=2x y x+.……………………………………………………3分 ∵3xy=, ∴3x y =. ………………………………………………………4分原式=32233y y y +=⨯.………………………………………… 5分 16. (海淀)解:∵22440,a ab b -+=2(2)0.a b -=∴………………………………………………………………………1分2.a b =∴……………………………………………………………………………2分∵0ab ≠, ∴2222()()()()a b a ba b a b a b a b a b ++⋅-=⋅---+2a ba b+=+………………………………………………………3分 222b bb b+=+………………………………………………………4分 4.3=……………………………………………………………5分 15(门头沟)解:y x y y x y x y xy x x-++-⋅+-2222222 =yx y y x y x y x y x x -+++-⋅-2))(()(22·················· 2分=yx y y x x -+-2)(2=)()(2y x y x -+. ·························· 3分当13x y =时,3y x =. ························ 4分 原式=2(3)(3)x x x x +-=-4. ······················· 5分16(石景山).解:将1x =代人22ax bx +2-=中,得22-=+b a ……………………………………………2分 当2x =时,2ax bx +=42a b +……………………………………… 3分2(2)a b =+4=- …………………………………………5分 16.(丰台)解:原式=32(1)1a 121a a a a +-÷+++=()3211a a a a ÷++ =23a 11a a a+⨯+()……………………………2分 =21a a + ……………………………………………3分 当2220a a --=时,222a a =+…………4分 原式=122a a ++=12……………………………………5分01722=-+x x ,分4 (1722)=+∴x x16.(怀柔) 解:2(21)(1)(-2)2x x x -+--.=222+2-1(-44)2x x x x x --+-. ………………………………………2分=2221+442x x x x +----. ………………………………………3分 =2+57x x -. ………………………………………4分当20+5+4=x x 时,原式=-4711-=-.………………………………………5分分分大兴)3.......................................................................10722.. (196231))3()23)(1(.(162222-+=+-+--+=+---+x x x x x x x x x 分5 (91))3()23)(1(2-=+---+∴x x x16. (某某)解:原式=2()()3()x y x y x y x y x y+-+⋅-+……………………………………………2 分 =3x y x y+-.…………………………………………………………3分 ∵ x -5y =0,∴ x =5y .…………………………………………………………………4分∴ 原式=5325y y y y+=-.…………………………………………………………5分 (密云)222242 1................2231016.=x x x =2x x ............................3x x =-1.......................................5-+-+----=原式分分当时,原式分四、解分式方程14. (房山)解:()242x x x +=- ..................................1分24x =-2x =- ..................................3分经检验:2x =-是原方程的解∴原方程的解为2x =- ..................................5分14. (通州)解:5113--=-x x x)1(53--=-x x ………………………………..(1分)84=x2=x ………………………………..(3分)经检验:2=x 是原方程的根∴原方程的根是2=x ………………………………..(4分)15. (西城)方程两边同时乘以24x -,得22(2)4x x x ++=-, ······· 3分 解得,3x =-. ··························· 4分经检验,3x =-是原方程的解3x =- ·················· 5分14. (门头沟)解: 去分母,得()()()1611x x x x --=+-. ……………………2分 解得5x =-. ……………………4分检验:把5x =-代入()()110x x +-≠所以5x =-是原方程的解. ……………………5分15(怀柔).解:11312=---x x x ,----------- 1分 132-=-x x , -----------2分34-=-x , ----------- 3分43=x .-----------4分 经检验,43=x 是原方程的解.----------- 5分 ∴原方程的解是43=x . 15.(某某) 解:将方程整理,得331022x x x -++=--. 去分母,得 x -3+3+x -2 = 0. ……………………………………………2分解得 x = 1. ……………………………………………3分经检验 x = 1是原分式方程的解. ………………………………………………4 分∴原分式方程的解为x = 1.…………………………………………………………5 分五、解方程:14.(东城)解:09102=+-x x.22212108.11025825.2(5)17.3555x x x x x x x -=--+=-+-==+=变形为分配方,分整理,得分解得,分 14. (海淀)323 1. x y x y +=⎧⎨-=⎩, ①② 解:由①3⨯+②得,510x =.解得,2x =. …………………………………………………………………………2分 把2x =代入①得,1y =. ……………………………………………………………4分 ∴原方程组的解为2,1.x y =⎧⎨=⎩……….……………………………………………………5分 15.(丰台)解:∆=244128-⨯⨯=,……………………1分∴x =,…………………………………3分∴1222x x ==……………5分14.(大兴)解:212x y x y +=⎧⎨-=⎩,①.② +①②得:23x x +=1x =. …………………………………………2分将1x =代入②得:12y -=,1-=y …………………………………………4分11x y =∴=-⎧⎨⎩原方程组的解是…………………………………………5分。
北京市石景山区2014-2015学年高一下学期期末考试数学试题_46240

石景山区2014—2015学年第二学期期末考试试卷高一数学考生须知 1. 本试卷为闭卷考试,满分为100分,考试时间为120分钟.2. 本试卷共8页,各题答案均答在本题规定的位置.一、选择题:本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后括号内. 1.下列结论正确的是 ( )A .若a b >,则ac bc >B .若a b >,则22a b >C .若a c b c +<+,0c <,则a b >D a b >a b >2.如图,矩形长为6,宽为4,在矩形内随机地撒 300颗黄豆,数得落在椭圆内的黄豆数为225颗,以此实验数据为依据可以估计出椭圆的面积约为( ). A .16B .17C .18D .193.下面关于算法的说法正确的是 ( )A .秦九韶算法是求两个数的最大公约数的方法B .更相减损术是求多项式的值的方法C .割圆术是采用正多边形面积逐渐逼近圆面积的算法计算圆周率πD .以上结论皆错4.设变量,x y 满足约束条件20,80,1,x y x y x -+≤⎧⎪+-≤⎨⎪≥⎩,则2z x y =-的最大值为( )A .5-B .1-C .1D .55. 已知△ABC 的三个内角满足sin :sin :sin 5:11:13A B C =,则△ABC 是( )A .等腰三角形B .锐角三角形C . 直角三角形D .钝角三角形6.某产品的广告费用x (万元)与销售额y (万元)的统计数据如右表,根据右表可得回归方程ˆˆˆybx a =+中的ˆ0a =,据此模型预报广告费用为6万元时销售额为( )A .50B .60C .63D . 59x 42 3 5y 38 20 31 517.设△ABC 的内角,,A B C 所对的边为,,a b c ,4a =,3b =4,30A =,则B =( )A .60B .60或120C .30D .30 或1508.在等差数列{}n a 中,若4681012240a a a a a ++++=,则91113a a -的值为( )A .30B .31C .32D . 339.执行如图所示的程序框图,若“否”箭头分别指向①和②,则输出的结果分别是 ( ) A .55,53 B .51,49C .55,49D .53,5110. 设{}n a 是公比为q 的等比数列,||1q >, 令1(1,2,)n n b a n =+=,若数列{}n b 有连续四项在集合{53,23,19,37,82}--中,则q = ( )A .32- B . 43- C .23-D .32二、填空题:本大题共4个小题,每小题3分,共12分.把答案填在题中横线上.11.某高中为了解在校高中生对参加某项社会实践活动的意向,拟采用分层抽样的方法从该校三个年级的高中生中抽取一个容量为300的样本进行调查.已知该校高一、高二、高三的人数之比为4∶5∶6,则应从高一年级抽取________名学生. 12.算式404-=⨯ 中,在方框中填入两个正整数...,使它们的乘积最大. 13.已知△ABC 在正方形网格中的位置如右图所示, 则cos ABC ∠=____________.14. 将数列{}n a 按如图所示的规律排成一个三角形表,并同时满足以下两个条件:结束否② ① 是 i =1S =1i =i +1 S =S +i 2S >50 输出S是开始a①各行的第一个数125,,a a a 构成公差为d 的等差数列; ②从第二行起,每行各数按从左到右的顺序构成 公比为q 的等比数列.若1351,4,3a a a ===,则d =_____________; 第n 行的和n T =__________________________.三、解答题:本大题共6个小题,共48分.写出必要的解题步骤及证明过程.15.设△ABC 的内角,,A B C 所对的边为,,a b c ,且有2sin cos sin cos cos sin B A A C A C =+. (Ⅰ)求角A 的大小; (Ⅱ)若2b =,3c =,D 为AC 的中点,求BD 的长.16.某超市从2014年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,整理得到数据分组及频率分布表.....和频率分布直方图: 分组(日销售量) 频率(甲种酸奶) [ 0,10] 0.10 (10,20] 0.20 (20,30] 0.30 (30,40] 0.25 (40,50]0.15(Ⅰ)写出频率分布直方图中的a 的值,并作出甲种酸奶日销售量的频率分布直方图;答:a =________________;乙种酸奶日销售量 10 20 30 40 50 0.030 频率组距0.025 0.0200.010a(Ⅱ)记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为21s ,22s , 试比较21s 与22s 的大小.(只需写出结论).答:21s ______________22s17.已知等差数列{}n a 满足:37a =,5726a a +=.{}n a 的前n 项和为n S . (Ⅰ)求n a 及n S ; (Ⅱ)令241n n b a =-(*n ∈N ),求数列{}n b 的前n 项和n T .10 20 30 40 50甲种酸奶日销售量/箱18.某商区停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过1小时收费6元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过4小时.(Ⅰ)设甲停车付费a 元.依据题意,填写下表:(Ⅱ)若每人停车的时长在每个时段的可能性相同,求甲、乙二人停车付费之和为36元的概率; (Ⅲ)若甲停车1小时以上且不超过2小时的概率为31,停车付费多于14元的概率为125,求甲停车付费恰为6元的概率.19.某机床厂2011年年初用98万元购进一台数控机床,并立即投入生产使用.计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元;该机床使用后,每年的总收入为50万元.设使用x 年后.数控机床的盈利额为y 万元. (Ⅰ)写出y 与x 之间的函数关系式;(Ⅱ)使用若干年后,对机床的处理方案有两种:方案一:当年平均盈利额达到最大值时,以30万元价格处理该机床; 方案二:当盈利额达到最大值时,以12万元价格处理该机床;请你研究一下哪种方案处理较为合理?并说明理由.20.已知数列{}n a 满足12112,8,(2),n n n a a a a ca n +-=⎧⎪=⎨⎪+=≥⎩(c 为常数,*n N ∈).(Ⅰ)当2c =时,求n a ;(Ⅱ)当1c =时,求2014a 的值;(Ⅲ)问:使3n n a a +=恒成立的常数c 是否存在?并证明你的结论.石景山区2014—2015学年第二学期期末考试试卷答案高一数学一、 选择题:题号 1 2 3 4 5 6 7 8 9 10 答案DCCCDBBCAA二、填空题:11.80 12.20,5 13. 3514.1d =,21(21)n n T n -=- 三、解答题:15.解:(Ⅰ)因为A B C π++=,所以A C B π+=-,,(0,)A B π∈,所以sin()sin 0A C B +=>;又2sin cos sin cos cos sin sin()sin B A A C A C A C B =+=+= ……………………2分 所以1cos ,2A =即3A π= ……………………4分 (Ⅱ)2b =可得1AD =, ……………………5分 在△ABD 由余弦定理得:2222cos 7BD AB AD AB AD A =+-⋅=,7BD =. ……………………8分16.解:(Ⅰ)0.015a =; ……………………2分……………………5分(Ⅱ)2212s s <. ……………………8分17.(Ⅰ)设等差数列{}n a 的公差为d , 因为37a =,5726a a +=,所以有112721026a d a d +=⎧⎨+=⎩,解得13,2a d ==, ……………………2分所以321)=2+1n a n n =+-(;n S =(-1)322n n n +⨯=22n n +. ……………………4分 (Ⅱ)241n n b a =-=2421)1n =+-(1(1)n n +=111n n -+, ……………………6分 所以n T =1111112231n n -+-++-+=111n -=+1nn +. ……………………8分18.(Ⅰ)(Ⅱ)解:甲停车付费a 元,设乙停车付费b 元,其中,6,14,22,30a b =.则甲、乙二人的停车费用构成的基本事件空间为:(6,6),(6,14),(6,22),(6,30),(14,6),(14,14),(14,22),(14,30),(22,6),(22,14),(22,22), (22,30),(30,6),(30,14),(30,22),(30,30),共16种情形.其中,(6,30),(14,22),(22,14),(30,6)这4种情形符合题意.故“甲、乙二人停车付费之和为36元”的概率为41164P ==. ………………6分 (Ⅲ)“甲临时停车付费恰为6元”为事件A , 则 41)12531(1)(=+-=A P .所以甲临时停车付费恰为6元的概率是41. ……………………8分 19.解:(Ⅰ)2(1)50[124]98240982x x y x x x x -=-+⨯-=-+-(0x >) ……………………2分(Ⅱ)方案一:989824040(2)y x x x x x=-+-=-+98228x x +≥=,所以9840(2)12y x x x =-+≤.当且仅当982x x=,即7x =时等号成立; 故到2018年,年平均盈利额达到最大值,工厂共获利12730114⨯+=(万元)……………………5分方案二:22240982(10)102y x x x =-+-=--+,当10x =时,y 有最大值102;故到2021年,盈利额达到最大值,工厂共获利10212114+=(万元).…………………7分 盈利额达到的最大值相同,而方案一所用的时间较短,故方案一较为合理.……………8分20.(Ⅰ)2c =时,112(2)n n n a a a n +-+=≥,11(2)n n n n a a a a n +-∴-=-≥112216n n n n a a a a a a ---∴-=-==-={}n a ∴是以2为首项,6为公差的等差数列64n a n ∴=- ……………………2分(Ⅱ)1c =时,11n n n a a a +-+=,(2)n ≥即11n n n a a a +-=-2111()n n n n n n n a a a a a a a ++--∴=-=--=-,(2)n ≥即对*n N ∈,3n n a a +=-,所以6n n a a +=.故201433564412a a a a ⨯+===-=-. ……………………5分 (Ⅲ)假设存在常数c ,使3n n a a +=恒成立. 由11(2)n n n a a ca n +-+=≥ ……①:21(1)n n n a a ca n +++=≥,又21n n a a +-=,代入上式得11(1)n n n a a ca n -++=≥ ……②①-②得11(),(2)n n n n a a c a a n ++-=-≥即1()(1)0,(2)n n a a c n +-+=≥10,2n n a a n +∴-=≥或1c =-.若10,2n n a a n +-=≥,可得3212828a ca a c a =-=-==,则54c =, 而此时4323524a a a a =-=≠,不合题意. 若1c =-,则11(2)n n n a a a n +-+=-≥,即110,(2)n n n a a a n +-++=≥则有*210,()n n n a a a n N ++++=∈ ……③ 同时,*3210,()n n n a a a n N +++++=∈……④④-③可得:3n n a a +=恒成立.高一数学试卷第11页(共11页) 综上,存在常数1c =-,使3n n a a +=恒成立 ……………………8分【若有不同解法,请酌情给分】。
北京市石景山区2014届高三数学上学期期末考试试题 理 新人教A版

石景山区2013—2014学年第一学期期末考试试卷高三数学〔理科〕本试卷共6页,总分为为150分,考试时间为120分钟.请务必将答案答在答题卡上,在试卷上作答无效,考试完毕后上交答题卡.第一局部〔选择题 共40分〕一、选择题共8小题,每一小题5分,共40分.在每一小题给出的四个选项中,选出符合题目要求的一项.1.集合{}2230M x x x =∈+-≤R ,{}10N x x =∈+<R ,那么MN =〔 〕A .{101}-,,B .{321}---,,C .{11}x x -≤≤D .{31}x x -≤<-2.复数1ii =-〔 〕 A .122i +B .122i - C .122i -+ D .122i -- 3.向量(1)x =,a ,(4)x =,b ,如此“2x =〞是“a ∥b 〞的〔 〕A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件4.数列为等差数列,,那么数列通项公式为〔 〕A .B .C .D .5.执行如下列图的程序框图,假设输入的x 的值为2, 如此输出的x 的值为〔 〕 A .3 B .126 C .127D .1286.在边长为1的正方形OABC 中任取一点P ,如此点P恰好落在正方形与曲线y =成的区域内(阴影局部)的概率为〔 〕A .12B .23 C .34D .457.用0到9这10个数字,可以组成没有重复数字的三位偶数的个数为〔 〕A .324B .328C .360D .6488.函数满足,当时,,假设在区间上方程有两个不同的实根,如此实数的取值范围是〔 〕A .B .C .D .第二局部〔非选择题 共110分〕二、填空题共6小题,每一小题5分,共30分. 9.圆C 的参数方程为12cos 2sin x y θθ+⎧⎨=⎩,,=(θ为参数),如此圆C 的直角坐标方程为_______________,圆心C 到直线:10l x y ++=的距离为______. 10.在ABC ∆中,角A B C ,,的对边分别为a b c ,,,假设=6a ,4c =,1cos =3B ,如此b =______.11. 假设x ,y 满足约束条件1020x y x y ≤⎧⎪≥⎨⎪-+≥⎩,,,如此z x y =+的最大值为.12.如图,在ABC ∆中,o 90B ∠=,O 是AB 上一点,以O 为圆心,OB 为半径的圆与AB 交于点E ,与AC 切 于点D ,2AD =,1AE =,如此AB 的长为,CD 的长为.13.抛物线24y x =的焦点为F ,准线为直线l ,过抛物线上一点P 作PE l ⊥于E ,假设直线EF 的倾斜角为o150,如此||PF =______.14. 四边形是边长为的正方形,且平面,为上动点,过且垂直于A DCBE.O1AP的平面交于,那么异面直线PC 与BD 所成的角的度数为,当三棱锥的体积取得最大值时, 四棱锥P ABCD -的高PA 的长为.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.〔本小题总分为13分〕函数()cos cos 21f x x x x =++. 〔Ⅰ〕求函数的单调递增区间;〔Ⅱ〕求函数在上的最小值,并写出取最小值时相应的值.16.〔本小题总分为13分〕市各级各类中小学每年都要进展“学生体质健康测试〞,测试总成绩总分为为100分,规定测试成绩在[85100],之间为体质优秀;在[7585),之间为体质良好;在[6075),之间为体质合格;在[060),之间为体质不合格.现从某校高三年级的300名学生中随机抽取30名学生体质健康测试成绩,其茎叶图如下:9 1 3 5 68 0 1 1 2 2 3 3 3 4 4 5 6 6 7 7 9 7 0 5 6 6 7 9 6 4 5 8 5 6〔Ⅰ〕试估计该校高三年级体质为优秀的学生人数;〔Ⅱ〕根据以上30名学生体质健康测试成绩,现采用分层抽样的方法,从体质为优秀和良好的学生中抽取5名学生,再从这5名学生中选出3人.〔ⅰ〕求在选出的3名学生中至少有1名体质为优秀的概率;〔ⅱ〕记X 为在选出的3名学生中体质为良好的人数,求X 的分布列与数学期望.17.〔本小题总分为14分〕如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是直角梯形,o 90ABC ∠=,AD ∥BC ,且2PA AD ==,1AB BC ==,E 为PD 的中点.〔Ⅰ〕求证:CD ⊥平面PAC ; 〔Ⅱ〕求二面角E AC D --的余弦值;〔Ⅲ〕在线段AB 上是否存在一点F 〔不与A B ,两点重合〕,使得AE ∥平面PCF ?假设存在,求出AF 的长;假设不存在,请说明理由.18.〔本小题总分为13分〕函数()xf x e ax =-〔e 为自然对数的底数〕.〔Ⅰ〕当2a =时,求曲线()f x 在点(0(0))f ,处的切线方程; 〔Ⅱ〕求函数()f x 的单调区间;〔Ⅲ〕函数()f x 在0x =处取得极小值,不等式()f x mx <的解集为P ,假设1{|2}2M x x =≤≤,且M P ≠∅,求实数的取值范围.19.〔本小题总分为14分〕椭圆:〔〕过点(20),,且椭圆的离心率为. 〔Ⅰ〕求椭圆的方程;〔Ⅱ〕假设动点在直线上,过作直线交椭圆于两点,且MP PN =,再过作直线.证明:直线恒过定点,并求出该定点的坐标.20.〔本小题总分为13分〕集合,对于数列中.〔Ⅰ〕假设50项数列{}n a 满足5019ii a==-∑,5021(1)107i i a =-=∑,如此数列{}n a 中有多A PEBDC少项取值为零?(121nin i aa a a n *==+++∈∑N ,)〔Ⅱ〕假设各项非零数列{}n a 和新数列{}n b 满足11i i i b b a ---=〔〕. 〔ⅰ〕假设首项10b =,末项1n b n =-,求证数列{}n b 是等差数列;〔ⅱ〕假设首项10b =,末项0n b =,记数列{}n b 的前n 项和为n S ,求n S 的最大值和最小值.石景山区2013—2014学年第一学期期末考试高三数学〔理科〕参考答案一、选择题共8小题,每一小题5分,共40分.二、填空题共6小题,每一小题5分,共30分.,2(两空的题目第一空2分,第二空3分)三、解答题共6小题,共80分. 15.〔本小题共13分〕解:〔Ⅰ〕()f x 2cos 2+1x x =+…………2分2sin 2+16x π=+(), ……………4分222262k x k πππππ-≤+≤+,k ∈Z , 36k x k ππππ-≤≤+,k ∈Z , ………6分所以函数)(x f 的单调递增区间为[]36k k ππππ-+,()k ∈Z .……………7分 〔Ⅱ〕因为,22363x πππ-≤+≤, ……………9分sin(2)126x π-≤+≤, 12sin 2+136x π≤+≤(), ……………11分所以当2=63x ππ+-,即=4x π-时,函数)(x f 取得最小值1.………13分16.〔本小题共13分〕人.…………3分〔Ⅱ〕依题意,体质为良好和优秀的学生人数之比为 15:103:2=.如此 3335C 9()1C 10P A =-=.故在选出的3名学生中至少有名体质为优秀的概率为910.……9分 〔ⅱ〕解:随机变量X 的所有取值为123,,.123235C C 3(1)C 10P X ⋅===,213235C C 6(2)C 10P X ⋅===,3335C 1(3)C 10P X ===.…………12分 所以,随机变量X 的分布列为:36191231010105EX =⨯+⨯+⨯=.……………13分 17.〔本小题共14分〕 〔Ⅰ〕证明:因为PA ⊥平面ABCD ,CD ⊂平面ABCD , 所以PA CD ⊥. ……………1分 取AD 的中点G ,连结GC ,因为底面ABCD 为直角梯形,AD ∥BC ,o90ABC ∠=,且1AB BC ==, 所以四边形ABCG 为正方形,所以CG AD ⊥,且1=2CG AD , 所以o=90ACD ∠,即AC CD ⊥................3分 又PA AC A =,所以CD ⊥平面PAC . (4)分〔Ⅱ〕解:如图,以A 为坐标原点,AB AD AP ,,所在直线分别为x y z ,,轴建立空间直角坐标系xyz A -.………5分如此(000)A ,,,(110)C ,,,(011)E ,,,(002)P ,,, A PEBDCG所以(002)AP =,,,(110)AC =,,,(011)AE =,,. 因为PA ⊥平面ABCD ,所以(002)AP =,,为平面ACD 的一个法向量. ……6分设平面EAC 的法向量为1()n x y z =,,, 由10n AC ⋅=,10n AE ⋅=得00x y y z +=⎧⎨+=⎩,,令1x =,如此1y =-,1z =,所以1(111)n =-,,是平面EAC 的一个法向量. ………8分所以1cos n AP <>==,因为二面角E AC D --为锐角, 所以二面角E AC D --的余弦值为3. ………9分 〔Ⅲ〕解:假设在线段AB 上存在点F 〔不与A B ,两点重合〕,使得AE ∥平面PCF . 设(00)F a ,,,如此(110)CF a =--,,,(112)CP =--,,. 设平面PCF 的法向量为2()n x y z =,,,由20n CF ⋅=,20n CP ⋅=得(1)020a x y x y z --=⎧⎨--+=⎩,,令1x =,如此1y a =-,2a z =, 所以2(11)2a n a =-,,是平面PCF 的一个法向量.…12分因为AE ∥平面PCF ,所以20AE n ⋅=,即(1)02aa -+=, ……………13分解得23a =,所以在线段AB 上存在一点F 〔不与A B ,两点重合〕,使得AE ∥平面PCF ,且2=3AF .……14分18.〔本小题共13分〕解:〔Ⅰ〕当2a =时,()2x f x e x =-,(0)1f =,()2xf x e '=-,得(0)1f '=-,………2分所以曲线()f x 在点(0(0))f ,处的切线方程为1y x =-+. ……………3分 〔Ⅱ〕()xf x e a '=-.当0a ≤时,()0f x '>恒成立,此时()f x 的单调递增区间为()-∞+∞,,无单调递减区间;………5分当0a >时,(ln )x a ∈-∞,时,()0f x '<,(ln )x a ∈+∞,时,()0f x '>, 此时()f x 的单调递增区间为(ln )a +∞,,单调递减区间为(ln )a -∞,.……7分 〔Ⅲ〕由题意知(0)0f '=得1a =,经检验此时()f x 在0x =处取得极小值.………8分因为M P ≠∅,所以()f x mx <在1[2]2,上有解,即1[2]2x ∃∈,使()f x mx <成立,…9分即1[2]2x ∃∈,使x e x m x ->成立, …………10分 所以min ()x e xm x->. 令()1x e g x x =-,2(1)()x x e g x x -'=,所以()g x 在1[1]2,上单调递减,在[12],上单调递增,如此min ()(1)1g x g e ==-, ……………12分 所以(1)m e ∈-∞,+. ……………13分 19.〔本小题共14分〕解:〔Ⅰ〕因为点(20),在椭圆C 上,所以22401a b+=, 所以24a =, …………1分 因为椭圆C 的离心率为12, 所以12c a =,即22214a b a -=,…………2分解得23b =, ……………4分所以椭圆C 的方程为22143x y +=. ……………5分 〔Ⅱ〕设0(1)P y -,,033()22y ∈-,, ①当直线MN 的斜率存在时,设直线MN 的方程为0(1)y y k x -=+,11()M x y ,,22()N x y ,,由2203412(1)x y y y k x ⎧+=⎨-=+⎩,,得22222000(34)(88)(48412)0k x ky k x y ky k ++++++-=, ………7分所以2012288+34ky k x x k +=-+, ……………8分因为MP PN =,即P 为MN 中点,所以12=12x x +-,即20288=234ky k k +--+. 所以003(0)4MN k y y =≠, ……………9分 因为直线l MN ⊥, 所以043l y k =-,所以直线l 的方程为004(1)3y y y x -=-+, 即041()34y y x =-+ ,显然直线l 恒过定点1(0)4-,. ……………11分②当直线MN 的斜率不存在时,直线MN 的方程为1x =-, 此时直线l 为x 轴,也过点1(0)4-,. ……………13分 综上所述直线l 恒过定点1(0)4-,. ……………14分 20.〔本小题共13分〕解:〔Ⅰ〕设数列{}n a 中项为110-,,分别有x y z ,,项.由题意知5094107x y z x y z y ++=⎧⎪-=-⎨⎪+=⎩,,,解得11z =.所以数列{}n a 中有11项取值为零. ……3分word11 / 11 〔Ⅱ〕〔ⅰ〕且11i i i b b a ---=,得到121(23)i i b a a a i n -=+++=,,,,假设1(121)i a i n ==-,,,,如此满足1n b n =-.此时11i i b b --=,数列{}n b 是等差数列;假设121n a a a -,,,中有*(0)p p p >∈,N 个1-,如此121n b n p n =--≠-不满足题意;所以数列{}n b 是等差数列. ……………7分 〔ⅱ〕因为数列{}n b 满足11i i i b b a ---=,所以121(23)i i b a a a i n -=+++=,,,, 根据题意有末项0n b =,所以1210n a a a -+++=.而,于是n 为正奇数,且121n a a a -,,,中有12n -个1和12n -个1-. 12112121()()n n n S b b b a a a a a a -=+++=+++++++121(1)(2)n n a n a a -=-+-++ 要求n S 的最大值,如此只需121n a a a -,,,前12n -项取1,后12n -项取1-, 所以2max (1)()(2)(4)14n n S n n -=-+-++=〔n 为正奇数〕. 要求n S 的最小值,如此只需121n a a a -,,,前12n -项取1-,后12n -项取1, 如此2min (1)()(2)(4)14n n S n n -=------=-〔n 为正奇数〕. …………13分【注:假设有其它解法,请酌情给分.】。
7.2013-2014第1学期初2数学期末考试题答案-石景山

石景山区2013-2014学年度第一学期期末考试初二数学答案及评分参考阅卷须知:为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数.二、填空题(本题共6道小题,每小题4分,共24分)11.3n m-; 12.3; 13.5; 14.36;(各2分)15.2; 162分,答对两个3分,答对3个4分)三、解答题(本题共4个小题,每小题5分,共20分)17. 解:原式=14- ………………………………………………………4分=3-- ………………………………………………………………5分18. 解:2(3)(1x x x ++-=-…………………………………………………1分224381x x x ++-=- …………………………………………………2分44x = …………………………………………………3分1x = ………………………………………………………4分 经检验:1x =是原方程的增根,所以原方程无解 ……………………………5分19. 解:原式…………………………………………3分…………………………………………4分……………………………………………………5分20. 解:原式=()()()22225213x y x y y x y x y +-⎡⎤-⨯⎢⎥--⎣⎦…………………………………………1分 =()()()()22522223y x y x y x y x y x y -+--⋅-- =()22293y x x y -- …………………………………………………………………2分=33y x y x +- ……………………………………………………………………3分解法一:∵23x y =,不妨设()2,30x k y k k ==≠ …………………………………4分∴原式=9292k kk k +-=117………………………………………5分 解法二:3333xy x y xy x y ++=-- ………………………………………4分∵23x y =∴原式=231132733+=- ………………………………………5分 (阅卷说明:如果学生直接将2,3x y ==代入计算正确者,本题扣1分)四、列方程解应用题(本题5分)21. 解:设原计划每天加工x 顶帐篷. ……………………………………………………1分1500300150030042x x ---= …………………………………………………2分解得 150x = ………………………………………………………………3分经检验,150x =是原方程的解,且符合题意. ………………………………4分答:原计划每天加工150顶帐篷.……………………………………………………5分五、解答题(本大题共3个小题,每题5分,共15分)22.证明:∵AE ∥DF ,∴∠AEB=∠DFC. …………………………………………………………1分 ∵BF=CE ,∴BF+EF =即=CF. …………………………2分在△ABE 和△DCF 中,AE DF AEB DFC BE CF =⎧⎪∠=∠⎨⎪=⎩ ………………………………………………………3分∴△ABE ≌△DCF ………………………………………………………4分∴AB=DC ………………………………………………………5分23. 解:AFB ∠=60° ………………………………………………………………1分证明:∵△ABC 是等边三角形∴CA=CB ,4∠=60° 2分 ∵∠2+∠4=∠5 C∠1+∠3=∠5且∠3=60°∴∠1=∠2 ……………… ………………3分又∵BE=AD∴△BCE ≌△ACD (SAS )∴CE=CD ,∠BCE=∠ACD ……………………………………………4分∴∠BCE -∠6=∠ACD -∠6即∠4=∠7=60°∴△ECD 是等边三角形 ………………………………………………5分24. 解:分类讨论(1)如图,过A 作AD ⊥BC 交BC (延长线)于D ,………………………1分∴∠D=90°,∴在Rt △ABD 中,∠B+∠BAD=90°,∴∠BAD =45°∴DA DB =, 又∵222AB DB DA =+,不妨设x DB DA ==则3222=+x x ,解得4=x ,∴DA=DB=4 ……………………………2分∵∠D=90°,∴在Rt △ACD 中,222AC DA DC =+3452222=-=-=AD AC CD ……………………………3分∴BC=BD-CD=4-3=1 ……………………………4分(2)如图:由(1)同理:DB=4,CD=3∴BC=BD+CD=4+3=7.综上所述:BC=1或BC=7 ……………………………5分 D C 'C B A(阅卷说明:只计算出一种情况,本题得4分)六、几何探究(本题6分)25. (1)证明:连结ND∵AO 平分BAC ∠, ∴12∠=∠∵直线l ⊥AO 于H ,∴4590∠=∠=︒ ∴67∠=∠∴AN AC =∴NH CH =∴AH 是线段NC 的中垂线∴DC DN =∴98∠=∠∴AND ACB ∠=∠∵3AND B ∠=∠+∠,2ACB B ∠=∠,∴3∠=∠B∴DN BN =∴BN DC = ……………………………………………………………………2分(2)当M BC 是中点时,CE 和CD 之间的等量关系为2CD CE =证明:过点C 作'CN AO ⊥交AB 于'N由(1)可得'BN CD =,',AN AC AN AE ==∴43∠=∠,'NN CE =过点C 作CG ∥AB 交直线l 于点G∴42∠=∠,1B ∠=∠∴23∠=∠∴CG =∵M BC 是中点, ∴BM CM = 在△BNM 和△CGM 1,,,B BM CM NMB GMC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BNM≌△CGM∴BN CG=∴BN CE=∴''2==+=……………………………CD BN NN BN CE……………4分(3)BN、CE、CD之间的等量关系:当点M在线段BC上时,CD BN CE=+;当点M在BC的延长线上时,CD BN CE=-;当点M在CB的延长线上时,=-………………………………6分CD CE BN(阅卷说明:三种情况写对一个给1分,全对给2分) 七、选作题螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈。
2014年北京市石景山中考二模数学试卷(纯WORD版,含答案)

北京市石景山区2014年初三第二次统一练习数 学 试 卷第Ⅰ卷(共32分)一、选择题(本题共32分,每小题4分)在每个小题给出的四个备选答案中,只有一个是正确的,请将所选答案前的字母填在题后括号内. 1.5-的倒数是( ).A .5B .5C .5-D .55-2.某省去年底森林面积为2801700公顷,将2801700用科学记数法表示应为( ). A .28017×102 B .2.8017×106 C .28.017×105 D .0.28017×107 3.四张质地、大小、背面完全相同的卡片上,正面分别画有圆、矩形、等腰三角形、平行四边形四个图案.现把它们的正面向下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案是中心对称图形的概率为( ). A.14B. 12C. 34D. 1 4.关于x 的一元二次方程2(2)10x m x m +-++=有两个相等的实数根,则m 的值是( ). A .0B .8C .4±D .0或85.如图,已知△ABC 中,∠B =50°,若沿图中虚线剪去 ∠B ,则∠1+∠2 等于( ). A. 130° B. 230° C. 270° D. 310°第5题图2150°CBA6.如图是石景山当代商场地下广场到地面广场 的手扶电梯示意图.其中AB 、CD 分别表示 地下广场、地面广场电梯口处的水平线,已 知∠ABC =135°,BC 的长约是26m ,则乘电 梯从点B 到点C 上升的高度h 是( )m .A .6B .24C .33D .237.下面一组数据是10名学生测试跳绳项目的成绩(单位:个/分钟).176 180 184 180 170 176 172 164 186 180 该组数据的众数、中位数、平均数分别为( ). A .180, 180, 178 B .180, 178, 178 C .180, 178, 176.8D .178, 180, 176.88.在平面直角坐标系xOy 中,矩形ABCD 的位置如图1所示,点A 的坐标为)0,2( ,点B 的坐标为)2,0(,点D 的坐标为(-3,1).矩形ABCD 以每秒1个单位长度的速度沿x 轴正方向运动,设运动时间为x (0≤x ≤3)秒,第一象限内的图形面积为y ,则下列图象中表示y 与x 的函数关系的图象大致是( ).A B C D第6题图 图1 图2 第8题图E D CBA 第Ⅱ卷(共88分)二、填空题(本题共16分,每小题4分)9.分解因式:=-224ay ax .10.已知二次函数82++=bx x y 的图象的顶点在y 轴右侧,则b 的一个值可为___________(只需写出符合条件的一个b 的值). 11.已知(1)A m -,与)3,2(-m B 是反比例函数xky =图象上的两个点.则m 的值= .12.如图,已知直线l :y =x ,过点A 1(1,0) 作x 轴的垂线交直线l 于点B 1,以A 1 B 1为 边作正方形A 1 B 1 C 1 A 2,过点A 2作x 轴的 垂线交直线l 于点B 2,以A 2 B 2为边作正方 形A 2 B 2 C 2 A 3,…;则点A 5的坐标为 , 点C n 的坐标为 .三、解答题(本题共30分,每小题5分) 13.)112sin 60()36-︒+-解:14.解不等式组211841x x x x -≥+⎧⎨+≤-⎩.解:15.已知:如图,点C 是线段AB 的中点,CE =CD ,∠ACD =∠BCE , 求证:AE =BD .证明:C 3C 2C 1y=xB 3B 2B 1A 4A 3A 2A 1O x y第12题图16.已知当1=x 时,22ax bx +的值为2-,求当2x =时,2ax bx + 的值.解:17.已知关于x 的方程0)12()2(2=-++-k x k x .(1)求证:方程恒有两个不相等的实数根;(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直 角三角形的周长. 解:18.北京某郊区景点门票价格:成人票每张40元,学生票每张是成人票的半价.小明和小华两家人买了12张门票共花了420元,求两家人的学生和成人各有几人? 解:四、解答题(本题共20分,每小题5分) 19.如图1,在△OAB 中,∠OAB =90°,∠AOB =30°,BA =2.以OB 为边,向外作等边△OBC ,D 是OB 的中点,连接AD 并延长交OC 于E . (1)求证:四边形ABCE 是平行四边形; (2)如图2,将图1中的四边形ABCO 折叠,使点C 与点A 重合,折痕为FG ,求OG 的长.解:20.以下是根据北京市国民经济和社会发展统计公报中的相关数据,绘制的北京B 图1 图2(1)根据北京市2009--2013年生产总值年增长率,请计算出2011年北京市年生产总值是_________(结果精确到1百亿元),并补全条形统计图;(2)若从2013年以后,北京市年生产总值都按15%的年增长率增长,则请你估算,若年生产总值不低于...2009年的2倍,至少要到_________年.(填写年份) (3)在(1)的条件下,2009--2013这四年间,比上一年增长的生产总值的平均数为多少百亿元?若按此平均数增长,请你预测2014年北京地区的生产总值多少百亿元? 解:21.如图,在△ABC 中,︒=∠90BCA ,以BC 为直径的⊙O 交AB 于点P ,Q 是AC 的中点.(1)求证:直线PQ 与⊙O 相切; (2)连结PO 并延长交⊙O 于点E 、 交AC 的延长线于点F ,连结PC , 若OC =5,21tan =∠OPC , 求EF 的长. 解:ABQC22.阅读下列材料:小明同学遇到了这样一个问题:如图,M 是边长为a 的正方形ABCD 内一定点,请在图中作出两条直线(要求其中一条直线必须过点M ),使它们将正方形ABCD 的面积分割成面积相等的四个部分.小明是这样思考的:数学课曾经做过一道类似的题目.如图2,O 是边长为a 的正方形ABCD 的中心,将以点O 为顶点的直角绕点O 任意旋转, 且直角两边与BA ,CB 相交,与正方形重叠部分(即阴影部分)的面积为一个确定的值.可以类比此问题解决.(1)请你回答图2中重叠部分(即阴影部分)的面积为________; 参考小明同学的想法,解答问题: (2)请你在图3中,解决原问题(3)如图4.在四边形ABCD 中,AB ∥CD ,AB +CD =BC ,点P 是AD 的中点,如果AB =a ,CD =b ,且b >a ,那么在边BC 上存在一点Q ,使PQ 所在直线将四边形ABCD 的面积分成相等的两部分,请你画出该直线,保留作图痕迹. 解:图2 图1 图3图4五、解答题(本题共22分,第23题7分,第24题8分,第25题7分) 23. 关于x 的一元二次方程023)1(32=+++-m x m x . (1)求证:无论m 为何值时,方程总有一个根大于0;(2)若函数23)1(32+++-=m x m x y 与x 轴有且只有一个交点,求m 的 值;(3)在(2)的条件下,将函数23)1(32+++-=m x m x y 的图象沿直线2=x 翻折,得到新的函数图象G .在x y ,轴上分别有点P (t ,0),Q (0,2t ),其中0t >,当线段PQ 与函数图象G 只有一个公共点时,求t 的值.解:24.将△ABC 绕点A 顺时针旋转α得到△ADE ,DE 的延长线与BC 相交于点 F ,连接AF .(1)如图1,若BAC ∠=α=︒60,BF DF 2=,请直接写出AF 与BF 的数量 关系;(2)如图2,若BAC ∠<α=︒60,BF DF 3=,猜想线段AF 与BF 的数量关 系,并证明你的猜想;(3)如图3,若BAC ∠<α,mBF DF =(m 为常数),请直接写出BFAF的值 (用含α、m 的式子表示). 解:25.在平面直角坐标系xoy中,射线l:()0y x=≥.点A是第一象限内.....一定点,OA=射线OA与射线l的夹角为30°.射线l上有一动点P从点O出发,以每秒l匀速运动,同时x轴上有一动点Q从点O出发,以相同的速度沿x轴正方向匀速运动,设运动时间为t秒.(1)用含t的代数式表示PQ的长.(2)若当P、Q运动某一时刻时,点A恰巧在线段PQ上,求出此时的t值.(3)定义M抛物线:顶点为P,且经过Q点的抛物线叫做“M抛物线”.若当P、Q运动t秒时,将△PQA绕其某边中点旋转180°后,三个对应顶点恰好都落在“M抛物线”上,求此时t的值.解:(1)(2)(3)备用图1备用图2备用图石景山区2014初三第二次统一练习数学参考答案一、选择题(本题共8道小题,每小题4分,共32分)9.(2)(2)a x y x y +-; 10. 0b <即可,答案不唯一; 11.2m =; 12.(16,0);(12,2n n -). 三、解答题(本题共6道小题,每小题5分,共30分) 13.解: 原式1623233-+⨯+= ……………………………………………4分534+= ………………………………………………………5分 14.解:21 1 84 1 x x x x -≥+⎧⎨+≤-⎩①②,解①得:2x ≥, (2)分 解②得:3x ≥. (4)分则不等式组的解集是:3x ≥. …………………………………5分 15.证明:∵点C 是线段AB 的中点,∴AC=BC , ………………………………………………………1分 ∵∠ACD=∠BCE,∴∠ACD+∠DCE=∠BCE+∠DCE, …………………………………………2分 即∠ACE=∠BCD,在△ACE 和△BCD 中,AC BC ACE BCD CE CD ⎧=⎪∠=∠⎨⎪=⎩…………………………………3分∴△ACE ≌△BCD (SAS )……………………………………………………4分 ∴AE=BD. ………………………………………………………5分16.解:将1x =代人22ax bx +2-=中,得22-=+b a ……………………………………………2分 当2x =时,2ax bx +=42a b + ……………………………………… 3分2(2)a b =+ 4=- …………………………………………5分 17. 解:(1)证明:∵)12(4)2(2--+=∆k k2(2)40k =-+>……………………………………… 2分∴方程恒有两个不相等的实数根.(2)解:根据题意得:0)12()2(1=-++-k k 解得:2=k则原方程为:0342=+-x x解得另一个根为3. ……………………………………… 3分① 当该直角三角形的两直角边是1、3时,由勾股定理得斜边的长为:10, 该直角三角形的周长为4+10; …………………………… 4分② 当该直角三角形的直角边和斜边分别是1、3时,由勾股定理得该直角三角形的另一直角边为22,该直角三角形的周长为4+22 .…………… 5分18.解:设两家人有学生x 人,成人y 人 ……………………………………… 1分据题意:⎩⎨⎧=+=+420402012y x y x (3)分 解之:⎩⎨⎧==93y x ……………………………………… 4分答:两家人的学生有3人,成人有9人. ……………………………………… 5分四、解答题(本题共20分,每小题5分)19. (1)证明:在R t △OAB 中, D 为OB 的中点∴DO =DA∴∠DAO =∠DOA =30°, ∠EOA =90° ∴∠AEO =60°又∵△OBC 为等边三角形 ∴∠BCO =∠AEO =60°∴BC ∥AE ……………….…………………………………………….1分∵∠BAO =∠COA =90° ∴OC ∥AB∴四边形ABCE 是平行四边形. ……….…………………………………2分(2)解:在Rt △ABO 中 ∵∠OAB =90°,∠AOB =30°,AB =2∴OA =AB ·tan60° .………………………………………..3分在Rt △OAG 中,222OA OG AG +=,设OG =x ,由折叠可知:AG =GC =4x -,可得(()2224x x +=- (4)分 解得,12x = ∴OG =12……………………………………………….………………..5分20.解:(1)163(数字1分,统计图1分) ……………………………………2分(2)2015年 ………………………………………… 3分(3)解:增长的生产总值的平均数:(195122)4-÷=18.25 ∴2009—2013这四年间,比上一年增长生产总值的平均18.25百亿元……4分195+18.25=213.25预测2014年北京地区的生产总值213.25百亿元. …………………………5分 21.解:(1)证明:连结PO 、PC . 是BC ⊙O 的直径, ︒=∠∴90BPC .B则︒=∠90APC .AQ CQ = 又,.21CQ AC PQ ==∴.P C Q C P Q ∠=∠∴. OC OP = ,O C PO P C ∠=∠∴,︒=∠=∠+∠=∠+∠∴90BCA PCQ OCP CPQ OPC ,∴直线PQ 与⊙O相切(2)解:连结.CEEP 是直径,.90︒=∠∴ECP.90︒=∠+∠OCP ECO 即,90︒=∠+∠ECF ECO 又 .OPC OCP ECF ∠=∠=∠∴F F ∠=∠且△EFC ∽△.CFP .EF CF CF PF∴= 1tan ,2Rt ECP EPC ∆∠=中,.21=∴CP CE 1.2EF CF CF PF ==则 ,2EF CF =∴EF CF PF 42==∴ EF PE 3=∴.352=EF 解得 ………………………………………………………………5分22.解:答案:214a ………………………………………….1分ABQC………………………………………….3分当BQ =CD =b 时,PQ 将四边形ABCD 面积二等分. (5)24题7分,第25题8分) 23.(1)证明:()()[]0231=+--m x x ∴11=x ,231+=m x ……………………………………………1分∵011>=x∴无论m 为何值时,方程总有一个根大于0; …………………………2分(2)解:∵若函数23)1(32+++-=m x m x y 与x 轴有且只有一个交点∴29(1)4(32)0m m ∆=+-+= …………………………………………3分∴31-=m ……………………………………………4分 (3)解: 当31-=m 时,函数()22112-=+-=x x x y 依题意,沿直线2=x 翻折后的解析式为:()96322+-=-=x x x y ,图象G 如图所示.可得,()96322+-=-=x x x y 与x ,y 轴的 交点分别为()0,3,()9,0.设直线PQ 的解析式为()0≠+=k b kx y ,由()0,t P ,Q (0,2t ).∴直线PQ 的解析式为t x y 22+-=………5分 ①当线段PQ 与函数图象G 相切时,96222+-=+-x x t x ()029416=--=∆t∴25=t ②当线段PQ 经过点()9,0时,92=t∴29=t综上:当25=t 或29>t 时,线段PQ 与函数图象G 只有一个公共点.……7分24. 解:(1)BF AF =; ……………1分 (2)解:猜想:BF AF 2=.证明:在DF 上截取BF DG =,连接AG (如图). 由旋转得AB AD =, ADG ∠=ABF ∠. ∴△ADG ≌△ABF .∴AF AG =,DAG ∠=BAF ∠. ∴ GAF GAB BAF ∠=∠+∠∴60GAB DAG DAB =∠+∠=∠=︒. ∴△GAF 是等边三角形. 又∵BF DF 3=.∴BF BF DF DG DF GF AF 2=-=-==.…5分(3)BFAF 2sin21α-=m . ……………7分 25. 解:(1)由射线l解析式为()0y x =≥∴∠POQ =60°. …………………………1分 ∵P ,Q 运动速度相同∴OP OQ == ∴△OPQ 是等边三角形∴PQ = ……………………………2分 (2)由题意:(6,A ,),3P t,(),0Q解法一:代数法),3Pt,(),0Q直线PQ解析式为6y t =+ …………3分 由于 A ,P ,Q三点共线,将(6,A 代入得:GABCD EFH FE D CBAG故 66t =+∴t =…………………………………4分 解法二:几何法过点A 作AB ⊥x 轴于B则AB =在Rt △ABQ 中,∠ABQ =90°,∠AQB =60°, ∴2BQ == ……………………………3分 ∴OQ =OB +BQ =8∴t ==…………………………4分 (3)由抛物线的对称性知:抛物线经过P 、Q 、O 三点),3Pt ,(),0Q ,()0,0O不妨设:抛物线M 的解析式为()y ax x =-将),3Pt 代入可得1a t =-∴抛物线的解析式为:21y x t=-+ …………………………5分显然:△PQA 绕PQ 中点旋转180°后,三个对应顶点在抛物线上 ……………6分 设A 的对应点为A’∴四边形P AQA’是平行四边形∵),3Pt ,(),0Q ,(6,A∴('6,3A t --, ……………………………………………………7分将('6,3A t --代入抛物线21y x t=-+∴ t =或t =∴当经过t =t =PQA 绕PQ 中点旋转180°后,三个对应顶点在“M 抛物线”上. ……………………………………………………8分。
北京市各区中考二模数学几何综合题题汇总含答案
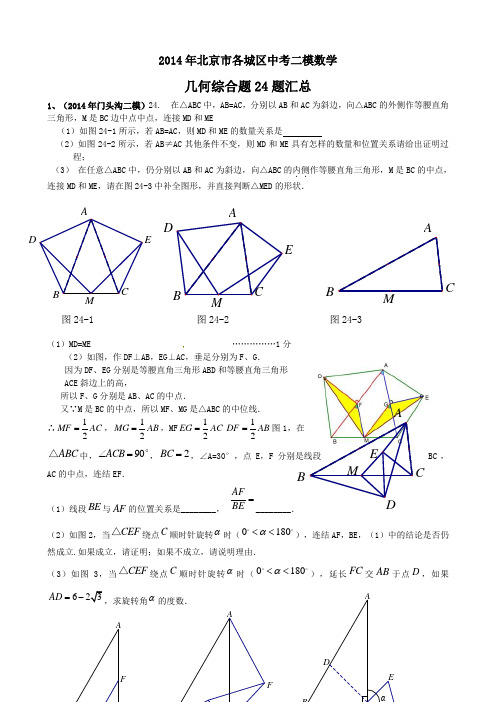
EDMBC AEDMBC AMBCAE MBC2014年北京市各城区中考二模数学几何综合题24题汇总1、(2014年门头沟二模)24. 在△ABC 中,AB=AC ,分别以AB 和AC 为斜边,向△ABC 的外侧作等腰直角三角形,M 是BC 边中点中点,连接MD 和ME(1)如图24-1所示,若AB=AC ,则MD 和ME 的数量关系是(2)如图24-2所示,若AB ≠AC 其他条件不变,则MD 和ME 具有怎样的数量和位置关系请给出证明过程;(3) 在任意△ABC 中,仍分别以AB 和AC 为斜边,向△ABC 的内侧..作等腰直角三角形,M 是BC 的中点,连接MD 和ME ,请在图24-3中补全图形,并直接判断△MED 的形状.(1)MD=ME ……………1分(2)如图,作DF ⊥AB ,EG ⊥AC ,垂足分别为F 、G .因为DF 、EG 分别是等腰直角三角形ABD 和等腰直角三角形 ACE 斜边上的高,所以F 、G 分别是AB 、AC 的中点.又∵M 是BC 的中点,所以MF 、MG 是△ABC 的中位线. ∴12MF AC =,12MG AB =,MF 12EG AC =12DF AB =图1,在ABC △中,90ACB ∠=°,2BC =,∠A=30°,点E ,F 分别是线段BC ,AC 的中点,连结EF .(1)线段BE 与AF 的位置关系是________, AFBE =________.(2)如图2,当CEF △绕点C 顺时针旋转α时(0180α<<),连结AF ,BE ,(1)中的结论是否仍然成立.如果成立,请证明;如果不成立,请说明理由.(3)如图3,当CEF △绕点C 顺时针旋转α时(0180α<<),延长FC 交AB 于点D ,如果623AD =-α的度数.DEAFAFA图24-1图24-2图24-3图2图1ED C A解:(12分 (2)答:(1)中结论仍然成立.…………………………………3分 证明:∵点E ,F 分别是线段BC ,AC 的中点,∴EC=12BC ,FC=12AC ∴12EC FC BC AC == ∵BCE ACF α∠=∠= BEC ∴∆∽AFC ∆13tan 30AF AC BE BC ∴===4分12∠=∠ , 延长BE 交AC 于点O ,交AF 于点M∵∠BOC=∠AOM ,∠1=∠2 ∴∠BCO=∠AMO=90°∴BE ⊥AF …………………………………………………5分 (3)∵∠ACB=90°,BC=2,∠A=30° ∴AB=4,∠B=60° 过点D作DH ⊥BC 于H∴DB=4(62--=∴1BH =,3DH =又∵21)3CH =-= ∴CH=BH ………………………………………………………6分∴∠HCD=45°∴∠DCA=45°18045135α∴=-=……………………………………7分 3、(2014年平谷二模)24.(1)如图1,在四边形ABCD 中,∠B=∠C=90°,E 为BC 上一点,且CE=AB ,BE=CD ,连结AE 、DE 、AD ,则△ADE 的形状是_________________________.(2)如图2,在90ABC A ∆∠=︒中,,D 、E 分别为AB 、AC 上的点,连结BE 、CD ,两线交于点P . ①当BD=AC ,CE=AD 时,在图中补全图形,猜想BPD ∠的度数并给予证明. ②当BD CEAC AD==时, BPD ∠的度数____________________.(1)等腰直角三角形 ----------------------------------------------------1分(2) 45°. ------------------------------------------------------------2分DH F EC BAαPFEAC图1F E DC BA 证明:过B 点作FB ⊥AB,且FB=AD. ∴90FBD A ∠=∠=︒,∵BD=AC ,∴△FBD ≌△DAC.∴∠FDB=∠DCA ,ED=DC∵∠DCA+∠CDA=90︒,∴∠FDB +∠CDA=90︒, ∴∠CDF=90︒,∴∠FCD=∠CFD =45︒. ∵AD=CE ,∴BF=CE∵90FBD A ∠=∠=︒,∴180FBD A ∠+∠=︒. ∴BF ∥EC.∴四边形BECF 是平行四边形. ∴BE ∥FC.∴45BPD FCD ∠=∠=︒.-------------------------------------------------6分 (3)60︒. --------------------------------------------7分4、(2014年顺义二模) 24.在△ABC 中, A B AC ,A 0,将线段 B C 绕点 B 逆时针旋转 60得到线段 B D ,再将线段BD 平移到EF ,使点E 在AB 上,点F 在AC 上.(1)如图 1,直接写出 A BD 和CFE 的度数; (2)在图1中证明: E CF ; (3)如图2,连接 C E ,判断△CEF 的形状并加以证明.(1)ABD= 15 °,CFE= 45 °.……………………………………… 2分(2)证明:连结CD 、DF .∵线段 B C 绕点 B 逆时针旋转 60得到线段 B D ,∴BD BC ,CBD 0. ∴△BCD 是等边三角形. ∴CD BD .∵线段BD 平移到EF ,∴EF ∥BD ,EF BD .∴四边形BDFE 是平行四边形,EF CD .……… 3分 ∵AB AC ,A 0, ∴ABC ACB .∴ABD ABCCBDACD . ∴DFE ABD ,AEF ABD .∴AEF ACD .………………………………………………… 4分 ∵CFE A+AEF ,∴CFD CFEDFE .∴ACFD .…………………………………………………… 5分 ∴△AEF ≌△FCD (AAS ).图2图1A DEFF E DA图2∴E CF . …………………………………………………………… 6分(3)解:△CEF 是等腰直角三角形.证明:过点E 作EG ⊥CF 于G ,∵CFE ,∴FEG . ∴EG FG . ∵A 0,AGE ,∴12EG AE =.∵E CF ,∴12EG CF =. ∴12FG CF =. ∴G 为CF 的中点.∴EG 为CF 的垂直平分线. ∴EF EC .∴CEF FEG=9.∴△CEF 是等腰直角三角形.………………………………………… 8分5、(2014年石景山二模)24.将△ABC 绕点A 顺时针旋转α得到△ADE ,DE 的延长线与BC 相交于点F ,连接AF .(1)如图1,若BAC ∠=α=︒60,BF DF 2=,请直接写出AF 与BF 的数量 关系;(2)如图2,若BAC ∠<α=︒60,BF DF 3=,猜想线段AF 与BF 的数量关 系,并证明你的猜想;(3)如图3,若BAC ∠<α,mBF DF =(m 为常数),请直接写出BFAF的值 (用含α、m 的式子表示). 解:解:( (2)解:猜想:BF AF 2=.证明:在DF 上截取BF DG =,连接AG (如图). 由旋转得AB AD =, ADG ∠=ABF ∠.∴△ADG ≌△ABF .∴AF AG =,DAG ∠=BAF ∠.∴ GAF GAB BAF ∠=∠+∠∴60GAB DAG DAB =∠+∠=∠=︒.G ABCDEFDAG∴△GAF 是等边三角形. 又∵BF DF 3=.∴BF BF DF DG DF GF AF 2=-=-==.…5分 (3)BFAF 2sin21α-=m . ……………7分6、(2014年海淀二模)24.在ABC △中,90ABC ∠=,D 为平面内一动点,AD a =,AC b =,其中a , b 为常数,且 a b <. 将ABD △沿射线BC 方向平移,得到FCE △,点A 、B 、D 的对应点分别为点F 、C 、E.连接BE .(1)如图1,若D 在ABC △内部,请在图1中画出FCE △;(2)在(1)的条件下,若AD BE ⊥,求BE 的长(用含, a b 的式子表示);(3)若=BAC α∠,当线段BE 的长度最大时,则BAD ∠的大小为__________;当线段BE 的长度最小时,则BAD ∠的大小为_______________(用含α的式子表示).图1 备用图解:(1)…………………………………………………2分(2)连接BF.∵将ABD △沿射线BC 方向平移,得到FCE △, ∴AD ∥EF, AD=EF ;AB ∥FC, AB=FC. ∵∠ABC=90°,∴四边形ABCF 为矩形.∴AC=BF. ……………………………………3分 ∵AD BE ⊥,∴EF BE ⊥. …………………………………4分 ∵AD a =,AC b =, ∴EF a =,BF b =.∴BE . ………………………………………………………………5分 (3)180α︒-; α . ……………………………………………………………7分7、(2014年西城二模)24.在△ABC ,∠BAC 为锐角,AB>AC , AD 平分∠BAC 交BC 于点D .(1)如图1,若△ABC 是等腰直角三角形,直接写出线段AC ,CD ,AB 之间的数量关系; (2)BC 的垂直平分线交AD 延长线于点E ,交BC 于点F .①如图2,若∠ABE=60°,判断AC ,CE ,AB 之间有怎样的数量关系并加以证明;②如图3,若AC AB +=,求∠BAC的度数.解:(1)AB=AC+CD ; ························ 1分 (2)①AB=AC+CE ; ························ 2分AB CAB证明:在线段AB 上截取AH=AC ,连接EH . ∵AD 平分∠BAC ∴12∠=∠. 又∵AE=AE ,∴△ACE ≌△AHE .∴CE=HE . ························ 3分 EF 垂直平分BC ,∴CE=BE . ························· 4分 又∠ABE=60°,∴△EHB 是等边三角形. ∴BH=HE .∴AB=AH+HB=AC+CE . ····················· 5分 ②在线段AB 上截取AH=AC ,连接EH ,作EM ⊥AB 于点M . 易证△ACE ≌△AHE , ∴CE=HE .∴△EHB 是等腰三角形. ∴HM=BM . ∴AC+AB=AH+AB=AM-HM+AM+MB =2AM .∵3AC AB AE +=, ∴3AM AE =. 在Rt △AEM 中,3cos AM EAM AE ∠==, ∴∠EAB=30°.∴∠CAB=2∠EAB=60°. ··················· 7分8、(2014年通州二模)23.已知:△ABD 和△CBD 关于直线BD 对称(点A 的对称点是点C ),点E 、F分别是线段BC 和线段BD 上的点,且点F 在线段EC 的垂直平分线上,连接AF 、AE ,AE 交BD 于点G .D M HFECAB(1)如图l ,求证:∠EAF =∠ABD ;(2)如图2,当AB =AD 时,M 是线段AG 上一点,连接BM 、ED 、MF ,MF 的延长线交ED 于点N ,∠MBF=12∠BAF ,AF =23AD ,请你判断线段FM 和FN 之间的数量关系,并证明你的判断是正确的.证明:(1)如图1,连接FE 、FC ∵点F 在线段EC 的垂直平分线上 ∴FE=FC∴∠FEC=∠FCE∵△ABD 和△CBD 关于直线BD 对称(点A 的对称点是点C ) ∴AB=CB ,∠ABD=∠CBD ∵在△ABF 与△CBF 中AB =CB∠ABD =∠CBD BF =BF ∴△ABF ≌△CBF (SAS ) ∴∠BAF=∠FCE ,FA=FC ∴FE=FA ,∠FEC=∠BAF ∴∠EAF=∠AEF∵∠FEC +∠BEF=180° ∴∠BAF+∠BEF=180°∵∠BAF+∠BEF+∠AFE+∠ABE=360°∴∠AFE+∠ABE=∠AFE+∠ABD+∠CBD =180° 又∵∠AFE+∠EAF+∠AEF=180° ∴∠EAF+∠AEF=∠ABD+∠CBD ∵∠ABD =∠CBD, ∠EAF=∠AEF∴∠EAF=∠ABD………………………………..(3分) (2)FM=72FN 证明: 由(1)可知∠EAF=∠ABD又∵∠AFB=∠GFA∴△AFG ∽△BFA∴∠AGF=∠BAF 又∵∠MBF=12∠BAF . GFCBDENG FDBEM图1图2G FCBDEDBAEQP DC BA∴∠MBF=12∠AGF又∵∠AGF=∠MBG+∠BMG∴∠MBG=∠BMG∴BG=MG∵AB=AD∴∠ADB=∠ABD=∠EAF 又∵∠FGA=∠AGD∴△AGF∽△DGAGF AG AFAG GD AD∴==∵AF=23AD23GF AGAG GD∴==设GF=2a AG=3a.∴GD=92a∴FD=52a∵∠CBD=∠ABD ∠ABD=∠ADB ∴∠CBD=∠ADB∴BE BG EGGD AG=23EG AGBG GD∴==54252===aaFDGFQEGQQEGQ54=4989k89k359k72MF MQFN QE∴==72(6分)9、(2014年东城二模)24.如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=4,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE ⊥AB于E,连接PQ交AB于D.(1)当∠BQD=30°时,求AP的长;(2)当运动过程中线段ED的长是否发生变化如果不变,求出线段ED的长;如果变化请说明理由;(3)在整个运动过程中,设AP为x,BD为y,求y关于x的函数关系式,并求出当△BDQ为等腰三角形时BD的值.FEQP DCBA解:(1)∵ ∠ACB=90°,AC=BC=4,设AP 为x , ∴PC=4-x ,CQ=4+x. ∵∠BQD=30°, ∴3CQ PC =. ∴43(4)x x +=-.解得843x =-.…………2分(2)当点P ,Q 运动时,线段DE 的长度不会改变.理由如下:作QF⊥AB,交直线AB 的延长线于点F , 又∵PE⊥AB 于E , ∴∠DFQ=∠AEP=90°,∵点P ,Q 做匀速运动且速度相同, ∴AP=BQ .∵△ABC 是等腰直角三角形, ∴可证 PE=QF=AE=BF. ∵∠PDE=∠QDF, ∴△PDE≌△QDF . ∴DE =DF. ∴DE=AB. 又∵AC =BC=4, ∴42AB =∴22DE =∴当点P ,Q 运动时,线段DE 的长度不会改变.…………5分 (3)∵AP =x ,∴22AE x =. ∵AB AE DE BD =++, ∵24222x y =+.即 222y x =-+(0<x <4). 当△BDQ 为等腰三角形时,x=y . ∴424x =-.…………7分 即BD 的值为424-.10、(2014年朝阳二模)24. 已知∠ABC=90°,D 是直线AB 上的点,AD=BC .(1)如图1,过点A 作AF ⊥AB ,并截取AF=BD ,连接DC 、DF 、CF ,判断△CDF 的形状并证明; (2)如图2,E 是直线BC 上的一点,直线AE 、CD 相交于点P ,且∠APD=45°,求证BD=CE .解:(1)△CDF 是等腰直角三角形 .………………1分 证明:∵∠ABC=90°,AF⊥AB, ∴∠FAD=∠DBC . ∵AD=BC,AF=BD ,∴△FAD≌△DBC .∴FD=DC .…………………………………………2分 ∠1=∠2. ∵∠1+∠3=90°, ∴∠2+∠3=90°.即∠CDF =90°. ……………………………………3分 ∴△CDF 是等腰直角三角形.(2)过点A 作AF⊥AB,并截取AF=BD ,连接DF 、CF .…………………………4分 ∵∠ABC =90°,AF⊥AB, ∴∠FAD=∠DBC .P EC 图2 C A B 图1 312CB∵AD=BC,AF=BD ,∴△FAD≌△DBC . ∴FD=DC ,∠1=∠2. ∵∠1+∠3=90°, ∴∠2+∠3=90°. 即∠CDF=90°.∴△CDF 是等腰直角三角形.………………………………………………………5分 ∴∠FCD=∠APD=45°. ∴FC∥AE.∵∠ABC =90°,AF⊥AB, ∴AF∥CE.∴四边形AFCE 是平行四边形. …………………………………………………6分 ∴AF=CE.∴BD=CE.……………………………………………………………………………7分11、(2014年密云二模)24.已知等腰Rt ABC ∆和等腰Rt AED ∆中,∠ACB=∠AED=90°,且AD=AC (1)发现:如(图1),当点E 在AB 上且点C 和点D 重合时,若点M 、N 分别是DB 、EC 的中点,则MN 与EC 的位置关系是 ,MN 与EC 的数量关系是(2)探究:若把(1)小题中的△AED 绕点A 旋转一定角度,如(图2)所示,连接BD 和EC,并连接DB 、EC 的中点M 、N,则MN 与EC 的位置关系和数量关系仍然能成立吗若成立,以顺时针旋转45°得到的图形(图3)为例给予证明数量关系成立,若不成立,请说明理由;请以逆时针旋转45°得到的图形(图4)为例给予证明位置关系成立,(1)1,2MN EC MN EC ⊥=.------------1分(2)连接EF并延长交BC 于F , ∵∠AED=∠ACB=90°(图2) (图1) (图3) A (图4)∴DE ∥BC∴∠DEM=∠AFM ,∠EDM=∠MBF 又BM=MD ∴△EDM ≌△FBM ∴BF=DE=AE,EM=FM∴1111()()2222MN FC BC BF AC AE EC ==-=-=--------------4分延长ED 到F ,连接AF 、MF ,则AF 为矩形ACFE 对角线,所以比经过EC 的中点N 且AN=NF=EN=NC. 在Rt △BDF 中,M 是BD 的中点,∠B=45° ∴FD=FB∴FM ⊥AB , ∴MN=NA=NF=NC∴点A 、C 、F 、M 都在以N 为圆心的圆上 ∴∠MNC=2∠DAC由四边形MACF 中,∠MFC=135° ∠FMA=∠ACB=90° ∴∠DAC=45°∴∠MNC=90°即MN ⊥FC-------------------7分12、(2014年延庆二模)13、(2014年房山二模) 24. 边长为2的正方形ABCD 的两顶点A 、C 分别在正方形EFGH 的两边DE 、DG 上(如图1),现将正方形ABCD 绕D 点顺时针旋转,当A 点第一次落在DF 上时停止旋转,旋转过程中,AB 边交DF 于点M ,BC 边交DG 于点N . (1)求边DA 在旋转过程中所扫过的面积;(2)旋转过程中,当MN 和AC 平行时(如图2),求正方形ABCD 旋转的度数;(3)如图3,设MBN ∆的周长为p ,在旋转正方形ABCD 的过程中,p 值是否有变化请证明你的结论. (1)∵A 点第一次落在DF 上时停止旋转, ∴DA 旋转了045.BNMDE∴DA 在旋转过程中所扫过的面积为24523602ππ⨯=......................................2分 (2)∵MN ∥AC ,∴45BMN BAC ∠=∠=︒,45BNM BCA ∠=∠=︒. ∴BMN BNM ∠=∠.∴BM BN =. 又∵BA BC =,∴AM CN =.又∵DA DC =,DAM DCN ∠=∠,∴DAM DCN ∆≅∆. ∴ADM CDN ∠=∠.∴1(90452ADM ∠=︒-︒)=22.5︒. ∴旋转过程中,当MN 和AC 平行时,正方形ABCD 旋转的度数为45︒-22.5︒=22.5︒ (5)分(3)证明:延长BA 交DE 轴于H 点,则045ADE ADM ∠=-∠,000904545CDN ADM ADM ∠=--∠=-∠,∴ADE CDN ∠=∠.又∵DA DC =,01809090DAH DCN ∠=-==∠. ∴DAH DCN ∆≅∆. ....................................................6分∴,DH DN AH CN ==.又∵045MDE MDN ∠=∠=,DM DM =,∴DMH DMN ∆≅∆. ........................................................7分∴MN MH AM AH ==+. ∴MN AM CN =+,∴4p MN BN BM AM CN BN BM AB BC =++=+++=+=.∴在旋转正方形ABCD 的过程中,p 值无变化............................8分14、(2014年昌平二模)24.【探究】如图1,在△ABC 中, D 是AB 边的中点,AE ⊥BC 于点E ,BF ⊥AC于点F ,AE ,BF 相交于点M ,连接DE ,DF. 则DE ,DF 的数量关系为 .【拓展】如图2,在△ A B C 中 ,C B = C A ,点 D 是AB 边的 中点 ,点M 在 △ A B C 的内部 ,且 ∠MBC =∠MAC . 过点M 作ME ⊥BC 于点E ,MF ⊥AC 于点F ,连接DE ,DF. 求证:DE=DF ;【推广】如图3,若将上面【拓展】中的条件“CB=CA ”变为“CB ≠CA ”,其他条件不变,试探究DE 与DF 之间的数量关系,并证明你的结论.ADBE CMFAD BECMF MABCDFE图3图2图1【探究】DE=DF. …………………………………………………………………………………1分【拓展】如图2,连接CD. ∵在△ A B C 中 ,C B = C A , ∴∠CAB=∠CBA. ∵∠MBC =∠MAC ,∴∠MAB=∠MBA. …………………………… 2分 ∴AM=BM.∵点 D 是 边 AB 的 中点 ,∴点M 在CD 上. ……………………………………………………………………… 3分 ∴CM 平分∠FCE. ∴∠FCD=∠ECD.∵ME ⊥BC 于E ,MF ⊥AC 于F , ∴MF=ME. 又∵CM=CM, ∴△CMF ≌△CME. ∴CF=CE. ∵CD=CD ,∴△CFD ≌△CED.∴DE=DF. ……………………………………………………………………………… 4分图2F MCE BD A【推广】 DE=DF.如图3,作AM 的中点G,BM 的中点H. ∵点 D 是 边 AB 的 中点 ,∴1//,.2DG BM DG BM =同理可得:1//,.2DH AM DH AM =∵ME ⊥BC 于E ,H 是BM 的中点, ∴在Rt △BEM 中, 1.2HE BM BH == ∴DG=HE. ………………………………………………………………………………… 5分 同理可得:.DH FG = ∵DG ∴∠DGM=∠DH M.∵∠MGF=2∠MAC, ∠MHE=2∠MBC, 又∵∠MBC =∠MAC , ∴∠MGF=∠MHE.∴∠DGM+∠MGF =∠DHM+∠MHE.∴∠DGF=∠DHE. ……………………………………………………………………… 6分 ∴△DHE ≌△FGD.∴DE=DF. ………………………………………………………………………………… 7分15、(2014年怀柔二模)24.已知△ABC 是等边三角形,E 是AC 边上一点,F 是BC 边延长线上一点,且CF=AE ,连接BE 、EF .(1)如图1,若E 是AC 边的中点,猜想BE 与EF 的数量关系为 .(2)如图2,若E 是线段AC 上的任意一点,其它条件不变,上述线段BE 、EF 的数量关系是否发生变化,写出你的猜想并加以证明.(3)如图3,若E 是线段AC 延长线上的任意一点,其它条件不变,上述线段BE 、EF 的数量关系是否发生变化,写出你的猜想并加以证明.解 :(1)猜想BE 与:BE=EF. …………………1分 (2)猜想BE=EF .证明:将线段BE 绕点B 顺时针旋转60°,AB EF 图AB C E F 图2 AB C E F 图3 图3H GF M CE BD A得线段BE ’,连接E ’C 、E ’E ,………………………………2分∴△EB E ’为等边三角形,∴BE=E E ’,又∵△ABC 为等边三角形,∴AB=BC ,∠ABC=∠ACB= 60°,∴∠1=∠2, ∴△ABE ≌△CB E ’(SAS ),………………………………3分∴AE=C E ’, ∠A=∠3=60°,又∵CF=AE , ∴C E ’=CF ,∵∠ACB=60°,∠3=60°,∴∠AC E ’=∠AC F=120°, ∵EC=EC∴△E C E ’≌△ECF (SAS ),………………………………4分 ∴E E ’=EF . ∴BE=EF .………………………………5分 (3)猜想BE=EF .证明:将线段BE 绕点B 顺时针旋转60°,得线段BE ’,连接E ’C 、E ’E ,∴△EB E ’为等边三角形,∴BE=E E ’, 又∵△ABC 为等边三角形,∴AB=BC ,∠ABC=∠ACB= 60°,∴∠ABE=∠CB E ’,∴△ABE ≌△CB E ’(SAS ),∴AE=C E ’, ∠A=∠B C E ’=60°, 又∵CF=AE ,∴C E ’=CF ,∵∠ACB=60°,∠B C E ’=60°,∴∠EC E ’=∠EC F=60°, ∵EC=EC∴△E E ’C ≌△EFC (SAS ),………………………………6分∴E E ’=EF .又∵BE=E E ’,∴BE=EF .………………………………7分16、(2014年大兴二模)25. 已知:E 是线段AC 上一点,AE=AB ,过点E 作直线EF ,在EF 上取一点D ,使得∠EDB=∠EAB ,联结AD.(1)若直线EF 与线段AB 相交于点P ,当∠EAB=60°时,如图1,求证:ED =AD+BD ;(2)若直线EF 与线段AB 相交于点P ,当∠EAB= α(0o ﹤α﹤90o )时,如图2,请你直接写出线段ED 、AD 、BD 之间的数量关系(用含α的式子表示);4321'F ECB A ABCE F E '(3)若直线EF 与线段AB 不相交,当∠EAB=90°时,如图3,请你补全图形,写出线段ED 、AD 、BD 之间的数量关系,并证明你的结论.(1)证明:作∠DAH=∠EAB 交DE 于点H. …………………………1分∴∠DAB=∠HAE.∵∠EAB=∠EDB ,∠APE=∠BPD , ∴∠ABD=∠AEH. ∵又AB=AE ,∴△ABD ≌△AEH. ………………2分 ∴BD=EH ,AD=AH. ∵∠DAH=∠EAB=60°, ∴△ADH 是等边三角形. ∴AD=HD. ∵ED = HD+EH∴ED =AD+BD. …………………………………………………………………3分 (2) BD AD ED +=2sin 2α ……………………5分(3)ED=BD -2AD ……………6分作∠DAH=∠EAB 交DE 于点H. ∴∠DAB=∠HAE. ∵∠EDB=∠EAB=90°,∴∠ABD+∠1=∠AEH+∠2 =90°. ∵∠1=∠2 ∴∠ABD=∠AEH.∵又AB=AE ,∴△ABD≌△AEH. ……………………………………………………7分 ∴BD=EH ,AD=AH. ∵∠DAH=∠EAB=90°, ∴△ADH 是等腰直角三角形.∵ED=EH-HD∴AD BD ED 2-=……………………………………………………8分17、(2014年燕山二模)24.如图1,已知ABC ∆是等腰直角三角形,︒=∠90BAC ,点D 是BC 的中点.作正方形DEFG ,使点A 、C 分别在DG 和DE 上,连接 AE ,BG .(1)试猜想线段BG 和AE 的数量关系是 ; (2)将正方形DEFG 绕点D 逆时针方向旋转)3600(︒≤<︒αα, ①判断(1)中的结论是否仍然成立请利用图2证明你的结论; ②若4==DE BC ,当AE 取最大值时,求AF 的值.图1 图2F GE DC A B B AC D EGF。
