第六章 轮系
机械设计基础:第六章 轮系

i 15
=
ω1 ω5
=
z2z3z4z5 z1z 2'z 3z4'
Z3:仅改变转向,惰轮
4
结论 :定轴轮系的传动比为组成该轮系的各对啮合齿
轮传动比的连乘积,其大小等于各对啮合齿轮中所有从动
轮齿数的连乘积与所有主动轮齿数的连乘积之比,即
i1k
= ω1 ωk
=
n1 nk
=
z2 Lzk z1 L zk−1
z1 z2 z3' z4'
= ω1 ω5
= i15
定轴轮系的传动比 = 组成该轮系各对齿轮传 动比的连乘积
定轴轮系的传动比
=
±
所有从动轮齿数的连乘积 所有主动轮齿数的连乘积
例2:设轮1为首轮,轮5为末轮,已知各轮齿数
为 z1,z2,…z5,求传动比i15 .
解:
i12
=
ω1 ω2
=
z2 z1
1
i 34
2 (d)
2 (e)
2、轮系的传动比
例1
i12
=
ω1 ω2
=
z2 z1
i3'4
=
ω 3' ω4
=
z4 z3'
i23
=
ω2 ω3
=
z3 z2
i4'5
=
ω 4' ω5
=
z5 z4'
i12
i• 23
i• 3'4
i• 4'5
=
ω1 ω2
ω2 ω •
3
ω 3' ω •
4
ω 4' ω •
5
=
第六章轮系解析

第六章轮系§6-1 轮系及其分类轮系是由一系列齿轮所组成的传动装置。
定义:这种由一系列齿轮组成的传动系统称为轮系。
它通常介于原动机和执行机构之间,把原动机的运动和动力传给执行机构。
工程实际中常用其实现变速、换向和大功率传动等,具有非常广泛的应用。
轮系的类型定轴轮系周转轮系混合轮系1、定轴轮系定义:组成轮系的所有齿轮几何轴线的位置在运转过程中均固定不变的轮系,称为定轴轮系,又称为普通轮系。
2、周转轮系定义:组成轮系的齿轮中至少有一个齿轮几何轴线的位置不固定,而是绕着其它定轴齿轮轴线回转的轮系,称为周转轮系。
周转轮系组成:2—行星轮1、3—中心轮H—系杆或行星架轮1与轮3轴线重合周转轮系的分类1. 根据周转轮系所具有的自由度数目不同(1)行星轮系周转轮系中,若将中心轮3(或1)固定,则整个轮系的自由度为1。
这种自由度为1的周转轮系称为行星轮系。
为了确定该轮系的运动,只需要给定轮系中一个构件以独立的运动规律即可。
(2)差动轮系周转轮系中,若中心轮1和3均不固定,则整个轮系的自由度为2。
这种自由度为2的周转轮系称为差动轮系。
为了使其具有确定的运动,需要两个原动件。
2. 根据周转轮系中基本构件的不同(1)2K-H型周转轮系单排式双排式双排式(2)3K型周转轮系具有三个中心轮的周转轮系一个周转轮系由行星轮、系杆和中心轮等几部分组成,其中,中心轮和系杆的运转轴线重合。
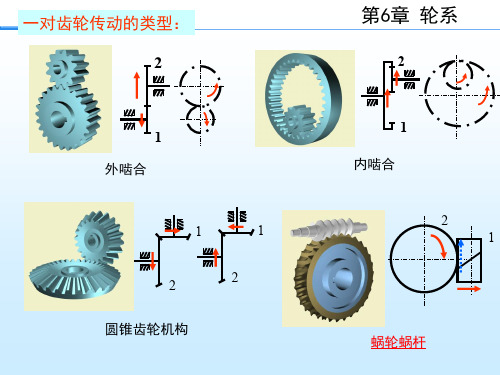
§6-2 定轴轮系的传动比1、传动比定义轮系中输入轴的角速度(或转速)与输出轴的角速度(或转速)之比,即:2、一对齿轮的传动比122112z z i ±==ωω正号:表示转向相同,用于内啮合负号:表示转向相反,用于外啮合3、传动比大小的计算举例说明传动比计算●主、从动轮转向关系的确定1、首末两轴平行,用“+”、“-”表示。
4——惰轮不改变传动比的大小,但改变轮系的转向2、首末两轴不平行用箭头表示所有主动轮齿数的乘积所有从动轮齿数的乘积定轴轮系传动比3、所有轴线都平行所有主动轮齿数的乘积所有从动轮齿数的乘积m i )1(51-==ωωm ——外啮合的次数4、所有齿轮的几何轴线不都平行,但首、尾两轮的轴线互相平行仍可在传动比的计算结果中加上"+"、"-"号来表示主、从动轮的转向关系。
第6章轮系

/
z 4 z 5 z / z 4 3
1 Ⅰ 2/ Ⅱ 2 5 Ⅴ 3 Ⅲ 4 Ⅳ 3/
z 2 z3 z 4 z5 z1 z 2 / z 3 / z 4
z 2 z3 z5 z1 z 2 / z 3 /
惰轮(介轮)
四、惰轮: 齿数z4在公式的分子和 分母上各出现一次,故不影 响传动比的大小。 这种不影响传动比数值 大小,只起改变转向作用的 齿轮称为惰轮或过桥齿轮。
4
H iGk iGk
例题1
求:nH。
3 2 2/ n3
已知:z1 15, z 2 25, z 2/ 20, z 3 60,n1 200r / min,n3 50r / min,转向如图。
解: i
H 13
n1 1
H
z 2 z3 n1 n H n3 n H z1 z 2 /
n 4; pL 4; pH 2 F 3 4 2 4 2 2
n 3; pL 3; pH 2 F 3 3 2 3 2 1
三、周转轮系传动比计算 周转轮系中,行星轮不是绕固定轴线转动,因此其传动 比不能直接用求解定轴轮系传动比的方法来计算。而是采用 转化机构的办法求解周转轮系的传动比。 基本思想是:设法把周转轮系转化为定轴轮系,然后 间接地利用定轴轮系的传动比公式求解周转轮系传动比。 采用反转法。设 ωH 为 转臂H的转速,若给整个轮系 加上一个与杆系H的速度大小 相等,方向相反的公共转速, 则杆系H的速度变为零,这时 并不影响轮系中各构件的相 对运动关系。
差动轮系F=?
行星轮系F=?
周 转 轮 系
两个中心轮都可以 动,F=?,差动轮系
两个中心轮有一个固 定,F=?,行星轮系
第六章 轮系

n4 z3 1 n3 z4 t n3 n3 tn4
齿轮2、齿轮1、齿轮3构成周转轮系。
z2 z3 n1 nH i n3 nH z1 z2 z2 z3 kn4 nH tn4 nH z1 z2
H 13
第三节 轮系的功用
1、实现远距离传动 2、获得较大的传动比 3、用作运动的合成
二、行星轮系各轮齿数和行星轮数目的选择(续) 3)装配条件 指为了使各行星轮能够均匀地装入两太阳轮之间, 行星轮的数目和各轮齿数之间所必须满足的关系。
设 k为均布的行星轮数,则相邻两行星轮之间的夹角为:
=360º /k。
(1)将第一个行星轮装于O2处; (2)固定轮3,使系杆转过 = 360º ,到达O2’ ,太阳轮1 /k 转过的角度为;
P143 例6-3
三、 复合齿轮系及其传动比
3 1 2 4 H 2'
1、复合齿轮系:既含有定轴齿轮系,又含有 行星齿轮系 , 或者含有多个行星齿轮系的 传动。
1
2
3
H
5
OH H'
2
H
2' 4
4
动比的计算方法
1)分清轮系 2)分列方程
3 2' 3
H
4
n1 z 2 n 2' nH z 3z4 1 , n2 z1 n 4 n H z 2'z 3 2 3)联立求解
1、传动比大小及方向的确定
1 z 2 i12 2 z1
1
1
1 2 (a)
2
2
(b)
1
(c)
1
2
(d)
2
(e)
例:设轮1为首轮,轮5为末轮,已知各轮齿数为 z1,z2,…z5,求传动比i15 . 1 1 z2 解: i12 2 z1 2 2' z 3 3 4 i 2' 3 3 z 2' 2´ 3 z 4 i 4' z5 i 34 4' 5 5 z4' 5 4 z 3 4´ 2' 2 , 4' 4
第6章-轮系

第6章轮系本章主要介绍轮系的分类和应用,轮系传动比的计算方法。
由单对齿轮组成的齿轮机构功能单一,不能满足工程上的复杂要求,故常采用若干对齿轮,组成轮系来完成传动要求。
按轮系运动时轴线是否固定,将其分为两大类:(1)定轴轮系轮系运动时,所有齿轮轴线都固定的轮系,称为定轴轮系,如图1-1所示。
(2)行星轮系轮系运动时,至少有一个齿轮的轴线可以绕另一根齿轮的轴线转动,这样的轮系称为行星轮系。
轴线可动的齿轮称为行星轮,如图1-2中轮2,它既绕本身的轴线自转,又绕O1或O H公转。
轮1与轮3的轴线固定不动,称为太阳轮。
图1-1图1-21.1 定轴轮系定轴轮系分为两大类:一类是所有齿轮的轴线都相互平行,称为平行轴定轴轮系(亦称平面定轴轮系);另一类轮系中有相交或交错的轴线,称之为非平行轴定轴轮系(亦称空间定轴轮系)。
轮系中,输入轴与输出轴的角速度或转速之比,称为轮系传动比。
计算传动比时,不仅要计算其数值大小,还要确定输入轴与输出轴的转向关系。
对于平行轴定轴轮系,其转向关系用正、负号表示:转向相同用正号,相反用负号。
对于非平行轴定轴轮系,各轮转动方向用箭头表示。
1.1.1 平行轴定轴轮系图1-1所示为各轴线平行的定轴轮系,输入轴与主动首轮1固联,输出轴与从动末轮5固联,所以该轮系传动比,就是输入轴与输出轴的转速比,其传动比i求法如下:(1)由图1-1所示轮系机构运动简图,可知齿轮动力传递线为:(1—2)=(2′—3)=(3′—4)=(4—5)上式括号内是一对啮合齿轮,其中轮1、2′、3′、4为主动轮,2、3、4、5为从动轮;以“—”所联两轮表示啮合,以“=”所联两轮同轴运转,它们的转速相等。
(2) 传动比i 的大小()4543321245342312354433221511i i i i z z z z z z z z n n n n n n n n n n i ⋅⋅⋅=⋅⋅⋅-=⋅⋅⋅=='''''' 上式表明,该定轴齿轮系的传动比等于各对啮合齿轮传动比的连乘积,也等于各对啮合齿轮中各从动轮齿数的连乘积与各主动轮齿数的连乘积之比,其正负号取决于轮系中外啮合齿轮的对数。
第6章 轮系

链传动 中心距变化范围 大载荷变化范围 大,平均传动比 较准确 瞬时传动比不准 确,在冲击振动 载茶下使用寿命 较低 0.95~0.98
中心距变化范围大,结 构简单,传动平稳,能 缓和冲击振动,起安全 装置作用 外廓尺寸大,轴上压力 较大,传动比不准确, 使用寿命较短 0.92~0.9——带轮小、速 度高时,效率较低。喧 传动效率也较低,平均 可取0.95
0.92~0.96(开式) 0.96~0.99(闭式) 0.4~0.45(自锁) 0.7~0.92(不自锁)
中小
中
瞬时传动比恒定,功率和速度适 应范围广,效率高,寿命长 传动比大,传动平稳,结构紧凑, 可实现自锁,但效率低 传动平稳,能自锁,增力效果好 平均传动比准确,可在高温下工 作,传动距离大,高速时有冲击 和振动 传动平稳,能保证恒定传动比 过载打滑,传动平稳,可在运转 中调节传动比 过载打滑,传动平稳,能缓冲吸 振传动距离大,不能保证定传动 比 从动件可实现各种运动,高副接 触磨损较大 结构简单,易制造,耐冲击,能 传递较大的载荷,可远距离传动
3
空间轮系【例】分析如图所示轮系传动路线。
i总=i19
传动路线:
z 2 z 4 z 6 z8 z 9 z1 z3 z5 z7 z8
i总=i19 z /z
7 8
/ 5/ 1/z n1 Ⅰ z22Ⅱ zz4 Ⅲ zz6 z4 z6 z39 z
8 9
/ Ⅳ 1 zz5zz7Ⅵ n9 z 3 z Ⅴ
二、轮系末端是螺旋传动的计算
z1 z3 z5 zk 1 n1Ph v nk Ph n1 Ph= z 2 z 4 z6 z k i
z1 z3 z5 zk 1 L Ph z 2 z 4 z6 z k
机械基础第6章轮系
第6章 轮系
2)周转轮系:至少有一个齿轮的轴线运动
3 2
O2
O1
OH
1
行星轮系
3 2
O2
O1
OH
O3
1
差动轮系
第6章 轮系 §6-2 定轴轮系及其传动比
(a) 传动比的大小
轮系的传动比:输入轴和输出轴的角速度(或转速)之比。
iab=a/b=na/nb
(b) 传动方向 确定首末两轮的转向关系。
1
n2
z 1 n4nH z2'z3
2
3)联立求解
4)注意符号
n1nH z2z3..z.k nknH z1z2'..z.k1'
3 4
2'
3
H
2'
OH
4
分清轮系的组成→分别写出各个轮系的传动比→找出轮 系之间的运动关系→联立方程解。
第6章 轮系
注意:
a、齿数比连乘积前的符号; b、已知转速应以代数量代入:即带“+”或“-” ; c、求出的转速也带有符号,“+”表示与假定的正方向相同,
4.式(5-2)只适于G、K轮与转臂H轴线平行时
例: 5
解:
求nH与n1的关系
i1H3
n1H n3H
n1 nH n3 nH
= -Z3/ Z1
第6章 轮系
注意n有符号
行星轮系
差动轮系
n3=0 n1= nH(1+ Z3/ Z1)
n1= nH(1+ Z3/ Z1) - n3 Z3/Z1
设n1为正,n3为负
→其齿数对传动比无影响
惰轮
作用: ①控制转向 ②中心距较大时可使机构紧凑
第6章 轮系讲解学习

n坯n9 分析题意可知:
1)齿坯由蜗轮9带动回转,所以
n刀64或n坯 1 n坯 n刀 64
2)滚刀回转1周,齿坯回转1个齿,即1/64周,所以
i刀坯 nn坯 刀zz12zz43zz65zz76zz98zz12zz43zz75zz98
3)由此可见
i7 5z z7 5z z1 2 z z4 3 z z9 8 n n 坯 刀 1 2 3 5 1 8 5 4 1 5 0 6 1 4 3 22 5 图 滚齿机工作台传动系统
1.平面定轴轮系传动比的计算 传动比大小的计算
i12
n1 n2
z2 z1
i23
n2 n3
z3 z2
i34
n3 n4
z4 z3
i45
n4 n5
z5 z4
i1 2 i2 3 i3 4 i4 5n n 1 2 n n 2 3 n n 3 4 n n 4 5z 2 z z2 3 z z3 4 z z4 5
解:
vn1zz2 1zz3 4ph50 5 2 6 5 8 3 7 8 35m 0/m min
Lz13p283831m 丝杠为右旋,砂轮架向右移动
图 磨床砂轮架进给机构
例:如图6-13所示轮系,齿轮1的转速为240r/min,求齿条10的 速度v10(齿轮9的模数为5mm) 。
解: 根据
d9=mz9 =5x65=325mm v10=v9 =πd9n9/(60×1000)= π×325×7.5/(60×1000) =0.128m/s v10的方向根据图示方向的判别竖直向下
定轴轮系
如图所示,黄色齿轮既自转又公转称为行星轮;绿色和白色齿轮和齿轮 的几何轴线的位置固定不动称为太阳轮,它们分别与行星轮相啮合;支持行 星轮作自转和公转的构件称为行星架或系杆。行星轮、太阳轮、行星架以及 机架组成周转轮系。一个基本周转轮系中,行星轮可有多个,太阳轮的数量 不多于两个,行星架只能有一个。
轮系

2. 根据周转轮系中基本构件的不同 (1)2K(1)2K- H型周转轮系
(2)3K型周转轮系 (2)3K型周转轮系
单排式
双排式
具有三个中心轮 的周Байду номын сангаас轮系
一个周转轮系由行星轮 系杆和 一个周转轮系由行星轮、系杆和中 行星轮、 心轮等几部分组成 其中, 等几部分组成, 心轮等几部分组成,其中,中心轮 和系杆的运转轴线重合。 和系杆的运转轴线重合。
由于ω =0,故得 由于ω3=0,故得 计算结果i 为正值,说明系杆与中心轮1 计算结果i1H为正值,说明系杆与中心轮1转向相同。
例3: 如下图所示的轮系中,已知各轮的齿数为: , 又n1=250r/min 转向如图所示。试求系杆的转速n 转向如图所示。试求系杆的转速nH的大小和方向。
解:这是一个由锥齿轮所组成的 周转轮系。先计算其转化机构的 传动比。
④实现多分路传动 机械式钟表机构就是一例 ⑤实现运动的合成与分解 利用差动轮系的双自由度特点, 可把两个运动合成为一个运动。 图示的差动轮系就常被用来进 行运动的合成。
差动轮系不仅能将两个独立地运动合成为一个运动,而且还可将 一个基本构件的主动转动,按所需比例分解成另两个基本构件的 不同运动。汽车后桥的差速器就利用了差动轮系的这一特性。
②实现变速、换向传动 ③实现结构紧凑的大功率传动 在周转轮系中,多采用多个 行星轮的结构形式,各行星 轮均匀地分布在中心轮四周, 如图所示。 这样,载荷由多对齿轮承受,可大大提高承载能力;又因多个 行星轮均匀分布,可大大改善受力状况此外,采用内啮合又有 效地利用了空间,加之其输入轴与输出轴共线,可减小径向尺 寸。因此可在结构紧凑的条件下,实现大功率传动。
双排式
§6-2 定轴轮系的传动比
第六章 轮系

1 2 3' 4' 1 i15 2 3 4 5 5
z 2 z 3 z4 z5 z1 z2 z3' z4'
图9-6
定轴轮系的传动比 组成该轮系各对齿轮传 动比的连乘积
所 有 从 动 轮 齿 数 的 连积 乘 定轴轮系的传动比 所 有 主 动 轮 齿 数 的 连积 乘
区分基本周转轮系的思路
系杆 基本周转轮系
啮合 中心轮
支 承
行星轮
啮合 中心轮
几何轴线与系杆重合
几何轴线与系杆重合
2 、复合轮系传动比的计算方法
1)分清轮系 2)分列方程
3 2' 3
H
4
n1 z 2 n 2' nH z 3z4 1 , n2 z1 n 4 n H z 2'z 3 2 n n ,n 0 3)联立求解
O1 O O11 O O O1 O1 O1 O1 OO1 1 O1
O
O
O
O
O
O
O
O
二、周转轮系的传动比的计算(反转法)
ωH
ω2=ω2-ωH ω3=ω3-ωH
O1 O
O1
ω2 O1 O ωH ω1
ω3
ω1=ω1-ωH
构件 1 2 3 H
周转轮系
图9-7
转化轮系
图9-8
1 2 3 H
1H= 1 - H 2H= 2 - H 3H= 3 - H
2 2 4
2' 4
OH
4)注意符号
z 2 z 3 ...z k n1 nH nk nH z1z 2' ...z k 1'
a、齿数比连乘积前的符号; b、已知转速应以代数量代入:即带“+”或“-” ;
机械原理 第六章 轮系

• 齿轮1、2-2’、3和H 组成一差动周转轮系。 • 其余的齿轮6、1”- 1’、5-5’、4组成一 定轴轮系。
2
H
(avi)
0
1 3
0
1 H 0
特点:① 有一个轴线不固定的 齿轮; ② 两个中心轮与系杆共轴线; ③ 一个中心轮固定为行星轮系; 中心轮都运动为差动轮系。
H
2 H
0 1 3 0 3
2
2
H
3
给整个周转轮系加一个与系杆H的角速度 大小相等、方向相反的公共角速度ωH
1 H
1
差 动 轮 系
实现大传动比的传动
例5:已知Z1=100 , Z2=101 , Z2′=100 , Z3=99 , 求iH1
H iH 1 10000 1
2.实现分路传动
单头滚刀 A B 9
齿坯 (avi) 右旋单头蜗杆 7
2 Ⅰ 1
8
3 4
6
5
机械式钟表机构
3.实现变速变向传动
y
x 1
n3Ⅲ
6 8 4
(avi)
输入轴与输出轴之间
的角速度之传动比:
i15
1 n1 5 n5
包含两个方面:大小与转向
i15
1 n1 5 n5
2
1
1 3
3' 4'
二、平面定轴轮系传动比的计算 轮系中各对啮合齿轮的传动比为:
4
5
5
z2 1 z3 z4 2 3' i12 = i3'4 = 2 = - z1 i23 = 3 = z2 4 = - z3' z5 4' i4‘5 = 5 = - z4' 且: 3 = 3 ' , 4 = 4 '
机械基础第六章轮系

定轴轮系
2.周转轮系
轮系运转时,至少有一个齿轮的几何轴线相 对于机架的位置是不固定的,而是绕另一个齿轮
的几何轴线转动 。
周转轮系
3.混合轮系 在轮系中,既有定轴轮系又有周转轮系。
二、轮系的应用特点
1.可获得很大的传动比 2.可作较远距离的传动 3.可以方便地实现变速和变向要求 4.可以实现运动的合成与分解
圆柱齿轮啮合-外啮合
转向用画箭头的方法 表示,主、从动轮转向相 反时,两箭头指向相反。
圆柱齿轮啮合-内啮合
主、从动轮转向相同 时,两箭头指向相同。
锥齿轮啮合传动
两箭头指向相背或相 向啮合点。
锥齿轮啮合传动
两箭头指向按第五章 讲过的规定标注。
对于轮系中各齿轮轴线相互平行时,其任意级从动轮 的转向可以通过在图上依次画箭头来确定,也可以数外啮 合齿轮的对数来确定,若齿轮的啮合对数是偶数,则首轮 与末轮的转向相同;若为奇数,则转向相反。
解题过程
三、轮系末端是齿条传动的计算
v?
nkπmz ?
n1
z1z3z5 ? z2 z4 z6 ?
zk ? 1 zk
πmz
L ? z1z3 z5 ? zk?1 πmz z2 z4 z6 ? zk
v ——齿轮沿齿条的移动速度,mm/min L——输入轴I每回转一周,齿轮沿齿条的移 动距离,mm
本章小结
第六章 轮系
§6-1 轮系分类及其应用特点 §6-2 定轴轮系传动比计算 §6-3 定轴轮系中任意从动齿轮的转速计算
轮系应用举例
§6-1 轮系分类及其应用特点
轮系——由一系列相互啮合的齿轮和轴组成的 传动系统。
一、轮系的分类 二、轮系的应用特点
轮系ppt课件

一、任意从动齿轮的转速计算
i1k
n1 nk
zz12zz34zz56 zzkk1
(不考虑齿轮旋转方向)
nk
n1 i1k
n1zz12zz34zz56 zzk k1
.
【例4】已知:z1=26,z2=51,z3 =42, z4=29,z5 =49, z6=36,z7=56,z8=43,z9=30,z10=90, 轴Ⅰ的转速nI = 200 r/min。试求当轴Ⅲ上的三联齿轮分别与轴Ⅱ上的三个 齿轮啮合时,轴Ⅳ的三种转速。
.
【例2】如图所示轮系,已知各程
.
【 例 3】 已 知 z1=24 , z2=28 , z3=20 , z4=60 , z5=20 , z6=20,z7=28,齿轮1为主动件。分析该轮系的传动路线并 求传动比i17;若齿轮1转向已知,试判定齿轮7的转向。
.
行星轮系
中心轮——位于中 心位置且绕轴线回转的 内齿轮或外齿轮。
行星轮——同时与中 心轮和齿圈啮合,既作自 转又作公转的齿轮。
行星架——支承行星 轮的构件。
差动轮系
.
3.混合轮系
在轮系中,既有定轴轮系又有周转轮系。
.
二、轮系的应用特点
1.可获得很大的传动比 2.可作较远距离的传动 3.可以方便地实现变速和变向要求 4.可以实现运动的合成与分解
滑移齿轮变速机构
.
利用中间齿轮变向机构
.
4.可以实现运动的合成与分解
采用行星轮系,可以将两个独立的运动合成为一个 运动,或将一个运动分解为两个独立的运动。
.
§6-2 定轴轮系传动比计算
一、定轴轮系中各轮转向的判断 二、传动比 三、惰轮的应用
.
一、定轴轮系中各轮转向的判断
第六章 轮系

第六章轮系§6-1 轮系及其分类轮系是由一系列齿轮所组成的传动装置。
定义:这种由一系列齿轮组成的传动系统称为轮系。
它通常介于原动机和执行机构之间,把原动机的运动和动力传给执行机构。
工程实际中常用其实现变速、换向和大功率传动等,具有非常广泛的应用。
轮系的类型定轴轮系周转轮系混合轮系1、定轴轮系定义:组成轮系的所有齿轮几何轴线的位置在运转过程中均固定不变的轮系,称为定轴轮系,又称为普通轮系。
2、周转轮系定义:组成轮系的齿轮中至少有一个齿轮几何轴线的位置不固定,而是绕着其它定轴齿轮轴线回转的轮系,称为周转轮系。
周转轮系组成:2—行星轮1、3—中心轮H—系杆或行星架轮1与轮3轴线重合周转轮系的分类1. 根据周转轮系所具有的自由度数目不同(1)行星轮系周转轮系中,若将中心轮3(或1)固定,则整个轮系的自由度为1。
这种自由度为1的周转轮系称为行星轮系。
为了确定该轮系的运动,只需要给定轮系中一个构件以独立的运动规律即可。
(2)差动轮系周转轮系中,若中心轮1和3均不固定,则整个轮系的自由度为2。
这种自由度为2的周转轮系称为差动轮系。
为了使其具有确定的运动,需要两个原动件。
2. 根据周转轮系中基本构件的不同(1)2K-H型周转轮系单排式双排式双排式(2)3K型周转轮系具有三个中心轮的周转轮系一个周转轮系由行星轮、系杆和中心轮等几部分组成,其中,中心轮和系杆的运转轴线重合。
§6-2 定轴轮系的传动比1、传动比定义轮系中输入轴的角速度(或转速)与输出轴的角速度(或转速)之比,即:2、一对齿轮的传动比122112z z i ±==ωω正号:表示转向相同,用于内啮合负号:表示转向相反,用于外啮合3、传动比大小的计算举例说明传动比计算●主、从动轮转向关系的确定1、首末两轴平行,用“+”、“-”表示。
4——惰轮不改变传动比的大小,但改变轮系的转向2、首末两轴不平行用箭头表示所有主动轮齿数的乘积所有从动轮齿数的乘积定轴轮系传动比3、所有轴线都平行所有主动轮齿数的乘积所有从动轮齿数的乘积m i )1(51-==ωωm ——外啮合的次数4、所有齿轮的几何轴线不都平行,但首、尾两轮的轴线互相平行仍可在传动比的计算结果中加上"+"、"-"号来表示主、从动轮的转向关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.首、末两轮轴线不平行:
在图上用箭头表示 首、末两轮的转向关系。 zz z i14 1 2 3 4 (首、末两轮的转向关系如图所示) 4 z1 z2 z3
图示的轮系中,已知各齿轮的齿数Z1=20, Z2=40, Z'2=15, Z3=60, Z‘3=18, Z4=18, Z7=20, 齿轮7的模数m=3mm, 蜗杆头数 为1(左旋),蜗轮齿数Z6=40。齿轮1为主动轮,转向如图所示, 转速n1=100r/min,试求齿轮7的速度和方向。
z z
从 mn
主 m n
k——外啮合齿轮对数
在图上用箭头表示 首、末两轮的转向关系,箭头同向取“+”;箭头反向取“-” 。
对于空间轮系:
i15
z z z z 1 2 3 4 5 5 z1 z2 z3 z4
传动比与齿轮2齿数无关,只对转向起作用, 齿轮2为惰轮。
H H- H
H
3 H=3- H
=0 O
1
1 H = - 3 1 1 H
1
周转轮系加上一公共角速度“-H”后,各构件的角速度: 构件 周转轮系角速度 转化轮系角速度
1
2 3
1
2 3 H
1- H = 1H 2- H = 2H
H
3- H = 3H H- H = 0
- H
O
O1 2 2 2- H
H- HH
1
H
3 H 3-
=0O
1 1- H
3
1
指给整个周转轮系加上一个“-H”的公共角速度,使系杆H变
为相对固定,从而得到假想定轴轮系。
——周转轮系的转化机构(转化轮系)
O1
H O
2
O1 3 O
-H
O1 2 2 2H = 2- H
传动比求解思路:将混合轮系分解为基本轮系,分别计算传
动比,然后根据组合方式联立求解。
求解要点:
1.分清轮系 ——首先找出其中的基本周转轮系 2.列出方程 ——分别列出基本周转轮系、定轴轮系的传动比方程 3.建立联系 ——找出运动相同的联系构件 4.联立求解
z2=(z3-z1)/2
z3z2‘=z1+z2
反方向
二.定轴轮系传动比大小的计算
1 2 i23 2 3 3 i3 4 4 i4 5 4 5
i12 z2 z1 z 3 z2 3 z4 4 z 3 z 4 5 5 z4 1 1 2 3 4 z z z z z z z i1 5 i1 2 i2 3 i3 4 i4 5 2 3 4 5 3 4 5 5 2 3 4 5 z1 z 2 z 3 z 4 z1 z 3 z 4
z z
从 mn
主 m n
2. 公式中各值均为矢量,计算时必须带“”号。
首、末两轮轴线平行,但中间一些齿轮轴线不平行: ——画虚线箭头来确定:箭头同向取“+”箭头反向取“”。
3. 如n轮固定,即n=0 ,则上式可写成:
i
H mn
m H H imH 1 即: imH 1 imn 0 H
2017年11月8日
例2:z1=z2=48,z2’=18, z3=24,
2H
w1=250 rad/s,w3= 100 rad/s,方向如 图所示。求:wH
2
1
2‘ H
3
1
H 1
3H
3
2017年11月8日
2
z1=20,z2=30, z2’=20, z3=40, z4=45, z4’=44, z5=81, z6=80 求: i16
条件有清楚的认识。
§6-1 齿轮系及其分类
一.轮系(gear train)
——由一系列齿轮组成的传动系统。
轮系应用举例
“红宝石”导弹发射快速反应装 置
仪表
二.轮系的分类
根据轮系在运转过程中各齿轮的几何轴线在空 间的相对位置关系是否变动,可以将轮系分为
定轴轮系 周转轮系 混合轮系
周转轮系传动比的一般公式为:
i
H mn
z z
从 mn
主 m n
三.注意事项
i
H mn H m H H m ( 1) k n H n
z z
从 mn
主 m n
1. m轮、n轮 及系杆H的轴线必须平行。
O1 O O1 O1 O1 O1
iH 1
1 n1 10000 nH
nH 10000 轮 1 转 1 转,其转向 n1 与系杆的转向相同。
当系杆转10000转时,
若将z3由99改为100,则
i1 H 1 i
H 13
z1=100 z2=101 z2=100 z3=99
iH 1
z 1 =100 z 2 =101 z2=100 z 3 =100
2 ‘
5 4
6
1
4 ‘ H
3
2017年11月8日
在图示的轮系中,已知各轮齿数为Z1=20,Z2=34,Z3=18, Z4=36,Z5=78, Z7=26,试求Z6转动比i1H
第6章 轮系
LOGO
第六章 轮系
本章教学内容
◆轮系的类型 ◆ 轮系的传动比
本章重点 周转轮系及复合轮系传动比的计算 本章难点 1. 周转轮系传动比计算中 的符号问题; 2. 混合轮系中基本轮系的 区别。
◆ 轮系的功用
本章基本要求 能正确划分轮系, 能计算定轴轮系、周转轮系、复合
轮系的传动比;
对轮系的主要功用有清楚的了解; 对确定行星轮系各齿轮齿数的四个
(2)根据基本构件的组成分:
2K-H型——有2个中心轮 3K型——有3个中心轮
3.混合轮系 (Composite gear train)
——由定轴—动轴或多个动轴轮系组成的轮系
3 H 1 2 2' 4
§6-2 定轴轮系及其传动比
轮系的传动比——输入轴与输出轴的角速度(或转速)之比,即: 大小 m imn n 转向
nH 100 n1
z2 z3 n1 101 100 1 1 1 z1 z2' 100 100 100 nH
复合轮系的传动比
3 H 1 2' 4 定轴轮系 周转轮系 2
定轴轮系
周转轮系
前面所介绍的2K-H型周转轮系,称为基本周转轮系(Elementary epicyclic gear train),通过一次反转可以得到一个定轴轮系(转化机构)。而对 于既包含定轴轮系又包含基本周转轮系的复合轮系 (Combined gear train), 不能通过一次反转得到一个定轴轮系。
一.一对齿轮的传动比
1. 大小
i12
1 z2 2 z1
2. 转向
圆柱 齿轮 空间 齿轮 外啮合——“-” 内啮合——“+”
1 1
2
2
圆锥齿轮传动
蜗杆蜗轮传动
——在图上以箭头表示
空间 齿轮
圆锥齿轮传动 蜗杆蜗轮传动
——在图上以箭头表示 左 旋 蜗 杆 用 左 手
1 2
2 1
右 2 旋 蜗 1 杆 用 四指为蜗杆转向,拇指为蜗杆相对于涡轮 右 前进的方向 手 涡轮相对于蜗杆的方向与此相反,为拇指
(1)
轮系的传动比
i1H 10
例1:z1=28,z2=18, z2’=24,z3=70,求: i1H
z2 z3 1H 1 H i H 3 3 H z1 z2
H 13
18 70 1.875 28 24
1 i1H 1 1.875 2.875 H
结论
定轴轮系的传动比 (imn )
z z
从 主
m m n所有从动轮齿数的乘积 n m n所有主动轮齿数的乘积
三.首、末两轮转向关系的确定
1.首、末两轮轴线平行:
对于平面轮系:
imn
m ( 1) k n
定轴轮系 周转轮系
n1 2 n 2
(1)
周转轮系部分
i2H 4 n2 n H z 4 n4 n H z 2
i
H 2 4
n2 n H z4 n4 n H z 2 n2 n H 4 nH
z1=20 z3=30
H
z4=80
由 n 4 0 , n 2 n 2 , z 2 2 0 , z 4 8 0
z2=40
z2=20
n2 5 nH
(2)
3)将(1)、(2)联立求解
n1 2n2 10n H
n1 2 n 2
i1 H n1 10 nH
§6-3 周转轮系及其传动比
一.周转轮系传动比计算的基本思路
周转轮系传动比不能直接计算,可以利用相对运动原理,将周 转轮系转化为假想的定轴轮系,然后利用定轴轮系传动比的计 算公式计算周转轮系传动比。 ——反转法或转化机构法
关键:设法使系杆H 固定不动,将周转轮系转化为定轴轮系。
O1 H O
2
O1 3
1. 定轴轮系(Ordinary gear train)
各齿轮轴线的位置都相对机架固定不动的齿轮传动系统。
组成
圆柱齿轮 圆锥齿轮 蜗轮蜗杆
2. 周转轮系 (Planetary gear train)
至少有一个齿轮的轴线(位置不固定)绕另一齿轮的轴线 转动的齿轮传动系统。
周转轮系的组成:
太阳轮(Sun gears)——周转轮系中轴线位置固定不动的齿轮 行星轮(Planet gears)——周转轮系中轴线不固定的齿轮 系杆H(行星架)(Planet carrier)——支撑行星轮的构件
