清华大学中学生标准学术能力诊断性测试2020届高三5月诊断考试理科综合试卷及答案
中学生标准学术能力诊断性测试理科综合试卷及答案(2020年5月)

2.双脱氧核苷三磷酸(ddNTP)属于非天然核苷酸,是桑格-库森法测定 DNA 序列的底物。ddNTP 与脱氧核苷三磷酸(dNTP)的结构如下图所示,根据所学知识判断下列选项错误的是
B.常温下,46g 的 NO2 和 N2O4 混合气体中含有的氮原子数为 NA
C.标准状况下,22.4L C3H6 分子中含有 NA 个碳碳双键 D.100mL0.1 mol·L−1CH3COONa 溶液中阴离子总数大于 0.01NA
10.下列实验操作及现象和结论均正确的是
实验操作
实验及现象
结论
A
取某 NaHSO3 溶液少量于试管 中,加入 BaCl2 溶液
加入 CCl4 振荡,静置
层溶液的棕黄色变浅
的氧化性
11.向 10mL 0.2mol·L−1 的 KIO3 溶液中逐渐加入 NaHSO3 粉末,生成的 I2 的物质的量随所加 NaHSO3
第 3 页 共 16 页
的物质的量变化如右图所示,下列说法不正确的是 A.A 点对应的 I2 的物质的量为 1.0×10−3mol B.0a:ab=5:1 C.当溶液中的 n(I2)=5×10−4 mol 时,加入 NaHSO3 的物质的
中学生标准学术能力诊断性测试 2020 年 5 月测试 理科综合试卷(一卷)
3.细胞自噬有助于人类更好地了解细胞如何实现自身的循环利用,帮助细胞适应饥饿和应对感染等 不良环境。下图表示细胞自噬作用的机理,请分析下列选项错误的是
本试卷共 300 分,考试时间 150 分钟。
可能用到的相对原子质量:H 1 O 16 C 12 N 14 Fe 56 Cr 52 S 32 I 127 Ba 137 一、选择题:本题共 13 小题,每小题 6 分,共 78 分。在每小题给出的四个选项中,只有一项是符合
THUSSAT中学生标准学术能力测试诊断性测试2020年5月测试测试清华大学理科综合一卷试题生物答案

暂时未被利用的能量
案 答 考
术 学
参准
标
生
学
中
32.(11 分,除标注外每空 1 分)
答案:
(1)染色体结构变异(染色体缺失) 用光学显微镜观察该植株分裂期(联会时期)细胞的装片
(2)让甲植株自交产生种子,种植后观察统计后代植株的产量 若子代全是高产植株,D 基因在 7 号正常染色体上 若子代高产植株:低产植株为 2:1,D 基因在 7 号异常染色体上
案 答 考
术 学
参准
标
生
学
中
中学生标准学术能力诊断性测试 2020 年 5 月测试
理科综合-生物参考答案(一卷)
一、选择题:本题共 13 小题,每小题 6 分。
1
2
3
4
5
6
BDDBDA
三、非选择题: (一)必考题
29.(10 分,除标注外每空 1 分)
答案:
(1)是否有成形的细胞核(是否有以核膜为界限的细胞核)
变,虾青素含量最高所对应的浓度即为最适 NaCl 浓度。(2 分)
30.(9 分,除标注外每空 1 分)
答案:
(1)减少 (突触小泡内)神经递质以胞吐形式释放(到突触间隙),Aβ 积累导致线粒体 膜损伤无法提供能量,神经纤维膜损伤无法正常胞吐释放神经递质 (2 分)
(2)大脑 (海马区) 低级中枢要受到高级中枢的调控 (3)通过促进小鼠脑细胞中 PSI 基因的表达,增加了 Aβ的含量 促进 Bax 基因表达,抑
导入重组质粒的受体细胞,蓝色菌落的没有导入重组细胞
或: 若子代无低产植株,D 基因在 7 号正常染色体上 若子代出现低产植株,D 基因在 7 号异常染色体上
(2 分) (2 分) (2 分) (2 分) (2 分) (2 分)
2020届清华大学中学生标准学术能力诊断性测试高三5月测试数学(理)试题(一卷)(解析版)

中学生标准学术能力诊断性测试2020年5月测试理科数学试卷(一卷)本试卷共150分,考试时间120分钟.一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合{}2log (2)0A x x =->,{}245,B y y xx x A ==-+∈,则A B =U ( )A.[)3,+∞B.[)2,+∞ C.()2,+∞D.()3,+∞【答案】C 【分析】先解对数不等式求出集合A ,再根据二次函数的单调性求出集合B ,然后根据并集的定义求解即可.【详解】解:∵2log (2)0x ->, ∴21x ->,即3x >, ∴()3,A =+∞,∴()2245212y x x x =-+=-+>, ∴()2,B =+∞,∴A B =U ()2,+∞,故选:C .【点睛】本题主要考查集合的并集运算,考查对数不等式的解法,考查二次函数的值域,属于基础题. 2.在复平面内,复数231ii+-的虚部为( )C. D. 【答案】B 【分析】根据复数代数形式的除法运算和复数的模先化简该复数,再根据虚部的定义得出结论.【详解】解:∵)()()231111122ii i i i i i ++===+---+,∴复数231i i +-的虚部为,故选:B .【点睛】本题主要考查复数代数形式的除法运算,考查复数的模和虚部的定义,属于基础题.3.已知单位向量a r ,br满足22a b a b +=-r r r r ,则()()3a b a b -⋅+=r rr r ( )A. 1B. 2C. 3D. 4【答案】B 【分析】由22a b a b +=-r r r r 可得0a b ⋅=r r ,再根据平面向量的数量积的定义即可求出答案. 【详解】解:∵22a b a b +=-r r r r ,∴()()2222a ba b+=-r r r r ,化简得0a b ⋅=r r ,∵1a =r,1=r b ,∴()()223322a b a b a b a b -⋅+=-+⋅=r r r r rr r r ,故选:B .【点睛】本题主要考查平面向量数量积的定义及其应用,属于基础题.4.下列程序框图的算法思想源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入16a =,10b =,则程序中需要做减法的次数为( )A. 6B. 5C. 4D. 3【答案】C 【分析】由循环结构的特点,先判断,再执行,分别计算出当前的,a b 的值,即可得到结论. 【详解】解:由16a =,10b =,满足a b ¹,满足a b >,则16106a =-=; 满足a b ¹,不满足a b >,则1064b =-=; 满足a b ¹,满足a b >,则642a =-=; 满足a b ¹,不满足a b >,则422b =-=;不满足a b ¹,则输出2a =; 则程序中需要做减法的次数为4, 故选:C .【点睛】本题主要考查算法和程序框图,主要考查循环结构的理解和运用,以及赋值语句的运用,属于基础题. 5.在()()252211x x x ++-的展开式中,4x 的系数为( )A. 6-B. 6C. 10D. 4【答案】A 【分析】 因为()()()()2545221111x x x x x ++-+-=,且()41+x 的展开式的通项公式为14r r r T C x +=,()51x -的展开式的通项公式为()5151kk k k T C x -+=⋅-⋅,令4r k +=,由此可求出答案.【详解】解:∵()()()()2545221111x x x x x ++-+-=,∵()41+x 的展开式的通项公式为41441rrr r rr T C x C x -+=⋅⋅=,()51x -的展开式的通项公式为()5151kkk k T C x -+=⋅-⋅,则展开式中含4x 的项需满足4r k +=,∴展开式中4x 的系数为()()20413454511C C C C ⋅-+⋅-()()342231454511C C C C +⋅-+⋅-()540451C C +⋅-54060201=-+-+-6=-,故选:A .【点睛】本题主要考查二项展开式的通项公式的应用,考查计算能力与推理能力,属于中档题. 6.在三角形ABC 中,a ,b ,c 分别为角A ,B ,C 的对边,且满足22265b c a bc +=+,则sin 2B C +⎛⎫=⎪⎝⎭( )A.2C.5【答案】D 【分析】根据余弦定理结合题意得3cos 5A =,而sin cos 22B C A +⎛⎫= ⎪⎝⎭,再根据半角公式求解即可.【详解】解:∵22265bc a bc +=+,即22265a b c bc -=+,由余弦定理可得2222cos a b c bc A =+-, ∴62cos 5bc A bc =, ∴3cos 5A =,则02A π<<, ∵ABC π++=, ∴1cos 25sin cos 222B C A A ++⎛⎫===⎪⎝⎭, 故选:D .【点睛】本题主要考查余弦定理的应用,考查半角公式的应用,属于基础题.7.函数()32x e f x x -=-的部分图像大致是( )A. B. C. D.【答案】A 【分析】根据指数函数的值域和绝对值的几何意义可知()302x e f x x -=>-,再结合导数求出函数在()2,+∞上的单调性,由此可得出答案.【详解】解:根据指数函数的值域和绝对值的几何意义可知()302x e f x x -=>-,则C 、D 错; 当2x >时,()32x x e f x --=,()()()23'32x f x x e x ---=, 由()'0f x >得3x >,由()'0f x <得23x <<,∴函数()f x 在()2,3上单调递减,在()3,+∞上单调递增,则A 对,B 错;故选:A .【点睛】本题主要考查函数图象的识别,考查利用导数研究函数的单调性,属于中档题.8.已知函数()31663x x f x x x e e -=--+-,若211011f f a a ⎛⎫⎛⎫+≤ ⎪ ⎪+-⎝⎭⎝⎭,则a 的取值范围为( ) A. (][),12,-∞-⋃+∞ B. ()1,2-C.()()1,00,1-UD.()[)1,12,-+∞U【答案】D 【分析】先判断函数的奇偶性,再求导研究函数的单调性,再结合奇偶性与单调性解不等式即可.【详解】解:∵()31663x x f x x x e e -=--+-,定义域为R ,∴()()31663x x f x x x e f x e --=+-+=-, ∴函数()f x 为奇函数,∵()21660x x f'x x e e -=---<-,∴函数()f x 在R 上单调递减,∵211011f f a a ⎛⎫⎛⎫+≤ ⎪ ⎪+-⎝⎭⎝⎭ ∴21111f f a a ⎛⎫⎛⎫≤-⎪ ⎪+-⎝⎭⎝⎭,则21111f f a a ⎛⎫⎛⎫≤ ⎪ ⎪+⎝-⎝⎭⎭, ∴21111a a ≥+-, ∴()()2011a a a +-≥-, ∴()()20110a a a -≤⎧⎨+-<⎩或()()20110a a a -≥⎧⎨+->⎩,解得11a -<<,或2a ≥, 故选:D .【点睛】本题主要考查利用函数的奇偶性与单调性解不等式,考查利用导数研究函数的单调性,考查分式不等式的解法,属于中档题. 9.已知等差数列{}n a 满足:11a =,4164a a +=,则1912222a a a⨯⨯⋅⋅⋅⨯=( )A. 382B. 192C. 162D. 762【分析】根据等差数列的性质和求和公式可得()()1194161219191922a a a a a a a ++++⋅⋅⋅+==,由此可求出答案. 【详解】解:∵等差数列{}n a 满足:11a =,4164a a +=,∴()()119416121919193822a a a a a a a ++++⋅⋅⋅+===,∴191219123822222a a a a a a ++⋅⋅⋅+⨯⨯⋅⋅⋅⨯==,故选:A .【点睛】本题主要考查等差数列的性质的应用,考查等差数列的求和公式,属于基础题.10.已知椭圆()222210x y a b a b +=>>21y x =+相切,则a =( )A. 2D. 1【答案】D 【分析】由题意可得222b c e a a b c =⎪==⎨⎪⎪-=⎪⎩,解出即可.【详解】解:由题意有,以原点为圆心以椭圆短半轴长为半径的圆的方程为222x y b +=, 直线21y x =+的一般式为210x y -+=,又椭圆22221x y a b+=,∴222b c e a a b c =⎪==⎨⎪⎪-=⎪⎩,解得1a b c ⎧⎪=⎪⎪=⎨⎪⎪=⎪⎩,【点睛】本题主要考查椭圆的标准方程及其几何性质,考查直线与圆的位置关系,属于中档题.11.设()f x 为定义于[]1,1-上的偶函数,当[]0,1x ∈时,()12f x x =-,则方程()()22xf f x =的实数解的个数为( ) A. 8 B. 6C. 4D. 2【答案】A 【分析】由题意可知,()()f f x 为偶函数,()[]0,1f x ∈,则()()()12f f x f x =-141,02134,12x x x x ⎧-≤≤⎪⎪=⎨⎪-<≤⎪⎩,画出函数()()f f x 和22x y =在[]0,1上的图象,结合图象即可得出结论.【详解】解:当[]0,1x ∈时,()112,0212121,12x x f x x x x ⎧-≤≤⎪⎪=-=⎨⎪-<≤⎪⎩,∴()[]0,1f x ∈,∴当[]0,1x ∈时,()()()12f f x f x =-()()11212,0211221,12x x x x ⎧--≤≤⎪⎪=⎨⎪--<≤⎪⎩141,02134,12x x x x ⎧-≤≤⎪⎪=⎨⎪-<≤⎪⎩114,041141,421334,24343,14x x x x x x x x ⎧-≤≤⎪⎪⎪-<≤⎪=⎨⎪-<≤⎪⎪⎪-<≤⎩,又()()()()f f x f f x -=,∴()()ff x 为偶函数,且22x y =为偶函数,画出函数()()f f x 和22x y =在[]0,1上的图象如图,由图可知,函数()()f f x 和22x y =的图象在[]0,1上有4个交点,∴由偶函数的性质可知,函数()()f f x 和22x y =的图象在[]1,0-上有4个交点,∴函数()()f f x 和22x y =的图象在[]1,1-上有8个交点,即方程()()22x f f x =的实数解的个数为8,故选:A .【点睛】本题主要考查方程的根与函数的零点以及函数图象的交点之间的关系,考查转化与化归思想,考查分类讨论思想,考查数形结合思想,考查计算能力与推理能力,属于难题. 12.已知当[]0,1x ∈时,不等式()()22cos 11sin 0x x x x θθ--+->恒成立,则θ的取值范围为( )A. π5πππ1212k k θ+<<+(k 为任意整数) B. π5πππ66k k θ+<<+(k 为任意整数) C. π5π2π2π1212k k θ+<<+(k 为任意整数) D. π5π2π2π66k k θ+<<+(k 为任意整数) 【答案】C 【分析】可设不等式左边为()f x 并化简,求出()f x 的最小值,令其大于0,得到θ的取值范围即可.【详解】解:设()()22()cos 11sin f x x x x x θθ=--+-2(1sin cos )(2sin 1)sin x x θθθθ=++-++,①若1cos sin 0θθ++=,即3222k k θππππ=++或时,原不等式不恒成立; ②若1cos sin 0θθ++≠即3222k k θππππ≠++或时,()f x Q 在[0,1]的最小值为(0)f 或()1f 或2sin 1[]2(1cos sin )f θθθ+++,∴(0)0(1)02sin 1[]02(1cos sin )f f f θθθ⎧⎪>⎪⎪>⎨⎪+⎪>++⎪⎩, ∴sin 0cos 01sin 22θθθ⎧⎪>⎪>⎨⎪⎪>⎩,解得522()1212k k k Z πππθπ+<<+∈, 故选:C .【点睛】本题主要考查不等式恒成立的问题,考查三角函数的性质,考查分类讨论思想,考查计算能力与转化能力,属于难题.二、填空题:本大题共4小题. 13.设数列{}n a 满足14a=,210a =,215n a a -=,3n ∀≥,则201920181ln ln 2a a -=______. 【答案】ln 5 【分析】由题意可得,(()21lnln 5n n a a -=,化简整理得112112ln ln ln ln ln 522n n n n a a a a ---⎛⎫⎛⎫---= ⎪ ⎪⎝⎭⎝⎭,令11ln ln 2n n n b a a +=-,可得()122ln5ln5n n b b ---=-,由此可得ln 5n b =,从而可求出答案.【详解】解:∵215n a a -=,3n ∀≥,∴当3n ≥时,(()21lnln 5n n a a -=,即2112ln ln ln 52ln 2n n na a a --+=+, ∴1212ln 2ln ln ln 52n n n a a a ---+=,∴112112ln ln ln ln ln 522n n n n a a a a ---⎛⎫⎛⎫---= ⎪ ⎪⎝⎭⎝⎭, 令11ln ln 2n n n b a a +=-,则122ln 5n n b b ---=,且1211ln ln ln 52a b a =-=,∴()122ln5ln5n n b b ---=-,又1ln 50b -=, ∴ln 5n b =,即11lnln ln 52n n a a +-=, ∴201920181ln ln ln 52a a -=, 故答案为:ln 5.【点睛】本题主要考查数列递推公式的应用,考查推理能力与计算能力,考查转化与化归思想,属于中档题.14.设实数x ,y 满足02203x y x y x -≥⎧⎪++≥⎨⎪≤⎩,则22x y +的最大值为______.【答案】73 【分析】画出不等式组表示的可行域,利用目标函数的几何意义(到原点的距离的平方)转化求解即可. 【详解】解:不等式组的图象如图:22x y +的几何意义是可行域内的点和原点的距离的平方,显然A 到原点的距离最大,由2203x y x ++=⎧⎨=⎩,解得()3,8A -,则22xy +的最大值为:96473+=,故答案为:73.【点睛】本题主要考查线性规划的应用,利用目标函数的几何意义,通过数形结合是解决本题的关键,属于基础题.15.假设抛一枚质地均匀的色子,若抛出的点数为1、2或3,我们称为“小”,否则,若抛出的点数为4、5或6,则称为“大”.独立重复地抛这枚色子两次,已知两次都为“大”,则第1次抛出的点数为6的概率______. 【答案】13【分析】由题意可知,第1次抛出的点数为4、5或6,根据相互独立的事件的概率互不影响即可求出答案. 【详解】解:由题意可知,第1次抛出的点数为4、5或6, ∵独立重复地抛这枚色子两次,两次抛掷互不影响, ∴第1次抛出的点数为6的概率13p =, 故答案为:13. 【点睛】本题主要考查独立重复试验的应用,属于基础题. 16.已知定义于实数R 上的奇函数()f x 满足()'2f x >-,则不等式()()()2132ln 312f x x x x -<-+-的解集为______. 【答案】()0,1【分析】 设()()()()2132ln 312,0g x f x x x x x =----->,则()()()2132ln 312f x x x x -<-+-()0g x ⇔<,()()''14ln 46g x f x x x x =-+-+,令()4ln 46h x x x x =-+,则()'4ln h x x =,求导后可得()()12h x h ≥=,结合题意可得()'220g x >-+=,得函数()gx 在()0+∞,上单调递增,而()10g =,由此可求出解集. 【详解】解:设()()()()2132ln 312,0g x f x x x x x =----->,则()()()2132ln 312f x x x x -<-+-()0g x ⇔<,∵()()''14ln 46g x f x x x x =-+-+,令()4ln 46h x x x x =-+,则()'4ln h x x =,由()'0hx >得1x >,由()'0h x <得01x <<,∴当1x =时,函数()h x 取得极小值同时也是最小值()12h =,∵()'12fx ->-,()2h x ≥,∴()'220gx >-+=,∴函数()g x 在()0+∞,上单调递增, 又()()()()2111132ln13120gf =-----=, ∴由()0gx <得()()1g x g <,∴01x <<, 故答案为:()0,1.【点睛】本题主要考查利用导数研究函数的单调性,考查利用函数的单调性解不等式,考查计算能力与推理能力,属于难题.三、解答题:解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:17.设ABC V 中,()cos cos cos 0C A A B +=,内角A 、B 、C 对应的对边长分别为a 、b 、c .(1)求角B 的大小; (2)若2248a c +=,求ABC V 面积S 的最大值,并求出S 取得最大值时b 的值.【答案】(1)π3B =(2)面积S 的最大值为b =【分析】(1)在三角形中,()cos cos cos cos sin sin C A B A B A B =-+=-+,结合条件可得π2sin sin 03A B ⎛⎫-= ⎪⎝⎭,由此可求出答案;(2)由2248a c +=可得2ac ≤,则11sin 222S ac B =≤⋅=,此时2a =,1c =,再由余弦定理即可求出答案.【详解】解:(1)∵()cos coscos cos sin sin C A B A B A B =-+=-+,∴()cos cos cos sin cos cos C A A B A B A B +=-π2sin sin 03A B ⎛⎫=-= ⎪⎝⎭,∵sin 0A >,0πB <<,∴πsin 03B ⎛⎫-= ⎪⎝⎭,则π3B =; (2)因a ,0c >,2248a c +=,2244a c ac +≥,故2ac ≤,于是,11sin 22222S ac B =≤⋅⋅=,∴ABC V 面积S 的最大值为2, 且当S 取得最大值时,2ac =,2a c =,可得2a =,1c =,由余弦定理,2222cos 3b a c ac B =+-=,即得b =【点睛】本题主要考查余弦定理的应用,考查三角形的面积公式,考查重要不等式的应用,属于基础题. 18.如下为简化的计划生育模型:每个家庭允许生男孩最多一个,即某一胎若为男孩,则不能再生下一胎,而女孩可以多个.为方便起见,此处约定每个家庭最多可生育3个小孩,即若第一胎或前两胎为女孩,则继续生,但若第三胎还是女孩,则不能再生了.设每一胎生男生女等可能,且各次生育相互独立.依据每个家庭最多生育一个男孩的政策以及我们对生育女孩的约定,令X 为某一家庭所生的女孩数,Y 为此家庭所生的男孩数.(1)求X ,Y 的分布列,并比较它们数学期望的大小;(2)求概率()()PX D X >,其中()D X 为X 的方差.【答案】(1)分布列见解析:EX EY =(2)14【分析】 (1)易知X 的取值为0,1,2,3,Y 的取值为0,1,利用相互独立的事件的概率公式求出相应概率,由此可得分布列,再根据数学期望的计算公式求出期望,进而比较大小;(2)结合公式()()22)(D X E X EX =-求出方差,再根据互斥事件的概率加法公式即可求出结果. 【详解】解:(1)易知X 的取值为0,1,2,3,对应取值的概率为别为:()102P X ==,()211124P X ⎛⎫=== ⎪⎝⎭,()311228P X ⎛⎫=== ⎪⎝⎭,()311328P X ⎛⎫=== ⎪⎝⎭ 即得X 的分布列如下类似地,Y 的取值为0,1,对应取值的概率分别为:()()1038P Y P X ====,()()71108P Y P Y ==-==;得Y 的分布列如下:X0 1P18 78由X ,Y 的分布列可得它们的期望分别为:11117()012324888E X =⨯+⨯+⨯+⨯=,177()01888E Y =⨯+⨯=,因此()()E X E Y =;(2)()()22222221111771(012)32488864D XE X EX ⎛⎫=-=⨯+⨯+⨯+⨯-=⎪⎝⎭, 故()()()()71123644PX D X P X P X P X ⎛⎫>=>==+== ⎪⎝⎭. 【点睛】本题主要考查离散型随机变量的分布列及数学期望、方差,考查计算能力与推理能力,属于中档题. 19.如图,已知四棱锥P ABCD -的底面ABCD 为边长为2的菱形,PA ⊥平面ABCD ,2PA =,60ABC ∠=︒,F 为棱PC 上一点,且:1:3PF FC =.(1)求证:BD AF ⊥;(2)求二面角A PD C--余弦值;(3)求三棱锥F APD -的体积V . 【答案】(1)证明见解析;(2)77(3)36【分析】(1)由PA ⊥平面ABCD 得PA BD ⊥,又底面ABCD 为菱形可得AC BD ⊥,则BD ⊥平面PAC ,从而BD AF ⊥;(2)设菱形ABCD 的对角线交点为O ,以O 为原点,分别以OC u u u r 、OD uuu r的方向为x ,y 轴建立空间直角坐标系,借助空间向量求出平面法向量的夹角,从而求出答案;(3)由图可知P ACD F ACD V V V --=-,由题意可知三棱锥P ACD -的高为3342PA =,由此可求出答案. 【详解】解:(1)因PA ⊥平面ABCD ,故PA BD ⊥, 又因底面ABCD 为菱形,故AC BD ⊥,又PA AC A =I,,PA AC ⊂平面PAC ,∴BD ⊥平面PAC , 而AF⊂平面PAC ,∴BD AF ⊥;(2)设菱形ABCD 的对角线交点为O ,因AC BD ⊥,PA ⊥平面ABCD ,以O 为原点,分别以OC u u u r 、OD uuu r的方向为x ,y 轴建立如图所示的空间直角坐标系,则()1,0,0A-,()1,0,2P -,()3,0D ,()1,0,0C ,∴()0,0,2AP =u u u r,()3,0AD =u u u r ,()2,0,2PC =-u u u r,()3,0CD =-u u u r ,∴平面APD 和平面PCD 的一个法向量分别为()13,1,0r =-r,23,1,3r =u r,∴1212127cos ,27r r r r r r ⋅===⋅⨯r r r rr r ,由图可知二面角A PD C --的平面角为锐角, ∴二面角A PD C --7(3)由图可知,P ACD F ACD V V V --=-,因:1:3PF FC =,可知三棱锥P ACD -的高为3342PA =,∴1311232326ACD VS ⎛⎫=⨯⨯-==⎪⎝⎭△. 【点睛】本题主要考查线面垂直的判定与性质,考查二面角的求法,考查三棱锥的体积的求法,考查计算能力与推理能力,属于中档题.20.已知双曲线C :()222210,0x y a b a b-=>>的离心率3e =,其左焦点1F到此双曲线渐近线的距离为(1)求双曲线C 的方程; (2)若过点()2,0D的直线l 交双曲线C 于AB 两点,且以AB 为直径的圆E 过原点O ,求圆E 的圆心到抛物线24x y =的准线的距离.【答案】(1)2218y x -=(21+1【分析】(1)由题意可得2223c e a a b c ⎧==⎪=+=⎪⎩,解出即可; (2)由题意设直线AB的方程为2x my =+,联立直线与椭圆的方程并消元,设()11,Ax y ,()22,B x y ,可得韦达定理的结论,又以AB 为直径的圆过原点O 得12120x x y y+=,代入可求得2=±m ,根据中点坐标公式求得圆E 的圆心的纵坐标,从而可求出答案.【详解】解:(1)由题意可得2223c e a a b c ⎧==⎪=+=⎪⎩, 解得13a b c =⎧⎪=⎨⎪=⎩,∴双曲线C 的方程为2218y x -=;(2)易知直线AB 与x 轴不重合,设直线AB 的方程为2x my =+,联立方程22182y x x my ⎧-=⎪⎨⎪=+⎩,可得()228132240m y my -++=, 上述方程式的判别式()232830m ∆=+>,以及2810m -≠(否则直线l 不能与双曲线交两点), 设()11,Ax y ,()22,B x y ,则1223281m y y m +=--,1222481y y m =-, 同时可得()()()2212121212284222481m x x my my m y y m y y m +=++=+++=--,以AB 为直径的圆过原点O ,知12120x x y y +=,结合2810m -≠,可知28424m +=,=m , ∴圆E 的圆心即AB中点的纵坐标为12216281y y m m +=-=-, ∵抛物线24x y =的准线方程为1y =-,∴圆E 的圆心到抛物线24x y =的准线距离为1+1. 【点睛】本题主要考查椭圆的标准方程及其几何性质,考查直线与椭圆的位置关系,考查计算能力,考查转化与化归思想,属于中档题. 21.设函数()3ln aef x x b x=-+,0x >,其中e 为欧拉数,a ,b 为未知实数,且0a >.如果()0,e 和(),e ∞均为函数()f x 的单调区间.(1)求a ; (2)若函数()()3hx f x cx =+在()()0,,e e ⋃∞上有极值点,c 为实数,求c 的取值范围.【答案】(1)3a =(2)22,0,e e ⎛⎫⎛⎫-⋃∞ ⎪ ⎪⎝⎭⎝⎭【分析】(1)令()3ln 3ln ae aeg x xx x x=-=-,0x >,求导得函数()g x 在()0,∞上单调递增,设()0g x =的唯一根为0x ,则0x 满足003ln aex x =,由题设得0x e =, 由此可得答案; (2)由题意得存在()()00,,x e e ∈⋃∞,使得()0h x '=,再分类讨论结合一元二次方程根的分布即可求出答案.【详解】解:(1)令()3ln 3ln ae aeg x xx x x=-=-,0x >, ∴()23)0aeg x x x'=+>(因0a >,0x >), ∴函数()gx 在()0,∞上单调递增,设()0gx =的唯一根为0x ,即0x 满足003ln ae x x =,(利用3ln x ,ae x的函数图象很容易确定) 于是,当()00,x x ∈时,()0g x <,而当()0,x x ∈∞时,()0g x >, 从而,当()00,x x ∈时,()3ln aef x x b x =-+, 当()0,x x ∈∞时,()3ln aef x x b x=-+, 可知,()00,x 为()f x 的单调递减区间,()0,∞x 为()f x 的单调递增区间,进而,由题设得0x e =, 因此,003ln 3x x a e==; (2)若函数()()3hx f x cx =+在()()0,,e e ⋃∞上有极值点,则易知存在()()00,,x e e ∈⋃∞,使得()0h x '=,注意到()()()22333,0,333,,e c x e x xh x e c x e x x ⎧--+∈⎪⎪=⎨⎪++∈'∞⎪⎩,①若23330e c x x --+=在()0,e 上有根,等价于20ey y c +-=在1,e ⎛⎫∞ ⎪⎝⎭上有解,由一元二次方程根的分布可得,只需满足2110e c e e⎛⎫+-< ⎪⎝⎭,解得2c e >; ②若23330e c x x ++=在(),e ∞上有根,等价于20ey y c ++=在10,e ⎛⎫⎪⎝⎭上有解, 由一元二次方程根的分布可得,只需满足0c <且2110e c e e⎛⎫++> ⎪⎝⎭,解得20c e -<<;综上,c 的取值范围为22,0,e e ⎛⎫⎛⎫-⋃∞ ⎪ ⎪⎝⎭⎝⎭. 【点睛】本题主要考查利用导数研究函数的单调性,考查分类讨论思想,考查计算能力与推理能力,属于难题. (二)选考题:共10分.请考生在第22,23题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号.[选修4-5:不等式选讲] 22.设()f x 为定义于()0,1上的函数,满足:(1)对任意()0,1x ∈,都有()0f x >;(2)对任意x ,()0,1y ∈,都有()()()()121f x f x f y f y -+≤-. 求证:()f x 在()0,1上的导数恒为零.【答案】证明见解析; 【分析】由题意可得,对任意x ,()0,1y ∈,都有()f x ,()1f x -,()f y ,()10f y ->, 由()()()()121f x f x f y f y -+≤-得()()()()()()1121f x f y f y f x f y f y -+-≤-,令1x y=-,可得()()()()()()221210f x f x f x f x +---≤,即()()()210f x f x --≤,则()()1f x f x =-,于是()()()()121f x f x f y f y -+≤-化为()()22f x f y ≤,即()()f x f y ≤,同理,亦有()()f y f x ≤,则()()f x f y =,由此得证.【详解】证明:要证明()f x 在()0,1上的导数恒为零,等价于证明()f x 在()0,1上恒为常数;因对任意()0,1x ∈,都有()0f x >,故对任意x ,()0,1y ∈,都有()f x ,()1f x -,()f y ,()10f y ->,对任意x ,()0,1y ∈,都有()()()()121f x f x f y f y -+≤-, 故有()()()()()()1121f x f y f y f x f y f y -+-≤-,因上式对于任意()0,1x ∈都成立,故令1x y =-,可得()()()()()()221210f x f x f x f x +---≤,即()()()210f x f x --≤,∴()()1f x f x =-,()0,1x ∀∈,于是,()()()()121f x f x f y f y -+≤-可化为()()22f x f y ≤,即()()f x f y ≤,x ∀,()0,1y ∈, 同理,亦有()()f y f x ≤,x ∀,()0,1y ∈, 因此,x ∀,()0,1y ∈,()()f x f y =,即得证()f x 在()0,1上恒为一个常数,∴()f x 在()0,1上的导数恒为零.【点睛】本题主要考查抽象函数的导数的应用,考查转化与化归思想,考查计算能力,属于难题. [选修2-2,推理与证明] 23.设数列{}n a 为非负实数列,且满足1220k k k a a a ++-+≥,11ki i a =≤∑,1k =,2,….求证:1220k k a a k +≤-<,1k =,2,….【答案】证明见解析; 【分析】先证10k k a a --≥,1k=,2,…,反证法,若存在某个01k ≥,使得001k k a a +<,则有从0k a 起,非负数列{}n a 单调递增,从而得出矛盾,得到假设不成立; 再证122kk a a k+-<,1k =,2,…,令10k k k b a a +=-≥,则1k k k a a b ++=,有题意可知1k k b b +≥,再由条件可得到123123k b b b kb ≥+++⋅⋅⋅+()()1122k k k k k b b +≥++⋅⋅⋅+=,由此即可证明. 【详解】证明:先证10k k a a --≥,1k=,2,…,21若存在某个01k ≥,使得001k k a a +<,则有000001122k k k k k a a a a a ++++≤-+<,即从0k a 起,非负数列{}n a 单调递增, ∴1kii a =∑将随着k 的增加而趋于正无穷,不可能永远小于等于1, 即与11k ii a =≤∑,1k =,2,…矛盾, 故10k k a a +-≥,1k=,2,…; 再证122k k a a k+-<,1k =,2,…, 令10k k k b a a +=-≥,1k =,2,…,则1k k k a a b ++=,由1220k k k a a a ++-+≥可知1k k b b +≥,1k=,2,…, 又因123411ki k i a a a a a a =≥=++++⋅⋅⋅+∑12342k b a a a a =++++⋅⋅⋅+12323k b b a a =+++⋅⋅⋅+123123k k b b b kb ka +=+++⋅⋅⋅++12323k b b b kb ≥+++⋅⋅⋅+,故有()()1231123122k k k k k b b b kb k b b +≥+++⋅⋅⋅+≥++⋅⋅⋅+=, ∴()2221k b k k k ≤<+,即证得122k k a a k +-<,1k =,2,…; 综上:1220k k a a k +≤-<,1k =,2,…. 【点睛】本题主要考查反证法证明不等式,考查数列的递推公式的应用,考查推理能力与计算能力,属于难题.。
清华大学中学生标准学术能力诊断性测试2020届高三5月测试理综试题 Word版含答案
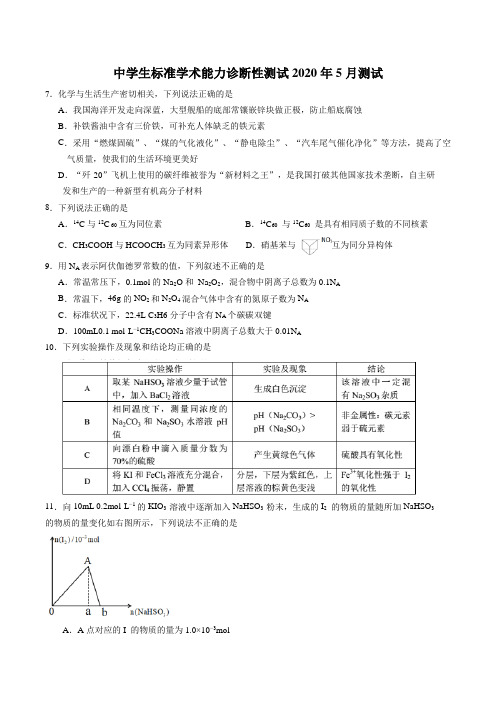
中学生标准学术能力诊断性测试2020年5月测试7.化学与生活生产密切相关,下列说法正确的是A.我国海洋开发走向深蓝,大型舰船的底部常镶嵌锌块做正极,防止船底腐蚀B.补铁酱油中含有三价铁,可补充人体缺乏的铁元素C.采用“燃煤固硫”、“煤的气化液化”、“静电除尘”、“汽车尾气催化净化”等方法,提高了空气质量,使我们的生活环境更美好D.“歼-20”飞机上使用的碳纤维被誉为“新材料之王”,是我国打破其他国家技术垄断,自主研发和生产的一种新型有机高分子材料8.下列说法正确的是A.14C与12C 60互为同位素B.14C60与12C60是具有相同质子数的不同核素C.CH3COOH与HCOOCH3互为同素异形体D.硝基苯与互为同分异构体9.用N A表示阿伏伽德罗常数的值,下列叙述不正确的是A.常温常压下,0.1mol的Na2O和Na2O2,混合物中阴离子总数为0.1N AB.常温下,46g的NO2和N2O4混合气体中含有的氮原子数为N AC.标准状况下,22.4L C3H6分子中含有N A个碳碳双键D.100mL0.1 mol·L−1CH3COONa溶液中阴离子总数大于0.01N A10.下列实验操作及现象和结论均正确的是11.向10mL 0.2mol·L−1的KIO3 溶液中逐渐加入NaHSO3 粉末,生成的I2的物质的量随所加NaHSO3的物质的量变化如右图所示,下列说法不正确的是A.A点对应的I 的物质的量为1.0×10−3molB.0a:ab=5:1C.当溶液中的n(I2)=5×10−4mol时,加入NaHSO3的物质的量可能为2.5×10−3mol或4.5×10−3mol D.由ab段反应可知,氧化性I2>HSO3−12.A、B、C、D为石墨电极,E、F分别为短周期相邻的两种活泼金属中的一种,且E能与NaOH 溶液反应。
按图接通线路,反应一段时间,当电路中通过1.0×10−3mol电子时,下列叙述正确的是A.U型管中的D端先变红,b烧杯中的溶液会变蓝B.a烧杯中最多有0.127gI2(KI足量)生成,甲池中的质量会减少0.04g(CuSO4溶液足量)C.A极产生气体的体积为5.6mL,甲池溶液的pH值为2D.E电极附近的溶液无明显现象产生13.常温下,将0.1mol·L−1的NaOH溶液逐渐加到5mL0.1mol·L−1的一元酸HA溶液中,测得混合溶液的BG(BG=-lg)与所加NaOH的体积的变化关系如图所示。
清华大学中学生标准学术能力诊断性测试2020届高三5月测试数学(理)试题(一卷)与答案

中学生标准学术能力诊断性测试2020年5月测试理科数学试卷(一卷)本试卷共150分,考试时间120分钟。
一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合{}2log (2)0A x x =->,{}245,B y y x x x A ==-+∈,则A B ⋃=( ) A .[)3,∞B .[)2,∞C .()2,∞D .()3,∞2.在复平面内,复数231ii+-的虚部为( )A B C .D . 3.已知单位向量a ,b 满足22a b a b +=-,则()()3a b a b -⋅+=( ) A .1B .2C .3D .44.下列程序框图的算法思想源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入16a =,10b =,则程序中需要做减法的次数为( )A .6B .5C .4D .35.在()()252211x x x ++-的展开式中,4x 的系数为( )A .6-B .6C .10D .46.在三角形ABC 中,a ,b ,c 分别为角A ,B ,C 的对边,且满足22265b c a bc +=+,则sin 2B C +⎛⎫=⎪⎝⎭( )A .2B C .5D7.函数()32x e f x x -=-的部分图像大致是( )A .B .C .D .8.已知函数()31663x x f x x x e e -=--+-,若211011f f a a ⎛⎫⎛⎫+≤ ⎪ ⎪+-⎝⎭⎝⎭,则a 的取值范围为( ) A .(][),12,-∞-⋃+∞ B .()1,2- C .()()1,00,1-⋃ D .()[)1,1$2,-⋃+∞9.已知等差数列{}n a 满足:11a =,4164a a +=,则1912222a a a⨯⨯⋅⋅⋅⨯=( )A .382B .192C .162D .76210.已知椭圆()222210x y a b a b +=>>21y x =+相切,则a =( )A .2BCD .111.设()f x 为定义于[]1,1-上的偶函数,当[]0,1x ∈时,()12f x x =-,则方程()()22x f f x =的实数解的个数为( ) A .8B .6C .4D .212.已知当[]0,1x ∈时,不等式()()22cos 11sin 0x x x x θθ--+->恒成立,则θ的取值范围为( ) A .π5πππ1212k k θ+<<+(k 为任意整数) B .π5πππ66k k θ+<<+(k 为任意整数) C .π5π2π2π1212k k θ+<<+(k 为任意整数) D .π5π2π2π66k k θ+<<+(k 为任意整数) 二、填空题:本大题共4小题.13.设数列{}n a 满足14a =,210a =,215n n a a -=,3n ∀≥,则201920181ln ln 2a a -=______. 14.设实数x ,y 满足02203x y x y x -≥⎧⎪++≥⎨⎪≤⎩,则22x y +的最大值为______.15.假设抛一枚质地均匀的色子,若抛出的点数为1、2或3,我们称为“小”,否则,若抛出的点数为4、5或6,则称为“大”。
2020年5月清华大学机考理综试题及答案

试管 编号
半粒种子 (10 粒)
赤霉素 (10-6g/mL)
赤霉素抑制剂 (5×10-4mol/L)
检测结果 (蓝色深浅)
A.若 X 表示 OH,该结构代表的物质 dNTP 可作为体内 DNA 分子复制的原料 B.若将 ddNTP 加到正在复制的 DNA 反应体系中,ddNTP 结合到子链后,子链的延伸会立即终
细胞中发生
4.水果玉米是鲜食玉米家族的重要成员,现将纯合的黄粒玉米植株与纯合的紫粒玉米植株杂交,F1
植株上全为黄粒,对 F1 自交的后代 F2 所结籽粒的粒色进行统计,结果为黄粒:紫粒:白粒为
422:108:35。现将 F2 的紫粒与白粒种子种在一起,让其随机传粉,每植株结实率相同。请分析下
列选项中正确的是
A.1、2 组结果可以说明小麦胚可以产生淀粉酶催化淀粉水解
B.3 组与 2、4 组结果不同,说明赤霉素可以促进无胚部分产生淀粉酶
C.1、3 组检测结果相同可能因为有胚部分的赤霉素促进淀粉酶的合成
D.根据表格可推测,小麦种子在成熟过程中赤霉素的含量逐渐增多
第 2 页 共 16 页
6.2018 年诺贝尔生理医学奖授予为癌症的免疫治疗方面作出贡献的美国科学家詹姆斯·艾利森和日
的物质的量变化如右图所示,下列说法不正确的是
本科学家本庶佑。他们的研究发现 PD-1 是活化的 T 淋巴细胞、B 淋巴细胞表面的一种免疫抑制 跨膜蛋白质分子,该蛋白质可以阻止 T 细胞全力攻击“入侵者”,起到免疫刹车的作用,研制的 PD-1 抗体(也称 PD-1 抑制剂)可以解除免疫刹车作用,是治疗一些晚期癌症的有效药物。下列 分析正确的是
中学生标准学术能力诊断性测试 2020 年 5 月测试 理科综合试卷(一卷)
2020清华测试5月-理综化学答案

中学生标准学术能力诊断性测试2020年5月测试理科综合-化学参考答案(一卷)一、选择题:本题共7小题,每小题6分,共42分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
三、非选择题:共58分。
(一)必考题:共43分。
26.(14分)答案:(一)(1)硫酸太稀,SO 2易溶于水不利于SO 2逸出;硫酸太浓,电离出的氢离子浓度减小,反应生成SO 2速率变小(2分,答对1点得1分)①干燥气体 ②控制流速,使二氧化硫与氧气的比例约为2:1 ③使两种气体均匀混合(2分,答对1点得1分)(2)排尽残留在装置中的SO 2与SO 3,使其被充分吸收,使测得的结果更准确(1分)(3)BaSO 4(1分) 80100%80233aa b ⨯+ (2分)(二)(1)HSO 3Cl+H 2O =HCl+H 2SO 4,HCl 气体在湿空气中形成盐酸小液滴(2分)(2)控制浓盐酸的流量,使其缓慢流入浓硫酸中(1分) 液体飞溅(或爆沸)(1分)(3)①吸收剩余的气体 ②防止空气中水分进入E (2分,答对1点得1分)27.(14分)答案:(1)AlO 2-+CO 2+2H 2O =Al(OH)3↓+HCO 3-(不加↓不扣分,2分)洗涤(1分) 灼烧(或煅烧)(1分)(2)V 2O 3+ Na 2CO 33+CO 2↑(不加↑不扣分,不加条件扣1分,2分)(3)VO 2++ H 2O VO 3-+2H +(反过来写也得分)(2分)(4)6(2分) 使VO 2++ H 2O VO 3-+2H +正向移动,VO 2-更多地转化为VO 3+(1分)NH 4VO 3(1分)(5)2NH 4O 5+2NH 3↑ +H 2O ↑ (不加↑不扣分,不加条件扣1分,2分)28.(15分)答案:(1)CH 3OH(l)+32O 2(g)=CO 2(g)+2H 2O(l) △H =3b+4d-a-c -a+1.5b-c+2d)2(或 (2分) (2)① Cr 2O 72-+6Fe 2++14H +=2Cr 3++6Fe 3++7H 2O (2分) ②8.4(2分)(3)①30(2分) ②小于(1分) ③大于(2分)(4)①c (Na +)﹥c (HA -)﹥c (H +)﹥c (A 2-)﹥c (OH -)(2分)② -7(a-0.1)100.2-a⨯(2分) (二)选考题:共15分。
2020届清华大学高三中学生标准学术能力诊断性测试(5月)理科综合生物试卷及解析

2020届清华大学高三中学生标准学术能力诊断性测试(5月)
理科综合生物试卷
★祝考试顺利★
一、选择题:
1.2019年诺贝尔生理医学奖授予了揭示“细胞如何感知和适应氧气”机理的三位科学家。
他们研究发现肾脏中有专门的细胞可以感受氧气水平的变化,当氧气供应不充足时,低氧诱导因子(HIF-1α)不被降解,细胞内积累的HIF-1α可促进促红细胞生成素(EPO)的合成;氧气供应充足时,HIF-1α合成后很快被降解,具体调节途径如下图所示。
请据图分析下列说法错误的是()
A. 低氧时,HIF-1α进入细胞核联合ARNT与EPO基因调控序列结合,增强EPO基因的表达,使细胞合成更多的EPO
B. 若将细胞中的脯氨酸酰羟化酶基因敲除,EPO基因的表达水平会下降,细胞合成的 EPO量减少
C. 正常条件下,人体细胞内HIF-1α含量较低,在医学上可尝试通过提高
HIF-1α的含量来治疗人类的贫血症
D. 高原反应时,EPO会刺激骨髓中的造血干细胞,使其增殖分化生成大量红细胞,提高氧气的运输能力,该调节方式属于激素调节
【答案】B
【分析】
在缺氧条件下,HIF-1α通过核孔进入细胞核内,促进EPO基因的表达,而使促红细胞生成素(EPO)增加,使得细胞适应低氧环境。
2020年5月北京市清华大学中学生标准学术能力诊断性测试THUSSAT诊断性测试理综试题物理答案

(1 分)
(二)选考题:共 15 分。请考生从 2 道物理题中任选一题作答。如果多做,则按所做的第 一题计分。
33.[物理—选修 3-3] (15 分) 答案: (1)BDE(5 分,选对一个 2 分,选对 2 个 4 分,选对 3 个 5 分,错选一个扣 3 分。最低 0
分) (2)(10 分)
第3页 共 5 页
设木板的长度为
L,则
d
−
L
=
1 2
a2t12
○13
解得 L = 3.5m
○14
小物块离开
D
点后做平抛运动,竖直方向
2R
=
1 2
gt22
○15
水平方向 x = vDt2
○16
解得 x = 4m
○17
(1 分) (1 分) (1 分)
(1 分) (1 分) (1 分) (1 分) (1 分)
由于 x L ,故小物块不能落在木板上 ○18
第2页 共 5 页
力 能 术 学 准 标
小物块通过 D 点时,mg = m vD2
③
R
从
C
点至
D
点,由机械能守恒定律得:1 2
mvC 2
=
2mgR
+
1 2
mvD2
④
解得: R = 2m ⑤
(2)由动能定理得:
(F
−
1mg)s
=
1 2
mvB 2
⑥
由牛顿第二定律得:F − 2mg = ma1
⑦
2mg − 3(M + m)g = Ma2
⑧
设小物块从 B 点运动至 C 点所需时间为 t1,则 vC = vB + a1t1
中学生标准学术能力诊断性测试2020年5月测试(全国I卷)理综化学试题 word

中学生标准学术能力诊断性测试2020年5月测试理科综合化学试卷(一卷)本试卷共300分,考试时间150分钟。
可能用到的相对原子质量:H 1 O 16 C 12 N 14 Fe 56 Cr 52 S 32 I 127 Ba 137一、选择题:本题共7小题,每小题6分,共42分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
7.化学与生活生产密切相关,下列说法正确的是A.我国海洋开发走向深蓝,大型舰船的底部常镶嵌锌块做正极,防止船底腐蚀B.补铁酱油中含有三价铁,可补充人体缺乏的铁元素C.采用“燃煤固硫”、“煤的气化液化”、“静电除尘”、“汽车尾气催化净化”等方法,提高了空气质量,使我们的生活环境更美好D.“歼-20”飞机上使用的碳纤维被誉为“新材料之王”,是我国打破其他国家技术垄断,自主研发和生产的一种新型有机高分子材料8.下列说法正确的是A.14C与12C 60互为同位素B.14C60与12C60是具有相同质子数的不同核素C.CH3COOH与HCOOCH3互为同素异形体.D.硝基苯与互为同分异构体9.用NA表示阿伏伽德罗常数的值,下列叙述不正确的是A.常温常压下,0.1mol的Na2O和Na2O2,混合物中阴离子总数为0.1N AB.常温下,46g的NO2和N2O4混合气体中含有的氮原子数为N AC.标准状况下,22.4L C3H6分子中含有N A个碳碳双键D.100mL0.1 mol·L−1CH3COONa溶液中阴离子总数大于0.01N A10.下列实验操作及现象和结论均正确的是11.向10mL 0.2mol·L−1的KIO3 溶液中逐渐加入NaHSO3 粉末,生成的I2的物质的量随所加NaHSO3的物质的量变化如右图所示,下列说法不正确的是A.A点对应的I 的物质的量为1.0×10−3molB.0a:ab=5:1C.当溶液中的n(I2)=5×10−4mol时,加入NaHSO3的物质的量可能为2.5×10−3mol或4.5×10−3mol D.由ab段反应可知,氧化性I2>HSO3−12.A、B、C、D为石墨电极,E、F分别为短周期相邻的两种活泼金属中的一种,且E能与NaOH 溶液反应。
THUSSAT中学生标准学术能力测试诊断性测试2020年5月测试测试清华大学理科综合一卷试题参考答案

或: 若子代无低产植株,D 基因在 7 号正常染色体上 若子代出现低产植株,D 基因在 7 号异常染色体上
CH3
(3)
SO3H
CH3
SO3H (2 分,每个 1 分)
SO3H
避免苯环上对位的氢原子也被硝基取代使产物不纯(或减少副产物也得分)(1 分)
(4)
(2 分)
(5)13 (2 分) (6)
(2 分,写错 1 步扣 1 分)
第2页 共2页
案 答 考
术 学
参准
标
生
学
中
中学生标准学术能力诊断性测试 2020 年 5 月测试
洗涤(1 分) 灼烧(或煅烧)(1 分)
(2)V2O3+ Na2CO3+O2 = 煅烧 2NaVO3+CO2↑(不加↑不扣分,不加条件扣 1 分,2 分) (3)VO2++ H2O VO3-+2H+(反过来写也得分)(2 分) (4)6(2 分) 使 VO2++ H2O VO3-+2H+正向移动,VO2-更多地转化为 VO3+(1 分)
100%
(2 分)
80 233
(二) (1)HSO3Cl+H2O=HCl+H2SO4,HCl 气体在湿空气中形成盐酸小液滴(2 分) (2)控制浓盐酸的流量,使其缓慢流入浓硫酸中(1 分) 液体飞溅(或爆沸)(1 分) (3)①吸收剩余的气体 ②防止空气中水分进入 E(2 分,答对 1 点得 1 分) 27.(14 分) 答案: (1)AlO2-+CO2+2H2O=Al(OH)3↓+HCO3-(不加↓不扣分,2 分)
清华大学2020届5月高三中学生标准学术能力诊断性测试 理综答案

中学生标准学术能力测试中学生标准学术能力诊断性测试2020年5月测试理科综合-物理参考答案(一卷)二、选择题:本题共8小题,每小题6分,共48分。
在每小题给出的四个选项中,第14~18题只有一项符合题目要求,第19~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
14 15 16 17 18 19 20 21B D D DC BD AD CD三、非选择题:共62分。
(一)必考题:共47分。
22 . (6分)答案:(1)1.050 (2分) (2)23 . (9分)答案:(2分) (3) (2分)(1)5409 ( 3 分)(2)实验电路如图所示,(3分)(3) (3分)24. (14分)解析:(1)设粒子不从MN 边界飞出的入射速度最小值为vmn, 对应的粒子在两个区域中做圆周运动的半径分别为r₁和r₂。
两圆心的连线与MN 的夹角为θ。
中学生标准学术能力测 试庄(x+2)sin θ=r ₂五+7cOS θ=h(1分)( 2 分 )( 1 分 )( 1 分 )( 1 分 )( 1 分 )(2)设粒子入射速度为v, 粒子在两区域中的运动半径分别为r ₁ 和 r ₂, 粒子第一次通过AB 时距离A 点为x ,由题意有(n=1,2,3 … …)x=√P²-(h-x)²可 得n<2.9则 n=1 时n=2 时25 . (18分)(1 分)( 1 分 )( 1 分 )( 1 分 )( 1 分 )( 1 分 )( 1 分 )解析:(1)由动能定理得:解得: d=8m( 1 分 )( 1 分 )②①THUSSAT中学生标准学术能力测试小物块通过D 点时,③( 1分)从C点至D 点,由机械能守恒定律得:④ ( 1 分)解得:R=2m ⑤( 1分)(2)由动能定理得:⑥( 1 分)由牛顿第二定律得:F-μmg=ma₁⑦(1分)μ₂mg- μ₃(M+m)g=Ma₂⑧( 1 分)设小物块从B点运动至C点所需时间为t,则vc=vg+at₁⑨(1分)木板到达凹槽右端时的速度v=a₂T₁⑩( 1 分)由题意可知v<vc 且a₂>0 ⑪( 1 分)解得②( 1 分)(3)当M=0.1kg时,由⑧得a₂=9m/s²设木板的长度为L, 则⑬( 1 分)解得L=3.5m ① ( 1 分)小物块离开D 点后做平抛运动,竖直方向 2 ⑮(1分)水平方向x=vo¹2 ⑩( 1 分)解得x = 4m ⑪( 1 分)由于x >L, 故小物块不能落在木板上⑩( 1 分)(二)选考题:共15分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
清华中学生标准学术能力诊断性测试2020届高三5月诊断考试
理科综合试卷
★祝考试顺利★
本试卷共300分,考试时间150分钟。
可能用到的相对原子质量:H 1 O 16 C 12 N 14 Fe 56 Cr 52 S 32 I 127 Ba 137
一、选择题:本题共13小题,每小题6分,共78分。
在每小题给出的四个选项中,只有一项是符合
题目要求的。
1.2019年诺贝尔生理医学奖授予了揭示“细胞如何感知和适应氧气”机理的三位科学家。
他们研究
发现肾脏中有专门的细胞可以感受氧气水平的变化,当氧气供应不充足时,低氧诱导因子(HIF-1α)
不被降解,细胞内积累的HIF-1α可促进促红细胞生成素(EPO)的合成;氧气供应充足时,HIF-1α
合成后很快被降解,具体调节途径如下图所示。
请据图分析下列说法错误的是
A.低氧时,HIF-1α进入细胞核联合ARNT与EPO基因调控序列结合,增强EPO基因的表达, 使细胞合成更多的EPO
B.若将细胞中的脯氨酸酰羟化酶基因敲除,EPO基因的表达水平会下降,细胞合成的EPO量减
少
C.正常条件下,人体细胞内HIF-1α的含量较低,在医学上可尝试通过提高HIF-1α的含量来治疗
人类的贫血症
D.高原反应时,EPO 会刺激骨髓中的造血干细胞,使其增殖分化生成大量红细胞,提高氧气
的
运输能力,该调节方式属于激素调节
2.双脱氧核苷三磷酸(ddNTP)属于非天然核苷酸,是桑格-库森法测定 DNA 序列的底物。
ddNTP 与脱氧核苷三磷酸(dNTP)的结构如下图所示,根据所学知识判断下列选项错误的是
A.若X表示OH,该结构代表的物质dNTP可作为体内DNA分子复制的原料
B.若将ddNTP加到正在复制的DNA反应体系中,ddNTP结合到子链后,子链的延伸会立即终止
C.ddNTP、dNTP以及磷脂分子的元素组成都为C、H、O、N、P
D.若X表示OH,碱基为A时,该物质可为细胞的各项生命活动直接提供能量
3.细胞自噬有助于人类更好地了解细胞如何实现自身的循环利用,帮助细胞适应饥饿和应对感染等
不良环境。
下图表示细胞自噬作用的机理,请分析下列选项错误的是
A.溶酶体起源于高尔基体,其中的水解酶在核糖体合成后需要转运至内质网以及高尔基体中加工
B.溶酶体膜能向其内部主动运输H,因此溶酶体的pH值低于细胞质基质中的pH值,若溶酶体+
膜发生破裂,释放的水解酶不会破坏细胞结构
C.细胞饥饿或机体感染病原体时,细胞的自噬作用会增强,该过程有利于维持机体的稳态 D.溶酶体还可以杀死侵入细胞的病原体,由于只有吞噬细胞中才有溶酶体,因此该过程只在吞噬
细胞中发生
4.水果玉米是鲜食玉米家族的重要成员,现将纯合的黄粒玉米植株与纯合的紫粒玉米植株杂交,F1。
