Origin 常用小技巧 分段线性拟合
origin8.0分层拟合问题

Origin8.0分层拟合问题
1)先输入所有的数据到origin中;再将所有的点作成散点
图,再将作的图缩小。
选择第一组数据,作散点图,可以改变一下图标的颜色,以免和后面的冲突。
再点击“图层1”右击选择隐藏图层。
2)可以直接点击快捷菜单上的“新建图层”(要么在空白处
右击,选择New layer);再右击图层,选择Layer contents,选择数据。
(如果此时出现的是一条线,而不是散点图,可以右击,选择Change plot to改为散点图),再改坐标。
注意:不同图层的坐标范围应一致。
3)分层时如果一个散点图的“图标”不见了,可以右击选择
“New Legend”
4)拟合时,选用“Fit Polynomial”拟合。
origin拟合函数

origin拟合函数Origin是一款功能强大的数据分析软件,它提供了丰富的数据分析工具来处理实验数据,其中包括曲线拟合功能。
本文将着重介绍Origin中的曲线拟合功能,包括常见的拟合函数及其应用。
一、拟合函数在Origin中,可以通过选择不同的拟合函数来拟合所需的曲线。
常见的拟合函数有线性函数、二次函数、三次函数、指数函数、对数函数、幂函数、指数增长函数、正弦函数、余弦函数等。
下面将对这些函数进行详细介绍。
1. 线性函数一元线性函数的表达式为y=a+bx,其中a和b分别为截距和斜率,x为自变量,y为因变量。
线性函数是最简单的拟合函数之一,适用于线性关系较为明显的数据。
例如,当我们在光电效应实验中测量出光电子的动能和光子的频率时,它们之间就存在着线性关系,此时可以使用线性函数来拟合数据。
2. 二次函数三次函数的表达式为y=a+bx+cx^2+dx^3,其中a、b、c和d分别为常数,x为自变量,y为因变量。
三次函数通常用于描述抛物线,这种函数在物理和工程学中经常被应用。
例如,在材料科学中可以使用三次函数来描述一个材料的弹性行为。
4. 指数函数指数函数的表达式为y=ae^(bx),其中a和b为常数,x为自变量,y为因变量。
指数函数适用于描述随时间或位置而变化的某些现象。
例如,当我们观察放射性衰变时,衰变速率随时间的变化可以使用指数函数来拟合。
8. 正弦函数正弦函数的表达式为y=a sin(bx+c),其中a、b和c为常数,x为自变量,y为因变量。
正弦函数适用于描述像周期性的变化,例如,天文学中的多个现象,如日、月、星星的运动都是可以用正弦函数表示的。
二、常见应用在实际应用中,我们可以使用Origin中的曲线拟合功能来解决各种问题。
下面列举几种常见的应用。
1. 数据分析在实验数据分析中,使用拟合函数可以帮助我们理解和预测实验数据的变化趋势。
例如,在物理实验中,我们可以使用线性函数来分析位移和时间的关系,使用指数函数来分析辐射物质的衰变过程。
用Origin软件的线性拟合和非线性曲线拟合功能处理实验数据

<
0.5,表明有95% 置信度认为可以拒绝零假
第6期
陈旭红:用 Origin 软件的线性拟合和非线性曲线拟合功能处理实验数据
89
设,也就是说可以接受拟合的参数的结果。 将相关的数据代入QV= Mm·C·ΔT,其中C为水当量,就可以求得QV:QV=- 5 541.8kJ·mol-1。 如果采用手工作图,不同的操作者处理同一组数据,得到的结果可能不同;即使由同一个操作者在不
摘 要:以物理化学实验中《 燃烧热的测定》实验为例,说明Origin软件在计算机上对实验数据进行作图、线性拟
合和非线性曲线拟合等处理而求得需要的实验参数,从而大大减少数据处理过程中产生的误差,而且方便快捷。
关键词:Origin软件;燃烧热;线性拟合;非线性曲线拟合
中图分类号:TP317
文献标识码:B
同时间处理同一组数据,其结果也不会完全一致。使用Origin软件可以克服上述问题,能够准确、快速、方 便地处理实验的数据。
参考文献:
[1] 郝红伟,施光凯. Origin6.0实例教程[M].北京:中国电力出版社,2000. [2] 夏春兰.Origin软件在物理化学实验数据处理中的应用[J].大学化学,2003,1(8 2):44- 46. [3] 复旦大学,武汉大学,中国科技大学.物理化学实验[M]. 3版.北京:高等教育出版社,2004.
0引言
提及Origin软件[1],许多人都知道它在实验数据作图上的应用。用Origin软件线性拟合和非线性曲线拟 合功能处理数据方面却很少有报道。实际上,Origin软件在线性拟合和非线性曲线拟合时,可屏蔽某些偏 差较大的数据点,以降低曲线的偏差[2],得到更为准确的结果,且方便快捷。
Origin软件有如下基本功能:①输入数据并作图。②将数据计算后作图。③数据排序。④选择需要的 数据范围作图。⑤数据点屏蔽。⑥Origin软件的线性拟合和非线性曲线拟合功能。
origin线性拟合的斜率和截距

origin线性拟合的斜率和截距
求origin线性拟合的斜率和截距,是求解一元线性回归问题的
基本步骤。
一元线性回归问题的模型可以表示为:y=ax+b,
其中a为斜率,b为截距。
要求求解origin线性拟合的斜率和截距,首先需要准备足够的
数据,即x和y的值,并将其分别放入x和y的数组中。
然后,根据x和y的值,计算出x的平均值和y的平均值,分别记为
x_mean和y_mean。
接下来,根据x和y的值,计算出x和y的方差,分别记为
x_var和y_var,以及x和y的协方差,分别记为x_cov和
y_cov。
最后,根据以上计算出的x_mean、y_mean、x_var、y_var、
x_cov和y_cov,可以计算出origin线性拟合的斜率a和截距b,其计算公式分别为:
a=x_cov/x_var
b=y_mean-a*x_mean
因此,求origin线性拟合的斜率和截距,需要准备足够的数据,并计算出x的平均值、y的平均值、x的方差、y的方差、x的
协方差和y的协方差,最后根据以上计算出的值,可以计算出origin线性拟合的斜率和截距。
Origin的使用方法汇总

Yi=β0+β1Xi+εi (i=1,2,···,n)
i,Yj)表示(X,Y)的第i个观测值,
β0 ,β1为参数,β0+β1Xi为反映统计关系直线的分量,
εi为反映在统计关系直线周围散布的随机分量, εi~N (0,σ2), εi 服从正态分布
Yi=β0+β1Xi+εi β0和β1均未知
根据样本数据 对 β 0和 β 1 进行估计
直线拟合上机练习2
2、Polynomial Fit 模型
yi 0 1 xi x
2 2 i
x i
k k i
k 9
Y A B1 X B2 X
2
Bk X
k
Fit Polynomial(多项式拟合)
步骤:
1、将x,y数据输入worksheet 2、绘制x,y的散点图 3、执行Polynomial Fit 4、结果在Results Log窗口中
fity列拟合数据residualy列剩余误差拟合图层中的所有曲线在resultlog中只显示简单的拟合结果在resultslog中显示所有的拟合结果绘制数据上下可信范围只对拟合过程中的误差参数有影响选中使用误差值作为权重如果激活的是worksheet必须选中一列y误差列如果激活的是graph图中必须有误差线绘制数据上下预期范围根据拟合公式计算的x值已知y值根据拟合公式计算的y值已知x值执行拟合指定多项式的阶数已知实验数据如0225064571335162171181935222575269929109311193413538134111944476548491551255353multipleregression多重回归bxcx1将多重回归的数据放在worksheet中2worksheet的第一列必须为y列后面的列为x列3拟合时用鼠标选中所有的x列y列不能选yintercept某省19781989年消费基金国民收入使用额和平均人口资料若1990年该省国民收入使用额为67十亿元平均人口为58百万人试估计1990年消费基金年份消费基金国民收入使用额平均人口数十亿元十亿元百万人1978121482197995129489198010168495419811061485025198212416451021983162209518419841772425276198520128156391986218301545519872533585535198831348556161989365485698二非线性模型origin中的非线性拟合功能origin解非线性拟合的算法levenbergmarquardtlmmethod马夸尔特法
origin分段函数拟合

origin分段函数拟合
拟合的函数形式为:
\[ f(x) =
\begin{cases}
a_1x + b_1 & \text{if } x < x_1 \\
a_2x + b_2 & \text{if } x_1 \leq x < x_2 \\
\vdots \\
a_{n-1}x + b_{n-1} & \text{if } x_{n-2} \leq x < x_{n-1} \\ a_nx + b_n & \text{if } x \geq x_{n-1} \\
\end{cases}
\]
其中,$a_i$和$b_i$为拟合参数,$x_i$为分段点。
拟合的过程可以分为以下几步:
1. 确定分段点$x_i$的个数和位置。
可以根据数据的分布情况和特点来选择合适的分段点。
2. 对每个区间$(x_{i-1}, x_i)$内的数据进行线性拟合,得到参数$a_i$和$b_i$。
3. 将每个区间的拟合结果拼接起来,得到最终的拟合函数。
具体的拟合算法可以使用最小二乘法来求解,最小化真实数据与拟合函数之间的误差。
可以使用数值优化算法,如梯度下降法或牛顿法来求解最优的参数值。
需要注意的是,拟合的结果可能会受到分段点的选择和初始参数值的影响,因此需要进行多次尝试和调整,以找到最优的拟合结果。
origin拟合曲线选取点

在Origin中拟合曲线时,选取合适的数据点非常重要。
以下是几个建议:
1. 代表性:选择具有代表性的数据点进行拟合。
这些点应该能够反映数据整体的变化规律。
2. 分布均匀:尽量选择分布均匀的数据点,避免在某些区域选择过多的点,而其他区域选择过少的点。
3. 考虑噪声和异常值:在选择数据点时,应考虑噪声和异常值的影响。
对于噪声,可以选择滤波或平滑处理来减少其影响。
对于异常值,可以将其去除或进行特殊处理。
4. 交互式拟合:可以在Origin中采用交互式拟合方式,即手动选择需要拟合的数据点,然后进行拟合。
这样可以更灵活地选择数据点,并获得更好的拟合效果。
5. 分段拟合:对于具有不同变化趋势的数据,可以考虑采用分段拟合方法。
这样可以更好地适应数据的局部变化规律,提高拟合精度。
6. 非线性拟合:如果数据呈现出非线性变化趋势,可以选择合适的非线性拟合函数进行拟合。
在Origin中,可以通过Analysis > Fitting > Nonlinear Curve Fit菜单进行非线性拟合。
7. 拟合曲线类型:根据数据的特征和变化规律,选择合适的拟合曲线类型。
例如,线性拟合、多项式拟合、指数拟合、对数拟合等。
总之,在Origin中拟合曲线时,需要仔细考虑数据点的选择,并根
据实际情况灵活调整拟合策略,以获得最佳的拟合效果。
Origin 7.5使用说明--直线拟合
Origin7.5使用说明--直线拟合我们根据数据作出y=a*x+b的直线拟合,具体使用origin7.5软件的方法如下:1、打开origin,输入数据
2、选中数据,并按图选择菜单。
3、出来如图菜单,点击“ok”。
4、这时会根据数据得出数点,如果不是线性关系,我们也可以在f(x)中选择Categories选中polynomial;Functions中选择Line。
就会得出如图线性关系,并拟合曲线。
下面就是我们想要得出直线的拟合曲线方程。
5、出现Select Function对话框,点击红框所示菜单
6、当出现下图图页时,我们要选择红框所示或者红线所示参数,并按Done确定。
7、我们就可以得出我们想要的直线拟合曲线,并附带方程。
8、经过加班熬夜的研究琢磨,终于得出我想要的结果了,很是高兴,于是写下方法,以备共鉴!谢谢大家@!。
线性拟合+数据计算origin小白教程
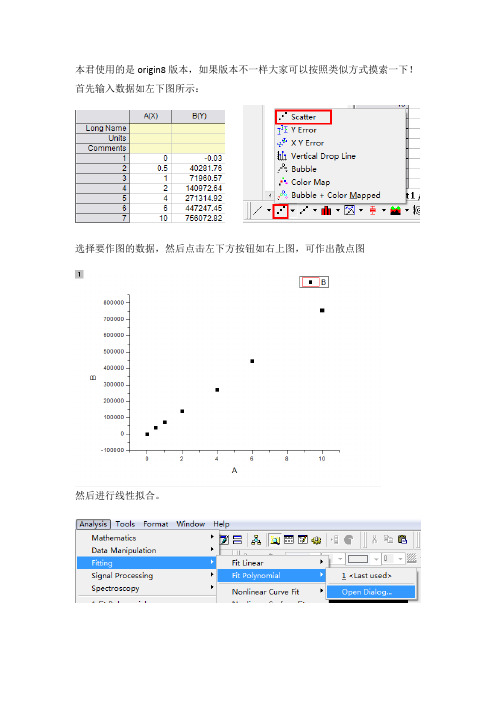
本君使用的是origin8版本,如果版本不一样大家可以按照类似方式摸索一下!首先输入数据如左下图所示:
选择要作图的数据,然后点击左下方按钮如右上图,可作出散点图
然后进行线性拟合。
然后在出现的对话框中选择拟合未知数的次数为1,即线性方程:
如果到时候需要用拟合方程来算具体的值,可以拉动滑动条在下面的对话框中选择:
这个就是看你是用X算Y还是Y算X了~
选择好以后点OK~以下就是算出来的图形。
(自己调整图表大小)
点击左侧菜单中的book1可以看到各种表:
从左至右依次是原始数据表格、拟合报告(可能有的人没有)、数据计算表格(?看起来貌似是根据拟合曲线算的数据)、计算实际数据用的表格(就是刚刚勾选的那个XY神马的~)
点击最后一个表,在左侧输入Y值右侧就可以得到对应的X值啦~
PS:还有一个问题就是如果计算的数据超过了范围的话可能会出现这样的哟~
即如框出来的那样没有数据!
这个时候就要改一下拟合函数的范围!
见下图所示:
点击左侧菜单中的graph重新点出图来。
然后点击上图中蓝框框出的绿色小锁,如图选择就会出现刚刚做拟合时的对话框。
拉动滑动条至下面这一栏:
选择X的范围为自定义,如下图:
出来的最大最小值大家自己填,只要包括自己要算的数据就可以啦~
然后点OK!
再回到刚刚计算XY的地方是不是先前是“---”的地方现在变得有数据啦~!
PS:本君自己也不是专业人士,这个是自己摸索出来的origin小白教程,希望对要使用origin8的各位化学同仁们有点小小帮助啦~。
Pl Origin 线性拟合

PL教程之Origin 拟合
一、 Origin数据线性拟合的方法
1.根据数据作散点图(plot-symbol-scatter)
2.点击散点图中的任意一个点,然后进入Analysis菜单,点击“Fit Linear-
Open Dialog”
3.设置拟合参数(如无需特殊要求,可以不作任何改变,系统自己会生产参数),
然后点击“OK”。
注意:Input Dat:拟合数据范围
Fit Option:拟合选项(包括是否给出固定的截距或者斜率等)
4.系统会自动给出结果,红色的线即为拟合得到的曲线,并提供了一张数据表。
Equation : 拟合方程
Adjusted R-squared: 调整后的离差平方和 Intercept: 截距
Slope: 斜率
Standard Error: 标准偏差
所以此数据拟合得到的拟合方程为所以此数据拟合得到的拟合方程为:: Y = -0.5536X + 6.2520
5. 拟合的详细情况, 可以通过双击工作表查看。
origin拟合曲线的方程并计算

origin拟合曲线的方程并计算一、Origin软件简介Origin是一款功能强大的数据分析和图形绘制软件,广泛应用于生物学、物理学、化学、工程学等领域。
通过Origin,我们可以进行数据拟合,从而得到曲线的方程,并对其进行计算和分析。
二、拟合曲线的方程拟合曲线通常是指通过给定的数据点,使用数学函数来拟合曲线,从而得到一条最佳拟合曲线。
在Origin中,常用的拟合方法包括线性拟合、多项式拟合、指数拟合、幂函数拟合等。
下面以线性拟合为例,介绍拟合曲线的方程。
线性拟合曲线方程为:y = mx + b,其中m为斜率,b为截距。
在Origin中,可以通过添加两个数据系列(x和y)来创建线性拟合图表,并通过“拟合”功能选择线性模型进行拟合。
三、计算步骤以下是使用Origin进行拟合曲线方程计算的一般步骤:1. 打开Origin软件并导入数据。
你可以将数据导入Origin中的数据表或从文件中导入。
确保数据具有相应的格式和准确性。
2. 创建一个新的图表,并将数据添加到图表中。
确保将正确的x 和y数据系列添加到图表中。
3. 选择“分析”菜单中的“拟合”选项,然后选择“线性”或其他适合的拟合模型。
在弹出的对话框中,输入拟合模型的参数值并进行其他必要的设置。
4. 执行拟合操作并得到拟合曲线和相关参数。
在拟合结果中,你将获得斜率和截距的值,即m和b。
这些值可用于后续的计算和分析。
5. 根据需要使用拟合曲线进行进一步的分析,如绘制其他图表、进行统计分析和建模等。
四、计算实例下面是一个简单的实例,演示如何使用Origin进行拟合曲线的方程计算。
假设我们有一组实验数据(x,y),并希望通过线性拟合得到拟合曲线的方程和相关参数。
1. 导入数据:打开Origin软件,并将实验数据导入数据表中。
确保数据具有相应的格式和准确性。
2. 创建图表:创建一个新的图表,并将x和y数据系列添加到图表中。
3. 进行拟合:选择“分析”菜单中的“拟合”选项,然后选择“线性”。
Origin8.5拟合两条直线

Origin8.5拟合两条直线
Origin 8.5拟合两条直线
1.将数据输入或复制到表格,选择全部数据,点击左下角三点标志,会出现一个散点图。
2.在表格中选择一条直线的几个点,点击Analysis,选择Fitting,点击Linear Fit,选择Open Dialog,点击OK。
3.回到表格,选择另一条直线的几个点,同2操作。
4.双击表格下面的散点图,右击左上角的1,选择Layer Contents,将左边的两个线性添加到右边,点击OK,这时会出现两条线性。
5.右击线性,选择Plot Details,修改Size,点击OK。
6.左击像锁一样的东西,选择Change Parameters,找到Fitted Curves Plot,找到Range,选择Custom,去掉Auto的勾,可以设置X的延伸范围。
利用Origin进行线性拟合

Polynomial Fit(多项式拟合工具)
使用【tools】菜单 【Ploynomial Fit 】命令用户可 以对多项式拟合过程中的参数进 行选择,使拟合过程按要求进行, 适合有具体要求的用户使用。
线性模型
线性模型,例如: y a bx y a bx cx
2 2
y a bx c sin x y a b1 x1 b2 x2
Origin 中的 Linear Model
basic linear regression model(线性回归)
where β0, β1 are coefficients and ε is the random error
根据样本数据 对β0和β1 进行估计
β0和β1的估计
值为b0和b1 建立一元线性回归方程
ˆ Y b0 b1 X
一般而言,所求的b0和b1应能使每个 样本观测点(Xi,Yi)与回归直线之间的偏 差尽可能小。
一元线性回归方程
Y与X之间 为线性关系
最小 二乘法
选出一条最能反 映Y与X之间关系 规律的直线
在Results Log中显示所有的拟合结果,除了上面介绍的 以外,还显示t-检验值和ANOVA(方差分析)列表
选中,则进行y=Bx回归分析,不选, 则执行标准线性回归分析 选中,则按指定的斜率值进行拟合,不选, 则执行标准线性回归分析 选中,使用误差值作为权重(如果激活的是 Worksheet,必须选中一列Y误差列,如果激 活的是Graph,图中必须有误差线) 只对拟合过程中的误差参数有影响 绘制数据上、下可信范围 绘制数据上、下预期范围 执行拟合 根据拟合公式计算的X值(已知Y值) 根据拟合公式计算的Y值(已知X值)
Origin拟合操作

a) 图 9 非线性拟合 Code 项 a) Function b) Parameter Init
-5-
b)
在 Parameters 页和 Bounds 页中可以对参数作系统的全面地修改和约束, 如图 10~11 所示。
图 10 非线性拟合 Parameters 项
图 11 非线性拟合 Bounds 项
-7-
a)
b)
图 8-
二、 多项式拟合
与线性拟合相比,多项式拟合仅多了一项功能,即选择拟合多项式的次数。如图 3 所示 的“Polynomial Order”选项。
三、 拟合报表
拟合报表是拟合操作完成后,Origin 会默认给出两个表单。可以根据需要在图 1 所示的 扩展选项中勾选相关功能,一般情况下,不需要输出报表的所有拟合相关结果,这样只会增 加寻找目标参数的时间。拟合报表是 Origin 拟合操作中的核心功能。我们不仅可以从中读取 到拟合曲线(曲面)的具体信息,还可以从概率论与数理统计的基础上获得大量拟合结果参 数,用于对各类模型或者试验离散点的拟合效果的对比。 图 4 和图 5 分别是拟合报表 1 和 2。表单名称为“Fit Linear 1”和“Fit Linear Curves 1” 。
a) 图 8 非线性拟合 Setting 项 a) Data Selection b) Function Selection
b)
“Code” , “Parameters”和“bounds”三页都是对已选拟合函数类型具体表达式和参数的 查看与修改。如图 9 所示,函数项(Function)在这里是不可编译的。而参数赋值和参数约束 项可以修改,注意使用 C 语言的格式。
一、 线性拟合
线性拟合(Linear Fitting)是最简单的一种拟合方式。线性回归拟合将选中的数据点拟合 为直线,选择 Analysis-Fit linear,那么 Origin 将曲线拟合为直线,以 X 为自变量,Y 为因变 量,回归拟合的函数形式为: y Ax b ,其中 A,b 为参数,由最小二乘法确定。对话框如 下图 1。
Origin7.5曲线拟合

使用Origin7.5来作演示1. 先随意输入一组数据吧
2. 选中这2列数据,然后点左下角的作scatter图的图标,
3. 然后就生成了散点图
4. 点击Analysis菜单中的Fit Polynomial,在弹出的对话框中,Order处设为1,这样就是作线性拟合,可能有人问,为什么不直接选择Fit Liner呢?因为只有选Fit Polynomial, 才能在图形上显示公式,也就是勾选对话框中的Show Flormula on graph。
(可能Origin的设计者认为线性拟合公式太简单,默认就不用显示了)
5. 点击OK后,就得到了拟合后的图形。
线性方程公式也显示在了图形上。
注意窗口的右下角。
点击那里的小箭头后,我们可以看到完整的拟合统计信息,如相关系数R2=0.9918
6. 好了,标准曲线知道了,现在就来计算IC50。
根据IC50定义,该例子中就是Y取中值时,X对应的数值,这里Y的中值是0.6,那根据线性方程就可以自己算出来对应的X值。
那如果不是线性方程,公式比较复杂手工计算就很麻烦了,所以还是用Origin中的功能吧。
点击Tools,Linear Fit,如果不是线性拟合的,请选择其他拟合方式,如果是S形曲线的,则需要选择Sigmoidal Fit.
7. 在弹出的对话框中,先点击Fit,然后在Find Y处输入0.6,点击Find X按钮,得到的数值就是IC50了。
同样的可以很方便的求得IC90,IC10,IC20 …。
Origin拟合操作

班门弄3 斧
报表都可以以PDF格式输出
2021/4/9
班门弄4 斧
原始数据 改变时的 重算功能
相关系数 (越接近正负1, 拟合效果越好)
拟合结果 重要!
2021/4/9
拟合的基本信息 数理统计值
输入的数据 (原始数据信息)
标准差
班门弄5 斧
重要信息汇总
不可编辑 的标志
拟合曲线图
2021/4/9
残差分析图 报方表差一分中析图形子置项信的概所率有值越接 数据(可以据此近画0图,)说明拟合
效果越显著
班门弄6 斧
拟合图形设置(与线性 拟合相同)
函数类型 具体函数
输入原始数据 Origin函内数置类了型20高0余级种选项
2021/4/9
原始数据的离散点图 图形形预览区
班门弄7 斧
2021/4/9
2021/4/9
空间拟合函数 残编设差辑置计函相数算和同结自果定在义函数 Message中显示
班门弄9 斧
Origin内置函数 (可修改)
自定义函数选取 完全自定义函数 函数方程,简图和说明
2021/4/9
班门1弄0 斧
自定义函数名称
函数存放路径与 简介
点我识别
再找我编译 参数设置
自变量,因变量和参量
函数表达式
参量设定
函数初始化参数
函数参数参约量束初始值的给 定参与量固值定变与化否范可围设定 加速迭代收敛
班门弄8 斧
近似化参数(赋完予整迭代按钮 保存已编辑大的体与目标曲线(趋达最大收敛
拟合函数 势近似的参数值次数迭代停止)
创建和编辑 恢复内置拟计合算拟单合步函迭数代按钮 拟合函数 函数初始值残差平方和
Origin的使用方法汇总

统计关系
即当X值确定后,Y值不是唯一确定的, 但大量统计资料表明,这些变量之间还 是存在着某种客观的联系。
回归分析(Regression Analysis)
• 应用统计方法,对大量的观测数据进行整 理、分析和研究,从而得出反映事物内部 规律性的一些结论。 • 描述不同变量之间的关系,找出相应函数 的系数,建立经验公式或数学模型。 • 只有一个或二个自变量时,回归分析的目 的就是找到符合数据的曲线或曲面,所以 回归分析也经常被称为 “curve fitting” 或 “surface fitting
最后得到的拟合曲线上点的个数 表示Graph窗口中拟合直线在两端多于曲线 X值范围的百分比 可信度,设置可信范围、预期范围 根据现有的坐标刻度进行拟合 在整个X轴坐标范围绘制拟合曲线,此时上面 设置的Range值无效 在相应的Worksheet窗口中生成两列: Fit(Y)列(拟合数据) Residual(Y)列(剩余误差) 拟合图层中的所有曲线 在Result Log中只显示简单的拟合结果 在Results Log中显示所有的拟合结果
y 0 -2.5 -4 -5.7 -3.5 -2 -1 2 3.5 4 7 7.5 9.9 10.9 11.9 13.5 13 11.9 9 6.5 4 1.5 0 -2.5 -5
某同学实验测得数据如左表所示, 设y和x之间满足: y b0 b1 x b2 x
2
bk x 。
k
分别就k 3和k 4两种情况, 在Origin中对表中的数据进行拟合, 求出b0 , b1 , b2 , , bk。
直线拟合上机练习2
2、Polynomial Fit 模型
yi 0 1 xi x
2 2 i
origin 分段函数拟合

origin 分段函数拟合
分段函数拟合是一种常用的数学方法,用于逼近复杂函数。
它将整个定义域分成多个段落,每个段落内使用简单的函数进行拟合。
这样做的目的是用一组简单的函数来近似整个函数的行为,从而简化计算和分析过程。
在分段函数拟合中,我们首先确定分段点,即将整个定义域划分为不同的段落。
然后,针对每个段落,选择一种适当的函数类型进行拟合。
常用的函数类型包括线性函数、二次函数、指数函数和对数函数等等。
在每个段落内,我们通过调整函数的参数,使得拟合函数与实际函数的取值尽可能接近。
这可以通过最小二乘法等统计方法来实现。
通过不断优化参数,我们可以得到一个在整个定义域上都较好逼近原函数的分段函数。
分段函数拟合可以应用于多个领域,如物理学、经济学和工程学等。
它可以用于描述非线性关系、曲线拟合和数据分析等问题。
通过将问题分解为多个简单的段落,分段函数拟合可以简化复杂问题的处理,并提高计算效率。
总的来说,分段函数拟合是一种有效的数学方法,可以将复杂函数近似为一组简单的函数。
通过合理选择分段点和拟合函数,我们可以得到一个在整个定义域上都较好逼近原函数的分段函数,从而简化计算和分析过程。
