浙大版概率论与数理统计答案---第六章
概率论与数理统计及其应用_习题答案_(浙大_盛骤谢式千版本)
《概率论与数理统计》习题解答教材：《概率论与数理统计及其应用》，浙江大学盛骤、谢式千编，高等教育出版社，2004年7月第一版目录第一章随机事件及其概率1第二章随机变量及其分布9第三章随机变量的数字特征25第四章正态分布33第五章样本及抽样分布39第六章参数估计42第七章假设检验53第一章 随机事件及其概率1、解：（1）{}67,5,4,3,2=S （2）{} ,4,3,2=S （3）{} ,,,TTH TH H S =（4）{}6,5,4,3,2,1,,T T T T T T HT HH S =2、设A , B 是两个事件，已知81)(,21)(,41)(===AB P B P A P ，求)(B A P ，)(B A P ，)(AB P ，)])([(AB B A P 解：81)(,21)(,41)(===AB P B P A P ∴)()()()(AB P B P A P B A P -+= 85812141=-+= )()()(AB P B P B A P -=838121=-=87811)(1)(=-=-=AB P AB P)])([(AB B A P )]()[(AB B A P -=)()(AB P B A P -= )(B A AB ⊂218185=-=3、解：用A 表示事件“取到的三位数不包含数字1”2518900998900)(191918=⨯⨯==C C C A P4、在仅由0，1，2，3，4，5组成且每个数字至多出现一次的全体三位数字中，任取一个三位数，（1）该数是奇数的概率；（2）求该数大于330的概率。
解：用A 表示事件“取到的三位数是奇数”，用B 表示事件“取到的三位数大于330”(1) 455443)(2515141413⨯⨯⨯⨯==A C C C C A P =0.48 2） 455421452)(251514122512⨯⨯⨯⨯+⨯⨯=+=A C C C A C B P =0.485、袋中有5只白球，4只红球，3只黑球，在其中任取4只，求下列事件的概率 （1）4只中恰有2只白球，1只红球，1只黑球； （2）4只中至少有2只红球； （3）4只中没有白球解：用A 表示事件“4只中恰有2只白球，1只红球，1只黑球”（1）412131425)(C C C C A P ==495120=338（2）用B 表示事件“4只中至少有2只红球”16567)(4124418342824=++=C C C C C C B P 或4124838141)(C C C C B P +-==16567495201= （3）用C 表示事件“4只中没有白球”99749535)(41247===C C C P 6、解：用A 表示事件“某一特定的销售点得到k 张提货单”nkn k n MM C A P --=)1()( 7、解：用A 表示事件“3只球至少有1只配对”，B 表示事件“没有配对”（1）3212313)(=⨯⨯+=A P 或321231121)(=⨯⨯⨯⨯-=A P （2）31123112)(=⨯⨯⨯⨯=B P 8、（1）设1.0)(,3.0)(,5.0)(===AB P B P A P ，求(),(),(),(),P A B P B A P A B P A A B(),()P AB A B P A AB ；（2）袋中有6只白球，5只红球每次在袋中任取一只球，若取到白球，放回，并放入1只白球，若取到红球不放回也不再放回另外的球，连续取球四次，求第一、二次取到白球且第三、四次取到红球的概率。
概率论和数理统计浙江大学第四版-课后习题答案解析[完全版]
![概率论和数理统计浙江大学第四版-课后习题答案解析[完全版]](https://img.taocdn.com/s3/m/2be46d428e9951e79b8927ce.png)
概率论与数理统计习题答案 第四版 盛骤 (浙江大学)浙大第四版（高等教育出版社） 第一章 概率论的基本概念1.[一] 写出下列随机试验的样本空间（1）记录一个小班一次数学考试的平均分数（充以百分制记分）（[一] 1）⎭⎬⎫⎩⎨⎧⨯=n n nn o S 1001, ，n 表小班人数（3）生产产品直到得到10件正品，记录生产产品的总件数。
（[一] 2）S={10，11，12，………，n ，………}（4）对某工厂出厂的产品进行检查，合格的盖上“正品”，不合格的盖上“次品”，如连续查出二个次品就停止检查，或检查4个产品就停止检查，记录检查的结果。
查出合格品记为“1”，查出次品记为“0”，连续出现两个“0”就停止检查，或查满4次才停止检查。
（[一] (3)）S={00，100，0100，0101，1010，0110，1100，0111，1011，1101，1110，1111，}2.[二] 设A ，B ，C 为三事件，用A ，B ，C 的运算关系表示下列事件。
（1）A 发生，B 与C 不发生。
表示为：C B A 或A － (AB+AC )或A － (B ∪C )（2）A ，B 都发生，而C 不发生。
表示为：C AB 或AB －ABC 或AB －C（3）A ，B ，C 中至少有一个发生表示为：A+B+C（4）A ，B ，C 都发生， 表示为：ABC（5）A ，B ，C 都不发生，表示为：C B A 或S － (A+B+C)或C B A ⋃⋃（6）A ，B ，C 中不多于一个发生，即A ，B ，C 中至少有两个同时不发生 相当于C A C B B A ,,中至少有一个发生。
故 表示为：C A C B B A ++。
（7）A ，B ，C 中不多于二个发生。
相当于：C B A ,,中至少有一个发生。
故 表示为：ABC C B A 或++ （8）A ，B ，C 中至少有二个发生。
相当于：AB ，BC ，AC 中至少有一个发生。
浙大《概率论与数理统计(第四版)简明本》盛骤著 课后习题解答
即样本空间 S={ 62 个基本事件}。事件 AB={两颗骰子点数之间和为 7，且有一颗为 1 点}，
两颗骰子点数之和为 7 的可能结果为 6 个，即
A={（1，6），（2，5），（3，4），（6，1），（5，2），（4，3）}
解 利用组合法计数基本事件数。从 10 人中任取 3 人组合数为 C130 ，即样本空间
{ } S= C130 = 120个基本事件 。
（1）令事件 A={最小号码为 5}。最小号码为 5，意味着其余号码是从 6，7，8，9，10 的 5
{ } 个号码中取出的，有 C52 种取法，故 A= C52 = 10个基本事件 ，所求概率为
其中由 P( AB) = P(BC) = 0, 而 ABC ⊂ AB 得 P( ABC) = 0 。
------------------------------------------------------------------------------6．在房间里有 10 个人，分别佩戴从 1 号到 10 号的纪念章，任选 3 人记录其纪念章的号码。 求 （1）最小号码为 5 的概率； （2）最大号码为 5 的概率。
∑200
P(B) = P( A2 ∪ A3 ∪⋯∪, A200）= P( Ai )
i=2
显然，这种解法太麻烦，用对立事件求解就很简单。令事件 B ={恰有 0 个次品或恰有
1 个次品}，即 B = A0 ∪ A1 ，而
P(B)
=
P( A0
∪
A1 )
=
P( A0 ) +
P( A1)
=
C 200 1100
推荐-概率论与数理统计答案浙江大学主编 精品
第一章 概率论的基本概念注意： 这是第一稿（存在一些错误）1解：该试验的结果有9个：（0，a ），（0，b ），（0，c ），（1，a ），（1，b ），（1，c ），（2，a ），（2，b ），（2，c ）。
所以，（1）试验的样本空间共有9个样本点。
（2）事件A 包含3个结果：不吸烟的身体健康者，少量吸烟的身体健康者，吸烟较多的身体健康者。
即A 所包含的样本点为（0，a ），（1，a ），（2，a ）。
（3）事件B 包含3个结果：不吸烟的身体健康者，不吸烟的身体一般者，不吸烟的身体有病者。
即B 所包含的样本点为（0，a ），（0，b ），（0，c ）。
2、解 （1）AB BC AC 或ABC ABC ABC ABC ；（2）ABBCAC（提示：题目等价于A ，B ，C 至少有2个发生，与（1）相似）； （3）ABC ABC ABC ；（4）AB C 或ABC ；（提示：A ，B ，C 至少有一个发生，或者A B C ，，不同时发生）； 3（1）错。
依题得()()()()0=-+=B A p B p A p AB p ,但空集≠B A ，故A 、B 可能相容。
（2）错。
举反例 （3）错。
举反例（4）对。
证明：由()6.0=A p ,()7.0=B p 知()()()()()3.03.1>-=-+=B A p B A p B p A p AB p ,即A 和B 交非空，故A 和B 一定相容。
4、解（1）因为A B ，不相容，所以A B ，至少有一发生的概率为：()()()=0.3+0.6=0.9P A B P A P B =+(2) A B ， 都不发生的概率为：()1()10.90.1P A B P A B =-=-=；（3）A 不发生同时B 发生可表示为：A B ，又因为A B ，不相容，于是()()0.6P A B P B ==；5解：由题知()3.0=BC AC AB p ,()05.0=ABC P .因()()()()()ABC p BC p AC p AB p BC AC AB p 2-++= 得，()()()()4.023.0=+=++ABC p BC p AC p AB p故A,B,C 都不发生的概率为()()C B A p C B A p -=1()()()()()()()()[]ABC p BC p AC p AB p C p B p A p +++-++-=1 ()05.04.02.11+--= 15.0=.6、解 设A ={“两次均为红球”}，B ={“恰有1个红球”}，C ={“第二次是红球”} 若是放回抽样，每次抽到红球的概率是：810，抽不到红球的概率是：210，则 （1）88()0.641010P A =⨯=； （2）88()210.321010P B =⨯⨯-=（）；（3）由于每次抽样的样本空间一样，所以：8()0.810P C == 若是不放回抽样，则（1）2821028()45C P A C ==；（2）118221016()45C C P B C ==； （3）111187282104()5A A A A P C A +==。
概率与数理统计第六章习题参考解答
《概率论与数理统计》第六章习题exe6-1解：10()0x b f x b ⎧<<⎪=⎨⎪⎩其他01()()2bb E X xf x dx x dx b +∞-∞==⋅=⎰⎰ 令11μ=A ，即2b X =，解得b 的矩估计量为ˆ2b X = 2ˆ2(0.50.60.1 1.30.9 1.60.70.9 1.0) 1.6899bx ==++++++++= exe6-2解：202()()()3x E X xf x dx x dx θθθθ+∞-∞-==⋅=⎰⎰令11μ=A ，即,3θ=X 解得θ的矩估计量为ˆ3X θ= Exe6-3解：（1）由于12222()()()()(1)()E X mpE X D X E X mp p mp μμ==⎧⎨==+=-+⎩令 ⎩⎨⎧==.2211μμA A 求解得221111p m p μμμμ⎧-=-⎪⎪⎨⎪=⎪⎩，p, m 的矩估计量为22211(1)ˆ11ˆˆA A n S pA nX X m p ⎧--=-=-⎪⎪⎨⎪=⎪⎩Exe6-4解：（1）()E X λ= 令11μ=A ，即,λ=X 解得λ的矩估计量为ˆX λ= {}),2,1,0(!===-x e x x X P xλλ{}),2,1,0(!===-i i xi x e x x X P iλλ似然函数11111(){}()!!niii x n nx ni ni i i ii eL P X x e x x λλλλλ=--===∑====∏∏∏11ln ()()ln ln(!)nni i i i L n x x λλλ===-+-∑∑1ln ()0nii x d L n d λλλ==-+=∑解得λ的最大似然估计值为 11ˆnii x x n λ===∑ （2）由（1）知1ˆ(6496101163710)7.210x λ==+++++++++= Exe6-5解：（1）似然函数1(1)111(){}(1)(1)ni i i nnx x ni i i L p P X x p p p p =--==∑===-=-∏∏∑-==-ni i nx np p 1)1(1ln ()ln (1)ln ni i L p n p x p ==+-⋅∑)1ln()(ln 1p n x p n ni i --+=∑=1(1)ln ()01nii x d L p ndp pp=-=-=-∑01)(ln 1=---=∑=pnxp n dp p L d ni i解得p 的最大似然估计值为 11ˆnii npxx===∑ （2）155ˆ5174926px ===++++ Exe6-6解：由22()2()x f x μσ--=（1）2σ已知，似然函数22122()()2211()(,)ni i i x nx n nii i L f x e μμσσμμ=----==∑===∏2211ln ())()2nii L n x μμσ==---∑21ln ()1(22)02nii d L x d μμμσ==--=∑即11()0nniii i x n xμμ==-=-=∑∑解得μ的最大似然估计值 1ˆnii xx nμ===∑（2）μ已知，似然函数为212222)(222)(12122121),()(σμσμπσσπσσ∑⎪⎭⎫ ⎝⎛====----==∏∏ni i i x n x ni n i i e ex f L21222)(21)ln(2)2ln(2)(ln μσσπσ-∑---==n i i x n n L 0)()(212)(ln 2122222=-+-=∑=μσσσσni ixn L d d解得∑=-=n i i x x n 122)(1ˆσ，故2σ的最大似然估计值为 .)(1ˆ122∑=-=n i i i x x n σ Exe6-7解：（1）矩估计量2220()()()(3)2xt x xt xx E X xf x dx x e dx e dx t e dt θθθθθθθθ=--+∞+∞+∞+∞--∞==⋅===Γ=⎰⎰⎰⎰令2X θ=，得ˆ/2X θ= 似然函数211()(,)ix n nii i i x L f x eθθθθ-====∏∏1111ln ()(ln 2ln )ln 2ln nnnii i i i i i x L x x n x θθθθθ====--=--∑∑∑令21ln ()210ni i d L n x d θθθθ==-+=∑解得θ的最大似然估计值为111ˆ22ni i x x n θ===∑ （2）2311()(,)2ixnni i i i x L f x e θθθθ-====∏∏331111ln ()[2ln ln(2)]2ln ln(2)nnnii i i i i i x L x x n x θθθθθ====--=--∑∑∑ 令2321ln ()1602nii d L n xd θθθθθ==-⋅-=∑013)(ln 1223=+⋅-=∑=ni ixn d L d θθθθθ解得θ的最大似然估计值为 111ˆ33n ii x x n θ===∑（3） ),(~p m B X ，m 已知{}∏∏=-=-===ni x m x x m ni i i i ip p C x X P p L 11)1()(1111ln ()[ln ln ()ln(1)]ln ln ln(1)()i inx m i i i nnnx m i i i i i L p C x p m x p C p x p nm x =====++--=++--∑∑∑∑令 11ln ()01n ni ii i x nm x d L p dp p p==-=-=-∑∑即1111(1)1n nniiii i i x xxnmppp p p===+==---∑∑∑ 解得p 的最大似然估计值为 1ˆnii xxpmnm===∑ Exe6-8解：(1)似然函数为{}{}{})1(2)1(2121)(522θθθθθθθ-=⋅-⋅==⋅=⋅==X P X P X P L)1ln(ln 52ln )(ln θθθ-++=L 令 0115)(ln =--=θθθθL d d 解得θ的最大似然估计值为.65ˆ=θ Exe6-9解：1212222)()(22)(12)(111212121),,(),,(),(σβαβασβασβασπσπσπβαβαβα∑∑⎪⎪⎭⎫⎝⎛=====+-+---+--=---===∏∏∏∏ni i ni i i i i i y x ny ni x ni n i i Y n i i X e eey f x f L))()((21ln 2)2ln(),(ln 21212βαβασσπβα+-∑+--∑---===ni i ni i y x n n L0))()((22),(ln 112=+-+--=∂∂∑∑==βαβασβααni i n i i y x L0)()((22),(ln 112=+----=∂∂∑∑==βαβασβαβni i n i i x x L 联立 解得,2ˆ,2ˆyx y x -=+=βα故βα,的最大似然估计量为 .2ˆ,2ˆYX Y X -=+=βαExe6-10解：（1）由1/2EX μθ==，得θ的矩估计量ˆ2X θ= ˆ()2()2()22E E X E X θθθ===⋅= 故θ的矩估计量ˆ2X θ=是θ的无偏估计量。
概率论与数理统计和应用课后标准答案答案最新版（浙江大学_盛骤版）
概率论与数理统计和应⽤课后标准答案答案最新版（浙江⼤学_盛骤版）第1章随机变量及其概率1，写出下列试验的样本空间：（1）连续投掷⼀颗骰⼦直⾄6个结果中有⼀个结果出现两次，记录投掷的次数。
（2）连续投掷⼀颗骰⼦直⾄6个结果中有⼀个结果接连出现两次，记录投掷的次数。
（3）连续投掷⼀枚硬币直⾄正⾯出现，观察正反⾯出现的情况。
（4）抛⼀枚硬币，若出现H 则再抛⼀次；若出现T ，则再抛⼀颗骰⼦，观察出现的各种结果。
解：（1）}7,6,5,4,3,2{=S ；（2）},4,3,2{Λ=S ；（3）},,,,{ΛTTTH TTH TH H S =；（4）}6,5,4,3,2,1,,{T T T T T T HT HH S =。
2，设B A ,是两个事件，已知,125.0)(,5.0)(,25.0)(===AB P B P A P ，求)])([(),(),(),(______AB B A P AB P B A P B A P ??。
解：625.0)()()()(=-+=?AB P B P A P B A P ，375.0)()(])[()(=-=-=AB P B P B A S P B A P ，875.0)(1)(___--=AB P AB P ，5.0)(625.0)])([()()])([()])([(___=-=?-?=-?=?AB P AB B A P B A P AB S B A P AB B A P3，在100，101，…，999这900个3位数中，任取⼀个3位数，求不包含数字1个概率。
解：在100，101，…，999这900个3位数中不包含数字1的3位数的个数为648998=??，所以所求得概率为72.0900648=4，在仅由数字0，1，2，3，4，5组成且每个数字⾄多出现⼀次的全体三位数中，任取⼀个三位数。
（1）求该数是奇数的概率；（2）求该数⼤于330的概率。
解：仅由数字0，1，2，3，4，5组成且每个数字之多出现⼀次的全体三位数的个数有100455=??个。
概率论与数理统计及其应用课后答案（浙江大学-盛骤版）
概率论与数理统计及其应用课后答案（浙江大学-盛骤版）
目录
第一章随机变量及其概率. (2)
第二章随机变量及其分布. (13)
第三章随机变量的数字特征. (30)
第四章正态分布. (39)
第五章样本及抽样分布. (49)
第六章参数估计. (55)
第七章假设检验. (68)
第一章随机变量及其概率
1,写出下列试验的样本空间：
（1）连续投掷一颗骰子直至6个结果中有一个结果出现两次，记录投掷的次数。
（2）连续投掷一颗骰子直至6个结果中有一个结果接连出现两次，记录投掷的次数。
（3）连续投掷一枚硬币直至正面出现，观察正反面出现的情况。
（4）抛一枚硬币，若出现H则再抛一次；若出现T，则再抛一颗骰子，观察出现的各种结果。
解:（1）S {2,345,6,7} ；（2）S {2,3,4, } ；（3）S
{H ,TH ,TTH ,TTTH , }；
（4）S {HH , HT,T1,T2,T3,T4,T5,T6} o
2，设A,B 是两个事件，已知P(A) 0.25,P(B) 0.5,P(AB) 0.125,，求
P(A B), P(AB), P(AB), P[( A B)(AB)]。
解：P(A B) P(A) P(B) P(AB) 0.625，
P(AB) P[(S A)B] P(B) P(AB) 0.375，
P(AB) 1 P(AB) 0.875，
P[(A B)(AB)] P[(A B)(S AB)] P(A B) P[(A B)( AB)] 0.625 P(AB) 0.5。
概率论与数理统计六七章习题答案
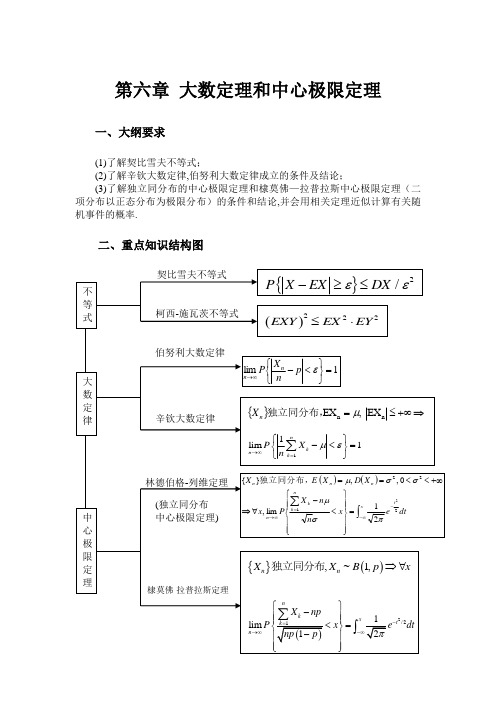
第六章大数定理和中心极限定理一、大纲要求(1)了解契比雪夫不等式；(2)了解辛钦大数定律,伯努利大数定律成立的条件及结论；(3)了解独立同分布的中心极限定理和棣莫佛—拉普拉斯中心极限定理（二项分布以正态分布为极限分布）的条件和结论,并会用相关定理近似计算有关随机事件的概率.二、重点知识结构图三、基本知识1. 马尔科夫不等式若X 为只取非负值的随机变量,则对任意常数0ε>,有{}EXP X εε≥≤.2. 契比雪夫不等式若DX 存在,则{}2DXP X EX εε-≥≤.3. 辛钦大数定律定理 1 设12,,,,n X X X 是独立同分布的随机变量序列，且具有有限的数学期望()a X E n =，则对任意的0ε>,有{}lim 0n n P X a ε→∞-≥=4. 伯努利大数定律定理2 设()p n B X n ,~，其中n=1,2, …，0<p<1 。
则对任意ε>0，有5．独立同分布的中心极限定理定理3 (林德伯格-列维定理) 设12,,,,n X X X 为独立同分布的随机变量,22,,0,i i EX a DX σσ==<<∞则对任意实数x 有12lim )()n n P X X X na x x →∞⎫++-≤=Φ⎬⎭式中, ()x Φ是标准正态分布(0,1)N 的分布函数,即2/2()t x e dt +∞--∞Φ=6. 棣莫佛-拉普拉斯中心极限定理定理3(棣莫佛-拉普拉斯定理) 设12,,,,n X X X 独立同分布,i X 的分布是{}{}1,01,(01)i i P X p P X p p ====-<<则对任意实数x ,有12lim )()n n P X X X np x x →∞⎧⎫⎪++-≤=Φ⎬⎪⎭0lim =⎭⎬⎫⎩⎨⎧≥-∞→εp n X P n n四、典型例题例1 设随机变量X 和Y 的数学期望分别为-2和2,方差分别为1和4,而相关系数为-0.5,则根据契比雪夫不等式{}6_____P X Y +≥≤.解 因为 ()0E X Y E X E Y +=+= ()2c o v (,D X Y D X D Y X Y +=++2DX DY ρ=++ 1420.52=+-⨯⨯= 根据契比雪夫不等式{}2DXP X EX εε-≥≤所以 {}3163612P X Y +≥≤= 例2 某保险公司经多年资料统计表明,在索赔户中被盗户占20%,在随意抽查的100家索赔户中以被盗的索赔户数为随机变量,利用中心极限定理,求被盗的索赔户大于14户且小于30户的概率近似值.[分析]本题的随机变量服从参数100,0.2n p ==的二项分布.如果要精确计算,就要用伯努利二项公式:{}291001001514300.20.8kk k k P X C -=<<=∑.如果求近似值,可用契比雪夫不等式估计.解 由于~(100,0.2)X N ,所以1000.220EX np ==⨯=168.02.0100)1(=⨯⨯=-=p np DX{}1430P X P <<=<<=Φ(2.5)-Φ(-1.5)()927.0)5.1(5.2=-Φ+Φ因此被盗的索赔户大于14户且小于30户的概率近似值为0.927.例3 某车间有200台机床,它们彼此工作独立,开工率都为0.6，工作时耗电都为1kW,问供电所至少给这个车间多少度电，才能以99.9%的概率保证这个车间不会因供电不足而影响生产.解 用X 表示工作的机床台数,则~(200,0.6)X B .设要向车间供电a kW,则有由棣莫佛-拉普拉斯定理得{}P o X a P ⎧⎫<≤=<≤020p q ⎛⎫⎛⎫⎫⎫≈Φ-≈⎪⎪⎪⎪⎪⎪⎭⎭⎭⎭()0.999 3.1≈Φ≥=Φ即3.1≥ 因此120 3.48141a ≥+= 例4 用契比雪夫不等式确定当掷一均匀硬币时,需掷多少次,才能保证使得出现正面的频率在0.4~0.6之间的概率不小于90%,并用正态逼近计算同一个问题.解 设需掷n 次，用n S 表示出现正面的次数，则1~(,)2n S B n ，有契比雪夫不等式得0.40.60.50.1n n S S P P n n ⎧⎫⎧⎫<<=-<⎨⎬⎨⎬⎩⎭⎩⎭211110022110.900.014n n n⨯⨯≥-=-≥ 所以10002504n ≥=. 由棣莫佛-拉普拉斯定理得0.40.6n S P P n ⎧⎫<<=<⎨⎬⎩⎭(((0.2210.90=Φ-Φ-=Φ-≥即(Φ≥0.95,查表得 1.645>,故68n ≥.例5 假设12,,,n X X X 是独立同分布的随机变量,且()k k i a X E =(1,2,3,4)k =,证明当n 充分大时,随机变量211n n i i Z X n ==∑近似服从正态分布,并指出其分布参数.证 由12,,,n X X X 是独立同分布的随机变量序列可知, 22212,,,nX X X 独立同分布,且有()22a X E i =, 2242i DX a a =-2211n n i i EZ EX a n ===∑, 2242211n n i i a a DZ DX n n=-==∑由林德伯格-列维定理可知,对任意x 有⎰∞--∞→=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧<--x t n n dte x n a a a Z P 22242221lim π即n Z 近似服从正态分布2422(,)a a N a n-. 例6 有一批建筑房屋用的木柱,其中80%的长度超过3m ，现从这批木柱中随机地取出100根，问其中至少有30根短于3m 的概率是多少？解 设10i X ⎧=⎨⎩()31,2,,1003i m i i m = 当所取的第根木柱短于当所取的第根木柱不短于 则()~1,0.2i X B ,记1001i i X X ==∑,则()~100,0.2X B .由棣莫佛-拉普拉斯定理得{}{}30130P X P X ≥=-<1P =-≤()302011 2.50.0062100.4-⎛⎫≈-Φ=-Φ= ⎪⨯⎝⎭例7 假设男婴的出生率为2243,某地区有7000多名产妇,试估计她们的生育情况.[分析] n 重伯努利实验中A 出现的频率nu n依概率收敛于它的概率p ，当n 很大时，有n u np ≈.解 设10i X ⎧=⎨⎩()1,2,,7000i i = 第名产妇生男婴否则显然, 12,,,n X X X 独立同分布且均服从01-分布2243p ⎛⎫= ⎪⎝⎭,1nn i i u X ==∑表示7000名产妇中生男婴的人数,有伯努利大数定理得()2243n u n n →→∞ 由于7000n =已是足够大,因此227000358143n u ≈⨯≈即该地区估计有3581名男婴出生.例8 某电视机厂每月生产10000台电视机,但它的显像管车间的正品率为0.8，为了以0.997的概率保证出厂的电视机都装上正品的显像管,该车间每月应生产多少只显像管?解 设显像管正品数为X ,月总产量为n ,则有()~,0.8X B n ,从而 0.8E X n =, ()n p np DX 16.01=-=为了使电视机都装上正品的显像管,则每月至少生产10000只正品显像管,即所求为{}100000.997P X n ≤<=由棣莫佛-拉普拉斯定理得{}100000.997P X n P ≤<=≤<=即997.05.016.08.016.08.010000=⎭⎬⎫⎩⎨⎧<-≤-n n n X n n P(0.997Φ-Φ=由题意可知,0<,且n 较大,即(1Φ≈,所以0.997Φ=2.75=,故)(1027.14只⨯≈n因此,每月至少要生产41027.1⨯只显像管才能以0.997的概率保证出厂的10000台电视机都能装上正品的显像管.例9 一养鸡场购进1万个良种鸡蛋,已知每个鸡蛋孵化成雏鸡的概率为0.84，每只雏鸡发育成种鸡的概率为0.90，试计算这批鸡蛋得到种鸡不少于7500只的概率.解 设{}k A k =第只鸡蛋孵化成雏鸡, {}k B k =第只鸡蛋育成种鸡,令 ()11,2,,100000k k k B X k B ⎧==⎨⎩ 当发生当不发生 则诸k A 独立同分布,且{}{}{}{}{}{}1k k k k k k k k P X P B P A P B A P A P B A ===+0.840.900.756=⨯+={}{}244.00===k k B P X P显然, 100001kk X X==∑表示10000个鸡蛋育成的种鸡数,则()~10000,0.756X B ,而64.1844244.07560)1(,7560756.010000=⨯=-=⨯=p np np根据棣莫佛-拉普拉斯定理可得()~0,1nkXnpN -=∑于是,所求概率为{}10000756075001k X P X P ⎧⎫-⎪⎪≥=≥≈-Φ⎪⎪⎩⎭∑()1.400.92=Φ= 因此,由这批鸡蛋得到的种鸡不少于7500只的概率为92%.五、课本习题全解6-1 设11nn i i Y X n ==∑,再对n Y 利用契比雪夫不等式:{}12222220n i i n n n n D X DY n P Y EY n n εεεε=→∞⎛⎫ ⎪⎝⎭-≥≤=≤−−−→∑ 故{}n X 服从大数定理. 6-2 设出现7的次数为X ,则有 ()~10000,0.1,1000,900X B E X n p D X === 由棣莫佛-拉普拉斯定理可得{}100096810001696810.14303015X P X P --⎧⎫⎛⎫<=<=-Φ=⎨⎬ ⎪⎩⎭⎝⎭6-3 11,212i i EX DX ==由中心极限定理可知,10110i X -⨯∑,所以101011616110.136i i i i P X P X ==⎧⎫⎧⎫>=-≤=-Φ=-Φ=⎨⎬⎨⎬⎩⎭⎩⎭∑∑6-4 设报各人数为X ,则.100,100==DX EX . 由棣莫佛-拉普拉斯定理可得()0228.021*********}120{=Φ-=⎭⎬⎫⎩⎨⎧-≥-=≥DX EX X P X P6-5 设()11,2,,100000i i X i i ⎧==⎨⎩ 第个人死亡第个人没有死亡,则{}{}10.006,00.994i i P X P X ====总保险费为51210000 1.210⨯=⨯(万元)(1) 当死亡人数在达到51.210/1000120⨯=人时,保险公司无收入.4100.00660,0.1295np =⨯==所以保险公司赚钱概率为)()12100000.129512060P X X X np ⎧⎫⎪++-≤⨯-⎬⎪⎭()7.771=Φ=因而亏本的概率为10P P '=-=.(2)若利润不少于40000，即死亡人数少于80人时,)()12100000.12958060P X X X np ⎧⎫⎪++-≤⨯-⎬⎪⎭()2.590.9952=Φ= 若利润不少于60000，即死亡人数少于60人时,)()12100000.12956060P X X X np ⎧⎫⎪++-≤⨯-⎬⎪⎭()00.5=Φ=若利润不少于80000，即死亡人数少于40人时,)()12100000.12954060P X X X np ⎧⎫⎪++-≤⨯-⎬⎪⎭()2.5920.0048=Φ-=6-6 设总机需备Y 条外线才能有95%的把握保证每个分机外线不必等候,设随机变量()11,2,,2600i i X i i ⎧==⎨⎩ 第架电话分机用外线第架电话分机不用外线,则{}{}10.04,00.96P X P X ====0.04,0.040.00160.0384i i EX DX ==-=由中心极限定理可得16%950384.026004.02602601≈=⎪⎭⎫⎝⎛⨯⨯-Φ=⎭⎬⎫⎩⎨⎧≤∑=Y Y Y X P i i6-7 密度函数为 ()10.50.50x f x -<<⎧=⎨⎩当其他故数学期望为 0.50.50E X x d x -==⎰()0.52220.5112DX EX EX x dx -=-==⎰(1)设i X 为第i 个数的误差,则9973.01)3(251515300130013001=-Φ=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧≤=⎭⎬⎫⎩⎨⎧≤∑∑∑===i i i i i i DX X P X P30030011151150.0027i i i i P X P X ==⎧⎫⎧⎫>=-≤=⎨⎬⎨⎬⎩⎭⎩⎭∑∑(2)110210.9440.77n i i P X n =⎧⎫≤=Φ-≥⇒≤⎨⎬⎩⎭∑ (3)3001210.99714.855i i Y P X Y Y =⎧⎫⎛⎫≤=Φ-≥⇒≤⎨⎬ ⎪⎝⎭⎩⎭∑6-8 kg kg EX 32105,105--⨯=⨯=σ (1)设i X 为第i 个螺钉的重量,则23100510,5100.05nEX --=⨯⨯⨯=0228.0)2(105.051.51.510011001=Φ-=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧->-=⎭⎬⎫⎩⎨⎧>∑∑==σn nEX X P X P i i i i(2)设()1.11,2,,5000.1i i Y i i ⎧==⎨⎩ 第个螺钉的重量超过5kg第个螺钉的重量不超过5kg,则33.3)1(4.11=-=p np np9951.0)58.2(33.34.1120)1(450050015001=Φ=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧->--=⎭⎬⎫⎩⎨⎧⨯<∑∑==p np np Y P Y P i i i i ％6-9 设随机变量()11,2,,10000i i X i ⎧==⎨⎩ 第个人按时进入掩体其他,按时进入掩体的人数为Y ,则()1,~10000,0.9ni i Y X Y B ==∑,所以有10000.9900,9000.190EY DY =⨯==⨯=设有k 人按时进入掩体，则916884645.19090095.090900===-=⎪⎪⎭⎫⎝⎛-Φk k k k 或所以至少有884人,至多有916.六、自测题及答案1.设随机变量X 服从(),B n p ,则对区间(),a b ,恒有lim _______.n P a b →∞⎧⎫⎪⎪<≤=⎨⎬⎪⎪⎩⎭2.一大批产品中优质品占一半,现每次抽取一个,看后放回再抽,问在100次抽 取中取到优质品次数不超过45的概率等于_______.3. 129,,X X X 相互独立, ()1,11,2,9i i EX DX i === ,则对任意给定的0ε>,有( ).9922119922111(A)11(B)119(C)91(D)919i i i i i i i i P X P X P X P X εεεεεεεε--==--==⎧⎫⎧⎫-<≥--<≥-⎨⎬⎨⎬⎩⎭⎩⎭⎧⎫⎧⎫-<≥--<≥-⎨⎬⎨⎬⎩⎭⎩⎭∑∑∑∑4.设12,,,,n X X X 为独立随机变量序列,且()1,2,i X i = 服从参数为λ的泊松分布,则有().()()()()111(A)lim (B)0,1(C),(D)n i n ni i n i i n i i X n P x x n X N n X N n n n P X x x λλλ→∞===⎧⎫-⎪⎪⎪≤=Φ⎬⎪⎪⎪⎩⎭⎧⎫≤=Φ⎨⎬⎩⎭∑∑∑∑当充分大的时，近似服从当充分大的时，近似服从当充分大的时，5.设12,,X X 为独立随机变量序列,且服从服从参数为λ的指数分布,则( ).()()()()112211(A)lim (B)lim 1(C)lim (D)lim n n i i i i n n nni i i n n n X X P x x P x x n X n X n P x x P x x n λλλλλλ==→∞→∞=→∞→∞⎧⎫⎧⎫--⎪⎪⎪⎪⎪⎪⎪⎪≤=Φ≤=Φ⎨⎬⎨⎬⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭⎩⎭⎧⎫⎧⎫--⎪⎪⎪⎪⎪⎪⎪≤=Φ≤=Φ⎬⎨⎬⎪⎪⎪⎪⎪⎪⎪⎩⎭⎩⎭∑∑∑∑6.设随机变量12,,,n X X X 相互独立, 12n X X X X =+++ ,根据林德伯格-列维定理,当n 充分大时, X 近似服从正态分布,只要12,,,n X X X ( )(A)(B)(C)(D)有相同的数学期望有相同的方差服从同一指数分布服从同一离散型分布7.某校有1000名学生,每人以80%的概率去图书馆自习,问图书馆至少应设多少个座位,才能以99%的概率保证去上自习的同学都有座位坐?8.某种电子器件的寿命(小时)具有数学期望μ(未知),方差2400σ=.为了估计μ,随机地取n 只这种器件,在时刻0t =投入测试(设测试是相互独立的)直到失败,测得寿命为12,,,nX X X ,以11ni i X X n ==∑作为μ的估计,为了使{}10.95P X μ-<≥,问n 至少为多少?9.利用中心极限定理证明11lim !2i n n n i n e i -→∞=⎡⎤=⎢⎥⎣⎦∑ [答案]1. 由棣莫佛-拉普拉斯定理可得22lim t b a n P a b dt -→∞⎧⎫⎪⎪<≤=⎨⎬⎪⎪⎩⎭⎰2. 令Y 表示100次抽取中取得优质品的次数()11,2,,1000i i X i i ⎧==⎨⎩ 当第次取到优质品当第次没有取到优质品则 ()1001,~100,0.5i i Y X Y B ==∑那么 1000.5,1000.50.E Y D Y =⨯=⨯⨯=由棣莫佛-拉普拉斯定理可得{}504515Y P Y P P -⎧⎫≤=≤=≤-⎨⎬⎩⎭()()11110.84130.1587≈Φ-=-Φ=-=3.由题意可得 99119,9i i i i EX EX DX DX ======∑∑又因为 9211i i DXP X EX εε=⎧⎫-<≥-⎨⎬⎩⎭∑故(D)项正确.4.因为()1,2,i X i = 服从参数为λ的泊松分布,故,i i EX DX λλ==,由林德伯格-列维定理得()lim n i n X n P x x λ→∞⎧⎫-⎪⎪⎪≤=Φ⎬⎪⎪⎪⎩⎭∑ 当n 充分大时,1nii X=∑近似服从(),N n n λλ分布,故C 项正确.5.由题意可知 211,i i EX DX λλ==由林德伯格-列维定理可得()22limntixnX nP x dt xμ-→∞⎧⎫-⎪⎪⎪≤==Φ⎬⎪⎪⎪⎩⎭∑⎰即()l i mninX nP x xλ→∞⎧⎫-⎪⎪⎪≤=Φ⎬⎪⎪⎪⎩⎭∑6.由于林德伯格-列维定理要求12,,,nX X X独立同分布,且具有有限的数学期望与方差.因此C项正确.7.设X表示同时去图书馆上自习的人数,并设图书馆至少有n个座位,才能以99%的概率保证去上自习的同学都有座位,即n满足{}0.99P X n≤≥.因为()~1000,0.8X B,所以{}⎪⎭⎫⎝⎛⨯⨯⨯-Φ-⎪⎭⎫⎝⎛⨯⨯⨯-Φ≈≤2.08.010008.01000`2.08.010008.01000`nnXP8000.9912.65n-⎛⎫=Φ≥⎪⎝⎭查表得8002.3312.65n-≥,故829.5n≥.因此图书馆至少应有830个座位.8.由于12,,,nX X X独立同分布,且2,400i iEX DXμσ===.由林德伯格-列维定理得{}1P X Pμ⎫⎛-<=<≈Φ-Φ⎝⎭⎝⎭21210.95=Φ-=Φ-≥⎝⎭⎝⎭即0.975Φ≥⎝⎭,查表得 1.9620≥,故2400 1.961536.64n≥⨯=.因此n至少为1537.9.设{}n X为独立同服从参数为1的泊松分布的随机变量序列,则1nkkX=∑服从参数为n的泊松分布,因此有101!!k k n n nn nn k k k k n n P X n e e e k k ---===⎧⎫≤==+⎨⎬⎩⎭∑∑∑由林德伯格-列维定理可得()11lim lim 02n k n k n n k X n P X n P →∞→∞=⎧⎫-⎪⎪⎧⎫≤=≤=Φ=⎨⎬⎩⎭⎪⎪⎩⎭∑∑ 所以11lim lim !k n n n n k n n k k n e P X n e k --→∞→∞==⎧⎫⎡⎤⎧⎫=≤-⎨⎨⎬⎬⎢⎥⎩⎭⎣⎦⎩⎭∑∑ 11lim lim 2n n k n n k P X n e -→∞→∞=⎧⎫=≤-=⎨⎬⎩⎭∑第7章数理统计的基础知识一、大纲要求(1)理解总体、简单随机样本、统计量、样本均值、样本方差及样本矩的概念,了解直方图和样本分布函数的意义和作用.(2)了解2χ分布、t分布、F分布的概念和性质,了解分位数的概念并掌握查表计算.(3)了解正态总体的抽样分布.二、重点知识结构图三、基本知识1.总体和个体在数理统计中,把研究对象的全体称为总体或母体,把组成总体的每一个研究对象(元素或单元)称为个体.总体分为有限总体和无限总体.有限总体是指其总体中的成员只有有限个.相应的,无限总体是指其总体中的成员有无限个.2．样本在一个总体中,抽取n 个个体12,,,n X X X ,这n 个个体总称为总体X 的样本或子样, n 称为样本容量.样本特性:① 代表性，样本中的每一个分量()1,2,i X i n = 与总体X 有相同的分布。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第六章 统计量与抽样分布注意： 这是第一稿（存在一些错误）1、解：易知的X 期望为μ，方差为2nσ，则()0,1X N μσ-近似地， 所以，()(0.10.10.909X P X P μσμσσ⎛⎫- ⎪-<=<≈Φ=⎪ ⎪⎪⎝⎭。
2、解 （1）由题意得：2222211111()()()()n n i i i i E X D X E X D X E X n n nσμ==⎛⎫=+=+=+ ⎪⎝⎭∑∑()2211111111()()n n i i i i E X X E X X E X X n n nσμ==⋅=⋅==+∑∑（2）1X X -服从正态分布，其中：1()0E X X -=，221122111()()()()n n n D X X D X D X n n nσ----=+= 从而 211~(0,)n X X N nσ-- 由于~(0,1)i X N μσ-，1,2,i n =，且相互独立，因此：()()2221~ni i X n μχσ=-∑~(0,1)X N μ-，所以()()222~1n X μχσ-由于()222(1)~1n S n χσ--，所以()()()222222(1)/~1,1(1)n X n X n SF n n S μμσσ---=--（3）由于()2/221~(/2)n i i X n μχσ=-∑，以及()221/2~(/2)ni i n X n μχσ=+-∑，因此有：()()()()22/2/2222211/211/2//~(,)22n nn ni i i i i i n i i n X X n n X X F μμμμσσ==+==+--=--∑∑∑∑3、解：（1）()1111111n nn iin n n i i n X X XX nX X ++++==+==+=+∑∑故1111n n n X nX X n n ++=+++ （2）()()()()122222111111n n nnn n in ini i nS n S X X XX XX ++++==----=---∑∑()()2211ni n i n i X XX X +=⎡⎤=---⎢⎥⎣⎦∑()()1112nin n nn i XX X XX ++==---∑()21n n n X X +=-()211111n n n n n X X X n +++⎧⎫⎡⎤=+--⎨⎬⎣⎦⎩⎭()2111n n X X n++=-()2111n n X X n++=- 4、解 用X 表示a~(0,1)X a N -。
由题意得：95%(0.5)2(0.5)121P X a P X a ≤-≤=-≤-=Φ- 经查表有：97n =5、解：（1）221111lim n n pi i n i i X X E n n σσ→∞==⎛⎫⎛⎫⎛⎫−−→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑∑， 因()0,1iX N σ，故()221ni i X n χσ=⎛⎫⎪⎝⎭∑，所以2211111lim 1n n i i n i i X X E E n n n n σσ→∞==⎛⎫⎛⎫⎛⎫⎛⎫==⋅= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭∑∑。
（2）因21n i i X E n σ=⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭∑，212n i i X D n σ=⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭∑，()20,1niXnN⎛⎫-⎪∑近似地，由分布函数的的右连续性知，()()limnnF x x→∞=Φ，即()()lim11nnF→∞=Φ。
（3）()()()()222111niiE X X X E n S nσ=⎛⎫--=-=-⎪⎝⎭∑()()()2211niiD X X X D n S DX=⎛⎫--=-+⎪⎝⎭∑()22421n SDnσσσ⎛⎫-=+⎪⎝⎭因()()22211n Snχσ--，故()()22121n SD nσ⎛⎫-=-⎪⎝⎭故()()224121niiD X X X nnσσ=⎛⎫--=-+⎪⎝⎭∑6、解（1）由题意得：()210221~(10)iiXμχσ=-∑，于是：()()210102222111(0.26 2.3)(2.623)0.978610iii iXP X Pμσμσσ==-≤-≤=≤≤=∑∑（2）由于()222(101)~1Snχσ--，即()210221~(9)iiX Xχσ=-∑，于是()()210102222111(0.26 2.3)(2.623)0.971910iii iX XP X X Pσσσ==-≤-≤=≤≤=∑∑7、解：()1120,8Y X X N=+，()23450,12Y X X X N=++，()367890,16Y X X X X N=+++，显然1Y，2Y和3Y相互独立。
()0,1N()0,1N，()30,14YN，取1a=，1b=，1c=，则()23Yχ8、 解 由题意得：91~(0,1)3ii X N =∑，以及()9221~9i i Y χ=∑，从而有91/~(9)3ii X t =∑，即91/~(9)i i X t =∑9、解：（1）1Y 和2Y 相互独立，13112X X X Y --=，31312X X X Y --=， 24222X X X Y --=，42422X X X Y --=， ()2130,2X X N σ-， ()2240,2X X N σ-，()()(((()()2213132224241,1X X X X Z F X X XX --==--，（2）22222213132222222424X X X X Z X X X X σσσσ++==++ 因()2221i X χσ，1,2,3,4i =，则()()()2222222222131313222222222224242422,22X X X X X X Z F X X X X X X σσσσσσσσ+++===+++10、解 （1）由题意得：()0E X =，()2D X =，从而()0E X =，21()10050D X ==（2）由题意可计算：()21001001002221111112*22()(2)(2)2999999100100i i i i i i E S E X XE X X X X ===⎛⎫=-=-+=-+= ⎪ ⎪⎝⎭∑∑∑（3）X 近似服从正态分布1~(0,)50X N ，于是(0.04)(220.7794P X P P >=>≈-Φ= 11、解：()10,1n X N +，10,XN n ⎛⎫ ⎪⎝⎭，()0,1XN ，()()2211n S nχ--，()1XY t n==-12、解（1）20.05(5)11.070χ=，20.06(5)10.596χ=，20.95(5) 1.145χ=，20.94(5) 1.250χ=（2）0.05(8) 2.306t=，0.06(8) 2.189t=，0.95(8)0.065t=，0.94(8)0.078t=，（3）0.05(3,5) 5.409F=，0.05(5,3)9.013F=，0.04(3,5) 6.098F=，0.04(5,3)10.617F=13、解：()1X和()1nX是统计量，()()()()()()()()1111111n n xXF x P X x P X x F x eλ-=≤=-≥=--=-，则()()1X E nλ，()()()()()11111111nx nxnnXx xF x P nX x P X F e en nλλ-⋅-⎛⎫⎛⎫⎛⎫=≤=-≥=--=-=-⎪ ⎪⎪⎝⎭⎝⎭⎝⎭，则()()1nX Eλ。
14、解由题意得：2122~(6,6)SFS，2221~(6,6)SFS，于是：2221212222120.05(max(,))2()S S SP C P CS S S=>=>，从而：0.025(6,6) 5.82C F==15、解：X和2S分别是总体X的期望EX和方差DX的无偏估计。
又12EX x dxθθθ==⎰，()222221412DX EX EX x dxθθθθ=-=-=⎰，故2E Xθ=，()2212E S DXθ==，()225522211114()()525415i ii iE X DX E X D X E X DXθθ==⎛⎫=+=+=+=⎪⎝⎭∑∑。
16、解（1）由于~(0,1)iXNμσ-，1,2,i n=，且相互独立，以及()22125~5Sχσ，因此：()26221~(6)i i X μχσ=-∑，()26221~(5)i i X Xχσ=-∑（2~(0,1)X N μ-，所以()()2226~1X μχσ-同时()()()2221222166/~1,5X X S F Sμμσσ--=（3）由题意得：0(())(()())0X YaE a E X E Y σσ-==-=2211()(()())4X Y a D a D X D Y a σσ⎛⎫-⎛⎫==+= ⎪ ⎪⎝⎭⎝⎭从而求得：2a = （4）由（3）知：2()~(0,1)X YN σ-，又22125~(5)S χσ和222211~(11)S χσ，于是222122511~(11)S S χσ+，从而2()/~(16)X Yt σ-化简后求得：8b = 17、解：()8218ii Xn χ=∑，()16298ii X n χ=∑，且81i i X =∑和169i i X =∑相互独立。
则()8116988,88ii ii XnF n n Xn==∑∑， 则()()88118,816169981110.58i i i i n n i i i i X X n P P F X X n ====⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪≤=≤== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭∑∑∑∑，又81169i i i i X X ==∑∑为连续分布，故8116910i i i i X P X ==⎛⎫⎪ ⎪== ⎪ ⎪⎝⎭∑∑。