同济大学朱慈勉-结构力学-第10章-结构动..习题答案
同济大学朱慈勉-结构力学-第10章-结构动..习题答案

同济大学朱慈勉 结构力学 第10章 结构动..习题答案10-1 试说明动力荷载与移动荷载的区别。
移动荷载是否可能产生动力效应10-2 试说明冲击荷载与突加荷载之间的区别。
为何在作厂房动力分析时,吊车水平制动力可视作突加荷载10-3 什么是体系的动力自由度它与几何构造分析中体系的自由度之间有何区别如何确定体系的 动力自由度10-4 将无限自由度的振动问题转化为有限自由度有哪些方法它们分别采用何种坐标 10-5 试确定图示各体系的动力自由度,忽略弹性杆自身的质量。
(a)(b)EI 1=∞EImyϕ分布质量的刚度为无穷大,由广义坐标法可知,体系仅有两个振动自由度y ,ϕ。
(c)](d)在集中质量处施加刚性链杆以限制质量运动体系。
有四个自由度。
10-6 建立单自由度体系的运动方程有哪些主要方法它们的基本原理是什么 10-7 单自由度体系当动力荷载不作用在质量上时,应如何建立运动方程10-8 图示结构横梁具有无限刚性和均布质量m ,B 处有一弹性支座(刚度系数为k ),C 处有一阻尼器(阻尼系数为c ),梁上受三角形分布动力荷载作用,试用不同的方法建立体系的运动方程。
解:1)刚度法该体系仅有一个自由度。
可设A 截面转角a 为坐标顺时针为正,此时作用于分布质量m 上的惯性力呈三角形分布。
其端部集度为..ml a 。
取A 点隔离体,A 结点力矩为:....3121233I M ml a l l mal =⨯⨯⨯= |由动力荷载引起的力矩为:()()2121233t t q l l q l ⋅⋅= 由弹性恢复力所引起的弯矩为:.2133la k l c al ⋅⋅+ 根据A 结点力矩平衡条件0I p s M M M ++=可得:()3 (322)1393t q l ka m al l c al ++=整理得:()...33t q ka c a m a l l l++= 2)力法.cα解:取AC 杆转角为坐标,设在平衡位置附近发生虚位移α。
结构力学课后习题答案

习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lfy )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
结构力学课后习题答案(朱慈勉)

朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a)(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aa aaa2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m 2m2mA2m2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F两铰的位lx l lx置。
结构力学1-9章答案
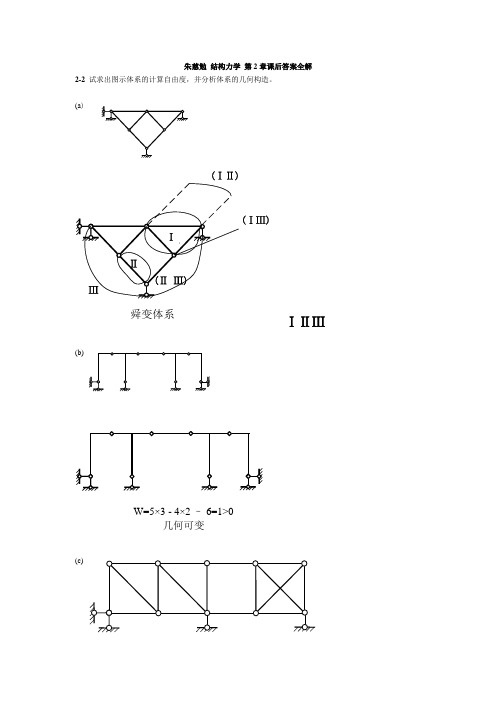
1 8
2 36
1 4
3 ( 1 3 2 1 6 2 (3) 1 (6))
6EI 2
2
+ 2 6 1 2 5 ()
6EI
2EI
(c)
2kN/m 6m
2kN 2kN
B 2EI C
EI
EI
1
A
D
3m 3m 3m
1 6
2
2
3
3
42
18
36
30
6
MP
M
xc
6
3 2EI
(2
18
2
0
C
F RC [( 1 ) a] a (方向与图示一致)
h
h
(b)
c1 c2 c3
A A′
2a
BC
D
B′ C′
D′
Δ C
a
2a
1
0.5
1.5
0
FR 图
yc
t h
M ds
t
5 4
5
+t 5 5 t (1) 12 t ( 1 4 3 2 4 3)
4
2
h2
54.5t()
5-10 试求图示结构在支座位移作用下的位移:(a) ΔC ;(b) ΔyC , ΔC 。 (a)
C D
D′
E E′
C′ΔC
h
b
A
l 2
B
B′
l 2
a
1
1
1
h
h
0
A
B
C
D
E
FG
H
2m 2m 2m 2m 2m 2m 2m 3m
A
M 7.5
结构力学课后习题答案
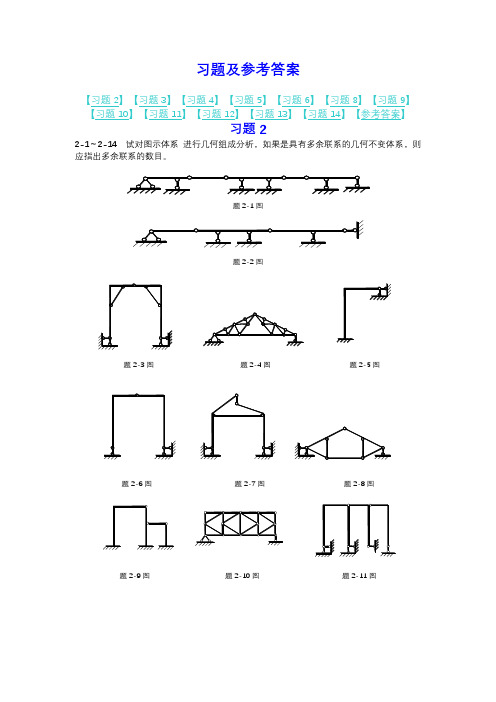
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
题3-1图3-2 试不计算反力而绘出梁的M 图。
题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
题4-1图4-2 作图示刚架的M 图。
(b)(a)20kN40kN20kN/m40kN(b)5kN/m40kN(a)(c)(b)(a)题4-2图4-3 作图示三铰刚架的M 图。
题4-3图4-4 作图示刚架的M 图。
题4-4图4-5 已知结构的M 图,试绘出荷载。
P(e)(d)(a)(b)(c)/4kN(b)(a)(a)(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
题4-6图习题55-1 图示抛物线三铰拱轴线方程,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程,求截面K 的弯矩。
题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(e)(g)(h)P(d)(c)(a)(b)(f)x x l l fy )(42-=x x l lfy )(42-=C题6-1图6-2 用结点法计算图示桁架中各杆内力。
题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(b)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
结构力学课后习题答案(朱慈勉)

朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aa aaa2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·m ABC D30303011010QM 210(c)45MQ(d)3m3m6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
结构力学课后习题答案

习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lfy )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
同济大学朱慈勉结构力学课后习题答案

更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
同济大学-朱慈勉版-结构力学-课后答案(上)

2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a)(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)【W=5×3 - 4×2 – 6=1>0几何可变(c)】有一个多余约束的几何不变体系(d)|2-3 试分析图示体系的几何构造。
(a)/W=3×3 - 2×2 – 4=1>0可变体系(ⅡⅢ) (b);Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变-(b)~(ⅠⅢ)(ⅡⅢ)几何不变~W=4×3 -3×2 -5=1>0几何可变体系(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体@(e)(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系…(f)?(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(g):(h)|二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)%(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)!Ⅲ(ⅡⅢ)(ⅠⅢ)`3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)%aa *a a2P F a 2P F a4P F Q34P F 2P F(b)"2020Q10/326/310(c){2m6m`4m2m3m2m2m3m3m4m18060(d)]7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)3m2m2m2m2m2m 2m2m4kNm%6m1k N /m2kNCB{242018616MQ18(b),30303011010QM 2106m10kN>3m3m40kNmAB CD:45MQ(d)…444444/32MQN3m3m6m)2m2m(e))4481``(f)#222220M…4m2m3m4m/3-4试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)—(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
结构力学章节习题及参考答案
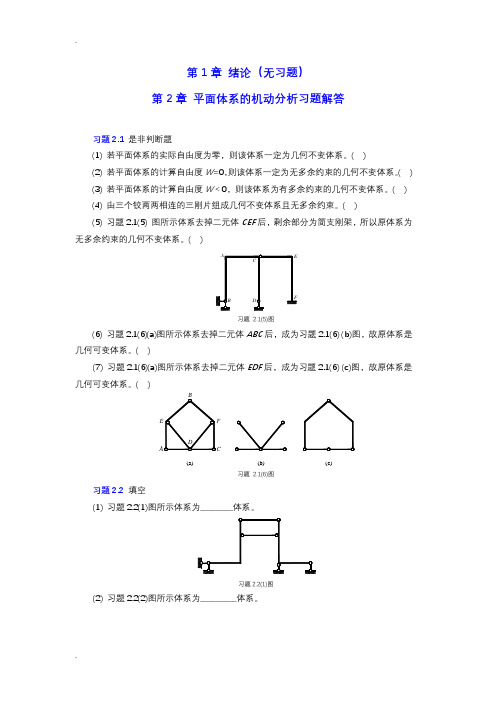
习题7.2填空题
(1)习题5.2(1)图(a)所示超静定梁的支座A发生转角,若选图(b)所示力法基本结构,则力法方程为_____________,代表的位移条件是______________,其中1c=_________;若选图(c)所示力法基本结构时,力法方程为____________,代表的位移条件是______________,其中1c=_________。
(a)
习题3.7改正习题3.7图所示刚架的弯矩图中的错误部分。
(a)(b)(c)
(d)(e)(f)
习题3.7图
习题3.8作习题3.8图所示刚架的内力图。
(a)
(b)
习题3.8图
第4章 静定拱习题解答
习题4.1是非判断题
(1) 三铰拱的水平推力不仅与三个铰的位置有关,还与拱轴线的形状有关。( )
(2) 所谓合理拱轴线,是指在任意荷载作用下都能使拱处于无弯矩状态的轴线。 ( )
习题3.2(2)图
习题3.3作习题3.3图所示单跨静定梁的M图和 图。
(a) (b)
(c) (d)
(e) (f)
习题3.3图
习题3.4作习题3.4图所示单跨静定梁的内力图。
(c)
习题3.4图
习题3.5作习题3.5图所示斜梁的内力图。
习题3.5图
习题3.6作习题3.6图所示多跨梁的内力图。
(a)
习题3.6图
(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。( )
(5) 习题2.1(5) 图所示体系去掉二元体CEF后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。( )
习题 2.1(5)图
《结构力学习题》(含答案解析)

第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
a a9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l /3 2 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
ql15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
q16、求图示刚架中D点的竖向位移。
EI =常数。
l/217、求图示刚架横梁中D点的竖向位移。
EI=常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/219、求图示结构A、B两截面的相对转角,EI=常数。
l/23l/320、求图示结构A、B两点的相对水平位移,E I = 常数。
ll21、求图示结构B点的竖向位移,EI = 常数。
同济大学朱慈勉-结构力学第10章-结构动力学

分析过程:
第1阶段:位移时间历史 y y(x)
第2阶段: 应力、应变及内力 (如何求?)
已知荷载的类型
周期荷载: 简谐荷载
复杂荷载
F
t
F
t
建筑物上的偏心电机
内燃机连杆
任意复杂周期荷载可以用傅里叶级数展开为简谐荷载
非周期荷载:
F
t
F
t
爆破
地震
§10-2 体系振动的自由度
(动力)自由度:确定体系上全部质量位置所需的独立参 数的数目
确定体系阻尼比的一种方法
▪ 阻尼体系动力反应:
y(t) et sin(dt )
▪ 体系的阻尼比可以通过测试体 系运动的衰减规律得到:
▪ 体系从任一时刻经几个周期后 的振幅比为:
y (t)
e tk
e (tk nT )
t
0 tk
t k + nT
e t
T 2/d
y e tk
tk
n T
2nπ d
my cy ky 0
(3-2)
▪ 特征方程:
s c
c
2
2
2m 2m
▪ 如果体系的阻尼比临界阻尼小,则显然有c/2m< ,这时,特 征方程根式中的值必然为负值,则s 值成为:
s c i 2 c 2
2m
2m
▪ 引入符号: c c cc 2m
c 2m
▪ 其中 表示体系阻尼与临界阻尼的比值,称为阻尼比,则:
y3 y2
y1
忽略楼板变形
3个自由度
y1 y2
2个自由度
1个自由度
y1
忽略杆件轴向变形
4个自由度
y1
结构力学朱慈勉版课后答案【重要】
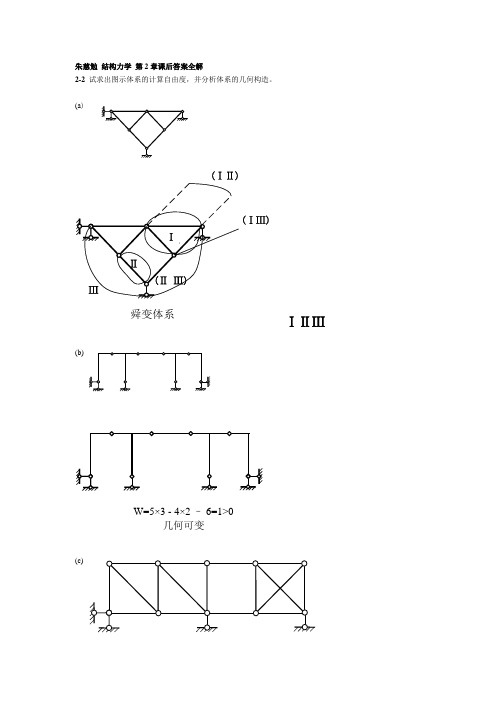
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aaaa a2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m 3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m 6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
结构力学课后习题答案

结构力学课后习题答案(总23页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN10kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)/20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lf y )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
同济大学朱慈勉版结构力学课后答案(上)之欧阳美创编
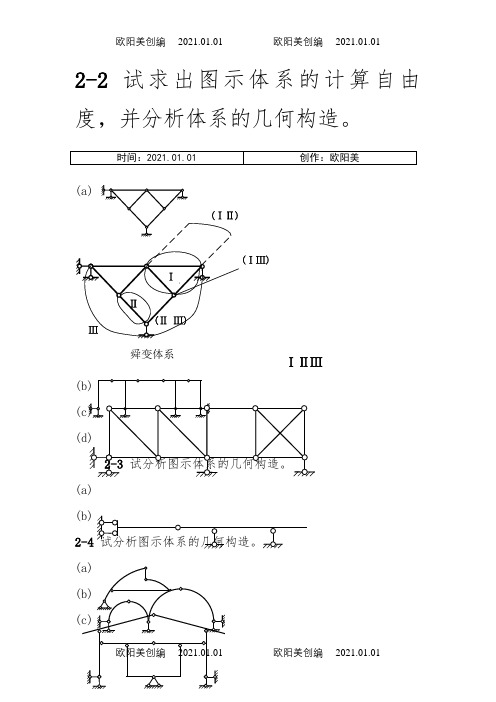
2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(ⅠⅢ)舜变体系ⅠⅡⅢ(a)(c) (d) (e) (f)3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝3-6 试作图示刚架的弯矩和剪力图。
(a) (b)14.25424213.5 1.50.2525.75A 72425 2.50.5()C 420.524 4.25()3.5(),0.25()5.752.1,24 4.253.752.5E K B B B B A A EF K M M R R H H V H Q Q =⨯-⨯⨯==⨯+⨯=⨯+⨯⨯=⨯→=-↓⨯⨯+⨯=⨯→=→∴=↑=←===⨯-=左对点求矩:对点求矩:2 2.1(c)l x l l x80/3Q8080380,61603330():(2023304)/2120():61201030420211320()380()3DA ED C C B B A M M H F V A V V V =⨯==⨯==←=⨯⨯+⨯=↑⨯+⨯=⨯+⨯⨯∴=-↓∴=↑对点求矩对点求矩(d)8/34/388414233:41614284()4:441426()38(),03DA B B B B A A M A V V C H H H V =⨯-⨯⨯=⨯⨯+⨯⨯=⨯→=↑⨯-⨯⨯=⨯→=←∴=←=对点求矩对点求矩(e)2FaF2Fa2Fa F F F2F----+2Fa2Fa2FaMQ02(),020322222(),2()4(),0C B p E B F BP H P F H P F P D P D M V F M H V MF a a H F a V aH F V F H F V =→=↑=→==→⨯+⨯=⨯+⨯∴=←=↓∴=→=∑∑∑(f)进一步简化BH IH 8:4(),4()4(),4(),42810B B I I A H KN V KN H KN V KN M N m=→=↓=-←=-↑=⨯=•可知84(g)2aqa22221.5()21.50 1.5()0,, 1.5C CA AGF GHHqaqa H a H qaqa a H a H qaH M qa M qa+=⨯→=→⨯+⨯=→=-←===对点求矩:对F点求矩:3-11试指出图示桁架中的零杆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
同济大学朱慈勉 结构力学 第10章 结构动..习题答案10-1 试说明动力荷载与移动荷载的区别。
移动荷载是否可能产生动力效应?10-2 试说明冲击荷载与突加荷载之间的区别。
为何在作厂房动力分析时,吊车水平制动力可视作突加荷载?10-3 什么是体系的动力自由度?它与几何构造分析中体系的自由度之间有何区别?如何确定体系的 动力自由度?10-4 将无限自由度的振动问题转化为有限自由度有哪些方法?它们分别采用何种坐标? 10-5 试确定图示各体系的动力自由度,忽略弹性杆自身的质量。
(a) (b)y ,ϕ。
(c)(d)10-6 10-710-8 m ,B 处有一弹性支座(刚度系数为k ),C 处有一阻尼器(阻尼系数为c ),梁上受三角形分布动力荷载作用,试用不同的方法建立体系的运动方程。
解:1)刚度法可设A 截面转角a 为..ml a 。
取A 点隔离体,A 结点力矩为: (3)121233I M ml a l l mal =⨯⨯⨯=由动力荷载引起的力矩为:()()2121233t t q l l q l ⋅⋅= 由弹性恢复力所引起的弯矩为:.2133la k l c al ⋅⋅+ 根据A 结点力矩平衡条件0I p s M M M ++=可得:整理得:()...33t q ka c a m a l l l++= 2)力法解:取AC 杆转角为坐标,设在平衡位置附近发生虚位移α。
根据几何关系,虚功方程为:() (2)01110333l t q l l k l l l c m x xdx ααααααα-⋅-⋅-⋅=⎰则同样有:()...33t q ka c a m a l l l++=。
t )10-9 图示结构AD 和DF 杆具有无限刚性和均布质量m ,A 处转动弹簧铰的刚度系数为k θ,C 、E 处弹簧的刚度系数为k ,B 处阻尼器的阻尼系数为c ,试建立体系自由振动时的运动方程。
解:取DF 隔离体,F M ∑取AE 隔离体:0AM=∑将R 代入,整理得:10-10 试建立图示各体系的运动方程。
(a)解:(处转角作为坐标,绘出梁的位移和受力图如下所示。
图中惯性力为三角形分布,方(2)画出p M 和1M 图(在B 点处作用一附加约束)(3)列出刚度法方程113EIk l=,()..3124pt m R l M α=- 代入1p R 、11k 的值,整理得: (b) 解:2M 图试用柔度法解题此体系自由度为1 。
设质量集中处的竖向位移y 为坐标。
y 是由动力荷载()p t F 和惯性力矩I M 共同引起的。
由图乘法: 惯性力矩为..m y l -经整理得,体系运动方程为:()..33516p t EI m y y F l +=。
10-11 试求图示各结构的自振频率,忽略杆件自身的质量。
(a)1M 图图乘得:31111225222223236a a a f a a a a EI EI⎛⎫=⨯⨯⨯⨯⨯+⨯⨯⨯=⎪⎝⎭(b)23。
ll2 m (t ) l2l 22aa a由此根据弯矩平衡可求得49P k =。
ω== (c)于是两者并联的柔度系数为331696102l EI EI EIl δ==+并(d)解:图 M 图10-12 10-13 比如何?10-14 什么是阻尼系数、临界阻尼系数、阻尼比和振幅的对数递减率?为什么阻尼对体系在冲击荷载作用下的动力响应影响很小?10-15 设已测得某单自由度结构在振动10周后振幅由1.188mm 减小至0.060mm ,试求该结构的阻尼比ξ。
解:0475.006.0188.1ln 201ln 21==≈+ππξn k k y y n 10-16 设有阻尼比ξ=0.2的单自由度结构受简谐荷载F P (t )= F t θsin 作用,且有ωθ75.0=。
若阻尼比降低至ξ=0.02,试问要使动位移幅值不变,简谐荷载的幅值应调整到多大?解:2222222411ωθξωθω+⎪⎪⎭⎫ ⎝⎛-⋅=m F A 已知ξ从0.2降低至0.02.ωθ75.0=,t F F θsin 1=,A 不变。
l 2 l2F 简谐荷载的幅值应调整到0.827F 。
10-17 试说明动力系数的含义及其影响因素。
单自由度体系质量动位移的动力系数与杆件内力的动力系数是否相同?10-18 什么是共振现象,如何防止结构发生共振?10-19 试求图示梁在简谐荷载作用下作无阻尼强迫振动时质量处以及动力荷载作用点的动位移幅值,并绘制最大动力弯矩图。
设36ml EI =θ。
(a)33l EI位移。
ω()32221sin sin 31t F Fl y t t EI m θθθωω=⋅=--即幅值为33Fl EI当幅值最大时,弯矩也最大。
max M 图(b)2M 图 (1)求结构运动方程 如所示弯矩图,图乘后,333112212215,,24348l l l f f f f EI EI EI====其中2*3245,2EI P F ml ω==稳态解:所示结构的运动方程为()35=sin 36t C Fl y t EI θC 点最大动位移幅值为3536Fl EI(2)求B 点的动位移反应B 点的动位移幅值为3121288Pl EI(3)绘制最大动力弯矩图1M 图 2M 图 最大动力弯矩图10-20 试求图示集中质量体系在均布简谐荷载作用下弹簧支座的最大动反力。
设杆件为无限刚性,弹簧的刚度系数为k 。
解:若()t q 已知图示体系为静定结构,具有一个自由度。
设为B 点处顺时针方向转角α为坐标。
建立动力方程:2l2ll 2l 2l tθ sin t θ sin则弹簧支座的最大动反力为l 891122⋅-ωθ。
10-21 设图a 所示排架在横梁处受图b 所示水平脉冲荷载作用,试求各柱所受的最大动剪力。
已知EI =6×106N ·m 2,t 1=0.1s ,F P0=8×104N 。
(a)解:求排架自振频率,横梁无限刚性,则各排架水平侧移相同。
可将排架柱视为三个并联的弹簧。
边柱刚度柔数k3.9773.91.01==T t 数值很小 所以认为当()t P F 作用结束时,结构位移很小,弹性力忽略不计,于是根据动量守恒原理可得:再根据势能守恒得:(b)10-22 设图a 所示排架横梁为无限刚性,并有图b 所示水平短时动力荷载作用,试求横梁的动位移。
(a)解:在三角形冲击荷载作用下单自由度体系的质点位移反应可分两个阶段考虑。
第一阶段(10t t ≤≤): 求T 的过程。
1M 图 第二阶段(1t t >)因为不受外力作用,所以横梁以1t 时刻的位移和速度为初始值做自由振动。
(b)10-23 设题10-22图a 所示刚架m =4000kg ,h =4m ,刚架作水平自由振动时因阻尼引起振幅的对数递减率γ=0.10。
若要求振幅在10秒内衰减到最大振幅的5%,试求刚架柱子的弯曲刚度EI 至少为何值。
解:(1)求周期数。
(2)求k :km n t n π2=两柱并联10-24 设某单自由度体系在简谐荷载F P (t )= F t θsin 作用下作有阻尼强迫振动,试问简谐荷载频率θ分别为何值时,体系的位移响应、速度响应和加速度响应达到最大?解:在简谐荷载F P (t )= F t θsin 作用下,稳态位移响应可表示为()()αθ-=t A y t sin6mEIEI 1=∞mhEIF P (t ) F P (t )t t 1 F P0 O F P (t )tF P0t 1O其中:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎭⎫⎝⎛-==+⎪⎪⎭⎫ ⎝⎛-⋅=-221222222212tan 411ωθωθξαμωθξωθωst y m F A(1)使动位移最大,即使μ最大,从而得出22222241ωθξωθ+⎪⎪⎭⎫ ⎝⎛-最小。
设()22222241ωθξωθθ+⎪⎪⎭⎫ ⎝⎛-=f 使()0='θf ,则221ξωθ-= (2)())cos(αθθ-='t A y t 设()222222222141141ωξωθθωθξωθθθ+⎪⎭⎫ ⎝⎛-=+⎪⎪⎭⎫ ⎝⎛-=g如果使速度响应最大,则()θg 最大,设()2221141ωξωθθθ+⎪⎭⎫⎝⎛-=g ,显然要求()θ1g 最小。
使:()01112221=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-='ωθωθθθg 得ωθ=。
(3)())sin(2αθθ--=''t A y t令()2222221411θωξωθθ+⎪⎭⎫ ⎝⎛-=h 显然要求()θ1h 最小。
则()02112221=--='ωξθθh 解的:221ξωθ-=10-25 结构自振频率的个数取决于何种因素?求解结构自振频率的问题在数学上属于何类问题? 10-26 试用柔度法求下列集中质量体系的自振频率和主振型。
(a) 解:2M 图(1)EIl f l l l l l l EIf 423222221232221231111=⇒⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯=(2)振型方程 令2312ωλml EI=,频率方程为: (3)振型图如下第一振型 第二振型(b)解:令ω21解得:3mlEI,332060.16675.23ml EIml EI =⋅=ω1773.2707.0414.211121-=--=λA A,1358.0707.0414.221222=--=λA A(c) 解:2M 图 (1)EI l f 3311=,EI l f 1213322=,EI l f f 12532112==(2)振型方程 令2312ωλml EI=,频率方程为: (3)当227.151==λλ时,设7227.0108112111=-=⇒=λA A当773.12==λλ时,设6227.0108122212-=-=⇒=λA A绘出振型图如下:第一振型 第二振型(d) 解: 2M 图频率方程为:aa alll l取3121,3m ma m ma ==代入整理得: 22444003a a λλ-+=其中3248EI a m λω= 振型方程为:将()1,11,2i i A i ωω===代入(a )式中的第一个方程中,得: 绘出振型图如下:第一振型 第二振型(e)解:2M 图(1)(2令λ振型图如下:第一振型 第二振型第三振型(f) 解: 1M 图 2M 图 3M 图(1)(2)振型方程为:令326EIml λω=,频率方程为: 10-27 试用刚度法求下列集中质量体系的自振频率和主振型。
(a) 解: 2M 图第二振型(b) 解:2F 图 令λ (c)aa a4mEI=常数aaEI解:1M 图 2M 图作出附加连杆移动单位位移的弯矩图 列出频率方程: 解得:结构自振频率分别为:求第一振型:令111A =得211A = 求第二振型:令121A =得221A =- 结构的振型向量形式为: 振型图如下:第一振型 第二振型 (d) 解:2M 图12k 列振型方程:()()12*160y A ⎨-=⎪⎩其中322ml y EI ω=列频率方程并求解: 求振型将11115,1y A ==代入方程组(*)中得:210A =,即()110A⎛⎫= ⎪⎝⎭ 将22216,1y A ==代入方程组(*)中得:220A =,即()201A ⎛⎫= ⎪⎝⎭振型图如下:第一振型 第二振型10-28 试说明在应用多自由度体系强迫振动的振幅方程(10-66)和(10-71)时,对动力荷载的性质、特点和作用位置分别有何要求?10-29 试说明为什么可以将惯性力幅值与简谐荷载幅值同时作用在体系上,按静力学方法计算体系的动内力幅值。
