第9章 噪声中信号的检测
高斯色噪声中信号的检测

104 高斯色噪声中信号检测的思路(1)色噪声:噪声的功率谱密度在整个频带内的分布是非均匀的。
色噪声的自相关函数不再是δ函数,故色噪声在任意两个不同时刻的取值不再是不相关的。
(2)高斯色噪声:服从高斯分布的色噪声。
(3)高斯色噪声中信号检测的基本方法:一种是白化处理方法,另一种是卡亨南-洛维(Karhunen-Loeve )展开方法。
(4)白化处理方法:先将含有高斯色噪声的接收信号通过一个白化滤波器,使输入白化滤波器的色噪声在输出端变为白噪声,然后再按白噪声中信号检测的方法进行处理。
(5)卡亨南-洛维展开方法:把含有高斯色噪声的信号表示成正交展开的形式,将正交展开的系数作为样本,从而使样本是相互统计独立的。
通过求取卡亨南-洛维展开系数的概率密度,并将它们相乘,得到所有卡亨南-洛维展开系数的联合概率密度(即含有高斯色噪声的信号的多维概率密度);再由卡亨南-洛维展开系数的联合概率密度得到不同假设下的似然函数,从而就可以进行似然比检测。
2 卡亨南-洛维展开1.随机信号的正交展开(1)正交函数集在时间),0(T 上定义的函数集},2,1),({ =k t f k ,如果满足⎰⎩⎨⎧≠==*Ti k ik ik t t f t f 001d )()( (5.2.1) 则称此函数集是正交函数集。
(2)完备的正交函数集如果在平方可积或能量有限的函数空间中,不存在另一个函数)(t g ,使⎰==*Tk k t t g t f 0,2,10d )()( (5.2.2)则正交函数集},2,1),({ =k t f k 称为完备的正交函数集。
(3)随机信号的正交展开在时间),0(T 上的任意平方可积随机信号)(t x 的正交展开表示为∑∑∞==∞→==11)()(lim)(k k k mk k km t f x t f xt x (5.2.3)其展开系数k x 为⎰==*Tk k k t t f t x x 0,2,1d )()( (5.2.4)105对于随机信号)(t x ,展开系数k x 是随机变量,因此随机信号)(t x 的正交展开应在平均意义上满足0)()(lim 21=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-∑=∞→m k k k m t f x t x E (5.2.5) 即正交展开的均方误差等于零,或者说正交展开均方收敛于)(t x 。
经典雷达资料-第9章 电子反干扰(ECCM)-3
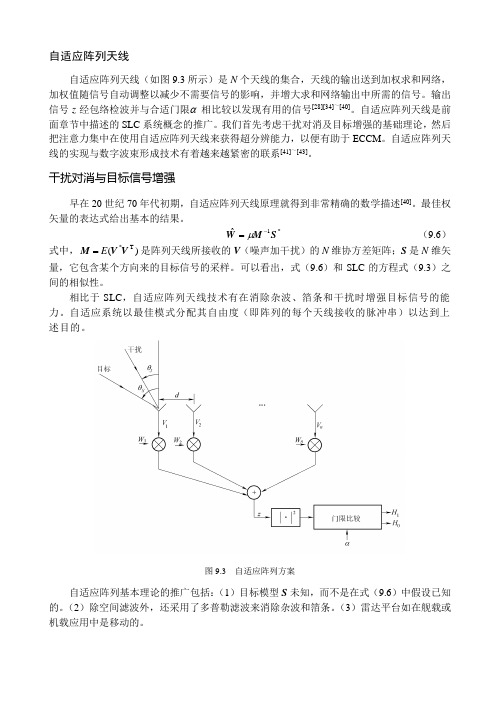
自适应阵列天线自适应阵列天线(如图9.3所示)是N 个天线的集合,天线的输出送到加权求和网络,加权值随信号自动调整以减少不需要信号的影响,并增大求和网络输出中所需的信号。
输出信号z 经包络检波并与合适门限α 相比较以发现有用的信号[28][34]~[40]。
自适应阵列天线是前面章节中描述的SLC 系统概念的推广。
我们首先考虑干扰对消及目标增强的基础理论,然后把注意力集中在使用自适应阵列天线来获得超分辨能力,以便有助于ECCM 。
自适应阵列天线的实现与数字波束形成技术有着越来越紧密的联系[41]~[43]。
干扰对消与目标信号增强早在20世纪70年代初期,自适应阵列天线原理就得到非常精确的数学描述[40]。
最佳权矢量的表达式给出基本的结果。
*1ˆS M W-=μ (9.6) 式中,)(T *V V M E =是阵列天线所接收的V (噪声加干扰)的N 维协方差矩阵;S 是N 维矢量,它包含某个方向来的目标信号的采样。
可以看出,式(9.6)和SLC 的方程式(9.3)之间的相似性。
相比于SLC ,自适应阵列天线技术有在消除杂波、箔条和干扰时增强目标信号的能力。
自适应系统以最佳模式分配其自由度(即阵列的每个天线接收的脉冲串)以达到上述目的。
图9.3 自适应阵列方案自适应阵列基本理论的推广包括:(1)目标模型S 未知,而不是在式(9.6)中假设已知的。
(2)除空间滤波外,还采用了多普勒滤波来消除杂波和箔条。
(3)雷达平台如在舰载或机载应用中是移动的。
第9章 电子反干扰(ECCM ) ·359·式(9.6)的最佳滤波的检测概率为[40])/1ln(2,(*1T FA D P Q P S M S -= (9.7)式中,Q (·,·)是Marcum Q 函数,P F A 是预先设定的虚警概率。
可以证明,式(9.6)中的权矢量提供最大的改善因子I f ,它由下式定义:输入端信干功率比输出端信干功率比=f I (9.8) 输入端信干功率比(SNR)I (相对于单个回波脉冲)在天线的输入端测量。
非高斯噪声中的信号检测

说明:非高斯噪声通 常具有较大的拖尾 拉普拉斯
-2
-1
0
1
2
3
4
5
1.非高斯噪声的性质
零均值PDF非高斯性描述:峰态(kurtosis)
E ( w [n]) 2 2 2 3 E ( w [n])
高斯PDF : 均匀PDF :
4
E (w [n]) 3 2 0
4 4
w[n] ~ U [ 32 , 32 ] 2 1.2
检测性能: PD Q[Q1 ( PF ) d 2 ]
2. 非高斯噪声中的确定性信号检测
p( w) w i ( A) dw p( w)
2
Fisher信息:
基于单个观测数据
例2: 拉普拉斯噪声中弱直流电平检验:
H 0 : z[n] w[n]
n 0,1,..., N 1
s[n]
n 0
N 1
H1 ' H0
非高斯噪声中确定性弱信号的NP检测器结构
2. 非高斯噪声中的确定性信号检测
pw ( z[n]) N 1 z[n] T (z ) s[n] pw ( z[n]) n 0
高斯分布时
1 T (z ) 2
1
0 1
p( w[n]) k
k 1 M 2 1 1 w [ n] exp 2 22 2 k k
权值因子:
k 1
M
k
1
2. 非高斯噪声中的确定性信号检测 例1: 非高斯噪声中直流电平检验:
H 0 : z[n] w[n]
h( y[n])
色高斯噪声中信号的检测

– 最优检测器与判决规则:
可编辑ppt
9
可编辑ppt
10
可编辑ppt
11
可编辑ppt
12
– 正交函数和卡亨南-洛维展开:
可编辑ppt
4
色高斯噪声中信号的检测
• 卡亨南-洛维(Karhunen-Loove)展开
– 正交函数和卡亨南-洛维展开:
可编辑ppt
5
可编辑ppt
6
可编辑ppt
7
色高斯噪声中信号的检测
• 问题和假设:
可编辑ppt
8
色高斯噪声中信号的检测
色高斯噪声中信号的检测
• 概述
可编辑ppt
1
色高斯噪声中信号的检测
• 卡亨南-洛维(Karhunen-Loove)展开
– 模型:
可编辑ppt
2
色高斯噪声中信号的检测
• 卡亨南-洛维(Karhunen-Loove)展开
– 模型:
可编辑ppt
3
色高斯噪声中信号的检测
• 卡亨南-洛维(Karhunen-Loove)展开
高斯白噪声中信号的检测

32 4.1 内容提要及结构本章首先介绍高斯白噪声统计特性及随机信号的采样定理,然后依次讨论高斯白噪声中二元确知信号检测、多元确知信号检测、二元随机参量信号检测以及多重二元信号的检测。
本章内容实际是将信号检测的基本理论具体应用到高斯白噪声信号检测的情况,并且主要讨论的是理想高斯白噪声中信号检测方法及性能分析方法;本章主要讨论一般的似然比检测方法,而不指定哪一个具体准则。
本章内容逻辑结构如图4.1.1所示。
4.2 目的及要求本章的目的是使学习者从概率分布、相关函数和功率谱密度等方面理解高斯白噪声的特点,熟悉随机信号的采样定理;掌握带限高斯白噪声和理想高斯白噪声中二元确知信号检测方法,尤其掌握理想高斯白噪声中观测信号的似然函数,掌握理想高斯白噪声中二元确知信号检测性能分析方法;掌握理想高斯白噪声中多元确知信号检测方法及性能分析方法;掌握理想高斯白噪声中二元随机参量信号检测方法及性能分析方法;理解和熟悉高斯白噪声中多重二元信号检测的概念及使用条件,掌握高斯白噪声中多重二元确知信号和二元随机参量信号检测方法及性能分析方法。
4.3 学习要点4.3.1 高斯白噪声● 内容提要:本小节从高斯噪声和白噪声两个方面论述高斯白噪声的概念,从概率分布、相关函数和功率谱密度等方面论述高斯白噪声的统计特性,简要讨论低通和带通随机信号采样定理。
● 关键点:从高斯噪声和白噪声两个方面理解高斯白噪声的概念,从概率分布、相关函数和功率谱密度等方面掌握高斯白噪声的统计特性,熟悉低通和带通随机信号采样定理。
1.噪声噪声是指与接收的有用信号混杂在一起而引起信号失真的不希望的信号,是一种随机信号或随机过程。
2.高斯白噪声 高斯白噪声是一种幅度分布服从高斯分布,功率谱密度在整个频带内为常数的随机信号或随机过程。
高斯白噪声既具有高斯噪声的特性,又具有白噪声的特性。
确知信号的检测二元确知信号 的检测 多元确知信号 的检测带限高斯白噪声中二元确知信号的检测理想高斯白噪声中二元 确知信号的检测二元随机振幅和相位信号的检测二元随机相位信号的检测3.高斯噪声1)高斯噪声定义高斯噪声是一种幅度分布服从高斯分布的随机信号或随机过程。
高斯白噪声中确知信号的波形检测

H1 kS1* e jt1 AkS e j e jt1 k S e j t1
国家重点实验室
4.2 匹配滤波器
3 匹配滤波的性质
3.3 匹配滤波器的鲁棒性
对于频移信号,匹配滤波器不具有适应性。 设信号s(t)的匹配滤波器的系统函数为 H kS* e jt0
国家重点实验室
4.2 匹配滤波器
3.4 匹配滤波器与相关器的关系
对于平稳输入信号 x1 t st nt 和 x2 t s0 t ,互相关 器的输出为:
rx1x2 x1 t x2 t dt
st nt s0 t dt
2
1 E n t 2
2 o
Pno d
2
1 2
H Pn d
国家重点实验室
4.2 匹配滤波器
def
2.4输出信号功率信噪比
so t 的峰值功率 SNRO no t 的平均功率
1 H S e jt0 d 2 1 2 H Pn d 2
4.3节将介绍一种正交级数展开方法
国家重点实验室
4.2 匹配滤波器
• 匹配滤波器的定义
• 匹配滤波器的设计 • 匹配滤波器的主要性质
国家重点实验室
4.2 匹配滤波器
1. 匹配滤波器的定义
若线性时不变滤波器输入的信号是确知信号,噪声是加性平稳噪声, 则在输入功率信噪比一定的条件下,使输出功率信噪比最大的滤波 器,即为与输入信号匹配的最佳滤波器,称为匹配滤波器。
H
S * e jt0 Pn Pn
第二讲噪声中非起伏信号的检测和非相参积累检测和处理

修正量
终 始 修正量
2
m 2
起始
终了
输入
单次虚警
目标
门限K=4 输出
方位角中心估计修正示意图
§3 二分层大滑窗检测器
二、性能
PF
qnCmK11
pnK
q 1 m n
K
pn
C K 1 m1
pnK
q mK 1 n
qn
pn
0 11011011....1101 1
求Min
Pd(m)
a(m)
单脉冲检测概率
所需信噪比
求最小信噪比
§3
一、原理
二分层大滑窗检测器
滑窗宽 m 波束内击中数 M
当m M 小滑窗 m M 大滑窗
§3 二分层大滑窗检测器
准则
起始: K m 终了: j m
一般j K 1或K 2
方位中心
终
始
2
始
其中: V0 2 ln Pf
Pd P 2ln Pf S N V dV
例: 虚警概率的确定
虚警持续时间
PFa
Td T fa
1 Tfa B
虚警间隔时间 例:B=1MHz,Tfa=1s,则PFa=10-6。
§2 连续信号检测
四、检波的影响
输入
检波器输出
包络检波器
门限
00 00
§1 引言
六、主要类型
*双门限成组检测器 *大滑窗检测器 *双极点滤波检测器
§2
工作方式
双门限成组检测器
连续发射m个脉冲
指向1
指向2
指向3
相控阵烧穿式(burn out)工作模式
现代通信理论与技术P9系统分析与设计XXXX.pdf

Pe
1 2
P(0 s1 ) P(1 s0 )
=
1 2
erfc
A 2σ
1 2
e
rfc
γ 2
2015/12/9
26
相干FSK系统的误码率
因为FSK信号的平均功率为
S
=
1 2
A2 cos2ωc1t A2 cos2ωc0t
A2 2
噪声功率为σ2,所以平均功率信噪比为
γ
A2 2σ 2
相干FSK系统的误码率:
通信系统的性能指标; 数字载波通信系统的抗噪声性能分析; 数字通信系统的通信链路分析; 数字通信系统设计。
2015/12/9
5
9.1 通信系统的主要性能指标 (Performance Measurements of
Communication Systems)
2015/12/9
6
通信的任务是传递信息,传输信息的有效 性和可靠性是通信系统最主要的性能指标。
2015/12/9
13
误码率的计算:
发 送 端 用 s1(t) 传 送 码 元“1”时,r(t)的条 件概 率密度函数和误码率分别 为:
p(r s1 )
1
(r-A)2
e 2 2
2
V
P(0 s1 ) p(r s1 )dr
发送端用s0(t)传送码元“0”时, r(t)的条件概率 密度函数和误码率分别为:
A
cos
0
c
t
0 t Tb , 以概率1 P传送码元“1”时 0 t Tb , 以概率P传送码元“0”时
带通滤波器让有用信号完整地通过,最大限度地 抑制输入噪声,其输出为
ri (t ) = s ASK (t ) + ni (t )
淹没在噪声或干扰中正弦信号的测量

淹没在噪声或干扰中正弦信号的测量实验目的了解淹没在噪声或干扰中的正弦信号的检测原理和方法。
了解锁定放大器抑制白噪声能力的概念与测量方法。
了解锁定放大器抑制不相干干扰能力的概念和测量方法。
掌握用锁定放大器测量淹没在噪声或干扰中的正弦信号的实际操作。
实验仪器HB~511型现代模拟电路实验测试系统A 分箱、C 分箱,双踪示波器,数字多用表。
实验内容实验步骤与操作(1)淹没在干扰信号中的微弱信号测量测量仪器框图如图7-29所示。
图中多功能信号源(A 分箱)作为信号源,频率为f ,输给衰减器输入端Vi,同时输给锁定放大器作为参考信号。
干扰源由C 分箱的信号源提供,频率为f 2,通过衰减器把信号与干扰信号混合成具有干扰的信号,送给锁定放大器进行测量。
衰减器Vp 输出插座接到示波器的输入端,可以观察被测信号被干扰信号淹没的波形,加强理解锁定放大器能抑制干扰、从干扰中检测信号的能力。
图7-29锁定放大器测量淹没在干扰信号中的微弱信号框图①仪器参数的设置:接通图7-29中所有仪器的电源。
>设置A 分箱多功能信号源的参数:被测信号设置频率f i=7 1 0 H z,输出电压值Vi=100mV,>设置C 分箱信号源的参数:干扰信号设置:频率fz=40kHz,输出电压值Vz=100 mV 。
>衰减器参数设置:K i=1 0-¹×1 0-1×1,K ₃=0.1(置1),K 4=0.1(置3),K 2根据测试需要选择,则输出电压为:加法器输出端:Vp=KVi+K ₂Vz=Vi ×10-2+K2V ₂ 输出 多功能 信号源(A 分箱)fi 衰减器 (C 分箱) '2 V 干扰信号源信号源 (C 1%i 双相锁定 (A衰减器输出端:V。
=VpK₃K₄=Vi×104+K2V₂×10-2被测信号为10μV,干扰信号由K2决定。
>双相锁定放大器参数设置:参考输入置“内”输入,输入模式置“A”输入。
信号检测与估计课程教学大纲

《信号检测与估计》课程教学大纲一、课程基本信息课程名称(中):信号检测与估计课程名称(英):Signal Detection and Estimation课程编号:××××××学时:48学时学分:2-3学分考核方式:闭卷笔试适用学科及专业:信息与通信工程、信号与信息处理、电子信息工程、通信工程、电子信息科学与技术、电子科学与技术适用对象:硕士、高年级本科生先修课程:概率论与数理统计,信号与系统,随机过程,数字信号处理二、课程的性质和任务本课程是“信息与通信工程”学科硕士研究生的重要基础课,是电子信息工程、通信工程、电子信息科学与技术等专业本科生的专业基础选修课。
本课程以信息传输系统为研究对象,主要研究随机信号统计处理的理论和方法,包括匹配滤波、信号检测及信号估计三个方面的内容。
它采用数理统计的方法,研究从噪声环境中检测出信号,并估计信号参量或信号波形的理论,是现代信息理论的一个重要分支,广泛应用于电子信息系统、自动控制、模式识别、射电天文学、气象学、地震学、生物医学工程及航空航天系统工程等领域。
三、课程的教学目的和要求通过本课程学习,使学生了解信号检测与估计的统计处理方法的特点,掌握信号检测与估计的基本概念、理论和方法,建立随机信号统计处理的观念和思维方法,提高用统计处理方法解决问题的能力,能对工程实际中应用的系统建立数学模型,并对数学模型进行统计求解,为今后的学习和工作打下良好基础。
四、教学内容及要求第一章绪论(1学时)教学内容:1.1 随机过程信号检测与估计的研究对象及应用1.2 信号检测与估计的内容及研究方法11.3 信号检测与估计课程与其他相关课程的关系1.4 内容编排和学习建议教学要求:深刻理解信号检测与估计的研究对象,了解信号检测与估计的应用,掌握信号检测与估计的基本概念、任务、内容及研究方法,熟悉信号检测与估计课程与其他相关课程的关系。
生物医学信号处理期末考试习题集

生物医学信号处理习题集第一章 生物医学信号处理绪论 ..................................................................................................... 1 第二章 数字信号处理基础 ............................................................................................................. 1 第三章 随机信号基础 ..................................................................................................................... 5 第四章 数字卷积和数字相关 ......................................................................................................... 9 第五章 维纳滤波 ........................................................................................................................... 10 第六章 卡尔曼滤波 ....................................................................................................................... 13 第七章 参数模型 ........................................................................................................................... 16 第八章自适应信号处理 (19)第一章 生物医学信号处理绪论1. 生物医学信号处理的对象是什么信号? 解答:包括生理过程自发产生的信号,如心电、脑电、肌电、眼电、胃电等电生理信号和血压、体温、脉搏、呼吸等非电生理信号;还有外界施加于人体的被动信号,如超声波、同位素、X 射线等。
光电检测技术与系统答案

光电检测技术与系统答案【篇一:光电检测课后习题部分答案】效应的工作原理.为什么光伏效应器件比光电导效应器件有更快的响应速度?答:(1)光生伏特效应的工作基础是内光电效应.当用适当波长的光照射pn 结时,由于内建场的作用(不加外电场),光生电子拉向n 区,光生空穴拉向p 区,相当于pn 结上加一个正电压. (2)光伏效应中,与光照相联系的是少数载流子的行为,因为少数载流子的寿命通常很短,所以以光伏效应为基础的检测器件比以光电导效应为基础的检测器件有更快的响应速度. 比较光电效应和光热效应在作用机理、性能及应用特点等方面的差异?1. 光电效应:指单个光子的性质对产生的光电子起直接作用的一类光电效应。
探测器吸收光子后,直接引起原子或分子的内部电子状态的改变。
光子能量的大小,直接影响内部电子状态的改变。
特点:光子效应对光波频率表现出选择性,响应速度一般比较快。
2. 光热效应:探测元件吸收光辐射能量后,并不直接引起内部电子状态的改变,而是把吸收的光能变为晶格的热运动能量,引起探测元件温度上升,温度上升的结果又使探测元件的电学性质或其他物理性质发生变化。
特点:原则上对光波频率没有选择性,响应速度一般比较慢。
(在红外波段上,材料吸收率高,光热效应也就更强烈,所以广泛用于对红外线辐射的探测。
第三章3-143-253-26第四章4-24-34-4第五章1 、直接检测系统的基本原理是什么?为什么说直接检测又叫包络检测?所谓光电直接检测是将待测光信号直接入射到光检测器光敏面上,光检测器响应于光辐射强度而输出相应的电流或电压。
光检测器输出的电流第一项为直流项,若光检测器输出端有隔直流电容,则输出光电流只包含第二项,这就是包络检测的意思。
2、何谓莫尔条纹?应用几何光学原理解释,为什么说莫尔条纹测试技术具有光学放大作用?若两块光栅相互重叠,并且使他们的栅线之间形成一个较小的夹角,当光栅对之间有相对运动时,透过光栅对看另一边的光源,就会发现有一组垂直于光栅运动方向的明暗相间的条纹移动,这就形成莫尔条纹。
光电检测习题解答

第1章1、举例说明你说知道的检测系统的工作原理。
(1)光电检测技术在工业生产领域中的应用:在线检测:零件尺寸、产品缺陷、装配定位…(2)光电检测技术在日常生活中的应用:家用电器——数码相机、数码摄像机:自动对焦---红外测距传感器自动感应灯:亮度检测---光敏电阻空调、冰箱、电饭煲:温度检测---热敏电阻、热电偶遥控接收:红外检测---光敏二极管、光敏三极管可视对讲、可视电话:图像获取---面阵CCD医疗卫生——数字体温计:接触式---热敏电阻,非接触式---红外传感器办公商务——扫描仪:文档扫描---线阵CCD红外传输数据:红外检测---光敏二极管、光敏三极管(3)光电检测技术在军事上的应用:夜视瞄准机系统:非冷却红外传感器技术激光测距仪:可精确的定位目标光电检测技术应用实例简介点钞机(1)激光检测—激光光源的应用用一定波长的红外激光照射第五版人民币上的荧光字,会使荧光字产生一定波长的激光,通过对此激光的检测可辨别钞票的真假。
由于仿制困难,故用于辨伪很准确。
(2)红外穿透检测—红外信号的检测红外穿透的工作原理是利用人民币的纸张比较坚固、密度较高以及用凹印技术印刷的油墨厚度较高,因而对红外信号的吸收能力较强来辨别钞票的真假。
人民币的纸质特征与假钞的纸质特征有一定的差异,用红外信号对钞票进行穿透检测时,它们对红外信号的吸收能力将会不同,利用这一原理,可以实现辨伪。
(3)荧光反应的检测—荧光信号的检测荧光检测的工作原理是针对人民币的纸质进行检测。
人民币采用专用纸张制造(含85%以上的优质棉花),假钞通常采用经漂白处理后的普通纸进行制造,经漂白处理后的纸张在紫外线(波长为365nm的蓝光)的照射下会出现荧光反应(在紫外线的激发下衍射出波长为420-460nm的蓝光),人民币则没有荧光反应。
所以,用紫外光源对运动钞票进行照射并同时用硅光电池检测钞票的荧光反映,可判别钞票真假。
(4)纸宽的检测—红外发光二极管及接收二极管的应用主要是用于根据钞票经过此红外发光及接收二极管所用的时间及电机的转速来间接的计算出钞票的宽度,并对机器的运行状态进行判断,比如有无卡纸等;同时也能根据钞票的宽度判断出其面值。
通信原理第9章 数字信号的最佳接收

(9.1 - 16)
fs1(y)和fs2(y)的曲线如图 8 - 2 所示。
若在观察时刻得到的观察值为yi,可依概率将yi判为r1或r2。 在yi附近取一小区间Δa,yi在区间Δa内属于r1的概率为
q1 a fs1(y)dy
(9.1 - 17)
9.1 最小差错概率接收准则
第9章 数字信号的最佳接收
根据fs1(y)和fs2(y)的单调性质, 在图 9 - 3 中y坐标上可以找 到一个划分点y′0 。在区间(-∞, y′0, q1>q2;在区间(y′0, ∞), q1<q2。 根据图 9- 3所分析的判决原理,当观察时刻得到的观 察值yi∈(-∞, y′0)时,判为r1出现;若观察时刻得到的观察值 yi∈(y′0, ∞)时,判为r2出现。
由于fs1(y)和fs2(y)的单调性质,图 9 - 2 所示的判决过程 可以简化为图 9 - 3 所示的判决过程。
9.1 最小差错概率接收准则
第9章 数字信号的最佳接收
r1 fs1( y)
P
r2
fs2( y) P
a1 y′0
a2
y
图 9 – 3 判决过程示意图 9.1 最小差错概率接收准则
第9章 数字信号的最佳接收
概率愈小愈好。
在噪声干扰环境中,按照何种方法接收信号才能使得错 误概率最小?我们以二进制数字通信系统为例分析其原理。
在二进制数字通信系统中,发送信号只有两种状态,假
设发送信号s1(t)和s2(t)的先验概率分别为P(s1)和P(s2),s1(t)和
s2(t)在观察时刻的取值分别为a1和a2,出现s1(t)信号时y(t)的概
在数字通信中,最常采用的最佳准则是输出信噪比最大准 则和差错概率最小准则。
第8章 噪声和混响背景下信号检测:检测阈

2020/1/30
第8章 噪声和混响背景下信号检测:检测阈
2
8.1 检测阈定义
定义解释:
—用于计算在预定置信 级下判断目标“有”、 “无”时所需要的接收 机输入端的信噪比。
意义:
(1)检测本身功能;
(2)在靠近接收系统 输出端的某处存在的一 个阈值。
2020/1/30
第8章 噪声和混响背景下信号检测:检测阈
波空
束间 信号+噪声 形 滤
成波 器器
带通带
滤波器 y
Hf
2
A f
z 比较器 T
空间滤波器输入端信号和噪声谱密度函数为Ssr(f)和Sn(f); 假设目标位于主响应轴上,空间滤波器的增益为单位值,平 方律检波器的输入端信号和噪声的谱密度分别为:
Ssr f H f 2 Sn f H f 2 A f
—上述两个概率随着 T的改变而 变化,且还与检测指数d有关。
注意:在心理学和听觉掩蔽理论 中,则经常采用检测指数的平方 根这个参数d′。
2020/1/30
第8章 噪声和混响背景下信号检测:检测阈
9
8.3 检测所需的输入信噪比
最佳接收机
—将ROC曲线与检测所需要接收机输入端信噪比联系起来。 —最佳接收机:满足某种最佳判决条件下定义的,即对每一个 输入进行计算,并在输出端绘出似然比的接收机。
第8章 噪声和混响背景下信号检测:检测阈
20
8.4 持续时间和带宽的影响
其它问题 检测阈确定:依据具体的处理系统以及信号和背景噪声的有关 性质。 —按照功率或强度比定义的检测阈 对利用信号和噪声的功率或能量的处理器(如平方律检波器) 是合适的; 对利用信号和噪声其它特征的高级处理系统仅仅是一个近似。
第三章 非高斯白噪声中的信号检测(已校)

若 同 时 满 足 C =1, 则 称 集 合 { fk(t)}, k=1,2,...为 归 一 化 的 正 交 函 数 集
。
利 用 { fk(t)},对 任 意 信 号 x(t),可 分 解 为
x ( t ) = x k . f k (t )
k
0 t T (3 .3 )
T 0
x ( t ) f i ( t ) dt
0
T
T 0
f i ( t1 ) f j ( t 2 )R n (t 1 -t 2 )d t 1 d t 2
T 0
*
T 0
f i ( t1 ) [
*
f j ( t 2 )R n (t 1 -t 2 )d t 2 ] d t 1 (3 .6 )
仅当
T 0
f j ( t 2 )R n (t 1 -t 2 )d t 2 j f j ( t1 )(3 .7 )
0
s1 ( t ) f k ( t ) d t
*
T 0
条件方差: V a r [ x i ] E { [ x i E ( x i )] } co v( x i , x i )
2
由 公 式 ( 3 - 6 ) an d ( 3 - 7 ) V a r[ xi ]
T 0
f i ( t1 ) i f i ( t1 ) d t1 i
基 于 和 信 号 与 噪 声 分 类 的 检 测
信号
确知信号 随机参量信号 随机信号
随相信号 随幅信号 随频信号 随机TOA 白噪声
加性噪声
高斯噪声
非高斯噪声
色噪声 白噪声
色噪声
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第9章 噪声中信号的检测前一章学习了经典假设检验理论,本章将要运用假设检验理论讨论噪声中信号的检测问题或最佳接收机的设计问题,在这里信号检测的含义是指从含有噪声的观测过程中判断是否有信号存在或区分几种不同的信号;而接收机实际上是对观测过程实施的数学运算。
为了设计最佳接收机,首先需要指定设计准则,这可以采用第8章介绍的判决准则,然后相对于选定的准则来设计接收机,在设计通信系统的接收机时,通常采用最小错误概率准则,而对于雷达和声纳系统则采用纽曼-皮尔逊(Neyman-Pearson )准则。
本章只介绍高斯白噪声环境下信号的检测问题,高斯有色噪声以及非高斯噪声环境下的检测问题请读者参看其它相关教材。
9.1 高斯白噪声中确定性信号的检测考虑一个简单的二元通信系统,系统发送信号)(0t y 或)(1t y ,两个信号是完全已知的,假定接收机的观测时间间隔为(0,T),由于信道噪声的影响,接收到的信号受到噪声的污染,因此接收机观测到的过程为:0011:()()()0:()()()0H z t y t v t t TH z t y t v t t T=+<<=+<< (9.1.1)其中噪声)(t v 假定是零均值的高斯白噪声,功率谱密度为2/0N 。
现在要设计一种接收机,通过对观测过程)(t z 的处理,对(9.1.1)式的两种假设作出判决。
由假设检验理论可知,最佳接收机的结构由似然比计算器与一个门限比较器组成,然而在第8章,涉及的观测数据都是离散的,因此要运用假设检验理论来解决噪声中信号的检测问题。
首先需要将连续的观测过程离散化,然后再计算似然比。
假定噪声)(t v 为一带限噪声,功率谱密度为 0()/2,v G N ω=ω<Ω (9.1.2)很显然,当Ω→∞时,带限过程趋于白噪声。
带限过程的相关函数为 τΩτΩ⋅πΩ=τ)sin(2)(0N R v (9.1.3) 噪声的方差为πΩ=σ202N v 当/τ=πΩ时,(/)0v R πΩ=,即(0),(/),(2/),...,v v v πΩπΩ是相互正交的随机变量序列,由于)(t v 是高斯的,故(0),(/),(2/),...,v v v πΩπΩ是相互独立的。
因此,如果以∆t=Ωπ/的间隔对观测过程进行均匀抽样,所得的观测值是相互独立的,且12/2122(|)(|)()1exp 22NN i k i k N N k ik k v v f H f z H z y ===⎡⎤-⎢⎥⎛⎫⎢⎥=- ⎪πσσ⎢⎥⎝⎭⎢⎥⎣⎦∏∑z /221001exp ()N Nk ik k t z y t N N =⎛⎫⎡⎤∆=--∆ ⎪⎢⎥π⎝⎭⎣⎦∑ i=0,1 (9.1.4) []21110001(()|)l i m (|)e x p ()()TN N t f z t H f H F z t y t d tN →∞∆→⎧⎫==--⎨⎬⎩⎭⎰z (9.1.5) 其中F 为常数,同理,[]20000001(()|)l i m (|)e x p ()()TN N t f z t H f H F z t y t d t N →∞∆→⎧⎫==--⎨⎬⎩⎭⎰z (9.1.6)10(()|)[()](()|)f z t H z t f z t H Λ=22100100000211exp{[()()()()()()]}22T T T T z t y t dt z t y t dt y t dt y t dt N =-+-⎰⎰⎰⎰ (9.1.7)22100100000211ln [()][()()()()()()]22T T T T z t z t y t dt z t y t dt y t dt y t dt N Λ=-+-⎰⎰⎰⎰ (9.1.8)所以判决表达式为10221001000000211[()()()()()()]ln 22H T T T T H z t y t dt z t y t dt y t dt y t dt N >-+-η<⎰⎰⎰⎰ (9.1.9)或122010010001()()()()ln [()()]22H TTT T H N z t y t dt z t y t dt y t dt y t dt >-⋅η+-=η<⎰⎰⎰⎰ (9.1.10)从(9.1.10)式可以看出,在白噪声环境下二元已知信号的检测可用相关接收机实现,接收机结构如图9.1所示。
图9.1 二元已知信号的检测的最佳接收机结构)(t z此外,根据3.6节介绍的匹配滤波理论,对信号y 1(t)的匹配滤波器的冲击响应为11()(),0h t y T t t T =-<< (9.1.11)观测过程z(t)通过匹配滤波器后,输出为 1110()()()()()Tz t z t h d z t y T d ττττττ∞-∞=-=--⎰⎰当t=T 时, 1110()()()()()TTz T z T y T d z t y t dt τττ=--=⎰⎰ (9.1.12)可见,相关积分可以用匹配滤波器来实现。
同理,对信号y 0(t)的匹配滤波器的冲击响应为00()(),0h t y T t t T =-<< (9.1.13)观测过程z(t)通过匹配滤波器后,在t=T 时的输出为 0000()()()()()TTz T z T y T d z t y t dt τττ=--=⎰⎰ (9.1.14)采用匹配滤波器的最佳接收机结构如图9.2所示。
图9.2 采用匹配滤波器的最佳接收机结构z9.2 最佳接收机的性能为了分析最佳接收机性能,定义一个检测统计量,22100101()()()()[()()]2TTT I z t y t dt z t y t dt y t y t dt =-+-⎰⎰⎰ (9.2.1)那么判决表达式(9.1.10)可表示为γ=η<>00ln 21N I H H (9.2.2) 虚警概率和漏警概率分别为 dI H I p P F ⎰∞γ=)|(0,⎰γ∞-=dI H I p P M )|(1 (9.2.3)因此要确定接收机的性能关键是要确定检测统计量I 在不同假设下的概率分布密度。
可以证明(参见习题9.1):⎭⎬⎫⎩⎨⎧ρ-ερ-ε+-ρ-επ=)1(2)]1([exp )1(21)|(0200N I N H I p (9.2.4)⎭⎬⎫⎩⎨⎧ρ-ερ-ε--ρ-επ=)1(2)]1([exp )1(21)|(0201N I N H I p (9.2.5)其中, 2000()Ty t dt ε=⎰, 2110()Ty t dt ε=⎰, )(2101ε+ε=ε (9.2.6) 01,εε和ε分别代表信号)(0t y ,)(1t y 的信号能量及它们的平均能量,010()()/Ty t y t dt ρ=ε⎰(9.2.7)为归一化相关系数,则虚警概率为 dI N I N P F ⎰∞γ⎭⎬⎫⎩⎨⎧ρ-ερ-ε+-ρ-επ=)1(2)]1([exp )1(21020 (9.2.8)在上式中令)1()1(0ρ-ερ-ε+=N I u ,则2()2F u P du Q ∞+⎛⎫=-=γ ⎪⎝⎭(9.2.9) 其中)1()1(0ρ-ερ-ε+γ=γ+N (9.2.10)漏警概率为20[(1)]1()2(1)M I P dI Q N γεργερ-⎧⎫--=-=-⎨⎬-⎩⎭⎰(9.2.11)其中)1()1(0ρ-ερ-ε-γ=γ-N (9.2.12)从(9.2.9)~(9.2.12)式可以看出,接收机的性能与信号的平均能量ε、归一化相关系数ρ、噪声的强度0N 以及判决门限0η有关,而与信号的波形是无关的。
如果采用最小总错误概率准则,且假定先验概率相等,即)()(10H P H P =,则10=η,0=γ,因此)1(N ρ-ε=γ-=γ-+ (9.2.13) 这时M F P P =,总的错误概率1()2e F M P P P Q =+= (9.2.14)当1-=ρ,也即)()(10t y t y -=时,e P Q = (9.2.15)这时总的错误概率是最小的,称这样的系统为理想二元通信系统。
例9.1 二元通信系统的检测性能分析解 采用最小总错误概率准则讨论一下常见的二元通信系统的性能。
对于相干相移键控(CPSK)系统,信号为t A t y 00sin )(ω=,t A t y 01sin )(ω-= 0t T ≤≤ 由于1-=ρ,所以这是一个理想的二元通信系统。
总的错误概率为212e P u du Q ∞⎛⎫=-= ⎪⎝⎭ 对于相干频移键控系统(CFSK),二元信号为t A t y 00sin )(ω=,t A t y 11sin )(ω=,0t T ≤≤适当地选择角频率ω0、ω1,例如01/m T ω+ω=π,10/n T ω-ω=π,其中m 和n 是正整数,那么两个信号是正交的,即0=ρ,这时总的错误概率为212e P u du Q ∞⎛⎫=-= ⎪⎝⎭ 对于启闭键控系统(OOK),二元信号为0)(0=t y ,t A t y 11sin )(ω=,f t t t ≤≤0 显然0=ρ,而2/1ε=ε,因此总的错误概率为212e P u du Q Q ∞⎛⎫=-== ⎪⎝⎭二元通信系统的检测性能曲线如图9.3所示。
图9.3 二元通信系统的检测性能0/()N dB εeP CFSK 系统ρ=CFSK 系统1ρ=-例9.2 雷达信号检测性能分析。
解 雷达信号的检测是一个二元假设检验问题,011:()()0:()()()0H z t v t t TH z t y t v t t T=<<=+<< (9.2.16)既相当于(9.1.1)式中y 0(t)=0的情况,那么,0ρ=,1/2ε=ε,由(9.2.9)和(9.2.10)可得F P Q ⎛⎫=(9.2.17)雷达信号检测经常采用纽曼--皮尔逊准则,门限由给定的虚警概率确定,因此,由(9.2.17)可得 ()11/2F P -γ=-ε(9.2.18)由(9.2.11)和(9.2.12)式可得检测概率为 1D M P P Q ⎛⎫=-= (9.2.19)将(9.2.18)式代入,得()(1D F P Q Q Q P -==- (9.2.20) 由上式可以看出,在高斯白噪声环境下,检测概率只与信号的能量和噪声谱密度之比有关,与信号的波形无关。
图9.4画出了以P F 为参数的D P 这一曲线称为雷达系统的检测性能曲线。
1010102/()N εdB DP 图9.4 雷达系统检测性能曲线P F =10-2-4-69.3高斯白噪声背景下随机信号的检测在前面两节讨论的检测问题中,信号是完全已知的,在实际中遇到的信号通常具有确定的形状,但信号的某些参数是未知的,某些参数甚至是随机的。
