圆孔衍射光学仪器的分辨率大学物理

合集下载

22单缝衍射圆孔衍射光学仪器的分辨率

2 f 3 x0 110 m a f x 0.5 10 3 m a
四. 光学仪器的分辨本领
1. 圆孔的夫琅禾费衍射 L 衍射屏
0
相对光强曲线
中央亮斑 (爱里斑)
孔径为D
f
经圆孔衍射后,一个点光源对应一个爱里斑爱里斑的半角宽度为
0 1.22

D
讨论：（1）给定λ，D 越小，
透镜

2
观测屏 x2 1 x1
1
x1
o
x1
0
衍射屏
x0
xk f tan k
中央明纹
f
角宽度 0 21 2 arcsin 线宽度 x0 2 x1 2 f tan1

a
第 1 级明纹角宽度 1 2 1 arcsin
2 arcsin a a 线宽度 x1 x2 x1 f tan2 f tan1 (k 1) k arcsin a a 线宽度 xk xk 1 xk f tank 1 f tank
D 5.0 mm 550 nm 眼睛的最小分辨角为 δ 1.22 d S δ D d Dd 5.0 103 1.20 3 S 8 . 94 10 m 9 1.22 1.22 550 10 d 120 cm
δ
观察者 S d =120 cm

a sin 0
a sin 2k
中央明纹

2 a sin (2k 1) 2 a sin k 2
k (k 1,2,)
干涉相消 ( 暗纹 ) 干涉加强(明纹)
(k 1,2,)
(k 0,1,2,) 介于明暗之间

圆孔衍射

6
S1 S2
可分辨此时两爱里斑重叠部分的光强为一个光斑中心最大值的 80％。％。
S1 S2
恰可分辨
两爱里斑中心距d 恰好等于爱里斑半径。两爱里斑中心距 0恰好等于爱里斑半径。
S1 S2
不可分辨
7
2.光学仪器分辨率光学仪器分辨率满足瑞利判据的两物点间的距离，满足瑞利判据的两物点间的距离，就是光学仪器所能分辨的最小距离。所能分辨的最小距离。此时两个物点对透镜中心所张的角δϕ称为最小分辨角。 δϕ称为最小分辨角的角δϕ称为最小分辨角。 d0为光学仪器可分辨的最小距离，即为两物点可为光学仪器可分辨的最小距离，分辨的最小距离，为圆孔到两物点的垂直距离，分辨的最小距离，L为圆孔到两物点的垂直距离，若为光学仪器，即为焦距f 为圆孔直径。光学仪器，则L即为焦距f。D为圆孔直径。光学仪器中将最小分辨角的倒数称为仪器的分辨率光学仪器中将最小分辨角的倒数称为仪器的分辨率。
4
二、光学仪器的分辨本领
一般光学仪器成像，一般光学仪器成像，光学仪器对点物成象是一个有一定大小的爱里斑。有一定大小的爱里斑。所以由于衍射现象会使图像边缘变得模糊不清，由于衍射现象，所以由于衍射现象，会使图像边缘变得模糊不清，使图像分辨率下降。使图像分辨率下降。点物S 象S’ 一个透镜成象的光路可用两个透镜的作用来 L 等效，如图所示：等效，如图所示： L1 L2 象点物就相当于在透点物物方焦点处，镜L1物方焦点处，经通 f1 f2 光孔径A，光孔径，进行夫琅和费衍射，在透镜L 费衍射，在透镜 2的象 A 方焦点处形成的中央零仅当通光孔径足够大时，仅当通光孔径足够大时，级明斑中心。级明斑中心。爱里斑才可能很小。 a >> λ 爱里斑才可能很小。 5

大学物理11-7 圆孔衍射光学仪器分辨率

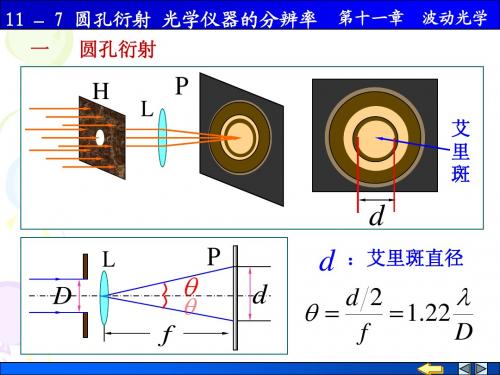
1.22 2.44 3 10 2 0 2 9 D D 0.5 30010 4.88103 rad 0.280
8
2.44
c
11 – 7 圆孔衍射光学仪器的分辨率第十一章波动光学例3 毫米波雷达发出的波束比常用的雷达波束窄，这使得毫米波雷达不易受到反雷达导弹的袭击. （1）有一毫米波雷达，其圆形天线直径为55cm，发射频率为220GHz的毫米波，计算其波束的角宽度；（2）将此结果与普通船用雷达发射的波束的角宽度进行比较，设船用雷达波长为1.57cm，圆形天线直径为2.33m . c 3 108 m/s 1 1.36103 m 解（1） 9
第十一章
波动光学
例4 (1)哈勃太空望远镜是1990年发射升空的天文望远镜（教材P213图14-34），它的主透镜直径为2.4m，是目前太空中的最大望远镜。试计算哈勃望远镜对波长为800nm的红外光的最小分辨角。解：（1）哈勃望远镜的最小分辨角
1.22 1.22 800 10 9 4.0 10 7 rad D 2.4
2.2 10 rad
（2）
4
L 0 L 2.2 104 rad 10m 2.2mm
11 – 7 圆孔衍射光学仪器的分辨率第十一章波动光学例11-14 设一雷达的圆形发射天线的直径 D 0.5m ，发射的无线电波频率 300 GHz 。求雷达发射的无线电束的角宽度。解雷达天线发射出去的无线电波，相当于通过天线圆孔后的衍射波。由于衍射的中央主级大（艾里斑）集中了绝大部分衍射波的能量，所以雷达波束的角宽度就是最小分辨角的角的两倍，即
D 6 2.5 D 2.4
11 – 7 圆孔衍射光学仪器的分辨率

《大学物理AII》作业 No.06光的衍射(参考答案)

《大学物理AII 》作业 No.06 光的衍射班级 ________ 学号 ________ 姓名 _________ 成绩 _______------------------------------------------------------------------------------------------------------- ****************************本章教学要求****************************1、理解惠更斯-菲涅耳原理以及如何用该原理解释光的衍射现象。

2、理解夫琅禾费衍射和菲涅耳衍射的区别，掌握用半波带法分析夫琅禾费单缝衍射条纹的产生，能计算明暗纹位置、能大致画出单缝衍射条纹的光强分布曲线；能分析衍射条纹角宽度的影响因素。

3、理解用振幅矢量叠加法求单缝衍射光强分布的原理。

4、掌握圆孔夫琅禾费衍射光强分布特征，理解瑞利判据以及光的衍射对光学仪器分辨率的影响。

5、理解光栅衍射形成明纹的条件，掌握用光栅方程计算主极大位置；理解光栅衍射条纹缺级条件，了解光栅光谱的形成以及光栅分辨本领的影响因素。

6、理解X 射线衍射的原理以及布拉格公式的意义，会用它计算晶体的晶格常数或X 射线的波长。

-------------------------------------------------------------------------------------------------------一、填空题1、当光通过尺寸可与（波长）相比拟的碍障物（缝或孔）时，其传播方向偏离直线进入障碍物阴影区，并且光强在空间呈现（非均匀分布）的现象称为衍射。

形成衍射的原因可用惠更斯-菲涅耳原理解释，即波阵面上各点都可以看成是（子波的波源），其后波场中各点波的强度由各子波在该点的（相干叠加）决定。

2、光源和接收屏距离障碍物有限远的衍射称为（菲涅尔衍射或近场衍射）；光源和接收屏距离障碍物无限远的衍射称为（夫琅禾费衍射）或者远场衍射。

15-(4-5)圆孔衍射光学仪器的分辨率

x 1.22

D
L
10
5500 10 3 1.22 160 10 3 5.0 10
21.4m
12
15-5 伦琴射线的衍射
13
1895年伦琴发现，受高速电子撞击的金属会发射一种穿透性很强的射线称Ｘ射线。
X 射线冷却水
(0.04 ~ 10nm)
K
E2
E1
劳厄斑点
0
f
l
l d 2 x 1.22 f f D L
1 D 1 D, 1.22
光学仪器分辨率

min
5
1990 年发射的哈勃太空望远镜的凹面物镜的直径为4.8m，最小分辨角 0 0.1' ' ，在大气层外 615km 高空绕地运行，可观察130亿光年远的太空深处, 发现了500 亿个星系。
对于两个强度相等的不相干的点光源（物点），一个点光源的衍射图样的主极大刚好和另一点光源衍射图样的第一极小相重合，这时两个点光源（或物点）恰为这一光学仪器所分辨。 4
三光学仪器的分辨本领 -- 两光点刚好能分辨
光学仪器的通光孔径D
x
s1 * s2*
min
L
最小分辨角 min
当两个爱里斑的中心恰好为 l d 2

o
C

d
A
B
2d sin k
k 0,1,2,
15
布拉格公式
2d sin k
k 0,1,2,
作业:练习十七
用途测量射线的波长研究X射线谱，进而研究原子结构；研究晶体的结构，进一步研究材料性能。例：对大分子DNA晶体的成千张的X射线衍射照片的分析，显示出DNA分子的双螺旋结构。

17、光的衍射-2

a+b 2 × 10
λ
θ 1= ± 140 28′
第三级明纹k=3 第三级明纹
3λ 3 × 500 × 10 9 sin θ 3 = ± =± = ±0.75 6 a+b 2 × 10
θ 3= ± 480 35′
2 × 10 6 = =4 9 500 × 10 即最多能看到第4级明条即最多能看到第级明条纹,考虑缺级 (a+b)/a=(a+a)/a=2. . 级明纹不出现, 第2,4级明纹不出现, , 级明纹不出现从而实际出现的只有级, 从而实际出现的只有级, 因而只能看到5条明纹条明纹. 因而只能看到条明纹.
2,光栅衍射的实验装置与衍射图样
反射光栅
屏幕上对应于光直线传播的成像位置上出现中央明纹; 屏幕上对应于光直线传播的成像位置上出现中央明纹; 屏幕上对应于光直线传播的成像位置上出现中央明纹在中央明纹两侧出现一系列明暗相间的条纹,两明条纹分在中央明纹两侧出现一系列明暗相间的条纹, 在中央明纹两侧出现一系列明暗相间的条纹得很开,明条纹的亮度随着与中央的距离增大而减弱; 得很开,明条纹的亮度随着与中央的距离增大而减弱; 明条纹的宽度随狭缝的增多而变细. 明条纹的宽度随狭缝的增多而变细. 明条纹的宽度随狭缝的增多而变细
θ=
代入数据,得: 代入数据,
1.5 × 4 × 10 3 S= = 8.9 × 10 3 m 1.22 × 5500 × 10 10
rD S= 1.22λ
r θ = θ 0 = 1.22 = D S
λ
S
§17-4 衍射光栅 -
引言:对于单缝: 引言:对于单缝: 若缝宽大,条纹亮,但条纹间距小, 若缝宽大,条纹亮,但条纹间距小,不易分辨若缝宽小,条纹间距大,但条纹暗, 若缝宽小,条纹间距大,但条纹暗,也不易分辨因而利用单缝衍射不能精确地进行测量. 因而利用单缝衍射不能精确地进行测量. 问题:能否得到亮度大,分得开,宽度窄的明条纹? 问题:能否得到亮度大,分得开,宽度窄的明条纹? 结论:利用衍射光栅所形成的衍射图样——光栅光谱结论:利用衍射光栅所形成的衍射图样光栅光谱应用: 应用: 精确地测量光的波长; 精确地测量光的波长; 是重要的光学元件,广泛应用于物理,化学,天文, 是重要的光学元件,广泛应用于物理,化学,天文, 地质等基础学科和近代生产技术的许多部门. 地质等基础学科和近代生产技术的许多部门.

光学仪器的分辨率

圆孔的直径为D。由理论计算可知，第一级暗环的衍射角（即艾
里斑张角的一半）θ为： d 1.22
2f
D
1.2 光学仪器里斑，物理学家瑞利提出了一条判据：当一个艾里斑的边缘正好与另一个艾里斑的中心重合时，两斑中心连线中点处的光强约为其中心光强的 80%，正常人的眼睛刚好能分辨出这是两个光点。这条判据称为瑞利判据。
如下图所示，两艾里斑恰好能被区分开时，其中心的距离 d0等于两个艾里斑的半径d/2。因此，两相邻物点的最小分辨角 θ0为：
0
d 2f
1.22
D
最小分辨角θ0越小，光学仪器的分辨本领越大。所以，常用最小分辨角的倒数来表示光学仪器的分辨率，即
1 D
0 1.22
上式表明，提高光学仪器分辨率的途径有两种：增大透镜直径D和减小入射光的波长λ。在天文望远镜中，为了提高分辨率，通常用直径很大的透镜作物镜；而在显微镜中，为了提高分辨率，通常采用波长较短的光进行照射，如紫外光和电子波（波长约为10-3nm）等。
物理学
光学仪器的分辨率
1.1 圆孔衍射
如左图所示，在单缝衍射实验装置中，用小圆孔代替单缝。当单色平行光垂直照射到小圆孔上时，会产生衍射，衍射光线被透镜会聚到屏幕上E上，形成明暗交替的环形衍射斑，其中，中央光斑较亮，它集中了绝大部分光强，称为中央亮斑或艾里斑，如右图所示。
设艾里斑的直径为d，透镜的焦距为f，入射光的波长为λ，
【例12-7】人眼的瞳孔直径约为2.5mm，在明亮的环境中，感觉最灵敏的是黄绿光（波长λ＝0.555μm），人眼中玻璃液的折射率为n＝1.336。试求：（1）人眼的最小分辨角；（2）若物体放在明视距离25cm处，则两点相距为多远时才能被分辨出。

大学物理3考试知识点

大学物理3预习指南及期末考点(20xx、春) (实验事实、模型建立、研究方法、概念引入、推导过程、公式意义、图片分析、结论应用)第一部分力学(分数分布20%)1-1质点模型及质点运动状态、状态变化与运动过程的描述；1-2恒力与变力作用下确定质点任一时刻的速度与位置的方法与步骤；2-1变力作用一段时间过程使质点状态发生变化的研究方法与动量原理及应用；2-2元分析法在计算变力做功中的应用与动能定理；2-3角动量与力矩概念的引入及右螺旋法则的应用；2-4质点系总动量的计算、变化、守恒判据与分动量守恒条件及应用；2-5质点系动能定理的表达式、势能属于系统的概念与机械能守恒与转换定律表述形式；2-6质点系角动量的计算、角动量定理与角动量守恒定律；3-1刚体模型及定轴转动的角量描述、力矩做功的计算与转动惯量的物理意义；3-2刚体定轴转动角动量定理与守恒定律的表述及应用；3-3弹性体模型及拉伸形变中形变与回复力的关系；3-4波在弹性介质中传播时质元既形变又加速的分析与描述；3-5理想流体模型及流速场描述方法与定常流连续性方程的建立、应用；3-6细流管中流体流动时的功能关系与伯努利方程的意义及应用；重点要求：第一章1-1.运动学方程(1)由位置矢量式写分量式(2)由运动学方程求位移、速度、加速度1-2.牛顿运动定律(1)积分法解一维变力f=f(x)情况下的运动问题；(2)积分法解一维变力f=f(v) 情况下的运动问题。

1-3.动量定理(1)冲量计算(2)求动量增量1-4动能定理变力的功计算1-5角动量定理(1)判断对不同参考点角动量(2)判断力矩方向(3)合力与力矩1-6 综述：模型方法的要点与应用(第一章第四节)第二章2-1保守力与非保守力的区分；2-1质点系内力的功之和不为零；2-3质点系内力矩之和为零；2-4机械能守恒定律；2-5动量守恒定律；第三章3-1 定轴转动(1)几个物理量；(2)角量与线量关系；(3)匀变速转动规律；3-2转动惯量数学表达式；3-3转动动能定理(1)转动动能计算(2)摩擦力矩简单计算3-4定轴转动中的角动量守恒3-5固体的弹性(1)胡克定律简单应用(2)应力定义叙述与公式3-6理想流体(1)定义叙述(2)定常流定义叙述(3)流量(4)连续性方程简单应用第二部分场(分数分布30%)4-1点电荷模型与静电力及静电场强弱的判断、检测、量度与计算的关系；4-2元分析法与场强叠加原理在连续分布电荷电场计算中的应用；4-3电场线与电通量的关系及高斯定理的意义与应用；4-4静电力的功、电势、环流与无旋场的相互关系及计算；5-1运动电荷在磁场受洛仑兹力与霍尔效应微观机理分析；5-2电流元模型及所受安培力的微观机理与平面线圈受磁力矩的分析、计算；5-3毕奥-沙伐尔定律中各量意义及积分计算中的几个关键步骤；5-4表征稳恒磁场无源、有旋性质的两定理的积分公式与应用；6-1法拉第电磁感应定律的物理意义及定律在互感、自感中的应用；6-2用洛仑兹力分析产生动生电动势的微观机理与计算电动势时的积分3要素；6-3磁场随时间变化在空间激发电场的现象、规律与感生电动势计算；6-4研究电容器充(放)电时提出位移电流所采用的几个基本概念与逻辑推理过程；第四章4-1库仑定律内容与应用4-2场强偶极子中垂线场强计算、带电细线旁一点的场强、带电圆线圈轴线上一点及圆心处场强、无限大带电平面的场强公式4-3高斯定理(1)数学表达式(2)用高斯定理求：球对称问题的场强、无限大带电平面的场强、柱对称问题的场强(3)电荷、场强与通量的关系4-4静电场环路定理(1)点电荷的电势(2)带电圆环中心的电势公式(3)带电圆环轴线上电势的积分计算(5-2-2)4-5 静电场是有源无旋场公式表述(8-1-5)第五章5-1洛伦兹力(1)磁场中电荷螺旋线运动参数计算(2)霍尔效应现象(3)霍尔电场场强与电势差的计算5-2安培定律(1)安培力方向的判断方法、带电半圆导线受力公式、带电直线受力、单匝与多匝带电线圈的磁矩公式、带电平面线圈受磁力矩定性分析。

大学物理第12讲：10.4 圆孔衍射、光学仪器的分辨率

4、分辨本领：最小分辨角的倒数
1 D 1 1.22 1
5、人眼的分辨本领
5 107 4 0 1.22 1.22 1 . 22 10 rad 3 D 5 10

思考：望远镜的分辨本领？
显微镜的分辨本领？
课堂练习2：在迎面驶来的汽车上，两盏前灯相距120cm，设夜间人眼瞳孔直径为5.0mm，入射光波长为500nm，问汽车离人多远的地方，眼睛恰可分辨这两盏灯？
欧洲南方天文台将在智利阿塔卡玛沙漠建造世界最大的天文望远镜。该望远镜镜片直径是一座足球场长度的一半，它对可见光和红外线的灵敏度将是现存望远镜的十倍。天文学家希望，这座望远镜能帮助人们破解有助于解释宇宙演化的暗物质秘密，甚至能探测到外星人的行踪。 2020年前投入使用
1990 年发射的哈勃太空望远镜的凹面物镜的直径为2.4m ，最小分辨角 0.1'' ，在大气层外615km 高空绕地运行 , 可观察130亿光年远的太空深处, 发现了500 亿个星系 .
英豪天文台卡塞格林折反射光路的500毫米望远镜，是目前华南地区最大的天文望远镜。
中国将在贵州建造世界上最大的望远镜
中国十一五期间，将投资60亿元用于十二项大科学工程的建设，并将在贵州建造世界上最大的望远镜，它将使中国
的天文观测能力延伸到宇宙边缘，寻找第一代诞生的天体。
智利阿塔卡玛沙漠建造世界最大望远镜
显镜的分辨本领
最小分辨角对于显微镜，孔径一定，波长越短，分辨率就越高，看得越细微。
1 D 1 1.22
1
孔径
波长
X射线的衍射
小结：
1、圆孔衍射 2、光学仪器的分辨能力
作业：
1、仔细阅读教材；

《大学物理III》教学大纲和考试大纲-64学时

《大学物理Ⅲ》课程简介课程名称：《大学物理Ⅲ》/College Physics Ⅲ课程代码：学时/学分：64/4课堂授课：64课程主要内容：本课程主要讲授力学、相对论、振动与波、波动光学、量子物理基础。

从经典力学拓宽到相对论力学；从宏观物体的运动学、动力学规律到三大守恒定律在宏观世界的应用；光的干涉、衍射及偏振现象与规律；普朗克量子假说、光的波粒二象性、德布罗意物质波及其统计解释、不确定关系、玻尔的氢原子理论，薛定谔方程及其初步应用等。

适用专业：先修课程：《高等数学》推荐教材：1．赵近芳王登龙编，《大学物理学》（第4版），北京邮电大学出版社，2014年。

参考书：1．张三慧主编，《大学基础物理学》，清华大学出版社，2003年；2．程守洙、江之永主编，《普通物理学》第5版，高等教育出版社，2001年；3、卢德馨主编，《大学物理学》，高等教育出版社，1998年；4．R.P.费曼，《费曼物理学讲义》，上海科学技术出版社，1983年；5．郭奕玲、沈慧君编著，《物理学史》，清华大学出版社，2005年。

《大学物理Ⅲ》课程教学大纲授课专业：学时数：64；学分数：4.0一、课程的性质和目的本课程是非物理专业的基础课程。

本课程的任务是通过讲授和讨论力学、相对论、振动与波、波动光学、量子物理基础等基础知识，使学生掌握力学、波动光学和近代物理的基本体系，认识光在传播过程中表现出的波动性以及在科学技术中的应用；了解量子力学的形成过程与基本规律，以及在微观领域所取得的巨大成就；了解物理学的新成就和发展方向，拓展学生视野，培养学生的创新意识，为后续课程的学习和将来进一步发展奠定良好的物理基础。

二、课程教学的基本要求本课程的教学环节以课堂讲授为主，辅以习题讨论、答疑、学生自学、课后作业、小测验和期末考试；通过上述教学环节，使学生学会从观察自然现象和总结实验事实入手，利用物理模型，掌握三大守恒定律在力学中的应用；理解经典时空观和相对论时空观的区别。

大学物理AII_衍射

缺级现象
缺级：由于单缝衍射的影响，在应该出现亮纹的地方，不再出现亮纹。缺极时衍射角同时满足：单缝衍射极小
a sin =k'
k'=±1, ±2,···
·· 缝间光束干涉极大 (a+ b )sin =k k=0,±1, ±2, ·
即： k =(a+b) /a· k'
k 就是所缺的级次
例 5：对某一定波长的垂直入射光，衍射光栅的屏幕上只能出现零级和一级主极大，欲使屏幕上出现更高级次的主极大，应该（（A）换一个光栅常数较小的光栅（B）换一个光栅常数较大的光栅（C）将光栅向靠近屏幕的方向移动 B ）
（D）将光栅向远离屏幕的方向移动
例 6：某单色光垂直入射到光栅上，衍射光谱中
ax / f k
f 暗纹坐标： x k a
k 1,2,3...
光强分布：
I
3 f 2 f f a a a
o
f a
2 f a
3 f a
xபைடு நூலகம்
中央明纹的宽度 l0 2 x1 2

a
f
思考：
进行下列操作，单缝衍射条纹将怎样变化？用白光光源进行实验。中央明纹两侧出现彩色条纹条纹变窄条纹不变条纹上移条纹消失条纹变宽
明纹
菲涅耳半波带法：
a sin 0
a sin 2k

中央明纹中心
2 a sin ( 2k 1) （明纹） 2 a sin k （介于明暗之间） 2
( k 1,2,3,)
k 干涉相消（暗纹）
例 1：
在单缝夫琅和费衍射实验中，屏上第三级暗纹对应于

大学物理课件---圆孔衍射--[福州大学李培官]

射，两光线在眼睛中的夹角为α，由n0α0= nα，即α0=nα 应用瑞利判据，当两光源恰好能分辨时这时两点光源对瞳孔的张角
S1
n0=1
n=1.33
1 . 22 min 0

n 1 . 22 1 . 22 0 mi n
nD

nD
D
三.解题举例
【例1】在通常亮度下，人眼的瞳孔直径约为3mm ，视觉感受的最灵敏的光波波长为 550 nm. 求：人眼的最小分辨角为多大？解：由题意有：
3 D 3 1 0 (2) 设两物点相距为d，则 d 人眼的最小分辨角为 d m i n
1 . 2 2 5 . 5 1 0 1 . 2 2 2 . 2 1 0 r a d
7 4
min
m in
l
l
则有：
2 4 5 d l
观察者 S
d =120 cm
x 恰能分辨时，有： 0 L
4 x L 25 2 . 3 10 0 . 058 ( mm ) 0
【例4】设人眼在正常照度下的瞳孔直径约3 mm ，而在可见光中，人眼最敏感的波长为 550nm ，问：(1) 人眼最小分辨角是多大？(2) 若物体放在明视距离25cm处，那么两物点相距为多远时恰能被分辨？解 (1) 人眼的最小分辨角为：
思考：如何提高仪器分辨率？
D R
提高光学
仪器的放大倍
数能提高角分辨率吗？望远镜：不可选择，可显微镜： D不会很大，可
D R
R
4.眼晴的分辨率
n n 0
视网膜上衍射图样衍射斑 0 S2 的半角宽度 λ D 1 . 22 1 . 22 0 D nD 当两光源对瞳孔的张角为α0时，由于前房液和玻璃状液的折

第三节圆孔衍射及光学仪器的分辨率

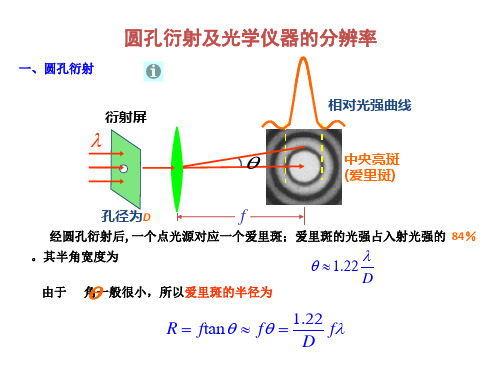
比较圆孔衍射与单缝衍射：
爱里斑的半角宽度为单缝衍射中央明纹半角宽度为
1.22
D sin
a
（式中D为圆孔的直径，a为单缝的宽度）
两式相对比：说明二者除在反映障碍物几何形状的系数不同以外，其在定性方面是一致的。
二、光学仪器的分辩率几何光学波动光学
物点
一一对应
像点
物点
一一对应像斑
而是物镜能分辨的最小距离z：
L
物空间
像空间
B
A
z
n n
B
z
A
f
由阿贝正弦条件
nz sin nzsin
又
n 1 sin D 2
f
z
f 0
1.22f
D
可得
z 0.61 ( n sin数值孔径 )
n sin
提高光学仪器分辨率的方法
由于光学仪器的分辨率与圆孔孔径成正比，与光波波长成反比，我们可以通过两个途径提高分辨率：
S
d =120 cm
可分辨
0
刚可分辨 0
不可分辨
0
瑞利判据:对于两个等光强的非相干物点,如果一个像斑中心恰好落在另一像斑的边缘(第一暗纹处),则此两像被认为是刚好能分辨。此时两像斑中心角距离为最小分辨角。
根据瑞利判据
0
1.22
D
光学仪器的分辨率为人眼的分辨率
1 0
L. Rayleigh （1842～1919）
例一直径为d1=2mm的氦氖激光束射向月球表面，其波长为λ=632.8 nm，已知
月球和地面的距离为
。
L 3.84105 km
求 (1)在月球上得到的光斑的直径D1有多大？ (2)如果这激光束经扩束器扩展成直径为d2=2m，则在月球表面上得到的光斑直径D1

11[1].6圆孔衍射和光学仪器的分辨率_750206138

2.44 × 3 × 10 8 = = 4.88 × 10 − 3 rad = 0.28° 0.5 × 300 × 10 9

11.6 圆孔衍射和光学仪器的分辨率 11.6.1 夫琅禾费圆孔衍射 11.6.2 光学仪器的分辨率在成像光学仪器中总有透镜的边框和光阑例如照相机中的光圈）（例如照相机中的光圈），它们限制通过仪器的光的波阵面，起到衍射圆孔的作用，的光的波阵面，起到衍射圆孔的作用，不可避免发生衍射现象。免发生衍射现象。如果光源离透镜很远，如果光源离透镜很远，并把光屏置于透镜的焦平面上，就会发生夫琅禾费圆孔衍射。的焦平面上，就会发生夫琅禾费圆孔衍射。夫琅禾费圆孔衍射
11.6.1 夫琅禾费圆孔衍射
艾里斑
艾里斑的角半径（半径对圆孔中心的张角）：艾里斑的角半径（半径对圆孔中心的张角）：
1.22 λ θ0 = D
λ：入射光波长，D：圆孔直径入射光波长，：
11.6.2 光学仪器的分辨率
两不相干物点两艾里斑
物点的像容易区分
刚能区分
不能区分
瑞利判据：瑞利判据：当一个艾里斑的边缘正好与另一个艾里斑的中心重合时，个艾里斑的中心重合时，这两个艾里斑刚好能被区分开。被区分开。
称为透 S1、S2对透镜中心的张角θ =θ0 → θ0 称为透镜的最小分辨角 1 D 透镜的分辨率：透镜的分辨率： R = = θ 0 1.22λ 望远镜： ↑ 望远镜：D↑， R↑; 电子显微镜：λ↓，R↑ ↑ 电子显微镜： ↑
【例 11.17】一雷达的圆形发射天线的直径】 D=0.5m，发射的无线电波的频率 ν=300GHz。，。求雷达发射的无线电波束的角宽度。求雷达发射的无线电波束的角宽度。解雷达天线发射的无线电波，相当于通过雷达天线发射的无线电波，天线圆孔后的衍射波。衍射中央主极大（天线圆孔后的衍射波。衍射中央主极大（艾里雷达波束角宽度雷达波束角宽度，斑）集中了绝大部分能量雷达波束角宽度，等于艾里斑角半径的两倍：等于艾里斑角半径的两倍： c 2.44 2.44λ ν θ = 2θ 0 = = D D

波动光学第4讲圆孔夫琅禾费衍射光学仪器的分辨本领光栅衍射

轮廓线
光强分布曲线
0
4
8 sin( /d )
5.缺级现象
光栅衍射加强条件
dsink k0,1,2,3,...
单缝衍射减弱条件
asin k k1,2,3,...
这样的主极大是不存在的, 称作缺级现象
两式相除 d k a k
k d k a
所缺级次
k1,2,3,...
光强曲线
I I0
N=4
-2(/d) -(/d-)(/4d)0/4d /d
I0 I单
单
sin
2/d
理论计算多缝干涉和单缝衍射共同决定的光栅衍射光强分布曲线如图
-2
-
1
光栅衍射光强曲线
-
-4
8
0
1
2 sin ( /a)
I N2I0单
N=4
主极大外形包络线
单缝衍射 d = 4a 为单缝衍射
例1：分光计作光栅实验，用波长 = 632.8 nm的激光照射光栅常数 d = 1/300 mm的光栅
上，问最多能看到几条谱线。
解：在分光计上观察谱线，最大衍射角为 90°,
d
(ab)sin k

(ab)si9n0
kmax

o
x
fP
kma x(ab)si9 n0
◆采用波长较短的光，也可提高分辨率。
电子显微镜用加速的电子束代替光束，其波长约 0.1nm，用它来观察分子结构。
电子显微镜拍摄的照片
第4节光栅衍射
一．光栅和光栅常数
1.光栅由大量彼此互相平行等间隔的透光（或反射光）的缝组成的光学器件。
透射式光栅
玻璃上刻出等宽等间距的刻痕，刻痕不透光

13-3圆孔衍射光学仪器分辨率

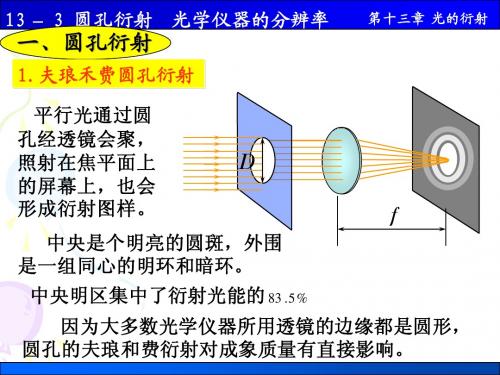
1.36103 m 1 2.44 2.44 0.00603 rad 2 D1 5510 m 2 1.57102 m 2.44 0.0164 rad （2） 2 2.44 D2 2.33m
1

22010 Hz
13 – 3 圆孔衍射
S1 S2
光学仪器的分辨率
第十三章光的衍射
可分辨
此时两爱里斑重叠部分的光 S1 恰可分辨强为一个 S2 光斑中心最大值的两爱里斑中心距d0恰好等于爱里斑半径。 80％。
S1 S2
不可分辨
第十三章光的衍射 13 – 3 圆孔衍射光学仪器的分辨率 2.光学仪器分辨率满足瑞利判据的两物点间的距离，就是光学仪器所能分辨的最小距离。此时两个物点对透镜中心所张的角称为最小分辨角。
1 2
500109 50102 光源 r01 1.22 3 2 0.110
所以：
S
R
f
1.5 10 m
9 2
3
圆孔
障碍物
E
接收屏
50010 5010 r02 1.22 1.5 104 m 2 1.0 103
13 – 3 圆孔衍射
二、光学仪器的分辨本领
同上所述，点物S和S1 对 S 1 透镜中心 O 所张的角，等于它们分别相应的中央 S 零级衍射中心S’、 S1’对 O所张的角。
S1 L1
O L L2
S’
S1’
如图所示，是可分 S’ 辨这两个物点的。 S O S1’ f1 当两个物点距离足够 f2 小时，就有能否分辨 A 的问题。瑞利给出恰可分辨两个物点的判据。 1.瑞利判据点物S1的爱里斑中心恰好与另一个点物S2的爱里斑边缘（第一衍射极小）相重合时，恰可分辨两物点。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第十一章光学
2
物理学
第五版
三
11-8 圆孔衍射光学仪器的分辨本领
光学仪器的分辨本领
光学仪器的通光孔径 D
s1 *
0
s2*
f
d 2 1.22
f
D
d 2
0
d f
2
1.22
D
第十一章光学仪器的分辨本领
第五版
最小分辨角
0
1.22
D
光学仪器分辨率 1 D D, 1
第十一章光学
9
物理学
11-8 圆孔衍射光学仪器的分辨本领
第五版
解 (1)
1
c
3108 m/s 220 109 Hz
1.36 103m
1
2.44
1
D1
1.36 103 m 2.44 55102m
0.006 03rad
(2)
2
2.44 2
D2
2.44 1.57 102 m 2.33m
0.016 4 rad
0 1.22
第十一章光学
4
物理学
11-8 圆孔衍射光学仪器的分辨本领
第五版
第十一章光学
5
物理学
11-8 圆孔衍射光学仪器的分辨本领
第五版
1990 年发射的哈勃太空望远镜的凹面
物镜的直径为2.4 m，最小分辨角 0 0.1"
在大气层外 615 km 高空绕地运行,可观察
130亿光年远的太空深处，发现了500 亿个
物理学
11-8 圆孔衍射光学仪器的分辨本领
第五版
二瑞利判据
0.8I 0
第十一章光学
1
物理学
11-8 圆孔衍射光学仪器的分辨本领
第五版
对于两个强度相等的不相干的点光源（物点），一个点光源的衍射图样的主极大刚好和另一点光源衍射图样的第一极小相重合，这时两个点光源（或物点）恰为这一光学仪器所分辨.
7
物理学
11-8 圆孔衍射光学仪器的分辨本领
第五版
解
(1)
0
1.22
D
1.22 5.510 7 m 310 3 m
2.2104 rad
(2) d l0 25 cm 2.2 10 4 0.0055cm 0.055mm
第十一章光学
8
物理学
11-8 圆孔衍射光学仪器的分辨本领
第五版
星系 .
第十一章光学
6
物理学
11-8 圆孔衍射光学仪器的分辨本领
第五版
例1 设人眼在正常照度下的瞳孔直径约为3 mm，而在可见光中，人眼最敏感的波长为550 nm，问
(1)人眼的最小分辨角有多大？
(2)若物体放在距人眼25 cm（明视距离）处，则两物点间距为多大时才能被分辨？
第十一章光学
例2 毫米波雷达发出的波束比常用的雷达波束窄，这使得毫米波雷达不易受到反雷达导弹的袭击.
(1)有一毫米波雷达，其圆形天线直径为55 cm，发射频率为220 GHz的毫米波，计算其波束的角宽度；
(2)将此结果与普通船用雷达发射的波束的角宽度进行比较，设船用雷达波长为 1.57 cm，圆形天线直径为2.33 m .
第十一章光学
10